Уравнение клапейрона имеет вид. Идеальные газы
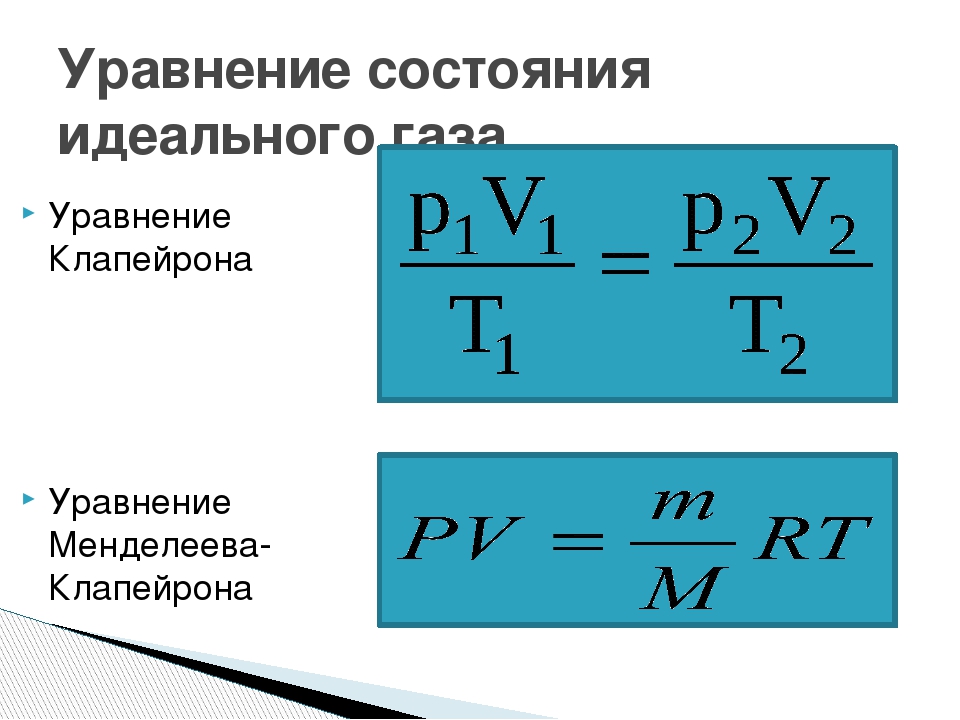
§2 Уравнение Менделеева-Клапейрона
Всякая система может находиться в различных состояниях, отличающихся температурой, давлением, объёмом и т.д.
Величины p , V , T и др. характеризующие состояние системы, называются параметрами состояния.
Если какой-либо из параметров меняется внутри системы от точки к точке, то такое состояние называется неравновесным . Если параметры системы во всех точках одинаковы при неизменных внешних условиях, то такое состояние называется равновесным .
Всякий процесс, т.е. переход системы из одного состояния в другое связанно с нарушением равновесия системы. Однако бесконечно медленный процесс будет состоять из последовательности равновесных состояний. Такой процесс называется равновесным
. При достаточно медленном протекании реальные процессы могут приближаться к равновесному.
Процесс, при котором система, пройдя ряд промежуточных состояний, возвращается в исходное состояние, называется круговым процессом или циклом : процесс 1-2-3-4-1 на рисунке.
Связь между параметрами состояния называется уравнением состояния : f (p , V , T )=0
Клапейрон, используя законы Бойля-Мариотта и Шарля вывел уравнение состояния идеального газа.
1 — 1’: T = const — закон Бойля — Мариотта: p 1 V 1 = p 1 ’ V 2 ;
1’ — 2: V = const — закон Шарля:
т.к. состояния 1и 2 выбраны произвольно, то для данной массы газа величина остается постоянной
— уравнение Клапейрона
В- газовая постоянная, различая для различных газов.
Менделеев объединил уравнение Клапейрона с законом Авогадро
() V m — молярный объём
Уравнение Менделеева-Клапейрона
R
— универсальная (молярная) газовая постоянная.
p = const; ;
Физический смысл R : численно равна работе, совершаемой газом при изобарическом ( p = const ) нагревании одного моля газа () на один Кельвин (?Т=1 К)
Введем постоянную Больцмана
тогда
p = n k T
p — давление идеального газа при данной температуре прямо пропорционально концентрации его молекул (или плотности газа). При одинаковых p и T все газы содержат в единице объёма одинаковое число молекул.
n — концентрация молекул (число молекул в единице объёма). Число молекул, содержащихся при нормальных условиях в 1 м 3 называется числом Лошмидта
§3 Основное уравнение молекулярно-кинетической теории (м.к.т.) газов.
При беспорядочном движении частицы газа сталкиваются между собой и со стенками сосуда. Механическое действие этих ударов о стенки сосуда воспринимается как давление на стенки. Выделим на стенке сосуда некую элементарную площадку
ΔS
и найдем давление, оказываемое на эту площадку.
Импульс, получаемый рассматриваемой стенкой, в результате удара одной молекулы будет равен
m 0 — масса одной молекулы
Уравнение Менделеева-Клапейрона — уравнение состояния для идеального газа, отнесенное к 1 молю газа. В 1874 г. Д. И. Менделеев на основе уравнения Клапейрона объединив его с законом Авогадро, используя молярный объем V m и отнеся его к 1 молю, вывел уравнение состояния для 1 моля идеального газа:
pV = RT , где R — универсальная газовая постоянная,
R = 8,31 Дж/(моль. К)
Уравнение Клапейрона-Менделеева показывает, что для данной массы газа возможно одновременно изменение трех параметров, характеризующих состояние идеального газа. Для произвольной массы газа М, молярная масса которого m: pV = (М/m) . RT . или pV = N А kT ,
где N А — число Авогадро, k — постоянная Больцмана.
Вывод уравнения:
С помощью уравнения состояния идеального газа
можно исследовать процессы, в которых масса газа и один из параметров —
давление, объем или температура — остается постоянным, а изменяются только
остальные два и получить теоретически газовые законы для этих условий изменения
состояния газа.
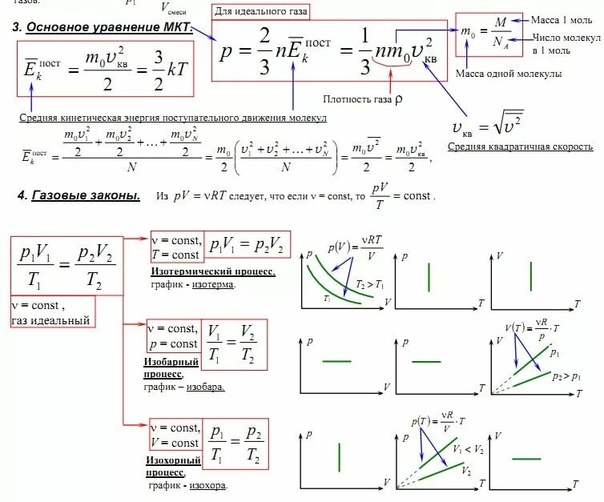
Такие процессы называют изопроцессами.
Законы, описывающие изопроцессы,
были открыты задолго до теоретического вывода уравнения состояния идеального
газа.
Изотермический процесс
— процесс изменения состояния системы при постоянной температуре.Для того, чтобы температура газа оставалась в процессе неизменной, необходимо, чтобы газ мог обмениваться теплотой с внешней большой системой — термостатом. Роль термостата может играть внешняя среда (воздух атмосферы). Согласно закону Бойля-Мариотта, давление газа обратно пропорционально его объему: P 1 V 1 =P 2 V 2 =const. Графическая зависимость давления газа от объема изображается в виде кривой (гиперболы), которая носит название изотермы. Разным температурам соответствуют разные изотермы.
Изобарный процесс
— процесс изменения состояния системы при
постоянном давлении. Для газа данной массы отношение объема газа к его
температуре остается постоянным, если давление газа не меняется
. Это закон Гей-Люссака.
Согласно закону Гей-Люссака, объем
газа прямо пропорционален его температуре: V/T=const. Графически эта
зависимость в координатах V-T изображается в виде прямой, выходящей из точки
Т=0. Эту прямую называют изобарой. Разным давлениям соответствуют разные
изобары. Закон Гей-Люссака не соблюдается в области низких температур, близких
к температуре сжижения (конденсации) газов.
Для газа данной массы отношение объема газа к его
температуре остается постоянным, если давление газа не меняется
. Это закон Гей-Люссака.
Согласно закону Гей-Люссака, объем
газа прямо пропорционален его температуре: V/T=const. Графически эта
зависимость в координатах V-T изображается в виде прямой, выходящей из точки
Т=0. Эту прямую называют изобарой. Разным давлениям соответствуют разные
изобары. Закон Гей-Люссака не соблюдается в области низких температур, близких
к температуре сжижения (конденсации) газов.
Изохорный процесс
— процесс изменения состояния системы при
постоянном объеме. Для данной массы газа отношение давления газа к его
температуре остается постоянным, если объем газа не меняется.
Этот газовый закон Шарля.
Согласно закону Шарля, давление газа
прямо пропорционально его температуре: P/T=const. Графически эта зависимость в
координатах P-Т изображается в виде прямой, выходящей из точки Т=0. Эту прямую
называют изохорой. Разным объемам соответствуют разные изохоры. Закон Шарля не
соблюдается в области низких температур, близких и температуре сжижения
(конденсации) газов.
Закон Шарля не
соблюдается в области низких температур, близких и температуре сжижения
(конденсации) газов.
Законы Бойля — Мариотта, Гей-Люссака и Шарля являются частными случаями объединенного газового закона: Отношение произведения давления газа и объема к температуре для данной массы газа — величина постоянная: PV/T=const.
Итак, из закона pV = (М/m) . RT выводятся следующие
законы:
T
=
const
=>
PV
=
const
— закон Бойля — Мариотта.
p = const
=> V/T = const
—
закон
Гей
—
Люссака
.
Если идеальный газ является смесью нескольких газов, то согласно закону Дальтона, давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов. Парциальное давление — это такое давление, которое производил бы газ, если бы он один занимал весь объем, равный объему смеси.
Некоторых, возможно,
интересует вопрос, каким образом удалось определить постоянную Авогадро N A
= 6,02·10 23 ? Значение числа
Авогадро было экспериментально установлено только в конце XIX – начале XX века.
В откачанный до глубокого вакуума сосуд объемом V = 30 мл поместили навеску элемента радия массой 0,5 г и выдержали там в течение одного года. Было известно, что за секунду 1 г радия испускает 3,7·10 10 альфа-частиц. Эти частицы представляют собой ядра гелия, которые тут же принимают электроны из стенок сосуда и превращаются в атомы гелия. За год давление в сосуде выросло до 7,95·10 -4 атм (при температуре 27 о С). Изменением массы радия за год можно пренебречь. Итак, чему равна N A ?
Сначала найдем, сколько альфа-частиц (то есть атомов гелия) образовалось за один год. Обозначим это число как N атомов:
N = 3,7·10 10 · 0,5 г · 60 сек · 60 мин · 24 час · 365 дней = 5,83·10 17 атомов.
Запишем уравнение Клапейрона-Менделеева PV =
N A = NRT = 5,83 . 10 17 . 0,0821 . 300 = 6,02 . 10 23
PV 7,95 . 10 -4 . 3 . 10 -2
В начале XX века этот способ
определения постоянной Авогадро был самым точным. Но почему так долго (в
течение года) длился эксперимент? Дело в том, что радий добывается очень
трудно. При его малом количестве (0,5 г) радиоактивный распад этого элемента
дает очень мало гелия. А чем меньше газа в замкнутом сосуде, тем меньшее он
создаст давление и тем большей будет ошибка измерения. Понятно, что ощутимое
количество гелия может образоваться из радия только за достаточно долгое время.
Но почему так долго (в
течение года) длился эксперимент? Дело в том, что радий добывается очень
трудно. При его малом количестве (0,5 г) радиоактивный распад этого элемента
дает очень мало гелия. А чем меньше газа в замкнутом сосуде, тем меньшее он
создаст давление и тем большей будет ошибка измерения. Понятно, что ощутимое
количество гелия может образоваться из радия только за достаточно долгое время.
Как уже указывалось, состояние некоторой массы газа определяется тремя термодинамическими параметрами: давлением р , объемом V и температурой Т . Между этими параметрами существует определенная связь, называемая уравнением состояния, которое в общем виде дается выражением
f (p , V , T ) = 0 ,
где каждая из переменных является функцией двух других.
Французский физик и инженер Б. Клапейрон (1799-1864) вывел уравнение состояния идеального газа, объединив законы Бойля — Мариотта и Гей-Люссака. Пусть некоторая масса газа занимает объем V
1 , имеет давление p
1 и находится при температуре Т
1 . Эта же масса газа в другом произвольном состоянии характеризуется параметрами p
2 , V
2 , Т 2 (рис.63). Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов:
Эта же масса газа в другом произвольном состоянии характеризуется параметрами p
2 , V
2 , Т 2 (рис.63). Переход из состояния 1 в состояние 2 осуществляется в виде двух процессов:
1) изотермического (изотерма 1 — 1 /),
2) изохорного (изохора 1 / — 2).
В соответствии с законами Бойля — Мариотта (41.1) и Гей-Люссака (41.5) запишем:
(42.1)
(42.2)
Исключив из уравнений (42.1) и (42.2) , получим
Так как состояния 1 и 2 были выбраны произвольно, то для данной массы газа
. (42.3)
Выражение (42.3) является уравнением Клапейрона , в котором В — газовая постоянная, различная для разных газов.
Русский ученый Д. И. Менделеев (1834-1907) объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (42.3) к одному молю, использовав молярный объем V m .
Согласно закону Авогадро, при одинаковых р
и Т
моли всех газов занимают одинаковый молярный объем V m
, поэтому постоянная В
будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R
и называется молярной газовой постоянной
. Уравнению
Эта общая для всех газов постоянная обозначается R
и называется молярной газовой постоянной
. Уравнению
(42.4)
удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа , называемым также уравнением Клапейрона — Менделеева .
Числовое значение молярной газовой постоянной определим из формулы (42.4), полагая, что моль газа находится при нормальных условиях ( = 1,013×10 5 Па, = 273,15 K, = 22,41×10 -3 м 3 /моль): R = 8,31 Дж/(моль×К).
От уравнения (42.4) для моля газа можно перейти к уравнению Клапейрона — Менделеева для произвольной массы газа. Если при некоторых заданных давлении и температуре один моль газа занимает молярный объем V m , то при тех же условиях масса m газа займет объем V = (m/M) V m , где М — молярная масса (масса одного моля вещества). Единица молярной массы — килограмм на моль (кг/моль). Уравнение Клапейрона — Менделеева для массы m газа
(42. 5)
5)
где = m/M — количество вещества.
Часто пользуются несколько иной формой уравнения состояния идеального газа, вводя постоянную Больцмана : = 1,38×10 -23 Дж/К.
Исходя из этого, уравнение состояния (42.4) запишем в виде
где — концентрация молекул (число молекул в единице объема). Таким образом, из уравнения
следует, что давление идеального газа при данной температуре прямо пропорционально концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1 м 3 газа при нормальных условиях, называется числом Лошмидта (И. Лошмидт (1821-1895) — австрийский химик и физик): 2,68×10 25 м -3 .
Как уже указывалось, состояние некоторой массы газа определяется тремя термодинамическими параметрами: давлением р
,объемом V
и температурой Т.
Между этими параметрами существует определенная связь, называемая уравнением состояния, которое в общем виде дается выражением: Рис. 7.4.
7.4.
F (p , V , T )=0,
где каждая из переменных является функцией двух других.
Французский физик и инженер Б. Клапейрон вывел уравнение состояния идеального газа, объединив законы Бойля — Мариотта и Гей-Люссака. Пусть некоторая масса газа занимает объем V 1 , имеет давление р 1 и находится при температуре T 1 . Эта же масса газа в другом произвольном состоянии характеризуется параметрами р 2 , V 2 , Т 2 (рис.7.4).
Переход из состояния 1 в состояние 2осуществляется в виде двух процессов: 1) изотермического (изотерма 1 – 1 /), 2) изохорного (изохора 1 / – 2).
В соответствии с законами Бойля- Мариотта (7.1) и Гей-Люссака (7.5) запишем:
р 1 V 1 =p / 1 V 2 , (7.6)
. (7.7)
Исключив из уравнений (7.6) и (7.7) p / 1 получим:
.
Так как состояния 1 и 2были выбраны произвольно, то для данной массы газа величина pV/T
остается постоянной, т. е.
е.
pV/T = В = const. (7.8)
Выражение (7.8) является уравнением Клапейрона , в котором В — газовая постоянная, различная для разных газов.
Д. И. Менделеев объединил уравнение Клапейрона с законом Авогадро, отнеся уравнение (7.8) к одному молю, использовав молярный объем V m . Согласно закону Авогадро, при одинаковых p и Τ моли всех газов занимают одинаковый молярный объем V m ,поэтому постоянная В будет одинаковой для всех газов. Эта общая для всех газов постоянная обозначается R и называется молярной газовой постоянной . Уравнению
pV m = RT (7.9)
удовлетворяет лишь идеальный газ, и оно является уравнением состояния идеального газа , называемым также уравнением Клапейрона — Менделеева .
Числовое значение молярной газовой постоянной определим из формулы (7.9), полагая, что моль газа находится при нормальных условиях (р
0 =
1,013×10 5 Па, T
0 =273,15 К, V m
=22,41×10 -3 м 3 /моль): R
=8,31 Дж/(моль К).
От уравнения (7.9) для моля газа можно перейти к уравнению Клапейрона — Менделеева для произвольной массы газа. Если при некоторых заданных p и T один моль газа занимает молярный объем V m , то масса т газа займет объем V= (m/М ) V m ,где Μ – молярная масса (масса одного моля вещества). Единица молярной массы – килограмм на моль (кг/моль). Уравнение Клапейрона — Менделеева для массы т газа
pV = RT = vRT ,(7.10)
где: v=m/M — количество вещества.
Часто пользуются несколько иной формой уравнения состояния идеального газа, вводя постоянную Больцмана
k=R/N A = 1,38∙10 -23 Дж/К.
Исходя из этого, уравнение состояния (2.4) запишем в виде
p= RT/V m = kN A T/V m = nkT ,
где N A /V m =n — концентрация молекул (число молекул в единице объема). Таким образом, из уравнения
p=nkT
(7. 11)
11)
следует, что давление идеального газа при данной температуре прямо пропорционально концентрации его молекул (или плотности газа). При одинаковых температуре и давлении все газы содержат в единице объема одинаковое число молекул. Число молекул, содержащихся в 1м 3 газа при нормальных условиях, называется числом Лошмидта:
N l = р 0 / (kТ 0)= 2,68∙10 25 м -3 .
Оно выведено на основе объединенного закона Бойля-Мариотта и Гей-Люссака с применением закона Авогадро. Для одной грамм-молекулы любого вещества, находящегося в идеальном газовом состоянии, уравнение Менделеева-Клапейрона имеет выражение:
Или PV = RT (11) .
В том случае, если имеется не один, а n молей газа выражение принимает вид:
где R- универсальная газовая постоянная, не зависящая от природы газа.
Так как число грамм-молей газа , где m- масса газа, а М- его молекулярная масса, то выражение (12) принимает вид:
Числовое значение R зависит от единицы измерения давления и объема.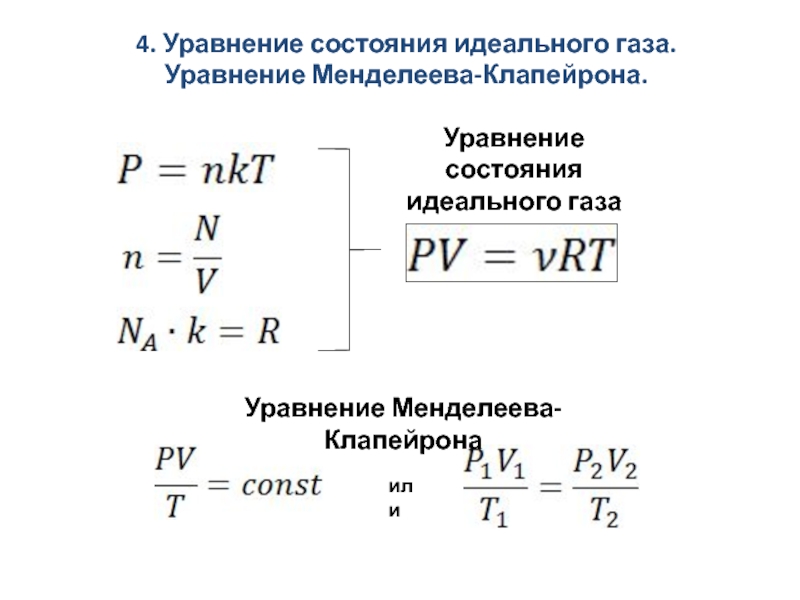 Величина ее выражается в единицах энергия/моль´град. Для нахождения числовых значений R
используем уравнение (11), применив его для 1 моля идеального газа, находящегося в нормальных условиях,
Величина ее выражается в единицах энергия/моль´град. Для нахождения числовых значений R
используем уравнение (11), применив его для 1 моля идеального газа, находящегося в нормальных условиях,
Подставив в уравнение (11) числовые значения Р=1 атм, T= 273° и V = 22,4 л, получаем
В международной системе единиц СИ давление выражается в ньютонах на м 2 (н/м 2), а объем в м 3 . Тогда .
Пользуясь уравнением Менделеева-Клапейрона можно производить следующие расчеты: а) нахождение физических параметров состояния газа по его молекулярной массе и другим данным, б) нахождение молекулярной массы газа по данным о его физическом состоянии (см. пример 22).
Пример 11. Сколько весит азот, находящийся в газгольдере диаметром 3,6 м и высотой 25 м при температуре 25ºС и давлении 747 мм рт. ст.?
IIример 12. В колбе емкостью 500 мл при 25ºС находится 0,615 г оксида азота (II). Каково давление газа в атмосферах, в н/м 2 ?
Пример 13. Масса колбы емкостью 750 см 3 , наполненной кислородом при 27°С, равна 83,35 г. Масса пустой колбы 82,11 г. Определить давление кислорода и мм рт.ст. на стенки колбы.
Масса колбы емкостью 750 см 3 , наполненной кислородом при 27°С, равна 83,35 г. Масса пустой колбы 82,11 г. Определить давление кислорода и мм рт.ст. на стенки колбы.
Закон Дальтона
Сформулирован этот закон так: общее давление смесей газов, не реагирующих друг с другом, равно сумме парциальных давлении составных частей (компонентов).
P = p 1 + p 2 + p 3 + ….. + p n (14)
где Р — общее давление смеси газов; p 1 , p 2 , p 3 , …., p n – парциальные давления компонентов смеси.
Парциальным давлением называется давление, оказываемое каждым компонентом газовой смеси, если представить этот компонент занимающим объем, равный объему смеси при той же температуре. Иными словами, парциальным давлением называется та часть общего давления газовой смеси, которая обусловлена данным газом.
Из закона Дальтона следует, что при наличии смеси газов п
в уравнении (12) представляет собой сумму числа молей всех компонентов, образующих данную смесь, а Р- общее давление смеси, занимающей при температуре Т
объем V.
Зависимость между парциальными давлениями и общим выражается уравнениями:
где n 1 , n 2 , n 3 — число молей компонента 1, 2, 3, соответственно, в смеси газов.
Отношения называются мольными долями данного компонента.
Если мольную долю обозначить через N, то парциальное давление любого i-го компонента смеси (где i = 1,2,3,…) будет равно:
Таким образом, парциальное давление каждого компонента смеси равно произведению его мольной доли па общее давление газовой смеси.
Помимо парциального давления у газовых смесей различают парциальный объем каждого из газов v 1 , v 2 , v 3 и т. д.
Парциальным называют объем, который занимал бы отдельный идеальный газ, входящий в состав идеальной смеси газов, если бы при том же количестве, он имел давление и температуру смеси.
Сумма парциальных объемов всех компонентов газовой смеси равна общему объему смеси
V = v 1 ,
+ v 2
+ v 3
+ . .. + v n
(16) .
.. + v n
(16) .
Отношение и т. д. называется объемной долей первого, второго и т.д. компонентов газовой смеси. Для идеальных газов мольная доля равна объемной доле. Следовательно, парциальное давление каждого компонента смеси равно также произведению его объемной доли на общее давление смеси.
; ; p i = r i ´P (17).
Парциальное давление обычно находят из величины общего давления с учетом состава газовой смеси. Состав газовой смеси выражают в весовых процентах, объемных процентах и в мольных процентах.
Объемным процентом называется объемная доля, увеличенная в 100 раз (число единиц объема данного газа, содержащегося в 100 единицах объема смеси)
Мольным процентом q называется мольная доля, увеличенная в 100 раз.
Весовой процент данного газа — число единиц массы его, содержащихся в 100 единицах массы газовой смеси.
где m 1 , m 2 – массы отдельных компонентой газовой смеси; m –
общая масса смеси.
Для перехода от объемных процентов к весовым, что бывает необходимым в практических расчетах, пользуются формулой:
где r i (%) — объемное процентное содержание i-гo компонента газовой смеси; M i -молекулярная масса этого газа; М ср — средняя молекулярная масса смеси газов, которую вычисляют по формуле
М ср = М 1 ´r 1 + M 2 ´r 2 + M 3 ´r 3 + ….. + M i ´r i (19)
где М 1 , M 2 , M 3 , M i — молекулярные мaccы отдельных газов.
Если состав газовой смеси выражен количеством масс отдельных компонентов, то среднюю молекулярную массу смеси можно выразить по формуле
где G 1 , G 2 , G 3 , G i – доли масс газов в смеси: ; ; и т.д.
Пример 14. 5 л азота под давлением 2 атм, 2 л кислорода под давлением 2,5 атм и 3 л углекислою газа под давлением 5 атм перемешаны, причем объем, предоставленный смеси, равен 15 л. Вычислить, под каким давлением находятся смесь и парциальные давления каждого газа.
Азот, занимавший объем 5 л при давлении Р 1 = 2 атм, после смешения с другими газами распространился в объеме V 2 = 15 л. Парциальное давление азота р N 2
= Р 2 находим из закона Бойля-Мариотта (P 1 V 1 = P 2 V 2). Откуда
Парциальное давление азота р N 2
= Р 2 находим из закона Бойля-Мариотта (P 1 V 1 = P 2 V 2). Откуда
Парциальное давления кислорода и углекислого газа находим аналогичным способом:
Общее давление смеси равно .
Пример 15. Смесь, состоящая из 2 молей водорода, некоторого количества молей кислорода и 1 моля азота при 20°С и давлении 4 атм, занимает объем 40 литров. Вычислить число молей кислорода в смеси и парциальные давления каждого из газов.
Из уравнения (12) Менделеева-Клапейрона находим общее число молей всех газов, составляющих смесь
Число молей кислорода в смеси равно
Парциальные давления каждого из газов вычисляем по уравнениям (15а):
Пример 17.
Состав паров бензольных углеводородов над поглотительным маслом в бензольных скрубберах, выраженный в единицах массы, характеризуется такими величинами: бензола C 6 H 6 — 73%, толуола С 6 Н 5 СН 3 — 21%, ксилола С 6 Н 4 (СН 3) 2 — 4%, триметилбензола С 6 Н 3 (СН 3) 3 — 2%. Вычислить содержание каждой составной части по объему и парциальные давления паров каждого вещества, если общее давление смеси равно 200 мм рт. ст.
Вычислить содержание каждой составной части по объему и парциальные давления паров каждого вещества, если общее давление смеси равно 200 мм рт. ст.
Для вычисления содержания каждой составной части смеси паров по объему используем формулу (18)
Следовательно, необходимо знать М ср, которую можно вычислить из формулы (20):
Парциальные давления каждого компонента в смеси вычисляем, используя уравнение (17)
p бензола = 0,7678´200 = 153,56 мм рт.ст. ; p толуола = 0,1875´200 = 37,50 мм рт.ст. ;
p ксилола = 0,0310´200 = 6,20 мм рт.ст. ; p триметилбензола = 0,0137´200 = 2,74 мм рт.ст.
Похожая информация.
Тест вопросы термодинамика
Вопрос 1. Во сколько раз увеличится объем воздушного шара, если его внести с улицы в теплое помещение? Температура на улице -30С, в помещении +270С.
Вопрос 2. Чтобы изотермически
уменьшить объема газа в цилиндре с поршнем в 3 раза, на поршень поместили груз
9 кг. Какой дополнительный груз (кг) следует поместить на поршень, чтобы объем
газа изотермически уменьшить еще в 2 раза?
Какой дополнительный груз (кг) следует поместить на поршень, чтобы объем
газа изотермически уменьшить еще в 2 раза?
Вопрос 3. Сосуд с газом плотно закрыт пробкой, площадь сечения которой 2,5 см2. Сила трения, удерживающая пробку, равна 12 Н. Начальное давление в сосуде 100 кПа, температура 270 К. Сосуд нагревают. Определите температуру (К), до которой нужно нагреть газ в сосуде, чтобы пробка вылетела.
Вопрос 4. Баллон объемом 50 л, содержащий воздух при давлении 120 кПа, соединяют с баллоном объемом 80 л. Давление в системе после соединения составило 150 кПа. Определите начальное давление (кПа) воздуха в баллоне объемом 80 л.
Вопрос 5. Мальчик накачивает мяч
емкостью 3 л при помощи поршневого насоса. За каждое качание насос захватывает
150 см3 при нормальном атмосферном давлении. Конечное давление
воздуха в мяче должно быть равно 200 кПа. Какое количество качаний необходимо
сделать, если считать процесс изотермическим.
Вопрос 6. В цилиндре под поршнем находится газ. Масса поршня 6 кг, площадь сечения поршня 20 см2, атмосферное давление 100 кПа. С какой добавочной силой надо действовать на поршень, чтобы объем газа в цилиндре уменьшился втрое?
Вопрос 7. В баллоне находилось некоторое количество газа при атмосферном давлении 100 кПа. При открытом вентиле баллон был нагрет, после чего вентиль закрыли и газ остыл до начальной температуры 283 К. Давление в баллоне упало до 70 кПа. Определите максимальное изменение температуры в баллоне.
Вопрос 8. Открытую стеклянную трубку постоянного сечения длиной 1 м погружают в ртуть на 1/4 ее длины. Затем трубку закрывают и вынимают. Если атмосферное давление равно 105 Па, то какой длины (см) останется столбик ртути в трубке?
Вопрос 9. Два одинаковых сосуда,
содержащие кислород при 300 К, соединены тонкой горизонтальной трубкой,
посередине которой находится столбик ртути. Объем сосудов 40 см3. Когда один сосуд нагрели на 3 К, а другой охладили на 3 К, столбик ртути
сместился на 1 см. Определите площадь (мм2) сечения трубки.
Когда один сосуд нагрели на 3 К, а другой охладили на 3 К, столбик ртути
сместился на 1 см. Определите площадь (мм2) сечения трубки.
Вопрос 10. Закрытый цилиндрический сосуд высотой 1 м разделен на две равные части тонким невесомым теплонепроницаемым поршнем, скользящим без трения. При застопоренном поршне давление в одной половине в 10 раз больше, чем в другой. На сколько (м) передвинется поршень, если снять стопор. Процесс изотермический.
Изопроцессы
Вариант 1
1. Два газа находятся в тепловом равновесии, при этом
у них имеются одинаковые физические параметры: . ..
..
А. Только температура.
Б. Только средняя квадратичная скорость молекул.
В. Температура и средняя квадратичная скорость молекул.
Г. Температура, давление и средняя квадратичная скорость молекул.
2. При одинаковой температуре Т и давлении р 1 моль любого газа занимает …
A. Одинаковый объем при нормальных условиях.
Б. Разный объем, значение которого не зависит от Т и р.
B. Одинаковый объем, значение которого зависит от Т пр.
Г. Разный объем, значение которого зависит от Т и р.
3. Количество молекул в 1 моль вещества определяет …
A. Число Авогадро.
Б. Универсальная газовая постоянная.
B. Постоянная Больцмана.
Г. Постоянная Лошмидта.
4. Из предложенных ответов выберите уравнение состояния идеального газа …
А. Б.
В. Г.
5. Уравнение идеального газа справедливо при условии …
A. m ≠ const, M = const, T = const.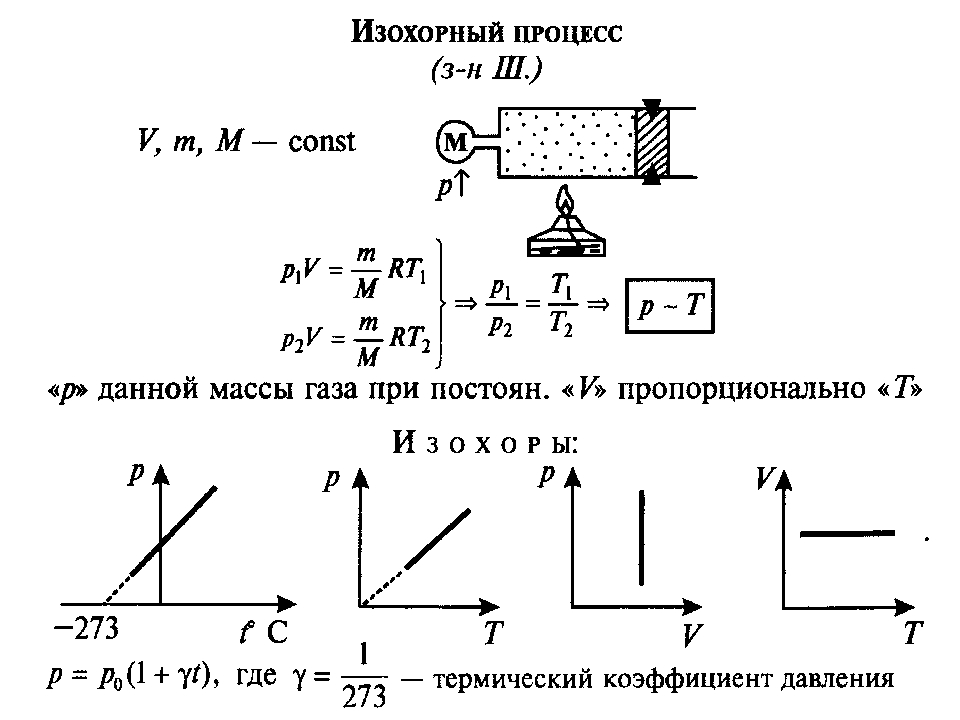
Б. m = const, T = const.
B. М = const, T = const.
Г. m = const, М = const, Т = const.
6. Единица измерения физической величины, определяемой выражением , в Международной
системе …
А. Па. Б. м3. В. кг/моль. Г. К.
7. Углекислый газ массой 88 кг при давлении 3 • 10 5 Па и температуре 27 °С занимает объем …
А. 16,62 м3. Б. 8,31м3.
В. 1,67 м3. Г. 0,0831 м3.
8.Для изохорного процесса в идеальном газе справедлива зависимость …
A. pV = const. Б.
В. . Г. .
9. Изобарному процессу в идеальном газе соответствует график …
p p V V
1 2 3 4
0 V 0 T 0 T 0 T
А. 1 Б. 2 В. 3 Г. 4
1 Б. 2 В. 3 Г. 4
10.При изотермическом расширении газа его давление уменьшается, так как уменьшается …
A. Концентрация молекул.
Б. Средняя кинетическая энергия молекул.
B. Масса газа. Г. Объем газа.
11. Определите изменения термодинамических параметров при переходе идеального газа из состояния 1 в состояние 2.
p 1 А. р — const, V — увеличился, Т — увеличилась.
Б. р — уменьшилось, V — const, T — уменьшилась.
В. р — увеличилось, V — уменьшился, Т — const.
2 Г. р — уменьшилось, V — увеличился, Т — const.
0 T
12. Объем, занимаемый кислородом массой 1 кг, увеличили в 2 раза с понижением температуры в 2 раза, при этом его давление …
A. Уменьшится в 2 раза. Б. Не изменится.
B. Увеличится в 4 раза. Г.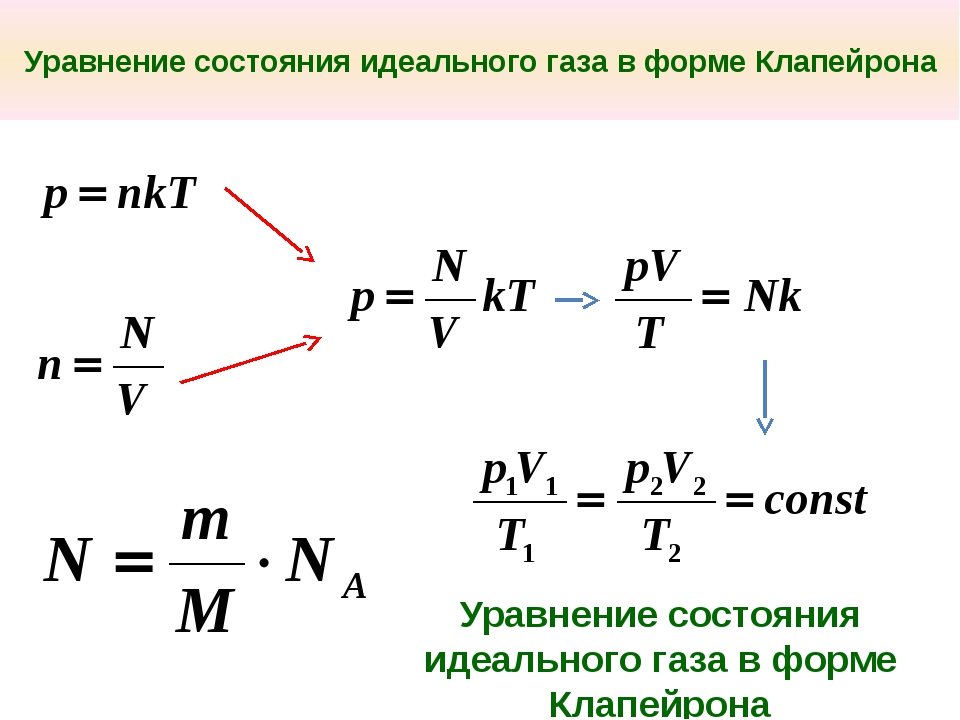 Уменьшится в 4
раза.
Уменьшится в 4
раза.
13. Определите по графику изменение объема идеального газа при переходах 1—2 и. 2—3.
А. 1—2 не изменится, 2—3 уменьшится. p 2
Б. 1—2 уменьшится, 2—3 уменьшится.
В. 1—2 не изменится, 2—3 увеличится. 1 3
Г. 1 — 2 увеличится ,2—3 увеличится. 0 T
14. Газ, имеющий температуру 300 К и давление 105 Па, изобарно нагревают до температуры 327 °С, при этом его концентрация …
A. Уменьшается в 2 раза. Б. Увеличивается в 2 раза.
B. Не изменяется. Г. Уменьшается в 4 раза.
15. Сравните термодинамические параметры
идеального газа, соответствующие состоянии V 2
1 и 2 данного графика, если масса газа неизменна. 1
А рl > р2, V1 < V2, Т1 < Т2
Б рl < р2, V1
< V2, Т1 < Т2. .
0 T
.
0 T
В. рl = р2, V1 > V2, Т1 < Т2. Г. рl = р2, V1 < V2, Т1 > Т2.
16. В результате нагревания изохорно давление газа в закрытом сосуде увеличилось в 4 раза, а средняя скорость движения молекул …
A. Увеличилась в 4 раза. Б. Уменьшилась в 4 раза.
B. Увеличилась в 2 раза Г. Уменьшилась в 2 раза.
17. При уменьшении давления в 1,5 раза и уменьшении массы в 6 раз установилась температура 600 К. Определите, на сколько градусов повысилась температура газа.
А. 450 К Б. 400 К. В. 150 К. Г. 100 К.
18. По графику зависимости р от V проследите, как изменилась температура идеального газа при переходе из состояния 1—2 в состояние 3—1.
A. 1—2 увеличилась, 2—3 увеличилась, 3—1 уменьшилась.
1—2 увеличилась, 2—3 увеличилась, 3—1 уменьшилась.
Б. 1—2 не изменилась, 2—3 увеличилась, 3—1 уменьшилась.
B. 1—2 уменьшилась, 2—3 увеличилась, 3—1 не изменилась
Г. 1—2 увеличилась, 2—3 уменьшилась, 3—1 увеличилась.
19. При переходе из состояния 1 в состояние 2 из сосуда выпустили половину молекул идеального газа. Проанализировав график, ответьте, как изменилась его температура.
A. Уменьшилась в 0,75 раза.
Б. Не изменилась.
B. Уменьшилась в 2,7 раза.
Г. Увеличилась в 2,7 раза.
20. В состоянии 1 давление идеального газа равно р0. По графику определите давление в состоянии 3.
А. 4р0
Б. 2 р0.
В. р0
Г. 0,5 р0
Изопроцессы
Вариант 2
1. К термодинамическим характеристикам состояния
идеального газа относятся . ..
..
А. Давление и масса.
Б. Объем, давление и молярная масса.
В. Температура, объем, давление.
Г. Температура, объем, масса.
2. У газов, имеющих одинаковые массу и объем, одинаковые …
A. Концентрации Б. Температуры.
B. Плотности. Г. Давления.
3. Изменение энергии 1 моль вещества при изменении температуры на 1 К определяет …
A. Число Авогадро.
Б. Универсальная газовая постоянная.
B. Постоянная Больцмана.
Г. Постоянная Лошмидта.
4. Из представленных ответов выберите уравнение Клапейрона для идеального газа.
А. Б.
В. Г.
5. Уравнение справедливо при условии …
A. m ≠ const, M = const, V = const.
Б. m = const, V = const.
B. М = const, V = const.
Г. m = const, М = const, V = const.
6. Единица измерения физической величины, определяемой
выражением , в Международной системе . ..
..
А. м3. Б. Па. В. кг/моль. Г. К.
7. Азот объемом 8,31м3 при давлении 3.105Па и температуре 27 °С имеет массу …
А. 14 кг. Б. 28 кг. В. 280 кг. Г. 140 кг.
8. Для изотермического процесса в идеальном газе справедливо уравнение …
A. pV = const. Б. = const.
B. = const. Г. .= const.
9. График изохорного процесса в идеальном газе имеет вид:
p p p V
1 2 3 4
0 V 0 T 0 T 0 T
А. 1 Б. 2 В. 3 Г. 4
10. При изотермическом расширении газа его давление
уменьшается, так как уменьшается . ..
..
A. Масса идеального газа.
Б. Средняя кинетическая энергия поступательного движения молекул.
B. Масса молекулы газа
Г. Концентрация молекул.
11. Определите по графику изменения термодинамических параметров при переходе идеального газа из состояния 1 в состояние 2.
A. р — const, V — увеличился, Т — увеличилась.
Б. р — уменьшилось, V — const, Т — уменьшилась.
B. р — увеличилось, V — уменьшился, Т — const.
Г. р — уменьшилось, V — увеличился, Т — const.
12. Если давление углекислого газа массой 2 кг уменьшилось в 3 раза, а объем увеличился в 3 раза, то его температура …
A. Уменьшилась в 2 раза. Б. Не изменилась.
B. Увеличилась в 9 раз. Г. Уменьшилась в 9 раз.
13. Определите по графику изменение температуры идеального газа при переходах 1 —2 и 2—3.
А. 1— 2 понижается, 2—3 повышается. p 2 1
Б. 1—2 повышается, 2—3 не изменяется.
В. 1—2 понижается, 2—3 понижается. 3
Г. 1—2 понижается, 2—3 не изменяется. 0 V
14. Изотермически уменьшают давление газа на 50%, при этом плотность газа …
A. Не изменится. Б. Уменьшится в 4 раза.
B. Увеличится в 2 раза Г. Уменьшится в 2 раза.
15. Сравните термодинамические параметры идеального газа, соответствующие состояниям 1 и 2 данного графика, если масса газа неизменна. p 1
А. рl > р2, V1 = V2, Т1 > Т2.
Б. рl > р2, V1 < V2, Т1 > Т2.
В. рl > р2, V1 > V2, Т1 > Т2. 2
Г. рl > р2,
V1 > V2,
Т1 < Т2.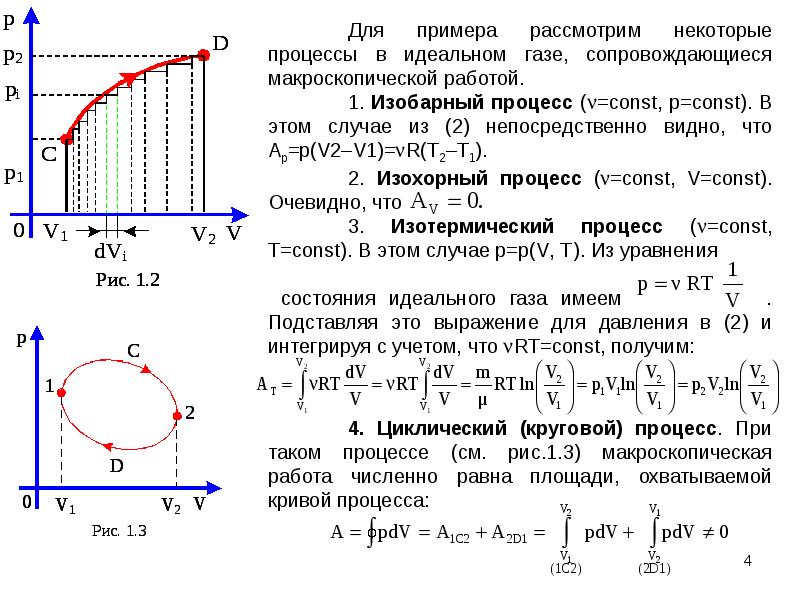 0
T
0
T
16. Объем идеального газа изобарно увеличился в 4 раза, а скорость движения молекул …
A. Не изменилась.
Б. Увеличилась в 2 раза.
B. Уменьшилась в 2 раза.
Г. Увеличилась в 2 раза.
17. При увеличении давления в 2 раза и температуры на 300 К плотность газа уменьшилась в 2 раза. Определите первоначальную температуру идеального газа.
А. 400 К. Б. 300 К. В. 200 К. Г. 100 К.
18. Проследите по графику изменения температуры идеального газа за весь цикл.
A. 1—2 увеличилась, 2—3 увеличилась, 3—4 уменьшилась, 4—1 уменьшилась.
Б. 1—2 увеличилась, 2—3 не изменилась, 3—4 уменьшилась, 4—1 уменьшилась.
B. 1—2 уменьшилась, 2—3 увеличилась, 3—4 не изменилась, 4—1 уменьшилась.
Г. 1—2 увеличилась, 2—3 не изменилась, 3—4 увеличилась, 4—1 увеличилась.
19. При
переходе из состояния 1 в состояние 2 из сосуда выпустили треть
молекул идеального газа. Проанализировав график, определите, как изменилось его давление.
При
переходе из состояния 1 в состояние 2 из сосуда выпустили треть
молекул идеального газа. Проанализировав график, определите, как изменилось его давление.
A.. Увеличилось в 8 раз.
Б. Уменьшилось в 8 раз.
B. Увеличилось в 6 раз.
Г. Уменьшилось в 6 раз.
20. В состоянии 1 температура идеального газа равна Tо. Определите по графику температуру газа в состоянии 3.
А. 4Т0
Б. Т0
В. 2 То.
Г. Т0 / 4
1. Какие параметры изменяются при протекании изотермического процесса в данной массе газа ?
2. Какие параметры изменяются при протекании изобарного
процесса в данной массе газа ?
Какие параметры изменяются при протекании изобарного
процесса в данной массе газа ?
3. Уравнение произвольного процесса в идеальном газе массой m
4. Уравнение состояния идеального газа
5. Укажите изохору идеального газа (рис 1.)
6. Укажите изобару идеального газа (рис 1.)
1)V 2) p 3) p 4) p
(рис 1)
T V T T
7.Укажите график изотермического расширения идеального газа (рис 2)
8.Укажите график изохорного нагревания газа (рис 2)
1) p 2) p 3) V 4) p
1. Какие параметры изменяются при протекании изобарного
процесса в данной массе газа ?
Какие параметры изменяются при протекании изобарного
процесса в данной массе газа ?
2.Какие параметры изменяются при протекании изотермического процесса в данной массе газа ?
3.Уравнение состояния идеального газа
4.Уравнение произвольного процесса в идеальном газе массой m
5.Укажите изобару идеального газа (рис 1.)
6.Укажите изохору идеального газа (рис 1.)
1)V 2) p 3) p 4) p
(рис 1)
T V T T
7.Укажите график изохорного нагревания газа (рис 2.)
8.Укажите график изотермического расширения идеального газа (рис 2.)
1) p 2) p 3) V 4) p
T V T
|
Тест по физике 11 кл.
1. Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 2. Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 3. Уравнение произвольного процесса в идеальном газе массой m 4. Уравнение состояния идеального газа 5. Укажите изохору идеального газа (рис 1.) 6. Укажите изобару идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1)
T V T T 7.Укажите график изотермического расширения идеального газа (рис 2) 8.Укажите график изохорного нагревания газа (рис 2) 1) p 2) p 3) V 4) p
T V T V |
Тест по физике 11 кл.
1.Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 2.Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 3.Уравнение состояния идеального газа 4.Уравнение произвольного процесса в идеальном газе массой m 5.Укажите изобару идеального газа (рис 1.) 6.Укажите изохору идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1)
T V T T 7.Укажите график изохорного нагревания газа (рис 2.) 8.Укажите график изотермического расширения идеального газа (рис 2.) 1) p 2) p 3) V 4) p
T V T V |
|
Тест по физике 11 кл.
1. Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 2. Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 3. Уравнение произвольного процесса в идеальном газе массой m 4. Уравнение состояния идеального газа 5. Укажите изохору идеального газа (рис 1.) 6. Укажите изобару идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1)
T V T T 7.Укажите график изотермического расширения идеального газа (рис 2) 8.Укажите график изохорного нагревания газа (рис 2) 1) p 2) p 3) V 4) p
T V T V |
Тест по физике 11 кл.
1.Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 2.Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 3.Уравнение состояния идеального газа 4.Уравнение произвольного процесса в идеальном газе массой m 5.Укажите изобару идеального газа (рис 1.) 6.Укажите изохору идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1)
T V T T 7.Укажите график изохорного нагревания газа (рис 2.) 8.Укажите график изотермического расширения идеального газа (рис 2.) 1) p 2) p 3) V 4) p
T V T V |
|
Тест по физике 11 кл.
1. Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 2. Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 3. Уравнение произвольного процесса в идеальном газе массой m 4. Уравнение состояния идеального газа 5. Укажите изохору идеального газа (рис 1.) 6. Укажите изобару идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1)
T V T T 7.Укажите график изотермического расширения идеального газа (рис 2) 8.Укажите график изохорного нагревания газа (рис 2) 1) p 2) p 3) V 4) p
T V T V |
Тест по физике 11 кл.
1.Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 2.Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 3.Уравнение состояния идеального газа 4.Уравнение произвольного процесса в идеальном газе массой m 5.Укажите изобару идеального газа (рис 1.) 6.Укажите изохору идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1)
T V T T 7.Укажите график изохорного нагревания газа (рис 2.) 8.Укажите график изотермического расширения идеального газа (рис 2.) 1) p 2) p 3) V 4) p
T V T V |
|
Тест по физике 11 кл.
1. Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 2. Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 3. Уравнение произвольного процесса в идеальном газе массой m 4. Уравнение состояния идеального газа 5. Укажите изохору идеального газа (рис 1.) 6. Укажите изобару идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1)
T V T T 7.Укажите график изотермического расширения идеального газа (рис 2) 8.Укажите график изохорного нагревания газа (рис 2) 1) p 2) p 3) V 4) p
T V T V |
Тест по физике 11 кл.
1.Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 2.Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 3.Уравнение состояния идеального газа 4.Уравнение произвольного процесса в идеальном газе массой m 5.Укажите изобару идеального газа (рис 1.) 6.Укажите изохору идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1)
T V T T 7.Укажите график изохорного нагревания газа (рис 2.) 8.Укажите график изотермического расширения идеального газа (рис 2.) 1) p 2) p 3) V 4) p
T V T V |
|
Тест по физике 11 кл.
1. Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 2. Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 3. Уравнение произвольного процесса в идеальном газе массой m 4. Уравнение состояния идеального газа 5. Укажите изохору идеального газа (рис 1.) 6. Укажите изобару идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1)
T V T T 7.Укажите график изотермического расширения идеального газа (рис 2) 8.Укажите график изохорного нагревания газа (рис 2) 1) p 2) p 3) V 4) p
T V T V |
Тест по физике 11 кл.
1.Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 2.Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 3.Уравнение состояния идеального газа 4.Уравнение произвольного процесса в идеальном газе массой m 5.Укажите изобару идеального газа (рис 1.) 6.Укажите изохору идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1)
T V T T 7.Укажите график изохорного нагревания газа (рис 2.) 8.Укажите график изотермического расширения идеального газа (рис 2.) 1) p 2) p 3) V 4) p
T V T V |
Тема занятия: « Внутренняя энергия»
Класс: 11 Дата:
Преподаватель:
Тобылбаева С. Т.
Т.
Цель урока: познакомить учащихся с законом, добиться его понимания и выработать начальные навыки по применению закона при решении простых задач.
Языковые цели: Тhe second law of motion: Тhe acceleration of an object is directly proportional to the net force acting on it and inversely proportional to its mass. Тhe third law of motion: ?
Задачи урока:
ОБРАЗОВАТЕЛЬНАЯ Формирование знаний об основных положениях МКТ, обобщение широкого круга физических явлений на основе данной теории. Систематизация понятий, их мировоззренческой интерпретации в современной научной картине мира.
РАЗВИВАЮЩАЯ формирование
умений самостоятельно приобретать и применять знания, наблюдать и объяснять
физические явления, а также умений пользоваться учебником, дополнительной
литературой. Развивать познавательный интерес к физике и технике, творческих
способностей. Формирование осознанных мотивов учения.
Формирование осознанных мотивов учения.
ВОСПИТЫВАЮЩАЯ Воспитание аккуратности, навыков письменной и устной речи. Воспитание способности следовать нормам поведения.
Основные ЗУН:
тепловое движение частиц, основные положения МКТ, температура как мера средней кинетической энергии, изопроцессы, идеальный газ. Основное уравнение МКТ, уравнение Менделеева-Клапейрона, уравнение внутренней энергии газа. Умения устанавливать
связь между средней кинетической энергией и температурой, рассчитывать значение внутренней энергии.
Тип урока: комбинированный по схеме «ВОР» ( Вызов Осмысление Рефлексия). Прием- ФИШБОУН.(рыба)
Этапы урока
1 Оргмомент. Постановка целей.
2 Вызов.
Граф Румфорд (англ.физик Томпсон) так объяснил свой
интерес к науке о теплоте : «Обедая, я часто замечал, что ….яблочные
пироги…оставались горячими удивительно долго.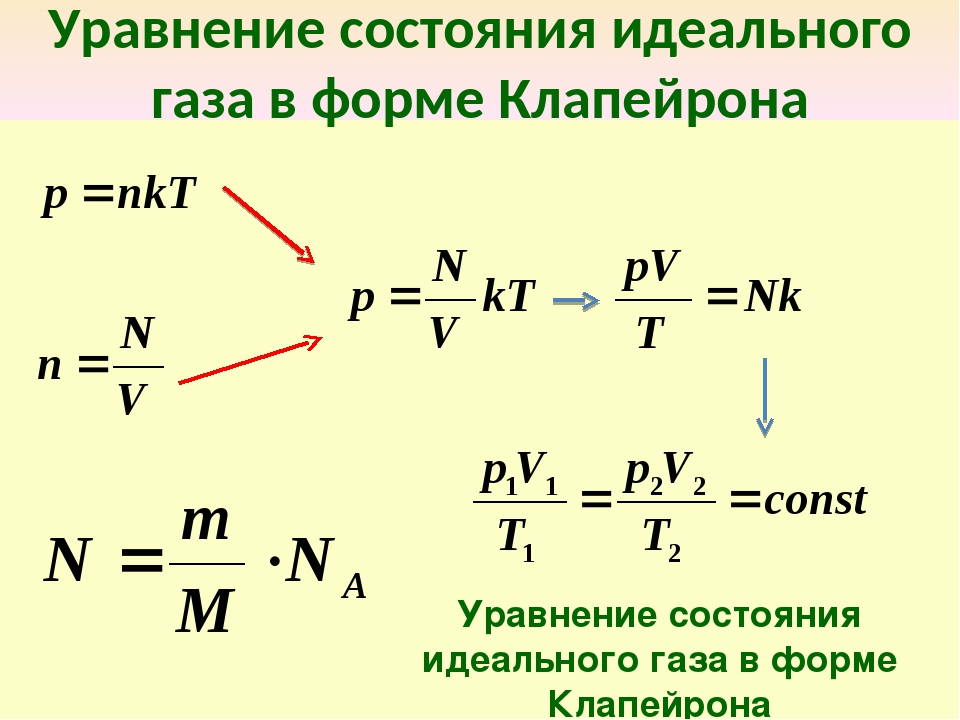 Сильно пораженный….я всегда
пытался, но все напрасно, найти хоть какое-нибудь объяснение удивительному
явлению».
Сильно пораженный….я всегда
пытался, но все напрасно, найти хоть какое-нибудь объяснение удивительному
явлению».
Вопрос: 1. К какому явлению относится данная ситуация?
- Какие понятия характеризуют тепловые явления? (8 класс)
- Осмысление.
Построение «рыбы», работа с учебником пар.54 : понятие внутренней энергии, положения о строении вещества, понятие идеального газа, различия в строении и виды веществ, количество теплоты, способы изменения внутренней энергии (работа по рисункам №195), теплообмен, тепловое равновесие.
4. Вывод формулы расчета внутренней энергии.
5..Рефлексия.
Выполнение задания на рефлексию с использованием подборки пословиц народов мира.
ЗАДАНИЕ:
- Выбрать номера пословиц, отражающие основные положения о строении веществ.
- Выбрать номера пословиц, отражающие способы
изменения внутренней энергии.

- Ответ на вопрос начала урока (вопрос графа Румфорда)
РЕШЕНИЕ ЗАДАЧ:
- При нагревании аргона, количество вещества которого 2 моля, внутренняя энергия увеличилась на 250Дж. Каково изменение температуры аргона?
- На сколько изменится внутренняя энергия одного моля одноатомного газа при его нагревании на 100К ?
Домашнее задание пар.54 «А» задача 1,2 «Б» № 621, 624
7. Итоговый тест-контроль.
8. Итог урока.
Рабочий лист ученика. Пар.54 «Внутренняя энергия»
- ответь на вопрос :
· Какое явление характеризует данная ситуация?
- Какие понятия характеризуют данное явление?
( ТЕРМИНЫ: Три положения о строении вещества, виды вещества, идеальный газ, Теплообмен, количество теплоты, способы изменения внутренней энергии)
- Изучив тексты пословиц и поговорок, выполни задание:
- Выбери № пословиц, отражающие основные положения
о строении веществ.

- Выбери № пословиц, отражающие способы изменения внутренней энергии.
ПОСЛОВИЦЫ И ПОГОВОРКИ.
- Как с гуся вода.
- Вода с водой – не гора с горой : сливаются.
- Возле огня ляжешь – обожжёшься.
- Масло с водой не смешаешь. Береги нос в большой мороз.
- Нарезанный лук сильнее пахнет. Тухлое яйцо всю кашу портит.
- На мешке с солью и верёвка солёная.
- Золотые цветы не пахнут. Овощной лавке и вывеска не нужна.
- Чем огонь просить, лучше его высечь.
- Работающей мельнице некогда мерзнуть.
- Где солнце пригреет, там и вода примлеет.
- Отрезанный ломоть к хлебу не приставишь.
- Помоги графу Румфорду ответить на вопрос:
Почему яблочный пирог долго не остывает?
- Решение задач.
- При нагревании аргона, количество вещества
которого 2 моля, внутренняя энергия увеличилась на 250Дж.
 Каково изменение
температуры аргона?
Каково изменение
температуры аргона? - На сколько изменится внутренняя энергия одного моля одноатомного газа при его нагревании на 100К ?
- Итоговый тест – контроль
1. Расставьте эти утверждения в порядке описания строения вещества.
А. Молекулы вещества взаимодействуют друг с другом.
Б. Вещества состоят из молекул.
В. Молекулы всех тел движутся непрерывно.
2. Расположите частицы в порядке сложности их строения.
А. Молекула Б. Электрон В. Атом.
3. Явление проникновения молекул одного вещества в межмолекулярное пространство другого вещества.
А. Конвекция, Б. Деформация. В. Диффузия.
4. Какие вещества не сохраняют ни формы, ни объема.
А. Кристаллические. Б. Газы. В.Жидкости.
5. Газ, взаимодействие между молекулами которого пренебрежимо мало…
А. Реальный. Б. Абсолютный. В.Свободный.
6. Как называются явления, обусловленные изменением температуры тела?
А. Тепловые Б.Электрические.
В.Магнитные.7. Значение температуры по шкале Кельвина определяется:
Тепловые Б.Электрические.
В.Магнитные.7. Значение температуры по шкале Кельвина определяется:
А.T=t- 273 Б.T=273t В.T=t+273
8. Состояние теплового равновесия тел характеризует..
А.Давление. Б.Объем. В.Температура.
Контрольная работа. ДАВЛЕНИЕ ТВЕРДЫХ ТЕЛ, ГАЗОВ И
ЖИДКОСТЕЙ. АРХИМЕДОВА СИЛА
ДАВЛЕНИЕ ТВЕРДЫХ ТЕЛ, ГАЗОВ И
ЖИДКОСТЕЙ. АРХИМЕДОВА СИЛА
Начальный уровень
ВАРИАНТ 1
1. Почему режущие и колющие инструменты оказывают на тела очень большое давление?
2. Какие примеры сообщающихся сосудов вы можете привести?
3. Будет ли свинцовый брусок плавать в ртути?
ВАРИАНТ 2
1. Почему у трактора делают широкие гусеницы? Почему не разрешено ездить по асфальту на гусеничных тракторах?
2. Кузов автомашины заполнили грузом. Изменилось ли давление в камерах колес автомашины?
3. Назовите металл, который тонет в ртути.
ВАРИАНТ 3
1. Для чего при шитье иголкой на палец надевают наперсток?
2. Почему мыльные пузыри круглые?
3. Будет ли кирпич плавать в серной кислоте?
ВАРИАНТ 4
1. Какая физическая величина характеризует действие силы на опору? В каких единицах ее измеряют?
2. Молоко вылили из бутылки в широкую
кастрюлю. Какие из следующих физических величин изменились и какие остались
неизменными: масса молока, объем молока, давление?
Молоко вылили из бутылки в широкую
кастрюлю. Какие из следующих физических величин изменились и какие остались
неизменными: масса молока, объем молока, давление?
3. Пользуясь таблицей плотностей, укажите 2-3 вещества, которые могут плавать в бензине.
ВАРИАНТ 5
1. Приведите примеры, показывающие, что давление зависит от площади опоры, на которую действует сила.
2. Где применяются сообщающиеся сосуды в домашних условиях? Приведите примеры домашней посуды, которая представляет собой сообщающиеся сосуды?
3. Будет ли парафиновый шарик плавать в ацетоне? Почему?
ВАРИАНТ 6
1. Приведите примеры использования больших площадей опоры для уменьшения давления.
2. Почему камень в воде легче поднимать, чем в воздухе?
3. Будет ли медная пластинка плавать в глицерине? Почему?
Средний уровень
ВАРИАНТ 1
1. В ведро или в бутылку нужно
перелить молоко из литровой банки, чтобы его давление на дно стало меньше?
В ведро или в бутылку нужно
перелить молоко из литровой банки, чтобы его давление на дно стало меньше?
2. При каком условии тело, например бревно, плавает на поверхности воды?
3. Сила 600 Н равномерно действует на площадь 0,2 м2. Как велико в данном случае давление?
ВАРИАНТ 2
1. Вам даны: колба, мензурка, стакан. Налейте в каждый из этих сосудов столько воды, чтобы давления на дно каждого из сосудов были равными. Какой прибор вам нужен для выполнения задания
2. При каком соотношении сил, действующих на опущенное в жидкость тело, оно будет тонуть? Приведите пример.
3. Трактор весом 112 кН оказывает давление на грунт 50 кПа. Определите площадь соприкосновения гусениц трактора с грунтом.
ВАРИАНТ 3
1. В чем суть закона Паскаля? Поясните его действие примерами.
2. В каких газах может всплыть пузырь, наполненный воздухом?
3. Вычислите давление жидкости
плотностью 1800 кг/м3 на дно цилиндрического сосуда, если высота ее
уровня 10 см.
Вычислите давление жидкости
плотностью 1800 кг/м3 на дно цилиндрического сосуда, если высота ее
уровня 10 см.
ВАРИАНТ 4
1. Оказывают ли давление газы? Почему?
2. Каково должно быть соотношение сил, действующих на опущенное в жидкость тело, чтобы оно стало всплывать? Приведите пример.
3. Сосуд с ртутью весит 32 Н. Рассчитайте давление, которое оказывает сосуд на стол, если площадь основания сосуда 0,008 м2.
ВАРИАНТ 5
1. Сформулируйте правило «поведения» однородной жидкости в сообщающихся сосудах. В каком случае оно не будет выполняться?
2. В мензурку налили керосин, а затем долили воду. Как расположатся в ней эти жидкости? Почему?
3. Давление, производимое на преграду штормовым ветром, достигает 1100 Па. Определите силу, с которой ветер давит на стену дома площадью 24 м2.
ВАРИАНТ 6
1. Каковы причины наличия у Земли
атмосферы?
Каковы причины наличия у Земли
атмосферы?
2. В каком случае тело, оказавшееся в жидкости, будет плавать внутри нее, не всплывая и не погружаясь на дно?
3. Рассчитайте давление воды на глубине 20 м, на которую может погружаться искусный ныряльщик.
Достаточный уровень
ВАРИАНТ 1
1. Какое давление оказывает на грунт стальной столб высотой 5 м?
2. Как узнать экспериментально (не пользуясь весами и мензуркой), больше или меньше плотности воды плотность ученической резинки?
3.
Подвешенные к коромыслу весов одинаковые шары погрузили в жидкость сначала так, как показано на рисунке а, а затем так, как показано на рисунке б. В каком случае равновесие весов нарушится? Почему?
4. Какую силу нужно приложить, чтобы удержать в воде стальной рельс объемом 0,7 м3?
ВАРИАНТ 2
1. Какая глубина в море соответствует
давлению воды, равному 412 кПа?
Какая глубина в море соответствует
давлению воды, равному 412 кПа?
2. Почему не только жидкости, но и газы передают производимое на них давление во все стороны одинаково?
3. В сосуде плавают одинакового размера деревянный и пробковый бруски. Какой из них деревянный, а какой пробковый?
4. Определите, что покажут пружинные весы, если тело объемом 100 см3 из алюминия взвешивать в керосине.
BAPИAHT 3
1. Человек оказывает на пол давление 1,5ּ104 Па. Площадь подошвы ботинка 0,02 м2. Определите массу человека.
2. Можно ли добиться того, чтобы тело, изготовленное из вещества с плотностью, большей плотности воды (например, из пластилина) плавало в ней? Как?
3. На поверхности воды плавают одинаковые по размерам бруски из дерева, льда и пробки. Изобразите примерную картину их расположения в воде.
4. Железную деталь размерами 20 х 20 х
25 см погружают в воду. Какую силу нужно приложить, чтобы удержать эту деталь
в воде?
Железную деталь размерами 20 х 20 х
25 см погружают в воду. Какую силу нужно приложить, чтобы удержать эту деталь
в воде?
ВАРИАНТ №4
1. Масса четырехколесного прицепа с грузом 2,5 т. Определите давление, оказываемое прицепом на дорогу, если площадь соприкосновения каждого колеса с дорогой 125 см2.
2. Объясните различие в передаче давления жидкостью и твердым телом на основе представлений об их внутреннем строении.
3.
На какой из опущенных в воду стальных шаров действует наибольшая выталкивающая сила? Почему?
4. Вес куска железа в воде 1,67 Н. Найдите его объем.
ВАРИАНТ №5
1. Какое давление оказывает на грунт гранитная колонна, объем которой 5 м3, если площадь основания 0,5 м2?
2.
Одинаковы ли причины давления газа
на стенки сосуда, в котором он находится, и давления твердого тела на опору?
Укажите эти причины.
3. Три несмешивающиеся между собой жидкости — вода, керосин, ртуть — налиты в сосуд. В каком порядке они расположились? Ответ обоснуйте. Сделайте рисунок.
4. Длина прямоугольной баржи 4 м, ширина 2 м. Определите вес помещенного на баржу груза, если после нагрузки она осела в воду на 0,5 м.
ВАРИАНТ №6
1. С какой силой давит атмосфера на поверхность страницы тетради, размер которой 16 х 20 см при атмосферном давлении 0,1 МПа?
2. Почему в самой жидкости (не зависимо от того, действуют ли на нее какие-либо силы или нет) должно возникать давление? Существует ли оно? Как это доказать?
3. На поверхности жидкости плавают два цилиндра одинакового размера — один деревянный (№ 1), а другой пробковый (№ 2). На какой из них можно положить больший груз, не утопив диска?
4.
После разгрузки баржи ее осадка в
реке уменьшилась на 60 см. Определите массу снятого с нее груза, если площадь
сечения баржи на уровне воды равна 240 м2.-reshenie-332.jpg)
Высокий уровень
ВАРИАНТ №1
1. Определите, с какой силой воздух давит на крышу дома размером 20 х 50 м при нормальном атмосферном давлении. Почему крыша не проваливается?
2. Стальной и стеклянный шарики имеют одинаковые массы. Какой из них легче поднять в воде?
3. Льдина объемом 5 м3 плавает на поверхности воды. Определите объем подводной и надводной части
4. Какова плотность подвешенного к динамометру бруска, если при полном погружении бруска в керосин показание динамометра уменьшается с 12Н до 8Н?
ВАРИАНТ 2
1. Принимая длину одной лыжи равной 1,8 м, а ширину 10 см, определите давление, которое оказывает на снег мальчик массой 54 кг.
2. Действует ли сила Архимеда в условиях невесомости? Почему?
3. Плотность жидкости в 5 раз больше плотности материала тела. Какая часть объема тела будет выступать над жидкостью, если тело поместить в жидкость?
4. Прямоугольная льдина длиной 52 м и
шириной 40 м плавает в море. Высота льдины, выступающей над поверхностью воды,
равна 1 м. Определите объем всей льдины.
Прямоугольная льдина длиной 52 м и
шириной 40 м плавает в море. Высота льдины, выступающей над поверхностью воды,
равна 1 м. Определите объем всей льдины.
BAPИAHТ 3
1. Ширина шлюза 10 м. Шлюз заполнен водой на глубину 5 м. С какой силой давит вода на ворота шлюза?
2. Стальной шарик плавает в ртути. Изменится ли погружение шарика в ртуть, если сверху налить воды?
3. Льдина плавает в воде. Объем ее подводной части 54 м3. Определите объем всей льдины.
4. Цинковый шар весит 3,6 Н, а при погружении в воду — 2,8 Н. Сплошной ли это шар или имеет полость? (Если полый, то чему равен объем полости?)
BAPИAHТ 4
1. Трактор массой 12 т имеет площадь опоры одной гусеницы 1,2 м2. Какое давление на грунт производит трактор?
2. Кусок мрамора весит столько, сколько весит медная гиря. Какое из этих тел легче удержать в воде?
3. Стержень плавает в воде таким
образом, что под водой находится 3/4 его объема. Определите плотность материала,
из которого изготовлен стержень.
Стержень плавает в воде таким
образом, что под водой находится 3/4 его объема. Определите плотность материала,
из которого изготовлен стержень.
4. При полном погружении полого латунного кубика массой 170 г в керосин на кубик действует архимедова сила 4 Н. Каков объем полости?
ВАРИАНТ 5
1. В гидравлической машине на малый поршень произвели давление 2 Н/см2. Какая сила будет действовать на большой поршень, если его площадь 20 см2? На каком свойстве жидкостей основано устройство гидравлической машины?
2. В сосуде с водой плавает стакан. Изменится ли уровень воды в сосуде, если, наклонив стакан, зачерпнуть им из сосуда немного воды и пустить стакан снова плавать?
3. Железный шар плавает в ртути. Какая часть его объема погружена в ртуть?
4. Полый медный шар плавает в воде во взвешенном состоянии. Чему равна масса шара, если объем воздушной полости равен 17,75 см3?
BAPИAHТ 6
1. Предел прочности гранита равен 270
МПа. Какой высоты можно было бы изготовить обелиск из цельного куска гранита,
чтобы он не разрушился под действием собственной тяжести?
Предел прочности гранита равен 270
МПа. Какой высоты можно было бы изготовить обелиск из цельного куска гранита,
чтобы он не разрушился под действием собственной тяжести?
2. Стальной шарик плавает в ртути. Изменится ли погружение шарика в ртуть, если сверху налить воды? Вес тела в воде в пять раз меньше, чем в воздухе. Какова плотность материала тела?
3. Какая архимедова сила действует на полностью погруженный в воду полый медный шар массой 890 г, если объем полости равен 40см3?
4. ДОМАШНЯЯ ЛАБОРАТОРНАЯ РАБОТА
5. 1.
Возьмите три стакана. В первый налейте кипяток, во второй теплую
и в третий холодную воду.
В каждый стакан бросить щепотку гранулированного чая. Что вы
заметили?.
6. 2.
Возьмите пустую пластиковую бутылку, предварительно охладив
ее, опустите горлышко в стакан с водой и обхватите
бутылку ладонями, но не нажимайте. Наблюдайте в течение
нескольких минут.
7. 3. На горлышко той же, но вновь охлажденной бутылки положите смоченную в воде перевернутую пробку и таккже обхватите ее теплыми ладонями. Наблюдайте в течение нескольких минут.
8. 4. Налейте в неглубокую тарелку воды на высоту 1 — 1,5 см, поставьте в нее перевернутый вверх дном и предварительно нагретый горячей водой стакан. Наблюдайте в течение нескольких минут.
9. Жду отчет с объяснениями увиденного. Кто первый?
10. ТЕМПЕРАТУРА
11. —
величина, которая характеризует тепловое состояние тела или иначе мера
«нагретости» тела.
Чем выше температура тела, тем большую в среднем энергию имеют его атомы и
молекулы.
12. Приборы, служащие для измерения температуры называются термометрами.
13. Принцип измерения температуры.
14. Температура
непосредственно не измеряется! Измеряется величина,
зависящая от температуры!
В современных жидкостных термометрах — это объем спирта или ртути ( в
термоскопе Галилея – объем газа). Термометр измеряет
собственную температуру! А, если мы хотим измерить с помощью термометра
температуру какого-либо другого тела, надо подождать некоторое время, пока
температуры тела и термометра уравняются, т.е. наступит тепловое равновесие
между термометром и телом.
Термометр измеряет
собственную температуру! А, если мы хотим измерить с помощью термометра
температуру какого-либо другого тела, надо подождать некоторое время, пока
температуры тела и термометра уравняются, т.е. наступит тепловое равновесие
между термометром и телом.
В этом состоит закон теплового равновесия:
у любой группы изолированных тел через какое-то время температуры становятся
одинаковыми,
т.е. наступает состояние теплового равновесия.
15. …
16. ПРОВЕДИ ДОМАШНИЙ ОПЫТ
17. Возьмите три тазика с водой: один — с очень горячей, другой — с умеренно теплой, а третий — с очень холодной. Теперь ненадолго опустите левую руку в тазик с горячей водой, а правую — с холодной. Через пару минут извлеките руки из горячей и холодной воды и опустите их в тазик с теплой водой. Теперь спросите каждую руку, что она «скажет» вам о температуре воды?
18. СДЕЛАЙ САМ:
19. Термометр.
Термометр.
20. Возьми
маленький стеклянный пузырек (в таких пузырьках в аптеках продают, например,
зеленку), пробку (лучше резиновую) и тоненькую прозрачную трубочку (можно взять
пустой прозрачный стерженек от шариковой ручки).
Проделай отверстие в пробке и закрой пузырек. Набери в трубочку капельку
подкрашенной воды и вставь стержень в пробку. Хорошенько загерметизируй щель
между пробкой и стержнем.
Термометр готов.
Теперь необходимо отградуировать его, т.е. сделать измерительную шкалу.
Понятно, что при нагревании воздуха в пузырьке он будет расширяться, и капелька
жидкости будет подниматься по трубочке вверх. Твоя задача отметить на
стерженьке или прикрепленной к нему картонке деления, соответствующие разным
температурам.
Для градуировки можно взять еще один готовый термометр и опустить оба
термометра в стакан с теплой водой. Показания термометров должны совпадать.
Поэтому, если готовый термометр показывает температуру, например, 40 градусов,
можете смело ставить отметинку 40 на стерженьке своего термометра в том месте,
где находится капелька жидкости. Вода в стакане будет остывать, и ты сможешь
таким образом разметить измерительную шкалу.
Вода в стакане будет остывать, и ты сможешь
таким образом разметить измерительную шкалу.
Можно сделать термометр, полностью заполнив его жидкостью.
21. А можно и иначе:
22.
23. Проделай
в крышке пластиковой бутылки отверстие и вставь тонкую пластиковую
трубочку.
Бутылку частично заполни водой и закрепи на стене. У свободного конца трубочки
разметь температурную шкалу. Отградуировать шкалу можно с помощью обычного
комнатного термометра.
При изменении температуры в комнате вода будет расширяться или сжиматься, и
уровень воды
в трубочке тоже «поползет» по шкале.
А можно и посмотреть, как работает термометр!
Обхвати бутылку руками и погрей ее.
Что произошло с уровнем воды в трубочке?
24. ТЕМПЕРАТУРНЫЕ ШКАЛЫ
|
|
Шкала |
Шкала |
Шкала |
Шкала |
|
Кем и |
А.
Цельсия |
Фаренгейт |
Реомюр
французский физик |
Томсон
|
|
Обозна- |
C |
F |
R |
К |
|
Наличие
положи- |
+ и – |
+ и – |
+ и – |
+ |
|
Опорные
|
0C |
32F |
0R |
0K –
абс.нуль, |
25.
ТЕРМОСКОП
26. Впервые прибор для определения температуры был изобретен Галилеем в 1592 г. Небольшой стеклянный баллон был припаян к тонкой трубке с открытым концом.
27.
28. Баллон нагревали руками и погружали конец трубки в сосуд с водой. Баллон охлаждался до температуры окружающего воздуха и уровень воды в трубке поднимался. Т.е. по изменению объема газа в сосуде можно было судить об изменении температуры. Здесь еще не было числовой шкалы, поэтому такой прибор назывался термоскопом. Измерительная шкала появилась только через 150 лет!
29.
ЗНАЕШЬ ЛИ ТЫ ?
30. Самая
высокая температура на Земле зарегистрированная в Ливии в 1922 году — +57,80С;
самая низкая температура, зарегистрированная на Земле, — –89,20С;
над головой у человека температура выше температуры окружающей среды на 1 –
1,50С;
средняя температура животных: лошади — 380С, овцы — 400С, курицы — 410С,
температурав центре Земли — 200000С;
температура на поверхности Солнца — 6000 К, в
центре — 20 млн.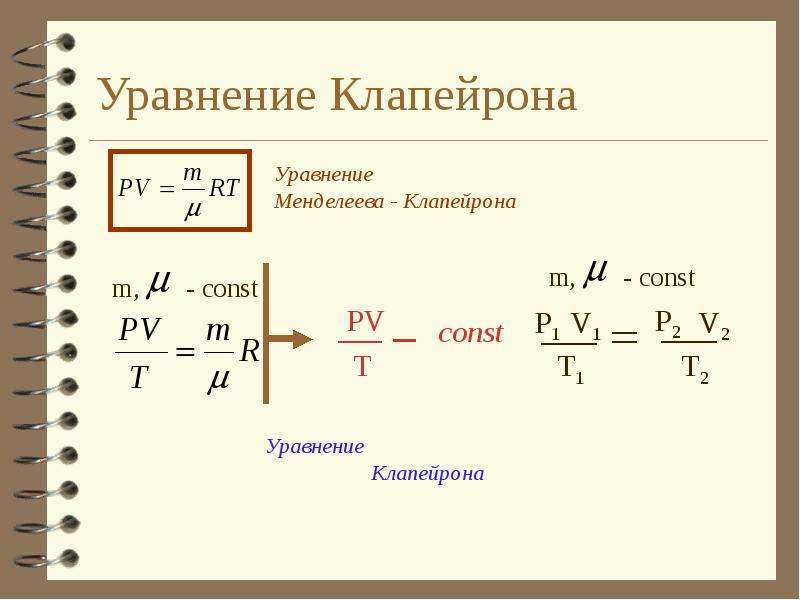 град К.
град К.
31. ___
32. А какова
температура недр Земли?
Раньше высказывались различные гипотетические предположения и приводились
расчеты, по которым температура на глубине 15 км получалась 100…400°C.
Теперь Кольская сверхглубокая скважина,
которая прошла отметку 12 км, дала точный ответ на поставленный вопрос. Вначале (до
3 км) температура росла на 1° через каждые 100 м проходки, далее этот
рост составил 2,5° на каждые новые 100 м. На глубине 10 км
температура недр Земли оказалась равной 180°C!
Наука и жизнь
33. ___
34. К концу 18 века число изобретенных температурных шкал достигало двух десятков.
35. ___
36. Итальянские
ученые-полярники, совершив экспедицию в Антарктиду, столкнулись с
удивительной загадкой. Близ залива Инглей они открыли ледяное ущелье, где постоянно
дует сверхскоростной и сверххолодный ветер. Поток воздуха температурой минус 90
градусов мчится со скоростью 200 км в час.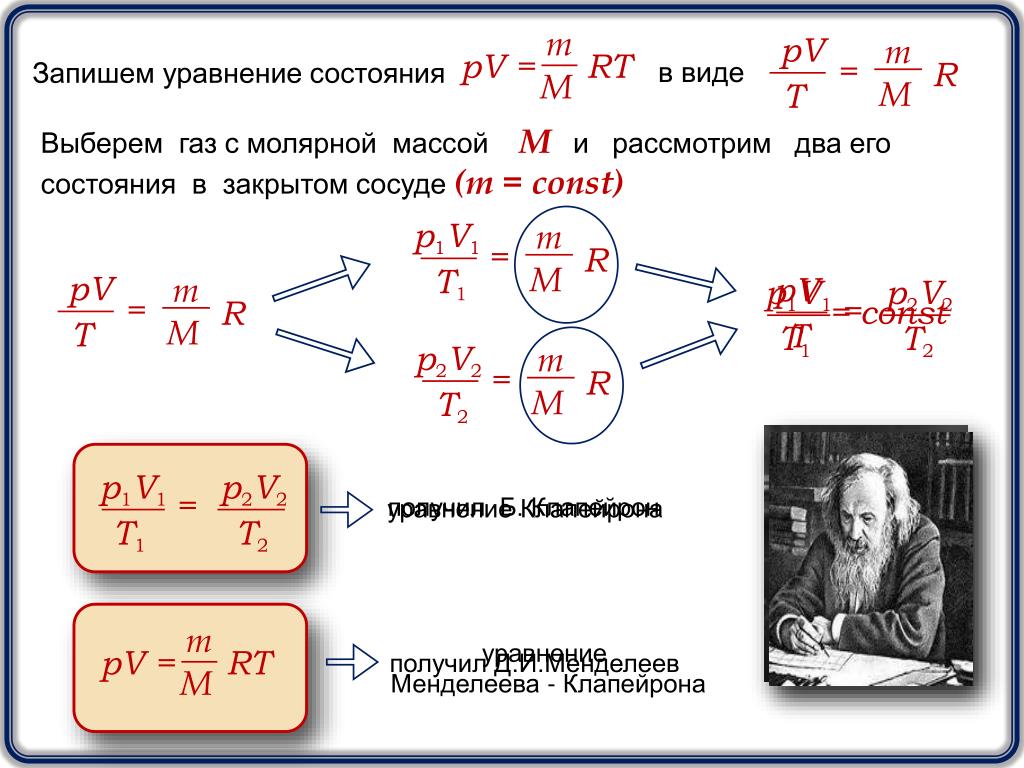 Неудивительно, что это ущелье
назвали «вратами ада» – никто не может находиться там без риска
для жизни больше одной минуты: ветер несет частицы льда с такой силой, что
мигом рвет одежду в клочья.
Неудивительно, что это ущелье
назвали «вратами ада» – никто не может находиться там без риска
для жизни больше одной минуты: ветер несет частицы льда с такой силой, что
мигом рвет одежду в клочья.
37.
ПОЛОМАЕМ ГОЛОВУ?
38.
39. ( или «5» светит )
40. КАВЕРЗНЫЕ ЗАДАЧИ
41. 1. Как измерить температуру тела муравья с помощью обычного термометра?
42.
43. 2. Существуют термометры, в которых используют воду. Почему такие водяные термометры неудобны для измерения температур, близких к температуре замерзания воды?
44. Жду ответа ( на уроке или по почте) !
45.
А ЭТО ТЫ ЗНАЕШЬ ?
46. На самом
деле шведский астроном и физик Цельсий предложил шкалу, в которой
точка кипения воды была обозначена числом 0, а точка таяния льда числом 100 !
«Зато зимой не будет отрицательных чисел!» -любил говорить Цельсий. Но потом шкалу «перевернули».
Но потом шкалу «перевернули».
47. ___
48. · Температура -40 градусов по Цельсию точно равна температуре -40 градусов по Фаренгейту. Это единственная температура, в которой две этих шкалы сходятся.
49. ___
50. Одно время в физических лабораториях пользовались для измерения температуры так называемым весовым термометром. Он состоял из полого платинового шара, заполненного ртутью, в котором было капиллярное отверстие. Об изменении термпературы судили по количеству ртути, вытекавшей из отверстия.
51. ___
52. Оказывается существует плоский термометр. Это «бумажка», которую накладывают на лоб больного. При высокой температуре «бумажка» становится красного цвета.
53. ___
54. Наши
ощущения, обычно надежные, могут подвести при
определении температуры Например, известен опыт, когда одну руку опускают в
горячую, а другую — в холодную воду.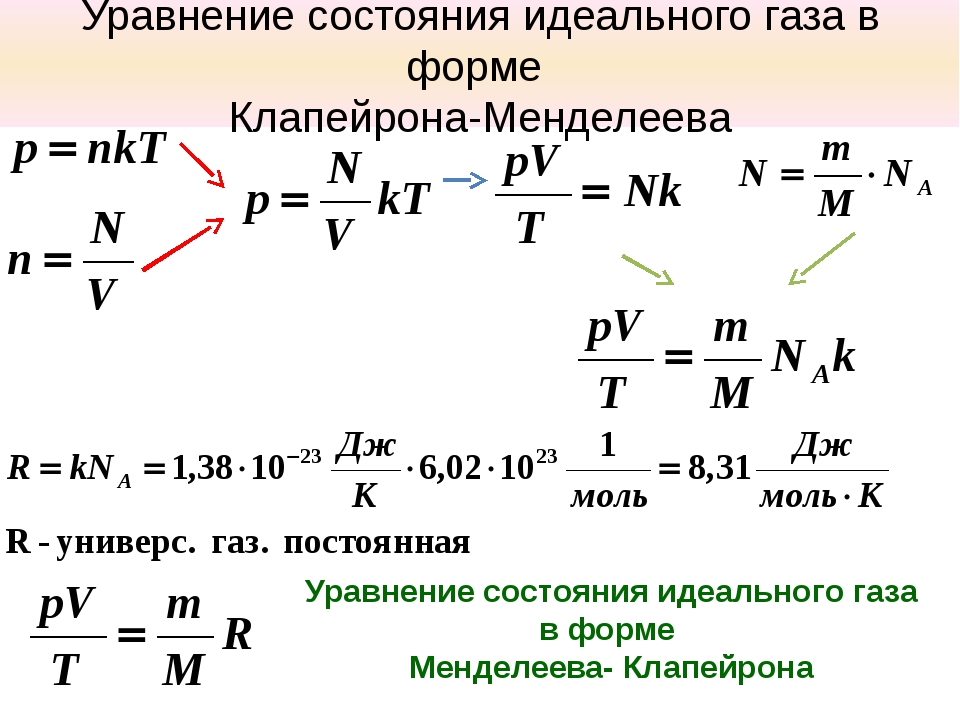 Если через некоторое время опустить обе
руки в теплую воду, то рука, которая до этого была в горячей воде, почувствует
холод, а рука, бывшая в холодной воде — жар!
Если через некоторое время опустить обе
руки в теплую воду, то рука, которая до этого была в горячей воде, почувствует
холод, а рука, бывшая в холодной воде — жар!
55. ___
56. Понятие температуры неприменимо к отдельной молекуле. О температуре можно говорить лишь в том случае, если имеется достаточно большая совокупность частиц.
57. ___
58. Чаще
всего физики измеряют температуру по шкале Кельвина:
0 градусов по шкале Цельсия = 273 градусам по шкале Кельвина!
59.
60.
ТЫ ХОЧЕШЬ ПЕРЕВЕСТИ ТЕМПЕРАТУРУ ИЗ ОДНОЙ ШКАЛЫ В ДРУГУЮ ?
61. — пожалуйста, жми здесь.
62.
63. Самая высокая температура.
64. Она
получена в центре взрыва термоядерной бомбы – около 300…400 млн°C.
Максимальная температура, достигнутая в ходе управляемой термоядерной реакции
на испытательной термоядерной установке ТОКАМАК в Принстонской лаборатории
физики плазмы, США, в июне 1986 г. , составляет 200 млн°C.
, составляет 200 млн°C.
65. Самая низкая температура.
66. Абсолютный нуль по шкале Кельвина (0 K) соответствует –273,15° по шкале Цельсия или –459,67° по шкале Фаренгейта. Самая низкая температура, 2·10–9 K (двухбиллионная часть градуса) выше абсолютного нуля, была достигнута в двухступенчатом криостате ядерного размагничивания в Лаборатории низких температур Хельсинкского технологического университета, Финляндия, группой учёных под руководством профессора Олли Лоунасмаа (род. в 1930 г.), о чём было объявлено в октябре 1989 г.
67. Самый миниатюрный термометр.
68. Д-р Фредерик Сакс, биофизик из Государственного университета штата Нью-Йорк, Буффало, США, сконструировал микротермометр для измерения температуры отдельных живых клеток. Диаметр наконечника термометра – 1 микрон, т.е. 1/50 часть диаметра человеческого волоса.
69.
Скачано с www. znanio.ru
znanio.ru
Графические задачи на газовые законы
Графические задачи на газовые законыМ.Л.Шифман,
ФМЛ № 30, г. Санкт-Петербург
Графические задачи заслуживают особого внимания, ибо, как показывает опыт, они представляют наибольшую трудность для абитуриентов. Причина проста: этому типу задач в школьном курсе уделяют неоправданно мало внимания – решают одну-две задачи, притом формально, не вникая в суть. Кроме того, в школе ограничиваются изопроцессами, когда масса газа постоянна. Именно поэтому на вступительных экзаменах абитуриенты теряются и не знают даже, с чего начать и каковы методы решения.
Напомним, как изображаются на диаграммах изотерма, изобара и изохора идеального газа.
Можно выделить несколько типов графических задач. В задачах первого типа графически задается какой-то изопроцесс в явной или неявной форме. Для решения таких задач можно предложить следующий «план действий»:
1. Установить характер изображенного процесса (если он очевиден).
2. Выбрать (на свое усмотрение) какой-либо из изопроцессов и изобразить его графически (провести изобару, изохору или изотерму).
3. Провести эту линию графика до пересечения с линией (или с линиями) представленного процесса (или процессов).
4. Спроецировать точку (или точки) пересечений этих линий на одну из координатных осей (выбор оси произволен).
5. Рассмотреть состояния данной массы газа, которым соответствуют эти проекции, и, используя известные газовые законы, ответить на поставленный в задаче вопрос.
Проиллюстрируем этот алгоритм примерами.
- Пример 1. Какая из двух линий графика соответствует большему давлению данной массы идеального газа?
Решение. Прежде всего установим, что это за
линии. Эти линии выражают прямо пропорциональную
зависимость между объемом газа и его
температурой, а это возможно для идеального газа
только при изобарическом процессе,
следовательно, изображенные линии графика –
изобары.
Проведем изотерму до пересечения с обеими изобарами, а точки их пересечения спроецируем на ось ординат (объемов). Из построения видно, что V2 > V1. Поскольку при изотермическом процессе газ подчиняется закону Бойля–Мариотта: р1V1 = р2V2, то р1 > р2. Напомним, что все точки, лежащие на одной изобаре, соответствуют состояниям с одинаковым давлением.
Читателю предоставляется возможность решить эту задачу путем построения изохоры и проецирования точек пересечения на ось температур (еще раз стоит напомнить, что выбор способа решения в задачах данного типа произволен).
- Пример 2. При нагревании идеального газа постоянной массы получена зависимость р(T) при переходе из состояния 1 в состояние 2. Как при этом переходе менялась плотность газа?
Решение. Прежде всего обратим внимание на то,
что линия графика не описывается ни одним из
изопроцессов («неявная форма»).
Проведем через начальную и конечную точки линии графика две изохоры.
Проведя еще изобару (или, как вариант, изотерму) и, спроецировав точки ее пересечения с изохорами на ось Т, убедимся, что Т2 > Т1. При изобарическом процессе, по закону Гей-Люссака, V ~ T, следовательно, V2 > V1. А т.к. плотность и объем связаны обратной зависимостью (при данной массе), то r1 > r2, откуда следует, что газ расширялся, а значит, его плотность уменьшилась.
В задачах второго типа в условии задан некий цикл, совокупность процессов, в результате которых данная масса газа возвращается в исходное состояние. Этот цикл может быть задан на разнообразных диаграммах: p, V; p, T; V, T и др. Как правило, в таких задачах требуется представить заданный цикл на других диаграммах. Эти задачи важны при рассмотрении первого закона термодинамики, когда совершается макроскопическая работа и происходит процесс теплообмена. Важно понимать, что цикл – это замкнутый процесс, и он должен быть замкнутым на любой диаграмме!
При решении предлагается следовать следующему алгоритму:
1.
Установить характер процесса на данном этапе.
2. Указать закон, по которому протекает процесс.
3. Отметить суть этого закона (как связаны между собой величины).
4. По графику выяснить, как меняется каждая величина.
Условимся для удобства обозначать ход процесса стрелками: – увеличение величины, Ї – уменьшение величины.
- Пример 3. На диаграмме р, T изображен цикл идеального газа постоянной массы. Изобразите его на диаграмме р, V.
Решение. Проведем поэтапный анализ представленного цикла:
1–2: изохорический процесс; закон Шарля; р ~ T; р, T.
2–3: изотермический процесс; закон Бойля–Мариотта; р ~ 1/V; рЇ; V
3–1: изобарический процесс; закон Гей-Люссака; V ~ T; TЇ; VЇ.
Теперь результаты поэтапного анализа перенесем на диаграмму р, V.
- Пример
4. Для постоянной массы идеального газа
представлен цикл на диаграмме р, V. Изобразить
этот цикл на диаграмме V, T.

Решение. Проведем поэтапный анализ:
1–2: изобарический процесс; закон Гей-Люссака; V~ T; V; T.
2–3: изохорический процесс; закон Шарля; р~ T; рЇ; TЇ.
3–4: изобарический процесс; закон Гей-Люссака; V ~ T; VЇ; TЇ.
4–1: изохорический процесс; закон Шарля; р ~ T; р; T.
- Пример 5. Изобразите на диаграмме р, Т цикл постоянной массы идеального газа, представленный на диаграмме р, V.
Решение
1–2: изотермический процесс; закон Бойля–Мариотта; р ~ 1/V; р; VЇ
2–3: изобарический процесс; закон Гей-Люссака; V~T; V; T
3–4: изотермический процесс; закон Бойля–Мариотта; р ~ 1/V; рЇ; V
4–1: изохорический процесс; закон Шарля; р ~ T; рЇ; TЇ.
А вот блок задач с необычной постановкой условия. Впрочем, и они решаются достаточно стандартными методами, а известные формулы начинают играть новыми красками. Давайте убедимся в этом.
- Пример 6. Как менялась температура постоянной идеального массы газа на протяжении цикла? Точки 1 и 2 лежат на одной изотерме.
Решение. Проведем изотермы через характерные точки 1, 2, 3 и касательную к участку 1–2. Как следует из теории, изотермы, более удаленные от координатных осей, соответствуют более высоким температурам. В этом можно убедиться, используя методы, предложенные в предыдущих задачах.
Проходим по циклу:
1–1*: переход на более «высокую» изотерму, значит, температура растет.
1*–2: переход на более «низкую» изотерму, следовательно, температура понижается.
2–3: переход на еще более «низкую» изотерму, это означает дальнейшее понижение температуры.
3–1: переход на более «высокую» изотерму, значит, температура повышается.
Как видим, ничего необычного в этой задаче нет, при решении использованы известные факты.
- Пример 7. Как менялась плотность идеального газа постоянной массы при переходе 1–2?
Решение. Проведем изохоры через характерные точки 1, А, В, 2. Проведем изотерму, пересекающую все изохоры, и спроецируем эти точки пересечения на ось р. Плотность r = m/V, т.е. плотность обратно пропорциональна объему. При изотермическом процессе р ~ 1/V. Таким образом, задача сводится к вопросу, каким изохорам соответствуют большие или меньшие объемы. Обратимся к графику:
1–А: р1 > рAЮ V1 < VAЮ r1 > rАЮ rЇ.
А–В: рВ > рАЮ VВ < VАЮ rВ > rАЮ r
В–2: рВ > р2Ю VВ < V2Ю rВ > r2Ю rЇ
Итак, сначала плотность уменьшается, затем увеличивается и снова уменьшается.
А это уже пример задачи, в которой «играют» формулы, позволяющие получить ответ, казалось бы, без конкретных данных.
- Пример 8. Дан цикл идеального газa постоянной массы. Указать в этом цикле пару точек равного давления.
Решение. В наших руках есть надежное «оружие» в виде уравнения Клапейрона–Менделеева! Применим его для двух произвольных состояний, учитывая, что в этих состояниях, по условию, давления одинаковы. Выразим объем через массу и плотность: V = m/r. Тогда:
р1V1 = р1m/r1 = nRT1;
р2V2 = p2 m/r2 = nRT2.
Теперь остается разделить одно уравнение на другое:
Но р1 = р2, значит, r1T1 = r2T2, или rT = const, или r ~ 1/T.
Как известно, обратно пропорциональная зависимость изображается гиперболой. Точки ее пересечения с циклом и будут соответствовать состояниям с одинаковым давлением. Заметим: любые другие гиперболы, пересекаясь с линией графика, будут давать пары состояний с одинаковым (но уже другим) давлением.
И в заключение рассмотрим три примера, о которых говорилось выше, – задачи, в которых масса газа меняется. К сожалению, как правило, подобные задачи в школьном курсе не рассматриваются. Это и приводит к неприятностям на вступительных экзаменах: срабатывает «фактор неожиданности», и абитуриент теряется…
- Пример 9. Идеальный газ с молярной массой М участвует в изотермическом процессе. При этом получена зависимость между объемом V и давлением р. Представьте этот цикл на диаграмме V, m.
Решение. Запишем уравнение Клапейрона–Менделеева:
По условию, T, M и R – постоянные, следовательно, m ~ рV.
Рассмотрим процессы цикла поэтапно:
1–2: T = const, V = const; m ~ р; р; m
2–3: T = const, р = const; m ~ V; V; m
3–4: T = const, V = const; m ~ р; pЇ; mЇ
4–1: T = const, р = const; m ~ V; VЇ; mЇ
- Пример 10. Идеальный газ с молярной массой М совершает изобарический процесс, что отражено на представленной диаграмме T, m. Изобразите этот цикл на диаграмме V, m.
Решение. Запишем уравнение
Клапейрона–Менделеева:
1–2: р = const; T = const; V ~ m; m; V.
2–3: р = const; m = const; V ~ T; T; V.
3–4: р = const; T = const; V ~ m; mЇ; VЇ
4–1: р = const; m = const; V ~ T; TЇ; VЇ.
Легко видеть, что ничего «необычного» в этих задачах нет, они решаются все теми же методами, которые рассматривались выше. Хочется надеяться, что после знакомства с ними у школьников и абитуриентов проблем уже не будет.
- Пример 11. Дан график зависимости р(V) для процессов, проводимых с идеальным газом неизменного химического состава при постоянной температуре. Кривые 2–3 и 4–1 – гиперболы. Изобразите эти процессы в координатах m, р.
Решение. Запишем уравнение Клапейрона–Менделеева: .
1–2: T = const, р = const; V ~ m; V; m
2–3: T = const, р ~ 1/V; m = const; рЇ
3–4: T = const, V = const; р ~ m; pЇ; mЇ
4–1: T = const, р ~ 1/V; m = const; р
Задачи для самостоятельного решения
- 1. Изобразите цикл постоянной массы идеального газа на диаграммах V, T; р, V.
- 2. Изобразите цикл постоянной массы идеального газа на диаграммах р, T; р, V.
- 3. Как менялась плотность постоянной массы идеального газа при переходе 1–2?
- 4. Изобразите цикл постоянной массы идеального газа на диаграммах р, V и р, T.
- 5. Идеальный газ постоянной массы расширяется по закону рV2 = const. Как при этом меняется температура газа: повышается или понижается?
- 6. Как менялась температура постоянной массы газа при переходе 1–2?
- 7. Дан цикл постоянной массы идеального газа. Указать на линии графика состояния, которым соответствуют экстремальные значения температуры.
- 8. Над постоянной массой идеального газа совершается работа по представленному циклу. Найти отношение экстремальных значений объема в цикле и изобразить цикл на диаграммах р, V; V, T.
| Тест по физике 11 кл. (Изопроцессы) Вариант 1 1. Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 2. Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 3. Уравнение произвольного процесса в идеальном газе массой m 4. Уравнение состояния идеального газа 5. Укажите изохору идеального газа (рис 1.) 6. Укажите изобару идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1) T V T T 7.Укажите график изотермического расширения идеального газа (рис 2) 8.Укажите график изохорного нагревания газа (рис 2) 1) p 2) p 3) V 4) p T V T V | Тест по физике 11 кл. (Изопроцессы) Вариант 2 1.Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 2.Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 3.Уравнение состояния идеального газа 4.Уравнение произвольного процесса в идеальном газе массой m 5.Укажите изобару идеального газа (рис 1.) 6.Укажите изохору идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1) T V T T 7.Укажите график изохорного нагревания газа (рис 2.) 8.Укажите график изотермического расширения идеального газа (рис 2.) 1) p 2) p 3) V 4) p T V T V | Тест по физике 11 кл. (Изопроцессы) Вариант 1 1. Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 2. Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 3. Уравнение произвольного процесса в идеальном газе массой m 4. Уравнение состояния идеального газа 5. Укажите изохору идеального газа (рис 1.) 6. Укажите изобару идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1) T V T T 7.Укажите график изотермического расширения идеального газа (рис 2) 8.Укажите график изохорного нагревания газа (рис 2) 1) p 2) p 3) V 4) p T V T V | Тест по физике 11 кл. (Изопроцессы) Вариант 2 1.Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 2.Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 3.Уравнение состояния идеального газа 4.Уравнение произвольного процесса в идеальном газе массой m 5.Укажите изобару идеального газа (рис 1.) 6.Укажите изохору идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1) T V T T 7.Укажите график изохорного нагревания газа (рис 2.) 8.Укажите график изотермического расширения идеального газа (рис 2.) 1) p 2) p 3) V 4) p T V T V | Тест по физике 11 кл. (Изопроцессы) Вариант 1 1. Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 2. Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 3. Уравнение произвольного процесса в идеальном газе массой m 4. Уравнение состояния идеального газа 5. Укажите изохору идеального газа (рис 1.) 6. Укажите изобару идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1) T V T T 7.Укажите график изотермического расширения идеального газа (рис 2) 8.Укажите график изохорного нагревания газа (рис 2) 1) p 2) p 3) V 4) p T V T V | Тест по физике 11 кл. (Изопроцессы) Вариант 2 1.Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 2.Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 3.Уравнение состояния идеального газа 4.Уравнение произвольного процесса в идеальном газе массой m 5.Укажите изобару идеального газа (рис 1.) 6.Укажите изохору идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1) T V T T 7.Укажите график изохорного нагревания газа (рис 2.) 8.Укажите график изотермического расширения идеального газа (рис 2.) 1) p 2) p 3) V 4) p T V T V | Тест по физике 11 кл. (Изопроцессы) Вариант 1 1. Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 2. Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 3. Уравнение произвольного процесса в идеальном газе массой m 4. Уравнение состояния идеального газа 5. Укажите изохору идеального газа (рис 1.) 6. Укажите изобару идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1) T V T T 7.Укажите график изотермического расширения идеального газа (рис 2) 8.Укажите график изохорного нагревания газа (рис 2) 1) p 2) p 3) V 4) p T V T V | Тест по физике 11 кл. (Изопроцессы) Вариант 2 1.Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 2.Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 3.Уравнение состояния идеального газа 4.Уравнение произвольного процесса в идеальном газе массой m 5.Укажите изобару идеального газа (рис 1.) 6.Укажите изохору идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1) T V T T 7.Укажите график изохорного нагревания газа (рис 2.) 8.Укажите график изотермического расширения идеального газа (рис 2.) 1) p 2) p 3) V 4) p T V T V | Тест по физике 11 кл. (Изопроцессы) Вариант 1 1. Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 2. Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 3. Уравнение произвольного процесса в идеальном газе массой m 4. Уравнение состояния идеального газа 5. Укажите изохору идеального газа (рис 1.) 6. Укажите изобару идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1) T V T T 7.Укажите график изотермического расширения идеального газа (рис 2) 8.Укажите график изохорного нагревания газа (рис 2) 1) p 2) p 3) V 4) p T V T V | Тест по физике 11 кл. (Изопроцессы) Вариант 2 1.Какие параметры изменяются при протекании изобарного процесса в данной массе газа ? 2.Какие параметры изменяются при протекании изотермического процесса в данной массе газа ? 3.Уравнение состояния идеального газа 4.Уравнение произвольного процесса в идеальном газе массой m 5.Укажите изобару идеального газа (рис 1.) 6.Укажите изохору идеального газа (рис 1.) 1)V 2) p 3) p 4) p (рис 1) T V T T 7.Укажите график изохорного нагревания газа (рис 2.) 8.Укажите график изотермического расширения идеального газа (рис 2.) 1) p 2) p 3) V 4) p T V T V |
Зависимость давления от объема газа формула. Компрессоры. Примеры решения задач
Закон Гей-Люссака: при постоянном давлении объем газа изменяется прямо пропорционально абсолютной температуре.
Закон Бойля-Мариотта: при постоянной температуре давление, производимое данной массой газа, обратно пропорционально объему газа.
Газовые законы
Изучение свойств газообразных веществ и химических реакций с участием газов сыграло настолько важную роль в становлении атомно-молекулярной теории, что газовые законы заслуживают специального рассмотрения.
Экспериментальные исследования, по изучению химических реакций между газообразными веществами, привели Ж.-Л. Гей-Люссака (1805) к открытиюзакона объемных отношений: при неизменных температуре и давлении объемы реагирующих газов относятся друг к другу и к объемам газообразных продуктов реакции как небольшие целые числа . Так, при образовании хлорида водорода из простых веществ (H 2 + Cl 2 = 2HCl), объемы реагирующих и полученных веществ относятся друг к другу как 1:1:2, а при синтезе Н 2 О из простых веществ (2H 2 + О 2 = 2H 2 О) это соотношение – 2:1:2.
Эти пропорции нашли объяснение в законе Авогадро: в равных объемах разных газов при одинаковых условиях (температуре и давлении) содержится равное количество молекул . Молекулы простых газообразных веществ, таких как водород, кислород, хлор и др., состоят из двух атомов.
Из закона Авогадро вытекает два важных следствия:
Молекулярная масса (н. у.) газа или пара (M 1) равна произведению его относительной плотности (D) к любому другому газу на молекулярную массу последнего (M 2)
M 1 = D ∙ M 2 ;
D = M 1 / M 2 – отношение массы данного газа к массе другого газа, взятого в том же объеме, при той же температуре и том же давлении.
Например, азот тяжелее гелия в 7 раз, поскольку плотность азота по гелию равна:
D He (N 2) = M (N 2) / М (Не) = 28/4 =7
— моль любого газа при нормальных условиях (Р 0 = 1 атм или 101,325 кПа или 760 мм.рт.ст. и температура Т 0 = 273,15 К или 0°С) занимает объем 22,4 л.
Газообразное состояние вещества заданной массы характеризуется тремя параметрами: давлением Р , объемом V и температурой Т . Между этими величинами были экспериментально установлены следующие соотношения.
Р 2 / Р 1 = V 1 / V 2 , или РV = const.
V 1 / Т 1 = V 2 / Т 2 , или V/Т = const.
Р 1 / Т 1 = Р 2 / Т 2 , или Р/Т = const.
Эти три закона можно объединить в один универсальный газовый закон :
Р 1 V 1 / Т 1 = Р 2 V 2 / Т 2 , или РV /Т = const.
Это уравнение было установлено Б. Клапейроном (1834 г.). Значение постоянной в уравнении зависит только от количества вещества газа. Уравнение для одного моля газа было выведено Д.И. Менделеевым (1874 г.). Для одного моля газа постоянная называется универсальной газовой постоянной и обозначается R = 8,314 Дж/(моль ∙К) = 0,0821 л∙атм/(моль∙К)
РV=RТ ,
Для произвольного количества газа ν правую часть этого уравнения надо умножить на ν :
РV= νRТ или РV= (т/М)RТ ,
которое называют уравнением Клапейрона-Менделеева. Это уравнение справедливо для всех газов в любых количествах и для всех значений Р, V и Т , при которых газы можно считать идеальными.
Темы кодификатора ЕГЭ : изопроцессы — изотермический, изохорный, изобарный процессы.На протяжении этого листка мы будем придерживаться следующего предположения: масса и химический состав газа остаются неизменными . Иными словами, мы считаем, что:
То есть нет утечки газа из сосуда или, наоборот, притока газа в сосуд;
То есть частицы газа не испытывают каких-либо изменений (скажем, отсутствует диссоциация — распад молекул на атомы).
Эти два условия выполняются в очень многих физически интересных ситуациях (например, в простых моделях тепловых двигателей) и потому вполне заслуживают отдельного рассмотрения.
Если масса газа и его молярная масса фиксированы, то состояние газа определяется тремя макроскопическими параметрами: давлением, объёмом и температурой . Эти параметры связаны друг с другом уравнением состояния (уравнением Менделеева — Клапейрона).
Термодинамический процесс (или просто процесс ) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры.
Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.
1. Изотермический процесс
идёт при постоянной температуре газа: .
2. Изобарный процесс
идёт при постоянном давлении газа: .
3. Изохорный процесс
идёт при постоянном объёме газа: .
Изопроцессы описываются очень простыми законами Бойля — Мариотта, Гей-Люссака и Шарля. Давайте перейдём к их изучению.
Изотермический процесс
Пусть идеальный газ совершает изотермический процесс при температуре . В ходе процесса меняются только давление газа и его объём.
Рассмотрим два произвольных состояния газа: в одном из них значения макроскопических параметров равны , а во втором — . Эти значения связаны уравнением Менделеева-Клапейрона:
Как мы сказали с самого начала,масса и молярная масса предполагаются неизменными.
Поэтому правые части выписанных уравнений равны. Следовательно, равны и левые части:
(1)
Поскольку два состояния газа были выбраны произвольно, мы можем заключить, что в ходе изотермического процесса произведение давления газа на его объём остаётся постоянным :
(2)
Данное утверждение называется законом Бойля — Мариотта .
Записав закон Бойля — Мариотта в виде
(3)
можно дать и такую формулировку: в изотермическом процессе давление газа обратно пропорционально его объёму . Если, например, при изотермическом расширении газа его объём увеличивается в три раза, то давление газа при этом в три раза уменьшается.
Как объяснить обратную зависимость давления от объёма с физической точки зрения? При постоянной температуре остаётся неизменной средняя кинетическая энергия молекул газа, то есть, попросту говоря, не меняется сила ударов молекул о стенки сосуда. При увеличении объёма концентрация молекул уменьшается, и соответственно уменьшается число ударов молекул в единицу времени на единицу площади стенки — давление газа падает. Наоборот, при уменьшении объёма концентрация молекул возрастает, их удары сыпятся чаще и давление газа увеличивается.
Графики изотермического процесса
Вообще, графики термодинамических процессов принято изображать в следующих системах координат:
-диаграмма: ось абсцисс , ось ординат ;
-диаграмма: ось абсцисс , ось ординат .
График изотермического процесса называется изотермой .
Изотерма на -диаграмме — это график обратно пропорциональной зависимости .
Такой график является гиперболой (вспомните алгебру — график функции ). Изотерма-гипербола изображена на рис. 1 .
Рис. 1. Изотерма на -диаграмме
Каждая изотерма отвечает определённому фиксированному значению температуры. Оказывается, что чем выше температура, тем выше лежит соответствующая изотерма на —диаграмме .
В самом деле, рассмотрим два изотермических процесса, совершаемых одним и тем же газом (рис. 2 ). Первый процесс идёт при температуре , второй — при температуре .
Рис. 2. Чем выше температура, тем выше изотерма
Фиксируем некоторое значение объёма . На первой изотерме ему отвечает давление , на второй — alt=»p_2 > p_1″> . Но при фиксированном объёме давление тем больше, чем выше температура (молекулы начинают сильнее бить по стенкам). Значит, alt=»T_2 > T_1″> .
В оставшихся двух системах координат изотерма выглядит очень просто: это прямая, перпендикулярная оси (рис. 3 ):
Рис. 3. Изотермы на и -диаграммах
Изобарный процесс
Напомним ещё раз, что изобарный процесс — это процесс, проходящий при постоянном давлении. В ходе изобарного процесса меняются лишь объём газа и его температура.
Типичный пример изобарного процесса: газ находится под массивным поршнем, который может свободно перемещаться. Если масса поршня и поперечное сечение поршня , то давление газа всё время постоянно и равно
где — атмосферное давление.
Пусть идеальный газ совершает изобарный процесс при давлении . Снова рассмотрим два произвольных состояния газа; на этот раз значения макроскопических параметров будут равны и .
Выпишем уравнения состояния:
Поделив их друг на друга, получим:
В принципе, уже и этого могло бы быть достаточно, но мы пойдём немного дальше. Перепишем полученное соотношение так, чтобы в одной части фигурировали только параметры первого состояния, а в другой части — только параметры второго состояния (иными словами, «разнесём индексы» по разным частям):
(4)
А отсюда теперь — ввиду произвольности выбора состояний! — получаем закон Гей-Люссака :
(5)
Иными словами, при постоянном давлении газа его объём прямо пропорционален температуре :
(6)
Почему объём растёт с ростом температуры? При повышении температуры молекулы начинают бить сильнее и приподнимают поршень. При этом концентрация молекул падает, удары становятся реже, так что в итоге давление сохраняет прежнее значение.
Графики изобарного процесса
График изобарного процесса называется изобарой . На -диаграмме изобара является прямой линией (рис. 4 ):
Рис. 4. Изобара на -диаграмме
Пунктирный участок графика означает, что в случае реального газа при достаточно низких температурах модель идеального газа (а вместе с ней и закон Гей-Люссака) перестаёт работать. В самом деле, при снижении температуры частицы газа двигаются всё медленнее, и силы межмолекулярного взаимодействия оказывают всё более существенное влияние на их движение (аналогия: медленный мяч легче поймать, чем быстрый). Ну а при совсем уж низких температурах газы и вовсе превращаются в жидкости.
Разберёмся теперь, как меняется положение изобары при изменении давления. Оказывается, что чем больше давление, тем ниже идёт изобара на
—диаграмме
.
Чтобы убедиться в этом, рассмотрим две изобары с давлениями и (рис. 5
):
Рис. 5. Чем ниже изобара, тем больше давление
Зафиксируем некоторое значение температуры . Мы видим, что . Но при фиксированной температуре объём тем меньше, чем больше давление (закон Бойля — Мариотта!).
Стало быть, alt=»p_2 > p_1″> .
В оставшихся двух системах координат изобара является прямой линией, перпендикулярной оси (рис. 6 ):
Рис. 6. Изобары на и -диаграммах
Изохорный процесс
Изохорный процесс, напомним, — это процесс, проходящий при постоянном объёме. При изохорном процессе меняются только давление газа и его температура.
Изохорный процесс представить себе очень просто: это процесс, идущий в жёстком сосуде фиксированного объёма (или в цилиндре под поршнем, когда поршень закреплён).
Пусть идеальный газ совершает изохорный процесс в сосуде объёмом . Опять-таки рассмотрим два произвольных состояния газа с параметрами и . Имеем:
Делим эти уравнения друг на друга:
Как и при выводе закона Гей-Люссака, «разносим» индексы в разные части:
(7)
Ввиду произвольности выбора состояний мы приходим к закону Шарля :
(8)
Иными словами, при постоянном объёме газа его давление прямо пропорционально температуре :
(9)
Увеличение давления газа фиксированного объёма при его нагревании — вещь совершенно очевидная с физической точки зрения. Вы сами легко это объясните.
Графики изохорного процесса
График изохорного процесса называется изохорой . На -диаграмме изохора является прямой линией (рис. 7 ):
Рис. 7. Изохора на -диаграмме
Смысл пунктирного участка тот же: неадекватность модели идеального газа при низких температурах.
Рис. 8. Чем ниже изохора, тем больше объём
Доказательство аналогично предыдущему. Фиксируем температуру и видим, что . Но при фиксированной температуре давление тем меньше, чем больше объём (снова закон Бойля — Мариотта). Стало быть, alt=»V_2 > V_1″> .
В оставшихся двух системах координат изохора является прямой линией, перпендикулярной оси (рис. 9 ):
Рис. 9. Изохоры на и -диаграммах
Законы Бойля — Мариотта, Гей-Люссака и Шарля называются также газовыми законами .
Мы вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.
«Физика — 10 класс»
Состояние какого газа описывает уравнение Менделеева-Клапейрона.
Можно ли универсальную газовую постоянную считать фундаментальной постоянной?
С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из трёх параметров — давление, объём или температура — остаются неизменными.
Количественные зависимости между двумя параметрами газа при фиксированном значении третьего называют газовыми законами .
Процессы, протекающие при неизменном значении одного из параметров, называют изопроцессами .
Слово «изопроцесс» — сложное слово, первая часть которого происходит от греческого слова isos — равный, одинаковый.
Отметим, что в действительности ни один процесс не может протекать при строго фиксированном значении какого-либо параметра. Всегда имеются те или иные воздействия, нарушающие постоянство температуры, давления или объёма. Лишь в лабораторных условиях удаётся поддерживать постоянство того или иного параметра с высокой точностью, но в действующих технических устройствах и в природе это практически неосуществимо. Изопроцесс — это идеализированная модель реального процесса, которая только приближённо отражает действительность.
Изотермический процесс.
Процесс изменения состояния системы макроскопических тел (термодинамической системы) при постоянной температуре называют изотермическим .
Слово «изотермический» происходит от греческих слов isos — равный, одинаковый и therme — теплота.
Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплом с большой системой — термостатом. Иначе при сжатии или расширении температура газа будет меняться. Термостатом может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса. Согласно уравнению состояния идеального газа (10.4), если масса газа не изменяется, в любом состоянии с неизменной температурой произведение давления газа на его объём остаётся постоянным:
pV = const при Т = const. (10.6)
Этот вывод был сделан английским учёным Р. Бойлем (1627-1691) и несколько позже французским учёным Э. Мариоттом (1620-1684) на основе эксперимента. Поэтому он носит название закона Бойля-Mapuoттa .
Для газа данной массы произведение давления газа на его объём постоянно.
Закон Бойля-Мариотта справедлив обычно для любых газов, а также и для их смесей, например для воздуха. Лишь при давлениях, в несколько сотен раз больших атмосферного, отклонения от этого закона становятся существенными.
Кривую, изображающую зависимость давления газа от объёма при постоянной температуре, называют изотермой .
Изотерма газа изображает обратно пропорциональную зависимость между давлением и объёмом. Кривую такого рода в математике называют гиперболой (рис. 10.1).
Различным постоянным температурам соответствуют различные изотермы. При повышении температуры газа давление согласно уравнению состояния (10.4) увеличивается, если V = const. Поэтому изотерма, соответствующая более высокой температуре Т 2 , лежит выше изотермы, соответствующей более низкой температуре Т 1 (см. рис. 10.1).
Для того чтобы процесс происходил при постоянной температуре, сжатие или расширение газа должно происходить очень медленно. Дело в том, что, например, при сжатии газ нагревается, так как при движении поршня в сосуде скорость и соответственно кинетическая энергия молекул после ударов о поршень увеличиваются, а следовательно, увеличивается и температура газа. Именно поэтому для реализации изотермического процесса надо после небольшого смещения поршня подождать, когда температура газа в сосуде опять станет равной температуре окружающего воздуха.
Кроме этого, отметим, что при быстром сжатии давление под поршнем сразу становится больше, чем во всём сосуде. Если значения давления и температуры в различных точках объёма разные, то в этом случае газ находится в неравновесном состоянии и мы не можем назвать значения температуры и давления, определяющие в данный момент состояние системы. Если систему предоставить самой себе, то температура и давление постепенно выравниваются, система приходит в равновесное состояние.
Равновесное состояние — это состояние, при котором температура и давление во всех точках объёма одинаковы.
Параметры состояния газа могут быть определены, если он находится в равновесном состоянии.
Процесс, при котором все промежуточные состояния газа являются равновесными, называют равновесным процессом .
Очевидно, что на графиках зависимости одного параметра от другого мы можем изображать только равновесные процессы.
Изобарный процесс
Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным .
Слово «изобарный» происходит от греческих слов isos — равный, одинаковый и baros — вес, тяжесть.
Согласно уравнению (10.4) в любом состоянии газа с неизменным давлением отношение объёма газа к его температуре остаётся постоянным:
Этот закон был установлен экспериментально в 1802 г. французским учёным Ж. Гей-Люссаком (1778-1850) и носит название закона Гей-Люссака .
Закона Гей-Люссака:
Для газа данной массы при постоянном давлении отношение объёма к абсолютной температуре постоянно.
Согласно уравнению (10.7) объём газа при постоянном давлении пропорционален температуре:
V = const Т. (10.8)
Прямую, изображающую зависимость объёма газа от температуры при постоянном давлении, называют изобарой .
Разным давлениям соответствуют разные изобары (рис. 10.2). Проведём на рисунке произвольную изотерму. С ростом давления объём газа при постоянной температуре согласно закону Бойля- Мариотта уменьшается. Поэтому изобара, соответствующая более высокому давлению р 2 , лежит ниже изобары, соответствующей более низкому давлению p 1 .
В области низких температур все изобары идеального газа сходятся в точке Т = 0. Но это не означает, что объём реального газа обращается в нуль. Все газы при сильном охлаждении превращаются в жидкости, а к жидкостям уравнение состояния (10.4) неприменимо. Именно поэтому, начиная с некоторого значения температуры, зависимость объёма от температуры проводится на графике штриховой линией. В действительности таких значений температуры и давления у вещества в газообразном состоянии быть не может.
Изохорный процесс
Процесс изменения состояния термодинамической системы при постоянном объёме называют изохорным .
Слово «изохорный» происходит от греческих слов isos — равный, одинаковый и chora — место, пространство, занимаемое чем-нибудь.
Из уравнения состояния (10.4) вытекает, что в любом состоянии газа с неизменным объёмом отношение давления газа к его температуре остаётся постоянным:
Этот газовый закон был установлен в 1787 г. французским физиком Ж. Шарлем (1746-1823) и носит название закона Шарля .
Для газа данной массы отношение давления к абсолютной температуре постоянно, если объём не меняется.
Согласно уравнению (10.9) давление газа при постоянном объёме пропорционально температуре:
р = const Т. (10.10)
Прямую, изображающую зависимость давления газа от температуры при постоянном объёме, называют изохорой.
Разным объёмам соответствуют разные изохоры. Также проведём на рисунке произвольную изотерму (рис. 10.3). С ростом объёма газа при постоянной температуре давление его, согласно закону Бойля- Мариотта, падает. Поэтому изохора, соответствующая большему объёму V 2 , лежит ниже изохоры, соответствующей меньшему объёму V 1 .
В соответствии с уравнением (10.10) все изохоры идеального газа начинаются в точке Т = 0. Значит, давление идеального газа при абсолютном нуле равно нулю.
Увеличение давления газа в любом сосуде или в электрической лампочке при нагревании можно считать изохорным процессом. Изохорный процесс используется в газовых термометрах постоянного объёма.
В заключение составим опорную схему (рис. 10.4) и покажем логические переходы связывающие различные законы и уравнения.
2. Изохорический процесс . V- постоянен. P и T изменяются. Газ подчиняется закону Шарля. Давление, при постоянном объёме, прямо пропорционально абсолютной температуре
3. Изотермический процесс . T- постоянна. P и V изменяются. В этом случае газ подчиняется закону Бойля — Мариотта. Давление данной массы газа при постоянной температуре обратно пропорциональна объёму газа .
4. Из большого числа процессов в газе, когда изменяются все параметры, выделяем процесс, подчиняющийся объединенному газовому закону. Для данной массы газа произведение давление на объём, делённое на абсолютную температуру есть величина постоянная .
Этот закон применим для большого числа процессов в газе, когда параметры газа меняются не очень быстро.
Все перечисленные законы для реальных газов являются приближёнными. Погрешности увеличиваются с ростом давления и плотности газа.
Порядок выполнения работы:
1. часть работы .
1. Шланг стеклянного шара опускаем в сосуд с водой комнатной температуры (рис.1 в приложении). Затем шар нагреваем (руками, тёплой водой).Считая давление газа постоянным, напишите как объём газа зависит от температуры
Вывод:………………..
2. Соединим шлангом цилиндрический сосуд с миллиманометром (рис. 2). Нагреем металлический сосуд и воздух в нём с помощью зажигалки. Считая объём газа постоянным, напишите, как зависит давление газа от температуры.
Вывод:………………..
3. Цилиндрический сосуд, присоединённый к миллиманометру сожмем руками, уменьшая его объём (рис.3). Считая температуру газа постоянной, напишите, как зависит давление газа от объёма.
Вывод:……………….
4. Соединим насос с камерой от мяча и закачаем несколько порций воздуха (рис.4). Как изменилось давление объём и температура закаченного в камеру воздуха?
Вывод:………………..
5. Нальём в бутылку около 2 см 3 спирта, закроем пробкой со шлангом (рис. 5) , прикреплённым к нагнетающему насосу. Сделаем несколько качков до момента вылета пробки из бутылки. Как изменяются давление объём и температура воздуха (и паров спирта) после вылета пробки?
Вывод:………………..
Часть работы.
Проверка закона Гей — Люссака.
1. Нагретую стеклянную трубку достаём из горячей воды и опускаем открытым концом в небольшой сосуд с водой.
2. Удерживаем трубку вертикально.
3. По мере охлаждения воздуха в трубке вода из сосуда заходит в трубку (рис 6).
4. Находим и
Длина трубки и столба воздуха (в начале опыта)
Объём тёплого воздуха в трубке,
Площадь поперечного сечения трубки.
Высота столба воды, зашедшей в трубке при остывании воздуха в трубке.
Длина столба холодного воздуха в трубке
Объём холодного воздуха в трубке.
На основании закона Гей-Люссака У нас для двух состояний воздуха
Или (2) (3)
Температура горячей воды в ведре
Комнатная температура
Нам нужно проверить уравнение (3) и, следовательно закон Гей – Люссака.
5. Вычислим
6. Находим относительную погрешность измерения при измерении длины принимая Dl=0.5 см.
7. Находим абсолютную погрешность отношения
=……………………..
8. Записываем результат показания
………..…..
9. Находим относительную погрешность измерения Т, принимая
10. Находим абсолютную погрешность вычисления
11. Записываем результат вычисления
12. Если интервал определения отношения температур (хотя бы частично) совпадает с интервалом определения отношения длин столбов воздуха в трубке, то уравнение (2) справедливо и воздух в трубке подчиняется закону Гей- Люссака.
Вывод:……………………………………………………………………………………………………
Требование к отчёту:
1. Название и цель работы.
2. Перечень оборудования.
3. Нарисовать рисунки с приложения и сделать выводы для опытов 1, 2, 3, 4.
4. Написать содержание, цель, расчёты второй части лабораторной работы.
5. Написать вывод по второй части лабораторной работы.
6. Построить графики изопроцессов (для опытов 1,2,3) в осях: ; ; .
7. Решить задачи:
1. Определить плотность кислорода, если его давление равно 152 кПа, а средняя квадратичная скорость его молекул -545 м/с.
2. Некоторая масса газа при давлении 126 кПа и температуре 295 К занимает объём 500 л. Найти объём газа при нормальных условиях.
3. Найти массу углекислого газа в баллоне вместимостью 40 л при температуре 288 К и давлении 5,07 МПа.
Приложение
ОПРЕДЕЛЕНИЕ
Процессы, при которых один из параметров состояния газа остается постоянным называют изопроцессами .
ОПРЕДЕЛЕНИЕ
Газовые законы — это законы, описывающие изопроцессы в идеальном газе.
Газовые законы были открыты экспериментально, но все они могут быть получены из уравнения Менделеева-Клапейрона.
Рассмотрим каждый из них.
Закон Бойля-Мариотта (изотермический процесс)
Изотермическим процессом называют изменение состояния газа, при котором его температура остаётся постоянной.
Для неизменной массы газа при постоянной температуре произведение давления газа на объем есть величина постоянная:
Этот же закон можно переписать в другом виде (для двух состояний идеального газа):
Этот закон следует из уравнения Менделеева — Клапейрона:
Очевидно, что при неизменной массе газа и при постоянной температуре правая часть уравнения остается постоянной величиной.
Графики зависимости параметров газа при постоянной температуре называются изотермами .
Обозначив константу буквой , запишем функциональную зависимость давления от объема при изотермическом процессе:
Видно, что давление газа обратно пропорционально его объему. Графиком обратной пропорциональности, а, следовательно, и графиком изотермы в координатах является гипербола (рис.1, а). На рис.1 б) и в) представлены изотермы в координатах и соответственно.
Рис.1. Графики изотермических процессов в различных координатах
Закон Гей-Люссака (изобарный процесс)
Изобарным процессом называют изменение состояния газа, при котором его давление остаётся постоянным.
Для неизменной массы газа при постоянном давлении отношение объема газа к температуре есть величина постоянная:
Этот закон также следует из уравнения Менделеева — Клапейрона:
изобарами .
Рассмотрим два изобарных процесса с давлениями и title=»Rendered by QuickLaTeX.com»>. В координатах и изобары будут иметь вид прямых линий, перпендикулярных оси (рис.2 а,б).
Определим вид графика в координатах .Обозначив константу буквой , запишем функциональную зависимость объема от температуры при изобарном процессе:
Видно, что при постоянном давлении объем газа прямо пропорционален его температуре. Графиком прямой пропорциональности, а, следовательно, и графиком изобары в координатах является прямая, проходящая через начало координат (рис.2, в). В реальности при достаточно низких температурах все газы превращаются в жидкости, к которым газовые законы уже неприменимы. Поэтому вблизи начала координат изобары на рис.2, в) показаны пунктиром.
Рис.2. Графики изобарных процессов в различных координатах
Закон Шарля (изохорный процесс)
Изохорным процессом называют изменение состояния газа, при котором его объем остаётся постоянным.
Для неизменной массы газа при постоянном объеме отношение давления газа к его температуре есть величина постоянная:
Для двух состояний газа этот закон запишется в виде:
Этот закон также можно получить из уравнения Менделеева — Клапейрона:
Графики зависимости параметров газа при постоянном давлении называются изохорами .
Рассмотрим два изохорных процесса с объемами и title=»Rendered by QuickLaTeX.com»>. В координатах и графиками изохор будут прямые, перпендикулярные оси (рис.3 а, б).
Для определения вида графика изохорного процесса в координатах обозначим константу в законе Шарля буквой , получим:
Таким образом, функциональная зависимость давления от температуры при постоянном объеме является прямой пропорциональностью, графиком такой зависимости является прямая, проходящая через начало координат (рис.3, в).
Рис.3. Графики изохорных процессов в различных координатах
Примеры решения задач
ПРИМЕР 1
| Задание | До какой температуры нужно изобарически охладить некоторую массу газа с начальной температурой , чтобы объем газа уменьшился при этом на одну четверть? |
| Решение | Изобарный процесс описывается законом Гей-Люссака:
По условию задачи объем газа вследствие изобарного охлаждения уменьшается на одну четверть, следовательно: откуда конечная температура газа: Переведем единицы в систему СИ: начальная температура газа . Вычислим: |
| Ответ | Газ нужно охладить до температуры . |
ПРИМЕР 2
| Задание | В закрытом сосуде находится газ под давлением 200 кПа. Каким станет давление газа, если температуру повысить на 30%? |
| Решение | Так как сосуд с газом закрытый, объем газа не меняется. Изохорный процесс описывается законом Шарля:
По условию задачи температура газа повысилась на 30%, поэтому можно записать: Подставив последнее соотношение в закон Шарля, получим: Переведем единицы в систему СИ: начальное давление газа кПа= Па. Вычислим: |
| Ответ | Давление газа станет равным 260 кПа. |
ПРИМЕР 3
| Задание | В кислородной системе, которой оборудован самолет, имеется кислорода при давлении Па. При максимальной высоте подъема летчик соединяет с помощью крана эту систему с пустым баллоном объемом . Какое давление установится в ней? Процесс расширения газа происходит при постоянной температуре. |
| Решение | Изотермический процесс описывается законом Бойля-Мариотта: |
2.1 Молекулярная модель идеального газа — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Применение закона идеального газа к ситуациям, связанным с давлением, объемом, температурой и числом молекул газа
- Использовать единицу измерения молей по отношению к числу молекул, а также молекулярной и макроскопической массе
- Объясните закон идеального газа с точки зрения количества молей, а не количества молекул
- Применение закона Ван-дер-Ваальса к ситуациям, когда закон идеального газа не подходит
В этом разделе мы исследуем тепловое поведение газов.Наше слово «газ» происходит от фламандского слова, означающего «хаос», впервые употребленного для паров химиком XVII века Дж. Б. ван Гельмонтом. Термин был более подходящим, чем он знал, потому что газы состоят из молекул, движущихся и сталкивающихся друг с другом случайным образом. Эта хаотичность делает связь между микроскопической и макроскопической областями более простой для газов, чем для жидкостей или твердых тел.
Чем отличаются газы от твердых тел и жидкостей? В обычных условиях, например в окружающем нас воздухе, разница состоит в том, что молекулы газов находятся гораздо дальше друг от друга, чем молекулы твердых и жидких тел.Поскольку типичные расстояния между молекулами велики по сравнению с размером молекулы, как показано на рис. 2.2, силы между ними считаются незначительными, за исключением случаев, когда они входят в контакт друг с другом во время столкновений. Кроме того, при температурах, значительно превышающих температуру кипения, движение молекул происходит быстро, и газы быстро расширяются, занимая весь доступный объем. Напротив, в жидкостях и твердых телах молекулы расположены ближе друг к другу, и поведение молекул в жидкостях и твердых телах сильно ограничено взаимодействием молекул друг с другом.Макроскопические свойства таких веществ сильно зависят от сил между молекулами, и, поскольку взаимодействуют многие молекулы, возникающие в результате «проблемы многих тел» могут быть чрезвычайно сложными (см. Физика конденсированного состояния).
Фигура 2.2 Атомы и молекулы в газе обычно далеко друг от друга. Так как силы между ними на этих расстояниях довольно слабы, свойства газа больше зависят от числа атомов в единице объема и от температуры, чем от типа атома.
Газовые законы
В предыдущей главе мы видели одно следствие большого межмолекулярного расстояния в газах: газы легко сжимаются. Таблица 1.2 показывает, что газы имеют больший коэффициент объемного расширения, чем твердые тела или жидкости. Эти большие коэффициенты означают, что газы очень быстро расширяются и сжимаются при изменении температуры. Мы также видели (в разделе о тепловом расширении), что большинство газов расширяются с одинаковой скоростью или имеют одинаковый коэффициент объемного расширения ββ.В связи с этим возникает вопрос: почему все газы ведут себя почти одинаково, тогда как все различные жидкости и твердые тела имеют сильно различающиеся скорости расширения?
Чтобы изучить взаимосвязь между давлением, температурой и объемом газа, рассмотрим, что происходит, когда вы накачиваете воздух в спущенную автомобильную шину. Объем шины сначала увеличивается прямо пропорционально количеству впрыскиваемого воздуха без значительного увеличения давления в шине. Как только шина расширилась почти до своего полного размера, стенки шины ограничивают ее объемное расширение.Если мы продолжаем накачивать воздух в шину, давление увеличивается. Когда автомобиль движется и шины изгибаются, их температура повышается, а следовательно, и давление увеличивается еще больше (рис. 2.3).
Фигура 2.3 (а) Когда воздух нагнетается в спущенную шину, ее объем сначала увеличивается без значительного увеличения давления. (b) Когда шина заполнена до определенной точки, стенки шины сопротивляются дальнейшему расширению, и давление увеличивается с увеличением количества воздуха. (c) Когда шина накачана, ее давление увеличивается с температурой.
На рис. 2.4 показаны данные экспериментов Роберта Бойля (1627–1691), иллюстрирующие то, что сейчас называется законом Бойля: при постоянной температуре и числе молекул абсолютное давление газа и его объем обратно пропорциональны. (Вспомните из механики гидродинамики, что абсолютное давление — это истинное давление, а манометрическое давление — это абсолютное давление за вычетом давления окружающей среды, обычно атмосферного давления.) График на рис. 2.4 отображает эту зависимость как обратную пропорциональную зависимость объема от давления.
Фигура 2,4 Роберт Бойль и его помощник обнаружили, что объем и давление обратно пропорциональны. Здесь их данные представлены как V против 1/ p ; линейность графика показывает обратную пропорциональность. Число, показанное как объем, на самом деле является высотой в дюймах воздуха в цилиндрической стеклянной трубке. Фактический объем представлял собой произведение высоты на площадь поперечного сечения трубы, которую Бойль не опубликовал. Данные взяты из книги Бойля «Защита доктрины о весне и весе воздуха» …, с.60.На рис. 2.5 показаны экспериментальные данные, иллюстрирующие то, что называется законом Шарля в честь Жака Шарля (1746–1823). Закон Шарля гласит, что при постоянном давлении и количестве молекул объем газа пропорционален его абсолютной температуре.
Фигура 2,5 Экспериментальные данные показывают, что при постоянном давлении объем примерно пропорционален температуре. Линия наилучшего соответствия проходит примерно через начало координат.Аналогично закону Амонтона или Гей-Люссака, который утверждает, что при постоянном объеме и количестве молекул давление пропорционально температуре.Этот закон лежит в основе газового термометра постоянного объема, рассмотренного в предыдущей главе. (История этих законов и соответствующая оценка их более сложны, чем можно обсудить здесь.)
Экспериментально известно, что для газов с малой плотностью (такой, что их молекулы занимают ничтожно малую долю общего объема) и при температурах, значительно превышающих точку кипения, эти пропорциональности выполняются в хорошем приближении. Неудивительно, что при прочих равных величинах давление или объем пропорциональны количеству молекул.Что еще более удивительно, когда пропорциональности объединены в одно уравнение, константа пропорциональности не зависит от состава газа. Полученное уравнение применимо для всех газов в пределе низкой плотности и высокой температуры; для кислорода это то же самое, что и для гелия или гексафторида урана. Газ на этом пределе называется идеальным газом; оно подчиняется закону идеального газа, который также называют уравнением состояния идеального газа.
Закон идеального газа
Закон идеального газа гласит, что
, где p — абсолютное давление газа, V — занимаемый им объем, N — число молекул в газе, T — его абсолютная температура.
Постоянная kBkB называется постоянной Больцмана в честь австрийского физика Людвига Больцмана (1844–1906) и имеет значение
. kB=1,38×10-23 Дж/К.kB=1,38×10-23 Дж/К.Закон идеального газа описывает поведение любого реального газа, когда его плотность достаточно низка или его температура достаточно высока, чтобы он был далек от сжижения. Это охватывает множество практических ситуаций. В следующем разделе мы увидим, почему он не зависит от типа газа.
Во многих случаях закон идеального газа применяется к образцу газа с постоянным числом молекул; например, газ может находиться в герметичном контейнере.Если N постоянно, то решение для N показывает, что pV / T является постоянным. Мы можем записать этот факт в удобной форме:
p1V1T1=p2V2T2,p1V1T1=p2V2T2,2.2
, где индексы 1 и 2 относятся к любым двум состояниям газа в разное время. Опять же, температура должна быть выражена в кельвинах, а давление должно быть абсолютным давлением, которое представляет собой сумму манометрического давления и атмосферного давления.
Пример 2.1
Расчет изменений давления из-за изменений температуры
Предположим, ваша велосипедная шина полностью накачана, с абсолютным давлением 7,00×105 Па7,00×105 Па (манометрическое давление чуть менее 90,0 фунтов/дюйм290,0 фунтов/дюйм2) при температуре 18,0°C.18,0°C. . Каково давление после повышения его температуры до 35,0°С35,0°С в жаркий день? Предположим, что нет заметных утечек или изменений объема.Стратегия
Давление в шине меняется только из-за изменения температуры.Мы знаем начальное давление p0=7,00×105 Па, p0=7,00×105 Па, начальную температуру T0=18,0°C, T0=18,0°C и конечную температуру Tf=35,0°C.Tf=35,0°C. Надо найти конечное давление pf.pf. Поскольку число молекул постоянно, мы можем использовать уравнение pfVfTf=p0V0T0.pfVfTf=p0V0T0.Поскольку объем постоянный, VfVf и V0V0 одинаковы и делятся. Следовательно,
Затем мы можем изменить это, чтобы найти pf:pf:
, где температура должна быть в кельвинах.
Решение
- Преобразование температуры из градусов Цельсия в кельвины Т0=(18.0+273)К=291К, Т0=(18,0+273)К=291К, Tf=(35,0+273)K=308K.Tf=(35,0+273)K=308K.
- Подставьте известные значения в уравнение, pf=p0TfT0=7,00×105 Па(308K291K)=7,41×105 Па.pf=p0TfT0=7,00×105 Па(308K291K)=7,41×105 Па.
Значение
Конечная температура примерно на 6%6% выше исходной температуры, поэтому конечное давление также примерно на 6%6% больше. Обратите внимание, что абсолютное давление (см. Гидромеханика) и абсолютная температура (см. Температура и тепло) должны использоваться в законе идеального газа.Пример 2.2
Расчет количества молекул в кубическом метре газа
Сколько молекул содержится в типичном объекте, например газе в шине или воде в стакане? Этот расчет может дать нам представление о том, насколько обычно велика N . Давайте подсчитаем количество молекул в воздухе, которое вдыхает типичный здоровый молодой взрослый человек за один вдох объемом 500 мл при стандартной температуре и давлении (СТД), которое определяется как 0ºC0ºC и атмосферное давление.(Наш молодой взрослый, по-видимому, находится на улице зимой.)Стратегия
Поскольку давление, объем и температура заданы, мы можем использовать закон идеального газа pV=NkBT,pV=NkBT, чтобы найти N .Решение
- Определите известное. T=0°C=273K,p=1,01×105 Па, V=500мл=5×10-4м3, kB=1,38×10-23Дж/KT=0°C=273K,p=1,01×105Па, V=500мл= 5×10−4 м3, кВ=1,38×10−23 Дж/К
- Подставьте известные значения в уравнение и найдите N . N=pVkBT=(1,01×105Па)(5×10-4м3)(1.38×10-23 Дж/К)(273К)=1,34×1022 молекул N=pVkBT=(1,01×105Па)(5×10-4м3)(1,38×10-23Дж/К)(273К)=1,34×1022молекул
Значение
N огромен даже в небольших объемах. Например, 1см31см3 газа при СТП содержит 2,68×10192,68×1019 молекул. Еще раз отметим, что наш результат для N одинаков для всех типов газов, включая смеси.Как мы отмечали в главе о механике жидкости, паскали равны Н/м2Н/м2, поэтому Па·м3=Н·м=Дж.Па·м3=Н·м=Дж. Таким образом, наш результат для N является безразмерным, чистым числом, которое можно получить путем подсчета (в принципе), а не измерения.Поскольку это количество молекул, мы ставим «молекулы» после числа, помня, что это скорее средство коммуникации, чем единица.
Кроты и число Авогадро
Часто бывает удобно измерять количество вещества единицей в более человеческом масштабе, чем молекулы. Единица СИ для этой цели была разработана итальянским ученым Амедео Авогадро (1776–1856). (Он исходил из гипотезы, что равные объемы газа при одинаковом давлении и температуре содержат одинаковое количество молекул, независимо от типа газа.Как упоминалось выше, эта гипотеза подтверждается, когда применяется приближение идеального газа.) Моль (сокращенно моль) определяется как количество любого вещества, которое содержит столько молекул, сколько атомов. (Технически мы должны говорить «формульные единицы», а не «молекулы», но это различие не имеет значения для наших целей.) Число молекул в одном моле называется числом Авогадро (NA), (NA), а значение числа Авогадро номер теперь известен как
NA = 6,02 × 1023 моль-1. NA = 6,02 × 1023 моль-1.Теперь мы можем написать N=NAnN=NAn, где n представляет количество молей вещества.
Число Авогадро связывает массу вещества в граммах с числом протонов и нейтронов в атоме или молекуле (12 для атома углерода-12), которые приблизительно определяют его массу. Естественно определить единицу массы так, чтобы масса атома была примерно равна количеству в нем нейтронов и протонов. Единицей такого рода, принятой для использования в СИ, является унифицированная атомная единица массы (u), называемая также дальтон .В частности, атом углерода-12 имеет массу ровно 12 u, так что его молярная масса M в граммах на моль численно равна массе одного атома углерода-12 в u. Это равенство справедливо для любого вещества. Другими словами, NANA — это не только преобразование числа молекул в моли, но и преобразование u в граммы: 6,02×1023u=1г.6,02×1023u=1г. См. рис. 2.6.
Фигура 2,6 Насколько велика родинка? На макроскопическом уровне количество шариков для настольного тенниса Авогадро покрыло бы Землю на глубину около 40 км.
Теперь, если msms обозначает массу образца вещества, мы имеем ms=nM.ms=nM. Приняв m за массу молекулы, мы имеем M=NAm.M=NAm.
Проверьте свое понимание 2.1
Проверьте свое понимание Рекомендуемая суточная доза витамина B3B3 или ниацина, C6NH5O2,C6NH5O2, для женщин, которые не беременны и не кормят грудью, составляет 14 мг. Найдите количество молекул никотиновой кислоты в этом количестве.
Проверьте свое понимание 2.2
Проверьте свои знания Плотность воздуха в классе (p=1,00 атм (p=1,00 атм и T=20°C)T=20°C) составляет 1,28 кг/м31,28 кг/м3. При каком давлении плотность 0,600 кг/м30,600 кг/м3, если температура поддерживается постоянной?
Закон об идеальном газе, переформулированный с использованием молей
Очень распространенное выражение закона идеального газа использует количество молей в образце, n , а не количество молекул, N . Начнем с закона идеального газа,
, умножьте и разделите правую часть уравнения на число Авогадро NA.Н/Д Это дает нам
Обратите внимание, что n=N/NAn=N/NA — количество молей. Мы определяем универсальную газовую постоянную как R=NAkB,R=NAkB и получаем закон идеального газа в молях.
Закон идеального газа (в молях)
С точки зрения числа молей n закон идеального газа записывается как
В единицах СИ,
R=NAkB=(6,02×1023моль-1)(1,38×10-23JK)=8,31Джмоль·K.R=NAkB=(6,02×1023моль-1)(1,38×10-23JK)=8,31Джмоль·K.В других единицах,
R=1,99 калмоль·K=0.0821 л·атммоль·K.R=1,99 калмоль·K=0,0821 л·атммоль·K.Вы можете использовать любое значение R , наиболее удобное для конкретной задачи.
Пример 2.3
Плотность воздуха в STP и на воздушном шаре
Рассчитайте плотность сухого воздуха (а) при стандартных условиях и (б) в воздушном шаре при температуре 120ºС120ºС. Сухой воздух содержит примерно 78% N2, 21% O2, 78% N2, 21% O2 и 1% Ar1% Ar.Стратегия и решение
- Нас просят найти плотность или массу на кубический метр.Начнем с нахождения молярной массы. Если у нас есть сто молекул, из которых 78 азота, 21 кислорода и 1 аргона, средняя молекулярная масса будет 78mN2+21mO2+mAr10078mN2+21mO2+mAr100, или масса каждого компонента, умноженная на его процентное содержание. То же самое относится и к молярной массе, которая, следовательно, M=0,78MN2+0,21MO2+0,01MAr=29,0 г/моль. M=0,78MN2+0,21MO2+0,01MAr=29,0 г/моль. Теперь мы можем найти количество молей на кубический метр. Мы используем закон идеального газа в молях, pV=nRT, pV=nRT, с p=1.00 атм.=1,00 атм, T=273KT=273K, V=1м3V=1м3 и R=8,31Дж/моль·KR=8,31Дж/моль·К. Наиболее удобным выбором для R в данном случае является R=8,31 Дж/моль·KR=8,31 Дж/моль·К, поскольку известные величины даны в единицах СИ: n=pVRT=(1,00×105Па)(1м3)(8,31Дж/моль·К)(273К)=44,1моль.n=pVRT=(1,00×105Па)(1м3)(8,31Дж/моль·К)(273К) =44,1 моль. Тогда масса msms этого воздуха равна ms=nM=(44,1 моль)(29,0 г/моль)=1290 г=1,28 кг.ms=nM=(44,1 моль)(29,0 г/моль)=1290 г=1,28 кг. Наконец, плотность воздуха в СТП равна ρ=msV=1,28 кг1м3=1,28 кг/м3.ρ=msV=1.28кг1м3=1,28кг/м3.
- Давление воздуха внутри шара по-прежнему составляет 1 атм, потому что нижняя часть шара открыта для атмосферы. Расчет такой же, за исключением того, что мы используем температуру 120ºC120ºC, что составляет 393 K. Мы можем повторить расчет в (a) или просто заметить, что плотность пропорциональна количеству молей, что обратно пропорционально температуре . Тогда, используя индексы 1 для воздуха на СТП и 2 для горячего воздуха, имеем ρ2=T1T2ρ1=273K393K(1,28кг/м3)=0.889кг/м3.ρ2=T1T2ρ1=273K393K(1,28кг/м3)=0,889кг/м3.
Значение
Используя методы закона Архимеда и плавучести, мы можем найти, что результирующая сила, действующая на 2200 м32200 м3 воздуха при температуре 120ºC120ºC, равна Fb−Fg=ρатмосферыVg−ρгорячего воздухаVg=8,49×103 Н, , или достаточно, чтобы поднять около 867 кг. Массовая плотность и молярная плотность воздуха при STP, найденные выше, часто являются полезными числами. По молярной плотности мы можем легко определить другое полезное число — объем моля любого идеального газа при СТП, который равен 22.4 л.
Проверьте свое понимание 2.3
Проверьте свое понимание Плотность жидкостей и твердых тел примерно в 1000 раз больше плотности газов. Объясните, как это означает, что расстояния между молекулами в газах примерно в 10 раз больше размеров их молекул.
Закон идеального газа тесно связан с энергией: единицами измерения в обеих частях уравнения являются джоули. Правая часть уравнения закона идеального газа есть NkBT.НкБТ. Этот термин приблизительно представляет собой полную кинетическую энергию поступательного движения (которая при обсуждении газов относится к энергии поступательного движения молекулы, а не к энергии вибрации ее атомов или вращения) N молекул при абсолютной температуре T , как мы увидим формально в следующем разделе. Левая часть уравнения закона идеального газа равна пВ . Как упоминалось в примере с числом молекул в идеальном газе, давление, умноженное на объем, имеет единицы энергии.Энергия газа может быть изменена, когда газ совершает работу по мере увеличения объема, что мы исследовали в предыдущей главе, а количество работы связано с давлением. Это процесс, происходящий в бензиновых или паровых двигателях и турбинах, как мы увидим в следующей главе.
Стратегия решения проблем
Закон идеального газа
Шаг 1. Изучите ситуацию, чтобы определить, что речь идет об идеальном газе. Большинство газов почти идеальны, если только они не близки к точке кипения или не находятся под давлением, намного превышающим атмосферное давление.
Шаг 2. Составьте список величин, которые даны или могут быть выведены из поставленной задачи (укажите известные величины).
Шаг 3. Точно определите, что нужно определить в задаче (идентифицируйте неизвестные величины). Письменный список полезен.
Этап 4. Определите, известно ли количество молекул или число молей или запрашивается, чтобы решить, следует ли использовать закон идеального газа как pV=NkBT,pV=NkBT, где N — количество молекул, или pV=nRT,pV=nRT, где n — количество молей.
Шаг 5. Преобразуйте известные значения в соответствующие единицы СИ (К для температуры, Па для давления, м3 м3 для объема, молекулы для N и моли для n ). Если единицы измерения согласуются с одним из несистемных значений R , вы можете оставить их в этих единицах. Обязательно используйте абсолютную температуру и абсолютное давление.
Шаг 6. Решите закон идеального газа для определяемой величины (неизвестной величины). Возможно, вам придется взять отношение конечных состояний к начальным состояниям, чтобы исключить неизвестные величины, которые остаются фиксированными.
Шаг 7. Подставьте известные величины вместе с их единицами измерения в соответствующее уравнение и получите численное решение с единицами измерения.
Шаг 8. Проверьте ответ, чтобы убедиться, что он разумен: Имеет ли он смысл?
Уравнение состояния Ван-дер-Ваальса
Мы неоднократно отмечали, что закон идеального газа является приближением. Как его можно улучшить? Уравнение состояния Ван-дер-Ваальса (названное в честь голландского физика Йоханнеса ван дер Ваальса, 1837–1923 гг.) улучшает его, учитывая два фактора.Во-первых, силы притяжения между молекулами, которые сильнее при большей плотности и снижают давление, учитываются добавлением к давлению члена, равного квадрату молярной плотности, умноженному на положительный коэффициент a . Во-вторых, объем молекул представлен положительной константой b , которую можно рассматривать как объем моля молекул. Это вычитается из общего объема, чтобы получить оставшийся объем, в котором могут двигаться молекулы.Константы a и b определяются экспериментально для каждого газа. В результате получится уравнение
. [p+a(nV)2](V-nb)=nRT.[p+a(nV)2](V-nb)=nRT.2,4
В пределе низкой плотности (малая n ) члены a и b пренебрежимо малы, и мы имеем закон идеального газа, как и при низкой плотности. С другой стороны, если V-nbV-nb мало, а это означает, что молекулы расположены очень близко друг к другу, давление должно быть выше, чтобы дать то же самое nRT , как и следовало ожидать в ситуации с сильно сжатым газом.Однако увеличение давления меньше, чем предполагает этот аргумент, потому что при высокой плотности член (n/V)2(n/V)2 значителен. Поскольку он положительный, он вызывает более низкое давление, чтобы дать тот же nRT .
Уравнение состояния Ван-дер-Ваальса хорошо работает для большинства газов в самых разных условиях. Как мы увидим в следующем модуле, он даже предсказывает переход газ-жидкость.
pV Диаграммы
Мы можем изучить аспекты поведения вещества, построив диаграмму pV , которая представляет собой график зависимости давления от объема.Когда вещество ведет себя как идеальный газ, закон идеального газа pV=nRTpV=nRT описывает соотношение между его давлением и объемом. На диаграмме pV принято изображать изотерму , которая представляет собой кривую, показывающую p как функцию V при фиксированном количестве молекул и температуре. Тогда для идеального газа pV=constant. pV=constant. Например, объем газа уменьшается по мере увеличения давления. Полученный график представляет собой гиперболу.
Однако, если мы примем уравнение состояния Ван-дер-Ваальса, изотермы станут более интересными, как показано на рис. 2.7. При высоких температурах кривые представляют собой примерно гиперболы, представляющие примерно идеальное поведение при различных фиксированных температурах. При более низких температурах кривые все меньше и меньше похожи на гиперболы, то есть газ ведет себя неидеально. Существует критическая температура TcTc, при которой кривая имеет точку с нулевым наклоном. Ниже этой температуры кривые не имеют монотонного убывания; вместо этого у каждого из них есть «горб», означающий, что для определенного диапазона объема увеличение объема увеличивает давление.
Фигура 2,7 pV диаграмма для газа Ван-дер-Ваальса при различных температурах. Красные кривые рассчитаны при температурах выше критической температуры, а синие кривые — при температурах ниже ее. Синие кривые имеют колебание, при котором объем ( V ) увеличивается с увеличением давления ( P ), что невозможно, поэтому их необходимо исправить, как показано на рисунке 2.8. (кредит: «Эман»/Wikimedia Commons)Такое поведение было бы совершенно нефизическим.Вместо этого кривые понимаются как описывающие фазовый переход жидкость-газ. Осциллирующая часть кривой заменена горизонтальной линией, показывающей, что по мере увеличения объема при постоянной температуре давление остается постоянным. Такое поведение соответствует кипению и конденсации; когда вещество находится при температуре кипения при определенном давлении, его объем может увеличиваться в объеме, когда часть жидкости превращается в газ, или уменьшаться, когда часть газа превращается в жидкость, без каких-либо изменений температуры или давления.
На рис. 2.8 показаны аналогичные изотермы, которые более реалистичны, чем изотермы, основанные на уравнении Ван-дер-Ваальса. Крутые участки кривых слева от переходной области показывают жидкую фазу, которая практически несжимаема — небольшое уменьшение объема требует большого увеличения давления. Плоские части показывают переход жидкость-газ; синие области, которые они определяют, представляют собой комбинации давления и объема, в которых жидкость и газ могут сосуществовать.
Фигура 2.8 pV диаграммы. (а) Каждая кривая (изотерма) представляет соотношение между p и V при фиксированной температуре; верхние кривые относятся к более высоким температурам. Нижние кривые не являются гиперболами, поскольку газ больше не является идеальным. (b) Расширенная часть диаграммы pV для низких температур, где фаза может переходить из газа в жидкость. Термин «пар» относится к газовой фазе, когда она существует при температуре ниже температуры кипения.
Изотермы выше TcTc не проходят через переход жидкость-газ. Следовательно, жидкость не может существовать выше этой температуры, которая является критической температурой (описанной в главе о температуре и теплоте). При достаточно низком давлении выше этой температуры газ имеет плотность жидкости, но не конденсируется; газ называется сверхкритическим. При более высоком давлении он твердый. Углекислый газ, например, не имеет жидкой фазы при температуре выше 31,0ºC31,0ºC. Критическое давление – это максимальное давление, при котором может существовать жидкость.Точка на диаграмме pV при критическом давлении и температуре является критической точкой (о которой вы узнали в главе о температуре и тепле). В Таблице 2.1 перечислены репрезентативные критические температуры и давления.
| Вещество | Критическая температура | Критическое давление | ||
|---|---|---|---|---|
| К | °С°С | Па | атм | |
| Вода | 647.4 | 374,3 | 22,12×10622,12×106 | 219,0 |
| Диоксид серы | 430,7 | 157,6 | 7,88×1067,88×106 | 78,0 |
| Аммиак | 405,5 | 132,4 | 11,28×10611,28×106 | 111,7 |
| Углекислый газ | 304,2 | 31,1 | 7,39×1067,39×106 | 73,2 |
| Кислород | 154.8 | –118,4 | 5,08×1065,08×106 | 50,3 |
| Азот | 126,2 | –146,9 | 3,39×1063,39×106 | 33,6 |
| Водород | 33,3 | –239,9 | 1,30×1061,30×106 | 12,9 |
| Гелий | 5,3 | –267,9 | 0,229×1060,229×106 | 2,27 |
Таблица 2.1 Критические температуры и давления для различных веществ
законов идеального газа | SpringerLink
К этому моменту мы получили выражение для разницы между теплоемкостью при постоянном давлении (изобарической) на моль идеального газа, C P , и постоянной объемной (изохорной) теплоемкостью на 1 моль идеального газа. моль идеального газа, C V . Наш термодинамический анализ показал, что C P – C V = ℜ, но у нас пока нет выражения ни для одного из уравнений теплоемкости, и поэтому мы не можем вычислить 90 состояния в уравнении(7.19) или для выражения в уравнении. (7.25), которое связывает изменения температуры с изменениями адиабатического давления. Чтобы вычислить C V для идеального газа, мы должны вернуться к нашей микроскопической модели и к теореме о равнораспределении в уравнении. (7.2).
7.2.1 Одноатомные (благородные) газы
Наше представление об атомах инертных газов как о «точечных частицах», отскакивающих друг от друга и от твердых стенок, но в остальном свободно летающих между столкновениями, подразумевало, что их единственная энергия была кинетической.2\right\rangle \right]=\frac{3}{2}{k}_BT $$(7.26)
Если просуммировать по молю частиц, то можно вычислить внутреннюю (тепловую) энергию 1 моль этого газа.$$ U=\frac{3}{2}{N}_A{k}_BT=\frac{3}{2}\mathit{\Re T} $$
(7.27)
Из нашего определения изохорная теплоемкость в уравнении. (7.11) теплоемкость 1 моля одноатомного (благородного) газа может быть выражена через универсальную газовую постоянную314462 Дж/моль-К.$$ {C}_V={\left(\frac{\partial U}{\partial T}\right)}_V=\frac{3}{2}\Re $$
(7,28)
Для благородные (одноатомные) идеальные газы, теплоемкость при постоянном объеме, Кл В = 1,5 ℜ ≅ 12,472 Дж/моль-К. Из уравнения (7.14), изобарная теплоемкость, Кл P = 2,5 ℜ ≅ 20,786 Дж/моль-К. Следовательно, теперь мы можем рассчитать отношение удельных теплоемкостей благородных газов: γ = C P /C V = 5/3.При достаточно низких давлениях этот результат настолько точен, что его использовали для определения универсальной газовой постоянной путем измерения скорости звука в гелии. [7]
В большинстве случаев интенсивная величина, называемая удельной теплоемкостью, используется для определения теплоемкости материала, поскольку интенсивная величина не зависит от размера системы. Наиболее распространенной удельной теплоемкостью является теплоемкость на единицу массы. 14 Используя соглашение о строчных переменных для интенсивных величин (наиболее заметным исключением является температура, T ), c V = 1.5 ℜ /M и c P = 2,5 ℜ /M , где M — атомная масса. Например, атомная масса гелия составляет M He = 4,0026 г/моль, поэтому для гелия при постоянном давлении -К.
7.2.2 Многоатомные газы
Если вместо благородного (одноатомного) газа мы имеем газ, состоящий из стабильных (т.е. не вступающих в химическую реакцию) многоатомных молекул , таких как N 2 , O 2 , HCl , H 2 O, CO 2 , CH 4 и т.д., то нам нужно вернуться к теореме о равнораспределении и вычислить количество «квадратичных» степеней свободы, которые имеют право на свою «справедливую долю» средней тепловой энергии: (½) k B T на степень свободы. Начнем с простой симметричной двухатомной молекулы, такой как N 2 или O 2 , схематично представленной в модели «шар-стержень» на рис. 7.3.Рис. 7.3Схематическое изображение двухатомной молекулы, состоящей из двух одинаковых атомов, разделенных средним расстоянием d
В дополнение к кинетической энергии движения центра масс молекулы вносят вклад три «поступательные» степени свободы , как выражено в уравнении(7.26), эта двухатомная молекула может вращаться вокруг своего центра масс вокруг двух перпендикулярных осей (третья ось, вдоль линии, соединяющей центры, не считается точечными массами), а также может колебаться вдоль линии, соединяющей две массы. Вращательная кинетическая энергия, (½) Iω 2 , и кинетическая и потенциальная энергии вибрации, KE = (½) мк v 2 и PE 3 70033 6 Κ= 1 (9004) 2 , также являются «квадратичными» степенями свободы (см.2.4.4), где I — момент инерции пары атомов относительно их центра масс, ω — угловая частота вращения, К — эффективная жесткость пружины для простых гармонических колебаний вдоль линии, соединяющей двух точечных масс (например, см. гл. 2, Prob. 13), а μ — (эффективная) приведенная масса пары (например, см. уравнение 2.147), чье зависящее от времени расстояние равно d + x ( т ).
Если суммировать квадратичные степени свободы, то получим три «поступательных», плюс две «вращательных», плюс две «колебательных» (т.е., одна кинетическая и одна потенциальная), всего семь «квадратичных» степеней свободы. Если это так, то C V = (7/2)ℜ и C P = (9/2)ℜ для двухатомного газа. Это не относится к азоту при комнатной температуре! Причина того, что результат неверен, можно проследить до квантовой механики. Помните, мы вернулись к «микроскопической» модели, и мир атомов и молекул управляется законами квантовой механики, а не классической механики.
В этом случае полезно оценить хотя бы один конкретный экземпляр, где Planck’s Constance , 15 H ≡ 6.62607015 × 10 -34 JS = 4.13566770 × 10 -15 EV-S входит акустика. В квантово-механических системах расстояние между энергетическими уровнями является дискретным, а не непрерывным. Мы редко видим прямое проявление квантовых эффектов в нашей повседневной жизни, потому что квант действия Планка, ч , настолько мал, что мы можем легко передать любое количество действия (произведение энергии, умноженной на количество времени, в течение которого она применяется). мы выбираем макроскопическую систему.Однако в атомном масштабе, если энергии недостаточно для изменения состояния атома или молекулы на один квантованный энергетический уровень, обмен энергией невозможен. 16
Как все это связано с удельной теплоемкостью двухатомной молекулы? Уровни энергии для вращения, E R R R ( j ) и вибрация E V ( N ), квантоваются с j и N , являющиеся положительными целыми числами .2}{I} $$(7.29)
I — момент инерции молекулы, ν — частота колебаний.Давайте начнем с расчета кванта вибрации, hν , для примера N 2 , затем сравним эту энергию со средней доступной кинетической энергией на степень свободы при температуре около комнатной ( T = 290 K ≅ 17 ° C): ( ½ ) k B T = 2 × 10 −21 J = 0.0125 эВ на степень свободы. (Электрон-вольты, как правило, являются более удобной мерой энергии отдельных атомов и молекул.)
Для N 2 частота колебаний, измеренная с помощью оптической спектроскопии, равна = 8,2082 × 10 13 Гц = 82 082 ГГц. Такие высокие частоты обычно выражаются соответствующей длиной волны света: λ EM = c / f , где c ≡ 299 792 458 м/с, что является скоростью света в вакууме.В этом случае λ EM = 3,65 мкм: длина волны в инфракрасной части электромагнитного спектра. При умножении на постоянную Планка E V ( N 2 ) = hν = 0,3395 эВ. Это соответствует колебательной температуре:{-E/{k}_BT} $$(7,30)
Для нашего примера с использованием частоты колебаний N 2 вероятность столкновения с молекулой, обладающей достаточной кинетической энергией для возбуждения колебательного режима, на основе уравнение (7.30), равно P ( E V ) = 1,25 × 10 −6 = 1,25 ч/млн при комнатной температуре, примерно один шанс на миллион. По этой причине колебательная степень свободы не дает вклада в теплоемкость N 2 при комнатных температурах.
для азота, температура вращения, T
3 R 6 = E 71 R R B = 2.86 K, так что по уравнению. (7.30), вероятность того, что атом средней комнатной температуры будет иметь достаточную энергию для возбуждения вращательной моды внеосевым столкновением, близка к единице: P ( E R ) = 0,99. Для двухатомной молекулы существуют только две вращательные степени свободы, поскольку вращение вокруг оси, соединяющей точечные частицы, не соответствует действительному вращению сферически-симметричных конечных масс (поскольку почти вся масса сосредоточена в ядре, а вращения вокруг этой оси равны нулю). неразличимы). 18Остается пять доступных «квадратичных» степеней свободы для азота вблизи комнатной температуры: три поступательных и две вращательных. Таким образом, удельная теплоемкость двухатомных газов равна c V = (5/2)ℜ и c p = (7/2)ℜ, поэтому 90 = 1 7,5 0 7,4 γ . Результаты для реальных двухатомных газов довольно хорошо согласуются с этой моделью. Для кислорода при 15 °C γ = 1,401; азот при 15 °C, γ = 1.404; и воздух при 0°C, γ = 1,403. Конечно, сухой воздух представляет собой смесь примерно 78,1 % N 2 , 20,9 % O 2 и 0,934 % Ar, а также около 415 частей на миллион CO 2 (и растет! 19 ), поэтому мы ожидаем, что значение γ воздуха должно быть немного больше 7/5 из-за вклада аргона, который является одноатомным и имеет γ Ar = 5/3.
График на рис. 7.4 демонстрирует влияние температуры на удельную теплоемкость H 2 .Температура вращения молекулы водорода, T 1 R R R 1 R 6 = 85,6 К, и колебательная температура, T V ≅ 6100 K. Ниже T R , молекула ведет себя в виде одноатомного газа и C V = (3/2) ℜ. Между 250 и 500 К могут участвовать две вращательные степени свободы и C V = (5/2) ℜ. При температуре выше 500 К две колебательные степени свободы также становятся совместными.После диссоциации количество «частиц» в газе (теперь это плазма?) удвоилось, поэтому теплоемкость должна быть 2(3/2) ℜ, так как имеется 2 моля одноатомного водорода. 20 Рис. 7.4Изменение молярной теплоемкости при постоянном объеме газа H 2 в зависимости от температуры. [8]
Мы можем продолжить применять это простое представление для более сложных молекул. Для молекулярных газов, таких как H 2 O и H 2 S, существуют три степени свободы вращения в дополнение к трем степеням свободы, связанным с движением центра масс молекулы; следовательно, мы ожидаем, что C V = 3ℜ и C P = 4ℜ, что дает γ = 4/3 = 1.33. Это довольно близко для пара при 100 °C ( γ = 1,324) и для H 2 S при 15 °C ( γ = 1,32). Ситуация для CO 2 при 15 °C ( γ = 1,304) немного сложнее. Основываясь на этом анализе, мы ожидаем, что более сложные молекулярные газы будут иметь еще меньшие значения γ . В любом случае коэффициент политропы для любого идеального газа ограничен: 1 < γ ≤ 5/3.
Как мы увидим позже в гл. 14, когда мы исследуем механизмы затухания в воздухе и морской воде, теплоемкость зависит не только от температуры, но и от времени.Например, рассмотрим громкоговоритель в контакте с воздухом. Воздействие диффузора динамика на молекулы воздуха передает только поступательную кинетическую энергию. Затем молекулы должны совершить несколько столкновений (в среднем около пяти), чтобы равномерно распределить дополнительную энергию между поступательными и вращательными модами, как это диктуется теоремой о равнораспределении, которая является утверждением о равновесии. Требуется ненулевое количество времени, чтобы восстановить это равновесие и «время релаксации» (см.4.4.1) для этого процесса, τ R , может вносить фазовые сдвиги и, следовательно, диссипацию. Эти эффекты релаксации обычно объединяют в термин, известный как «объемная вязкость». 21
Сохранение массы с использованием контрольных объемов
Сохранение массы с использованием контрольных объемовСохранение массы с использованием контрольных объемов
Сохранение массы
В транспортной теореме Рейнольдса для сохранения массы пусть B = m , т.е.е. B сис = м сис = масса системы,
Для нашей системы мы знаем, что
Итак, Транспортная теорема Рейнольдса (R.T.T.) становится
ИЛИ,
- Проанализируем последний член уравнения:
- n = единичный вектор внешней нормали (перпендикулярно поверхности элемент площади dA)
- V = вектор скорости, который может быть в любом произвольном направлении
- Напомним, из определения скалярного произведения:
- Выходы: В есть наружу (массовый выход С.В.)
- Входы: В — внутрь (масса на входе C.V.)
- Теперь получается, что
= масса скорость потока наружу через поверхность
, поэтому, если мы проинтегрируем по всей поверхности,
и уравнение сохранения массы примет вид:
*это наиболее полезная форма.
- напр. Дано : Жесткий резервуар объемом V с p = p 0
при t = 0. Воздух нагнетается с постоянным массовым расходом
изотермически.
Найдите: p в резервуаре как функцию времени
Решение: сначала нарисуйте C.V. внутри всего бака.
Теперь воспользуемся нашим уравнением сохранения массы.
Предположим, что плотность везде в резервуаре одинакова и меняется только со временем. Выходов нет, и единственный оставшийся срок — это массовый срок. на входе:
Это дифференциальное уравнение, которое мы должны решить, разделив переменные и интегрирование от t=0 до некоторого произвольного t.
Наконец, используйте закон идеального газа, чтобы получить давление.Таким образом,
(ПРИМЕЧАНИЕ: давление изменяется линейно с t)Особый случай : СТАЦИОНАРНЫЙ ПОТОК
Для установившегося потока ничто не зависит от времени, член d/dt в уравнении сохранения массы уходит.
, другими словами, «То, что входит, должно выйти наружу»
Если внутрь входит больше, чем выходит, масса со временем будет накапливаться внутри контрольный объем, и это не было бы устойчивым состоянием!! (и вам нужно включить нестационарный объемный член)
-
Поскольку плотность постоянна,
взять плотность вне интеграла
Таким образом, интегральный член равен Q, объемный расход
т.е.е. где массовый расход расход = плотность X объемный расходТаким образом, уравнение сохранения массы принимает вид:
«объемный расход it» = «объемный расход ставка»
-
Еще одно упрощение: входы и выходы 1-D
(для несжимаемого потока)
Рассмотрим торговую точку:
Где:- 1-D выпускное отверстие означает, что скорость параллельна n , единичный вектор нормали.
- В = постоянная на выходе.
-
Плотность
= постоянная на выходе
и
мы обычно говорим:
.так как отрицательный знак учитывается в уравнение сохранения массы,
то есть
-
Средняя скорость
Если вход или выход , а не 1-D, мы все равно можем использовать, но V AV должно быть средним значением скорость
-
ПРИМЕР 3.14 в тексте:
Емкость с водой,
Дано: В АВ , Q 3 , D 1 , D 2 и h равны константам.
В 1 = 3 м/с; Q 3 = 0,01 м 3 /с; ч = постоянная; Д 1 = 0,05 м; D 2 = 0,07 м
Найти: Средняя скорость выхода В 2
Решение: Использовать сохранение массы.Сначала нарисуйте C.V. показано.
Поскольку он устойчивый и несжимаемый,
Используя приведенные выше уравнения, найдите V 2 :
%PDF-1.3 % 2 0 объект > ручей БТ /TT4 1 тф 17.2154 0 0 17.2154 72 707.1831 Тм 0 г /GS1 г 0 Тс 0 тв [(Состояние)-250.1(Уравнения)]TJ ET 71,97 690,249 447,741 -0,398 рэ ф 71,97 689,822 0,399 -84,332 рэ ф 0 0 0 0 к 78,376 686,311 71,605 -77,776 рэ ф д 1 я 78.376 686.311 71.604 -77.774 ре W н 0 0 0 1 к д 71,6044 0 0 -77,7746 78,3761 686,3107 см /Im1 Делать Вопрос Вопрос БТ /TT6 1 тф 11,9552 0 0 11,9552 165,9895 666,4917 Тм 0 г -0,0001 Тс [(Чтение)-2871,3(P)-0,1(r)20,1(o)-0,3(b)9,7(l)-0,3(ems)]TJ /TT2 1 тф -0,556 -1,2083 ТД 0 Тс (6-4)Тдж /F4 1 тф 1,583 0 ТД ()Tj /TT2 1 тф 1,4 0 ТД (6-12)Тж ET 519,33 689,822 0,398 -84,332 рэ ф 71,97 605,529 447,741 -0,399 рэ ф БТ /TT8 1 тф 17,2154 0 0 17,2154 72 561,5054 Тм [(В)-250,1(Т)0(Гермодинамика)-249,8(Г)-250(Состояние)]ТДж /TT4 1 тф 14,3462 0 0 14,3462 72 531.1482 тм -0,0001 Тс [(ИДЕАЛЬНЫЙ)-250,2(ГАЗ)]ТДж /TT2 1 тф 11,9552 0 0 11,9552 72 491,8755 Тм 0,0001 Тс [(The)-250,1(d)0,1(e)]TJ /TT9 1 тф 2,749 0 ТД 0 Тс ()Tj /TT2 1 тф 0,556 0 ТД -0,0002 Тс [(нинг)-250,2(уравнение)-250,2(фор)-250,2(а)-250,4(и)-0,4(сделка)-250,4(газ)-250(и)-0,3(с)]TJ /F3 1 тф -0,7571 -3,0693 ТД 0,1597 Тс (Pv)Tj ET 102,45 449,409 17,771 -0,398 рэ ф БТ 11,9552 0 0 11,9552 106,5863 437,2154 Тм 0 Тс (Т)Тj /F2 1 тф 1,5608 0,7562 ТД (=)Tj /F3 1 тф 1.1944 0 ТД (постоянная)Tj /F2 1 тф 4.8382 0 ТД (=)Tj /F3 1 тф 1.1945 0 ТД (R)Tj /TT2 1 тф -11,6809 -3,6728 ТД [(Kno)25(w)0,2(ing)-250(t)-0,2(hat)]TJ /F3 1 тф 5,6969 0 ТД (v)Тj /F2 1 тф 0,9232 0 ТД (=)Tj /F3 1 тф 1.1944 0 ТД 0,1278 Тс [(В/)127,8(м)] ТДж -5,2603 -3,1029 ТД 0,1597 Тс (PV)Tj ET 102,45 359,529 21,863 -0,398 рэ ф БТ 11,9552 0 0 11,9552 102,4608 347,2847 Тм (Тм)Тj /F2 1 тф 2,2482 0,7562 ТД 0 Тс (=)Tj /F3 1 тф 1.1944 0 ТД (постоянная)Tj /F2 1 тф 4.8382 0 ТД (=)Tj /F3 1 тф 1.1945 0 ТД (R)Tj /TT2 1 тф -12,0232 -3,6089 ТД (где)Tj /F3 1 тф 2,693 0 ТД (R)Tj /TT2 1 тф 1.1265 0 ТД 0,0001 Тс [(есть)-249,7(а)-250,1(г)5,1(а)-249,7(константа)-250,1(е)0,2(или)-249,9(а)-250,1(р)0,1(суставной)-249,9(г )5,1(а)-0,1(с)-249,7(\()0,1(ас)-249,7(ги)24,9(в)15,1(д)-0,1(н)-249,9(и)-0,1(н)-249,9 (C)0,1(&B)-249,9(T)79,9(a)-0,1(bles)-249,7(A-1)-249,9(a)-0,1(nd)-249,9(A-2\).)]TJ /TT8 1 тф 17,2154 0 0 17,2154 72 260,4772 Тм 0 Тс [(Ан)-249,9(Исентр)17,9(о)0(пик)-250,1(П)-0,2(р)17,9(о)0(цесс)-249,8(ж)25(о)0(р)-250,1 (a)0(n)-249,9(Идеал)-250,1(Газ)]ТДж /TT2 1 тф 11,9552 0 0 11,9552 72 233,1088 Тм -0.0001 ТК [(Gi)24,7(v)14,9(e)-0,3(n:)]TJ /F5 1 тф 1,4583 -3,3333 ТД 0 Тс ()Tj /TT2 1 тф 0,9896 0 ТД 0,0001 Тс [(константа)-250,1(удельно)] ТДж /TT9 1 тф 5.6379 0 ТД 0 Тс ()Tj /TT2 1 тф 0,556 0 ТД 0,0001 Тс [(c)-250,1(h)0,1(ест)-249,7(o)15,1(v)15,1(e)-0,1(r)-249,9(a)-250,1(широкий)-250,1(диапазон)-250,1(из )-249,9(температура)] ТДж /F5 1 тф -7,1835 -2,0833 ТД 0 Тс ()Tj /F3 1 тф 0,9896 0 ТД (дс)Tj /F2 1 тф 1.4604 0 ТД 0,3194 Тс (=0)Tj /F5 1 тф -2,45 -2,4167 ТД 0 Тс ()Tj /F3 1 тф 0,9896 0 ТД (дю) Tj /F2 1 тф 1.6102 0 ТД (=)Tj /F3 1 тф 1.1944 0 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 140,9325 137,6668 Тм (v)Тj /F3 1 тф 11,9552 0 0 11,9552 146,5604 139,4601 Тм (дТ)Тj /F4 1 тф 1,7255 0 ТД ()Tj /F3 1 тф 1.2139 0 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 187,8396 137,6668 Тм (v)Тj /F2 1 тф 11,9552 0 0 11,9552 197,2872 139,4601 Тм (=)Tj /F1 1 Тф 9,9626 0 0 9,9626 211,5666 156,9943 Тм ()Tj /F3 1 тф 11,9552 0 0 11,9552 221,339 148,3865 Тм 0,0639 Тс (и)Tj ET 220,65 142,689 17,797 -0,398 рэ ф БТ 11,9552 0 0 11,9552 220,6496 130,4199 Тм (Т)Тj /F1 1 Тф 9.9626 0 0 9,9626 239,6423 156,9943 Тм 0 Тс ()Tj /F6 1 тф 7,6513 0 0 7,9701 247,5298 127,0066 Тм (В)Tj /F5 1 тф 11,9552 0 0 11,9552 89,4346 98,114 Тм ()Tj /F3 1 тф 0,9896 0 ТД (дч)Tj /F2 1 тф 1,5967 0 ТД (=)Tj /F3 1 тф 1.1944 0 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 140,7721 96,3208 Тм (р)Tj /F3 1 тф 11,9552 0 0 11,9552 146,389 98,114 Тм (дТ)Тj /F4 1 тф 1,7255 0 ТД ()Tj /F3 1 тф 1.2139 0 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 187,6682 96,3208 Тм (р)Tj /F2 1 тф 11,9552 0 0 11,9552 197,1039 98,114 Тм (=)Tj /F1 1 Тф 9.9626 0 0 9,9626 211,3843 115,6493 Тм ()Tj /F3 1 тф 11,9552 0 0 11,9552 221,2364 107,0416 Тм 0,0639 Тс (ч)Tj ET 220,41 101,288 17,797 -0,398 рэ ф БТ 11,9552 0 0 11,9552 220,4662 89,0749 Тм (Т)Тj /F1 1 Тф 9,9626 0 0 9,9626 239,46 115,6493 Тм 0 Тс ()Tj /F6 1 тф 7,6513 0 0 7,9701 247,3465 85,6607 Тм (П)Тj /TT2 1 тф 11,9552 0 0 11,9552 303,0117 23,2499 Тм (1)Tj ET конечный поток эндообъект 3 0 объект > /XОбъект > /ExtGState > >> эндообъект 19 0 объект > ручей БТ /TT2 1 тф 11,9552 0 0 11,9552 72 707.1831 тм 0 г /GS1 г 0,0001 Тс 0 тв [(Гибб) 55,1 (с) — 249,7 (е) — 0,1 (выражение) — 249,9 (можно) — 249,9 (быть) — 250,1 (написано) — 249,9 (как)] TJ /F3 1 тф 2,4479 -3,3291 ТД 0,1597 Тс [(Тд) 159,7 (с)] ТДж /F2 1 тф 2.2567 0 ТД 0 Тс (=)Tj /F3 1 тф 1.1944 0 ТД (дю) Tj /F2 1 тф 1,5463 0 ТД (+)Tj /F3 1 тф 1.1305 0 ТД 0,1597 Тс [(Pd) 159,7 (v)] ТДж /F2 1 тф 2.4157 0 ТД 0 Тс (=)Tj /F3 1 тф 1.1945 0 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 223,8246 665,5901 Тм (v)Тj /F3 1 тф 11,9552 0 0 11,9552 229,4525 667,3833 Тм (дТ)Тj /F2 1 тф 1,6616 0 ТД (+)Tj /F3 1 тф 1.1306 0 ТД 0,1597 Тс [(Pd) 159,7 (v)] ТДж /F2 1 тф 2.4157 0 ТД 0 Тс [(=)-319,4(0)-3011,3(\(1\))]TJ /TT2 1 тф -18,3781 -3,329 ТД (где)Tj /F3 1 тф 2,693 0 ТД (дс)Tj /F2 1 тф 1.4604 0 ТД 0,3194 Тс (=0)Tj /TT2 1 тф 2,0069 0 ТД 0 Тс [(потому что)-250,2(мы)-250,1(га)19,8(в)14,9(д)-250,2(предполагается)-250(ан)-250(изэнтропия)-250,2(процесс.)]TJ -6,1603 -2,25 ТД 0,0001 Тс [(The)-250,1(d)0,1(e)]TJ /TT9 1 тф 2,749 0 ТД 0 Тс ()Tj /TT2 1 тф 0,556 0 ТД 0,0001 Тс [(нитион)-249,9(из)-249,9(энтальп)10,1(г)-249,9(и)-0,1(с)]ТДж /F3 1 тф -0.8571 -3,3291 ТД 0 Тс (ч)Tj /F2 1 тф 0,987 0 ТД (=)Tj /F3 1 тф 1.1944 0 ТД (и)Tj /F2 1 тф 0,9366 0 ТД (+)Tj /F3 1 тф 1.1306 0 ТД 0,1597 Тс (Pv)Tj /TT2 1 тф -6,6965 -3,3291 ТД 0,0001 Тс [(T)79,9(a)-0,1(король)-249,9(the)-250,1(d)0,1(eri)25(v)25,1(ati)24,9(v)15,1(e)-250,1(урожайность)]TJ /F3 1 тф 2,4479 -3,329 ТД 0 Тс (дч)Tj /F2 1 тф 1,5967 0 ТД (=)Tj /F3 1 тф 1.1944 0 ТД (дю) Tj /F2 1 тф 1,5463 0 ТД (+)Tj /F3 1 тф 1.1305 0 ТД 0,1597 Тс [(Pd) 159,7 (v)] ТДж /F1 1 Тф 9,9626 0 0 9,9626 134,6341 475,6085 Тм 0 Тс ()Tj ET 139.17 476,846 19,565 -1,196 рэ ф БТ 9,9626 0 0 9,9626 158,6819 475,6085 Тм ()Tj ET 167,61 476,846 19,565 -1,196 рэ ф БТ 9,9626 0 0 9,9626 187,214 475,6085 Тм ()Tj /F8 1 тф 7,6513 0 0 7,9701 151,198 465,4247 Тм ()Tj /F6 1 тф 0,9924 0 ТД 0,162 Тс [(Тд) 179,6 (с)] ТДж /F2 1 тф 11,9552 0 0 11,9552 193,9885 481,2872 Тм 0 Тс (+)Tj /F3 1 тф 0,875 0 ТД 0,037 Тк [(vd)37(P)]TJ -8,6309 -4,2828 ТД 0 Тс (дч)Tj /F2 1 тф 1,5967 0 ТД (=)Tj /F3 1 тф 1.1944 0 ТД 0,1597 Тс [(Тд) 159,7 (с)] ТДж /F2 1 тф 2.1929 0 ТД 0 Тс (+)Tj /F3 1 тф 1.1305 0 ТД 0,0371 Тс [(vd)37.1(P)]TJ /F4 1 тф 2,9157 0 ТД 0 Тс ()Tj /F3 1 тф 1,9694 0 ТД 0,1598 Тс [(Тд) 159,8 (с)] ТДж /F2 1 тф 2,2568 0 ТД 0,3194 Тс (=0=)Tj /F3 1 тф 3.2708 0 ТД 0 Тс (дч)Tj /F4 1 тф 1,5328 0 ТД ()Tj /F3 1 тф 1.15 0 ТД 0,037 Тк [(vd)37(P)]TJ ET 225,45 402,009 102,027 -0,399 рэ ф 225,45 401,593 0,398 -17,623 рэ ф БТ 11,9552 0 0 11,9552 228,792 390,2855 Тм 0 Тс (с)Tj /F6 1 тф 7,6513 0 0 7,9701 234,93 388,4922 Тм (р)Tj /F3 1 тф 11,9552 0 0 11,9552 240,547 390,2855 Тм (дТ)Тj /F4 1 тф 1,6617 0 ТД ()Tj /F3 1 тф 1.15 0 ТД 0,037 Тк [(vd)37(P)]TJ /F2 1 тф 2.4157 0 ТД 0,3194 Тс (=0)Tj ET 327,09 401,593 0,398 -17,623 рэ ф 225,45 384,009 102,027 -0,399 рэ ф БТ 11,9552 0 0 11,9552 369,4097 390,2855 Тм 0 Тс (\(2\))Tj /TT2 1 тф -24,8771 -3,4198 ТД [(приравнивая)-250(E)-0,2(qs.)-310(\()0,1(1\))-250(и)-250(\(2\))-250(через)-250( )]ТДЖ /F3 1 тф 15.2799 0 ТД (дТ)Тj /TT2 1 тф 1,6561 0 ТД 0,0001 Тс [(срок) -250,1(г)0,1(и)24,9(в)15,1(эс)]TJ /F3 1 тф -14,3881 -3,0732 ТД 0 Тс (дП)Tj ET 102,45 306,969 17,843 -0,399 рэ ф БТ 11.9552 0 0 11,9552 106,1051 294,6919 Тм (П)Тj /F2 1 тф 1,6071 0,7562 ТД (=)Tj /F4 1 тф 1.1945 0 ТД ()Tj /F3 1 тф 0,9948 0,7467 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 157,6309 310,8662 Тм (р)Tj ET 151,53 306,969 11,766 -0,399 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 151,4869 294,6919 Тм (с)Tj /F6 1 тф 7,6513 0 0 7,9701 157,6249 292,8986 Тм (v)Тj /F3 1 тф 11,9552 0 0 11,9552 168,6326 312,6595 Тм (дв)Тдж ET 168,69 306,969 14,507 -0,399 рэ ф БТ 11,9552 0 0 11,9552 172,277 294,6919 Тм (v)Тj /F2 1 тф 4,0198 0,7562 ТД (\(3\))Tj /TT2 1 тф -12.4076 -3,7505 ТД 0,0001 Тс [(Инте)14,9(решетка)-249,9(\()0,2(3\))-249,9(от)-250,1(его)-249,7(исходное)-250,1(состояние)-250,1(до)-249,9(а) ]TJ /TT9 1 тф 15,8168 0 ТД 0 Тс ()Tj /TT2 1 тф 0,556 0 ТД 0,0002 Тс [(нал)-250(с)0,4(тейт)]ТДж /F3 1 тф -13,9248 -3,3291 ТД 0 Тс (П)Тj /F7 1 тф 7,9701 0 0 7,9701 109,9098 217,3011 Тм (1)Tj /F3 1 тф 11,9552 0 0 11,9552 115,2897 219,0944 Тм (v)Тj /F6 1 тф 7,6513 0 0 7,9701 122,5066 224,0309 Тм (к)Tj /F7 1 тф 7,9701 0 0 7,9701 122,0643 215,3972 Тм (1)Tj /F2 1 тф 11,9552 0 0 11.9552 132.0488 219.0944 Тм (=)Tj /F3 1 тф 1.1944 0 ТД (П)Тj /F7 1 тф 7,9701 0 0 7,9701 154,9728 217,3011 Тм (2)Tj /F3 1 тф 11,9552 0 0 11,9552 160,3527 219,0944 Тм (v)Тj /F6 1 тф 7,6513 0 0 7,9701 167,5706 224,0309 Тм (к)Tj /F7 1 тф 7,9701 0 0 7,9701 167,1273 215,3972 Тм (2)Tj /F2 1 тф 11,9552 0 0 11,9552 177,1128 219,0944 Тм (=)Tj /F3 1 тф 1.1944 0 ТД (постоянная)Tj /F2 1 тф 4.8382 0 ТД (=)Tj /F3 1 тф 1.1944 0 ТД 0,1597 Тс (Pv)Tj /F6 1 тф 7,6513 0 0 7,9701 281,2842 224,0309 Тм 0 Тс (к)Tj /TT2 1 тф 11.9552 0 0 11,9552 72 179,2946 Тм (где)Tj /F3 1 тф 2,4479 -3,329 ТД (к)Tj /F2 1 тф 0,9417 0 ТД (=)Tj /F3 1 тф 1,2949 0,7467 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 134,142 146,6291 Тм (р)Tj ET 128,01 142,689 11,766 -0,398 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 127,998 130,4557 Тм (с)Tj /F6 1 тф 7,6513 0 0 7,9701 134,136 128,6625 Тм (v)Тj /TT2 1 тф 11,9552 0 0 11,9552 72 92,9375 Тм 0,0001 Тс [(The)-250,1(продукт)-250,1(о)0,1(f)]TJ /F3 1 тф 6.193 0 ТД 0 Тс (П)Тj /F4 1 тф 1.1383 0 ТД ()Tj /F3 1 тф 0,575 0 ТД (v)Тj /F6 1 тф 7.6513 0 0 7,9701 173,7385 97,2762 Тм (к)Tj /TT2 1 тф 11,9552 0 0 11,9552 182,4508 92,9375 Тм 0,0001 Тс [(остается)-249,7(константа)-250,1(для)-249,9(ан)-249,9(идеальный)-250,1(г)5,1(а)-0,1(т)-249,7(ш)0,3(курица:)]TJ /F5 1 тф -7,7804 -3,3291 ТД 0 Тс ()Tj /TT2 1 тф 0,9896 0 ТД (специфический)Tj /TT9 1 тф 2.0549 0 ТД ()Tj /TT2 1 тф 0,556 0 ТД 0,0001 Тс [(с)-250,1(ч)0,1(ест)-249,7(ар)-250,1(с)0(постоянно)]ТДж 14.2643 -2,5 ТД 0 Тс (2)Tj ET конечный поток эндообъект 20 0 объект > /ExtGState > >> эндообъект 24 0 объект > ручей БТ /F5 1 тф 11.9552 0 0 11,9552 89,4346 707,1831 Тм 0 г /GS1 г 0 Тс 0 тв ()Tj /TT2 1 тф 0,9896 0 ТД 0,0001 Тс [(the)-250.1(g)5.1(as)-249.7(under)18.1(goes)-249.7(a)-0.1(n)-249.9(i)-0.1(sentropic)-250.1(процесс)]TJ /F4 1 тф 16.0288 0 ТД 0 Тс ()Tj /TT2 1 тф 1,4 0 ТД 0,0001 Тс [(re)24,9(v)15,1(e)0(rsible)-250,1(+)-249,9(a)-0,1(диабатический)]TJ -19,8768 -3,3334 ТД [(Объединение)-249,9(это)-249,7(результат)-250,1(с)-249,9(это)-250,1(и)-0,1(сделка)-250,1(г)5,1(а)-0,1(с)-249,7 (e)-0,1(квант)-249,9(оф)-249,9(состояние)]TJ ET 218.49 638,889 174,961 -0,398 рэ ф 218,49 638,419 0,398 -38,689 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 223,1024 623,6254 Тм 0 Тс (Т)Тj /F7 1 тф 7,9701 0 0 7,9701 230,7138 621,8322 Тм (2)Tj ET 223,05 617,889 12,991 -0,398 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 223,1024 605,6588 Тм (Т)Тj /F7 1 тф 7,9701 0 0 7,9701 230,7138 603,8655 Тм (1)Tj /F2 1 тф 11,9552 0 0 11,9552 241,1078 614,6989 Тм (=)Tj /F1 1 Тф 9,9626 0 0 9,9626 255,3873 632,2332 Тм ()Tj /F3 1 тф 11,9552 0 0 11,9552 264,4702 623,6254 Тм (v)Тj /F7 1 тф 7.9701 0 0 7,9701 271,2448 621,8322 Тм (1)Tj ET 264,45 617,889 12,154 -0,398 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 264,4702 605,6588 Тм (v)Тj /F7 1 тф 7,9701 0 0 7,9701 271,2448 603,8655 Тм (2)Tj /F1 1 Тф 9,9626 0 0 9,9626 277,8202 632,2332 Тм ()Tj /F6 1 тф 7,6513 0 0 7,9701 285,7076 629,4765 Тм (к)Tj /F8 1 тф 0,6828 0 ТД ()Tj /F7 1 тф 7,9701 0 0 7,9701 298,5255 629,4766 Тм (1)Tj /F2 1 тф 11,9552 0 0 11,9552 307,725 614,6989 Тм (=)Tj /F1 1 Тф 9,9626 0 0 9,9626 322,0045 632,2332 Тм ()Tj /F3 1 тф 11,9552 0 0 11.9552 331.0874 623.6254 Тм (П)Тj /F7 1 тф 7,9701 0 0 7,9701 339,732 621,8322 Тм (2)Tj ET 331,05 617,889 14,024 -0,398 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 331,0874 605,6588 Тм (П)Тj /F7 1 тф 7,9701 0 0 7,9701 339,732 603,8655 Тм (1)Tj /F1 1 Тф 9,9626 0 0 9,9626 346,3073 632,2332 Тм ()Tj /F7 1 тф 7,9701 0 0 7,9701 354,1938 629,4765 Тм (\()Tj /F6 1 тф 7,6513 0 0 7,9701 357,9915 629,4766 Тм (к)Tj /F8 1 тф 0,6828 0 ТД ()Tj /F7 1 тф 7,9701 0 0 7,9701 370,8094 629,4766 Тм (1\))Tj /F6 1 тф 7,6513 0 0 7,9701 379.4879 629,4766 тм -0,017 Тс (/к)Tj ET 393,09 638,419 0,398 -38,689 рэ ф 218,49 599,769 174,961 -0,398 рэ ф БТ /TT2 1 тф 11,9552 0 0 11,9552 72 549,3599 Тм 0,0001 Тс [(The)-250,1(i)-0,1(сентропический)-250,1(процесс)-249,7(i)-0,1(s)-249,7(a)-250(особый)-250,1(случай)-250,1(o)0,1 (f)-249,8(а)-250,1(подробнее)-250,1(общий)-250,1(процесс)-249,7(kno)25,1(wn)-249,9(as)-249,7(a)-250,1(политропный)-250,1( процесс)]TJ ET 443,85 545,529 87,989 -0,398 рэ ф БТ 11,9552 0 0 11,9552 110,9888 522,4608 Тм 0 Тс (где)Tj /F4 1 тф 2.693 0 ТД ()Tj /F3 1 тф 1,4 0 ТД 0,1597 Тс (Pv)Tj /F6 1 тф 7,6513 0 0 7,9701 177,6926 526,7985 Тм 0 Тс (н)Tj /F2 1 тф 11,9552 0 0 11,9552 188,1295 522,4608 Тм (=)Tj /F3 1 тф 1.1944 0 ТД (постоянная)Tj /TT2 1 тф 4.7687 0 ТД 0,0001 Тс (и)Tj /F3 1 тф 1,694 0 ТД 0 Тс (н)Tj /TT2 1 тф 0,9629 0 ТД 0,0001 Тс [(есть)-249,7(ан)15,1(у)-249,9(число)55,1(.)]TJ /TT8 1 тф -18,3338 -3,5833 ТД 0 Тс [(Особый)-250,1(С)0,2(аз)]ТДж /F3 1 тф 0,5 -2,1327 тд (н)Tj /F2 1 тф 1.0324 0 ТД 0,3194 Тс (=1)Тj /F3 1 тф 6.7534 0 ТД 0.1597 тк (Pv)Tj /F2 1 тф 1,8059 0 ТД 0 Тс (=)Tj /F3 1 тф 1.1944 0 ТД 0,0042 Тс (РТ)Tj /F2 1 тф 1,9924 0 ТД 0 Тс (=)Tj /F3 1 тф 1.1944 0 ТД (постоянная)Tj /F4 1 тф 5.3382 0 ТД ()Tj /TT2 1 тф 1,4 0 ТД 0,0001 Тс [(изотермический)-250,1(процесс)]ТДж /F3 1 тф -20,7112 -2,4167 ТД 0 Тс (н)Tj /F2 1 тф 1.0324 0 ТД 0,3194 Тс (=0)Tj /F3 1 тф 6.7534 0 ТД 0,1597 Тс (Pv)Tj /F7 1 тф 7,9701 0 0 7,9701 188,8299 429,5721 Тм 0 Тс (0)Тдж /F2 1 тф 11,9552 0 0 11,9552 198,0284 425,2334 Тм (=)Tj /F3 1 тф 1.1944 0 ТД (постоянная)Tj /F2 1 тф 4.8382 0 ТД (=)Tj /F3 1 тф 1.1944 0 ТД (П)Тj /F4 1 тф 1.7022 0 ТД ()Tj /TT2 1 тф 1,4 0 ТД [(изобарическая)-250,2(процесс)-249,8(\()0(постоянная)-250,2(давление\))]ТДж /F3 1 тф -20,3711 -2,4167 ТД (н)Tj /F2 1 тф 1.0324 0 ТД (=)Tj /F3 1 тф 1.1944 0 ТД 4,9553 Тс [(кП)4795,6(в)]ТДж /F6 1 тф 7,6513 0 0 7,9701 188,8299 400,6805 Тм 0 Тс (к)Tj /F2 1 тф 11,9552 0 0 11,9552 198,3721 396,3417 Тм (=)Tj /F3 1 тф 1.1944 0 ТД (постоянная)Tj /F4 1 тф 5.3382 0 ТД ()Tj /TT2 1 тф 1,4 0 ТД [(изоэнтропический)-250,2(процесс)-249,8(\()]ТДж /F3 1 тф 7.7759 0 ТД (к)Tj /F2 1 тф 0,9417 0 ТД (=)Tj /F3 1 тф 1.1944 0 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 417,8451 394,5484 Тм (р)Tj /F3 1 тф 11,9552 0 0 11,9552 423,462 396,3417 Тм (/с)Tj /F6 1 тф 7,6513 0 0 7,9701 436,4742 394,5484 Тм (v)Тj /TT2 1 тф 11,9552 0 0 11,9552 442,1021 396,3417 Тм (\))Tj /F3 1 тф -30,4575 -2,4167 ТД (н)Tj /F2 1 тф 1.0324 0 ТД (=)Tj /F4 1 тф 1.1944 0 ТД ()Tj /F3 1 тф 5.559 0 ТД 0,1597 Тс (Pv)Tj /F8 1 тф 7,6513 0 0 7,9701 188,8299 371,7888 Тм 0 Тс ()Tj /F2 1 тф 11,9552 0 0 11,9552 202.9101 367,4501 Тм (=)Tj /F3 1 тф 1.1944 0 ТД (постоянная)Tj /F4 1 тф 5.3382 0 ТД ()Tj /TT2 1 тф 1,3999 0 ТД 0,0001 Тс [(изохорный)-250,1(процесс)-249,7(\()0,1(константа)-250,1(v)20,1(колум\))]TJ /TT8 1 тф 17.2154 0 0 17.2154 72 305.0281 Тм 0 Тс [(Отн.)9,8(v)10(e)-250,1(Pr)17,9(essur)17,9(e)-250,2(a)0(nd)-249,9(Relati)9,8(v)10(e)-250,1( Спец)] TJ /TT12 1 тф 15,5328 0 ТД ()Tj /TT8 1 тф 0,556 0 ТД [(с)-250,1(В)100,2(количество)]ТДж /F5 1 тф 11,9552 0 0 11,9552 89,4346 284,6336 Тм ()Tj /TT2 1 тф 0,9896 0 ТД 0.0001 ТК [(обычно)-249,9(мы)-250,1(предположим)-250,1(удельно)]TJ /TT9 1 тф 10.4148 0 ТД 0 Тс ()Tj /TT2 1 тф 0,556 0 ТД 0,0001 Тс [(с)-250,1(ч)0,1(есть)-250,1(к)-249,9(бэ)-250,1(константа)-250,1(ш)0,3(ит)-249,9(отн.)-250,1(к)-249,9( температура)]TJ /F5 1 тф -11,9604 -2,0833 ТД 0 Тс ()Tj /TT11 1 тф 0,9896 0 ТД -0,02 Тс [(бу)-20(т)]ТДж /TT2 1 тф 1,526 0 ТД 0,0001 Тс [(когда)-249,9(температура)-250,1(колебания)-249,7(есть)-250,1(с)0,3(зажигание)]TJ /TT9 1 тф 13,8858 0 ТД 0 Тс ()Tj /TT2 1 тф 0,556 0 ТД 0,0001 Тс [(не могу)-249.9(т)-0,1(его)-249,7(а)-0,1(предположение)-249,9(можно)-249,9(привести)-249,9(к)-249,9(неточности,)-249,9(т.е.)]TJ /F3 1 тф -15,4678 -2,5623 ТД 0 Тс (Т)Тj /F2 1 тф 1.0463 0 ТД (\()Tj /F3 1 тф 0,4375 0 ТД (К)Tj /F2 1 тф 1.0409 0 ТД (\))Tj /F3 1 тф 2,4375 0 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 172,7063 227,3006 Тм (р)Tj /F2 1 тф 11,9552 0 0 11,9552 181,3121 229,0939 Тм (\()Tj /F3 1 тф 0,4375 0 ТД [(к)-18,5(Дж)-36,8(/к)-18,5(г)]ТДж /F4 1 тф 3.3249 0 ТД ()Tj /F3 1 тф 0,575 0 ТД (К)Tj /F2 1 тф 1,041 0 ТД (\))Tj /TT8 1 тф 1.4375 0 ТД 0,0001 Тс [(%)-249,9(d)0,3(диффер)17,9(e)0(nce)]TJ ET 101,25 224,769 233,359 -0,398 рэ ф БТ /TT2 1 тф 11,9552 0 0 11,9552 124,7243 199,8037 Тм 0 Тс [(300)-4149,7(1,0057)]ТДж -0,5 -1,2083 ТД [(1000)-4149,7(1,1417)-5028,6(13,5)]ТДж Т* [(2500)-4399,7(1,688)-5278,6(67,8)]ТДж ET 101,25 152,169 233,359 -0,399 рэ ф БТ /F5 1 тф 11,9552 0 0 11,9552 89,4346 120,6666 Тм ()Tj /TT2 1 тф 0,9896 0 ТД 0,0001 Тс [(the)-403,1(r)0,1(elati)24,9(v)15,1(e)-403,1(давление)-403,1(and)-403(r)0,1(elati)24,9(v)15,1(e)-403 .1(v)20.1(o)0.1(lume)-403.1(tables)-402.7(\(C&B)-402.8(T)79.9(able)-403.1(A-17\),)-441.2(pro)15( v) 0,1(ide)-403,1(a)-0,1(n)-402,9(точно)]TJ 0 -1,25 ТД [(w)10,3(a)-0,1(y)-349,6(o)0,1(f)-349,6(i)-0,1(nвключая)-349,6(the)-349,7(температура)-349,7(ef)25,1(загрязняет )-349,4(на)-349,6(удельно)]TJ /TT9 1 тф 20.4075 0 ТД 0 Тс ()Tj /TT2 1 тф 0,556 0 ТД -0,0001 Тс [(в)-349,9(ч)-0,1(ед)-349,9(фор)-349,8(идеальный)-250,3(газы)-249,9(во время)-250,1(изоэнтропический)]ТДж ET 403,65 101,889 136,407 -0,398 рэ ф БТ 11,9552 0 0 11.9552 101,2653 90,7786 Тм 0 Тс (процессы)Tj ET 101,25 87,009 45,811 -0,398 рэ ф БТ /F5 1 тф 11,9552 0 0 11,9552 89,4346 65,8719 Тм ()Tj /TT2 1 тф 0,9896 0 ТД 0,0001 Тс [(примечание:) -295,8(в)-221,6(с)0,3(пеци)]TJ /TT9 1 тф 5.7942 0 ТД 0 Тс ()Tj /TT2 1 тф 0,556 0 ТД 0,0001 Тс [(c)-221,6(h)0,1(еда)-221,6(r)0,1(atio)-221,5(term)-221,7(gi)24,9(v)15,1(e)-0,1(n)-221,5(b) 0,1(г)] ТДж /F3 1 тф 10.2873 0 ТД 0 Тс (к)Tj /F2 1 тф 0,9417 0 ТД (=)Tj /F3 1 тф 1.1944 0 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 331,8456 64,0797 Тм (р)Tj /F3 1 тф 11.9552 0 0 11,9552 337,4625 65,8719 Тм (/с)Tj /F6 1 тф 7,6513 0 0 7,9701 350,4747 64,0797 Тм (v)Тj /TT2 1 тф 11,9552 0 0 11,9552 358,7517 65,8719 Тм [(будет)-221,7(также)-221,6(будет)-221,7(в)]TJ /TT9 1 тф 5,5536 0 ТД ()Tj /TT2 1 тф 0,556 0 ТД 0,0001 Тс [(с учетом)-221,5(по)-221,5(температура)]TJ -10,772 -3,5652 ТД 0 Тс (3) Тдж ET конечный поток эндообъект 25 0 объект > /ExtGState > >> эндообъект 29 0 объект > ручей БТ /F5 1 тф 11,9552 0 0 11,9552 89,4346 707,1831 Тм 0 г /GS1 г 0 Тс 0 тв ()Tj /TT8 1 тф 0.9896 0 ТД 0,0001 Тс [(Pr) 17,9 (процесс) 17,9 (e:)] TJ 1,1645 -2,3333 ТД 0 Тс ()Tj /TT2 1 тф 0,9896 0 ТД [(gi)24,8(v)15(e)-0,2(n)]TJ /F3 1 тф 2.432 0 ТД (Т)Тj /F7 1 тф 7,9701 0 0 7,9701 163,7041 677,4944 Тм (1)Tj /F3 1 тф 11,9552 0 0 11,9552 169,0839 679,2877 Тм 0,1916 Тс (,P)Tj /F7 1 тф 7,9701 0 0 7,9701 183,8386 677,4944 Тм 0 Тс (1)Tj /TT2 1 тф 11,9552 0 0 11,9552 192,2072 679,2877 Тм 0,0001 Тс (и)Tj /F3 1 тф 1,694 0 ТД 0 Тс (П)Тj /F7 1 тф 7,9701 0 0 7,9701 221,1039 677,4944 Тм (2)Tj /TT2 1 тф 11,9552 0 0 11.9552 229,4725 679,2877 Тм 0,0001 Тс [(для)-249,9(ан)-249,9(изоэнтропический)-250,1(процесс)]ТДж /TT8 1 тф -9,5595 -1,6667 ТД 0 Тс ()Tj /TT2 1 тф 0,9896 0 ТД 0,0001 Тс (определить)Tj /F3 1 тф 4.249 0 ТД 0 Тс (П)Тj /F6 1 тф 7,6513 0 0 7,9701 186,4598 657,5692 Тм (р)Tj /F7 1 тф 7,9701 0 0 7,9701 191,2578 657,5692 Тм (1)Tj /TT2 1 тф 11,9552 0 0 11,9552 199,6264 659,3624 Тм 0,0002 Тс (в)Tj /F3 1 тф 0,9719 0 ТД 0 Тс (Т)Тj /F7 1 тф 7,9701 0 0 7,9701 218,8573 657,5692 Тм (1)Tj /TT2 1 тф 11,9552 0 0 11,9552 227.2259 659,3624 тм [(от)-250,2(Т)79,8(а)-0,2(бле)-250,2(А)0,2(-17)]ТДж /TT8 1 тф -9,3716 -1,6667 ТД ()Tj /TT2 1 тф 0,9896 0 ТД 0,0002 Тс (рассчитать)Tj /F3 1 тф 3.804 0 ТД 0 Тс (П)Тj /F6 1 тф 7,6513 0 0 7,9701 181,1397 637,6439 Тм (р)Tj /F7 1 тф 7,9701 0 0 7,9701 185,9367 637,6439 Тм (2)Tj /TT2 1 тф 11,9552 0 0 11,9552 191,3176 639,4371 Тм 0,0001 Тс [(,)-249,9(w)0,4(здесь)]TJ /F1 1 Тф 9,9626 0 0 9,9626 156,2829 625,7883 Тм 0 Тс ()Tj /F3 1 тф 11,9552 0 0 11,9552 165,3659 617,1806 Тм (П)Тj /F7 1 тф 7.9701 0 0 7,9701 174,0105 615,3873 Тм (2)Tj ET 165,33 611,409 14,024 -0,398 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 165,3659 599,2139 Тм (П)Тj /F7 1 тф 7,9701 0 0 7,9701 174,0105 597,4207 Тм (1)Tj /F1 1 Тф 9,9626 0 0 9,9626 180,5858 625,7883 Тм ()Tj /F6 1 тф 7,6513 0 0 7,9701 188,4732 595,8008 Тм (с)Tj /F7 1 тф 7,9701 0 0 7,9701 192,9584 595,8008 Тм (=)Tj /F6 1 тф 7,6513 0 0 7,9701 200,5529 595,8008 Тм -0,014 Тс [(con)9(s)-5(t)]TJ /F2 1 тф 11,9552 0 0 11,9552 228,3258 608,254 Тм 0 Тс (=)Tj /F3 1 тф 1.2944 0,7467 ТД (П)Тj /F6 1 тф 7,6513 0 0 7,9701 252,4453 615,3873 Тм (р)Tj /F7 1 тф 7,9701 0 0 7,9701 257,2433 615,3873 Тм (2)Tj ET 243,81 611,409 18,822 -0,398 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 243,8008 599,2139 Тм (П)Тj /F6 1 тф 7,6513 0 0 7,9701 252,4453 597,4207 Тм (р)Tj /F7 1 тф 7,9701 0 0 7,9701 257,2433 597,4207 Тм (1)Tj /TT8 1 тф 11,9552 0 0 11,9552 115,187 576,1405 Тм ()Tj /TT2 1 тф 0,9896 0 ТД 0,0002 Тс (читать) Тдж /F3 1 тф 1,971 0 ТД 0 Тс (Т)Тj /F7 1 тф 7,9701 0 0 7,9701 158,1928 574,3472 Тм (2)Tj /TT2 1 тф 11.9552 0 0 11,9552 166,5614 576,1405 Тм 0,0001 Тс [(от)-250,1(Т)79,9(а)-0,1(бле)-250,1(А)0,3(-17)-249,9(за)-249,9(т)-250,1(расчетно)-249,9(в)25,1( алуе)-250,1(о)0,1(ж)] ТДж /F3 1 тф 17.6118 0 ТД 0 Тс (П)Тj /F6 1 тф 7,6513 0 0 7,9701 385,7584 574,3472 Тм (р)Tj /F7 1 тф 7,9701 0 0 7,9701 390,5565 574,3472 Тм (2)Tj /F5 1 тф 11,9552 0 0 11,9552 89,4346 548,2451 Тм ()Tj /TT2 1 тф 0,9896 0 ТД [(использование)-250,2(а)-250,1(аналогично)-250(процедура)-250,2(и)-0,2(е)-250(в)20(колум)-250,2(и)-0,2(с)-249,8 (kno)25(wn)-250(вместо)-250(of)-250(давление)-250(w)0.2 (здесь)] TJ /F1 1 Тф 9,9626 0 0 9,9626 130,5295 526,3293 Тм ()Tj /F3 1 тф 11,9552 0 0 11,9552 139,6124 517,7225 Тм (v)Тj /F7 1 тф 7,9701 0 0 7,9701 146,387 515,9293 Тм (2)Tj ET 139,65 511,929 12,154 -0,399 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 139,6124 499,756 Тм (v)Тj /F7 1 тф 7,9701 0 0 7,9701 146,387 497,9626 Тм (1)Tj /F1 1 Тф 9,9626 0 0 9,9626 152,9624 526,3293 Тм ()Tj /F6 1 тф 7,6513 0 0 7,9701 160,8498 496,3417 Тм (с)Tj /F7 1 тф 7,9701 0 0 7,9701 165,336 496,3418 Тм (=)Tj /F6 1 тф 7,6513 0 0 7.9701 172,9295 496,3418 Тм -0,014 Тс [(con)9(s)-5(t)]TJ /F2 1 тф 11,9552 0 0 11,9552 200,7024 508,795 Тм 0 Тс (=)Tj /F3 1 тф 1,2944 0,7467 ТД (v)Тj /F6 1 тф 7,6513 0 0 7,9701 222,9519 515,9293 Тм (р)Tj /F7 1 тф 7,9701 0 0 7,9701 227,7499 515,9293 Тм (2)Tj ET 216,21 511,929 16,952 -0,399 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 216,1773 499,756 Тм (v)Тj /F6 1 тф 7,6513 0 0 7,9701 222,9519 497,9626 Тм (р)Tj /F7 1 тф 7,9701 0 0 7,9701 227,7499 497,9626 Тм (1)Tj /TT8 1 тф 17,2154 0 0 17,2154 72 452,6993 Тм -0.0001 ТК [(В)-249,9(Сводка)]TJ /TT2 1 тф 11,9552 0 0 11,9552 72 425,331 Тм 0,0001 Тс [(F)15,3(o)0,1(r)-249,9(a)-0,1(n)-249,9(i)-0,1(сделка)-250,1(g)5,1(a)-0,1(s)-249,7(w )0,3(ит)-249,9(константа)] ТДж /F3 1 тф 12.2009 0 ТД 0 Тс (с)Tj /F6 1 тф 7,6513 0 0 7,9701 224,002 423,5377 Тм (р)Tj /TT2 1 тф 11,9552 0 0 11,9552 232,6077 425,331 Тм 0,0001 Тс (и)Tj /F3 1 тф 1,694 0 ТД 0 Тс (с)Tj /F6 1 тф 7,6513 0 0 7,9701 258,9978 423,5377 Тм (v)Тj /F3 1 тф 11,9552 0 0 11,9552 127,3405 388,4692 Тм 0,1597 Тс (Pv)Tj /F2 1 тф 2.3198 0 ТД 0 Тс (=)Tj /F3 1 тф 1.7083 0 ТД 0,0042 Тс (РТ)Tj -6.2092 -2.1984 ТД 0 Тс (и)Tj /F7 1 тф 7,9701 0 0 7,9701 109,4067 360,3935 Тм (2)Tj /F4 1 тф 11,9552 0 0 11,9552 117,8421 362,1868 Тм ()Tj /F3 1 тф 1.15 0 ТД (и)Tj /F7 1 тф 7,9701 0 0 7,9701 139,732 360,3935 Тм (1)Tj /F2 1 тф 11,9552 0 0 11,9552 155,0745 362,1868 Тм (=)Tj /F3 1 тф 1.7083 0 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 181,6359 360,3935 Тм (v)Тj /F2 1 тф 11,9552 0 0 11,9552 187,2638 362,1868 Тм (\()Tj /F3 1 тф 0,4375 0 ТД (Т)Тj /F7 1 тф 7.9701 0 0 7,9701 200,1046 360,3935 Тм (2)Tj /F4 1 тф 11,9552 0 0 11,9552 208,54 362,1868 Тм ()Tj /F3 1 тф 1.15 0 ТД (Т)Тj /F7 1 тф 7,9701 0 0 7,9701 229,8999 360,3935 Тм (1)Tj /F2 1 тф 11,9552 0 0 11,9552 235,2797 362,1868 Тм (\))Tj /F3 1 тф -11.1829 -2.1984 ТД (ч)Tj /F7 1 тф 7,9701 0 0 7,9701 109,5671 334,1111 Тм (2)Tj /F4 1 тф 11,9552 0 0 11,9552 118,0025 335,9044 Тм ()Tj /F3 1 тф 1.15 0 ТД (ч)Tj /F7 1 тф 7,9701 0 0 7,9701 139,732 334,1111 Тм (1)Tj /F2 1 тф 11,9552 0 0 11,9552 155,0745 335,9044 Тм (=)Tj /F3 1 тф 1.7083 0 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 181,6359 334,1111 Тм (р)Tj /F2 1 тф 11,9552 0 0 11,9552 187,2528 335,9044 Тм (\()Tj /F3 1 тф 0,4375 0 ТД (Т)Тj /F7 1 тф 7,9701 0 0 7,9701 200,0937 334,1111 Тм (2)Tj /F4 1 тф 11,9552 0 0 11,9552 208,529 335,9044 Тм ()Tj /F3 1 тф 1.15 0 ТД (Т)Тj /F7 1 тф 7,9701 0 0 7,9701 229,8889 334,1111 Тм (1)Tj /F2 1 тф 11,9552 0 0 11,9552 235,2687 335,9044 Тм (\))Tj /TT2 1 тф -13,6568 -4,0833 ТД 0,0001 Тс [(Там)-250,1(а)-0,1(ре)-250,1(3)-249,9(формы)-249,7(о)0,1(е)-249.9(а)-250,1(изменение)-250,1(в)-249,9(энтроп)10,1(у)-249,9(а)-0,1(с)-249,7(а)-250,1(функция)-249,9(о)0,1( е)]TJ /F3 1 тф 23.0108 0 ТД 0 Тс (Т)Тj /F2 1 тф 1.0463 0 ТД (&)Tj /F3 1 тф 1,125 0 ТД (v)Тj /TT2 1 тф 0,6037 0 ТД (,)Tj /F3 1 тф 0,5 0 ТД (Т)Тj /F2 1 тф 1.0464 0 ТД (&)Tj /F3 1 тф 1,125 0 ТД (П)Тj /TT2 1 тф 0,8827 0 ТД 0,25 Тс [(,a)249,8(n)250(d)]TJ /F3 1 тф 2.194 0 ТД 0 Тс (П)Тj /F2 1 тф 1.1328 0 ТД (&)Tj /F3 1 тф 1,125 0 ТД (v)Тj /TT2 1 тф 0,6037 0 ТД (.)Tj /F3 1 тф -31,9476 -5,8495 ТД (с)Tj /F7 1 тф 7.9701 0 0 7,9701 107,6164 215,3624 Тм (2)Tj /F4 1 тф 11,9552 0 0 11,9552 116,0508 217,1556 Тм ()Tj /F3 1 тф 1.15 0 ТД (с)Tj /F7 1 тф 7,9701 0 0 7,9701 136,1504 215,3624 Тм (1)Tj /F2 1 тф 11,9552 0 0 11,9552 151,4929 217,1556 Тм (=)Tj /F3 1 тф 1.7083 0 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 178,0543 215,3624 Тм (v)Тj /F2 1 тф 11,9552 0 0 11,9552 185,9746 217,1556 Тм (ln)Tj /F3 1 тф 1,2292 0,7467 ТД (Т)Тj /F7 1 тф 7,9701 0 0 7,9701 208,2799 224,2899 Тм (2)Tj ET 200,61 220,329 12,991 -0,399 рэ ф БТ /F3 1 тф 11.9552 0 0 11,9552 200,6695 208,1165 Тм (Т)Тj /F7 1 тф 7,9701 0 0 7,9701 208,2799 206,3232 Тм (1)Tj /F2 1 тф 11,9552 0 0 11,9552 217,9108 217,1556 Тм (+)Tj /F3 1 тф 1.1305 0 ТД (R)Tj /F2 1 тф 1,0683 0 ТД (ln)Tj /F3 1 тф 1,2292 0,7467 ТД (v)Тj /F7 1 тф 7,9701 0 0 7,9701 265,6667 224,2899 Тм (2)Tj ET 258,93 220,329 12,154 -0,399 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 258,8922 208,1165 Тм (v)Тj /F7 1 тф 7,9701 0 0 7,9701 265,6667 206,3232 Тм (1)Tj /F2 1 тф 11,9552 0 0 11,9552 151,4929 176,8588 Тм (=)Tj /F3 1 тф 1.7083 0 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 178,0543 175,0655 Тм (р)Tj /F2 1 тф 11,9552 0 0 11,9552 185,9626 176,8588 Тм (ln)Tj /F3 1 тф 1,2292 0,7467 ТД (Т)Тj /F7 1 тф 7,9701 0 0 7,9701 208,269 183,992 Тм (2)Tj ET 200,61 180,009 12,991 -0,399 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 200,6575 167,8186 Тм (Т)Тj /F7 1 тф 7,9701 0 0 7,9701 208,269 166,0254 Тм (1)Tj /F4 1 тф 11,9552 0 0 11,9552 217,8999 176,8588 Тм ()Tj /F3 1 тф 1.15 0 ТД (R)Tj /F2 1 тф 1,0682 0 ТД (ln)Tj /F3 1 тф 1,2292 0,7467 ТД (П)Тj /F7 1 тф 7.9701 0 0 7,9701 267,7579 183,992 Тм (2)Tj ET 259,17 180,009 14,024 -0,399 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 259,1133 167,8186 Тм (П)Тj /F7 1 тф 7,9701 0 0 7,9701 267,7579 166,0254 Тм (1)Tj /F2 1 тф 11,9552 0 0 11,9552 151,4929 136,5609 Тм (=)Tj /F3 1 тф 1.7083 0 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 178,0543 134,7676 Тм (р)Tj /F2 1 тф 11,9552 0 0 11,9552 185,9626 136,5609 Тм (ln)Tj /F3 1 тф 1,2292 0,7467 ТД (v)Тj /F7 1 тф 7,9701 0 0 7,9701 207,4321 143,6941 Тм (2)Tj ET 200,61 139,809 12,154 -0,398 рэ ф БТ /F3 1 тф 11.9552 0 0 11,9552 200,6575 127,5208 Тм (v)Тj /F7 1 тф 7,9701 0 0 7,9701 207,4321 125,7275 Тм (1)Tj /F2 1 тф 11,9552 0 0 11,9552 217,063 136,5609 Тм (+)Tj /F3 1 тф 1.1306 0 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 236,7173 134,7676 Тм (v)Тj /F2 1 тф 11,9552 0 0 11,9552 244,6366 136,5609 Тм (ln)Tj /F3 1 тф 1,2292 0,7467 ТД (П)Тj /F7 1 тф 7,9701 0 0 7,9701 267,9761 143,6941 Тм (2)Tj ET 259,29 139,809 14,024 -0,398 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 259,3315 127,5208 Тм (П)Тj /F7 1 тф 7,9701 0 0 7,9701 267.9761 125,7275 тм (1)Tj /F3 1 тф 11,9552 0 0 11,9552 101,2653 91,6224 Тм (R)Tj /F2 1 тф 1.196 0 ТД (=)Tj /F3 1 тф 1.1944 0 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 135,9811 89,8292 Тм (р)Tj /F4 1 тф 11,9552 0 0 11,9552 144,6535 91,6224 Тм ()Tj /F3 1 тф 1.15 0 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 164,54 89,8292 Тм (v)Тj /TT2 1 тф 11,9552 0 0 11,9552 303,0117 23,2499 Тм (4)Тдж ET конечный поток эндообъект 30 0 объект > /ExtGState > >> эндообъект 32 0 объект > ручей БТ /TT8 1 тф 17.2154 0 0 17.2154 72 707.1831 тм 0 г /GS1 г 0 Тс 0 тв [(A)-249,8(G)-0,2(общий)-250,2(F)24,8(состав)]TJ /TT2 1 тф 11,9552 0 0 11,9552 72 679,8148 Тм 0,0001 Тс [(Устойчиво)-392,4(S)0,3(tate)-428,1(Устойчиво)-392,4(F)0,3(lo)25,1(w)-392,2(i)-0,1(n)-392,4(a)-392,6( Flo)25,1(w)-392,2(канал)-392,6(o)0,1(f)-392,4(A)0,3(rbitrary)-392,4(поперечное сечение)-392,4(w)0,3(ith)-392,4(W) 79,9(орк)-392,4(и)-392,4(Н)0,3(ед)]ТДж 0 -1,25 ТД [(T)34,9(r)0,1(ответ)]TJ ET 0 0 0 1 К 0 Дж 0 Дж 0,147 Вт 2,613 М []0 д 1 я 146,669 539,578 м 198.807 567.144 251,179 603,739 302,058 598,989 в 353,686 594,169 404,412 605,598 456,456 625,638 в 154,199 520,197 м 201,671 549,33 238,813 494,893 272,768 501,98 в 319,302 511,694 367,267 564,298 472,591 603,032 в С 0,341 ш [1,705 1,705 ]0 д 274,134 597,671 м 271,983 501,4 л 311,688 597,577 м 309,536 516,997 л С 0,682 Вт []0 д 302,101 555,089 м 317,43 555,089 л С 0 0 0 1 к 319,849 555,089 м 315,037 557,151 л 315,724 555,776 315,724 554,401 315,037 553,026 в 319,849 555,089 л е* 262,746 554,995 м 278.075 554.995 л С 280,494 554,995 м 275,682 557,057 л 276,369 555,682 276,369 554,307 275,682 552,932 в 280,494 554,995 л е* 288,117 624,562 м 288,117 593,635 л С 288,117 591,217 м 290,18 596,029 л 288,805 595,342 287,43 595,342 286,055 596,029 в 288,117 591,217 л е* 295,647 519,686 м 282,356 475,213 л С 281,663 472,896 м 285,017 476,916 л 283,503 476,651 282,186 477,045 281,065 478,097 в 281,663 472,896 л е* 0,147 Вт 240,789 433,097 49,48 50,555 рэ С 0,682 Вт 133,762 519,148 м 170,866 537,955 л С 173 023 539.048 м 167,798 538,712 л 169,033 537,796 169,655 536,57 169,663 535,033 в 173,023 539,048 л е* 439,246 604,125 м 474,093 617,255 л С 476,356 618,108 м 471,125 618,341 л 472,254 617,297 472,738 616,01 472,58 614,481 в 476,356 618,108 л е* 0,341 ш [1,705 1,023 ]0 д 148,821 554,645 м 166.031 514.846 л 445,606 630,384 м 462,816 590,585 л С 258,109 451,829 м 258,109 450,43 л 254,153 450,43 л 254,153 440,088 л 252,538 440,088 л 252,538 450,43 л 248,583 450,43 л 248,583 451,829 л 258,109 451,829 л е* 259.702 451,829 м 268,26 451,829 л 268,26 450,389 л 261,252 450,389 л 261,252 446,827 л 267,733 446,827 л 267,733 445,468 л 261,252 445,468 л 261,252 441,488 л 268,38 441,488 л 268,38 440,088 л 259,702 440,088 л 259,702 451,829 л е* 275,909 446,45 м 276,654 446,45 277,246 446,6 277,679 446,897 в 278,113 447,195 278,331 447,735 278,331 448,512 в 278,331 449,35 278,026 449,92 277,42 450,223 в 277,096 450,381 276,659 450,463 276,116 450,463 в 272,232 450,463 л 272,232 446,45 л 275,909 446,45 л час 270,641 451.829 м 276,078 451,829 л 276,973 451,829 277,709 451,699 278,29 451,437 в 279,392 450,937 279,946 450,013 279,946 448,665 в 279,946 447,961 279,799 447,386 279,51 446,938 в 279,218 446,491 278,812 446,131 278,29 445,858 в 278,749 445,673 279,092 445,427 279,324 445,124 в 279,556 444,819 279,687 444,328 279,714 443,646 в 279,769 442,072 л 279,785 441,624 279,824 441,289 279,881 441,07 в 279,976 440,699 280,148 440,459 280,394 440,353 в 280,394 440,088 л 278,443 440,088 л 278,389 440,189 278,348 440.32 278,315 440,481 в 278,282 440,639 278,255 440,948 278,236 441,406 в 278,138 443,365 л 278,102 444,131 277,816 444,647 277,284 444,909 в 276,981 445,05 276,503 445,124 275,854 445,124 в 272,232 445,124 л 272,232 440,088 л 270,641 440,088 л 270,641 451,829 л е* 127,288 509,423 м 128,709 509,423 л 128,709 508,206 л 129,05 508,629 129,358 508,935 129,637 509,126 в 130,111 509,45 130,649 509,614 131,252 509,614 в 131,934 509,614 132,482 509,445 132,897 509,109 в 133,131 508,918 133,344 508,637 133.538 508,264 с 133,857 508,722 134,233 509,06 134,664 509,281 в 135,095 509,502 135,581 509,614 136,118 509,614 в 137,27 509,614 138,053 509,199 138,467 508,367 в 138,691 507,92 138,803 507,317 138,803 506,561 в 138,803 500,862 л 137,31 500,862 л 137,31 506,809 л 137,31 507,38 137,166 507,77 136,882 507,982 в 136,596 508,195 136,249 508,304 135,837 508,304 в 135,273 508,304 134,787 508,113 134,381 507,737 в 133,971 507,358 133,77 506,725 133,77 505,841 в 133,77 500,862 л 132,307 500,862 л 132.307 506.449 л 132,307 507,03 132,236 507,453 132,097 507,721 в 131,879 508,119 131,473 508,318 130,875 508,318 в 130,332 508,318 129,839 508,108 129,394 507,688 в 128,949 507,268 128,726 506,504 128,726 505,402 в 128,726 500,862 л 127,288 500,862 л 127,288 509,423 л е* 473,015 633,028 м 474,436 633,028 л 474,436 631,812 л 474,777 632,234 475,085 632,54 475,364 632,731 в 475,838 633,056 476,376 633,219 476,979 633,219 в 477,66 633,219 478,209 633,05 478,624 632,715 в 478,858 632,524 479,071 632,243 479,265 631.869 с 479,584 632,327 479,96 632,666 480,391 632,887 в 480,822 633,108 481,308 633,219 481,845 633,219 в 482,996 633,219 483,779 632,805 484,194 631,973 в 484,418 631,525 484,53 630,922 484,53 630,167 в 484,53 624,468 л 483,037 624,468 л 483.037 630.415 л 483,037 630,985 482,893 631,375 482,609 631,588 в 482,323 631,801 481,976 631,91 481,564 631,91 в 481 631,91 480,514 631,719 480,108 631,343 в 479,698 630,963 479,496 630,33 479,496 629,447 в 479,496 624,468 л 478.034 624.468 л 478.034 630.055 л 478.034 630,636 477,963 631,059 477,824 631,326 в 477,606 631,724 477,2 631,924 476,602 631,924 в 476,059 631,924 475,565 631,714 475,121 631,293 в 474,676 630,873 474,453 630,109 474,453 629,007 в 474,453 624,468 л 473,015 624,468 л 473,015 633,028 л е* 260,928 589,021 м 262,792 589,021 л 264,756 586,006 л 266,747 589,021 л 268,504 589,021 л 265,612 584,847 л 268,624 580,46 л 266,785 580,46 л 264,66 583,674 л 262,598 580,46 л 260,776 580,46 л 263,79 584,847 л 260,928 589,021 л е* 252,256 554,989 м 253.639 554,989 л 255.097 552.751 л 256,575 554,989 л 257,879 554,989 л 255,733 551,891 л 257,968 548,635 л 256,603 548,635 л 255,026 551,02 л 253,495 548,635 л 252,143 548,635 л 254,38 551,891 л 252,256 554,989 л е* 317,4 590,096 м 319,263 590,096 л 321,227 587,082 л 323,219 590,096 л 324,975 590,096 л 322.084 585.923 л 325,095 581,536 л 323,257 581,536 л 321,132 584,75 л 319,069 581,536 л 317,247 581,536 л 320,261 585,923 л 317,4 590,096 л е* 326,206 585,036 м 326,206 586,378 л 329,692 586,378 л 329.692 589,889 л 331,059 589,889 л 331,059 586,378 л 334,542 586,378 л 334,542 585,036 л 331.059 585.036 л 331,059 581,536 л 329,692 581,536 л 329,692 585,036 л 326,206 585,036 л е* 336,853 585,715 м 336,853 584,799 337,047 584,032 337,437 583,413 в 337,824 582,796 338,449 582,488 339,305 582,488 в 339,971 582,488 340,52 582,775 340,948 583,348 в 341,376 583,92 341,591 584,742 341,591 585,811 в 341,591 586,894 341,37 587,693 340,929 588,214 в 340,487 588,732 339,941 588,992 339,289 588,992 в 338 566 588.992 337,977 588,716 337,527 588,162 в 337,077 587,608 336,853 586,793 336,853 585,715 в час 339,019 590,246 м 339,674 590,246 340,222 590,11 340,664 589,832 в 340,92 589,671 341,21 589,393 341,537 588,992 в 341,537 593,315 л 342,917 593,315 л 342,917 581,536 л 341,624 581,536 л 341,624 582,728 л 341,289 582,199 340,891 581,82 340,432 581,585 в 339,974 581,351 339,45 581,233 338,858 581,233 в 337,903 581,233 337,079 581,634 336,381 582,436 в 335,683 583,238 335,334 584,305 335,334 585,636 в 335 334 586.883 335,653 587,963 336,288 588,877 в 336,927 589,791 337,835 590,246 339,019 590,246 в е* 344,227 590,096 м 346,09 590,096 л 348,054 587,082 л 350.046 590.096 л 351,802 590,096 л 348,911 585,923 л 351,922 581,536 л 350.084 581.536 л 347,959 584,75 л 345,896 581,536 л 344,074 581,536 л 347,088 585,923 л 344,227 590,096 л е* 334,992 559,247 м 336,375 559,247 л 337,833 557,01 л 339,311 559,247 л 340,615 559,247 л 338,469 556,149 л 340,704 552,893 л 339,339 552,893 л 337,762 555,278 л 336,231 552,893 л 334.879 552,893 л 337,116 556,149 л 334,992 559,247 л е* 341,528 555,491 м 341,528 556,487 л 344,116 556,487 л 344,116 559,093 л 345,13 559,093 л 345,13 556,487 л 347,716 556,487 л 347,716 555,491 л 345,13 555,491 л 345,13 552,893 л 344,116 552,893 л 344,116 555,491 л 341,528 555,491 л е* 349,431 555,995 м 349,431 555,315 349,575 554,746 349,864 554,286 в 350,152 553,829 350,616 553,6 351,252 553,6 в 351,746 553,6 352,153 553,812 352,47 554,238 в 352,788 554,663 352,948 555,272 352,948 556,066 в 352.948 556,87 352,784 557,463 352,456 557,85 в 352,128 558,235 351,723 558,427 351,239 558,427 в 350,703 558,427 350,265 558,223 349,931 557,811 в 349,597 557,4 349,431 556,795 349,431 555,995 в час 351,039 559,358 м 351,525 559,358 351,932 559,257 352,26 559,051 в 352,45 558,931 352,665 558,725 352,908 558,427 в 352,908 561,636 л 353,932 561,636 л 353,932 552,893 л 352,973 552,893 л 352,973 553,778 л 352,723 553,385 352,428 553,104 352,088 552,93 в 351,748 552,756 351,359 552,668 350,919 552,668 в 350.211 552,668 349,599 552,966 349,081 553,561 в 348,562 554,157 348,303 554,948 348,303 555,936 в 348,303 556,862 348,54 557,664 349,012 558,342 в 349,486 559,02 350,16 559,358 351,039 559,358 в е* 354,904 559,247 м 356,287 559,247 л 357,745 557,01 л 359,223 559,247 л 360,527 559,247 л 358,381 556,149 л 360,616 552,893 л 359,251 552,893 л 357,674 555,278 л 356,143 552,893 л 354,791 552,893 л 357,028 556,149 л 354,904 559,247 л е* 324,475 566,924 м 333,033 566,924 л 333,033 565,484 л 326,025 565,484 л 326.025 561,921 л 332,506 561,921 л 332,506 560,562 л 326,025 560,562 л 326,025 556,582 л 333,153 556,582 л 333,153 555,183 л 324,475 555,183 л 324,475 566,924 л е* 241,556 564,141 м 250,114 564,141 л 250,114 562,701 л 243,106 562,701 л 243,106 559,138 л 249,587 559,138 л 249,587 557,779 л 243,106 557,779 л 243,106 553,799 л 250,234 553,799 л 250,234 552,4 л 241,556 552,4 л 241,556 564,141 л е* 289,008 630,892 м 289,008 629,976 289,202 629,209 289,592 628,59 в 289,98 627,974 290,604 627,665 291,461 627.665 с 292,126 627,665 292,675 627,952 293,103 628,525 в 293,531 629,098 293,747 629,919 293,747 630,988 в 293,747 632,071 293,526 632,87 293,084 633,391 в 292,642 633,91 292,096 634,169 291,444 634,169 в 290,722 634,169 290,132 633,893 289,682 633,34 в 289,232 632,786 289,008 631,97 289,008 630,892 в час 291,174 635,424 м 291,829 635,424 292,377 635,287 292,819 635,009 в 293,076 634,848 293,365 634,57 293,692 634,169 в 293,692 638,493 л 295,073 638,493 л 295,073 626,713 л 293,78 626,713 л 293,78 627.906 л 293,444 627,376 293,046 626,997 292,588 626,762 в 292,129 626,528 291,605 626,411 291,014 626,411 в 290,059 626,411 289,235 626,812 288,537 627,614 в 287,838 628,415 287,489 629,482 287,489 630,813 в 287,489 632,06 287,808 633,14 288,444 634,054 в 289,082 634,968 289,99 635,424 291,174 635,424 в е* 298,163 638,454 м 300,379 628,904 л 303,03 638,454 л 304,757 638,454 л 307,411 628,904 л 309,624 638,454 л 311,367 638,454 л 308,282 626,713 л 306,612 626,713 л 303,903 636,447 л 301,178 626,713 л 299.506 626,713 л 296,437 638,454 л 298,163 638,454 л е* 297,076 494,285 м 297,076 493,369 297,269 492,602 297,66 491,983 в 298,047 491,366 298,672 491,058 299,528 491,058 в 300,194 491,058 300,742 491,344 301,17 491,917 в 301,599 492,49 301,814 493,311 301,814 494,381 в 301,814 495,464 301,593 496,263 301,151 496,784 в 300,709 497,302 300,164 497,562 299,512 497,562 в 298,789 497,562 298,2 497,286 297,75 496,732 в 297,299 496,178 297,076 495,363 297,076 494,285 в час 299,242 498,816 м 299,897 498,816 300.445 498,68 300,887 498,402 в 301,143 498,241 301,432 497,962 301,76 497,562 в 301,76 501,885 л 303,14 501,885 л 303,14 490,106 л 301,847 490,106 л 301,847 491,298 л 301,512 490,769 301,113 490,39 300,655 490,155 в 300,197 489,92 299,673 489,803 299,081 489,803 в 298,126 489,803 297,302 490,204 296,604 491,006 в 295,905 491,808 295,556 492,875 295,556 494,206 в 295,556 495,453 295,875 496,533 296,511 497,447 в 297,149 498,361 298,058 498,816 299,242 498,816 в е* 316,199 490,139 м 315,4 489,17 л 313.585 490,553 л 313,146 490,313 312,674 490,122 312,167 489,978 в 311,657 489,833 311,1 489,762 310,5 489,762 в 308,678 489,762 307,248 490,36 306,215 491,552 в 305,303 492,714 304,848 494,168 304,848 495,917 в 304,848 497,504 305,243 498,863 306,032 499,992 в 307,044 501,441 308,542 502,166 310,522 502,166 в 312,595 502,166 314,131 501,501 315,127 500,167 в 315,904 499,13 316,294 497,799 316,294 496,181 в 316,294 495,423 316,202 494,697 316,013 493,999 в 315,732 492,932 315,255 492,065 314,584 491.393 с 316,199 490,139 л час 310,691 491,186 м 311,021 491,186 311,329 491,208 311,619 491,252 в 311,905 491,298 312,156 491,388 312,369 491,522 в 311.084 492.528 л 311,883 493,511 л 313,416 492,321 л 313,902 492,875 314,229 493,494 314,404 494,182 в 314,576 494,869 314,663 495,526 314,663 496,157 в 314,663 497,537 314,303 498,647 313,58 499,487 в 312,857 500,33 311,872 500,751 310,62 500,751 в 309,352 500,751 308,348 500,347 307,606 499,539 в 306,866 498,735 306,495 497,491 306,495 495,813 в 306 495 494.4 306,85 493,276 307,562 492,438 в 308,274 491,604 309,316 491,186 310,691 491,186 в е* 0,147 Вт []0 д 139,572 568,09 м 139,572 570,054 140,263 571,727 141,648 573,112 в 143,033 574,497 144,705 575,188 146,669 575,188 в 148,63 575,188 150,306 574,497 151,688 573,112 в 153,073 571,727 153,767 570,054 153,767 568,09 в 153,767 566,126 153,073 564,453 151,688 563,069 в 150,306 561,684 148,63 560,993 146,669 560,993 в 144,705 560,993 143,033 561,684 141,648 563,069 в 140,263 564,453 139,572 566,126 139.572 568,09 в час 140,522 568,09 м 140,522 566,388 141,121 564,941 142,319 563,74 в 143,517 562,542 144,967 561,943 146,669 561,943 в 148,368 561,943 149,822 562,542 151,023 563,74 в 152,225 564,941 152,827 566,388 152,827 568,09 в 152,827 569,793 152,225 571,243 151,023 572,444 в 149,822 573,646 148,368 574,248 146,669 574,248 в 144,967 574,248 143,517 573,646 142,319 572,444 в 141,121 571,243 140,522 569,793 140,522 568,09 в час 146,198 563,592 м 146,198 571,649 л 144,781 571,649 л 144,781 572,395 л 147.39 572,618 л 147,39 563,592 л 146,198 563,592 л б* 438,065 643,386 м 438,065 645,35 438,755 647,023 440,14 648,407 в 441,525 649,792 443,198 650,483 445,162 650,483 в 447,123 650,483 448,799 649,792 450,18 648,407 в 451,565 647,023 452,259 645,35 452,259 643,386 в 452,259 641,422 451,565 639,749 450,18 638,364 в 448,799 636,979 447,123 636,289 445,162 636,289 в 443,198 636,289 441,525 636,979 440,14 638,364 в 438,755 639,749 438,065 641,422 438,065 643,386 в час 439,014 643,386 м 439,014 641,683 439.613 640,237 440,811 639,035 в 442,009 637,837 443,459 637,238 445,162 637,238 в 446,861 637,238 448,314 637,837 449,516 639,035 в 450,717 640,237 451,319 641,683 451,319 643,386 в 451,319 645,088 450,717 646,538 449,516 647,74 в 448,314 648,941 446,861 649,543 445,162 649,543 в 443,459 649,543 442,009 648,941 440,811 647,74 в 439,613 646,538 439,014 645,088 439,014 643,386 в час 442,563 639,012 м 442,563 640,057 л 442,9 640,862 443,6 641,742 444,661 642,695 в 445,342 643,317 л 446,219 644,106 446,658 644.892 446,658 645,677 в 446,658 646,214 446,517 646,617 446,236 646,882 в 445,954 647,147 445,532 647,278 444,969 647,278 в 444,363 647,278 443,633 647,039 442,782 646,561 в 442,782 647,615 л 443,574 647,992 444,366 648,182 445,152 648,182 в 445,99 648,182 446,661 647,952 447,165 647,501 в 447,669 647,046 447,925 646,45 447,925 645,707 в 447,925 645,17 447,794 644,695 447,538 644,283 в 447,283 643,87 446,808 643,366 446,111 642,77 в 445,65 642,378 л 444,703 641,566 444,153 640,793 444 640,057 в 447.885 640,057 л 447,885 639,012 л 442,563 639,012 л б* 132,877 512,04 м 132,487 512,04 132,156 512,177 131,885 512,452 в 131,613 512,727 131,477 513,059 131,477 513,449 в 131,477 513,837 131,613 514,166 131,886 514,438 в 132,16 514,709 132,49 514,845 132,877 514,845 в 133,264 514,845 133,592 514,709 133,86 514,438 в 134,129 514,166 134,263 513,837 134,263 513,449 в 134,263 513,059 134,127 512,727 133,855 512,452 в 133,584 512,177 133,258 512,04 132,877 512,04 в б* 478,604 635,645 м 478,214 635,645 477.883 635,783 477,611 636,058 в 477,34 636,333 477,204 636,665 477,204 637,055 в 477,204 637,443 477,34 637,771 477,613 638,043 в 477,887 638,315 478,217 638,451 478,604 638,451 в 478,991 638,451 479,319 638,315 479,587 638,043 в 479,856 637,771 479,99 637,443 479,99 637,055 в 479,99 636,665 479,854 636,333 479,582 636,058 в 479,311 635,783 478,985 635,645 478,604 635,645 в б* 245,188 566,804 м 244,798 566,804 244,467 566,941 244,196 567,216 в 243,924 567,491 243,788 567,823 243,788 568,213 в 243 788 568.601 243,924 568,93 244,198 569,202 в 244,471 569,473 244,802 569,609 245,188 569,609 в 245,576 569,609 245,903 569,473 246,172 569,202 в 246,44 568,93 246,574 568,601 246,574 568,213 в 246,574 567,823 246,438 567,491 246,167 567,216 в 245,895 566,941 245,569 566,804 245,188 566,804 в б* 328,457 569,399 м 328,067 569,399 327,736 569,537 327,465 569,811 в 327,193 570,087 327,057 570,419 327,057 570,808 в 327,057 571,196 327,193 571,525 327,466 571,797 в 327,74 572,068 328,07 572,204 328,457 572,204 в 328.844 572,204 329,172 572,068 329,44 571,797 в 329,709 571,525 329,843 571,196 329,843 570,808 в 329,843 570,419 329,707 570,087 329,435 569,811 в 329,164 569,537 328,838 569,399 328,457 569,399 в б* 303,623 641,642 м 303,233 641,642 302,902 641,78 302,631 642,055 в 302,359 642,33 302,223 642,662 302,223 643,052 в 302,223 643,44 302,359 643,768 302,632 644,04 в 302,906 644,312 303,236 644,448 303,623 644,448 в 304,01 644,448 304,338 644,312 304,607 644,04 в 304,875 643,768 305,009 643,44 305,009 643.052 с 305,009 642,662 304,873 642,33 304,601 642,055 в 304,33 641,78 304,004 641,642 303,623 641,642 в б* 310,077 504,228 м 309,687 504,228 309,356 504,366 309,085 504,641 в 308,813 504,916 308,677 505,248 308,677 505,638 в 308,677 506,026 308,813 506,354 309,086 506,626 в 309,36 506,898 309,69 507,034 310,077 507,034 в 310,464 507,034 310,792 506,898 311,06 506,626 в 311,329 506,354 311,463 506,026 311,463 505,638 в 311,463 505,248 311,327 504,916 311,055 504,641 в 310,784 504,366 310,458 504,228 310.077 504.228 с б* БТ /F3 1 тф 11,9552 0 0 11,9552 101,2653 352,265 Тм 0 г 0 Тс (г)Tj /F2 1 тф 0,9816 0,2417 ТД ()Tj /F3 1 тф -0,3719 -0,2417 ТД (Е)Tj /F2 1 тф 1,6979 0 ТД (=)Tj 2,0803 0,2417 ТД ()Tj /F3 1 тф -0,3719 -0,2417 ТД (Е)Tj /F6 1 тф 7,6513 0 0 7,9701 158,9609 350,4717 Тм 0,1147 Тс [(fi)134,5(n)137,7(a)132,4(l)]TJ /F4 1 тф 11,9552 0 0 11,9552 186,121 352,265 Тм 0 Тс ()Tj /F2 1 тф 1,5219 0,2417 ТД ()Tj /F3 1 тф -0,3719 -0,2417 ТД (Е)Tj /F6 1 тф 7,6513 0 0 7,9701 209,5542 350,4717 Тм -0,0203 Тс (начальный)Tj /F2 1 тф 11.9552 0 0 11,9552 128,8528 325,9825 Тм 0 Тс (=)Tj 2,0803 0,2417 ТД ()Tj /F3 1 тф -0,3719 -0,2417 ТД (Е)Tj /F6 1 тф 7,6513 0 0 7,9701 158,9609 324,1893 Тм (х)Тj /F7 1 тф 7,9701 0 0 7,9701 164,532 324,1893 Тм (+)Tj /F6 1 тф 7,6513 0 0 7,9701 172,1255 324,1893 Тм -0,0176 Тс (дх)Tj /F4 1 тф 11,9552 0 0 11,9552 186,3681 325,9825 Тм 0 Тс ()Tj /F2 1 тф 1,5219 0,2417 ТД ()Tj /F3 1 тф -0,3719 -0,2417 ТД (Е)Tj /F6 1 тф 7,6513 0 0 7,9701 209,8012 324,1893 Тм (х)Тj /TT2 1 тф 11,9552 0 0 11,9552 72 274,7866 Тм (где)Tj /F2 1 тф 2.8198 -2,8034 ТД ()Tj /F3 1 тф -0,3718 -0,2417 ТД (Е)Tj /F2 1 тф 1,6979 0 ТД 1.1933 Тк (=)Tj /F3 1 тф 1.7083 0 ТД 0 Тс (м)Tj /F2 1 тф 1.0323 0 ТД (\()Tj /F3 1 тф 0,4375 0 ТД (е)Tj /F2 1 тф 0,8092 0 ТД (+)Tj /F3 1 тф 1.1306 0 ТД 0,1597 Тс (Pv)Tj /F2 1 тф 1,4865 0 ТД 0 Тс (\))Tj -6,6044 -2,821 ТД 1.1933 Тк (=)Tj /F3 1 тф 1.7083 0 ТД 0 Тс (м)Tj /F2 1 тф 1.0323 0 ТД (\()Tj /F3 1 тф 0,4375 0 ТД (и)Tj /F2 1 тф 0,9366 0 ТД (+)Tj 1,2306 0,7467 ТД (\()Tj /F3 1 тф 0,4375 0 ТД (v)Тj /F8 1 тф 7,6513 0 0 7,9701 197.9158 217,9218 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 203,2956 213,5841 Тм (\))Tj /F7 1 тф 7,9701 0 0 7,9701 208,526 217,9218 Тм (2)Tj ET 185,49 207,849 28,437 -0,399 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 196,3248 195,6165 Тм (2)Tj 1,8262 0,7562 ТД (+)Tj /F3 1 тф 1.1306 0 ТД 0,037 Тк (gz)Tj /F2 1 тф 1.4347 0 ТД 0 Тс (+)Tj /F3 1 тф 1.1306 0 ТД 0,1597 Тс (Pv)Tj /F2 1 тф 1,4865 0 ТД 0 Тс (\))Tj /TT2 1 тф -17,4078 -4,3166 ТД [(С)-250,2(с)-250,2(1)0(ст)-250,2(ла)14,8(ж)]ТДЖ /F3 1 тф 2,8646 -2,9735 ТД [(р)-31.9(ат)-250(оф)-360,5(энер)-32(г)-37(у)]TJ 1,8277 -1,2083 ТД [(стор)-32(аг)-37(е)]TJ /F2 1 тф 6,4241 0,5958 ТД (=)Tj /F3 1 тф 1,6111 0,6125 ТД [(р)-32(ел)-250(из)]TJ 0,5244 -1,2083 ТД 0,0299 Тс [(wo)29.9(rk)]TJ /F2 1 тф 3,8234 0,5958 ТД 0 Тс (+)Tj /F3 1 тф 3,292 0,6125 ТД [(р)-31,9(ел)-250(из)]ТДж -1,7447 -1,2083 ТД [(тепло)-250(tr)-31,9(ansf)-110,4(er)]TJ /F2 1 тф 7,8373 0,5958 ТД (+)Tj /F3 1 тф 1,6607 0,6125 ТД [(нетто)-250(r)-32(ate)-250(of)-360,4(ener)-32(g)-37(y)]TJ -0,1134 -1,2083 ТД [(l)-8,8(eav)-37(ing)-287.1(т)-250(с)-37,1(стебель)]ТЖ -25,4591 -3,1726 ТД (dE)Tj /F6 1 тф 7,6513 0 0 7,9701 119,4341 63,3346 Тм 0,0555 Тс (CV)Tj ET 102,45 59,409 32,831 -0,398 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 112,7492 47,1611 Тм 0 Тс (дт)Tj /F2 1 тф 2,305 0,7561 ТД (=)Tj /F3 1 тф 1.1944 0 ТД (г)Tj /F2 1 тф 1,0798 0,2417 ТД ()Tj /F3 1 тф -0,4701 -0,2417 ТД (Вт)Tj /F4 1 тф 1,5083 0 ТД ()Tj /F3 1 тф 1.15 0 ТД (г)Tj /F2 1 тф 0,9837 0,2417 ТД ()Tj /F3 1 тф -0,3739 -0,2417 ТД (Q)Tj /F4 1 тф 1.1242 0 ТД ()Tj /F3 1 тф 1.15 0 ТД (г)Tj /F2 1 тф 0.9816 0,2417 ТД ()Tj /F3 1 тф -0,3718 -0,2417 ТД (Е)Tj /F2 1 тф 3,8757 0 ТД (\(1\))Tj /TT2 1 тф 1,7778 -2,7562 ТД (5) Тдж ET конечный поток эндообъект 33 0 объект > /ExtGState > >> эндообъект 35 0 объект > ручей БТ /TT2 1 тф 11,9552 0 0 11,9552 72 701,9089 Тм 0 г /GS1 г 0 Тс 0 тв (где)Tj /F3 1 тф 2,793 0,7468 ТД (dE)Tj /F6 1 тф 7,6513 0 0 7,9701 122,3641 709,0431 Тм 0,0555 Тс (CV)Tj ET 105,45 705,129 32,831 -0,398 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 115,6792 692,8688 Тм 0 Тс (дт)Tj /F2 1 тф 2.305 0,7562 ТД 0,3194 Тс (=0)Tj /TT2 1 тф 2,0069 0 ТД 0,0001 Тс [(для)-249,9(постоянно)-249,9(с)0,3(тат.)]TJ -7,9655 -2,5215 ТД [(Уравнение)-249,9(\(1\))-249,9(становится)]TJ /F2 1 тф 2,4479 -3,9223 ТД 0,3194 Тс (0=)Tj /F3 1 тф 2.0763 0 ТД 0 Тс (г)Tj /F2 1 тф 1,0799 0,2417 ТД ()Tj /F3 1 тф -0,4702 -0,2417 ТД (Вт)Tj /F4 1 тф 1,5083 0 ТД ()Tj /F3 1 тф 1.15 0 ТД (г)Tj /F2 1 тф 0,9836 0,2417 ТД ()Tj /F3 1 тф -0,3739 -0,2417 ТД (Q)Tj /F4 1 тф 1.1242 0 ТД ()Tj /F2 1 тф 1,51 0 ТД ()Tj /F3 1 тф -0,36 0 ТД 0,25 Тс (мд)Tj /F1 1 Тф 9.9626 0 0 9,9626 224,5479 642,406 Тм 0 Тс ()Tj /F3 1 тф 11,9552 0 0 11,9552 230,3592 624,8718 Тм (и)Tj /F2 1 тф 0,9366 0 ТД (+)Tj /F3 1 тф 1.1306 0 ТД 0,1597 Тс (Pv)Tj /F2 1 тф 1,742 0 ТД 0 Тс (+)Tj 1,2306 0,7467 ТД (\()Tj /F3 1 тф 0,4375 0 ТД (v)Тj /F8 1 тф 7,6513 0 0 7,9701 303,0575 638,137 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 308,4374 633,7983 Тм (\))Tj /F7 1 тф 7,9701 0 0 7,9701 313,6678 638,137 Тм (2)Tj ET 290,61 628,089 28,437 -0,398 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 301,4665 615,8317 Тм (2)Tj 1.8262 0,7562 ТД (+)Tj /F3 1 тф 1.1306 0 ТД 0,037 Тк (gz)Tj /F1 1 Тф 9,9626 0 0 9,9626 350,9121 642,406 Тм 0 Тс ()Tj /F2 1 тф 11,9552 0 0 11,9552 395,0147 624,8718 Тм (\(2\))Tj /TT2 1 тф -27,0188 -3,8487 ТД [(От)-250,2(в)-250,2(2-й)-250(ла)14,8(ш)]TJ /F3 1 тф 3,0545 -3,0245 ТД [(р)-32(ел)-250(из)]TJ -0,1899 -1,2083 ТД [(энтр)-32(опы)]TJ 0,0976 -1,2083 ТД [(стор)-31,9(аг)-37,1(е)]TJ /F2 1 тф 4,6939 1,2 ТД (=)Tj /F1 1 Тф 9,9626 0 0 9,9626 177,8102 552,0668 Тм ( )Tj 0 -0,9 ТД (\012)Tj 0 -0,3 ТД ()Tj 0 -1.8 ТД (\012)Tj 0 -0,3 ТД ()Tj /F3 1 тф 11,9552 0 0 11,9552 193,9178 542,7019 Тм [(р)-31,9(ел)-250(из)]ТДж -0,1899 -1,2083 ТД [(вход)-31.9(оп)]TJ 0,2291 -1,2083 ТД [(инф)-110,5(л)-8,8(о)0(ш)]ТДж /F4 1 тф 4.4986 1,2 ТД ()Tj /F3 1 тф 1,809 1,2167 ТД [(р)-32(ел)-250(из)]TJ -0,1899 -1,2083 ТД [(энтр)-32(опы)]TJ -0,0525 -1,2083 ТД [(выход)-110,5(л)-8,9(о)0(ш)]ТДж /F1 1 Тф 9,9626 0 0 9,9626 321,6159 552,0668 Тм (\015)Tj 0 -0,9 ТД (\012)Tj 0 -0,3 ТД ()Tj 0 -1,8 ТД (\012)Tj 0 -0,3 ТД ()Tj /F2 1 тф 11,9552 0 0 11.9552 339,5049 528,1564 Тм (+)Tj /F3 1 тф 3,0435 1,2167 ТД [(р)-32(ел)-250(из)]TJ -0,1899 -1,2083 ТД [(энтр)-32(опы)]TJ -0,8064 -1,2083 ТД [(pr)-32(производство)]TJ -21,8749 -3,4653 ТД (dS)Tj /F6 1 тф 7,6513 0 0 7,9701 118,0314 470,5883 Тм 0,0555 Тс (CV)Tj ET 102,45 466,689 31,427 -0,398 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 112,0468 454,415 Тм 0 Тс (дт)Tj /F2 1 тф 2,2463 0,7562 ТД 0,3195 Тс [(=[)-40.4()]ТДж /F3 1 тф 1,507 0 ТД -0,0001 Тс (мс)Tj /F2 1 тф 1,5636 0 ТД 0 Тс (])Tj /F6 1 тф 7,6513 0 0 7,9701 179.3474 461,6618 тм (х)Тj /F4 1 тф 11,9552 0 0 11,9552 188,4722 463,4551 Тм ()Tj /F2 1 тф 1.15 0 ТД 0,3599 Тк ([)Tj /F3 1 тф 0,3125 0 ТД 0 Тс (мс)Tj /F2 1 тф 1,5637 0 ТД (])Tj /F6 1 тф 7,6513 0 0 7,9701 228,3866 461,6618 Тм (х)Тj /F7 1 тф 7,9701 0 0 7,9701 233,9566 461,6618 Тм (+)Tj /F6 1 тф 7,6513 0 0 7,9701 241,5512 461,6619 Тм -0,0176 Тс (дх)Tj /F4 1 тф 11,9552 0 0 11,9552 255,7938 463,4551 Тм 0 Тс ()Tj /F3 1 тф 1,742 0,7467 ТД (г)Tj /F2 1 тф 0,9836 0,2418 ТД ()Tj /F3 1 тф -0,3739 -0,2418 ТД (Q)Tj ET 270.69 466,689 29,438 -0,398 рэ ф БТ 11,9552 0 0 11,9552 270,7377 454,415 Тм (Т)Тj /F6 1 тф 7,6513 0 0 7,9701 278,3482 452,6217 Тм 0,162 Тс [(TE)119,9(R)]TJ /F2 1 тф 11,9552 0 0 11,9552 304,4254 463,4551 Тм 0 Тс (+)Tj 1,5174 0,2417 ТД ()Tj /F4 1 тф -0,3868 -0,2417 ТД (П)Тj /F6 1 тф 7,6513 0 0 7,9701 327,6234 461,6618 Тм (S)Tj /TT2 1 тф 11,9552 0 0 11,9552 72 397,5342 Тм (где)Tj /F3 1 тф 2,793 0,7467 ТД (dS)Tj /F6 1 тф 7,6513 0 0 7,9701 120,9614 404,6685 Тм 0,0555 Тс (CV)Tj ET 105,45 400,689 31,427 -0.398 ре ф БТ /F3 1 тф 11,9552 0 0 11,9552 114,9768 388,4941 Тм 0 Тс (дт)Tj /F2 1 тф 2,2463 0,7562 ТД 0,3195 Тс (=0)Tj /TT2 1 тф 2,007 0 ТД 0,0001 Тс [(для)-249,9(постоянно)-249,9(с)0,3(тат.)]TJ /F2 1 тф -5,4003 -4,6056 ТД 0,3194 Тс (0=)Tj /F4 1 тф 2.0763 0 ТД 0 Тс ()Tj /F2 1 тф 1.2544 0 ТД ()Tj /F3 1 тф -0,3599 0 ТД -0,0001 Тс (мдс) Tj /F4 1 тф 2.4289 0 ТД 0 Тс ()Tj /F3 1 тф 1,742 0,7467 ТД (г)Tj /F2 1 тф 0,9836 0,2417 ТД ()Tj /F3 1 тф -0,3739 -0,2417 ТД (Q)Tj ET 180,81 345,609 29,438 -0,398 рэ ф БТ 11.9552 0 0 11,9552 180,7641 333,4336 Тм (Т)Тj /F6 1 тф 7,6513 0 0 7,9701 188,3746 331,6404 Тм 0,162 Тс [(TE)119,9(R)]TJ /F2 1 тф 11,9552 0 0 11,9552 214,4518 342,4738 Тм 0 Тс (+)Tj 1,5174 0,2417 ТД ()Tj /F4 1 тф -0,3868 -0,2417 ТД (П)Тj /F6 1 тф 7,6513 0 0 7,9701 237,6498 340,6805 Тм (S)Tj /TT2 1 тф 11,9552 0 0 11,9552 72 300,2979 Тм (или)Tj /F3 1 тф 2,4479 -3,3333 ТД (г)Tj /F2 1 тф 0,9836 0,2417 ТД ()Tj /F3 1 тф -0,3739 -0,2417 ТД (Q)Tj /F2 1 тф 1.1881 0 ТД (=)Tj /F3 1 тф 1.1944 0 ТД (Т)Тj /F6 1 тф 7.6513 0 0 7,9701 144,6486 258,6541 Тм 0,1619 Тс [(TE)119,8(R)]ТДж /F2 1 тф 11,9552 0 0 11,9552 171,0994 263,3364 Тм 0 Тс ()Tj /F4 1 тф -0,3868 -0,2417 ТД (П)Тj /F6 1 тф 7,6513 0 0 7,9701 176,1574 258,6541 Тм (S)Tj /F4 1 тф 11,9552 0 0 11,9552 185,9586 260,4473 Тм ()Tj /F3 1 тф 1.15 0 ТД (Т)Тj /F6 1 тф 7,6513 0 0 7,9701 207,3186 258,6541 Тм 0,1619 Тс [(TE)119,6(R)]TJ /F2 1 тф 11,9552 0 0 11,9552 233,4486 260,4473 Тм 0 Тс ()Tj /F3 1 тф -0,36 0 ТД (мдс) Tj /F2 1 тф 5.1847 0 ТД (\(3\))Tj /TT2 1 тф -18,3292 -3.3333 ТД [(Объединение)-250(\(2\))-250(а)-0,2(й)-250(\(3\))-250(через)]TJ /F3 1 тф 12,6379 0 ТД (г)Tj /F2 1 тф 0,9836 0,2417 ТД ()Tj /F3 1 тф -0,3738 -0,2417 ТД (Q)Tj ET 103,41 192,128 349,25 -0,398 рэ ф 103,41 191,705 0,399 -36,335 рэ ф БТ 11,9552 0 0 11,9552 106,8035 170,3163 Тм (Т)Тj /F6 1 тф 7,6513 0 0 7,9701 114,4149 168,5231 Тм 0,1619 Тс [(TE)119,8(R)]ТДж /F2 1 тф 11,9552 0 0 11,9552 143,8545 173,2055 Тм 0 Тс ()Tj /F4 1 тф -0,3868 -0,2417 ТД (П)Тj /F6 1 тф 7,6513 0 0 7,9701 148,9116 168,5231 Тм (S)Tj /F4 1 тф 11.9552 0 0 11,9552 158,7138 170,3163 Тм ()Tj /F3 1 тф 1.15 0 ТД (Т)Тj /F6 1 тф 7,6513 0 0 7,9701 180,0737 168,5231 Тм 0,1619 Тс [(TE)119,8(R)]ТДж /F2 1 тф 11,9552 0 0 11,9552 209,1925 170,3163 Тм 0 Тс ()Tj /F3 1 тф -0,36 0 ТД (мдс) Tj /F2 1 тф 2,4928 0 ТД (=)Tj /F3 1 тф 1.1944 0 ТД (г)Tj /F2 1 тф 1,0798 0,2417 ТД ()Tj /F3 1 тф -0,4701 -0,2417 ТД (Вт)Tj /F4 1 тф 1,5083 0 ТД ()Tj /F2 1 тф 1,5099 0 ТД ()Tj /F3 1 тф -0,3599 0 ТД 0,25 Тс (мд)Tj /F1 1 Тф 9,9626 0 0 9,9626 312,9525 187,8505 Тм 0 Тс ()Tj /F3 1 тф 11.9552 0 0 11,9552 320,8399 170,3163 Тм (и)Tj /F2 1 тф 0,9366 0 ТД (+)Tj /F3 1 тф 1.1305 0 ТД 0,1597 Тс (Pv)Tj /F2 1 тф 1.7421 0 ТД 0 Тс (+)Tj 1,2306 0,7468 ТД (\()Tj /F3 1 тф 0,4375 0 ТД (v)Тj /F8 1 тф 7,6513 0 0 7,9701 393,5382 183,5815 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 398,9181 179,2439 Тм (\))Tj /F7 1 тф 7,9701 0 0 7,9701 404,1485 183,5815 Тм (2)Tj ET 381,09 173,529 28,437 -0,399 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 391,9472 161,2762 Тм (2)Tj 1,8262 0,7562 ТД (+)Tj /F3 1 тф 1.1306 0 ТД 0,037 Тк (gz)Tj /F1 1 Тф 9.9626 0 0 9,9626 441,3918 187,8505 Тм 0 Тс ()Tj ET 452,25 191,705 0,398 -36,335 рэ ф 103,41 155,409 349,25 -0,399 рэ ф БТ /TT2 1 тф 11,9552 0 0 11,9552 494,6441 170,3163 Тм (\(4\))Tj -35,3524 -4,132 ТД [(Уравнение)-250(\(4\))-250(можно)-250(b)0(e)-250.2(u)0(sed)-250(for)-250(an)15(y) -250(SS-SF)-249,8(проц.)]TJ 19.3232 -8.1695 ТД (6)Тдж ET конечный поток эндообъект 36 0 объект > /ExtGState > >> эндообъект 38 0 объект > ручей БТ /TT8 1 тф 17.2154 0 0 17.2154 72 707.1831 Тм 0 г /GS1 г 0 Тс 0 тв [(Особый)-250.2(C)0,2(аза)]TJ 14,3462 0 0 14,3462 72 676,8259 Тм [(Re)14,9(v)10(e)-0,2(rsible,)-250(SS-SF)-250,1(Pr)17,9(процесс)]TJ /TT2 1 тф 11,9552 0 0 11,9552 72 637,5532 Тм 0,0001 Тс [(Re)24,9(v)15,1(e)-0,1(rsible)-250,1(подразумевается)]TJ /F4 1 тф 7,6819 0 ТД 0 Тс ()Tj /F2 1 тф 1,8562 0,2417 ТД ()Tj /F4 1 тф -0,3868 -0,2417 ТД (П)Тj /F6 1 тф 7,6513 0 0 7,9701 191,0874 635,7599 Тм (S)Tj /F2 1 тф 11,9552 0 0 11,9552 201,6538 637,5532 Тм 0,3194 Тс (=0)Tj /F5 1 тф -9,3867 -3,0833 ТД 0 Тс ()Tj /TT2 1 тф 0,9896 0 ТД 0.0001 ТК [(без трения)-249,7(процесс)]TJ /F5 1 тф -0,9896 -2,0833 ТД 0 Тс ()Tj /TT2 1 тф 0,9896 0 ТД 0,0001 Тс [(тепло)-250(передача)-249,9(ис)-249,7(алло)25,1(ср)-249,9(б)20,1(ут)-250,1(должно)-250,1(быть)-250,1(поперек)]TJ /F2 1 тф 17.1738 0 ТД 0 Тс ()Tj /F3 1 тф 0,9375 0 ТД (Т)Тj /F4 1 тф 1,1158 0 ТД ()Tj /F2 1 тф 1.4694 0 ТД (0)Тдж /F5 1 тф -21,6861 -2,0833 ТД ()Tj /TT2 1 тф 0,9896 0 ТД 0,0001 Тс [(что)-249,9(означает)]TJ /F3 1 тф 5.4989 0 ТД 0 Тс (Т)Тj /F6 1 тф 7,6513 0 0 7,9701 174,6172 549,085 Тм 0.1619 тк [(TE)119,8(R)]ТДж /F4 1 тф 11,9552 0 0 11,9552 200,262 550,8782 Тм 0 Тс ()Tj /F3 1 тф 1.2139 0 ТД (Т)Тj /F6 1 тф 7,6513 0 0 7,9701 222,3851 549,085 Тм 0,0555 Тс (CV)Tj /F2 1 тф 11,9552 0 0 11,9552 242,0613 550,8782 Тм 0 Тс (=)Tj /F3 1 тф 1.1944 0 ТД (Т)Тj /TT2 1 тф -15,4193 -3,0833 ТД 0,0001 Тс [(Уравнение)-249,9(4)-249,9(b)0,1(выходит)]TJ /F3 1 тф 2,5479 -3,3193 ТД 0 Тс (г)Tj /F2 1 тф 1,0798 0,2417 ТД ()Tj /F3 1 тф -0,4702 -0,2417 ТД (Вт)Tj ET 102,45 468,609 22,266 -0,398 рэ ф БТ /F2 1 тф 11.9552 0 0 11,9552 111,726 456,3666 Тм ()Tj /F3 1 тф -0,36 0 ТД (м)Tj /F2 1 тф 1,8669 0,7562 ТД (=)Tj /F4 1 тф 1.1944 0 ТД ()Tj /F3 1 тф 0,8944 0 ТД 0,1598 Тс [(Тд) 159,8 (с)] ТДж /F2 1 тф 2.1929 0 ТД 0 Тс (+)Tj /F3 1 тф 2,5125 0 ТД (дю) Tj /F2 1 тф 1,5463 0 ТД (+)Tj /F3 1 тф 1.1306 0 ТД (г)Tj /F2 1 тф 0,6097 0 ТД (\()Tj /F3 1 тф 0,4375 0 ТД 0,1597 Тс (Pv)Tj /F2 1 тф 1,4865 0 ТД 0 Тс (\))Tj /F1 1 Тф 9,9626 0 0 9,9626 210,9679 458,2336 Тм ()Tj ET 215,49 459,446 24,795 -1,196 рэ ф БТ 9,9626 0 0 9,9626 240.2461 458,2336 тм ()Tj ET 249,21 459,446 24,795 -1,196 рэ ф БТ 9,9626 0 0 9,9626 274,0075 458,2336 Тм ()Tj /F7 1 тф 7,9701 0 0 7,9701 194,4468 445,2822 Тм (=)Tj /F3 1 тф 11,9552 0 0 11,9552 202,0403 445,2823 Тм (дю) Tj /F2 1 тф 1,5463 0 ТД (+)Tj /F3 1 тф 1.1306 0 ТД 0,1597 Тс [(Pd) 159,7 (v)] ТДж /F1 1 Тф 9,9626 0 0 9,9626 202,0403 439,6035 Тм 0 Тс ()Tj ET 206,49 440,846 19,565 -1,196 рэ ф БТ 9,9626 0 0 9,9626 226,0882 439,6035 Тм ()Tj ET 235,05 440,846 19,565 -1,196 рэ ф БТ 9,9626 0 0 9,9626 254,6202 439.6035 тм ()Tj /F9 1 тф 5,9776 0 0 5,9776 220,3596 430,6371 Тм (=)Tj /F10 1 тф 5,5592 0 0 5,9776 226,7467 430,6372 Тм 0,1789 Тс [(Td)205,6(s)]TJ /F7 1 тф 7,9701 0 0 7,9701 260,7303 445,2822 Тм 0 Тс (+)Tj /F3 1 тф 11,9552 0 0 11,9552 269,9517 445,2823 Тм 0,037 Тк [(vd)37(P)]TJ /F1 1 Тф 9,9626 0 0 9,9626 269,9517 441,0979 Тм 0 Тс ()Tj ET 274,41 442,286 3,564 -1,196 рэ ф БТ 9,9626 0 0 9,9626 277,9985 441,0979 Тм ()Tj ET 287,01 442,286 3,564 -1,196 рэ ф БТ 9,9626 0 0 9,9626 290,5285 441,0979 Тм ()Tj /F2 1 тф 11.9552 0 0 11,9552 297,3031 465,4067 Тм (+)Tj /F3 1 тф 0,875 0 ТД (г)Tj /F1 1 Тф 9,9626 0 0 9,9626 317,345 482,941 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 326,4279 474,3343 Тм (\()Tj /F3 1 тф 0,4375 0 ТД (v)Тj /F8 1 тф 7,6513 0 0 7,9701 338,8752 478,673 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 344,255 474,3343 Тм (\))Tj /F7 1 тф 7,9701 0 0 7,9701 349,4854 478,673 Тм (2)Tj ET 1 я 326,37 468,21 28,437 0,398 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 337,2842 456,3666 Тм (2)Tj /F1 1 Тф 9,9626 0 0 9,9626 356,0608 482.941 тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 367,0038 465,4067 Тм (+)Tj /F3 1 тф 1.1305 0 ТД (г)Tj /F2 1 тф 0,6098 0 ТД (\()Tj /F3 1 тф 0,4375 0 ТД 0,037 Тк (gz)Tj /F2 1 тф 1.1792 0 ТД 0 Тс [(\))-3011.3(\(5\))]TJ /TT2 1 тф -28,0327 -5,9236 ТД 0,0001 Тс (Поэтому)Tj /F3 1 тф 2,5479 -3,1148 ТД 0 Тс (г)Tj /F2 1 тф 1,0798 0,2417 ТД ()Tj /F3 1 тф -0,4702 -0,2417 ТД (Вт)Tj ET 102,45 351,609 22,266 -0,398 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 111,726 339,3843 Тм ()Tj /F3 1 тф -0,36 0 ТД (м)Tj /F2 1 тф 1,8669 0.7562 ТД (=)Tj /F3 1 тф 1.1944 0 ТД 0,0371 Тс [(vd)37.1(P)]TJ /F2 1 тф 2.3518 0 ТД 0 Тс (+)Tj /F3 1 тф 1.1305 0 ТД (г)Tj /F1 1 Тф 9,9626 0 0 9,9626 195,2339 365,9587 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 204,3168 357,3509 Тм (\()Tj /F3 1 тф 0,4375 0 ТД (v)Тj /F8 1 тф 7,6513 0 0 7,9701 216,7641 361,6897 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 222,144 357,3509 Тм (\))Tj /F7 1 тф 7,9701 0 0 7,9701 227,3743 361,6897 Тм (2)Tj ET 204,33 351,609 28,437 -0,398 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 215,1731 339.3843 тм (2)Tj /F1 1 Тф 9,9626 0 0 9,9626 233,9497 365,9587 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 244,8916 348,4244 Тм (+)Tj /F3 1 тф 1.1306 0 ТД (г)Tj /F2 1 тф 0,6098 0 ТД (\()Tj /F3 1 тф 0,4375 0 ТД 0,037 Тк (gz)Tj /F2 1 тф 1.1792 0 ТД 0 Тс [(\))-3011.2(\(6\))]TJ /TT2 1 тф -17,8187 -3,8487 ТД 0,0001 Тс [(Inte)14,9(решетка)-249,9(E)0(q.)-309,9(\(6\))-249,9(между)-249,9(the)-250,1(i)-0,1(nlet)-250,1( а)-249,9(т)-0,1(он)-250,1(на выходе)]ТДж /F2 1 тф 3,018 -3,1292 ТД 0 Тс ()Tj /F3 1 тф -0,4701 -0,2417 ТД (Вт)Tj ET 102.45 256,329 14,977 -0,399 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 108,0807 244,1464 Тм ()Tj /F3 1 тф -0,3599 0 ТД (м)Tj /F2 1 тф 1,562 0,7562 ТД (=)Tj /F1 1 Тф 9,9626 0 0 9,9626 136,7322 267,2448 Тм ()Tj /F6 1 тф 7,6513 0 0 7,9701 146,6949 264,0906 Тм -0,0124 Тс [(ou)10,6(t)]TJ -0,5788 -2,4445 ТД -0,0197 Тс (в)Tj /F3 1 тф 11,9552 0 0 11,9552 161,5392 253,1866 Тм 0,037 Тк [(vd)37(P)]TJ /F2 1 тф 2.3517 0 ТД 0 Тс (+)Tj 1,3306 0,7467 ТД (\()Tj /F3 1 тф 0,4375 0 ТД (v)Тj /F8 1 тф 7,6513 0 0 7,9701 218,0095 266.4518 тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 223,3893 262,1141 Тм (\))Tj /F7 1 тф 7,9701 0 0 7,9701 228,6197 266,4518 Тм (2)Tj ET 205,53 256,329 28,437 -0,399 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 216,4184 244,1464 Тм (2)Tj /F1 1 Тф 9,9626 0 0 9,9626 235,195 271,1193 Тм ()Tj 0 -0,6 ТД ()Tj Т* ()Tj Т* ()Tj Т* ()Tj /F6 1 тф 7,6513 0 0 7,9701 238,5166 268,4333 Тм -0,0124 Тс [(ou)10,6(t)]TJ 0 -3,4755 ТД -0,0198 Тс (в)Tj /F1 1 Тф 9,9626 0 0 9,9626 203,1711 236,5489 Тм 0 Тс ()Tj ET 207,69 237,686 16,129 -1.196 ре ф БТ 9,9626 0 0 9,9626 223,7828 236,5489 Тм ()Tj ET 232,77 237,686 16,129 -1,196 рэ ф БТ 9,9626 0 0 9,9626 248,8777 236,5489 Тм ()Tj /F7 1 тф 7,9701 0 0 7,9701 216,2222 226,4308 Тм ()Tj /F6 1 тф 7,6513 0 0 7,9701 224,3586 226,4308 Тм 0,06 Тс (КЭ)Tj /F2 1 тф 11,9552 0 0 11,9552 255,6523 253,1866 Тм 0 Тс (+)Tj /F3 1 тф 1.1667 0 ТД 0,037 Тк (gz)Tj /F1 1 Тф 9,9626 0 0 9,9626 283,6971 271,1193 Тм 0 Тс ()Tj 0 -0,6 ТД ()Tj Т* ()Tj Т* ()Tj Т* ()Tj /F6 1 тф 7,6513 0 0 7,9701 287,0177 268,8607 Тм -0.0124 Тс [(ou)10,6(t)]TJ 0 -3,5291 ТД -0,0197 Тс (в)Tj /F1 1 Тф 9,9626 0 0 9,9626 268,4045 236,5489 Тм 0 Тс ()Tj ET 272,85 237,686 7,763 -1,196 рэ ф БТ 9,9626 0 0 9,9626 280,6496 236,5489 Тм ()Tj ET 289,65 237,686 7,763 -1,196 рэ ф БТ 9,9626 0 0 9,9626 297,3788 236,5489 Тм ()Tj /F7 1 тф 7,9701 0 0 7,9701 273,7415 226,4308 Тм ()Tj /F6 1 тф 7,6513 0 0 7,9701 281,878 226,4308 Тм 0,1667 Тс (PE)Tj /F2 1 тф 11,9552 0 0 11,9552 337,862 253,1866 Тм 0 Тс (\(7\))Tj /TT2 1 тф -22,2383 -5,1741 ТД -0,02 Тс [(бу)-20(т)]ТДж /F2 1 тф 1.508 0 ТД 0 Тс ()Tj /F3 1 тф 0,9375 0 ТД 0,0698 Тс (КЭ)Tj /TT2 1 тф 2.1555 0 ТД 0,0001 Тс (и)Tj /F2 1 тф 1,694 0 ТД 0 Тс ()Tj /F3 1 тф 0,9375 0 ТД 0,1597 Тс (PE)Tj /TT2 1 тф 1,9974 0 ТД 0,0001 Тс [(есть)-250,1(и)0,1(сулл)-249,9(н)0,1(е)14,9(г)0,1(приемлемо.)]TJ -9,2299 -2,25 ТД 0 Тс (Если)Tj /F2 1 тф 0,916 0 ТД ()Tj /F3 1 тф 0,9375 0 ТД 0,0698 Тс (КЭ)Tj /TT2 1 тф 2.1555 0 ТД 0 Тс (+)Tj /F2 1 тф 0,814 0 ТД ()Tj /F3 1 тф 0,9375 0 ТД 0,1597 Тс (PE)Tj /F2 1 тф 2,0668 0 ТД 0,3195 Тс (=0)Tj ET 231,93 138.489 92,11 -0,398 рэ ф 231,93 138,186 0,398 -35,136 рэ ф БТ 11,9552 0 0 11,9552 242,1898 126,8383 Тм 0 Тс ()Tj /F3 1 тф -0,4701 -0,2417 ТД (Вт)Tj ET 236,61 118,209 14,977 -0,398 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 242,1898 105,9815 Тм ()Tj /F3 1 тф -0,3599 0 ТД (м)Tj /F2 1 тф 1,562 0,7562 ТД (=)Tj /F1 1 Тф 9,9626 0 0 9,9626 270,8414 129,0799 Тм ()Tj /F6 1 тф 7,6513 0 0 7,9701 280,804 125,9258 Тм -0,0124 Тс [(ou)10,6(t)]TJ -0,5788 -2,4445 ТД -0,0197 Тс (в)Tj /F3 1 тф 11,9552 0 0 11,9552 295,6483 115.0216 Тм 0,037 Тк [(vd)37(P)]TJ ET 323,73 138,186 0,398 -35,136 рэ ф 231,93 102,969 92,11 -0,398 рэ ф БТ /TT2 1 тф 11,9552 0 0 11,9552 366,0732 115,0216 Тм 0 Тс (\(8\))Tj -24,598 -3,8881 ТД 0,0001 Тс [(Уравнение)-249,9(может)-249,9(быть)-250(используется)-249,9(для)-249,9(а)-250,1(r)0,1(е)24,9(v)15,1(используемый,)-249,9( СС-СФ)]TJ /TT9 1 тф 18.0958 0 ТД 0 Тс ()Tj /TT2 1 тф 0,556 0 ТД 0,0001 Тс [(о)25,1(в)-249,7(в)-249,9(а)-250,1(жидкость)-249,9(о)0,1(г)-249,9(а)-250,1(г)5,1(а)-0,1(с) .)]ТДЖ 0,6713 -3,7882 ТД 0 Тс (7)Тдж ET конечный поток эндообъект 39 0 объект > /ExtGState > >> эндообъект 43 0 объект > ручей БТ /TT2 1 тф 11.9552 0 0 11,9552 72 707,1831 Тм 0 г /GS1 г 0,0001 Тс 0 тв [(Если)-249,9(мы)-250,1(k)10,1(eep)-249,9(в)-249,9(ум)]TJ /F3 1 тф 2,4479 -3,0233 ТД 0 Тс ()Tj /F6 1 тф 7,6513 0 0 7,9701 108,5788 669,2463 Тм -0,0184 Тс (жидк.)Tj /F3 1 тф 11,9552 0 0 11,9552 124,1554 671,0397 Тм 0 Тс [(>>)-319.5()]ТД /F6 1 тф 7,6513 0 0 7,9701 156,6745 669,2463 Тм 0,022 Тс [(ga)39.6(s)]TJ /F4 1 тф 11,9552 0 0 11,9552 187,727 671,0397 Тм 0 Тс ()Tj /F3 1 тф 2,4694 0 ТД (v)Тj /F6 1 тф 7,6513 0 0 7,9701 224,0239 669,2463 Тм -0.0184 Тс (жидк.)Tj /F3 1 тф 11,9552 0 0 11,9552 239,5995 671,0397 Тм 0 Тс [()Tj /F3 1 тф 11,9552 0 0 11,9552 155,5536 634,8962 Тм 0,5698 Тс (С)Tj /F2 1 тф 2.318 0 ТД 0 Тс [(=)-319,4(997)]ТДж /F3 1 тф 3.1319 0 ТД 0,0185 Тс [(кг)-18,5(/)18,5(м)]ТДж /F7 1 тф 7,9701 0 0 7,9701 254,3213 639,2339 Тм 0 Тс (3) Тдж /TT2 1 тф 11,9552 0 0 11,9552 262,6899 634,8962 Тм 0,0002 Тс [(и)-249,8(воздух)-249,8(@)]ТДж /F2 1 тф 4.17 0 ТД 0 Тс (25)Тдж /F8 1 тф 7,6513 0 0 7,9701 328,9814 639,2339 Тм ()Tj /F3 1 тф 11,9552 0 0 11,9552 334.3612 634,8962 Тм 0,5698 Тс (С)Tj /F2 1 тф 2.318 0 ТД 0,3194 Тс (=1)Тj /F3 1 тф 1,7569 0 ТД 0 Тс (.)Tj /F2 1 тф 0,3194 0 ТД (18)Тж /F3 1 тф 1,375 0 ТД 0,0186 Тс [(кг)-18,4(/)18,6(м)]ТДж /F7 1 тф 7,9701 0 0 7,9701 436,9475 639,2339 Тм 0 Тс (3) Тдж /TT2 1 тф 11,9552 0 0 11,9552 72 607,9971 Тм 0,0001 Тс (Поэтому)Tj /F1 1 Тф 9,9626 0 0 9,9626 101,2653 585,2593 Тм 0 Тс ()Tj 0 -1,8 ТД ()Tj /F2 1 тф 11,9552 0 0 11,9552 116,798 576,5519 Тм ()Tj /F3 1 тф -0,4701 -0,2417 ТД (Вт)Tj ET 111,21 567,969 14,977 -0.398 ре ф БТ /F2 1 тф 11,9552 0 0 11,9552 116,798 555,6962 Тм ()Tj /F3 1 тф -0,3599 0 ТД (м)Tj /F1 1 Тф 9,9626 0 0 9,9626 127,3504 585,2593 Тм ()Tj 0 -1,8 ТД ()Tj /F6 1 тф 7,6513 0 0 7,9701 136,0677 549,2932 Тм -0,0184 Тс (жидк.)Tj /F3 1 тф 11,9552 0 0 11,9552 151,6433 564,7363 Тм 0 Тс ()Tj Т* ()Tj /F2 1 тф 11,9552 0 0 11,9552 192,3826 576,5519 Тм ()Tj /F3 1 тф -0,4702 -0,2417 ТД (Вт)Tj ET 1 я 186,81 567,57 14,977 0,398 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 192,3826 555,6962 Тм ()Tj /F3 1 тф -0,36 0 ТД (м)Tj /F1 1 Тф 9.9626 0 0 9,9626 202,934 585,2593 Тм ()Tj 0 -1,8 ТД ()Tj /F6 1 тф 7,6513 0 0 7,9701 211,6513 549,2932 Тм 0,0221 Тс [(ga)39.8(s)]TJ /TT2 1 тф 11,9552 0 0 11,9552 72 517,3948 Тм 0,0001 Тс [(F)15,3(o)0,1(r)-354,6(e)14,9(пример:)-519,4(t)-0,1(he)-354,6(w)10,3(ork)-354,6(требуется)-354,5(t )-0,1(о)-354,6(работа)-354,6(а)-354,7(насос)-354,6(и)0(с)-354,4(м)-0,1(уч)-354,6(л)0(эсс)- 354,4(т)-0,1(хат)-354,6(т)-0,1(хат)-354,7(р)0,1(требуется)-354,6(т)-0,1(о)-354,6(работа)-354,7(а)]TJ 0 -1,25 ТД 0 Тс [(компрессор)55(.)]ТДЖ /TT8 1 тф 14,3462 0 0 14,3462 72 438,2934 Тм [(Incompr)17,9(e)-0,2(ssible)-250,1(Вещество)]TJ /TT2 1 тф 11,9552 0 0 11,9552 72 399,0207 Тм 0,0001 Тс [(Это)-249,7(есть)-249,7(а)-250,1(ы)0,3(особые)-250,1(случай)-250(о)0,1(ф)-249,9(Э)-0,1(кв.)-309,9 (\(8\))-249,9(где)]TJ /F3 1 тф 15.4998 0 ТД 0 Тс (v)Тj /F2 1 тф 0,9232 0 ТД (=)Tj /F3 1 тф 1.1944 0 ТД (постоянная)Tj /F2 1 тф 4.8382 0 ТД (=)Tj /F3 1 тф 1.1944 0 ТД (v)Тj /F6 1 тф 7,6513 0 0 7,9701 361,5143 397,2274 Тм -0,0197 Тс (в)Tj /F4 1 тф 11,9552 0 0 11.9552 374,6162 399,0207 Тм 0 Тс ()Tj /F3 1 тф 1.1499 0 ТД (v)Тj /F6 1 тф 7,6513 0 0 7,9701 395,1382 397,2274 Тм -0,0124 Тс [(ou)10,5(t)]TJ /TT2 1 тф 11,9552 0 0 11,9552 409,9836 399,0207 Тм 0 Тс (.)Tj -28.2709 -2.25 ТД [(От)-250.2(Уравнение)-250(\(8\))]TJ /F2 1 тф 3,018 -2,7675 ТД ()Tj /F3 1 тф -0,4701 -0,2417 ТД (Вт)Tj ET 102,45 330,369 14,977 -0,398 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 108,0807 318,1798 Тм ()Tj /F3 1 тф -0,3599 0 ТД (м)Tj /F2 1 тф 1,562 0,7561 ТД (=)Tj /F3 1 тф 1.1945 0 ТД (v)Тj /F6 1 тф 7.6513 0 0 7,9701 143,5068 325,4257 Тм -0,0198 Тс (в)Tj /F2 1 тф 11,9552 0 0 11,9552 153,5522 327,2189 Тм 0 Тс (\()Tj /F3 1 тф 0,4375 0 ТД (П)Тj /F6 1 тф 7,6513 0 0 7,9701 167,4272 325,4257 Тм -0,0124 Тс [(ou)10,5(t)]TJ /F4 1 тф 11,9552 0 0 11,9552 185,327 327,2189 Тм 0 Тс ()Tj /F3 1 тф 1.15 0 ТД (П)Тj /F6 1 тф 7,6513 0 0 7,9701 207,7201 325,4257 Тм -0,0197 Тс (в)Tj /F2 1 тф 11,9552 0 0 11,9552 217,7654 327,2189 Тм 0 Тс [(\))-3011.2(\(9\))]TJ /TT2 1 тф -12.1927 -3.2988 ТД 0,0001 Тс [(The)-331.8(w)10.3(орк)-331,6(срок)-331,8(р)0,1(представляет)-331,5(т)-0,1(он)-331,8(минимум)-331,8(ж)10,3(орк)-331,7(требуется)-331,6( т)-0,1(о)-331,6(насос)-331,6(а)-331,9(жидкость)-331,7(ж)0,1(ром)]TJ /F3 1 тф 32.0668 0 ТД 0 Тс (П)Тj /F6 1 тф 7,6513 0 0 7,9701 464,009 285,9875 Тм -0,0198 Тс (в)Tj /TT2 1 тф 11,9552 0 0 11,9552 478,0204 287,7808 Тм 0,0002 Тс (к)Tj /F3 1 тф 1,1098 0 ТД 0 Тс (П)Тj /F6 1 тф 7,6513 0 0 7,9701 499,9332 285,9875 Тм -0,0124 Тс [(ou)10,6(t)]TJ /TT2 1 тф 11,9552 0 0 11,9552 518,7438 287,7808 Тм 0.0001 ТК (с)Tj -37,3683 -1,25 ТД [(ne)14,9(неразборчиво)]TJ /F2 1 тф 4.2349 0 ТД 0 Тс ()Tj /F3 1 тф 0,9375 0 ТД 0,0698 Тс (КЭ)Tj /TT2 1 тф 2.1556 0 ТД 0,0001 Тс (и)Tj /F2 1 тф 1,694 0 ТД 0 Тс ()Tj /F3 1 тф 0,9375 0 ТД 0,1597 Тс (PE)Tj /TT2 1 тф 1,7474 0 ТД 0 Тс (.)Tj /TT8 1 тф 14,3462 0 0 14,3462 72 224,6197 Тм [(Incompr)17,9(e)-0,2(ssible)-250,1(вещество)-250,1(and)]TJ /F3 1 тф 13.1778 0 ТД (г)Tj /F2 1 тф 1,0799 0,2417 ТД ()Tj /F3 1 тф -0,4701 -0,2417 ТД (Вт)Tj /F2 1 тф 1,5722 0 ТД 0,3194 Тс (=0)Tj /TT2 1 тф 11.9552 0 0 11,9552 72 185,3469 Тм 0 Тс [(От)-250,2(уравнение)-310(\(6\))]TJ /F3 1 тф 2,4479 -3,6123 ТД 0,037 Тк [(vd)37(P)]TJ /F2 1 тф 2.3518 0 ТД 0 Тс (+)Tj /F3 1 тф 1.1306 0 ТД (г)Tj /F1 1 Тф 9,9626 0 0 9,9626 152,4772 159,6961 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 161,5602 151,0885 Тм (\()Tj /F3 1 тф 0,4375 0 ТД (v)Тj /F8 1 тф 7,6513 0 0 7,9701 174,0075 155,4271 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 179,3873 151,0885 Тм (\))Tj /F7 1 тф 7,9701 0 0 7,9701 184,6177 155,4271 Тм (2)Tj ET 161,61 145,329 28.437 -0,398 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 172,4164 133,1218 Тм (2)Tj /F1 1 Тф 9,9626 0 0 9,9626 191,194 159,6961 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 202,136 142,1618 Тм (+)Tj /F3 1 тф 1.1306 0 ТД (г)Tj /F2 1 тф 0,6097 0 ТД (\()Tj /F3 1 тф 0,4375 0 ТД 0,037 Тк (gz)Tj /F2 1 тф 1.1792 0 ТД 0 Тс [(\))-319,4(=)-319,5(0)-3011,2(\(10\))]TJ /TT2 1 тф -14,2423 -3,5386 ТД 0,0001 Тс (Поэтому)Tj /F3 1 тф 2,4479 -3,4078 ТД 0 Тс (г)Tj /F1 1 Тф 9,9626 0 0 9,9626 110,8453 76,6506 Тм ()Tj /F3 1 тф 11,9552 0 0 11.9552 119,9283 68,0428 Тм (П)Тj ET 119,97 62,288 10,554 -0,398 рэ ф БТ 11,9552 0 0 11,9552 121,5482 50,0762 Тм ()Tj /F1 1 Тф 9,9626 0 0 9,9626 131,6782 76,6506 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 142,6202 59,1163 Тм (+)Tj /F3 1 тф 1.1306 0 ТД (г)Tj /F1 1 Тф 9,9626 0 0 9,9626 165,7166 76,6506 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 174,7995 68,0428 Тм (\()Tj /F3 1 тф 0,4375 0 ТД (v)Тj /F8 1 тф 7,6513 0 0 7,9701 187,2468 72,3816 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 192,6266 68,0428 Тм (\))Tj /F7 1 тф 7.9701 0 0 7,9701 197,857 72,3816 Тм (2)Tj ET 174,81 62,288 28,437 -0,398 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 185,6558 50,0762 Тм (2)Tj /F1 1 Тф 9,9626 0 0 9,9626 204,4324 76,6506 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 215,3753 59,1163 Тм (+)Tj /F3 1 тф 1.1305 0 ТД (г)Tj /F2 1 тф 0,6098 0 ТД (\()Tj /F3 1 тф 0,4375 0 ТД 0,037 Тк (gz)Tj /F2 1 тф 1.1792 0 ТД 0,3195 Тс (\)=0)Tj /TT2 1 тф 3,9735 -3,0001 ТД 0 Тс (8)Тдж ET конечный поток эндообъект 44 0 объект > /ExtGState > >> эндообъект 46 0 объект > ручей БТ /F3 1 тф 11.9552 0 0 11,9552 101,2653 700,7363 Тм 0 г /GS1 г 0 Тс 0 тв (г)Tj /F1 1 Тф 9,9626 0 0 9,9626 110,8453 718,2705 Тм ()Tj /F3 1 тф 11,9552 0 0 11,9552 119,9283 709,6638 Тм (П)Тj ET 119,97 703,929 10,554 -0,399 рэ ф БТ 11,9552 0 0 11,9552 121,5482 691,6962 Тм ()Tj /F2 1 тф 1,1028 0,7562 ТД (+)Tj 1,2306 0,7467 ТД (\()Tj /F3 1 тф 0,4375 0 ТД (v)Тj /F8 1 тф 7,6513 0 0 7,9701 161,8919 714,0015 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 167,2717 709,6638 Тм (\))Tj /F7 1 тф 7,9701 0 0 7,9701 172,5021 714,0015 Тм (2)Tj ET 149.49 703,929 28,437 -0,399 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 160,3009 691,6962 Тм (2)Tj 1,8262 0,7562 ТД (+)Tj /F3 1 тф 1.1306 0 ТД 0,037 Тк (gz)Tj /F1 1 Тф 9,9626 0 0 9,9626 209,7464 718,2705 Тм 0 Тс ()Tj /F2 1 тф 11,9552 0 0 11,9552 221,4525 700,7363 Тм [(=)-319,4(0)-3011,2(\(11\))]TJ /TT2 1 тф -12,5011 -3,8193 ТД 0,0001 Тс [(Inte) 14,9 (решетка) -249,9 (g) 0,1 (i) 25 (v) 15 (es)] TJ /F3 1 тф 2,5479 -3,1462 ТД 0 Тс (П)Тj ET 102,45 611,769 10,554 -0,398 рэ ф БТ 11,9552 0 0 11,9552 104,0807 599,4949 Тм ()Tj /F2 1 тф 1.1028 0,7562 ТД (+)Tj 1,2306 0,7467 ТД (\()Tj /F3 1 тф 0,4375 0 ТД (v)Тj /F8 1 тф 7,6513 0 0 7,9701 144,4244 621,8002 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 149,8042 617,4625 Тм (\))Tj /F7 1 тф 7,9701 0 0 7,9701 155,0346 621,8002 Тм (2)Tj ET 131,97 611,769 28,437 -0,398 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 142,8334 599,4949 Тм (2)Tj 1,8262 0,7562 ТД (+)Tj /F3 1 тф 1.1305 0 ТД 0,0371 Тс (gz)Tj /F2 1 тф 1,4987 0 ТД 0 Тс (=)Tj /F3 1 тф 1.1944 0 ТД (постоянная)Tj /F2 1 тф 7.53 0 ТД (\(12\))Tj /TT2 1 тф -19.1047 -3,7698 ТД 0,0001 Тс [(Уравнение)-309,9(\(12\))-310(is)-309,7(Бернулли)55,1(s)-309,8(уравнение)-310(для)-309,9(без трения)]TJ /TT9 1 тф 21.6131 0 ТД 0 Тс ()Tj /TT2 1 тф 0,556 0 ТД 0,0001 Тс [(о)25,1(ш)-309,7(с)-310(константа)-310,2(д)0,1(энт)65,1(.)-490,1(Т)-0,1(он)-310,1(константа)-310,1(я )-0,1(с)] ТДж -22,1691 -1,25 ТД [(Бернулли) 55,1 (с) — 348,6 (постоянная) — 373,4 (ш) 0,3 (ч) — 348,6 (остатки) — 348,5 (с) — 0,1 (постоянная) — 348,8 (вдоль) — 348,6 (а) — 348,8 (с) 0,3 (тракт) — 348,8 (фор) — 348,6 (стационарно) 65,1 (,) — 373.4(без трения,)-373,3(инком-)]TJ Т* 0 Тс (нажимаемый)Tj /TT9 1 тф 3.8049 0 ТД ()Tj /TT2 1 тф 0,556 0 ТД -0,025 Тс [(вл)40,2(.)]ТД /TT8 1 тф 14,3462 0 0 14,3462 72 484,9076 Тм 0 Тс [(Изотермический)-250,2(Идеальный)-250,2(Газ)-250(Компрессор)17,9(д)-0,1(Секция/Расширение)]ТДж /TT2 1 тф 11,9552 0 0 11,9552 72 445,6349 Тм 0,0001 Тс [(Это)-249,7(есть)-249,7(а)-250,1(ы)0,3(особые)-250,1(случай)-250(о)0,1(ф)-249,9(Э)-0,1(кв.)-309,9 (\(8\))-249,9(для)-249,9(ан)-249,9(идеальный)-250,1(г)5,1(а)-0,1(с)-249,7(ш)0,3(здесь)]TJ /F3 1 тф 21.8818 0 ТД 0,1597 Тс (Pv)Tj /F2 1 тф 1,806 0 ТД 0 Тс (=)Tj /F3 1 тф 1.1944 0 ТД 0,0042 Тс (РТ)Tj -22,4342 -3,3039 ТД 0,1597 Тс (Pv)Tj /F2 1 тф 1,8059 0 ТД 0 Тс (=)Tj /F3 1 тф 1.1944 0 ТД (постоянная)Tj /F2 1 тф 4.8383 0 ТД 0,3194 Тс (=\()Tj /F3 1 тф 1,6319 0 ТД 0,1597 Тс (Pv)Tj /F2 1 тф 1,4865 0 ТД 0 Тс (\))Tj /F6 1 тф 7,6513 0 0 7,9701 237,4884 404,3427 Тм -0,0197 Тс (в)Tj /F2 1 тф 11,9552 0 0 11,9552 251,3534 406,136 Тм 0,3194 Тс (=\()Tj /F3 1 тф 1,6319 0 ТД 0,1597 Тс (Pv)Tj /F2 1 тф 1,4865 0 ТД 0 Тс (\))Tj /F6 1 тф 7.6513 0 0 7,9701 293,865 404,3427 Тм -0,0124 Тс [(ou)10,5(t)]TJ /F2 1 тф 11,9552 0 0 11,9552 108,0807 369,2941 Тм 0 Тс ()Tj /F3 1 тф -0,4701 -0,2417 ТД (Вт)Tj ET 102,45 360,609 14,977 -0,398 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 108,0807 348,4373 Тм ()Tj /F3 1 тф -0,3599 0 ТД (м)Tj /F2 1 тф 1,562 0,7562 ТД (=)Tj /F1 1 Тф 9,9626 0 0 9,9626 136,7322 371,5357 Тм ()Tj /F6 1 тф 7,6513 0 0 7,9701 146,6949 368,3815 Тм -0,0124 Тс [(ou)10,6(t)]TJ -0,5788 -2,4445 ТД -0,0197 Тс (в)Tj /F3 1 тф 11,9552 0 0 11,9552 161.5392 357,4774 тм 0,037 Тк [(vd)37(P)]TJ /F2 1 тф 2.4157 0 ТД 0 Тс (=)Tj /F1 1 Тф 9,9626 0 0 9,9626 204,6984 371,5357 Тм ()Tj /F6 1 тф 7,6513 0 0 7,9701 214,661 368,3815 Тм -0,0124 Тс [(ou)10,5(t)]TJ -0,5786 -2,4445 ТД -0,0198 Тс (в)Tj /F2 1 тф 11,9552 0 0 11,9552 229,5053 357,4774 Тм 0 Тс (\()Tj /F3 1 тф 0,4375 0 ТД 0,1597 Тс (Pv)Tj /F2 1 тф 1,4865 0 ТД 0 Тс (\))Tj /F6 1 тф 7,6513 0 0 7,9701 257,7375 355,6841 Тм -0,0197 Тс (в)Tj /F3 1 тф 11,9552 0 0 11,9552 268,9793 366,405 Тм 0 Тс (дП)Tj ET 269.01 360,609 17,843 -0,398 рэ ф БТ 11,9552 0 0 11,9552 272,6237 348,4373 Тм (П)Тj /TT2 1 тф -16,7813 -2,8192 ТД 0,0001 Тс (Поэтому)Tj ET 205,41 289,089 135,197 -0,398 рэ ф 205,41 288,581 0,399 -38,051 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 215,6603 277,3489 Тм 0 Тс ()Tj /F3 1 тф -0,4701 -0,2417 ТД (Вт)Tj ET 210,09 268,689 14,977 -0,398 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 215,6603 256,4922 Тм ()Tj /F3 1 тф -0,3599 0 ТД (м)Tj /F2 1 тф 1,562 0,7562 ТД (=)Tj /F3 1 тф 1.1945 0 ТД (П)Тj /F6 1 тф 7,6513 0 0 7.9701 252,9564 263,739 Тм -0,0197 Тс (в)Tj /F3 1 тф 11,9552 0 0 11,9552 263,0017 265,5323 Тм 0 Тс (v)Тj /F6 1 тф 7,6513 0 0 7,9701 269,7763 263,739 Тм -0,0197 Тс (в)Tj /F2 1 тф 11,9552 0 0 11,9552 282,1141 265,5323 Тм 0 Тс (ln)Tj /F1 1 Тф 9,9626 0 0 9,9626 295,6135 283,0665 Тм ()Tj /F3 1 тф 11,9552 0 0 11,9552 304,6954 274,4598 Тм (П)Тj /F6 1 тф 7,6513 0 0 7,9701 313,34 272,6665 Тм -0,0124 Тс [(ou)10,5(t)]TJ ET 304,65 268,689 23,489 -0,398 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 307,0954 256,4922 Тм 0 Тс (П)Тj /F6 1 тф 7.6513 0 0 7,9701 315,74 254,6989 Тм -0,0198 Тс (в)Tj /F1 1 Тф 9,9626 0 0 9,9626 329,3799 283,0665 Тм 0 Тс ()Tj ET 340,29 288,581 0,398 -38,051 рэ ф 205,41 250,569 135,197 -0,398 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 382,6321 265,5323 Тм (\(13\))Tj /TT8 1 тф 14,3462 0 0 14,3462 72 208,5718 Тм [(Исентр)17,9(опик)-250,1(Идеал)-250,2(Г)-0,2(ас)-250(С)0,2(омпр)17,9(е)-0,2(ссион/Расширение)]TJ /TT2 1 тф 11,9552 0 0 11,9552 72 169,2991 Тм 0,0001 Тс [(Изэнтропия)-308,1(подразумевается)-307,8(а)-308,1(r)0,1(е)24,9(v)15.1(эмульсионный)-308,1(а)-0,1(й)-307,9(адиабатический)-308,1(процесс)-307,7(ш)0,3(здесь)]TJ /F3 1 тф 24.251 0 ТД 0 Тс (с)Tj /F2 1 тф 0,9743 0 ТД (=)Tj /F3 1 тф 1,318 0 ТД (постоянная)Tj /TT2 1 тф 4.5187 0 ТД 0,0001 Тс [(.)-484(W)39,9(ит)-308(ан)-307,9(идеальный)-308,1(г)5,1(ас,)]TJ /F3 1 тф -31,0621 -1,25 ТД 0,1597 Тс (Pv)Tj /F6 1 тф 7,6513 0 0 7,9701 89,7713 158,6938 Тм 0 Тс (к)Tj /F2 1 тф 11,9552 0 0 11,9552 99,3136 154,3551 Тм (=)Tj /F3 1 тф 1.1944 0 ТД (постоянная)Tj /TT2 1 тф 4.7687 0 ТД 0,0001 Тс (и)Tj /F2 1 тф 1.694 0 ТД 0 Тс (\()Tj /F3 1 тф 0,4375 0 ТД 0,1597 Тс (Pv)Tj /F6 1 тф 7,6513 0 0 7,9701 213,858 158,6938 Тм 0 Тс (к)Tj /F2 1 тф 11,9552 0 0 11,9552 219,5806 154,3551 Тм (\))Tj /F6 1 тф 7,6513 0 0 7,9701 224,811 152,5619 Тм -0,0197 Тс (в)Tj /F2 1 тф 11,9552 0 0 11,9552 238,676 154,3551 Тм 0,3195 Тс (=\()Tj /F3 1 тф 1,632 0 ТД 0,1597 Тс (Pv)Tj /F6 1 тф 7,6513 0 0 7,9701 275,9582 158,6938 Тм 0 Тс (к)Tj /F2 1 тф 11,9552 0 0 11,9552 281,6807 154,3551 Тм (\))Tj /F6 1 тф 7,6513 0 0 7,9701 286,9111 152,5619 Тм -0.0124 Тс [(ou)10,5(t)]TJ /TT2 1 тф 11,9552 0 0 11,9552 301,7554 154,3551 Тм 0 Тс (.)Tj -19,2181 -2,25 ТД 0,0001 Тс [(Уравнение)-249,9(\(8\))-249,9(становится)]TJ /F2 1 тф 3,018 -3,1741 ТД 0 Тс ()Tj /F3 1 тф -0,4701 -0,2417 ТД (Вт)Tj ET 102,45 80,889 14,977 -0,398 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 108,0807 68,6536 Тм ()Tj /F3 1 тф -0,3599 0 ТД (м)Tj /F2 1 тф 1,562 0,7562 ТД (=)Tj /F1 1 Тф 9,9626 0 0 9,9626 136,7322 91,7519 Тм ()Tj /F6 1 тф 7,6513 0 0 7,9701 146,6949 88,5967 Тм -0,0124 Тс [(ou)10,6(t)]TJ -0.5788 -2,4444 ТД -0,0197 Тс (в)Tj /F3 1 тф 11,9552 0 0 11,9552 161,5392 77,6937 Тм 0,037 Тк [(vd)37(P)]TJ /F2 1 тф 2.4157 0 ТД 0 Тс (=)Tj /F1 1 Тф 9,9626 0 0 9,9626 204,6984 91,7519 Тм ()Tj /F6 1 тф 7,6513 0 0 7,9701 214,661 88,5967 Тм -0,0124 Тс [(ou)10,5(t)]TJ -0,5786 -2,4444 ТД -0,0198 Тс (в)Tj /F1 1 Тф 9,9626 0 0 9,9626 231,7968 95,2279 Тм 0 Тс ()Tj /F2 1 тф 11,9552 0 0 11,9552 238,8045 86,6201 Тм (\()Tj /F3 1 тф 0,4375 0 ТД 0,1597 Тс (Pv)Tj /F6 1 тф 7,6513 0 0 7,9701 261,8062 90,9589 Тм 0 Тс (к)Tj /F2 1 тф 11.9552 0 0 11,9552 267,5287 86,6201 Тм (\))Tj /F6 1 тф 7,6513 0 0 7,9701 272,7592 84,8269 Тм -0,0197 Тс (в)Tj ET 238,77 80,889 44,001 -0,398 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 255,5278 68,6536 Тм 0 Тс (П)Тj /F1 1 Тф 9,9626 0 0 9,9626 284,001 95,2279 Тм ()Tj /F7 1 тф 7,9701 0 0 7,9701 289,8122 93,339 Тм (1)Tj /F6 1 тф 7,6513 0 0 7,9701 294,6939 93,339 Тм -0,0171 Тс (/к)Tj /F3 1 тф 11,9552 0 0 11,9552 310,5793 77,6937 Тм 0 Тс (дП)Tj /TT2 1 тф -0,633 -4,554 ТД (9)Тдж ET конечный поток эндообъект 47 0 объект > /ExtGState > >> эндообъект 49 0 объект > ручей 0 г /GS1 г 100.17 719,169 345,83 -0,398 рэ ф 100,17 718,733 0,398 -41,843 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 110,3442 706,6451 Тм 0 Тс 0 тв ()Tj /F3 1 тф -0,4702 -0,2417 ТД (Вт)Tj ET 104,73 698,049 14,977 -0,398 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 110,3442 685,7893 Тм ()Tj /F3 1 тф -0,3599 0 ТД (м)Tj /F2 1 тф 1,562 0,7562 ТД (=)Tj /F1 1 Тф 9,9626 0 0 9,9626 138,9948 712,3636 Тм ()Tj /F3 1 тф 11,9552 0 0 11,9552 159,8416 703,7559 Тм (к)Tj ET 148,05 698,049 30,967 -0,398 рэ ф БТ 11,9552 0 0 11,9552 148,0777 685.7893 тм (к)Tj /F4 1 тф 0,8777 0 ТД ()Tj /F2 1 тф 1.15 0 ТД (1)Tj /F1 1 Тф 9,9626 0 0 9,9626 180,2401 712,3636 Тм ()Tj /F2 1 тф 11,9552 0 0 11,9552 190,4189 694,8295 Тм (\()Tj /F3 1 тф 0,4375 0 ТД 0,1597 Тс (Pv)Tj /F2 1 тф 1,4865 0 ТД 0 Тс (\))Tj /F6 1 тф 7,6513 0 0 7,9701 218,6511 693,0361 Тм -0,0197 Тс (в)Tj /F1 1 Тф 9,9626 0 0 9,9626 230,9878 715,3525 Тм 0 Тс ()Tj 0 -1,8 ТД ()Tj 0,6667 1,5 ТД ()Tj /F3 1 тф 11,9552 0 0 11,9552 246,7128 703,7559 Тм (П)Тj /F6 1 тф 7,6513 0 0 7,9701 255,3574 701,9626 Тм -0.0124 Тс [(ou)10,6(t)]TJ ET 246,69 698,049 23,489 -0,398 рэ ф БТ /F3 1 тф 11,9552 0 0 11,9552 249,1118 685,7893 Тм 0 Тс (П)Тj /F6 1 тф 7,6513 0 0 7,9701 257,7564 683,9961 Тм -0,0197 Тс (в)Tj /F1 1 Тф 9,9626 0 0 9,9626 271,3973 712,3636 Тм 0 Тс ()Tj /F7 1 тф 7,9701 0 0 7,9701 279,2847 709,6069 Тм (\()Tj /F6 1 тф 7,6513 0 0 7,9701 283,0815 709,6069 Тм (к)Tj /F8 1 тф 0,6828 0 ТД ()Tj /F7 1 тф 7,9701 0 0 7,9701 295,9004 709,6069 Тм (1\))Tj /F6 1 тф 7,6513 0 0 7,9701 304,5788 709,6069 Тм -0,0171 Тс (/к)Tj /F4 1 тф 11.9552 0 0 11,9552 318,2386 694,8295 Тм 0 Тс ()Tj /F2 1 тф 1.15 0 ТД (1)Tj /F1 1 Тф 9,9626 0 0 9,9626 338,7119 715,3525 Тм ()Tj 0 -1,8 ТД ()Tj /F2 1 тф 11,9552 0 0 11,9552 349,1726 694,8295 Тм (=)Tj /F3 1 тф 1.1944 0 ТД (с)Tj /F6 1 тф 7,6513 0 0 7,9701 369,59 693,0361 Тм (р)Tj /F2 1 тф 11,9552 0 0 11,9552 375,207 694,8295 Тм (\()Tj /F3 1 тф 0,4375 0 ТД (Т)Тj /F6 1 тф 7,6513 0 0 7,9701 388,0488 693,0361 Тм -0,0124 Тс [(ou)10,6(t)]TJ /F4 1 тф 11,9552 0 0 11,9552 405,9487 694,8295 Тм 0 Тс ()Tj /F3 1 тф 1.15 0 ТД (Т)Тj /F6 1 тф 7,6513 0 0 7,9701 427,3076 693,0361 Тм -0,0197 Тс (в)Tj /F2 1 тф 11,9552 0 0 11,9552 437,3539 694,8295 Тм 0 Тс (\))Tj ET 445,53 718,733 0,399 -41,843 рэ ф 100,17 676,929 345,83 -0,399 рэ ф БТ 11,9552 0 0 11,9552 487,9492 694,8295 Тм (\(14\))Tj /TT2 1 тф -34,7924 -4,3945 ТД 0,0001 Тс [(The)-268,6(r)0,1(right)-268,7(side)-268,6(of)-268,4(Eq.)-365,6(\(14\))-268,4(is)-268,2(основано)-268,4 (о)0,1(н)-268,5(т)-0,1(он)-268,6(ф)10,1(акт)-268,6(та)]ТДж /F2 1 тф 20.3893 0 ТД 0 Тс ()Tj /F3 1 тф 0.9375 0 ТД 0,0698 Тс (КЭ)Tj /F2 1 тф 2.1769 0 ТД 0,2713 Тс (+)Tj /F3 1 тф 2,0838 0 ТД 0,1597 Тс (PE)Tj /F2 1 тф 2.1063 0 ТД 0,3589 Тк (=0)Tj /TT2 1 тф 2,065 0 ТД 0,0001 Тс (и)Tj /F3 1 тф 1,7125 0 ТД 0 Тс (дч)Tj /F2 1 тф 1,6362 0 ТД (=)Tj /F3 1 тф 1,2339 0 ТД (дю) Tj /F2 1 тф 1,5621 0 ТД (+)Tj /F3 1 тф 1.1463 0 ТД [(дП)-159,8(об)] ТДж /TT2 1 тф -37,05 -1,4757 ТД 0,0001 Тс (и)Tj /F3 1 тф 1,694 0 ТД 0 Тс (дю) Tj /F2 1 тф 1.6102 0 ТД 0,3194 Тс (=0)Tj /TT2 1 тф 1,7569 0 ТД 0,0002 Тс [(.)-309,8(W)0(высокий)-249.8(отводит)-249,6(т)0(о)] ТДж /F3 1 тф 6.809 0 ТД 0 Тс (ч)Tj /F2 1 тф 0,987 0 ТД (=)Tj /F1 1 Тф 9,9626 0 0 9,9626 239,988 638,7079 Тм ()Tj /F3 1 тф 11,9552 0 0 11,9552 250,4488 624,6496 Тм 0,0371 Тс [(vd)37.1(P)]TJ /TT2 1 тф 2.0962 0 ТД 0 Тс (.)Tj -17,0228 -2,4829 ТД 0,0001 Тс [(Примечание:)-310,1(для)-249,9(в)-250,1(с)0,3(аме)-250,1(вход)-250(состояние)-250,1(и)-249,9(давление)-250,1(отношение)] ТиДжей /F4 1 тф 2,4479 -4,1332 ТД 0 Тс ()Tj /F1 1 Тф 9,9626 0 0 9,9626 118,8324 566,0762 Тм ()Tj 0 -1,8 ТД ()Tj /F2 1 тф 11.9552 0 0 11,9552 134,3661 557,3699 Тм ()Tj /F3 1 тф -0,4702 -0,2417 ТД (Вт)Tj ET 128,73 548,769 14,977 -0,398 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 134,3661 536,5131 Тм ()Tj /F3 1 тф -0,36 0 ТД (м)Tj /F1 1 Тф 9,9626 0 0 9,9626 144,9176 566,0762 Тм ()Tj 0 -1,8 ТД ()Tj /F6 1 тф 7,6513 0 0 7,9701 153,6349 530,1111 Тм 0,0203 Тс [(ре)34,2(в.)36,8(,)36,9(и)40(с)29,4(о)32,7(т)42,3(ч)38(д)34,2(г)-0,8(м)44(а) 37,9 (л)] ТДж /F3 1 тф 11,9552 0 0 11,9552 226,7148 545,5532 Тм 0 Тс ()Tj Т* ()Tj /F2 1 тф 11,9552 0 0 11.9552 256,7611 557,3699 Тм ()Tj /F3 1 тф -0,4702 -0,2417 ТД (Вт)Tj ET 251,13 548,769 14,977 -0,398 рэ ф БТ /F2 1 тф 11,9552 0 0 11,9552 256,7611 536,5131 Тм ()Tj /F3 1 тф -0,36 0 ТД (м)Tj /F1 1 Тф 9,9626 0 0 9,9626 267,3126 566,0762 Тм ()Tj 0 -1,8 ТД ()Tj /F6 1 тф 7,6513 0 0 7,9701 276,0299 530,1111 Тм -0,0186 Тс [(r)-39,8(e)-4,7(v)-38(.)-2(,adiab)-6,2(atic)]TJ /TT2 1 тф 11,9552 0 0 11,9552 300,0229 23,2499 Тм 0 Тс (10)Тдж ET конечный поток эндообъект 50 0 объект > /ExtGState > >> эндообъект 15 0 объект > ручей
Задача о вертикальном шприце.Шприц, содержащий идеальный газ и…
Контекст 1
… исследования на университетском уровне, два из которых имеют непосредственное отношение к нашему исследованию, были проведены Розье и 4,5 Вьено во Франции и Мельцером в Соединенные Штаты. В нашем исследовании приняли участие более 1000 студентов четырех университетов. Большинство из них были зачислены на лекционные и лабораторные секции физики, основанной на алгебре, или на курс теплофизики для второкурсников в Университете Вашингтона. Другими участниками были студенты, изучающие физику в Университете Цинциннати, Университете Мэриленда и Сиракузском университете.Студенты вводной химии в Сиракузах также приняли участие. Во всех этих курсах обсуждались закон идеального газа, первый закон термодинамики и связь между внутренней энергией и температурой идеального газа. Наше решение сосредоточиться на законе идеального газа было мотивировано предварительными результатами более раннего исследования понимания студентами первого закона термодинамики. Мы обнаружили, что многие студенты неуместно ссылались на закон идеального газа, пытаясь ответить на вопросы, требующие применения первого закона.Студенты выявили не только недостаточное понимание первого закона, особенно роли работы, но и продемонстрировали глубокое непонимание уравнения состояния идеального газа. Эти открытия побудили нас предпринять параллельное исследование, связанное с законом идеального газа. Настоящее исследование началось с индивидуальных интервью, проведенных с 45 студентами UW, которые были зачислены или закончили вторую четверть основанного на алгебре курса N = 16 или курса теплофизики для второкурсников ͑ N = 29 ͒ .8 Многие посвятили год изучению химии. Почти все выступили на уровне или выше среднего в своих классах. Большинство интервью проходило в течение нескольких недель до и после выпускных экзаменов студентов. Адиабатические и изобарические процессы, лежащие в основе вопросов, были вдохновлены работами Розье и Вьенно. В интервью студентам показывали пластиковый велосипедный насос, наполненный воздухом. Их попросили предсказать, что произойдет с температурой воздуха, если отверстие насоса закрыть и быстро втолкнуть поршень.В этом примерно адиабатическом процессе температура будет повышаться — предсказание, которое большинство студентов сделало, но не смогло оправдать. Почти никто не упоминал первый закон термодинамики и понятие работы. Они опирались только на закон идеального газа, который не годится для предсказания повышения температуры. Студенты также часто приводили неверные микроскопические аргументы. В некоторых интервью студентам давали второе задание, чтобы проверить их понимание давления. Их спросили, можно ли уменьшить объем воздуха в насосе, не изменяя давления, и объяснили свои рассуждения.Многие из студентов утверждали, что любое уменьшение объема приведет к увеличению давления, не признавая, что уменьшение объема может быть достигнуто за счет снижения температуры. Характер и распространенность ошибок, допущенных студентами, побудили нас глубже изучить их понимание макроскопических переменных давления, температуры и объема. Для этой цели мы разработали несколько типов письменных задач. Все они включали качественные вопросы, для ответа на которые требовались объяснения рассуждений.Наш анализ результатов позволил разработать учебную программу для решения конкретных проблем. Наша группа оценивает обучение учащихся с помощью предварительных и посттестов. Обычно предварительные тесты проводятся после стандартного рассмотрения темы, но до обучения, основанного на исследованиях. Когда это возможно, пост-тесты проводятся на экзаменах или 9 на неоцененных викторинах. Последующие тесты требуют применения понятий в ситуациях, несколько отличных от тех, которые встречаются на предварительных тестах или во время обучения.Запоминание недостаточно помогает. Результаты можно сравнить с результатами соответствующих предварительных испытаний. ͑ Сходство предтеста и посттеста практически не влияет на успеваемость учащихся. В качестве альтернативы можно провести сравнение с пост-тестами в классах, в которых проводилось только стандартное обучение. Наш опыт работы с другими темами показал, что результаты наших оценок аналогичны для аналогичных классов с аналогичными инструкциями. Поэтому мы объединили результаты из нескольких разделов одного и того же курса, округлили количество студентов и присвоили процент правильных и неправильных ответов с точностью до 5%.В качестве ориентира для разработки и оценки учебной программы этот диапазон воспроизводимости успеваемости учащихся оказался достаточным. Ниже мы обсудим три примера задач, предназначенных для проверки понимания учащимися закона идеального газа с макроскопической точки зрения. Для каждой задачи мы даем правильный ответ и отмечаем преобладание правильных ответов. Более подробный анализ следует в гл. IV. Учащиеся считают идеальным стеклянный шприц, содержащий газ, с которым им предлагается обращаться (см. рис.1 ͒ . Шприц запечатан без трения поршнем массы М и первоначально находится в тепловом равновесии с баней со льдом и водой. Затем шприц помещают в стакан с кипящей водой, где он достигает теплового равновесия. Студентов просят сравнить давления и объемы газа в начальном и конечном состояниях равновесия. Чтобы ответить правильно, они должны признать, что сила, действующая на поршень со стороны атмосферы, и сила тяжести одинаковы в начальном и конечном состояниях.Следовательно, чтобы поршень находился в механическом равновесии как до, так и после расширения, сила, действующая на заключенный в нем газ, а значит, и давление, должны быть одинаковыми. Из закона идеального газа повышение температуры должно быть связано с увеличением объема. Результаты представлены в таблице I. На вводных курсах физики ͑ N Ͼ 1000 ͒ ответы не сильно зависели от типа курса (основанного на алгебре или математическом анализе), времени ͑ до или после обучения ͒ или условий ͑ лекция или лаборатория ͒ .Около 30% студентов поняли, что начальное и конечное давление равны. ͑ Правильно рассуждали около 10%. ͒ При вводе в химию после изучения закона идеального газа только около 15% сказали, что давления равны. По курсу теплофизики правильный ответ дали около 45%. На всех курсах самым частым неверным ответом было то, что конечное давление будет больше, чем начальное давление. На рис. 2 показаны три одинаковых цилиндра A, B и C, которые содержат неуказанные количества различных идеальных газов.Они уплотнены одинаковыми поршнями без трения. Цилиндры А и В имеют одинаковую температуру, но содержат разные газы. Их поршни находятся на разной высоте. Баллоны B и C содержат один и тот же тип газа, но имеют разную температуру. Их поршни находятся на одной высоте. Учащимся предлагается сравнить давления газов в цилиндрах А и В, а также в В и С. Для правильного ответа необходимо отметить, что атмосферное давление и вес поршня одинаковы для каждого цилиндра.Поэтому у всех должно быть одинаковое давление. Результаты суммированы в Таблице II. Для случая, когда поршни находятся на разной высоте (цилиндры A и B), около 30% студентов, изучающих физику для вводного курса (N ϳ 250), правильно заявили, что давления одинаковы. Из остальных студентов примерно такой же процент сказал, что либо у А, либо у В более высокое давление. Для газов с разными температурами (цилиндры B и C) около 40% признали, что давления равны. Почти все остальные сказали, что давление в C ͑ выше, температура ͒ больше.Правильное сравнение давления во всех трех цилиндрах сделали только около 15% первокурсников. Около 40 % студентов-теплофизиков ͑ N ϳ 65 ͒ правильно оценили все три давления. Ошибки были те же, что и на вводных курсах. Несколько небольших масс постепенно добавляют к верхней части поршня без трения, который герметизирует изолированный цилиндр, содержащий идеальный газ (см. рис. 3). Учащихся спрашивают, как ͑ изменяются ли вообще ͒ давление, температура и объем.Им необходимо признать, что положительная работа совершается над газом, когда поршень движется вниз. ͑ Студенты не должны были оправдываться тем, что поршень упадет. ͒ Поскольку цилиндр изолирован, теплопередача незначительна или отсутствует. По первому закону термодинамики внутренняя энергия газа внутри цилиндра должна возрастать. Внутренняя энергия пропорциональна температуре, которая, следовательно, также будет увеличиваться. В конечном положении поршень будет ниже, чем первоначально, что указывает на уменьшение объема газа.Поскольку система поршня и грузов имеет больший вес, чем раньше, и снова находится в покое, давление газа должно было увеличиться. Эта задача была задана примерно 180 студентам курса алгебры. Около 70% студентов поняли, что объем уменьшится. Только около 10% дали правильный ответ относительно температуры. Многочисленные неправильные ответы студентов указывают на то, что после стандартного обучения у многих студентов, изучающих вводную физику и химию, а также более специализированные курсы по теплофизике, возникают серьезные трудности в интерпретации и применении закона идеального газа.В последующем анализе эти трудности организованы в категории, которые не исключают друг друга. Концептуальные, логические и математические трудности часто переплетаются и не могут быть полностью разделены. Ни в одной из задач, рассмотренных в гл. III — закон идеального газа, достаточный, чтобы предсказать, изменится ли какая-либо из переменных и насколько сильно. Делая прогнозы, многие студенты сосредоточились на единственном соотношении между двумя величинами, которое справедливо только в том случае, если другие постоянны.Неверно предполагая, что P всегда κ 1 / V . Следующая цитата взята из интервью со студентом курса теплофизики, который пытался применить …
Тест №1: 25.01.02
Если g(N,s) = N!/[(0,5N +s)!(0,5N-s)!], то что g(N,s) представляют?
G(N,s) дает кратность (т.е. количество различных способами), в которых N элементов с двумя состояниями (например, бинарные спины, монеты и т. д.) могут иметь спин превышение 2с.
Если P(s) указывает на функцию распределения вероятностей,
тогда мы можем написать
Мы не можем использовать g(N,s) потому что он не нормализован. То есть скажем ∑g(N,s) ≠ 1
Тест №2: 27.01.03
Что вы можете сказать о g(U1,U2) для двух систем в тепловом равновесие?
Максимальное значение ценность.
Тест №3: 31.01.03
Почему изолированная система из 4-х гармонических осцилляторов не работает? у вас когда-нибудь была отрицательная (абсолютная) температура?
Количество квантов состояния, доступные системе, не ограничены, поэтому при добавлении энергии энтропия продолжает увеличиваться.
Тест №4: 03.02.03
Если P(e s ) — вероятность нахождения системы в
конкретного состояния s, запишите выражение для U (т.е.
U = e с P(e с )
Тест №5: 11.02.03
О чем говорит следующее уравнение? (т.е. Что именно
?)
<с>
= 1/(exp( ч вес/т)-1)
Это дает среднее число фотонов в моде частоты w в системе при температуре t.
Тест №6: 14.02.03
Какая связь между излучением в полости и излучение черного тела?
При любой заданной температуре излучение, выходящее из небольшого отверстия в резонаторе, будет иметь такое же спектр как энергия, излучаемая черным телом. При этом суммарный поток энергии от отверстия и тела (на единицу площади) будет отличаться только простым геометрическим фактором.
Тест №7: 17.02.03
Что такое фонон?
Фонон – это квант энергия, связанная с упругими волнами в твердых материалах.
Тест №8: 21.02.03
Что движет потоком частиц из одной системы в Другая?
Градиент в хим. потенциал. (или, что то же самое, возможность увеличить общую энтропию).
Тест №9: 28.02.03
Учитывая, что Z = S exp [(Нм — е с(Н) )/т], напишите выражение для среднего квадрата энергии.
< e 2 > = S e с(Н) 2 exp [(Нм — e с(Н) )/t] / Z
Тест №10: 03.03.03
Каковы возможные значения ферми-дирака функция распределения f(e)?
1 ф(е) 0
Тест №11: 07.03.03
Что определяет классический предел идеального газа?
Концентрация большая меньше квантовой концентрации.В качестве альтернативы, средняя занятость каждой орбитали намного меньше, чем один.
Тест №12: 28.03.03
Каково определение энергии Ферми?
Энергия высшей занятой орбитали ферми-газа в его основном состоянии.
Тест №13: 04.04.03
Что такое конденсат Бозе-Эйнштейна?
Те атомы в бозоне газа, которые находятся в основном состоянии системы.
Тест №14: 11.04.03
При изотермическом расширении газ совершает работу окружение, но энергия газа остается неизменной (U = 3/2 NkbT и T фиксированный). Как это может быть?
Энергия поступает как тепло из окрестностей.
Тест №15: 14.04.03
Что такое тепловая машина?
Тепловая машина – это устройство преобразующий теплоту в работу (т.е. передача энергии за счет теплового градиента и передача энергии механическим путем).
Что такое холодильник?
Холодильник – это устройство который использует работу для перемещения тепла от холодного резервуара к горячему резервуару.
Тест №16: 21.04.03
При каких экспериментальных условиях Гиббс свободен энергия соответствующее количество?
Когда система поддерживается при постоянном давлении.
Тест №17: 25.04.03
Что такое экстенсивное свойство системы?
Свойство, значение которого изменения, если система дублируется, обширны.
Тест №18: 30.04.03
О чем говорит нам следующее выражение? P(v) = 4p (M/2pt) 3/2 v 2 exp(-mv 2 /2t)
Это скорость Максвелла распределения и дает вероятность найти молекулу (массы m)
идеального газа (при температура t), движущаяся со скоростью в интервале между v и v + dv.
Тест №19: 02.05.03
Транспортные процессы характеризуются соотношением Поток = коэффициент х движущая сила.
Выберите транспортный процесс и приведите конкретные примеры эти 2 термина.
Вот примеры:
Тепловой поток: энергия, теплопроводность, температурный градиент
Распространение: частицы, коэффициент диффузии, градиент концентрации
Импульсный транспорт: импульс, вязкость, скорость сдвига
Электропроводность: заряд, проводимость, электрический потенциал
lectnotes3-09All101812 — Cálculo II — 2
- e1 = ∫ 2 1 диск + ∫ 2 1 дв .(1.1) Тепло, добавленное в систему, ∫ dq, и работа, проделанная над системой, ∫ дв зависит по конкретному пути интеграции. Первый закон (1.1) применим к любому пути. это удобно записать это для бесконечно малого изменения как де знак равно dq + dw . (1.2) Второй закон термодинамики вводит энтропию, которая удовлетворяет следующее неравенство: s2 − s1 ≥ ∫ 2 1 дисквалификация Т . (1.3) 2 Б. Гроссман Конспект лекций № 3 Для обратимого процесса справедлива часть равенства (1.3), так что (dq)об = Tds .(1.4) Можно также утверждать, что если работа, совершаемая над системой, совершается посредством обратимого процесс, затем (dw)rev = −pdv . (1,5) Теперь рассмотрим переход между теми же состояниями 1 и 2, что и в (1.1), но это время обратимыми процессами. Тогда из (1.4) и (1.5) е2 - е1 = ∫ 2 1 TDS- ∫ 2 1 пдв. (1.6) Сравнивая (1.6) с (1.1), мы должны иметь ∫ 2 1 диск + ∫ 2 1 дв = ∫ 2 1 TDS- ∫ 2 1 пдв , где dq и dw соответствуют присоединенной теплоте и работе, выполненной через произвольный процесс, обратимый или необратимый.Отсюда не следует, что dq = Tds или dw = −pdv, но это означает, что dq + dw должно равняться Tds − pdv. Это следствие эл. будучи переменной состояния. Следовательно, в общем случае мы можем утверждать, что de = Tds− pdv . (1.7) Это соотношение справедливо как для обратимых, так и для необратимых процессов. Это какой- раз называется фундаментальным уравнением или комбинированным первым и вторым законом. В этих примечания, мы будем называть его первым законом термодинамики. Другую форму первого закона можно получить, введя энтальпию: h ≡ e+ pv, откуда получаем dh = Tds+ vdp .(1.8) Вводя свободную энергию Гиббса на единицу массы, g ≡ h− Ts , (1.9) и свободная энергия Гельмгольца на единицу массы f ≡ e− Ts , (1.10) приводит к dg = −sdT + vdp (1.11) и df = −sdT − pdv . (1.12) Понятия газовой динамики 3 1.2 Производные отношения Уравнения (1.7), (1.8), (1.11) и (1.12) могут быть использованы для получения соотношения Максвелла. ции. Например, если мы рассмотрим e = e(s, v), то de = (∂e/∂s)vds + (∂e/∂v)sdv и, сравнивая с (1.7), получаем( ∂е ∂s ) в = Т , ( ∂е ∂v ) с = -р . (1.13) Аналогично, рассматривая h = h(s, p), получаем из (1.8)( ∂ч ∂s ) п = Т , ( ∂ч ∂p ) с = в . (1.14) Использование g = g(T, p) и (1.11) дает( ∂г ∂Т ) п = −s , ( ∂г ∂p ) Т = v , (1.15) и f = f(T, v) и (1.12) приводит к ( ∂f ∂Т ) в = −s , ( ∂f ∂v ) Т = -р . (1.16) Другой набор полезных отношений, называемый отношениями взаимности, может быть разработан. начиная с e = e(v, T ) и s = s(v, T ) и (1.7) где( ∂е ∂v ) Т дв + ( ∂е ∂Т ) в дТ = Т [( ∂s ∂v ) Т дв + ( ∂s ∂Т ) в дТ ] − пдв. Поскольку dv и dT должны быть независимы друг от друга, ( ∂е ∂v ) Т = Т ( ∂s ∂v ) Т − р ,( ∂е ∂Т ) в = Т ( ∂s ∂Т ) в .(1.17) Теперь мы можем исключить энтропию путем перекрестного дифференцирования приведенных выше выражений. Дифференцируя первое из (1.17) по T и второе по v дает ∂2e ∂v∂T = Т ∂2с ∂v∂T + ( ∂s ∂v ) Т − ( ∂p ∂Т ) в , ∂2e ∂T∂v = Т ∂2с ∂T∂v . 4 Б. Гроссман Конспект лекций № 3 Предполагая непрерывность вторых производных, мы можем поменять местами сложение и вычитание дает ( ∂s ∂v ) Т знак равно ( ∂p ∂Т ) в . Подставляя теперь этот результат в первое из (1.17), получаем ( ∂е ∂v ) Т = −p+ Т ( ∂p ∂Т ) в .(1.18) Это называется отношениями взаимности, и мы будем использовать их в нашем обсуждении. уравнение состояния. Другая форма отношения взаимности, связанная с энтальпией, может быть получается из h = h(p, T ) и s = s(p, T ) и (1.7), что приводит к ( ∂ч ∂p ) Т = Т ( ∂s ∂p ) Т + в ,( ∂ч ∂Т ) п = Т ( ∂s ∂Т ) п . (1.19) Опять же, устранение s путем перекрестного дифференцирования дает отношение взаимности в терминах энтальпии как: ( ∂ч ∂p ) Т = v - Т ( ∂v ∂Т ) п . (1.20) 1.3 Тепловое уравнение состояния В широком диапазоне условий поведение большинства газов описывается как совершенный или идеальный газ.Из физики газов анализ, основанный на кинетических теория газов и статистическая механика (см. Винченти и Крюгер (1965), §II.3 и §IV.9), можно использовать для построения уравнения состояния в виде pV = NkT, (1.21) где N — число молекул, а постоянная Больцмана k равна 1,38054× 10−23 Дж/◦K/молекула. Сделанные допущения включают понятие слабой взаимодействующий газ, где межмолекулярными силами пренебрегают. Мы можем написать результат в пересчете на количество молей газа N по соотношению N = N N̂, где Число Авогадро N̂ = 6.02252 × 1023 молекул/моль. Мы получаем pV = N R̂T , (1.22) Понятия газодинамики 5 где универсальная газовая постоянная R̂ = N̂k = 8314,3 Дж/(кг-моль ◦K). Этот результат согласуется с ранними экспериментами Бойля, Шарля и Гей-Люссака. Мы можем записать уравнение состояния в терминах массы M, введя молекулярная масса (масса на моль) M̂ = M/N и газовая постоянная R = R̂/M̂ так что pV = МРТ. (1.23) Наконец, разделив на M, мы получим известный закон идеального газа рв = РТ, (1.24) или р = ρRT.(1,25) Этот результат называется тепловым уравнением состояния, и газы, подчиняющиеся этому закону, называются называется термически совершенным. (Термин идеальный газ иногда используется для обозначения газа который термически совершенен и имеет постоянную удельную теплоемкость. Поэтому, чтобы избежать амби- Правильно, мы будем использовать термин термически совершенный, когда будем иметь в виду газ, где p = ρRT.) Условия, при которых газ не может быть термически совершенным, включают очень высокие давления вблизи тройной точки газа. Здесь используется уравнение состояния Ван-дер-Ваала, см., Липманн и Рошко (1957), стр.9, где р = ρРТ ( 1 1 − βρ − αρ РТ ) , (1.26) β = RTc/8pc, α = 27βRTc/8, где Tc и pc — критическая температура. и критическое давление соответственно. Значения pc и tc для некоторых распространенных газообразных виды представлены в таблице 1.1. Видно, что эффект реального газа важен при очень высоких давлениях и низких температурах. Например, двухатомный азот. N2 имеет критические свойства pc = 33,5 атм и Tc = 126 К. При умеренном температуре 315 К уравнение состояния Ван-дер-Ваала будет отклоняться от термически совершенного уравнения состояния на 1% при давлении выше 67 атм.При более низкой температуре 210 К изменение на 1% происходит при давлениях выше 4,9 атм. Таблица 1.1 Критические давления и температуры O2 N2 NO h3 He A CO2 пк (атм) 49,7 33,5 65,0 12,8 2,26 48,0 73,0 Tc (◦K) 154,3 126,0 179,1 33,2 5,2 151,1 304,2 На рис. 1.1 мы представляем график зависимости z = p/ρRT от log10 p для азота N2 при температуры 200, 300 и 400 градусов Кельвина. Пунктирная кривая представляет Случай T = 200K, а штрихпунктирная кривая соответствует случаю T = 400K. Таким образом, мы видим, что -0,5 0 0,5 1 1,5 2 2.5 журнал p 0,8 0,85 0,9 0,95 1 1,05 1.1 1,15 Z 6 Б. Гроссман Конспект лекций № 3 Рисунок 1.1. Термическое несовершенство для N2 при T = 200K, T = 300K, T = 400K, Z = p/ρRT. основные тепловые уравнения несовершенства состояния возникают при сочетании очень высоких давление и низкие температуры для этих газов. С другой стороны, при очень высоких температурах и низких давлениях газ может диссоциировать и ионизироваться и больше не будет вести себя как термически совершенный газ. Тем не мение, даже если реакции будут иметь место, отдельные виды будут вести себя как термически совершенные газа, но смеси не будет.Например, рассматривая чистый N2 при температурах выше 4500K начинают присутствовать значительные количества диссоциированного азота. То закон идеального газа по-прежнему будет выполняться для каждого вида, pN2 = ρN2RN2T и pN = ρNRNT. Для смеси N и N2 имеем p = pN + pN2 = ρR̃T, где ρ — масса плотность смеси, а R̃ — «постоянная» газовая смесь. Но, как будет показано далее в этой главе R̃ будет зависеть от массовых долей видов, которые, в свою очередь, зависят от давления и температуры и, следовательно, не будут постоянными.

 (Изопроцессы) Вариант 1
(Изопроцессы) Вариант 1 (Изопроцессы) Вариант 2
(Изопроцессы) Вариант 2 (Изопроцессы) Вариант 1
(Изопроцессы) Вариант 1 (Изопроцессы) Вариант 2
(Изопроцессы) Вариант 2 (Изопроцессы) Вариант 1
(Изопроцессы) Вариант 1 (Изопроцессы) Вариант 2
(Изопроцессы) Вариант 2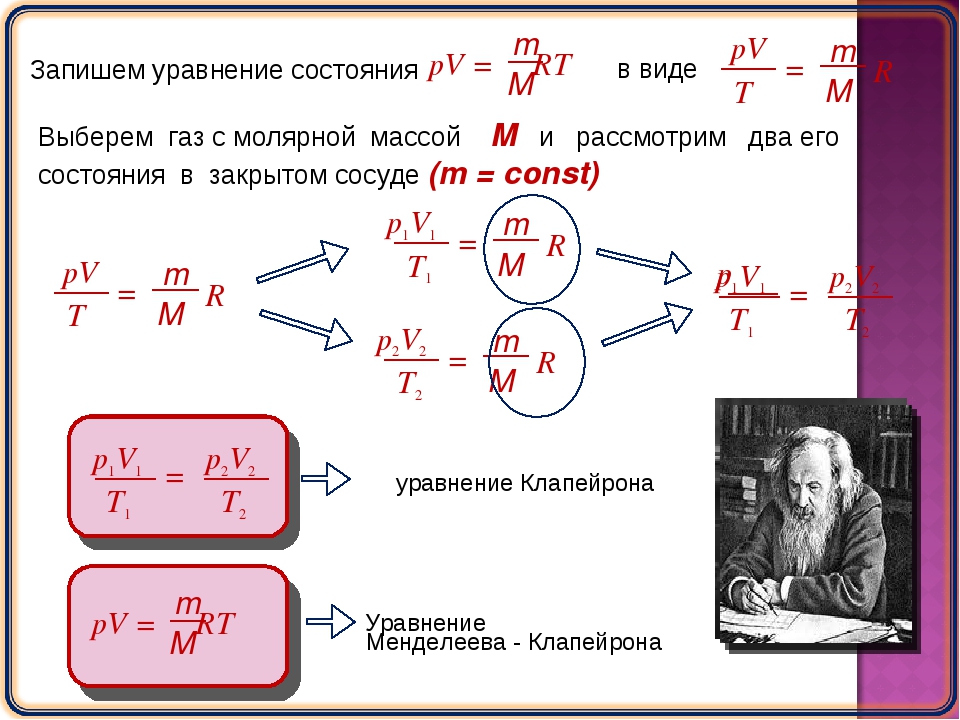 (Изопроцессы) Вариант 1
(Изопроцессы) Вариант 1 (Изопроцессы) Вариант 2
(Изопроцессы) Вариант 2 (Изопроцессы) Вариант 1
(Изопроцессы) Вариант 1 (Изопроцессы) Вариант 2
(Изопроцессы) Вариант 2
 кипения воды.
кипения воды.