|
Языковые цели
|
Учащиеся будут: оперировать терминами данного раздела; комментировать вывод формул тригонометрических функций суммы и разности аргументов аргументировать выбор формул при преобразовании тригонометрических выражений. Предметная лексика и терминология синус/косинус/тангенс/котангенс суммы аргументов; синус/косинус/тангенс/котангенс разности аргументов; Серия полезных фраз для диалога/письма применим к выражению формулу тригонометрических функций суммы/разности аргументов; |
Начало урока 10 минут
|
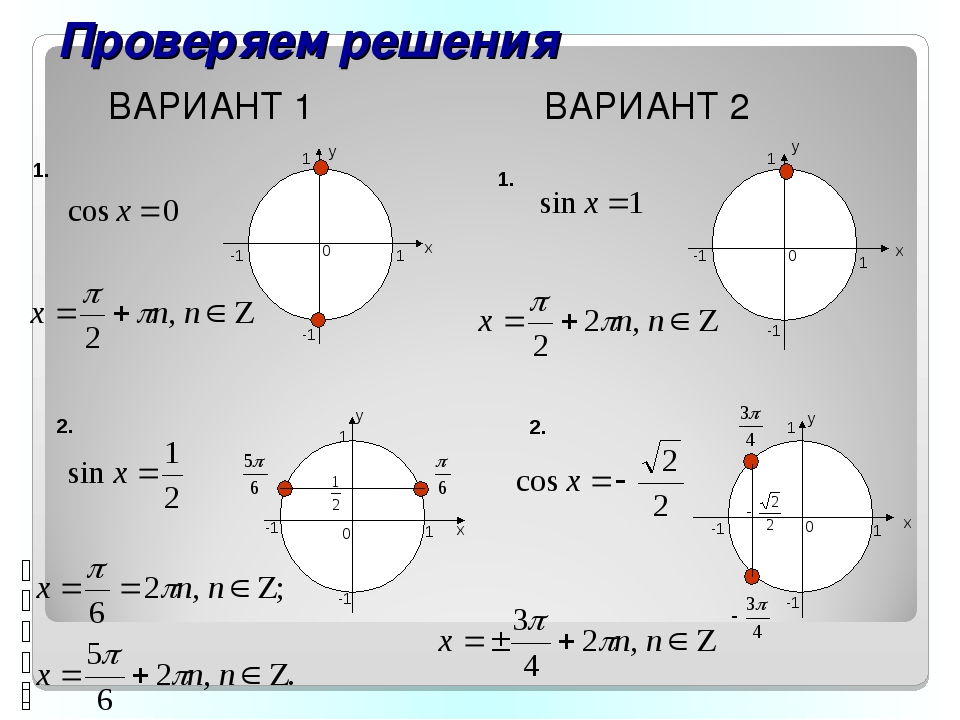
Актуализация знаний 1. 1).Упростить: а)cos (3π/2 + α) = ; б) tg(3600 – α) = ; в) sin (π – α) = ; г) sin( π/2 + α) = ; д) tg ( 2π + α) = ; е) cos ( π/2 – α) = ; ж) ctg ( π/2 + α ) = ; з) tg ( π + α) = . 2). Вычислите: а) cos 30o = б) – 2 tg2 450 = в) а sin 1800 = г) 2sin 300 = д) sin 1350= е) sin 750 = ж) sin 150 = з) cos 1050 = . Вызов. Определение проблемы Чтобы вычислить sin 750, надо применить формулу синус суммы, а sin 150 формулу синус разности. |
|
Середина урока 10 минут
15 минут
10 минут
10 минут
15 минут
|
На данном этапе можно
организовать просмотр ролика https://www.
Самостоятельное обучение. Вывод формулы косинуса разности аргументов самостоятельно, представив разность аргументов α – β, как сумму α и (-β). Объединение учащихся в группы, учитывая индивидуальные способности учащихся и уровень математической подготовки. Используяформулы приведения и основные тригонометрические тождества, ученики самостоятельно должны вывести формулы синуса/ тангенса/ котангенса суммы и разности аргументов. Каждая группа демонстрирует классу результаты своей работы.
Для быстрого запоминания формул можно
предложить учащимся устные упражнения. Или предложить каждому ученику
записывать свой ответ на ламинированных листах формата А4. Упростить: Вычислить:
Парная работа. Закрепление. Вычислите: 1) Ответ: -1 2) Ответ: 1 Проверку можно провести по готовым ответам. Если необходимо, то разобрать решение у доски.
Разберите с учащимися следующие задания на применение формул суммы и разности аргументов. Используя формулы сложения, вычислите: ; ; . Дополнительно: можно предложить учащимся решить геометрические задачи. При решении данных задач нельзя использовать калькулятор. 1) Найдите х. 2) На рисунке показаны три точки L (-2, 1), M (0, 2) и N (3, -2), соединенные в треугольник. Углы α и β и точка P показаны на рисунке. (i) Покажите, что . И запишите значение cosα. (ii) Найти значения sin β и cos β. (iii) Покажите, что . (iv) Покажите, что . |
Мордкович А. Г. Алгебра и начала математического анализа. 10 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобраз-х учреждений (профильный уровень) / А. Г. Мордкович, П. В. Семенов. — 6-е изд., стер. — М. : Мнемозина, 2009. — 424 с. : ил.
Макарычев Ю. Н. Алгебра. 9 класс : учеб.для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М. : Мнемозина, 2008. — 447 с. : ил. |
Дифференциация может быть выражена в подборе заданий, в ожидаемом результате от конкретного ученика
|
Используйте данный раздел для записи методов,
которые Вы будете использовать для оценивания того, чему учащиеся научились
во время урока. \(\blacktriangleright\) Формулы произведения функций: \[\begin{array}{|c|} \hline \\ \sin\alpha\sin\beta=\dfrac12\bigg(\cos{(\alpha-\beta)}-\cos{(\alpha+\beta)}\bigg)\\\\ \cos\alpha\cos\beta=\dfrac12\bigg(\cos{(\alpha-\beta)}+\cos{(\alpha+\beta)}\bigg)\\\\ \sin\alpha\cos\beta=\dfrac12\bigg(\sin{(\alpha-\beta)}+\sin{(\alpha+\beta)}\bigg)\\\\ \hline \end{array}\] \(\blacktriangleright\) Формулы суммы/разности функций: \[\begin{array}{|lc|cr|} \hline &&&\\ \sin\alpha+\sin\beta=2\sin{\dfrac{\alpha+\beta}2}\cos{\dfrac{\alpha-\beta}2} &&& \sin\alpha-\sin\beta=2\sin{\dfrac{\alpha-\beta}2}\cos{\dfrac{\alpha+\beta}2}\\&&&\\ \cos\alpha+\cos\beta=2\cos{\dfrac{\alpha+\beta}2}\cos{\dfrac{\alpha-\beta}2} &&& \cos\alpha -\cos\beta=-2\sin{\dfrac{\alpha-\beta}2}\sin{\dfrac{\alpha+\beta}2}\\&&&\\ \mathrm{tg}\, \alpha \pm \mathrm{tg}\, \beta=\dfrac{\sin{(\alpha\pm\beta)}}{\cos\alpha\cos\beta} &&& \mathrm{ctg}\, \alpha\pm \mathrm{ctg}\, \beta= — \dfrac{\sin{(\alpha\pm \beta)}}{\sin\alpha\sin\beta}\\&&&\\ \hline \end{array}\] \(\blacktriangleright\) Выражение синуса и косинуса через тангенс половинного угла: \[\begin{array}{|l|r|} \hline &\\ \sin{2\alpha}=\dfrac{2\mathrm{tg}\, \alpha}{1+\mathrm{tg}^2\, \alpha} & \cos{2\alpha}=\dfrac{1-\mathrm{tg}^2\, \alpha}{1+\mathrm{tg}^2\, \alpha}\\&\\ \cos\alpha\ne 0 & \sin\alpha\ne 0\\ \hline \end{array}\] \(\blacktriangleright\) Формула вспомогательного аргумента: \[\begin{array}{|c|} \hline \text{Частный случай}\\ \hline \\ \sin\alpha\pm \cos\alpha=\sqrt2\cdot \sin{\left(\alpha\pm \dfrac{\pi}4\right)}\\\\ \sqrt3\sin\alpha\pm \cos\alpha=2\sin{\left(\alpha\pm \dfrac{\pi}6\right)}\\\\ \sin\alpha\pm \sqrt3\cos\alpha=2\sin{\left(x\pm \dfrac{\pi}3\right)}\\\\ \hline \text{Общий случай}\\ \hline\\ a\sin\alpha\pm b\cos\alpha=\sqrt{a^2+b^2}\cdot \sin{(\alpha\pm \phi)}, \ \ \cos\phi=\dfrac a{\sqrt{a^2+b^2}}, \ \sin\phi=\dfrac b{\sqrt{a^2+b^2}}\\\\ \hline \end{array}\] Зная идею вывода формул, вы можете запомнить лишь несколько из них.
3) \(\sin(\alpha-\beta)=\sin(\alpha+(-\beta))=\sin\alpha\cos(-\beta)+\sin(-\beta)\cos\alpha=\sin\alpha\cos\beta-\sin\beta\cos\alpha\)
4) \(\mathrm{tg}\,(\alpha\pm\beta)=\dfrac{\sin (\alpha\pm\beta)}{\cos (\alpha\pm\beta)}=\dfrac{\sin\alpha\cos\beta\pm\sin\beta\cos\alpha}{\cos\alpha\cos\beta\mp\sin\alpha\sin\beta}=\)
разделим числитель и знаменатель дроби на \(\cos\alpha\cos\beta\ne
0\)
\(=\dfrac{\mathrm{tg}\,\alpha\pm\mathrm{tg}\,\beta}{1\mp\mathrm{tg}\,\alpha\cdot \mathrm{tg}\,\beta}\)
Таким образом, данная формула верна только при \(\cos\alpha\cos\beta\ne 0\).
5) Аналогично, только делением на \(\sin\alpha\sin\beta\ne 0\), выводится формула котангенса суммы/разности двух углов.
Заметим, что в данных формулах степень синуса/косинуса равна \(2\) в левой части, а в правой части степень косинуса равна \(1\).
\(\blacktriangleright\) Вывод формул произведения функций:
1) Сложим формулы косинуса суммы и косинуса разности двух углов:
\(\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\)
\(\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\)
Получим: \(\cos(\alpha+\beta)+\cos(\alpha-\beta)=2\cos\alpha\cos\beta \Rightarrow \cos\alpha\cos\beta=\dfrac12\Big(\cos(\alpha-\beta)+\cos(\alpha+\beta)\Big)\)
2) Если вычесть из формулы косинуса суммы косинус разности, то получим:
\(\sin\alpha\sin\beta=\dfrac12\Big(\cos(\alpha-\beta)-\cos(\alpha+\beta)\Big)\)
3) Сложим формулы синуса суммы и синуса разности двух углов:
\(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\sin\beta\cos\alpha\)
\(\sin(\alpha-\beta)=\sin\alpha\cos\beta-\sin\beta\cos\alpha\)
Получим: \(\sin\alpha\cos\beta=\dfrac12\Big(\sin(\alpha-\beta)+\sin(\alpha+\beta)\Big)\)
\(\blacktriangleright\) Вывод формул суммы/разности функций:
Обозначим \(\alpha+\beta=x, \alpha-\beta=y\).
1) \(2\cos{\dfrac{x+y}2}\cos{\dfrac{x-y}2}=\cos x+\cos y\)
Получили формулу суммы косинусов.
2) \(2\sin {\dfrac{x+y}2}\sin {\dfrac{x-y}2}=\cos y-\cos x\)
Получили формулу разности косинусов.
3) \(2\sin {\dfrac{x+y}2}\cos {\dfrac{x-y}2}=\sin y+\sin x\)
Получили формулу суммы синусов.
4) Формулу разности синусов можно вывести из формулы суммы синусов:
\(\sin x-\sin y=\sin x+\sin(-y)=2\sin {\dfrac{x-y}2}\cos {\dfrac{x+y}2}\)
5) \(\mathrm{tg}\,\alpha\pm\mathrm{tg}\,\beta=\dfrac{\sin\alpha}{\cos\alpha}\pm\dfrac{\sin\beta}{\cos\beta}=\dfrac{\sin\alpha\cos\beta\pm\sin\beta\cos\alpha}{\cos\alpha\cos\beta}=\dfrac{\sin(\alpha\pm\beta)}{\cos\alpha\cos\beta}\)
Аналогично выводится формула суммы котангенсов.
\(\blacktriangleright\) Вывод формул выражения синуса и косинуса через тангенс половинного угла:
1) \(\sin2\alpha=\dfrac{\sin2\alpha}1=\dfrac{2\sin\alpha\cos\alpha}{\sin^2\alpha+\cos^2\alpha}=\)
(разделим числитель и знаменатель дроби на \(\cos^2\alpha\ne 0\) (при \(\cos\alpha=0\) и \(\sin2\alpha=0\)):)
\(=\dfrac{2\mathrm{tg}\,\alpha}{1+\mathrm{tg}^2\,\alpha}\)
2) Так же, только делением на \(\sin^2\alpha\), выводится формула для косинуса.
\(\blacktriangleright\) Рассмотрим некоторые частные случаи формул вспомогательного угла:
\(a) \ \sin x\pm\cos x=\sqrt2\,\left(\dfrac1{\sqrt2}\sin x\pm\dfrac1{\sqrt2}\cos x\right)=\sqrt2\, \sin \left(x\pm\dfrac{\pi}4\right)\)
\(b) \ \sqrt3\sin x\pm\cos x=2\left(\dfrac{\sqrt3}2\sin x\pm \dfrac12\cos x\right)=2\, \sin \left(x\pm\dfrac{\pi}6\right)\)
\(c) \ \sin x\pm\sqrt3\cos x=2\left(\dfrac12\sin x\pm\dfrac{\sqrt3}2\cos x\right)=2\,\sin\left(x\pm\dfrac{\pi}3\right)\)
Урок алгебры в 9-м классе по теме «Тригонометрические формулы и приемы их запоминания»Цель урока: познакомить учащихся с мнемоническими правилами для
запоминания формул приведения и значений тригонометрических функций некоторых
углов; способствовать развитию логического мышления и устной математической речи
при поиске решения поставленной проблемы; Замечание: при проведении этого урока использовалась интерактивная доска
и пульты дистанционного тестирования Activote, но провести его можно без этого
оборудования, при помощи прилагаемой презентации. Ход урока I. Организационный момент/ – Здравствуйте, ребята! Тригонометрия – один из интереснейших разделов
математики, но почему-то большинство учащихся считают его самым трудным.
Объяснить это, скорее всего можно тем, что в этом разделе формул больше, чем в
любом другом – формулы приведения, формулы сложения, формулы двойного и
половинного аргументов, формулы суммы и разности тригонометрических функций,
формулы преобразования произведения тригонометрических функций в сумму. И самая
первая группа формул, с которой вы познакомились в курсе геометрии 8 класса –
основные тригонометрические тождества. Без знаний этих формул ни одно
тригонометрическое выражение не преобразуешь. Сегодня на уроке, я хочу
познакомить вас с некоторыми приемами запоминания тригонометрических формул. II. Входное (интерактивное) тестирование/ – Перед вами на парте лежат пульты дистанционного тестирования. Я предлагаю вам выполнить тест на знание тригонометрических формул и значений тригонометрических функций некоторых углов. Чтобы ответить на вопрос вам необходимо нажать на пульте кнопку с выбранным вами вариантом ответа.
III. Изучение нового материала (знакомство с приемами запоминания тригонометрических формул). 1. Табличные значения тригонометрических функций. Вы уже знаете, что тригонометрическую функцию любого угла можно выразить через тригонометрическую функцию угла, не превышающего 90º. Поэтому необходимо знать табличные значения углов первой четверти. Для запоминания значений синуса и косинуса для углов в 30º, 45º и 60º я предлагаю своим ученикам притчу. – Пошли три дамы гулять.
Чтобы указать значения тангенса и котангенса тех же углов достаточно вспомнить ОТТ, т.е , а котангенс взаимно обратная функция для тангенса. 2. Формулы приведения Тригонометрические функции углов видамогут быть выражены через функции угла α с помощью формул, которые называют формулами приведения. Но запоминать эти формулы не обязательно. Для преобразования таких выражений достаточно знать знаки тригонометрических функций по четвертям и еще одну притчу. – Жил забывчивый математик, и каждый раз преобразовывая тригонометрические
функции углов вида
,
он спрашивал у своей лошади, жующей за окном сено, надо менять функцию на
конфункцию или нет.
3. Формулы сложения. Формулы сложения – это та, группа формул которую нужно знать наизусть. Но для их запоминания можно тоже воспользоваться ассоциативным приемом. У косинуса функции одноименные, а у синуса разноименные. Не все в нашей жизни бывает “гладко” за белой полосой идет черная, и наоборот. Так и у наших функций, если функции идут одноименные, то знаки не совпадают, а если разноименные, то совпадают. cos (α β ) = cos
α cos β
+ sin α sin β; Для получения формулы тангенса суммы и тангенса разности достаточно применить ОТТ и разделить числитель и знаменатель полученной дроби на cos α cos β, где cos α ≠ 0 и cos β ≠ 0. Например, сos 97º cos 67º + sin 97º sin 67º = ños (97º– 67º) = ños 30º = ; sin 25º сos 20º + cos 25º sin 20º = sin (25º + 20º) = sin 45º = .4. Формулы двойного угла Чтобы получить тригонометрические формулы двойного аргумента достаточно в формулах сложения β заменить на α. Например, cos 2α = cos (α + α ) = cos α cos α – sin α sin α = cos²α – sin²α; sin 2α = sin (α + α ) = sin α cos α + sin α cos α = 2sin α cos α tg2α = tg (α + α ) = . Поэтому, 2 sin 65º cos 65º = sin (2∙ 65º) = sin130º = sin (180º – 50º) = sin 50º Формулы суммы и разности тригонометрических функций Если сложить косинус разности с косинусом суммы двух углов,то мы получим формулу суммы косинусов: cos (α – β ) = cos
α cos β
+ sin α sin β; Обозначим α – β ηа х, а α
+ β ηа у, тогда α =
(х
+ у) и β =(х
– у). cos х + cos у = 2 cos(х+у) cos(х-у). Если обе части равенства (*) разделить на два, то мы получим формулу, позволяющую представлять произведение косинусов двух углов в виде суммы: cos α cos β =(cos (α – β ) + cos (α + β )). ΐналогичным способом мы получим: cos х – cos у = -2 sin(х + у) sin(х – у) и sin α sin β = (cos (α – β ) – cos (α + β )). Если сложить синус разности с синусом суммы двух углов, то мы получим формулу суммы синусов: sin (α – β ) = sin
α cos β
– cos α sin β; Из чего мы получаем: sin α cos β =(sin (α – β ) + sin (α + β )) θ sin х + sin у = 2 sin(х + у) cos (х – у). Например, cos 80º–
cos 40º = -2 sin(80º
+ 40º) sin(80º
– 40º) = -2 sin60º sin 20º = -√3sin
20º. sin 35º + sin 55º = 2 sin (35º + 55º) cos (35º – 55º) = 2 sin45º cos 10º = √2 cos 10º.IV. Инструктаж домашнего задания. В качестве домашнего задания ребятам можно предложить, используя рассмотренные на уроке приемы, записать тригонометрические формулы. И сделать это нужно несколько раз. V. Итог урока (интерактивное тестирование).
На интерактивной доске демонстрируются результаты тестирования на входе и выходе. Конспект по алгебре на тему «Формулы двойного угла» (10 класс)Урок по теме: «Формулы двойного угла» Цели урока: Учиться применять формулы для упрощения тригонометрических выражений. Ход урока
Актуализация знаний. Мы живём в реальном мире, и для его познания нам необходимы знания. — Тригонометрия помогает рассчитывать влияние ветра на полет самолета. Треугольник скоростей – это треугольник, образованный вектором воздушной скорости (V), вектором ветра( W), вектором путевой скорости (Vп). ПУ – путевой угол, УВ – угол ветра, КУВ – курсовой угол ветра.
— При плавании тело рыбы принимает форму кривой, которая напоминает график функции y=tgx. — Модель биоритмов можно построить с помощью тригонометрических функций. Для построения модели биоритмов необходимо ввести дату рождения человека, дату отсчета (день, месяц, год) и длительность прогноза (количество дней). Даже некоторые участки головного мозга называются синусами. Прием «Мозговой штурм»: Перечислите все известные понятия, связанные с тригонометрией. Прием «Ключевые слова». Ниже записаны ключевые слова по теме тригонометрия. Учащимся необходимо записать, пользуясь учебником 1-2 формулы, связанные с каждым понятием. 1) Синус, косинус, тангенс, котангенс 2) Плюс, минус 3) Зависимость 4) Тождество 5)Абсцисса, ордината. 6) –α 7) 1 2.Изучение нового материала. Метод «Активной беседы. А) Какие формулы мы изучали на прошлом уроке? (синус, косинус и тангенс суммы и разности углов) П 28 стр 144 — 146. Б) Могут ли углы быть равными? (да) В) Что получим, применив формулу. Вывод формул двойного аргумента:
Д) Как можно назвать данные формулы? (синус и косинус двойного угла). Это и есть тема нашего урока. Ж) Какая цель нашей дальнейшей работы на уроке? (научиться применять данные формулы) 3.Закрепление изученного материала. Рассмотрим применение формул двойного угла для нахождения значений тригонометрических функций и преобразования тригонометрических выражений. Пример 1. Известно, что . Найти Вопросы учащимся: Какой четверти принадлежит угол ? Какой знак имеет синус в этой четверти? Мы знаем, что , так как нам известен остается найти . Для этого какой формулой воспользуемся?:
значение синуса берем с плюсом так, как синус в первой четверти принимает положительное значение.
Пример 2. Упростите выражение: самостоятельная домашняя работа Упростите 1). 2). 3). 4). 5) 6). Известно, что Найдите: Основные формулы тригонометрии
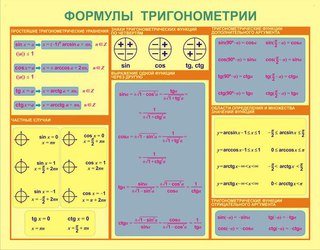
Тригонометрические выражения – это выражения, в котором переменная содержится под знаком тригонометрических функций. Их всего четыре:
Существует два способа решения тригонометрических уравнений: Первый способ — с использованием формул. | \( \displaystyle -\dfrac{\pi }{2}+2\pi n \) | \( \displaystyle \pi n \) | \( \displaystyle \dfrac{\pi }{2}+2\pi n \) |
| \( \displaystyle \cos x=A \) | \( \displaystyle \pm \arccos \alpha +2\pi n \) | \( \displaystyle \pi +2\pi n \) | \( \displaystyle \dfrac{\pi }{2}+\pi n \) | \( \displaystyle 2\pi n \) |
| \( \displaystyle tgx=A \) | \( \displaystyle arctg\alpha +\pi n \) | \( \displaystyle -\dfrac{\pi }{4}+\pi n \) | \( \displaystyle \pi n \) | \( \displaystyle \dfrac{\pi }{4}+\pi n \) |
| \( \displaystyle ctgx=A \) | \( \displaystyle arcctg\alpha +\pi n \) | \( \displaystyle \dfrac{3\pi }{4}+\pi n \) | \( \displaystyle \dfrac{\pi }{2}+\pi n \) | \( \displaystyle \dfrac{\pi }{4}+\pi n \) |
Второй способ — через тригонометрическую окружность.
Тригонометрическая окружность позволяет измерять углы, находить их синусы, косинусы и прочее. {2}}a=1 \]
{2}}a=1 \]
Выражение тангенса через синус и косинус (по сути альтернативное определение тангенса)
\[ \displaystyle tg\ \alpha =\dfrac{sin\ \alpha }{cos\ \alpha } \]
Выражение котангенса через синус и косинус или через тангенс (по сути альтернативное определение котангенса)
\[ \displaystyle ctg\ \alpha =\dfrac{cos\ \alpha }{sin\ \alpha }=\dfrac{1}{tg\ \alpha } \]
Синус суммы и разности:
\[ \displaystyle \sin \left( \alpha \pm \beta \right)=sin\alpha \cdot cos\beta \pm cos\alpha \cdot sin\beta \]
Косинус суммы и разности:
\[ \displaystyle \cos \left( \alpha \pm \beta \right)=cos\alpha \cdot cos\beta \mp sin\alpha \cdot sin\beta \]
Тангенс суммы и разности:
\[ \displaystyle tg\left( \alpha \pm \beta \right)=\dfrac{tg\alpha \pm tg\beta }{1\mp tg\alpha \cdot tg\beta } \]
Формулы понижения степени:
Данная группа формул позволяет перейти от любого тригонометрического выражения к рациональному.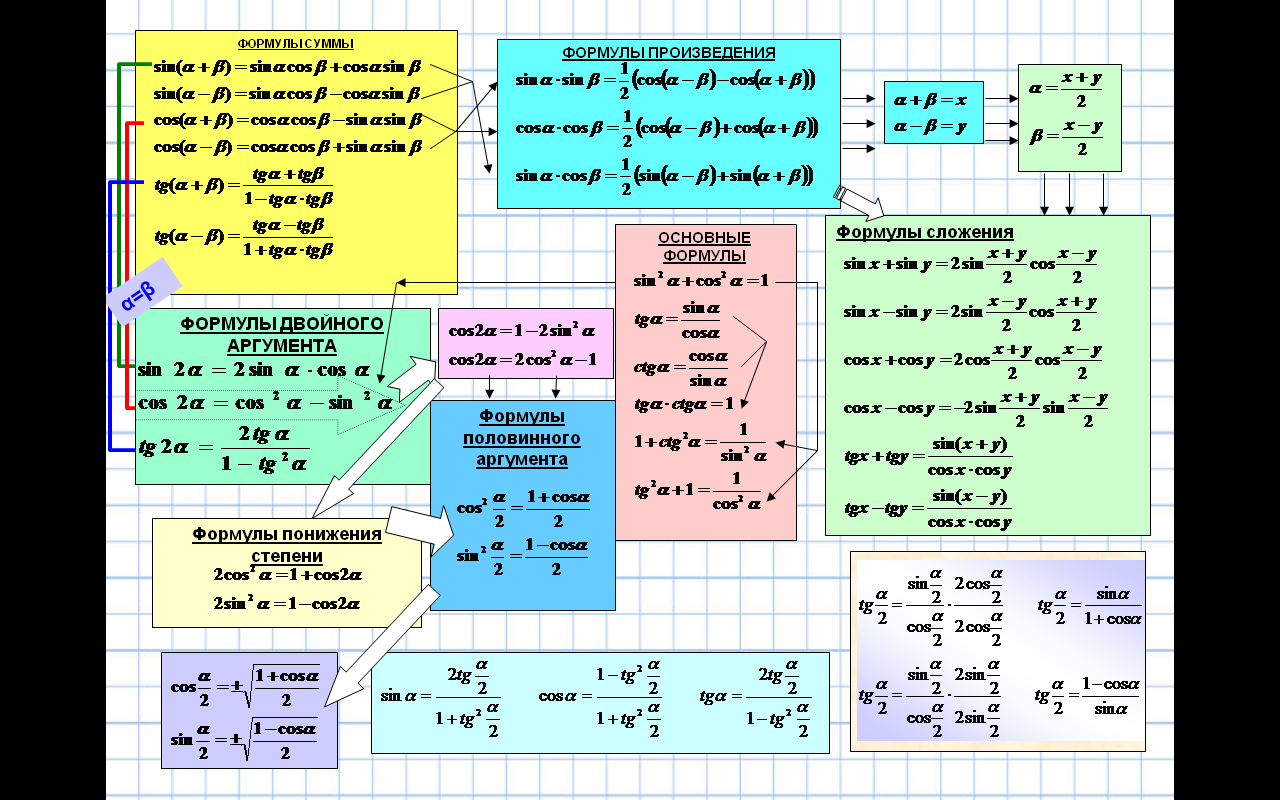 {2}}\alpha } \]
{2}}\alpha } \]
Формулы преобразования суммы функций
Данная группа формул позволяет преобразовать произведение в сумму и сумму в произведение.
\[ \displaystyle sin\alpha \pm sin\beta =2sin\dfrac{\alpha \pm \beta }{2}cos\dfrac{\alpha \mp \beta }{2} \]
\[ \displaystyle cos\alpha +cos\beta =2cos\dfrac{\alpha +\beta }{2}cos\dfrac{\alpha -\beta }{2} \]
\[ \displaystyle cos\alpha -cos\beta =-2sin\dfrac{\alpha +\beta }{2}sin\dfrac{\alpha -\beta }{2} \]
\[ \displaystyle tg\alpha \pm tg\beta =\dfrac{\text{sin}\left( \alpha \pm \beta \right)}{cos\alpha cos\beta } \]
\[ \displaystyle ctg\alpha \pm ctg\beta =\dfrac{\text{sin}\left( \beta \pm \alpha \right)}{sin\alpha sin\beta } \]
Формулы преобразования произведений функций
\[ \displaystyle sin\alpha sin\beta =\dfrac{\cos \left( \alpha -\beta \right)-\text{cos}\left( \alpha +\beta \right)}{2} \]
\[ \displaystyle sin\alpha cos\beta =\dfrac{\sin \left( \alpha +\beta \right)+\text{sin}\left( \alpha -\beta \right)}{2} \]
\[ \displaystyle cos\alpha cos\beta =\dfrac{\cos \left( \alpha -\beta \right)+\text{cos}\left( \alpha +\beta \right)}{2} \]
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Больше интересного в телеграм @calcsbox| Главная > Учебные материалы > Математика: Тригонометрические формулы | ||||
|
1.Знаки тригонометрических функций. |
||||
| 1 2 3 4 5 6 7 8 | ||||
Знаки тригонометрических функций по четвертям в тригонометрическом круге |
||||
Значения тригонометрических функций для некоторых углов |
||||
Основные тригонометрические тождества |
Формулы приведения |
|||
Формулы преобразования суммы |
Формулы сложения |
|||
Формулы половинного аргумента |
Формулы понижения степени |
|||
Формулы двойного угла |
Переход от произведения к сумме |
|||
Формулы тройного угла |
||||
Обратные тригонометрические функции и их свойства |
||||
Равносильные переходы с обратными тригонометрическими функциями |
||||
Одноименные обратные тригонометрические функции |
||||
Разноименные обратные тригонометрические функции |
||||
| 1 2 3 4 5 6 7 8 | ||||
Как не заучивать формулы приведения
Как не заучивать формулы приведения.
При решении тригонометрических уравнений или совершении тригонометрических преобразований первым делом нужно минимизировать количество различных аргументов тригонометрических функций. Для этого нужно все углы привести к углам первой четверти, воспользовавшись формулами приведения. Я хочу познакомить вас с мнемоническим правилом, которое позволяет не заучивать формулы приведения. Это правило в шутку называется «Лошадиное правило».
В этом ВИДЕОУРОКЕ я расскажу, как пользоваться этим правилом: приводить тригонометрическую функцию произвольного угла к углу первой четверти, освободив себя от необходимости запоминать формулы приведения:
Итак, «лошадиное правило» звучит так:
Если мы откладываем угол от вертикальной оси, лошадь говорит «да» (киваем головой вдоль оси OY) и приводимая функция меняет свое название: синус на косинус, косинус на синус, тангенс на котангенс, котангенс на тангенс.
Если мы откладываем угол от горизонтальной оси, лошадь говорит «нет» (киваем головой вдоль оси OХ) и приводимая функция не меняет свое название.
Знак правой части равенства совпадает со знаком приводимой функции, стоящей в левой части равенства.
Приведу несколько примеров использования формул приведения:
1. Найти значение выражения:
1. Выделим целую часть в дроби :
2. Так как период функции равен , выделим «холостые обороты»:
Теперь наш аргумент находится в пределах от нуля до , и самое время применить «лошадиное правило»:
Чтобы попасть в точку, соответствующую углу поворота на , мы сначала совершаем поворот на радиан, а потом из этой точки откладывает угол радиан:
Мы отложили угол от горизонтальной оси (лошадь говорит «нет») — не меняет свое названия, угол расположен в третьей четверти, в которой косинус отрицателен, следовательно приводимая функция отрицательна. Получаем:
Получаем:
2. Найти значение выражения:
Разберемся по отдельности с каждой функцией:
— мы сначала совершаем поворот на радиан, а затем откладываем угол 1 радиан от вертикальной оси в отрицательном направлении и попадаем в третью четверть:
Следовательно, приводимая функция меняет свое название, приводимая функция больше нуля (тангенс угла третьей четверти больше нуля): .
:
Сначала совершаем поворот на радиан, а затем из этой точки двигаемся на 1 радиан в отрицательном направлении. Откладываем угол 1 радиан от горизонтальной оси (синус не меняет свое название) и попадаем во вторую четверть, в которой синус больше нуля:
.
:
Сначала совершаем поворот на радиан, а затем из этой точки двигаемся на 1 радиан в положительном направлении. Откладываем угол 1 радиан от горизонтальной оси (косинус не меняет свое название) и попадаем в третью четверть, в которой косинус меньше нуля:
Вернемся к исходному примеру:
Ответ: 0
И. В. Фельдман, репетитор по математике.
В. Фельдман, репетитор по математике.
Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и С1»
Тригонометрических идентичностей
Вы могли бы сначала прочитать о тригонометрии!
Прямой треугольник
Тригонометрические идентичности — это уравнения, которые верны для прямоугольных треугольников. (Если это не прямоугольный треугольник, перейдите на страницу «Треугольники».)
Каждая сторона прямоугольного треугольника имеет имя:
Соседний всегда находится рядом с углом
И Напротив находится напротив угла
Мы скоро будем играть со всеми видами функций, но помните, что все возвращается к этому простому треугольнику с:
- Угол θ
- Гипотенуза
- Соседний
- Напротив
Синус, косинус и тангенс
Три основных функции в тригонометрии — это синус, косинус и тангенс.
Это всего лишь длины одной стороны делится на еще
Для прямоугольного треугольника с углом θ :
| Функция синуса: |
sin ( θ ) = Противоположно / Гипотенуза |
| Функция косинуса: |
cos ( θ ) = Соседний / Гипотенуза |
| Касательная функция: |
tan ( θ ) = напротив / рядом |
Для заданного угла θ каждое отношение остается неизменным
независимо от того, насколько большой или малый треугольник
Когда мы разделим синус на косинус, получим:
sin (θ) cos (θ) = Противоположный / Гипотенуза Соседний / Гипотенуза = Противоположный Соседний = tan (θ)
Итак, мы можем сказать:
Это наш первый Тригонометрический идентификатор .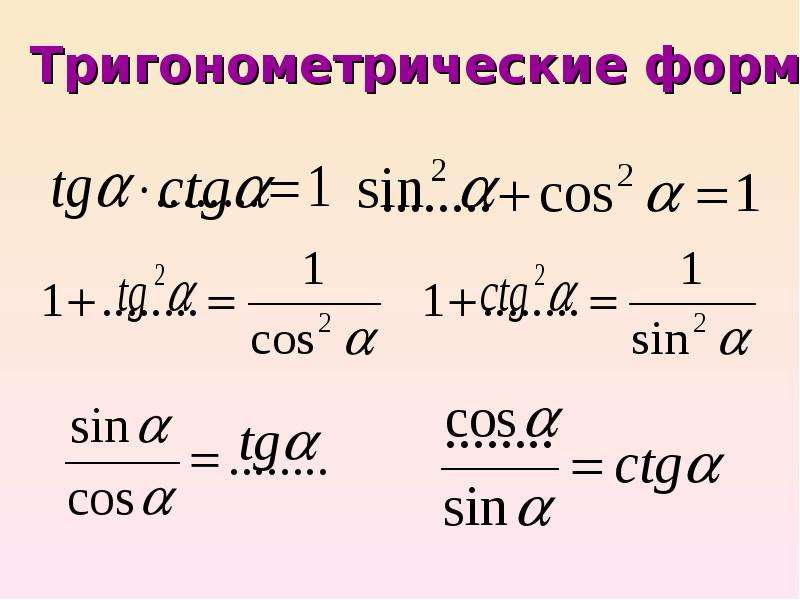
Косеканс, секанс и котангенс
Мы также можем разделить «наоборот» (например, Соседний / Противоположный вместо Противоположный / Соседний ):
| Косекансная функция: |
csc ( θ ) = Гипотенуза / Напротив |
| Секущая функция: |
сек ( θ ) = Гипотенуза / Соседняя |
| Котангенс Функция: |
детская кроватка ( θ ) = рядом / напротив |
Пример: когда Противоположность = 2 и Гипотенуза = 4, тогда
sin (θ) = 2/4 и csc (θ) = 4/2
На основании всего, что мы можем сказать:
грех (θ) = 1 / csc (θ)
cos (θ) = 1 / сек (θ)
загар (θ) = 1 / детская кроватка (θ)
И наоборот:
csc (θ) = 1 / sin (θ)
сек (θ) = 1 / cos (θ)
детская кроватка (θ) = 1 / tan (θ)
А еще у нас есть:
детская кроватка (θ) = cos (θ) / sin (θ)
Теорема Пифагора
Следующие тригонометрические тождества мы начнем с теоремы Пифагора:
| Теорема Пифагора гласит, что в прямоугольном треугольнике квадрат a плюс квадрат b равен квадрату c: a 2 + b 2 = c 2 |
Делим на c 2 дает
а 2 с 2 + б 2 с 2 знак равно с 2 с 2
Это можно упростить до:
( a с ) 2 + ( б с ) 2 = 1
Теперь, a / c равно Противоположно / Гипотенуза , что составляет sin (θ)
И b / c — это Соседний / Гипотенуза , что составляет cos (θ)
Так (a / c) 2 + (b / c) 2 = 1 также можно записать:
Примечание:- sin 2 θ означает найти синус θ, , затем возвести результат в квадрат и
- sin θ 2 означает возвести θ в квадрат, , затем выполнить синусоидальную функцию
Пример: 32 °
Использование только 4 десятичных разряда :
- sin (32 °) = 0.
 5299 …
5299 … - cos (32 °) = 0,8480 …
Теперь посчитаем sin 2 θ + cos 2 θ :
0,5299 2 + 0,8480 2
= 0,2808 … + 0,7191 …
= 0,9999 …
Мы очень близки к 1, используя всего 4 десятичных знака. Попробуйте это на своем калькуляторе , возможно, вы получите лучшие результаты!
Связанные идентификационные данные включают:
sin 2 θ = 1 — cos 2 θ
cos 2 θ = 1 — sin 2 θ
tan 2 θ + 1 = sec 2 θ
tan 2 θ = sec 2 θ — 1
детская кроватка 2 θ + 1 = csc 2 θ
детская кроватка 2 θ = csc 2 θ — 1
Как вы их помните? Упомянутые до сих пор личности можно запомнить
|
Но погоди.
 .. Это еще не все!
.. Это еще не все!
Есть еще много идентификаторов … вот некоторые из наиболее полезных:
Идентичности с противоположным углом
грех (-θ) = -sin (θ)
cos (−θ) = cos (θ)
тангенс (-θ) = -тан (θ)
Double Angle Identities
Идентификаторы Half Angle
Обратите внимание, что «±» означает, что это может быть или один , в зависимости от значения θ / 2
Идентификаторы суммы углов и разностей
Обратите внимание, что это означает, что вы можете использовать плюс или минус, а средство — использовать противоположный знак.
sin (A B) = sin (A) cos (B) cos (A) sin (B)
cos (A B) = cos (A) cos (B) sin (A) sin (B)
загар (A B) = загар (A) загар (B) 1 загар (A) загар (B)
детская кроватка (A B) = детская кроватка (A) детская кроватка (B) 1 детская кроватка (B) детская кроватка (A)
Треугольники
Существуют также идентичности треугольников, которые применяются ко всем треугольникам (а не только к прямоугольным треугольникам).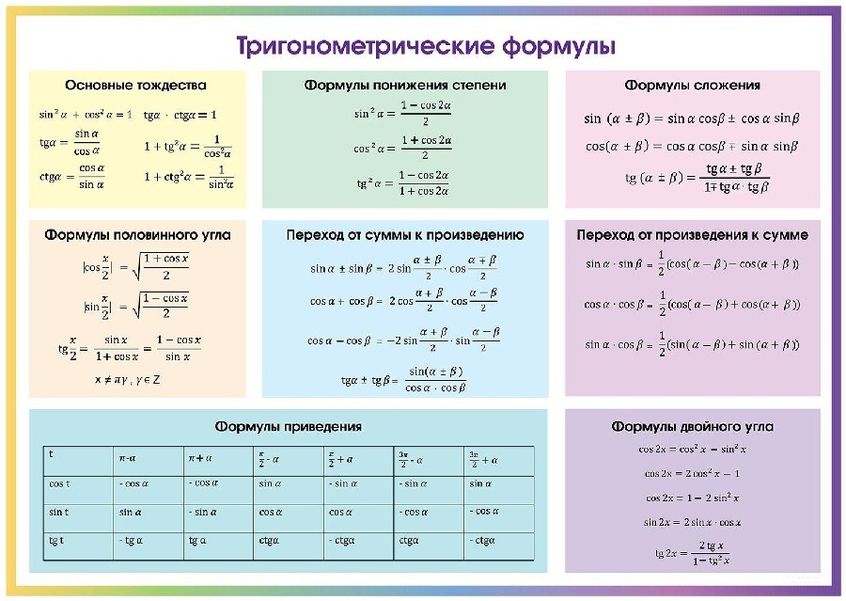
Решение простых (и средней сложности) триггерных уравнений
Purplemath
При решении тригонометрических уравнений используются как исходные углы, так и тригонометрические тождества, которые вы запомнили, а также большая часть изученной вами алгебры.Будьте готовы к тому, что для решения этих уравнений потребуется думать .
Далее предполагается, что вы хорошо разбираетесь в значениях триггерного отношения в первом квадранте, как работает единичный круг, соотношение между радианами и градусами и как выглядят кривые различных триггерных функций на минимум по первому периоду. Если вы не уверены в себе, вернитесь и сначала просмотрите эти темы.
MathHelp.
 com
com
-
Решите sin (
x ) + 2 = 3 в интервале 0 ° & leq; x <360 °
Как и в случае с линейными уравнениями, я сначала выделю член, содержащий переменную:
грех ( x ) + 2 = 3
грех ( x ) = 1
Теперь я буду использовать запомненные углы отсчета, чтобы получить окончательный ответ.
Примечание. В инструкциях указан интервал в градусах, что означает, что я должен давать свой ответ в градусах. Да, синус в первом периоде принимает значение 1 при
π / 2 радиан, но это не тот тип угловой меры, который им нужен, и использование его в качестве моего ответа, вероятно, приведет к моему как минимум проигрышу. несколько моментов по этому вопросу.
несколько моментов по этому вопросу.
Итак, в градусах мой ответ:
-
Решить tan
2 (θ) + 3 = 0 на интервале 0 ° & leq; θ <360 ° 90 481
Есть соблазн быстро вспомнить, что тангенс 60 ° включает в себя квадратный корень из 3, и отбросить ответ, но это уравнение на самом деле не имеет решения.Я вижу это, когда замедляюсь и делаю шаги. Мой первый шаг:
Может ли любой квадрат (касательной или любой другой триггерной функции) быть отрицательным ? Нет! Итак, мой ответ:
-
Решить в интервале 0 ° & leq;
x <360 °
Левая часть этого уравнения множится.
2 y 2 + 3 y = 0
y (2 y + 3) = 0
… и затем решить каждый из факторов. То же самое и здесь. Чтобы решить уравнение, которое они мне дали, я начну с факторинга:
Я занимался алгеброй; то есть, я провел факторинг, а затем решил каждое из двух уравнений, связанных с факторами.Это создало два триггерных уравнения. Итак, теперь я могу сделать триггер; а именно решение этих двух результирующих тригонометрических уравнений, используя то, что я запомнил о косинусоидальной волне. Из первого уравнения я получаю:
Из второго уравнения я получаю:
Соединяя эти два набора решений вместе, я получаю решение для исходного уравнения следующим образом:
x = 30 °, 90 °, 270 °, 330 °
-
Решить sin
2 (θ) — sin (θ) = 2 на интервале 0 & leq; θ <2π
Во-первых, перенесу все по одну сторону от знака «равно»:
грех 2 (θ) — грех (θ) — 2 = 0
Это уравнение является «квадратичным по синусу»; то есть форма уравнения — это формат квадратного уравнения:
В случае уравнения, которое они хотят, чтобы я решил, X = sin (θ), a = 1, b = –1 и c = –2.
Поскольку это квадратичная форма, я могу применить некоторые методы квадратного уравнения. В случае этого уравнения я могу разложить на множители квадратичный:
грех 2 (θ) — грех (θ) — 2 = 0
(грех (θ) — 2) (грех (θ) + 1) = 0
Первый множитель дает мне соответствующее тригонометрическое уравнение:
Но синус никогда не бывает больше 1, поэтому это уравнение не разрешимо; у него нет решения.
Другой фактор дает мне второе связанное тригонометрическое уравнение:
грех (θ) + 1 = 0
sin (θ) = –1
θ = (3/2) π
Тогда мой ответ:
(Если в своем классе вы выполняете решения только для ученых степеней, указанное выше значение решения равно «270 °». )
)
-
Решить cos
2 (α) + cos (α) = sin 2 (α) на интервале 0 ° & leq; x <360 °
Я могу использовать триггерное тождество, чтобы получить квадратичный косинус:
cos 2 (α) + cos (α) = sin 2 (α)
cos 2 (α) + cos (α) = 1 — cos 2 (α)
2cos 2 (α) + cos (α) — 1 = 0
(2cos (α) — 1) (cos (α) + 1) = 0
cos (α) = 1/2, cos (α) = –1
Первое тригонометрическое уравнение, cos (α) = 1/2, дает мне α = 60 ° и α = 300 °.Второе уравнение дает мне α = 180 °. Итак, мое полное решение:
-
Решить sin (β) = sin (2β) на интервале 0 ° & leq; β
<360 ° 90 481
Я могу использовать обозначение с двумя углами в правой части, а также переставлять и упрощать; тогда я фактор:
sin (β) = 2sin (β) cos (β)
sin (β) — 2sin (β) cos (β) = 0
sin (β) (1-2cos (β)) = 0
sin (β) = 0, cos (β) = 1/2
Синусоидальная волна (из первого триггерного уравнения) равна нулю при 0 °, 180 ° и 360 °. Но в исходном упражнении 360 ° не включены, поэтому значение последнего решения в данном конкретном случае не учитывается.
Косинус (из второго триггерного уравнения) равен
1/2 при 60 ° и, следовательно, также при 360 ° — 60 ° = 300 °. Итак, полное решение:β = 0 °, 60 °, 180 °, 300 °
-
Решите sin (
x ) + cos ( x ) = 1 на интервале 0 ° & leq; x <360 °
Хм… Я действительно ничего здесь не вижу. Было бы неплохо, если бы одно из этих триггерных выражений было возведено в квадрат …
Хорошо, почему бы мне не возвести обе стороны в квадрат и посмотреть, что произойдет?
(sin ( x ) + cos ( x )) 2 = (1) 2
sin 2 ( x ) + 2sin ( x ) cos ( x ) + cos 2 ( x ) = 1
[sin 2 ( x + cos 2 ( x )] + 2sin ( x ) cos ( x ) = 1
1 + 2sin ( x ) cos ( x ) = 1
2sin ( x ) cos ( x ) = 0
sin ( x ) cos ( x ) = 0
Ха; иди и подумай: я возведен в квадрат и получил кое-что, с чем я мог бы работать с . Хороший!
Хороший!
Из последней строки выше, либо синус равен нулю, либо косинус равен нулю, поэтому мое решение выглядит следующим образом:
x = 0 °, 90 °, 180 °, 270 °
Однако (и это важно!), Чтобы получить это решение, я возведен в квадрат, а возведение в квадрат — это «необратимый» процесс.
(Почему? Если вы возведете что-то в квадрат, вы не сможете просто извлечь квадратный корень, чтобы вернуться к тому, с чего начали, потому что возведение в квадрат могло где-то изменить знак.)
Итак, чтобы быть уверенным в своих результатах, мне нужно проверить свои ответы в исходном уравнении , чтобы убедиться, что я случайно не создал решения, которые на самом деле не учитываются. Подключаю обратно, вижу:
sin (0 °) + cos (0 °) = 0 + 1 = 1
. .. поэтому решение « x = 0 °» работает
.. поэтому решение « x = 0 °» работает
sin (90 °) + cos (90 °) = 1 + 0 = 1
…поэтому решение « x = 90 °» тоже работает
sin (180 °) + cos (180 °) = 0 + (–1) = –1
… ну ладно, значит « x = 180 °» НЕ работает
sin (270 °) + cos (270 °) = (–1) + 0 = –1
… так что « x = 270 °» тоже не работает,
Хорошо, что я проверил свои решения, потому что два из них на самом деле не работают.Они были созданы путем возведения в квадрат.
Мое фактическое решение :
Примечание. В приведенном выше описании я мог бы остановиться на этой строке:
… и использовал тождество с двойным углом для синуса, наоборот, вместо разделения 2 в предпоследней строке в моих вычислениях. Ответ был бы таким же, но мне нужно было бы учесть интервал решения:
Ответ был бы таким же, но мне нужно было бы учесть интервал решения:
2sin ( x ) cos ( x ) = sin (2 x ) = 0
Тогда 2 x = 0 °, 180 °, 360 °, 540 ° и т. Д., И разделение 2 из x даст мне x = 0 °, 90 °, 180 °, 270 °, это то же самое почти решение, что и раньше.После выполнения необходимой проверки (из-за возведения в квадрат) и отбрасывания посторонних решений мой окончательный ответ был бы таким же, как и раньше.
Трюк с возведением в квадрат в последнем примере, приведенном выше, встречается нечасто, но если все остальное не работает, возможно, стоит попробовать. Имейте это в виду для следующего теста.
URL: https://www.purplemath.com/modules/solvtrig.htm
Решение тригонометрических уравнений алгебраическими методами
Уравнение, содержащее
тригонометрические функции
называется
тригонометрическое уравнение
.
Пример:
грех 2 Икс + потому что 2 Икс знак равно 1 2 грех Икс — 1 знак равно 0 загар 2 2 Икс — 1 знак равно 0
Решение тригонометрических уравнений
Чтобы решить тригонометрическое уравнение, мы используем правила алгебры, чтобы изолировать тригонометрическую функцию по одну сторону от знака равенства.Затем мы используем наши знания о значениях тригонометрических функций для определения переменной.
Когда вы решаете тригонометрическое уравнение, которое включает только одно тригонометрическое выражение, начните с выделения выражения.
Если тригонометрические функции не могут быть объединены на одной стороне уравнения, попробуйте разложить уравнение на множители, а затем применить
свойство нулевого продукта
для решения уравнения. Если уравнение имеет квадратную форму, по возможности используйте первый множитель. Если это невозможно, примените
квадратичная формула
для решения уравнения.
Если уравнение имеет квадратную форму, по возможности используйте первый множитель. Если это невозможно, примените
квадратичная формула
для решения уравнения.
Пример :
Решать 2 грех Икс — 1 знак равно 0 .
Чтобы решить уравнение, мы начинаем его переписывать так, чтобы sin Икс изолирован с левой стороны. Итак, сначала добавьте 1 в каждую сторону, а затем разделите каждую сторону на 2 .
2 грех Икс знак равно 1 грех Икс знак равно 1 2
С
грех
Икс
имеет период
2
π
, сначала находим все решения в интервале
[
0
,
2
π
]
.
Решения Икс знак равно π 6 и Икс знак равно 5 π 6 .
Решения на интервале ( — ∞ , ∞ ) затем находятся путем сложения целых чисел, кратных 2 π . Добавление 2 п π к каждому из решений получаем общее решение данного уравнения.Следовательно, общий вид решений имеет вид Икс знак равно π 6 + 2 п π и Икс знак равно 5 π 6 + 2 п π где п любое целое число.
Тригонометрические уравнения
Тригонометрические тождества верны для всех замещающих значений переменных, для которых определены обе части уравнения. Условные тригонометрические уравнения верны только для некоторых значений замены. Решения в определенном интервале, например 0 ≤ x ≤ 2π, обычно называются первичными решениями . Общее решение — это формула, в которой перечислены все возможные решения.
Условные тригонометрические уравнения верны только для некоторых значений замены. Решения в определенном интервале, например 0 ≤ x ≤ 2π, обычно называются первичными решениями . Общее решение — это формула, в которой перечислены все возможные решения.
Процесс решения общих тригонометрических уравнений не является однозначным. Не существует правил, которые всегда приводят к решению. Процедура обычно включает использование тождеств, алгебраические манипуляции, проб и ошибок.Следующие рекомендации могут помочь найти решение.
Если уравнение содержит более одной тригонометрической функции, используйте тождества и алгебраические манипуляции (например, разложение на множители), чтобы переписать уравнение в терминах только одной тригонометрической функции. Найдите выражения в квадратичной форме и решите их с помощью разложения на множители. Не все уравнения имеют решения, но те, которые имеют, обычно могут быть решены с использованием соответствующих тождеств и алгебраических манипуляций. Ищите шаблоны. Нет замены опыту.
Ищите шаблоны. Нет замены опыту.
Пример 1: Найдите точное решение:
Сначала преобразуйте уравнение, используя тождество sin 2 α + cos2α = 1.
Следовательно,
Таким образом,
Пример 2: Решите cos 2 x = 3 (sin x — 1) для всех действительных значений x .
Первый ответ, −2,351, не является решением, так как функция синуса должна находиться в диапазоне от -1 до 1.Второй ответ, 0,8508, является допустимым значением. Таким образом, если k — целое число,
В радианах,
По специальности,
Пример 3 : Найдите точное решение:
Сначала преобразуйте уравнение, используя тождество двойного угла cos 2θ = 2 cos 2 θ — 1.
Следовательно,
Таким образом,
Вся элементарная математика — Учебное пособие — Тригонометрия
Тригонометрические уравнения. Простейшие тригонометрические уравнения.
Простейшие тригонометрические уравнения. Методы решения: алгебраический метод, факторинг, редукция
к однородному уравнению, переход к полууголу,
вводим вспомогательный угол, превращая изделие в
сумма, универсальная замена.
Тригонометрические уравнения. Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим .
Простейшие тригонометрические уравнения.
Методы решения тригонометрических уравнений. Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнение для получения его простейшего вида (см. выше) и решение полученного простейшего тригонометрического уравнения. Есть семь основных методов решения тригонометрических уравнений.
1. Алгебраический метод. Этот метод хорошо известен нам из алгебры (обмен и
метод подстановки).
2. Факторинг. Рассмотрим этот метод на примерах.
E x a m p l e 1. Решите уравнение: sin x + cos x = 1.
С о л ю т и н. Перенесите все термины влево:
sin x + cos x 1 = 0,преобразовать и разложить на множители левое выражение:
Е х а м п л е 2.Решите уравнение: cos² x + sin x cos x = 1.
С о л ю т и н. cos ² x + sin x cos x sin² x cos ² x = 0,
sin x cos x sin² х = 0, sin x (cos x sin x ) = 0,E x a m p l e 3. Решите уравнение: cos 2 x cos 8 x + cos 6 x = 1.
С о л ю т и н. cos 2 x + cos 6 x = 1 + cos 8 x ,
2 cos 4 x cos 2 x = 2 cos ² 4 x ,
cos 4 x (cos 2 x cos 4 x ) = 0,
cos 4 x 2 sin 3 x sin x = 0,
1). cos 4 x = 0, 2). грех 3 х = 0
, 3). грех x = 0,
cos 4 x = 0, 2). грех 3 х = 0
, 3). грех x = 0,
| 3. | Приведение к однородному уравнению. Уравнение называется однородным уравнением в
sin и cos , если и только если все его члены имеют одинаковую степень в sin и cos
того же угла. Для решения однородного уравнения необходимо: а ) перенести все термины в левую часть; b ) убрать все общие множители за скобки; c ) приравнять все множители и скобки к нулю; d ) скобки, приравненные к нулю, дают однородное уравнение меньшего градус, который следует разделить на cos (или sin ) более высокой степени; e ) для решения полученного алгебраического уравнения в tan . E x a m p l e. Решите уравнение: 3 sin ²
x + 4 sin x cos x + 5 cos ² x = 2. С о л ю т и н. 3 греха ² x + 4 sin x cos x + 5 cos ² x = 2sin ² x + 2cos ² x , sin ² x + 4 sin x cos x + 3 cos ² х = 0, tan ² x + 4 tan x + 3 = 0, следовательно, y ² + 4 y +3 = 0, корни этого уравнения: y 1 = –1 , y 2 = –3, отсюда 1) tan x = –1, 2) tan x = –3,
|
4.Переход на полуугол. Рассмотрим этот метод на примере:
E x a m p l e. Решите уравнение: 3 sin x 5 cos x = 7.
С о л ю т и н. 6 sin ( x /2) cos ( x /2) 5 cos ² ( x /2) + 5 sin ² ( x /2) =
= 7 sin ² ( x 900 10/2) + 7 cos ² ( x /2),
2 sin ² ( x /2) 6 sin ( x /2) cos ( x /2) + 12 cos ² ( x /2) = 0,
желтовато-коричневый ² ( x /2) 3 коричневый ( x /2) + 6 = 0,
. . . . . . . . . .
. . . . . . . . .
5. Введение вспомогательного уголка. Рассмотрим уравнение формы:
a sin x + b cos x = c ,
, где коэффициенты a , b , c ; x неизвестно.
Новые коэффициенты в левой части имеют свойства синуса и косинуса: модуль
(по модулю) каждого из них не более 1, а сумма их квадратов равна
к 1.Итак, мы можем отметить их как cos и
грех соответственно; вот так
называется
вспомогательным уголком .
Теперь наше уравнение имеет форму:
6. Преобразование произведения в сумму. Здесь используются соответствующие формулы.
Е х а м п л е. Решите уравнение: 2 sin 2 x sin 6 x = cos 4 x .
cos 4 x cos 8 x = cos 4 x ,
cos 8 x = 0,
7.Универсальная подмена. Рассмотрим этот метод на примере.
Е х а м п л е. Решите уравнение: 3 sin x 4 cos x = 3.
Итак, только первый случай дает решение.
Что такое тригонометрия? — Функции, формулы и приложения — Видео и стенограмма урока
Тригонометрия и треугольники
Однако не любой треугольник подходит для тригонометрии. Это должен быть прямоугольный треугольник, в котором один из углов равен 90 градусам.
Что такого особенного в прямоугольном треугольнике, скажете вы? Что ж, просто посмотрев на это, мы видим, что у прямоугольного треугольника есть имена для всех трех сторон. Но держите лошадей. Имена не всегда остаются прежними! Гипотенуза всегда находится на стороне прямого угла; однако две другие стороны переключаются в зависимости от того, под каким углом вы имеете в виду. Видите ли, соседняя сторона, как следует из названия, всегда находится рядом с углом.
Видите ли, соседняя сторона, как следует из названия, всегда находится рядом с углом.
Итак, если бы наш угол находился под пустым углом, тогда соседние и противоположные стороны наверху поменялись бы местами.
Эти три стороны составляют тригонометрию. Да, тригонометрия — это соотношение сторон. Синус, косинус и тангенс — это разные отношения этих трех сторон.
| Тригонометрическая функция | Коэффициент |
|---|---|
| Синус: sin (x) = | Напротив / Гипотенуза |
| Косинус: cos (x) = | Смежный / Гипотенуза |
| Касательная: tan (x) = | Напротив / рядом |
Это основа всей тригонометрии! Легкий способ запомнить эти соотношения — произнести слово SOHCAHTOA.Это помогает мне запоминать соотношения. SOH — синус с отношением противоположности к гипотенузе. CAH — косинус с отношением, смежным с гипотенузой. И TOA — это касательная с отношением, противоположным соседнему. Вы видите, как вы сократили отношения к первой букве каждого слова? Запомните это одно слово, и оно вам пригодится в тригонометрии. Хотя есть и другие тригонометрические функции, все они связаны с этими тремя основными.
CAH — косинус с отношением, смежным с гипотенузой. И TOA — это касательная с отношением, противоположным соседнему. Вы видите, как вы сократили отношения к первой букве каждого слова? Запомните это одно слово, и оно вам пригодится в тригонометрии. Хотя есть и другие тригонометрические функции, все они связаны с этими тремя основными.
Тригонометрия и круги
Итак, как все эти вещи о треугольниках связаны с кругами? Потому что, путешествуя по кругу, вы можете создавать все треугольники, необходимые для решения задач тригонометрии.
Этот конкретный круг с радиусом, равным единице, называется единичным кругом. Поместив круг в декартовую координату с центром круга в качестве начала координат, мы получим отрицательные стороны. Принятие отношения с отрицательным числом даст нам взамен отрицательное число. Так обстоит дело со всеми тремя тригонометрическими функциями. Есть определенные углы, которые дадут отрицательный ответ. Вы можете проверить это с помощью единичной окружности, нарисовав треугольник с гипотенузой, проведенной под углом.Угол треугольника соответствует правилам декартовых координат, увеличиваясь при движении против часовой стрелки от положительной стороны оси x.
Вы можете проверить это с помощью единичной окружности, нарисовав треугольник с гипотенузой, проведенной под углом.Угол треугольника соответствует правилам декартовых координат, увеличиваясь при движении против часовой стрелки от положительной стороны оси x.
Немного изучите единичный круг, и вы найдете несколько интересных тригонометрических соотношений. Например, углы 20 и 160 дают одинаковый синус. Глядя на единичный круг и рисуя треугольник под обоими углами, мы видим, что треугольники имеют одинаковую высоту. Поскольку коэффициент синуса относится к противоположной стороне угла, он одинаков для обоих градусов.
Как это поможет мне в реальной жизни?
Возможно, вы удивитесь, насколько полезны треугольники в реальном мире. Двумя важными приложениями являются строительство дорог на склонах холмов или гор и траектория полета приземляющегося самолета. Давайте посмотрим на пару примеров.
Учитывая конкретный склон холма, городу необходимо знать, какой длины дорога должна быть построена.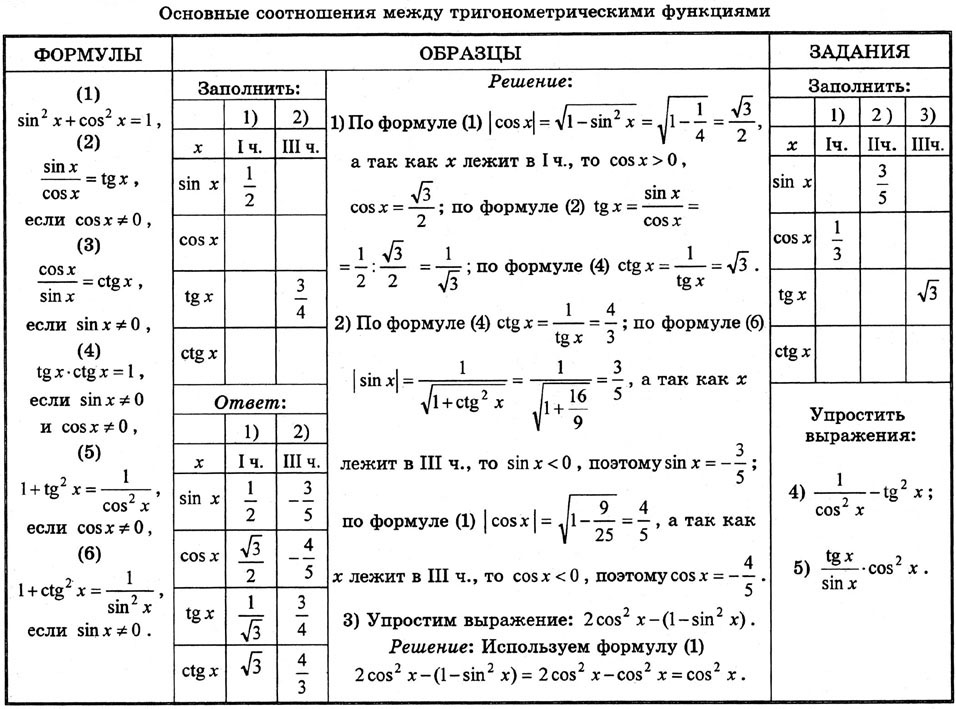 Конечно, город как бы застраивать на склоне холма не собирается. Это было бы слишком ухабисто. Сначала нужно было немного выровнять склон холма.На каком уровне нужно проводить прокачку? Чтобы добраться до вершины холма, вы не можете срезать середину холма, вам нужно постепенно подниматься вверх. Итак, какой наклон нужен?
Конечно, город как бы застраивать на склоне холма не собирается. Это было бы слишком ухабисто. Сначала нужно было немного выровнять склон холма.На каком уровне нужно проводить прокачку? Чтобы добраться до вершины холма, вы не можете срезать середину холма, вам нужно постепенно подниматься вверх. Итак, какой наклон нужен?
Вот здесь-то и вступает в игру тригонометрия. Вы можете сфотографировать холм и нарисовать треугольник, где гипотенуза представляет дорогу. Измеряя нижнюю часть треугольника и высоту треугольника, вы можете определить угол или уклон, необходимый для правильного движения дороги по склону.
Аналогичным образом, когда самолет заходит на посадку, пилот должен определить расстояние до взлетно-посадочной полосы и свою высоту. Это определит его скорость снижения или его угол снижения. Это аналогичный процесс с использованием треугольника и нахождением угла. В качестве альтернативы, если ему задан требуемый угол снижения, он должен вычислить расстояние, на котором ему нужно начать снижение.
Краткое содержание урока
Тригонометрия буквально означает измерение треугольников.Но его можно определить как часть геометрии, которая имеет дело с вычислениями. Тригонометрия — это когда вы напрягаете мышцы своего мозга и решаете проблемы в функциональной форме, а не в форме. В реальном мире у тригонометрии есть реальные применения, которые важны для вашей безопасности.
|
Функция ABS |
Возвращает абсолютное значение числа |
|
Функция ACOS |
Возвращает арккосинус числа . |
|
Функция ACOSH |
Возвращает обратный гиперболический косинус числа .
|
|
Функция ACOT
|
Возвращает арккотангенс числа . |
|
Функция ACOTH
|
Возвращает гиперболический арккотангенс числа . |
|
АГРЕГАТ (функция АГРЕГАТ) |
Возвращает агрегат в списке или базе данных |
|
АРАБСКИЙ (функция)
|
Преобразует римское число в арабское как число |
|
Функция ASIN |
Возвращает арксинус числа .
|
|
Функция ASINH |
Возвращает обратный гиперболический синус числа . |
|
Функция ATAN |
Возвращает арктангенс числа . |
|
Функция ATAN2 |
Возвращает арктангенс от x- и y-координат |
|
Функция ATANH |
Возвращает обратный гиперболический тангенс числа . |
|
ОСНОВНАЯ функция
|
Преобразует число в текстовое представление с заданным основанием системы счисления |
|
ПОТОЛОК (функция ПОТОЛОК) |
Округляет число до ближайшего целого или до ближайшего значения, кратного значению |
|
ПОТОЛОК. |
Округляет число до ближайшего целого или до ближайшего значения, кратного значению |
|
ПОТОЛОК.ТОЧНАЯ функция |
Округляет число до ближайшего целого или до ближайшего кратного значимости.Независимо от знака числа, число округляется в большую сторону. |
|
Функция КОМБИНАР |
Возвращает количество комбинаций для заданного количества объектов |
|
Функция КОМБИНА
|
Возвращает количество комбинаций с повторениями для заданного количества элементов. |
|
Функция COS |
Возвращает косинус числа . |
|
Функция COSH |
Возвращает гиперболический косинус числа . |
|
Функция СОТ
|
Возвращает котангенс угла. . |
|
COTH функция
|
Возвращает гиперболический котангенс числа . |
|
Функция CSC
|
Возвращает косеканс угла. |
|
Функция CSCH
|
Возвращает гиперболический косеканс угла . |
|
ДЕСЯТИЧНАЯ функция
|
Преобразует текстовое представление числа с заданным основанием в десятичное число. |
|
ГРАДУСЫ (функция ГРАДУСЫ) |
Преобразует радианы в градусы |
|
ЧЕТНАЯ функция |
Округляет число до ближайшего четного целого |
|
Функция EXP |
Возвращает e в степени заданного числа |
|
ФАКТ (функция ФАКТ) |
Возвращает факториал числа .
|
|
Функция ФАКТДВОБЛЕ |
Возвращает двойной факториал числа . |
|
Функция ПОЛ |
Округляет число до нуля |
|
ЭТАЖ.МАТЕМАТИЧЕСКАЯ функция
|
Округляет число до ближайшего целого или до ближайшего значения, кратного значению |
|
Функция FLOOR.PRECISE |
Округляет число до ближайшего целого числа или до ближайшего кратного значимости. |
|
Функция НОД |
Возвращает наибольший общий делитель . |
|
Функция INT |
Округляет число до ближайшего целого числа |
|
ISO.ПОТОЛОК (функция ПОТОЛОК)
|
Возвращает число, округленное в большую сторону до ближайшего целого числа или до ближайшего кратного значения |
|
Функция НОК |
Возвращает наименьшее общее кратное .
|
|
LN функция |
Возвращает натуральный логарифм числа . |
|
ЖУРНАЛ функция |
Возвращает логарифм числа по указанному основанию. |
|
Функция LOG10 |
Возвращает десятичный логарифм числа . |
|
Функция МДЕТЕРМ |
Возвращает определитель матрицы массива |
|
Функция МИНВЕРСИ |
Возвращает матрицу, обратную массиву |
|
Функция ММУЛЬМ |
Возвращает матричное произведение двух массивов |
|
Функция MOD |
Возвращает остаток от деления .
|
|
ОКРУГЛ. Функция |
Возвращает число, округленное до желаемого кратного. |
|
МНОГОЧИСЛЕННАЯ функция |
Возвращает многочлен набора чисел . |
|
MUNIT (функция MUNIT)
|
Возвращает единичную матрицу или указанное измерение |
|
НЕЧЕТНАЯ функция |
Округляет число до ближайшего нечетного целого числа |
|
Функция PI |
Возвращает значение пи .
|
|
Функция МОЩНОСТЬ |
Возвращает результат возведения числа в степень . |
|
Функция ПРОДУКТ |
Умножает свои аргументы |
|
ЧАСТИЧНАЯ функция |
Возвращает целую часть деления. . |
|
РАДИАНЫ (функция РАДИАНЫ) |
Преобразует градусы в радианы |
|
СЛУЧАЙ (функция СЛЧИС) |
Возвращает случайное число от 0 до 1 |
|
СЛУЧАЙНАЯ функция |
Возвращает массив случайных чисел от 0 до 1. |
|
СЛУЧМЕЖДУ функция |
Возвращает случайное число между указанными вами числами |
|
РИМСКАЯ функция |
Преобразует арабскую цифру в римскую как текст |
|
ОКРУГЛ (функция ОКРУГЛ.) |
Округляет число до указанного количества цифр |
|
Функция ОКРУГЛВНИЗ |
Округляет число до нуля |
|
Функция ОКРУГЛВЕРХ |
Округляет число до нуля |
|
Функция SEC
|
Возвращает секанс угла. |
|
Функция SECH
|
Возвращает гиперболический секанс угла. . |
|
Функция СЕРИЕСУМ |
Возвращает сумму степенного ряда по формуле . |
|
ЗНАК функция |
Возвращает знак числа |
|
Функция SIN |
Возвращает синус заданного угла. |
|
Функция SINH |
Возвращает гиперболический синус числа .
|
|
КОРЕНЬ (функция КОРЕНЬ) |
Возвращает положительный квадратный корень . |
|
Функция КОРЕНЬПИ |
Возвращает квадратный корень из (число * пи) . |
|
ПРОМЕЖУТОЧНЫЙ ИТОГ |
Возвращает промежуточный итог в списке или базе данных |
|
СУММ (функция СУММ) |
Добавляет аргументы |
|
СУММЕСЛИ функция |
Добавляет ячейки, указанные в критериях |
|
СУММЕСЛИМН (функция СУММЕСЛИМН) |
Добавляет ячейки в диапазон, удовлетворяющий нескольким критериям |
|
Функция СУММПРОИЗВ |
Возвращает сумму произведений соответствующих компонентов массива |
|
СУММКВ функция |
Возвращает сумму квадратов аргументов. |
|
СУММХ2МИ2 (функция СУММХ2МИ2) |
Возвращает сумму разницы квадратов соответствующих значений в двух массивах |
|
СУММХ2ПИ2 (функция СУММХ2ПИ2) |
Возвращает сумму суммы квадратов соответствующих значений в двух массивах |
|
СУММКВМ2 (функция СУММКВМ2) |
Возвращает сумму квадратов разностей соответствующих значений в двух массивах. |
|
Функция TAN |
Возвращает тангенс числа .
|


 youtube.com/watch?v=z47QtuD5lS0с последующим обсуждением либо вывод
формулы косинуса суммы аргументов можно продемонстрировать учителю
самостоятельно, используя поворот начального радиуса, около начала координат,
на угол α и на угол β, и привлекая учащихся к обсуждению данного
вывода.
youtube.com/watch?v=z47QtuD5lS0с последующим обсуждением либо вывод
формулы косинуса суммы аргументов можно продемонстрировать учителю
самостоятельно, используя поворот начального радиуса, около начала координат,
на угол α и на угол β, и привлекая учащихся к обсуждению данного
вывода.

 2\alpha=\dfrac{1+\cos{2\alpha}}2\\&&&\\
\hline
\end{array}\]
2\alpha=\dfrac{1+\cos{2\alpha}}2\\&&&\\
\hline
\end{array}\] \circ-\alpha)\sin\beta=\sin\alpha\cos\beta+\cos\alpha\sin\beta\)
\circ-\alpha)\sin\beta=\sin\alpha\cos\beta+\cos\alpha\sin\beta\) 2\alpha=\dfrac{1-\cos2\alpha}2\)
2\alpha=\dfrac{1-\cos2\alpha}2\)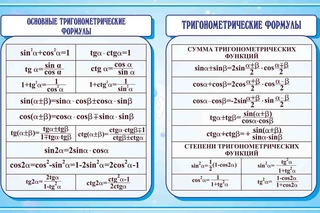 Тогда: \(\alpha=\dfrac{x+y}2, \ \beta=\dfrac{x-y}2\). Подставим эти значения в предыдущие три формулы:
Тогда: \(\alpha=\dfrac{x+y}2, \ \beta=\dfrac{x-y}2\). Подставим эти значения в предыдущие три формулы:  2}\,\cos (x-\phi)\]
2}\,\cos (x-\phi)\] Можно провести числовой анализ
на каждом этапе тестирования – на начальном и итоговом, а можно сделать
сравнительный анализ в конце урока, в качестве подведения итогов.
Можно провести числовой анализ
на каждом этапе тестирования – на начальном и итоговом, а можно сделать
сравнительный анализ в конце урока, в качестве подведения итогов. Может, некоторые из них вам уже знакомы.
Может, некоторые из них вам уже знакомы. Первая дама, вторая дама и третья дама. И неожиданно
пошел дождь. Все дамы открыли зонтики, и одели по паре калош. Прогулка была
закончена, и дамы вернулись домой. Первая дама, вторая дама и третья дама пошли
домой. (Сначала, в таблице, во второй строке по порядку указываются номера
дам. За тем изображают корни – “зонтики”, и “надевают калоши” – в знаменателях
пишут 2).
Первая дама, вторая дама и третья дама. И неожиданно
пошел дождь. Все дамы открыли зонтики, и одели по паре калош. Прогулка была
закончена, и дамы вернулись домой. Первая дама, вторая дама и третья дама пошли
домой. (Сначала, в таблице, во второй строке по порядку указываются номера
дам. За тем изображают корни – “зонтики”, и “надевают калоши” – в знаменателях
пишут 2). А лошадь кивала головой по той оси, на которой располагался
угол
являющиеся границами первой и третьей четвертей соответственно, лежат на оси Оу,
то лошадь кивком головы подтверждала смену функции на конфункцию. А для углов
наоборот отрицала. Математику оставалось лишь записывать ответ, указывая знак
данной функции.
А лошадь кивала головой по той оси, на которой располагался
угол
являющиеся границами первой и третьей четвертей соответственно, лежат на оси Оу,
то лошадь кивком головы подтверждала смену функции на конфункцию. А для углов
наоборот отрицала. Математику оставалось лишь записывать ответ, указывая знак
данной функции.
 Следовательно,
Следовательно, 
 Сегодня мы поднимемся на следующую ступеньку наших знаний по теме: «Тригонометрия». Перед тем как запишем тему нашего урока сначала мы должны убедиться , что все что мы изучаем, находит применение в жизни.
Сегодня мы поднимемся на следующую ступеньку наших знаний по теме: «Тригонометрия». Перед тем как запишем тему нашего урока сначала мы должны убедиться , что все что мы изучаем, находит применение в жизни.


 {n}}\arcsin \alpha +\pi n \)
{n}}\arcsin \alpha +\pi n \)

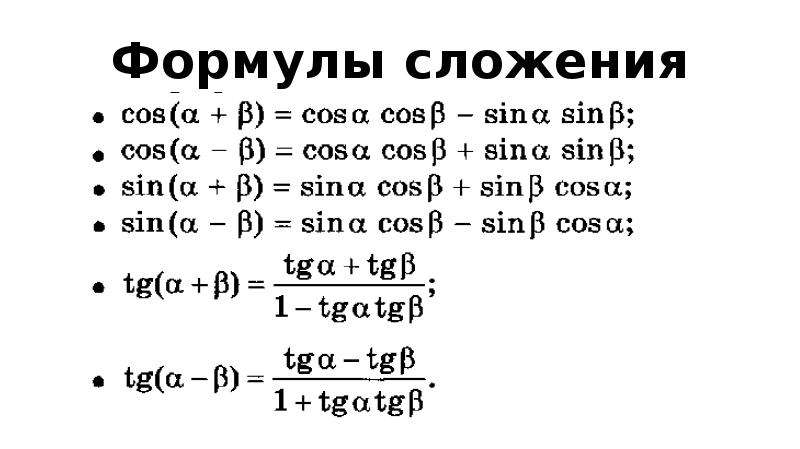 МАТЕМАТИЧЕСКАЯ функция
МАТЕМАТИЧЕСКАЯ функция


 Независимо от знака числа, число округляется в меньшую сторону.
Независимо от знака числа, число округляется в меньшую сторону.  Однако вы можете указать количество строк и столбцов для заполнения, минимальные и максимальные значения, а также указать, возвращать ли целые числа или десятичные значения.
Однако вы можете указать количество строк и столбцов для заполнения, минимальные и максимальные значения, а также указать, возвращать ли целые числа или десятичные значения. 
