Posted in Разное

Тригонометрические уравнения самостоятельная работа 10 класс – Самостоятельная работа в 10 классе по теме: «Тригонометрические уравнения»

Самостоятельные работы по теме «Решение тригонометрических уравнений» для 10-х классов физико-математического профиля

Разделы: Математика

Класс:

Тригонометрические уравнения традиционно входят в число задач, предлагаемых на едином государственном экзамене по математике. Косвенно это обусловлено тем, что не существует единого универсального метода решения тригонометрических уравнений. И решение каждого конкретного уравнения требует хорошего владения навыками тригонометрических преобразований, умения выбрать нужную формулу для упрощения тригонометрического выражения и сведения его к более простому уравнению.

В данном пособии представлены самостоятельные работы для отработки и закрепления навыков решения тригонометрических уравнений.

Самостоятельные работы рассчитаны на учащихся физико-математического классов, однако, могут использоваться и для хорошо успевающих учащихся общеобразовательных учреждений. За каждую из проведенных работ выставляется оценка, что послужит достаточной мотивацией для наиболее полной и качественной домашней проработки пройденного накануне материала, а также для дополнительного повторения и лучшего запоминания формул тригонометрических преобразований, а также методов решения тригонометрических уравнений.

В Приложении 1 приведен математический диктант – задание для проверки усвоения учащимися основных базовых навыков по пройденному материалу. Эту работу полезно использовать и в средней общеобразовательной школе для лучшего запоминания и усвоения основных понятий по данной теме. В Приложении 2 содержится самостоятельная работа, в которой требуется решить уравнения несколько более сложные. Приложение 3 содержит самостоятельную работу, где нужно решить тригонометрические уравнения различными методами. В Приложении 4 содержатся задания, требующие проверки найденных корней на соответствие с ограничениями в исходном уравнении, что является еще более сложной задачей.

Самостоятельные работы составлены в четырех вариантах эквивалентной сложности, которые удобно использовать для промежуточного контроля знаний учащихся, отработки практических навыков решения задач по теме «Решение тригонометрических уравнений».

Представленные в пособии работы позволяют учащимся лучше усвоить пройденный материал по указанной теме, что подтверждено практикой.

Все самостоятельные работы содержат ответы, что позволит значительно сократить время проверки работ преподавателем.

Данное пособие также может быть использовано для организации повторения при подготовке учащихся старших классов к успешной сдаче единого государственного экзамена по математике.

Литература:

  1. Мордкович А.Г., Денищева Л.О., Звавич Л.И., Корешкова Т.А., Мишустина Т.Н., Рязановский А.Р., Семенов П.В. Алгебра и начала математического анализа 10 класс. Ч. 2. – М.: «Издательство Мнемозина»: ОАО «Московские учебники», 2009.
  2. Шестаков С.А., Захаров П.И. ЕГЭ 2013. Математика. Задача С1. Уравнения и системы уравнений. – М. : Издательство МЦНМО, 2013.
  3. Сергеев И.Н., Панферов В.С. ЕГЭ 2013. Математика. Задача С3. Уравнения и неравенства. – М. : Издательство МЦНМО, 2013.
  4. Ершова А.П., Нелин Е.П. Самостоятельные и контрольные работы по алгебре и началам математического анализа для 10 класса. – М.: Илекса, 2011.

6.05.2013

Поделиться страницей:

urok.1sept.ru

Конспект урока в 10 классе по теме «Тригонометрические уравнения.»

Муниципальное бюджетное общеобразовательное учреждение

«Гимназия №3» городского округа город Октябрьский Республики Башкортостан

План проведения открытого урока

по алгебре в 10 классе

по теме «Тригонометрические уравнения»

Учитель Балашова Светлана Владимировна.

Тема. Тригонометрические уравнения.

Цели урока:

  1. Систематизировать, обобщить знания учащихся по теме «Тригонометрические уравнения», проверить уровень усвоения темы.

  2. Развивать навык решения тригонометрических уравнений, умение анализировать, применять полученные знания к решению заданий по теме урока, навык самостоятельной работы.

  3. Воспитывать мотивацию к учению, развивать познавательный интерес к предмету.

План урока.

1.Организационный момент. Постановка целей и задач урока.

2.Основная часть.

1. Теоретический опрос.

2. Устная работа.

3.Работа у доски и в тетрадях по теме урока.

4.Физминутка.

5. Домашняя работа.

6.Самостоятельная работа с взаимопроверкой.

3.Итог урока, выставление оценок.

Уравнение представляет

собой наиболее серьёзную и

важную вещь в математике.

Оливер Лодж, английский

физик и изобретатель.

Ход урока.

1.Организационный момент. Постановка целей и задач урока.

Тема нашего урока « Тригонометрические уравнения». Эпиграфом к уроку я взяла слова английского физика и изобретателя Оливера Лоджа «Уравнение представляет

собой наиболее серьёзную и важную вещь в математике».

На предыдущих уроках мы работали над этой темой, изучили формулы корней простейших тригонометрических уравнений, узнали способы и методы решения тригонометрических уравнений, сегодня на уроке мы обобщим и закрепим эту тему.

2.Основная часть.

1. Теоретический опрос.

Хочется вспомнить слова английского философа, Герберт Спенсер говорил: «Дороги не те знания, которые откладываются в мозгу, как жир, а те, которые превращаются в умственные мышцы». Давайте накачивать «умственные мышцы», начнём урок с устного счёта ( разминка для ума).

Повторим решение простейших тригонометрических уравнений ( с места по цепочке).

Для решения уравнений, необходимо знание основных тригонометрических формул, давайте их вспомним (один человек письменно на доске).

Sin2x= 2 sinx cosx

Sin(x+ y)= sinx cosy + siny cosx

2. Устная работа.

А) выбери правильный ответ.

а)

б)

г) нет решения

Б) найди ошибки в решении.

Ответ:

В) составь алгоритм решения уравнения.

2 cos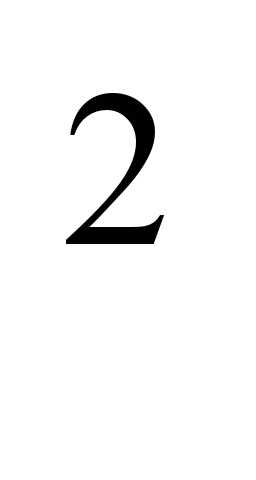x + sin x+1=0

3 sin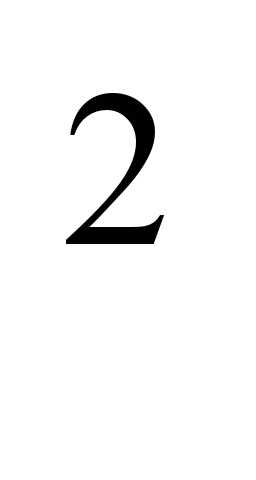x — 4sin x cos x + cos 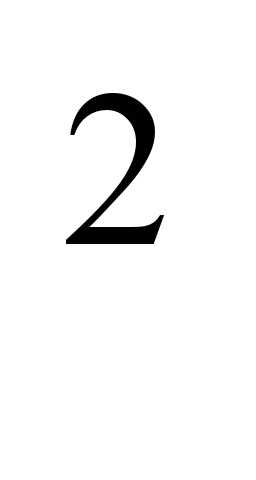x=0

2 sinx=

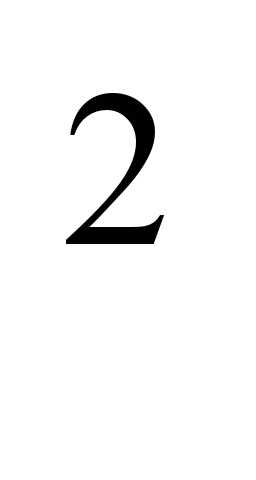sin 2x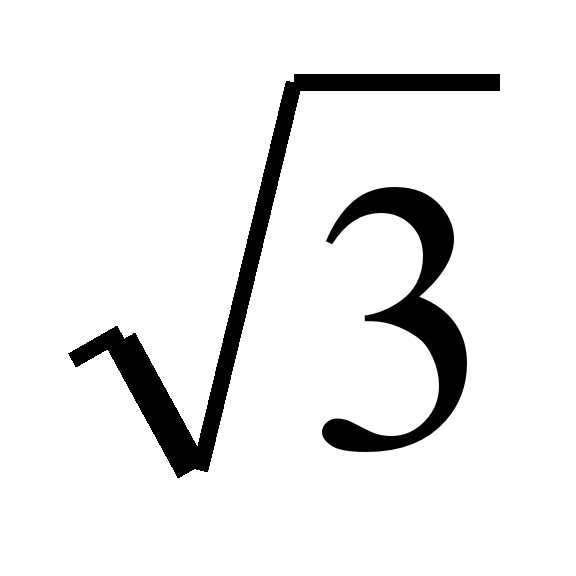

Sin x+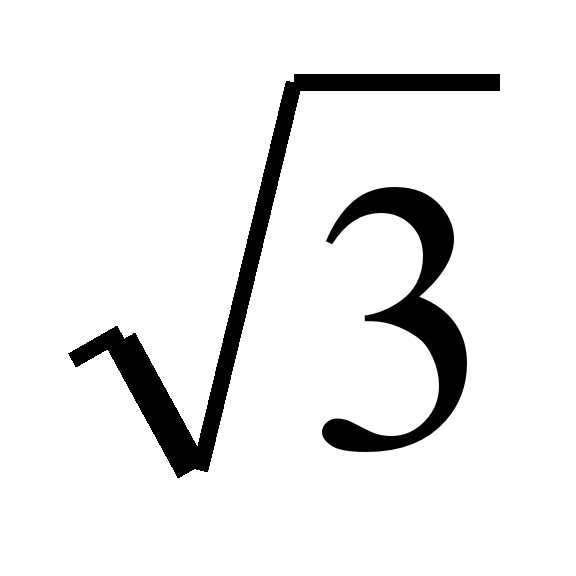cos x=2

3 cos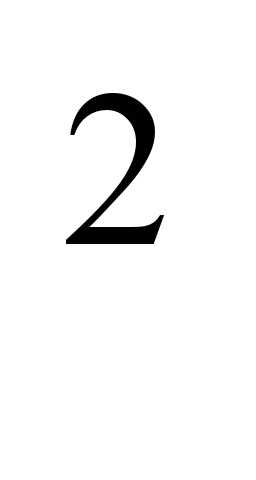x – 10 cos x+3=0

Cos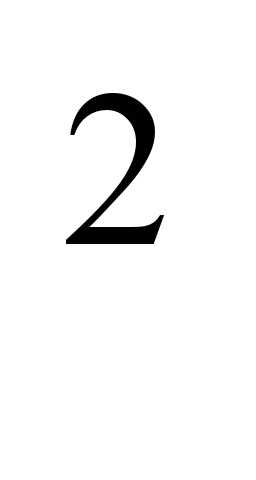x -2 cos x=0

Sin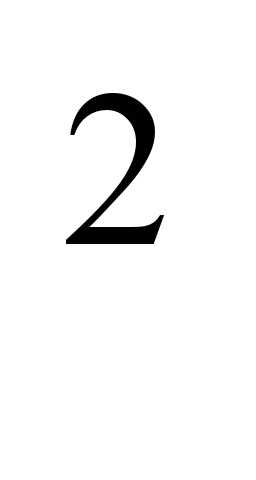 x-16=0

Cos 3x +sin 3x=0

6sin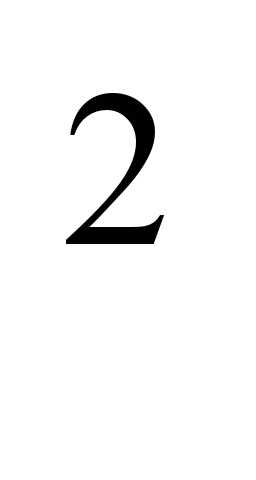x- sin x cos x-cos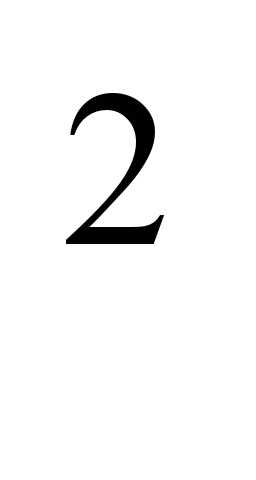x=3

Sin 2x+cos x=2

3sin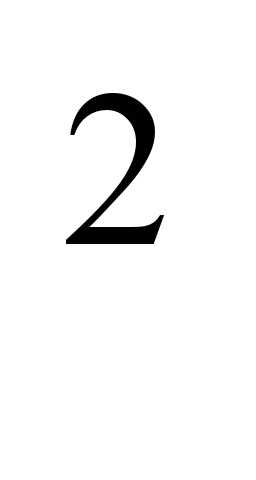x+ sin x cos x = 2 cos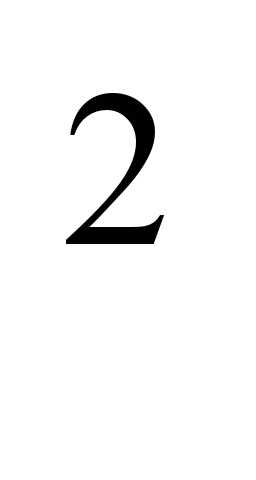

x

2ctgx – 3 tgx+5=0

Альберт Эйнштейн говорил: «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно».

Давайте решим некоторые из данных уравнений. (Один человек у доски, остальные в тетрадях).

1) введение новой переменной, приведение к квадратному.

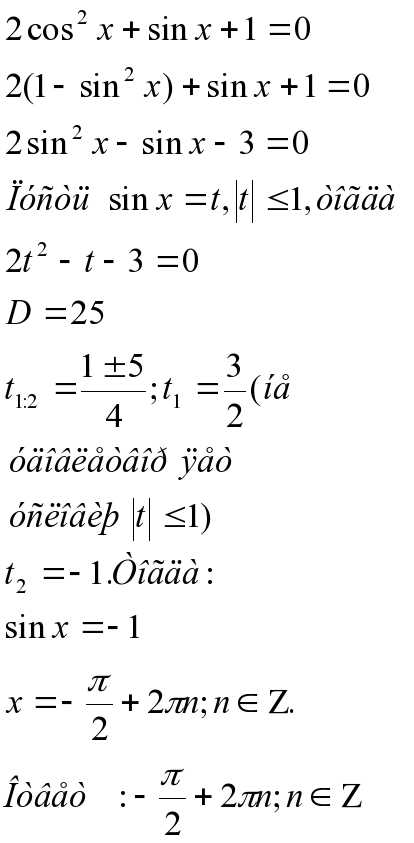
2) однородное тригонометрическое уравнение второй степени ( делим на косинус в квадрате икс):

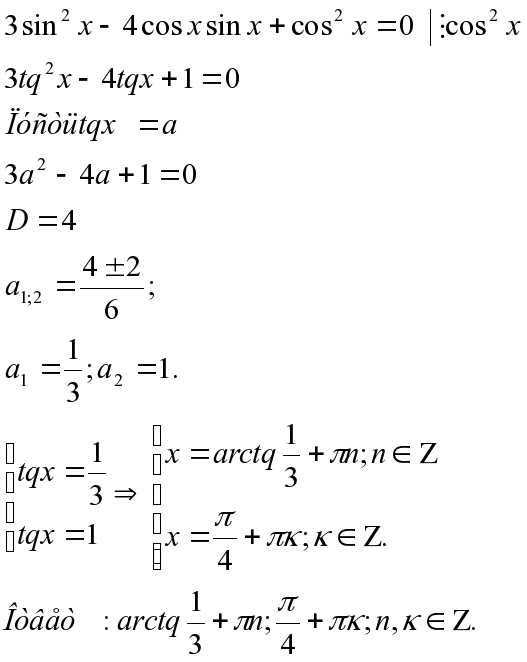
3) разложение на множители:

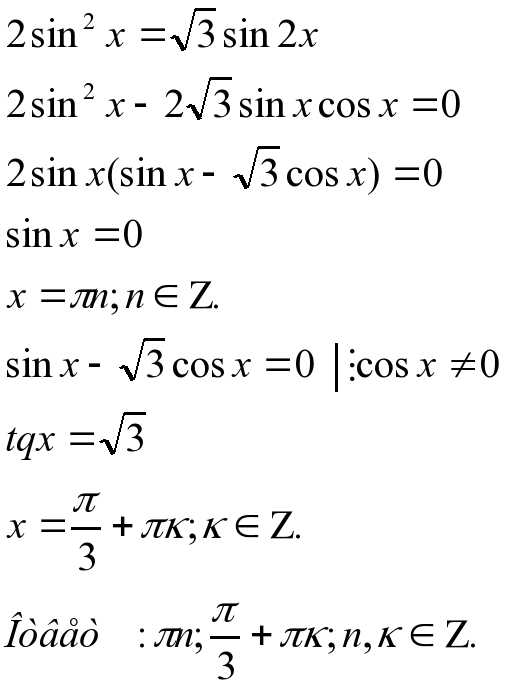
4)введение вспомогательного аргумента:

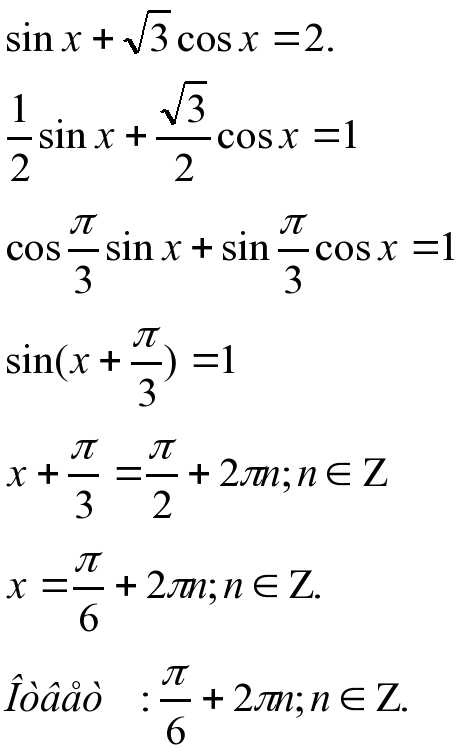
4.Физминутка.

Французский писатель Анатоль Франс говорил: «Учиться надо весело… Чтобы переваривать знания, надо поглощать их с аппетитом».Чтобы «нагулять аппетит» проведём физминутку.

5. Домашняя работа.

На домашнюю работу остаются остальные уравнения.

6.Самостоятельная работа с взаимопроверкой.

Древнегреческий поэт Нивей утверждал: «Математику нельзя изучать, наблюдая, как это делает сосед», поэтому выполним небольшую самостоятельную работу.

Вариант 1. Вариант 2.



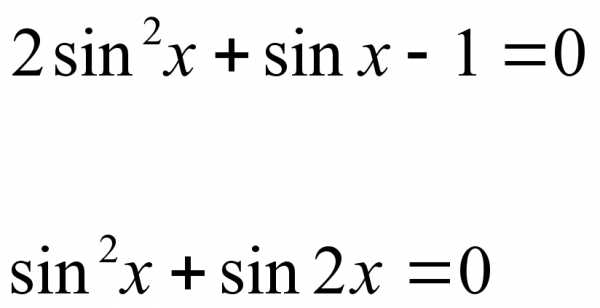
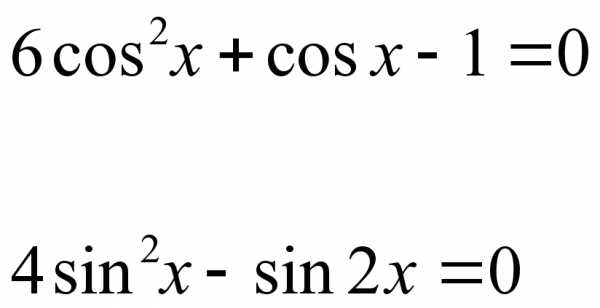
Ответы:

(взаимопроверка).

Вариант1 Вариант2


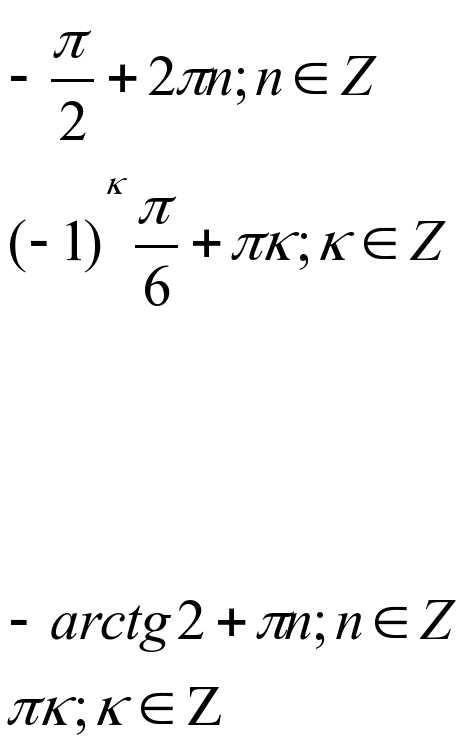
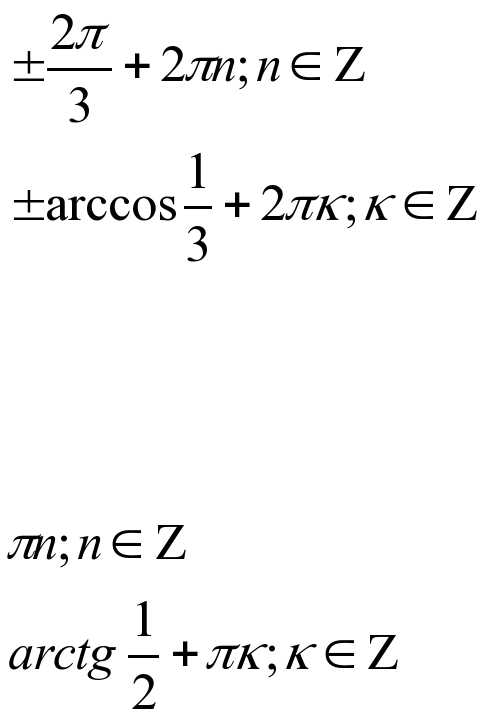
3.Итог урока, выставление оценок.

Давайте вспомним некоторые тригонометрические понятия, решим кроссворд.

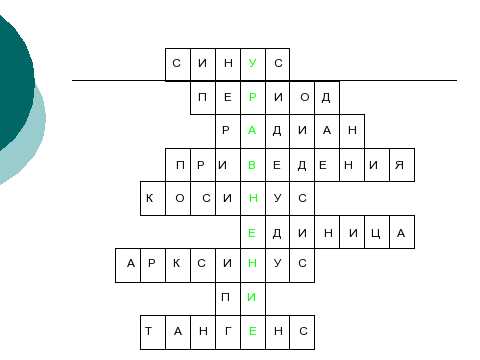
По горизонтали.

1.Ордината точки на единичной окружности? (синус).

2.2пn для функций у= sinx y=cosx? (период).

3. Угловая величина дуги, длина которой равна её радиусу (радиан).

4.Формулы вида …. называются? (приведения).

5.Абсцисса точки на единичной окружности? (косинус).

6.Сумма квадратов синуса и косинуса одного аргумента равна…?(единица).

7. Число из отрезка…,синус которого равен а? (арксинус).

8.Математическая постоянная = 3,14? (пи).

9. Отношение синуса числа к косинусу того же числа (тангенс).

3.Итог урока, выставление оценок.

Чем занимались на уроке?

Что интересное узнали на уроке?

Какие ещё высказывания о математике известных людей вы знаете?

Пожалуйста, поднимите руку те, кто считает, что эту тему понял очень хорошо?

Кто считает, что ещё нужно поработать?

Кто совсем плохо понял эту тему?

Молодцы, хорошо работали, думаю, с целями справились.

В заключении урока я хочу вам прочитать стихотворение:

“Музыка может возвышать или умиротворять душу,

Живопись – радовать глаз,

Поэзия — пробуждать чувства,

Философия – удовлетворять потребности разума,

Инженерное дело – совершенствовать материальную сторону жизни людей,

а математика способна достичь всех этих целей”.

Так сказал американский математик Морис Клайн.

Спасибо за урок!

kopilkaurokov.ru

Методическая разработка по алгебре (10 класс) по теме: Самостоятельная работа по теме «Простейшие тригонометрические уравнения».

10 класс

Самостоятельная работа

по теме  «Простейшие тригонометрические уравнения».

1 вариант.

Решите уравнения:

1)   2

2)   2

3)   2

4)   2

5)

6)

10 класс

Самостоятельная работа

по теме  «Простейшие тригонометрические уравнения».

2 вариант.

Решите уравнения:

  1. 2
  2. 2
  4. 2
  5. 2(=

1

2

3

4

5

6

1вариант

+6

4

2вариант

nsportal.ru

Тест по алгебре (10 класс) по теме: Самостоятельная работа «Тригонометрические уравнения»

По теме: методические разработки, презентации и конспекты

Контрольная работа №1, самостоятельные работы «Совместные действия обыкновенных и десятичных дробей», «Решение уравнений ( совместные действия)» в 6классе по математике

Данный материал оформлен в виде раздаточных карточек  для распечатки. Материал работ взят из сборника «Самостоятельные и контрольные работы по математике для 6 класса  » Е.С.С…

Самостоятельная работа по теме «Неполные квадратные уравнения»

Самостоятельная работа по теме «Неполные квадратные уравнения», на 4 варианта…

Самостоятельная работа по алгебре по теме:Решение уравнений 7 класс

Данная работа рекомендована для учащихся 7 класса, обучающихся по стандартной школьной программе….

Самостоятельная работа (5-10 мин.) «Коэффициенты квадратного уравнения»

Самостоятельная работа (5-10 мин.) «Коэффициенты квадратного уравнения» к УМК Алимова…

Самостоятельная работа по алгебре 8 класс( Ш.А. Алимов) «Квадратные уравнения»

Работа содержит 16 различных вариантов,выполнение  расчитано на 20-25 мин., может использоваться как самостоятельная работа обучающего  или контролирующего характера. В работе содержится 5 у…

самостоятельная работа по теме «Уравнения» 7 класс

Самостоятельная работа по алгебре для учеников 7 класса по теме «Решение уравнений» представлена в 30 вариантах (с ответами)….

7 класс, алгебра, обучающая самостоятельная работа по алгебре по теме: «Решение уравнений и задач на составление уравнений»

В самостоятельной работе даётся образец  типичного уравнения с пошаговым его решением. Далее предлагается решить четыре уравнения, постепенно, усложняя их.Так же разобран пример решения типичной …

nsportal.ru

Самостоятельная работа Тригонометрические уравнения», 10 класс

МБОУ города Иркутска СОШ №11 с углубленным изучением отдельных предметов

Самостоятельная работа по теме «Тригонометрические уравнения» 10 класс

Дмитриева Надежда Ивановна

30.03.2017

Тема: Самостоятельная работа по теме «Решение простейших тригонометрических уравнений» 10 класс.

Цель:

-проверка знаний формул решения простейших тригонометрических уравнений и тригонометрических формул;

-уметь распознавать формулы, типы уравнений и методы их решения.

Оборудование: раздаточный материал карточки-задания 6 вариантов, листочки для записи ответов, презентация для проведения самопроверки.

Ход работы

  1. Раздать карточки-задания.

  2. Решить задания карточки в тетрадях.

  3. Ответы дети записывают на листочке и сдают учителю.

  4. Самопроверка и самооценка с помощью презентации. Выписать букву, соответствующую ответу каждого задания. Оценить себя по критериям:

отметка «5»-если правильно решены 5 заданий;

отметка «4»-если правильно решены 4 задания;

отметка «3»-если правильно решены 3 задания.

  1. Анализ допущенных ошибок совместно.

  1. Карточки-задания

В-1

Решите уравнение:

  2. sin- cos=

  3. sin(2x+)=1

  4. cos(3x-)=-1

  5. 2sin2x+3cosx=0

В-2

Решите уравнение:

  1. 6cos2x+13sinx-12=0

  2. cos5xcos3x+sin5xsin3x=1

  4. sin(3x+)=0

  5. cos(4x+)=1

В-3

Решите уравнение:

  1. cos22x+2sin2x-1=0

  3. — sin2x=1

  4. sin(2x-)=0

  5. tq(

В-4

Решите уравнение:

  1. cos23x+sin3x+1=0

  2. cos(4x-)=1

  4. — cos2x=0

  5. ctq(2x-)=-

В-5

Решите уравнение:

  1. sin(

  2. cos()=1

  3. 2cos2cos+3=0

  4. — sin2x=1

В-6

Решите уравнение:

  1. sinx+cos2x=

  3. — sin2x=1

  4. sin(2x-)=-1

  5. cos()=0

  1. Таблица проверки (слайд)

а) Рядом с ответом напишите букву, соответствующую ответу из таблицы.

б) Выпишите полученное слово.

в) Оцените свой ответ.

Отметка «5»-если правильно решены 5 заданий.

Отметка «4»-если правильно решены 4 задания

Отметка «3»-если правильно решены 3 задания.

Вариант\задание

1

2

3

4

5

I

Ж

И

З

Н

Ь

II

С

Л

А

В

А

III

Ж

Е

Т

О

Н

IV

Г

О

В

О

Р

V

К

А

П

О

Т

VI

М

Е

Ч

Т

Ы

  1. Слайд проверки

А

Г

В

Е

Ж

З

И

п

К

Л

М

Н

О

Р

С

Т

Ч

Ы

Ь

Где n

infourok.ru

Самостоятельная работа по теме «Тригонометрические уравнения», 10 класс

А

Г

В

Е

Ж

З

И

п

К

Л

М

Н

О

Р

С

Т

Ч

Ы

Ь

Где n

Вариант\задание

1

2

3

4

5

I

Ж

И

З

Н

Ь

II

С

Л

А

В

А

III

Ж

Е

Т

О

Н

IV

Г

О

В

О

Р

V

К

А

П

О

Т

VI

М

Е

Ч

Т

Ы

Самостоятельная работа по теме «Решение простейших тригонометрических уравнений» 10 класс. Учитель Дмитриева Н.И.

Цель: контроль умения решать простейшие тригонометрические уравнения, знание тригонометрических формул.

Пояснения: решите уравнение, найдите в таблице свой ответ и поставьте соответствующую числу букву

Критерии оценки: «5»-5 правильных ответов; «4»-4, «3»-3, меньше- трех правильных ответов-«2»

В-1

Решите уравнение:

  2. sin- cos=

  3. sin(2x+)=1

  4. cos(3x-)=-1

  5. 2sin2x+3cosx=0

В-2

Решите уравнение:

  1. 6cos2x+13sinx-12=0

  2. cos5xcos3x+sin5xsin3x=1

  4. sin(3x+)=0

  5. cos(4x+)=1

В-3

Решите уравнение:

  1. cos22x+2sin2x-1=0

  3. — sin2x=1

  4. sin(2x-)=0

  5. tq(

В-4

Решите уравнение:

  1. cos23x+sin3x+1=0

  2. cos(4x-)=1

  4. — cos2x=0

  5. ctq(2х-)=-

В-5

Решите уравнение:

  1. sin(

  2. cos()=1

  3. 2cos2cos+3=0

  4. — sin2x=1

В-6

Решите уравнение:

  1. sinx+cos2x=

  3. — sin2x=1

  4. sin(2x-)=-1

  5. cos()=0

infourok.ru

Методическая разработка по алгебре (10 класс) по теме: Однородные тригонометрические уравнения.

. Урок по теме 

«Однородные тригонометрические уравнения» 

(10-й класс)

Цель:

  1. ввести понятие однородных тригонометрических уравнений I и II степени ;
  2. сформулировать и отработать алгоритм решения однородных тригонометрических уравнений I и II степени;
  3. научить учащихся решать однородные тригонометрических уравнений I и II степени;
  4. развивать умение выявлять закономерности, обобщать;
  5. стимулировать интерес к предмету, развивать чувство солидарности и здорового соперничества.

Тип урока: урок формирования новых знаний.

Форма проведения: работа в группах.

Оборудование: компьютер, мультимедийная установка

Ход урока

I. Организационный момент

На уроке рейтинговая система оценки знаний (учитель поясняет систему оценки знаний, заполнение оценочного листа независимым экспертом, выбранным учителем из числа учащихся). Урок сопровождается презентацией. Приложение 1.

Оценочный лист№

п\п        

Фамилия имя        

Домашнее задание

Познавательная активность

Решение уравнений

Самостоятельная

работа        

        Оценка

1

2

3

4

II. Актуализация опорных знаний..

Мы продолжаем изучение темы “Тригонометрические уравнения”. Сегодня на уроке мы познакомимся с вами с еще одним видом тригонометрических уравнений и методами их решения и поэтому повторим изученное. Все виды тригонометрических уравнений при решении сводятся к решению простейших тригонометрических уравнений. Вспомним основные виды простейших тригонометрических уравнений. Поставьте с помощью стрелок соответствии между выражениями.

III. Мотивация обучения.

 Нам предстоит работа по разгадыванию кроссворда. Разгадав его, мы узнаем название нового вида уравнений, которые научимся решать сегодня на уроке.

Вопросы спроецированы на доску. Учащиеся отгадывают, независимый эксперт заносит в оценочный лист баллы отвечающим учащимся.

Разгадав кроссворд, ребята прочитают слово “однородные”.

Кроссворд.

Если вписать верные слова, то получится название одного из видов тригонометрических уравнений.

1.Значение переменной, обращающее уравнение в верное равенство? (Корень)

2.Единица измерения углов? (Радиан)

3.Числовой множитель в произведении? (Коэффициент)

4.Раздел математики, изучающий тригонометрические функции? (Тригонометрия)

5.Какая математическая модель необходима для введения тригонометрических функций? (Окружность)

6.Какая из тригонометрических функций четная? (Косинус)

7.Как называется верное равенство? (Тождество)

8.Равенство с переменной? (Уравнение)

9.Уравнения, имеющие одинаковые корни? (Равносильные)

10.Множество корней уравнения? (Решение)

IV. Объяснение нового материала.

 Тема урока “Однородные тригонометрические уравнения”. (Презентация)

Примеры:

  1. sin x + cos x = 0
  2. √3cos x + sin x = 0
  3. sin 4x = cos 4x
  4. 2sin2 x + 3 sin x cos x + cos2 x = 0
  5. 4 sin2 x – 5 sin x cos x – 6 cos2 x = 0
  6. sin2 x + 2 sin x cos x – 3cos2 x + 2 = 0
  7. 4sin2 x – 8 sin x cos x + 10 cos2 x = 3
  8. 1 + 7cos2 x = 3 sin 2x
  9. sin 2x + 2cos 2x = 1

        

V. Самостоятельная работа

 Задачи: всесторонне проверить знания учащихся при решении всех видов тригонометрических уравнений, стимулировать учащихся к самоанализу, самоконтролю.
Учащимся предлагается выполнить письменную работу на 10 минут.  
Учащиеся выполняют на чистых листочках под копировку. По истечении времени собираются вершки самостоятельной работы, а решения под копировку остаются у учащихся.
Проверка самостоятельной работы (3 мин) проводится взаимопроверкой.
. Учащиеся цветной ручкой проверяют письменные работы своего соседа и записывают фамилию проверяющего. Затем сдают листочки.

Потом сдают независимому эксперту.

1 вариант:   1) sin x =  √3cos x                                                

                    2) 3sin2 x – 7sin x cos x + 2 cos2 x = 0

                    3) 3sin x – 2sin x cos x = 1

                    4) sin 2x⁄sin x =0

2 вариант:    1) cosx  + √3sin x = 0

                     2)2sin2 x + 3sin x cos x – 2 cos2 x = 0

                     3)1 + sin2 x = 2 sin x cos x

                     4) cos 2x ⁄  cos x = 0

VI. Подведение итогов урока

VII. Задание на дом:

Рейтинговая система оценки знаний

Домашнее задание – 12 баллов (на дом было задано 3 уравнения 4 х 3 = 12)

Активность уч-ся – 1ответ – 1 балл (4 балла максимально)

Решение уравнений 1 балл

Самостоятельная работа – 4 балла

nsportal.ru

Author: alexxlab

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *