Тест по теме «Тригонометрические функции»
Тест для самоконтроля
Тема: «Тригонометрические функции»
Вариант № 1
Задание 1. (выберите два варианта ответов) Какие из углов являются углами II четверти?
Варианты ответов:
1) 2) 3) 4)
Задание 2. (выберите один вариант ответа) Углом какой четверти является угол , если ?
Варианты ответов:
1) I 2) II 3) III 4) IV
Задание 3. (выберите один вариант ответа) Вычислите: sin1200.
Варианты ответов:
1) 2) 3) 4)
Задание 4. (выберите варианты ответов согласно тексту задания) Установите соответствие, чтобы получились верные равенства.
А) cos () = Б) cos () = В) cos () = Г) cos () =
Варианты ответов:
1) cos α 2) sin α 3) – sin α 4) – cos α
Задание 5. (выберите один вариант ответа) Упростите выражение
1 — sin.
Варианты ответов:
1) 2) 1 3) 2cos 4)
Задание 6. (выберите один вариант ответа) Чему равно значение выражения ?
Варианты ответов:
1) – 1 2) 0 3) 1 4) – 0,5
Задание 7. (выберите один вариант ответа) Укажите неверное тригонометрическое тождество.
Варианты ответов:
1) sin 2α = 2 sin α cos α 2) cos 2α = 2cos2 α – 13) 1– tg2 α = sec2 α 4) 1 + ctg2 α = cosec2 α
Задание 8. (выберите один вариант ответа) Вычислите: arcsin + arctg (–).
Варианты ответов:
1) – 2) 0 3) 4)
Задание 9. (выберите один вариант ответа) Решите уравнение: cos 2x = 1
Варианты ответов:
1) 2)
3) 4)
Задание 10. (выберите один вариант ответа) Укажите уравнение, которому соответствует решение: .
Варианты ответов:
1) tg x = 1 2) cos x = 0 3) sin x = – 1 4) ctg x =
Тест для самоконтроля
Тема: «Тригонометрические функции»
Вариант № 1
Задание 1. (выберите один вариант ответа) Какой их углов является граничным углом III и IV четвертей?
Варианты ответов:
1) 2 2) 3) 4)
Задание 2. (выберите один вариант ответа) Сравните с нулем выражения sin 1400 и cos 1850. Выберите правильную серию ответов.
Варианты ответов:
1) – – 2) – + 3) + – 4) + +
Задание 3. (выберите один вариант ответа) Вычислите: cos1500.
Варианты ответов:
1) 2) 3) 4)
Задание 4. (выберите один вариант ответа) Упростите .
Варианты ответов:
1) sin α 2) – sin α 3) cos α 4) – cos α
Задание 5. (выберите один вариант ответа) Упростите выражение .
Варианты ответов:
1) 2) 3) 4)
Задание 6. (выберите один вариант ответа) Упростите выражение .
Варианты ответов:
1) 2) 2 3) 2 4) 2
Задание 7. (выберите два варианта ответов) Укажите неверное тригонометрическое тождество.
Варианты ответов:
1) sin 2α = 2 sin α 2) cos 2α = cos2 α –
3) 1– tg2 α = sec2 α 4) 1 + tg2 α = sec2 α
Задание 8.
Варианты ответов:
1) – 2) 3) 4)
Задание 9. (выберите один вариант ответа) Укажите уравнение, которому соответствует решение
Варианты ответов:
1) ctg x = 1 2) sin x = 3) cos x = 4) tg x = – 1
Задание 10. (выберите варианты ответов согласно тексту задания) Установите соответствие между уравнением и его решением.
А) cos x = – 1 Б) cos x = 1 В) cos x = 0 Г) cos x = a
Варианты ответов:
1) 2)
3) 4)
Тест для самоконтроля
Тема: «Тригонометрические функции»
Вариант № 1
Задание 1. (выберите один вариант ответа) Какой из углов является граничным углом II и III четвертей?
Варианты ответов:
1) 2 2) 3) 4)
Задание 2. (выберите два варианта ответов) Косинусы углов какой четверти имеют знак «+»?
Варианты ответов:
1) I 2) II 3) III 4) IV
Задание 3. (выберите варианты ответов согласно тексту задания) Расположите числа в порядке возрастания.
Варианты ответов:
1) sin 1200 2) sin 1800 3) sin 900 4) sin 2000
Задание 4. (выберите один вариант ответа) Упростите выражение tg ().
Варианты ответов:
1) tg α 2) ctg α 3) – tg α 4) – ctg α
Задание 5. (выберите один вариант ответа) Упростите выражение: sin · cos · ctg – 1.
Варианты ответов:
1) 0 2) cos2 3) – sin2 4) sin2
Задание 6. (выберите один вариант ответа) Вычислите: 2sin 150 · cos 150.
Варианты ответов:
1) 2) 3) 4)
Задание 7. (выберите один вариант ответа) Укажите неверное тригонометрическое тождество.
Варианты ответов:
1) sin 2α = 2 sin α cos α 2) cos 2α = cos2 α –
3) 1 + tg2 α = sec2 α 4) 1 – tg2 α = sec2 αЗадание 8. (выберите один вариант ответа) Вычислите: arccos 1 + arcsin(–).
Варианты ответов:
1) 2) 3) – 4)
Задание 9. (выберите один вариант ответа) Решите уравнение: sin x – = 0.
Варианты ответов:
1) 2)
3) 4)
Задание 10. (выберите один вариант ответа) Укажите уравнение, которому соответствует решение
Варианты ответов:
1) tg x = 0 2) cos x = 1 3) cos x = – 1 4) сtg x = 0
Тест для самоконтроля
Тема: «Тригонометрические функции»
Задание 1. (выберите один вариант ответа) В какой четверти находится угол ?
Варианты ответов:
1) I 2) II 3) III 4) IV
Задание 2. (выберите один вариант ответа) Какой четверти принадлежит угол , если cos α < 0 и sin α < 0?
Варианты ответов:
1) I 2) II 3) III 4) IV
Задание 3. (выберите один вариант ответа) Сравните с нулем выражения: sin 140º , cos 285º, ctg 152º. Выберите правильную серию ответов.
Варианты ответов:
1) + – – 2) – + – 3) + + + 4) + + –
Задание 4. (выберите один вариант ответа) Упростите выражение ctg ().
Варианты ответов:
1) tg α 2) ctg α 3) – tg α 4) – ctg α
Задание 5. (выберите один вариант ответа) Упростите выражение 9 + 5sin + 5cos.
Варианты ответов:
1) 14 2) 5 3) 9 + 5cos 2 4) 9 – 5cos 2
Задание 6. (выберите один вариант ответа) Упростите выражение .
Варианты ответов:
1) 2) 3) cos 4α 4)
Задание 7. (выберите варианты ответов согласно тексту задания) Установите соответствие, чтобы получились верные равенства.
А) cos2 α – = Б) sin2 α + cos2 α = В) 2 sin α cos α = Г) 1 + tg2 α =
Варианты ответов:
sin 2α 2) cos 2α 3) sec2 α 4) 1
Задание 8. (выберите один вариант ответа) Вычислите: arccos () – arctg 1.
Варианты ответов:
1) 2) 3) – 4)
Задание 9. (выберите один вариант ответа) Найдите решение уравнения
sin x = 0.
Варианты ответов:
1) 2)
3) 4)
Задание 10. (выберите два варианта ответов) Укажите уравнение, для которого является решением
Варианты ответов:
1) tg x = – 1 2) sin x = – 1 3) cos x = – 1 4) сtg x = – 1
Ответы на тест
13 баллов
«5» — 12, 13 баллов
«4» — 10, 11 баллов
«3» — 7, 8, 9 баллов
«2» — 6 и менее баллов
infourok.ru
Тест по теме «Тригонометрические функции, их свойства и графики»
Тест
Вариант I
А1. Значение sin равно:
а) б) — ; в) ; г) — .
А2. Найдите множество значений функции: y = 1 + 2 cos 3x
а) ; б) ; в) ; г)
А3. Какие из функций являются чётными:
1) у = sin 3x; 2) y = x sin5x; 3) y = x3 – sin 2x; 4) y = .
3) 1 и 3; б) 2 и 3; в) 2 и 4; г) 3 и 4.
А4. Период функции y = sin равен:
а) ; б) ; в) ; г) .
А5. Укажите область определения функции у = 6 + 5cosx.
а) множество действительных чисел;
б) множество действительных чисел, кроме чисел вида 𝜋n, n ∊ Z;
в) множество действительных чисел, кроме чисел вида ;
г) .
А6. График какой функции изображён на рисунке?
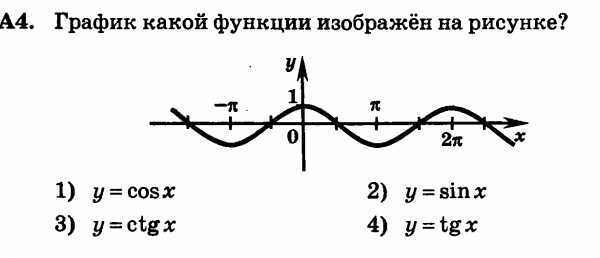
а) у = cosx; б) y = sinx; в ) y = ctgx; г ) y = tgx.
А7. Найдите координаты всех точек пересечения графика функции у = сtgx с осью абсцисс.
а) ; б) ;
в) ; г) нет точек пересечения.
В1. Укажите наименьшее значение функции у = — sinx — 6
B2. Найдите ординату точки пересечения графика функции у = 5 — 2sinx с осью ординат.
Тест
Вариант II
А1. Значение cos ( — равно:
а) б) — ; в) ; г) — .
А2. Найдите область значений функции: у = 3 – 4 sin 5x.
а) ; б) ; в) ; г) .
А3. Какие из функций являются нечётными:
1) y = cos 5x; 2) y = x – sin 5x; 3) y = 1 + tg x; 4) y = x cos x.
а) 1 и 3; б) 2 и 4; в) 2 и 3; г) 1 и 4.
А4. Период функции y = cos равен:
а) ; б) ; в) ; г) .
А5. Укажите область определения функции у = 1 — 4tgx
а) ;
б) множество действительных чисел;
в) множество действительных чисел, кроме чисел вида 𝜋n, n ∊ Z;
г) множество действительных чисел, кроме чисел вида .
А6. График какой функции изображён на рисунке?
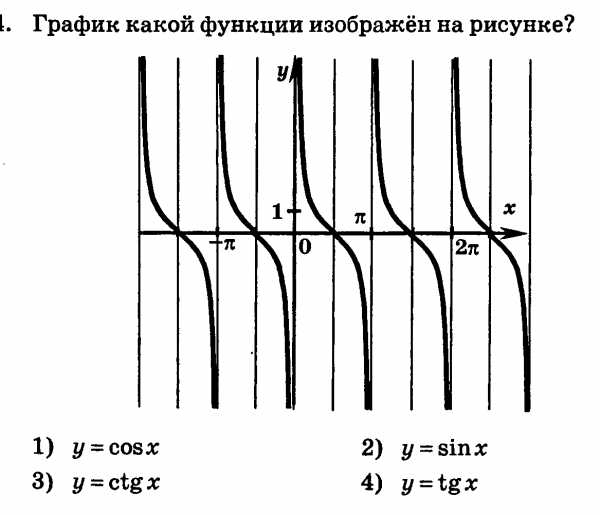
а) у = cosx; б) y = sinx; в ) y = ctgx; г ) y = tgx.
А7. Найдите координаты всех точек пересечения графика функции у = sinx с осью абсцисс.
а) ; б) ;
в) ; г) нет точек пересечения
В1. Укажите наибольшее значение функции у = — 7 — cosx.
В2. Найдите ординату точки пересечения графика функции у = 1 — 5cosx с осью ординат.
infourok.ru
Тест «Обратные тригонометрические функции»
5.
Лист эталонных ответов
Контрольный талон
Фамилия_____________
Вариант______________
Ответы:
_____
_____
_____
_____
_____
Оценка_____
Контрольный талон
Фамилия_____________
Вариант______________
Ответы:
_____
_____
_____
_____
_____
Оценка_____
Контрольный талон
Фамилия_____________
Вариант______________
Ответы:
_____
_____
_____
_____
_____
Оценка_____
Контрольный талон
Фамилия_____________
Вариант______________
Ответы:
_____
_____
_____
_____
_____
Оценка_____
Контрольный талон
Фамилия_____________
Вариант______________
Ответы:
_____
_____
_____
_____
_____
Оценка_____
Контрольный талон
Фамилия_____________
Вариант______________
Ответы:
_____
_____
_____
_____
_____
Оценка_____
Контрольный талон
Фамилия_____________
Вариант______________
Ответы:
_____
_____
_____
_____
_____
Оценка_____
Контрольный талон
Фамилия_____________
Вариант______________
Ответы:
_____
_____
_____
_____
_____
Оценка_____
Контрольный талон
Фамилия_____________
Вариант______________
Ответы:
_____
_____
_____
_____
_____
Оценка_____
infourok.ru
Тест для проведения дифференцированного зачета по математике по теме «Тригонометрические функции»
Тест для проведения дифференцированного зачета
по математике по теме «Тригонометрические функции»
Цель: установление уровня сформированности предметных, метапредметных и личностных результатов обучающихся по теме «Тригонометрические функции» .
Требования стандарта:
Личностные результаты:
формирование ответственного отношения к учению,
формирование готовности и способности обучающегося к саморазвитию и самообразованию на основе мотивации к обучению и познанию.
Метапредметные результаты:
умение осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач,
умение оценивать правильность выполнения учебной задачи.
Предметные результаты:
Овладение приемами исследования функций на периодичность, на возрастание и убывание, на нахождение множества значений, на наибольшее и наименьшее значение функции.
Развитие умения использовать функционально-графические представления для решения различных математических задач.
Инструкция по выполнению работы
На выполнение всей работы отводится 40 минут.
Работа состоит из 7 заданий. Среди них 3 задания с выбором одного верного ответа из предложенных (задания 1 – 3), 1 задание на соотнесение (задание 4), 1 задание с кратким ответом (задание 6), 1 задание на составление тригонометрического неравенства (задание 6) и задание, требующее подробное аргументированное решение.(задание 7)
Задания 1 – 3. К каждому заданию приводятся варианты ответа, один из которых верный. За каждое верно выполненное задание выставляется 1 балл.
Задание 4 на соотнесение. Учащиеся вписывают в приведенную в ответе таблицу под каждой цифрой соответствующую букву. За каждую верно указанную пару начисляется 1 балл. Максимальный балл за задание 4.
Задание 5 со свободным ответом. Учащиеся представляют решение на черновике и выписывают в бланк полученный ответ. Максимальный балл за задание 4.
Задание 6 на составление тригонометрического неравенства по заданным условиям и на основе имеющихся знаний по теме. Максимальный балл за задание 3.
Задание 7 предусматривает подробное решение. Максимальный балл за задание 4.
Максимальное количество баллов за всю работу – 18
Диагностическая работа по теме « Тригонометрические функции»
Вариант 1
Укажите наименьший положительный период функции у=, выпишите правильный ответ
1); 2); 3)-2
Выясните при каких значениях х функция у= существует? выпишите правильный ответ
1)хk,k
2)х,k
3)х+k, k
Запишите в порядке возрастания значения в ответе запишите номер верного ряда
Установите соответствие между графиками и их формулами. Ответ запишите в таблицу.
А
У=
Б
У=
В
У=
Г
У=
Д
У=tgх
1
2
3
4
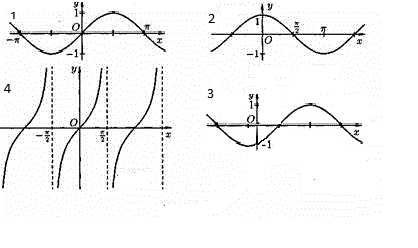
Найдите наибольшее значение функции у=2- 3 и выпишите правильный ответ
Подберите числа А и С и по данному рисунку составьте неравенство, решите его и запишите полученный ответ.
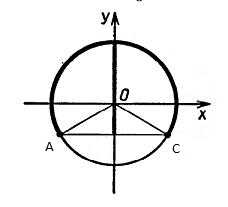
7. Постройте график функции у=2sin(х-), и опишите шаги построения.
Диагностическая работа по теме « Тригонометрические функции»
Вариант 2
Укажите наименьший положительный период функции у=, выпишите правильный ответ
1); 2); 3)-2
Выясните при каких значениях х функция у= существует? выпишите правильный ответ
1)х,k
2)х,k
3)хk, k
Запишите в порядке возрастания значения в ответе запишите номер верного ряда
Установите соответствие между графиками и их формулами. Ответ запишите в таблицу.
А
У=)
Б
У=
В
У=
Г
У=
Д
У=tgх
1
2
3
4

5. Найдите наименьшее значение функции у=1- 4 и выпишите правильный ответ.
6. Подберите числа А и С и по данному рисунку составьте неравенство, решите его и запишите полученный ответ.
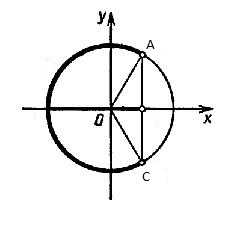
7. Постройте график функции у=3 sin (х- ), и опишите шаги построения.
Критерии оценивания тестового контроля знаний
Оценка «отлично»
77 – 100 % правильных ответов
14 – 18баллов
Оценка «хорошо»
45 – 75 % правильных ответов
8 – 13 баллов
Оценка «удовлетворительно»
22 – 40 % правильных ответов
4 – 7 баллов
Оценка «неудовлетворительно»
20% и менее правильных ответов
0 – 3 балла
Содержание заданий
Уровни деятельности
УУД
Критерии
№ задания
Макс. балл
Эмоц.-психол.
Личностные
Знание определения периодичности тригонометрических функций. Знание свойств тригонометрических функций.
1
1
Регуля-тивный
Регуля-тивные
Знание понятия области определения функций
2
Знание алгоритма решения тригонометрического уравнения, умение находить область определения функции , знание значений арксинуса и арккосинуса числа.
2
1
Регулятивный
Регулятивные-
Знание чётности и нечётности тригонометрических функций.
3
1
Знание свойств возрастания и убывания тригонометрических функций и Умение осознанно применять их .
Соци-альный
Комму-
никати-вные
Умение распознать по графику функцию
4
4
Знание свойств функций
Анали-тичес-кий
Позна-
ватель-
ные
Знание понятия множество значений функции.
5
4
Умение находить множество значений тригонометрической функции
Умение отыскать наибольшее или наименьшее значение
Умение применить алгоритм решения данной задачи
Умение оценивать правильность выполнения учебной задачи
Умение осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач.
Творчс-кий
Личност-ные
Умение составить тригонометрическое неравенство по заданным условиям и на основе имеющихся знаний по теме.
6
3
Готовность и способность обучающегося к саморазвитию и самообразованию на основе мотивации к обучению и познанию.
Самосовершенствова-ния
Регуля-
тивные
Построение графика тригонометрической функции с помощью сдвигов (многошаговая задача).
7
4
Готовность и способность обучающегося к саморазвитию и самообразованию на основе мотивации к обучению и познанию.
Ответы
№ задания
1
2
3
4
5
6
6
Ответ
1 вар
4
1
3
БГДВ
5
Sinх≥ —
х[-], k
2 вар
4
3
1
БДГА
-3
Cos х
х+2 ;+2
№ задания
Критерии оценки
Балл
5
верно выполнена запись множества значений функции
представлено правильное решение
выписан верный ответ.
4
выполнены все условия, но допущена вычислительная ошибка, с ее учетом все шаги выполнены верно.
2
2
1
0
6
верно подобраны числа А и С
правильно составлено неравенство, выбран знак неравенства в соответствии с условием,
безошибочно использована закрашенная часть окружности и записан верный ответ
3
выполнены два условия из трех,
выполнены все условия, но допущена вычислительная ошибка, с ее учетом все шаги выполнены верно.
2
1
0
7
4
3
2
1
0
infourok.ru
Тесты по тригонометрии
Разделы: Математика
Вариант № 1
Часть 1
- Выразить в радианах угол α = 20°
1) π/5 2) π/7 3) π/9 4) π/10
- Выразить в градусах угол α = 4π/45
1) 16º 2) 15º 3) 20º 4) 35º
- Какой четверти числовой окружности принадлежит точка t = 19π/4
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: 3cos2α — 6 + 3sin2α
1) 1 2) -5 3) 3 4) -3
- Найти значение выражения 4cos2x + 2 , если sin2x = 0,6
1) 4,56 2) 3,6 3) 4,6 4) 8,4
- Упростить выражение: sin4α — sin6α + cos2α + cos4α — cos6α
1) cos10α + cos2α 2) 2cos2α 3) cosα — cos6α 4) cos2α + sin10α
- Упростить выражение
1) sinα 2) -sinα 3) 2cosα + sinα 4) cosα + sinα
- Найти область значений функции y = sin2x
1) [-1;1] 2) [-2;2] 3) [0;-2] 4) [-2;0]
- Найти tgα, если cosα = -2/3 и
- Решить уравнение sin2x = 1/2
Часть 2
- Найти значение выражения .
- Решить уравнение 2sin22x + 7cos2x = 3
- Решить уравнение 6sin2x + sinx — cosx — cos2x = 2
- Найти значение выражения 169sin2x, если cosx = -5/13, -π < x < 0
- Сколько корней имеет уравнение
- Найти наименьшее целое значение функции .
Вариант № 2
Часть 1
- Выразить в радианах угол α = 240°
1) 4π/5 2) 2π/3 3) 4π/3 4) 3π/2
- Выразить в градусах угол α = 5π/36
1) 40º 2) 35º 3) 25º 4) 50º
- Какой четверти числовой окружности принадлежит точка t = -23π/6
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: 9cos2α — 16 + 9sin2α
1) 2 2) -25 3)-15 4) -7
- Найти значение выражения 3 — 2tg2x · cos2x, если sinx = 0,1
1) 2,8 2) 1,02 3) 2,98 4) 3,02
- Упростить выражение: cos3α — cos2α — cosα — sin3α — sin2α
1) cos5α — cosα 2) 0 3) sinα — cosα 4) cos5α + cosα
- Упростить выражение
1) 3cosα 2) cosα 3) 0 4) 2cosα — sinα
- Найти множество значений функции y = sinx — 3
1) [-4;0] 2) [-4;-2] 3) [-3;3] 4) [-3;-2]
- Найти значение выражения
- Решить уравнение
Часть 2
- Найти значение выражения .
- Решить уравнение 2sin2x + 7cosx + 2 = 0
- Решить уравнение 2sin2x -3sinx · cosx + 3cos2x = 2
- Найти значение выражения 5sin2x, если
- Сколько корней имеет уравнение
- Найти наибольшее целое значение функции
Вариант № 3
Часть 1
- Выразить в радианах угол α = 50°
1) 3π/5 2) 6π/7 3) 4π/9 4) 5π/18
- Выразить в градусах угол α = 49π/36
1) 230º 2) 245º 3) 240º 4) 265º
- Какой четверти числовой окружности принадлежит точка t = 37π/4
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: -3cos2α + 8 — 3sin2α
1) 5 2) -5 3)3 4) -3
- Найти значение выражения 3 + 2tg2x · cos2x, если sinx = 0,3
1) 3,18 2) 3,6 3) 4,8 4) 4,82
- Упростить выражение: cos5α · cos7α — cosα + sin5α · sin7α
1) cos12α — cosα 2) sin12α — cosα 3) sin2α — cosα 4) cos2α — cosα
- Упростить выражение
1) sin2α 2) cos2α 3) 3cos2α 4) cos3α
- Найти множество значений функции y = 3sinx — 2
1) [-5;1] 2) [-1;1] 3) (-∞; +∞) 4) [-1;5]
- Найти значение выражения
1) √3 2) √3 + 1 3) 1/2 + 3√3 4) 1
- Решить уравнение 2cos2x — 3sinx = 1/2
Часть 2
- Найти значение выражения
- Решить уравнение 2sin2x + 1 = 5cosx
- Решить уравнение 4sin2x + sinx — cosx + cos2x = 2
- Найти значение выражения 26sin2x, если
- Сколько корней имеет уравнение
- Найти наибольшее целое значение функции
Вариант № 4
Часть 1
- Выразить в радианах угол α = 315°
1) 7π/4 2) 4π/7 3) 5π/9 4) 3π/10
- Выразить в градусах угол α = 13π/9
1) 245º 2) 250º 3) 275º 4) 260º
- Какой четверти числовой окружности принадлежит точка t = 27π/4
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: 1,5cos2α — 6,5 + 1,5sin2α
1) 1 2) -5 3)3 4) -3
- Найти значение выражения 7sin2x — 3, если cos 2x = 0,7
1) 1 2) -0,9 3) -1,2 4) -1
- Упростить выражение: 2cosα — cosα + sin2α — sinα — sin(α — 6π)
1) cos3α + sinα 2) 2sinα 3) 0 4) cos3α — sinα
- Упростить выражение
1) sin2x 2) -sin2x 3) 4) cos2x
- Найти множество значений функции y = cosx — 3
1) [-1;1] 2) [2;4] 3) [-4;-2] 4) [-3;-2]
- Найти значение выражения
1)1,5 2) 2√3 3) 1 — √3 4) 0,5
- Решить уравнение 2cos 2x — 3sinx = 0
Часть 2
- Найти значение выражения
- Решить уравнение 2cos 2x + 9sinx = 6
- Решить уравнение 4sin2x — 4sinx — cosx + 6cos2x = 3
- Найти значение выражения 7tg2α, если
- Сколько корней имеет уравнение
- Найти наименьшее значение функции
Вариант № 5
Часть 1
- Выразить в радианах угол α = 210°
1) 7π/5 2) 5π/7 3) 7π/6 4) 4π/5
- Выразить в градусах угол α = 19π/9
1) 320º 2) 365º 3) 380º 4) 375º
- Какой четверти числовой окружности принадлежит точка t = 31π/3
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: 10cos2α — 7 + 10sin2α
1) 1 2) -5 3)3 4) -3
- Найти значение выражения 6sin2x — 3, если cos2x = 0,3
1) -1,4 2) -0,2 3) 1,2 4) 0,8
- Упростить выражение: sin3α — cos2α + sin2α — cos3α — cos(2π -α)
1) cos3α + sinα 2) 2sinα 3)0 4) cos3α — sinα
- Упростить выражение
1) -6sinx 2) 2sinx 3) 3cosx — sinx 4) -2sinx
- Найти множество значений функции y = sinx + 2
1) [-1;1] 2) [0;2] 3) [1;3] 4) [2;3]
- Найти значение tgα, если
1) -2 2) 2 3) 0,5 4) -0,5
- Решить уравнение 1 + 2cosx — sin2x = 0
Часть 2
- Найти значение выражения
- Решить уравнение 2cos2x = 11sinx + 7
- Решить уравнение sin2x — 2sinx — cosx = cos2x + 1
- Найти значение выражения
- Сколько корней имеет уравнение
- Найти наибольшее целое значение функции
Вариант № 6
Часть 1
- Выразить в радианах угол α = 330°
1) 11π/6 2) 11π/5 3) 10π/9 4) 9π/10
- Выразить в градусах угол α = 2π/5
1) 72º 2) 75º 3) 65º 4) 52º
- Какой четверти числовой окружности принадлежит точка t = -41π/3
1) первой 2) второй 3) третьей 4) четвёртой
- Упростить выражение: 13cos2α — 15 + 13sin2α
1) 2 2) -2 3) 0 4) 28
- Найти значение выражения 5cos2x — 3, если sin2x = 0,2
1) 1,2 2) 2,1 3) -1 4) 1
- Упростить выражение: sin2,5α — cos1,5α + sin1,5α — cos2,5α + cos(4π — α)
1) sin4α — cosα 2) sinα + cosα 3) sinα — cosα 4) cosα + sin4α
- Упростить выражение
1) sinα 2) cosα 3) cosα + 2sinα 4) 2cosα + sinα
- Найти наибольшее значение функции y = 2cosx — 14
1) -16 2) 2 3) -14 4) -12
- Найти значение выражения
- Решить уравнение
Часть 2
- Найти значение выражения
- Решить уравнение cos2x + 2 sinx = 2
- Решить уравнение 8sin2x + 3sinx — cosx + cos2x = 3
- Найти значение выражения
- Найти сумму корней уравнения принадлежащих промежутку [0; -2π]
- Найти наименьшее целое значение функции
8.07.2010
urok.1sept.ru
Тематический тест на тему «Тригонометрические функции» (10 класс)
Тест 2. «Тригонометрические функции»
Вариант 1
Часть В.
В 1. Арксинус — это угол…
а) танген которого равен б) синус которого равен а
в) косинус которого равен
В2. sinx=a. Чему равно значение х?
а) ±arccos a + 2πn б) (-1)ͫ arcsin a + πn в) не знаю
В 3. Чему равен синус 60° ?
а) ½ б) 1 в) г)
В 4. Укажите множество значений функции y=sin3x+2.
а) (-5; 5) б) (1; 5) в) [ 1; 3] г) [ 1; 5]
В 5. Укажите наибольшее число из области значений функции y=2cos(3x/2)-4.
а) -6 б) 6 в) -2 г) -4
Часть С.
С 1. sin(arccos 12/13)=?
Ответ:
С 2. Известно, что cos α = , Найдите значение sin α.
Ответ:
Вариант 2
Часть В.
В 1. Аркосинус — это угол…
а) танген которого равен б) синус которого равен а
в) косинус которого равен
В 2. cos x = a. Чему равно значение х?
а) ±arccos a + 2πn б) (-1)ͫ arcsin a + πn в) не знаю
В 3. Чему равен косинус 30° ?
а) 1 б) ½ в) г)
В 4. Укажите множество значений функции y=cos2x+3.
а) (-5; 5) б) (1; 4) в) [ 2; 4] г) ( 2; 4)
В 5. Укажите наименьшее целое число из области значений функции y=12,7+5sin(3x-2).
а) -5 б) 8 в) 5 г) 17
Часть С.
С 1. Найдите tg(arcsin 3/5)=?
Ответ:
С 2. Известно, что sin α = — 0,8, π ˂ α ˂ Найдите значение cos α.
Ответ:
infourok.ru
Тест по теме «Основы тригонометрии»
Дисциплина «Математика».
Раздел «Основы тригонометрии».
Тест разработан для учащихся 10-11 классов, а также студентов 1 курса СПО, обучающихся на базе 9 классов.
Вопросы теста
Косинусом называется … точки единичной окружности.
абсцисса
ордината
координата
затрудняюсь ответить
Тангенс углаопределяется отношением
нет правильного ответа
Если угол содержит градусов, то его радианная мера равна
При каких значениях угла (в градусной мере) не существует тангенс?
Установите соответствие между видами тригонометрических уравнений.
-
Тригонометрическое уравнение, приводимое к квадратному
Однородное тригонометрическое уравнение
Простейшее тригонометрическое уравнение
Тригонометрическое уравнение, решаемое с помощью формул преобразования суммы одноименных тригонометрических функций в произведении
Если существует такое число Т (называемое периодом), что для всех х выполняется равенство и , то функция называется …
периодической
тригонометрической
нечетной
простейшей
Укажите функцию с периодом :
На единичной окружности тангенс – это
ордината
абсцисса
отношение абсциссы к ординате
отношение ординаты к абсциссе
установите соответствие:
-
основное тригонометрическое тождество
формула половинного аргумента
формула сложения аргументов
формула двойного аргумента
Сжатие функции произойдет, если
Установите соответствие между тригонометрическим уравнением и его решением
При , какое из уравнений не будет иметь решения?
Область определения функции
R
Q
Ординатой точки единичной окружности называется:
косинусом
котангенсом
синусом
тангенсом
Абсциссой точки единичной окружности называется:
котангенсом
синусом
тангенс
косинусом
Основное тригонометрическое тождество имеет вид:
sin2 х — cos2х = 1
sin х + cos x = 0
sin2x + cos 2х= 1
sin x + cos x — 1
Какая из функций является четной:
tg х
Укажите неверное утверждение
-
 a.
a.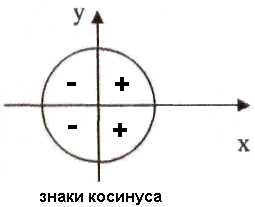 b.
b.c.
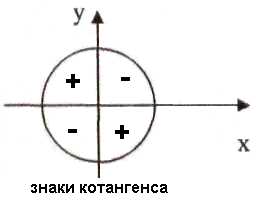 d.
d.
Продолжить выражение …
cos 2x
sin 2x
tg 2x
нет ни одного верного
Множество значений функций у = sin x, у = cos x является отрезок:
[-1;1)
(-1;1]
(-1;0)
[-1;1]
Арккосинусом числа а называется такое число из отрезка … косинус которого равен а
Период функций у = cos x, у = sin x равен
Определить соответствие
-
tga ctga
1
-cos2a — sin2a
cos2a — sin2a
cos2a
-1
Установите соответствие между радианной и градусной мерой
-
2100
1500
750
2250
При построении графика функции у = sin2x произойдет
растяжение по оси ОУ
сжатие по оси ОУ
сжатие по оси ОХ
растяжение по оси ОХ
Какие из функций являются нечетными
у = tg х, у = ctg x, у = cos х
у = tg x, у = sin x, у = cos х
у = tg х, у = ctg х, y = sin x
у = ctg x , у = sin x, у = cos х
Арктангенсом числа a называется такое число из интервала …, тангенс которого равен α.
Арккотангенсом числа а называется такое число из интервала …, котангенс которого равен α.
Синус двойного аргумента определяется формулой
2sin а + 2cos а
в радианной мере угол в 1200
Выразите в градусах
900
1800
2700
1500
Установите соответствие
При построение графика функции у = 2sin x произойдет:
растяжение функции у = sin x вдоль оси ОХ
сужение функции у = sin x вдоль оси ОХ
растяжение функции у = sin x вдоль оси 0Y
сужение функции у = sin x вдоль оси 0Y
Найдите число arctg 0
0
затрудняюсь ответить
Существует ли arсctg 0
да
нет
затрудняюсь ответить
Продолжить выражение cos cos + sin sin
cos ( — )
sin ( — )
cos ( + )
sin ( + )
Упростите
a.
b.
c.
d.
Укажите выражения, имеющие знак плюс
cos 2500·sin 3300
tg 1750·ctg 2000
cos 1000·sin 1000
cos 1500·sin 1500
Преобразуйте
cos2
sin2
sin ·cos
затрудняюсь ответить
Какая функция на отрезке является возрастающей
sin x
tg x
cos x
ctg x
Ключи к тесту.
-
1
2
3
4
5
6
7
8
9
10
a
a
b
c
1a, 2d,
3c, 4b
a
b
d
1a, 2c, 3b, 4d
c
-
11
12
13
14
15
16
17
18
19
20
1c, 2b, 3d, 4a
a
c
c
d
c
b
d
b
d
-
21
22
23
24
25
26
27
28
29
30
a
c
1a, 2d, 3c, 4b
1b, 2c, 3a, 4d
c
c
d
c
a
b
-
31
32
33
34
35
36
37
38
39
40
c
1d, 2a, 3c, 4b
c
b
a
a
d
a
b
c
Шарапова Юлия Владимировна,
преподаватель математики
ОАОУ СПО «Астраханский социально педагогический колледж»,
414040 г. Астрахань, ул. Коммунистическая , 48
infourok.ru
