Теория решение уравнений: Базовые методы решения уравнений и неравенств - Математика - Теория, тесты, формулы и задачи - Управленческое образование

Содержание

Базовые методы решения уравнений и неравенств — Математика — Теория, тесты, формулы и задачи

Знание базовых методов решения уравнений и неравенств является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Базовые методы решения уравнений и неравенств, которые надежно усвоены и отработаны учеником — это один из основных инструментов, которым он должен оперировать при решении математических задач. На этой странице сайта представлены примеры применения базовых методов решения уравнений и неравенств из школьной математики.

Изучать базовые методы решения уравнений и неравенств из школьной математики онлайн:

Как успешно подготовиться к ЦТ по физике и математике?

Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:

Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.

Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
Посетить все три этапа репетиционного тестирования по физике и математике.
Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка.

Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

Теория линейных уравнений и задачи

Значение неизвестной величиной, для которой из данного уравнения мы получим истинное числовое равенство, называется корнем этого уравнения. Два уравнения называются эквивалентными, если множества их корней совпадают, корни первого уравнения являются также корнями второго и наоборот. Действуют следующие правила:
1. Если в данном уравнении значение заменяется другим, но идентичным, мы получаем уравнение, эквивалентное данному.
2. Если в данном уравнении некоторое значение переносится из одной стороны на другую с противоположным знаком, мы получаем уравнение, эквивалентное (равное) заданному.

3. Если мы умножаем или делим обе стороны уравнения на одно и то же число, отличное от нуля, мы получаем уравнение, эквивалентное заданному.
Уравнение вида $ax + b = 0$, где $a, b$ — заданные числа, называется простым уравнением по отношению к неизвестной величине $х$.

Задача 1 Решите уравнение:
A) $16x + 10 – 32 = 35 – 10x — 5$
B) $y + \frac{3}{2}y + 25 = \frac{1}{2}y + \frac{3}{4}y – \frac{5}{2}y + y + 37$
C) $7u – 9 – 3u + 5 = 11u – 6 – 4u$

Решение:

A)После проведения некоторых действий, получаем
$16х – 22 = 30 – 10x$
После использования правила 2 мы находим, что $16x + 10x = 30 + 22$
После сложения получаем $26x = 52$
Мы находим неизвестную величину, разделив произведение на другой множитель.
Тогда $x = \frac{52}{26}$
Отсюда $x = 2$

B) По аналогии с A) мы находим:

$y\left(1 + \frac{3}{2}\right) + 25 = y\left(\frac{1}{2} + \frac{3}{4} – \frac{5}{2} + 1\right) + 37 \Leftrightarrow$
$\frac{5}{2}y + 25 = -\frac{1}{4}y + 37 \Leftrightarrow \frac{5}{2}y + \frac{1}{4}y = 37 — 25 \Leftrightarrow$
$\frac{11}{4}y = 12 \Leftrightarrow y = \frac{12 \cdot 4}{11} \Leftrightarrow y = \frac{48}{11}$

C) $4u – 4 = 7u – 6 \Leftrightarrow 6 – 4 = 7u – 4u \Leftrightarrow 2 = 3u \Leftrightarrow u = \frac{2}{3}$

Задача 2 Решите уравнение:
A) $7(3x – 6) + 5(x — 3) — 2(x — 7) = 5$
B) $(x -3)(x + 4) — 2(3x — 2) = (x — 4)^2$
C) $(x + 1)^3 – (x — 1)^3 = 6(x^2 + x + 1)$

Решение:

A) $21x — 42 + 5x — 15 — 2x + 14 = 5\Leftrightarrow$
$21x + 5x — 2x = 5 + 42 + 15 — 14 \Leftrightarrow$
$24x = 48 \Leftrightarrow x = 2$

B) $x^2 + 4x — 3x — 12 — 6x + 4 = x^2 — 8x + 16 \Leftrightarrow$
$x^2 — 5x – x^2 + 8x = 16 + 12 – 4 \Leftrightarrow$
$3x = 24 \Leftrightarrow x = 8$

C) $x^3 + 3x^2 + 3x + 1 – (x^3 — 3x^2 + 3x — 1) = 6x^2 + 6x + 6 \Leftrightarrow$
$x^3 + 3x^2 + 3x + 1 – x^3 + 3x^2 + 1 = 6x^2 + 6x + 6 \Leftrightarrow$
$2 = 6x + 6 \Leftrightarrow 6x = -4 \Leftrightarrow x = -\frac{2}{3}$

Задача 3 Решите уравнение:
A) $\frac{5x-4}{2} = \frac{0,5x+1}{3}$
B) $1 –\left[\frac{x-3}{5}\right] = \frac{-3x+3}{3}$
C) $\frac{x+1}{3} – \frac{2x+5}{2} = -3$
D) $\frac{3(x-1)}{2} + \frac{2(x+2)}{4} = \frac{3x+4,5}{5}$

Решение:

A) $\frac{5x-4}{2} – \frac{0,5x+1}{3} \Leftrightarrow$
$3(5x — 4) = 2(0,5x + 1) \Leftrightarrow$
$15x — 12 = x + 2 \Leftrightarrow$
$15x – x = 12 + 2\Leftrightarrow$
$14x = 14 \Leftrightarrow x = 1$

B) $1 – \left[\frac{x-3}{5}\right] = \frac{3(1-x)}{3}\Leftrightarrow$
$1 –\left[\frac{x-3}{5}\right] = 1 – x \Leftrightarrow$
$-x + 3 = — 5x \Leftrightarrow$
$5x – x = — 3 \Leftrightarrow$
$x = -\frac{3}{4}$

C) $\frac{2(x+1)-3(2x+5)}{6} = — 3 \Leftrightarrow$
$\frac{2x+2-6x-15}{6} = — 3 \Leftrightarrow$
$-4x — 13 = -18 \Leftrightarrow$
$-4x = -18 + 13 \Leftrightarrow$
$-4x = -5 \Leftrightarrow x = \frac{5}{4}$

D) После нахождения и сокращения общего знаменателя, который для 2, 4 и 5 есть 20
$\frac{3(x-1)}{2} + \frac{2(x+2)}{4} = \frac{3x+4,5}{5} \Leftrightarrow$
$30(x — 1) + 10(x + 2) = 4(3x + 4,5) \Leftrightarrow$
$30x — 30 + 10x + 20 = 12x + 18 \Leftrightarrow$
$40x — 12x = 18 + 10 \Leftrightarrow$
$28x = 28 \Leftrightarrow x = 1$

Задача 4 Докажите, что любое значение неизвестной величины является корнем уравнения:
A) $7x — 13 = — 13 + 7x$
B) $\left(\frac{1}{2} – x\right)^2 – \left(\frac{1}{2} + x\right)^2 = -2x$
C) $3x — 3x = 26 — 2(7 + 6)$
D) $\frac{-3x+4x^2}{5} = (0,8x — 0,6)x$

Решение: Для простого уравнения с неизвестной величиной $x$ любое x является решением, если уравнение сокращается к следующему эквивалентному уравнению 0. 2 — 12x — 8 \Leftrightarrow$
$0 = 9 \Rightarrow$ нет решения

Задача 7 Решите уравнение:
A) $\frac{6x-1}{5} — \frac{1-2x}{2} = \frac{12x+49}{10}$
B) $\frac{x-3}{2} + \frac{2x-2}{4} = \frac{7x-6}{3}$

Решение:

A)После нахождения и сокращения общего знаменателя, мы получаем:
$12x — 2 — 5 +10x = 12x + 49 \Leftrightarrow$
$22x — 12x = 49 + 7 \Leftrightarrow$
$10x = 56 \Leftrightarrow x = 5,6$

B) $\frac{x-3}{2} + \frac{2x-2}{4} = \frac{7x-6}{3} \Leftrightarrow$
$\frac{x-3+x-1}{2} = \frac{7x-6}{3} \Leftrightarrow$
$3(2x — 4) = 2(7x — 6) \Leftrightarrow$
$6x -12 = 14x — 12 \Leftrightarrow$
$8x = 0 \Leftrightarrow x = 0$

Задача 8 Дана функция $f(x) = x + 4$. Решите уравнение:
$\frac{3f(x-2)}{f(0)} + 4 = f(2x + 1)$

Решение:

Мы вычисляем $f(0), f(x -2), f(2x +1)$. То есть, $f(0) = 0 + 4 = 4$;
$f(x — 2) = x — 2 + 4 = x + 2$;
$f(2x + 1) = 2x + 1 + 4 = 2x + 5$. 2 + 9 = x + \frac{1}{4} \Leftrightarrow$
$9 = x + 2x \Leftrightarrow$
$9 = 3x \Leftrightarrow x = 3$

Задача 13 Докажите, что уравнения эквивалентны:
A) $\frac{x-5}{2} + \frac{x-1}{8} = \frac{1,5x-10}{4}$ и $\frac{x+6}{2} – \frac{5,5-0,5x}{3} = 1,5$
B) $x – \frac{8x+7}{6} + \frac{x}{3} = -1.\left(\frac{1}{6}\right)$ и $2x – \frac{6-x}{3} — 2\left(\frac{1}{3}\right)x = -2$

Решение:

A) Для первого уравнения получаем:
$4(x — 5) + x — 1 = 2(1,5x — 10) \Leftrightarrow$
$4x — 20 + x — 1 = 3x — 20 \Leftrightarrow$
$5x – 3x = — 20 + 21 \Leftrightarrow$
$2x = 1 \Leftrightarrow x = \frac{1}{2}$,
для второго уравнения получаем
$3(x + 6) — 2(5,5 — 0,5y) = 6 \cdot 1,5 \Leftrightarrow$
$3x + 18 — 11 + x = 9 \Leftrightarrow$
$4y = 9 — 7 \Leftrightarrow$
$x = \frac{2}{4} \Leftrightarrow x = \frac{1}{2}$ Поэтому, уравнения являются эквивалентными (равными).

B) Aналогично A), попробуйте решить это самостоятельно

Задача 14 Решите уравнение:
A) $(2x + 1)^2 – x(1 — 2x)(1 + 2x) = (2x — 1)^2 + 4x^3 — 3$
B) $(2x — 1)^2 + (x — 2)^3 = x^2(x — 2) + 8x — 7$
C) $(x + 2)(x^2 — 2x + 4) + x(1 – x)(1 + x) = x — 4$
D) $\frac{8x+5}{4} – \frac{1}{2}\left[2 – \frac{3-x}{3}\right] = 2x + \frac{5}{6}$
E) $\frac{x}{3} — \frac{x + 3}{4} = x-\frac{1}{3}\left[1 — \frac{3 — 24x}{8}\right]$
F) $\frac{x}{5}- \left[\frac{(2x — 3)^2}{3}\right] = \frac{1}{5}\left[ 5 — \frac{(20x — 43x)}{3}\right]$

Решение:

A) $4x^2 + 4x + 1 – x(1 — 4x^2) = 4x^2 — 4x + 1 + 4x^3 — 3 \Leftrightarrow$
$4x – x + 4x^3 = -4x + 4x^3 -3 \Leftrightarrow$
$3x + 4x = -3 \Leftrightarrow$
$7x = — 3 \Leftrightarrow x = -\frac{3}{7}$

B) $4x^2 — 4x + 1 + x^3 — 3x^2\cdot2 + 3x\cdot2^2 — 8 = x^3 -2x^2 + 8x — 7 \Leftrightarrow$
$4x^2 — 6x^2 — 4x + 1 + 12x — 8 = — 2x^2 + 8x -7 \Leftrightarrow$
$-2x^2 + 8x — 7 = — 2x^2 + 8x — 7 \Leftrightarrow$
$0 = 0 \Rightarrow$ любое x есть решением;

C) $x^3 + 2x^2 — 2x^2 — 4x + 4x + 8 + x(1 – x^2) = x — 4 \Leftrightarrow$
$x^3 + 8 + x – x^3 = x — 4 \Leftrightarrow$
$8 = -4$, что невозможно. 2 + 43x \Leftrightarrow$
$63x — 43x = 15 + 45 \Leftrightarrow$
$20x = 60 \Leftrightarrow x = 3$

Решение уравнений с модулем

Решение уравнений и неравенств с модулем часто вызывает затруднения. Однако, если хорошо понимать, что такое модуль числа, и как правильно раскрывать выражения, содержащие знак модуля, то наличие в уравнении выражения, стоящего под знаком модуля, перестает быть препятствием для его решения.

Немного теории. Каждое число имеет две характеристики: абсолютное значение числа, и его знак.

Например, число +5, или просто 5 имеет знак «+» и абсолютное значение 5.

Число -5 имеет знак «-» и абсолютное значение 5.

Абсолютные значения чисел 5 и -5 равны 5.

Абсолютное значение числа х называется модулем числа и обозначается |x|.

Как мы видим, модуль числа равен самому числу, если это число больше или равно нуля, и этому числу с противоположным знаком, если это число отрицательно.

Это же касается любых выражений, которые стоят под знаком модуля.

Правило раскрытия модуля выглядит так:

|f(x)|= f(x), если f(x) ≥ 0, и

|f(x)|= — f(x), если f(x) < 0

Например |x-3|=x-3, если x-3≥0 и |x-3|=-(x-3)=3-x, если x-3<0.

Чтобы решить уравнение , содержащее выражение, стоящее под знаком модуля, нужно сначала раскрыть модуль по правилу раскрытия модуля.

Тогда наше уравнение или неравенство преобразуется в два различных уравнения, существующих на двух различных числовых промежутках.

Одно уравнение существует на числовом промежутке, на котором выражение, стоящее под знаком модуля неотрицательно.

А второе уравнение существует на промежутке, на котором выражение, стоящее под знаком модуля отрицательно.

Рассмотрим простой пример.

Решим уравнение:

|x-3|=-x²+4x-3

1.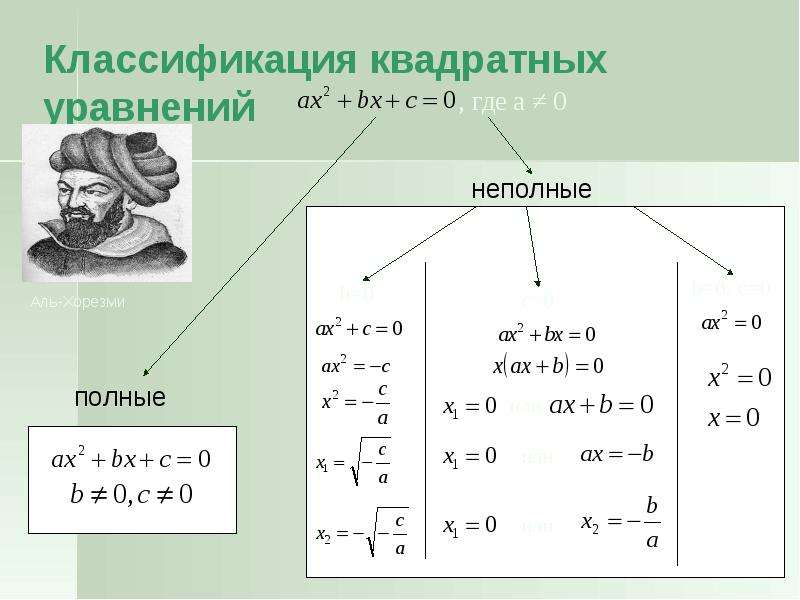 Раскроем модуль.

|x-3|=x-3, если x-3≥0, т.е. если х≥3

|x-3|=-(x-3)=3-x, если x-3<0, т.е. если х<3

2. Мы получили два числовых промежутка: х≥3 и х<3.

Рассмотрим, в какие уравнения преобразуется исходное уравнение на каждом промежутке:

А) При х≥3 |x-3|=x-3, и наше уранение имеет вид:

x-3=-x²+4x-3

Внимание! Это уравнение существует только на промежутке х≥3!

Раскроем скобки, приведем подобные члены:

x² -3х=0

и решим это уравнение.

Это уравнение имеет корни:

х₁=0, х₂=3

Внимание! поскольку уравнение x-3=-x²+4x-3 существует только на промежутке х≥3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х₂=3.

Б) При x<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:

3-x=-x²+4x-3

Внимание! Это уравнение существует только на промежутке х<3!

Раскроем скобки, приведем подобные члены.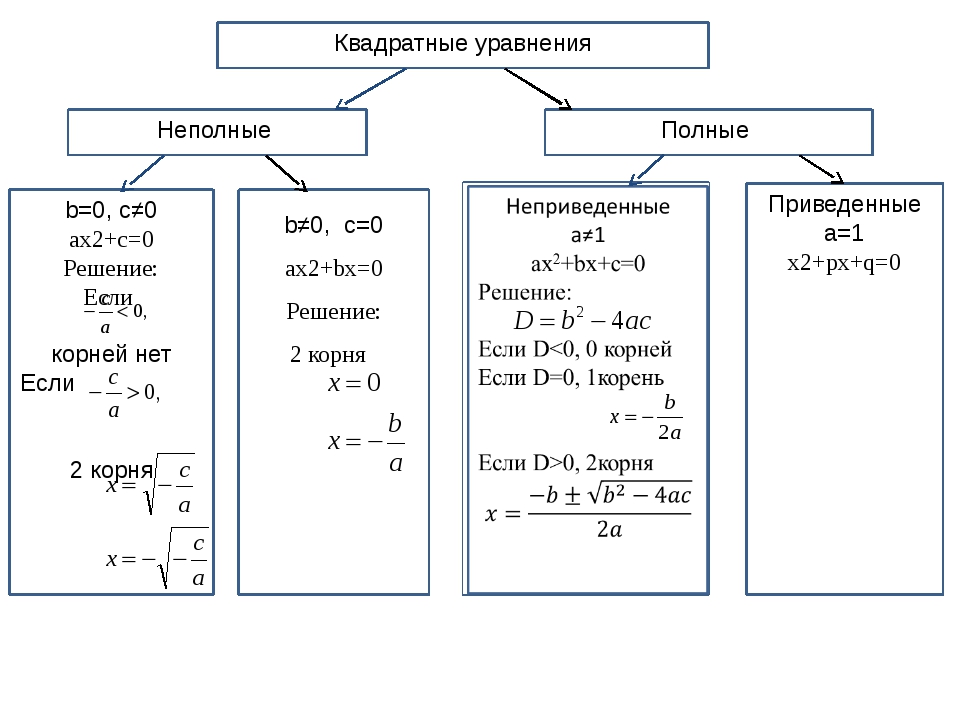 Получим уравнение:

x²-5х+6=0

х₁=2, х₂=3

Внимание! поскольку уравнение 3-х=-x²+4x-3 существует только на промежутке x<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х₁=2.

Итак: из первого промежутка мы берем только корень х=3, из второго — корень х=2.

Ответ: х=3, х=2

Урок 49. уравнения. методы решения уравнений — Алгебра и начала математического анализа — 11 класс

Алгебра и начала математического анализа, 11 класс

Урок №49. Уравнения. Методы решения уравнений.

Перечень вопросов, рассматриваемых в теме:

Методы решения уравнений.
Применение методов решения к уравнениям различного вида.
Примеры решения задач государственной итоговой аттестации

Глоссарий по теме

Уравнение.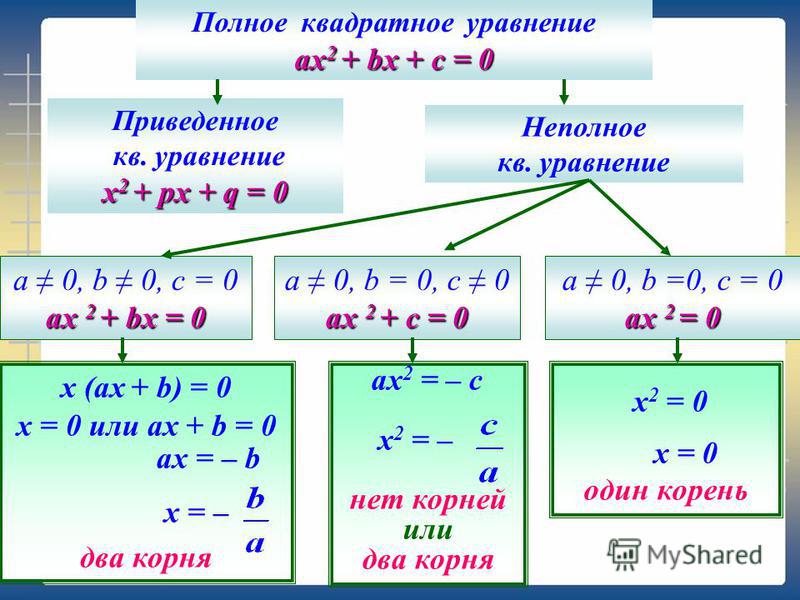 Пусть заданы функции f(x) и g(x). Если относительно равенства поставлена задача отыскания всех значений переменной, при которых получается верное числовое равенство, то говорят, что задано уравнение с одной переменной.

Основная литература

Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. Под ред. А.Б. Жижченко. Алгебра и начала математического анализа. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни. – 2-е изд. – М.: Просвещение, 2010.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.

Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.

Теоретический материал для самостоятельного изучения

Основные методы решения уравнений

Метод разложения на множители

Рассмотрим пример.

Решить уравнение:

ООУ:

Преобразуем обе части уравнения

Это уравнение равносильно совокупности двух уравнений

или

Первое уравнение

имеет множество корней

Второе уравнение

равносильно и его корни

Ответ:

Метод замены переменной

Рассмотрим пример.

ООУ:

Так как в уравнении присутствует повторяющееся выражение, введем новую переменную

и получи уравнение

, корни которого

Возвращаемся к первоначальной переменной

или

Ответ:

Метод решения однородных уравнений.

Рассмотрим пример

Решить уравнение:

ООУ: x – любое действительное число

Все слагаемые в правой части уравнения имеют равные степени, поэтому разделим обе части уравнения на и получим

Решаем полученное уравнение методом замены переменной

или

Ответ: 1; 2

Итак, можно сделать следующие выводы.

Наличие в уравнении повторяющихся элементов позволяет сделать предположение, что в его решении можно применить метод замены переменной. Наличие общих множителей выводит на применение метода разложение на множители. Если же в одной из частей уравнения стоит однородный многочлен, то применяем метод решения однородных уравнений.

Примеры и разбор решения заданий тренировочного модуля

Пример 1.

Решите уравнение

Выберите ответ из предложенных.

Варианты ответов:

10
-10
100
-100
1000
-1000

Решение

ООУ:

Преобразуем левую часть уравнения

Введем новую переменную

Получим уравнение

Возвращаемся к первоначальной переменной

Ответ: — 1000

Пример 2.

Решите уравнение

Выберите корень из списка:

Решение:

ООУ:

Возведем обе части уравнения в квадрат

Повторно возведем в квадрат при условии

Корни этого уравнения

Учитывая все ограничения, получаем ответ .

Теория решений простейших уравнений B5 на ЕГЭ. Виртуальная помощь репетитора

В задаче B5 на ЕГЭ по математике Вам будет предложено решить какое-нибудь простенькое уравнение на одну из тем школьной программы (алгебра 9 — 11 класс). Повторите логарифмы, простейшие свойства показательной функции, квадратные корни, алгебраические дроби (и даже формулу дискриминанта квадратного уравнения — 8 класс).

Мини-урок подготовки к ЕГЭ по математике с виртуальным репетитором

Перечислим основные виды типовых уравнений, наиболее часто встречающиеся на реальном ЕГЭ. Подготовку к их упешному освоению репетитор по математике проводит в начале своего курса в том случе, если нет глубоких проблем с предметом, уходящих в далекие 5 — 9 классы.

1) Простейшие логарифмические уравнения:

Вместо буквы а составитель задачи B5 на ЕГЭ, скорее всего поставит некоторое положительное число (не равное единице), а вместо f (x) и g (x) — некие буквенные выражения (или одно из них тоже будет числом).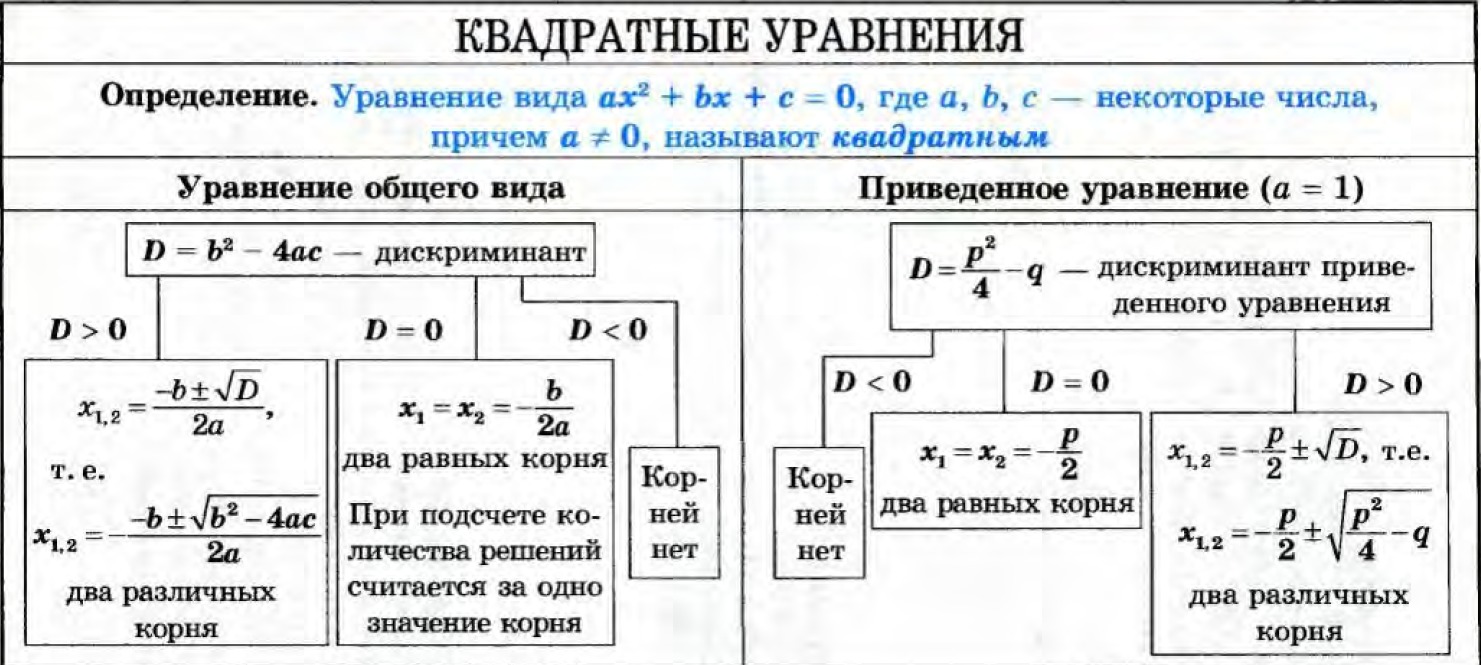 Для решения данного уравнения нужно составить новое равенство f (x)=g (x) и проверить полученные от него корни на предмет выполнения условия f (x)>0 или g (x)>0 (на Ваш выбор). Прошедшие такую проверку числа нужно записать в ответ. Все!

Пример репетитора по математике: решить уравнение

Приравняем выражения под логарифмами

Перенесем все слагаемые в одну часть

Решив его при помощи дискриминанта по формуле мы получим следующие корни и . Удобнее проверить выполнение условие x-2>0, которое окажется неверным, если вместо икса подставить число . Тогда в ответ попадает только .

2) Показательные уравнения

Простейшими показательными являются уравнения следующего вида:

Именно на них нужно обратить внимание при непрофильной подготовке к ЕГЭ по математике: Здесь, как и в случае с логарифмами проверять не нужно.

3) Иррациональные уравнения

На ЕГЭ Вам предложат, скорее всего, уравнение такого вида

, где (обычно без каких-либо степеней). Его корень — ответ задачи B5 Вашего ЕГЭ.
Пример репетитора: решить уравнение

Возводим это равенство в квадрат:

Cокращаем знак квадратного корня:

Ответ: x=19

Качественная подготовка к ЕГЭ по математике, безусловно, не ограничивается такими примерами и не начинается с подобных объяснений. Репетитор проводит определенный анализ возможностей и знаний ученика и выстраивает систему объяснений (и упражнений) в зависимости от полученных результатов тестирования на первых занятиях. Это очень важно, ибо типовой стандарт B5 на реальном ЕГЭ может несколько измениться и тогда натасканный репетитором по математике ученик не справится даже с такими легкими номерами. Поэтому необходимо начинать подготовку к экзамену как можно раньше. Не затягивайте с занятиями!

Удачи на реальном ЕГЭ. Колпаков А.Н. Репетитор по математике для ЕГЭ. Москва, Строгино.

Качественная теория дифференциальных уравнений. Часть 1

Спецкурс для студентов 2-5 курсов и аспирантов. В курсе излагаются основы качественной теории обыкновенных дифференциальных уравнений. Наряду с фундаментальными методами излагаются современные методы исследования, в том числе, разработанные автором применительно к нелинейным дифференциальным уравнениям высокого порядка. Обсуждаются сложные задачи об исследовании поведения решений, а также актуальные нерешенные задачи.

Список всех тем лекций

Лекция 1. Уравнение Риккати.
Вступительное слово к курсу Качественная теория дифференциальных уравнений Обращение решения в нуль Область максимальной определенности Другие качественные свойства решений Уравнение Риккати Пример Замена переменной Канонический вид уравнения Риккати Структура общего решения уравнения Риккати Случаи интегрируемости уравнения Риккати

Лекция 2. Интегрируемость уравнения Риккати и качественное свойство его решений.
Повторение пройденного Специальное уравнение Риккати Замена Обратные замены Случаи интегрируемости Пример №1 Пример №2 Упражнения Свойства решений уравнения Риккати Доказательство Следствие теоремы Домашнее задание

Лекция 3. Качественные свойства уравнения Риккати.
Упражнения с прошлого занятия Свойства решений уравнения Риккати Доказательство теоремы Пример и доказательство Случай Теорема Домашнее задание

Лекция 4. Асимптотические и качественные свойства уравнения Риккати.
План лекции Случай с двумя различными корнями Теорема Доказательство теоремы Свойство Пример Случай комплексных корней уравнения Пример Теорема о непрерывной зависимости решения уравнения от начальных условий и правой части Задача Обозначения Теорема о сжимающих отображениях Доказательство Домашнее задание

Лекция 5. Качественные свойства решения полиномиальных уравнений первого порядка.
Полиномиальное уравнение первого порядка Определение главного члена полинома Доказательство Опровержение первого пункта Отношение членов полинома Опровержение второго пункта План следующей лекции и домашнее задание

Лекция 6. Продолжение темы: полиномиальные уравнения.
Повторение пройденного Опровержение второго пункта Первое неравенство Второе неравенство Лемма Для уравнений второго порядка Пример План следующей лекции

Лекция 7. Асимптотические формулы решений полиномиальных уравнений.
Повторение пройденного Дробно-рациональное уравнение Лемма и её доказательство Следствия Теорема Харди Доказательство Четыре различных случая Случай 2 Случай 3 Вопрос по решению домашнего задания

Лекция 8. Теорема Харди. Линейные уравнения второго порядка.
План лекции Доказательство теоремы Харди с предыдущей лекции Случаи Линейные уравнения второго порядка Задача Коши Общее решение уравнения (1) Общее решение уравнения (2) Приведение к простейшим формам Уравнение без первой производной Домашняя задача Приведение к самосопряженному виду Задача: привести уравнение Бесселя Представление Валле-Пуссена

Лекция 9. Линейные уравнения второго порядка.
Представление оператора высокого порядка с непрерывными коэффициентами в виде оператора квазипроизводной Обсуждение линейного уравнения второго порядка Определения неколеблющегося и колеблющегося решений Определение колеблющегося решения на полуоси Определение неколеблющегося решения на полуоси Теорема и её доказательство Доказательство Доказательство Теорема Шпета Теорема об ограниченности решений Аналогии теоремы Штурма для порядка выше двух Теоремы Штурма и Кондратьева

О теореме Абеля-Руффини без групп и теории Галуа / Хабр

Историческая справка

Поиск решения алгебраических уравнений оказал колоссальное влияние на развитие математики. Формула решения общего кубического уравнения впервые была получена итальянскими математиками 16-го века. Это событие ставшее первопричиной рассмотрения комплексных чисел, считается одним из поворотных моментов в истории математики. Судьбы Джероламо Кардано, Никколо Тартальи, Сципиона дель Ферро и их поисков решения кубического уравнения заслуживают отдельного романа со своими интригами, скандалами и расследованиями. Столь яркие истории достаточно редки в математике.

Начиная с 19-го века поиск формул для решения уравнений произвольных степеней положил начало теории групп и абстрактной алгебре, которые преобразили практически все разделы современной математики. Думаю, многие, кто интересовался историей и развитием алгебры, знают, что формулы для решения общего алгебраического уравнения степени выше четвертой не существует. Как сообщается, первое доказательство этого факта было дано итальянским математиком Паоло Руффини в самом конце восемнадцатого века, оно составляло около 500 страниц и все же содержало некоторые пробелы. Хотя отдельные математики, как Огюстен Коши, и признавали данное доказательство, но ввиду столь большого объема и сложности изложения, оно так и не было принято математическим сообществом. Считается, что первое полное доказательство дано норвежским математиком Нильсом Абелем и содержалось в двух работах, изданных в 1824 и 1826 годах. С тех пор оно носит название теоремы Абеля или теоремы Абеля-Руффини.

Если вы попытаетесь изучить это доказательство в его современном изложении, то окажется, что оно практически полность опирается на Теорию Галуа. Эварист Галуа был французским математиком 19-го века и современником Нильса Абеля. Помимо занятий математикой он вел активную политическую жизнь из-за чего несколько раз попадал в тюрьму. В возрасте всего двадцати лет был застрелен на дуэли, поводом для которой послужила любовная интрига, хотя есть предположения, что дуэль была подстроена его политическими противниками. Об этой истории написано достаточно много, кроме того, имеется перевод на русский язык его мемуаров и писем. Последнее письмо его другу Огюсту Шевалье было написано в ночь накануне дуэли, в нем он наспех излагает свои последние идеи. Несмотря на столь короткую жизнь, Эварист Галуа считается одним из родоначальников современной алгебры. Хотел бы заметить, что в популярном изложении создается некий романтический образ Галуа, как подростка-гения, который в одиночку, с нуля создал теорию групп и преобразил всю алгебру. Несомненно его идеи сыграли огромную роль, но если почитать его сочинения, то мы увидим, что он хорошо знал и опирался на знаменитые работы Лагранжа, Эйлера, Гаусса, Абеля, Якоби. Зачатки теории групп и перестановок появляются еще в работах Жозефа Луи Лагранжа по теории алгебраических уравнений, а также Карла Фридриха Гаусса в его знаменитых «Арифметических исследованиях». К тому же, теория Галуа в современном изложении была оформлена многими последующими математиками — Дедекиндом, Кронекером, Гильбертом, Артином и другими.

Мотивация данной статьи

Чуть менее года назад меня сильно увлекла статья об истории решения кубического уравнения и последующих безуспешных поисков формулы уравнения 5-й степени, длившихся почти триста лет. Сразу хочу отметить, что специального математического образования у меня нет и поэтому, попробовав прочесть современную версию доказательства теоремы Абеля-Руффини, я естественно ничего не понял. В моем сознании термины группа, кольцо и поле никак не ассоциировались с алгебраическими структурами. Но желание разобраться было столь велико, что я принялся за изучение курса высшей алгебры.

На первых этапах абстрактная алгебра была наверное самым сложным из того, что мне приходилось изучать ранее. Объем новых терминов и определений просто зашкаливал: группы, факторгруппы, моноиды, поля, кольца, тела, модули, идеалы, ядра, векторные пространства, биекции, сюръекции, инъекции, изоморфизмы, автоморфизмы, гомоморфизмы, эндоморфизмы и тд. Спустя несколько месяцев упорных занятий, я начал понимать формальную часть, но, к сожалению, интуитивного понимания, которое и являлось моей изначальной целью, я так и не достиг.

Дело в том, что практически все современные доказательства неразрешимости уравнений 5-й степени в радикалах сводятся к следующему. Рассматривается некоторое неприводимое уравнение, например x⁵-10x+2, после чего методами мат анализа определяется, что оно имеет три действительных и два комплексно-сопряженных корня. После чего заключается, что группой Галуа данного уравнения есть группа S₅, которая не является разрешимой, и следовательно данное уравнение неразрешимо в радикалах. Доказательство теоремы Абеля-Руффини о неразрешимости общего уравнения также сводится к неразрешимости группы S_n. Для меня данные доказательства были слишком абстрактными и оторванными от конкретных уравнений. Когда я пытался представить их в терминах элементарных алгебраических операций, чтобы понять в чем заключается главная причина неразрешимости уравнений, у меня ничего не получалось. Возможно для тех, кто занимается этим достаточно долго, эти вещи могут казаться интуитивно понятными.

Немного иной подход описан в книге Алексеева «Теорема Абеля в задачах и решениях», основанной на лекциях Владимира Арнольда, но в изложенном там доказательстве помимо теории групп используются элементы комплексного анализа и Римановых поверхностей. Я также находил похожие статьи, использующие топологические аргументы в виде комбинаций петель и коммутаторов, но мне хотелось найти что-то чисто алгебраическое.

Параллельно изучая историю математики и понимая, что современная формулировка и доказательство сильно отличаются от того, как излагали свои идеи Лагранж, Руффини, Абель и Галуа, я решил прочесть первоисточники. К сожалению, на русский или английский по этой теме переведены лишь сочинения Галуа и одна из работ Абеля.

После некоторых поисков я наткнулся на статью 1845 года французского математика Пьера Лорана Ванцеля, в которой он переработал и сильно упростил доказательство Абеля-Руффини, о чем он пишет во введении. В этой работе, он так же упоминает мемуары Галуа и отмечает, что они будут опубликованы в скором времени. Для заметки — работы Галуа были опубликованы лишь в 1846 году Жозефом Лиувиллем, спустя почти 15 лет после смерти Галуа. Кстати, Пьер Лоран Ванцель, также был первым, кто доказал неразрешимость трисекции угла и удвоения куба с помощью циркуля и линейки — знаменитых задач стоявших еще со времен античности. Доказательства Ванцеля были изложены без использования абстрактной алгебры и теории Галуа, поскольку на тот момент они еще не были разработаны. Хотя работа и была доступна лишь на французском, которого я до этого практически не знал, но ввиду специфической темы, небольшого размера (всего 7 страниц) и наличия гугл переводчика, я справился достаточно быстро. По моему субъективному мнению, его доказательство теоремы Абеля-Руффини является наиболее простым для понимания.

Уже позже я нашел пример подобного доказательства основанного на работе Руффини в книге Чеботарёва “Основы Теории Галуа”. Далее я постараюсь кратко изложить принцип решения уравнений в радикалах и идею доказательства неразрешимости уравнения 5-й степени.

Решения уравнений в радикалах

Для дальнейшего понимания, потребуются минимальные пререквизиты:

Формулы Виета — напомню, что коэффициенты произвольного уравнения являются элементарными симметрическими функциями от его корней, то есть функциями, которые не меняют своего значения при любых перестановках корней. Примеры: x₁ + x₂ + x₃, x₁x₂x₃, x₁x₂ + x₁x₃ + x₂x₃.

Теорема о симметрических многочленах — каждую симметрическую функцию от корней, можно выразить с помощью элементарных симметрических функций (коэффициентов уравнения).

Первообразные корни n-й степени из единицы — комплексные величины не равные единице, но n-я степень которых, равна единице. Примеры: (-1)² = 1, (-1/2 + sqrt(-3)/2)³ = 1, i⁴ = 1 соответственно квадратный, кубический и биквадратный корни из единицы.

Основная теорема алгебры — гласит о том, что уравнение n-й степени с комплексными коэффициентами имеет ровно n комплексных корней с учетом кратности (корни могут быть одинаковые).

Первоначальная идея восходит к работе Жозефа Луи Лагранжа “Размышления о решении уравнений” 1770-1771 годов. Это достаточно объемное сочинение и я не нашел его перевода на русский или английский язык. Как указывается в разных источниках, в попытке найти формулу для уравнения 5-й степени, Лагранж проанализировал все имеющиеся к тому времени способы решения уравнений и выделил общий принцип, позволяющий решить уравнения 4-й и низших степеней. В этой же работе, изучая перестановки корней, он пришел к теореме, которая сейчас носит его имя. Принцип, открытый Лагранжем, заключался в том, чтобы найти выражения от корней заданного уравнения n-й степени, которые при всех возможных перестановках этих корней принимали n-1 значений, но в тоже время через них выражались первоначальные корни. На эти значения, можно составить уравнение n-1 степени и повторить операцию, тем самым сводя изначальное уравнение к цепочке уравнений меньших степеней, решив которые, можно получить корни первоначального уравнения. Рассмотрим один из примеров:

Пусть f(x) = x⁴ + ax³ + bx² + cx + d общее уравнение 4-й степени с произвольными коэффициентами a, b, c, d и x₁, x₂, x₃, x₄ его корни.

Напомним, что его коэффициенты — это элементарные симметрические функции от корней, в чем можно убедиться просто раскрыв скобки в выражении (x — x₁)(x -x₂)(x — x₃)(x — x₄):

x₁ + x₂ + x₃ + x₄ = -a

x₁x₂ + x₁x₃ + x₁x₄ + x₂x₃ + x₂x₄ + x₃x₄ = b

x₁x₂x₃ + x₁x₂x₄ + x₁x₃x₄ + x₂x₃x₄ = -c

x₁x₂x₃x₄ = d

Так как корни являются произвольными, то существует 4! = 24 различных вариантов их расположения, но можно составить выражение x₁x₂ + x₃x₄, которое принимает всего три разных значения при всех 24-х перестановках корней:

x₁x₂ + x₃x₄ = y₁

x₁x₃ + x₂x₄ = y₂

x₁x₄ + x₂x₃ = y₃

На эти три значения мы можем составить уже кубическое уравнение, корнями которого они и будут являться. Таким образом, мы сводим решение уравнения 4-й степени к уравнению 3-й степени. Для решения кубического уравнения мы можем воспользоваться резольвентой Лагранжа (y₁ + wy₂ + w²y₃)³, где w — это кубический корень из единицы. Данное выражение принимает всего два разных значения при всех возможных 3! = 6 перестановках. Оно будет сохранять значение при циклических перестановках и менять знак при любой транспозиции. Получим:

(y₁ + wy₂ + w²y₃)³ = z₁

(y₁ + w²y₂ + wy₃)³ = z₂

Теперь составим квадратное уравнение на z₁ и z₂:

(t — z₁)(t — z₂) = t² — t(z₁+z₂) + z₁z₂

z₁+z₂ и z₁z₂ — будут симметрическими функциями от корней нашего изначального уравнения f(x), следовательно, по теореме о симметрических многочленах, напрямую выражаться через коэффициенты a, b, c, d. Решив квадратное уравнение мы получим значения z₁, z₂. После чего, извлекая кубические корни из z₁, z₂, и складывая с коэффициентом b, сможем выразить y₁. Далее, c помощью y₁ и коэффициентов a, b, d, решив два квадратных уравнения, мы доберемся до корней x₁, x₂, x₃, x₄ изначального уравнения.

Данный пример показывает, что произвольное уравнение 4-й степени решается путем составления вспомогательных кубического и квадратных уравнений. Далее я приведу рассуждение, почему подобный прием невозможен для общего уравнения 5-й степени.

Неразрешимость уравнения 5-й степени

Итак, мы хотим показать, что ни один корень общего уравнения 5-й степени не может быть выражен через его коэффициенты путем решения цепочки вспомогательных двучленных уравнений низших степеней.

Пусть f(x) = x⁵ + ax⁴ + bx³ + cx² + xd + e общее уравнение 5-й степени с произвольными коэффициентами a, b, c, d, e и x₁, x₂, x₃, x₄, x₅его корни. Обозначим за y₁ первый радикал входящий в значение x₁ в порядке вычисления. Пусть y₁ⁿ = p, где p будет какой-то симметрической функцией от корней и, следовательно, напрямую выражаться через коэффициенты a, b, c, d, e. Заметим, что y₁ уже не будет симметрической, а лишь рациональной функцией g от корней — g(x₁, x₂, x₃, x₄, x₅). Следовательно, g должно менять значение при перестановке любых двух корней. Тогда эти значения будут являться корнями уравнения y₁ⁿ = p, которые имеют вид g, zg, z²g, z³g … z^n-1g, где z — первообразный корень n-й степени из единицы (zⁿ=1). Рассмотрим произвольную транспозицию, например (x₁, x₂), тогда

g(x₂, x₁, x₃, x₄, x₅) = zg(x₁, x₂, x₃, x₄, x₅)

если мы применим ее еще раз, то получим:

g(x₁, x₂, x₃, x₄, x₅) = zg(x₂, x₁, x₃, x₄, x₅)

что равносильно g(x₁, x₂, x₃, x₄, x₅) = z²g(x₁, x₂, x₃, x₄, x₅)

Из этого следует, что z² = 1, то есть z должен быть квадратным корнем из единицы (z = -1) и соответственно первый радикал y₁ будет квадратным. Поясним: так как корни являются произвольными, то g должно сохранять значение при любых четных перестановках корней и менять знак при нечетных. Теперь покажем, что значение функции g не будет меняться при циклической перестановке трех корней (x₁, x₂, x₃). Здесь стоит пояснить, что циклическая перестановка (x₁, x₂, x₃) четная и может быть представлена, как произведение транспозиций (x₁, x₂)(x₂, x₃). То есть, функция g не поменяет своего значения при данной перестановке. Еще заметим, что функция g не изменится при циклической перестановке пяти корней, так как она так же раскладывается в произведение четного количества транспозиций. Присоединяя радикал y₁ к выражениям от коэффициентов с помощью базовых арифметических операций, мы будем получать симметрические функции относительно всех циклов на трех и пяти корнях и вообще любых четных перестановок, но при перестановке содержащей нечетное количество транспозиций, y₁ будет менять знак. Дальнейшее присоединение квадратных радикалов не даст нам ничего нового. Теперь предположим, что мы пришли к радикалу, который меняет свое значение лишь при тройных циклах. Обозначим его y₂, тогда y₂ⁿ = q, где q — это рациональная функция от коэффициентов a, b, c, d, e и радикала y₁.

g(x₂, x₃, x₁, x₄, x₅) = zg(x₁, x₂, x₃, x₄, x₅)

g(x₃, x₁, x₂, x₄, x₅) = zg(x₂, x₃, x₁, x₄, x₅)

g(x₁, x₂, x₃, x₄, x₅) = zg(x₃, x₁, x₂, x₄, x₅)

что равносильно g(x₁, x₂, x₃, x₄, x₅) = z³g(x₁, x₂, x₃, x₄, x₅)

В данном случае z³ = 1, то есть z здесь будет кубическим корнем из единицы.

Теперь произведем циклическую перестановку 5-и корней

g(x₂, x₃, x₄, x₅, x₁) = zg(x₁, x₂, x₃, x₄, x₅)

g(x₃, x₄, x₅, x₁, x₂) = zg(x₂, x₃, x₄, x₅, x₁)

g(x₄, x₅, x₁, x₂, x₃) = zg(x₃, x₄, x₅, x₁, x₂)

g(x₅, x₁, x₂, x₃, x₄) = zg(x₄, x₅, x₁, x₂, x₃)

g(x₁, x₂, x₃, x₄, x₅) = zg(x₅, x₁, x₂, x₃, x₄)

Так как z должен быть кубическим корнем из единицы, как мы выяснили ранее, то единственным вариантом будет z = 1 и g должна быть инвариантна при любой из этих циклических перестановок. Но тогда она должна быть инвариантна и при циклической перестановке x₃,x₂,x₅,x₁,x₄ -> x₂,x₅,x₁,x₄,x₃. Отсюда, одной транспозицией мы можем получить, что

g(x₃, x₄, x₅, x₁, x₂) = g(x₂, x₃, x₁, x₄, x₅)

но, выше мы уже видели, что

g(x₁, x₂, x₃, x₄, x₅) = g(x₃, x₄, x₅, x₁, x₂)

а из этого следует

g(x₁, x₂, x₃, x₄, x₅) = g(x₂, x₃, x₁, x₄, x₅)

что приводит нас к противоречию, так как мы предполагали, что g меняет значение при циклической перестановке трех корней (x₁, x₂, x₃).

Еще одним вариантом, было бы показать что все четные перестановки на пяти корнях порождаются тройными циклами, то есть, если есть тройные циклы, то никаких выражений от корней, которые бы сохраняли набор значений при всех четных перестановках, не существует. Если теперь перевести это на теоретико-групповой язык, то получается, что группа общего уравнения пятой степени есть симметрическая группа S₅, в которой существует 5! = 120 различных перестановок пяти корней. Далее, путем присоединения квадратного корня из дискриминанта, мы можем понизить ее до знакопеременной группы четных перестановок A₅, которая содержит 120/2 = 60 перестановок. Но A₅ является простой группой, в которой нет никаких нетривиальных нормальных подгрупп, которым бы соответствовали выражения от корней сохраняющие значения при определенных перестановках, из чего следует, что присоединение любых дополнительных радикалов не приблизит нас к решению.

Заключение

Поводом для написания данной статьи послужило желание структурировать свои мысли по этой теме и представить идеи о неразрешимости уравнений в радикалах без привлечения абстрактной алгебры и теории Галуа. По моему мнению, в подавляющем большинстве современных изложений теряется связь между областью, в которой происходит доказательство и конкретными уравнениями. Если у кого-то есть замечания, дополнения или ссылки на подобные элементарные изложения, буду рад услышать.

Теория системы линейных уравнений | Математические упражнения

Простейший метод решения системы линейных уравнений состоит в многократном исключении переменных.

шагов:

1. В первом уравнении решить уравнение для переменной относительно остальной части уравнения

Введите это выражение в другие уравнения. Это оставит систему уравнений с уравнением с меньшей переменной.

Повторяйте этот метод до тех пор, пока не будет получено одно линейное уравнение с одной переменной

Решите это уравнение

Заменяет результат переменной в приведенных выше уравнениях до тех пор, пока окончательное уравнение не будет решено

Самый простой способ решения системных уравнений — повторное исключение переменных.

шагов:

1.В первом уравнении решите уравнение относительно переменной относительно остальной части уравнения

Введите это выражение в другие уравнения. Это оставит систему уравнений с уравнением с меньшей переменной.

Повторяйте этот метод до тех пор, пока не будет получено одно линейное уравнение с одной переменной

Решите, применяя следующую формулу:

Биопроф |Теория систем уравнений| 01

Существует несколько различных методов, которые приведут к получению одинаковых результатов:

Метод замещения.
Метод выравнивания.
Метод редукции.
Метод Гаусса.
Метод обратной матрицы.
Правило Крамера.

Метод замены:

Решите одно из неизвестных в одном из уравнений.
Выражение этой тайны заменяется в другом уравнении, таким образом получается уравнение с одним неизвестным.
Полученное уравнение решено.
Полученное значение подставляется в уравнение, которое появилось ясно-неизвестно.
Это уравнение решено, и два полученных значения являются решением системы.

Пример:

Биопрофе |Теория систем уравнений| 02

Решаем неизвестное x во втором уравнении:

Биопрофе |Теория систем уравнений| 03

И заменяется в первом уравнении:

Биопрофе |Теория систем уравнений| 04

Он уже решил линейное уравнение с одним неизвестным:

Биопрофе |Теория систем уравнений| 05

Полученное значение подставляем в первое решенное уравнение:

Биопрофе |Теория систем уравнений| 06

РЕШЕНИЕ:

х= 1; у = 3

Метод выравнивания:

1.Решите одно из неизвестных в обоих уравнениях.

2. Приравниваем полученные выражения и получаем уравнение с одним неизвестным

3.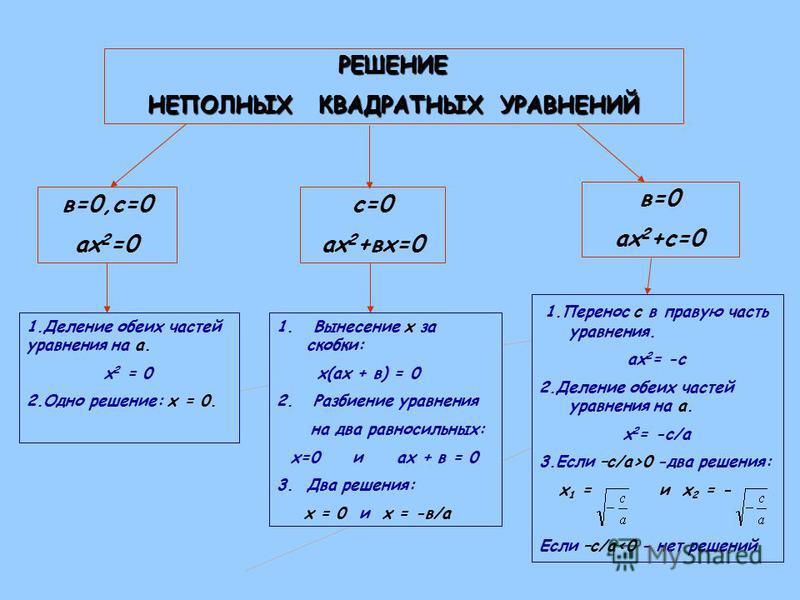 Уравнение решено.

4. Полученное значение подставляется в одно из двух выражений, появившихся четкими, в другое неизвестное.

5. Два полученных значения являются решением системы.

Пример:

Биопрофе |Теория систем уравнений| 07

Решаем одно и то же неизвестное в обоих уравнениях:

Биопрофе |Теория систем уравнений| 08

Приравниваем два выражения:

Биопрофе |Теория систем уравнений| 09

Подставляя его в любое очищенное выражение:

Биопрофе |Теория систем уравнений| 10

РЕШЕНИЕ:

Х= 4; у = -3

Метод сокращения:

Уравнения составлены, умножаем их на соответствующее число.
2. Вычесть их для упрощения, и тогда одно из неизвестных исчезнет.
3. Решить полученное уравнение.
4. Полученное значение подставляется в одно из исходных уравнений и решается.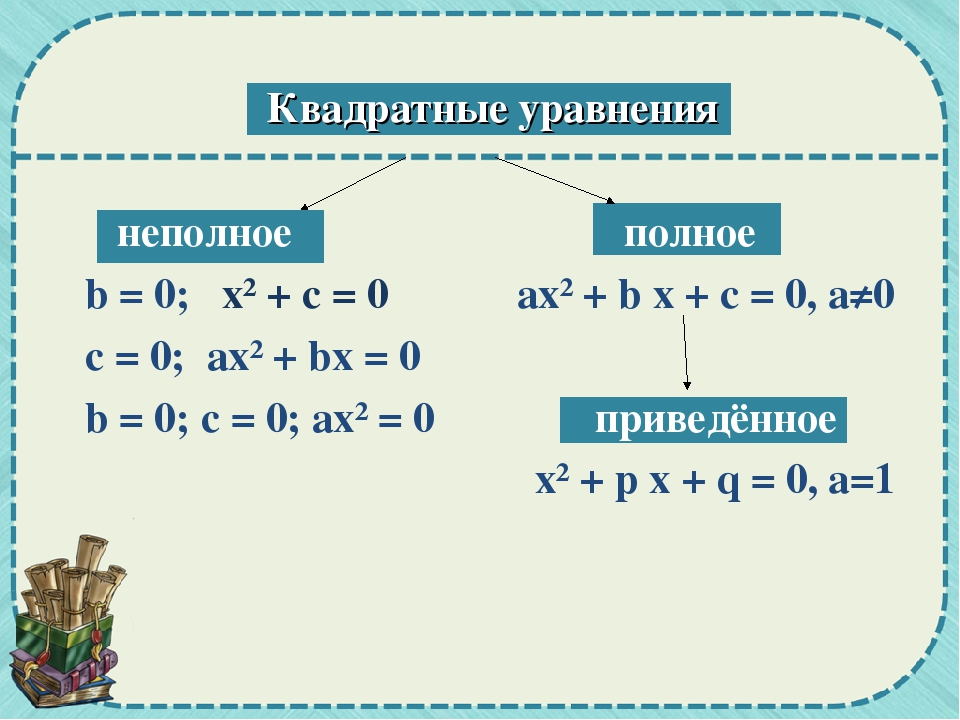
5. Два полученных значения являются решением системы.

Пример:

Биопрофе |Теория систем уравнений| 11

Уравнения подготовлены для вычитания. Неизвестный «y» подавляется, оставаясь:

Биопрофе |Теория систем уравнений| 12

Заменяется значение, полученное в одном из исходных уравнений:

Биопрофе |Теория систем уравнений| 13

РЕШЕНИЕ:

х= 2; у=3

Эта теория о Системе Линейных Уравнений продолжится в следующем посте «Теория Системы Уравнений II»

Решение уравнений | Brilliant Math & Science Wiki

Решать 3X4+6X3-123X2-126X+1080=0.2 + 20,25 Y &= 0\\ Y(Y-1)(Y-20,25)&=0. \end{выровнено}Y3 +2f×Y2 +16f2 −4h×Y-64g2Y3 –21,25Y2 +161806,25–(4×370,5625)×Y-6402Y3 -21,25Y2 +16(1806,25–1482,25) ×Y−0Y3 −21,25Y2 +20,25YY(Y−1)(Y−20,25)=0=0=0=0=0. Тогда 3 корня уравнения равны Y1=0, Y2=1,Y3= 20,25.Y_1= 0, \quad Y_2= 1, \quad Y_3= 20,25.Y1=0, Y2=1,Y3= 20,25. Теперь пусть ppp и qqq будут квадратными корнями из любых двух ненулевых из Y1,Y2,Y_1, Y_2,Y1,Y2 или Y3:Y_3:Y3: p=20,25=4,5,q=1=1.p=\sqrt{20,25} = 4,5, \quad q=\sqrt{1}= 1.р=20,25=4,5, q=1=1. потом r=-g8×pq=0,s=b4×a=64×3=0,5.r= \frac{-g}{8\times pq} = 0, \quad s=\frac{b}{4\ раз a}= \frac {6}{4×3} = 0,5.r=8×pq−g=0,s=4×ab=4×36=0,5. Тогда четыре корня уравнения четвертой степени равны X1=p+q+r-s=4,5+1+0-0,5=5X2=p-q-r-s=4,5-1-0-0,5=3X3=-p+q-r-s=-4,5+ 1-0-0,5=-4X4=-p-q+r-s=-4,5-1+0-0,5=-6. □\begin{выровнено} X_1&= p + q + r -s = 4,5 + 1 + 0 — 0,5 = 5\\ X_2&= p — q — r -s = 4,5 — 1 — 0 — 0,5 = 3\\ X_3&= -p + q — r -s = -4,5 + 1 — 0 — 0,5 = -4\\ X_4&= -p — q + r -s = -4.5 — 1 + 0 — 0,5 = -6.\ _\квадрат \end{выровнено} X1X2X3X4=p+q+r-s=4.5+1+0-0.5=5=p-q-r-s=4.5-1-0-0.5=3 =-p+q-r-s=-4,5+1-0-0,5=-4=-p-q+r-s=-4,5-1+0-0,5=-6. □

Правило Крамера

Магазин Крамера Правило

Дана система линейных уравнения, правило Крамера — удобный способ решить только одну из переменных без решения всей системы уравнений. Обычно они не преподавать правило Крамера таким образом, но это должно быть точкой Правило: вместо решения всей системы уравнений можно использовать Крамера, чтобы решить только для одной единственной переменной.

Давайте использовать следующее система уравнений:

У нас левая сторона системы с переменными («матрица коэффициентов») а правая часть со значениями ответов.Позволять Д – определитель матрицы коэффициентов вышеуказанной системы, и пусть D _x быть определителем, образованным заменой x -столбца значения со значениями столбца ответов:

система из уравнений	коэффициент матрицы определитель	ответ столбец	D _x : определитель коэффициента с ответом-столбец значения в x -столбец
2 х + 1 г + 1 из = 3 1 х 1 г 1 z = 0 1 х + 2 у + 1 из = 0

Оценка каждого определителя (используя описанный здесь метод), получаем:

Правило Крамера гласит, что x = Д _х Д , г = Д _у Д , и з = D _z D . То есть:

x = ³ / ₃ = 1, y = ⁶ / ₃ = 2 , и z = ⁹ / ₃ = 3

Это все, что нужно Крамеру Правило.Чтобы найти любую переменную, которую вы хотите (назовите ее «» или «бета»), просто оцените определяющее частное D _{Д . (Пожалуйста
не просите меня объяснить, почему это работает. Просто поверь мне, что детерминанты
может творить многие виды магии.)}

Учитывая следующее системы уравнений, найдите значение z .

Решить только для z , Сначала я нахожу определитель коэффициента.

Затем я формирую D _z заменив третий столбец значений столбцом ответа:

Затем я составляю частное и упростить:

Суть правила Крамера заключается в том, что вам не нужно решать всю систему, чтобы получить одно значение тебе нужно.Это сэкономило мне немало времени на некоторых тестах по физике. я забыть то, над чем мы работали (что-то с проводами и токами, я думаю), но правило Крамера было намного быстрее, чем любой другой метод решения (и Видит Бог, мне нужно было дополнительное время). Не позволяйте всем подпискам и прочему запутать вас; Правило действительно довольно простое. Вы просто выбираете переменную вы хотите решить, замените столбец значений этой переменной в определитель коэффициента со значениями столбца ответов, оцените, что определителя и разделить на определитель коэффициента.это все к этому.

Почти.

Что делать, если определитель коэффициента ноль? На ноль делить нельзя, так что это значит? я не могу пойти в технические подробности, но » D = 0″ означает, что система уравнений не имеет единственного решения. Система может быть несовместимой (вообще нет решения) или зависимые (бесконечное решение, которое может быть выражается в виде параметрического решения, такого как «( a , и + 3, и 4)»).Согласно правилу Крамера, « D = 0″ означает, что вам придется использовать какой-то другой метод (например, матричный операции со строками) для решить систему. Если Д = 0, вы не можете использовать Крамера Правило.

Топ | Вернуться к индексу

Процитировать эту статью как:

Стапель, Элизабет.«Правило Крамера». Пурпурная математика . Доступно с
https://www.purplemath.com/modules/cramers.htm . Доступ [Дата] [Месяц] 2016

Системы нелинейных уравнений — ChiliMath

« система уравнений » — это набор двух или более уравнений , которые решаются одновременно. Ранее я рассмотрел несколько примеров, показывающих, как решать систему линейных уравнений с помощью методов замены и исключения.Это считается линейной системой, потому что все уравнения в наборе являются линиями.

Что такое нелинейная система уравнений?

С другой стороны, нелинейная система – это набор уравнений, которые могут содержать некоторые уравнения прямой, но не все . В этом уроке мы будем иметь дело только с системой нелинейных уравнений с двумя уравнениями с двумя неизвестными, x и y.

В этом уроке семь (7) примеров.

Примеры решения систем нелинейных уравнений

Пример 1: Решите приведенную ниже систему нелинейных уравнений.

Эта система имеет по два уравнения каждого вида: линейное и нелинейное. Начните с первого уравнения, так как оно линейное. Вы можете решить для x или y. Для этого давайте найдем у через х.

Подставьте значение y во второе уравнение, а затем найдите x. В этой задаче переместите все в одну часть уравнения, оставив противоположную сторону равной нулю. После этого вынесите простой трехчлен на множители, а затем установите каждый множитель равным нулю, чтобы найти x.

Решив уравнение, мы получили два значения x. Подставьте эти числовые значения в любое из двух исходных уравнений. Однако выберите «более простое» уравнение, чтобы упростить вычисления. Очевидно, что линейное уравнение x + y = 1 — лучший выбор!

Ответ: (– 3, 4)

Ответ: (2, –1)

Таким образом, множество решений данной системы нелинейных уравнений состоит из двух точек: (– 3, 4) и (2, –1) .2}.

Я заменю выражение y, которое равно \color{blue}x+3, из нижнего уравнения на y из верхнего уравнения. Тогда мы должны быть в состоянии найти x.

Используйте эти значения x, чтобы найти соответствующие значения y. Я бы выбрал более простое уравнение (нижнее уравнение) y=x+3 для решения для y.

Ответ: (0, 3)

Ответ: (– 3, 0)

Конечными ответами являются точки (0, 3) и (– 3, 0) . Это точки пересечения заданной прямой и окружности с центром в начале координат.

Пример 3: Решите приведенную ниже систему уравнений.

Эта проблема очень похожа на проблему №2. У нас есть прямая (верхнее уравнение), которая пересекает окружность (нижнее уравнение) в двух точках.

Шаг 1 : Решите первое уравнение для y.

Шаг 2 : Подставьте значение y в нижнее уравнение. Вам нужно будет возвести в квадрат двучлен, объединить одинаковые члены и вынести трехчлен, чтобы получить значения x.Вот решение:

Следовательно, значения x равны

Шаг 3 : Обратно подставьте эти x{\rm{ — значения}} в верхнее уравнение x + y = — 1, чтобы получить соответствующие y{\rm{ — значения}}.

Ответ: (– 3, 2)

Ответ: (2, – 3)

Шаг 4 : Вот график линии, пересекающей окружность в точках (– 3, 2) и (2, – 3) .

Пример 4: Решение системы нелинейных уравнений

Подставить выражение y из верхнего уравнения на y из нижнего уравнения.Примените распределительное свойство, затем переместите все влево. Вынесите трехчлен на множители, затем установите каждый множитель равным нулю, чтобы найти x.

Итак, у нас есть

Поскольку теперь у нас есть значения x, выберите любое из исходных уравнений для решения относительно y. Очевидным выбором является y=x+3, потому что он намного проще, чем другой.

Ответ: (–1, 2)

Ответ: (– 2, 1)

На графике показано пересечение косой гиперболы и прямой в точках (–1, 2) и (– 2, 1) .

Пример 5: Решение системы нелинейных уравнений

Обратите внимание, что первое уравнение представляет собой окружность с центром в точке (-2, 2) и радиусом 1. Второе уравнение представляет собой параболу стандартной формы с вершиной в точке (-2, 3). Мы ожидаем, что решениями этой системы нелинейных уравнений являются точки, в которых парабола (квадратичная функция) пересекает заданную окружность.

Мы решим это двумя способами. Сначала методом замещения, затем методом исключения.2} второго уравнения и подставьте его в первое уравнение.

Затем подставьте это во второе уравнение, которое дает нам уравнение с одной переменной только в y.

Приравняв каждый множитель к нулю и найдя у, мы получим

Теперь мы хотим найти соответствующие значения x, когда y=2 и y=3. Я буду использовать уравнение окружности, чтобы сделать именно это.

Ответ: (–1, 2) и (– 3, 2)

Ответ: (– 2, 3)

Следовательно, полными решениями являются точки пересечения квадратичной функции и окружности (–1, 2) , (– 3, 2) и (– 2, 3) .2} терм исчез, у нас осталось простое квадратное уравнение с переменной y, и только тогда его можно решить с помощью факторизации.

Начните с расширения биномиального члена, объедините одинаковые члены, переместите все влево, разложите полученный трехчлен на множители и приравняйте каждый множитель к нулю, чтобы найти y.

Приравняв каждый множитель к нулю и найдя у, мы получим

Обратите внимание, что мы получили те же значения y, используя метод подстановки, как показано выше. С этого момента решение теперь такое же, как показано выше, поэтому я не буду показывать остальную часть.2, а затем применяя квадратный корень с обеих сторон, чтобы получить значения x. Не забывайте прикреплять знак плюс или минус всякий раз, когда вы получаете квадратный корень из чего-либо.

Выберите любое из двух исходных уравнений и найдите значения y, когда \color{blue}x = \pm\, 3. Я буду использовать первое уравнение, потому что оно намного проще!

Ответ: (3, 1) и (3, –1)

Ответ: (– 3, 1) и (– 3, –1)

Решения этой системы нелинейных уравнений состоят из четырех точек пересечения:

(3, 1), (3, –1), (– 3, 1) и (– 3, –1)

Фактически это точки пересечения заданного эллипса (первое уравнение) и гиперболы (второе уравнение). 2, а затем извлекаем квадратный корень из обеих частей уравнения.

Обратно подставьте значения x в любое из исходных уравнений, чтобы найти y. Используем первое уравнение.

Ответ: (3, 2) и (3, – 2)

Ответ: (– 3, 2) и (– 3, – 2)

Решениями этой нелинейной системы являются точки пересечения заданного эллипса и гиперболы.

Теория линейных уравнений и задачи

Значение неизвестной величины, для которого из данного уравнения получается истинное числовое равенство, называется корнем этого уравнения.Два уравнения называются эквивалентными, когда совпадают множества их корней, корни первого уравнения также являются корнями второго и наоборот. Действуют следующие правила:
1. Если в данном уравнении одно выражение заменить другим тождественным, то получится уравнение, эквивалентное данному.
2. Если в данном уравнении какое-то выражение перенести из одной части в другую с обратным знаком, то получится уравнение, эквивалентное данному.
3. Если обе части данного уравнения умножить или разделить на одно и то же число, отличное от нуля, то получится уравнение, эквивалентное данному.
Уравнение вида $ax + b = 0$, где $a, b$ — заданные числа, называется простое уравнение относительно неизвестной величины $x$.

Задача 1 Решите уравнение:
A) 16x + 10 – 32 = 35 – 10x — 5
B) $y + \frac{3}{2y} + 25 = \frac{1}{2}y + \ frac{3}{4}y – \frac{5}{2}y + y + 37$
C) 7u – 9 – 3u + 5 = 11u – 6 – 4u

Решение :

А) Выполним некоторые действия макрода и получим
16х – 22 = 30 – 10х
После использования правила 2 находим 16х + 10х = 30 + 22
После сложения 26х = 52
Находим неизвестный множитель делением произведение на другой множитель.
Поэтому $x = \frac{52}{26}$
Следовательно, x = 2

Б) По аналогии с А) находим:
$y\left(1 + \frac{3}{2}\right) + 25 = y\left(\frac{1}{2} + \frac{3} {4} – \frac{5}{2} + 1\right) + 37 \Leftrightarrow$
$\frac{5}{2}y + 25 = -\frac{1}{4}y + 37 \Leftrightarrow \frac{5}{2}y + \frac{1}{4}y = 37 — 25 \Leftrightarrow$
$\frac{11}{4}y = 12 \Leftrightarrow y = \frac{12. 4}{11 } \Leftrightarrow y = \frac{48}{11}$

C) 4u – 4 = 7u – 6 6 – 4 = 7u – 4u 2 = 3u $u = \frac{2}{3}$

Задача 2 Решите уравнение:
A) 7(3x – 6) + 5(x — 3) — 2(x — 7) = 5
B) (x -3)(x + 4) — 2(3x — 2) = (х — 4) ²
С) (х + 1) ³ – (х — 1) ³ = 6(х ² + х + 1)

Решение :

А) 21x — 42 + 5x — 15 — 2x + 14 = 5
21x + 5x — 2x = 5 + 42 + 15 — 14
24x = 48 x = 2

B) x ² + 4x — 3x — 12 — 6x + 4 = x ² — 8x + 16
x ² — 5x – x ² + 8x = 16 + 12 – 4
3x = 16 + 12 – 4
3x = = 8

C) x ³ + 3x ² + 3x + 1 — (x ³ — 3x ² + 3x — 1) = 6x ² + 6x + 6
x ³ + 3x ² + 3x + 1 – x ³ + 3x ² + 1 = 6x ² + 6x + 6
2 = 6x + 6 6x = -4 $x = -\frac{2}{3}$

Задача 3 Решите уравнение:
A) $\frac{5x — 4}{2} = \frac{0. 5x + 1}{3}$
B) $1 –\frac{x — 3}{5} = \frac{-3x + 3}{3}$
C) $\frac{x + 1}{3} – \frac{2x + 5}{2} = -3$
D) $\frac{3(x — 1)}{2} + \frac{2(x + 2)}{4} = \frac{ 3x + 4,5}{5}$

Решение :

A) $\frac{5x — 4}{2} – \frac{0,5x + 1}{3} \Leftrightarrow$
3(5x — 4) = 2(0,5x + 1)
15x — 12 = x + 2
15х – х = 12 + 2
14х = 14 х = 1

B) $1 – \frac{x — 3}{5} = \frac{3(1 — x)}{3}\Leftrightarrow$
$1 –\frac{x — 3}{5} = 1 – x\Leftrightarrow $
-x + 3 = — 5x
5x – x = — 3
$x = -\frac{3}{4}$

C) $\frac{3(x — 1)}{2} + \frac{2(x + 2)}{4} = \frac{3x + 4.5}{5} \Leftrightarrow$
$\frac{2(x + 1) — 3(2x + 5)}{6} = — 3 \Leftrightarrow$
$\frac{2x + 2 — 6x -15}{ 6} = — 3 \Leftrightarrow$
-4x — 13 = -18
-4x = -18 + 13
-4x = -5 $x = \frac{5}{4}$

D) Приводим к общему знаменателю, который для 2, 4 и 5 равен 20
$\frac{3(x — 1)}{2} + \frac{2(x + 2)}{4} = \frac{ 3x + 4,5}{5} \Leftrightarrow$
30(x — 1) + 10(x + 2) = 4(3x + 4,5)
30x — 30 + 10x + 20 = 12x + 18
40x — 12x = 18 + 10
28 х = 28 х = 1

Задача 4 Доказательство того, что каждое значение неизвестной величины является корнем уравнения:
A) 7x — 13 = — 13 + 7x
B) $(\frac{1}{2} – x)^2 – (\ frac{1}{2} + x)^2 = -2x$
C) 3x — 3x = 26 — 2(7 + 6)
D) $\frac{-3x + 4x^2}{5} = ( 0. 2 = — 2x$
-2x = -2x
-2x + 2x = 0
0.x = 0 Следовательно, каждый x является решением.

C) 0.x = 26 — 2,13
0.x = 26 — 26
0.x = 0 каждый x является решением.

D) -3x + 4x ² = 5(0,8x — 0,6)x
-3x + 4x ² = (4x — 3)x
-3x + 4x ² = 4x ² — 3x каждый x является решением.

Задача 5 Доказательство отсутствия корней уравнения:
A) 0.x = 34
B) 5 — 3x = 7 — 3x
C) $\frac{x — 3}{4} = \frac{x + 5}{4}$
D) 2(3x — 1) – 3(2x + 1) = 6

Решение :

A) Для левой стороны мы получим значение 0 для каждого x, а для правой стороны 34, т.е.е. число, отличное от 0. Следовательно, нет такого x, чтобы получить истинное числовое равенство;

Б) 5 — 3х = 7 — 3х 3х — 3х = 7 — 5 0.х = 2 0 = 2, что невозможно при любом х

C) $\frac{x — 3}{4} = \frac{x + 5}{4}$ x — 3 = x + 5 x – x = 5 + 3 0 = 8 => решения нет;

Г) 2(3x — 1) — 3(2x + 1) = 6 6x — 2 — 6x — 3 = 6 0. x = 6 + 5 0 = 11 нет решения.

Задача 6 Решите уравнение:
A) 2x ² — 3(1 – x)(x + 2) + (x — 4)(1 — 5x) + 58 = 0
B) 3.(x + 1) ² – (3x + 5).x = x + 3
C) x ² – (x — 1).(x + 1) = 4
D) (x — 1). (х ² + х + 1) = (х — 1) ³ + 3х(х — 1)
E) (3х — 1) ² – х(15х + 7) = х(х + 1 ).(х — 1) – (х + 2) ³

Решение :

A) 2x ² — 3(x + 2 – x ² — 2x) + x — 5x ² — 4 + 20x + 58 = 0
2x ² — 3x — 6 + 3x ^{2 2 6х + х — 5х ² — 4 + 20х + 58 = 0
0.х ² + 24х + 48 = 0
24х = — 48 х = -2}

Б) 3(х ² + 2х + 1) — 3х ² — 5х = 3х ² + 6х + 3 — 3х ² -5х = х + 3
(3 — 3)х ² + (6 — 5).x – x = 3 — 3
0 = 0 => каждый x является решением

C) x ² – (x ² -1) = 4
x ² – x ² + 1 = 4
0 = 3 => нет решения

Г) х ³ + х ² + х – х ² – х — 1 = х ³ — 3х ² + 3х — 1 + 3х ² — 3х
=> 0 х это решение

E) 9x ² — 6x + 1 — 15x ² — 7x = x ³ -x ² + x ² — x — x — x ³ — 6x ² — 12x — 8
0 = 9 => нет решения

Задача 7 Решить уравнение:
A) $\frac{6x — 1}{5} — \frac{1 — 2x}{2} = \frac{12x + 49}{10}$
B) $\ frac{x — 3}{2} + \ frac{2x — 2}{4} = \ frac{7x — 6}{3}$

Решение :

А) Приводим к общему знаменателю и получаем:
12х — 2 — 5 +10х = 12х + 49
22х — 12х = 49 + 7
10х = 56 х = 5. 6

Б) $\frac{x — 3}{2} + \frac{2x — 2}{4} = \frac{7x — 6}{3}$
$\frac{x -3 + x — 1}{ 2} = \frac{7x — 6}{3}$
3(2x — 4) = 2(7x — 6)
6x -12 = 14x — 12
8x = 0 x = 0

Задача 8 Дана функция f(x) = x + 4. Решите уравнение:
$\frac{3f(x — 2)}{f(0)} + 4 = f(2x + 1)$

Решение :

Мы вычисляем f(0), f(x-2), f(2x+1), а именно f(0) = 0 + 4 = 4;
f(х — 2) = х — 2 + 4 = х + 2;
f(2x + 1) = 2x + 1 + 4 = 2x + 5 Уравнение примет такой вид
$\frac{3(x + 2)}{4} + 4 = 2x + 5$
3(x + 2 ) +16 = 4(2x + 5)
3x + 6 +16 = 8x + 20
22 — 20 = 8x — 3x
2 = 5x x = 0.4

Задача 9 Решите уравнение:
(2x — 1) ² – x(10x + 1) = x(1 – x)(1 + x) – (2 – x) ³

Решение :

(2x — 1) ² – x(10x + 1) = x(1 – x)(1 + x) – (2 – x) ³
4x ² — 4x + 1-10x ² – x = x – x ³ — 8 + 12x — 6x ² + x ³
18x = 9 $x = \frac{1}{2}$

Задача 10 Решите уравнение:
(2x + 3) ² –x(1 + 2x)(1 — 2x) = (2x — 1) ² + 4x ³ — 1

Решение :

(2x + 3) ² – x(1 + 2x)(1 — 2x) = (2x — 1) ² + 4x ³ -1
4x ² + 12x + 9 – x(1 — 4x ² ) = 4x ² — 4x + 1 + 4x ³ — 1
12x + 9 — x + 4x ³ = — 4x + 4x ^{3 9044 $ 15x 4 9020 фракция{3}{5}$}

Задача 11 Решите уравнение:
(2x — 1) ³ + 2x(2x — 3). 2 + 9 = x + \frac{1}{4}$
9 = x + 2x
9 = 3x x = 3

Задача 13 Доказательство эквивалентности двух уравнений:
A) $\frac{x — 5}{2} + \frac{x — 1}{8} = \frac{1.5x — 10}{4}$ и $\frac{x + 6}{2} – \frac{5,5 — 0,5x}{3} = 1,5$
B) $x – \frac{8x + 7}{6 } + \frac{x}{3} = -1\left(\frac{1}{6}\right)$ и $2x – \frac{6 – x}{3} — 2\left(\frac{ 1}{3}\справа)х = -2$

Решение :

А) Для первого уравнения получаем последовательно:
4(х — 5) + х — 1 = 2(1,5х — 10)
4х — 20 + х — 1 = 3х — 20
5х — 3х = — 20 + 21
2x = 1 $x = \frac{1}{2}$,
для второго уравнения имеем
3(x + 6) — 2(5,5 — 0.5г) = 6 . 1.5
3x + 18 — 11 + x = 9
4y = 9 — 7
$x = \frac{2}{4}$ $x = \frac{1}{2}$ Следовательно, уравнения эквивалентны.

Б) Аналогично А) Попробуйте сами

Задача 14 Решите уравнение:
A) (2x + 1) ² – x(1 — 2x)(1 + 2x) = (2x — 1) ² + 4x ³ — 3
B) (2x — 1) ² + (x — 2) ³ = x ² (x — 2) + 8x — 7
C) (x + 2)(x ² — 2x + 4) + x(1 – x)(1 + x) = x – 4
D) $\frac{8x + 5}{4} – \frac{1}{2\left[2 – \frac{3 – x}{ 3}\right]} = 2x + \frac{5}{6}$
E) $\frac{x}{3} – \frac{x + 3}{4} = x – \frac{1}{ 3\left[1 — \frac{3 — 24x}{8}\right]}$
F) $\frac{x}{5} — \frac{(2x — 3)^2}{3} = \ frac{1}{5}\left[5 – \frac{20x — 43x}{3}\right]$

Решение :

A) 4x ² + 4x + 1 – x(1 — 4x ² ) = 4x ² — 4x + 1 + 4x ³ — 3
4x – x + 4x ^{3 9044 4 — ³ -3
3x + 4x = -3
7x = — 3 $x = -\frac{3}{7}$}

Б) 4x ² — 4x + 1 + x ³ — 3x ² . 2 + 3x.2 ² — 8 = x ³ -2x ² + 8x — 7
4x ² — 6x ² — 4x + 1 + 12x — 8 = — 2x -7
-2x ² + 8x — 7 = — 2x ² + 8x — 7
0 = 0 => каждый x является решением;

C) x ³ + 2x ² — 2x ² — 4x + 4x + 8 + x(1 – x ² ) = x — 4
x ³ + 8 + x – x ^{3 = x — 4
8 = — 4, что невозможно. Следовательно, уравнение не имеет решения;}

D) $\frac{8x + 5}{4} — 1 + \frac{3 — x}{6} = 2x + \frac{5}{6} \Leftrightarrow$
3(8x + 5) — 12 + 2(3 – х) = 24х + 2.2 — 43x}{15} \Leftrightarrow$
3x — 5(4x ² -12x + 9) = 15 — 20x ² + 43x
3x — 20x ² + 60x — 45 = 15 — 200 + 43х
63х — 43х = 15 + 45
20х = 60 х = 3

Подробнее об уравнениях на математическом форуме

Регистрация на форуме

Дифференциальные уравнения — Системы дифференциальных уравнений

Показать мобильное уведомление Показать все примечания Скрыть все примечания
Похоже, вы используете устройство с «узкой» шириной экрана ( i. е. вы, вероятно, на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Раздел 5-4: Системы дифференциальных уравнений
Во введении к этому разделу мы кратко обсудили, как система дифференциальных уравнений может возникнуть из проблемы популяции, в которой мы отслеживаем популяцию как жертвы, так и хищника.Имеет смысл, что количество присутствующей добычи повлияет на количество присутствующего хищника. Точно так же количество присутствующих хищников повлияет на количество присутствующих жертв. Следовательно, дифференциальное уравнение, определяющее популяцию либо жертвы, либо хищника, должно каким-то образом зависеть от популяции другого. Это приведет к двум дифференциальным уравнениям, которые необходимо решить одновременно, чтобы определить популяции жертвы и хищника.
Весь смысл этого в том, чтобы заметить, что системы дифференциальных уравнений могут довольно легко возникать из естественных ситуаций.{\ text {th}} \) также линейные дифференциальные уравнения порядка. Однако, прежде чем мы углубимся в это, давайте запишем систему и избавимся от некоторой терминологии.
Мы будем рассматривать линейные системы дифференциальных уравнений первого порядка. Эти термины означают то же самое, что они означали до сих пор. Наибольшая производная в любом месте системы будет первой производной, а все неизвестные функции и их производные будут встречаться только в первой степени и не будут умножаться на другие неизвестные функции.Вот пример системы линейных дифференциальных уравнений первого порядка.
\[\begin{align*}{{x’}_1} & = {x_1} + 2{x_2}\\ {{x’}_2} & = 3{x_1} + 2{x_2}\end{align* }\]
Мы называем такую систему -сопряженной системой , поскольку для нахождения $x_{1}$ требуется знание $x_{2}$, а также знание $x_{1}$ требуется найти $x_{2}$. Мы будем беспокоиться о том, как решить их позже. На данный момент нас интересует только знакомство с некоторыми основами систем.{\text{th}}\) линейное дифференциальное уравнение порядка как система. Давайте посмотрим, как это можно сделать.
Пример 1 Напишите следующее дифференциальное уравнение 2 ^nd порядка в виде системы линейных дифференциальных уравнений первого порядка. \[2y» — 5y’ + y = 0\hspace{0.25in}y\left( 3 \right) = 6\,\,\,\,\,\,\,\,\,y’\left ( 3 \справа) = — 1\] Показать решение
Мы можем записать дифференциальные уравнения высшего порядка в виде системы с очень простой заменой переменной.Мы начнем с определения следующих двух новых функций.
\[\begin{align*}{x_1}\left( t \right) & = y\left( t \right)\\ {x_2}\left( t \right) & = y’\left( t \right )\конец{выравнивание*}\]
Теперь заметьте, что если мы продифференцируем обе стороны, мы получим
\[\begin{align*}{{x’}_1} & = y’ = {x_2}\\ {{x’}_2} & = y» = — \frac{1}{2}y + \ frac{5}{2}y’ = — \frac{1}{2}{x_1} + \frac{5}{2}{x_2}\end{align*}\]
Обратите внимание на использование дифференциального уравнения во втором уравнении. Мы также можем преобразовать начальные условия в новые функции.
\[\begin{align*}{x_1}\left( 3 \right) & = y\left( 3 \right) = 6\\ {x_2}\left( 3 \right) & = y’\left( 3 \справа) = — 1\конец{выравнивание*}\]
Собирая все это вместе, мы получаем следующую систему дифференциальных уравнений.
\[\begin{align*}{{x’}_1} & = {x_2} & \hspace{0,25in}{x_1}\left( 3 \right) & = 6\\ {{x’}_2} & = — \frac{1}{2}{x_1} + \frac{5}{2}{x_2} & \hspace{0.2}\hspace{0.25in}y\left( 0 \right) = 1\,\,\,\,y’\left( 0 \right) = 2\,\,\,\,y»\left ( 0 \справа) = 3\,\,\,\,y»’\слева( 0 \справа) = 4\] Показать решение
Как и в предыдущем примере, нам нужно определить несколько новых функций. На этот раз нам понадобятся 4 новые функции.
\[\begin{align*}{x_1} & = y & \Rightarrow \hspace{0.25in}{{x’}_1} & = y’ = {x_2}\\ {x_2} & = y’ & \Rightarrow \hspace{0.25in}{{x’}_2} & = y» = {x_3}\\ {x_3} & = y» & \Rightarrow \hspace{0. 2} & \hspace{0.25in}{x_4}\left( 0 \right) & = 4\end{align*}\]
Теперь, когда мы, наконец, приступим к их решению, мы увидим, что обычно мы не решаем системы в том виде, в каком мы их дали в этом разделе. Системы дифференциальных уравнений можно преобразовать в матричную форму , и это форма, которую мы обычно используем при решении систем.
Пример 3 Преобразуйте следующую систему в матричную форму. \[\begin{align*}{{x’}_1} & = 4{x_1} + 7{x_2}\\ {{x’}_2} & = — 2{x_1} — 5{x_2}\end{ выровнять*}\] Показать решение
Сначала напишите систему так, чтобы каждая сторона была вектором.
\[\left( {\begin{array}{*{20}{c}}{{{x’}_1}}\\{{{x’}_2}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}{4{x_1} + 7{x_2}}\\{ — 2{x_1} — 5{x_2}}\end{массив}} \ правильно)\]
Теперь правую часть можно записать как умножение матриц,
\[\left( {\begin{array}{*{20}{c}}{{{x’}_1}}\\{{{x’}_2}}\end{array}} \right) = \left( {\begin{array}{*{20}{c}}4&7\\{ — 2}&{ — 5}\end{array}} \right)\left( {\begin{array}{* {20}{c}}{{x_1}}\\{{x_2}}\end{массив}} \right)\]
Теперь, если мы определим,
\[\vec x = \left( {\begin{array}{*{20}{c}}{{x_1}}\\{{x_2}}\end{array}} \right)\]
затем
\[\vec x’ = \left( {\begin{array}{*{20}{c}}{{{x’}_1}}\\{{{x’}_2}}\end{массив} } \правильно)\]
Тогда система может быть записана в матричной форме,
\[\vec x’ = \left( {\begin{array}{*{20}{c}}4&7\\{ — 2}&{- 5}\end{array}} \right)\vec x\ ] Пример 4 Преобразуйте системы из примеров 1 и 2 в матричный вид. Показать решение
Начнем с системы из примера 1.
\[\begin{align*}{{x’}_1} & = {x_2}\hspace{0,25in}{x_1}\left( 3 \right) = 6\\ {{x’}_2} & = — \frac{1}{2}{x_1} + \frac{5}{2}{x_2}\hspace{0.25in}{x_2}\left( 3 \right) = — 1\end{align*}\]
Первое определение,
\[\vec x = \left( {\begin{array}{*{20}{c}}{{x_1}}\\{{x_2}}\end{array}} \right)\]
Система тогда,
\[\vec x’ = \left( {\begin{array}{*{20}{c}}0&1\\{ — \frac{1}{2}}&{\frac{5}{2}} \end{массив}} \right)\vec x\hspace{0.25in}\vec x\left( 3 \right) = \left( {\begin{array}{*{20}{c}}{{x_1}\left( 3 \right)}\\{{x_2}\ влево( 3 \вправо)}\конец{массив}} \вправо) = \влево( {\начать{массив}{*{20}{c}}6\\{ — 1}\конец{массив}} \вправо )\]
Теперь давайте сделаем систему из примера 2.
\[\begin{align*}{{x’}_1} & = {x_2}\hspace{0,25in}{x_1}\left( 0 \right) = 1\\ {{x’}_2} & = { x_3}\hspace{0. 2}}\end{массив}} \right)\]
Теперь первый вектор можно записать как умножение матриц, и мы оставим второй вектор в покое.2}}\end{массив}} \right)\hspace{0.25in}\vec x\left( 0 \right) = \left( {\begin{array}{*{20}{c}}1\\ 2\\3\\4\конец{массив}} \справа)\]
где,
\[\vec x\left( t \right) = \left( {\begin{array}{*{20}{c}}{{x_1}\left( t \right)}\\{{x_2}\ влево( t \вправо)}\\{{x_3}\влево( t \вправо)}\\{{x_4}\влево( t \вправо)}\конец{массив}} \вправо)\]
Обратите внимание, что иногда для таких «больших» систем, как эта, мы делаем еще один шаг вперед и записываем систему как
. \[\vec x’ = A\vec x + \vec g\left( t \right)\]
Последнее, что нам нужно сделать в этом разделе, — это избавиться от терминологии.Начиная с
\[\vec x’ = A\vec x + \vec g\left( t \right)\]
мы говорим, что система однородна , если $\vec g\left( t \right) = \vec 0$, и мы говорим, что система неоднородна , если $\vec g\left( t \right ) \ne \vec 0$.
Системы линейных уравнений: исключение Гаусса
Решение линейной системы с матрицами с помощью исключения Гаусса
После нескольких уроков, в которых мы неоднократно упоминали, что мы охватываем основы, необходимые для того, чтобы позже научиться решать системы линейных уравнений, пришло время для нашего урока сосредоточиться на полной методологии, которой нужно следовать, чтобы найти решения. для таких систем.
Что такое исключение Гаусса
Исключение по Гауссу — это название метода, который мы используем для выполнения трех типов операций со строками над расширенной матрицей, полученной из линейной системы уравнений, чтобы найти решения для такой системы. Этот метод также называется сокращением строк и состоит из двух этапов: прямое исключение и обратная замена.
Эти два шага метода исключения Гаусса отличаются не операциями, которые вы можете использовать через них, а результатом, который они дают.Шаг прямого исключения относится к сокращению строк, необходимому для упрощения рассматриваемой матрицы до ее эшелонированной формы. Такой этап имеет целью продемонстрировать, имеет ли изображенная в матрице система уравнений единственное возможное решение, бесконечно много решений или вообще не имеет решения. Если установлено, что система не имеет решения, то нет смысла продолжать сокращение строки матрицы до следующего этапа.
Если возможно получить решения для переменных, входящих в линейную систему, то выполняется этап исключения Гаусса с обратной подстановкой.Этот последний шаг создаст уменьшенную форму эшелона матрицы, которая, в свою очередь, обеспечивает общее решение системы линейных уравнений.
Правила исключения Гаусса такие же, как правила для трех элементарных операций со строками, другими словами, вы можете алгебраически работать со строками матрицы следующими тремя способами (или комбинацией):
Замена двух рядов
Умножение строки на константу (любую константу, отличную от нуля)
Добавление строки к другой строке
Итак, решение линейной системы с матрицами методом исключения Гаусса оказывается структурированным, организованным и достаточно эффективным методом.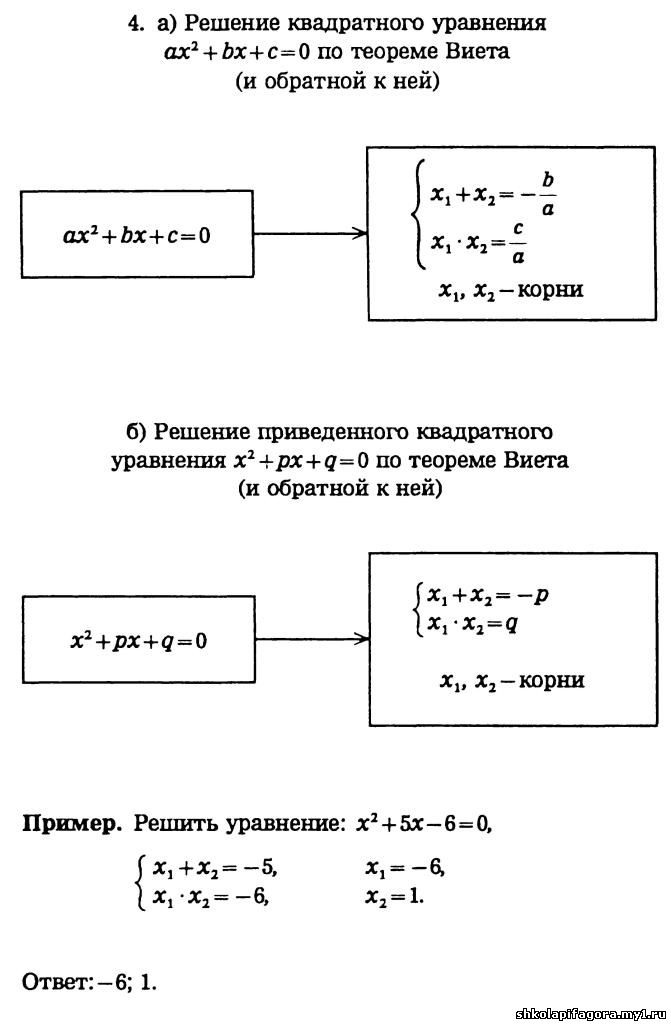
Как выполнить исключение Гаусса
На самом деле это не установленный набор шагов исключения Гаусса, которым нужно следовать, чтобы решить систему линейных уравнений, все дело в матрице, которая у вас есть в руках, и необходимых операциях над строками для ее упрощения. Для этого давайте поработаем над нашим первым примером исключения Гаусса, чтобы вы могли начать изучать весь процесс и интуицию, которая необходима при работе с ними:
Пример 1
Обратите внимание, что в этот момент мы можем наблюдать, что эта система линейных уравнений разрешима с уникальным решением для каждой из ее переменных.То, что мы до сих пор выполняли, — это первый этап сокращения строк: прямое исключение. Мы можем еще больше упростить эту матрицу (что приведет нас ко второму этапу обратной подстановки), но на самом деле в этом нет необходимости, так как на этом этапе система легко решаема. Таким образом, смотрим на получившуюся систему, чтобы решить ее напрямую:
Уравнение 5: Результирующая линейная система уравнений для решения
Из этого набора мы можем автоматически заметить, что значение переменной z равно: z=-2. Мы используем это знание, чтобы подставить его во вторые уравнения для решения для y и подставить значения y и z в первые уравнения для решения для x:
В последний раздел этого урока добавлено больше задач на исключение Гаусса. Обязательно проработайте их, чтобы попрактиковаться.
Разница между исключением Гаусса и исключением Гаусса Джордана
Разница между методом исключения Гаусса и методом исключения Гаусса Жордана заключается в том, что один из них создает матрицу в форме эшелона строк, а другой — матрицу в форме сокращенного ряда строк.Матрица формы эшелона строк имеет верхний треугольный состав, где любые нулевые строки находятся внизу, а все ведущие члены находятся справа от старшего члена из строки выше. Сокращенная форма эшелона выходит за рамки простого упрощения (иногда даже достигая формы единичной матрицы).
Уравнение 8: Разница между формой эшелона и формой эшелона строки
История исключения Гаусса и его названия довольно интересна, вы будете удивлены, узнав, что название «гауссова» было присвоено этой методологии по ошибке в прошлом веке. На самом деле было обнаружено, что алгоритм одновременного решения системы линейных уравнений с использованием матриц и редукции строк в той или иной форме записан в древних китайских текстах, которые датируются еще до нашей эры. Затем, в конце 1600-х годов, Исаак Ньютон составил по ней урок, чтобы заполнить то, что он считал пробелом в книгах по алгебре. После того, как в 1950-х годах уже было установлено название «гауссовский», термин «гауссово-иорданский» был принят, когда геодезист У. Джордан усовершенствовал технику, чтобы он мог использовать такие расчеты для обработки своих наблюдаемых данных геодезической съемки.Если вы хотите продолжить чтение об увлекательной истории о математиках исключения Гаусса, не стесняйтесь нажать на ссылку и прочитать.
На самом деле нет физической разницы между методом исключения Гаусса и методом исключения Гаусса-Жордана, оба процесса следуют одному и тому же типу операций со строками и их комбинаций, их различие заключается в результатах, которые они производят. Многие математики и учителя во всем мире будут ссылаться на исключение Гаусса и исключение Гаусса-Жордана как на методы создания матрицы ступенчатой формы по сравнению с методом создания матрицы уменьшенной ступенчатой формы, но на самом деле они говорят о двух этапах сокращения строк. мы объяснили в самом первом разделе этого урока (прямое исключение и обратная замена), поэтому вы просто применяете операции со строками, пока не упростите рассматриваемую матрицу.Если вы пришли к эшелонированной форме, вы обычно можете решить с ней систему линейных уравнений (до сих пор это называлось исключением Гаусса). Если вам нужно продолжить упрощение такой матрицы, чтобы получить непосредственно общее решение системы уравнений, над которой вы работаете, в этом случае вы просто продолжаете работать с матрицей до тех пор, пока не упростите ее до редуцированной ступенчатой формы. (это было бы то, что мы называем частью Гаусса-Жордана, и которую можно рассматривать также как поворотное исключение Гаусса).
Мы оставим подробное объяснение сокращения строк и эшелонированных форм для следующего урока, а сейчас вам нужно знать, что, если у вас нет единичной матрицы в левой части решаемой вами расширенной матрицы (в этом случае вы не не нужно ничего делать для решения системы уравнений, связанных с матрицей), метод исключения Гаусса (регулярное сокращение строк) всегда будет использоваться для решения линейной системы уравнений, которая была преобразована в матрицу.
Примеры исключения Гаусса
В качестве последнего раздела позвольте нам выполнить еще несколько упражнений по методу исключения Гаусса (сокращение строк), чтобы вы могли попрактиковаться в этой методологии.На многих будущих уроках этого курса линейной алгебры вы обнаружите, что сокращение строк является одним из наиболее важных инструментов при работе с матричными уравнениями. Поэтому убедитесь, что вы понимаете все шаги, связанные с решением следующих проблем.
Пример 2
Пример 3
Мы знаем, что для этой системы мы получим расширенную матрицу с тремя строками (поскольку система содержит три уравнения) и тремя столбцами слева от вертикальной линии (поскольку есть три разных переменных). В этом случае мы перейдем непосредственно к сокращению строк, и поэтому первая матрица, которую вы увидите в этом процессе, — это та, которую вы получите, транскрибируя систему линейных уравнений в расширенную матрицу.
Уравнение 15: Строка, уменьшающая расширенную матрицу
Обратите внимание, как мы можем сразу сказать, что переменная z равна нулю для этой системы, так как третья строка результирующей матрицы показывает уравнение -9z = 0 . Мы используем это знание и проверяем вторую строку матрицы, которая дает уравнение 2y — 6z = 0 , подставляя значение z = 0 \, в это уравнение получается y \, также равное нулю.Таким образом, мы, наконец, подставляем оба значения y и z \ в уравнение, полученное из первой строки матрицы: x + 4y + 3z = 1 , так как оба , равны нулю, то это дает нам x = 1 . Итак, окончательное решение этой системы уравнений выглядит следующим образом:
Уравнение 16: Окончательное решение системы уравнений
Пример 4
Отсюда видно, что последняя строка дает уравнение: 6z = 3 и, следовательно, z = 1/2. Подставим это в уравнения, полученные из второй и первой строки (в таком порядке), чтобы вычислить значения переменных x и y:
Пример 5
Решите следующую линейную систему, используя исключение Гаусса: Уравнение 21: Система линейных уравнений с двумя переменными
Преобразование линейной системы в виде расширенной матрицы и сокращения строк: Уравнение 22: Строка, уменьшающая расширенную матрицу
Что автоматически говорит нам y = 8 .И так, подставляя это значение в уравнение из первой строки получаем: 4x — 5y = 4x — 5(8) = 4x — 40 = -6 4x = 34 \, и, следовательно, значение x равно: x = 172\frac{\small17}{\small2} 217 . И окончательное решение этой системы уравнений:
Уравнение 23: Окончательное решение системы уравнений
Пример 6
В завершение нашего сегодняшнего урока у нас есть рекомендательная ссылка, которая дополнит ваши исследования: Исключение по Гауссу, статья, которая содержит дополнительную информацию о сокращении строк, включая введение в тему и еще несколько примеров.