1. Однородные члены предложения, знаки препинания при них
Здравствуй, мой друг. Я очень рад нашей новой встрече. И сегодня мы будем изучать однородные члены предложения, правила постановки знаков препинания между ними.
Однородными членами предложения называются члены, которые относятся к одному слову и отвечают на один вопрос. Однородными могут быть все члены предложения.
Однородные подлежащие.
Маша и Витя встретились случайно.
Грибы и ягоды росли на поляне в изобилии.
Однородные сказуемые.
Я одновременно слушаю и пишу.
Ласточки кружатся над озером и ловят мошек.
Однородные дополнения.
Мы увидели тебя и маму ещё возле магазина.
Я люблю булочки и пирожки.
Однородные определения.
Ветер гнал жёлтые и красные листья клёнов по улице.
Нежные и трепетные слова мама произнесла в день рождения своей мамы.
Однородные обстоятельства.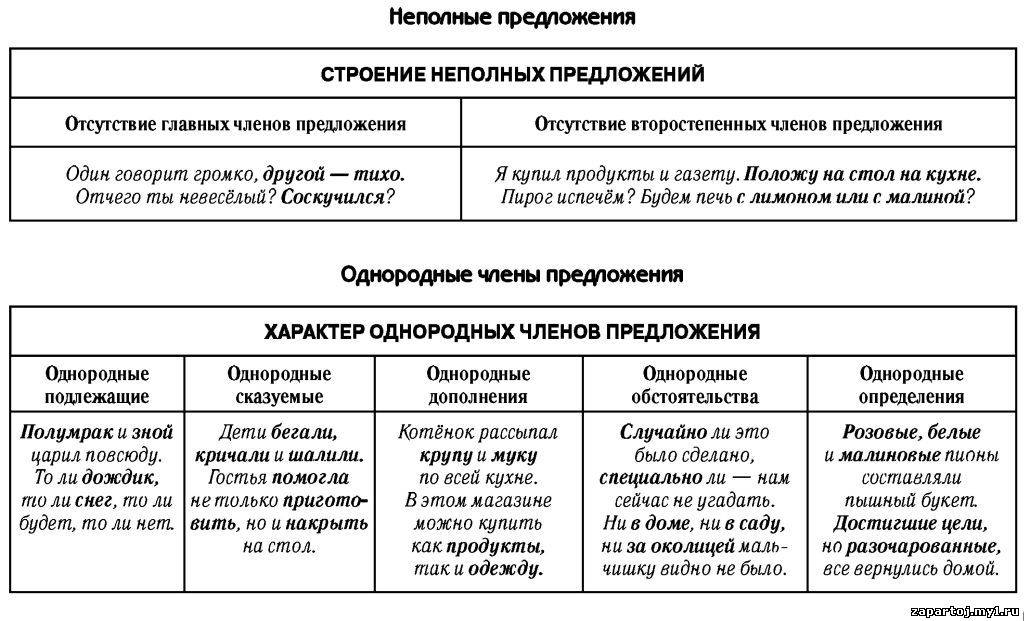
Я быстро и чётко проговорил слово.
Грибы росли быстро и всюду.
Знаки препинания при однородных членах
Если однородные члены предложения соединены без союзов, то между ними всегда ставится запятая.
Дома, улицы, переулки мелькали из окна машины со скоростью человеческой мысли.
О, О, О
Запятая ставится и перед союзами А, НО, которые связывают однородные члены.
Не высокий, а низкий клён рос возле дома со стороны улицы.
О, а О
Он подошёл ближе, но всё равно не смог прочитать объявление.
О, но О
Запятая не ставится, если между однородными членами один раз употребляется союз и.
Мел и губка лежали возле доски.
О и О
Коты и собаки не любят друг друга.
О и О
Союз И может связывать однородные члены, которые повторяются.
Мальчики и девочки, взрослые и дети прыгнули с палубы в море.
О и О, О и О
Я читал и Пушкина, и Лермонтова, и Державина.
И О, и О, и О
В схемах однородные члены обозначаются заглавной буквой О.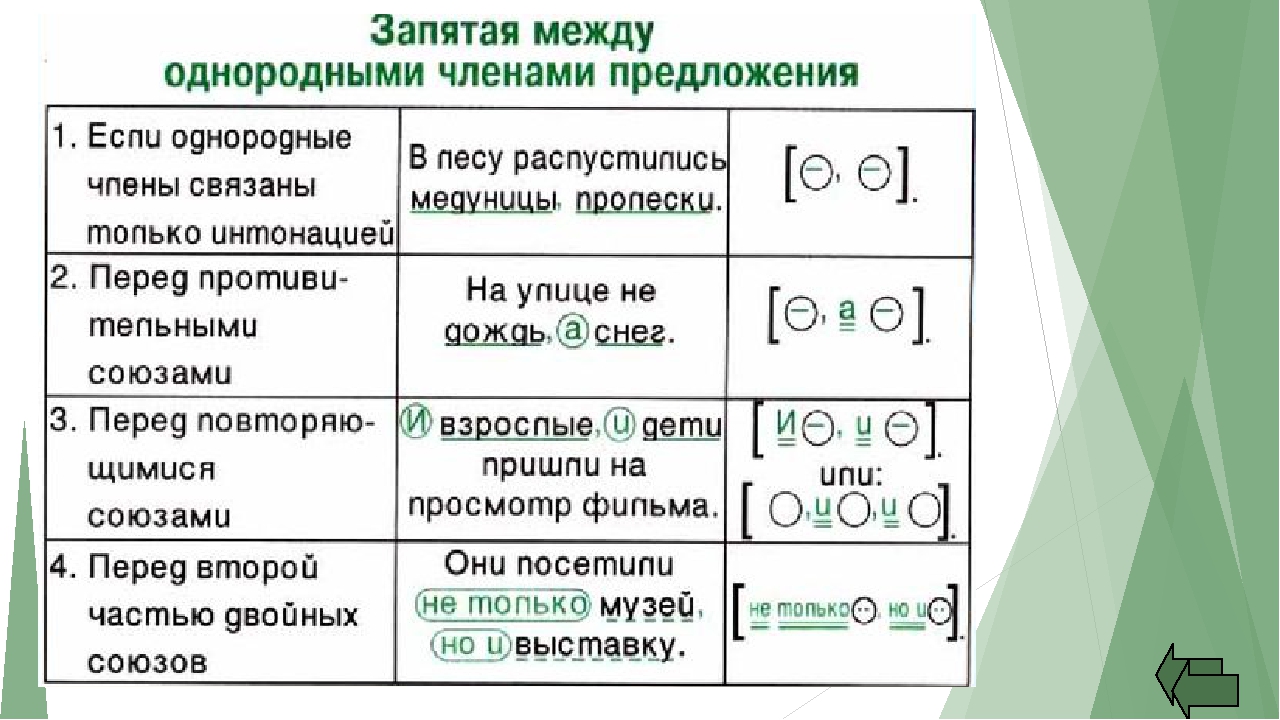 Схемы помогают лучше понять, какие знаки препинания необходимо ставить при однородных членах предложения.
Схемы помогают лучше понять, какие знаки препинания необходимо ставить при однородных членах предложения.
Обрати внимание!
1. Однородными называются такие члены предложения, которые отвечают на один вопрос и относятся к одному слову.
2. Могут быть однородными и главные, и второстепенные члены предложения.
3. Запятая при однородных членах обязательно ставится перед союзами а, но, а при союзе и — только если он повторяется.
Однородные члены предложения — урок. Русский язык, 8 класс.
Однородными называются члены предложения, которые относятся к одному и тому же члену предложения, отвечают на один и тот же вопрос и выполняют одинаковую синтаксическую функцию.
Пример:
«Он любил (Что?) степи, и широкие реки, и дремучие леса своей родины».
Однородные члены соединены между собой сочинительной связью (интонацией перечисления, сочинительными союзами).
Пример:
«По утрам солнце бьёт в беседку сквозь пурпурную, лиловую, зелёную и лимонную листву» (К. Паустовский).
Паустовский).
Первые три определения связаны интонацией перечисления; третье и четвёртое — соединительным союзом и.
Однородными могут быть как главные, так и второстепенные члены предложения.
Пример:
«Люди и животные пытались спастись от дождя и ветра».
Однородные члены предложения могут иметь при себе зависимые слова.
Пример:
«Люди и животные пытались спастись от потоков (Каких?) воды и свирепого (Какого?) ветра».
Пример:
«Он говорил медленно (нареч.), с большими паузами (сущ. с предл.), покачиваясь из стороны в сторону» (дееприч. об.).
Однородные и неоднородные определения
Однородные определения характеризуют определяемое слово с одной и той же стороны (размер, цвет, качество, материал, физическое состояние и т. п.).Пример:
«Могучий, оглушительный ливень хлынул на город» (сила ливня).
Однородные определения произносятся с перечислительной интонацией. Между ними обычно можно вставить союзы и, но.
Между ними обычно можно вставить союзы и, но.
Пример:
«Счастливая (и) озорная улыбка осветила его лицо».
Определения, стоящие после определяемого слова (инверсия), обычно однородны. Пример:«Она смотрела на меня глазами добрыми, улыбчивыми, родными».
Неоднородные определения характеризуют предмет (лицо) с разных сторон.Пример:
«Отец нёс большой кожаный чемодан (размер и материал)».
Между однородными определениями, соединёнными бессоюзной связью, ставится запятая, а между неоднородными — не ставится.
Однородные члены, связанные сочинительными союзами, и знаки препинания при них
Союзы | Соединительные союзы | Противительные союзы | Разделительные союзы |
| Одиночные | и, да (\(=\) и) | а, но, да (\(=\) но), однако, же, зато | или, либо |
| Повторяющиеся | и. .. и; ни… ни .. и; ни… ни | то… то; не то… не то; либо… либо, то ли… то ли | |
| Двойные | не только… но и; как так… и |
Запятая ставится между однородными членами, если они соединены:
- одиночными противительными союзами.
Пример:
«Она шила не одежду, а игрушки»;
- повторяющимися союзами.
Пример:
«Она шила и одежду, и игрушки»;
- двойными союзами.
Пример:
«Она шила не только одежду, но и игрушки».
Обрати внимание!
Запятая не ставится во фразеологических оборотах: ни конца ни края, и стар и млад, ни дать ни взять, и днём и ночью и др.
Запятые при повторяющемся союзе и ставятся в следующих случаях:
- [и О, и О, и О].
Пример:
«Сестра и шьёт, и готовит, и вяжет».
- [О и О, О и О].
Пример:
«В нашем лесу живут белки и зайцы, лисы и волки».
Обрати внимание!
Запятая не ставится, если союз и соединяет разные пары однородных членов:«Дети и взрослые шумели и смеялись по поводу и без повода».
Союз и может соединять части сложносочинённого предложения:
[Стало холодно], и [утром выпал снег].
Обобщающие слова при однородных членах
В предложении с однородными членами может быть обобщающее слово или словосочетание, дающее общее (обобщённое) название однородным членам.
Обобщающее слово и уточняющие его однородные члены отвечают на один и тот же вопрос и являются одним членом предложения.
Пример:
«Всё мы видели: и дома, и парки, и музеи». Обощающее слово всё.
Наличие обобщающего слова в предложении и его место по отношению к однородным членам — это условие, от которого зависит постановка знаков препинания.
- [ʘ: О, О, О].
Пример:
«Всюду слышны голоса: в поле, в роще, в садах».
- [О, О, О — ʘ].
Пример:
«В поле, в роще, в садах — всюду слышны голоса».
- [ʘ: О, О, О — …].
Пример:
«Всюду: в поле, в роще, в садах — слышны голоса».

Предложения с однородными членами. Знаки препинания в предложениях с однородными членами
Цели: повторить ранее изученный материал по теме; отработать умение правильно ставить знаки препинания в предложениях, осложненных однородными членами; закрепить навыки пунктуационного анализа предложений.
Ход урока
I. Словарно-семантическая разминка
— Запишите слова в тетрадь, расставьте ударения. Укажите твердое или мягкое произношение согласного звука перед буквой “е”.
Адекватный, антитеза, астероид, афера, де-юре, камбала, маркетинг, менеджмент, мизерный, рефери, пустячный, демагогия.
— Объясните лексическое значение слов.
II. Проверка домашнего задания
Устное сообщение об односоставных предложениях (два человека). Класс оценивает ответы, комментирует оценки.III. Повторение, обобщение теоретического материала об однородных членах предложения
Примечание.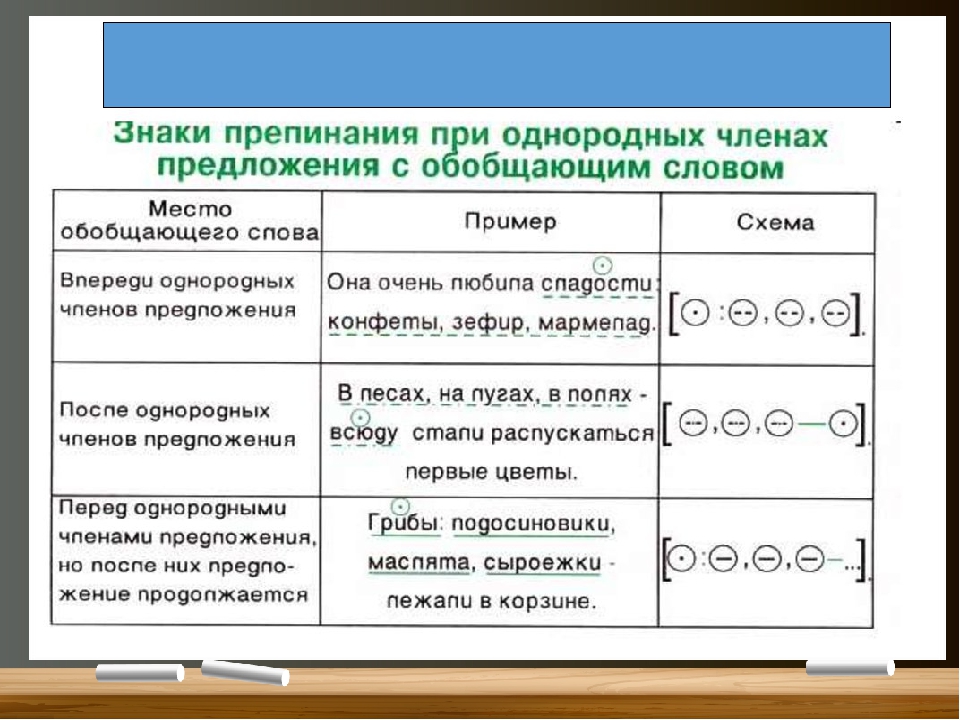 Прежде чем говорить об однородности, необходимо разобраться в двух ключевых понятиях синтаксиса — сочинении и подчинении. Сочинение — это равноправие каких-либо элементов языка, а подчинение — это неравноправие, зависимость одного элемента от другого. Отношения сочинения возникают между отдельными словами (однородными членами предложения), придаточными частями сложноподчиненного предложения и отдельными частями в составе сложносочиненного предложения. Принцип постановки знаков препинания в первом и втором случае одинаков: если между сочинительными частями нет союзов или есть союзы повторяющиеся, то между ними ставится запятая. Иной принцип действует в сложносочиненных предложениях, где запятая ставится между частями всегда (исключая сложносочиненные предложения с общим второстепенным членом — детерминантом).
Прежде чем говорить об однородности, необходимо разобраться в двух ключевых понятиях синтаксиса — сочинении и подчинении. Сочинение — это равноправие каких-либо элементов языка, а подчинение — это неравноправие, зависимость одного элемента от другого. Отношения сочинения возникают между отдельными словами (однородными членами предложения), придаточными частями сложноподчиненного предложения и отдельными частями в составе сложносочиненного предложения. Принцип постановки знаков препинания в первом и втором случае одинаков: если между сочинительными частями нет союзов или есть союзы повторяющиеся, то между ними ставится запятая. Иной принцип действует в сложносочиненных предложениях, где запятая ставится между частями всегда (исключая сложносочиненные предложения с общим второстепенным членом — детерминантом).
1. Беседа с классом.
— Дайте понятие однородности.
— Какая связь между однородными членами предложения?
— Какая интонация при однородных членах?
— Назовите морфологическое выражение однородных членов.
— Назовите условие, когда повторяющиеся слова не являются однородными членами предложения.
— Перечислите знаки препинания между однородными членами предложения.
2. Чтение § 79—83, составление таблиц.
(Составляются таблицы по теме “Знаки препинания при однородных членах”, примеры к таблицам подбираются из упражнений к параграфам. Проверка таблиц и приведенных к ним примеров с комментированием учащимися.)
— Какие группы союзов вы знаете?
— Что, кроме однородных членов, соединяют сочинительные союзы?
— Назовите группы сочинительных союзов по значению, особенностям употребления, составу.
— Зависит ли постановка знаков препинания от группы сочинительного союза, от его повторяемости (неповторяемости)?
— Назовите случаи, когда не ставится запятая между однородными членами.
(Учитель обращает внимание на правильность составленных схем, особое внимание — на расстановку запятых при повторе союза и (да — и), так как здесь учащиеся допускают ошибок больше всего.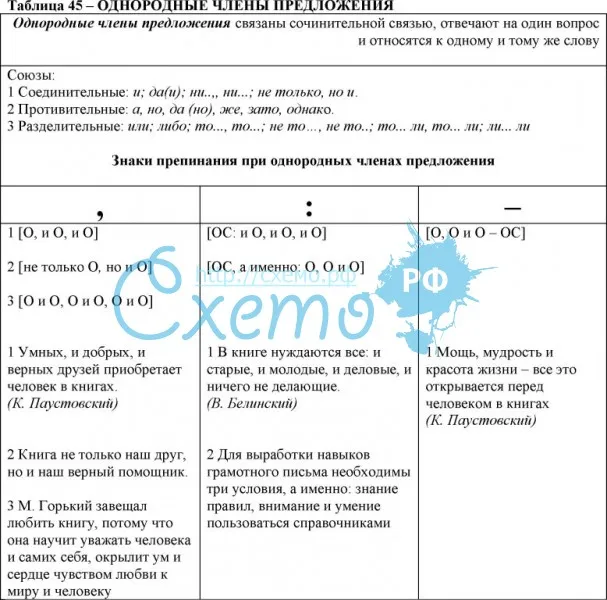 )
)
IV. Закрепление материала
Выполнение упражнений 391, 392 (устно), 393 (письменно).
Таблица 30
Соединение однородных членов в предложении
|
Бессоюзной связью (интонацией перечисления) |
Одиночными союзами |
|
Двойными союзами |
|
Искусство должно отражать жизнь человека целостно, синтетично, во взаимоотношении разных сторон |
По вечерам старички смотрели телевизор или играли в шашки |
Горный поток и шумел, и пенился, и бился о скалы |
Он интересуется как физикой, так и математикой |
Таблица 31
Выражение однородных членов в предложении
|
Отдельные слова |
Словосочетания (в том числе деепричастные и причастные обороты) |
Придаточные предложения |
|
Семейка воробьев прыгала бойко, забавно, самонадеянно |
Вынув из кармана маленький пистолет и вложив его в ухо голодному зверю, Дефорш выстрелил |
Весной он снова поверил, что силы вернутся к нему, что он вовремя закончит книгу, что счастье еще ему улыбнется |
Примечание. Может быть несколько рядов однородных членов: былые невзгоды (1), и беды (1), и горе (1) промчатся (2), как воды, забудутся (2) вскоре. Первый ряд однородных членов — подлежащие, второй — сказуемые.
Может быть несколько рядов однородных членов: былые невзгоды (1), и беды (1), и горе (1) промчатся (2), как воды, забудутся (2) вскоре. Первый ряд однородных членов — подлежащие, второй — сказуемые.
— Определите, сколько рядов однородных членов в предложении.
Солнце светило ласково и нежно и согревало своим теплом лес, луг, озеро.
V. Итог урока
Домашнее задание
1. § 79—83.
2. Упражнение 394.
Однородные члены предложения
Раздел VІ.Вода-источник жизни Урок: 61
|
Вода на службе у человека |
Школа№104 Проверила: Сыдыкжанова Л.У. |
|||||||||||||||
|
Дата: |
ФИО учителя |
|||||||||||||||
|
КЛАСС 8 «В», «А» |
Количество присутствующих |
Количество отсутствующих |
||||||||||||||
|
Цели обучения, которые необходимо достичь на данном уроке |
С. П8.4.3.1 – представлять информацию в виде презентации, в том числе содержащей таблицу, схему, диаграмму, график |
|||||||||||||||
|
яяяяя
Ожидаемый результат |
Все учащиеся смогут: находить однордные члены предложения в тексте |
|||||||||||||||
|
Большинство учащихся будут уметь прогнозировать содержание по отрывку произведения; определяя роль однородных членов предложения в тексте |
||||||||||||||||
|
Некоторые учащиеся смогут: аргументировать свою точку зрения, представляя информацию об однордных членах предложения в виде таблицы |
||||||||||||||||
|
Критерий успеха |
Узнают, какую службу несёт вода; Определяют роль однородных членов предложения |
|||||||||||||||
|
Языковая цель |
Учащиеся могут: строить логично и последовательно речь, соблюдая нормы устной и письменной речи Ключевые слова и фразы: микроорганизмы – өте ұсақ, біржасушалы микроағзалар, бактерия – простые одноклеточные микроскопические организмы, Используемый язык для диалога/письма на уроке: русский. Вопросы для обсуждения: Что мы узнаем об однородных членах предложения? |
|||||||||||||||
|
Предыдущее обучение |
Этот раздел построен на знаниях и навыках, приобретенных в предыдущих классах, в том числе на тех, которые направлены на восприятие и оценку аудиоматериалов, на анализ текста, на формирование грамотности речи. |
|||||||||||||||
|
Плани- руемые Сроки |
Планируемые действия |
Ресурсы |
||||||||||||||
|
0–2 мин |
I. Организационный момент. Психологический настрой. Приём «Поляна снежинок» У кого отличное настроение поднимают белые снежинки, у кого среднее голубые |
Компьютер. |
||||||||||||||
|
Начало урока |
Актуализация знаний. Прослушайте стихотворение. —О чём говорится в стихотворений? — Обратите внимание на следующие слова (Река, и озеро, и пруд) -Скажите, пожалуйста, на какие вопросы отвечают и какими членами предложениями являются данные слова? -Как называются такие члены предложения? -А теперь, ребята, определите тему и цели нашего урока (Деятельность учащихся) (К) Прогнозирование учащимися темы и цели урока Выбор капитанов команды. Раздать им оценочные листы Деление на группы. Игра «Найди пару» 1 группа-соединительные союзы Рубаха расшита красными, черными и белыми нитками. Девочки пели и танцевали. 2 группа-противительные союзы Витя предложил повернуть не влево, а вправо. Задача трудная, зато интересная; 3 группа разделительные союзы Снаружи раздался крик не то сойки, не то ребенка. . Я успею сделать химию или биологию. Изучение нового материала. К)-Ребята, давайте просмотрите презентацию Выступления учащихся своими аргументами Работа с учебником.Работа с текстом. Прочитайте текст. Выполните задания в группе Упр. 5 «А есть ли вода в живой природе?». Задания для первой группы -Определите тезис текста. -Ддокажите, что однородные члены в 3-м предложении 1-го абзаца с помощью интонации и сочинительных союзов Задания для первой группы -Найдите в тексте ключевое предложение, -докажите, что однородные члены в предпоследнем предложении 2-го абзаца с помощью интонации иразделительного союза Задания для первой группы Текст «Подводный мир» Деятельность учащихся) Учащиеся рассказывают о службе воды Критерий оценивания групп ФО. |
Учебник Аудиоматериал Река, и озеро, и пруд Всегда нас летом в гости ждут, В жару приятно очутиться И у ручья — воды напиться. Повсюду, всем вода нужна: Она и кораблям важна, Плывут что на морском просторе, Пшенице, спеющей на поле… И для людей, и для зверей Нет ничего воды ценней. Водой всем нужно дорожить, Ведь без нее нам не прожить! |
||||||||||||||
|
Середина урока |
IV. Освоение изученного материала. Приём «Бинго» Г)Опрежающий метод (ученицам раздала признаки ОЧП) С каждой команды вступают ученицы Капитан 1 группы -расскажет об однородных членах предложения Капитан 2группы -расскажет о знаках препинаниях ОЧП(запятая ставится) Капитан 3группы- расскажет о знаках препинаниях ОЧП(запятая не ставится) (Деятельность учащихся) Учащиеся играют
в бинго,
после игры каждый член группы делает выводы. П) Работа у доски. 1пара -пишет предложение с однородными членами и разберет их по членам 2пара- начертит схему, делает выводы ФО Смайлики (оценочный лист) Работа с учебником (Деятельность учащихся) Учащиеся выполняют работу в группах, выступают, аргументируют свою точку зрения. V. Закрепление изученного материала. С.Т) Составьте предложения по схеме. Сделайте синтаксический разбор предложения 1 группа О и О 2 группа О, а О. 3 группа О и О, и О Взаимооценивание Г) Приём «Творческая матрица» Дети заполняют таблицу
И)Работа с таблицей. Задания для капитанам команды Роль однородных членов предложения в тексте ФО Самооценивание Г(И) (Деятельность учащихся) Учащиеся выполняют задания, выступают своими аргументами Выступления капитанов команды с оценочными листами |
Учебник
Оценочный лист |
||||||||||||||
|
Конец урока |
Домашнее задание. Подготовьте презентацию на тему «Вода на службе у человека», используя интернет-ресурсы. Составьте тематическую группу слов на основе прочитанных текстов урока. Приём «Поляна снежинок». Учащиеся поднимут те снежинки, которые выражают их настроения в конце урока. Рефлексия. На доске прикреплены строки стихотворения и учащиеся вывешивают свои снежинки Урок полезен, все понятно. Лишь кое-что чуть-чуть неясно. Еще придется потрудиться. Да, трудно все-таки учиться!
|
|
||||||||||||||
Таблица Роль однородных членов предложения в тексте
|
Роль |
Примеры |
|
Конкретизация, уточнение |
На столе стояла чистая посуда: чашки, тарелки, соусник, два стакана. |
|
Называние одновременно происходящих действий |
На школьном концерте мы пели и танцевали. |
|
Противопоставление |
Мы договорились встретиться не вечером, а утром. |
|
Выражение эмоциональной окрашенности, экспрессивности |
Вершины старых лип покрылись узором юной листвы, поднялись и
протянулись над садом. |
|
Выражение градации, где каждый последующий однородный член усиливает или ослабляет значение предыдущего |
За эти дни он многое обдумал, пересмотрел, переоценил. |
Какую роль играют однородные члены в предложении?
В предложении однородные члены могут выполнять любую синтаксическую роль, то есть выступать любым членом предложения.
|
Какую синтаксическую роль выполняют |
Примеры предложений с однородными членами |
|
Подлежащее |
У нас в лесу водятся зайцы, белки и лисы. |
|
Сказуемое |
Маша закрыла дверь и открыла окно. |
|
Определение |
Саша купил синие и серые брюки. |
|
Обстоятельство |
Справа и слева от дороги росли березки. |
|
Дополнение |
Девочка кормила голубей хлебом и семечками. |
Важно! При описаниях предметов, людей, природы, интерьера
|
Задания Имя ученика
|
Работа в группе |
|
|
|
|
|
|
Урок полезен, все понятно.
Лишь кое-что чуть-чуть неясно.
Еще придется потрудиться.
Да, трудно все-таки учиться!
|
Тип связи |
Союзы между однородными членами |
Знаки препинания между однородными членами |
|
Примеры предложений |
|
Союзная (однородные члены предложения связаны союзами и интонацией) |
одиночные соединительные и разделительные |
и, да, или, либо |
не ставятся |
Я хорошо рисую и танцую. Возьми толстую или тонкую тетрадь. |
|
|
одиночные противительные |
но, а, зато, да, хотя |
запятая перед союзом |
Ученик не сделал домашнее задание, но решил сложную задачу на уроке. Мне нравится не апельсиновый, а вишневый сок. |
|
|
повторяющиеся |
и…и; или…или; то…то; да…да; ни…ни и др. |
запятая перед вторым и последующим союзами |
Он не нашел ни чистых, ни грязных вещей. Из яблок мама приготовила и варенье, и компот, и мармелад. |
|
|
составные |
как…так и; не только…но и; если не…то и др. |
запятая перед второй частью союза |
Как работает, так и ест. Девушка не только полила кусты, но и срезала сухие листья. |
|
Бессоюзная (однородные члены предложения связаны только интонацией) |
запятая |
|
|
Саше нравится математика, физика, химия. У папы были рубашки из хлопка, льна, шелка. |
Союзная (однородные члены предложения связаны союзами и интонацией)
одиночные соединительные и разделительные
и, да, или, либо не ставятся
одиночные противительные но, а, зато, да, хотя[WU1] , повторяющиеся союзы
Бессоюзная (однородные члены предложения связаны только интонацией)
Однородные члены – это члены предложения, которые обычно отвечают на один и тот же вопрос и связаны с одним и тем же словом в предложении.
Однородные члены – это одинаковые члены предложения, объединённые друг с другом сочинительной связью.
Если однородные члены предложения соединены неповторяющимися соединительными или разделительными союзами, то запятая между ними не ставится (В класс зашли Марина и Ольга
|
№
гр. |
Правильность изложения материала |
Логика изложения материала, чёткость |
Культура изложения материала |
Дополнения других групп |
Поведение в группе, умение сотрудничать |
|
I |
|
|
|
|
|
|
II |
|
|
|
|
|
|
III |
|
|
|
|
|
|
IV |
|
|
|
|
|
Критерии для оценивания выступления от группы:
1. Время
Время
2. Правильность
3. Доступность изложения
4. Логика изложения
Однородные члены предложения — это такие члены предложения, которые выражены одной и той же частью речи, имеют одну и ту же грамматическую форму и выполняют одну и ту же синтаксическую функцию в предложении (являются одними и тем же членом предложения). Однородными бывают абсолютно все члены предложения — как главные, так и второстепенные:
Хлынул дождь, и все вокруг сразу намокло: трава, асфальт, деревья, машины и даже дети во дворе.
Запятая в предложениях с однородными членами ставится:
1.Между однородными членами с повторяющимися союзами и, ни, да, либо, или, то, не то:
Снаружи раздался крик не то сойки, не то ребенка.
2.Между двумя и более однородных членов без союзов:
На улице было холодно, сыро, скользко.
3.Между однородными членами, связанными противительными союзами а, но, хотя, да (в значении но):
Мал золотник, да дорог.
4. Раздел VІІІ. Планетыи спутники Урок: 80
|
УРОК §75 Тема урока: Солнечная система: наши соседи |
Школа: №104 Проверила: Сыдыкжанова Л.О. |
|||||||
|
Дата: 08.04-09.04 |
Ф.И.О. преподавателя: Сагындыкова К.Б. |
|||||||
|
КЛАСС:6«Ә», «Б» |
Количество присутствующих:
|
Количество отсутствующих:
|
||||||
|
Цели обучения, которые необходимо достичь на данном уроке |
Ч6. П6.4.2.1 – излагать подробно содержание текста на основе прослушанного, прочитанного и/или аудиовизуального материала |
|||||||
|
Критерий успеха |
Учащийся достиг цели обучения, еслинаучится производить разбор словосочетания;различает и выделяет словосочетания по заданным схемам; будет строить высказывание с опорой на иллюстрацию;сформулирует вопросы, направленные на оценку содержаниятекста;: |
|||||||
|
Цели урока
|
Все учащиеся смогут:производить разбор словосочетания; различать и выделять словосочетания по заданным схемам;строить высказвание с опорой на иллюстрацию; формулировать вопросы, направленные на оценку содержания тексты; отвечать на «тонкие» и «толстые» вопросы; участвовать в исследовательскойработе. |
|||||||
|
Большинство учащихся смогут: определять главные и зависимые слова; составлять из словосочетаний распространенные и различные по цели высказывания предложения. |
||||||||
|
Некоторые учащиеся смогут:формулировать вопросы, направленные на оценку содержания текста, и отвечать на вопросы, выражая свое мнение по теме. |
||||||||
|
Языковаяцель |
Учащиеся могут: строить речь логично и последовательно, демонстрируя нормы устной и письменной речи. Ключевые слова и фразы: солнечная система, признаков жизни, созвездия. Используемый язык для диалога/письма на уроке: русский. Вопросы для обсуждения:Что мы узнали о Солнечной системе? |
|||||||
|
Ожидаемый результат |
Развиваться интерес детей к
изучению русского языка, расширять активный словарь, кругозор, прививать
любовь к русскому слову. |
|||||||
|
План урока |
||||||||
|
Планируемое время |
Запланированная деятельность (впишите свои задания, вместо изложенных ниже) |
Ресурсы |
||||||
|
Начало урока
|
Оргмомент. Создание коллаборативной среды. Компьютер. Игра«Хорошее настроение». Похлопайте в ладоши те, у кого сегодня хорошее настроение. А теперь мы должны развеселить тех, у кого плохое настроение. Посмотрите друг на друга – улыбнитесь!– Проверка домашнего задания. II. Актуализация знаний. (К) Догадайтесь по названию урока, о каких соседях пойдет речь. (Деятельность учащихся) Ученики отвечают на вопрос, делают выводы |
Иллюстрации На доске написаны:
|
||||||
|
Середина урока
15 минут |
ІІІ. (К) Упр. 1. Рассмотрите иллюстрацию. Сколько планет в нашей Солнечной системе? Какие из них находятся ближе к Солнцу, а какие удалены от него? (К) Упр. 2. Прочитайте текст «Существуют ли планеты, похожие на Землю?». Сформулируйте к нему вопросы таким образом, чтобы в ответах были причинные и изъяснительные союзы. Ответьте на них. П) Работа с текстом. Чтение по цепочке. №3 1 пара-читает текст, определяя его смысл, выделяя словосочетания, 2 пара-выделяет основную информацию и определяя тему текста, выписывая ключевые слова и С/С IV. Освоение изученного материала. (Г) Работа в группах Деление на группы. (главное и зависимое слово) Деление класса на группы. Работа в группах по стратегии «Корзина идей» 1 группа-№4 Определите количество С/С. Прил+сущ. Выпишите их и обозначьте грамматические связи 2 группа-№3 выпишите С/С
глагол +сущ. Физкультурная минутка V. Закрепление изученного материала Упр. Спишите, вставляя пропущенные буквы. Обозначьте главное и зависимое слова в данных словосочетаниях. Как бы вы озаглавили текст? Укажите, верно ли утверждение, что в словосочетании из водяного пара прилагательное водяного является главным словом? Обоснуйте свой ответ. Упр. Проверьте себя, умеете ли вы образовывать формы степеней сравнения. Г) Приём «Слепая схема». Заполнение таблиц в группе Подготовьте сообщение об астрономии как науке по РАФТ, используя материал урока и интернет-ресурсы. Критерий оценивания: научатся производить разбор словосочетания; различают и выделяют словосочетания по заданным схемам; будут строить высказывание с опорой на иллюстрацию; формулируют вопросы, направленные на оценку содержания текста; отвечают на «тонкие» и «толстые» вопросы; участвуют
в исследовательской работе. К.П. (Деятельность учащихся) Ученики выполняют задания, проводят взаимооценивание по стратегии «2 звезды и 1пожелание». |
Видеоматериал Предлоги
|
||||||
|
Конец урока Минут |
Рефлексия. Выберите одно из утверждений. Своей работой на уроке я: а) доволен (довольна), потому что … б) не совсем доволен (довольна), потому что… в) не доволен (не довольна), потому что… |
стикеры |
||||||
|
Домашнее задание: Составить свою опору по теме «Словосочетание» |
||||||||
|
Дополнительная информация |
||||||||
|
Дифференция |
Оценивание – |
Междисциплинарные связи |
||||||
|
рефлексия.
|
Проводит рефлексию.
|
|||||||
|
Итоговая оценка
|
1. 2. 1. 2. |
|||||||
5.
6.
7.
8.
Скачано с www.znanio.ru
“Стрекозы, мушки, мошки…”
“Стрекозы, мушки, мошки…”Изучение однородных членов предложения – одной из важных тем русского языка – можно сделать интересным. Главное условие успеха – использование различных активных форм работы, создающих основу для сознательного употребления членов предложения. Мария ТАМАРКОВА, учитель начальных классов школы № 562 г. Москвы, знакомит вас c такими формами.
3-й класс (1–3)
Тема. “Однородные члены предложения”
Цели и задачи. Познакомить
детей с понятием однородные члены предложения,
научить видеть их в предложении, правильно
ставить знаки препинания между ними; создать
основу для сознательного употребления
однородных членов предложения в речи.
Познакомить
детей с понятием однородные члены предложения,
научить видеть их в предложении, правильно
ставить знаки препинания между ними; создать
основу для сознательного употребления
однородных членов предложения в речи.
Оборудование. Доска с заданиями, книжки-карточки, плакаты с заданиями, таблица на доске, индивидуальные таблицы, индивидуальные карточки с проверочными заданиями.
Ход урока
I. Организационный момент
Учитель. Здравствуйте!
Откройте тетради и запишите сегодняшнее число.
Над какой большой темой мы работали на
предыдущих уроках?
Дети. Над темой “Предложение”.
У. Запишите название темы в тетрадях. Новую
подтему мы запишем в процессе урока.
II. Повторение изученного ранее
У. Ребята, посмотрите на
доску. Что записано на доске?
Запись на доске.
В саду растут сливы.
Д. Предложение.
У. Докажите, что это предложение.
Д. Слова связаны между собой и выражают
законченную мысль.
Слова связаны между собой и выражают
законченную мысль.
У. Дайте определение, что такое
предложение.
Д. Предложение – это слово или несколько
слов, выражающих законченную мысль.
Запись на доске.
У. Посмотрите на доску.
О чем я хочу вас спросить?
Д. О членах предложения.
У. Какие бывают члены предложения?
Д. Члены предложения бывают главными и
второстепенными.
У. Расскажите о них.
Д. Главные члены предложения – это
подлежащее и сказуемое. Подлежащее отвечает на
вопросы кто? что? Его подчеркиваем одной
чертой.
– Сказуемое отвечает на вопросы что делать? что
сделать? Его подчеркиваем двумя чертами.
У. Расскажите о второстепенных членах
предложения.
Д. Второстепенные члены предложения:
определение – отвечает на вопрос какой? какая?
какое? какие?; дополнение – отвечает на вопросы
косвенных падежей; обстоятельство – где? куда?
откуда? как?
У. Проверим на практике, насколько хорошо
вы усвоили этот материал. Работаем по вариантам.
Задание самостоятельно выполнить в тетрадях.
Затем я проверю тетради.
Проверим на практике, насколько хорошо
вы усвоили этот материал. Работаем по вариантам.
Задание самостоятельно выполнить в тетрадях.
Затем я проверю тетради.
I вариант (для сильных)
Составьте предложение по схеме, разберите по членам, надпишите части речи.
II вариант (для средних)
Допишите предложение, разберите по членам, надпишите части речи.
III вариант (для слабых)
Разберите предложение по членам, надпишите части речи.
III. Знакомство с новым материалом (работа по вариантам)
У. У вас на столах маленькие книжки. Прочитайте предложение на левых страницах книг. На правых страницах книг “соберите” эти предложения в одно так, чтобы одни и те же слова три раза не повторялись.
I вариант
| В саду растут
сливы. В саду растут вишни. В саду растут яблони. |
II вариант
В роще птицы
свистят. В роще птицы поют. В роще птицы щебечут. |
III вариант
| Стайка птиц
помчалась за леса.
Стайка птиц помчалась Стайка птиц помчалась |
Дети выполняют задание.
– Сравните предложения. В чем их сходство? Какие слова в них перечисляются?
Д. Сходство в том, что
первые слова в предложении одинаковые. Смысл
предложений остается прежним.
Дети перечисляют в I варианте обстоятельства,
во II – варианте сказуемые, в III – варианте
подлежащие.
У. На какой вопрос отвечают перечисленные
слова и к какому слову они относятся?
Д. В первом варианте отвечают на вопрос куда?,
относятся к слову помчались.
– Во втором варианте отвечают на вопрос что
делают?, относятся к слову птицы.
– В третьем варианте отвечают на вопрос что?,
относятся к слову растут.
У. Сформулируйте правило, какие слова
можно называть однородными.
Д. Однородными словами называются слова,
которые отвечают на один и тот же вопрос и
относятся к одному и тому же слову.
У. А какими членами предложения могут быть
однородные слова?
Д. И главными, и второстепенными.
У. Принято говорить не однородные слова, а
однородные члены предложения. Учитывая
последние замечания, сформулируйте правило.
Д. Члены предложения, которые отвечают на
один и тот же вопрос и относятся к одному и тому
же слову, называются однородными. Однородными
могут быть и главные, и второстепенные члены
предложения.
У. Давайте это докажем на практике, для
чего выполним следующее задание: спишите
стихотворение Льдова, найдите и подчеркните
однородные члены предложения. Если однородные
члены – подлежащее, то подчеркивается одной
чертой, если сказуемое – двумя и т. д.
д.
На доске.
Как-то летом на лужайке
Господин учитель Жук
Основал для насекомых
Школу чтенья и наук.
Вот стрекозы, мушки, мошки,
Пчелы, осы и шмели,
Муравьи, сверчки, козявки
На урок к Жуку пришли.
Проверка выполненного
задания.
– Какие однородные члены вам встретились в
этом стихотворении? Назовите их.
Д. Чтенья и наук.
– Стрекозы, мушки, мошки, пчелы, осы, шмели,
муравьи, сверчки, козявки.
У. Какими членами предложения они
являются?
Д. В первом случае дополнениями.
– Во втором – подлежащими.
У. Подчеркните однородные члены.
IV. Самостоятельная работа
У. Вставьте то, что считаете нужным, запишите и подчеркните однородные члены предложения.
Подлежащее,
____________ – главные члены предложения. Существительное, прилагательное, ______________ – части речи. Корень, __________ , __________ , __________ – части слова. |
V. Физкультминутка
VI. Углубление ранее изученного
У. В предыдущем задании
вы писали предложения с однородными членами. А
как выделяются однородные члены на письме?
Д. Запятыми.
У. На самом деле однородные члены не всегда
выделяются запятыми, и в этом нам поможет
разобраться следующее упражнение. У вас на
столах есть карточки, у меня такие же карточки на
доске. Ваша задача расставить знаки препинания,
но прежде ответьте на вопрос: какие союзы вам
известны?
Д. Союзы и, а.
У. Еще нам часто встречаются союзы или
и но. Приведите примеры.
Д. Темный или холодный.
– Веселый или грустный.
– Высокий, но худой.
– Бедный, но добрый.
У. Хорошо. А как же ставить знаки
препинания, когда есть союзы? Давайте это
выясним. Итак, берем в руки карточки. Что есть в
этом предложении?
Итак, берем в руки карточки. Что есть в
этом предложении?
Карточка 1
Д. Однородные члены.
У. Для удобства однородные члены будем
обозначать .
Расставьте запятые. Тогда у нас получится схема . Объясните ее.
Д. Однородные члены отделяются запятыми.
У. Прочитайте предложение на карточке 2,
назовите однородные члены, подчеркните их.
Карточка 2
– Запомните: перед союзом но
всегда ставится запятая.
Аналогично рассматривается карточка 3.
Карточка 3
– Посмотрите на карточки 4 и 5. Чем они похожи и чем отличаются?
Карточка 4
Карточка 5
Д. Похожи тем, что
одинаковые однородные члены, а отличаются тем,
что в карточке 5 союз и повторяется и
перед ним ставятся запятые, союзы можно назвать
однородными.
Аналогично рассматриваются карточки 6 и 7.
Карточка 6
Карточка 7
У. Дети, у нас получилась
таблица постановки запятых при однородных
членах. Ее надо запомнить. А сейчас работаем по
вариантам. На доске три столбика предложений с
пропущенными союзами. Надо вставить пропущенные
союзы и составить схему. В тетрадях вы
записывайте только схемы.
Дети, у нас получилась
таблица постановки запятых при однородных
членах. Ее надо запомнить. А сейчас работаем по
вариантам. На доске три столбика предложений с
пропущенными союзами. Надо вставить пропущенные
союзы и составить схему. В тетрадях вы
записывайте только схемы.
К доске от команды выходят по пять человек по
очереди. Побеждает команда, которая выполнит
быстро и правильно.
I вариант
II вариант
III вариант
– Проведем самостоятельную работу по вариантам. Задание на индивидуальных карточках.
I вариант (для сильных)
II вариант (для средних)
III вариант (для слабых)
VII. Подведение итогов урока
VIII. Выставление оценок
IX. Домашнее задание
У. Придумайте семь предложений с однородными членами.
Урок «Знаки препинания при однородных членах предложения» – Документ 1 – УчМет
6. Самостоятельное составление текста-описания весеннего цветка
по данному началу, концу и опорным
словам.
— Ребята, мы подошли к самому сложному и ответственному заданию.
Вы, наверное, не раз видели, как люди, соскучившись за зиму по ярким краскам и приятным запахам, весной срывают только что распустившиеся цветы, чтобы недолгое время полюбоваться ими, а потом выбросить, ведь век сорванного цветка так недолог.
Нам нужно составить для нашей газеты текст-описание весеннего цветка. Так, чтобы, этот текст не просто рассказал о цветке, а тронул души людей. Чтобы каждый человек, прежде чем сорвать цветок, сначала задумался: «А стоит ли это делать?».
Послушайте стихотворение и догадайтесь, описание какого весеннего цветка мы должны составить.
-
Белые жемчужины прилепились в ряд
К стебелёчку тонкому. Дарят аромат.
В мае распускается и цветёт в лесу.
Даже Книга Красная бережёт красу.
И лисичка рыжая рядышком пройдёт,
Белый и душистый цветик не сомнёт.
— Рассмотрите таблицу. В каком столбике даны слова и выражения для описания предмета в научном
стиле, а в каком – для художественного описания?
-
Предмет
….стиль
…стиль
Ландыш
травянистое растение;
продолговатые листья;
тонкий стебель;
в виде колокольчиков.

в лесной глуши; расцветает;
прячется;
от посторонних глаз;
крупные гладкие
блестящие;
выглядывает, тоненький
белые воздушные
как на ниточках,
жемчужинки, дрожат.
— Как вы думаете, в каком стиле мы должны описывать цветок, чтобы достичь своей цели?
(в художественном стиле).
— Оставьте строку для заглавия.
— Запишите начало текста в тетрадь. Как запишем начало текста? (с красной строки).
С приходом весны всё оживает.
— Распределите опорные слова
соответственно частям цветка.
Что делает? Где? От чего?
1. ландыш расцветает в лесной глуши
2. хрупкий цветок прячется от посторонних лаз
У чего? Какие?
3. листья у цветка крупные гладкие блестящие
у него
Какой? Что делает? Между чем?
4. стебель тоненький выглядывает между листьями
стебелёк
Какие? Что делают? Как? На чём?
5. цветки
белые дрожат как
на ниточках на стебельке
цветки
белые дрожат как
на ниточках на стебельке
жемчужинки на нём
— Составьте предложения устно по опорным словам.
— Запишите основную часть. Как запишем? (с красной строки).
— Запишите заключение (с красной строки).
Эти хрупкие цветы украшают лес. Не рви их.
— Как можно озаглавить наш текст? Запишите заголовок.
(1 человек пишет на карточке).
— Прочитайте текст, который у вас получился.
— Как вы думаете, справились ли мы с задачей?
(Текст прикрепляется на страницу газеты).
Готовимся к ЕГЭ по русскому языку. : Однородные члены предложения.
Знаки препинания в простом осложненном предложении (однородные члены предложения)| 1) отвечают на один и тот же вопрос | |
| Однородные члены предложения | 2) зависят от одного и того же слова |
| 3) произносятся с перечислительной интонацией |
 Самое главное, чтобы они отвечали на один и тот же
вопрос и зависели от одного слова!
Во-вторых, однородными могут быть ЛЮБЫЕ ЧЛЕНЫ предложения: и
подлежащее, и сказуемое, и определение, и дополнение, и обстоятельство.
Обозначим однородный член знаком Ο.
Самое главное, чтобы они отвечали на один и тот же
вопрос и зависели от одного слова!
Во-вторых, однородными могут быть ЛЮБЫЕ ЧЛЕНЫ предложения: и
подлежащее, и сказуемое, и определение, и дополнение, и обстоятельство.
Обозначим однородный член знаком Ο.
| Однородные члены предложения могут использоваться | |||
| с одиночными союзами | с повторяющимися союзами | с двойными союзами | |
| В саду расцвели розы, лилии, ромашки. |
соединительными союзами и, да(=и), или
Вдруг налетела буря с крупным И частым
градом.
Осеннею свежестью,
листвой И плодами
благоухает сад. противительными союзами а, но, да(=но),
зато, однако
Не железным ключом
открывается сердце, А добротой.
противительными союзами а, но, да(=но),
зато, однако
Не железным ключом
открывается сердце, А добротой.
|
или Ο, или Ο, или Ο Мне чудятся ТО шумные пиры, ТО ратный стан, ТО схватки боевые. Ты меня не слышишь, ИЛИ не понимаешь, ИЛИ просто игнорируешь. Метели И вьюга, стужа И темнота не помешали полярникам высадиться на льдины. | не только… но и не столько сколько Запятая ставится перед второй часть союза! не только Ο, но и Ο Эти нормы под силу вспомнить КАК мастерам спорта, ТАК И новичкам. |
В предложении может быть несколько рядов однородных
членов, поэтому различай конструкции с однородными членами предложения,
соединенными повторяющимися союзами, и
конструкции с несколькими рядами однородных членов, которые внутри ряда
соединены одиночным союзом.
(Это предложение с тремя рядами однородных членов: двумя однородными подлежащими, двумя однородными сказуемыми и двумя однородными обстоятельствами)
Запятые нигде не ставятся!
Тонкий дожди сеялся и на леса, и на поля, и на широкий Днепр. Это один ряд однородных членов, так они зависят от одного глагола «сеялся», отвечают на один вопрос – Куда? и являются обстоятельствами, поэтому запятая ставится как при повторяющихся союзах. Фразеологические обороты (устойчивые сочетания слов): Ни с того ни с сего Ни взад ни вперед Запятая внутри них не ставится! Ни за что ни про что Ни рыба ни мясо Ни свет ни заря
Ни слуху ни духу
Алгоритм действий 1) В каждом предложении найди однородные члены предложения (см. три признаки однородных членов в самом начале главы). 2) Определи, сколько рядов однородных членов есть в предложении. Каждый из рядов рассматривай отдельно друг от друга.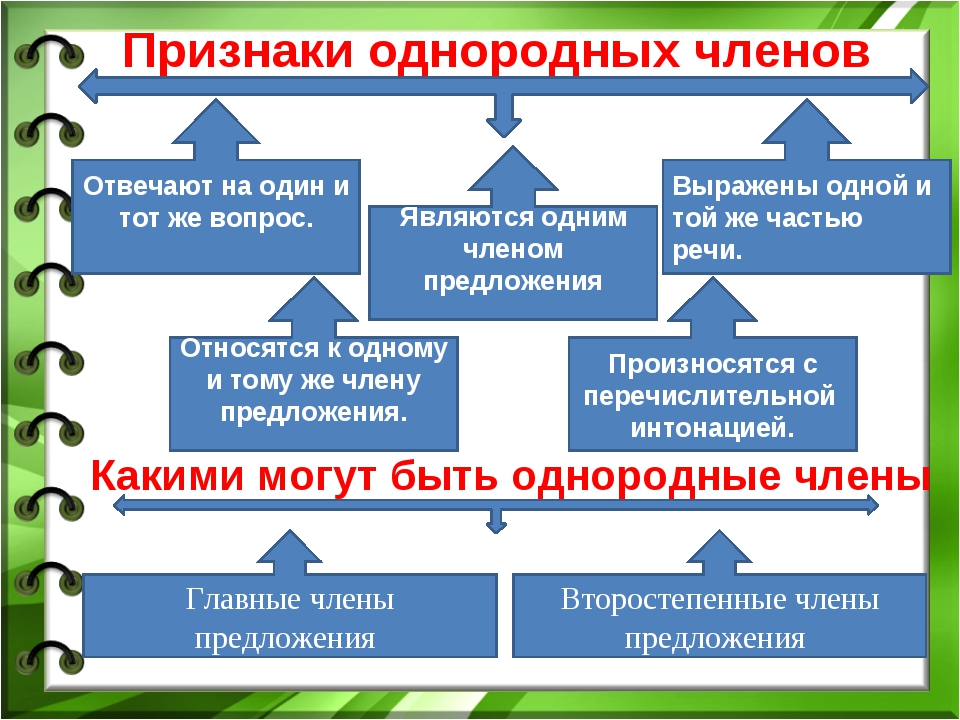 3) Отметь, какими
союзами они связаны: без союза, одиночным, повторяющимся или двойным союзом.
4) Построй схему и
расставь запятые.
ÑРазбор задания
Укажите
предложение, в котором нужно поставить одну запятую. (Знаки препинания не
расставлены.)
1)
По сторонам тропы
высокими и крутыми стенами стоял шиповник и цвел алым и влажным огнем.
2)
Видны были только
верхушки деревьев да извилистый край противоположного берега.
3)
Рука его и лицо и
синяя спецовка лоснились от сажи и машинного масла.
4)
В атмосфере тайных
обществ проходила жизнь Пушкина как в Петербурге так и в дальнейшем на юге.
Вариант ответа №1.
Прочитай еще раз Ловушку №1
Находим однородные члены предложения. Здесь их три
ряда: высокими и крутыми (какими?,
зависят от слова «стенами»),
стоял и цвел (что делал?), алым и
влажным (каким?, зависят от слова «огнем).
3) Отметь, какими
союзами они связаны: без союза, одиночным, повторяющимся или двойным союзом.
4) Построй схему и
расставь запятые.
ÑРазбор задания
Укажите
предложение, в котором нужно поставить одну запятую. (Знаки препинания не
расставлены.)
1)
По сторонам тропы
высокими и крутыми стенами стоял шиповник и цвел алым и влажным огнем.
2)
Видны были только
верхушки деревьев да извилистый край противоположного берега.
3)
Рука его и лицо и
синяя спецовка лоснились от сажи и машинного масла.
4)
В атмосфере тайных
обществ проходила жизнь Пушкина как в Петербурге так и в дальнейшем на юге.
Вариант ответа №1.
Прочитай еще раз Ловушку №1
Находим однородные члены предложения. Здесь их три
ряда: высокими и крутыми (какими?,
зависят от слова «стенами»),
стоял и цвел (что делал?), алым и
влажным (каким?, зависят от слова «огнем). Три ряда однородных членов предложения, каждый из которых внутри
связан одиночным союзом И, поэтому запятых не требуется.
Вариант ответа №2.
В предложении один ряд однородных членов: верхушки да край (что?, зависят от слова
«были видны»). Они соединены одиночным союзом да в значении и, поэтому
запятой не требуется.
Вариант ответа №3.
В предложении два ряда однородных членов.
Во-первых, рука и лицо и спецовка
(что? являются подлежащими), которые соединены повторяющимся союзом и. Расставляем запятые после каждого
однородного члена предложения: Рука его,
и лицо, и синяя спецовка. Во-вторых,
от сажи и масла (от чего? зависят от
«лоснились»), они соединены одиночным союзом и, поэтому запятой не требуется.
Вариант ответа №4.
Один ряд однородных членов предложения: как в Петербурге так и на юге (где?,
зависят от слова «проходила»). Они связаны двойным союзом как… так и, поэтому запятую поставим только перед второй частью союза, то есть: как в Петербурге, так и на юге.
Три ряда однородных членов предложения, каждый из которых внутри
связан одиночным союзом И, поэтому запятых не требуется.
Вариант ответа №2.
В предложении один ряд однородных членов: верхушки да край (что?, зависят от слова
«были видны»). Они соединены одиночным союзом да в значении и, поэтому
запятой не требуется.
Вариант ответа №3.
В предложении два ряда однородных членов.
Во-первых, рука и лицо и спецовка
(что? являются подлежащими), которые соединены повторяющимся союзом и. Расставляем запятые после каждого
однородного члена предложения: Рука его,
и лицо, и синяя спецовка. Во-вторых,
от сажи и масла (от чего? зависят от
«лоснились»), они соединены одиночным союзом и, поэтому запятой не требуется.
Вариант ответа №4.
Один ряд однородных членов предложения: как в Петербурге так и на юге (где?,
зависят от слова «проходила»). Они связаны двойным союзом как… так и, поэтому запятую поставим только перед второй частью союза, то есть: как в Петербурге, так и на юге. Таким образом, правильный вариант – ответ №4.
? Потренируйся
1. Укажите предложение, в котором нужно поставить одну запятую. (Знаки препинания не
расставлены.)
1) Официальная медицина выступает против
самолечения и лечения непроверенными средствами.
2) Северные районы оказались неравноценны как по
численности жителей так и по возможностям экономического развития.
3) Иногда лекарственные растения полностью теряют
свои лечебные свойства или сохраняют их в незначительной степени.
4) Лебеди величаво плыли по реке либо кружили над
водой либо отдыхали у своего домика.
2. Укажите предложение, в котором нужно поставить одну запятую. (Знаки препинания не
расставлены.)
1) На одном и том же кусте сирени я увидел желтые
листья и начавшие набухать почки.
2) Гусак разговаривал сам с собой сипловатым басом
и подбирал просыпанные семечки.
3) Культура наша сильна не только и не столько
столичными деятелями сколько жителями глубинки.
4) Очевидны факты изменения животных и растений под
влиянием селекции.
Таким образом, правильный вариант – ответ №4.
? Потренируйся
1. Укажите предложение, в котором нужно поставить одну запятую. (Знаки препинания не
расставлены.)
1) Официальная медицина выступает против
самолечения и лечения непроверенными средствами.
2) Северные районы оказались неравноценны как по
численности жителей так и по возможностям экономического развития.
3) Иногда лекарственные растения полностью теряют
свои лечебные свойства или сохраняют их в незначительной степени.
4) Лебеди величаво плыли по реке либо кружили над
водой либо отдыхали у своего домика.
2. Укажите предложение, в котором нужно поставить одну запятую. (Знаки препинания не
расставлены.)
1) На одном и том же кусте сирени я увидел желтые
листья и начавшие набухать почки.
2) Гусак разговаривал сам с собой сипловатым басом
и подбирал просыпанные семечки.
3) Культура наша сильна не только и не столько
столичными деятелями сколько жителями глубинки.
4) Очевидны факты изменения животных и растений под
влиянием селекции. 3. Укажите предложение, в котором нужно поставить одну запятую. (Знаки препинания не
расставлены.)
1) Разговор перескакивал с предмета на предмет и
становился бессмысленным и ненужным.
2) Тут были старинный сундучок и часы в футляре и
комод со множеством отделений.
3) Дом невелик да лежать не велит.
3. Укажите предложение, в котором нужно поставить одну запятую. (Знаки препинания не
расставлены.)
1) Разговор перескакивал с предмета на предмет и
становился бессмысленным и ненужным.
2) Тут были старинный сундучок и часы в футляре и
комод со множеством отделений.
3) Дом невелик да лежать не велит.
4) Репин писал Пушкина то с вдохновленным лицом то улыбающимся то смотрящим куда-то вдаль.
Однородными называются такие члены предложения, которые:
1) играют в предложении одну и ту же синтаксическую роль;
2) связаны с одним и тем же главным словом посредством одного и того же
вопроса;
3) соединены между собой сочинительной связью, что говорит об их смысловом
равноправии в предложении;
4) часто бывают выражены одной и той же частью речи.
Разъясним сказанное схемой:
Она любила танцы, книги и романтические встречи.
Перед нами ряд однородных дополнений (танцы, книги, встречи), все они зависят от одного и того же сказуемого, отвечают на один и тот же вопрос и являются равноправными по смыслу.

Однородные члены предложения (ОЧП) могут быть связаны между собой как бессоюзной связью, так и с помощью сочинительных союзов:
| Средства связи между ОЧП | Пример |
| Однородные члены связаны бессоюзной связью | Айболит по лесам, по болотам идет. |
| Однородные члены связаны соединительными союзами и, да (в значении и), ни — ни, не только — но и, как — так и, не столько — сколько и др. | Да здравствует мыло душистое, и полотенце пушистое,
и зубной порошок! (К. Чуковский). Ни страны, ни погоста не хочу выбирать! (И. Бродский). Он не столько беден, сколько жаден. |
| Однородные члены связаны противительными союзами а, но, да (в значении но), зато | Звезды падают им на плечи, а не в ладони. Мал золотник, да дорог.  Блоха мала, зато зла. |
| Однородные члены связаны разделительными союзами или (иль), либо, то — то, не то — не то | Я или зарыдаю, или закричу, или в обморок упаду. Там где-то есть город либо село с таким названием. |
Ветер носился во дворах, стучал в окна, зарывался в листья.
Ответы должны быть полными, четкими, краткими.
В некоторых предложениях для большей выразительности слова могут повторяться. Между ними также ставится запятая, однако они не считаются однородными членами.
Шла она, шла и наконец пришла.
И стало ему жалко, жалко своей уходящей жизни.
Для однородных членов, связанных сочинительными союзами, существуют следующие правила расстановки знаков препинания:
| Случаи, когда однородные члены разделяются запятой | Случаи, когда однородные члены не разделяются запятой |
При одиночных союзах а, но, зато, да (в значении но). Мал золотник, да дорог. |
При одиночных союзах и, или, либо, да (в значении и). Слышался шум леса_ да треск сучьев в костре. Внутри групп однородных членов, соединенных попарно союзами и, или, либо, да (в значении и). Он так ходил летом и зимой, осенью и весной. |
| При повторяющихся союзах и — и, ни — ни, то — то, не то — не то, или —
или, либо — либо, да — да. Ни я, ни мой друг не устали. |
|
| При всех двойных союзах: как — так и, не только — но и, где — там и,
настолько — насколько, хотя и — но и др. Его уважали как друзья, так и враги. Он был хотя и стар, но крепок. |
Обратите внимание! Повторяющийся союз может по-разному располагаться относительно ряда однородных членов. Обычно союз ставится перед каждым членом однородного ряда. В этом случае запятая ставится между всеми однородными членами, в том числе и после первого из них: Работу он и знал, и любил, и умел ее делать.  Звезды то едва горели, то пропадали, то вдруг ярко вспыхивали на небе. Иногда перед первым членом однородного ряда нет союза. В подобных случаях запятая также ставится между всеми однородными членами, в том числе и после первого из них. Оставил себе только саблю, да трубку, да ружьишко отцово. Он тогда недовольно морщился, или хмурился, или поджимал губы. В русском языке есть немало фразеологизмов, построенных на базе ряда однородных членов. В таких фразеологизмах запятые не ставятся. Запомните основные из них: |
||
| и то и сё; ни то ни сё; и так и сяк; |
ни свет ни заря; и туда и сюда; ни рыба ни мясо; |
ни днем ни ночью; ни дать ни взять; ни взад ни вперед |
| Возможные трудности | Добрые советы |
Можно допустить ошибку при расстановке запятых в следующем случае.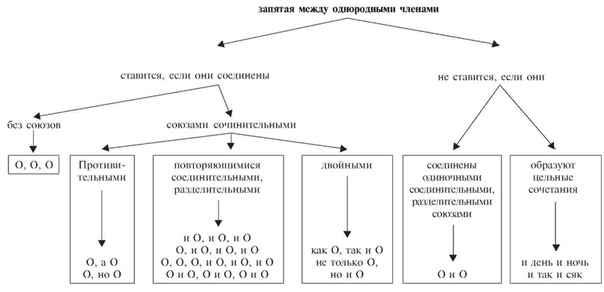 Ветер срывал с берез мокрые_ и пахучие листья_ и бросал в траву. |
Перед нами два однородных ряда (мокрые и пахучие; срывал и бросал), члены
каждого из них соединены одиночным союзом и. Запятые в этом случае не нужны. Ветер срывал с берез мокрые и пахучие листья и бросал в траву. |
| Можно допустить ошибку при расстановке запятых в следующем случае. Оставил себе только саблю_ да трубку_ да ружьишко отцово. Он тогда недовольно морщился_ или хмурился_ или поджимал губы. |
Иногда при повторяющемся союзе и (да), или, либо перед первым членом
однородного ряда нет союза. В подобных случаях запятая ставится между всеми
однородными членами, в том числе и после первого из них. Оставил себе только саблю, да трубку, да ружьишко отцово. Он тогда недовольно морщился, или хмурился, или поджимал губы. |
| Можно допустить ошибку при расстановке запятых в следующих случаях. Его уважали _ как друзья_ так и враги. Он был _ хотя и стар_ но крепок.  |
При всех двойных союзах (как …, так и …; хотя и …, но …и так далее) между
однородными членами ставится запятая. Перед первой частью союза она не нужна. Его уважали как друзья, так и враги. Он был хотя и стар, но крепок. |
К так называемой «ползучей» инфляции финансовые, производственные, фискальные структуры приспосабливаются лучше, чем к резким скачкам курса валют.
На практике отличить однородные определения от неоднородных бывает трудно. Сделать это поможет материал следующей таблицы.
| Однородные определения характеризуют разные предметы. | Красные, желтые, сиреневые брызги разорвали ночное небо (одни брызги — красные, другие — желтые и т. д.). |
Однородные определения связаны друг с другом в предложении по смыслу как
причина / следствие, условие / следствие, уточняемое / уточняющее и т. д. д. |
Им противостоял опытный, опасный враг (опытный, поэтому опасный — причина
и следствие). Это был усталый, измученный человек (второе определение уточняет, поясняет первое). |
| Определения являются однородными, если обозначают различные признаки одного и того же предмета, характеризуя его с одной стороны. В этом случае между определениями можно вставить союз И. | Буйный, оглушительный ливень хлынул на степь. Он погрузился в крепкий, неподвижный сон. |
| Определения обычно считаются однородными, если вторым компонентом является причастный оборот либо оборот на базе прилагательного. | Высокие, иссушенные солнцем деревья стояли вдоль дороги. Яркие, полные света блики заиграли на стеклах. |
| Определения, стоящие после определяемого слова, считаются однородными. | Морские волны, упругие, холодноватые, казались ему кожаными. |
Зачастую вопрос об однородности определений (а значит, и вопрос о знаках препинания при них) может быть решен только при учете интонации предложения (говорящий обычно интонационно подчеркивает однородные определения). Если обобщающее слово стоит перед однородными членами, то после него ставится двоеточие.
За полчаса снегом покрылась вся улица: и тротуар, и крыши домов, и спины прохожих.
Если обобщающее слово стоит после однородных членов, то перед ним ставится тире.
Гайки, обломки деталей, ветошь — всё это представляло теперь огромную ценность.
Если обобщающее слово стоит перед однородными членами, а после них предложение продолжается, то перед однородными членами ставится двоеточие, а после них перед остальной частью предложения — тире.
Все они: и лейтенант, и Игорь Иванович, и даже Петька — Соколик — стояли молча, не глядя по сторонам.
Следует запомнить особый случай, когда в книжной речи после обобщающих слов перед однородными членами стоят слова как-то, а именно, например, указывающие на перечисление.
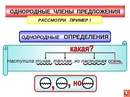 В таких случаях после этих слов
ставится двоеточие, а перед ними — запятая.
В таких случаях после этих слов
ставится двоеточие, а перед ними — запятая.Здесь водились разные звери, как-то: волки, лисы, бобры и т. д.
Обобщающее слово при однородных членах предложения. Обобщающее слово – это слово, являющееся общим по отношению к однородным членам предложения. Однородные члены предложения уточняют, конкретизируют обобщающее слово. Обобщающим словом могут быть определительные местоимения и наречия (все, всегда, везде, всюду), а также другие члены предложения и цельные словосочетания. Обобщающие слова являются тем же членом предложения, что и однородные члены. В зависимости от позиции выделяют три типа конструкций:| …: Ο,Ο,Ο. | Всё в нем нравилось Арбузову: веселый характер, щедрость, утонченная деликатность. |
| Ο,Ο,Ο — … |
Веселый характер,
щедрость, утонченная деликатность – всё в нем нравилось Арбузову.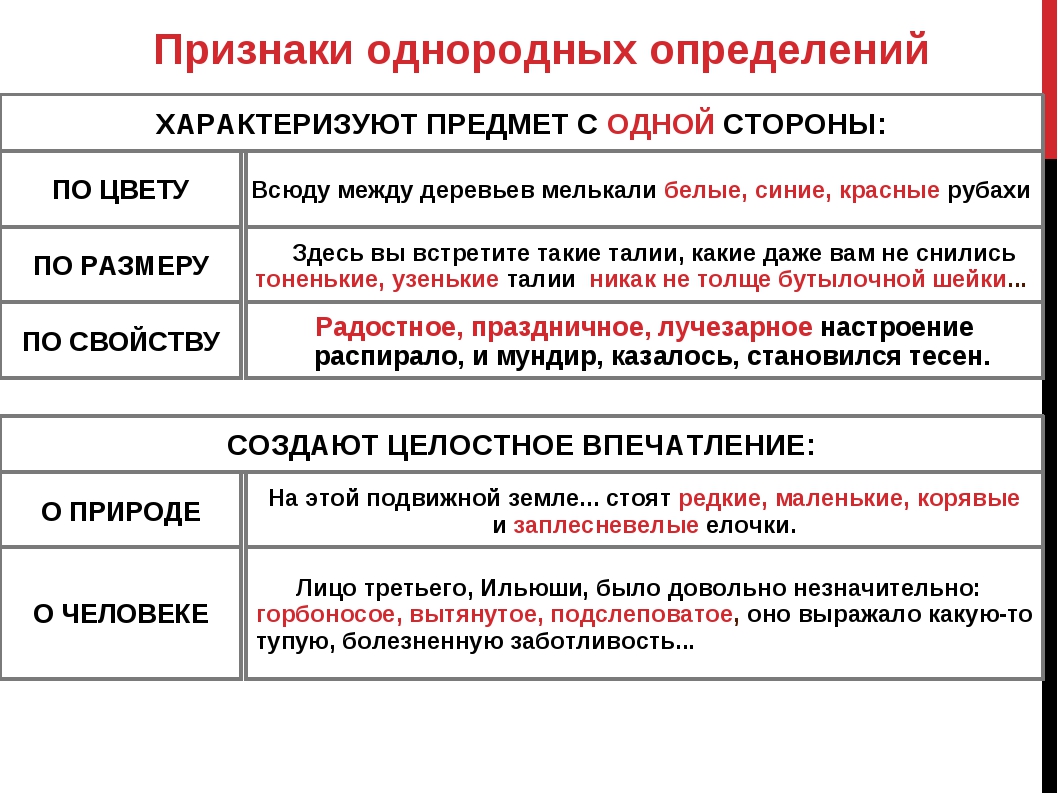
|
| : Ο,Ο,Ο — … | Всё: веселый характер, щедрость, утонченная деликатность — в нем нравилось Арбузову. |
[PDF] Единство в разнообразии: изучение распределенного гетерогенного представления предложений для экстрактивного суммирования
ПОКАЗЫВАЕТ 1-10 ИЗ 33 ССЫЛОК
СОРТИРОВАТЬ ПО Релевантности Статьи, на которые оказали наибольшее влияние Дата последнего
Гибридная MemNet для экстрактивного суммирования
Полностью управляемая данными конечная точка сеть, которая называется Hybrid MemNet для задачи обобщения одного документа, которая изучает непрерывное унифицированное представление документа перед генерацией его резюме. Развернуть- Просмотр 1 отрывка, справочная информация
Нейронное суммирование путем извлечения предложений и слов
В этой работе разрабатывается общая структура для суммирования отдельных документов, состоящая из иерархического кодировщика документов и экстрактора на основе внимания, который допускает различные классы суммирования модели, которые могут извлекать предложения или слова. Развернуть
Развернуть - Просмотр 9 отрывков, справочная информация, справочная информация и методы
Обучающая сводка Предварительное представление для экстрактивного суммирования
Разработана новая сводная система, называемая PriorSum, которая применяет усовершенствованные сверточные нейронные сети для захвата сводных предварительных характеристик, полученных из фраз с переменной длиной в рамках регрессии и объединены с зависимыми от документа функциями для ранжирования предложений. Развернуть- Просмотреть 12 выдержек, справочную информацию и методы
Обобщение документов с использованием условных случайных полей
Представлена структура на основе условных случайных полей (CRF), позволяющая сохранить достоинства двух вышеуказанных подходов, избегая при этом их недостатков. результаты предыдущих методов как функции и легко интегрируют их.Развернуть- Просмотр 1 отрывок, ссылки на методы
Экстрактивное суммирование с использованием моделей непрерывного векторного пространства
В этой статье предлагается использование непрерывных векторных представлений для семантически осознанных представлений предложений в качестве основы для измерения сходства и оценки различных композиций для представления предложений на стандартный набор данных с использованием критериев оценки ROUGE.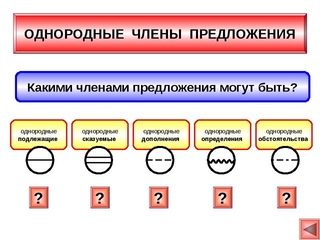 Развернуть
Развернуть - Просмотреть 1 отрывок, ссылки на методы
Сиамские рекуррентные архитектуры для обучения схожести предложений
Представлена сиамская адаптация сети долгосрочной краткосрочной памяти для помеченных данных, состоящих из пар последовательностей переменной длины, которые заставляют представления предложений Модель научилась формировать высоко структурированное пространство, геометрия которого отражает сложные семантические отношения.Развернуть- Просмотреть 2 выдержки, справочную информацию и методы
Многодокументное обобщение для левого и правого полушарий
С тех пор, как мы начали участвовать в DUC в 2001 году, наш сумматор был основан на HMM (скрытой модели Маркова) для выбор предложения в документе и поворотный алгоритм QR для создания… Развернуть
- Просмотреть 3 выдержки, ссылки на методы и фон
Может ли обезьяна создать предложение? на JSTOR
Абстрактный Было проанализировано более 19 000 многосигнальных высказываний младенца шимпанзе (ним) на предмет синтаксических и семантических закономерностей.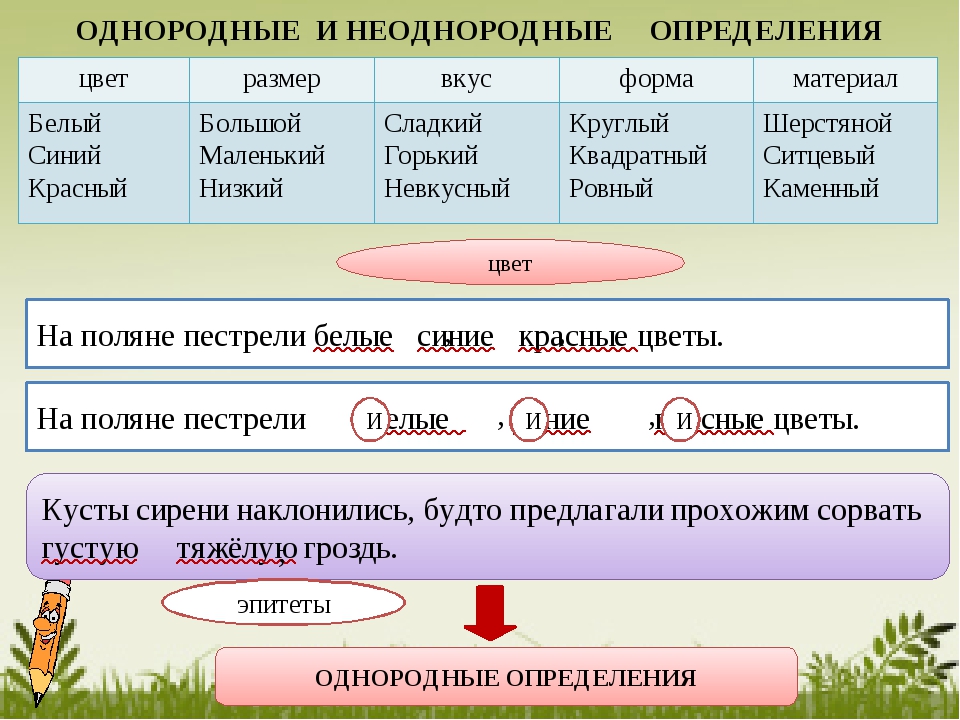 Лексические закономерности наблюдались в случае двухзнаковых сочетаний: определенные знаки (например, больше) имели тенденцию встречаться в определенной позиции. Эти закономерности нельзя было отнести к запоминанию или позиционным привычкам, предполагая, что они были структурно ограниченными. Этот вывод, однако, был опровергнут анализом видеозаписей, который показал, что большинство высказываний Нима было вызвано предыдущим высказыванием его учителя, и что Ним прерывал своих учителей в гораздо большей степени, чем ребенок прерывает речь взрослого.Подписанные высказывания других обезьян (показанные в фильмах) выявили аналогичные нечеловеческие модели дискурса.
Лексические закономерности наблюдались в случае двухзнаковых сочетаний: определенные знаки (например, больше) имели тенденцию встречаться в определенной позиции. Эти закономерности нельзя было отнести к запоминанию или позиционным привычкам, предполагая, что они были структурно ограниченными. Этот вывод, однако, был опровергнут анализом видеозаписей, который показал, что большинство высказываний Нима было вызвано предыдущим высказыванием его учителя, и что Ним прерывал своих учителей в гораздо большей степени, чем ребенок прерывает речь взрослого.Подписанные высказывания других обезьян (показанные в фильмах) выявили аналогичные нечеловеческие модели дискурса.
Science, основанный Томасом А. Эдисоном в 1880 году и издаваемый AAAS, сегодня является крупнейшим в мире общенаучным журналом с тиражом. Издается 51 раз в год, журнал Science известен своими высоко цитируемыми, рецензируемыми научными работами, своей особой силой в дисциплинах наук о жизни и отмеченным наградами освещением последних научных новостей. Интернет-издание включает в себя не только полный текст текущих выпусков, но и научные архивы, относящиеся к первому изданию Эдисона в 1880 году. В журнале Science Careers, в печатном и в Интернете, публикуются соответствующие статьи о карьере, которые публикуются еженедельно, тысячи объявлений о вакансиях обновляются несколько раз в неделю. неделя и другие услуги, связанные с карьерой. В интерактивном научном мультимедийном центре представлены научные подкасты, изображения и слайд-шоу, видео, семинары и другие интерактивные функции. Для получения дополнительной информации посетите www.sciencemag.org.
Интернет-издание включает в себя не только полный текст текущих выпусков, но и научные архивы, относящиеся к первому изданию Эдисона в 1880 году. В журнале Science Careers, в печатном и в Интернете, публикуются соответствующие статьи о карьере, которые публикуются еженедельно, тысячи объявлений о вакансиях обновляются несколько раз в неделю. неделя и другие услуги, связанные с карьерой. В интерактивном научном мультимедийном центре представлены научные подкасты, изображения и слайд-шоу, видео, семинары и другие интерактивные функции. Для получения дополнительной информации посетите www.sciencemag.org.
AAAS, основанная в 1848 году, превратилась в крупнейшее в мире междисциплинарное научное общество, насчитывающее почти 130 000 членов и подписчиков. Миссия «продвигать науку, технику и инновации во всем мире на благо всех людей» вывела организацию на передний план национальных и международных инициатив. Глобальные усилия включают программы и партнерства по всему миру, от Азии до Европы и Африки, а также обширную работу в области прав человека с использованием геопространственных технологий для подтверждения нарушений. Программы по науке и политике включают в себя крупный ежегодный форум по политике в области науки и технологий, стипендии в рамках политики в области науки и технологий в Конгрессе США и правительственных учреждениях, а также отслеживание финансирования США исследований в области НИОКР. Инициативы в области естественнонаучного образования заложили основу для обучения на основе стандартов и предоставляют учителям инструменты поддержки в Интернете. Мероприятия по привлечению общественности создают открытый диалог с учеными по таким социальным вопросам, как глобальное изменение климата. AAAS также действует как зонтичная организация для федерации, состоящей из более чем 270 аффилированных научных групп.Расширенная серия веб-сайтов включает в себя исчерпывающие ресурсы по развитию карьеры. Для получения дополнительной информации посетите www.aaas.org.
Программы по науке и политике включают в себя крупный ежегодный форум по политике в области науки и технологий, стипендии в рамках политики в области науки и технологий в Конгрессе США и правительственных учреждениях, а также отслеживание финансирования США исследований в области НИОКР. Инициативы в области естественнонаучного образования заложили основу для обучения на основе стандартов и предоставляют учителям инструменты поддержки в Интернете. Мероприятия по привлечению общественности создают открытый диалог с учеными по таким социальным вопросам, как глобальное изменение климата. AAAS также действует как зонтичная организация для федерации, состоящей из более чем 270 аффилированных научных групп.Расширенная серия веб-сайтов включает в себя исчерпывающие ресурсы по развитию карьеры. Для получения дополнительной информации посетите www.aaas.org.
Однородный случай Определение | Law Insider
Относится к
Однородный случай Фильтрация из диатомовой земли означает процесс, приводящий к значительному удалению твердых частиц, в котором (i) слой фильтрующего материала из диатомита осаждается на опорной мембране (перегородке), и ( ii) в то время как вода фильтруется путем прохождения через лепешку на перегородке, к питательной воде непрерывно добавляется дополнительная фильтрующая среда, известная как основной корм, чтобы поддерживать проницаемость фильтрационной корки.
Документ технических спецификаций индикатора MSAA означает, в зависимости от контекста, один или оба документа, озаглавленные «Соглашение о многосекторной подотчетности за услуги (MSAA) 2019-20 Технические спецификации индикатора 5 ноября 2018 года, версия 1.3», и документ, озаглавленный «Соглашение о подотчетности многосекторальных услуг (MSAA) на 2019-2020 гг.
Инвазивные виды растений означают виды растений, которые исторически не встречались в Калифорнии, которые распространяются за пределы возделываемых территорий и могут нанести ущерб окружающей среде или экономическим ресурсам.Инвазивные виды могут регулироваться сельскохозяйственными агентствами округа как вредные. Списки инвазивных растений хранятся в Калифорнийской инвентаризации инвазивных растений и в базе данных по инвазивным и ядовитым сорнякам Министерства сельского хозяйства США.
Партия урожая означает определенное количество обработанной розничной марихуаны, однородной по штамму, выращенной с использованием тех же пестицидов и других сельскохозяйственных химикатов и собранной в одно и то же время.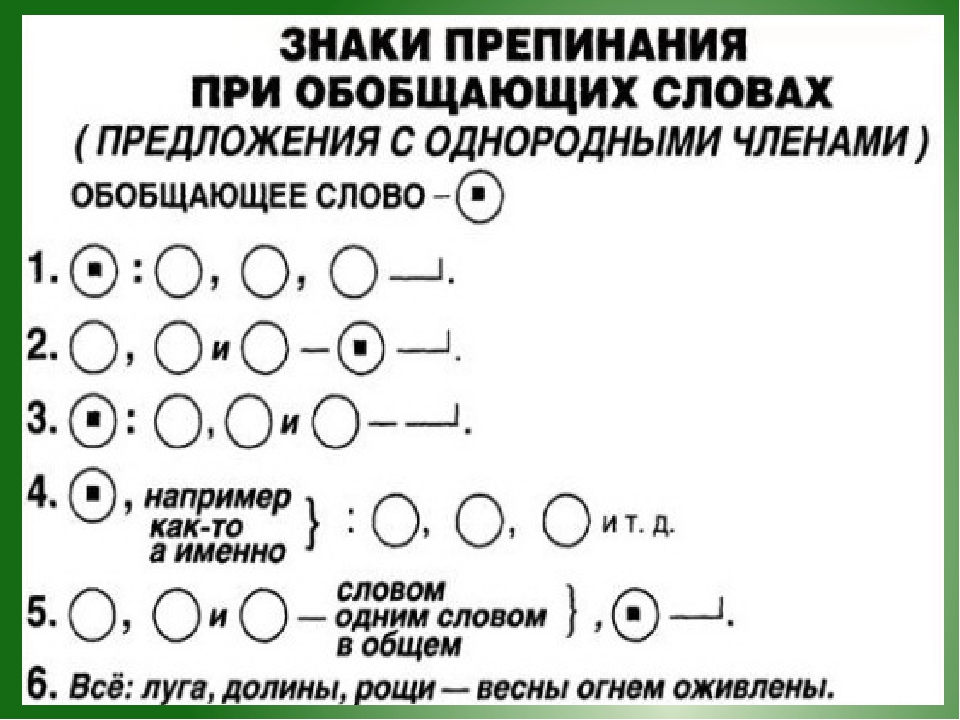
спецификация охраны труда и техники безопасности означает документ, относящийся к объекту, деятельности или проекту, подготовленный заказчиком и относящийся ко всем требованиям охраны труда и техники безопасности, связанным со строительными работами;
Образец ДНК означает любой материал, полученный из человеческого тела и состоящий из человеческих клеток или включающий их;
Водные инвазивные виды означают любые инвазивные, запрещенные, регулируемые, нерегулируемые или не включенные в перечень виды водных животных или растений, как они определены в подразделах (3), (28), (40), (44), (58) и ( 59) этого раздела, водные ядовитые сорняки, как определено в RCW 17.26.020 (5) (c), и виды, причиняющие вред водной среде, как определено в RCW 77.60.130 (1).
Генетическое тестирование означает анализ генетических маркеров для исключения или идентификации мужчины как отца или женщины как матери ребенка. Термин включает анализ одного или их комбинации:
Термин включает анализ одного или их комбинации:
Корректирующая мера Подрядчик отремонтирует или заменит поврежденную черепицу в соответствии с рекомендациями по производительности.
Охватываемые виды означает виды, для которых был учрежден Банк и для которых были выделены Кредиты, как указано в Приложении F-1.
Узел формирования рентгеновских изображений означает подсистему, в которой рентгеновские фотоны создают набор рентгеновских изображений или рентгеновских изображений, записанных с приемника рентгеновских изображений. Он включает в себя рецепторы изображения, электрические блокировки, если таковые имеются, и конструкционный материал, обеспечивающий связь между рецептором изображения и сборкой диагностического источника.
Инвазивные виды означают чужеродные виды, интродукция которых причиняет или может причинить экономический или экологический ущерб или вред здоровью человека.
Аборигенные виды в отношении конкретной экосистемы означают виды, которые, кроме как в результате интродукции, исторически встречались или встречаются в этой экосистеме в настоящее время.
Взять пробу означает индивидуальную пробу, отобранную менее чем за 15 минут, в сочетании с мгновенным измерением расхода.
Пищевой продукт каннабиса означает продукт каннабиса, который предназначен для использования, полностью или частично, для потребления человеком, включая, помимо прочего, жевательную резинку, но исключая продукты, указанные в Подразделе 15 (начиная с Раздела 32501). ) Продовольственного и сельскохозяйственного кодекса.Съедобный продукт каннабиса не считается пищей, как это определено в разделе 109935 Кодекса здоровья и безопасности, или лекарством, как определено в разделе 109925 Кодекса здоровья и безопасности.
Тест на ВИЧ означает тест на выявление ВИЧ-инфекции.
техническая спецификация означает требование тендера, которое:
Тестовый образец означает любое телесное вещество, включая, помимо прочего, кровь или мочу, взятые у лошади под наблюдением ветеринарного врача комиссии и в соответствии с предписаниями комиссии для цель анализа.
Генетический тест означает анализ ДНК, РНК, хромосом, белков или метаболитов человека, который выявляет генотипы, мутации или хромосомные изменения. Термин «генетический тест» не означает анализ белков или метаболитов, который не обнаруживает генотипы, мутации или хромосомные изменения; или анализ белков или метаболитов, который непосредственно связан с проявленным заболеванием, нарушением или патологическим состоянием, которое может быть разумно обнаружено медицинским работником, имеющим соответствующую подготовку и опыт в соответствующей области медицины.
Phase I Study означает клиническое испытание на людях в любой стране, которое удовлетворяет требованиям 21 C.F.R. § 312.21 (a) (FDCA), с поправками, которые время от времени вносятся, и его иностранный эквивалент.
Коррозионно-стойкий материал означает материал, который сохраняет приемлемые характеристики очищаемости поверхности при длительном воздействии продуктов питания, с которыми будет контактировать, при нормальном использовании чистящих составов и дезинфицирующих растворов, а также в других условиях окружающей среды.
Материал, произведенный ускорителем. означает любой материал, который стал радиоактивным с помощью ускорителя частиц.
Испытание фазы III означает клиническое испытание Лицензионного продукта на людях, которое обозначено как испытание фазы III или базовое испытание и предназначено (а) для подтверждения того, что Лицензионный продукт безопасен и эффективен для предполагаемого использования. использовать; (b) для определения предупреждений, мер предосторожности и побочных реакций, связанных с Лицензионным продуктом, в предписанном диапазоне доз; и (c) быть, само по себе или вместе с одним или несколькими другими клиническими испытаниями, имеющими сопоставимый дизайн и размер, окончательным клиническим испытанием на людях в поддержку нормативного утверждения лицензированного продукта, и (d) соответствовать 21 CFR § 312.21 (c) (с изменениями и дополнениями, приведенными ниже) и любые его зарубежные эквиваленты.
Трансграничное перемещение означает любое перемещение опасных или других отходов из района, находящегося под национальной юрисдикцией одного государства, в район или через район, находящийся под национальной юрисдикцией другого государства, либо в район или через район, не находящийся под национальной юрисдикцией какого-либо государства.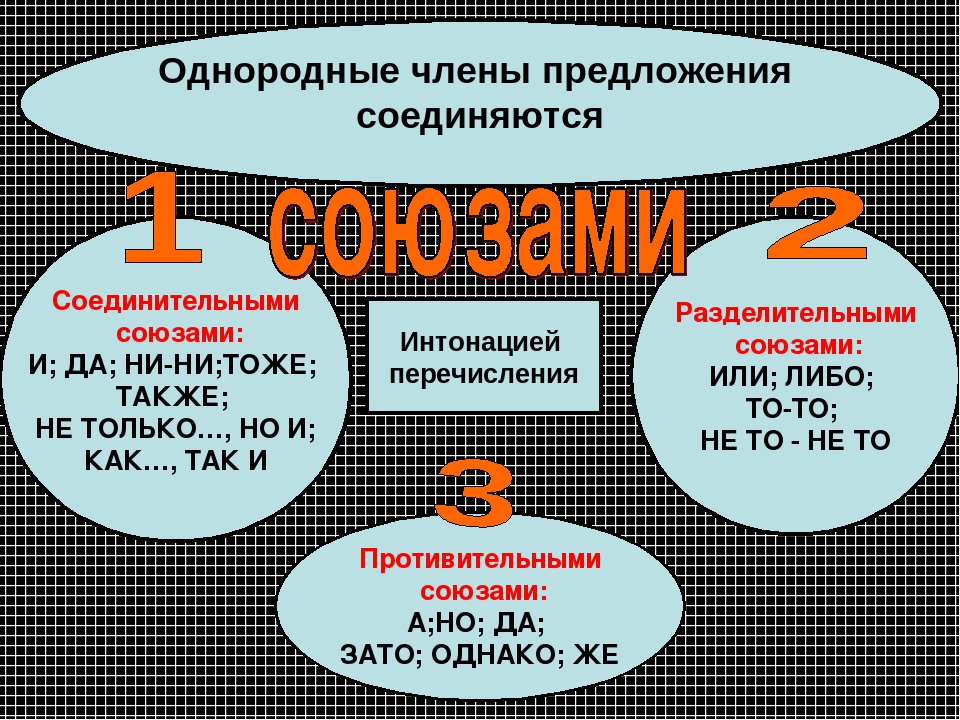 Государство, при условии, что в движении участвуют как минимум два государства;
Государство, при условии, что в движении участвуют как минимум два государства;
Испытание фазы II означает клиническое испытание Лицензионного продукта на пациентах, включая, возможно, фармакокинетические исследования и исследования диапазона доз, основными целями которых являются предварительное определение безопасности такого Лицензионного продукта для предполагаемого использования и получение достаточная информация об эффективности такого Лицензионного продукта для планирования дальнейших клинических испытаний и в целом соответствует требованиям 21 CFR §312.21 (b), или его последующее постановление, или эквивалентное в любой зарубежной стране.
Сердечно-легочная реанимация (СЛР) означает меры по восстановлению сердечной функции или поддержке дыхания в случае остановки сердца или дыхания или сбоя в работе. «СЛР» включает, помимо прочего, искусственную вентиляцию легких, компрессию грудной клетки, нанесение электрического шока, установку трубок в дыхательные пути для облегчения дыхания или другие базовые и расширенные методы реанимации.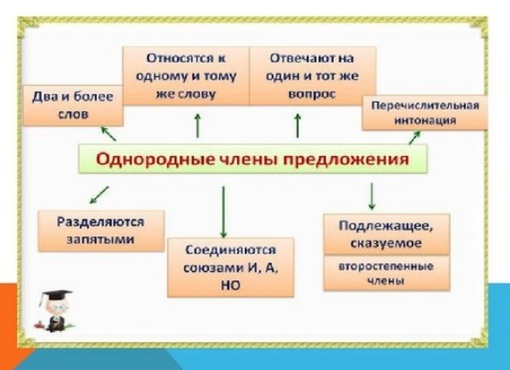
Учебные группы студентов: однородные или неоднородные?
«Хорошо, ребята, сегодня мы будем учиться в группах.Каждой группе нужен математик, ведущий, писатель / редактор и иллюстратор. Вы решаете, кто что делает. Вы рассмотрите лучшие способы решения полиномиальных задач. Вытащите инструкции и рубрику для этого задания. Как группа, ваша задача — создать одностраничный пошаговый процесс, которому кто-то может следовать, чтобы прийти к решению. У вас есть 15 минут, чтобы выполнить это задание в соответствии с заданной мной рубрикой. На старт, внимание, марш!»
Учитель, который дает эти инструкции, затем тратит следующие 15 минут, блуждая по классу, проверяя прогресс каждой группы и задавая вопросы, чтобы помочь отдельным группам прояснить свое мышление.
Группировка звучит так просто. В приведенном выше примере мы не видим того, как учитель организовал учеников в группы для достижения наилучших результатов. Некоторые преподаватели твердо убеждены в том, что учитель должен смешивать группы так, чтобы в каждой группе были представлены ученики всех уровней (разнородная группа учеников), в то время как другие считают, что учитель должен организовать учеников по уровням способностей (однородная группировка учеников). Роберт Марцано, Дебра Пикеринг и Джейн Поллок объясняют в книге « Классная инструкция, которая работает» (первое издание), что у обоих методов есть преимущества в зависимости от того, что хочет делать учитель.
Роберт Марцано, Дебра Пикеринг и Джейн Поллок объясняют в книге « Классная инструкция, которая работает» (первое издание), что у обоих методов есть преимущества в зависимости от того, что хочет делать учитель.
Определение целей
Если целью группового обучения является помощь учащимся, испытывающим трудности, исследование показывает, что разнородные группы могут помочь больше всего. С другой стороны, если цель состоит в том, чтобы стимулировать группы со средними способностями к обучению на высоких уровнях, однородное группирование было бы лучше.
Я усвоил это как учитель, когда одна из моих одаренных и талантливых учениц сказала мне по секрету, что она действительно ненавидит все время находиться в разнородных группах (она говорила это, конечно, по-другому), потому что по умолчанию другие члены группы ожидали она должна быть лидером, организовывать дела и делать всю работу.
Это был переломный момент для меня, потому что он заставил меня осознать, что я не группировал студентов для углубленного изучения. Я использовал группировку в основном как инструмент управления дисциплиной, и на самом деле моя попытка увеличить вовлеченность студентов полностью обернулась. Всегда следя за тем, чтобы «умные» студенты и учащиеся, испытывающие трудности, были поровну разделены на группы, я фактически ограничивал участие студентов фактическими лидерами групп.
Я использовал группировку в основном как инструмент управления дисциплиной, и на самом деле моя попытка увеличить вовлеченность студентов полностью обернулась. Всегда следя за тем, чтобы «умные» студенты и учащиеся, испытывающие трудности, были поровну разделены на группы, я фактически ограничивал участие студентов фактическими лидерами групп.
Выбор лучшего
Из-за этого прозрения я помню, как пообещал, что буду и дальше дифференцировать свое обучение, также ища способы дать ученикам старших классов сложные и увлекательные учебные задания.Я пообещал прекратить использовать «хороших детей» в надежде, что часть их «доброты» отразится на других учениках. Интересный случай произошел, когда я сгруппировал студентов по способностям. Сформировались новые структуры лидерства, и студенты, которые раньше никогда не участвовали активно в группах, внезапно продемонстрировали навыки и креативность, о которых я даже не подозревал.
Студенты умны и могут легко понять, что мы делаем на самом деле. Учащиеся в наших классах знают, когда их группируют в основном для наставничества и исправления менее способных учеников и… большую часть времени они возмущены этим. Мы также можем отметить их, когда мы формируем группы исключительно в целях дисциплины, помещая спокойных, послушных учеников в каждую группу, чтобы отделить и успокоить непослушных. Моя дочь Мерседес, которая попадает в обе указанные выше категории, сказала, что, когда учителя делают это с ней, она не учится, и это не доставляет удовольствия ни ей, ни другим ученикам. Возможно, чаще всего ученики достаточно сообразительны, чтобы подыгрывать, когда понимают, что группировка — это не более чем рутинный способ провести время и вообще не имеет реальной учебной цели.
Учащиеся в наших классах знают, когда их группируют в основном для наставничества и исправления менее способных учеников и… большую часть времени они возмущены этим. Мы также можем отметить их, когда мы формируем группы исключительно в целях дисциплины, помещая спокойных, послушных учеников в каждую группу, чтобы отделить и успокоить непослушных. Моя дочь Мерседес, которая попадает в обе указанные выше категории, сказала, что, когда учителя делают это с ней, она не учится, и это не доставляет удовольствия ни ей, ни другим ученикам. Возможно, чаще всего ученики достаточно сообразительны, чтобы подыгрывать, когда понимают, что группировка — это не более чем рутинный способ провести время и вообще не имеет реальной учебной цели.
Если у учащихся есть выбор, они предпочитают учиться в группах своих сверстников и друзей (однородные группы), но они также ценят возможность узнавать что-то новое и учиться у других членов класса. Это требует, чтобы мы доверяли учащимся принимать правильные решения и требовали от них ответственности за соблюдение норм обучения в группах.
По мнению Марцано, Пикеринга и Поллока, эффективное обучение в группах должно включать как минимум следующие элементы:
- В работе должен участвовать каждый член группы.
- У каждого человека есть допустимая работа с известным уровнем завершения.
- Каждый участник вкладывается в выполнение задачи или учебной цели.
- Каждый член несет индивидуальную и коллективную ответственность.
Помните, что столы не прикреплены к полу — мы можем смешивать вещи в разнородные и однородные группы интересными и творческими способами: по цвету глаз, леворукости или праворукости, предпочтительным начинкам для пиццы, количеству братьев и сестер, музыкальным предпочтениям и т. Д. пол, национальность, длина волос, шнурки для обуви, генетические особенности, стили обучения и т. д.
Гомогенная смесь | Определение и примеры
Определение однородной смеси
Гомогенная смесь — это смесь веществ, смешанных так тщательно, что вы не можете увидеть отдельные вещества. Каждый образец смеси покажет одинаковое количество каждого вещества. Гомогенные смеси могут быть твердыми, жидкими, газовыми или плазменными.
Каждый образец смеси покажет одинаковое количество каждого вещества. Гомогенные смеси могут быть твердыми, жидкими, газовыми или плазменными.
Свойства однородных смесей
Гомогенные смеси имеют несколько идентифицирующих свойств:
- Гомогенные смеси, тщательно перемешанные до уровня молекул, называются растворами.
- Однородные смеси существуют в одной фазе вещества одновременно. Вы не увидите жидкую воду и твердую воду вместе в однородной смеси. Это означает, что ваш стакан с ледяной водой с плавающими в нем кубиками льда представляет собой неоднородную смесь гомогенных смесей.
- Гомогенные смеси нельзя выразить химическими формулами.
- Чтобы точно описать любую гомогенную смесь, вам нужно назвать компоненты и указать их пропорцию или соотношение в смеси.
- Как и все смеси, гомогенные смеси можно разделить на компоненты, обычно используя их физические свойства, такие как температура кипения или магнетизм.
Морская вода — это пример гомогенной смеси, которую можно легко разделить испарением.
Многие страны используют испарение для улавливания чистой питьевой воды из морской воды, оставляя после себя соль, которую можно продать с целью получения прибыли.
Сахарная вода — еще один пример гомогенной смеси, которую можно разделить выпариванием.
Гомогенное соединение
Смесь не является соединением. В химии чистые вещества могут быть химически связаны с образованием соединений . Если вещества не связываются химически, они образуют смесей .
Примером гомогенного соединения является чистая вода (h3O). Водород связан с кислородом.
Двуокись углерода — еще один пример гомогенного соединения.
Однако воздух, которым вы дышите, представляет собой однородную смесь.Каждый вдох представляет собой смесь азота, кислорода, аргона, углекислого газа, водяного пара и некоторых других веществ. Тоже хорошо, иначе ты можешь потерять сознание.
Однородный Vs. Гетерогенная смесь
В химии мы можем иметь два типа смесей: гомогенные смеси и гетерогенные смеси :
- Однородная смесь: смешанная настолько тщательно, что выглядит как одно вещество — однородный состав.

- Гетерогенная смесь: смешанная не полностью, поэтому вы можете увидеть и выделить отдельные части смеси.
Прежде чем углубляться в эти смеси, давайте научимся их правильно произносить. Это пяти- и шестисложные слова:
- Однородный: ho-mo- gee -nee-us
- Гетерогенный: het-er-oh- gee -nee-us
Оба слова являются прилагательными, а не существительными. Вы должны использовать их, чтобы описать что-то еще, например, смесь. Вы не можете сказать: «Это неоднородно».
Приставка «гомосексуалы» означает «одинаковые», а префикс «гетеро» означает «разные».«Корень слова« родственный »- это греческое слово « генос », означающее группу, тип или род. Таким образом, однородный означает одну и ту же группу, а гетерогенный означает все разные группы вместе.
Представьте себе две разные тарелки супа: томатный суп однородный, а овощной суп неоднородный.
Вот еще три примера гетерогенных смесей:
- Студенты на занятиях
- Трейл микс
- Загрузка белья
Примеры гомогенных смесей
Если внимательно осмотреться в собственном доме, можно увидеть множество примеров однородных смесей в вашем доме.
Вот список бытовых однородных смесей:
- Мойщик окон
- Лосьон
- Жидкое мыло
- Молоко
- Дезинфицирующее средство для рук
- Напитки безалкогольные
- Лимонад (если процедить все семена и мякоть)
Это могло показаться очевидным. Учтите и это:
- Водопроводная вода (составной является только вода лабораторного класса; большая часть воды содержит растворенные газы и твердые вещества)
- Глина и графит в грифеле по дереву.«
- Чернила в ручке
- Цемент (не путать с бетоном)
- Пластмассы
- Бензин
- Свечи
- Бидоны металлические
- Жидкое средство для мытья посуды или стирки
Это все смеси, однородные во всем, если смотреть невооруженным глазом.
Никогда не пробуйте, не прикасайтесь и не нюхайте химические вещества дома или в научной лаборатории. Вы можете взглянуть на некоторые предметы и сразу увидеть, что это однородные смеси. Все смешано, и вы не можете выбрать ни один элемент в смеси.
Все смешано, и вы не можете выбрать ни один элемент в смеси.
Гомогенные смеси Quiz
Проверьте свои знания об однородных смесях, ответив на следующие вопросы:
- Что означает гомогенная смесь?
- Является ли чашка кофе однородной смесью?
- Как выглядит однородная смесь?
- Является ли раствор однородной смесью?
- Какие из вариантов ниже являются однородными?
- Мешок trail mix
- Воздух
- Итальянская заправка для салатов (масло, специи и уксус)
- Шоколадный молочный коктейль
- Морская вода
- Мост стальной
Не путайте! Сначала выполните работу, а затем проверьте свои ответы ниже.
- Определение гомогенной смеси — это смесь, которая перемешана настолько тщательно, что вы не можете увидеть отдельные компоненты или части.
- Заварной кофе представляет собой однородную смесь.
- Однородная смесь выглядит как одно целое, хотя и состоит из разных компонентов.
 Воздух невидим; морская вода — это жидкость, которая выглядит прозрачной; стальные ножки классного стула изготовлены из сплава, однородной смеси.
Воздух невидим; морская вода — это жидкость, которая выглядит прозрачной; стальные ножки классного стула изготовлены из сплава, однородной смеси. - Да, раствор представляет собой однородную смесь.Пример однородного раствора — безалкогольный напиток.
- Из вариантов, представленных ниже, все являются однородными смесями, за исключением a., Trail mix и c., Итальянской заправки.
- Мешок trail mix
- Воздух
- Итальянская заправка для салатов (масло, специи и уксус)
- Шоколадный молочный коктейль
- Морская вода
- Мост стальной
ОДНОРОДНАЯ СМЕСЬ | Определение
в кембриджском словаре английского языка Клинкер из портландцемента получают путем нагрева во вращающейся печи при высокой температуре гомогенной смеси сырья.ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Следовательно, в одном измерении трудно получить однородную смесь , , , , если начальное возмущение не направлено только к одному из минимумов.Гомогенная смесь , в которой присутствуют как растворенное вещество, так и растворитель, также является раствором.
Из
Следовательно, в одном измерении трудно получить однородную смесь , , , , если начальное возмущение не направлено только к одному из минимумов.Гомогенная смесь , в которой присутствуют как растворенное вещество, так и растворитель, также является раствором.
Из Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Когда кофе добавляется к смазке таким образом, может получиться однородная смесь , , в которой не будет эффекта красных глаз. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Как гомогенная смесь , раствор имеет одну фазу (жидкость), хотя растворенное вещество и растворитель могут варьироваться: например, соленая вода.
Из
Как гомогенная смесь , раствор имеет одну фазу (жидкость), хотя растворенное вещество и растворитель могут варьироваться: например, соленая вода.
Из Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.С химической точки зрения космолин представляет собой гомогенную смесь масляных и воскообразных длинноцепочечных неполярных углеводородов. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Эти плиты изготовлены из однородной смеси и, следовательно, имеют однослойную форму любой толщины.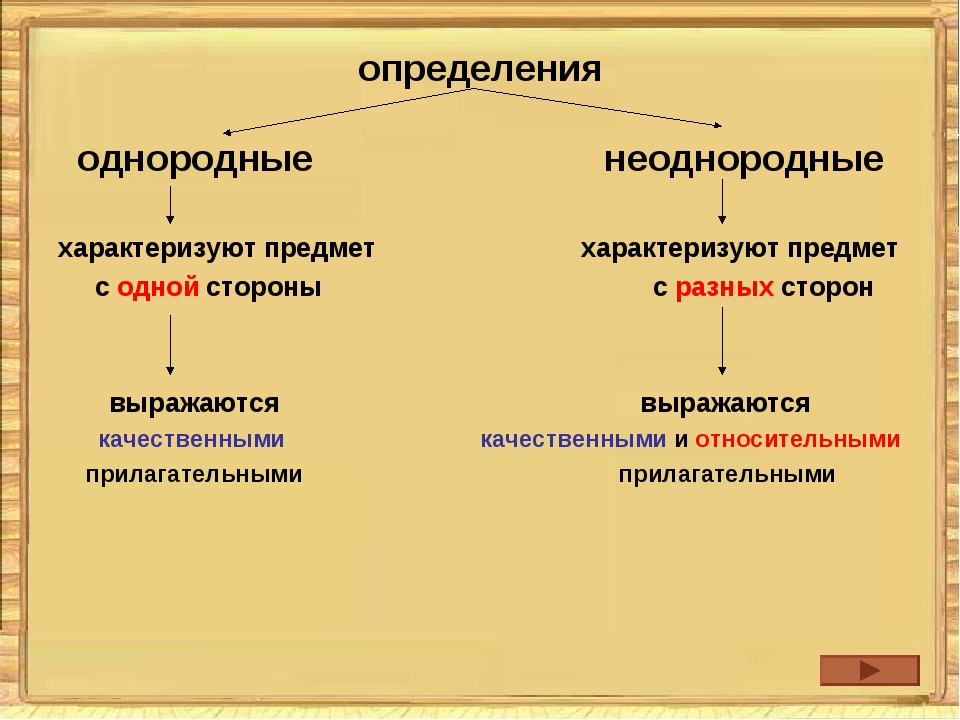 Из
Из Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Контроль осуществлялся путем расслоения заряда при низких и средних нагрузках и с помощью гомогенной смеси при высоких нагрузках. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Это указывает на то, что плод некоторое время назад прошел через меконий, так что произошло достаточное перемешивание, чтобы образовалась гомогенная смесь , , . ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. При выпечке эти ингредиенты объединяются в однородную смесь , похожую на карамель.
Из
При выпечке эти ингредиенты объединяются в однородную смесь , похожую на карамель.
Из Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Мельница непрерывного действия может получить тщательно перемешанную смесь , гомогенную, , , за несколько секунд. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Примером гомогенной смеси является воздух. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA. Порошкообразное лекарственное средство и наполнитель (обычно инертный сахар) добавляют к жидкому раствору и быстро перемешивают с получением гомогенной смеси .
Из
Порошкообразное лекарственное средство и наполнитель (обычно инертный сахар) добавляют к жидкому раствору и быстро перемешивают с получением гомогенной смеси .
Из Википедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.Это основная причина для разработки реакторов с дискретным твердым топливом, разделенным замедлителем, вместо использования более гомогенной смеси двух материалов. ИзВикипедия
Этот пример взят из Википедии и может быть повторно использован по лицензии CC BY-SA.В этом контексте пены обычно моделируются как однородные смеси.
Эти примеры взяты из корпусов и из источников в Интернете.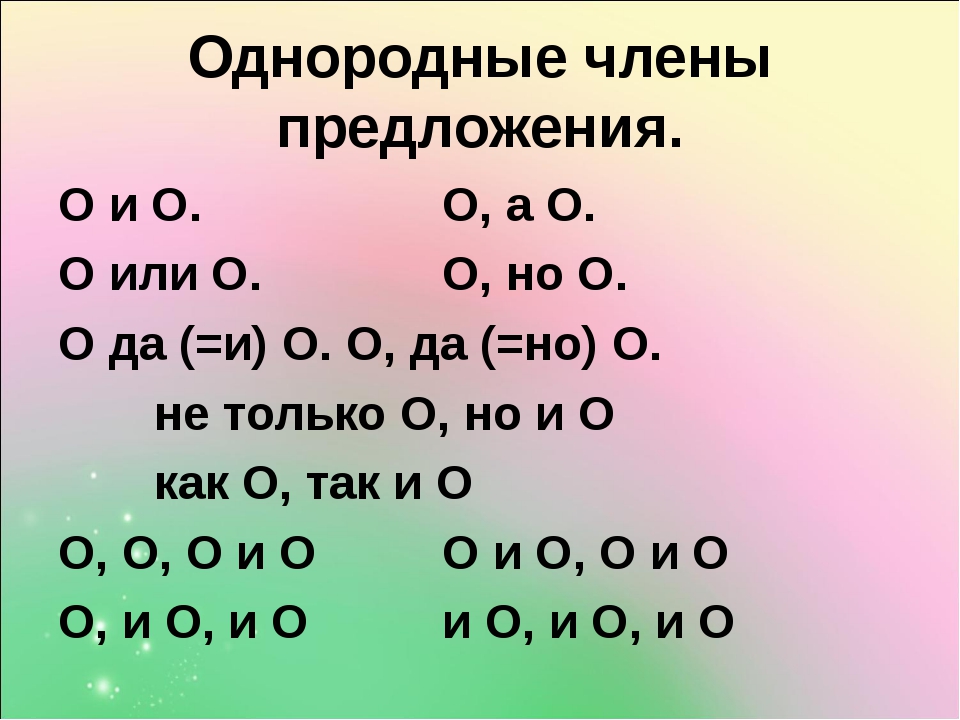 Любые мнения в примерах не отражают мнение редакторов Cambridge Dictionary, Cambridge University Press или его лицензиаров.
Любые мнения в примерах не отражают мнение редакторов Cambridge Dictionary, Cambridge University Press или его лицензиаров.
Обобщение данных
Обобщение данных Обобщение данных
Описательная статистика
Первым шагом в решении проблем в области общественного здравоохранения и принятии решений, основанных на фактических данных, является сбор точных данных, их описание, обобщение и представление таким образом, чтобы их можно было использовать для решения проблем.Информация состоит из элементов данных или точек данных , которые представляют интересующие переменные. При решении проблем общественного здравоохранения единицами измерения чаще всего являются отдельные люди, хотя, если бы мы изучали различия в медицинской практике в США, объектами или единицами измерения могли бы быть больницы. Популяция состоит из всех представляющих интерес субъектов, в отличие от выборки , которая является подмножеством интересующей совокупности. Как правило, невозможно собрать информацию обо всех представителях интересующей группы населения. Вместо этого мы выбираем выборку из представляющей интерес совокупности, и обобщения о совокупности основываются на предположении, что выборка является репрезентативной для той совокупности, из которой она была взята.
Как правило, невозможно собрать информацию обо всех представителях интересующей группы населения. Вместо этого мы выбираем выборку из представляющей интерес совокупности, и обобщения о совокупности основываются на предположении, что выборка является репрезентативной для той совокупности, из которой она была взята.
После завершения этого модуля студент сможет:
- Различайте дихотомические, порядковые, категориальные и непрерывные переменные.
- Определите соответствующие числовые и графические сводки для каждого типа переменной.
- Вычислить среднее значение, медианное значение, стандартное отклонение, квартили и диапазон для непрерывной переменной.
- Создайте таблицу частотного распределения для дихотомических, категориальных и порядковых переменных.
- Приведите пример, когда среднее значение является лучшим показателем центральной тенденции (местоположения), чем медиана.
- Интерпретировать стандартное отклонение непрерывной переменной.

- Создайте и интерпретируйте коробчатую диаграмму для непрерывной переменной.
- Создание и интерпретация бок о бок боксовых диаграмм.
- Различия между гистограммой и гистограммой.
Процедуры обобщения данных и выполнения последующего анализа различаются в зависимости от типа данных (или переменных), которые доступны.В результате важно иметь четкое представление о том, как классифицируются переменные.
Существует три общих классификации переменных:
1) Дискретные переменные : переменные, которые принимают только конечное число значений, например, раса, отнесенная к категории белых неиспаноязычных, испаноязычных, чернокожих, азиатских и других. Дискретные переменные можно подразделить на:
- Дихотомические переменные
- Категориальные переменные (или номинальные переменные)
- Порядковые переменные
2) Непрерывные переменные : их иногда называют количественными или измерительными переменными; они могут принимать любое значение в диапазоне возможных значений.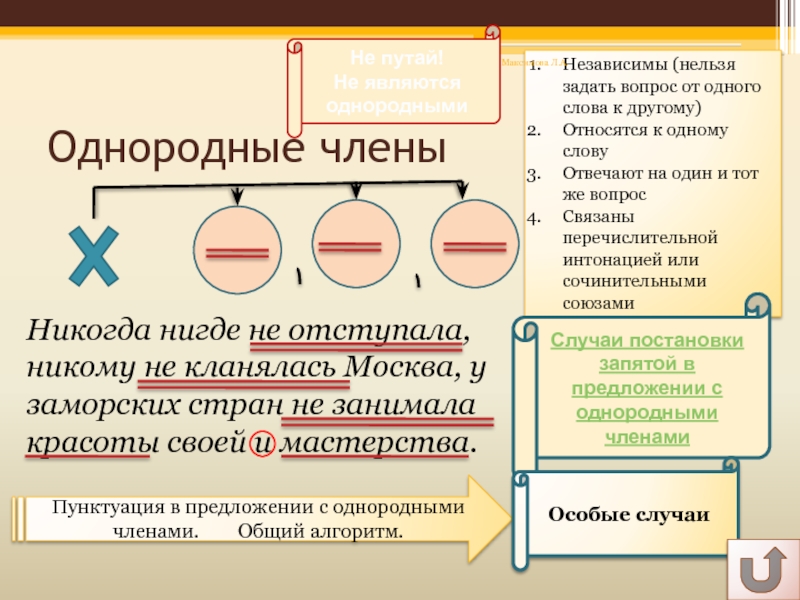 Например, общий уровень холестерина в сыворотке, рост, вес и систолическое артериальное давление являются примерами непрерывных переменных.
Например, общий уровень холестерина в сыворотке, рост, вес и систолическое артериальное давление являются примерами непрерывных переменных.
3) Переменные времени до события : они отражают время до определенного события, такого как сердечный приступ, ремиссия рака или смерть.
Таблицы частотного распределения — это распространенный и полезный способ обобщения дискретных переменных. Типичные примеры показаны ниже.
Таблицы распределения частот для дихотомических переменных
В когорте потомков Фрамингемского исследования сердца 3539 человек прошли седьмой осмотр в период с 1998 по 2001 год, который включал обширный медицинский осмотр.Одной из записанных переменных был пол, как показано ниже в таблице частотного распределения.
Таблица 1 — Таблица распределения частот для пола
|
Пол |
Частота |
Относительная частота,% |
|---|---|---|
|
Мужской |
1,625 |
45. |
|
Женский |
1 914 |
54,1 |
|
Итого |
3,539 |
100,0 |
Обратите внимание, что третий столбец содержит относительные частоты, которые вычисляются путем деления частоты в каждой категории ответов на размер выборки (например,г., 1,625 / 3,539 = 0,459). В случае дихотомических переменных относительные частоты часто выражаются в процентах (путем умножения на 100).
Исследователи также записали, лечились ли субъекты антигипертензивными препаратами, как показано ниже.
Таблица 2 — Таблица распределения частот для лечения гипотензивными препаратами
|
Лечение |
Частота |
Относительная частота (%) |
|---|---|---|
|
№ |
2,313 |
65. |
|
Есть |
1,219 |
34,5 |
|
Итого |
3,532 |
100,0 |
Отсутствующие данные
Обратите внимание, что в таблице выше имеется только n = 3 532 действительных ответа, хотя размер выборки был n = 3 539.Это указывает на то, что у семи человек отсутствовали данные по этому конкретному вопросу. Отсутствие данных в исследованиях происходит по разным причинам. Если имеется большое количество отсутствующих данных или если существует систематический образец отсутствующих ответов, результаты анализа могут быть смещенными (см. Более подробную информацию в модуле «Смещение для EP713»). Существуют методы обработки отсутствующих данных, но они выходят за рамки объем данного курса
Иногда представляет интерес сравнить две или более групп на основе дихотомической переменной результата. Например, предположим, что мы хотим сравнить степень лечения антигипертензивными препаратами у мужчин и женщин, как показано в таблице ниже.
Например, предположим, что мы хотим сравнить степень лечения антигипертензивными препаратами у мужчин и женщин, как показано в таблице ниже.
Таблица 3 — Лечение гипотензивными препаратами у мужчин и женщин
|
Пол |
Номер обращения / n |
Относительная частота,% |
|---|---|---|
|
Мужской |
611/1622 |
37.7 |
|
Женский |
608/1 910 |
31,8 |
|
Итого |
1,219 / 3,532 |
34,5 |
Здесь и пол, и статус лечения являются дихотомическими переменными. Поскольку количество мужчин и женщин неравно, относительную частоту лечения для каждого пола необходимо рассчитывать путем деления количества пациентов, получающих лечение, на размер выборки для каждого пола. Число мужчин и женщин, получающих лечение (частота), почти одинаково, но относительные частоты показывают, что лечение проходит у мужчин больше, чем у женщин. Также обратите внимание, что сумма в крайнем правом столбце не равна 100,0%, как это было в предыдущих примерах, потому что это указывает на относительную частоту лечения среди всех участников (мужчин и женщин) вместе взятых.
Число мужчин и женщин, получающих лечение (частота), почти одинаково, но относительные частоты показывают, что лечение проходит у мужчин больше, чем у женщин. Также обратите внимание, что сумма в крайнем правом столбце не равна 100,0%, как это было в предыдущих примерах, потому что это указывает на относительную частоту лечения среди всех участников (мужчин и женщин) вместе взятых.
Таблицы распределения частот для категориальных переменных
Напомним, что категориальные переменные — это переменные с двумя или более разными неупорядоченными ответами.Некоторые примеры категориальных переменных, измеряемых в Framingham Heart Study, включают семейное положение, правую или левую руку и статус курения. Поскольку ответы неупорядочены, порядок ответов или категорий в сводной таблице можно изменить, например, представив категории в алфавитном порядке или, возможно, от наиболее частых к наименее частым.
В таблице 4 ниже обобщены данные о семейном положении из исследования сердца Фрамингема. Взаимоисключающие и исчерпывающие категории показаны в первом столбце таблицы.Частоты или количество участников в каждой категории ответов показаны в среднем столбце, а относительные частоты в процентах показаны в крайнем правом столбце.
Взаимоисключающие и исчерпывающие категории показаны в первом столбце таблицы.Частоты или количество участников в каждой категории ответов показаны в среднем столбце, а относительные частоты в процентах показаны в крайнем правом столбце.
Таблица 4 — Таблица распределения частот для семейного положения
|
Семейное положение |
Частота |
Относительная частота,% |
|---|---|---|
|
Одноместный |
203 |
5.8 |
|
женат |
2,580 |
73,1 |
|
Вдовы |
334 |
9,5 |
|
В разводе |
367 |
10,4 |
|
Отдельно |
46 |
1. |
|
Итого |
3,530 |
100,0 |
На вопрос о семейном положении дано n = 3 530 действительных ответов (9 участников не предоставили данные о семейном положении). Большая часть выборки состоит в браке (73,1%), и примерно 10% выборки в разводе. Еще 10% овдовели, 6% не замужем и 1% разделились.
Таблицы распределения частот для порядковых переменных
Некоторые дискретные переменные по своей сути порядковые. В дополнение к упорядоченным по своей природе категориям (например, отлично, очень хорошо, хорошо, удовлетворительно, плохо) исследователи иногда собирают информацию о непрерывно распределенных показателях, но затем классифицируют эти измерения, поскольку это облегчает принятие клинических решений. Например, NHLBI (Национальный институт сердца, легких и крови и Американская кардиологическая ассоциация используют следующую классификацию артериального давления:
- Нормально: систолическое артериальное давление <120 и диастолическое артериальное давление <80
- Предварительная гипертензия: систолическое артериальное давление от 120 до 139 или диастолическое артериальное давление от 80 до 89
- Артериальная гипертензия I стадии: систолическое артериальное давление от 140 до 159 или диастолическое артериальное давление от 90 до 99
- Артериальная гипертензия II стадии: систолическое артериальное давление 160 и более или диастолическое артериальное давление 100 и более
Американская кардиологическая ассоциация использует следующую классификацию уровней общего холестерина:
- Желательно: общий холестерин <200 мг / дл,
- Граница высокого риска: общий холестерин от 200–239 мг / дл до
- Высокий риск: общий холестерин 240 мг / дл или выше
Индекс массы тела (ИМТ) рассчитывается как отношение веса в килограммах к росту в квадратных метрах, и часто используются следующие категории:
- Недостаточный вес: ИМТ <18.
 5
5 - Нормальный вес: ИМТ от 18,5 до 24,9
- Избыточный вес: ИМТ от 25 до 29,9
- Ожирение: ИМТ 30 или выше
Это все примеры общих непрерывных мер, которые были разделены на категории для создания порядковых переменных. В таблице ниже представлена таблица частотного распределения для порядковой переменной артериального давления. Взаимоисключающие и исчерпывающие категории показаны в первом столбце таблицы. Частоты или количество участников в каждой категории ответов показаны в среднем столбце, а относительные частоты в процентах показаны в крайних правых столбцах.Ключевыми сводными статистическими данными для порядковых переменных являются относительные частоты и совокупные относительные частоты.
Таблица 5 — Распределение частот для категории артериального давления
|
Артериальное давление |
Частота |
Относительная частота (%) |
Накопленная частота |
Накопленная относительная частота,% |
|---|---|---|---|---|
|
Обычный |
1 206 |
34. |
1 206 |
34,1 |
|
До гипертонии |
1,452 |
41,1 |
2 658 |
75,2 |
|
Гипертония I стадии |
653 |
18.5 |
3 311 |
93,7 |
|
Гипертония II стадии |
222 |
6,3 |
3,533 |
100,0 |
|
Итого |
3,533 |
100.0 |
|
|
Обратите внимание, что совокупные частоты отражают количество пациентов с определенным уровнем артериального давления или ниже . Например, 2658 пациентов имеют нормальное артериальное давление или предгипертонию. Есть 3311 пациентов с нормальной гипертензией, гипертензией до гипертензии или гипертонией I стадии. Совокупные относительные частоты очень полезны для суммирования порядковых переменных и показывают долю (от 0 до 1) или процент (от 0 до 100%) пациентов на определенном уровне или ниже.В этом примере 75,2% пациентов НЕ классифицируются как гипертоники (т. Е. У них нормальное артериальное давление или предгипертония). Обратите внимание, что для последней (самой высокой) категории артериального давления кумулятивная частота равна размеру выборки (n = 3,533), а кумулятивная относительная частота составляет 100%, что указывает на то, что все пациенты находятся на самом высоком уровне или ниже.
Например, 2658 пациентов имеют нормальное артериальное давление или предгипертонию. Есть 3311 пациентов с нормальной гипертензией, гипертензией до гипертензии или гипертонией I стадии. Совокупные относительные частоты очень полезны для суммирования порядковых переменных и показывают долю (от 0 до 1) или процент (от 0 до 100%) пациентов на определенном уровне или ниже.В этом примере 75,2% пациентов НЕ классифицируются как гипертоники (т. Е. У них нормальное артериальное давление или предгипертония). Обратите внимание, что для последней (самой высокой) категории артериального давления кумулятивная частота равна размеру выборки (n = 3,533), а кумулятивная относительная частота составляет 100%, что указывает на то, что все пациенты находятся на самом высоком уровне или ниже.
Таблица 6 — Таблица распределения частот для статуса курения
|
Статус курения |
Частота |
Относительная частота,% |
|---|---|---|
|
Некурящие |
1,330 |
37. |
|
Бывшая |
1,724 |
48,8 |
|
Текущий |
482 |
13,6 |
|
Итого |
3,536 |
100.0 |
Столбчатые диаграммы для дихотомических и категориальных переменных
Графические изображения очень полезны для суммирования данных, а дихотомические и неупорядоченные категориальные переменные лучше всего суммировать с помощью гистограмм. Варианты ответа (например, да / нет, присутствует / отсутствует) показаны на горизонтальной оси, а частоты или относительные частоты нанесены на вертикальную ось. На рисунке 1 ниже представлена гистограмма частот , которая соответствует табличному представлению в таблице 1 выше.
Рисунок 1 — Гистограмма частот
Обратите внимание, что для дихотомических и категориальных переменных должен быть пробел между вариантами ответа. Аналогичное графическое представление для порядковой переменной не имеет пробелов между полосами, чтобы подчеркнуть, что существует неотъемлемый порядок.
Аналогичное графическое представление для порядковой переменной не имеет пробелов между полосами, чтобы подчеркнуть, что существует неотъемлемый порядок.
Напротив, на рисунке 2 ниже показана гистограмма
относительной частоты распределения лечения гипотензивными препаратами.Это графическое представление соответствует табличному представлению в последнем столбце Таблицы 2 выше.Рисунок 2 — Гистограмма относительной частоты
Частотная гистограмма семейного положения может выглядеть, как на Рисунке 3 ниже.
Рисунок 3
Рассмотрим графическое представление данных в таблице 3 выше, сравнивая относительную частоту приема гипотензивных препаратов между мужчинами и женщинами.Это уместно выглядело бы, как показано на рисунке ниже. Обратите внимание, что для вертикальной оси был выбран диапазон от 0 до 40.
Рисунок 4
Ловушка:
Для приведенного выше примера относительные частоты составляют 31,8% и 37,7%, поэтому масштабирование вертикальной оси от 0 до 40% подходит для размещения данных. Однако можно визуально ввести читателя в заблуждение относительно сравнения, используя вертикальную шкалу, которая либо слишком широка, либо слишком ограничительна.Рассмотрим две гистограммы ниже (рисунки 5 и 6).
Однако можно визуально ввести читателя в заблуждение относительно сравнения, используя вертикальную шкалу, которая либо слишком широка, либо слишком ограничительна.Рассмотрим две гистограммы ниже (рисунки 5 и 6).
Рисунок 5
Рисунок 6
На этих гистограммах отображаются одинаковые относительные частоты, т. Е. 31,8% и 37,7%. Однако гистограмма слева минимизирует разницу, потому что вертикальный масштаб слишком большой и находится в диапазоне от 0 до 100%. С другой стороны, линейчатая диаграмма справа визуально преувеличивает разницу, потому что вертикальный масштаб слишком ограничен, в пределах 30-40%.
Гистограммы порядковых переменных
Отличительной чертой столбчатых диаграмм для дихотомических и неупорядоченных категориальных переменных является то, что столбцы разделены пробелами, чтобы подчеркнуть, что они описывают неупорядоченные категории. Однако, когда мы имеем дело с порядковыми переменными, подходящим графическим форматом является гистограмма . Гистограмма похожа на гистограмму, за исключением того, что соседние столбцы примыкают друг к другу, чтобы усилить идею о том, что категории имеют внутренний порядок.Гистограмма частот ниже суммирует данные артериального давления, которые были представлены в табличном формате в таблице 4 на предыдущей странице. Обратите внимание, что на вертикальной оси отображается частота или количество участников, отнесенных к каждой категории.
Гистограмма похожа на гистограмму, за исключением того, что соседние столбцы примыкают друг к другу, чтобы усилить идею о том, что категории имеют внутренний порядок.Гистограмма частот ниже суммирует данные артериального давления, которые были представлены в табличном формате в таблице 4 на предыдущей странице. Обратите внимание, что на вертикальной оси отображается частота или количество участников, отнесенных к каждой категории.
Рисунок 7 Частотная гистограмма артериального давления
Эта гистограмма сразу передает сообщение о том, что большинство участников относятся к двум нижним категориям распределения.Небольшое количество участников относится к категории гипертонии II стадии. Гистограмма ниже представляет собой гистограмму относительной частоты для тех же данных. Обратите внимание, что рисунок такой же, за исключением вертикальной оси, которая масштабирована для размещения относительных частот вместо частот.
Рисунок 8 — Гистограмма относительной частоты для артериального давления
Чтобы предоставить подробное описание вычислений, используемых для числовых и графических сводок непрерывных переменных, мы выбрали небольшую подгруппу (n = 10) участников Фрамингемского исследования сердца. Значения данных для этих десяти участников показаны в таблице ниже. Крайний правый столбец содержит индекс массы тела (ИМТ), рассчитанный с использованием измерений роста и веса.
Значения данных для этих десяти участников показаны в таблице ниже. Крайний правый столбец содержит индекс массы тела (ИМТ), рассчитанный с использованием измерений роста и веса.
Таблица 8 — Значения данных для небольшой выборки
|
ID участника |
Систолическое артериальное давление |
Диастолическое артериальное давление |
Общий холестерин сыворотки |
Масса |
Высота |
Индекс массы тела |
|---|---|---|---|---|---|---|
|
1 |
141 |
76 |
199 |
138 |
63.00 |
24,4 |
|
2 |
119 |
64 |
150 |
183 |
69,75 |
26,4 |
|
3 |
122 |
62 |
227 |
153 |
65. |
24,9 |
|
4 |
127 |
81 |
227 |
178 |
70,00 |
25,5 |
|
5 |
125 |
70 |
163 |
161 |
70.50 |
22,8 |
|
6 |
123 |
72 |
210 |
206 |
70,00 |
29,6 |
|
7 |
105 |
81 |
205 |
235 |
72.00 |
31,9 |
|
8 |
113 |
63 |
275 |
151 |
60,75 |
28,8 |
|
9 |
106 |
67 |
208 |
213 |
69.00 |
31,5 |
|
10 |
131 |
77 |
159 |
142 |
61,00 |
26,8 |
Первая сводная статистика, которую важно сообщить для непрерывной переменной (а также для любой дискретной переменной), — это размер выборки (в данном примере размер выборки равен n = 10).Большие размеры выборки дают более точные результаты и, следовательно, имеют больший вес. Однако есть момент, когда увеличение размера образца существенно не повысит точность анализа. Вычисления размера выборки будут подробно обсуждаться в следующем модуле.
Поскольку эта выборка мала (n = 10), ее легко обобщить, проверив наблюдаемые значения, например, перечислив диастолическое артериальное давление в порядке возрастания:
62 63 64 67 70 72 76 77 81 81
Диастолическое артериальное давление <80 мм рт. Ст. Считается нормальным, и мы видим, что последние два значения едва превышают верхний предел.Однако для большой выборки проверка отдельных значений данных не дает содержательной сводной информации, и необходимы сводные статистические данные. Два ключевых компонента полезной сводки для непрерывной переменной:
- описание центра или «среднего» данных (т.е. какое типичное значение?) И
- указывает на изменчивость данных.
Среднее значение
В биостатистике термин «средний» — это очень общий термин, который может рассматриваться с помощью нескольких статистических данных.Наиболее знакомым является выборочное среднее, которое вычисляется путем суммирования всех значений и деления на размер выборки. Для образца диастолического артериального давления в таблице выше среднее значение образца рассчитывается следующим образом:
Среднее значение = (62 + 63 + 64 + 67 + 70 + 72 + 76 + 77 + 81 + 81) / 10 = 71,3
Чтобы упростить формулы для статистики выборки (и для параметров генеральной совокупности), мы обычно обозначаем интересующую переменную как «X». X — это просто заполнитель для анализируемой переменной.Здесь X = диастолическое артериальное давление.
Общая формула для выборочного среднего:
Значок X с полосой над ним представляет выборочное среднее значение и читается как «столбик X». Знак Σ обозначает суммирование (то есть сумму X или сумму диастолического артериального давления в этом примере).
При составлении сводной статистики для непрерывной переменной принято указывать на один десятичный знак больше, чем количество измеренных десятичных знаков.Систолическое и диастолическое артериальное давление, общий холестерин в сыворотке и вес измерялись с точностью до ближайшего целого числа, поэтому итоговая статистика приводится с точностью до десятого. Высота измерялась с точностью до четверти дюйма (сотых долей), поэтому сводная статистика приводится с точностью до тысячных долей. Индекс массы тела рассчитан с точностью до десятых, сводная статистика приведена с точностью до сотых.
Медиана
Вторая мера «среднего» значения — это медиана выборки, которая является средним значением в упорядоченном наборе данных или значением, отделяющим верхние 50% значений от нижних 50%.Когда в выборке есть нечетное количество наблюдений, медиана — это значение, которое содержит столько значений над ним, сколько под ним в упорядоченном наборе данных. Когда в выборке четное количество наблюдений (например, n = 10), медиана определяется как среднее из двух средних значений в упорядоченном наборе данных. В выборке из n = 10 диастолического артериального давления два средних значения — 70 и 72, и, таким образом, медиана составляет (70 + 72) / 2 = 71. Половина диастолического артериального давления выше 71, а половина — ниже.В этом случае среднее значение выборки и медиана выборки очень похожи.
Среднее значение и медиана предоставляют различную информацию о среднем значении непрерывной переменной. Предположим, что выборка из 10 значений диастолического артериального давления выглядела следующим образом:
62 63 64 67 70 72 76 77 81 140
В этом случае выборочное среднее (x «полоса») = 772/10 = 77,2, но это не кажется нам «типичным» значением, поскольку большинство диастолических артериальных давлений в этом образце ниже 77.2. Экстремальное значение 140 влияет на вычисление среднего. Для этого же образца медиана составляет 71. На медиана не влияют экстремальные или выпадающие значения. По этой причине медиана предпочтительнее среднего, когда есть экстремальные значения (очень маленькие или очень большие значения по сравнению с другими). Когда нет экстремальных значений, среднее значение является предпочтительной мерой типичного значения, отчасти потому, что каждое наблюдение учитывается при вычислении среднего. Если в выборке нет экстремальных значений, среднее и медианное значение в выборке будут близкими по величине.Ниже мы предлагаем более формальный метод определения крайних значений и, следовательно, использования медианы.
В таблице 9 показаны выборочные средние и медианы для каждой из непрерывных мер для выборки n = 10 в таблице 8.
Таблица 9 — Средние и медианы переменных в подвыборке размера n = 10
|
Переменная |
Среднее |
Медиана |
|---|---|---|
|
Диастолическое артериальное давление |
71.3 |
71 |
|
Систолическое артериальное давление |
121,2 |
122,5 |
|
Общий холестерин сыворотки |
202,3 |
206,5 |
|
Масса |
176.0 |
169,5 |
|
Высота |
67,175 |
69,375 |
|
Индекс массы тела |
27,26 |
26,60 |
Для каждой непрерывной переменной, измеренной в подвыборке из n = 10 участников, средние и медианы не идентичны, но относительно близки по значению, что позволяет предположить, что среднее является наиболее подходящим обобщением типичного значения для каждой из этих переменных.(Если среднее значение и медиана сильно различаются, это говорит о наличии выбросов, влияющих на среднее значение.)
Режим
Третьим показателем «типичного» значения для непрерывной переменной является режим, который определяется как наиболее частое значение. В таблице 8 выше режим диастолического артериального давления равен 81, режим общего уровня холестерина — 227, режим высот — 70,00, потому что каждое из этих значений появляется дважды, тогда как другие значения появляются только один раз. Для каждой из других непрерывных переменных существует 10 различных значений, поэтому режима нет, поскольку ни одно значение не появляется чаще, чем любое другое.
Предположим, что диастолическое артериальное давление было:
62 63 64 64 70 72 76 77 81 81
В этом примере есть два режима: 64 и 81. Этот режим представляет собой полезную сводную статистику для непрерывной переменной. Он не отображается вместо среднего или медианного значения, а скорее в дополнение к среднему значению или медиане.
Диапазон
Второй аспект непрерывной переменной, который необходимо резюмировать, — это изменчивость выборки.Относительно грубым, но важным показателем изменчивости в выборке является диапазон выборки. Диапазон выборки вычисляется следующим образом:
Диапазон выборки = Максимум — Минимальное значение
В таблице 10 показаны диапазоны выборки для каждой из непрерывных мер в подвыборке из n = 10 наблюдений.
Таблица 10 Диапазоны переменных в подвыборке размера n = 10
|
Переменная |
Минимум |
Максимум |
Диапазон |
|---|---|---|---|
|
Диастолическое артериальное давление |
62 |
81 |
19 |
|
Систолическое артериальное давление |
105 |
141 |
36 |
|
Общий холестерин сыворотки |
150 |
275 |
125 |
|
Масса |
138 |
235 |
97 |
|
Высота |
60.75 |
72,00 |
11,25 |
|
Индекс массы тела |
22,8 |
31,9 |
9,1 |
Диапазон переменной зависит от масштаба измерения. Артериальное давление измеряется в миллиметрах ртутного столба; общий холестерин измеряется в миллиграммах на децилитр, вес — в фунтах и так далее.Диапазон общего холестерина в сыворотке велик с минимальным и максимальным значениями в выборке размером n = 10, различающихся на 125 единиц. Напротив, рост участников более однороден с диапазоном 11,25 дюйма. Диапазон — важная описательная статистика для непрерывной переменной, но он основан только на двух значениях в наборе данных. Как и на среднее значение, на диапазон выборки могут влиять экстремальные значения, поэтому к его интерпретации следует относиться с осторожностью. Наиболее широко используемая мера изменчивости для непрерывной переменной называется стандартным отклонением, которое проиллюстрировано ниже.
Если нет крайних или выпадающих значений переменной, среднее значение является наиболее подходящим обобщением типичного значения, и для обобщения изменчивости данных мы специально оцениваем изменчивость в выборке вокруг выборочного среднего. Если все наблюдаемые значения в выборке близки к выборочному среднему, стандартное отклонение будет небольшим (то есть близким к нулю), а если наблюдаемые значения сильно различаются вокруг выборочного среднего, стандартное отклонение будет большим.Если все значения в выборке идентичны, стандартное отклонение выборки будет равно нулю.
При обсуждении выборочного среднего мы обнаружили, что выборочное среднее для диастолического артериального давления составило 71,3. В таблице ниже показано каждое из наблюдаемых значений вместе с соответствующим отклонением от выборочного среднего.
Таблица 11 — Диастолическое артериальное давление и отклонение от среднего значения
|
X = диастолическое артериальное давление |
Отклонение от среднего |
|---|---|
|
76 |
4.7 |
|
64 |
-7,3 |
|
62 |
-9,3 |
|
81 |
9,7 |
|
70 |
-1,3 |
|
72 |
0.7 |
|
81 |
9,7 |
|
63 |
-8,3 |
|
67 |
-4,3 |
|
77 |
5,7 |
|
|
|
Отклонения от среднего значения отражают, насколько далеко диастолическое артериальное давление каждого человека от среднего диастолического артериального давления.Диастолическое артериальное давление первого участника на 4,7 единицы выше среднего, а диастолическое артериальное давление второго участника на 7,3 единицы ниже среднего. Нам нужна сводка этих отклонений от среднего, в частности, мера того, насколько в среднем каждый участник находится от среднего диастолического артериального давления. Если мы вычислим среднее значение отклонений, суммируя отклонения и разделив их на размер выборки, мы столкнемся с проблемой. Сумма отклонений от среднего равна нулю.Так будет всегда, поскольку это свойство выборочного среднего, т.е. сумма отклонений ниже среднего всегда будет равна сумме отклонений выше среднего. Однако цель состоит в том, чтобы зафиксировать величину этих отклонений в виде сводной меры. Чтобы решить эту проблему суммирования отклонений до нуля, мы могли бы взять абсолютные значения или возвести в квадрат каждое отклонение от среднего. Оба метода решат проблему. Более популярный метод суммирования отклонений от среднего включает возведение отклонений в квадрат (абсолютные значения затруднены в математических доказательствах).Таблица 12 ниже отображает каждое из наблюдаемых значений, соответствующие отклонения от выборочного среднего и квадратичные отклонения от среднего.
Таблица 12
|
X = диастолическое артериальное давление |
Отклонение от среднего
|
Квадратное отклонение от среднего
|
|
76 |
4.7 |
22.09 |
|
64 |
-7,3 |
53,29 |
|
62 |
-9,3 |
86,49 |
|
81 |
9,7 |
94.09 |
|
70 |
-1,3 |
1,69 |
|
72 |
0,7 |
0,49 |
|
81 |
9,7 |
94,09 |
|
63 |
-8.3 |
68,89 |
|
67 |
-4,3 |
18,49 |
|
77 |
5,7 |
32,49 |
|
|
|
|
Квадрат отклонений интерпретируется следующим образом.Отклонение в квадрате первого участника составляет 22,09, что означает, что его / ее диастолическое артериальное давление составляет 22,09 единиц в квадрате от среднего диастолического артериального давления, а диастолическое артериальное давление второго участника составляет 53,29 единиц в квадрате от среднего диастолического артериального давления. Величина, которая часто используется для измерения изменчивости в выборке, называется дисперсией выборки, и по сути представляет собой среднее значение квадратов отклонений. Выборочная дисперсия обозначается s 2 и рассчитывается следующим образом:
В этой выборке из n = 10 диастолического артериального давления дисперсия выборки составляет s 2 = 472.10/9 = 52,46. Таким образом, в среднем диастолическое артериальное давление составляет 52,46 единиц в квадрате от среднего диастолического артериального давления. Из-за возведения в квадрат дисперсию нельзя особо интерпретировать. Более распространенной мерой изменчивости в выборке является стандартное отклонение выборки, определяемое как квадратный корень из дисперсии выборки:
Когда набор данных имеет выбросы или экстремальные значения, мы суммируем типичное значение, используя медианное значение вместо среднего.Когда в наборе данных есть выбросы, изменчивость часто суммируется статистикой, называемой межквартильным диапазоном , который представляет собой разницу между первым и третьим квартилями. Первый квартиль, обозначенный Q 1 , представляет собой значение в наборе данных, которое содержит 25% значений ниже it. Третий квартиль, обозначенный Q 3 , представляет собой значение в наборе данных, которое содержит 25% значений выше it. Квартили можно определить с помощью того же подхода, который мы использовали для определения медианы, но теперь мы рассмотрим каждую половину набора данных отдельно.Межквартильный размах определяется следующим образом:
Межквартильный размах = Q 3 -Q 1
с четным размером выборки:
Для выборки (n = 10) среднее диастолическое артериальное давление составляет 71 (50% значений выше 71, а 50% ниже). Квартили можно определить так же, как мы определили медианное значение, за исключением того, что мы рассматриваем каждую половину набора данных отдельно.
Рисунок 9 — Межквартильный размах при четном размере выборки
Есть 5 значений ниже медианы (нижняя половина), среднее значение — 64, что является первым квартилем.Есть 5 значений выше медианы (верхняя половина), среднее значение — 77, что является третьим квартилем. Межквартильный размах 77 — 64 = 13; Межквартильный диапазон — это диапазон средних 50% данных.
————————————————- ————————————————— ————————————————— ————
с нечетным размером выборки:
Если размер выборки нечетный, медиана и квартили определяются таким же образом.Предположим, что в предыдущем примере было исключено самое низкое значение (62), а размер выборки был n = 9. Медиана и квартили указаны ниже.
Рисунок 10 — Межквартильный размах при нечетном размере выборки
Когда размер выборки равен 9, медиана — это среднее число 72. Квартили определяются таким же образом, глядя на нижнюю и верхнюю половины, соответственно. В нижней половине есть 4 значения, первый квартиль является средним из двух средних значений в нижней половине ((64 + 64) / 2 = 64).Тот же подход используется в верхней половине для определения третьего квартиля ((77 + 81) / 2 = 79).
Выбросы и заборы Tukey:
Если в выборке нет выбросов, среднее и стандартное отклонение используются для суммирования типичного значения и изменчивости в выборке, соответственно. Если в выборке есть выбросы, медиана и межквартильный размах используются для обобщения типичного значения и вариабельности в выборке, соответственно.
|
Туки заборы Существует несколько методов определения выбросов в выборке.Очень популярный метод основан на следующем:
Выбросы — это значения ниже Q 1 -1,5 (Q 3 -Q 1 ) или выше Q 3 +1,5 (Q 3 -Q 1 ) или эквивалентные значения ниже Q 1 -1,5 IQR или выше Q 3 +1,5 IQR. Они называются ограждениями Тьюки. 6 Для диастолического артериального давления нижний предел составляет 64 — 1,5 (77-64) = 44,5, а верхний предел — 77 + 1.5 (77-64) = 96,5. Диастолическое артериальное давление колеблется от 62 до 81. Следовательно, нет никаких отклонений. Лучшее обобщение типичного диастолического артериального давления — это среднее значение (в данном случае 71,3), а наилучшее обобщение вариабельности — стандартное отклонение (s = 7,2). |
В таблице 13 показаны средние значения, стандартные отклонения, медианы, квартили и межквартильные диапазоны для каждой из непрерывных переменных в подвыборке из n = 10 участников, принявших участие в седьмом экзамене Framingham Offspring Study.
Таблица 13 — Итоговая статистика по n = 10 участникам
|
Характеристика |
Среднее |
Стандартное отклонение |
Медиана |
1 квартал |
3 квартал |
IQR |
|---|---|---|---|---|---|---|
|
Систолическое артериальное давление |
121.2 |
11,1 |
122,5 |
113,0 |
127,0 |
14,0 |
|
Диастолическое артериальное давление |
71,3 |
7,2 |
71,0 |
64.0 |
77,0 |
13,0 |
|
Общий холестерин сыворотки |
202,3 |
37,7 |
206,5 |
163,0 |
227,0 |
64,0 |
|
Масса |
176.0 |
33,0 |
169,5 |
151,0 |
206,0 |
55,0 |
|
Высота |
67,175 |
4.205 |
69,375 |
63.0 |
70,0 |
7,0 |
|
Индекс массы тела |
27,26 |
3,10 |
26,60 |
24,9 |
29,6 |
4,7 |
В таблице 14 показаны наблюдаемые минимальные и максимальные значения, а также пределы для определения выбросов с использованием правила квартилей для каждой из переменных в подвыборке из n = 10 участников.Есть ли выбросы по какой-либо из переменных? Какие статистические данные наиболее подходят для суммирования среднего или типичного значения и дисперсии?
Таблица 14 — Пределы для оценки выбросов в характеристиках, измеренных в n = 10 участниках
|
Характеристика |
Минимум |
Максимум |
Нижний предел 1 |
Верхний предел 2 |
|---|---|---|---|---|
|
Систолическое артериальное давление |
105 |
141 |
92 |
148 |
|
Диастолическое артериальное давление |
62 |
81 |
44.5 |
96,5 |
|
Общий холестерин сыворотки |
150 |
275 |
67 |
323 |
|
Масса |
138 |
235 |
68.5 |
288,5 |
|
Высота |
60,75 |
72,00 |
52,5 |
80,5 |
|
Индекс массы тела |
22,8 |
31,9 |
17.85 |
36,65 |
1 Определено Q 1 -1,5 (Q 3 -Q 1 )
2 Определено Q 3 +1,5 (Q 3 -Q 1 )
Поскольку в подвыборке из n = 10 участников нет предполагаемых выбросов, среднее и стандартное отклонение являются наиболее подходящими статистическими данными для суммирования средних значений и дисперсии, соответственно, каждой из этих характеристик.
Полная фрамингемская когорта
Для ясности мы до сих пор использовали очень небольшое подмножество Framingham Offspring Cohort, чтобы проиллюстрировать вычисления сводной статистики и определение выбросов. Для вашего интереса в таблице 15 показаны средние значения, стандартные отклонения, медианы, квартили и межквартильные диапазоны для каждой непрерывной переменной, представленной в таблице 13 в полной выборке (n = 3539) участников, которые посетили седьмой экзамен Фрамингема. Исследование потомства.
Таблица 15 — Сводная статистика по выборке из (n = 3539) участников
|
Характеристика |
Среднее значение
|
Стандартное отклонение (т) |
Медиана |
1 квартал |
3 квартал |
IQR |
|
Систолическое артериальное давление |
127.3 |
19,0 |
125,0 |
114,0 |
138,0 |
24,0 |
|
Диастолическое артериальное давление |
74,0 |
9,9 |
74,0 |
67.0 |
80,0 |
13,0 |
|
Общий холестерин сыворотки |
200,3 |
36,8 |
198,0 |
175,0 |
223,0 |
48,0 |
|
Масса |
174.4 |
38,7 |
170,0 |
146,0 |
198,0 |
52,0 |
|
Высота |
65.957 |
3,749 |
65.750 |
63.000 |
68.750 |
5,75 |
|
Индекс массы тела |
28,15 |
5,32 |
27,40 |
24,5 |
30,8 |
6,3 |
В таблице 16 показаны наблюдаемые минимальные и максимальные значения, а также пределы для определения выбросов с использованием правила квартилей для каждой из переменных в полной выборке (n = 3 539).
Таблица 16 — Пределы для оценки выбросов в характеристиках, представленных в таблице 15
|
|
|
|
Туки заборы |
|
|
Характеристика |
Минимум |
Максимум |
Нижний предел 1 |
Верхний предел 2 |
|---|---|---|---|---|
|
Систолическое артериальное давление |
81.0 |
216,0 |
78 |
174 |
|
Диастолическое артериальное давление |
41,0 |
114,0 |
47,5 |
99,5 |
|
Общий холестерин сыворотки |
83.0 |
357,0 |
103 |
295 |
|
Масса |
90,0 |
375,0 |
68,0 |
276,0 |
|
Высота |
55.00 |
78,75 |
54,4 |
77,4 |
|
Индекс массы тела |
15,8 |
64,0 |
15,05 |
40,25 |
1 Определено Q 1 -1.5 (Q 3 -Q 1 )
2 Определено Q 3 +1,5 (Q 3 -Q 1 )
Популярным графическим дисплеем для непрерывной переменной является диаграмма «усы-коробочка» . Выбросы или экстремальные значения также могут быть оценены графически с помощью диаграмм типа «усы». Для подвыборки из n = 10 участников Фрамингема, которых мы рассматривали ранее, мы вычислили следующую сводную статистику диастолического артериального давления:
|
Минимум: К 1 : Медиана: К 3 : Максимум: |
62 64 71 77 81 |
Иногда их называют квантилями или процентилями распределения.Конкретный квантиль или процентиль — это значение в наборе данных, которое содержит определенный процент значений на уровне или ниже. Первый квартиль , например, является 25 -м процентилем , что означает, что он содержит 25% значений, равных ему или ниже. Медиана — это процентиль 50 , третий квартиль — процентиль 75 , а максимум — процентиль 100 (т. Е. 100% значений находятся на его уровне или ниже).
График прямоугольного уса представляет собой графическое отображение этих процентилей.На рисунке 11 показан график диастолического артериального давления, измеренного в подвыборке из n = 10 участников, описанной выше в таблице 14. Горизонтальные линии представляют (сверху) максимум, третий квартиль, медианное значение (также обозначено точка), первый квартиль и минимум. Заштрихованный прямоугольник представляет средние 50% распределения (между первым и третьим квартилями). График коробчатого уса предназначен для быстрого отображения распределения переменной. Мы определили, что не было никаких выбросов в распределении диастолического артериального давления в подвыборке из n = 10 участников, которые присутствовали на седьмом экзамене Framingham Offspring Study.
Рисунок 11 — График диастолического артериального давления в подвыборке из n = 10.
Рис. 12 представляет собой график диастолического артериального давления, измеренного в полной выборке (n = 3 539) участников. Напомним, что в полной выборке мы определили, что были выбросами как на нижнем, так и на верхнем конце (см. Таблицу 16). На рисунке 12 выбросы отображаются в виде горизонтальных линий вверху и внизу распределения.В нижней части распределения есть 5 значений, которые считаются выбросами (т. Е. Значения ниже 47,5, которые были нижним пределом для определения выбросов). В верхней части распределения есть 12 значений, которые считаются выбросами (т. Е. Значения выше 99,5, которые были верхним пределом для определения выбросов). «Усы» графика (жирные горизонтальные скобки) — это пределы, которые мы определили для обнаружения выбросов (47,5 и 99,5).
Рисунок 12 — График диастолического артериального давления с усами-коробкой для полной выборки (n = 3539) участников
Диаграммы коробчатого уса очень полезны для сравнения распределений.На рисунке 13 ниже показаны бок-о-бок графики распределения веса в фунтах для мужчин и женщин в исследовании Framingham Offspring Study. На рисунке отчетливо виден сдвиг в распределении мужчин с гораздо большим весом. Фактически, 25 -й процентиль веса у мужчин составляет примерно 180 фунтов и равен 75 -му процентилю у женщин. В частности, 25% мужчин весят 180 или меньше по сравнению с 75% женщин. Как среди мужчин, так и среди женщин в верхней части распределения есть много выбросов.Среди мужчин есть две очень низкие ценности.
Рисунок 13 — Графики веса мужчин и женщин, расположенные бок о бок в исследовании Framingham Offspring
Поскольку мужчины обычно выше женщин (см. Рис. 14 ниже), неудивительно, что мужчины имеют больший вес, чем женщины.
Рис. 14 — График роста мужчин и женщин, построенный бок о бок с прямоугольными усами, в исследовании Framingham Offspring Study
Поскольку мужчины выше ростом, более уместным сравнением является индекс массы тела, см. Рис. 15 ниже.
Рисунок 15 — Графики индекса массы тела у мужчин и женщин, расположенные бок о бок в исследовании Framingham Offspring
Распределение индекса массы тела одинаково для мужчин и женщин. И снова наблюдается много выбросов как у мужчин, так и у женщин. Однако, принимая во внимание рост (сравнивая индекс массы тела вместо сравнения только веса), мы видим, что наиболее резко отклоняющиеся значения наблюдаются среди женщин.
На графиках «ящик-ус» выбросы — это значения, которые либо превышают Q 3 + 1.5 IQR или падение ниже Q 1 — 1,5 IQR. Некоторые пакеты статистических вычислений используют следующее для определения выбросов: значения, которые либо превышают Q 3 + 3 IQR, либо падают ниже Q 1 -3 IQR, что приведет к тому, что меньшее количество наблюдений будет классифицировано как выбросы. 7,8 Правило, использующее 1,5 IQR, является наиболее часто применяемым правилом для определения выбросов.
Первым важным аспектом любого статистического анализа является соответствующая сводка ключевых аналитических переменных.Это включает в себя сначала определение типа анализируемой переменной. Этот шаг чрезвычайно важен, поскольку соответствующие числовые и графические сводки зависят от типа анализируемой переменной. Переменные бывают дихотомическими, порядковыми, категориальными или непрерывными. Лучшие числовые сводки для дихотомических, порядковых и категориальных переменных включают относительные частоты. Лучшие числовые сводки для непрерывных переменных включают среднее и стандартное отклонение или медианный и межквартильный размах, в зависимости от того, есть ли в распределении выбросы.Среднее и стандартное отклонение или медиана и межквартильный размах суммируют центральную тенденцию (также называемую местоположением) и дисперсию, соответственно. Лучшая графическая сводка для дихотомических и категориальных переменных — это гистограмма, а наилучшая графическая сводка для порядковой переменной — это гистограмма. Как гистограммы, так и гистограммы могут быть предназначены для отображения частот или относительных частот, причем последний является более популярным дисплеем. Графики прямоугольных усов представляют собой очень полезную и информативную сводку для непрерывных переменных.Графики прямоугольного уса также полезны для сравнения распределений непрерывной переменной среди взаимоисключающих (т. Е. Неперекрывающихся) групп сравнения.
В следующей таблице приведены основные статистические данные и графические изображения, организованные по типам переменных.
|
Тип переменной |
Статистика |
Определение |
|---|---|---|
|
Дихотомические, порядковые или категориальные |
Относительная частота |
ф / п |
|
Дихотомия или категоричность |
Гистограмма частоты или относительной частоты |
|
|
Гистограмма частоты или относительной частоты |
|
|
|
Непрерывный |
Среднее |
|
|
Стандартное отклонение |
|
|
|
Медиана |
Среднее значение в упорядоченном наборе данных |
|
|
Первый квартиль
Третий квартиль |
Q 1 = Значение, удерживающее 25% на уровне или ниже Q 3 = Значение, удерживающее 25% на уровне или выше |
|
|
Межквартильный размах |
К 3 — К 1 |
|
|
Критерии выбросов |
Значения ниже Q 1 -1.5 (Q 3 -Q 1 ) или выше Q 3 +1,5 (Q 3 -Q 1 ) |
|
|
Участок с усами |
|
- Национальный институт сердца, легких и крови. Доступно на: http://www.nhlbi.nih.gov.
- Sullivan LM. Повторные мероприятия. Тираж (в печати).
- Little RJ, Рубин ДБ.Статистический анализ с отсутствующими данными. Нью-Йорк, штат Нью-Йорк: John Wiley and Sons, Inc .; 1987.
- Американская кардиологическая ассоциация. Доступно на: http://www.americanheart.org.
- Экспертная панель. Группа экспертов по обнаружению, оценке и лечению повышенного холестерина в крови у взрослых: резюме второго отчета экспертной группы NCEP (Группа лечения взрослых II). Журнал Американской медицинской ассоциации. 1993; 269: 3015-3023.
- Хоаглин, округ Колумбия.Джон В. Тьюки и анализ данных. Статистические науки .

 8.1.5.1 – прогнозировать
содержание по отрывку прослушанного текста
8.1.5.1 – прогнозировать
содержание по отрывку прослушанного текста
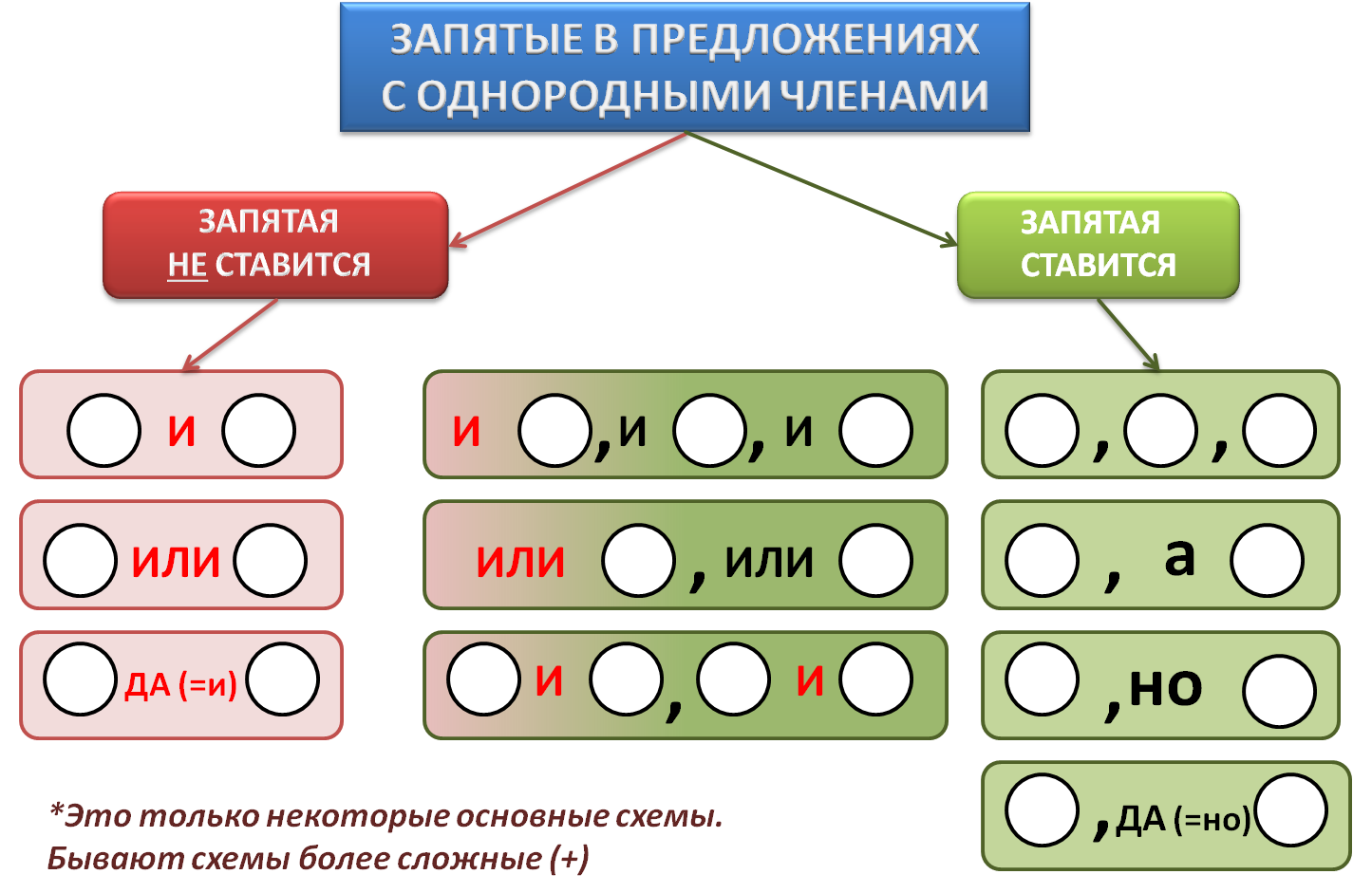 Интерактивная доска, снежинки из бумаг
Интерактивная доска, снежинки из бумаг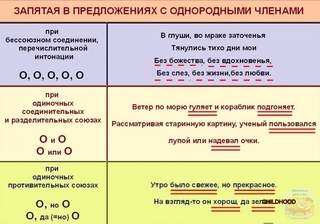
 «Большой палец»
«Большой палец» Капитаны команды оценивают
членов своих команд
Капитаны команды оценивают
членов своих команд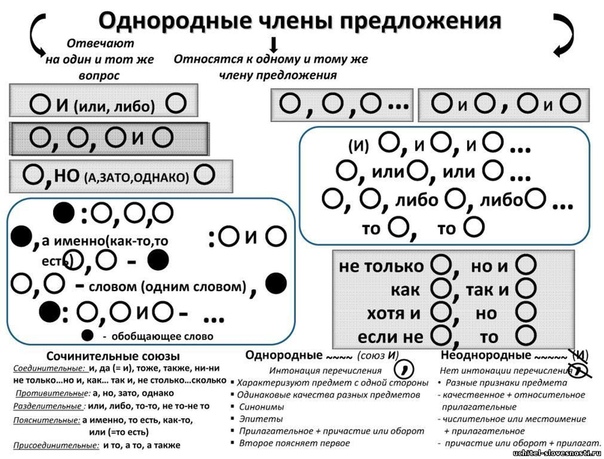 Соотнесите примеры с ролью ОЧП
Соотнесите примеры с ролью ОЧП 





 .3.1.1 – понимать
основную информацию, определяя тему, цель или назначение текста;
.3.1.1 – понимать
основную информацию, определяя тему, цель или назначение текста;

 Изучение нового материала.
Изучение нового материала.  Графически обозначьте. Трансформируйте их на именные (сущ+сущ)
Графически обозначьте. Трансформируйте их на именные (сущ+сущ)

 9
9  5
5  3
3  1
1 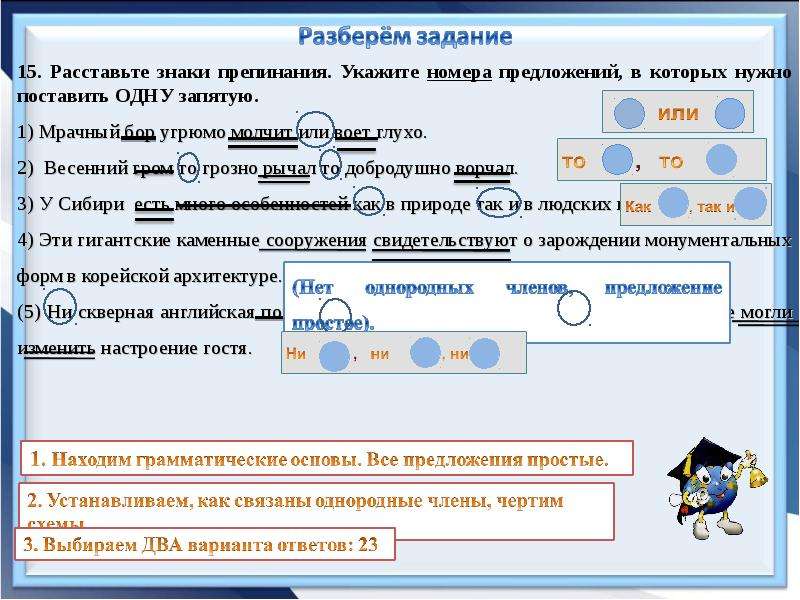 6
6  75
75