Справочный материал тригонометрия: Справочный материал - "Тригонометрия вне школы" - Управленческое образование

Содержание

Справочный материал — «Тригонометрия вне школы»

Формулы тригонометрических функций суммы углов.

Формулы тригонометрических функций разницы углов.

Формулы тригонометрических функций двойного

sin(2α)- через sin и cos:

sin(2α)- через tg и ctg:

cos(2α)- через sin и cos:

cos(2α)- через tg и ctg:

tg(2α) и сtg(2α):

Формулы тригонометрических функций тройного угла

Синус, косинус, тангенс, котангенс половинного угла

Формулы суммы тригонометрических функций

Формулы разницы тригонометрических функций

Формулы произведения тригонометрических функций, (sin cos tg ctg)

Квадрат синуса, косинуса, тангенса, котангенса (альфа)

Уравнения разложения тригонометрических функций:

квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.

Синус, косинус в кубе

Тригонометр

Практическая тетрадь по теме «Тригонометрия»

ПРАКТИЧЕСКАЯ ТЕТРАДЬ

по теме «Тригонометрия»

Пояснительная записка:

Практическая тетрадь «Тригонометрия» предназначена в первую очередь для самоконтроля учащихся усвоения ЗУН по вышеуказанной теме. Учителя могут использовать данный материал при подготовке учащихся средней школы к итоговой аттестации по алгебре и началам анализа.

Тема: ТРИГОНОМЕТРИЯ

СПРАВОЧНЫЙ МАТЕРИАЛ

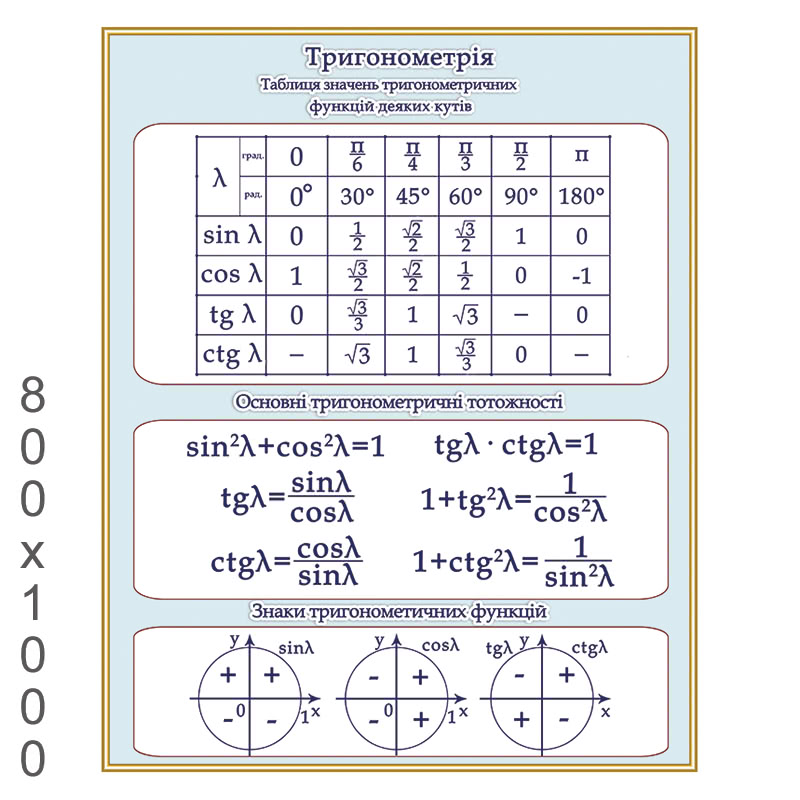
1)Значение тригонометрических функций

Угол	Функция	00	0	300	450	600	900	1800	2700	3600
sinα							1	0	-1		0
cosα		1					0	-1	0		1
tgα		0			1		—	0	—		0
ctgα					1		0	—	0		—

2)Знаки синуса, косинуса, тангенса, котангенса в каждой из координатных четвертей.

Знаки синуса Знаки косинуса Знаки тангенса и

котангенса

+ + — + — +

— — — + + —

3) sin(-α) = -sinα нечетная функции

tg (-α) = -tgα нечетная функции

ctg (-α) = -ctgα нечетная функции

cos (-α) = cosα} – четная функция

Формулы тригонометрии

Основные тригонометрические тождества

Формулы двойного угла

sin2α +cos2α =1

tgα ∙ctgα =1

sin2α = 2sinα ∙ cosα

cos2α = cos2α – sin2α

cos2α = 1-sin2α

cos2α =2cos2α -1

Формулы половинного угла

Формулы сложения

sin (α+β) =sinα cosβ +cosα sinβ

sin (α-β) =sinα cosβ-cosα sinβ

cos (α+β) = cosα cosβ -sinα sinβ

cos (α-β) = cosα cosβ +sinα sinβ

Формулы суммы и разност

Тема: ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ

СПРАВОЧНЫЙ МАТЕРИАЛ

Решите уравнение:

1. arcsin(-a) = -arcsin a arcsin = ; arcsin(- ) = —

2. arccos(-a) = π – arccos a arccos = ; arccos(- ) = π — = π

3. arctg(-a) = -arctg a arctg1 = ; arctg(-1) = —

4. arcctg(-a) = π – arcctg a arcctg1 = ; arcctg(-1) = π — = π

5. sin (arcsin a) = a

cos (arccos a) = a

6. arcsin (sin х) = х

arccos (cos х) = х

7 .tg (arctg a) = a

arctg (tg х) = х, если х€

Найдите значение выражения:

a) arcsin 1 г) arctg 0 ж) arccos (-)

б) arcsin (- ) д) arctg (-) з) arcctg (-)

в) arccos е) arcctg ()

Тема: ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ

СПРАВОЧНЫЙ МАТЕРИАЛ

Уравнения вида sin x = a, cos x = a, tg x = a, ctg x =a называются простейшими тригонометрическими уравнениями. Любое другое тригонометрическое уравнение с помощью преобразований можно привести к простейшим.

1) sin x = a, -1 ≤ a ≤ 1

х = (-1)k arcsin a + πk, k€z

Частные случаи

sinx = 0; x = πk, k€z

sinx = 1; x = + 2πk, k€z

sinx = -1; x = — + 2πk, k€z

sin2x = a; x = ±arcsin + πn

2) cos x = a, -1 ≤ a ≤ 1

х = ±arccos a + 2πk, k€z

Частные случаи

cosx = 0; x = — + πk, k€z

cosx = 1; х=2πk, k€z

cosx = -1; х= π + 2πk, k€z

cos2x = ±arccos + πn, n€z

3) tg x = a

х = arctg a + πk, k€z

УПРАЖНЕНИЯ С РЕШЕНИЯМИ

Пример 1. Решить уравнение:

sinx = —

x = (-1)k arcsin (- ) + πk, k€z

x = (-1)k+1 + πk, k€z

Ответ: x = (-1)k+1 + πk, k€z

Пример 3. Решить уравнение:

sin2x =

2x = (-1)k arcsin + πk, k€z

2x = (-1)k + πk, k€z

х = (-1)k + k, k€z

Ответ: х = (-1)k + k, k€z

Пример 2. Решить уравнение:

2 cosx + 1 = 0

2cosx = -1

cosx = —

x = ±arccos(- ) + 2πk, k€z

x = ±() + 2πk, k€z

Ответ: x = ±() + 2πk, k€z

Пример 4. Решить уравнение:

3tgx -1 = 0

tgx =

x = arctg + πk, k€z

Ответ: x = arctg + πk, k€z

ДИДАКТИЧЕСКИЙ МАТЕРИАЛ

Решите уравнения:

1. cos x = 7. sin x = -0,6

2. cos x = -1 8. cos (-4x )= 0

3. sin(- x) = 0,5 9. cos = —

4. 2 sin x = 0 10. tg( x+π/4) =

5. ctg х + 1 = 0 11. 2 sin x + = 0

6. sin 3x = 12. cos x = 3

Тема: РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Уравнения, сводящиеся к квадратным

(Виды уравнений: а sin2x + b sinx + c= 0, а cos2x + b sinx + c = 0)

Алгоритм решения:

а) Выполнить преобразования, приводящие к уравнению с одной функцией

б) Решить квадратное уравнение относительно данной функции

в) Решить простейшие тригонометрические уравнения

Пример: 2 sin2 x + 5 sin x – 3 = 0

Замена: sinx = t , |t| ≤ 1

2 t2 + 5 t – 3 = 0 , t = -3

t = Обратная замена: sin x=-3 нет решения,

sinx = (простейшее уравнение)

(см. таблицу)

2) Уравнения вида a sinx + b cosx = 0 (однородное уравнение первого порядка)

Решается делением на sin x ≠ 0 или cos х ≠ 0

Например: поделим на cos x, получим уравнение а tgx + b = 0

tgx = — (простое тригонометрическое уравнение)

Уравнения, решаемые разложением левой части на множители, если справа 0

(левую часть уравнения раскладываем на множители, затем каждый из сомножителей приравниваем к нулю)

а sin2x + b sinxcosx = 0 (вынесем за скобки sin х)

sinx (a sinx + b cosx) = 0 (данное уравнение распадается на 2 уравнения:

1) sinx = 0 (прост. триг. уравнение) . 2) а sinx + b cosx = 0 (однородное триг. уравнение 1-го порядка, смотри пункт 2)

4) Однородные тригонометрические уравнения 2-го порядка

а sin2 x + b sinx cosx + c cos2x = 0 Примечание: если уравнение имеет вид

а sin2 x + bsinx cosx + c cos2x = d, то правую часть

уравнения умножаем на 1, т.е.

Решается делением на сos2 х≠ 0

a tg2x + b tgx + c = 0 (смотри пункт 1)

замена: tgx = t

at2 + bt + c =0 …

ДИДАКТИЧЕСКИЙ МАТЕРИАЛ

Решите уравнение

1.2 cos2x + 9 sinx + 3 = 0, (указание: заменить на 1-sin2x) 2. sinx + cosx = 0

Ответ: — + πn, n€z Ответ: (-1)n+1 + πn, n€z

3. 2sin cosx – sinx = 0 4. 3 sin2x + sinxcosx = 2cos2x

Ответ: x = — + πn, x = arctg + πn, n€z Ответ: x = ± + 2πn, n€z, x = πn, n€z

ТЕСТ № 1

1. Решите уравнение: sinx =

А) (-1)k + πk, k€z B) ± + 2πk C) (-1)k + πk D) (-1)k + 2πk

2. Решите уравнение: 2 cos2x =

A) + 2πk B) ± + πk C) + πk D) ± + 2πk

3. Решите уравнение: 3tg3x = 3

A) + k B) — + πk C)k D) +

4. Решите уравнение: 2cos2x – 5cosx = -3

A) 2πn, n€z B) нет решения C) πn, n€z D) π + 2πn, n€z

5. Решите уравнение: sin2x – 2sinx = 0

A) πn, n€z B) (-1)k + πк C) ± + 2πn D) π + 2πn, n€z

6. Решите уравнение:

A) нет решения B) C) D) ± + 2πn, n€z

7. Решите уравнение: 2sin + = 0

A) (-1)k + 2πk B) (-1)k + 1 + 2πk C) (-1)k + πk D) (-1)k + 1 + πk

8. Решите уравнение: sinx – cosx = 0

A) + πn B) + πn C) ± +2 πn D) ± + πn

9. Решите уравнение: sin2 + sin cos = 0

A) — + 2 πn, n€z, 2πn, n€z B) + 2 πn, n€z C) + πn, n€z D) — + πn, n€z, πn, n€z

10. Решите уравнение: 3tg6x + = 0

A) + πn, n€z B) + 6 πn, n€z C) + 3 πn, n€z D) — n, n€z

ТЕСТ №2

1. Решите уравнение:

А) В) С)D)

2. Решите уравнение если

А) В) С) D)

3. Решите уравнение:

А); В);

С); D).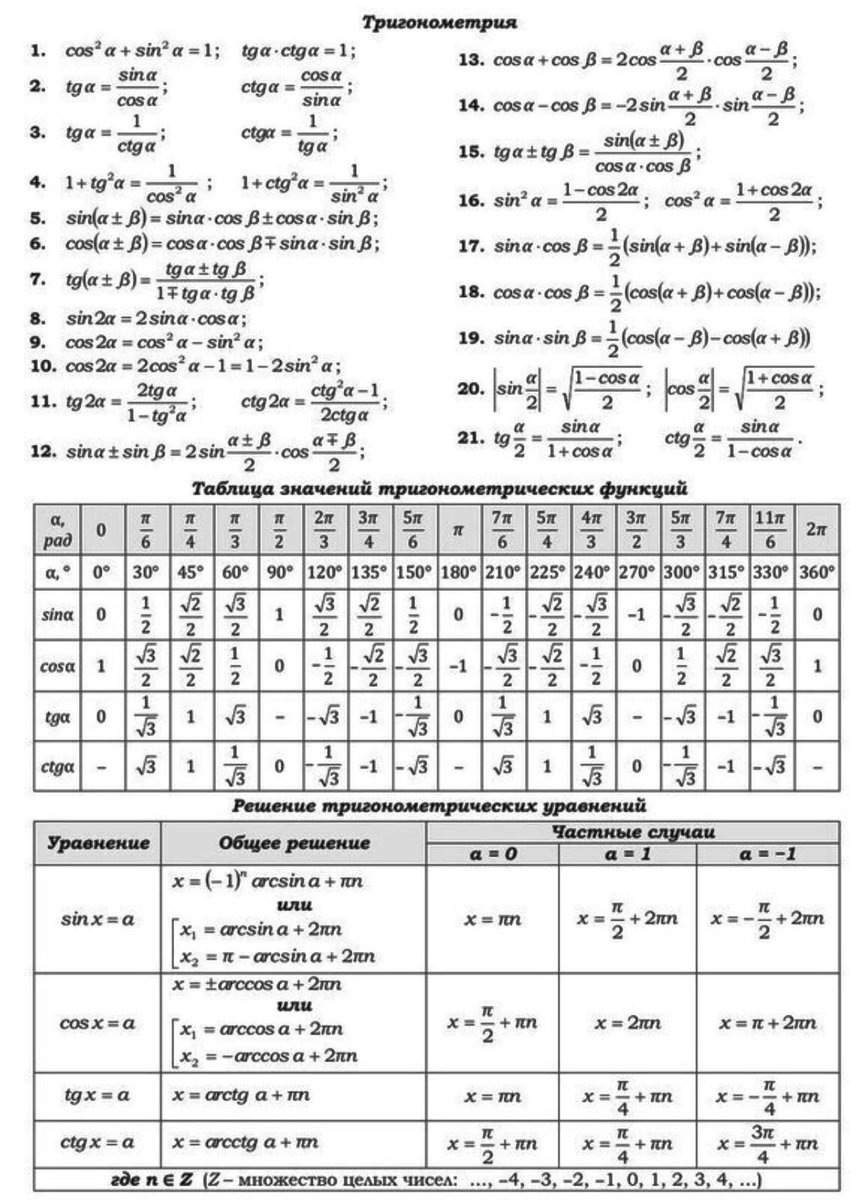

4. Решите уравнение: .

А); В); С); D).

5. Найдите корень уравнение принадлежащий []

А)300; В)450; С)200; D)150.

6. Решите уравнение: .

А) В) С)D)

7. Решите уравнение:

А) В) С) D)

8. Решите уравнение: .

А); В); С) ; D).

9. Решите уравнение: .

А); В);

С) ; D).

10. Решите уравнение:

А) ; В) ;

С) ; D) .

Частные случаи решения тригонометрических уравнений. Тригонометрические уравнения — формулы, решения, примеры. Решение тригонометрических уравнений через разложение на множители

Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!

Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.

Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.

Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.

Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.

Тригонометрические уравнения.

Простейшие тригонометрические уравнения

Методы решения тригонометрических уравнений.

Тригонометрические уравнения. Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим .

Простейшие тригонометрические уравнения.

Методы решения тригонометрических уравнений. Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида (см. выше ) и решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения тригонометрических уравнений.

1. Алгебраический метод.

Этот метод нам хорошо известен из алгебры

(метод замены переменной и подстановки).

2. Разложение на множители.

Этот метод рассмотрим на примерах.

П р и м е р 1. Решить уравнение:

sin x + cos x = 1 .

Р е ш е н и е. Перенесём все члены уравнения влево:

Sin x + cos x – 1 = 0 ,

Преобразуем и разложим на множители выражение в

Левой части уравнения:

П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.

Р е ш е н и е. cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,

Sin x · cos x – sin 2 x = 0 ,

Sin x · (cos x – sin x ) = 0 ,

П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.

Р е ш е н и е. cos 2 x + cos 6 x = 1 + cos 8 x ,

2 cos 4x cos 2

x = 2 cos ² 4x ,

Cos 4x · (cos 2x – cos 4x ) = 0 ,

Cos 4x · 2 sin 3x · sin x = 0 ,

1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,

Приведение к однородному уравнению. Уравнение называется однородным от носительно sin и cos , если все его члены одной и той же степени относительно sin и cos одного и того же угла . Чтобы решить однородное уравнение, надо:

а ) перенести все его члены в левую часть;

б ) вынести все общие множители за скобки;

в ) приравнять все множители и скобки нулю;

г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на

cos (или sin ) в старшей степени;

д ) решить полученное алгебраическое уравнение относительно tan .

П р и м е р. Решить уравнение: 3 sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.

Р е ш е н и е. 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,

Sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,

Tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,

Корни этого уравнения: y 1 = — 1, y 2 = — 3, отсюда

1) tan x = –1, 2) tan x = –3,

4. Переход к половинному углу. Рассмотрим этот метод на примере:

П р и м е р. Решить уравнение: 3 sin

x – 5 cos x = 7.

Р е ш е н и е. 6 sin (x / 2) · cos (x / 2) – 5 cos ² (x / 2) + 5 sin ² (x / 2) =

7 sin ² (x / 2) + 7 cos ² (x / 2) ,

2 sin ² (x / 2) – 6 sin (x / 2) · cos (x / 2) + 12 cos ² (x / 2) = 0 ,

tan ² (x / 2) – 3 tan (x / 2) + 6 = 0 ,

. . . . . . . . . .

5. Введение вспомогательного угла. Рассмотрим уравнение вида :

a sin x + b cos x = c ,

Где a , b , c – коэффициенты; x – неизвестное.

Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого

Соотношения между основными тригонометрическими функциями – синусом, косинусом, тангенсом и котангенсом — задаются

тригонометрическими формулами . А так как связей между тригонометрическими функциями достаточно много, то этим объясняется и обилие тригонометрических формул. Одни формулы связывают тригонометрические функции одинакового угла, другие – функции кратного угла, третьи – позволяют понизить степень, четвертые – выразить все функции через тангенс половинного угла, и т.д.

В этой статье мы по порядку перечислим все основные тригонометрические формулы, которых достаточно для решения подавляющего большинства задач тригонометрии. Для удобства запоминания и использования будем группировать их по назначению, и заносить в таблицы.

Навигация по странице.

Основные тригонометрические тождества

Основные тригонометрические тождества задают связь между синусом, косинусом, тангенсом и котангенсом одного угла. Они вытекают из определения синуса, косинуса, тангенса и котангенса, а также понятия единичной окружности . Они позволяют выразить одну тригонометрическую функцию через любую другую.

Подробное описание этих формул тригонометрии, их вывод и примеры применения смотрите в статье .

Формулы приведения

Формулы приведения следуют из свойств синуса, косинуса, тангенса и котангенса , то есть, они отражают свойство периодичности тригонометрических функций, свойство симметричности, а также свойство сдвига на данный угол. Эти тригонометрические формулы позволяют от работы с произвольными углами переходить к работе с углами в пределах от нуля до 90 градусов.

Обоснование этих формул, мнемоническое правило для их запоминания и примеры их применения можно изучить в статье .

Формулы сложения

Тригонометрические формулы сложения показывают, как тригонометрические функции суммы или разности двух углов выражаются через тригонометрические функции этих углов. Эти формулы служат базой для вывода следующих ниже тригонометрических формул.

Формулы двойного, тройного и т.д. угла

Формулы двойного, тройного и т.д. угла (их еще называют формулами кратного угла) показывают, как тригонометрические функции двойных, тройных и т.д. углов () выражаются через тригонометрические функции одинарного угла . Их вывод базируется на формулах сложения.

Более детальная информация собрана в статье формулы двойного, тройного и т.д. угла .

Формулы половинного угла

Формулы половинного угла показывают, как тригонометрические функции половинного угла выражаются через косинус целого угла . Эти тригонометрические формулы следуют из формул двойного угла.

Их вывод и примеры применения можно посмотреть в статье .

Формулы понижения степени

Тригонометрические формулы понижения степени призваны содействовать переходу от натуральных степеней тригонометрических функций к синусам и косинусам в первой степени, но кратных углов. Иными словами, они позволяют понижать степени тригонометрических функций до первой.

Формулы суммы и разности тригонометрических функций

Основное предназначение формул суммы и разности тригонометрических функций заключается в переходе к произведению функций, что очень полезно при упрощении тригонометрических выражений. Указанные формулы также широко используются при решении тригонометрических уравнений, так как позволяют раскладывать на множители сумму и разность синусов и косинусов.

Формулы произведения синусов, косинусов и синуса на косинус

Переход от произведения тригонометрических функций к сумме или разности осуществляется посредством формул произведения синусов, косинусов и синуса на косинус .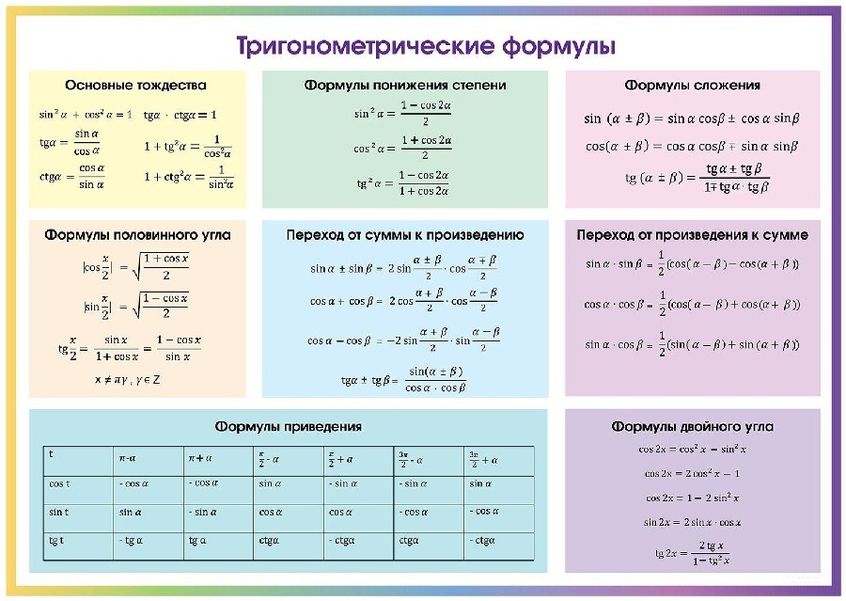

Универсальная тригонометрическая подстановка

Обзор основных формул тригонометрии завершаем формулами, выражающими тригонометрические функции через тангенс половинного угла. Такая замена получила название

универсальной тригонометрической подстановки . Ее удобство заключается в том, что все тригонометрические функции выражаются через тангенс половинного угла рационально без корней.

Список литературы.

Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004. — 384 с.: ил.- ISBN 5-09-013651-3.
Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.

Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта , включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.

Концепция решения тригонометрических уравнений.

Для решения тригонометрического уравнения преобразуйте его в одно или несколько основных тригонометрических уравнений. Решение тригонометрического уравнения в конечном итоге сводится к решению четырех основных тригонометрических уравнений.

Решение основных тригонометрических уравнений.

Существуют 4 вида основных тригонометрических уравнений:
sin x = a; cos x = a
tg x = a; ctg x = a
Решение основных тригонометрических уравнений подразумевает рассмотрение различных положений «х» на единичной окружности, а также использование таблицы преобразования (или калькулятора).
Пример 1. sin x = 0,866. Используя таблицу преобразования (или калькулятор), вы получите ответ: х = π/3. Единичная окружность дает еще один ответ: 2π/3. Запомните: все тригонометрические функции являются периодическими, то есть их значения повторяются. Например, периодичность sin x и cos x равна 2πn, а периодичность tg x и ctg x равна πn. Поэтому ответ записывается следующим образом:
x1 = π/3 + 2πn; x2 = 2π/3 + 2πn.
Пример 2. соs х = -1/2. Используя таблицу преобразования (или калькулятор), вы получите ответ: х = 2π/3. Единичная окружность дает еще один ответ: -2π/3.
x1 = 2π/3 + 2π; х2 = -2π/3 + 2π.
Пример 3. tg (x — π/4) = 0.
Ответ: х = π/4 + πn.
Пример 4. ctg 2x = 1,732.
Ответ: х = π/12 + πn.

Преобразования, используемые при решении тригонометрических уравнений.

Для преобразования тригонометрических уравнений используются алгебраические преобразования (разложение на множители, приведение однородных членов и т. д.) и тригонометрические тождества.
Пример 5. Используя тригонометрические тождества, уравнение sin x + sin 2x + sin 3x = 0 преобразуется в уравнение 4cos x*sin (3x/2)*cos (x/2) = 0. Таким образом, нужно решить следующие основные тригонометрические уравнения: cos x = 0; sin (3x/2) = 0; cos (x/2) = 0.
Нахождение углов по известным значениям функций.
- Перед изучением методов решения тригонометрических уравнений вам необходимо научиться находить углы по известным значениям функций. Это можно сделать при помощи таблицы преобразования или калькулятора.
- Пример: соs х = 0,732. Калькулятор даст ответ х = 42,95 градусов. Единичная окружность даст дополнительные углы, косинус которых также равен 0,732.
Отложите решение на единичной окружности.
- Вы можете отложить решения тригонометрического уравнения на единичной окружности. Решения тригонометрического уравнения на единичной окружности представляют собой вершины правильного многоугольника.
- Пример: Решения x = π/3 + πn/2 на единичной окружности представляют собой вершины квадрата.
- Пример: Решения x = π/4 + πn/3 на единичной окружности представляют собой вершины правильного шестиугольника.
Методы решения тригонометрических уравнений.
- Если данное тригонометрическое уравнение содержит только одну тригонометрическую функцию, решите это уравнение как основное тригонометрическое уравнение. Если данное уравнение включает две или более тригонометрические функции, то существуют 2 метода решения такого уравнения (в зависимости от возможности его преобразования).
- Преобразуйте данное уравнение в уравнение вида: f(x)*g(x)*h(x) = 0, где f(x), g(x), h(x) — основные тригонометрические уравнения.
- Пример 6. 2cos x + sin 2x = 0. (0
- Решение. Используя формулу двойного угла sin 2x = 2*sin х*соs х, замените sin 2x.
- 2соs х + 2*sin х*соs х = 2cos х*(sin х + 1) = 0. Теперь решите два основных тригонометрических уравнения: соs х = 0 и (sin х + 1) = 0. 2 — 1) = 0. Теперь найдите t, а затем найдите х для t = tg х.

Урок и презентация на тему: «Решение простейших тригонометрических уравнений»

Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.

Пособия и тренажеры в интернет-магазине «Интеграл» для 10 класса от 1С
Решаем задачи по геометрии. Интерактивные задания на построение в пространстве
Программная среда «1С: Математический конструктор 6.1»

Что будем изучать:
1. Что такое тригонометрические уравнения?

3. Два основных метода решения тригонометрических уравнений.
4. Однородные тригонометрические уравнения.
5. Примеры.

Что такое тригонометрические уравнения?

Ребята, мы с вами изучили уже арксинуса, арккосинус, арктангенс и арккотангенс. Теперь давайте посмотрим на тригонометрические уравнения в общем.

Тригонометрические уравнения – уравнения в котором переменная содержится под знаком тригонометрической функции. n – минус один в степени n.

Ещё примеры тригонометрических уравнений.

Решить уравнения: а) cos(x/5)=1 б)tg(3x- π/3)= √3

Решение:

А) В этот раз перейдем непосредственно к вычислению корней уравнения сразу:

X/5= ± arccos(1) + 2πk. Тогда x/5= πk => x=5πk

Ответ: x=5πk, где k – целое число.

Б) Запишем в виде: 3x- π/3=arctg(√3)+ πk. Мы знаем что: arctg(√3)= π/3

3x- π/3= π/3+ πk => 3x=2π/3 + πk => x=2π/9 + πk/3

Ответ: x=2π/9 + πk/3, где k – целое число.

Решить уравнения: cos(4x)= √2/2. И найти все корни на отрезке .

Решение:

Решим в общем виде наше уравнение: 4x= ± arccos(√2/2) + 2πk

4x= ± π/4 + 2πk;

X= ± π/16+ πk/2;

Теперь давайте посмотрим какие корни попадут на наш отрезок. При k При k=0, x= π/16, мы попали в заданный отрезок .
При к=1, x= π/16+ π/2=9π/16, опять попали.
При k=2, x= π/16+ π=17π/16, а тут вот уже не попали, а значит при больших k тоже заведомо не будем попадать.

Ответ: x= π/16, x= 9π/16

Два основных метода решения.

Мы рассмотрели простейшие тригонометрические уравнения, но существуют и более сложные. Для их решения применяют метод ввода новой переменной и метод разложения на множители. Давайте рассмотрим примеры.

Решим уравнение:

Решение:
Для решения нашего уравнения воспользуемся методом ввода новой переменной, обозначим: t=tg(x).

В результате замены получим: t 2 + 2t -1 = 0

Найдем корни квадратного уравнения: t=-1 и t=1/3

Тогда tg(x)=-1 и tg(x)=1/3, получили простейшее тригонометрическое уравнение, найдем его корни.

X=arctg(-1) +πk= -π/4+πk; x=arctg(1/3) + πk.

Ответ: x= -π/4+πk; x=arctg(1/3) + πk.

Пример решения уравнения

Решить уравнений: 2sin 2 (x) + 3 cos(x) = 0

Решение:

Воспользуемся тождеством: sin 2 (x) + cos 2 (x)=1

Наше уравнение примет вид:2-2cos 2 (x) + 3 cos (x) = 0

2 cos 2 (x) — 3 cos(x) -2 = 0

Введем замену t=cos(x): 2t 2 -3t — 2 = 0

Решением нашего квадратного уравнения являются корни: t=2 и t=-1/2

Тогда cos(x)=2 и cos(x)=-1/2.

Т.к. косинус не может принимать значения больше единицы, то cos(x)=2 не имеет корней.

Для cos(x)=-1/2: x= ± arccos(-1/2) + 2πk; x= ±2π/3 + 2πk

Ответ: x= ±2π/3 + 2πk

Однородные тригонометрические уравнения.

Определение: Уравнение вида a sin(x)+b cos(x) называются однородными тригонометрическими уравнениями первой степени.

Уравнения вида

однородными тригонометрическими уравнениями второй степени.

Для решения однородного тригонометрического уравнения первой степени разделим его на cos(x): Делить на косинус нельзя если он равен нулю, давайте убедимся что это не так:
Пусть cos(x)=0, тогда asin(x)+0=0 => sin(x)=0, но синус и косинус одновременно не равны нулю, получили противоречие, поэтому можно смело делить на ноль.

Решить уравнение:
Пример: cos 2 (x) + sin(x) cos(x) = 0

Решение:

Вынесем общий множитель: cos(x)(c0s(x) + sin (x)) = 0

Тогда нам надо решить два уравнения:

Cos(x)=0 и cos(x)+sin(x)=0

Cos(x)=0 при x= π/2 + πk;

Рассмотрим уравнение cos(x)+sin(x)=0 Разделим наше уравнение на cos(x):

1+tg(x)=0 => tg(x)=-1 => x=arctg(-1) +πk= -π/4+πk

Ответ: x= π/2 + πk и x= -π/4+πk

Как решать однородные тригонометрические уравнения второй степени?
Ребята, придерживайтесь этих правил всегда!

1. Посмотреть чему равен коэффициент а, если а=0 то тогда наше уравнение примет вид cos(x)(bsin(x)+ccos(x)), пример решения которого на предыдущем слайде

2. Если a≠0, то нужно поделить обе части уравнения на косинус в квадрате, получим:

Делаем замену переменной t=tg(x) получаем уравнение:

Решить пример №:3

Решить уравнение:
Решение:

Разделим обе части уравнения на косинус квадрат:

Делаем замену переменной t=tg(x): t 2 + 2 t — 3 = 0

Найдем корни квадратного уравнения: t=-3 и t=1

Тогда: tg(x)=-3 => x=arctg(-3) + πk=-arctg(3) + πk

Tg(x)=1 => x= π/4+ πk

Ответ: x=-arctg(3) + πk и x= π/4+ πk

Решить пример №:4

Решить уравнение:

Решение:
Преобразуем наше выражение:

Решать такие уравнение мы умеем: x= — π/4 + 2πk и x=5π/4 + 2πk

Ответ: x= — π/4 + 2πk и x=5π/4 + 2πk

Решить пример №:5

Решить уравнение:

Решение:
Преобразуем наше выражение:

Введем замену tg(2x)=t:2 2 — 5t + 2 = 0

Решением нашего квадратного уравнения будут корни: t=-2 и t=1/2

Тогда получаем: tg(2x)=-2 и tg(2x)=1/2
2x=-arctg(2)+ πk => x=-arctg(2)/2 + πk/2

2x= arctg(1/2) + πk => x=arctg(1/2)/2+ πk/2

Ответ: x=-arctg(2)/2 + πk/2 и x=arctg(1/2)/2+ πk/2

Задачи для самостоятельного решения.

1) Решить уравнение

А) sin(7x)= 1/2 б) cos(3x)= √3/2 в) cos(-x) = -1 г) tg(4x) = √3 д) ctg(0.5x) = -1.7

2) Решить уравнения: sin(3x)= √3/2. И найти все корни на отрезке [π/2; π ].

3) Решить уравнение: ctg 2 (x) + 2ctg(x) + 1 =0

4) Решить уравнение: 3 sin 2 (x) + √3sin (x) cos(x) = 0

5) Решить уравнение:3sin 2 (3x) + 10 sin(3x)cos(3x) + 3 cos 2 (3x) =0

6)Решить уравнение:cos 2 (2x) -1 — cos(x) =√3/2 -sin 2 (2x)

Справочные материалы. Алгебра. Тригонометрия | ISBN: 978-985-15-3237-3

Аннотация

Справочный материал «Алгебра. Тригонометрия».

Дополнительная информация

Регион (Город/Страна где издана):	Минск
Год публикации:	2016
Тираж:	1000
Страниц:
Ширина издания:	145
Высота издания:	110
Вес в гр.:	5
Язык публикации:	Русский
Тип обложки:	Мягкий / Полужесткий переплет
Цвета обложки:	Голубой, Белый
Полный список лиц указанных в издании:

Алгебра, 10-й класс.

Урок по теме «Построение графиков тригонометрических функций»

Цели урока:

сформировать умение и навыки построения графиков тригонометрических функций, используя геометрические преобразования;
закрепить основные формулы тригонометрии;
способствовать самостоятельной деятельности учащихся;
развивать логическое мышление.

Оборудование:

интерактивная доска;
компьютеры;
раздаточный материал;
справочный материал.

Ход урока

I. Организационный момент. Сообщение темы и цели урока. (Приложение 1, слайд 1)

II. Актуализация опорных знаний. Устная работа.

1) разгадывание ребусов (Приложение 1, слайды 2,3)

2) повторение основных свойств тригонометрических функций (Приложение 1, слайды 4-7)

III.
Практическая работа, с использованием интерактивной доски.

1) Построение графиков тригонометрических функции. (Приложение 1, слайды 8-11)

Построение графиков осуществляется учащимися у доски, а остальные учащиеся выполняют построение графиков на рабочих листах. (Приложение 2)

2) Найди ошибку и исправь её. (Приложение 1 , слайды 12-13)

Учащиеся должны найти ошибку в построении графиков тригонометрических функций и исправить её. Собрать рабочие листы для проверки.

IV. Разгадывание кроссворда. (Приложение 1, слайд 14)

Учащиеся должны разгадать кроссворд и узнать великого математика 18 века.

V. Исторический материал. Сообщение об Эйлере. (Приложение 1, слайд15)

Из истории тригонометрии.

Леонард Эйлер – крупнейший математик 18-го столетия. Родился в Швейцарии. Долгие годы жил и работал в России, член Петербургской академии.

Почему же мы должны знать и помнить имя этого ученого?

К началу 18 века тригонометрия была еще недостаточно разработана: не было условных обозначений, формулы записывались словами, усваивать их было трудно, неясным был и вопрос о знаках тригонометрических функций в разных четвертях круга, под аргументом тригонометрической функции понимали только углы или дуги. Только в трудах Эйлера тригонометрия получила современный вид. Именно он стал рассматривать тригонометрическую функцию числа, т.е. под аргументом стали понимать не только дуги или градусы, но и числа. Эйлер вывел все тригонометрические формулы из нескольких основных, упорядочил вопрос о знаках тригонометрической функции в разных четвертях круга. Для обозначения тригонометрических функций он ввел символику: sin x, cos x, tg x, ctg x.

На пороге 18-го века в развитии тригонометрии появилось новое направление – аналитическое. Если до этого главной целью тригонометрии считалось решение треугольников, то Эйлер рассматривал тригонометрию как науку о тригонометрических функциях. Первая часть: учение о функции – часть общего учения о функциях, которое изучается в математическом анализе. Вторая часть: решение треугольников – глава геометрии. Такие вот нововведения были сделаны Эйлером.

Учащиеся, которые изучают свойства тригонометрических функции, решают уравнения, неравенства, пользуются формулами тригонометрии должны помнить имя этого ученого.

VI. Повторение

1) Тест. Выполнение теста учащиеся осуществляют на компьютере. (Приложение 3) 2) Игра “Собери формулу”. (Приложение 1,слайды 16,17). Учащиеся разделяются на две команды.

3) Итоги игры.

VII. Итоги урока:

1) Что нового вы узнали сегодня на уроке?

2) Что еще вы хотите узнать?

3) Выставление оценок.

VIII. Домашнее задание. Тест.

Персональный сайт — Краткий справочник

Справочный материал ( формулы,таблицы)

Арифметика 1.Arifmetika.doc

Законы арифметических действий.

Правила знаков при умножении (делении) чисел.

Правила действий с рациональными числами ( дробями).

Арифметическая прогрессия.

Геометрическая прогрессия.

Некоторые числовые ряды (Конечные).

Золотое сечение.

Свойства степени.

Свойства квадратного (арифметического) корня.

Формулы сокращенного умножения.

Пропорции .

Среднее арифметическое.

Среднее квадратичное.

Среднее геометрическое ( среднее пропорциональное).

Алгебра 2.Algebra.doc

Определение степени и корня

Свойства степени. Правила действий со степенями.

Правила действий с радикалами .Свойства квадратного(арифметического) корня.

Модуль и его свойства.

Формулы сокращенного умножения.

Бином Ньютона.

Выделение квадрата из квадратного трёхчлена.

Теорема Виета ( свойство корней).

Формула корней квадратного уравнения.

Формула Кардано.

Координаты вершины параболы.

Определение логарифма.

Свойства логарифма.

Действия с логарифмами.

Факториал. Основное свойство факториала.

Формула Стирлинга.

Соединения: размещения , перестановки, сочетания.

Неравенства

Комплексные числа.

Комплексно-сопряженные числа.

Действия с комплексными числами.

Тригонометрическая форма записи комплексных чисел.

Модуль комплексного числа.

Аргумент комплексного числа.

Показательная форма записи комплексных чисел.

Формула Эйлера.

Произведение и частное комплексных чисел

Тригонометрия 3.Trigonometriya.doc

Тригонометрические формулы в прямоугольном треугольнике.

Тригонометрические тождества.

Формулы сложения тригонометрических функций.

Тригонометрические функции кратных углов.

Тригонометрические функции половинного угла.

Сумма тригонометрических функций.

Понижение степени тригонометрических функций.

Произведение тригонометрических функций.

Формулы приведения тригонометрических функций.

Соотношения между обратными тригонометрическими функциями.

Начала анализа 4.Nachala_analiza.doc

Предел функции. Свойства.

Пределы некоторых последовательностей.

Производные некоторых функций.

Правила вычисления производных.

Производная сложной функции.

Свойства производных высшего порядка.

Геометрический, физический смыслы производной.

Первообразная.

Неопределенный интеграл.

Основное свойство.

Интегралы некоторых функций.

Основные правила интегрирования.

Формула Ньютона-Лейбница.

Свойства определенного интеграла.

Площадь криволинейной трапеции.

Длина кривой.

Площадь поверхности вращения.

Объём тела вращения.

Несобственные интегралы.

Значение некоторых несобственных интегралов.

Геометрия. 5.Geometriya.doc

Треугольник.

Площадь треугольника. Медиана, биссектриса, высота .

Высоты и стороны треугольника.

Теорема косинусов, теорема синусов, теорема тангенсов.

Прямоугольный треугольник, Теорема Пифагора.

Равносторонний треугольник.

Квадрат.

Прямоугольник,

Параллелограмм.

Ромб.

Трапеция.

Произвольный выпуклый четырехугольник.

Правильный многоугольник( n сторон).

Окружность и круг

Длина окружности,

Свойства хорд, секущих и касательной.

Углы в окружности.

Площадь круга.

Сегмент и сектор.

Многогранники

Призма.

Параллелепипед,

Куб.

Пирамида, усеченная пирамида.

Формула Эйлера.

Куб, тетраэдр, октаэдр, додекаэдр, икосаэдр.

Тела вращения

Цилиндр.

Конус, усеченный конус.

Шар. Шаровой сектор, шаровой сегмент, шаровой слой.

Декартовы координаты на плоскости.

Расстояние между точками.

Деление отрезка в заданном отношении.

Координаты середины отрезка.

Уравнение прямой на плоскости.

Расстояние от точки (х_0,y₀) до прямой ax+by+c=0.

Взаимное расположение прямых .

Уравнение кривых на плоскости.

Формулы преобразования декартовых координат.

Полярные координаты.

Декартовы координаты в пространстве.

Уравнение плоскости.

Угол между плоскостями.

Условие параллельности двух плоскостей.

Условие перпендикулярности двух плоскостей.

Расстояние от точки до плоскости.

Уравнение прямой в пространстве.

Угол между прямыми, между прямой и плоскостью.

Условие параллельности, перпендикулярности прямой и плоскости.

Уравнения плоскостей второго порядка.

Эллипсойд

Сфера.

Гиперболойд(однополостный, двуполостный)

Конус.

Параболоид ( эллиптический ,гиперболический).

Цилиндр ( эллиптический, гиперболический, парболический).

Векторы

Координаты вектора.

Сумма векторов.

Умножение вектора на число.

Свойства проекций вектора на ось.

Скалярное произведение.Свойства.

Длина вектора.

Угол между векторами.

Условия коллинеарности, ортогональности векторов.

Векторное произведение векторов..

Свойства векторного произведения.

Смешанное произведения векторов.

Определители

Определители второго, третьего порядка.

Основные свойства определителей.

Справочные таблицы

Квадраты натуральных чисел от 11 до 99.

Кубы натуральных чисел.

Простые числа от 2 до 997.

Факториалы чисел от 0 до 10.

Степени чисел 2,3, 5.

Значения функций y=e^x

Десятичные логарифмы чисел

Натуральные логарифмы чисел.

Некоторые значения тригонометрических функций.

Правильные многоугольники.

Правильные многогранники.

Длина окружности диаметра d.

Площадь круга диаметра d.

Ручная тригонометрия — Урок — TeachEngineering

(1 оценка)

Быстрый просмотр

Уровень: 11 (9-12)

Необходимое время: 15 минут

Урок Зависимость: Нет

предметных областей: Геометрия, измерение

Резюме

Учащиеся изучают концепцию подобных прямоугольных треугольников и то, как они применяются к тригонометрическим отношениям.

Используйте этот урок, чтобы напомнить, что такое коэффициенты срабатывания и как они работают. В дополнение к тригонометрии учащиеся изучают приложение клинометра на устройстве Android® или iOS® и то, как его можно использовать для проверки математики, лежащей в основе тригонометрии. Это готовит учащегося к соответствующей деятельности, во время которой каждая группа проверяет клинометр, чтобы лучше понять тригонометрию.

Инженерное подключение

Некоторые объекты и расстояния в нашем мире очень трудно — даже невозможно — измерить напрямую вручную или с помощью инструментов.Инженеры, которые проектируют различные типы конструкций, невероятно больших или очень маленьких, или машины, которые могут перемещаться на большие расстояния глубоко под водой или далеко в космос, должны иметь точное представление о длинах и размерах, даже если их невозможно измерить. Часто в таких случаях инженеры используют тригонометрию и другие математические соотношения, чтобы найти очень точное приближение к длинам и размерам. При проектировании больших конструкций инженеры должны обеспечить баланс сил, действующих на конструкцию, чтобы они оставались неподвижными.Инженеры используют тригонометрию для учета вертикальных и горизонтальных составляющих различных сил, действующих на конструкции, таким образом определяя, сможет ли конструкция устоять без разрушения еще до того, как она будет построена. Эти стратегии, основанные на математических знаниях, позволяют инженерам разрабатывать решения проблем, которые иначе были бы неразрешимы.

Цели обучения

После этого урока учащиеся должны уметь:

Опишите, как инженеры могут использовать клинометр.
Используйте клинометр для измерения углов.

Образовательные стандарты

Каждый урок или занятие TeachEngineering связано с одной или несколькими науками K-12, технологические, инженерные или математические (STEM) образовательные стандарты.
Все более 100 000 стандартов K-12 STEM, включенных в TeachEngineering , собираются, поддерживаются и упаковываются сетью стандартов достижений (ASN) , проект D2L (www.достижениястандарты.org).
В ASN стандарты структурированы иерархически: сначала по источнику; напр. по штатам; внутри источника по типу; напр. , естествознание или математика; внутри типа по подтипу, затем по классу, и т.д. .
Общие базовые государственные стандарты — математика
Поймите, что по подобию отношения сторон в прямоугольных треугольниках являются свойствами углов в треугольнике, что приводит к определениям тригонометрических отношений для острых углов.(Оценки 9 — 12) Подробнее
Посмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
Используйте тригонометрические соотношения и теорему Пифагора для решения прямоугольных треугольников в прикладных задачах. (Оценки 9 — 12) Подробнее
Посмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
Международная ассоциация преподавателей технологий и инженерии — Технология
ГОСТ Предложите выравнивание, не указанное выше
Какое альтернативное выравнивание вы предлагаете для этого контента?
Рабочие листы и вложения
Посетите [www. Teachengineering.org/lessons/view/uno_handheld_lesson01] для печати или загрузки.
Больше учебных программ, подобных этому
Предварительные знания
Учащиеся должны пройти курс геометрии в средней школе и понимать конгруэнтность и подобие геометрических фигур. Студенты также должны иметь начальные знания тригонометрии.
Учитель должен уметь работать с приложением клинометр для iOS или Android.Большинство клинометров говорят сами за себя с небольшим опытом. Если вы используете клинометр с открытым кодом (предложенный в списке материалов), лучше всего держать мобильное устройство вертикально с 0°, отображаемым в верхней части клинометра, а затем поворачивать мобильное устройство влево или вправо так, чтобы верхняя или нижняя часть устройство выравнивается по наклонной стороне измеряемого угла. Другая сторона угла должна быть выровнена по горизонтали. Градус, отображаемый на клинометре, является градусной мерой угла. Дополнительная информация представлена в разделе «Основные сведения и концепции для учителей».
Введение/Мотивация
Тригонометрия — это раздел математики, изучающий взаимосвязь между длинами сторон и углов треугольника. Инженеры обычно используют тригонометрические концепции для вычисления углов. Инженеры-строители и инженеры-механики используют тригонометрию для расчета крутящего момента и силы на таких объектах, как мосты или строительные балки.Примером может служить расчет статических сил на объект, который не движется, например мост. Причина, по которой мост статичен (не движется), заключается в том, что силы, действующие на него, уравновешиваются (уравновешивают друг друга). Инженеры используют тригонометрию для разложения сил на горизонтальные и вертикальные компоненты, которые можно анализировать.
Понимание сил, действующих на объекты, является важной частью статики, важной области инженерии. Изучение статики и связанные с ней расчеты используются инженерами, чтобы гарантировать, что здания и мосты не рухнут из-за действующих на них сил.
Для начала я хочу, чтобы все нарисовали два прямоугольных треугольника с конгруэнтными соответствующими углами (см. рис. 1), из чего следует, что треугольники подобны . Подобие — это геометрическое понятие, означающее, что все соответствующие углы на конгруэнтны на , а отношения на соответствующих сторон равны. С точки зрения непрофессионала, подобные фигуры являются большими или меньшими ( в масштабе ) копиями друг друга. От геометрической концепции сходства вы перейдете к тригонометрии.Рисунок 1. Подобные прямоугольные треугольники. Copyright
Copyright © 2014 Scott Burns, College of Information Science & Technology, University of Nebraska-Omaha
Рассмотрите эти вопросы, связанные с вашими нарисованными фигурами:
Что вы заметили в углах этих двух треугольников? ( Ответ: Все соответствующие углы равны. )
Откуда вы знаете, что ВСЕ соответствующие углы равны, даже если не все отмечены как таковые? ( Ответ: Поскольку сумма всех углов в евклидовом треугольнике должна составлять 180 градусов, а два соответствующих угла уже конгруэнтны, можно сделать объяснение, используя свойство транзитивности или замену, чтобы показать конгруэнтность третьих углов. )
Сколько сторон/углов прямоугольного треугольника нужно знать, чтобы вычислить все остальные стороны/углы? ( Ответ: знание хотя бы одного острого угла и одной стороны позволяет обнаружить все остальные части прямоугольного треугольника .) -Омаха
Запомните три тригонометрических соотношения. (Покажите учащимся рисунок 2 при рассмотрении тригонометрических соотношений, используя стороны a, b и c и острый угол θ для моделирования отношений.)
Синус противоположен гипотенузе в прямоугольном треугольнике. Это означает, что sin(θ) = y/r.
Косинус примыкает к гипотенузе. Это означает, что cos(θ) = x/r.
Касательная противоположна смежной в прямоугольном треугольнике. Это означает, что tan(θ) = y/x.
Почему это работает? Подумайте о подобных треугольниках. Помните, что углы равны, а соответствующие стороны находятся в равных отношениях.
Затем извлеките устройство Android или iOS и запустите приложение клинометра (см. рис. 3).Поэкспериментируйте с приложением, чтобы увидеть, что оно делает. Как можно использовать это приложение для изучения триггерных коэффициентов? (Много возможных ответов, но цель состоит в том, чтобы дать учащимся понять, что они могут измерить угол и стороны прямоугольного треугольника и проверить правильность тригонометрических соотношений). Обратитесь к соответствующему упражнению «Тригонометрия через мобильное устройство», чтобы узнать, как интегрировать мобильные устройства с этим уроком.
Рисунок 3. Скриншот приложения клинометра. Copyright
Copyright © 2014 Скотт Бернс, Колледж информационных наук и технологий, Университет Небраски, Омаха
(Чтобы подвести итог введению и заставить учащихся задуматься о возможных применениях тригонометрии и клинометров и о том, как каждый из них может применяться в инженерии, проведите мозговой штурм, ответив на следующие вопросы всем классом. ) В каких профессиях можно использовать тригонометрию и клинометрию? Где инженеры могут использовать тригонометрию? Для каких типов проектов инженеры могут использовать клинометры?
(После обсуждения попросите пары учащихся воспользоваться Интернетом, чтобы подтвердить свои мысли и/или найти другие возможные ответы. возможные инженерные применения тригонометрии и использование клинометра.)
Предыстория урока и концепции для учителей
Подобные треугольники являются основой тригонометрии прямоугольного треугольника. Поскольку прямые углы конгруэнтны, любые прямоугольные треугольники, у которых есть еще один конгруэнтный соответствующий угол, будут подобны в соответствии с геометрическим постулатом сходства углов. Если треугольники подобны, отношения соответствующих сторон будут равны. Тригонометрия использует это свойство подобных треугольников, вычисляя отношения двух сторон в треугольнике.Например, синус – это отношение катета, противолежащего углу, к гипотенузе в прямоугольном треугольнике. Это означает, что любой прямоугольный треугольник с острым углом 30° будет иметь отношение противоположной стороны к гипотенузе 1:2.
Клинометр — это устройство, которое можно использовать для измерения углов. Приложение на мобильном устройстве позволяет использовать мобильное устройство для измерения углов. Используя приложение в виде простого кода с 0° в верхней части клинометра (как показано на рисунке 3), вы можете использовать верхнюю или нижнюю часть мобильного устройства для измерения угла.Поместив устройство на наклонную поверхность и используя приложение клинометра, можно определить угол наклонной поверхности.
Клинометры
можно использовать для измерения углов между объектами или наклона неподвижного объекта, что позволяет косвенно измерять расстояние с помощью тригонометрии. Устройство Android или iOS должно быть почти вертикально, чтобы использовать функцию измерения угла клинометра, когда оно находится в режиме, соответствующем рисунку 3. Когда приложение клинометра соответствует рисунку 3, с 0° в верхней части клинометра, поверните поворачивайте устройство Android или iOS влево или вправо, пока верхняя или нижняя часть устройства не совпадет с наклонной стороной угла. Другая сторона угла должна быть выровнена по горизонтали. Затем градусную меру угла можно считать с клинометра. На рис. 4 показано расположение клинометра при измерении угла. Рис. 4. Измерение угла с помощью клинометра. Самсон, программа ITL, Инженерный колледж Университета Колорадо в Боулдере
Инженерам-строителям часто приходится измерять очень большие объекты, такие как небоскребы и мосты.Нецелесообразно, а часто и невозможно измерять эти объекты рулеткой. Когда прямые измерения невозможны, вместо них используются технологии и математика. Тригонометрия прямоугольного треугольника использует одну известную сторону треугольника в сочетании с известным углом для вычисления других сторон треугольника (которые могут быть, например, высотой или длиной здания). Инженеры используют такие устройства, как клинометры, для измерения угла, необходимого для выполнения тригонометрических вычислений.
Различные определения основных тригонометрических функций
Распознаваемые термины:
Триггерные функции — это отношения катетов и гипотенузы прямоугольных треугольников, используемые в теореме Пифагора. Основные триггерные функции связаны с опорным углом (заданным углом или его эквивалентом).
Концептуально:
Если мы посмотрим на прямоугольную систему координат и поместим угол (θ) так, чтобы его вершина находилась в начале координат, а смежный катет угла лежал на оси абсцисс, основные тригонометрические функции этого угла определяются как :
Синус – отношение длины катета, противолежащего исходному углу, к длине гипотенузы.
Косинус – отношение длины катета, примыкающего к опорному углу, к длине гипотенузы.
Тангенс – отношение длины стороны, противоположной опорному углу, к длине стороны, примыкающей к опорному углу.
В математических терминах:
Основные триггерные функции для угла θ, расположенного, как указано выше, определены следующим образом:
sin θ = г/г
потому что θ = x/r
тангенс θ = у/х
(Помните из теоремы Пифагора, что x ² + y ² = r ² ).
Рисунок 5. Прямоугольный треугольник в окружности на координатной плоскости. Авторские права
Copyright © 2014 Карли Самсон, программа ITL, Инженерный колледж Университета Колорадо в Боулдере
В процессе работы:
На рис. 5 показан прямоугольный треугольник, расположенный на координатной плоскости, одна из вершин которого находится в начале координат на плоскости и в центре окружности. Одна сторона треугольника находится в направлении х, начинается в начале координат и имеет длину х.Другая сторона треугольника находится в направлении y и простирается от точки (x, 0) до (x, y). Гипотенуза имеет длину r и простирается от (0,0) до (x,y). Поскольку тригональные функции угла определяются как соотношения, указанные выше, и эти отношения не меняются в зависимости от положения точки (x, y) на гипотенузе, синус, косинус и тангенс связаны с углом θ и а не точка (x, y), выбранная для расчета отношений.
Связанные виды деятельности
Тригонометрия с помощью мобильного устройства. Учащиеся исследуют отношения между углами и длинами сторон в прямоугольных треугольниках с помощью материалов, найденных в классе, и электронного устройства.Используя всю или часть измерительной линейки или дюбеля и учебники или другие материалы, учащиеся строят прямоугольные треугольники и измеряют углы с помощью приложения клинометра на устройстве Android (телефон или планшет) или iOS (iPhone® или iPad®). Затем им предлагается составить треугольник с заданной длиной стороны и одним углом. Электронное устройство используется для измерения точности их построения.
Словарь/Определения
клинометр: прибор для измерения углов наклона, возвышения или депрессии объекта по отношению к силе тяжести.
косинус: отношение длины катета, примыкающего к опорному углу, к длине гипотенузы.
синус: Отношение длины катета, противоположного опорному углу, к длине гипотенузы.
Тангенс : Отношение длины стороны, противоположной опорному углу, к длине стороны, прилегающей к опорному углу.
тригонометрия: изучение отношений между углами и сторонами прямоугольных треугольников.
Оценка
Оценка перед уроком
Обсуждение в классе: Задайте классу следующие вопросы, чтобы проверить их знания тригонометрии:
Что вы знаете о тригонометрии? ( Пример ответа: Это предмет изучения математики, в котором содержится информация об отношениях сторон прямоугольных треугольников. )
Какие инструменты доступны для измерения угла наклонной поверхности? ( Возможные ответы: Транспортир, уровень, транзит, клинометр .)
Как можно измерить высоту дерева или флагштока? ( Пример ответа: Измерьте тень очень высокого объекта и измерьте угол от кончика тени до вершины объекта. Затем используйте тангенс триггерной функции, чтобы найти противоположную сторону треугольника [высота объекта ].)
Оценка после внедрения
Наблюдения : Во время урока учащиеся бродят по комнате, задавая вопросы и/или наблюдая за работой учащихся; задайте себе следующие (или похожие) вопросы:
Могут ли учащиеся объяснить, что такое коэффициенты триггера?
Могут ли учащиеся продемонстрировать, что они знают, как подобные треугольники связаны с тригонометрией?
Понимают ли учащиеся, как можно использовать клинометр для решения задач по тригонометрии?
Итоги урока Оценка
Тест: Проведите тест после урока, чтобы оценить понимание учащимися тригонометрии, клинометров и того, как инженеры используют тригонометрию и клинометры в реальных проектах.
авторское право
© 2014 Регенты Университета Колорадо; оригинал © 2013 Университет Небраски
Авторы
Скотт Бернс
Программа поддержки
Программа IMPART RET, Колледж информационных наук и технологий, Университет Небраски, Омаха
Благодарности
Содержание этой учебной программы цифровой библиотеки было разработано в рамках сайта RET в области инженерии и компьютерных наук по внедрению прикладных исследований мобильной платформы в программу обучения (IMPART) Университета Небраски в Омахе в рамках гранта Национального научного фонда RET номер CNS 1201136 .Однако это содержание не обязательно отражает политику NSF, и вы не должны предполагать, что оно одобрено федеральным правительством.
Последнее изменение: 15 января 2022 г.
Исторические размышления о преподавании тригонометрии
За прошедшие годы в журналах Национального совета учителей математики (NCTM) было опубликовано множество статей по истории математики и ее использованию в обучении. Эти журналы включают «Обучение детей математике», «Преподавание математики в средней школе», и «Учитель математики». Соредактор-основатель Convergence Фрэнк Свец договорился с NCTM о переиздании в Convergence (в формате pdf) избранных статей из Mathematics Teacher, , начиная с 2015 года. Одним из вариантов, выбранных редактором в этом году, является статья Дэвида Брессуда. о происхождении тригонометрии и о том, как история предмета предлагает новый подход к тригонометрии в наших современных школах:
Дэвид М.Брессоуд, «Исторические размышления о преподавании тригонометрии», Учитель математики, Том. 104, № 2 (сентябрь 2010 г.), стр. 106–112, плюс три дополнительных раздела: «Гиппарх», «Евклид» и «Птолемей». Перепечатано с разрешения Учитель математики, © 2010 Национальный совет учителей математики. Все права защищены.
Недавно Брессо вспомнил, как он пришел к написанию этой статьи:
«Исторические размышления о преподавании тригонометрии» был основан на докладе, который я сделал на ежегодном собрании NCTM 2009 года «Уроки истории математики». «Заголовок был заполнителем, когда я решил, о чем я хочу поговорить. Два обстоятельства убедили меня в том, что я должен говорить о тригонометрии. Одним из них был визит Мэрилин Карлсон и Пэт Томпсон в Университет штата Аризона, где я узнал об их работе и работе Кевина Мура, в то время аспиранта, о трудностях студентов при переходе от тригонометрических функций как отношений сторон прямоугольных треугольников к функциональному пониманию тригонометрических функций.В то же время я только что прочитал Глена Вана Замечательная книга Брюммлена, Математика неба и земли: ранняя история тригонометрии , которая показала, что функциональный подход, синус и косинус как функции длины дуги, является историческим подходом.Эл Гетц, в то время редактор журнала «Учитель математики , », присутствовал на моем выступлении и убедил меня написать его для журнала. Моя первоначальная заявка включала материал из трех дополнений к статье. Я не удивился, когда Ал сказал, что это слишком долго, поэтому я вырезал их как онлайн-приложения.
В статье «Исторические размышления о преподавании тригонометрии» (скачать ее здесь) сначала рассматривается изобретение «круговой тригонометрии» греческими астрономами II века до н. э., которые, зная длину дуги, соединяющей две точки на окружности, искали длину хорды, соединяющей две точки.К концу V века н.э. индийские астрономы вместо этого сосредоточились на полухорде, или синусе , , и это соглашение было принято более поздними арабскими и европейскими астрономами. Именно Эйлер окончательно установил радиус определяющего круга равным 1. Брессо признает, что «тригонометрия треугольника», имеющая древние корни в измерении теней, также важна. Однако он утверждает, что для того, чтобы лучше всего помочь учащимся понять тригонометрические функции , учителя должны сначала сосредоточиться на исходных функциональных отношениях круговой тригонометрии; а именно, длина хорды как функция длины дуги.
Об авторе
Дэвид М. Брессоуд — профессор математики им. ДеВитта Уоллеса в колледже Макалестер в Сент-Поле, штат Миннесота. Он много публиковался по истории математики и ее использованию в обучении, в том числе книги MAA «Радикальный подход к реальному анализу», «Радикальный подход к теории интеграции Лебега», и «Доказательства и подтверждения: история переменного знака». Матричная гипотеза . Он был президентом MAA в 2009 и 2010 годах, а в настоящее время является директором Совета по математическим наукам (CBMS).
О NCTM
Национальный совет учителей математики (NCTM) является общественным голосом в области математического образования, поддерживая учителей в обеспечении справедливого обучения математике самого высокого качества для всех учащихся посредством дальновидности, лидерства, профессионального развития и исследований. Он издает пять журналов, по одному для каждого класса, а также один по последним исследованиям и еще один для педагогов-педагогов. NCTM, насчитывающая 80 000 членов и более 200 филиалов, является крупнейшей в мире организацией, занимающейся улучшением математического образования в дошкольных учреждениях до 12 класса. Для получения дополнительной информации о членстве в NCTM посетите сайт http://www.nctm.org/membership.
Другое
Учитель математики Статьи в Конвергенция
Патриция Р. Аллер и Роберт Э. Брэдли, «Геометрические подходы к квадратичным уравнениям из других времен и мест», Учитель математики, Vol. 94, № 4 (апрель 2001 г.), стр. 308–313, 319.
Ричард М. Дэвитт, «Эволюционный характер математики», Учитель математики , Vol.93, № 8 (ноябрь 2000 г.), стр. 692–694.
Кейт Девлин, «Соответствие Паскаля-Ферма: как на самом деле делается математика», Учитель математики, Vol. 103, № 8 (апрель 2010 г.), стр. 578–582.
Дженнифер Хорн, Эми Замеровски и Рита Баргер, «Переписка математиков», Учитель математики , том 93, № 8 (ноябрь 2000 г.), стр. 688–691.
Шон П. Мэдден, Джоселин М. Комсток и Джеймс П. Даунинг, «Столбы, парковки и гора Питон: занятия в классе, сочетающие астрономию, историю и математику», Учитель математики , Vol. 100, № 2 (сентябрь 2006 г.), стр. 94–99.
Питер Н. Оливер, «Пьер Вариньон и теорема о параллелограмме», Учитель математики, Том. 94, № 4 (апрель 2001 г.), стр. 316–319.
Питер Н. Оливер, «Последствия теоремы о параллелограмме Вариньона», Учитель математики, Том. 94, № 5 (май 2001 г.), стр. 406–408.
Рета Н. Рубенштейн и Рэнди К. Шварц, «История слов: объединение математики и значений», Учитель математики , Vol.93, № 8 (ноябрь 2000 г.), стр. 664–669.
Шай Симонсон, «Математика Леви бен Гершона», Учитель математики, Том. 93, № 8 (ноябрь 2000 г.), стр. 659–663.
Фрэнк Шветц, «Нагромождение квадратов в Древнем Китае», Учитель математики , Vol. 73, № 1 (январь 1977 г.), стр. 72–79.
Разгадана математическая тайна древней глиняной таблички
Ученые из Университета Нового Южного Уэльса, Сидней, выяснили назначение знаменитой вавилонской глиняной таблички возрастом 3700 лет, и выяснилось, что это самая старая и самая точная тригонометрическая таблица в мире, которая, возможно, использовалась древними математическими писцами для расчета способов строительства дворцов и храмов и строительства каналов.
Новое исследование показывает, что вавилоняне, а не греки, были первыми, кто начал изучать тригонометрию — науку о треугольниках — и раскрывает древнюю математическую изощренность, которая была скрыта до сих пор.
Небольшая табличка, известная как Плимптон 322, была обнаружена в начале 1900-х годов на территории нынешнего южного Ирака археологом, академиком, дипломатом и торговцем древностями Эдгаром Бэнксом, человеком, с которого был основан вымышленный персонаж Индиана Джонс.
Он состоит из четырех столбцов и 15 рядов чисел, написанных на нем клинописью того времени с использованием шестидесятеричной системы счисления.
«Плимптон 322 озадачивает математиков уже более 70 лет, так как выяснилось, что он содержит особый набор чисел, называемый пифагорейскими тройками», — говорит доктор Дэниел Мэнсфилд из Школы математики и статистики факультета естественных наук Университета Нового Южного Уэльса.
«Огромной загадкой до сих пор было его предназначение — почему древние писцы выполняли сложную задачу по генерации и сортировке чисел на табличке.
«Наше исследование показывает, что Plimpton 322 описывает формы прямоугольных треугольников, используя новый тип тригонометрии, основанный на соотношениях, а не на углах и окружностях.Это увлекательная математическая работа, демонстрирующая несомненную гениальность.
«Таблица содержит не только старейшую в мире тригонометрическую таблицу; это также единственная полностью точная тригонометрическая таблица из-за совершенно другого вавилонского подхода к арифметике и геометрии».
Plimpton 322, вавилонская табличка возрастом 3700 лет, хранящаяся в Библиотеке редких книг и рукописей Колумбийского университета в Нью-Йорке.
Новое исследование доктора Мэнсфилда и доцента UNSW Нормана Вильдбергера опубликовано в Historia Mathematica , официальном журнале Международной комиссии по истории математики.
Тригонометрическая таблица позволяет использовать одно известное отношение сторон прямоугольного треугольника для определения двух других неизвестных отношений.
Греческий астроном Гиппарх, живший около 120 лет до нашей эры, долгое время считался отцом тригонометрии, а его «таблица аккордов» на окружности считалась древнейшей тригонометрической таблицей.
«Плимптон 322 старше Гиппарха более чем на 1000 лет, — говорит доктор Вильдбергер. «Это открывает новые возможности не только для современных математических исследований, но и для математического образования.С Plimpton 322 мы видим более простую и точную тригонометрию, которая имеет явные преимущества перед нашей собственной.
«Существует кладезь вавилонских табличек, но пока изучена лишь часть из них. Математический мир только начинает осознавать тот факт, что эта древняя, но очень сложная математическая культура может многому нас научить».
Доктор Мэнсфилд случайно прочитал о Плимптоне 322, когда готовил материалы для студентов-первокурсников-математиков Университета Нового Южного Уэльса. Он и доктор Вильдбергер решили изучить вавилонскую математику и изучить различные исторические интерпретации значения таблички после того, как поняли, что она имеет параллели с рациональной тригонометрией из книги доктора Вильдбергера «Божественные пропорции: рациональная тригонометрия к универсальной геометрии ».
15 рядов на табличке описывают последовательность из 15 прямоугольных треугольников, наклон которых постоянно уменьшается.

Исследователи UNSW обнаружили, что Плимптон 322, вавилонская табличка возрастом 3700 лет, старше Пифагора на 1000 лет.
Левый край таблички сломан, и исследователи UNSW опираются на предыдущие исследования, чтобы представить новые математические доказательства того, что изначально было шесть столбцов и что табличка должна была быть заполнена 38 строками.
Они также демонстрируют, как древние писцы, которые использовали числовую арифметику с основанием 60, аналогичную нашим часам, а не систему счисления с основанием 10, которую мы используем, могли генерировать числа на табличках, используя свои математические методы.
Исследование UNSW Science представляет собой альтернативу широко распространенному мнению о том, что планшет был помощником учителя для проверки решения учащихся квадратичных задач.
«Plimpton 322 был мощным инструментом, который можно было использовать для съемки полей или выполнения архитектурных расчетов при строительстве дворцов, храмов или ступенчатых пирамид», — говорит доктор Мэнсфилд.
Табличка, которая, как считается, была найдена в древнем шумерском городе Ларса и датируется периодом между 1822 и 1762 годами до нашей эры. Сейчас он находится в Библиотеке редких книг и рукописей Колумбийского университета в Нью-Йорке.
Пифагорова тройка состоит из трех положительных целых чисел a, b и c, таких что a ² + b ² = c ² . Целые числа 3, 4 и 5 являются хорошо известным примером пифагорейской тройки, но значения на Плимптоне 322 часто значительно больше, например, первая строка ссылается на тройку 119, 120 и 169.
Название происходит от теоремы Пифагора о прямоугольных треугольниках, которая гласит, что квадрат гипотенузы (диагональная сторона, противоположная прямому углу) равен сумме квадратов двух других сторон.
Ссылки для новостных СМИ:
Исследовательская работа в Historia Mathematica
изображения доктора Мэнсфилда и Плимптона 322 в Библиотеке редких книг и рукописей Колумбийского университета в Нью-Йорке. Предоставлено: UNSW/Эндрю Келли.
Справочная информация о Плимптоне 322 и тригонометрии.
Статья о находке в Разговор доктора Мэнсфилда и доцента Вильдбергера

Heavenly Mathematics: The Forgotten Art of Spherical Trigonometry: 9780691175997: Van Brummelen, Glen: Books
«Одно из лучших научных званий 2013 г.»
«Сферическая тригонометрия, когда-то составлявшая основу математики, больше не фигурирует в школьных программах.Здесь Глен Ван Браммелен подтверждает важность этой области, подробно рассказывая о том, как она фигурирует в астрономии, картографии и нашем понимании вращения Земли». ; это оставляет ясное впечатление, что автор намеревался полюбить — не просто представить и научить — сферическую тригонометрию читателю. Хотя это и не книга по истории, в ней есть отдельные главы, проливающие свет на подходы к этому предмету в древности, средневековье и современности.Есть также главы по сферической геометрии, многогранникам, стереографической проекции и искусству навигации. Книга хорошо иллюстрирована и читается с удовольствием. Главы заканчиваются упражнениями; приложения содержат длинный список доступных и не очень доступных учебников и рекомендации для дальнейшего чтения, организованные по отдельным главам. Книга стала ценным дополнением к моей библиотеке. Я смело рекомендую ее учителям математики и любознательным старшеклассникам.» —Александр Богомольный, CTK Insights
«Серьезное введение в сферическую тригонометрию.― Book News, Inc.
«Прекрасная популярная книга». ― ThatsMaths.com
«Эта книга, наполненная академическим, учебным содержанием, доставляет удовольствие студентам, изучающим математику. Так что, если вы хотите совершить путешествие в мир сферической тригонометрии, возьмите эту книгу. Ван Браммелен дает упражнения в конце глав, которые могут быть забавными.» — Р. Балашанкар, Организатор
» Небесная математика — действительно приятное описание несколько забытой науки сферической тригонометрии.. . . Когда читатели откроют для себя эту дисциплину, они также оценят красоту, присущую этой теме.» ― Choice
» Небесная математика доказывает ценность того, что увлекательный фрагмент математической истории доступен широкому читателю.» — Флорин Диаку, Литературное обозрение Канады
«Ван Браммелен написал замечательное предисловие. . . это опирается на историю [сферической тригонометрии], чтобы осветить саму математику и в то же время дает читателям реальное представление о том, что такое исследования в истории ранней математики.» ― Metascience
«[ Heavenly Mathematics ] — отличный обзор сферической тригонометрии. . . . Просто оценка прекрасного утраченного предмета с историческим подтекстом. . . . [D]отличается привлекательным свежим стилем». ― Mathematical Reviews
«[ Heavenly Mathematics ] — прекрасная книга для чтения. . . . [A] прекрасное введение для всех, кто хочет узнать больше об этом предмете. . . . Я полностью согласен с автором в том, что сферическую тригонометрию следует донести до более широкой аудитории, и я считаю, что эта книга как раз для этого.» ― Mathematics Today
«Увлекательно, понятно и не слишком технично; Вы можете смело одолжить эту книгу своим друзьям на историческом факультете. . . . [ Heavenly Mathematics ] превосходно.» ― Zentralblatt MATH
» Heavenly Mathematics будет представлять интерес для математически склонных историков науки, а также для студентов, изучающих математику и инженерию. Поскольку сферическая тригонометрия актуальна для приложений современной науки, эта элегантная книга может даже способствовать возрождению предмета.» — Ян П. Хогендейк, Исида
«Эта книга может служить отличным учебником для любого класса средней школы по математике на уровне или выше геометрии и, конечно же, тригонометрии; как основа для отличников средней школы; или в качестве темы учебника и семинара для студентов колледжей». — Тереза Флойд, Учитель математики
«Любой читатель этой книги (а таких должно быть много) увидит, как современная математика может рассматриваться через калейдоскоп своего исторического происхождения.. . . Глен Ван Браммелен написал прекрасно оформленную книгу, включающую увлекательные биографические подробности на каждом этапе своего повествования. учителя тригонометрии и все, кто интересуется историей математики». — Элизабет Хэмм, Aestimatio Critical Reviews in the History of Science
Живопись кубизма, геометрия треугольника, тригонометрия, веселье Красочный геометрический треугольник, ромб, фон PNG
Живопись кубизма, геометрия треугольника, тригонометрия, веселье, красочный геометрический треугольник, ромб, фон PNG | HiClipart живопись кубизма, геометрия треугольника, тригонометрия, веселье, красочный геометрический треугольник, ромб, фон PNG
Ключевые слова
PNG Информация о клипарте
Размеры PNG 625x625px
PNG Размер файла 129. 64 КБ
MIME-тип Изображение/png
Доминирующий цвет PNG серый
Лицензия
HiClipart — это открытое сообщество, где пользователи могут обмениваться изображениями в формате PNG. Все PNG-клипарты в HiClipart предназначены для некоммерческого использования, указание авторства не требуется. Если вы являетесь автором и обнаружите, что этот PNG распространяется без вашего разрешения, сообщите о нарушении DMCA, свяжитесь с нами.
Геометрия треугольника, красочный алмазный фон, серый и синий 3D PNG 2078x2315px Размер файла: 974.48 КБ
синий и зеленый, треугольник геометрической формы узор, красочный геометрический PNG 1000x768px 1000x768px Размер файла: 379.18 КБ
org/ImageObject»> Евклидова геометрия, красочная абстрактная геометрическая радиальная перспектива, иллюстрация зеленого, синего и желтого цветов PNG 568x569px 568x569px Размер файла: 36,3 КБ
иллюстрация рисунка зеленой иллюзии, полигон геометрии, неправильный геометрический фон PNG 1300x1300px Размер: 1.77 МБ
Геометрия Евклидова икона, Неправильный геометрический фон, разноцветные геометрические изображения PNG 2800x3664px Размер файла: 781.45KB
ледяной коллаж, геометрия многоугольника евклидова, красочный фон многоугольной геометрии PNG 2488x3358px 2488x3358px Размер файла: 1,45 МБ
Геометрия Абстрактное искусство Иллюстрация, Красочные абстрактные геометрические квадраты, разноцветные графические изображения PNG 1171x1122px 1171x1122px Размер файла: 346. 58 КБ
Геометрическая текстура модного справочного материала, красный и серый логотип PNG 896x896px Размер файла: 140,56 КБ
Угол геометрии, треугольный космический фон, серые и бежевые точки с линейной иллюстрацией PNG 743x862px 743x862px Размер файла: 127,89 КБ
Простые абстрактные линии фоновые линии, черная, зеленая и синяя абстрактная живопись PNG 1024x969px 1024x969px Размер файла: 1,37 МБ
Абстрактная дифференциальная геометрия, евклидова, геометрическая текстура, модный справочный материал, синие и красные волнистые PNG 945x945px 945x945px Размер файла: 228.78 КБ
org/ImageObject»> синий геометрический фон, синий и белый PNG 2579x2456px Размер файла: 1,12 МБ
Низкополигональная полигональная текстура, блюз абстрактный фон большой лингге, сине-белое абстрактное искусство PNG 3000x2000px 3000x2000px Размер файла: 3,22 МБ
серые линии, белая симметричная структура, дневное освещение, технологический смысл геометрических линий PNG 650x487px Размер файла: 796.08 КБ
фиолетовая и красная абстрактная иллюстрация, цвет геометрии, красочный технологический фон PNG 1300x1539px Размер файла: 1,2 МБ
бирюзово-оранжевая абстрактная живопись, полигональная геометрия, весело красочный геометрический треугольник ромбовидный фон PNG 625x625px 625x625px Размер файла: 165. 28 КБ
Геометрия Геометрическая абстракция Евклидова, Абстрактная геометрия, три розовые, желтые и зеленые абстрактные картины PNG 1240x1058px 1240x1058px Размер файла: 178.1 КБ
разноцветная абстрактная иллюстрация, цвет полигональной геометрии, цветная абстрактная графика PNG 6070x2879px 6070x2879px Размер файла: 1,7 МБ
Затенение фона треугольной формы, черно-белый абстрактный PNG 2480x3508px Размер файла: 524.6KB
Geometry Curve Icon, геометрическая текстура, модный справочный материал, серый и синий PNG 792x1000px 792x1000px Размер файла: 133.38 КБ
org/ImageObject»> черно-бело-красная иллюстрация, полигональная геометрия, 3D геометрические узоры PNG 1000x1000px 1000x1000px Размер файла: 464.39 КБ
разные цвета, геометрический узор, красочная заливка PNG 1150x1686px 1150x1686px Размер файла: 311.97 КБ
Цветные линии геометрические узоры PNG 2529x2497px Размер файла: 174.04 КБ
абстрактная черная точка, черно-белый узор, алмазная геометрическая градиентная заливка PNG 1920x815px 1920x815px Размер файла: 771.79 КБ
синие и розовые шестиугольники, шестиугольник, евклидов градиент, синий цвет, наука и техника PNG 1000x749px 1000x749px Размер файла: 1001.05 КБ
org/ImageObject»> Шаблон красочных квадратов, креативные красочные квадраты, розовое, зеленое и синее цифровое искусство PNG 799x1660px 799x1660px Размер файла: 520.61 КБ
синяя трапециевидная форма, ковровая плитка для ванной комнаты, синий геометрический узор затенения PNG 1420x2270px Размер файла: 12,3 МБ
красный, геометрическая текстура мода справочный материал PNG 1229x854px Размер файла: 112,3 КБ
Brand Angle, геометрическая текстура, модный справочный материал, черно-белая лестница PNG 979x583px Размер файла: 99.28 КБ
Кривая геометрии Геометрическая форма, геометрическая текстура, модный справочный материал, красная и серая цифровая иллюстрация PNG 979x979px 979x979px Размер файла: 174. 02 КБ
Геометрия Многоугольник Треугольник, Красочный фон многоугольной геометрии PNG 4252x4598px 4252x4598px Размер файла: 1,5 МБ
Геометрическая текстура моды справочный материал, абстрактная иллюстрация PNG 1260x945px 1260x945px Размер файла: 158.08 КБ
Геометрический номер, четырехслойная диаграмма параметров PNG 1084x620px Размер файла: 144.13 КБ
Графический дизайн Shape Square, Красочный бриллиантовый декор PNG 958x1091px 958x1091px Размер файла: 367,96 КБ
разноцветные треугольники, треугольник, элемент треугольника тренда PNG 554x664px 554x664px Размер файла: 132,9 КБ
org/ImageObject»> коричнево-черные абстрактные произведения искусства, евклидова геометрия, темные красочные геометрические PNG 500x592px Размер файла: 294.32 КБ
Черно-белая геометрия Геометрическая абстракция Pattern, Technology Triangle Cover, черно-серый шестиугольный скриншот PNG 2430x2447px Размер файла: 258.18 КБ
Цвет, цветной всплеск порохового дыма, крупный план взрыва фиолетового пороха PNG 600x623px Размер файла: 460.84KB
иллюстрация синего треугольника, геометрия треугольника, евклидова тригонометрия, геометрический треугольник PNG 2362x2541px Размер файла: 832.4 КБ
фиолетово-белая абстрактная живопись, евклидова геометрия, весело красочный геометрический треугольник ромбовидный фон PNG 503x529px 503x529px Размер файла: 354. 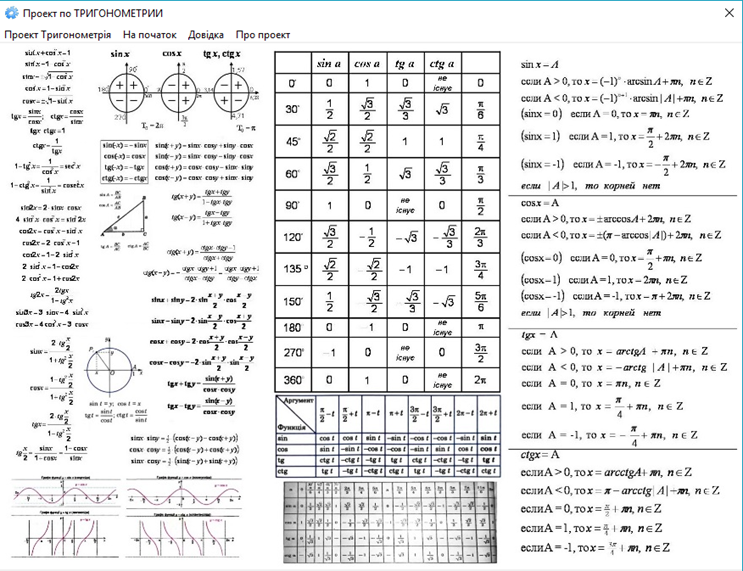79 КБ
Квадрат, синий квадрат абстрактный справочный материал, синяя рамка PNG 1024x1024px 1024x1024px Размер файла: 885.52 КБ
Blue Polygon Abstraction, небесно-голубые многоугольники абстрактный фон, чирок и синяя рамка иллюстрации PNG 800x800px Размер файла: 226.02 КБ
абстрактная живопись, программное обеспечение для абстракции геометрии, красочные квадраты PNG 2244x3390px Размер файла: 49.06 КБ
разноцветная абстракция, геометрия светлый квадрат геометрическая форма, красочный куб PNG 1200x1289px 1200x1289px Размер файла: 955.89KB
Угловой узор, треугольник фон PNG 1100x574px Размер файла: 135. 18 КБ
разноцветная плитка, цветной узор мозаики, красочная геометрическая абстракция PNG 800x394px Размер: 51.36 КБ
Цвет синий, красочный справочный материал, иллюстрация карты PNG 456x720px Размер файла: 1,25 МБ
Геометрия Треугольник Геометрическая форма, геометрический фон розового треугольника, красная и разноцветная абстрактная живопись PNG 1180x990px 1180x990px Размер файла: 290.14 КБ
разноцветная абстрактная иллюстрация], абстрактное искусство, кривая красочных абстрактных геометрических квадратов PNG 672x571px Размер файла: 278.65 КБ
org/ImageObject»> Синий, Синий абстрактная графика, синий фон PNG 3553x5075px 3553x5075px Размер файла: 726.6KB
Белый узор симметрии, абстрактный геометрический градиентный блок затенения PNG 650x650px Размер файла: 394.14 КБ
абстрактная графика, шаблон Adobe Illustrator, красочный геометрический модный справочный материал PNG 1693x1763px Размер файла: 201.47 КБ
разноцветный, круг, красочный геометрический PNG 1042x1042px Размер файла: 394.13 КБ
желто-синяя коробка, блок орнамента геометрии, абстрактные геометрические блоки трехмерных фигур PNG 937x1184px 937x1184px Размер файла: 355.32 КБ
org/ImageObject»> треугольник ассорти, геометрия треугольник абстракция евклидова, красочный абстрактный геометрический треугольник PNG 814x966px 814x966px Размер файла: 80 КБ
Акварельная живопись, красочные чернила, красная, синяя, фиолетовая и желтая абстрактная живопись PNG 1000x771px 1000x771px Размер: 1.73 МБ
Геометрический круг Евклидова иллюстрация, Красочный абстрактный геометрический точечный круг, иллюстрация кругов разных цветов PNG 702x1076px 702x1076px Размер файла: 134.43 КБ
красная этикетка, Line Geometry Free Компьютерный файл, Геометрические линии PNG 1675x962px Размер файла: 51,94 КБ
Квадрат, Мода Квадрат фон симметрия PNG 650x607px Размер файла: 304. 32 КБ
Геометрия, Геометрический фон, разноцветное искусство PNG 3543x5315px Размер: 4.92 МБ
Геометрическая форма Абстрактное искусство, абстрактные формы, разноцветные PNG 2480x2480px Размер файла: 96,51 КБ
оранжево-синяя спираль, геометрия, цветной геометрический абстрактный фон PNG 801x1055px Размер файла: 84,88 КБ
Color Shape Графический дизайн, красочный технологический фон, оранжевый, зеленый, синий, розовый и красный абстрактный декор PNG 1024x1024px 1024x1024px Размер файла: 369.39 КБ
квадратная иллюстрация разных цветов, геометрический узор, трехмерные абстрактные геометрические квадраты PNG 650x435px Размер файла: 44. 16 КБ
Цветной дым, красный дым PNG 4206x2722px Размер файла: 14,77 МБ
Многоугольник Геометрия Треугольник Евклидов, Многоугольник PNG 500x500px Размер файла: 61,81 КБ
Абстрактное искусство Blue Geometry illustration, Фон дизайна элементов научной фантастики, пиксельный PNG 800x797px Размер файла: 712.46 КБ
зеленый, серый и бежевый, геометрия ромба, абстрактный материал в форме ромба PNG 1024x1024px Размер файла: 100,76 КБ
квадратная черная рамка, геометрическая форма, ромб, квадрат, треугольник, ромбовидная форма PNG 2208x2229px Размер файла: 133. 33 КБ
красная и фиолетовая абстрактная живопись, джазовый плакат саксофон, красочный фон плаката PNG 2053x3582px 2053x3582px Размер: 2.17 МБ
разноцветные цветочные, симфония, красочная абстрактная геометрическая тема PNG 1564x1654px Размер файла: 846.84KB
цветные брызги, светлая растровая графика, абстракция, цветные линии PNG 800x800px Размер файла: 1,5 МБ
Абстракция Евклидова, Концепция абстрактного фона, Логотип заголовка PNG 800x800px Размер файла: 17,56 КБ
иллюстрация желтой, красной, черной, оранжевой и синей волны, линия, абстрактная цветная линия PNG 2083x1771px 2083x1771px Размер: 1. 41 МБ
Линия Абстрактное искусство Евклидово, геометрические многоугольники и круги, разноцветные PNG 1501x1558px Размер файла: 102 КБ
Загрузить больше PNG-клипартов
Мы используем файлы cookie для анализа нашего трафика и улучшения предоставляемых нами услуг. Продолжая использовать этот веб-сайт, вы соглашаетесь на использование нами файлов cookie, как это определено в нашей политике конфиденциальности. принимать
Новый угол древней тригонометрии
Эта статья впервые появилась в Cosmos Weekly 6 августа 2021 года.Чтобы узнать больше подобных историй, подпишитесь на Cosmos Weekly.
У некоторых людей слово «тригонометрия» вызывает в воображении образы прямоугольных треугольников или, может быть, даже наших старых знакомых синус , косинус и тангенс . И это может означать кровавые слезы, поскольку «тригонометрия» для многих является триггером со школьных времен.
Но без «триггера» архитекторы испортили бы вашу новую пристройку, GPS не существовало бы, и мне бы очень не хотелось видеть, что с вами сделает компьютерная томография, если бы мы не понимали тригонометрические функции, когда снимали рентгеновские снимки в вашем доме. плоть.
Вы можете вспомнить старого грека Пифагора и некоторые из многих открытий, приписываемых его имени. Наиболее известной, пожалуй, является теорема Пифагора, которая дает нам уравнение Пифагора: a ² + b ² = c ² . Это говорит нам о том, что если у нас есть любой прямоугольный треугольник, сумма квадратов перпендикулярных сторон равна квадрату длины гипотенузы.
Любые три положительных целых числа, удовлетворяющих уравнению Пифагора, известны как «тройки Пифагора».Например, (3,4,5) является пифагоровой тройкой, потому что 3 ² + 4 ² = 5 ² . Менее очевидная пифагорейская тройка — это (140, 171, 221), и мы знаем, что, как это часто бывает в математике, таких элементов бесконечное множество.
Однако более чем за тысячу лет до того, как Пифагор ступил на Землю, вавилоняне не только знали о пифагорейских тройках, но и изощренно использовали их.
Без «триггера» архитекторы испортили бы вашу новую пристройку, GPS не существовало бы — и мне бы очень не хотелось видеть, что с вами сделает компьютерная томография, если бы мы не понимали тригонометрические функции, когда снимали рентгеновские снимки в вашем доме. плоть.
Введите Плимптон 322, вавилонскую глиняную табличку, найденную в древнем шумерском городе Ларса (на территории современного Ирака) и датируемую периодом между 1822 и 1762 годами до нашей эры. Этот частично разрушенный математический документ, которому около 3700 лет, представляет собой просто таблицу чисел (написанную клинописью), состоящую из четырех столбцов и 15 строк. чудесная особенность этой таблички заключается не только в том, что каждая строка содержит два из трех чисел ряда пифагорейских троек, но и в том, что эти числа записаны в шестидесятеричной системе счисления (с основанием 60), что обеспечивает математические преимущества при записи и вычислении. дроби.
Plimpton 322: первая в мире тригонометрическая таблица. Предоставлено: UNSW/Эндрю Келли.
Мы выражаем числа в десятичной системе счисления, или в системе счисления с основанием 10, в которой мы используем 10 уникальных цифр или символов, 0, 1, 2, …, 9. Шестидесятеричная система счисления, используемая вавилонянами, имеет уникальные символы (или уникальные комбинации символов) для представления чисел от 1 до 59.
Причина того, что 60 является выгодным основанием, связана с количеством общих факторов, которые оно имеет. Число 60 — это то, что мы бы назвали «превосходным составным числом», которое, как вы знаете, должно быть хорошим из-за двойной превосходной степени.Его можно разделить точно на 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 и 60, тогда как 10 можно разделить точно только на 1, 2, 5 и 10. И это становится важным. когда мы смотрим на информацию, содержащуюся на планшете.
Для упрощения обсуждения возьмем прямоугольный треугольник с более короткой перпендикулярной стороной s , более длинной перпендикулярной стороной l и диагональю d , так что s ² + l ² = d ² .
Столбцы два и три Plimpton 322 просто содержат значения для s и d соответственно для серий пифагорейских троек. Четвертый столбец — это просто список чисел от 1 до 15, поэтому мы можем запомнить, до какой строки мы дошли. Но в первом столбце представлено отношение d ² / l ² , и поскольку в третьем столбце нам дано значение d , мы можем вычислить l , и voila … полная пифагорейская тройка ( s , l , d ) раскрывается!
Так работает Плимптон 322.Тем не менее, были некоторые споры о назначении этого планшета. Многие историки считали, что это просто учебное пособие. Но в основе этих споров лежит идея о том, что существует точное (и более простое в вычислительном отношении) описание тригонометрии, предшествующее древним грекам, которым обычно приписывают открытие тригонометрии.
Прямоугольные треугольники на планшете Plimpton 322: первая в мире тригонометрическая таблица. Предоставлено: UNSW/Эндрю Келли.
Получайте обновления научных статей прямо на свой почтовый ящик.
В 2017 году два исследователя из Университета Нового Южного Уэльса, доктор Дэниел Мэнсфилд и профессор Норман Вильдбергер, заявили, что числовая сложность Плимптона 322 делает его исторически и математически значимым, поскольку это одновременно первая тригонометрическая таблица и Единственная тригонометрическая таблица, которая является точной.
Однако некоторые историки не были убеждены, что эта табличка была ничем иным, как простым школьным текстом писцов.Этот скептицизм поставил Мэнсфилда перед миссией. «Что делали жители Месопотамии?» он спросил.
Подобно современному Индиане Джонсу, он искал в музеях, частных коллекциях и библиотеках по всему миру подобные типы математических документов того же периода, которые также содержали пифагорейские тройки.
Единственный действительно очевидный ответ, который он мог придумать, был: обследование.
Подобно современному Индиане Джонсу, он искал в музеях, частных коллекциях и библиотеках по всему миру подобные типы математических документов того же периода, которые также содержали пифагорейские тройки.Так получилось, что недостающая часть головоломки пряталась у всех на виду, выставленная в Археологическом музее Стамбула.
Си. 427, линзовидная табличка древневавилонского периода, содержала не менее трех пифагорейских троек — (5, 12, 13) дважды и (8, 15, 17) — и использовалась геодезистами для исключительно точного распределения частных земель. путем построения перпендикулярных границ поля с использованием этих пифагорейских троек.
Раньше геодезические документы представляли собой просто сельскохозяйственные оценки.Но люди начали беспокоиться о точных границах, когда они стали владеть землей в частном порядке.
Это открытие позволило Мэнсфилду прийти к новой гипотезе относительно истинной цели Плимптона 322: теоретическое исследование по поиску прямоугольников с правильными сторонами, возможно, вдохновленное необходимостью таких прямоугольников в геодезии. «Обычный» здесь означает, что длина стороны равна 60.
Plimpton 322 в Библиотеке редких книг и рукописей Колумбийского университета в Нью-Йорке.Предоставлено: UNSW/Эндрю Келли.
«Чтобы использовать пифагорейские тройки для съемки, нужно знать, какие прямоугольники можно использовать», — объясняет Мэнсфилд.
Таким образом, простая пифагорейская тройка, такая как (5, 12, 13), не особенно полезна, потому что 13 не является множителем 60 и, следовательно, не появляется на Плимптоне 322. «Они прошли через все пифагорейские тройки. они могли подумать, а затем посмотрели на них, чтобы сказать, какие стороны являются правильными», — говорит Мэнсфилд.
Это откровение о Плимптоне 322 поддерживает как идею о том, что это могло быть просто теоретическое исследование по поиску прямоугольников с правильными сторонами, так и то, что эта теоретическая работа, возможно, была мотивирована практической потребностью в таких прямоугольниках при съемке.
Чистая математика и прикладная математика объединяются, как настоящие друзья, которыми они должны быть.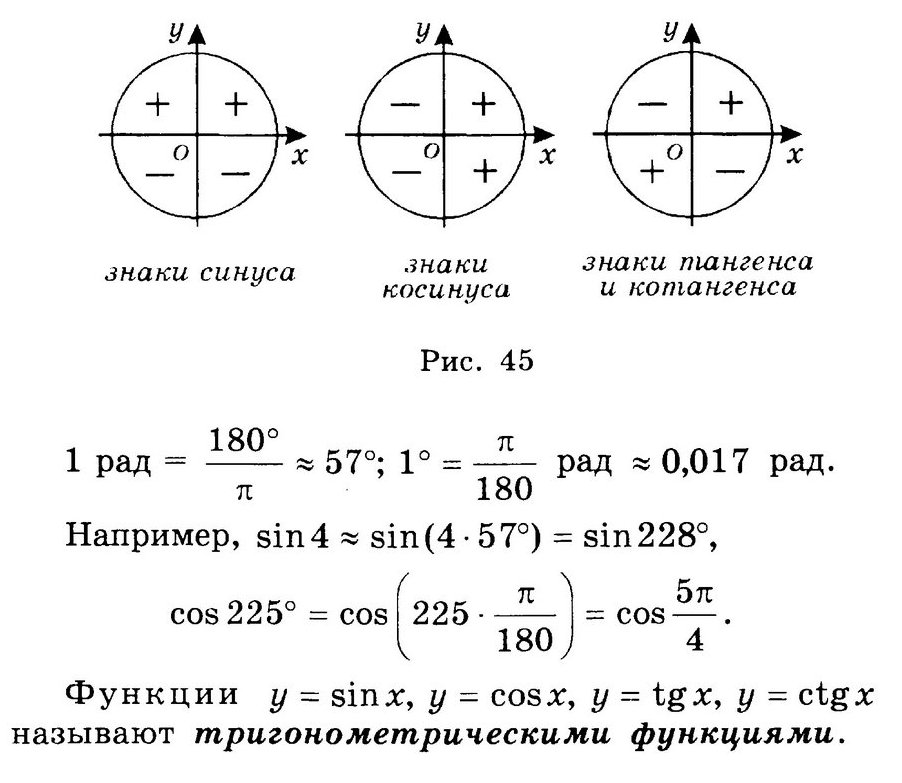
Эта статья впервые появилась в Cosmos Weekly 6 августа 2021 года. Чтобы увидеть больше подобных подробных историй, подпишитесь сегодня и получите доступ к нашей еженедельной электронной публикации, а также доступ ко всем предыдущим выпускам Cosmos Weekly .
Как сдать тригонометрию | Study.com
Повторите, что вы узнали на предыдущих занятиях
Прежде чем приступить к занятиям по тригонометрии, убедитесь, что вы твердо стоите на ногах.Курсы математики, как правило, опираются друг на друга, и тригонометрия ничем не отличается; предполагается, что у вас есть хорошие знания в области алгебры и геометрии. Возможно, вы уже вкратце коснулись тригонометра в конце курса алгебры (или предварительного исчисления), но прежде чем начать курс тригонометра, было бы неплохо убедиться, что вы хотя бы понимаете:
Теорема Пифагора
Как вычислить наклон и середину отрезка, а также расстояние между его концами
Уравнения для парабол, гипербол, окружностей и эллипсов
Как вычислить длину окружности и площадь круга
Как вычислить площадь прямоугольного треугольника
Если вы уже какое-то время не занимались математикой, полезно повторить перед началом урока.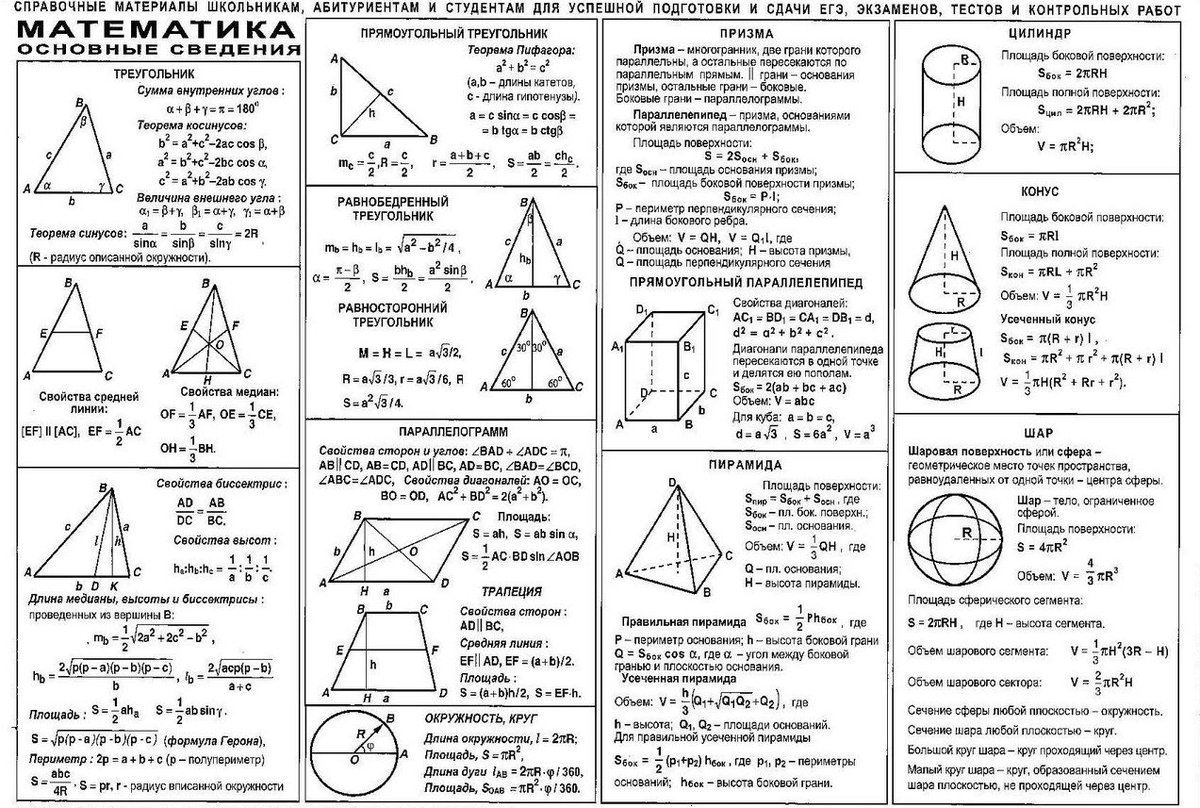 Таким образом, вы не будете тратить драгоценное время, пытаясь запомнить основы! Чувствуете себя немного ржавым? Study.com поможет вам изучить основы с помощью этих карточек по геометрии. Распечатайте их или используйте в цифровом формате.
Стань звездным учеником
Стремись посещать все занятия. В конце концов, ваш учитель может охватить много важного материала всего за один урок! Во время занятий слушайте инструктора и делайте хорошие заметки. Слушайте ключевые термины и старайтесь изо всех сил воспроизвести все, что инструктор пишет на доске (это может быть сложно!).
Будьте активным участником вашего класса триггеров. Если что-то в лекции кажется неясным или вы думаете, что что-то совсем упустили, не бойтесь попросить разъяснений. Вы также можете помочь своим одноклассникам.
Триггер не заканчивается у двери в класс
Выполнение домашних заданий и регулярная учеба вне класса жизненно важны для такого предмета, как тригонометрия, особенно потому, что многие из них зависят от запоминания формул и вашей способности применять эти формулы к конкретным задачам. .Когда вы делаете свою домашнюю работу, не переключайтесь сразу на ключ ответа, чтобы вы могли просто найти все проблемы и получить простые ответы. Вместо этого постарайтесь сначала решить их самостоятельно. Если вы немного боретесь, ключ ответа может помочь вам понять, где вы идете не так, чтобы вы могли выполнить оставшуюся домашнюю работу, не нуждаясь в книге. Но если вы сильно боретесь, простое списывание ответов совсем не поможет вам усвоить материал.
Обратитесь за помощью
Всякий раз, когда вы сталкиваетесь с проблемой домашнего задания, которую не можете решить, запишите ее и обсудите с инструктором или другом.В конце концов, домашняя работа предназначена для того, чтобы помочь вам усвоить материал, поэтому не смущайтесь, если вам понадобится дополнительная помощь. Чем раньше вы столкнетесь с этими проблемами, тем раньше сможете их решить.
В учебной группе вы можете встречаться с другими студентами, делиться стратегиями тригонометрии и обмениваться заметками; у ваших друзей могут быть разные способы обучения, которые могут помочь и вам, и наоборот.
В качестве альтернативы вы можете назначить время один на один с наставником. Многие школы и университеты предлагают бесплатные программы репетиторства или лабораторные занятия для студентов, изучающих математику; подробности узнайте у своего преподавателя или на математическом факультете.
Если вы ищете удобный и доступный способ закрепить основы в свободное время, курс «Фундаментальная тригонометрия» от Study.com может быть именно тем, что вам нужно. Курс охватывает широкий спектр соответствующих тем, от линейных уравнений до тригонометрических функций, векторов и параметрических уравнений, и вы также можете получить помощь от экспертов в предметной области, когда вам это нужно.
Находить время
Не ждите до последней минуты перед выполнением домашних заданий, учебой или получением дополнительной помощи, если она вам нужна.Если вы не понимаете одну концепцию, у вас могут возникнуть трудности с пониманием и последующих концепций.
Избавьте себя от необходимости зубрить двухмесячный материал за час до экзамена! Вместо этого учитесь понемногу каждый день и выполняйте свои задания задолго до их срока.