Скорость реакции прямой — Справочник химика 21
Закон действующих масс — закон, учитывающий соотношение между скоростью химической реакции и концентрацией реагентов при постоянной температуре скорость реакции прямо пропорциональна концентрации реагирующих веществ. [c.372]Равновесие и константа равновесия. Скорость реакции. Прямая и обратная реакции. [c.167]
При равновесии скорости прямой и обратной реакций равны. Но скорость реакции прямо пропорциональна концентрациям реагирующих веществ в степенях, равных стехиометрическим коэффициентам, т. е. [c.247]
Реакции замещения, в свою очередь, делятся на мономолекулярные и бимолекулярные. В реакции мономолекулярного замещения весь процесс лимитирует диссоциация субстрата на ионы и скорость суммарного процесса замещения не зависит (слабо зависит) от концентрации атакующего агента.
В отличие от гомогенного катализа, при котором скорость реакции прямо пропорциональна количеству катализатора, при гетерогенном катализе скорость сильно зависит от степени его измельчения (активная поверхность). Диспергированные частицы металлических катализаторов, например, имеют размеры 10″ —10 см. [c.242]
Итак, во-первых, скорость реакции прямо пропорциональна концентрации катализатора, во-вторых, кинетически уравнение дает дробный порядок процесса, лежащий между нулевым и л-ым. Действительно, если К[А]» 1 (равновесие сдвинуто в сторону образования промежуточного продукта), формальный [c.282]
При больших различиях в скоростях реакций прямого и обратного направления для самопроизвольных процессов и > >0, 1 >0.
СТОЯНКОЙ [N 2 ] оказывает на скорость реакции точно такое же влияние. Отсюда следует, что скорость реакции прямо пропорциональна концентрации. Общую зави симость скоросги от концентраций реагентов можно выразить соотнощением [c.9]
В обоих случаях скорость реакции прямо пропорциональна концентрации катализатора. Порядок реакции по исходным веществам различен и принимает значение, равное единице или двум. Вне указанных предельных случаев значение порядка реакции лежит между единицей и двумя. [c.344]
По зависимости начальной скорости реакции от исходной концентрации реагента. Начальная скорость реакции прямо пропорциональна Ао- Проведя серию опытов с разными исходными концентрациями реагента и построив логарифмическую анаморфозу (рис. 3)
Участие катализатора в реакции не отражается на ее стехио-метрическом уравнении. Однако в первом приближении скорость реакции прямо пропорциональна количеству катализатора. [c.292]
[c.292]
Таким образом, скорость реакции прямо пропорциональна давлению слабо адсорбирующегося газа и обратно пропорциональна давлению хорошо адсорбирующегося газа. [c.410]
Из полученного уравнения видно, что скорость реакции прямо пропорциональна концентрации катализатора (это хорошо согласуется с опытом). [c.325]
Уравнение (7) представляет собой математическое выражение закона действия масс скорость реакции прямо пропорциональна произведению концентраций реагирующих веществ, возведенных в степени, равные соответствующим коэффициентам в уравнении реакции. [c.57]
При одинаковой степени раздробления угля скорость реакции прямо пропорциональна концентрации кислорода. [c.80]
Основополагающим в химической кинетике является понятие о скорости химических реакций. Скорость химической реакции зависит от многих факторов, но важнейшими являются природа реагирующих веществ, концентрация, температура, давление и действие катализаторов. При постоянной температуре скорость реакции прямо пропорциональна концентрации реагирующих веществ. Данное количественное соотношение известно как закон действующих масс. [c.90]
При постоянной температуре скорость реакции прямо пропорциональна концентрации реагирующих веществ. Данное количественное соотношение известно как закон действующих масс. [c.90]
Очевидно, что скорость реакции прямо пропорциональна произведению концентраций веществ, участвующих в лимитирующей стадии процесса. Для взаимодействия Н2 и 1а у=кн,,иСп,Си. Для тримолекулярной реакции в формулу дл расчета скорости и должны входить кроме константы реакции три концентрационных сомножителя. Например, при образовании озона в присутствии азота
Очевидно, что скорость реакции прямо пропорциональна произведению концентраций веществ, участвующих в лимитирующей стадии процесса. Для взаимодействия Н, и 12 V = = кщ Д тримолекулярной реакции в формулу для [c.175]
Гомогенный катализ — процессы, в которых катализатор и реагирующие вещества находятся в одном агрегатном состоянии, жидком или газообразном. Для гомогенного катализа характерно проявление активности отдельным ионом или молекулой катализатора. Поэтому, как правило, увеличение скорости реакции прямо пропорционально концентрации введенного катализатора. Процесс в гомогенном катализе развивается через образование лабильных [c.4]
Поэтому, как правило, увеличение скорости реакции прямо пропорционально концентрации введенного катализатора. Процесс в гомогенном катализе развивается через образование лабильных [c.4]
Если, однако, одно из веществ адсорбируется сильно, например, А, г В слабо, то кинетика реакции в этом случае сильно изменяется. При этом газ А займет почти всю поверхность катализатора и будет препятствовать адсорбции газа В, что будет приводить к замедлению реакции. Можно показать, что в этом случае скорость реакции прямо пропорциональна рв и обратно пропорциональна Ра. Подобный ход реакции наблюдается при реакции С0- -+О2 на платине, где хорошо адсорбирующимся газом является СО. [c.278]
Скорости реакций — прямой (разряда) и обратной (ионизации) — зависят от концентраций окисленной Со и восстановленной Св форм реагирующих частиц [c.268]
Согласно основному закону химической кинетики скорость реакции прямо пропорциональна произведению концентраций реагирующих веществ, возведенных в степени их стехиометрических коэффициентов [c.
Выражения для весов дуг получаются, если скорости реакций (прямой и обратной), которым соответствуют дуги графа, разделить на концентрации участвующих в реакции промежуточных веществ [c.73]
Фишер окислял парафин с температурой плавления 52° воздухом методом барботирования при температуре 170° и давлениях до 60 ат и нашел, что скорость реакции прямо пропорциональна давлению воздуха [121] при 15 ат длительность процесса 8 час., при 30 ат 4 часа, при 60 аш [c.464]
Дк-н> >н-Од. Энергия активации этой реакции практически равна ее эндотермичности [33] =[9]=Дн н—221 кДж/моль. Скорость реакции прямо пропорциональна концентрации углеводорода и парциальному давлению О2 [c.38]
Химические реакции являются двухсторонними, то есть они одновременно протекают как в сторону продуктов реакции, так и в сторону образования исходных веществ со скоростями Ццр — прямой реакции и Иобр — обратной реакции.
Для определения закона, по которому происходит накопление перекисей и альдегидов, авторы рассматривают полулогарифмическую анаморфозу концентрационных кривых этих веществ для верхнетемпературного и для холоднопламепного окисления были получены, вплоть до момента максимальной скорости реакции, прямые линии (рис. 150 и 151). Накопление перекисей и альдегидов происходит, следовательно, в обоих случаях по экспоненциальному закону. [c.376]
Все химические реакции одновременно протекают в двух направлениях в сторону образования продуктов реакции (вправо — прямая реакция) и в сторону преврапдения продуктов в исходные вещества (влево—обратная реакция). Вследствие химической обратимости реакции не доходят до конца. Так как скорость реакции прямо пропорциональна концентрации, то с течением времени скорость прямой реакции будет уменьшаться, а скорость обратной расти.
К каталитическим реакциям, проходящим через стадию образования активного комплекса, приложимы кинетические закономерности, используемые в теории переходного состояния. Скорость образования активного комплекса выше скорости его распада на продукты и катализатор, поэтому скорость процессов в целом определяется скоростью распада активного комплекса. Скорость реакции прямо пропорциональна концентрации каталиэ атора. [c.70]
Увеличение или уменьшение концентрации одного из ионоп, образующихся при диссоциации эле1стролита ( одноименного иона ), увеличивает или уменьшает скорость реакции (прямой или обратной) и приводит к сдвигу равновесия в соответствующем направлении. [c.101]
[c.101]
Зависимость скорости реакции от концентрации реагирующих веществ выражена в законе действия масс Скорость реакции прямо пропорциональна произведению концентраций реагируюи их веществ [c.78]
Согласно чако.ч действия масс при постоянной температуре скорость реакции прямо пропорциональна произведению концентраций реагируюишх веществ, взятых в степенях, равньк их стехиометрическим коэффициентам. Например, для реакции [c.28]
Основопологающим в химической кинетике является понятие о скорости химических реакций. Скорость химической 15сакции зависит от многих факторов, но важнейшими являются природа реагируюгцих веществ, концентрация, температура, давление и действие катализаторов. При постоянной температуре скорость реакции прямо пропорциональна концентрации реагирующих веществ. Данное количественное соотношение известно как закон действующих масс. Зависимость скорости реакции от температуры выражается правилом Вант-Гоффа.
Зависимость скорости реакции от концентрации реагентов впервые была установлена К- Гульдбергом и П. Вааге в 1867 г. скорость реакции прямо пропорциональна произведению концентраций реагентов, возведенных в степени, равные коэффицентам в уравнении лимитируюш,ей стадии, сумма которых равна порядку реакции. [c.134]
1.4.3 Скорость реакции, её зависимость от различных факторов
Видеоурок: Введение в кинетику
Лекция: Скорость реакции, её зависимость от различных факторов
Понятие скорости реакцииЧасто бывает так, что химические реакции происходят мгновенно. Например, происходит взрыв кислородно-водородной смеси. Другие реакции проходят быстро, например горение веществ. А еще одни происходят медленно. К «медленным» реакциям можно отнести коррозию. Так же существуют очень медленные реакции. Реакции, имеющие такую минимальную скорость, человек практически не может заметить. К данному типу реакции можно отнести преобразование гранита в песок и глину, которое происходит в течении долгого времени. Исходя из таких примеров, следует, что химические реакции проходят с различной скоростью.
Например, происходит взрыв кислородно-водородной смеси. Другие реакции проходят быстро, например горение веществ. А еще одни происходят медленно. К «медленным» реакциям можно отнести коррозию. Так же существуют очень медленные реакции. Реакции, имеющие такую минимальную скорость, человек практически не может заметить. К данному типу реакции можно отнести преобразование гранита в песок и глину, которое происходит в течении долгого времени. Исходя из таких примеров, следует, что химические реакции проходят с различной скоростью.
Скорость гомогенной реакции – это определенное изменение количества вещества, происходящее за одну единицу времени в одной конкретной единице объема.
Скорость гетерогенной реакции – это определенное изменение количества вещества, происходящее за одну единицу времени на единице поверхности раздела фаз.
Скорость реакции измеряется по формуле: V=+ n2-n1/ t2-t1 * 1/v
N1 и N2 – количество вещества (измеряется в молях) в определенный момент времени t1 и t2 в системе с объемом V.
Скорость гетерогенной реакции – это такое изменение молярной концентрации вещества, которое проходит во время химической реакции за одну единицу времени.
Факторы скорости реакцииСуществует ряд факторов, влияющих на скорость реакций. Для того чтобы реакция прошла успешно, необходимо, чтобы произошло столкновение молекул исходных веществ — это самый минимальный фактор.
В случае повышения количества молекул, в какой — либо единице объема, число происходящий столкновений будет расти. Таким образом, скорость реакции начинает расти при увеличении концентрации реагирующих в процессе реакции веществ. Если реагентом является газ, скорость реакции возрастет при повышении давления. Почему? Происходит это, потому что давление газа прямо пропорционально концентрации составляющих его молекул. Столкновение частиц — не является достаточным условием протекания реакции. С помощью проведенных расчетов доказано, что количество столкновений молекул реагирующих веществ при их разумной концентрации достаточно велико. Поэтому, реакции должны протекать достаточно быстро. Но это происходит не всегда. Так как не каждое столкновение молекул реагентов будет достаточно эффективным. Многие соударения являются упругими, а при упругом столкновении, молекулы отскакивают друг от друга.
Поэтому, реакции должны протекать достаточно быстро. Но это происходит не всегда. Так как не каждое столкновение молекул реагентов будет достаточно эффективным. Многие соударения являются упругими, а при упругом столкновении, молекулы отскакивают друг от друга.
Для успешной реакции необходимо, чтобы молекулы обладали достаточно большой кинетической энергией. Энергия активации является самой минимальной энергией, которой должны обладать молекулы реагирующих веществ. Данная энергия необходима для того, чтобы реакция прошла. Энергия обозначается как Еа. В системе, которая состоит из достаточно большого количества молекул, существует определенное разделение молекул по энергии. Какие — то из них имеют низкую, или недостаточную энергию, другая часть — высокую и среднюю. Из всех этих молекул только у небольшой части молекул энергия превышает энергию активации. Температура фактически считается мерой кинетической энергии частиц, из которых состоит, какое — либо вещество. Иными словами, чем больше скорость движения частиц, составляющих вещество, тем выше температура этого вещества. Значит, повышая температуру, можно увеличить кинетическую энергию молекул. В результате можно получить следующее: начинается рост доли молекул с энергией, превышающей Еа. Столкновение данных молекул обязательно приведет к химической реакции. Скорость химической реакции может вырасти в 2-4 раза, если повысить температуру на 10 градусов по Цельсию.
Значит, повышая температуру, можно увеличить кинетическую энергию молекул. В результате можно получить следующее: начинается рост доли молекул с энергией, превышающей Еа. Столкновение данных молекул обязательно приведет к химической реакции. Скорость химической реакции может вырасти в 2-4 раза, если повысить температуру на 10 градусов по Цельсию.
Достаточно часто случается, что химическая реакция «не хочет» проходить сама по себе. В таком случае скорость реакций повышается с помощью катализа — химического процесса, при котором используются катализаторы. Это такие вещества, которые способны ускорить протекание реакции. При этом сами катализаторы не расходуются.
Как же действуют катализаторы? Во время химической реакции они вступают во взаимодействие с реагентами. При этом образуются промежуточные соединения. К концу реакции катализаторы освобождаются и возвращаются к прежнему состоянию.
Существуют два вида катализаторов. Гомогенный и гетерогенный. Первый вместе с реагентами находится в одной фазе, к примеру, жидкости или газе. Тогда как второй образует самомстоятельную от реагентов фазу. К гомогенным относятся кислоты и основания, к гетерогенным простые вещества, оксиды и сульфиды металлов.
Тогда как второй образует самомстоятельную от реагентов фазу. К гомогенным относятся кислоты и основания, к гетерогенным простые вещества, оксиды и сульфиды металлов.
Если постороннее вмешательство приводит к еще большему замедлению то, речь идет об ингибиторах. Они тоже нужны человеку, к примеру, для того чтобы защитить металл от коррозии.
Скорость реакции так же зависит от площади соприкосновения использующихся реагентов. На скорость гетерогенной реакции, в процессе которой реагирует твердое вещество с газообразным или жидким, оказывает влияние и перемешивание. Данный фактор связан с тем, что в результате перемешивания, удается достичь исчезновения из места реакции скапливающихся молекул продуктов реакции и «поднести» новые молекулы реагента.
Подводя итог можно сказать, что скорость реакции зависит от следующих факторов:
От концентрации реагентов. То есть чем выше концентрация, тем больше скорость реакции.
От температуры.
 То есть с ростом температуры, скорость любой реакции увеличивается.
То есть с ростом температуры, скорость любой реакции увеличивается. От площади соприкосновения реагирующих веществ. Чем больше площадь контакта реагентов, тем выше скорость реакции.
От перемешивания. То есть, если реакция происходит между твердым веществом, жидкостью, газом, перемешивание может ее ускорить.
Тест по теме » Скорость химических реакций.» ( формат 2017 года)
Задание №21 «Скорость реакции, её зависимость от различных факторов»
1)От увеличения площади поверхности соприкосновения реагентов не зависит скорость реакции между
30) Из предложенного перечня внешних воздействий выберите два воздействия, которые приводят к увеличению скорости реакции между газообразными веществами.1.повышение температуры и увеличение давления
2.понижение температуры и уменьшение давления
3. увеличение концентрации исходных веществ
увеличение концентрации исходных веществ
4.повышение давления и понижение температуры
5.понижение давления и повышение температуры
31)Скорость реакции 2SO2 + O2 = 2SO3 + Q увеличится при
1. внесении катализатора 2. Нагревании 3. уменьшении концентрации кислорода
4. уменьшении давления в системе 5. увеличении концентрации SO3
32)Увеличение давления в системе в наибольшей степени скажется на скорости химической реакции между 1. пропеном и водородом 2. магнием и хлором
3. сульфатом железа(III) и хлоридом бария
4. оксидом меди(II) и серной кислотой 5. алюминием и раствором щёлочи
33)Скорость реакции Zn + h3SO4 = ZnSO4 + Н2 уменьшится при
1. внесении катализатора 2. Нагревании 3. уменьшении концентрации кислоты
4. уменьшении давления в системе 5. добавлении ингибитора
34)Уменьшение давления в системе в наибольшей степени скажется на скорости химической реакции между 1. цинком и соляной кислотой 2. азотом и водородом
цинком и соляной кислотой 2. азотом и водородом
3. хлоридом алюминия и гидроксидом калия
4. растворами фосфорной кислоты и щёлочи 5. этиленом и водородом
35)Скорость химической реакции Fe + h3SO4(20%-ный раствор) — FeSO4 + Н2
при обычных условиях больше, чем скорость реакции
1. 2Fe + 6h3SO4(96%-ный раствор) = Fe2(SO4)3 + 3SO2 + 6Н2О
2. Mg + h3SO4(20%-ный раствор) = MgSO4 + Н2
3. Zn + h3SO4(20%-ный раствор) = ZnSO4 + Н2
4. 2Na + h3SO4(5%-ный раствор) = Na2SO4 + h3
5. Fe + h3SO4(5%-ный раствор) = FeSO4 + h3
36)Скорость реакции Fe + 2НСl(р-р) = FeCl2 + Н2 увеличится при
1. добавлении ингибитора 2. Нагревании 3. увеличении концентрации FeCl2
4. увеличении давления в системе 5. увеличении концентрации кислоты
37)Скорость реакции N2 + ЗН2 = 2Nh4 + Q уменьшится при
1. внесении катализатора 2. Нагревании 3. уменьшении концентрации аммиака
4. уменьшении давления в системе 5. уменьшении концентрации N2
уменьшении концентрации N2
38)Из предложенного перечня внешних воздействий выберите два воздействия, которые приводят к уменьшению скорости реакции этилена с водородом. 1. понижении температуры 2. увеличении концентрации этилена 3. использовании катализатора 4. уменьшение концентрации водорода 5. повышении давления в системе
39)Скорость реакции 2NO + O2 = 2NO2 + Q уменьшится при 1. внесении катализатора 2. уменьшении концентрации NO2 3. увеличении концентрации NO2 4. уменьшении давления в системе 5. уменьшении концентрации кислорода
40)Увеличение давления в системе в наибольшей степени скажется на скорости химической реакции между 1. азотом и водородом 2. железом и серной кислотой
3. сульфатом алюминия и раствором щёлочи 4. сернистым газом и кислородом
5. растворами серной кислоты и щёлочи
Химия — 8
12. Факторы, влияющие на скорость химических реакций
1. Влияние на скорость химических реакций химической природы веществ (реагентов). Химическая природа веществ определяется их составом, строением и типом связи между частицами. Обусловленные этими факторами различные вещества, обладая различной природой, при взаимодействии с одним и тем же веществом будут иметь разные скорости реакций. Например, при изучении химических свойств кислот в 6-ой теме мы наблюдали различные скорости реакций металлов Мп, Zn, Fе с соляной кислотой, имеющей в каждом случае одну и ту же концентрацию. Следовательно, чем активнее металл, тем быстрее будет протекать реакция.
Химическая природа веществ определяется их составом, строением и типом связи между частицами. Обусловленные этими факторами различные вещества, обладая различной природой, при взаимодействии с одним и тем же веществом будут иметь разные скорости реакций. Например, при изучении химических свойств кислот в 6-ой теме мы наблюдали различные скорости реакций металлов Мп, Zn, Fе с соляной кислотой, имеющей в каждом случае одну и ту же концентрацию. Следовательно, чем активнее металл, тем быстрее будет протекать реакция.
2. Влияние концентрации на скорость реакции. Влияние концентрации веществ на скорость реакции в основном имеет отношение к реакциям, протекающим в газообразной среде и в растворе.
HВ гомогенных
реакциях скорость реакции прямо пропорциональна произведению концентраций реагентов (исходных веществ). Эта зависимость для гомогенных реакций была установлена в 1867 году норвежскими учеными К.Гульдбергом и П.Вааге, и названа законом влияния масс. Для реакций, выраженных уравнением
A(г) + B(г)=AB(г)
Для реакций, выраженных уравнением
A(г) + B(г)=AB(г)
V = k•CA•CB где
CA и CB молярная концентрация исходных веществ, к — константа скорости реакции. Значение константы скорости реакции может меняться в зависимости от природы веществ и температуры. к — не зависит от других факторов.
Если реагенты имеют коэффициенты, например: mA(г)+ nB(г) = AmBn(г), в таком случае,
V = k • CAm • CBn.
Формула скорости, показывающая зависимость скорости реакции от концентрации реагентов, называется кинетическим уравнением скорости реакции. В кинетическом уравнении выражение концентрации увеличивается до коэффициента реагента. Подобного типа кинетические уравнения и относящиеся к ним задачи верны только для таких простых реакций, как:
A(г) + B(г) =AB(г) ; A(г) + 2B(г) =AB2(г); 2A(г) + B(г) =A2B(г)
A(ж) + B(ж)=AB(ж); A(ж) + 2B(ж)=AB2(ж) и т. д.
д.
Если коэффициенты обоих исходных веществ одинаковы, то при увеличении их концентрации в 2 раза скорость реакции увеличится в 4 раза. Например: для реакции
A(г) + B(г)=AB(г)V = k • CA • CB
Если увеличим концентрацию А и В в 2 раза, тогда:
Если в гомогенных реакциях при увеличении концентрации реагентов в 2 раза скорость реакции увеличивается в 8 раз, тогда коэффициент одного из веществ будет равен 1, а другого — 2. Например:
Скорость химической реакции | himiyaklas.ru
Скорость машины – это расстояние, которое она проезжает за единицу времени.
А скорость реакции – это сколько продукта образуется или исходного вещества расходуется за единицу времени.
То, с какой скоростью будет образовываться продукт, зависит от того, насколько часто будут друг с другом встречаться молекулы реагирующих веществ. Ведь реакция может произойти только, если молекулы реагирующих веществ будут в непосредственной близости друг с другом.
Чтобы молекуле преобразоваться, то есть вступить в реакцию, она должна обладать некоторой энергией. Минимальная энергия, которая необходима для осуществления реакции называется энергией активации. Только молекула, обладающая энергией активации, может вступить в реакцию. То есть энергия активации – это барьер, который должны преодолеть молекулы исходных веществ, чтобы стать продуктами. Соответственно, чем больше молекул в данный момент времени обладают энергией активации, тем выше скорость реакции.
Это основной принцип. И с пониманием этого принципа мы сможем рассмотреть, как меняется скорость реакции при том или ином воздействии.
При повышении концентрации исходного вещества скорость реакции увеличивается
Во-первых, из-за того, что расстояние между реагирующими молекулами становится меньше и они с большей вероятностью провзаимодействуют.
А во-вторых, чем больше концентрация вещества, тем больше молекул в данный момент времени будут обладать энергией достаточной, чтобы преодолеть «барьер» и вступить в химическое превращение.
То есть элементарно возрастает вероятность превращения из-за увеличения «попыток».
Важное следствие: в начале химической реакции исходного вещества больше, чем в конце, потому что оно расходуется. В ходе химической реакции концентрация исходного вещества падает. Следовательно, с течением реакции ее скорость уменьшается.
При повышении температуры скорость реакции возрастает
Повышая температуру, мы сообщаем молекулам энергию. Молекулы приобретают энергию активации, преодолевают барьер и ступают в реакцию.
При повышении температуры, молекулы начинают двигаться быстрее и с большей вероятностью будут сталкиваться друг с другом.
Эмпирически даже было выведено, что увеличение температуры на каждые 10° скорость реакции возрастает в 2-4 раза. Это называется правило Вант-Гоффа.
При увеличении площади контакта реагирующих веществ друг с другом скорость реакции увеличивается
Логика такая же: чем больше площадь соприкосновения, тем больше реагирующих молекул будут в непосредственной близости друг с другом:
Поэтому для увеличения скорости реакции, твердые вещества-реагенты измельчают. Так достигается большая площадь соприкосновения.
Так достигается большая площадь соприкосновения.
Разберем на примере, возьмем кусочек сахара и внесем в пламя горелки – он обуглится. А если разотрем его в пудру и распылим в воздухе – получится взрывоопасная смесь. Потому что суммарная площадь поверхности сахара в измельченном виде больше.
Следствие из 3 пункта – гомогенные реакции идут быстрее
Скорость реакции между веществами: газ – газ, жидкость – жидкость идет быстрее, чем при других комбинациях: газ – жидкость, газ – твердое тело, жидкость – твердое тело, твердое тело – твердое тело.
В системах газ – газ и жидкость – жидкость молекулы равномерно распределены друг относительно друга. Нет конкретной границы раздела фаз. Поэтому вероятность столкновения реагирующих молекул велика. Реакция идет по всему объему смеси.
А в системах газ – жидкость, газ – твердое тело, жидкость – твердое тело, твердое тело – твердое тело есть четкая граница раздела фаз, молекулы реагирующих веществ не так близко прилежат друг к другу. И реакция идет только на поверхности: в точках соприкосновения веществ.
И реакция идет только на поверхности: в точках соприкосновения веществ.
Рассмотрим реакцию уксуса с содой, всем нам хорошо знакомую в быту. Если мы сыпем соду в уксус, реакция идет медленнее, чем если мы заранее соду растворим в воде.
Если одно из исходных веществ – газ, то при повышении давления скорость реакции будет увеличиваться
Из курса физики вам должно быть известно, что газ имеет способность сжиматься. При сжимании плотность газа увеличивается: между молекулами уменьшается расстояние. Поэтому при повышении давление возрастает концентрация газа. Молекулы будут находиться ближе друг к другу и, соответственно, увеличивается вероятность «встречи» реагирующих молекул. Скорость реакции увеличивается.
Катализатор ускоряет химическую реакцию
Катализаторы – это вещества, которые участвуют в реакции, но не расходуются и их участие заставляет протекать реакцию быстрее.
Механизмам действия катализа посвящен целый раздел химии (он называется химия катализа). Этих механизмов множество, но суть их одна: катализатор уменьшает энергию активации данной реакции.
Этих механизмов множество, но суть их одна: катализатор уменьшает энергию активации данной реакции.
Поэтому молекулам достаточно более низкой энергии, чтобы вступить в реакцию. Следовательно, в данный момент времени больше молекул обладают нужной энергией, следовательно, скорость реакции больше. Раз «барьер» ниже, то и преодолеть его могут больше молекул.
Если, например, просто оставить в пробирке перекись водорода Н2О2 на длительное время, она довольно нескоро вся разложится до воды и молекулярного кислорода. Но стоит добавить катализатор MnO2 реакция пойдет куда быстрее. И через считанные минуты от перекиси не останется и следа:
Последний, но самый важный пункт – природа реагирующих веществ
С него следовало бы начать, но мы умышленно его поместили в конце, потому что про этот самый важный принцип чаще всего забывают. Первое, что должны мы ответить на вопрос: «от чего зависит скорость химической реакции?», прежде температуры и площади соприкосновения мы должны ответить: «от природы реагирующих веществ». Натрий с водой будет реагировать быстрее, чем железо. Бензин горит быстрее угля. Метиловый спирт убивает быстрее, чем водка.
Натрий с водой будет реагировать быстрее, чем железо. Бензин горит быстрее угля. Метиловый спирт убивает быстрее, чем водка.
И если другие параметры: температуру, давление, степень измельченности, агрегатное состояние мы можем изменять, то с природой реагирующих веществ мы ничего поделать не можем. Нам всегда нужно иметь ввиду свойства самого вещества.
Вот эти нехитрые принципы, которые нужно понять и запомнить, чтобы успешно справляться с заданиями по теме «скорость химической реакции».
Энергия активации
Энергия активации
Для эффективного соударения молекул (частиц), приводящего к химической реакции, требуется определенная энергия.Минимальное количество энергии, необходимое для прохождения реакции называют энергией активации.
Эта энергия требуется для достижения системой переходного состояния и образования активированного (переходного) комплекса, который превращается в продукты реакции уже самопроизвольно (примечаниеТермины «переходное состояние» и «переходный комплекс» часто используют как взаимозаменяемые, хотя переходное состояние – это уровень энергии на пути реакции, а переходный комплекс — группировка атомов, находящаяся в переходном состоянии. ).
Изменение энергии реагирующей системы можно показать на примере элементарной реакции А + В АВ:
Энергия активации Еа равна разности энергий переходного (ЕПС) и исходного (Еисх) состояний:
Еа = ЕПС – Еисх.
Величина Еа служит важной характеристикой любой реакции. Она зависит от природы реагирующих веществ и наличия катализатора, влияющего на энергию переходного состояния, но не зависит от температуры.
Энергия активации определяет скорость реакции: чем меньше значение Еа, тем выше скорость реакции. Эта зависимость выражается уравнением Аррениуса, которое связывает константу скорости реакции Константа скорости реакции (k) – коэффициент пропорциональности, численно равный скорости реакции, когда произведение молярных концентраций реагентов равно 1. Константа скорости реакции зависит от температуры, от природы реагирующих веществ, но не зависит от их концентрации.
).
Изменение энергии реагирующей системы можно показать на примере элементарной реакции А + В АВ:
Энергия активации Еа равна разности энергий переходного (ЕПС) и исходного (Еисх) состояний:
Еа = ЕПС – Еисх.
Величина Еа служит важной характеристикой любой реакции. Она зависит от природы реагирующих веществ и наличия катализатора, влияющего на энергию переходного состояния, но не зависит от температуры.
Энергия активации определяет скорость реакции: чем меньше значение Еа, тем выше скорость реакции. Эта зависимость выражается уравнением Аррениуса, которое связывает константу скорости реакции Константа скорости реакции (k) – коэффициент пропорциональности, численно равный скорости реакции, когда произведение молярных концентраций реагентов равно 1. Константа скорости реакции зависит от температуры, от природы реагирующих веществ, но не зависит от их концентрации. с энергией активации и температурой. Уравнение Аррениуса более точно, чем правило Вант-ГоффаПравило Вант-Гоффа: «При повышении температуры на 10°С скорость реакции увеличивается в 2-4 раза».
с энергией активации и температурой. Уравнение Аррениуса более точно, чем правило Вант-ГоффаПравило Вант-Гоффа: «При повышении температуры на 10°С скорость реакции увеличивается в 2-4 раза». Это правило является приближенным и применимо лишь для ориентировочной оценки влияния температуры на скорость реакций, протекающих при температурах, близких к комнатной (энергия активации таких реакций 50-150 кДж/моль). отражает зависимость скорости (константы скорости) реакции от температуры.
Лимитирующая стадия – элементарная стадия сложной реакции, которая имеет наиболее высокую энергию активации и протекает намного медленнее остальных, ограничивая общую скорость процесса.
Для примера рассмотрим изменение энергии в ходе двухстадийной реакции: В данном случае стадия 1 является лимитирующей, так как имеет более высокую энергию переходного состояния ПС1. Следовательно, для осуществления двухстадийной реакции в целом требуется энергия Еа, активирующая стадию 1.
Следовательно, для осуществления двухстадийной реакции в целом требуется энергия Еа, активирующая стадию 1.
Константа скорости реакции (k) – коэффициент пропорциональности, численно равный скорости реакции, когда произведение молярных концентраций реагентов равно 1. Константа скорости реакции зависит от температуры, от природы реагирующих веществ, но не зависит от их концентрации.
Скорость реакции не зависит от A Химический температурный класс 12 CBSE
Подсказка: Скорость реакции представляет собой отношение изменения концентрации реагента ко времени, необходимому для этого изменения. Скорость реакции также выражается как отношение изменения парциального давления реагента ко времени, необходимому для этого изменения. Факторы, увеличивающие количество эффективных столкновений в единицу времени, также увеличивают скорость реакции. Полный ответ:
Рассмотрим общую реакцию \[{\text{A}} \to {\text{продукты}}\] . n\]
n\]
Скорость реакции также увеличивается в присутствии катализатора. Катализатор увеличивает скорость прямой и обратной реакции. Таким образом, равновесие достигается быстро. Катализатор обеспечивает альтернативный путь с меньшей энергией активации.
Изменение температуры также влияет на скорость химической реакции: когда температура повышается примерно на \[{\text{10 K}}\], скорость реакции удваивается. Влияние температуры на скорость химической реакции имеет промышленное значение, так как замес в установке может быть завершен за меньшее время за счет повышения температуры, так что скорость реакции увеличивается.
Таким образом, правильный ответ D).
Примечание: Существует два типа катализа: положительный катализ и отрицательный катализ. Положительный катализатор увеличивает скорость реакции, а отрицательный катализатор снижает скорость реакции. Отрицательный катализатор действует как яд.
Константа скорости реакции — обзор
Знание сложной последовательности газофазных и гетерогенных реакций, участвующих в CVD/CVI, имеет центральное значение для контроля всего процесса. Экспериментальные данные в основном получают в специальных лабораторных CVD/CVI реакторах с горячими стенками с диагностикой, такой как измерение поглощения массы, с использованием микровесов, ex-situ измерения толщины образцов, либо плоских, либо пористых, и анализ газовой фазы, либо на месте или на выходе из реактора, с помощью газофазной хроматографии (ГПХ), возможно, в сочетании с масс-спектрометрией (ГХ/МС) или инфракрасной спектроскопией с преобразованием Фурье (FTIR). Результаты касаются основных обнаруживаемых химических соединений; большинство радикалов и менее устойчивых видов остаются скрытыми для прямого наблюдения.
Экспериментальные данные в основном получают в специальных лабораторных CVD/CVI реакторах с горячими стенками с диагностикой, такой как измерение поглощения массы, с использованием микровесов, ex-situ измерения толщины образцов, либо плоских, либо пористых, и анализ газовой фазы, либо на месте или на выходе из реактора, с помощью газофазной хроматографии (ГПХ), возможно, в сочетании с масс-спектрометрией (ГХ/МС) или инфракрасной спектроскопией с преобразованием Фурье (FTIR). Результаты касаются основных обнаруживаемых химических соединений; большинство радикалов и менее устойчивых видов остаются скрытыми для прямого наблюдения.
Поэтому крайне желательно связать экспериментальные определения с моделями газофазной и гетерогенной химии, учитывающими термодинамические и кинетические аспекты. Действительно, термодинамика полезна для предсказания равновесного состава данной газовой фазы в реакторе, но часто случается, что время пребывания и контакта слишком мало, чтобы позволить этому равновесию полностью наступить; поэтому кинетические данные также представляют большой интерес. Общая блок-схема вычислительных подходов к химии реакторов CVD/CVI представлена на рис.21. Конечная цель подхода заключается в определении критических газообразных соединений, ответственных за качество отложений и скорость отложений. Для этого проводятся термохимические расчеты и расчеты кинетики реакций, которые, возможно, вводятся в модель реактора CFD. Они основаны на существовании надежной, непротиворечивой базы данных, описывающей свойства всех реагентов и законы скоростей всех реакций. Это, в свою очередь, зависит от получения термохимических данных и данных о скорости реакции. Если экспериментальные или литературные значения недоступны, необходимы теоретические химические расчеты.Во-первых, на основе квантово-химических расчетов вычисляются равновесные геометрические параметры, частоты гармонических колебаний и поверхности потенциальной энергии выбранного набора химических соединений. Популярное программное обеспечение для квантовой химии часто основано на DFT и работает с довольно высокими уровнями теории.
Общая блок-схема вычислительных подходов к химии реакторов CVD/CVI представлена на рис.21. Конечная цель подхода заключается в определении критических газообразных соединений, ответственных за качество отложений и скорость отложений. Для этого проводятся термохимические расчеты и расчеты кинетики реакций, которые, возможно, вводятся в модель реактора CFD. Они основаны на существовании надежной, непротиворечивой базы данных, описывающей свойства всех реагентов и законы скоростей всех реакций. Это, в свою очередь, зависит от получения термохимических данных и данных о скорости реакции. Если экспериментальные или литературные значения недоступны, необходимы теоретические химические расчеты.Во-первых, на основе квантово-химических расчетов вычисляются равновесные геометрические параметры, частоты гармонических колебаний и поверхности потенциальной энергии выбранного набора химических соединений. Популярное программное обеспечение для квантовой химии часто основано на DFT и работает с довольно высокими уровнями теории. Затем статистические суммы, энтропии и теплоемкости получаются из стандартных статистических уравнений. 202
Затем статистические суммы, энтропии и теплоемкости получаются из стандартных статистических уравнений. 202
Рис. 21. Полная стратегия химического моделирования CVI, начиная с квантово-химических расчетов и заканчивая глобальными результатами в масштабе реактора.
Воспроизведено из Reinisch, G., Leyssale, J.-M., Patel, S., et al. ., 2013. Исследования реакционной способности газовой фазы во время химического осаждения из паровой фазы карбида бора. В: Кривен, В.М., Гьекенези, А.Л., Вестин, Г., Ван, Дж. (ред.), Разработки в области стратегических материалов и вычислительного дизайна III. В: Halbig, M., Mathur, S. (Vol. Eds.), Ceramics Engineering and Science Proceedings, Vol. 33, выпуск 10. Нью-Йорк: John Wiley & Сыновья, стр. 105–116. Вклад некоторых мод свободных колебаний (качание и виляние) в статистическую сумму нескольких молекул и переходных состояний может быть критическим.Если гармонического приближения и приближения свободного ротора достаточно при соответственно низких и высоких температурах, значения в промежуточной области может быть сложно оценить, что потребует опять-таки специальных методов, 210 , среди которых недавно разработанный метод 1DQ. 211
211
5.4.3.3.1 Термодинамика
Первым теоретическим подходом к получению предварительных знаний о химической системе CVD/CVI является термодинамика, которая позволяет получить данные о гетерогенном равновесии газ-твердое тело.Для любых экспериментальных условий (т. е. температуры, давления и начального состава газовой фазы) в соответствии с гипотезой равновесия можно рассчитать (1) теоретический состав месторождения (которое может быть однофазным или состоять из нескольких фаз). ) и газовой фазе и (2) термодинамические выходы. Можно вывести наиболее термодинамически вероятные реакции, что даст информацию об образовании отложений, наличии газообразных побочных продуктов и возможном травлении подложки.Такой термодинамический подход обычно осуществляется по методу минимизации общей свободной энтальпии системы. 213 В качестве примера, CVD Zirconia (который был инфильтрирован как матрица CMC 79 от ZRCL 4 — CO 2 — H 2 — AR Система) , было исследовано с термодинамической точки зрения. 214 На инертной подложке чистый ZrO 2 может быть нанесен со 100% выходом при избытке водяного пара в равновесии, в то время как совместное осаждение углерода и диоксида циркония может быть получено для H 2 -богатый исходные композиции.В условиях ZrO 2 выход близок к 100 %, углеродная подложка оказывается окисленной, а муллитовая термодинамически устойчивой. Такие прогнозы, подтвержденные экспериментально, очень важны, поскольку позволяют, например, правильно выбрать волокнистую заготовку для получения новых КМЦ методом ХВН. Другой пример термодинамического исследования включал расчет как гетерогенного, так и гомогенного равновесия в системе CH 3 SiCl 3 – H 2 для CVD карбида кремния. 215 Во-первых, было показано, что в реакторе с горячими стенками молекула-предшественник CH 3 SiCl 3 не является исходным веществом, а разлагается на промежуточные соединения SiCl и CH 4 , возможные исходные соединения для Si и C соответственно в самом общем случае (рис.
214 На инертной подложке чистый ZrO 2 может быть нанесен со 100% выходом при избытке водяного пара в равновесии, в то время как совместное осаждение углерода и диоксида циркония может быть получено для H 2 -богатый исходные композиции.В условиях ZrO 2 выход близок к 100 %, углеродная подложка оказывается окисленной, а муллитовая термодинамически устойчивой. Такие прогнозы, подтвержденные экспериментально, очень важны, поскольку позволяют, например, правильно выбрать волокнистую заготовку для получения новых КМЦ методом ХВН. Другой пример термодинамического исследования включал расчет как гетерогенного, так и гомогенного равновесия в системе CH 3 SiCl 3 – H 2 для CVD карбида кремния. 215 Во-первых, было показано, что в реакторе с горячими стенками молекула-предшественник CH 3 SiCl 3 не является исходным веществом, а разлагается на промежуточные соединения SiCl и CH 4 , возможные исходные соединения для Si и C соответственно в самом общем случае (рис. 23), согласно следующей последовательности реакций:
23), согласно следующей последовательности реакций:
Рис. 23. Расчетные парциальные давления газообразные виды по сравнению сОтношение начальной композиции α = N ° = N ° ( H ° 2 ) / N ° ( CH 3 SICL 3 ) на 1200 K и 10 кПа для CH 3 SiCl 3 – H 2 система в гипотезе (а) гомогенного равновесия и (б) гетерогенного равновесия. 215
[1]Ch4SiCl3+h3→Ch5+SiCl2+HClгомогенная реакцияCh5+SiCl2→SiC+2HCl+h3гетерогенная реакция равновесие, высокие значения которого можно соотнести с режимом зародышеобразования. 216 Наконец, на основе термодинамических данных была предложена оценка концентраций различных химических соединений, хемосорбированных на поверхностях SiO 2 или β – SiC ; отмечено значение хемосорбции радикалов SiCl 3 и H на атомах C и радикалов CH 3 и Cl на атомах Si и различные механизмы образования Получена керамика на основе SiC . 217
217
Необходимые термохимические данные обычно извлекаются из имеющихся таблиц. 218–220 Однако иногда значения могут быть сомнительными; соответственно растет интерес к оценке этих констант на основе квантово-химических расчетов. Были проведены многочисленные исследования, результаты которых приведены в таблице 2; полученные данные в целом хорошо согласуются с имеющимися экспериментами.
Таблица 2. Некоторые термохимические базы данных, относящиеся к CVI, изученные квантовой химией
| | метод | ссылки | | | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| General Custrial | G2, G3 | 221 | 148 | |||||||||||||||||||||||
| BAC-G3B3 | 222 | 155 | B — CL — H — H | BAC-MP4 1 BH I CL CL J J ( I + J + J ≤ 3)|||||||||||||||||||||||
| + N -Conting Molecules | 1||||||||||||||||||||||||||
| G2 | 224 1 BH I I I I I Cl j ( i + j ≤ 3) | |||||||||||||||||||||||||
| G3B3 | 225 | |||||||||||||||||||||||||
| SI — C — C CL — CL — H | H CCSDT226 | 50 световых видов | ||||||||||||||||||||||||
| G3B3 | 227 | 163 света | ||||||||||||||||||||||||
| B — C — C — CL — H — H | H3B3 / G3MP2228 | 1 154 светлых видов 1 8SI — B — CL — H | H 1 BAC-MP4229 2 1 Si I B J J J HCl ( I ≤ 2, J ≤ 2) | ≤ 2)
5.
 4.3.3.2 Кинетика
4.3.3.2 Кинетика В реакторе CVD/CVI из-за непрерывного потока прекурсоров гетерогенное равновесие никогда не достигается, за исключением очень специфических условий. Необходимо учитывать кинетические факторы. Экспериментальное исследование изменений скорости осаждения в зависимости от различных экспериментальных параметров обычно проводится для получения более полных знаний о химической системе (таблица 3).
Таблица 3. Некоторые кинетические газофазные реакции механизма базы данных
| Химическая система | тип работы | ссылки | |||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C — H — H | Подробная компиляция | 230-232 | 1 C 3 H 8 Pyrolyse и CVD|||||||||||||||||||||||||||||||||||||||||||
| снижена модель | 1 44 1 CH 4 Pyrolysis И CVD|||||||||||||||||||||||||||||||||||||||||||||
| Подробные компиляции | 294 1 CH 4 Pyrolysis и CVD 9003 8 2 C — H — CL — CL | 1 Компиляция235 2 C 6 H 5 Cl пиролиз | |||||||||||||||||||||||||||||||||||||||||||
| Компиляция | 236 | 1 CH 3 CL — O O 2 Pyrolisiz||||||||||||||||||||||||||||||||||||||||||||
| Компиляция | 1 237 1 CH 4 — CL 2 Pyrolyse 2|||||||||||||||||||||||||||||||||||||||||||||
| B — H — H — CL — CL — CL | 1 Теория G2 1 238 2 1 BCL 3 — H 2 H 2 CVD 2|||||||||||||||||||||||||||||||||||||||||||||
| 31 Reaubs | |||||||||||||||||||||||||||||||||||||||||||||
| Теория — G3B3 Метод | 1 212,225 1 BCL 3 — H — H — H 2 H 2 2|||||||||||||||||||||||||||||||||||||||||||||
Exptl. Измерения Измерения | 239 | 1 BCL 3 — H — O — OH — OH 8 B — C — CL — H 2 H 1 Exptl.73,240 | |||||||||||||||||||||||||||||||||||||||||||
| Теория | 9021 | SI — C — CL — H — H — H 2 1 Теория — CCSDT 1 241 2 1 CH 3 3 SICL 3 3 — H — H 2 CVD 9007 | Теория — BAC-MP4 // RRKM | 1 CH CH 3 SICL 3 Разложение 1||||||||||||||||||||||||||||||||||||||||||
| Экспериментальный | 243244 | ||||||||||||||||||||||||||||||||||||||||||||
| Si — B — Cl — Н | Теория — ДПФ | 245 | ХОП из Б Si, легированных ионами от | ||||||||||||||||||||||||||||||||||||||||||
| SICL 2 H 2 — B 2 H 6 — H 2 2 | |||||||||||||||||||||||||||||||||||||||||||||
| Si – B – C | Расш. | 76–78 | |||||||||||||||||||||||||||||||||||||||||||
| – Cl – H |
Кинетика этой реакции определяется условиями первой стадии исследования. Влияние температуры осаждения, представленное в виде графика Аррениуса, часто используется для определения режимов химического и массообмена. Когда энергия активации очень низкая, т.е. ниже 20 кДж моль -1 , кинетика ограничивается массопереносом, в то время как при более высокой энергии активации, обычно наблюдаемой в более низком температурном диапазоне, кинетический процесс определяется химическими реакциями. , как показано на рис.24 для осаждения SiC из CH 3 SiCl 3 – H 2 прекурсор. 246
Рис. 24. Скорость осаждения керамики на основе SiC в зависимости от обратной температуры для соотношения составов α=3, общего расхода Q =200 см3/мин и трех полных давлений в CH 3 SiCl 3 – H 2 система. 246
246
Переход между этими двумя кинетическими режимами можно обнаружить и по изменению суммарного расхода (рис. 25). Если скорость осаждения увеличивается с увеличением общего расхода, что обычно имеет место при наименьших значениях этого параметра, массоперенос является управляющей стадией процесса. Если при более высокой общей скорости потока скорость роста становится постоянной или уменьшается с увеличением общей скорости потока, считается, что кинетический процесс контролируется химическими реакциями.Химический процесс, приводящий к образованию твердого осадка, может включать гомогенные реакции. Возможным следствием гомогенных реакций является уменьшение скорости осаждения при увеличении общего расхода или уменьшении времени пребывания газообразного прекурсора в горячей зоне реакции, как это видно на примере осаждения пироуглеродов из различных углеводородов (рис. 26). 18,30–33,42 В этой системе увеличение времени пребывания в большей или меньшей степени способствует превращению прекурсора в результате газофазных реакций, называемых «созреванием», с образованием более или менее эффективных промежуточных частиц для образования различных типов пироуглеродов. 18,19,28,44,45
18,19,28,44,45
Рис. 25. Скорость осаждения керамики на основе SiC в зависимости от общей скорости потока для соотношения составов α =3 в CH 3 SiCl 3 – H 2 система. 246
Рис. 26. Скорость осаждения пироуглерода в зависимости от времени пребывания при полном давлении пропана P =2 кПа и различных температурах: (а) T =905 °C, (б) T =950°С, (в) Т =992°С и (г) Т =1035°С. 19
Значения энергий активации являются результатом общего химического пути, и чем больше последовательных стадий включает этот путь, тем выше кажущаяся энергия активации. В особых случаях, когда скорость осаждения не зависит от общей скорости потока или времени пребывания, кинетический процесс контролируется только гетерогенными реакциями. В таких условиях экспериментально определенная энергия активации может быть напрямую связана с химическим процессом на поверхности, а кинетические законы могут быть получены путем изменения парциального давления различных частиц-предшественников и определения порядков реакции по отношению к этим частицам. Например, такие кинетические данные были получены для процесса осаждения SiC из прекурсора CH 3 SiCl 3 – H 2 . 247 Кроме того, путем добавления к прекурсору возрастающих концентраций соединений, образующихся в результате реакций осаждения, например, HCl для роста SiC или H 2 для роста пироуглерода, можно оценить эффекты ингибирования, которые могут играть важную роль в процессе CVI, поскольку такие виды ингибиторов могут сильно ограничивать скорость осаждения внутри преформы и приводить к заметным градиентам инфильтрации. 30-32,39,247-250 в атмосферном давлении CVD от CH 3 3 SICL 3 — H 2 , добавление HCL может привести к внезапному переходу к чистому росту пироарбона; уменьшение количества HCl позволяет вернуться к росту SiC с явным гистерезисом.
Например, такие кинетические данные были получены для процесса осаждения SiC из прекурсора CH 3 SiCl 3 – H 2 . 247 Кроме того, путем добавления к прекурсору возрастающих концентраций соединений, образующихся в результате реакций осаждения, например, HCl для роста SiC или H 2 для роста пироуглерода, можно оценить эффекты ингибирования, которые могут играть важную роль в процессе CVI, поскольку такие виды ингибиторов могут сильно ограничивать скорость осаждения внутри преформы и приводить к заметным градиентам инфильтрации. 30-32,39,247-250 в атмосферном давлении CVD от CH 3 3 SICL 3 — H 2 , добавление HCL может привести к внезапному переходу к чистому росту пироарбона; уменьшение количества HCl позволяет вернуться к росту SiC с явным гистерезисом. 251 Влияние гистерезисной химии на многослойное осаждение также теоретически обсуждалось в случае пироуглеродного осаждения. 252
251 Влияние гистерезисной химии на многослойное осаждение также теоретически обсуждалось в случае пироуглеродного осаждения. 252
Чтобы лучше понять этапы гомогенной реакции перед осаждением, можно проанализировать газовую фазу, окружающую подложку. Действительно анализы in situ при высоких температурах очень трудно выполнить. Несколько экспериментальных исследований с помощью FTIR-спектроскопии можно упомянуть в случаях осаждения SiC и PyC . 18,253
Более популярные анализы выполняются на выходе из горячей зоны: в случае углеводородов/ H 2 систем часто используется газофазная хроматография; 30–33,42,230–232,254 Характеристики тяжелых молекул MALDI-ToF 45 дали интересную дополнительную информацию о текстурном переходе в зависимости от экспериментальных параметров. 28 ИК-Фурье-спектроскопия также использовалась, сначала по всему реактору, с усреднением по верхней, горячей и нижней зонам, 18 , затем только на выходе в случае B – C – Cl – H система. 240
240
Влияние смешивания, скоростей реакций и стехиометрии на выход чувствительных реакций смешивания — Часть I: Разработка модели
Существует два класса чувствительных к смешиванию реакций: конкурентно-последовательные и конкурентно-параллельные.Выход желаемого продукта из этих сопряженных реакций зависит от того, насколько быстро реагенты объединяются. Недавние экспериментальные результаты показали, что эффект смешивания может сильно зависеть от стехиометрии реакций. Чтобы исследовать это, была разработана одномерная безразмерная модель реакции-диффузии в масштабе микроперемешивания. Предполагая постоянную массовую концентрацию и массовую диффузию, системы PDE были получены на основе массовой доли для обоих типов реакций. В результате анализа были получены два безразмерных отношения скоростей реакций и одно общее число Дамкелера.Полученные безразмерные уравнения были использованы для исследования влияния перемешивания, отношения скоростей реакции и стехиометрии реакции. Как и ожидалось, уменьшение либо толщины страты, либо безразмерного соотношения скоростей максимизирует выход, стехиометрия реакции оказывает значительное влияние на выход, и все три переменные сильно взаимодействуют.
Как и ожидалось, уменьшение либо толщины страты, либо безразмерного соотношения скоростей максимизирует выход, стехиометрия реакции оказывает значительное влияние на выход, и все три переменные сильно взаимодействуют.
1. Введение
Смешивание и кажущаяся скорость реакции неразрывно связаны: реакции с участием нескольких реагентов не могут происходить без тесного контакта реагентов на молекулярном уровне.В реакторе реагенты добавляются в макро- или мезомасштабе. Чтобы реакция произошла, чистые реагенты должны быть гомогенизированы на молекулярном уровне, чтобы молекулы могли столкнуться. Если смешивание происходит достаточно быстро, внутренняя химическая кинетика определяет скорость образования новых видов. Это требует уменьшения масштаба и различий в концентрации, что является самим определением смешивания, поскольку оно относится к химическим реакциям.
В двух известных классах реакций ход реакции в значительной степени зависит от того, насколько быстро реагенты объединяются. Эти реакции состоят из двух или более конкурирующих реакций, протекающих либо параллельно, когда две или более реакций с участием одних и тех же реагентов протекают одновременно, либо в последовательной последовательности, когда желаемый продукт одной из реакций участвует во второй нежелательной реакции. реакция с исходными реагентами. Оба типа схем реакции могут включать значительное образование нежелательных побочных продуктов, несмотря на то, что желаемая реакция протекает в миллион раз быстрее, чем нежелательная реакция.
Эти реакции состоят из двух или более конкурирующих реакций, протекающих либо параллельно, когда две или более реакций с участием одних и тех же реагентов протекают одновременно, либо в последовательной последовательности, когда желаемый продукт одной из реакций участвует во второй нежелательной реакции. реакция с исходными реагентами. Оба типа схем реакции могут включать значительное образование нежелательных побочных продуктов, несмотря на то, что желаемая реакция протекает в миллион раз быстрее, чем нежелательная реакция.
Типичные представления этих схем реакции приведены в таблице 1. В обоих случаях , является желаемым продуктом, а является нежелательным побочным продуктом. Поэтому для совершенно гомогенной смеси реагентов, находящихся в стехиометрическом соотношении один (), выход побочного продукта должен быть очень мал. Хорошо известно (Балдыга и Борн [1], Паттерсон и др. [2]), что выход побочного продукта действительно может быть весьма значительным: эффект, который возникает из-за несовершенного перемешивания. Эти классические стехиометрии широко изучались (Балдыга и Борн [1, 3], Балдыга и др.[4], Кокс и соавт. [5], Клиффорд и соавт. [6], Cox [7] и Patterson et al. [2]). Основной целью данной статьи является изучение влияния различной общей стехиометрии реакции на выход желаемого продукта и ограничения диффузионного массопереноса, связанные с этим различием.
Эти классические стехиометрии широко изучались (Балдыга и Борн [1, 3], Балдыга и др.[4], Кокс и соавт. [5], Клиффорд и соавт. [6], Cox [7] и Patterson et al. [2]). Основной целью данной статьи является изучение влияния различной общей стехиометрии реакции на выход желаемого продукта и ограничения диффузионного массопереноса, связанные с этим различием.
| ||||||||||||
Число Дамкелера — это безразмерное число, используемое для приведения скорости смешивания к скорости реакции для любой конкретной реакции, чувствительной к смешиванию.Существует несколько форм числа Дамкелера, при этом смешивающее число Дамкелера (Da) определяется формулой (Паттерсон и др.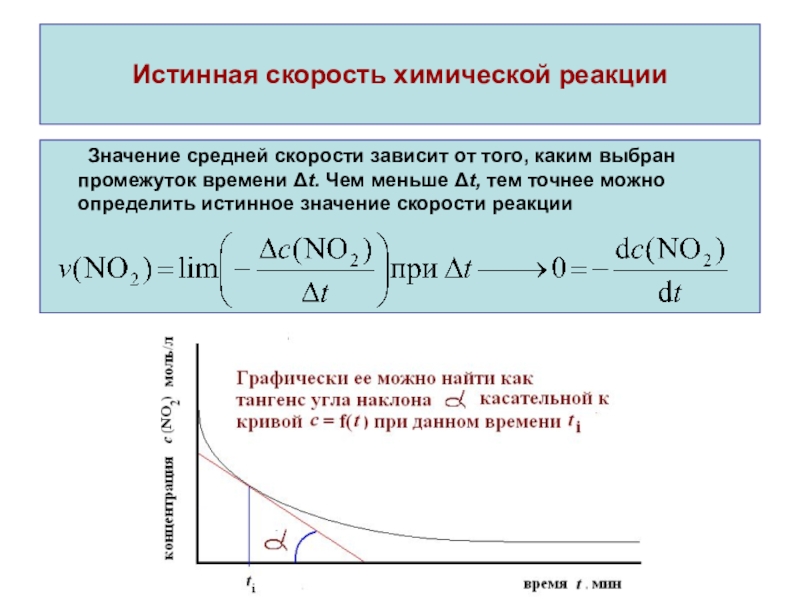 [2]):
где – характерное время перемешивания, – характерное время реакции. Академические и промышленные сообщества предложили несколько определений , , и Da применительно к проблеме реагирующего потока, и некоторые из этих усилий суммированы в следующих разделах.
[2]):
где – характерное время перемешивания, – характерное время реакции. Академические и промышленные сообщества предложили несколько определений , , и Da применительно к проблеме реагирующего потока, и некоторые из этих усилий суммированы в следующих разделах.
2. Обзор литературы
Обзор литературы построен следующим образом.Во-первых, представлен обзор литературы по химической технологии, в которой основное внимание уделяется схемам конкурентно-последовательных и конкурентно-параллельных реакций. Затем следует обзор литературы по динамике нелинейных реакций, в которой основное внимание уделяется тем же схемам реакций, но с точки зрения прикладной математики.
2.1. Модели смешивания
Исследования выхода гомогенных реакций проводились инженерами-химиками в течение достаточно долгого времени, начиная с Данквертса [8, 9] и Левеншпиля [10], которые предоставили аналитические решения для выхода любой реакции при условии, что она идеально смешана.Поскольку идеальное мгновенное смешивание практически невозможно реализовать на практике, также был проведен ряд исследований влияния несовершенного смешивания на конечный выход желаемого продукта (например, Паттерсон и др. [2], Балдыга и Борн [1, 3], Балдыга и др. [4] и Бхаттачарья [11]).
[2], Балдыга и Борн [1, 3], Балдыга и др. [4] и Бхаттачарья [11]).
В тонкой химической промышленности реакции часто проводятся в полупериодических мешалках. Перемешивание и турбулентность очень тесно связаны между собой, и на скорость перемешивания большое влияние оказывает интенсивность турбулентности внутри резервуара, которая может варьироваться на порядки в разных частях резервуара.Максимальная интенсивность обычно приходится на крыльчатку, а минимальная — в основном в объеме резервуара. Следовательно, для большинства реакций, чувствительных к смешиванию, реагенты впрыскиваются в рабочее колесо.
С более теоретической стороны основное внимание уделяется простой геометрии с лагранжевыми моделями микроперемешивания Балдыги, Борна и других (Балдыга и Похорецкий [12], Балдыга и Борн [1] и Виллермо и Фальк [13] ). Они очень недороги в вычислительном отношении и в некоторых случаях имеют аналитические решения.Модели микроперемешивания эволюционировали от ранних чередующихся полос реагентов до модели поглощения (Балдыга и Борн [1]), которая широко считается лучшей доступной в настоящее время моделью микроперемешивания. Масштабы этих моделей обычно находятся на уровне или ниже колмогоровского масштаба турбулентных вихрей, поэтому предполагается, что они не зависят от крупномасштабной механики жидкости. Обобщенная модель смешения, предложенная Виллермо и Фальком [13], представляет собой аналогичную модель, расширенную для учета эффектов мезосмешивания.
Масштабы этих моделей обычно находятся на уровне или ниже колмогоровского масштаба турбулентных вихрей, поэтому предполагается, что они не зависят от крупномасштабной механики жидкости. Обобщенная модель смешения, предложенная Виллермо и Фальком [13], представляет собой аналогичную модель, расширенную для учета эффектов мезосмешивания.
Также были попытки интегрировать вычислительную гидродинамику (CFD) с моделями микросмешивания. Фокс [14, 15] объединил Обобщенную модель перемешивания Виллермо и Фалька [13] и CFD для моделирования турбулентного перемешивания. Muzzio и Liu [16] использовали аналогичный подход, объединив модель микросмешивания и CFD для ламинарного смешивания.
Задача реагирующего потока для множественных конкурирующих реакций также привлекла внимание физиков и математиков, поскольку она демонстрирует интересное нелинейное поведение.Краткое изложение их усилий дано в следующем разделе.
2.2. Обзор литературы по динамике нелинейных реакций
Реакция CC представляет интересную нелинейную проблему, которая широко исследовалась физиками и математиками хаоса, такими как Кокс, Клиффорд и другие (Клиффорд [17], Клиффорд и Кокс [18] , Клиффорд и др. [6, 19–21], Кокс [7] и Кокс и др. [5]). Схема реакции CP представляла меньший интерес для сообщества математиков и физиков, и с ней связано меньшее количество работ (Hecht and Taitelbaum [22], Sinder [23], Sinder et al.[24] и Taitelbaum et al. [25]).
[6, 19–21], Кокс [7] и Кокс и др. [5]). Схема реакции CP представляла меньший интерес для сообщества математиков и физиков, и с ней связано меньшее количество работ (Hecht and Taitelbaum [22], Sinder [23], Sinder et al.[24] и Taitelbaum et al. [25]).
Реакции, чувствительные к смешиванию, демонстрируют интересное поведение на границе раздела реагентов. Есть несколько исследований, изучающих это поведение для реакций. Корнелл и Дроз [26] являются примером такого исследования, где исследовалось поведение фронта реакции для общей одностадийной реакции . Кокс и др. [5], а позже Кокс и Финн [27] подробно исследовали поверхность раздела для классической реакции CC. Они предоставили цифры и аналитические выражения для профилей каждого вида на поверхности реакции с использованием модели, состоящей из чередующихся одномерных полос реагентов различной толщины.Полосы имели одинаковые начальные концентрации, для которых они написали дифференциальные уравнения в частных производных (PDE) мольного баланса для каждого из видов, участвующих в реакции.
В длительных исследованиях Cox et al. [5] сначала начали со стационарных и сегрегированных полос чередующихся реагентов, то есть «полос зебры», с однородными начальными концентрациями реагентов по всей полосе. Они выполнили молярный баланс и вывели уравнения в молярных концентрациях. Их уравнения были обезразмерены с использованием константы скорости и концентраций, а толщина страты была исключена.Их безразмерные уравнения:
где и — размерное и безразмерное время, пространство и концентрация для видов соответственно. — константа скорости желаемой реакции, — начальная концентрация лимитирующего реагента, — коэффициент диффузии, который считался одинаковым для всех четырех участвующих частиц. Это эквивалентно таблице 1. Они использовали страты разной толщины в пределах одного и того же домена, поэтому толщину страты нельзя было использовать в качестве безразмерного параметра.Поскольку они рассмотрели только один тип стехиометрии, их выражения скорости являются постоянными и являются очевидным выбором для обезразмеривания.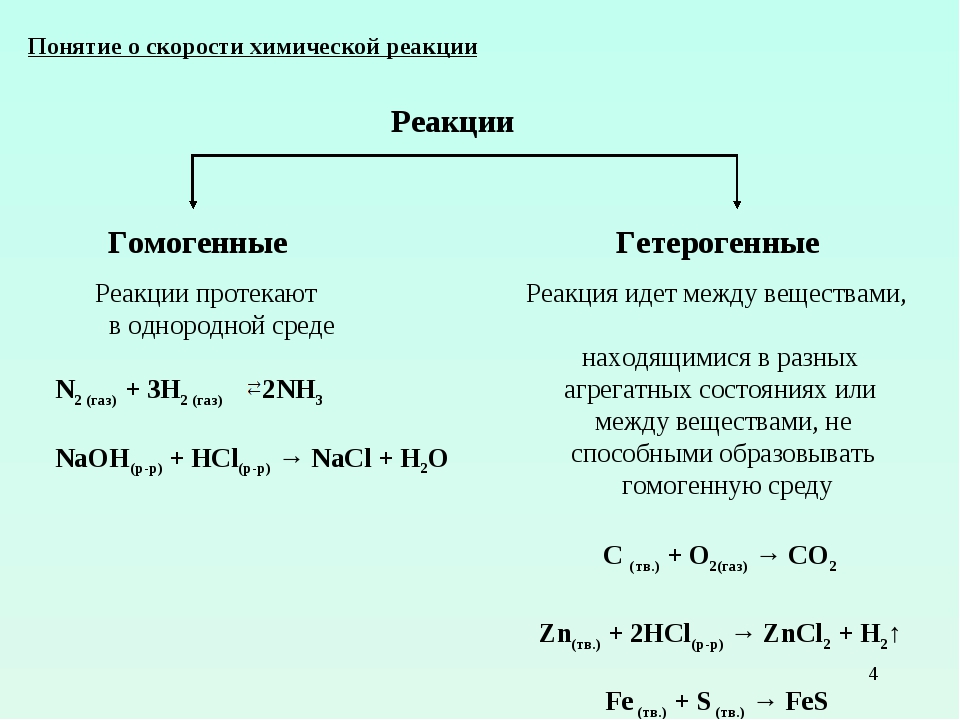
Первоначально они рассмотрели модель, которая имела единую толщину страты первоначально разделенных реагентов (Кокс и др. [5]). Они исследовали влияние начального масштаба сегрегации, то есть толщины полос, и отношения скоростей реакции для классической схемы конкурентных последовательных реакций. Они обнаружили, что уменьшение масштаба сегрегации, то есть толщины полос и соотношения скоростей реакции (), было благоприятным.Формулировки числа Дамкелера и соотношения скоростей реакции, которые они нашли, были следующими:
где представляет собой начальную толщину страты реагентов, представляет собой скорость реакции желаемой реакции, представляет собой молярную концентрацию, представляет собой коэффициент диффузии и представляет собой отношение скоростей реакции. Используя эту модель, они исследовали выход полосок зебры одинаковой толщины (Клиффорд и др. [6]) и подтвердили, что уменьшение масштаба сегрегации может иметь значительное положительное влияние на выход желаемого продукта.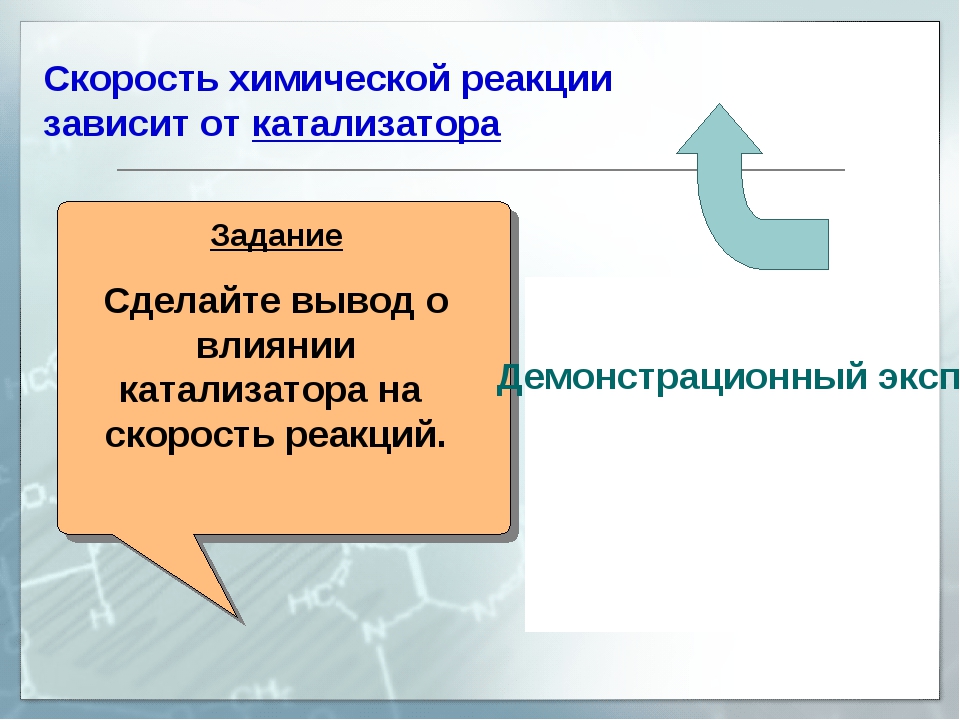 Они также включили параметр, позволяющий учитывать нестехиометрические начальные концентрации реагентов, и довольно широко исследовали влияние наличия более , менее и стехиометрической смеси. Они также обнаружили, что если начальное соотношение реагентов () меньше 1, выход будет равен нулю, и только если начальное соотношение выше 1, может быть значительный выход желаемого продукта.
Они также включили параметр, позволяющий учитывать нестехиометрические начальные концентрации реагентов, и довольно широко исследовали влияние наличия более , менее и стехиометрической смеси. Они также обнаружили, что если начальное соотношение реагентов () меньше 1, выход будет равен нулю, и только если начальное соотношение выше 1, может быть значительный выход желаемого продукта.
Клиффорд [17] и Клиффорд и Кокс [18] развили модель постоянной толщины страты, предполагая более реалистичное гауссово распределение концентрации реагентов внутри страты.Они сравнили полные дифференциальные уравнения в частных производных (PDE) модели Гаусса с моделью однородной концентрации и моделью обыкновенного дифференциального уравнения (ODE). Было обнаружено, что модель с однородной концентрацией дает завышенный прогноз выхода, а модель ODE довольно хорошо согласуется с результатами полного раствора PDE. Это было своего рода отклонением от остальной литературы по этому вопросу, но дает интересный взгляд на проблему.
Следующим шагом, который предприняли Клиффорд, Кокс и Робертс, было введение в модель нескольких начальных толщин борозд, так называемой модели «штрих-кода» (Clifford et al.[20, 21]). Это дает более точное представление о распределении полос в ситуации хаотического перемешивания. Они варьировали общее количество и расположение бороздок и обнаружили, что группировка бороздок одинакового размера вместе максимизирует выход желаемого продукта. Использование средней толщины бороздки для системы дало завышенный прогноз выхода для небольшой выборки, но увеличение количества борозд в модели приблизило два значения друг к другу.
Клиффорд и др. В работе [20] исследовано влияние расположения страт чередующихся реагентов ( и ) различной толщины на выход.Расположение было выбрано таким образом, чтобы ширина чередующихся реагентов была положительно коррелирована, отрицательно коррелирована или размещена случайным образом. Из-за больших вычислительных требований они применили метод Гаусса, разработанный Клиффордом [17]. Они обнаружили, что положительная корреляция между толщинами бороздок, то есть сгруппированных вместе бороздок одинаковой толщины, обеспечивает самый высокий выход желаемого продукта для промежуточных периодов времени, но что существует пересечение на больших временах, когда на самом деле случайное расположение обеспечивает наибольший конечный выход целевого продукта.Случай с отрицательной корреляцией, то есть чередование «толстых» и «тонких» полос, давал наихудший выход. Последним шагом в поисках моделирования реальности Клиффорда, Кокса и Робертса было включение параметра растяжения, чтобы преобразовать модель реакции-диффузии в модель реакции-диффузии-адвекции (Клиффорд и др. [19]). Кокс резюмирует эти попытки свести поле хаотического смешения к одномерной модели, двумерной модели и другим сокращенным моделям, включая различные модели хаотического смешения, такие как модель карты Бейкера для моделирования растяжения и складывания в [7].Он обнаружил, что выход желаемого продукта в реакции CC недооценивается одномерной ламеллярной моделью, которая игнорирует эффекты перемешивания жидкости, но переоценивается двумя другими ламеллярными моделями (непрерывное растяжение и дискретное растяжение и складывание (карта Бейкера)), которые включают перемешивание жидкости.
Они обнаружили, что положительная корреляция между толщинами бороздок, то есть сгруппированных вместе бороздок одинаковой толщины, обеспечивает самый высокий выход желаемого продукта для промежуточных периодов времени, но что существует пересечение на больших временах, когда на самом деле случайное расположение обеспечивает наибольший конечный выход целевого продукта.Случай с отрицательной корреляцией, то есть чередование «толстых» и «тонких» полос, давал наихудший выход. Последним шагом в поисках моделирования реальности Клиффорда, Кокса и Робертса было включение параметра растяжения, чтобы преобразовать модель реакции-диффузии в модель реакции-диффузии-адвекции (Клиффорд и др. [19]). Кокс резюмирует эти попытки свести поле хаотического смешения к одномерной модели, двумерной модели и другим сокращенным моделям, включая различные модели хаотического смешения, такие как модель карты Бейкера для моделирования растяжения и складывания в [7].Он обнаружил, что выход желаемого продукта в реакции CC недооценивается одномерной ламеллярной моделью, которая игнорирует эффекты перемешивания жидкости, но переоценивается двумя другими ламеллярными моделями (непрерывное растяжение и дискретное растяжение и складывание (карта Бейкера)), которые включают перемешивание жидкости.
Вся эта работа была выполнена для схемы реакции C-C и классической стехиометрии. Схема реакции CP имеет значительно меньший объем работ, при этом большинство публикаций сосредоточено на поведении фронта реакции (Taitelbaum et al.[25], Синдер [23], Синдер и др. [24] и Хехта и Тайтельбаума [22]) и классической стехиометрии.
Число Дамкелера для классической реакции CC было предложено Cox et al. [5], но нет такого предложения для схемы реакции C-C с общей стехиометрией. Аналогичное отсутствие определения для схемы реакции CP.
2.3. Соотношение скоростей смешивания и реакции
Идеальное смешивание для реакций определяется как мгновенное восстановление до однородного поля концентрации.Это также соответствует идеально микроперемешанному условию смешивания (Левеншпиль [10]). Хорошее перемешивание быстро приближается к идеально гомогенному состоянию и, следовательно, приближается к максимальному выходу желаемого продукта.
На другом конце спектра находится полная сегрегация реагентов без диффузии и с минимальной площадью поверхности для контакта. В этом случае реакция может протекать только на границе раздела, а затем полностью останавливается, поэтому выход целевого продукта сводится к минимуму. В отсутствие диффузии единственный способ увеличить выход — увеличить площадь контакта между реагентами, и в этом случае степень реакции полностью зависит от масштаба сегрегации.Ситуация значительно улучшается с введением диффузии, потому что тогда реагентам, удаленным от интерфейсов, предоставляется доступ друг к другу. Диффузия является конечным агентом смешивания в мельчайших масштабах сегрегации. Когда масштаб сегрегации варьируется путем регулирования начальной толщины бороздки реагентов, предел идеального смешения — это случай, когда толщина бороздки стремится к нулю, а предел идеальной сегрегации возникает, когда имеется только одна граница раздела.
В этом случае реакция может протекать только на границе раздела, а затем полностью останавливается, поэтому выход целевого продукта сводится к минимуму. В отсутствие диффузии единственный способ увеличить выход — увеличить площадь контакта между реагентами, и в этом случае степень реакции полностью зависит от масштаба сегрегации.Ситуация значительно улучшается с введением диффузии, потому что тогда реагентам, удаленным от интерфейсов, предоставляется доступ друг к другу. Диффузия является конечным агентом смешивания в мельчайших масштабах сегрегации. Когда масштаб сегрегации варьируется путем регулирования начальной толщины бороздки реагентов, предел идеального смешения — это случай, когда толщина бороздки стремится к нулю, а предел идеальной сегрегации возникает, когда имеется только одна граница раздела.
Вторым аспектом модели является кинетика реакции.Чем быстрее идет желаемая реакция по сравнению с нежелательной реакцией, тем больше будет конечный выход желаемого продукта (Левеншпиль [10] и Фоглер [28]). Поскольку цель состоит в том, чтобы максимизировать выход желаемого продукта, очень маленькое значение является благоприятным, а очень большое нежелательным.
Поскольку цель состоит в том, чтобы максимизировать выход желаемого продукта, очень маленькое значение является благоприятным, а очень большое нежелательным.
Целью данной статьи является предоставление некоторой информации специалистам-химикам, занимающимся проектированием реактора для ранее неисследованной реакции, чувствительной к смешению. Прогнозирование выхода для чувствительных к смешению реакций было особенно сложным, как описано в , глава 13, Справочника по промышленному смешиванию [2], в основном из-за отсутствия информации о схемах реакций, соотношениях скоростей реакций, требованиях к смешиванию. , и так далее.Большая часть работы по смешиванию чувствительных реакций предназначена для конкретных известных реакций, поэтому результаты нельзя напрямую перенести на новую реакцию, и любая общая обработка была ограничена конкретными стехиометриями, все с коэффициентами, равными единице. Конструкции, включающие более сложные реакции, часто основаны на опыте, пробах и ошибках или на обширных испытаниях в пилотном масштабе.
С более теоретической точки зрения было немало споров о формулировке числа Дамкелера для двухстадийных реакций: следует ли использовать скорость первой реакции, второй реакции или реакции, для которой информация доступна? Каково подходящее время смешивания? Как только будет определено стандартное число Дамкелера, станет возможным разработать структуру, на основе которой можно будет создавать диаграммы или цифры, прогнозирующие выход для чувствительных к смешению реакций, что облегчит практикующему инженеру-химику работу со сложными реакционными системами, включающими множество взаимодействующих параметров. .Даже если модель не служит для точного предсказания выхода, она, по крайней мере, послужит основой для анализа новых схем реакций. Эта статья улучшит понимание требований к конструкции реакторов для смешивания чувствительных реакций путем уточнения доминирующих переменных и взаимодействий между ними.
В оставшейся части этой статьи представлен вывод модели влияния начальных условий смешивания, отношения скоростей реакции и стехиометрии на два типа реакций, чувствительных к смешиванию: конкурентно-последовательная (CC) реакция и конкурентно-параллельная (CP) реакция. реакция.
реакция.
Основные результаты: (1) Разработка модели с общим числом Дамкелера для любой чувствительной к смешиванию реакции с переменной стехиометрией. (2) Инструменты, которые позволяют исследовать влияние стехиометрии, смешивания и относительных скоростей реакции на конечный выход желаемого продукта для смешивания чувствительных реакций обоих типов: CC и CP. (3) Моделирование переходного поведения интерфейса реакции для коротких и длинных времен.
3. Модель и основные уравнения
Разработанная модель основана на идеализированной одномерной геометрии первоначально чередующихся слоев реагентов в масштабе микроперемешивания с поперечным сечением, как показано на рисунке 1(а).На рис. 1(b) изображен изолированный сегмент общей структуры вблизи , который расположен на границе между общими смесями реагентов и , тем самым создавая интересующую область, ограниченную симметричными границами нулевого потока в срединных плоскостях. этих слоев. В этой формулировке смеси и могут принимать различные составы частиц в зависимости от рассматриваемой схемы реакции и заданной стехиометрии. На рис. 1(в) показана геометрия для частного случая чистых страт и .
На рис. 1(в) показана геометрия для частного случая чистых страт и .
Система безразмерных реактивно-диффузионных уравнений в частных производных (УЧП), основанная на балансе масс, была разработана для каждого из компонентов в реакционной системе. Предполагается, что жидкость в системе остается однородной по фазе и имеет постоянную температуру, а также находится в состоянии покоя. С учетом этих допущений общее нестационарное уравнение реакции-диффузии баланса массы одномерных видов имеет вид:
где — массовая концентрация отдельных частиц, — диффузионная способность отдельных частиц по отношению к смеси, и представляет условия источника/поглотителя реакции.и – пространственная и временная координаты соответственно. В модели предполагается, что начальные толщины страт смесей реагентов равны, как показано на рис. 1(б) при . Одна из целей этой модели состоит в том, чтобы позволить исследовать начальные условия смешения, варьируя начальную толщину страты. Пространство () и время () обезразмерены с помощью начальной толщины страты и коэффициента молекулярной диффузии:
Выбор и обезразмеривание уравнений был сделан потому, что далее в этой статье состав слоя должен быть ограничен смесью, содержащей только инертный и/или лимитирующий реагент , который всегда считается лимитирующим реагентом реакция вне зависимости от схемы, эффективно проводящая и , как показано в (5). Свойства лимитирующего реагента использовались для обезразмеривания. Массовые концентрации видов () были преобразованы в массовые доли () с использованием:
Используя (5)-(6) для модификации (4), безразмерное общее уравнение видов для нестационарной одномерной, стационарной, реактивно-диффузионной системы задается следующим образом:
Также применялось допущение о том, что все частицы имеют одинаковую диффузионную способность, поэтому коэффициент эллиптического члена в (7) был равен единице и давал:
Уравнение (8) представляет собой уравнение реакции-диффузии для некоторой произвольной реакции, представленной членом источника/стока .Детали этого термина определяются сами по себе, когда указана схема реакции. Для целей данной статьи схема реакции будет определена как обобщенная конкурентно-последовательная (C-C) или конкурентно-параллельная (C-P) реакция между двумя слоями. Для этих целей предполагалось, что слой состоит из гомогенной смеси лимитирующего реагента , и инертного вещества , а слой состоит либо из одного реагента , либо из двух реагентов и , опять же с примесью инертного вещества в этот слой .
Свойства лимитирующего реагента использовались для обезразмеривания. Массовые концентрации видов () были преобразованы в массовые доли () с использованием:
Используя (5)-(6) для модификации (4), безразмерное общее уравнение видов для нестационарной одномерной, стационарной, реактивно-диффузионной системы задается следующим образом:
Также применялось допущение о том, что все частицы имеют одинаковую диффузионную способность, поэтому коэффициент эллиптического члена в (7) был равен единице и давал:
Уравнение (8) представляет собой уравнение реакции-диффузии для некоторой произвольной реакции, представленной членом источника/стока .Детали этого термина определяются сами по себе, когда указана схема реакции. Для целей данной статьи схема реакции будет определена как обобщенная конкурентно-последовательная (C-C) или конкурентно-параллельная (C-P) реакция между двумя слоями. Для этих целей предполагалось, что слой состоит из гомогенной смеси лимитирующего реагента , и инертного вещества , а слой состоит либо из одного реагента , либо из двух реагентов и , опять же с примесью инертного вещества в этот слой . В таблице 2 показаны обобщенные схемы реакций для двух типов реакций, чувствительных к смешиванию, которые будут исследованы. Влияние диффузии видов в данной работе не исследовалось.
В таблице 2 показаны обобщенные схемы реакций для двух типов реакций, чувствительных к смешиванию, которые будут исследованы. Влияние диффузии видов в данной работе не исследовалось.
| ||||||||||||
и представляют собой исходные реагенты для схемы СС., и представляют исходные реагенты для схемы CP. является желаемым продуктом и нежелательным продуктом для обеих схем реакции. Инертный , также присутствует, но в реакции не участвует. и представляют собой константы скоростей желаемой и нежелательной реакций соответственно, а , , , – стехиометрические коэффициенты.
Если предположить, что реакции элементарны, то выражения для можно записать априори в виде выражений для молярных скоростей. Для использования в (8) эти основанные на молях выражения преобразуются в выражения массовой доли с использованием молекулярных масс каждого вида.Чтобы сосредоточить внимание на эффектах стехиометрии, далее предполагалось, что молекулярные массы , , и были идентичными (). Например, исходный термин для видов как для СС, так и для СР определяется следующим образом:
Затем эти выражения массовой доли помещаются в (8). Молекулярные массы и зависят от стехиометрии и рассчитываются по закону действующих масс. Например, молекулярная масса для схемы CP будет:
Выражения для условий источника и стока для всех участвующих видов могут быть записаны так, как показано для видов в (9).Следует отметить, что термины источник/сток содержат всю информацию для интересующей схемы реакции. Условия для других видов значительно различаются для схемы реакции СС и СР. Системы дифференциальных уравнений в частных производных (УЧП) разрабатываются отдельно в следующих подразделах.
Для использования в (8) эти основанные на молях выражения преобразуются в выражения массовой доли с использованием молекулярных масс каждого вида.Чтобы сосредоточить внимание на эффектах стехиометрии, далее предполагалось, что молекулярные массы , , и были идентичными (). Например, исходный термин для видов как для СС, так и для СР определяется следующим образом:
Затем эти выражения массовой доли помещаются в (8). Молекулярные массы и зависят от стехиометрии и рассчитываются по закону действующих масс. Например, молекулярная масса для схемы CP будет:
Выражения для условий источника и стока для всех участвующих видов могут быть записаны так, как показано для видов в (9).Следует отметить, что термины источник/сток содержат всю информацию для интересующей схемы реакции. Условия для других видов значительно различаются для схемы реакции СС и СР. Системы дифференциальных уравнений в частных производных (УЧП) разрабатываются отдельно в следующих подразделах.
3.1. Схема конкурентно-последовательной (C-C) реакции
Схема реакции C-C представляет собой схему реакции, в которой желаемый продукт (), однажды образовавшись, участвует в нежелательной реакции с одним из исходных реагентов (в данном случае ). В реакции принимают участие виды , , и . Желаемый продукт и нежелательный побочный продукт . Общая стехиометрия для этого типа схемы реакции приведена в таблице 2. Выражения источника и поглотителя для , , , и инертного для схемы реакции СС получают по процедуре, аналогичной показанной в (9). После подстановки этих выражений в (8) и упрощения получается следующая система уравнений:
Чтобы сравнить влияние относительных скоростей желаемых и нежелательных реакций при различной стехиометрии реакций, необходимо представить безразмерное выражение для соотношения скоростей желаемых и нежелательных реакций.Использование соотношения недостаточно, так как это соотношение будет иметь разные размеры для каждой стехиометрии реакции, что затрудняет сравнение. Идеальное безразмерное отношение должно давать относительные скорости желаемой реакции к нежелательной реакции, сохраняя при этом физический смысл, который можно понять интуитивно. Это может быть достигнуто путем сравнения скоростей массового превращения, связанных с первой и второй реакциями.
В реакции принимают участие виды , , и . Желаемый продукт и нежелательный побочный продукт . Общая стехиометрия для этого типа схемы реакции приведена в таблице 2. Выражения источника и поглотителя для , , , и инертного для схемы реакции СС получают по процедуре, аналогичной показанной в (9). После подстановки этих выражений в (8) и упрощения получается следующая система уравнений:
Чтобы сравнить влияние относительных скоростей желаемых и нежелательных реакций при различной стехиометрии реакций, необходимо представить безразмерное выражение для соотношения скоростей желаемых и нежелательных реакций.Использование соотношения недостаточно, так как это соотношение будет иметь разные размеры для каждой стехиометрии реакции, что затрудняет сравнение. Идеальное безразмерное отношение должно давать относительные скорости желаемой реакции к нежелательной реакции, сохраняя при этом физический смысл, который можно понять интуитивно. Это может быть достигнуто путем сравнения скоростей массового превращения, связанных с первой и второй реакциями. Для схемы С-С это было сделано путем сравнения массовой скорости потребления целевого продукта во второй реакции с массовой скоростью образования в первой реакции:
Цель состоит в том, чтобы сделать это соотношение как можно меньше, чтобы максимизировать объем производства.Используя выражения для массовой скорости вместо утверждений в (12) и затем упрощая полученное выражение, безразмерное отношение скоростей реакции для общей схемы реакции C-C становится следующим:
Это физически значимое улавливает как влияние стехиометрии, так и влияние констант скорости двух реакций, а также имеет преимущество значительного упрощения (11), чтобы дать:
Изучение (14) показывает, что существует выражение, общее для всех четырех уравнений, включающих реакции, которое принимает форму числа Дамкелера (Da), определяемого как:
Этот Da зависит от константы скорости желаемой реакции и начальной толщины страты реагентов.Он масштабирует скорость диффузии при наименьшем масштабе смешивания с желаемой скоростью реакции.
Для схемы С-С это было сделано путем сравнения массовой скорости потребления целевого продукта во второй реакции с массовой скоростью образования в первой реакции:
Цель состоит в том, чтобы сделать это соотношение как можно меньше, чтобы максимизировать объем производства.Используя выражения для массовой скорости вместо утверждений в (12) и затем упрощая полученное выражение, безразмерное отношение скоростей реакции для общей схемы реакции C-C становится следующим:
Это физически значимое улавливает как влияние стехиометрии, так и влияние констант скорости двух реакций, а также имеет преимущество значительного упрощения (11), чтобы дать:
Изучение (14) показывает, что существует выражение, общее для всех четырех уравнений, включающих реакции, которое принимает форму числа Дамкелера (Da), определяемого как:
Этот Da зависит от константы скорости желаемой реакции и начальной толщины страты реагентов.Он масштабирует скорость диффузии при наименьшем масштабе смешивания с желаемой скоростью реакции. Влияние второй скорости реакции учитывается через отношение скоростей . Глядя на (15), малое число Дамкелера указывает на то, что диффузия в наименьшей бороздке происходит быстрее по сравнению с желаемой/быстрой реакцией, а большое число Дамкелера указывает на то, что диффузия идет медленно по сравнению с быстрой реакцией. Ожидается, что небольшой Da даст высокий урожай.
Влияние второй скорости реакции учитывается через отношение скоростей . Глядя на (15), малое число Дамкелера указывает на то, что диффузия в наименьшей бороздке происходит быстрее по сравнению с желаемой/быстрой реакцией, а большое число Дамкелера указывает на то, что диффузия идет медленно по сравнению с быстрой реакцией. Ожидается, что небольшой Da даст высокий урожай.
Формулировки числа Дамкелера и безразмерного отношения скоростей реакции для классической схемы реакции C-C, полученные Кохом и др. [5], получены из наших общих форм числа Дамкелера (15) и безразмерного отношения скоростей реакций (13).Установка , , и равными 1 дает классическую схему реакции СС. Коэффициент 0,5 появляется в соотношении, потому что мы использовали массовый баланс при выводе уравнений, а Кокс и др. использовал моль баланса.
Подстановка (15) в (14) дает окончательный набор уравнений:
Используя (16), можно исследовать влияние скоростей реакций и толщины полос на реакции С-С, используя безразмерное отношение скоростей реакций () и число Дамкелера (Da).
3.2. Схема конкурентно-параллельной (КП) реакции
В схеме реакции КП один из исходных реагентов (в данном случае ) участвует в двух реакциях одновременно. Общая стехиометрия для этого типа реакции показана в таблице 2. Условия источника и стока для , , , , и инертных для схемы реакции CP были разработаны в соответствии с той же процедурой, что и для схемы реакции CC выше, а затем заменены в (8) получить набор УЧП для схемы реакции СР.
Как и в схеме реакции C-C, переменная стехиометрия требует введения физически значимого безразмерного соотношения скоростей реакции для схемы C-P.Поскольку в схеме реакции КП имеется только один реагент (), участвующий в обеих реакциях, безразмерное соотношение скоростей реакции для схемы КП принимает вид:
что при подстановке скоростных выражений можно записать в виде:
Как и в случае отношения, определенного для схемы реакции C-C, минимизация этого отношения приведет к максимальному желаемому продукту (). Это также включает влияние стехиометрии и констант скорости реакции для двух реакций. Подстановка (18) в УЧП CP и упрощение дает то же число Дамкелера, которое появилось в уравнениях реакции CC, что дает уравнения CP для численного моделирования:
Эта формулировка как для схем СС, так и для схем СР позволяет использовать одно число Дамкелера для описания смешивания относительно желаемой скорости реакции. Он также обеспечивает физически значимое безразмерное отношение скоростей реакции для описания относительных скоростей реакции. Хотя нет явного выражения для влияния стехиометрии, обе безразмерные меры включают стехиометрические коэффициенты, показывающие, что стехиометрия схемы реакции влияет как на перемешивание, так и на относительную скорость реакции.
Подстановка (18) в УЧП CP и упрощение дает то же число Дамкелера, которое появилось в уравнениях реакции CC, что дает уравнения CP для численного моделирования:
Эта формулировка как для схем СС, так и для схем СР позволяет использовать одно число Дамкелера для описания смешивания относительно желаемой скорости реакции. Он также обеспечивает физически значимое безразмерное отношение скоростей реакции для описания относительных скоростей реакции. Хотя нет явного выражения для влияния стехиометрии, обе безразмерные меры включают стехиометрические коэффициенты, показывающие, что стехиометрия схемы реакции влияет как на перемешивание, так и на относительную скорость реакции.
4. Численное решение уравнений
Две системы уравнений для схем реакции C-C (16) и C-P (19) были решены с помощью COMSOL Multi-physics 3.4, коммерческого решателя дифференциальных уравнений методом конечных элементов. Была использована одномерная переходная модель конвекции и диффузионного массопереноса с массовыми долями для каждого вида, указанными как независимые переменные. Элементы задавались как квадратичные по Лагранжу. Одномерная геометрическая линия единичной длины поровну разделена на две области ( и ), и была сгенерирована сетка из 2048 равноотстоящих друг от друга элементов.Граничные условия (ГУ) для всех случаев задавались как
Общие начальные условия для двух схем реакции показаны в таблице 3. Начальные условия были выбраны для воспроизведения условия сегрегации модели.
Элементы задавались как квадратичные по Лагранжу. Одномерная геометрическая линия единичной длины поровну разделена на две области ( и ), и была сгенерирована сетка из 2048 равноотстоящих друг от друга элементов.Граничные условия (ГУ) для всех случаев задавались как
Общие начальные условия для двух схем реакции показаны в таблице 3. Начальные условия были выбраны для воспроизведения условия сегрегации модели.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Последнее ограничение, налагаемое на моделирование, заключается в том, что реагенты должны присутствовать в стехиометрических количествах. Используя это ограничение, можно выразить начальные массовые доли как функцию исходной массовой доли ограничивающего реагента , как показано в таблице 4. Для случая C-C первоначально присутствуют только реагенты и . Следовательно, чередующиеся страты имели бы массовые доли единицы для и единицы для . Однако для случаев CP присутствуют три исходных реагента. В этой модели предполагается, что реагенты и хорошо перемешаны и присутствуют в страте, а лимитирующий реагент находится в страте.Инертным веществам позволяли присутствовать как в полосах, так и в полосах, как это требовалось для поддержания постоянной массовой концентрации в полосах, и предполагалось, что они хорошо перемешаны с другими реагентами. Еще одно условие, указанное для случая CP, состоит в том, что отношения , , и таковы, что либо или могут потреблять все доступные , поэтому всегда является ограничивающим реагентом.
Используя это ограничение, можно выразить начальные массовые доли как функцию исходной массовой доли ограничивающего реагента , как показано в таблице 4. Для случая C-C первоначально присутствуют только реагенты и . Следовательно, чередующиеся страты имели бы массовые доли единицы для и единицы для . Однако для случаев CP присутствуют три исходных реагента. В этой модели предполагается, что реагенты и хорошо перемешаны и присутствуют в страте, а лимитирующий реагент находится в страте.Инертным веществам позволяли присутствовать как в полосах, так и в полосах, как это требовалось для поддержания постоянной массовой концентрации в полосах, и предполагалось, что они хорошо перемешаны с другими реагентами. Еще одно условие, указанное для случая CP, состоит в том, что отношения , , и таковы, что либо или могут потреблять все доступные , поэтому всегда является ограничивающим реагентом.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Моделирование обеих схем реакции проводилось до эквивалента в случае Da = 1. Поскольку симуляции решаются во времени, безразмерные времена, до которых выполнялись симуляции, были масштабированы в соответствии с числом Дамкелера. Следовательно, = 500 при равно при и при , т. е. значения равны для всех случаев. Фактически эквивалентно безразмерному времени реакции, где . Таким образом, запуск симуляций до аналогичен запуску симуляций для 500 раз реакции. Все эти безразмерные времена на самом деле равны в реальном времени. В большинстве случаев было замечено, что весь ограничивающий реагент расходуется или эквивалентен.COMSOL вернул профили массовой доли различных видов в безразмерном пространстве для каждого безразмерного временного шага.
Поскольку симуляции решаются во времени, безразмерные времена, до которых выполнялись симуляции, были масштабированы в соответствии с числом Дамкелера. Следовательно, = 500 при равно при и при , т. е. значения равны для всех случаев. Фактически эквивалентно безразмерному времени реакции, где . Таким образом, запуск симуляций до аналогичен запуску симуляций для 500 раз реакции. Все эти безразмерные времена на самом деле равны в реальном времени. В большинстве случаев было замечено, что весь ограничивающий реагент расходуется или эквивалентен.COMSOL вернул профили массовой доли различных видов в безразмерном пространстве для каждого безразмерного временного шага.
5. Результаты и обсуждение
Результаты и обсуждение представлены следующим образом. Во-первых, представлена и обсуждена временная эволюция видовых профилей в отдельных полосах для конкурентно-последовательных и конкурентно-параллельных реакций. Это обсуждение включает в себя влияние, которое смешивание и соотношение скоростей реакции оказывают на профили видов.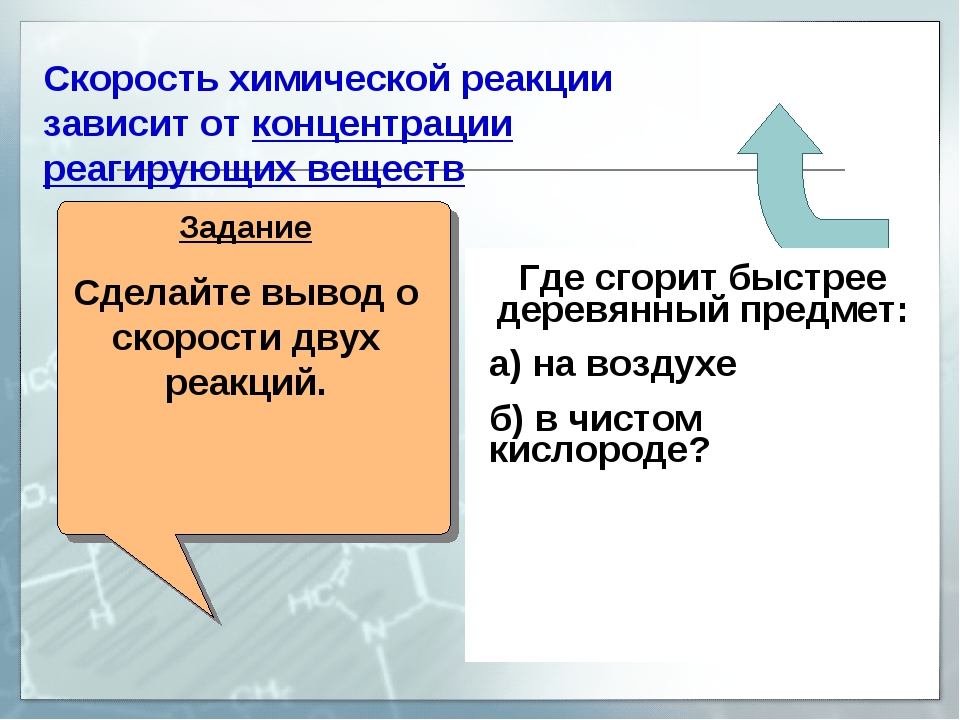 После этого представлено определение выхода целевого продукта и показаны результаты, показывающие изменение выхода целевого продукта во времени для обеих схем реакции. Затем следует обсуждение влияния смешения и соотношения скоростей реакции на выход целевого продукта для обеих схем реакции.
После этого представлено определение выхода целевого продукта и показаны результаты, показывающие изменение выхода целевого продукта во времени для обеих схем реакции. Затем следует обсуждение влияния смешения и соотношения скоростей реакции на выход целевого продукта для обеих схем реакции.
5.1. Конкурентно-последовательная (CC) реакция
Для проверки модели реакции CC значения Da и были присвоены значениям, приведенным в таблице 5. Все стехиометрические коэффициенты были установлены равными 1, чтобы соответствовать классической схеме реакции, используемой Кокс и другие (Muzzio and Liu [16], Clifford et al.[6, 19–21], Клиффорд [17], Клиффорд и Кокс [18] и Кокс [7]). Это позволяет сравнивать результаты по влиянию толщины страты и скорости реакции с их данными. Начальные условия были выбраны такими, чтобы в системе присутствовали только чистые и.
| ||||||||||||||||||||||||
Глядя на случаи CC в таблице 5, значения и Da для случая 1 являются благоприятными условиями для высокого выхода, то есть и . Для случая 4 выход должен быть мал, т.е. Эти два случая предназначены для представления двух крайностей: очень благоприятного соотношения скоростей реакции и идеального перемешивания и очень неблагоприятной кинетики и плохих условий перемешивания. Случаи 2 и 3 имеют хорошее с плохим смешиванием и плохое с хорошим смешиванием. Решения, возвращаемые COMSOL, представляют собой профили массовой доли различных видов в безразмерном пространстве для каждого временного шага. На рис. 2 показана пространственная и временная эволюция видов на одной безразмерной страте.Прежде чем подробно обсуждать профили, важно отметить пару моментов о профилях. Вертикальная линия представляет собой четкую границу раздела. Изогнутая линия представляет собой градиент концентрации. Наконец, горизонтальная линия представляет собой однородную концентрацию по всему пространству.
Для случая 4 выход должен быть мал, т.е. Эти два случая предназначены для представления двух крайностей: очень благоприятного соотношения скоростей реакции и идеального перемешивания и очень неблагоприятной кинетики и плохих условий перемешивания. Случаи 2 и 3 имеют хорошее с плохим смешиванием и плохое с хорошим смешиванием. Решения, возвращаемые COMSOL, представляют собой профили массовой доли различных видов в безразмерном пространстве для каждого временного шага. На рис. 2 показана пространственная и временная эволюция видов на одной безразмерной страте.Прежде чем подробно обсуждать профили, важно отметить пару моментов о профилях. Вертикальная линия представляет собой четкую границу раздела. Изогнутая линия представляет собой градиент концентрации. Наконец, горизонтальная линия представляет собой однородную концентрацию по всему пространству.
Глядя на рисунки 2(a) и 2(c), можно увидеть, что все виды равномерно распределены для всех временных шагов, превышающих . Это не относится к рисункам 2(b) и 2(d). Это можно объяснить меньшими толщинами полос, то есть меньшим числом Дамкелера, для случаев 1 и 3.Поскольку бороздки в этих случаях тоньше, виды могут полностью диффундировать за более короткий промежуток времени, чем в случаях 2 и 4, где бороздки в 100 раз толще. Более толстые полосы учитывают пространственную неоднородность вида. Меньшая толщина штриховок учитывает различия только во временном, а не в пространственном распределении видов. Более толстые полосы вызывают различия как во временном, так и в пространственном распределении. На рисунках 2(b) и 2(d) также показана поверхность раздела между реагентами, тогда как на рисунках 2(a) и 2(c) ее нет.
Это можно объяснить меньшими толщинами полос, то есть меньшим числом Дамкелера, для случаев 1 и 3.Поскольку бороздки в этих случаях тоньше, виды могут полностью диффундировать за более короткий промежуток времени, чем в случаях 2 и 4, где бороздки в 100 раз толще. Более толстые полосы учитывают пространственную неоднородность вида. Меньшая толщина штриховок учитывает различия только во временном, а не в пространственном распределении видов. Более толстые полосы вызывают различия как во временном, так и в пространственном распределении. На рисунках 2(b) и 2(d) также показана поверхность раздела между реагентами, тогда как на рисунках 2(a) и 2(c) ее нет.
Несмотря на то, что в обоих случаях происходит полное смешивание, существует очень большая разница в выходе для этих двух случаев. Для варианта 1, который характеризуется как хорошим перемешиванием, так и благоприятным соотношением скоростей реакции, большая часть присутствующей массы приходится на массу желаемого продукта (рис. 2(a)-(iii)). Однако для случая 3 массовая доля нежелательного продукта всегда выше, чем доля желаемого продукта (рис. 2(c)-(iii)). Наблюдается значительное падение массовой доли от 0.от 99 до 0,25, что свидетельствует о сильном влиянии отношения скоростей реакции при тех же условиях смешивания.
2(a)-(iii)). Однако для случая 3 массовая доля нежелательного продукта всегда выше, чем доля желаемого продукта (рис. 2(c)-(iii)). Наблюдается значительное падение массовой доли от 0.от 99 до 0,25, что свидетельствует о сильном влиянии отношения скоростей реакции при тех же условиях смешивания.
Глядя на рисунки 2(b)-(iii) и 2(d)-(iii), наблюдается такое же обращение и. Соотношение скоростей реакции оказывает сильное влияние на выход желаемого продукта, который не зависит от перемешивания. Когда соотношение скоростей реакции хорошее, нежелательная реакция не участвует. Все продукты формируются на границе раздела и В, делая профиль массовой доли симметричным относительно срединной плоскости, как показано на рисунках 2(b)-(ii) и 2(b)-(iii).Когда нежелательная побочная реакция протекает со скоростью, сравнимой со скоростью желаемой реакции, видна значительная асимметрия в профилях массовой доли для всех видов (рис. 2(d)-(ii) и 2(d)-( III)). Это можно объяснить тем, что вторая реакция происходит только с правой стороны от места контакта с . Это вызывает реакцию формы, когда она подвергается воздействию с одной стороны.
Это вызывает реакцию формы, когда она подвергается воздействию с одной стороны.
Основные результаты заключаются в следующем: во-первых, малая толщина штрихов обеспечивает однородную концентрацию частиц, т. е. идеальное смешивание, в то время как большие штрихи могут вызывать пространственные неоднородности массовой доли частиц.Во-вторых, соотношение скоростей реакции является независимым фактором, который может значительно изменить выход целевого продукта независимо от условий смешивания. Этот эффект предсказуем в том смысле, что если соотношение хорошее, то урожай будет хорошим, а если соотношение плохим, то и урожай будет плохим. Наконец, для больших толщин бороздок хорошее отношение реакции вызывает симметричные профили концентрации желаемого продукта, в то время как плохое соотношение вызывает перекос профилей продукта в сторону бороздок.Идеальное перемешивание упрощает анализ реакции и сокращает время реакции. Благоприятная кинетика значительно повышает урожайность.
Изменение стехиометрии не повлияло на профили видов в случае хорошего соотношения скоростей реакции () как для хороших, так и для плохих условий смешивания. Профили всех видов были идентичны представленным выше. Профили видов для различных стехиометрий с плохим соотношением скоростей реакции () и хорошим перемешиванием выглядят аналогично показанным здесь, но количество и производимые изменения.В случае как плохого соотношения скоростей (), так и плохого смешивания всегда производилось большее количество продукции, чем , и все профили были смещены в сторону . Количество произведенного и варьируется в зависимости от стехиометрии, и профили искажаются в большей или меньшей степени в зависимости от стехиометрии.
Профили всех видов были идентичны представленным выше. Профили видов для различных стехиометрий с плохим соотношением скоростей реакции () и хорошим перемешиванием выглядят аналогично показанным здесь, но количество и производимые изменения.В случае как плохого соотношения скоростей (), так и плохого смешивания всегда производилось большее количество продукции, чем , и все профили были смещены в сторону . Количество произведенного и варьируется в зависимости от стехиометрии, и профили искажаются в большей или меньшей степени в зависимости от стехиометрии.
5.2. Конкурентно-параллельная (C-P) реакция
В таблице 6 показаны переменные настройки для моделирования CP. Четыре случая идентичны случаям, используемым для моделирования CC, за исключением определения .Проиллюстрированная стехиометрия представляет собой классическую схему реакции CP со всеми стехиометрическими коэффициентами, равными 1. Начальные условия были выбраны таким образом, что , а начальные количества , и , присутствующих в системе, были рассчитаны по формулам в Таблице 4. Решения COMSOL возвращает – профили массовой доли различных видов в безразмерном пространстве для каждого временного шага. На рис. 3 показана пространственная и временная эволюция видов, в том числе инертных.
Решения COMSOL возвращает – профили массовой доли различных видов в безразмерном пространстве для каждого временного шага. На рис. 3 показана пространственная и временная эволюция видов, в том числе инертных.
| ||||||||||||||||||||||||
Профили корпусов C-P во многом совпадают с характеристиками корпусов C-C.Случаи 1 и 3 с более тонкими начальными штрихами снова показывают пространственную однородность для всех видов по всей толщине штрихов, тогда как случаи 2 и 4 демонстрируют пространственные вариации массовой доли для всех видов по всей толщине штрихов. Выходы и изменяются при изменении отношения реакции от благоприятного () к неблагоприятному. Случаи 1 и 2 имеют высокий выход ; Случаи 3 и 4 имеют равный выход и . Случаи с большими толщинами штрихов показывают симметрию в профилях массовой доли продукта примерно, когда вторая реакция незначительна () и значительную асимметрию, когда он активно участвует в реакции.Основное различие между реакциями С-С и С-П заключается в том, что после того, как продукт образуется в реакции С-П, он не расходуется побочной реакцией. Следовательно, с точки зрения измерения выхода , схема реакции CP намного менее чувствительна к смешиванию, чем схема реакции СС. Для реакции CC чем дольше он находится в контакте с , тем выше вероятность того, что выход снизится.
Выходы и изменяются при изменении отношения реакции от благоприятного () к неблагоприятному. Случаи 1 и 2 имеют высокий выход ; Случаи 3 и 4 имеют равный выход и . Случаи с большими толщинами штрихов показывают симметрию в профилях массовой доли продукта примерно, когда вторая реакция незначительна () и значительную асимметрию, когда он активно участвует в реакции.Основное различие между реакциями С-С и С-П заключается в том, что после того, как продукт образуется в реакции С-П, он не расходуется побочной реакцией. Следовательно, с точки зрения измерения выхода , схема реакции CP намного менее чувствительна к смешиванию, чем схема реакции СС. Для реакции CC чем дольше он находится в контакте с , тем выше вероятность того, что выход снизится.
Изменение стехиометрии для реакций C-P привело к некоторым нелинейным изменениям профиля.В то время как профили для хорошо перемешанных случаев оставались одинаковыми по всей бороздке, величины желаемого и нежелательного продукта изменились. Профили для плохо смешанных случаев выглядят иначе, чем профили, представленные здесь, отчасти из-за других начальных условий, необходимых при изменении стехиометрии, а также из-за самих стехиометрий. Во второй статье [29] выход используется для учета всех этих изменений как для схем реакции CP, так и для схем реакции C-C.
Профили для плохо смешанных случаев выглядят иначе, чем профили, представленные здесь, отчасти из-за других начальных условий, необходимых при изменении стехиометрии, а также из-за самих стехиометрий. Во второй статье [29] выход используется для учета всех этих изменений как для схем реакции CP, так и для схем реакции C-C.
5.3. Выход желаемого продукта
Чтобы оценить выход для неоднородных профилей массовой доли, профили были интегрированы для получения общей массы присутствующих в системе в момент времени:
Отслеживание во времени дает прогрессию доходности во времени. На рис. 4 показан выход во времени по мере развития реакции для четырех случаев С-С, а на рис. 5 показаны те же результаты для четырех случаев С-П. Построение по оси — позволяет отображать все четыре кривые на одном рисунке.Эти цифры подтверждают выводы, сделанные выше, о том, что хорошее перемешивание и хорошее соотношение скоростей реакции максимизируют выход целевого продукта (случай 1 на рисунках 4 и 5), а плохое смешивание с неблагоприятным соотношением скоростей реакции сводит к минимуму выход целевого продукта (см.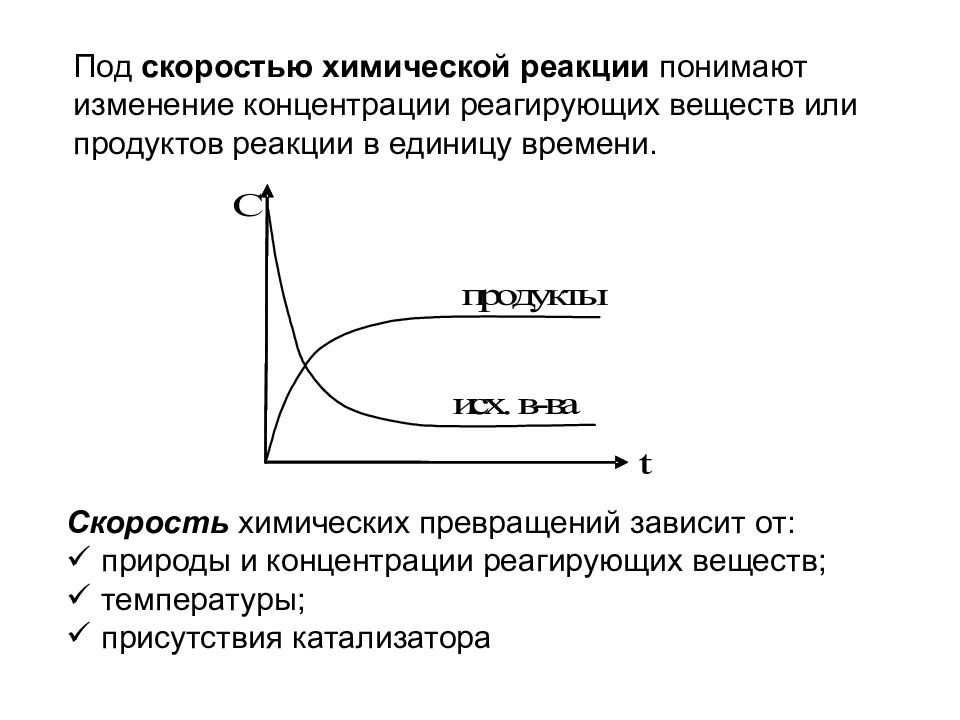 Случай 4 для рисунков 4 и 5). Это также подтверждает мнение о желательности минимизации отношения числа Дамкелера и скорости реакции. Выводы Clifford et al. [6] для классической стехиометрии C-C совпадают с нашими.Количественное сравнение невозможно, потому что наш выбор характерной длины и шкалы времени отличается от их выбора.
Случай 4 для рисунков 4 и 5). Это также подтверждает мнение о желательности минимизации отношения числа Дамкелера и скорости реакции. Выводы Clifford et al. [6] для классической стехиометрии C-C совпадают с нашими.Количественное сравнение невозможно, потому что наш выбор характерной длины и шкалы времени отличается от их выбора.
5.4. Влияние отношения скоростей реакции на выход
На рисунках 4 и 5 показано, что соотношение скоростей реакций влияет на количество образующегося продукта независимо от условий смешивания. Это видно при сравнении Случаев 1 и 3, которые хорошо перемешаны, и Случаев 2 и 4, которые плохо перемешаны. Благоприятное соотношение скоростей реакции (случаи 1 и 2) всегда обеспечивает более высокий конечный выход .Невозможно получить хороший выход целевого продукта, если соотношение скоростей реакции неблагоприятно, независимо от условий смешивания (варианты 3 и 4). Клиффорд и др. [6] пришли к такому же выводу относительно влияния соотношения скоростей реакций. Меньшее соотношение скоростей реакции благоприятно для максимизации выхода желаемого продукта.
Меньшее соотношение скоростей реакции благоприятно для максимизации выхода желаемого продукта.
5.5. Влияние смешивания на выход
На рисунках 4 и 5 видно значительное влияние смешивания. 1 и 2 на обоих рисунках (до 1 для CC и до 1 для CP).Если соотношение скоростей реакции неблагоприятное, аналогичный благоприятный эффект смешивания виден при сравнении случаев 3 и 4, хотя он не так значителен, как при хорошем соотношении скоростей реакции (до 0,24 для С-С и до 0,5 для С-Р). Это показывает, что эффект смешивания ограничен соотношением скоростей реакции, то есть соотношение скоростей реакций определяет конечный выход, и хорошее перемешивание помогает реализовать это асимптотическое значение выхода. Для случаев с хорошим перемешиванием (случаи 1 и 3) окончательный выход достигается намного быстрее, поэтому перемешивание также определяет скорость реакции.В случае С-С, благодаря характеру реакции, это оказывает значительное положительное влияние на конечный выход . К такому же выводу пришли Кокс и др. (Кокс и др. [5] и Клиффорд и др. [6]): минимизация числа Дамкелера приводит к увеличению выхода целевого продукта.
(Кокс и др. [5] и Клиффорд и др. [6]): минимизация числа Дамкелера приводит к увеличению выхода целевого продукта.
6. Выводы
Новые определения числа Дамкелера (Da) и безразмерного соотношения скоростей реакций () были получены для исследования влияния стехиометрии, смешения и соотношения скоростей реакций для конкурентно-последовательных и конкурентно-параллельных реакций с общей стехиометрией .При разработке модели учитываются обе схемы реакции, что ранее было недоступно. Для обоих типов реакций, чувствительных к смешиванию, было найдено одно число Дамкелера. Это обнадеживает, поскольку ранее было много споров о формулировке числа Дамкелера для этих конкурирующих реакций, например, должно ли оно быть основано на первой или второй реакции. Иметь только одно выражение для описания смешивания более физически, поскольку смешивание не должно зависеть от схемы реакции.Общее выражение для числа Дамкелера применительно к классическим схемам реакций сводится к выражениям, использованным в предыдущих исследованиях Cox et al. [5] в частности. Схемы реакций С-С и С-П, однако, сильно различаются, и эти различия отражаются в конкретных соотношениях скоростей реакций для двух типов стехиометрии реакций, которые должны использоваться в модели.
[5] в частности. Схемы реакций С-С и С-П, однако, сильно различаются, и эти различия отражаются в конкретных соотношениях скоростей реакций для двух типов стехиометрии реакций, которые должны использоваться в модели.
Влияние соотношения скоростей смешивания и реакции на выход целевого продукта было исследовано для классических схем конкурентно-последовательной и конкурентно-параллельной реакции.Соотношение скоростей реакции в конечном счете ограничивает конечный выход желаемого продукта. Смешивание определяет, достигается ли этот выход, и скорость, с которой достигается окончательный выход. Соотношение скоростей реакции и число Дамкелера должны быть сведены к минимуму для достижения максимального выхода продукта. Результаты модели согласуются с ожидаемыми результатами и с результатами предыдущих исследований, в которых варьировались как смешивание, так и соотношение скоростей реакции. Улучшение смешивания и химии за счет минимизации числа Дамкелера и соотношения скоростей реакции является желательным и приводит к увеличению выхода желаемого продукта.
Это подтверждение модели позволяет провести будущую работу, в которой будет исследовано влияние стехиометрии, смешивания и соотношений на выход для общей чувствительной к смешиванию реакции с различной стехиометрией.
Хотя модель позволяет исследовать влияние начальных концентраций реагентов, это не было сделано в текущем исследовании, и это еще один возможный путь для дальнейших исследований. Также признано, что одномерная модель не является точным описанием реального турбулентного перемешивания, но это исследование должно было стать первым набегом на эффект стехиометрии реакций, чувствительных к перемешиванию, поэтому была желательна простота.Дополнительные сложности включают в себя введение в модель потока жидкости, например учет ламинарного растяжения бороздок, 2D-деформации и, в конечном итоге, 3D-деформации, аналогично работам Кокса [7] и Балдыги и Борна [1]. Конечной целью было бы интегрировать уравнения реакционной диффузии в модель поглощения Балдыги и Борна [1]. Эта модель также может быть интегрирована в трехмерные модели мезо-смешивания, чтобы лучше аппроксимировать реальную промышленную ситуацию.
Эта модель также может быть интегрирована в трехмерные модели мезо-смешивания, чтобы лучше аппроксимировать реальную промышленную ситуацию.
Номенклатура
| Молярная концентрация по Cox et al.[5] [кмоль/] | ||
| : | Исходная концентрация ограничивающего реагента в Cox et al. [5] [кмоль/] | |
| : | Номер Дамкелера [–] | |
| Da II : | Номер Дамкелера в Cox et al. [5] [–] | |
| : | Коэффициент диффузии, [/с] | |
| : | Безразмерная концентрация видов в Cox et al. [5] [–] | |
| : | Константа скорости 1 в Cox et al.[5] [/кмоль с] | |
| : | Константа скорости 2 в Cox et al. [5]. | |
| : | : | Толщина отпуска [M] |
| : | Молекулярная масса [кг / кг / кг] | |
| : | Срок реакции [кг / с] | |
| : | Время [S ] | |
| : | Безразмерное время [–] | |
| : | Безразмерное время в Cox et al. [5] [–] [5] [–] | |
| : | Массовая доля [–] | |
| : | Толщина штриховки в Cox et al. [5] [м] | |
| : | Расстояние [м] | |
| : | Безразмерное расстояние [–] | |
| 1 : | 2 Безразмерное расстояние. [5] | |
| : | Выход желаемого продукта [–]. |
Греческие буквы
| : | Стехиометрические коэффициенты [–] |
| : | Соотношение скоростей реакций Cox et al.[5] [–] |
| : | Массовая концентрация [кг/] |
| : | Время перемешивания [с] |
| время реакции [с]. |
подписка
| : | вид (реактива) | : | : |
| : | Виды (реагенты) | |
| : | вид, или | |
| : | Виды (инертные) | |
| : | Любые виды в Cox et al. [5] [5] | |
| 0: | Начальное значение | |
| : | ||
| : | вид (продукт) | |
| : | вид (побочный продукт) | |
| : | Всего | |
| : | Смеси видов. |
Благодарности
Авторы хотели бы поблагодарить NSERC Canada и MITACS за финансирование, предоставленное для проведения этого исследования.
Помогите с этими вопросами по кинетике о порядке реакции по отношению к одному реагенту A??
Выделите, чтобы открыть ответы, как только вы это выяснили.п#. Что такое #bbn# на этот раз? (Чем возводится #2#, что коррелирует с квадратным корнем?) Реакция этого #n#-го порядка по отношению к #A#.
#4)#
Он обсуждает первый и второй периоды полураспада и утверждает, что они равны. Это как раз говорит о том, что период полураспада (ТАКОГО порядка) не зависит от того, с какой концентрации вы начинаете.

Смотри выше. Период полураспада какого порядка не зависит от #[A]_0#? Подсказка: это не простое число.0 = к#
Элементы технологии химических реакций, часто задаваемые вопросы
В литературе есть таблицы. Для газофазной реакции первого порядка значение порядка величины равно A=10 13 с -1 . Обычно частотный фактор не зависит от температуры, однако иногда он может слабо зависеть от температуры. См. стр.944
Если в качестве основы для расчетов выбран предельный реагент , а не , можно рассчитать ОТРИЦАТЕЛЬНУЮ концентрацию. См. пример 3-5 (стр. 90).
и k в норме законов?
K C – константа равновесия, а k – константа удельной скорости, выраженная в единицах времени.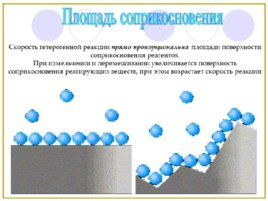 Константа равновесия концентрации K C не имеет значения.
Константа равновесия концентрации K C не имеет значения.
ТОЛЬКО в очень очень редких случаях при очень высоких давлениях, таких как 6000 атм, есть функция давления. См. стр. 220 и компакт-диск «Критика прочитанного».
Уравнение Аррениуса k = Ae-E/RT
Коэффициент частоты, A, является коэффициентом экспоненциального члена.
Он имеет те же единицы измерения, что и k.
Это связано с количеством столкновений между молекулами.
См. стр. 942 и 943.
Можно классифицировать реакции по их общему порядку реакции.
Их можно найти в литературе, журналах, книгах, таблицах и т. д.,
см. сноску на стр. 75.
Их также можно определить в лаборатории.
См. гл. 5
д.,
см. сноску на стр. 75.
Их также можно определить в лаборатории.
См. гл. 5
Закон скорости определяется только из эксперимента, см. главу 5.Также см. главу 7 для обсуждения неэлементарных реакций.
Это функция концентрации частиц, участвующих в реакции. и есть ли катализатор.
Так что -r A всегда имеет одни и те же единицы измерения (моль/дм3 с), независимо от порядок реакции.
Изменение общего количества молей (для полной конверсии) на моль лимитирующий реагент.
е=у Ао д
Это изменение общего количества молей при полной конверсии (т. е. X = 1).
на общее количество молей, подаваемых в реактор.Параметр е
может быть как положительным, так и отрицательным (см. Упр. 3-7, стр. 100).
е. X = 1).
на общее количество молей, подаваемых в реактор.Параметр е
может быть как положительным, так и отрицательным (см. Упр. 3-7, стр. 100).
Энергия активации является константой для каждой реакции (по крайней мере, в диапазон температур). Это связано с прочностью химических связей, которые должны быть разорваны и сформированы, чтобы произошла химическая реакция.
Например, если закон скорости, мы можем видеть, что для больших значений k 2 C A ( k 2 C A >> 1) закон скорости принимает вид , т.е.е. кажущийся нулевой порядок. Если в реакторе периодического действия проводится реакция нулевого порядка, концентрация является линейной функцией времени (т. е. dC/dt = k и C A = C Ao — kt).
CSTR всегда считается идеально смешанным. Проба реакционной смеси, взятая из любого места внутри реактора, будет такой же, как и на выходе.Следовательно, выход
конверсии и, таким образом, 1/r A на выходе такие же, как и внутри реактора. С другой стороны, в ПФР
преобразование (и, следовательно, 1/r A ) изменяется по длине
реактор; скорость велика на входе, где концентрации реагентов высоки, а конверсия
низкий и малый на выходе, где концентрации реагентов низкие, а конверсия высокая.
Проба реакционной смеси, взятая из любого места внутри реактора, будет такой же, как и на выходе.Следовательно, выход
конверсии и, таким образом, 1/r A на выходе такие же, как и внутри реактора. С другой стороны, в ПФР
преобразование (и, следовательно, 1/r A ) изменяется по длине
реактор; скорость велика на входе, где концентрации реагентов высоки, а конверсия
низкий и малый на выходе, где концентрации реагентов низкие, а конверсия высокая.
CSTR используются для жидкофазных реакций.Они дешевле, проще в использовании, а так как реагенты хорошо перемешаны, нет горячих точки (горячие точки могут привести к взрыву).
Нет! Стехиометрия зависит только от химии реакции и инертных газов. или присутствующие жидкости.
или присутствующие жидкости.
Уравнения для концентрации с точки зрения конверсии изменятся, как только начнется фазовый переход.Следовательно, выражение для закона скорости как функции преобразования могло бы иметь разные выражения для разных диапазонов преобразования. См. пример 3-10, стр. 108.
Это зависит от крутизны функции, которую вы хотите интегрировать. Чем больше крутизна, тем большее количество точек вы должны набрать. использовать.Квадратурные методы приведены в разделе A.4, стр. 924.
Определение скорости реакции с помощью кинетики действия масс — MATLAB & Simulink
Определение скорости реакции с помощью кинетики массового действия
Используйте кинетику действующих масс для определения нулевого, первого,
реакции второго порядка и обратимые реакции.
Определение кинетики действия масс
Действие масс описывает поведение реагентов и продуктов в элементарной химической реакции.Кинетика действующих масс описывает это поведение как уравнение, в котором скорость или скорость химического реакция прямо пропорциональна концентрации реагирующих веществ.
Реакции нулевого порядка
При реакции нулевого порядка скорость реакции не зависит
по концентрации реагентов. Примеры реакций нулевого порядка
являются синтезом из нулевых видов и моделированием
исходный вид, который добавляется в систему с определенной скоростью.
реакция: null -> P
скорость реакции: к моль/сек
виды: P = 0 моль
параметры: k = 1 моль/сек Примечание
скорость должна быть определена в единицах количества в единицу времени, а не концентрации в единицу времени.
Ввод приведенной выше реакции в программное обеспечение и имитация дает следующий результат:
Кинетика действия масс нулевого порядка
Примечание
Если количество реагента с кинетикой нулевого порядка достигает
ноль перед окончанием симуляции, то количество реагента может
опускаться ниже нуля независимо от установленного решателя или допусков.
Реакции первого порядка
При реакции первого порядка скорость реакции пропорциональна до концентрации одного реагента.Пример первого порядка реакция – радиоактивный распад.
реакция: R -> P
скорость реакции: k*R моль/(литр*секунда)
виды: R = 10 моль/л
Р = 0 моль/л
параметры: k = 1 1/сек.
Ввод приведенной выше реакции в программное обеспечение и имитация дает следующие результаты:
Кинетика действия масс первого порядка
Реакции второго порядка
Скорость реакции второго порядка пропорциональна квадрату или концентрации одного реагента или пропорциональна на два реагента.2 моль/(литр*секунда) виды: R = 10 моль/л Р = 0 моль/л параметры: k = 1 литр/(моль*секунда)
Ввод приведенной выше реакции в программное обеспечение и имитация дает следующие результаты:
Кинетика второго порядка с одним реагентом
С двумя реагентами скорость реакции зависит от концентрации
из двух реагентов.
реакция: R1 + R2 -> P
скорость реакции: k*R1*R2 моль/(литр*секунда)
виды: R1 = 10 моль/л
R2 = 8 моль/л
Р = 0 моль/л
параметры: k = 1 литр/(моль*секунда)
Введите приведенную выше реакцию в программное обеспечение, и имитация приведет к следующие результаты.Разница в окончательных значениях есть, потому что начальное количество одного из реагентов меньше, чем другого. После израсходования первого реагента реакция останавливается.
Кинетика второго порядка с двумя реагентами
Обратимое действие масс
Вы можете моделировать обратимые реакции с двумя отдельными реакциями или с одной реакцией. При одной обратимой реакции реакция скорости прямой и обратной реакции объединены в одну выражение.Обратите внимание на угловые скобки до и после дефиса представить обратимую реакцию.
реакция: R <-> P
скорость реакции: kf*R - kr*P моль/(литр*секунда)
виды: R = 10 моль/л
Р = 0 моль/л
параметры: kf = 1 1/сек. кр = 0,2 1/сек.
кр = 0,2 1/сек.
Ввод приведенной выше реакции в программное обеспечение и имитация
дает следующие результаты. В состоянии равновесия, когда скорость
прямая реакция равна обратной реакции, v = kf*R -
kr*P = 0 и P/R = kf/kr .
Кинетика реакций — вопросы и ответы по органической химии
Этот набор вопросов и ответов с несколькими вариантами ответов (MCQ) по органической химии посвящен «кинетике реакций».
1. Для приведенной ниже реакционной системы объем резко уменьшается до половины своего значения при увеличении давления на нее. Как изменится скорость реакции, если реакция первого порядка по O 2 и второго порядка по NO?
2NO(г) + O 2 (ж) + 2NO 2 (ж)
а) уменьшить до одной четверти исходного значения
б) уменьшить до одной восьмой исходного значения
в) увеличить в восемь раз от исходного значения
d) увеличить в четыре раза от исходного значения
Посмотреть ответ
Объяснение:
2.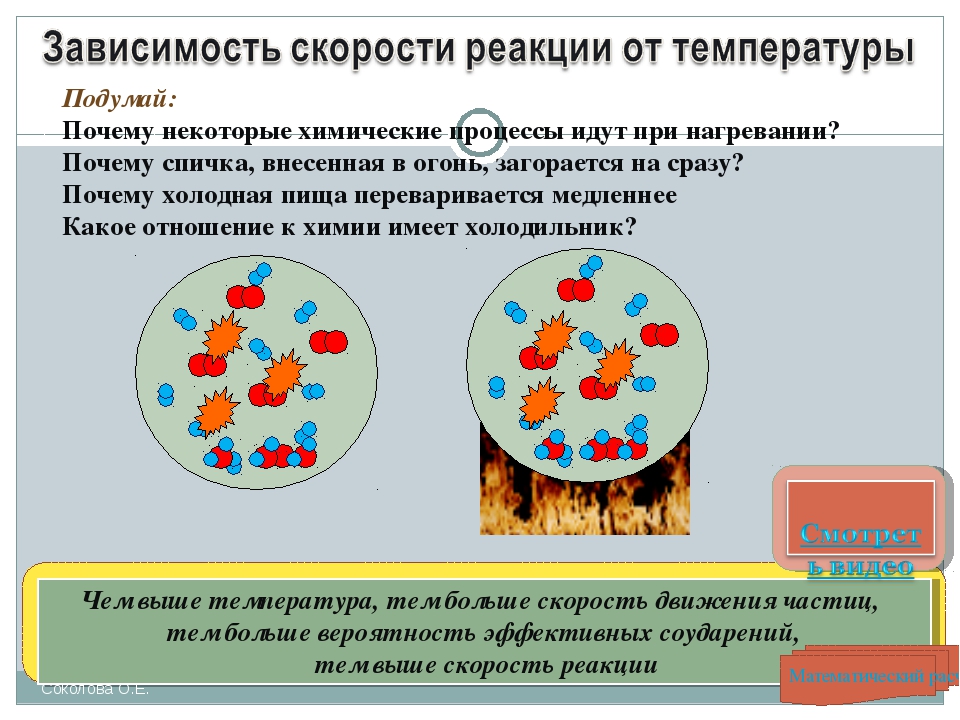 Закон скорости реакции между веществами А и В определяется выражением скорость = K[A]n [B]m. При удвоении концентрации А и уменьшении вдвое концентрации В. Каково будет отношение новой скорости к прежней скорости реакции?
Закон скорости реакции между веществами А и В определяется выражением скорость = K[A]n [B]m. При удвоении концентрации А и уменьшении вдвое концентрации В. Каково будет отношение новой скорости к прежней скорости реакции?
a) (\(\frac{1}{2}\)) m+n
b) m+n
c) n-m
d) 2 n-m
Посмотреть ответ
Объяснение:
3. Скорость = Если объем реакционного сосуда внезапно уменьшается до \(\frac{1}{4}\) th от начального значения.Как повлияет новая ставка?
a) \(\frac{1}{10}\)
b) \(\frac{1}{8}\)
c) 8
d) 16
Посмотреть ответ
Объяснение:
4. От какого фактора не зависит константа скорости реакции?
а) температура
б) энергия активации
в) катализатор
г) концентрация реагентов и продуктов реагента и продукта).
5. Скорость реакции, продукты A + B, определяется уравнением r = k[A][B]. Если В взять в избытке, каков будет порядок реакции?
а) 2
б) 1
в) ноль
г) непредсказуемый
Посмотреть ответ
Ответ: б
Объяснение: А + В → Произведения
Н = k[А][В] [если В взять в большом избытке затем по реакции псевдопервого порядка. B принимается постоянным]. Итак, порядок = 1.
B принимается постоянным]. Итак, порядок = 1.
6. В реакции 2А 2 + В 2 → 2А 2 В, когда исчезнет реагент А?
a) половина скорости уменьшения B
b) такая же скорость уменьшения B
c) удвоенная скорость уменьшения A2B
d) удвоенная скорость уменьшения B
Просмотреть ответ
Объяснение:
Таким образом, реагент А исчезнет, когда А удвоится со скоростью, по которой В уменьшится.
7. Скорость реакции, в которой не участвуют газы, не зависит от _____________
а) давления
б) температуры
в) концентрации
г) катализатора
Посмотреть Ответ
Ответ: а
Пояснение: Скорость реакции, которая не включает газы, не зависит от давления.
8. Что неверно для редукции второго порядка?
a) Он может иметь константу скорости 1 x 10 -2 л моль -1 с -1
b) Его период полувыведения обратно пропорционален его начальной концентрации
c) Время до завершения 75% реакции равно удвоенный период полураспада
d) T 50 = 1/(k a ⋅A 0 )
Посмотреть ответ
Объяснение:
но т 75 = 3 * т 50
Таким образом, вариант Время завершения 75% реакции в два раза больше периода полураспада является неверным утверждением для n = 2.

9. Скорость разложения вещества увеличивает концентрацию вещества при той же температуре. Выясните порядок реакции.
a) 1
b) 2
c) 3
d) 0
Посмотреть ответ
Ответ: b
Объяснение: Rate = k [A] α
R 1 = k[A] 8 7 R 2 = k [1,5 A] n = 2,25 R 1
k(1,5 A) n = 2,25*k*[A] n
(1,7 * 9003] n = 2,25*[A] n
n log (1.5) = log (2,25)
n = 2,
10. Если реакция n th порядка период полураспада ________ от начальной концентрации реагентов.
a) не зависит
b) изменяется обратно пропорционально (n-1) -й степени
c) изменяется обратно пропорционально n -й степени
d) изменяется прямо как (n-1) -й степени
Посмотреть ответ
Объяснение: для n-го порядка; Итак, изменяется обратно пропорционально как (n – 1) -я -я степень.

