Онлайн калькулятор систем счисления с решением онлайн
Переведем целую часть 12 числа 12.310 в 2-ичную систему счисления, при помощи последовательного деления на 2, до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.| 12 | : | 2 | = | 6 | остаток: 0 |
| 6 | : | 2 | = | 3 | остаток: 0 |
| 3 | : | 2 | = | 1 | остаток: 1 |
| 1 | : | 2 | = | 0 | остаток: 1 |
1210 = 11002
Переведем дробную часть 0.3 числа 12.310 в 2-ичную систему счисления, при помощи последовательного умножения на 2, до тех пор, пока в дробной части произведения не получиться ноль или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.
В результате будет получено число из целых частей произведений, записанное слева направо.
| 0.3 | · | 2 | = | 0.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1. 2 2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1.2 |
| 0.2 | · | 2 | = | 0.4 |
| 0.4 | · | 2 | = | 0.8 |
| 0.8 | · | 2 | = | 1.6 |
| 0.6 | · | 2 | = | 1. 2 2 |
0.310 = 0.0100110011001100110011001100112
12.310 = 1100.0100110011001100110011001100112
Опубликованные материалы на сайте СМИ «Солнечный свет». Статья Решение задач по теме: «Системы счисления. Автор: Мещерякова Елена Владимировна.
Автор: Мещерякова Елена Владимировна
Моделирование урока по теме: Решение задач по теме «Системы счисления». 8 класс 1 год обучения
Автор: Мещерякова Елена Владимировна
Моделирование урока
Тема урока: Решение задач по теме Системы счисления
8 класс, 2 урок, 1 год обучения
Дорогу осилит идущий, а информатику – мыслящий
Цели урока:
Образовательные: — продолжить работу по формированию навыков решения задач с применением знаний по теме Системы счисления
— закрепить знания учащихся по теме Системы счисления
Развивающие: — развитие алгоритмического мышления, памяти, внимания, логического мышления;
— развитие познавательного интереса и творческой активности учащихся.
Воспитательные: — воспитание активности учащихся;
— привитие навыков самостоятельной работы;
— сплочение коллектива класса.
Тип урока: урок — закрепления и обобщения.
Вид урока: Урок- брейн-ринг, выполняя различные задания, учащиеся закрепляют навыки решения задач с применением знаний по теме Системы счисления.
Средства обучения: компьютер, операционная среда Windows XP, Power Point, Word, мультимедийный проектор, раздаточный материал, авторская презентация.
Межпредметные связи: математика.
Ход занятия
Организационный момент. (1 мин)
Проверка наличия учащихся в классе.
Разминка. (4 мин)
(Этап подготовки к активной учебно-познавательной деятельности и проверки знаний учащихся).
На предыдущих уроках мы с вами познакомились с различными системами счисления, научились переводить числа из одной системы счисления в другую (письменно или с помощью программы калькулятор) и решали задачи.

Чтобы проверить, как вы усвоили материал прошедших уроков, проведем небольшую разминку.
Задание на внимание.
(Учащиеся несколько секунд смотрят на таблицу и затем отвечают на вопросы.)
1510410
112 12
12 +12
1112 02
Вопросы
Какими цветами записаны выражения?
Произведение каких чисел записано красным цветом? Чему оно равно?
Чему равно произведение чисел, записанных синим цветом?
Какое выражение записано зеленым цветом? Чему равно его значение?
Чему равно значение выражения, записанного черным цветом?
Сообщение темы и постановка целей урока (2мин)
Сегодня мы с вами занятие проведем в форме брейн-ринга, то есть в каждом конкурсе команды соревнуются не только в том, чтобы правильно выполнить предложенные задания, но и в том, чтобы опередить соперника. Для этого разобьемся на две команды, выберем в каждой команде капитана. Выиграет та команда, которая наберет наибольшее количество баллов.
( Группа делится на две команды. Каждая из команд садится за свой игровой стол, выбирает капитана.

Брейн-ринг. (32 мин)
Конкурс на сообразительность.(3 мин)
Восстановите двоичные цифры:
**0*0*1**1+10111*1001=101*0*00010
Ответ: 1000001001+1011111001=10100000010
Конкурс капитанов.(4 мин)
Задание: Найдите в примерах ошибки и исправьте их
102•12 = 102
102+ 12 = 112
102 • 12 = 112
1012 • 02 = 1012
1012 +102 =1112
1012 • 1002 = 101002
10102 + 02 =02
112 + 1002 =1112
12 • 12 = 102
12 +12 = 102
12 • 02 = 12
1210 = 148
13. 310 =112
(3. 102 • 12 = 102 ; 4. 1012 • 02 = 02; 7. 10102 + 02 = 10102; 9. 12 • 12 =12 ; 11. 12 • 02 =02 )
Какое из заданий не смогли проверить? Почему? Какие цифры можем использовать в восьмеричной системе счисления? Как вы думаете, что надо сделать, чтобы перевести число из десятичной системы счисления в восьмеричную систему счисления?
Конкурс художников. (15 мин).
Каждый ученик получает карточку с заданием.
Задание. Перевести координаты точек, представленных в недесятичных системах счисления, в их обычный десятичный вид записи числа (можно воспользоваться программой Калькулятор).
 Затем эти координаты использовать при построении рисунка в текстовом редакторе Word (на рис.1 представлена сетка для построения, которая приготовлена заранее).
Затем эти координаты использовать при построении рисунка в текстовом редакторе Word (на рис.1 представлена сетка для построения, которая приготовлена заранее).Вариант №1
Координаты точек представлены в недесятичной системе счисления. Выполните перевод координат в десятичную систему счисления и отметьте точки на координатной плоскости. Правильно сделав перевод и соединив последовательно все точки, получите некий рисунок.
1
2
3
4
5
6
7
8
9
10
11
12
X
100002
11102
11102
11002
11002
11012
11102
11102
1116
1416
1416
1516
Y
1002
1002
102
102
10102
10102
101102
1816
1616
А16
С16
продолжение таблицы
13
14
15
16
17
18
19
20
21
22
23
X
1616
1616
1416
248
228
228
208
208
218
228
228
Y
А16
216
216
48
48
28
28
128
148
128
48
Результат построения на рис.
 2
2Вариант №2
Координаты точек представлены в недесятичной системе счисления. Выполните перевод координат в десятичную систему счисления и отметьте точки на координатной плоскости. Правильно сделав перевод и соединив последовательно все точки, получите некий рисунок.
1
2
3
4
5
6
7
8
9
X
10102
10002
100102
100102
11102
228
128
128
228
Y
102
10002
1102
101102
101012
248
208
148
108
продолжение таблицы
10
11
12
13
14
15
X
168
1216
1216
1С16
1А16
А16
Y
168
1416
616
816
216
216
Результат построения на рис.3
Вариант №3
Координаты точек представлены в недесятичной системе счисления. Выполните перевод координат в десятичную систему счисления и отметьте точки на координатной плоскости. Правильно сделав перевод и соединив последовательно все точки, получите некий рисунок.
1
2
3
4
5
6
7
8
X
100002
100002
10102
100002
11002
208
168
228
Y
102
1002
1002
10102
10102
168
168
248
продолжение таблицы
9
10
11
12
13
14
15
16
X
268
248
1816
1416
1А16
1416
1416
1016
Y
168
168
А16
А16
416
416
216
216
Результат построения на рис.

Вариант №4
Координаты точек представлены в недесятичной системе счисления. Выполните перевод координат в десятичную систему счисления и отметьте точки на координатной плоскости. Правильно сделав перевод и соединив последовательно все точки, получите некий рисунок.
1
2
3
4
5
6
7
8
9
X
1102
10102
100002
100102
1416
1616
1416
1316
1A16
Y
11102
100002
11102
11112
F16
E16
E16
D16
816
продолжение таблицы
10
11
12
13
14
15
16
17
18
X
1D16
348
348
328
158
138
11002
10002
1102
Y
916
78
48
68
118
108
10102
11002
11102
Результат построения на рис.5
Первые 2 человека в каждом варианте получают – 5, вторые – 4 и т.д.
Физкультминутка.(2 мин)
А сейчас немного отдохнем перед следующей работой.
Гимнастика для глаз (все упражнения делаются сидя)
1.
 Закройте глаза, расслабьте мышцы лица, свободно, без напряжения откиньтесь на спинку стула, положите руки на бедра (10-15 секунд).
Закройте глаза, расслабьте мышцы лица, свободно, без напряжения откиньтесь на спинку стула, положите руки на бедра (10-15 секунд).2. Продолжая держать глаза закрытыми, выполните движение глаз по часовой стрелке и обратно. Повторите упражнение еще раз.
3. Посмотрите на метку на окне, отведите глаза в даль, затем посмотрите на метку.
4. Расслабьтесь, руки опустите вниз, руки поднимаем вверх, смотрим за движением рук вверх, опускаем руки.
5. Руки кладем на пояс, посмотрите на свой левый локоть, посмотрите на правый локоть.
Конкурс Считай и не зевай. (3 мин)
(5 баллов каждому из команды-победителей, если задание сделано идеально, 4 балла, если были набольшие погрешности, 3 – если грубые ошибки, 2 – задание не выполнено).
Задание: Выполнить следующие арифметические действия:
1. Количество базисных цифр в двоичной системе счисления сложить с количеством бит в одном байте.

3. К полученному результату прибавить отличную школьную оценку.
4. Ответ перевести в двоичную систему счисления.
Оценивается правильность и скорость выполнения заданияОтвет:(2+8)*4+5=45 4510 = 1011012.
Контроль и самоконтроль. (5 мин)
Работа в группах по 2 человека.
Выполните задание.
Зачеркните в таблицах те столбики, где стоят числа, которые вы получили выполняя задания, и прочитайте текст.
1 вариант.
2 вариант.
Перевести числа в восьмеричную систему счисления
1) 1710
1) 1910
2) 3710
2) 3610
Перевести числа в десятичную систему счисления
1) 1038
1)1108
2) 718
2)738
…Первый портативный электронный калькулятор был выпущен американским филиалом японской фирмы
Ш
Т
А
Р
О
К
М
П
228
218
278
328
238
448
458
548
в
1
8
9
9
6
7
4
9
6310
6710
5810
5710
6410
5910
7210
7410
году. Он весил около килограмма и “знал” только четыре действия арифметики.
 (“Шарп”, 1969).
(“Шарп”, 1969).Выполнив задание ученики меняются тетрадями и проверив задание, выставляют оценку.
Подведение итогов. (4 мин)
Оценивание работы команд и отдельных учащихся.
6. Домашнее задание. (2 мин)
Придумать и оформить аналогичные 2 задачи по теме Системы счисления
Используемая литература:
А.Г. Гейн, А.И. Сенокосов Информатика 7-9 класс. – М: Дрофа., 2001 год.
Н.Б. Демидович, В.М. Монахов Программирование и ЭВМ. Учебное пособие. – М. Просвещение, 1980.
М.Долинский “Алгоримизация и программирование…” ПИТЕР, 2005 год.
С. Окулов Основы программирования. – М: БИНОМ, 2005 год.
Н.Угринович “Информатика и информационные технологии” 8 класс. – М.: БИНОМ, 2005 год.
А.Ф. Чернов, А.А. Чернов Информатика: тесты к олимпиадам и итоговому тестированию. – Волгоград: Учитель, 2006 год.
Скачать работу comments powered by HyperComments
Задачи по теме Системы счисления Примеры решения
Задачи по теме «Системы счисления»
Примеры решения
Задание №1.
Сколько значащих цифр в записи десятичного числа 357 в системе
счисления с основанием 3?
Решение:
Переведём число 35710 в троичную систему счисления:
Итак, 35710 = 1110203. Число 1110203 содержит 6
значащих цифр.
Ответ: 6.
Задание №2.
Дано А=A715, B=2518. Какое из чисел C, записанных в двоичной
системе, отвечает условию A<c<b?
1) 101011002
2) 101010102
3) 101010112
4) 101010002
Решение:
Переведём числа А=A715 и B=2518 в двоичную систему
счисления, заменив каждую цифру первого числа соответствующей тетрадой, а
каждую цифру второго числа – соответствующей триадой: A715= 1010 01112;
2518 = 010 101 0012.
Условию a<b<c Ответ: 101010002 (вариант 4).
Задание №3.
На какую цифру оканчивается запись десятичного числа 123 в
системе счисления с основанием 6?
Решение:
Переведём число 12310 в систему счисления с основанием
6:
12310 = 3236.
Ответ: Запись числа 12310 в системе счисления с основанием
6 оканчивается на цифру 3.
Задания на выполнение арифметических действий над числами,
представленными в разных системах счисления
Задание №4.
Вычислите сумму чисел X и Y, если X=1101112, Y=1358. Результат
представьте в двоичном виде.
1) 100100112 2) 100101002 3) 110101002 4)
101001002
Решение:
Переведём число Y=1358 в двоичную систему счисления,
заменив каждую его цифру соответствующей триадой: 001 011 1012. Выполним
сложение:
Ответ: 100101002 (вариант 2).
Задание №5.
Найдите среднее арифметическое чисел 2368, 6С16 и 1110102.
Ответ представьте в десятичной системе счисления.
Решение:
Переведём числа 2368, 6С16 и 1110102 в десятичную
систему счисления:
Вычислим среднее арифметическое чисел: (158+108+58)/3 =
10810.
Ответ: среднее арифметическое чисел 2368, 6С16 и
1110102 равно 10810.
Задание №6.
Вычислите значение выражения 2068 + AF16 ? 110010102. Вычисления
производите в восьмеричной системе счисления. Переведите ответ в десятичную
систему.
Переведите ответ в десятичную
систему.
Решение:
Переведём все числа в восьмеричную систему счисления:
2068 = 2068; AF16 = 2578; 110010102 = 3128
Сложим числа:
Переведём ответ в десятичную систему:
Ответ:51110.
Задания на нахождение основания системы счисления
Задание №7.
В саду 100q фруктовых деревьев: из них 33q яблони,
22q груши, 16q слив и 17q вишен. Найдите основание системы
счисления, в которой посчитаны деревья.
Решение:
Всего в саду 100q деревьев: 100q =
33q+22q+16q+17q.
Пронумеруем разряды и представим данные числа в развёрнутой
форме:
Ответ: Деревья посчитаны в системе счисления с основанием
9.
Задание №8.
Найдите основание x системы счисления, если известно, что
2002x = 13010.
Решение:
Пронумеруем разряды и запишем данные числа в развёрнутой
форме:
Ответ:4.
Задание №9.
В системе счисления с некоторым основанием десятичное число 18
записывается в виде 30. Укажите это основание.
Укажите это основание.
Решение:
Примем за х основание неизвестной системы счисления и составим
следующее равенство:
1810 = 30x;
Пронумеруем разряды и запишем данные числа в развёрнутой
форме:
Ответ: десятичное число 18 записывается в виде 30 в системе
счисления с основанием 6.
Читать «Как решать задачи на системы счисления? ЕГЭ. Информатика. Задание № 10» — Теплоухова Елена — Страница 1
Введение
В ЕГЭ по предмету информатика одной из главных тем являются системы счисления. Тема сложная для самостоятельного изучения и требующая понимания ее сути. На сайте К.Полякова для тренировки представлены сотни задач различных уровней сложности. Вроде бы столько возможностей хорошо подготовиться к ЕГЭ, много систематизированных заданий – берите и решайте. Но, прочитывая задачи, вы понимаете, что не знаете как их решить. На занятиях с репетитором вы разбирали подобные задачи, но немного измененные условия в задаче вводят в ступор. И появляется страх, что на экзамене попадется именно эта формулировка задачи.
И появляется страх, что на экзамене попадется именно эта формулировка задачи.
Вы начинаете поиск подобных заданий на системы счисления, которыми пестрят книги и сайты по подготовке к ЕГЭ, но объяснения представлены сложными способами, мало пояснений к решениям, не все нюансы разных условий задач отражены. После поисков в интернете, зачастую безрезультатных, и блужданий по сомнительным форумам, чаще всего приходится ждать следующей консультации с репетитором. Все, что вам нужно в этой ситуации для экономии времени и денег – это иметь простые и понятные алгоритмы, чтобы решать любые формулировки заданий и понимать суть их решения. Это дает уверенность в своих силах, систематизирует знания и формирует опыт решения таких задач.
Работая учителем информатики, я столкнулась с необходимостью систематизировать свои знания по теме системы счисления. Многие задачи оказались для меня хорошим поводом углубиться в эту тему, найти более простые и понятные способы решения, а также написать для себя алгоритмы решений. Моей целью было не только прорешать все задания, но сгруппировать их – такая систематизация позволит намного быстрее усвоить алгоритмы решения и безошибочно определить – какой путь решения выбрать для той задачи, с которой вы столкнулись. Результатом систематизации стал сборник задач, выстроенный от самых простых задач до задач повышенной сложности. В нем представлены решения 45 заданий, что собраны для тренировки К.Поляковым к заданию №10.
Моей целью было не только прорешать все задания, но сгруппировать их – такая систематизация позволит намного быстрее усвоить алгоритмы решения и безошибочно определить – какой путь решения выбрать для той задачи, с которой вы столкнулись. Результатом систематизации стал сборник задач, выстроенный от самых простых задач до задач повышенной сложности. В нем представлены решения 45 заданий, что собраны для тренировки К.Поляковым к заданию №10.
На каждую из формулировок, которая встречается в заданиях, составлены простые понятные пошаговые алгоритмы и решения с пояснениями каждого действия. К каждому алгоритму прописаны номера подобных заданий, тем самым и вы легко сможете решить, например задачи №1, 34 и 85. Это позволит вам не только разобраться со способом решения, но и самостоятельно нарешивать подобные задания, они перестанут казаться для вас непонятным хаосом разных формулировок. А если у вас возникнут вопросы, вы сразу можете найти решение того задания, в котором вы испытали затруднение и увидеть на каком шаге вы допустили ошибку. Часто возникает проблема, что прочитав теорию, не понимаешь на каком шаге решения задачи ее применить. Готовые алгоритмы решения задач помогут и в этом, потому что теория дана не отдельно от решения – она встроена последовательно, пошагово с подробными пояснениями. Сборник позволит вам с минимальными временными и финансовыми затратами на репетитора самим освоить тему. Он выстроен таким образом, что вы ощутите себя на индивидуальном занятии и сможете продвигаться в своем темпе.
Часто возникает проблема, что прочитав теорию, не понимаешь на каком шаге решения задачи ее применить. Готовые алгоритмы решения задач помогут и в этом, потому что теория дана не отдельно от решения – она встроена последовательно, пошагово с подробными пояснениями. Сборник позволит вам с минимальными временными и финансовыми затратами на репетитора самим освоить тему. Он выстроен таким образом, что вы ощутите себя на индивидуальном занятии и сможете продвигаться в своем темпе.
Разбор задания №10.
Задание этого типа относится к базовому уровню и на его решение выделяют 4 минуты. Основная тема задания это кодирование данных, комбинаторика и системы счисления.
Мы рассмотрим в этом разделе только те формулировки задач, что относятся к теме системы счисления. На сайте К. Полякова представлены все формулировки задач, которые относятся к 10 заданию. Для удобства работы с данным сайтом, нумерация задач в книге полностью сохранена.
Основные знания, которыми необходимо обладать для решения задач этого типа – это принципы работы с числами, записанными в позиционных системах счисления. Самый простой способ решать задачи этого типа – это использование систем счисления. В данном задании существует всего 6 разных формулировок заданий и на основе них составлены алгоритмы решения. Алгоритмы расписаны очень подробно и исчерпывающе, в конце алгоритма указаны подобные задания. Для удобства в решении подписан номер алгоритма, на основе которого задание решено.
Самый простой способ решать задачи этого типа – это использование систем счисления. В данном задании существует всего 6 разных формулировок заданий и на основе них составлены алгоритмы решения. Алгоритмы расписаны очень подробно и исчерпывающе, в конце алгоритма указаны подобные задания. Для удобства в решении подписан номер алгоритма, на основе которого задание решено.
Задачи для тренировки к Заданию №10
1
:
Задача №1. Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Вот начало списка:
1. ААААА
2. ААААО
3. ААААУ
4. АААОА
……
Запишите слово, которое стоит на 101-м месте от начала списка.
Решение задачи №1. (По алгоритму 10.1.)
1. ААААА = 00000 это троичная А=0
2. ААААО = 00001 система О=1
3. ААААУ = 00002 счисления У=2
4. АААОА = 00010 ОА=10
10010= А3
100
3
-99
33
3
1
–33
11
3
0
–9
3
3
2
–3
1
0
10010 = 102013
№
Слово, которое стоит на 101-м месте от начала списка.
Число
101
1 0 2 0 13
О А У А О
10010
Ответ: ОАУАО
Формулировка
Алгоритм решения (10.1):
Задача №2.
Все 5-буквенные слова, составленные из букв А, О, У, записаны в алфавитном порядке. Вот начало списка:
1. ААААА
2. ААААО
3. ААААУ
4. АААОА
Запишите слово, которое стоит на 125-м месте от начала списка.
Подобные задачи №1-8, 17-20.
1. Читаем в задаче, какое количество букв используется для составления слов.
3 буквы (А, О, У) – очевидно, что это троичная система счисления.
2. Переведем буквенные слова в их числовые коды, чтобы определить какой букве какая относится цифра. (Обращаем внимание на порядок записи – алфавитный и дано начало списка):
1. ААААА это троичная А=0
2. ААААО система О=1
3. ААААУ счисления У=2
4. АААОА ОА=10
3. По условию задачи нам необходимо найти слово, которое стоит на 125-м месте от начала списка.
Помним, что на первом месте стоит число ноль, на втором месте стоит число один. Следовательно, на 125-м месте стоит число 124.
№
Число
1
0
2
1
….
125
124
4. Число 12410 в десятичной системе счисления. Слово, которое мы ищем, записано в троичной системе счисления. Переведем найденное число из десятичной системы счисления в троичную систему счисления.
12410= А3
124
3
-123
41
3
1
–39
13
3
2
–12
4
3
1
–3
1
1
12410 = 111213
5. Получили следующее:
№
Слово, которое стоит на 125-м месте от начала списка.
Число
125
111213
12410
Двоичная система счисления перевод обычных чисел. Перевод чисел в различные системы счисления с решением
Самой короткой системой счисления является двоичная. Она полностью основана на позиционной форме
записи числа. Основной характеристикой считается принцип удвоения цифры
при выполнении перехода от определённой позиции к последующей. Из одной системы счисления в другую можно осуществить перевод как при помощи специальной программы, так и вручную.
Она полностью основана на позиционной форме
записи числа. Основной характеристикой считается принцип удвоения цифры
при выполнении перехода от определённой позиции к последующей. Из одной системы счисления в другую можно осуществить перевод как при помощи специальной программы, так и вручную.
Вконтакте
Историческое признание
Появление двоичной СС в истории связано с учёным математиком В.Г. Лейбницем. Именно он впервые заговорил о правилах выполнения операций с числовыми значениями данного рода. Но первоначально этот принцип остался невостребованным . Мировое признание и применение алгоритм получил на заре возникновения вычислительных машин.
Удобство и несложность выполнения операций привели к необходимости более детального изучения данного подраздела арифметики, который стал незаменимым при развитии компьютерной технологии с программным обеспечением. Впервые такие механизмы появились на немецком и французском рынках.
Внимание!
Конкретную точку над превосходством двоичной системы по отношению десятичной, именно в данной отрасли, было поставлено в 1946 году и обосновано в статье А. Бекса, Х. Гольдстайна и Дж.Фон Неймана.
Бекса, Х. Гольдстайна и Дж.Фон Неймана.
Перевод числа из десятичной системы счисления в двоичную.
Особенности двоичной арифметики
Вся двоичная СС основана на применении только двух символов , которые очень точно совпадают с особенностями цифровой схемы. Каждый из символов отвечает за определённое действие, которое зачастую подразумевает два состояния:
- наличие отверстия или его отсутствие, к примеру, перфокарты или перфоленты;
- на магнитных носителях отвечает за состояние намагничивания или размагничивания;
- по уровню сигнала, высокий или низкий.
В науке, в которой применяется СС, введена определённая терминология, суть ее состоит в следующем:
- Бит – двоичный разряд , который состоит из двух составляющих, несущих в себе определённый смысл. Размещённый слева, определяется как старший и является приоритетным, а справа – младшим, являющийся менее весомым.
- Байт – это единица, которая состоит из восьми битов
.
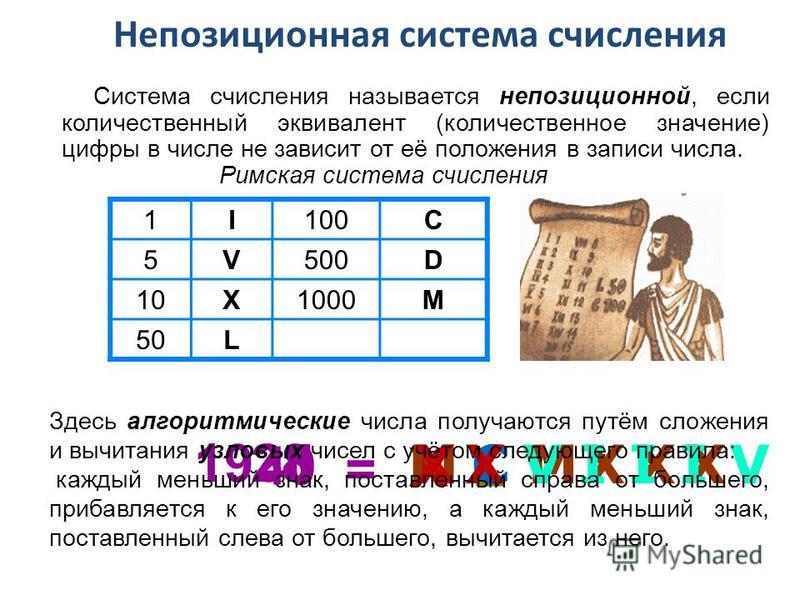
Многие модули воспринимают и обрабатывают информацию порциями или словами . Каждое слово имеет разный вес и может состоять из 8-ми, 16-ти или 32-х битов .
Правила переводов из одной системы в другую
Одним из важнейших факторов арифметики машин является перевод из одной СС в другую . Поэтому обратим внимание на основные алгоритмы выполнения процесса, который покажет, как перевести число в двоичную систему.
Переводим десятичную систему в двоичную
Первоначально обратимся к вопросу, как осуществить перевод системы из десятичной в двоичную систему счисления. Для этого существует правило перевода из десятичных чисел в двоичный код, которое подразумевает математические действия .
Необходимо число, записанное в десятичном виде разделить на 2 . Деление выполнять до тех пор, пока в частном не останется единица . Если необходима двоичная система счисления перевод осуществляется так:
186:2=93 (ост. 0)
0)
93:2=46 (ост. 1)
46:2=23 (ост. 0)
23:2=11 (ост. 1)
11:2=5 (ост. 1)
5:2=2 (ост.1)
После того, как процесс деления закончен, то единицу в частном и все остатки записываем последовательно в обратном делению порядке . То есть, 18610=1111010. Правило перевода десятичных чисел в СС надо соблюдать всегда.
Перевод числа из десятичной системы в двоичную.
Перевод из десятичной СС в восьмеричную
Аналогичный процесс проводится при переводе из десятичной СС в восьмеричную. Его ещё называют «правилом замещения ». Если в предыдущем примере деление данных осуществлялось на 2, то здесь необходимо делить на 8. Алгоритм перевода числа X10 в восьмеричную состоит из следующих шагов:
- Число X10 начинают делить на 8. Полученное частное берём для следующего деления, а остаток записывается, как бит младшего порядка .
- Продолжаем деление до тех пор, пока не получим в результат частного равного нулю
или остаток, который по своему значению меньше восьми
.
 При этом все остатки записываем, как младшие порядки бита
.
При этом все остатки записываем, как младшие порядки бита
.
К примеру, необходимо перевести число 160110 в восьмеричное.
1601:8=200 (ост. 1)
200:8=25 (ост. 0)
25:8=3 (ост.1)
Итак, получим: 161010=31018.
Перевод из десятичной системы в восьмеричную.
Записываем десятичное число шестнадцатеричным
Перевод из десятичной в шестнадцатиричную СС осуществляется аналогично с использованием системы замещения. Но кроме цифр применяют ещё и буквы латинского алфавита A, B, C, D, E, F. Где A обозначает остаток 10, а F остаток 15. Десятичное число делят на 16. К примеру, переводим 10710 в шестнадцатеричную:
107:16=6 (ост. 11 – заменяем В)
6 – меньше, чем шестнадцать. Деление прекращаем и записываем 10710=6В16.
Переходим из другой системы в двоичную
Следующий вопрос, как преобразовать из восьмеричной в двоичную запись числа. Перевод чисел из любой системы в двоичную выполняется достаточно просто.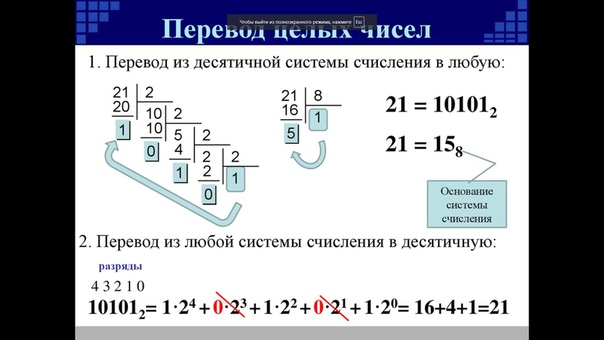 Помощником в этом деле выступает таблица для систем счисления
.
Помощником в этом деле выступает таблица для систем счисления
.
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней двойки:
Таблица 4. Степени числа 2
Пример.
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 5. Степени числа 8
Пример. Число перевести в десятичную систему счисления.
3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 6. Степени числа 16
Степени числа 16
Пример. Число перевести в десятичную систему счисления.
4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в двоичную систему счисления.
5. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в восьмеричную систему счисления.
6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в шестнадцатеричную систему счисления.
Замечание 1
Если вы хотите перевести число из одной системы счисления в другую, то удобнее для начала перевести его в десятичную систему счисления, и уже только потом из десятичной перевести в любую другую систему счисления.
Правила перевода чисел из любой системы счисления в десятичную
В вычислительной технике, использующей машинную арифметику, большую роль играет преобразование чисел из одной системы счисления в другую. Ниже приведем основные правила таких преобразований (переводов).
- Для перевода числа из десятичной системы счисления в двоичную его необходимо последовательно делить на $2$ до тех пор, пока не останется остаток, меньший или равный $1$. Число в двоичной системе представить как последовательность последнего результата деления и остатков от деления в обратном порядке.
- Для перевода числа из десятичной системы счисления в восьмеричную его необходимо последовательно делить на $8$ до тех пор, пока не останется остаток, меньший или равный $7$. Число в восьмеричной системе счисления представить как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
- Для перевода числа из десятичной системы счисления в шестнадцатеричную систему его необходимо последовательно делить на $16$ до тех пор, пока не останется остаток, меньший или равный $15$. Число в шестнадцатеричной системе представить как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
- Чтобы перевести число из двоичной системы счисления в восьмеричную, его необходимо разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, затем каждую триаду заменить соответствующей восьмеричной цифрой согласно таблице 4.
- Чтобы перевести число из двоичной системы счисления в шестнадцатеричную, его следует разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, затем каждую тетраду заменить соответствующей восьмеричной цифрой согласно таблице 4.

- Перевод десятичных чисел в двоичную систему счисления в 2019
- Для образца возьмем число 156, записанное в привычной нам десятичной форме, и попробуем перевести его в двоичный вид.
- Алгоритм будет выглядеть следующим образом — начальное число понадобится разделить на два, затем еще раз на 2, и еще раз на 2 до тех пор, пока в ответе не останется единица.
- При совершении деления для перевода в двоичный код имеют значения не целые числа — а остатки. Если при делении в ответе получилось четное число, то остаток записывается в виде цифры 0, если нечетное — то в виде цифры 1.
- На практике можно легко убедиться, что начальный двоичный ряд остатков для числа 156 будет выглядеть следующим образом — 00111001.
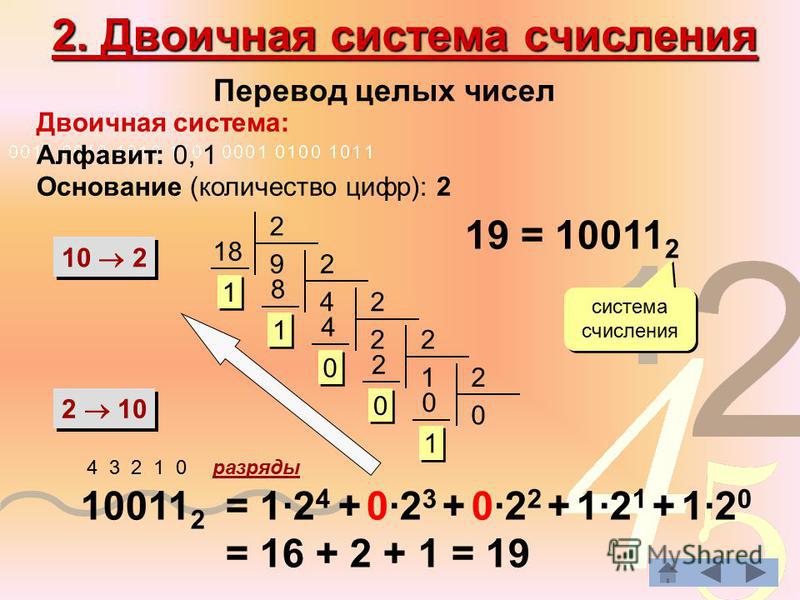 Для того, чтобы превратить его в полноценный двоичный код, этот ряд понадобится записать в обратном порядке — то есть, 10011100.
Для того, чтобы превратить его в полноценный двоичный код, этот ряд понадобится записать в обратном порядке — то есть, 10011100. - Метод удвоения основан на том, что при каждом шаге вычисления берут так называемый предыдущий итог и прибавляют к нему следующую цифру.
- Поскольку на первом шаге предыдущего итога еще не существует, здесь всегда берут 0, удваивают его и прибавляют к нему первую цифру выражения. В нашем примере это будет 0 * 2 + 1 = 1.
- На втором шаге мы уже располагаем предыдущим итогом — он равен 1.
 Это цифру нужно удвоить, а потом прибавить к ней следующую по порядку, то есть — 1 * 2 + 0 = 2.
Это цифру нужно удвоить, а потом прибавить к ней следующую по порядку, то есть — 1 * 2 + 0 = 2. - На третьем, четвертом и последующем шагах все так же берутся предыдущие итоги и складываются с последующей цифрой в выражении.
- 132 = 81 + 27 + 2 ∙ 9 + 2 ∙ 3 = 1 ∙ 34 + 1 ∙ 33 + 2 ∙ 32 + 2 ∙ 31 + 0 = (11220)3.

- 132 = 1 ∙ 53 + 0 ∙ 52 + 1 ∙ 5 + 2 = (1012)5.
- 132 = 2 ∙ 72 + 4 ∙ 7 + 6 = (246)7.
- Какое из следующих чисел является нечетным простым числом?
Ответ и объяснение
Ответ : Вариант 3
Среди данных вариантов 3 является нечетным простым числом. Следовательно, ответ — вариант 3. - Какая наименьшая цифра должна стоять вместо # в 9-значном числе 15549#325, для которого число делится на 3?
Ответ и объяснение
Ответ: Вариант 3
Число, если оно делится на 3, если сумма цифр кратна 3. В 15549#325,
В 15549#325,
Сумма цифр = 1 + 5 + 5 + 4 + 9 + # + 3 + 2 + 5 = 34 + # = 34 + 2 = 36, что делится на 3. - Каково произведение наименьших 15 целых чисел?
Ответ и объяснение
Ответ : Вариант 2
Наименьшие 15 целых чисел: 0, 1, 2, 3, 4,…..14. Так как эти числа содержат ноль, то и произведение будет равно нулю. Итак, ответ — вариант 2. - Какова сумма первых 10 совершенных кубов?
Ответ и объяснение
Ответ: Вариант 1
Сумма 1 st 10 совершенных кубов :- = 1 3 + 2 3 + 3 3 ______ + 10 3 + (10(10) 2 = 3025 Следовательно, правильный ответ — вариант 1 - В чем разница между самым большим пятизначным числом и самым маленьким пятизначным числом?
Ответ и объяснение
Ответ: Вариант 2
Наибольшее 5-значное число = 99999
Наименьшее 5-значное число = 10000.
Искомая разница = 99999 – 10000 = 89999
Итак, ответ вариант 2. - В группе 20 человек. Если каждый человек пожимает руку каждому другому человеку, каково общее количество рукопожатий?
Ответ и объяснение
Ответ : Вариант 4
1 st человек пожмет руку 19 другим людям. 2 и человек пожмут руку оставшимся 18 людям и так далее.
Следовательно, общее количество рукопожатий.
= 19 + 18 + 17+ ……………………+ 3 + 2 + 1 = Σ19 =(19(19+1)/2) =190
Итак, правильный ответ – вариант 4. - 107-значное число получается путем написания первых 58 натуральных чисел рядом друг с другом. Найдите остаток при делении числа на 8.
Ответ и объяснение
Ответ: Вариант 1
Чтобы найти остаток на 8, мы делим только число, образованное последними 3 цифрами, на 8. Последние 3 цифры дадут число 758. Остаток при делении 758 на 8 = 6.Итак, ответ — вариант 1. - Пятизначное число 7500A8 делится на 4.
 Сколько значений A возможно?
Сколько значений A возможно?
Ответ и объяснение
Ответ : Вариант 3
Чтобы найти делимость на 4, нам нужно рассмотреть две последние цифры числа, они должны делиться на 4. Следовательно, A может принимать значения, равные 0, 2, 4, 6 и 8. Следовательно, 5 значения возможны. Итак, правильный ответ — вариант 3. - Чему равна сумма этого ряда 1 + 1 + 2 + 8 + 3+ 27 + 4 + 64 +_______10 + 1000?
Ответ и объяснение
Ответ : Вариант 4
Здесь нам дана комбинация двух рядов
(1+2+3+4+…………………+10) + (1 + 8 + 27 + 64 +…………+1000)
= (1 + 2 + 3 + 4 +…………………+10) + (1 3 +2 3 +3 3 + 4 3 +……………….+10 3 )
(10(10+1)/2) + ((10 × 11)/2) 2 = 3080. Значит, правильный ответ — вариант 4. - Какое из следующих чисел не является рациональным?
Ответ и объяснение
Ответ: Вариант 3
Здесь, 0,2333, 0. 56666 и 7 — рациональные числа, поскольку их можно представить в виде p/q.√3 — не рациональное число, поэтому ответ — вариант 3.
56666 и 7 — рациональные числа, поскольку их можно представить в виде p/q.√3 — не рациональное число, поэтому ответ — вариант 3. -
\[\frac{9}{25}\]
-
\[\frac{37}{78}\]
-
\[0.
 \overline{6}\]
\overline{6}\] -
\[0.\overline{43} \]
- \(ш + г = г + ш\)
- \(и + (w + z) = (u + w) + z\)
- Комплексное число \(0 = 0 + 0i\) является аддитивным тождеством, то есть \(z + 0 = z\).
 {2} — x +2 = 0\) в виде комплексных чисел вида \(r + si\) и \(u + vi\) для некоторых действительных чисел \(r\), \(s\), \(u\) и \(v\).
{2} — x +2 = 0\) в виде комплексных чисел вида \(r + si\) и \(u + vi\) для некоторых действительных чисел \(r\), \(s\), \(u\) и \(v\).
( Подсказка : Помните: \(i = \sqrt{-1}\). Таким образом, мы можем переписать что-то вроде \(\sqrt{-4}\) как \(\sqrt{-4} = \sqrt{ 4}\sqrt{-1} = 2i\).)
- Ответить
-
Мы используем формулу квадрата для решения уравнения и получаем \[x = \dfrac{1 \pm \sqrt{-7}}{2}.\]
Затем мы можем написать \(\sqrt{-7} = i\sqrt{7}\). Таким образом, два решения квадратного уравнения:
\[\begin{align*} x &= \dfrac{1 \pm i\sqrt{7}}{2} \\[4pt] &= \dfrac{1}{2} \pm \dfrac{\sqrt {7}}{2}i \\[4pt] \end{align*}\]
Отдел комплексных чисел
Мы можем складывать, вычитать и умножать комплексные числа, поэтому естественно спросить, можем ли мы делить комплексные числа.Проиллюстрируем на примере.
Пример \(\PageIndex{2}\): деление на комплексное число
Запишите частное \(\dfrac{2 + i}{3 + i}\) как комплексное число в форме \(a + bi\).

Раствор
Эта задача рационализирует знаменатель, поскольку \(i = \sqrt{-1}\). Так что в данном случае нам нужно «убрать» мнимую часть из знаменателя. Напомним, что произведение комплексного числа на его сопряженное является действительным числом, поэтому, если мы умножим числитель и знаменатель \(\dfrac{2 + i}{3 + i}\) на комплексно-сопряженное число знаменателя, мы можно переписать знаменатель как действительное число.{2}} = \dfrac{7 + i}{10} \номер\]
Теперь мы можем записать окончательный результат в стандартной форме как
.\[\dfrac{7 + i}{10} = \dfrac{7}{10} + \dfrac{1}{10}i. \номер\]
Пример \(\PageIndex{2}\) иллюстрирует общий процесс деления одного комплексного числа на другое. В общем, мы можем записать частное \(\dfrac{a + bi}{c + di}\) в форме \(r + si\), умножив числитель и знаменатель нашей дроби на сопряженное \(c — di \) из \(c + di\), чтобы увидеть, что
\[\dfrac{a + bi}{c + di} = \left(\dfrac{a + bi}{c + di}\right)\left(\dfrac{c — di}{c — di}\ справа) = \dfrac{(ac + bd) + (bc — ad)i}{c^{2} + d^{2}} = \dfrac{ac + bd}{c^{2} + d^{ 2}} + \dfrac{bc — ad}{c^{2} + d^{2}}i\]
Таким образом, у нас есть формула отношения двух комплексных чисел.
 {2}}i\]
{2}}i\] при условии \(c + di \neq 0\).
Упражнение \(\PageIndex{3}\)
Пусть \(z = 3 + 4i\) и \(w = 5 — i\).
- Запишите \(\dfrac{w}{z} = \dfrac{5 — i}{3 + 4i}\) как комплексное число в форме \(r + si\), где \(r\) и \ (s\) — некоторые действительные числа. Проверьте результат, умножив частное на \(3 + 4i\). Равно ли это произведение \(5 — i\)?
- Найдите решение уравнения \((3 + 4i)x = 5 — i\) в виде комплексного числа в виде \(x = u + vi\), где \(u\) и \(v\) некоторые действительные числа.{2} = \left(\dfrac{33}{25} + \dfrac{92}{25}\right) + \left(-\dfrac{69}{25}i + \dfrac{44}{25} я\справа) = 5 — я\]
- Мы можем найти \(x\), разделив обе части уравнения на \(3 + 4i\), чтобы увидеть, что \[x = \dfrac{5 — i}{3 + 4i} = \dfrac{11} {25} — \dfrac{23}{25}i\]
Геометрические представления комплексных чисел
Каждая упорядоченная пара \((a , b)\) действительных чисел определяет:
- Точка на координатной плоскости с координатами \((a , b)\).

- Комплексное число \(a + bi\)
- Вектор \(a\textbf{i} + b\textbf{j} = ( a, b )\)
Это означает, что мы можем геометрически представить комплексное число \(a + bi\) вектором в стандартном положении с конечной точкой \((a , b)\). Следовательно, мы можем рисовать изображения комплексных чисел на плоскости. Когда мы это делаем, горизонтальная ось называется реальной осью , а вертикальная ось называется воображаемой осью . Кроме того, координатная плоскость тогда называется комплексной плоскостью .То есть, если \(z = a + bi\), мы можем думать о \(z\) как о направленном отрезке прямой от начала координат до точки (a, b), где конечная точка отрезка равна \( а\) единиц от мнимой оси и \(б\) единиц от действительной оси. Например, комплексные числа \(3 + 4i\) и \(-8 + 3i\) показаны на рис. 5.1.
Рисунок \(\PageIndex{1}\): Два комплексных числа.
Кроме того, сумму двух комплексных чисел можно представить геометрически, используя векторные формы комплексных чисел.
 Нарисуйте параллелограмм, определяемый \(w = a + bi\) и \(z = c + di\). Сумма \(w\) и \(z\) представляет собой комплексное число, представленное вектором из начала координат в вершину параллелограмма, противоположного началу координат, как показано векторами \(w = 3 + 4i\) и \ (z = -8 + 3i\) на рисунке \(\PageIndex{2}\).
Нарисуйте параллелограмм, определяемый \(w = a + bi\) и \(z = c + di\). Сумма \(w\) и \(z\) представляет собой комплексное число, представленное вектором из начала координат в вершину параллелограмма, противоположного началу координат, как показано векторами \(w = 3 + 4i\) и \ (z = -8 + 3i\) на рисунке \(\PageIndex{2}\). Упражнение \(\PageIndex{4}\)
Пусть \(w = 2 + 3i\) и \(z = -1 + 5i\).
- Запишите комплексную сумму \(w + z\) в стандартной форме.
- Нарисуйте рисунок, чтобы проиллюстрировать сумму, используя векторы для представления \(w\) и \(z\).
- Ответить
-
1. Сумма равна \(w + z = (2 — 1) + (3 + 5)i = 1 + 8i\).
2. Представление комплексной суммы с использованием векторов показано на рисунке ниже.
Теперь мы расширим использование представления комплексного числа в виде вектора в стандартной позиции, включив в него понятие длины вектора.
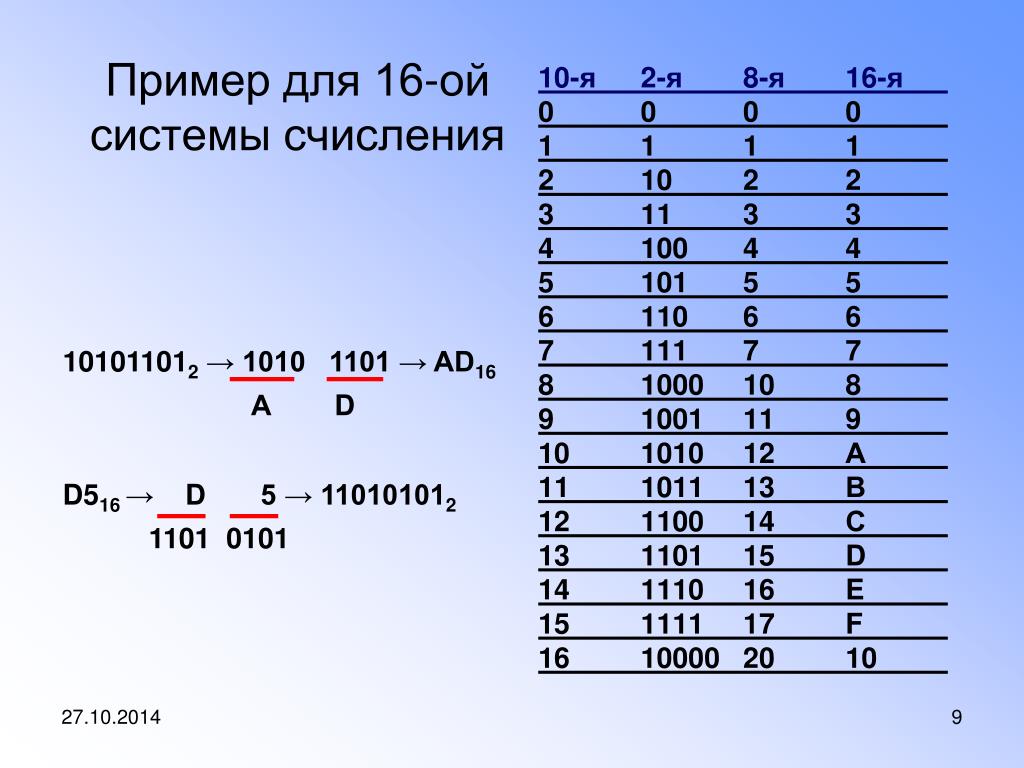 {2}}.{2},\], и поэтому \[|z| = \sqrt{z\bar{z}}\]
{2}}.{2},\], и поэтому \[|z| = \sqrt{z\bar{z}}\] Упражнение \(\PageIndex{5}\)
Пусть \(w = 2 + 3i\) и \(z = -1 + 5i\)
- Найти \(\bar{w}\) и \(\bar{z}\).
- Вычислить \(|w|\) и \(|z|\).
- Вычислить \(w\bar{w}\) и \(z\bar{z}\).
- Что такое \(\bar{z}\), если \(z\) — действительное число?
- Ответить
-
1. Используя определение сопряженного комплексного числа, находим, что \(\bar{w} = 2 — 3i\) и \(\bar{z} = -1 — 5i\).{2}} = \sqrt{26}\).
3. Используя определение произведения комплексных чисел, находим, что\[w\bar{w} = (2 + 3i)(2 — 3i) = 4 + 9 = 13\]
\[z\bar{z} = (-1 + 5i)(-1 — 5i) = 1 + 25 = 26\]
4. Пусть \(z = a + 0i\) для некоторого \(a \in \mathbb{R}\). Тогда \(\bar{z} = a — 0i\). Таким образом, \(\bar{z} = z\), когда \(z \in \mathbb{R}\).
Резюме
В этом разделе мы изучили следующие важные концепции и идеи:
- Комплексное число — это объект вида \(a + bi\), где \(a\) и \(b\) — действительные числа, а \(i^{2} = -1\).
 {2}}i\nonumber\] при условии \(c + di \neq 0\)
{2}}i\nonumber\] при условии \(c + di \neq 0\)
- Комплексное число \(a + bi\) может быть представлено геометрически вектором в стандартном положении с конечной точкой \((a, b)\).Когда мы это делаем, горизонтальная ось называется реальной осью , а вертикальная ось называется воображаемой осью . Кроме того, координатная плоскость тогда называется комплексной плоскостью . То есть, если \(z = a + bi\), мы можем думать о \(z\) как о направленном отрезке прямой от начала координат до точки \((a, b)\), где конечная точка отрезка это единицы от мнимой оси и \(b\) единиц от действительной оси.
- норма (или модуль ) комплексного числа \(z = a + bi\) есть расстояние от начала координат до точки \((a, b)\) и обозначается \(|z |\).{2} \номер\]
Двоичная система счисления
Двоичное число состоит только из 0 с и 1 с.

110100
Пример двоичного числа В двоичном формате нет 2, 3, 4, 5, 6, 7, 8 или 9!
Двоичные числа широко используются в математике и не только.
На самом деле в цифровом мире используются двоичные числа.Как считать с помощью двоичного кода?
Это похоже на десятичный счет, за исключением того, что мы достигаем 10 намного раньше.
Двоичный 0 Начнем с 0 1 Затем 1 ??? Но тогда нет символа 2 … что мы делаем? Ну как считать в десятичной системе? 0 Начать с 0 .  ..
.. Сосчитайте 1,2,3,4,5,6,7,8, а затем… 9 Это последняя цифра в десятичном формате .10 Итак, мы снова начинаем с 0, но добавляем 1 слева То же самое делается в двоичном формате…
Двоичный 0 Начать с 0 • 1 Затем 1 •• 10 Теперь снова начните с 0, но добавьте 1 слева ••• 11 еще 1 •••• ??? Но что СЕЙЧАС … ? Что происходит в Decimal? 99 Когда у нас заканчиваются цифры, мы. 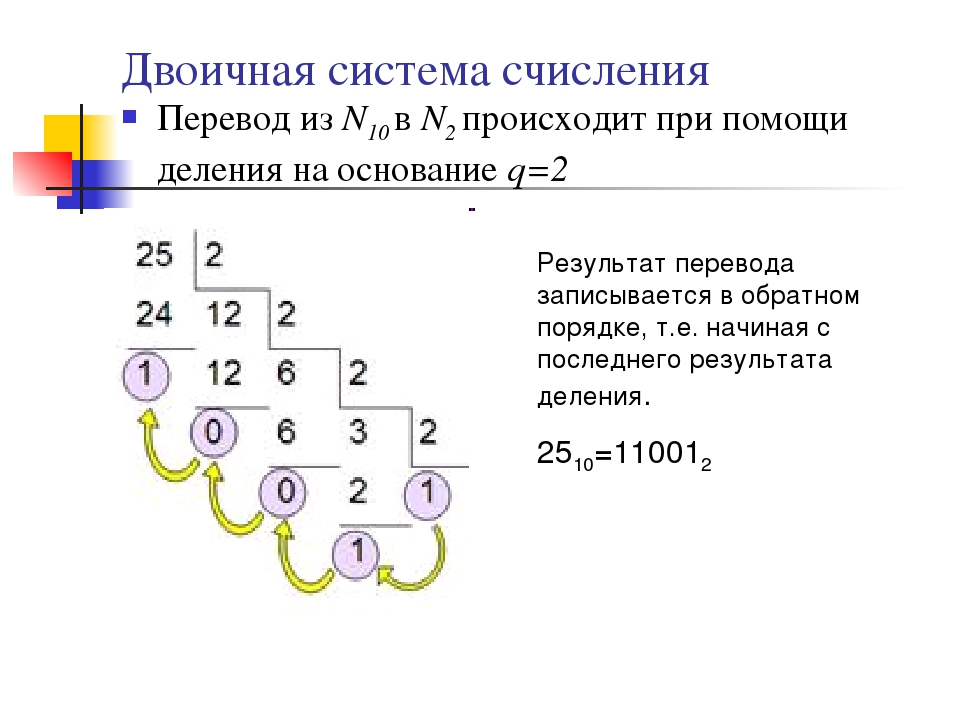 ..
.. 100 … снова начать с 0, но добавить 1 слева
И это то, что мы делаем в двоичном формате …
Двоичный 0 Начать с 0 • 1 Затем 1 •• 10 Снова начать с 0, но добавить 1 слева ••• 11 •••• 100 снова начните с 0 и добавьте единицу к числу слева…
… но это число уже равно 1, поэтому оно также возвращается к 0 …
… и 1 добавляется к следующей позиции слева••••• 101 •••••• 110 ••••••• 111 •••••••• 1000 Снова начать с 0 (для всех 3 цифр),
добавить 1 слева••••••••• 1001 И так далее! Посмотрите, как это делается в этой небольшой демонстрации (нажмите кнопку воспроизведения):
Десятичный против двоичного
Вот некоторые эквивалентные значения:
Десятичный: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Двоичный: 0 1 10 11 100 101 110 111 1000 1001 1010 1011 1100 1101 1110 1111 Симметрия
Двоичные числа также имеют красивый и элегантный узор:
Вот несколько больших значений:
Десятичный: 20 25 30 40 50 100 200 500 Двоичный: 10100 11001 11110 101000 110010 1100100 11001000 111110100 «Двоичный код так же прост, как 1, 10, 11.
 »
» Теперь посмотрите, как использовать Binary для счета на пальцах после 1000:
Позиция
В десятичной системе есть единицы, десятки, сотни и т. д.
В Двоичный есть Единицы, Двойки, Четверки и т. д., например:
Это 1×8 + 1×4 + 0×2 + 1 + 1×(1/2) + 0×(1/4) + 1×(1/8)
= 13,625 в десятичном форматеЦифры можно размещать слева или справа от точки, чтобы показать значения больше единицы и меньше одного.
10,1 Число слева от точки целое число (например, 10) По мере того, как мы двигаемся дальше влево, каждый числовой разряд
получает 2 раз больше .Первая цифра справа означает половинок (1/2). По мере того, как мы движемся дальше вправо, каждый числовой разряд
становится в 2 раза меньше (в два раза больше).
Пример: 10.1
- «10» означает 2 в десятичной системе,
- «.1» означает половину,
- Таким образом, «10,1» в двоичном формате равно 2,5 в десятичном виде
Вы можете выполнять преобразования в Конвертер двоичных и десятичных чисел в шестнадцатеричные.
слов
Слово двоичное происходит от «Би-», что означает два. Мы видим «би-» в таких словах, как «велосипед» (два колеса) или «бинокль» (два глаза).
Когда вы произносите двоичное число, произносите каждую цифру (например, двоичное число «101» произносится как «один ноль один» , или иногда «один-о-один» ). Таким образом, люди не путаются с десятичным числом. Одна двоичная цифра (например, «0» или «1») называется «бит».
Например, 11010 имеет длину пять бит.
Слово бит составлено из слов « b inary dig it »
Как показать, что число является двоичным
Чтобы показать, что число является двоичным числом , добавьте к нему маленькую двойку, например: 101 2
Таким образом, люди не будут думать, что это десятичное число «101» (сто один).
Примеры
Пример: Что такое 1111
2 в десятичном формате?- «1» слева находится в позиции «2×2×2», что означает 1×2×2×2 (=8)
- Следующая «1» находится в позиции «2×2», так что это означает 1×2×2 (=4)
- Следующая «1» находится в позиции «2», так что это означает 1×2 (=2)
- Последняя «1» стоит в позиции единиц, значит 1
- Ответ: 1111 = 8+4+2+1 = 15 в десятичной системе счисления
Пример: Что такое 1001
2 в десятичном формате?- «1» слева находится в позиции «2×2×2», что означает 1×2×2×2 (=8)
- «0» стоит в позиции «2×2», значит, 0×2×2 (=0)
- Следующий «0» находится в позиции «2», что означает 0×2 (=0)
- Последняя «1» стоит в позиции единиц, значит 1
- Ответ: 1001 = 8+0+0+1 = 9 в десятичной системе счисления
Пример: Что такое 1.1
2 в десятичной системе?- «1» слева стоит в позиции единиц, значит 1.

- 1 справа находится в положении «половинки», значит, 1×(1/2)
- Итак, 1,1 — это «1 и 1 половина» = 1,5 в десятичной системе счисления
Пример. Что такое 10.11
2 в десятичном формате?- «1» стоит в позиции «2», значит 1×2 (=2)
- «0» стоит в позиции единиц, значит 0
- «1» справа от точки находится в положении «половинки», так что это означает 1×(1/2)
- Последняя «1» справа стоит в позиции «четверти», значит, 1×(1/4)
- Итак, 10.11 равно 2+0+1/2+1/4 = 2,75 в десятичной системе счисления .
«В мире есть 10 типов людей,
тех, кто понимает двоичные числа, и тех, кто не понимает.»Решения NCERT для математики класса 9, глава 1 Система счисления
Решения NCERT для математики класса 9, глава 1 Системы счисления Ex 1.1 являются частью решений NCERT для математики класса 9. Здесь мы предоставили решения NCERT для математики класса 9, глава 1, системы счисления, пример 1.
 1.
1. Решения NCERT для математики класса 9 Глава 1 Системы счисления Ex 1.1
Упр. 1.1 Класс 9 Математика Вопрос 1.
Является ли ноль рациональным числом? Можете ли вы записать его в виде \(\frac { p }{ q }\), где p и q — целые числа, а q ≠0?
Решение:
Да, ноль — рациональное число, его можно записать в виде \(\frac { p }{ q }\).
0 = \(\frac { 0 }{ 1 }\) = \(\ frac { 0 }{ 2 }\) = \(\ frac { 0 }{ 3 }\) и т. д. Знаменатель q также можно принять в виде отрицательное целое число.Пример 1.1 Класс 9 Математика Вопрос 2.
Найдите шесть рациональных чисел между 3 и 4.
Решение:
Пусть q i будет рациональным числом между 3
и 4, где j = от 1 до 6.
∴ Шесть рациональных чисел равны следует:
Таким образом, шесть рациональных чисел между 3 и 4 равны
Упражнение 1.1. Математика для 9 класса. Вопрос 3.
Найдите пять рациональных чисел между \(\frac { 3 }{ 5 }\) и \(\frac { 4 }{ 5 }\).
Решение:
Так как нам нужно найти пять рациональных чисел, значит, умножаем числитель и знаменатель на 6.
Упражнение 1.1 Класс 9 Математика Вопрос 4.
Укажите, верны или нет следующие утверждения. Обоснуйте свои ответы.
(i) Каждое натуральное число является целым числом.
(ii) Каждое целое число является целым числом.
(iii) Каждое рациональное число является целым числом.
Решение:
(i) Верно
∵ Совокупность всех натуральных чисел и 0 называется целыми числами.
(ii) Ложь
∵ Целые отрицательные числа не являются целыми числами.
(iii) Ложь
∵ Рациональные числа имеют вид p/q, q ≠ 0 и q не делит полностью p, если они не являются целыми числами.NCERT Solutions for Class 9 Math Chapter 1 Системы счисления (Hindi Medium) Ex1.1
Решения NCERT для математики класса 9 Глава 1 Системы счисления Ex 1.2
Упр. 1.2 Класс 9 Математика Вопрос 1.
Укажите, верны или нет следующие утверждения. Обоснуйте свои ответы.
Обоснуйте свои ответы.
(i) Каждое иррациональное число является действительным числом.
(ii) Каждая точка на числовой прямой имеет вид √m , где m — натуральное число.
(iii) Каждое действительное число является иррациональным числом.
Решение:
(i) Верно
Потому что все рациональные числа и все иррациональные числа образуют группу (набор) действительных чисел.
(ii) False
Потому что отрицательные числа не могут быть квадратным корнем любого натурального числа.
(iii) Ложь
Потому что рациональные числа также являются частью действительных чисел.Упражнение 1.2. Математика для 9 класса. Вопрос 2.
Являются ли квадратные корни всех натуральных чисел иррациональными? Если нет, приведите пример квадратного корня из числа, которое является рациональным числом.
Решение:
Нет, если мы возьмем положительное целое число, скажем, 9, его квадратный корень равен 3, что является рациональным числом.Упражнение 1.2.
 Математика для 9 класса. Вопрос 3.
Математика для 9 класса. Вопрос 3.
Покажите, как √5 может быть представлено на числовой прямой.
Решение:
Нарисуйте числовую прямую и отметьте на ней точки О и А так, что ОА = 1 единица. Нарисуйте BA ⊥ OA, так как BA = 1 единица. Присоединяйтесь к OB = √2 единицы.
Теперь нарисуйте BB 1 ⊥ OB так, чтобы BB 1 = 1 единица. Присоединяйтесь к OB 1 = √3 единиц.
Затем нарисуйте B 1 B 2 ⊥ OB 1 так, что B 1 B 2 = 1 единица.
Присоединиться к OB 2 = шт.
Снова нарисуйте B 2 B 3 ⊥OB 2 так, что B 2 B 3 = 1 единица.
Присоединиться к OB 3 = √5 единиц.
Возьмите O в качестве центра и OB 3 в качестве радиуса, нарисуйте дугу, которая пересекает числовую прямую в точке D.
Точка D
представляет √5 на числовой прямой.Упражнение 1.
 2. Математика для 9 класса. Вопрос 4.
2. Математика для 9 класса. Вопрос 4.
Возьмите большой лист бумаги и постройте «спираль квадратного корня» следующим образом.Начните с точки O и начертите отрезок OP 1 единичной длины Нарисуйте отрезок P 1 , P 2 перпендикулярно OP 1 единичной длины (см. рисунок). Теперь нарисуйте отрезок P 2 P 3 перпендикулярно OP 2 . Затем начертите отрезок P 3 P 4 перпендикулярно OP 3 . Продолжая в том же духе, вы можете получить отрезок P n-1 P n , нарисовав отрезок единичной длины перпендикулярно OP n – 1 .Таким образом, вы создадите точки P 2 , P 3 ,…… P n ,….. и соедините их, чтобы создать красивую спираль, изображающую √2,√3,√4,……
Решение:
Сделай сам.Решения NCERT для математики класса 9 Глава 1 Системы счисления Ex 1.3
Упр. 1.3 Класс 9 Математика Вопрос 1.

Запишите следующее в десятичной форме и скажите, какое десятичное разложение имеет каждый
Решение:
(i) Имеем, \(\frac { 36 }{ 100 }\) = 0 .36
Таким образом, десятичное расширение \(\frac { 36 }{ 100 }\) заканчивается.(ii) Разделив 1 на 11, мы получим
Таким образом, десятичное расширение \(\frac { 1}{11}\) является непрерывным повторением.(iii) Имеем 4\(\frac { 1 }{ 8 }\) = \(\frac { 33 }{ 8 }\)
Разделив 33 на 8, получим
∴ 4\(\frac { 1 }{ 8 }\) = 4,125. Таким образом, десятичное разложение числа 4\(\frac { 1 }{ 8 }\) заканчивается.(iv) Разделив 3 на 13, мы получим
Здесь повторяющийся блок цифр равен 230769
∴ \(\frac { 3 }{ 13 }\) = 0.23076923… = 0.\(\bar { 230769 }\)
Таким образом, десятичное расширение \(\frac { 3 }{ 13 }\) является непрерывным повторением.(v) Разделив 2 на 11, получим
Здесь повторяющийся блок цифр равен 18.
∴ \(\frac { 2 }{ 11 }\) = 0,1818… = 0. \(\bar { 18 } \)
\(\bar { 18 } \)
Таким образом, десятичное расширение \(\frac { 2 }{ 11 }\) является непрерывным повторением.(vi) Разделив 329 на 400, получим
∴ \(\frac { 329}{400}\) = 0,8225. Таким образом, десятичное расширение \(\frac { 329 }{ 400 }\) заканчивается.Пример 1.3. Математика для 9 класса. Вопрос 2.
Вы знаете, что \(\frac { 1 }{ 7 }\) = \(\bar { 0,142857 }\). Можете ли вы предсказать, что десятичные разложения \(\frac { 2 }{ 7 }\) , \(\ frac { 13 }{ 7 }\) , \(\ frac { 4 }{ 7 }\) , \(\ frac { 5 }{ 7 }\) , \(\ frac { 6 }{ 7 }\) , без фактического деления в большую сторону? Если да, то как?
Решение:
Нам дано, что \(\frac { 1 }{ 7 }\) = \(\bar {0,142857 }\).
∴ \(\frac { 2 }{ 7 }\) = 2 x \(\frac { 1 }{ 7 }\) = 2 x (\(\bar {0,142857 }\)) =\(\bar { 0 .285714 }\)
\(\frac { 3 }{ 7 }\) = 3 x \(\frac { 1 }{ 7 }\) = 3 x (\(\bar {0,142857 }\)) = \(\ бар {0,428571}\)
\(\frac {4}}{7}\) = 4 x \(\frac {1}{7}\) = 4 x (\(\bar {0,142857}\)) = \ (\ bar { 0,571 428 }\)
\(\ frac { 5 }{ 7 }\) = 5 x \(\ frac { 1 }{ 7 }\) = 5 x (\(\ bar {0,142857 }\) ) = \(\bar { 0,714285 }\)
\(\frac { 6 }{ 7 }\) = 6 x \(\frac { 1 }{ 7 }\) = 6 x (\(\ bar { 0,142857 } \)) = \(\bar { 0,8571 42 }\)
Таким образом, фактически не выполняя длинное деление, мы можем предсказать десятичные разложения заданных рациональных чисел.
Упр. 1.3. Математика для 9 класса. Вопрос 3.
Представить следующее в виде \(\frac { p }{ q }\), где p и q — целые числа, а q ≠ 0.
(i) 0.\(\bar { 6 }\)
(ii) 0,4\(\bar { 7 }\)
(iii) 0.\(\overline { 001 }\)
Решение:
(i) Пусть x = 0.\(\bar { 6 }\) = 0,6666… … (1)
Поскольку имеется только одна повторяющаяся цифра,
умножая (1) на 10 с обеих сторон, мы получаем
10x = 6,6666… … (2)
Вычитая (1) из (2) ), получаем
10x – x = 6,6666… -0,6666…
⇒ 9x = 6 ⇒ x = \(\frac { 6 }{ 9 }\) = \(\frac { 2 }{ 3 }\)
Таким образом, 0.\(\бар {6}\) = \(\фракция {2}{3}\)(ii) Пусть x = 0,4\(\bar { 7 }\) = 0,4777… … (1)
Поскольку имеется только одна повторяющаяся цифра, умножив (1) на lo с обеих сторон, мы получим
10x = 4,777
Вычитая (1) из (2), получаем
10x – x = 4,777…… – 0,4777…….
⇒ 9x = 4,3 ⇒ x = \(\frac { 43 }{ 90 }\)
Таким образом, 0,4\(\bar { 7 }\) = \(\frac { 43 }{ 90 }\)(iii) Пусть x = 0.
 \(\overline { 001 }\) = 0,001001… … (1)
\(\overline { 001 }\) = 0,001001… … (1)
Поскольку имеется 3 повторяющихся цифры,
умножая (1) на 1000 с обеих сторон, мы получаем
1000x = 1 .001001 … (2)
Вычитая (1) из (2), получаем
1000x – x = (1,001…) – (0,001…)
⇒ 999x = 1 ⇒ x = \(\frac { 1 }{ 999 }\ )
Таким образом, 0.\(\overline { 001 }\) = \(\frac { 1 }{ 999 }\)Ex 1.3 Class 9 Maths Вопрос 4.
Выразите 0,99999… в форме \(\frac { p }{ q }\)Вы удивлены своим ответом? С учителем и одноклассниками обсудите, почему ответ имеет смысл.
Решение:
Пусть x = 0,99999….. …. (i)
Поскольку есть только одна повторяющаяся цифра,
умножая (i) на 10 с обеих сторон, мы получаем
10x = 9.9999 … (ii)
Вычитая (i) из (ii), получаем
10x – x = (99999) – (0,9999)
⇒ 9x = 9 ⇒ x = \(\frac { 9 }{ 9 }\) = 1
Таким образом, 0,9999 = 1
Поскольку 0,9999… продолжается вечно, нет такой большой разницы между 1 и 0,9999
Следовательно, оба равны.Пример 1.
 3 Математика для 9 класса. Вопрос 5.
3 Математика для 9 класса. Вопрос 5.
Какое максимальное количество цифр может быть в повторяющемся блоке цифр в десятичной записи \(\frac { 1 }{ 17 }\)? Выполните деление, чтобы проверить свой ответ.
Решение:
В \(\frac { 1 }{ 17 }\), В делитель равно 17.
Так как количество записей в повторяющемся блоке цифр меньше делителя, то максимальное количество цифр в повторяющемся блоке равно 16.
Разделив 1 на 17, получим
с которого мы начали деление.
∴ \(\frac { 1 }{ 17 }\) = 0.\(\overline { 0588235294117647 }\)
Таким образом, в десятичном разложении \(\frac { 1 }{) в повторяющемся блоке 16 цифр. 17 }\).
Значит, наш ответ подтвержден.Пример 1.3 Математика для 9 класса Вопрос 6.
Посмотрите на несколько примеров рациональных чисел в форме \(\frac { p }{ q }\) (q ≠ 0). Где p и q — целые числа без общих делителей, кроме 1, и имеющие завершающие десятичные представления (расширения). Можете ли вы угадать, какому свойству q должно удовлетворять?
Решение:
Давайте посмотрим на десятичное разложение следующих конечных рациональных чисел:
Мы видим, что простая факторизация q (т. е. знаменатель) имеет только степени 2 или степени 5 или степени обоих.
е. знаменатель) имеет только степени 2 или степени 5 или степени обоих.Упражнение 1.3 Класс 9 Математика Вопрос 7.
Напишите три числа, чьи десятичные разложения не заканчиваются и не повторяются.
Решение:
√2 = 1,414213562 ………..
√3 = 1,732050808 …….
√5 = 2,23606797 …….Упражнение 1.3. Математика для 9 класса. Вопрос 8.
Найдите три различных иррациональных числа между рациональными числами \(\frac { 5}{ 7 }\) и \(\frac { 9 }{ 11 }\) .
Решение:
У нас есть,
Три иррациональных числа между 0.\(\overline { 714285 }\) и 0.\(\overline { 81 }\) равны
(i) 0,750750075000 …..
(ii) 0,767076700767000 ……
(iii) 0,78080078008000 ……Упражнение 1.3 Класс 9 Математика Вопрос 9.
Классифицируйте следующие числа как рациональные или иррациональные (iv) 7,478478…..
(v) 1,101001000100001………
Решение:
(1) ∵ 23 не является полным квадратом.
∴ \(\sqrt { 23 }\) — иррациональное число.
(ii) ∵ 225 = 15 x 15 = 15 2
∴ 225 — полный квадрат.
Таким образом, \(\sqrt { 225 }\) — рациональное число.
(iii) ∵ 0,3796 — конечный десятичный знак.
∴ Это рациональное число.
(iv) 7,478478… = 7.\(\overline { 478 }\)
Так как 7.\(\overline { 478 }\) является непрерывающимся повторяющимся (повторяющимся) десятичным числом.
∴ Это рациональное число.
(v) Так как 1.101001000100001… — это бесконечное, неповторяющееся десятичное число.
∴ Это иррациональное число.Решения NCERT для математики класса 9, глава 1, системы счисления, пример 1.4
Упр. 1.4 Класс 9 Математика Вопрос 1.
Визуализируйте 3,765 на числовой прямой, используя последовательное увеличение.
Решение:
3,765 лежит между 3 и 4.
Пример 1.4 Математика для 9 класса Вопрос 2.
Визуализируйте 4.\(\bar { 26 }\) в числовой строке, до 4 знаков после запятой.
Решение:
4.\(\bar { 26 }\) или 4,2626 лежит между 4 и 5.
Решения NCERT для математики класса 9, глава 1, системы счисления, пример 1.5
Упр. 1.5 Класс 9 Математика Вопрос 1.
Классифицируйте следующие числа как рациональные или иррациональные.
Решение:
(i) Так как это разность рационального и иррационального числа.
∴ 2 – √5 – иррациональное число.
(ii) 3 + \( \sqrt{23} \) – \( \sqrt{23} \) = 3 + \( \sqrt{23} \) – \( \sqrt{23} \) = 3
что является рациональным числом.
(iii) Поскольку \(\frac { 2\sqrt { 7 } }{ 7\sqrt { 7 } }\) = \(\frac { 2\times\sqrt { 7 } }{ 7\times\sqrt { 7 } }\) = \(\frac { 2 }{ 7 }\) , что является рациональным числом.
(iv) ∵ Частное рационального и иррационального числа является иррациональным числом.
∴ \(\frac { 1 }{ \sqrt { 2 } }\) — иррациональное число.
(v) ∵ 2π = 2 x π = Произведение рационального и иррационального чисел является иррациональным числом.
∴ 2π — иррациональное число.Упр. 1.5 Класс 9 Математика Вопрос 2.
Упростите каждое из следующих выражений
Решение:
(i) (3 + √3)(2 + √2)
= 2(3 + √3) + √2(3 + √3)
= 6 + 2√3 + 3√2 + √6
Таким образом, (3 + √3)(2 + √2) = 6 + 2√3 + 3√2 + √6
(ii) (3 + √3)(3 – √3) = (3) 2 – (√3) 2
= 9 – 3 = 6
Таким образом, (3 + √3)(3 – √3) = 6
(iii) (√5 + √2) 2 = (√5) 2 + (√2) 2 + 2(√5)(√2)
= 5 + 2 + 2√10 = 7 + 2√10
Таким образом, (√5 + √2 ) 2 = 7 + 2√10
(iv) (√5 – √2)(√5 + √2) = (√5) 2 – (√2) 2 = 5 – 2 = 3
Таким образом, (√5 – √2) (√5 + √2) = 3Пример 1.5 Класс 9 Математика Вопрос 3.
Напомним, π определяется как отношение длины окружности (скажем, c) круга к его диаметру (скажем, d). То есть π = \ (\ frac { c }{ d } \). Кажется, это противоречит тому факту, что n иррационально. Как вы разрешите это противоречие?
Решение:
Когда мы измеряем длину линии с помощью весов или любого другого устройства, мы получаем лишь приблизительное ациональное значение, т. е. c и d оба иррациональны.
е. c и d оба иррациональны.
∴ \(\frac { c }{ d }\) иррационально и, следовательно, π иррационально.
Таким образом, нет никакого противоречия в том, что оно иррационально.Пример 1.5 Класс 9 Математика Вопрос 4.
Представьте \( \sqrt{9.3} \) в числовой строке.
Решение:
Нарисуйте отрезок AB = 9,3 единицы и продлите его до C так, чтобы BC = 1 единица.
Найдите середину АС и обозначьте ее как O.
Нарисуйте полукруг, взяв центр O и радиус AO. Нарисуйте BD ⊥ AC.
Начертите дугу, в центре которой находится B, а в качестве радиуса — BD, пересекающую AC, образующуюся в точке E, так что BE = BD = \(\sqrt { 9.3 }\) единиц.
Упражнение 1.5 Класс 9 Математика Вопрос 5.
Рационализируйте знаменатель следующего
Решение:
Решения NCERT для математики класса 9 Глава 1 Системы счисления Ex 1.6
Упр. 1.6 Класс 9 Математика Вопрос 1.
Найти:
Решение:
(i) 64 = 8 x 8 = 8 2
∴ (64) 1/2 = (82) 1/2
8 2 x 1/2 = 8 [(a m ) n = a m x n ]
(ii) 32 = 2 x 2x 2 x 2 x 2 = 2 5- ∴ 1/5 = (2 5 ) 1/5 = 2 5 x 1/5 = 2 [(a m ) n = a mxn ] 5 x 5 x 5 = 5 3
м ) n = a mxn ]
∴ (125) 1/3 = (5 3 ) 1/3 = 5 3 x 1/3 = 5 [(aПример 1.
 { n } }\) ]
{ n } }\) ] Пример 1.6 Математика для 9 класса Вопрос 3.
Упростить:
Решение:
(i) 2 2/3 . 2 1/5 = 2 2/3 + 1/5 = 2 13/15
[a m . a n = a m + n
(iv) 7 1/2 .8 1/2 = (7 x 8) 1/2 = (56) 1/2 a м xb м = (ab) м ]Мы надеемся, что решения NCERT для класса 9 по математике, глава 1, системы счисления, пример 1.1, помогут вам.Если у вас есть какие-либо вопросы относительно решений NCERT для математики класса 9, глава 1, системы счисления, пример 1.1, оставьте комментарий ниже, и мы свяжемся с вами в ближайшее время.
Решение уравнений в действительной системе счисления
Решение уравнения с целыми числами
Уравнение для примера 1 В нашем первом примере мы решим уравнение -5 x + 3 = -17.
 Помните, что цель состоит в том, чтобы изолировать переменную x , отменив целые числа, которые находятся на одной стороне уравнения с ней.Целое число -5 умножается на x , поэтому мы можем использовать противоположную операцию, деление, чтобы отменить это. Мы также можем отменить тройку, вычитая ее.
Помните, что цель состоит в том, чтобы изолировать переменную x , отменив целые числа, которые находятся на одной стороне уравнения с ней.Целое число -5 умножается на x , поэтому мы можем использовать противоположную операцию, деление, чтобы отменить это. Мы также можем отменить тройку, вычитая ее. Важно, чтобы числа исключались в определенном порядке, соблюдая порядок операций в обратном порядке. Порядок операций заканчивается сложением и вычитанием, поэтому мы начинаем решать уравнения. После этого мы можем отменить умножение и деление, за которыми следуют показатели степени, а затем члены в скобках.Все, что мы делаем с одной частью уравнения, должно быть сделано с обеих сторон. Это уравновешивает уравнение.
Решение для примера 1 Уравнение считается решенным, когда переменная сама по себе находится в одной части уравнения, а число (решение) — в другой.
 Затем мы можем проверить решение, подставив его вместо переменной в исходном уравнении. Если обе части уравнения упрощаются до одного и того же числа, то решение верное.
Затем мы можем проверить решение, подставив его вместо переменной в исходном уравнении. Если обе части уравнения упрощаются до одного и того же числа, то решение верное.Проверка решения для примера 1 Решение уравнений с рациональными числами
Уравнение для примера 2 В этом примере мы решим уравнение, в котором рациональные числа представлены в виде дробей и десятичных знаков. Мы будем следовать тому же процессу, что и в первом примере, рассматривая рациональные числа так же, как и целые числа.Дробь одна пятая умножается на x и вычитается восьмерка. Можно использовать противоположные операции, чтобы исключить рациональные числа, оставив x на этой стороне уравнения. Число, оставшееся справа, и будет решением.
Решение для примера 2 Наконец, решение можно проверить, подставив 46,5 вместо x в исходное уравнение.
 После упрощения получается 1,3 = 1,3. Это верное утверждение, дающее нам понять, что 46,5 — правильное решение уравнения.
После упрощения получается 1,3 = 1,3. Это верное утверждение, дающее нам понять, что 46,5 — правильное решение уравнения. Проверка решения для примера 2 Резюме урока
При решении уравнения противоположные операции используются для исключения чисел, которые находятся на той же стороне уравнения, что и переменная. Какие бы операции ни выполнялись с одной стороны, они должны выполняться и с другой стороны уравнения.Уравнение решено, когда переменная стоит одна на одной стороне уравнения, а число на другой стороне. Это число представляет 90 685 решений 90 686 уравнения.
Лучшие альтернативные решения для системы Take-a-Number
Не все системы управления очередью одинаковы.
В нашем быстро меняющемся мире системы очередей, как и все остальное, должны учиться развиваться и адаптироваться. К сожалению, лишь немногие из них готовы принять цифровые достижения.

Одним из таких пережитков среди систем управления очередями является так называемая система . Несмотря на свой возраст, мы все еще можем видеть, как его используют в DMV, ресторанах быстрого питания, банках, почтовых отделениях, аптеках и т. д. возьмите распечатанный номерной билет и ждите своей очереди.
Звучит хорошо на первый взгляд, но не забудьте прочитать мелкий шрифт. Чего вам не говорят о системах выдачи билетов в очереди, так это того, что вы вынуждены проводить каждую минуту бодрствования, приклеившись к экрану , в ожидании мучительно долгого периода, пока наконец не появится ваш номер.
«Ну и ну! Вот что значит стоять в очереди», — можете сказать вы. И это именно та проблема, с которой мы сталкиваемся — вместо того, чтобы улучшать ситуацию с очередями, системы «принимай число» программируют нас на то, чтобы воспринимать это ужасное ожидание как должное.
В этой статье мы рассмотрим некоторые насущные проблемы, связанные с использованием в вашем бизнесе систем очередей по принципу «бери число», и предложим решение, которое вам необходимо принять немедленно.
Давайте начнем наш список проблем с обычного примера.
Отсутствие четкого объяснения: взгляд на систему самообслуживания McDonald’s
Когда McDonald’s впервые обнародовал свой план по внедрению киосков самообслуживания, в ряде статей выражалось беспокойство. Люди боялись, что McDonald’s якобы заменит 2500 человек-кассиров цифровыми киосками.
В действительности, однако, McDonald’s хотел внедрить эти киоски совместно с людьми. Цель развертывания киосков самообслуживания — позволить клиентам делать заказы и оплачивать их, не усугубляя проблему ожидания.
Несмотря на общие успехи, у этой системы есть свои недостатки . Давайте посмотрим на основной.
Несмотря на то, что система самообслуживания в McDonald’s использует, казалось бы, систему нумерованных билетов, нет особого смысла называть ее нумерованной системой.
Представьте себе: вы приходите в Макдональдс, видите, что в очереди слишком много людей, и поворачиваетесь к киоскам самообслуживания.
 Вы делаете заказ без заминок и получаете номер, который поможет вам отследить ваш заказ.
Вы делаете заказ без заминок и получаете номер, который поможет вам отследить ваш заказ.Естественно, если номер вашего заказа, скажем, 090, вы ожидаете, что он будет выполнен до 091. Однако обычно это не так.
На самом деле заказы 091, 092 и даже 099 могут подняться раньше вашего.
Теоретически это звучит логично. Некоторые заказы занимают больше времени, некоторые заказы пересекаются — в конце концов, быстрее подать пять разных Биг-Маков, чем пять разных блюд.
Но тогда для чего эти цифры? Даже зная причину, по которой ваш заказ пришел позже других, оставляет у вас ощущение, что ваши надежды возродились и быстро рухнули .
Это относится не только к ресторанам быстрого питания. Проблема в том, что система нумерации не учитывает внутреннюю систему приоритетов.
Даже если система работает как задумано, факт в том, что система продажи билетов не сообщает о продолжительности вашего ожидания. Ваш номер может быть следующим в очереди, и все же вы можете подождать еще час, прежде чем вас обслужат.

Короче говоря, системы «возьми число» создают ожидания, которые они просто не могут удовлетворить . А если говорить о проблемах с билетными автоматами, то мы только начинаем.
Отсюда все идет под откос.
Отсутствие персонализации
Еще один, и некоторые могут сказать, что самый важный недостаток системы с номерными билетами заключается в том, что она игнорирует личную информацию ваших клиентов. Применение унифицированного подхода уничтожает любую возможность персонализации процесса для ваших клиентов.
В теории одинаковое отношение ко всем звучит хорошо. Если одному покупателю присваивается номер, то же самое присваивается и каждому другому покупателю.
Но вы не можете игнорировать силу запоминания имен ваших клиентов .
Когда компания прилагает усилия, чтобы запомнить ваше имя, это радует. Конечно, могут быть случаи, когда имена произносятся неправильно, но важна мысль.
И да, никому не нравится, когда их имена вырезают, но им вообще не присваивают имени? Это прямо унизительно.
Сейчас номер вместо имени дают только бездушной технике, быдлу или сокамерникам. И даже тогда многие тюрьмы знают, что лучше не продолжать дегуманизировать заключенных.
(Эй, коровы тоже заслуживают вашего уважения!)
Так что же сделали ваши клиенты, чтобы с ними обращались так? Как бизнес, вы должны приложить все усилия, чтобы лучше понять своих клиентов .Практика обмена именами является признаком взаимного уважения и большого уровня комфорта.
С точки зрения бизнеса, это первый шаг к обеспечению превосходного качества обслуживания клиентов. Но почему-то многие компании продолжают настаивать на разыгрывании этой нелепой игры:
- Привет, рад иметь с тобой дело! Меня зовут Джеймс.
- Ого, слишком много букв, чтобы запомнить. С этого момента мы будем называть вас № 104865.
Конечно, есть смысл использовать коды в местах с большим совпадением названий, например, в университете.Даже в этом случае эти номера следует использовать вместе с настоящими именами.

Однако в большинстве случаев имени и инициала достаточно, чтобы узнать человека .
Присвоение номера своим клиентам — это верный способ сказать им: «Вы будете говорить, когда к вам обращаются». Для клиента нет ничего более удручающего, чем осознание того, что единственное, что видят в нем компании, — это их деньги.
Отсутствие подхода, основанного на данных
По сравнению с цифровыми решениями для организации очередей, системы Take-a-Number практически не предоставляют полезной бизнес-информации .
При регистрации клиенты могут в лучшем случае выбрать очередь. Это предупреждает персонал о прибытии клиента, но не дает соответствующей информации для работы до начала фактического обслуживания.
Какова цель их визита? Какие вопросы должны решить эти клиенты? Есть ли у них особые требования? Вашим сотрудникам необходимо подготовить документы?
Ни на один из этих вопросов нельзя ответить с помощью простой системы «возьми-число».

Имейте в виду: сбор данных о клиентах — не очень приятный бонус.Это обязательное условие, которое должна обеспечивать система управления очередью. Цель сбора данных состоит в том, чтобы как лучше обслуживать клиентов , так и лучше понимать их .
Кроме того, есть внутренняя информация — например, время ожидания, время обслуживания, время простоя, количество неявок и т. д. Эти данные в основном остаются невидимыми для клиентов, но они могут значительно помочь вам в дальнейшем улучшить ваш сервис.
Например, узнав, что в одной точке обслуживания клиентов больше, чем в остальных, можно делегировать туда больше сотрудников или открыть новую аналогичную службу поддержки.
Суть в том, что вы получаете точное число, на котором основываете свои решения. В современном деловом мире, где все играют в эту игру с числами, важно ошибаться в пользу получения большего количества данных — и большего количества отзывов клиентов.

Система считывания просто не может с ней конкурировать. Поскольку пронумерованные билеты существуют за пределами цифровой сферы, те немногие номера, которые они предоставляют, недостаточно надежны.
Системы Take-a-Number тратят ресурсы впустую
Последний пункт незначителен, но все же звучит правдоподобно.Одним из недостатков системы управления «бери номер» является то, что она опирается на печатные материалы .
Для распечатки номерных билетов автомат использует бумажные рулоны, которые установлены внутри него.
Мы уже говорили о том, как один канадский колледж отказался от бумажной очереди в пользу более экологичных систем. Поскольку охрана окружающей среды становится главной темой для разговора, ваш бизнес не может свободно игнорировать это.
Но даже если исключить из уравнения растрату бумаги — в конце концов, это может быть переработка бумажных материалов без каких-либо затрат для Матери-природы — остается проблема использования реальных, материальных ресурсов.

А что самое худшее в такого рода ресурсах? Они могут закончиться в самый неподходящий момент.
Приходилось ли вам когда-нибудь ждать несколько минут на кассе, чтобы заменить рулон кассового аппарата? Помните: последние моменты опыта покупки — самые важные.
Хотя это ни в коем случае не конец света, это может и негативно повлиять на ваших клиентов. Когда вы пытаетесь сделать путь клиента максимально гладким, каждая мелочь имеет значение .
Цифровое решение для организации очередей не имеет этой проблемы. В нем используются настоящие технологические достижения, поэтому он кажется современным, гладким и инновационным.
Кроме того, это экологично.
Надеемся, нам удалось не только убедить вас в том, что системы «набери номер» устарели, но и помочь вам понять, что система управления электронной очередью — это шаг вперед, который нужен вашему бизнесу.
Qminder — это комплексных бизнес-решений «все в одном», с которыми билетные автоматы не могут конкурировать с .

При переводе двоичного числа в десятичное требуется представить двоичное число в виде многочлена , каждый элемент которого представлен в виде произведения цифры числа и соответствующей степени числа основания, в данном случае $2$, а затем нужно вычислить многочлен по правилам десятичной арифметики:
$X_2=A_n \cdot 2^{n-1} + A_{n-1} \cdot 2^{n-2} + A_{n-2} \cdot 2^{n-3} + . 0 =61440 + 3840 + 160 + 2 = 65442_{10}$
0 =61440 + 3840 + 160 + 2 = 65442_{10}$
Правила перевода чисел из десятичной системы счисления в другую
Пример 4
Число $22_{10}$ перевести в двоичную систему счисления.
Решение:
Рисунок 4.
$22_{10} = 10110_2$
Пример 5
Число $571_{10}$ перевести в восьмеричную систему счисления.
Решение:
Рисунок 5.
$571_{10} = 1073_8$
Пример 6
Число $7467_{10}$ перевести в шестнадцатеричную систему счисления.
Решение:
Рисунок 6.
$7467_{10} = 1D2B_{16}$
Для того чтобы перевести правильную дробь из десятичной системы счисления в недесятичную, необходимо дробную часть преобразуемого числа последовательно умножить на основание той системы, в которую ее требуется перевести. Дробь в новой системе будет представлена в виде целых частей произведений, начиная с первого.
Например: $0,3125_{(10)}$ в восьмеричной системе счисления будет выглядеть как $0,24_{(8)}$.
В данном случае можно столкнуться с проблемой, когда конечной десятичной дроби может соответствовать бесконечная (периодическая) дробь в недесятичной системе счисления. В данном случае количество знаков в дроби, представленной в новой системе, будет зависеть от требуемой точности. Также нужно отметить, что целые числа остаются целыми, а правильные дроби — дробями в любой системе счисления.
Правила перевода чисел из двоичной системы счисления в другую
Рисунок 7. Таблица 4
Пример 7
Число $1001011_2$ перевести в восьмеричную систему счисления.
Решение . Используя таблицу 4, переведем число из двоичной системы счисления в восьмеричную:
$001 001 011_2 = 113_8$
Использование привычной всем десятичной системы в компьютерной документации и программировании очень неудобно. Преобразования из двоичной в десятичную системы и обратно — весьма трудоемкие процессы.
Происхождение восьмеричной системы, так же как и десятичной, связывают со счетом на пальцах. Но считать нужно не пальцы, а промежутки между ними. Их как раз восемь.
Решением проблемы стала восьмеричная . По крайней мере на заре компьютерной техники. Когда разрядность процессоров была невелика. Восьмеричная система позволила с легкостью переводить как двоичные числа в восьмеричные, так и наоборот.
Восьмеричная система счисления — система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.
Преобразование
Для того чтобы перевести число в двоичное, необходимо заменить каждую цифру восьмеричного числа на тройку из двоичных цифр. Важно лишь запомнить, какая двоичная комбинация соответствует цифрам числа. Их совсем немного. Всего восемь!Во всех системах счисления, кроме десятичной, знаки читаются по одному. Например, в восьмеричной системе число 610 произносится «шесть, один, ноль».
Видео по теме
У компонентов электронных машин, к которым относятся и компьютеры, есть только два различимых состояния: есть ток и нет тока. Их обозначают «1» и «0» соответственно. Поскольку таких состояний только два, многие процессы и операции в электронике можно описать с помощью двоичных чисел.
Инструкция
Делим десятичное число на два до тех пор, пока не получим неделимый на два остаток. На шаге получим остаток 1 (если число было нечетным) или 0 (если делимое делится на два без остатка). Все эти остатки обязательно должны быть учтены. Последнее частное, полученное в результате такого пошагового деления, всегда будет единицей.
Последнее частное, полученное в результате такого пошагового деления, всегда будет единицей.
Записываем последнюю единицу в старший разряд искомого двоичного , а полученные в процессе остатки записываем за этой единицей в обратном порядке. Здесь надо быть внимательным и не пропускать нули.
Таким образом, числу 235 в двоичном коде будет соответствовать число 11101011.
Теперь переведем в двоичную систему счисления дробную часть десятичного числа. Для этого последовательно умножаем дробную часть числа на 2 и фиксируем целые полученных . Эти целые части дописываем к полученному в предыдущем шаге числу после двоичной в прямом порядке.
Тогда десятичному дробному числу 235.62 соответствует двоичное дробное 11101011.100111.
Видео по теме
Обратите внимание
Двоичная дробная часть числа будет конечной, только если дробная часть исходного числа конечна и заканчивается на 5. Простейший случай: 0.5 х 2 = 1, следовательно 0.5 в десятичной системе — это 0. 1 в двоичной.
1 в двоичной.
Источники:
Двоичная или бинарная система счисления применяется для отображения электронной информации. Любое число можно записать в двоичном виде. Двоичная система используется во всех вычислительных машинах. Каждая запись в них кодируется по определенным правилам с помощью набора двух символов: 0 и 1. Перевести двоичное число в его десятичное представление, более удобное пользователю, можно с помощью разработанного алгоритма.
Инструкция
Представьте число в виде записи степеней по 2. Для этого все восемь цифр последовательно умножаем на число 2, возведенное в . Степень должна соответствовать разряду цифры. Разряд считается от нуля, начиная с младшего, самого правого символа двоичного числа . Все восемь составленных произведений запишите в .
Десятичная система счисления
– одна из самых распространенных в математической теории. Однако с появлением информационных технологий, двоичная система получила не менее широкое распространение, поскольку она является основным способом представления информации в компьютерной памяти.
Однако с появлением информационных технологий, двоичная система получила не менее широкое распространение, поскольку она является основным способом представления информации в компьютерной памяти.
Инструкция
Преобразование из десятичной системы в двоичную реализуется как для целых чисел, так и для дробных. Перевод целого десятичного числа производится методом последовательного деления его на 2. При этом количество итераций (действий) увеличивается до тех пор, пока частное не станет равно нулю, а итоговое двоичное число записывается в виде полученных остатков справа налево.
Например, преобразования числа 19 выглядит так:19/2 = 18/2 + 1 = 9, в остатке – 1, пишем 1;9/2 = 8/2 + 1 = 4, в остатке – 1, пишем 1;4/2 = 2, остаток отсутствует, пишем 0;2/2 = 1, остаток отсутствует, пишем 0;1/2 = 0 + 1, в остатке – 1, пишем 1.Итак, после метода последовательного деления к числу 19 получилось двоичное число 10011.
В повседневной жизни мы привыкли пользоваться десятичной системой счисления, знакомой нам еще со школьной скамьи. Однако помимо нее, существует и множество других систем. Как записывать цифры не в десятичной, а, например, в
?
Однако помимо нее, существует и множество других систем. Как записывать цифры не в десятичной, а, например, в
?
Как перевести в двоичную любое число из десятичной системы
Необходимость перевести десятичное число в двоичный вид выглядит пугающей только на первый взгляд. На самом деле это довольно просто — необязательно искать даже онлайн-сервисы для совершения операции.
Двоичное число 10011100, полученное в результате нехитрой операции, и будет двоичным выражением числа 156.
Ещё один пример, но уже на картинке
Перевод двоичного числа в десятичную систему
Обратный перевод — из двоичной в десятичную систему — может показаться чуть более сложным. Но если использовать простой метод удвоения, то и с этой задачей получится справиться за пару минут. Для примера возьмем все то же число, 156, но в двоичном виде — 10011100.
Когда в двоичной записи останется только одна последняя цифра, и прибавлять больше будет нечего, операция будет завершена. При помощи нехитрой проверки можно убедиться, что в ответе получится нужное десятичное число 156.
1.1.4. Системы счисления
Глава 1. Арифметика
1.1.
1.1.4.
Система счисления – это совокупность приёмов и правил для записи чисел цифровыми знаками. Системы счисления делятся на позиционные и непозиционные.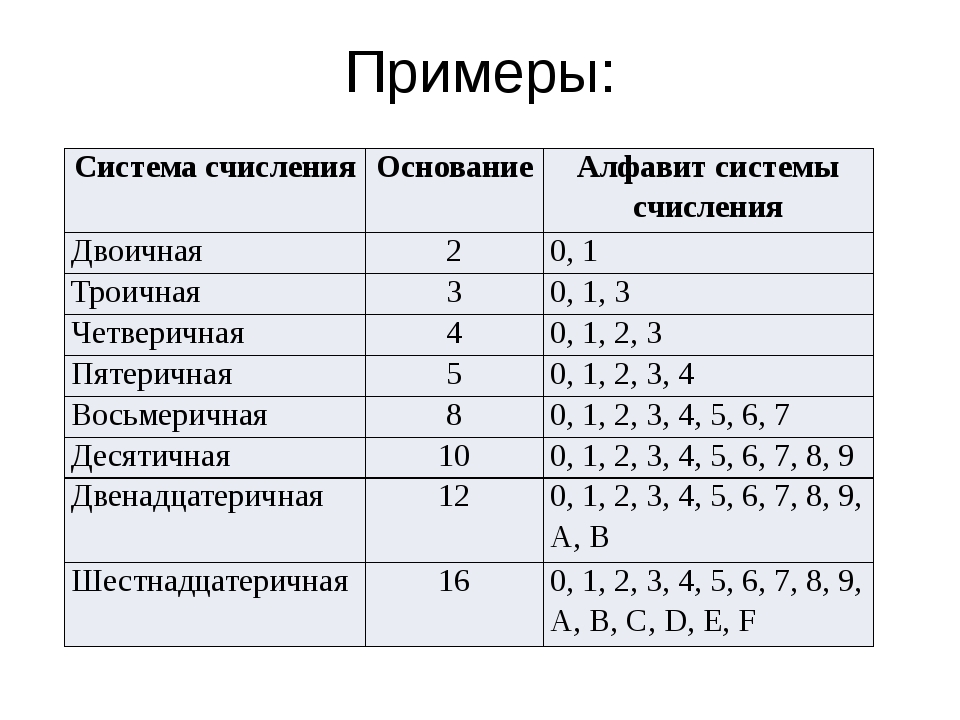 Позиционной называется система счисления, в которой используется определённое число знаков для обозначения чисел, но значение каждого символа зависит от того, как этот символ расположен по отношению к другим символам в том же числе. Непозиционной называется система счисления, в которой используется определённое число знаков для обозначения чисел, но значение каждого символа не зависит от того, как этот символ расположен по отношению к другим символам в том же числе, и всегда одно и то же.
Позиционной называется система счисления, в которой используется определённое число знаков для обозначения чисел, но значение каждого символа зависит от того, как этот символ расположен по отношению к другим символам в том же числе. Непозиционной называется система счисления, в которой используется определённое число знаков для обозначения чисел, но значение каждого символа не зависит от того, как этот символ расположен по отношению к другим символам в том же числе, и всегда одно и то же.
В процессе развития человеческой цивилизации люди использовали различные системы счисления, однако самой удобной для практических нужд оказалась десятичная система счисления. Разумеется, во многом это было связано с физиологическими особенностями человеческого тела; в самом деле, ведь у человека на руках десять пальцев. Конечно же, не нужно думать, что другие системы счисления совсем не используются. Например, для различных машинных вычислений необыкновенно эффективны вычисления в двоичной системе счисления.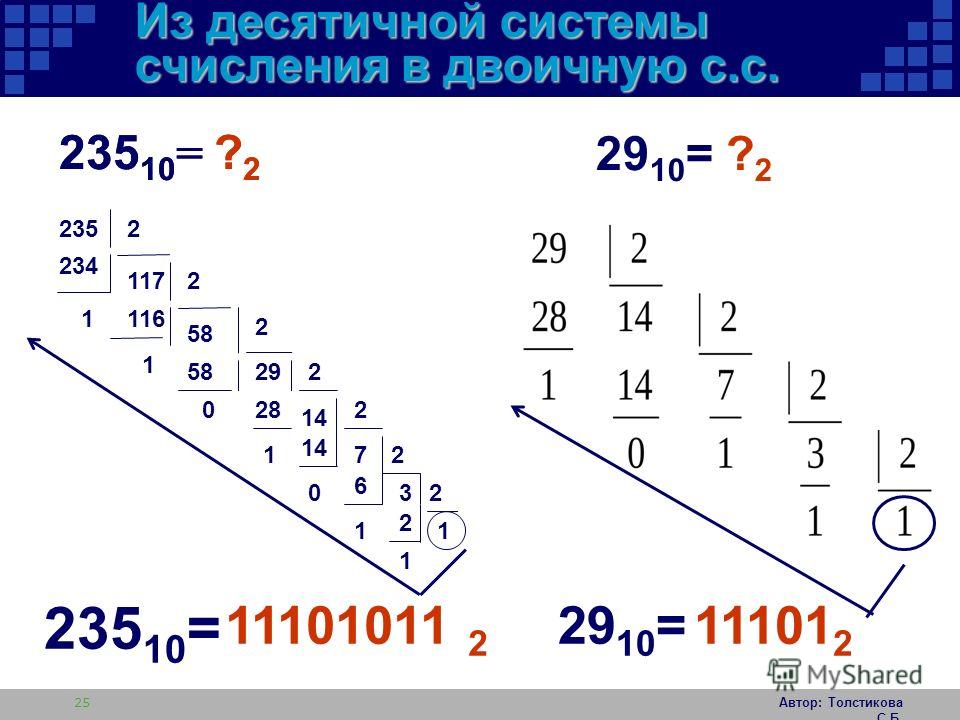 Познакомимся же с принципом записи числа в позиционной системе счисления.
Познакомимся же с принципом записи числа в позиционной системе счисления.
| 1 |
| Рисунок 1.1.4.1. В разное время арабские цифры выглядели по-разному |
Любое натуральное число n может быть представлено в q-ичной системе счисления:
|
В частности, десятичная система счисления основана на представлении чисел в виде:
| (2) |
 .., ak – числа от 0 до 9, причём ak ≠ 0. Если справедливо последнее соотношение, то число n записывают коротко так:
.., ak – числа от 0 до 9, причём ak ≠ 0. Если справедливо последнее соотношение, то число n записывают коротко так:
Для того, чтобы перевести число, записанное в q-ичной системе счисления, в десятичную систему счисления, нужно просто провести все вычисления в формуле (1). Для того, чтобы перевести число из десятичной системы счисления в q-ичную, можно попытаться представить его в виде (1).
Пример 1Записать число 132 в 1) троичной; 2) пятеричной; 3) семеричной; 4) двенадцатеричной.
|
Так, буква B последнем примере обозначает цифру «11» в двенадцатеричной системе счисления. Ответ. 1) (11220)3, 2) (1012)5, 3) (246)7, 4) (B0)12 |
Для того чтобы перевести число, записанное в десятичной системе, в любую q-ичную систему счисления, можно использовать следующее наблюдение. Перепишем формулу (1) в виде:
 Понятно, что так можно найти все числа ak.
Пример 2
Понятно, что так можно найти все числа ak.
Пример 2Записать число 4784 в восьмеричной системе счисления.
|
Стратегии и приемы решения вопросов по системе счисления
Вопросы по системе счисления – решенные примеры и практические вопросы
Система счисления – важная глава математики. Студент должен хорошо разбираться в основах системы счисления, чтобы решать другие задачи, связанные с математикой. Некоторые учащиеся сталкиваются с трудностями при решении сумм в системе счисления. Итак, здесь, в этой статье, мы представили некоторые важные суммы, относящиеся к системе счисления.Учащийся может попрактиковаться в этих вопросах, и ему/ей будет легко понять главу. В этой статье мы предоставили различные вопросы, основанные на системах счисления, таких как вопросы и ответы по системам счисления, вопросы по практике работы с системами счисления, MCQ по системам счисления и многие другие важные вопросы.
Вопросы и ответы по системе счисления
Q1. Определите, являются ли числа рациональными или иррациональными.
Ответ. Рациональное число — это число, которое может быть представлено в виде p/q, тогда как иррациональное число не может быть представлено в виде p/q.Итак,
√2 иррационально.
1.5 Рационал.
√100 — рациональное.
3.14 Иррационально.
Q2. Без фактического деления укажите, какое из следующих чисел является конечным десятичным числом.
Ответ. В \[\frac{9}{25}\] простые множители знаменателя 25 равны 5,5. Таким образом, это завершающая десятичная дробь. В \[\frac{37}{78}\] простые множители знаменателя 78 равны 2, 3 и 13.Таким образом, это неконечная десятичная дробь.
Q3. Выразите каждое из следующих чисел как рациональное число в форме p/q, где q ≠ 0,
Ответ. 1. Пусть x = 0,6666 …..(i)
Умножая обе части уравнения (i) на 10, мы получаем
10x = 6,6666…..(ii)
Теперь, вычитая уравнение (i) из уравнения ( ii) получаем
10x = 6,6666
x = 0,6666
9x = 6.
⇒ x = 6/9, что равно ⅔, поэтому искомая дробь равна ⅔.
2. Пусть x = 0,43434343….(i)
Умножая обе части уравнения (i) на 100, получаем (ii) мы получаем,
100x = 43,43434343
x = 0,43434343
99x = 43
⇒ x = 43/99, следовательно, дробь равна 43/99.
Q4. Найдите 4 рациональных числа от 1 до 2.
Ответ. Чтобы найти 4 рациональных числа между 1 и 2, нам нужно разделить и умножить оба числа на (4 + 1), что равно 5. Итак, мы получаем,
Итак, мы получаем,
1 х 5/5 = 5/5 и 2 х 5/5 = 10/5, Следовательно, рациональные числа:
5/5, 6/5, 7/5, 8/5, 9/5, 10/5.
Q5. Сравните следующие числа.
(i) 0 и -9/5.
(ii) -17/20 и -13/20.
(iii) 40/29 и 141/29.
Ответ. (i) Мы знаем, что отрицательное число всегда меньше 0. Следовательно,
0 > — 9/5.
(ii) Здесь знаменатель тот же, и мы знаем, что -17 < -13. Следовательно,
-17/20 < -13/20.
(iii) Здесь знаменатель тот же, и мы знаем, что 40 < 141. Следовательно,
40/29 < 141/29.
Q6. Запишите следующее десятичным числом и укажите, какое это расширение.
(i) 40/100 (ii) 9/10 (iii) 9/37 (iv) 103/5
Отв. (i) 40/100 — это 0,40, и он завершается.
(ii) 9/10 равен 0,9, и срок его действия истекает.
(iii) 9/37 — это 0,243243… он неограничен.
(iv) 103/5 — 20,6, и он заканчивается.
Q7. Вставьте одно рациональное число между ⅗ и 7/9.
Ответ. Если a и b два рациональных числа, то одно рациональное число между этими двумя будет
\[\frac{a + b}{2}\]. Следовательно, искомое рациональное число будет
\[\frac{1}{2} (\frac{3}{5} + \frac{7}{9}) = \frac{1}{2} (\frac {27 + 35}{45}) = \frac{1}{2} \times \frac{62}{45} = \frac{31}{45}\]
Таким образом, рациональное число равно 31/45. .
Вопросы по преобразованию системы счисления
Здесь мы предоставили некоторые математические вопросы по системе счисления, основанные на преобразовании системы счисления.
Q1. Преобразуйте каждое из следующих чисел в десятичное число.
(i) \[\frac{4}{15}\]
(ii) \[2\frac{5}{12}\]
(iii) \[\frac{9}{27} \]
(iv) \[5\frac{31}{55}\]
Q2.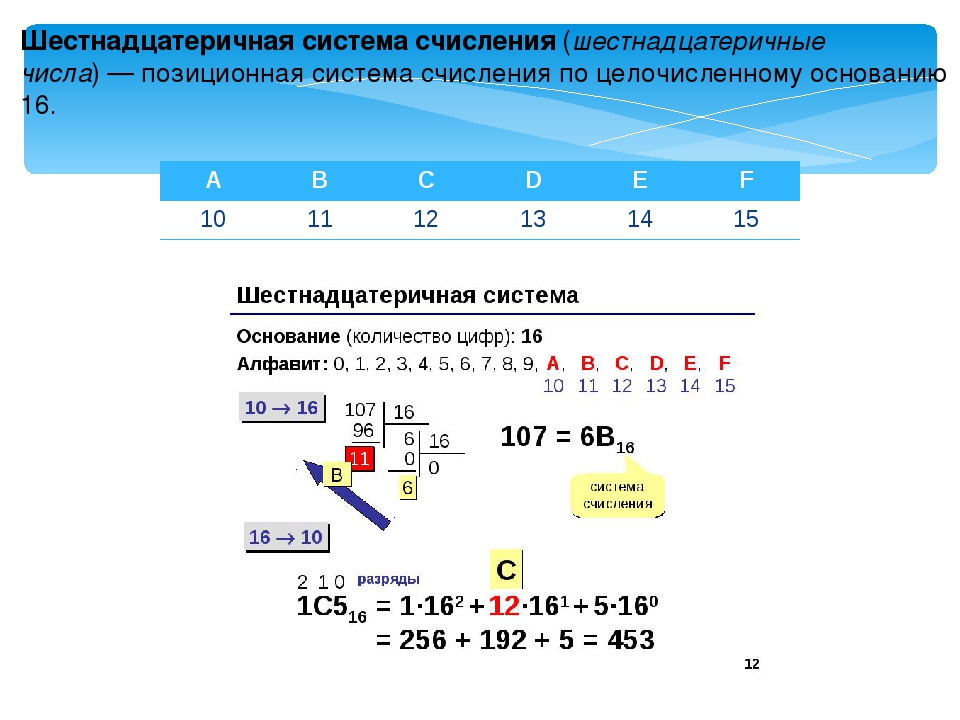 Преобразуйте следующее число в рациональное.
Преобразуйте следующее число в рациональное.
(i) \[0.\overline{227}\]
(ii) \[0.\overline{2104}\]
Практические вопросы по системе счисления
Как мы знаем, практика делает каждого совершенным, поэтому для лучшего понимания студентов, мы предоставили несколько важных вопросов по системе счисления для практики.
Q1. Покажите цифру √5 на числовой прямой.
Q2. Вставьте три рациональных числа между 4 и 5.
Q3. Представьте следующие рациональные числа в десятичной форме:
(i) 18/42 (ii) -11/13
Q4. Рационализируйте знаменатель \[\frac{1}{3 — \sqrt{5}}\].
Q5. Упростите следующее выражение (2 4 — 3 2 ). ( 5 + 2 3 )
5.1: Комплексная система счисления
Основные вопросы
Следующие вопросы помогут нам изучить материал этого раздела.Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы. {2} = -1\), число \(\sqrt{-1}\) не является действительным числом.{2} = -1\).
{2} = -1\), число \(\sqrt{-1}\) не является действительным числом.{2} = -1\).
Форма \(a + bi\), где a и b — действительные числа, называется стандартной формой для комплексного числа. Когда у нас есть комплексное число вида \(z = a + bi\), число \(a\) называется действительной частью комплексного числа \(z\), а число \(b\) называется мнимой частью оператора \(z\). Поскольку i не является вещественным числом, два комплексных числа \(a + bi\) и \(c + di\) равны тогда и только тогда, когда \(a = c\) и \(b = d\).
Существует арифметика комплексных чисел, которая определяется сложением и умножением комплексных чисел.{2} \\[4pt] &= (ac — bd) + (ad + bc)i \end{align*}\]
Свойства комплексного номера
Можно показать, что комплексные числа обладают многими полезными и знакомыми свойствами, которые аналогичны свойствам действительных чисел. Если \(u\), \(w\) и \(z\) — комплексные числа, то
