Как решать уравнения с модулем
Одна из самых сложных тем для учащихся – это решение уравнений, содержащих переменную под знаком модуля. Давайте разберемся для начала с чем же это связано? Почему, например, квадратные уравнения большинство детей щелкает как орешки, а с таким далеко не самым сложным понятием как модуль имеет столько проблем?
На мой взгляд, все эти сложности связаны с отсутствием четко сформулированных правил для решения уравнений с модулем. Так, решая квадратное уравнение, ученик точно знает, что ему нужно сначала применять формулу дискриминанта, а затем формулы корней квадратного уравнения. А что делать, если в уравнении встретился модуль? Постараемся четко описать необходимый план действий на случай, когда уравнение содержит неизвестную под знаком модуля. К каждому случаю приведем несколько примеров.
Но для начала вспомним определение модуля. Итак, модулем числа a называется само это число, если a неотрицательно и  Записать это можно так:
Записать это можно так:
|a| = a, если a ≥ 0 и |a| = -a, если a < 0
Говоря о геометрическом смысле модуля, следует помнить, что каждому действительному числу соответствует определенная точка на числовой оси – ее координата. Так вот, модулем или абсолютной величиной числа называется расстояние от этой точки до начала отсчета числовой оси. Расстояние всегда задается положительным числом. Таким образом, модуль любого отрицательного числа есть число положительное. Кстати, даже на этом этапе многие ученики начинают путаться. В модуле может стоять какое угодно число, а вот результат применения модуля всегда число положительное.
Теперь перейдем непосредственно к решению уравнений.
1. Рассмотрим уравнение вида |x| = с, где с – действительное число. Это уравнение можно решить с помощью определения модуля.
Все действительные числа разобьем на три группы: те, что больше нуля, те, что меньше нуля, и третья группа – это число 0. Запишем решение в виде схемы:
Запишем решение в виде схемы:
{±c, если с > 0
Если |x| = c, то x = {0, если с = 0
{нет корней, если с < 0
Примеры:
1) |x| = 5, т.к. 5 > 0, то x = ±5;
2) |x| = -5, т.к. -5 < 0, то уравнение не имеет корней;
3) |x| = 0, то x = 0.
2. Уравнение вида |f(x)| = b, где b > 0. Для решения данного уравнения необходимо избавиться от модуля. Делаем это так: f(x) = b или f(x) = -b. Теперь необходимо решить отдельно каждое из полученных уравнений. Если в исходном уравнении b< 0, решений не будет.
Примеры:
1) |x + 2| = 4, т.к. 4 > 0, то
x + 2 = 4 или x + 2 = -4
x = 2 x = -6
2) |x2 – 5| = 11, т.к. 11 > 0, то
x2 – 5 = 11 или x2 – 5 = -11
x2 = 16 x2 = -6
x = ± 4 нет корней
3) |x2 – 5x| = -8 , т. к. -8 < 0, то уравнение не имеет корней.
3. Уравнение вида |f(x)| = g(x). По смыслу модуля такое уравнение будет иметь решения, если его правая часть больше или равна нулю, т.е. g(x) ≥ 0. Тогда будем иметь:
f(x) = g(x) или f(x) = -g(x).
Примеры:
1) |2x – 1| = 5x – 10. Данное уравнение будет иметь корни, если 5x – 10 ≥ 0. Именно с этого и начинают решение таких уравнений.
1. О.Д.З. 5x – 10 ≥ 0
5x ≥ 10
x ≥ 2.
2. Решение:
2x – 1 = 5x – 10 или 2x – 1 = -(5x – 10)
3x = 9 7x = 11
x = 3 x = 11/7
3. Объединяем О.Д.З. и решение, получаем:
Корень x = 11/7 не подходит по О.Д.З., он меньше 2, а x = 3 этому условию удовлетворяет.
Ответ: x = 3
2) |x – 1| = 1 – x2.
1. О.Д.З. 1 – x2 ≥ 0. Решим методом интервалов данное неравенство:
(1 – x)(1 + x) ≥ 0
-1 ≤ x ≤ 1
2. Решение:
Решение:
x – 1 = 1 – x2 или x – 1 = -(1 – x2)
x2 + x – 2 = 0 x2 – x = 0
x = -2 или x = 1 x = 0 или x = 1
3. Объединяем решение и О.Д.З.:
Подходят только корни x = 1 и x = 0.
Ответ: x = 0, x = 1.
4. Уравнение вида |f(x)| = |g(x)|. Такое уравнение равносильно двум следующим уравнениям f(x) = g(x) или f(x) = -g(x).
Пример:
1) |x2 – 5x + 7| = |2x – 5|. Данное уравнение равносильно двум следующим:
x2 – 5x + 7 = 2x – 5 или x2 – 5x +7 = -2x + 5
x2 – 7x + 12 = 0 x2 – 3x + 2 = 0
x = 3 или x = 4 x = 2 или x = 1
Ответ: x = 1, x = 2, x = 3, x = 4.
5. Уравнения, решаемые методом подстановки (замены переменной). Данный метод решения проще всего объяснить на конкретном примере. Так, пусть дано квадратное уравнение с модулем:
x2 – 6|x| + 5 = 0. По свойству модуля x2 = |x|2, поэтому уравнение можно переписать так:
По свойству модуля x2 = |x|2, поэтому уравнение можно переписать так:
|x|2 – 6|x| + 5 = 0. Сделаем замену |x| = t ≥ 0, тогда будем иметь:
t2 – 6t + 5 = 0. Решая данное уравнение, получаем, что t = 1 или t = 5. Вернемся к замене:
|x| = 1 или |x| = 5
x = ±1 x = ± 5
Ответ: x = -5, x = -1, x = 1, x = 5.
Рассмотрим еще один пример:
x2 + |x| – 2 = 0. По свойству модуля x2 = |x|2, поэтому
|x|2 + |x| – 2 = 0. Сделаем замену |x| = t ≥ 0, тогда:
t2 + t – 2 = 0. Решая данное уравнение, получаем, t = -2 или t = 1. Вернемся к замене:
|x| = -2 или |x| = 1
Нет корней x = ± 1
Ответ: x = -1, x = 1.
6. Еще один вид уравнений – уравнения со «сложным» модулем. К таким уравнениям относятся уравнения, в которых есть «модули в модуле». Уравнения данного вида можно решать, применяя свойства модуля.
Примеры:
1) |3 – |x|| = 4. Будем действовать так же, как и в уравнениях второго типа. Т.к. 4 > 0, то получим два уравнения:
3 – |x| = 4 или 3 – |x| = -4.
Теперь выразим в каждом уравнении модуль х, тогда |x| = -1 или |x| = 7.
Решаем каждое из полученных уравнений. В первом уравнении нет корней, т.к. -1 < 0, а во втором x = ±7.
Ответ x = -7, x = 7.
2) |3 + |x + 1|| = 5. Решаем это уравнение аналогичным образом:
3 + |x + 1| = 5 или 3 + |x + 1| = -5
|x + 1| = 2 |x + 1| = -8
x + 1 = 2 или x + 1 = -2. Нет корней.
x = 1 x = -3
Ответ: x = -3, x = 1.
Существует еще и универсальный метод решения уравнений с модулем. Это метод интервалов. Но мы его рассмотрим в дальнейшем.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Уравнение с модулем
Уравнение с модулем достаточно сложная тема для начинающих.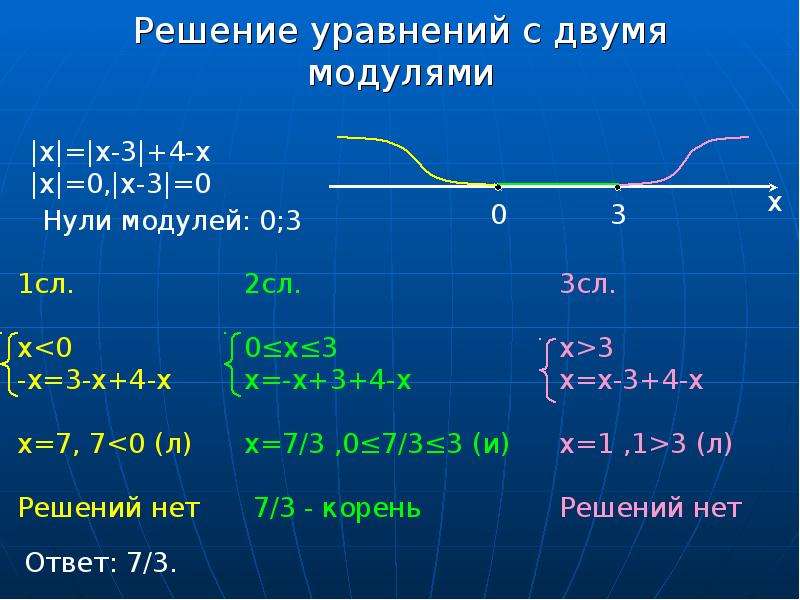
Что такое уравнение с модулем и как его решить?
В уравнениях с модулем неизвестное значение содержится под знáком модуля. Например:
|x − 2| = 5
Уравнения с модулем бывают разными и решаются они различными методами. Нельзя сказать что какой-то метод наиболее рационален. Всё зависит от исходного уравнения.
Например, в каких-то уравнениях можно просто угадать корень, в то время как в других нужно логически мыслить, раскрывать модули, выполнять тождественные преобразования. Человек волен выбирать каким методом решения пользоваться.
К примеру, решим вышеприведённое уравнение |x − 2| = 5. Допустим, что мы не знаем ни одного метода решения. Как бы мы его решили?
Прежде всего заметим, что правая часть данного уравнения равна числу 5. Слева же располагается модуль из выражения |x − 2|. Это означает что подмодульное выражение
Значит нужно выяснить при каких значениях переменной x подмодульное выражение x − 2 будет обращаться в число 5 или −5.
Искомые значения x найдутся если приравнять подмодульное выражение к числу 5 и −5, а затем поочерёдно решить каждое из уравнений:
Значит корнями уравнения |x − 2| = 5 являются числа 7 и −3.
Большинство элементарных уравнений с модулем можно решить используя правило раскрытия модуля. Для этого раскрывают модуль содержащийся в уравнении, затем получившееся выражение подставляют в исходное уравнение вместо выражения с модулем.
Раскрывать модуль нужно для каждого из случаев: когда подмодульное выражение больше или равно нулю, и когда подмодульное выражение меньше нуля.
Решим наше уравнение |x − 2| = 5 с помощью правила раскрытия модуля. Выпишем отдельно его модуль и раскроем его:
В этой конструкции говорится, что если подмодульное выражение x − 2 больше или равно нулю, то модуль раскроется как x − 2, и тогда исходное уравнение примет вид x − 2 = 5, откуда x = 7
А если же подмодульное выражение x − 2 меньше нуля, то модуль раскроется как −(x − 2). Тогда исходное уравнение примет вид −(x − 2) = 5, откуда x = −3
Тогда исходное уравнение примет вид −(x − 2) = 5, откуда x = −3
Итак, уравнение |x − 2|= 5 имеет корни 7 и −3. Для проверки подстáвим числа 7 и −3 в исходное уравнение вместо x. Тогда получим верное равенство:
Подмодульное выражение как правило содержит такое x, которое может обращать всё подмодульное выражение как в положительное число, так и в отрицательное, либо вообще в ноль.
Поэтому модуль и раскрывается для каждого из случаев: когда подмодульное выражение больше или равно нулю, и когда подмодульное выражение меньше нуля. Каждый из случаев будет давать независимое уравнение со своим корнем.
Вернёмся теперь к моменту, где мы раскрывали модуль:
Условия x − 2 ≥ 0 и x − 2 < 0 являются неравенствами, которые можно решить, тем самым приведя их к простому виду:
Символ ⇔ означает равносильность. В данном случае указывается, что условие x − 2 ≥ 0 равносильно условию x ≥ 2, а условие x − 2 < 0 равносильно условию x < 2.
Такой вид записи условий позволяет однозначно сказать при каких x модуль будет раскрываться с плюсом, а при каких с минусом.
В первом случае получилось условие x ≥ 2. Это значит что при всех x бóльших либо равных 2, модуль |x − 2| будет раскрываться с плюсом. Так, при x = 7, подмодульное выражение станет равно 5
|7 − 2| = |5|
А значит дальнейшее раскрытие будет с плюсом
|7 − 2| = |5| = 5
Таким же образом модуль |x − 2| будет вести себя и с другими значениями x на промежутке x ≥ 2. То есть, будет раскрываться с плюсом. Примеры:
При x = 3, |3 − 2|=|1| = 1
При x = 4, |4 − 2|=|2| = 2
При x = 2, |2 − 2|=|0| = 0
При x = 13, |13 − 2|=|11| = 11
А во втором случае получилось условие x < 2. Это значит что при всех x мéньших 2, модуль будет раскрываться с минусом. Так, при x = −3, подмодульное выражение опять же станет равно 5. Но в промежуточных вычислениях можно увидеть, что модуль раскрывается с минусом:
Но в промежуточных вычислениях можно увидеть, что модуль раскрывается с минусом:
|−3 − 2| = |−5| = −(−5) = 5
Модуль |x − 2| будет вести себя так же и с другими значениями x на промежутке x < 2. Примеры:
При x = 1, |1 − 2|=|−1| = −(−1) = 1
При x = 0, |0 − 2|=|−2| = −(−2) = 2
При x = −1, |−1 − 2|=|−3| = −(−3) = 3
При x = −9,|−9 − 2|=|−11| = −(−11) = 11
Число 2 является своего рода точкой перехода, в которой модуль |x − 2| меняет свой порядок раскрытия.
Можно представить как модуль |x − 2| двигался по маршруту от минус бесконечности до числа 2, раскрываясь в каждой точке с минусом. Попав в точку 2, модуль поменял свой порядок раскрытия — а именно раскрывшись в точке 2 с плюсом, он далее стал раскрываться с плюсом, двигаясь в правую часть к плюс бесконечности.
С помощью координатной прямой это можно представить так:
Красные знаки минуса и плюса указывают, как будет раскрываться модуль |x − 2| на промежутках x < 2 и x ≥ 2.
Точку перехода можно найти для любого модуля. Для этого нужно узнать при каких x подмодульное выражение равно нулю. Ноль это то значение, до и после которого модуль всегда сохраняет свой знак. Это следует из правила раскрытия модуля:
В этом примере в момент когда x станет равным нулю, модуль |x| раскроется с плюсом и далее при всех x, бóльших нуля, будет раскрываться с плюсом. Напротив, при всех x, мéньших нуля модуль будет раскрываться с минусом:
А например для модуля |2x + 6| точкой перехода будет число −3, потому что при его подстановке в подмодульное выражение 2x + 6 вместо x, данное подмодульное выражение станет равно нулю. Изобразим это на рисунке:
При всех x, бóльших либо равных −3, модуль будет раскрываться с плюсом. Примеры:
При x = −3, |2 × (−3) + 6| = |0| = 0
При x = 4, |2 × 4 + 6| = |14| = 14
При x = 5, |2 × 5 + 6| = |16| = 16
А при всех x, мéньших 3, модуль будет раскрываться с минусом. Примеры:
Примеры:
При x = −4, |2 × (−4) + 6| = |−2| = −(−2) = 2
При x = −5, |2 × (−5) + 6| = |−4| = −(−4) = 4
При x = −6, |2 × (−6) + 6| = |−6| = −(−6) = 6
Пример 2. Решить уравнение |x| + 3x = −2
Решение
Раскроем модуль, который содержится в левой части уравнения:
Если x ≥ 0, то модуль раскроется со знаком плюс и тогда исходное уравнение примет вид x + 3x = −2. Сразу решим это уравнение:
Теперь рассмотрим второй случай — когда x < 0. В этом случае модуль в исходном уравнении раскроется со знаком минус, и тогда получится уравнение −x + 3x = −2. Решим и это уравнение:
Получили корни и −1.
Выполним проверку, подставив найденные корни в исходное уравнение. Проверим корень
Видим, что при подстановке корня исходное уравнение не обращается в верное равенство. Значит не является корнем исходного уравнения.
Значит не является корнем исходного уравнения.
Проверим теперь корень −1
Получили верное равенство. Значит из двух найденных решений только −1 является корнем уравнения.
Ответ: −1.
Здесь можно сделать важный вывод. В уравнениях с модулем найденные корни не всегда удовлетворяют исходному уравнению. Чтобы убедиться в правильности своего решения, нужно выполнять проверку, подставляя найденные корни в исходное уравнение.
Кроме того, проверить является ли найденное значение корнем уравнения можно с помощью условия, согласно которому был раскрыт модуль.
Так, в данном примере мы раскрывали модуль |x| для случаев когда подмодульное выражение больше или равно нулю, и когда подмодульное выражение меньше нуля:
Условия x≥0 и x<0 являются неравенствами. В эти неравенства можно подставлять найденные корни. Если неравенства окажутся верными, значит корни удовлетворяют исходному уравнению.
Так, при раскрытии модуля со знаком плюс, получилось уравнение x + 3x = −2. Корнем этого уравнения стало число . Это число не удовлетворяет условию x ≥ 0, согласно которому был раскрыт модуль |x| и согласно которому было получено уравнение x + 3x = −2. Действительно, при подстановке числа в неравенство x ≥ 0 получается неверное неравенство.
А при раскрытии модуля со знаком минус, получилось уравнение −x + 3x = −2. Корнем этого уравнения стало число −1. Это число удовлетворяет условию x<0, согласно которому был раскрыт модуль |x| и согласно которому было получено уравнение −x + 3x = −2. Действительно, при подстановке числа −1 в неравенство x < 0 получается верное неравенство.
Пример 3. Решить уравнение |1 − 2x| − 4x = −6
Решение
Раскроем модуль:
При раскрытии модуля |1 − 2x| со знаком плюс, получим уравнение 1 − 2x − 4x = −6. Решим его:
Решим его:
При раскрытии модуля |1 − 2x| со знаком минус, получим уравнение −1 + 2x − 4x = −6. Решим его:
Получили корни и .
Корень не удовлетворяет условию , значит не является корнем исходного уравнения.
Корень удовлетворяет условию , значит является корнем исходного уравнения. Проверка также покажет это:
Ответ: .
Пример 4. Решить уравнение |x2 − 3x| = 0
Решение
Если модуль числа равен нулю, то подмодульное выражение тоже равно нулю:
То есть можно не раскрывать модуль. Достаточно узнать при каких значениях x подмодульное выражение равно нулю. В данном случае для этого нужно решить неполное квадратное уравнение:
Получили корни 0 и 3. Оба корня удовлетворяют исходному уравнению. Проверка показывает это:
Пример 5. Решить уравнение x2 − 5|x| + 6 = 0
Выпишем отдельно модуль |x| и раскроем его:
При раскрытии модуля |x| со знаком плюс, исходное уравнение примет вид x2 − 5x + 6 = 0. Это квадратное уравнение. Решим его с помощью дискриминанта:
Это квадратное уравнение. Решим его с помощью дискриминанта:
Оба корня удовлетворяют условию x ≥ 0, значит являются корнями исходного уравнения.
При раскрытии модуля |x| со знаком минус, исходное уравнение примет вид x2 + 5x + 6 = 0. Это тоже квадратное уравнение. Решим его как и предыдущее:
При условии x ≥ 0, модуль из уравнения раскрылся с плюсом, получились корни 3 и 2. Оба корня удовлетворяют условию x ≥ 0, значит удовлетворяют и исходному уравнению.
При условии x < 0, модуль из уравнения раскрылся с минусом, получились корни −2 и −3. Оба корня удовлетворяют условию x < 0, значит удовлетворяют и исходному уравнению.
Ответ: 3, 2, −2 и −3.
Сведéние уравнения с модулем в совокупность
Большинство элементарных уравнений с модулем можно решить сведéнием их к так называемой совокупности уравнений.
Элементарными мы будем называть те уравнения с модулем, в которых левая часть является модулем из какого-то выражения, а правая часть — числом. Например, |x| = 3 или |2x − 1| = 3.
Решим наше самое первое уравнение |x − 2| = 5 сведéнием его к совокупности уравнений. Корнями этого уравнения были числа 7 и −3. Это уравнение тоже считается элементарным.
Если раскрыть модуль |x − 2| со знаком плюс, то уравнение |x − 2| = 5 примет вид x − 2 = 5.
Если раскрыть модуль |x − 2| со знаком минус, то уравнение |x − 2| = 5 примет вид −(x − 2) = 5, то есть −x + 2 = 5.
Видим, что из уравнения |x − 2| = 5 получилось два уравнения: x − 2 = 5 и −x + 2 = 5. Причём каждое из уравнений имеет свой собственный корень. Уравнение x − 2 = 5 имеет корень 7, а уравнение −x + 2 = 5 — корень −3
Выпишем уравнения x − 2 = 5 и −x + 2 = 5 и объединим их квадратной скобкой:
Такой вид записи называют совокупностью уравнений.
Совокупность уравнений — это несколько уравнений, объединённых квадратной скобкой, и имеющих множество решений, которые удовлетворяют хотя бы одному из уравнений, входящих в данную совокупность.
Так, число 7 является решением совокупности потому что это число удовлетворяет первому уравнению х − 2 = 5.
Число −3 тоже является решением данной совокупности, поскольку удовлетворяет второму уравнению −х + 2 = 5.
Вместе же числа 7 и −3 образуют множество решений данной совокупности.
В отличие от системы уравнений, совокупность состоит из уравнений, которые не зависят друг от друга. Для каждого уравнения, входящего в совокупность, значение переменной x будет разным. А в системе уравнений значение переменной x удовлетворяет как первому уравнению, так и второму.
Решить совокупность уравнений означает найти множество решений, которые удовлетворяют хотя бы одному из уравнений, входящих в данную совокупность.
Решим каждое уравнение совокупности по-отдельности. Это обычные линейные уравнения, которые легко решаются:
Символ ⇔ как было ранее сказано означает равносильность. В данном случае он указывает на то, что все получающиеся совокупности равносильны друг другу.
Итак, мы получили корни 7 и −3. Поскольку эти два числа являются решениями совокупности , то значит являются и решениями уравнения |x − 2| = 5.
В исходную совокупность можно включать условия, согласно которым был раскрыт модуль. В этом случае каждое уравнение вместе со своим условием обрамляется знаком системы.
Дополним предыдущую совокупность условиями, согласно которым был раскрыт модуль. К первому уравнению x − 2 = 5 добавим условие x − 2 ≥ 0, а ко второму уравнению −x + 2 = 5 добавим условие x − 2 < 0
Решение каждого уравнения должно удовлетворять своему условию. Поэтому условия и уравнения обрамлены знáком системы.
Решим получившуюся совокупность с условиями. Условия являются неравенствами, которые тоже можно решать:
В первом случае получили корень 7, который удовлетворяет своему условию x ≥ 2. Во втором случае получили корень −3, который удовлетворяет своему условию x < 2.
Не следует бояться таких записей. Это лишь подробное решение, показывающее что откуда взялось. Чаще всего решение можно записать покороче.
Существует схема для сведéния в совокупность уравнения вида |x| = a. Выглядит эта схема так:
Данная схема легко позволяет свести уравнение с модулем в совокупность. Эту схему можно прочитать так: «Если выражение |x| равно a, то подмодульное выражение равно a или −a»
Квадратная скобка в совокупностях заменяет собой слово «или».
Например, уравнение |x| = 5 можно свести в совокупность, рассуждая так: если выражение |x| равно 5, то подмодульное выражение равно 5 или −5.
А применительно к нашему предыдущему примеру можно рассуждать так: если |x − 2| равно 5, то подмодульное выражение равно 5 или −5
Это та же самая совокупность, что и в прошлый раз. Убедитесь в этом, умножив обе части второго уравнения на −1.
В уравнениях где слева модуль, а справа число, мы будем чаще использовать именно такой способ записи совокупности. Он позволяет не прибегать к правилу раскрытия модуля, а сразу получить совокупность.
Но надо помнить, что эта схема будет работать только для уравнений вида |x| = a. То есть для уравнений, у которого слева модуль, а справа число.
Пример 2. Решить уравнение |2x − 1| = 3
Решение
У этого уравнения слева модуль, а справа число. Значит его можно свести в совокупность, воспользовавшись схемой
Если выражение |2x − 1| равно 3, то подмодульное выражение 2x − 1 равно 3 или −3
Теперь решим каждое уравнение совокупности по отдельности:
Ответ: 2 и −1.
Пример 3. Решить уравнение |x + 2| − 3 = 8
Решение
В некоторых случаях прежде чем свести исходное уравнение в совокупность, его следует упростить.
Так, в данном случае −3 следует перенести в правую часть, изменив знак:
Получили уравнение |x + 2| = 11. Если выражение |x + 2| равно 11, то подмодульное выражение x + 2 равно 11 или −11
Решим данную совокупность:
Ответ: 9 и −13.
Пример 4. Решить уравнение 4|x| + 4 = 2|x| + 10
Решение
Перенесём 2|x| из правой части в левую часть, а 4 перенесём из левой части в правую часть:
4|x| − 2|x| = 10 − 4
2|x| = 6
Разделим обе части получившегося уравнения на 2. Тогда получится простое уравнение с модулем:
Ответ: 3 и −3.
Пример 5. Решить уравнение
Решить уравнение
Решение
Если выражение |2 − 5x2| равно 3, то подмодульное выражение 2 − 5x2 равно 3 или −3
В обоих уравнениях перенесём 2 в правую часть, изменив знак:
В первом уравнении разделим обе части на −5. Во втором уравнении так же разделим обе части на −5. Тогда получим два квадратных уравнения
Первое уравнение не имеет корней, потому что квадрат любого числа положителен, а в данном случае он равен отрицательному числу. Корнями второго уравнения являются числа 1 и −1, поскольку вторая степень этих чисел равна единице.
Ответ: 1 и −1.
Пример 6. Решить уравнение |x + 6| + 4x = 5
Решение
Данное уравнение не является уравнением вида |x| = a, значит не получится воспользоваться схемой .
Чтобы свести данное уравнение в совокупность, нужно сначала раскрыть его модуль, затем записать совокупность из получившихся уравнения.
Раскроем модуль |x + 6|
Если x + 6 ≥ 0 , то модуль раскроется со знаком плюс и тогда исходное уравнение примет вид x + 6 + 4x = 5
Если x + 6 < 0, то модуль раскроется со знаком минус и тогда исходное уравнение примет вид −x − 6 + 4x = 5. Получим следующую совокупность:
Дальнейшее решение элементарно:
Из найденных корней только является корнем исходного уравнения, поскольку удовлетворяет условию x ≥ −6. А корень не является корнем уравнения, поскольку не удовлетворяет условию x < −6.
Ответ:
Наиболее простой вид
Наиболее простой вид уравнения с модулем выглядит так:
| x | = a
где x — корень уравнения, a — произвольное число, бóльшее или рáвное нулю. То есть a ≥ 0
Если условие a ≥ 0 не выполнено, то уравнение |x|= a корней не имеет. Это следует из определения модуля. Действительно, модуль всегда неотрицателен.
Это следует из определения модуля. Действительно, модуль всегда неотрицателен.
Приведем несколько примеров уравнений вида |x| = a
Пример 1. Решить уравнение |x| = 2
Решение
В данном случае сразу видно, что корнями являются числа 2 и −2. Ведь если вместо x подставить эти числа, то получим верное равенство: |−2| = 2 и |2| = 2. Решение для этого уравнения можно записать, сведя его в совокупность:
«Если выражение |x| равно 2, то подмодульное выражение x равно 2 или −2«
Ответ: 2 и −2
Пример 2. Решить уравнение |−x| = 4
Решение
Если выражение |−x| равно 4, то подмодульное выражение равно 4 или −4
Умножим оба уравнения на −1
Ответ: −4 и 4.
Пример 3. Решить уравнение |x| = −7
В данном случае корней нет, поскольку модуль всегда неотрицателен. А в данном случае модуль равен отрицательному числу.
А в данном случае модуль равен отрицательному числу.
Если уравнение с модулем не имеет корней, обычно пишут что x принадлежит пустому множеству:
x ∈ ø
Напомним, что пустым называют множество, не имеющее элементов.
Модуль внутри модуля
Рассмотрим уравнение:
В этом уравнении слева располагается модуль, который в свою очередь содержит внутри себя другой модуль, а справа уравнения располагается число. Такой вид уравнения с модулем можно решить, сведя его в совокупность с помощью схемы, которую мы рассмотрели ранее:
В нашем случае если выражение равно 9, то подмодульное выражение |2 + x| + 3 равно 9 или −9
В получившейся совокупности имеется два уравнения с модулем. Эти уравнения тоже в свою очередь следует свести в совокупность. Но сначала немного упростим эти уравнения. В первом и во втором уравнении перенесем 3 в правую часть, изменив знак. Тогда получим:
Теперь сведём эти уравнения в совокупности. Первое уравнение распадётся на следующую совокупность:
Первое уравнение распадётся на следующую совокупность:
Сразу решим совокупность . Первый корень равен 4, второй −8.
Теперь решим второе уравнение |2 + x| = −12. Но замечаем, что его правая часть равна отрицательному числу. Это уравнение не имеет корней, потому что модуль не может равняться отрицательному числу.
Значит уравнение имеет корни 4 и −8. Проверим эти корни, подставив их в исходное уравнение
В данном случае оба корня удовлетворяют исходному уравнению.
Ответ: 4 и −8.
Вообще, уравнение с модулем внутри которого содержится другой модуль, тоже решается различными способами. Какой способ использовать зависит от самогó уравнения. Решим например следующее уравнение:
Здесь уже нельзя использовать схему потому что слева располагается не только модуль, но и переменная x. Конечно, переменную x можно перенести в правую часть, и тогда можно будет свести данное уравнение в совокупность:
Но тогда справа появляется переменная x, на которую нужно будет вводить дополнительное ограничение, чтобы правая часть уравнения не стала отрицательной. Такой способ решения мы рассмотрим позже. А пока решим исходное уравнение с помощью правила раскрытия модуля.
Такой способ решения мы рассмотрим позже. А пока решим исходное уравнение с помощью правила раскрытия модуля.
Чтобы раскрыть модули данного уравнения нужно сначала определиться где внешний и где внутренний модуль.
В уравнении внешним модулем является полностью левая часть , а внутренним модулем — выражение
Значение внешнего модуля зависит от внутреннего модуля, и раскрываться внешний модуль будет исходя от результата который получился в результате вычисления его подмодульного содержимого.
Например, если x = 3, то внутренний модуль |3 − x| примет значение 0, и в результате всё подмодульное выражение внешнего модуля станет равно −2. А это значит что внешний модуль будет раскрываться с минусом.
||3 − x| − x + 1| = ||3 − 3| − 3 + 1| = ||0| − 3 + 1| = |−2| = −(−2) = 2
А если например x = −2, то внутренний модуль |3 − x| примет значение 5, и в результате всё подмодульное выражение внешнего модуля станет равно 8. А это значит что внешний модуль будет раскрываться с плюсом:
А это значит что внешний модуль будет раскрываться с плюсом:
||3 − x| − x + 1| = ||3 − (−2)| − (−2) + 1| = ||5| − (−2) + 1| = | 8 |=8
Поэтому решение будем начинать с раскрытия внутреннего модуля.
Если внутренний модуль раскроется с плюсом, то есть если 3 − x ≥ 0 (что равносильно неравенству x ≤ 3), то исходное уравнение примет вид:
Теперь уравнение имеет только внешний модуль. Решим его раскрыв модуль:
Если −2x + 4 ≥ 0, то:
Сейчас нас интересуют только те значения x при которых внутренний модуль раскрывается с плюсом, а это произойдет при условии x ≤ 3. Поэтому для наглядности рядом с найденным корнем указано, что он удовлетворяет условию x ≤ 3
Решаем далее. Если −2x + 4 < 0, то:
Несмотря на то, что оба найденных корня удовлетворяют уравнению |−2x+4|=6−x, мы исключаем корень из решений, потому что нас сейчас интересуют только те значения x, при которых внутренний модуль изначального уравнения раскрывается с плюсом. Поэтому рядом с корнем указано, что он не удовлетворяет условию x ≤ 3.
Поэтому рядом с корнем указано, что он не удовлетворяет условию x ≤ 3.
Итак, если внутренний модуль раскрывается с плюсом, исходное уравнение принимает вид |−2x + 4| = 6 − x и корнем этого уравнения является число −2.
Теперь решим исходное уравнение для случая, когда внутренний модуль раскрывается с минусом, то есть когда 3 − x < 0 (что равносильно неравенству x > 3). Внутренний модуль будет раскрываться с минусом при всех значениях x больших 3.
Если внутренний модуль раскроется с минусом, то исходное уравнение примет вид:
Модуль −2 равен 2. Тогда получаем простейшее линейное уравнение, корень которого равен 4
Получили корень 4, который удовлетворяет условию x > 3.
В итоге корнями уравнения являются числа −2 и 4.
Ответ: 2 и 4.
Пример 3. Решить уравнение ||x − 1| − 7| = 10
Решить уравнение ||x − 1| − 7| = 10
Решение
Слева располагается модуль, а справа число, значит можно применить схему:
В данном случае если выражение ||x − 1| − 7| равно 10, то подмодульное выражение |x − 1| − 7 равно 10 или −10. Получится совокупность из двух уравнений:
Упростим получившиеся уравнения. Перенесём число −7 в обоих уравнениях в правую часть, изменив знак:
Второе уравнение корней не имеет. Первое уравнение распадется на совокупность , корни которой 18 и −16.
Ответ: 18 и −16.
Решим это же уравнение с помощью раскрытия модулей. Начнем с внутреннего модуля.
Если x − 1 ≥ 0 (что равносильно x ≥ 1), то исходное уравнение примет вид:
Решим получившееся уравнение раскрыв модуль:
Далее решаем уравнение для случаев когда x − 8 ≥ 0 и x − 8 < 0
Сейчас нас интересуют те значения, при которых внутренний модуль исходного уравнения раскрывается с плюсом. А это будет при условии, что x ≥ 1. Этому условию удовлетворяет только значение 18, поэтому мы пометили его зеленой галочкой для наглядности.
А это будет при условии, что x ≥ 1. Этому условию удовлетворяет только значение 18, поэтому мы пометили его зеленой галочкой для наглядности.
Теперь решим исходное уравнение для случая, когда внутренний модуль раскрывается с минусом, то есть когда x − 1 < 0 (или что равносильно неравенству x < 1).
Если x − 1 < 0, то исходное уравнение примет вид:
Решим получившееся уравнение раскрыв модуль:
Далее решаем уравнение для случаев когда −x − 6 ≥ 0 и −x − 6 < 0
Из найденных корней только −16 удовлетворяет условию x < 1.
В итоге корнями уравнения ||x − 1| − 7| = 10 являются числа 18 и −16.
Видно, что с помощью схемы данное уравнение решилось легче и быстрее, чем способом раскрытия модулей.
Слева модуль, а справа выражение с переменной
Решим следующее уравнение с модулем:
|4x − 3| = 3x
Здесь так же применима схема:
То есть, если выражение |4x − 3| равно 3x, то подмодульное выражение 4x − 3 должно равняться 3x или −3x.
Но в исходном уравнении переменная x содержится не только под знáком модуля, но и в правой части. Нам пока неизвестно какое значение примет переменная x. Если x примет отрицательное значение, то правая часть станет полностью отрицательной. В этом случае корней не будет, потому что модуль не может равняться отрицательному числу.
Поэтому, если мы хотим решить данное уравнение, то при сведéнии его в совокупность, дополнительно следует ввести ограничение в виде условия 3x ≥ 0. Это будет означать, что правая часть уравнения |4x − 3| = 3x должна быть больше либо равна нулю:
Совокупность и условие обрамлены знаком системы, потому что решения совокупности должны удовлетворять условию 3x ≥ 0.
Итак, решим совокупность. Условие 3x ≥ 0 является неравенством, которое тоже можно решить:
Получившиеся корни можно подставить в условие x ≥ 0 и посмотреть выполняется ли оно. Если выполняется, то найденные корни удовлетворяют уравнению. В данном случае при подстановке обеих корней в неравенство, оно выполняется. Проверка также показывает, что корни удовлетворяют уравнению:
Пример 2. Решить уравнение |2x − 1| = 5x − 10
Решение
Решим это уравнение таким же образом, как и предыдущее. Введём условие, требующее чтобы правая часть была больше либо равна нулю:
В данном случае только значение 3 удовлетворяет условию x ≥ 2. Оно же является единственным корнем исходного уравнения. Проверка показывает это:
А число не удовлетворяет условию x ≥ 2 и не является корнем исходного уравнения. Проверка также показывает это:
Видим, что модуль стал равен отрицательному числу, а это противоречит определению модуля и нашему условию x ≥ 2.
Пример 3. Решить уравнение
Решение
Это уравнение мы решили, когда учились решать уравнения с модулем внутри которых другой модуль. Теперь данное уравнение можно решить, сведя его в совокупность.
Для начала перенесём x в правую часть, изменив знак:
Теперь сведём данное уравнение в совокупность. Дополнительно введём условие в виде неравенства 6 − x ≥ 0
В левой части первого уравнения оставим модуль, остальные члены перенесём в правую часть. Тоже самое сделаем и со вторым уравнением. Также будем решать неравенство 6 − x ≥ 0, оно позволит в конце проверять найденные корни на соответствие:
Решим первое уравнение. Оно распадётся на следующую совокупность:
Получились корни −2 и 8. Из них только −2 удовлетворяет условию x ≤ 6.
Теперь решим второе уравнение. Оно является уравнением, содержащим переменную в правой части. При сведении его в совокупность дополним его условием −7 + 2x ≥ 0
Дальнейшее элементарно:
При решении второго уравнения получились корни и 4. Прежде чем сверять их с условием x ≤ 6 следует сверить их с условием под которое решалось уравнение |3 − x| = −7 + 2x. Условию удовлетворяет только корень 4.
Прежде чем сверять их с условием x ≤ 6 следует сверить их с условием под которое решалось уравнение |3 − x| = −7 + 2x. Условию удовлетворяет только корень 4.
В итоге корнями исходного уравнения являются числа −2 и 4.
Пример 4. Решить уравнение |4x + 20| = −6x
Решение
На первый взгляд покажется, что данное уравнение не имеет решений, потому что правая часть отрицательна. Но это не совсем так. Правая часть содержит переменную x, которая может принять отрицательное значение или ноль, и это приведёт к тому что правая часть станет положительной либо равной нулю. А такое уравнение имеет право на существование.
В данном случае мы решим это уравнение, сведя его в совокупность. Но при этом укажем, что правая часть должна быть больше или равна нулю:
Из найденных корней только корень −2 удовлетворяет исходному уравнению. Также он удовлетворяет нашему условию x ≤ 0.
Ответ: −2.
Когда обе части — модули
Решим следующее уравнение:
|x + 7| = |1 + 3x|
Обе части этого уравнения являются модулями. Раскроем эти модули. Будем учитывать все возможные случаи при их раскрытии.
Случай 1. Если x + 7 ≥ 0 и 1 + 3x ≥ 0, то модули в обеих частях раскроются со знаком плюс и тогда исходное уравнение примет вид:
x + 7 = 1 + 3x
Это простейшее линейное уравнение. Решим его:
Случай 2. Если x + 7 < 0 и 1 + 3x < 0, то модули в обеих частях раскроются со знаком минус и тогда исходное уравнение примет вид:
−(x + 7) = −(1 + 3x)
Раскроем скобки, получим:
−x − 7 = −1 − 3x
Замечаем, что если умножить обе части этого уравнения на −1, то получается уравнение x + 7 = 1 + 3x. А это уравнение мы получали в результате раскрытия модулей со знаком плюс.
То есть уравнения x + 7 = 1 + 3x и −x − 7 = −1 − 3x являются равносильными, а значит имеют одни и те же корни. Убедимся в этом, решив уравнение −x − 7 = −1 − 3x
Поэтому, раскрыв модули со знаком плюс, нет необходимости раскрывать их со знаком минус, потому что в обоих случаях получаются уравнения, имеющие одни и те же корни.
Следующий случай это когда x + 7 ≥ 0 и 1 + 3x < 0. Тогда исходное уравнение примет вид x + 7 = −1 − 3x. Найдём корень этого уравнения:
И последний случай это когда x + 7 < 0 и 1 + 3x ≥ 0. Тогда уравнение примет вид −x − 7 = 1 + 3x. Если умножить это уравнение на −1, то получим уравнение x + 7 = −1 − 3x. А это уравнение мы получали, когда рассматривали предыдущий случай (случай x + 7 ≥ 0 и 1 + 3x < 0).
Следовательно, уравнение −x − 7 = 1 + 3x равносильно предыдущему уравнению x + 7 = −1 − 3x. Убедимся в этом решив уравнение −x − 7 = 1 + 3x
Убедимся в этом решив уравнение −x − 7 = 1 + 3x
Значит раскрыв левую часть со знаком плюс, а правую часть со знаком минус, нет необходимости раскрывать левую часть со знаком минус, а правую часть со знаком плюс, потому что в обоих случаях получаются уравнения, имеющие одни и те же корни.
Вообще, если в уравнении обе части являются модулями как в данном примере, то это уравнение можно свести в следующую совокупность:
В этой конструкции уравнение вида |a| = |b| сведено в совокупность из двух уравнений a = b и a = −b. Видно что первое уравнение получается путем раскрытия обоих модулей со знаком плюс, а второе уравнение — путем раскрытия модуля |a| со знаком плюс, а модуля|b|— со знаком минус.
Важно. Данная схема работает только тогда, когда обе части являются модулями без посторонних членов. Проще говоря, если будет дано уравнение, например |a| = |b| + c, то приведенную схему использовать нельзя.
Пример 2. Решить уравнение |2 − 3x| = |x + 5|
Решение
Обе части данного уравнения являются модулями. Воспользуемся схемой:
У нас получится совокупность из двух уравнений. В первом уравнении оба модуля будут раскрыты со знаком плюс, во втором уравнении — модуль |2 − 3x| будет раскрыт со знаком плюс, а модуль |x + 5| со знаком минус:
Выполним проверку:
Ответ: и
Пример 3. Решить уравнение |x2 − 13x + 35|=|35 − x2|
Решение
Обе части данного уравнения являются модулями. Воспользуемся схемой:
У нас получится совокупность из двух уравнений. В первом уравнении оба модуля будут раскрыты со знаком плюс. Во втором уравнении — модуль |x2 − 13x + 35| будет раскрыт со знаком плюс, а модуль |35 − x2| со знаком минус:
Приведём подобные члены в обоих уравнениях:
Первое уравнение является неполным квадратным. Решим его, вынеся x за скобки. Второе уравнение решается элементарно:
Решим его, вынеся x за скобки. Второе уравнение решается элементарно:
Ответ: , , 0.
Когда решение — числовой промежуток
Нередко приходиться решать уравнения с модулем, где корнями являются не один или два числа, а числовой промежуток. Таковым, например, является уравнение:
|5x + 3| = −5x − 3
Раскроем модуль этого уравнения:
Если раскрыть модуль со знаком плюс, то получается уравнение 5x + 3 = −5x − 3. Решим его:
А если раскрыть модуль со знаком минус, то получится уравнение −5x − 3 = −5x − 3. В этом уравнении обе части являются одинаковыми, а значит данное равенство является тождеством. Оно будет верно при любом значении x. Значит корнями уравнения −5x − 3 = −5x − 3 являются все числа от минус бесконечности до плюс бесконечности:
x ∈ (−∞; +∞)
Но надо помнить про условия, согласно которым были раскрыты модули. В первом случае мы получили корень . Он будет верен только при условии что . Это условие соблюдено. Проверка также показывает что корень подходит:
В первом случае мы получили корень . Он будет верен только при условии что . Это условие соблюдено. Проверка также показывает что корень подходит:
Значит один из корней уравнений равен
Во втором случае мы получили множество корней от минус бесконечности до плюс бесконечности. Но это будет верно только при условии что
Например, если взять любое число из промежутка (−∞; +∞), но которое не будет удовлетворять условию , то это число не будет обращать наше уравнение в верное равенство.
Например, число 2 принадлежит промежутку (−∞; +∞), но не удовлетворяет условию , а значит число 2 не является корнем исходного уравнения. Проверка также покажет это:
А если взять к примеру число −5, то оно будет принадлежать промежутку (−∞; +∞) и удовлетворять условию , а значит будет обращать исходное уравнение в верное равенство:
Поэтому ответ надо записать так, чтобы были выполнены оба условия и . Для наглядности нарисуем координатную прямую и обозначим её как x
Отметим на ней наш первый корень
Раскрыв модуль со знаком минус и решив получившееся уравнение, мы получили в ответе множество всех чисел от минус бесконечности до плюс бесконечности, но при этом было дано условие . Значит более точным ответ в этом случае будет таким:
Значит более точным ответ в этом случае будет таким:
Корнями уравнения −5x − 3 = −5x − 3 при условии являются все числа от минус бесконечности до
Значит на координатной прямой нужно заштриховать область слева от числа . Они будут иллюстрировать числа, меньшие
Число тоже является верным корнем исходного уравнения. Он был получен при раскрытии модуля со знаком плюс. Поэтому на координатной прямой пустой кружок нужно закрасить. Так мы включим число во множество решений:
Тогда окончательный ответ будет выглядеть так:
Ответ:
Также, можно решить это уравнение сведя его в совокупность, дополнительно указав, что правая часть должна быть больше либо равна нулю:
Пример 2. Решить уравнение |2x − 3| = 3 − 2x
Решение
Решим исходное уравнение для случаев когда 2x − 3 ≥ 0 и 2x − 3 < 0
Ответ:
Использование координатной прямой
Рассмотрим ещё один способ решения элементарных уравнений с модулем — с помощью координатной прямой. Этот способ используется редко, но знать о нём не помешает.
Этот способ используется редко, но знать о нём не помешает.
Решим наше самое первое уравнение |x − 2| = 5 с помощью координатной прямой. Напомним, что корнями этого уравнения были числа 7 и −3.
Модуль есть расстояние от начала координат до точки A. Либо расстояние между двумя числами на координатной прямой.
Расстояние между двумя числами выражается в виде разности |x1 − x2|, где x1 — первое число, x2 — второе число.
Если внимательно посмотреть на уравнение |x − 2|= 5, то можно увидеть что его левая часть это расстояние от x до 2 (или от 2 до x) и это расстояние равно 5. Отмéтим на координатной прямой число x и число 2
Правая часть уравнения |x − 2|= 5 говорит о том, что расстояние от x до 2 составляет пять единиц:
Если расстояние от x до 2 равно 5, то и расстояние от 2 до x тоже равно 5. Это позволяет отсчитать пять целых шагов от числа 2 к числу x и таким образом узнать значение x
Это позволяет отсчитать пять целых шагов от числа 2 к числу x и таким образом узнать значение x
Видно, что отсчитав пять шагов влево мы попали в точку с координатой −3. А это один из корней, который мы находили для уравнения |x − 2|= 5.
Но пять целых шагов от числа 2 можно отсчитать не только влево, но и вправо:
Если отсчитать пять целых шагов вправо, то попадём в точку с координатой 7. Это тоже был корень уравнения |x − 2|= 5
Несколько модулей в одной части
Решим следующее уравнение:
|x − 5| − |x| = 1
Это уравнение содержит два модуля в левой части. Чтобы решить данное уравнение нужно раскрыть его модули. Рассмотреть нужно каждый из случаев:
- когда оба модуля больше либо равны нулю;
- когда оба модуля меньше нуля;
- когда первый модуль больше либо равен нулю, а второй модуль меньше нуля;
- когда первый модуль меньше нуля, а второй модуль больше либо равен нулю.

Не будем комментировать каждый случай, а сразу приведём решение:
Первые два случая корней не дали. В третьем случае нашелся корень 3, но он не удовлетворяет условиям x − 5 ≥ 0 и x < 0, поэтому не является корнем исходного уравнения.
В четвёртом случае нашёлся корень 2, который удовлетворяет условиям x − 5 < 0 и x ≥ 0. Также он удовлетворяет исходному уравнению.
Заметно, что такой способ решения уравнения неудобен. Если модулей в уравнении будет три, четыре или более, то придётся рассматривать намного больше случаев. Человек запутавшись, может забыть рассмотреть какой-то из случаев, и получится что уравнение решено не полностью.
Поэтому такой вид уравнения как в данном примере удобнее решать методом интервалов. Об этом мы поговорим в следующем уроке.
Задания для самостоятельного решения
Задание 1. Решить уравнение:
Решение:
Задание 2. Решить уравнение:
Решить уравнение:
Решение:
Задание 3. Решить уравнение:
Решение:
Задание 4. Решить уравнение:
Решение:
Ответ: .Задание 5. Решить уравнение:
Решение:
Ответ: .Задание 6. Решить уравнение:
Решение:
Ответ: .Задание 7. Решить уравнение:
Решение:
Ответ: .Задание 8. Решить уравнение:
Решение:
Ответ: .Задание 9. Решить уравнение:
Решение:
Ответ: .Задание 10. Решить уравнение:
Решение:
Ответ: .Задание 11. Решить уравнение:
Решение:
Ответ: .Задание 12. Решить уравнение:
Решение:
Ответ: 0, 5.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Модуль числа.
 Простое уравнение с модулем. Корень уравнения с модулем.
Простое уравнение с модулем. Корень уравнения с модулем.
Наиболее часто возникают ошибки при решении уранений с модулем. Давайте разберем решение простейших уравнений с модулем. Чтобы решить уранения с модулем, надо знать определение модуля. Модуль обозначает абсолютное значение числа и записывается вертикальными черточками:
\(|a|\) — читается как модуль числа \(a\).
Определение модуля:
Модуль числа \(|-5|\) из определения является расстоянием от \(-5\) до \(0\).
- Если модуль числа равен положительному значению, то уравнение имеет два корня.
- Если модуль числа равен нулю, то уравнение имеет один корень.
- Если модуль равен отрицательному значению, то уравнение не имеет корней.
Пример 1. Решите \(|x|=3\)
Решение:
\(|x|=3\)
\(x = 3\) или \(x = -3\)
Уранение имеет два корня
Ответ: \(x = 3\) или \(x = -3\).
Пример 2. Решите \(|x|=0\)
Решение:
\(|x|=0\)
\(x = 0\)
Уравнение имеет один корень
Ответ: \(x = 0\).
Пример 3. Решите \(|x|=-3\)
Решение:
Модуль не может быть равен отрицательному значению!!!
корней нет
Ответ: корней нет.
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявкуРепетитор по математике
Минский государственный лингвистический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-9 классов. Я фанат английского языка. Хочу, чтобы и мои ученики выучили английский язык даже так же как и я и даже лучше! Коммуникативная методика, преподавание с креативом и энергией, индивидуальный подход к каждому ученику.
Я фанат английского языка. Хочу, чтобы и мои ученики выучили английский язык даже так же как и я и даже лучше! Коммуникативная методика, преподавание с креативом и энергией, индивидуальный подход к каждому ученику.
Репетитор по математике
Гомельский государственный университет им. Ф. Скорины
Ф. Скорины
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике 8-11 классов. Люблю математику за четкость и логичность. Объясняю материал доступно и столько раз, сколько потребуется для его усвоения. Стремлюсь к тому, чтобы ученик почувствовал уверенность в своих знаниях. Учу искать нестандартные решения. Мои ученики успешно учатся в ведущих вузах России, Белоруссии, Чехии и Польши. Многие из них уже получили дипломы и работают в разных странах.
Люблю математику за четкость и логичность. Объясняю материал доступно и столько раз, сколько потребуется для его усвоения. Стремлюсь к тому, чтобы ученик почувствовал уверенность в своих знаниях. Учу искать нестандартные решения. Мои ученики успешно учатся в ведущих вузах России, Белоруссии, Чехии и Польши. Многие из них уже получили дипломы и работают в разных странах.
Репетитор по математике
Марийский государственный педагогический институт им. Н.К. Крупской
Н.К. Крупской
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по русскому языку 5-9 классов. Люблю свой предмет! Готовлю к ОГЭ. Русский язык помогает вникать в тонкости построения отдельных слов и предложений. Предлагаю окунуться в это увлекательное путешествие прямо сейчас!
Люблю свой предмет! Готовлю к ОГЭ. Русский язык помогает вникать в тонкости построения отдельных слов и предложений. Предлагаю окунуться в это увлекательное путешествие прямо сейчас!
Похожие статьи
Записаться на бесплатный урок
Рассказываю как решить уравнение с модулем из ОГЭ | ВЛАДИМИР. МАТЕМАТИКА И ФИЗИКА
Доброго времени суток, уважаемые читатели! Для тех, кто меня не знает, представлюсь. Меня зовут Владимир. Я работаю преподавателем в университете, увлекаюсь наукой (магнитные колебания и волны) и время от времени стараюсь делиться с Вами полезной информацией на канале. Сегодня мы рассмотрим решение ещё одного уравнения из ОГЭ.
На этот раз мне на глаза попалось интересное уравнение с модулем числа |x-7|=2.
Для того, чтобы решить данное уравнение, первым делом позвольте Вам напомнить, что такое модуль числа.
Вам нравятся уравнения с модулем?:)Вам нравятся уравнения с модулем?:)
Модуль числа — это положительное число или число равное 0. Это значит, что, каким бы не был x, мы всегда будем получать положительное число.Следующим шагом, нужно рассмотреть 2 случая значений выражения под модулем x-7.
Первый случай, когда x-7>0.
В этом случае |x-7| будет равен просто x-7. Следовательно, наше уравнение запишется в следующем виде:
x-7=2 при x-7>0
Переносим -7 в правую часть уравнения x-7=2 и неравенства x-7>0.
Получаем:
x=9 при x>7.
Таким образом, получаем первое решение уравнения: x=9
Второй случайУравнение |x-7|=2 имеет ещё один корень. Для того, чтобы найти второй корень уравнения, нужно рассмотреть случай, когда x-7<0. То есть случай, когда x<7. При этом модуль принимает следующее значение:
|x-7|=-(x-7)=-x+7
Таким образом, уравнение будет принимать следующий вид для x<7:
-x+7=2
Решая уравнение получим:
x=5
В итоге получаем два корня уравнения:
x1=9, x2=5
Если у Вас возникли вопросы, обязательно задавайте их в комментариях. Мой опыт занятий с детьми показывает, что многие школьники не понимают, как решать задачи с модулями.
Спасибо за внимание! Ваш лайк очень важен для развития моего небольшого блога.
Решение уравнений с модулем (часть 1)
Уравнения с модулем с решениями (часть 1)
перейти к содержанию
Свойства модуля (справочник)
1. Найдите корни уравнения
Решение
Так как и для любого , то . Поэтому и уравнение принимает вид , откуда . Условию удовлетворяет только число .
Ответ:
2. Найдите сумму корней уравнения
Решение
www.itmathrepetitor.ru Раскроем модуль. Для этого рассмотрим первый случай: . Тогда . Корнями этого уравнения являются числа и . После проверки остается только .
Второй случай: . Тогда , откуда . Условию удовлетворяет только .
Сумма корней равна
Ответ:
3. Найдите произведение корней уравнения .
Решение
Пусть , тогда , откуда или , то есть или . Первое уравнение имеет корни , второе уравнение корней не имеет, так как . Значит, произведение корней исходного уравнения равно .
Ответ:
4. Найдите сумму корней уравнения
Решение
www.itmathrepetitor.ru , что равносильно при условии . Корнями первого уравнения совокупности являются числа и , корнями второго — числа и . Неравенству удовлетворяют только и . Значит, сумма корней исходного уравнения равна .
Ответ:
5. Найдите разность между наибольшим и наименьшим корнями уравнения
Решение
. Пусть , тогда и , то есть или . Первое уравнение корней не имеет, так как . Из второго следует, что . Сумма этих корней равна .
Ответ:
6. Найдите сумму корней уравнения
Решение
Уравнение равносильно совокупности , откуда Избавимся от знаменателя: .
Ответ:
7. Найдите сумму корней уравнения
Решение
www.itmathrepetitor.ru Уравнение равносильно совокупности , откуда . Сумма корней равна .
Ответ:
8. Решите уравнение
Решение
Нули модулей равны и . Рассмотрим три случая: . Для каждого из них модули раскрываются с определенным знаком.
Рассмотрим три случая: . Для каждого из них модули раскрываются с определенным знаком.
Первый случай.
, то есть — любое число. С учетом ограничения случая, .
Второй случай.
. С учетом ограничения случая, корней нет.
Третий случай.
, то есть корней нет.
Ответ:
9. Найдите сумму корней уравнения
Решение
Нули модулей равны и . Рассмотрим три случая: . Для каждого из них модули раскрываются с определенным знаком.
Первый случай.
. Найденный корень удовлетворяет ограничению случая.
Второй случай.
. С учетом ограничения случая, корней нет.
Третий случай.
. Найденный корень удовлетворяет ограничению случая.
Сумма корней исходного уравнения равна .
Ответ:
10. Найдите произведение корней уравнения
Решение
Уравнение равносильно совокупности , откуда . Произведение корней равно .
Ответ:
смотрите раздел «Математика»
Решение уравнений и неравенств c модулем
Версия для печати
1.
 4`;
4`;
1.3 Модуль неизвестного числа
`abs(x)=[({(x >= 0),(abs(x) = x):}), ({(x1.4 Упражнения к определению модуля
1.4.1 Решить уравнение `abs(2x-1)=2x-1`
`2x-1>=0`; `x >= 1/2`Ответ: `[1/2; +infty)`
1.4.2 Решить уравнение `abs(7x-14)=14-7x`
`7x-14 <= 0`; `x <= 2`Ответ: `(-infty; 2]`
1.4.3 Решить уравнение `abs(3x-19)=1`
`[(3x-19=1), (3x-19=-1) :}`; `[(x=20/3), (x=6) :}`Ответ: `{6; 20/3}`
1.4.4 Решить уравнение `abs(5x-11)=3x+4`
`{( 3x+4 >= 0 ), ( [(5x-11=3x+4), (5x-11=-3x-4):}) :}`; `{(x >= -4/3), ( [(x=15/2), (x=7/8):} ) :}`;Ответ: `{7/8; 15/2}`
1.
 4.5 Решить неравенство `abs(x+4) <=1`
4.5 Решить неравенство `abs(x+4) <=1`
`-1
`-5
Ответ: `[-5; -3]`
1.4.6 Решить неравенство `1/5 abs(1-7x) > 3`
`abs(1-7x) > 15`;
`[(1-7x > 15), (1 — 7x < -15) :}`; `[(7x < -14), ( 7x > 16) :}`;
`[(x < -2), (x > 16/7) :}`
Ответ: `(-infty; -2) uu (16/7; +infty)`
2. Решение уравнений, содержащих неизвестную функцию под знаком модуля
`abs(f(x))=varphi(x)`
— Если `varphi(x) >= 0`, то решаем систему:
`{( varphi(x) >= 0 ), ( [(f(x)=varphi(x)), (f(x)=-varphi(x)) :}) :}`
Примеры уравнений, содержащих неизвестную функцию под знаком модуля
Решить уравнение `abs(x^2-x)=3x-4`
`{( 3x-4 >= 0 ), ( [ (x^2-x=3x-4), (x^2-x=4-3x) :}) :}`; `{ (x >= 4/3 ), ( [ (x^2-4x+4 = 0), (x^2+2x-4=0) :}) :}`;`[( { (x >= 4/3), ((x-2)^2=0) :} ), ( { (x >= 4/3), (x^2+2x-4=0) :}) :}`; `[( { (x >= 4/3), (x=2) :} ), ( { (x >= 4/3), ([(x=-1-sqrt5),(x=-1+sqrt5):}) :}) :}`;
Сравним `4/3 vv sqrt5-1`
`4 vv 3sqrt5-3`; `7 vv 3sqrt5`; `49 vv 45 (>)`
`4/4 > sqrt5-1`
Ответ: 2
3.
 10`
10`
Итоговое объединение двух систем: `x < -5/3 uu [-3/2; 2] uu x>=2`
Ответ: `(-infty; -5/3) uu (-3/2; +infty)`
3.1.3 Найти область определения функции `f(x)=sqrt(1/2-abs(3/(5-x))`
`D_f(x)`:`1/2-abs(3/(5-x)) >= 0`;
`abs(3/(5-x))
` -1/2
`{( 3/(5-x) <= 1/2), ( 3/(5-x) >= -1/2) :}`; `{( 3/(5-x) — 1/2 <= 0), ( 3/(5-x) + 1/2 >= 0):}`;
`{( (6-5+x)/(2(5-x)) <= 0 ), ( (6+5-x)/(2(5-x)) >= 0 ):}`; `2 > 0`; `{( (x +1)/(5-x) <= 0 ), ( (11-x)/(5-x) >= 0 ):}`;
Ответ: `(-infty; -1] uu [11; +infty)`
3.
 2/(x-1) <= 0) :} ) :}`; `[({(x <= 1/2), (x-1 > 0):}), ({(x <= 1/2), (-(x+1) <= 0):}) :}`; `[(emptyset), ({(x <= 1/2), (x+1 >= 0):}) :}`; `{(x <= 1/2), (x >= -1):}`
2/(x-1) <= 0) :} ) :}`; `[({(x <= 1/2), (x-1 > 0):}), ({(x <= 1/2), (-(x+1) <= 0):}) :}`; `[(emptyset), ({(x <= 1/2), (x+1 >= 0):}) :}`; `{(x <= 1/2), (x >= -1):}`
В ответ: `[-1; 1/2]` (б)
В ответ `[ ( a: (1/2; 1) uu (1; +infty)), ( б: [-1; 1/2]) :}`
Ответ: `[-1; 1) uu (1; +infty)`
4. Уравнения и неравенства, содержащие неизвестные под несколькими модулями
4.1 Решить неравенство `abs(x-4)-2abs(1-x) >= 1`
На числовом луче отметим значения x, при которых подмодульные значения обращаются в «0»: `x=1; x=4`. Луч разбился на три интервала.Необходимо на каждом интервале найти решение данного неравенства, то есть решить совокупность трёх систем неравенств:
`[
(
{
(x <= 1), (4-x-2(1-x) >= 1)
:}
),
(
{(1 < x <= 4), (4-x+2(1-x) >= 1) :}
),
(
{(x > 4), (x-4+2(1-x) >= 1) :}
)
:}` ;
`[
(
{
(x <= 1), (4-x-2+2x >= 1)
:}
),
(
{(1 < x <= 4), (4-x+2-2x >= 1) :}
),
(
{(x > 4), (x-4+2-2x >= 1) :}
)
:}` ;
`[
(
{
(x <= 1), (x+1 >= 0)
:}
),
(
{(1 < x <= 4), (5-3x >= 0) :}
),
(
{(x > 4), (-x-3 >= 0) :}
)
:}` ;
`[
(
{
(x <= 1), (x >= -1)
:}
),
(
{(1 < x <= 4), (x <= 5/3) :}
),
(
{(x > 4), (x <= -3) :}
)
:}` ;
Ответ: `[-1; 5/3]`
4.
 2 -3abs(x)+1)`
Ответ: `(-infty; -5/3] uu {-1} uu {1} uu [5/3; +infty)`
2 -3abs(x)+1)`
Ответ: `(-infty; -5/3] uu {-1} uu {1} uu [5/3; +infty)`
6.9 Решить неравенство `3x — abs(x+8) — abs(1-x) <= -6`
Ответ: `(-infty; 1]`Много задач с решениями на неравенства с модулем можно посмотреть здесь:
Решения неравенств с модулем
Чему равен модуль х 2. Как решать уравнения с модулем: основные правила
Инструкция
Если модуль представлен в виде непрерывной функции, то значение ее аргумента может быть как положительным, так и отрицательным: |х| = х, х ≥ 0; |х| = — х, х
Модуль нулю, а модуль любого положительного числа – ему . Если аргумент отрицательный, то после раскрытия скобок его знак меняется с минуса на плюс. На основании этого вытекает вывод, что модули противоположных равны: |-х| = |х| = х.
Модуль комплексного числа находится по формуле: |a| = √b ² + c ², а |a + b| ≤ |a| + |b|. Если в аргументе присутствует в виде множителя положительное число, то его можно вынести за знак скобки, например: |4*b| = 4*|b|.
Если аргумент представлен в виде сложного числа, то для удобства вычислений допускается порядка членов выражения, заключенного в прямоугольные скобки: |2-3| = |3-2| = 3-2 = 1, поскольку (2-3) меньше нуля.
Возведенный в степень аргумент одновременно находится под знаком корня того же порядка – он решается при помощи : √a² = |a| = ±a.
Если перед вами задача, в которой не указано условие раскрытия скобок модуля, то избавляться от них не нужно – это и будет конечный результат. А если требуется их раскрыть, то необходимо указать знак ±. Например, нужно найти значение выражения √(2 * (4-b)) ². Его решение выглядит следующим образом: √(2 * (4-b)) ² = |2 * (4-b)| = 2 * |4-b|. Поскольку знак выражения 4-b неизвестен, то его нужно оставить в скобках. Если добавить дополнительное условие, например, |4-b| >
Модуль нуля равен нулю, а модуль любого положительного числа – ему самому. Если аргумент отрицательный, то после раскрытия скобок его знак меняется с минуса на плюс. На основании этого вытекает вывод, что модули противоположных чисел равны: |-х| = |х| = х.
На основании этого вытекает вывод, что модули противоположных чисел равны: |-х| = |х| = х.
Модуль комплексного числа находится по формуле: |a| = √b ² + c ², а |a + b| ≤ |a| + |b|. Если в аргументе присутствует в виде множителя целое положительное число, то его можно вынести за знак скобки, например: |4*b| = 4*|b|.
Отрицательным модуль быть не может, поэтому любое отрицательное число преобразуется в положительное: |-x| = x, |-2| = 2, |-1/7| = 1/7, |-2,5| = 2,5.
Если аргумент представлен в виде сложного числа, то для удобства вычислений допускается изменение порядка членов выражения, заключенного в прямоугольные скобки: |2-3| = |3-2| = 3-2 = 1, поскольку (2-3) меньше нуля.
Если перед вами задача, в которой не указано условие раскрытия скобок модуля, то избавляться от них не нужно – это и будет конечный результат. А если требуется их раскрыть, то необходимо указать знак ±. Например, нужно найти значение выражения √(2 * (4-b)) ². Его решение выглядит следующим образом: √(2 * (4-b)) ² = |2 * (4-b)| = 2 * |4-b|. Поскольку знак выражения 4-b неизвестен, то его нужно оставить в скобках. Если добавить дополнительное условие, например, |4-b| > 0, то в итоге получится 2 * |4-b| = 2 *(4 — b). В качестве неизвестного элемента также может быть задано конкретное число, которое следует принимать во внимание, т.к. оно будет влиять на знак выражения.
Поскольку знак выражения 4-b неизвестен, то его нужно оставить в скобках. Если добавить дополнительное условие, например, |4-b| > 0, то в итоге получится 2 * |4-b| = 2 *(4 — b). В качестве неизвестного элемента также может быть задано конкретное число, которое следует принимать во внимание, т.к. оно будет влиять на знак выражения.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
А вычисляется в соответствии с такими правилами:
Для краткости записи применяют |а| . Так, |10| = 10; — 1 / 3 = | 1 / 3 |; | -100| =100 и т. д.
Всякой величине х соответствует достаточно точная величина |х |. И значит тождество у = |х | устанавливает у как некоторую функцию аргумента х .
График этой функции представлен ниже.
Для x
> 0 |x
| = x
, а для x
x
|= —x
; в связи с этим линия у = |x
| при x
> 0 совмещена с прямой у =х
(биссектриса первого координатного угла), а при х
у = -х
(биссектриса второго координатного угла).
Отдельные уравнения включают в себя неизвестные под знаком модуля .
Произвольные примеры таких уравнений — |х — 1| = 2, |6 — 2х | =3х + 1 и т. д.
Решение уравнений содержащих неизвестную под знаком модуля базируется на том, что если абсолютная величина неизвестного числа х равняется положительному числу а, то само это число х равняется или а, или -а.
Например :, если |х | = 10, то или х =10, или х = -10.
Рассмотрим решение отдельных уравнений .
Проанализируем решение уравнения |х — 1| = 2.
Раскроем модуль тогда разность х — 1 может равняться или + 2, или — 2. Если х — 1 = 2, то х = 3; если же х — 1 = — 2, то х = — 1. Делаем подставновку и получаем, что оба эти значения удовлетворяют уравнению.
Ответ. Указанное уравнение имеет два корня: x 1 = 3, x 2 = — 1.
Проанализируем решение уравнения
| 6 — 2х
| = 3х
+ 1.
После раскрытия модуля получаем: или 6 — 2х = 3х + 1, или 6 — 2х = — (3х + 1).
В первом случае х = 1, а во втором х = — 7.
Проверка. При х = 1 |6 — 2х | = |4| = 4, 3x + 1 = 4; от суда следует, х = 1 — корен ь данного уравнения .
При x = — 7 |6 — 2x | = |20| = 20, 3x + 1= — 20; так как 20 ≠ -20, то х = — 7 не является корнем данного уравнения.
Ответ. У уравнения единственный корень: х = 1.
Уравнения такого типа можно решать и графически .
Так решим, например , графически уравнение |х- 1| = 2.
Первоначально выполним построение графика функции у = |x — 1|. Первым начертим график функции у =х- 1:
Ту часть этого графика
, которая расположена выше оси х
менять не будем. Для нее х
— 1 > 0 и потому |х
-1|=х
-1.
Часть графика, которая расположена под осью х , изобразим симметрично относительно этой оси. Поскольку для этой части х — 1 х — 1|= — (х — 1). Образовавшаяся в результате линия (сплошная линия) и будет графиком функции у = |х —1|.
Эта линия пересечется с прямой у = 2 в двух точках: M 1 с абсциссой -1 и М 2 с абсциссой 3. И, соответственно, у уравнения |х — 1| =2 будет два корня: х 1 = — 1, х 2 = 3.
Одна из самых сложных тем для учащихся – это решение уравнений, содержащих переменную под знаком модуля. Давайте разберемся для начала с чем же это связано? Почему, например, квадратные уравнения большинство детей щелкает как орешки, а с таким далеко не самым сложным понятием как модуль имеет столько проблем?
На мой взгляд, все эти сложности связаны с отсутствием четко сформулированных правил для решения уравнений с модулем. Так, решая квадратное уравнение, ученик точно знает, что ему нужно сначала применять формулу дискриминанта, а затем формулы корней квадратного уравнения.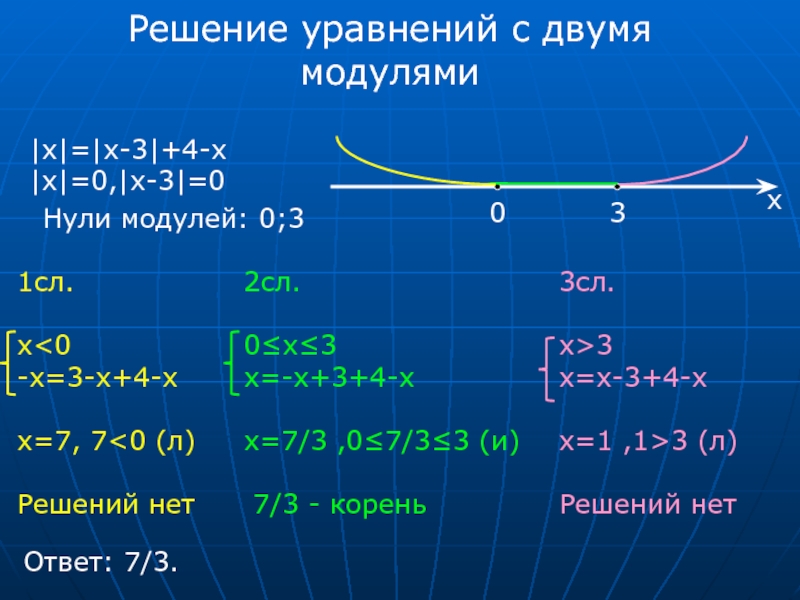 А что делать, если в уравнении встретился модуль? Постараемся четко описать необходимый план действий на случай, когда уравнение содержит неизвестную под знаком модуля. К каждому случаю приведем несколько примеров.
А что делать, если в уравнении встретился модуль? Постараемся четко описать необходимый план действий на случай, когда уравнение содержит неизвестную под знаком модуля. К каждому случаю приведем несколько примеров.
Но для начала вспомним определение модуля . Итак, модулем числа a называется само это число, если a неотрицательно и -a , если число a меньше нуля. Записать это можно так:
|a| = a, если a ≥ 0 и |a| = -a, если a
Говоря о геометрическом смысле модуля, следует помнить, что каждому действительному числу соответствует определенная точка на числовой оси – ее координата. Так вот, модулем или абсолютной величиной числа называется расстояние от этой точки до начала отсчета числовой оси. Расстояние всегда задается положительным числом. Таким образом, модуль любого отрицательного числа есть число положительное. Кстати, даже на этом этапе многие ученики начинают путаться. В модуле может стоять какое угодно число, а вот результат применения модуля всегда число положительное.
Теперь перейдем непосредственно к решению уравнений.
1. Рассмотрим уравнение вида |x| = с, где с – действительное число. Это уравнение можно решить с помощью определения модуля.
Все действительные числа разобьем на три группы: те, что больше нуля, те, что меньше нуля, и третья группа – это число 0. Запишем решение в виде схемы:
{±c, если с > 0
Если |x| = c, то x = {0, если с = 0
{нет корней, если с
1) |x| = 5, т.к. 5 > 0, то x = ±5;
2) |x| = -5, т.к. -5
3) |x| = 0, то x = 0.
2. Уравнение вида |f(x)| = b, где b > 0. Для решения данного уравнения необходимо избавиться от модуля. Делаем это так: f(x) = b или f(x) = -b. Теперь необходимо решить отдельно каждое из полученных уравнений. Если в исходном уравнении b
1) |x + 2| = 4, т.к. 4 > 0, то
x + 2 = 4 или x + 2 = -4
2) |x 2 – 5| = 11, т.к. 11 > 0, то
x 2 – 5 = 11 или x 2 – 5 = -11
x 2 = 16 x 2 = -6
x = ± 4 нет корней
3) |x 2 – 5x| = -8 , т. к. -8
к. -8
3. Уравнение вида |f(x)| = g(x). По смыслу модуля такое уравнение будет иметь решения, если его правая часть больше или равна нулю, т.е. g(x) ≥ 0. Тогда будем иметь:
f(x) = g(x) или f(x) = -g(x) .
1) |2x – 1| = 5x – 10. Данное уравнение будет иметь корни, если 5x – 10 ≥ 0. Именно с этого и начинают решение таких уравнений.
1. О.Д.З. 5x – 10 ≥ 0
2. Решение:
2x – 1 = 5x – 10 или 2x – 1 = -(5x – 10)
3. Объединяем О.Д.З. и решение, получаем:
Корень x = 11/7 не подходит по О.Д.З., он меньше 2, а x = 3 этому условию удовлетворяет.
Ответ: x = 3
2) |x – 1| = 1 – x 2 .
1. О.Д.З. 1 – x 2 ≥ 0. Решим методом интервалов данное неравенство:
(1 – x)(1 + x) ≥ 0
2. Решение:
x – 1 = 1 – x 2 или x – 1 = -(1 – x 2)
x 2 + x – 2 = 0 x 2 – x = 0
x = -2 или x = 1 x = 0 или x = 1
3. Объединяем решение и О.Д.З.:
Подходят только корни x = 1 и x = 0.
Ответ: x = 0, x = 1.
4. Уравнение вида |f(x)| = |g(x)|. Такое уравнение равносильно двум следующим уравнениям f(x) = g(x) или f(x) = -g(x).
1) |x 2 – 5x + 7| = |2x – 5|. Данное уравнение равносильно двум следующим:
x 2 – 5x + 7 = 2x – 5 или x 2 – 5x +7 = -2x + 5
x 2 – 7x + 12 = 0 x 2 – 3x + 2 = 0
x = 3 или x = 4 x = 2 или x = 1
Ответ: x = 1, x = 2, x = 3, x = 4.
5. Уравнения, решаемые методом подстановки (замены переменной). Данный метод решения проще всего объяснить на конкретном примере. Так, пусть дано квадратное уравнение с модулем:
x 2 – 6|x| + 5 = 0. По свойству модуля x 2 = |x| 2 , поэтому уравнение можно переписать так:
|x| 2 – 6|x| + 5 = 0. Сделаем замену |x| = t ≥ 0, тогда будем иметь:
t 2 – 6t + 5 = 0. Решая данное уравнение, получаем, что t = 1 или t = 5. Вернемся к замене:
|x| = 1 или |x| = 5
x = ±1 x = ± 5
Ответ: x = -5, x = -1, x = 1, x = 5.
Рассмотрим еще один пример:
x 2 + |x| – 2 = 0. По свойству модуля x 2 = |x| 2 , поэтому
По свойству модуля x 2 = |x| 2 , поэтому
|x| 2 + |x| – 2 = 0. Сделаем замену |x| = t ≥ 0, тогда:
t 2 + t – 2 = 0. Решая данное уравнение, получаем, t = -2 или t = 1. Вернемся к замене:
|x| = -2 или |x| = 1
Нет корней x = ± 1
Ответ: x = -1, x = 1.
6. Еще один вид уравнений – уравнения со «сложным» модулем. К таким уравнениям относятся уравнения, в которых есть «модули в модуле». Уравнения данного вида можно решать, применяя свойства модуля.
1) |3 – |x|| = 4. Будем действовать так же, как и в уравнениях второго типа. Т.к. 4 > 0, то получим два уравнения:
3 – |x| = 4 или 3 – |x| = -4.
Теперь выразим в каждом уравнении модуль х, тогда |x| = -1 или |x| = 7.
Решаем каждое из полученных уравнений. В первом уравнении нет корней, т.к. -1
Ответ x = -7, x = 7.
2) |3 + |x + 1|| = 5. Решаем это уравнение аналогичным образом:
3 + |x + 1| = 5 или 3 + |x + 1| = -5
|x + 1| = 2 |x + 1| = -8
x + 1 = 2 или x + 1 = -2. Нет корней.
Нет корней.
Ответ: x = -3, x = 1.
Существует еще и универсальный метод решения уравнений с модулем. Это метод интервалов. Но мы его рассмотрим в дальнейшем.
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Модуль числа легко найти, и теория, которая лежит в его основе, важна при решении задач.
Свойства и правила раскрытия, используемые при решении упражнений и на экзаменах, будут полезны школьникам и студентам. Заработай деньги с помощью своих знаний на https://teachs.ru !
Что такое модуль в математике
Модуль числа описывает расстояние на числовой линии от нуля до точки без учета того, в каком направлении от нуля лежит точка. Математическое обозначение: |x|.
Иными словами, это абсолютная величина числа. Определение доказывает, что значение никогда не бывает отрицательным.
Свойства модуля
Важно помнить о следующих свойствах:
Модуль комплексного числа
Абсолютной величиной комплексного числа называют длину направленного отрезка, проведенного от начала комплексной плоскости до точки (a, b).
Этот направленный отрезок также является вектором, представляющим комплексное число a + bi , поэтому абсолютная величина комплексного числа – это то же самое, что и величина (или длина) вектора, представляющего a+ bi .
Как решать уравнения с модулем
Уравнение с модулем – это равенство, которое содержит выражение абсолютного значения. Если для действительного числа оно представляет его расстояние от начала координат на числовой линии, то неравенства с модулем являются типом неравенств, которые состоят из абсолютных значений.
Уравнения типа |x| = a
Уравнение |x| = a имеет два ответа x = a и x = –a , потому что оба варианта находятся на координатной прямой на расстоянии a от 0.
Равенство с абсолютной величиной не имеет решения, если величина отрицательная.
Если |x|
Уравнения типа |x| = |y|
Когда есть абсолютные значения по обе стороны уравнений, нужно рассмотреть обе возможности для приемлемых определений – положительные и отрицательные выражения.
Например, для равенства |x − a| = |x + b| есть два варианта: (x − a) = − (x + b) или (x − a) = (x + b).
Уравнения типа |x| = y
Уравнения такого вида содержат абсолютную величину выражения с переменной слева от нуля, а справа – еще одну неизвестную. Переменная y может быть как больше, так и меньше нуля.
Для получения ответа в таком равенстве нужно решить систему из нескольких уравнений, в которой нужно убедиться, что y – неотрицательная величина:
Решение неравенств с модулем
Чтобы лучше понять, как раскрыть модуль в разных типах равенств и неравенств, нужно проанализировать примеры.
Уравнения вида |x| = a
Пример 1 (алгебра 6 класс). Решить: |x| + 2 = 4.
Решение.
Такие уравнения решаются так же, как и равенства без абсолютных значений. Это означает, что, перемещая неизвестные влево, а константы – вправо, выражение не меняется.
После перемещения константы вправо получено: |x| = 2
.
Поскольку неизвестные связаны с абсолютным значением, это равенство имеет два ответа: 2 и −2 .
Ответ: 2 и −2 .
Пример 2 (алгебра 7 класс). Решить неравенство |x + 2| ≥ 1.
Решение.
Первое, что нужно сделать, это найти точки, где абсолютное значение изменится. Для этого выражение приравнивается к 0 . Получено: x = –2 .
Это означает, что –2 – поворотная точка.
Разделим интервал на 2 части:
- для x + 2 ≥ 0
[−1; + ∞).
- для х + 2
Общим ответом для этих двух неравенств является интервал (−∞; –3].
Окончательное решение – объединение ответов отдельных частей:
x ∈ (–∞; –3] ∪ [–1; + ∞).
Ответ: x ∈ (–∞; –3] ∪ [–1; + ∞) .
Уравнения вида |x| = |y|
Пример 1
(алгебра 8 класс). Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.
Решить уравнение с двумя модулями: 2 * |x – 1| + 3 = 9 – |x – 1|.
Решение:
Ответ: x 1 = 3; x 2 = − 1.
Пример 2 (алгебра 8 класс). Решить неравенство:
Решение:
Уравнения вида |x| = y
Пример 1 (алгебра 10 класс). Найти x:
Решение:
Очень важно провести проверку правой части, иначе можно написать в ответ ошибочные корни. Из системы видно, что не лежит в промежутке.
Ответ: x = 0 .
Модуль суммы
Модуль разности
Абсолютная величина разности двух чисел x и y равна расстоянию между точками с координатами X и Y на координатной прямой.
Пример 1.
Пример 2.
Модуль отрицательного числа
Для нахождения абсолютного значения числа, которое меньше нуля, нужно узнать, как далеко оно расположено от нуля. Поскольку расстояние всегда является положительным (невозможно пройти «отрицательные» шаги, это просто шаги в другом направлении), результат всегда положительный. То есть,
То есть,
Проще говоря, абсолютная величина отрицательного числа имеет противоположное значение.
Модуль нуля
Известно свойство:
Вот почему нельзя сказать, что абсолютная величина – положительное число: ноль не является ни отрицательным, ни положительным.
Модуль в квадрате
Модуль в квадрате всегда равен выражению в квадрате:
Примеры графиков с модулем
Часто в тестах и на экзаменах встречаются задания, которые возможно решить, лишь проанализировав графики. Рассмотрим такие задания.
Пример 1.
Дана функция f(x) = |x|. Необходимо построить график от – 3 до 3 с шагом 1.
Решение:
Объяснение : из рисунка видно, что график симметричен относительно оси Y.
Пример 2 . Необходимо нарисовать и сравнить графики функций f(x) = |x–2| и g(x) = |x|–2.
Решение:
Объяснение: константа внутри абсолютной величины перемещает весь график вправо, если ее значение отрицательное, и влево, если положительное. Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2
в функции g (x))
.
Но постоянная снаружи будет передвигать график вверх, если значение положительное, и вниз, если оно отрицательное (как –2
в функции g (x))
.
Координата вершины x (точка, в которой соединяются две линии, вершина графа) – это число, на которое график сдвигается влево или вправо. А координата y – это значение, на которое график сдвигается вверх или вниз.
Строить такие графики можно с помощью онлайн приложений для построения. С их помощью можно наглядно посмотреть, как константы влияют на функции.
Метод интервалов в задачах с модулем
Метод интервалов – один из лучших способов найти ответ в задачах с модулем, особенно если в выражении их несколько.
Для использования метода нужно совершить следующие действия:
- Приравнять каждое выражение к нулю.
- Найти значения переменных.
- Нанести на числовую прямую точки, полученные в пункте 2.
- Определить на промежутках знак выражений (отрицательное или положительное значение) и нарисовать символ – или + соответственно.
 Проще всего определить знак с помощью метода подстановки (подставив любое значение из промежутка).
Проще всего определить знак с помощью метода подстановки (подставив любое значение из промежутка). - Решить неравенства с полученными знаками.
Пример 1 . Решить методом интервалов.
Решение:
Решение простых уравнений с абсолютной величиной | Пурпурная математика
Пурпурная математика
Когда мы берем абсолютное значение числа, мы всегда получаем положительное число (или ноль). Независимо от того, был ли ввод положительным или отрицательным (или нулем), вывод всегда положительный (или нулевой). Например, | 3 | = 3 и | –3 | = 3 также.
Это свойство — то, что и положительное, и отрицательное становятся положительными — делает решение уравнений с абсолютными значениями немного сложным.Но как только вы научитесь «трюку», они не так уж и плохи. Начнем с простого:
.
MathHelp.com
Я уже почти решил это, в моем обсуждении выше:
Итак, x должно быть равно 3 или равно -3.
Но как мне это решить, если я не знаю ответа? Я буду использовать положительное/отрицательное свойство абсолютного значения, чтобы разделить уравнение на два случая, и я буду использовать тот факт, что знак «минус» в отрицательном случае указывает на «противоположный знак», а не на «отрицательное число».
Например, если у меня x = –6, то «– x » означает «противоположное x » или, в данном случае, –(–6) = +6, положительное число.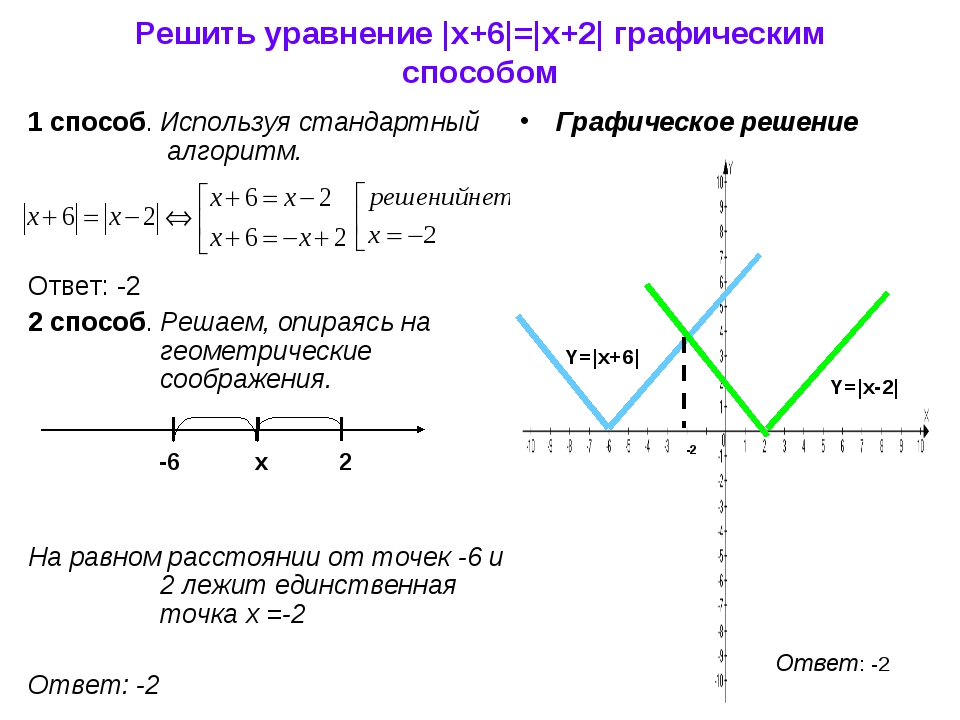 Знак «минус» в «– x » как раз указывает на то, что я меняю знак на x . , а не указывает на отрицательное число. Это различие имеет решающее значение!
Знак «минус» в «– x » как раз указывает на то, что я меняю знак на x . , а не указывает на отрицательное число. Это различие имеет решающее значение!
Каким бы ни было значение x , абсолютное значение x делает его положительным. Поскольку x изначально могло быть положительным, а могло изначально быть отрицательным, я должен признать этот факт, когда удаляю столбцы абсолютного значения.Я делаю это, разбивая уравнение на два случая. Для этого упражнения эти случаи следующие:
а. Если значение x было неотрицательным (то есть, если оно было положительным или нулевым) для начала, то я могу вывести это значение из столбцов абсолютных значений, не меняя его знака, что даст мне уравнение x = 3.
б. Если значение x изначально было отрицательным, то я могу вывести это значение из столбцов абсолютных значений, изменив знак на x , что даст мне уравнение — x = 3, которое решается как х = –3.
Тогда мое решение
Мы можем, кстати, проверить приведенное выше решение графически. Когда мы пытаемся решить уравнение абсолютного значения | х | = 3, мы, по сути, устанавливаем два линейных уравнения равными друг другу и находим, где они пересекаются. Например:
Выше я построил график y 1 = | x | (это синяя линия, похожая на букву «V») и y 2 = 3 (это зеленая горизонтальная линия).Эти два графика пересекаются при x = –3 и x = +3 (две красные точки).
Если вы хотите проверить свои ответы на тесте (перед тем, как сдать его), может быть полезно ввести каждую часть исходного уравнения абсолютного значения в ваш калькулятор как свои собственные функции; затем запросите у калькулятора точки пересечения.
Конечно, любое решение также можно проверить, подключив его к исходному упражнению и подтвердив, что левая часть (левая часть) уравнения упрощается до того же значения, что и правая часть (правая часть) уравнения. уравнение.Для уравнения выше, вот мой чек:
Если вы когда-либо сомневались в своем решении уравнения, попробуйте построить график или попытаться снова включить свое решение в исходный вопрос. Проверка вашей работы всегда в порядке!
Описанный выше шаг, когда уравнение абсолютного значения было переформулировано в двух формах, одна с «плюсом», а другая с «минусом», дает нам удобный способ упростить ситуацию: когда мы выделили абсолютное значение и перейти к снятию баров, мы можем разделить уравнение на два случая; мы обозначим эти случаи, поставив «минус» на противоположной стороне уравнения (для одного случая) и «плюс» на противоположной стороне (для другого). Вот как это работает:
Вот как это работает:
-
Решить |
х + 2 | = 7 и проверьте свои решения.
Абсолютное значение изолировано в левой части уравнения, поэтому я уже настроил разделение уравнения на два случая. Чтобы очистить столбцы абсолютных значений, я должен разделить уравнение на два возможных случая, по одному на случай, если содержимое столбцов абсолютных значений (то есть, если «аргумент» абсолютного значения) является отрицательным, и если он неотрицательный (то есть положительный или нулевой).Для этого я создаю два новых уравнения, единственная разница между которыми заключается в знаке в правой части. Сначала я сделаю «минусовый» регистр:
х + 2 = –7
х + 2 = –7
х = –9
Теперь я займусь неотрицательным случаем, где я могу просто отбросить столбцы и решить:
Теперь мне нужно проверить свои решения. Я сделаю это, подставив их обратно в исходное уравнение, поскольку оценщик не может видеть, как я проверяю графики на своем графическом калькуляторе.
Я сделаю это, подставив их обратно в исходное уравнение, поскольку оценщик не может видеть, как я проверяю графики на своем графическом калькуляторе.
Оба решения проверяются, поэтому мой ответ:
-
Решить | 2
х – 3 | – 4 = 3
Сначала я выделю абсолютную часть уравнения; то есть я получу выражение абсолютного значения с одной стороны знака «равно», а все остальное с другой стороны:
| 2 х – 3 | – 4 = 3
| 2 х – 3 | = 7
Теперь я уберу столбцы абсолютных значений, разделив уравнение на два случая, по одному для каждого знака аргумента.Сначала я возьму отрицательный регистр:
.2 х – 3 = –7
2 х = –4
х = –2
И тогда я сделаю неотрицательный случай:
2 х – 3 = 7
2 х = 10
х = 5
В упражнении не сказано проверять, поэтому я не буду. нан, где ааа — заданное положительное целое число.n=\text {произведение нескольких выражений}, = произведение нескольких выражений. В частности, если aaa простое число, то по основной теореме арифметики мы можем заключить, что каждый множитель произведения является степенью этого простого числа. Даже если aaa является составным, он часто сводится к рассмотрению случаев после рассмотрения наибольшего общего делителя. Мы даем следующий пример, чтобы проиллюстрировать эту технику:
нан, где ааа — заданное положительное целое число.n=\text {произведение нескольких выражений}, = произведение нескольких выражений. В частности, если aaa простое число, то по основной теореме арифметики мы можем заключить, что каждый множитель произведения является степенью этого простого числа. Даже если aaa является составным, он часто сводится к рассмотрению случаев после рассмотрения наибольшего общего делителя. Мы даем следующий пример, чтобы проиллюстрировать эту технику:
Найдите (p,n,x)(p,n,x)(p,n,x) в следующем диофантовом уравнении с простым ppp и положительными целыми числами x,n:x,n:x,n:
п+1=х2.z.3x+4y=5z.
Подсказка: покажите, что x=y=2x=y=2x=y=2 являются единственными решениями.
Расчет объема по частям — Математические модули Ohlone Biotechnology
Прежде чем мы начнем решать уравнения, мы должны понять, что такое уравнение. Уравнение — это утверждение о том, что две величины равны.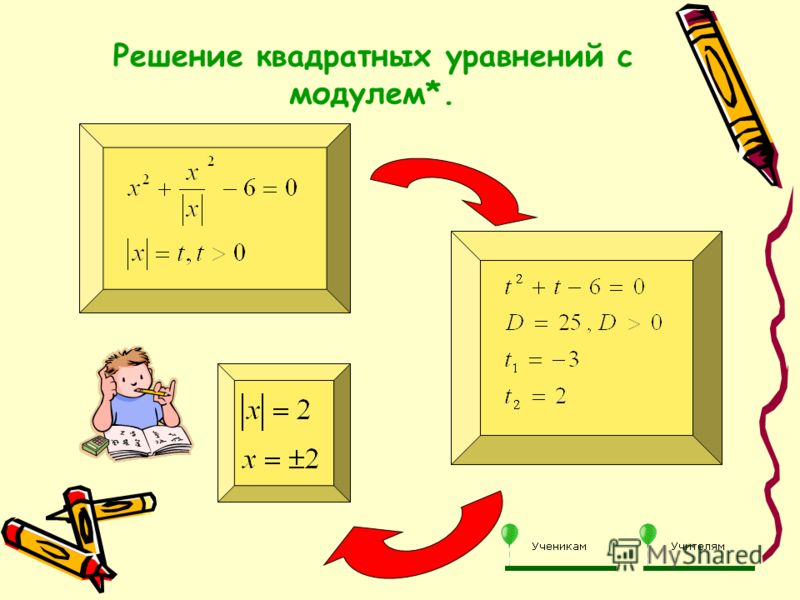 Уравнения обычно обозначаются символом равенства (=) .
Уравнения обычно обозначаются символом равенства (=) .
Давайте начнем с нескольких ключевых терминов, которые мы можем использовать для понимания различных частей уравнения.Читая эти словарные термины, рассмотрите уравнение
12x=8
и используйте приведенный ниже рисунок — Части уравнения — в качестве руководства для понимания того, как используются эти словарные термины.
Словарь
- Переменная – это символ, представляющий неизвестную величину. В качестве переменных чаще всего используются буквы, такие как x, y и z.
- Коэффициент – это число, которое умножается на переменную.
- Решение : Значение переменной (например, x, y и z), которая делает уравнение верным.
- Эквивалентные уравнения : Два (или более) уравнения, имеющие одно и то же решение.
Использование эквивалентных уравнений
При решении уравнения цель состоит в том, чтобы создать эквивалентные уравнения — исходное уравнение и его решение . Вы можете думать об этом как о поиске «ответа» или поиске решения. Решение уравнения также является эквивалентным уравнением , то есть решение эквивалентно исходному уравнению.
Вы можете думать об этом как о поиске «ответа» или поиске решения. Решение уравнения также является эквивалентным уравнением , то есть решение эквивалентно исходному уравнению.
Например, уравнения x + 4 = 7 и x = 3 эквивалентны. x = 3 также является решением.
Откуда мы знаем, что эти два уравнения эквивалентны друг другу?
В обоих случаях, если переменная x равна 3, уравнение истинно. Подставляя x = 3 в уравнение x + 4 = 7, 3 + 4 = 7 и 3 = 3.
Вероятно, вы можете посмотреть на этот пример и определить значение x, которое делает это утверждение верным. Но не все эквивалентные уравнения столь очевидны. Рассмотрим два уравнения:
0.05x — 0,2 = 0,6 и 0,5x = 8 эквивалентных уравнений?
Так и есть, но наиболее ценным эквивалентным уравнением было бы то, которое читается как x = 16. Почему это так? Подстановка x = 16 в уравнение делает каждое уравнение верным. Это уравнение (решение), которое мы хотим найти, потому что оно легче всего читается и сообщает нам решение уравнений.
Мы будем использовать идею эквивалентных уравнений в свойстве сложения равенства, а затем в свойстве умножения равенства. Давайте сначала рассмотрим свойство сложения равенства.
Аддитивное свойство равенства
Для любых действительных чисел a , b и c :
, если a = b , то
а + в = б + в
Давайте посмотрим, что означает это свойство. Если a равно b …, то a плюс c равно b плюс c .«Плюс с» — самая важная часть этого уравнения. Другими словами, вы можете создавать эквивалентные уравнения, добавляя одно и то же число к обеим частям уравнения. Давайте посмотрим на пример :
Исходное уравнение: x — 5 = 7
Добавьте 5 к обеим сторонам: x — 5 + 5 = 7 + 5
Эквивалентное уравнение (решение): x = 12
Свойство равенства при сложении также работает для вычитания путем замены знаков: Для любых действительных чисел a, b и c: если a = b, то a — c = b — c. Пример ниже:
Пример ниже:
Исходное уравнение: у + 8 = 20
Вычесть 8 с обеих сторон: у + 8 — 8 = 20 — 8
Эквивалентное уравнение: y = 12
[содержимое после окна объявлений]
Проверка понимания № 1: свойство равенства сложения
Решите следующие уравнения, используя свойство равенства сложения/вычитания. Решения находятся в конце этого руководства.
- х-6=-3
- р+1=4.2
- х+13=223
- с-0,03=0,4
- 12=2-14+х
- 6,1=х+3,25
Свойство равенства умножения
Для любых действительных чисел a , b и c :
, если a = b , то
а.к. = до н.э.
Идея, лежащая в основе свойства равенства умножения, аналогична идее свойства равенства сложения.Для любых действительных чисел a, b и c, если a равно b, то a · c = b · c. Другими словами, вы можете составить эквивалентные уравнения, умножив обе части уравнения на одну и ту же величину . Например:
Например:
Исходное уравнение: r4=6
Умножить обе части на 4: r4·4=6·4
Эквивалентное уравнение: r=24
Умножая обе части уравнения на 4, мы можем составить эквивалентное уравнение, r = 24, что делает решение понятным.
Свойство равенства умножения также применимо к делению обеих частей уравнения: для любых действительных чисел a, b и c, если a = b, то ac=bc
Исходное уравнение: 8y=88Делить обе части на 8: 8y8=888Эквивалентное уравнение: y=11
Проверка понимания #2: свойство равенства умножения
Решите следующие уравнения и посмотрите, сможете ли вы определить закономерность для значения, которое вы умножаете или делите на обе части уравнения (решения находятся на последней странице этого руководства).
- х3=-2
- 4x=36
- у5=110
- -3м=4,2
- 23x=12
- -34i=32
Некоторые уравнения будут похожи на приведенные выше, но решить другие будет сложнее. Всякий раз, когда вам нужно решить уравнение, полезно иметь стратегию, которая поможет вам начать работу.
Всякий раз, когда вам нужно решить уравнение, полезно иметь стратегию, которая поможет вам начать работу.
Например, в уравнении
3x-7=11
Должны ли мы начать с деления обеих частей на 3? Или было бы лучше добавить 7 к обеим сторонам?
Ответить на этот вопрос может быть сложно, если у вас нет стратегии.Прямо сейчас мы можем использовать два инструмента, которые помогут нам: свойства сложения и умножения равенства, которые мы рассмотрели ранее.
Возможно, для решения уравнения необходимо использовать оба свойства, но большинство, если не все, алгебраические уравнения можно решить, используя только одно из этих свойств.
Прежде чем мы напишем стратегию решения уравнений, давайте взглянем на решение приведенного выше уравнения двумя способами: сначала путем деления на 3, а затем путем прибавления 7 к обеим частям.
-
3x-7=11Если мы разделим обе части на 3:3×3-73=113Добавим 73 к каждой части уравненияx=113+73 ⇒ x=183Упростим каждую часть уравненияx=6
-
3x-7=11Если мы добавим 7 к обеим сторонам:3x-7+7=11+7и упростим3x=18разделим обе стороны на 33×3=183упростим x=6
Оба варианта работают и дают одинаковое решение. Сложение перед делением сделано для менее сложных эквивалентных уравнений. Сначала можно разделить, но деление МОЖЕТ привести к дробным константам (например, 7/3) и дробным коэффициентам. Теперь мы можем написать стратегию решения уравнения:
Сложение перед делением сделано для менее сложных эквивалентных уравнений. Сначала можно разделить, но деление МОЖЕТ привести к дробным константам (например, 7/3) и дробным коэффициентам. Теперь мы можем написать стратегию решения уравнения:
Стратегия решения уравнения
- Сложите или вычтите обе стороны, чтобы изолировать переменную.
- Разделите обе части на коэффициент переменного члена.
- Проверьте правильность своего решения.
Используйте свои знания о свойствах сложения равенства и свойства умножения равенства, чтобы решить следующие уравнения.
Проверка понимания #3: Решение уравнений с использованием обоих свойств
Используйте описанную выше стратегию, чтобы решить следующие уравнения. Проверьте свои решения, чтобы убедиться, что они верны. (Ответы на эти упражнения находятся на странице «Решения» в этом руководстве).
- 3n-8=7
- 2г+4=-3
- 34x-18=14
- 21.
 8=2,4х+9,8
8=2,4х+9,8 - 0,24x-2=4,3
- 0,25х+0,3=1,26
Проверка понимания № 1: свойство равенства сложения
- x-6=-3
Прибавьте 6 к обеим сторонам ⇒ x=3 - p+1=-4,2
Вычесть 1 с обеих сторон ⇒ p=3,2 - x+13=223
Вычесть 13 из обеих сторон ⇒ x=213 - c-0,03=0,4
Добавить 0,03 к обеим сторонам ⇒ 0,43 - 12=2-14+x
Прибавьте 14 к обеим сторонам ⇒ x=34 - 6.1=х+3.25
Вычтите 3,25 с обеих сторон ⇒ x=2,85
Проверка понимания #2: свойство равенства умножения
- x3=-2
Умножить обе части на 3 ⇒ x=-6 - 4x=36
Разделите обе части на 4 ИЛИ умножьте обе части на 14 ⇒ x=9 - y5=110
Умножить обе части на 5 ⇒ y=12 - -3m=4,2
Разделите обе части на -3 ⇒ m=-1,4 - 23x=12
Разделите каждую сторону на 23 или умножьте каждую сторону на 32 ⇒ x=18 - -34i=32
Умножьте обе части на 4-3 ⇒ x=-2
Проверка понимания #3: Решение уравнений с использованием обоих свойств
- 3n-8=7
Прибавить 8 к каждой стороне ⇒ 3n=15
Разделить обе стороны на 3 ⇒ n=5
Проверить: 3(5)-8=7 ⇒
Проверить: 15-8=7 ✔ - 2y+4=-3
Вычесть 4 с обеих сторон ⇒ 2y=-7
Разделить обе стороны на 2 ⇒ (y=-72=-3. 5)
5)
Проверка: 2(-3,5)+4=-3
Проверка: -7+4=-3 ✔ - 34x-18=14
Прибавь 18 к обеим сторонам ⇒ 34x=38
Умножь обе стороны на 43 ⇒ х=12 - 21,8=2,4x+9,8
Вычесть 9,8 с обеих сторон ⇒12=2,4x
Разделить обе стороны на 2,4 ⇒ 5=x
Проверить: 21,8=2,4(5)+9,8
Проверить: 21,8=12+9,8 ✔ - 0,24x-2=4,3
Прибавить 2 к обеим сторонам ⇒ 0,24x=6,3
Разделить обе стороны на 0,24 ⇒x=26,25
Проверить: 0,24(26,25)-3=4.3
Проверить: 6,3-3=4,3 ✔ - 0,25x+0,3=1,26
Вычесть 0,3 с обеих сторон ⇒0,25x=0,96
Разделить обе стороны на 0,25 ⇒ x=3,84
Проверить: 0,25(3,84)+0,3=1,26
(PDF) Решение уравнений и систем линейных уравнений в модуле
Журнал Иракского общества Аль-Хорезми (JIKHS) Том:2 Выпуск:2 Декабрь 2018 Страницы: 33-48
33
Решение уравнений и систем линейные уравнения в модуле
Amjad Hamead Alhusiny
Педагогический колледж чистых наук, Университет Кербелы, Кербела, Ирак
amjad. [email protected]
[email protected]
Abstract:
В этой статье мы сосредоточимся на решении типов уравнений в кольце и предложили несколько методов решения
системы линейных уравнений в модуле, в которых их матрицы необратимы. .
1. Введение:
Почему именно?. «В 8-битном изображении с оттенками серого имеется 256 уровней серого, а интенсивность каждого пикселя может иметь значение от 0 до
255, где 0 — черный, а 255 — белый» [1].С другой стороны, уравнения модульной арифметики предназначены для всех, от
аспирантов компьютерных наук, инженерии или экономики до специалистов по алгебраической геометрии. В частности, алгебра и
теория чисел нашли широкое применение в теоретической информатике для проверки делимости и блочных шифров в
криптографии и безопасности, теории кодирования и многом другом. Китайская теорема об остатках (CRT) — одна из старейших теорем
в математике; он использовался для расчета календарей еще в первом веке нашей эры [2]. Диксон [3] приводит в качестве первой ссылки
Диксон [3] приводит в качестве первой ссылки
Шонемана, который рассмотрел в 1839 году уравнения вида где — простое число. Это был
, вероятно, Гаусс, который впервые рассмотрел системы n линейных уравнений с n неизвестными относительно различных модулей [2]. Мы знаем, что
для всех и всех , все целые числа, которые удовлетворяют , даны как , для . То есть
непосредственно из определения конгруэнтности: для некоторых [3]. В этой статье мы привели некоторые
свойств кольца и рассмотрели его идеалы.Затем мы дали понятие и докажем, что . В четвертой главе
мы предлагаем два метода решения уравнения вида , и корней уравнения вида
, и одновременных уравнений в . В то время как в пятой главе приведены достаточные условия для того, чтобы матрица
была обратимой, и несколько методов решения системы линейных уравнений, с некоторыми примерами, рассмотренными на протяжении всей нашей работы.
2. Кольцо:
Примечание 2.1. : Все операции, которые мы будем использовать в нашей работе, являются операциями по модулю, то есть:
: Все операции, которые мы будем использовать в нашей работе, являются операциями по модулю, то есть:
Предлог 2.2. Все подгруппы циклические.
Доказательство: Позвольте быть подгруппой , так как конечно, предположим, что , пусть
, то принадлежат , то . Это означает, что , и, следовательно,
.
Мы дадим в следующем предлоге общий вид подгрупп .
Предлог 2.3. Для каждой подгруппы существует , с .
Доказательство: прямо из предлога privies.
Развлечение с модульной арифметикой – BetterExplained
Недавно один читатель предложил мне написать о модульной арифметике (она же «вычитание остатка»). Я не особо задумывался об этом, но понял, что модуль чрезвычайно мощный: он должен быть в нашем умственном наборе инструментов рядом со сложением и умножением.
Вместо того, чтобы бить вас формулами по лицу, давайте рассмотрим идею, которую мы ненавязчиво вынашивали годами. Есть хорошая статья о модульной арифметике, которая вдохновила меня на этот пост.
Нечетный, четный и тричетный
Вскоре после открытия целых чисел (1, 2, 3, 4, 5…) мы поняли, что они делятся на две группы:
- Четное: делится на 2 (0, 2, 4, 6..)
- Нечетное: не делится на 2 (1, 3, 5, 7…)
Почему это различие важно? Это начало абстракции — мы замечаем свойств числа (например, четность или нечетность), а не только само число («37»).
Это огромно — это позволяет нам исследовать математику на более глубоком уровне и находить отношения между типами чисел, а не конкретными.Например, мы можем создать такие правила:
.- Чет x Чет = Чет
- Нечетное x Нечетное = Нечетное
- Чет x Нечет = Чет
Эти правила являются общими — они работают на уровне свойства. (Интуитивно у меня есть химическая аналогия, что «четность» — это молекула, которую имеют некоторые числа, и ее нельзя удалить путем умножения.)
Но четное/нечетное — очень специфическое свойство: деление на 2. А как насчет числа 3? Как насчет этого:
А как насчет числа 3? Как насчет этого:
- «Три» означает, что число делится на 3 (0, 3, 6, 9…)
- «Тродд» означает, что вы , а не делитесь на 3 (1, 2, 4, 5, 7, 8…)
Странно, но работает.Вы заметите несколько вещей: есть два типа throdd. Такое число, как «4», на 1 меньше, чем тричетырнадцать (остаток 1), а число 5 — на два (остаток 2).
Быть «три» — это еще одно свойство числа. Возможно, это не так полезно сразу, как чет/нечет, но оно есть: мы можем создавать правила, такие как «три семь х тривен = тривен» и так далее.
Но это сводит с ума. Мы не можем все время составлять новые слова.
Введите модуль
Операция по модулю (сокращенно «mod» или «%» во многих языках программирования) — это остаток при делении.Например, «5 mod 3 = 2», что означает, что 2 — это остаток при делении 5 на 3.
Преобразование повседневных терминов в математические: «четное число» — это число, у которого «0 по модулю 2», то есть оно дает остаток 0 при делении на 2. Нечетное число — «1 по модулю 2» (имеет остаток 1) .
Нечетное число — «1 по модулю 2» (имеет остаток 1) .
Почему это круто? Итак, наши правила «чет/нечет» становятся такими:
.- Четный x Четный = 0 x 0 = 0 [четный]
- Нечетное x Нечетное = 1 x 1 = 1 [нечетное]
- Четный x Нечетный = 0 x 1 = 0 [четный]
Круто, да? Довольно легко разобраться — мы преобразовали «свойства» в настоящие уравнения и нашли несколько новых фактов.
Сколько будет четное x четное x нечетное x нечетное? Ну, это 0 x 0 x 1 x 1 = 0. На самом деле, вы можете видеть, что если где-нибудь умножить на четное, то весь результат будет равен нулю… Я имею в виду даже :).
Математика часов
Коварная особенность модульной математики заключается в том, что мы уже использовали ее для измерения времени — иногда называемую «арифметикой часов».
Например: сейчас 7:00 (утра/вечера не имеет значения). Где будет часовая стрелка через 7 часов?
грн. 7 + 7 = 14, но мы не можем показать «14:00» на часах. Значит, должно быть 2. Рассуждаем интуитивно и в математических терминах:
Значит, должно быть 2. Рассуждаем интуитивно и в математических терминах:
- (7 + 7) по модулю 12 = (14) по модулю 12 = 2 по модулю 12 [2 — это остаток от деления 14 на 12]
Уравнение «14 mod 12 = 2 mod 12» означает, что «14 часов» и «2 часа» выглядят одинаково на 12-часовых часах. Они конгруэнтны , обозначены тройным знаком равенства: 14 ≡ 2 по модулю 12.
Другой пример: сейчас 8:00. Где будет большая рука через 25 часов?
Вместо того, чтобы прибавлять 25 к 8, вы можете понять, что 25 часов — это просто «1 день + 1 час».Таким образом, часы переведутся на 1 час вперед, в 9:00.
- (8 + 25) mod 12 ≡ (8) mod 12 + (25) mod 12 ≡ (8) mod 12 + (1) mod 12 ≡ 9 mod 12
Вы интуитивно преобразовали 25 в 1 и добавили это к 8.
Забавное свойство: математика просто работает
Используя в качестве аналогии часы, мы можем выяснить, «просто работают» ли правила модульной арифметики (работают).
Сложение/вычитание
Допустим, два времени на наших часах выглядят одинаково («2:00» и «14:00»).Если мы добавим к ним одинаковые «x» часов, что произойдет?
Ну меняют на столько же на часах! 2:00 + 5 часов ≡ 14:00 + 5 часов — оба будут показывать 7:00.
Почему? Ну, нас никогда не волновали лишние «12:00», которые таскал с собой 14-й. Мы можем просто добавить 5 к остатку 2, который есть у обоих, и они продвинутся одинаково. Для всех конгруэнтных чисел (2 и 14) сложение и вычитание дают одинаковый результат.
Умножение
Труднее понять, остается ли умножение прежним.Если 14 ≡ 2 (mod 12), можем ли мы умножить обе части и получить тот же результат?
Посмотрим — что получится, если умножить на 3?
Ну, 2 часа * 3 ≡ 6 часов. Но что такое «14:00» * 3?
Помните, 14 = 12 + 2. Итак, мы можем сказать
.- 14 * 3 = (12 + 2) * 3 = (12 * 3) + (2 * 3) mod 12
Первую часть (12 * 3) можно игнорировать! «12-часовое переполнение», которое носит с собой 14, просто повторяется несколько раз. Но кого это волнует? Мы все равно игнорируем переполнение.
Но кого это волнует? Мы все равно игнорируем переполнение.
При умножении важен только остаток, который равен 2 часам для 14:00 и 2:00. Интуитивно я вижу, что умножение не меняет отношения с модульной математикой (вы можете умножить обе части модульного отношения и получить тот же результат). Смотрите ссылку выше для более строгих доказательств — это мои интуитивные карандашные линии.
Использование модульной арифметики
Теперь самое интересное — чем полезна модульная арифметика?
Простые расчеты времени
Мы делаем это интуитивно, но неплохо дать ему имя.Ваш рейс прибывает в 15:00. Задержка на 14 часов. В какое время он приземлится?
Итак, 14 ≡ 2 mod 12. Поэтому я думаю об этом как о «2 часах и переключении утра/после полудня», поэтому я знаю, что это будет «3 + 2 = 5 утра».
Это немного сложнее, чем простой оператор по модулю, но принцип тот же.
Размещение элементов в случайных группах
Предположим, у вас есть люди, купившие билеты в кино, с номером подтверждения. Вы хотите разделить их на 2 группы.
Вы хотите разделить их на 2 группы.
Что ты делаешь? «Шансы здесь, четы там». Вам не нужно знать, сколько билетов было выдано (первая половина, вторая половина), каждый может определить свою группу мгновенно (без обращения в центральный орган), и схема работает по мере того, как все больше людей покупают билеты.
Нужно 3 группы? Разделите на 3 и возьмите остаток (он же мод 3). У вас будут группы «0», «1» и «2».
В программировании по модулю можно помещать элементы в хэш-таблицу: если в вашей таблице N записей, преобразуйте ключ элемента в число, выполните mod N и поместите элемент в это ведро (возможно, сохраняя связанный список там).По мере увеличения размера вашей хэш-таблицы вы можете пересчитать модуль для ключей.
Выбор случайного предмета
Я использую модуль в реальной жизни. Действительно. У нас есть 4 человека, играющих в игру, и нужно выбрать кого-то, кто пойдет первым. Сыграй в мини-игру мод N! Дайте людям номера 0, 1, 2 и 3.
Теперь все идут «раз, два, три, стрелять!» и высовывает случайное количество пальцев. Сложите их и разделите на 4 — тот, кто точно наберет остаток, ходит первым.(Например: если сумма пальцев равна 11, тот, у кого было «3», ходит первым, так как 11 по модулю 4 = 3).
Это быстро и работает.
Запуск задач в цикле
Предположим, задачи должны выполняться по определенному расписанию:
- Задача A выполняется 3 раза в час
- Задача B выполняется 6 раз в час
- Задача C выполняется 1 раз в час
Как вы храните эту информацию и составляете расписание? В одну сторону:
- Таймер должен запускаться каждую минуту (отслеживайте минуты как «n»)
- 3x/час означает один раз каждые 60/3 = 20 минут.Таким образом, задача A запускается всякий раз, когда «n % 20 == 0»
- Задача B запускается всякий раз, когда «n % 10 == 0»
- Задача C запускается всякий раз, когда «n % 60 == 0»
О, вам нужна задача C1, которая выполняется 1 раз в час, но не в то же время, что и задача C? Конечно, запустите его, когда «n mod 60 == 1» (по-прежнему один раз в час, но не так, как C1).
Мысленно я вижу цикл, который хочу «побить» с различными интервалами, поэтому вставляю мод. Удобно то, что хиты могут перекрываться независимо друг от друга. В этом отношении это немного похоже на XOR (каждое XOR может быть многоуровневым — но это уже другая статья!).
Аналогично, при программировании вы можете распечатать каждый сотый элемент журнала, выполнив: if (n % 100 == 0){ print… }.
Это очень гибкий и простой способ запуска элементов по расписанию. На самом деле, это способ ответить на проверку вменяемости FizzBuzz. Если в вашем batbelt нет операции по модулю, вопрос становится намного сложнее.
Нахождение свойств чисел
Допустим, я сказал вам следующее:
Что вы можете сделать быстро? Что ж, «а» должно быть четным, поскольку оно равно чему-то, что включает умножение на 2.
Если бы я также сказал вам:
Ты бы отказался. Не потому, что вы «знаете», что два продукта разные, а потому, что один явно четный, а другой нечетный. Есть проблема: a не может быть одним и тем же числом в обоих случаях, поскольку свойства не совпадают с .
Есть проблема: a не может быть одним и тем же числом в обоих случаях, поскольку свойства не совпадают с .
Такие вещи, как «четный», «три» и «mod n», являются более общими, чем отдельные числа, и мы можем проверить их согласованность. Таким образом, мы можем использовать модуль, чтобы выяснить, согласуются ли числа, не зная, что они собой представляют!
Если я скажу вам это:
Можно ли решить эти уравнения с целыми числами? Посмотрим:
- 3a + 5b = 8… давайте «mod 3 it»: 0 + 2b ≡ 2 mod 3 или b ≡ 1 mod 3
- 3a + b = 2… давайте «mod 3 it»: 0 + b ≡ 2 mod 3), или b ≡ 2 mod 3
Противоречие, молодцы! Б не может быть одновременно «1 по модулю 3» и «2 по модулю 3» — это так же абсурдно, как быть четным и нечетным одновременно!
Но есть одна загвоздка: числа типа «1.5” не четные и не нечетные — это не целые числа! Модульные свойства применяются к целым числам, поэтому мы можем сказать, что b не может быть целым числом .
Потому что на самом деле мы можем решить это уравнение:
- (3а + 5б) – (3а +б) = 8 – 2
- 4б = 6
- б = 1,5
- 3а + 1,5 = 2, поэтому 3а = 0,5 и а = 1/6
Не соблазняйтесь силой модуля! Знайте его пределы: это относится к целым числам.
Криптография
Игра с числами имеет очень важное применение в криптографии.Это слишком много, чтобы охватить здесь, но модуль используется в обмене ключами Диффи-Хеллмана — используется при настройке SSL-соединений для шифрования веб-трафика.
Простой английский
Компьютерщики любят использовать технические слова в обычном контексте. Вы можете услышать «X такое же, как Y по модулю Z», что примерно означает «Игнорируя Z, X и Y одинаковы».
Например:
- b и B идентичны, капитализация по модулю
- iTouch и iPad идентичны по модулю размера 😉
Далее и выше
Странно думать о «полезности» оператора по модулю — это все равно, что кто-то спрашивает, почему экспоненты полезны. В повседневной жизни не очень, но это инструмент для понимания закономерностей в мире и создания своих.
В повседневной жизни не очень, но это инструмент для понимания закономерностей в мире и создания своих.
В общем, я вижу несколько общих вариантов использования:
- Редуктор диапазона: введите ввод по модулю N, и вы получите число от 0 до N-1.
- Назначение группы: возьмите ввод, мод N, и вы пометите его как группу от 0 до N-1. Эта группа может быть согласована любым количеством сторон — например, разные серверы, которые знают N = 20, могут договориться о том, к какой группе принадлежит ID=57.
- Вывод свойств: обработка чисел в соответствии со свойствами (четные, тричетные и т. д.) и разработка принципов, полученных на уровне свойств
Я уверен, что есть еще десятки применений, которые я пропустил — не стесняйтесь комментировать ниже.Удачной математики!
Другие сообщения из этой серии
- Методы сложения чисел от 1 до 100
- Переосмысление арифметики: наглядное руководство
- Quick Insight: интуитивное значение подразделения
- Краткий обзор: вычитание отрицательных чисел
- Удивительные закономерности в квадратных числах (1, 4, 9, 16…)
- Развлечение с модульной арифметикой
- Учимся считать (избегая проблемы с ограждением)
- Причудливое введение в системы счисления
- Еще один взгляд на простые числа
- Интуиция для золотого сечения
- Различные интерпретации числа ноль
Модульный анализ методов последовательного решения почти блочно-диагональных систем уравнений
Почти блочно-диагональных линейных систем уравнений можно представить на примере двух модулей. Это позволяет построить все последовательные формы методов исключения полос и/или блоков. Это также позволяет легко оценивать методы на основе количества операций, потребностей в памяти и допустимости частичного поворота. Результатом анализа и внедрения является открытие новых методов, которые превосходят хорошо известные методы, модификация которых поэтому рекомендуется.
Это позволяет построить все последовательные формы методов исключения полос и/или блоков. Это также позволяет легко оценивать методы на основе количества операций, потребностей в памяти и допустимости частичного поворота. Результатом анализа и внедрения является открытие новых методов, которые превосходят хорошо известные методы, модификация которых поэтому рекомендуется.
1. Введение
Системы уравнений с почти блочно-диагональной (АБД) матрицей коэффициентов часто встречаются при численном решении систем обыкновенных дифференциальных уравнений или уравнений в частных производных.Несколько таких ситуаций были описаны Amodio et al. [1], который также сделал обзор последовательных и параллельных решателей для систем ABD и пришел к выводу, что последовательные методы решения не нуждаются в дальнейшем изучении.
Традиционно последовательные методы решения систем ABD выполняли декомпозицию матрицы коэффициентов либо посредством леночного (скалярного) исключения, либо блочного трехдиагонального исключения. Знаменитый алгоритм COLROW [2], получивший высокую оценку за свою производительность, был включен в несколько приложений [3–7].Он использует переменный поворот столбца/строки Лама [8] и соответственно чередующееся скалярное исключение столбца/строки Вараха [9]. Эффективные блочные трехдиагональные методы включали метод исключения блочного трехдиагонального ряда (BTDR) Келлера [10, раздел 5, случай i] и метод исключения блочного трехдиагонального столбца (BTDC) Эль-Мистикави [11]. Оба метода могут применять подходящую форму смешанной пивотной стратегии Келлера [10], которая дороже, чем стратегия Лама.
Знаменитый алгоритм COLROW [2], получивший высокую оценку за свою производительность, был включен в несколько приложений [3–7].Он использует переменный поворот столбца/строки Лама [8] и соответственно чередующееся скалярное исключение столбца/строки Вараха [9]. Эффективные блочные трехдиагональные методы включали метод исключения блочного трехдиагонального ряда (BTDR) Келлера [10, раздел 5, случай i] и метод исключения блочного трехдиагонального столбца (BTDC) Эль-Мистикави [11]. Оба метода могут применять подходящую форму смешанной пивотной стратегии Келлера [10], которая дороже, чем стратегия Лама.
Настоящая статья предназначена для изучения других вариантов разложения .Он не следует традиционным подходам обработки матрицы коэффициентов как ленточной матрицы или приведения ее к блочной трехдиагональной форме. Скорее, он использует новый подход, модульный анализ , который предлагает простой и унифицированный способ выражения и оценки методов решения для систем ABD.
Матрица коэффициентов (точнее, ее значащая часть, содержащая ненулевые блоки) разбирается на упорядоченный набор модулей. (Фактически идентифицируются два разных набора модулей.) Каждый модуль представляет собой сущность, имеющую голову и хвост. Располагая модули таким образом, что головка модуля добавляется к хвосту следующего, можно собрать значительную часть модуля. Модуль иллюстрирует матрицу, но его намного легче анализировать.
(Фактически идентифицируются два разных набора модулей.) Каждый модуль представляет собой сущность, имеющую голову и хвост. Располагая модули таким образом, что головка модуля добавляется к хвосту следующего, можно собрать значительную часть модуля. Модуль иллюстрирует матрицу, но его намного легче анализировать.
Все возможные методы разложения могут быть сформулированы как разложения . Это привело к открытию двух новых многообещающих методов: устранение блочного столбца/блочной строки (BCBR) и устранение блочного столбца/скалярной строки (BCSR).
Достоверность и стабильность методов исключения имеют первостепенное значение как для численных аналитиков, так и для пользователей алгоритмов. Валидность означает, что никогда не встречается деление на ноль, тогда как стабильность защищает от роста ошибки округления. Для обеспечения достоверности и достижения стабильности требуется поворот [12]. Полный поворот требует больших вычислительных ресурсов, требуя полного двумерного поиска поворотов. Более того, это разрушает ленточный вид матрицы коэффициентов. Стратегии частичного поворота, хотя потенциально менее стабильны, значительно дешевле.Однонаправленный поворот (строка или столбец) вносит незначительные изменения в форму, добавляя несколько посторонних элементов. Переменный поворот Лама [8], который включает в себя чередующиеся последовательности поворота строки и поворота столбца, поддерживает форму . Когда не является сингулярным, поворот Лама гарантирует достоверность, а если за ним следует соответствующее альтернативное исключение, он дает множители, ограниченные единицей, что повышает стабильность. Этот подход был предложен Варахом [9] в его методе декомпозиции.Впоследствии он был преобразован в более эффективную версию, названную здесь устранением скалярных столбцов/скалярных строк (SCSR), которая была принята решателем COLROW [2].
Более того, это разрушает ленточный вид матрицы коэффициентов. Стратегии частичного поворота, хотя потенциально менее стабильны, значительно дешевле.Однонаправленный поворот (строка или столбец) вносит незначительные изменения в форму, добавляя несколько посторонних элементов. Переменный поворот Лама [8], который включает в себя чередующиеся последовательности поворота строки и поворота столбца, поддерживает форму . Когда не является сингулярным, поворот Лама гарантирует достоверность, а если за ним следует соответствующее альтернативное исключение, он дает множители, ограниченные единицей, что повышает стабильность. Этот подход был предложен Варахом [9] в его методе декомпозиции.Впоследствии он был преобразован в более эффективную версию, названную здесь устранением скалярных столбцов/скалярных строк (SCSR), которая была принята решателем COLROW [2].
Настоящий подход модульного анализа показывает, что поворот Лама (с расположением Вараха) также применим к методам исключения BCBR и BCSR. Это даже относится к двухблочным трехдиагональным методам исключения BTDR и BTDC, вопреки распространенному мнению. Также определена более надежная, хотя и более дорогая стратегия, Local Pivoting .Он выполняет полный поворот над теми же сегментами (или ), к которым применяется поворот Лама. Смешанный поворот Келлера [10] занимает промежуточное положение между поворотом Лама и локальным поворотом.
Это даже относится к двухблочным трехдиагональным методам исключения BTDR и BTDC, вопреки распространенному мнению. Также определена более надежная, хотя и более дорогая стратегия, Local Pivoting .Он выполняет полный поворот над теми же сегментами (или ), к которым применяется поворот Лама. Смешанный поворот Келлера [10] занимает промежуточное положение между поворотом Лама и локальным поворотом.
Модульный анализ также позволяет легко оценить количество операций и потребности в памяти, выявляя метод с наилучшей производительностью для каждой учетной записи. Методом с наименьшим количеством операций является устранение BCBR, тогда как методом, требующим наименьшего объема памяти, является устранение BTDC [11]. Оба метода обеспечивают экономию первостепенной важности для больших размеров блоков по сравнению с другими методами.
На основе предыдущей оценки и осознания того, что программные факторы могут повлиять на производительность, были реализованы четыре конкурирующих метода исключения. Алгоритм COLROW, который был разработан для обеспечения наилучшей производительности исключения SCSR, был модифицирован для выполнения вместо этого исключения BTDC, BCBR или BCSR. Четыре метода были применены к одним и тем же задачам, и время выполнения было записано. Устранение BCSR оказалось эффективной модификацией алгоритма COLROW.
Алгоритм COLROW, который был разработан для обеспечения наилучшей производительности исключения SCSR, был модифицирован для выполнения вместо этого исключения BTDC, BCBR или BCSR. Четыре метода были применены к одним и тем же задачам, и время выполнения было записано. Устранение BCSR оказалось эффективной модификацией алгоритма COLROW.
2.Описание задачи
Рассмотрим почти блочно-диагональную систему уравнений, расширенная матрица коэффициентов которой имеет вид (1) Блоки с ведущими символами , , и имеют столбцы , , и соответственно. Блоки с ведущим символом имеют столбцы, указывающие столько же правых сторон. Завершающий символ или (и впоследствии) указывает количество строк блока или порядок квадратной матрицы, такой как единичная матрица и нижняя или верхняя треугольная матрица.Пробелы обозначают нулевые блоки.
Матрица неизвестных записывается аналогично, как где верхний индекс обозначает транспонирование.
Такая система уравнений приводит, например, к конечно-разностному решению ОДУ первого порядка на сетке точек с условиями на одной стороне, которые должны быть отмечены, и условиями на другой стороне, которые должны быть отмечены . Тогда каждый столбец подматрицы содержит неизвестные th узла сетки, соответствующие правой части.
Тогда каждый столбец подматрицы содержит неизвестные th узла сетки, соответствующие правой части.
3. Модульный анализ
Описание методов разложения расширенной матрицы коэффициентов можно сделать простым и кратким за счет введения модулей . Идентифицируются два разных модуля:
Выровненный модуль ( A -Модуль) (3) Смещенный модуль ( D -Модуль) (4) (Для удобства мы иногда будем опускать нижний индекс и/или верхний индекс, идентифицирующие модуль и его компоненты (данные позже), а также нижний индекс, идентифицирующий его блоки.)
Как правило, пунктирная линия определяет разделение на левые и правые объекты. Пунктирные линии определяют разбиение (5) на следующие компоненты: стебель, голова, плавники и .
У каждого модуля есть хвост. Для , который определяется через соотношение «голова-хвост» (6)
Для которого также определяется соотношением «голова-хвост» (7)
Это позволяет построить значимую часть , расположив каждый набор модулей таким образом, что хвост добавляется к началу , для . Незначительные корректировки нужно только вызывать на обоих концах . В частности, мы определяем усеченные модули
(8)
Незначительные корректировки нужно только вызывать на обоих концах . В частности, мы определяем усеченные модули
(8)
Глава модуля еще не определена. Считается, что он связан с другими компонентами чтобы допустить разложения вида (10)
Соотношения общего положения , , , и тогда выполняются, что приводит к определению в (9).
3.1. Методы исключения
Все методы исключения могут быть выражены в терминах разложения основы.Здесь представлены только те заслуживающие внимания методы, которые допускают чередование поворота и исключения столбца/строки. Задействовано несколько перегибов блоков, которые определены в разделе приложения. Последовательность, в которой манипулируют блоками для: разложения стебля, обработки плавников и обработки головы (оценка головы и применение отношения голова-хвост для определения хвоста последующего модуля), упоминается вместе с уравнениями ( из раздела приложения). Правильность разложений можно проверить, выполнив умножение матриц, используя равенства раздела приложения и сравнив с неразложенной формой модуля.
Следующие три метода могут быть сгенерированы из любого модуля. Они будут даны в терминах выровненного модуля.
3.1.1. Исключение скалярного столбца/скалярного ряда (SCSR)
Это метод, реализованный алгоритмом COLROW. Он выполняет скалярную декомпозицию стебля. Треугольные матрицы и появляются явно. Если диагональ единичная, они отмечены циркумфлексом: (11)
Применяется следующая последовательность манипуляций: Шток: , , , , .Плавники: , , , , .Голова: , .
3.1.2. Block Column/Block Row (BCBR) Elimination
Метод выполняет блочную декомпозицию стебля, при которой разлагаются опорные блоки и появляются: (12)
Применяется следующая последовательность манипуляций: Носик:, , , , .Плавники:, , .Голова:, .
3.1.3. Блочный столбец/скалярный ряд (BCSR) Исключение
Метод имеет декомпозицию (13)
Применяется следующая последовательность манипуляций: Шток:, , , , .Плавники:, , , .Голова:, .
3.1.4. Блочный трехдиагональный ряд (BTDR) Исключение
Этот метод может быть сгенерирован только из выровненного модуля. Он выполняет тождественную декомпозицию, приводящую к декомпозиции
(14)
Он выполняет тождественную декомпозицию, приводящую к декомпозиции
(14)
В [10, § 5, случай (i)] для получения разложенного ствола использовалось скалярное исключение строк . Однако к настоящему времени его можно получить любым из нетождественных (скалярных и/или блочных) методов декомпозиции, приведенных в разделах 3.1.1–3.1.3.
При использовании исключения SCSR применяется следующая последовательность манипуляций:Ствол:, , , , .Плавники:, , , , , .Голова:, .
3.1.5. Блок-трехдиагональная колонна (BTDC) Исключение
Этот метод может быть создан только из смещенного модуля. Он выполняет тождественную декомпозицию, приводящую к декомпозиции (15)
В [11] получено скалярным исключением столбцов. Как и в случае исключения BTDR, к настоящему моменту его можно получить из любого из нетождественных разложений, приведенных в разделах 3.1.1–3.1.3.
При использовании исключения SCSR применяется следующая последовательность манипуляций:Ствол:, , , , . Плавники:, , , , , .Голова:, .
Плавники:, , , , , .Голова:, .
3.2. Процедура решения
Процедура решения матричного уравнения , которая может быть описана в терминах манипулирования расширенной матрицей , аналогичным образом может быть описана в терминах манипулирования расширенным модулем . Манипуляция применяет прямую развертку, соответствующую разложению, за которым следует обратная развертка, соответствующая разложению . Точно так же манипулирование применяет прямую развертку, включающую два шага.Первый шаг выполняет декомпозицию. На втором этапе оценивается голова, затем применяется отношение «голова-хвост» для определения хвоста . При обратном проходе к модулю решения применяются два шага. При известном, первый шаг использует в обратной замене отношение к контракту на . Второй шаг решает, для чего эквивалентно разложению .
3.3. Количество операций и потребность в хранении
Модули, представленные ранее, позволяют легко оценить методы исключения.Количество операций измеряется количеством умножений (mul) при том понимании, что количество сложений сопоставимо. Потребности в хранении измеряются количеством мест (loc), необходимых для хранения массивов, рассчитанных в прямом цикле для использования в обратном цикле, при условии, что элементы массива не сохраняются, а генерируются по мере необходимости, как это обычно делается в численном анализе. например, решение набора ОДУ.
Потребности в хранении измеряются количеством мест (loc), необходимых для хранения массивов, рассчитанных в прямом цикле для использования в обратном цикле, при условии, что элементы массива не сохраняются, а генерируются по мере необходимости, как это обычно делается в численном анализе. например, решение набора ОДУ.
Для каждого модуля (т. е. для каждой точки сетки) каждому методу требуется столько операций для манипулирования , сколько требуется для манипулирования .Все методы требуют (mul) для разложения ствола, pmn (mul) для оценки головы и (mul) для обработки правильного модуля. Методы различаются только количеством операций для обработки ребер и , при этом устранение BCBR требует наименьшего количества pmn (mul).
Для каждого модуля каждый метод требует столько мест хранения, сколько необходимо для хранения . Все методы требуют pr (loc) для хранения файлов . Они различаются количеством мест, необходимых для хранения ‘s, при этом для устранения BTDC требуется наименьшее число pn (loc). Обратите внимание, что в исключениях SCSR и BCSR квадратные блоки должны быть зарезервированы для хранения треугольных блоков и/или .
Обратите внимание, что в исключениях SCSR и BCSR квадратные блоки должны быть зарезервированы для хранения треугольных блоков и/или .
Таблица 1 содержит эту информацию, что позволяет провести четкое сравнение методов. Например, при исключении BCBR достигается экономия на операциях, имеющих значение ведущего порядка и соответственно в двух выделенных пределах и , по сравнению с устранением SCSR.
| |||||||||||||||||||||||||||
3.
 4. Стратегии поворота
4. Стратегии поворота Переменный поворот Лама [8] применяет поворот столбца для формирования и декомпозиции несингулярного опорного блока и поворот строки для формирования и декомпозиции несингулярного опорного блока . Это допустимые процессы, так как имеет ранг m и ранг , как можно показать, следуя рассуждениям Келлера [10, § 5, теорема].
Для дальнейшего повышения стабильности мы вводим стратегию локального поворота, которая применяет полный поворот (стратегия максимального поворота) к сегментам и .Обратите внимание, что смешанный поворот Келлера [10], если его интерпретировать как применение полного поворота к и поворота строки к , занимает промежуточное положение между поворотом Лама и локальным поворотом.
Ламовская, Келлеровская и локальная развороты применяются ко всем методам исключения из Раздела 3.1. Более того, в любой заданной задаче каждая стратегия разворота будет производить одну и ту же последовательность разворотов, независимо от используемого метода исключения.
4. Реализация
Алгоритм COLROW, основанный на исключении SCSR, модифицирован для выполнения вместо этого исключения BTDC, BCBR или BCSR.В качестве иллюстрации четыре метода применяются к трем системам уравнений с расширенной матрицей, приведенной в (1), с и . Процедуры решения повторяются несколько раз, чтобы можно было записать и сравнить разумное время выполнения. Все расчеты выполняются с двойной точностью с помощью оптимизированного по скорости Compaq Visual Fortran (версия 6.6) на процессоре Pentium 4 с тактовой частотой 2 ГГц и 750 МБ ОЗУ.
Первая система имеет и . Рассматриваются различные комбинации , 9/2, 8/3, 7/4 и 6/5.Время выполнения без поворота приведено в таблице 2. Все записи включают ≈ 22 секунды, которые требуются для чтения, записи и запуска пустых циклов Fortran-Do-Loop. Для разворота требуется дополнительно ≈ 20 секунд во всех методах.
| |||||||||||||||||||||||||||||||||||||||||

Вторая (третья) система имеет (51) и (10 4 ). Времена выполнения с поворотом Лама приведены в таблице 3 (4) для различных комбинаций .
| ||||||||||||||||||||||||||||||||||||||||||||||||
. | ||||||||||||||||||||||||||||||||||||||||||||||||
Хотя модифицированные алгоритмы COLROW могут не обеспечивать наилучшие характеристики исключения BTDC, BCBR и BCSR, таблицы 2, 3 и 4 ясно показывают, что в некоторых случаях (когда ) они превосходят алгоритм COLROW, который разработан, чтобы обеспечить устранение SCSR с максимальной эффективностью.
| ||||||||||||||||||||||||||||||||||||||||||||||
5. Заключение
Используя новый подход модульного анализа, мы проанализировали последовательные методы решения почти блочно-диагональных систем уравнений. Были определены два модуля, которые позволили выразить и оценить все возможные методы устранения полос и блоков.Основываясь на количестве операций, потребностях в памяти и допустимости частичного поворота, мы определили четыре различных метода: исключение блочного столбца/блочного ряда (BCBR) (с наименьшим количеством операций), исключение блочного трехдиагонального столбца (BTDC) (имеющее наименьшая потребность в хранении), устранение блочного столбца/скалярной строки (BCSR) и устранение скалярного столбца/скалярной строки (SCSR) (реализовано в хорошо известном алгоритме COLROW). Применение этих методов в алгоритме COLROW показывает, что они превосходят устранение SCSR в случаях большого отношения строк верхнего блока к нижнему блоку.В таких случаях устранение BCSR рекомендуется как эффективная модификация алгоритма COLROW.
Применение этих методов в алгоритме COLROW показывает, что они превосходят устранение SCSR в случаях большого отношения строк верхнего блока к нижнему блоку.В таких случаях устранение BCSR рекомендуется как эффективная модификация алгоритма COLROW.
Приложение
В разделе 3 два модуля и матрицы коэффициентов вводятся и разлагаются для генерации методов исключения. Процесс включает перегибы блоков , которые протекают для блока , скажем, по следующей схеме:
Следующие равенства используются для определения блоков с подчеркнутым ведущим символом.Количество задействованных умножений указано в фигурных скобках:
— Блоки -Блоки (разобранные поворотные блоки)
— Блоки и -блоки
%PDF-1.2 % 89 0 объект > эндообъект внешняя ссылка 89 333 0000000016 00000 н 0000007009 00000 н 0000009935 00000 н 0000010150 00000 н 0000010393 00000 н 0000010779 00000 н 0000010957 00000 н 0000011305 00000 н 0000011639 00000 н 0000011931 00000 н 0000012245 00000 н 0000012595 00000 н 0000012922 00000 н 0000013251 00000 н 0000013513 00000 н 0000013834 00000 н 0000014105 00000 н 0000014402 00000 н 0000014716 00000 н 0000015123 00000 н 0000015520 00000 н 0000015817 00000 н 0000016158 00000 н 0000016528 00000 н 0000016890 00000 н 0000017218 00000 н 0000017501 00000 н 0000017841 00000 н 0000018133 00000 н 0000018453 00000 н 0000018834 00000 н 0000019196 00000 н 0000019500 00000 н 0000019846 00000 н 0000020123 00000 н 0000020330 00000 н 0000020565 00000 н 0000020780 00000 н 0000020948 00000 н 0000021118 00000 н 0000021453 00000 н 0000021736 00000 н 0000022101 00000 н 0000022447 00000 н 0000022791 00000 н 0000023124 00000 н 0000023400 00000 н 0000023719 00000 н 0000023910 00000 н 0000024259 00000 н 0000024526 00000 н 0000024578 00000 н 0000024799 00000 н 0000025285 00000 н 0000025782 00000 н 0000026041 00000 н 0000026331 00000 н 0000026619 00000 н 0000026872 00000 н 0000027088 00000 н 0000027328 00000 н 0000027626 00000 н 0000027883 00000 н 0000028136 00000 н 0000028402 00000 н 0000028700 00000 н 0000028969 00000 н 0000029089 00000 н 0000029263 00000 н 0000029446 00000 н 0000029658 00000 н 0000029825 00000 н 0000030003 00000 н 0000030276 00000 н 0000030528 00000 н 0000030777 00000 н 0000031046 00000 н 0000031098 00000 н 0000031289 00000 н 0000031522 00000 н 0000031775 00000 н 0000031827 00000 н 0000031936 00000 н 0000032189 00000 н 0000032379 00000 н 0000032558 00000 н 0000032707 00000 н 0000032985 00000 н 0000033263 00000 н 0000033542 00000 н 0000033822 00000 н 0000034071 00000 н 0000034246 00000 н 0000034612 00000 н 0000034664 00000 н 0000034869 00000 н 0000035164 00000 н 0000035409 00000 н 0000035715 00000 н 0000035952 00000 н 0000036167 00000 н 0000036421 00000 н 0000036656 00000 н 0000036826 00000 н 0000037156 00000 н 0000037491 00000 н 0000037818 00000 н 0000038079 00000 н 0000038384 00000 н 0000038718 00000 н 0000038936 00000 н 0000039390 00000 н 0000039442 00000 н 0000039581 00000 н 0000039877 00000 н 0000040179 00000 н 0000040417 00000 н 0000040705 00000 н 0000040979 00000 н 0000041229 00000 н 0000041531 00000 н 0000041790 00000 н 0000042119 00000 н 0000042366 00000 н 0000042589 00000 н 0000042765 00000 н 0000043045 00000 н 0000043291 00000 н 0000043658 00000 н 0000044013 00000 н 0000044347 00000 н 0000044715 00000 н 0000045148 00000 н 0000045513 00000 н 0000045877 00000 н 0000046141 00000 н 0000046448 00000 н 0000046626 00000 н 0000046826 00000 н 0000046994 00000 н 0000047268 00000 н 0000047568 00000 н 0000047870 00000 н 0000048198 00000 н 0000048562 00000 н 0000048881 00000 н 0000049262 00000 н 0000049448 00000 н 0000049786 00000 н 0000050119 00000 н 0000050481 00000 н 0000050717 00000 н 0000051014 00000 н 0000051244 00000 н 0000051531 00000 н 0000051711 00000 н 0000051988 00000 н 0000052225 00000 н 0000052521 00000 н 0000053198 00000 н 0000053649 00000 н 0000053987 00000 н 0000054232 00000 н 0000054474 00000 н 0000054827 00000 н 0000055118 00000 н 0000055430 00000 н 0000055728 00000 н 0000056074 00000 н 0000056353 00000 н 0000056727 00000 н 0000057207 00000 н 0000057489 00000 н 0000057733 00000 н 0000057936 00000 н 0000058201 00000 н 0000058561 00000 н 0000058859 00000 н 0000059157 00000 н 0000059209 00000 н 0000059456 00000 н 0000059813 00000 н 0000060043 00000 н 0000060386 00000 н 0000060731 00000 н 0000061079 00000 н 0000061347 00000 н 0000061634 00000 н 0000061805 00000 н 0000062062 00000 н 0000062238 00000 н 0000062588 00000 н 0000063001 00000 н 0000063344 00000 н 0000063682 00000 н 0000064058 00000 н 0000064356 00000 н 0000064666 00000 н 0000064851 00000 н 0000065134 00000 н 0000065479 00000 н 0000065755 00000 н 0000066011 00000 н 0000066376 00000 н 0000066602 00000 н 0000066788 00000 н 0000067043 00000 н 0000067422 00000 н 0000067634 00000 н 0000067960 00000 н 0000068193 00000 н 0000068434 00000 н 0000068716 00000 н 0000069004 00000 н 0000069276 00000 н 0000069503 00000 н 0000069777 00000 н 0000070779 00000 н 0000071315 00000 н 0000071601 00000 н 0000071940 00000 н 0000072259 00000 н 0000072578 00000 н 0000072880 00000 н 0000073225 00000 н 0000073453 00000 н 0000073746 00000 н 0000074050 00000 н 0000074344 00000 н 0000074617 00000 н 0000074899 00000 н 0000075082 00000 н 0000075361 00000 н 0000075659 00000 н 0000075902 00000 н 0000076105 00000 н 0000076349 00000 н 0000076590 00000 н 0000076612 00000 н 0000077477 00000 н 0000077704 00000 н 0000077934 00000 н 0000078107 00000 н 0000078293 00000 н 0000078345 00000 н 0000078439 00000 н 0000078540 00000 н 0000078796 00000 н 0000079042 00000 н 0000079275 00000 н 0000079297 00000 н 0000080195 00000 н 0000080555 00000 н 0000080906 00000 н 0000081293 00000 н 0000081616 00000 н 0000081985 00000 н 0000082306 00000 н 0000082699 00000 н 0000082985 00000 н 0000083350 00000 н 0000083673 00000 н 0000084044 00000 н 0000084276 00000 н 0000084573 00000 н 0000084995 00000 н 0000085346 00000 н 0000085563 00000 н 0000085740 00000 н 0000086041 00000 н 0000086093 00000 н 0000086367 00000 н 0000086672 00000 н 0000086931 00000 н 0000087304 00000 н 0000087497 00000 н 0000087845 00000 н 0000088231 00000 н 0000088568 00000 н 0000088916 00000 н 0000089323 00000 н 0000089666 00000 н 00000
00000 н 0000000000 н 00000
00000 н 00000 00000 н 0000092185 00000 н 0000092630 00000 н 0000092981 00000 н 0000093244 00000 н 0000093564 00000 н 0000093862 00000 н 0000094127 00000 н 0000094433 00000 н 0000094745 00000 н 0000095098 00000 н 0000095375 00000 н 0000095690 00000 н 0000096030 00000 н 0000096395 00000 н 0000096720 00000 н 0000096996 00000 н 0000097332 00000 н 0000097623 00000 н 0000097958 00000 н 0000098276 00000 н 0000098298 00000 н 0000099112 00000 н 0000099134 00000 н 0000099902 00000 н 0000100125 00000 н 0000100393 00000 н 0000100611 00000 н 0000100663 00000 н 0000100925 00000 н 0000101018 00000 н 0000101115 00000 н 0000101357 00000 н 0000101679 00000 н 0000101922 00000 н 0000101944 00000 н 0000102773 00000 н 0000102795 00000 н 0000103657 00000 н 0000103679 00000 н 0000104515 00000 н 0000104719 00000 н 0000104741 00000 н 0000105531 00000 н 0000007064 00000 н 0000009912 00000 н трейлер ] >> startxref 0 %%EOF 90 0 объект > эндообъект 420 0 объект > ручей HWhCB@H ҫ0 0I!»C@j!@(Gp(tT@Efgf9{v{ソ}
.

 12
12