Решение уравнений по физике: Решение уравнений бесплатно — Калькулятор Онлайн

Уравнения математической физики, с примерами

Дифференциальные уравнения математической физики

Математические модели естественнонаучных явлений и процессов зачастую представляют собой задачи, содержащие дифференциальные уравнения с частными производными первого и второго порядков. Дифференциальные уравнения существенные для физики, механики техники называют дифференциальными уравнениями математической физики.

Каждое уравнение математической физики описывает бесконечное множество качественно аналогичных явлений или процессов, так как дифференциальные уравнения, которыми занимается математическая физика, имеют бесконечное множество частных решений. Конкретное решение, описывающее рассматриваемое физическое явление, выделяется из множества частных решений с помощью начальных и граничных условий.

Общий вид дифференциального уравнения в частных производных первого порядка относительно неизвестной искомой функции таков:

   

Если F является линейной функцией относительно старших производных, то есть:

   

   

данное уравнение называется квазилинейным дифференциальным уравнением.

Если функции не зависят от u, а зависимость P от u линейна, то есть , тогда уравнение (2) называется линейным. Если , то уравнение (2) называется однородным линейным дифференциальным уравнением в частных производных первого порядка.

Решений уравнений математической физики

Рассмотрим квазилинейное дифференциальное уравнение в частных производных первого порядка:

   

Для получения общего решения уравнения (3) рассматривают характеристическую систему обыкновенных дифференциальных уравнений:

   

Если с=0, то система сводится к одному уравнению .

Если общий интеграл уравнения, тогда – общее решение.

Само дифференциальное уравнение содержит в себе только самую общую информацию об описываемом процессе. Необходимо задание начальных и граничных условий, для конкретизации.

Дифференциальные уравнения математической физики второго порядка

Большое количество процессов и явлений в физике описывается с помощью дифференциальных уравнений второго порядка в частных производных, это связано с тем, что фундаментальные законы физики – законы сохранения – записываются в терминах вторых производных. Методы решения уравнений математической физики зависят от типа к которому принадлежит рассматриваемое уравнение. Выделяют три основных типа дифференциальных уравнений с частными производными второго порядка, поиск решения которых имеют качественные различия: уравнения параболического, гиперболического и эллиптического типов.

Рассмотрим линейное уравнение с частными производными второго порядка с двумя независимыми переменными:

   

где a, b, c некоторые функции от x, y, имеющие непрерывные производные до второго порядка включительно.

Уравнение (5) принадлежит в точке (x, y)

1. параболическому типу, если Канонический вид такого уравнения:
      

   где — независимые переменные. Кроме того — дважды дифференцируемая функция в рассматриваемой области. Уравнение (6) так же как и уравнение теплопроводности имеет только один член высшей производной.

2. гиперболическому типу, если Канонический вид такого уравнения:

   первая каноническая форма:

      

   где — независимые переменные,

   вторая каноническая форма:

      

   где . Левая часть уравнения (8) полностью совпадает с частью волнового уравнения.

3. эллиптическому типу, если Канонический вид такого уравнения:

      

   где — независимые переменные. Левая часть этого уравнения совпадает с левой частью уравнения Лапласа.

Для того чтобы привести уравнение (5) к каноническому виду, надо записать так называемое характеристическое уравнение (10):

   

которое распадается на два уравнения:

   

   

и найти их общие интегралы.

В общем случае линейное уравнение с частными производными второго порядка параболического типа с n независимыми переменными можно записать так:

   

где

   

   

Уравнения параболического типа описывают неустановившиеся тепловые, диффузионные процессы, которые зависят от времени.

Уравнение (13) называют однородным, если =0.

Довольно часто при решении уравнения (13) ставят так называемую задачу Коши. В которой, требуется найти функцию w, удовлетворяющую уравнению (13) (при -эвклидово пространство) и начальном условии w=f(x) при t=0 и граничному условию:

   

В общем случае — линейный дифференциальный оператор первого порядка по пространственным переменным, коэффициенты которого зависят от x и t.

Начальное условие называют однородным, если f(x)=0. Граничное условие называют однородным, если .

В общем случае линейное уравнение с частными производными второго порядка гиперболического типа с n независимыми переменными можно записать так:

   

где линейный дифференциальный оператор определен формулам (14). Уравнениями гиперболического типа описываются неустановившиеся волновые процессы, зависящие от времени.

При решении уравнения (15) ставят задачу Коши. В которой, требуется найти функцию w, удовлетворяющую уравнению (15) (при и начальным условиям:

   

   

Граничные условия задаются (14).

Уравнения эллиптического типа

В общем случае линейное уравнение с частными производными второго порядка эллиптического типа с n независимыми переменными можно записать в виде:

   

где

   

   

Уравнения эллиптического типа описывают установившиеся тепловые, диффузионные и другие процессы, которые не зависят от времени.

Уравнение (18) называется однородным, если

Граничные условия для эллиптического уравнения записывают так:

   

В общем случае — линейный дифференциальный оператор первого порядка.

Наиболее часто в прикладных примерах при описании различных процессов, происходящих в изотропных средах коэффициенты

   

таковыми и мы будем считать коэффициенты .

Для любых уравнений в частных производных второго порядка в зависимости от вида граничных условий принято выделять четыре типа краевых задач.

Первая краевая задача. На границе области S функция w(x,t) принимает заданные значения:

   

Вторая краевая задача. На границе области S задается производная по (внешней) нормали:

   

Третья краевая задача. На границе области S задана линейная связь между искомой функцией и ее производной по нормали:

   

Чаще всего В задачах массопереноса, где w – концентрация, граничное условие (22) при описывает поверхностную химическую реакцию.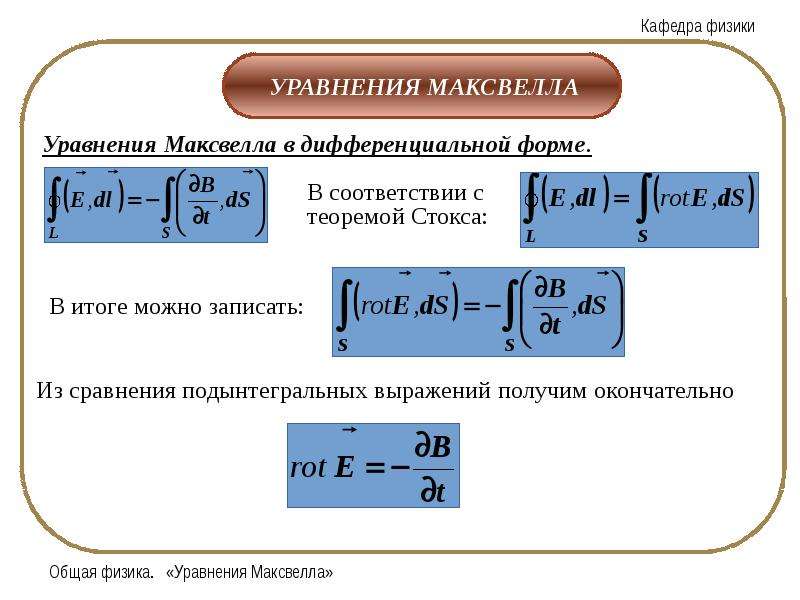

Смешанные краевые задачи. В этом случае на различных участках границы S задают различные граничные условия.

Методы решения уравнений математической физики

Все методы решения уравнений математической физики можно разделить на две большие группы:

1. аналитические методы решения уравнений, которые основаны на сведении уравнения в частных производных к обыкновенному или системе обыкновенных уравнений;
2. численные методы решения (с помощью ЭВМ).

Среди аналитических методов решения уравнений следует выделить:

1. Метод характеристик.
2. Метод разделения переменных.
3. Метод Фурье.
4. Метод Деламбера.
5. Метод интегральных преобразований.
6. Преобразование Лапласа.
7. Представление решений через функцию Грина.

Среди численных методов решения уравнений математической физики следует выделить:

1. метод сеток;
2. метод конечных разностей;
3. методы расщепления: метод переменных направлений, метод дробных шагов;
4. методы Эйлера;
5. методы Рунге-Кутта;
6. метод Адамса;
7. символьно-численный метод.

Примеры решения задач

Уравнения математической физики | Решатель

У физиков есть шутка с бородой: “Женщина-физик: еще не физик, но уже не женщина!”. С математической физикой примерно та же история. Это уже не чистая математика, а ее приложение к реальным физическим задачам. Однако, от привычной физики с ее экспериментами и рассуждениями, она тоже отличается.

 

Что касается масштабов бедствия, данная дисциплина охватывает почти все разделы физики, изложенные в 10 томах Ландау-Лифшица: электромагнетизм, гидро- и газодинамика, теория теплопереноса, упругости.
 

В рамках курса “уравнения математической физики”, очевидно, вы будете иметь дело с уравнениями, но не далеко не простыми. Забудьте о заданиях с уравнениями типа 2x+5=9. Да здравствуют дифференциальные уравнения с частными производными! А это вам не шутки.
 

В большинстве случаев вы будете рассматривать случай двух независимых переменных и уравнение второго порядка вида (хотя, конечно, для полноценного рассмотрения многих физических задач для реального мира необходимо рассматривать трехмерный случай):
 

 

Но не так страшно уравнение, каким оно кажется на первый вид.

На самом деле далеко не каждое уравнение такого общего вида годится для моделирования физического явления, и вы будете сталкиваться с уравнениями одного и того же типа.
 

Итак, начнем наше знакомство с теми уравнениями, которые запишутся в ваш новый список друзей.
 

1) Одномерное волновое уравнение:

 

 

u(x,t) может быть, например, давлением или плотностью для упругих волн в газах, напряженностью электрического или магнитного поля,a a есть скорость распространения волн в рассматриваемой среде. Это уравнение является уравнением гиперболического типа; оно будет с вами, когда вы будете изучать процессы поперечных колебаний струны, электрических колебаний в проводе, колебаний газа и жидкости.
 

2) Ваш друг номер два:

 
 

Это уравнение параболического типа, известное в народе также как уравнение теплопроводности, где u(x,t)представляет собой температуру. С этим уравнением вы будете сталкиваться каждый раз, когда заинтересуетесь вопросом распространения тепла, фильтрации газа и жидкости.

 

3) Двумерное уравнение Лапласа:

 

 

Это уравнение эллиптического типа, которое необходимо при рассмотрении задач об электрических и магнитных полях (например, таким уравнением описывается потенциал электростатического поля при отсутствии зарядов), а также задач гидродинамики и диффузии.
 

Испугались? В действительности, не все так плохо. Уравнения такого типа можно научиться очень быстро решать, даже если вы перед этим не штудировали учебники по дифференциальным уравнениям.
 

Мы покажем на примере первого уравнения (2), как можно с ними дружить.
 

Мы можем заметить, что правая часть зависит только от t, а левая часть — только от x. Равенство между ними возможно только при условии, что обе части равны константе, это значит, что решение уравнения есть произведение одной функции от t и другой функции от x:
 

 

Подставив это выражение в исходное уравнение, получаем систему двух простых дифференциальных уравнений:
 

 

А для того, чтобы решить такие уравнения, достаточно знать, как решать квадратное уравнение (это под силу даже школьнику), ведь для решения подобного уравнения (дифференциального однородного уравнения второго порядка)
 

 

необходимо всего лишь решить квадратное уравнение
 

 

и тогда решение уравнения (7) есть:
 

 

В зависимости от условий конкретной физической задачи, вы будете иметь дело с определенными граничными условиями, например, f(x=0)=0, применяя которые, легко можно найти постоянную λ в системе уравнений (6) и постоянные A₁ и A₂ в каждом решении вида (9).
 

Хотите знать больше?

Тогда бегом в библиотеку за следующими учебниками:

• А.Н.Тихонов, А.А.Самарский, “Уравнения математической физики”. М. “Наука”, 1972.
• В.С. Владимиров “Уравнения математической физики”. М. “Наука”, 1988.
• Смирнов М.М. “Дифференциальные уравнения в частных производных второго порядка”. М. “Наука”, 1964.
• Полянин А.Д. “Справочник по линейным уравнениям математической физики”. М.: Физматлит, 2001.
• Полянин А.Д., Зайцев В.Ф. “Справочник по нелинейным уравнениям математической физики: Точные решения”. М.: Физматлит, 2002.

 
 

Хотите заказать решение у нас?

Автор данной статьи также берется за решение уравнений математической физики на заказ.
Узнать цену работы можно на странице заказа. Для этого нужно всего лишь прикрепить файл с заданием и указать сроки.

Статья по физике по теме » Использование линейных уравнений для решения задач по физике» (7, 9 классы)

М. В. Русинова

МБОУ «Средняя общеобразовательная школа № 80»

г. Кемерово,

M. V. Rusinova

MBOU «Srednyaya obshcheobrazovatel‘naya shkola № 80»

Kemerovo

E-mail: rusinova1975@inbox.ru

Использование линейных уравнений для решения задач по теме «Равномерное движение»

Use linear equations to solve problems on the topic of «Uniform motion»

Материал статьи посвящен интеграции двух предметов школьного курса: физики и математики. Авторы обращают внимание на необходимость взаимосвязей между учебными предметами для отражения целостной картины мира, природы «в голове ученика», для создания истинной системы знаний и миропонимания.

The article is devoted to the integration of the two subjects of the school course of physics and mathematics. The authors draw attention to the need relationships between subjects to reflect a holistic picture of the world of nature «in the mind of the disciple», to create true knowledge and understanding of the world.

Ключевые слова: интеграция, математика, физика, равномерное движение, линейные уравнения, школьный курс

Математика и физика обычно считаются наиболее трудными предметами школьного курса. Эти направления научной мысли развивались взаимосвязано во все периоды формирования человеческого сознания, стимулируя обоюдный процесс. На всех уровнях изучения физики в школьном преподавании, интеграция с математикой может сделать изложение предметов более ясным и доступным. Общение с учениками показывает, что непонимание ими какого- либо вопроса из курса физики или неумение решить физическую задачу часто связаны с неумением проводить алгебраические преобразования и геометрические построения, отсутствием навыка анализа функциональных зависимостей, составления и решения математических уравнений.

Современное обучение требует сочетания экспериментального и теоретического методов изучения физики, выявления сути физических законов на основе доступных ученикам понятий элементарной математики.

Такой подход одновременно обеспечивает повышение уровня математических знаний, формирует логическое мышление, осознание единства материального мира. Ученики начинают испытывать удовлетворение, замечая, что абстрактные математические формулы и уравнения имеют реальное воплощение в физических процессах.

Приведем примеры изложения некоторых вопросов физики с использованием доступного учащимся математического аппарата.

Английский физик Поль Адриен Морис Дирак писал: «Физический закон должен быть математически красивым»

Простейший вид механического движения — движение тела вдоль прямой линии с постоянной по модулю и направлению скоростью такое движение называется равномерным. При равномерном движении тело за любые равные промежутки времени проходит равные пути.

Изучая равномерное движение на уроках физики в 7 и 9 классах, учащиеся вспоминают линейные уравнения вида y=kx+b из курса математики.

Уравнение y=kx+b, называют линейным уравнением с двумя переменными х и у. Решением данного уравнения является пара чисел (х; у), которая удовлетворяет этому уравнению. Графиком такого уравнения является прямая.

Учащимся предлагается сравнить «математическое» уравнение y=kx+b и «физическое» x=x₀₌ +v_xt, являющееся закономерностью изменения координаты х от времени t при равномерном движении. Данное сравнение позволяет учащимся сделать вывод, что выражение x=x₀₌+v_xt- линейная функция, где время t служит аргументом, а х— функцией. Уравнение x=x₀₌+v_xt. -уравнение равномерного прямолинейного движения точки, записанное в координатной форме. Оно позволяет найти координату х тела при этом движении в любой момент времени, если известны проекция его скорости на ось Ох и его начальная координата x₀.

В природе очень мало примеров равномерного движения. Почти равномерно всплывают мелкие пузырьки в газированной воде, падают капли дождя, падает парашютист с раскрытым парашютом и т.д.

В различных равномерных движениях перемещения тел за одинаковые промежутки времени могут быть различными, а значит одинаковые перемещения будут совершаться ими за разное время.

Так, при прохождении расстояния между двумя остановками, автобус затратит времени меньше, чем велосипедист. Чтобы количественно охарактеризовать это различие между равномерными движениями, вводится новая физическая величина- скорость движения.

Скорость- одна из основных кинематических характеристик движения материальной точки, определяемая отношением перемещения ко времени, в течении которого оно произошло. Скорость обозначаем буквой v. Так как при равномерном движении скорость не меняется, то графиком зависимости v_x(t) является прямая, параллельная оси t.

Порядок построения графиков зависимости х=х(t) для равномерного движения можно задать в виде таблицы, содержащей определенное значение промежутка времени и длины пройденного пути, что соответствует

Алгоритм построения графика уравнения х=х(t) аналогичен построению графика у=f(х):

1. Переменной t придается конкретное значение t=t₁; из уравнения x =x₀₌ +v_xt находим соответствующее значение х₁.

2. Переменной t придается другое значение t=t₂, находим соответствующее значение х=х₂.

3. Построить координатные плоскости хОt, выбирая необходимый масштаб.

4. На координатной плоскости хОt построить две точки (t₁, х₁) и (t_2, х₂).

5. Провести через эти точки прямую, являющуюся графиком уравнения x=x₀₌+v_xt.

С помощью графиков можно легко решать разные задачи о движении.

По графику движения можно судить о скорости движущейся точки, определять перемещение за любой промежуток времени и находить координату тела в данный момент времени.

Рассмотрим законы равномерного прямолинейного движения на конкретных примерах.

Уравнение координаты тела задается линейной функцией времени

x =x₀₌ +v_xt.

Из уравнения определяем: х₀₌ 10м, v₀₌ 10 м/c

Через 0 c тело будет иметь следующую координаты: x₁(0) = 10, через 2 с , x₂(2) = 30.

Строим координатную плоскость хОt, выбирая масштаб по оси х и оси t.

Отмечаем точки (0,10) и (2,30). Соединяем эти точки, получаем график зависимости х(t), являющийся прямой.

рис.1 График зависимости х(t).

Пример 2. По графику зависимости v(t), рис.2, определите скорость тела, найдите пройденный путь через 5 с от начала движения.

Решение: По графику v(t) определяем скорость движения. v=8м/с. Для определения пройденного пути воспользуемся формулой : s=vt. При t=5с, s = 40 м. Путь можно также найти как площадь фигуры под графиком скорости, ограниченной справа и слева линиями времени, данного по условию задачи.

рис. 2 График зависимости v(t)

Таким образом, при изучении равномерного прямолинейного движения опираемся на знания учащихся, полученные на уроках математики по теме «Линейная функция и ее график». Если учащиеся хорошо владеют данным материалом, то они успешно справляются с заданиями по физике на построение графиков зависимости скорости, пути и координаты от времени, а также, читая графики, определяют промежуточные величины.

Межпредметные связи способствует систематизации, а, следовательно, глубине и прочности знаний, дает ученикам целостную картину мира.

В заключении можно сказать:

«О, физика, наука из наук!

Все впереди! Как мало за плечами!

Пусть химия нам будет вместо рук,

Пусть будет математика очами.

Не разлучайте этих трех сестер

Познание всего в подлунном мире,

Тогда лишь будет ум и глаз остер

И знанья человеческие шире».

(М. Алигер)

Литература

1. Перышкин, А. В. Физика. 7 класс [Текст] : учебник для общеобразовательных учебных заведений. ФГОС / А. В. Перышкин. – 4-е изд., стререотип. – М. : Дрофа, 2015.

2. Перышкин, А. В. Физика. 9 класс [Текст] : учебник для общеобразовательных учреждений. / А. В. Перышкин, Е. М. Гутник. – М. : Дрофа, 2014.

3. Макарычев Ю.Н. Алгебра. 7 класс [Текст] : учебник для общеобразовательных учебных заведений. ФГОС / Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др./Под ред. Теляковского С.А.- М: Просвещение,2013.

4. Г.В. Дорофеев. Алгебра 7 класс [Текст] : учебник для общеобразовательных учебных заведений. ФГОС Г.В.Дорофеев, С.Б. Суворова, Е.А. Бунимович и др.; под ред.  Г.В. Дорофеева. — М.: Просвещение, 2008.

Уравнения математической физики. Часть 1. Семинары

Семинары по первой части курса «Уравнения математической физики»

Список всех тем лекций

Семинар 1. Уравнения с частными производными первого порядка.
Обзор курса Задача №1168 Линейное однородное уравнение в частных производных первого порядка Линейное неоднородное уравнение Квазилинейное уравнение Задача № 1202 Домашнее задание и подведение итогов семинара

Семинар 2. Линейные уравнения первого порядка.
Типы линейных уравнений и их решения Теорема существования и единственности решения Квазилинейное уравнение с одной пространственной переменной (из сборника задач) Теорема о существовании решения

Семинар 3. Классические решения.
Классические решения методами обыкновенных дифференциальных уравнений и №334 Решение задачи Коши Возникновение сильного разрыва

Семинар 4. Обобщённые решения.
Обобщённое решение Когда кусочно-гладкая функция является обобщённым решением Теорема (кусочно-гладкие решения) Решение задачи №4. 11 Единственность решения задачи

Семинар 5. Задача Римана о распаде разрыва. Часть 1.
Обобщённые решения Решение задач 4.4, 4.5 Разрывы Условие допустимости разрыва Задача Римана о распаде разрыва Автомодельные решения Задачи для самостоятельного решения

Семинар 6. Задача Римана о распаде разрыва. Часть 2.
Постановка задачи Автомодельные решения Случай выпуклой функции f (задача 6.2.2) Автомодельные решения в общем виде Решение задачи 6.2.4 Случай невыпуклой функции

Семинар 7.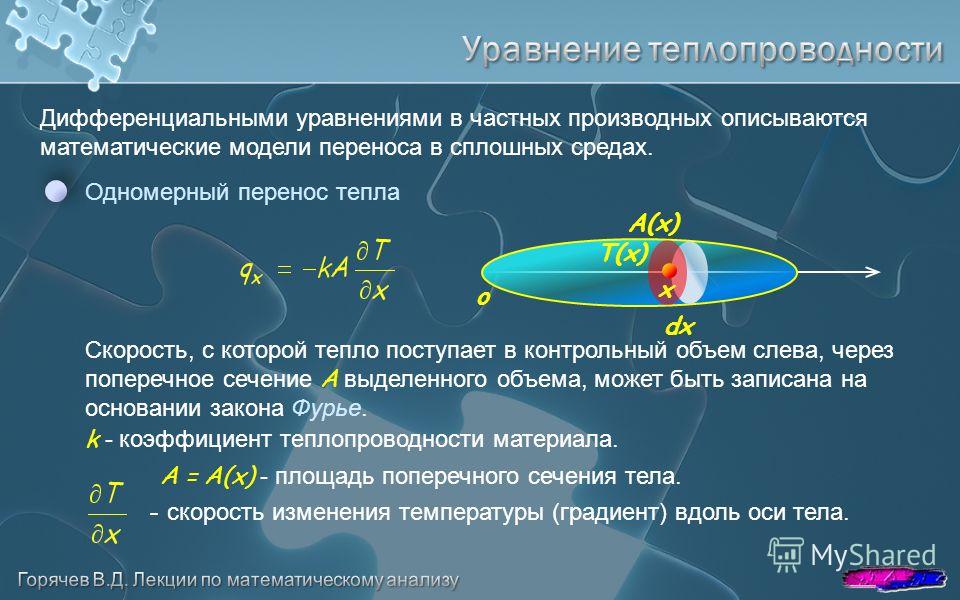 Приведение к каноническому виду уравнений в двумерной области.
Понятие линейного уравнения с частными производными второго порядка Характеристическая точка (определение) Характеристика (определение) Утверждение (понятие характеристики — геометрическое понятие) Гиперболическое уравнение (дискриминант больше нуля) Эллиптическое уравнение (дискриминант меньше нуля) Параболическое уравнение (дискриминант равен нулю) Решение уравнения Домашнее задание

Семинар 8. Задача Коши.
Комментарии к решению уравнений из домашнего задания Общее решение уравнения с частными производными Начальные условия задачи Коши Домашнее задание и комментарии к нему Единственность решения задачи Коши Домашнее задание и комментарии к нему (дополнение)

Семинар 9.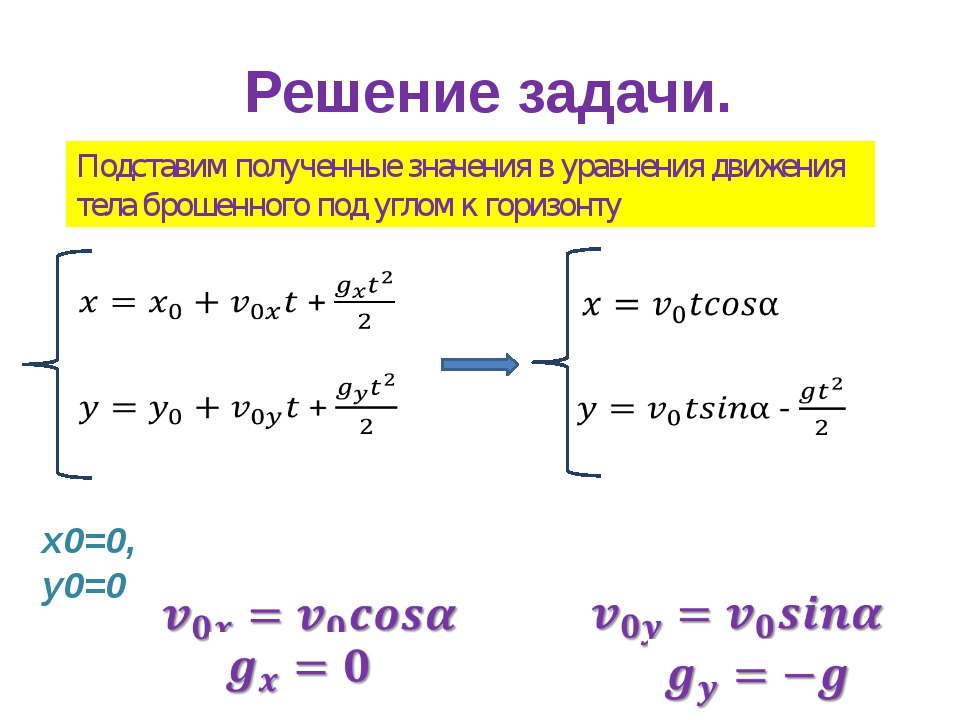 Классификация линейных уравнений второго порядка.
Классификация линейных уравнений второго порядка Приведение к каноническому виду (привести к каноническому виду) Уравнение струны Домашнее задание

Семинар 10. Полуограниченная струна.
(из домашнего задания) Задача (нарисовать положение струны) Задача (нарисовать положение струны) — второй вариант Постановка и решение задачи Домашнее задание

Семинар 11. Отражение волн полуограниченной струны.
Полуограниченная струна Решение аналитической задачи о полуограниченной струне Домашнее задание

Семинар 12. Метод Даламбера.
Повторение изученного на предыдущих семинарах Неоднородное уравнение струны Обзор задач 21.19, 21.14, 21.16, 21.18 Метод Дюамеля Уравнение упругих продольных колебаний стержня

Семинар 13. Метод Фурье.
Уравнение струны Задача Штурма — Лиувилля Теорема (свойства собственных значений и векторов) Ряд Фурье Домашнее задание

Семинар 14. Неоднородные задачи. Часть 1.
из домашнего задания из домашнего задания Неоднородные уравнения Неоднородные краевые условия Домашнее задание

Семинар 15. Неоднородные задачи. Часть 2.
Физическое и математическое описание Задача Штурма — Лиувилля Продолжение решения Задача (с условием резонанса) Домашнее задание

Семинар 16. Уравнение теплопроводности. Часть 1.
Решение задач из домашнего задания п.4 Задача теплопроводности Задача (соединили два нагретых стержня (до заданной температуры) и теплоизолировали) Домашнее задание

Семинар 17. Уравнение теплопроводности. Часть 2.
Ряды Фурье для краевой задачи для уравнения струны (уравнение теплопроводности) из домашнего задания (уравнение теплопроводности) из домашнего задания (уравнение теплопроводности) из домашнего задания Домашнее задание

Семинар 18. Уравнение Лапласа.
Уравнение Лапласа Задача Дирихле Задача Дирихле в кольце Задача Дирихле в круге Решение задачи 16.6 Задача Дирихле в прямоугольнике Домашнее задание

Издания | Библиотечно-издательский комплекс СФУ

Все года изданияТекущий годПоследние 2 годаПоследние 5 летПоследние 10 лет

Все виды изданийУчебная литератураНаучная литератураЖурналыМатериалы конференций

Все темыЕстественные и точные наукиАстрономияБиологияГеографияГеодезия. КартографияГеологияГеофизикаИнформатикаКибернетикаМатематикаМеханикаОхрана окружающей среды. Экология человекаФизикаХимияТехнические и прикладные науки, отрасли производстваАвтоматика. Вычислительная техникаБиотехнологияВодное хозяйствоГорное делоЖилищно-коммунальное хозяйство. Домоводство. Бытовое обслуживаниеКосмические исследованияЛегкая промышленностьЛесная и деревообрабатывающая промышленностьМашиностроениеМедицина и здравоохранениеМеталлургияМетрологияОхрана трудаПатентное дело. Изобретательство. РационализаторствоПищевая промышленностьПолиграфия. Репрография. ФотокинотехникаПриборостроениеПрочие отрасли экономикиРыбное хозяйство. АквакультураСвязьСельское и лесное хозяйствоСтандартизацияСтатистикаСтроительство. АрхитектураТранспортХимическая технология. Химическая промышленностьЭлектроника. РадиотехникаЭлектротехникаЭнергетикаЯдерная техникаОбщественные и гуманитарные наукиВнешняя торговляВнутренняя торговля. Туристско-экскурсионное обслуживаниеВоенное делоГосударство и право. Юридические наукиДемографияИскусство. ИскусствоведениеИстория. Исторические наукиКомплексное изучение отдельных стран и регионовКультура. КультурологияЛитература. Литературоведение. Устное народное творчествоМассовая коммуникация. Журналистика. Средства массовой информацииНародное образование. ПедагогикаНауковедениеОрганизация и управлениеПолитика и политические наукиПсихологияРелигия. АтеизмСоциологияФизическая культура и спортФилософияЭкономика и экономические наукиЯзыкознаниеХудожественная литератураХудожественные произведения

Все институтыВоенно-инженерный институтБазовая кафедра специальных радиотехнических системВоенная кафедраУчебно-военный центрГуманитарный институтКафедра ИТ в креативных и культурных индустрияхКафедра истории России, мировых и региональных цивилизацийКафедра культурологии и искусствоведенияКафедра рекламы и социально-культурной деятельностиКафедра философииЖелезногорский филиал СФУИнженерно-строительный институтКафедра автомобильных дорог и городских сооруженийКафедра инженерных систем, зданий и сооруженийКафедра проектирования зданий и экспертизы недвижимостиКафедра строительных конструкций и управляемых системКафедра строительных материалов и технологий строительстваИнститут архитектуры и дизайнаКафедра архитектурного проектированияКафедра градостроительстваКафедра дизайнаКафедра дизайна архитектурной средыКафедра изобразительного искусства и компьютерной графикиИнститут горного дела, геологии и геотехнологийКафедра геологии месторождений и методики разведкиКафедра геологии, минералогии и петрографииКафедра горных машин и комплексовКафедра инженерной графикиКафедра маркшейдерского делаКафедра открытых горных работКафедра подземной разработки месторожденийКафедра технической механикиКафедра технологии и техники разведкиКафедра шахтного и подземного строительстваКафедра электрификации горно-металлургического производстваИнститут инженерной физики и радиоэлектроникиБазовая кафедра «Радиоэлектронная техника информационных систем»Базовая кафедра инфокоммуникацийБазовая кафедра физики конденсированного состояния веществаБазовая кафедра фотоники и лазерных технологийКафедра нанофазных материалов и нанотехнологийКафедра общей физикиКафедра приборостроения и наноэлектроникиКафедра радиотехникиКафедра радиоэлектронных системКафедра современного естествознанияКафедра теоретической физики и волновых явленийКафедра теплофизикиКафедра экспериментальной физики и инновационных технологийКафедры физикиИнститут космических и информационных технологийБазовая кафедра «Интеллектуальные системы управления»Базовая кафедра геоинформационных системКафедра высокопроизводительных вычисленийКафедра вычислительной техникиКафедра информатикиКафедра информационных системКафедра прикладной математики и компьютерной безопасностиКафедра разговорного иностранного языкаКафедра систем автоматики, автоматизированного управления и проектированияКафедра систем искусственного интеллектаИнститут математики и фундаментальной информатикиБазовая кафедра вычислительных и информационных технологийБазовая кафедра математического моделирования и процессов управленияКафедра алгебры и математической логикиКафедра высшей и прикладной математикиКафедра математического анализа и дифференциальных уравненийКафедра математического обеспечения дискретных устройств и системКафедры высшей математики №2афедра теории функцийИнститут нефти и газаБазовая кафедра пожарной и промышленной безопасностиБазовая кафедра химии и технологии природных энергоносителей и углеродных материаловКафедра авиационных горюче-смазочных материаловКафедра бурения нефтяных и газовых скважинКафедра геологии нефти и газаКафедра геофизикиКафедра машин и оборудования нефтяных и газовых промысловКафедра разработки и эксплуатации нефтяных и газовых месторожденийКафедра технологических машин и оборудования нефтегазового комплексаКафедра топливообеспеченя и горюче-смазочных материаловИнститут педагогики, психологии и социологииКафедра информационных технологий обучения и непрерывного образованияКафедра общей и социальной педагогикиКафедра психологии развития и консультированияКафедра современных образовательных технологийКафедра социологииИнститут торговли и сферы услугБазовая кафедра таможенного делаКафедра бухгалтерского учета, анализа и аудитаКафедра гостиничного делаКафедра математических методов и информационных технологий в торговле и сфере услугКафедра технологии и организации общественного питанияКафедра товароведения и экспертизы товаровКафедра торгового дела и маркетингаОтделение среднего профессионального образования (ОСПО)Институт управления бизнес-процессамиКафедра бизнес-информатики и моделирования бизнес-процессовКафедра маркетинга и международного администрированияКафедра менеджмент производственных и социальных технологийКафедра цифровых технологий управленияКафедра экономики и управления бизнес-процессамиКафедра экономической и финансовой безопасностиИнститут физ. культуры, спорта и туризмаКафедра медико-биологических основ физической культуры и оздоровительных технологийКафедра теоретических основ и менеджмента физической культуры и туризмаКафедра теории и методики спортивных дисциплинКафедра физической культурыИнститут филологии и языковой коммуникацииКафедра восточных языковКафедра журналистики и литературоведенияКафедра иностранных языков для гуманитарных направленийКафедра иностранных языков для естественнонаучных направленийКафедра иностранных языков для инженерных направленийКафедра романских языков и прикладной лингвистикиКафедра русского языка и речевой коммуникацииКафедра русского языка как иностранногоКафедра теории германских языков и межкультурной коммуникацииИнститут фундаментальной биологии и биотехнологииБазовая кафедра «Медико-биологические системы и комплексы»Базовая кафедра биотехнологииКафедра биофизикиКафедра водных и наземных экосистемКафедра геномики и биоинформатикиКафедра медицинской биологииИнститут цветных металлов и материаловеденияБазовая кафедра «Технологии золотосодержащих руд»Кафедра автоматизации производственных процессов в металлургииКафедра аналитической и органической химииКафедра инженерного бакалавриата СDIOКафедра композиционных материалов и физико-химии металлургических процессовКафедра литейного производстваКафедра металловедения и термической обработки металловКафедра металлургии цветных металловКафедра обогащения полезных ископаемыхКафедра обработки металлов давлениемКафедра общаей металлургииКафедра техносферной безопасности горного и металлургического производстваКафедра физической и неорганической химииКафедра фундаментального естественнонаучного образованияИнститут экологии и географииКафедра географииКафедра охотничьего ресурсоведения и заповедного делаКафедра экологии и природопользованияИнститут экономики, государственного управления и финансовКафедра бухгалтерского учета и статистикиКафедра международной и управленческой экономикиКафедра социально-экономического планированияКафедра теоретической экономикиКафедра управления человеческими ресурсамиКафедра финансов и управления рискамиКрасноярская государственная архитектурно-строительная академияКрасноярский государственный технический университетКрасноярский государственный университетМежинститутские базовые кафедрыМежинститутская базовая кафедра «Прикладная физика и космические технологии»Политехнический институтБазовая кафедра высшей школы автомобильного сервисаКафедра конструкторско-технологического обеспечения машиностроительных производствКафедра материаловедения и технологии обработки материаловКафедра машиностроенияКафедра прикладной механикиКафедра робототехники и технической кибернетикиКафедра стандартизации, метрологии и управления качествомКафедра тепловых электрических станцийКафедра теплотехники и гидрогазодинамикиКафедра техногенных и экологических рисков в техносфереКафедра техносферной и экологической безопасностиКафедра транспортаКафедра транспортных и технологических машинКафедра химииКафедра электроэнергетикиХакасский технический иститутЮридический институтКафедра гражданского праваКафедра иностранного права и сравнительного правоведенияКафедра конституционного, административного и муниципального праваКафедра международного праваКафедра предпринимательского, конкурентного и финансового праваКафедра теории и истории государства и праваКафедра теории и методики социальной работыКафедра трудового и экологического праваКафедра уголовного праваКафедра уголовного процеса и криминалистики

По релевантностиСначала новыеСначала старыеПо дате поступленияПо названиюПо автору

Алгоритм решения задач по физике » 4ЕГЭ

Советы по основным типам заданий.

Алгоритм решения задач по физике
1. Внимательно прочти условие задачи.
2. Произведи краткую запись условия задачи с помощью общепринятых буквенных обозначений (СИ).
3. Выполни рисунки или чертежи задачи.
4. Определи, каким методом будет решаться задача.
5. Запиши основные уравнения, описывающие процессы, предложенные задачной системой.
6. Найди решение в общем виде, выразив искомые величины, через заданные.
7. Проверь правильность решения задачи в общем виде, произведя действия с наименованием величин.
8. Произведи вычисления.
9. Произведи оценку реальности полученного решения.
10. Запиши ответ.

Алгоритм решения задач по кинематике
1. Проанализировать условие задачи: определить движение тела и характер этого движения.
2. Записать краткое условие задачи в единицах СИ.
3. Сделать чертёж. Записать кинематические законы движения для тела в векторной форме.
4. Спроецировать векторные величины на оси х и у.
5. Вывести формулу для расчёта искомой величины.
6. Вычислить значение искомой величины.
7. Проконтролировать размерность и ответ.

Алгоритм решения задач по динамике
1. Проанализировать условие задачи: выяснить характер движения.
2. Записать краткое условие задачи в единицах СИ.
3. Сделать чертеж с указанием все сил, действующих на тело, векторы ускорений и системы координат.
4. Записать уравнение второго закона Ньютона в векторной форме.
5. Записать уравнение второго закона Ньютона в проекциях на оси координат с учетом направления осей координат и векторов.
6. Вывести формулу для расчёта искомой величины.
7. Вычислить значение искомой величины.
8. Проконтролировать размерность и ответ.

Алгоритм решения задач на применение закона сохранения импульса.
1. Проанализировать условие задачи: проверить систему взаимодействующих тел на замкнутость.
2. Записать краткое условие задачи в единицах СИ.
3. Изобразить на чертеже векторы импульсов тел системы до и после взаимодействия.
4. Записать закон сохранения импульса в векторной форме.
5. Спроецировать векторные величины на оси х и у; записать закон сохранения импульса в скалярной форме.
6. Вывести формулу для расчёта искомой величины.
7. Вычислить значение искомой величины.
8. Проконтролировать размерность и ответ.

Алгоритм решения задач на закон сохранения и превращения энергии
1. Проанализировать условие задачи: проверить систему взаимодействующих тел на замкнутость.
2. Записать краткое условие задачи в единицах СИ.
3.Сделать чертёж с указанием положения системы для различных моментов времени.
4. Записать формулы для определения полной механической энергии в начальный и конечный момент времени.
5. Вывести формулу для расчёта искомой величины.
6. Вычислить значение искомой величины.
7. Проконтролировать размерность и ответ.

Алгоритм решения задач на «Газовые законы»
1. Проанализировать условие задачи: выяснить, сколько состояний газа рассматривается в задаче.
2. Записать краткое условие задачи в единицах СИ.
3. Записать параметры p,V и T, характеризующие каждое состояние газа. Определить какой процесс произошёл.
4. Записать уравнение закон Клапейрона — Менделеева для данных состояний.
5. Вывести формулу для расчёта искомой величины.
6. Вычислить значение искомой величины.
7. Проконтролировать размерность и ответ.

Алгоритм решения задач на «Основы термодинамики»
1. Проанализировать условие задачи: проверить систему тел на замкнутость; определить, какие тела участвуют в теплообмене.
2. Записать краткое условие задачи в единицах СИ.
3. Определить для каждого тела, какие процессы с ним происходят при теплообмене.
4. Записать для каждого процесса формулу для вычисления количества теплоты, выделенной или поглощённой.
4. Составить уравнение теплового баланса.
5. Вывести формулу для расчёта искомой величины.
5. Вычислить значение искомой величины.
6. Проконтролировать размерность и ответ.

Алгоритм решения задач на тему «Электростатика»
1. Проанализировать условие задачи: выяснить, какая система зарядов создаёт электростатическое поле.
2. Записать краткое условие задачи в единицах СИ.
3. Сделать чертёж; определить направление векторов напряжённости, которые создаются в данной точке, каждым из зарядов.
4. Рассчитать модули векторов напряжённости.
5. Вывести формулу для расчёта искомой величины, используя принцип суперпозиции для напряжённости.
6. Вычислить значение искомой величины.
7. Проконтролировать размерность и ответ.

Типовые задачи на уравнения и графики прямолинейного равномерного движения. Примеры решения задач по физике. 9-10 класс

Типовые задачи на уравнения и графики прямолинейного равномерного движения. Примеры решения задач по физике. 9-10 класс

Подробности

Просмотров: 1628

Задачи по физике — это просто!

Не забываем, что решать задачи надо всегда в системе СИ!

А теперь к задачам!

Элементарные задачи из курса школьной физики по кинематике.

Задача на составление описания движения и составление уравнения движения по заданному графику движения

Дано: график движения тела

Найти:
1. составить описание движения
2. составить уравнение движения тела.

Проекцию вектора скорости определяем по графику, выбрав любой удобный для рассмотрения отрезок времени.
Здесь удобно взять t=4c

Тогда:

Составляем уравнение движения тела:

Записываем формулу уравнения прямолинейного равномерного движения.

Подставляем в нее найденный коэффициент V_x (не забываем о минусе!).
Начальная координата тела (X_о) соответствует началу графика, тогда X_о=3

Составляем описание движения тела:

Желательно сделать чертеж, это поможет не ошибиться!
Не забываем, что все физические величины имеют единицы измерения, их необходимо указывать!

Тело движется прямолинейно и равномерно из начальной точки X_о=3м со скоростью 0,75 м/с противоположно направлению оси X.

Задача на определение места и времени встречи двух движущихся тел (при прямолинейном равномерном движении)

Движение тел задано уравнениями движения для каждого тела.

Дано:
1. уравнение движения первого тела
2. уравнение движения второго тела

Найти:
1. координату места встречи
2. момент время (после начала движения), когда произойдет встреча тел

По заданным уравнениям движения строим графики движения для каждого тела в одной системе координат.

Точка пересечения двух графиков движения определяет:

1. на оси t — время встречи ( через сколько времени после начала движения произойдет встреча)
2. на оси X — координату места встречи (относительно начала координат)

В результате:

Два тела встретятся в точке с координатой -1,75 м через 1,25 секунд после начала движения.

Для проверки полученных графическим способом ответов можно решить систему уравнений из двух заданных
уравнений движения:

Все было верно!

Для тех, кто почему-то забыл, как построить график прямолинейного равномерного движения:

График движения — это линейная зависимость ( прямая), строится по двум точкам.
Выбираем два любых удобных для простоты расчета значения t₁ и t₂.
Для этих значений t подсчитываем соответствующие значения координат X₁ и X₂.
Откладываем 2 точки с координатами (t₁, X₁) и (t₂, X₂) и соединяем их прямой — график готов!

Задачи на составление описания движения тела и построение графиков движения по заданному уравнению прямолинейного равномерного движения

Задача 1

Дано: уравнение движения тела

Найти:
1. составить описание движения
2. построить график движения

Заданное уравнение сравниваем с формулой и определяем коэффициенты.
Не забываем делать чертеж, чтобы еще раз обратить внимание на направление вектора скорости.

Задача 2

Дано: уравнение движения тела

Найти:
1. составить описание движения
2. построить график движения

Задача 3

Дано: уравнение движения тела

Найти:
1. составить описание движения
2. построить график движения

Задача 4

Дано: уравнение движения тела

Найти:
1. составить описание движения
2. построить график движения

Описание движения:

Тело находится в состоянии покоя в точке с координатой X=4м (состояние покоя — это частный случай движения, когда скорость тела равна нулю).

Задача 5

Дано:
начальная координата движущейся точки xo=-3 м
проекция вектора скорости Vx=-2 м/с

Найти:
1. записать уравнение движения
2. построить график движения
3. показать на чертеже векторы скорости и перемещения
4. найти координату точки через 10 секунд после начала движения

Физические калькуляторы

Плотность, Сила, Энергия, Работа

Плотность

р = м/В

Е = мс ²

Е = мс ²

Сила

F =

мА

Гравитационный потенциал

ЧЭ = мгч

Закон Гука

Ф _с = -кх

Закон идеального газа

PV = нРТ

Импульс

Дж =

футов

Импульс-Импульс

FΔt = мΔv

Кинетическая энергия

КЭ = 1/2М * v ²

Импульс

р = мв

Работа

Вт = Фс

---

Уравнение среднего ускорения

Среднее ускорение как изменение скорости за изменение времени

\( \overline{a} = \dfrac{\Delta v}{\Delta t} = \dfrac{v_f — v_i}{t_f — t_i}\)

Уравнение средней скорости

Средняя скорость как перемещение во время изменения времени

\( \overline{v} = \dfrac{\Delta x}{\Delta t} = \dfrac{x_f — x_i}{t_f — t_i}\)

с отличием Физика: кинематические уравнения

Разработка набора инструментов

Графики движения, такие как графики положение-время, скорость-время и ускорение-время, являются прекрасными инструментами для понимания движения.Однако бывают случаи, когда графическое изображение движения может быть не самым эффективным или действенным способом понимания движения объекта. Чтобы помочь в таких ситуациях, вы можете добавить набор уравнений для решения задач в свой набор физических инструментов, известных как кинематические уравнения. Эти уравнения могут помочь вам найти ключевые переменные, описывающие движение объекта при постоянном ускорении. Как только вы узнаете значения любых трех переменных, вы можете использовать кинематические уравнения для решения двух других!

Ключевые переменные кинематики

Переменная	Значение
v 0	Начальная скорость
против	Конечная скорость
Δx	Рабочий объем
и	Ускорение
т	Время истекло

 

 

 

 

 

 

Стратегия решения проблем

При использовании этих уравнений для решения задач движения важно позаботиться о настройке анализа, прежде чем приступать к решению. Ключевые шаги для решения проблем кинематики включают в себя:

1. Маркировка анализа для горизонтального (ось X) или вертикального (ось Y) движения.
2. Выбор и указание положительного направления (обычно направление начального движения).
3. Создание таблицы анализа движения (v ₀ , v, Δx, a, t). Обратите внимание, что Δx — это изменение положения или смещения, и его можно переписать как x-x ₀ .
4. Используя то, что вы знаете о проблеме, заполните свои «данные» в таблице.
5. Как только вы узнаете три элемента в таблице, используйте кинематические уравнения для решения любых неизвестных.
6. Убедитесь, что ваше решение имеет смысл.

Взгляните на пример задачи, чтобы увидеть, как можно использовать эту стратегию.

Примеры задач

Эти уравнения и этапы решения задач применимы как к задачам горизонтального, так и вертикального движения. Давайте попробуем их:

Эта стратегия решения задач и кинематические уравнения работают и для задач вертикального движения:

В некоторых случаях вы, возможно, не сможете найти количество «найти» напрямую.В этих случаях вы можете сначала найти другую неизвестную переменную, а затем выбрать уравнение, которое даст вам окончательный ответ:

 

Вопрос: Космонавт сбрасывает молот с высоты 2,0 метра над поверхностью Луны. Если ускорение свободного падения на Луне составляет 1,62 метра в секунду ² , то через какое время молот упадет на поверхность Луны?

Ответ:

 

несколько простых примеров из Physclips

Дифференциальные уравнения включают в себя дифференциал количества: как быстро это количество изменяется по отношению к изменению другого. Например, обыкновенное дифференциальное уравнение относительно x(t) может включать x, t, dx/dt, d 2 x/dt 2 и, возможно, другие производные. Ниже мы рассмотрим два простых примера обыкновенных дифференциальных уравнений, решим их двумя разными способами и покажем, что в них нет ничего страшного — ну, по крайней мере, не в тех простых, с которыми вы встретитесь во вводном курсе физики. (И к тому времени, когда вы столкнетесь со сложными уравнениями на курсах физики второго и старшего курсов, вы уже будете более формально изучать дифференциальное исчисление по своим предметам математики.) Мы предполагаем, что вы уже немного знакомы с математикой. Если нет, сначала см. это введение. Методы решения дифференциальных уравнений Существует несколько различных способов решения дифференциальных уравнений, которые я перечислю в приблизительном порядке популярности. Я также классифицирую их способом, который отличается от того, что можно найти в учебниках. Знай или ищи .Конечно! Уже решено очень много дифференциальных уравнений. Некоторые из них вы узнаете, а другие вы можете найти. Это , безусловно, наиболее распространенный способ, которым ученые или математики «решают» дифференциальные уравнения. Это также то, как некоторые (нечисловые) компьютерные программы решают дифференциальные уравнения. Замена . Часто дифференциальное уравнение можно упростить, заменив одну или другую переменную. Это может сделать ее уже решенной (см. выше) или решаемой одним из других методов.(Программные пакеты тоже делают это.) Эта категория решений включает в себя ряд методов, которые вы изучите на курсе математики второго года обучения. Угадай и попробуй . Другой очень распространенный метод решения дифференциальных уравнений: угадать, каким может быть решение, подставить его и, если это не решение или не полное решение, изменить предположение, пока не будет получено полное решение. Это используется часто — чаще, чем можно было бы предположить, читая книги и статьи, где процесс обычно кажется довольно элегантным.Во многих случаях вы знаете что-то об изучаемой системе, что дает вам подсказку. Опыт, конечно, тоже помогает. Однако ниже мы увидим, что угадывать иногда несложно. Изменить более простое решение . Если вы знаете решение уравнения, которое является упрощенной версией того, с которым вы столкнулись, попробуйте изменить решение более простого уравнения, чтобы сделать его решением более сложного. Трансформация .Некоторые дифференциальные уравнения легче решать при математическом преобразовании. Это основное применение преобразований Лапласа. Численное решение. Если все вышеперечисленное не помогло, то алгоритм, обычно реализованный на компьютере, может решить ее явно, вычислив производные как отношения. Обычно это крайний метод по двум причинам. Во-первых, это дает вам решение только для одного конкретного набора граничных условий и параметров, тогда как все вышеперечисленное дает вам общие решения. Во-вторых, он имеет ограниченную точность: числовые производные по своей природе зашумлены. Интеграция . Эта техника элегантна, но часто трудна (или невозможна). Иногда можно умножить уравнение на интегрирующий коэффициент, чтобы сделать интегрирование возможным. Специальные типы . Это расплывчатое название должно включать в себя специальные методы, которые работают для определенных типов уравнений. Это тоже для изучения на курсах математики в старших классах. Аналоговое решение. Некоторые дифференциальные уравнения легко решаются на аналоговых компьютерах. Они очень быстрые и поэтому подходят для задач управления в реальном времени. Их недостатками являются ограниченная точность и то, что аналоговые компьютеры сейчас редкость. Ниже приведены два примера решения общих уравнений. Они простые, потому что имеют только постоянные коэффициенты, но именно с ними вы столкнетесь на первом курсе физики. Эти уравнения могут быть решены несколькими способами, указанными выше, но мы проиллюстрируем только два метода. Пример 1: Экспоненциальный рост и затухание Одним из распространенных примеров является рост популяции простых организмов, не ограниченных пищей, водой и т. д. Пусть количество организмов в любой момент времени t равно x(t). Скорость образования новых организмов (dx/dt) пропорциональна количеству уже существующих организмов с константой пропорциональности α. Итак, дифференциальное уравнение: Прежде чем идти дальше, , что мы уже знаем? Подумайте, что означает эта ситуация: если число удваивается за один день (скажем), то на второй день их становится вдвое больше, поэтому на второй день популяция снова удвоится и так далее.Это говорит нам, какое решение мы ищем: геометрическое или экспоненциальное увеличение (пример нарисован справа: больше об экспоненциальной функции по этой ссылке). Поскольку это простое уравнение, давайте решим его интегрированием. Для этого уравнения можно разделить переменные , т. е. перестроить уравнение так, чтобы в одну сторону входили только х, а в другую только t. Здесь мы получаем где C — постоянная интегрирования.(Подробнее о логарифмической функции и константах интегрирования в исчислении Physclips.) Константа (константы) интегрирования обычно находится из граничных условий: что в данном случае означает знание x при некотором значении t. Для этого примера предположим, что мы знаем, что в момент времени t = 0 x = x 0 . Замена дает Разница между двумя логарифмами является логарифмом отношения, поэтому и, взяв антилогарифмы (или возведя каждую сторону в степень e): Проверим размеры. e αt — это число, поэтому x имеет те же размеры и единицы измерения, что и x 0 : это хорошо! Аргумент экспоненциальной функции должен быть числом, а это означает, что a имеет размеры обратного времени. α — пропорциональная скорость прироста населения, так что это доля за время, так что да, размеры верны. Из-за этих размерностей обычно определяют τ  = 1/α , что дает решение В примере справа τ (или 1/α) называется постоянной времени или характеристическим временем.Его смысл теперь ясен: когда   t  =  τ,   x/x 0 равно e 1   = 2,72. По истечении двух постоянных времени (когда t   = 2τ) мы имеем x/x 0  = e 2 = 7,39 и т. д. x растет в e раз за каждый временной интервал τ. (Подробнее об экспоненциальной функции по этой ссылке.) Кстати, здесь стоит остановиться и отметить, что дифференциальные уравнения почти всегда являются лишь приближениями. Невозможно иметь систему, описываемую этим уравнением. Например, популяция любого вида не может расти экспоненциально. Приведу лишь одно ограничение: когда организмы занимают твердую сферу, радиус которой увеличивается со скоростью света, дальнейший рост не может быть экспоненциальным. (Об этом стоит помнить, когда политики становятся одержимыми достижением роста чего-либо, но особенно населения.) Экспоненциальное уменьшение В приведенном выше примере α был положительным. Рассмотрим теперь случай, когда коэффициент при t отрицателен, например радиоактивный распад.Если имеется N(t) радиоактивных ядер в момент времени t и N 0 в момент t = 0, и если скорость их распада (-dN/dt) пропорциональна числу нераспавшихся ядер с константой пропорциональности α, то Делая то же интегрирование, что и выше, мы имеем где в этом случае τ — время, необходимое для изменения популяции в e −1  = 0,37, и так далее. Пример 2: Простое гармоническое движение Мы рассмотрим простое гармоническое движение в Physclips, сначала кинематически (т.е. описание и количественная оценка движения), затем физически в колебаниях. В последнем случае мы приводим решение и показываем, что оно действительно удовлетворяет дифференциальному уравнению. Давайте посмотрим повнимательнее и используем его как пример решения дифференциального уравнения. В направлении x второй закон Ньютона говорит нам, что F = ma = m.d 2 x/dt 2 , и здесь сила равна −kx. Это дает нам дифференциальное уравнение: где x — отклонение массы m от равновесия в момент времени t, а k — жесткость пружины, к которой прикреплена масса. Что мы уже знаем? Теперь, даже если мы никогда не видели груз, прикрепленный к пружине, мы можем догадаться о его поведении. Первый тривиальный: если масса покоится и находится в равновесии, то она там и останется. Поведение. Если мы сместим массу и отпустим ее, пружина разгонит ее к положению равновесия (x = 0). Когда он достигает этого места, сила на нем равна нулю, но он движется с ненулевой скоростью.Таким образом, из-за своей инерции он промахивается: он продолжает двигаться за пределами x = 0. Однако по эту сторону от x = 0 пружина замедляет его, в конечном итоге останавливая. Но сила пружины теперь велика, поэтому она ускоряется в противоположном направлении, возвращаясь к точке x = 0. Достигнув ее, она промахивается… Хорошо, она колеблется. Так что мы будем искать решение, которое колеблется . Другое дело, что мы пренебрегли трением, чтобы получить это уравнение.Так что нечему преобразовывать механическую энергию, поэтому система будет колебаться вечно. Это важно и в нашем решении. Размеры также помогают. Левая часть представляет собой ускорение, поэтому к/м должно иметь размерность (время) −2 . Таким образом, характерное время τ в этом уравнении определяется как τ −2 = k/m или τ = (m/k) ½ . Обратная величина времени — это частота, поэтому 1/τ может быть частотой или, возможно, угловой частотой, или, по крайней мере, связана с ними.Мы узнаем. Сейчас самое время использовать метод решения «Угадай и попробуй ». Нам нужно решение, которое колеблется вечно и обладает тем свойством, что его вторая производная пропорциональна самой себе, но отрицательна. Функция синуса делает все это. Теперь мы не можем написать x = sin t по причинам размерности: аргумент функции синуса не может иметь размерности: он дается в радианах (что является отношением или числом).Мы можем написать sin (2πft) или, что то же самое,          sin (ωt), где f — циклическая частота (количество полных циклов синусоиды в единицу времени), а ω = 2πf — угловая частота (количество радиан в единицу времени). Однако sin (ωt) — это число, и нам нужно, чтобы длина имела те же размеры, что и x, поэтому возможное решение: . Когда мы описывали простое гармоническое движение, мы называли А амплитудой : функция синуса изменяется от -1 до +1, поэтому движение изменяется от -А до +А. Однако с этим предлагаемым решением есть проблема: оно имеет x = 0, когда t = 0. Было бы нормально, если бы я дал ему толчок, чтобы запустить его из состояния покоя, но что, если я выпущу массу из состояния покоя в точке, удаленной от равновесия? В последнем случае мне понадобится x = A cos (ωt). Общее решение должно учитывать эти и любые другие начальные условия. Поэтому вместо этого мы пишем: . Может ли это быть решением? Берем производные и получаем Итак, это решение, если ω 2   = k/m.Или, если хотите, мы можем записать общее решение в виде Однако для элегантности мы обычно пишем Итак, вернемся к рассмотрению φ. Если мы начнем движение (t = 0) с v = 0 при x = A, то φ должно быть равно 90°: вместо синуса мы имеем косос-функцию. В качестве альтернативы, если мы начнем с максимальной (положительной) скорости при x = 0, тогда нам нужно φ = 0. Мы приводим примеры этих случаев на странице фона для колебаний.Однако мы могли бы начать с любой комбинации начального смещения x = x 0 и v = v 0 . Итак, для общего случая (x 0 ≠ 0, v 0 ≠ 0) мы можем подставить, чтобы получить Мы можем решить их через A и φ, сначала разделив два уравнения, затем возведя их в квадрат и сложив. Итак, для этих заданных начальных условий мы можем найти комбинацию констант A и φ, так что это общее решение. Сколько граничных условий? В нашем первом примере нам нужно было найти только одну константу интегрирования, поэтому нужно было найти только одно начальное условие (или другое граничное условие). Второй пример представлял собой уравнение второго порядка, требующее двух интегрирований или двух граничных условий. Здесь мы можем указать два из начальных перемещений, скорость и ускорение, или какие-то другие два параметра. Затухающие и вынужденные колебания Выше мы решили уравнение d 2 x/dt 2  + ω 2  x  =  0 ,      где ω 2   =  k/m . Теперь добавим дополнительный член: линейный член в dx/dt.Это дает уравнение для затухающих колебаний: d 2 x/dt 2  + β dx/dt +     2  x  =  0 ,      , где ω 2   =  k/m и где β > 0. Физически этот термин соответствует силе, пропорциональной скорости. Что мы можем предположить о решении и как нам изменить решение, которое мы получили выше, чтобы оно удовлетворяло нашему новому дифференциальному уравнению? Опять же, мы можем использовать наши знания о физической системе: когда мы прикладываем силу, направление которой противоположно скорости, мы замедляем ее. Таким образом, мы можем ожидать одного из двух возможных ответов: либо он должен колебаться, причем амплитуда колебаний постепенно уменьшается с течением времени, либо (если затухание достаточно велико) он может замедлиться до полной остановки, даже не колеблясь. Это наводит нас на мысль о возможности решения вида Мы можем попробовать это уже. Но это не совсем решение. Ну, а если демпфирующая сила замедляет вибрацию? Почему бы не попробовать (ω + δω) вместо ω = k/m и посмотреть, даст ли это решение для подходящего значения δω? Добавим еще одно усложнение: давайте начнем трясти частицу с дополнительной колебательной силой, скажем, F = F 0  sin Ωt.Это дает нам новое дифференциальное уравнение: d 2 x/dt 2  + β dx/dt +  ω 2  x  =  F 0  sin Ωt. Это уравнение вынужденных колебаний. Что произойдет, если мы позволим этой системе развиваться до тех пор, пока ее поведение не станет стабильным? Здесь мы снова можем угадать решение, подставить его в дифференциальное уравнение, а затем попытаться изменить его или подобрать соответствующие значения его параметров. Почему бы не попробовать сначала и, если вы хотите проверить, перейти к Затухающим колебаниям и Принудительным колебаниям, где мы обсуждаем физику, показываем примеры и решаем уравнения. Уравнения в частных производных: волновое уравнение Когда у нас есть функция y(t), мы можем легко определить dy/dx как наклон графика y(x). Но теперь рассмотрим y(x,t). В нашем примере это будет смещение y точки на струне в зависимости от положения на струне x и времени t. Итак, теперь мы можем думать о двух разных производных. Мы пишем их по-разному. (Мы также представили их в разделе на странице исчисления.) Здесь мы будем решать волновое уравнение, уравнение движения волны в струне.(См. введение в Волны I и Волны II.) ∂y/∂x. Подумайте об этом как dy/dx в заданное постоянное время, t. Представьте, что вы фотографируете (время постоянно): на изображении в момент времени t это наклон формы y(x) в момент фотографирования. ∂y/∂t. Подумайте об этом как dy/dt в данной позиции, x. Это просто скорость в направлении y в конкретной точке x на струне. (Кстати, не скорость волны). Возьмем стандартный пример.Бегущая синусоида с амплитудой A, частотой f = 2πω и длиной волны λ = 2π/k имеет уравнение y  =  A sin(kx − ωt),    так что ∂y/∂x =  kA cos(kx − ωt), который представляет собой наклон строки в позиции x и момент времени t, и ∂y/∂t =  − ωA cos(kx − ωt), которая является скоростью точки струны в точках x и t. Теперь все эти три выражения являются функциями y(x,t): это кривые y(x), которые меняются с течением времени t. Таким образом, следующая анимация рисует их таким образом (чего не могут сделать учебники!).Вы можете приостановить анимацию, чтобы проверить наклоны y(x), а также проверить правильность формы выражения скорости. Два нижних графика представляют собой вторые производные по тем же переменным: ∂y 2 /∂x 2  =  − k 2 A sin(kx − ωt), скорость изменения наклона струны при изменении x, и указать на строку. Они имеют важное физическое значение: первое определяет кривизну струны. Если ∂y 2 /∂x 2 = 0, то наклон постоянный, поэтому он прямой. Это означает, что натяжение T действует в противоположных направлениях на противоположных концах, не создавая результирующей силы. Однако если сегмент изогнут (∂y 2 /∂x 2 ≠ 0), на него действует сила. При постоянной кривизне на малой длине L результирующая сила пропорциональна L. Нам известно ускорение, поэтому мы можем применить второй закон Ньютона. Масса сегмента равна µL, где µ – масса единицы длины µ. Запись закона Ньютона в виде a = F/m дает: ∂y 2 /∂t 2   =  ( T /μ)∂y 2 /∂x 2 Оглядываясь назад на наши выражения для двух вторых производных, мы видим, что они представляют собой наши простые константы, умноженные на нашу исходную функцию y  =  A sin(kx − ωt). Это означает, что y =  A sin(kx − ωt) является решением волнового уравнения при условии, что T /µ = ω 2 /к 2 . Мы также видели, в Волны I, что ω/k — скорость волны, v. Что, наконец, связывает скорость волны с физическими свойствами T и μ струны: Скорость волны больше, если струна натянута сильнее, и меньше, если струна имеет большую массу на единицу длины.

Мотивирующие уравнения в физике. Уравнения в физике помогают нам решать… | Томас Чилимамп | ноябрь 2021 г.

Уравнения в физике помогают решать задачи, но ученикам это не сразу очевидно.Я пытаюсь мотивировать полезность уравнений на своих уроках, следуя аналогичному методу для каждого уравнения. Здесь я буду использовать пример расчета работы, проделанной при толкании объекта. Вдохновением для этого послужила статья Гетина Джонса в журнале «Воздействие на p-prims» — как научить учащихся понимать, являются ли отношения пропорциональными, обратно пропорциональными или чем-то еще. Я хочу, чтобы учащиеся «увидели физику», а затем использовали свои знания, чтобы чувствовать себя уверенно при выполнении расчетов, понимая, почему они полезны и как они соотносятся с базовой концепцией физики.

Я начинаю с того, что рисую ситуацию, которая обычно представляет собой сравнение двух разных сценариев (отмеченный призом рисунок) соседний учитель естественных наук (или ученик в первом ряду). Затем я добавляю «цифры», чтобы ученики могли сравнить.

Итак, процесс начинается с очень конкретного примера, при этом основная концепция становится еще более конкретной за счет сравнения двух разных ситуаций.

Я намеренно оставляю одно и то же и меняю только одну переменную. Я не буду явно подсчитывать проделанную работу, но мы обсудим, что главный человек (да, это я в очках) проделал больше работы, потому что ему пришлось применить больше силы.

Затем я настрою второй сценарий, в котором я изменю другую переменную (и оставлю первую прежней) большое расстояние.

Сейчас мы, вероятно, остановимся на некоторых основных вопросах, чтобы прояснить эту взаимосвязь «по мере увеличения силы выполняется больше работы» и т. д.Мы могли бы провести еще несколько простых сравнений и использовать интерактивные доски, чтобы убедиться, что они могут легко видеть, когда выполняется дополнительная работа в сценариях, где отличается только одна переменная.

Теперь учащиеся умеют говорить: «В сценарии А выполняется больше работы, потому что…». Теперь я мотивирую использование уравнений, давая сравнение, подобное этому

больше работы, мы заставили сделать расчет. Некоторые учащиеся очень хорошо умеют выводить ответы, что показывает, что они думают об отношениях e.г. «сила в А больше половины силы В, а расстояние более чем в два раза, значит, это А» — у меня с этим проблем нет. Я отмечаю, что написание этого занимает больше времени, чем выполнение двух расчетов (но это отличный пример того, как мыслить как физик и осыпать их похвалами). Вы можете адаптировать числа в примере, чтобы сделать это настолько простым или сложным, насколько вам нужно.

Гарри Флетчер Вуд обсуждает мотивацию учащихся в своей книге «Привычки к успеху » и в различных подкастах и ​​приводит пример продавца аспирина.Идеальным покупателем для продажи аспирина является человек со слабой головной болью — люди не оценят аспирин, если он им не нужен, и с этической точки зрения вы не должны навязывать его им. Аспирин здесь «использует формулу для выполнения вычислений», и я создал головную боль, обеспечив отсутствие прямого сравнения между двумя сценариями. Студенты теперь должны (теоретически) приходить ко мне за решением — и они, безусловно, находят это гораздо более удовлетворительным.

Это наводит на мысль, что, возможно, вы могли бы вместо этого начать с последнего примера, так как это головная боль.Но учащиеся не смогли бы понять основную концепцию физики без этих более простых и менее вызывающих головную боль примеров.

Если вы хотите узнать больше об обучении на примерах, см. мой предыдущий пост. Дайте мне знать в Твиттере (@tchillimamp), как вы мотивируете уравнения на своих уроках.

Почему важны уравнения?

Почему уравнения важны? декабрь 2002 г. Учитывая часы, которые учителя математики тратят обучая учащихся решать уравнения, легко было бы предположить, что наиболее важным что делать с уравнением, чтобы найти решение. Но это бывает редко. Большинство уравнений которые возникают в контексте реального мира, не могут быть решены. Даже если они могут, часто проще и быстрее использовать вычислительный метод, чтобы найти численное решение. Настоящая сила уравнений в том, что они предоставить очень точный способ описать различные особенности мира. (Вот почему решение уравнение может быть полезным, когда его можно найти. )

Прежде чем я окажусь заваленным сотнями разгневанных электронные письма от учителей, которые не хотят, чтобы их ученики понять, что научиться решать уравнения не важно, я должен сказать, что это действительно важное упражнение.Но причина не в том, что студент, скорее всего, найдет ее или себя на самом деле решение уравнений — вне урока математики, т.е. Скорее, овладение процессами, необходимыми для решения уравнения, возможно, лучший способ стать адептом в понимании того, что говорят нам уравнения. Это, из Конечно, это та же причина, по которой учителя английского языка спрашивают своим ученикам писать рефераты. Мало таких студентов могут стать писателями или журналистами, но написание эссе — лучший способ научиться использовать письменный язык.

Одна из самых драматичных иллюстраций неважность — вне самой математики — решение уравнений предусмотрено современной физикой. Фундаментальная теория материи, которую физики работа с сегодняшним днем ​​является самой точной научной теорией мир когда-либо знал. Прогнозы, сделанные на основу фундаментальных уравнений материи имеют проверено экспериментально во многих местах десятичные дроби. И все же ни одно из этих уравнений не было решено.Вы должны вернуться в 1920-е годы, чтобы найти уравнения материи, которые кто-либо смог решать.

Жить, как мы, в мире, наполненном высокими технологиями гаджеты, которые зависят от современной физики — компьютер, на котором я это пишу, и проигрыватель компакт-дисков это развлекает меня, потому что я просто два таких — очевидно, что отсутствие решения вряд ли сдерживал физиков, или инженеры, которые принимают современную физическую теорию и превратить его в продукты. Без точного понимания предоставленные уравнениями, в мире не было бы кремниевые чипы, проигрыватели компакт-дисков, медицинские МРТ экзамены или многие другие вещи, которые мы сейчас принимаем как должное. Но ни одно из этих приложений требуется, чтобы эти уравнения решались в строгий математический смысл.

Физики потратили последние восемьдесят лет, пытаясь найти единую структуру, которая объясняет, что сейчас считается (единственными) четырьмя фундаментальными силами природа: электромагнетизм, гравитация, сильное ядерное сила и слабое ядерное взаимодействие.Большая часть усилий был направлен на разработку расширения квантовой теории, которую физики называют «квантовой теория поля» (КТП). Картина материи, которую дает КТП данный нам, который представляет наши лучшие текущие знания о природа материала, из которого состоит вселенная, обычно называют «стандартной моделью частиц». физика.»

Эдвард Виттен из Института перспективных исследований в Принстон, штат Нью-Джерси, один из нынешних лидеров этого продолжающееся исследование, описал текущую версию КТП как «научная теория двадцатого века, использующая Математика двадцать первого века. «Под этим он подразумевает, что многое из математики еще предстоит проработать — в Другими словами, математикам еще предстоит решить уравнения!

Может показаться, что Виттен жестоко обращается с математиками. за опоздание, а на самом деле он просто реалистичный. Ученые и математики были в это положение раньше. Большая часть науки Ньютона зависела о методах исчисления, которые он изобрел для цель, но детали исчисления не были полностью разрабатывалась как математическая теория до двухсот лет спустя!

Конкретная нерешенная математическая проблема, возникающая Исследование QFT было выбрано в качестве одного из семи Проблемы тысячелетия, которые Глиняная математика Институт объявил в 2000 году, предложить приз в размере 1 миллиона долларов тому, кто первым решить каждую проблему.(Я описываю эти семь проблем в как можно ближе к терминам непрофессионала в моей недавней книге Проблемы тысячелетия: семеро Величайшие нерешенные математические загадки нашего времени. ) Эта конкретная проблема тысячелетия, единственная на список, который исходит из современной физики, требует решения (при определенных условиях) в Yang-Mills уравнения (квантовый полевой аналог уравнений Максвелла для электромагнетизма), вместе с последующим объяснение, основанное на этом решении, так называемого «массовый разрыв» (предполагаемое и наблюдаемое до сих пор минимальный уровень массы, которую может иметь любая материя).

Несмотря на свое происхождение в физике, проблема в том виде, в каком она сформулирована по существу является математическим. Действительно, многие физики рассматривают проблему как в значительной степени уже решено. Фрэнк Вильчек из Массачусетского технологического института, одна из ведущих фигур в КТП и один из инициаторов квантовой хромодинамика (КХД), наиболее полная теория в рамках общей структуры QFT, комментарии:

«В частности, имеются прямые доказательства существования из основных элементов теории [КХД] — кварки и глюонов — и для основных взаимодействий постулаты теории. Большая часть доказательств получена из исследований струй в высокоэнергетических процессах и сравнение их наблюдаемые свойства с очень точными и однозначными расчеты в КХД… Другой вид доказательств взят из фактически интегрируя полные уравнения напрямую, используя мощные компьютеры. Эта работа непосредственно адресована и к меня эффективно решает, проблема Клэя. Мы не только знаем что есть массовый разрыв, но рассчитали его, и удачно сравнил с реальностью.Конечно я понимать, что численные результаты, какими бы убедительными и хорошо контролируются, традиционно не считаются математические доказательства.»

Если физики вроде Вильчека рассматривают проблему Клея как уже решено, почему Институт Клэя включил он в их списке семи самых сложных и важные нерешенные математические задачи на старте третьего тысячелетия? Ответ предоставлен Артур Джаффе из Гарвардского университета, эксперт в области математика квантовой теории поля и до недавнего времени директор Института Клэя. Он сказал: «В проблема теории Янга-Миллса и массового разрыва Гипотеза была выбрана в качестве проблемы тысячелетия, потому что ее решение ознаменовало бы начало новой крупной область математики, имеющая глубокие и основательные связи с нашим нынешним пониманием вселенной.» Другими словами, решение уравнений — это важная цель в математике.

Замечание Яффе, однако, не означает, что решение теории Янга-Миллса и массового разрыва проблема, если бы она была обнаружена на следующей неделе, не имеют серьезные последствия для физики.Напротив, это почти наверняка привело бы со временем к увеличению понимание материи, а оттуда к черт знает чему новые технологические гаджеты для улучшения и улучшения наших Мир. Но — и именно поэтому Вильчек и Яффе не в конфликте здесь — приложения почти наверняка начинать не с решения , а с как такового, а будет исходить из методов , которые использовали, чтобы найти это решение. Как это часто бывает в математике, в в долгосрочной перспективе метод, вероятно, будет более важным чем ответ.

Помните, все вы, студенты, я не говорю что решение уравнений не имеет значения. Это важно по нескольким причинам. Скорее, я хочу сказать, что это вообще-то не а самое главное что нужно сделать уравнение, реальная сила которого так же формальна и точна описание нашего мира.

Мы также должны помнить, что любая новая математическая результат может изменить мир. У многих есть.

---

Угол Девлина обновлен в начале каждого месяца.

---

Математик Кит Девлин (англ. [email protected]) является Исполнительный директор Центра Изучение языка и информации в Стэнфорде Университет и «Парень-математик» на NPR Выпуск выходного дня. Его книга Проблемы тысячелетия: семь величайших Нерешенные математические загадки нашего времени был только что опубликован Basic Books.

---

2.6: Решение уравнений движения в трех частных случаях

В разделе 2.3 мы видели несколько примеров уравнений движения, вытекающих из второго закона Ньютона. Для довольно распространенного случая, когда масса интересующего нас объекта постоянна, его траектория будет задана как решение обыкновенного дифференциального уравнения второго порядка со временем в качестве нашей переменной. В общем случае сила во втором законе Ньютона может зависеть от времени и положения, а также от первой производной положения, т.е.д., скорость. Таким образом, в одном измерении мы имеем

\[m \ddot{x}=F(x, \dot{x}, t) \label{force}\]

Уравнение \ref{force} может быть сложно решить для сложных функций F. Однако в каждом из частных случаев, когда сила зависит только от одной из трех переменных, мы можем записать общее решение, хотя и в виде интеграла по сила, которую мы можем или не можем вычислить явно.

Случай 1: F=F(t)

Если сила зависит только от времени, мы можем решить уравнение (\ref{сила}) путем прямого интегрирования.{\prime} \label{case1}\]

Случай 2: F=F(x)

Если сила зависит только от положения в пространстве (как в случае гармонического осциллятора), мы не можем интегрировать по времени, так как для этого нам уже нужно знать x(t). {2} \ справа] \label{fxsoln}\]

Чтобы получить x(t), мы используем соотношение \({dx \over dt}=v(x)\).{\prime} \label{case3}\]

Из уравнения (\ref{case3}) мы можем получить v(x) путем инвертирования и x(t) из уравнения (\ref{case2}). Обратите внимание, что уравнение (\ref{case3}) не дает нам \(x(t)\) напрямую, так как \(x\) является переменной в этом уравнении.

пример 2.6.4: скорость гармонического осциллятора

Может показаться, что то, что мы сделали до сих пор в этом разделе, едва ли помогло делу: найденные нами «решения» содержат интегралы, и их часто нужно инвертировать, чтобы получить желаемую функцию \(x(t)\) (или, в зависимости от изучаемой проблемы, \(v(t)\) или \(v(x)\)).Чтобы показать вам, как эти решения могут быть полезны, давайте рассмотрим конкретный пример: гармонический осциллятор, состоящий из массы на пружине Гука с

\[F=F(x)=-k x. \номер\]

Раствор

Мы уже записали уравнение движения (уравнение 2. 3.4) и его общее решение (уравнение 2.3.5). Общее решение можно найти путем замены экспонент, как мы это сделаем в разделе 8.1. Однако мы также можем узнать кое-что полезное, написав уравнение движения в форме (\ref{fx}).{2}\справа)} \номер\]

для \(v(x)\). Хотя \(x(t)\) и \(v(t)\) легче получить из решения, данного в уравнении 2.3.5, это решение не даст вам \(v(x)\), и его вывод сложно. Здесь мы получаем его почти бесплатно. Более того, как вы, наверное, заметили, уравнение \ref{harmosc} связывает кинетическую энергию с потенциальной энергией гармонического осциллятора — частный случай сохранения энергии, который мы обсудим в следующем разделе.

Определение уравнения в физике.

Примеры уравнений в следующих темах:

• Приложения

  • Существуют четыре кинематических уравнения , которые описывают движение объектов без учета его причин.
  • Обратите внимание, что четыре кинематических уравнения включают пять кинематических переменных: $d$, $v$, $v_0$, $a$ и $t$. \mu_{;\mu}=0$ если частицы сохраняются, то уравнения Лиовиля и Больцмана не могут выполняться, если $\nabla_{\bf p} \cdot F \neq 0$ и частицы сохраняются.

• Методы решения проблем

  • Определите проблему и решите соответствующее уравнение или уравнение для определяемой величины.
  • Решите соответствующее уравнение или уравнения для определяемой величины (неизвестной).
  • Мы не можем использовать любое уравнение , которое включает t, чтобы найти ω, потому что уравнение будет иметь как минимум два неизвестных значения.
  • Уравнение $\omega 2=\omega 02+2$ будет работать, потому что мы знаем значения всех переменных, кроме ω.
  • Извлечение квадратного корня из уравнения и ввод известных значений дает

• Атомная структура

  • Волновая функция развивается вперед во времени в соответствии с зависящим от времени уравнением Шрёдингера
  • Если гамильтониан не зависит от времени, мы можем решить это уравнение с помощью
  • Эта реализация позволяет нам написать уравнение которому волновая функция атома должна удовлетворять
  • Для большинства атомных состояний эти эффекты можно рассматривать при возмущениях. Мы можем упростить эти уравнения , используя
  • Это дает следующее безразмерное уравнение

• Решение проблем

  • Закон идеального газа — это уравнение состояния гипотетического идеального газа.
  • Вариации уравнения идеального газа могут помочь легко решить проблему.
  • Подставить известные значения в уравнение .
  • Выберите соответствующее газовое уравнение уравнение , которое позволит вам вычислить неизвестную переменную: Мы можем использовать общее уравнение газа для решения этой задачи: $\frac{P_1 V_1}{T_1} = \frac{P_2 V_2} {T_2}$.
  • Подставить известные значения в уравнение .

• Общий подход

  • Следующим шагом является использование того, что известно, чтобы найти соответствующее уравнение , чтобы найти то, что неизвестно.
  • Хотя легче всего найти уравнение , которое оставляет только одно неизвестное, иногда это невозможно.
  • В этих ситуациях вы можете решить несколько уравнений , чтобы найти правильный ответ.
  • Помните, что уравнения представляют физические принципы и взаимосвязи, поэтому используйте уравнения и рисунки в тандеме.2 = (\partial P/\partial \rho)_s$.
  • Давайте решим это уравнение для давления,

• Применение уравнения Бернулли: давление и скорость

  • Это просто добавляет еще один член к приведенной выше версии уравнения Бернулли и приводит к
  • Уравнение Бернулли может быть применено при перекачивании жидкости между двумя резервуарами.
  • Уравнение Бернулли может быть адаптировано к потокам, которые являются как нестационарными, так и сжимаемыми.
  • Однако предположение о невязком течении остается как в нестационарной, так и в сжимаемой версиях уравнения .
  • Адаптация уравнения Бернулли для нестационарных или сжимаемых течений

• Математическое представление бегущей волны

  • является решением волнового уравнения для $c= \frac{\omega}{k}$. 2 = k/m$ )
  • уравнения несвязаны в том смысле, что каждое неизвестное ( $x,y,z$ ) встречается только в одном уравнении ; таким образом, мы можем найти $x$, игнорируя $y$ и $z$.
  • Подставляя их в уравнения для $x$ и $y$, мы получаем два уравнения амплитуды
  • Мы можем использовать первое уравнение для вычисления $x_0$ через $y_0$, а затем подставить его во второе уравнение , чтобы получить

.