Правила математике: Книга: "Правила по математике. Начальная школа". Купить книгу, читать рецензии | ISBN 978-5-408-05702-3 - Управленческое образование

Содержание

Сложение и вычитание отрицательных и положительных чисел. Решение примеров.

Существуют разные типы чисел — четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов — положительные числа и отрицательные числа. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны — положительные.

Ноль — это нейтральный элемент относительно сложения целых чисел. В основном в этой статье мы будем изучать операции сложения и вычитания с отрицательными числами. Существуют определенные правила для знаков при сложении и вычитании:

Для того чтобы сложить два отрицательных числа, надо сложить два числа и поставить знак минус.

$(-2)+(-3)=-5$

Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:

$(-8)+4=4-8=-4$

$9+(-4)=9-4=5$

Для каждого числа кроме $0$ существует противоположный элемент, при сумме с ним образуется ноль:

$-9+9=0$ $7,1+(-7,1)=0$

При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс. То есть, если стоят рядом два минуса, в сумме получается плюс.

$(-7)-(-6)=(-7)+6=(-1)$

Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.

$7-9=-2$ так как $9>7$

Также не стоит забывать минус на минус дает плюс:

$7-(-9)=7+9=16$

Задача 1. Вычислите:

$4+(-5)$
$-36+15$
$(-17)+(-45)$
$-9+(-1)$

Решение:

$4+(-5)=4-5=-1$
$-36+15=-21$
$(-17)+(-45)$ $=-17-45=-62$
$-9+(-1)=-9-1=-10$

Задача 2. Вычислите:

$3-(-6)$
$-16-35$
$-27-(-5)$
$-94-(-61)$

Решение:

$3-(-6)=3+6=9$
$-16-35=-51$
$-27-(-5)=-27+5=-22$
$-94-(-61)=-94+61=-33$

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

Наши преподаватели

Оставить заявку

Репетитор по математике

Уральский государственный педагогический университет

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по химии 8-11 классов.

Готовлю к ЕГЭ и ОГЭ по химии. Просто повышаю уровень знаний по химии. Объясняю простым и доступным языком. Даю прочные и необходимые знания для успешной сдачи экзаменов. Люблю химию за уникальность и исключительность. Могу заниматься бесконечно решением задач, составлением химических уравнений, выявлением закономерностей. Репетитор по математике 1-9 класс. Занимаюсь подготовкой к ОГЭ. Люблю математику за точность, рациональность и развитие логического мышления. Объясняю простым и доступным языком. Учу ребят рассуждать, говорить, мыслить и анализировать. Даю детям прочные знания. С любовью отношусь к своему делу и прививаю любовь к обучению детям.

Оставить заявку

Репетитор по математике

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по математике 1-4 классы и русскому языку 1-4 классы.

Математика — точная наука, которая развивает логическое мышление, учит думать и является основой для дальнейшего изучения школьных предметов в старшей школе. Главное, чтобы ребенок перестал боятся задач, «трудных» уравнений и «длинных» примеров. Результат работы — мои ученики победители и призеры муниципальных и краевых олимпиад. Сейчас работаю по программе «Школа России». Есть несколько выпусков по программе»ХХI век» и опыт работы по учебнику математики Л.Петерсон.

Оставить заявку

Репетитор по математике

БГПУ им. М.Танка

Проведенных занятий:

Форма обучения:

Дистанционно (Скайп)

Репетитор по химии для 7-10 классов. Тестируем уровень знаний и выявляем пробелы, для дальнейшего повышения уровня знаний. Решаем домашнее задание. Готовимся к урокам вместе. Химия — это интересно не только для меня, но и для вас.

Функция

— Индивидуальные занятия
— В любое удобное для вас время
— Бесплатное вводное занятие

Векторы

— Индивидуальные занятия
— В любое удобное для вас время
— Бесплатное вводное занятие

Правила по математике в схемах и таблицах

ББК 74. 102

П 68

данное пособие предназначено как для занятий на уроках математики, так и для самостоятельной работы дома. Учебный материал представлен в таблицах, что способствует его лучшему запоминанию, а также развитию зрительной памяти.

lSBN 978-5-00061-110-4 С) Оформление ООО «Искательпресс», 2016

о, 1 , 2, 3, 4, 5, 6, 7,

Это арабские цифры. Их всего десять.

Натуральные числа — это числа, которые применяют при счёте. Нуль не относится к натуральным числам.

> больше	плюс, знак сложения
М е НЬИје	— минус, знак вычитания
= равно	• или х умножение

: деление

Знак «РАВНО» = означает, что числа, находящиеся слева и справа от этого знака, одинаковые, то есть равны друг другу.

Знак «БОЛЬШЕ» > означает, что число, находящееся слева от этого знака, больше, чем число, находящееся справа от него.

Знак «МЕНЬШЕ» < означает, что число, находящееся слева от этого знака, меньше, чем число, находящееся справа от него.

Число 7 больше 5, но меньше 9

Числовая лесенка

Числа чётные и нечётные

Числа, которые делятся на 2, называются ЧЁТНЫМИ: 2, 4, 6, 8, 10 и так далее.

Числа, которые не делятся на 2, называются НЕЧЁТНЫМИ: 1 , З, 5, 7, 9, 1 1 и так далее.

При сложении чётных чисел получается чётное число, при сложении двух нечётных тоже получается чётное число:

6+4= 10

5+7= 12

При сложении нечётного числа с чётным в ответе будет нечётное число:

Сложение

первое слагаемое

второе слагаемое

сумма

2 Переместительный закон сложения

От перестановки мест слагаемых сумма не меняется:

9 9

Связь между суммой и слагаемыми 6

первое второе сумма

слагаемое слагаемое

Чтобы получить первое слагаемое, надо из суммы вычесть второе слагаемое: 6 4 2

сумма второе первое

слагаемое слагаемое

Чтобы получить второе слагаемое, надо из суммы вычесть первое слагаемое: 6 2 4

сумма первое второе

слагаемое слагаемое

Сочетательный закон сложения

Чтобы к сумме двух чисел прибавить третье число, нужно к первому числу прибавить сумму второго и третьего чисел.

Пример:

8 8

3 + (3 + 2) = (3 + 2) + 3 = (3 + 3) + 2

Если одно из слагаемых равно 0, то сумма равна другому слагаемому: а+О=а, О+а=а, 3+0=3, 0+3=3

Вычитание

Уменьшаемое— число, из которого вычитают. Вычитаемое— число, которое вычитают.

Правила вычитания

(7—6) +4= 1 +4=5

Если перед скобкой стоит МИНУС,то при раскрытии скобок знаки меняются на противоположные.

a-(b+c)=a-b—c а-(Ь -с) =a-b с

или

(а

Таблица сложения и вычитания

ппааиввпвп вааааааввш ававаавашш ааааааашше

5	6 7 8			9 10 1 1			12 13 14
б	7 8			9 10 11			12 13 14 15
7	8	9	10	11	12	13	14	15	16

9	10	11	12	13	14	15	16	17	18

Пример:

Эти цифры обозначены стрелками.

Там, где стрелки пересекаются, находим число 12.

Сложение и вычитание чисел с переходом через десяток

Одно из слагаемых надо разложить так, чтобы одна из сумм была равна 10. в= 7 + (З +5) 15

Таким же способом можно решать примеры на вычитание.

12-5 = 12—(2 +3)

Счёт сотнями

Сто (100) — это одна сотня, двести (200) —две сотни, триста (300) — три сотни и так далее.

Тысяча — это десять сотен, то есть 10 раз по 100.

Число575содержит

5 сотен, 7 десятков, 5 единиц

Сложение и вычитание чисел в «столбик»

При сложении двузначных или трёхзначных чисел единицы складываются с единицами, десятки с десятками, а сотни с сотнями.

	243 + 516 = 759	аз

аз

12+ 14=26

При вычитании двузначных или трёхзначных чисел единицы вычитаются из единиц, десятки из десятков, сотни из сотен.

аэ	759 -516= 243	аэе

па		аза

26- 14= 12

Проверка сложения и вычитания

Сложение можно проверить вычитанием. Нужно из суммы вычесть одно из слагаемых, если получится другое слагаемое — сложение выполнено верно.

пример: проверка:

15 + 40 = 55 55-15=40 55-40= 15

a+b=c с—а=Ь с—Ь =а

Вычитание можно проверить сложением.

Нужно к разности прибавить вычитаемое, если получится уменьшаемое — вычитание выполнено верно.

пример:	проверка:
78- 27=51	27+51 = 78
а-Ь=с	c+b=a

Умножение

Знаки умножения: ( е ) или (х)

з 0 2 = 6

• 7= 21

5 . 5 = 25

Правила умножения

Если один из множителей равен О, то и произведение равно О.

а • 0=0 или Оха = О

5 . или 0х5=0

Если один из множителей равен то произведение равно другому множителю:

а • 1 = а или 1 • а= а

4 . или 1 .

От перестановки множителей значение произведения не меняется.

a • b = b • a з . 5 = 5 . з

Распределительный закон умножения

(а + Ь) • с = а c+b • c

Сочетательный закон умножения

или

15 -60

Правила деления

Самое большое число в частном— делимое.

Деление суммы на число

Можно решить так:

Если делимое не делится на делитель, например 9 : 2, то надо подобрать ближайшее число, меньшее 9, которое делится на 2 без остатка.

1 ) : (остаток ) .

Остаток всегда должен быть меньше делителя.

Признаки делимости чисел

На делятся числа, оканчивающиеся на чётную цифру 12, 16 и так далее).

На З делятся числа, сумма цифр которых делится на з.

225 : 3=75 2+2+5=9, 9 делится на З.

4 делятся числа, если двузначное число, образованное двумя последними цифрами, делится на 4.

На 5 делятся числа, оканчивающиеся на 5 О.

40 : 5=8

155 : 5 =31

На 10 делятся числа, которые оканчиваются на О.

1000 : 100= 10

Проверка умножения

Если произведение двух чисел разделить на один из множителей, то получится другой множитель.

а . b = c с .• b = a

С : a = b

Проверка: 18 : З—- 6,

Проверка деления

Если делимое разделить на частное, получится делитель.

а: Ь=с а:с=Ь

Проверка:

Если делитель умножить на частное, получится делимое.

а: Ь=с

Проверка: 15 : 5 = 3,

Таблица умножения Пифагора

пвааавппапш ввававвпвпш
	2	4	6	8	10	12	14	16	18	20
з	з	6	9	12	15	18	21	24	27	зо
	4	8	12	16		24	28	32	36	40
	5	10	15	20	25	зо	35	40	45	50
	6	12		24	зо	36	42	48	54	60
	7	14	21	28	35	42	49	56	63	70
	8		24	32	40	48	56	64	72	80
	9		27	36	45	54	63	72	81	90
	10	20	30	40	50	60	70	80	90	100

Пример:

Эти цифры обозначены

стрелками.

Там, где стрелки

пересекаются, находим число

Порядок действий

В выражениях со скобками сначала выполняются действия в скобках, затем действия умножения и деления, а после этого остальные действия по порядку.

В выражениях без скобок сначала выполняются действия умножения и деления, а после этого остальные действия по порядку.

Запомни

Увеличить число на несколько единиц значит прибавить.

Увеличить число в несколько раз — значит умножить.

Уменьшить число на несколько единиц — значит вычесть.

8-2=6

Уменьшить число несколько раз — значит разделить.

Решение уравнений

Неизвестные числа обозначают латинскими буквами:

Х — «икс», У — «игрек» илиZ — «ЗЭТ»

Пример: Х = 21

х = 21 -4, Х = 17

Проверка. 17=21

Дроби и доли

— обыкновенная дробь,

а — числитель,

Ь — знаменатель,

Пример:

Числитель — сколько равных частей взяли.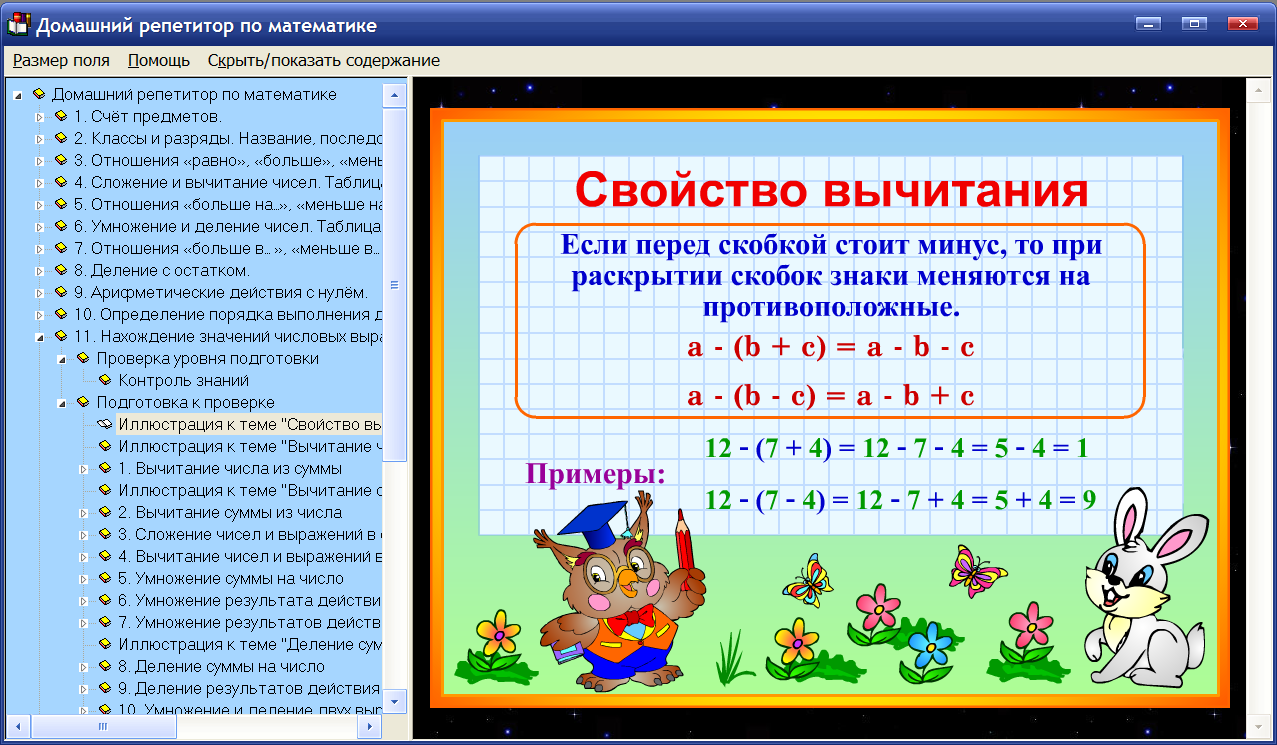

Знаменатель — на сколько равных частей разделили.

Правильные и неправильные дроби

Дробь правильная, если её числитель меньше, чем знаменатель.

а< Ь, то есть З, 5 и так далее.

Дробь неправильная, если её числитель больше, чем знаменатель.

5 13

а> Ь, то есть — —и так далее.

Сравнение дробей

11 1 1

—>—>—

ъ.) 24

со

Нахождение числа по доле

Если доля числа равна 2,

то всё число равно

Нахождение доли числа

Если всё число равно 12 то 3 доля от него равна

12 : 3 =4

Разряды и классы

Класс миллионов

Класс тысяч

Класс единиц

сотни миллионов

десятки мил-

ЛИОНОВ

единицы миллионов

сотни тысяч

десятки тысяч

единицы тысяч

сотни

десятки

едини цы

В числе 547375242

547375242 единицы

54737524 десятка

5473752 сотни

547375 единиц тысяч

54737 десятков тысяч

5473 сотни тысяч

547 единиц миллионов

54 десятка миллионов

ъ. ) 5 сотен миллионов

Римские цифры

Геометрические

с	D с
Треугольник	Многоугольник	Круг

Четырёхугольник Прямоугольник Квадрат а

в В

с с

АВ

в— диаметр

ОС — радиус

Периметр

Периметр — это сумма сторон любой геометрической фигуры, обозначается латинской буквой Р.

Единицы измерения — миллиметры (мм), сантиметры (см) метры (м) и так далее.

Периметр прямоугольника Периметр квадрата равен сумме всех его сторон равен его стороне, умноженной на 4

а— ширина прямоугольника, а— сторона квадрата Ь — длина прямоугольника.

Периметр многоугольника

Периметр треугольника равен сумме всех его сторон равен сумме всех его сторон

Рмн = a+b+c+d+e

Рд = а+Ь+с а с

Площа

дь

Площадь — это внутренняя часть любой геометрической фигуры, обозначается латинской буквой s.

Единицы измерения — квадратные километры (км ²) , квадратные метры (м ²) квадратные сантиметры (см ²) и так далее.

Площадь прямоугольника равна произведению длин его сторон.

а— ширина прямоугольника, длина прямоугольника.

Площадь квадрата равна квадрату длины его стороны.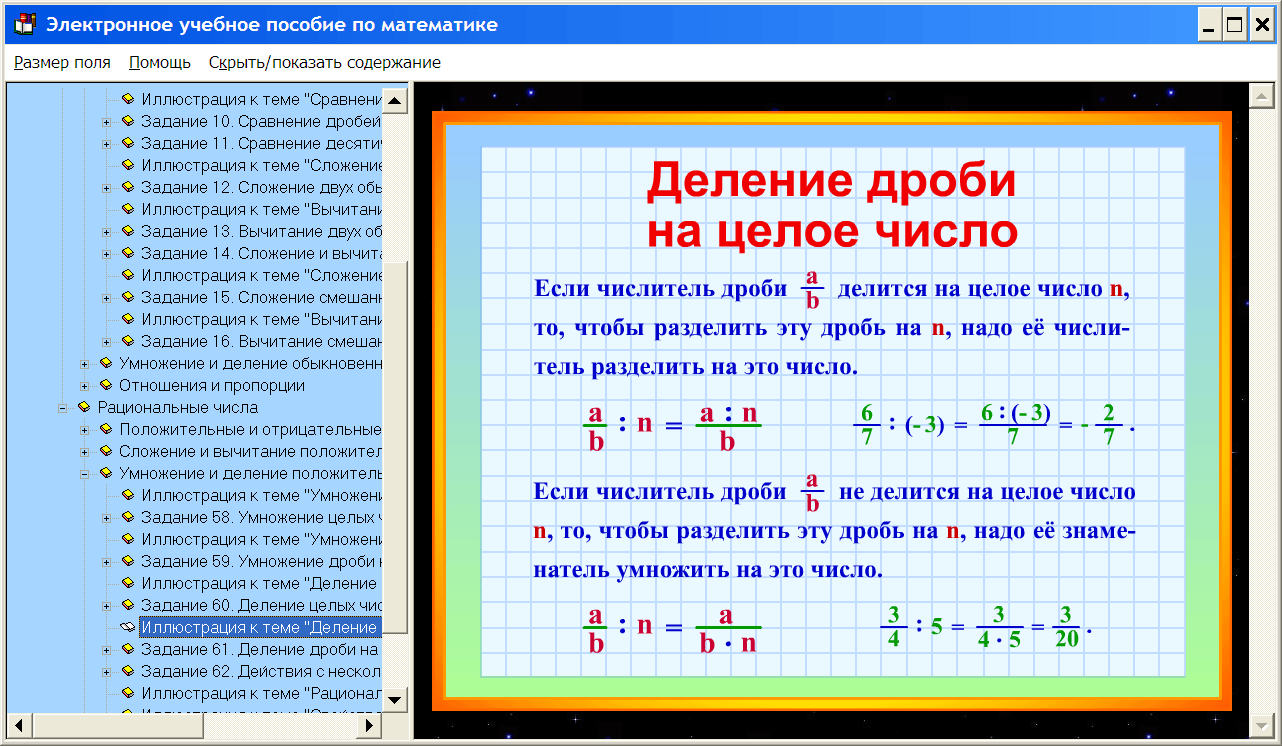

а — сторона квадрата

Единицы измерения времени

1 минута = 60 секунд -1 неделя суток

¹/4 часа = 15 минут 1 месяц = 30 или 31 день

¹/2 часа = 30 минут (полчаса¹/4 года = З месяца (квартал

1 час = 60 минут ¹/2 года = 6 месяцев (полгода

¹/2 суток = 12 часов= 365 или 366суток — 12— месяцев 1 сутки часа 1 век = 100лет

В феврале 28 дней.

В феврале високосного года 29 дней.

Високосный год встречается один раз в четыре года.

Неделя — семь дней (суток)

1 . Понедельник— день получил такое название, так как шёл после недели, а неделей называли день ОТДЫХа (от слов «не делаты»).

2. Вторник — второй день. З. Среда — середина недели. 4. Четверг — четвёртый день.

5. Пятница — пятый день.

б. Суббота — название этого дня недели произошло от слова «шаббат» — так у еврейского народа назывался день отдыха.

7. Воскресенье — день, в который, согласно Библии, воскрес Иисус Христос.

Единицы измерения длины

1 миллиметрмм

1сантиметр см = 10 мм

1 дециметрдм = 10 см

1 метр —1 м = 10дм = 100 см

1километркм

Единицы измерения площади

1 кв. миллиметр = 1 мм ²

1 кв, сантиметр (см ²) = 100 кв. мм (мм ²)

1 кв. дециметр дм ²) = 100 кв, см (см ²)

1 кв. метр (м ²100 кв. дм (дм ²)

1 гектар 1 га) = 10 000 кв. м (м ²)

1 кв, километр (кг“) = 1 000 000 кв, м (м ²)

Единицы измерения массы

1 миллиграмм = 1 мг = 1/1000 г

1 грамм = 1 г = 1000 мг

1 килограмм = 1 кг = 1000 г

1 центнер = 1 ц = 100 кг

1 тонна = 1 т = 1000 кг = 10 ц

Скорость, время, расстояние

Скорость — это расстояние, преодолеваемое предметом за единицу времени.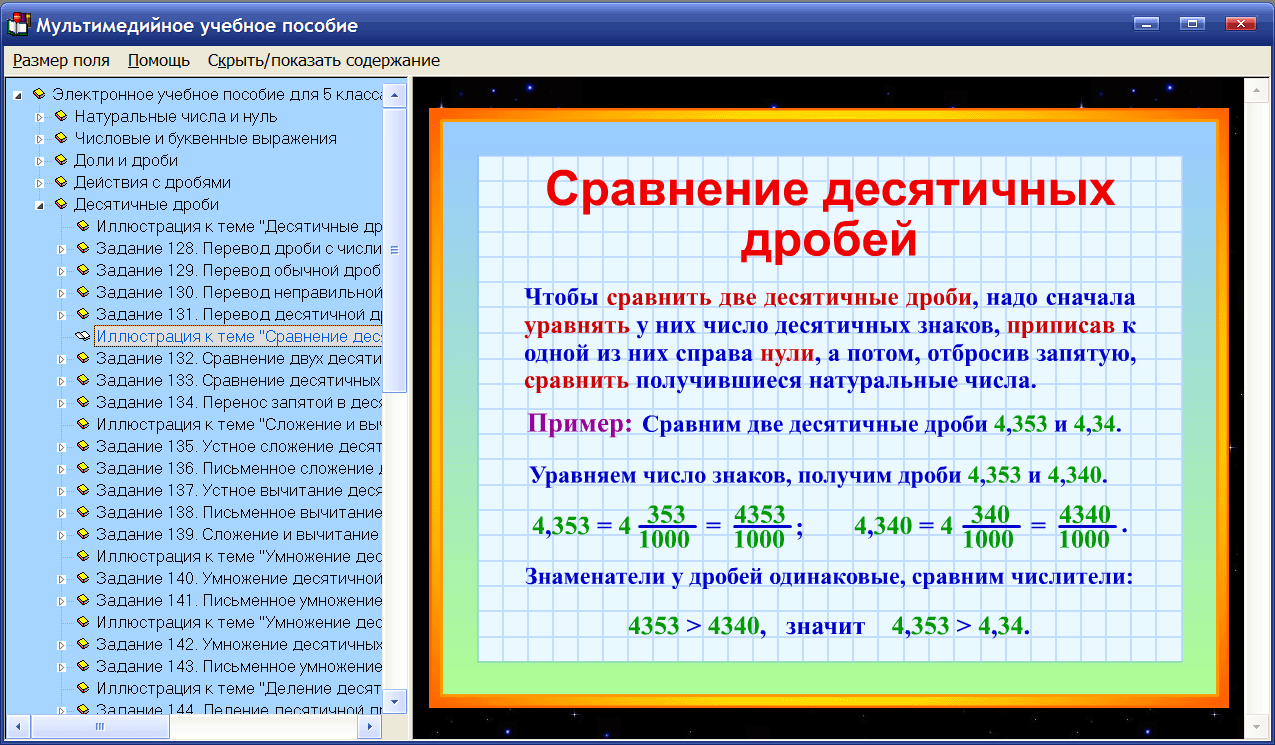 Измеряется в км/ч, км/с, м/мин, м/с.

Скорость — V. Время — t. Расстояние — S.

Чтобы найти СКОРОСТЬ, нужно расстояние разделить на время:

V=S : t

Чтобы найти ВРЕМЯ, надо расстояние разделить на скорость:

Чтобы найти РАССТОЯНИЕ, надо скорость умножить на время:

Цена, стоимость, количество

цена — это стоимость одного предмета, одной единицы товара.

Ц — цена

Ст — общая стоимость Ст —

К— количество ст : ц

Как быстро выучить правила по математике

Математика по праву считается среди детей одним из самых сложных школьных предметов. Способности к изучению математики обуславливаются несколькими факторами. В первую очередь это связано с предрасположенностью самого ребенка к точным или гуманитарным наукам. Во вторую очередь важна база, заложенная в начальных классах. В третью очередь имеет значение наличие желания у ребенка обучению.

Тем не менее, существуют методики, которые помогут быстрее выучить правила математики даже тем, кто считает себя абсолютно не предрасположенным к этой науке. Кроме того такие методики помогают в изучении не только математики, но и других предметов. На сегодняшний день существует много онлайн-ресурсов, предлагающих современные методики школьного образования, среди которых выделяется образовательный портал на сайте https://uchi.ru/.

Чтобы правильно организовать процесс изучения математики существует несколько способов, которые прошли проверку на практике.

Первый способ направлен на устранение пробелов в математических знаниях ближе к окончанию школы. При подготовке к экзамену по математике не нужно пытаться объять необъятное и повторить все сразу или за короткий срок выучить все темы. Во-первых, нужно определить конкретные темы, которые являются трудными для ученика. Это могут быть любые темы за любой предыдущий класс – в этом нет ничего страшного. Нужен конкретный перечень тем для повторения. Затем важно в выбранной теме изучить и понять основные определения. Важно именно понять, а не зазубрить. Далее нужно переходить к практическим заданиям, так как практика является самым лучшим способом усвоения математического материала.

Второй способ основан на четком планировании своей деятельности. В начале изучения ставится конкретная цель. Например, изучить квадратные уравнения. Затем, при необходимости можно разбить цель на подцели (если цель слишком большая). После этого нужно составить план, указав, что именно и в каике сроки нужно выучить. Математика – наука точная, поэтому и подходить к ее изучению нужно рационально и точно. Составление такого плана не только поможет быстрее выучить предмет, но и позволит научиться дисциплинированности и ответственности.

Вконтакте

Facebook

Twitter

Google+

Одноклассники

Четыре математических правила

Четыре правила математики

Понятия сложения, вычитания, умножения и деления представляют собой сложные абстрактные понятия, которые взаимосвязаны.

1. Правила добавления:

положительный + положительный = (добавить) положительный

Пример: 2 + 1 = 3

отрицательный + отрицательный = (добавить) отрицательный

Пример: −3+ (−5) = −8

минус + плюс = (вычесть)

Пример: 2 + (-10) = -8

Возьмите знак числа с наибольшим абсолютным значением

Пример: −14 + 16 = 2

Примечание: −(−7) означает обратное (−7) = 7

2.Правила вычитания:

Замените все вычитанием на сложение и возьмите противоположный знак следующего числа, затем следуйте правилам сложения.

Пример: −7 −(9)

означает -7 +(-9) = -16

Пример: −3 −(−10)

−3 + (10) = 7

Пример:

−8 + (−9) −(−1)−2 (изменить все знаки вычитания)

−8 + (−9)+ (1) + (−2) (выполнять сложение и вычитание слева направо)

−17 +(1)+ (−2)

−16 +(−2) = −18

Сложение и вычитание с отрицательными числами:

При сложении и вычитании положительных и отрицательных чисел полезно помнить следующие правила.

Если операция и знак совпадают, они работают как сложение (положительного) числа, так что

− ⁻ работает как +plus; ⁺

Если операция и знак различны, они работают как вычитание (положительного) числа, так что

+ ⁻ работает как − ^+;

3 и 4. Правила умножения/деления:

Правила умножения и деления одинаковы.

положительный (&крест или ÷) положительный = положительный

Пример: 10 ÷ 2 = 5

отрицательный (&крест; или ÷) отрицательный = положительный

Пример: −4 ✗(−3) = 12

отрицательный (&крест или ÷) положительный = отрицательный

Пример: 18 ÷ (−2) −9

Умножение и деление отрицательных чисел:

При перемножении пар положительных и отрицательных чисел полезно помнить следующие правила: Когда знаки чисел совпадают, ответ — положительное число.

(+) &крест; (+) , ответ (+)

(-) &крест; (−) , ответ (+)

(+) ÷ (+) , ответ (+)

(-) ÷ (-) , ответ (+)

Когда знаки чисел различны, ответ — отрицательное число.

(+) &крест; (-) , ответ (-)

(-) &крест; (+) , ответ (-)

(+) ÷ (-) , ответ (-)

(-) ÷ (+) , ответ (-)

Математические правила — Scientific American

В своей новой книге « В погоне за неизвестным: 17 уравнений, изменивших мир » Ян Стюарт рассказывает об одной из худших шуток в истории науки.Вы можете разработать свою собственную установку, исходя из первых принципов, как только узнаете изюминку: «Скво на бегемоте равно сумме скво на двух других шкурах». Неважно, как коренные американцы завладели бегемотом — важно то, что теорема Пифагора настолько хорошо известна, что авторы комедий считают ее честной игрой, даже если эта игра не может быть найдена на правильном континенте.

Стюарт, ранее писавший колонку «Математические развлечения» для журнала Scientific American , приглашает читателя в увлекательное путешествие по математике, жизненно важной для современного мира.Мы идем от прямоугольного треугольника Пифагора (a ² + b ² = c ²) — хорошо — к закону всемирного тяготения Ньютона (F = G) — хорошо — к специальной теории относительности Эйнштейна (E = mc ^{). 2} ) — все еще с вами — к уравнению Навье-Стокса, управляющему движением жидкостей, — что в значительной степени убедило меня изменить траекторию моей карьеры с науки на научную журналистику.

Я настоятельно рекомендую чудесно доступную книгу Стюарта, а теперь делюсь с вами некоторыми дополнительными уравнениями, не находящимися на ее страницах, но важными для меня лично.

HA > H в любое время ( t )
Технически неравенство HA > H (t) означает, что в любой момент времени ( t ) количество лошадиных ослов (HA) превысит количество лошадей ( H ). (Следует понимать, что время ограничено периодом, начинающимся с эволюции современного человека и заканчивающимся нашим окончательным вымиранием.)

Эта концепция настолько очевидна, что практически имеет статус аксиоматической истины.Неравенство явно сохраняется на ипподромах и конных соревнованиях, где HA может лишь немного превосходить по численности H . (Вы видели шляпы, которые носят некоторые из этих лошадей?) Однако его истинная способность описывать реальность проявляется в ситуациях, когда H может исчезнуть до 0, например, в профессиональной борьбе или в подавляющем большинстве программ на C. -Охватывать.

P _СМ (Д) = 0
Кто-то выигрывает в лотерею, но не я.

M _{S1 + S2} + 3d = WTS
Я обнаружил это уравнение только в последние несколько месяцев, когда путешествовал и работал ненормированные часы, вплоть до отказа от обычных ежедневных омовений.Уравнение утверждает, что через три дня (3d) после вашего последнего душа ( S1 ) и бритья ( S2 ) любой мужчина ( M ) будет выглядеть в точности как Уильям Текумсе Шерман.

20x + 10y + 5z = 0 _С
Это уравнение ясно показывает, что при попытке использовать торговый автомат, принимающий одиночные, у вас будет несколько целых чисел 20, 10 и пятерок, но не будет единиц — и, следовательно, не будет конфет.

OPS = [AB × (H + BB + HBP) + TB × (AB + BB + SF + HBP)] /
[AB × (AB + BB + SF + HBP) ]
Когда мне было 10 лет, я начал посвящать невероятное количество времени анализу и созданию бейсбольной статистики.В то время это было примерно так же сложно, как отбить среднее число попаданий, деленное на у летучих мышей. Теперь, благодаря Биллу Джеймсу и другим поклонникам математики, у нас есть гораздо более ценные статистические данные, такие как база плюс пробивка (OPS), что также означает реакцию более случайных фанатов на чьи-то высказывания по этому поводу, а именно: «О, пожалуйста, встряхнись.

0,5х = 100
Это уравнение оказало сильное влияние на моего друга, которое перешло в мою сторону. Друг хотел быть автомобильным инженером.Но он плохо учился по алгебре в средней школе и знал, что на пути к любой инженерной карьере есть более сложная математика. Так что мы много часов работали над основами алгебры. По истечении указанных часов мой друг смог определить, что 0,5 × 100 равно 50. Но скачок к определению X в 0,5X = 100 остался незамеченным, что привело к моему совету, что он считает карьеру полезно как автомобильная инженерия, избегающая сложных вычислений. Он стал специалистом по автомобильному страхованию и является для меня бесценным помощником всякий раз, когда мою машину сбивает какой-нибудь HA .

Эта статья была опубликована в печати под названием «Математические правила».

Использование скобок в математике: правила и примеры — видео и стенограмма урока

Когда использовать скобки с калькуляторами

Это дополнение к уроку поможет учащимся понять, что в некоторых задачах необходимо использовать круглые скобки, чтобы ввести задачу в калькулятор, даже если круглых скобок не было изначально. Рассмотрим следующую задачу 2/(7 + 3)

Мы знаем, что сначала нужно упростить знаменатель, а затем упростить дробь (и преобразовать в десятичную, если мы предпочитаем)

2/(7 + 3) = 2/10 = 1/5 = 0. 2

Учащиеся умеют группировать члены в знаменателе, потому что их научили распознавать дробную черту как разделение числителя и знаменателя на группы. Но что, если мы попробуем ввести это в калькулятор без предварительного упрощения?

Попросите ученика ввести задачу в калькулятор точно так, как она написана: 2/(7 + 3) и нажать Enter. Калькулятор скажет 3,2857142857142…, возможно, с более или менее десятичными знаками. Это не правильный ответ.Что случилось?

Калькуляторы и компьютеры запрограммированы на выполнение операций в определенном порядке. Когда студент ввел 2/(7 + 3), калькулятор вычислил выражение так, как оно было напечатано: он выполнил деление перед сложением, как указано в порядке операций. Калькулятор вычислил 2/7 +3, что мы не планировали. Чтобы решить эту проблему, предложите учащемуся попробовать использовать круглые скобки вокруг знаменателя, чтобы указать калькулятору сначала упростить 7 + 3. Попросите ученика ввести 2/(7+3) и нажать Enter. Теперь калькулятор скажет 0,2, что правильно.

Практические задачи

Есть и другие ситуации, когда нам нужно было бы ввести круглые скобки в калькуляторе, когда они явно не указаны в задаче. Попросите учащихся решить задачи, набрав их в калькуляторе. Чтобы получить правильный ответ, необходимо добавить скобки. Ответ, если он введен правильно, будет указанным ответом. Попросите учащихся найти, где следует использовать скобки, чтобы получить правильный результат.

1. (2 + 5)/5 Ответ должен быть 1,4

2. (3 — 7)/(2 — 1) Ответ должен быть 4

3. 2(3 + 1) Ответ должен быть 16

Решения для ввода

Чтобы получить правильные ответы, перечисленные выше, задачи должны быть набраны следующим образом:

1. (2 + 5)/5

Группировать члены числителя скобками

2. (3 — 7)/(2 — 1)

Сгруппируйте члены числителя в круглые скобки и сгруппируйте члены знаменателя в круглые скобки.

3. 2(3+1)

Сгруппировать весь показатель в круглых скобках.

Порядок действий — определение, правила, примеры, задачи

Порядок операций — это набор правил, которым необходимо следовать в определенной последовательности при решении выражения. В математике под словом «операции» мы подразумеваем процесс вычисления любого математического выражения, включающий арифметические операции, такие как деление, умножение, сложение и вычитание. Давайте подробно узнаем о правилах порядка действий и о том, насколько хорошо мы можем запомнить правила, используя короткие трюки.

Каков порядок операций?

Порядок Операций — это правило в математике, которое гласит, что сначала мы вычисляем круглые скобки/квадратные скобки, затем степени/порядки, затем деление или умножение (слева направо, в зависимости от того, что наступит раньше) и сложение или вычитание в последнюю очередь. (слева направо, в зависимости от того, что наступит раньше). В математике при вычислении выражения может быть выполнено несколько операций, и упрощение в конце дает разные результаты. Однако у нас может быть только один правильный ответ для любого вида выражения. Чтобы определить правильный ответ, мы упрощаем любое заданное математическое выражение, используя определенный набор правил. Эти правила вращаются вокруг всех основных операторов, используемых в математике. Такие операторы, как сложение (+), вычитание (-), деление (÷) и умножение (×). Посмотрите на данное изображение, чтобы получить представление о том, как точно выглядит порядок операций.

Определение порядка операций

Как мы обсуждали выше, порядок операций можно определить как набор основных правил приоритета, которые мы используем при решении любого математического выражения, включающего несколько операций.Когда подвыражение появляется между двумя операторами, оператор, который идет первым в соответствии со списком, приведенным ниже, должен применяться первым. Порядок действий, правила изложены здесь:

Скобки ( ), { }, [ ]
Экспоненты
Деление (÷) и умножение (×)
Сложение (+) и вычитание (-)

Вышеупомянутый набор правил всегда варьируется в соответствии с заданными математическими выражениями.

Порядок действий Правила

При выполнении любой операции над соответствующими числами, присутствующими в выражении, мы будем следовать заданным основным правилам в конкретной последовательности.

Порядок действий Правило 1: Соблюдайте выражение. Первое правило состоит в том, чтобы решить числа, присутствующие в скобках или скобках. Мы решаем операции группировки изнутри наружу. Обратите внимание на шаблон скобок, присутствующих в выражении, существует особый порядок решения скобок, т.е.е., [ { ( ) } ]. Сначала решите круглые скобки ( ) → фигурные скобки { } → квадратные скобки [ ]. Внутри скобок соблюдается порядок действий.
Порядок действий Правило 2: После решения чисел в скобках найдите любой термин, представленный в виде показателей степени, и решите его.
Порядок операций Правило 3: Теперь у нас остались четыре основных оператора. Найдите числа с действием умножения или деления, решите их слева направо.
Порядок действий Правило 4: Наконец, найдите условия со сложением или вычитанием и решите их слева направо.

Эти правила имеют специальное название аббревиатуры. Мы называем их PEMDAS или BODMAS. Давайте теперь узнаем, что такое PEMDAS или BODMAS.

Порядок действий — PEMDAS против BODMAS

PEMDAS или BODMAS — это две разные аббревиатуры, данные для изучения правил. Эти два имени указывают порядок, в котором должны выполняться операции в выражении.Вот подробный термин для каждой буквы, используемой в упомянутых аббревиатурах. Во-первых, мы обсудим PEMDAS.

Порядок действий PEMDAS

P означает Скобки ( ), { }, [ ]
E означает Экспоненты (a ²) (Например, здесь a — число с показателем степени 2 )
M означает умножение (×)
D означает подразделение (÷)
A означает Дополнение (+)
S означает вычитание (-)

Порядок операций БОДМАС

B означает Кронштейны ( ), { }, [ ]
O означает заказ

D означает подразделение (÷)
M означает умножение (×)
A означает Дополнение (+)
S означает вычитание (-)

С помощью приведенных выше обозначений мы можем легко решить математические выражения и получить правильный ответ.

Как использовать порядок операций?

Давайте рассмотрим различные примеры, упомянутые ниже, чтобы понять точность правил, используемых в порядке операций.

1) Для решения круглых скобок в порядке операций :

Выражение: 4 × (5 + 2)
Решение: 4 × ( 7 ) = 28 (Верно (✔). Это правильный способ решения скобок)
Давайте рассмотрим другой подход для того же выражения.
4 × ( 5 + 2) = 20 + 2 = 22 (Неверно (✘). Это неправильный способ решения скобок)

2) Для решения показателей в порядке операций

Выражение: 4 × (5 ² )
Решение: 4 × ( 25 ) = 100 (Верно (✔). Это правильный способ решения показателей)
Давайте рассмотрим другой подход для того же выражения.
4 × ( 5 ² ) = 20 ² = 400 ((Неверно (✘).Это неправильный способ решения показателей)

3) Для умножения или деления и сложения или вычитания

Выражение: 3 + 5 × 2
Решение: 3 + 5 × 2 = 3 + 10 = 13 (Верно (✔). Это правильный способ.)
Давайте рассмотрим другой подход для того же выражения.
3 + 5 × 2 = 8 × 2 = 16 (Неверно (✘). Это неверный способ. )

Выражение: 3 — 6 ÷ 2
Решение: 3 — 6 ÷ 2 = 3 — 3 = 0 (Верно (✔).Это правильный путь.)
Давайте рассмотрим другой подход для того же выражения.
3 — 6 ÷ 2 = (-3) ÷ 2 = -3/2 (Неверно (✘). Это неверный способ.)

Всегда помните, следуя правилам порядка операций, перед сложением или вычитанием выполняйте умножение или деление

Способы запомнить порядок действий

Мы только что прочитали о двух разных словах PEMDAS и BODMAS.Это лучший способ запомнить порядок операций. PEMDAS можно запомнить по фразе «Пожалуйста, извините мою дорогую тетю Салли». В порядке операций это означает «круглые скобки, показатели степени, умножение и деление, сложение и вычитание». Здесь умножение и деление, сложение и вычитание вместе. Точно так же мы можем запомнить порядок действий со словом BODMAS (скобки, порядок, деление, умножение, сложение и вычитание).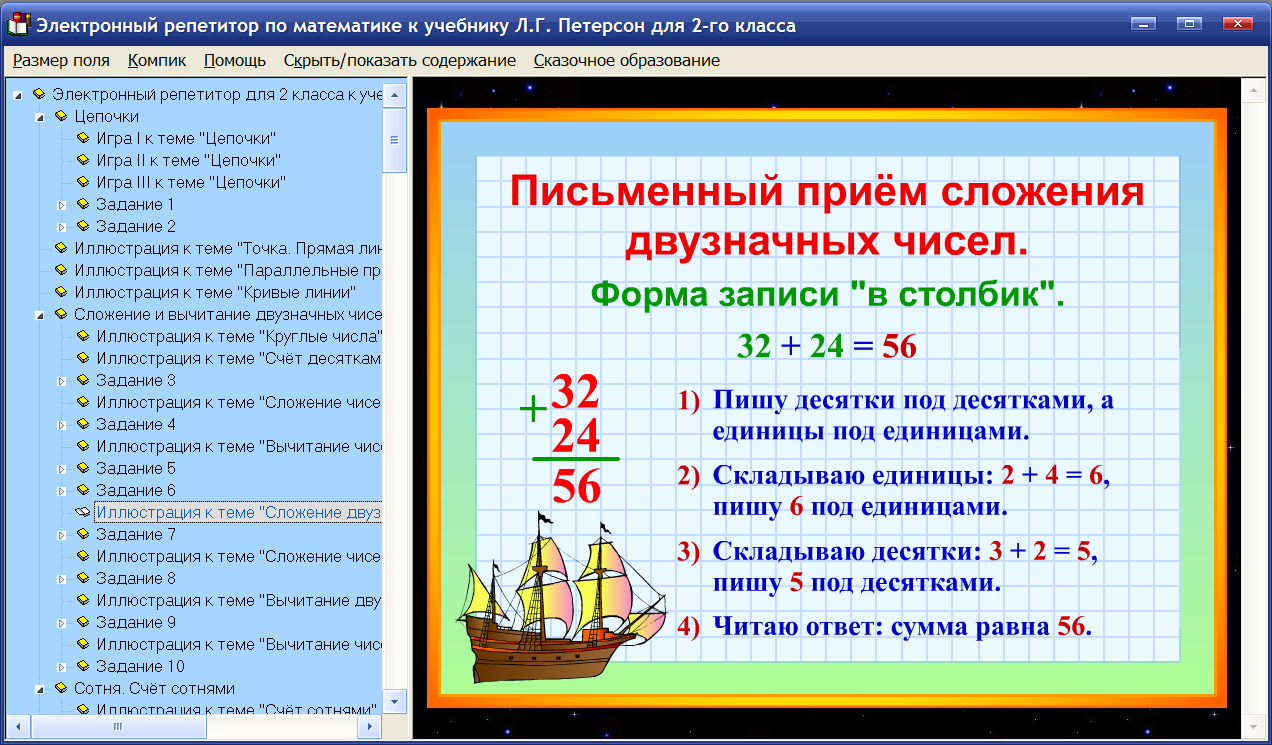

Самый простой способ узнать порядок действий — выполнить указанные шаги:

Сначала начните упрощать термины в скобках
Решите экспоненциальные члены.
Выполнить деление или умножение.
Выполнить сложение или вычитание.

Примечание: Выполняя порядок операций над любым заданным выражением, мы должны соблюдать шаблон операторов.

Реальные приложения порядка операций

Многие действия в нашей жизни требуют определенного порядка операций, чтобы выполнять их хорошо. Возьмем повседневную проблему. Предположим, вы купили пять пицц с пепперони по 20 долларов каждая и хотите поровну разделить общую стоимость на 5 человек.Чтобы узнать, сколько каждый человек должен заплатить, воспользуемся здесь порядком операций.

Общее количество людей = 5
Общее количество пицц = 5
Стоимость одной пиццы = 20
$ Сформулируем выражение, используя PEMDAS:
Выражение: (20 + 20 + 20 + 20 + 20) ÷ 5 или (5 × 20) ÷ 5
Решение: В соответствии с PEMDAS или BODMAS мы сначала решим скобки.
(100) ÷ 5 = 20
Согласно порядку операций, каждый человек должен заплатить 20 долларов.

Подобно вышеупомянутой проблеме, у нас есть много повседневных реальных случаев, когда мы используем порядок операций для решения наших проблем.

☛Связанные статьи о порядке операций

Ознакомьтесь с интересными статьями ниже и узнайте больше о порядке операций и его приложениях.

Часто задаваемые вопросы о порядке операций

Каков порядок операций в математике?

Порядок действий в математике — это набор правил, вращающихся вокруг 4 основных операторов.В соответствии с порядком операций существует определенная последовательность, которой мы должны следовать на каждом операторе при решении данного математического выражения.

Как решить порядок операций?

Чтобы решить порядок операций, сначала посмотрите на выражение и обратите внимание, какому образцу оно точно следует. Теперь начните использовать PEMDAS или BODMAS для решения данного выражения. В соответствии с правилами порядка операций сначала ищите круглые скобки, затем показатели степени, затем переходите к умножению или делению и сложению или вычитанию слева направо.

Как сделать порядок операций с целыми числами?

Мы знаем, что целые числа бывают положительными и отрицательными числами. Мы можем легко выполнить порядок операций с целыми числами, выполнив указанные шаги:

Найдите целые числа в круглых или квадратных скобках и решите их.
После решения целых чисел в скобках найдите любой целочисленный термин, представленный в виде показателей степени, и решите его.
Теперь у нас остались четыре основных оператора, которые нужно выполнять над целыми числами.Найдите целые числа с операцией умножения или деления и решите их слева направо.
Наконец, найдите целые числа с помощью сложения или вычитания и решите их.
В случае с целыми числами нам нужно убедиться, что мы правильно умножаем знаки. Так что (-) × (-) = + и (+) × (-) = —

Как запомнить порядок действий?

Чтобы запомнить порядок операций, мы используем две известные аббревиатуры, т. е.е. ПЕМДАС и БОДМАС. Мы используем любой из двух в соответствии с правилами порядка операций. PEMDAS или BODMAS помогают запомнить процесс решения любого порядка операций для любого n числа выражений.

Как выполнить порядок операций с экспонентами?

Согласно PEMDAS, буква E обозначает показатели степени, которые идут вторым шагом в порядке выполнения операций. Давайте посмотрим на данный пример, чтобы четко понять, как сделать порядок операций с показателями.
Выражение: 7 × (2 ² )
Решение: 7 × ( 4 ) = 28 (Верно (✔). Это правильный способ решения показателей)
Давайте рассмотрим другой подход для того же выражения.
7 × ( 2 ² ) = 14 ² = 196 ((Неверно (✘). Это неправильный порядок выполнения операций с показателями)

Каков правильный порядок операций?

Правильный порядок операций можно легко выразить с помощью слова PEMDAS или BODMAS. Эти два слова можно описать как PEMDAS (круглые скобки, экспоненты, умножение или деление и сложение или вычитание). Аналогично для BODMAS (скобки, порядки, деление, умножение, сложение и вычитание).

Какой порядок операций без скобок?

Следуя правилам порядка выполнения операций, если убрать скобки, то останется EMDAS. EMDAS означает (экспоненты, умножение или деление, сложение или вычитание). Если в выражении у нас нет экспоненциального члена, то нам нужно сначала выполнить умножение или деление, а затем перейти к сложению или вычитанию.Ситуация может варьироваться в зависимости от операторов, присутствующих в данном выражении

Когда мы используем порядок операций?

Многие случаи в нашей жизни проходят через определенный порядок операций, чтобы выполнить ее хорошо. Каждый день мы сталкиваемся с таким сценарием. Например, отправляясь на продуктовый рынок и покупая вещи, мы быстро проделываем в голове порядок действий. Это помогает нам сократить время работы на кассе.

Какая операция выполняется первой в порядке операций?

В предыдущих разделах мы читали о двух аббревиатурах BODMAS и PEMDAS.Согласно обоим аббревиатурам, в порядке операций мы сначала упрощаем скобки или квадратные скобки.

Для чего нужен калькулятор порядка операций?

Калькулятор порядка операций — это онлайн-инструмент и самый быстрый метод, с помощью которого мы можем вычислить любое заданное числовое выражение с учетом правил порядка операций. Чтобы использовать калькулятор порядка операций, нам нужно ввести числовое выражение в правильном формате. Попробуйте калькулятор порядка операций Cuemath и быстро решите выражения в течение нескольких секунд.

☛Также проверьте:

Для большей практики попробуйте эти:

Что такое 4 порядка операций?

4 основных порядка операций:

Скобки.
Экспоненциальный член.
Умножение или деление.
В конце сложения или вычитания.

Четыре порядка операций можно легко вспомнить в любой момент времени, заучив аббревиатуры PEMD AS или B ODMAS .

Экспоненциальные правила | Законы показателей

Правила экспоненты, законы экспоненты и примеры.

Что такое показатель степени

Основание a, возведенное в степень n, равно произведению a, n раз:

а ^н = × × … ×

n раз

а — основание, а n — показатель степени.

Примеры

3 ¹ = 3

3 ² = 3 × 3 = 9

3 ³ = 3 × 3 × 3 = 27

3 ⁴ = 3 × 3 × 3 × 3 = 81

3 ⁵ = 3 × 3 × 3 × 3 × 3 = 243

Экспоненты правила и свойства

Имя правила	Правило	Пример
Правила продукта	a ⁿ ⋅ a ^м = a ^n+m	2 ³ ⋅ 2 ⁴ = 2 ³⁺⁴ = 128
Правила продукта	а ^н ⋅ б ^н = ( а ⋅ б ) ^{1 н 0}	3 ² ⋅ 4 ² = (3⋅4) ² = 144
Частные правила	a ⁿ / a ^м = a ⁿ ^{— м}	2 ⁵ / 2 ³ = 2 ^5-3 = 4
Частные правила	а ^н / б ^н = ( а / б ) ^н	4 ³ / 2 ³ = (4/2) ³ = 8
Силовые правила	( б ^н ) ^м = б ^н⋅м	(2 ³ ) ² = 2 ^3⋅2 = 64
	_б н ^м _{= б} ( н ^{м )}	₂ 3 ² _{= 2} (3 ² ) _{= 512}
	^м √( б ^н ) = б ^{н / м}	² √(2 ⁶ ) = 2 ^6/2 = 8
	б ^{1/ н} = ^н √ б	8 ^1/3 = ³ √8 = 2
Отрицательные показатели степени	б ^-н = 1 / б ^п	2 ^-3 = 1/2 ³ = 0. 125
Нулевые правила	б ⁰ = 1	5 ⁰ = 1
Нулевые правила	0 ⁿ = 0 , для n >0	0 ⁵ = 0
Одно правило	б ¹ = б	5 ¹ = 5
Одно правило	1 ^п = 1	1 ⁵ = 1
Минус одно правило		(-1) ⁵ = -1
Производное правило	( x ⁿ ) ‘ = n ⋅ x ⁿ ^-1	( х ³ ) ‘ = 3⋅ х ^3-1
Интегральное правило	∫ x ⁿ dx = x ⁿ ⁺¹ /( n +1)+ C	∫ x ² dx = x ²⁺¹ /(2+1)+ C

Экспоненты правила продукта

Правило продукта с той же базой

a ⁿ ⋅ a ^м = a ^n+m

Пример:

2 ³ ⋅ 2 ⁴ = 2 ³⁺⁴ = 2 ⁷ = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128

Правило произведения с одинаковым показателем

а ^н ⋅ б ^н = ( а ⋅ б ) ^н

Пример:

3 ² ⋅ 4 ² = (3⋅4) ² = 12 ² = 12⋅12 = 144

См. : Умножение показателей степени

Частные правила степени

Правило частных с тем же основанием

a ⁿ / a ^м = a ⁿ ^{— м}

Пример:

2 ⁵ / 2 ³ = 2 ^5-3 = 2 ² = 2⋅2 = 4

Частное правило с одинаковым показателем

a ⁿ / b ⁿ = ( a / b ) ⁿ

Пример:

4 ³ / 2 ³ = (4/2) ³ = 2 ³ = 2⋅2⋅2 = 8

См.: Показатель степени деления

Экспоненты степенных правил

Силовое правило I

( a ⁿ ) ^м = a ^нм

Пример:

(2 ³ ) ² = 2 ^3⋅2 = 2 ⁶ = 2⋅2⋅2⋅2⋅2⋅2 = 64

Силовое правило II

_A ^N ^м 9061 = _A ( N ^M)

Пример:

₂ 3 ² _{= 2} (3 ² ) _{= 2} (3⋅3) _{= 2} 9 _{= 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512}

Силовое правило с радикалами

^м √( a ⁿ ) = a ⁿ ^{/ м}

Пример:

² √(2 ⁶ ) = 2 ^6/2 = 2 ³ = 2⋅2⋅2 = 8

Правило отрицательных показателей степени

б ^-н = 1 / б ^п

Пример:

2 ^-3 = 1/2 ³ = 1/(2⋅2⋅2) = 1/8 = 0.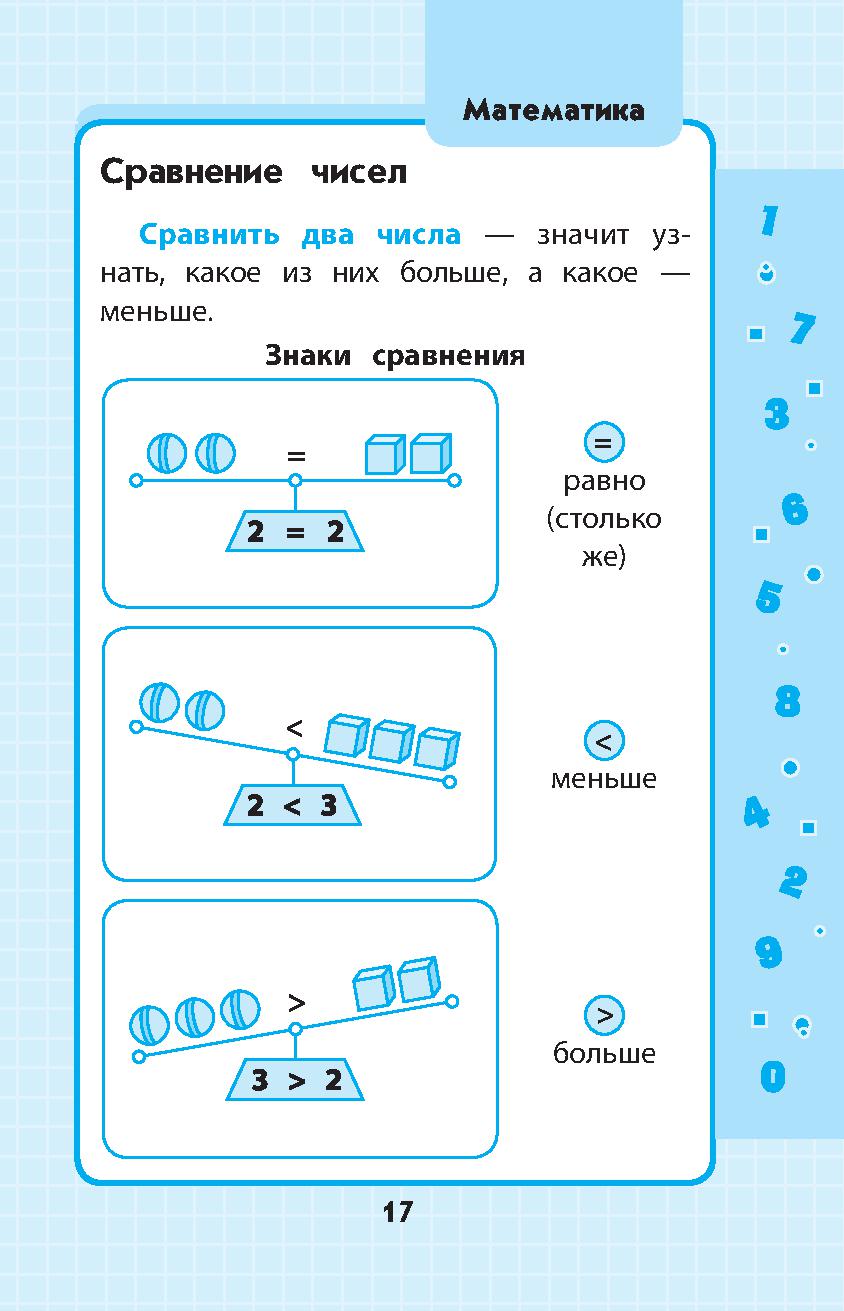 125

См.: Отрицательные показатели степени

Калькулятор экспоненты ►

См. также

Каков порядок операций? [Видео и практика]

«Пожалуйста, извините, моя дорогая тетя Салли».

Теперь я знаю, о чем вы думаете: «Что на самом деле означает эта фраза?» На самом деле довольно много, потому что это высказывание дает ключ к запоминанию важного математического понятия: порядка операций.

Порядок операций — одна из наиболее важных математических концепций, которую вы изучите, потому что она определяет, как мы вычисляем задачи.Он дает нам шаблон, чтобы все решали математические задачи одинаково.

Начнем с простого вопроса. Что такое операция?

Операция — это математическое действие. Сложение, вычитание, умножение, деление и вычисление корня — все это примеры математических операций. Давайте посмотрим на эту задачу:

$7\times 4-6=?$

Выглядит просто, правда? Что ж, это было бы не так просто, если бы мы не понимали порядок, в котором выполняются математические операции. Если бы у нас не было правил, определяющих, какие вычисления мы должны произвести в первую очередь, мы бы пришли к другим ответам.

Следует ли начать с вычитания 4 минус 6, а затем умножения на 7?

Нет. Порядок операций говорит нам, как решить математическую задачу. И это возвращает нас к тете Салли.

Каков порядок операций?

Операции имеют определенный порядок, и это то, что «Пожалуйста, извините, моя дорогая тетя Салли» помогает нам понять. Это аббревиатура, которая говорит нам, в каком порядке мы должны решать математическую задачу.

«Пожалуйста» означает « скобки », поэтому сначала мы решаем все, что находится внутри скобок.

Затем «Извините», что означает « Экспоненты ». Мы решаем это после того, как решим все в скобках.

Умножение , то есть «Мое», и это происходит слева направо.

А затем деление , то есть «Дорогой», что тоже бывает слева направо.

А дальше у нас сложение и вычитание , что тоже происходит слева направо, а это «Тетя» и «Салли».

Порядок операций Примеры

Итак, теперь, когда мы знаем порядок операций, давайте применим его к нашей задаче и решим ее.

$7\times 4-6=?$

У нас нет круглых скобок и у нас нет показателей степени, но у нас есть умножение, поэтому мы делаем это до того, как будем выполнять сложение или вычитание. Давайте продолжим и умножим $7\х4$. Это дает нам 28.

$28-6$

А теперь мы вычитаем 6, что дает нам 22.

$28-6=22$

Теперь давайте рассмотрим другую задачу.

$7+7\умножить на 3$

Без операций эту задачу можно вычислить как $7+7=14\умножить на 3=42$.

И это было бы неправильно!

Помните, вы умножаете, прежде чем складывать. Таким образом, уравнение должно выглядеть так:

$7+(7\times 3)$
$=7+21$
$=28$

Итак, когда мы решаем задачи таким образом, мы можем использовать круглые скобки, чтобы сгруппировать наши числа, которые будут занимать первое место. {2})\)

$=6\умножить на 9$

$=54$

Видите? Решение уравнения в правильном порядке дает правильный ответ.

Давайте попробуем еще одну задачу. Этот немного сложнее, но он прекрасно иллюстрирует порядок операций.

$5\умножить на 10-(8\умножить на 6$$-15)+4\умножить на 20\дел 4$

Запомнить порядок. Что мы делаем в первую очередь? Цифры в скобках. Итак, $8\times 6=48$, затем мы вычитаем 15, и это дает нам 33.Вот как теперь выглядит задача:

$5\times 10-33+4\times 20\div 4$

Итак, наш следующий шаг — умножение и деление, поэтому давайте решим все наши задачи на умножение и деление и тогда посмотрим, что у нас осталось.

$50-33+80\дел 4$
$50-33+20$

Теперь закончим со сложением и вычитанием, вот что у нас есть:

$50- 33+20$
$=50-13$
$=37$

И наш ответ 37!

Есть исключение. Если уравнение имеет только одно выражение, вам не нужно соблюдать порядок операций.

Вот несколько примеров одиночных выражений.

$10+10$: Ну, других операций нет, так что просто сложите их и получите 20. То же самое с вычитанием, умножением и делением. Все это единичные выражения.

Итак, ребята, это наше видео о порядке действий. Я надеюсь, что это было полезно!

Увидимся в следующий раз!

Правило 3: прямое и обратное

В сегодняшней статье мы будем работать над пропорциями .На этот раз мы рассмотрим способ решения прямой и обратной пропорции: правило 3 .

Что такое правило 3?

Правило из 3 — это операция, которая помогает нам быстро решать как прямые, так и обратные пропорции словесных задач.

Чтобы использовать правило 3, нам нужны три значения: два пропорциональных друг другу и третье. Оттуда мы вычислим четвертое значение .

Прямое правило 3

Начнем с рассмотрения того, как применить в случае прямых пропорций .

Мы поместим 3 значения (которые мы назовем «a» , «b» и «c» ) и неизвестное значение, которое мы хотим вычислить ( «x» ) в таблице. Далее применим следующую формулу:

В качестве примера решим следующую задачу:

По прибытии в отель персонал дал нам карту с указанием достопримечательностей города и сказал нам, что 5 сантиметров на карте соответствуют 600 метрам в действительности.Сегодня мы хотим отправиться в парк, который находится в 8 сантиметрах от отеля на карте. Как далеко от отеля парк?

Давайте составим таблицу с тремя значениями и неизвестным значением («x»), и мы найдем «x» с помощью только что изученной формулы .

Сантиметры на карте Метры в реальности

Ответ: Парк находится в 960 метрах от отеля.

Обратное правило 3

Теперь посмотрим, как применить правило 3 в случае обратных пропорций .

Мы поместим 3 значения и неизвестное значение в таблицу , так же, как мы сделали в предыдущем случае, , но мы применим другую формулу:

Давайте рассмотрим пример:

Вчера 2 грузовика перевезли товар из порта на склад.Сегодня 3 грузовика того же размера, что и вчера, должны будут совершить 6 рейсов, чтобы перевезти такое же количество товаров со склада в торговый центр. Сколько рейсов грузовики сделали вчера?

Мы помещаем значения в таблицу и применяем формулу для обратного правила 3  :

Грузовые автомобили Необходимые поездки

Ответ: Вчера 2 грузовика совершили 9 рейсов.