Показательные неравенства с разными основаниями как решать: Решение показательного неравенства с разными основаниями - Управленческое образование

{\log_{0,2}{4}}\)

Избавимся от оснований с переменой знака т.к. $0,2<1$

$-7x+4≤\log_{0,2}⁡{4}$

$\log_{0,2}{⁡4}$ – число некрасивое, но все-таки число, т.е. перед нами обычное линейное неравенство.
Будем выражать $x$, для этого перенесем $4$ в правую часть

$-7x≤\log_{0,2}{⁡4}-4$

Поделим обе части на $-7$

$x≥$ $\frac{4-\log_{0,2}{⁡4}}{7}$

Ответ: $x∈$$[\frac{4-\log_{0,2}{⁡4}}{7}$$;∞)$

Знаю, выглядит не очень, но ответ не выбирают.

x>-5\) будет любое число: $x∈(-∞;∞)$.

Смотрите также:
Показательные уравнения
Логарифмические уравнения
Равносильные преобразования неравенств
Логарифмические неравенства

Содержание

Показательные неравенства — как решать? Примеры, методы решения и свойства

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение показательных неравенств

Показательными считаются неравенства, которые включают в себя показательную функцию. Другими словами, это неравенства с переменной в показателе степени: a^f(x) > a^g(x), a^f(x) < a^g(x)

Из них показательно-степенными неравенствами являются те, в которых есть переменные и в показателе степени, и в основании.

Для изучения этой темы стоит повторить:

И, конечно, для решения тригонометрических и логарифмических показательных неравенств также придется вспомнить формулы соответствующих разделов алгебры.

Если все это еще свежо в памяти, давайте приступим. Как и к показательным уравнениям, к неравенствам стоит подходить, помня о свойствах показательной функции. Напомним, что она выглядит так: y = a^x, где a > 0 и a ≠ 1. Два графика ниже дают представление о том, на что похожа такая функция, когда основание степени а больше и меньше единицы. Наверняка вы уже догадались, каково главное свойство этой функции. Да, она монотонна.

При этом заметьте — значения а всегда больше нуля. На практике в этом несложно убедиться, если возводить какое-либо число во всевозможные степени, включая отрицательные. Например: 2^-2 = 4, 2^-4 = 1/16 и т. д. Значение функции будет уменьшаться, но никогда не достигнет нуля.

Для любых а и х верно неравенство a^x > 0, т. е. показательная функция не принимает отрицательных значений.

Запишем следствие монотонности показательной функции в виде формул:

a^f(x) > a^g(x) <-> f(x) > g (x), когда функция возрастает, т. е. а > 1;
a^f(x) > a^g(x) <-> f(x) < g (x), когда функция убывает, т. е. 0 < а < 1.

На этом свойстве показательных неравенств так или иначе основываются все методы решения, и сейчас мы разберемся, как им пользоваться.

Как решать показательные неравенства

Как мы уже говорили, для успешного освоения этой темы нужно хорошенько повторить все, что касается показательных уравнений. Способы решения показательных неравенств выглядят примерно так же — мы будем пытаться упростить выражение, получить одинаковые степени или одинаковые основания, по возможности свести все к квадратному или рациональному уравнению. Но есть и свои тонкости…

Допустим, у нас есть простейшее показательное неравенство:

3^х > 9

Если вы помните, как решались показательные уравнения, не придется долго думать, что делать с таким неравенством — приведем его к одинаковому основанию:

3^х > 3²

х > 2

Казалось бы, все логично, но всегда ли можно смело вычеркивать одинаковые основания степеней? А что, если вместо 3 у нас основание степени будет 0,5? Посмотрим:

0,5^х > 0,5²

Проверим, верно ли в таком случае х > 2.

0,5² = 0,25;

0,5³ = 0, 125 и т. д.

Как видите, на самом деле в этом случае х < 2. Неудивительно, если вспомнить, о чем мы писали в самом начале, когда рисовали графики возрастающей и убывающей показательной функции.

Если а > 1, то a^x > aⁿ <-> a > n, и при решении неравенства можно просто убрать одинаковые основания степени.

Если 0 < а < 1, то a^x > aⁿ <-> a < n, т. е. одинаковые основания по-прежнему можно убрать, но при этом необходимо поменять знак неравенства.

Если a = 1, то решений нет, т. к. единица в любой степени равна сама себе.

Наконец, если рассмотреть случай, когда а < 0, получится неопределенность. Допустим:

(-3)^х > 9

(-3)^х > 3²

Логичное, на первый взгляд, предположение, что х > 2, не выдержит проверки, потому что:

х = 3 -> (-3)³ = -27

х = 4 -> (-3)⁴ = 81

х = 5 -> (-3)⁵ = -243

Если продолжить этот ряд, знаки будут чередоваться, и наш корень будет попеременно то меньше, то больше 2. Поэтому для ясности всегда предполагается, что основание степени — положительное число.

Это были общие правила, а сейчас рассмотрим разные виды показательных неравенств и примеры с решениями.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Показательные неравенства, сводящиеся к простейшим

Решая показательные уравнения, вы наверняка первым делом исследовали их на возможность приведения к одинаковым основаниям или одинаковым степенным функциям. Так вот, с неравенствами можно делать то же самое! Помните лишь о смене знака, если основание степени меньше единицы. И да пребудет с вами сила. 😎

Попробуем на примере несложного показательного неравенства с разными основаниями.

Пример 1

3^х < 243

3^х < 3⁵

Поскольку 3 больше 1, знак не меняем:

х < 5

Ответ: х (5; +∞).

Пример 2

(1/2)^х > √8

(1/2)^х > 2^3/2

(1/2)^х > (1/2)^-3/2

х < -3/2, обратите внимание — мы поменяли знак, поскольку 1/2 < 1.

Ответ: х ∈ (-∞; -3/2).

Показательные неравенства, сводящиеся к квадратным

Снова давайте вспомним, как аналогичный метод применялся к показательным уравнениям. Если все переменные имели общий множитель, его можно было обозначить новой переменной — в итоге у нас, как правило, получалось квадратное уравнение. Нужно было лишь найти дискриминант и произвести обратную замену. И снова алгоритм решения показательных неравенств будет совершенно таким же.

Пример 1

9^х + 27 < 12 × 3^х

Наименьший общий множитель в данном случае будет 3^х, обозначим его новой переменной у и перенесем все слагаемые в левую сторону.

9^х + 27 < 12 × 3^х

(3^х)²

— 12 × 3^х + 27 < 0

3^х = у

y² — 12y + 27 < 0

3 < y < 9

Пришло время выполнить обратную замену.

3 < 3^х < 9

3¹ < 3^х < 3²

Поскольку 3 > 1, мы не меняем знак.

1 < х < 2

Ответ: х ∈ (1;2).

Пример 2

2sin²x — 5 sinx + 2 < 0

Это более сложное показательное неравенство, но и в нем можно угадать скрытое уравнение квадратичной функции — достаточно заменить sinx на новую переменную.

sinx = y

2y²— 5y + 2 < 0

y = 2

y = 1/2

1/2 < y < 2

Произведем обратную замену:

1/2 < sinx < 2

Поскольку sinx и так меньше 1, а значит, точно меньше 2, мы можем отбросить правую часть неравенства и сосредоточиться только на левой.

1/2 < sinx

Воспользуемся формулой х c (arcsina + 2πn; π — arcsina + 2πn), n ∈ z

х c (arcsin 1/2 + 2πn; π — arcsin 1/2 + 2πn), n ∈ z

х c (π/6 + 2πn; π — π/6 + 2πn), n ∈ z

х c (π/6 + 2πn; 5π/6 + 2πn), n ∈ z

Ответ: х ∈ (π/6 + 2πn; 5π/6 + 2πn), n ∈ z

Показательные неравенства, сводящиеся к рациональным

Как вы, наверное, помните из предыдущего курса алгебры, рациональные показательные неравенства — это такие, в которых левая и правая часть представляют собой дробно-рациональные функции. Метод их решения таков: нужно перенести все в левую часть, чтобы в правой остался лишь ноль, и привести к общему знаменателю. Далее решаем уравнение, отмечаем все корни на оси и применяем метод интервалов (если забыли, что это такое — повторите).

Важно помнить: если в числителе и знаменателе встретятся одинаковые множители с переменной, сокращать их нельзя.

Пример 1

Преобразуем неравенство указанным выше способом:

(обратите внимание, мы избавились от минуса в числителе и поменяли знак неравенства).

Поскольку выражение 2^х + 2 в любом случае будет больше нуля, мы можем смело его исключить из неравенства.

(2^х— 2) × (2^х— 1/2) × (2^х— 3) > 0

1/2 < 2^х < 2

2^х > 3

-1 < х < 1

х > log₂3

Ответ: х ∈ (-1;1) U (log₂3; +∞)

Пример 2

Обозначим 3^х через новую переменную y:

3^х = y, при условии что 3^х > 0.

Применим метод интервалов и получим:

y c (1/3; 3)

Вернем на место нашу старую переменную:

3^-1 < 3^х <= 3

Поскольку 3 больше 1, знаки не меняем:

-1 < х <= 1

Ответ: х ∈ (-1;1).

Однородные показательные неравенства

Однородными называются такие показательные неравенства, где в каждом слагаемом сумма степеней одинакова.

Иногда такие выражения бывают очень длинными и запутанными, но не стоит этого пугаться. Практически все неравенства с однородными показательными функциями решаются по одному принципу: стараемся упростить выражение, разделив его на одночлен, а затем при необходимости делаем замену переменных.

Пример 1

4^х — 2 × 5^2х — 2^х × 5^х > 0

2 × 2^х — 2 × 5^2х — 2^х × 5^х > 0

В левой части неравенства мы видим однородные функции относительно 2^х и 5^х. Следовательно, можно разделить обе части на 2^2х или 5^2х. Выберем 5^2х, т. е. 25^х. В итоге у нас получится:

Если обозначить (2/5)^х новой переменной y, получим квадратное неравенство:

y²— y — 2 > 0

y₁ > 2

y₂ < -1

Исходя из этого, у нас образуется следующее неравенство:

Поскольку 2/5 меньше 1, функция убывающая и мы должны поменять знак:

х < log_2/52

Ответ: х ∈ (-∞; log_2/52).

Пример 2

Но где здесь одинаковая сумма степеней? Сейчас будет:

Ответ: х ∈ (-∞; +∞) / (-2; 3)

Неравенства, решаемые графическим методом

Этот метод решения показательных неравенств — самый наглядный, и для многих он может показаться самым простым. Нужно лишь построить графики функций, заданных в левой и правой части выражения, а затем посмотреть, в какой точке они пересекаются. Если бы мы имели дело с уравнением, эта точка стала бы корнем.

Но поскольку мы рассматриваем неравенства, нужно будет выделить искомую область. Для неравенства f(x) > g(x) это будет та область, где график функции f(x) находится выше.

Пример 1

2^х <= 3-х

Итак, нам нужны графики двух функций: 2^х и 3 — х, а также точка их пересечения.

Очевидно, что точкой пересечения является х = 1, при этом график функции 2^х ниже в области от -∞ до 1.

Ответ: х ∈ (-∞; 1).

Пример 2

(1/2)^х > х + 3

Начертим графики этих двух функций, чтобы найти точку пересечения.

Искомой точкой будет х = -1, а областью, где функция (1/2)^х находится выше — диапазон от -∞ до -1.

Ответ: х ∈ (-∞; — 1).

«Показательные уравнения и показательные неравенства»

Исходя из этого и применяя теорему о корне, получим, что уравнение a x = b иметь один единственный корень, при b>0 и положительном a не равном единице. Чтобы его найти, необходимо представить b в виде b = a c .
Тогда очевидно, что с будет являться решением уравнения a x = a c .

Рассмотрим следующий пример: решить уравнение 5 (x 2 — 2*x — 1) = 25.

Представим 25 как 5 2 , получим:

5 (x 2 — 2*x — 1) = 5 2 .

Или что равносильно:

x 2 — 2*x — 1 = 2.

Решаем полученное квадратное уравнение любым из известных способов. Получаем два корня x = 3 и x = -1.

Ответ: 3;-1.

Решим уравнение 4 x — 5*2 x + 4 = 0. Сделаем замену: t=2 x и получим следующее квадратное уравнение:

t 2 — 5*t + 4 = 0.
Решаем это уравнение любым из известных способов. Получаем корни t1 = 1 t2 = 4

Теперь решаем уравнения 2 x = 1 и 2 x = 4.

Ответ: 0;2.

Решение показательных неравенств

Решение простейших показательных неравенств основывается тоже на свойствах возрастания и убывания функции. Если в показательной функции основание a больше единицы, то функция будет возрастающей на всей области определения.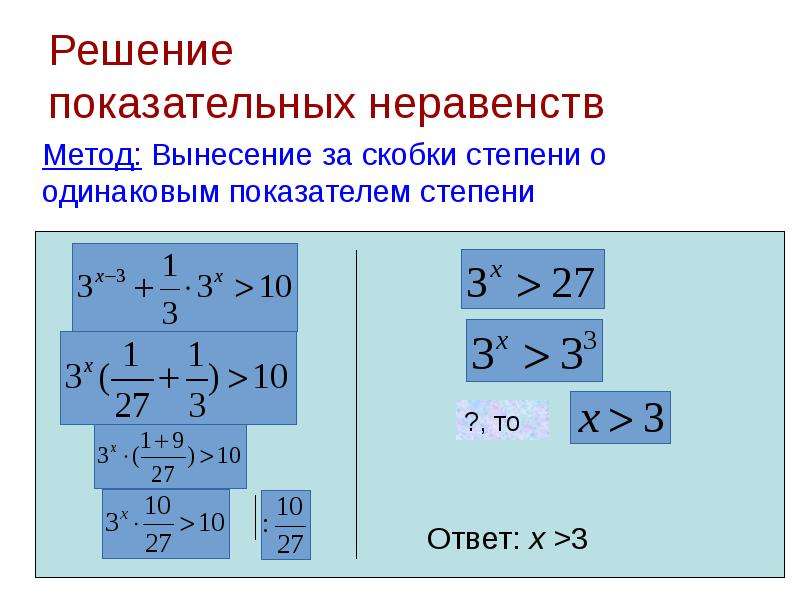 Если в показательной функции для основания а выполнено следующее условие 0, то данная функция будет убывающей на всем множестве вещественных чисел.

Рассмотрим пример: решить неравенство (0.5) (7 — 3*x)

Заметим, что 4 = (0.5) 2 . Тогда неравенство примет вид (0.5)(7 — 3*x)

Получим: 7 — 3*x>-2.

Отсюда: х

Ответ: х

Если бы в неравенстве основание было больше единицы, то при избавлении от основания, знак неравенства менять было бы не нужно.

На данном уроке мы рассмотрим различные показательные неравенства и научимся их решать, основываясь на методике решения простейших показательных неравенств

1. Определение и свойства показательной функции

Напомним определение и основные свойства показательной функции. Именно на свойствах базируется решение всех показательных уравнений и неравенств.

Показательная функция — это функция вида , где основание степени и Здесь х — независимая переменная, аргумент; у — зависимая переменная, функция.

Рис. 1. График показательной функции

На графике показаны возрастающая и убывающая экспоненты, иллюстрирующие показательную функцию при основании большем единицы и меньшем единицы, но большим нуля соответственно.

Обе кривые проходят через точку (0;1)

Свойства показательной функции :

Область определения: ;

Область значений: ;

Функция монотонна, при возрастает, при убывает.

Монотонная функция принимает каждое свое значение при единственном значении аргумента.

При , когда аргумент возрастает от минус до плюс бесконечности, функция возрастает от нуля не включительно до плюс бесконечности, т. е. при данных значениях аргумента мы имеем монотонно возрастающую функцию (). При наоборот, когда аргумент возрастает от минус до плюс бесконечности, функция убывает от бесконечности до нуля не включительно, т. е. при данных значениях аргумента мы имеем монотонно убывающую функцию ().

2. Простейшие показательные неравенства, методика решения, пример

На основании вышесказанного приведем методику решения простейших показательных неравенств:

Методика решения неравенств:

Уравнять основания степеней;

Сравнить показатели, сохранив или изменив на противоположный знак неравенства.

Решение сложных показательных неравенств заключается, как правило, в их сведении к простейшим показательным неравенствам.

Основание степени больше единицы, значит, знак неравенства сохраняется:

Преобразуем правую часть согласно свойствам степени:

Основание степени меньше единицы, знак неравенства необходимо поменять на противоположный:

Для решения квадратного неравенства решим соответствующее квадратное уравнение:

По теореме Виета находим корни:

Ветви параболы направлены вверх.

Таким образом, имеем решение неравенства:

Несложно догадаться, что правую часть можно представить как степень с нулевым показателем:

Основание степени больше единицы, знак неравенства не меняется, получаем:

Напомним методику решения таких неравенств.

Рассматриваем дробно-рациональную функцию:

Находим область определения:

Находим корни функции:

Функция имеет единственный корень,

Выделяем интервалы знакопостоянства и определяем знаки функции на каждом интервале:

Рис. 2. Интервалы знакопостоянства

Таким образом, получили ответ.

Ответ:

3. Решение типовых показательных неравенств

Рассмотрим неравенства с одинаковыми показателями, но различными основаниями.

Одно из свойств показательной функции — она при любых значениях аргумента принимает строго положительные значения, значит, на показательную функцию можно разделить. Выполним деление заданного неравенства на правую его часть:

Основание степени больше единицы, знак неравенства сохраняется.

Проиллюстрируем решение:

На рисунке 6.3 изображены графики функций и . Очевидно, что когда аргумент больше нуля, график функции расположен выше, эта функция больше. Когда же значения аргумента отрицательны, функция проходит ниже, она меньше. При значении аргумента функции равны, значит, данная точка также является решением заданного неравенства.

Рис. 3. Иллюстрация к примеру 4

Преобразуем заданное неравенство согласно свойствам степени:

Приведем подобные члены:

Разделим обе части на :

Теперь продолжаем решать аналогично примеру 4, разделим обе части на :

Основание степени больше единицы, знак неравенства сохраняется:

4. Графическое решение показательных неравенств

Пример 6 — решить неравенство графически:

Рассмотрим функции, стоящие в левой и правой части и построим график каждой из них.

Функция — экспонента, возрастает на всей своей области определения, т. е. при всех действительных значениях аргумента.

Функция — линейная, убывает на всей своей области определения, т. е. при всех действительных значениях аргумента.

Если данные функции пересекаются, то есть система имеет решение, то такое решение единственное и его легко можно угадать. Для этого перебираем целые числа ()

Несложно заметить, что корнем данной системы является :

Таким образом, графики функций пересекаются в точке с аргументом, равным единице.

Теперь нужно получить ответ. Смысл заданного неравенства в том, что экспонента должна быть больше или равна линейной функции, то есть быть выше или совпадать с ней. Очевиден ответ: (рисунок 6.4)

Рис. 4. Иллюстрация к примеру 6

Итак, мы рассмотрели решение различных типовых показательных неравенств. Далее перейдем к рассмотрению более сложных показательных неравенств.

Список литературы

Мордкович А. Г. Алгебра и начала математического анализа. — М.: Мнемозина. Муравин Г. К., Муравина О. В. Алгебра и начала математического анализа. — М.: Дрофа. Колмогоров А. Н., Абрамов А. М., Дудницын Ю. П. и др. Алгебра и начала математического анализа. — М.: Просвещение.

Math. md . Mathematics-repetition. com . Diffur. kemsu. ru .

Домашнее задание

1. Алгебра и начала анализа, 10-11 класс (А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын) 1990, № 472, 473;

2. Решить неравенство:

3. Решить неравенство.

Способы решения систем уравнений

Для начала кратко вспомним, какие вообще существуют способы решения систем уравнений.

Существуют четыре основных способа решения систем уравнений:

Способ подстановки: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x. $ После этого мы легко можем вычислить переменную $y.$

Способ сложения: в данном способе необходимо умножать одно или оба уравнения на такие числа, чтобы при сложении вместе обоих одна из переменных «исчезла».

Графический способ: оба уравнения системы изображается на координатной плоскости и находится точка их пересечения.

Способ введения новых переменных: в этом способе мы делаем замену каких-либо выражений для упрощения системы, а потом применяем один из выше указанных способов.

Системы показательных уравнений

Определение 1

Системы уравнений, состоящие из показательных уравнений, называются системой показательных уравнений.

Решение систем показательных уравнений будем рассматривать на примерах.

Пример 1

Решить систему уравнений

Рисунок 1.

Решение.

Будем пользоваться первым способом для решения данной системы. Для начала выразим в первом уравнении $y$ через $x$.

Рисунок 2. {\varphi (x)} $, где $a >0,a\ne 1$ равносильна совокупности двух систем

\U}

Как решать показательные неравенства | Логарифмы

Рассмотрим, как решать показательные неравенства, содержащих степени с разными основаниями. Решение таких неравенств аналогично решению соответствующих показательных уравнений.

Группируем степени с одинаковыми основаниями. Удобнее для этого развести их по разные стороны неравенства:

Из каждой пары степеней выносим за скобки общий множитель — степень с меньшим показателем. Вынести за скобки общий множитель- значит, каждое слагаемое разделить на этот множитель. При делении степеней с одинаковыми основаниями основание оставляем прежним, а показатели вычитаем:

Делить можно сразу на 20 (20=4∙5), но практика показывает, что деление в два этапа позволяет избежать возможных ошибок:

Так как основание 2/5<1, показательная функция

убывает, поэтому знак неравенства между показателями степеней изменяется на противоположный:

Квадратичное неравенство решим методом интервалов. Нули функции, стоящей в левой части неравенства — x1=-1; x2=2. Отмечаем их на числовой прямой.

Для проверки знака возьмем нуль: 0²-0-2=-2, в промежуток, которому принадлежит нуль, ставим «-«. Остальные знаки расставляем в шахматном порядке. Так как решаем неравенство, в котором левая часть меньше нуля, выбираем промежуток со знаком «-«.

Ответ: x ∈ (-1; 2).

Вариант неравенств такого вида — все степени имеют одинаковые основания, но отличаются коэффициентами при x в показателях.

В левой части выносим за скобки степень с наименьшим показателем

Пришли к показательному неравенству простейшего вида. Так как основание 7>1, функция

возрастает, знак неравенства между показателями не изменяется:

Чтобы решить это неравенство методом интервалов перенесем все слагаемые в левую часть и приведём дроби к наименьшему общему знаменателю:

Полученные точки отмечаем на числовой прямой (с учётом ОДЗ x≠0). x — 3} \geqslant 2.`

На этом все. Если объяснение понятное, то ставьте лайки, а если остались вопросы, оставляйте их в комментариях.

Как обычно, видео с этим материалом прилагается.

Решение показательных неравенств

3 января 2017

Многие считают, что показательные неравенства — это что-то такое сложное и непостижимое. И что научиться их решать — чуть ли не великое искусство, постичь которое способны лишь Избранные…

Полная брехня! Показательные неравенства — это просто. И решаются они всегда просто. Ну, почти всегда.:)

Сегодня мы разберём эту тему вдоль и поперёк. Этот урок будет очень полезен тем, кто только начинает разбираться в данном разделе школьной математики. Начнём с простых задач и будем двигаться к более сложным вопросам. Никакой жести сегодня не будет, но того, что вы сейчас прочитаете, будет достаточно, чтобы решить большинство неравенств на всяких контрольных и самостоятельных работах. {n}}$. До тех пор, пока у вас слева или справа есть какие-то левые множители, дополнительные константы и т.д., никакую рационализацию и «зачёркивание» оснований выполнять нельзя! Бесчисленное множество задач было выполнено неправильно из-за непонимания этого простого факта. Я сам постоянно наблюдаю эту проблему у моих учеников, когда мы только-только приступаем к разбору показательных и логарифмических неравенств.

Но вернёмся к нашей задаче. Попробуем в этот раз обойтись без рационализации. Вспоминаем: основание степени больше единицы, поэтому тройки можно просто зачеркнуть — знак неравенства при этом не поменяется. Получим:

\[\begin{align} & -\frac{8x}{3} \lt 4-4x; \\ & 4x-\frac{8x}{3} \lt 4; \\ & \frac{4x}{3} \lt 4; \\ & 4x \lt 12; \\ & x \lt 3. \\\end{align}\]

Вот и всё. Окончательный ответ: $x\in \left( -\infty ;3 \right)$.

Выделение устойчивого выражения и замена переменной

В заключение предлагаю решить ещё четыре показательных неравенства, которые уже являются довольно сложными для неподготовленных учеников. {5}}=3125. \\\end{align}\]

Конечно, все эти числа при желании можно восстановить в уме, просто последовательно умножая их друг на друга. Однако, когда вам предстоит решить несколько показательных неравенств, причём каждое следующее сложнее предыдущего, то последнее, о чём хочется думать — это степени каких-то там чисел. И в этом смысле данные задачи являются более сложными, нежели «классические» неравенства, которые решаются методом интервалов.

Надеюсь, этот урок помог вам в освоении данной темы. Если что-то непонятно — спрашивайте в комментариях. И увидимся в следующих уроках.:)

Смотрите также:

Простейшие показательные уравнения
Преобразование показательных уравнений
Сравнение дробей
Задача B8: отрезки и углы в треугольниках
Быстрое возведение чисел в квадрат без калькулятора
Задача B4: строительные бригады

Показательные уравнения и неравенства online. Показательные уравнения и неравенства

Рассмотрим следующий пример: решить уравнение 5 (x 2 — 2*x — 1) = 25.

Представим 25 как 5 2 , получим:

5 (x 2 — 2*x — 1) = 5 2 .

Или что равносильно:

x 2 — 2*x — 1 = 2.

Решаем полученное квадратное уравнение любым из известных способов. Получаем два корня x = 3 и x = -1.

Ответ: 3;-1.

Решим уравнение 4 x — 5*2 x + 4 = 0. Сделаем замену: t=2 x и получим следующее квадратное уравнение:

t 2 — 5*t + 4 = 0.
Решаем это уравнение любым из известных способов. Получаем корни t1 = 1 t2 = 4

Теперь решаем уравнения 2 x = 1 и 2 x = 4.

Ответ: 0;2.

Решение показательных неравенств

Рассмотрим пример: решить неравенство (0.5) (7 — 3*x)

Заметим, что 4 = (0.5) 2 . Тогда неравенство примет вид (0.5)(7 — 3*x)

Получим: 7 — 3*x>-2.

Отсюда: х

Ответ: х

1. Определение и свойства показательной функции

Рис. 1. График показательной функции

Обе кривые проходят через точку (0;1)

Свойства показательной функции :

Область определения: ;

Область значений: ;

Функция монотонна, при возрастает, при убывает.

Монотонная функция принимает каждое свое значение при единственном значении аргумента.

2. Простейшие показательные неравенства, методика решения, пример

На основании вышесказанного приведем методику решения простейших показательных неравенств:

Методика решения неравенств:

Уравнять основания степеней;

Сравнить показатели, сохранив или изменив на противоположный знак неравенства.

Основание степени больше единицы, значит, знак неравенства сохраняется:

Преобразуем правую часть согласно свойствам степени:

Основание степени меньше единицы, знак неравенства необходимо поменять на противоположный:

Для решения квадратного неравенства решим соответствующее квадратное уравнение:

По теореме Виета находим корни:

Ветви параболы направлены вверх.

Таким образом, имеем решение неравенства:

Несложно догадаться, что правую часть можно представить как степень с нулевым показателем:

Основание степени больше единицы, знак неравенства не меняется, получаем:

Напомним методику решения таких неравенств.

Рассматриваем дробно-рациональную функцию:

Находим область определения:

Находим корни функции:

Функция имеет единственный корень,

Выделяем интервалы знакопостоянства и определяем знаки функции на каждом интервале:

Рис. 2. Интервалы знакопостоянства

Таким образом, получили ответ.

Ответ:

3. Решение типовых показательных неравенств

Рассмотрим неравенства с одинаковыми показателями, но различными основаниями.

Основание степени больше единицы, знак неравенства сохраняется.

Проиллюстрируем решение:

Рис. 3. Иллюстрация к примеру 4

Преобразуем заданное неравенство согласно свойствам степени:

Приведем подобные члены:

Разделим обе части на :

Теперь продолжаем решать аналогично примеру 4, разделим обе части на :

Основание степени больше единицы, знак неравенства сохраняется:

4. Графическое решение показательных неравенств

Пример 6 — решить неравенство графически:

Рассмотрим функции, стоящие в левой и правой части и построим график каждой из них.

Несложно заметить, что корнем данной системы является :

Таким образом, графики функций пересекаются в точке с аргументом, равным единице.

Рис. 4. Иллюстрация к примеру 6

Список литературы

Math. md . Mathematics-repetition. com . Diffur. kemsu. ru .

Домашнее задание

1. Алгебра и начала анализа, 10-11 класс (А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын) 1990, № 472, 473;

2. Решить неравенство:

3. Решить неравенство.

Показательными уравнениями и неравенствами считают такие уравнения и неравенства, в которых неизвестное содержится в показателе степени.

Решение показательных уравнений часто сводится к решению уравнения а х = а b , где а > 0, а ≠ 1, х – неизвестное. Это уравнение имеет единственный корень х = b, так как справедлива следующая теорема:

Теорема. Если а > 0, а ≠ 1 и а х 1 = а х 2 , то х 1 = х 2 .

Обоснуем рассмотренное утверждение.

Предположим, что равенство х 1 = х 2 не выполняется, т.е. х 1 1, то показательная функция у = а х возрастает и поэтому должно выполняться неравенство а х 1 а х 2 . В обоих случаях мы получили противоречие условию а х 1 = а х 2 .

Рассмотрим несколько задач.

Решить уравнение 4 ∙ 2 х = 1.

Решение.

Запишем уравнение в виде 2 2 ∙ 2 х = 2 0 – 2 х+2 = 2 0 , откуда получаем х + 2 = 0, т.е. х = -2.

Ответ. х = -2.

Решить уравнение 2 3х ∙ 3 х = 576.

Решение.

Так как 2 3х = (2 3) х = 8 х, 576 = 24 2 , то уравнение можно записать в виде 8 х ∙ 3 х = 24 2 или в виде 24 х = 24 2 .

Отсюда получаем х = 2.

Ответ. х = 2.

Решить уравнение 3 х+1 – 2∙3 х — 2 = 25.

Решение.

Вынося в левой части за скобки общий множитель 3 х — 2 , получаем 3 х — 2 ∙ (3 3 – 2) = 25 – 3 х — 2 ∙ 25 = 25,

откуда 3 х — 2 = 1, т. е. х – 2 = 0, х = 2.

Ответ. х = 2.

Решить уравнение 3 х = 7 х.

Решение.

Так как 7 х ≠ 0, то уравнение можно записать в виде 3 х /7 х = 1, откуда (3/7) х = 1, х = 0.

Ответ. х = 0.

Решить уравнение 9 х – 4 ∙ 3 х – 45 = 0.

Решение.

Заменой 3 х = а данное уравнение сводится к квадратному уравнению а 2 – 4а – 45 = 0.

Решая это уравнение, находим его корни: а 1 = 9, а 2 = -5, откуда 3 х = 9, 3 х = -5.

Уравнение 3 х = 9 имеет корень 2, а уравнение 3 х = -5 не имеет корней, так как показательная функция не может принимать отрицательные значения.

Ответ. х = 2.

Решение показательных неравенств часто сводится к решению неравенств а х > а b или а х

Рассмотрим некоторые задачи.

Решить неравенство 3 х

Решение.

Запишем неравенство в виде 3 х 1, то функция у = 3 х является возрастающей.

Следовательно, при х

Таким образом, при х 3 х

Ответ. х

Решить неравенство 16 х +4 х – 2 > 0.

Решение.

Обозначим 4 х = t, тогда получим квадратное неравенство t2 + t – 2 > 0.

Это неравенство выполняется при t 1.

Так как t = 4 х, то получим два неравенства 4 х 1.

Первое неравенство не имеет решений, так как 4 х > 0 при всех х € R.

Второе неравенство запишем в виде 4 х > 4 0 , откуда х > 0.

Ответ. х > 0.

Графически решить уравнение (1/3) х = х – 2/3.

Решение.

1) Построим графики функций у = (1/3) х и у = х – 2/3.

2) Опираясь на наш рисунок, можно сделать вывод, что графики рассмотренных функций пересекаются в точке с абсциссой х ≈ 1. Проверка доказывает, что

х = 1 – корень данного уравнения:

(1/3) 1 = 1/3 и 1 – 2/3 = 1/3.

Иными словами, мы нашли один из корней уравнения.

3) Найдем другие корни или докажем, что таковых нет. Функция (1/3) х убывающая, а функция у = х – 2/3 возрастающая. Следовательно, при х > 1 значения первой функции меньше 1/3, а второй – больше 1/3; при х 1 и х

Ответ. х = 1.

Заметим, что из решения этой задачи, в частности, следует, что неравенство (1/3) х > х – 2/3 выполняется при х 1.

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Решение экспоненциальных уравнений из определения

Пурпурная математика

Чтобы решить экспоненциальные уравнения без логарифмов, вам нужно иметь уравнения со сравнимыми экспоненциальными выражениями по обе стороны от знака «равно», чтобы вы могли сравнить степени и решить. Другими словами, у вас должно быть «(некоторая база) в (некоторая степень) равна (той же основе) в (какая-то другая степень)», где вы устанавливаете две степени равными друг другу и решаете полученное уравнение. Например:

Поскольку основания (в каждом случае «5») одинаковы, то единственный способ, которым два выражения могут быть равны, — это чтобы степени также были одинаковыми. То есть:

MathHelp.com

Это решение демонстрирует логическую основу того, как решается весь этот класс уравнений: если основания одинаковы, то и степени должны быть равны; это единственный способ, чтобы две части уравнения были равны друг другу.Поскольку степени должны быть одинаковыми, мы можем положить две степени равными друг другу и решить полученное уравнение.

Так как основания одинаковые, то я могу приравнять силы и решить:

1 – х = 4

1 – 4 = х

–3 = х

Тогда мое решение:

Не все экспоненциальные уравнения даны в терминах одного и того же основания по обе стороны от знака «равно».Иногда нам сначала нужно преобразовать одну или другую сторону (или обе) в какое-то другое основание, прежде чем мы сможем установить степени равными друг другу. Например:

Поскольку 9 = 3 ² , мне действительно нужно решить:

Преобразовав 9 в 3 ² , я преобразовал правую часть уравнения так, чтобы она имела то же основание, что и левая часть. Поскольку базы теперь одинаковы, я могу установить две степени равными друг другу:

В этом случае у меня есть экспонента с одной стороны от «равно», а число с другой. Я могу решить уравнение, если я могу выразить «27» как степень числа 3. Поскольку 27 = 3 ³ , я могу преобразовать и перейти к решению:

3 ^{2 х –1} = 27

3 ^{2 х –1} = 3 ³

2 х – 1 = 3

2 х = 4

х = 2

Если я не уверен в своем ответе или хочу проверить его перед сдачей (например, на тесте), я могу проверить его, вставив его обратно в исходное упражнение.Степень в левой части исходного уравнения упростилась бы как:

А 3 ³ = 27, что является правой частью исходного уравнения. Тогда мое (подтвержденное) решение:

Как вы, вероятно, уже заметили, вам нужно хорошенько освоить свои числовые степени, такие как степени от 2 до 2 ⁶ = 64, степени от 3 p до 3 ⁵ = 243, степени 4 до 4 ⁴ = 256, степени 5 до 5 ⁴ = 625, степени 6 до 6 ³ = 216, и все квадраты.

Не планируйте во всем полагаться на свой калькулятор, потому что необходимость находить для каждого значения в вашем калькуляторе может привести к пустой трате времени. Вы захотите иметь определенную степень легкости (то есть определенную степень знакомства и скорости) к тому времени, когда вы достигнете теста, поэтому ознакомьтесь с меньшими способностями сейчас.

Примечание по форматированию: HTML обычно не любит вложенные надстрочные индексы, поэтому в приведенном выше примере для обозначения степени используется нотация «карат».2–3 x = 3 ⁴

х ² – 3 х = 4

х ² – 3 х – 4 = 0

( х – 4)( х + 1) = 0

х = –1, 4

Итак, мой ответ:

Это уравнение похоже на два предыдущих, но не совсем то же самое, потому что 8 не является степенью числа 4. 2+4 х = 2 ³

4 х ² + 4 х = 3

4 х ² + 4 х – 3 = 0

(2 х – 1)(2 х + 3) = 0

х = ¹ / ₂ , ^–3 / ₂

Отрицательные показатели степени могут использоваться для обозначения того, что основание принадлежит другой стороне дробной линии.Поскольку 64 = 4 ³ , то я могу использовать отрицательные показатели степени, чтобы преобразовать дробь в экспоненциальное выражение:

Используя это, я могу решить уравнение:

4 ^{x +1} = ¹ / ₆₄

4 ^{x +1} = 4 ^–3

х + 1 = –3

х = –4

Чтобы решить это, мне сначала нужно вспомнить, что квадратные корни — это то же самое, что и половинные степени, и преобразовать радикал в экспоненциальную форму. Тогда я могу решить уравнение:

8 ^{x –2} = кв [8]

8 ^{x –2} = 8 ^1/2

х – 2 = 1/2

x = 2 + ¹ / ₂ = ⁵ / ₂

Тогда мой ответ:

Ниже приведен пример обычного вопроса с подвохом:

Подумайте об этом: какая степень положительного числа «2» может , возможно, дать отрицательное число? Число никогда не может перейти от положительного к отрицательному, взяв степени; Я никогда не смогу превратить положительную двойку в отрицательную что-либо , четверку или что-то еще, умножая два на себя, независимо от того, сколько раз я выполняю умножение. Возведение в степень просто так не работает. Итак, ответ здесь:

URL: https://www.purplemath.com/modules/solvexpo.htm

Экспоненциальные уравнения — определение, решение и примеры

Экспоненциальные уравнения, как следует из их названия, включают показатели степени.Мы знаем, что показатель степени числа (основания) показывает, сколько раз число (основание) умножается. Но что произойдет, если степень числа является переменной? Когда мощность является переменной и если она является частью уравнения, то это называется показательным уравнением. Нам может понадобиться использовать связь между показателями степени и логарифмами для решения экспоненциальных уравнений.

Давайте изучим определение показательных уравнений вместе с процессом их решения, когда основания одинаковы и когда основания не совпадают, а также несколько решенных примеров и практических вопросов.

Что такое экспоненциальные уравнения?

Показательное уравнение – это уравнение с показателями степени, где показатель степени (или часть показателя степени) является переменной. Например, 3 ^x = 81, 5 ^{x — 3} = 625, 6 ^{2y — 7} = 121 и т. д. являются примерами экспоненциальных уравнений. Мы можем столкнуться с использованием экспоненциальных уравнений при решении задач алгебры, сложных процентов, экспоненциального роста, экспоненциального убывания и т. д.

Типы экспоненциальных уравнений

Существует три типа экспоненциальных уравнений. Они следующие:

Уравнения с одинаковыми основаниями с обеих сторон. (Пример: 4 ^x = 4 ² )
Уравнения с разными основаниями можно сделать одинаковыми. (Пример: 4 ^x = 16, что можно записать как 4 ^x = 4 ² )
Уравнения с разными основаниями, которые нельзя сделать одинаковыми. (Пример: 4 ^x = 15)

Формулы экспоненциальных уравнений

При решении экспоненциального уравнения основания в обеих частях могут совпадать или не совпадать. Вот формулы, которые используются в каждом из этих случаев, которые мы подробно изучим в следующих разделах.

Свойство равенства для экспоненциальных уравнений

Это свойство полезно для решения показательного уравнения с теми же основаниями.В нем говорится, что если основания в обеих частях экспоненциального уравнения равны, то показатели степени также должны быть равны. то есть a ^x = a ^y ⇔ x = y .

Экспоненциальные уравнения в логарифмической форме

Мы знаем, что логарифмы не что иное, как показатели степени, и наоборот. Следовательно, показательное уравнение может быть преобразовано в логарифмическое уравнение. Это помогает в процессе решения показательного уравнения с разными основаниями. Вот формула для преобразования показательных уравнений в логарифмические уравнения.

б ^х = а ⇔ log _б а = х

Решение экспоненциальных уравнений с одинаковыми основаниями

Иногда показательное уравнение может иметь одинаковые основания в обеих частях уравнения. Например, 5 ^x = 5 ³ имеет одинаковое основание 5 с обеих сторон. Иногда, хотя показатели с обеих сторон неодинаковы, их можно сделать одинаковыми. Например, 5 ^x = 125. Хотя у него разные основания в обеих частях уравнения, их можно сделать одинаковыми, записав как 5 ^x = 5 ³ (поскольку 125 = 5 ³ ).Чтобы решить показательные уравнения в каждом из этих случаев, мы просто применяем свойство равенства показательных уравнений, используя которое, мы устанавливаем показатели равными и решаем для переменной.

Вот еще пример, где базы не одинаковые, но можно сделать одинаковыми.

Пример: Решить показательное уравнение 7 ^{y + 1} = 343 ^y .

Решение:

Мы знаем, что 343 = 7 ³ .Используя это, данное уравнение можно записать как

7 ^{у + 1} = (7 ³ ) ^у

7 ^{г + 1} = 7 ^{3 года}

Теперь базы с обеих сторон одинаковые. Таким образом, мы можем установить показатели степени одинаковыми.

года + 1 = 3 года

Вычитание у с обеих сторон,

2 года = 1

Деление обеих частей на 2,

г = 1/2

Решение экспоненциальных уравнений с разными основаниями

Иногда основания в обеих частях экспоненциального уравнения могут не совпадать (или) не могут быть сделаны одинаковыми.Мы решаем показательные уравнения с помощью логарифмов, когда основания не совпадают в обеих частях уравнения. Например, 5 ^x = 3 не имеет одинаковых оснований с обеих сторон, и основания не могут быть одинаковыми. В таких случаях мы можем сделать одну из следующих вещей.

Преобразуйте экспоненциальное уравнение в логарифмическую форму, используя формулу b ^x = a ⇔ log _b a = x, и найдите переменную.
Примените логарифм (log) к обеим частям уравнения и найдите переменную.В этом случае нам придется использовать свойство логарифма, log a ^m = m log a.

Решим уравнение 5 ^x = 3 каждым из этих способов.

Метод 1:

Преобразуем 5 ^х = 3 в логарифмическую форму. Тогда мы получаем,

журнал ₅ 3 = х

Использование изменения базового свойства,

х = (лог. 3) / (лог. 5)

Метод 2:

Приложим лог с обеих сторон 5 ^х = 3.Тогда мы получаем log 5 ^x = log 3. Используя свойство log a ^m = m log a в левой части уравнения, мы получаем x log 5 = log 3. Разделив обе части на log 5,

х = (лог. 3) / (лог. 5)

Важные примечания:

Вот несколько важных замечаний относительно экспоненциальных уравнений.

Чтобы решить экспоненциальные уравнения с одинаковыми основаниями, просто приравняйте показатели степени.
Чтобы решить показательные уравнения по разным основаниям, примените логарифмирование к обеим частям.
Показательные уравнения с теми же основаниями также могут быть решены с использованием логарифмов.
Если экспоненциальное уравнение имеет 1 с любой стороны, то мы можем записать его как 1 = a ⁰ для любого ‘a’. Например, чтобы решить 5 ^x = 1, мы можем записать это как 5 ^x = 5 ⁰ , тогда мы получим x = 0,
Чтобы решить экспоненциальное уравнение с помощью логарифмов, мы можем либо применить «log», либо применить «ln» к обеим сторонам.

Связанные темы:

Вот связанные темы экспоненциальных уравнений.

Часто задаваемые вопросы по экспоненциальным уравнениям

Что такое экспоненциальные уравнения?

Показательное уравнение — это уравнение, которое имеет переменную в показателе(ях). Например, 5 ^{2x — 3} = 125, 3 ^{7 — 2x} = 91 и т. д. являются показательными уравнениями.

Какие бывают типы экспоненциальных уравнений?

Существует три типа экспоненциальных уравнений. Они,

Показательные уравнения с одинаковыми основаниями с обеих сторон.
Показательные уравнения с разными основаниями с обеих сторон, которые можно сделать одинаковыми.
Показательные уравнения с разными основаниями с обеих сторон, которые нельзя сделать одинаковыми.

Как решать экспоненциальные уравнения?

Чтобы решить показательные уравнения с одинаковыми основаниями, мы приравняем показатели степени, тогда как для решения показательных уравнений с разными основаниями мы применим логарифмирование с обеих сторон.

Как записать экспоненциальное уравнение в логарифмической форме?

Запись показательного уравнения в логарифмической форме помогает нам решить его.Это можно сделать по формуле b ^x = a ⇔ log _b a = x.

Что такое свойство равенства экспоненциальных уравнений?

Свойство равенства экспоненциальных уравнений говорит об установлении показателей степени равными всякий раз, когда основания в обеих частях уравнения равны. т. е. а ^х = а ^у ⇔ х = у.

Как решать экспоненциальные уравнения с одинаковыми основаниями?

Если экспоненциальное уравнение имеет одинаковые основания с обеих сторон, просто приравняйте показатели степени и найдите переменную.Вот пример: 4 ^{2x — 1} = 4 ^{1 — x}. Здесь основания с обеих сторон равны. Таким образом, мы можем установить показатели равными.
2х — 1 = 1 — х
3x = 2
х = 2/3.

Как решать показательные уравнения с разными основаниями?

Если экспоненциальное уравнение имеет разные основания с обеих сторон, примените log к обеим сторонам и найдите переменную. Вот пример, 4 ^{х — 5} = 8. Берем бревно с двух сторон,
журнал 4 ^{х — 5} = журнал 8
(x — 5) журнал 4 = журнал 8
х — 5 = (логарифм 8) / (логарифм 4)
х = [(журнал 8) / (лог 4)] + 5.

Как решать экспоненциальные уравнения с помощью логарифмов?

Мы решаем показательные уравнения с помощью логарифмов двумя способами.

Преобразуйте экспоненциальное уравнение в логарифмическое, используя b ^x = a ⇔ log _b a = x.
Нанесите «log» или «ln» на обе стороны и решите.

Решение экспоненциальных уравнений с использованием логарифмов

На предыдущем уроке вы научились решать показательные уравнения без логарифмов.На этот раз мы хотим решить экспоненциальные уравнения , требующие использования логарифмов . Почему? Причина в том, что мы не можем манипулировать экспоненциальным уравнением, чтобы иметь одинаковую или общую основу в обеих частях уравнения. Если вы столкнулись с такой проблемой, предлагаем следующие шаги:

Этапы решения экспоненциальных уравнений с использованием логарифмов

1) Оставьте экспоненциальное выражение отдельно в одной части уравнения.

2) Получите логарифмы обеих частей уравнения.{2x}} = 21,

В этом уравнении хорошо то, что экспоненциальное выражение уже изолировано в левой части. Теперь мы можем взять логарифмы обеих частей уравнения. Не имеет значения, какое основание логарифма использовать. Окончательный ответ должен получиться таким же. Лучший выбор для основания логарифмической операции — 5, так как это основание самого экспоненциального выражения. Однако мы также будем использовать в расчетах общее основание 10 и естественное основание \color{red}e (обозначаемое \color{blue}ln), просто чтобы показать, что в конце концов все они дают одинаковые ответы. .{х — 5}}} \справа) = 12 .

Как видите, экспоненциальное выражение слева не само по себе. Мы должны исключить число 2, которое умножает экспоненциальное выражение. Для этого разделите обе части на 2. У нас останется только экспоненциальное выражение слева и 6 справа после упрощения.

Пришло время взять бревно с обеих сторон. Поскольку экспоненциальное выражение имеет основание 3, его удобно использовать для логарифмических операций. Кроме того, мы также решим это, используя натуральное основание e, просто чтобы сравнить, совпадают ли наши окончательные результаты.{x — 2}}}}}}} \right) — 7 = 13 .

Сначала это выглядит как беспорядок. Однако, если вы знаете, с чего начать, решение этой проблемы станет проще простого. Что мы должны сделать в первую очередь, так это упростить выражение внутри круглых скобок. Воспользуйтесь правилом деления экспоненты, скопировав общее основание e и вычтя верхнюю часть из нижней степени.

Теперь изолируйте экспоненциальное выражение, добавив обе части на 7, а затем разделив все уравнение на 2.

Возьмем логарифм обеих частей.х} + 3 = 53 .

Обратите внимание, что экспоненциальное выражение возводится в x. Упростите это, применив силу к силовому правилу. Сделайте это, скопировав основание 10 и умножив его показатель на внешний показатель. Это должно выглядеть так после этого.

Теперь мы можем изолировать экспоненциальное выражение, вычитая обе части на 3 и затем умножая обе части на 2.

Возьмем логарифм обеих сторон по основанию 10. Если вы просто видите красное поле без какого-либо определенного основания, считается, что оно имеет 10 в качестве основания.х снова.

Наконец, приравняйте каждый множитель к нулю и найдите x, как обычно, используя логарифмы.

Вас также может заинтересовать:

Решение экспоненциальных уравнений без логарифмов

Экспоненциальные и логарифмические уравнения – Алгебра и тригонометрия

Цели обучения

В этом разделе вы:

Используйте одинаковые основания для решения экспоненциальных уравнений.
Используйте логарифмы для решения экспоненциальных уравнений.
Используйте определение логарифма для решения логарифмических уравнений.
Используйте свойство логарифмов «один к одному» для решения логарифмических уравнений.
Решение прикладных задач на экспоненциальные и логарифмические уравнения.

Рисунок 1. Дикие кролики в Австралии. Популяция кроликов в Австралии росла так быстро, что это событие стало известно как «кроличья чума». (кредит: Ричард Тейлор, Flickr)

В 1859 году австралийский землевладелец Томас Остин выпустил на охоту 24 кролика.Поскольку в Австралии было мало хищников и достаточно еды, популяция кроликов резко возросла. Менее чем за десять лет популяция кроликов исчислялась миллионами.

Неконтролируемый рост популяции, как у диких кроликов в Австралии, можно смоделировать с помощью экспоненциальных функций. Уравнения, полученные из этих экспоненциальных функций, можно решать для анализа и прогнозирования экспоненциального роста. В этом разделе мы изучим методы решения экспоненциальных функций.

Использование одинаковых оснований для решения экспоненциальных уравнений

В первом методе используются две функции с одинаковыми основаниями.{T}\,[/latex] тогда и только тогда, когда

Другими словами, когда показательное уравнение имеет одинаковое основание с каждой стороны, показатели степени должны быть равны. Это также применимо, когда показатели степени являются алгебраическими выражениями. Следовательно, мы можем решить многие экспоненциальные уравнения, используя правила экспонент, чтобы переписать каждую сторону как степень с одним и тем же основанием. Затем мы используем тот факт, что экспоненциальные функции являются взаимно однозначными, чтобы установить показатели степени равными друг другу и найти неизвестное.

Например, рассмотрим уравнение. Чтобы решить для, мы используем свойство деления показателей степени, чтобы переписать правую часть так, чтобы обе части имели общее основание. Затем мы применяем свойство степени однозначности, устанавливая показатели степени равными друг другу. и решение для

Использование однозначности экспоненциальных функций для решения экспоненциальных уравнений

Для любых алгебраических выражений и любого положительного действительного числа

Решение экспоненциального уравнения с общим основанием

Решить

[reveal-answer q=»fs-id1165137655365″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137655365″] [/ скрытый ответ]

Попробуйте

Решить

[reveal-answer q=»fs-id1165137730366″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137730366″]

[/скрытый ответ]

Переписать уравнения так, чтобы все степени имели одно основание

Иногда общее основание экспоненциального уравнения не отображается явно.В этих случаях мы просто переписываем члены уравнения в виде степеней с общим основанием и решаем, используя свойство взаимно однозначности.

Например, рассмотрим уравнение. Мы можем переписать обе части этого уравнения в виде степени. Затем мы применяем правила экспоненты вместе со свойством однозначности, чтобы найти

Как

Имея показательное уравнение с разными основаниями, используйте для его решения свойство однозначности.

Перепишите каждую часть уравнения как степень с общим основанием.
Используйте правила экспоненты для упрощения, если это необходимо, чтобы результирующее уравнение имело вид
Используйте свойство «один к одному», чтобы установить равные степени.
Решите полученное уравнение относительно неизвестного.

Решение уравнений путем переписывания их так, чтобы они имели общее основание

Решить

[reveal-answer q=»fs-id1165137552155″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137552155″] [/ скрытый ответ]

Попробуйте

Решить

[reveal-answer q=»fs-id1165137810723″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137810723″]

[/скрытый ответ]

Решение уравнений путем перезаписи корней с дробными показателями для получения общего основания

Решить

[reveal-answer q=»fs-id1165137722496″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137722496″] [/ скрытый ответ]

Попробуйте

Решить

[reveal-answer q=»fs-id1165137678183″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137678183″]

[/скрытый ответ]

Все ли показательные уравнения имеют решение? Если нет, то как мы можем узнать, есть ли решение в процессе решения проблемы?

№Напомним, что диапазон экспоненциальной функции всегда положителен. При решении уравнения может получиться неопределенное выражение.

Решение уравнения с положительными и отрицательными степенями

Решить

[reveal-answer q=»fs-id1165137723720″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137723720″]

Это уравнение не имеет решения. Не существует действительного значения, которое сделало бы уравнение верным утверждением, потому что любая степень положительного числа положительна.

[/скрытый ответ]

Анализ

(рисунок) показывает, что два графика не пересекаются, поэтому левая сторона никогда не равна правой стороне. Таким образом, уравнение не имеет решения.

Рис. 2.

Попробуйте

Решить

[reveal-answer q=»fs-id1165137844325″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137844325″]

Уравнение не имеет решения.

[/скрытый ответ]

Решение экспоненциальных уравнений с использованием логарифмов

Иногда члены экспоненциального уравнения не могут быть переписаны с общим основанием. В этих случаях мы решаем, логарифмируя каждую сторону. Напомним, поскольку это эквивалентно, мы можем применять логарифмы с одним и тем же основанием к обеим частям экспоненциального уравнения.

Как

Для заданного показательного уравнения, в котором невозможно найти общее основание, найдите неизвестное.

Примените логарифм обеих частей уравнения.
- Если один из членов уравнения имеет основание 10, используйте десятичный логарифм.
- Если ни один из членов уравнения не имеет основание 10, используйте натуральный логарифм.
Используйте правила логарифмирования, чтобы найти неизвестное.

Решение уравнения, содержащего степени разных оснований

Решить

[reveal-answer q=»fs-id1165135194651″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165135194651″] [/ скрытый ответ]

Попробуйте

Решить

[reveal-answer q=»fs-id1165137605315″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137605315″]

[/скрытый ответ]

Есть ли способ решить

Да. Решение

Посторонние растворы

Иногда методы, используемые для решения уравнения, вводят постороннее решение, которое является решением, правильным алгебраически, но не удовлетворяющим условиям исходного уравнения. Одна из таких ситуаций возникает при решении, когда обе части уравнения логарифмируются. В таких случаях помните, что аргумент логарифма должен быть положительным. Если число, которое мы оцениваем в логарифмической функции, отрицательное, выходных данных нет.

Решение показательных функций в квадратичной форме

Решить

[reveal-answer q=»70562″]Показать решение[/reveal-answer]
[скрытый ответ = ”70562″][/скрытый ответ]

Анализ

Когда мы планируем использовать факторинг для решения проблемы, мы всегда получаем ноль в одной части уравнения, потому что ноль обладает уникальным свойством: когда произведение равно нулю, один или оба множителя должны быть равны нулю. Мы отвергаем уравнение, потому что положительное число никогда не равно отрицательному числу. Решение не является действительным числом, и в действительной системе счисления это решение отбрасывается как постороннее решение.

Попробуйте

Решить

[reveal-answer q=»fs-id1165135638513″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165135638513″]

[/скрытый ответ]

Каждое ли логарифмическое уравнение имеет решение?

Нет. Имейте в виду, что мы можем применять логарифм только к положительному числу.Всегда проверяйте наличие посторонних решений.

Использование свойства «один к одному» логарифмов для решения логарифмических уравнений

Как и в случае экспоненциальных уравнений, мы можем использовать свойство «один к одному» для решения логарифмических уравнений. Свойство логарифмических функций «один к одному» говорит нам, что для любых действительных чисел и любого положительного действительного числа, где

Например,

Таким образом, если мы можем решить forи мы получаемПроверить, мы можем подставить в исходное уравнение: Другими словами, когда логарифмическое уравнение имеет одинаковое основание с каждой стороны, аргументы должны быть равны. Это также применимо, когда аргументы являются алгебраическими выражениями. Поэтому, когда у нас есть уравнение с логарифмами одинакового основания на каждой стороне, мы можем использовать правила логарифмирования, чтобы переписать каждую сторону как один логарифм. Затем мы используем тот факт, что логарифмические функции являются взаимно однозначными, чтобы установить аргументы равными друг другу и найти неизвестное.

Например, рассмотрим уравнение. Чтобы решить это уравнение, мы можем использовать правила логарифмирования, чтобы переписать левую часть как одиночный логарифм, а затем применить свойство один к одному для решения для

Для проверки результата подставьте

Как

Имея уравнение, содержащее логарифмы, решите его, используя свойство однозначности.

Используйте правила логарифмирования, чтобы объединить одинаковые члены, если это необходимо, чтобы результирующее уравнение имело вид
Используйте свойство «один к одному», чтобы установить равные аргументы.
Решите полученное уравнение относительно неизвестного.

Попробуйте

Решить

[reveal-answer q=»fs-id1165137724842″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137724842″]

или

[/скрытый ответ]

Решение прикладных задач с использованием экспоненциальных и логарифмических уравнений

В предыдущих разделах мы изучили свойства и правила как для экспоненциальной, так и для логарифмической функции.Мы видели, что любую экспоненциальную функцию можно записать в виде логарифмической функции и наоборот. Мы использовали показатели степени для решения логарифмических уравнений и логарифмы для решения показательных уравнений. Теперь мы готовы объединить наши навыки для решения уравнений, моделирующих реальные ситуации, независимо от того, находится ли неизвестное в показателе степени или в аргументе логарифма.

Одно из таких применений находится в науке при расчете времени, необходимого для распада половины нестабильного материала в образце радиоактивного вещества, называемого периодом полураспада. (Рисунок) показывает период полураспада нескольких наиболее распространенных радиоактивных веществ.

Вещество	Использовать	Период полураспада
галлий-67	ядерная медицина	80 часов
кобальт-60	производство	5,3 года
технеций-99м	ядерная медицина	6 часов
америций-241	строительство	432 года
углерод-14	археологические датировки	5715 лет
уран-235	атомная энергия	703 800 000 лет

Мы можем видеть, насколько сильно различаются периоды полураспада этих веществ. Зная период полураспада вещества, мы можем рассчитать количество, оставшееся после определенного времени. Мы можем использовать формулу радиоактивного распада:

где

Использование формулы радиоактивного распада для определения количества вещества

Сколько времени потребуется для распада десяти процентов 1000-граммовой пробы урана-235?

[reveal-answer q=»fs-id1165137628663″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137628663″] [/ скрытый ответ]

Анализ

Десять процентов от 1000 граммов составляют 100 граммов.Если 100 граммов распадаются, количество оставшегося урана-235 составляет 900 граммов.

Попробуйте

Сколько времени пройдет, прежде чем двадцать процентов нашей 1000-граммовой пробы урана-235 распадутся?

[reveal-answer q=»fs-id1165137426971″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137426971″]

[/скрытый ответ]

Ключевые понятия

Мы можем решить многие экспоненциальные уравнения, используя правила экспонент, чтобы представить каждую часть как степень с одним и тем же основанием. Затем мы используем тот факт, что экспоненциальные функции являются взаимно однозначными, чтобы установить показатели степени равными друг другу и найти неизвестное.
Когда нам дано экспоненциальное уравнение, в котором основания явным образом показаны как равные, приравняйте показатели степени друг к другу и найдите неизвестное. См. (Рисунок).
Когда нам дано экспоненциальное уравнение, в котором основания , а не явно показаны равными, перепишем каждую часть уравнения как степени одного и того же основания, затем приравняем показатели степени и найдем неизвестное.См. (Рисунок), (Рисунок) и (Рисунок).
Если показательное уравнение нельзя переписать с общим основанием, решите его, логарифмируя каждую часть. См. (Рисунок).
Мы можем решать экспоненциальные уравнения с основанием, применяя натуральный логарифм обеих частей, потому что экспоненциальные и логарифмические функции являются обратными друг другу. См. (Рисунок) и (Рисунок).
После решения экспоненциального уравнения проверьте каждое решение в исходном уравнении, чтобы найти и исключить любые посторонние решения. См. (Рисунок).
Когда дано уравнение формы где есть алгебраическое выражение, мы можем использовать определение логарифма, чтобы переписать уравнение как эквивалентное показательное уравнение и найти неизвестное. См. (Рисунок) и (Рисунок).
Мы также можем использовать графическое изображение для решения уравнений в форме Мы наносим оба уравнения на одну и ту же координатную плоскость и идентифицируем решение как x- значение точки пересечения. См. (Рисунок).
Когда дано уравнение вида где и являются алгебраическими выражениями, мы можем использовать свойство взаимно однозначного логарифмирования для решения уравнения относительно неизвестного.См. (Рисунок).
Объединяя навыки, полученные в этом и предыдущем разделах, мы можем решать уравнения, моделирующие реальные ситуации, независимо от того, находится ли неизвестное в показателе степени или в аргументе логарифма. См. (Рисунок).

Раздел Упражнения

Устный

Как решить показательное уравнение?

[reveal-answer q=»fs-id1165137643496″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137643496″]

Сначала определите, можно ли переписать уравнение так, чтобы каждая сторона использовала одно и то же основание. Если да, то показатели степени можно установить равными друг другу. Если уравнение нельзя переписать так, чтобы каждая сторона использовала одно и то же основание, то примените логарифм к каждой стороне и используйте для решения свойства логарифмов.

[/скрытый ответ]

Когда появляется посторонний раствор? Как распознать постороннее решение?

Когда можно использовать свойство логарифмов «один к одному» для решения уравнения? Когда его нельзя использовать?

[reveal-answer q=»fs-id1165135203846″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165135203846″]

Свойство «один к одному» можно использовать, если обе части уравнения можно переписать в виде одинарного логарифма с одним и тем же основанием.Если это так, аргументы можно положить равными друг другу, а полученное уравнение решить алгебраически. Свойство «один к одному» нельзя использовать, если каждую часть уравнения нельзя переписать в виде одинарного логарифма с одним и тем же основанием.

[/скрытый ответ]

Алгебраический

В следующих упражнениях используйте одинаковые основания для решения экспоненциального уравнения.

[reveal-answer q=»fs-id1165137409289″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137409289″]

[/скрытый ответ]

[reveal-answer q=»fs-id1165135187451″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165135187451″]

[/скрытый ответ]

[reveal-answer q=»fs-id1165137418206″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137418206″]

[/скрытый ответ]

Для решения следующих упражнений используйте логарифмы.

[reveal-answer q=»fs-id1165137425852″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137425852″]

[/скрытый ответ]

[reveal-answer q=»fs-id1165135173523″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165135173523″]

Нет решения

[/скрытый ответ]

[reveal-answer q=»fs-id1165135188812″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165135188812″]

[/скрытый ответ]

[reveal-answer q=»fs-id1165137667780″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137667780″]

[/скрытый ответ]

[reveal-answer q=»fs-id1165135253221″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165135253221″]

[/скрытый ответ]

[reveal-answer q=»fs-id1165137658150″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137658150″]

[/скрытый ответ]

[reveal-answer q=»fs-id1165135475913″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165135475913″]

[/скрытый ответ]

[reveal-answer q=»225493″]Показать решение[/reveal-answer]
[скрытый ответ = ”225493″]

[/скрытый ответ]

[reveal-answer q=»fs-id1165135195715″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165135195715″]

[/скрытый ответ]

В следующих упражнениях используйте определение логарифма, чтобы переписать уравнение как показательное уравнение.

[reveal-answer q=»fs-id1165135487112″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165135487112″]

[/скрытый ответ]

В следующих упражнениях используйте определение логарифма для решения уравнения.

[reveal-answer q=»fs-id1165137652929″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137652929″]

[/скрытый ответ]

[reveal-answer q=»fs-id1165135570427″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165135570427″]

[/скрытый ответ]

[reveal-answer q=»fs-id1165134232199″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165134232199″]

[/скрытый ответ]

Для решения следующих упражнений используйте свойство логарифмов «один к одному».

[reveal-answer q=»fs-id1165137424487″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137424487″]

[/скрытый ответ]

[reveal-answer q=»fs-id1165137436082″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137436082″]

Нет решения

[/скрытый ответ]

[reveal-answer q=»fs-id1165135511361″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165135511361″]

Нет решения

[/скрытый ответ]

[reveal-answer q=»fs-id1165134388216″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165134388216″]

[/скрытый ответ]

В следующих упражнениях решите каждое уравнение относительно числа

[reveal-answer q=»fs-id1165135182927″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165135182927″]

[/скрытый ответ]

[reveal-answer q=»988487″]Показать решение[/reveal-answer]
[скрытый ответ = ”988487″]

[/скрытый ответ]

[reveal-answer q=»fs-id1165137793981″]Показать решение[/reveal-answer]
[скрытый ответ = ”fs-id1165137793981″]

[/скрытый ответ]

Глоссарий

посторонний раствор: решение введено при решении уравнения, которое не удовлетворяет условиям исходного уравнения

Алгебра колледжа
Учебник 45: Экспоненциальные уравнения

Цели обучения

После завершения этого руководства вы сможете:

Решение показательных уравнений.

Введение

В этом уроке я покажу вам, как решать уравнения, которые имеют экспоненциальные выражения. В этих уравнениях вы заметите что переменная, которую мы ищем, находится в показателе степени. Мы привыкли видеть переменную в базе. Мы будем использовать инверсию операции, как мы делаем в линейных уравнениях, обратная операция, которую мы будем использовать здесь логарифмы.Если вам нужен обзор определения функций журнала, не стесняйтесь переходить к Tutorial 43: Логарифмические функции . Если вам нужен обзор свойств журнала, смело переходите к Tutorial 44: Логарифмические свойства . Я думаю, вы готовы начать.

Учебник

Решение экспоненциальных уравнений,
, где x в показателе степени, НО
основания НЕ СООТВЕТСТВУЮТ.

Шаг 1: Изолировать экспоненциальное выражение.

Получите экспоненциальное выражение на одной стороне всего за пределами экспоненциальное выражение на другой стороне вашего уравнения.

Шаг 2: Возьмите натуральный лог обеих сторон.

Обратной операцией экспоненциального выражения является логарифм. Убедитесь, что вы делаете то же самое с обеими частями вашего уравнения, чтобы держать их равными друг другу.

Шаг 3: Использование в свойствах логов вытащить х из экспоненты.

Теперь, когда переменная вышла за пределы экспоненты, найдите переменную используя обратные операции для решения задачи.

Специальное примечание:
Единственный способ получить эту переменную из экспоненты, когда базы не совпадают, это использовать логи. 3-й шаг позволяет нам сделать это. При решении уравнения не имеет значения, что вы делаете, чтобы уравнение до тех пор, пока вы делаете то же самое с обеими сторонами — это сохраняет обе стороны равны. Кроме того, причина, по которой мы берем натуральный логарифм обоих сторон, потому что у нас есть естественный логарифмический ключ на калькуляторе — так что мы сможет найти его значение в конце.

Пример 1 : Решите показательное уравнение . Округлите ответ до двух знаков после запятой.

Это уже сделано за нас в этой задаче.

*Возьмите натуральное бревно с ОБЕИХ сторон

*Инверсия множ.на 3ln e разделить на 3ln e

*Используйте калькулятор, чтобы найти ln 50
*ln e равно 1

Пример 2 : Решите показательное уравнение .

Округлите ответ до двух знаков после запятой.

*Инверсия множ. на 5 делить на 5

*Экспоненциальное выражение изолировано

*Возьмите натуральное бревно с ОБЕИХ сторон

*Инверсия множ.на ln 10 делить на № 10

*Инверсия добавления 1 является вспомогательной. 1

*Используйте калькулятор, чтобы найти ln 2. 4 и ln 10

Пример 3: Решите показательное уравнение . Округлите ответ до двух знаков после запятой.

*Инверсия добавления 4 является вспомогательной. 4

*Экспоненциальное выражение изолировано

*Возьмите натуральное бревно с ОБЕИХ сторон

*Инверсия множ.на .2ln 2 делить на . 2ln 2

*Используйте калькулятор, чтобы найти ln 21 и ln 2

Пример 4: Решите показательное уравнение . Округлите ответ до двух знаков после запятой.

Обратите внимание, что у нас есть два экспоненциальных члена с разными показателями степени. Мы не смогли бы изолировать оба. Нам придется придумать другой способ переписать его, чтобы мы могли продолжить шаги.

Обратите внимание, что у нас есть трехчлен и что e в 2 x равно e в x в квадрате. Это означает, что оно квадратично в от. Таким образом, мы можем разложить его так же, как трехчлен вида .

*Установите 1-й коэффициент = 0
*Выделите экспоненциальное выражение

*Установите второй множитель = 0
*Выделите экспоненциальное выражение

Обратите внимание, что поскольку e является положительным основанием, независимо от того, какой показатель степени у x , это экспоненциальное выражение НЕ МОЖЕТ равняться -2.

Итак, мы можем решить только одно уравнение .

*Возьмите натуральное бревно с ОБЕИХ сторон

*Инверсия множ. на ln e разделить на ln e

*Используйте калькулятор, чтобы найти ln 4
*ln e = 1

Практические задачи

Это тренировочные задачи, которые помогут вам перейти на следующий уровень. Это позволит вам проверить и понять, понимаете ли вы эти виды проблем. Математика работает так же, как и все в противном случае, если вы хотите добиться в этом успеха, вам нужно практиковаться. Даже лучшие спортсмены и музыканты получали помощь на этом пути и много практиковаться, практиковаться, практиковаться, чтобы преуспеть в своем виде спорта или игре на инструменте. На самом деле практики много не бывает.

Чтобы получить максимальную отдачу от них, вы должны решить проблему на свой собственный, а затем проверьте свой ответ, нажав на ссылку для ответа/обсуждения для этой проблемы .По ссылке вы найдете ответ а также любые шаги, которые привели к поиску этого ответа.

Практические задачи 1a — 1c: Решите данное показательное уравнение. Круглый ваш ответ с точностью до двух знаков после запятой.

Нужна дополнительная помощь по этим темам?

Последняя редакция Ким Сьюард от 24 марта 2011 г.
Авторские права на все содержимое (C) 2002–2011, WTAMU и Ким Сьюард. Все права защищены.

3.

{x — 5}\).{2x — 10}\hfill & \text{Чтобы взять степень степени, умножьте показатели степени}.\hfill\\ 8=2x — 10\hfill & \text{Примените свойство взаимно однозначности показателей степени}. \hfill \\ 18=2x\hfill & \text{Добавить 10 к обеим сторонам}.\hfill \\ x=9\hfill & \text{Разделить на 2}.\hfill \end{массив}\)

Логарифм, обратный экспоненте

Использование однозначного свойства может быть переформулировано с точки зрения обратного. Вы использовали обратные функции для решения уравнений с тех пор, как начали заниматься алгеброй.Например, если вы хотите решить уравнение:

$х-7=2$

вы бы добавили $7$ к обеим сторонам . Это работает, потому что операция сложения «отменяет» операцию вычитания. $+7$ и $-7$ сокращаются.

Если вы хотите решить уравнение:

$3\cdot х=15$

вы бы разделили обе части на $3$ . Это работает, потому что операция деления «отменяет» операцию умножения. $\div 3$ и $3\cdot$ сокращаются.х\вправо)=\mathrm{log}_{10}\влево(30\вправо)\)

Использовать правило степени для логарифмов

$x\cdot \mathrm{log}_{10}\left(2\right)=\mathrm{log}_{10}\left(30\right)$

Разделить, чтобы изолировать $x$

$\ displaystyle x = \ frac {\ mathrm {log} _ {10} \ left (30 \ right)} {\ mathrm {log} _ {10} \ left (2 \ right)} = \ frac {\ mathrm {LOG}\влево(30\вправо)}{\mathrm{LOG}\влево(2\вправо)}\приблизительно\фракция{1,4771}{0,3010}=4,907$

Вы можете ввести [LOG] из 30 и [LOG] из 2 в калькулятор, чтобы найти ответ очень быстро. Этот процесс хорошо работает для многих примеров «из реальной жизни», которые включают беспорядочные числа, которые не имеют простых экспоненциальных форм.x\right)&=\mathrm{log}_{2}\left(30\right)\end{align*}\)

Поскольку логарифм и экспонента обратны, логарифм по основанию 2 «отменяет» экспоненту по основанию 2, и в левой части уравнения остается только $x$.

$x=\mathrm{log}_{2}\left(30\right)$

Однако мы уже знаем, что решение также можно записать:

$\displaystyle x=\frac{\mathrm{LOG}\left(30\right)}{\mathrm{LOG}\left(2\right)}$

Это означает, что один логарифм можно выразить как долю двух других логарифмов с другим основанием:

$\ displaystyle \ mathrm {log} _ {2} \ left (30 \ right) = \ frac {\ mathrm {LOG} \ left (30 \ right)} {\ mathrm {LOG} \ left (2 \ right) }$

Иногда вы можете увидеть эту эквивалентность, выраженную как изменение базовой формулы

$\ displaystyle \ mathrm {log} _ {b} \ left (A \ right) = \ frac {\ mathrm {log} _n \ left (A \ right)} {\ mathrm {log} _n \ left (b \ правильно)}$

В упражнениях из учебника вам чаще будут давать числа, которые можно решить без калькулятора, при условии, что вы сможете найти общие основания. {4x+4}\hfill & \text{Чтобы взять степень степени, умножьте показатели степени}.\hfill \\ \text{ }3x+6=4x+4\hfill & \text{Используйте один-к- одно свойство для установки показателей равными}.\hfill \\ \text{ }x=2\hfill & \text{Решить для }x.\hfill \end{массив}\)

В общем, вот несколько шагов, которые следует учитывать при решении экспоненциальных уравнений. Хорошим первым шагом всегда является определение того, можете ли вы переписать термины с общей основой.

Перепишите каждую часть уравнения как степень с общим основанием.{Т}\).
Используйте свойство «один к одному», чтобы установить равные степени.
Решите полученное уравнение S = T для неизвестного.

Подумай об этом

Все ли показательные уравнения имеют решение? Если нет, то как мы можем узнать, есть ли решение в процессе решения проблемы? Напишите свои мысли в текстовом поле ниже, прежде чем проверить предложенный нами ответ.

Показать ответ

Нет. Напомним, что диапазон экспоненциальной функции всегда положителен.{у}=х\). Мы можем использовать этот факт вместе с правилами логарифмирования для решения логарифмических уравнений, где аргументом является алгебраическое выражение.

Например, рассмотрим уравнение ${\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x — 5\right)=3 $. Чтобы решить это уравнение, мы можем использовать правила логарифмирования, чтобы переписать левую часть в компактной форме, а затем применить определение журналов для решения x :

$\ begin{array}{c}{\mathrm{log}}_{2}\left(2\right)+{\mathrm{log}}_{2}\left(3x — 5\right) =3\hfill & \hfill \\ \text{ }{\mathrm{log}}_{2}\left(2\left(3x — 5\right)\right)=3\hfill & \text{Применить правило произведения логарифмов}.{3}.\hfill \\ \text{ }18=6x\hfill & \text{Добавить 10 к обеим сторонам}.\hfill \\ \text{ }x=3\hfill & \text{Разделить на 6}. \hfill\конец{массив}$

В нашем первом примере мы покажем, как использовать методы решения линейных уравнений для решения логарифмического уравнения.

Пример

Решите $2\cdot\mathrm{ln}x+3=7$.

Показать ответ

$\begin{array}{c}2\cdot\mathrm{ln}\left(x\right)+3=7\hfill & \hfill \\ \text{ }2\cdot\mathrm{ln}\left (x\right)=4\hfill & \text{Вычесть 3}.{\ влево (\ гидроразрыва {7} {2} \ вправо)} $

Приблизительный ответ: $x\примерно{5,5}$

В следующем примере мы покажем вам возможности использования графиков для анализа решений логарифмических уравнений. Превратив каждую часть уравнения в функцию и нанеся их на один и тот же набор осей, мы сможем увидеть, как они взаимодействуют друг с другом. В этом случае мы получаем логарифмическую функцию и горизонтальную линию и обнаруживаем, что решением является точка, в которой они пересекаются.

Пример

Решите $\mathrm{ln}\left(x\right)=3$.3,3\справа)\), что приблизительно равно (20,0855, 3).

Точно так же, как история может помочь вам понять сложную концепцию, графики могут помочь нам понять широкий спектр концепций в математике. Визуальные представления частей уравнения можно создать, превратив каждую часть в функцию и нанеся функции на один и тот же набор осей.

Использовать свойство логарифмов «один к одному» для решения логарифмических уравнений

Как и в случае экспоненциальных уравнений, мы можем использовать свойство «один к одному» для решения логарифмических уравнений.Свойство взаимно однозначности логарифмических функций говорит нам, что для любых действительных чисел $M \gt 0$ и $N \gt 0$ и любого положительного действительного числа $b$, где $b \ne 1$,

${\mathrm{log}}_{b}\left(M\right)={\mathrm{log}}_{b}\left(N\right)$ тогда и только тогда, когда $M= Н$

Например,

$\ text{If }{\mathrm{log}}_{2}\left(x — 1\right)={\mathrm{log}}_{2}\left(8\right),\text {тогда}х — 1=8$.

Итак, если $x — 1=8$, то мы можем найти x , и мы получим x = 9.Для проверки подставим x = 9 в исходное уравнение: ${\mathrm{log}}_{2}\left(9 — 1\right)={\mathrm{log}}_{2} \влево(8\вправо)=3$. Другими словами, когда логарифмическое уравнение имеет одинаковое основание с каждой стороны, аргументы должны быть равны. Это также применимо, когда аргументы являются алгебраическими выражениями. Поэтому, когда у нас есть уравнение с логарифмами одинакового основания на каждой стороне, мы можем использовать правила логарифмирования, чтобы переписать каждую сторону как один логарифм. Затем мы используем тот факт, что логарифмические функции являются взаимно однозначными, чтобы установить аргументы равными друг другу и найти неизвестное.

Пример

Решите $\mathrm{log}\left(3x — 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\right)$

Проверьте свои результаты.

Показать ответ

\(\begin{array}{c}\mathrm{log}\left(3x — 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left(x+4\ справа)\hfill & \hfill \\ \text{ }\mathrm{log}\left(\frac{3x — 2}{2}\right)=\mathrm{log}\left(x+4\right)\ hfill & \text{Применить правило отношения логарифмов}.

\hfill \\ \text{ }\frac{3x — 2}{2}=x+4\hfill & \text{Применить свойство «один к одному» логарифма }.\hfill \\ \text{ }3x — 2=2x+8\hfill & \text{Умножьте обе части уравнения на }2.\hfill \\ \text{ }x=10\hfill & \text{Вычтите 2 }x\text{ и добавьте 2}.\hfill \end{массив}\)

Чтобы проверить результат, подставьте x = 10 в $\mathrm{log}\left(3x — 2\right)-\mathrm{log}\left(2\right)=\mathrm{log}\left (х+4\справа)$.

$\begin{array}{c}\mathrm{log}\left(3\left(10\right)-2\right)-\mathrm{log}\left(2\right)=\mathrm{log }\left(\left(10\right)+4\right)\hfill & \hfill \\ \text{ }\mathrm{log}\left(28\right)-\mathrm{log}\left(2\ right)=\mathrm{log}\left(14\right)\hfill & \hfill \\ \text{ }\mathrm{log}\left(\frac{28}{2}\right)=\mathrm{log }\left(14\right)\hfill & \text{Проверка решения}.\hfill\конец{массив}$

Ответить

х = 10

Обратите внимание: при решении уравнения с логарифмами всегда проверяйте правильность ответа или наличие постороннего решения.

Применение логарифмических уравнений

В предыдущих разделах мы изучили свойства и правила как для экспоненциальной, так и для логарифмической функции. Мы видели, что любую экспоненциальную функцию можно записать в виде логарифмической функции и наоборот.Мы использовали показатели степени для решения логарифмических уравнений и логарифмы для решения показательных уравнений. Теперь мы готовы объединить наши навыки для решения уравнений, моделирующих реальные ситуации, независимо от того, находится ли неизвестное в показателе степени или в аргументе логарифма.

Одно из таких приложений называется периодом полураспада , , который относится к количеству времени, необходимому для распада половины заданного количества радиоактивного материала. В таблице ниже указаны периоды полураспада некоторых наиболее распространенных радиоактивных веществ.

Вещество	Использовать	Период полураспада
галлий-67	ядерная медицина	80 часов
кобальт-60	производство	5,3 года
технеций-99м	ядерная медицина	6 часов
америций-241	строительство	432 года
углерод-14	археологические датировки	5715 лет
уран-235	атомная энергия	703 800 000 лет

Мы можем видеть, насколько сильно различаются периоды полураспада этих веществ. {\ гидроразрыва {т} {T}} \)

где

$A$ — количество вещества, присутствующего после времени $t$
${A}_{0}$ — сумма, первоначально представленная
$T$ — период полураспада вещества
$t$ — период времени, в течение которого изучается вещество

Пример

Сколько времени потребуется для распада десяти процентов 1000-граммовой пробы урана-235?

Показать ответ

После распада 10% останется 900 грамм.{т/703,800,000}\справа)\
\mathrm{log}\left(0.9\right)&=\frac{t}{703 800 000} \cdot \mathrm{log}\left(0.5\right) \\
\ frac {\ mathrm {log} \ left (0,9 \ right)} {\ mathrm {log} \ left (0,5 \ right)} & = \ frac {t} {703 800 000} \\
703 800 000 \cdot \frac{\mathrm{log}\left(0,9\right)}{\mathrm{log}\left(0,5\right)}&=t \\ \\ t&=106 979 777\text{лет} \end {выровнять*}\)

Температура

Тепло течет быстро, когда очень горячий объект находится в очень холодной среде, но тепло течет медленно, когда объект лишь немного теплее, чем окружающая среда. Когда объект имеет ту же температуру, что и окружающая среда, тепло не течет вообще. Когда объекты остывают, их температура падает экспоненциально. В следующем примере мы воспользуемся парой измерений, чтобы найти скорость экспоненциального затухания, а затем воспользуемся экспоненциальной моделью, чтобы предсказать будущую температуру.

Пример

Горячий железный стержень погружают в ванну с ледяной водой, чтобы охладить его. Через 10 секунд температура стержня падает до 172°F, а через 5 секунд температура стержня достигает 160°F.

Что такое «период полураспада» экспоненциального распада?
Какой была начальная температура непосредственно перед погружением бруска в ледяную воду?
Какой будет температура после охлаждения бруска в течение 30 секунд?
Как долго брусок должен остыть, прежде чем с ним можно будет безопасно обращаться (110°F)?

Покажи ответ

1. Мы знаем, что для охлаждения бруска с 172°F до 160°F требуется 5 секунд. Мы можем использовать эту информацию, чтобы найти период полураспада или период полураспада.{5/T}\right)\\\text{ }\\
\mathrm{log}_{0,5}(0,9302)&=5/T \\\text{ }\\
T\cdot \mathrm{log }_{0,5}(0,9302)&=5 \\\text{ }\\ T&=\displaystyle \frac{5}{\mathrm{log}_{0,5}(0,9302)}\\\text{ }\\ T&\приблизительно 48\текст{секунд} \end{выравнивание*}\)

Скорее всего, мы застряли с калькулятором, который имеет только натуральные и общие журналы. В этом случае мы логарифмируем обе части уравнения, используя основание $е$ или $10$, и используем свойства логарифмов, чтобы изолировать $Т$.{t/48}\right) \\\text{ }\\ \mathrm{LOG}(0,5528)&= (t/48)\cdot\mathrm{LOG}(0,5) \\\text{ }\\ \ displaystyle \frac{48\cdot\mathrm{LOG}(0,5528)}{\mathrm{LOG}(0,5)}&= t \\\text{ }\\ t&\примерно 41\text{секунды}\end{align *}\)

Ответить

Период полураспада составляет около 48 секунд, а начальное значение было около 199°F. Плитка охлаждается примерно до 129 ° F за 30 секунд, и для безопасного обращения с ней требуется не менее 41 секунды.

рН

В химии рН используется как мера кислотности или щелочности вещества.{+}\справа]\). Как изменится рН, если увеличить концентрацию ионов водорода в жидкости вдвое?

Показать ответ

Предположим, что C — исходная концентрация ионов водорода, а P — исходный pH жидкости. Тогда изначально $P=-\mathrm{log}\left(C\right)$. Если концентрацию удвоить, новая концентрация будет 2 C . Тогда рН новой жидкости будет

$\text{pH}=-\mathrm{log}\left(2C\right)$

Использование правила произведения журналов

$\text{pH}=-\mathrm{log}\left(2C\right)=-\left(\mathrm{log}\left(2\right)+\mathrm{log}\left(C\ вправо)\вправо)=-\mathrm{лог}\влево(2\вправо)-\mathrm{лог}\влево(С\вправо)$

Поскольку $P=-\mathrm{log}\left(C\right)$, новый pH равен

$\text{pH}=P-\mathrm{log}\left(2\right)\приблизительно P — 0.301$

Когда концентрация ионов водорода удваивается, pH уменьшается примерно на 0,301.

Шкала Рихтера

Шкала Рихтера энергии землетрясения

Шкала Рихтера — это логарифмическая функция, используемая для измерения магнитуды землетрясений. Сила землетрясения связана с тем, сколько энергии высвобождается при землетрясении. Инструменты, называемые сейсмографами, обнаруживают движение земли; наименьшее движение, которое можно обнаружить, отображается на сейсмографе в виде волны с амплитудой $A_{0}$.

Магнитуда землетрясения по шкале Рихтера $R$ рассчитывается по формуле:

$R=\mathrm{log}\left(\frac{A}{A_{0}}\right)$

$A$ — мера амплитуды волны землетрясения
$A_{0}$ — амплитуда наименьшей обнаруживаемой волны (или стандартной волны)

Интенсивность землетрясения обычно составляет от 2 до 10 баллов по шкале Рихтера. Любые землетрясения, зарегистрированные ниже 5 баллов, довольно незначительны; они могут немного сотрясать землю, но редко бывают достаточно сильными, чтобы нанести большой ущерб. Землетрясения с баллом по шкале Рихтера от 5 до 7,9 являются гораздо более сильными, и любое землетрясение с баллом выше 8 может привести к огромным разрушениям. (Самый высокий рейтинг, когда-либо зарегистрированный для землетрясения, был 9,5 во время землетрясения в Вальдивии в 1960 году в Чили.)

Пример

Измерено землетрясение с амплитудой волны, в 392 раза превышающей $A_{0}$. Какова магнитуда этого землетрясения по шкале Рихтера с точностью до десятых?

Показать ответ

Используйте уравнение шкалы Рихтера.

$R=\mathrm{log}\left(\frac{A}{A_{0}}\right)$

Так как A в 392 раза больше, чем $A_{0}$, $A=392A_{0}$. Подставьте это выражение вместо A.

$R=\mathrm{log}\left(\frac{392A_{0}}{A_{0}}\right)$

Упростите аргумент логарифма, затем используйте калькулятор для вычисления.

$\begin{array}{c}R=\mathrm{log}\left(\frac{392A_{0}}{A_{0}}\right)\\=\mathrm{log}\left(392\ справа)\\=2,5932\\\приблизительно{2,6}\конец{массив}$

Ответить

Землетрясение силой 2,6 балла по шкале Рихтера.

Разница в 1 балл по шкале Рихтера соответствует 10-кратной разнице в амплитуде землетрясения (которая связана с силой волны). Это означает, что землетрясение силой 3,6 балла по шкале Рихтера имеет амплитуду в 10 раз больше, чем землетрясение силой 2,6 балла.

В примере по шкале Рихтера амплитуда волны землетрясения была в 392 раза больше нормальной. Что, если бы амплитуда была в 10 раз больше или в 3920 раз больше нормы? Чтобы найти измерение землетрясения такого размера по шкале Рихтера, вы найдете $\mathrm{log}\left(3920\right)$.Калькулятор дает значение 3,5932…или 3,6 при округлении до десятых. Один дополнительный балл по шкале Рихтера может означать гораздо большее потрясение!

децибел

Убавь звук

Звук измеряется в логарифмической шкале с использованием единицы, называемой децибел. Формула похожа на шкалу Рихтера:

$d=10\cdot\mathrm{log}\left(\frac{P}{P_{0}}\right)$

, где $P$ — мощность или интенсивность звука, а $P_0$ — самый слабый звук, который может слышать человеческое ухо. В следующем примере мы обнаружим, насколько интенсивнее шум посудомоечной машины, чем шум насоса горячей воды.

Пример

Уровень шума одного насоса горячей воды составляет 50 децибел. Однако одна посудомоечная машина имеет рейтинг шума 62 децибела. Шум посудомоечной машины во сколько раз интенсивнее шума насоса горячей воды?

Показать ответ

Нам даны децибелы $d$, но мы хотим сравнить звуковые мощности $P$, поэтому начнем с выделения $P$ в формуле децибел.{1,2}\) (или примерно в 15,85) раз интенсивнее, чем у насоса горячей воды.

Применение логарифмов и экспонент в науке повсюду. Мы надеемся, что приведенные здесь примеры дали вам представление о том, насколько полезными они могут быть.

Резюме

6.6 Экспоненциальные и логарифмические уравнения — Алгебра колледжа

Цели обучения

В этом разделе вы будете:

Использовать одинаковые основания для решения экспоненциальных уравнений.
Используйте логарифмы для решения экспоненциальных уравнений.
Используйте определение логарифма для решения логарифмических уравнений.
Используйте свойство логарифмов «один к одному» для решения логарифмических уравнений.
Решение прикладных задач на экспоненциальные и логарифмические уравнения.

Рисунок 1 Дикие кролики в Австралии. Популяция кроликов в Австралии росла так быстро, что это событие стало известно как «кроличья чума». (Фото: Ричард Тейлор, Flickr)

В 1859 году австралийский землевладелец по имени Томас Остин выпустил на охоту 24 кролика.Поскольку в Австралии было мало хищников и достаточно еды, популяция кроликов резко возросла. Менее чем за десять лет популяция кроликов исчислялась миллионами.

Использование одинаковых оснований для решения экспоненциальных уравнений

В первом методе используются две функции с одинаковыми основаниями.Напомним, что свойство взаимно однозначности экспоненциальных функций говорит нам, что для любых действительных чисел b,b, S,S и T,T, где b>0,b≠1,b>0,b≠1, bS=bTbS=bT тогда и только тогда, когда S=TS=T.

Например, рассмотрим уравнение 34x−7=32×3,34x−7=32×3. Чтобы найти x,x, мы используем свойство деления показателей степени, чтобы переписать правую часть так, чтобы обе части имели общее основание, 3.3. Затем мы применяем взаимно однозначное свойство показателей, устанавливая показатели равными друг другу и решая для xx:

34x−7=32x334x−7=32×31Перепишем 3 как 31,34x−7=32x−1Используем свойство деления показателей .4x-7=2x-1Применить свойство степени однозначности.2x=6Вычесть 2xи добавить 7 к обеим частям.x=3Делить на 3,34x−7=32x334x−7=32×31Переписать 3 как 31,34x−7=32x−1Использовать свойство деления показателей степени.4x−7=2x−1Применить свойство степени однозначности.2x=6Вычесть 2xи прибавить 7 к обеим сторонам.x=3Разделить на 3.

Использование свойства однозначности экспоненциальных функций для решения экспоненциальных уравнений

Для любых алгебраических выражений Sand T,Sand T и любых положительных вещественных чисел b≠1,b≠1,

bS=bTif и только еслиS=TbS=bTif и только еслиS=T

Как

Имея показательное уравнение вида bS=bT,bS=bT, где SS и TT — алгебраические выражения с неизвестным, найдите неизвестное.

Используйте правила возведения в степень для упрощения, если необходимо, чтобы результирующее уравнение имело вид bS=bT.bS=bT.
Используйте свойство «один к одному», чтобы установить равные степени.
Решите полученное уравнение S=T,S=T относительно неизвестного.

Пример 1

Решение экспоненциального уравнения с общим основанием

Решите 2x−1=22x−4,2x−1=22x−4.

Решение

2x−1=22x−4Общее основание равно 2.x−1=2x−4По свойству «один к одному» показатели степени должны быть равны.x=3Найти x. 2x−1=22x−4Общее основание равно 2.x−1=2x−4По свойству «один к одному» показатели степени должны быть равны.x=3Найти x.

Попробуйте #1

Решите 52x=53x+2,52x=53x+2.

Переписать уравнения так, чтобы все степени имели одно основание

Иногда общее основание экспоненциального уравнения не отображается явно. В этих случаях мы просто переписываем члены уравнения в виде степеней с общим основанием и решаем, используя свойство взаимно однозначности.

Например, рассмотрим уравнение 256=4x−5.256=4x−5. Мы можем переписать обе части этого уравнения в виде степени 2,2. Затем мы применяем правила возведения в степень вместе со свойством однозначности, чтобы найти x:x:

256=4x−528=(22)x−5. Перепишем каждую сторону как степень с основанием 2,28=22x−10. свойство экспоненты «один к одному».8=2x-10Применить свойство экспоненты «один-к-одному».18=2xДобавить 10 к обеим частям.x=9Разделить на 2,256=4x-528=(22)x-5Переписать каждый сторону как степень с основанием 2,28=22x−10Использовать свойство степени однозначности.8=2x−10Применить свойство степени однозначности степени.18=2xПрибавить 10 к обеим сторонам.x=9Разделить на 2.

Как сделать

Имея показательное уравнение с разными основаниями, используйте для его решения свойство однозначности.

Перепишите каждую часть уравнения как степень с общим основанием.
Используйте правила возведения в степень, чтобы упростить, если это необходимо, чтобы результирующее уравнение имело вид bS=bT.bS=bT.
Используйте свойство «один к одному», чтобы установить равные степени.
Решите полученное уравнение S=T,S=T относительно неизвестного.

Пример 2

Решение уравнений путем их перезаписи для получения общей базы

Решите 8x+2=16x+1,8x+2=16x+1.

Решение

8x+2=16x+1(23)x+2=(24)x+1Запишите 8 и 16 как степени 2,23x+6=24x+4Чтобы взять степень степени, умножьте показатели степени.3x+6=4x+4Используйте единицу- к одному свойству, чтобы установить показатели степени равными. степень, умножить показатели степени.3x+6=4x+4Используйте свойство «один к одному», чтобы установить степени равными.x=2Найти x.

Попробуйте #2

Решите 52x=253x+2,52x=253x+2.

Пример 3

Решение уравнений путем перезаписи корней с дробными показателями для получения общего основания

Решите 25x=2,25x=2.

Решение

25x=212Запишите квадратный корень из 2 в виде степени 2.x=12Используйте свойство «один к одному». одно свойство.x=110Решить forx.

Вопросы и ответы

Пример 4

Решение уравнения с положительными и отрицательными степенями

Решить 3x+1=-2,3x+1=-2.

Решение

Это уравнение не имеет решения. Не существует действительного значения xx, которое сделало бы уравнение верным утверждением, потому что любая степень положительного числа положительна.

Анализ

На рис. 2 показано, что два графика не пересекаются, поэтому левая сторона никогда не равна правой стороне.Таким образом, уравнение не имеет решения.

Рисунок 2

Попробуйте #4

Решите 2x=-100,2x=-100.

Решение экспоненциальных уравнений с использованием логарифмов

Иногда члены экспоненциального уравнения не могут быть переписаны с общим основанием. В этих случаях мы решаем, логарифмируя каждую сторону. Напомним, поскольку log(a)=log(b)log(a)=log(b) эквивалентно a=b,a=b, мы можем применять логарифмы с одинаковым основанием к обеим частям экспоненциального уравнения.

Как

Для заданного показательного уравнения, в котором невозможно найти общее основание, найдите неизвестное.

Примените логарифм обеих частей уравнения.
1. Если один из членов уравнения имеет основание 10, используйте десятичный логарифм.
2. Если ни один из членов уравнения не имеет основание 10, используйте натуральный логарифм.
Используйте правила логарифмирования, чтобы найти неизвестное.

Пример 5

Решение уравнения, содержащего степени разных оснований

Решите 5x+2=4x.5х+2=4х.

Решение

5x+2=4xНет простого способа получить силы, имеющие одинаковую основу. xln5−xln4=−2ln5Получить термины, содержащие x с одной стороны, термины без x с другой.x(ln5−ln4)=−2ln5В левой части вынести x.xln(54)=ln(125)Использовать логарифмические законы. x=ln(125)ln(54) Разделите на коэффициент x.5x+2=4xНет простого способа получить степени, имеющие одинаковое основание.ln5x+2=ln4xВозьмем ln с обеих сторон.(x+2)ln5=xln4Используем законы логарифмического распределения.

xln5+2ln5=xln4Используем закон дистрибутивности.xln5−xln4=−2ln5Получим члены, содержащие x на одной стороне, члены без x на другой.x(ln5 −ln4)=−2ln5. В левой части вынесите x.xln(54)=ln(125)Используйте законы логарифмов.x=ln(125)ln(54) Разделите на коэффициент x.

Вопросы и ответы

Есть ли способ решить 2x=3x?2x=3x?

Да. Решение 0,0.

Уравнения, содержащие

Одним из распространенных типов показательных уравнений являются уравнения с основанием e.е. Эта константа снова и снова встречается в природе, в математике, в науке, в технике и в финансах. Когда у нас есть уравнение с основанием ee с обеих сторон, мы можем использовать натуральный логарифм для его решения.

Как

Для заданного уравнения вида y=Aekt,y=Aekt найдите t. t.

Разделите обе части уравнения на A.A.
Примените натуральный логарифм к обеим частям уравнения.
Разделите обе части уравнения на k.к.

Пример 6

Решить уравнение вида

y = Ae ^kt

Решите 100=20e2t.100=20e2t.

Решение

100=20e2t5=e2tРазделите на коэффициент мощности.ln5=2tВозьмите ln обеих сторон. Используйте тот факт, что ln(x) и ex представляют собой обратные функции. Используйте тот факт, что ln(x) и ex — обратные функции.t=ln52Разделить на коэффициент при t.

Анализ

Используя законы журналов, мы также можем записать этот ответ в виде t=ln5.t=ln5. Если мы хотим десятичную аппроксимацию ответа, мы используем калькулятор.

Попробуйте #6

Решите 3e0. 5t=11.3e0.5t=11.

Вопросы и ответы

Каждое ли уравнение вида y=Aekty=Aekt имеет решение?

Нет. Существует решение, когда k≠0,k≠0, и когда yy и AA либо оба равны 0, либо ни один из них не равен 0, и они имеют одинаковый знак.Примером уравнения этой формы, не имеющего решения, является 2=-3et.2=-3et.

Пример 7

Решение уравнения, которое можно упростить до вида

y = Ae ^kt

Решите 4e2x+5=12,4e2x+5=12.

Решение

4e2x+5=124e2x=7Объедините одинаковые члены.e2x=74Разделите на коэффициент степени.2x=ln(74)Возьмите ln обеих сторон.x=12ln(74)Найдите x.4e2x+5=124e2x=7Объедините подобные terms.e2x=74Разделить на коэффициент мощности.2x=ln(74)Возьмите ln обеих сторон.

x=12ln(74)Найдите x.

Попробуйте #7

Решите 3+e2t=7e2t.3+e2t=7e2t.

Посторонние растворы

Иногда методы, используемые для решения уравнения, вводят постороннее решение, которое является решением, правильным алгебраически, но не удовлетворяющим условиям исходного уравнения. Одна из таких ситуаций возникает при решении, когда обе части уравнения логарифмируются. В таких случаях помните, что аргумент логарифма должен быть положительным.Если число, которое мы оцениваем в логарифмической функции, отрицательное, выходных данных нет.

Пример 8

Решение показательных функций в квадратичной форме

Решите e2x-ex=56.e2x-ex=56.

Решение

e2x-ex=56e2x-ex-56=0Получите одну часть уравнения равной нулю.(ex+7)(ex-8)=0Разложите по методу FOIL.ex+7=0или ex-8=0Если произведение ноль, то один множитель должен быть равен нулю.

ex=−7или ex=8Изолировать экспоненты.ex=8Отклонить уравнение, в котором степень равна отрицательному числу.x=ln8Решить уравнение, в котором степень равна положительному числу.e2x−ex=56e2x−ex−56=0Получить одну часть уравнения равной нулю.(ex+7)(ex−8)=0Помножить методом FOIL .ex+7=0или ex-8=0Если произведение равно нулю, то один множитель должен быть равен нулю.ex=-7или ex=8Выделить экспоненты.ex=8Отклонить уравнение, в котором степень равна отрицательному числу.x=ln8Решить уравнение, в котором мощность равна положительному числу.

Анализ

Когда мы планируем использовать факторинг для решения проблемы, мы всегда получаем ноль в одной части уравнения, потому что ноль обладает уникальным свойством: когда произведение равно нулю, один или оба множителя должны быть равны нулю.Мы отвергаем уравнение ex=−7ex=−7, потому что положительное число никогда не равняется отрицательному числу. Решение ln(−7)ln(−7) не является вещественным числом, и в действительной системе счисления это решение отбрасывается как лишнее.

Вопросы и ответы

Каждое ли логарифмическое уравнение имеет решение?

Нет. Имейте в виду, что мы можем применять логарифм только к положительному числу. Всегда проверяйте наличие посторонних решений.

Использование определения логарифма для решения логарифмических уравнений

Мы уже видели, что каждое логарифмическое уравнение logb(x)=ylogb(x)=y эквивалентно показательному уравнению by=x.по=х. Мы можем использовать этот факт вместе с правилами логарифмирования для решения логарифмических уравнений, где аргументом является алгебраическое выражение.

Например, рассмотрим уравнение log2(2)+log2(3x−5)=3. log2(2)+log2(3x−5)=3. Чтобы решить это уравнение, мы можем использовать правила логарифмирования, чтобы переписать левую часть в компактной форме, а затем применить определение логов для решения x:x:

log2(2)+log2(3x−5)=3log2(2( 3x−5))=3Применить правило произведения логарифмов.

log2(6x−10)=3Распределить.23=6x−10Применить определение логарифма.8=6x−10Вычислить 23.18=6xПрибавить 10 к обеим сторонам.x=3Разделить на 6.log2(2)+log2(3x−5)=3log2(2(3x−5))=3Применить правило произведения логарифмов.log2( 6x−10)=3Распределить.23=6x−10Применить определение логарифма.8=6x−10Вычислить 23.18=6xПрибавить 10 к обеим сторонам.x=3Разделить на 6.

Использование определения логарифма для решения логарифмических уравнений

Для любого алгебраического выражения SS и вещественных чисел bb и c,c, где b>0,b≠1,b>0,b≠1,

logb(S)=cif и только если bc=Slogb(S)=cif и только еслиbc=S

Пример 9

Использование алгебры для решения логарифмического уравнения

Решите 2lnx+3=7.2lnx+3=7.

Решение

2lnx+3=72lnx=4Вычесть 3.lnx=2Разделить на 2.x=e2Переписать в экспоненциальной форме.2lnx+3=72lnx=4Вычесть 3.lnx=2Разделить на 2.x=e2Переписать в экспоненциальной форме.

Пример 10

Использование алгебры до и после использования определения натурального логарифма

Решите 2ln(6x)=7,2ln(6x)=7.

Решение

2ln(6x)=7ln(6x)=72Разделите на 2,6x=e(72)Используйте определение ln.x=16e(72)Разделите на 6,2ln(6x)=7ln(6x)=72Разделите на 2.6x=e(72)Используйте определение ln.x=16e(72)разделите на 6.

Попробуйте #10

Решите 2ln(x+1)=10,2ln(x+1)=10.

Пример 11

Использование графика для понимания решения логарифмического уравнения

Решите lnx=3.lnx=3.

Решение

lnx=3x=e3Используйте определение натурального логарифма. lnx=3x=e3Используйте определение натурального логарифма.

На рис. 3 представлен график уравнения. На графике x координата точки пересечения двух графиков близка к 20.Другими словами, e3≈20.e3≈20. Калькулятор дает более точное приближение: e3≈20,0855.e3≈20,0855.

Рисунок 3 Графики y=lnxy=lnx и y=3y=3 пересекаются в точке (e3,3),(e3,3), что приблизительно равно (20,0855, 3).

Попробуйте #11

С помощью графического калькулятора вычислите приблизительное решение логарифмического уравнения 2x=10002x=1000 с точностью до 2 знаков после запятой.

Использование свойства взаимно однозначности логарифмов для решения логарифмических уравнений

Как и в случае экспоненциальных уравнений, мы можем использовать свойство «один к одному» для решения логарифмических уравнений.Свойство логарифмических функций «один к одному» говорит нам, что для любых действительных чисел x>0,x>0, S>0,S>0, T>0T>0 и любых положительных действительных чисел b,b, где b ≠1,b≠1,

logbS=logbTif и только если S=T.logbS=logbTif и только если S=T.

Например,

Если log2(x−1)=log2(8), то x−1=8. Если log2(x−1)=log2(8), то x−1=8.

Итак, если x−1=8,x−1=8, то мы можем найти x,x и получить x=9. x=9. Для проверки мы можем подставить x=9x=9 в исходное уравнение: log2(9−1)=log2(8)=3.log2(9−1)=log2(8)=3.Другими словами, когда логарифмическое уравнение имеет одинаковое основание с каждой стороны, аргументы должны быть равны. Это также применимо, когда аргументы являются алгебраическими выражениями. Поэтому, когда у нас есть уравнение с логарифмами одинакового основания на каждой стороне, мы можем использовать правила логарифмирования, чтобы переписать каждую сторону как один логарифм. Затем мы используем тот факт, что логарифмические функции являются взаимно однозначными, чтобы установить аргументы равными друг другу и найти неизвестное.

Например, рассмотрим уравнение log(3x−2)−log(2)=log(x+4).лог(3х-2)-лог(2)=лог(х+4). Чтобы решить это уравнение, мы можем использовать правила логарифмирования, чтобы переписать левую часть как одиночный логарифм, а затем применить свойство «один к одному» для решения x:x:

log(3x−2)−log(2)=log(x+4)log(3x−22)=log(x+4)Применить правило частного логарифмов.

3x−22=x+4Применить свойство один к одному логарифма.3x−2=2x+8Умножить обе части уравнения на 2.x=10Вычесть 2xи добавить 2.log(3x−2)−log(2)=log(x+4)log(3x−22) =log(x+4)Применить правило отношения логарифмов.3x−22=x+4Применить свойство один к одному логарифма.3x−2=2x+8Умножьте обе части уравнения на 2.x=10Вычтите 2x и прибавьте 2.

Чтобы проверить результат, подставьте x=10x=10 в log(3x−2)−log(2)=log(x +4).log(3x−2)−log(2)=log(x+4).

log(3(10)−2)−log(2)=log((10)+4)log(28)−log(2)=log(14)log(282)=log(14) Решение проверяет. log(3(10)−2)−log(2)=log((10)+4)log(28)−log(2)=log(14)log(282)=log(14) Решение проверяет.

Использование свойства взаимно однозначности логарифмов для решения логарифмических уравнений

Для любых алгебраических выражений SS и TT и любых положительных действительных чисел b,b, где b≠1,b≠1,

logbS=logbTif и только еслиS=TlogbS=logbTif и только еслиS=T

Обратите внимание: при решении уравнения с логарифмами всегда проверяйте, правильный ли ответ или это постороннее решение.

Как

Дано уравнение, содержащее логарифмы, решить его, используя свойство однозначности.

Используйте правила логарифмирования для комбинирования одинаковых членов, если необходимо, чтобы результирующее уравнение имело вид logbS=logbT.logbS=logbT.
Используйте свойство «один к одному», чтобы установить равные аргументы.
Решите полученное уравнение S=T,S=T относительно неизвестного.

Пример 12

Решение уравнения с использованием свойства однозначности логарифмов

Решить ln(x2)=ln(2x+3).ln(x2)=ln(2x+3).

Решение

ln(x2)=ln(2x+3)x2=2x+3Используйте свойство однозначности логарифма.x2−2x−3=0Получите ноль с одной стороны перед разложением на множители.(x−3)(x+1 )=0Множитель с использованием FOIL.x−3=0или x+1=0Если произведение равно нулю, один из множителей должен быть равен нулю.

x=3orx=-1Решить для x.ln(x2)=ln(2x+3)x2 =2x+3Использовать свойство один к одному логарифма.x2−2x−3=0Получить ноль с одной стороны перед разложением на множители.(x−3)(x+1)=0Разложить на множители, используя FOIL.x−3=0или x +1=0Если продукт равен нулю, один из факторов должен быть равен нулю.x=3orx=−1Найти x.

Анализ

Есть два решения: 33 или -1.-1. Решение −1−1 отрицательно, но оно проверяется при подстановке в исходное уравнение, потому что аргумент логарифмических функций по-прежнему положителен.

Попробуйте #12

Решить ln(x2)=ln1.ln(x2)=ln1.

Решение прикладных задач с использованием экспоненциальных и логарифмических уравнений

Одно из таких применений находится в науке при расчете времени, необходимого для распада половины нестабильного материала в образце радиоактивного вещества, называемого периодом полураспада.В таблице 1 приведены периоды полураспада некоторых наиболее распространенных радиоактивных веществ.

Вещество	Использовать	Период полураспада
галлий-67	ядерная медицина	80 часов
кобальт-60	производство	5,3 года
технеций-99м	ядерная медицина	6 часов
америций-241	строительство	432 года
углерод-14	археологические датировки	5715 лет
уран-235	атомная энергия	703 800 000 лет

Таблица 1

A(t)=A0eln(0,5)TtA(t)=A0eln(0,5)tTA(t)=A0(eln(0,5))tTA(t)=A0(12)tTA(t)=A0eln(0,5)TtA( t)=A0eln(0,5)tTA(t)=A0(eln(0,5))tTA(t)=A0(12)tT

, где

A0A0 — первоначальное количество
TT – период полураспада вещества
tt – период времени, в течение которого изучается вещество
A(t)A(t) – количество вещества, присутствующего после времени tt

Пример 13

Использование формулы радиоактивного распада для определения количества вещества

Сколько времени потребуется для распада десяти процентов 1000-граммовой пробы урана-235?

Решение

у=1000eln(0.5)703 800 000t900=1000eln(0,5)703800000tПосле 10% распадов остается 900 граммов. .ln(0.9)=ln(0.5)703,800,000tln(eM)=Mt=703,800,000×ln(0,9)ln(0,5)yearsРешите fort.

t≈106,979,777 yearsy=1000eln(0,5)703,800,000t900=1000eln(0,5) % распадается, осталось 900 грамм. (eM)=Mt=703 800 000×ln(0.9)ln(0,5)yearsРешите fort.t≈106 979 777 лет

Анализ

Десять процентов от 1000 граммов составляют 100 граммов. Если 100 граммов распадаются, количество оставшегося урана-235 составляет 900 граммов.

Попробуйте #13

Сколько времени пройдет, прежде чем двадцать процентов нашей 1000-граммовой пробы урана-235 распадутся?

6.6 Упражнения по секциям

Вербальные

Как решить показательное уравнение?

Когда появляется посторонний раствор? Как распознать постороннее решение?

Алгебраический

В следующих упражнениях используйте одинаковые основания для решения экспоненциального уравнения.

4-3v-2=4-v4-3v-2=4-v

32x+1⋅3x=24332x+1⋅3x=243

2−3n⋅14=2n+22−3n⋅14=2n+2

625⋅53х+3=125625⋅53х+3=125

363b362b=2162−b363b362b=2162−b

10.

(164)3n⋅8=26(164)3n⋅8=26

Для решения следующих упражнений используйте логарифмы.

13.

er+10−10=−42er+10−10=−42

15.

−8⋅10p+7−7=−24−8⋅10p+7−7=−24

16.

7e3n−5+5=−897e3n−5+5=−89

18.

−5e9x−8−8=−62−5e9x−8−8=−62

19.

−6e9x+8+2=−74−6e9x+8+2=−74

21.

e2x-ex-132=0e2x-ex-132=0

22.

7e8x+8−5=−957e8x+8−5=−95

24.

4e3x+3−7=534e3x+3−7=53

25.

8e-5x-2-4=-908e-5x-2-4=-90

27.

e2x-ex-6=0e2x-ex-6=0

28.

3e3−3x+6=−313e3−3x+6=−31

29.

лог(1100)=-2лог(1100)=-2

30.

log324(18)=12log324(18)=12

В следующих упражнениях используйте определение логарифма для решения уравнения.

34.

2log(8n+4)+6=102log(8n+4)+6=10

35.

10−4ln(9−8x)=610−4ln(9−8x)=6

Для решения следующих упражнений используйте свойство логарифмов «один к одному».

36.

ln(10−3x)=ln(−4x)ln(10−3x)=ln(−4x)

37.

log13(5n−2)=log13(8−5n)log13(5n−2)=log13(8−5n)

38.

лог(х+3)-лог(х)=лог(74)лог(х+3)-лог(х)=лог(74)

39.

ln(−3x)=ln(x2−6x)ln(−3x)=ln(x2−6x)

40.

log4(6-м)=log43mlog4(6-м)=log43м

41.

ln(x−2)−ln(x)=ln(54)ln(x−2)−ln(x)=ln(54)

42.

log9(2n2-14n)=log9(-45+n2)log9(2n2-14n)=log9(-45+n2)

43.

пер(х2-10)+пер(9)=пер(10)пер(х2-10)+пер(9)=пер(10)

В следующих упражнениях решите каждое уравнение относительно x.Икс.

44.

лог(х+12)=лог(х)+лог(12)лог(х+12)=лог(х)+лог(12)

45.

ln(x)+ln(x−3)=ln(7x)ln(x)+ln(x−3)=ln(7x)

47.

пер(7)+пер(2−4×2)=пер(14)пер(7)+пер(2−4×2)=пер(14)

48.

log8(x+6)−log8(x)=log8(58)log8(x+6)−log8(x)=log8(58)

49.

ln(3)−ln(3−3x)=ln(4)ln(3)−ln(3−3x)=ln(4)

50.

log3(3x)−log3(6)=log3(77)log3(3x)−log3(6)=log3(77)

Графический

Для следующих упражнений решите уравнение относительно x,x, если есть решение . Затем начертите обе части уравнения и посмотрите на точку пересечения (если она существует), чтобы проверить решение.

51.

log9(x)−5=−4log9(x)−5=−4

55.

log(4)+log(-5x)=2log(4)+log(-5x)=2

56.

−7+log3(4−x)=−6−7+log3(4−x)=−6

57.

ln(4x−10)−6=−5ln(4x−10)−6=−5

58.

лог(4-2х)=лог(-4х)лог(4-2х)=лог(-4х)

59.

log11(-2×2-7x)=log11(x-2)log11(-2×2-7x)=log11(x-2)

60.

пер(2х+9)=пер(-5х)пер(2х+9)=пер(-5х)

61.

log9(3-x)=log9(4x-8)log9(3-x)=log9(4x-8)

62.

лог(х2+13)=лог(7х+3)лог(х2+13)=лог(7х+3)

63.

3log2(10)-log(x-9)=log(44)3log2(10)-log(x-9)=log(44)

64.

ln(x)−ln(x+3)=ln(6)ln(x)−ln(x+3)=ln(6)

В следующих упражнениях найдите указанное значение и постройте график ситуации, показывающий точку решения.

65.

Счет с первоначальным депозитом в размере 6500 долларов США 6500 долларов США приносит 7,25% 7,25% годовых процентов, которые непрерывно начисляются.Сколько будет стоить аккаунт через 20 лет?

66.

Формула для измерения интенсивности звука в децибелах DD определяется уравнением D=10log(II0),D=10log(II0), где II – интенсивность звука в ваттах на квадратный метр, а I0=10−12I0=10 −12 — это самый низкий уровень звука, который может слышать обычный человек. Сколько децибел излучает реактивный самолет с интенсивностью звука 8,3⋅1028,3⋅102 ватт на квадратный метр?

67.

Население небольшого города моделируется уравнением P=1650e0.5tP=1650e0,5t, где tt измеряется в годах. Примерно через сколько лет население города достигнет 20 000?20 000?

Технология

В следующих упражнениях решите каждое уравнение, переписав экспоненциальное выражение, используя указанный логарифм. Затем с помощью калькулятора аппроксимируйте переменную до 3 знаков после запятой.

68.

1000(1,03)t=50001000(1,03)t=5000 с использованием общего журнала.

69.

e5x=17e5x=17 с использованием натурального логарифма

70.

3(1.04)3t=83(1.04)3t=8 с использованием общего журнала

71.

34x−5=3834x−5=38 с использованием общего журнала

72.

50e-0,12t=1050e-0,12t=10 с использованием натурального бревна

В следующих упражнениях используйте калькулятор для решения уравнения. Если не указано иное, округлить все ответы до десятитысячных.

73.

7e3x−5+7,9=477e3x−5+7,9=47

74.

ln(3)+ln(4,4x+6,8)=2ln(3)+ln(4,4x+6,8)=2

75.

log(-0,7x-9)=1+5log(5)log(-0.7x−9)=1+5log(5)

76.

Атмосферное давление PP в фунтах на квадратный дюйм представлено формулой P=14,7e−0,21x,P=14,7e−0,21x, где xx — количество миль над уровнем моря. Какова с точностью до фута вершина горы с атмосферным давлением 8,3698,369 фунтов на квадратный дюйм? ( Подсказка : в миле 5280 футов)

77.

Магнитуда землетрясения M представлена уравнением M=23log(EE0)M=23log(EE0), где EE — количество энергии, высвобождаемой землетрясением, в джоулях, а E0=104.4E0=104,4 – заданная минимальная мера, высвобождаемая землетрясением. Какова будет с точностью до сотой магнитуда землетрясения, высвободившего 1,4⋅10131,4⋅1013 джоулей энергии?

Удлинители

78.

Используйте определение логарифма вместе со свойством логарифмов «один к одному», чтобы доказать, что blogbx=x.blogbx=x.

79.

Вспомните формулу постоянного начисления процентов: y=Aekt.y=Aekt. Используйте определение логарифма вместе со свойствами логарифмов, чтобы решить формулу для времени tt так, чтобы tt было равно единичному логарифму.

80.

Вспомните формулу сложных процентов A=a(1+rk)kt.A=a(1+rk)kt. Используйте определение логарифма вместе со свойствами логарифмов, чтобы решить формулу для времени t.t.

81.

Закон охлаждения Ньютона гласит, что температура TT объекта в любой момент времени t может быть описана уравнением T=Ts+(T0−Ts)e−kt, T=Ts+(T0−Ts)e−kt, где TsTs — температура окружающей среды, T0T0 — начальная температура объекта, kk — скорость охлаждения.