Показательные неравенства — как решать? Примеры, методы решения и свойства
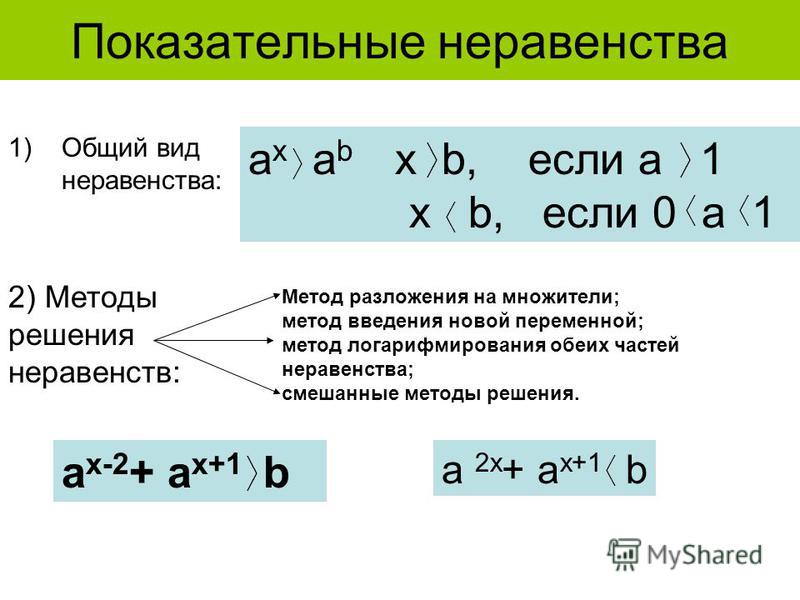
Определение показательных неравенств
|
Показательными считаются неравенства, которые включают в себя переменную, стоящую в показателе степени: . Из них показательно-степенными неравенствами являются те, в которых есть переменные и в показателе степени, и в основании. |
Для изучения этой темы стоит повторить:
показательные уравнения;
метод интервалов;
разложение многочлена на множители;
свойства степенной функции.

И, конечно, для решения смешанных неравенств, включающих в себя тригонометрические и логарифмические, также придется вспомнить формулы соответствующих разделов алгебры.
Если все это еще свежо в памяти, давайте приступим. Как и к показательным уравнениям, к неравенствам стоит подходить, помня о свойствах показательной функции. Напомним, что она выглядит так: y = ax, где a > 0 и a ≠ 1. Два графика ниже дают представление о том, на что похожа такая функция, когда основание степени а положительно, но не равно единице. Наверняка вы уже догадались, каково главное свойство этой функции. Да, она монотонна.
При этом заметьте — значения функции всегда больше нуля. На практике в этом несложно убедиться, если возводить какое-либо число (большее нуля) во всевозможные степени, включая отрицательные.
Для любых а и х верно неравенство ax > 0, т. е. показательная функция не принимает отрицательных значений.
Запишем следствие монотонности показательной функции в виде формул:
, когда функция возрастает, т. е. ;
, когда функция убывает, т. е. .
На этом свойстве показательных неравенств так или иначе основываются все методы решения, и сейчас мы разберемся, как им пользоваться.
Демо урок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Как решать показательные неравенства
Как мы уже говорили, для успешного освоения этой темы нужно хорошенько повторить все, что касается показательных уравнений. Способы решения показательных неравенств выглядят примерно так же — мы будем пытаться упростить выражение, получить одинаковые степени или одинаковые основания, по возможности свести все к квадратному или рациональному уравнению. Но есть и свои тонкости…
Способы решения показательных неравенств выглядят примерно так же — мы будем пытаться упростить выражение, получить одинаковые степени или одинаковые основания, по возможности свести все к квадратному или рациональному уравнению. Но есть и свои тонкости…
Допустим, у нас есть простейшее показательное неравенство:
3х > 9
Если вы помните, как решались показательные уравнения, не придется долго думать, что делать с таким неравенством — приведем его к одинаковому основанию:
3х > 32
х > 2
Казалось бы, все логично, но всегда ли можно смело вычеркивать одинаковые основания степеней? А что, если вместо 3 у нас основание степени будет 0,5? Посмотрим:
0,5х > 0,52
Проверим, верно ли в таком случае х > 2.
0,52 = 0,25;
0,53 = 0, 125 и т. д.
д.
Как видите, на самом деле в этом случае х < 2. Неудивительно, если вспомнить, о чем мы писали в самом начале, когда рисовали графики возрастающей и убывающей показательной функции.
|
Если а > 1, то , и при решении неравенства можно просто убрать одинаковые основания степени. Если 0 < а < 1, то , т. е. одинаковые основания по-прежнему можно убрать, но при этом необходимо поменять знак неравенства. |
Для ясности всегда предполагается, что основание степени — положительное число.
Это были общие правила, а сейчас рассмотрим разные виды показательных неравенств и примеры с решениями.
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Показательные неравенства, сводящиеся к простейшим
Решая показательные уравнения, вы наверняка первым делом исследовали их на возможность приведения к одинаковым основаниям или одинаковым степенным функциям. Так вот, с неравенствами можно делать то же самое! Помните лишь о смене знака, если основание степени меньше единицы. 😎
Попробуем на примере несложного показательного неравенства с разными основаниями.
Пример 1
3х < 243
3х < 35
Поскольку 3 больше 1, знак не меняем:
х < 5
Ответ: х ∈ (−∞; 5).
Пример 2
, обратите внимание — мы поменяли знак, поскольку .
Ответ: .
Показательные неравенства, сводящиеся к квадратным
Снова давайте вспомним, как аналогичный метод применялся к показательным уравнениям. Если все переменные имели общий множитель, его можно было обозначить новой переменной — в итоге у нас, как правило, получалось квадратное уравнение. Нужно было лишь найти дискриминант и произвести обратную замену. И снова алгоритм решения показательных неравенств будет совершенно таким же.
Если все переменные имели общий множитель, его можно было обозначить новой переменной — в итоге у нас, как правило, получалось квадратное уравнение. Нужно было лишь найти дискриминант и произвести обратную замену. И снова алгоритм решения показательных неравенств будет совершенно таким же.
Пример 1
9х + 27 < 12 × 3х
Наименьший общий множитель в данном случае будет 3х, обозначим его новой переменной у и перенесем все слагаемые в левую сторону.
9х + 27 < 12 × 3х
(3х)2— 12 × 3х + 27 < 0
3х = у при y > 0
y2 — 12y + 27 < 0
3 < y < 9
Пришло время выполнить обратную замену.
3 < 3х < 9
31 < 3х < 32
Поскольку 3 > 1, мы не меняем знак.
1 < х < 2
Ответ: х ∈ (1;2).
Показательные неравенства, сводящиеся к рациональным
Как вы, наверное, помните из предыдущего курса алгебры, рациональные показательные неравенства — это такие, в которых левая и правая часть представляют собой дробно-рациональные функции. Метод их решения таков: нужно перенести все в левую часть, чтобы в правой остался лишь ноль, и привести к общему знаменателю. Далее решаем уравнение, отмечаем все корни на оси и применяем метод интервалов (если забыли, что это такое — повторите).
Важно помнить: если в числителе и знаменателе встретятся одинаковые множители с переменной, сокращать их нельзя.
Пример 1
Преобразуем неравенство:
(обратите внимание, мы избавились от минуса в числителе и поменяли знак неравенства).
Поскольку выражение 2х + 2 всегда больше нуля, мы можем домножить на него все неравенство и сократить.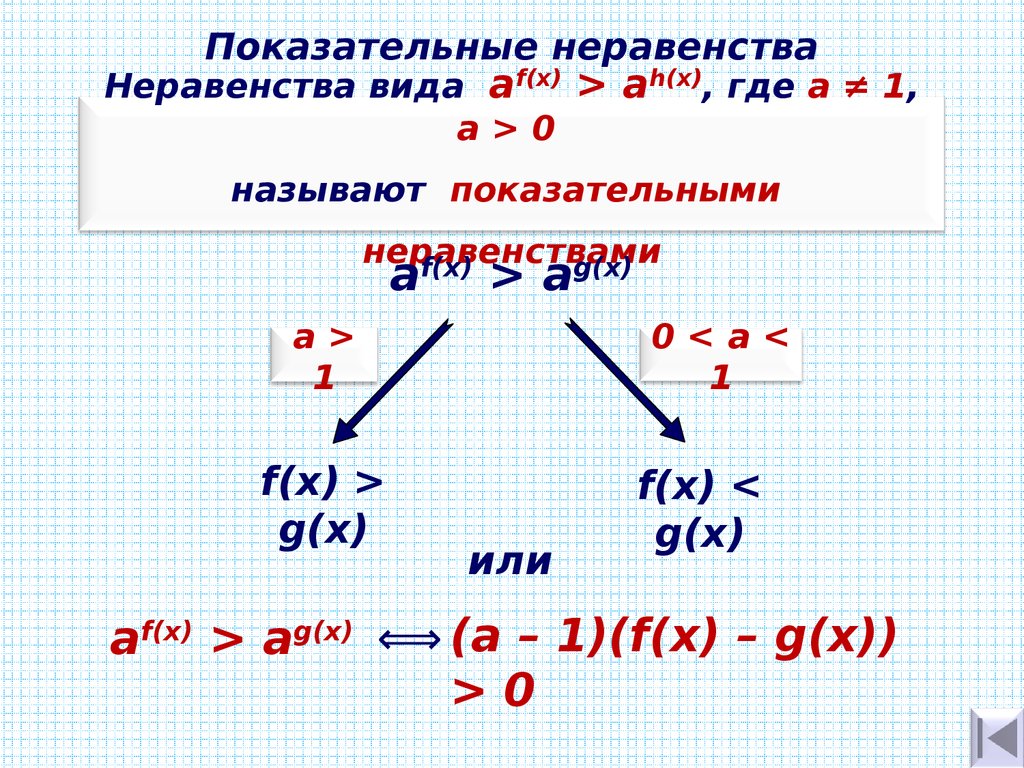
и
Ответ:
Пример 2
Обозначим 3х через новую переменную y:
3х = y, при условии что y > 0.
Применим метод интервалов и получим:
Произведем обратную замену:
Поскольку 3 больше 1, знаки не меняем:
Ответ: .
Однородные показательные неравенства
|
Однородными называются такие показательные неравенства, где в каждом слагаемом сумма степеней одинакова. |
Иногда такие выражения бывают очень длинными и запутанными, но не стоит этого пугаться. Практически все неравенства с однородными показательными функциями решаются по одному принципу: стараемся упростить выражение, разделив его на одночлен, а затем при необходимости делаем замену переменных.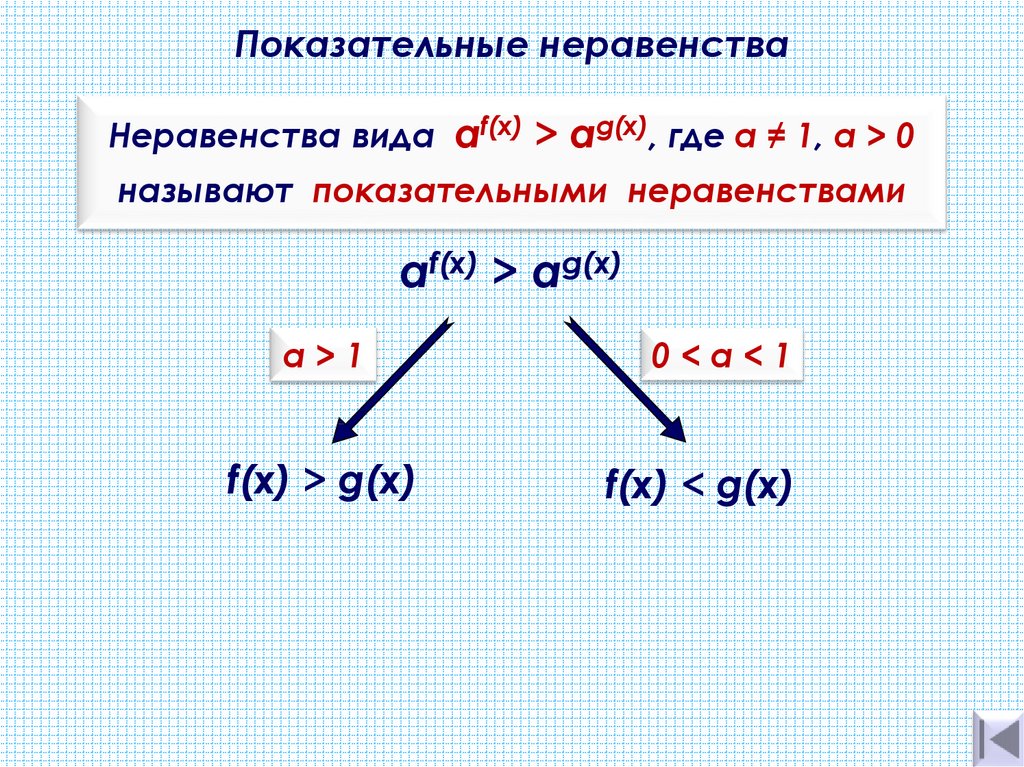
Пример 1
В левой части неравенства мы видим однородные функции относительно 2х и 5х. Следовательно, можно разделить обе части на 22х или 52х. Выберем 52х, т. е. 25х. В итоге у нас получится:
Если обозначить новой переменной y (при условии, что y > 0), получим квадратное неравенство:
y2— y — 2 > 0
y1 > 2
y2 < -1
Исходя из этого, у нас образуется следующее неравенство:
Поскольку меньше 1, функция убывающая и мы должны поменять знак:
Ответ: .
Пример 2
Но где здесь одинаковая сумма степеней? Сейчас будет:
Ответ:
Неравенства, решаемые графическим методом
Этот метод решения показательных неравенств — самый наглядный, и для многих он может показаться самым простым. Нужно лишь построить графики функций, заданных в левой и правой части выражения, а затем посмотреть, в какой точке они пересекаются. Но для использования данного метода точки пересечения должны быть целыми числами. Если бы мы имели дело с уравнением, такие точки стали бы его корнями.
Нужно лишь построить графики функций, заданных в левой и правой части выражения, а затем посмотреть, в какой точке они пересекаются. Но для использования данного метода точки пересечения должны быть целыми числами. Если бы мы имели дело с уравнением, такие точки стали бы его корнями.
Но поскольку мы рассматриваем неравенства, нужно будет выделить искомую область. Для неравенства f(x) > g(x) это будет та область, где график функции f(x) находится выше.
Пример 1
Итак, нам нужны графики двух функций: и , а также точка их пересечения.
Очевидно, что абсциссой точки пересечения является х = 1, при этом график функции ниже в области .
Ответ: .
Пример 2
Начертим графики этих двух функций, чтобы найти точку пересечения.
Искомой точкой будет х = -1, а областью, где функция находится выше — диапазон значений х от -∞ до -1. {\log_{0,2}{4}}\)
{\log_{0,2}{4}}\)
Избавимся от оснований с переменой знака т.к. \(0,2<1\)
\(-7x+4≤\log_{0,2}{4}\)
\(\log_{0,2}{4}\) – число некрасивое, но все-таки число, т.е. перед нами обычное линейное неравенство.
Будем выражать \(x\), для этого перенесем \(4\) в правую часть
\(-7x≤\log_{0,2}{4}-4\)
Поделим обе части на \(-7\)
\(x≥\) \(\frac{4-\log_{0,2}{4}}{7}\)
Ответ: \(x∈\)\([\frac{4-\log_{0,2}{4}}{7}\)\(;∞)\)
Знаю, выглядит не очень, но ответ не выбирают. x>-5\) будет любое число: \(x∈(-∞;∞)\).
x>-5\) будет любое число: \(x∈(-∞;∞)\).
Смотрите также:
Показательные уравнения
Логарифмические уравнения
Равносильные преобразования неравенств
Логарифмические неравенства
Иногда члены экспоненциального уравнения не могут быть переписаны с общим основанием. В этих случаях мы решаем, логарифмируя каждую сторону. Напомним, поскольку [latex]\mathrm{log}\left(a\right)=\mathrm{log}\left(b\right)[/latex] можно переписать как a = b , мы можем применить логарифмы с одинаковым основанием в обеих частях показательного уравнения. 9{х}[/латекс].
Показать решение
В общем случае мы можем решать показательные уравнения, члены которых не имеют одинаковых оснований, следующим образом:
- Прологарифмируйте обе части уравнения.
 {kt}[/latex]. Эта формула используется в бизнесе, финансах и во многих приложениях биологических и физических наук. В нашем следующем примере мы покажем, как решить это уравнение для [latex]t[/latex], прошедшего времени для рассматриваемого поведения.
9{2t}[/латекс].
{kt}[/latex]. Эта формула используется в бизнесе, финансах и во многих приложениях биологических и физических наук. В нашем следующем примере мы покажем, как решить это уравнение для [latex]t[/latex], прошедшего времени для рассматриваемого поведения.
9{2t}[/латекс]. Показать решение
Посторонние растворы
Иногда методы, используемые для решения уравнения, вводят постороннее решение , которое является решением, правильным алгебраически, но не удовлетворяющим условиям исходного уравнения. Одна из таких ситуаций возникает, когда обе части уравнения логарифмируются. В таких случаях помните, что аргумент логарифма должен быть положительным. Если число, которое мы оцениваем в логарифмической функции, отрицательное, выходных данных нет. 9{x}=56[/латекс].
Показать решение
Анализ решения
Решение показательных уравнений с разными основаниями — Концепция
Иногда нам дают показательные уравнения с разными основаниями на членах.
 Чтобы решить эти уравнения, мы должны знать логарифмы и уметь их использовать с возведением в степень. Мы можем получить доступ к переменным в экспоненте в экспоненциальных уравнениях с разными основаниями , используя логарифмы и правило степени логарифмов, чтобы избавиться от основания и получить только показатель степени.
Чтобы решить эти уравнения, мы должны знать логарифмы и уметь их использовать с возведением в степень. Мы можем получить доступ к переменным в экспоненте в экспоненциальных уравнениях с разными основаниями , используя логарифмы и правило степени логарифмов, чтобы избавиться от основания и получить только показатель степени. экспоненциальная функция журнал обеих сторон
Теперь мы собираемся поговорить о решении показательных уравнений, когда наши базы различны. Итак, прямо здесь у меня есть показательное уравнение, и мы пытаемся найти x, хорошо? Для этой конкретной задачи мы знаем, что числа 8 и 16 имеют общее основание 2, поэтому мы можем переписать их как степени двойки, чтобы получилось 2 в кубе до 2x, а 16 — это 2 до четвертого до x+4. Используя степени логарифмов, умножьте степени 2 на 6x, получится 2 на 4x+16, наши основания одинаковы, поэтому мы можем просто установить наши показатели степени равными 6x равно 4x+16, 2x равно 16, x равно равно 8.
 Итак, когда наши базы имеют по крайней мере общую мощность, их довольно легко решить, вы получаете, что их базы одинаковы, поэтому их показатели равны.
Итак, когда наши базы имеют по крайней мере общую мощность, их довольно легко решить, вы получаете, что их базы одинаковы, поэтому их показатели равны.
Жизнь не всегда так проста, хорошо? Итак, мы собираемся поговорить о том, когда у нас есть базы, которые не разделяют силу, хорошо? Здесь у нас есть 7 и 12, есть 2 разных способа сделать это хорошо. Я хочу, чтобы мы привыкли к первому способу, и он заключается в том, чтобы найти способ каким-то образом снизить этот показатель, хорошо? Что мы собираемся использовать, так это правило степени от логарифмов, хорошо? Мы можем взять журнал с обеих сторон, не имеет значения, какой журнал мы делаем, пока он одинаков, поэтому для этого я буду использовать натуральный журнал, если вы хотите использовать журнал с основанием 10, он будет работать очень хорошо, поэтому, если я возьми естественное бревно с обеих сторон, хорошо? Когда у нас есть a, получение естественного журнала становится просто операцией. Я могу добавить 4 к обеим сторонам, это нормально, я могу разделить на 2 с обеих сторон, это нормально, пока мы берем натуральный логарифм обеих сторон, это точно так же, как и все остальное, хорошо? Итак, когда у нас есть натуральный логарифм впереди, мы можем перенести этот показатель на передний план, так что на самом деле мы имеем здесь x натуральный логарифм 7 равен натуральному логарифму 12. Натуральный логарифм 7 — это просто число, ладно, это уродливое число, мы его не знаем, мы можем подключить его к нашему калькулятору и узнать, но это просто число, так что мы можем на него поделить, ладно? И в итоге мы получаем, что x равен натуральному логарифму 12 больше натурального логарифма 7, хорошо? Это то, что просто называется формой готовности к калькулятору, потому что натуральный логарифм — это логарифм, который мы можем поместить в наш калькулятор, чтобы мы могли довольно легко просто подставить натуральный логарифм 12 к натуральному логарифму 7, чтобы выяснить, какой x в порядке?
Натуральный логарифм 7 — это просто число, ладно, это уродливое число, мы его не знаем, мы можем подключить его к нашему калькулятору и узнать, но это просто число, так что мы можем на него поделить, ладно? И в итоге мы получаем, что x равен натуральному логарифму 12 больше натурального логарифма 7, хорошо? Это то, что просто называется формой готовности к калькулятору, потому что натуральный логарифм — это логарифм, который мы можем поместить в наш калькулятор, чтобы мы могли довольно легко просто подставить натуральный логарифм 12 к натуральному логарифму 7, чтобы выяснить, какой x в порядке?
Идти по другому пути, как некоторые из вас могут захотеть, начать делать это, но в конечном итоге мы захотим как бы отказаться от этого, потому что это не всегда будет работать, хорошо? Так что у меня точно такая же проблема, хорошо? 7x равно 7, x равно 12, если вы помните, это называется экспоненциальной формой, хорошо, у нас есть 7 в степени, равной 12, мы могли бы довольно легко представить это в логарифмической форме, опустив 7 и что мы в конце концов, x равен логарифму по основанию 7 из 12, хорошо? Итак, теперь у нас есть логарифмическая база 7 из 12, и мы не знаем, как ее оценить, потому что логарифмической базы 7 нет в нашем калькуляторе.

