Урок 16. окружность. задачи на построение — Геометрия — 7 класс
Геометрия
7 класс
Урок № 16
Окружность. Задачи на построение
Перечень рассматриваемых вопросов:
- Геометрическое место точек, примеры ГМТ.
- Изображение на рисунке окружности и ее элементов.
- Решение задач на построение.
- Выполнение построений прямого угла, отрезка, угла равного данному, биссектрисы угла, перпендикулярных прямых, середины отрезка с помощью циркуля и линейки.
Тезаурус:
Радиус окружности – отрезок соединяющий центр окружности с какой-либо точкой окружности.
Окружность – это геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Хорда – отрезок, соединяющий две точки окружности.
Диаметр – хорда, проходящая через центр окружности.
Основная литература:
- Атанасян Л.
Дополнительная литература:
- Атанасян Л. С. Геометрия: Методические рекомендации 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А. и др. – М.: Просвещение, 2019. – 95 с.
- Зив Б. Г. Геометрия: Дидактические материалы 7 класс. // Зив Б. Г., Мейлер В. М. – М.: Просвещение, 2019. – 127 с.
- Мищенко Т. М. Дидактические материалы и методические рекомендации для учителя по геометрии 7 класс. // Мищенко Т. М., – М.: Просвещение, 2019. – 160 с.
- Атанасян Л. С. Геометрия: Рабочая тетрадь 7 класс. // Атанасян Л. С., Бутузов В. Ф., Глазков Ю. А., Юдина И. И. – М.: Просвещение, 2019. – 158 с.
- Иченская М.А. Геометрия: Самостоятельные и контрольные работы 7–9 классы. // Иченская М.А. – М.: Просвещение, 2019. – 144 с.
Теоретический материал для самостоятельного изучения.
Ранее мы узнали некоторые геометрические фигуры, например, угол, отрезок, треугольник, научились их строить и измерять.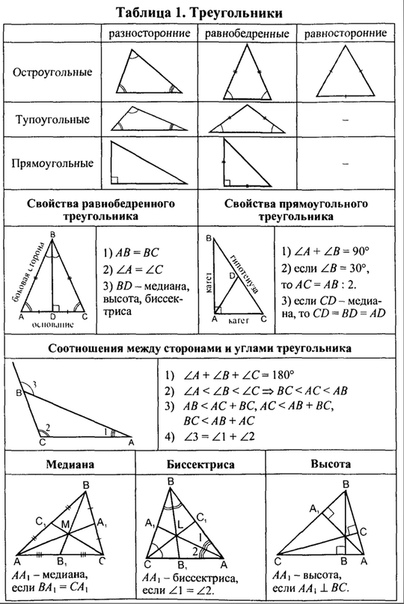
Сегодня мы введём определение ещё одной фигуры – окружности, рассмотрим её элементы и выполним построения геометрических фигур с помощью циркуля и линейки.
Для начала дадим определение геометрической фигуры, называемой окружностью.
Окружность – это геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Но можно использовать и другое определение окружности.
Окружность ‑ это геометрическое место точек, удалённых на одно и то же расстояние от точки, называемой центром окружности. Это расстояние называют радиусом окружности. В нашем случае точки О.
При этом стоит пояснить, что геометрическое место точек – это фигура речи, употребляемая в математике для определения геометрической фигуры, как множества всех точек, обладающих некоторым свойством.
Вспомним элементы окружности.
Радиус окружности – отрезок соединяющий центр окружности с какой-либо точкой окружности.
По определению окружности все её радиусы имеют одну и ту же длину.
OM = OA
Отрезок, соединяющий две точки окружности, называется хордой.
AC, BD – хорды
Хорда, проходящая через центр окружности, называется диаметром.
AB – диаметр,
OB – радиус,
AB = 2OB,
O – середина диаметра.
Любые две точки окружности делят её на две части. Каждая из этих частей называется дугой окружности.
AMB, ALB – дуги окружности.
Построим окружность радиусом 3 см. Для этого поставим точку О. Возьмём циркуль и выставим с помощью линейки расстояние между ножками циркуля, равное 3 см. Поставим иголочку циркуля в точку О и построим окружность, вращая ножку циркуля с грифелем вокруг этой точки. Грифель описывает замкнутую кривую линию, которую называют окружностью.
Часть плоскости, которая лежит внутри окружности, вместе с самой окружностью, называют кругом, т. е. окружность ‑ граница круга.
Итак, мы можем с помощью циркуля строить окружность, но с его помощью можно построить и угол равный данному.
Для построения воспользуемся ещё и линейкой.
Дано: A, OM – луч.
Построить: EOМ = A.
Построение.
1. Окр. (A; r), r – произвольный радиус.
2. Окр. (A; r) ∩ AB = B.
3. Окр. (A; r) ∩ AС = С.
4. Окр. (O; r) ∩ OM = D.
5. Окр. (D; BС) ∩ Окр. (O; r) = E
6. OЕ, ЕОD = BAC (из равенства ∆ОЕD и ∆ABC). EOM – искомый.
Теперь выполним построение биссектрисы угла.
Построить: AE – биссектриса CAB.
Построение.
- Окр. (A; r), r – произвольный радиус.
- Окр. (A; r) ∩ AB = B.
- Окр. (A; r) ∩ AC = C.
- Окр. (C; CB) ∩ Окр. (B; CB) = E.
- AE – искомая биссектриса BAC, т. к. ABE =CBE (из равенства ∆ACE и ∆ABE).
Рассмотрим ещё одно построение с помощью циркуля и линейки. Построим середину отрезка АВ.
Для этого построим две окружности с центрами на концах отрезка , т. е. в точках А и В.
Окружности пересекутся в точках Р и Q. Проведём прямую через точки Р и Q. Прямая РQ пересечёт прямую АВ в точке О, которая и будет являться искомой серединой отрезка АВ. Докажем это. Для этого рассмотрим ∆APQ и ∆BPQ. Они равны по трём сторонам, следовательно, ∠1 = ∠2, поэтому РО– биссектриса равнобедренного ∆АВР, а соответственно РО ещё и медиана. Следовательно, точка О – середина отрезка АВ.
Разбор заданий тренировочного модуля.
№ 1. АВ и СК – диаметры окружности, с центром в точке О. По какому признаку равенства треугольников равны треугольники АОС и ОКВ?
Решение:
Так как О – центр окружности, то точка О делит диаметры пополам, следовательно отрезки АО, ОВ, ОС, ОК равны. ∠СОА = ∠КОВ (как вертикальные). Поэтому треугольники АОС и ОКВ равны по первому признаку равенства треугольников (по двум сторонам и углу между ними).
Ответ: 1 признак равенства треугольников.
№ 2. На рисунке O – центр окружности, АВ – диаметр окружности.
Отрезки АD и ВС, перпендикулярны к отрезку АВ. АВ = 8 см, ОС = 5 см, СВ = 3 см. Чему равен периметр ∆AOD?
Решение:
Периметр треугольника AOD равен сумме сторон АО, AD, DO. Найдём эти стороны.
По условию O – центр окружности, то она делит диаметр пополам, следовательно отрезок АО равен отрезку ОВ, т. е. АО = АВ:2 = 8 см :2 = 4 см.
По условию отрезки АD и ВС, перпендикулярны к отрезку АВ, следовательно ∠СВО = ∠ОАD = 90°, ∠АОD = ∠СОВ (как вертикальные). Поэтому ∆АОD = ∆СОВ (по 2 признаку равенства треугольников). Следовательно, AD = СВ = 3 см, DO = ОС = 5 см.
Р∆AOD = АО + AD + DO = 4 см + 3 см + 5 см = 12 см.
Ответ: Р∆AOD = 12 см.
Дополнительные главы геометрии. 7 класс: О курсе
Курс ориентирован на слушателей, владеющих школьной программой 7 класса по геометрии. Учащиеся познакомятся с яркими геометрическими сюжетами, систематизируют теоретические знания, научатся решать задачи повышенной сложности.
Курс поможет школьникам не только на уроках геометрии в школе, но и позволит успешнее выступать на олимпиадах, а учителям математики — лучше понять аспекты теории и задачные акценты, примыкающие к школьной программе и характерные для математических олимпиад, использовать задачную базу курса на занятиях в школе.
Курс состоит из 21 обязательного учебного модуля, 69 видеолекций с конспектами, 378 обязательных упражнений и факультативных задач для самостоятельного решения. На старте курса ученикам будет предложено пройти входное тестирование, по итогам которого будет определен начальный уровень ученика и, соответственно, определена индивидуальная образовательная траектория. По итогам тестирования может быть зачтена часть учебных модулей.
В курсе содержатся материалы двух уровней сложности. Первый уровень сложности: рассказываются базовые вещи, даны наиболее простые упражнения и задачи. Второй уровень сложности иногда содержит дополнительную теорию, задачи и упражнения, для того, чтобы можно было углубить свои знания в соответствующей теме.
Учебные модули
— Признаки равенства треугольников
— Равнобедренные треугольники и ГМТ
— Параллельность и сумма углов треугольника
— Параллелограмм и другие четырехугольники
— Прямоугольный треугольник
— Средняя линия
— Геометрия на клетчатой бумаге
— Симметрия
— Ошибки в геометрических доказательствах
— Примеры и контрпримеры
— Дополнительные построения
— Неравенство треугольника
— Перекладывание площадей
— Замечательные точки треугольника
Внутри каждого модуля есть:
— видео с кратким конспектом, где обсуждается теория и разбираются примеры решения задач,
— упражнения с автоматической проверкой, позволяющие понять, как усвоена теория,
— задачи для самостоятельного решения, которые не учитываются в прогрессе и не идут в зачет по модулю, но позволяют качественно повысить свой уровень.
В каждом разделе есть ответы на популярные вопросы, где можно уточнить свое понимание теории или условия задачи, но нельзя получить подсказки по решению.
По итогам обучения выдается электронный сертификат. Для его получения необходим зачет по всем учебным модулям, кроме лекционных. Условие получения зачета по модулю — успешное выполнение не менее 70% упражнений. Сертификаты могут учитываться при отборе на очные программы по направлению «Наука».
Если ученик не успеет получить зачет по отдельным модулям, то он не сможет получить сертификат, но сможет возобновить обучение, когда курс стартует в следующий раз. При этом выполнять пройденные модули заново не потребуется (но может быть предложено, если соответствующие учебные материалы обновятся).
В следующий раз курс будет открыт осенью 2020 года.
Зачёт по геометрии за 7 класс
Вопросы по геометрии. 7 класс1. Сколько прямых можно провести через две точки?
2. Сколько общих точек могут иметь две прямые?
3. Что такое отрезок? Начертить, обозначить и объяснить? Какая точка называется серединой отрезка?
4. Что такое луч? Как обозначаются лучи?
5.
Какая фигура называется углом? Объясните, что такое вершина и стороны угла.
6. Какие фигуры называются равными?
7. Как сравнить два угла? Какой луч называется биссектрисой угла?
8. Какой угол называется острым? прямым? тупым?
9. Какие углы называются смежными? Чему равна сумма смежных углов? Уметь их строить.
10. Какие углы называются вертикальными? Каким свойством обладают вертикальные углы? Уметь их строить.
11. Какие прямые называются перпендикулярными? Уметь их строить Объясните, почему две прямые, перпендикулярные к третьей, не пересекаются?
12. Объясните, какая фигура называется треугольником. Начертите треугольник и покажите его стороны, вершины и углы. Что такое периметр треугольника?
13. Какие треугольники называются равными?
14. Что такое теорема и доказательство теоремы?
15. Сформулируйте первый признак равенства треугольников.
16. Какой отрезок называется медианой треугольника? Сколько медиан имеет треугольник? Уметь их строить.
17. Какой отрезок называется биссектрисой треугольника? Сколько биссектрис имеет треугольник? Уметь их строить.
18. Какой отрезок называется высотой треугольника? Сколько высот имеет треугольник? Уметь их строить.
19. Какой треугольник называется равнобедренным? Уметь его строить. Как называются его стороны?
20. Какой треугольник называется равносторонним? Уметь его строить. Сформулировать основные свойства равнобедренного треугольника.
21. Сформулируйте второй признак равенства треугольников.
22. Сформулируйте третий признак равенства треугольников.
23. Что такое определение? Дайте определение окружности. Что такое центр, радиус, хорда и диаметр окружности?
24. Объясните, как отложить от данного луча в данную плоскость угол, равный данному.(с помощью циркуля и линейки)
25. Объясните как построить биссектрису данного угла.( с помощью циркуля и линейки)
26. Объясните, как построить прямую, проходящую через данную точку, лежащую на данной прямой, и перпендикулярную к этой прямой.
.(с помощью циркуля и линейки)
27. Объясните, как построить середину данного отрезка. .(с помощью циркуля и линейки)
28. Дайте определение параллельных прямых. Какие два отрезка называются параллельными?
29. Что такое секущая? Назовите пары углов, которые образуются при пересечении двух прямых секущей. Уметь их построить , показать и обозначить.
30. Сформулируйте признаки параллельности прямых ?
31. Что такое аксиома? Приведите примеры. Сформулируйте аксиому параллельных прямых.
32. Какая теорема называется обратная данной теореме? Приведите примеры теорем, обратных данным.
33. Сформулируйте теоремы об углах, образованных двумя параллельными прямыми и секущей.
34. Сформулируйте теорему о сумме углов треугольника.
35. Какой угол называется внешним углом треугольника? Уметь его строить. Сформулируйте, чему равен внешний угол в треугольнике.
36. Какой треугольник называют остроугольным? Какой треугольник называется тупоугольным? Уметь их строить.
37. Какой треугольник называется прямоугольным? Как называются стороны прямоугольного треугольника?
38. Сформулируйте соотношения между сторонами и углами. Почему в прямоугольном треугольнике гипотенуза больше катета?
39. Сформулируйте теорему о неравенстве треугольника.
40. Сформулируйте некоторые свойства прямоугольных треугольников.
41. Сформулируйте признаки равенства прямоугольных треугольников.
42. Что называется расстоянием от точки до прямой?
43. Что называется расстоянием между двумя параллельными прямыми?
44. Объясните, как построить треугольник по двум сторонам и углу между ними.
45. Объясните, как построить треугольник по стороне и двум прилежащим к ней углам.
46. Объясните, как построить треугольник по трём сторонам. Всегда ли эта задача имеет решение?
Задачи к зачету по геометрии. 7 класс
Задача №1. В равнобедренном треугольнике угол при основании в 2 раза меньше, чем угол при вершине. Найдите все углы треугольника.
Задача №2. Высота АD равностороннего треугольника ВАС с основанием ВС равна 10 см, периметр треугольника АDС равен 70 см. Найдите периметр треугольника АВС.
Задача №3. Первый угол треугольника равен 40градусов, а второй больше третьего на 16 градусов. Найдите эти углы треугольника.
Задача №4. В равнобедренном треугольнике периметр равен 150 см, боковая сторона больше основания на 15 см. Найдите все стороны треугольника.
Задача №5. В равнобедренном прямоугольном треугольнике гипотенуза равна 42 см. Найдите высоту проведённую из вершины прямого угла.
Задача №6. В равнобедренном треугольнике внешний угол при вершине равен 40 градусов. Найдите углы этого треугольника.
Задача №7. В равнобедренном треугольнике СDЕ с основанием СЕ проведена биссектриса СF. Найдите угол ЕСF, если угол D равен 54 градуса.
Задача №8. Один из углов прямоугольного треугольника равен 60 градусов, а сумма гипотенузы и меньшего катета равна 30 см. Найдите гипотенузу треугольника.
Задача №9. Один из внешних углов равнобедренного треугольника равен 110 градусов. Найдите все углы данного треугольника.
Задача №10. Периметр равнобедренного треугольника равен 65 см, его боковая сторона на 5 см меньше основания. Найдите стороны треугольника.
Задача №11. Периметр равнобедренного тупоугольного треугольника равен 77 см, а одна из его сторон больше другой на 17см. Найдите стороны этого треугольника.
Задача №12. Сумма вертикальных углов АОВ и СОD, образованных при пересечении прямых АD и ВС, равна 108 градусов. Найдите угол ВОD.
Задача №13. В остроугольном треугольнике МNP биссектриса угла М пересекает высоту NК в точке О. причём ОК равно 9 см.
Найдите расстояние от точки О до прямой МN.
Задача №14. Отрезки АВ и СD- диаметры окружности с центром О. Найдите периметр треугольника АОD, если хорда СВ равна 10 см, диаметр АВ равен 12 см.
Задача №15. Найдите все неразвёрнутые углы, образованные при пересечении двух прямых, если сумма двух из них равна 296 градусов.
Задача №16. Луч ОС делит угол АОВ на два угла. Найдите угол СОВ, если угол АОВ равен 110 градусов, а угол АОС на 18 градусов меньше угла ВОС.
Задача №17. Углы треугольника относятся как 2: 3: 4. Найдите их градусные меры.
Задача №18. В равнобедренном треугольнике АВС с основанием АС равно 38 см внешний угол при вершине В равен 60 градусов. Найдите расстояние от вершины С до прямой АВ.
Задача №19. Один из углов при пересечении двух параллельных прямых третьей прямой в 2 раза больше другого. Найдите остальные углы.
Задача №20. Один из углов при пересечении двух параллельных прямых третьей прямой на 20 градусов меньше другого. Найдите остальные углы.
Задача №21. В равнобедренном треугольнике АВС с основанием АС равно 42см, внешний угол при вершине С равен 120 градусов. Найдите боковые стороны треугольника АВС.
geo7.docx
ГДЗ (решебник) Геометрия 7 класс Мерзляк
Сложный предмет – геометрия в 7 классе
Уже после окончания младшей школы большинство учеников четко понимает свои предпочтения – точные, либо гуманитарные науки.
Чем помогут решебники Мерзляка
Действительно, появившаяся лишь в седьмом классе новая дисциплина геометрия требует от учеников не только знание теории, но и умение полноценно применять ее при решении практических задач. Вряд ли многие родители смогут оказать помощь в изучении предмета, с которым они сами не сталкивались около двадцать лет. Гораздо эффективнее использовать помощь профессионалов в этой науке — пособий «ГДЗ по Геометрии 7 класс Мерзляк».
С помощью представленных решебников школьники смогут:
- Улучшить качество д/з.
- Всесторонне исследовать непонятные моменты.
- Заранее подготовиться к проверочным мероприятиям.
- Самостоятельно справиться с работой над ошибками.
- Повысить свою активность в классе и поднять успеваемость.
С данными пособиями очень удобно работать, т.к. они всегда доступны онлайн. При этом заметно сократится время, затрачиваемое на выполнение домашних заданий. А самое главное — ребята начнут безоговорочно разбираться в материале.
Что входит в состав решебников по геометрии
Пособия предлагают задания ко всем параграфам основного курса геометрии для седьмого класса. Четкие и конкретные задачи охватывают все темы учебного года:
- Найти геометрическое место центров окружностей.
- Построить треугольник по заданным параметрам.
- Найти точки, принадлежащие окружности и равноудаленные от концов отрезка.
Удобная навигация решебников позволяет быстро найти нужное упражнение и верный ответ на него.
Онлайн тести з геометрії
Створюйте онлайн-тести
для контролю знань і залучення учнів
до активної роботи у класі та вдома
6
Геометрія, 11 клас
Створено 29 січня
Приклад запитання: В основі прямої призми лежить прямокутний трикутник, катети якого дорівнюють 8 см і 6 см. Висота призми дорівнює 11 см. Знайдіть об’єм призми.
14
Геометрія, 9 клас
Приклад запитання: Знайдіть третю сторону трикутника, якщо відомі дві сторони 3 і 8 см та кут між ними 120°.
8
Геометрія, 10 клас
Створено 29 січня
Приклад запитання: Якщо дві прямі перпендикулярні до однієї і тієї самої площини,
6
Геометрія, 7 клас
Створено 29 січня
Приклад запитання: Як називаються кути 1 і 2?
45
Геометрія, 7 клас
Створено 29 січня
Приклад запитання: Чи існує трикутник зі сторонами 13см, 5см і 4 см?
10
Геометрія, 11 клас
Приклад запитання: Обчисліть об’єм правильної чотирикутної призми зі стороною основи 3√3 см і довжиною бічного ребра 2 см.
6
Геометрія, 7 клас
Приклад запитання: Як можуть розташовуватися два кола?
7
Геометрія, 9 клас
Приклад запитання: Чому дорівнює скалярний добуток векторів a̅(-1;2) і b̅(-5;7)?
7
Геометрія, 9 клас
Створено 28 січня
Приклад запитання: Знайти координати центра О і радіус R кола, заданого рівнянням ( х -3)2 + ( у + 4)2 = 16
12
Геометрія, 8 клас
Приклад запитання: Сторони подібних трикутників…
12
Геометрія, 7 клас
Приклад запитання: Периметр рівнобедреного трикутника 19 см, а основа 7 см. Чому дорівнюють бічні сторони трикутника?
11
Геометрія, 7 клас
Приклад запитання: За якою ознакою рівні трикутники на малюнку?
8
Геометрія, 9 клас
Приклад запитання: Дано ā(1; -3). Знайдіть координати вектора 2ā
5
Геометрія, 9 клас
Приклад запитання: Площа трикутника дорівнює 84 см2.
Знайти висоту трикутника, проведену до сторони довжиною 8 см.
14
Геометрія, 10 клас
Створено 28 січня
Приклад запитання: Якщо пряма перпендикулярна до двох прямих, що лежатьу площині та перетинаються,
9
Геометрія, 8 клас
Приклад запитання: У прямокутному трикутнику відношення протилежного катета до гіпотенузи називається…
6
Геометрія, 8 клас
Приклад запитання: Знайдіть гіпотенузу прямокутного трикутника, якщо його катети дорівнюють 10 см і 24 см.
6
Геометрія, 8 клас
Приклад запитання: Знайдіть гіпотенузу прямокутного трикутника, якщо його катети дорівнюють 10 см і 24 см.
8
Геометрія, 9 клас
Створено 28 січня
Приклад запитання: Сторона трикутника дорівнює 8см, а висота, проведена до неї — 4,5см. Знайти площу трикутника.
3
Геометрія, 8 клас
Приклад запитання: Сторони прямокутника дорівнюють 8 см і 15 см.
Знайдіть діагональ прямокутника.
8
Геометрія, 9 клас
Приклад запитання: Знайти площу трикутника зі сторонами 2см, 6см і кутом між ними 30°
4
Геометрія, 9 клас
Приклад запитання: Знайти міру внутрішнього кута правильного трикутника.
8
Геометрія, 8 клас
Приклад запитання: Сторони прямокутника дорівнюють 8 см і 15 см. Знайдіть діагональ прямокутника.
13
Геометрія, 9 клас
Приклад запитання: У трикутнику проти більшої сторони лежить…
7
Геометрія, 9 клас
Приклад запитання: Який із записів правильний:
6
Геометрія, 8 клас
Створено 28 січня
Приклад запитання: Сторони прямокутника дорівнюють 8 см і 15 см. Знайдіть діагональ прямокутника.
8
Геометрія, 9 клас
Приклад запитання: Квадрат будь-якої сторони трикутника дорівнює сумі квадратів двох інших сторін без подвоєного добутку цих сторін на косинус кута між ними.
Це теорема…
12
Геометрія, 7 клас
Створено 28 січня
Приклад запитання: Бічна сторона рівнобедреного трикутника дорівнює 14 см, основа на 5 см більша. Знайдіть периметр трикутника
8
Геометрія, 9 клас
Приклад запитання: Між сторонами b i c знаходиться кут..
18
Геометрія, 9 клас
Створено 27 січня
Приклад запитання: Які з наведених величин є векторною?
Доказательства по геометрии 7 класс. | Геометрия
Доказательства по геометрии 7 класс. | Геометрия — просто!Добрый день, дорогие друзья! Сегодня мы с вами поговорим про задачи на доказательства по геометрии 7 класса.
В геометрии, в отличии от алгебры, есть очень много задач на доказательство тех или иных тем.
В таких задачах, как правило, очень мало вычислительного материала, зато очень много логических рассуждений, связанных между собой цепочкой доказательств.
Здесь важно выделить конец доказательства, а затем, идя к началу, раскручивать его.
Как это происходит, мы сегодня разберём.
Задача 1. Докажите, что медианы, проведённые к боковым сторонам равнобедренного треугольника, равны.
Доказательство. Предположим, что мы доказали равенство медиан.
Смотрим, в каких фигурах эти медианы находятся, и что можно сказать об этих фигурах.
Итак, медианы АМ и СК находятся в треугольниках АМС и АКС или в треугольниках АВМ и СВК. Для доказательства равенства медиан надо доказать равенство треугольников.
Выбираем первую пару. Треугольники АМС и СКА. Поскольку треугольник АВС равнобедренный, то АВ=ВС.
Но медиана делит противоположную сторону треугольника пополам. Отсюда АК=КВ=СМ=ВМ. Или АК=СМ.
Углы при основании равнобедренного треугольника равны. Получается ∠А=∠С. Теперь вернёмся опять к треугольникам АМС и СКА. У них АК=СМ.
Угол МСА равен углу КАС, а сторона АС — общая.
Получается, треугольники равны по первому признаку равенства треугольников.
А в равных треугольниках против равных углов лежат равные стороны.
Против угла МСА в треугольнике АМС лежит сторона АМ, а против угла КАС в треугольнике СКА лежит сторона КС. Значит, эти стороны равны.
Медианы, проведённые к боковым сторонам равнобедренного треугольника, равны.
Задача 2. Докажите, что диагональ параллелограмма разбивает его на 2 равных треугольника.
Доказательство. И опять, как в задаче 1. Предположим, что треугольники АВД и ВСД равны.
Диагональ параллелограмма принадлежит обоим треугольникам. Т.е. у них одна сторона общая.
Осталось найти либо 2 пары равных углов, либо равные стороны и два равных угла, либо по две равных стороны.
У параллелограмма, как мы знаем, противоположные стороны равны.
Имеем АД=ВС, АВ=СД. Получается, что треугольники равны по трем сторонам.
Можно доказать по другому, согласно 2 признаку равенства треугольников.
В треугольниках АВД и ВСД углы
СВД и ВДА равны, как накрест лежащие
при параллельных прямых ВС и АД и секущей ВД.
Углы ВДС и АВД равны, как накрест лежащие при параллельных прямых АВ и СД и секущей ВД.
Получается, что треугольники равны по стороне и двум прилежащим к ней углам.
Задача 3. Докажите, что отрезки касательных, проведённых к окружности из одной точки, равны.
Доказательство. Нам дано, что из точки С проведены 2 касательных АС и ВС к окружности.
Для того, чтобы провести доказательство равенства сторон, сделаем дополнительные построения.
Проведём радиусы ОА и ОВ, а также прямую ОС. Доказав равенство треугольников ОАС и ОВС, мы сможем доказать равенство сторон АС и ВС.
Мы знаем, что радиусы, проведённые в точку касания перпендикулярны касательной. Поэтому, углы ОАС и ОВС — прямые.
Отсюда, треугольники САО и СВО — прямоугольные.
Эти треугольники равны, т.к. катеты ОА и ОВ равны, а гипотенуза ОС у них общая. Прямоугольные треугольники равны по катету и гипотенузе.
А в равных треугольниках против равных сторон лежат равные углы.
Против стороны ОА лежит угол АСО, а против стороны ОВ — угол ВСО.Эти углы равны. А если 2 угла одного треугольника соответственно равны двум углам другого треугольника, то и третьи углы у них равны.
Значит, углы ВОС и АОС равны.
А в равных треугольниках против равных углов лежат равные стороны.
Против угла АОС лежит сторона АС, а против угла ВОС — сторона ВС.
Углы равны, значит и стороны АС и ВС равны.
На сегодня, пожалуй, достаточно. Ведь скоро Новый Год, все мысли о нём,
так что геометрию ненадолго отложим в сторону.
Спасибо всем и с НОВЫМ ГОДОМ!
Вам так же будет интересно:
Оставить комментарий
Учебный план для 7 класса
Ниже перечислены необходимые навыки со ссылками на ресурсы, которые помогут с этими навыками. Мы также поощряем множество упражнений и работу с книгами.
Curriculum Home
Важно: это только руководство.
Обратитесь в местное управление образования, чтобы узнать их требования.
7 класс | Раздел
☐ Понимать и уметь пользоваться Длинным разделом
7 класс | Числа
☐ Различать различные подмножества действительных чисел (счетные/натуральные числа, целые числа, целые числа, рациональные числа и иррациональные числа)
☐ Определите простую факторизацию заданного числа и запишите в экспоненциальной форме
☐ Упростите выражения, используя порядок операций (Примечание: выражения могут включать абсолютное значение, квадратные корни и/или целые показатели степени больше 0.)
☐ Складывать, вычитать, умножать и делить целые числа
☐ Сложите два целых числа (с использованием числовой прямой и без нее)
☐ Развить концептуальное представление об отрицательных и нулевых показателях степени с основанием десять и соотноситься с дробями и десятичными знаками (например, 10 -2 = 0,01 = 1/100)
☐ Распознать и назвать значение квадратного корня из полного квадрата (до 225)
☐ Определите квадратный корень из неполных квадратов (или более сложных полных квадратов) с помощью калькулятора
☐ Классифицировать иррациональные числа как неповторяющиеся/бесконечные десятичные дроби
☐ Определите два последовательных целых числа, между которыми лежит квадратный корень из неполного квадратного целого числа меньше 225 (с использованием числовой прямой и без нее)
☐ Знать разницу между рациональными и иррациональными числами (например,г.
, исследуйте различные приближения числа пи)
☐ Поместите рациональные и иррациональные числа (аппроксимации) на числовую прямую и обоснуйте размещение.
☐ Запишите числа в экспоненциальном представлении
☐ Заменить числа, записанные в экспоненциальном представлении, на обычные числа
☐ Сравните числа, записанные в экспоненциальном представлении
☐ Найдите общие делители и наибольший общий делитель двух или более чисел
☐ Определить кратные и наименьшее общее кратное двух или более чисел
☐ Вычесть два целых числа (с использованием и без использования числовой прямой)
☐ Сравните и упорядочите целые числа от -10 до 10
☐ Распознать и назвать значение кубического корня из полного куба (до 216)
☐ Определите кубический корень несовершенных кубов (или более сложных совершенных кубов) с помощью калькулятора
☐ Определите два последовательных целых числа, между которыми лежит кубический корень несовершенного кубического целого числа меньше 216 (с использованием числовой прямой и без нее)
☐ Знать и понимать основную теорему арифметики.
7 класс | Дроби
☐ Сложение и вычитание комбинации из трех или более дробей с разными знаменателями
7 класс | Проценты
☐ Рассчитайте полную сумму (100%), если дан другой процент от той же суммы, например. Если вы знаете 25%, что такое 100%?
7 класс | Соотношения
☐ Расчет расстояния с использованием масштаба карты или масштаба модели
☐ Расчет масштабов карт, чертежей или моделей в масштабе как пропорций
7 класс | Измерение
☐ Определение личных эталонов для метрических единиц массы
☐ Обоснование обоснованности массы объекта (метрические единицы)
☐ Перевести емкости и объемы в метрическую систему
☐ Определите метрические единицы массы
☐ Перевести массу в метрическую систему
☐ Нарисуйте центральные углы в данной окружности с помощью транспортира (круговые диаграммы)
☐ Определить инструменты и методы, необходимые для измерения массы с соответствующим уровнем точности (метрические единицы)
☐ Знать метрические единицы площади: квадратный миллиметр, квадратный сантиметр, квадратный метр, гектар и квадратный километр; и как конвертировать между ними.
☐ Определение личных эталонов для стандартных единиц массы США
☐ Обоснуйте разумность массы объекта (стандартные единицы США)
☐ Преобразование мощностей и объемов в системе США
☐ Определите стандартные единицы массы США
☐ Преобразование массы в системе США
☐ Определить инструменты и методы, необходимые для измерения массы с соответствующим уровнем точности (стандартные единицы США)
☐ Знать стандартные единицы площади США: квадратный дюйм, квадратный фут, квадратный ярд, акр, квадратная миля; и как конвертировать между ними.
7 класс | Геометрия (плоскость)
☐ Построить шаблон для разработки правила определения суммы внутренних углов многоугольников
☐ Рассчитайте радиус или диаметр, зная длину окружности или площадь круга
☐ Найдите недостающий угол по заданным углам четырехугольника
☐ Поймите, что углы на прямой в сумме составляют 180 градусов, а углы вокруг точки в сумме составляют 360 градусов
☐ Понимание тесселяции и того, что подразумевается под обычными и полуправильными тесселяциями.
☐ Знать названия многоугольников с 5, 6 и 8 сторонами, знать величины их внутренних углов, знать, что называют правильными, неправильными, вогнутыми и выпуклыми многоугольниками.
7 класс | Геометрия (тело)
☐ Рассчитайте объемы призм и цилиндров, используя заданные формулы и калькулятор
☐ Определите двумерные фигуры, составляющие грани и основания трехмерных фигур (призмы, цилиндры, конусы и пирамиды)
☐ Определите площади поверхности призм и цилиндров с помощью калькулятора и различных методов
7 класс | Алгебра
☐ Сложение и вычитание одночленов с показателями единицы
☐ Оценить формулы для заданных входных значений (задачи площади поверхности, скорости и плотности)
☐ Запишите обратную величину алгебраического выражения
☐ Сложение и вычитание простых многочленов с показателями степени не выше 3
7 класс | Показатель степени
☐ Разработайте законы показателей степени для умножения и деления
7 класс | Неравенства
☐ Решить одношаговые неравенства (только положительные коэффициенты)
☐ Нарисуйте набор решений неравенства (только с положительными коэффициентами) на числовой прямой.
7 класс | Линейные уравнения
☐ Преобразование словесных выражений, состоящих из двух шагов, в алгебраические выражения
☐ Решайте многошаговые уравнения, комбинируя одинаковые члены, используя свойство дистрибутивности или перемещая переменные в одну часть уравнения
7 класс | Тригонометрия
☐ Определение прямого угла, гипотенузы и катетов прямоугольного треугольника
☐ Исследуйте взаимосвязь между длинами трех сторон прямоугольного треугольника, чтобы вывести теорему Пифагора
☐ Используйте теорему Пифагора, чтобы определить неизвестную длину стороны прямоугольного треугольника
☐ Определите, является ли данный треугольник прямоугольным, применив теорему Пифагора и используя калькулятор
7 класс | Многочлены
☐ Определить многочлен как алгебраическое выражение, содержащее один или несколько членов
7 класс | Функции
☐ Напишите уравнение для представления функции из таблицы значений
7 класс | Данные
☐ Выявление и сбор данных с использованием различных методов
☐ Предсказать исход эксперимента
☐ Разработайте и проведите эксперимент для проверки предсказаний
☐ Сравните фактические результаты с прогнозируемыми
☐ Отображение данных в виде круговой диаграммы (круговой диаграммы)
☐ Преобразование необработанных данных в двойные гистограммы и двойные линейные графики
☐ Рассчитать диапазон для заданного набора данных
☐ Чтение и интерпретация данных, представленных в графическом виде (пиктограмма, гистограмма, гистограмма, линейный график, двойная линия/гистограмма или круговая диаграмма)
7 класс | Оценка
☐ Оценка площади поверхности
☐ Обоснуйте обоснованность ответов, используя оценку
☐ Оцените площади плоских фигур, посчитав количество квадратов, необходимых для покрытия фигуры.
7 класс | Графики
☐ Нарисуйте графическое представление шаблона из уравнения или из таблицы данных
7 класс | Вероятность
☐ Интерпретировать данные, чтобы обеспечить основу для прогнозов и установить экспериментальные вероятности
7 класс | Статистика
☐ Выберите соответствующую меру центральной тенденции
☐ Определить достоверность методов выборки для прогнозирования результатов
7 класс | Деньги
☐ Рассчитайте цену за единицу, используя пропорции
☐ Сравните цены за единицу
☐ Конвертируйте деньги в разные валюты с помощью таблицы обменных курсов и калькулятора
Математика — В: 7 класс
Математика Академические стандарты Индианы предоставляют преподавателям и администраторам полный набор академических стандартов штата Индиана по математике для K-12.Школы должны работать над тем, чтобы привести учебный план и оценивание в классе в соответствие с новыми стандартами.
В то время как стандарты устанавливают ожидания для обучения студентов, они не предписывают, как стандарты должны преподаваться.
Учителя должны использовать свои навыки, опыт, таланты и ресурсы для организации уроков в классе с учетом индивидуальных потребностей своих учеников. С введением этих новых академических стандартов учащиеся в Индиане будут хорошо оснащены навыками и знаниями, чтобы подготовить их к будущему.
В: 7 класс
Академические стандарты Индианы по математике включают стандарты для учащихся седьмого класса.
Алгебраические понятия
Блок алгебраических понятий включает в себя компетенции / цели, которые сосредоточены на алгебраических уравнениях и операциях. Этот блок включает в себя изучение систем счисления, операций и форм. Учащиеся изучают символическую природу алгебраических понятий, выявляя и расширяя закономерности в алгебре, следуя алгебраическим процедурам и доказывая теоремы со свойствами.
Десятичные числа
Блок десятичных знаков включает в себя компетенции / цели, которые сосредоточены на смысле чисел и операциях с десятичными знаками. Блок десятичных знаков включает в себя сравнение, вычисления, деньги, оценку, решение проблем и рассуждение.
Дроби
Модуль «Дроби» включает в себя компетенции/цели, которые фокусируются на смысле чисел и операциях с дробями.Блок дробей включает в себя сравнение, упорядочивание, части дроби, оценку, рассуждение и решение проблем.
Функции
Блок функций включает изучение полиномиальных, рациональных, экспоненциальных, логарифмических, тригонометрических и круговых функций.
Геометрия
Блок геометрии включает в себя компетенции / цели, которые сосредоточены на изучении геометрических концепций с разных точек зрения.Блок геометрии включает в себя свойства и построение фигур, доказательства и теоремы, историю геометрии, преобразования, логику и решение задач.
Целые числа
Модуль «Целые числа» включает в себя компетенции / цели, которые сосредоточены на смысле чисел и операциях с целыми числами. Этот блок включает в себя сравнение целых чисел, выполнение операций с целыми числами, преобразование целых чисел в другие числовые формы, использование манипуляций для демонстрации целых чисел и решение проблем с целыми числами в реальных контекстах.
Математические процессы
Блок математических процессов фокусируется на математических связях, коммуникации, моделировании, концепциях и процедурах.
Измерение
Блок измерения включает в себя компетенции/цели, которые сосредоточены на концепциях измерения, приложениях и анализе. Единица измерения включает в себя понятия длины, площади, окружности, периметра, объема, веса, формул, расстояния, календаря, денег, инструментов, точности, единиц, построений, шаблонов и решения задач.
Теория чисел
Блок теории чисел фокусируется на манипулировании числовыми формами и классификациями.
Учащиеся устанавливают связи между числовыми формами и их реальными приложениями.
Нумерация
Блок счисления фокусируется на изучении порядкового номера, выявлении и расширении шаблонов чисел, сравнении чисел и демонстрации отношений между числами.
Проценты
Процентная единица фокусируется на понятии процентов. Этот модуль включает в себя выполнение операций с процентами, преобразование процентов в другие числовые формы, использование манипуляций для демонстрации процентов и решение проблем с процентами в реальных контекстах.
Взгляд/роль в обществе
Блок «Перспектива / роль в обществе» фокусируется на реальной математике.Эти блоки включают математику в обществе и роль математики в личных финансах и карьере.
Вероятность/статистика
Группа вероятностей/статистики занимается анализом данных и вероятностными концепциями. Этот модуль включает в себя сбор, анализ и осмысление реальных данных (включая перекрывающиеся данные, неубедительные данные и т.
д.).
Решение проблем
Группа решения проблем фокусируется на усилиях по решению проблем.Этот модуль включает в себя анализ проблем, оценку решений, исследование проблем и стратегии.
Рациональные и иррациональные числа
Модуль рациональных и иррациональных чисел включает в себя манипулирование, сравнение и выполнение операций с рациональными числами.
Вещественные числа и координатная плоскость
Модуль «Вещественные числа и координатная плоскость» включает графические уравнения и установление связей между алгебраическими понятиями и их геометрическими соответствиями.
Math Beasts Camp 7-9 (подготовка к алгебре и геометрии)
Выберите правильный уровень
Лагерь Math Beasts Camp 7-9 предназначен для учащихся, прошедших курс предварительной алгебры, такой как математика с отличием 6 или соревновательная математика 6.
Учебная программа
Наши опытные инструкторы используют материалы, разработанные командой по учебной программе «Искусство решения задач», для обучения Math Beasts Camp 7–9.
Будучи углубленным исследованием сложной математики, учебная программа AoPS готовит студентов к успеху в лучших университетах и
конкурентоспособные карьеры.Для этого класса книги не требуются.
Math Beasts Camp 7-9 включает в себя занятия по математическим исследованиям и решению задач.
Наши занятия Mathematical Exploration предназначены для того, чтобы вооружить учащихся общими математическими стратегиями, которые помогут быть полезным на протяжении всего обучения. Мы вводим темы, с которыми большинство учащихся столкнутся гораздо позже в школе. Учащиеся изучают криптографию, начиная с шифров Цезаря, шифров ключевых слов и других методов, а затем знакомятся с основы современной криптографии — строительные блоки теории чисел.Студенты закончат курс с благодарностью для криптографических концепций безопасности в Интернете.
Сессии по решению проблем сосредоточены на логическом мышлении, обеспечивая при этом обзор ключевых математических концепций.
Студенты участвуют
в широком спектре математических игр и головоломок, которые призваны подтолкнуть учащихся к пониманию знакомых тем далеко за пределы
стандартный уровень обучения.
Формат
Наши преподаватели проводят занятия виртуально, в небольшом (10-16 человек) классе видеоконференцсвязи.
Домашнее задание
Нет обязательных домашних заданий для Лагеря математических зверей 7-9. Однако мы подготовили больше материалов, чем можем охватить
во время урока, и многие ученики продолжают работать над ними после урока для дополнительной практики.
Политики удаления и возврата
Если вы откажетесь от летнего курса до начала вашего первого занятия, мы полностью вернем вам деньги за
курс обучения. Возврат средств за отказ от летнего курса после начала первого занятия не производится.
сессия.
Расписание
Наши летние курсы проходят пять дней в неделю, с понедельника по пятницу.
Мы предлагаем этот курс в два раза
форматы. Оба охватывают один и тот же материал курса.
- Двухнедельный курс проводится по 3 часа каждый день.
- Четырехнедельный курс проводится по 1,5 часа каждый день.
Что такое геометрия? — Определение, факты и примеры
Что такое геометрия?
Геометрия — это раздел математики, изучающий размеры, формы, положения, углы и размеры вещей.
Плоские формы, такие как квадраты, круги и треугольники, являются частью плоской геометрии и называются двумерными фигурами. Эти формы имеют только 2 измерения: длину и ширину.
Примеры двумерных форм в плоской геометрии
Твердые объекты также известны как трехмерные объекты, имеющие третье измерение высоты или глубины.
Примеры трехмерных фигур в твердотельной геометрии
Угол :
Вершина фигуры, где два ребра пересекаются, образуя угол.
Различные фигуры в геометрии имеют разные меры угла.
Например :
Треугольник представляет собой трехстороннюю фигуру, а мера трех внутренних углов равна 180˚
Квадрат, прямоугольник или четырехугольник имеют четыре стороны, а мера их внутренних углов равна 360˚
Другие многоугольники, такие как пятиугольник, шестиугольник, семиугольник, восьмиугольник, имеют 5, 6, 7, 8 сторон соответственно и разные углы.
Примеры различных многоугольников с их углами и сторонами
Мы изучаем различные аспекты форм, такие как измерение углов, длины сторон, площади, объема и т. д. в геометрии.
Подобие и конгруэнтность — два важных аспекта геометрии.
Сходство : Сходство — это когда две формы одинаковы, но их размеры могут различаться.
Конгруэнтность : Конгруэнтность — это когда две фигуры совершенно одинаковы по форме и размеру.
Координатная плоскость :
Координатная плоскость — это двухмерная поверхность, образованная двумя числовыми линиями, пересекающимися под прямым углом.
Горизонтальная числовая линия — это ось x, а вертикальная числовая линия — ось y.
Пересечение двух осей является координатой (0,0).
Используя координатную плоскость, мы наносим точки, линии и т. д. Соединяя различные точки на координатной плоскости, мы можем создавать формы.
Мы используем формулу и теоремы для решения задач по геометрии.
Формула — это математическое уравнение для решения задачи геометрии, а теорема — это утверждение, которое доказывается с использованием ранее известных фактов.
Например, « Теорема Пифагора » доказала, что a2 + b2 = c2 для прямоугольного треугольника, где a и b — стороны прямоугольного треугольника, а c — гипотенуза.
Однако, a2 + b2 = c2 — это формула для нахождения гипотенузы прямоугольного треугольника.
Интересные факты |
Конспекты курсов 7-го класса — Средняя школа Фрелингхейзена
Краткое содержание курса для 7 класса
Средняя школа Фрелингхейзена
7 класс
Краткое содержание курса
Все учебные программы FMS соответствуют стандартам Common Core Curriculum Standards штата Нью-Джерси.
Для получения дополнительной информации посетите: http://www.state.nj.us/education/cccs/
МАТЕМАТИКА
В 7 классе учащиеся программы по математике будут: (1) развивать понимание пропорциональных отношений и применять их; (2) развитие понимания операций с рациональными числами и работы с выражениями и линейными уравнениями; (3) решение задач, связанных с чертежами в масштабе и неформальными геометрическими построениями, а также работа с двух- и трехмерными формами для решения задач, связанных с площадью, площадью поверхности и объемом; и (4) делать выводы о популяциях на основе выборок.
Цели нашей программы: использовать подход к решению проблем, в котором особое внимание уделяется стандартам NCTM, развивать уверенность, знания и методы использования математики для рассуждений и решения проблем в повседневной жизни, а также уметь математически общаться, а также помогать учащимся. ценить математику и ее связь со всеми предметами.
АЛГЕБРА I
Программа алгебры для 7 класса знакомит учащихся с понятиями алгебры в программе подготовки к колледжу. Объем расширяет математические знания студентов с помощью различных видов деятельности, которые включают в себя рассуждение, решение проблем и общение.
Учащиеся должны: 1) продемонстрировать концептуальное понимание свойств и операций с действительными числами с акцентом на отношения, доли и пропорции, а также числовые выражения, содержащие экспоненты и радикалы, 2) работать с полиномиальными выражениями, факторизовать полиномиальные выражения и использовать алгебраические радикальные выражения, 3) анализировать, представлять и отображать линейные функции, включая те, которые включают абсолютное значение, а также распознавать и использовать линейные модели, 4) решать и строить графики линейных уравнений и неравенств и использовать их для представления контекстуальных ситуаций, 5) решать системы линейных уравнений и моделировать с одной переменной линейные уравнения, неравенства с одной или двумя переменными или системы уравнений, 6) демонстрировать способность оценивать и проверять решения линейных уравнений, используя для этого соответствующие технологии, 7) представлять простые квадратичные функции несколькими способами и использовать квадратичные модели, а также решать квадратные уравнения и устанавливать связи через интер создание линейных тенденций в данных, сравнение данных с использованием сводной статистики, принципов вероятности и подсчета, а также оценка основанных на данных отчетов в СМИ.
ИСКУССТВО ЯЗЫКА
Учебная программа по словесности в седьмом классе объединяет чтение и письмо, побуждая учащихся выйти за рамки базовых навыков чтения и письма, чтобы иметь дело с абстрактными понятиями и символикой. По мере того, как учащиеся будут ценить язык и условности авторов, которых они читают, они будут оттачивать свои навыки письма, сочиняя, набрасывая и публикуя для различных целей.
Цели: для успешного завершения элементов чтения этого курса учащиеся продемонстрируют способность: определять характеристики разных жанров; использовать стратегии чтения, соответствующие задаче; отрегулируйте скорость чтения, чтобы просматривать, сканировать и читать для получения подробной информации; улучшить беглость речи; прогнозировать результаты внутри и за пределами структуры текста; выявлять, обобщать и оценивать элементы художественной литературы; объяснить основную идею логической последовательностью идей, деталей и реакций; анализировать текст по назначению, тону и стилю; подкреплять утверждения и мнения доказательствами из текста; улучшить навыки логического вывода; и сравнить различные произведения одного и того же автора.
Чтобы успешно завершить письменные элементы этого курса, студенты продемонстрируют способность: использовать различные техники для генерации идей для письма; разрабатывать и использовать разнообразные подготовительные упражнения; использовать приемы черчения для создания законченного произведения; подготовьте окончательный вариант так, как удобно для аудитории; сосредоточьте письмо, чтобы ответить на идентифицируемую цель; использовать стиль и тон, соответствующие предполагаемой аудитории и цели; и используйте правильное написание, пунктуацию, синтаксис и использование слов.Обучение чтению основано на жанровых единицах, которые прогрессируют в течение периода маркировки. Единицы: рассказ, научно-популярная литература, фэнтези и историческая фантастика.
ОБЩЕСТВЕННЫЕ НАУКИ
Учебная программа по общественным наукам для 7-го класса разделена на шесть разделов всемирной истории: Эпохи палеолита и кочевников; География; религия; Правительство; экономика; и Общество.
Акцент делается на значимых событиях, которые повлияли на цивилизации во всем мире. Цели: Учащиеся смогут: 1) Читать из различных первичных и вторичных источников (художественной и научной литературы) для получения информации, 2) Расширить навыки критического мышления, 3) Развить и закрепить навыки письма в области содержания, 4 ) расширить учебные и исследовательские навыки, 5) получить представление об историческом вкладе, сформировавшем общество.
НАУКА
Этот курс предназначен для того, чтобы познакомить учащихся с основными понятиями, навыками и отношениями, связанными с наукой. Через различные независимые учебные блоки студенты будут подвергаться научной методологии, выполняя соответствующие лабораторные и другие практические действия. Особое внимание будет также уделяться процедурам безопасности в научных классах/лабораториях, знакомству со сбором, анализом и интерпретацией эмпирических данных, а также развитию чувства признательности и понимания научного вклада представителей различных культур и этнических групп.
Цели: Учащийся продемонстрирует способность: 1) безопасно и совместно работать в лаборатории, 2) использовать единицы метрической системы, 3) применять научный метод для решения задач, 4) умело использовать составной микроскоп, 5 ) Использовать клеточную теорию для исследования живых существ, 6) Объяснять, как живые существа функционируют и реагируют/взаимодействуют с окружающей средой, 7) Использовать и разрабатывать различные системы классификации, 8) Распознавать взаимосвязь между функциями, структурой и поведением организмов.
МИРОВЫЕ ЯЗЫКИ
Философия этой программы 2-го года сосредоточена на повышении способности учащихся говорить, слушать и писать на изучаемом языке. Кроме того, расширяются знания учащихся о культуре и взаимосвязи между языком и культурой. Целями программы 7-го класса являются: 1) дальнейшее развитие навыков устной речи для успешного общения на различные темы на изучаемом языке; и 2) повышать и поощрять осведомленность и понимание культурного разнообразия.
6-8-й учебный план мировых языков
(PDF) Навыки геометрического мышления учащихся седьмого класса на тему треугольника и четырехугольника на основе теории обучения геометрии Ван Хиле
анализировать свойства геометрических фигур и делать математические выводы о геометрических
отношениях с использованием визуализации, пространственного мышления и геометрии моделирование для решения задач.
Математические способности учащихся все еще низкие. Доказано результатами Международной программы оценки исследований
(PISA), проведенной в 2015 году для индонезийских учащихся младших классов средней школы, которые заняли 63 место из
из 70 стран в области тестов математических способностей.Индонезия получила 386 баллов, при этом средний балл всех 490 стран составил 90 003 90 002 (OECD, 2016). Согласно опросу Trends in International Mathematics
и Science Study (TIMSS) в 2011 году, Индонезия заняла 38-е место из 42 стран в области
тестов математических навыков.
Индонезия набрала 386 баллов, при этом средний балл всех 90 003 90 002 стран-участниц составил 500 (Ina VS Mullis, 2012). Основываясь на результатах экзаменов
Национальной средней школы за 2018 учебный год, процент освоения математических задач
в материале «Геометрия и измерения» составил 42.80% на национальном уровне.
Согласно теории Ван Хиле (Usiskin, 1982), существует пять фаз изучения геометрии,
а именно: информация, ориентация, эксплуатация, свободная ориентация и интеграция. Теория
Ван Хиле утверждает, что навыки геометрического мышления имеют 5 (пять) уровней, а именно: 1) Уровень 0 Визуализация, 2)
Уровень 1 Анализ, 3) Уровень 2 Неформальная дедукция, 4) Уровень 3 Дедукция, 5) Уровень 4 Строгость (Кроули,
1987).На уровне 0 учащиеся узнают геометрические фигуры. На уровне 1 учащиеся знакомы с
свойствами геометрии. На уровне 2 учащиеся знают отношения между геометрическими фигурами и другими
геометрическими фигурами.
На уровне 3 учащиеся могут делать дедуктивные выводы, а именно выводы из
различных конкретных вещей. На уровне 4 учащиеся понимают, насколько важна точность основных принципов
, лежащих в основе доказательства, и понимают, почему что-то используется в качестве постулата или предложения
(Purwoko, 2019).Согласно Yildiz (2009), 7-й класс неполной средней школы получил неформальный вычет
(уровень 2) навыков геометрического мышления ван Хиле. Это означает, что учащиеся 7-го класса средней школы
могут достичь уровня 0, уровня 1 и уровня 2 навыков геометрического мышления Ван Хиле, и ни один ученик
не может достичь уровня 3.
Навыки геометрического мышления учащихся могут быть показатель успешности изучения математики.
Если навыки геометрического мышления у учащихся высокие, это означает, что изучение математики выполнено хорошо, а
низкие навыки геометрического мышления учащихся указывают на то, что имевшее место изучение математики было
менее успешным.
Учитель должен уметь помочь учащимся улучшить навыки геометрического мышления.
Первый шаг, который необходимо сделать, это проанализировать навыки геометрического мышления учащихся. По этой причине
необходимо провести исследование навыков геометрического мышления учащихся в качестве материала для оценки
учителем того, хорошо ли идет текущее изучение геометрии. Это исследование направлено на определение
навыков геометрического мышления учащихся 7-го класса средней школы, особенно на треугольниках и
четырехугольниках, и описание фактов, обнаруженных в ходе исследования.
2. Методы исследования
Этот тип исследования был количественным описательным исследованием. Количественное описательное исследование — это один из
видов исследований, целью которого является систематическое, фактическое и точное описание фактов и
характеристик конкретных групп населения или попытка подробного описания явлений (Lehmann, 1979).
Количественное описательное исследование представляет собой сознательную и систематическую попытку дать ответы на проблему
и/или получить более глубокую и обширную информацию о явлении с использованием этапов исследования
с количественным подходом (Yusuf, 2014).
Согласно Arikunto (2006), количественные описательные исследования не предназначены для проверки гипотез, а только описывают то, что они касаются переменной.
По словам Эрика (2015), количественные описательные исследования проводятся в виде чисел и процентов.
Что касается переменной в данном исследовании, то это были навыки геометрического мышления, при этом предметом исследования были
учащиеся 7-х классов средней школы.
Методы сбора данных проводились путем предоставления письменных тестов учащимся 7-х классов и
анализа ответов учащихся по каждому пункту.Тест был использован для выявления, как геометрическое мышление
навыков учащихся 7-х классов, особенно в предмете треугольники и четырехугольники. Методика анализа данных
использовала интервальную шкалу. Согласно Джаали и соавт. (2000), интервальная шкала — это шкала, которая имеет
одинаковое расстояние между одними данными и другими данными. Шкала интервалов идентична действительному числу.
Согласно Suryabrata (2003), шкалы интервалов взаимоисключающие; категории данных являются логическими,
Математика 7-го класса — Раздел 6: Геометрия
Обзор блока
В Разделе 6 учащиеся седьмого класса изучают широкий спектр тем, от соотношения углов до окружностей и многоугольников и объемных фигур.Стандарты по геометрии для седьмого класса относятся к категории дополнительных стандартов, однако в этом разделе есть несколько возможностей, когда учащиеся занимаются основной работой в классе. В начале раздела учащиеся используют и решают уравнения для представления взаимосвязей между углами и находят отсутствующие угловые меры. Исследуя круги, учащиеся обнаруживают пропорциональную связь между длиной окружности и ее диаметром и понимают π как отношение этих двух величин.Студенты также будут использовать свои навыки выражения для написания числовых выражений, которые можно использовать для нахождения площади поверхности и объема трехмерных фигур.
На протяжении всего раздела учащиеся сталкиваются с несколькими словарными словами, такими как дополнительные углы, вертикальные углы, радиус и окружность. Многие из этих слов позволяют учащимся быть более точными в общении друг с другом (MP.6). Студенты также столкнутся со сложными диаграммами углов и трехмерными фигурами, где им нужно будет понять, какую информацию они могут извлечь из диаграммы, и спланировать путь решения, прежде чем прыгать (MP.1). Учащиеся должны иметь доступ к нескольким инструментам, которые они могут использовать на протяжении всего раздела, включая линейки, транспортиры, циркуль и справочные листы (MP.5).
Основополагающие навыки для стандартов в этом подразделении формируются в классах с четвертого по шестой. В четвертом классе учащиеся изучали понятия измерения угла и понимали, что мера угла является аддитивной. В пятом классе учащиеся развили понимание трехмерного объема, которое они получили в шестом классе.Учащиеся шестого класса также начали различать трехмерное пространство, которое занимает объект, и площадь поверхности, которая его покрывает.
В восьмом классе учащиеся будут увеличивать прямоугольные треугольники и применять теорему Пифагора для определения длин сторон в прямоугольных треугольниках. Они также продолжат решать реальные приложения площади поверхности и объема с добавлением конусов, сфер и цилиндров.
Темп: 23 учебных дня (21 урок, 1 гибкий день, 1 контрольный день)
Для получения рекомендаций по корректировке темпа на 2021–2022 учебный год см. Рекомендуемые корректировки объема и последовательности для 7-го класса.
.
