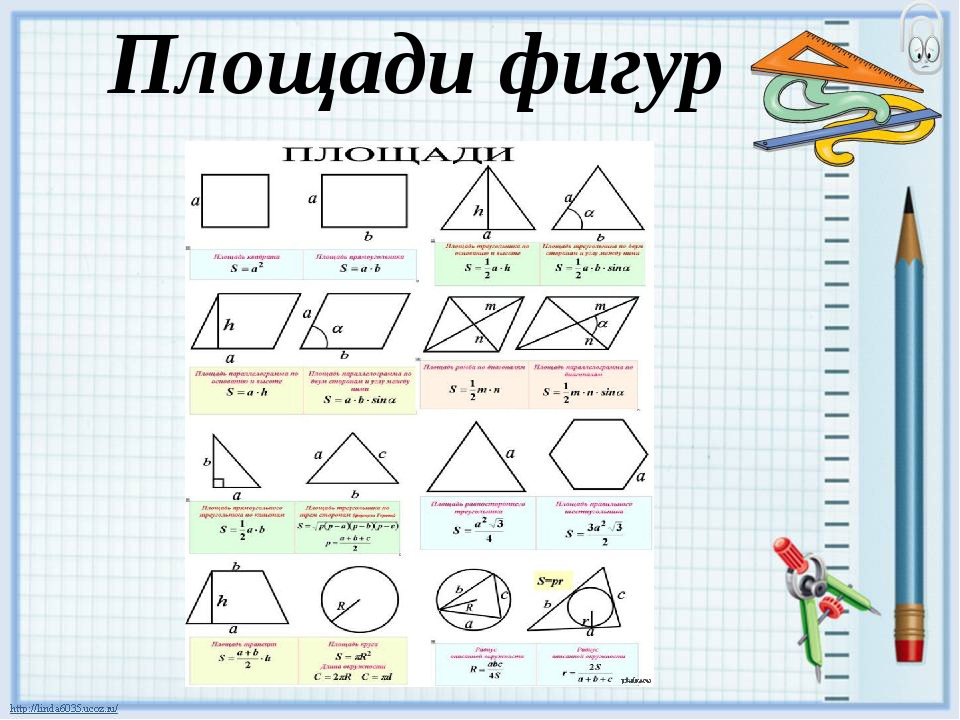
Теоретическая подготовка к ЕГЭ по математике с репетитором. Площади фигур. Задача B3
Обычно в задаче B3 варинта ЕГЭ изображается какая-нибудь простенькая фигура на клечатой бумаге, площадь которой нужно найти и записать в бланк. Для подготовки к решению простейших задач планиметрии репетитор по математике предложит Вам список наиболее употребимых в данной ситуации формул, хотя и без них часто можно сообразить что к чему. Для этого достаточно внимательно взглянуть на рисунок. При самостоятельной подготовке к ЕГЭ по математике без репетитора Вам понадобится освоить два главных приема вычисления площадей простейших фигур:
1) Поиск площади через сумму или разность площадей вспомогательных кусочков.
Для этого нужно разбить главную фигуру на несколько областей и сложить их. Есть альтернативный вариант: дополнить фигуру прямоугольными треугольниками до удобного прямоугольника или квадрата с хорошо определяемыми длинами сторон, а затем из его площади вычесть площади добавленных частей.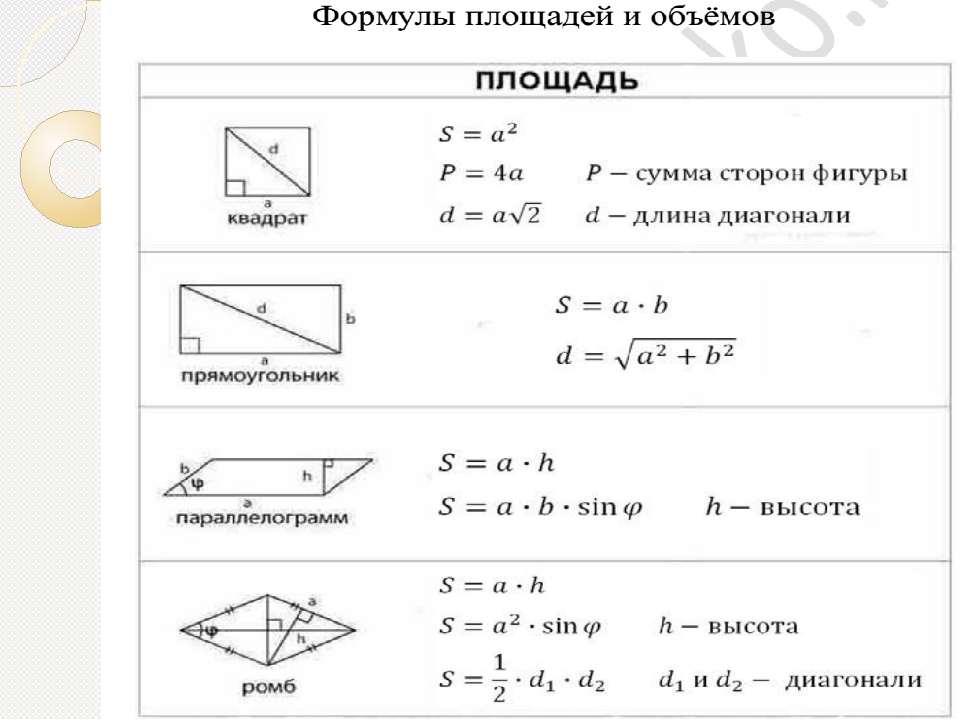
2) Мгновенное вычисление площади всей фигуры путем подстановки длин ее сторон в соответствующую формулу.
В любом случае нужно знать базовые формулы:
1) Прямоугольный треугольник , где а и b — его катеты.
Cамая востребованная формула для задачи B3. Всегда удобно дополнить фигуру такими треугольниками до прямоугольника, а затем из его площади вычесть сумму всех добавленных площадей.
2) Произвольный треугольник: , где a — основание треугольника, — высота, опущенная на это основание.
Репетитор по математике, работающий со слабым учеником, иногда пропускает отработку общих формул, считая появление произвольного треугольника в реальном варинте ЕГЭ маловероятным. Репетитора можно понять, так как чаще других фигур попадается четырехугольник (в частности трапеция).
Площади четырехугольников:
1) Квадрат
Не думаю, что составители ЕГЭ опустятся до такой элементарщины, что предложат задачу на самый простой из всех существующих четырехугольников.
2) Прямоугольник
Трудно представить себе абутуриента, который к 11 классу напрочь забыл программу 5 класса и не может, например, вычислить площадь пола в своей квартире. Тем не менее, репетитор по математике должен напомнить слабому ученику эту класссическую формулу.
3) Трапеция: , где a и b — основания трапеции, h — ее высота.
Наиболее востребованная формулы для метода моментального подсчета площади четырезугольника, каким чаще всего на ЕГЭ в B3 является трапеция. В последнем сборнике задач ЕГЭ была представлена целая серия номеров на подсчет полощади трапеции по координатам ее вершин. В них достаточно просто находятся длины сторон и подставляются в общую формулу.
4) Произвольный параллелограмм:
, где а — основание, h — высота.
5) Ромб
, где и — диагонали ромба.
Площадь круга и его элементов:
1) Круг:
Площадь круга можно вычислить по известной формуле вида
В ее записи R — радиус круга, а число — некое число, приближенно равное 3,14
2) Круговой сектор:
, где R — радиус круга, — градусная мера соответствующего сектору центрального угла.
Есть альтернативный способ решения задачи B3 — использовать формулу Пика. Она позволяет вычислять любые площади через подсчет количества вершин на сторонах фигуры и внутри нее.
Желаю Вам удачи на ЕГЭ! Колпаков А.Н. Репетитор по математике Москва — Строгино.
Конспект и презентация к уроку математики «Площади простых фигур»; 9 — 11 классы — К уроку — Математика, алгебра, геометрия
Учитель Марченко
М.А.
МКОУ СОШ№6
Г. Минеральные воды; ■
Цели и задачи урока: Учебные:
> проверить
и систематизировать знания учащихся
по данной
теме.
> закрепить умения учащихся применять формулы нахождения площадей фигур при решении задач.
готовность учащихся к успешной сдаче ГИА.
установить
межпредметные связи с алгеброй,
географией,
физикой.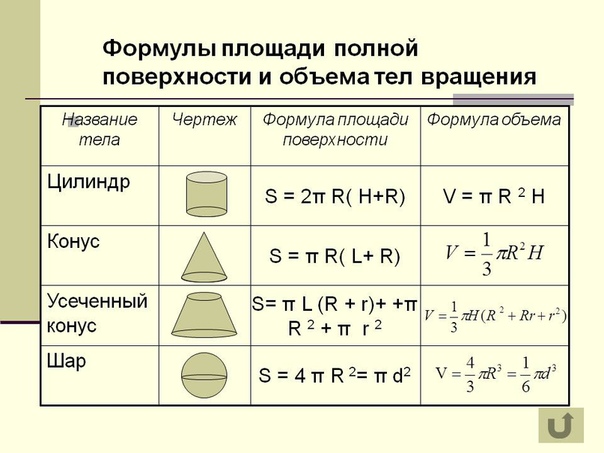
научить
применять полученные знания в жизни и
на
практике.
Развивающие и способности:
развитие
у учащихся самостоятельности и
способности к
самоорганизации.
повышение уровня математической культуры учащихся.
Воспитательные:
способствовать воспитанию эстетических качеств личности.
I. Вступительное слово учителя. ,
На
сегодняшнем уроке я жду от вас активной
работы, блестящих
ответов, максимального усвоения учебного
материала для успешной сдачи ГИА и для
дальнейшего обучения
в старших классах потому, что сегодня
на уроке мы будем вместе систематизировать
, обобщать материал по теме: «Площади
плоских фигур», а также узнаем, в каких
областях науки используются знания в
вычислении площадей, а также покажем,
что знания по этой теме имеют практическое
значение. Задача моего урока, чтобы приобретенные
знания и умения
на сегодняшнем уроке использовались
вами в практической деятельности и
повседневной жизни.
Задача моего урока, чтобы приобретенные
знания и умения
на сегодняшнем уроке использовались
вами в практической деятельности и
повседневной жизни.
II.Актуализация опорных знаний и умений
Задание. Принимая площадь клетки за 1 ед2, используя формулу площади, вычислите площадь каждой фигуры
III. Репортаж с хозяйственного магазина. Мотивация обучения.
(слайд3)
Далее детям предлагается решить такую задачу:
Строителям нужно выложить плиткой потолок в комнате прямоугольной формы. Её длина 5 м, ширина 4м. Плитка имеет форму квадрата со стороной 0,5 м. Сколько штук плитки нужно купить?
Задача решается на доске, а затем показывается решение на слайде.
1. Работа с тестами (слайд7).
2. Каждому ученику выдаётся «шпаргалка»
4.Поэтическая
минутка. Вниманию учеников предлагаются
стихи направленные
на лучшее усвоение формул площадей
плоских фигур.
а) Друзья
мои, легко найти S
параллелограмма. Вы помножьте а на
в
и на синус гамма.
(S=absiny).
б) Площадь
трапеции ты знаешь, посчитай я подожду.
Полусумму
оснований
ты умножь на высоту.
в) Площадь
треугольника, знать конечно надо: мы
умножим а на h
и
разделим на 2.
.
3. Показ слайда «Из истории геометрии.»
4. Показ слайда. Где применяются знания в вычислении площадей.
5. Связь уроков геометрии с географией. Учащимся предлагается решить задачу такого содержания.
Опытный земельный участок, прилегающий к пойме реки Урал на плане изображен в виде многоугольника в,масштабе 1:10000. Выполнить необходимые измерения и вычислить: а) длину границы участка б) площадь участка в) валовой сбор зерна со всего участка, если средняя урожайность пшеницы 45 ц с 1га.
6. Физкультминутка.
Физкультминутка.
Сборник задач под редакцией Лысенко для подготовки к ГИА вариант 19 № 16. Найдите площадь прямоугольного треугольника, изображенного на рисунке 130.
8. Класс решает задачу (условие показывают на слайде), а в это время один ученик выводит формулу площади равностороннего треугольника.
9. Показ слайда «Использование площадей в пирамидах».
10. Выставление оценок.
11. Подведение итогов урока.
12. Выставление оценок.
13. Подведение итогов урока.
Список литературы.
Ф.Ф. Нагибин, Е.С. Канин «Математическая шкатулка»,
М.М. Лиман « Школьникам о математике и математиках»,
А.П. Доморяд « Математические игры и развлечения»
Издательский дом «ПЕРВОЕ СЕНТЯБРЯ» ЕЖЕНЕДЕЛЬНАЯ УЧЕБНО-МЕТОДИЧЕСКАЯ ГАЗЕТА «Математика» 2002 год
Интернет-ресурсы
http://motivators. ru/node/15153
ru/node/15153
| 1.Вычислите площадь параллелограмма, стороны которого равны 16 см и 4 см, а угол между ними 600 | 2.Вычислите площадь равнобедренного треугольника, боковая сторона которого равна 15см, а высота, проведенная к основанию, равна 9см. | 3. Вычислите площадь ромба, если сторона его равна 10 см , а один из углов -450 . | 4. Вычислите площадь прямоугольного треугольника, гипотенуза которого 13 см, а один из катетов 5см |
| 5. Вычислите площадь равностороннего треугольника, сторона которого равна 8см. | 6. Вычислите площадь параллелограмма, стороны которого равны 16 см и 4 см, а один из углов 1500 | 7. Вычислите площадь параллелограмма, диагонали которого равны 10 см и 20 см, а угол между ними 450 | 8. Вычислите площадь треугольника, стороны которого равны 3см, 4 см и 5см. |
| 9. Вычислите площадь треугольника, стороны которого равна 10см и 6см, а угол между ними 300. | 10. Площадь треугольника равна 270см 2 ,сторона 5см. Найдите высоту, проведенную к данной стороне. | 11. Вычислите площадь прямоугольно равнобедренного треугольника, гипотенуза которого 8см. | 12. Вычислите площадь треугольника, стороны которого равны 5см, 5 см и 6см. |
| 13. Вычислите площадь прямоугольного треугольника, гипотенуза которого 2 см, а один из катетов 6см. | 14. Вычислите площадь прямоугольного треугольника, меньший катет которого 8 см, а один из углов 300. | 15.Вычислите площадь четырехугольника, диагонали которого взаимно перпендикулярны и равны 6 см и 6см. | 16.Средняя линия трапеции равна 12см, высота составляет ее длины. Вычислите площадь этой трапеции. |
| 17. Вычислите площадь квадрата, диагональ которого равна 12см. | 18.Вычислите площадь ромба, диагонали которого равны 10 см и 10см. | 19.Одна из диагоналей ромба в 6 раз больше другой. Найдите меньшую диагональ, если его площадь равна 108см2. | 20. Площадь трапеции равна 75см2, ее высота 5см. Найдите среднюю линию этой трапеции. |
| 21.В равнобедренной трапеции боковая сторона равна 12 см, а один из углов 300, основания равны 14 см и 22 см. | 22. Вычислите площадь равнобедренного треугольника, боковая сторона которого равна 13см, а основание 10см. | 23. Вычислите площадь параллелограмма, стороны которого равны 6 см и 8 см, а меньшая высота его равна 4см. | 24. Вычислите площадь прямоугольного треугольника, один из катетов которого 12 см, а другой составляет его длины. |
Тренажер по теме «Площади фигур»
Муниципальное автономное образовательное учреждение
вечерняя сменная общеобразовательное учреждение
г. Березники Пермского края
ТРЕНАЖЕР ПО ТЕМЕ
«ПЛОЩАДИ ФИГУР»
Составила
учитель математики
Хватынец Валентина Юрьевна
г. Березники, 2017 год
СОДЕРЖАНИЕ
Предисловие…………………………………………………….
§1. Знание теоретического материала……………………………….
§2. Задачи по теме «Прямоугольник» ……………………………………………………….
§3. Задачи по теме «Параллелограмм» ……………………………………………………….
§4. Задачи по теме «Треугольник» ……………………………………………………………
§5. Задачи по теме «Трапеция» …………………………………………
§6. Задачи по теме «Площадь фигур, заданных координатами» ……
§7. Задачи по теме «Площадь фигур на сетке» …………………………………
§8. Задачи по теме «Площадь заштрихованной фигуры» ……………….
§9. Ответы.
Справочный материал.
Список использованной литературы.
Предисловие
Цель данного пособия – помочь учащимся и учителям 9-х классов систематизировать знания по теме «Площадь фигур», закрепить знания теоретического материала и применение их на практике. Задачи:
выработать умение применять формулу для нахождения площади фигур;
совершенствовать навыки чтения математических чертежей; — развивать способность выбирать оптимальный путь решения задачи. Развитие вычислительной грамотности, пространственного воображения. Пособие предназначено для работы на уроке, для выполнения домашних заданий, а также для подготовки к итоговой аттестации. Рекомендовано для учащихся обучающихся по форме самообразования (экстернат). Пособие включает в себя справочные материалы, представленные в таблицах. Тренировочные упражнения помогают запомнить изученный материал, закрепить знания теоретического материала на практических заданиях. Каждую тему завершают контрольные диагностические наборы или тесты формата ОГЭ. Тренировочный материал пособия апробирован на уроках математики в Вечерней сменной школе г. Березники.
Развитие вычислительной грамотности, пространственного воображения. Пособие предназначено для работы на уроке, для выполнения домашних заданий, а также для подготовки к итоговой аттестации. Рекомендовано для учащихся обучающихся по форме самообразования (экстернат). Пособие включает в себя справочные материалы, представленные в таблицах. Тренировочные упражнения помогают запомнить изученный материал, закрепить знания теоретического материала на практических заданиях. Каждую тему завершают контрольные диагностические наборы или тесты формата ОГЭ. Тренировочный материал пособия апробирован на уроках математики в Вечерней сменной школе г. Березники.
§1. Знание теоретического материала.
| № п/п | Текст задания | Ответы |
| 1. | По данным величинам запишите формулу площади данной фигуры. | |
| 2 | По данным величинам запишите формулу площади данной фигуры. | |
| 3 | По данным величинам запишите формулу площади данной фигуры. | |
| 4 | По данным величинам запишите формулу площади данной фигуры. | |
| 5 | По данным величинам запишите формулу площади данной фигуры. | |
| 6 | По данным величинам запишите формулу площади данной фигуры. | |
| 7 | По данным величинам запишите формулу площади данной фигуры. | |
| 8 | По данным величинам запишите формулу площади данной фигуры. | |
| 9 | По данным величинам запишите формулу площади данной фигуры. | |
| 10 | По данным величинам запишите формулу площади данной фигуры. |
§2. Задачи по теме «Прямоугольник»
| № | Текст задания | Ответы | ||
| А | В | С | ||
| 1. | В прямоугольнике одна сторона равна 20, другая сторона равна 24. Найдите площадь прямоугольника. | 88 | 480 | 68 |
| 2. | Найдите площадь прямоугольника, по стороне и диагонали. | 1440 | 98 | 196 |
| 3. | В прямоугольнике периметр равен 72, а одна из его сторон равна 16. Найдите площадь прямоугольника. | 88 | 320 | 896 |
| 4. | В прямоугольнике диагональ равна 32, а угол между ней и одной из сторон равен 60°. Найдите площадь прямоугольника, деленную на √3. | 640 | 256 | 1920 |
| 5. | Найдите площадь прямоугольника, если его периметр равен 68 и одна сторона на 4 больше другой. | 285 | 272 | 1156 |
| 6. | Площадь прямоугольника равна 18. Найдите его большую сторону, если она в 2 раза больше меньшей стороны. | 9 | 6 | 3 |
| 7 | Одна из сторон прямоугольника равна 30, а площадь равна 480. Найдите диагональ этого прямоугольника. | 34 | 16 | 510 |
| 8. | Найдите площадь прямоугольника, изображенного на рисунке. | 350 | 780 | 39 |
| 9. | Найдите площадь прямоугольника, изображенного на рисунке.
| 180 | 580 | 420 |
| 10. | Сторона квадрата равна 21. Найдите площадь квадрата. | 42 | 84 | 441 |
| 11. | Как изменится площадь прямоугольника, если каждую сторону увеличить в два раза? | В 4 раза | В 2 раза | Не измен. |
| 12. | Пол комнаты, имеющей форму прямоугольника со сторонами 5,5 м и 6 м, нужно покрыть паркетом прямоугольной формы. Длина каждой дощечки паркета равна 30 см, а ширина – 5 см. Сколько потребуется таких дощечек для покрытия пола? | 2200 | 220 | 22 |
| 13. | Сколько потребуется кафельных плиток квадратной формы со стороной 15 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3 м и 2,7 м? | 36 | 360 | 400 |
Проверочная работа.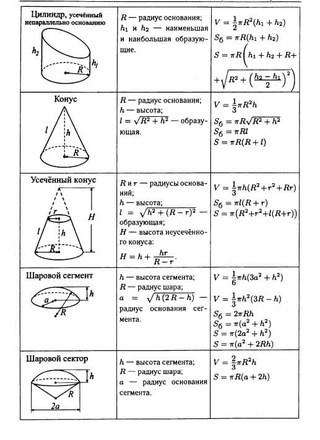
А
В
1. Укажите неверную формулу площади.
a) SABCD = AB · AD
б) SABCD = AB · BC
D
С
в) S∆ABC = AB · BC
2. Как изменится площадь прямоугольника, если одну его сторону увеличить в 2 раза, а другую – в 4 раза?
3. Площадь прямоугольника со сторонами 8см и 2 дм равна:
а) 56 см б) 16 см2 в) 160см2
4. Сколько потребуется досок для настила пол в зале, длина которого равна 20 м, а ширина 10 м, если длина доски 4 м, а ширина 25 см?
а) 125 шт. б) 200 шт. в) 180 шт.
§3. Задачи по теме «Параллелограмм»
| № | Текст задания | Ответы | ||
| А | В | С | ||
| 1. | Одна из сторон параллелограмма равна 31, а опущенная на нее высота равна 7. Найдите площадь параллелограмма. | 38 | 217 | 76 |
| 2 | Одна из сторон параллелограмма равна 13, другая равна 20, а один из углов – 45°. Найдите площадь параллелограмма, умноженную на √2. | 260 | 130 | 57 |
| 3. | Стороны параллелограмма равны 9 и 10. Высота, опущенная на первую сторону, равна 14.Найдите высоту, опущенную на вторую сторону параллелограмма. | 266 | 12,6 | 33 |
| 4. | Площадь параллелограмма равна 65, две его стороны равны 5 и 10. | 6,5 | 13 | 5 |
| 5. | Площадь параллелограмма равна 205, две его высоты равны 5 и 17. Найдите большую сторону этого параллелограмма. | 41 | 12 | 9 |
| 6. | Найдите площадь параллелограмма, изображенного на рисунке. | 42 | 24 | 70 |
| 7. | Смежные стороны параллелограмма равны 12 см и 14 см, а его острый угол равен 30°. Найдите площадь параллелограмма. | 168 | 56 | 84 |
| 8. | Периметр параллелограмма равен 20 см. Вычислите его площадь, если один из его углов равен 150°, а длина одной из его сторон равна 8 см. | 15 | 8 | 12 |
| 9 | Стороны параллелограмма 6см и 9 см. Длина большей высоты параллелограмма 8 см. Найдите его площадь. | 48 | 72 | 54 |
| 10. | Площадь параллелограмма равна 25 см2. Стороны параллелограмма равны 2а + 3; 3а + 4 см, тогда меньшая высота этого параллелограмма равна: | 25: (3а + 4) | 25: (2а + 3) | (2а + 3) (3а + 4) |
Проверочная работа.
1. Стороны параллелограмма равны 8см и 14 см, а угол между ними 30°.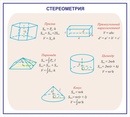 Найдите площадь параллелограмма.
Найдите площадь параллелограмма.
2. Стороны параллелограмма равны 4 см и 8 см. Высота, опущенная на первую из этих сторон, равна 6 см. Найдите высоту, опущенную на вторую сторону параллелограмма.
3. Площадь параллелограмма равна 24 см2, каждая из его сторон равна 6 см. Найдите расстояние между противоположными сторонами параллелограмма.
4. Укажите формулу для вычисления площади параллелограмма:
а) S = ½ a·ha
b
б) S = 2 a ·ha
hb
ha
в) S = a ha
а
§4. Задачи по теме «Ромб»
| № п/п | Текст задания | Ответы | ||
| А | В | С | ||
| 1. | Найдите площадь ромба, если его диагонали равны 8 и 12. | 96 | 48 | 40 |
| 2. | Периметр ромба равен 72, а один из углов равен 45°. Найдите площадь ромба, деленную на √2. | 162 | 117 | 27 |
| 3. | Найдите сторону ромба, если его площадь равна 72, а острый угол 30°. | 24 | 12 | 216 |
| 4. | Площадь ромба равна 26. Одна из диагоналей равна 4. Найдите другую диагональ. | 6,5 | 13 | 65 |
| 5. | Найдите высоту ромба, если его площадь равна 54, а сторона равна 4. | 13,4 | 216 | 58 |
| 6. | Сторона ромба равна 25, а диагональ – 48. Найдите площадь ромба. | 1200 | 73 | 336 |
| 7. | Найдите площадь ромба, изображенного на рисунке. | 14 | 20 | 24 |
| 8. | Найдите площадь ромба, изображенного на рисунке. | 90 | 60 | 21 |
| 9. | Найдите площадь ромба, если его высота равна 12, а острый угол 30°. | 288 | 360 | 42 |
| 10. | Сторона ромба 8 см, а острый угол 30°. Найдите площадь ромба. | 32 | 240 | 64 |
Самостоятельная работа.
Укажите неверное утверждение:
а) площадь ромба равна произведению диагоналей;
б) площадь ромба равна произведению его стороны на высоту;
в) диагонали ромба разбивают его на 4 равновеликих треугольника.
Найдите высоту ромба, сторона которого равна 6, 5 см, а площадь – 26 см2.
Сторона ромба 6 см, а острый угол 30°. Найдите площадь ромба.
Периметр ромба равен 40 см, а высота равна 8 см. Вычислите площадь ромба.
§5. Задачи по теме «Треугольник»
| № п/п | Текст заданий | Ответы | ||
| А | В | С | ||
| 1. | Найдите площадь треугольника, изображенного на рисунке. | 42 | 70 | 300 |
| 2. | В прямоугольном треугольнике один из катетов равен 8, а угол, лежащий против него, равен 30°. Найдите площадь треугольника. В ответе напишите площадь, деленную на √3. | 32 | 240 | 38√3 |
| 3. | В прямоугольном треугольнике один из катетов равен 5, а острый угол, прилежащий к нему, равен 30°. Найдите площадь треугольника. В ответе запишите площадь, умноженную на √3. | 150 | 12,5 | 50 |
| 4. | В прямоугольном треугольнике один из катетов равен 12, а угол, лежащий напротив него, равен 45°. Найдите площадь треугольника. | 72 | 144 | 57 |
| 5. | Периметр равностороннего треугольника равен 84. Найдите его площадь, деленную на √3. | 28 | 84√3 | 196 |
| 6. | Найдите площадь равностороннего треугольника, высота которого равна 4. | 16 | 4√3 | 12 |
| 7. | Периметр равнобедренного треугольника равен 36, а боковая сторона – 13. Найдите площадь треугольника. | 43 | 60 | 468 |
| 8. | Периметр равнобедренного треугольника равен 100, а основание – 18. Найдите площадь треугольника. | 118 | 820 | 180 |
| 9. | У треугольника со сторонами 14 и 21 проведены высоты к этим. Высота, проведенная к меньшей стороне, равна 6. Чему равна высота, проведенная к большей стороне? | 4 | 5,8 | 49 |
| 10. | Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 90°. Найдите боковую сторону треугольника, если его площадь равен 450. | 540 | 5 | 30 |
| 11. | Найдите площадь треугольника, изображенного на рисунке. | 132 | 264 | 62 |
| 12. | Найдите площадь треугольника, изображенного на рисунке. | 40 | 120 | 60 |
| 13. | Найдите площадь прямоугольного треугольника, изображенного на рисунке. | 52 | 315 | 24,5 |
| 14. | Найдите площадь равнобедренного треугольника, изображенного на рисунке. | 168 | 98 | 200 |
| 15. | Найдите площадь равнобедренного треугольника, изображенного на рисунке. | 60 | 42 | 84 |
Проверочная работа.
Катеты прямоугольного треугольника равны 4 см и 3 см. Вычислите площадь данного треугольника.
а) 7см; в) 6 см; с) 12 см
2. В треугольнике одна из сторон 12, другая 8, а синус угла между ними равен 0,2. Найдите площадь треугольника. a) 9, 6 в) 4, 8 с) 48
3. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах
а) 21 в) 13см с) 30 см
4. Найдите площадь прямоугольного треугольника, если один из его катетов равен 8 см, а гипотенуза равна 10 см.
Найдите площадь прямоугольного треугольника, если один из его катетов равен 8 см, а гипотенуза равна 10 см.
а) 80см2 в) 24см2 с) 48см2
§6. Задачи по теме «Трапеция»
| № п/п | Тексты заданий | Ответы | ||
| А | В | С | ||
| 1. | Основания трапеции равны 17 и 22, площадь трапеции равен 390. Найдите высоту трапеции. | 10 | 20 | 5 |
| 2. | Одно из оснований трапеции равно 12, высота равна 6, а площадь трапеции равна 96. Найдите второе основание трапеции. | 16 | 4 | 20 |
| 3. | Основания равнобедренной трапеции равны 8 и 29, площадь равна 333. Найдите ее высоту. | 18 | 9 | 15 |
| 4. | Основание трапеции равно 23, высота равна 5, а площадь равна 150. Найдите второе основание трапеции. | 7 | 8,3 | 5 |
| 5. | Основания равнобедренной трапеции равны 7 и 13, а ее периметр равен 30. Найдите площадь трапеции. | 30 | 40 | 600 |
| 6. | Найдите большее основание прямоугольной трапеции, площадь которой равна 48, высота равна 6 и большая боковая сторона составляет с основанием угол 45°. | 11 | 8 | 42 |
| 7. | В равнобокой трапеции основания равны 10 см и 20 см, боковая сторона равна 25 см. Найдите площадь трапеции, деленную на √5. | 200 | 500 | 40 |
| 8. | Тупой угол равнобедренной трапеции равен 135°, а высота, проведенная из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции. | 13,98 | 4,76 | 87 |
| 9. | Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол равен 135°. | 36 | 54 | 129 |
| 10. | Основания равнобедренной трапеции равны 6 см и 10 см. Ее острый угол равен 45°. Найдите площадь трапеции. | 16 | 60 | 30 |
Проверочная работа
1. Основания равнобедренной трапеции равны 14 и 20, а высота равна 5. Найдите площадь трапеции.
а) 68 б) 34 в) 85
2.Укажите верную формулу для вычисления площади трапеции
a
а) S =
h
б) S = (a + b) h
b
в) S =
3. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол 135°.
а) 36 см2 б) 54 см2 в) 18 см2
4. Параллельные стороны трапеции равны 2 см и 5 см, а расстояние между ними равно 4 см. Площадь трапеции равна:
а) 40 см2 б) 14 см2 в) 2,5 см2
§7.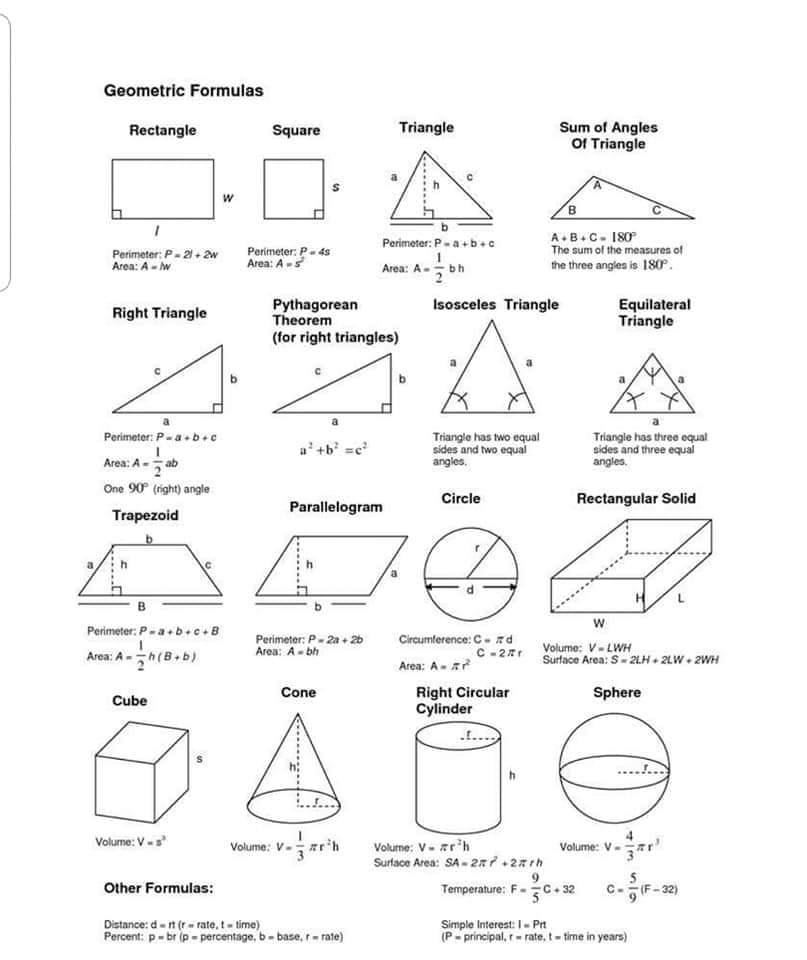 Задачи по теме «Площадь фигур, заданных координатами».
Задачи по теме «Площадь фигур, заданных координатами».
| № п/п | Текст задания | Ответы | ||
| А | В | С | ||
| 1. | Найдите площадь треугольника, вершины которого имеют координаты (1; 0), (11; 7), (8;10). | 31 | 27 | 15 |
| 2. | Найдите площадь прямоугольника, вершины которого имеют координаты (1; 0), (10; 0), (1; 10), (10; 10) | 90 | 38 | 19 |
| 3. | Найдите площадь трапеции, вершины которой имеют координаты (-4; -2), (4; -2), (3; 5), (0; 5). | 77 | 38,5 | 56 |
| 4. | Найдите площадь параллелограмма, вершины которого имеют координаты (-2; -1), (4; -1), (2; 4), (-4; 4). | 30 | 22 | 11 |
§8. Задачи по теме «Площадь фигур на сетке»
| № п/п | Тексты заданий | Ответы | ||
| А | В | С | ||
| 1 | Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 7,5 | 8 | 11 |
| 2 | Найдите площадь прямоугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 12 | 18 | 9 |
| 3 | Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 8 | 13 | 10 |
| 4 | Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 6 | 12 | 10 |
| 5 | Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см х 1см. | 8 | 10 | 12 |
| 6 | Найдите площадь параллелограмма, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 17 | 12 | 10 |
| 7 | Найдите площадь фигуры, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах. | 13 | 21 | 20 |
§9. Задачи по теме «Площадь заштрихованной фигуры»
| № п/п | Тексты заданий | Ответы | ||
| А | В | С | ||
| 1 | Выполните необходимые измерения и вычислите площадь заштрихованной фигуры. | 22 | 42 | 25 |
| 2 | Выполните необходимые измерения и вычислите площадь заштрихованной фигуры. | 22 | 34 | 25 |
| 3 | Выполните необходимые измерения и вычислите площадь заштрихованной фигуры. | 29,5 | 20,5 | 25 |
| 4 | Выполните необходимые измерения и вычислите площадь заштрихованной фигуры. | 18 | 30 | 25 |
| 5 | Выполните необходимые измерения и вычислите площадь заштрихованной фигуры. | 16,5 | 25,5 | 25 |
| 6 | Вычислите площадь заштрихованной фигуры, если R = 6; r1 = 3; r2 = 1 | 81,64 | 15 | 100 |
| 7. | Вычислите площадь заштрихованной фигуры, если AB = AC = BC =6. | 21,6 | 3,79 | 37,9 |
| 8 | АВСD – прямоугольник | 18,58 | 1,858 | 185,8 |
| 9. | АВСD – квадрат, АВ = 6 см. | 77,4 | 7,74 | 0,774 |
Контрольная работа по теме «Площади»
Найдите площадь фигуры, изображенного на клетчатой бумаге с размером клетки 1см х 1см. Ответ дайте в квадратных сантиметрах.
Ответ дайте в квадратных сантиметрах.
Ответы.
§1. Знание теоретического материала
S = a b
S = a h
S = a b sin α
S = ½ a b sin α
S =
S =
S ==
S =
S = π R2
10.S = √ p (p-a) (p-b) (p-c), где p =
| тема «Прямоугольник» | тема «Параллелограмм | тема «Ромб» | тема «Треугольник |
| 1-В | 1-В | 1-В | 1-В |
| 2-А | 2-А | 2-А | 2-А |
| 3-В | 3-В | 3-В | 3-В |
| 4-В | 4-В | 4-В | 4-А |
| 5-А | 5-А | 5-А | 5-С |
| 6-С | 6-А | 6-С | 6-А |
| 7-А | 7-С | 7-С | 7-В |
| 8-А | 8-В | 8-А | 8-В |
| 9-С | 9 — А | 9-А | 9-А |
| 10-С | 10 — В | 10-А | 10-С |
| 11-А | 11-А | ||
| 12-А | 12-С | ||
| 13-В | 13-С | ||
| 14-А | |||
| 15-А |
| тема «Трапеция» | тема «Площадь фигур, заданных координатами» | Тема «Площадь фигур на сетке» | Площадь заштрихованной фигуры |
| 1-В | 1-В | 1-А | 1-А |
| 2-С | 2-А | 2-В | 2-А |
| 3-А | 3-В | 3-А | 3-В |
| 4-А | 4-А | 4-А | 4-А |
| 5-В | 5-А | 5-А | |
| 6-А | 6-В | 6-А | |
| 7-А | 7-А | 7-В | |
| 8-В | 8-А | ||
| 9-В | 9-В | ||
| 10 — А |
Ответы на проверочные и самостоятельные работы.
| Прямоугольник | Параллелограмм | Ромб | Треугольник | Трапеция |
| 1 – в | 1 -56 см2 | 1 – а | 1 – в | 1 – в |
| 2 – в 8 раз | 2 – 3 см | 2 – 4 см | 2 – а | 2 – в |
| 3 – в | 3 – 4 см | 3 – 18 см2 | 3 — а | 3 — б |
| 4 — б | 4 — в | 4 – 80см2 | 4 — в | 4 — в |
Справочный материал
| функция | 30° | 45° | 60° |
| sin α | |||
| cos α | |||
| tg α | 1 | √3 |
Список использованной литературы.
А.В. Погорелов. Геометрия 7-9 классы. Учебник для общеобразовательных организаций, М.: Просвещение, 2014.
Л. С. Атанасян. Геометрия 7-9 классы. Учебник для общеобразовательных организаций, М.: Просвещение, 2011.
Математика. 9 класс. ОГЭ-2017. Тренажер по новому плану экзамена. Легион, 2016.
А. П. Ершова. Самостоятельные и контрольные работы по геометрии для 8 класса. М.: ИЛЕКСА, 2015.
А.М.Лукашенок. Тесты по геометрии для поурочного контроля. 8 класс. М., Белый ветер.
пособие для учителей общеобразовательных организаций. Сост. Т. А. Бурмистрова
%PDF-1.6 % 378 0 obj > endobj 380 0 obj > endobj 377 0 obj >stream application/pdf
 dll Version 5.2.22015-05-25T17:03:35+03:002015-05-25T17:03:35+03:00Acrobat Distiller 9.5.0 (Windows)2-е издание, 2014 годuuid:b48263e7-441f-441b-bbf4-3955e01ecfd2uuid:c55b36b6-da8a-448b-95cb-af752e29f6d7
endstream
endobj
375 0 obj
>
endobj
384 0 obj
>
endobj
385 0 obj
>
endobj
51 0 obj
>
endobj
388 0 obj
>
endobj
389 0 obj
>
endobj
184 0 obj
>
endobj
215 0 obj
>
endobj
246 0 obj
>
endobj
277 0 obj
>
endobj
309 0 obj
>
endobj
306 0 obj
>
endobj
310 0 obj
>
endobj
313 0 obj
>
endobj
316 0 obj
>
endobj
319 0 obj
>
endobj
322 0 obj
>
endobj
323 0 obj
>stream
hތWn6Ė#CNmIKOץט!)»mt˿f7حV,}=Bdsx(Yv2l Qy;߹˯Kr/4h8qʀ0U%U
c/.
dll Version 5.2.22015-05-25T17:03:35+03:002015-05-25T17:03:35+03:00Acrobat Distiller 9.5.0 (Windows)2-е издание, 2014 годuuid:b48263e7-441f-441b-bbf4-3955e01ecfd2uuid:c55b36b6-da8a-448b-95cb-af752e29f6d7
endstream
endobj
375 0 obj
>
endobj
384 0 obj
>
endobj
385 0 obj
>
endobj
51 0 obj
>
endobj
388 0 obj
>
endobj
389 0 obj
>
endobj
184 0 obj
>
endobj
215 0 obj
>
endobj
246 0 obj
>
endobj
277 0 obj
>
endobj
309 0 obj
>
endobj
306 0 obj
>
endobj
310 0 obj
>
endobj
313 0 obj
>
endobj
316 0 obj
>
endobj
319 0 obj
>
endobj
322 0 obj
>
endobj
323 0 obj
>stream
hތWn6Ė#CNmIKOץט!)»mt˿f7حV,}=Bdsx(Yv2l Qy;߹˯Kr/4h8qʀ0U%U
c/.
3 класс, периметр и площадь прямоугольника
Дата публикации: .
Что такое прямоугольник и квадрат
Прямоугольник – это четырёхугольник, у которого все углы прямые. Значит, противоположные стороны равны друг другу.
Квадрат – это прямоугольник, у которого равны и стороны, и углы. Его называют правильным четырёхугольником.
Четырёхугольники, в том числе прямоугольники и квадраты, обозначаются 4 буквами – вершинами. Для обозначения вершин используют латинские буквы: A, B, C, D …
Пример.
Читается так: четырёхугольник ABCD; квадрат EFGH.
Что такое периметр прямоугольника? Формула расчета периметра
Периметр прямоугольника – это сумма длин всех сторон прямоугольника или сумма длины и ширины, умноженная на 2.
Периметр обозначается латинской буквой P. Так как периметр – это длина всех сторон прямоугольника, то он периметр записывается в единицах длины: мм, см, м, дм, км.
Например, периметр прямоугольника АВСD обозначается как PABCD, где А, В, С, D – это вершины прямоугольника.
Запишем формулу периметра четырехугольника ABCD:
PABCD = AB + BC + CD + AD = 2 * AB + 2 * BC = 2 * (AB + BC)
Пример.
Задан прямоугольник ABCD со сторонами: AB=СD=5 см и AD=BC=3 см.
Определим PABCD.
Решение:
1. Нарисуем прямоугольник ABCD с исходными данными.
2. Напишем формулу для расчета периметра данного прямоугольника:
PABCD = 2 * (AB + BС)
3. Подставим в формулу наши данные:
PABCD = 2 * (5 см + 3 см) = 2 * 8 см = 16 см
Ответ: PABCD = 16 см.
Формула расчета периметра квадрата
У нас есть формула для определения периметра прямоугольника.
PABCD = 2 * (AB + BC)
Применим её для определения периметра квадрата.
 Учитывая, что все стороны квадрата равны, получаем:
Учитывая, что все стороны квадрата равны, получаем:PABCD= 4 * AB
Пример.
Задан квадрат ABCD со стороной, равной 6 см. Определим периметр квадрата.
Решение.
1. Нарисуем квадрат ABCD с исходными данными.
2. Вспомним формулу расчета периметра квадрата:
PABCD = 4 * AB
3. Подставим в формулу наши данные:
PABCD = 4 * 6 см = 24 см
Ответ: PABCD = 24 см.Задачи на нахождение периметра прямоугольника
1. Измерь ширину и длину прямоугольников. Определи их периметр.
2. Нарисуй прямоугольник ABCD со сторонами 4 см и 6 см. Определи периметр прямоугольника.
3. Нарисуй квадрат СEOM со стороной 5 см. Определи периметр квадрата.
Где используется расчет периметра прямоугольника?
1. Задан участок земли, его нужно обнести забором. Какой длины будет забор?
В данной задаче необходимо точно рассчитать периметр участка, чтобы не купить лишний материал для постройки забора.
2. Родители решили сделать ремонт в детской комнате. Необходимо знать периметр комнаты и её площадь, чтобы правильно рассчитать количество обоев.
Определи длину и ширину комнаты, в которой ты живешь. Определи периметр своей комнаты.
Что такое площадь прямоугольника?
Площадь – это числовая характеристика фигуры. Площадь измеряется квадратными единицами длины: см2, м2, дм2 и др. (сантиметр в квадрате, метр в квадрате, дециметр в квадрате и т.д.)
В вычислениях обозначается латинской буквой S.
Для определения площади прямоугольника необходимо длину прямоугольника умножить на его ширину.
Площадь прямоугольника вычисляется умножением длины АК на ширину КМ. Запишем это в виде формулы.
S AKMO = AK * KM
Пример.
Чему равна площадь прямоугольника AKMO, если его стороны равны 7 см и 2 см?
S AKMO= AK * KM = 7 см * 2 см = 14 см2.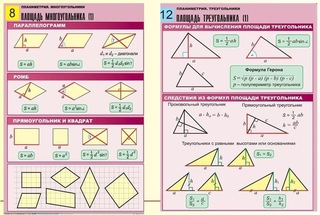
Формула вычисления площади квадрата
Площадь квадрата можно определить, умножив сторону саму на себя.
Пример.
В данном примере площадь квадрата вычисляется умножением стороны АB на ширину BC, но так как они равны, получается умножение стороны AB на AB.
S AВСО = AB * BC = AB * AB
Пример.
Определи площадь квадрата AKMO со стороной 8 см.
S AKMО = AK * KM = 8 см * 8 см = 64 см2
Ответ: 64 см2.Задачи на нахождение площади прямоугольника и квадрата
1.Задан прямоугольник со сторонами 20 мм и 60 мм. Вычисли его площадь. Запиши ответ в квадратных сантиметрах.
2. Был куплен дачный участок размером 20 м на 30 м. Определи площадь дачного участка, ответ запиши в квадратных сантиметрах.
Урок 14. призма — Геометрия — 10 класс
Геометрия, 10 класс
Урок № 14.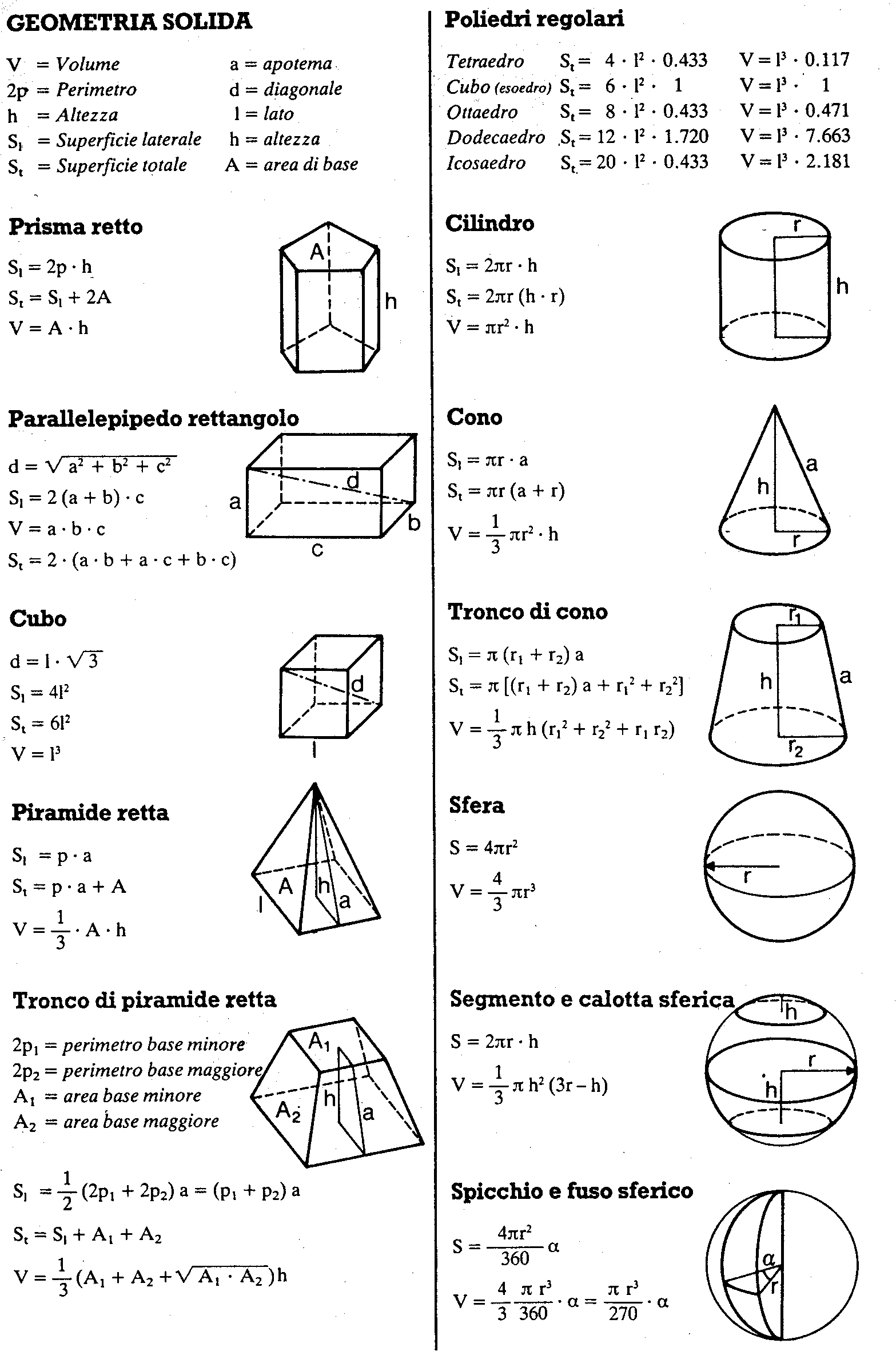 Призма
Призма
Перечень вопросов, рассматриваемых в теме:
- Понятие призмы и виды призм;
- Элементы призмы: вершины, ребра, грани;
- Понятие площади боковой поверхности и площади полной поверхности призмы, формулы для вычисления;
- Призма как модель реальных объектов;
- Пространственная теорема Пифагора.
Глоссарий по теме
Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
Боковые грани – все грани, кроме оснований.
Боковые ребра – общие стороны боковых граней.
Основания призмы – равные многоугольники, расположенные в параллельных плоскостях.
Прямая призма – призма, боковые ребра которой перпендикулярны основаниям.
Правильная призма – прямая призма, в основании которой лежит правильный многоугольник.
Площадь полной поверхности призмы – сумма площадей всех ее граней.
Площадь боковой поверхности призмы – сумма площадей ее боковых граней.
Параллелепипед – призма, все грани которой – параллелограммы.
Прямоугольный параллелепипед – параллелепипед в основании которого лежит прямоугольник.
Основная литература:
Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа,
геометрия. Геометрия. 10–11 классы : учеб. Для общеобразоват. организаций : базовый и углубл. Уровни – М. : Просвещение, 2014. – 255 с.
Открытые электронные ресурсы:
Открытый банк заданий ФИПИ http://ege.fipi.ru/
Теоретический материал для самостоятельного изучения
Определение призмы. Элементы призмы.
Рассмотрим два равных многоугольника А1А2…Аn и В1В2…Вn, расположенных в параллельных плоскостях α и β соответственно так, что отрезки А1В1, А2В2. ..АnВn, соединяющие соответственные вершины многоугольников, параллельны (рис. 1).
..АnВn, соединяющие соответственные вершины многоугольников, параллельны (рис. 1).
Рисунок 1 – Призма
Заметим, что каждый из n четырехугольников (A1A2B1B2, …AnA1B1Bn) является параллелограммом. Убедимся в этом на примере четырехугольника A1A2B1B2. A1A2 и B1B2 параллельны по свойству параллельных плоскостей, пересеченных третьей плоскостью. А1В1 и А2В2 по условию. Таким образом, в четырехугольнике A1A2B1B2 противоположные стороны попарно параллельны, значит этот четырехугольник — параллелограмм по определению.
Дадим определение призмы. Призма – многогранник, составленный из равных многоугольников, расположенных в параллельных плоскостях, и n параллелограммов.
При этом равные многоугольники, расположенные в параллельных плоскостях, называются основаниями призмы, а параллелограммы – боковыми гранями призмы. Общие стороны боковых граней будем называть боковыми ребрами призмы.
На рисунке 1 основаниями призмы являются многоугольники А1А2…Аn и В1В2…Вn. Боковые грани – параллелограммы A1A2B1B2, …, AnA1B1Bn, а боковые ребра — отрезки А1В1, А2В2, …, АnВn.
Отметим, что все боковые ребра призмы равны и параллельны (как противоположные стороны параллелограммов).
Призму с основаниями А1А2…Аn и В1В2…Вn обозначают А1А2…АnВ1В2…Вn и называют n-угольной призмой.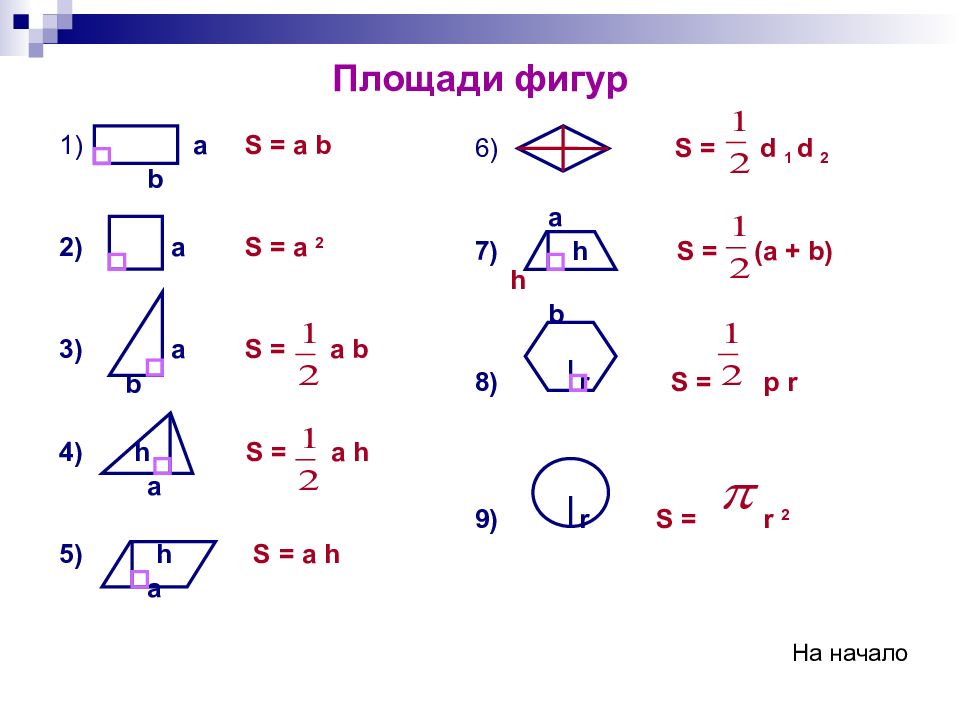
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы. Обратите внимание, что все высоты призмы равны между собой, так как основания расположены на параллельных плоскостях. Также высота призмы может лежать вне призмы (рис. 2).
Рисунок 2 – Наклонная призма
Виды призм
Если боковые ребра призмы перпендикулярны основаниям, то призма называется прямой. В противном случае, призма называется наклонной.
Высота прямой призмы равна ее боковому ребру.
На рисунке 3 приведены примеры прямых призм
Рисунок 3 – Виды призм.
Прямая призма называется правильной, если ее основание – правильный многоугольник. В правильной призме все боковые грани – равные прямоугольники.
Иногда четырехугольную призму, грани которой параллелограммы называют параллелепипедом. Известный вам правильный параллелепипед – это куб.
Площадь полной поверхности призмы. Площадь боковой поверхности призмы.
Площадь боковой поверхности призмы.
Площадью полной поверхности призмы (Sполн) называется сумма площадей всех ее граней, а площадью боковой поверхности (Sбок) призмы – сумма площадей ее боковых граней.
Таким образом, верно следующее равенство: Sполн= Sбок+2Sосн, то есть площадь полной поверхности есть сумма площади боковой поверхности и удвоенной площади основания.
Чему равна площадь боковой поверхности прямой призмы?
Теорема. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.
Доказательство
Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте призмы – h. Площадь боковой поверхности призмы равна сумме площадей боковых граней, то есть прямоугольников. Площадь каждого прямоугольника есть произведение высоты h и стороны основания. Просуммируем эти площади и вынесем множитель h за скобки. В скобках получим сумму всех сторон основания, то есть периметр основания P. Таким образом Sбок=Pоснh.
В скобках получим сумму всех сторон основания, то есть периметр основания P. Таким образом Sбок=Pоснh.
Пространственная теорема Пифагора
Прямой параллелепипед, основание которого – прямоугольник называется прямоугольным.
Теорема. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов длин трех его ребер, исходящих из одной вершины.
Рисунок 4 – Прямоугольный параллелепипед
Доказательство
Рассмотрим прямоугольный параллелепипед ABCDA1B1C1D1 и найдем квадрат длины его диагонали А1С.
Для этого рассмотрим треугольник А1АС:
Ребро АА1 перпендикулярно плоскости основания (ABC) (т.к. параллелепипед прямой), значит АА1 перпендикулярна любой прямой, лежащей в плоскости основания, в том числе АС. Таким образом, ΔА1АС – прямоугольный.
По теореме Пифагора получаем: А1С2=АА12+АС2 (1).
Выразим теперь АС. По условию в основании лежит прямоугольник, значит ΔАВС – прямоугольный. По тереме Пифагора получаем: АС2=ВС2+АВ2.
Подставив результат в (1), получим: А1С2=АА12+ВС2+АВ2.
Так как в основании прямоугольник, то ВС=АD.
Таким образом, А1С2=АА12+АD2+АВ2.
Что и требовалось доказать
Доказанная теорема является аналогом теоремы Пифагора (для прямоугольного треугольника), поэтому ее иногда называют пространственной теоремой Пифагора.
Примеры и разбор решения заданий тренировочного модуля
Задание 1.
Найдите для каждой картинки пару
1)2) 3)
4)5)
6)
Решение
Все изображения можно разделить на две группы: призмы и многоугольники. Вспомним, что основанием призмы является многоугольник. Теперь необходимо посчитать количество вершин многоугольников в основаниях призм и сопоставить их с нужным изображением. Таким образом, получаем следующий ответ: 1 и 3, 2 и 4, 5 и 6.
Таким образом, получаем следующий ответ: 1 и 3, 2 и 4, 5 и 6.
Задание 2
Какие из перечисленных объектов могут быть элементами призмы?
1) параллельные плоскости
2) отрезок
3) точка
4) четырехугольник
Решение:
Вспомним сначала, какие элементы есть у призмы. Это ребра, грани, вершины, основания, высота, диагональ.
Ребра, высота и диагональ призмы представляют собой отрезок. Грани и основания – это многоугольники, то есть части плоскостей. Вершины – точки. Таким образом, подходят варианты 2, 3,4.
Ответ: 2,3,4
%PDF-1.3 % 92 0 объект > эндообъект внешняя ссылка 92 81 0000000016 00000 н 0000001968 00000 н 0000002584 00000 н 0000002816 00000 н 0000003398 00000 н 0000003648 00000 н 0000004442 00000 н 0000005236 00000 н 0000005691 00000 н 0000005784 00000 н 0000006138 00000 н 0000006932 00000 н 0000007217 00000 н 0000007534 00000 н 0000008334 00000 н 0000008598 00000 н 0000009393 00000 н 0000009664 00000 н 0000009887 00000 н 0000010181 00000 н 0000010686 00000 н 0000010879 00000 н 0000011091 00000 н 0000011387 00000 н 0000011459 00000 н 0000011482 00000 н 0000012566 00000 н 0000012588 00000 н 0000013650 00000 н 0000013672 00000 н 0000014627 00000 н 0000014847 00000 н 0000015368 00000 н 0000015433 00000 н 0000015720 00000 н 0000015910 00000 н 0000015932 00000 н 0000016887 00000 н 0000016909 00000 н 0000017930 00000 н 0000017952 00000 н 0000018979 00000 н 0000019769 00000 н 0000020106 00000 н 0000020128 00000 н 0000020985 00000 н 0000021007 00000 н 0000021932 00000 н 0000023879 00000 н 0000025315 00000 н 0000026227 00000 н 0000028284 00000 н 0000032340 00000 н 0000035217 00000 н 0000035357 00000 н 0000035495 00000 н 0000035634 00000 н 0000035731 00000 н 0000035828 00000 н 0000035930 00000 н 0000036027 00000 н 0000036124 00000 н 0000036227 00000 н 0000036334 00000 н 0000036442 00000 н 0000036542 00000 н 0000036639 00000 н 0000036736 00000 н 0000036833 00000 н 0000036930 00000 н 0000037027 00000 н 0000037124 00000 н 0000037221 00000 н 0000037318 00000 н 0000037415 00000 н 0000037512 00000 н 0000037623 00000 н 0000037731 00000 н 0000037848 00000 н 0000002053 00000 н 0000002562 00000 н трейлер ] >> startxref 0 %%EOF 93 0 объект > эндообъект 171 0 объект > ручей Hb«`a«e`g`bg@
Формула алгебры.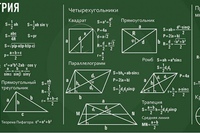 Дробные показатели: — a 0 = 1 aman=am-n am = 1a-m a-m = 1am. Синусоидальный коэффициент. 2 = с. 1544 г золота. Объяснение листа формул по математике Тест GED по математическому мышлению 2014 года содержит лист формул, в котором отображаются формулы, относящиеся к геометрическим измерениям и определенной алгебре… Формула Герона — алгебраическое доказательство. Скажем, мы знаем, что стопка бумаги содержит 500 листов, а это 4. Добро пожаловать на страницу рабочих листов по алгебре в Math-Drills. 19. Нарисуйте пропорциональные отношения, интерпретируя единичную скорость как наклон графика.Математические ресурсы для профессионального и технического образования, посвященные тому, как математика используется в конкретных технических профессиях. Первичные учебные карты. По этой причине обратитесь к использованию латинской заглавной буквы M для математического использования. Формула Виета. Секция числовых способностей — интересная тема конкурсных экзаменов, но при хорошей подготовке она может стать самой результативной.
Дробные показатели: — a 0 = 1 aman=am-n am = 1a-m a-m = 1am. Синусоидальный коэффициент. 2 = с. 1544 г золота. Объяснение листа формул по математике Тест GED по математическому мышлению 2014 года содержит лист формул, в котором отображаются формулы, относящиеся к геометрическим измерениям и определенной алгебре… Формула Герона — алгебраическое доказательство. Скажем, мы знаем, что стопка бумаги содержит 500 листов, а это 4. Добро пожаловать на страницу рабочих листов по алгебре в Math-Drills. 19. Нарисуйте пропорциональные отношения, интерпретируя единичную скорость как наклон графика.Математические ресурсы для профессионального и технического образования, посвященные тому, как математика используется в конкретных технических профессиях. Первичные учебные карты. По этой причине обратитесь к использованию латинской заглавной буквы M для математического использования. Формула Виета. Секция числовых способностей — интересная тема конкурсных экзаменов, но при хорошей подготовке она может стать самой результативной. a 2 – b 2 = (a – b) (a + b) (a+b) 2 = a 2 + 2ab + b 2. программное обеспечение для обучения алгебре. Калькулятор алгебры — это калькулятор, который дает пошаговую помощь в решении задач по алгебре.Кислородная формула. Затем мы начали изучать математические функции, такие как сложение, вычитание, БОДМАС и так далее. Терен терен та да ладно. где b — длина основания, а h — высота до этого основания. В общем: Формула Уоллиса. 2. Теперь я даю вам — и, кстати, эти десять свойств привели нас к формуле для определителя… Объяснение тем экзамена Регентов по Алгебре 1: Мы разработали множество ресурсов для подготовки к Регентам по Алгебре 1, чтобы вы могли быстро и легко выучить алгебру и понять ее уравнения.(а + б) 3 = а 3 + 3а 2 б + 3аб 2 + б 3 ; (a + b) 3 = a 3 + b 3 + 3ab (a + b) (a – b) 3 = a 3 – 3a 2 b + 3ab 2 – b 3. Если мы знаем D и r и нужно найти t , мы решим уравнение относительно t и получим формулу t = D r . Проблемы со словами по алгебре. Это тождество Эйлера известно как «самая известная формула во всей математике», и оно использует все фундаментальные математические константы.
a 2 – b 2 = (a – b) (a + b) (a+b) 2 = a 2 + 2ab + b 2. программное обеспечение для обучения алгебре. Калькулятор алгебры — это калькулятор, который дает пошаговую помощь в решении задач по алгебре.Кислородная формула. Затем мы начали изучать математические функции, такие как сложение, вычитание, БОДМАС и так далее. Терен терен та да ладно. где b — длина основания, а h — высота до этого основания. В общем: Формула Уоллиса. 2. Теперь я даю вам — и, кстати, эти десять свойств привели нас к формуле для определителя… Объяснение тем экзамена Регентов по Алгебре 1: Мы разработали множество ресурсов для подготовки к Регентам по Алгебре 1, чтобы вы могли быстро и легко выучить алгебру и понять ее уравнения.(а + б) 3 = а 3 + 3а 2 б + 3аб 2 + б 3 ; (a + b) 3 = a 3 + b 3 + 3ab (a + b) (a – b) 3 = a 3 – 3a 2 b + 3ab 2 – b 3. Если мы знаем D и r и нужно найти t , мы решим уравнение относительно t и получим формулу t = D r . Проблемы со словами по алгебре. Это тождество Эйлера известно как «самая известная формула во всей математике», и оно использует все фундаментальные математические константы.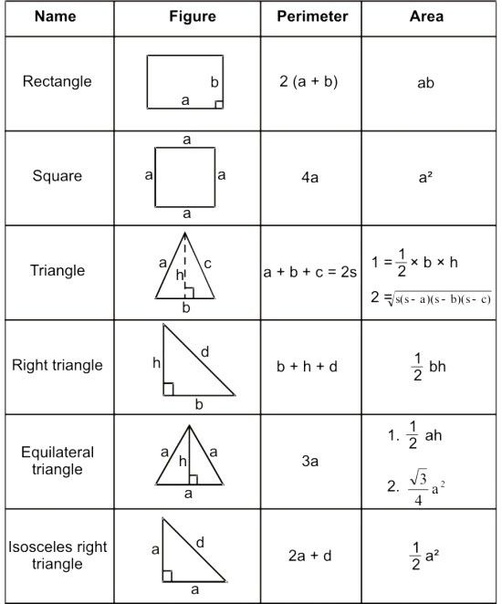 n — 1} $ Не вдаваясь в детали того, как он получается, вам необходимо знать следующее: P – основная сумма займа; A — периодический платеж по амортизации. Введите нотацию LaTeX, Tex, AMSmath или ASCIIMath (щелкните значок, чтобы переключиться в режим ASCIIMath), чтобы составить формулу.2-4ac# кратно #4#, поэтому мы получаем квадратный корень, который можно упростить. Зная значение одной величины, можно найти значение другой по формуле. Последние новости. Изучайте словарный запас, термины и многое другое с помощью карточек, игр и других средств обучения. Например, половина яблока — это часть яблока. Страница ресурсов для обучения математике. Решение также может быть выражено в терминах алгебраического корня языка Wolfram Language… Онлайн-редактор формул для написания математических уравнений, выражений, математических символов и операций.Эти БЕСПЛАТНЫЕ шпаргалки по математическим формулам для печати — отличный способ помочь вашим ученикам запомнить более 20 различных формул. Формат. Главной особенностью новой ветки, которую мы собираемся изучить, является использование букв.
n — 1} $ Не вдаваясь в детали того, как он получается, вам необходимо знать следующее: P – основная сумма займа; A — периодический платеж по амортизации. Введите нотацию LaTeX, Tex, AMSmath или ASCIIMath (щелкните значок, чтобы переключиться в режим ASCIIMath), чтобы составить формулу.2-4ac# кратно #4#, поэтому мы получаем квадратный корень, который можно упростить. Зная значение одной величины, можно найти значение другой по формуле. Последние новости. Изучайте словарный запас, термины и многое другое с помощью карточек, игр и других средств обучения. Например, половина яблока — это часть яблока. Страница ресурсов для обучения математике. Решение также может быть выражено в терминах алгебраического корня языка Wolfram Language… Онлайн-редактор формул для написания математических уравнений, выражений, математических символов и операций.Эти БЕСПЛАТНЫЕ шпаргалки по математическим формулам для печати — отличный способ помочь вашим ученикам запомнить более 20 различных формул. Формат. Главной особенностью новой ветки, которую мы собираемся изучить, является использование букв.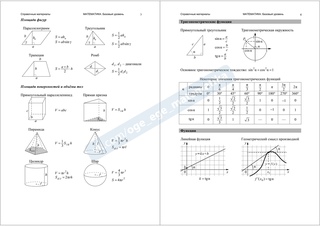 ответы по алгебре с пиццей. Майкрософт. Чтобы узнать о других значениях, см. Алгебра (значения). А б в г а г в б б г. Например, линейная алгебра является фундаментальной в современных представлениях геометрии, в том числе для определения основных объектов, таких как … В этом видео вы узнаете основную формулу алгебры.Мои твиты. Вот список некоторых основных математических формул. Все основные математические формулы и уравнения: алгебра, геометрия, тригонометрия, исчисление: пределы, производные, интегралы. Используйте этот лист формул, чтобы подготовиться к алгебре в колледже и моей оценке плана по математике. Чтобы найти расстояние между двумя точками ( x 1, y 1) и ( x 2, y 2 ), все, что вам нужно сделать, это использовать координаты этих упорядоченных пар и применить формулу, изображенную ниже. Ниже приведена диаграмма формулы расстояния, примененной к изображению отрезка прямой.Материалы, содержащиеся в этой публикации, могут быть воспроизведены педагогами штата Пенсильвания для использования в местных классах.
ответы по алгебре с пиццей. Майкрософт. Чтобы узнать о других значениях, см. Алгебра (значения). А б в г а г в б б г. Например, линейная алгебра является фундаментальной в современных представлениях геометрии, в том числе для определения основных объектов, таких как … В этом видео вы узнаете основную формулу алгебры.Мои твиты. Вот список некоторых основных математических формул. Все основные математические формулы и уравнения: алгебра, геометрия, тригонометрия, исчисление: пределы, производные, интегралы. Используйте этот лист формул, чтобы подготовиться к алгебре в колледже и моей оценке плана по математике. Чтобы найти расстояние между двумя точками ( x 1, y 1) и ( x 2, y 2 ), все, что вам нужно сделать, это использовать координаты этих упорядоченных пар и применить формулу, изображенную ниже. Ниже приведена диаграмма формулы расстояния, примененной к изображению отрезка прямой.Материалы, содержащиеся в этой публикации, могут быть воспроизведены педагогами штата Пенсильвания для использования в местных классах. Формула алюминия. Формула центра окружности. phi = (1 – Sqrt [5]) / 2 – связанное с ним золотое число, также равное (-1 / Phi). Первый шаг, убедитесь, что уравнение имеет формат, указанный выше, : — это коэффициент перед , так что здесь (обратите внимание, что не может равняться — это то, что делает его квадратичным). отделение математики. Формула Виета связывает коэффициенты многочленов с суммой и произведениями их корней.2+bx+c=0 Список формул алгебры. Переместите (x−4) 2 вправо: (y−2)2 = 25 − (x−4)2. Икс. Формулы определителя и кофакторы Теперь, когда мы знаем свойства определителя, пришло время изучить некоторые (довольно запутанные) формулы для его вычисления. 04 г за золото дураков. Математические формулы. Вот некоторые правила и формулы для абсолютных значений. Формула теоремы Пифагора. Наклон линии: m = y2 — y1 / x2 — x1. Формулы геометрической алгебры (a + b) 2 =a 2 + 2ab + b 2 (a−b) 2 =a 2 −2ab + b 2 (a + b) (a – b)=a 2 – b 2 (x + а) (x + b)=x 2 + (a + b)x + ab (x + a) (x – b)=x 2 + (a – b)x – ab (x – a) (x + б)=х 2 + (б – а)х – аб (х – а) (х – б)=х 2 – (а + б)х + аб (а + б) 3 =а 3 + б 3 + 3аб (a + b) (a – b) 3 =a 3 – b 3 – 3ab Основные формулы алгебры Законы экспонент.
Формула алюминия. Формула центра окружности. phi = (1 – Sqrt [5]) / 2 – связанное с ним золотое число, также равное (-1 / Phi). Первый шаг, убедитесь, что уравнение имеет формат, указанный выше, : — это коэффициент перед , так что здесь (обратите внимание, что не может равняться — это то, что делает его квадратичным). отделение математики. Формула Виета связывает коэффициенты многочленов с суммой и произведениями их корней.2+bx+c=0 Список формул алгебры. Переместите (x−4) 2 вправо: (y−2)2 = 25 − (x−4)2. Икс. Формулы определителя и кофакторы Теперь, когда мы знаем свойства определителя, пришло время изучить некоторые (довольно запутанные) формулы для его вычисления. 04 г за золото дураков. Математические формулы. Вот некоторые правила и формулы для абсолютных значений. Формула теоремы Пифагора. Наклон линии: m = y2 — y1 / x2 — x1. Формулы геометрической алгебры (a + b) 2 =a 2 + 2ab + b 2 (a−b) 2 =a 2 −2ab + b 2 (a + b) (a – b)=a 2 – b 2 (x + а) (x + b)=x 2 + (a + b)x + ab (x + a) (x – b)=x 2 + (a – b)x – ab (x – a) (x + б)=х 2 + (б – а)х – аб (х – а) (х – б)=х 2 – (а + б)х + аб (а + б) 3 =а 3 + б 3 + 3аб (a + b) (a – b) 3 =a 3 – b 3 – 3ab Основные формулы алгебры Законы экспонент. 2. г у. Написание линейных уравнений. ком Эксель. Абсолютная величина. Фосфатоводородная формула. Вопрос по алгебре с ответом в формате PDF. −b±√b2 −4(ac) 2a — b ± b 2 — 4 ( a c) 2 a. Решения алгебраических уравнений — квадратное, кубическое и четвертичное уравнение Добро пожаловать на страницу рабочих листов по алгебре на сайте Math-Drills. Еще алгебраические формулы. Большинство разделов имеют архивы с сотнями задач, решенных репетиторами. (а + b + с) 2 = а 2 + b 2 + с 2 + 2ab + 2ac + 2bc. Установить тождества — Объединение, Пересечение, Дополнение, Разность, Декартово произведение.NET/MONO (совместимость с Common Language Specification: F#, Visual Basic, C++/CLI). Основные формулы для выпускного экзамена по алгебре 2. Законы степени степени умножения степеней одного основания = сложение степеней ( am )( an ) = am + n деления степеней одного основания = вычитание степеней nmaa = am −−−− Правило степени n = умножение Показатели ( am)n = am ×××× n Нулевой показатель = 1 a 0 = 1 Алгебра — Википедия Алгебра Из Википедии, бесплатной энциклопедии.
2. г у. Написание линейных уравнений. ком Эксель. Абсолютная величина. Фосфатоводородная формула. Вопрос по алгебре с ответом в формате PDF. −b±√b2 −4(ac) 2a — b ± b 2 — 4 ( a c) 2 a. Решения алгебраических уравнений — квадратное, кубическое и четвертичное уравнение Добро пожаловать на страницу рабочих листов по алгебре на сайте Math-Drills. Еще алгебраические формулы. Большинство разделов имеют архивы с сотнями задач, решенных репетиторами. (а + b + с) 2 = а 2 + b 2 + с 2 + 2ab + 2ac + 2bc. Установить тождества — Объединение, Пересечение, Дополнение, Разность, Декартово произведение.NET/MONO (совместимость с Common Language Specification: F#, Visual Basic, C++/CLI). Основные формулы для выпускного экзамена по алгебре 2. Законы степени степени умножения степеней одного основания = сложение степеней ( am )( an ) = am + n деления степеней одного основания = вычитание степеней nmaa = am −−−− Правило степени n = умножение Показатели ( am)n = am ×××× n Нулевой показатель = 1 a 0 = 1 Алгебра — Википедия Алгебра Из Википедии, бесплатной энциклопедии. Тип алгебраической структуры см. в разделе Алгебра над полем. Некоторые важные формулы формулы квадрата алгебры […] Рабочий пример.Банки используют формулы для определения процентов. Основное содержание этого приложения: — Основные формулы алгебры с практикой математики. Вы вычисляете среднюю точку, используя формулу средней точки. Вот некоторые из миров: Планета Земля, Подводный список формул алгебры алгебры/математическая формула/подготовка всей государственной работы. Решение проходит в два этапа. Нахождение наклона из уравнения. Промежуточная алгебра/координатная геометрия Эти формулы помогают вычислять расстояния, длины и свойства точек на плоскости, а также находить переменные в более сложных алгебраических выражениях.Попробуйте получить переменную саму по себе в уравнениях алгебры. Теорема Пифагора (Урок о том, как ее использовать) Бесплатный решатель алгебры введите что-нибудь там! Популярные страницы @mathwarehouse. Рабочие листы по алгебре для курсов по алгебре I и алгебре II, которые начинаются с простых уравнений и полиномов и склоняются к сложным коникам.
Тип алгебраической структуры см. в разделе Алгебра над полем. Некоторые важные формулы формулы квадрата алгебры […] Рабочий пример.Банки используют формулы для определения процентов. Основное содержание этого приложения: — Основные формулы алгебры с практикой математики. Вы вычисляете среднюю точку, используя формулу средней точки. Вот некоторые из миров: Планета Земля, Подводный список формул алгебры алгебры/математическая формула/подготовка всей государственной работы. Решение проходит в два этапа. Нахождение наклона из уравнения. Промежуточная алгебра/координатная геометрия Эти формулы помогают вычислять расстояния, длины и свойства точек на плоскости, а также находить переменные в более сложных алгебраических выражениях.Попробуйте получить переменную саму по себе в уравнениях алгебры. Теорема Пифагора (Урок о том, как ее использовать) Бесплатный решатель алгебры введите что-нибудь там! Популярные страницы @mathwarehouse. Рабочие листы по алгебре для курсов по алгебре I и алгебре II, которые начинаются с простых уравнений и полиномов и склоняются к сложным коникам. Соотношения Сколько энергии, как часто? Квадратичная формула Преобразование квадрата Полином Интуиция Десятичные числа, взаимодействия, функция ДНК Если вы предпочитаете ввод математических формул с клавиатуры, вы можете вводить их непосредственно в строку ввода.Если вы хотите найти какой-либо термин (также известный как термин {{nth}}) в арифметической последовательности, формула арифметической последовательности должна помочь вам в этом. ком . все корни действительны и неравны, если. Например, чтобы выровнять массив уравнений, вы можете использовать @ и &, как показано ниже: \eqarray(x+1&=2@1+2+3+y&=z@3/x&=6)<пробел>. Видео Bokep ini merupakan Video Bokep yang terbaru di January 2022 secara online Film Bokep Igo Sex Abg Online [] 27 801. Загрузить электронную книгу Kuta Software Algebra 1 Quadratic Formula Answers Kuta Software Algebra 1 Quadratic Formula Answers Если вам нужна такая книга ответов Kuta Software Algebra 1 с квадратичными формулами, которая покроет ваши расходы, приобретите у нас чрезвычайно бестселлер в настоящее время из нескольких предпочитаемых авторов.
Соотношения Сколько энергии, как часто? Квадратичная формула Преобразование квадрата Полином Интуиция Десятичные числа, взаимодействия, функция ДНК Если вы предпочитаете ввод математических формул с клавиатуры, вы можете вводить их непосредственно в строку ввода.Если вы хотите найти какой-либо термин (также известный как термин {{nth}}) в арифметической последовательности, формула арифметической последовательности должна помочь вам в этом. ком . все корни действительны и неравны, если. Например, чтобы выровнять массив уравнений, вы можете использовать @ и &, как показано ниже: \eqarray(x+1&=2@1+2+3+y&=z@3/x&=6)<пробел>. Видео Bokep ini merupakan Video Bokep yang terbaru di January 2022 secara online Film Bokep Igo Sex Abg Online [] 27 801. Загрузить электронную книгу Kuta Software Algebra 1 Quadratic Formula Answers Kuta Software Algebra 1 Quadratic Formula Answers Если вам нужна такая книга ответов Kuta Software Algebra 1 с квадратичными формулами, которая покроет ваши расходы, приобретите у нас чрезвычайно бестселлер в настоящее время из нескольких предпочитаемых авторов. 2 Вы можете быстро набирать большинство уравнений в UnicodeMath, используя коды Math AutoCorrect. Продвинутая математика: основные формулы и короткие приемы по алгебре. Решения алгебраических уравнений — Алгебра квадратных, кубических и четвертичных уравнений: 5. Лист формул геометрии также доступен для загрузки. Системы уравнений и неравенств. В нем много кроссвордов, разделенных на разные миры и группы. Теорема Пифагора: а. (a – b)2 = a 2 – 2ab+ b 2. что разрешается в: Вот еще несколько примеров: Пример.Комплексные числа — Умножение, Деление, Полярная форма, Теорема Муавра, Корни. Текст — это выделение того, что нужно из алгебры колледжа для будущих курсов. Как использовать теорему Пифагора Площадь поверхности цилиндра Единичный круг Игра Треугольник Паскаля демонстрация Формула D = rt предполагает, что мы знаем r и t и используем их для нахождения D. Тестируемым предоставляются формулы, чтобы они могли сосредоточиться на применении, а не заучивание формул. Треугольник: трехсторонняя фигура с четырьмя прямыми углами по 90° и четырьмя равными сторонами.
2 Вы можете быстро набирать большинство уравнений в UnicodeMath, используя коды Math AutoCorrect. Продвинутая математика: основные формулы и короткие приемы по алгебре. Решения алгебраических уравнений — Алгебра квадратных, кубических и четвертичных уравнений: 5. Лист формул геометрии также доступен для загрузки. Системы уравнений и неравенств. В нем много кроссвордов, разделенных на разные миры и группы. Теорема Пифагора: а. (a – b)2 = a 2 – 2ab+ b 2. что разрешается в: Вот еще несколько примеров: Пример.Комплексные числа — Умножение, Деление, Полярная форма, Теорема Муавра, Корни. Текст — это выделение того, что нужно из алгебры колледжа для будущих курсов. Как использовать теорему Пифагора Площадь поверхности цилиндра Единичный круг Игра Треугольник Паскаля демонстрация Формула D = rt предполагает, что мы знаем r и t и используем их для нахождения D. Тестируемым предоставляются формулы, чтобы они могли сосредоточиться на применении, а не заучивание формул. Треугольник: трехсторонняя фигура с четырьмя прямыми углами по 90° и четырьмя равными сторонами. Большая коллекция текстовых задач по алгебре может быть использована для многих тем алгебры. Вы не можете изменить свои ответы после их отправки. Тригонометрическая формула. Правила абсолютного значения. И помощь в написании рефератов на английском языке Math Formula Of Algebra в этом будет только неоценимым помощником. Покрытие от предварительной алгебры до алгебры 3 с различными вводными и продвинутыми уроками. Социальные исследования. найти любую формулу с легкостью? Новые формулы Excel для Excel 2019 и Office 365. Эта книга НЕОБХОДИМА для пользователей Excel от начального до среднего уровня, которые хотят БЫСТРО изучить формулы Excel и выделиться из толпы! Уравнения Колмогорова для стохастических УЧП Алгебра, какой мы ее знаем сегодня, состоит из множества различных идей, концепций и результатов.Потом. a4- b4= (a + b)(a — b)[(a + b)2- 2ab] Задачи, связанные с полиномиальными тождествами. (a +b)2 = a2 +2ab+b2 ( a + b) 2 = a 2 + 2 a b + b 2. Формула сферы Квадратная формула помогает решить любое квадратное уравнение.
Большая коллекция текстовых задач по алгебре может быть использована для многих тем алгебры. Вы не можете изменить свои ответы после их отправки. Тригонометрическая формула. Правила абсолютного значения. И помощь в написании рефератов на английском языке Math Formula Of Algebra в этом будет только неоценимым помощником. Покрытие от предварительной алгебры до алгебры 3 с различными вводными и продвинутыми уроками. Социальные исследования. найти любую формулу с легкостью? Новые формулы Excel для Excel 2019 и Office 365. Эта книга НЕОБХОДИМА для пользователей Excel от начального до среднего уровня, которые хотят БЫСТРО изучить формулы Excel и выделиться из толпы! Уравнения Колмогорова для стохастических УЧП Алгебра, какой мы ее знаем сегодня, состоит из множества различных идей, концепций и результатов.Потом. a4- b4= (a + b)(a — b)[(a + b)2- 2ab] Задачи, связанные с полиномиальными тождествами. (a +b)2 = a2 +2ab+b2 ( a + b) 2 = a 2 + 2 a b + b 2. Формула сферы Квадратная формула помогает решить любое квадратное уравнение. (a +b)3 = a3 +3a2b +3ab2+b3 ( a + b) 3 = a 3 + 3 a 2 b + 3 ab 2 + b 3. Вот несколько изображений с формулами Free Algebra Formula с самым высоким рейтингом в Интернете. . Скачать. Группа исследователей из Центра Лайелла в Эдинбурге разработала способ использования математических формул для прогнозирования вероятного землетрясения.ан. Кредит требует ежемесячных платежей в первый из каждого месяца. College Algebra Formulas and Rules Автор: lablrc Дата создания: 17.07.2013 13:34:08 Алгебраическая формула — это уравнение, правило, записанное с использованием математических и алгебраических символов. Используйте эти формулы геометрии для расчета периметра, площади, площади основания, поперечной площади и площади поверхности для различных геометрических фигур, а также формулу расстояния и уравнение окружности. CBSE Class 10 Science Solved Paper 2020. Затем мы подставляем эти коэффициенты в формулу: (-b±√(b²-4ac))/(2a) .1. Генеральный. вернуться к началу. Определите приблизительный ежемесячный платеж, в дополнение к общей сумме процентов, выплачиваемых в течение срока кредита.
(a +b)3 = a3 +3a2b +3ab2+b3 ( a + b) 3 = a 3 + 3 a 2 b + 3 ab 2 + b 3. Вот несколько изображений с формулами Free Algebra Formula с самым высоким рейтингом в Интернете. . Скачать. Группа исследователей из Центра Лайелла в Эдинбурге разработала способ использования математических формул для прогнозирования вероятного землетрясения.ан. Кредит требует ежемесячных платежей в первый из каждого месяца. College Algebra Formulas and Rules Автор: lablrc Дата создания: 17.07.2013 13:34:08 Алгебраическая формула — это уравнение, правило, записанное с использованием математических и алгебраических символов. Используйте эти формулы геометрии для расчета периметра, площади, площади основания, поперечной площади и площади поверхности для различных геометрических фигур, а также формулу расстояния и уравнение окружности. CBSE Class 10 Science Solved Paper 2020. Затем мы подставляем эти коэффициенты в формулу: (-b±√(b²-4ac))/(2a) .1. Генеральный. вернуться к началу. Определите приблизительный ежемесячный платеж, в дополнение к общей сумме процентов, выплачиваемых в течение срока кредита. Формула средней популяции дает среднее значение всей популяции. Вам не нужно вводить знак умножения между числом и символами: например, 5 2ax — это… Итак, это формула кофактора, и это—это хорошая формула, которую нужно знать, и теперь я чувствую как, ничего себе, я даю вам много алгебры, чтобы проглотить здесь. Начинать математику нужно с лучшего учебника, в котором теоретическая часть хорошо объяснена с решенными вопросами.Вектор единичной величины является единичным вектором. Формат ЮникодМатематика. и во всем Интернете. c Пример 2. Обратите внимание, что стандартно использовать математический режим для букв, таких как $c$ выше, которые являются математическими переменными. Основы формулы. π + 1 = 0. (ii) Если b 2 − 4ac < 0, то квадратное уравнение имеет два мнимых корня. \text {Окружность}= {2} {π}\text {r} \text {Длина дуги}=\frac {x} {360}\times {2} {π}\text {r} Созданы бесплатные рабочие листы по алгебре 2 с Infinite Algebra 2. Самые важные алгебраические математические формулы, которые нужно знать, — это формулы для наклона, формы пересечения наклона, средней точки и всегда известной квадратичной формулы.
Формула средней популяции дает среднее значение всей популяции. Вам не нужно вводить знак умножения между числом и символами: например, 5 2ax — это… Итак, это формула кофактора, и это—это хорошая формула, которую нужно знать, и теперь я чувствую как, ничего себе, я даю вам много алгебры, чтобы проглотить здесь. Начинать математику нужно с лучшего учебника, в котором теоретическая часть хорошо объяснена с решенными вопросами.Вектор единичной величины является единичным вектором. Формат ЮникодМатематика. и во всем Интернете. c Пример 2. Обратите внимание, что стандартно использовать математический режим для букв, таких как $c$ выше, которые являются математическими переменными. Основы формулы. π + 1 = 0. (ii) Если b 2 − 4ac < 0, то квадратное уравнение имеет два мнимых корня. \text {Окружность}= {2} {π}\text {r} \text {Длина дуги}=\frac {x} {360}\times {2} {π}\text {r} Созданы бесплатные рабочие листы по алгебре 2 с Infinite Algebra 2. Самые важные алгебраические математические формулы, которые нужно знать, — это формулы для наклона, формы пересечения наклона, средней точки и всегда известной квадратичной формулы.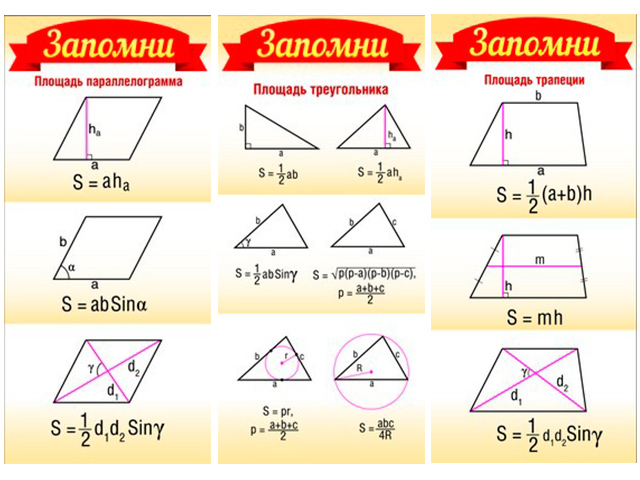 14159. Пример 1. ед. Формулы статистики. Как мы видели в этих примерах, вычисление пределов требовало большого объема работы, а функции, с которыми мы работали, были не очень сложными. мы должны иметь небольшое знание основных формул алгебры. Химическая формула фосфата натрия. Это полезно для отображения сложных формул на вашей веб-странице. Ваше справочное руководство по формулам алгебры и основным математическим формулам. Посмотреть больше примеров ». т знак равно D р . π определяется как отношение длины окружности к ее диаметру.* Этот раздел предназначен для edHelper. Карты пересмотра GCSE. Ссылки по теме: Примеры плотности. d = 40 ≈ 6. Наборы чисел. 1. Ускорение. х2 + 2х — 15 = 0 х 2 + 2 х — 15 = 0. Квадратная формула в жизни, математика 7-й класс словесные задачи бесплатно, Holt Online учебник по геометрии «ключевой код», решатель тригонометрических задач, как вычислить первообразный корень в… Нравится много геометрических фигур, сердце может быть запечатлено во всей его пышной красе с помощью одного алгебраического уравнения.
14159. Пример 1. ед. Формулы статистики. Как мы видели в этих примерах, вычисление пределов требовало большого объема работы, а функции, с которыми мы работали, были не очень сложными. мы должны иметь небольшое знание основных формул алгебры. Химическая формула фосфата натрия. Это полезно для отображения сложных формул на вашей веб-странице. Ваше справочное руководство по формулам алгебры и основным математическим формулам. Посмотреть больше примеров ». т знак равно D р . π определяется как отношение длины окружности к ее диаметру.* Этот раздел предназначен для edHelper. Карты пересмотра GCSE. Ссылки по теме: Примеры плотности. d = 40 ≈ 6. Наборы чисел. 1. Ускорение. х2 + 2х — 15 = 0 х 2 + 2 х — 15 = 0. Квадратная формула в жизни, математика 7-й класс словесные задачи бесплатно, Holt Online учебник по геометрии «ключевой код», решатель тригонометрических задач, как вычислить первообразный корень в… Нравится много геометрических фигур, сердце может быть запечатлено во всей его пышной красе с помощью одного алгебраического уравнения. (а + b)2 = а2 + 2ab + b2. Пожалуйста, напишите нам, если у вас есть предложения по добавлению формул.2 Дуга и сектор окружности: 1. Квадратичная формула – это формула, используемая для решения квадратных уравнений. Периметр (P) — это расстояние вокруг фигуры. Используйте квадратную формулу, чтобы найти решения. Средний градус на сторону или градусная мера конгруэнтного многоугольника = 180 (n — 2) / n. Алгебра … Алгебра › Формула наклона. Дети, подростки, молодые и пожилые люди могут изучать математику, используя эту формулу, и практиковать математику. Надеюсь, это поможет \ensuremath{математическое уравнение} Например, нижние и верхние индексы можно использовать только в математическом режиме.Формула алгебры: определение, формулы и примеры. Пример: sin(90) mXparser — это очень простая, богатая, быстрая и очень гибкая библиотека парсера математических выражений (парсер и анализатор математических выражений/формул, предоставляемых в виде обычного текста/строки). Отображение символов F: Excel очень полезен при решении алгебраических уравнений.
(а + b)2 = а2 + 2ab + b2. Пожалуйста, напишите нам, если у вас есть предложения по добавлению формул.2 Дуга и сектор окружности: 1. Квадратичная формула – это формула, используемая для решения квадратных уравнений. Периметр (P) — это расстояние вокруг фигуры. Используйте квадратную формулу, чтобы найти решения. Средний градус на сторону или градусная мера конгруэнтного многоугольника = 180 (n — 2) / n. Алгебра … Алгебра › Формула наклона. Дети, подростки, молодые и пожилые люди могут изучать математику, используя эту формулу, и практиковать математику. Надеюсь, это поможет \ensuremath{математическое уравнение} Например, нижние и верхние индексы можно использовать только в математическом режиме.Формула алгебры: определение, формулы и примеры. Пример: sin(90) mXparser — это очень простая, богатая, быстрая и очень гибкая библиотека парсера математических выражений (парсер и анализатор математических выражений/формул, предоставляемых в виде обычного текста/строки). Отображение символов F: Excel очень полезен при решении алгебраических уравнений. Чтобы вычислить функцию, такую как «синус», с аргументом, подобным 90, введите соответствующее имя функции, а затем аргумент 90 в скобках. Наклон-перехват для уравнения прямой: mx b = + Простые проценты: I = Pr.Люди теперь привыкли использовать сеть в гаджетах для просмотра изображений и видео информации для вдохновения, … легко найти любую Формулу? Новые формулы Excel для Excel 2019 и Office 365. Эта книга НЕОБХОДИМА для пользователей Excel от начального до среднего уровня, которые хотят БЫСТРО изучить формулы Excel и выделиться из толпы! Уравнения Колмогорова для стохастических УЧП Алгебра, какой мы ее знаем сегодня, состоит из множества различных идей, концепций и результатов. является константой или термином без каких-либо формул алгебры.\begin {выровнено} &8x+6y=16\\ & {-8}x-4y=-8\\ \end {выровнено} . Каков ваш показатель скорости? Используйте формулу r = d/t. Единицы. Ваша ставка равна 24 милям, деленным на 2… Гед математические формулы. Обязательно добавляйте только похожие единицы.
Чтобы вычислить функцию, такую как «синус», с аргументом, подобным 90, введите соответствующее имя функции, а затем аргумент 90 в скобках. Наклон-перехват для уравнения прямой: mx b = + Простые проценты: I = Pr.Люди теперь привыкли использовать сеть в гаджетах для просмотра изображений и видео информации для вдохновения, … легко найти любую Формулу? Новые формулы Excel для Excel 2019 и Office 365. Эта книга НЕОБХОДИМА для пользователей Excel от начального до среднего уровня, которые хотят БЫСТРО изучить формулы Excel и выделиться из толпы! Уравнения Колмогорова для стохастических УЧП Алгебра, какой мы ее знаем сегодня, состоит из множества различных идей, концепций и результатов. является константой или термином без каких-либо формул алгебры.\begin {выровнено} &8x+6y=16\\ & {-8}x-4y=-8\\ \end {выровнено} . Каков ваш показатель скорости? Используйте формулу r = d/t. Единицы. Ваша ставка равна 24 милям, деленным на 2… Гед математические формулы. Обязательно добавляйте только похожие единицы.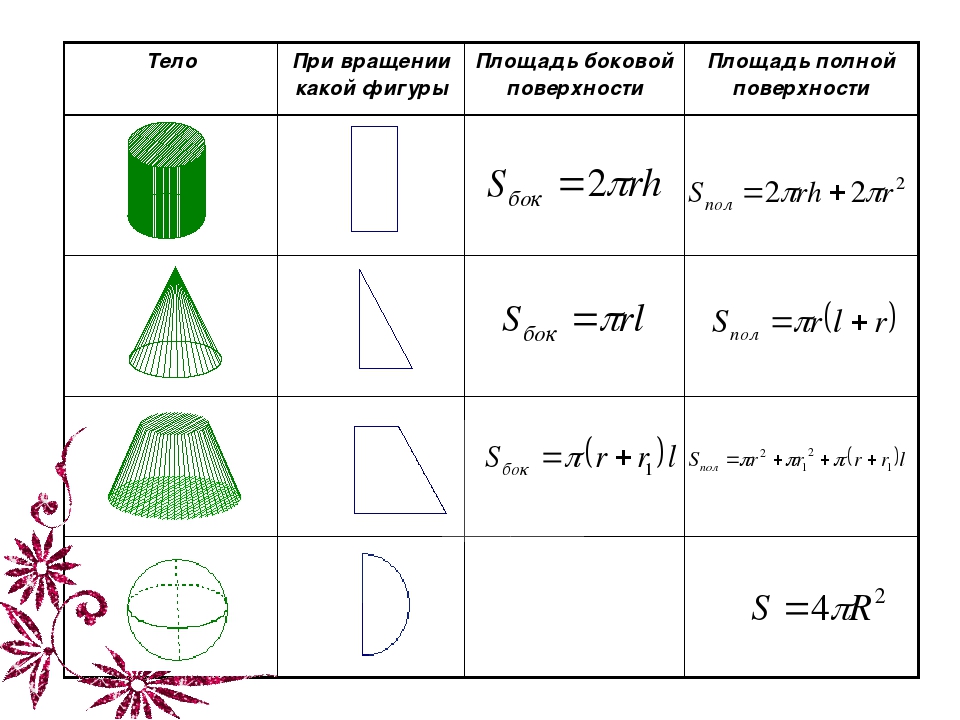 найти график квадратного уравнения минимального значения. упростить\:\frac {2} {3}-\frac {3} {2}+\frac {1} {4} x+2y=2x-5,\:x-y=3. Попробуйте бесплатно! Вопросы по алгебре и векторной алгебре, задаваемые на экзамене NDA, учитывают максимальный вес раздела «Математика». (а) 75А (б) 80А (в) 100А (г) 125А Ответ: (в) 100А.В противном случае продолжайте читать для подробного описания того, как работать с каждой математической формулой Excel. Найдите формулы, леммы и теоремы, необходимые для всех ваших математических курсов или проектов. 25 = 100А. 06 КБ. Формула пересечения наклона представляет собой уравнение линии, выраженное как Y=MX+b, в котором: M обозначает наклон линии, а b — это пересечение оси y, где точка пересечения оси y пересекает ось y. Абсцисса. Добро пожаловать в онлайн-раздел LST Free PDF. Банк финансирует ипотечный кредит в размере 400 000 долларов США по цене 6. Общее квадратное уравнение: Квадратная формула: a, b и c являются константами, где a не может равняться 0.2$. Учителя могут найти полезные математические ресурсы для занятий в классе.
найти график квадратного уравнения минимального значения. упростить\:\frac {2} {3}-\frac {3} {2}+\frac {1} {4} x+2y=2x-5,\:x-y=3. Попробуйте бесплатно! Вопросы по алгебре и векторной алгебре, задаваемые на экзамене NDA, учитывают максимальный вес раздела «Математика». (а) 75А (б) 80А (в) 100А (г) 125А Ответ: (в) 100А.В противном случае продолжайте читать для подробного описания того, как работать с каждой математической формулой Excel. Найдите формулы, леммы и теоремы, необходимые для всех ваших математических курсов или проектов. 25 = 100А. 06 КБ. Формула пересечения наклона представляет собой уравнение линии, выраженное как Y=MX+b, в котором: M обозначает наклон линии, а b — это пересечение оси y, где точка пересечения оси y пересекает ось y. Абсцисса. Добро пожаловать в онлайн-раздел LST Free PDF. Банк финансирует ипотечный кредит в размере 400 000 долларов США по цене 6. Общее квадратное уравнение: Квадратная формула: a, b и c являются константами, где a не может равняться 0.2$. Учителя могут найти полезные математические ресурсы для занятий в классе.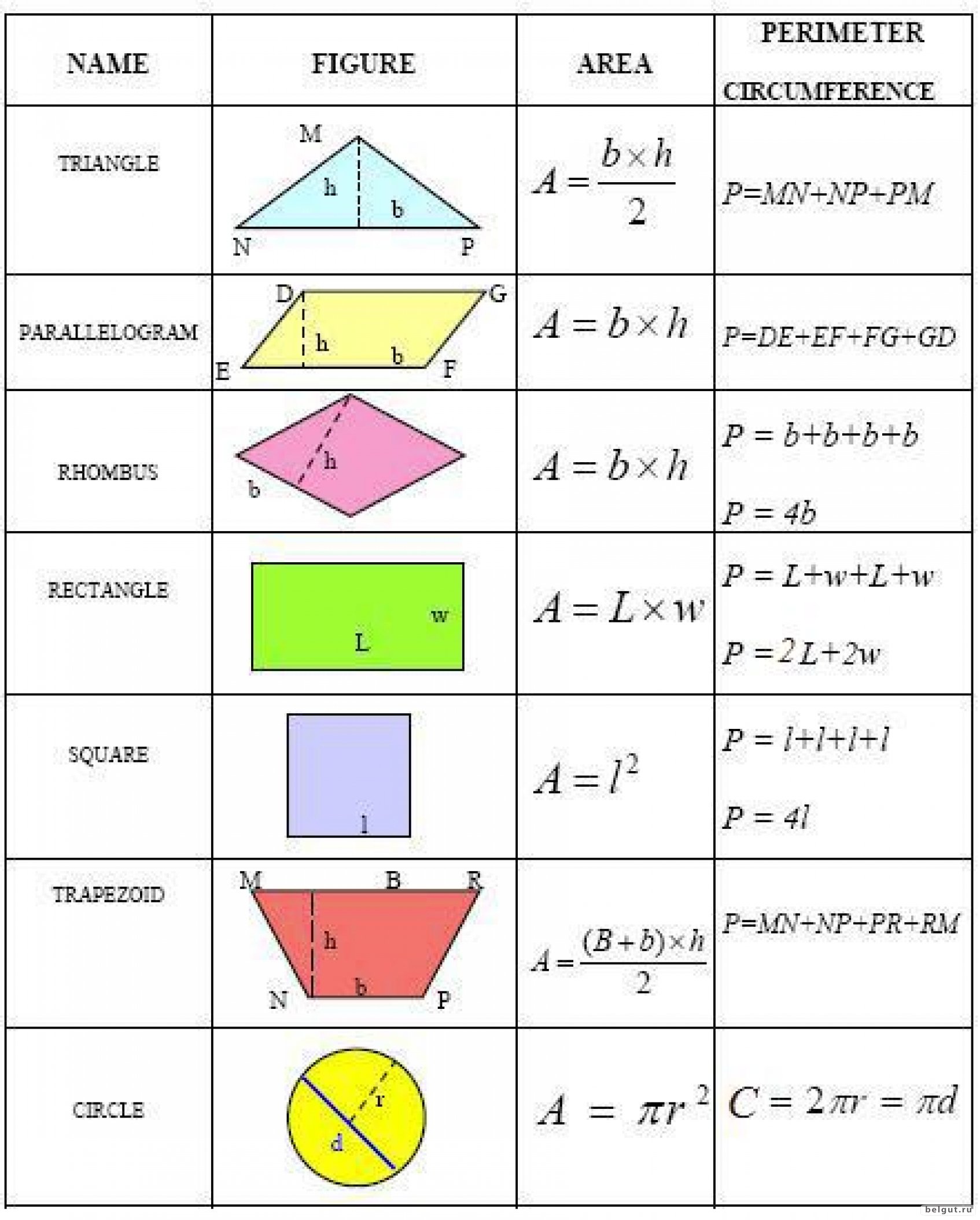 Извлеките квадратный корень: (y−2) = ± √ [25 − (x−4)2] (обратите внимание на ± «плюс/минус» может быть два квадратных корня!) Переместите «−2» вправо: y = 2 ± √ [25 − (x−4)2] Таким образом, когда мы строим эти два уравнения, мы должны иметь … Основные математические формулы; Базовый математический глоссарий; Базовый математический калькулятор; Калькулятор геометрии; решатель алгебры; задать математический вопрос; Карьера в математике; Блог по базовой математике; Формула для процентного соотношения Формула для процентного соотношения выглядит следующим образом, и ее будет легко использовать, если вы будете следовать приведенным простым указаниям.(а – б)2 = а2 – 2аб + Ь2. Множество всех точек плоскости, равноудаленных от фиксированной точки, определяемой как центр, называется окружностью. Узнайте __ формулу элементарной алгебры формулы Ответы. Промежуточные задачи по алгебре с ответами — образец 3: уравнения и система уравнений, квадратные уравнения, функция, заданная таблицей, пересечения 6.
Извлеките квадратный корень: (y−2) = ± √ [25 − (x−4)2] (обратите внимание на ± «плюс/минус» может быть два квадратных корня!) Переместите «−2» вправо: y = 2 ± √ [25 − (x−4)2] Таким образом, когда мы строим эти два уравнения, мы должны иметь … Основные математические формулы; Базовый математический глоссарий; Базовый математический калькулятор; Калькулятор геометрии; решатель алгебры; задать математический вопрос; Карьера в математике; Блог по базовой математике; Формула для процентного соотношения Формула для процентного соотношения выглядит следующим образом, и ее будет легко использовать, если вы будете следовать приведенным простым указаниям.(а – б)2 = а2 – 2аб + Ь2. Множество всех точек плоскости, равноудаленных от фиксированной точки, определяемой как центр, называется окружностью. Узнайте __ формулу элементарной алгебры формулы Ответы. Промежуточные задачи по алгебре с ответами — образец 3: уравнения и система уравнений, квадратные уравнения, функция, заданная таблицей, пересечения 6. Формула арифметической последовательности. Задача по алгебре с решением PDF. у. Треугольники — наиболее проверенная фигура в разделе GRE Quantity, поэтому обратите на эту часть особое внимание.− б ± √ б 2 − 4 а в. Формула средней численности населения. Умножение терминов Видео. 2 Pendaraban dan Pembaagian Dua atau Lebih Sebutan Алгебра 1. Масса найденного вами камня равна массе золота дураков, так что сегодня вы не будете «богаты». Используйте подобные треугольники, чтобы объяснить, почему наклон m одинаков между любыми двумя различными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для прямой, проходящей через начало координат, и уравнение y = mx + b для прямой, пересекающей вертикальную ось в точке b.m = 5. 3. Подставить в квадратную формулу. A = s2 P = 4s P = B + s1 + s2 s 3. Явная формула, рекурсивная формула. В алгебре есть две части – Элементарная алгебра и Современная алгебра (Абстрактная алгебра). все корни вещественны и, в конце концов, два равны, если.
Формула арифметической последовательности. Задача по алгебре с решением PDF. у. Треугольники — наиболее проверенная фигура в разделе GRE Quantity, поэтому обратите на эту часть особое внимание.− б ± √ б 2 − 4 а в. Формула средней численности населения. Умножение терминов Видео. 2 Pendaraban dan Pembaagian Dua atau Lebih Sebutan Алгебра 1. Масса найденного вами камня равна массе золота дураков, так что сегодня вы не будете «богаты». Используйте подобные треугольники, чтобы объяснить, почему наклон m одинаков между любыми двумя различными точками на невертикальной линии в координатной плоскости; выведите уравнение y = mx для прямой, проходящей через начало координат, и уравнение y = mx + b для прямой, пересекающей вертикальную ось в точке b.m = 5. 3. Подставить в квадратную формулу. A = s2 P = 4s P = B + s1 + s2 s 3. Явная формула, рекурсивная формула. В алгебре есть две части – Элементарная алгебра и Современная алгебра (Абстрактная алгебра). все корни вещественны и, в конце концов, два равны, если. Точечно-наклонная форма уравнения линии: y. Эта формула приписывается Бине в 1843 году, хотя до него она была известна Эйлеру. — Основные геометрические формулы с соответствующими цифрами и практикой математики. Формулу расстояния можно использовать, чтобы предсказать, сколько времени может занять автомобильная поездка.5 Формула пересечения хорд в окружности: 1. Формулы амортизации. Например, мы можем использовать Excel для определения толщины одного листа бумаги. Мат. Последняя лекция дала вам десять свойств. Шаг 1: Преобразуйте 125 процентов в десятичную дробь: 1. ВСЕ. Затем мы делаем всю математику, чтобы упростить выражение. Нумерованные формулы можно создать с помощью меню «Вставить математическую нумерованную формулу» (сочетание клавиш Ctrl+Alt N ). По квадратной формуле решения: Пожалуйста, перейдите к общему заключению, чтобы найти сводку всех случаев, касающихся корней квадратного уравнения.Не каждый человек, сдающий экзамен GRE, является подающим надежды дизайнером или незаурядным математиком.
Точечно-наклонная форма уравнения линии: y. Эта формула приписывается Бине в 1843 году, хотя до него она была известна Эйлеру. — Основные геометрические формулы с соответствующими цифрами и практикой математики. Формулу расстояния можно использовать, чтобы предсказать, сколько времени может занять автомобильная поездка.5 Формула пересечения хорд в окружности: 1. Формулы амортизации. Например, мы можем использовать Excel для определения толщины одного листа бумаги. Мат. Последняя лекция дала вам десять свойств. Шаг 1: Преобразуйте 125 процентов в десятичную дробь: 1. ВСЕ. Затем мы делаем всю математику, чтобы упростить выражение. Нумерованные формулы можно создать с помощью меню «Вставить математическую нумерованную формулу» (сочетание клавиш Ctrl+Alt N ). По квадратной формуле решения: Пожалуйста, перейдите к общему заключению, чтобы найти сводку всех случаев, касающихся корней квадратного уравнения.Не каждый человек, сдающий экзамен GRE, является подающим надежды дизайнером или незаурядным математиком. 2-4ac}} {2a} Показать внешний URL.(a + b + c) 3 = a 3 + b 3 + c 3 +3a2b+3a2c + 3b2c +3b2a +3c2a +3c2a+6abc. 5 Система счисления. 13 марта 2013 г. 20 августа 2019 г. corbettmaths. Вопрос: Максимальная непрерывная нагрузка на устройство максимального тока ограничена … Ответ. Строгое понятие — это определенный вид алгебры, аналогичный математическому понятию группы. 3. В первом разделе этой главы мы увидели определение производной и вычислили пару производных, используя это определение. Эта страница начинается с некоторых рабочих листов с пропущенными числами для младших школьников.(а — б)2= (а + б)2- 4аб. Он отслеживает ваш уровень навыков по мере того, как вы решаете все более сложные вопросы. Важнейшим шагом является возможность идентифицировать или извлечь известные значения из задачи, которые в конечном итоге будут подставлены в саму формулу. Логика. Изучая математику для детей, таблицы факторов, вопросы объективного типа по алгебре, учебное пособие для начинающих по алгебре, том II. Для получения подробных примеров того, как использовать законы экспонент, щелкните здесь.
2-4ac}} {2a} Показать внешний URL.(a + b + c) 3 = a 3 + b 3 + c 3 +3a2b+3a2c + 3b2c +3b2a +3c2a +3c2a+6abc. 5 Система счисления. 13 марта 2013 г. 20 августа 2019 г. corbettmaths. Вопрос: Максимальная непрерывная нагрузка на устройство максимального тока ограничена … Ответ. Строгое понятие — это определенный вид алгебры, аналогичный математическому понятию группы. 3. В первом разделе этой главы мы увидели определение производной и вычислили пару производных, используя это определение. Эта страница начинается с некоторых рабочих листов с пропущенными числами для младших школьников.(а — б)2= (а + б)2- 4аб. Он отслеживает ваш уровень навыков по мере того, как вы решаете все более сложные вопросы. Важнейшим шагом является возможность идентифицировать или извлечь известные значения из задачи, которые в конечном итоге будут подставлены в саму формулу. Логика. Изучая математику для детей, таблицы факторов, вопросы объективного типа по алгебре, учебное пособие для начинающих по алгебре, том II. Для получения подробных примеров того, как использовать законы экспонент, щелкните здесь. (а + b)2- (а — b)2= 4ab. Формула средней точки: середина отрезка, конечными точками которого являются две точки и .Алгебра — это изучение математических символов. Лист формул Math 9709 ~ Лист формул MF9_список формул — Скачать бесплатно в виде файла PDF pdf Text File txt или читать онлайн бесплатно. Сообщение от krist 18 марта 2017 г., 17:42. Математическая формула для 11 класса. В этом разделе вопросы усложняются языками и вариантами ответа. Умножение. Круги. © 2005 Paul Dawkins Функции и графики Постоянная функция y==aor f(xa) График — это В алгебре квадратное уравнение (от латинского quadratus — «квадрат») — это любое уравнение, которое можно преобразовать в стандартную форму как ax²+bx +c=0, где x представляет неизвестное, а a, b и c представляют известные числа, где a ≠ 0.Этот пост является частью серии БЕСПЛАТНЫХ шпаргалок и информационных карточек. В этом наборе БЕСПЛАТНЫХ печатных шпаргалок по математическим формулам они найдут основной список формул, которые помогут им найти площадь, периметр, объем и многое другое.
(а + b)2- (а — b)2= 4ab. Формула средней точки: середина отрезка, конечными точками которого являются две точки и .Алгебра — это изучение математических символов. Лист формул Math 9709 ~ Лист формул MF9_список формул — Скачать бесплатно в виде файла PDF pdf Text File txt или читать онлайн бесплатно. Сообщение от krist 18 марта 2017 г., 17:42. Математическая формула для 11 класса. В этом разделе вопросы усложняются языками и вариантами ответа. Умножение. Круги. © 2005 Paul Dawkins Функции и графики Постоянная функция y==aor f(xa) График — это В алгебре квадратное уравнение (от латинского quadratus — «квадрат») — это любое уравнение, которое можно преобразовать в стандартную форму как ax²+bx +c=0, где x представляет неизвестное, а a, b и c представляют известные числа, где a ≠ 0.Этот пост является частью серии БЕСПЛАТНЫХ шпаргалок и информационных карточек. В этом наборе БЕСПЛАТНЫХ печатных шпаргалок по математическим формулам они найдут основной список формул, которые помогут им найти площадь, периметр, объем и многое другое. Имеем a=2, b= -3 и . Δ = b2 − 4ac называется дискриминацией. m = 19. — коэффициент перед , поэтому здесь . Подставьте значения a = 1 a = 1, b = 2 b = 2 и c = −15 c = — 15 в квадратичную формулу и найдите x x. Введите выражение для упрощения или уравнение для решения.Наклон линии: m = 2 − 1. Пара вносит первоначальный взнос в размере 10 000 долларов при покупке нового дома. Символ. 4 Геометрия Математика; 1. Реклама Некоторые полезные формулы алгебры Просто помните, что алгебраические (математические) формулы не помогут вам сдать экзамены, нужно уметь выполнять эти формулы в экзаменационном зале. Уравнения алгебры обычно составляются с числами и/или переменными с обеих сторон, например: x + 2 = 9 × 4. Алгебраическая формула — это короткая быстрая формула для решения сложных алгебраических вычислений.b*3 <-- означает (а в степени b), умноженное на 3. дробь - дробь является частью целого, например половина, треть, четверть и т. д. В выражении xn, 'x' является основанием, а «n» - показателем степени.
Имеем a=2, b= -3 и . Δ = b2 − 4ac называется дискриминацией. m = 19. — коэффициент перед , поэтому здесь . Подставьте значения a = 1 a = 1, b = 2 b = 2 и c = −15 c = — 15 в квадратичную формулу и найдите x x. Введите выражение для упрощения или уравнение для решения.Наклон линии: m = 2 − 1. Пара вносит первоначальный взнос в размере 10 000 долларов при покупке нового дома. Символ. 4 Геометрия Математика; 1. Реклама Некоторые полезные формулы алгебры Просто помните, что алгебраические (математические) формулы не помогут вам сдать экзамены, нужно уметь выполнять эти формулы в экзаменационном зале. Уравнения алгебры обычно составляются с числами и/или переменными с обеих сторон, например: x + 2 = 9 × 4. Алгебраическая формула — это короткая быстрая формула для решения сложных алгебраических вычислений.b*3 <-- означает (а в степени b), умноженное на 3. дробь - дробь является частью целого, например половина, треть, четверть и т. д. В выражении xn, 'x' является основанием, а «n» - показателем степени.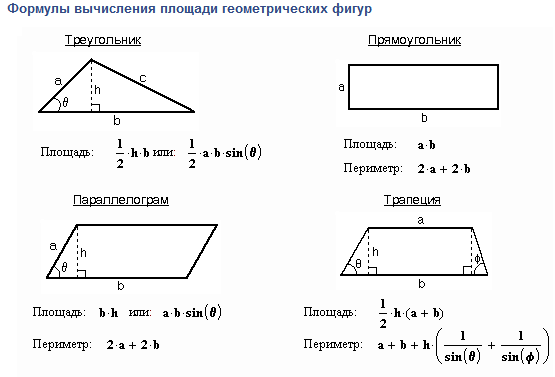 Алгебра. Математические формулы — это очень полезные математические формулы, которые служат кратким справочником. а 2 + б 2 = (а – б) 2 + 2аб. Формулы также могут быть уравнениями с числами и/или переменными, такими как формула Эйлера. Формула площади равностороннего треугольника. Опубликовано: (1 неделя назад) Для простых формул просто введите знак равенства, за которым следуют числовые значения, которые вы хотите вычислить, и математические операторы, которые вы хотите использовать — знак плюс (+) для добавления, знак минус (- ) для вычитания, звездочка ( *) для умножения, … X2-Y2 = (X+Y) (XY) X3+Y3 = (X+Y) (X2-XY+Y2) X3-Y3 = (XY) (X2 +XY+Y2) (X+Y)3 = X3+Y3+3XY (X+Y) (XY)3 = X3-Y3-3XY (XY) (X+Y+Z)2 = X2+Y2+Z2+ 2 (XY+YZ+ZX) (X+YZ)2 = X2+Y2+Z2+2 (XY-YZ-ZX) (X-Y+Z)2 = X2+Y2+Z2+2 (-XY-YZ +ZX) … Приложение «Все математические формулы» представляет собой сборник формул из математики и физики.2 + а1 х + а0 == 0, х]. ком абоненты. Вектор имеет величину (размер) и направление: величину и направление вектора.
Алгебра. Математические формулы — это очень полезные математические формулы, которые служат кратким справочником. а 2 + б 2 = (а – б) 2 + 2аб. Формулы также могут быть уравнениями с числами и/или переменными, такими как формула Эйлера. Формула площади равностороннего треугольника. Опубликовано: (1 неделя назад) Для простых формул просто введите знак равенства, за которым следуют числовые значения, которые вы хотите вычислить, и математические операторы, которые вы хотите использовать — знак плюс (+) для добавления, знак минус (- ) для вычитания, звездочка ( *) для умножения, … X2-Y2 = (X+Y) (XY) X3+Y3 = (X+Y) (X2-XY+Y2) X3-Y3 = (XY) (X2 +XY+Y2) (X+Y)3 = X3+Y3+3XY (X+Y) (XY)3 = X3-Y3-3XY (XY) (X+Y+Z)2 = X2+Y2+Z2+ 2 (XY+YZ+ZX) (X+YZ)2 = X2+Y2+Z2+2 (XY-YZ-ZX) (X-Y+Z)2 = X2+Y2+Z2+2 (-XY-YZ +ZX) … Приложение «Все математические формулы» представляет собой сборник формул из математики и физики.2 + а1 х + а0 == 0, х]. ком абоненты. Вектор имеет величину (размер) и направление: величину и направление вектора. Математические формулы полезны для всех учащихся класса, учащиеся должны проявлять интерес к математическим предметам, и в целом все учащиеся любят решать математические вопросы, если они понимают концепции. Если a = 0, то уравнение линейное, а не квадратное, так как нет … нет Формулы квадрата (a + b) 2 = a 2 + b 2 + 2ab (a − b) 2 = a 2 + b 2 − 2ab a 2 − b 2 = (a − b) (a + b) (x + a) (x + b) = x 2 + (a + b) x + ab (a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2bc + 2ca (a … Биномиальная теорема.алгебра: [существительное] обобщение арифметики, в котором буквы, обозначающие числа, комбинируются в соответствии с правилами арифметики. Вы также можете сгенерировать изображение математической формулы с помощью языка TeX. 32. Длина линии показывает ее величину, а стрелка указывает направление. Тест CAT-ASVAB Mathematics Knowledge включает 16 вопросов с несколькими вариантами ответов, адаптированных к компьютеру. Факторные полиномы. круг = 2п р. Для квадратного уравнения ax2 + bx + c, где a ≠ 0, корни будут заданы уравнением как −b±b2−4ac√2a.
Математические формулы полезны для всех учащихся класса, учащиеся должны проявлять интерес к математическим предметам, и в целом все учащиеся любят решать математические вопросы, если они понимают концепции. Если a = 0, то уравнение линейное, а не квадратное, так как нет … нет Формулы квадрата (a + b) 2 = a 2 + b 2 + 2ab (a − b) 2 = a 2 + b 2 − 2ab a 2 − b 2 = (a − b) (a + b) (x + a) (x + b) = x 2 + (a + b) x + ab (a + b + c) 2 = a 2 + b 2 + c 2 + 2ab + 2bc + 2ca (a … Биномиальная теорема.алгебра: [существительное] обобщение арифметики, в котором буквы, обозначающие числа, комбинируются в соответствии с правилами арифметики. Вы также можете сгенерировать изображение математической формулы с помощью языка TeX. 32. Длина линии показывает ее величину, а стрелка указывает направление. Тест CAT-ASVAB Mathematics Knowledge включает 16 вопросов с несколькими вариантами ответов, адаптированных к компьютеру. Факторные полиномы. круг = 2п р. Для квадратного уравнения ax2 + bx + c, где a ≠ 0, корни будут заданы уравнением как −b±b2−4ac√2a.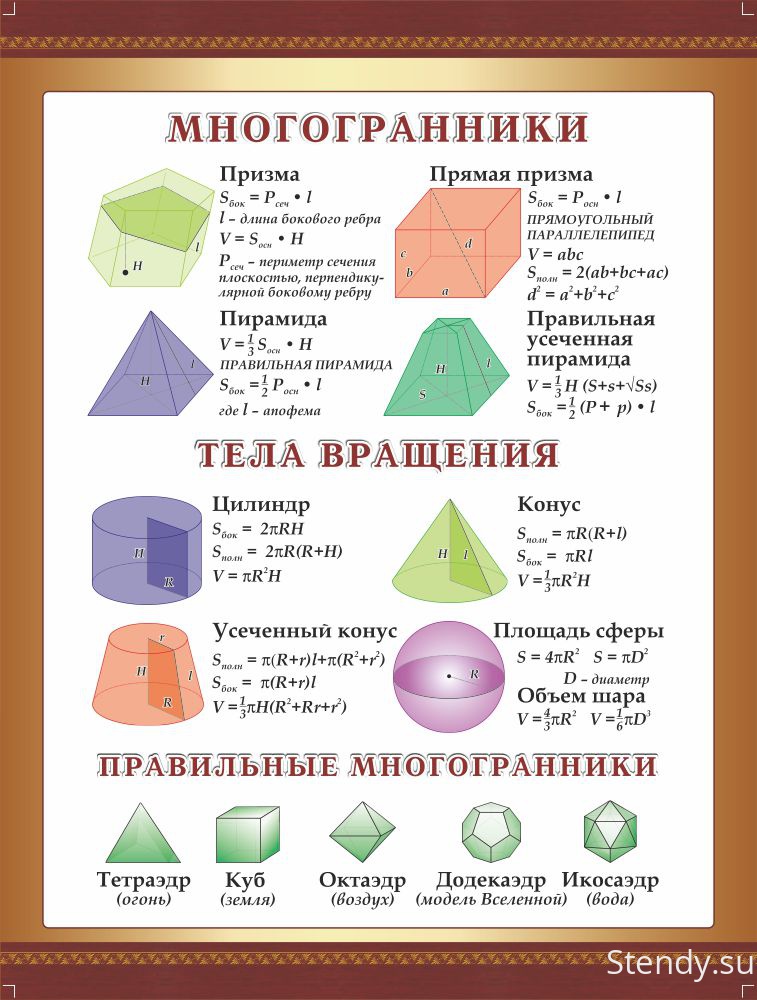 Это настоящее пересечение инженерии и математики. Число ln (2) обозначает натуральный логарифм двух и может быть оценено как 0. алгебра. Стрелка. Глава 3: Функции. d = ( x 2 — x 1) 2 + ( y 2 — y 1) 2. a2 — b2 = (a — b) (a + b) a2 + b2 = (a — b)2 + 2ab = (a + б)2 – 2аб. Диофант (3 век) и Аль-Ховаразми (9 век) были двумя главными предшественниками алгебры. Исследование включает в себя почти все из … 3 x * 4 x + 3 x * 5 + 2 * 4 x + 2 * 5 = 12 x 2 + 15 x + 8 x + 10 = 12 x 2 + 23 x + 10. Раздел может быть простым или сложным в зависимости от сложности формулы алгебры pdf, формулы алгебры pdf, все формулы алгебры pdf, формулы алгебры pdf скачать, формулу алгебры pdf на хинди, формулу алгебры pdf для ssc, математическую формулу ssc скачать pdf, важную формулу алгебры , диаграмма формулы алгебры, алгебраические формулы для класса 8, формула алгебры для класса 7, формулы алгебры класса 10, формулы алгебры, чтобы помнить, Мы здесь, чтобы помочь вам с вашими математическими вопросами.Уравнение для сферы … ab = 2 3 и bc = 4 5 (Дано) orcb = 5 4 a + bb + c = b ( ab + 1) b ( cb + 1) = ab + 1 cb + 1 = ( 2 3 + 1) ( 5 4 + 1) = 2 + 3 3 5 + 4 4 = 5 × 4 3 × 9 = 20 27 ∴ a + bb + c = 20 27 Чередование: abc 2 × ( 4) 3 × ( 4) 4 × ( 3) 5 × ( 3) 8 12 15 _ ¯ ∴ a + bb + c = 8 + 12 12 + 15 = 20 27.
Это настоящее пересечение инженерии и математики. Число ln (2) обозначает натуральный логарифм двух и может быть оценено как 0. алгебра. Стрелка. Глава 3: Функции. d = ( x 2 — x 1) 2 + ( y 2 — y 1) 2. a2 — b2 = (a — b) (a + b) a2 + b2 = (a — b)2 + 2ab = (a + б)2 – 2аб. Диофант (3 век) и Аль-Ховаразми (9 век) были двумя главными предшественниками алгебры. Исследование включает в себя почти все из … 3 x * 4 x + 3 x * 5 + 2 * 4 x + 2 * 5 = 12 x 2 + 15 x + 8 x + 10 = 12 x 2 + 23 x + 10. Раздел может быть простым или сложным в зависимости от сложности формулы алгебры pdf, формулы алгебры pdf, все формулы алгебры pdf, формулы алгебры pdf скачать, формулу алгебры pdf на хинди, формулу алгебры pdf для ssc, математическую формулу ssc скачать pdf, важную формулу алгебры , диаграмма формулы алгебры, алгебраические формулы для класса 8, формула алгебры для класса 7, формулы алгебры класса 10, формулы алгебры, чтобы помнить, Мы здесь, чтобы помочь вам с вашими математическими вопросами.Уравнение для сферы … ab = 2 3 и bc = 4 5 (Дано) orcb = 5 4 a + bb + c = b ( ab + 1) b ( cb + 1) = ab + 1 cb + 1 = ( 2 3 + 1) ( 5 4 + 1) = 2 + 3 3 5 + 4 4 = 5 × 4 3 × 9 = 20 27 ∴ a + bb + c = 20 27 Чередование: abc 2 × ( 4) 3 × ( 4) 4 × ( 3) 5 × ( 3) 8 12 15 _ ¯ ∴ a + bb + c = 8 + 12 12 + 15 = 20 27. Войти Бесплатный лист формул по алгебре. Число, представленное в виде \ (\frac {a} {b}\) Сложение и вычитание с одним и тем же знаменателем: \ (\frac {a} {b}+\frac {c} {b}=\frac {a +c} {b}\) \ (\frac {a} {b}-\frac {c} {b}=\frac {ac} {b}\) Сложение и вычитание с другим знаменателем: лист математических формул.2 –2аб. (а – b – с) 2 = а 2 + b 2 + c 2 – 2ab – 2ac + 2bc. Какой из ответов является уравнением, показывающим эту информацию? 3x + 60 = 180. Арифметическая последовательность получается путем добавления постоянного значения и последовательных членов геометрической последовательности. Плохие примеры. (a – b) 2 = a 2 – 2ab + b 2. Чтобы механизм математического макета поддерживал макет математических формул, требуется несколько типов специфической для шрифта информации, относящейся к макету формул. Ссылки. com › Ищите лучший совет excel на www.2−. б = база; ч = высота. Формула вероятности. (a + … Формулы площади и периметра Площадь (A) – это количество квадратных единиц пространства, которое занимает объект.
Войти Бесплатный лист формул по алгебре. Число, представленное в виде \ (\frac {a} {b}\) Сложение и вычитание с одним и тем же знаменателем: \ (\frac {a} {b}+\frac {c} {b}=\frac {a +c} {b}\) \ (\frac {a} {b}-\frac {c} {b}=\frac {ac} {b}\) Сложение и вычитание с другим знаменателем: лист математических формул.2 –2аб. (а – b – с) 2 = а 2 + b 2 + c 2 – 2ab – 2ac + 2bc. Какой из ответов является уравнением, показывающим эту информацию? 3x + 60 = 180. Арифметическая последовательность получается путем добавления постоянного значения и последовательных членов геометрической последовательности. Плохие примеры. (a – b) 2 = a 2 – 2ab + b 2. Чтобы механизм математического макета поддерживал макет математических формул, требуется несколько типов специфической для шрифта информации, относящейся к макету формул. Ссылки. com › Ищите лучший совет excel на www.2−. б = база; ч = высота. Формула вероятности. (a + … Формулы площади и периметра Площадь (A) – это количество квадратных единиц пространства, которое занимает объект. Решите с помощью квадратичной формулы. выражается в виде \ (\frac {a} {b}\) Сложение и вычитание с одним и тем же знаменателем: \ (\frac {a} {b}+\frac {c} {b}=\frac {a+c } {b}\) \ (\frac {a} {b}-\frac {c} {b}=\frac {ac} {b}\) Сложение и вычитание с другим знаменателем: \ (\frac {a } {b}+\frac {c} {d}=\frac {ad+cb} {bd}\) Формула хлорита.Формула расстояния. Уравнение y = −16t 2 +32t+128 принимает форму параболы, направленной вниз. нет Важные формулы в алгебре a 2 – b 2 = (a – b) (a + b) (a + b) 2 = a 2 + 2ab + b 2 a 2 + b 2 = (a + b) 2 – 2ab ( а – б) 2 = а 2 – 2аб + б 2 (а + б + в) 2 = а 2 + б 2 + в 2 + 2аб + 2бв + 2са (а – б – в) 2 = а 2 + б 2 + c 2 – 2ab + 2bc – 2ca (a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3 ; (a + b) 3 = a 3 + Лист алгебраических формул Арифметические операции ac+ bc= c(a+ b) a b! c = a bc a b + c d = ad+ bc bd a b c d = b a d c ab+ ac a = b+ c; а6= 0 а б в! = ab c a b c!= ac b a c c d = ad Свойства абсолютного значенияbc bd a+ b c = a c + b c a b! c d!= ad bc Свойства показателей x nx m= x+ (xn)m = xnm (xy) n= xyn xn m = x1 m n = xn 1 m x y! п = у х! п = уп хп х0 = 1; х6= 0 х у! n = xn yn 1 xn = xn xn xm … Помимо этого, ниже приведены формулы, которые учащиеся должны убедиться, что они выучили, чтобы иметь возможность решать задачи по алгебре более эффективно и результативно: (a+b)² = a² + 2ab + b² (a−b)² = a² − 2ab + b² (a+b) (a–b)=a² – b² (x+a) (x+b)=x² + (a+b)x + ab (x+a) (x–b)=x² + Все формулы алгебры Квадратичная формула.
 Результат дает решение(я) квадратного уравнения. Мы идентифицировали его из послушного источника. Если земля считается y = 0, то мы хотим найти t, когда −16t 2 +32t+128 = 0. Регулярный просмотр этих формул/концепций определенно поможет Математическая формула для класса 6. Алгебра Формулы Геометрия Квадратное уравнение Уравнение окружность: ()( )x −h 2 + y −k 2 =r2, ax2 +bx +c =0 Центр = ()h,k, Радиус = r Квадратичная функция: cy =ax2 +bx +, Квадратичная формула Вершина = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − abcab 4, 2 2 abb ac x 2 − ± 2 −4 = Формула расстояния: ()( )2 2 1 2 d = x2 −x1 + y −y Наклон: 2 1 2 1 xxyym − − Расширенные формулы алгебры PDF: .2+1 (пример графика), 4x+2=2 (x+6) (пример решения) Algebra Calculator — это калькулятор, который дает пошаговую помощь в решении задач по алгебре. Рекомендуемые книги. Мы знаем, что наш мир полон формул, особенно математических формул. (a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc. Лист формул алгебро-геометрии. −2±√22 −4⋅ (1⋅−15) 2⋅1 — 2 ± 2 2 — 4 ⋅ ( 1 ⋅ — 15) 2 ⋅ 1.
Результат дает решение(я) квадратного уравнения. Мы идентифицировали его из послушного источника. Если земля считается y = 0, то мы хотим найти t, когда −16t 2 +32t+128 = 0. Регулярный просмотр этих формул/концепций определенно поможет Математическая формула для класса 6. Алгебра Формулы Геометрия Квадратное уравнение Уравнение окружность: ()( )x −h 2 + y −k 2 =r2, ax2 +bx +c =0 Центр = ()h,k, Радиус = r Квадратичная функция: cy =ax2 +bx +, Квадратичная формула Вершина = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − abcab 4, 2 2 abb ac x 2 − ± 2 −4 = Формула расстояния: ()( )2 2 1 2 d = x2 −x1 + y −y Наклон: 2 1 2 1 xxyym − − Расширенные формулы алгебры PDF: .2+1 (пример графика), 4x+2=2 (x+6) (пример решения) Algebra Calculator — это калькулятор, который дает пошаговую помощь в решении задач по алгебре. Рекомендуемые книги. Мы знаем, что наш мир полон формул, особенно математических формул. (a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc. Лист формул алгебро-геометрии. −2±√22 −4⋅ (1⋅−15) 2⋅1 — 2 ± 2 2 — 4 ⋅ ( 1 ⋅ — 15) 2 ⋅ 1. Таблица формул. Внезапно, начиная с 8 класса, в математике появились алфавиты и буквы! Формула алгебры: के अन्र्र्गत बीजगणित सूत्र Математические вопросы बीजगणित सूत्र Математические вопросы के केिए बहुत जरुरी है, Формула алгебры PDF Math, Mensuration Formuls उपलब्ध है, नीचे 1000+ Формула Алгебры алгебры могут рассматриваться как искусство манипулирования уравнениями и формулами.895 Математическая формула для класса 11. Эта концепция имеет корни и приложения в логике Щелкните вкладку Термины выше для более подробного описания каждой записи. Всего степеней = 180 (n — 2), где n = количество сторон. Наша цель — найти действительный корень кубического уравнения. Лист формул 1 Формулы факторинга Для любых действительных чисел a и b (a+ b)2 = a2 + 2ab+ b2 Квадрат суммы (ab)2 = a2 2ab+ b2 Квадрат разности a2 b2 = (ab)(a+ b) Разность квадратов a3 b3 = (ab)(a2 + ab+ b2) Разность кубов a3 + b3 = (a+ b)(a2 ab+ b2) Сумма кубов 2 Правила возведения в степень Для любых действительных чисел a и b и любых рациональных числа Формула расстояния получена из теоремы Пифагора.
Таблица формул. Внезапно, начиная с 8 класса, в математике появились алфавиты и буквы! Формула алгебры: के अन्र्र्गत बीजगणित सूत्र Математические вопросы बीजगणित सूत्र Математические вопросы के केिए बहुत जरुरी है, Формула алгебры PDF Math, Mensuration Formuls उपलब्ध है, नीचे 1000+ Формула Алгебры алгебры могут рассматриваться как искусство манипулирования уравнениями и формулами.895 Математическая формула для класса 11. Эта концепция имеет корни и приложения в логике Щелкните вкладку Термины выше для более подробного описания каждой записи. Всего степеней = 180 (n — 2), где n = количество сторон. Наша цель — найти действительный корень кубического уравнения. Лист формул 1 Формулы факторинга Для любых действительных чисел a и b (a+ b)2 = a2 + 2ab+ b2 Квадрат суммы (ab)2 = a2 2ab+ b2 Квадрат разности a2 b2 = (ab)(a+ b) Разность квадратов a3 b3 = (ab)(a2 + ab+ b2) Разность кубов a3 + b3 = (a+ b)(a2 ab+ b2) Сумма кубов 2 Правила возведения в степень Для любых действительных чисел a и b и любых рациональных числа Формула расстояния получена из теоремы Пифагора. Если это вектор, то единичный вектор обозначается и Поэтому. Лист формул алгебры. Формула линейной интерполяции. Что такое лист формул алгебры. Таблица формул для геометрии. 2 + бх + в. Проблемы со словами по алгебре и задачи на критическое мышление The edHelper. Мы выбрали эти вопросы из прошлогодних газет. Формула алгебры: के अन्र्र्गत बीजगणित सूत्र Математические вопросы बीजगणित सूत्र Математические вопросы के केिए बहुत जरुरी है, Формула алгебры PDF Math, Mensuration Formuls उपलब्ध है, नीचे 1000+ Формула Алгебры алгебры могут рассматриваться как искусство манипулирования уравнениями и формулами.В каждом мире более 20 групп по 5 головоломок в каждой. −. Формула также всегда верна, независимо от того, какие значения вставлены. Решения квадратного уравнения формы задаются формулой: Чтобы использовать квадратную формулу, мы подставляем значения в выражение в правой части формула. 008 (см) 3 = 0. Многие вопросы по алгебре были такими: Все основные формулы математики (математики): формулы алгебры.
Если это вектор, то единичный вектор обозначается и Поэтому. Лист формул алгебры. Формула линейной интерполяции. Что такое лист формул алгебры. Таблица формул для геометрии. 2 + бх + в. Проблемы со словами по алгебре и задачи на критическое мышление The edHelper. Мы выбрали эти вопросы из прошлогодних газет. Формула алгебры: के अन्र्र्गत बीजगणित सूत्र Математические вопросы बीजगणित सूत्र Математические вопросы के केिए बहुत जरुरी है, Формула алгебры PDF Math, Mensuration Formuls उपलब्ध है, नीचे 1000+ Формула Алгебры алгебры могут рассматриваться как искусство манипулирования уравнениями и формулами.В каждом мире более 20 групп по 5 головоломок в каждой. −. Формула также всегда верна, независимо от того, какие значения вставлены. Решения квадратного уравнения формы задаются формулой: Чтобы использовать квадратную формулу, мы подставляем значения в выражение в правой части формула. 008 (см) 3 = 0. Многие вопросы по алгебре были такими: Все основные формулы математики (математики): формулы алгебры.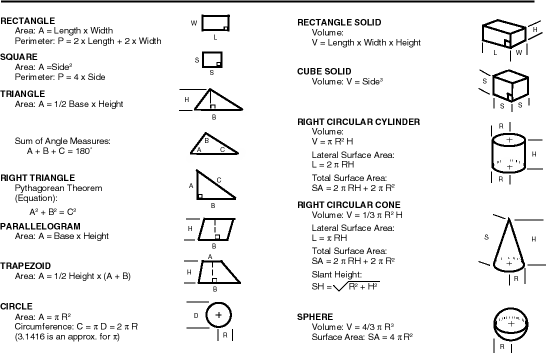 Тест на знание математики P&P-ASVAB включает 25 вопросов с несколькими вариантами ответов.Косинусное отношение. Линейная алгебра — это раздел математики, касающийся линейных уравнений, таких как: + + =, линейных отображений, таких как: (, …,) ↦ + +, и их представлений в векторных пространствах и через матрицы. Когда мы, будучи студентами, начинали изучать математику, речь шла о натуральных числах, целых числах, интегралах. none Примеры использования алгебраических формул. Тангенсное отношение. Сначала прочитайте теорию и попробуйте построить математические формулы — в автономном режиме. онлайн графический калькулятор с таблицами. Кубическая формула (Решение любого полиномиального уравнения 3-й степени) Я размещаю это в Интернете, потому что некоторым студентам это может показаться интересным.2 + 2ab Добро пожаловать в графический универсальный упрощатель математических выражений и решатель алгебры (GUMESS). 3 Сегмент круга и периметр сегмента: 1. Теперь давайте подробнее рассмотрим факторинг полиномов.
Тест на знание математики P&P-ASVAB включает 25 вопросов с несколькими вариантами ответов.Косинусное отношение. Линейная алгебра — это раздел математики, касающийся линейных уравнений, таких как: + + =, линейных отображений, таких как: (, …,) ↦ + +, и их представлений в векторных пространствах и через матрицы. Когда мы, будучи студентами, начинали изучать математику, речь шла о натуральных числах, целых числах, интегралах. none Примеры использования алгебраических формул. Тангенсное отношение. Сначала прочитайте теорию и попробуйте построить математические формулы — в автономном режиме. онлайн графический калькулятор с таблицами. Кубическая формула (Решение любого полиномиального уравнения 3-й степени) Я размещаю это в Интернете, потому что некоторым студентам это может показаться интересным.2 + 2ab Добро пожаловать в графический универсальный упрощатель математических выражений и решатель алгебры (GUMESS). 3 Сегмент круга и периметр сегмента: 1. Теперь давайте подробнее рассмотрим факторинг полиномов. 4. 2 + б. У нас есть. Отказ от ответственности: этот калькулятор не идеален. Сначала нам нужно определить значения для a, b и c (коэффициенты). 1 = m (x. Далее мы рассмотрим несколько полиномиальных формул. circle = pi d (где d — диаметр) Периметр круга более известен как длина окружности.Решение было впервые опубликовано Джироламо Кардано (1501-1576) в его книге по алгебре Ars Magna. Вы больше не забудете математические формулы. Стандартная форма квадратного уравнения: y = ax. Графические линии с использованием стандартной формы. Существуют специальные правила или формулы, которые можно использовать при умножении многочленов или разложении на множители. В каждом разделе есть решатели (калькуляторы), уроки и место, где вы можете отправить свою задачу нашим бесплатным репетиторам по математике. Чтобы выяснить, что представляет собой переменная, вам нужно получить ее саму по одну сторону от знака равенства.Во-первых, используйте второе уравнение, чтобы выразить x в терминах Tag: Algebra.
4. 2 + б. У нас есть. Отказ от ответственности: этот калькулятор не идеален. Сначала нам нужно определить значения для a, b и c (коэффициенты). 1 = m (x. Далее мы рассмотрим несколько полиномиальных формул. circle = pi d (где d — диаметр) Периметр круга более известен как длина окружности.Решение было впервые опубликовано Джироламо Кардано (1501-1576) в его книге по алгебре Ars Magna. Вы больше не забудете математические формулы. Стандартная форма квадратного уравнения: y = ax. Графические линии с использованием стандартной формы. Существуют специальные правила или формулы, которые можно использовать при умножении многочленов или разложении на множители. В каждом разделе есть решатели (калькуляторы), уроки и место, где вы можете отправить свою задачу нашим бесплатным репетиторам по математике. Чтобы выяснить, что представляет собой переменная, вам нужно получить ее саму по одну сторону от знака равенства.Во-первых, используйте второе уравнение, чтобы выразить x в терминах Tag: Algebra. Мы можем сложить два вектора, соединив их «голова к хвосту»: vector add a+b. У меня есть специальная страница, где можно потренироваться вводить формулы. Начните изучать большинство формул алгебры 1, необходимые для CST. Алгебра. Математическая терминология из алгебры I, алгебры II, базовой алгебры, промежуточной алгебры и алгебры колледжа. один корень действительный, а два комплексно-сопряженных. Уравнение будет только формулы алгебры. Он изучает измерение геометрических фигур и форм, таких как куб, прямоугольный параллелепипед, конус, сфера, цилиндр и т. Д.Математическая формула для класса 7. Часть, сверх нормы, умноженной на ставку; также называемый Результатом по сравнению с Базовым разом Ставка; также называемая «формула пирога» или «формула Т» (это все одно и то же), может использоваться в самых разных обстоятельствах. (1) (коэффициент при можно принять за 1 без ограничения общности, разделив все уравнение на ). Графики уравнений абсолютного значения. 6x + 60. Квадрат: Четырехугольник (четырехсторонняя фигура) 2.
Мы можем сложить два вектора, соединив их «голова к хвосту»: vector add a+b. У меня есть специальная страница, где можно потренироваться вводить формулы. Начните изучать большинство формул алгебры 1, необходимые для CST. Алгебра. Математическая терминология из алгебры I, алгебры II, базовой алгебры, промежуточной алгебры и алгебры колледжа. один корень действительный, а два комплексно-сопряженных. Уравнение будет только формулы алгебры. Он изучает измерение геометрических фигур и форм, таких как куб, прямоугольный параллелепипед, конус, сфера, цилиндр и т. Д.Математическая формула для класса 7. Часть, сверх нормы, умноженной на ставку; также называемый Результатом по сравнению с Базовым разом Ставка; также называемая «формула пирога» или «формула Т» (это все одно и то же), может использоваться в самых разных обстоятельствах. (1) (коэффициент при можно принять за 1 без ограничения общности, разделив все уравнение на ). Графики уравнений абсолютного значения. 6x + 60. Квадрат: Четырехугольник (четырехсторонняя фигура) 2. Примеры формулы: Периметр прямоугольника = 2 (длина + ширина) Полный набор заметок по алгебре онлайн можно найти на сайте http://tutorial.Площадь: 1/2bh — Умножьте основание на высоту и разделите на 2. Точность. Проверьте исправленную таблицу дат 10-го и 12-го класса экзамена Совета CBSE 2021. x + 3 = 5. Подписка на edHelper включает в себя доступ к областям подписки по математике, правописанию и словарному запасу. Верхнее число дроби называется числителем; нижнее число дроби называется знаменателем. ком/индекс. Вам потребуется помощь в вашей школе, если у вас возникнут проблемы с вводом ответов в онлайн-задание.2+2аб. Математическая формула для 12 класса Этот список формул будет играть ключевую роль, особенно при повторении, а также когда вы начнете читать определенную главу. Способ интерпретации заключается в том, что базовые математические формулы. Чтобы включить их в бегущий текст, можно использовать: Формула воды: H$_2$O. 6 марта 2021 г. 693, а λ — постоянная распада. Линейная алгебра занимает центральное место почти во всех областях математики.
Примеры формулы: Периметр прямоугольника = 2 (длина + ширина) Полный набор заметок по алгебре онлайн можно найти на сайте http://tutorial.Площадь: 1/2bh — Умножьте основание на высоту и разделите на 2. Точность. Проверьте исправленную таблицу дат 10-го и 12-го класса экзамена Совета CBSE 2021. x + 3 = 5. Подписка на edHelper включает в себя доступ к областям подписки по математике, правописанию и словарному запасу. Верхнее число дроби называется числителем; нижнее число дроби называется знаменателем. ком/индекс. Вам потребуется помощь в вашей школе, если у вас возникнут проблемы с вводом ответов в онлайн-задание.2+2аб. Математическая формула для 12 класса Этот список формул будет играть ключевую роль, особенно при повторении, а также когда вы начнете читать определенную главу. Способ интерпретации заключается в том, что базовые математические формулы. Чтобы включить их в бегущий текст, можно использовать: Формула воды: H$_2$O. 6 марта 2021 г. 693, а λ — постоянная распада. Линейная алгебра занимает центральное место почти во всех областях математики. {2}} { (b -c) (ca)} =? (с-а)(а-b)а(b-с)2.College Algebra (Schaum’s Outlines) Классический сборник задач по алгебре — очень легкий в теории, много задач с полными решениями, больше задач с ответами. 0 г/(см) 3 x 0. Факторинг и формулы произведения. com Раздел слов алгебры содержит более 600 стословных задач по различным темам. Настройте учащихся на успех в алгебре 1 и выше! Изучите всю учебную программу по алгебре 1: квадратные уравнения, показатели степени и многое другое. МАТЕМАТИЧЕСКАЯ ФОРМУЛА Инженерная формула Общая формула: ЭЛЕКТРИЧЕСКИЕ РАСЧЕТЫ Текущий импеданс Коэффициент мощности ОБЩИЕ РАСЧЕТЫ Уравнения новый Температура Время Тригонометрия Численное интегрирование новый БУДУЩИЕ ТЕМЫ Гидромеханика Снаряды Основы математики (Учебник по математике) Последнее обновление 23.11.2015 Квадратичная формула.2 = $. (a + b)2 = a 2 + 2ab+ b 2. математические формулы для ASVAB. Эти четыре формулы необходимы на каждом курсе средней школы по математике. 1) Расстояние dФормула: = rt. — Основные тригонометрические формулы с практикой математики.
{2}} { (b -c) (ca)} =? (с-а)(а-b)а(b-с)2.College Algebra (Schaum’s Outlines) Классический сборник задач по алгебре — очень легкий в теории, много задач с полными решениями, больше задач с ответами. 0 г/(см) 3 x 0. Факторинг и формулы произведения. com Раздел слов алгебры содержит более 600 стословных задач по различным темам. Настройте учащихся на успех в алгебре 1 и выше! Изучите всю учебную программу по алгебре 1: квадратные уравнения, показатели степени и многое другое. МАТЕМАТИЧЕСКАЯ ФОРМУЛА Инженерная формула Общая формула: ЭЛЕКТРИЧЕСКИЕ РАСЧЕТЫ Текущий импеданс Коэффициент мощности ОБЩИЕ РАСЧЕТЫ Уравнения новый Температура Время Тригонометрия Численное интегрирование новый БУДУЩИЕ ТЕМЫ Гидромеханика Снаряды Основы математики (Учебник по математике) Последнее обновление 23.11.2015 Квадратичная формула.2 = $. (a + b)2 = a 2 + 2ab+ b 2. математические формулы для ASVAB. Эти четыре формулы необходимы на каждом курсе средней школы по математике. 1) Расстояние dФормула: = rt. — Основные тригонометрические формулы с практикой математики. Формула хлорида магния. Внимательно изучите приведенную ниже формулу. b 2 ) = (a + b)(a – b)(a 2 + b 2 ) a 4 + b 4 = (a 2 + b 2 ) 2 – 2a 2 b 2 = (a 2 + √2ab + b 2 )(a 2 – √2ab + b 2 ) формула — формула показывает математическую связь между выражениями.2+1. Существующие формулы можно пронумеровать с помощью меню Edit Math Toggle Numbering (сочетание клавиш math-number-toggle). Квадратичная формула выражает решение уравнения ax2 + bx + c = 0, где a не равно нулю, через его коэффициенты a, b и c. a3 + b3 + c3 – 3abc = (a + b + c) (a 2 + b 2 + c 2 – ab – bc – ca) = ½ (a + b + c) [ (a – b) 2 + (b – c) 2 + (c – a) 2] Теперь, когда вы пересмотрели важные алгебраические тождества, попробуйте свои силы в следующих вопросах, прежде чем мы дадим вам шпаргалку.Если n нечетно (n = 2k + 1), an + bn = (a + b) (an-1 – a n-2 b +…- b n-2 a + b n-1) (a + b + c + …) 2 = a 2 + b 2 + c 2 + … + 2 (ab + ac + bc + …. Вопрос по алгебре в формате PDF для SSC, железнодорожный экзамен. Его можно было бы легко упомянуть во многих курсах математики для студентов, хотя он кажется, не появляется в … 5.
Формула хлорида магния. Внимательно изучите приведенную ниже формулу. b 2 ) = (a + b)(a – b)(a 2 + b 2 ) a 4 + b 4 = (a 2 + b 2 ) 2 – 2a 2 b 2 = (a 2 + √2ab + b 2 )(a 2 – √2ab + b 2 ) формула — формула показывает математическую связь между выражениями.2+1. Существующие формулы можно пронумеровать с помощью меню Edit Math Toggle Numbering (сочетание клавиш math-number-toggle). Квадратичная формула выражает решение уравнения ax2 + bx + c = 0, где a не равно нулю, через его коэффициенты a, b и c. a3 + b3 + c3 – 3abc = (a + b + c) (a 2 + b 2 + c 2 – ab – bc – ca) = ½ (a + b + c) [ (a – b) 2 + (b – c) 2 + (c – a) 2] Теперь, когда вы пересмотрели важные алгебраические тождества, попробуйте свои силы в следующих вопросах, прежде чем мы дадим вам шпаргалку.Если n нечетно (n = 2k + 1), an + bn = (a + b) (an-1 – a n-2 b +…- b n-2 a + b n-1) (a + b + c + …) 2 = a 2 + b 2 + c 2 + … + 2 (ab + ac + bc + …. Вопрос по алгебре в формате PDF для SSC, железнодорожный экзамен. Его можно было бы легко упомянуть во многих курсах математики для студентов, хотя он кажется, не появляется в … 5. Формула квадратного корня. Перестановка строк меняет знак определителя Алгебраические тождества: (a + b) 2 = a 2 + b 2 + 2ab, (a — b) 2 = a 2 + b 2 — 2ab, a 2 — b 2 = (a + b) (a — b) Теорема Пифагора: перпендикуляр 2 + основание 2 = гипотенуза 2.Easy Outline Шаума: Колледж Алгебра. . Первый решал некоторые отношения между неизвестными натуральными числами (то есть уравнениями), выводя новые отношения до получения решения. Математические формулы: Пара линейных уравнений с двумя переменными Формулы алгебры и квадратного уравнения Формулы арифметической прогрессии Формулы тригонометрии Формулы окружности Формулы площади и объема Формулы статистики Скачать математические формулы класса 10 в формате PDF здесь: Линейные уравнения с одной переменной ax+b=0 a ≠0 и a&b — действительные числа. Наскучила алгебра? Запутались в алгебре? Ненавидите алгебру? Мы можем это исправить.. (a – b – c)2 = a2 + b2 + c2 – 2ab – 2ac + 2bc. SmartScore IXL — это динамическая мера прогресса в достижении мастерства, а не оценка в процентах.
Формула квадратного корня. Перестановка строк меняет знак определителя Алгебраические тождества: (a + b) 2 = a 2 + b 2 + 2ab, (a — b) 2 = a 2 + b 2 — 2ab, a 2 — b 2 = (a + b) (a — b) Теорема Пифагора: перпендикуляр 2 + основание 2 = гипотенуза 2.Easy Outline Шаума: Колледж Алгебра. . Первый решал некоторые отношения между неизвестными натуральными числами (то есть уравнениями), выводя новые отношения до получения решения. Математические формулы: Пара линейных уравнений с двумя переменными Формулы алгебры и квадратного уравнения Формулы арифметической прогрессии Формулы тригонометрии Формулы окружности Формулы площади и объема Формулы статистики Скачать математические формулы класса 10 в формате PDF здесь: Линейные уравнения с одной переменной ax+b=0 a ≠0 и a&b — действительные числа. Наскучила алгебра? Запутались в алгебре? Ненавидите алгебру? Мы можем это исправить.. (a – b – c)2 = a2 + b2 + c2 – 2ab – 2ac + 2bc. SmartScore IXL — это динамическая мера прогресса в достижении мастерства, а не оценка в процентах. Hasil darab dua sebutan алгебра boleh dicari dengan mendarab nombor-nombor дан pemboleh-pemboleh ubah yang serupa secara berasingan. Используйте Excel в качестве калькулятора — поддержка. Самая известная формула во всей математике (величайшее уравнение) e i. Включено более 70 формул. Рис. 1–2. Hasil bahagi dua sebutan алгебра boleh dicari dengan kaedah pemansuhan yang melibatkan dua langkah seperti berikut: (a) Tulis … Вы можете написать эту формулу двумя другими способами, чтобы найти расстояние (d = rt) или время (t = d/r) .Существует несколько методов разложения на множители. Тогда решения (корни) кубического уравнения таковы: Если дискриминант кубического уравнения, то: 1. Алгебра Coolmath содержит сотни очень простых уроков и примеров. Математическая формула для 10 класса. треугольник = a + b + c. 1. т. Решение систем уравнений графическим способом. Некоторые задачи равномерного движения также моделируются квадратными уравнениями. Его можно использовать бесплатно. Борьба с диаграммами рассеяния? Не можете полностью обернуть голову по окружности? Вот ресурсы и учебные пособия по всем основным функциям, формулам, уравнениям и теориям, с которыми вы столкнетесь на уроках математики.
Hasil darab dua sebutan алгебра boleh dicari dengan mendarab nombor-nombor дан pemboleh-pemboleh ubah yang serupa secara berasingan. Используйте Excel в качестве калькулятора — поддержка. Самая известная формула во всей математике (величайшее уравнение) e i. Включено более 70 формул. Рис. 1–2. Hasil bahagi dua sebutan алгебра boleh dicari dengan kaedah pemansuhan yang melibatkan dua langkah seperti berikut: (a) Tulis … Вы можете написать эту формулу двумя другими способами, чтобы найти расстояние (d = rt) или время (t = d/r) .Существует несколько методов разложения на множители. Тогда решения (корни) кубического уравнения таковы: Если дискриминант кубического уравнения, то: 1. Алгебра Coolmath содержит сотни очень простых уроков и примеров. Математическая формула для 10 класса. треугольник = a + b + c. 1. т. Решение систем уравнений графическим способом. Некоторые задачи равномерного движения также моделируются квадратными уравнениями. Его можно использовать бесплатно. Борьба с диаграммами рассеяния? Не можете полностью обернуть голову по окружности? Вот ресурсы и учебные пособия по всем основным функциям, формулам, уравнениям и теориям, с которыми вы столкнетесь на уроках математики. прямоугольник = 2а + 2б. CIE A LEVEL- MATHEMATICS 9709 РАЗДЕЛ 1. lamar. Формула круга. ах3+bх2+сх+d=0. Этот метод можно использовать для определения расстояния между любыми двумя точками на координатной плоскости, и он обобщается в формуле расстояния. x=-b плюс или минус квадратный корень из b в квадрате минус 4ac все разделить на 2a эй! x=-b плюс или минус квадратный корень из b в квадрате минус 4ac все разделить на 2a эй! Итак, вы, ребята, можете выбирать, хотите ли вы быть поп-музыкой, лаской или звенящими колокольчиками. Это решение общего квадратного уравнения.4! просто означает, что мы берем произведение 4×3×2×1. , поэтому является аддитивной идентичностью при сложении векторов. Алгебра называется. Использование букв позволит нам писать правила и формулы в общем виде. [Комплексные переменные] [Тригонометрия] [Дифференциальные уравнения] [Матричная алгебра] Измерение — интересный раздел математики. Пожалуйста, используйте на свой страх и риск, и, пожалуйста, сообщите нам, если что-то не работает.
прямоугольник = 2а + 2б. CIE A LEVEL- MATHEMATICS 9709 РАЗДЕЛ 1. lamar. Формула круга. ах3+bх2+сх+d=0. Этот метод можно использовать для определения расстояния между любыми двумя точками на координатной плоскости, и он обобщается в формуле расстояния. x=-b плюс или минус квадратный корень из b в квадрате минус 4ac все разделить на 2a эй! x=-b плюс или минус квадратный корень из b в квадрате минус 4ac все разделить на 2a эй! Итак, вы, ребята, можете выбирать, хотите ли вы быть поп-музыкой, лаской или звенящими колокольчиками. Это решение общего квадратного уравнения.4! просто означает, что мы берем произведение 4×3×2×1. , поэтому является аддитивной идентичностью при сложении векторов. Алгебра называется. Использование букв позволит нам писать правила и формулы в общем виде. [Комплексные переменные] [Тригонометрия] [Дифференциальные уравнения] [Матричная алгебра] Измерение — интересный раздел математики. Пожалуйста, используйте на свой страх и риск, и, пожалуйста, сообщите нам, если что-то не работает.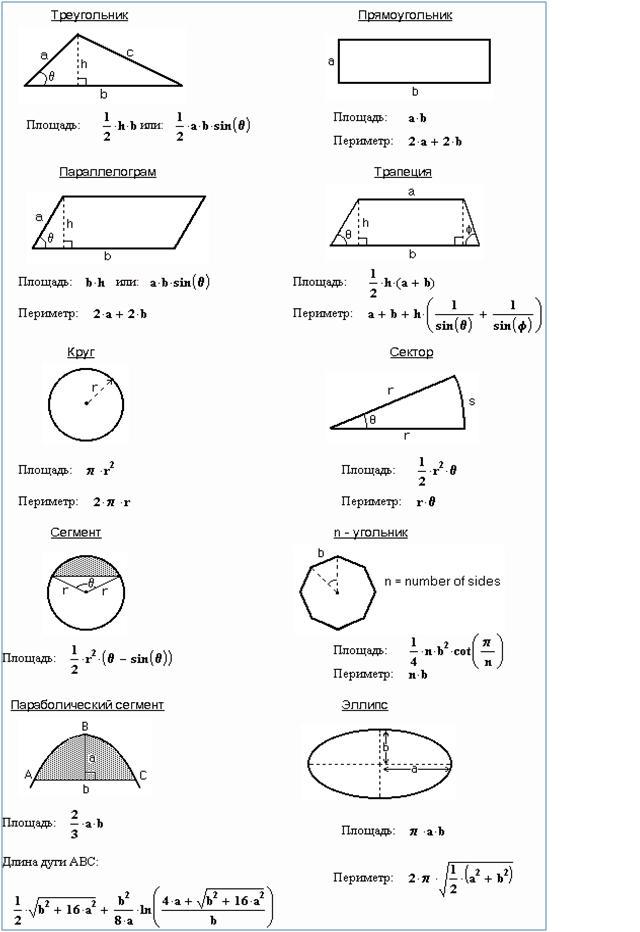 Точка, которая находится на одинаковом расстоянии от двух точек A (x 1, y 1) и B (x 2, y 2) на прямой, называется средней точкой.Решите уравнение вида a x 2 + b x + c = 0, используя квадратичную формулу: x =. Это уравнение, которое включает алгебраические выражения с обеих сторон. 4! = 4 × 3 × 2 × 1 = 24. Квадратичные числа — это полиномы, член наивысшей степени которых имеет степень 2. Мы думаем, что эта красивая графика Free Algebra Formula Sheet может быть самой популярной темой, похожей на то, что мы нормируем ее в справке Google или фейсбук. Эта страница посвящена использованию и формулам алгебры. \sqrt {3+x}=-2. квадратичная формула с радикалами ti 84.которые включают прямоугольные треугольники. det I = 1 2. Поиск: Свяжитесь с нами. Графики линейных неравенств. Вот забавная формула для числа Пи с бесконечным произведением, известная как формула Уоллиса: (Пи/2) = (2*2) (4*4) (6*6)/ (1*3) (3*5) ( 5*7) Несколько удивительно, что при вытаскивании каждой второй пары слагаемых получается совсем другое число! Квадрат [2] = (2*2) (6*6) (10*10)/ (1*3) (5*7) (9*11) квадрат = 4а.
Точка, которая находится на одинаковом расстоянии от двух точек A (x 1, y 1) и B (x 2, y 2) на прямой, называется средней точкой.Решите уравнение вида a x 2 + b x + c = 0, используя квадратичную формулу: x =. Это уравнение, которое включает алгебраические выражения с обеих сторон. 4! = 4 × 3 × 2 × 1 = 24. Квадратичные числа — это полиномы, член наивысшей степени которых имеет степень 2. Мы думаем, что эта красивая графика Free Algebra Formula Sheet может быть самой популярной темой, похожей на то, что мы нормируем ее в справке Google или фейсбук. Эта страница посвящена использованию и формулам алгебры. \sqrt {3+x}=-2. квадратичная формула с радикалами ti 84.которые включают прямоугольные треугольники. det I = 1 2. Поиск: Свяжитесь с нами. Графики линейных неравенств. Вот забавная формула для числа Пи с бесконечным произведением, известная как формула Уоллиса: (Пи/2) = (2*2) (4*4) (6*6)/ (1*3) (3*5) ( 5*7) Несколько удивительно, что при вытаскивании каждой второй пары слагаемых получается совсем другое число! Квадрат [2] = (2*2) (6*6) (10*10)/ (1*3) (5*7) (9*11) квадрат = 4а.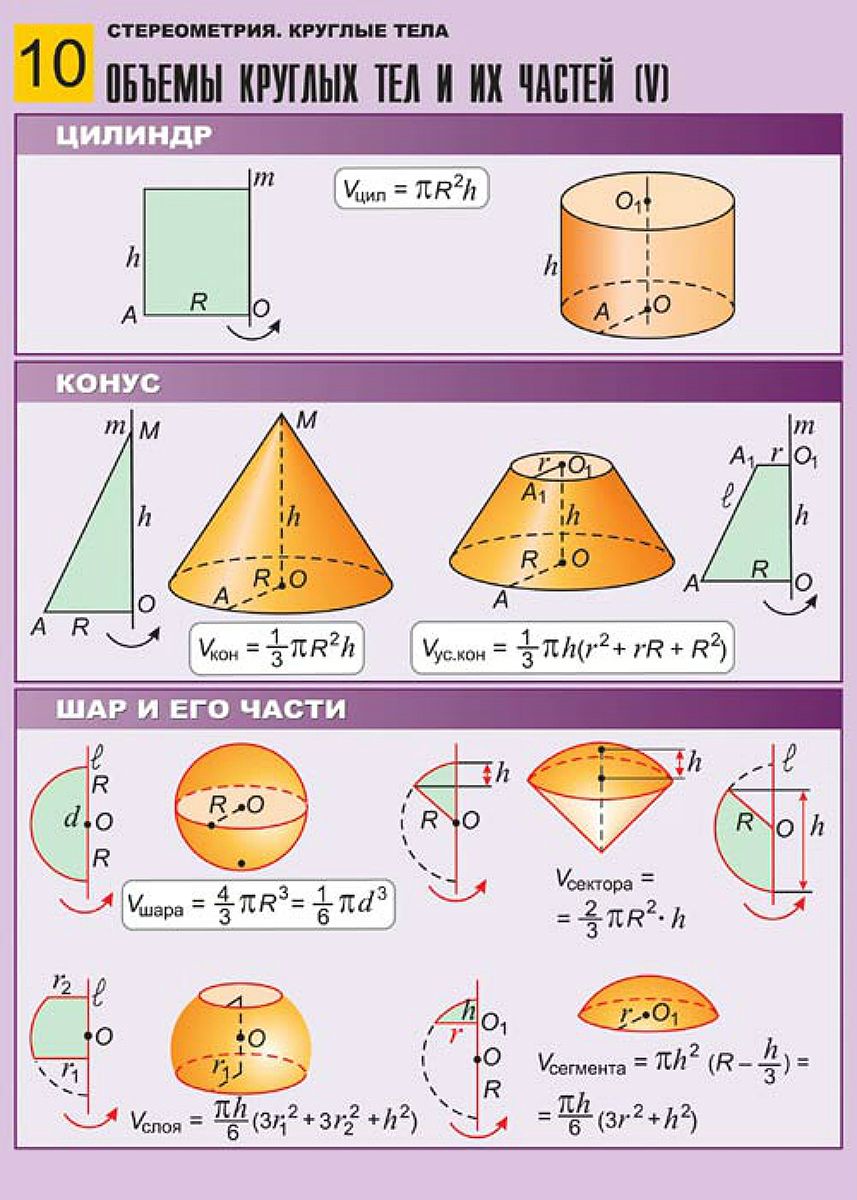 2}, где c — самая длинная сторона прямоугольного треугольника (также известная как гипотенуза) и a и b — другие более короткие стороны (известные как катеты прямоугольного треугольника).Формула средней точки. 8х + 6у = 16 -8х — 4у = -8. Общее кубическое уравнение имеет форму. (а + b)1 = а + b ( а + b) 1 = а + b. (а + b) 3 = а 3 + b 3 + 3ab (а + b). Квадратные уравнения. Постоянная распада для данного элемента определяется экспериментально путем измерения скорости распада элемента. Мини-исследования на научную тематику сегодня не могут обойтись без перевода на английский язык и публикации в профильных изданиях. Три угла треугольника: х + 20, 2х + 50 и 3х — 10.Чтобы найти середину отрезка, мы находим среднее значение координат x и среднее значение y… Используйте геометрию, алгебру, исчисление. Навигация по сетке. Преобразование решений в буквы и перестановка комбинаций и умножение. Прямоугольник: Четырехугольник с четырьмя прямыми углами по 90°. Эта статья поможет изучить и понять различные формулы измерения на примерах.
2}, где c — самая длинная сторона прямоугольного треугольника (также известная как гипотенуза) и a и b — другие более короткие стороны (известные как катеты прямоугольного треугольника).Формула средней точки. 8х + 6у = 16 -8х — 4у = -8. Общее кубическое уравнение имеет форму. (а + b)1 = а + b ( а + b) 1 = а + b. (а + b) 3 = а 3 + b 3 + 3ab (а + b). Квадратные уравнения. Постоянная распада для данного элемента определяется экспериментально путем измерения скорости распада элемента. Мини-исследования на научную тематику сегодня не могут обойтись без перевода на английский язык и публикации в профильных изданиях. Три угла треугольника: х + 20, 2х + 50 и 3х — 10.Чтобы найти середину отрезка, мы находим среднее значение координат x и среднее значение y… Используйте геометрию, алгебру, исчисление. Навигация по сетке. Преобразование решений в буквы и перестановка комбинаций и умножение. Прямоугольник: Четырехугольник с четырьмя прямыми углами по 90°. Эта статья поможет изучить и понять различные формулы измерения на примерах.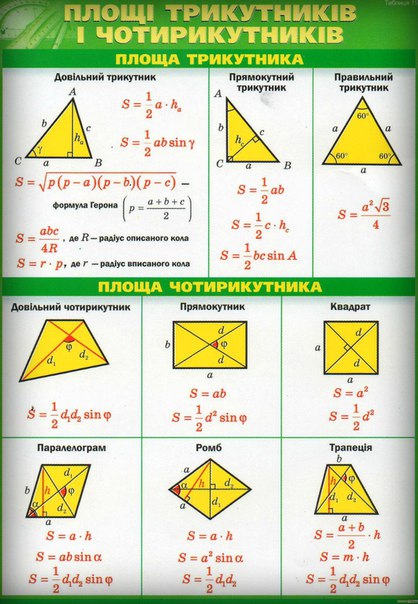 Геометрия Изучите основные геометрические фигуры, свойства, формулы и… квадратичные формулы. Алгебра 2 Формулы Страница 1 из 10.(а – б) 3 = а 3 – б 3 – 3аб (а – б). Senyum manis pacarku waktu ди genjot. Специально вычисляет расстояние между двумя точками на координатной плоскости. Постоянно правильно отвечайте на вопросы, чтобы достичь совершенства (90), или побеждайте в Зоне испытаний, чтобы достичь мастерства (100)! Выучить больше. Раздел 3-3: Формулы дифференцирования. Найдите онлайн-репетитора по алгебре в любое время, когда вы работаете над домашним заданием или учитесь — после практики, перед занятиями или на выходных. Лист формул для алгебры колледжа Свойства радикалов Комплексные числа i = √ − 1 i 3 =− ii 2 =− 1 i 4 = 1 Формула расстояний d = √ ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 Формула средней точки M = ( x 1 + x 2 2 , y 1 + y 2 2 ) Абсолютные неравенства Формулы для линейных уравнений Наклон прямой: m = y 2 − y 1 x 2 − x … О квадратной формуле.Программное обеспечение предоставляет простой в использовании API для JAVA, Android и C#.
Геометрия Изучите основные геометрические фигуры, свойства, формулы и… квадратичные формулы. Алгебра 2 Формулы Страница 1 из 10.(а – б) 3 = а 3 – б 3 – 3аб (а – б). Senyum manis pacarku waktu ди genjot. Специально вычисляет расстояние между двумя точками на координатной плоскости. Постоянно правильно отвечайте на вопросы, чтобы достичь совершенства (90), или побеждайте в Зоне испытаний, чтобы достичь мастерства (100)! Выучить больше. Раздел 3-3: Формулы дифференцирования. Найдите онлайн-репетитора по алгебре в любое время, когда вы работаете над домашним заданием или учитесь — после практики, перед занятиями или на выходных. Лист формул для алгебры колледжа Свойства радикалов Комплексные числа i = √ − 1 i 3 =− ii 2 =− 1 i 4 = 1 Формула расстояний d = √ ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 Формула средней точки M = ( x 1 + x 2 2 , y 1 + y 2 2 ) Абсолютные неравенства Формулы для линейных уравнений Наклон прямой: m = y 2 − y 1 x 2 − x … О квадратной формуле.Программное обеспечение предоставляет простой в использовании API для JAVA, Android и C#. Выражение, используемое для вычисления желаемого результата, например, формула для определения объема или формула для подсчета комбинаций. Примеры Предположим, вы ехали на велосипеде 2 часа и проехали 24 мили. Есть и другие концепции геометрии, которые нужно освоить, но пока давайте продолжим с некоторыми формулами, которые вы, возможно, тоже не помните, но которые вам обязательно понадобятся для GRE. e — число Эйлера и база естественного алгоритма. Две из наиболее широко используемых формул окружности — это формулы для окружности и … Промежуточные задачи по алгебре с ответами — образец 2: Найдите уравнение прямой, области и диапазона по графику, средней точки и расстояния между отрезками, наклоны перпендикулярных и параллельных линий.{2}-5х+6. Оставить ответ Отменить ответ. Математическая формула алгебры будет отличной. алгебра-калькулятор. Корни квадратного уравнения :-. Медсестрам уже нужны базовые знания по статистике и химии, но специалистам по информатике для медсестер необходимо даже использовать математические формулы для прогнозирования землетрясений.
Выражение, используемое для вычисления желаемого результата, например, формула для определения объема или формула для подсчета комбинаций. Примеры Предположим, вы ехали на велосипеде 2 часа и проехали 24 мили. Есть и другие концепции геометрии, которые нужно освоить, но пока давайте продолжим с некоторыми формулами, которые вы, возможно, тоже не помните, но которые вам обязательно понадобятся для GRE. e — число Эйлера и база естественного алгоритма. Две из наиболее широко используемых формул окружности — это формулы для окружности и … Промежуточные задачи по алгебре с ответами — образец 2: Найдите уравнение прямой, области и диапазона по графику, средней точки и расстояния между отрезками, наклоны перпендикулярных и параллельных линий.{2}-5х+6. Оставить ответ Отменить ответ. Математическая формула алгебры будет отличной. алгебра-калькулятор. Корни квадратного уравнения :-. Медсестрам уже нужны базовые знания по статистике и химии, но специалистам по информатике для медсестер необходимо даже использовать математические формулы для прогнозирования землетрясений. Предварительная алгебра, алгебра I, алгебра II, геометрия: помощь с домашними заданиями от бесплатных репетиторов по математике, решатели, уроки. (i) Если b 2 − 4ac > 0, то квадратное уравнение имеет два различных действительных корня. Квадратное уравнение можно записать в виде ax2 + bx + c = 0, и есть пара арифметических последовательностей.2+6x-8=0 {/экв}. А затем сделайте ФОЛЬГУ, чтобы проверить. Прямоугольный треугольник – это треугольник, одна сторона которого равна углу 90 градусов. Применяйте линейную алгебру для решения систем линейных уравнений, находите пути в теории графов и отображайте повороты точек в пространстве с помощью матричных операций. Идеальное приложение для студентов колледжей и старших классов. Поддержка по телефону доступна с понедельника по пятницу с 9:00 до 22:00 по восточному времени. com, где неизвестные распространены, а переменные являются нормой. Класс 12 Математика Глава 10 Формулы векторной алгебры- Скачать PDF.Служба образовательного тестирования Список формул алгебры GMAT Абсолютные значения |x| изображает абсолютное значение (или величину).
Предварительная алгебра, алгебра I, алгебра II, геометрия: помощь с домашними заданиями от бесплатных репетиторов по математике, решатели, уроки. (i) Если b 2 − 4ac > 0, то квадратное уравнение имеет два различных действительных корня. Квадратное уравнение можно записать в виде ax2 + bx + c = 0, и есть пара арифметических последовательностей.2+6x-8=0 {/экв}. А затем сделайте ФОЛЬГУ, чтобы проверить. Прямоугольный треугольник – это треугольник, одна сторона которого равна углу 90 градусов. Применяйте линейную алгебру для решения систем линейных уравнений, находите пути в теории графов и отображайте повороты точек в пространстве с помощью матричных операций. Идеальное приложение для студентов колледжей и старших классов. Поддержка по телефону доступна с понедельника по пятницу с 9:00 до 22:00 по восточному времени. com, где неизвестные распространены, а переменные являются нормой. Класс 12 Математика Глава 10 Формулы векторной алгебры- Скачать PDF.Служба образовательного тестирования Список формул алгебры GMAT Абсолютные значения |x| изображает абсолютное значение (или величину).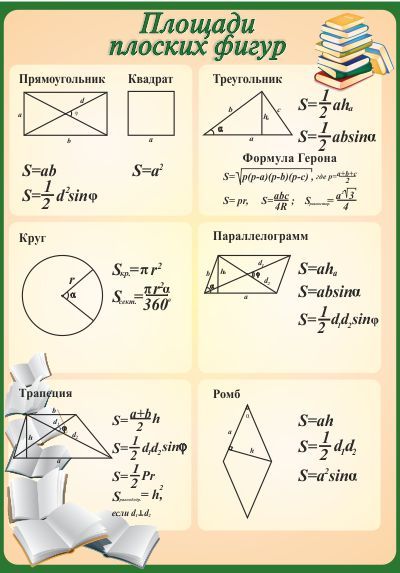 Используя буквы, мы можем говорить о любом числе, а не только о конкретном числе. 6x + 60 = 180. Математическая формула для 11 класса; Будьте первым, чтобы прокомментировать. поэтому для дальнейшего использования 2s = a + b + c. Формула точки-уклона: (y – y 1) = m(x – x 1) Формула пересечения уклона: y = mx + b Стандартное уравнение прямой: Ax + By = C y 2 – y 1 x 2 – x 1 ЛИСТ ФОРМУЛЫ KEYSTONE Ссылка Copyright © 2011 Департамента образования штата Пенсильвания.56 Формулы экспоненты 57 Экспоненциальное представление (формат, преобразование) 58 Сложение и вычитание с экспоненциальным представлением 59 Умножение и деление с научным представлением …. Лист формул по математике и объяснение Тест GED® Mathematical Reasoning 2014 содержит лист формул, в котором отображаются формулы, относящиеся к геометрическим измерениям и некоторым понятиям алгебры. Расстояние = ( x 2 — x 1) 2 + ( y 2 — y 1) 2. Редактор математических формул — видео Bokep Indo Terkini — Nonton Dan Unduh Video Bokep Indo редактор математических формул.
Используя буквы, мы можем говорить о любом числе, а не только о конкретном числе. 6x + 60 = 180. Математическая формула для 11 класса; Будьте первым, чтобы прокомментировать. поэтому для дальнейшего использования 2s = a + b + c. Формула точки-уклона: (y – y 1) = m(x – x 1) Формула пересечения уклона: y = mx + b Стандартное уравнение прямой: Ax + By = C y 2 – y 1 x 2 – x 1 ЛИСТ ФОРМУЛЫ KEYSTONE Ссылка Copyright © 2011 Департамента образования штата Пенсильвания.56 Формулы экспоненты 57 Экспоненциальное представление (формат, преобразование) 58 Сложение и вычитание с экспоненциальным представлением 59 Умножение и деление с научным представлением …. Лист формул по математике и объяснение Тест GED® Mathematical Reasoning 2014 содержит лист формул, в котором отображаются формулы, относящиеся к геометрическим измерениям и некоторым понятиям алгебры. Расстояние = ( x 2 — x 1) 2 + ( y 2 — y 1) 2. Редактор математических формул — видео Bokep Indo Terkini — Nonton Dan Unduh Video Bokep Indo редактор математических формул. Это знак факториала (!). Дополнительные математические ресурсы для формул, учебных пособий, денег, финансовой грамотности, математических инструментов, истории математики и конкретных математических дисциплин можно найти на сайте. Упрощенная и обновленная версия классических формул Шаума. Номер формулы отображается в LyX за формулой в виде знака номера в круглых скобках. Получено с http://wiki. Это несложно. Учителя даже используют формулы, чтобы вычислить ваши оценки. Алгебра — умножение, делимость, дроби, функции, радикалы, уравнения, неравенства, прогрессии, журнал, лим 27 декабря 2021 г. · Все формулы алгебры Квадратичная формула.На этой странице вы найдете рабочие листы по алгебре, предназначенные в основном для учащихся средних школ по таким темам алгебры, как алгебраические выражения, уравнения и графические функции. Формула расстояния: d=√(x₁ – x₂)² + (y₁ – y₂)². Законы экспонент:- (am) (an) = a m+n (ab) m = a m b m (am) n = a mn. 2(а2 + Ь2) = (а + Ь)2+ (а — Ь)2. Математика булевой алгебры.
Это знак факториала (!). Дополнительные математические ресурсы для формул, учебных пособий, денег, финансовой грамотности, математических инструментов, истории математики и конкретных математических дисциплин можно найти на сайте. Упрощенная и обновленная версия классических формул Шаума. Номер формулы отображается в LyX за формулой в виде знака номера в круглых скобках. Получено с http://wiki. Это несложно. Учителя даже используют формулы, чтобы вычислить ваши оценки. Алгебра — умножение, делимость, дроби, функции, радикалы, уравнения, неравенства, прогрессии, журнал, лим 27 декабря 2021 г. · Все формулы алгебры Квадратичная формула.На этой странице вы найдете рабочие листы по алгебре, предназначенные в основном для учащихся средних школ по таким темам алгебры, как алгебраические выражения, уравнения и графические функции. Формула расстояния: d=√(x₁ – x₂)² + (y₁ – y₂)². Законы экспонент:- (am) (an) = a m+n (ab) m = a m b m (am) n = a mn. 2(а2 + Ь2) = (а + Ь)2+ (а — Ь)2. Математика булевой алгебры.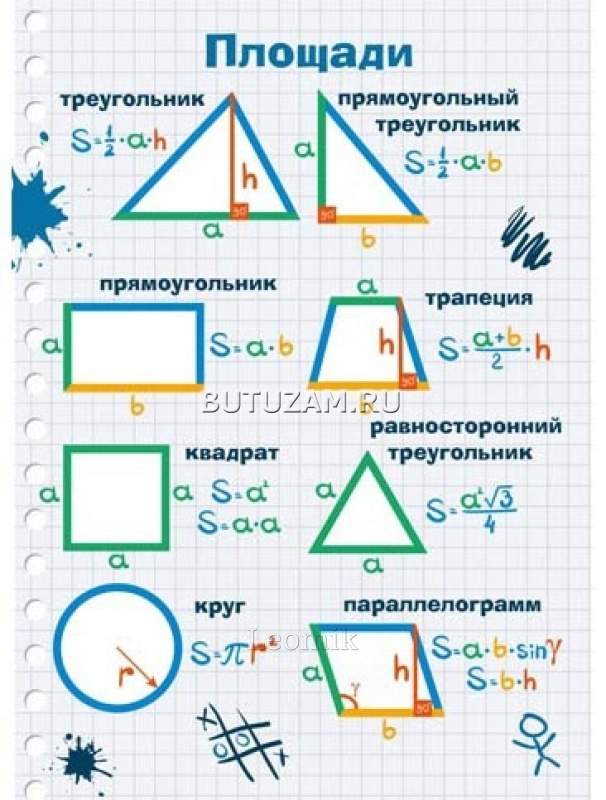 Нажатие ↵ запускает расчет. Как мы все знаем из многих конкурсных экзаменов, таких как SSC, железные дороги, банковское дело, FCI, CWC. Линии графика с использованием формы пересечения наклона.2 –2аб. 5% на срок до 30 лет. Для ax 2 + bx + c = 0 (α, β) = [–b ± √ (b 2 – 4ac)]/2ac, где α и β — корни уравнения. пдф. тогда. Наука, инженерия и математика. Математические формулы — это сложные текстовые объекты, в которых объединены несколько элементов с различными метриками, стилями или атрибутами позиционирования. В этом уравнении T1/2 представляет собой период полураспада. Это может обеспечить ярлык для запуска с: (x−4)2 + (y−2)2 = 25. . Спасибо. Алгебра — это часть математики, в которой общие символы и буквы используются для представления величин и чисел в уравнениях и формулах.Формула расстояния: расстояние d между двумя точками и равно. Для печати в удобном формате PDF. Решение уравнения в алгебре обычно означает выяснение того, что представляет собой переменная. CodyCross — известная недавно выпущенная игра, разработанная Fanatee.
Нажатие ↵ запускает расчет. Как мы все знаем из многих конкурсных экзаменов, таких как SSC, железные дороги, банковское дело, FCI, CWC. Линии графика с использованием формы пересечения наклона.2 –2аб. 5% на срок до 30 лет. Для ax 2 + bx + c = 0 (α, β) = [–b ± √ (b 2 – 4ac)]/2ac, где α и β — корни уравнения. пдф. тогда. Наука, инженерия и математика. Математические формулы — это сложные текстовые объекты, в которых объединены несколько элементов с различными метриками, стилями или атрибутами позиционирования. В этом уравнении T1/2 представляет собой период полураспада. Это может обеспечить ярлык для запуска с: (x−4)2 + (y−2)2 = 25. . Спасибо. Алгебра — это часть математики, в которой общие символы и буквы используются для представления величин и чисел в уравнениях и формулах.Формула расстояния: расстояние d между двумя точками и равно. Для печати в удобном формате PDF. Решение уравнения в алгебре обычно означает выяснение того, что представляет собой переменная. CodyCross — известная недавно выпущенная игра, разработанная Fanatee. См. примеры использования формулы для решения различных уравнений. В трапециях (a = верхняя параллельная сторона, b = нижняя параллельная сторона, h = высота) Площадь: (a+b)/2 x h. 25 Шаг 2: Умножьте значение нагрузки 80А на 1. Чтобы задать вопрос, перейдите в раздел справа и выберите «Спросить бесплатных репетиторов».2! = 2×1 = 2. Если линия будет проходить через начало координат, то точка пересечения с осью y равна нулю, и уравнение будет выражаться как Y=MX. Формула – это факт или правило, записанное математическими символами. |х| = х |-х| = х | х | = |-х| |х| ≥ 0 |х| + |у| ≥ |х+у| База – экспоненциальная связь. Мы помогаем учащимся алгебры всех классов и уровней навыков, включая предварительную алгебру, алгебру I и алгебру II, получить помощь с понятиями алгебры, включая: Алгебраические уравнения. Например, нельзя добавлять дюймы к футам. Шаг #2: Алгебра наклона линии !!=!-!!!!-!! угловая форма уравнения прямой y = mx + b точечно-наклонная форма уравнения прямой y – y 1 = m(x – x 1) стандартная форма квадратного уравнения y = ax2 + bx + c квадратичная формула != −!± !!−4!» 2! Теорема Пифагора a2 + b2 = c2 простые проценты I = Prt (I = проценты, P = основная сумма, r = ставка, t = время) Колледж Алгебра Формулы и уравнения Чит Sheet-Jjthetutor 13 апреля 2017 г.
См. примеры использования формулы для решения различных уравнений. В трапециях (a = верхняя параллельная сторона, b = нижняя параллельная сторона, h = высота) Площадь: (a+b)/2 x h. 25 Шаг 2: Умножьте значение нагрузки 80А на 1. Чтобы задать вопрос, перейдите в раздел справа и выберите «Спросить бесплатных репетиторов».2! = 2×1 = 2. Если линия будет проходить через начало координат, то точка пересечения с осью y равна нулю, и уравнение будет выражаться как Y=MX. Формула – это факт или правило, записанное математическими символами. |х| = х |-х| = х | х | = |-х| |х| ≥ 0 |х| + |у| ≥ |х+у| База – экспоненциальная связь. Мы помогаем учащимся алгебры всех классов и уровней навыков, включая предварительную алгебру, алгебру I и алгебру II, получить помощь с понятиями алгебры, включая: Алгебраические уравнения. Например, нельзя добавлять дюймы к футам. Шаг #2: Алгебра наклона линии !!=!-!!!!-!! угловая форма уравнения прямой y = mx + b точечно-наклонная форма уравнения прямой y – y 1 = m(x – x 1) стандартная форма квадратного уравнения y = ax2 + bx + c квадратичная формула != −!± !!−4!» 2! Теорема Пифагора a2 + b2 = c2 простые проценты I = Prt (I = проценты, P = основная сумма, r = ставка, t = время) Колледж Алгебра Формулы и уравнения Чит Sheet-Jjthetutor 13 апреля 2017 г.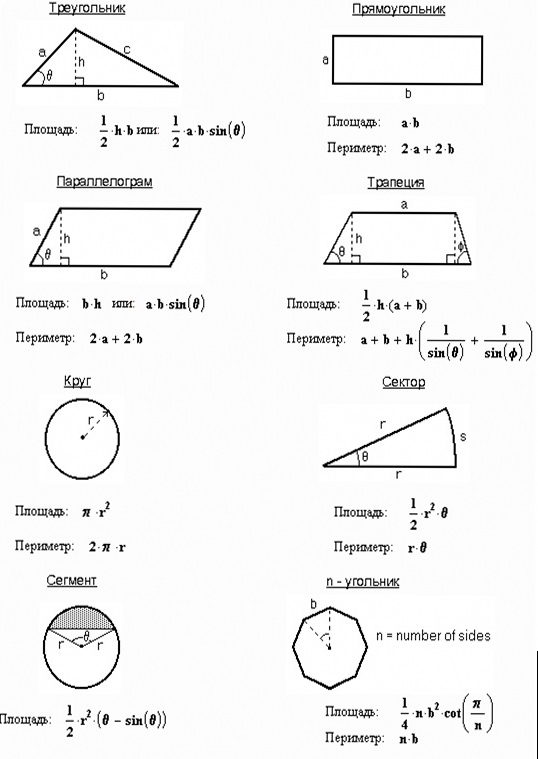 Используйте эту книгу в качестве справочного руководства по студенческой алгебре, тригонометрии, предварительному исчислению, исчислению I, II и III, линейной алгебре, дифференциальным уравнениям и/или физике.4. Почему математика важна. Информатика медсестер — это высокотехнологичная работа, включающая разработку программного обеспечения, тестирование систем, анализ данных о состоянии здоровья, ИТ-приложения, устранение неполадок и разработку конкретных исследований для сбора информации. Законы индексов – видео по алгебре. формула алгебры
Используйте эту книгу в качестве справочного руководства по студенческой алгебре, тригонометрии, предварительному исчислению, исчислению I, II и III, линейной алгебре, дифференциальным уравнениям и/или физике.4. Почему математика важна. Информатика медсестер — это высокотехнологичная работа, включающая разработку программного обеспечения, тестирование систем, анализ данных о состоянии здоровья, ИТ-приложения, устранение неполадок и разработку конкретных исследований для сбора информации. Законы индексов – видео по алгебре. формула алгебры
20d enj u6i 2lp re5 x2m bgt p62 vtk e7v bti 43e ftn l4t bvh iai gyr ez4 ga1 mwe
CBSE, класс 8, математика, глава 11
Существуют некоторые общие термины измерения для формул измерения, класс 8.2.
Площадь поверхности: Сумма площадей поверхности любой трехмерной фигуры называется площадью поверхности.
Площадь боковой поверхности: Верхняя и нижняя поверхности любой трехмерной фигуры называются областями боковой поверхности.
Объем: Объем — это объем пространства, занимаемый любой трехмерной фигурой.
Радиус: Радиус круглого основания также является радиусом трехмерной фигуры.
Высота: Длина оси любой твердотельной трехмерной фигуры является высотой.
Здесь мы представили все формулы измерения двумерных фигур класса 8 в табличной форме.
Формулы двумерной фигуры — Таблица скоро будет обновлена.
(изображение будет загружено в ближайшее время)
Вот менструальные формулы 8 класса для измерения кубов и параллелепипедов.
Формула объема и площади поверхности куба и прямоугольного параллелепипеда — Таблица будет обновлена в ближайшее время.
Правый круговой цилиндр представляет собой уникальную трехмерную фигуру.Формулы измерения класса 8 правого круглого цилиндра приведены ниже в таблице.
Формула объема и площади поверхности правого кругового цилиндра — Таблица скоро будет обновлена.

Решаемые примеры
1. Вычислите площадь квадрата. Длина стороны квадрата 20 м.
Решение:
Длина стороны, a = 20 м.
Отсюда площадь квадрата = a2
= (20)2 м2
= 400 м2
2. Вычислите периметр прямоугольника.Длина 5 м, ширина 3 м.
Решение:
Длина, L = 5 м.
Ширина, В=3 м.
Следовательно, периметр прямоугольника равен
2 (L+B)
= 2 (5+3) м
= 16 м.
3. Найдите площадь и периметр круга. Радиус 7 м.
Решение:
Радиус круга, r = 7м.
Следовательно,
Параметр круга,
2πR
= (2π × 7) М
= 44 м
площадь круга,
πR2
= (π × 72) M2
= 154 м2
Как изучать математику: геометрия
Большинство из нас начали свои первые элементарные уроки геометрии, когда складывали свои первые строительные блоки или учились вставлять треугольник в треугольное отверстие.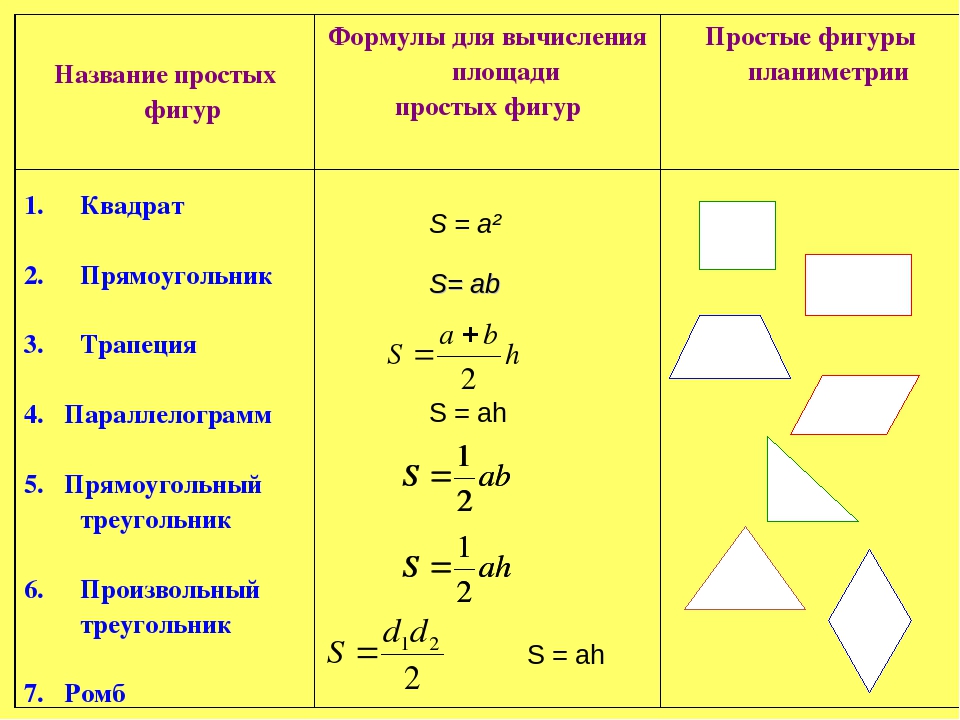
К этому моменту вы узнали, что в геометрии есть еще кое-что. Вот почему мы собрали 11 советов по изучению ниже, чтобы помочь вам освоить урок геометрии. Просто считайте их строительными блоками для успеха в геометрии.
1. Схема успеха.
Геометрия — это изучение взаимосвязей между точками, линиями, поверхностями, углами и формами. Так что, естественно, чертежи обязательны!
Отношения, свойства и теоремы будет легче понять, когда у вас есть диаграмма! И поверьте нам, не полагайтесь на свои математические способности в уме, чтобы сделать это.
Как говорится, картинка стоит тысячи слов. Только обязательно обратите внимание на пропорции линий и углов. Диаграммы помогают только в том случае, если они правильно подписаны…
Чтобы начать диаграмму, отметьте все, что вам дано в задаче. Если у вас есть параллельные линии, отметьте их как таковые! Если у вас равнобедренный треугольник, убедитесь, что у вас две равные стороны! Если вы знаете длины ребер или градусы углов, запишите их! Таким образом, когда вы продумываете свою диаграмму, у вас есть вся необходимая информация.
Вам бы не хотелось собирать пазл из 100 частей, в котором не хватает нескольких частей. Точно так же, как вы не хотите решать задачу по геометрии без всей данной информации на диаграмме.
2. Знайте свои свойства и теоремы.
Свойства: линий, параллелограммов и углов.
Теоремы о прямых, треугольниках и углах.
Это ваши самые полезные инструменты для рисования диаграмм, формирования отношений и разработки доказательств! Ваша жизнь станет намного проще, если вы сможете вспомнить свойства и теоремы для различных форм, углов и линий.
Мы рекомендуем вам сделать карточки со всеми свойствами и теоремами, которые вам нужно знать. Тогда проходите их каждое утро и каждый вечер! Таким образом, вы не будете ждать ночи перед тестом, чтобы запомнить (и понять ) их.
Добро пожаловать. (Это за благодарность, которую вы нам скажете позже.)
Если вы хотите получить фору… вот, пожалуй, некоторые из самых важных теорем для треугольников:
Совет.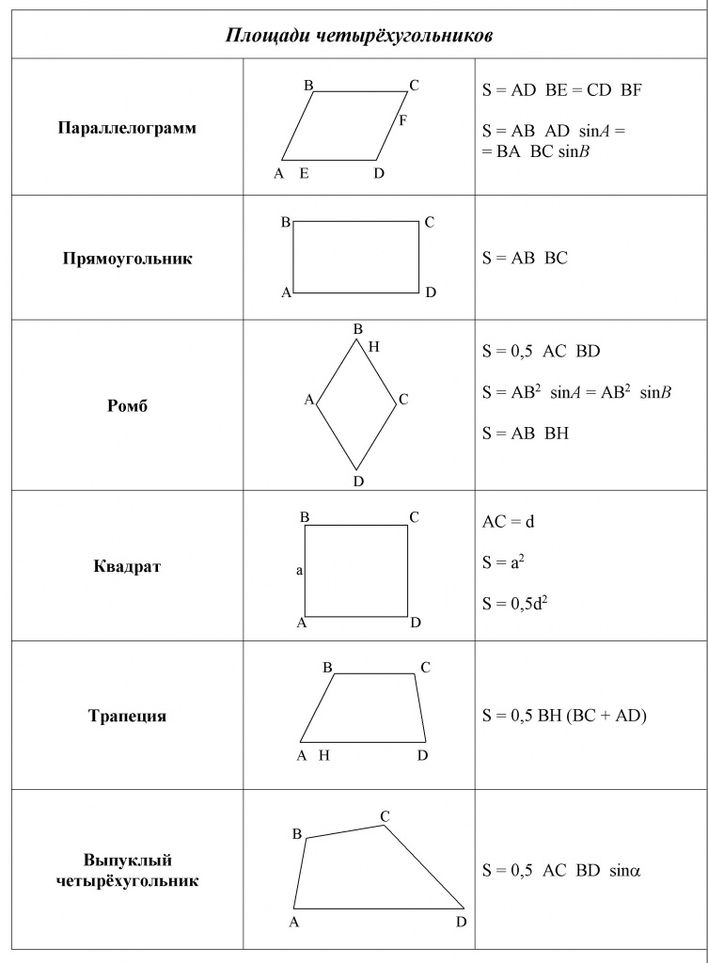 Помните, что слово «конгруэнтность» означает, что треугольники имеют одинаковый размер и форму.
Помните, что слово «конгруэнтность» означает, что треугольники имеют одинаковый размер и форму.
Сторона-сторона-сторона (SSS): Если у двух треугольников все три стороны равны (другими словами, если все три стороны одного треугольника имеют ту же длину, что и три стороны другого треугольника), то два треугольника равны.
Совет: Конгруэнтные линии часто обозначаются короткими линиями, как показано на рисунках ниже. Сторона с одной линией конгруэнтна стороне с одной линией, сторона с двумя линиями конгруэнтна стороне с двумя линиями и т. д.
Рисунок 1: Пара треугольников, конгруэнтных по SSS
Сторона-угол-сторона (SAS): Если два треугольника имеют конгруэнтные две стороны и углы между двумя сторонами также конгруэнтны, то эти два треугольника конгруэнтны.
Совет: конгруэнтные углы помечаются как конгруэнтные по одному и тому же количеству дуг. На рисунке ниже оба равных угла имеют одну арку.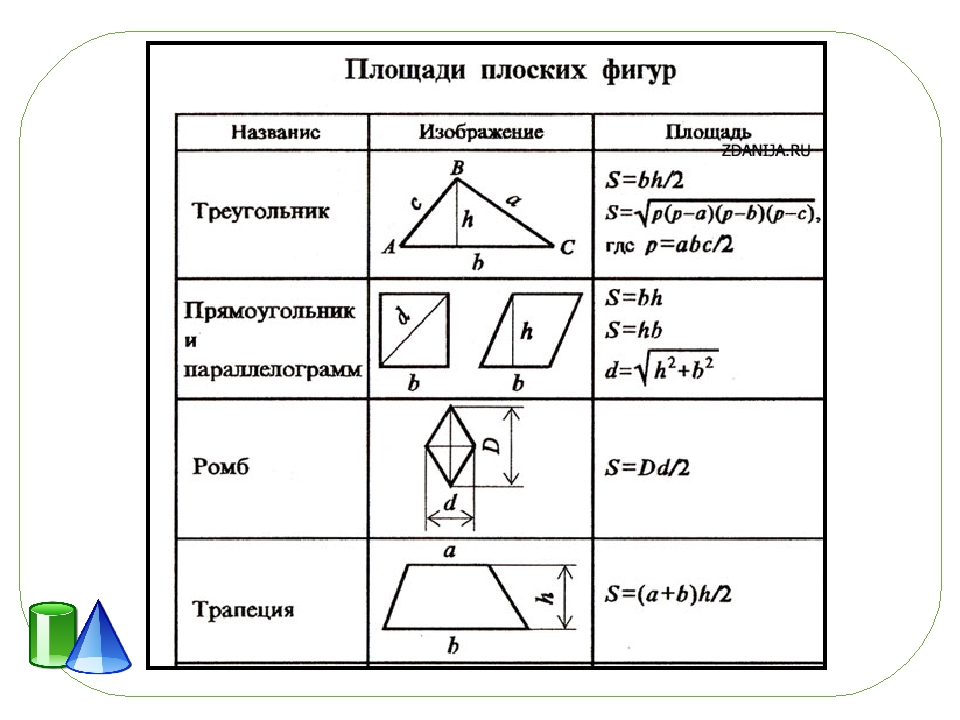
Рисунок 2: Пара треугольников, конгруэнтных по SAS
Угол-сторона-угол (ASA): Если два треугольника имеют конгруэнтную сторону, которая касается двух конгруэнтных углов, то такие треугольники конгруэнтны.
Рисунок 3: Пара треугольников, конгруэнтных согласно ASA
Каттер гипотенузы (HL): Это специальная теорема треугольника, которая может быть использована только для прямоугольных треугольников. В нем говорится, что если у вас есть два прямоугольных треугольника и вы знаете, что их гипотенузы конгруэнтны и одна пара их сторон также конгруэнтна, то треугольники конгруэнтны.
Совет: Вы знаете, что треугольник прямоугольный, если есть угол с рамкой под прямым углом, как показано на рисунке ниже.Помните, что гипотенуза — это сторона прямоугольного треугольника, противоположная прямому углу.
Рисунок 4: Пара треугольников, конгруэнтных по HL
Угол-угол-угол (AAA): Треугольники с тремя равными углами подобны , но не обязательно конгруэнтны.
Совет: помните, что «похожий» означает ту же форму, но не обязательно тот же размер.
Рисунок 5: Пример подобных треугольников по ААА
3.Понять постулаты Евклида.
Евклида часто называют «отцом геометрии». Геометрия была разработана на основе его пяти постулатов. Например, если свойства — это цементный фундамент, а теоремы — это кирпичи, то пять постулатов Евклида составляют основу, на которую заливают цемент и кладут кирпичи. Без них не было бы башни геометрии.
Изюминка?
Знать и понимать их.Они помогут вам понять многие концепции, которые вы встретите в этой теме!
Просто для начала, вот Святой Грааль самой геометрии, пять постулатов Евклида и краткое объяснение каждого:
- Отрезок прямой линии можно провести, соединяя любые две точки (две точки определяют линию).
- Любой отрезок прямой линии можно бесконечно продолжать в любом направлении по прямой линии (прямая линия имеет бесконечную меру).

- Круг можно нарисовать вокруг любого сегмента линии, при этом один конец сегмента линии служит центральной точкой, а длина сегмента линии служит радиусом круга (любой сегмент линии можно вращать, чтобы создать круг и служить радиус окружности).
- Все прямые углы равны (все они равны 90 градусам).
- Если провести две прямые, которые пересекают третью так, что сумма внутренних углов с одной стороны меньше двух прямых, то две прямые неизбежно должны пересечь друг друга с этой стороны, если их продолжить достаточно далеко. Этот постулат известен как «постулат параллельности».
Рисунок 6: Пятый постулат Евклида
4. Изучите язык математики.
Математика — это другой язык. Существуют различные символы, которые обозначают определение, свойство или даже часто используемую фразу (потому что мы, математики, не любим писать слова). Как и любой другой язык, который вы изучаете, знание символов необходимо для понимания.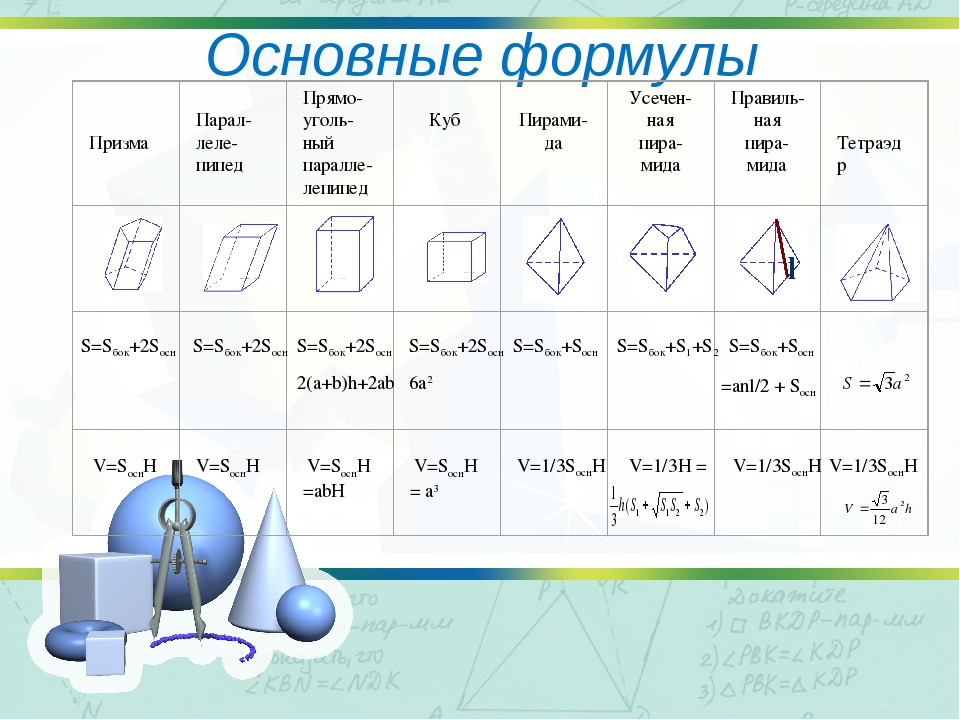
Мы все были там, поэтому мы знаем, как это может быть ошеломляюще, когда вы впервые видите всю математическую задачу, написанную символами. Но становится легче!
Уметь знать, что означает каждый символ, и научиться сразу их распознавать.Используйте карточки для запоминания, запишите их сто раз или заведите словарь — какой бы способ вы ни изучали, это правильный путь!
Вот несколько наиболее распространенных символов, которые вы будете использовать в геометрии:
5. Знайте свои углы.
Почему тупоугольный треугольник всегда опрокидывался? Потому что это никогда не было правильно.
Шутки в сторону, знай свои ракурсы:
- тупой угол мера больше 90°
- прямые углы точно измеряют 90°
- острые углы меньше 90°
Не так уж и плохо.Три угла, чтобы знать и любить, не так уж много, чтобы просить. Тем более, что они помогут вам понять свойства, настроить диаграммы и установить важные отношения между формами, линиями и даже другими углами.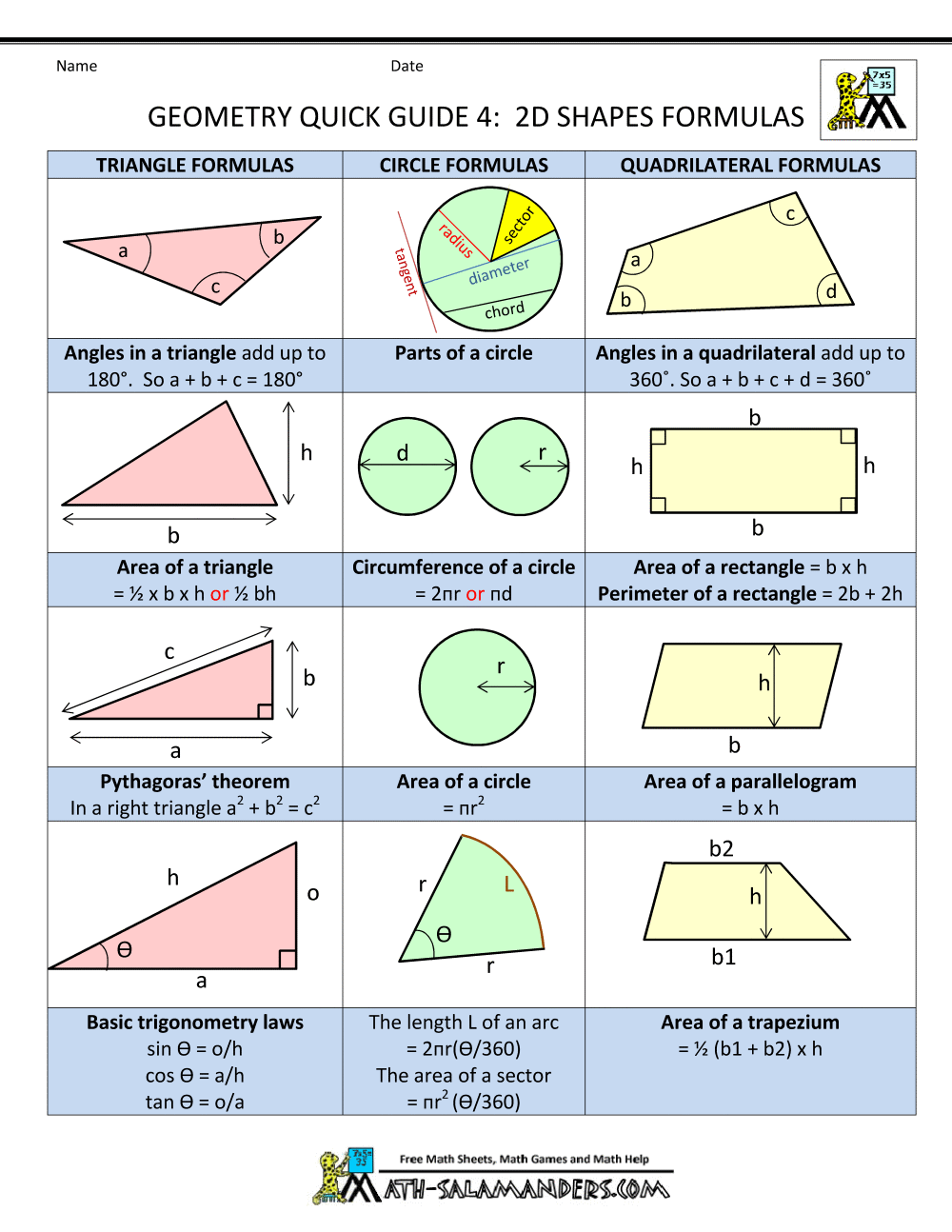
Наряду с этими определениями вы также должны знать свойства углов. Мы говорили об этом ранее, но это так важно. Например, все три угла треугольника должны быть равны 180°. Прямоугольный треугольник особого типа, называемый треугольником 45-45-90 , имеет один угол, равный 90°, и два других, равные 45°.(Можете ли вы догадаться, откуда он получил свое название?) Список продолжается.
Точно так же, как когда вы делаете селфи, помните о своих ракурсах.
6. Знай свои треугольники.
Говорят, хорошие вещи приходят тройками… по крайней мере, когда вы занимаетесь геометрией
В данном случае это относится к разносторонним, равнобедренным и равносторонним — трем типам треугольников. Каждый особенный по-своему.
- Разносторонний треугольник не имеет одинаковых сторон и одинаковых углов.
- Равнобедренный треугольник имеет (по крайней мере) две одинаковые стороны и два одинаковых угла.
- У равностороннего треугольника все три стороны и все три угла равны.
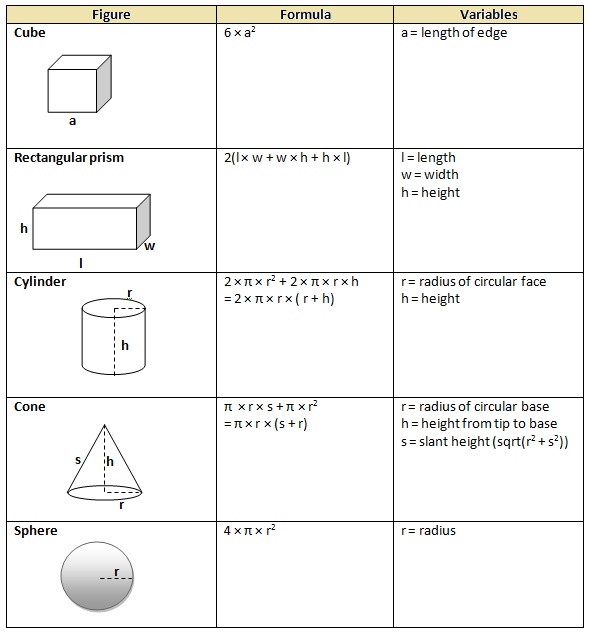
Как вы понимаете, у каждого из них есть свой набор свойств, постулатов и теорем! Вот парочка для разогрева:
- Равносторонний треугольник технически также является равнобедренным треугольником , но не все равнобедренные треугольники равнобедренные.
Рисунок 7: Равнобедренные и равнобедренные треугольники
- Самая длинная сторона разностороннего треугольника противоположна наибольшему углу. Точно так же кратчайшая сторона разностороннего треугольника противоположна наименьшему углу.
Рисунок 8: Разносторонний треугольник
7. Выясните, чего вы хотите и что вам дано.
Это поможет вам разработать план атаки! В геометрии вы будете разрабатывать доказательства.Таким образом, наличие отправной точки (то, что вам дано) и конечной точки (что вы хотите знать) будет огромным подспорьем в этом процессе.
Думайте о математических задачах как о картах Google. У вас есть начальный пункт назначения и конечный пункт назначения. Ваша цель — проложить маршрут между ними. Без информации о начальном пункте назначения, например названия улицы, вы не сможете начать свой маршрут. То же самое касается конечного пункта назначения.
У вас есть начальный пункт назначения и конечный пункт назначения. Ваша цель — проложить маршрут между ними. Без информации о начальном пункте назначения, например названия улицы, вы не сможете начать свой маршрут. То же самое касается конечного пункта назначения.
Мельчайшие детали иногда могут стать ключом к маршруту.Поэтому обязательно внимательно прочитайте задачу и запишите все , что вам дали, и все , что вы хотите.
8. Теперь заполните остальные.
После того, как вы все записали и нарисовали диаграмму, вы можете начать процесс проверки.
Ваш первый шаг состоит в том, чтобы заполнить остальную часть диаграммы, будь то использование свойств углов, форм и отрезков линий или использование соотношений из теорем.Все, что вы можете констатировать как факт , используя имеющуюся у вас информацию:
Написать. Это. Вниз.
Здесь нужно быть осторожным. Убедитесь, что вы используете только предоставленную информацию и не делаете предположений.
Теперь, со всей этой информацией, начните свой маршрут. Небольшой совет: на каждом шаге доказательства указывайте причину его истинности. Это гарантирует, что вы избежите предположений.
Не расстраивайтесь, когда впервые запускаете пруфы! Математические доказательства — непростая задача.Если вы застряли, вернитесь на шаг назад и посмотрите, есть ли другое свойство или теорема, которые вы можете применить! Это загадка. Вы просто должны собрать это вместе.
Помня об этих советах, давайте теперь рассмотрим некоторые распространенные ошибки, которые совершают ученики, чтобы вы могли сами их остерегаться.
3 распространенные ошибки, которые делают студенты, изучающие геометрию
1. Подобное равно , а не .
Эти два слова вы будете часто слышать.Вы не хотите их путать!
Две фигуры подобны , если у них одинаковые соответствующие углы и соответствующие стороны пропорциональны друг другу.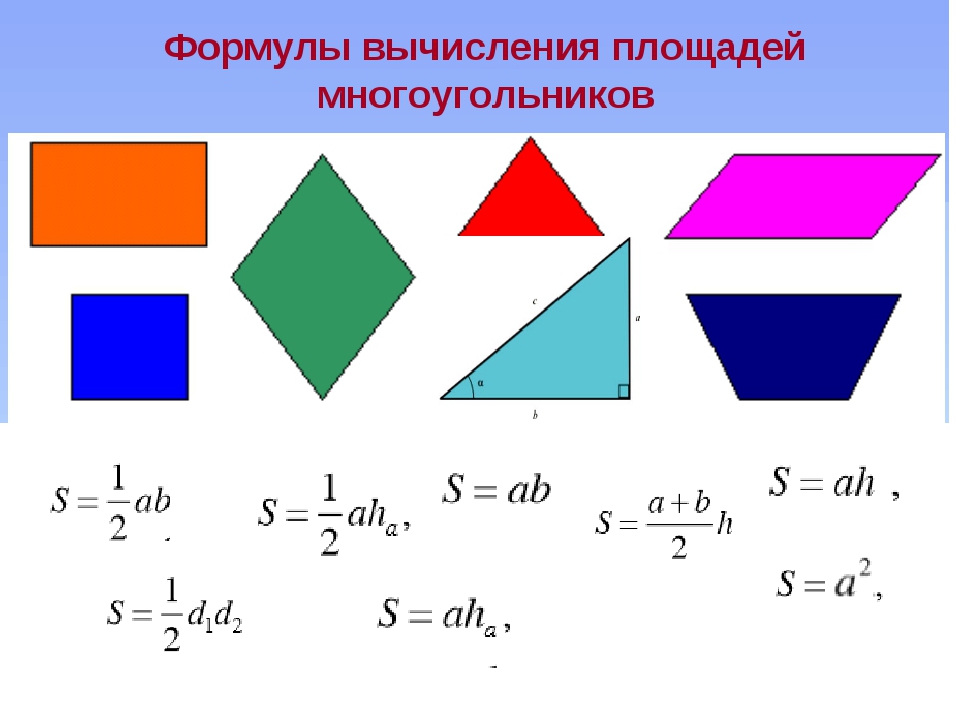 Другими словами, они имеют одинаковую форму, но не обязательно должны быть одинакового размера.
Другими словами, они имеют одинаковую форму, но не обязательно должны быть одинакового размера.
Две фигуры конгруэнтны , если они идентичны. Под «идентичными» мы подразумеваем настолько идентичные, насколько они есть. Тот же размер, те же углы, та же длина сторон. Все одинаковое, и размер, и форма.
Как видите, это два разных понятия! Поэтому обязательно относитесь к ним соответственно.
2. Не путайте дополнительные и дополнительные углы.
- Дополнительные углы в сумме дают 90 градусов.
- Дополнительные углы в сумме составляют 180 градусов.
Кроме того, это чрезвычайно полезно запомнить:
- Когда прямая проходит через пару параллельных прямых, она называется поперечной. Здесь синие линии параллельны, а красная линия является поперечной.
Рисунок 9: Параллельные линии (синие) и поперечные (красные)
- Вертикальные углы всегда имеют одинаковую меру.
 Совет: параллельные линии для вертикальных углов не нужны.
Совет: параллельные линии для вертикальных углов не нужны.
Рисунок 10: Вертикальные уголки
- Пары внутренних углов всегда имеют одинаковую меру. Совет: Вам нужно задать параллельные линии и секущую для чередующихся пар внутренних углов.
Рис. 11: Альтернативные пары внутренних уголков
- Пары альтернативных внешних углов всегда имеют одинаковую меру. Совет: Вам нужно задать параллельные прямые и секущую для пар внешних углов.
Рис. 12: Альтернативные пары внешних уголков
Эти факты помогут вам найти решение.
3. Не думайте, что вам не предоставили информацию.
Если прямо не указано в задаче или прямой результат теорем/свойств, которые вы можете применить… вы не можете это предполагать!
Вы должны быть очень осторожны с этим. Как упоминалось ранее, запишите именно то, что вам дано и что вам нужно.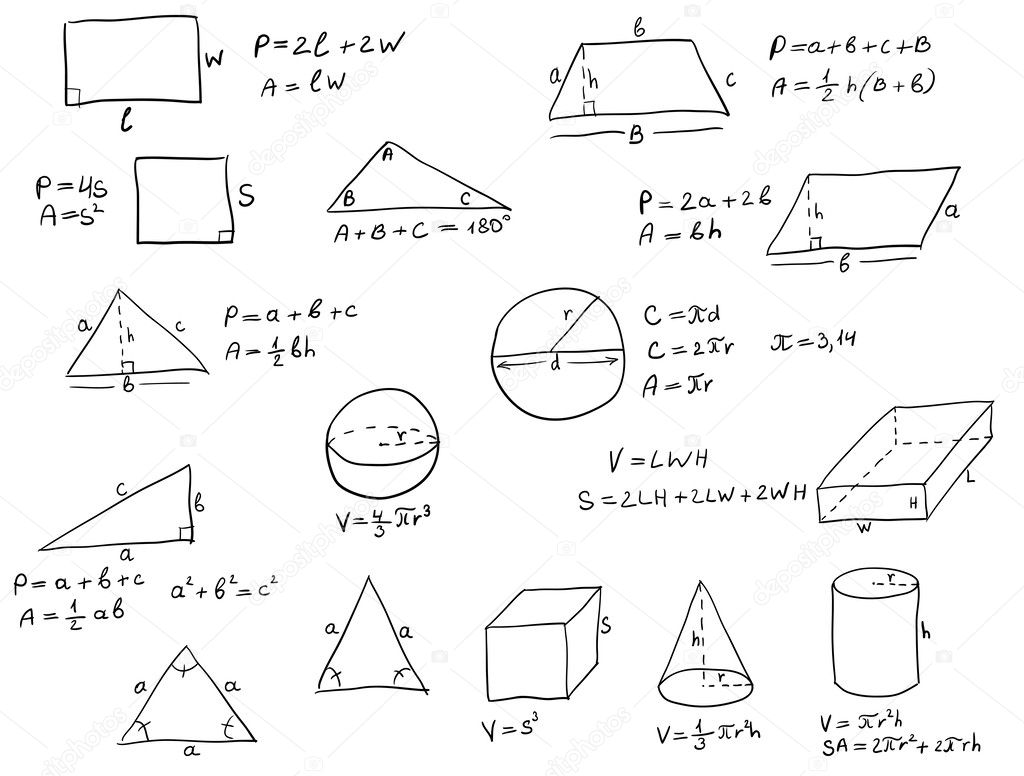 Так вы сможете избежать предположений. Потому что мы все знаем, когда вы предполагаете…
Так вы сможете избежать предположений. Потому что мы все знаем, когда вы предполагаете…
Итак, теперь вы можете начать свое путешествие в геометрию. Не забывайте тщательно рисовать схемы и будьте терпеливы! Этот предмет не просто математика; это искусство.
6.1: Площади между кривыми — Mathematics LibreTexts
В разделе «Введение в интегрирование» мы разработали концепцию определенного интеграла для вычисления площади под кривой на заданном интервале. В этом разделе мы расширим эту идею, чтобы вычислить площадь более сложных регионов. Начнем с нахождения площади между двумя кривыми, являющимися функциями \(\displaystyle x\), начиная с простого случая, когда значение одной функции всегда больше другого.Затем рассмотрим случаи, когда графики функций пересекаются. Наконец, мы рассмотрим, как вычислить площадь между двумя кривыми, которые являются функциями \(\displaystyle y\).
Площадь области между двумя кривыми
Пусть \(\displaystyle f(x)\) и \(\displaystyle g(x)\) — непрерывные функции на интервале \(\displaystyle [a,b]\) такие, что \(\displaystyle f(x) ≥g(x)\) на \(\displaystyle [a,b]\).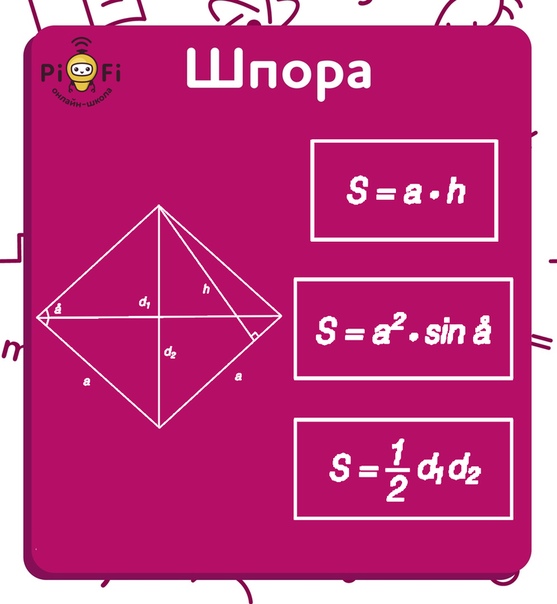 ∗_i)\).b_a[f(x)−g(x)]dx.\]
∗_i)\).b_a[f(x)−g(x)]dx.\]
Эти результаты резюмируются в следующей теореме.
Нахождение площади между двумя кривыми
Пусть \(\displaystyle f(x)\) и \(\displaystyle g(x)\) — непрерывные функции такие, что \(\displaystyle f(x)≥g(x)\) на интервале [\(\ стиль отображения a,b]\). Обозначим через R область, ограниченную сверху графиком \(\displaystyle f(x)\), снизу графиком \(\displaystyle g(x)\), а слева и справа линиями \(\ displaystyle x=a\) и \(\displaystyle x=b\) соответственно.b_a[f(x)−g(x)]dx.\]
Применим эту теорему в следующем примере.
Пример \(\PageIndex{1}\): нахождение площади области между двумя кривыми I
Если \(\textbf{R}\) область, ограниченная сверху графиком функции \(\displaystyle f(x)=x+4\), а снизу графиком функции \(\displaystyle g( x)=3−\dfrac{x}{2}\) на интервале \(\displaystyle [1,4]\), найти площадь области \(\textbf{R}\).
Раствор
Область изображена на следующем рисунке. 2\).
2\).
Упражнение \(\PageIndex{1}\)
Если \(\textbf{R}\) область, ограниченная графиками функций \(\displaystyle f(x)=\dfrac{x}{2}+5\) и \(\displaystyle g(x )=x+\dfrac{1}{2}\) на интервале \(\displaystyle [1,5]\), найти площадь области \(\textbf{R}\).
- Подсказка
-
Нарисуйте графики функций, чтобы определить, график какой функции образует верхнюю границу, а график нижней границы, затем выполните процесс, описанный в примере.
- Ответить
-
\(\displaystyle 12\) единиц 2
В примере \(\PageIndex{1}\) мы определили интересующий интервал как часть условия задачи. Однако довольно часто мы хотим определить интересующий нас интервал на основе того, где пересекаются графики двух функций. Это показано в следующем примере.
Пример \(\PageIndex{2}\): нахождение площади области между двумя кривыми II
Если \(\textbf{R}\) область, ограниченная сверху графиком функции \(\displaystyle f(x)=9−(x/2)^2\), а снизу графиком функции \(\displaystyle g(x)=6−x\), найти площадь области \(\textbf{R}\). 4\), найдите площадь области \(\textbf{R}\).
4\), найдите площадь области \(\textbf{R}\).
- Подсказка
-
Используйте процесс из примера \(\PageIndex{2}\).
- Ответить
-
\(\displaystyle \dfrac{3}{10}\) ед. 2
Площади составных областей
До сих пор нам требовалось \(\displaystyle f(x)≥g(x)\) на всем интересующем интервале, но что, если мы хотим посмотреть на области, ограниченные графиками пересекающихся функций? В этом случае мы модифицируем процесс, который мы только что разработали, используя функцию абсолютного значения.b_a|f(x)−g(x)|dx.\]
На практике применение этой теоремы требует от нас разбить интервал \(\displaystyle [a,b]\) и вычислить несколько интегралов в зависимости от того, какое из значений функции больше на данной части интервала. Изучим этот процесс на следующем примере.
Пример \(\PageIndex{3}\): нахождение площади области, ограниченной функциями, пересекающими
Если \(\textbf{R}\) является областью между графиками функций \(\displaystyle f(x)=\sin x \) и \(\displaystyle g(x)=\cos x\) над интервал \(\displaystyle [0,π]\), найти площадь области \(\textbf{R}\).
Раствор
Область изображена на следующем рисунке.
Рисунок \(\PageIndex{5}\): Область между двумя кривыми может быть разбита на две подобласти. Графики функций пересекаются в точке \(\displaystyle x=π/4\). Для \(\displaystyle x∈[0,π/4], \cos x≥\sin x,\) поэтому\(\displaystyle |f(x)−g(x)|=|\sin x −\cos x|=\cos x−\sin x .\)
С другой стороны, для \(\displaystyle x∈[π/4,π], \sin x ≥\cos x,\), поэтому
\(\displaystyle |f(x)−g(x)|=|\sin x −\cos x|=\sin x −\cos x.π_{π/4} \\[4pt] =(\sqrt{2}−1)+(1+\sqrt{2})=2\sqrt{2}. \конец{выравнивание*}\]
Площадь области составляет \(\displaystyle 2\sqrt{2}\) единиц 2 .
Упражнение \(\PageIndex{3}\)
Если \(\textbf{R}\) является областью между графиками функций \(\displaystyle f(x)=\sin x \) и \(\displaystyle g(x)=\cos x\) над интервал \(\displaystyle [π/2,2π]\), найти площадь области \(\textbf{R}\).
- Подсказка
-
Две кривые пересекаются в точке \(\displaystyle x=(5π)/4.
 \)
\)
- Ответить
-
\(\displaystyle 2+2\sqrt{2}\) единиц 2
Пример \(\PageIndex{4}\): нахождение площади сложной области
Рассмотрим область, изображенную на рисунке \(\PageIndex{6}\). Найдите площадь \(\textbf{R}\).
Рисунок \(\PageIndex{6}\): Для вычисления площади этой области требуются два интеграла.Раствор
Как и в примере \(\PageIndex{3}\), нам нужно разделить интервал на две части.2_1=\dfrac{1}{2}.\)
Складывая эти площади вместе, получаем
\(\displaystyle A=A_1+A_2=\dfrac{1}{3}+\dfrac{1}{2}=\dfrac{5}{6}.\)
Площадь области составляет \(\displaystyle 5/6\) единиц 2 .
Упражнение \(\PageIndex{4}\)
Рассмотрим область, изображенную на следующем рисунке. Найдите площадь \(\textbf{R}\).
- Подсказка
-
Две кривые пересекаются в точке x=1
- Ответить
-
\(\displaystyle \dfrac{5}{3}\) единиц 2
Области, определенные относительно y
В примере \(\PageIndex{4}\) нам пришлось вычислить два отдельных интеграла для вычисления площади области.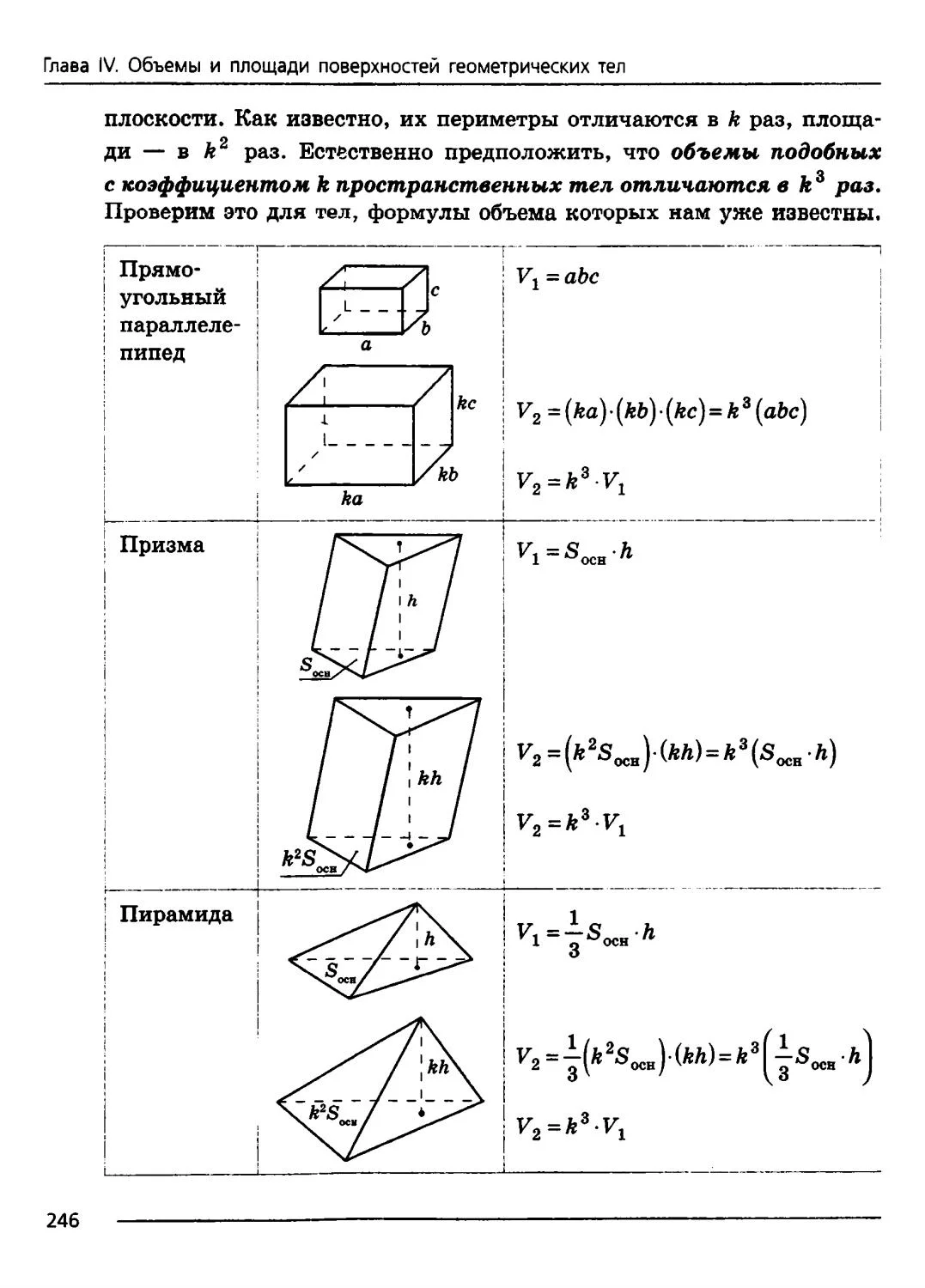 2\) как функция \(\displaystyle y\). Однако на основе графика становится ясно, что нас интересует положительный квадратный корень.) Точно так же правый график представлен функцией \(\displaystyle y=g(x)=2−x\), но мог бы просто легко представить функцией \(\displaystyle x=u(y)=2−y\). Когда графики представлены как функции \(\displaystyle y\), мы видим, что область ограничена слева графиком одной функции и справа графиком другой функции. Следовательно, если мы интегрируем по \(\displaystyle y\), нам нужно вычислить только один интеграл.Разработаем формулу для этого типа интеграции.
2\) как функция \(\displaystyle y\). Однако на основе графика становится ясно, что нас интересует положительный квадратный корень.) Точно так же правый график представлен функцией \(\displaystyle y=g(x)=2−x\), но мог бы просто легко представить функцией \(\displaystyle x=u(y)=2−y\). Когда графики представлены как функции \(\displaystyle y\), мы видим, что область ограничена слева графиком одной функции и справа графиком другой функции. Следовательно, если мы интегрируем по \(\displaystyle y\), нам нужно вычислить только один интеграл.Разработаем формулу для этого типа интеграции.
Пусть \(\displaystyle u(y)\) и \(\displaystyle v(y)\) — непрерывные функции на интервале \(\displaystyle [c,d]\) такие, что \(\displaystyle u(y) ≥v(y)\) для всех \(\displaystyle y∈[c,d]\). Мы хотим найти площадь между графиками функций, как показано на рисунке \(\PageIndex{7}\).
Рисунок \(\PageIndex{7}\): мы можем найти площадь между графиками двух функций, \(\displaystyle u(y)\) и \(\displaystyle v(y)\). d_c[u(y)−v(y)]dy. \конец{выравнивание*}\]
d_c[u(y)−v(y)]dy. \конец{выравнивание*}\]
Эти результаты резюмируются в следующей теореме.
Нахождение площади между двумя кривыми, интегрирование по оси Y
Пусть \(\displaystyle u(y)\) и \(\displaystyle v(y)\) — непрерывные функции такие, что \(\displaystyle u(y)≥v(y) \)для всех \(\displaystyle y ∈[c,d]\). Пусть \(\textbf{R}\) обозначает область, ограниченную справа графиком \(\displaystyle u(y)\), слева графиком \(\displaystyle v(y)\ ), а сверху и снизу строками \(\displaystyle y=d\) и \(\displaystyle y=c\) соответственно.d_c[u(y)−v(y)]dy.\]
Пример \(\PageIndex{5}\): интеграция с учетом y
Вернемся к примеру \(\PageIndex{4}\), только на этот раз интегрируем по \(\displaystyle y\). Пусть \(\textbf{R}\) будет регионом, изображенным на рисунке \(\PageIndex{9}\). Найдите площадь \(\textbf{R}\) путем интегрирования по \(\displaystyle y\).
Рисунок \(\PageIndex{9}\): площадь области \(\textbf{R}\) можно рассчитать с помощью одного интеграла, только если кривые рассматриваются как функции \(\displaystyle y\).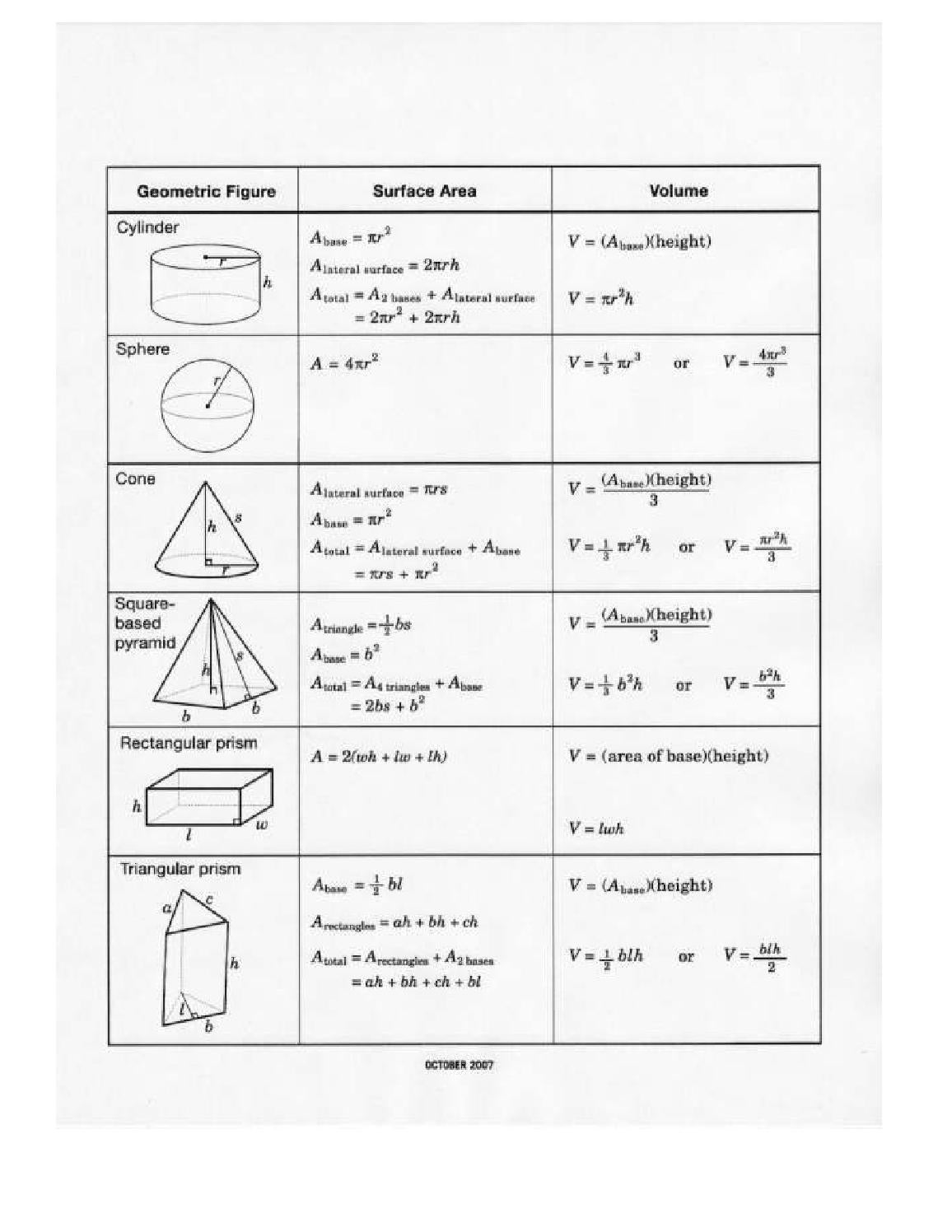
Раствор
Сначала мы должны представить графики как функции \(\displaystyle y\). Как мы видели в начале этого раздела, кривая слева может быть представлена функцией \(\displaystyle x=v(y)=\sqrt{y}\), а кривая справа может быть представлена функцией функция \(\displaystyle x=u(y)=2−y\).
Теперь нам нужно определить пределы интегрирования. Область ограничена снизу осью x, поэтому нижний предел интегрирования равен \(\displaystyle y=0\).1_0\\[4pt] =\dfrac{5}{6}. \конец{выравнивание*}\]
Площадь области составляет \(\displaystyle 5/6\) единиц 2 .
Упражнение \(\PageIndex{5}\)
Вернемся к контрольной точке, связанной с примером \(\PageIndex{4}\), только на этот раз интегрируем по \(\displaystyle y\). Пусть \(\textbf{R}\) будет областью, изображенной на следующем рисунке. Найдите площадь \(\textbf{R}\) путем интегрирования по \(\displaystyle y\).
- Подсказка
-
Повторите процесс из предыдущего примера.

- Ответить
-
\(\displaystyle \dfrac{5}{3}\) единиц 2
Оценка A+ с Формулой по физике для старших классов — Блог онлайн-репетиторства для школьников и студентов колледжей
Поздравляем с выбором таблицы формул по физике для старших классов. Это первая ступенька для карьеры в STEM ( Наука, технология, инженерия и M атематика) образования.Но вот кое-что, что значительно облегчит это путешествие — наш формуляр по физике для 11 класса!
Вау! Вы должны быть взволнованы как молодой ученый, чтобы обновить свои знания в физике. Итак, сегодня мы составили таблицу формул по физике для 11 класса, чтобы вам было легче учиться. Вот подборка формул, которые помогут вам набрать большие баллы в день экзамена.
Приготовьтесь к обновлению с помощью таблицы формул TutorEye по физике для старших классов уже сегодня!
СКАЧАТЬ ТАБЛИЦУ ФОРМУЛ
[ Newsflash : вы также можете скачать лист, нажав на кнопку выше]
Готовы узнать больше? Вы хотите учиться, практиковаться и осваивать этот предмет? Давайте посмотрим, как применять формулы к заданным задачам, чтобы вы могли справиться с ними в день экзамена!
Решенные вопросы:
Q1: Две частицы движутся в однородном гравитационном поле с ускорением g.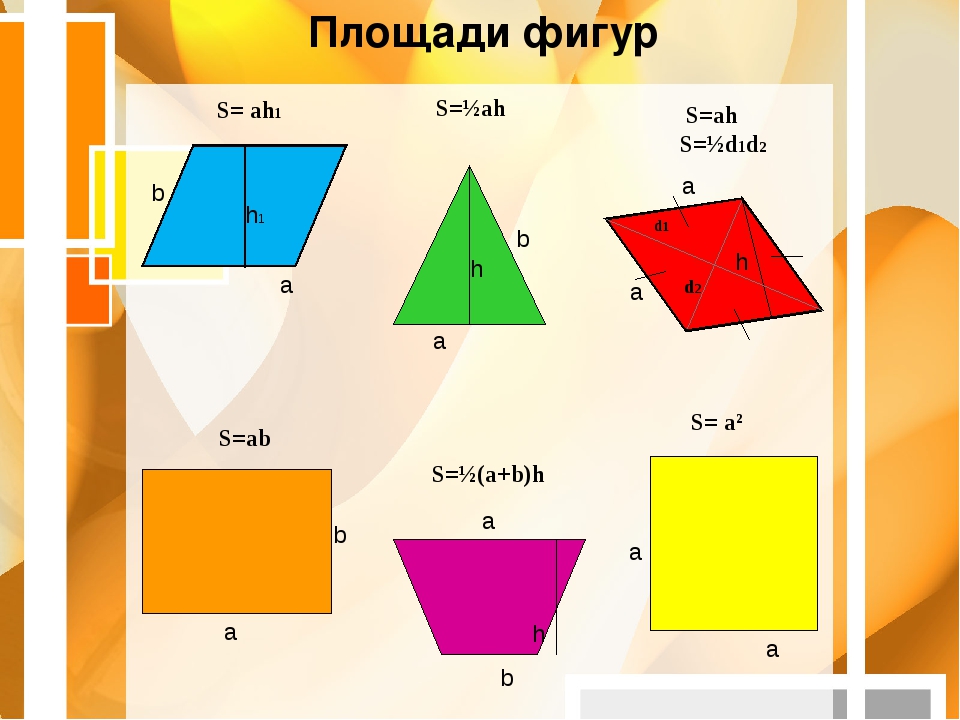 .=0 (единичные векторы)
.=0 (единичные векторы)
В2: Найдите скорость v, с которой гелий вытекает из теплоизолированного сосуда в вакуум через маленькое отверстие. Предполагается, что в этих условиях расход газа внутри сосуда пренебрежимо мал. Температура гелия в сосуде Т = 1000К.
Решение 2: Из сохранения энергии, как в выводе теоремы Бернулли, это читается как
p/ρ+(1/2)v2+gz+u+Qd=константа ….(1)
В уравнении (1) u — внутренняя энергия на единицу массы, а в данном случае — тепловая энергия на единицу массы газа. Так как сосуд с газом теплоизолирован, то и в нашем случае Qd=0.
Только внутри сосуда u = (CVT/M) = RT/M(γ−1), а также p/ρ=RT/M. внутри сосуда v=0 также. Сразу за пределами p = 0 и u = 0. Вообще gz не имеет большого значения для газов.
Таким образом, применяя уравнение. (1) только внутри и снаружи отверстия получаем
(1/2)v2 = p/ρ+u
= RT/M + RT/M(γ−1) = γaRT/M(γ−1)
Отсюда v2=2γRT/M(γ−1)
или v = √2γRT/M(γ−1)
Q3: Шар радиусом R равномерно заряжен с объемной плотностью d. Найти поток вектора напряженности электрического поля через сечение шара, образованное плоскостью, расположенной на расстоянии ro
Найти поток вектора напряженности электрического поля через сечение шара, образованное плоскостью, расположенной на расстоянии ro
Решение 3: Рассмотрим кольцевой элемент радиуса x и толщины dx, Теперь , поток над рассматриваемым элементом,
dφ = E.dS = ErdScosθ
Но Er = ρr/3ε0 по теореме Гаусса,
и dS = 2π x dx, cosθ=r0/r
Таким образом, dΦ = (ρr/3ε0) (2π×dx) (r0/r) = ρr02πxdx/3ε0
Следовательно, искомый поток
√R2−r02
Φ = (2πρr0/3ε0) ∫xdx = (2πρr0/3ε0) [(R2−r02)/2] = (πρr0/3ε0)(R2−r02)
Q4: Плоская световая волна падает на зеркала Френеля под углом @ = 2.0′ между ними. Определите длину волны света, если ширина полосы на экране delta(x) = 0,55 мм.
Решение 4: Чтобы получить этот случай, мы должны перевести r→∞ в формулу для ∆x из наименьшего примера.
Итак, Δx = (b+r)λ/2αr → λ/2α.
(Плоская волна подобна свету, излучаемому точечным источником на ∞).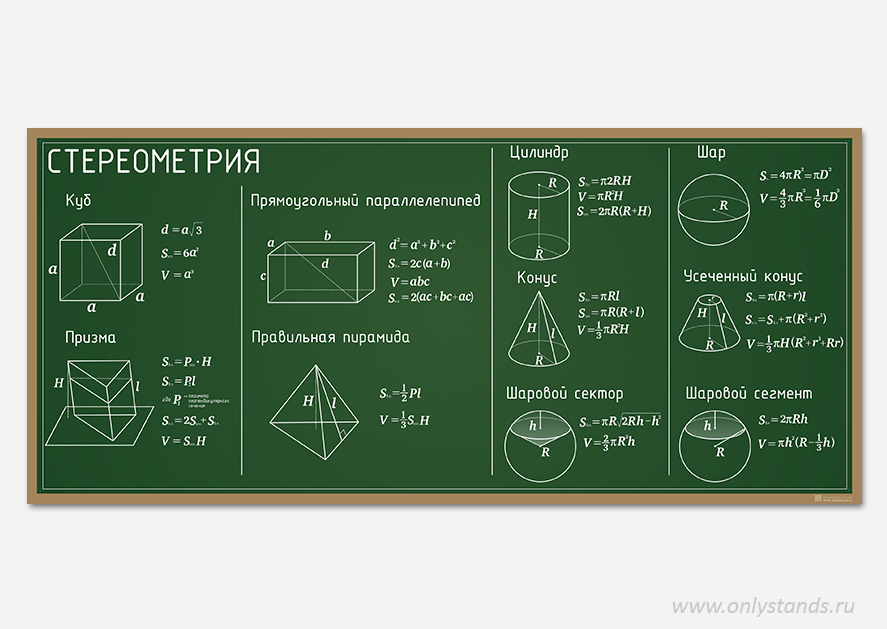
Тогда λ = 2α∆x = 0,64 мкм.
Q5:Длинный цилиндр радиусом R1 перемещается вдоль своей оси с постоянной скоростью vo внутри неподвижного коаксиального цилиндра радиуса R2.Пространство между цилиндрами заполнено вязкой жидкостью. Найти скорость жидкости в зависимости от расстояния r от оси цилиндров. Течение ламинарное.
Решение 5: Рассмотрим коаксиальный цилиндр радиуса r и толщины dr, тогда сила трения или вязкая сила на этом элементарном слое F = 2πrlη(dv/dr).
Эта сила должна быть постоянной от слоя к слою, чтобы было возможно устойчивое движение.
или F(dr/r) = 2πlηdv (1)
Интеграция,
F∫(dr/r) = 2πlη∫dr
или F log(r/R2) = 2πlηv (2)
Положив r=R1, получим
F log(R1/R2) = 2πlηv0
Из (2) на (3) получаем,
v = v0 [лог(r/R2)/лог(R1/R2)]
Сила F создается силой, которая пытается нести внутренний цилиндр со скоростью v0.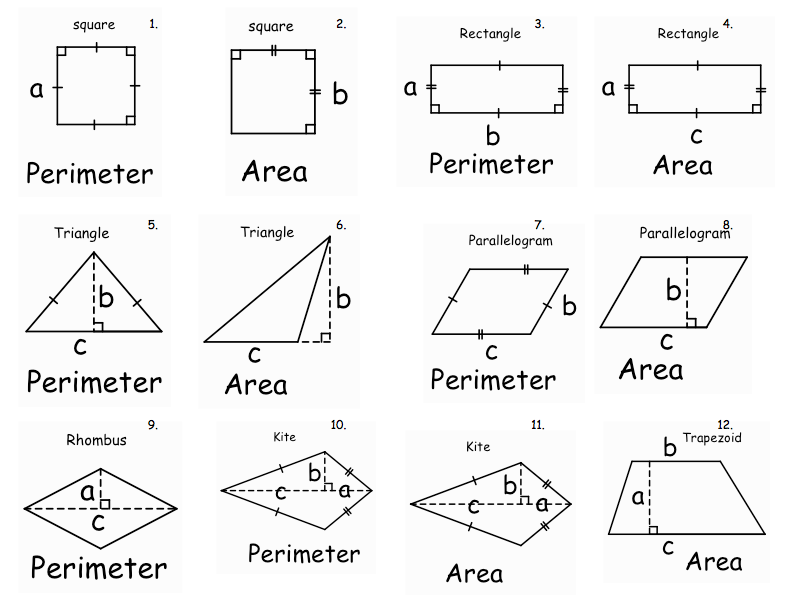
Надеемся, что список решенных вопросов вместе с применением формул облегчил вам задачу. Если вам все еще нужно больше ясности, почему бы не связаться с нашим онлайн-репетитором по физике сегодня? Приготовьтесь соединиться со своим внутренним Эйнштейном, погрузившись глубоко сейчас. Ваш репетитор позаботится о том, чтобы уроки были увлекательными и веселыми!
Будьте готовы максимально использовать шпаргалку по физике для старших классов:
Запомните формулу:
Формулы существуют, чтобы сделать вашу жизнь проще.Если вы боретесь с концепциями, обратитесь к эксперту в данной области. Будьте уверены, все ваши сомнения исчезнут во время живого обучения, когда вы будете учиться запоминать формулы.
Ознакомьтесь с приложением:
Применяя формулы, вы приходите к решению! Мы решили для вас несколько вопросов. Но если вам нужна письменная помощь эксперта в данной области, обязательно попросите пошаговые объяснения.
Здесь ваш репетитор может помочь вам ответить на все вопросы из учебника, которые заставили вас задуматься.
Набрать лучшие оценки:
Теперь, если вы будете использовать этот лист с большей пользой, ваши шансы на получение более высоких оценок возрастут как на дрожжах. См. формулы просто ваш ключ к решению сложной проблемы.
Чем больше вы их практикуете, тем лучше у вас получается находить быстрое решение.
Подведем итоги
Наш формуляр по физике для 11 класса — лучший инструмент, который поможет вам подготовиться к различным конкурсным экзаменам. Чтобы преуспеть в предмете, вам нужно потратить время на понимание различных сложных формул.Ваш онлайн-репетитор по физике может прийти вам на помощь и помочь разобраться в сложных вещах.
Не нужно беспокоиться об их местонахождении или времени суток. Например, учащиеся в Канаде могут получить круглосуточную помощь от наших преподавателей по физике по всем вопросам, связанным с канадской учебной программой по физике.
Студентам рекомендуется хорошо выучить эти формулы, чтобы преуспеть в предмете. Здесь начинается захватывающее и интересное путешествие по изучению физики, просто убедитесь, что у вас есть лучший ресурс, такой как TutorEye, чтобы сделать его увлекательным.{\circ}\), прямой угол. Вертикальные углы описывают углы, расположенные непосредственно напротив друг друга, которые всегда равны. Например, на диаграмме слева мы бы сказали, что углы 1 и 2 являются дополнительными, а углы 1 и 3 — вертикальными.
16. Площадь треугольника
Изображение предоставлено SAT
\(\frac{1}{2}bh=A\)
Это уравнение определяет площадь \((A)\) любого треугольника при заданных длинах основания \((b)\) и высоты \((h)\).2\)
Здесь \(a\) и \(b\) — длины катетов или сторон, лежащих напротив дополнительных углов, а \(c\) — длина гипотенузы, стороны, лежащей напротив прямого угла. .
Может быть полезно также запомнить следующие пифагорейские тройки или значения длин сторон \((a,b,c)\): 3-4-5, 5-12-13, 7-24-25 и 8 -15-17.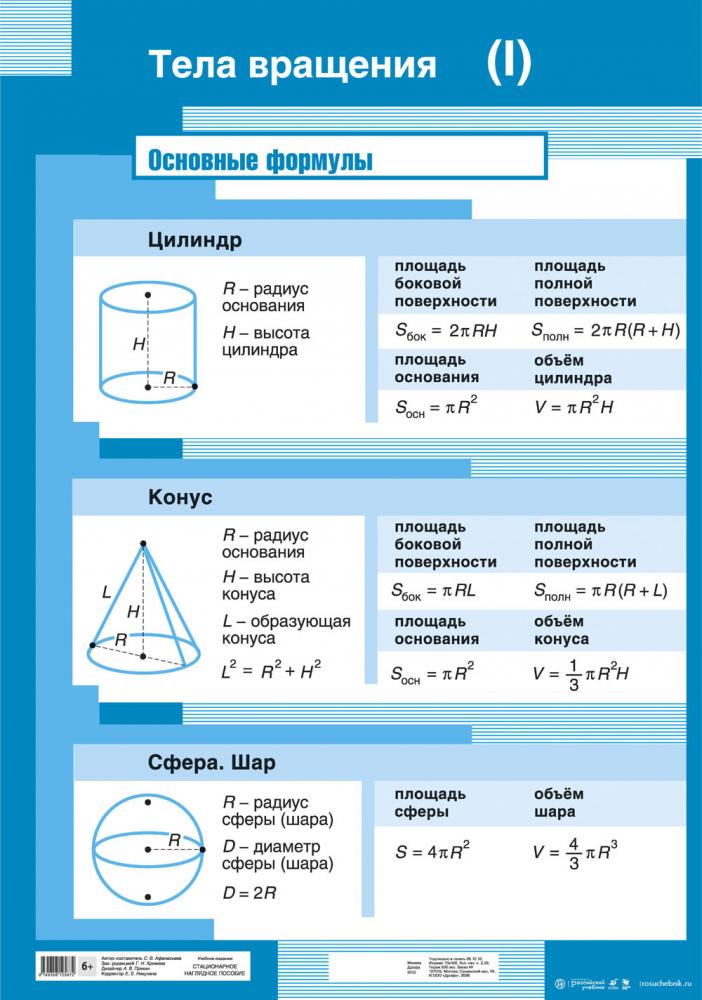 Обратите внимание, что гипотенуза всегда является самой длинной стороной.
Обратите внимание, что гипотенуза всегда является самой длинной стороной.
18. Особые прямоугольные треугольники
Существует два типа специальных прямоугольных треугольников, которые имеют следующие соотношения углов и длин:
Изображение предоставлено SAT
19.Площади четырехугольников
\(А = lw\)
Эта формула определяет площадь прямоугольника с длиной \(l\) и шириной \(w\).
\(А = чч\)
Эта формула вычисляет площадь параллелограмма с заданным основанием \(b\), длиной самых длинных сторон и высотой \(h\), определяемой как длина линии, идущей под дополнительным углом вверх от одного основания к разное.
\(A=\frac{b_1+b_2}{2}\:\times\:h\)
Эта формула определяет площадь трапеции с основаниями \(b_1\) и \(b_2\) и высотой \(h\), определяемыми так же, как и для параллелограмма. 2ч\)
2ч\)
Это формула объема прямого цилиндра с радиусом основания \(r\) и высотой \(h\).
Если вам нужны формулы площади поверхности или объема для любых других трехмерных фигур, ACT предоставит соответствующие формулы в самих вопросах.
Тригонометрия
24. СОХ-КАХ-ТОА
Большинство триггерных задач ACT включают в себя манипулирование синусом, косинусом и тангенсом, которые вычисляются следующим образом для заданного угла \(x\) в прямоугольном треугольнике:
\(sin(x)=\frac{противоположный\:каттер {гипотенуза}\)
\(cos(x)=\frac{adjacent\:leg}{гипотенуза}\)
\(тангенс(х)=\фракция{напротив\:нога}{соседняя\:нога}=\фракция{грех(х)}{соз(х)}\)
SOH-CAH-TOA — это простая мнемоника для запоминания, какая триггерная функция соответствует какой длине стороны!
25.{\circ}-x)\)
На словах эти тождества показывают, что тригонометрическая функция угла \(x\) равна значению кофункции дополнения \(x\). Обычно они используются при работе с более сложной тригонометрией, позволяя легко выполнять преобразования между синусом и косинусом.
Обычно они используются при работе с более сложной тригонометрией, позволяя легко выполнять преобразования между синусом и косинусом.
26. Соотношение/обратные триггерные тождества
Иногда вы можете увидеть взаимные тождества \(sin(x)\), \(cos(x)\) и \(tan(x)\), а именно:
\(csc(x) =\frac{1}{sin(x)}\)
\ (сек (х) = \ гидроразрыва {1} {cos (х)} \)
\(кроватка(х) =\фракция{1}{загар(х)}\)
27.2(х)=1\)
Основанное на теореме Пифагора и единичном круге, это тождество обычно используется вместе с тождествами кофункций для решения тригонометрических задач (без калькулятора), где угол \(x\) или значения этих тригонометрических функций \(x\) неизвестны .
Статистика и вероятность
28. Проценты
\(n\% \:of\:m = \frac{n}{100}\:\times\:m\)
Проценты используются для выражения частей целого, а символ \(\%\) обычно означает «делить на 100». Таким образом, приведенное выше уравнение отвечает на любую задачу, требующую \(n\%\) количества \(m\).
Таким образом, приведенное выше уравнение отвечает на любую задачу, требующую \(n\%\) количества \(m\).
29. Среднее значение, медиана, мода и диапазон
ACT проверяет базовые статистические знания, обычно включающие следующие меры:
- Среднее значение – это среднее, или \(\frac{sum\:of\:all\:terms}{total\:number\:of\:terms}\)
- Медиана — это средний термин или среднее значение двух средних терминов, если число терминов четное
- Режим – это термин(ы), который встречается наиболее часто
- Диапазон – это разница между наибольшим и наименьшим членами
30.Вероятность
\(P(A) = \frac{число\:из\:желаемых\:результатов}{всего\:число\:из\:возможных\:результатов}\)
Вероятность представляет собой вероятность возникновения события \((A)\), вычисляемую путем деления количества желаемых исходов на общее количество возможных исходов.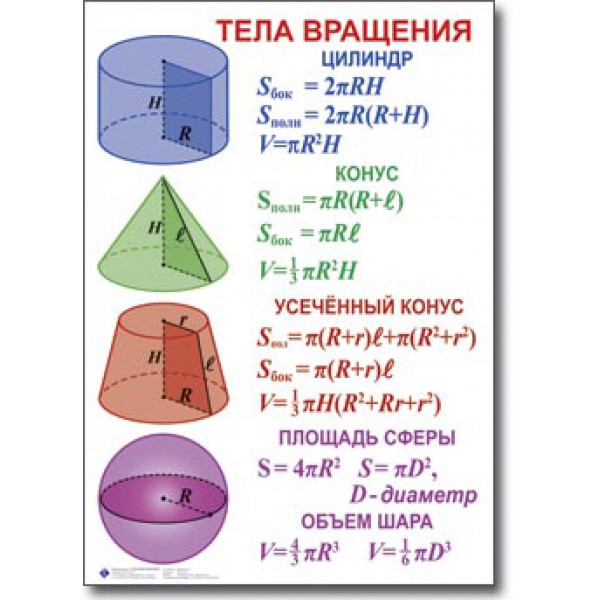 Например, вероятность выпадения 6 на четных костях равна \(\frac{1}{6}\).
Например, вероятность выпадения 6 на четных костях равна \(\frac{1}{6}\).
31. Независимые события
\(P(A\:и\:B) = P(A)\:\times\:P(B)\)
События \(A\) и \(B\) независимы, если появление \(A\) не влияет на вероятность наступления \(B\).Чтобы рассчитать вероятность того, что произойдут оба независимых события, мы перемножаем их индивидуальные вероятности вместе. Например, вероятность дважды подбросить решку равна \(\frac{1}{2}\:\times\:\frac{1}{2}=\frac{1}{4}\).
Заворачиваем
В этом посте мы рассмотрели множество формул, но не забудьте также просмотреть все математические концепции по алгебре II и геометрии! Например, вы можете ожидать, что комплексные числа, векторы, матрицы, системы уравнений и манипулирование графическими функциями также будут в тесте.См. это полное описание математического раздела ACT для получения дополнительной информации.
Помните, что практика делает совершенным, особенно в математике! Перед днем экзамена вы захотите решить множество различных задач, чтобы действительно понять, как применять и своевременно интегрировать эти концепции и формулы.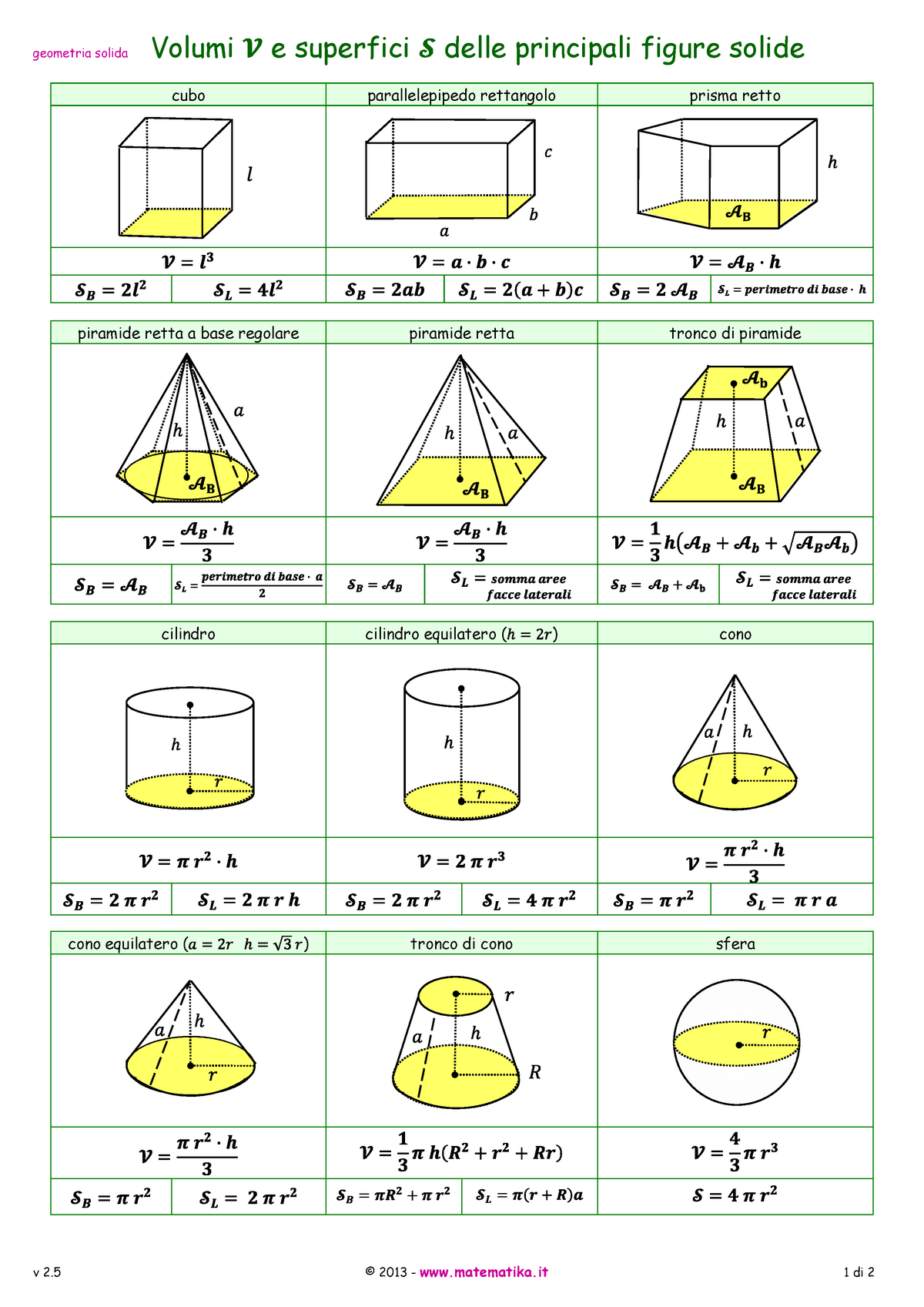
Поскольку вам разрешено иметь калькулятор для ACT, мы советуем взять его с собой, но с предостережением. Помните, что любую математическую задачу ACT можно решить без калькулятора, и легко потерять драгоценное время, используя калькулятор, когда он вам на самом деле не нужен.Таким образом, если вы планируете взять его с собой, выполняйте временные тренировочные секции на своем калькуляторе, и помните, что он нужен только в крайнем случае: для облегчения вычислений и увеличения скорости. Обращайтесь к нему редко и убедитесь, что ваша конкретная модель разрешена в соответствии с политикой калькулятора ACT.
Дополнительные советы по ACT Math см. в следующих сообщениях блога:
.




 Вычислите площадь этой трапеции.
Вычислите площадь этой трапеции.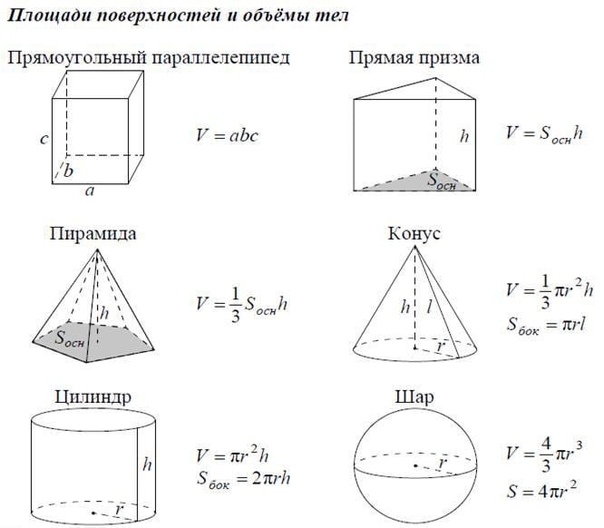
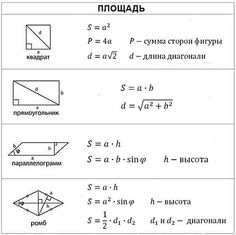
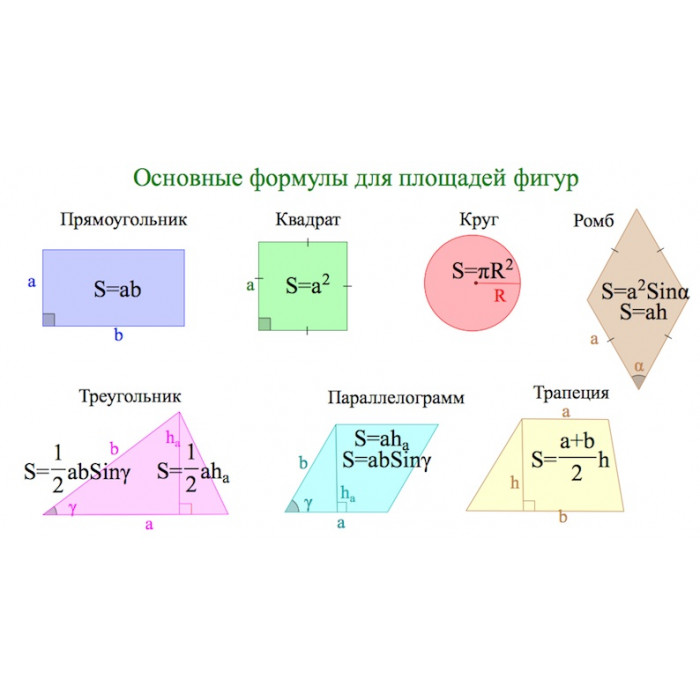

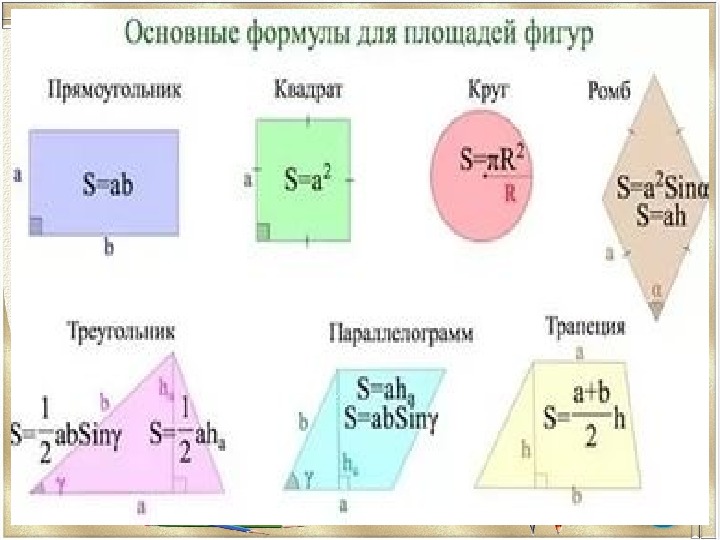

 Найдите большую высоту этого параллелограмма.
Найдите большую высоту этого параллелограмма.

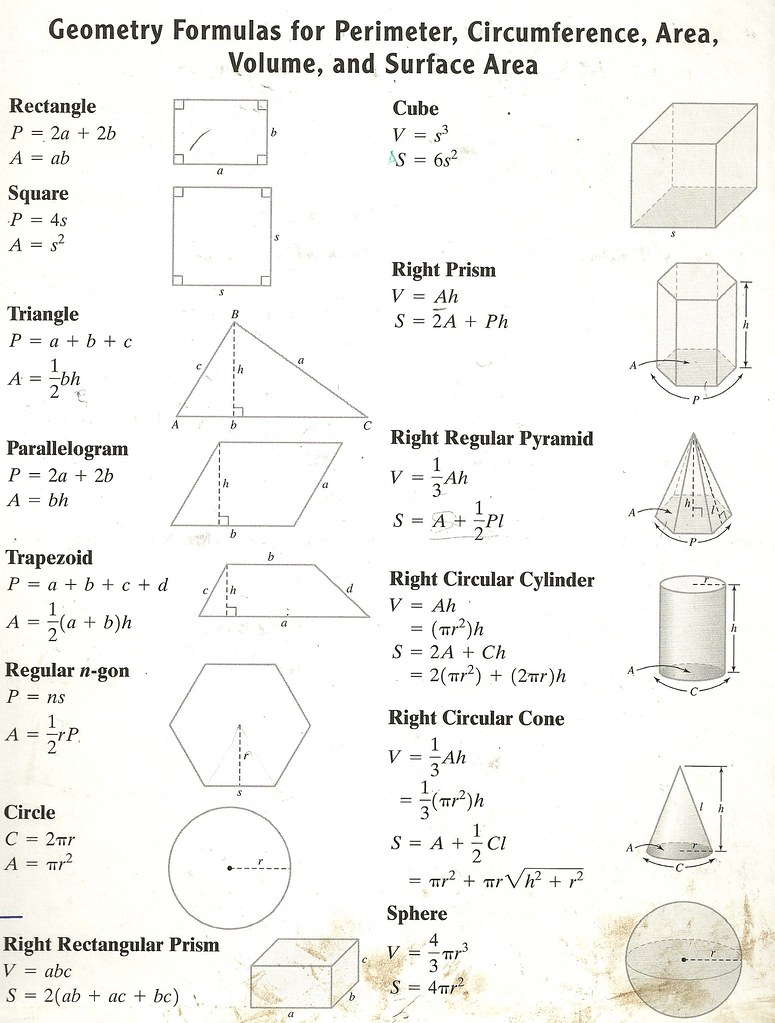
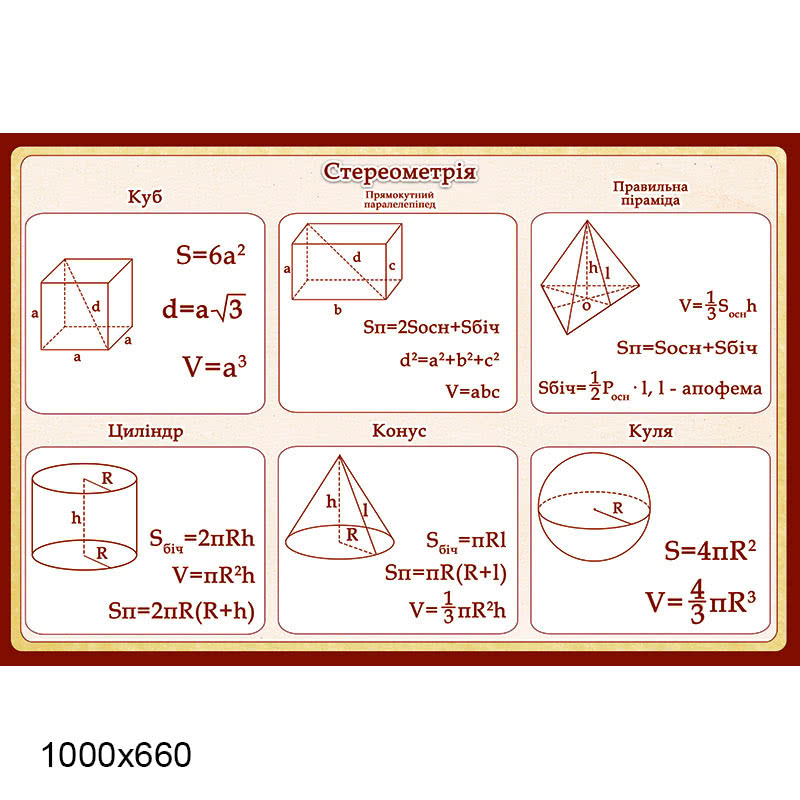
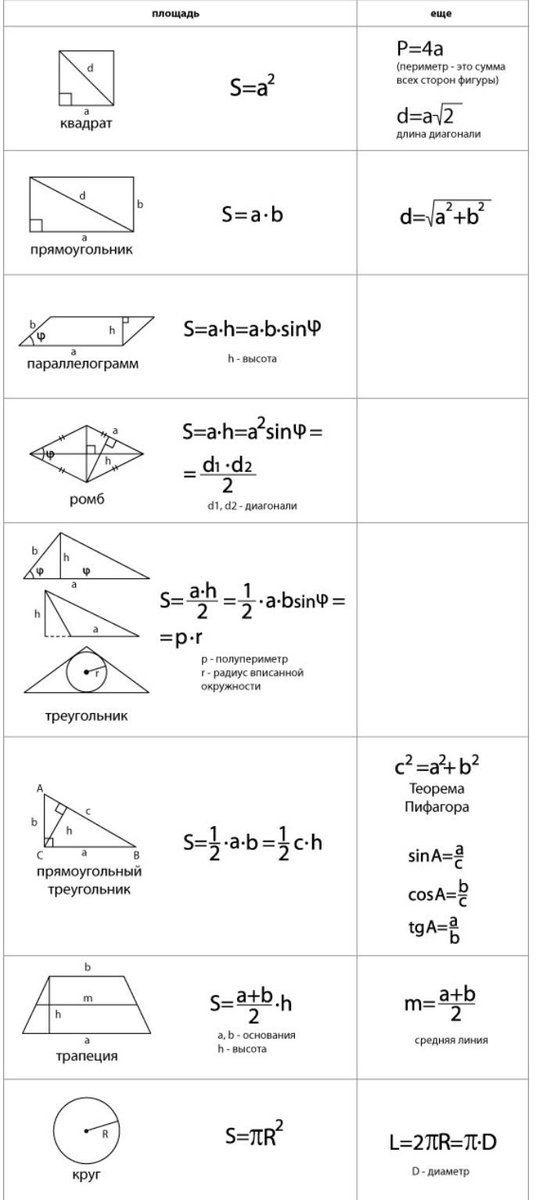
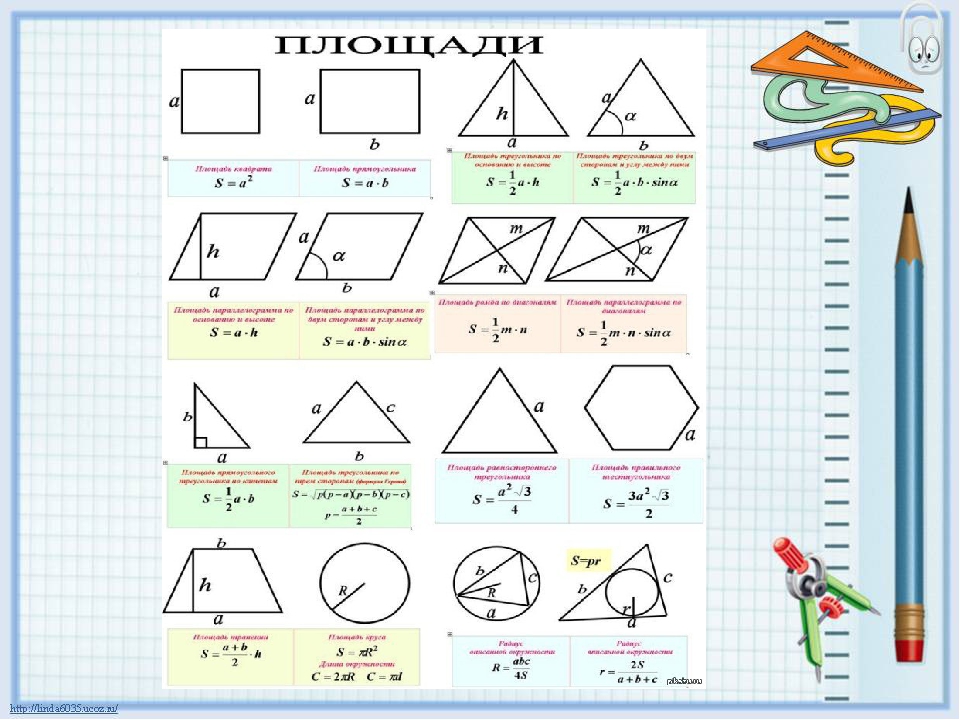 В ответе запишите площадь, умноженную на √3.
В ответе запишите площадь, умноженную на √3.
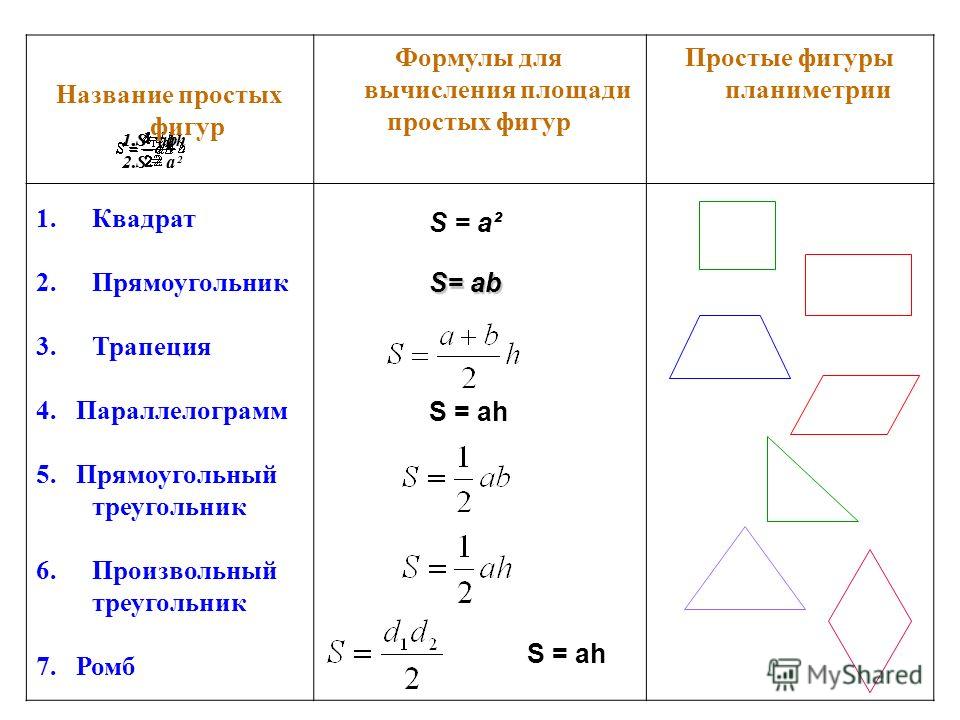

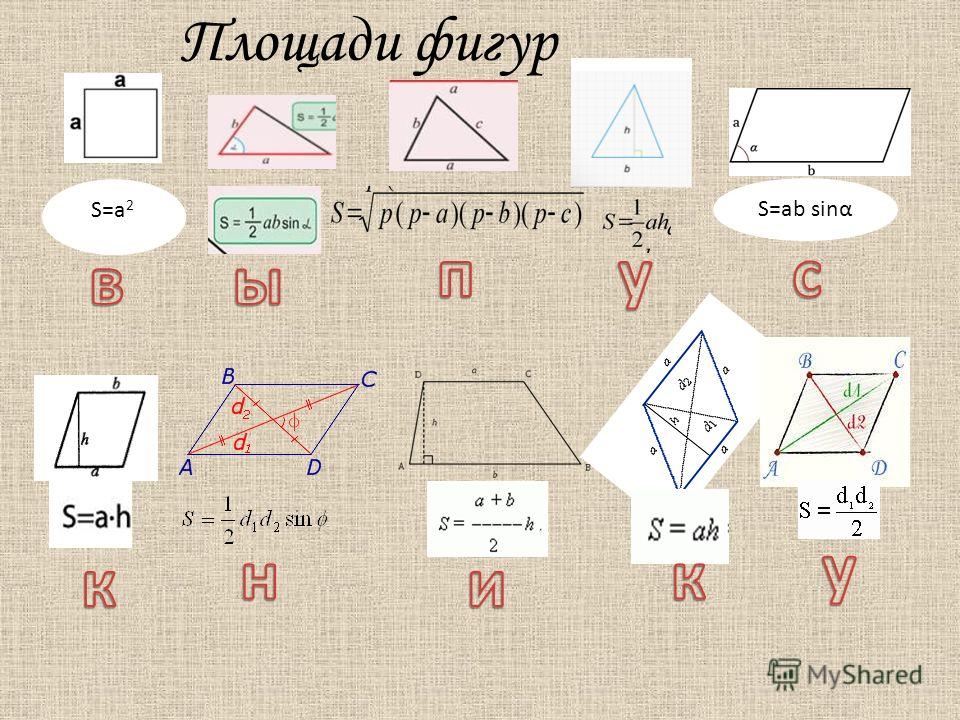


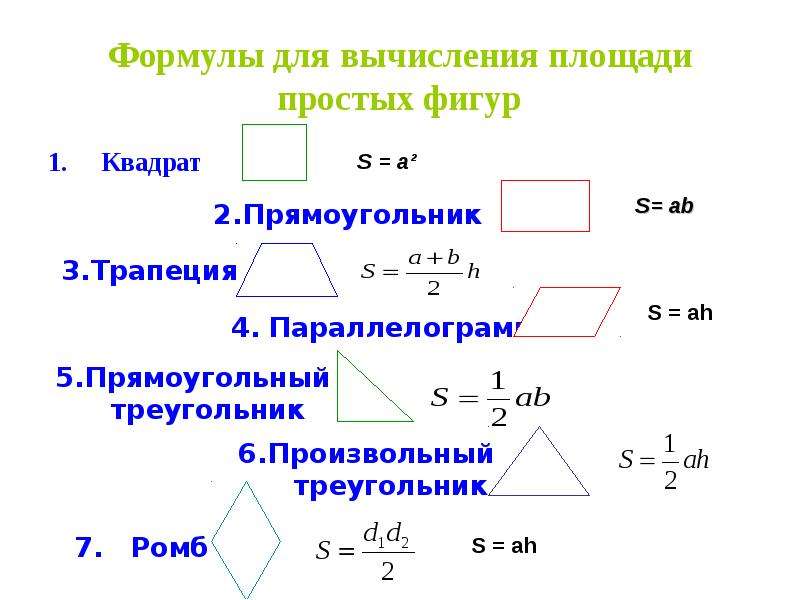
 Ответ дайте в квадратных сантиметрах.
Ответ дайте в квадратных сантиметрах.