Период и частота формулы: Период и частота колебаний, теория и онлайн калькуляторы

Амплитуда, частота, период колебаний — урок. Физика, 9 класс.

Рассмотрим величины, с помощью которых можно охарактеризовать колебания.

 

Рис. \(1\). Движение пустых качелей и качелей с мальчиком

 

Сравним колебания двух качелей на рисунке \(1\) — пустых качелей и качелей с мальчиком. Качели с мальчиком колеблются с большим размахом, то есть их крайние положения находятся дальше от положения равновесия, чем у пустых качелей.

Амплитудой колебаний \(A\) называется максимальное отклонение колеблющегося тела от положения равновесия.

\([A]=1~м\)

Полным колебанием называют движение, за которое тело возвращается в исходную точку (из которой началось колебание).

За одно полное колебание тело дважды максимально отклоняется от положения равновесия, поэтому один полный путь одного полного колебания равен четырём амплитудам: \(s=4A\).

  

Период колебаний — это промежуток времени, за который тело совершает одно полное колебание.
\([T]=1~с\) 

Пример:

ударим по столу двумя линейками — металлической и деревянной (рис. \(2\)) Линейки после этого начнут колебаться, но за один и тот же промежуток времени металлическая линейка (B) сделает больше колебаний, чем деревянная (A).

 

 

Рис. \(2\). Колебания металлической (B) и деревянной (A) линеек

Число колебаний в единицу времени называется частотой колебаний.

Обрати внимание!

Обозначается частота греческой буквой ν («ню»). За единицу частоты принято одно колебание в секунду. Эта единица в честь немецкого учёного Генриха Герца названа герцем (Гц).

Период колебания \(T\) и частота колебаний ν связаны следующей зависимостью:

T=1ν.

Свободные колебания в отсутствие трения и сопротивления воздуха называются собственными колебаниями, а их частота — собственной частотой колебательной системы.

Для описания закономерностей колебательной системы необходимо учитывать зависимость параметров колебания от параметров системы. Например, период колебаний и их частота зависят от массы груза и жёсткости пружины для физического маятника.

 

Рис. \(3\). Движение пустых качелей и качелей с мальчиком

 

Рассмотрим колебания двух одинаковых пустых качелей на рисунке \(3\). В один и тот же момент времени красные качели из положения равновесия начинают движение вперед, а зелёные качели из положения равновесия движутся назад. Движение качелей таково, что их амплитуды и периоды колебаний одинаковы. А если одинаковы периоды, то и частота колебаний совпадает. Однако, направлений движения качелей противоположно. О таких движениях говорят, что они движутся в противофазах.

 

Красные пустые качели и качели с мальчиком тоже колеблются с одинаковыми частотами. Направление скоростей этих качелей тоже совпадает. Это означает, что колебания происходят в одинаковых фазах, т.е. совпадают по фазе.

Фаза — физическая величина. Её используют для описания колебания тела.

 

Исходя из выше сказанного следует, что характеристиками колебательного движения являются:

• амплитуда,
• частота (можно использовать период),
• фаза.

Источники:

Рис. 1, 3. Движение пустых качелей и качелей с мальчиком.

Рис. 2. Колебания металлической и деревянной линеек.

Период, частота, амплитуда и фаза переменного тока

Период и частота переменного тока

Время, в течение которого совершается одно полное изме­нение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания пере­менного тока (рисунок 1).

Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.

Период выражают в секундах и обозначают буквой Т.

Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.

1 мс =0,001сек =10^-3сек.

1 мкс=0,001 мс = 0,000001сек =10^-6сек.

1000 мкс = 1 мс.

Число полных изменений ЭДС или число оборотов ради­уса-вектора, то есть иначе говоря, число полных циклов колеба­ний, совершаемых переменным током в течение одной секунды, называется

частотой колебаний переменного тока.

Частота обо­значается буквой f и выражается в периодах в секунду или в герцах.

Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.

1000 Гц = 10³ Гц = 1 кГц;

1000 000 Гц = 10⁶ Гц = 1000 кГц = 1 МГц;

1000 000 000 Гц = 10⁹ Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;

Чем быстрее происходит изменение ЭДС, то есть чем бы­стрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.

Математическая связь между периодом и частотой переменного тока и напряжения выра­жается формулами

Например, если частота тока равна 50 Гц, то период будет равен:

Т = 1/f = 1/50 = 0,02 сек.

И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек.), то частота будет равна:

f = 1/T=1/0,02 = 100/2 = 50 Гц

Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.

Частоты от 20 до 20 000 Гц называются звуковыми часто­тами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие вы­сокие частоты называются радиочастотами или колебаниями высокой частоты.

Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.

Амплитуда переменного тока

Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется

амплитудой ЭДС или силы переменного тока. Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно бук­вами Im, Em и Um (рисунок 1).

Угловая (циклическая) частота переменного тока.

Скорость вращения радиуса-вектора, т. е. изменение ве­личины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (оме­га). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.

Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.

Рисунок 2. Радиан.

Тогда,

1рад = 360°/2

Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в тече­ние одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f, то за одну секунду его ко­нец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ?.

Итак,

?= 6,28*f = 2f

Фаза переменного тока.

Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока. Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза пока­зывает, убывает ли ЭДС или возрастает.

Рисунок 3. Фаза переменного тока.

Полный оборот радиуса-вектора равен 360°. С началом но­вого оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следова­тельно, все фазы ЭДС будут повторяться в прежнем поряд­ке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обо­их этих случаях радиус-вектор занимает одинаковое положе­ние, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Как найти период колебаний волны. Основные формулы по физике

При изучении этого раздела следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебани.

Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивления среды, т.е. колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания и логарифмический декремент затухани.

Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает. Это явление называется резонансом.

Переходя к изучению электромагнитных волн нужно четко представлять, что электромагнитная волна — это распространяющееся в пространстве электромагнитное поле. Простейшей системой, излучающей электромагнитные волны, является электрический диполь. Если диполь совершает гармонические колебания, то он излучает монохроматическую волну.

Таблица формул: колебания и волны

Физические законы, формулы, переменные	Формулы колебания и волны
Уравнение гармонических колебаний: где х — смещение (отклонение) колеблющейся величины от положения равновесия; А — амплитуда; ω — круговая (циклическая) частота; α — начальная фаза; (ωt+α) — фаза.
Связь между периодом и круговой частотой:
Частота:
Связь круговой частоты с частотой:
Периоды собственных колебаний 1) пружинного маятника: где k — жесткость пружины; 2) математического маятника: где l — длина маятника, g — ускорение свободного падения; 3) колебательного контура: где L — индуктивность контура, С — емкость конденсатора.
Частота собственных колебаний:
Сложение колебаний одинаковой частоты и направления: 1) амплитуда результирующего колебания где А 1 и А 2 — амплитуды составляющих колебаний, α 1 и α 2 — начальные фазы составляющих колебаний; 2) начальная фаза результирующего колебания
Уравнение затухающих колебаний: е = 2,71. .. — основание натуральных логарифмов.
Амплитуда затухающих колебаний: где А 0 — амплитуда в начальный момент времени; β — коэффициент затухания;
Коэффициент затухания: колеблющегося тела где r — коэффициент сопротивления среды, m — масса тела; колебательного контура где R — активное сопротивление, L — индуктивность контура.
Частота затухающих колебаний ω:
Период затухающих колебаний Т:
Логарифмический декремент затухания:
Связь логарифмического декремента χ и коэффициента затухания β:

Характеристика колебаний

Фаза определяет состояние системы, а именно координату, скорость, ускорение, энергию и др.

Циклическая частота

характеризует скорость изменения фазы колебаний.

Начальное состояние колебательной системы характеризует начальная фаза

Амплитуда колебаний A — это наибольшее смещение из положения равновесия

Период T — это промежуток времени, в течение которого точка выполняет одно полное колебание.

Частота колебаний — это число полных колебаний в единицу времени t.

Частота, циклическая частота и период колебаний соотносятся как

Виды колебаний

Колебания, которые происходят в замкнутых системах называются свободными или собственными колебаниями. Колебания, которые происходят под действием внешних сил, называют вынужденными . Встречаются также автоколебания (вынуждаются автоматически).

Если рассматривать колебания согласно изменяющихся характеристик (амплитуда, частота, период и др.), то их можно разделить на гармонические , затухающие , нарастающие (а также пилообразные, прямоугольные, сложные).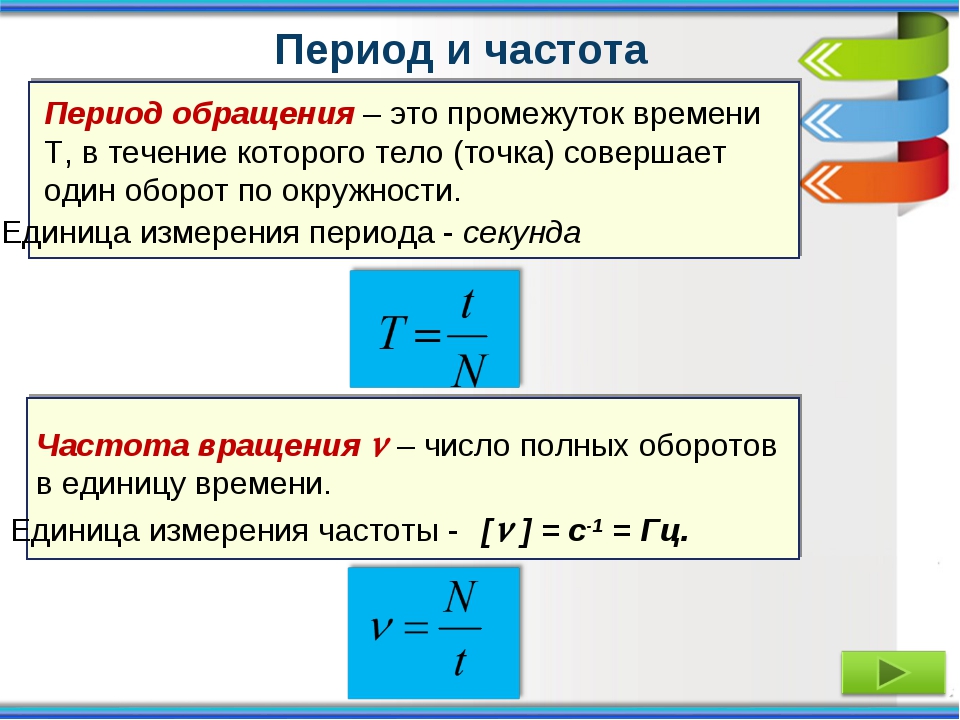

При свободных колебаниях в реальных системах всегда происходят потери энергии. Механическая энергия расходуется, например, на совершение работы по преодолению сил сопротивления воздуха. Под влиянием силы трения происходит уменьшение амплитуды колебаний, и через некоторое время колебания прекращаются. Очевидно, что чем больше силы сопротивления движению, тем быстрее прекращаются колебания.

Вынужденные колебания. Резонанс

Вынужденные колебания являются незатухающими. Поэтому необходимо восполнять потери энергии за каждый период колебаний. Для этого необходимо воздействовать на колеблющееся тело периодически изменяющейся силой. Вынужденные колебания совершаются с частотой, равной частоте изменения внешней силы.

Вынужденные колебания

Амплитуда вынужденных механических колебаний достигает наибольшего значения в том случае, если частота вынуждающей силы совпадает с частотой колебательной системы. Это явление называется резонансом .

Например, если периодически дергать шнур в такт его собственным колебаниям, то мы заметим увеличение амплитуды его колебаний.

Если влажный палец двигать по краю бокала, то бокал будет издавать звенящие звуки. Хотя это и незаметно, палец движется прерывисто и передает стеклу энергию короткими порциями, заставляя бокал вибрировать

Стенки бокала также начинают вибрировать, если на него направить звуковую волну с частотой, равной его собственной. Если амплитуда станет очень большой, то бокал может даже разбиться. По причине резонанса при пении Ф.И.Шаляпина дрожали (резонировали) хрустальные подвески люстр. Возникновение резонанса можно проследить и в ванной комнате. Если вы будете негромко пропевать звуки разной частоты, то на одной из частот возникнет резонанс.

В музыкальных инструментах роль резонаторов выполняют части их корпусов. Человек также имеет собственный резонатор — это полость рта, усиливающая издаваемые звуки.

Явление резонанса необходимо учитывать на практике. В одних явлениях он может быть полезен, в других — вреден. Резонансные явления могут вызывать необратимые разрушения в различных механических системах, например, неправильно спроектированных мостах. Так, в 1905 году рухнул Египетский мост в Санкт-Петербурге, когда по нему проходил конный эскадрон, а в 1940 — разрушился Такомский мост в США.

Явление резонанса используется, когда с помощью небольшой силы необходимо получить большое увеличение амплитуды колебаний. Например, тяжелый язык большого колокола можно раскачать, действуя сравнительно небольшой силой с частотой, равной собственной частоте колебаний колокола.

ЧАСТОТА КОЛЕБАНИЙ, числоколебаний в 1 с. Обозначается. Если T -периодот колебаний, то= 1/T; измеряется в герцах (Гц).Угловая частотаколебаний= 2= 2/T рад/с.

ПЕРИОД колебаний, наименьший промежуток времени, через который совершающая колебания системавозвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. Период -величина, обратная частоте колебаний.Понятие»период» применимо, например, в случае гармонических колебаний, однако часто применяется и для слабо затухающих колебаний.

Круговая или циклическая частотаω

При изменении аргумента косинуса, либо синуса на 2π эти функции возвращаются к прежнему значению. Найдем промежуток времени T, в течение которого фаза гармонической функции изменяется на 2π .

ω(t + T) + α = ωt + α + 2π, или ωT = 2π.

Время T одного полного колебания называется периодом колебания. Частотой ν называют величину, обратную периоду

Единица измерения частоты — герц (Гц), 1 Гц = 1 с -1 .

Круговая, или циклическая частоты ω в 2π раз больше частоты колебаний ν. Круговая частота — это скорость изменения фазы со временем. Действительно:

.

АМПЛИТУДА (от латинского amplitudo — величина), наибольшее отклонение от равновесного значения величины, колеблющейся по определенному, в том числе гармоническому, закону; смотри такжеГармонические колебания.

ФАЗА КОЛЕБАНИЙ аргумент функцииcos (ωt + φ), описывающей гармонический колебательный процесс (ω — круговая частота, t — время, φ — начальная фаза колебаний, т. е. фаза колебаний вначальный момент времениt = 0)

Смещение, скорость, ускорение колеблющейся системы частиц.

Энергия гармонических колебаний.

Гармонические колебания

Важным частным случаем периодических колебаний являются гармонические колебания, т.е. такие изменения физической величины, которые идут по закону

где . Из курса математики известно, что функция вида (1) меняется в пределах от А до -А, и что наименьший положительный период у нее. Поэтому гармоническое колебание вида (1) происходит с амплитудой А и периодом.

Не следует путать циклическую частоту и частоту колебаний. Между ними простая связь. Так как, а, то.

Величина называется фазой колебания. При t=0 фаза равна, потомуназывают начальной фазой.

Отметим, что при одном и том же t:

где — начальная фаза.Видно, что начальная фаза для одного и того же колебания есть величина, определенная с точнотью до. Поэтому из множества возможных значений начальной фазы выбирается обычно значение начальной фазы наименьшее по модулю или наименьшее положительное. Но делать это необязательно. Например, дано колебание, то его удобно записать в видеи работать в дальнейшем с последним видом записи этого колебания.

Можно показать, что колебания вида:

где имогут быть любого знака, с помощью простых тригонометрических преобразований всегда приводится к виду (1), причем,, ане равна, вообще говоря. Таким образом, колебания вида (2) являются гармоническими с амплитудойи циклической частотой. Не приводя общего доказательства, проиллюстрируем это на конкретном примере.

Пусть требуется показать, что колебание

будет гармоническим и найти амплитуду , циклическую частоту, периоди начальную фазу. Действительно,

—

Видим, что колебание величины S удалось записать в виде (1). При этом ,.

Попробуйте самостоятельно убедится, что

.

Естественно, что запись гармонических колебаний в форме (2) ничем не хуже записи в форме (1), и переходить в конкретной задаче от записи в данной форме к записи в другой форме обычно нет необходимости. Нужно только уметь сразу находить амплитуду, циклическую частоту и период, имея перед собой любую форму записи гармонического колебания.

Иногда полезно знать характер изменения первой и второй производных по времени от величины S, которая совершает гармонические колебания (колеблется по гармоническому закону). Если , то дифференцирование S по времени t дает,. Видно, что S» и S»» колеблются тоже по гармоническому закону с той же циклической частотой, что и величина S, и амплитудамии, соответственно. Приведем пример.

Пусть координата x тела, совершающего гармонические колебания вдоль оси x, изменяется по закону , где х в сантиметрах, время t в секундах. Требуется записать закон изменения скорости и ускорения тела и найти их максимальные значения. Для ответа на поставленный вопрос заметим, что первая производная по времени от величины х есть проекция скорости тела на ось х, а вторая производная х есть проекция ускорения на ось х:,. Продифференцировав выражение для х по времени, получим,. Максимальные значения скорости и ускорения:.

Гармонические колебания – колебания, совершаемые по законам синуса и косинуса. На следующем рисунке представлен график изменения координаты точки с течением времени по закону косинуса.

картинка

Амплитуда колебаний

Амплитудой гармонического колебания называется наибольшее значение смещения тела от положения равновесия. Амплитуда может принимать различные значения. Она будет зависеть от того, насколько мы сместим тело в начальный момент времени от положения равновесия.

Амплитуда определяется начальными условиями, то есть энергией сообщаемой телу в начальный момент времени. Так как синус и косинус могут принимать значения в диапазоне от -1 до 1, то в уравнении должен присутствовать множитель Xm, выражающий амплитуду колебаний. Уравнение движения при гармонических колебаниях:

x = Xm*cos(ω0*t).

Период колебаний

Период колебаний – это время совершения одного полного колебания. Период колебания обозначается буквой Т. Единицы измерения периода соответствуют единицам времени. То есть в СИ — это секунды.

Частота колебаний – количество колебаний совершенных в единицу времени. Частота колебаний обозначается буквой ν. Частоту колебаний можно выразить через период колебания.

ν = 1/Т.

Единицы измерения частоты в СИ 1/сек. Эта единица измерения получила название Герца. Число колебаний за время 2*pi секунд будет равняться:

ω0 = 2*pi* ν = 2*pi/T.

Частота колебаний

Данная величина называется циклической частотой колебаний. В некоторой литературе встречается название круговая частота. Собственная частота колебательной системы – частота свободных колебаний.

Частота собственных колебаний рассчитывается по формуле:

Частота собственных колебаний зависит от свойств материала и массы груза. Чем больше жесткость пружины, тем больше частота собственных колебаний. Чем больше масса груза, тем меньше частота собственных колебаний.

Эти два вывода очевидны. Чем более жесткая пружина, тем большее ускорение она сообщит телу, при выведении системы из равновесия. Чем больше масса тела, тем медленнее будет изменяться это скорость этого тела.

Период свободных колебаний :

T = 2*pi/ ω0 = 2*pi*√(m/k)

Примечателен тот факт, что при малых углах отклонения период колебания тела на пружине и период колебания маятника не будут зависеть от амплитуды колебаний.

Запишем формулы периода и частоты свободных колебаний для математического маятника.

тогда период будет равен

T = 2*pi*√(l/g).

Данная формула будет справедлива лишь для малых углов отклонения. Из формулы видим, что период колебаний возрастает с увеличением длины нити маятника. Чем больше будет длина, тем медленнее тело будет колебаться.

От массы груза период колебаний совершенно не зависит. Зато зависит от ускорения свободного падения. При уменьшении g, период колебаний будет увеличиваться. Данное свойство широко используют на практике. Например, для измерения точного значения свободного ускорения.

1. Вспомним, что называется частотой и периодом колебаний.

Время, за которое маятник совершает одно полное колебание, называют периодом колебаний.

Период обозначают буквойT и измеряют в секундах (с).

Число полных колебаний за одну секунду, называют частотой колебаний. Частоту обозначают буквой n.

1 Гц = .

Единица частоты колебаний в Ш — герц (1 Гц ).

1 Гц — это частота таких колебаний, при которых за 1 с совершается одно полное колебание .

Частота колебаний и период связаны соотношением:

n = .

2. Период колебаний рассмотренных нами колебательных систем — математического и пружинного маятников — зависит от характеристик этих систем.

Выясним, от чего зависит период колебаний математического маятника. Для этого проделаем опыт. Будем менять длину нити математического маятника и измерять время нескольких полных колебаний, например 10. В каждом случае определим период колебаний маятника, разделив измеренное время на 10. Опыт показывает, что чем больше длина нити, тем больше период колебаний.

Теперь поместим под маятником магнит, увеличивая тем самым силу тяжести, действующую на маятник, и измерим период его колебаний. Заметим, что период колебаний уменьшится. Следовательно, период колебаний математического маятника зависит от ускорения свободного падения: чем оно больше, тем меньше период колебаний.

Формула периода колебаний математического маятника имеет вид:

где l — длина нити маятника, g — ускорение свободного падения.

3. Определим экспериментально, от чего зависит период колебаний пружинного маятника.

Будем подвешивать к одной и той же пружине грузы разной массы и измерять период колебаний. Заметим, что чем больше масса груза, тем больше период колебаний.

Затем будем к пружинам разной жесткости подвешивать один и тот же груз. Опыт показывает, что чем больше жесткость пружины, тем меньше период колебаний маятника.

Формула периода колебаний пружинного маятника имеет вид:

где m — масса груза, k — жесткость пружины.

4. В формулы периода колебаний маятников входят величины, характеризующие сами маятники. Эти величины называют параметрами колебательных систем.

Если в процессе колебаний параметры колебательной системы не меняются, то период (частота) колебаний остается неизменным. Однако в реальных колебательных системах действуют силы трения, поэтому период реальных свободных колебаний с течением времени уменьшается.

Если же предположить, что трение отсутствует и система совершает свободные колебания, то период колебаний меняться не будет.

Свободные колебания, которые могла бы совершать система в отсутствие трения, называют собственными колебаниями.

Частота таких колебаний называется собственной частотой . Она зависит от параметров колебательной системы.

Вопросы для самопроверки

1. Что называют периодом колебаний маятника?

2. Что называют частотой колебаний маятника? Какова единица частоты колебаний?

3. От каких величин и как зависит период колебаний математического маятника?

4. От каких величин и как зависит период колебаний пружинного маятника?

5. Какие колебания называют собственными?

Задание 23

1. Каков период колебаний маятника, если 20 полных колебаний он совершает за 15 с?

2. Чему равна частота колебаний, если период колебаний равен0,25 с?

3. Какой должна быть длина маятника в маятниковых часах, чтобы период его колебаний был равен 1 с? Считать g = 10 м/с 2 ; p 2 = 10.

4. Чему равен период колебаний маятника, длина нити которого равна 28 см, на Луне? Ускорение свободного падения на Луне 1,75 м/с 2 .

5. Определите период и частоту колебаний пружинного маятника, если жесткость его пружины равна 100 Н/м, а масса груза 1 кг.

6. Во сколько раз изменится частота колебаний автомобиля на рессорах, если в него положить груз, масса которого равна массе ненагруженного автомобиля?

Лабораторная работа № 2

Изучение колебаний
математического и пружинного маятников

Цель работы:

исследовать, от каких величин зависит, а от каких не зависит период колебаний математического и пружинного маятников.

Приборы и материалы:

штатив, 3 груза разной массы (шарик, груз массой 100 г, гирька), нить длиной 60 см, 2 пружины разной жесткости, линейка, секундомер, полосовой магнит.

Порядок выполнения работы

1. Изготовьте математический маятник. Наблюдайте его колебания.

2. Исследуйте зависимость периода колебаний математического маятника от длины нити. Для этого определите время 20 полных колебаний маятников длиной 25 и 49 см. Вычислите период колебаний в каждом случае. Результаты измерений и вычисленийс учетом погрешности измерений занесите в таблицу 10. Сделайте вывод.

Таблица 10

l , м	n	t д Dt, с	T д DT, с
0,25	20
0,49	20

3. Исследуйте зависимость периода колебаний маятника от ускорения свободного падения. Для этого под маятником длиной 25 см поместите полосовой магнит. Определите период колебаний, сравните его с периодом колебаний маятника в отсутствие магнита. Сделайте вывод.

4. Покажите, что период колебаний математического маятника не зависит от массы груза. Для этого к нити неизменной длины подвешивайте грузы разной массы. Для каждого случая определите период колебаний, сохраняя одинаковой амплитуду. Сделайте вывод.

5. Покажите, что период колебаний математического маятника не зависит от амплитуды колебаний. Для этого маятник отклоните сначала на 3 см, а затем на 4 см от положения равновесия и определите период колебаний в каждом случае. Результаты измерений и вычислений занесите в таблицу 11. Сделайте вывод.

Таблица 11

A , см	n	t + Dt , с	T + DT , с

6. Покажите, что период колебаний пружинного маятника зависит от массы груза. Прикрепляя к пружине грузы разной массы, определите период колебаний маятника в каждом случае, измерив время 10 колебаний. Сделайте вывод.

7. Покажите, что период колебаний пружинного маятника зависит от жесткости пружины. Сделайте вывод.

8. Покажите, что период колебаний пружинного маятника не зависит от амплитуды. Результаты измерений и вычислений занесите в таблицу 12. Сделайте вывод.

Таблица 12

A , см	n	t + Dt , с	T + DT , с

Задание 24

1 э. Исследуйте область применимости модели математического маятника. Для этого изменяйте длину нити маятника и размеры тела. Проверьте, зависит ли период колебаний от длины маятника, если тело имеет большие размеры, а длина нити мала.

2. Вычислите длины секундных маятников, установленных на полюсе (g = 9,832 м/с 2), на экваторе (g = 9,78 м/с 2), в Москве (g = 9,816 м/с 2), в Санкт‑Петербурге (g = 9,819 м/ с 2).

3 * . Как влияют изменения температуры на ход маятниковых часов?

4. Как изменится частота маятниковых часов при подъеме в гору?

5 * . Девочка качается на качелях. Изменится ли период колебаний качелей, если на них сядут две девочки? Если девочка будет качаться не сидя, а стоя?

Лабораторная работа № 3*

Измерение ускорения свободного падения
с помощью математического маятника

Цель работы:

научиться измерять ускорение свободного падения, используя формулу периода колебаний математического маятника.

Приборы и материалы:

штатив, шарик с прикрепленной к нему нитью, измерительная лента, секундомер (или часы с секундной стрелкой).

Порядок выполнения работы

1. Подвесьте к штативу шарик на нити длиной 30 см.

2. Измерьте время 10 полных колебаний маятника и вычислите его период колебаний. Результаты измерений и вычисления занесите в таблицу 13.

3. Пользуясь формулой периода колебаний математического маятника T = 2p, вычислите ускорение свободного падения по формуле: g = .

4. Повторите измерения, изменив длину нити маятника.

5. Вычислите относительную и абсолютную погрешность изменения ускорения свободного падения для каждого случая по формулам:

dg ==+ ; Dg = g dg .

Считайте, что погрешность измерения длины равна половине цены деления измерительной ленты, а погрешность измерения времени — цене деления секундомера.

6. Запишите значение ускорения свободного падения в таблицу 13 с учетом погрешности измерений.

Таблица 13

№ опыта	l д Dl , м	n	t д Dt , с	T д DT , с	g , м/с2	Dg , м/с2	g д Dg , м/с2

Задание 25

1. Изменится ли, и если да, то как, погрешность измерения периода колебаний маятника, если увеличить число колебаний с 20 до 30?

2. Как влияет на точность измерения ускорения свободного падения увеличение длины маятника? Почему?

Формула частоты период времени частота цикл в секунду герц Гц амплитуда продолжительность периодический период времени к угловой частоте формула длина волны акустическое уравнение отношение длина волны Гц миллисекунда расчет мс расчет калькулятор t=1/f Гц герц в мс T в f рабочий лист

Формула частоты период время частота цикл в секунду герц Гц амплитуда продолжительность периодический период времени к угловой частоте формуляр длины волны акустическое уравнение соотношение длина волны Гц миллисекунды расчет мс вычислить калькулятор t=1/f Гц герц в мс рабочий лист T в f — sengpielaudio Sengpiel Berlin
 

Заполните серое поле выше и щелкните на панели расчета соответствующего столбца.

Частота означает количество колебаний (циклов) в секунду в Гц = герц = 1/с.
1 секунда = 1 с = 1000 мс | 1 мс = 0,001 с | 1 мкс = 0,000001 с
cps = число циклов в секунду

Чтобы использовать калькулятор, просто введите значение. Калькулятор работает в обе стороны от знака ↔ .

Осциллоскоп: Ввод ящиков (разд.) и временная развертка (Y) дают частоту.

Формула периода (длительности цикла) T

Физическое значение	символ	шт.	аббревиатура	формула
Длительность цикла	Т = 1/ф	второй	с	Т = λ/с
Частота	f = 1/T	Гц	Гц = 1/с	f = с / λ
Длина волны	λ	счетчик	м	λ = к/ф
Скорость волны	с	метр в секунду	м/с	с = λ × f

 

Преобразование во времени — По ходу времени

Формулы и уравнения для частоты и длины волны

Формула для частоты: f (частота) = 1 / T (период). f = c / λ = скорость волны c (м/с) / длина волны λ (м). Формула для времени: T (период) = 1 / f (частота). Формула для длины волны λ (m) = C / F λ = C / F = скорость волны C (м / с) / частота f (Гц). Единица измерения герц (Гц) когда-то называлась cps = циклы в секунду.

c = λ × f          λ = c / f = c × T          f = c / λ
Дифференцировать скорость среды:
Скорость звука или скорость света

Выберите: Скорость звука в воздухе при температуре 20°C: c = 343 м/с или скорость радиоволн и света в вакууме: c = 299 792 458 м/с.   Скорость распространения электрических сигналов по оптоволокну составляет около 9/10 . скорость света, то есть ≈ 270 000 км/с. Скорость распространения электрических сигналов по медным кабелям составляет около 2/3 скорость света, то есть ≈ 200 000 км/с.   Скорость звука c = 343 м/с также равна 1235 км / ч, 767 миль в час, 1125 фут/с.

  Волна состоит из четырех частей:
длина волны, период, частота и амплитуда
Изменение частоты (герц, Гц) никогда не меняет амплитуду и наоборот

Угловая частота равна ω = 2 π × f

Дано уравнение: y = 50 sin (5000 t) Определить частоту и амплитуду. Ответ: амплитуда составляет 50 и Ω = 5000. , поэтому частота F = 1/ T = ω /2 π = 795,77 Гц.

Чтобы использовать калькулятор, просто введите значение. Калькулятор работает в обе стороны от знака ↔ .

Преобразование: частота в длину волны и наоборот

Синусоида или синусоида и период T

В физике и электротехнике для синусоидального процесса часто используется угловая частота ω вместо частоты f .Скорость или частота вращения размер при — предпочтительно механических — вращательных движениях с указанием частоты революций. Например, это важная функция для двигателей. Это будет дано в 1/мин, как число оборотов в минуту или как число оборотов в минуту.

 

Ось y показывает звуковое давление p (амплитуда звукового давления). Если на графике по оси X отобразить время t , мы увидим период T = 1 / f . Если на графике по оси x отобразить расстояние d , мы увидим длину волны λ . Наибольшее отклонение или удлинение называется амплитудой a .

Амплитуда не имеет абсолютно никакого отношения к частоте… тоже ничего с длиной волны.

 
● Графики волн ●

Волны могут быть отображены в виде графика в зависимости от времени или расстояния. Одна частота волна будет выглядеть как синусоида (синусоида) в любом случае. С расстояния график длина волны может быть определена. На временном графике период и частоту можно получить. От обоих вместе скорость волны может быть определенный. Источник: http://hyperphysics.phy-astr.gsu.edu/hbase/sound/wavplt.html

 

В акустике выражение для синусоиды записывается в виде y = A sin (2 π f T + φ ).Где ω = 2 π f и A — амплитуда и где f — частота волны, измеряемая в герцах. Сравнивая математическую форму y = A sin ( B T + φ ): С этой акустической формой мы видим, что | Б | = 2 π f . Следовательно, у нас есть частота f = | Б | / 2 π и период T = 2 π / | Б | = 1/ f .

 
 

Кратность SI для герц (Гц)
Значение	Символ	Имя		Значение	Символ	Имя
10 −1 Гц	дБ	децигерц		10 1 Гц	даГц	декагерц
10 −2 Гц	Гц	сантигерц		10 2 Гц	Гц	гектогерц
10 −3 Гц	МГц	миллигерц		10 3 Гц	кГц	килогерц
10 −6 Гц	мкГц	микрогерц		10 6 Гц	МГц	мегагерц
10 −9 Гц	нГц	наногерц		10 9 Гц	ГГц	гигагерц
10 −12 Гц	пГц	пикогерц		10 12 Гц	ТГц	терагерц
10 −15 Гц	фГц	фемтогерц		10 15 Гц	Гц	петагерц
10 −18 Гц	Гц	аттогерц		10 18 Гц	Гц	экзагерц
10 −21 Гц	Гц	зептогерц		10 21 Гц	Гц	зеттагерц
10 −24 Гц	Гц	йоктогерц		10 24 Гц	Гц	йоттагерц
Единицы с общим префиксом выделены жирным шрифтом.

Типичный вопрос: как связаны длина волны, температура и частота?

Объясните взаимосвязь между расстоянием, временем и частотой при определении Длина волны или: Что такое уравнение с частотой, расстоянием и временем? Скорость = расстояние/время Скорость = длина волны × частота поэтому Длина волны × частота = расстояние/время поэтому Длина волны = расстояние / (время × частота)

Калькулятор Masterclock (тактовая частота)

Чтобы использовать калькулятор, просто введите значение. Калькулятор работает в обе стороны от знака ↔ .

Калькулятор опорной частоты

Для настройки вниз можно изменить опорную частоту и настройку фортепиано.
 
100 центов эквивалентны полутону (полутону).

Названия примечаний: сравнение английской и немецкой систем
 
Расчет гармоник по основной частоте

Частотная формула — что такое частотная формула? Примеры

Формула частоты используется для определения частоты волны.Частота определяется как количество циклов, совершаемых в единицу времени. Он также говорит о том, сколько гребней проходит через фиксированную точку в единицу времени. Иногда его называют обратным времени. Частота выражается в герцах (Гц). Частотная формула используется для определения частоты волны. Давайте лучше поймем это на решенных примерах.

Что такое формула частоты?

Частота — это общее количество повторений повторяющегося события в единицу заданного времени. Существуют различные частотные формулы для расчета частоты в зависимости от известных величин.Формула частоты волны используется для определения частоты (f), периода времени (T), скорости волны (V) и длины волны (λ). 1 Герц относится к одному циклу в секунду.

Формула частоты

Формула частоты задается как

.

Формула 1:  Формула частоты во времени имеет вид:

f = 1/T

где,

• f — частота в герцах, измеренная в м/с, а
• T — время выполнения одного цикла в секундах

Формула 2:  Формула частоты с учетом длины волны и скорости волны имеет вид

.

f = 𝜈/λ

где,

• 𝜈 — скорость волны в м/с, а
• λ — длина волны в м

Формула 3:  Частота в терминах угловой частоты выражается как

f = ω/2π

где ω — угловая частота

Давайте лучше поймем формулу частоты на нескольких решенных примерах.

Хотите найти сложные математические решения за считанные секунды?

Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.

Записаться на бесплатный пробный урок

Примеры использования формулы частоты

Пример 1: Используя частотную формулу, найдите частоту волны, один цикл которой завершается за 0,5 с.
Решение:     

Найти: Частота

Дано:

Время = 0.5с

Использование формулы частоты

ф = 1/Т

f = 1/0,5

ф = 2

Ответ: Частота 2 Гц.

Пример 2: Найдите частоту световой волны, если длина волны света составляет 600 нм.
Решение:     

Найти: Частота

Дано: Длина волны = 600 нм = 600 × 10 ^-9 м

= 6 × 10 ^-7  м

Мы знаем, что скорость света = 3 × 10 ⁸  м/с

Использование формулы частоты

f = 𝜈 / λ

f = 3 × 10 ⁸  / 6 × 10 ^-7                                         

f = 5 × 10 ¹⁴  с ^-1

Ответ: Частота равна 5 × 10 90 539 14 90 540 Гц.

Пример 3: Определите частоту маятника, совершающего один оборот за 4 секунды.
Решение:

Найти: Частота

Дано:

Время = 4 с

Использование формулы частоты

ф = 1/Т

ф = 1/4

f = 0,25

Ответ: Частота 0,25 Гц.

Часто задаваемые вопросы о частоте

Что такое формула частоты?

Формула частоты определяется как формула для определения частоты волны.Формула частоты используется для определения частоты (f), периода времени (T), скорости волны (V) и длины волны (λ).

Каковы применения формулы частоты?

Применение формулы частоты:

• Частота считается важным параметром в области науки и техники и формула частоты тоже.
• Формула для частоты используется для определения скорости колебательных и вибрационных явлений, в основном механических колебаний, звуковых сигналов (звука), радиоволн и световых волн.
• Формула частоты используется для определения частоты (f), периода времени (T), скорости волны (V) и длины волны (λ), а также для получения других связанных формул.

Как применяется формула частоты для заданных значений?

Процентная формула дается как,

• Формула частоты в единицах времени имеет следующий вид: f = 1/T, где f — частота в герцах, а T — время, необходимое для завершения одного цикла в секундах
• Формула частоты для длины волны и скорости волны задается следующим образом: f = 𝜈/λ, где 𝜈 – скорость волны, а λ – длина волны
• Формула частоты в терминах угловой частоты задается как f = ω/2π, где ω – угловая частота

Что такое «T» в частотной формуле?

В частотной формуле f = 1/T, T — период времени.T – время выполнения одного цикла (в секундах). Период времени обратно пропорционален частоте.

Формула частоты

Частота — это количество циклов в единицу времени. «Циклы» могут быть движениями чего-либо с периодическим движением, например, пружины, маятника, чего-то вращающегося или волны. Частота равна 1, деленной на период, который представляет собой время, необходимое для одного цикла.

Производной единицей СИ для частоты является герц, названный в честь Генриха Рудольфа Герца (обозначение гц).Один герц — это один цикл в секунду.

f = частота, количество циклов в единицу времени

T = период, время, необходимое для одного цикла времени

Формула частоты Вопросы:

1) Длинному маятнику требуется 5,00 с , чтобы совершить один возвратно-поступательный цикл. Какова частота движения маятника?

Ответ: Маятник проходит 5.00 с для завершения одного цикла, так что это его период, T. Частота может быть найдена с помощью уравнения:

f = 0,20 циклов/с

Частота маятника 0,20 циклов /с . Единицы циклов/с часто записывают как «Герц» с символом «Гц».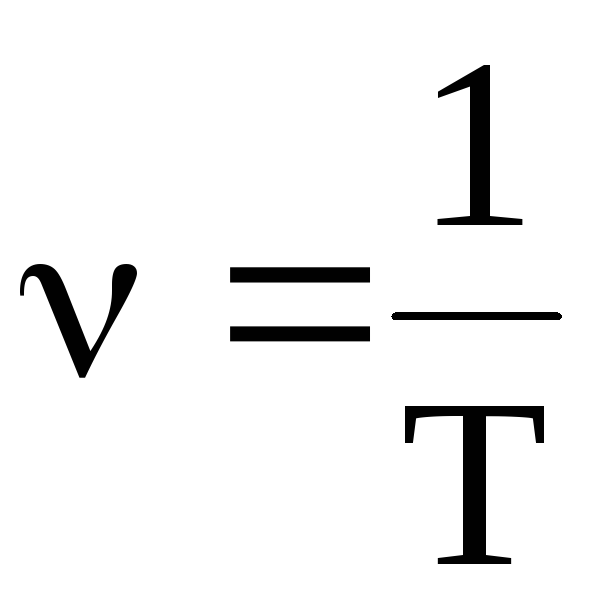 Таким образом, частоту этого маятника также можно определить как 0,20 Гц.

2) Тахометр в автомобиле измеряет обороты шин в минуту (обороты и циклы — одно и то же).Автомобиль движется с постоянной скоростью, а тахометр показывает 2400 оборотов в минуту. Какова частота вращения шин, выраженная в циклах в секунду? Что такое период в секундах?

Ответ: Количество циклов (оборотов) для рассмотрения равно 2400 . Это количество циклов, происходящих за одну минуту, что равно 60 секундам. Итак, частоту можно найти по уравнению:

f = 40 циклов/с

Частота вращения шин равна 40 циклов/с , что также можно записать как 40 Гц.Чтобы найти из этого период, переформулируйте уравнение, связывающее период и частоту:

T = 0,025 с

Период вращения шин равен 0,025 секунд.

13.2 Свойства волн: скорость, амплитуда, частота и период — физика

Раздел Цели обучения

К концу этого раздела вы сможете делать следующее:

• Определение амплитуды, частоты, периода, длины волны и скорости волны
• Связь частоты волны, периода, длины волны и скорости
• Решение задач, связанных со свойствами волн

Поддержка учителей

Поддержка учителей

Цели обучения в этом разделе помогут вашим ученикам освоить следующие стандарты:

• (7) Научные концепции. Учащийся знает характеристики и поведение волн. Ожидается, что студент:
  • (Б) исследовать и анализировать характеристики волн, включая скорость, частоту, амплитуду и длину волны, и рассчитывать, используя взаимосвязь между скоростью волны, частотой и длиной волны;
  • (Д) исследовать поведение волн, включая отражение, преломление, дифракцию, интерференцию, резонанс и эффект Доплера.

Основные термины раздела

Служба поддержки учителей

Служба поддержки учителей

[BL][OL][AL] Проверьте амплитуду, период и частоту простого гармонического движения.

Волновые переменные

В главе о движении в двух измерениях мы определили следующие переменные для описания гармонического движения:

• Амплитуда — максимальное смещение от положения равновесия объекта, колеблющегося вокруг такого положения равновесия
• Частота — количество событий в единицу времени
• Период — время, необходимое для совершения одного колебания

Для волн эти переменные имеют одинаковый основной смысл. Однако полезно сформулировать определения более конкретным образом, применимым непосредственно к волнам:

• Амплитуда — расстояние между положением покоя и максимальным смещением волны
• Частота — количество волн, проходящих через определенную точку в секунду
• Период — время, необходимое для завершения одного цикла волны

Волны характеризуют не только амплитуда, частота и период, но и их длина волны и скорость волны.Длина волны λλ — это расстояние между соседними одинаковыми частями волны, параллельными направлению распространения. Скорость волны vwvw — это скорость, с которой движется возмущение.

Советы для достижения успеха

Скорость волны иногда также называют скоростью распространения или скоростью распространения , потому что возмущение распространяется из одного места в другое.

Рассмотрим периодическую волну воды на рис. 13.7. Его длина волны — это расстояние от гребня до гребня или от впадины до впадины.Длину волны также можно рассматривать как расстояние, пройденное волной за один полный цикл или один период. Время одного полного движения вверх-вниз равно периоду простой водной волны T . На рисунке сама волна движется вправо с волновой скоростью v _w . Его амплитуда X — это расстояние между положением покоя и максимальным смещением — гребнем или впадиной — волны. Важно отметить, что это движение волны на самом деле является возмущением , движущимся вправо, а не самой водой; в противном случае птица двигалась бы вправо.Вместо этого чайка качается вверх и вниз на месте, когда под ней проходят волны, преодолевая общее расстояние 2 X за один цикл. Однако, как упоминалось в текстовой статье о серфинге, настоящие океанские волны более сложны, чем этот упрощенный пример.

Рисунок 13.7 Волна имеет длину волны λ , что является расстоянием между соседними идентичными частями волны. Возмущение поверхности вверх-вниз распространяется параллельно поверхности со скоростью v _w .

Смотреть физику

Амплитуда, период, частота и длина волны периодических волн

Это видео является продолжением видео «Введение в волны» из раздела «Виды волн». В нем обсуждаются свойства периодической волны: амплитуда, период, частота, длина волны и скорость волны.

Советы для успеха

Гребень волны иногда также называют вершиной .

Проверка захвата

Смотреть Физика: амплитуда, период, частота и длина волны периодических волн.В этом видео представлены несколько концепций звука; амплитуда, период, частота и длина волны периодических волн.

Если вы находитесь на лодке в ложбине волны в океане, и амплитуда волны составляет 1\,\text{м}, какова высота волны с вашего местоположения?

1. 1\,\текст{м}
2. 2\,\текст{м}
3. 4\,\текст{м}
4. 8\,\текст{м}

Взаимосвязь между частотой волны, периодом, длиной волны и скоростью

Поскольку частота волны — это количество волн в секунду, а период — это, по существу, количество секунд на волну, связь между частотой и периодом равна

или

так же, как и в случае гармонического движения объекта. Из этого соотношения видно, что более высокая частота означает более короткий период. Напомним, что единицей измерения частоты является герц (Гц), а 1 Гц — это один цикл — или одна волна — в секунду.

Скорость распространения v _w — это расстояние, которое волна проходит за заданное время, которое составляет одну длину волны за время одного периода. В форме уравнения это записывается как

или

Из этого соотношения мы видим, что в среде, где v _w постоянно, чем выше частота, тем меньше длина волны.См. рисунок 13.8.

Рис. 13.8 Поскольку в данной среде они распространяются с одинаковой скоростью, низкочастотные звуки должны иметь большую длину волны, чем высокочастотные звуки. Здесь низкочастотные звуки излучаются большим динамиком, называемым низкочастотным динамиком, а высокочастотные звуки излучаются маленьким динамиком, называемым твитером.

Поддержка учителя

Поддержка учителя

[BL] Для звука более высокая частота соответствует более высокому тону, а более низкая частота соответствует более низкому тону. Амплитуда соответствует громкости звука.

[BL][OL] Поскольку звук на всех частотах имеет одинаковую скорость в воздухе, изменение частоты означает изменение длины волны.

[Поддержка рисунка] Один и тот же динамик способен воспроизводить как высокочастотные, так и низкочастотные звуки. Однако высокие частоты имеют более короткую длину волны и, следовательно, лучше всего воспроизводятся динамиком с маленьким, твердым и плотным диффузором (твитер), тогда как более низкие частоты лучше всего воспроизводятся с большим и мягким диффузором (вуфер).

Эти фундаментальные соотношения справедливы для всех типов волн. Например, для волн на воде v _w — это скорость поверхностной волны; для звука v _w — скорость звука; а для видимого света v _w — это скорость света. Амплитуда X совершенно не зависит от скорости распространения v _w и зависит только от количества энергии в волне.

Лаборатория Snap

Волны в миске

В этой лаборатории вы проведете измерения, чтобы определить, как передача энергии от пробки, брошенной в воду, влияет на амплитуду и период волн.Пробка изначально обладает некоторой потенциальной энергией, когда ее держат над водой — чем больше высота, тем выше потенциальная энергия. Когда пробка падает, такая потенциальная энергия преобразуется в кинетическую энергию, когда пробка падает. Когда пробка ударяется о воду, эта энергия распространяется по воде волнами.

• Большая миска или таз
• Вода
• Пробка (или шарик для пинг-понга)
• Секундомер
• Рулетка

Инструкции

Процедура

1. Наполните большую миску или таз водой и подождите, пока вода не осядет, чтобы не было ряби.
2. Аккуратно бросьте пробку в середину чаши.
3. Оцените длину волны и период колебаний водной волны, распространяющейся от пробки. Вы можете оценить период, подсчитав количество ряби от центра к краю чаши, пока ваш партнер измеряет это время. Эта информация в сочетании с измерением чаши даст вам длину волны при использовании правильной формулы.
4. Выньте пробку из миски и подождите, пока вода снова не осядет.
5. Аккуратно бросьте пробку с высоты, отличной от высоты первого падения.
6. Повторите шаги с 3 по 5, чтобы собрать второй и третий наборы данных, опуская пробку с разной высоты и записывая полученные длины волн и периоды.
7. Интерпретируйте свои результаты.

Проверка захвата

Пробка падает в бассейн с водой, создавая волны. Зависит ли длина волны от высоты над водой, с которой брошена пробка?

1. Нет, влияет только на амплитуду.
2. Да, длина волны затронута.

Поддержка учителей

Поддержка учителей

Учащиеся могут заранее измерить чашу, чтобы лучше оценить длину волны.

Ссылки на физику

Геология: физика сейсмических волн

Рис. 13.9 Разрушительный эффект землетрясения является ощутимым свидетельством энергии, переносимой волнами землетрясения. Оценка землетрясений по шкале Рихтера связана как с их амплитудой, так и с энергией, которую они несут.(старшина 2-го класса Кэндис Вильярреал, ВМС США)

Геологи в значительной степени полагаются на физику при изучении землетрясений, поскольку землетрясения связаны с несколькими типами волновых возмущений, включая возмущение поверхности Земли и возмущения давления под поверхностью. Поверхностные волны землетрясения подобны поверхностным волнам на воде. Волны под поверхностью Земли имеют как продольную, так и поперечную составляющие. Продольные волны при землетрясении называются волнами давления (P-волнами), а поперечные волны называются поперечными волнами (S-волнами).Эти два типа волн распространяются с разными скоростями, и скорость, с которой они распространяются, зависит от жесткости среды, в которой они распространяются. Во время землетрясений скорость Р-волн в граните значительно превышает скорость S-волн. Оба компонента землетрясений распространяются медленнее в менее жестких материалах, таких как отложения. P-волны имеют скорость от 4 до 7 км/с, а S-волны — от 2 до 5 км/с, но обе они быстрее в более жестких материалах. P-волна постепенно опережает S-волну по мере того, как они проходят через земную кору.По этой причине разница во времени между продольными и поперечными волнами используется для определения расстояния до их источника — эпицентра землетрясения.

Из сейсмических волн, создаваемых землетрясениями, мы знаем, что части недр Земли жидкие. Сдвиговые или поперечные волны не могут проходить через жидкость и не передаются через ядро ​​Земли. Напротив, волны сжатия или продольные волны могут проходить через жидкость и проходят через ядро.

Все волны несут энергию, и энергию волн землетрясений легко наблюдать, основываясь на количестве повреждений, оставшихся после того, как земля перестала двигаться. Землетрясения могут сровнять с землей целые города, выполняя работу тысяч шаров-разрушителей. Количество энергии в волне связано с ее амплитудой. Землетрясения большой амплитуды вызывают большие смещения грунта и больший ущерб. По мере распространения волн землетрясения их амплитуда уменьшается, поэтому чем дальше они удаляются от источника, тем меньше повреждений.

Проверка захвата

Какая связь между скоростью распространения, частотой и длиной волны S-волн при землетрясении?

1. Соотношение между скоростью распространения, частотой и длиной волны vw=fλ.vw=fλ.
2. Соотношение между скоростью распространения, частотой и длиной волны vw=fλ.vw=fλ.
3. Соотношение между скоростью распространения, частотой и длиной волны vw=λf.vw=λf.
4. Соотношение между скоростью распространения, частотой и длиной волны vw=fλ.vw=fλ.

Виртуальная физика

Волна на струне

В этой анимации посмотрите, как струна вибрирует в замедленном темпе, выбрав параметр «Замедленное движение». Выберите параметры «Без конца» и «Вручную» и покачивайте конец струны, чтобы создавать волны самостоятельно. Затем переключитесь на настройку Oscillate для автоматического создания волн. Отрегулируйте частоту и амплитуду колебаний, чтобы увидеть, что произойдет. Затем поэкспериментируйте с регулировкой демпфирования и натяжения.

Проверка захвата

Какая из настроек — амплитуда, частота, затухание или натяжение — изменяет амплитуду волны при ее распространении? Что он делает с амплитудой?

1. Частота; он уменьшает амплитуду волны по мере ее распространения.
2. Частота; он увеличивает амплитуду волны по мере ее распространения.
3. Демпфирование; он уменьшает амплитуду волны по мере ее распространения.
4. Демпфирование; он увеличивает амплитуду волны по мере ее распространения.

Решение волновых задач

Рабочий пример

Расчет скорости распространения волны: чайка в океане

Рассчитайте скорость морской волны на предыдущем рисунке, если расстояние между гребнями волн равно 10. 0 м, а время покачивания чайки вверх и вниз составляет 5,00 с.

Стратегия

Даны значения длины волны (λ=10,0 м)(λ=10,0 м) и периода (T=5,00 с)(T=5,00 с), и нас просят найти vwvw Следовательно, мы можем использовать vw=λTvw =λT, чтобы найти скорость волны.

Решение

Введите известные значения в vw=λTvw=λT

vw=10,0 м5,00 с=2,00 м/с. vw=10,0 м5,00 с=2,00 м/с.

13,5

Обсуждение

Такая низкая скорость кажется приемлемой для океанской волны.Обратите внимание, что на рисунке волна движется вправо с этой скоростью, которая отличается от переменной скорости, с которой чайка качается вверх и вниз.

Рабочий пример

Расчет периода и скорости волны игрушечной пружины

Женщина на рис. 13.3 создает две волны каждую секунду, встряхивая игрушечную пружину вверх и вниз. а) Каков период каждой волны? (b) Если каждая волна проходит 0,9 метра после одного полного волнового цикла, какова скорость распространения волны?

Стратегия ДЛЯ (А)

Чтобы найти период, мы решаем T=1fT=1f, учитывая значение частоты (f=2s−1). (f=2с−1).

Раствор для (а)

Введите известное значение в T=1fT=1f

T=12 с-1=0,5 с. T=12 с-1=0,5 с.

13,6

Стратегия ДЛЯ (B)

Поскольку одним из определений длины волны является расстояние, пройденное волной за один полный цикл или один период, приводятся значения длины волны (λ=0,9 м)(λ=0,9 м), а также частоты. Следовательно, мы можем использовать vw=fλvw=fλ, чтобы найти скорость волны.

Решение для (б)

Введите известные значения в vw=fλvw=fλ

vw=fλ=(2 s−1)(0.9 м) = 1,8 м/с. vw=fλ=(2 с−1)(0,9 м) = 1,8 м/с.

Обсуждение

Мы могли бы также использовать уравнение vw=λTvw=λT для определения скорости волны, поскольку мы уже знаем значение периода (T=0,5 с)(T=0,5 с) из нашего расчета в части (a), и мы пришли бы к тому же ответу.

Практические задачи

7.

Частота волны 10 Гц. Каков его период?

1. Период волны 100 с.
2. Период волны 10 с.
3. Период волны 0,01 с.
4. Период волны 0,1 с.

8.

Какова скорость волны с длиной волны 2 м и частотой 5 Гц?

1. 20 м/с
2. 2,5 м/с
3. 0,4 м/с
4. 10 м/с

Проверьте свое понимание

Служба поддержки учителей

Служба поддержки учителей

Используйте эти вопросы для оценки достижений учащихся в соответствии с целями обучения раздела.Если учащиеся борются с определенной целью, эти вопросы помогут определить такую ​​цель и направить их к соответствующему содержанию.

9.

Какова амплитуда волны?

1. Четверть общей высоты волны
2. Половина общей высоты волны
3. В два раза больше общей высоты волны
4. В четыре раза больше общей высоты волны

10.

Что понимается под длиной волны?

1. Длина волны — это расстояние между соседними одинаковыми частями волны, параллельными направлению распространения.
2. Длина волны — это расстояние между соседними одинаковыми частями волны, перпендикулярное направлению распространения.
3. Длина волны — это расстояние между гребнем и прилегающей впадиной волны, параллельное направлению распространения.
4. Длина волны — это расстояние между гребнем и прилегающей впадиной волны, перпендикулярное направлению распространения.

11.2

12.

Когда длина волны прямо пропорциональна периоду волны?

1. Когда скорость волны уменьшается вдвое
2. Когда скорость волны постоянна
3. Когда скорость волны удваивается
4. Когда скорость волны утроится

Период и частота — AP Physics 1

Объяснение:

Мы можем начать с сохранения энергии, чтобы решить эту проблему:

Постановка задачи говорит нам, что цилиндр изначально покоится, поэтому мы можем исключить начальную кинетическую энергию.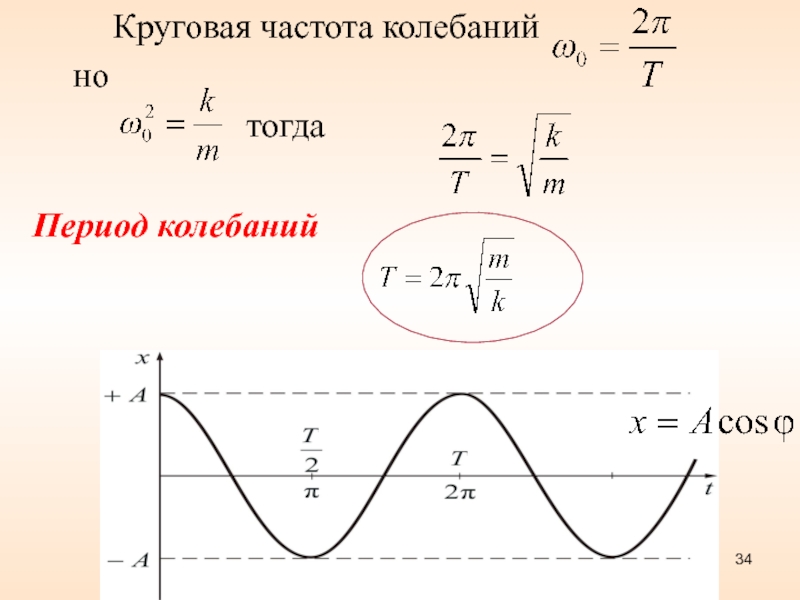 Если мы предположим, что высота цилиндра, когда он достигает периода 0,2 с, имеет высоту 0, мы можем исключить конечную потенциальную энергию. Следовательно, получаем:

Расширив эти условия и убедившись, что у нас есть как линейная, так и вращательная составляющая кинетической энергии, мы получаем уравнение (1):

Прежде чем мы двинемся дальше, мы знаем, что нам нужно вычислить что-то, что мы можем использовать для определения периода цилиндра. Мы знаем, что период — это время, за которое цилиндр совершает один полный оборот.Думая практически, мы можем использовать длину окружности цилиндра и линейную скорость для определения периода:

Используя переменные, мы получаем уравнение:

Переставляя конечную скорость, получаем уравнение (2):

Теперь мы знаем, что период зависит от конечной линейной скорости. Мы еще вернемся к этому уравнению. Теперь мы можем вернуться к уравнению (1) и начать подставлять выражения для неизвестных переменных, двигаясь слева направо. Первая переменная, которую мы не знаем, это начальная высота. Однако мы можем использовать расстояние, пройденное цилиндром, и угол наклона:

Переставляя по начальной высоте, получаем уравнение (3):

Идем дальше, следующий неизвестный термин — конечная скорость. Мы можем заменить уравнение (2), которое мы уже получили:

Идем дальше, следующий неизвестный термин — это момент инерции. Используя выражение для цилиндра, получаем уравнение (4):

Идем дальше, последний неизвестный член — это конечная скорость вращения.Мы можем использовать соотношение между этим и линейной скоростью:

Теперь подставляя уравнение (2), получаем уравнение (5):

Теперь мы можем подставить уравнения 2, 3, 4 и 5 в уравнение (1):

Исключение массы из обеих частей уравнения и расширение каждого члена:

Объединение терминов справа:

Изменение длины:

Проверьте свои единицы и убедитесь, что у вас есть секунды, прежде чем двигаться дальше!

Мы знаем значения для каждой переменной, так что пора втыкать и пыхтеть:

Объясните связь между частотой и периодом времени

Мы знаем, что число полных колебаний колеблющейся частицы за одну секунду называется ее частотой. Частота обозначается f. Опять же, период времени — это время одной полной вибрации. Частота и период являются обратно пропорциональными величинами. Частота (f) волны — это количество полных сигналов, генерируемых в секунду. Это то же самое, что количество повторений в секунду или количество колебаний в секунду.

Период времени (T) — количество секунд на сигнал или количество секунд на колебание. Ясно, что частота и период времени обратны.

Если период времени равен T, то за T секунд количество вибраций равно 1

Следовательно, количество вибраций в одну секунду равно 1/T

Количество вибраций в 1 секунду равно частоте.Итак, частота f = 1/T

Частота относится к тому, как часто что-то происходит; тогда как период относится ко времени, которое требуется для того, чтобы что-то произошло. Частота означает, сколько раз периодическое событие происходит в секунду.
Период — это время между любыми двумя событиями. Как правило, период должен быть обратен частоте, отсюда и уравнение: Период = 1/Частота.

Частота, f, представляет собой количество циклов колебаний в секунду и измеряется в циклах в секунду или герцах (Гц).Период волны Т — это время, за которое волна совершает один полный цикл колебаний. Эти два члена обратно пропорциональны друг другу: f = 1/T и T = 1/f.

Например, если волне требуется 1 секунда, чтобы колебаться вверх и вниз, период волны равен 1 секунде. Частота обратно пропорциональна 1 циклу в секунду, потому что в секунду происходит только один цикл.

Математический пример: Длина волны звука, производимого объектом в воздухе, составляет 20 см.Если скорость звука в воздухе 340 мс ^-1 , найдите частоту и период объекта.

Здесь, Длина волны, γ = 20 см = 0,2 м

Скорость звука = 340 мс ^-1

Частота, f =?

Период (время), T = ?

Мы знаем, Скорость = fγ

Итак, f = v/γ = 340 мс ^-1 / 0,20 м = 1700 Гц

А T = 1/f = 1 / 1700 с ^-1 = 0,000 = 5,88 x 10 ^-4 с

Частота 1700 Гц; Период (время) 5. 88 x 10 ^-4 с (Обратное, потому что если частота высока, то период времени низок).

Частота является величиной скорости. Период – это величина времени. Частота — это количество циклов в секунду, обозначаемое как Герц (Гц). Период — секунды/цикл. Период – во времени – измеряется в секундах, часах, днях или годах.

Период формулы и уравнения волны | Как найти период волны — видео и расшифровка урока

Что такое период волны?

Большинство людей знакомы с понятием волны.Их можно увидеть в океане, на струнах таких инструментов, как гитары, в скакалках на детской площадке, в ряби в пруду или даже на спортивных мероприятиях в толпе. Волны также существуют таким образом, что их структура не видна невооруженным глазом, например, звуковые волны или электромагнитные волны (свет). У них есть определенные свойства, которые делают их уникальными: верхняя и нижняя точки, которые колеблются в непрерывном цикле.

Этот непрерывный цикл называется волновым циклом и определяется как пика волны до пика или впадины до впадины, где пик или гребень является высшей точкой волны и впадиной. является самой низкой точкой волны.Расстояние между пиком волны или впадиной до впадины одинаково и также известно как длина волны , потому что оно измеряет длину цикла волны.

Простая волна, длину волны которой можно измерить от пика до пика или от впадины до впадины.

Скажем, волне требуется две секунды, чтобы пройти от пика к пику или от впадины к впадине. Это измерение времени будет известно как период волны .Период волны — это время, необходимое волне для завершения одного полного цикла, измеряемое в секундах. Его можно определить или рассчитать несколькими способами, и он имеет множество полезных применений.

Частота волны

Другим свойством волны является ее частота . Подобно периоду волны, частота волны связана со временем и циклом волны. Однако частота относится к тому, сколько циклов волны проходит в данный промежуток времени.

Например, было заявлено, что волне в предыдущем примере потребовалось две секунды, чтобы завершить один цикл, известный как период волны.Теперь скажем, что одна и та же волна наблюдалась в течение десяти секунд. Сколько раз волна повторила свой цикл?

Так как волна может завершить один цикл за две секунды, то она совершит пять циклов за десять секунд. Это означает, что волна имеет частоту пяти циклов в течение десяти секунд. Однако частота обычно измеряется количеством циклов, которые происходят всего за секунд , поэтому частота этой волны будет составлять половину цикла в секунду. Другими словами, эта волна может завершить только половину своего цикла за одну секунду.

Волны различаются по частоте, и хорошим примером этого является спектр видимых волн света. Помните, что свет состоит из всех цветов радуги.

Сравнение различных частот, составляющих видимый спектр света.

Это представление различных частот, составляющих цвета света, причем красный цвет имеет самую низкую частоту, а фиолетовый — самую высокую. Частоты можно найти путем подсчета пиков, поскольку все они отображаются в одном временном интервале.

Красный имеет самую низкую частоту, потому что здесь меньше всего пиков. С другой стороны, фиолетовый имеет самую высокую частоту, потому что он имеет наибольшее количество пиков. Глядя на рисунок, можно увидеть, насколько тесно связана частота с длиной волны. Красный цвет имеет не только самую низкую частоту, но и самую большую длину волны. Это имеет смысл, потому что, если волна длиннее, она не сможет завершить столько же циклов в заданный период времени, сколько более короткая волна.

Частоту можно найти, взяв скорость волны ({eq}v {/eq}) и разделив ее на длину волны ({eq}\lambda {/eq}):

{eq}f = \frac {v}{\lambda} {/eq}

, где {eq}f {/eq} – частота, измеряемая в циклах в секунду или Герцах (Гц), {eq}v {/eq} – скорость в метрах. в секунду, а {eq}\lambda {/eq} – длина волны в метрах.

Это означает, что количество волновых циклов, проходящих за заданный промежуток времени, зависит от скорости движения волны и ее длины.

Как найти период волны?

Как было сказано ранее, частота и период волны тесно связаны. Частота описывает, как часто или как часто волна будет проходить свой цикл за заданный промежуток времени, а период описывает, сколько времени требуется волне для завершения одного цикла. Следовательно, если волна имеет более короткий период, что означает, что она может завершить цикл за короткий промежуток времени, то за заданный промежуток времени может пройти больше циклов, что увеличивает частоту.Другими словами, с меньшим периодом волна будет иметь более высокую частоту и наоборот. В математическом мире говорят, что эти две величины обратно пропорциональны друг другу, где значение одной увеличивается, а другой уменьшается.

Формула периода волны

Из-за обратно пропорциональной зависимости между частотой и периодом волны, формула для периода волны просто обратна частоте волны:

{eq}T = \frac{1}{f} \ \ T = \frac{\lambda}{v} \\ {/eq}

, где {eq}T {/eq} — период в секундах, {eq}f {/eq} — частота волны, {eq }\lambda {/eq} – длина волны в метрах, а {eq}v {/eq} – скорость в метрах в секунду.