Основные формулы тригонометрии (таблица) — математика, кабинет
Просмотр
содержимого документа
|
О С Н О В Н Ы Е Ф О Р М У Л Ы Т Р И Г О Н О М Е Т Р И И |
|||
|
ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА |
ФОРМУЛЫ ДВОЙНОГО АРГУМЕНТА |
СУММА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ |
|
|
ФОРМУЛЫ СЛОЖЕНИЯ АРГУМЕНТОВ |
|||
|
ПРОИЗВЕДЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ |
|||
|
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ОТРИЦАТЕЛЬНОГО АРГУМЕНТА |
|||
|
ЗНАКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ |
|||
Основные формулы по тригонометрии — Математика — Теория, тесты, формулы и задачи
Знание формул по тригонометрии является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по тригонометрии, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении тригонометрических задач. На этой странице сайта представлены основные формулы по школьной тригонометрии.
Формулы по тригонометрии, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении тригонометрических задач. На этой странице сайта представлены основные формулы по школьной тригонометрии.
Изучать основные формулы по школьной тригонометрии онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.

- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Тригонометрические свойства. Основные формулы тригонометрии
В этой статье собраны таблицы синусов, косинусов, тангенсов и котангенсов
. Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360
градусов (0, π/6, π/4, π/3, π/2, …, 2π
радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.
После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.
Навигация по странице.
Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Гусев В. А., Мордкович А.
 Г.
Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Г.
Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил. - Брадис В. М. Четырехзначные математические таблицы: Для общеобразоват. учеб. заведений. — 2-е изд. — М.: Дрофа, 1999.- 96 с.: ил. ISBN 5-7107-2667-2
Позволяют установить ряд характерных результатов – свойств синуса, косинуса, тангенса и котангенса . В этой статье мы рассмотрим три основных свойства. Первое из них указывает знаки синуса, косинуса, тангенса и котангенса угла α в зависимости от того, углом какой координатной четверти является α . Дальше мы рассмотрим свойство периодичности, устанавливающее неизменность значений синуса, косинуса, тангенса и котангенса угла α при изменении этого угла на целое число оборотов. Третье свойство выражает зависимость между значениями синуса, косинуса, тангенса и котангенса противоположных углов α и −α .
Если же Вас интересуют свойства функций синуса, косинуса, тангенса и котангенса, то их можно изучить в соответствующем разделе статьи .
Навигация по странице.
Знаки синуса, косинуса, тангенса и котангенса по четвертям
Ниже в этом пункте будет встречаться фраза «угол I , II , III и IV координатной четверти». Объясним, что же это за углы.Возьмем единичную окружность , отметим на ней начальную точку А(1, 0) , и повернем ее вокруг точки O на угол α , при этом будем считать, что мы попадем в точку A 1 (x, y) .
Говорят, что угол α является углом I , II , III , IV координатной четверти , если точка А 1 лежит в I , II , III , IV четверти соответственно; если же угол α таков, что точка A 1 лежит на любой из координатных прямых Ox или Oy , то этот угол не принадлежит ни одной из четырех четвертей.
Для наглядности приведем графическую иллюстрацию. На чертежах ниже изображены углы поворота 30 , −210 , 585 и −45 градусов, которые являются углами I , II , III и IV координатных четвертей соответственно.
Углы 0, ±90, ±180, ±270, ±360, …
градусов не принадлежат ни одной из координатных четвертей.
Теперь разберемся, какие знаки имеют значения синуса, косинуса, тангенса и котангенса угла поворота α в зависимости от того, углом какой четверти является α .
Для синуса и косинуса это сделать просто.
По определению синус угла α — это ордината точки А 1 . Очевидно, что в I и II координатных четвертях она положительна, а в III и IV четвертях – отрицательна. Таким образом, синус угла α имеет знак плюс в I и II четвертях, а знак минус – в III и VI четвертях.
В свою очередь косинус угла α — это абсцисса точки A 1 . В I и IV четвертях она положительна, а во II и III четвертях – отрицательна. Следовательно, значения косинуса угла α в I и IV четвертях положительны, а во II и III четвертях – отрицательны.
Чтобы определить знаки по четвертям тангенса и котангенса нужно вспомнить их определения: тангенс – это отношение ординаты точки A 1
к абсциссе, а котангенс – отношение абсциссы точки A 1
к ординате. Тогда из
правил деления чисел
с одинаковыми и разными знаками следует, что тангенс и котангенс имеют знак плюс, когда знаки абсциссы и ординаты точки A 1
одинаковые, и имеют знак минус – когда знаки абсциссы и ординаты точки A 1
различны. Следовательно, тангенс и котангенс угла имеют знак +
в I
и III
координатных четвертях, и знак минус – во II
и IV
четвертях.
Следовательно, тангенс и котангенс угла имеют знак +
в I
и III
координатных четвертях, и знак минус – во II
и IV
четвертях.
Действительно, например, в первой четверти и абсцисса x , и ордината y точки A 1 положительны, тогда и частное x/y , и частное y/x – положительно, следовательно, тангенс и котангенс имеют знаки + . А во второй четверти абсцисса x – отрицательна, а ордината y – положительна, поэтому и x/y , и y/x – отрицательны, откуда тангенс и котангенс имеют знак минус.
Переходим к следующему свойству синуса, косинуса, тангенса и котангенса.
Свойство периодичности
Это и понятно: при изменении угла на целое число оборотов мы из начальной точки А
всегда будем попадать в точку А 1
на единичной окружности, следовательно, значения синуса, косинуса, тангенса и котангенса остаются неизменными, так как неизменны координаты точки A 1
.
С помощью формул рассматриваемое свойство синуса, косинуса, тангенса и котангенса можно записать так: sin(α+2·π·z)=sinα , cos(α+2·π·z)=cosα , tg(α+2·π·z)=tgα , ctg(α+2·π·z)=ctgα , где α — угол поворота в радианах, z – любое , абсолютная величина которого указывает количество полных оборотов, на которые изменяется угол α , а знак числа z указывает направление поворота.
Если же угол поворота α задан в градусах, то указанные формулы перепишутся в виде sin(α+360°·z)=sinα , cos(α+360°·z)=cosα , tg(α+360°·z)=tgα , ctg(α+360°·z)=ctgα .
Приведем примеры использования этого свойства. Например, , так как , а . Вот еще пример: или .
Это свойство вместе с формулами приведения очень часто используется при вычислении значений синуса, косинуса, тангенса и котангенса «больших» углов.
Рассмотренное свойство синуса, косинуса, тангенса и котангенса иногда называют свойством периодичности.
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
Пусть А 1
– точка, полученная в результате поворота начальной точки А(1, 0)
вокруг точки O
на угол α
, а точка А 2
– это результат поворота точки А
на угол −α
, противоположный углу α
.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов базируется на достаточно очевидном факте: упомянутые выше точки А 1
и А 2
либо совпадают (при ), либо располагаются симметрично относительно оси Ox
. То есть, если точка A 1
имеет координаты (x, y)
, то точка А 2
будет иметь координаты (x, −y)
. Отсюда по определениям синуса, косинуса, тангенса и котангенса записываем равенства и .
Сопоставляя их, приходим к соотношениям между синусами, косинусами, тангенсами и котангенсами противоположных углов α
и −α
вида .
Это и есть рассматриваемое свойство в виде формул.
Приведем примеры использования этого свойства. Например, справедливы равенства и .
Остается лишь заметить, что свойство синусов, косинусов, тангенсов и котангенсов противоположных углов, как и предыдущее свойство, часто используется при вычислении значений синуса, косинуса, тангенса и котангенса, и позволяет полностью уйти от отрицательных углов.
Список литературы.
- Алгебра: Учеб. для 9 кл. сред. шк./Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского.- М.: Просвещение, 1990.- 272 с.: ил.- ISBN 5-09-002727-7
- Алгебра и начала анализа: Учеб. для 10-11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
- Башмаков М. И. Алгебра и начала анализа: Учеб. для 10-11 кл. сред. шк. — 3-е изд. — М.: Просвещение, 1993. — 351 с.: ил. — ISBN 5-09-004617-4.
- Гусев В. А., Мордкович А. Г. Математика (пособие для поступающих в техникумы): Учеб. пособие.- М.; Высш. шк., 1984.-351 с., ил.
Тригонометрия — раздел математической науки, в котором изучаются тригонометрические функции и их использование в геометрии. Развитие тригонометрии началось еще во времена античной Греции. Во времена средневековья важный вклад в развитие этой науки внесли ученые Ближнего Востока и Индии.
Данная статья посвящена базовым понятиям и дефинициям тригонометрии. В ней рассмотрены определения основных тригонометрических функций: синуса, косинуса, тангенса и котангенса. Разъяснен и проиллюстрирован их смысл в контексте геометрии.
Yandex.RTB R-A-339285-1
Изначально определения тригонометрических функций, аргументом которых является угол, выражались через соотношения сторон прямоугольного треугольника.
Определения тригонометрических функций
Синус угла (sin α) — отношение противолежащего этому углу катета к гипотенузе.
Косинус угла (cos α) — отношение прилежащего катета к гипотенузе.
Тангенс угла (t g α) — отношение противолежащего катета к прилежащему.
Котангенс угла (c t g α) — отношение прилежащего катета к противолежащему.
Данные определения даны для острого угла прямоугольного треугольника!
Приведем иллюстрацию.
В треугольнике ABC с прямым углом С синус угла А равен отношению катета BC к гипотенузе AB.
Определения синуса, косинуса, тангенса и котангенса позволяют вычислять значения этих функций по известным длинам сторон треугольника.
Важно помнить!
Область значений синуса и косинуса: от -1 до 1. Иными словами синус и косинус принимают значения от -1 до 1. Область значений тангенса и котангенса — вся числовая прямая, то есть эти функции могут принимать любые значения.
Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от — ∞ до + ∞ .
В данном контексте можно дать определение синуса, косинуса, тангенса и котангенса угла произвольной величины. Представим единичную окружность с центром в начале декартовой системы координат.
Начальная точка A с координатами (1 , 0) поворачивается вокруг центра единичной окружности на некоторый угол α и переходит в точку A 1 .
Синус (sin) угла поворота
Синус угла поворота α — это ордината точки A 1 (x , y). sin α = y
Косинус (cos) угла поворота
Косинус угла поворота α — это абсцисса точки A 1 (x , y). cos α = х
Тангенс (tg) угла поворота
Тангенс угла поворота α — это отношение ординаты точки A 1 (x , y) к ее абсциссе. t g α = y x
Котангенс (ctg) угла поворота
Котангенс угла поворота α — это отношение абсциссы точки A 1 (x , y) к ее ординате. c t g α = x y
Синус и косинус определены для любого угла поворота. Это логично, ведь абсциссу и ординату точки после поворота можно определить при любом угле. Иначе обстоит дело с тангенсом и котангенсом. Тангенс не определен, когда точка после поворота переходит в точку с нулевой абсциссой (0 , 1) и (0 , — 1). В таких случаях выражение для тангенса t g α = y x просто не имеет смысла, так как в нем присутствует деление на ноль. Аналогично ситуация с котангенсом. Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Отличием состоит в том, что котангенс не определен в тех случаях, когда в ноль обращается ордината точки.
Важно помнить!
Синус и косинус определены для любых углов α .
Тангенс определен для всех углов, кроме α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z)
Котангенс определен для всех углов, кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z)
При решении практических примеров не говорят «синус угла поворота α «. Слова «угол поворота» просто опускают, подразумевая, что из контекста и так понятно, о чем идет речь.
Числа
Как быть с определением синуса, косинуса, тангенса и котангенса числа, а не угла поворота?
Синус, косинус, тангенс, котангенс числа
Синусом, косинусом, тангенсом и котангенсом числа t называется число, которое соответственно равно синусу, косинусу, тангенсу и котангенсу в t радиан.
Например, синус числа 10 π равен синусу угла поворота величиной 10 π рад.
Существует и другой подход к определению синуса, косинуса, тангенса и котангенса числа. Рассмотрим его подробнее.
Рассмотрим его подробнее.
Любому действительному числу t ставится в соответствие точка на единичной окружности с центром в начале прямоугольной декартовой системы координат. Синус, косинус, тангенс и котангенс определяются через координаты этой точки.
Начальная точка на окружности — точка A c координатами (1 , 0).
Положительному числу t
Отрицательному числу t соответствует точка, в которую перейдет начальная точка, если будет двигаться по окружности против часовой стрелки и пройдет путь t .
Теперь, когда связь числа и точки на окружности установлена, переходим к определению синуса, косинуса, тангенса и котангенса.
Синус (sin) числа t
Синус числа t — ордината точки единичной окружности, соответствующей числу t. sin t = y
Косинус (cos) числа t
Косинус числа t — абсцисса точки единичной окружности, соответствующей числу t. cos t = x
Тангенс (tg) числа t
Тангенс числа t
— отношение ординаты к абсциссе точки единичной окружности, соответствующей числу t. t g t = y x = sin t cos t
t g t = y x = sin t cos t
Последние определения находятся в соответствии и не противоречат определению, данному в начале это пункта. Точка на окружности, соответствующая числу t , совпадает с точкой, в которую переходит начальная точка после поворота на угол t радиан.
Тригонометрические функции углового и числового аргумента
Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α , отличным от α = 90 ° + 180 ° · k , k ∈ Z (α = π 2 + π · k , k ∈ Z) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α , кроме α = 180 ° · k , k ∈ Z (α = π · k , k ∈ Z).
Можно сказать, что sin α , cos α , t g α , c t g α — это функции угла альфа, или функции углового аргумента.
Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t
соответствует определенное значение синуса или косинуса числа t
. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.
Основные функции тригонометрии
Синус, косинус, тангенс и котангенс — основные тригонометрические функции.
Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.
Вернемся к данным в самом начале определениям и углу альфа, лежащему в пределах от 0 до 90 градусов. Тригонометрические определения синуса, косинуса, тангенса и котангенса полностью согласуются с геометрическими определениями, данными с помощью соотношений сторон прямоугольного треугольника. Покажем это.
Возьмем единичную окружность с центром в прямоугольной декартовой системе координат. Повернем начальную точку A (1 , 0) на угол величиной до 90 градусов и проведем из полученной точки A 1 (x , y) перпендикуляр к оси абсцисс. В полученном прямоугольном треугольнике угол A 1 O H равен углу поворота α , длина катета O H равна абсциссе точки A 1 (x , y) . Длина катета, противолежащего углу, равна ординате точки A 1 (x , y) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
Длина катета, противолежащего углу, равна ординате точки A 1 (x , y) , а длина гипотенузы равна единице, так как она является радиусом единичной окружности.
В соответствии с определением из геометрии, синус угла α равен отношению противолежащего катета к гипотенузе.
sin α = A 1 H O A 1 = y 1 = y
Значит, определение синуса острого угла в прямоугольном треугольнике через соотношение сторон эквивалентно определению синуса угла поворота α , при альфа лежащем в пределах от 0 до 90 градусов.
Аналогично соответствие определений можно показать для косинуса, тангенса и котангенса.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
С центром в точке A
.
α
— угол, выраженный в радианах.
Определение
Синус (sin α)
— это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус — нечетная. Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | -1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Изначально синус и косинус возникли из-за необходимости рассчитывать величины в прямоугольных треугольниках. Было замечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается всегда одинаковым.
Было замечено, что если значение градусной меры углов в прямоугольном треугольнике не менять, то соотношение сторон, насколько бы эти стороны ни изменялись в длине, остается всегда одинаковым.
Именно так и были введены понятия синуса и косинуса. Синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – прилежащего к гипотенузе.
Теоремы косинусов и синусов
Но косинусы и синусы могут применяться не только в прямоугольных треугольниках. Чтобы найти значение тупого или острого угла, стороны любого треугольника, достаточно применить теорему косинусов и синусов.
Теорема косинусов довольно проста: «Квадрат стороны треугольника равен сумме квадратов двух других сторон за вычетом удвоенного произведения этих сторон на косинус угла между ними».
Существует две трактовки теоремы синусов: малая и расширенная. Согласно малой: «В треугольнике углы пропорциональны противолежащим сторонам». Данную теорему часто расширяют за счет свойства описанной около треугольника окружности: «В треугольнике углы пропорциональны противолежащим сторонам, а их отношение равно диаметру описанной окружности».
Производные
Производная — математический инструмент, показывающий, как быстро меняется функция относительно изменения ее аргумента. Производные используются , геометрии, и , ряде технических дисциплин.
При решении задач требуется знать табличные значения производных тригонометрических функций: синуса и косинуса. Производной синуса является косинус, а косинуса — синус, но со знаком «минус».
Применение в математике
Особенно часто синусы и косинусы используются при решении прямоугольных треугольников и задач, связанных с ними.
Удобство синусов и косинусов нашло свое отражение и в технике. Углы и стороны было просто оценивать по теоремам косинусов и синусов, разбивая сложные фигуры и объекты на «простые» треугольники. Инженеры и , часто имеющие дело с расчетами соотношения сторон и градусных мер, тратили немало времени и усилий для вычисления косинусов и синусов не табличных углов.
Тогда «на подмогу» пришли таблицы Брадиса, содержащие тысячи значений синусов, косинусов, тангенсов и котангенсов разных углов. В советское время некоторые преподаватели заставляли своих подопечных страницы таблиц Брадиса наизусть.
В советское время некоторые преподаватели заставляли своих подопечных страницы таблиц Брадиса наизусть.
Радиан — угловая величина дуги, по длине равной радиусу или 57,295779513° градусов.
Градус (в геометрии) — 1/360-я часть окружности или 1/90-я часть прямого угла.
π = 3.141592653589793238462… (приблизительное значение числа Пи).
Таблица косинусов для углов: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330°, 360°.
| Угол х (в градусах) | 0° | 30° | 45° | 60° | 90° | 120° | 135° | 150° | 180° | 210° | 225° | 240° | 270° | 300° | 315° | 330° | 360° |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Угол х (в радианах) | 0 | π/6 | π/4 | π/3 | π/2 | 2 x π/3 | 3 x π/4 | 5 x π/6 | π | 7 x π/6 | 5 x π/4 | 4 x π/3 | 3 x π/2 | 5 x π/3 | 7 x π/4 | 11 x π/6 | 2 x π |
| cos x | 1 | √3/2 (0,8660) | √2/2 (0,7071) | 1/2 (0,5) | 0 | -1/2 (-0,5) | -√2/2 (-0,7071) | -√3/2 (-0,8660) | -1 | -√3/2 (-0,8660) | -√2/2 (-0,7071) | -1/2 (-0,5) | 0 | 1/2 (0,5) | √2/2 (0,7071) | √3/2 (0,8660) | 1 |
Рекомендуем также
| (1) | Основное тригонометрическое тождество | sin2(α) + cos2(α) = 1 | |||||||||||||||
| (2) | Основное тождество через тангенс и косинус | 1 + tg2(α) = 1/cos2(α) | |||||||||||||||
| (3) | Основное тождество через котангенс и синус | 1 + ctg2(α) = 1/sin2(α) | |||||||||||||||
| (4) | Соотношение между тангенсом и котангенсом | tg(α)ctg(α) = 1 | |||||||||||||||
| (5) | Синус двойного угла | sin(2α) = 2sin(α)cos(α) | |||||||||||||||
| (6) | Косинус двойного угла | cos(2α) = cos2(α) – sin2(α) = 2cos2(α) – 1 = 1 – 2sin2(α) | |||||||||||||||
| (7) | Тангенс двойного угла |
| |||||||||||||||
| (8) | Котангенс двойного угла |
| |||||||||||||||
| (9) | Синус тройного угла | sin(3α) = 3sin(α)cos2(α) – sin3(α) | |||||||||||||||
| (10) | Косинус тройного угла | cos(3α) = cos3(α) – 3cos(α)sin2(α) | |||||||||||||||
| (11) | Косинус суммы/разности | cos(α±β) = cos(α)cos(β) ∓ sin(α)sin(β) | |||||||||||||||
| (12) | Синус суммы/разности | sin(α±β) = sin(α)cos(β) ± cos(α)sin(β) | |||||||||||||||
| (13) | Тангенс суммы/разности | tg(α±β) = (tg(α) ± tg(β))/(1 ∓ tg(α)tg(β)) | |||||||||||||||
| (14) | Котангенс суммы/разности | ctg(α±β) = (-1 ± ctg(α)ctg(β))/(ctg(&alpha) ± ctg(β)) | |||||||||||||||
| (15) | Произведение синусов | sin(α)sin(β) = ½(cos(α–β) – cos(α+β)) | |||||||||||||||
| (16) | Произведение косинусов | cos(α)cos(β) = ½(cos(α+β) + cos(α–β)) | |||||||||||||||
| (17) | Произведение синуса на косинус | sin(α)cos(β) = ½(sin(α+β) + sin(α–β)) | |||||||||||||||
| (18) | Сумма/разность синусов | sin(α) ± sin(β) = 2sin(½(α±β))cos(½(α∓β)) | |||||||||||||||
| (19) | Сумма косинусов | cos(α) + cos(β) = 2cos(½(α+β))cos(½(α–β)) | |||||||||||||||
| (20) | Разность косинусов | cos(α) – cos(β) = –2sin(½(α+β))sin(½(α–β)) | |||||||||||||||
| (21) | Сумма/разность тангенсов | tg(α) ± tg(β) = sin(α±β)/cos(α)cos(β) | |||||||||||||||
| (22) | Формула понижения степени синуса | sin2(α) = ½(1 – cos(2α)) | |||||||||||||||
| (23) | Формула понижения степени косинуса | cos2(α) = ½(1 + cos(2α)) | |||||||||||||||
| (24) | Сумма/разность синуса и косинуса | sin(α) ± cos(α) = &sqrt;2sin(α±π/4) | |||||||||||||||
| (25) | Сумма/разность синуса и косинуса с коэффициентами | Asin(α) ± Bcos(α) = Корень(A²+B²)(sin(α ± arccos(A/Корень(A²+B²))) | |||||||||||||||
| (26) | Основное соотношение арксинуса и арккосинуса | arcsin(x) + arccos(x) = π/2 | |||||||||||||||
| (27) | Основное соотношение арктангенса и арккотангенса | arctg(x) + arcctg(x) = π/2 |
| α | 0 | π/6 | π/4 | π/3 | π/2 | 2π/3 | 3π/5 | 5π/6 | π | 7π/6 | 5π/4 | 4π/3 | 3π/2 | 5π/3 | 7π/4 | 11π/6 | 2π |
| sin(α) | 0 | 1/2; | √2/2 | √3/2 | 1 | √3/2 | √2/2 | 1/2 | 0 | -1/2 | -√2/2 | -√3/2 | -1 | -√3/2 | -√2/2 | -1/2 | 0 |
| cos(α) | 1 | √3/2 | √2/2 | 1/2 | 0 | -1/2 | -√2/2 | -√3/2 | -1 | -√3/2 | -√2/2 | -1/2 | 0 | 1/2 | √2/2 | √3/2 | 1 |
| tg(α) | 0 | 1/√3 | 1 | √3 | — | -√3 | -1 | -1/√3 | 0 | 1/√3 | 1 | √3 | — | -√3 | -1 | -1/√3 | 0 |
| ctg(α) | — | √3 | 1 | 1/√3 | 0 | -1/√3 | -1 | -√3 | — | √3 | 1 | 1/√3 | 0 | -1/√3 | -1 | -√3 | — |
триггерных тождеств и формул | Список тригонометрических тождеств — видео и расшифровка урока
Основные тригонометрические тождества
Все тригонометрические тождества выводятся с использованием шести основных тригонометрических соотношений. Это синус (sin), косинус (cos), тангенс (tan), косеканс (csc), секанс (sec) и котангенс (cot).
Это синус (sin), косинус (cos), тангенс (tan), косеканс (csc), секанс (sec) и котангенс (cot).
На рис. 1 показана таблица, которую можно использовать для запоминания шести основных тригонометрических соотношений.Значения этих шести тригонометрических отношений остаются положительными в первом квадранте координатной плоскости xy и в одном другом квадранте. Тогда их оценочные значения будут отрицательными в двух других квадрантах. Все это можно увидеть на рис. 2.
Sin Cos и Tan Trig Тождества
Внимательное изучение таблицы на рис. 1 покажет, как были получены основные тригонометрические тождества, показанные ниже.Эти тождества также называют взаимными тождествами.
Синус
{экв}sin \; \ тета = \ гидроразрыва {1} {csc \; \тета}\; \: \; \;\; \: \; \;\; \: \; \;\; \: \; \; csc \; \ тета = \ гидроразрыва {1} {грех \; \theta} {/eq}
Косинус
{eq}cos \; \ тета = \ гидроразрыва {1} {сек \; \тета}\; \: \; \;\; \: \; \;\; \: \; \;\; \: \; \; сек \; \ тета = \ гидроразрыва {1} {cos \; \theta } {/eq}
Тангенс
{eq}tan \; \ тета = \ гидроразрыва {1} раскладушка \; \тета}\; \: \; \;\; \: \; \;\; \: \; \;\; \: \; \; детская кроватка \; \ тета = \ гидроразрыва {1} {загар \; \theta } {/eq}
Дополнительные тождества углов
Еще одно триггерное свойство, которое можно использовать для получения других тождеств, — это свойство дополнительных углов.Напомним, что сумма дополнительных углов равна 90 градусов. Алгебраически говоря, углы, измеряющие {eq}\theta {/eq} и {eq}90 — \theta {/eq}, являются дополнительными углами. Используя это свойство триггера, можно получить дополнительные тождества. Это связано с тем, что шесть триггерных функций равны кофункции, оцениваемой под дополнительным углом. {2}\;\theta {/eq} и упрощение аналогичным образом даст тождество ниже.{2}\;\тета {/экв}
{2}\;\theta {/eq} и упрощение аналогичным образом даст тождество ниже.{2}\;\тета {/экв}
Эти тождества можно использовать как есть при решении тригонометрических задач. Кроме того, использование тригонометрического соотношения или 1 в качестве предмета любого из них оказывается полезным во многих ситуациях.
Другие тригонометрические тождества
Другие важные и полезные тригонометрические тождества рассматриваются ниже.
Сумма или разность углов
Для двух углов {eq}\alpha {/eq} и {eq}\beta {/eq} тождества, включающие их сумму или разность, следующие.
- {eq}sin(\alpha + \beta)=sin(\alpha) cos (\beta)+cos (\alpha)sin(\beta) {/eq}
- {eq}sin(\alpha — \beta)=sin(\alpha) cos (\beta)-cos (\alpha)sin(\beta) {/eq}
- {eq} cos(\alpha + \beta)=cos(\alpha) cos (\beta)+sin (\alpha)sin(\beta) {/eq}
- {eq} cos(\alpha — \beta)=cos(\alpha) cos (\beta)-sin (\alpha)sin(\beta) {/eq}
- {eq} tan (\ alpha + \ beta) = \ frac {tan (\ alpha) + tan (\ beta)} {1-tan (\ alpha) tan (\ beta)} {/eq}
- {eq} tan (\ alpha — \ beta) = \ frac {tan (\ alpha) -tan (\ beta)} {1+tan (\ alpha) tan (\ beta)} {/eq}
Идентификаторы продуктов
Сумму или разность идентичностей углов можно использовать для получения идентичностей продуктов. Например, возьмем
Например, возьмем
{eq}sin(\alpha + \beta)=sin(\alpha) cos (\beta)+cos (\alpha)sin(\beta) {/eq}
и сделать {eq}sin(\alpha) cos (\beta) {/eq} предметом уравнения:
{eq}sin(\alpha) cos (\beta)= sin(\alpha + \beta) — cos(\alpha)sin(\beta) {/eq}. Обозначьте это уравнение цифрой 1.
Затем переставьте
{eq}sin(\alpha — \beta)=sin(\alpha) cos (\beta)-cos (\alpha)sin(\beta) {/eq}
как
{eq} cos (\alpha)sin(\beta) = sin(\alpha) cos (\beta) — sin(\alpha — \beta) {/eq}.Обозначьте это уравнение цифрой 2.
Теперь подставьте уравнение 2 в уравнение 1 и упростите.
{eq}sin(\alpha)cos(\beta)=sin(\alpha+\beta)-[sin(\alpha)cos(\beta)-sin(\alpha-\beta)] {/eq}
{eq}\Rightarrow sin(\alpha)cos(\beta)=sin(\alpha+\beta)-sin(\alpha)cos(\beta)+sin(\alpha-\beta) {/eq}
{eq}\Rightarrow sin(\alpha)cos(\beta)+ sin(\alpha)cos(\beta)=sin(\alpha+\beta)+sin(\alpha-\beta) {/eq}
{ eq}\Rightarrow 2sin(\alpha)cos(\beta)=sin(\alpha+\beta)+sin(\alpha-\beta) {/eq}
{eq}\Rightarrow sin(\alpha)cos(\ beta)=\frac{1}{2}[sin(\alpha+\beta)+sin(\alpha-\beta)] {/eq}
Это идентификатор продукта. {2}\альфа} {/экв}
{2}\альфа} {/экв}
Примечание : Каждое из тождеств, включающих {eq}cos(2\alpha) {/eq}, можно изменять по мере необходимости.{2}(\alpha)= \frac{1-cos(2\alpha)}{2} {/eq}
{eq}\Rightarrow sin(\alpha)=\pm \sqrt{\frac{1- cos(2\alpha)}{2}} {/eq}
В этом тождестве {eq}\theta {/eq} можно заменить на {eq}\frac{\theta}{2} {/eq} чтобы прийти к тождеству половинного угла для синуса.
{eq} \ Rightarrow sin (\ frac {\ alpha} {2}) = \ pm \ sqrt {\ frac {1-cos \; 2(\frac{\alpha}{2})}{2}} {/eq}
{eq}\Rightarrow sin(\frac{\alpha}{2})=\pm \sqrt{\frac{1 -cos(\alpha)}{2}} {/eq}
Аналогичным образом можно вывести формулы половинного угла для тангенса и косинуса.Полный список ниже.
- {eq}sin(\frac{\alpha}{2})=\pm \sqrt{\frac{1-cos(\alpha)}{2}} {/eq}
- {eq} cos (\ frac {\ alpha} {2}) = \ pm \ sqrt {\ frac {1 + cos (\ alpha)} {2}} {/eq}
- {eq}tan(\frac{\alpha}{2})=\pm \sqrt{\frac{1-cos(\alpha)}{1+cos(\alpha)}} {/eq}
- {eq} tan (\ frac {\ alpha} {2}) = \ frac {1-cos (\ alpha)} {sin (\ alpha)} {/eq}
- {экв} tan(\frac{\alpha}{2})=\frac{sin(\alpha)}{1+cos(\alpha)} {/eq}
Краткий обзор урока
Тригонометрические тождества представляют собой уравнения, определяющие взаимосвязь между тригонометрическими отношениями и истинные для всех значений. Эти тригонометрические тождества используют шесть основных тригонометрических функций, как показано ниже.
Эти тригонометрические тождества используют шесть основных тригонометрических функций, как показано ниже.
- синус
- косинус
- тангенс
- косецент
- сек
- котангенс
Тождества, использующие эти функции, варьируются от базовых тождеств до более сложных тождеств, таких как пифагорейские тождества, дополнительные тождества, тождества суммы или разности, произведения, двойного тождества и тождества половинного угла, которые получаются с использованием базовых тождеств. Тригонометрические тождества полезны для решения тригонометрических задач, поскольку их можно использовать для управления и упрощения сложных уравнений.{2} (\ альфа) = 1 {/экв}.
Производные тригонометрических функций — веб-формулы
Общее дифференцирование|
Функция |
Производное |
|
грех х |
cos х |
|
cos х |
— грех х |
|
грех 2 х |
2∙ sin x∙ cos x = sin 2 x |
|
cos 2 х |
-2∙ sin x∙ cos x = — sin 2 x |
|
тангенс х = с 2 х |
1/( cos 2 x) = 1+ тангенс 2 x |
|
детская кроватка x = — csc 2 x |
-1/( sin 2 x) = -1- кроватка 2 x |
|
сек х |
сек х∙ загар х |
|
csc х |
— csc x∙ детская кроватка x |
|
arcsin x = sin -1 x |
1/√(1-х 2 ) |
|
arccos x = cos -1 x |
-1/√(1-x 2 ) |
|
арктан х = тан -1 х |
1/(1+х 2 ) |
|
arccot x = кроватка -1 x |
-1/(1+x 2 ) |
|
угловых секунд x = секунд -1 x |
1/(|х|∙√(х 2 -1)) |
|
arccsc x = csc -1 x |
-1/(|х|∙√(х 2 -1)) |
В следующей таблице приведены производные шести тригонометрических функций, а также их эквиваленты по цепному правилу (то есть синус, косинус и т. д.).функции).
д.).функции).
Пример 1:
Пример 2: Найдите производную от y = 3 sin 3 (2x 4 + 1) .
Положить u = 2x 4 + 1 и v = sin u
Итак, и = 3 v 3
Пример 3: Дифференцировать
Сначала примените правило отношения, тогда мы получим
Теперь примените правило произведения в первой части числителя, результат g'(x) будет:
Пример 4: Дифференцируем y = cos 3 (загар (3x)).
Формулы, тождества, функции и задачи
Тригонометрия — это раздел математики, который в основном занимается конкретными функциями углов, их приложениями и их вычислениями. Всего в математике существует шесть различных типов тригонометрических функций: синус (sin), косинус (cos), секанс (sec), косеканс (cosec), тангенс (tan) и котангенс (cot). Эти шесть различных типов тригонометрических функций символизируют соотношение между отношениями различных сторон прямоугольного треугольника.Эти тригонометрические функции также можно назвать круговыми функциями, поскольку их значения можно описать как отношения координат x и y окружности радиуса 1, которые соприкасаются с углами в стандартных положениях.
Эти шесть различных типов тригонометрических функций символизируют соотношение между отношениями различных сторон прямоугольного треугольника.Эти тригонометрические функции также можно назвать круговыми функциями, поскольку их значения можно описать как отношения координат x и y окружности радиуса 1, которые соприкасаются с углами в стандартных положениях.
Связь между этими тригонометрическими тождествами со сторонами треугольников может быть представлена следующим образом: \theta) = \frac {Adjacent}{Hypotenuse} \]
\[Tan (\theta) = \frac {Opposite}{Adjacent} \]
\[Cot (\theta) = \frac {Смежный}{Напротив} \]
\[Косек (\theta) = \frac {Гипотенуза}{Напротив} \]
\[Сек (\theta) = \frac {Гипотенуза}{Смежный} \]
Тригонометрические функции очень важны для изучения треугольников, света, звука или волн. Значения этих тригонометрических функций в разных областях и диапазонах могут использоваться из следующей таблицы:
Значения этих тригонометрических функций в разных областях и диапазонах могут использоваться из следующей таблицы:
значения этих тригонометрических функций в разных доменах и диапазонах
| тригонометрические функции | Домен | 1 3 1 |
| \ [SIN X \] | \ [R \] | \ [- 1 ≤ sin x ≤ 1 \] |
| \ [cos x x \] | \[R\] | \[-1 ≤ cos x ≤ 1 \] |
| \[Tan x \] | 90 {n 1) \frac{\pi}{2}, n \epsilon I }\] | \[R \] |
| \[Cosec x \] | \[R – {n \pi, n \epsilon I }\] | \[R – {x: -1 < x < 1} \] |
| \[S ec x \] | \[R – {(2n + 1) \frac{\pi}{2}, n \epsilon I }\] | \[R – {x: -1 < x < 1} \] |
| \[Cot x \] | \[R – {n \pi, n \epsilon I }\] | 5 1 \[R \] 9000 |
Значения различных тригонометрических функций на разных углах приведены в следующей таблице, через которую его можно напрямую использовать в задачах:
| Углы | \ [0 ^{\circ} \] | \[30^{\circ} \] | \[45^{\circ} \] | \[60^{\circ} \] | \ [90 ^ {\ Circ} \] | |
| 1 \ [SIN \] | 0 | \ [\ FRAC {1} {2} \] | \ [ \frac{1}{\sqrt{2}}\] | \[ \ frac{\ sqrt {3}} {2} \] | 1 | |
| \[cos] | 1 | \[ \frac{1}{\sqrt{2}}\] | \[ \frac{1}{2}\] | 0 | ||
| 0 | \[ \frac{1}{\sqrt{3}}\] | 1 | 9063 [0\rt | undefined | ||
| \ [COSEC \] | undefined | 2 |
\ [\ \ frac {2} { \ SQRT {3}} \]
1
\ [\ frac {2} {\ sqrt {3}} \]
\[\sqrt{2}\]
2
у ndefined
\ [COT \]
undefined
| 1 | \ [\ frac {1} {\ sqrt { 3}} \] | 0 |
Некоторые общие тождества и формулы, обычно используемые при нахождении тригонометрических соотношений, приведены ниже: cos x \]
2)\[ cos2x = cos^{2}x – sin^{2}x = 1 – 2sin^{2}x = 2cos^{2}x – 1\]
3)\ [ tan 2x = \frac {2 tan x}{(1-tan^{2}x)} \]
4) \[sin 3x = 3 sin x – 4 sin^{3}x \]
5 ) \[cos3x = 4 cos^{3}x – 3 cos x \]
6) \[tan 3x = \frac {(3 tan x – tan^{3}x)}{(1- 3tan^{ 2}x)}\]
Формулы суммы и разности различных тригонометрических функций следующие:
1) \[sin (\alpha + \beta) = sin(\alpha) cos(\beta) + cos(\ альфа) грех(\бета) \]
2) \[грех (\alpha — \beta) = sin(\alpha) cos(\beta) — cos(\alpha) sin(\beta) \]
3) \[cos (\alpha + \beta) = cos(\alpha ) cos(\beta) – sin(\alpha) sin(\beta) \]
4) \[cos (\alpha – \beta) = cos(\alpha) cos(\beta) + sin(\alpha) sin(\beta) \]
5) \[tan (\alpha + \beta) = \frac {tan(\alpha)+tan(\beta)}{1–tan(\alpha)tan(\beta) } \]
6) \[tan (\alpha – \beta) = \frac{tan(\alpha)–tan(\beta)}{ 1+tan(\alpha)tan(\beta)} \]
7) \[tan (\frac{\pi}{4} + \theta) = \frac {(1 + tan \theta)}{(1 – tan \theta)} \]
8) \[tan (\frac{\pi}{4} — \theta) = \frac {(1 — tan \theta)}{(1 + tan \theta)} \]
9) \[cot (\alpha + \beta ) = \ frac {cot (\ alpha). кроватка(\бета)–1}{кроватка(\альфа)+кот(\бета)} \]
кроватка(\бета)–1}{кроватка(\альфа)+кот(\бета)} \]
10) \[кроватка (\альфа – \бета) = \фракция {кот(\альфа).кот(\ beta)+1} {cot(\beta)–cot(\alpha)} \]
Для тройного угла используются указанные ниже тригонометрические функции:
1)\[sin (A+B+C) = sinAcosBcosC + cosAsinBcosC + cosAcosBsinC – sinAsinBsinC.\]
2)\[ cos (A+B+C) = cosAcosBcosC – cosAsinBsinC – sinAcosBsinC – sinAsinBcosC.\]
3) \[tan (A+B+C) =\ frac { tanA + tanB + tanC – tanA tanB tanC}{ 1 – tanA tanB – tanB tanC – tanA tanC}\]
4) \[cot (A+B+C) = \frac {cotA cotB cotC – cotA– cotB–cotC}{cotA cotB + cotB cotC + cotA cotC – 1} \]
Соотношения между различными тригонометрическими функциями следующие:
1) \[Sin A = \frac {1}{cosec A} \]
2) \[Cos A = \frac {1}{sec A} \]
3) \[Sec A = \frac{1}{cos A} \]
4) \[Cosec A = \ frac{1}{sin A} \]
5) \[Tan A = \frac {1}{cot A}, \frac {sin A}{cos A }\]
6) \[Cot A = \frac {1}{tan A}, \frac {cos A}{sin A } \]
Для тождеств периодичности между тригонометрическими функциями:
1) \[Sin (x + 2\pi) = sinx \]
2) \[Cos (x + 2\pi ) = Cosx \]
3) \[Tan (x + \pi ) = Tanx \]
4) \[Cot (x + \ pi ) = Cotx \]
Для функций тригонометрии половинного угла:
1) \[Sin \frac{x}{2}= ± \sqrt{(1-cos x)}{2} \]
2) \[Cos \frac{x}{2}= ± \sqrt{(1+cos x)}{2} \]
3) \[Tan \frac{x}{2}= \sqrt{(1- cos x)}{(1+ cos x)} , \frac{(1- cos x)}{sin x} \]
Для суммы тригонометрических тождеств произведения:
1) \[Sin \alpha ± sin \ бета = 2 sin ^ {\ frac {1} {2}} (\ alpha ± \ beta) Cos ^ {\ frac {1} {2}} (\ alpha ∓ \ beta) \]
2) \[Cos \alpha + Cos \beta=2 Cos^{\frac{1}{2}} (\alpha + \beta) Cos^{\frac{1}{2}} (\alpha — \beta) \]
3) \[Cos \alpha – Cos \beta = — 2 sin (\alpha + \beta)/2 sin (\alpha – \beta)/2 \]
Формулы квадратного закона:
906 31 1) \[Sin 2x + cos 2x = 1 \]2) \[Tan2x = 1 + sec 2x \]
3) \[Cot2x = 1 + cosec 2x \]
Наряду со знанием того, что два острых угла дополняют друг друга, т. {\circ}\] и вы можете решить любой прямоугольный треугольник:
{\circ}\] и вы можете решить любой прямоугольный треугольник:
Если вы знаете две из трех сторон, вы можете найти третью сторону и оба острых угла.
Если вы знаете один острый угол и одну из трех сторон, вы можете найти другой острый угол и две другие стороны.
Знаки тригонометрических функций играют важную роль в их формулах, так как знак меняется при изменении квадранта. В основном, знак основан на квадранте, в котором лежит угол.
В первом квартале все тригонометрические коэффициенты положительны.{\circ} — \theta ) = — Cos \theta \]
Некоторые важные обратные тригонометрические формулы можно легко запомнить с помощью следующей области и диапазона обратных тригонометрических тождеств:
обратные тригонометрические формулы с их областью определения и диапазоном значений
| 1 Домен | 1 4 |
-1,1
-1,1
\[-\frac{\pi}{2}, \frac{\pi}{2} \]
\[- \frac{\pi}{2}, \frac{\pi}{2 } \]
\[Cos-1 x \]
-1,1
-1,1
\[0,\031 \[0,\03 \] 9 pi \]
\[Tan-1 x \]
\[R \]
\[-\frac{\pi}{2}, \frac{\pi}{ 2} \]
\[-\frac{\pi}{2}, \frac{\pi}{2} \]
\[Cot-1 x \]
\[R \]
\[0,\pi \]
[1 0,\pi \]
\[Sec-1 x \]
\[R — (-1,1) \]
\[0,\pi \] 5 \[ — \frac{\pi}{2}, \frac{\pi}{2} \]
\[Cosec-1 x \]
\[R — (-1, 1) \]
\[-\frac{\pi}{2},\frac{\pi}{2} \]
0, 0
Приведенная выше таблица доменов и диапазонов тригонометрических тождеств показывает, что \[sin^{-1} x\] имеет бесконечно много решений в точке x € -1, и существует только одно значение, которое лежит в интервалах \[\frac{\pi}{2 },\frac{\pi}{2}\], которое называется главным значением.
Все таблицы функций тригонометрии Формулы для класса 10
Формулытригонометрии класса 10 приведены в таблице ниже. Список тригонометрических формул для 10-го числа. Применяя теорему Пифагора для данного прямоугольного треугольника, мы имеем: (перпендикуляр) 2 + (основание) 2 = (гипотенуза) 2 ⇒ (P) 2 + (B) 2 = (H) 2. Тригонометрические формулы приведены ниже. :
sin (2π + A) = sin A & cos (2π + A) = cos A. Все тригонометрические тождества цикличны по своей природе. Они повторяются после этой постоянной периодичности.Эта константа периодичности различна для разных тригонометрических тождеств. tan 45° = tan 225°, но это верно для cos 45° и cos 225°.
Какие тригонометрические формулы для классов 10, 11 и 12?
Эти формулы включают в себя все тригонометрические соотношения, тригонометрические тождества, тригонометрическое правило знаков, правило квадрантов и некоторые значения тригонометрических функций определенных степеней. Тригонометрические тождества очень полезны при решении вопросов, которые охватывают большую часть математики в 10, 11 и 12 классах.
Как называются шесть тригонометрических функций?
Всего существует 6 тригонометрических функций, а именно Sin, Cos, Tan, Sec, Cosec и Cot. Существуют тригонометрические соотношения, которые помогают вывести текущую длину и угол. Все формулы тригонометрии, приемы и вопросы по тригонометрии вращаются вокруг этих 6 функций.
Как найти тригонометрические числа в таблице?
Используя таблицу тригонометрии или метод SOHCATOA, вы можете легко найти основные тригонометрические числа наиболее распространенных углов.Создайте пустую тригонометрическую таблицу. Нарисуйте свою таблицу, чтобы иметь 6 строк и 6 столбцов. В первом столбце запишите тригонометрические отношения (синус, косинус, тангенс, косеканс, секанс и котангенс).
Каковы тригонометрические функции для CBSE Class 11?
CBSE Class 11 Math Trigonometric Functions Formulas 1. sin A = противоположность/гипотенуза = a/c. 2. cos A = смежный/гипотенуза = b/c. 3. тангенс A = противоположный/прилегающий = a/b = (a/c)/ (b/c) = sin A/cos A. 4. cosec A = 1/sin A= гипотенуза/противоположный = c/a.5. sec A = 1/cos A= гипотенуза/прилегающая = c/b. 6. детская кроватка
4. cosec A = 1/sin A= гипотенуза/противоположный = c/a.5. sec A = 1/cos A= гипотенуза/прилегающая = c/b. 6. детская кроватка
Тригонометрические формулы для 10 класса
Формула для шести тригонометрических функций: Синус A = Противоположная сторона/Гипотенуза Cos A = Прилегающая сторона/Гипотенуза Tan A = Противоположная сторона/Прилегающая сторона Cot A = Прилегающая сторона/противоположная сторона Sec A = Гипотенуза/Прилежащая сторона Cosec A = Гипотенуза / Противоположная сторона
Основные тригонометрические формулы. sinθ = противолежащая сторона гипотенузы. cosθ = смежная гипотенуза. tanθ = Противоположная Сторона AdiacentSide.secθ = гипотенуза AdjacentSide. θ = гипотенуза на противоположной стороне. cotθ = СмежнаяСторона ПротивоположнаяСторона.
Домен — это все значения q, которые можно вставить в функцию. sinq, q может быть любым углом cosq, q может быть любым углом tanq, 1,0,1,2, 2 qpnn æö „ç÷+=–– Łł K cscq, qp„nn,=0,––1,2 ,K secq, 1,0,1,2, 2 qpnn æö „ç÷+=–– Łł K cotq, qp„nn,=0,––1,2,K Range Диапазон – это все возможные значения для вывода функции.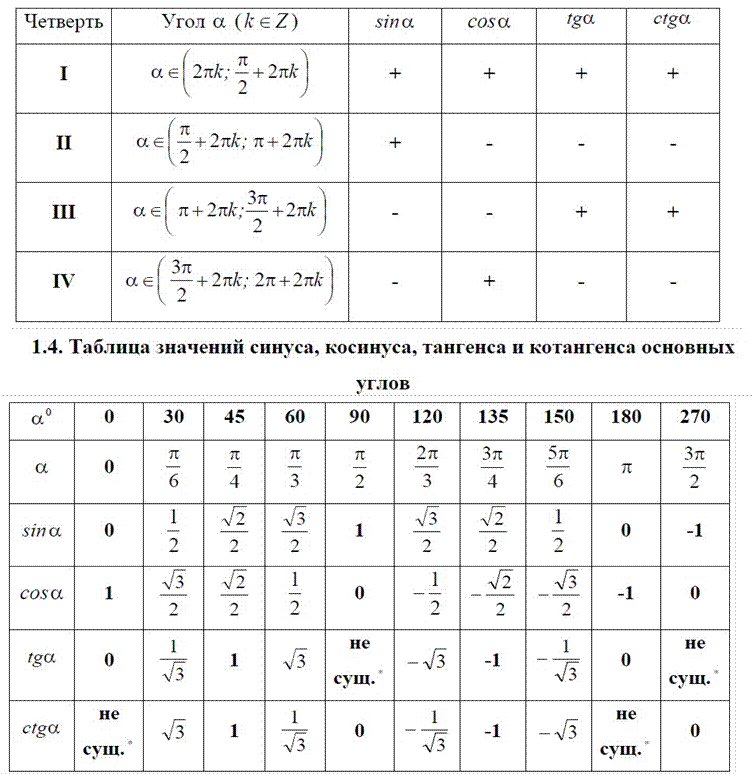
Все формулы главы тригонометрии представлены здесь для учащихся, чтобы помочь им быстро решать задачи.Тригонометрические формулы. грех (-θ) = -sin θ. потому что (-θ) = потому что θ. тангенс (-θ) = -тангенс θ. cosec(−θ) = −cosecθ. сек (-θ) = сек θ. раскладушка (-θ) = — раскладушка θ. Продукт для суммирования формул.
Для прямой ΔABC, направленной под прямым углом к ∠B, тригонометрические отношения ∠A следующие: sin A=противоположная сторона/гипотенуза=BC/AC. cos A=прилежащая сторона/гипотенуза=AB/AC. загар A=противоположная сторона/прилегающая сторона=BC/AB. cosec A=гипотенуза/противоположная сторона=AC/BC. сек A=гипотенуза/прилежащая сторона=AC/AB.
Тригонометрические формулы и тождества (полный список)
Диапазоны функций запуска 1 sin 1 1 cos 1 1 tan 1 csc 1 и csc 1 sec 1 и sec 1 1 cot 1 Периоды функций запуска Периодом функции является число T, такое что f ( +T ) = ж ( ) .Итак, если ! — фиксированное число и любой угол, у нас есть следующие периоды. sin(!) )T= 2ˇ! cos(!) )T= 2ˇ! загар(!) )T= ˇ! csc(!) )T= 2ˇ! сек(!) )T= 2ˇ! раскладушка(!
sin(!) )T= 2ˇ! cos(!) )T= 2ˇ! загар(!) )T= ˇ! csc(!) )T= 2ˇ! сек(!) )T= 2ˇ! раскладушка(!
Таблица и список формул тригонометрии. Таблица формул тригонометрии от А до Я и список тождеств с загрузкой в формате PDF: мы уже изучили, что такое тригонометрия и все основные тригонометрические тождества. Здесь мы подробно получим таблицу всех формул тригонометрии и список всех тригонометрических тождеств. Мы обсудим каждую формулу тригонометрии от уровня 10, 11, 12 класса до уровня колледжа.
Тригонометрические функции формируются при изучении тригонометрических соотношений в терминах радианной меры для любого угла (0, 30, 90, 180, 270…). Они также определяются в терминах функций синуса и косинуса. В этой статье мы предоставим вам все подробности о тригонометрических функциях, таких как значение в градусах, радианах, полную тригонометрическую таблицу и другую соответствующую информацию.
Ответ. Все формулы тригонометрии в одном месте помогут вам в выполнении обеих глав тригонометрии в 10 классе. Вы можете выучить все формулы тригонометрии 10 класса и использовать их на практике и при повторении главы для экзаменов. Это поможет также в повторении формул обеих глав непосредственно перед экзаменом.
Вы можете выучить все формулы тригонометрии 10 класса и использовать их на практике и при повторении главы для экзаменов. Это поможет также в повторении формул обеих глав непосредственно перед экзаменом.
Вы можете найти формулы по всем темам, изложенным в разделе «Введение в тригонометрию 10 класса», в деталях и получить хорошее представление о них. Пересмотрите все понятия разумным образом, воспользовавшись помощью Математических формул для 10 класса. Введение в тригонометрию.
Тригонометрия (таблица, формулы и примеры решения)
Перед попыткой начать лучше постараться запомнить эти значения и знать следующие тригонометрические формулы. sin x = cos (90°− x) cos x = sin (90°− x) tan x = cot (90°− x) cot x = tan (90°− x) sec x = cot (90°− x) cot x = sec (90°− x) 1/sin x = 1/cos x = sin x. 1/cos х = сек х.
Тригонометрические функции: Существует 6 различных тригонометрических функций: Синус x, записываемый как sin(x) Косинус x, записываемый как cos(x) Тангенс x, записываемый как Tan(x) Котангенс x, записываемый как Cot(x) ) Секанс x, записывается как Sec(x) Косеканс x, записывается как Cosec(x) Тригонометрические отношения: Существуют три основных тригонометрических отношения.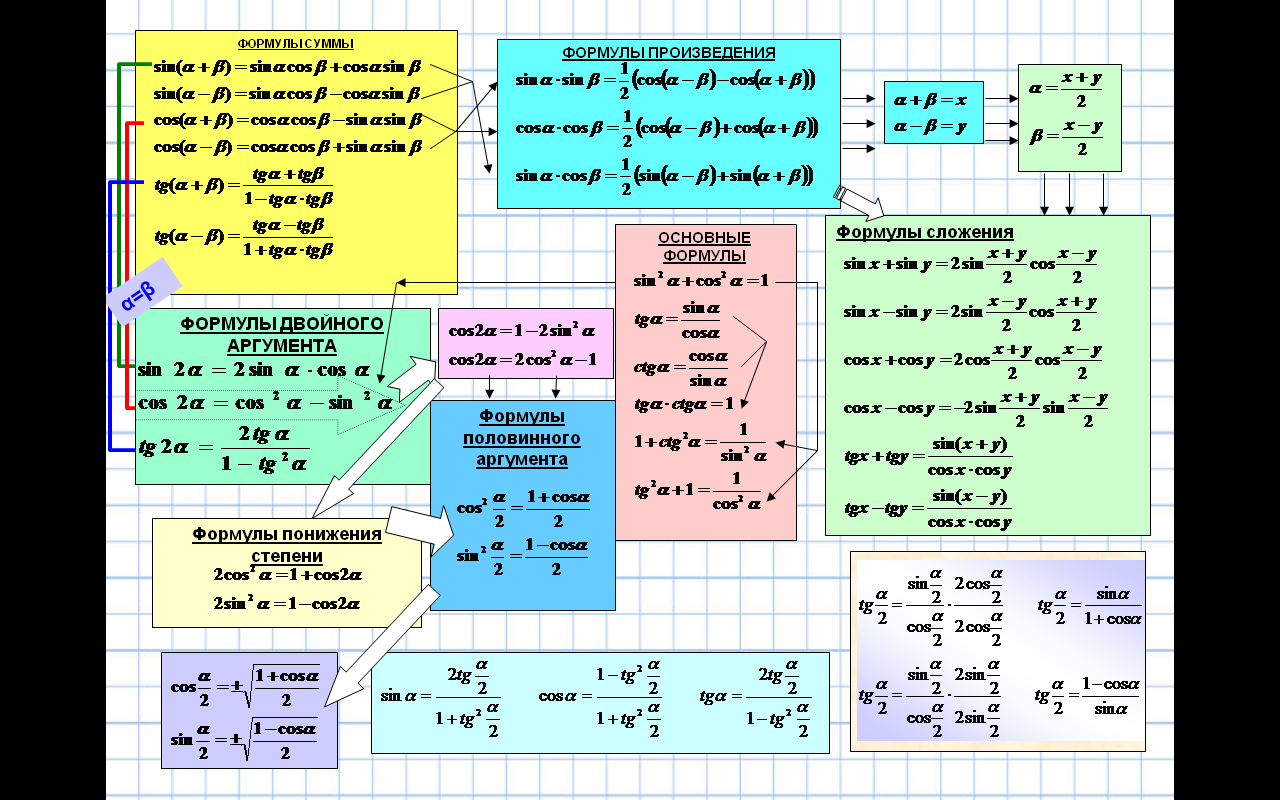 Они следующие:
Они следующие:
Привет всем, вот список формул тригонометрии, которые помогут вам решить задачи по математике для 10 класса. Тригонометрия – это наука о соотношениях между сторонами и углами треугольника. В прямоугольном треугольнике ABC, прямоугольном в точке B, sin A = сторона, противолежащая углу A/гипотенуза, cos A = сторона, прилежащая к углу A/гипотенуза.
Список тригонометрических тождеств 2 Тригонометрические функции Основными тригонометрическими функциями являются синус и косинус угла.Иногда они обозначаются аббревиатурой sin(θ) и cos(θ) соответственно, где θ — угол, но скобки вокруг угла часто опускаются, например, sin θ и cos θ. Тангенс (тангенс) угла – это отношение синуса к косинусу:
Тригонометрические формулы Это общие формулы, используемые в главах с 9 по 14 Учебника по алгебре и тригонометрии класса XI, Совет по учебникам Пенджаба, Лахор. Этот раздаточный материал очень помогает запомнить формулы. Все эти формулы даны для вещественнозначных и определенных тригонометрических функций. Файл PDF можно скачать для высококачественной печати.
Файл PDF можно скачать для высококачественной печати.
Тригонометрические формулы для 11 класса
Содержание. Формулы тригонометрических функций для 11 класса по математике Глава 3. Взаимные тождества задаются как: Тригонометрические значения особых углов. Тригонометрические формулы произведения: Тригонометрические формулы суммы в произведение: Тригонометрические формулы Пифагора. Пифагорейцы в радикальной форме Тригонометрические формулы.
В этом посте мы приводим все основные тригонометрические формулы с доказательством простейшим методом с уловками.Все эти основные формулы тригонометрии наиболее важны для 10 класса, глава 8 по математике, тригонометрические функции 11 класса и т. д. Прежде чем начать, пожалуйста, прочитайте нашу 1-ю часть, если вы не читали — Перейти к курсу по тригонометрии Часть — 1
Тригонометрия — это раздел математики, изучающий треугольники, особенно треугольники на плоскости, где один угол треугольника равен 90 градусов. Тригонометрия занимается именно отношениями между сторонами и углами треугольника, т. 2 (\ alpha) = 1 sin 2 (α) + cos 2 (α) = 1: α \alpha α — значение угла, sin — синус угловой функции, cos — косинус угловой функции.
2 (\ alpha) = 1 sin 2 (α) + cos 2 (α) = 1: α \alpha α — значение угла, sin — синус угловой функции, cos — косинус угловой функции.
Введение в тригонометрию Класс 10 Глава 8 Примечания
Формула тригонометрии для 12 класса Тригонометрия — это часть математики, где мы исследуем связь между точками и длинами треугольника. В арифметике 12-го класса мы изучаем жизненно важные идеи, такие как математика, трехмерность и т. д. Практически на каждом уроке мы решаем математические задачи с помощью геометрических уравнений.
Таблица тригонометрических функций – точные значения специальных углов Angle θ Значения тригонометрических функций в градусах в радианах sin(θ) cos(θ) tan(θ) cot(θ) sec(θ) csc(θ)
Обзор тригонометрии с единичным кругом: все триггеры.вам когда-либо понадобится знать в исчислении Цели: это ваш обзор тригонометрии: углы, шесть триггеров. функции, тождества и формулы, графики: область определения, диапазон и преобразования. Измерение угла Углы можно измерять двумя способами: в градусах или в радианах. На следующем рисунке показан
На следующем рисунке показан
В этой брошюре мы рассмотрим определение этих тригонометрических отношений и расширим понятия косинуса, синуса и тангенса. Мы определяем косинус, синус и тангенс как функции всех действительных чисел. Эти тригонометрические функции чрезвычайно важны в естественных науках, технике и математике, и в большинстве
случаев предполагается некоторое знакомство с ними.Просмотр загрузки таблицы тригонометрии.docx из MATH 4U1 Университетского института Лестера Б. Пирсона. таблица тригонометрии скачать Скачать файл Справочник по тригонометрии со всеми этими тождествами, формулами, а также
Таблица тригонометрических формул Определение триггерных функций
Тригонометрия — раздел математики, изучающий взаимосвязь между сторонами треугольника (прямоугольного треугольника) и его углами. Отношение представлено как отношение сторон, являющихся тригонометрическими соотношениями.Шесть тригонометрических соотношений: синус, косинус, тангенс, котангенс, секанс и косеканс.
ГЛАВА 1 1 Углы и их применение 1.1 Введение Тригонометрия — это раздел математики, связанный с измерением частей, сторон и углов треугольника. Плоская тригонометрия, которая является темой этой книги, ограничивается треугольниками, лежащими на плоскости. Тригонометрия основана на определенных соотношениях, называемых тригонометрическими функциями, которые будут определены в следующей главе.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ Определения тригонометрических соотношений и функций В тригонометрии существует шесть тригонометрических соотношений, которые связывают меры углов прямоугольного треугольника с длинами его сторон.(Помните, что прямоугольный треугольник содержит угол 90 °) Прямоугольный треугольник может быть образован из начальной стороны x и конечной стороны r, где r
Основные идентификаторы триггеров. Базовые тригонометрические тождества или фундаментальные тригонометрические тождества на самом деле являются теми тригонометрическими функциями, которые верны каждый раз для переменных. Таким образом, эти тригонометрические тождества отображают определенные функции хотя бы одного угла (может быть больше углов). Он отождествляется с единичным кругом, где связь между прямыми и углами в декартовой плоскости.
Таким образом, эти тригонометрические тождества отображают определенные функции хотя бы одного угла (может быть больше углов). Он отождествляется с единичным кругом, где связь между прямыми и углами в декартовой плоскости.
Тригонометрическая таблица 12 класс pdf Тригонометрическая таблица 12 класс pdf. Тригонометрическая таблица 12 класс. Формулы тригонометрии Список тригонометрических формул для 10 и 11 классов был представлен учащимся в новом учебнике по математике для 10 класса. Тригонометрические формулы и тождества являются полезными инструментами для студентов при изучении приложений тригонометрии.
Математический справочник формул, процессов и приемов
Область тригонометрических функций, диапазон и графики тригонометрических функций.Приведем эти формулы ниже.
Функция f(x) называется периодической, если существует действительное число T > 0 такое, что f(x + T)= f(x) для всех x. T называется периодом функции, все тригонометрические функции периодические. Максимальное и минимальное значения тригонометрических выражений Тригонометрические отношения сложных углов
Максимальное и минимальное значения тригонометрических выражений Тригонометрические отношения сложных углов
Тригонометрия в основном используется в случае прямоугольных треугольников. Тригонометрические функции определяют отношения между тремя сторонами и углами треугольника.В основном есть 6 тригонометрических функций. Прежде чем приступить к изучению тригонометрических функций, мы узнаем о трех сторонах прямоугольного треугольника.
Рисунок 1.7.3.1: Диаграмма, демонстрирующая тригонометрические функции в единичном круге., \). Значения других тригонометрических функций могут быть выражены через x, y и r (рис. 1.7.3). Рисунок 1.7.3.2: Для точки P = (x, y) на окружности радиуса r координаты x и y удовлетворяют условиям x = rcosθ и y = rsinθ.
В этом разделе мы дадим краткий обзор триггерных функций.Мы рассмотрим основные обозначения, взаимосвязь между тригонометрическими функциями, определение прямоугольного треугольника тригонометрических функций. Мы также рассмотрим вычисление триггерных функций, а также единичный круг (одна из наиболее важных идей класса триггеров!) и то, как его можно использовать для вычисления тригонометрических функций.
Математические формулы 10 класса
Формула Пифагора для синусов и косинусов. Это, вероятно, самая важная триггерная идентичность. Тождества, выражающие триггерные функции через их дополнения.В этом нет ничего особенного. Каждая из шести триггерных функций равна своей кофункции, оцениваемой под дополнительным углом. Периодичность триггерных функций.
Здесь мы получим таблицу всех формул тригонометрии и подробный список всех тригонометрических тождеств. Мы обсудим каждую формулу тригонометрии от уровня 10, 11, 12 класса до уровня колледжа. Мы также будем изучать от основных тригонометрических тождеств до формул обратной тригонометрии. Помните, что множественное число формулы — это формулы, а не формулы.
Краткий факт: все тригонометрические функции в Python предполагают, что входной угол выражается в радианах. Кроме того, поскольку мы изучаем математику, пи/2 равно 90 градусам, а пи/3 равно 60 градусам, математический модуль в python предоставляет константу пи, которая представляет число пи, которое можно использовать с тригонометрической функцией.
Проверьте таблицу формул интегрирования. Темы включают Основные формулы интегрирования Интеграл специальных функций Интеграл по частным дробям Интегрирование по частям Другие специальные интегралы Площадь как сумма Свойства определенного интегрирования Интегрирование тригонометрических функций, Свойства определенного интегрирования упоминаются здесь.
Сделайте тригонометрию своим приоритетом в классе. Старайтесь не использовать время занятий для общения или выполнения домашних заданий для другого класса. Когда вы находитесь на уроке тригонометрии, вы должны сосредоточиться на лекциях и практических задачах. Записывайте все заметки, которые инструктор делает на доске или отмечает как важные.
Тригонометрические функции с их формулами
Тригонометрические функции для углов единичной окружности можно запомнить и вызвать, используя набор правил.Знак тригонометрической функции зависит от квадранта, в который попадает угол, и мнемоническая фраза «Класс интеллектуальных триггеров» используется для определения того, какие функции положительны в каком квадранте.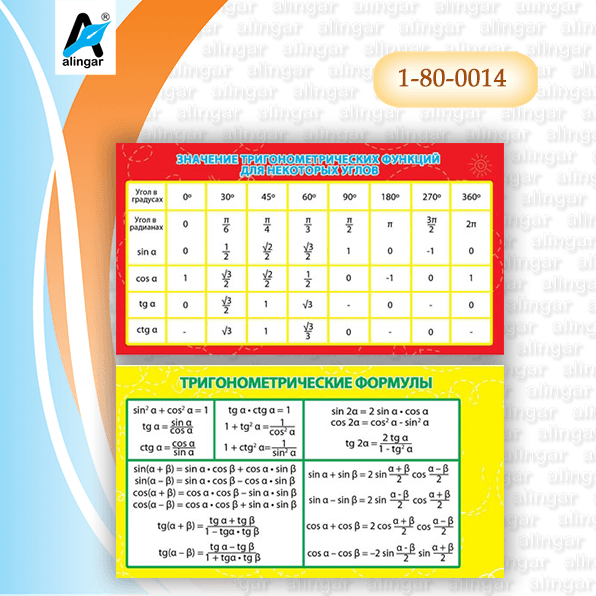
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ 2.1 Обзор 2.1.1 Обратная функция Обратная функция f существует, если функция является взаимно однозначной и однонаправленной, т. е. взаимно однозначной. Поскольку тригонометрические функции являются многоединичными над своими областями, мы ограничиваем их области определения и ко-области, чтобы сделать их взаимно-однозначными и затем найти их обратную.
6.2 Тригонометрические тождества (EMBHH) Тождество – это математическое утверждение, приравнивающее одну величину к другой. Тригонометрические тождества позволяют упростить данное выражение, чтобы оно содержало только отношения синуса и косинуса. Это позволяет нам решать уравнения, а также доказывать другие тождества.
Представлены задачи и вопросы по тригонометрии для 10 класса с ответами и решениями. Проблемы. Найдите x и H в прямоугольном треугольнике ниже. Найдите длины всех сторон прямоугольного треугольника, если его площадь равна 400.BH перпендикулярна AC.
1. Контрольные работы по тригонометрии для 11 класса по всем важным темам, которые могут быть включены в ваши школьные экзамены, скачать в формате pdf бесплатно. Всего существует 6 тригонометрических функций, а именно Sin, Cos, Tan, Sec, Cosec и Cot. Введение в нашу электронную книгу «Учебное пособие по географии 11» Добро пожаловать в учебное пособие по географии для 11 класса.
Контрольные работы по тригонометрии для 11 класса по всем важным темам, которые могут быть включены в ваши школьные экзамены, скачать в формате pdf бесплатно. Всего существует 6 тригонометрических функций, а именно Sin, Cos, Tan, Sec, Cosec и Cot. Введение в нашу электронную книгу «Учебное пособие по географии 11» Добро пожаловать в учебное пособие по географии для 11 класса.
CBSE Class 10 Math Chapter 8
Для пределов мы ставим значение и проверяем, имеет ли оно вид 0/0, ∞/∞, 1 ∞. Если он имеет такую форму, мы не можем найти пределы, ставя значения.п Формула.
Родственные
Формулы тригонометрии PDF —
Привет, студенты, добро пожаловать в блоги Amans Maths (AMB) . В этом посте вы получите все формулы тригонометрии . Это поможет вам решить вопросы по тригонометрии. Эта формула тригонометрии очень полезна для пересмотра перед школьными экзаменами или конкурсными экзаменами, такими как SSC, IBPS, CAT, NTSE и т. Д. Это в виде файла PDF, поэтому вы можете загрузить его на свой мобильный телефон / ноутбук и сохранить этот файл PDF. постоянно.
Д. Это в виде файла PDF, поэтому вы можете загрузить его на свой мобильный телефон / ноутбук и сохранить этот файл PDF. постоянно.
Тригонометрические формулы: градусы в радианы
Чтобы преобразовать угол в градусах в радианы, нам нужно умножить π/180 на градус.
Например: 30 градусов = 30 x π/180 = π/6 радиан.
Тригонометрические формулы: радианы в градусы
Чтобы преобразовать угол в радианах в градусы, нам нужно умножить 180/π на градусы.
Например: π/6 радиан = π/6 x 180/π = 30 градусов.
Тригонометрические формулы: длина дуги и угол сектора окружности
Если дуга образует угол θ (в радианах) в центре окружности, радиус которой равен r, то длина дуги дуги равна s = rθ .Следовательно, мы можем сказать, что угол θ = s/r радиан.
Тригонометрические формулы: Теорема Пифагора
В прямоугольном треугольнике сумма квадрата его перпендикуляра и квадрата его основания равна квадрату гипотенузы. Это известно как теорема Пифагора .
На рисунке ниже ABC представляет собой прямоугольный треугольник с прямым углом при вершине B. В этом треугольнике сторона, противоположная прямому углу B, является гипотенузой (h = AC), а сторона, противоположная углу ACB = θ, равна перпендикуляр (p = AB), а сторона BC является основанием (b).
Таким образом, по теореме Пифагора p 2 + b 2 = h 2 .
Мы также можем записать это как p 2 = h 2 – b 2 или b 2 = h 2 – p 2 .
Тригонометрические формулы: тригонометрические отношения
В тригонометрии мы изучаем отношения между сторонами и углами прямоугольного треугольника. Для этого определяются шесть тригонометрических соотношений, как показано ниже.
1.Синус θ обозначается как sinθ и представляет собой отношение перпендикуляра (p) к гипотенузе (h). Это означает, что
sinθ = p/h = AB/AC.
2. Косинус θ обозначается как cosθ и представляет собой отношение основания (b) и гипотенузы (h). Это означает, что
cosθ = b/h = BC/AC.
3. Тангенс θ обозначается как tanθ и представляет собой отношение перпендикуляра (p) к основанию (b). Это означает, что
tanθ = p/b = AB/BC.
4.Косеканс θ обозначается как cosecθ или cscθ и представляет собой отношение гипотенузы (h) к перпендикуляру (p). Это означает, что
cosecθ или cscθ = h/p = AC/AB.
5. Секанс θ обозначается как secθ и представляет собой отношение гипотенузы (h) к основанию (b). Это означает, что
секθ = h/b = AC/BC.
6. Котангенс θ обозначается как cotθ и представляет собой отношение основания (b) и гипотенузы (h). Это означает, что
cotθ = b/p = BC/AB.
Прочтите: Вопросы и ответы по тригонометрическим отношениям
Тригонометрические формулы: частные тождества
час). Таким образом,
tanθ = sinθ / cosθ .
Поскольку sinθ = p/h, cosθ = b/h и cotθ = b/p, то cotθ = (b/h) / (p/h). Таким образом,
cotθ = cosθ / sinθ .
Тригонометрические формулы: тождества взаимности
Поскольку sinθ = p/h и cosecθ = h/p, то
sinθ x cosecθ = 1 или sinθ = 1/ cosecθ и
cosec
Поскольку cosθ = b/h и secθ = h/b, то
cosθ x secθ = 1 или cosθ = 1/secθ и secθ = 1/cosθ .
Так как tanθ = p/b и cotθ = b/p, то
tanθ x cotθ = 1 или tanθ = 1/ cotθ и cotθ = 1/ tanθ .
Тригонометрические формулы: тригонометрические тождества
Используя теорему Пифагора p 2 + b 2 = h 2 и основное определение тригонометрических отношений, мы получаем три тригонометрических тождества, как показано ниже.
SIN 2 θ + COS 2 θ = 1
θ — Tan 2 θ = 1
COSEC 2 θ — COT 2 θ = 1
Используя a 2 – b 2 = (a + b)(a – b) в с 2 θ – tan 2 + 90 с (secθ – tanθ) = 1. Таким образом, мы получаем результаты как
secθ + tanθ = 1 / (secθ – tanθ)
и
secθ – tanθ = 1 / (secθ 5 900 ) где θ nπ + π/2
Используя a 2 – b 2 = (a + b)(a – b) в cosec 2 θ = ctg 3 2 мы получить (cosecθ + cotθ) (cosecθ – cotθ) = 1.Таким образом, мы получаем результаты как cosecθ + cotθ = 1 / (cosecθ – cotθ) и cosecθ – cotθ = 1 / (cosecθ + cotθ) , 90π 005, где 9.θn Читайте : Тригонометрические тождества Вопросы и ответы Существуют определенные тригонометрические значения определенных углов, которые приведены ниже в тригонометрической таблице. Читайте : Тригонометрическая таблица Вопросы и ответы Тригонометрические формулы : Тригонометрическая таблица

Тригонометрические формулы : Тригонометрические значения , 225, 240, 270, 300, 315, 330 и 360 градусов, как указано в приведенной выше тригонометрической таблице.
1. SIN15 O = COS75 O =,
2. COS15 O = SIN75 O =,
3. TAN15 O = COT75 O =,
4. COT15 o = TAN75 O =,
5. SIN22.5 O = COS67.5 O =,
6. COS22.5 O = SIN67.5 O =,
7. tan22.5 o = ,
8. cot22.5 o = ,
9.SIN18 O = COS72 =,
o =,10. Cos18 O = SIN72 o =,
11. SIN36 O = COS54 O =,
12. COS36 O = sin54 o = ,
Тригонометрические формулы : знак тригонометрических отношений
Знак тригонометрических отношений (sinθ, cosθ, tanθ, cosecθ, secθ, cotθ) зависит от угла θ, в котором они лежат в квадрантах.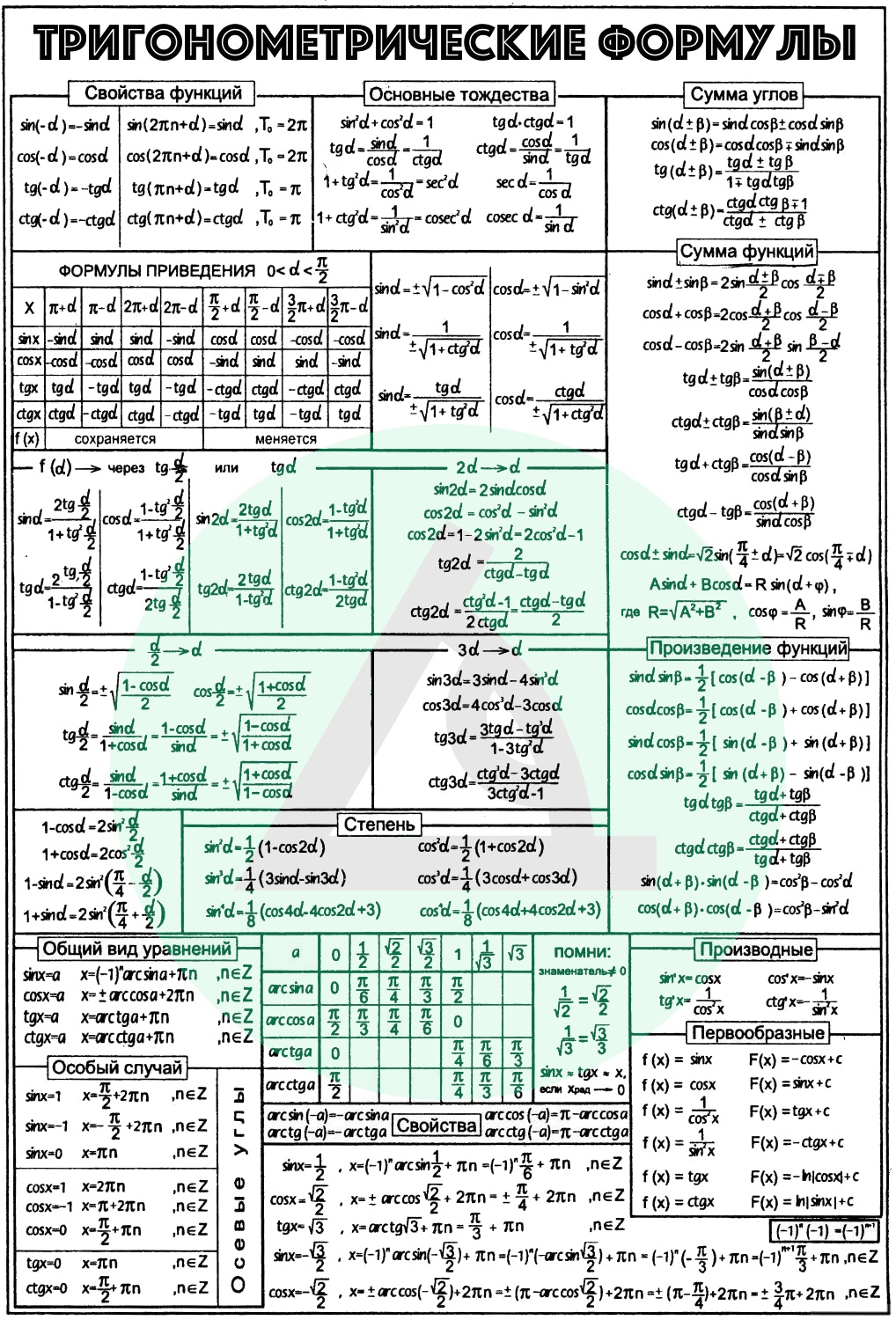 Для этого мы используем концепцию правила ASTC .
Для этого мы используем концепцию правила ASTC .
A находится в первой позиции (означает 1 st квадрант) в ASTC , что означает Все ( A означает Все ). Это означает, что все тригонометрические отношения угла θ в первом квадранте (0 o < θ < 90 o ) являются положительными .
S находится в позиции второй (означает 2 и квадрант) в ASTC , что означает Sin и обратное значение Cosec ( S означает Sin и Cosec ).Это означает, что только Sin и Cosec угла θ во втором квадранте (90 o < θ < 180 o ) являются положительными , а остальные тригонометрические отношения (cosθ, tanθ, secθ, cotθ) отрицательны.
T находится в третьем положении (означает 3 rd квадрант) в ASTC , что означает Tan и его обратный Cot ( T означает Tan & Cot ). Это означает, что только Tan и Cot угла θ в третьем квадранте (180 o < θ < 270 o ) являются положительными , а остальные тригонометрические отношения (sinθ, cosθ, cosecθ, secθ) отрицательны.
Это означает, что только Tan и Cot угла θ в третьем квадранте (180 o < θ < 270 o ) являются положительными , а остальные тригонометрические отношения (sinθ, cosθ, cosecθ, secθ) отрицательны.
C находится в четвертом положении (означает 4 й квадрант) в ASTC , что означает Cos и его обратную Sec ( C означает Cos и Sec ). Это означает, что только Cos и Sec угла θ в четвертом квадранте (270 o < θ < 360 o ) являются положительными , а остальные тригонометрические отношения (sinθ, tanθ, cosecθ, cotθ) отрицательны.
Тригонометрические формулы: союзные углы Формула
Углы O θ , 180 o θ , 270 , 270 o θ o 360 o θ — это Knwon AS углы . Значение тригонометрических отношений этих смежных углов соответствует правилу ASTC, как обсуждалось выше.
Значение тригонометрических отношений этих смежных углов соответствует правилу ASTC, как обсуждалось выше.
Здесь также используется другое правило, известное как нечетного и четного умножения 90 o .
o o = 1 x o o o o o = 3 x o = 3 x
| Функции | Значение |
| грех А | \(\ гидроразрыва{P}{H}\) |
| потому что А | \(\ frac{B}{H}\) |
| желто-коричневый А | \(\ гидроразрыва{P}{B}\) |
| косек А | \(\ гидроразрыва{H}{P}\) |
| сек А | \(\ гидроразрыва{H}{B}\) |
| кроватка А | \(\ гидроразрыва {B}{P}\) |
Тригонометрические формулы на основе соотношений:
| Функции | Отношения |
| желто-коричневый А | \(\frac{sin\:A}{cos\:A}\) |
| кроватка А | \(\frac{cos\:A}{sin\:A}\) |
| сек А | \(\frac{1}{cos\:A}\) |
| косек А | \(\frac{1}{sin\:A}\) |
Отрицательный знак тригонометрической функции:
Знак минус (-A) имеет обычное значение в терминах (2π – A).
| Серийный номер | Функция |
| 1. | sin(-A) = – sin A |
| 2. | cos(-A) = cos A |
| 3. | тангенс(-А) = – тангенс А |
| 4. | косек(-А) = – косек А |
| 5. | сек(-А) = сек А |
| 6. | детская кроватка(-A) = – детская кроватка A |
Правила знаков в тригонометрии:
Также часто используемая функция в квадрантах:
Знак в этом квадранте запоминается как
.«От школы до колледжа»
т.е.
- Все положительные для 1 ст. квадранта,
- Sin и cosec положительны для 2 -го квадранта,
- Tan and cot положительный для 3 rd квадранта,
- Cos и сек положительны в 4 th .
| Серийный номер | Значение |
| 1. | sin(90⁰-A) = cos A |
| 2. | cos(90⁰-A) = sin A |
| 3. | загар(90⁰-A) = детская кроватка A |
| 4. | косек(90⁰-А) = сек А |
| 5. | сек(90⁰-А) = косек А |
| 6. | детская кроватка(90⁰-A) = загар A |
Ежедневно пересматривайте эти тригонометрические формулы, чтобы получить более высокие баллы на экзаменах, а также на JEE, SSC и т. д., таких как конкурсные экзамены.
Тригонометрические тождества:
| Серийный номер | Личности |
1. |
sin 2 А + cos 2 А = 1 |
| 2. | сек 2 А – рыжевато-коричневый 2 А = 1 |
| 3. | cosec 2 A – раскладушка 2 A = 1 |
Тригонометрическая формула как правило произведения:
| Серийный номер | Правила |
| 1. | sin (A + B) = sin A cos B + cos A sin B |
| 2. | sin (A – B) = sin A cos B – cos A sin B |
| 3. | cos (A + B) = cos A cos B – sin A sin B |
| 4. | cos (A – B) = cos A cos B + sin A sin B |
| 5. | tan (A + B) = \(\frac{tanA + tanB}{1 – tanA\: tanB}\) |
6. |
tan (A – B) = \(\frac{tanA – tanB}{1 + tanA\: tanB}\) |
Тригонометрические формулы для двойного угла:
| С.{2}А – 1}\) |
Преобразование тригонометрического произведения:
| Серийный номер | Формулы |
| 1. | \(\frac{cos(A – B) – cos(A+B)}{2}\) = sinA.sinB |
| 2. | \(\ frac{cos(A – B) + cos(A+B)}{2}\) = cosA.cosB |
| 3. | \(\frac{sin(A + B) + sin(A – B)}{2}\) = sinA.cosB |
| 4. | \(\frac{cos(A + B) + sin(A — B)}{2}\) = cosA.sinB |
Расширенное правило продукта:
| Серийный номер | Формулы |
1. |
sinA.sinB = \(\frac{cos\frac{(A + B)}{2}.cos\frac{(AB)}{2}}{2}\) |
| 2. | cosA.cosB = \(\frac{cos\frac{(A + B)}{2}.sin\frac{(AB)}{2}}{2}\) |
| 3. | sinA.cosB = \(\frac{sin\frac{(A + B)}{2}.cos\frac{(AB)}{2}}{2}\) |
| 4. | cosA.sinB = \(\frac{sin\frac{(A + B)}{2}.sin\frac{(AB)}{2}}{2}\) |
Тригонометрические тождества полууглов:
| Серийный номер | Формулы |
| 1. | \(\sin\frac{x}{2}=\pm \sqrt{\frac{1-\cos\: x}{2}}\) |
| 2. | \(\cos\frac{x}{2}=\pm \sqrt{\frac{1+\cos\: x}{2}}\) |
| 3. | \(\tan(\frac{x}{2}) = \sqrt{\frac{1-\cos(x)}{1+\cos(x)}}\) |
4.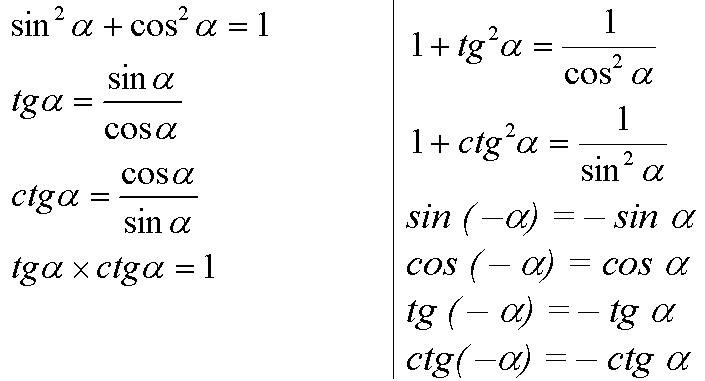 |
\(\tan(\frac{x}{2}) = \sqrt{\frac{1-\cos(x)}{1+\cos(x)}}\) Кроме того, \(\tan(\ frac{x}{2}) =\frac{1-\cos(x)}{\sin(x)}\) |
Тригонометрические формулы облегчат вам решение вопросов. Сохраните этот сайт в закладки, чтобы регулярно его изучать и пересматривать. Тригонометрическая формула 10 класса здесь с полной оценкой.
Тригонометрическое соотношение некоторых конкретных углов:
Тригонометрическое отношение 0°, 30°, 45°, 60°, 90° указано ниже. взгляните на это.
| ∠ А | 0⁰ | 30⁰ | 45⁰ | 60⁰ | 90⁰ |
| грех А | 0 | \(\ гидроразрыва{1}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\ гидроразрыва {\ sqrt {3}} {2} \) | 1 |
| cos A | 1 | \(\ гидроразрыва {\ sqrt {3}} {2} \) | \(\frac{1}{\sqrt{2}}\) | \(\ гидроразрыва{1}{2}\) | 0 |
| желто-коричневый А | 0 | \(\frac{1}{\sqrt{3}}\) | 1 | \(\sqrt{3}\) | Не определено |
| сек А | 1 | \(\frac{2}{\sqrt{3}}\) | \(\sqrt{2}\) | 2 | Не определено |
| кроватка A | Не определено | \(\sqrt{3}\) | 1 | \(\frac{1}{\sqrt{3}}\) | 0 |
| косек А | Не определено | 2 | \(\sqrt{2}\) | \(\frac{2}{\sqrt{3}}\) | 1 |
Математические навыки: Тригонометрия
Темы по математике
Тригонометрия
Печатные материалы
Материалы для печати, чтобы помочь с любыми предварительными требованиями по математике, требуемыми в курсах USQ. Эти материалы основаны на программе подготовки к высшему образованию USQ. Математические модули представлены в возрастающем уровне сложности и сложности от уровня A до уровня D.
Эти материалы основаны на программе подготовки к высшему образованию USQ. Математические модули представлены в возрастающем уровне сложности и сложности от уровня A до уровня D.
Сравнение номеров (только часть модуля)
- Сравнение количеств вычитания
- Сравнение количеств по разделам (включая проценты)
- Соотношения (включая соотношения в квадратах, прямоугольниках, кругах и треугольниках )
- Тарифы
Тригонометрия (Уровень B)
- Синус (включая коэффициент синуса, функцию синуса, функцию, обратную синусоиде, градусы, минуты и секунды, амплитуду и период)
- Косинус (включая отношение косинуса, функцию косинуса, функцию, обратную косинусу, амплитуду и период)
- Тангенс (включая отношение тангенса, функцию тангенса, функцию, обратную тангенсу, амплитуду и период)
Тригонометрические функции (уровень C)
- Радианная мера (включая то, что такое радианы, преобразование из градусов в радианы, преобразование из радианов в градусы, использование радианной меры в реальных приложениях)
- Графики функций синуса, косинуса и тангенса
- Моделирование с использованием тригонометрических функций (включая амплитуду, вертикальный сдвиг, период тригонометрических функций, фазу тригонометрических функций)
- Обратные функции
- Решение тригонометрических уравнений
Тригонометрия (уровень D)
- Радиан
- Полярные координаты
- Тригонометрические тождества и формулы кратных углов
- Решение тригонометрического уравнения
- Периодичность
- Амплитуда
- Треугольное решение
- Составные углы
- Решение уравнений с тригонометрическими функциями
Видеоматериалы
Введение в тригонометрию (раздаточный материал для печати)
Это 20-минутное видео представляет:
- маркировка треугольников для тригонометрии
- Теорема Пифагора
- тригонометрические соотношения 90 109 обработанных примеров с использованием тригонометрических соотношений 90 110
Решение треугольников с использованием правил синусов и косинусов
Это 18-минутное видео показывает, как использовать правила синуса и косинуса (то есть, когда у вас нет прямоугольных треугольников.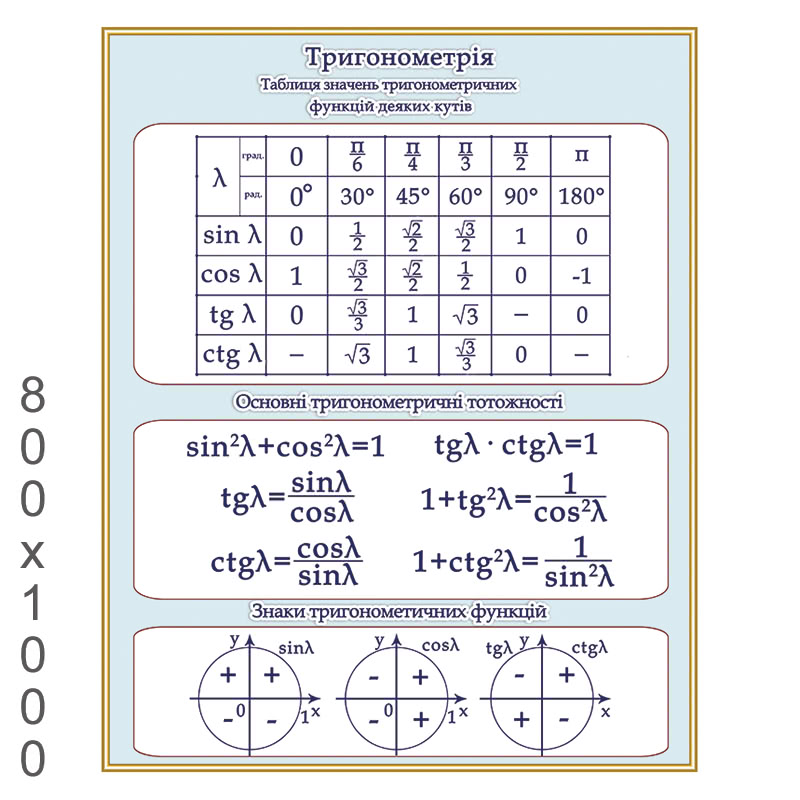
Использование тригонометрических тождеств
В этом 11-минутном видеоролике есть несколько рабочих примеров использования тригонометрических тождеств.
Вы также можете получить помощь Освоение калькулятора – бесплатные, простые в использовании онлайн-буклеты по целому ряду научных калькуляторов.
.

 {2}(\alpha)
$$
{2}(\alpha)
$$
 Напоминаем, что Π приблизительно равняется 3.14 радиан. Более точное значение числа Π можно посмотреть тут: Число Пи с точностью до 100000 знаков.
Напоминаем, что Π приблизительно равняется 3.14 радиан. Более точное значение числа Π можно посмотреть тут: Число Пи с точностью до 100000 знаков.  В этом случае тригонометрические отношения НЕ изменены.Это означает
В этом случае тригонометрические отношения НЕ изменены.Это означает 


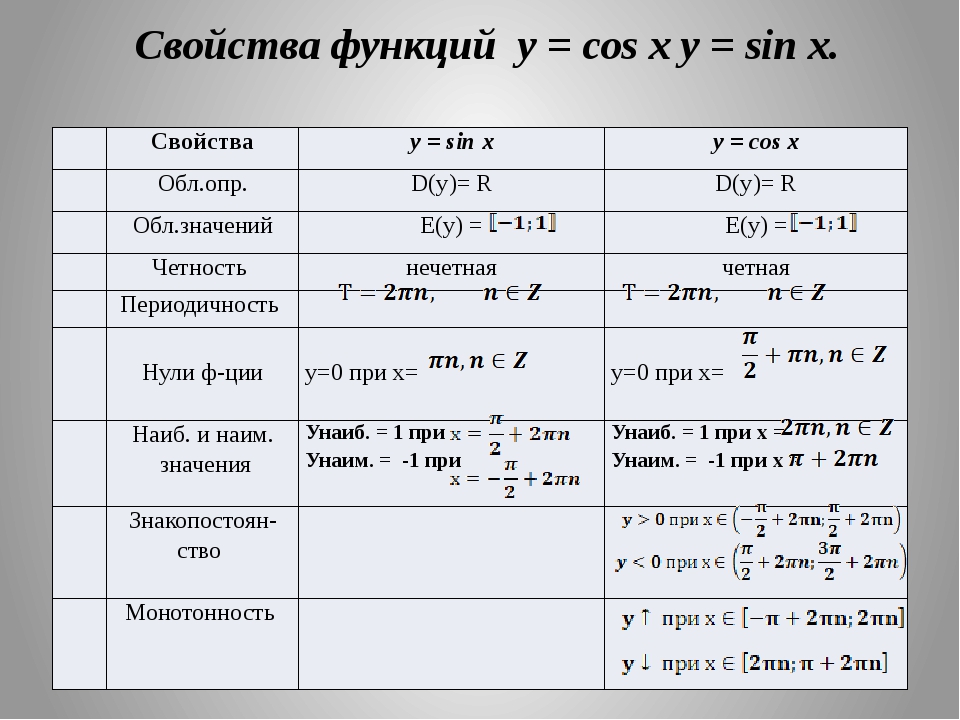
 Полный список тригонометрической формулы поможет вам в любое время и в любом месте.
Полный список тригонометрической формулы поможет вам в любое время и в любом месте.