Сила Лоренца – сила действующая со стороны магнитного
Такие поля, как мы уже говорили называются вихревыми или соленоидальными.
Магнитному полю нельзя приписывать потенциал, как у электрического поля. Этот потенциал не был бы однозначным – после каждого обхода по контуру он получал бы приращение μ0I.
Линии напряженности электрического поля начинаются и заканчиваются на зарядах. А магнитных зарядов в
природе нет. Опыт показывает, что линии |
всегда |
замкнуты. Поэтому теорему BГаусса для вектора магнитной |
|
индукции можно записать так: |
B |
Bdl 0 |
(18.7.4) |

18.8. Магнитное поле соленоида
B |
, |
|
|
Ii , для |
Применим теорему о циркуляции |
Bdl μμ0 |
|
вычисления простейшего магнитного поля – бесконечно длинного соленоида представляющий собой тонкий провод намотанный плотно виток к витку на цилиндрический каркас (рис.18.10).
Соленоид можно представить в виде системы одинаковых круговых токов с общей прямой осью.
Бесконечно |
длинный |
соленоид |
Рис. 18.10 |
|
симметричен любой, перпендикулярной |
|
|||
к его оси плоскости. Взятые попарно (рис. 18.11) |
|
|||
симметричные относительно такой плоскости витки создают |
|
|||
поле, в котором |
перпендикулярна плоскости витка, т.е |
B |
||
|
B |
|
|
|
имеет направление только параллельно оси соленоида |
|
|||
studfiles.net
Материал презентаций по физике / Часть 2 / Лекция 9 / Лекция 9
13
Лекция 9
Магнитное поле в вакууме
Вопросы
Действие магнитного поля на проводник с током. Сила Ампера.
Взаимодействие параллельных проводников с током.
Действие магнитного поля на движущийся заряд. Сила Лоренца.
Эффект Холла.
1. Действие магнитного поля на проводник с током. Сила Ампера
Действие магнитного поля на проводник с током изучалось Эрстедом и Ампером. Сила, действующая со стороны магнитного поля на проводник с током, называется силой Ампера.
, (1)
, (2)
Раскрытие векторного произведения
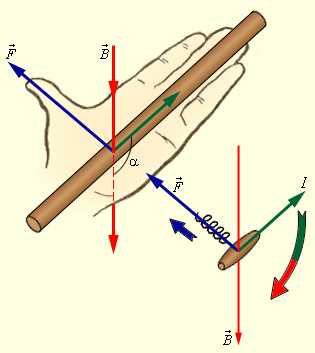
Правило левой руки
Если
расположить левую руку так, чтобы линии
 индукции входили в ладонь, а вытянутые
пальцы были направлены вдоль тока, то
отведенный большой палец укажет
направление силы, действующей на
проводник.
индукции входили в ладонь, а вытянутые
пальцы были направлены вдоль тока, то
отведенный большой палец укажет
направление силы, действующей на
проводник.
Правило буравчика (правого винта)
Воображаемый
буравчик располагается перпендикулярно
плоскости, содержащей вектор
 и
проводник с током, затем его рукоятка
поворачивается от направления тока к
направлению вектора
и
проводник с током, затем его рукоятка
поворачивается от направления тока к
направлению вектора
 .Поступательное
перемещение буравчика показывает
направление силы Ампера
.Поступательное
перемещение буравчика показывает
направление силы Ампера
 .
.
Сила Ампера – нецентральная сила (в отличие от центральных сил (Кулона, тяжести и др.). При = /2 , отсюда
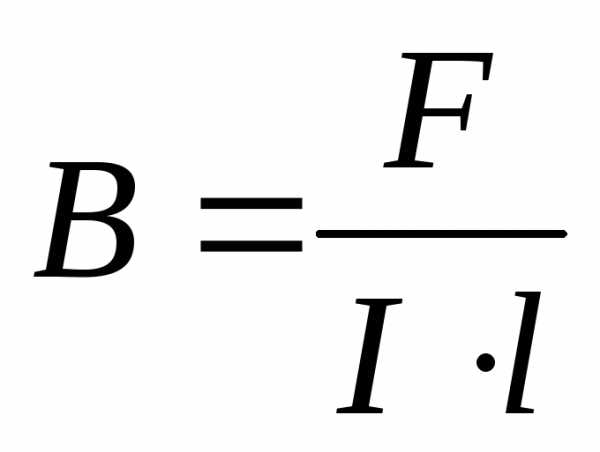 ,
.
(3)
,
.
(3)
В системе единиц СИ за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила Ампера 1 Н. Эта единица называется тесла (Тл).
Тесла – очень крупная единица. Магнитное поле Земли приблизительно равно 0,5·10–4 Тл. Большой лабораторный электромагнит может создать поле не более 5 Тл.
Принцип суперпозиции
Для
нахождения результирующей силы,
действующей на криволинейный участок
проводника с током в магнитном поле,
нужно разбить его на малые прямолинейные
отрезки, затем определить силы Ампера,
действующие на каждый такой отрезок и
вычислить векторную сумму полученных
сил, т.е. в пределе нужно взять интеграл
вдоль всей длины провода
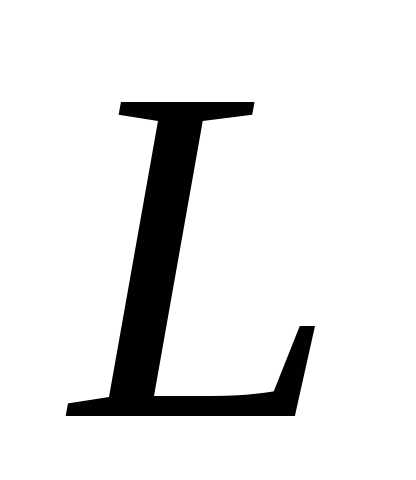 :
:
. (4)
Пример 1. Определить результирующую силу Ампера, действующую на проводник ADC с током
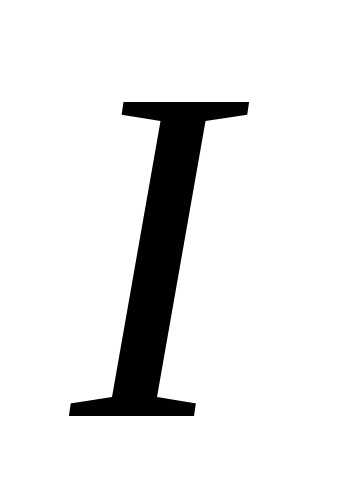 ,
находящийся в однородном магнитном
поле с вектором индукции
,
находящийся в однородном магнитном
поле с вектором индукции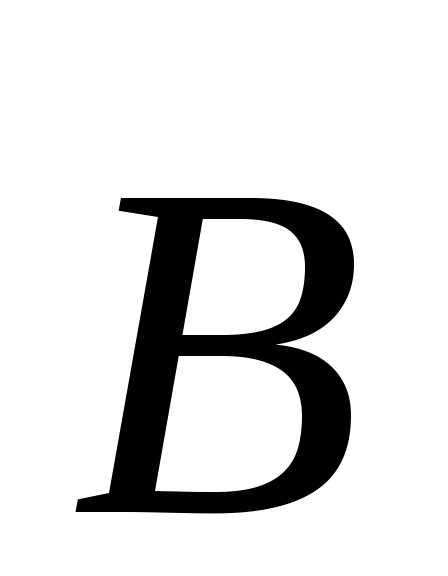 .
.
Пусть
 ,
,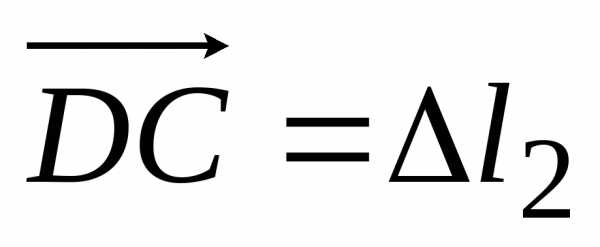 ,
,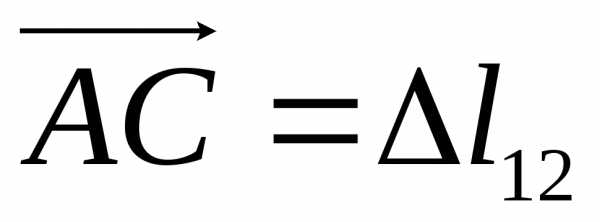 .
Тогда силы Ампера, действующие на участки
проводника:
.
Тогда силы Ампера, действующие на участки
проводника:
, .
Результирующая сила Ампера, действующая на проводник
.
Фактически при вычислении силы Ампера ломаный проводник ADC можно заменить прямолинейным проводником АС.
Отсюда следует важный вывод: сила Ампера, действующая на криволинейный участок проводника с током в однородном магнитном поле, не зависит от формы проводника, а зависит только от расстояния между началом и концом этого участка (т. е. фактически от координат начала и конца участка).
Результаты примера 1 позволяют сделать еще один вывод: сила Ампера, действующая на замкнутый проводник с током (рамку, виток с током) в однородном магнитном поле, равна нулю.
2. Взаимодействие параллельных проводников с током
Для бесконечно длинного проводника 1
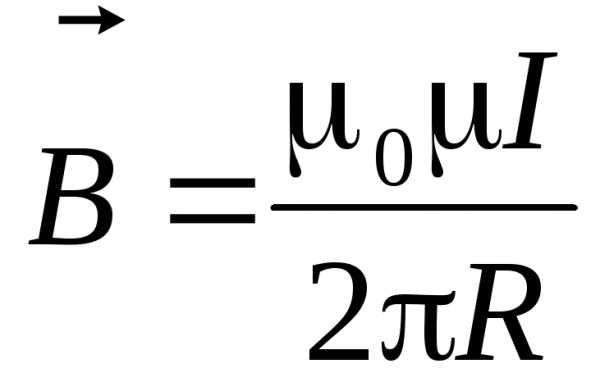

 ,
(5)
,
(5). (6)
Аналогично
. (6а)
При
 ,
,
 .
(7)
.
(7)
Если по двум параллельным проводникам электрические токи текут в одну и ту же сторону, то наблюдается взаимное притяжение проводников. В случае, когда токи текут в противоположных направлениях, проводники отталкиваются.
Из (7) следует эталон силы тока: 1Ампер – это сила постоянного тока при длине проводников и расстоянию между ними в 1 м в вакууме, равная 210-7 Н.
Из (7) следует также значение магнитной постоянной (при I1 = I2 = I)
,
где Гн – Генри, единица индуктивности.
3. Действие магнитного поля на движущийся заряд. Сила Лоренца
Сила Ампера, действующая на отрезок проводника длиной dl с силой тока I, находящемся в магнитном поле B,
(8)
может быть выражена через силы, действующие на отдельные носители заряда. Элемент тока
(9)
Подставив (9) в (8) и поделив на число частиц dn, получим силу, действующую на одну заряженную частицу (силу Лоренца
)(10)
Направление
силы Лоренца, действующей на положительно
заряженную частицу, может быть найдено
по правилу
левой руки.
Если
расположить левую руку так, чтобы линии
 индукции магнитного поля входили в
ладонь, а вытянутые пальцы были направлены
вдоль скорости движения частицы, то
отведенный большой палец укажет
направление силы Лоренца.
индукции магнитного поля входили в
ладонь, а вытянутые пальцы были направлены
вдоль скорости движения частицы, то
отведенный большой палец укажет
направление силы Лоренца.
Сила Лоренца всегда направлена перпендикулярно скорости, поэтому при движении заряженной частицы в магнитном поле сила Лоренца работы не совершает.
Частные случаи
Рис. 6. Круговое движение заряженной частицы
магнитном поле
Частица движется вдоль линии (
= /2;
sin
= 0; Fл
= 0). Движение
равномерное, прямолинейное.
(
= /2;
sin
= 0; Fл
= 0). Движение
равномерное, прямолинейное.Частица движется перпендикулярно линиям
 (
= 0; sin
=1; Fл
= qvB).
Движение равномерное,
по окружности
(
= 0; sin
=1; Fл
= qvB).
Движение равномерное,
по окружности


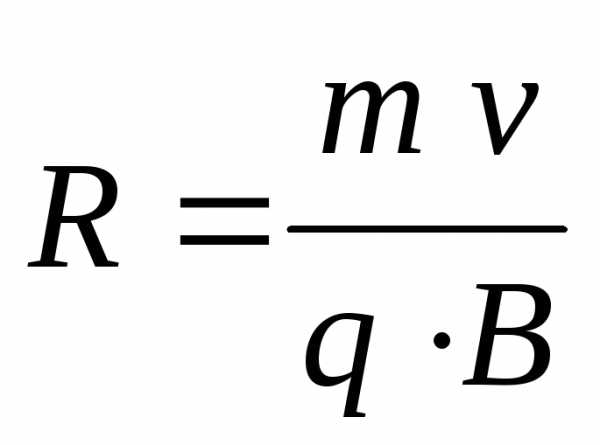

, (11)
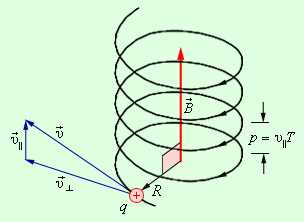
Рис. 7. Движение заряженной частицы по спирали
т.е. частица движется по окружности с периодом Т, не зависящим от скорости.Частица движется под углом к линиям
 ().
().
Радиус
спирали:
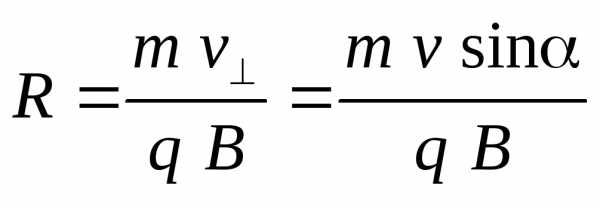 ,
,
Шаг спирали:
Угловая скорость движения заряженной частицы по круговой траектории
 (12)
(12)
называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов).
В общем случае, когда на заряженную частицу действуют электрическое и магнитное поля:
. (13)
Силу, определяемую формулой (13), называют обобщенной силой Лоренца. Учитывая действие двух полей, электрического и магнитного, говорят, что на заряженную частицу действует электромагнитное поле.
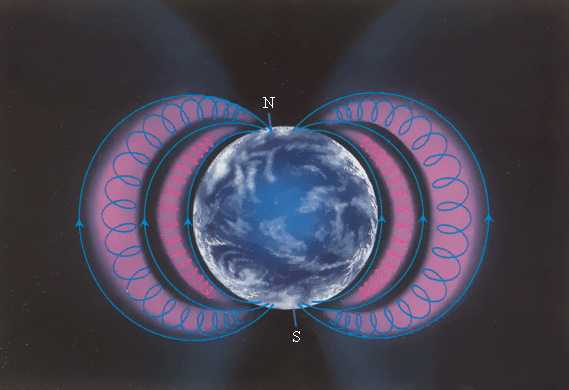
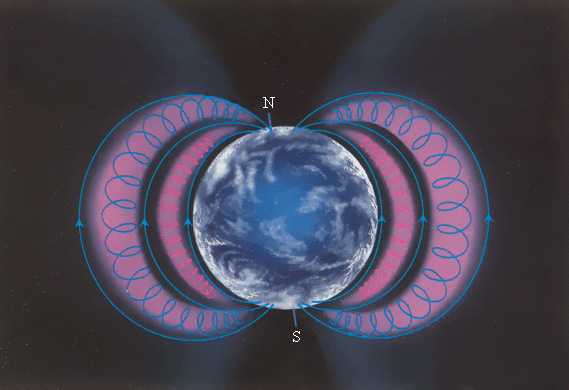
Рис. 8. Радиационные пояса Земли
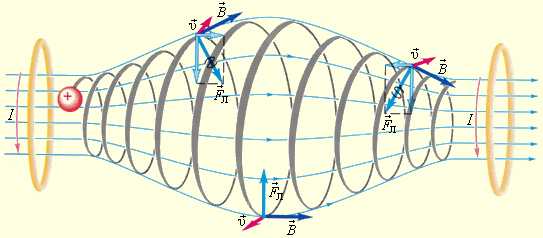
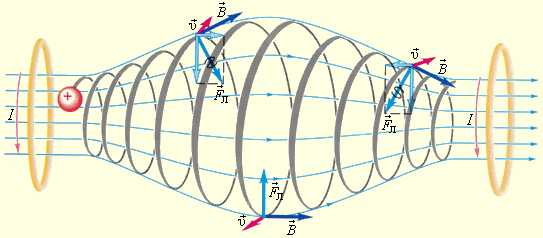
Магнитное поле Земли является защитой для всего живого от потоков заряженных частиц из космического пространства. Быстрые заряженные частицы из космоса «захватываются» магнитным полем Земли и образуют радиационные пояса, в которых частицы, как в магнитных ловушках, перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за времена порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния. Радиационные пояса Земли простираются от расстояний порядка 500 км до десятков земных радиусов.4. Эффект Холла
При размещении проводника с током в магнитное поле внутри проводника возникает электрическое поле, направленное перпендикулярно направлению тока и магнитному полю. Это явление и называется эффектом Холла.
Вычислим
разность потенциалов, возникающую
между боковыми границами проводника

холловскую разность потенциалов.
Процесс накопления зарядов прекращается,
когда электрическая сила уравновесит
силу Лоренца:
холловскую разность потенциалов.
Процесс накопления зарядов прекращается,
когда электрическая сила уравновесит
силу Лоренца:
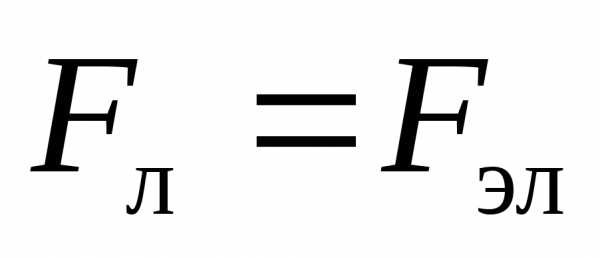


 .
.
Тогда
получаем:
,
где

толщина проводника.
толщина проводника.
Средняя скорость упорядоченного движения электронов (дрейфовая скорость)

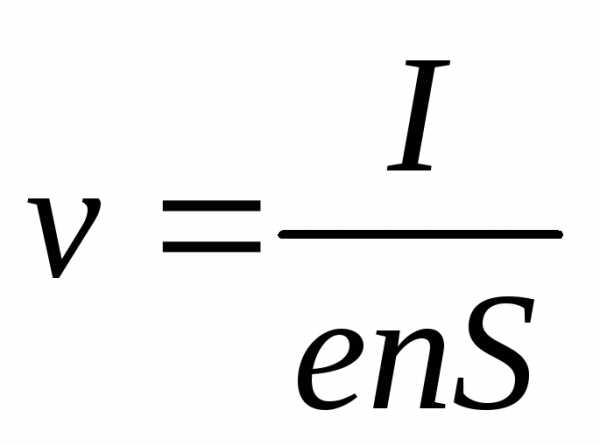 .
.
Тогда холловская разность потенциалов:
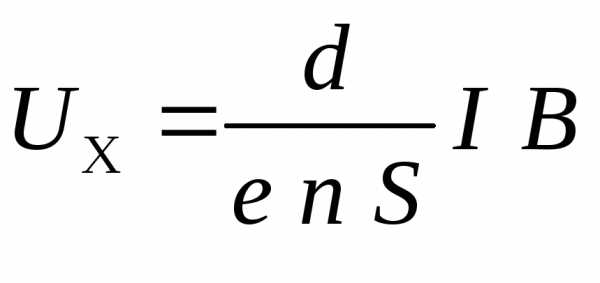 . (14)
. (14)
Применение эффекта Холла: датчики Холла для измерения В, v, n .
Магнитное поле
Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B,
может быть выражена через силы, действующие на отдельные носители заряда.
Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение nqυS, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S– площадь поперечного сечения проводника, равно току, текущему по проводнику:
Выражение для силы Ампера можно записать в виде:
|
F = qnSΔlυB sin α. |
Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно nSΔl, то сила, действующая на одну заряженную частицу, равна
Эту силу называют силой Лоренца. Угол α в этом выражении равен углу между скоростью ивектором магнитной индукцииНаправление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено поправилу левой руки или по правилу буравчика. Взаимное расположение векторов ,идля положительно заряженной частицы показано на рис. 1.18.1.
Сила Лоренца направлена перпендикулярно векторам и
При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется.
Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной векторуто частица будет двигаться по окружности радиуса
|
|
Сила Лоренца в этом случае играет роль центростремительной силы (рис. 1.18.2).
|
Рисунок 1.18.2. Круговое движение заряженной частицы в однородном магнитном поле. |
Период обращения частицы в однородном магнитном поле равен
|
|
Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории R.
Угловая скорость движения заряженной частицы по круговой траектории
называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов). Принципиальная схема циклотрона приведена на рис. 1.18.3.
|
|
|
Рисунок 1.18.3. Движение заряженных частиц в вакуумной камере циклотрона. |
Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода в виде полых металлических полуцилиндров (дуантов). К дуантам приложено переменное электрическое напряжение, частота которого равна циклотронной частоте. Заряженные частицы инжектируются в центре вакуумной камеры. Частицы ускоряются электрическим полем в промежутке между дуантами. Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Каждый раз, когда частица пролетает через зазор между дуантами, она ускоряется электрическим полем. Таким образом, в циклотроне, как и во всех других ускорителях, заряженная частица ускоряется электрическим полем, а удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ.
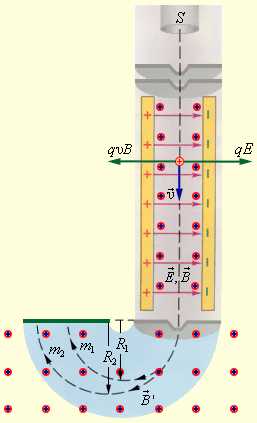
Однородные магнитные поля используются во многих приборах и, в частности, в масс-спектрометрах – устройствах, с помощью которых можно измерять массы заряженных частиц – ионов или ядер различных атомов. Масс-спектрометры используются для разделения изотопов, то есть ядер атомов с одинаковым зарядом, но разными массами (например, 20Ne и 22Ne). Простейший масс-спектрометр показан на рис. 1.18.4. Ионы, вылетающие из источника S, проходят через несколько небольших отверстий, формирующих узкий пучок. Затем они попадают в селектор скоростей, в котором частицы движутся в скрещенных однородных электрическом и магнитном полях. Электрическое поле создается между пластинами плоского конденсатора, магнитное поле – в зазоре между полюсами электромагнита. Начальная скорость заряженных частиц направлена перпендикулярно векторами
На частицу, движущуюся в скрещенных электрическом и магнитном полях, действуют электрическая сила имагнитная сила Лоренца. При условии E = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B.
Далее частицы с одним и тем же значением скорости попадают в камеру масс-спектрометра, в которой создано однородное магнитное поле Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусовR = mυ / qB’. Измеряя радиусы траекторий при известных значениях υ и B’ можно определить отношение q / m. В случае изотопов (q1 = q2) масс-спектрометр позволяет разделить частицы с разными массами.
Современные масс-спектрометры позволяют измерять массы заряженных частиц с точностью выше 10–4.
|
Рисунок 1.18.4. Селектор скоростей и масс-спектрометр. |
Если скорость частицы имеет составляющуювдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спиралиR зависит от модуля перпендикулярной магнитному полю составляющей υ┴ вектора а шаг спиралиp – от модуля продольной составляющей υ|| (рис. 1.18.5).
|
|
|
Рисунок 1.18.5. Движение заряженной частицы по спирали в однородном магнитном поле. |
Таким образом, траектория заряженной частицы как бы навивается на линии магнитной индукции. Это явление используется в технике для магнитной термоизоляции высокотемпературной плазмы, то есть полностью ионизированного газа при температуре порядка 106 K. Вещество в таком состоянии получают в установках типа «Токамак» при изучении управляемых термоядерных реакций. Плазма не должна соприкасаться со стенками камеры. Термоизоляция достигается путем создания магнитного поля специальной конфиругации. В качестве примера на рис. 1.18.6 изображена траектория движения заряженной частицы в магнитной «бутылке» (или ловушке).
|
|
|
Рисунок 1.18.6. Магнитная «бутылка». Заряженные частицы не выходят за пределы «бутылки». Магнитное поле «бутылки» может быть создано с помощью двух круглых катушек с током. |
Аналогичное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Быстрые заряженные частицы из космоса (главным образом от Солнца) «захватываются» магнитным полем Земли и образуют так называемые радиационные пояса (рис. 1.18.7), в которых частицы, как в магнитных ловушках, перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за времена порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния. Радиационные пояса Земли простираются от расстояний порядка 500 км до десятков земных радиусов. Следует вспомнить, что южный магнитный полюс Земли находится вблизи северного географического полюса (на северо-западе Гренландии). Природа земного магнетизма до сих пор не изучена.
studfiles.net
Действие магнитного поля на движущийся заряд. Сила Лоренца — Мегаобучалка
Электрический ток – это совокупность упорядоченно движущихся заряженных частиц. Поэтому действие магнитного поля на проводник с током есть результат действия поля на движущиеся заряженные частицы внутри проводника.
Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца.
Модуль силы Лоренца равен отношению модуля силы Ампера, действующей на участок проводника, к числу заряженных частиц в этом участке проводника:
Сила Ампера равна , сила тока равна (см. стр. 12). Подставив эти выражения в формулу для силы Лоренца, получим:
где — угол между векторами скорости и магнитной индукции.
Направление силы Лоренца определяют для положительного заряда по правилу левой руки. (Для отрицательного заряда сила Лоренца будет направлена в противоположную сторону).
Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работу. А, согласно теореме о кинетической энергии, это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.
Закон Ампера
Поместим в магнитное поле проводник длинной l, по которому течет ток I. На проводник действует сила, прямо пропорциональная силе тока, текущего по проводнику, индукции магнитного поля, длине проводника, и зависящая от ориентации проводника в магнитном поле. |F|=IBlsina, где a — угол между направлением тока в проводнике и направлением вектора магнитной индукции B, Направление силы Ампера определяется по правилу левой руки: если левую руку расположить так, что магнитные силовые линии входят в ладонь, четыре вытянутых пальца направить по току, то отогнутый большой палец укажет направление силы. Очевидно, что сила Ампера равна нулю, если проводник расположен вдоль силовых линий поля и максимальна, если проводник перпендикулярен силовым линиям. Движение заряженных частиц в магнитном поле. На проводник с током в магнитном поле действует сила Ампера FА IBlsina.Ток, в свою очередь, это направленное движение заряженных частиц. Сила тока равна I=qnvS, где q – заряд частицы, n-концентрация движущихся заряженных частиц, v-средняя скорость их направленного движения, S-площадь поперечного сечения проводника. Подставив I в выражение для FА, получим FА= qnvSBlsina, где nsl=N – общее число частиц, создающих ток. Тогда сила, действующая на отдельный движущийся заряд – сила Лоренца, равна Fл=qvBsina. где a — угол между векторами скорости и магнитной индукции. Направление силы Лоренца определяется для положительно заряженной частицы по правилу левой руки.
Закон Ампера
Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Экспериментальное изучение магнитного взаимодействия показывает, что модуль силы Ампера пропорционален длине проводника с током, силе тока и зависит от ориентации проводника в магнитном поле.
Опыт показывает, что магнитное поле, вектор индукции которого направлен вдоль проводника с током, не оказывает влияния на ток. Поэтому модуль силы зависит лишь от модуля составляющей вектора магнитной индукции, перпендикулярной проводнику.
Закон Ампера заключается в следующем. Сила Ампера равна произведению магнитной индукции поля на силу тока, длину участка проводника и на синус угла между магнитной индукцией и участком проводника:
Направление силы ампера определяется по правилу левой руки: если левую руку расположить так, чтобы перпендикулярная составляющая магнитной индукции входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 большой палец покажет направление силы, действующей на отрезок проводника.
Магнитное взаимодействие проводников с током используется в Международной системе для определения единицы сила тока –ампера.
Ампер –сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывал бы между этими проводниками силу магнитного взаимодействия, равную Н на каждый метр длины.
megaobuchalka.ru
. Сила Лоренца
Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B,
может быть выражена через силы, действующие на отдельные носители заряда.
Пусть концентрация носителей свободного заряда в проводнике есть n, а q – заряд носителя. Тогда произведение n q υ S, где υ – модуль скорости упорядоченного движения носителей по проводнику, а S – площадь поперечного сечения проводника, равно току, текущему по проводнику:
Выражение для силы Ампера можно записать в виде:
|
F = q n S Δl υB sin α. |
Так как полное число N носителей свободного заряда в проводнике длиной Δl и сечением S равно n S Δl, то сила, действующая на одну заряженную частицу, равна
|
Эту силу называют силой Лоренца. Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика. Взаимное расположение векторов , и для положительно заряженной частицы показано на рис. 1.18.1.
Сила Лоренца направлена перпендикулярно векторам и
При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает. Поэтому модуль вектора скорости при движении частицы не изменяется.
Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору то частица будет двигаться по окружности радиуса
|
|
Сила Лоренца в этом случае играет роль центростремительной силы (рис. 1.18.2).
|
Рисунок 1.18.2. Круговое движение заряженной частицы в однородном магнитном поле |
Период обращения частицы в однородном магнитном поле равен
|
|
Это выражение показывает, что для заряженных частиц заданной массы m период обращения не зависит от скорости υ и радиуса траектории R.
Угловая скорость движения заряженной частицы по круговой траектории
называется циклотронной частотой. Циклотронная частота не зависит от скорости (следовательно, и от кинетической энергии) частицы. Это обстоятельство используется в циклотронах – ускорителях тяжелых частиц (протонов, ионов). Принципиальная схема циклотрона приведена на рис. 1.18.3.
|
Рисунок 1.18.3. Движение заряженных частиц в вакуумной камере циклотрона |
Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода в виде полых металлических полуцилиндров (дуантов). К дуантам приложено переменное электрическое напряжение, частота которого равна циклотронной частоте. Заряженные частицы инжектируются в центре вакуумной камеры. Частицы ускоряются электрическим полем в промежутке между дуантами. Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Каждый раз, когда частица пролетает через зазор между дуантами, она ускоряется электрическим полем. Таким образом, в циклотроне, как и во всех других ускорителях, заряженная частица ускоряется электрическим полем, а удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ.
Однородные магнитные поля используются во многих приборах и, в частности, в масс-спектрометрах – устройствах, с помощью которых можно измерять массы заряженных частиц – ионов или ядер различных атомов. Масс-спектрометры используются для разделения изотопов, то есть ядер атомов с одинаковым зарядом, но разными массами (например, 20Ne и 22Ne). Простейший масс-спектрометр показан на рис. 1.18.4. Ионы, вылетающие из источника S, проходят через несколько небольших отверстий, формирующих узкий пучок. Затем они попадают в селектор скоростей, в котором частицы движутся в скрещенных однородных электрическом и магнитном полях. Электрическое поле создается между пластинами плоского конденсатора, магнитное поле – в зазоре между полюсами электромагнита. Начальная скорость заряженных частиц направлена перпендикулярно векторам и
На частицу, движущуюся в скрещенных электрическом и магнитном полях, действуют электрическая сила и магнитная сила Лоренца. При условии E = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B.
Далее частицы с одним и тем же значением скорости попадают в камеру масс-спектрометра, в которой создано однородное магнитное поле Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = mυ / qB’. Измеряя радиусы траекторий при известных значениях υ и B’ можно определить отношение q / m. В случае изотопов (q1 = q2) масс-спектрометр позволяет разделить частицы с разными массами.
Современные масс-спектрометры позволяют измерять массы заряженных частиц с точностью выше 10–4.
|
Рисунок 1.18.4. Селектор скоростей и масс-спектрометр |
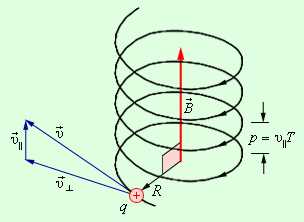
Если скорость частицы имеет составляющую вдоль направления магнитного поля, то такая частица будет двигаться в однородном магнитном поле по спирали. При этом радиус спирали R зависит от модуля перпендикулярной магнитному полю составляющей υ┴ вектора а шаг спирали p – от модуля продольной составляющей υ|| (рис. 1.18.5).
|
|
|
Рисунок 1.18.5. Движение заряженной частицы по спирали в однородном магнитном поле |
Таким образом, траектория заряженной частицы как бы навивается на линии магнитной индукции. Это явление используется в технике для магнитной термоизоляции высокотемпературной плазмы, то есть полностью ионизированного газа при температуре порядка 106 K. Вещество в таком состоянии получают в установках типа «Токамак» при изучении управляемых термоядерных реакций. Плазма не должна соприкасаться со стенками камеры. Термоизоляция достигается путем создания магнитного поля специальной конфигурации. В качестве примера на рис. 1.18.6 изображена траектория движения заряженной частицы в магнитной «бутылке» (или ловушке).
|
|
|
Рисунок 1.18.6. Магнитная «бутылка». Заряженные частицы не выходят за пределы «бутылки». Магнитное поле «бутылки» может быть создано с помощью двух круглых катушек с током |
Аналогичное явление происходит в магнитном поле Земли, которое является защитой для всего живого от потоков заряженных частиц из космического пространства. Быстрые заряженные частицы из космоса (главным образом от Солнца) «захватываются» магнитным полем Земли и образуют так называемые радиационные пояса (рис. 1.18.7), в которых частицы, как в магнитных ловушках, перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за времена порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния. Радиационные пояса Земли простираются от расстояний порядка 500 км до десятков земных радиусов. Следует вспомнить, что южный магнитный полюс Земли находится вблизи северного географического полюса (на северо-западе Гренландии). Природа земного магнетизма до сих пор не изучена.
|
|
|
Рисунок 1.18.7. Радиационные пояса Земли. Быстрые заряженные частицы от Солнца (в основном электроны и протоны) попадают в магнитные ловушки радиационных поясов. Частицы могут покидать пояса в полярных областях и вторгаться в верхние слои атмосферы, вызывая полярные сияния |
Контрольные вопросы
1.Опишите опыты Эрстеда и Ампера.
2.Что является источником магнитного поля?
3. В чем состоит гипотеза Ампера, объясняющая существования магнитного поля постоянного магнита?
4.В чем состоит принципиальное отличие магнитного поля от электрического?
5.Сформулируйте определение вектора магнитной индукции.
6. Почему магнитное поле называется вихревым?
7. Сформулируйте законы:
А) Ампера;
Б) Био-Савара-Лапласа.
8. Чему равен модуль вектора магнитной индукции поля прямого тока?
9. Сформулируйте определение единицы силы тока (ампера) в Международной системе единиц.
10. Запишите формулы, выражающую величину:
А) модуля вектора магнитной индукции;
Б) силы Ампера;
В) силы Лоренца;
Г) периода обращения частицы в однородном магнитном поле;
Д) радиуса кривизны окружности, при движении заряженной частицы в магнитном поле;
Тест для самоконтроля
Что наблюдалось в опыте Эрстеда?
1) Взаимодействие двух параллельных проводников с током.
2) Взаимодействие двух магнитных стрелок
3) Поворот .магнитной стрелки вблизи проводника при пропускании через него тока.
4) Возникновение электрического тока в катушке пнри вдвигании в нее магнита.
Ответ:
Как взаимодействуют два параллельных проводника, если по ним пропускают токи в одном направлении?
Притягиваются;
Отталкиваются;
Сила и момент сил равны нулю.
Сила равна нулю, но момент сил не равен нулю.
Ответ:
Какая формула определяет выражение модуля силы Ампера?

Ответ:
Какая формула определяет выражение модуля силы Лоренца?
А)
Б)
В)
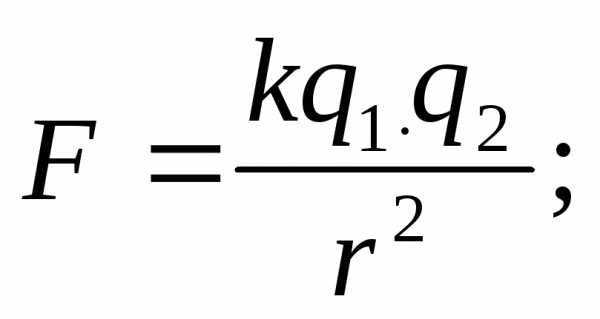
Г)
Ответ:
Прямолинейный проводник с током длиной l= 10см, сила тока в котором I=3 А, находится в однородном магнитном поле с индукцией И= 4 Тл и расположен под углом =600 к вектору
 Чему равна сила, действующая на
проводник со стороны магнитного поля?
Чему равна сила, действующая на
проводник со стороны магнитного поля?
0,6 Н; 2) 1 Н; 3) 1,4 Н; 4) 2,4 Н.
Ответ:
Прямоугольную рамку с током поместили в однородное магнитное поле, линии индукции
 которого
оказались параллельными её плоскости.
При силе тока в рамке I=4
А на неё стал действовать момент сил
М=2 Нм.
Чему равен модуль индукции магнитного
поля? Площадь рамки равна S=0,5
м2.
которого
оказались параллельными её плоскости.
При силе тока в рамке I=4
А на неё стал действовать момент сил
М=2 Нм.
Чему равен модуль индукции магнитного
поля? Площадь рамки равна S=0,5
м2.
1) 0,5 Тл; 2) 1 Тл; 3) 2 Тл; 4) 0,8 Тл.
Ответ:
Электрон со скоростью V влетает в магнитное поле с модулем индукции В перпендикулярно магнитным линиям. Какое выражение соответствует радиусу орбиты электрона?
Ответ:
1)
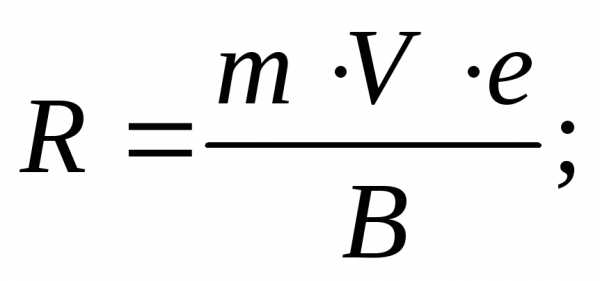 2)
2)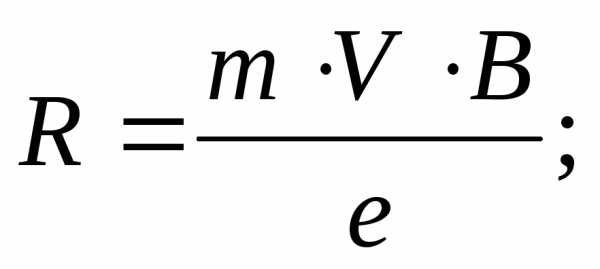
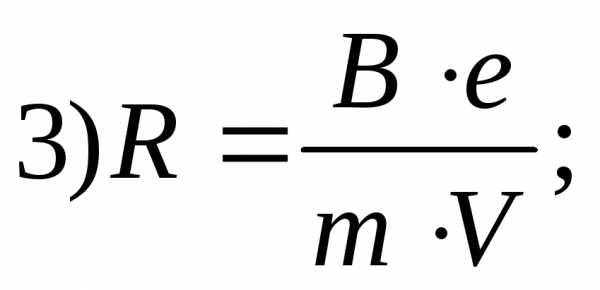 4)
4)
8. Как изменится период обращения заряженной частицы в циклотроне при увеличении её скорости в 2 раза? ( V<<c).
1) Увеличится в 2 раза; 2) Увеличится в 2 раза;
3) Увеличится в 16 раз; 4) Не изменится.
Ответ:
9.Какой формулой определяется модуль индукции магнитного поля, созданного в центре кругового тока с радиусом окружности R?
1)
 2)
2)
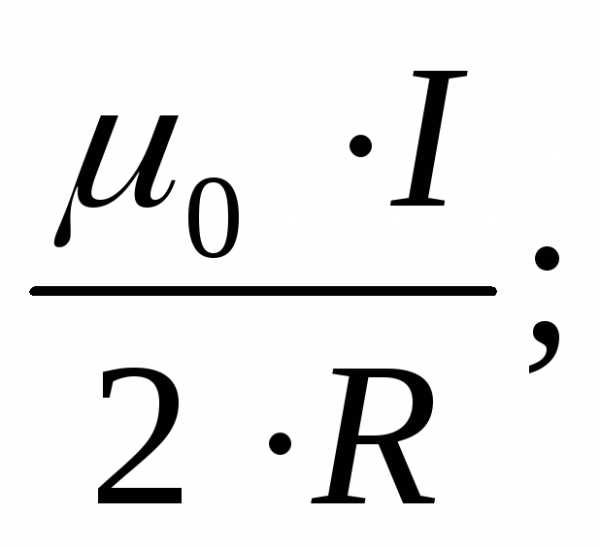 3)
3)
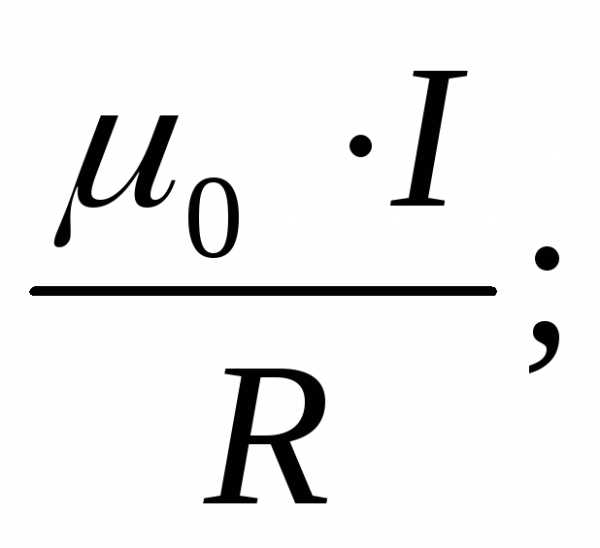 4)
4)
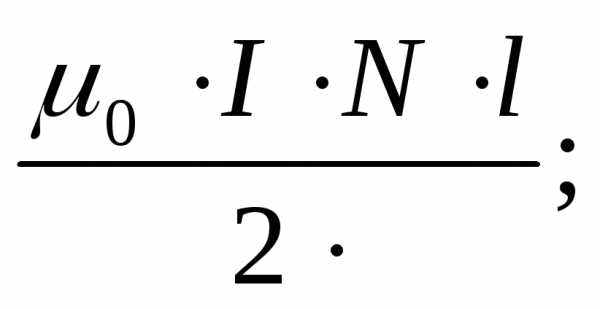
Ответ:
10.Сила тока в катушке равна I. Какой из формул определяется модуль индукции магнитного поля в середине катушки длиной l c числом витков N?
1)
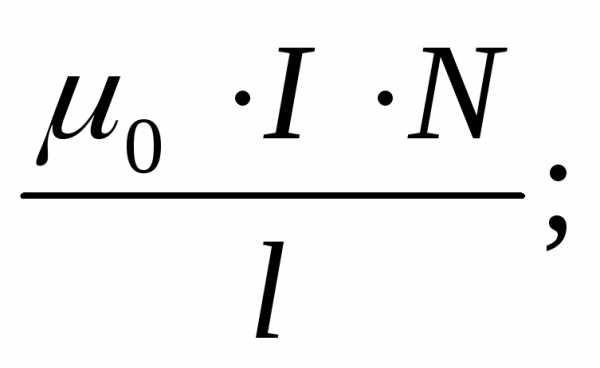 2)
2)
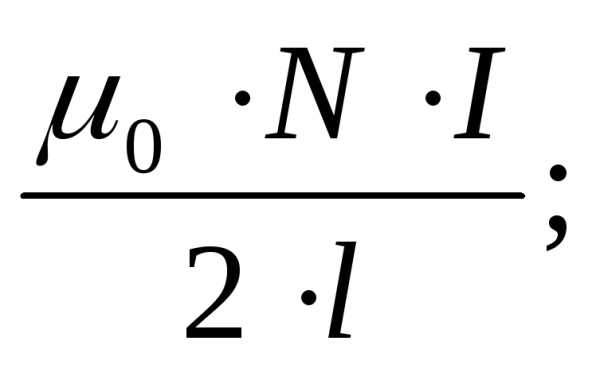 3)
3)
 4)
4)
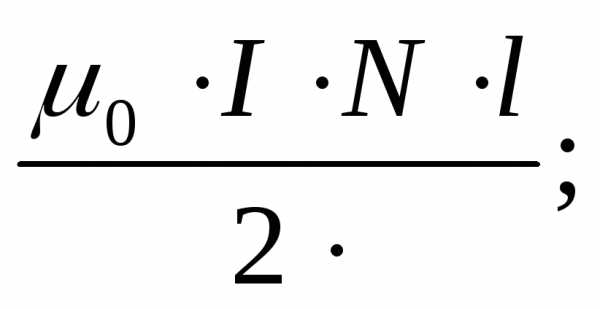
Лабораторная работа №
Определение горизонтальной составляющей индукции магнитного поля Земли.
Краткая теория к лабораторной работе.
Магнитное поле это материальная среда, передающая так называемые магнитные взаимодействия. Магнитное поле является одной из форм проявления электромагнитного поля.
Источниками магнитных полей являются движущиеся электрические заряды, проводники с током и переменные электрические поля. Порождаясь движущимися зарядами (токами), магнитное поле, в свою очередь, действует только на движущиеся заряды (токи), на неподвижные же заряды оно действия не оказывает.
Основной
характеристикой магнитного поля является
вектор магнитной индукции
 :
:
|
|
(1) |
Модуль
вектора магнитной индукции численно
равен максимальной силе, действующей
со стороны магнитного поля на проводник
единичной длины, по которому протекает
ток единичной силы. Вектор
 образует
правую тройку с вектором силы и
направлением тока. Таким образом,
магнитная индукция это силовая
характеристика магнитного поля.
образует
правую тройку с вектором силы и
направлением тока. Таким образом,
магнитная индукция это силовая
характеристика магнитного поля.
Единицей магнитной индукции в СИ является Тесла (Тл).
Силовыми линиями магнитного поля называются воображаемые линии, в каждой точке которых касательные совпадают с направлением вектора магнитной индукции. Магнитные силовые линии всегда замкнуты, никогда не пересекаются.
Закон Ампера определяет силовое действие магнитного поля на проводник с током.
Если
в магнитное поле с индукцией
 помещен
проводник с током, то на каждый направленный
по току элемент
помещен
проводник с током, то на каждый направленный
по току элемент
 проводника
действует сила Ампера, определяемая
соотношением
проводника
действует сила Ампера, определяемая
соотношением
|
. |
(2) |
Направление
силы Ампера совпадает с направлением
векторного произведения
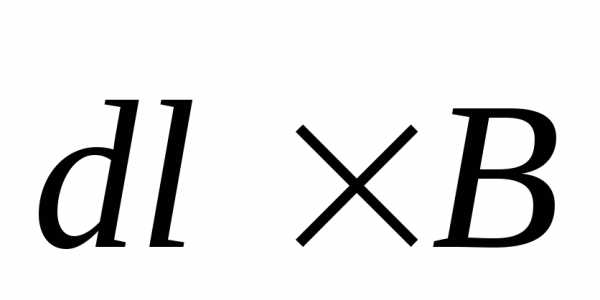 ,
т.е.
она перпендикулярна плоскости, в которой
лежат векторы
,
т.е.
она перпендикулярна плоскости, в которой
лежат векторы
 и
и
 (рис.1).
(рис.1).
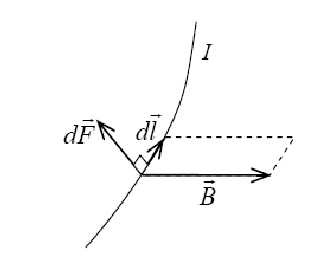
Рис. 1. К определению направления силы Ампера
Если
 перпендикулярен
перпендикулярен
 ,
то
направление силы Ампера можно определить
по правилу левой руки: четыре вытянутых
пальца направить по току, ладонь
расположить перпендикулярно силовым
линиям, тогда большой палец покажет
направление силы Ампера. Закон Ампера
положен в основу определения магнитной
индукции, т.е. соотношение (1) следует из
формулы (2), записанной в скалярном виде.
,
то
направление силы Ампера можно определить
по правилу левой руки: четыре вытянутых
пальца направить по току, ладонь
расположить перпендикулярно силовым
линиям, тогда большой палец покажет
направление силы Ампера. Закон Ампера
положен в основу определения магнитной
индукции, т.е. соотношение (1) следует из
формулы (2), записанной в скалярном виде.
Сила Лоренца – это сила, с которой электромагнитное поле действует на движущуюся в этом поле заряженную частицу. Формула силы Лоренца была впервые получена Г. Лоренцем как результат обобщения опыта и имеет вид:
|
. |
(3) |
где
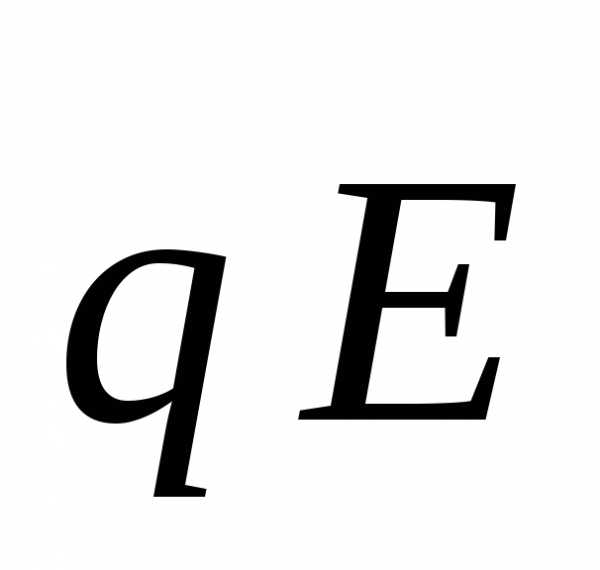 –
сила, действующая на заряженную частицу
в электрическом поле с напряженностью
–
сила, действующая на заряженную частицу
в электрическом поле с напряженностью
 ;
;
 – сила,
действующая на заряженную частицу в
магнитном поле.
– сила,
действующая на заряженную частицу в
магнитном поле.
Формулу для магнитной составляющей силы Лоренца можно получить из закона Ампера, учитывая, что ток – это упорядоченное движение электрических зарядов. Если бы магнитное поле не действовало на движущиеся заряды, оно не оказывало бы действия и на проводник с током. Магнитная составляющая силы Лоренца определяется выражением:
|
. |
(4) |
Направлена
эта сила перпендикулярно плоскости, в
которой лежат векторы скорости
 и
индукции магнитного поля
и
индукции магнитного поля
 ;
её
направление совпадает с направлением
векторного произведения
;
её
направление совпадает с направлением
векторного произведения
 для
q
>
0 и с направлением
для
q
>
0 и с направлением
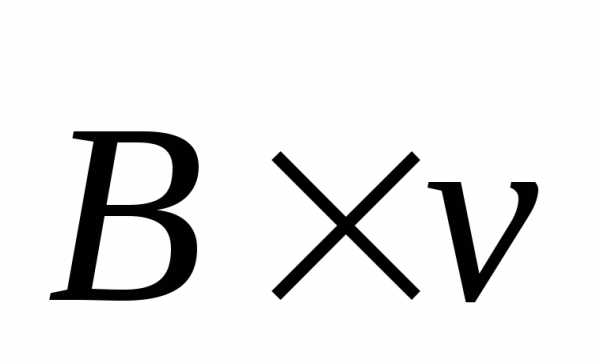 для
q>0
(рис.
2).
для
q>0
(рис.
2).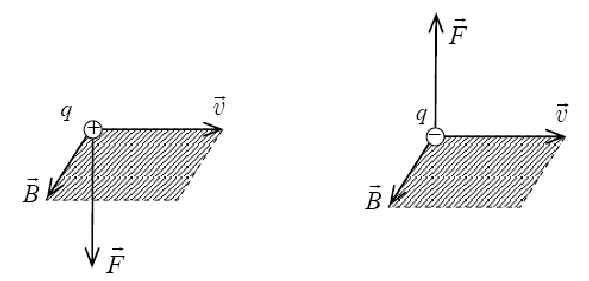
Рис. 2. К определению направления магнитной составляющей силы Лоренца
Если
вектор
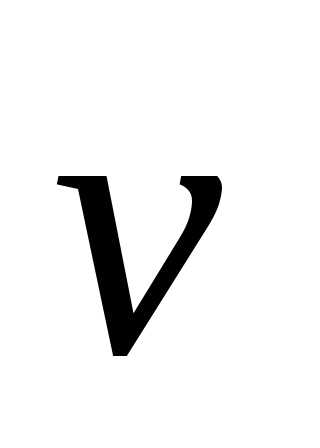 перпендикулярен
вектору
перпендикулярен
вектору
 ,
то
направление магнитной составляющей
силы Лоренца для положительно заряженных
частиц можно найти по правилу левой
руки, а для отрицательно заряженных
частиц по правилу правой руки. Так как
магнитная составляющая силы Лоренца
всегда направлена перпендикулярно
скорости
,
то
направление магнитной составляющей
силы Лоренца для положительно заряженных
частиц можно найти по правилу левой
руки, а для отрицательно заряженных
частиц по правилу правой руки. Так как
магнитная составляющая силы Лоренца
всегда направлена перпендикулярно
скорости
 ,
то
работы по перемещению частицы она не
совершает. Она может лишь изменять
направление скорости
,
то
работы по перемещению частицы она не
совершает. Она может лишь изменять
направление скорости
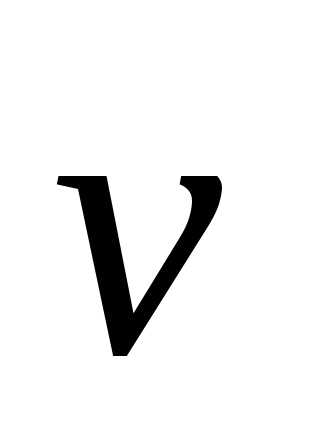 ,
искривлять
траекторию движения частицы, т.е.
выполнять роль центростремительной
силы.
,
искривлять
траекторию движения частицы, т.е.
выполнять роль центростремительной
силы.
Закон
Био-Савара-Лапласа служит для расчёта
магнитных полей (определения
 ),
создаваемых
проводниками с током.
),
создаваемых
проводниками с током.
Согласно
закону Био-Савара-Лапласа, каждый
направленный по току элемент проводника
 создаёт
в точке, находящейся на расстоянии
создаёт
в точке, находящейся на расстоянии
 от
этого элемента, магнитное поле, индукция
которого определяется соотношением:
от
этого элемента, магнитное поле, индукция
которого определяется соотношением:
|
. |
(5) |
где Гн/м – магнитная постоянная;µ – магнитная проницаемость среды.
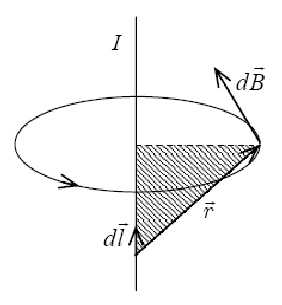
Рис. 3. К закону Био-Савара-Лапласа
Направление
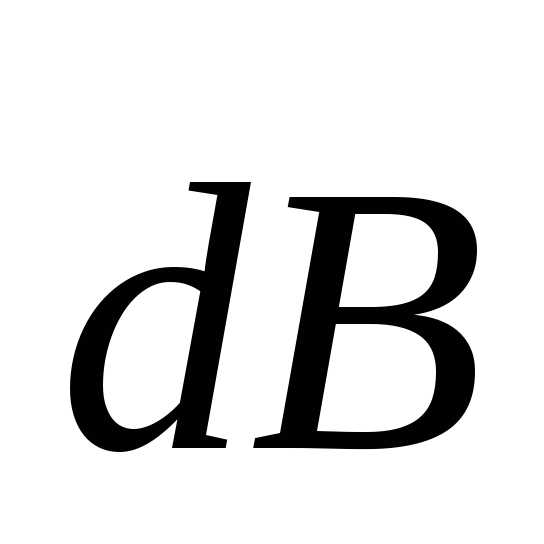 совпадает
с направлением векторного произведения
совпадает
с направлением векторного произведения
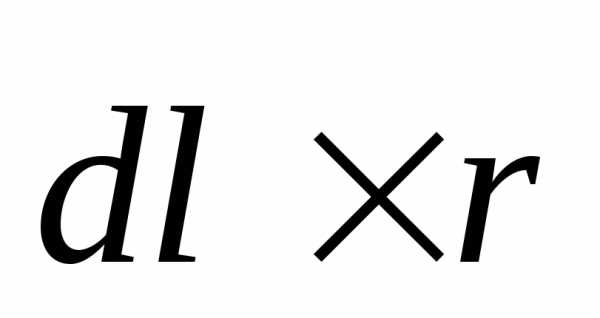 ,
т.е.
,
т.е.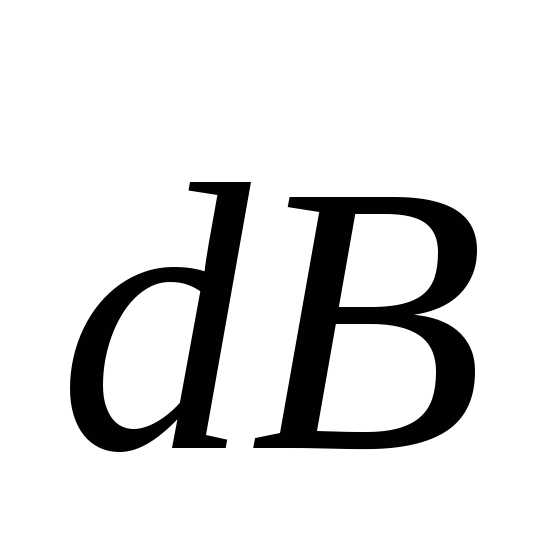 перпендикулярен
плоскости, в которой лежат векторы
перпендикулярен
плоскости, в которой лежат векторы
 и
и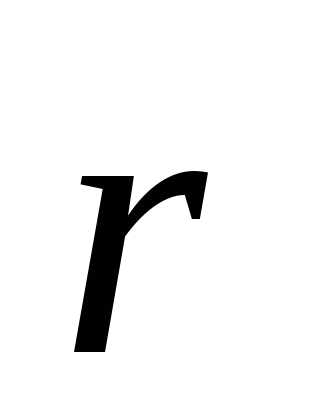 .
Одновременно
.
Одновременно является
касательной к силовой линии, направление
которой можно определить по правилу
буравчика: если поступательное движение
острия буравчика направить по току, то
направление вращения рукоятки определит
направление силовой линии магнитного
поля (рис. 3).
является
касательной к силовой линии, направление
которой можно определить по правилу
буравчика: если поступательное движение
острия буравчика направить по току, то
направление вращения рукоятки определит
направление силовой линии магнитного
поля (рис. 3).
Чтобы найти магнитное поле, создаваемое всем проводником, нужно применить принцип суперпозиции полей:
|
|
(6) |
Например, вычислим магнитную индукцию в центре кругового тока (рис. 4).
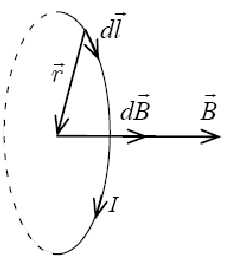 Рис.
4. К расчёту поля в центре кругового тока
Рис.
4. К расчёту поля в центре кругового тока
Для
кругового тока
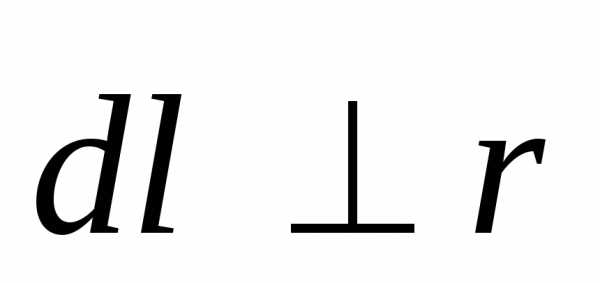 и
и ,
поэтому соотношение (5) в скалярной форме
имеет вид:
,
поэтому соотношение (5) в скалярной форме
имеет вид:
|
. |
(7) |
Все
элементы
 создадут
в т. O
магнитные
поля с одинаковым направлением
создадут
в т. O
магнитные
поля с одинаковым направлением
 ,
поэтому результирующая магнитная
индукция
,
поэтому результирующая магнитная
индукция
|
. |
(8) |
Закон полного тока (теорема о циркуляции магнитной индукции) является ещё одним законом для расчёта магнитных полей.
Закон полного тока для магнитного поля в вакууме имеет вид:
|
|
(9) |
где
Bl
– проекция
 на
элемент проводника
на
элемент проводника
 ,
направленный по току.
,
направленный по току.
Циркуляция вектора магнитной индукции по любому замкнутому контуру равна произведению магнитной постоянной на алгебраическую сумму токов, охватываемых этим контуром.
Теорема Остроградского-Гаусса для магнитного поля выглядит следующим образом:
|
|
(10) |
где
Bn
– проекция
вектора
 на
нормаль
на
нормаль
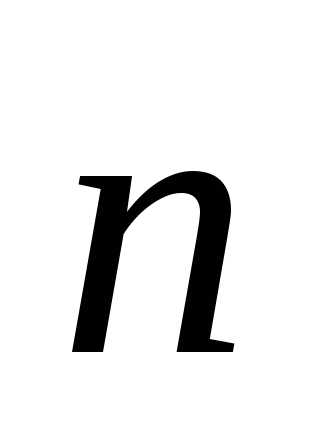 к
площадке dS.
к
площадке dS.
Поток вектора магнитной индукции через произвольную замкнутую поверхность равен нулю.
Характер магнитного поля следует из формул (9), (10).
Условием
потенциальности электрического поля
является равенство нулю циркуляции
вектора напряженности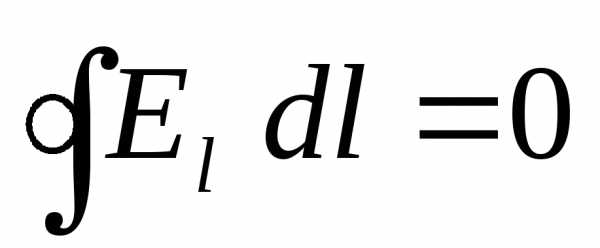 .
.
Потенциальное электрическое поле порождается неподвижными электрическими зарядами; силовые линии поля не замкнуты, начинаются на положительных зарядах и кончаются на отрицательных.
Из формулы (9) мы видим, что в магнитном поле циркуляция вектора магнитной индукции отлична от нуля, следовательно, магнитное поле потенциальным не является.
Из соотношения (10) следует, что магнитных зарядов, способных создавать потенциальные магнитные поля, не существует. (В электростатике аналогичная теорема тлеет вид .
Магнитные силовые линии замыкаются сами на себя. Такое поле называется вихревым. Таким образом, магнитное поле – это вихревое поле. Направление силовых линий поля определяется правилом буравчика. У прямолинейного бесконечно длинного проводника с током силовые линии имеют вид концентрических окружностей, охватывающих проводник (рис. 3).
studfiles.net
1.4. Сила Лоренца. Правило левой руки для определения направления силы Лоренца
Силу,
действующую на движущуюся заряженную
частицу со стороны магнитного поля,
называют силой
Лоренца.
Опытным путём установлено, что сила,
действующая в магнитном поле на заряд
 ,
перпендикулярна векторам
,
перпендикулярна векторам и
и ,
а ее модуль определяется формулой:
,
а ее модуль определяется формулой:
,
где
 – угол между векторами
– угол между векторами
 и
и .
.
Направление
силы Лоренца
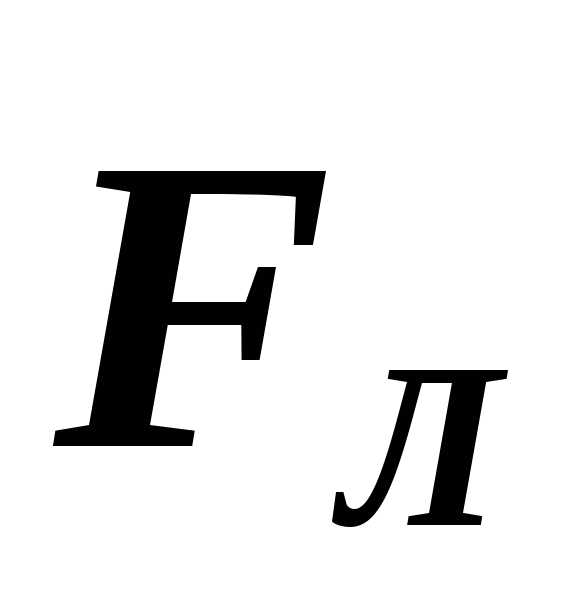 определяется
правилом
левой руки
(рис. 6):
определяется
правилом
левой руки
(рис. 6):
если
вытянутые пальцы расположить по
направлению скорости положительного
заряда, а силовые линии магнитного поля
будут входить в ладонь, то отогнутый
большой палец укажет направление силы
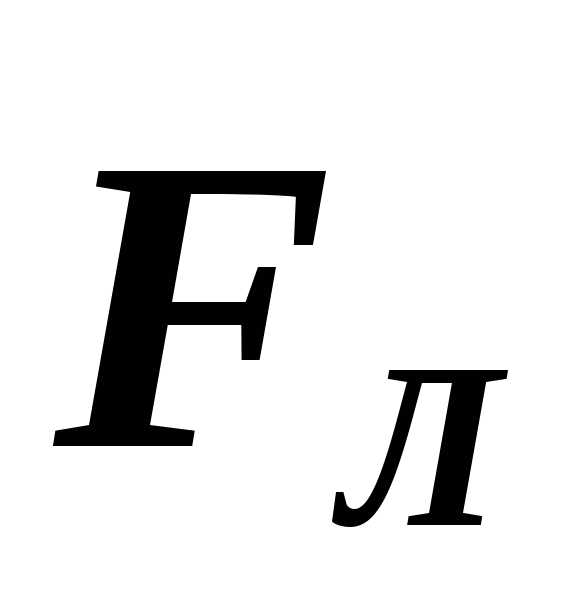 ,
действующей на заряд со стороны магнитного
поля.
,
действующей на заряд со стороны магнитного
поля.
Для
отрицательного заряда направление
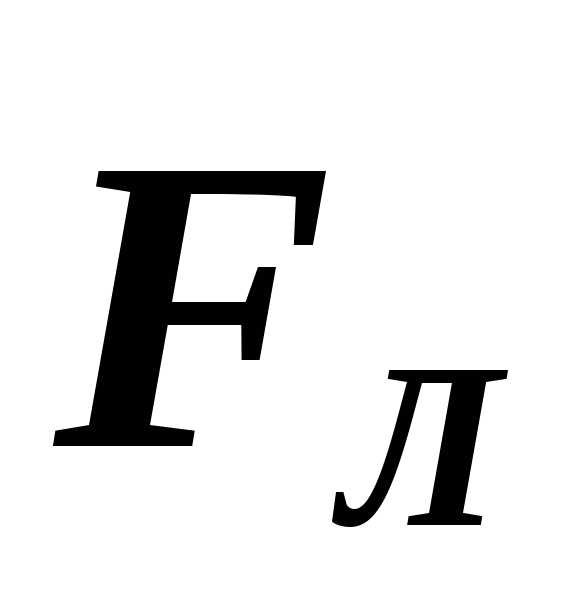 следует изменить на противоположное.
следует изменить на противоположное.

Рис. 6. Правило левой руки для определения направления силы Лоренца.
1.5. Сила Ампера. Правило левой руки для определения направления силы Ампера
Экспериментально установлено, что на проводник с током, находящийся в магнитном поле, действует сила, получившая название силы Ампера (см. п. 1.3.). Направление силы Ампера (рис. 4) определяется правилом левой руки (см. п. 1.3).
Модуль силы Ампера вычисляется по формуле
,
где
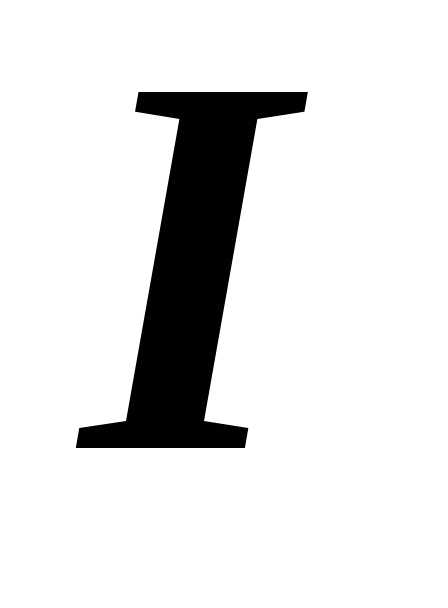 –
сила тока в проводнике,
–
сила тока в проводнике, —
индукция магнитного поля,
—
индукция магнитного поля,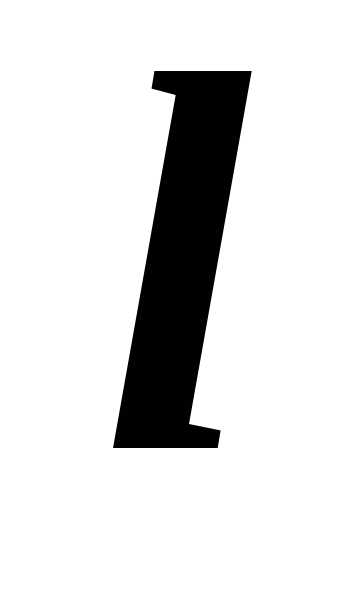 —
длина проводника,
—
длина проводника, —
угол между направлением тока и вектором
—
угол между направлением тока и вектором .
.
1.6. Магнитный поток
Магнитным
потоком
 сквозь
замкнутый контур называется скалярная
физическая величина, равная произведению
модуля вектора
сквозь
замкнутый контур называется скалярная
физическая величина, равная произведению
модуля вектора
 на площадь
на площадь контура и на косинус угла
контура и на косинус угла между
вектором
между
вектором
 и
нормалью
и
нормалью
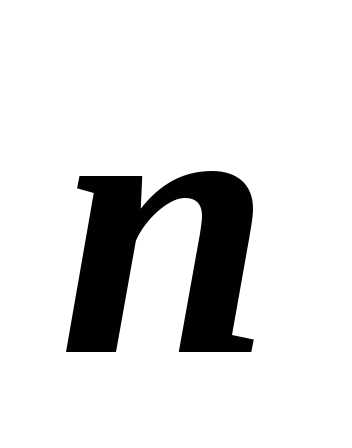 к контуру (рис. 7):
к контуру (рис. 7):

Рис. 7. К понятию магнитного потока
Магнитный
поток наглядно можно истолковать как
величину, пропорциональную числу линий
магнитной индукции, пронизывающих
поверхность площадью
 .
.
Единицей магнитного потока является вебер .
Магнитный поток в 1 Вб создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м2, расположенную перпендикулярно вектору магнитной индукции:
1 Вб =1 Тл·м2.
2. Электромагнитная индукция
2.1. Явление электромагнитной индукции
В 1831г. Фарадей обнаружил физическое явление, получившее название явления электромагнитной индукции (ЭМИ), заключающееся в том, что при изменении магнитного потока, пронизывающего контур, в нем возникает электрический ток. Полученный Фарадеем ток называется индукционным.
Индукционный ток можно получить, например, если постоянный магнит вдвигать внутрь катушки, к которой присоединен гальванометр (рис. 8, а). Если магнит вынимать из катушки, возникает ток противоположного направления (рис. 8, б).
Индукционный ток возникает и в том случае, когда магнит неподвижен, а движется катушка (вверх или вниз), т.е. важна лишь относительность движения.
Но не при всяком движении возникает индукционный ток. При вращении магнита вокруг его вертикальной оси тока нет, т.к. в этом случае магнитный поток сквозь катушку не изменяется (рис. 8, в), в то время как в предыдущих опытах магнитный поток меняется: в первом опыте он растет, а во втором – уменьшается (рис. 8, а, б).
Направление индукционного тока подчиняется правилу Ленца:
возникающий в замкнутом контуре индукционный ток всегда направлен так, чтобы создаваемое им магнитное поле противодействовало причине, его вызывающей.
Индукционный ток препятствует внешнему потоку при его увеличении и поддерживает внешний поток при его убывании.
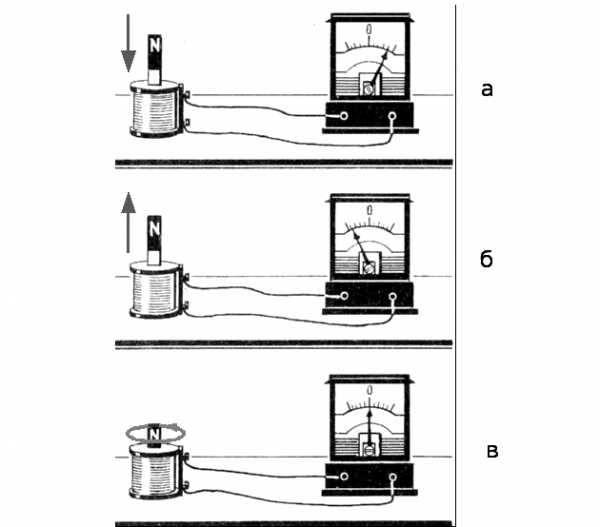
Рис. 8. Явление электромагнитной индукции
Ниже
на левом рисунке (рис. 9) индукция внешнего
магнитного поля
 ,
направленного «от нас» (+) растет
(
,
направленного «от нас» (+) растет
(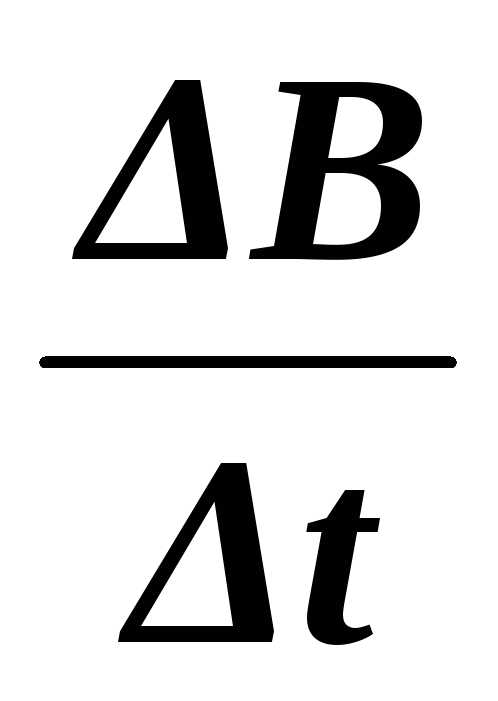 >0),
на правом – убывает (
>0),
на правом – убывает (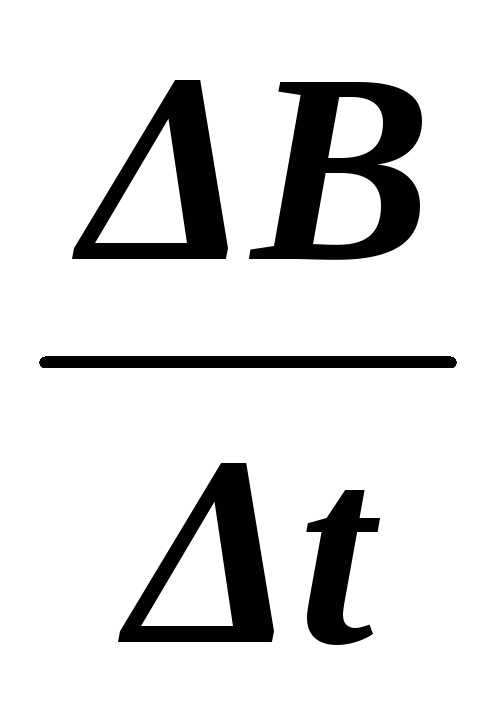 <0).
Видно, чтоиндукционный
ток
направлен так, что его собственное
магнитное
поле препятствует изменению внешнего
магнитного потока, вызвавшего этот ток.
<0).
Видно, чтоиндукционный
ток
направлен так, что его собственное
магнитное
поле препятствует изменению внешнего
магнитного потока, вызвавшего этот ток.

Рис. 9. К определению направления индукционного тока
studfiles.net
Проверочная работа 9 класс на использование правила левой руки
1Определите направление действия силы Ампера со стороны магнитного поля на участок проводника с током
Определите направление действия силы Лоренца со стороны магнитного поля на движущуюся в нем заряженную частицу
Вариант №2
Определите направление действия силы Ампера со стороны магнитного поля на участок проводника с током
Определите направление действия силы Лоренца со стороны магнитного поля на движущуюся в нем заряженную частицу
Вариант №4
Определите направление действия силы Ампера со стороны магнитного поля на участок проводника с током
Определите направление действия силы Лоренца со стороны магнитного поля на движущуюся в нем заряженную частицу
Вариант №5
Определите направление действия силы Ампера со стороны магнитного поля на участок проводника с током
Определите направление действия силы Лоренца со стороны магнитного поля на движущуюся в нем заряженную частицу
Вариант №6
Определите направление действия силы Ампера со стороны магнитного поля на участок проводника с током
Определите направление действия силы Лоренца со стороны магнитного поля на движущуюся в нем заряженную частицу
Вариант №7
Определите направление действия силы Ампера со стороны магнитного поля на участок проводника с током
Определите направление действия силы Лоренца со стороны магнитного поля на движущуюся в нем заряженную частицу
Вариант №8
Определите направление действия силы Ампера со стороны магнитного поля на участок проводника с током
Определите направление действия силы Лоренца со стороны магнитного поля на движущуюся в нем заряженную частицу
Вариант №9
Определите направление действия силы Ампера со стороны магнитного поля на участок проводника с током
Определите направление действия силы Лоренца со стороны магнитного поля на движущуюся в нем заряженную частицу
Вариант №10
Определите направление действия силы Ампера со стороны магнитного поля на участок проводника с током
Определите направление действия силы Лоренца со стороны магнитного поля на движущуюся в нем заряженную частицу
Вариант №11
Определите направление действия силы Ампера со стороны магнитного поля на участок проводника с током
Определите направление действия силы Лоренца со стороны магнитного поля на движущуюся в нем заряженную частицу
Вариант №12
Определите направление действия силы Ампера со стороны магнитного поля на участок проводника с током
Определите направление действия силы Лоренца со стороны магнитного поля на движущуюся в нем заряженную частицу
13 EMBED PBrush 1415
Вариант №13
Определите
profhelp.net


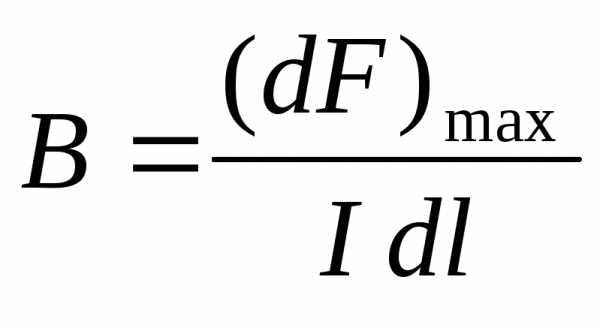
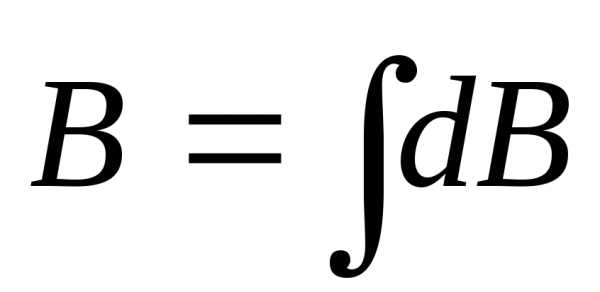 .
.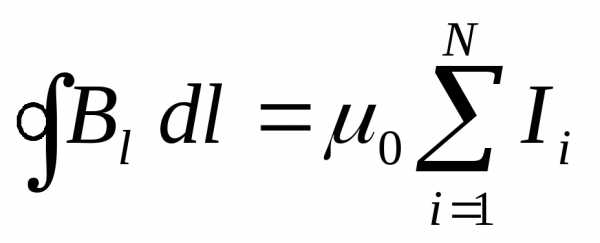 .
.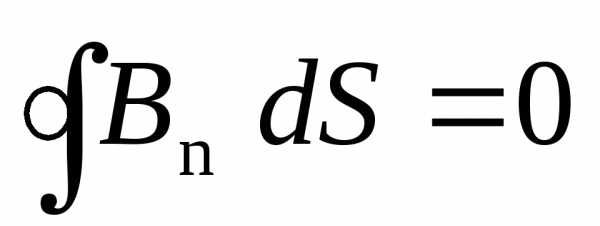 .
.