Одз что это алгебра: Как найти Область Допустимых Значений (ОДЗ)

Как найти Область Допустимых Значений (ОДЗ)

Допустимые и недопустимые значения переменных

В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.

Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений. 

Чтобы дать верное определение области допустимых значений, разберемся, что  такое допустимые и недопустимые значения переменной. 

Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.

Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.

Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.

Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.

Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.

Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.

Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.

Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми. 

В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного. 

Пример 1

Рассмотрим выражение

В выражении три переменные (a, b, c). 

Запишем значения переменных в виде: a = 0, b = 1, c = 2.

Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:

Таким же образом можем выяснить, какие значения переменных  — недопустимые. 

a = 1, b = 2, c = 1.

Подставим значения переменных в выражение

На ноль делить нельзя. 

Что такое ОДЗ

ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».

Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.

Запоминаем!

ОДЗ относится к выражениям. Область определения функции относится к функциям и не относится к выражениям.

Пример 2

Рассмотрим выражение

ОДЗ такого выражения выглядит следующим образом: ( — ∞; 3) ∪ (3; +∞).

Читать запись нужно вот так:
Область допустимых значений переменной x для выражения  — это числовое множество ( — ∞; 3) ∪ (3; +∞).

Пример 3
Рассмотрим выражение

ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.

Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курс подготовки к ЕГЭ по математике (профиль).

Как найти ОДЗ: примеры решения

Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.

Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено. 

Мы не можем вычислить значение выражения, если:

• требуется извлечение квадратного корня из отрицательного числа;
• присутствует деление на ноль (математическое правило номер раз: никогда не делите на ноль).

Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам. 

Давайте потренируемся находить ОДЗ.

Пример 4

Найдем область допустимых значений переменной выражения a³ + 4 * a * b − 6.

Как решаем:

В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a³ + 4 * a * b − 6 при любых значениях переменной. 

ОДЗ переменных  a и b — это множество таких пар допустимых значений (a, b), где a — любое число и  b — любое число. 

Ответ: (a и b), где a — любое число и b — любое число.

Пример 5

Найдем область допустимых значений (ОДЗ) переменной выражения 

Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль. 

Это значит, что мы может сказать, что ОДЗ переменной a в выражении — пустое множество.

Пустое множество изображается в виде вот такого символа Ø.

Пример 6

Найдем область допустимых значений (ОДЗ) переменных в выражении

Если  есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.

Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.

Лайфхак

Чтобы не потратить зря время на решение нерешаемого примера, всегда обращайтесь к списку условий, при которых выражение не может быть решено.

Запомните

• Если число входит в ОДЗ, то около числа ставим квадратные скобки.
• Если число не входит в ОДЗ, то около него ставятся круглые скобки. 

Например, если х > 6, но х < 8, то  записываем интервал [6; 8).

Зачем учитывать ОДЗ при преобразовании выражения

Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.

Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.

Тождественное преобразование может:

• расширить ОДЗ
• никак не повлиять на ОДЗ
• сузить ОДЗ

Рассмотрим каждый случай в отдельности.

Пример 7

Рассмотрим выражение a + 4/a — 4/a

Поскольку мы должны следить за тем, чтобы в выражении не возникало деление на ноль, определяем условие a ≠ 0.

Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).

В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a. 

ОДЗ для a — это R — множество всех вещественных чисел. 

Преобразование расширило ОДЗ — добавился ноль. 

Пример 8

Рассмотрим выражение a² + a + 4 * a

ОДЗ a для этого выражения — множество R.

В выражении есть подобные слагаемые, выполним тождественное преобразование. 

После приведения подобных слагаемых выражение приняло вид  a

2 + 5 * a 

ОДЗ переменной a для этого выражения — множество R.

Это значит, что тождественное преобразование никак не повлияло на ОДЗ. 

Пример 9

Рассмотрим выражение

ОДЗ a определяется неравенством (a — 1) * (a — 4) ≥ 0.

Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).

Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.

Приведем выражение к виду

ОДЗ переменной a для этого выражения определяется неравенствами:
a — 1 ≥ 0
a — 4 ≥ 0

Решив систему линейных неравенств, получаем множество [4; + ∞).

Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).

Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.

Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.

Область допустимых значений

Область допустимых значений алгебраического выражения (сокращенно ОДЗ) — это множество значений переменной, при которых это выражение  определено.

В школьном курсе алгебры есть всего пять элементарных функций, которые имеют ограниченную область определения. Вот они:

1.    ОДЗ:

Выражение, стоящее под знаком корня четной кратности, должно быть больше или равно нулю.

2.          ОДЗ:

 

Выражение, стоящее в знаменателе дроби, не может быть равно нулю.

3.          ОДЗ:  

 

Выражение, стоящее под знаком логарифма, должно быть строго больше нуля; выражение, стоящее в основании логарифма  должно быть строго больше нуля и отлично от единицы.

4.  , ОДЗ:

5. Есть две функции, которые содержат «скрытую» дробь:

и

6.   ОДЗ:

Степень корня — натуральное число, отличное от 1.

Таким образом, функции  и имеют разную область определения.

 

Если выражение содержит одну или несколько функций, которые определены на ограниченном множестве значений аргумента, то для того, чтобы найти ОДЗ выражения, нужно учесть все ограничения, которые накладываются этими функциями.

Чтобы найти область допустимых значений выражения, нужно исследовать, присутствуют ли в выражении функции, которые я перечислила выше. И по мере обнаружения этих функций, записывать задаваемые ими ограничения, двигаясь «снаружи» «внутрь».

Поясню на примере:

Найти область определения функции:

 

Чтобы найти область определения функции, нужно найти область допустимых значений выражения, которое стоит в правой части уравнения функции

Я специально выбрала «страшную», на первый взгляд,  функцию, чтобы показать вам, на какие простые операции разбивается процесс нахождения области допустимых значений.

«Просканируем» выражение, стоящее в правой части равенства:

 

1. Мы видим дробь:

Знаменатель дроби не равен нулю. Записываем:

2. Мы видим в знаменателе логарифм:

Выражение, стоящее под знаком логарифма должно быть строго больше нуля; выражение, стоящее в основании логарифма  должно быть строго больше нуля и отлично от единицы.

Записываем:

 

3.Мы видим квадратный корень:

Выражение, стоящее под знаком корня четной кратности, должно быть больше или равно нулю.

Записываем:

Теперь запишем все ограничения в систему неравенств:

   

 

Решение этой системы неравенств посмотрите в ВИДЕУРОКЕ:

 

И.В. Фельдман, репетитор по математике

ОДЗ | Алгебра

Найти ОДЗ — область допустимых значений — задание, которое в алгебре встречается как в виде самостоятельных примеров, так и при решении уравнений, неравенств и их систем.

   

   

ОДЗ многочлена — любое значение переменной.

   

Дробь имеет смысл, если знаменатель отличен от нуля.

Следовательно, ОДЗ дроби — все значения переменной, за исключением тех, в которых знаменатель обращается в нуль.

   

Выражение, стоящее под знаком корня чётной степени (в том числе, под знаком квадратного корня), должно быть неотрицательным.

Следовательно, ОДЗ выражения, содержащего переменную под знаком корня чётной степени — все значения переменной, при которых это выражение больше либо равно нуля.

   

Выражение, стоящее под знаком корня чётной степени (в том числе, под знаком квадратного корня) в знаменателе дроби, должно быть положительным.

То есть ОДЗ выражения с корнем чётной степени в знаменателе — множество значений переменной, при котором это выражение строго больше нуля.

   

Выражение, стоящее под знаком логарифма, должно быть положительным.

Выражение, стоящее в основании логарифма, должно быть положительным и не равным единице.

   

Выражение, стоящее под знаком синуса, может принимать любые значения (ОДЗ синуса — любые значения переменной).

   

Выражение, стоящее под знаком косинуса, может принимать любые значения (ОДЗ косинуса — любые значения переменной).

   

ОДЗ тангенса можно рассматривать как ОДЗ дроби

   

   

ОДЗ котангенса находим как ОДЗ дроби

   

   

Выражение, стоящее под знаком арксинуса, должно быть не меньшим -1 и не большим 1 (то есть ОДЗ арксинуса — промежуток [-1;1]).

   

Выражение, стоящее под знаком арккосинуса, должно быть не меньшим -1 и не большим 1 (ОДЗ арккосинуса — промежуток [-1;1]).

   

Выражение, стоящее под знаком арктангенса, может принимать любые значения (ОДЗ арктангенса — любые значения f(x)).

   

Выражение, стоящее под знаком арккотангенса, может принимать любые значения (ОДЗ арккотангенса — любые значения f(x)).

   

   

Выражение, стоящее в показателе степени, основание которой — положительное число, может принимать любые значения.

В ходе изучения темы «Степенная функция» обобщается информация по области допустимых значений степени и корня.

   

• Если α — натуральное число, то f(x)∈R.
• Если α — целое отрицательное число или нуль, то f(x)≠0.
• Если α — нецелое положительное число, то то f(x)≥0.
• Если α — нецелое отрицательное число, то то f(x)>0.

Функции и графики — Математика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Координаты и базовые понятия о функциях

К оглавлению…

Длина отрезка на координатной оси находится по формуле:

Длина отрезка на координатной плоскости ищется по формуле:

Для нахождения длины отрезка в трёхмерной системе координат используется следующая формула:

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы) вычисляются по формулам:

Функция – это соответствие вида y = f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины, y (зависимой переменной, иногда это значение просто называют значением функции). Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у. При этом одно и то же значение у может быть получено при различных х.

Область определения функции – это все значения независимой переменной (аргумента функции, обычно это х), при которых функция определена, т.е. ее значение существует. Обозначается область определения D(y). По большому счету Вы уже знакомы с этим понятием. Область определения функции по другому называется областью допустимых значений, или ОДЗ, которую Вы давно умеете находить.

Область значений функции – это все возможные значения зависимой переменной данной функции. Обозначается Е(у).

Функция возрастает на промежутке, на котором большему значению аргумента соответствует большее значение функции. Функция убывает на промежутке, на котором большему значению аргумента соответствует меньшее значение функции.

Промежутки знакопостоянства функции – это промежутки независимой переменной, на которых зависимая переменная сохраняет свой положительный или отрицательный знак.

Нули функции – это такие значения аргумента, при которых величина функции равна нулю. В этих точках график функции пересекает ось абсцисс (ось ОХ). Очень часто необходимость найти нули функции означает необходимость просто решить уравнение. Также часто необходимость найти промежутки знакопостоянства означает необходимость просто решить неравенство.

Функцию y = f(x) называют четной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:

Это означает, что для любых противоположных значений аргумента, значения четной функции равны. График чётной функции всегда симметричен относительно оси ординат ОУ.

Функцию y = f(x) называют нечетной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:

Это означает, что для любых противоположных значений аргумента, значения нечетной функции также противоположны.  График нечётной функции всегда симметричен относительно начала координат.

Сумма корней чётной и нечетной функций (точек пересечения оси абсцисс ОХ) всегда равна нулю, т.к. на каждый положительный корень х приходится отрицательный корень –х.

Важно отметить: некоторая функция не обязательно должна быть четной либо нечетной. Существует множество функций не являющихся ни четными ни нечетными. Такие функции называются функциями общего вида, и для них не выполняется ни одно из равенств или свойств приведенных выше.

 

График линейной функции

К оглавлению…

Линейной функцией называют функцию, которую можно задать формулой:

График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k > 0, в этом случае функция возрастающая; для случая k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону — слева направо):

 

График квадратичной функции (Парабола)

К оглавлению. ..

График параболы задается квадратичной функцией:

Квадратичная функция, как и любая другая функция, пересекает ось ОХ в точках являющихся её корнями: (x₁; 0) и (x₂; 0). Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (x₀; 0) квадратичная функция только касается оси ОХ, но не пересекает её. Квадратичная функция всегда пересекает ось OY в точке с координатами: (0; c). График квадратичной функции (парабола) может выглядеть следующим образом (на рисунке примеры, которые далеко не исчерпывают все возможные виды парабол):

При этом:

• если коэффициент a > 0, в функции y = ax² + bx + c, то ветви параболы направлены вверх;
• если же a < 0, то ветви параболы направлены вниз.

Координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):

Игрек вершины (q — на рисунках выше) параболы или максимальное, если ветви параболы направлены вниз (a < 0), либо минимальное, если ветви параболы направлены вверх (a > 0), значение квадратного трехчлена:

 

Графики других функций

К оглавлению…

Степенной функцией называют функцию, заданную формулой:

Приведем несколько примеров графиков степенных функций:

Обратно пропорциональной зависимостью называют функцию, заданную формулой:

В зависимости от знака числа k график обратно пропорциональной зависимости может иметь два принципиальных варианта:

Асимптота — это линия, к которой линия графика функции бесконечно близко приближается, но не пересекает. Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.

Показательной функцией с основанием а называют функцию, заданную формулой:

В зависимости от того больше или меньше единицы число a график показательной функции может иметь два принципиальных варианта (приведем также примеры, см. ниже):

Логарифмической функцией называют функцию, заданную формулой:

В зависимости от того больше или меньше единицы число a график логарифмической функции может иметь два принципиальных варианта:

График функции y = |x| выглядит следующим образом:

 

Графики периодических (тригонометрических) функций

К оглавлению…

Функция у = f(x) называется периодической, если существует такое, неравное нулю, число Т, что f(x + Т) = f(x), для любого х из области определения функции f(x).  Если функция f(x) является периодической с периодом T, то функция:

где: A, k, b – постоянные числа, причем k не равно нулю, также периодическая с периодом T₁, который определяется формулой:

Большинство примеров периодических функций — это тригонометрические функции. Приведем графики основных тригонометрических функций. На следующем рисунке изображена часть графика функции y = sinx (весь график неограниченно продолжается влево и вправо), график функции y = sinx называют синусоидой:

График функции y = cosx называется косинусоидой. Этот график изображен на следующем рисунке. Так как и график синуса он бесконечно продолжается вдоль оси ОХ влево и вправо:

График функции y = tgx называют тангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.

Ну и наконец, график функции y = ctgx называется котангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических и тригонометрических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.

алгебра / Есть ли более легкий способ решить неравенство? / Математика

Здесь на чём-то сэкономить можно, но не сильно. Прежде всего, обращает на себя внимание «узость» ОДЗ. И лучше с ним ничего не пересекать, а действовать только в этих рамках. Нули числителя и знаменателя придётся находить так и так. Лучше начать со знаменателя, и тогда сразу ясно, что будут два случая: $%x < 2$% и $%x > 2$% — в пределах ОДЗ. При этом ясен также знак у знаменателя. Останется проанализировать числитель, где одно слагаемое равно $%x-2$%, и сразу ясно, что при $%x > 2$% числитель заведомо положителен. А при $%x < 2$% надо будет сравнить между собой два неотрицательных числа: квадратный корень и $%2-x$%. Тут сразу ясно что надо возвести в квадрат. То есть тут пример так подобран, что весь этот анализ проводится легко — почти устно.

Ответ, кстати, у Вас получился неверный: если $%x=2,1$%, то в числителе явно плюс, а в знаменателе минус. То есть надо пересчитать всё, не производя никаких сложных операций.

Добавление. Тут уже многие написали, и рассуждения у всех в основе своей похожи, но я продемонстрирую свой ход мысли в той форме, как он у меня сам собой сложился.

Начинаем со знаменателя, из которого $%x < 2,5$%. Приравниваем знаменатель к нулю, получаем $%x=2$%. Так быть не должно, поэтому имеем два случая, в каждом из которых знак знаменателя однозначно определяется.

1) $%x > 2$% (не забываем также про $%x < 2,5$%) Знаменатель отрицателен, а числитель явно положителен: сумма корня квадратного и $%x-2$%. Ничего не вычисляем, а в ответ включаем $%x\in(2;2,5)$%. 2-3x+1\ge0$%. Корни квадратного трёхчлена равны $%(3\pm\sqrt{5})/2$%, и множество решений неравенства состоит из двух лучей. Правый луч нам заведомо не подходит, так как там все точки больше двух (и даже не входят в область определения дроби из условия). Остаётся заметить, что число $%(3-\sqrt{5})/2$% положительно, но при этом меньше $%2$%, поэтому в пересечении мы имеем $%x\in[1-\sqrt{3};(3-\sqrt{5})/2]$%.

Осталось объединить множество решений для первого и второго случая, что даёт окончательный ответ $%x\in[1-\sqrt{3};(3-\sqrt{5})/2]\cup(2;2,5)$%.

ГДЗ по алгебре 8 класс Дорофеев, Суворова Просвещение ответы и решения онлайн

Для того, чтобы результат был видим и существенен, необходимо соблюдать простые правила работы с гдз по алгебре за 8 класс Дорофеев, среди которых — ежедневность такой работы и её постоянство. Специалисты рекомендуют уделять подготовке минимум час в день, а если материал вызывает сложности, полтора-два часа. Кроме того, не стоит делать долгосрочных, превышающих 10 дней подряд, перерывов в занятиях. Поскольку длительное отсутствие работы способствует забыванию значительной части пройденного материала. Впоследствии придется изучать его большими блоками, что отрицательно скажется как на запоминание важных правил и порядка их применения, так и на состоянии ученика. Усталость и потеря интереса — частые спутники форсированного обучения, которых стоит избегать.

Приоритетные группы пользователей онлайн сборников готовых решений

В числе тех, кто постоянно или часто использует подробные решения по алгебре за 8 класс Дорофеев, можно встретить:

• восьмиклассников, готовящихся к тематическим предметным конкурсам. Особенно если в классе они изучают дисциплину по другим учебникам и УМК. Ресурс позволит им расширить свои знания, подключив дополнительные источники информации, что положительно скажется на результате;
• подростков, которые по тем или иным причинам (болезнь, посещение сборов и конкурсов, спортивных и творческих), часто пропускают школьные уроки. Чтобы понять тему, научиться грамотно выполнять решения, они прибегают к сборнику;
• школьников, переведенных на дистанционную форму обучения или избравших домашний/семейный формат образования. Для них такой ресурс — прекрасная альтернатива или дополнение к объяснению учителя, которое они не получают в достаточном объеме;
• школьных педагогов, которым нужно проверить большое количество ученических тетрадей за короткий срок. Учитывая, как много работы у современного учителя, в том числе — организационно-плановой, воспитательной, отчетной, материалы станут для них незаменимым подспорьем в их труде;
• родителей восьмиклассников, стремящихся проверить знания и уровень подготовки своего ребенка, не вникая глубоко в суть школьной программы по предмету, но будучи уверенными в качестве результата такой проверки.

Какими достоинствами обладает онлайн справочник по алгебре 8 класс (авторы Дорофеев, Суворова)?

Несмотря на то, что и сегодня есть те, кто недооценивает полезность еуроки ГДЗ, полагая материалы используются исключительно для механического переписывания правильных ответов, многие уже оценили плюсы ресурса:

• возможность организации разноплановой работы, в том числе — для самостоятельного повышения уровня и качества своих знаний;
• его круглосуточную доступность для всех пользователей;
• экономическую выгоду, использование как альтернативы репетиторам, дорогостоящим математическим курсам;
• соответствие информации требованиям Стандартов образования.

Изучив быстрые ответы, научившись ими пользоваться, школьники приобретут полезные навыки работы со справочниками в условиях ограниченного времени на выполнение поставленной задачи.

решите систему неравенств. растолкуйте пожалуйста как осознать одз и что делать

Малюсенько баллов 🙁

Попробую начать с ОДЗ. Заметим, что в первом неравенстве знаменатель не обязан быть равен 0. То есть

 

 

— это и есть ОДЗ.

 

Попробую решить поначалу первое неравенство.

 

 

 

 

 

 

 

 

Сократим обе доли на 2.

 

 

 

Заметим, что числитель при всех х будет неотрицательным. Только при х=1. Дробь обращается в 0 и удовлетворяет неравенству.

Означает все остальное зависит от знаменателя. Нам необходимо решить довольно простое неравенство 2х-1lt;0. Равенство невероятно, так как противоречит ОДЗ.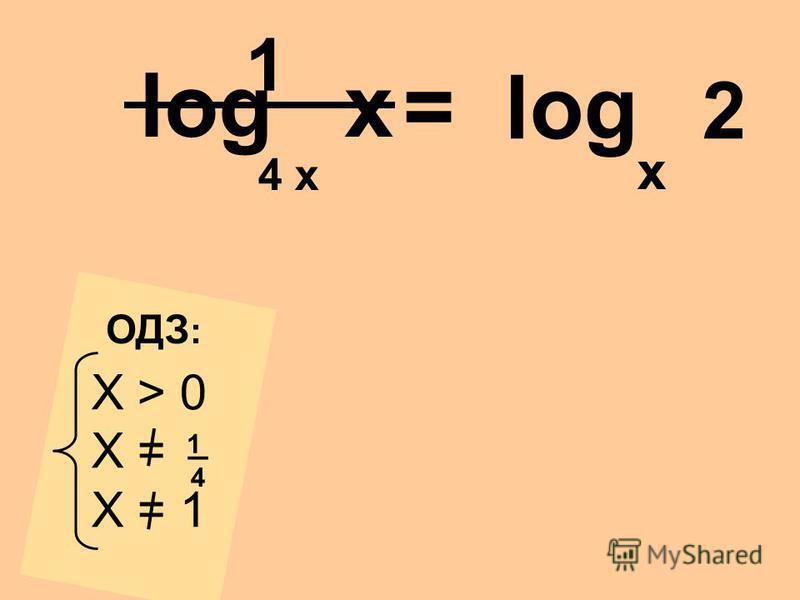 хlt;0,5.

 

Означает решением этого неравенства будет

 

 

Сейчас попытаемся решить второе неравенство, беря во внимание 1-ое.

 

 

Выделим полный квадрат в левой доли

 Обозначим через t=3-5x. Тогда t — неотрицательно. Перепишем неравенство

 

 

 

Так как t — неотрицательно, то все зависит от второго множителя.

 

t-3lt;0

 

3-5x-3lt;0 (*)

 

Осмотрим 2 случая

 

 

 

 

 

 

Тогда модуль раскрывается в неравенстве (*)

 

 (3-5х)-3lt;0

3-5x-3lt;0

-5хlt;0

xgt;0

Беря во внимание (**) решением этого случая будет

 

 

 

Тогда модуль раскрывается в виде

-(3-5х)-3lt;0

-3+5x-3lt;0

-6+5xlt;0

5xlt;6

xlt;1,2 

Беря во внимание, условие  (***)

Во втором неравенстве объединяется оба случая. Так как это решения в двух различных случаях. Соединеньем будет

 

Решением систему неравенств будет скрещение решений первого и второго неравенств.

 

То есть

По правилам пересечений и соединения множеств

 

 

Ответ:

 

теория, примеры, решения. Как найти область определения математических функций

Шамшурин А.В. один

Гагарина Н.А. один

1 Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа № 31»

Текст работы размещается без изображений и формул.
Полная версия работы доступна во вкладке «Рабочие файлы» в формате PDF

Введение

Я начал с просмотра многих тем по математике в Интернете и выбрал эту тему, потому что я убежден, что важность нахождения DHS играет огромную роль при решении уравнений и задач.В своей исследовательской работе я рассматривал уравнения, в которых достаточно только найти ОДЗ, опасность, необязательность, ограничения ОДЗ, некоторые запреты в математике. Самое главное для меня – хорошо сдать ЕГЭ по математике, а для этого нужно знать: когда, зачем и как найти ОДЗ. Это побудило меня к исследованию темы, целью которого было показать, что освоение этой темы поможет студентам правильно выполнять задания на экзамене. Для достижения этой цели я изучил дополнительную литературу и другие источники.Мне стало интересно, и учащиеся нашей школы знают: когда, зачем и как найти ДГС. Поэтому я провел тест на тему «Когда, зачем и как найти ODU?» (было дано 10 уравнений). Количество студентов — 28. Справились — 14 %, опасность ОДУ (учтена) — 68 %, факультативна (учтена) — 36 %.

Цель : определение: когда, почему и как найти DHS.

Задача: уравнения и неравенства в которых нужно найти ОДВ не нашли места в курсе алгебры систематического изложения, возможно поэтому я и мои сверстники часто допускаем ошибки при решении таких примеров, тратя много времени на их решение, забыв про ОДВ.

Задачи:

1. Показать значение ОДЗ при решении уравнений и неравенств.
2. Провести практическую работу по данной теме и подвести ее итоги.

Думаю, что полученные знания и навыки помогут мне решить вопрос: искать ОДЗ или нет? Я перестану делать ошибки, научившись правильно делать ODD. Время покажет, смогу ли я это сделать, а точнее ЕГЭ.

Глава 1

Что такое ODU?

ОДЗ — это диапазон допустимых значений , то есть это все значения переменной, для которых выражение имеет смысл.

Важно. Не решаем пример найти ОДЗ! Решаем кусочки примера, чтобы найти запрещенные места.

Некоторые запреты в математике. Таких запрещенных действий в математике очень мало. Но не все их помнят…

• Выражения с четной кратностью или должны быть > 0 или равны нулю, ОДЗ: f(x)
• Выражение в знаменателе дроби не может быть равно нулю, ОДЗ: f(x)
• | ф (х) | = г(х), ОДЗ: г(х) 0

Как записать ОДЗ? Очень просто.Всегда пишите ОДЗ рядом с примером. Под этими известными буквами, глядя на исходное уравнение, напишите значения х, допустимые для исходного примера. Преобразование примера может изменить LDO и, соответственно, ответ.

Алгоритм поиска ОДЗ:

1. Определить тип запрета.
2. Найдите значения, которые делают выражение бессмысленным.
3. Исключить эти значения из множества действительных чисел R.

Решить уравнение: =

Без ОДЗ	С ОДЗ
Ответ: х = 5	ОДЗ: => => Ответ: нет корней

Диапазон допустимых значений защищает нас от таких серьезных ошибок.Если честно, то именно из-за ОДЗ многие «ударники» превращаются в «троечников». Считая, что поиск и учёт ОДВ — незначительный шаг в решении, пропускают его, а потом недоумевают: «почему учитель поставил 2?». И поэтому я поставил, что ответ неверный! Это не «придирка» учителя, а вполне конкретная ошибка, как просчет или потерянный знак.

Дополнительные уравнения:

а) =; б) -42 = 14х+; в) = 0; г) | х-5 | = 2x-2

Глава 2

ОДЗ.Зачем? Когда? Как?

Диапазон допустимых значений — есть решение

1. ОДЗ — пустое множество, значит исходный пример не имеет решений

Ответ: корней нет.

Ответ: корней нет.

0, уравнение не имеет корней

Ответ: корней нет.

Дополнительные примеры:

а) + = 5; б) + = 23х-18; в) = 0,

1. ОДЗ содержит одно или несколько чисел, и простая подстановка быстро определяет корни.

ОДЗ: х = 2, х = 3

Проверка: х = 2, +, 0

Проверка: х = 3, +, 0

Ответ: х = 2, х = 3.

Проверить: x = 0,>, 0> 0, неправильно

Проверка: x = 1,>, 1> 0, верно

Ответ: х = 1.

Проверить: + = 3, 0 = 3, неправильно.

Ответ: корней нет.

Дополнительные примеры:

а) =; б) + = 0; в) + = х -1

Опасность ДЛО

Обратите внимание, что идентичные преобразования могут:

• не влияют на LDU;
• ведут на расширенную ЛДЗ;
• приводят к сужению ОДЗ.

Также известно, что в результате некоторых преобразований, изменяющих исходный HLO, это может привести к неправильным решениям.

Поясним каждый случай на примере.

1) Рассмотрим выражение x + 4x + 7x, ОДЗ переменной x для него есть множество R. Приведем аналогичные термины. В результате он примет вид х 2 + 11х. Очевидно, что LDV переменной x этого выражения также является множеством R. Таким образом, выполненное преобразование не изменило LDV.

2) Возьмем уравнение х + — = 0. В этом случае ОДЗ: х ≠ 0. В этом выражении есть и аналогичные слагаемые, после приведения которых приходим к выражению х, для которого ОДЗ есть R. Что имеем см.: в результате преобразования ОДЗ была расширена (к ОДЗ переменной x для исходного выражения добавлено число ноль).

3) Возьмем выражение. ОДВ переменной x определяется неравенством (x − 5) · (x − 2) ≥0, ОДВ: (−∞, 2] ∪∪ / Режим доступа: Материалы сайтов www.fipi.ru, www.eg

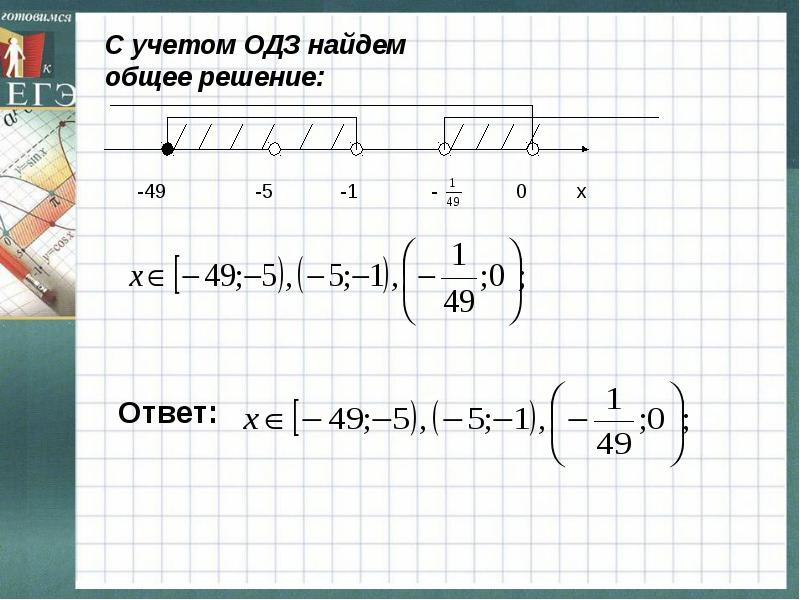Диапазон допустимых значений — решение [Электронный ресурс]/Режим доступа: rudocs. exdat.com ›docs/index-16853.html

ОДЗ — область допустимых значений, как найти ОДЗ [Электронный ресурс]/Режим доступа: smartstudents.ru ›expressions/odz.html

Диапазон допустимых значений: теория и практика [Электронный ресурс]/Режим доступа: pandia.ru ›text/78/083/13650.php

Что такое ОДЗ [Электронный ресурс] / Режим доступа: www.cleverstudents.ru ›odz.html

Что такое LDO и как его найти — объяснение и пример. Электронный ресурс]/Режим доступа: cos-cos.ru ›math/82/

Приложение 1

Практикум «ОДЗ: когда, почему и как?»

Опция 1	Опция 2
│х + 14│ = 2 — 2х
	│3-х│ = 1 — 3х

Приложение 2

Ответы на задания практикума «ОДЗ: когда, почему и как?»

Опция 1	Опция 2
Ответ: нет корней	Ответ: х — любое число, кроме х = 5
9х + = +27 ОДЗ: х ≠ 3 Ответ: нет корней	ОДЗ: х=-3, х=5. Ответ: -3; 5.
г = -убывание, г = -увеличивается Следовательно, уравнение имеет не более одного корня. Ответ: х = 6.	ОДЗ: → → х≥5 Ответ: х≥5, х≤-6.
│х + 14│ = 2-2х ОДЗ: 2-2х≥0, х≤1 х=-4, х=16, 16 не относится к ОДЗ	Уменьшается, -увеличивается У уравнения не более одного корня. Ответ: корней нет.
0, ОДЗ: х≥3, х≤2 Ответ: x≥3, x≤2	8х + = -32, ОДЗ: х ≠ -4. Ответ: корней нет.
х = 7, х = 1. Ответ: нет решений	Увеличение — уменьшение Ответ: х = 2.
0 ОДЗ: х ≠ 15 Ответ: x — любое число, кроме x = 15.	│3-х│ = 1-3х, ОДЗ: 1-3х≥0, х≤ х=-1, х=1 не принадлежит ОДЗ. Ответ: х = -1.

Ваша конфиденциальность важна для нас. По этой причине мы разработали Политику конфиденциальности, в которой описывается, как мы используем и храним вашу информацию. Пожалуйста, ознакомьтесь с нашей политикой конфиденциальности и сообщите нам, если у вас есть какие-либо вопросы.

Сбор и использование личной информации

Личная информация относится к данным, которые могут быть использованы для идентификации конкретного лица или связи с ним.

Вас могут попросить предоставить личную информацию в любое время, когда вы свяжетесь с нами.

Ниже приведены некоторые примеры типов личной информации, которую мы можем собирать, и того, как мы можем использовать такую ​​информацию.

Какую личную информацию мы собираем:

• Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваше имя, номер телефона, адрес электронной почты и т.д.

Как мы используем вашу личную информацию:

• Личная информация, которую мы собираем, позволяет нам связываться с вами и сообщать об уникальных предложениях, рекламных акциях и других событиях и предстоящих событиях.
• Время от времени мы можем использовать вашу личную информацию для отправки важных уведомлений и сообщений.
• Мы также можем использовать личную информацию для внутренних целей, таких как проведение аудитов, анализ данных и различные исследования, чтобы улучшить предоставляемые нами услуги и предоставить вам рекомендации относительно наших услуг.
• Если вы участвуете в розыгрыше призов, конкурсе или аналогичном рекламном мероприятии, мы можем использовать предоставленную вами информацию для управления такими программами.

Раскрытие информации третьим лицам

Мы не раскрываем полученную от Вас информацию третьим лицам.

Исключения:

• В случае необходимости — в соответствии с законом, постановлением суда, в судебном порядке и/или на основании публичных запросов или запросов государственных органов на территории Российской Федерации — раскрыть свои персональная информация. Мы также можем раскрыть информацию о вас, если решим, что такое раскрытие необходимо или уместно в целях безопасности, правоохранительных органов или по другим общественно важным причинам.
• В случае реорганизации, слияния или продажи мы можем передать собираемую нами личную информацию соответствующему третьему лицу — правопреемнику.

Защита личной информации

Мы принимаем меры предосторожности, в том числе административные, технические и физические, для защиты вашей личной информации от потери, кражи и злоупотребления, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.

Соблюдение вашей конфиденциальности на уровне компании

Для того, чтобы убедиться, что ваша личная информация в безопасности, мы доводим до наших сотрудников правила конфиденциальности и безопасности, строго следим за выполнением мер конфиденциальности.

Как найти область действия функции? Ученикам средней школы часто приходится сталкиваться с этой задачей.

Родители должны помочь своим детям разобраться в этом вопросе.

Назначение функций.

Напомним основные термины алгебры. Функция в математике — это зависимость одной переменной от другой.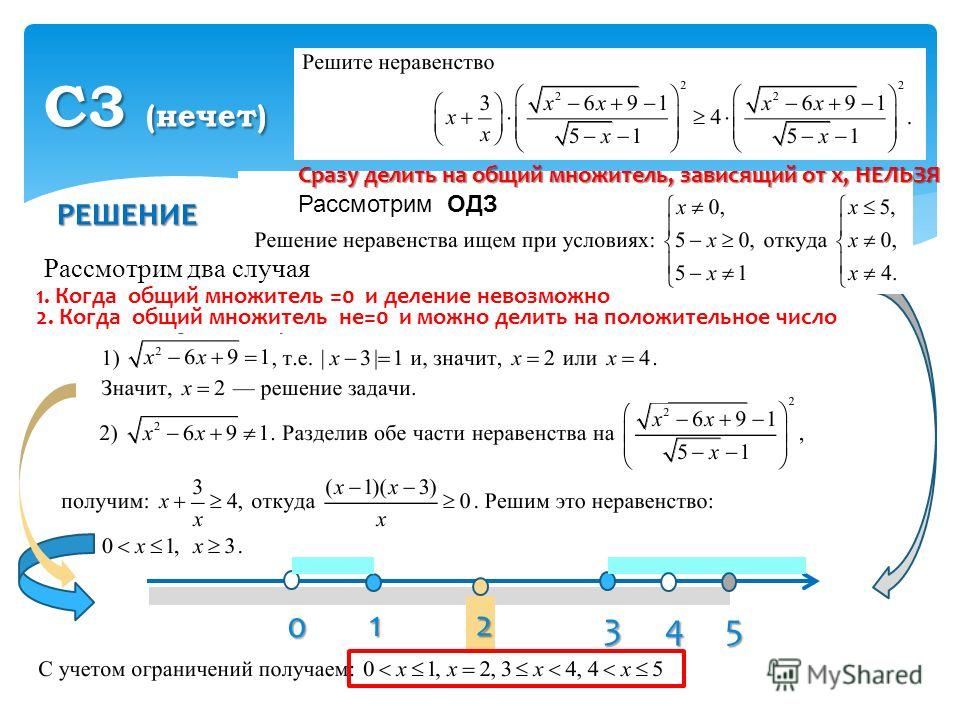 Можно сказать, что это строгий математический закон, связывающий определенным образом два числа.

В математике при анализе формул числовые переменные заменяются буквенными символами.Чаще всего используются x («x») и y («y»). Переменная x называется аргументом, а переменная y называется зависимой переменной или функцией x.

Существуют различные способы установки зависимостей переменных.

Давайте перечислим их:

1. Аналитический тип.
2. Табличный вид.
3. Графический дисплей.

Аналитический метод представлен формулой. Рассмотрим примеры: y = 2x + 3, y = log(x), y = sin(x). Формула y = 2x + 3 типична для линейной функции.Подставляя числовое значение аргумента в заданную формулу, получаем значение y.

Табличный метод представляет собой таблицу с двумя столбцами. Первый столбец отводится для значений x, а игровые данные записываются в следующий столбец.

Наиболее наглядным считается графический метод. График называется отображением множества всех точек на плоскости.

Для построения графика используется декартова система координат. Система состоит из двух перпендикулярных прямых.На оси отложены такие же единичные отрезки. Отсчет ведется от центральной точки пересечения прямых.

Независимая переменная указана на горизонтальной линии. Она называется осью абсцисс. Вертикальная линия (ось ординат) отображает числовое значение зависимой переменной. На пересечении перпендикуляров к данным осям отмечены точки. Соединив точки друг с другом, мы получим сплошную линию. Это основа расписания.

Типы переменных зависимостей

Определение.

В общем виде зависимость представляется в виде уравнения: y = f(x). Из формулы следует, что каждому значению числа x соответствует определенное число y. Значение игры, соответствующее числу x, называется значением функции.

Все возможные значения, которые получает независимая переменная, образуют область определения функции. Соответственно весь набор чисел зависимой переменной определяет диапазон значений функции. Область видимости — это все значения аргумента, для которых f(x) имеет смысл.

Первоначальная проблема при изучении математических законов состоит в том, чтобы найти область определения. Этот термин должен быть правильно определен. В противном случае все дальнейшие расчеты будут бесполезны. Ведь объем значений формируется на основе элементов первого набора.

Объем функции напрямую зависит от ограничений. Ограничения связаны с невозможностью выполнения некоторых операций. Существуют также ограничения на использование числовых значений.

Не ограничено, областью действия является все числовое пространство. Знак бесконечности имеет горизонтальную восьмерку. Весь набор чисел записывается следующим образом: (-∞; ∞).

В некоторых случаях набор данных состоит из нескольких подмножеств. Рамки числовых лакун или пробелов зависят от вида закона изменения параметров.

Вот список факторов, влияющих на ограничения:

• обратная пропорциональность;
• арифметический корень;
• возведение в степень;
• логарифмическая зависимость;
• тригонометрических формы.

Если таких элементов несколько, то поиск ограничений разделяется для каждого из них. Самая большая проблема заключается в выявлении критических точек и пробелов. Решением задачи будет объединение всех числовых подмножеств.

Набор и подмножество чисел

О наборах.

Домен выражается как D (f), а знак объединения представлен символом ∪. Все числовые пробелы заключены в круглые скобки. Если граница участка не входит в комплект, то ставят полукруглую скобу.В противном случае, когда число включено в подмножество, используются квадратные скобки.

Обратная пропорциональность выражается формулой y = k/x. График функции представляет собой кривую линию, состоящую из двух ветвей. Обычно его называют гиперболой.

Поскольку функция выражается дробью, нахождение области определения сводится к анализу знаменателя. Известно, что деление на ноль в математике запрещено. Решение задачи сводится к приравниванию знаменателя к нулю и нахождению корней.

Приведем пример:

Дано: y = 1 / (x + 4). Найдите домен.

1. Установить знаменатель равным нулю.
   х + 4 = 0
2. Найдите корень уравнения.
   х = -4
3. Определяем множество всех возможных значений аргумента.
   D (f) = (- ∞; -4) ∪ (-4; + ∞)

Ответ: Областью действия функции являются все действительные числа, кроме -4.

Значение числа под знаком квадратного корня не может быть отрицательным.В этом случае определение функции с корнем сводится к решению неравенства. Подкоренное выражение должно быть больше нуля.

Домен корня связан с четностью показателя корня. Если показатель делится на 2, то выражение имеет смысл только в том случае, если его значение положительно. Нечетное число показателя указывает на допустимость любого значения подкоренного выражения: как положительного, так и отрицательного.

Неравенство решается так же, как уравнение.Есть только одно отличие. Умножив обе части неравенства на отрицательное число, поменяйте знак на противоположный.

Если корень квадратный в знаменателе, то следует наложить дополнительное условие. Значение числа не должно быть равно нулю. Неравенство переходит в разряд строгих неравенств.

Логарифмические и тригонометрические функции

Логарифмическая форма имеет смысл, когда числа положительные. Таким образом, область определения логарифмической функции аналогична функции извлечения квадратного корня, за исключением нуля.

Рассмотрим пример логарифмической зависимости: y = log (2x-6). Найдите домен.

Ответ: (3; + ∞).

Область значений y = sin x и y = cos x представляет собой множество всех действительных чисел. Существуют ограничения для тангенса и котангенса. Они связаны с делением на косинус или синус угла.

Тангенс угла определяется отношением синуса к косинусу. Укажем значения углов, при которых значение тангенса не существует. Функция y = tg x имеет смысл при всех значениях аргумента, кроме x = π/2 + πn, n∈Z.

Областью определения функции y = ctg x является все множество действительных чисел, исключая x = πn, n∈Z. Если аргумент равен π или кратен π, синус угла равен нулю. В этих точках (асимптотах) котангенс не может существовать.

Первые задания на выявление области определения начинаются на уроках в 7 классе. При первом знакомстве с этим разделом алгебры учащийся должен четко усвоить тему.

Следует отметить, что данный термин будет сопровождать студента, а затем студента на протяжении всего периода обучения.

Дробные уравнения. ОДЗ.

Внимание!
В Спецразделе 555 есть дополнительные материалы
.
Для очень «не очень…»
И для «очень даже…»)

Продолжаем осваивать уравнения. Мы уже умеем работать с линейными и квадратными уравнениями. Остается последний вид — дробных уравнений … Или их еще называют гораздо солиднее — дробных рациональных уравнений … Это то же самое.

Дробные уравнения.

Как следует из названия, в этих уравнениях всегда присутствуют дроби. Но не просто дроби, а дроби, у которых в знаменателе неизвестных … Хотя бы один. Например:

Напомню, что если в знаменателях только числа , то это линейные уравнения.

Как решить дробное уравнение ? Прежде всего, избавьтесь от дробей! После этого уравнение, чаще всего, превращается в линейное или квадратное.И тогда мы знаем, что делать… В некоторых случаях это может превратиться в тождество, например 5 = 5, или в неверное выражение, например 7 = 2. Но такое случается редко. Я упомяну об этом ниже.

Но как избавиться от дробей!? Очень простой. Применив все те же одинаковые преобразования.

Нам нужно умножить все уравнение на одно и то же выражение. Чтоб все знаменатели сводились! Все сразу станет легче. Поясню на примере. Предположим, нам нужно решить уравнение:

Как вы учили в младших классах? Переводим все в одну сторону, приводим к общему знаменателю и т.д.Забудь его, как страшный сон! Это следует делать при сложении или вычитании дробных выражений. Или работа с неравенствами. А в уравнениях сразу обе части умножаем на выражение, которое даст нам возможность привести все знаменатели (т.е., по сути, на общий знаменатель). А что это за выражение?

Слева умножение на х + 2 … А справа умножение на 2. Это значит, что уравнение нужно умножить на 2 (х + 2) … Умножаем:

Это обычное умножение дробей, но напишу подробно:

Обратите внимание, что я пока не раскрываю скобки. (х + 2) ! Итак, в целом, я пишу это:

Слева уменьшается целиком (x+2) , а справа 2. Что и требуется! После приведения получаем линейное уравнение:

И это уравнение решит каждый! х = 2 .

Решим еще один пример, чуть посложнее:

Если вспомнить, что 3 = 3/1, а 2x = 2x / 1, можно написать:

И снова избавляемся от того, что нам не очень нравится — от дробей.

Видим, что для сокращения знаменателя с х нужно дробь умножить на (х — 2) … Несколько нам не помеха. Что ж, умножаем. Вся левая сторона и вся правая сторона:

Снова скобки (x — 2) Не раскрываю.Я работаю со скобками целиком, как если бы это было одно число! Это нужно делать всегда, иначе ничего не уменьшится.

С чувством глубокого удовлетворения разрезаем (х — 2) и получаем уравнение без дробей, в линейку!

А теперь раскрываем скобки:

Отдаем подобные, переносим все на левую сторону и получаем:

Но перед этим мы научимся решать другие задачи.Интерес. Вот грабли, кстати!

Если вам нравится этот сайт…

Кстати, у меня для вас есть еще парочка интересных сайтов. )

Вы можете попрактиковаться в решении примеров и узнать свой уровень. Мгновенное проверочное тестирование. Учимся — с интересом!)

вы можете ознакомиться с функциями и производными.

В математике существует бесконечное количество функций. И у каждого свой характер.) Для работы с самыми разнообразными функциями нужен единый подход.Иначе какая же это математика?!) И такой подход есть!

При работе с любой функцией мы представляем ее стандартным набором вопросов. И первый, самый главный вопрос — это объем функции. Иногда эту область называют набором допустимых значений аргументов, областью определения функции и т. д.

Какова область действия функции? Как его найти? Эти вопросы часто кажутся сложными и непонятными… Хотя на самом деле все предельно просто.В чем вы можете убедиться сами, прочитав эту страницу. Идти?)

Ну что тут сказать… Только респект.) Да! Естественный домен функции (о котором мы здесь говорим) соответствует с выражениями ODZ, включенными в функцию. Соответственно, они и разыскиваются по тем же правилам.

Теперь давайте посмотрим на не совсем естественную область определения.)

Дополнительные ограничения на объем функции.

Здесь речь пойдет об ограничениях, которые накладывает задание.Те. задача содержит некоторые дополнительные условия, которые придумал компилятор. Или ограничения выплывают из самого способа определения функции.

Что касается ограничений в задании, тут все просто. Обычно ничего искать не нужно, в задаче все уже сказано. Напомню, что ограничения, написанные автором задания, никоим образом не отменяют фундаментальных ограничений математики. Нужно только не забывать учитывать условия задания.

Например, такая задача:

Найти домен функции:

на множестве положительных чисел.

Выше мы нашли естественную область определения этой функции. Этот район:

Д (ж) = ( -∞ ; -1) ∪ (-1; 2] ∪ ∪

При словесном способе определения функции нужно внимательно прочитать условие и найти там ограничения на крестики. Иногда глаза ищут формулы, а слова свистят мимо сознания да…) Пример из предыдущего урока:

Функция задается условием: каждому значению натурального аргумента x ставится в соответствие сумма цифр, составляющих значение x.

Здесь следует отметить, что мы говорим только о естественных значениях х. Потом и Д(ф) мигом записали:

Г (е): х е Н

Как видите, область действия функции не такое уж сложное понятие.Нахождение этой области сводится к исследованию функции, записи системы неравенств и решению этой системы. Конечно, есть всякие системы, простые и сложные. Но…

Открою вам маленький секрет. Иногда функция, для которой нужно найти область применения, выглядит просто устрашающе. Хочется побледнеть и заплакать.) Но стоит записать систему неравенств… И вдруг система оказывается элементарной! Причем часто чем страшнее функция, тем проще система…

Мораль: глаза боятся, голова решает!)

 

РЕШЕНО:el / 2 (+15(+3)0-odz для |zl-=2

Стенограмма видео

проблема. Нас просят вычислить последнее преобразование функции e к отрицательному знаку t в t. И чтобы сделать это, мы просто будем работать непосредственно с определениями, интегрируя каждое из отрицательных x t раз, используя отрицательный знак t до t t T.Теперь, чтобы интегрировать это, мы просто применим интеграцию по горшкам. В данном случае мы собираемся объединить эти два термина, чтобы получить отрицательную реакцию тимуса на единицу плюс. Если мы выполним интегрирование по частям, не дифференцируя это, мы получим значение, отрицательное на единицу, плюс s, соответствующее этому отрицательному значению, плюс спросим его, умноженное на E, чтобы получить отрицательное значение, плюс знак s T, чтобы t оценивалось как ноль. Знак бесконечности минус дифференцирующий знак перед t дает вам знак Coast t. Таким образом, это уравнение представляет собой отрицательное уравнение от e плюс s t Coast к t.Хорошая вещь здесь в том, что вы также можете выполнить интеграцию по частям, чтобы оценить эту сторону на dhe. Эта сторона полностью аннулируется, потому что знак нуля равен нулю, и каждая отрицательная бесконечность есть бесконечность, выполняя интегрирование по шине снова. Это равно отрицательному значению более одного плюс s в квадрате, умноженному на e в отрицательной форме, плюс st побережье до t, оцененное в нуле и бесконечности, плюс удвоенный интеграл каждого из отрицательных единиц плюс st побережья True T. Теперь, к сожалению, эти термины уничтожаются.Если мы не сможем бороться, они обнаружат, что ценность бесконечности равна нулю. Но значение нуля равно единице, чтобы получить, что это равно отрицательному значению более одного плюс s в квадрате минус четыре на один плюс s в квадрате, умноженному на этот интеграл, который вы распознаете как последнее черное преобразование. Посмотрите на отрицательную оценку береговой пошлины. s, что хорошо, потому что мы выразили отсутствие последнего преобразования функции в терминах самой функции. Если вы перестроите это уравнение, вы получите, э-э, это, э-э, это, э-э, один плюс четыре на один плюс s в квадрате, умноженный на нехватку жизни, превратится с вами в родной знак t в t, оцененный. Это люди, которые больше одного плюс х в квадрате. А теперь разделив на эту сторону и упростив, мы получили круг. Последнее преобразование будет равно двум на один плюс Х в квадрате плюс четыре

Все возрасты в App Store

Практические, наглядные задания по алгебре, которые помогут вам по-новому взглянуть на математику.

«Мне 48. Я всю жизнь хотел изучать алгебру. Перепробовал все виды книг, но безрезультатно. Ваше приложение работает для меня. Я так взволнован.Открывается целый новый мир.» — Салли Г.

Algebra Touch — это дополнительное учебное пособие, которое дает вам возможность играть непосредственно с алгеброй… и делает невозможным совершение ошибок.

Свободно ковыряться. реагировать так, как вы думали? Нет? Что ж, пора обновить вашу внутреннюю модель понимания и попробовать еще раз. Так люди учатся.

«Серьезно потрясающее приложение. Я профессиональный преподаватель математики и физики для учащихся средних школ и студентов колледжей. и взрослые.Я использовал ваше приложение с несколькими моими учениками…. И это было похоже на волшебство. Визуальный и кинестетический подход к «движущейся математике» такой мощный!»

* Пользовательские манипуляции для каждой темы алгебры
* Случайно генерируемые практические задачи — столько, сколько вы хотите!
* Режим испытаний в конце каждого модуля, чтобы действительно проверить свое понимание способ увидеть, о чем идет речь, это попробовать.

«С помощью этого приложения автор успешно сделал алгебру красивой. Я бы очень хотел, чтобы это приложение существовало, когда я изучал алгебру 25 лет назад.» — geekswithjuniors.com

Более 1 миллиона загрузок по всему миру! (включая старую версию)

Текущий материал охватывает:
Упрощение, Подобные термины, Коммутативность, Порядок операций, Факторизация, Простые числа, Исключение, Изоляция, Переменные, Одношаговые уравнения, Двухшаговые уравнения. Переменные с обеих сторон уравнения, распределение, факторизация, правило произведения экспоненты, правило экспонентного частного и логарифмы.

Вопросы? Комментарии?
Электронная почта [email protected] для реального ответа.

Бюллетень бакалавриата

Stony Brook — весна 2022 г. BulletinMAP

КАРТА 101: Основы арифметики и алгебры

Арифметика: дроби, десятичные дроби и проценты. Алгебра: числа со знаком, одночлены, линейные уравнения с одним неизвестным и текстовые задачи. Этот курс предназначен для студентов, которые никогда не изучали алгебру.Не соответствует вступительным требованиям по математике или требованиям D.E.C. Требование категории С. Учащиеся, которые во всем остальном удовлетворили D.E.C. категория C не может регистрироваться на этот курс. Студенты с избыточной квалификацией, выявленные в результате вступительного теста, могут быть сняты с регистрации и направлены на перевод на другой курс. Не засчитывается для получения диплома. Только оценки от A до C/неудовлетворительно. Опция Pass/No Credit не может быть использована.

3 кредита

​

КАРТА 102: обзор знаний по алгебре

Незачетный онлайновый интенсивный обзор тем из школьной алгебры в качестве подготовки к изучению статистики, предварительного исчисления, исчисления и другой математики.Численные и алгебраические операции, показатели степени, многочлены, рациональные выражения, построение графиков, аналитическая геометрия линий, решение линейных и квадратных уравнений с одной переменной, решение линейных систем с двумя переменными, многочлены, разложение алгебраических выражений на множители, абсолютное значение, неравенства и биномиальная теорема. . Окончательной оценкой в ​​этом курсе будет вступительный экзамен по математике в Стоуни-Брук; удовлетворительное завершение курса соответствует уровню размещения 3 или выше. Только оценки от A до C/неудовлетворительно. Этот курс имеет соответствующую плату. Пожалуйста, посетите www.stonybrook.edu/coursefees для получения дополнительной информации.

Необходимое условие: разрешение отдела

0 кредит

​

КАРТА 103: Знание алгебры

Интенсивный обзор школьной алгебры в качестве подготовки к математическим вычислениям и другой математике.Возможности с показателями, основные графики, решение линейных и квадратных уравнений с одной переменной, решение линейных систем с двумя переменными, многочлены, факторизация алгебраических выражений, биномиальная теорема и неравенства. Алгебраические операции, аналитическая геометрия линий. Не засчитывается для получения диплома. Только оценки от A до C/неудовлетворительно. Опция Pass/No Credit не может быть использована.