Формулы комбинаторики с примерами. Основные формулы комбинаторики: сочетания, размещения, перестановки
Учитесь решать задачи по комбинаторике? На самом начальном этапе нужно изучить основные формулы комбинаторики: сочетания, размещения, перестановки (смотрите подробнее ниже) и научиться их применять для решения задач.
Как выбрать формулу комбинаторики?
Мы подготовили для вас наглядную схему с примерами решений по каждой формуле комбинаторики:
- алгоритм выбора формулы (сочетания, перестановки, размещения с повторениями и без),
- рекомендации по изучению комбинаторики,
- 6 задач с решениями и комментариями на каждую формулу.
Перестановки
Пусть имеется $n$ различных объектов.
Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок).
Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.
Пример всех перестановок из $n=3$ объектов (различных фигур) — на картинке справа. Согласно формуле, их должно быть ровно $P_3=3!=1\cdot 2\cdot 3 =6$, так и получается.
С ростом числа объектов количество перестановок очень быстро растет и изображать их наглядно становится затруднительно. Например, число перестановок из 10 предметов — уже 3628800 (больше 3 миллионов!).
Еще: онлайн калькулятор перестановок.
Размещения
Пусть имеется $n$ различных объектов.
Будем выбирать из них $m$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются
размещениями из $n$ объектов по $m$, а их число равно
 m \cdot P_m.$$
m \cdot P_m.$$
Удобный и бесплатный онлайн калькулятор сочетаний.
Решебник задач по комбинаторике
Изучаем комбинаторику: полезные ссылки
Перестановки сочетания и размещения (с и без повторений) в к…
Привет, сегодня поговорим про перестановки, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое перестановки, сочетания,размещения,перестановки с повторениями ,перестановки без повторений,соединения в комбинаторике , настоятельно рекомендую прочитать все из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Таблица Отличие и признаки сочетаний, размещений и перестановок
| Признаки | |||
| перестановки | сочетания | размещения | |
| Порядок следования элементов | + | – | + |
| Состав элементов | – | + | + |
Сводка формул для всех видов соединений в комбинаторике
6 перестановок 3-х шаров
В комбинаторике перестановка — это упорядоченный набор чисел обычно трактуемый как биекция на множестве , которая числу i ставит в соответствие i-й элемент из набора. Число n при этом называется порядком перестановки. Как синоним слову «перестановка» в этом смысле некоторые авторы используют слово расстановка.
Число n при этом называется порядком перестановки. Как синоним слову «перестановка» в этом смысле некоторые авторы используют слово расстановка.
В теории групп под перестановкой произвольного множества подразумевается биекция этого множества на себя. Как синоним слову «перестановка» в этом смысле некоторые авторы используют слово подстановка. (Другие авторы подстановкой называют наглядный способ записи перестановки.)
Свойства перестановок
- Число всех перестановок порядка равно числу размещений из n по n, то есть факториалу:[
Связанные определения
Специальные типы перестановок
Подстановка
Перестановка множества может быть записана в виде подстановки, например:
где и
Произведения циклов и знак перестановки[править ]
Любая перестановка может быть разложена в произведение (композицию) непересекающихся циклов длины причем единственным образом с точностью до порядка следования циклов в произведении. Например:
Например:
Любой цикл может быть разложен в произведение (не обязательно непересекающихся) транспозиций. Для произвольного цикла длины разложение можно написать так: Циклы длины 1 действуют как тождественная перестановка и тоже могут быть легко разложены, так как квадрат любой транспозиции есть тождественная перестановка: Такое разложение циклов на произведение транспозиций не будет единственным:
Таким образом любая перестановка может быть разложена в произведение транспозиций. Хотя это разложение и не будет единственным, но четность числа транспозиций, входящих в разложение, сохраняется. Пусть перестановка разложена в произведение транспозиций, тогда знаком перестановки (иначе:четностью перестановки или сигнатурой перестановки) называют число при этом называют четной перестановкой, если инечетной перестановкой, если
Знак перестановки также может быть определен через число инверсий в этой перестановке:
Замечание. Имеется два соглашения по умножению перестановок и циклов:
Имеется два соглашения по умножению перестановок и циклов:
1) .
Например: .
2) .
Например: .
Перестановки с повторением в комбинаторике
Рассмотрим n элементов m различных типов, причем в каждом типе все элементы одинаковы. Тогда перестановки из всех этих элементов с точностью до порядка следования однотипных элементов называются перестановками с повторением. Если ki — количество элементов i-го типа, то и количество всевозможных перестановок с повторениями равно мультиномиальному коэффициенту
Случайная перестановка
Обобщенная схема размещения
Случайной перестановкой называется случайный вектор все элементы которого принимают натуральные значения от 1 до и при этом вероятность совпадения любых двух элементов равна 0.
Независимой случайной перестановкой
для некоторых таких что
Если при этом не зависят от , то перестановку называют одинаково распределенной. Если же нет зависимости от , то есть то называют однородной.
Если же нет зависимости от , то есть то называют однородной.
В комбинаторике размещением (из n по k) называется упорядоченный набор из k различных элементов из некоторого множества различных n элементов.
Пример 1: — это 4-элементное размещение из 6-элементного множества .
Пример 2: некоторые размещения элементов множества по 2: … … …
В отличие от сочетаний, размещения учитывают порядок следования предметов. Так, например, наборы и являются различными, хотя состоят из одних и тех же элементов (то есть совпадают как сочетания).
Пример
• В фирме работают 8 человек одинаковой квалификации, среди них Иванов, Петров, Сидоров. Сколькими способами можно случайно выбратьтрех из восьми?
Решение
• Всего вариантов — выбрать три из восьми без повторения, т.к. один и тот же не может выполнять две работы
Количество размещений
Количество размещений из n по k, обозначаемое , равно убывающему факториалу:
Последнее выражение имеет естественную комбинаторную интерпретацию: каждое размещение из n по k однозначно соответствует некоторому сочетанию из nпо k и некоторой перестановке элементов этого сочетания; число сочетаний из n по k равно биномиальному коэффициенту , в то время как перестановок наk элементах ровно k! штук.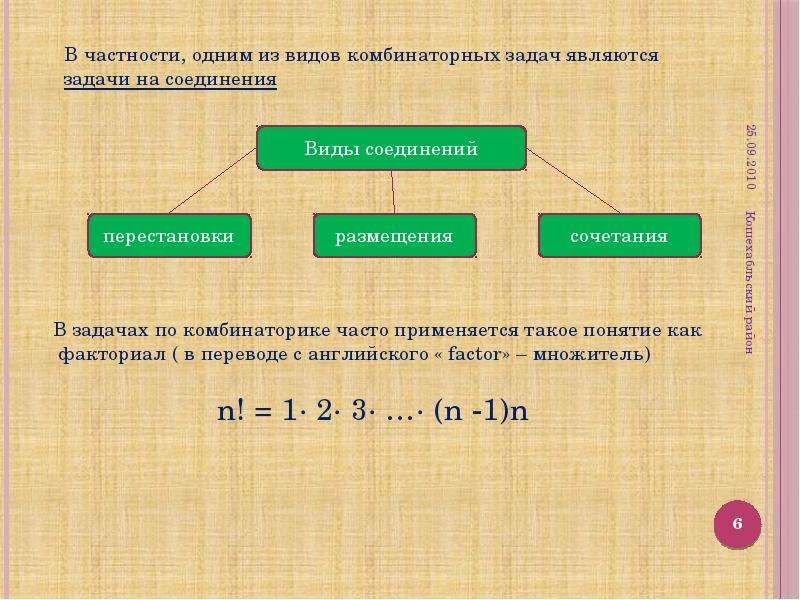
При k=n количество размещений равно количеству перестановок порядка
Размещение с повторениями
Размещение с повторениями или выборка с возвращением — это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз.
Пример задач
Замок камеры хранения имеет четыре диска, каждый из которых разделен на 10 секторов; насекторах каждого из дисков написаны цифры 0, 1, …, 9.
• Какова вероятность открыть закрытую камеру для человека:
1. забывшего все, что он набрал на дисках, закрывая камеру;
2. помнящего только цифру, набранную на первом диске;
3. помнящего только, что ни на втором, ни на третьем, ни на четвертом, диске не набирал цифру 6?
. Решение
3) Всего вариантов N=10*9*9*9
Количество размещений с повторениями
По правилу умножения количество размещений с повторениями из n по k, обозначаемое , равно:
Например, количество вариантов 3-значного кода, в котором каждый знак является цифрой от 0 до 9 и может повторяться, равно:
Еще один пример: размещений с повторениями из 4 элементов a, b, c, d по 2 равно эти размещения следующие:
В комбинаторике сочетанием из по называется набор элементов, выбранных из данного множества, содержащего различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Так, например, наборы (3-элементные сочетания, подмножества, ) {2, 1, 3} и {3, 2, 1} 6-элементного множества {1, 2, 3, 4, 5, 6} () являются одинаковыми (в то время как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.
В общем случае число, показывающее, сколькими способами можно выбрать элементов из множества, содержащего различных элементов, стоит на пересечении -й диагонали и -й строки треугольника Паскаля.
Пример
В чемпионате по шахматам участвовало 40 спортсменов. Каждый с каждым сыграл по одной партии. Сколько всего партий было сыграно?
Число сочетаний
Биномиальный коэффициент
Число сочетаний из по равно биномиальному коэффициенту
При фиксированном производящей функцией последовательности чисел сочетаний , , , … является:
Двумерной производящей функцией чисел сочетаний является
Сочетания с повторениями
Сочетанием с повторениями называются наборы, в которых каждый элемент может участвовать несколько раз.
Число сочетаний с повторениями из по равно биномиальному коэффициенту
Доказательство
Пусть имеется типов объектов, причем объекты одного типа неотличимы. Пусть имеется неограниченное (или достаточно большое, во всяком случае, не меньше ) количество объектов каждого типа. Из этого ассортимента выберем объектов; в выборке могут встречаться объекты одного типа, порядок выбора не имеет значения. Обозначим через количество выбранных объектов -го типа, , . Тогда . Но число решений этого уравнения легко подсчитывается с помощью «шаров и перегородок»: каждое решение соответствует расстановке в ряд шаров и перегородок так, чтобы между -й и -й перегородками находилось ровно шаров. Но таких расстановок в точности , что и требовалось доказать.
При фиксированном производящей функцией чисел сочетаний с повторениями из по является:
Двумерной производящей функцией чисел сочетаний с повторениями является:
Пример Имеется 2 типа цветов, количество цветов не ограничено.
 Сколько различных букетов можно составить из 3-х цветов?
Сколько различных букетов можно составить из 3-х цветов?• 111
• 222
• 122
• 211
• Всего 4 различных букета
Пример Имеется 5 типов цветов, количество цветов не ограничено. Сколько различных букетов можно составить из 3-х цветов?
Решение
• Сочетание с повторением:
(5+3-1)!/(3!*(5-1) !)=35
См. также
Понравилась статья про перестановки? Откомментируйте её Надеюсь, что теперь ты понял что такое перестановки, сочетания,размещения,перестановки с повторениями ,перестановки без повторений,соединения в комбинаторике и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Дискретная математика. Теория множеств . Теория графов . Комбинаторика.
Комбинаторика: основные правила и формулы.

КОМБИНАТОРИКА
Комбинаторика – раздел математики, который изучает задачи выбора и расположения элементов из некоторого основного множества в соответствии с заданными правилами. Формулы и принципы комбинаторики используются в теории вероятностей для подсчета вероятности случайных событий и, соответственно, получения законов распределения случайных величин. Это, в свою очередь, позволяет исследовать закономерности массовых случайных явлений, что является весьма важным для правильного понимания статистических закономерностей, проявляющихся в природе и технике.
Правила сложения и умножения в комбинаторике
Правило суммы. Если два действия А и В взаимно исключают друг друга, причем действие А можно выполнить m способами, а В – n способами, то выполнить одно любое из этих действий (либо А, либо В) можно n + m способами.
Пример 1.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить одного дежурного?
Сколькими способами можно назначить одного дежурного?
Решение
Дежурным можно назначить либо мальчика, либо девочку, т.е. дежурным может быть любой из 16 мальчиков, либо любая из 10 девочек.
По правилу суммы получаем, что одного дежурного можно назначить 16+10=26 способами.
Правило произведения. Пусть требуется выполнить последовательно k действий. Если первое действие можно выполнить n1 способами, второе действие n2 способами, третье – n3 способами и так до k-го действия, которое можно выполнить nk способами, то все k действий вместе могут быть выполнены:
способами.
Пример 2.
В классе учится 16 мальчиков и 10 девочек. Сколькими способами можно назначить двух дежурных?
Решение
Первым дежурным можно назначить либо мальчика, либо девочку. Т.к. в классе учится 16 мальчиков и 10 девочек, то назначить первого дежурного можно 16+10=26 способами.
После того, как мы выбрали первого дежурного, второго мы можем выбрать из оставшихся 25 человек, т.е. 25-ю способами.
По теореме умножения двое дежурных могут быть выбраны 26*25=650 способами.
Сочетания без повторений. Сочетания с повторениями
Классической задачей комбинаторики является задача о числе сочетаний без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать m из n различных предметов?
Пример 3.
Необходимо выбрать в подарок 4 из 10 имеющихся различных книг. Сколькими способами можно это сделать?
Решение
Нам из 10 книг нужно выбрать 4, причем порядок выбора не имеет значения. Таким образом, нужно найти число сочетаний из 10 элементов по 4:
.
Рассмотрим задачу о числе сочетаний с повторениями: имеется по r одинаковых предметов каждого из n различных типов; сколькими способами можно выбрать m () из этих (n*r) предметов?
.
Пример 4.
В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и слоеные. Сколькими способами можно купить 7 пирожных?
Решение
Т.к. среди 7 пирожных могут быть пирожные одного сорта, то число способов, которыми можно купить 7 пирожных, определяется числом сочетаний с повторениями из 7 по 4.
.
Размещения без повторений. Размещения с повторениями
Классической задачей комбинаторики является задача о числе размещений без повторений, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n различных предметов?
Пример 5.
В некоторой газете 12 страниц. Необходимо на страницах этой газеты поместить четыре фотографии. Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Сколькими способами можно это сделать, если ни одна страница газеты не должна содержать более одной фотографии?
Решение.
В данной задаче мы не просто выбираем фотографии, а размещаем их на определенных страницах газеты, причем каждая страница газеты должна содержать не более одной фотографии. Таким образом, задача сводится к классической задаче об определении числа размещений без повторений из 12 элементов по 4 элемента:
Таким образом, 4 фотографии на 12 страницах можно расположить 11880 способами.
Также классической задачей комбинаторики является задача о числе размещений с повторениями, содержание которой можно выразить вопросом: сколькими способами можно выбрать и разместить по m различным местам m из n предметов, среди которых есть одинаковые?
Пример 6.
У мальчика остались от набора для настольной игры штампы с цифрами 1, 3 и 7. Он решил с помощью этих штампов нанести на все книги пятизначные номера– составить каталог. Сколько различных пятизначных номеров может составить мальчик?
Решение
Можно считать, что опыт состоит в 5-кратном выборе с возращением одной из 3 цифр (1, 3, 7). Таким образом, число пятизначных номеров определяется числом размещений с повторениями из 3 элементов по 5:
.
Перестановки без повторений. Перестановки с повторениями
Классической задачей комбинаторики является задача о числе перестановок без повторения, содержание которой можно выразить вопросом: сколькими способами можно разместить n различных предметов на n различных местах?
Пример 7.
Сколько можно составить четырехбуквенных «слов» из букв слова«брак»?
Решение
Генеральной совокупностью являются 4 буквы слова «брак» (б, р, а, к). Число «слов» определяется перестановками этих 4 букв, т. е.
Для случая, когда среди выбираемых n элементов есть одинаковые (выборка с возвращением), задачу о числе перестановок с повторениями можно выразить вопросом: сколькими способами можно переставить n предметов, расположенных на n различных местах, если среди n предметов имеются k различных типов (k < n), т. е. есть одинаковые предметы.
Пример 8.
Сколько разных буквосочетаний можно сделать из букв слова «Миссисипи»?
Решение
Здесь 1 буква «м», 4 буквы «и», 3 буквы «c» и 1 буква «п», всего 9 букв. Следовательно, число перестановок с повторениями равно
ОПОРНЫЙ КОНСПЕКТ ПО РАЗДЕЛУ «КОМБИНАТОРИКА»
перестановка — Перестановки, размещения и сочетания
Подборка по базе: Гостиница, как средство размещения.
 docx, Стратегии размещения рекламы.docx, Задание «Вставка изображения и способы его размещения в документ, КТ 3 для размещения.docx, Пудровые оттенки и их сочетания.docx, 9.2. Законодательная и нормативно-правовая база размещения госуд, Форма размещения информации об ответственном.docx, Реферат по экологии (Экологические проблемы размещения вредных д, Гармоничные сочетания цветов в маникюре.docx, ПЛАНИРОВАНИЕ РАЗМЕЩЕНИЯ ЭЛЕМЕНТОВ ИНФРАСТРУКТУРЫ.docx
docx, Стратегии размещения рекламы.docx, Задание «Вставка изображения и способы его размещения в документ, КТ 3 для размещения.docx, Пудровые оттенки и их сочетания.docx, 9.2. Законодательная и нормативно-правовая база размещения госуд, Форма размещения информации об ответственном.docx, Реферат по экологии (Экологические проблемы размещения вредных д, Гармоничные сочетания цветов в маникюре.docx, ПЛАНИРОВАНИЕ РАЗМЕЩЕНИЯ ЭЛЕМЕНТОВ ИНФРАСТРУКТУРЫ.docxТема урока: Перестановки, размещения и сочетания.
Цели урока:
Образовательная:
познакомить с понятием «комбинаторика»;
познакомить с правилами комбинаторики;
обеспечить в ходе урока усвоение понятия размещений, перестановок и сочетаний;
сформировать умения решать комбинаторные задачи.
Воспитательная:
воспитание интереса к дисциплине, честности, аккуратности, эстетического отношения к оформлению математических решений;
воспитание умения слушать и вступать в диалог, участвовать в коллективном обсуждении проблем.

Развивающая:
развитие логического мышления посредством решения комбинаторных задач, сообразительности;
развитие математической речи, внимания.
Обучающийся должен:
знать:
определения трех важнейших понятий комбинаторики:
размещения из n элементов по m;
сочетания из n элементов по m;
перестановки из n элементов;
основные комбинаторные формулы
уметь:
отличать задачи на «перестановки», «сочетания», «размещения» друг от друга;
применять основные комбинаторные формулы при решении простейших комбинаторных задач.
Методы обучения:
словесно-информационный (рассказ),
словесно-репродуктивный(опрос),
практически-репродуктивный( выполнение заданий),
наглядно-иллюстративный .

Структура урока
Организационный момент
Мотивация учебной деятельности
Сообщение темы и цели урока.
Объяснение нового материала.
Формирование умений и навыков в решении комбинаторных задач.
Домашнее задание
Подведение итогов
Список литературы
Ход урока
Организационный момент
Приветствие, определение отсутствующих, проверка готовности учащихся к уроку.
Мотивация учебной деятельности
Задача из басни С. Крылова «Квартет»
Проказница Мартышка
Осёл,
Козёл,
Да косолапый Мишка
Затеяли играть квартет
…
Стой, братцы стой! –
Кричит Мартышка, — погодите!
Как музыке идти?
Ведь вы не так сидите…
И так, и этак пересаживались – опять музыка на лад не идет.
Вот пуще прежнего пошли у них разборы
И споры,
Кому и как сидеть…
— Как вы думаете сколько различных вариантов расположения музыкантов возможно? (учащиеся предлагают свои варианты)
— В конце урока вы узнаете кто дал правильный ответ.
3. Сообщение темы и цели урока.
Тема сегодняшнего урока «Основы комбинаторики. Размещения, перестановки, сочетания». Сегодня на уроке вам предстоит рассмотреть общие правила комбинаторики, ознакомится с основными понятиями комбинаторики (размещения, сочетания, перестановки), научиться решать простейшие комбинаторные задачи.
4.Объяснение нового материала.
Одним из важнейших понятий современной математики является понятие множества. Говорят о множестве учащихся в группе, о множестве букв в алфавите, о множестве изделий в упаковке и т.д.
Понятие множества относится к первоначальным, простейшим, понятиям и формально через другие более простые понятия не определяется. Оно воспринимается конкретно, посредством знакомства с различными примерами множества. Множество характеризуется объединением некоторых однородных объектов в одно целое. Объекты, образующие множество, называются элементами множества.
Оно воспринимается конкретно, посредством знакомства с различными примерами множества. Множество характеризуется объединением некоторых однородных объектов в одно целое. Объекты, образующие множество, называются элементами множества.
Множество будем записывать, располагая его элементы в фигурных скобка {a, b, c, … , e, f}.
Во множестве порядок элементов роли не играет, так {a, b} = {b, a}.
Множество, не содержащее ни одного элемента, называется пустым множествоми обозначается символом ø.
Если каждый элемент множества А является элементом множества В, то говорят, что множество А является подмножеством множества В
Множество {a, b} является подмножеством множества {a, b, c, … , e, f}.
Задача: Перечислите возможные варианты подмножества множества {3, 4, 5, 7, 9}.
При решении многих практических задач часто приходится имеющиеся предметы (элементы) соединять в разные наборы (комбинации). Например — парфюмерные наборы, конфеты, инструменты, спортивные команды. Задачи которые рассматривают такие соединения и находится число различных соединений, называют комбинаторными.
Комбинаторикой называется область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов, принадлежащих заданному множеству. В каждой из них требуется подсчитать число возможных вариантов осуществления некоторого действия, ответить на вопрос «сколькими способами». Комбинаторика возникла и развивалась одновременно с теорией вероятностей. И первоначально комбинаторные задачи касались в основном азартных игр.
Комбинаторика – раздел математики, который занят поисками ответов на вопросы: сколько всего есть комбинаций в том или ином случае, как из всех этих комбинаций выбрать наилучшую. Слово «комбинаторика» происходит от латинского слова «combinare», что в переводе на русский означает – «сочетать», «соединять». Термин «комбинаторика» был введён знаменитым Готфридом Вильгельмом Лейбницем, — всемирно известным немецким учёным.
Комбинаторика является важным разделом математики, который исследует закономерности расположения, упорядочения, выбора и распределения элементов с фиксированного множества.
При большом числе возможных последствий испытания способы прямого перебора возможных вариантов малоэффективны. На помощь приходят комбинаторные методы, в основе которых лежат два следующих правила называемых соответственно правилами умножения и сложения.
ПРАВИЛО СУММИРОВАНИЯ
Если два взаимоисключающие действия могут быть выполнены в соответствии и способами, тогда какое-то одно из этих действий можно выполнить способами.
Пример №1
Из города А в город В можно добраться 12 поездами, 3 самолетами, 23 автобусами. Сколькими способами можно добраться из города А в город В?
Решение. Проезд из А в В на поезде, самолете или автобусе являются событиями, которые не могут выполняться одновременно одним человеком (взаимоисключающими), поэтому общее количество маршрутов можно вычислить суммированием способов передвижения
N=12+13+23=38
Пример № 2
В ящике имеется n разноцветных шариков. Произвольным образом вынимаем один шарик. Сколькими способами это можно сделать?
Решение. Конечно, n способами.
Теперь эти n шариков распределены по двум ящикам: В первом m шариков, во втором k. Произвольно из какого-нибудь ящика вынимаем один шарик. Сколькими разными способами это можно сделать?
Решение. Из первого ящика шарик можно вытянуть m различными способами, из второго k различными способами, всего N = m + k способами.
ПРАВИЛО ПРОИЗВЕДЕНИЯ
Пусть две выполняемые одно за другим действия могут быть осуществлены в соответствии и способами. Тогда обе они могут быть выполнены способами.
Пример № 3
В турнире принимают участие 8 хоккейных команд. Сколько существует способов распределить первое, второе и третье места?
Решение. Первое место займет одна из 8 команд, второе — одна из 7, третье — одна из 6, так как каждая из них не может претендовать одновременно на два призовых места. Поэтому таких способов будет ровно
N=8 7 6 =336
Пример № 4
Сколько можно записать двузначных чисел в десятичной системе счисления?
Решение. Поскольку число двузначное, то число десятков (m) может принимать одно из девяти значений: 1,2,3,4,5,6,7,8,9. Число единиц (k) может принимать те же значения и может, кроме того быть равным нулю. Отсюда следует, что m = 9, а k= 10. Всего получим двузначных чисел
N = m ·k = 9·10 =90.
Пример № 5
В студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать, для выполнения различных заданий, двух студентов одного пола?
Решение. По правилу умножения двух девушек можно выбрать 14 ·13 = 182 способами, а двух юношей 6·5 = 30 способами. Следует выбрать двух студентов одного пола: двух студентов или студенток. Согласно правилу сложения таких способов выбора будет N =182 + 30 = 212.
Типы соединений
Множества элементов называются соединениями.
Различают три типа соединений:
перестановки из n элементов;
размещения из n элементов по m;
сочетания из n элементов по m (m n).
Перестановки. Число перестановок
На практике часто возникают задачи, связанные с установлением порядка во множестве. Например, число мест равно количеству людей, на которых мы должны разместить их. Такая ситуация встречается часто – рассадить n человек на n мест, или приписать каждому человеку номер. Первый человек может выбрать любое из n мест, второй человек выбирает из (n — 1) оставшихся мест, третий человек может выбрать из уже (n — 2) мест, …, предпоследний человек выбирает из 2 мест, последний человек получает последнее место. Мы получаем произведение всех целых чисел от n до 1.
В общем виде произведение всех целых чисел от 1 до n включительно обозначают
n! = 1·2·3…(n – 2) · (n – 1) · n.
Установленный в конечном множестве порядок называют перестановкой его элементов.
Определение: Перестановкой из n элементов называется любое упорядоченное множество из n элементов.
Иными словами, это такое множество, для которого указано, какой элемент находится на первом месте, какой – на втором, какой- на третьем, …, какой – на n-м месте.
Перестановки можно образовывать из элементов любого конечного множества. Число перестановок из n элементов обозначают Рn. Возьмем одноэлементное множество {a}. Ясно, что один элемент можно упорядочить единственным образом, следовательно, Р1 = 1.
Перестановки– это такие соединения по n элементам из данных элементов, которые отличаются одно от другого порядком элементов.
Возьмем двух элементное множество {a, b}. В нем можно установить два порядка: {a, b} или {b, a}. Следовательно, число перестановок из двух элементов Р2 = 2.
Три буквы во множестве {a, b, c} можно расположить, по порядку шестью способами: {a, b, c}{a, c, b}{b, a, c}{b, c, a}{c, b, a}{c, a, b}.
Следовательно, общее число способов упорядочения трех элементов множества
Р3 = 3 · Р2 = 3 · 2 · 1 = 6.
Рn = n · (n — 1) · (n – 2) · … · 2 · 1 = n!
Определение: Пусть n — натуральное число. Через n! (читается «эн факториал») обозначается число, равное произведению всех натуральных чисел 1 от до n:
n! = 1 · 2 · 3 · … · n.
В случае, если n = 0, по определению полагается: 0! = 1.
Пример № 6
Найдем значения следующих выражений:
1! = 1
2! = 1 · 2 = 2
3! = 1 · 2 · 3 = 6
Пример № 7
Чему равно а)Р5 ; б) Р3.
Решение.
Рn = n! =n · (n — 1) · (n – 2) · … · 2 · 1
Р5=5! = 5 · 4 · 3 · 2 ·1 = 120
Р3=3! = 1 · 2 · 3 = 6
Пример № 8
Упростите
а) 7! · 8 = 8!
б) 12! · 13 ·14 = 14!
в) κ! · (κ + 1) = (κ + 1)!
Пример № 9
Сколькими способами можно расставить 8 участниц финального забега на восьми беговых дорожках?
Решение.
n =8
Р8=8! = 8·7·6·5 · 4 · 3 · 2 ·1 =40320
Размещения.
Размещениями из m элементов по n элементов ( n ≤ m ) называются такие соединения, каждое из которых содержит n элементов, взятых из m данных разных элементов, и которые отличаются одно от другого либо самими элементами, либо порядком их расположения.
Определение. Размещением из n элементов по m называется любое упорядоченное множество из m элементов, состоящее из элементов n элементного множества.
Число размещений из m элементов по n обозначают (от французского «arrangement» — «размещение») и вычисляют по формуле:
Пример № 9
Учащиеся 11-го класса изучают 9 учебных предметов. В расписании учебных занятий на один день можно поставить 4 различных предмета. Сколько существует различных способов составления расписания на один день?
Решение.
Имеем 9-элементное множество, элементы которого учебные предметы. При составлении расписания мы будем выбирать 4-элементное подмножество (урока) и устанавливать в нем порядок. Число таких способов равно числу размещений из девяти по четыре, то есть A94:
Пример № 10
Сколькими способами из класса, где учатся 24 ученика, можно выбрать старосту и помощника старосты?
Решение.
Имеем 24-элементное множество, элементы которого ученики класса. При выборах старосты и помощника старосты мы будем выбирать 2-элементное подмножество (ученика) и устанавливать в нем порядок. Число таких способов равно числу размещений из девяти по четыре(m=24, n=2), то есть A242:
Сочетания.
Сочетаниями из m элементов по n элементов ( n ≤ m ) называются такие соединения, каждое из которых содержит n элементов, взятых из m данных элементов, и которые отличаются друг от друга по крайней мере одним элементом.
Определение. Сочетанием без повторений из n элементов по m -называется любое m элементное подмножество n -элементного множества
Число сочетаний из n элементов по m обозначают (от французского «combination» — «сочетание») и вычисляют по формуле:
Пример № 11
Сколькими способами из класса, где учатся 24 ученика, можно выбрать два дежурных ?
Решение.
n =24, m=2
5.Формирование умений и навыков в решении комбинаторных задач.
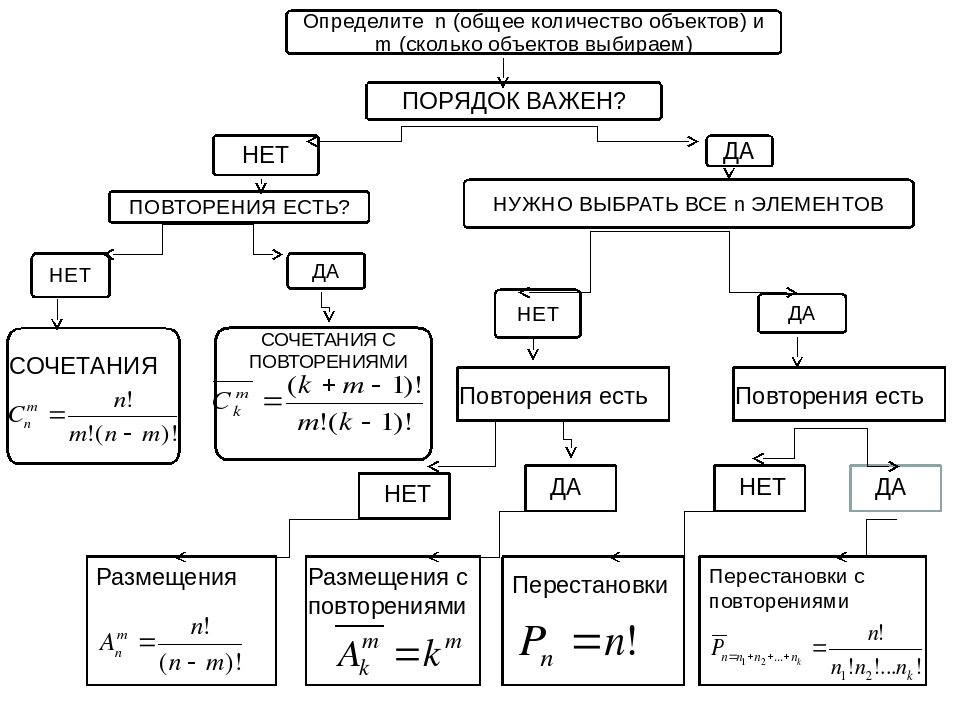
При решении комбинаторных задач и выборе типа соединений важно ответить на следующие вопросы:
Учитывается ли порядок следования элементов в соединении?
Все ли элементы входят в соединение?
Определить к какому типу относится соединений относится задача.
Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков?
Учитывается ли порядок следования элементов в соединении? ( да)
Все ли элементы входят в соединение? (да)
Вывод: перестановка
В 9«Б» классе 12 учащихся. Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?
Учитывается ли порядок следования элементов в соединении? (нет)
Все ли элементы входят в соединение? (на этот вопрос ответ не нужен)
Вывод: сочетания
3. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?
Учитывается ли порядок следования элементов в соединении? ( да)
Все ли элементы входят в соединение? (нет)
Вывод: размещение
Решить задачи:
У нас имеется 5 книг. Известно, что у нас всего одна полка, и на ней вмещается лишь 3 книги. Сколькими способами можно расставить на полке 3 книги?
Решение.
Учитывается ли порядок следования элементов в соединении? ( да)
Все ли элементы входят в соединение? (нет)
Вывод: размещение
n =5, m=3
Сколькими способами можно расставить 3 тома на книжной полке, если выбирать их из имеющихся в наличии внешне неразличимых 5 книг?
Решение.
Учитывается ли порядок следования элементов в соединении? (нет)
Все ли элементы входят в соединение? (на этот вопрос ответ не нужен)
Вывод: сочетания
n =5, m=3
Сколькими способами могут занять I, II, III места 8 участниц финального забега на дистанции 100 м?
Решение.
Учитывается ли порядок следования элементов в соединении? (да)
Все ли элементы входят в соединение? (нет)
Вывод: сочетания
n =8, m=3
Вернемся к решению задачи о музыкальном квартете
Проказница Мартышка
Осёл,
Козёл,
Да косолапый Мишка
Затеяли играть квартет
…
Стой, братцы стой! –
Кричит Мартышка, — погодите!
Как музыке идти?
Ведь вы не так сидите…
И так, и этак пересаживались – опять музыка на лад не идет.
Вот пуще прежнего пошли у них разборы
И споры,
Кому и как сидеть…
Сколько различных вариантов расположения музыкантов возможно?
Решение.
Учитывается ли порядок следования элементов в соединении? ( да)
Все ли элементы входят в соединение? (да)
Вывод: перестановка
Рn = n! =n · (n — 1) · (n – 2) · … · 2 · 1
n =4
Р4 = 4! = 4 · 3 · 2 ·1=24
Работа в группе
В результате решения заданий учащиеся ответят на вопрос: кто является автором высказывания «Рано или поздно всякая правильная математическая идея находит применение в том или ином деле»? (русский математик, физик, механик, кораблестроитель Алексей Николаевич Крылов).
Задания для групп
Первая группа
| № задания | Задания | Ответ | Буква |
| | | ||
| | Сколькими способами могут занять I, II, III места 8 участниц финального забега на дистанции 100 м? | ||
| | Сколькими различными способами для участия в конференции из 9 членов научного общества можно выбрать трех студентов? | ||
| | Сколькими способами могут встать в очередь в билетную кассу 5 человек? | ||
| | | ||
| | Сколькими способами из 15 учеников класса можно выбрать трёх для участия в праздничном концерте? |
Вторая группа
| № задания | Задания | Ответ | Буква |
| | | ||
| | | ||
| | | ||
| | Сколькими способами можно установить дежурство по одному человек в день среди семи учащихся класса в течении семи дней? | ||
| | -2168 | ||
| | В теннисном турнире участвуют 10 спортсменов. Сколькими способами теннисисты могут завоевать золото, серебро и бронзу? |
Третья группа
| № задания | Задания | Ответ | Буква |
| | — 3 | ||
| | Сколькими различными способами для участия в конференции из 9 членов научного общества можно выбрать четырех студентов? | ||
| | | ||
| | | ||
| | | ||
| | Сколькими способами можно рассадить четверых детей на четырех стульях в столовой? |
Четвертая группа
| № задания | Задания | Ответ | Буква |
| | | ||
| | | ||
| | Из 30 обучающихся группы надо выбрать старосту и помощника старосты. Сколькими способами это можно сделать | ||
| | | ||
| | (подсказка 0!=1) |
Ответы к заданиям
Задания для первой группы:
| № задания | Задания | Буква | Ответы |
| | = | А | 12 |
| | Сколькими способами могут занять I, II, III места 8 участниц финального забега на дистанции 100 м? | Л | Размещение |
| | Сколькими различными способами для участия в конференции из 9 членов научного общества можно выбрать трех студентов? | Е | Сочетания |
| | Сколькими способами могут встать в очередь в билетную кассу 5 человек? | К | Перестановки |
| | = | С | 21 |
| | Сколькими способами из 15 учеников класса можно выбрать трёх для участия в праздничном концерте? | Е | Сочетания |
Задания для второй группы:
Задания для третьей группы:
| № задания | Задания | Буква | Ответы |
| | – 3= -3=5 -3=12 | А | 12 |
| | Сколькими различными способами для участия в конференции из 9 членов научного общества можно выбрать четырех студентов? | Е | Сочетания |
| | | В | 720 |
| | | И | 56 |
| | = | Ч | 6720 |
| | Сколькими способами можно рассадить четверых детей на четырех стульях в столовой? | К | Перестановки |
Задания для четвертой группы:
| № задания | Задания | Буква | Ответы |
| | | Р | 5040 |
| | | Ы | 9 |
| | Из 30 обучающихся группы надо выбрать старосту и помощника старосты. Сколькими способами это можно сделать | Л | Размещение |
| | = | О | 132 |
| | = (подсказка 0!=1) | В | 720 |
6. Домашнее задание
Выучить конспект и формулы.
С. 143 № 7,8,9
С. 145 №1,4
С. 145 №5
7. Подведение итогов урока
Какие типы соединений вы знаете?
В чем отличие перестановок и размещений?
В чем отличие размещений и сочетаний?
Список литературы
Математика автор: Л.П.Стойлова
Комбинаторика в Excel
Комбинаторика в Excel
Комбинаторика — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения элементов) и отношения на них. Термин комбинаторика был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». Excel поддерживает ряд функций комбинаторики. Чтобы разобраться, какую формулу использовать, следует ответить на ряд вопросов:
- Исходное множество содержит только уникальные элементы, или некоторые из них могут повторяться?
- Операция выполняется со всеми элементами множества, или только с некоторой выборкой из них?
- Важен ли порядок элементов в выборке?
- После выбора элемента мы его возвращаем назад?
Рис. 1. Дерево решений, какую формулу комбинаторики использовать
Скачать заметку в формате Word или pdf, примеры в формате Excel
Перестановки без повторений
Возьмем несколько различных элементов (предметов) и будем переставлять их всевозможными способами, оставляя неизменным их число и меняя только их порядок (рис. 2). Каждая из получившихся таким образом комбинаций носит название перестановки. Перестановкой из n элементов называется упорядоченное множество, составленное из всех элементов множества.
Рис. 2. Перестановки (картинка взята здесь)
Если все n элементы разные, то число перестановок обозначается Pn от perturbation.
С другой стороны, произведение n первых натуральных чисел называется n-факториал и обозначается n!
Например
По определению: 1! = 1; 0! = 1.
Функция в Excel =ФАКТР(n). Факториал растет очень быстро. Существенно быстрее экспоненты (рис. 3).
Рис. 3. Расчет числа перестановок без повторений с помощью факториала
Перестановки с повторениями
Если в основном n множестве не все элементы разные, то число перестановок будет меньше n! Например, если наше множество состоит из трех яблок и одной груши, то всего возможно 4 перестановки (рис. 4). Груша может быть первой, второй, третьей или четвертой, а яблоки неразличимы).
Рис. 4. Перестановки с повторениями (картинка найдена здесь)
В общем случае, можно сказать: последовательность длины n, составленная из k разных символов, первый из которых повторяется n1 раз, второй – n2 раз, третий – n3 раз, …, k-й – nk раз (где n1 + n2 + … + nk = n) называется перестановкой с повторениями из n элементов.
Пример. Сколько различных пятибуквенных слов можно составить из букв слова «манна»?
Решение. Буквы а и н повторяются 2 раза, а буква м один раз.
Размещение без повторений
Размещением из n элементов по m называется упорядоченный набор из m различных элементов, выбранных из n-элементного множества (все элементы множества уникальны; позиции элементов в выборке важны). Число размещений обозначается от arrangement.
Например, два элемента из трех можно выбрать и расположить шестью способами (рис. 4):
Рис. 5. Размещение без повторений (картинка из презентации)
Если m = n количество элементов совпадает с количеством имеющихся мест для размещения. Знаменатель в формуле (4) превращается в 0! = 1. Остается только числитель n! А это – изученная выше перестановка без повторений; см. формулу (1).
Название функции в Excel несколько обескураживает. Но… что поделаешь: =ПЕРЕСТ(n;m)
Рис. 6. Размещение без повторений; обратите внимание на смешанные ссылки, которые позволяют протянуть формулу на всю таблицу
Размещение с повторениями
Размещение с повторениями по смыслу отличается от перестановок с повторением. Перестановки с повторением – это операция над множеством, которое состоит из нескольких видов элементов, так что каждый вид представлен несколькими одинаковыми элементами. Размещение с повторениями – выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором.
Например, если у вас множество, включающее грушу, яблоко и лимон, и вам нужно выбрать два элемента, так что после первого выбора вы возвращаете выбранный предмет назад, то существует девять различных комбинаций (рис. 7).
Рис. 7. Размещение с повторениями
В общем случае размещение с повторениями или выборка с возвращением – это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз. По правилу умножения количество размещений с повторениями из n по k:
В Excel используется функция ПЕРЕСТА(n;k).
Задача. Сколько различных номеров можно составить в одном коде региона?
Подсказка. В номере используется 12 букв алфавита, также существующих и в латинском алфавите (А, В, Е, К, М, Н, О, Р, С, Т, У, Х).
Рис. 8. Номер автомобиля
Решение. Можно воспользоваться формулой для размещения с повторениями:
Каждую цифру можно выбрать 10 способами, а всего цифр 3, при этом они могут повторяться, и их порядок важен. Каждую букву можно выбрать 12 способами, при этом буквы могут повторяться, и их порядок важен.
Сочетания без повторений
Сочетаниями из n множества по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (в сочетаниях не учитывается порядок элементов).
Например, два элемента из 4 сочетаются 6 способами (порядок следования не важен):
Рис. 9. Сочетания без повторений из 4 по 2
Сочетания без повторений образуют знаменитый треугольник Паскаля (рис. 10). В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Числа в строках, составляющие треугольник Паскаля, являются сочетаниями
где n – номер строки, m – номер элемента в строке, начиная с нулевого. Например, в строке 7:
Рис. 10. Треугольник Паскаля; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
В Excel используется функция =ЧИСЛКОМБ(n;m).
Сочетания с повторениями
Сочетания с повторениями по смыслу похожи на размещение с повторениями – это выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором. При этом порядок в выборке не важен.
Например, два предмета из четырех можно выбрать 10 способами, если после каждого выбора предмет возвращается назад (рис. 11).
Рис. 11. Сочетания с повторениями
В общем случае, число сочетаний с повторениями:
Для нашего примера с фруктами
В Excel для подсчета числа сочетаний с повторениями используется функция =ЧИСЛКОМБА(n;m). В нашем примере =ЧИСЛКОМБА(4;2) = 10.
КОМБИНАТОРИКА — это… Что такое КОМБИНАТОРИКА?
- КОМБИНАТОРИКА
- КОМБИНАТОРИКА
-
(лат. ars combinatoria). Наука о законах сочетания известных предметов.
- КОМБИНАТОРИКА
-
лат. ars combinatoria. Наука о законах сочетания известных предметов.
- комбинато́рика
-
(лат. combinare соединять, сочетать) раздел математики, в котором изучаются соединения ; к простейшим соединениям относятся: перестановки, размещения, сочетания, напр., из трех элементов а, ь, с можно получить шесть перестановок: abc, bca, cab, cba, bac, acb.
- комбинаторика
-
[] – отдел математики, изучающий приёмы вычисления числа различных соединений (комбинаций): перестановок, размещений, сочетаний, составляемых при определённых условиях из данных предметов; например, из трёх чисел a, b, c можно получить шесть перестановок: abc, bca, cab, cba, bac, acb.
- комбинаторика
-
и, мн. нет, ж. (нем. Kombinatorik лат. combinātio сочетание, соединение).
Раздел математики, в котором изучаются перестановки, размещения, сочетания элементов.
Словарь иностранных слов, вошедших в состав русского языка.- Чудинов А.Н., 1910.
Объяснение 25000 иностранных слов, вошедших в употребление в русский язык, с означением их корней.- Михельсон А.Д., 1865.
Новый словарь иностранных слов.- by EdwART, , 2009.
Большой словарь иностранных слов.- Издательство «ИДДК», 2007.
Толковый словарь иностранных слов Л. П. Крысина.- М: Русский язык, 1998.
.
- КОМБИНАЦИОННЫЙ
- КОМБИНАТОРНЫЙ
Смотреть что такое «КОМБИНАТОРИКА» в других словарях:
КОМБИНАТОРИКА — раздел математики, в котором изучаются простейшие соединения . Перестановки соединения, которые можно составить из n предметов, меняя всеми возможными способами их порядок; число ихРазмещения соединения, содержащие по m предметов из числа n… … Большой Энциклопедический словарь
КОМБИНАТОРИКА — КОМБИНАТОРИКА, и, жен. Раздел дискретной математики, изучающий всевозможные сочетания и расположения предметов. | прил. комбинаторный, ая, ое. К. анализ. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
КОМБИНАТОРИКА — раздел математики, где рассматриваются сочетания, размещения, перестановки элементов и связанные с ними задачи. Широко применяется при вероятностном моделировании геол. процессов. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н … Геологическая энциклопедия
комбинаторика — — [http://www.dunwoodypress.com/148/PDF/Biotech Eng Rus.pdf] Тематики биотехнологии EN combinatorics … Справочник технического переводчика
КОМБИНАТОРИКА — раздел математики, посвящённый решению задач выбора и расположения элементов из некоторого основного (обычно конечного) множества в соответствии с заданными правилами. Простейшими задачами К. являются перестановки, сочетания и размещения … Большая политехническая энциклопедия
Комбинаторика — (Комбинаторный анализ) раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика связана со многими другими… … Википедия
комбинаторика — и; ж. [лат. combinare соединять] Раздел математики, изучающий все возможные способы простейших перестановок элементов, цифр, каких л. данных. * * * комбинаторика раздел математики, в котором изучаются простейшие «соединения». Перестановки … … Энциклопедический словарь
Комбинаторика — 1) то же, что математический Комбинаторный анализ. 2) Раздел элементарной математики, связанный с изучением количества комбинаций, подчинённых тем или иным условиям, которые можно составить из заданного конечного множества объектов… … Большая советская энциклопедия
Комбинаторика — ж. Раздел математики, изучающий различного рода соединения элементов: перестановки, сочетания, размещения. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
комбинаторика — комбинаторика, комбинаторики, комбинаторики, комбинаторик, комбинаторике, комбинаторикам, комбинаторику, комбинаторики, комбинаторикой, комбинаторикою, комбинаториками, комбинаторике, комбинаториках (Источник: «Полная акцентуированная парадигма… … Формы слов
Книги
- Комбинаторика., Виленкин Н.Я.. Область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов, называется комбинаторикой.… Подробнее Купить за 1626 грн (только Украина)
- Комбинаторика., Виленкин Н.Я.. Область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов, называется комбинаторикой.… Подробнее Купить за 1446 руб
- Комбинаторика, Виленкин Наум Яковлевич, Виленкин Александр Наумович, Виленкин Павел Александрович. В книге в популярной форме рассказывается о комбинаторике, методах решения комбинаторных задач, о рекуррентных соотношениях и производящих функциях. Материал частично захватывает области,… Подробнее Купить за 493 руб
Школьнику: Комбинаторика — размещения, перестановки, сочетания
Основные понятия
- Размещением из n элементов по k называется упорядоченный набор из k различных элементов некоторого n-элементного множества.
Пример задачи: Сколько трехзначных чисел можно создать из цифр от 1 до 5?
Комментарий: В данном случае n=5 (мы можем использовать пять вариантов элементов — числа 1…5), а k=3 (три позиции для размещения элементов, так как число трехзначное). - Перестановкой из n элементов (например чисел 1, 2, … n) называется всякий упорядоченный набор из этих элементов. Перестановка также является размещением из n элементов по n.
Пример задачи: Сколькими способами можно создать числа, переставляя цифры в числе 12345?
Комментарий: В данном случае n=5 (пять вариантов элементов — числа 1…5). - Сочетанием из n по k называется набор k элементов, выбранных из данных n элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.
Пример задачи: В вазе есть тюльпаны пяти цветов: белые, желтые, оранжевые, красные и розовые. Сколькими способами можно создать букет из трех тюльпанов, если в букете должно быть по одному цветку каждого цвета?
Комментарий: Очевидно, что данный вариант размещения элементов отличается от примера с размещением цифр в числе, так как цветы в букете не имеют своего номера (позиции) и совершенно неважно, в каком порядке мы добавляем в него цветы. В данном случае n=5 (пять вариантов цветов тюльпанов), а k=3 (букет нужно собрать из трех тюльпанов).
Перестановки
Обычно начинают объяснять с размещений, но я сознательно хочу начать с перестановок, так как на их примере проще понять логику вычисления.
Итак, вернемся к задаче из примера: Сколькими способами можно создать числа, переставляя цифры в числе 12345?
У нас есть пять цифр (пусть это будет пять кубиков с цифрами): 1,2,3,4,5.
У нас есть пять, пока еще свободных, позиций под их размещение (пусть это будут пустые коробочки): ▢▢▢▢▢.
Начинаем постепенно заполнять эти позиции: на первую позицию (в первую коробочку) мы можем поместить одну из пяти цифр (один из пяти кубиков). То есть у нас есть пять вариантов заполнения первой позиции.
Предположим, мы взяли кубик с номером 4.
Теперь у нас осталось четыре цифры (кубика): 1,2,3,5.
Позиций (коробочек) у нас осталось пять, но первая уже заполнена, то есть свободных позиций четыре: 4▢▢▢▢.
На размещение во второй коробочке у нас осталось 4 «претендента». Мы взяли кубик с номером 4. Но если бы мы взяли любой из других кубиков, у нас все равно было бы 4 варианта заполнения второй коробочки (просто мы выбирали бы из другого набора ставшихся кубиков), то есть на каждый вариант заполнения первой коробочки у нас приходится по четыре варианта заполнения второй.
Значит у нас есть 5⋅ 4 = 20 — двадцать вариантов заполнения первых двух позиций (коробочек).
Предположим, мы взяли кубик с номером 1.
У нас осталось три цифры (кубика): 2,3,5.
Позиций (коробочек) у нас осталось пять, но первые две уже заполнены: 41▢▢▢.
Продолжая по аналогии, мы получим, что у нас есть 5⋅ 4⋅ 3 = 60 — шестьдесят вариантов заполнения первых трех позиций (коробочек).
Заполнить первые четыре позиции мы можем 5⋅ 4⋅ 3⋅ 2 = 120 способами, а все пять — 5⋅ 4⋅ 3⋅ 2⋅ 1 = 120 — тоже ста двадцатью способами.
Почему последние два числа совпадают? Все просто: на последнем этапе у нас остается всего один кубик, но и одна пустая коробочка. То есть у нас уже нет вариантов размещения. Поэтому последний шаг уже не оказывает влияния на число перестановок.
Нетрудно догадаться, что сколько бы элементов (цифр, чисел, воздушных шариков и так далее) нам ни дали, мы можем узнать число из перестановок умножая последовательно число элементов на все целые числа меньше него.
В математике для подобной операции существует функция, которая называется факториал и обознается восклицательным знаком, стоящим за числом, факториал которого нужно вычислить.
6! = 6⋅ 5⋅ 4⋅ 3⋅ 2⋅ 1
3! = 3⋅ 2⋅ 1
Обозначается число перестановок из n так:
\[P_{n}\]
В итоге мы получаем следующую формулу для вычисления количества перестановок для n элементов:
\[P_{n}=n!=1\cdot 2\cdot \dots \cdot n\]
Размещения
Размещение очень похоже на перестановку, с одной лишь разницей: у нас обычно «не хватает» позиций (коробочек) для размещения всех элементов (кубиков).{k}}\]
Начнем заполнять «коробочки».
У нас есть пять кубиков с цифрами: 1,2,3,4,5.
У нас есть пять, пока еще свободных, позиций под их размещение (пусть это будут пустые коробочки): ▢▢▢▢▢.
Положим, в первую мы кладем номер 4.
Значит у нас осталось четыре свободных «коробочки»: 4▢▢▢▢.
Начинаем заполнять вторую коробочку. Их у нас четыре, как я уже сказал. Но кубиков у нас, в отличии от размещения без повторения осталось всё равно пять. Значит у нас на каждый вариант заполения первой коробочки приходится пять вариантов заполения второй.
Соотвественно две первые коробочки мы можем заполнить 5⋅ 5 = 25 способами (а не 5⋅ 4 = 20, как в случае без повторения).
Повторяя рассуждения мы вычислим, что три коробочки мы можем заполнить 5⋅ 5⋅ 5 = 125 способами.6=\frac{(3+6-1)!}{(3-1)!\cdot 6!}=\frac{8!}{2! \cdot 6!}=28\]
Перестановка и комбинация — GeeksforGeeks
Перестановка и комбинация
- Перестановка: это различные расположения заданного количества элементов, взятых один за другим, или некоторые, или все одновременно. Например, если у нас есть два элемента A и B, то есть два возможных варианта: AB и BA.
- Количество перестановок, когда элементы «r» скомпонованы из общего количества элементов «n», составляет n P r = n! / (п — г)! . Например, пусть n = 4 (A, B, C и D) и r = 2 (все перестановки размера 2).Ответ — 4! / (4-2)! = 12. Двенадцать перестановок: AB, AC, AD, BA, BC, BD, CA, CB, CD, DA, DB и DC.
- Комбинация: это различные выборы заданного количества элементов, взятые один за другим, или несколько, или все одновременно. Например, если у нас есть два элемента A и B, то есть только один способ выбрать два элемента, мы выбираем их оба.
- Количество комбинаций при выборе элементов «r» из общего количества элементов «n» составляет n C r = n! / [(г!) х (п — г)! ].Например, пусть n = 4 (A, B, C и D) и r = 2 (все комбинации размера 2). Ответ: 4! / ((4-2)! * 2!) = 6. Шесть комбинаций: AB, AC, AD, BC, BD, CD.
- n C r = n C (n — r)
ПРИМЕЧАНИЕ: В том же примере у нас есть разные случаи для перестановки и комбинации. Для перестановки AB и BA — это две разные вещи, но для выбора AB и BA одинаковы.
Примеры задач
Вопрос 1: Сколько слов можно составить, используя 3 буквы из слова «DELHI»?
Решение: Слово «ДЕЛИ» состоит из 5 разных слов.
Следовательно, необходимое количество слов = 5 P 3 = 5! / (5 — 3)!
=> Требуемое количество слов = 5! / 2! = 120/2 = 60
Вопрос 2: Сколько слов можно составить, используя буквы слова «ВОДИТЕЛЬ», чтобы все гласные всегда были вместе?
Решение: В вопросах такого типа мы предполагаем, что все гласные — это один символ, то есть «IE» — это один символ.
Итак, теперь у нас в слове всего 5 символов, а именно D, R, V, R, IE.
Но, R встречается 2 раза.
=> Количество возможных расположений = 5! / 2! = 60
Теперь две гласные могут быть расположены в 2! = 2 способа.
=> Общее количество возможных слов, при которых гласные всегда вместе = 60 x 2 = 120
Вопрос 3: Сколько способов мы можем выбрать команду из 4 учеников из заданного выбора из 15?
Решение: Количество возможных вариантов выбора = 15 C 4 = 15! / [(4!) X (11!)]
=> Количество возможных способов выбора = (15 x 14 x 13 x 12) / (4 x 3 x 2 x 1) = 1365
Вопрос 4: Какими способами можно сформировать группу из 5 человек, выбрав 3 мальчика из 6 и 2 девочки из 5?
Решение: Количество способов выбора 3 мальчиков из 6 = 6 C 3 = 6! / [(3!) X (3!)] = (6 x 5 x 4) / (3 x 2 x 1) = 20
Количество способов выбора 2 девушек из 5 = 5 C 2 = 5! / [(2!) X (3!)] = (5 x 4) / (2 x 1) = 10
Следовательно, общее количество способов формирования группы = 20 x 10 = 200
Вопрос 5: Сколько слов можно составить, используя буквы слова «ВОДИТЕЛЬ», чтобы все гласные никогда не совпадали?
Решение: мы предполагаем, что все гласные являются одним символом, т.е.е. «IE» — это одиночный символ.
Итак, теперь у нас в слове всего 5 символов, а именно D, R, V, R, IE.
Но, R встречается 2 раза.
=> Количество возможных расположений = 5! / 2! = 60
Теперь две гласные могут быть расположены в 2! = 2 способа.
=> Общее количество возможных слов, при которых гласные всегда вместе = 60 x 2 = 120
Кроме того, общее количество возможных слов = 6! / 2! = 720/2 = 360
Следовательно, общее количество возможных слов, в которых гласные никогда не встречаются вместе = 360 — 120 = 240Проблемы перестановки и сочетания | Набор-2
Викторина по перестановке и комбинации
Практические вопросы по перестановке и комбинации.Автор статьи: Nishant Arora . Пожалуйста, напишите комментарии, если у вас есть какие-либо сомнения по теме, обсужденной выше, или если вы столкнулись с трудностями в каком-либо вопросе, или если вы хотите обсудить вопрос, отличный от упомянутых выше.
Пожалуйста, напишите комментарии, если вы обнаружите что-то неправильное или хотите поделиться дополнительной информацией по теме, обсужденной выше
Комбинаторика | Безграничная алгебра
Правила и методы подсчета
Комбинаторика — это раздел математики, изучающий конечные или счетные дискретные структуры.
Цели обучения
Описать различные правила и свойства комбинаторики
Основные выводы
Ключевые моменты
- Правило суммы (правило сложения), правило произведения (правило умножения) и принцип включения-исключения часто используются для целей перечисления.
- Биективные доказательства используются, чтобы продемонстрировать, что два набора имеют одинаковое количество элементов.
- Двойной счет — это метод, используемый для демонстрации равенства двух выражений.Принцип «ящика» часто устанавливает наличие чего-либо или используется для определения минимального или максимального количества чего-либо в дискретном контексте.
- Генерирующие функции и рекуррентные отношения — мощные инструменты, которые можно использовать для управления последовательностями, и они могут описывать, если не разрешать многие комбинаторные ситуации.
- Двойной счет — это метод, используемый для демонстрации равенства двух выражений.
Ключевые термины
- полином : выражение, состоящее из суммы конечного числа членов: каждый член является произведением постоянного коэффициента и одной или нескольких переменных, возведенных в неотрицательную целую степень.
- комбинаторика : Раздел математики, изучающий (обычно конечные) совокупности объектов, удовлетворяющих указанным критериям.
Комбинаторика — это раздел математики, изучающий конечные или счетные дискретные структуры. Комбинаторные методы применимы ко многим областям математики, и знание комбинаторики необходимо для создания прочных знаний в области статистики. Он включает в себя перечисление, комбинацию и перестановку наборов элементов и математических отношений, которые характеризуют их свойства.
Аспекты комбинаторики включают: подсчет структур данного вида и размера, решение, когда могут быть соблюдены определенные критерии, а также создание и анализ объектов, соответствующих критериям. Аспекты также включают поиск «наибольших», «наименьших» или «оптимальных» объектов, изучение комбинаторных структур, возникающих в алгебраическом контексте, или применение алгебраических методов к комбинаторным задачам.
Комбинаторные правила и методы
Общепризнано и используется несколько полезных комбинаторных правил или комбинаторных принципов.Каждый из этих принципов используется для определенной цели. Правило суммы (правило сложения), правило произведения (правило умножения) и принцип включения-исключения часто используются для целей перечисления. Биективные доказательства используются, чтобы продемонстрировать, что два набора имеют одинаковое количество элементов. Двойной счет — это способ показать, что два выражения равны. Принцип «ящика» часто устанавливает наличие чего-либо или используется для определения минимального или максимального количества чего-либо в дискретном контексте.Формирующие функции и рекуррентные отношения — мощные инструменты, которые можно использовать для управления последовательностями, и они могут описывать, если не разрешать многие комбинаторные ситуации. Каждый из этих методов более подробно описан ниже.
Правило суммы
Правило суммы — это интуитивный принцип, гласящий, что если есть [латекс] а [/ латекс] возможные способы сделать что-то, и [латекс] b [/ латекс] возможные способы сделать что-то еще, и эти две вещи могут » Если и то и другое будет сделано, то есть [latex] a + b [/ latex] все возможные способы сделать что-то одно.Более формально сумма размеров двух непересекающихся множеств равна размеру объединения этих множеств.
Правило продукта
Правило продукта — это еще один интуитивный принцип, гласящий, что если есть [latex] a [/ latex] способы сделать что-то и [latex] b [/ latex] способы сделать что-то другое, то есть [latex] a \ cdot b [/ latex] способов сделать и то, и другое.
Принцип включения-исключения
Принцип включения-исключения — это метод подсчета, который используется для получения количества элементов в объединении нескольких наборов.Этот метод подсчета гарантирует, что элементы, которые присутствуют более чем в одном наборе в объединении, не будут подсчитаны более одного раза. Он учитывает размер каждого набора и размер пересечения наборов. Самый маленький пример — когда есть два набора: количество элементов в объединении [latex] A [/ latex] и [latex] B [/ latex] равно сумме количества элементов в [latex] A [/ latex] и [latex] B [/ latex], за вычетом количества элементов на их пересечении. См. Схему ниже для примера с тремя наборами.
Биективное доказательство
Биективное доказательство — это метод доказательства, который находит биективную функцию [латекс] f: A \ rightarrow B [/ latex] между двумя конечными наборами [latex] A [/ latex] и [latex] B [/ latex], что доказывает что у них одинаковое количество элементов, [латекс] | A | = | B | [/ латекс]. Биективная функция — это функция, в которой существует взаимно однозначное соответствие между элементами двух множеств. Другими словами, каждый элемент в наборе [latex] B [/ latex] сопряжен ровно с одним элементом в наборе [latex] A [/ latex].Этот метод полезен, если мы хотим узнать размер [латекса] A [/ latex], но не можем найти прямого способа подсчета его элементов. Если [латекс] B [/ латекс] легче подсчитать, установление биекции от [латекса] A [/ latex] к [латексу] B [/ latex] решает проблему.
Двойной счет
Двойной счет — это комбинаторный метод доказательства равенства двух выражений. Это делается путем демонстрации того, что два выражения представляют собой два разных способа подсчета размера одного набора.В этом методе конечный набор [latex] X [/ latex] описывается с двух точек зрения, что приводит к двум различным выражениям для размера набора. Поскольку оба выражения равны размеру одного и того же набора, они равны друг другу.
Принцип голубятни
Принцип «ящика» гласит, что если каждый предмет [latex] a [/ latex] помещается в одну из коробок [latex] b [/ latex], где [latex] a> b [/ latex], то по крайней мере один из коробки содержат более одного предмета. Этот принцип позволяет продемонстрировать наличие некоторого элемента в наборе с некоторыми специфическими свойствами.Например, рассмотрим комплект из трех перчаток. {n} [/ latex]
, коэффициенты которого дают последовательность [латекс] \ left \ {a_ {0}, a_ {1}, a_ {2},… \ right \} [/ latex].
Отношение повторения
Рекуррентное отношение определяет каждый член последовательности в терминах предыдущих терминов. Другими словами, как только даны один или несколько начальных терминов, каждый из следующих членов последовательности является функцией предыдущих терминов.
Последовательность Фибоначчи — один из примеров рекуррентного отношения. Каждый член последовательности Фибоначчи определяется как [латекс] F_ {n} = F_ {n-1} + F_ {n-2} [/ latex] с начальными значениями [латекс] F_ {0} = 0 [/ latex ] и [латекс] F_ {1} = 1 [/ латекс].Таким образом, начинается последовательность чисел Фибоначчи:
[латекс] \ displaystyle 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,… [/ латекс]
Перестановки
Перестановка набора объектов — это расположение этих объектов в определенном порядке; количество перестановок можно подсчитать.
Цели обучения
Рассчитать количество расположений упорядоченных объектов с помощью перестановок
Основные выводы
Ключевые моменты
- Неформально перестановка набора объектов — это расположение этих объектов в определенном порядке.Например, существует шесть вариантов набора [latex] {1,2,3} [/ latex], а именно [latex] (1,2,3) [/ latex], [latex] (1,3,2 ) [/ латекс], [латекс] (2,1,3) [/ латекс], [латекс] (2,3,1) [/ латекс], [латекс] (3,1,2) [/ латекс] , и [латекс] (3,2,1) [/ латекс].
- Количество перестановок [latex] n [/ latex] различных объектов равно [latex] n \ cdot (n — 1) \ cdot (n — 2) \ cdots 2 \ cdot 1 [/ latex]. Это называется [латекс] п [/ латекс] факториал и пишется [латекс] п! [/ Латекс].
- При принятии решения о перестановках подмножества из большего набора часто бывает полезно разделить один факториал на другой, чтобы определить количество возможных перестановок.Например, первые шесть карт из колоды карт будут иметь [латекс] \ frac {52!} {46! } [/ latex] возможных перестановок, или около 14,7 миллиарда.
Ключевые термины
- факториал : Результат умножения заданного количества последовательных целых чисел из [latex] 1 [/ latex] на заданное число. В уравнениях он обозначается восклицательным знаком ([латекс]! [/ Латекс]). Например, [латекс] 5! = 1 \ cdot 2 \ cdot 3 \ cdot 4 \ cdot 5 = 120 [/ латекс].
- перестановка : упорядочение конечного набора различных элементов.
Перестановки
Перестановка набора объектов — это расположение этих объектов в определенном порядке. Например, существует шесть вариантов набора [латекс] {1,2,3} [/ латекс]: [латекс] (1,2,3) [/ латекс], [латекс] (1,3,2) [/ латекс], [латекс] (2,1,3) [/ латекс], [латекс] (2,3,1) [/ латекс], [латекс] (3,1,2) [/ латекс], и [латекс] (3,2,1) [/ латекс]. Можно определить анаграмму слова как перестановку его букв.
6 перестановок 3 шаров: Если у одного есть три шара разного цвета, есть шесть различных способов их упорядочить, как показано.Эти шесть различных порядков следующие: красный-зеленый-синий, красный-синий-зеленый, зеленый-красный-синий, зеленый-синий-красный, синий-красный-зеленый и сине-зеленый-красный.
Количество перестановок [latex] n [/ latex] различных объектов определяется по формуле:
[латекс] \ displaystyle n \ cdot (n — 1) \ cdot (n — 2) \ cdots 2 \ cdot 1 [/ латекс]
Это называется факториалом [латекс] n [/ latex] и записывается как [латекс] n! [/ Латекс].
Другими словами, факториал — это умножение всех чисел от [latex] 1 [/ latex] до этого числа.Итак, [латекс] 5! [/ Латекс] означает [латекс] 1 \ cdot 2 \ cdot 3 \ cdot 4 \ cdot 5 = 120 [/ latex]. Таким образом, [latex] 120 [/ latex] — это количество перестановок, возможных для набора из пяти различных объектов.
Пример
В игре «Пасьянс» вначале раздаются семь карт: одна лицом вверх, а остальные шесть рубашкой вверх. Полная колода карт состоит из [латексных] 52 [/ латексных] карт. Если предположить, что единственная видимая карта — это [латекс] 7 [/ латекс] пик, сколько возможных «рук» (остальные шесть карт) может быть внизу? Проблема перестановки состоит в том, что порядок имеет значение: если где-то в этих шести картах прячется туз, имеет значение, находится ли туз на первой позиции, на второй и т. Д.Проблемы перестановки всегда можно рассматривать как пример правила умножения с одним небольшим поворотом.
Одна стопка карт в пасьянсе: Чтобы узнать, сколько возможных комбинаций карт ниже семерки пик, мы используем концепцию перестановок для вычисления возможных комбинаций карт.
Сколько карточек может быть на первой позиции, прямо под показом [latex] 7 [/ latex]? Ответ — 51. Эта карта может быть чем угодно, кроме [латекса] 7 [/ латекса] пик.
Если какая-либо карта находится на первой позиции, сколько карт может быть на второй позиции? Ответ [латекс] 50 [/ латекс]. Сданы семерка пик и следующая карта. Так что для второй позиции остались возможные карты.
Итак, сколько возможностей существует для первых двух позиций вместе? Ответ [латекс] 51 \ cdot 50 [/ латекс].
Сколько возможностей существует для всех шести позиций? Ответ: [латекс] 51 \ cdot 50 \ cdot 49 \ cdot 48 \ cdot 47 \ cdot 46 [/ latex], или приблизительно [латекс] 1.{10} [/ латекс]; о [латексе] 13 [/ латексе] миллиардов возможностей!
Этот результат можно выразить более кратко, используя факториалы.
Обратите внимание, что [латекс] \ frac {7!} {5! } [/ latex] также можно записать как [latex] \ frac {1 \ cdot 2 \ cdot 3 \ cdot 4 \ cdot 5 \ cdot 6 \ cdot 7} {1 \ cdot 2 \ cdot 3 \ cdot 4 \ cdot 5 }[/латекс]. Большинство условий отменяют, оставляя только [латекс] 6 × 7 = 42 [/ латекс].
Рассмотрим другой пример, [латекс] \ frac {51!} {45! }[/латекс]. Если все термины выписаны, первые [latex] 45 [/ latex] термины отменяются, оставляя [latex] 46 \ cdot 47 \ cdot 48 \ cdot 49 \ cdot 50 \ cdot 51 [/ latex] в числителе.Вместо того, чтобы вводить в калькулятор шесть чисел для умножения или шестьдесят чисел или шестьсот в зависимости от задачи, ответ на проблему перестановки можно найти, разделив два факториала. По этой причине во многих калькуляторах факториал находится в меню «вероятность».
Общие положения
В математике понятие перестановки используется в нескольких немного разных значениях, и все они связаны с актом перестановки (перестановки) объектов или значений.Неформально перестановка набора объектов — это упорядочение этих объектов в определенном порядке (
). Изучение перестановок обычно относится к области комбинаторики.
Перестановки происходят более или менее заметным образом почти во всех областях математики. Они часто возникают при рассмотрении различных порядков на определенных конечных наборах, возможно, только потому, что кто-то хочет игнорировать такие порядки и должен знать, сколько конфигураций идентифицируется таким образом. По аналогичным причинам при изучении алгоритмов сортировки в информатике возникают перестановки.
Перестановки различимых объектов
Количество перестановок отдельных элементов может быть вычислено, если используются не все элементы из данного набора.
Цели обучения
Подсчитайте количество перестановок [латекс] n [/ латекс] объектов, взятых [латекс] k [/ латекс] за раз
Основные выводы
Ключевые моменты
- Если все рассматриваемые объекты различны, они могут быть расположены в перестановках [latex] n! [/ Latex], где [latex] n [/ latex] представляет количество объектов.
- Если не все объекты в наборе уникальных элементов [latex] n [/ latex] выбраны, приведенная выше формула может быть изменена на: [latex] \ displaystyle \ frac {n!} {(N-k)! } [/ latex], где [latex] k [/ latex] представляет количество выбранных элементов.
- При вычислении частных факториалов члены знаменателя могут сокращаться с членами числителя, таким образом исключая, возможно, большинство членов, подлежащих умножению.
Ключевые термины
- факториал : Результат умножения заданного количества последовательных целых чисел из [latex] 1 [/ latex] на заданное число.В уравнениях он обозначается восклицательным знаком ([латекс]! [/ Латекс]). Например, [латекс] 5! = 1 \ cdot 2 \ cdot 3 \ cdot 4 \ cdot 5 = 120 [/ латекс].
- перестановка : упорядочение конечного набора различных элементов.
Напомним, что, если все объекты в наборе различны, то они могут быть расположены в [latex] n! [/ Latex] возможных перестановках, где [latex] n [/ latex] представляет количество объектов. Количество [латекс] n! [/ Латекс] определяется по формуле:
[латекс] \ Displaystyle п \ cdot (n-1) \ cdot (n-2) \ cdots 2 \ cdot 1 [/ латекс]
Эту формулу достаточно легко использовать для подсчета числа возможных перестановок набора различных объектов; например, количество перестановок трех разноцветных шаров.Однако рассмотрим ситуацию, когда не все элементы в наборе отдельных объектов используются в каждой перестановке. Например, что, если карты [latex] 7 [/ latex] выбраны из полной колоды [latex] 52 [/ latex]? В этом случае не все карты из колоды выбираются для каждой возможной перестановки. Существует формула для решения проблемы перестановки, подобной этой, которую иначе было бы почти невозможно определить.
Перестановки частичного множества
Если выбраны не все объекты в наборе уникальных элементов, используется следующая формула.Эта формула определяет количество возможных перестановок элементов [latex] k [/ latex], выбранных из набора элементов [latex] n [/ latex]:
[латекс] \ displaystyle \ frac {n!} {(N-k)! } [/ латекс]
Чтобы понять применение этой концепции, рассмотрим гонку, в которой [латекс] 3 [/ латекс] различных призов присуждаются лучшим [латексным] 3 [/ латексным] спортсменам. Если в гонке участвуют участники [latex] 25 [/ latex], в каком количестве различных порядков могут быть присуждены призы [latex] 3 [/ latex]?
Чтобы решить эту проблему, мы хотим оценить количество возможных перестановок элементов [latex] 3 [/ latex] из набора элементов [latex] 25 [/ latex]; другими словами, [латекс] k = 3 [/ латекс] и [латекс] n = 25 [/ латекс].Подставляя эти значения в формулу, получаем:
[латекс] \ displaystyle \ frac {25!} {(25–3)! } = \ frac {25!} {22!} [/ latex]
Помните, что и [латекс] 25! [/ Латекс], и [латекс] 22! [/ Латекс] содержат термины [латекс] 22 \ cdot 21 \ cdots 2 \ cdot 1 [/ latex]. Таким образом, эти значения исключаются из числителя и знаменателя, и уравнение можно упростить:
[латекс] [/ латекс]
[латекс] \ displaystyle \ begin {align} \ frac {25!} {22!} & = \ Frac {25 \ cdot 24 \ cdot 23 \ cdot 22 \ cdot 21 \ cdots 2 \ cdot 1} {22 \ cdot 21 \ cdots 2 \ cdot 1} \\ & = 25 \ cdot 24 \ cdot 23 \\ & = 13,800 \ end {align} [/ latex]
Существует 13 800 [/ latex] возможных перестановок, в которых главные призы [latex] 3 [/ latex] могут быть присуждены участникам гонки [latex] 25 [/ latex].
Общие положения
Стоит отметить, что эта формула не исключает того, что мы могли бы назвать «повторяющимися» перестановками. Другими словами, порядок выбранных элементов имеет значение. Рассмотрим [латексные] 3 [/ латексные] карты, вытянутые из колоды: туз пик, [латекс] 10 [/ латекс] бубен и [латекс] 3 [/ латекс] треф. Рука в точности такая же, как следующая: [латекс] 10 [/ латекс] бубен, туз пробелов и [латекс] 3 [/ латекс] треф. Если вы играете в игру, в которой порядок ваших карт не имеет значения , , вам нужно будет подсчитывать каждую перестановку карт только один раз.Представленная здесь формула не применима к таким ситуациям.
[латекс] [/ латекс]
Перестановки неотличимых объектов
Выражение, показывающее количество перестановок отдельных элементов, можно изменить, если не все элементы в наборе различны.
Цели обучения
Вычислить количество перестановок данного набора объектов, некоторые из которых неразличимы
Основные выводы
Ключевые моменты
- Некоторые наборы включают повторения определенных элементов.В этих случаях количество возможных перестановок элементов не может быть выражено с помощью [latex] n! [/ Latex], где [latex] n [/ latex] представляет количество элементов, потому что это вычисление будет включать в себя множество возможных состояния.
- Чтобы исправить множественность определенных перестановок, разделите факториал общего количества элементов на произведение факториалов количества каждого повторяющегося элемента.
- Выражение для количества перестановок с повторяющимися элементами: [latex] \ frac {n!} {N_1! N_2! N_3!…} [/ Latex], где [latex] n [/ latex] — общее количество терминов в a sequence, а [latex] n_1 [/ latex], [latex] n_2 [/ latex] и [latex] n_3 [/ latex] — это количество повторений различных элементов.
Ключевые термины
- кратность : количество значений, для которых выполняется данное условие.
- перестановка : упорядочение конечного набора различных элементов.
Напомним, что количество возможных перестановок набора из [latex] n [/ latex] различных элементов определяется как [latex] n! [/ Latex]:
[латекс] \ Displaystyle п \ cdot (n-1) \ cdot (n-2) \ cdots 2 \ cdot 1 [/ латекс]
Это легко проверить.Число [латекс] 1 [/ латекс] можно расположить всего одним способом [латекс] 1! [/ Латекс]. Номера [latex] 1 [/ latex] и [latex] 2 [/ latex] можно расположить двумя способами [latex] 2! [/ Latex]: [latex] (1,2) [/ latex] и [latex] ] (2,1) [/ латекс]. Номера [латекс] 1 [/ латекс], [латекс] 2 [/ латекс] и [латекс] 3 [/ латекс] могут быть расположены [латекс] 3! [/ Латекс] способами: [латекс] (1, 2,3) [/ латекс], [латекс] (1,3,2) [/ латекс], [латекс] (2,1,3) [/ латекс], [латекс] (2,3,1) [ / латекс], [латекс] (3,1,2) [/ латекс] и [латекс] (3,2,1) [/ латекс]. Это правило справедливо для наборов любого размера, пока все элементы различны.Но что, если некоторые элементы повторяются?
Повторение некоторых элементов усложняет вычисление перестановок, поскольку позволяет использовать несколько способов упорядочивания элементов в определенном порядке. Например, учитывая номера [латекс] 1 [/ латекс], [латекс] 3 [/ латекс] и [латекс] 3 [/ латекс] в наборе, есть 2 способа получить заказ [латекс] (3 , 1,3) [/ латекс].
Чтобы исправить «множественность» определенных перестановок, мы должны разделить факториал общего количества элементов на произведение факториалов количества каждого повторяющегося элемента.Обычно это можно представить как:
[латекс] \ displaystyle \ frac {n!} {N_1! N_2! N_3!…} [/ Латекс]
Где [latex] n [/ latex] — общее количество терминов в последовательности, а [latex] n_1 [/ latex], [latex] n_2 [/ latex] и [latex] n_3 [/ latex] представляют количество повторений разных элементов.
Чтобы понять, почему мы делим на количество повторов, примите во внимание, что элементы [latex] 2 [/ latex] могут быть расположены в общей сложности [latex] 2! [/ Latex] различными способами, [latex] 3 [/ latex ] элементы можно расположить [латексом] 3! [/ латексом] различными способами и так далее.Когда мы сталкиваемся с множественностью в перестановке, мы должны учесть ее, разделив эти возможные расстановки из общего числа перестановок, которые были бы возможны, если бы все элементы были различными.
Пример: Рассмотрим набор чисел:
[латекс] \ displaystyle (15, 17, 24, 24, 28) [/ латекс]
Есть пять терминов, поэтому [латекс] n = 5 [/ латекс]. Однако два термина одинаковы; их стоимость [латекс] 24 [/ латекс]. Таким образом, количество возможных различных перестановок в наборе составляет:
[латекс] \ displaystyle {\ frac {5!} {2! } = 60} [/ латекс]
Та же логика применима к более сложным системам.
Пример: Рассмотрим набор:
[латекс] \ displaystyle (0, 0, 0, 2, 4, 4, 7, 7, 7, 7, 7, 8, 8) [/ латекс]
Всего [latex] 13 [/ latex] элементов. Они включают в себя множество повторов: [латекс] 0 [/ латекс] встречается 3 раза, [латекс] 4 [/ латекс] и [латекс] 8 [/ латекс] каждый наблюдается дважды, и есть [латекс] 5 [/ латекс ] экземпляры числа [латекс] 7 [/ латекс]. Таким образом, количество возможных различных перестановок можно рассчитать по формуле:
[латекс] \ displaystyle \ frac {13! } {2! \ Cdot 2! \ Cdot 3! \ Cdot 5! } = 2 162 160 [/ латекс]
Эту логику можно применить к задачам, связанным с анаграммами заданных слов.
Пример. Подумайте, сколько различных способов упорядочить буквы слова «водопад».
Слово водопад состоит всего из [латекс] 9 [/ латекс] букв, поэтому [латекс] n = 9 [/ латекс]. Буква «а» появляется дважды, что дает значение [латекс] 2 [/ латекс] для [латекс] n_ {1} [/ латекс]. Точно так же буква «l» появляется дважды, что дает [латекс] n_ {2} = 2 [/ latex]. Таким образом, количество различных перестановок букв в «водопаде» можно рассчитать как:
[латекс] \ displaystyle \ frac {9! } {2! \ Cdot 2!} = 90,720 [/ латекс]
Комбинации
Комбинация — это способ выбора нескольких вещей из большей группы, где (в отличие от перестановок) порядок не имеет значения.
Цели обучения
Рассчитайте количество способов выбора нескольких вещей из большей группы (где порядок не имеет значения) с помощью комбинаций
Основные выводы
Ключевые моменты
- Комбинация — это математическая концепция, при которой подсчитывается количество способов, которыми можно выбрать несколько элементов из большей группы.
- В отличие от перестановки, при определении количества комбинаций порядок не имеет значения.
- Формально, [latex] k [/ latex] -комбинация набора [latex] S [/ latex] является подмножеством [latex] k [/ latex] отдельных элементов [latex] S [/ latex].Если в наборе есть [latex] n [/ latex] элементов, то количество [latex] k [/ latex]-комбинаций равно биномиальному коэффициенту: [latex] \ begin {pmatrix} n \\ k \ end {pmatrix} = \ frac {n (n-1)… (n-k + 1)} {k (k-1)… 1} [/ latex], который можно записать с использованием факториалов как [latex] \ frac {n!} {к! (нк)! } [/ latex] всякий раз, когда [latex] k \ le n [/ latex] и который равен нулю, когда [latex] k> n [/ latex].
Ключевые термины
- комбинация : способ выбора элементов из набора, где порядок не имеет значения.п [/ латекс].
В математике комбинация — это способ выбора нескольких вещей из большей группы, где (в отличие от перестановок) порядок не имеет значения. В меньших случаях можно подсчитать количество комбинаций. Например, даны [latex] 3 [/ latex] кусочка фруктов: яблоко, апельсин и груша. Есть [latex] 3 [/ latex] комбинации [latex] 2 [/ latex], которые можно извлечь из этого набора: яблоко и груша, яблоко и апельсин или груша и апельсин.
Комбинации могут относиться к комбинации [латекс] n [/ латекс] вещей, взятых [латекс] k [/ латекс] за один раз с или без повторения.В приведенном выше примере повторение было запрещено. Однако, если бы [латекс] 2 [/ латекс] был возможен из любого фрукта [латекс] 1 [/ латекс], то было бы [латекс] 3 [/ латекс] больше комбинаций: [латекс] 2 [/ латексные] яблоки, [латексные] 2 [/ латексные] апельсины и [латексные] 2 [/ латексные] груши.
Чтобы понять разницу между перестановкой и комбинацией, рассмотрим колоду из [латексных] 52 [/ латексных] карт, из которой раздается покерная рука ([латексные] 5 [/ латексные] карты). Сколько существует возможных покерных комбинаций?
На первый взгляд это может показаться вопросом перестановки, когда можно подумать о том, сколько различных способов собрать стопку карт.Однако есть одно важное отличие: порядок в этой задаче не имеет значения. При раздаче покерной руки во время игры порядок не имеет значения, поэтому у вас будет одна и та же рука независимо от порядка, в котором раздаются карты. Комбинированные задачи включают такие сценарии.
Чтобы подойти к такому вопросу, начнем с перестановок: сколько существует возможных покерных рук, если порядок имеет значение?
Вспомните формулу перестановки: [latex] \ displaystyle {\ frac {n!} {(Nk)!}} [/ Latex], где [latex] n [/ latex] — количество различных объектов в наборе, а [latex] k [/ latex] — количество выбранных объектов.В этом случае мы можем рассчитать количество перестановок как:
[латекс] [/ латекс] [латекс] \ displaystyle \ begin {align} \ frac {52!} {(52-5)!} & = \ Frac {52!} {47!} \\ & = 52 \ cdot 51 \ cdot 50 \ cdot 49 \ cdot 48 \ end {align} [/ latex]
Это дает приблизительно [латекс] 311,9 [/ латекс] миллиона возможных покерных рук. Однако в этом подсчете нужно пересчитывать все возможные руки много раз. Сколько раз подсчитывается каждая отдельная рука?
Ключевым моментом является ответ на второй вопрос: «Сколько раз можно считать каждую отдельную руку?» сам по себе вопрос перестановки.Это то же самое, что и вопрос «Сколько разных способов переставить эти пять карт в руке?» Возможности [latex] 5 [/ latex] для первой карты, [latex] 4 [/ latex] для второй и так далее. Ответ — [латекс] 5! [/ Латекс], то есть [латекс] 120 [/ латекс]. Итак, поскольку каждая возможная рука была подсчитана [латекс] 120 [/ латекс] раз, разделите наш предыдущий результат на [латекс] 120 [/ латекс], чтобы найти [латекс] \ frac {52!} {(47! ) (5!)} [/ Latex], или примерно [latex] 2,6 [/ latex] миллиона возможных покерных комбинаций.
У комбинацийоказалось удивительно большое количество применений. Обдумайте следующие вопросы:
- Школа предлагает 50 классов [/ латекса]. Каждый ученик должен выбрать [латекс] 6 [/ латекс] из них, чтобы заполнить расписание. Сколько возможных графиков можно составить?
- В баскетбольной команде есть [латекс] 12 [/ латекс] игроков, но только [латекс] 5 [/ латекс] будут стартовать. Сколько возможных стартовых команд они смогут выставить?
- На вашем компьютере есть [latex] 300 [/ latex] видео, но вы можете разместить только [latex] 10 [/ latex] из них на вашем телефоне.Сколько возможных способов загрузить свой телефон?
Каждый из этих вопросов представляет собой комбинационный вопрос, и на него можно ответить точно так же, как и в карточном сценарии. Поскольку этот тип вопросов возникает в очень разных контекстах, ему дается особое имя и символ. Последний вопрос будет называться «[латекс] 300 [/ латекс] выбрать [латекс] 10 [/ латекс]» и писать [латекс] \ begin {pmatrix} 300 \\ 10 \ end {pmatrix} [/ latex] . Он рассчитывается как [латекс] \ frac {300!} {(290!) (10!)} [/ Латекс] по причинам, описанным выше.
Каждая возможная комбинация различных элементов [latex] k [/ latex] набора [latex] S [/ latex] известна как [latex] k [/ latex] -комбинация. Если в наборе есть [latex] n [/ latex] элементов, количество [latex] k [/ latex] -комбинаций равно
.[латекс] \ begin {pmatrix} n \\ k \ end {pmatrix} = \ dfrac {n (n-1)… (n-k + 1)} {k (k-1)… 1} [/ latex ]
Что можно записать с использованием факториалов как
[латекс] \ dfrac {n!} {K! (N-k)! } [/ латекс]
Каждый раз, когда [латекс] k \ leq n [/ latex], и который равен нулю, когда [латекс] k> n [/ latex].п [/ латекс]. [латекс] [/ латекс]
Мир математики — Mathigon
Введение
Леонард Эйлер (1707 — 1783)
Комбинаторика — это раздел математики, который насчитывает около при подсчете — и мы откроем для себя много захватывающих примеров «вещей», которые вы можете сосчитать.
Первые комбинаторные задачи изучались математиками Древней Индии, Арабских стран и Греции. Интерес к этому предмету увеличился в 19 и 20 веках вместе с развитием теории графов и таких проблем, как теорема о четырех цветах.Среди ведущих математиков — Блез Паскаль (1623–1662), Якоб Бернулли (1654–1705) и Леонард Эйлер (1707–1783).
Комбинаторика имеет множество приложений в других областях математики, включая теорию графов, кодирование и криптографию, а также вероятность.
Факториалы
Комбинаторика может помочь нам подсчитать количество заказов , в которых что-то может случиться. Рассмотрим следующий пример:
В классе В.CombA1 учеников и стульев V.CombA1, стоящих в ряд, стульев. В скольких различных порядках ученики могут сидеть на этих стульях?
Перечислим возможности — в этом примере V.CombA1 разных зрачков представлены V.CombA1 разных цветов стульев.
Существует {2: 2, 3: 6, 4: 24, 5: 120} [V.CombA1] различных возможных порядков. Обратите внимание, что количество возможных порядков очень быстро увеличивается по мере увеличения количества учеников.У 6 учеников есть 720 различных возможностей, и перечислять их все становится непрактично. Вместо этого нам нужна простая формула, которая говорит нам, сколько имеется заказов на n человек, чтобы сесть на n стулья. Затем мы можем просто заменить 3, 4 или любое другое число на n , чтобы получить правильный ответ.
Предположим, у нас есть стульев V.CombB1 и мы хотим разместить V.CombB1 == 1? ‘Один ученик’: V.CombB1 == 2? ‘Два ученика’: V.CombB1 == 3? ‘Три ученика ‘: V.CombB1 == 4? ‘Четыре ученика’: V.CombB1 == 5? ‘Пять учеников’: V.CombB1 == 6? ‘Шесть учеников’: ‘семь учеников’ на них. {7: «Семь учеников могут сесть на первый стул. Затем есть 6 учеников, которые могли бы сесть на второй стул. Есть 5 вариантов для третьего стула, 4 варианта для четвертого стула, 3 варианта для пятого стула, 2 варианта для шестого стула и только один вариант для последнего стула. ‘, 6: «Есть 6 учеников, которые могли бы сесть на первый стул. Затем есть 5 учеников, которые могли бы сесть на второй стул.Есть 4 варианта для третьего стула, 3 варианта для четвертого стула, 2 варианта для пятого стула и только один вариант для последнего стула. ‘, 5: «Пятеро учеников могли бы сесть на первый стул. Затем есть 4 ученика, которые могут сесть на второй стул. Есть 3 варианта для третьего стула, 2 варианта для четвертого стула и только один вариант для последнего стула. ‘, 4: «Есть 4 ученика, которые могли бы сесть на первый стул. Затем есть 3 ученика, которые могут сесть на второй стул.Есть 2 варианта для третьего стула и только один вариант для последнего стула. ‘, 3: «Есть 3 ученика, которые могут сесть на первый стул. Затем есть 2 ученика, которые могут сесть на второй стул. Наконец, остался только один ученик, чтобы сесть на третий стул. ‘, 2: «Есть 2 ученика, которые могут сесть на первый стул. Далее остается только один ученик, который может сесть на второй стул. ‘, 1: ‘Это только один вариант для одиночного стула.’} [V.CombB1] Всего
возможности.Чтобы упростить обозначения, математики используют знак «!» называется факториалом. Например, 5! («Пять факториалов») то же самое, что 5 × 4 × 3 × 2 × 1. Выше мы только что показали, что существует n ! возможности заказать н предметов.
Насколько разными способами 23 ребенка могли сесть на 23 стула в классе математики? Если у вас 4 урока в неделю, а в году 52 недели, сколько лет нужно, чтобы изучить все возможности? Примечание: Возраст Вселенной составляет около 14 миллиардов лет.
Для 23 детей, чтобы сесть на 23 стула, их 23! = 25 852 016 738 884 800 000 000 возможностей (это число слишком велико для отображения на экране калькулятора). Испытание всех возможностей займет
23! 4 × 52 = 124 288 542 000 000 000 000 лет.
Это почти в 10 миллионов раз больше нынешнего возраста Вселенной!
Перестановки
Вышеупомянутый метод требовал, чтобы у нас было столько же учеников, сколько стульев, на которых можно было бы сидеть.Но что будет, если стульев не хватит?
Сколько различных возможностей существует для любых Math.min (V.CombC1, V.CombC2) из V.CombC1 учеников, чтобы сесть на Math.min (V.CombC1, V.CombC2) стульев? Обратите внимание, что Math.max (0, V.CombC1-V.CombC2) останется включенным, и мы не должны включать его при перечислении возможностей.
Давайте начнем снова, перечислив все возможности:
Чтобы найти простую формулу, подобную приведенной выше, мы можем думать о ней очень похожим образом. «Есть ученики« + V.CombC1 + », которые могут сесть на первый стул. ‘+ (((Math.min (V.CombC1, V.CombC2)) == 2 || (Math.min (V.CombC1, V.CombC2)) == 3 || (Math.min (V.CombC1, V .CombC2)) == 4)? ‘Тогда есть’ + (V.CombC1-1) + ‘ученики, которые могли бы сесть на второй стул.’: ») + (((Math.min (V.CombC1, V.CombC2)) == 3 || (Math.min (V.CombC1, V.CombC2)) == 4)? ‘Тогда есть’ + (V.CombC1 -2) + ‘ученики, которые могли бы сесть на третий стул.’: ») + (((Math.min (V.CombC1, V.CombC2)) == 4)? ‘Наконец, остался один ученик, который сядет на последний стул.’:’ ‘) + ((V.CombC1- (Math.min (V.CombC1, V.CombC2)) == 1 || V.CombC1- (Math.min (V.CombC1, V.CombC2)) == 2 || V. CombC1- (Math.min (V.CombC1, V.CombC2)) == 3)? ‘Нас не волнуют оставшиеся’ + (V.CombC1-V.CombC2) + ‘дети, оставшиеся стоять.’: ‘ ‘) Всего
возможности. Мы снова должны подумать об обобщении этого. Мы начинаем так же, как и с факториалами, но останавливаемся, не дойдя до 1. Фактически, мы останавливаемся, как только достигаем числа студентов без стула. При размещении 7 студентов на 3 стульях их
7 × 6 × 5 = 7 × 6 × 5 × 4 × 3 × 2 × 17 × 6 × 5 × 4 × 3 × 2 × 1 = 7 ! 4! = 7 ! ( 7 — 3 )!
возможности, так как 4 × 3 × 2 × 1 будут компенсировать друг друга.Опять же, для этого есть более простое обозначение: 7 P 3 . Если мы хотим разместить n объектов на m позиции, то будет
n P м = n ! ( n — м )!
возможности. P означает « p перестановок», поскольку мы подсчитываем количество перестановок (порядков) объектов. Если m и n такие же, как и в задаче в начале этой статьи, мы имеем
n P n = n ! ( n — n )! = n ! 0 !.
Чтобы понять это, мы определяем 0! = 1. Теперь n P n = n ! как и следовало ожидать от нашего решения первой проблемы.
К сожалению, вы не можете вспомнить код своего четырехзначного замка. Вы только знаете, что не использовали ни одну цифру более одного раза. Сколько разных способов вы должны попробовать? Что вы делаете о безопасности этих замков?
Имеется 10 цифр (0, 1,…, 9), каждая из которых встречается не более одного раза.Число порядков этих цифр составляет 10 P 4 = 5040. Проверка такого количества комбинаций займет очень много времени, поэтому 4-значные блокировки очень безопасны.
Комбинации
Перестановки используются, когда вы выбираете объекты и заботитесь об их порядке — например, о порядке детей на стульях. Однако в некоторых задачах вы не заботитесь о порядке и просто хотите знать, сколько есть способов выбрать определенное количество объектов из большего набора.
В магазине есть пять разных футболок, которые вам нравятся: красного, синего, зеленого, желтого и черного цветов.К сожалению, у вас достаточно денег, чтобы купить три из них. Сколько существует способов выбрать три футболки из пяти, которые вам нравятся?
Здесь нас не волнует порядок (неважно, покупаем ли мы сначала черный, а затем красный или сначала красный, а затем черный), а только количество комбинаций футболок. Возможностей
, итого их 10. Если бы мы вычислили 5 P 3 = 60, мы бы дважды подсчитали некоторые возможности, как показано в следующей таблице:
При перестановках мы считаем каждую комбинацию из трех футболок 6 раз, потому что их 3! = 6 способов заказать три футболки.Чтобы получить количество комбинаций из количества перестановок, нам просто нужно разделить на 6. Мы пишем
5 C 3 = 5 P 33! = 606 = 10.
Здесь C означает « c комбинаций». В общем, если мы хотим выбрать r объектов из общего числа n , то будет
n C r = n P r r ! = n ! р ! ( n — r )!
различных комбинаций.Вместо n C r математики часто пишут n C r = ( n r ), как дробь в скобках, но без промежуточной линии. (Для упрощения набора мы продолжим использовать первую строчную нотацию.)
(a) В вашем классе 10 детей, но вы можете пригласить только пятерых на свой день рождения. Сколько разных комбинаций друзей вы могли бы пригласить? Объясните, следует ли использовать комбинации или перестановки.
(б) На вечеринке 75 человек. Каждый раз всем пожимает руку. Как часто в целом рукопожатие? Подсказка: сколько людей участвует в рукопожатии?
(a) Количество комбинаций друзей, которых вы можете пригласить, составляет 10 C 5 = 252. Мы использовали комбинации, потому что не имеет значения, в каком порядке мы приглашаем друзей, на какие мы приглашаем.
(b) Вы хотите найти количество всех возможных пар гостей вечеринки.Это просто 75 C 2 = 2775 (это много рукопожатий!)
Комбинаторика и треугольник Паскаля
Рассчитаем некоторые значения n C r . Начнем с 0 C 0. Затем находим 1 C 0 и 1 C 1. Затем 2 C 0, 2 C 1 и 2 C 2. Затем 3 C 0 , 3 C 1, 3 C 2 и 3 C 3. Мы можем записать все эти результаты в таблицу:
| 0 С 0 = 1 | |||||||||||
| 1 С 0 = 1 | 1 С 1 = 1 | ||||||||||
| 2 С 0 = 1 | 2 С 1 = 2 | 2 С 2 = 1 | |||||||||
| 3 С 0 = 1 | 3 С 1 = 3 | 3 С 2 = 3 | 3 С 3 = 1 | ||||||||
| 4 С 0 = 1 | 4 С 1 = 4 | 4 С 2 = 6 | 4 С 3 = 4 | 4 С 4 = 1 | |||||||
| 5 С 0 = 1 | 5 С 1 = 5 | 5 С 2 = 10 | 5 С 3 = 10 | 5 С 4 = 5 | 5 С 5 = 1 | ||||||
Это в точности треугольник Паскаля, который мы исследовали в статье о последовательностях.Его можно создать проще, если учесть, что любая ячейка представляет собой сумму двух ячеек, указанных выше. В треугольнике Паскаля скрыто бесчисленное множество узоров и числовых последовательностей.
Теперь мы также знаем, что число r в строке n также задается как n C r (но мы всегда должны начинать отсчет с 0, поэтому первая строка или столбец фактически нулевой ряд). Если мы применим то, что мы знаем о создании треугольника Паскаля, к нашим комбинациям, мы получим
( n r ) + ( n r + 1) знак равно ( n + 1 r + 1) .
Это известно как идентификатор Паскаля . Вы можете получить его, используя определение n C r в терминах факториалов, или вы можете думать об этом следующим образом:
Мы хотим выбрать r + 1 объектов из набора n + 1 объектов. Это в точности то же самое, что пометить один объект из n + 1 , который будет называться X, и либо выбрать X плюс r других (из оставшихся n), либо не выбрать X и r + 1 других ( от оставшихся n).
У многих задач комбинаторики есть простое решение, если вы подумаете о нем правильно, и очень сложное решение, если вы просто попытаетесь использовать алгебру…
Звезды и решетки
Решение
Пример
Зеленщик на рынке хранит большое количество различных видов фруктов. Какими способами мы можем составить пакет из или фруктов? Обратите внимание, что r может быть меньше, равно или больше n .
Обратите внимание, что с r ≤ n существует n C r способ выбрать по одному фрукту каждого вида. Однако мы также можем съесть более одного фрукта каждого вида, например, два яблока, одну клубнику и один банан.
Мы можем представить любой допустимый выбор фруктов цепочкой звезд и полосок, как показано в этом примере:
| ★★★ | | | ★★ | | | | | ★★ | | | ★ | |
| 3 типа 1 | 2 типа 2 | 0 типа 3 | 2 типа 4 | 1 типа 5 |
Всего r звездочек ( r фруктов, которые нам разрешено есть) и n — 1 столбик (деление n разных фруктов).Это составляет r + n — всего 1 место. Любой заказ на r звездочек и n — 1 батончик соответствует ровно одному действительному выбору фруктов.
Теперь мы можем применить наши комбинаторные инструменты: есть r + n — 1 мест, и мы хотим выбрать n — 1 из них как столбцы (все остальные — звездочки). Что есть ровно ( r + n — 1) C ( n — 1) возможностей для этого!
Предположим, есть пять видов фруктов, и мы хотим взять десять штук.Исходя из того, что мы подсчитали выше, всего
(10 + 5 — 1) C (5 — 1) = 14 C 4 = 24 024
возможности. Подумайте об этом в следующий раз, когда пойдете за покупками!
Комбинаторика и вероятность
Комбинаторика имеет множество приложений в теории вероятностей. Вы часто хотите найти вероятность одного конкретного события, и вы можете использовать уравнение
P ( X ) = вероятность того, что X произойдет = количество исходов, при которых X случится, общее количество возможных исходов
Вы можете использовать комбинаторику, чтобы вычислить «общее количество возможных результатов».Вот пример:
Четверо детей, которых зовут A, B, C и D, случайным образом сидят на четырех стульях. Какова вероятность того, что А сядет на первый стул?
Мы уже показали, что всего существует 24 способа сесть на четыре стула. Если вы посмотрите на наше решение, вы также обнаружите, что А сидит на первом стуле в шести случаях. Следовательно,
P (A сидит на первом стуле) = количество результатов, где A сидит на первом стуле, общее количество возможных результатов = 624 = 14.
Этот ответ был ожидаемым, поскольку каждый из четырех детей с одинаковой вероятностью сядет на первый стул. Но в других случаях все не так просто…
(a) Почтальон должен доставить четыре письма в четыре разных дома на улице. К сожалению, дождь стер адреса, поэтому он просто раздает их случайным образом, по одной букве на дом. Какова вероятность, что каждый дом получит нужную букву? (☆ Какова вероятность, что каждый дом получит неправильную букву?)
(b) В лотерее нужно угадать 6 номеров из 49.Какова вероятность того, что вы все сделаете правильно? Если каждую неделю отправлять 100 предположений, сколько времени в среднем вам понадобится, чтобы выиграть?
(a) Всего 4! = 24 способа случайного распределения букв и только один способ получить их все правильно. Таким образом, вероятность того, что каждое письмо будет доставлено в нужный дом, составляет 1/24 = 0,0417 = 4,17%.
Определить вероятность того, что каждое письмо будет доставлено не в тот дом, немного сложнее.Это не просто 1 — 0,0417, так как во многих случаях один или два, но не всех домов получают правильную букву. В этом простом случае самым простым решением было бы записать все 24 варианта. Вы обнаружите, что в 9 из 24 случаев каждый дом получает неправильную букву, что дает вероятность 0,375 = 37,5%. Если домов слишком много, чтобы записать все возможности, вы можете использовать идею под названием Принцип исключения включения .
(b) Существует 49 C 6 = 13 983 816 возможных результатов лотереи, поэтому вероятность получить правильное решение составляет 1/49 C 6 = 0.000000072.
В среднем также потребуется 13 983 816 попыток, чтобы выиграть. Если мы отправляем 100 предположений каждую неделю, это соответствует 139 838 неделям, что равняется 2689 годам. Урок, который нужно усвоить: не играйте в лото!
комбинаций против перестановок. Мы используем термин «комбинация»… | Бретт Берри | Math Hacks
Разница между комбинациями и перестановками — это порядок. При перестановках мы заботимся о порядке элементов, а при комбинациях — нет.
Например, скажем, ваш шкафчик «комбо» — 5432. Если вы введете 4325 в свой шкафчик, он не откроется, потому что это другой порядок (также известный как перестановка).
Перестановки из 2, 3, 4, 5:
- 5432, 5423, 5324, 5342, 5234, 5243, 4532, 4523, 4325, 4352, 4253, 4235, 3542, 3524, 3425 , 3452, 3254, 3245, 2543, 2534, 2435, 2453, 2354, 2345
«Комбинация» вашего шкафчика — это определенная комбинация 2, 3, 4 и 5. Если ваш шкафчик действительно работал по комбинации, вы можете ввести любой из вышеперечисленных перестановок, и он откроется!
Предположим, вы хотите узнать, сколько существует перестановок чисел 2, 3, 4, 5, не перечисляя их, как я сделал выше.Как бы вы этого добились?
Давайте использовать линейную диаграмму, чтобы помочь нам визуализировать проблему.
Мы хотим найти, сколько возможных 4-значных перестановок можно сделать из четырех различных чисел. Начните с рисования четырех линий, представляющих 4 цифры.
Первая цифра может быть любой из 4 цифр, поэтому поставьте «4» в первый пробел.
Теперь для второго пустого поля осталось 3 варианта, потому что вы уже использовали одно из чисел в первом пустом поле. Поставьте цифру «3» в следующем месте.
Для третьей позиции у вас осталось два числа.
И на последней позиции осталось одно число, поэтому поставьте там «1».
Принцип умножения
Используя принцип умножения комбинаторики, мы знаем, что если есть x способ сделать одно и y способ сделать другое, то общее количество способов сделать и то, и другое равно x • y . Это означает, что нам нужно умножить, чтобы найти общие перестановки.
Это отличная возможность использовать сокращенную факториальную нотацию (!) :
Есть 24 перестановки, которые соответствуют листингу, который мы сделали в начале этого поста.
Что, если бы я хотел найти общее количество перестановок, включающих числа 2, 3, 4 и 5, но хотел бы включить такие порядки, как 5555 или 2234, где используются не все числа, а некоторые используются более одного раза ?
Сколько существует этих перестановок?
Это простой расчет.Мы снова составляем 4-значное число, поэтому нарисуйте 4 линии для представления цифр.
В первой позиции у нас есть 4 варианта чисел, поэтому, как и раньше, поместите «4» в первый пробел. Поскольку нам разрешено повторно использовать числа, теперь у нас есть 4 варианта чисел, доступных для второй, третьей и четвертой цифр.
Это то же самое, что:
Допуская повторение чисел, мы получаем 256 перестановок!
Давайте поднимем ставку, решив более сложную задачу:
Сколько разных комбинаций из 5 карт можно собрать из стандартной колоды карт?
В этой задаче порядок не имеет значения, поскольку не имеет значения, в каком порядке мы выбираем карты.
Мы начнем с пяти линий, представляющих нашу руку из 5 карт.
Предполагая, что никто другой не берет карты из колоды, в первом розыгрыше доступно 52 карты, поэтому поместите «52» в первое поле.
После того, как вы выберете карту, в следующем розыгрыше будет на одну карту меньше. Таким образом, у второго бланка будет 51 вариант. В следующем розыгрыше в колоде будет на две карты меньше, поэтому теперь есть 50 вариантов и так далее.
Это 311 875 200 перестановок .
Это перестановки, а не комбинации. Чтобы исправить это, нам нужно разделить на количество рук с разными перестановками, но с одинаковой комбинацией.
Это то же самое, что сказать , сколькими различными способами я могу расположить 5 карточек?
Примечание: это математически аналогично поиску различных перестановок нашей комбинации шкафчикаТаким образом, количество комбинаций рук из пяти карт равно:
Приложив немного изобретательности, мы можем переписать приведенный выше расчет, используя факториалы.
Мы знаем 52! = 52 • 51 • 50 •… • 3 • 2 • 1, но нам нужны только произведения целых чисел от 52 до 48. Как мы можем выделить только эти целые числа?
Мы хотим разделить все целые числа, кроме от 48 до 52. Для этого разделите на 47! так как это произведение целых чисел от 47 до 1.
Задачи перестановок и комбинаций | GMAT GRE Maths Tutorial
В этой статье вы узнаете о задачах перестановки и комбинирования: определение, формулы, решенные примеры и викторину с практическими вопросами.
Перестановки
Определение
Перестановки — это различные способы организации коллекции элементов.
Например:
Различные способы группировки алфавитов A, B и C, взятые одновременно, — это ABC, ACB, BCA, CBA, CAB, BAC.
Обратите внимание, что ABC и CBA не совпадают, так как порядок расположения отличается. То же правило применяется при решении любой задачи в перестановках.
Количество способов, которыми могут быть расположены n вещей, взятых одновременно, n P n = n !, называемых «n факториалами».
Факториальная формула
Факториал числа n определяется как произведение всех чисел от n до 1.
Например, факториал 5, 5! = 5 * 4 * 3 * 2 * 1 = 120.
Таким образом, количество способов, которыми можно расположить 3 буквы за один раз, равно 3! = 3 * 2 * 1 = 6 способов.
Число перестановок n вещей, взятых r за раз, обозначается следующим образом:
Например:
Различные способы расположения трех букв, взятых по две за раз, — это 3! / (3-2)! = 3! / 1! = 6 способов.
Важные формулы перестановки
1! = 1
0! = 1
Давайте посмотрим на несколько примеров:
Задача 1: Найдите количество слов со смыслом или без него, которые могут быть образованы буквами слова «СТУЛ».
Решение :
«СТУЛ» состоит из 5 букв.
Следовательно, количество слов, которые могут быть образованы из этих 5 букв, = 5! = 5 * 4 * 3 * 2 * 1 = 120.
Задача 2: Найдите количество слов со смыслом или без него, которые могут быть образованы буквами слова «ИНДИЯ».
Решение :
Слово «ИНДИЯ» состоит из 5 букв, а «я» встречается дважды.
Когда буква встречается в слове более одного раза, мы делим факториал числа всех букв в слове на количество появлений каждой буквы.
Следовательно, количество слов, образованных словом «ИНДИЯ» = 5! / 2! = 60,
Задача 3: Найдите количество слов со смыслом или без него, которые можно составить из букв слова «ПЛАВАНИЕ?
Решение :
Слово «ПЛАВАНИЕ» состоит из 8 букв.Из них I встречается дважды, а M — дважды.
Следовательно, количество слов, образованных этим словом = 8! / (2! * 2!) = 10080.
Задача 4: Сколько разных слов можно составить из букв слова «SUPER», чтобы гласные всегда сходились?
Решение :
Слово «СУПЕР» состоит из 5 букв.
Чтобы найти количество перестановок, которые могут быть образованы, когда две гласные U и E объединяются.
В этих случаях мы группируем буквы, которые должны объединиться, и рассматриваем эту группу как одну букву.
Итак, буквы — S, P, R, (UE). Теперь количество слов 4.
Следовательно, количество способов расположения 4 букв равно 4!
В U и E количество способов упорядочения U и E равно 2!
Следовательно, общее количество способов, которыми буквы «SUPER» могут быть расположены так, чтобы гласные всегда были вместе, равно 4! * 2! = 48 способов.
Задача 5: Найдите количество разных слов, которые можно составить из букв слова «МАСЛО», чтобы гласные всегда были вместе.
Решение :
Слово «МАСЛО» состоит из 6 букв.
Буквы U и E всегда должны совпадать. Итак, буквы — B, T, T, R, (UE).
Количество способов расположения вышеприведенных букв = 5! / 2! = 60 (поскольку буква «Т» повторяется дважды).
Количество способов расположения U и E = 2! = 2 пути
Следовательно, общее количество возможных перестановок = 60 * 2 = 120 способов.
Задача 6: Найдите количество перестановок букв в слове «ОСТАЛОСЬ», при котором гласные всегда встречаются в нечетных местах.
Решение :
Слово «ОСТАЛОСЬ» состоит из 7 букв.
В нем 4 согласных и 3 гласных.
Написание следующего текста упрощает решение вопросов такого типа.
(1) (2) (3) (4) (5) (6) (7)
Количество способов 3 гласные могут встречаться в 4 разных местах = 4 P 3 = 24 способа.
После 3 гласных занимают 3 места, нет. способов 4 согласных могут занимать 4 места = 4 P 4 = 4! = 24 способа.
Следовательно, общее количество возможных перестановок = 24 * 24 = 576 способов.
Комбинации
Определение
Различные варианты выбора из набора элементов называются комбинациями.
Различные варианты выбора из набора элементов называются комбинациями.
Например:
Различные варианты выбора из алфавитов A, B, C, взятые по 2 за раз, — это AB, BC и CA.
Не имеет значения, выбираем ли мы A после B или B после A. Порядок выбора не важен в комбинациях.
Чтобы найти количество возможных комбинаций из данной группы элементов n, взятых по r за раз, формула, обозначенная как n C r , равна
n C r = n! / [р! * (н-р)!]Например, проверяя приведенный выше пример, различные варианты выбора из алфавитов A, B, C, взятые по два за раз, равны
3 С 2 = 3! / (2! * (3-2)!) = 3 возможных выбора (т. Е.е., AB, BC, CA)
Важные формулы комбинирования
n C n = 1
n C 0 = 1
n C 1 = n
n C r = n C (n-r)
Число возможных вариантов выбора с использованием A, B, C, взятых одновременно, равно 3 C 3 = 1 (т.е. ABC)
Решенные примеры комбинации
Давайте рассмотрим несколько примеров, чтобы понять, как работают комбинации:
Задача 1: Какими способами можно сформировать комитет из 1 мужчины и 3 женщин из группы из 3 мужчин и 4 женщин?
Решение :
№способов 1 человека можно выбрать из группы 3 мужчин = 3 C 1 = 3! / 1! * (3-1)! = 3 способа.
Количество способов выбрать 3 женщины из группы из 4 женщин = 4 C 3 = 4! / (3! * 1!) = 4 способа.
Задача 2: Среди набора из 5 черных шаров и 3 красных шаров, сколько можно выбрать из 5 шаров, чтобы по крайней мере 3 из них были черными шарами.
Решение :
Выбор по крайней мере 3 черных шаров из набора из 5 черных шаров в общем выборе 5 шаров может быть
3 Б и 2 Р
4 B и 1 R и
шариков 5 B и 0 R.
Следовательно, выражение нашего решения выглядит так.
5 C 3 * 3 C 2 + 5 C 4 * 3 C 1 + 5 C 5 * 3 C 0 = 46 способами.
Задача 3: Сколько четырехзначных чисел, которые делятся на 10, можно составить из чисел 3, 5, 7, 8, 9, 0, чтобы ни одно число не повторялось?
Решение :
Если число делится на 10, то его место в единицах должно содержать 0.
_ _ _ 0
После того, как 0 будет помещен в разряд единиц, разряд десятков можно заполнить любыми другими 5 цифрами.
Выбор одной цифры из 5 цифр можно выполнить 5 способами. 5 C 1 = 5.
После заполнения разряда десятков у нас остается 4 цифры. Выбрать 1 цифру из 4 цифр можно четырьмя способами: 4 C 1 = 4.
После заполнения разряда сотен можно заполнить разряды тысяч 3 C 1 = 3 способами.
Следовательно, общее количество возможных комбинаций = 5 * 4 * 3 = 60.
Тест на перестановки и комбинации
Попробуйте эти практические задачи.
Проблема 1
Решите следующее.
i) 30 P 2
ii) 30 C 2
А. 870, 435
Б. 435, 870
С. 870, 470
Д. 435, 835
Ответ 1
А
Пояснение:
30 П 2 = 30! / 28! = 30 * 29 * 28! / 28! = 30 * 29 = 870.
30 С 2 = 30! / (2! * 28!) = 435,
Задача 2
Сколько различных возможных перестановок можно сделать из слова «BULLET», чтобы гласные никогда не совпадали?
А. 360
Б. 120
С. 480
Д. 240
Ответ 2
Д.
Пояснение :
Слово «ПУЛЯ» состоит из 6 букв, из которых 1 буква встречается дважды = 6! / 2! = 360
№возможных перестановок с гласными всегда вместе = 5! * 2! / 2! = 120
Количество возможных перестановок гласных никогда не бывает вместе = 360-120 = 240.
Задача 3
Какими способами можно выбрать 3 мужчин и 2 женщин из группы из 5 мужчин и 5 женщин?
A. 10
B. 20
C. 30
D. 100
Ответ 3
Д.
Пояснение :
5 C 3 * 5 C 2 = 100
Концепции и формулы перестановки и комбинирования способностей
Что нужно помнить:
1) Факториал:
Факториал можно определить как произведение числа (для которого мы должны найти факториал) на его последователя, пока оно не достигнет единицы.
Мы можем записать это как, n! (Факториал n) = n (n-1) (n-2) …. 1
Например: Факториал 3:
3! = 3 * 2 * 1 = 6
Примечание: Факториал нуля (0) всегда равен 1, потому что пустой набор может быть организован только одним способом.
2) Перестановка: Это относится к количеству способов, которыми может быть организован конкретный набор, причем порядок расположения имеет значение. Кодовый замок можно назвать замком перестановки.
Например:
i) Пусть у нас есть три буквы a, b и c, и мы должны расположить по две буквы за раз.
Итак, в этом случае перестановки двух букв = ab, ba, bc, cb, ac и ca.
ii) Если нам нужно расположить все буквы (a, b, c) одновременно, перестановка будет такой: abc, acb, bac, bca, cab и cba.
Формула для вычисления количества возможных перестановок r элементов из набора n за один раз выглядит следующим образом:
n P r = n (n — 1) (n — 2) (n — 3 )… (п — г + 1) =
Например:
и. 8 P 3 = = = (8 * 7 * 6) = 336
ii. 7 P 5 = = = 2520
iv. Количество перестановок или расстановок всех n вещей за раз = n! (Факториал n).
т.е. n = 3, поэтому 3! = 3 * 2 * 1 = 6 (количество перестановок = 6)
3) Комбинации:
Это относится к количеству способов, которыми может быть организован конкретный набор, где порядок расположения не имеет значения, что означает, что для комбинации n количества вещей могут быть разные порядки.
Формула для вычисления возможной комбинации для r вещей из набора n объектов за раз имеет следующий вид:
n C r = =
Примечание:
i) n C n = 1
ii) n C 0 = 1
iii) n C r = n C (n-r)
Например:
и. 8 С 3 = = = = (8 * 7) = 56
Или, 8 C 3 = 8 C (8-3) = 8 C 5 = = 8 * 7 = 56
ii. 7 C 5 = 7 C (7-5) = 7 C 2 = = 21
Примечание:
- Когда количество элементов равно x, y и z, тогда количество комбинаций, принимающих по две за раз, будет xy, yz и zx.
Примечание: xy и yx в комбинации совпадают.
- Комбинация всех вещей одновременно — это xyz.
Тестовая бумага на перестановку и комбинацию 1
Тестовая бумага на перестановку и комбинацию 2
простых перестановок и комбинаций — лучше объяснение
Я всегда путала «перестановку» и «комбинацию» — какая из них какая?
Вот простой способ запомнить: перестановка звучит сложно , не так ли? И это.При перестановках важна каждая мелочь. Алиса, Боб и Чарли отличаются от Чарли, Боба и Алисы (вставьте сюда имена своих друзей).
С другой стороны, комбинациидовольно просты. Детали значения не имеют. Алиса, Боб и Чарли такие же, как Чарли, Боб и Алиса.
Перестановки предназначены для списков (порядок имеет значение), а комбинации — для групп (порядок не имеет значения).
Вы знаете, «кодовый замок» действительно следует называть «блокировкой перестановки».Порядок, в котором вы ставите числа, имеет значение.
Настоящий «кодовый замок» примет правильными и 10-17-23, и 23-17-10.
Перестановки: волосатые детали
Давайте начнем с перестановок, или всех возможных способов, что-то сделать. Мы используем модный термин «перестановка», поэтому мы позаботимся о каждой детали, включая порядок каждого элемента. Допустим, у нас 8 человек:
1: Алиса
2: Боб
3: Чарли
4: Дэвид
5: Ева
6: Фрэнк
7: Джордж
8: Горацио
Какими способами мы можем присуждать призы за 1, 2 и 3 места среди восьми участников? (Золото / Серебро / Бронза)
Мы собираемся использовать перестановки, так как порядок, в котором мы раздаем эти медали, имеет значение.Вот как он распадается:
- Золотая медаль: 8 вариантов: A B C D E F G H (Я умело заставлял имена совпадать с буквами, а?). Скажем, A выигрывает золото.
- Серебряная медаль: 7 вариантов: B C D E F G H. Допустим, B выигрывает серебро.
- Бронзовая медаль: 6 вариантов: C D E F G H. Скажем,… C выигрывает бронзу.
Мы выбрали определенных людей, которые выиграют, но детали не имеют значения: сначала у нас было 8 вариантов, затем 7, затем 6. Общее количество вариантов составило 8 долларов * 7 * 6 = 336 долларов.
Давайте посмотрим на детали. Нам пришлось заказать 3 человека из 8. Для этого мы начали со всеми вариантами (8), затем забирали их по одному (7, затем 6), пока у нас не закончились медали.
Мы знаем, что факториал:
К сожалению, этого уже слишком! Нам нужно всего 8 * 7 * 6 $. Как мы можем «остановить» факториал на 5?
Вот где перестановки становятся крутыми: обратите внимание, как мы хотим избавиться от $ 5 * 4 * 3 * 2 * 1 $. Как еще это назвать? 5 факториал!
Итак, если мы сделаем 8! / 5! получаем:
А почему мы использовали цифру 5? Потому что это осталось после того, как мы выбрали 3 медали из 8.Итак, лучший способ написать это:
где 8! / (8-3)! это просто причудливый способ сказать «Используйте первые 3 цифры из 8!». Если у нас всего n товаров и мы хотим забрать k в определенном порядке, мы получим:
И это причудливая формула перестановки: у вас есть n элементов и вы хотите найти количество способов, которыми можно заказать k элементов:
Комбинации, Хо!
Комбинации просты.Порядок не имеет значения. Вы можете смешать это, и он выглядит так же. Допустим, я скряга и не могу позволить себе раздельные золотые, серебряные и бронзовые медали. Фактически, я могу позволить себе только пустые консервные банки.
Сколько способов я могу подарить 3 консервные банки 8 людям?
Ну, в этом случае порядок, в котором мы отбираем людей, не имеет значения. Если я дам банку Алисе, Бобу, а затем Чарли, это то же самое, что дать Чарли, Алисе и затем Бобу. В любом случае они одинаково разочарованы.
Это вызывает интересный момент — здесь у нас есть некоторые дублирования.Алиса Боб Чарли = Чарли Боб Алиса. На мгновение давайте просто разберемся, сколькими способами мы можем переставить трех человек.
Итак, у нас есть 3 варианта для первого лица, 2 для второго и только 1 для последнего. Итак, у нас есть 3 * 2 * 1 $ способов перераспределить 3 человека.
Погодите … это немного похоже на перестановку! Ты обманул меня!
Верно. Если у вас N человек, и вы хотите знать, сколько аранжировок существует для всех из них, это просто N факториал или N!
Итак, если у нас есть 3 жестяных банки, которые можно раздать, их будет 3! или 6 вариантов на каждый выбор, который мы выберем.Если мы хотим выяснить, сколько у нас комбинаций, мы просто создаем все перестановки и делим на все избыточности . В нашем случае мы получаем 336 перестановок (сверху), делим на 6 избыточностей для каждой перестановки и получаем 336/6 = 56.
Общая формула
, что означает «Найдите все способы выбрать k человек из n и разделить на k! варианты ». Записав это, мы получаем нашу формулу комбинирования или количество способов комбинировать k элементов из набора n:
Иногда C (n, k) записывается как:
, который является биномиальным коэффициентом.
Несколько примеров
Вот несколько примеров комбинаций (порядок не имеет значения) из перестановок (порядок имеет значение).
-
Комбинация: Выбор команды из 3 человек из группы из 10 человек. $ C (10,3) = 10! / (7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120 $.
Перестановка: выбор президента, вице-президента и водяного мальчика из группы из 10 человек.
