Гармонические колебания — формулы, законы, примеры
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Механические колебания
Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.
Колебания делятся на два вида: свободные и вынужденные.
Свободные колебания
Это колебания, которые происходят под действием внутренних сил в колебательной системе.
Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.
Вынужденные колебания
А вот вынужденные колебания восполняют запас энергии внешним воздействием
 Если это происходит каждый период, то колебания вообще затухать не будут.
Если это происходит каждый период, то колебания вообще затухать не будут.
Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.
Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.
Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.
Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.
Автоколебания
Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.
У автоколебательной системы есть три важных составляющих:
- сама колебательная система
- источник энергии
- устройство обратной связи, обеспечивающей связь между источником и системой
Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.
Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.
Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.
Характеристики колебаний
Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.
Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.
|
Формула периода колебаний T = t/N T — период [с] t — время [с] N — количество колебаний [—] |
Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.
Она показывает, сколько колебаний совершает система в единицу времени.
|
Формула частоты ν = N/t = 1/T ν — частота [Гц]t — время [с] T — период [с] N — количество колебаний [—] |
Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо xmax.
Она используется в уравнении гармонических колебаний:
Гармонические колебания
Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:
|
Уравнение гармонических колебаний x = xmaxcos(2πνt) x — координата в момент времени t [м] xmax — амплитуда [м] ν — частота [Гц] t — момент времени [с] π = 3,14 |
(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ
Ее обозначают греческой буквой φ
|
Фаза колебаний φ = 2πνt φ — фаза [рад] ν — частота [Гц] t — момент времени [с] π = 3,14 |
Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.
Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.
Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.
На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.
В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.
Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.
Математический маятник
Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.
Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.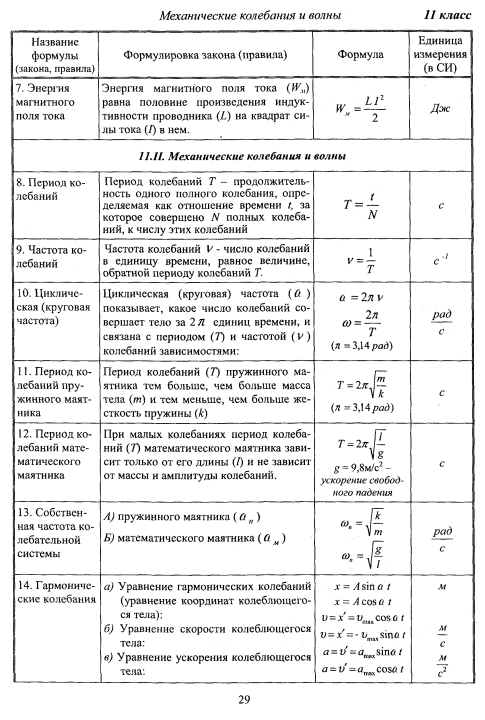
Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).
Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:
|
Формула периода колебания математического маятника
T — период [с] l — длина нити [м] g — ускорение свободного падения [м/с2] На планете Земля g = 9,8 м/с2 π = 3,14 |
Пружинный маятник
Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.
В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.
|
Формула периода колебания пружинного маятника T — период [с] m — масса маятника [кг] k — жесткость пружины [Н/м] π = 3,14 |
Закон сохранения энергии для гармонических колебаний
Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.
Рассмотрим его на примере математического маятника.
- Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
- Когда маятник опускается, потенциальная энергия переходит в кинетическую.
 Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.
Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.
Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!
| 1. |
Механические волны (теоретические задания)
Сложность: лёгкое |
1 |
2.
|
Длина волны (определение и формула)
Сложность: лёгкое |
1 |
| 3. |
Длина волны (вариант 1)
Сложность: лёгкое |
1 |
4.
|
Продольные или поперечные?
Сложность: среднее |
2 |
| 5. |
Частота и период колебаний
Сложность: среднее |
2 |
6.
|
Скорость волн
Сложность: среднее |
2 |
| 7. |
Направление движения волны
Сложность: сложное |
3 |
8.
|
Направление движения частицы
Сложность: сложное |
3 |
| 9. |
Частота колебаний
Сложность: сложное |
3 |
11-ж.
 Электромагнитные колебания
Электромагнитные колебания § 11-ж. Электромагнитные колебания
Как вы уже знаете, переменные токи, создаваемые индукционными генераторами, имеют частоту 50 Гц (см. § 10-ж). Однако для работы многих электронных устройств необходимы токи более высоких частот, измеряемых килогерцами (кГц) и мегагерцами (МГц). Для их генерирования служат специальные электрические цепи – колебательные контуры.
Любой колебательный контур всегда состоит из конденсатора и катушки индуктивности (см. § 8-е, § 10-б). Рассмотрим явления в колебательном контуре на опыте. Для этого соберём цепь по левой схеме (рис. «а»).
Сначала конденсатор получает энергию от источника постоянного тока. При этом верхняя пластина заряжается положительно, а нижняя отрицательно – на ней скапливается избыток электронов.
Переключим конденсатор на катушку индуктивности (рис. «б»). Избыток электронов с нижней пластины конденсатора устремится через катушку к верхней пластине, и в цепи возникнет ток. Поэтому катушка индуктивности создаст вокруг себя магнитное поле.
Поэтому катушка индуктивности создаст вокруг себя магнитное поле.
Можно предположить, что когда конденсатор разрядится, ток в контуре прекратится. Проверим эту гипотезу. Для этого присоединим к катушке осциллограф и повторим наблюдение. Осциллограмма показывает, что сила тока в контуре колеблется, периодически бывая равной нулю, и существует намного дольше, чем длится одно колебание.
Осциллограмма показывает также, что колебания являются затухающими. Так происходит потому, что катушка индуктивности и соединительные провода обладают электрическим сопротивлением. И, по закону Джоуля-Ленца, электрическая энергия будет постепенно превращаться в теплоту. Поэтому свободные колебания в контуре всегда являются затухающими.
Рассмотрим колебания в контуре, содержащем конденсатор и катушку индуктивности с точки зрения превращений энергии.
Возникающий при разрядке конденсатора ток непостоянен, значит, непостоянно и магнитное поле катушки. Оно усиливается и достигает максимума, когда конденсатор полностью отдаст свой заряд (рис. «в»). Следовательно, энергия электрического поля конденсатора полностью превратится в энергию магнитного поля катушки (см. § 8-е, § 10-б).
Оно усиливается и достигает максимума, когда конденсатор полностью отдаст свой заряд (рис. «в»). Следовательно, энергия электрического поля конденсатора полностью превратится в энергию магнитного поля катушки (см. § 8-е, § 10-б).
Однако после разряда конденсатора ток не прекратится. Магнитное поле катушки, оставшись «без подпитки», начнёт ослабевать (рис. «г»). Запасённая им энергия будет постепенно передаваться электронам катушки. Они придут в движение, создав индукционный ток такого направления, что электроны из нижней пластины, проходя через катушку к верхней пластине, придадут ей отрицательный заряд (рис.«д»). Поскольку ранее эта пластина была положительно заряженной, говорят, что произошла перезарядка конденсатора: плюс и минус на нём поменялись местами.
Теперь, когда конденсатор вновь заряжен, он может снова создавать ток, правда, уже противоположного направления (рис. «е»). Так будет повторяться до тех пор, пока вся энергия, полученная конденсатором от источника тока, не превратится в теплоту.
Одной из характеристик электромагнитных колебаний является период – наименьшее время, за которое происходит двойная перезарядка конденсатора (или полный цикл изменения магнитного поля катушки). Единица периода колебаний – 1 секунда.
Величину, обратную периоду, называют частотой колебаний. Единица частоты – 1 герц (1 Гц = 1/с). Частота колебаний зависит от размеров и формы конденсатора и катушки, а также от свойств среды внутри и вокруг них.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
Больше интересного в телеграм @calcsboxВопросы на зачёт по физике за первое полугодие (11 класс)
Вопросы на зачёт за первое полугодие по физике 11 класс
1.Вектор магнитной индукции. Формула. Единицы измерения? Показать на рисунке?
2. Сила Ампера? Показать на рисунке. Формула? Применение?
3. Сила Лоренца. Показать на рисунке. Формула. Применение? Радиус траектории заряженной частицы и формула периода вращения. (Стр.19. Формулы 1.6 и 1.7)
Сила Лоренца. Показать на рисунке. Формула. Применение? Радиус траектории заряженной частицы и формула периода вращения. (Стр.19. Формулы 1.6 и 1.7)
4. Явление электромагнитной индукции. Привести примеры.
5.Магнитный поток. Формула и ед. измерения?
(Формулы 2.1стр.31, также 2.7 2.8 стр.46)
6.Правило Ленца. Направление индукционного тока?
7. Закон электромагнитной индукции. (2.4, Стр.35)
ЭДС в движущихся проводниках (формула 2.6, Стр.36)
8.Энергия магнитного поля п.16
9.Формулы периода, частоты, циклической частоты, фазы, амплитуды и координаты при механических колебаниях. Уметь на рисунке показывать характеристики колебаний. Выбор закона синуса или косинуса?
10.Превращение энергии при механических колебаниях. Резонанс?
11. Аналогия между механическими колебаниями и электромагнитными? Уметь объяснять механизм появления переменного тока в цепи и колебательном контуре?
12. Формулы периода, частоты, циклической частоты, фазы, амплитуды и координаты при электромагнитных колебаниях?
13. Колебательный контур. Переменный ток. Виды сопротивлений при переменном токе? Формулы и рисунок?
Колебательный контур. Переменный ток. Виды сопротивлений при переменном токе? Формулы и рисунок?
14. Виды силы переменного тока. Формулы и их понимание?
15. Виды напряжения переменного тока. Формулы и их понимание?
16. Формулы ЭДС переменного тока и их понимание?
17. Закон сохранения энергии в колебательном контуре? Превращения энергии?
18. Трансформаторы. Принцип действия трансформатора.
Коэффициент трансформации? Особенности передачи электрической энергии на расстоянии.
19. Механические волны. Поперечные волны. Продольные волны. Длина волны и период волны. Показать на рисунке длину волны?
Механические колебания и волны. Примеры решения задач по физике. 9-10 класс
Механические колебания и волны. Примеры решения задач по физике. 9-10 класс
- Подробности
- Просмотров: 1166
Задачи по физике — это просто!
Вспомним
Формула длины волны:
Период колебаний:
А теперь к задачам!
Элементарные задачи из курса школьной физики на механические колебания и волны.
Задача 1
Определить длину волны с частотой 300 Гц, которая распространяется в воздухе со скоростью 340 м/с.
Задача 2
Найти период колебания плота на волнах озера, если длина волны составляет 4 метра, а скорость распространения волн равна 2,5 м/с.
Задача 3
Определить сколько колебаний за 1 минуту совершает буек на воде, если скорость распространения волн составляет 3 м/с, а длина волны равна 5 метрам.
Задача 4
По поверхности воды идут волны. Определить параметры волны (период колебания, длину волны, скорость распространения), если расстояния между 1 и 4 гребнями волн составляет 9 метров, а мимо наблюдателя за 10 секунд проходят 5 гребней волн.
Задача 5
Поплавок удочки рыбака за 40 секунд сделал 20 колебаний, а расстояние между соседними гребнями волн составило 2 метра. Какова была скорость распространения волны?
Задача 6
С лодки в воду бросили камень. По воде пошли круги-волны. Расстояние между соседними гребнями волн составило 1 метр, а время за которое волна дошла до берега — 1 минута. Причем волны накатывались на берег с интервалом в 2 секунды. На каком расстоянии от берега бросили камень?
По воде пошли круги-волны. Расстояние между соседними гребнями волн составило 1 метр, а время за которое волна дошла до берега — 1 минута. Причем волны накатывались на берег с интервалом в 2 секунды. На каком расстоянии от берега бросили камень?
Задача 7
За время полета 30 секунд муха делает 15000 взмахов крыльями, а период колебания крыла комара составляет 1,6 миллисекунд. Во сколько раз отличаются частоты колебаний крыльев мухи и комара?
4) волны, классическое уравнение движения / Хабр
1.
Шар на пружине, ньютоновская версия2.
Квантовый шар на пружине3.
Волны, классический вид4.
Волны, классическое уравнение движения5.
Квантовые волны6.
Поля7.
Частицы – это кванты8.
Как частицы взаимодействуют с полямиВернёмся к уравнению колебаний шара на пружине
В
одной из первых статейцикла мы сначала вывели формулу для колебательного движения шара
А затем нашли уравнение движения, для которого эта формула была решением
Здесь
• d
2z/dt
2 обозначает изменение по времени изменения по времени z(t).
• K – сила пружины, М – масса шара, z
0— равновесное положение.
• ν = √ K/M / 2π
Ключевым шагом для получения последнего уравнения частоты, выраженной через К и М был подсчёт d2z/dt2 для колебательного движения шара z(t) = z0 + A cos [ 2 π ν t ]. Мы нашли, что
Уравнение движения волн
Теперь мы хотим сделать то же самое для волн. Мы нашли формулу для формы и движения волны, колеблющейся как в пространстве, так и во времени.
Среди решений какого уравнения движения есть такая формула? Можно представить себе ответ. Очевидно, в него входят:
1. d2Z/dt2, изменение по времени изменения по времени Z(x,t).
2. d2Z/dx2, изменение в пространстве изменения в пространстве Z(x,t).
Естественным образом мы можем догадаться, что уравнение должно выглядеть как-то так:
Где C
t, C
xи C
0 – константы. Отмечу, что если Где C
Отмечу, что если Где C
= 1, C
x= 0, а C
0= -K/M, вы вернёмся к уравнению колебания шара на пружине. Какие же это константы в нашем случае?
Мы всегда можем положить Ct = 1. Если бы вы захотели, допустим, положить Ct = 5, я бы просто попросил вас разделить всё уравнение на 5, что и дало бы вам эквивалент варианта, в котором Ct = 1, просто с другими значениями остальных констант.
После этого оказывается, что значения Cx и C0 оказываются разными в различных физических системах. Мы изучим два разных класса волн, отличающихся разными константами.
У обеих классов Cx будет отрицательным, (здесь cw обозначает скорость перемещения высокочастотных волн).
Различаться эти классы будут тем, что у первого класса, Класс 1, C0 будет отрицательным, и будет равняться –(2 π μ)2, а у второго, Класс 0, C0 будет равно нулю.
Исследуем теперь свойства волн двух этих классов уравнений. Но до этого нужно провести ещё одно вычисление, которое мы уже делали ранее.
Но до этого нужно провести ещё одно вычисление, которое мы уже делали ранее.
Быстрый подсчёт
Для нашей бесконечной волны
Нам нужно будет знать d
2Z/dt
2и d
2Z/dx
2. В предыдущей статье мы уже показали, что для шара на пружине, движущегося согласно z(t) = z
0+ A cos [ 2 π ν t ], получается, что
. Изменение по времени даёт нам множитель 2 π ν, а изменение по времени изменения по времени даёт нам два множителя. Кроме того, тут есть общий знак минуса. Поэтому вас не удивит, что:
•
•
Каждое изменение по времени даёт нам множитель ν = 1/T (чем больше период, тем медленнее идёт изменение по времени), а каждое изменение в пространстве даёт нам множитель 1/λ (чем длиннее волна, тем медленнее изменение в пространстве).
Доказательство
Для бесконечной волны у нас есть основное уравнение
И мы хотим показать, что
Несколько фактов:
• Z – Z0 = A cos (2π [ν t – x/λ]) (просто в основном уравнении перенесли Z0 в левую часть)
• Поскольку Z0 — константа, не зависящая от времени и пространства, dZ0/dt = 0 and dZ0/dx = 0.
• d(cos t)/dt = – sin t, и d(sin t)/dt = + cos t
• d(F[a t +b x])/dt = a d(F[a t +b x])/d(a t+ b x), где a и b – константы, а F – любая функция от (a t + b x).
• d[A f(t)]/dt = A d[f(t)]/dt, где f(t) – любая функция от t, а A — константа
Всё вместе это означает, что:
и
Поскольку основная формула для волны не изменится при замене (ν t) на (-x/λ), вычисление d
2Z/dx
2не отличается от вычисления d
2Z/dt
2, просто вместо d/dt, дающего множитель (2π ν), у нас будет d/dx, дающий множитель (- 2π/λ). Но, поскольку в ответе есть два таких множителя, мы просто заменим (2π ν)
2на (- 2π/λ)
2= (+2π/λ)
2; минус значения не имеет (общий минус в сложении остаётся). Как нам и требовалось доказать,
Мелкий шрифт: все указанные выше производные на самом деле являются частными производными.
Класс 0: волны любой частоты и равных скоростей
В этом классе волн уравнение движения будет таким:
Подключив формулу Z(x,t) для бесконечной волны и используя только что сделанные нами подсчёты, мы находим, что:
Поделим уравнение на
, мы получим
Поскольку частоты, скорости и длины волн положительные, можно извлечь корень и получить
ν = cw/λ, или, если хотите, λ = cw/ν = cw T
Из этой формулы мы узнаём, что:
• Изначально у нашей волны, так, как мы её записали, могла быть любая частота и любая длина волны. Но уравнение движения заставляет их зависеть друг от друга. Для волн класса 0 можно выбрать любую частоту, но после этого длина волны определяется через λ = cw/ν.
Но уравнение движения заставляет их зависеть друг от друга. Для волн класса 0 можно выбрать любую частоту, но после этого длина волны определяется через λ = cw/ν.
• Все волны класса 0, вне зависимости от частоты, перемещаются со скоростью cw. Это следует из формулы λ = cw T и рис. 3 предыдущей статьи. Понаблюдайте, как волна проходит один цикл колебаний за время одного периода Т. Что происходит? Волна выглядит точно так же после Т, но каждый гребень сместился туда, где был его сосед – на расстояние λ. Это значит, что гребень передвигается на расстояние λ за время Т – одна длина волны за один период колебаний – и значит, что гребни движутся со скоростью λ / T = cw. Это верно для всех частот и их периодов, и всех длин волн!
• Как и в случае с шаром на пружине, амплитуда А этих волн может быть любой, сколь угодно большой или малой. И это так для всех частот.
Класс 1: волны с частотой больше минимальной, с разными скоростями
Для этого класса волн наше уравнение движение будет таким:
Подставив формулу Z(x,t) для бесконечной волны и использовав быстрое вычисление, указанное выше, мы найдём, что
Поделив уравнение на
, мы получим
Поскольку частоты, скорости и длины волн положительные, мы можем извлечь квадратный корень и получить
Напомню, что y
1/2 — это то же самое, что √y.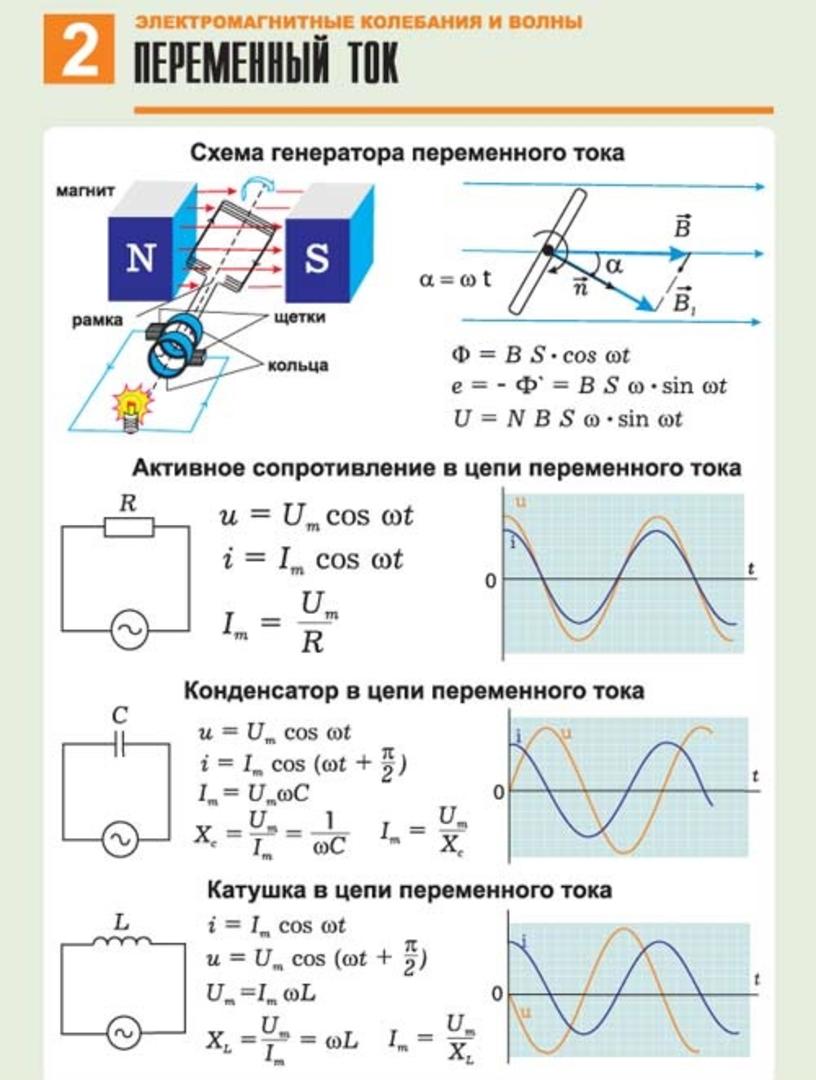
Эта формула сильно отличается от формулы для волн класса 0, как и последствия её применения.
Во-первых, уравнение движения говорит о наличии минимально допустимой частоты. Поскольку (cw/λ) 2 всегда положительно,
Чтобы приблизиться к ν = μ, необходимо увеличивать λ. Для очень больших длин волн частота приближается к μ, но меньше её стать не может. Для волн класса 0 это было не так. У них было ν = cw / λ, так что для них, чем больше вы делаете λ, тем сильнее ν приближается к нулю. Для волн класса 1 возможно любое значение ν, большее μ.
Во-вторых, мы нашли доказательство того, что у всех волн класса 0 скорость одинакова, но он не работает для волн класса 1. Единственный вариант, в котором он может сработать, если взять ν очень сильно больше, чем μ; для этого нам нужно сделать λ очень маленьким (и, соответственно, 1/ λ очень большим). В этом случае
То есть, на очень больших частотах и малых длинах волн у волн класса 1 будет примерно такое же соотношение между частотой и длиной волны, как у волн класса 0, поэтому по тем же причинам, что и волны класса 0, такие волны будут перемещаться со скоростью, (примерно) равной cw.
Что верно для волн обоих классов, так это то, что амплитуда А может быть любой, сколь угодно малой или большой, и не зависит от частоты.
Рис. 1. Для волн класса 0 и 1 уравнение движение даёт взаимосвязь между частотой, или периодом, и длиной волны, или 1/длину волны. На каждом из графиков показана взаимосвязь этих величин в зависимости от уравнения движения. Три графика показывают одно и то же, но построены они на разных переменных. Голубые линии относятся к волнам класса 0. Красные обозначают волны класса 1, скорость которых получается такой же на очень высоких частотах и малых длинах волн, когда они совпадают с голубыми линиями. Но на минимальной частоте μ (и с максимальным периодом 1/μ), обозначенных зелёным, две кривые расходятся при увеличении длин волн.
Мелкий шрифт: возможно, вы заметили, что я немножечко схитрил. Я не подсчитывал скорость волн класса 1. Дело в том, что здесь притаился очень хитрый подвох. У волн класса 0 я подсчитывал их скорость, следя за перемещениями гребней. Это работает потому, что в классе 0 волны всех частот перемещаются на одной скорости. Но у класса 1, или у любого другого, где волны разной частоты перемещаются с разной скоростью, скорость реальной волны не задаётся скоростью перемещения её гребней! Оказывается, что гребни движутся быстрее, чем cw, но скорость волны получается меньше, чем cw. Чтобы это понять, необходимо использовать весьма неочевидную логику и разницу между «групповой» и «фазовой» скоростью. Я пока обойду этот подвох; просто хотел обратить ваше внимание на его существование, чтобы вы не получили неправильное представление.
Это работает потому, что в классе 0 волны всех частот перемещаются на одной скорости. Но у класса 1, или у любого другого, где волны разной частоты перемещаются с разной скоростью, скорость реальной волны не задаётся скоростью перемещения её гребней! Оказывается, что гребни движутся быстрее, чем cw, но скорость волны получается меньше, чем cw. Чтобы это понять, необходимо использовать весьма неочевидную логику и разницу между «групповой» и «фазовой» скоростью. Я пока обойду этот подвох; просто хотел обратить ваше внимание на его существование, чтобы вы не получили неправильное представление.
Финальные комментарии по поводу классических волн
Можно найти много знакомых примеров волн класса 0, включая звук в воздухе, воде или металле (где cw – скорость звуковых волн в материале), свет, и другие электромагнитные волны (где cw = с в вакууме), и волны на верёвках или струнах, как на рис. 2 в предыдущей статье. Поэтому волнам класса 0 обучают в начальных курсах физики. Не могу привести примера волн класса 1 в обычной жизни, но вскоре мы увидим, что эти волны так же важны для Вселенной.
У нас есть удобная формула E = 2 π2 ν2 A2 M для энергии шара массы М на пружине. Формулы для других осцилляторов зависят от их природы, но их форма примерно такая же. Но в случае волн мы не упоминали их энергию. В частности из-за того, что мы для упрощения математики изучали волны с бесконечным числом гребней. Интуитивно понятно, что какая-то энергия должна храниться в движении и форме каждого гребня и впадины, и с бесконечным количеством гребней и впадин количество энергии в волне будет бесконечным. Это можно обойти двумя путями. Точные формулы зависят от типа волны, но давайте рассмотрим волны класса 0 на верёвке.
• Количество энергии на одну длину волны (хранящееся в промежутке между точкой x и точкой x + λ), конечно, и равно 2 π2 ν2 A2 Mλ, где Mλ — масса отрезка верёвки длиной λ.
• В реальности волны не бывают бесконечными. Как импульс из нескольких гребней и впадин, показанный на рис. 2 в прошлой статье, любая волна будет конечной, у неё будет конечное количество гребней и впадин. Если она протянется на длину L, то есть, у неё будет L/λ гребней, тогда переносимая ей энергия будет равнятся 2 π2 ν2 A2 ML, где ML — масса отрезка верёвки длиной L. Это просто L/λ, умноженное на энергию на одну длину волны.
2 в прошлой статье, любая волна будет конечной, у неё будет конечное количество гребней и впадин. Если она протянется на длину L, то есть, у неё будет L/λ гребней, тогда переносимая ей энергия будет равнятся 2 π2 ν2 A2 ML, где ML — масса отрезка верёвки длиной L. Это просто L/λ, умноженное на энергию на одну длину волны.
Для волн, распространяющихся не по верёвкам, детали уравнений будут отличаться, но энергия на одну длину волны простой колебательной системы всегда будет пропорциональной ν2 A2.
В классе 1 существует очень интересная волна, которой не бывает в классе 0. Это случай, когда ν = μ, минимальному значению, а λ = бесконечности. В этом случае волна принимает вид
Эта волна не зависит от x в любое время, то есть Z(x,t) будет константой по всему пространству, а Z колеблется во времени точно так, как шар на пружине с частотой μ. Такая стационарная волна, показанная на рис. 2, окажется очень важной в дальнейших рассуждениях.
Рис. 2
Квантовые волны
Для шара на пружине разница между классической и квантовой системой была в том, что в первом случае амплитуда могла принимать произвольные значения, как и энергия, а в квантовом случае амплитуда и энергия квантовались. Для любой похожей колебательной системы это работает таким же образом. Возможно, мы можем догадаться, что это выполняется и для волн…
7. Колебания, волны — Физика62
1.1. Физические термины и классификация колебаний, волн
Колебание — это движение, которое периодически повторяется около точки равновесия.
Виды колебаний по физической природе:
1. Механические — колеблется материя.
Маятник
— это система, в которой физическое тело колеблется. Осциллятор — это
колеблющееся тело. Математический маятник — это материальная точа
подвешенная на нерастяжимой, неупругой нити. Пружинный — это тело
подвешенное на пружину при малых деформациях, масса которой пренебрежимо мала относительно массы тела. Физический
— это любое абсолютно неупругое тело.
Физический
— это любое абсолютно неупругое тело.
2. Электромагнитные — колеблется электрическое и магнитное поле. Колебательный контур — это совокупность катушки и конденсатора, в которых возникают электромагнитные колебания.
Основные характеристики механических колебаний:
1. Амплитуда — это максимальное смещение от точки равновесия (A, x0). СИ: [x0]=1м.
2. Период — это время одного полного колебания, когда тело проходит одну и туже точку дважды (T). [T]=1с (секунда).
3. Частота — количество колебаний за одну секундe (ν). СИ: [ν]=1 Гц (Герц)=1с-1 (секунда в минус первой степени)
4. Фаза — это состояние колебательной системы, которая характеризуется определенным положением тела s(t) и направлением движения (φ). [φ]=1рад (радиан)
5. Циклическая
частота (по определению угловая скорость при вращениях за один оборот) — это число колебаний, совершаемых за 2π секунд (ω0). СИ: [ω0]=1
рад/c
(радиан
в секунду). Как, проще запомнить: по определению угловая скорость это ω=∆φ/∆t, где ∆φ — изменение угла, ∆t — изменение времени. Угловая скорость за один полный оборот 360 град. или 2π рад.: ω=2π/T, где T — время одного оборота. Формулы для циклической частоты точно такая же, поэтому ω0=2π/T=2πν=2πN/t, если подставить 2π вместо t, то слагаемые 2π/2π сокращаются и получается, что ω0=N за t=2π (с).
СИ: [ω0]=1
рад/c
(радиан
в секунду). Как, проще запомнить: по определению угловая скорость это ω=∆φ/∆t, где ∆φ — изменение угла, ∆t — изменение времени. Угловая скорость за один полный оборот 360 град. или 2π рад.: ω=2π/T, где T — время одного оборота. Формулы для циклической частоты точно такая же, поэтому ω0=2π/T=2πν=2πN/t, если подставить 2π вместо t, то слагаемые 2π/2π сокращаются и получается, что ω0=N за t=2π (с).
Виды колебаний по характеру взаимодействия с окружающей средой:
1. Вынужденные — колебание возникающие из-за внешней периодической силы.
2. Свободное — колебание происходящее за счет внутренних сил и переданной начальной энергии.
Виды колебаний по функции смещения s(t):
1. Гармонические — по закону синуса и косинуса s(t)=x*sin(ω)
2. Линейные — по функции линий s(t)=±|x| /\/\/\/\/\
3. Модульные — в виде двоичного кода: -_-_-_-
Виды колебаний по изменению энергии:
1. Затухающие — механическая энергия и амплитуда маятника убывает из-за внешнего взаимодействия
или сил трения.
2. Незатухающие — механическая энергия маятника и амплитуда не меняются.
Резонанс — это резкое возрастание амплитуды колебаний тела, если собственная частота колебаний тела совпадает с частотой колебаний внешней силы.
Волна — это колебание среды, которое распространяется в пространстве с конечной скоростью без переноса вещества.
Виды волн: механические (звуковые — воздух при н.у.V=330м/с), электромагнитные (свет в вакууме V=3*108м/с).
Длина волны — это расстояние между двумя одинаковыми фазами смещения.
Эхо — это явление отражения звуковой волны.
Виды волн по распространению:
1. Продольная – это волна, у которой частицы среды колеблются вдоль скорости ее распространения.
1.2. Формулы для колебаний и волн
2.
Доплеровский сдвиг: определение и формулы — видео и расшифровка урока
Уравнение эффекта Доплера
Однако эффект Доплера не является полностью теоретическим. Мы можем использовать уравнение эффекта Доплера для расчета скорости источника и наблюдателя, исходной частоты звуковых волн и наблюдаемой частоты звуковых волн.
Мы можем использовать уравнение эффекта Доплера для расчета скорости источника и наблюдателя, исходной частоты звуковых волн и наблюдаемой частоты звуковых волн.
Использование уравнения в различных сценариях
Хотя существует только одно уравнение эффекта Доплера, оно изменяется в различных ситуациях в зависимости от скорости наблюдателя или источника звука.Давайте посмотрим, как мы можем применить уравнение эффекта Доплера в различных ситуациях.
Примените уравнение
1. Источник движется к наблюдателю в состоянии покоя
Представьте снова нашу машину скорой помощи. В этом сценарии вы стоите на месте, а скорая помощь движется к вам. Вернемся к нашему уравнению. Скорость наблюдателя равна нулю, поэтому vo равно нулю. Подставив это в уравнение выше, мы получим уравнение, когда источник движется к неподвижному наблюдателю:
2.
 Источник, удаляющийся от покоящегося наблюдателя
Источник, удаляющийся от покоящегося наблюдателя Теперь представьте, что мимо вас проехала скорая помощь. Скорая помощь едет со скоростью 25 м/с, но вы все еще стоите на месте. Частота звука, издаваемого машиной скорой помощи, составляет 1000 Гц, а звуковые волны распространяются со скоростью 343 м/с. Поскольку ваша скорость равна нулю, мы можем снова исключить vo из уравнения. Но на этот раз машина скорой помощи удаляется от вас, поэтому ее скорость отрицательна, чтобы указать направление. Вставка наших чисел в уравнение дает нам:
Частота, воспринимаемая наблюдателем, меньше фактической частоты, излучаемой сиреной, как мы и ожидаем от эффекта Доплера.
3. Наблюдатель движется к стационарному источнику
Теперь представьте, что вы едете в машине на шумную вечеринку. Когда вы приближаетесь к динамикам, звуковые волны сближаются, а частота увеличивается. В этом случае вы двигаетесь, а источник нет. Итак, vs будет равно нулю, и мы получим следующее уравнение:
Когда вы приближаетесь к динамикам, звуковые волны сближаются, а частота увеличивается. В этом случае вы двигаетесь, а источник нет. Итак, vs будет равно нулю, и мы получим следующее уравнение:
4.Наблюдатель, удаляющийся от стационарного источника
Вы минуете шумную вечеринку и отправитесь в более спокойную обстановку. Теперь вы удаляетесь от звуковых волн, и частота уменьшается. Итак, поскольку вы уходите, ваша скорость становится отрицательной. Итак, вместо прибавления vo мы теперь вычитаем, так как vo отрицательно.
5.И Наблюдатель, и Источник движутся навстречу друг другу
Теперь представьте себе движение по шоссе. Вы движетесь вперед со скоростью 30 м/с, а полицейская машина мчится по противоположной стороне шоссе к вам со скоростью 40 м/с. Поскольку источник движется к вам, его скорость положительна. Вы тоже движетесь к ней, так что ваша скорость тоже положительна. Скорость излучаемых звуковых волн составляет 343 м/с, а частота — 900 Гц. Итак, какова воспринимаемая вами частота?
Вы движетесь вперед со скоростью 30 м/с, а полицейская машина мчится по противоположной стороне шоссе к вам со скоростью 40 м/с. Поскольку источник движется к вам, его скорость положительна. Вы тоже движетесь к ней, так что ваша скорость тоже положительна. Скорость излучаемых звуковых волн составляет 343 м/с, а частота — 900 Гц. Итак, какова воспринимаемая вами частота?
Подставляя наши переменные, мы получаем 1108 Гц, более высокую воспринимаемую частоту, поскольку звуковые волны сжимаются.
6. Наблюдатель и источник удаляются друг от друга
Теперь вы и полицейская машина пересеклись и находитесь на противоположных траекториях. Поскольку вы оба удаляетесь друг от друга, воспринимаемая частота должна быть меньше, чем излучаемая автомобилем. Поскольку теперь вы оба удаляетесь, обе ваши скорости отрицательны.
7.Наблюдатель, движущийся к источнику, удаляющемуся
Теперь скорая помощь начинает преследовать полицейскую машину со скоростью 35 м/с. Врач скорой помощи, управляющий машиной скорой помощи, является наблюдателем, а полицейская машина — источником. Поскольку наблюдатель движется к источнику, скорость положительна. Источник удаляется, так что скорость отрицательна. Снова подставив наши числа в первое уравнение эффекта Доплера, мы получим:
8.Источник движется к удаляющемуся наблюдателю
Теперь представьте, что машина скорой помощи проезжает мимо полицейской машины. Источник, полицейская машина, теперь движется к машине скорой помощи, поэтому ее скорость положительна. Наблюдатель, скорая помощь, удаляется от источника, поэтому его скорость отрицательна. Используя наше уравнение эффекта Доплера, мы получаем:
Наблюдатель, скорая помощь, удаляется от источника, поэтому его скорость отрицательна. Используя наше уравнение эффекта Доплера, мы получаем:
Резюме урока:
Эффект Доплера — это сдвиг частоты звуковых волн из-за движения наблюдателя, источника или того и другого.Когда один объект удаляется от другого, их скорость отрицательна, а когда они движутся навстречу друг другу, скорость положительна. Используя основное уравнение для эффекта Доплера, мы можем рассчитать наблюдаемую частоту звука в любом количестве ситуаций. Вот снова это уравнение:
Что такое электромагнитные волны — определения, примечания, формулы, уравнения и книги
Волна — это не что иное, как образец возмущения, которое распространяется и несет с собой энергию. Вы можете создать волну на веревке, перемещая один конец веревки вверх и вниз. Волне, создаваемой на веревке, нужна среда для распространения, и здесь средой является сама веревка. Этот тип волн известен как механические волны. Но в случае электромагнитных волн им не нужна среда для распространения. Электромагнитные волны — это волны, возникающие в результате вариаций электрического поля и магнитного поля. Или мы можем сказать, что электромагнитные волны есть не что иное, как изменяющиеся магнитные и электрические поля.Известно также, что электромагнитные волны являются решениями уравнений Максвелла. А уравнения Максвелла являются фундаментальными уравнениями электродинамики. Электромагнитные волны могут передавать энергию и проходить через вакуум. световые волны являются примерами электромагнитных волн. Обычно электромагнитные волны изображаются синусоидальным графиком.
Вы можете создать волну на веревке, перемещая один конец веревки вверх и вниз. Волне, создаваемой на веревке, нужна среда для распространения, и здесь средой является сама веревка. Этот тип волн известен как механические волны. Но в случае электромагнитных волн им не нужна среда для распространения. Электромагнитные волны — это волны, возникающие в результате вариаций электрического поля и магнитного поля. Или мы можем сказать, что электромагнитные волны есть не что иное, как изменяющиеся магнитные и электрические поля.Известно также, что электромагнитные волны являются решениями уравнений Максвелла. А уравнения Максвелла являются фундаментальными уравнениями электродинамики. Электромагнитные волны могут передавать энергию и проходить через вакуум. световые волны являются примерами электромагнитных волн. Обычно электромагнитные волны изображаются синусоидальным графиком.
Как показано на рисунке Электромагнитные волны состоят из переменных во времени электрического и магнитного полей, и они перпендикулярны друг другу И эти оба поля также перпендикулярны направлению распространения волн. И из-за этого Электромагнитные волны имеют поперечный характер.
И из-за этого Электромагнитные волны имеют поперечный характер.
Электромагнитные волны — одна из самых важных глав современной физики при подготовке ко всем конкурсным экзаменам, потому что она помогает понять важные свойства электромагнитных волн. Эта глава также поможет вам понять различные типы электромагнитных волн и их применение. Это простая для понимания и высоко оцениваемая тема. Иногда Концепция электромагнитных волн и другие разделы физики смешиваются с разными вопросами, которые задают на различных конкурсных экзаменах.
Онлайн-подготовка к JEE Main/NEETCrack JEE 2021 с онлайн-программой подготовки к JEE/NEET
Начинай сейчас
Заметки об электромагнитных волнах
Итак, мы шаг за шагом обсудим важные темы этой главы, а затем сделаем обзор этой главы. Тогда мы поймем важные формулы из этой главы. Запоминание этих формул повысит вашу скорость при решении вопросов.
Электромагнитные волны Темы
-
Электромагнитные волны и их характеристики.
 Поперечный характер электромагнитных волн.
Поперечный характер электромагнитных волн. -
Электромагнитный спектр (микроволны, инфракрасные, видимые, радиоволны, рентгеновские лучи, ультрафиолетовые, гамма-лучи). Применение э.м. волны.
Электромагнитные волны Обзор
В главе «Электромагнитные волны» мы изучим электромагнитные волны, их все важные свойства, их типы и области их применения. Так мы узнаем о
-
Уравнения Максвелла- Поскольку электромагнитные волны также являются решениями уравнений Максвелла.Поэтому важно узнать о них. Джеймс С. Максвелл заметил непоследовательность в законе Ампера и асимметрию в законах электромагнетизма. Таким образом, он представил некоторые предложения в этих законах. Например, он предложил идею тока смещения, чтобы устранить это противоречие в законе Ампера. Таким образом, он представил модифицированную версию этих законов с помощью уравнений Максвелла, которые приведены ниже.

-
Первое уравнение Максвелла — Закон Гаусса для электростатики
-
Второе уравнение Максвелла: закон Гаусса в магнетизме
-
3-е уравнение Максвелла-закон Фарадея
-
4-е уравнение Максвелла-закон Ампера
-
Эти волны не требуют среды для распространения и имеют поперечный характер.
-
Эти волны распространяются в пространстве со скоростью света в вакууме.
-
Волна, имеющая более высокую частоту, будет иметь более высокую энергию, связанную с ней.
-
Может использоваться для переноса информации.
-
Он движется по прямой.
-
Его можно разделить и рекомбинировать для формирования интерференционной/дифракционной картины.

-
Может отражаться или преломляться.
Одним из очень важных типов электромагнитных волн являются синусоидальные плоские волны. Все электромагнитные волны можно рассматривать как линейную суперпозицию синусоидальных плоских волн, распространяющихся в произвольных направлениях.
Например- Плоская волна, распространяющаяся в направлении x, имеет форму
А если E находится в плоскости y-z, то
Где E – электрическое поле при (x,t)
— Амплитуда электрического поля
= Угловая частота
c = скорость света в вакууме
Точно так же B находится в плоскости y-z
Где B = магнитное поле при (x,t)
= Амплитуда магнитного поля
Вы узнаете о некоторой физической величине, приведенной ниже-
-
Интенсивность электромагнитной волны
-
Импульс электромагнитной волны
-
Плотность энергии электромагнитной волны
-
Длина волны электромагнитной волны
-
Частота электромагнитной волны
Типы электромагнитных волн и их применение
В зависимости от диапазона частоты волны существуют различные типы электромагнитной волны. И эти волны имеют различное применение в нашей повседневной жизни. Ниже приведены некоторые типы электромагнитной волны
И эти волны имеют различное применение в нашей повседневной жизни. Ниже приведены некоторые типы электромагнитной волны
-
γ — луч (гамма-луч) — полезен при обнаружении дефектов, трещин, дефектов, отверстий в металлах.
-
Рентгеновские лучи — полезны при рентгенотерапии.
-
Ультрафиолетовое излучение — помогает в изучении молекулярной структуры.
-
Инфракрасные волны — помогают фотографировать в тумане или дыму
-
Микроволны — используются в радио- и телекоммуникациях.
Формулы электромагнитных волн
E находится в плоскости y-z
B находится в плоскости y-z
- Ток смещения Максвелла-
- Закон Гаусса для электричества-
- Закон Гаусса для магнетизма-
- Связь между и —
- Плотность энергии ЭМ волны-
- Интенсивность электромагнитной волны-
Как подготовить электромагнитные волны
- Во-первых, вы должны хорошо разбираться в концепциях электромагнитных волн, а также уметь применять их во время вступительного экзамена или при решении вопросов.
- Пожалуйста, постарайтесь понять каждое понятие из этой главы с помощью теории, вопросов с решениями и видеолекций по каждому важному понятию.
- Для каждой концепции отработайте достаточное количество задач, чтобы у вас было полное понимание концепции.
- Решите все вопросы дома с должной концентрацией и попробуйте сделать все расчеты самостоятельно, не видя сначала решения.
- При решении задач волнового уравнения необходимо также учитывать направление соответствующих векторов.
- Пожалуйста, хорошо разбирайтесь в спектре электромагнитных волн и применении различных электромагнитных волн.
- Вспомните все формулы Энергии, импульса, частоты Электромагнитных волн. Это поможет вам при решении вопросов.
Наконечники для электромагнитных волн
- Составьте план подготовки к этой главе и придерживайтесь расписания.
- Ставьте умные и реалистичные цели и старайтесь их достичь.

- Сначала изучите концепцию, а затем начинайте решать вопросы. Не задавайте вопросы напрямую, не зная концепции.
- Формулы из этой главы очень важны с точки зрения конкурсного экзамена. Поэтому, пожалуйста, запомните их и решите множество вопросов на основе этих формул.
- Решить вопрос предыдущего года различных экзаменов из этой главы.
- Используйте умные методы для решения вопросов.
Книги об электромагнитных волнах
Для Электромагнитных волн понятий главы в NCERT достаточно, но вам придется практиковать множество вопросов, включая вопросы предыдущего года, и вы можете следовать другим стандартным книгам, доступным для подготовки к конкурсным экзаменам, таким как Concepts of Physics (HC Verma) и Understanding Physics by DC Pandey. (Арихант Публикации).
Примечания по главам физики для технических и медицинских экзаменов
Интенсивность – Гиперучебник по физике
Обсуждение
интенсивность против.
 амплитуда
амплитуда
Амплитуда звуковой волны может быть количественно определена несколькими способами, каждый из которых является мерой максимального изменения величины, которое происходит, когда волна распространяется через некоторую область среды.
- Амплитуды, связанные с изменением кинематических величин частиц, составляющих среду
- Амплитуда смещения представляет собой максимальное изменение положения.
- Амплитуда скорости — это максимальное изменение скорости.
- Амплитуда ускорения — это максимальное изменение ускорения.
- Амплитуды, связанные с изменением объемных свойств сколь угодно малых участков среды
- Амплитуда давления представляет собой максимальное изменение давления (максимальное манометрическое давление).
- Амплитуда плотности — это максимальное изменение плотности.
Измерение смещения может оказаться невозможным. Для типичных звуковых волн максимальное смещение молекул в воздухе всего в сто или тысячу раз больше, чем сами молекулы — да и какие вообще существуют технологии для отслеживания отдельных молекул? Изменения скорости и ускорения, вызванные звуковой волной, одинаково трудно измерить в частицах, составляющих среду.
Колебания плотности ничтожны и недолговечны. Период звуковой волны обычно измеряется в миллисекундах. Есть некоторые оптические методы, которые позволяют изобразить сильные сжатия и разрежения, связанные с ударными волнами в воздухе, но это не те звуки, с которыми мы сталкиваемся в нашей повседневной жизни.
Колебания давления, вызванные звуковыми волнами, гораздо легче измерить. Животные (включая людей) уже несколько сотен миллионов лет делают это с помощью устройств, называемых ушами.Люди уже около сотни лет делают это с помощью электромеханических устройств, называемых микрофонами. Все типы амплитуд в равной степени подходят для математического описания звуковых волн, но амплитуды давления — это то, с чем мы, люди, имеем самую тесную связь.
В любом случае, результаты таких измерений редко публикуются. Вместо этого измерения амплитуды почти всегда используются в качестве исходных данных в некоторых вычислениях. Когда это делается электронной схемой (например, схемой в телефоне, которая подключается к микрофону), результирующее значение называется интенсивностью. Когда это делается нейронной цепью (например, цепью в вашем мозгу, которая связана с вашими ушами), результирующее ощущение называется громкостью.
Когда это делается нейронной цепью (например, цепью в вашем мозгу, которая связана с вашими ушами), результирующее ощущение называется громкостью.
Интенсивность звуковой волны представляет собой комбинацию ее скорости и плотности передачи энергии. Это объективная величина, связанная с волной. Громкость — это реакция восприятия на физическое свойство интенсивности. Это субъективное качество, связанное с волной, и оно немного сложнее. Как правило, чем больше амплитуда, тем больше интенсивность, тем громче звук.Звуковые волны с большой амплитудой называются «громкими». Звуковые волны с малой амплитудой называются «тихими» или «мягкими». Слово «низкий» иногда также используется для обозначения тихого, но этого следует избегать. Используйте «low» для описания звуков низкой частоты. Громкость будет рассмотрена в конце этого раздела, после определения термина «уровень» и его единицы децибел.
По определению, интенсивность ( I ) любой волны представляет собой усредненную по времени мощность (⟨ P ⟩), которую она передает на единицу площади ( A ) через некоторую область пространства. Традиционный способ указать усредненное по времени значение переменной величины — заключить его в угловые скобки (⟨⟩). Они похожи на символы «больше» и «меньше», но они выше и менее заострены. Это дает нам уравнение, которое выглядит так…
Традиционный способ указать усредненное по времени значение переменной величины — заключить его в угловые скобки (⟨⟩). Они похожи на символы «больше» и «меньше», но они выше и менее заострены. Это дает нам уравнение, которое выглядит так…
Единицей мощности в СИ является ватт, единицей площади в СИ является квадратный метр, поэтому единицей интенсивности в СИ является ватт на квадратный метр — единица, не имеющая специального названия.
| ⎡ ⎢ ⎣ |
Вт | = | Вт | ⎤ ⎥ ⎦ |
| м 2 | м 2 |
интенсивность и смещение
Для простых механических волн, таких как звук, интенсивность связана с плотностью среды и скоростью, частотой и амплитудой волны.Это можно показать длинным ужасным расчетом. Если вам не нравится смотреть, как делают колбасу внизу, переходите к уравнению прямо перед ярким столом.
Начните с определения интенсивности. Замените мощность энергией (как кинетической, так и упругой) с течением времени (один период для удобства).
|
Поскольку кинетическая и упругая энергии всегда положительны, мы можем разделить усредненную по времени часть на две части.
|
|||||||
|
|||||||
Механические волны в сплошной среде можно рассматривать как бесконечный набор бесконечно малых связанных гармонических осцилляторов. Маленькие массы соединены с другими маленькими массами маленькими пружинками, насколько хватает глаз. В среднем половина энергии простого гармонического осциллятора приходится на кинетическую, а половина на упругую. Тогда усредненная по времени полная энергия либо удваивает среднюю кинетическую энергию, либо удваивает среднюю потенциальную энергию.
Маленькие массы соединены с другими маленькими массами маленькими пружинками, насколько хватает глаз. В среднем половина энергии простого гармонического осциллятора приходится на кинетическую, а половина на упругую. Тогда усредненная по времени полная энергия либо удваивает среднюю кинетическую энергию, либо удваивает среднюю потенциальную энергию.
| ⟨ P ⟩ = | 2⟨ К ⟩ | = | 2⟨ U с ⟩ | |
| Т | Т | |||
Давайте поработаем над кинетической энергией и посмотрим, куда она нас приведет.Он состоит из двух важных частей — массы и скорости.
К = ½ мв 2
Частицы в продольной волне смещаются из положения равновесия функцией, которая колеблется во времени и пространстве. Используйте для этого одномерное волновое уравнение.
| ∆ с ( x , t ) = ∆ с sin | ⎡ ⎢ ⎣ |
2π | ⎛ ⎜ ⎝ |
футов — | х | ⎞⎤ ⎟⎥ ⎠⎦ |
| λ |
где…
| ∆ с ( x , t ) = | мгновенное перемещение в любом положении ( x ) и времени ( t ) |
| ∆ с = | амплитуда смещения |
| ƒ = | частота |
| λ = | длина волны|
| π = | всеми любимая математическая константа |
Возьмите производную по времени, чтобы получить скорость частиц в среде (а не скорость волны в среде).
|
||||||||
|
Затем возведите его в квадрат.
| δ V V 2 2 ( x , T ) = |
⎡ ⎢ ⎣ |
2π | ⎛ ⎜ ⎝ |
футов — | х | ⎞⎤ ⎟⎥ ⎠⎦ |
| λ |
На массу. Плотность, умноженная на объем, равна массе. Объем материала, который нас интересует, представляет собой коробку, площадь которой представляет собой поверхность, по которой распространяется волна, а длина — расстояние, которое проходит волна.За один период волна будет двигаться вперед на одну длину волны (λ).
Плотность, умноженная на объем, равна массе. Объем материала, который нас интересует, представляет собой коробку, площадь которой представляет собой поверхность, по которой распространяется волна, а длина — расстояние, которое проходит волна.За один период волна будет двигаться вперед на одну длину волны (λ).
м = ρ В = ρ А λ
В объеме, охватываемом одной длиной волны, все частицы материи движутся с разными скоростями. Исчисление необходимо для объединения множества различных значений в одно интегрированное значение. Здесь мы имеем дело с периодической системой, которая повторяется снова и снова. Мы можем начать наш расчет в любое время, если мы закончим на один цикл позже.Для удобства выберем время равным нулю — началу синусоидальной волны.
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
Очистить константы.
½ (ρ A ) (4π 2 F 2 Δ S 2 2 ) = 2π 2 ρ AF 2 Δ S 2
Затем поработайте над интегралом. Это может выглядеть тяжело, но это не так. Просто визуализируйте кривую квадрата косинуса, вычерченную за один цикл. Видите, как он делит ограничивающий его прямоугольник на равные половины?
Высота этого прямоугольника равна единице (как в числе 1 без единиц измерения), а ширина равна одной длине волны.Это дает площадь в одну длину волны и половину площади в половину длины волны.
| λ | ||||||
| ⌠ ⎮ ⌡ |
потому что 2 | ⎡ ⎢ ⎣ |
– 2π | х | ⎤ ⎥ ⎦ |
дх = ½λ |
| λ | ||||||
| 0 | ||||||
Сложите константы вместе с интегралом и разделите на один период, чтобы получить усредненную по времени кинетическую энергию. (Помните, что длина волны, деленная на период, равна скорости волны.)
(Помните, что длина волны, деленная на период, равна скорости волны.)
|
||||||||
|
На этом сложная часть завершена.Удвойте приведенное выше уравнение и разделите на площадь…
|
||||||
|
Еще немного алгебры, и все готово.
I = 2π 2 ρ f 2 v ∆ s 2
Теперь у нас есть уравнение, связывающее интенсивность ( I ) с амплитудой смещения (∆ с ).
Имеет ли смысл эта формула? Давайте проверим, как каждый из факторов влияет на интенсивность.
| коэффициент | комментариев |
|---|---|
| I ∝ ρ | Чем плотнее среда, тем интенсивнее волна.В этом есть смысл. Плотная среда упаковывает больше массы в любой объем, чем разреженная среда, и кинетическая энергия идет с массой. |
| I ∝ f 2 | Чем чаще волна сотрясает среду, тем интенсивнее волна. Я вижу это мысленным взором. Тусклая волна, которая просто не приводит в движение среду, не будет нести столько энергии, сколько волна, которая сотрясает среду как сумасшедшая. |
| I ∝ v | Чем быстрее распространяется волна, тем быстрее она передает энергию.Здесь вы должны помнить, что интенсивность измеряет не столько количество переданной энергии, сколько скорость передачи этой энергии. |
| I ∝ ∆ с 2 | Чем больше амплитуда смещения, тем интенсивнее волна. Просто подумайте об океанских волнах на мгновение. Водяная стена, движимая ураганом, дает гораздо больше силы, чем рябь в ванне. Метафора визуально неверна, поскольку звуковые волны продольные, а океанские волны сложны, но интуитивно она верна. |
Движение частиц можно описать в терминах смещения, скорости или ускорения. Интенсивность также может быть связана с этими величинами. Мы только что завершили тяжелую работу по связыванию интенсивности ( I ) с амплитудой смещения (∆ с ). Для полноты (и почему бы и нет) давайте также выведем уравнения для интенсивности через амплитуду скорости (∆ v ) и амплитуду ускорения (∆ a ).
интенсивность и скорость
Как интенсивность связана с максимальной скоростью (амплитуда скорости)? Давайте разберемся.Начните с одномерного волнового уравнения.
| ∆ с ( x , t ) = ∆ с sin | ⎡ ⎢ ⎣ |
2π | ⎛ ⎜ ⎝ |
футов — | х | ⎞⎤ ⎟⎥ ⎠⎦ |
| λ |
Напомним, что скорость — это производная смещения по времени.
|
||||||||
|
Перед функцией косинуса стоит амплитуда скорости.
∆ v = 2π f ∆ с
Решите это для амплитуды смещения.
Совсем недавно мы вывели уравнение для интенсивности через амплитуду смещения.
I = 2π 2 ρ f 2 v ∆ s 2
Объединить эти два уравнения…
| I = 2π 2 ρ f 2 v | ⎛ ⎜ ⎝ |
∆ по сравнению с | ⎞ 2 ⎟ ⎠ |
| 2π ф |
и упростите.
Теперь у нас есть уравнение, связывающее интенсивность ( I ) с амплитудой скорости (∆ v ).
интенсивность и ускорение
Как интенсивность связана с максимальным ускорением (амплитуда ускорения)? Еще раз, давайте узнаем. Опять же, начнем с одномерного волнового уравнения.
| ∆ с ( x , t ) = ∆ с sin | ⎡ ⎢ ⎣ |
2π | ⎛ ⎜ ⎝ |
футов — | х | ⎞⎤ ⎟⎥ ⎠⎦ |
| λ |
Напомним, что скорость — это производная смещения по времени…
|
||||||||
|
и что ускорение есть производная скорости по времени.
|
||||||||
|
Амплитуда ускорения — это то, что стоит перед функцией синуса (без учета знака минус).
∆ a = 4π 2 f 2 ∆ s
Измените это, чтобы сделать амплитуду смещения предметом.
Пришло время вернуться к нашему уравнению для интенсивности через амплитуду смещения.
I = 2π 2 ρ f 2 v ∆ s 2
Объединить два предыдущих уравнения…
| I = 2π 2 ρ f 2 v | ⎛ ⎜ ⎝ |
∆ и | ⎞ 2 ⎟ ⎠ |
| 4π 2 ф 2 |
и упростите.
Теперь у нас есть уравнение, связывающее интенсивность ( I ) с амплитудой ускорения (∆ a ).
интенсивность и давление
Амплитуда звуковой волны может быть гораздо легче измерена с помощью давления (объемное свойство материала, такого как воздух), чем смещение (смещение субмикроскопических молекул, из которых состоит воздух). Вот быстрый и грязный вывод более полезного уравнения интенсивность-давление из фактически бесполезного уравнения интенсивности-смещения.
Начните с уравнения, связывающего интенсивность с амплитудой смещения.
I = 2π 2 ρ f 2 v ∆ s 2
Теперь давайте поиграем в небольшую игру с символами — в игру под названием алгебра. Обратите внимание, что многие символы в приведенном выше уравнении возведены в квадрат. Возведите их все в квадрат, умножив числитель и знаменатель на 2ρ v .
| I = | 4π 2 ρ 2 f 2 v 2 ∆ с 2 |
| 2р v |
Запишите числитель как количество в квадрате.
| I = | (2πρ fv ∆ с ) 2 |
| 2р v |
Посмотрите на набор символов в скобках.
2πρ fv ∆ с
Посмотрите единицы измерения каждой физической величины.
| ⎡ ⎢ ⎣ |
кг | 1 | м | м | ⎤ ⎥ ⎦ |
|||
| м 3 | с | с | 1 |
Еще немного магии — на этот раз не алгебра, а анализ измерений.
| ⎡ ⎢ ⎣ |
кг | = | кг м | = | Н | = Па | ⎤ ⎥ ⎦ |
| м с 2 | м 2 с 2 | м 2 |
Единицами этой мешанины являются паскали, поэтому величина в скобках в предыдущем уравнении — это давление, точнее максимальное манометрическое давление. Теперь у нас есть уравнение, связывающее интенсивность с амплитудой давления.
где…
| I = | интенсивность [Вт/м 2 ] |
| ∆ P = | амплитуда давления [Па] |
| ρ = | плотность [кг/м 3 ] |
| v = | скорость волны [м/с] |
Вот медленный и четкий вывод уравнения интенсивность-давление. Начните с версии закона Гука, в которой используется объемный модуль ( K ).
Дробь слева представляет собой сжимающее напряжение, также известное как давление ( P ). Дробь справа представляет собой деформацию сжатия, также известную как дробное изменение объема (θ). Последний из этих двух интересует нас прямо сейчас. Представьте себе звуковую волну, которая растягивает и сжимает среду только в одном направлении. Если это так, то дробное изменение объема фактически совпадает с дробным изменением длины.
| θ = | ∆ В | = | ∂∆ с ( x , т ) |
| В 0 | ∂ х |
Здесь мы должны использовать исчисление, чтобы получить это дробное изменение, поскольку бесконечно малые кусочки и кусочки среды сжимаются и растягиваются с разной скоростью в разных точках пространства. Изменения длины описываются одномерным волновым уравнением.
| ∆ с ( x , t ) = ∆ с sin | ⎡ ⎢ ⎣ |
2π | ⎛ ⎜ ⎝ |
футов — | х | ⎞⎤ ⎟⎥ ⎠⎦ |
| λ |
Его пространственная производная такая же, как и дробное изменение объема.
| θ = | ∂∆ с ( x , т ) | = − | 2π | ∆ с соз | ⎡ ⎢ ⎣ |
2π | ⎛ ⎜ ⎝ |
футов — | х | ⎞⎤ ⎟⎥ ⎠⎦ |
| ∂ х | λ | λ |
Интересно отметить, что изменения объема не совпадают по фазе со смещениями, поскольку взятие производной изменило синус на отрицательный косинус. Изменения объема отстают на 90° от смещения, поскольку отрицательный косинус отстает на 90° от синуса. Наиболее резкие изменения объема происходят в местах, где частицы возвращаются в свои равновесные положения.
Изменения объема отстают на 90° от смещения, поскольку отрицательный косинус отстает на 90° от синуса. Наиболее резкие изменения объема происходят в местах, где частицы возвращаются в свои равновесные положения.
Интересно, но сейчас не очень полезно. Нас больше волнует , где эти экстремальные значения, чем , где они встречаются. Для этого мы заменяем выражение отрицательного косинуса его крайним абсолютным значением +1. Это оставляет нам это выражение для максимальной деформации (∆θ).
Подставив это обратно в уравнение объемного модуля, мы получим максимальное манометрическое давление.
| ∆ P = K | 2π | ∆ с |
| λ |
А теперь о грязной работе. Вспомним эти два уравнения для скорости звука.
Подставить в предыдущее уравнение…
| ∆ P = v 2 ρ | 2π ж | ∆ с |
| v |
и упростите.
∆ P = 2πρ fv ∆ с
Знакомый? Он находится в числителе выражения, которое появилось ранее.
| I = | (2πρ fv ∆ с ) 2 |
| 2р v |
Замените стопку символов в скобках и вот. Мы снова получаем эту вещь — соотношение интенсивности и амплитуды давления.
где…
| I = | интенсивность [Вт/м 2 ] |
| ∆ P = | амплитуда давления [Па] |
| ρ = | плотность [кг/м 3 ] |
| v = | скорость волны [м/с] |
интенсивность и плотность
Изменения плотности среды, связанные со звуковой волной, прямо пропорциональны изменениям давления.Отношения следующие…
Это похоже на уравнение Ньютона-Лапласа для скорости звука в идеальном газе, но в нем отсутствует коэффициент теплоемкости γ (гамма). Почему?
Почему?
Предполагая, что первое уравнение правильное, решите его для ∆ρ.
Возьмем зависимость амплитуды давления от амплитуды смещения…
∆ P = 2πρ fv ∆ с
замена…
| ∆ρ = | 2πρ fv ∆ с |
| v 2 |
и упростим, чтобы получить соотношение плотности и амплитуды смещения.
Немного забавно. Давайте попробуем что-нибудь еще.
Опять же, предполагая, что первое уравнение правильное, решите его для ∆ P .
∆ P = ∆ρ v 2
Возьмем уравнение, связывающее интенсивность с амплитудой давления…
сделать аналогичную замену…
и упростите, чтобы получить уравнение, связывающее интенсивность с амплитудой плотности.
Не очень интересно, но теперь наш список завершен.
| амплитуда | интенсивность | соединение | |||
|---|---|---|---|---|---|
| смещение |
|
||||
| скорость | ∆ v = 2π f ∆ с | ||||
| ускорение | ∆ a = 2π f ∆ v | ||||
| давление | |||||
| плотность |
уровень
НАПИСАТЬ ЭТУ ЧАСТЬ
Что такое уровень?
Типы уровней.
Я избавляюсь от всей своей мебели. Все это. И я собираюсь построить эти разные уровни со ступенями, и все это будет покрыто множеством подушек. Знаете, как в Древнем Египте.
Космо Крамер, 1991
Для любого периодического сигнала уровень его интенсивности ( L I ) в бел [B] определяется как логарифм по основанию десяти отношения его интенсивности к интенсивности опорного сигнала .Так как для большинства целей эта единица великовата, принято делить бел на десятые доли или децибел [дБ]. Бел — безразмерная единица.
| l | l i = 10 log | ⎛ ⎜ ⎝ | ⎝ | i | ⎞ ⎟ ⎠ |
| 1 I |
Когда сигнал звуковая волна, эта величина называется уровнем интенсивности звука , часто сокращенно SIL .
давление
уровень звукового давления, SPL
|
|
||||||||||
|
|
||||||||||
|
|
Text
| l p = 20 log | ⎛ ⎜ ⎝ | Δ P | ⎞ ⎟ ⎠ |
| Δ P 7 0 |
Примечания
- Условно звук имеет уровень 0 дБ при силе давления 20 мкПа и частоте 1000 Гц.
 Это общепринятый 90 519 порог слышимости 90 520 для людей. Звуки с интенсивностью ниже этого значения неслышны (вполне возможно) каждому человеку.
Это общепринятый 90 519 порог слышимости 90 520 для людей. Звуки с интенсивностью ниже этого значения неслышны (вполне возможно) каждому человеку. - Для звука в воде и других жидкостях используется эталонное давление 1 мкПа.
- Диапазон интенсивности слышимого звука настолько велик, что требуется шесть порядков величины, чтобы добраться от порога слышимости (20 мкПа~0,5 пВт/м 2 ) до порога боли (20 Па~0,5 Вт/м). м 2 ).
- Звонок был изобретен инженерами телефонной сети Bell в 1923 году и назван в честь изобретателя телефона Александра Грэхема Белла.
- Уровень 0 дБ не совпадает с интенсивностью 0 Вт/м 2 или амплитудой давления 0 Па или амплитудой смещения 0 м.
- Сигналы ниже порогового или эталонного значения являются отрицательными. Тишина имеет уровень отрицательной бесконечности.
- Поскольку десятичный логарифм 2 равен примерно 0,3, каждые дополнительные 3 дБ уровня соответствуют примерно удвоению амплитуды.

- Увеличение на 10 децибел воспринимается людьми как примерно вдвое более громкое.
- Другие примеры логарифмических шкал включают в себя: магнитуды землетрясений (часто называемые по устаревшему названию шкалой Рихтера), рН, звездные величины, диаграммы электромагнитного спектра, … что-то еще?
- Преобразуйте уравнение децибел для уровня из отношения в разницу.
- Извержение 1883 года в Кракатау, Индонезия (часто неправильно пишется Кракатау), имело интенсивность 180 дБ и было слышно на расстоянии 5 000 км на Маврикии. Взрыв Кракатау зарегистрировал 172 децибела на расстоянии 100 миль от источника.
В равной степени разумно было бы использовать натуральные логарифмы вместо десятичной системы счисления, но это встречается гораздо реже. Для любого периодического сигнала отношение натурального логарифма его интенсивности к эталонному сигналу является мерой уровня его интенсивности ( L ) в непер [Np]. Как и в случае с белом, непер принято делить на десятые доли или децинепер [dNp]. Непер также является безразмерной единицей.
Непер также является безразмерной единицей.
|
|||||
|
Непер и децибел настолько редки по сравнению с белами и децибелами, что по сути являются ответом на простой вопрос.
Примечания и цитаты.
- Цитата Расса Роулетта из Университета Северной Каролины: «[Непер] признает британского математика Джона Нейпира, изобретателя логарифма. Нейпир часто произносил свое имя по буквам Джон Непер, а в своих трудах он использовал латинскую форму Иоанна Наперо».
 AHD «Шотландский математик, который изобрел логарифмы и ввел использование десятичной точки в записи чисел».
AHD «Шотландский математик, который изобрел логарифмы и ввел использование десятичной точки в записи чисел». - Значение в неперах разности уровней двух значений ( F 1 и F 2 ) величины поля получается путем возведения натурального логарифма отношения двух значений, Δ L N = ln F 1 / F 2 .Для так называемых величин мощности (см. ниже) в определение разности уровней включен коэффициент 0,5: Два уровня величины поля отличаются на 1 Np, когда значения величины различаются на коэффициент e (основание натуральных логарифмов). (Уровни двух степенных величин различаются на 1 Np, если величины различаются в 2 раз.) и может быть представлен как «один.«Из этой меры нельзя сделать вывод, о каком количестве идет речь, так что во всех случаях приходится четко указывать вид количества».
| уровень (дБ) | источник |
|---|---|
| −∞ | абсолютная тишина |
| −24 | звучит тише этого невозможно из-за хаотического движения молекул воздуха при комнатной температуре (∆ P = 1. 27 мкПа) 27 мкПа) |
| −20,6 | самая тихая комната в мире на данный момент (Microsoft Building 87, Редмонд, Вашингтон) |
| −9,4 | бывшая самая тихая комната в мире (Orfield Laboratories, Миннеаполис, Миннесота) |
| 0 | порог слышимости, эталонное значение звукового давления (∆ P 0 = 20 мкПа) |
| 10–20 | обычное дыхание, шелест листьев |
| 20–30 | шепчет на высоте 5 футов |
| 30–40 | |
| 40–50 | кофеварка, библиотека, тихий офис, тихий жилой район |
| 50–60 | посудомоечная машина, электробритва, электрическая зубная щетка, большой офис, дождевик, холодильник |
| 60–70 | кондиционер, салон автомобиля, будильник, фоновая музыка, обычный разговор, телевизор, пылесос, стиральная машина |
| 70–80 | кофемолка, унитаз со сливом, движение по автостраде, фен |
| 80–90 | блендер, дверной звонок, салон автобуса, кухонный комбайн, вывоз мусора, интенсивное движение, ручная пила, газонокосилка, станки, шумный ресторан, тостер, звонок телефона, чайник со свистком |
| >85 | OSHA 1910.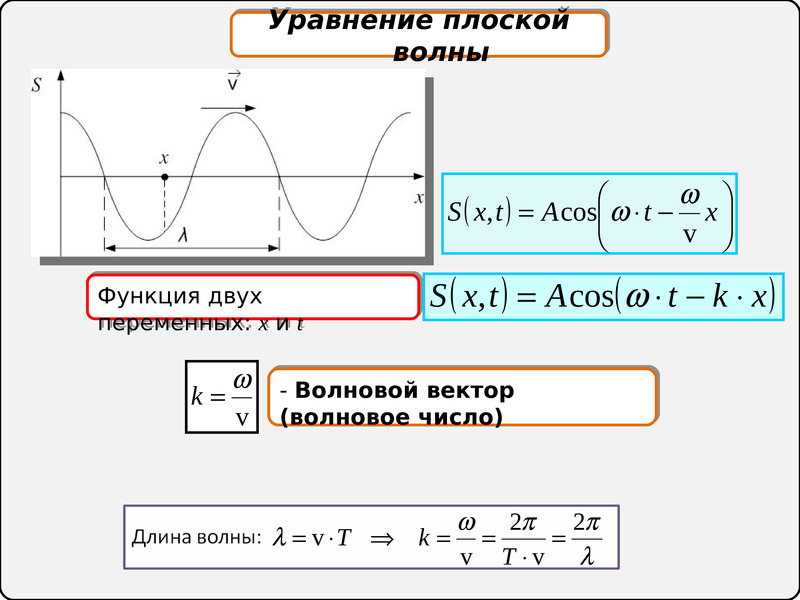 95(i)(1): Работодатели должны предоставить средства защиты органов слуха всем сотрудникам, подвергающимся воздействию средневзвешенного по времени 85 децибел или выше за 8 часов бесплатно для сотрудников. 95(i)(1): Работодатели должны предоставить средства защиты органов слуха всем сотрудникам, подвергающимся воздействию средневзвешенного по времени 85 децибел или выше за 8 часов бесплатно для сотрудников. |
| 090–100 | электродрель, кричал разговор, трактор, грузовик |
| 100–110 | детский плач, магнитола, заводское оборудование, мотоцикл, школьные танцы, снегоуборочная машина, снегоход, пищащая игрушка, которую держат возле уха, поезд метро, класс деревообработки |
| 110–120 | сирена скорой помощи, автомобильный гудок, бензопила, дискотека, игра в футбол, реактивный самолет на рампе, воздуходувка, персональный музыкальный проигрыватель на высоких частотах, электропила, рок-концерт, крик в ухо, симфонический концерт, игровые автоматы, |
| 113 | самый громкий хлопок (Аластер Галпин, Новая Зеландия, 2008 г.) |
| 120–130 | болевой порог (∆ P = 20 Па), автостерео, ленточный концерт, цепная пила, молоток на гвозде, тяжелая техника, пневматические дрели, гонки на серийных автомобилях, гром, дрель, секция перкуссии в симфонии |
| 125 | самая громкая птица (белый колокольчик, Procnias albus ) |
| 130–140 | сирена воздушной тревоги, взлет реактивного самолета, отбойный молоток |
| 140–150 | |
| 150–160 | артиллерийский огонь на высоте 500 футов, взрыв воздушного шара, капсюль, петарда, взлет реактивного двигателя |
| 160–170 | фейерверк, пистолет, винтовка |
| 170–180 | дробовик |
| 180–190 | запуск ракеты, 1883 г. извержение вулкана Кракатау, 1908 г. Тунгусский метеор извержение вулкана Кракатау, 1908 г. Тунгусский метеор |
| 194 | самый громкий звук, возможный в атмосфере Земли |
| +∞ | бесконечно громко |
слух
- громкость
- Громкость — это реакция восприятия на физическое свойство интенсивности.
- Повышение уровня на 10 дБ воспринимается большинством слушателей как удвоение громкости
- Изменение уровня на 1 дБ едва заметно для большинства слушателей
- Поскольку громкость зависит как от частоты, так и от интенсивности, для громкости был разработан специальный блок — фон. Один фон — это громкость звука в 1 дБ с частотой 1000 Гц; 10 фон – громкость звука 10 дБ с частотой 1000 Гц; и так далее.
- Если положить руку за ухо, уровень громкости усилится на 6–8 дБ.
- Просьба к кому-либо высказаться обычно приводит к увеличению громкости говорящего примерно на 10 дБ.
- поиск источника звука
- Разность фаз — это один из способов локализации звуков.
 Эффективен только для длин волн, превышающих 2 диаметра головы (расстояние от уха до уха). также известная как межушная разница во времени (ITD)
Эффективен только для длин волн, превышающих 2 диаметра головы (расстояние от уха до уха). также известная как межушная разница во времени (ITD) - Звуковые волны легко преломляются на длинах волн, превышающих диаметр человеческой головы (длина волны около 500 Гц равна 69 см).На более высоких частотах голова отбрасывает «тень». Звуки в одном ухе будут громче, чем в другом. также известная как интерауральная разница уровней (ILD)
- Разность фаз — это один из способов локализации звуков.
- Человеческое ухо может различить некоторые…
- 280 различных уровней интенсивности (кажется маловероятным)
- рыба
- В отличие от наших ушей и гидрофонов, рыбьи уши не обнаруживают звукового давления, то есть сжатия молекул. Вместо этого они воспринимают движение частиц, крошечные возвратно-поступательные движения частиц в ответ на звуковые волны.
сейсмические волны
Расширенная цитата, которую необходимо перефразировать.
Шкалы магнитуд являются количественными.
С помощью этих шкал измеряется размер землетрясения, выраженный амплитудой сейсмической волны (количество сотрясений в точке, удаленной от землетрясения), а не интенсивностью или степенью разрушительности. Большинство шкал магнитуд имеют логарифмическую основу, так что увеличение одного целого числа соответствует землетрясению в 10 раз сильнее, чем землетрясение, указанное следующим меньшим числом.Это означает примерно 30-кратное увеличение количества высвобождаемой энергии. Таким образом, магнитуда 5 представляет собой движение грунта примерно в 10 раз больше, чем магнитуда 4, и примерно в 30 раз больше высвобождаемой энергии. Землетрясение силой 5 баллов представляет собой 100-кратное движение грунта и 900-кратное выделение энергии при землетрясении магнитудой 3.
Шкала Рихтера была создана Чарльзом Рихтером в 1935 году в Калифорнийском технологическом институте. Он был создан для сравнения силы землетрясений.Одним из самых ценных вкладов доктора Чарльза Ф. Рихтера было признание того, что сейсмические волны, излучаемые всеми землетрясениями, могут дать хорошие оценки их магнитуд.
Он собрал записи сейсмических волн от большого количества землетрясений и разработал калиброванную систему измерения их магнитуды. Он откалибровал свою шкалу магнитуд, используя измеренные максимальные амплитуды поперечных волн на сейсмометрах, особенно чувствительных к поперечным волнам с периодами около одной секунды. Записи должны были быть получены с помощью специального прибора, называемого сейсмографом Вуда-Андерсона.Хотя его работа изначально была откалибрована только для этих конкретных сейсмометров и только для землетрясений в южной Калифорнии, сейсмологи разработали масштабные коэффициенты, чтобы распространить шкалу магнитуд Рихтера на многие другие типы измерений на всех типах сейсмометров по всему миру. На самом деле, были сделаны оценки магнитуд тысяч лунотрясений и двух землетрясений на Марсе.
Большинство оценок энергии исторически основывались на эмпирическом соотношении, разработанном Бено Гутенбергом и Чарльзом Рихтером.
log 10 E с = 4,8 + 1,5 M с
где энергия, E s , выражена в джоулях.
Недостатком этого метода является то, что 90 521 M 90 587 с 90 588 90 522 вычисляется из полосы пропускания примерно от 18 до 22 с. В настоящее время известно, что энергия, излучаемая землетрясением, концентрируется в другой полосе пропускания и на более высоких частотах. Обратите внимание, что это не полная «внутренняя» энергия землетрясения, переданная от источников, таких как гравитационная энергия, или к поглотителям, таким как тепловая энергия.Это только количество, излучаемое землетрясением в виде сейсмических волн, которое должно составлять небольшую долю от общей энергии, передаваемой во время процесса землетрясения.
С появлением во всем мире современных цифровых записывающих сейсмографов с широкой полосой пропускания компьютеризированные методы теперь могут производить точные и подробные оценки энергии на регулярной основе для всех крупных землетрясений. Теперь можно определить магнитуду, основанную на энергии, излучаемой землетрясением, M e .Эти величины энергии рассчитываются на основе излучаемой энергии с использованием формулы Choy and Boatwright (1995)
.
M e = ⅔ log 10 E s − 2,9
, где E s — излучаемая сейсмическая энергия в джоулях. M e , рассчитанный по высокочастотным сейсмическим данным, является мерой сейсмического потенциала повреждения.
Формула амплитуды
Для объекта, находящегося в периодическом движении, амплитуда представляет собой максимальное отклонение от равновесия.Например, маятник проходит через точку равновесия (прямо вниз), а затем отклоняется на максимальное расстояние от центра. Это расстояние представляет собой амплитуду A. Полный диапазон колебаний маятника имеет величину 2A. Периодическое движение также применимо к таким вещам, как пружины и волны. Функция синуса колеблется между значениями +1 и -1, поэтому она используется для описания периодического движения. Единицей амплитуды являются метры (м).
положение = амплитуда x функция синуса (угловая частота x время + разность фаз)
х = A sin(ωt + ϕ)
x = водоизмещение (м)
A = амплитуда (м)
ω = угловая частота (радиан/с)
t = время (с)
ϕ = фазовый сдвиг (радианы)
Формула амплитуды Вопросы:
1) Маятник качается взад и вперед. Угловая частота колебаний ω = π радиан/с, фазовый сдвиг ϕ = 0 радиан. В момент времени t = 8,50 с маятник находится на расстоянии 14,0 см от положения равновесия. Какова амплитуда колебаний?
Угловая частота колебаний ω = π радиан/с, фазовый сдвиг ϕ = 0 радиан. В момент времени t = 8,50 с маятник находится на расстоянии 14,0 см от положения равновесия. Какова амплитуда колебаний?
Ответ: Положением маятника в данный момент времени является переменная x, которая имеет значение x = 14,0 см или x = 0,140 м. Амплитуда A может быть найдена перестановкой формулы:
Синус 8,50 π можно решить (учитывая, что значение выражено в радианах) с помощью калькулятора:
грех(8.50 π) = 1
Следовательно, амплитуда в момент времени t = 8,50 с равна:
А = 0,140 м
Амплитуда колебаний маятника А = 0,140 м = 14,0 см
2) Голова игрушки Джек из коробки подпрыгивает вверх и вниз на пружине. Угловая частота колебаний ω = π/6 рад/с, фазовый сдвиг ϕ = 0 рад. Амплитуда подпрыгивания 5,00 см. Каково положение головы чертика из табакерки относительно положения равновесия в следующие моменты времени:
а) 1. 00 с
00 с
б) 6,00 с
в) 11,0 с
Ответ: Амплитуда подпрыгивания A = 5,00 см = 0,500 м. Положение головы чертика из табакерки относительно равновесия равно x и может быть найдено по формуле.
а) t = 1,00 с
х = A sin(ωt + ϕ)
x = (0,500 м) sin[(π/6 радиан/с)(1,00 с) + 0]
x = (0,500 м) sin(π/6 радиан)
х = (0,500 м)(0.500)
x = 0,250 м
x = 2,50 см
В момент времени t = 1,00 с голова находится на 2,50 см выше положения равновесия.
б) t = 6,00 с
х = A sin(ωt + ϕ)
x = (0,500 м) sin[(π/6 радиан/с)(6,00 с) + 0]
x = (0,500 м) sin(π радиан)
х = (0,500 м)(0,00)
x = 0,00 м
В момент времени t = 6.00 с головка находится в положении x = 0,00 м, что является положением равновесия.
в) t = 11,0 с
х = A sin(ωt + ϕ)
x = (0,500 м) sin[(π/6 радиан/с)(11,0 с) + 0]
x = (0,500 м) sin(11π/6 радиан)
x = (0,500 м)(-0,500)
x = -0,250 м
х = -2,50 см
В момент времени t = 11,0 с голова находится в положении x = -2,50 см, что равно 2. {-1}$}\)
{-1}$}\)
\(\lambda =\) длина волны в \(\text{м}\)
\(f =\) частота в \(\text{Гц}\)
Рабочий пример 1: Скорость продольных волн
Музыкальная нота «ля» — это звуковая волна.Заметка имеет частоту \(\text{440}\) \(\text{Гц}\) и длина волны \(\text{0,784}\) \(\text{m}\). Вычислите скорость музыкальной ноты.
Определить, что дано и что требуется
Использование:
\начать{выравнивать*} f & = \text{440}\text{ Гц} \\ \лямбда & = \текст{0,784}\текст{м} \конец{выравнивание*}Нам нужно рассчитать скорость музыкальной ноты «Ля».
Определить, как подойти на основе того, что дано
Нам даны частота и длина волны ноты.{−1}$}\).
temp textРабочий пример 2: Скорость продольных волн
Продольная волна распространяется в среде, в которой ее скорость увеличивается. Как это влияет на его… (напишите
только увеличивается, уменьшается, остается прежним ).
Как это влияет на его… (напишите
только увеличивается, уменьшается, остается прежним ).
-
период?
-
длина волны
?
Определить, что требуется
Нам нужно определить, как изменяются период и длина волны продольной волны при увеличении ее скорости.
Определить, как подойти на основе того, что дано
Нам нужно найти связь между периодом, длиной волны и скоростью волны.
Обсудите, как меняется период
Мы знаем, что частота продольной волны зависит от частоты колебаний, приводящих к созданию продольной волны. Поэтому частота всегда неизменна, независимо ни от чего. изменения скорости.Поскольку период обратно пропорционален частоте, период остается неизменным.
Обсудите, как изменяется длина волны
Частота остается неизменной. По волновому уравнению
По волновому уравнению
, если \(f\) остается прежним, а \(v\) увеличивается, то \(λ\), длина волны, также должна увеличиваться.
temp text| [1] | R.П. Фейнман, Р. Б. Лейгтон, М. Сэндс, «Фейнмановские лекции по физике», Массачусетс, Лондон. Том. 1, 1963. | |
| [2] | Киттель К., Найт В.Д., Рудерман М.А. Механика. Курс физики Беркли». Книжная компания McGraw-Hill, Vol. 1, 1965. | |
| [3] | Ландау Л.Д., Лифшиц Е.М. «Механика и электродинамика», Наука, Москва, Вып. 1, 1969, (на русском языке). | |
| [4] | Т. Фиппс, «Старая физика для новой: мировоззрение теории относительности Эйнштейна», Апейрон, Монреаль, 2012. | |
| [5] | Л. Д. Ландау, Е. М. Лифшиц, “Теоретическая физика. Теория поля”, Наука, Москва, Vol. 2, 509 с., 1988, (на русском языке). Д. Ландау, Е. М. Лифшиц, “Теоретическая физика. Теория поля”, Наука, Москва, Vol. 2, 509 с., 1988, (на русском языке). | |
| [6] | Р. П. Фейнман, Р. Б. Лейгтон, М. Сэндс, «Фейнмановские лекции по физике», Массачусетс, Лондон, Vol. 2, 1964. | |
| [7] | EF Taylor, JA Wheeler, «Физика пространства-времени», Freeman, 1963. пресс, 1967. | |
| [9] | С. Н. Артеха, “Об основах специальной теории относительности. Электродинамика Галилея», специальные выпуски 14/2, осень, стр. 23–28, 2003 г. | |
| [10] | Мэтью Д. Швардс, «Квантовая теория поля и стандартная модель», University Press, Cambridge, New York, 1 st Edition, март 2014 г. DOI: http:/doi.org/10.5281/zenodo. 2578864. | |
| [11] | Алан П., Лайтман, Уильям Х. Пресс, Ричард Х.Прайс, Сол А. Теукольский, «Сборник задач по теории относительности и гравитации», Princeton University Press, Принстон, Нью-Джерси, 1975. | |
| [12] | С. Н. Артеха, «Критические комментарии к релятивистской динамике. Пространство-время и вещество», (4), №5/20, с. 216-224, 2003. | |
| [13] | Р.И. Храпко, «Что такое масса», УФН, №12, Том. 170, 2000, (на русском языке). | |
| [14] | Ю.Е. Хорошавцев, “Релятивистское сложение ускорений”, Вестник инженеров-строителей.№1(10), Санкт-Петербург, стр. 88-90, 2007. ISBN 5-9227-0059-6, (на русском языке) | |
| [15] | Гарри Э. Фиппс. Принцип относительности. Очерки физики», Университет Торонто. Том. 29(1), стр. 62–64, март 2016 г. DOI: 10.4006/0836-1398-29.1.62. | |
| [16] | Гарри Х. Рикер, «Эмпирическая интерпретация замедления времени в специальной теории относительности», 114. Parkway, Newport News, VA 23606, 2011. «Волны де Бройля, уравнение Шредингера и теория относительности», Honda Electronics Co. , Ltd, Япония, 2015 г. , Ltd, Япония, 2015 г. | |
| [18] | П. Хат, М., Дж. Рис, «Насколько стабилен наш вакуум?» Nature, 302(5908), pp. 508-509, 1983. | |
| [19] | М. Е. Пескин, Д. В. Шредер, «Введение в квантовую теорию поля», Addison-Wessely, 1995. 20] | Р.Э. Ван, «Вакуум и возбужденные состояния Кулона – калибровочные SU(n) поля Янга-Миллса», Physical Review D, №37, 3024, 1988. DOI: https://doi.org/10.1103/PhysRevD.37.3024. |
| [21] | Павлов Г.Г., Шибанов Ю.А., Гнедин Ю.Н. Влияние поляризации на циклотронное излучение тепловой плазмы в сильном магнитном поле // Письма в журнале экспериментальной и теоретической физики. Том. 30(2), стр. 137-142, 1979, (на русском языке). | |
| [22] | Кохри Казунори, Мацуи, Хироки, «Электрослабая нестабильность вакуума и перенормированные флуктуации вакуумного поля на фоне Фридмана-Лемэтра-Робертсона-Уокера», Physical Review D, 2018, 98(10): 103521. DOI: 10.1103/PhysRevD.98.103521. DOI: 10.1103/PhysRevD.98.103521. | |
| [23] | Ю.Е. Хорошавцев, “Волновая интерпретация уравнений релятивистской динамики”, Математическое моделирование, цифровые методы и программные комплексы, Архитектурный государственный университет, -Санкт-Петербург. 2004. № 10. С. 164–172. | |
| [24] | Ю.Е. Хорошавцев”, Решение волнового уравнения в классе комплексных чисел путем введения гиперболических координат”, Международный журнал прикладной математики и теоретической физики.Том 4, №2, стр. 61-66, июнь 2018 г., doi: 10.11648/j.ijampt. 20180402.15. | |
| [25] | Р. П. Фейнман, Р. Б. Лейгтон, М. Сэндс, «Фейнмановские лекции по физике. Упражнения», издательство Addison Wesley, Лондон, 1964–1966 годы. |
(PDF) Флуктуационная формула Эйнштейна и дуальность волна-частица127–128).
32 Он также отверг предположение о том, что энергия не сохраняется, когда оно появилось в печати в теории Бора, Крамерса и Слейтера 1924 года: Считайте, что это настоящий парень». [«Diese Idee ist ein
[«Diese Idee ist ein
alter Bekannter von mir, den ich aber fur keinen reelen Kerl halte».] (Эйнштейн —
Ehrenfest, 31 мая 1924 г., EA 10-088)
33 «die Fragestellung prinzipieller Natur, die WIR NUN AUF DEM GEBIETE DER
Licherscheinungen Haben, Gipffelt Dirin, Entweder, Zu Zeigen, Daß Die Korpuskular-
Теория DAS Wawre Wesen des Lichtes Erfaßt, ODER, DAß RIDIGHTSTHEORIE
Richtig Ist und Das Quantenhafte Nur Scheanbar Ist, Oder endlich, daß beide
Auffassungen dem wahren Wesen des Lichts entsprechen und das Licht sowohl
Quanteneigenschaften als undulatorische Eigenschaften hat.Mansuchte nun eine
Synthese dieser beiden Eigenschaften zu finden, was bisher mathematisch noch
nicht gelungen ist. Der letzte große fortschritt, der in der Physik des lichts
Gemacht Wurde, IST DADERCH ERREICHT WORDEN, DAß MAN SICH Wieder von der
KorpuskularaufassAssung Entfernt Hat und Wieder Einen Schritt Gemacht Hat, Der
Umgekehrt Ist Demjenigen, Der Von Der UndulationStheorie zur Korpuskulartheorie
geführt шляпа. Einstein verweist Hier auf die Arbeiten von De Broglie und Schrödin-
Einstein verweist Hier auf die Arbeiten von De Broglie und Schrödin-
ger.. . . die Natur fordert von uns eine Synthese beider Auffassungen, die bis jetzt
allerdings noch über die Denkkräfte der Physiker hinausgegangen ist» (Эйнштейн
1927, стр. 546). О нежелании Эйнштейна принять двойственность в смысле квантовой
механики см. также Bach 1989, p. 174.
34 «Dein Gehirn sieht, weiß der Himmel, reinlicher aus. Seine Produkte sind
klar, einfach und treffen die Sache. Wir kapieren es dann zur Not ein paar Jahre
später.So ist es uns auch mit Deiner Gasentartung und der Boseschen Statistik
gegangen. Glücklicherweise erschien Ehrenfest hier und hat uns ein Licht
aufgesteckt. Darauf habe ich die Arbeit von Louis de Broglie gelesen und bin
allmählich auchhinter Deine Schliche gekommen. Jetzt glaube ich, daß die
‘Wellentheorie der Materie’ eine sehr gewichtige Sache werden kann» (Борн и
Эйнштейн, 1969, стр.