Глава 11. Механические колебания и волны
Колебательным называется любое периодически повторяющееся движение. Поэтому зависимости координаты и скорости тела от времени при колебаниях описываются периодическими функциями времени. В школьном курсе физики рассматриваются такие колебания, в которых зависимости и скорости тела представляют собой тригонометрические функции , или их комбинацию, где — некоторое число. Такие колебания на-зываются гармоническими (функции и часто называют гармоническими функциями). Для решения задач на колебания, входящих в программу единого государственного экзамена по физике, нужно знать определения основных характеристик колебательного движения: амплитуды, периода, частоты, круговой (или циклической) частоты и фазы колебаний. Дадим эти определения и свяжем перечисленные величины с параметрами зависимости координаты тела от времени , которая в случае гармонических колебаний всегда может быть представлена в виде
(11. |
где , и — некоторые числа.
Амплитудой колебаний называется максимальное отклонение колеблющегося тела от положения равновесия. Поскольку максимальное и минимальное значение косинуса в (11.1) равно ±1, то амплитуда колебаний тела, совершающего колебания (11.1), равна величине . Период колебаний — это минимальное время, через которое движение тела повторяется. Для зависимости (11.1) период можно установить из следующих соображений. Косинус — периодическая функция с периодом . Поэтому движение полностью повторяется через такое значение , что . Отсюда получаем
| (11.2) |
Частотой колебаний тела называется число колебаний, совершаемых в единицу времени. Очевидно, что частота колебаний связана с периодом колебаний по формуле
| (11.3) |
Круговой (или циклической) частотой колебаний называется число колебаний, совершаемых за единиц времени. Из формулы (11.3) заключаем, что круговой частотой является величина из формулы (11.1).
Из формулы (11.3) заключаем, что круговой частотой является величина из формулы (11.1).
Фазой колебаний называется аргумент тригонометрической функции, описывающей зависимость координаты от времени. Из формулы (11.1) видим, что фаза колебаний тела, движение которого описывается зависимостью (11.1), равна . Значение фазы колебаний в момент времени = 0 называется начальной фазой. Для зависимости (11.1) начальная фаза колебаний равна величине . Очевидно, начальная фаза колебаний зависит от выбора начала отсчета времени (момента = 0), которое всегда является условным. Изменением начала отсчета времени начальная фаза колебаний всегда может быть «сделана» равной нулю, а синус в формуле (11.1) «превращен» в косинус или наоборот.
В программу единого государственного экзамена входит также знание формул для частоты колебаний пружинного и математического маятников. Пружинным маятником принято называть тело, которое может совершать колебания на гладкой горизонтальной поверхности под действием пружины, второй конец которой закреплен (левый рисунок). Математическим маятником называется массивное тело, размерами которого можно пренебречь, совершающее колебания на длинной, невесомой и нерастяжимой нити (правый рисунок). Название этой системы – «математический маятник» связано с тем, что она представляет собой абстрактную математическую модель реального (физического) маятника. Необходимо помнить формулы для периода (или частоты) колебаний пружинного и математического маятников. Для пружинного маятника
Математическим маятником называется массивное тело, размерами которого можно пренебречь, совершающее колебания на длинной, невесомой и нерастяжимой нити (правый рисунок). Название этой системы – «математический маятник» связано с тем, что она представляет собой абстрактную математическую модель реального (физического) маятника. Необходимо помнить формулы для периода (или частоты) колебаний пружинного и математического маятников. Для пружинного маятника
| (11.4) |
где — коэффициент жесткости пружины, — масса груза. Период колебаний математического маятника определяется следующим соотношением
| (11.5) |
где — длина нити, — ускорение свободного падения. Рассмотрим применение этих определений и законов на примере решения задач.
Чтобы найти циклическую частоту колебаний груза в задаче 11.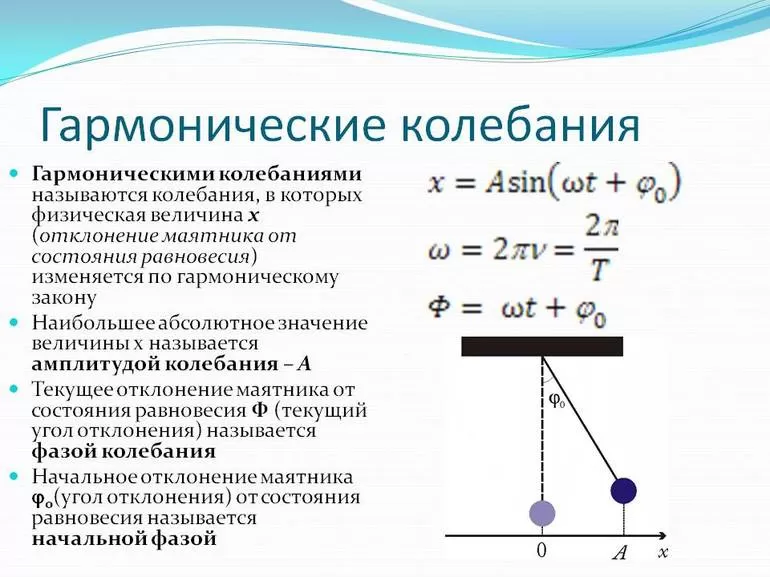 1.1 найдем сначала период колебаний, а затем воспользуемся формулой (11.2). Поскольку 10 м 28 с — это 628 с, и за это время груз совершает 100 колебаний, период колебаний груза равен 6,28 с. Поэтому циклическая частота колебаний равна 1 c-1 (ответ 2). В задаче 11.1.2 груз за 600 с совершил 60 колебаний, поэтому частота колебаний — 0,1 с
1.1 найдем сначала период колебаний, а затем воспользуемся формулой (11.2). Поскольку 10 м 28 с — это 628 с, и за это время груз совершает 100 колебаний, период колебаний груза равен 6,28 с. Поэтому циклическая частота колебаний равна 1 c-1 (ответ 2). В задаче 11.1.2 груз за 600 с совершил 60 колебаний, поэтому частота колебаний — 0,1 с
Чтобы понять, какой путь пройдет груз за 2,5 периода (задача 11.1.3), проследим за его движением. Через период груз вернется назад в точку максимального отклонения, совершив полное колебание. Поэтому за это время груз пройдет расстояние, равное четырем амплитудам: до положения равновесия — одна амплитуда, от положения равновесия до точки максимального отклонения в другую сторону — вторая, назад в положение равновесия — третья, из положения равновесия в начальную точку — четвертая. За второй период груз снова пройдет четыре амплитуды, а за оставшиеся половину периода — две амплитуды. Поэтому пройденный путь равен десяти амплитудам (ответ 4).
Поэтому пройденный путь равен десяти амплитудам (ответ 4).
Величина перемещения тела — расстояние от начальной точки до конечной. За 2,5 периода в задаче 11.1.4 тело успеет совершить два полных и половину полного колебания, т.е. окажется на максимальном отклонении, но с другой стороны от положения равновесия. Поэтому величина перемещения равна двум амплитудам (ответ 3).
По определению фаза колебаний — это аргумент тригонометрической функции, которой описывается зависимость координаты колеблющегося тела от времени. Поэтому правильный ответ в задаче 11.1.5 — 3.
Период — это время полного колебания. Это значит, что возвращение тела назад в ту же точку, из которой тело начало движение, еще не означает, что прошел период: тело должно вернуться в ту же точку с той же скоростью. Например, тело, начав колебания из положения равновесия, за период успеет отклониться на максимальную величину в одну сторону, вернуться назад, отклонится на максимум в другую сторону и снова вернуться назад. Поэтому за период тело успеет два раза отклониться на максимальную величину от положения равновесия и вернуться обратно. Следовательно, на прохождение от положения равновесия до точки максимального отклонения (
Поэтому за период тело успеет два раза отклониться на максимальную величину от положения равновесия и вернуться обратно. Следовательно, на прохождение от положения равновесия до точки максимального отклонения (
Гармоническими называются такие колебания, при которых зависимость координаты колеблющегося тела от времени описывается тригонометрической (синус или косинус) функцией времени. В задаче 11.1.7 таковыми являются функции и , несмотря на то, что входящие в них параметры обозначены как 2 и 2. Функция же — тригонометрическая функция квадрата времени. Поэтому гармоническими являются колебания только величин и (ответ 4).
При гармонических колебаниях скорость тела изменяется по закону , где — амплитуда колебаний скорости (начало отсчета времени выбрано так, чтобы начальная фаза колебаний равнялась бы нулю). Отсюда находим зависимость кинетической энергии тела от времени (задача 11. 1.8). Используя далее известную тригонометрическую формулу, получаем
1.8). Используя далее известную тригонометрическую формулу, получаем
Из этой формулы следует, что кинетическая энергия тела изменяется при гармонических колебаниях также по гармоническому закону, но с удвоенной частотой (ответ 2).
За соотношением между кинетической энергий груза и потенциальной энергией пружины (задача 11.1.9) легко проследить из следующих соображений. Когда тело отклонено на максимальную величину от положения равновесия, скорость тела равна нулю, и, следовательно, потенциальная энергия пружины больше кинетической энергии груза. Напротив, когда тело проходит положение равновесия, потенциальная энергия пружины равна нулю, и, следовательно, кинетическая энергия больше потенциальной. Поэтому между прохождением положения равновесия и максимальным отклонением кинетическая и потенциальная энергия один раз сравниваются. А поскольку за период тело четыре раза проходит от положения равновесия до максимального отклонения или обратно, то за период кинетическая энергия груза и потенциальная энергия пружины сравниваются друг с другом четыре раза (ответ

Амплитуду колебаний скорости (задача 11.1.10) проще всего найти по закону сохранения энергии. В точке максимального отклонения энергия колебательной системы равна потенциальной энергии пружины , где — коэффициент жесткости пружины, — амплитуда колебаний. При прохождении положения равновесия энергия тела равна кинетической энергии , где — масса тела, — скорость тела при прохождении положения равновесия, которая является максимальной скоростью тела в процессе колебаний и, следовательно, представляет собой амплитуду колебаний скорости. Приравнивая эти энергии, находим
(ответ 1), где использовано выражение для круговой частоты колебаний груза на пружине:
По формуле (11.4) получаем в задаче 11.2.1
(ответ 4).
Из формулы (11.5) заключаем (задача 11. 2.2), что от массы математического маятника его период не зависит, а при увеличении длины в 4 раза период колебаний увеличивается в 2 раза (ответ 1).
2.2), что от массы математического маятника его период не зависит, а при увеличении длины в 4 раза период колебаний увеличивается в 2 раза (ответ 1).
Часы — это колебательный процесс, который используется для измерения интервалов времени (задача 11.2.3). Слова часы «спешат» означают, что период этого процесса меньше того, каким он должен быть. Поэтому для уточнения хода этих часов необходимо увеличить период процесса. Согласно формуле (11.5) для увеличения периода колебаний математического маятника необходимо увеличить его длину (ответ
Чтобы найти амплитуду колебаний в задаче 11.2.4, необходимо представить зависимость координаты тела от времени в виде одной тригонометрической функции. Для данной в условии функции это можно сделать с помощью введения дополнительного угла. Умножая и деля эту функцию на и используя формулу сложения тригонометрических функций, получим
где — такой угол, что .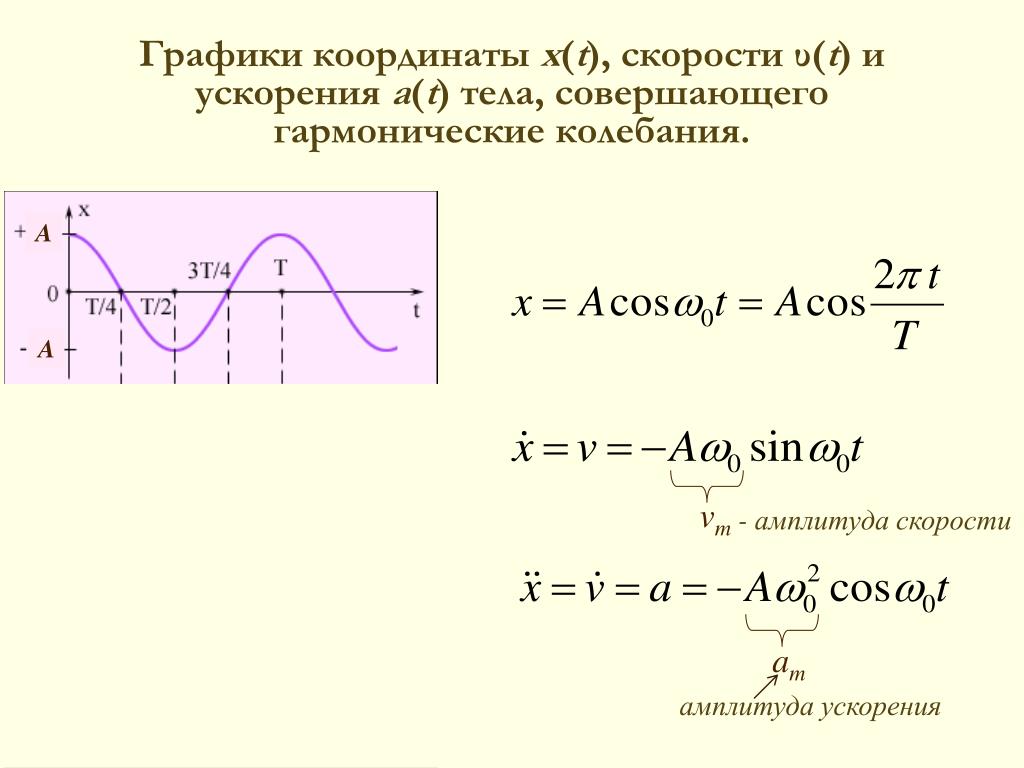 Из этой формулы следует, что амплитуда колебаний тела — (ответ 4).
Из этой формулы следует, что амплитуда колебаний тела — (ответ 4).
В задаче 11.2.5 имеем при см. Откуда см (ответ 2).
Задачи 11.2.6 и 11.2.7 посвящены механическим волнам. Волна – некоторый колебательный процесс, который может распространяться в среде. При этом каждая точка среды совершает колебания около определенного положения и в среднем не перемещается в пространстве. Волна характеризуется периодом (или связанной с ним частотой ), скоростью и длиной волны , которая определяется как минимальное расстояние между точками, колеблющимися в одинаковой фазе. Для решения задач ЕГЭ по этой теме необходимо помнить формулу, дающую связь между параметрами волны
| (11.6) |
которую легко запомнить, поскольку эта связь имеет такой же вид как обычное соотношение между расстоянием, скоростью и временем. Например, в задаче 11.2. 6 по формуле (11.6) находим длину волны м (ответ 2).
6 по формуле (11.6) находим длину волны м (ответ 2).
Как следует из рисунка в задаче 11.2.7 длина волны, распространяющейся по шнуру, равна м. Поэтому по формуле (11.6) имеем Гц (ответ 4).
Поскольку в момент максимального отклонения пружинного маятника, механическая энергия системы равна потенциальной энергии пружины, то
где — амплитуда колебаний, — жесткость пружины. Поэтому при увеличении механической энергии пружинного маятника в 2 раза амплитуда колебаний увеличилась в раз (задача 11.2.8 – ответ 1).
Используя известную тригонометрическую формулу, получим в задаче 11.2.9
Эта зависимость представляет собой гармоническую функцию, но колеблющуюся вокруг точки . Амплитудой этих колебаний является множитель перед косинусом — (так как сам косинус меняется в интервале от -1 до 1). Циклической частотой — величина (ответ 4).
Циклической частотой — величина (ответ 4).
Вертикальный пружинный маятник отличается от горизонтального (задача 11.2.10) наличием силы тяжести. Однако сила тяжести приводит только к сдвигу положения равновесия маятника, а возвращающая сила по прежнему будет зависеть от смещения маятника от положения равновесия по закону (так как возвращающей силой будет разность силы упругости и постоянной силы тяжести). Поэтому период колебаний груза на вертикальной и горизонтальной пружине — одинаков (конечно, при условии, что и сам груз и пружины одинаковы). Правильный ответ в задаче — 3.
Задачи для самостоятельного решения — Студопедия
Задача № 1. Какова длина математического маятника, совершающего гармонические колебания с частотой 0,5 Гц на поверхности Луны? Ускорение свободного падения на поверхности Луны 1,6 м/с2.
Задача № 2. Груз массой 400 г совершает колебания на пружине с жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.
Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.
Задача №3. Частота колебаний крыльев вороны в полете равна в среднем 3 Гц. Сколько взмахов крыльями сделает ворона, пролетев путь 650 м со скоростью 13 м/с?
Задача № 4. Гармоническое колебание описывается уравнением
Чему равны циклическая частота колебаний, линейная частота колебаний, начальная фаза колебаний?
Задача № 5. Математический маятник длиной 0,99 м совершает 50 полных колебаний за 1 мин 40 с. Чему равно ускорение свободного падения в данном месте на поверхности Земли? (Можно принять π2 = 9,87.)
Задача № 6. Как и во сколько раз изменится период колебаний пружинного маятника, если шарик на пружине заменить другим шариком, радиус которого вдвое меньше, а плотность — в два раза больше?
Задача № 7. Два математических маятника за одно и то же время совершают — первый N1 = 30, а второй — N2 = 40 колебаний. Какова длина каждого из них, если разность их длин Δl= 7 см?
Два математических маятника за одно и то же время совершают — первый N1 = 30, а второй — N2 = 40 колебаний. Какова длина каждого из них, если разность их длин Δl= 7 см?
Опорный конспект
| Вопросы по теме «МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ» |
1. Что является наиболее характерным признаком колебательного движения?
2. При каких условиях в системе возникают свободные колебания?
3. При каких условиях реальные колебания можно рассматривать как гармонические?
4. Какова связь между частотой и периодом колебаний? Как связана циклическая частота с периодом гармонических колебаний?
5. Чем отличаются графики гармонических колебаний, у которых разные амплитуды? частоты? начальные фазы?
6. Как амплитуда скорости гармонических колебаний зависит от амплитуды смещения? периода? В чем отличие графиков координаты и скорости?
7. Как связаны ускорение и координата при гармонических колебаниях?
8. Чему равен сдвиг фаз между ускорением колеблющейся точки и скоростью?
9. От чего зависит ускорение тела, колеблющегося под действием силы упругости? Ускорение математического маятника? Что общего в уравнениях движения этих систем?
10. В каких точках скорость(ускорение) колеблющегося маятника максимальна?
11. Является ли движение математического маятника к положению равновесия равноускоренным?
12. От чего зависит период свободных колебаний математического маятника? пружинного маятника?
13. Почему изменится период колебаний математического маятника, если поднять его на высокую гору?
14. Будут ли отличаться периоды колебаний тел разной массы на нитях одинаковой длины? на пружинах одинаковой жесткости?
15. Что произойдет с частотой колебаний тела, если пружину, на которой оно подвешено, укоротить?
16. Будет ли продолжать колебания математический маятник при свободном падении?
17. Как связаны ускорение и координата при гармонических колебаниях?
8. Чему равен сдвиг фаз между ускорением колеблющейся точки и скоростью?
9. От чего зависит ускорение тела, колеблющегося под действием силы упругости? Ускорение математического маятника? Что общего в уравнениях движения этих систем?
10. В каких точках скорость(ускорение) колеблющегося маятника максимальна?
11. Является ли движение математического маятника к положению равновесия равноускоренным?
12. От чего зависит период свободных колебаний математического маятника? пружинного маятника?
13. Почему изменится период колебаний математического маятника, если поднять его на высокую гору?
14. Будут ли отличаться периоды колебаний тел разной массы на нитях одинаковой длины? на пружинах одинаковой жесткости?
15. Что произойдет с частотой колебаний тела, если пружину, на которой оно подвешено, укоротить?
16. Будет ли продолжать колебания математический маятник при свободном падении?
17. Можно ли считать, что при гармонических колебаниях зависимость кинетической и потенциальной энергии от времени является гармонической? Чему равен период изменения этих энергий?
18. В каких положениях колеблющейся точки максимальна кинетическая энергия? потенциальная энергия?
19. Как зависят максимальные значения кинетической и потенциальной энергии при гармонических колебаниях от амплитуды? от периода? Сохраняется ли при гармонических колебаниях полная механическая энергия?
20. В чем состоит отличие вынужденных колебаний от свободных? Чем отличаются вынужденные колебания от затухающих?
21. При каких условиях возникает явление резонанса? От чего зависит «острота» резонансной кривой? Чем определяется амплитуда колебаний при резонансе?
22. Механические волны: свойства и характеристики.
23. Звуковые волны.
24. Ультразвук. Инфразвук. Можно ли считать, что при гармонических колебаниях зависимость кинетической и потенциальной энергии от времени является гармонической? Чему равен период изменения этих энергий?
18. В каких положениях колеблющейся точки максимальна кинетическая энергия? потенциальная энергия?
19. Как зависят максимальные значения кинетической и потенциальной энергии при гармонических колебаниях от амплитуды? от периода? Сохраняется ли при гармонических колебаниях полная механическая энергия?
20. В чем состоит отличие вынужденных колебаний от свободных? Чем отличаются вынужденные колебания от затухающих?
21. При каких условиях возникает явление резонанса? От чего зависит «острота» резонансной кривой? Чем определяется амплитуда колебаний при резонансе?
22. Механические волны: свойства и характеристики.
23. Звуковые волны.
24. Ультразвук. Инфразвук.
|
Механические колебания — материалы для подготовки к ЕГЭ по Физике
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ : гармонические колебания; амплитуда, период, частота, фаза колебаний; свободные колебания, вынужденные колебания, резонанс.
Колебания — это повторяющиеся во времени изменения состояния системы. Понятие колебаний охватывает очень широкий круг явлений.
Колебания механических систем, или механические колебания — это механическое движение тела или системы тел, которое обладает повторяемостью во времени и происходит в окрестности положения равновесия. Положением равновесия называется такое состояние системы, в котором она может оставаться сколь угодно долго, не испытывая внешних воздействий.
Например, если маятник отклонить и отпустить, то начнутся колебания. Положение равновесия — это положение маятника при отсутствии отклонения. В этом положении маятник, если его не трогать, может пребывать сколь угодно долго. При колебаниях маятник много раз проходит положение равновесия.
Сразу после того, как отклонённый маятник отпустили, он начал двигаться, прошёл положение равновесия, достиг противоположного крайнего положения, на мгновение остановился в нём, двинулся в обратном направлении, снова прошёл положение равновесия и вернулся назад. Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.
Совершилось одно полное колебание. Дальше этот процесс будет периодически повторяться.
Амплитуда колебаний тела — это величина его наибольшего отклонения от положения равновесия.
Период колебаний — это время одного полного колебания. Можно сказать, что за период тело проходит путь в четыре амплитуды.
Частота колебаний — это величина, обратная периоду: . Частота измеряется в герцах (Гц) и показывает, сколько полных колебаний совершается за одну секунду.
Гармонические колебания.
Будем считать, что положение колеблющегося тела определяется одной-единственной координатой . Положению равновесия отвечает значение . Основная задача механики в данном случае состоит в нахождении функции , дающей координату тела в любой момент времени.
Для математического описания колебаний естественно использовать периодические функции. Таких функций много, но две из них — синус и косинус — являются самыми важными. У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.
У них много хороших свойств, и они тесно связаны с широким кругом физических явлений.
Поскольку функции синус и косинус получаются друг из друга сдвигом аргумента на , можно ограничиться только одной из них. Мы для определённости будем использовать косинус.
Гармонические колебания — это колебания, при которых координата зависит от времени по гармоническому закону:
(1)
Выясним смысл входящих в эту формулу величин.
Положительная величина является наибольшим по модулю значением координаты (так как максимальное значение модуля косинуса равно единице), т. е. наибольшим отклонением от положения равновесия. Поэтому — амплитуда колебаний.
Аргумент косинуса называется фазой колебаний. Величина , равная значению фазы при , называется начальной фазой. Начальная фаза отвечает начальной координате тела: .
Величина называется циклической частотой. Найдём её связь с периодом колебаний и частотой . Одному полному колебанию отвечает приращение фазы, равное радиан: , откуда
(2)
(3)
Измеряется циклическая частота в рад/с (радиан в секунду).
В соответствии с выражениями (2) и (3) получаем ещё две формы записи гармонического закона (1):
.
График функции (1), выражающей зависимость координаты от времени при гармонических колебаниях, приведён на рис. 1.
| Рис. 1. График гармонических колебаний |
Гармонический закон вида (1) носит самый общий характер. Он отвечает, например, ситуации, когда с маятником совершили одновременно два начальных действия: отклонили на величину и придали ему некоторую начальную скорость. Имеются два важных частных случая, когда одно из этих действий не совершалось.
Пусть маятник отклонили, но начальной скорости не сообщали (отпустили без начальной скорости). Ясно, что в этом случае , поэтому можно положить . Мы получаем закон косинуса:
.
График гармонических колебаний в этом случае представлен на рис. 2.
Рис.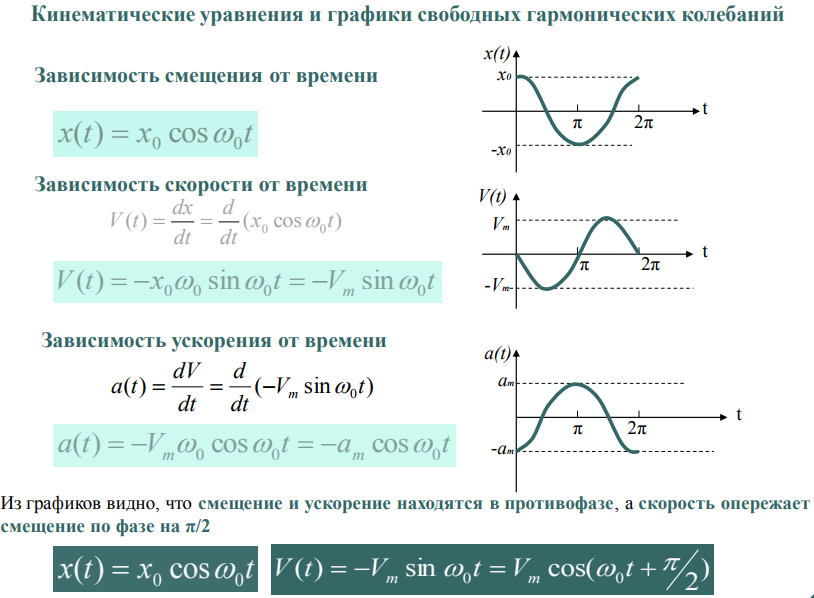 2. Закон косинуса 2. Закон косинуса |
Допустим теперь, что маятник не отклоняли, но ударом сообщили ему начальную скорость из положения равновесия. В этом случае , так что можно положить . Получаем закон синуса:
.
График колебаний представлен на рис. 3.
| Рис. 3. Закон синуса |
Уравнение гармонических колебаний.
Вернёмся к общему гармоническому закону (1). Дифференцируем это равенство:
. (4)
Теперь дифференцируем полученное равенство (4):
. (5)
Давайте сопоставим выражение (1) для координаты и выражение (5) для проекции ускорения. Мы видим, что проекция ускорения отличается от координаты лишь множителем :
. (6)
Это соотношение называется уравнением гармонических колебаний. Его можно переписать и в таком виде:
. (7)
C математической точки зрения уравнение (7) является дифференциальным уравнением. Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Решениями дифференциальных уравнений служат функции (а не числа, как в обычной алгебре).
Так вот, можно доказать, что:
-решением уравнения (7) является всякая функция вида (1) с произвольными ;
-никакая другая функция решением данного уравнения не является.
Иными словами, соотношения (6), (7) описывают гармонические колебания с циклической частотой и только их. Две константы определяются из начальных условий — по начальным значениям координаты и скорости.
Пружинный маятник.
Пружинный маятник — это закреплённый на пружине груз, способный совершать колебания в горизонтальном или вертикальном направлении.
Найдём период малых горизонтальных колебаний пружинного маятника (рис. 4). Колебания будут малыми, если величина деформации пружины много меньше её размеров. При малых деформациях мы можем пользоваться законом Гука. Это приведёт к тому, что колебания окажутся гармоническими.
Трением пренебрегаем. Груз имеет массу , жёсткость пружины равна .
Координате отвечает положение равновесия, в котором пружина не деформирована. Следовательно, величина деформации пружины равна модулю координаты груза.
| Рис. 4. Пружинный маятник |
В горизонтальном направлении на груз действует только сила упругости со стороны пружины. Второй закон Ньютона для груза в проекции на ось имеет вид:
. (8)
Если (груз смещён вправо, как на рисунке), то сила упругости направлена в противоположную сторону, и . Наоборот, если , то . Знаки и всё время противоположны, поэтому закон Гука можно записать так:
Тогда соотношение (8) принимает вид:
или
.
Мы получили уравнение гармонических колебаний вида (6), в котором
.
Циклическая частота колебаний пружинного маятника, таким образом, равна:
. (9)
Отсюда и из соотношения находим период горизонтальных колебаний пружинного маятника:
. (10)
Если подвесить груз на пружине, то получится пружинный маятник, совершающий колебания в вертикальном направлении. Можно показать, что и в этом случае для периода колебаний справедлива формула (10).
Математический маятник.
Математический маятник — это небольшое тело, подвешенное на невесомой нерастяжимой нити (рис. 5). Математический маятник может совершать колебания в вертикальной плоскости в поле силы тяжести.
| Рис. 5. Математический маятник |
Найдём период малых колебаний математического маятника. Длина нити равна . Сопротивлением воздуха пренебрегаем.
Запишем для маятника второй закон Ньютона:
,
и спроектируем его на ось :
.
Если маятник занимает положение как на рисунке (т. е. ), то:
.
Если же маятник находится по другую сторону от положения равновесия (т. е. ), то:
.
Итак, при любом положении маятника имеем:
. (11)
Когда маятник покоится в положении равновесия, выполнено равенство . При малых колебаниях, когда отклонения маятника от положения равновесия малы (по сравнению с длиной нити), выполнено приближённое равенство . Воспользуемся им в формуле (11):
,
или
.
Это — уравнение гармонических колебаний вида (6), в котором
.
Следовательно, циклическая частота колебаний математического маятника равна:
. (12)
Отсюда период колебаний математического маятника:
. (13)
Обратите внимание, что в формулу (13) не входит масса груза. В отличие от пружинного маятника, период колебаний математического маятника не зависит от его массы.
Свободные и вынужденные колебания.
Говорят, что система совершает свободные колебания, если она однократно выведена из положения равновесия и в дальнейшем предоставлена сама себе. Никаких периодических внешних
воздействий система при этом не испытывает, и никаких внутренних источников энергии, поддерживающих колебания, в системе нет.
Рассмотренные выше колебания пружинного и математического маятников являются примерами свободных колебаний.
Частота, с которой совершаются свободные колебания, называется собственной частотой колебательной системы. Так, формулы (9) и (12) дают собственные (циклические) частоты колебаний пружинного и математического маятников.
В идеализированной ситуации при отсутствии трения свободные колебания являются незатухающими, т. е. имеют постоянную амплитуду и длятся неограниченно долго. В реальных колебательных системах всегда присутствует трение, поэтому свободные колебания постепенно затухают (рис. 6).
| Рис. 6. Затухающие колебания |
Вынужденные колебания — это колебания, совершаемые системой под воздействием внешней силы , периодически изменяющейся во времени (так называемой вынуждающей силы).
Предположим, что собственная частота колебаний системы равна , а вынуждающая сила зависит от времени по гармоническому закону:
.
В течение некоторого времени происходит установление вынужденных колебаний: система совершает сложное движение, которое является наложением выужденных и свободных колебаний. Свободные колебания постепенно затухают, и в установившемся режиме система совершает вынужденные колебания, которые также оказываются гармоническими. Частота установившихся вынужденных колебаний совпадает с частотой
вынуждающей силы (внешняя сила как бы навязывает системе свою частоту).
Амплитуда установившихся вынужденных колебаний зависит от частоты вынуждающей силы. График этой зависимости показан на рис. 7.
| Рис. 7. Резонанс |
Мы видим, что вблизи частоты наступает резонанс — явление возрастания амплитуды вынужденных колебаний. Резонансная частота приближённо равна собственной частоте колебаний системы: , и это равенство выполняется тем точнее, чем меньше трение в системе. При отсутствии трения резонансная частота совпадает с собственной частотой колебаний, , а амплитуда колебаний возрастает до бесконечности при .
Скорость и ускорение гармонического колебания
Скорость и ускорение гармонического колебания [c.288]На этом примере видно, что в случае сложных колебаний, составленных из нескольких гармонических, скорость и ускорение суммарного колебания складываются из скоростей и ускорений составляющих колебаний. [c.173]
Следовательно, в этом движении и скорость, и ускорение точки изменяются с течением времени по гармоническому закону. По знакам v м а легко проверить, что когда точка движется к центру колебаний, ее движение является ускоренным, а когда от центра колебаний,— замедленным. [c.112]
Доказать, что движение точки является гармоническим колебательным движением. Определить амплитуду и период колебаний. Найти скорость и ускорение точки. [c.244]
Доказать, что точка совершает гармоническое колебательное движение. Определить амплитуду, период колебаний, а также скорость и ускорение точки. [c.245]
Скорость и ускорение при гармонических колебаниях. Най- [c.216]
Отсюда следует, что при гармонических колебаниях точки ускорение но величине пропорционально расстоянию от центра колебания, причем точка движется ускоренно, приближаясь к центру, и замедленно, удаляясь от него. В самом деле, при приближении к центру со стороны отрицательных абсцисс Vx > 0, X о, т. е. движение ускоренное при х > 0 приближение к центру совершается при н проекции скорости и ускорения имеют опять одинаковый знак и движение ускоренное. Точно так же можно показать, что при удалении точки от центра движение будет замедленным. [c.170]
От результатов, полученных нами для амплитуды и фазы смещения при вынужденных колебаниях, можно перейти к амплитудам и фазам скорости и ускорения. Когда вынужденные колебания являются гармоническими, то амплитуда скорости [c.608]
Дело в том, что, говоря о форме колебаний, можно подразумевать не только закон изменения смещения, но и закон изменения скорости и, наконец,, закон изменения ускорения. В случае, если смещение изменяется по гармоническому закону, скорость и ускорение также меняются по гармоническому закону (ибо производная от гармонической функции есть также гармоническая функция). Если же форма колебаний смещения отлична от гармонической, то форма колебаний скорости не только отлична от гармонической, но и отлична от формы колебаний смещения то же относится к скорости и ускорению, так как ни одна периодическая функция, кроме гармонической, не имеет производной, которая по форме совпадала бы с самой функцией. Поэтому только в специальном случае действия гармонической внешней силы на линейную систему гармонической оказывается форма колебаний как для смещений, так и для скоростей и ускорений. Для определенности мы будем ниже везде (если не оговорено иное) под формой колебаний понимать закон изменения смещения.- [c.620]
Итак, смещение, скорость и ускорение при гармонических колебаниях изменяются гармонически. [c.168]
Таким образом скорость v t) и ускорение w t) при гармонических колебаниях также изменяются во времени по синусоидальному закону с той же частотой, что и перемещение u t). Амплитуды скорости и ускорения равны соответственно соЛ и мМ. [c.19]
СКОРОСТЬ и УСКОРЕНИЕ ТОЧКИ ПРИ ГАРМОНИЧЕСКОМ КОЛЕБАНИИ [c.317]
Каковы амплитуды скорости и ускорения материальной точки, совершающей гармоническое колебание по следующему закону [c.329]
Скорость и ускорение точки, совершающей гармоническое колебание, соответственно будут [c.168]
При гармонических колебаниях скорость и ускорение меняются также по гармоническому закону [c.216]
Из полученного соотношения для скорости следует, что изображающий ее вектор повернут на я/2 вперед по отношению к вектору положения колеблющейся точки и имеет в (Оо раз большую амплитуду. Аналогично, вектор. Представляющий ускорение опережает вектор положения на л и имеет в соо раз большую амплитуду. На рис.4 приведены векторные диаграммы для координаты, скорости и ускорения при гармонических колебаниях. [c.120]
Динамика вибрационного воздействия на жидкий металл. Если принять, что несжимаемая жидкость в вертикально расположенной трубе с жесткими стенками и дном подвергается прямолинейному гармоническому колебанию (рис. 34), то скорость и ускорение каждой точки среды могут быть рассчитаны с использованием зависимостей из теории колебания. [c.36]
Задача Т. Точка совершает гармонические колебания с периодом 2,0 с. Амплитуда колебания 10 см. Найти смещение, скорость и ускорение точки спустя 0,20 с после ее прохождения через положение равновесия. Начало колебания совпадало с положением равновесия. [c.290]
Таким образом, скорость и ускорение при гармоническом колебании также изменяются со временем по закону гармонического колебания с той же частотой, что и координата, [c.108]
Часовой балансир совершает крутильные гармонические колебания с периодом 7= 1/2 с. Наибольший угол отклонения точки обода балансира от положения равновесия а = я/2 рад. Найти угловую скорость и угловое ускорение баланса через 2 с после момента, когда балансир проходит положение равновесия. [c.108]
Из закона движения следует, что груз совершает вдоль траектории гармонические колебания с дуговой амплитудой А. В крайних положениях (а точках В, и Bj) sin kt= 1, а следовательно, os kt=Q. Поэтому в точках и скорость и нормальное ускорение обращаются в нуль касательное же ускорение имеет здесь наибольшее по модулю значение [c.114]
В первом случае (рис. 424, а) начальные отклонения всех трех масс подобраны так, что результирующие силы, действующие на них со стороны пружин, пропорциональны смещениям этих масс. Можно рассчитать величину отклонений, при которых соблюдается это требование. Если начальные отклонения будут подобраны так, что силы будут пропорциональны начальным смещениям, то и ускорения, и достигнутые скорости все время будут пропорциональны смещениям. Все три массы будут двигаться, сохраняя свое взаимное расположение, и будут совершать одно гармоническое колебание с одной и той же частотой. Это будет первое нормальное колебание системы. [c.651]
Для определения потенциала ускорения Ф, а затем гидродинамических коэффициентов Су и необходимо предварительно найти постоянную интегрирования с (i) в (IV.3.5). Рассматривая гармонические колебания профиля, представим потенциал ускорения и вызванные скорости в комплексной форме [c.184]
В качестве приемников вибрации применяются емкостные, индуктивные или пьезоэлектрические преобразователи. Они могут быть выполнены в виде приемников колебательного смещения скорости I и ускорения . При определенной градуировке приемников можно измерять все перечисленные параметры вибрации, так как для гармонических колебаний они связаны между собой. [c.46]
Тогда переменгение, скорость и ускорение точки, совершающей гармонические колебания, может быть представлена простой векторной диаграммой (рис. 5.5), где проекция скорости движения представляется 12 [c.355]
В качестве примера вычисления скорости и ускорения при гармоническом колебательном движении найдем максимал1зные значения скорости и ускорения средней точки рессоры, если амплитуда ее колебаний а = 4 мм, а период Т 0,1 с. По форч мулам (33) и (34) имеем [c.171]
То оСстоятельство, что при гармонических колебаниях смещение, скорость и ускорение пропорциональны друг другу и изменяются со временем по одинаковому (гармоническому) закону, является специальным свойством гармонических колебаний, которое выделяет их из всех колебаний любых иных форм. [c.592]
При исследовании малых колебаний в выражешш для работы инутренних сил (1.21) пренебрежем слагаемыми третьего и четвертого порядков малости. Предположим также, что конструкхщя совершает гармонические колебания, причем узловые перемещения изменяются по акону = а начальные скорости и ускорения равны нулю. При [c.33]
В отличие от свободных колебаний поведение колебательных систем под действием гармонической силы определяется не только параметрами системы, но и частотой внешнего воздействия. Мы видим, что смещение, скорость и ускорение вынужденных колеба1 ий имеют частоту, не зависящую от параметра колебательной системы, и выражаются, формулами [c.21]
Скорость и ускорение при гармоническом колебательном движении. Пусть материальная точка совершает гармоническое колебание вдоль оси Ох и ее координата изменяется по закону (34.1), причем для простоты положим = 0 x(t) = Aan аХ. Получим формулы для скорости и ускорения точки, которые, очевидно, направлены вдоль оси Ох. Для проекции скорости точки v, согласно (2.4) и (34.1) имеем v,=dx ldt = rf(y4 sin at) dt = A a os at. Дифференцируя v, no времени, получим согласно (3.4) проекцию ускорения a,=dvjdt= d(.Aeo o mt) dt =-Аа шт1. Чтобы сравнивать фазы колебаний координаты, скорости и ускорения, их формулы должны быть записаны в одинаковой форме, например, в виде asin.(), где а>0. Выражая в формуле для V, косинус через синус, а в формуле для а, синус со знаком минус через синус со знаком плюс, получаем следующие формулы для скорости и ускорения точки [c.107]
На рис. 43, б показаны графики изменения г, 2 н г в зависимости от времени /, причем график z t) дает также в другом масштабе график изменения уиругоР силы пружины. Штрихиунктириой линией показано значение 2 в положении статического равновесия. В отличие от обычь ых гармонических колебаний егце до истечения времени, равного периоду колебаний с собственной частотой, скорость ползуна, достигнув значения V( , перестает возрастать, несмотря на то, что ускорение ползуна в этот момент времени остается положительным. Скорость ползуна не может превысить скорость движущейся поверхности 1>о, так как при 2>1>о изменяется знак относительной скорости 2—Уо и, следовательно, изменяется направление силы трения, которая из силы движущей для ползуна превращается в силу сопротивления. В этот момент времени движущаяся со скоростью Уо плоскость подхватывает ползун, их относительное движение прекращается и сила трения вновь становится силой трения покоя до следующего срыва ползуна. [c.107]
Наиболее существенная информация, получаемая с помощью гармонического анализатора Фурье, — зависимость динамических перемещений от частоты колебаний. При этом одновременно проводятся экспериментальные замеры, которые с помощью ЭВМ обрабатываются для получения истории изменения возбуждающей колебания силы и ускорения. Эти данные с помощью гармонического анализатора Фурье позволяют вычислять спектральные автокорреляционные функции ускорений, скоростей или перемещений (дуу), сил (Gxx), а также смешант ные спектральные функции Gyx и функцию распределения частот Я(f) [c.189]
МЕТАЛЛОФИЗИКА — раздел физики, в котором изучаются структура и свойства металлов МЕТОД [аналогии состоит в изучении какого-либо процесса путем замены его процессом, описываемым таким же дифференциальным уравнением, как и изучаемый процесс векторных диаграмм служит для сложения нескольких гармонических колебаний путем представления их посредством векторов встречных пучков используется для увеличения доли энергии, используемой ускоренными частицами для различных ядерных реакций Дебая — Шеррера применяется при исследовании структуры монохроматических рентгеновских излучений затемненного поля служит для наблюдения частиц, когда направление наблюдения перпендикулярно к направлению освещения Лагранжа в гидродинамике состоит в том, что движение жидкости задается путем указания зависимости от времени координат всех ее частиц ин1 ерференционного контраста служит для получения изображений микроскопических объектов путем интерференции световых воли, прошедших и не прошедших через объект меченых атомов состоит в замене атомов исследуемого вещества, участвующего в каком-либо процессе, их радиоактивными изотопами моделирования — метод исследования сложных объектов, явлений или процессов на их моделях или на реальных установках с применением методов подобия теории при постановке и обработке эксперимента статистический служит для изучения свойств макроскопических систем на основе анализа, с помощью математической статистики, закономерностей теплового движения огромного числа микрочастиц, образующих эти системы совнадений в ядерной физике состоит в выделении определенной группы одновременно происходящих событий термодинамический служит для изучения свойств системы взаимодействующих тел путем анализа условий и количественных соотношений происходящих в системе превращений энергии Эйлера в гидродинамике заключаегся в задании поля скоростей жидкости для кинематического описания г чения жидкости] [c.248]
U>l/(,g os а) 1,85, т е. примерно при ускорении поперечных колебаний, меньшем в 2 «раза. Отношение средних скоростей движения частиць (при гармонических продольных колебаниях) согласно (31) и (102) = 05,/2И2. Таким образом, средняя скорость в случае двух поверхностей может быть сохранена на прежнем уровне, если принять частоту колебаний вдвое меньшей, чем а случае одной поверхности. Для получения необходимого значения w-> = 1,85 при этом, очевидно, потребуется увеличить амплитуду колебаний каждой из двух поверхностен также примерно в 2 раза частота воздействия на частицу в обоих случаях будет одинакова. Ины.мн словами, можно ожидать, что устройства с двумя гармонически вибрирующими поверхностями, работающие, например, при частоте п, = = 1000 кол/мин и амплитуде мм (с ускорением 3g), окажутся столь же эффективными, как н устройства с одной поверхностью, вибрирующей с частотой ni = = 2000 кол/мин н амплитудой = 1,5 мм (с ускорением gg). [c.58]
Исследуемая механическая система при изменении гармонического возбуждения отзывается как набор осцилляторов. Рассмотрим методы определения характеристик собственных колебаний для систем с одной степенью свободы. Практически одним из простых и тотаых способов определения собственной частоты является ее определение по нулевому фазовому СДВИ1У сигналов скорости колебаний и вынуждающей силы. Максимальная амплитуда измеряется датчиком скорости при резонансной частоте (частоте фазового резонанса). Фазовый сдвиг перемещения (и ускорения) для этой частоты составляет 90 . [c.354]
Стержень в свою очередь совершает гармонические колебания в вертикальной плоскости ху ио закону ф = фо81по)о . Найти угловую скорость и угловое ускорение диска в зависимости от времени. [c.33]
Гармонические колебания
Теперь зная, как связаны между собой ускорение и координата колеблющегося тела, можно найти зависимость координаты от времени. Для этого давайте с вами рассмотрим равномерное вращение материальной точки по окружности известного радиуса. Пусть рассматриваемое движение происходит против хода часовой стрелки. Выберем систему координат ХОY так, как это показано на рисунке.
Теперь предположим, что через некоторый промежуток времени Δt материальная точка повернулась на угол φ. Давайте вспомним, что придвижении по окружности материальная точка обладает линейной скоростью, направленной по касательной в каждой точке траектории, и центростремительным ускорением, направленным всегда по радиусу к центру окружности. Спроецируем на ось OX радиус-вектор движущейся точки, её линейную скорость и центростремительное ускорение.
Проекция радиус-вектора в положении «Эм» (М) (это точка В) является смещением материальной точки от центра окружности вдоль оси Ох. Следовательно, на выбранной оси этому смещению соответствует координата х точки В.
Поскольку при равномерном вращении точки по окружности её координата (смещение) будет периодически изменяться от xmin = –R до хmax = +R, то можно сказать, что точка В совершает колебательное движение вдоль оси Ох, а её координата х является координатой колеблющейся точки.
Соответственно будут изменяться и проекция линейной скорости (от +υ0 = ωR до –υ0 = –ωR) и проекция центростремительного ускорения материальной точки (от +a0 = ω2R до –a0 = ω2R).
Теперь вспомним, что угол поворота материальной точки при её движении по окружности можно найти, как произведение угловой скорости точки и времени поворота:
Так как при равномерном вращении по окружности линейная скорость направлена по касательной, а центростремительное ускорение — к центру окружности, то изменение координаты, проекции скорости и центростремительного ускорения материальной точки будут описываться уравнениями, которые вы сейчас видите на экране:
Перепишем данные уравнения, выразив начальную скорость и ускорение точки через угловую скорость:
Поскольку функции синуса и косинуса являются периодическими, то через промежуток времени, равный периоду, все характеристики движения точки В вдоль оси Ох примут прежние значения, то есть значения характеристик периодически повторяются. А как мы говорили на прошлом уроке, повторяемость — это основной признак периодического движения.
Обратим внимание на то, что проекция ускорения точки B в любой момент времени пропорционально смещению и противоположно ей по знаку:
Перепишем это равенство так, как это показано на экране:
Колебания, описываемые полученным уравнением, называются гармоническими, а система, совершающая такие колебания, — гармонической колебательной системой, или гармоническим осциллятором.
Гармоническими колебаниями называются колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса:
Термин «гармонические колебания» впервые был введён в науку швейцарским физиком Даниилом Бернулли.
В записанных уравнениях φ0 — это начальная фаза колебаний, которая определяет состояние колебательной системы в начальный момент времени.
xmax — это максимальное смещение материальной точки от положения устойчивого равновесия, называемое также амплитудой колебаний:
Она определяется энергией, которую сообщают точке в начальный момент времени.
ω — это циклическая частота. Она показывает, какое число полных колебаний материальная точка совершает за 2π секунд:
Наименьший промежуток времени, по истечении которого повторяются значения всех физических величин, характеризующих колебание, называется периодом колебаний:
А число полных колебаний, совершаемых в единицу времени, называется частотой колебаний:
Так как в СИ единицей периода колебаний является секунда, то единицей частоты в СИ служит с–1. Она носит название герц в честь первооткрывателя электромагнитных волн Генриха Герца.
С учётом определения периода и частоты колебаний, можно получить ещё две формулы для определения циклической частоты:
Ещё одной важной характеристикой гармонических колебаний является их фаза. Фазой колебания называется аргумент периодической функции, определяющий значение физической величины в любой момент времени. Единицей фазы в СИ является радиан.
Зависимость координаты точки от времени называется кинематическим законом (или уравнением) гармонических колебаний, поскольку позволяет определить положение точки, её скорость и ускорение в произвольный момент времени.
Скорость будет являться первой производной смещения по времени:
А ускорение — это первая производная скорости по времени или вторая производная смещения по времени:
Теперь давайте сравним уравнение гармонических колебаний с динамическими уравнениями математического и пружинного маятников, полученные нами на прошлом уроке:
Не трудно заметить, что вот эти вот величины, являются квадратом циклической частоты маятников. Извлекая квадратный корень из этих двух выражений, найдём формулы, по которым можно рассчитать циклические частоты математического и пружинного маятников:
Учитывая, что период колебаний обратно пропорционален циклической частоте (T = 2π/ω), получим формулы для определения периода колебаний пружинного и математического маятников:
Как видно из формул, период, а, следовательно, и частота колебаний пружинного маятника не зависят от амплитуды его колебаний (в пределах выполнимости закона Гука). Он определяется лишь массой груза и жёсткостью пружины.
А период и частота математического маятника не зависят от массы маятника и амплитуды его колебаний, а определяются только его длиной и модулем ускорения свободного падения.
Кстати, впервые формулу для периода математического маятника получил ученик Исаака Ньютона Христиан Гюйгенс. Поэтому она называется формулой Гюйгенса.
Давайте с вами для примера определим амплитуду, циклическую частоту, период и начальную фазу колебаний тела массой пол килограмма, подвешенного к вертикальной пружине, если известно, что в состоянии покоя тело растягивает пружину на расстояние 5 мм и для возбуждения колебаний его смещают вниз на расстояние 20 мм от положения равновесия и отпускают.
В заключении урока отметим, что гармонические колебания полностью подчиняются закону сохранения энергия. Полная механическая энергия при гармонических колебаниях равна сумме кинетической и потенциальной энергий колебательной системы:
При этом, если в колеблющейся системе отсутствуют силы сопротивления, то её полная механическая энергия остаётся неизменной. Она равна либо потенциальной энергии в момент максимального отклонения от положения равновесия, либо же кинетической энергии в момент, когда тело проходит положение равновесия.
Гармонические колебания и их характеристики
15. Гармонические колебания иих характеристики
Колебаниями или колебательными движениями
называются движения или изменения состояния,
обладающие той или иной степенью повторяемости во
времени.
Периодом колебания Т называется наименьший
промежуток
времени,
по
истечении
которого
повторяются значения всех величин, характеризующих
колебательное движение. За это время совершается
одно полное колебание.
f (t ) f (t T )
t
T
N
Частотой
периодических
колебаний
называется число полных колебаний, которые
совершаются за единицу времени:
N 1
t T
Циклической (круговой) частотой периодических
колебаний называется число полных колебаний,
которые совершаются за 2 секунд:
2
2
T
Получить уравнение простейшего колебания можно,
установив
аналогию
между
вращательным
и
колебательным движением.
При вращении с постоянной
скоростью проекция вектора
на ось Х равна:
x A cos
t 0
Угол поворота определяет значение х в данный момент
времени и называется фазой колебания.
В результате простейшее периодические колебаний
совершается по гармоническому закону:
x A cos( t 0 )
Скорость при гармоническом колебании
x A sin( t 0 )
0 sin( t 0 )
0 A
– амплитуда скорости.
Ускорение при гармоническом колебании
a x A cos( t 0 )
2
a 0 A
2
— амплитуда ускорения.
0 0
x A cos( t 0 )
A sin( t 0 ) A cos( t 0 2)
a A 2 cos( t 0 )
Графическое изображение гармонических колебаний
посредством
вращающегося
вектора
амплитуды
называется методом векторных диаграмм.
Графическое изображение гармонических колебаний
посредством
вращающегося
вектора
амплитуды
называется методом векторных диаграмм.
Ускорение и координата при гармонических колебаниях в
любой момент времени связаны соотношением
a x
2
или
x x
2
x x 0
2
представляющим
собой
дифференциальное
уравнение гармонических колебаний. Решением
уравнения является гармоническая функция.
Согласно формуле Эйлера
ei cos i sin
i 1
Уравнение гармонического колебания в комплексной
форме имеет вид
i t 0
~
x x0 e
Физический смысл имеет лишь действительная
часть, обозначаемая
~
Re x x0 cos t 0
14. 16. Квазиупругая сила. Период колебаний пружинного, математического и физического маятников.
Пружинный маятник. Колебания груза массой m напружине жесткостью k совершаются под действием
силы упругости пружины
F kx
Ускорение телу сообщает сила упругости
kx ma
kx mx
k
x x 0
m
k
2
m
k
m
m
T 2
k
16. Тело совершает гармонические колебания в случае действия на него квазиупругой возвращающей силы. Для определения частоты необходимо уста
Тело совершает гармонические колебания вслучае действия на него квазиупругой
возвращающей силы.
Для определения частоты необходимо
установить квазиупругий характер
возвращающей силы, определить k.
k
квазиупруг ий фактор
m
масса системы
Математический маятник представляет собой
материальную точку, подвешенную на невесомой
нерастяжимой нити и совершающую движение в
вертикальной плоскости под действием
силы
тяжести
W mgh
l l h x
2
2
2
2
x
h
2l
2
2
mgx
kx
W
2l
2
mg
k
l
k
m
g
l
l
T 2
g
l – длина подвеса,
g – ускорение свободного падения.
19. Физический маятник представляет собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром
масс этоготела,
или
неподвижной
оси,
перпендикулярной
направлению действия сил и не проходящей через центр
масс этого тела.
20. Колебания происходят под действием момента силы тяжести.
M IM mgd sin
mgd sin I
sin
mgd I
mgd
I
Для угла отклонения получаем дифференциальное
уравнение гармонических колебаний
mgd
0
I
mgd
I
22. l* — приведенная длина физического маятника
Период колебаний физического маятника*
I
l
T 2
2
mgd
g
I
l
md
*
l* — приведенная длина физического маятника
23. 17. Превращение и изменение энергии в системе
Превращение энергии рассмотрим на примерепружинного маятника. Пусть колебания происходят по
закону
x A cos t
При гармонических колебаниях пружинного маятника
происходят превращения потенциальной энергии
упругой деформации
2
kx
U
2
в его кинетическую энергию и наоборот
m
E
2
2
Полная
энергия
колебательной
определяется суммой энергий:
системы
m 2 kx2 m( A sin t ) 2 k ( A cos t ) 2
W
2
2
2
2
m 2 A2 sin 2 t m 2 A2 cos2 t m 2 A2
2
2
2
m A
W
2
2
2
Колебание энергий происходит с удвоенной частотой
по сравнению с колебаниями координаты.
27. Колебания кинетической и потенциальной энергии в колебательной системе происходит с удвоенной частотой 2.
Колебания кинетической и потенциальнойэнергии в колебательной системе происходит с
удвоенной частотой 2 .
m A
1
2
2
E
sin t E0 sin t W 1 cos 2 t
2
2
m 2 A2
1
2
2
U
cos t E0 cos t W 1 cos 2 t
2
2
2
2
Превращения
энергии
при
колебаниях
пружинного
маятника
происходят
в
соответствии
с
законом
сохранения
механической
энергии.
Максимальные
значения энергий равны друг другу:
2
m 0
kA
2
2
2
В любой момент сумма кинетической и
потенциальной энергии постоянна и равна
полной энергии.
2
m 0
m
kx
kA
2
2
2
2
2
2
2
Физическая величина определяющая скорость изменения фазы колебаний. Изучаем колебания – фаза колебаний
Колебаниями называются движения или процессы, которые характеризуются определенной повторяемостью во времени. Колебания широко распространены в окружающем мире и могут иметь самую различную природу. Это могут быть механические (маятник), электромагнитные (колебательный контур) и другие виды колебаний. Свободными , или собственными колебаниями, называются колебания, которые происходят в системе предоставленной самой себе, после того как она была выведена внешним воздействием из состояния равновесия. Примером могут служить колебания шарика, подвешенного на нити. Гармоническими колебаниями называются такие колебания, при которых колеблющаяся величина меняется от времени по закону синуса или косинуса . Уравнение гармонических колебаний имеет вид: , где A — амплитуда колебаний (величина наибольшего отклонения системы от положения равновесия) ; — круговая (циклическая) частота. Периодически изменяющийся аргумент косинуса — называется фазой колебаний . Фаза колебаний определяет смещение колеблющейся величины от положения равновесия в данный момент времени t. Постоянная φ представляет собой значение фазы в момент времени t = 0 и называется начальной фазой колебания .. Этот промежуток времени T называется периодом гармонических колебаний. Период гармонических колебаний равен : T = 2π/.Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения . Период малых собственных колебаний математического маятника длины L неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит от амплитуды колебаний и массы маятника.Физический маятник — Осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
24. Электромагнитные колебания. Колебательный контур. Формула Томсона.
Электромагнитные колебания — это колебания электрического и магнитного полей, которые сопровождаются периодическим изменением заряда, силы тока и напряжения. Простейшей системой, где могут возникнуть и существовать свободные электромагнитные колебания, является колебательный контур. Колебательный контур — это цепь, состоящая из катушки индуктивности и конденсатора (рис. 29, а). Если конденсатор зарядить и замкнуть на катушку, то по катушке потечет ток (рис. 29, б). Когда конденсатор разрядится, ток в цепи не прекратится из-за самоиндукции в катушке. Индукционный ток, в соответствии с правилом Ленца, будет иметь то же направление и перезарядит конденсатор (рис. 29, в). Процесс будет повторяться (рис. 29, г) по аналогии с колебаниями маятниками. Таким образом, в колебательном контуре будут происходить электромагнитные колебания из-за превращения энергии электрического поля конденсатора () в энергию магнитного поля катушки с током (), и наоборот. Период электромагнитных колебаний в идеальном колебательном контуре зависит от индуктивности катушки и емкости конденсатора и находится по формуле Томсона . Частота с периодом связана обратно пропорциональной зависимостью .
Но т.к. витки сдвинуты в пространстве, то наводимая в них ЭДС будет достигать амплитудных и нулевых значений не одновременно.
В начальный момент времени ЭДС витка будет:
В этих выражениях углы и называются фазными , или фазой . Углы и называются начальной фазой . Фазный угол определяет значение ЭДС в любой момент времени, а начальная фаза определяет значение ЭДС в начальный момент времени.
Разность начальных фаз двух синусоидальных величин одинаковой частоты и амплитуды называется углом сдвига фаз
Разделив угол сдвига фаз на угловую частоту, получим время, прошедшее с начала периода:
Графическое изображение синусоидальных величинU = (U 2 a + (U L — U c) 2)
Таким образом, из-за наличия угла сдвига фаз напряжение U всегда меньше алгебраической суммы U a + U L + U C . Разность U L — U C = U p называется реактивной составляющей напряжения .
Рассмотрим, как изменяются ток и напряжение в последовательной цепи переменного тока.
Полное сопротивление и угол сдвига фаз. Если подставить в формулу (71) значения U a = IR; U L = lL и U C =I/(C), то будем иметь: U = ((IR) 2 + 2), откуда получаем формулу закона Ома для последовательной цепи переменного тока:
I = U / ((R 2 + 2)) = U / Z (72)
где Z = (R 2 + 2) = (R 2 + (X L — X c) 2)
Величину Z называют полным сопротивлением цепи , оно измеряется в омах. Разность L — l/(C) называют реактивным сопротивлением цепи и обозначают буквой X. Следовательно, полное сопротивление цепи
Z = (R 2 + X 2)
Соотношение между активным, реактивным и полным сопротивлениями цепи переменного тока можно также получить по теореме Пифагора из треугольника сопротивлений (рис. 193). Треугольник сопротивлений А’В’С’ можно получить из треугольника напряжений ABC (см. рис. 192,б), если разделить все его стороны на ток I.
Угол сдвига фаз определяется соотношением между отдельными сопротивлениями, включенными в данную цепь. Из треугольника А’В’С (см. рис. 193) имеем:
sin ? = X / Z; cos? = R / Z; tg? = X / R
Например, если активное сопротивление R значительно больше реактивного сопротивления X, угол сравнительно небольшой. Если в цепи имеется большое индуктивное или большое емкостное сопротивление, то угол сдвига фаз возрастает и приближается к 90°. При этом, если индуктивное сопротивление больше емкостного, напряжение и опережает ток i на угол; если же емкостное сопротивление больше индуктивного, то напряжение и отстает от тока i на угол.
Идеальная катушка индуктивности, реальная катушка и конденсатор в цепи переменного тока.
Реальная катушка в отличии от идеальной имеет не только индуктивность, но и активное сопротивление, поэтому при протекании переменного тока в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в тепло в соответствии с законом Ленца — Джоуля .
Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р , а изменение энергии в магнитном поле — реактивной мощностью Q .
В реальной катушке имеют место оба процесса, т. е. ее активная и реактивная мощности отличны от нуля. Поэтому одна реальная катушка в схеме замещения должна быть представлена активным и реактивным элементами.
4 Кинематическая связь между круговым движением и гармоническим колебательным движением. Пусть точка движется по окружности радиуса R с постоянной угловой скоростью ω. Тогда проекция x-радиус – вектора этой точки на горизонтальную ось OX (рис.11, а) выразится так:
Но α = ωt. Поэтому:
Это значит, что проекция точки, движущейся по окружности, на ось OX совершает гармонические колебания с амплитудой x m = R и циклической частотой ω. Это используется в так называемом кулисном механизме, предназначенном для преобразования вращательного движения в колебательное. Рассмотрим устройство кулисного механизма на простейшей его модели (рис.11б). На оси электродвигателя 1 укреплён кривошип 2, а на кривошипе – палец 3. При работе двигателя палец движется по окружности радиуса R. Палец вставлен в прорезь кулисы 4, которая может двигаться по направляющим 5. Поэтому палец давит на кулису и заставляет её смещаться то
вправо, то влево. Кулиса приходит в колебательное движение. Колебания кулисы – гармонические, так как прорезь в кулисе как бы проецирует движение пальца на горизонтальную ось.
Фаза колебаний. Разность фаз
1 Понятие фазы колебаний. Так как амплитудные значения смещения (x m), скорости (υ m) и ускорения(a m) при гармонических колебаниях постоянны, то мгновенные значения этих величин, как видно из формул смещения, скорости и ускорения, определяются значением аргумента
называемого фазой колебаний.
Таким образом, фазой колебания называется физическая величина, определяющая (при данной амплитуде) мгновенные значения смещения, скорости и ускорения.
Из формулы
x = x m sin ω 0 t
видно, что при t = 0 смещение x также равно нулю. Но всегда ли будет так?
Допустим для конкретности, что мы наблюдаем движение кулисного механизма, отсчитывая время по положению стрелки секундомера. В этом случае момент t= 0 есть момент пуска секундомера. Запись «x = 0 при t= 0» означает, что секундомер был пущен в один из тех моментов, когда кулиса находилась в среднем (нулевом) положении (рис. 12, а). В этом случае
x = x m sin ω 0 t
Предположим теперь, что секундомер был включен тогда, когда кулиса уже сместилась на расстояние x’ (рис. 12, б). В этом случае смещение кулисы через промежуток времени t, отмеченный секундомером, определится формулой
x = x m sin ω 0 (t + t «)
где t » – время, необходимое на смещение кулисы на величину x’.
Преобразуем эту формулу
x = x m sin (ω 0 t + ω 0 t «),
x = x m sin (ω 0 t + φ 0),
где φ 0 = ω 0 t- начальная фаза колебаний. Мы видим, что начальная фаза зависит от выбора начала отсчёта времени. Если начало отсчёта времени ведётся с момента, когда смещение равно нулю(x = 0), то начальная фаза равна нулю. Изменение мгновенного значения
смещения в этом случае описывается формулой
x = x m sin ω 0 t
Если же за начало отсчёта времени берётся момент, когда изменяющееся смещение достигло наибольшего значения x = x m , то начальная фаза равна π/2 и изменение мгновенного значения смещения описывается формулой
x = x m sin (ω 0 t + ) = x m sin ω 0 t
2 Разность фаз двух гармонических колебаний. Возьмём два одинаковых маятника. Подтолкнув маятники в разные моменты времени t 1 и t 2 , запишем осциллограммы их колебаний (рисунок 13). Анализ осциллограмм показывает, что колебания маятников имеют одинаковую частоту, но не совпадают по фазе. Колебания первого маятника опережают колебания второго маятника на одну и ту же постоянную величину.
Уравнения колебаний маятников запишутся так:
x 1 = x m sin (ω 0 t + φ 1),
x 2 = x m sin (ω 0 t + φ 2)
Величина φ 1 -φ 2 – называется разностью фаз или сдвигом фаз.
Из осциллограммы видно, что перенос начала отсчёта времени не изменяет разности фаз. Следовательно, разность фаз гармонических колебательных движений, имеющих одинаковую частоту, не зависит от выбора начала отсчёта времени. На рисунке 14 представлены графики смещения, скорости и ускорения для одного и того же гармонически колеблющегося тела. Как видно из рисунка, колебания этих величин происходят с различными начальными фазами.
>> Фаза колебаний
§ 23 ФАЗА КОЛЕБАНИЙ
Введем еще одну величину, характеризующую гармонические колебания , — фазу колебаний.
При заданной амплитуде колебаний координата колеблющегося тела в любой момент времени однозначно определяется аргументом косинуса или синуса :
Величину , стоящую под знаком функции косинуса или синуса, называют фазой колебаний, описываемой этой функцией. Выражается фаза в угловых единицах радианах.
Фаза определяет не только значение координаты, но и значение других физических величин, например скорости и ускорения, изменяющихся также по гармоническому закону. Поэтому можно сказать, что фаза определяет при заданной амплитуде состояние колебательной системы в любой момент времени. В этом состоит значение понятия фазы.
Колебания с одинаковыми амплитудами и частотами могут различаться фазами.
Отношение указывает, сколько периодов прошло от момента начала колебаний. Любому значению времени t, выраженному в числе периодов Т, соответствует значение фазы , выраженное в радианах. Так, по прошествии времени t = (четверти периода) , по прошествии половины периода = , по прошествии целого периода = 2 и т. д.
Можно изобразить на графике зависимость координаты колеблющейся точки не от времени, а от фазы. На рисунке 3.7 показана та же косинусоида, что и на рисунке 3.6, но на горизонтальной оси отложены вместо времени различные значения фазы .
Представление гармонических колебаний с помощью косинуса и синуса. Вы уже знаете, что при гармонических колебаниях координата тела изменяется со временем по закону косинуса или синуса. После введения понятия фазы остановимся на этом подробнее.
Синус отличается от косинуса сдвигом аргумента на , что соответствует, как видно из уравнения (3.21), промежутку времени, равному четверти периода:
Но при этом начальная фаза, т. е. значение фазы в момент времени t = 0, равна не нулю, а .
Обычно колебания тела, прикрепленного к пружине, или колебания маятника мы возбуждаем, выводя тело маятника из положения равновесия и затем отпуская его. Смещение от гихпожения равновесия максимально в начальной момент. Поэтому для описания колебаний удобнее пользоваться формулой (3.14) с применением косинуса, чем формулой (3.23) с применением синуса.
Но если бы мы возбудили колебания покоящегося тела кратковременным толчком, то координата тела в начальный момент была бы равна нулю, и изменения координаты со временем было бы удобнее описывать с помощью синуса, т. е. формулой
x = x m sin t (3.24)
так как при этом начальная фаза равна нулю.
Если в начальный момент времени (при t = 0) фаза колебаний равна , то уравнение колебаний можно записать в виде
x = x m sin(t + )
Сдвиг фаз. Колебания, описываемые формулами (3.23) и (3.24), отличаются друг от друга только фазами. Разность фаз, или, как часто говорят, сдвиг фаз, этих колебаний составляет . На рисунке 3.8 показаны графики зависимости координат от времени колебаний, сдвинутых по фазе на . График 1 соответствует колебаниям, совершающимся по синусоидальному закону: x = x m sin t а график 2 — колебаниям, совершающимся по закону косинуса:
Для определения разности фаз двух колебаний надо в обоих случаях колеблющуюся величину выразить через одну и ту же тригонометрическую функцию — косинус или синус.
1. Какие колебания называют гармоническими!
2. Как связаны ускорение и координата при гармонических колебаниях!
3. Как связаны циклическая частота колебаний и период колебаний!
4. Почему частота колебаний тела, прикрепленного к пружине, зависит от его массы, а частота колебаний математического маятника от массы не зависит!
5. Каковы амплитуды и периоды трех различных гармонических колебаний, графики которых представлены на рисунках 3.8, 3.9!
Простое гармоническое движение — Концепции
Введение
Вы когда-нибудь задумывались, почему напольные часы показывают точное время? Движение маятника — это особый вид повторяющегося или периодического движения, называемого простым гармоническим движением или SHM. Положение колеблющегося объекта изменяется синусоидально со временем. Многие объекты колеблются взад и вперед. Движение ребенка на качелях можно представить себе как синусоидальное и, следовательно, можно рассматривать как простое гармоническое движение.Некоторые сложные движения, такие как турбулентные волны на воде, не считаются простым гармоническим движением. Когда объект находится в простом гармоническом движении, можно легко определить скорость, с которой он колеблется взад и вперед, а также его положение относительно времени. В этой лабораторной работе вы проанализируете простой маятник и систему пружина-масса, которые демонстрируют простое гармоническое движение.Обсуждение принципов
Частица, которая колеблется вертикально в простом гармоническом движении, перемещается вверх и вниз между двумя крайними значениями y = ± A .Максимальное смещение A называется амплитудой . Это движение показано графически на графике зависимости положения от времени на рисунке 1. Одно полное колебание или цикл или колебание — это движение, например, отy = −A
доy = + A
и обратно доy = −A.
Интервал времени T , необходимый для завершения одного колебания, называется периодом . Связанная величина — частота f , которая представляет собой количество колебаний, которые система делает за единицу времени.Частота обратно пропорциональна периоду и измеряется в герцах, сокращенно Гц;1 Гц = 1 с −1 .
Если частица колеблется вдоль оси y , ее положение на оси y в любой момент времени t , измеренное от начала колебания, определяется уравнением Напомним, что скорость объекта — это первая производная, а ускорение — вторая производная функции смещения по времени.Скорость v и ускорение a частицы в момент времени t определяются следующим образом.(3)
v = 2 π fA cos (2 π фут)
(4)
a = — (2 π f) 2 [A sin (2 π ft)]
Обратите внимание, что скорость и ускорение также синусоидальны. Однако функция скорости имеет разность фаз 90 ° или π /2, в то время как функция ускорения имеет разность фаз 180 ° или π относительно функции смещения.Например, когда смещение является положительным максимумом, скорость равна нулю, а ускорение — отрицательному максимуму. Подстановка из уравнения 2 в уравнение 4 дает Из уравнения 5 мы видим, что ускорение объекта в SHM пропорционально смещению и имеет противоположный знак. Это основное свойство любого объекта, совершающего простое гармоническое движение. Рассмотрим несколько критических точек в цикле, как в случае колебательной системы пружина-масса. Система пружина-масса состоит из массы, прикрепленной к концу пружины, подвешенной на стойке.Масса слегка опускается и отпускается, чтобы заставить пружину и массу колебаться в вертикальной плоскости. На рисунке 2 показаны пять критических точек, когда нагрузка на пружину проходит полный цикл. Положение равновесия для системы пружина-масса — это положение массы, когда пружина не растягивается и не сжимается. Масса завершает полный цикл, перемещаясь из положения A в положение E. Описание каждой позиции приводится ниже. Положение A: пружина сжата; масса выше точки равновесия наy = A
и вот-вот будет выпущена.Положение B: Масса движется вниз, проходя через точку равновесия. Положение C: Груз на мгновение находится в состоянии покоя в самой нижней точке перед тем, как начать движение вверх. Положение D: Масса движется вверх, проходя через точку равновесия. Положение E: гиря на мгновение находится в состоянии покоя в наивысшей точке, прежде чем снова начать движение вниз. Отметив время, когда возникают отрицательное максимальное, положительное максимальное и нулевое значения для положения, скорости и ускорения колеблющегося объекта, вы можете построить график функции синуса (или косинуса).Это сделано для случая колеблющейся системы пружина-масса в таблице ниже, а три функции показаны на рисунке 3. Обратите внимание, что положительное направление обычно выбирается как направление, в котором пружина растягивается. Следовательно, положительное направление в этом случае — вниз, а начальное положение A на рисунке 2 фактически является отрицательным значением. Самый сложный параметр для анализа — это ускорение. Это помогает использовать второй закон Ньютона, который говорит нам, что отрицательное максимальное ускорение происходит, когда результирующая сила равна отрицательному максимуму, положительное максимальное ускорение происходит, когда результирующая сила равна положительному максимуму, и ускорение равно нулю, когда результирующая сила равна нулю.Для этого конкретного начального условия (начальное положение в точке A на рисунке 2) кривая положения является функцией косинуса (фактически отрицательной функцией косинуса), кривая скорости является функцией синуса, а кривая ускорения является просто отрицательной функцией кривой положения. .Масса и пружина
Масса, подвешенная на конце пружины, растянет ее на некоторое расстояние х . Сила, с которой пружина тянет вверх груз, определяется формулой Hooke ‘ s law где k — жесткость пружины, а y — растяжение пружины при приложении к ней силы F .Константа пружины k является мерой жесткости пружины. Жесткость пружины может быть определена экспериментально, позволяя грузу неподвижно висеть на пружине, а затем добавляя дополнительную массу и записывая дополнительное растяжение пружины, как показано ниже. На рисунке 4а подвеска груза подвешена к концу пружины. На рисунке 4b к подвеске была добавлена дополнительная масса, и теперь пружина выдвинута на величинуΔy.
Эта экспериментальная установка также показана на фотографии устройства на рисунке 5.Когда масса неподвижна, ее ускорение равно нулю. Следовательно, согласно второму закону Ньютона, результирующая сила должна быть равна нулю. На массу действуют две силы: сила тяжести, направленная вниз, и сила пружины, направленная вверх. См. Диаграмму свободного тела на Рисунке 6 ниже. Итак, второй закон Ньютона дает нам гдеΔm
— изменение массы, аΔy
— изменение растяжения пружины, вызванное изменением массы, g — ускорение свободного падения, а k — жесткость пружины.Уравнение 7 также можно выразить как Второй закон Ньютона, примененный к этой системе, равенma = F = −ky.
Подставим из уравнения 5a = −4 π 2 f 2 y.
для разгона получить(9)
м (−4 π 2 f 2 y) = −ky
откуда получаем выражение для частоты f и периода T .(10)
f =(11)
Т = 2 πT 2
по сравнению с м будет прямой линией, и жесткость пружины может быть определена по наклону.Простой маятник
Другой пример простого гармонического движения, который вы исследуете, — это простой маятник . Простой маятник состоит из массы м , называемой бобом маятника, прикрепленной к концу веревки. Длина L простого маятника измеряется от точки подвешивания струны до центра боба, как показано на Рисунке 7 ниже. Если боб перемещен из положения покоя на некоторый угол смещения θ , как на фиг. 8, возвращающая сила вернет боб обратно в положение равновесия.Силы, действующие на боб, — это сила тяжести и сила натяжения струны. Сила натяжения струны уравновешивается составляющей силы тяжести, которая соответствует струне (то есть перпендикулярна движению боба). Возвращающей силой здесь является тангенциальная составляющая гравитационной силы. Когда мы применяем тригонометрию к меньшему треугольнику на рисунке 8, мы получаем величину возвращающей силы | F | = мг sin θ .Эта сила зависит от массы боба, ускорения свободного падения g и синуса угла, на который натянута струна. Снова должен применяться второй закон Ньютона, поэтому(13)
ma = F = −mg sin θ
где отрицательный знак означает, что возвращающая сила действует противоположно направлению движения боба. Поскольку боб движется по дуге окружности, угловое ускорение определяется какα = a / L.
Из уравнения 13 получаем На рисунке 9 синяя сплошная линия представляет собой график зависимости sin ( θ ) от θ , а прямая линия представляет собой график θ в градусах против θ в радианах. Для малых углов эти две кривые почти неразличимы. Следовательно, пока смещение θ мало, мы можем использовать приближение sin θ ≈ θ . В этом приближении уравнение 14 принимает вид Уравнение 15 показывает (угловое) ускорение, пропорциональное отрицательному значению (углового) смещения, и поэтому движение боба является простым гармоническим, и мы можем применить уравнение 5a = −4 π 2 f 2 г.
получить Комбинируя уравнение 15 и уравнение 16 и упрощая, мы получаем(17)
f =(18)
Т = 2 πCopyright © 2013 Advanced Instructional Systems, Inc. и Государственный университет Северной Каролины | Кредиты
Harmonic Motion — обзор
Чувствительный прибор весом W = 30 кН устанавливается в месте, где окружающая среда вызывает вертикальное гармоническое движение с циклической частотой f = 15 Гц и максимальной амплитудой u0 = 0.02м. Для изоляции движения инструмент размещается на упругом слое с жесткостью k = 28 кН / м и демпфированием ξ = 0,1. Определите (i) ускорение, передаваемое на инструмент, и (ii) если для бесперебойной работы инструмента требуется, чтобы приложенное к нему ускорение было меньше 0,1g, укажите, как обеспечить это, используя тот же эластичный слой.
Расчет передаточного числа TR
Масса и собственная частота инструмента
m = Wg = 30 кН9.81 м / с2 = 3,058 кНм − 1 с2
ω = км = 283,058 = 3,026 с − 1
Круговая частота гармонического движения и максимальное ускорение составляют
ω¯ = 2πf = 94,248 с − 1
u¨gmax = ω¯2u0 = 177,653 = 18,109gg = 9,81 мс − 2
, следовательно,β = ω¯ω = 31,147
иTR = 1 + 2ξβ21 − β22 + 2ξβ2 = 0,0065
Следовательно, максимальное ускорение, передаваемое на прибор, равно
u¨totmax = TR × u¨gmax = 0,118g
Модификация системы так, чтобы u¨totmax <0.1g
Это должно быть
TR = 1 + 2ξβ21 − β22 + 2ξβ2 = u¨totmaxu¨gmax <0,1g18.109g = 0,0055
Для одного и того же упругого слоя жесткость k и коэффициент демпфирования c не изменяются. Следовательно, передаточное отношение TR может быть изменено, если передаточное отношение β изменяется. Но поскольку задано ω¯, это соотношение можно изменить, только если изменить собственную частоту ω. Это возможно, если изменить массу системы (инструмента) на шаг Δm.
Пусть m ′ = m + Δm — новая масса, а ξ ′, ω ′ — новый коэффициент демпфирования и частота системы (прибора), соответственно.Тогда у нас будет
(1) ω′ω = mm ′
c = 2mωξ = 2m′ω′ξ ′
, что дает(2) ξ ′ = ξmωm′ω ′ = ξmm ′
Кроме того, мы имеем
(3) β ′ = ω¯ω ′ = βm′m
Из ур. (2), (3) получаем
ξ′β ′ = ξβ = 3,115
Следовательно, должно быть
TR = 1 + 2ξ′β′21 − β′22 + 2ξ′β′2 = 1 + 2 × 3,11521 − β′22 + 2 × 3,1152 <0,0055
, что справедливо, если33,885 <β ′ = βm ′ / morm ′> 3,619 кНм − 1s2
Следовательно, Δm≥0,561 кНм − 1s2.
механики | Определение, примеры, законы и факты
механика , наука, изучающая движение тел под действием сил, включая особый случай, когда тело остается в покое.В первую очередь проблема движения — это силы, которые тела действуют друг на друга. Это приводит к изучению таких тем, как гравитация, электричество и магнетизм, в зависимости от природы задействованных сил. Учитывая силы, можно искать способ движения тел под действием сил; это предмет собственно механики.
Британская викторина
Викторина «Все о физике»
Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какая единица измерения для циклов в секунду? Проверьте свою физическую хватку с помощью этой викторины.
Исторически сложилось так, что механика была одной из первых возникших точных наук. Его внутренняя красота как математической дисциплины и ранний замечательный успех в количественном учете движений Луны, Земли и других планетных тел оказали огромное влияние на философскую мысль и послужили толчком для систематического развития науки.
Механику можно разделить на три раздела: статика, которая имеет дело с силами, действующими на покоящееся тело и в нем; кинематика, описывающая возможные движения тела или системы тел; и кинетика, которая пытается объяснить или предсказать движение, которое произойдет в данной ситуации.В качестве альтернативы механику можно разделить по типу изучаемой системы. Простейшей механической системой является частица, определяемая как настолько маленькое тело, что его форма и внутренняя структура не имеют значения в данной задаче. Более сложным является движение системы из двух или более частиц, которые действуют друг на друга и, возможно, испытывают силы, действующие со стороны тел вне системы.
Принципы механики были применены к трем общим областям явлений.Движение таких небесных тел, как звезды, планеты и спутники, можно предсказать с большой точностью за тысячи лет до того, как они произойдут. (Теория относительности предсказывает некоторые отклонения от движения в соответствии с классической или ньютоновской механикой; однако они настолько малы, что их можно наблюдать только с помощью очень точных методов, за исключением задач, затрагивающих всю или большую часть обнаруживаемой Вселенной. ) Как вторая область, обычные объекты на Земле вплоть до микроскопических размеров (движущиеся со скоростью намного ниже скорости света) правильно описываются классической механикой без значительных исправлений.Инженер, проектирующий мосты или самолеты, может с уверенностью использовать ньютоновские законы классической механики, даже если силы могут быть очень сложными, а вычислениям не хватает прекрасной простоты небесной механики. Третья область явлений включает поведение материи и электромагнитного излучения в атомном и субатомном масштабах. Хотя вначале были достигнуты ограниченные успехи в описании поведения атомов в терминах классической механики, эти явления должным образом рассматриваются в квантовой механике.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчасКлассическая механика занимается движением тел под действием сил или равновесием тел, когда все силы уравновешены. Предмет можно рассматривать как разработку и применение основных постулатов, впервые сформулированных Исааком Ньютоном в его Philosophiae Naturalis Principia Mathematica (1687), широко известном как Principia . Эти постулаты, называемые законами движения Ньютона, изложены ниже.Их можно использовать для предсказания с большой точностью самых разных явлений, от движения отдельных частиц до взаимодействий очень сложных систем. В этой статье обсуждается множество этих приложений.
В рамках современной физики классическую механику можно понять как приближение, вытекающее из более глубоких законов квантовой механики и теории относительности. Однако такой взгляд на место объекта сильно недооценивает его важность в формировании контекста, языка и интуиции современной науки и ученых.Наш современный взгляд на мир и место человека в нем прочно укоренен в классической механике. Более того, многие идеи и результаты классической механики выживают и играют важную роль в новой физике.
Центральными понятиями классической механики являются сила, масса и движение. Ни сила, ни масса не были четко определены Ньютоном, и оба они были предметом многих философских спекуляций со времен Ньютона. Оба они наиболее известны своими эффектами. Масса — это мера склонности тела сопротивляться изменениям в состоянии движения.С другой стороны, силы ускоряют тела, то есть они изменяют состояние движения тел, к которым они приложены. Взаимодействие этих эффектов — основная тема классической механики.
Хотя законы Ньютона фокусируют внимание на силе и массе, три другие величины приобретают особое значение, потому что их общее количество никогда не меняется. Эти три величины — энергия, (линейный) импульс и угловой момент. Любой из них может быть перемещен из одного тела или системы тел в другое.Кроме того, энергия может менять форму, будучи связанной с единственной системой, проявляясь как кинетическая энергия, энергия движения; потенциальная энергия, энергия позиции; тепло или внутренняя энергия, связанная со случайными движениями атомов или молекул, составляющих любое реальное тело; или любая комбинация из трех. Тем не менее полная энергия, импульс и угловой момент во Вселенной никогда не меняются. Этот факт выражается в физике, говоря, что энергия, импульс и угловой момент сохраняются.Эти три закона сохранения вытекают из законов Ньютона, но сам Ньютон их не выражал. Их нужно было обнаружить позже.
Примечателен тот факт, что, хотя законы Ньютона больше не считаются фундаментальными и даже не совсем правильными, три закона сохранения, выведенные из законов Ньютона — сохранение энергии, импульса и момента количества движения — остаются в точности верными даже в квантовая механика и теория относительности. Фактически, в современной физике сила больше не является центральным понятием, а масса — лишь одним из множества атрибутов материи.Однако энергия, импульс и угловой момент по-прежнему прочно занимают центральное место. Сохраняющаяся важность этих идей, унаследованных от классической механики, может помочь объяснить, почему этот предмет сохраняет такое большое значение в современной науке.
Учебное пособие по физике: движение маятника
Простой маятник состоит из относительно массивного объекта, подвешенного на веревке к неподвижной опоре. Обычно он висит вертикально в положении равновесия. Этот массивный объект ласково называют маятником bob .Когда боб смещается из состояния равновесия, а затем отпускается, он начинает свое возвратно-поступательное колебание относительно своего фиксированного положения равновесия. Движение регулярное и повторяющееся, пример периодического движения. Движение маятника было описано ранее в этом уроке, когда мы пытались понять природу вибрирующих объектов. Маятник снова обсуждался, когда мы рассматривали математические свойства объектов, находящихся в периодическом движении. Здесь мы исследуем движение маятника еще более подробно, поскольку мы сосредоточимся на том, как различные величины меняются с течением времени.Такие величины будут включать силы, положение, скорость и энергию — как кинетическую, так и потенциальную энергию.
Расчет силы маятника
Ранее в этом уроке мы узнали, что на объект, который вибрирует, действует восстанавливающая сила. Возвратная сила заставляет вибрирующий объект замедляться при удалении от положения равновесия и ускоряться при приближении к положению равновесия. Именно эта восстанавливающая сила отвечает за вибрацию.Итак, какие силы действуют на качение маятника? А какова восстанавливающая сила маятника? На маятник bob постоянно действуют две доминирующие силы во время его движения. Есть сила тяжести, которая действует на боб. Это результат того, что масса Земли притягивает массу боба. И есть сила натяжения, действующая вверх и к точке поворота маятника. Сила натяжения возникает в результате натяжения струны на боб маятника.В нашем обсуждении игнорирует влияние сопротивления воздуха — третьей силы, которая всегда противодействует движению боба, когда он качается взад и вперед. Сила сопротивления воздуха относительно мала по сравнению с двумя доминирующими силами.
Сила тяжести очень предсказуема; она всегда в одном направлении (вниз) и всегда одной величины — масса * 9,8 Н / кг. Сила натяжения значительно менее предсказуема. И его направление, и величина меняются по мере того, как боб качается взад и вперед.Направление силы натяжения всегда к точке поворота. Таким образом, когда боб качается влево от своего положения равновесия, сила натяжения находится под углом — направлена вверх и вправо. И когда боб качается вправо от своего положения равновесия, натяжение направляется вверх и влево. На приведенной ниже диаграмме показано направление этих двух сил в пяти разных положениях на пути маятника.
В физических ситуациях, когда силы, действующие на объект, не имеют одинаковых, противоположных или перпендикулярных направлений, принято разделять одну или несколько сил на компоненты.Эта практика использовалась при анализе задач по вывешиванию знаков и задач с наклонной плоскостью. Обычно одна или несколько сил разделяются на перпендикулярные составляющие, которые лежат вдоль координатных осей, направленных в направлении ускорения или перпендикулярно ему. Таким образом, в случае маятника разрешается сила тяжести, поскольку сила натяжения уже направлена перпендикулярно движению. На диаграмме справа показан маятник в положении справа от его положения равновесия и на полпути к точке максимального смещения.Система координатных осей изображена на схеме, а сила тяжести разделена на две составляющие, лежащие вдоль этих осей. Одна из составляющих направлена по касательной к дуге окружности, по которой движется маятник; эта компонента помечена как Fgrav-касательная. Другой компонент направлен перпендикулярно дуге; он обозначен как Fgrav-perp. Вы заметите, что перпендикулярная составляющая силы тяжести находится в направлении, противоположном силе натяжения. Вы также можете заметить, что сила натяжения немного больше, чем этот компонент силы тяжести.Тот факт, что сила натяжения (Ftens) больше, чем перпендикулярная составляющая силы тяжести (Fgrav-perp), означает, что будет чистая сила, перпендикулярная дуге движения боба. Это должно быть так, поскольку мы ожидаем, что объекты, движущиеся по круговой траектории, будут испытывать внутреннюю или центростремительную силу. Тангенциальная составляющая силы тяжести (F-тангенс) неуравновешивается любой другой силой. Таким образом, существует результирующая сила, направленная по другим координатным осям. Именно этот тангенциальный компонент силы тяжести действует как восстанавливающая сила.Когда маятник движется вправо от положения равновесия, эта составляющая силы направляется против его движения назад к положению равновесия.
Приведенный выше анализ применим для одного места вдоль дуги маятника. В других местах по дуге сила натяжения будет изменяться. Тем не менее, процесс разделения гравитации на две составляющие вдоль осей, перпендикулярных и касательных к дуге, остается прежним. На диаграмме ниже показаны результаты силового анализа для нескольких других положений.
Осталось сделать пару комментариев. Во-первых, обратите внимание на диаграмму, когда боб смещен до максимального смещения вправо от положения равновесия. Это положение, в котором маятник на мгновение имеет скорость 0 м / с и меняет свое направление. Сила натяжения (Ftens) и перпендикулярная составляющая силы тяжести (Fgrav-perp) уравновешивают друг друга. В этот момент времени нет результирующей силы, направленной вдоль оси, перпендикулярной движению.Поскольку движение объекта приостановлено на мгновение , центростремительная сила не нужна.
Во-вторых, обратите внимание на диаграмму, когда боб находится в положении равновесия (струна полностью вертикальна). В этом положении компонент силы в касательном направлении отсутствует. При перемещении через положение равновесия восстанавливающая сила на мгновение отсутствует. После того, как вернул в положение равновесия, восстанавливающая сила отсутствует.Возвратная сила необходима только тогда, когда маятник смещен из положения равновесия. Вы также можете заметить, что сила натяжения (Ftens) больше, чем перпендикулярная составляющая силы тяжести (Fgrav-perp), когда боб движется через это положение равновесия. Поскольку боб движется по дуге окружности, в этом положении должна быть чистая центростремительная сила.
Синусоидальная природа движения маятника
В предыдущей части этого урока мы исследовали синусоидальный характер движения массы на пружине.Мы проведем аналогичное исследование здесь для движения маятника. Предположим, что мы можем измерить величину, на которую маятник смещается влево или вправо от своего положения равновесия или покоя с течением времени. Смещение вправо от положения равновесия будет рассматриваться как положительное смещение; а смещение влево будет рассматриваться как отрицательное смещение. Используя эту систему отсчета, положение равновесия будет рассматриваться как нулевое положение.И предположим, что мы построили график, показывающий изменение положения во времени. Полученный график зависимости положения от времени показан ниже. Подобно тому, что наблюдалось для груза на пружине, положение маятника (измеренное по дуге относительно его положения покоя) является функцией синуса времени.
Теперь предположим, что мы используем наш детектор движения, чтобы исследовать, как скорость маятника изменяется во времени.По мере того как маятник совершает движение вперед и назад , скорость непрерывно изменяется. Бывают моменты, когда скорость является отрицательной величиной (для движения влево), а в другие моменты времени она будет положительной (для движения вправо). И, конечно же, будут моменты времени, когда скорость будет равна 0 м / с. Если бы были нанесены изменения скорости с течением времени, результирующий график был бы похож на показанный ниже.
Теперь давайте попробуем понять взаимосвязь между положением боба по дуге его движения и скоростью, с которой он движется.Предположим, мы идентифицируем несколько точек вдоль дуги, а затем связываем эти положения со скоростью качания маятника. На рисунке ниже показана попытка установить такую связь между положением и скоростью.
Как часто говорят, картинка стоит тысячи слов. А вот и слова. График выше основан на положении равновесия (D), обозначенном как нулевое положение. Смещение влево от положения равновесия считается отрицательным положением.Смещение вправо считается положительной позицией. Анализ графиков показывает, что скорость наименьшая, когда смещение наибольшее. И скорость наибольшая, когда смещение боба наименьшее. Чем дальше боб отошел от положения равновесия, тем медленнее он движется; и чем ближе боб находится к положению равновесия, тем быстрее он движется. Это можно объяснить тем, что по мере того, как боб движется от положения равновесия, возникает возвращающая сила, которая препятствует его движению.Эта сила замедляет качание. Таким образом, когда боб движется влево из положения D в E, затем из положения F в G, сила и ускорение направляются вправо, а скорость уменьшается по мере его движения по дуге от D к G. В G — максимальное смещение влево — маятник. Боб имеет скорость 0 м / с. Вы можете думать о бобе как о , который на мгновение остановился, и готов изменить свое направление. Затем боб движется вправо по дуге от G к F, от E к D. При этом восстанавливающая сила направляется вправо в том же направлении, что и боб.Эта сила ускоряет боб, придавая ему максимальную скорость в положении D — положении равновесия. Когда боб движется мимо позиции D, он движется вправо по дуге в направлении C, затем B и затем A. При этом возникает восстанавливающая сила влево, противодействующая его движению и заставляющая его замедляться. Таким образом, когда смещение увеличивается от D до A, скорость уменьшается из-за противодействующей силы. Как только боб достигает положения А — максимального смещения вправо — он достигает скорости 0 м / с.Еще раз, скорость боба наименьшая, когда смещение наибольшее. Боб завершает свой цикл, перемещаясь влево от A к B к C к D. По этой дуге от A к D восстанавливающая сила действует в направлении движения, тем самым ускоряя боб вверх. Таким образом, было бы логично заключить, что по мере уменьшения положения (по дуге от A до D) скорость увеличивается. Попав в положение D, боб будет иметь нулевое смещение и максимальную скорость. Скорость наибольшая, когда смещение наименьшее.Анимация справа (используется с разрешения Wikimedia Commons; особая благодарность Hubert Christiaen) визуально отображает эти принципы. Показанный вектор ускорения объединяет как перпендикулярное, так и тангенциальное ускорения в один вектор. Вы заметите, что этот вектор полностью касается дуги при максимальном смещении; это согласуется с анализом сил, обсужденным выше. И вектор вертикальный (по направлению к центру дуги) в положении равновесия.Это также согласуется с анализом сил, рассмотренным выше.
Энергетический анализ
В предыдущей главе Учебника по физике обсуждалась энергия, которой обладает маятник. Мы продолжим это обсуждение здесь, поскольку мы попытаемся связать описанные выше характеристики движения с концепциями кинетической энергии, потенциальной энергии и полной механической энергии.
Кинетическая энергия, которой обладает объект, — это энергия, которой он обладает из-за своего движения.Это количество, которое зависит как от массы, так и от скорости. Уравнение, связывающее кинетическую энергию (KE) с массой (m) и скоростью (v), составляет
KE = ½ • м • v 2
Чем быстрее движется объект, тем большей кинетической энергией он будет обладать. Мы можем объединить эту концепцию с обсуждением выше, как скорость изменяется в ходе движения. Такое смешение концепций привело бы нас к выводу, что кинетическая энергия качающегося маятника увеличивается по мере приближения качки к положению равновесия.И кинетическая энергия уменьшается по мере того, как боб перемещается дальше от положения равновесия.
Потенциальная энергия, которой обладает объект, — это запасенная энергия положения. В Учебнике по физике обсуждаются два типа потенциальной энергии — гравитационная потенциальная энергия и упругая потенциальная энергия. Упругая потенциальная энергия присутствует только тогда, когда пружина (или другая упругая среда) сжимается или растягивается. Простой маятник не состоит из пружины.Форма потенциальной энергии, которой обладает маятник, — это потенциальная энергия гравитации. Количество гравитационной потенциальной энергии зависит от массы (m) объекта и высоты (h) объекта. Уравнение для гравитационной потенциальной энергии (PE):
PE = м • г • ч
, где g представляет собой напряженность гравитационного поля (иногда называемую ускорением свободного падения) и имеет значение 9,8 Н / кг.
Высота объекта выражается относительно некоторого произвольно назначенного нулевого уровня .Другими словами, высота должна измеряться как расстояние по вертикали над некоторой исходной позицией. Для маятникового боба принято называть самое низкое положение опорным положением или нулевым уровнем. Таким образом, когда боб находится в положении равновесия (самое нижнее положение), его высота равна нулю, а его потенциальная энергия равна 0 Дж. Поскольку маятник совершает движения вперед и назад , бывают моменты, в течение которых боб движется от положение равновесия. При этом его высота увеличивается по мере того, как он движется все дальше и дальше.Он достигает максимальной высоты, когда достигает положения максимального смещения от положения равновесия. По мере того, как боб движется к своему положению равновесия, он уменьшает свою высоту и снижает свою потенциальную энергию.
Теперь давайте объединим эти две концепции кинетической энергии и потенциальной энергии, когда мы рассмотрим движение маятника, движущегося по дуге, показанной на диаграмме справа. Мы будем использовать гистограмму энергии, чтобы представить изменения в двух формах энергии.Количество каждой формы энергии представлено полосой. Высота планки пропорциональна количеству этой формы энергии. Помимо столбца потенциальной энергии (PE) и столбца кинетической энергии (KE), есть третий столбец, обозначенный TME. Полоса TME представляет собой общее количество механической энергии, которой обладает маятник. Полная механическая энергия — это просто сумма двух форм энергии — кинетической и потенциальной. Найдите время, чтобы изучить гистограммы, показанные ниже, для положений A, B, D, F и G.Что ты заметил?
Когда вы просматриваете гистограммы, становится очевидно, что по мере того, как боб движется от A к D, кинетическая энергия увеличивается, а потенциальная энергия уменьшается. Однако общее количество этих двух форм энергии остается постоянным. Потенциальная энергия, которая теряется при переходе из положения A в положение D, отображается как кинетическая энергия. Потенциальная энергия трансформируется в кинетическую, когда боб перемещается из положения A в положение D.Однако общая механическая энергия остается постоянной. Мы бы сказали, что механическая энергия сохраняется. Когда боб перемещается из положения D в положение G, наблюдается обратное. Кинетическая энергия уменьшается по мере того, как боб движется вправо и (что более важно) вверх к положению G. Существует увеличение потенциальной энергии, сопровождающее это уменьшение кинетической энергии. Энергия трансформируется из кинетической формы в потенциальную. Тем не менее, как показано на шкале TME, общее количество механической энергии сохраняется.Этот самый принцип сохранения энергии был объяснен в главе «Энергия» учебного пособия по физике.
Период маятника
Наше последнее обсуждение будет относиться к периоду маятника. Как уже говорилось ранее в этом уроке, период — это время, за которое вибрирующий объект завершает свой цикл. В случае маятника настало время для маятника начать с одного крайнего положения , переместиться на противоположный крайний предел , а затем вернуться в исходное положение.Здесь нас будет интересовать вопрос Какие переменные влияют на период маятника? Мы займемся возможными переменными. Переменными являются масса маятника, длина веревки, на которой он висит, и угловое смещение . Угловое смещение или угла дуги — это угол, который образует струна с вертикалью при выходе из состояния покоя. Эти три переменные и их влияние на период легко изучаются и часто находятся в центре внимания физической лаборатории на вводном уроке физики.В таблице данных ниже представлены репрезентативные данные для такого исследования.
|
Пробная |
Масса (кг) |
Длина (м) |
Угол дуги (°) |
Период (ы) |
|
1 |
0.02- |
0,40 |
15,0 |
1,25 |
|
2 |
0,050 |
0,40 |
15,0 |
1,29 |
|
3 |
0.100 |
0,40 |
15,0 |
1,28 |
|
4 |
0.200 |
0,40 |
15,0 |
1,24 |
|
5 |
0.500 |
0,40 |
15,0 |
1,26 |
|
6 |
0.200 |
0.60 |
15,0 |
1,56 |
|
7 |
0.200 |
0,80 |
15,0 |
1,79 |
|
8 |
0.200 |
1,00 |
15,0 |
2,01 |
|
9 |
0.200 |
1,20 |
15,0 |
2,19 |
|
10 |
0.200 |
0,40 |
10,0 |
1,27 |
|
11 |
0.200 |
0,40 |
20,0 |
1,29 |
|
12 |
0.200 |
0,40 |
25,0 |
1,25 |
|
13 |
0.200 |
0,40 |
30,0 |
1,26 |
В опытах с 1 по 5 масса боба систематически изменялась, при этом другие величины оставались постоянными. Таким образом экспериментаторы смогли исследовать возможное влияние массы на период. Как видно из этих пяти испытаний, изменение массы мало влияет на период маятника.
В испытаниях 4 и 6-9 масса остается постоянной на уровне 0,200 кг, а угол дуги — на уровне 15 °. Однако длина маятника различна. Таким образом экспериментаторы смогли исследовать возможное влияние длины струны на период. Как видно из этих пяти испытаний, изменение длины определенно влияет на период маятника. По мере удлинения струны период маятника увеличивается. Между периодом и длиной существует прямая зависимость.
Наконец, экспериментаторы исследовали возможное влияние угла дуги на период в опытах 4 и 10-13. Масса остается постоянной на уровне 0,200 кг, а длина струны остается постоянной на уровне 0,400 м. Как видно из этих пяти испытаний, изменение угла дуги практически не влияет на период маятника.
Итак, вывод из такого эксперимента состоит в том, что единственная переменная, влияющая на период маятника, — это длина струны.Увеличение длины приводит к увеличению периода. Но расследование не должно останавливаться на достигнутом. Количественное уравнение, связывающее эти переменные, может быть определено, если данные нанесены на график и выполнен линейный регрессионный анализ. Два графика ниже представляют такой анализ. На каждом графике значения периода (зависимой переменной) отложены по вертикальной оси. На графике слева длина маятника отложена по горизонтальной оси. Форма кривой указывает на какое-то соотношение мощности между периодом и длиной.На графике справа нанесен квадратный корень из длины маятника (длина в ½ степени). Показаны результаты регрессионного анализа.
|
Угловой коэффициент: 1.7536 |
Наклон: 2.0045 |
Анализ показывает, что данные и линия регрессии лучше подходят для графика справа. Таким образом, график справа является основой уравнения, связывающего период и длину. Для этих данных уравнение:
Период = 2,0045 • Длина 0,5 + 0,0077
Используя T как символ периода и L как символ длины, уравнение можно переписать как
Т = 2.0045 • L 0,5 + 0,0077
Обычно сообщается уравнение, основанное на теоретических разработках:
T = 2 • Π • (л / г) 0,5
, где g — постоянная, известная как сила гравитационного поля или ускорение свободного падения (9,8 Н / кг). Значение 2,0045, полученное в результате экспериментального исследования, хорошо согласуется с тем, что можно было бы ожидать из этого теоретически описанного уравнения. Подставляя значение g в это уравнение, получаем константу пропорциональности 2Π / g 0.5 , что равно 2,0071, очень похоже на константу пропорциональности 2,0045, разработанную в эксперименте.
Расследовать! Используйте виджет Investigating a Pendulum ниже, чтобы исследовать влияние длины маятника на период маятника. Просто введите значение длины в поле ввода и нажмите кнопку Отправить . Поэкспериментируйте с различными значениями длины маятника.
Проверьте свое понимание
1. Маятниковый качающийся рычаг возвращается в положение A и освобождается из состояния покоя. Боб движется по своей обычной дуге окружности и застревает в позиции C. Определите позицию (A, B, C или все то же самое), где…
а. … Сила тяжести самая большая?
б. … Восстанавливающая сила самая большая?
c. … Скорость самая большая?
d.… Потенциальная энергия велика?
е. … Кинетическая энергия самая большая
f. … Общая механическая энергия самая большая?
2. Воспользуйтесь функцией энергосбережения, чтобы заполнить пропуски на следующей диаграмме.
3. Пара танцоров-трапеций в цирке раскачивается на веревках, прикрепленных к большой возвышенной платформе. Предположим, что исполнителей можно рассматривать как простой маятник длиной 16 м.Определите период для одного полного цикла вперед-назад.
4. Какая из частот вибрации будет самой высокой?
Маятник A: Груз весом 200 г, прикрепленный к веревке длиной 1,0 м
Маятник B: гиря массой 400 г, прикрепленная к струне длиной 0,5 м
5. Анна Литикал хочет сделать простой маятник, который будет служить устройством отсчета времени. Она планирует сделать его таким, чтобы его период равнялся 1.00 секунд. Какой длины должен быть маятник?
За пределами скорости и ускорения: рывки, рывки и более высокие производные
Высшие производные движения редко обсуждаются в преподавании классической механики твердого тела; тем не менее, мы ощущаем эффект не только ускорения, но также рывков и рывков. В этой статье мы обсудим производные смещения третьего и более высокого порядка по времени, используя батуты и американские горки в тематических парках, чтобы проиллюстрировать эту концепцию.Мы также обсудим влияние на человеческое тело различных типов ускорения, рывков, рывков и более высоких производных, а также то, как их можно использовать в физическом образовании для дальнейшего улучшения обучения и, следовательно, понимания концепций классической механики.
Ежедневно мы подвергаемся большому количеству внешних движений и движений. От вождения автомобиля до подъема на лифте наши тела постоянно подвергаются воздействию внешних сил, действующих на нас, что приводит к ускорению.
Изменения в движении и движениях могут иметь значительные биомеханические эффекты на человеческое тело, и, как правило, мы стараемся свести к минимуму воздействие движений.Большинство транспортных средств предназначены для уменьшения ускорения, насколько это практически возможно. С другой стороны, аттракционы уникальны тем, что они специально созданы, чтобы мы могли испытывать большие и меняющиеся типы движений.
Все мы знакомы с терминами «смещение», «скорость» и «ускорение». Мы ощущаем скорость, когда движемся, и ускорение, когда меняем скорость, с которой мы движемся. Наше тело не ощущает скорости, а только изменение скорости, то есть ускорение, вызванное силой, прилагаемой объектом к нашему телу.Например, пассажир в постоянно ускоряющемся автомобиле будет ощущать постоянную силу сиденья на своем теле.
Не считая силы тяжести, которой все мы подвержены каждую минуту, концепция постоянной силы редко встречается в нашей повседневной жизни. Ускорения, которые мы обычно испытываем и поэтому чувствуем, непостоянны. Когда мы находимся в машине и ускоряемся, когда загорается зеленый свет, наше ускорение не является постоянным. В этой ситуации наше ускорение меняется, поэтому ощущение движения, которое мы ощущаем, более вероятно, является рывком и даже щелчком, поскольку есть изменение в рывке.В качестве конкретных иллюстраций концепций мы представляем некоторые подробные примеры американских горок и батутов, используя достоверные данные.
Нет согласия в названиях производных высших порядков [1]. Термин «привязка» будет использоваться в этой статье для обозначения четвертой производной смещения по времени. Другое название этой четвертой производной — скачок. Пятая и шестая производные по времени называются треском и треском соответственно.
Термины «рывок» и «щелчок» мало что значат для большинства людей, включая физиков и инженеров.Что такое рывки и щелчки? Математически рывок — это третья производная от нашего положения по времени, а привязка — это четвертая производная от нашего положения по времени.
Разгон без рывков — просто следствие статической нагрузки. Рывок ощущается как изменение силы; толчок может ощущаться как возрастающая или уменьшающаяся сила на теле. Обратите внимание на следующее. Скорость не включается внезапно, а растет с нуля. Итак, должно быть какое-то ускорение. Точно так же ускорение не включается внезапно, а растет с нуля.Значит, тут должен быть какой-то придурок. Но рывок вдруг не включается, с нуля тоже растет. Так что тут должен быть какой-то щелчок. Но оснастка вдруг не включается, с нуля тоже растет. Так что тут должен быть какой-то треск. Но треск вдруг не включается, с нуля тоже нарастает. Так что здесь должна быть какая-то поп-музыка и так далее.
Нам известны термины «смещение», «скорость» и «ускорение», «где» и. Таким образом, изменение скорости должно сопровождаться силой, воздействующей на каждую часть тела, хотя демпфирование человеческого тела приводит к некоторому ослаблению быстрых изменений.
В школе учащихся изучают второму закону Ньютона, обычно в форме, где м — масса, а — — ускорение. Чего студентов обычно не учат, так это того, что точная формулировка, которую использовал Ньютон, была Lex II: Mutationem motus ratioalem esse vi motrici impressionae, et fieri secundum lineam rectam qua vis illa imprimitur. (Закон II: изменение движения пропорционально приложенной движущей силе и происходит вдоль прямой линии, на которой действует эта сила.) [2]. Эту формулировку также можно интерпретировать как импульсную силу, при которой сила действует в течение определенного периода времени. Если сила импульсная, значит, ускорение не может быть постоянным (если масса тела остается неизменной).
Изменение силы приводит к изменению ускорения, которое может быть выражено, например, как j = d a / d t = (d F / d t ) / m , где мы ввели рывок, j . Точно так же мы можем определить щелчок, s , потрескивание, c , и хлопок, p , как:
Что физически такое щелчок, треск и треск? Ниже мы рассмотрим численные примеры в связи с несколькими знакомыми ситуациями.
Большинство поездок, которые мы совершаем, таких как езда на лифте, поездка на поезде, плавание на корабле или полет на самолете, специально разработаны для минимизации биомеханического воздействия на нас. Не так с аттракционами на американских горках. Аттракционы на американских горках специально созданы для стимуляции сенсорной системы человека, в первую очередь зрительной, слуховой и вестибулярной. Пользователи аттракционов намеренно подвергаются повышенному ускорению, при котором контролируется величина, продолжительность и скорость изменения ускорения.Эти биомеханические параметры увеличиваются для усиления сенсорной стимуляции, но также ограничиваются для обеспечения безопасности езды [3].
Не все биомеханические эффекты повышенных ускорений доставляют удовольствие. Если поездка на американских горках была неправильно спроектирована или неисправна, биомеханические эффекты могли бы вызвать чувство дискомфорта или даже нанести вред здоровью пассажиров.
Способность человеческого тела выдерживать экстремальные нагрузки g была экспериментально подтверждена в конце 1940-х годов полковником.Джон Стэпп из ВВС США [4, 5]. Стапп спланировал и провел серию тестов на себе, используя сани с ракетным двигателем, известные как «Джи-свист» или «Звуковой ветер». Он пристегнулся к сани, повернувшись назад, отказавшись от анестезии, потому что хотел узнать свои реакции из первых рук. Двигаясь со скоростью более 65 м / с −1 , он был резко остановлен менее чем за 6 мс, так как был прижат к спинке сиденья. Ему приписывают доказательство того, что человеческое тело может выдержать повышенную силу g и выдержать удар, хотя в процессе он страдал от головных болей, сотрясения мозга, перелома ребра и запястья и кровоизлияния в сетчатку [3, 5].
На рисунке 1 показана система координат, используемая для описания сил, действующих на пассажира. Например, когда американские горки ускоряются при запуске, мы ощущаем «глаза назад» или это прижимает наше тело к сиденью назад. Общая сила X на кузов от американских горок также должна компенсировать силу тяжести, так что общее ускорение будет, тогда как нагрузка на кузов характеризуется величиной. В контексте биомеханических эффектов все еще принято называть «ускорение».
Увеличить Уменьшить Сбросить размер изображения
Рис. 1. Трехосная система координат ускорения для сидящего пассажира американских горок на основе [6]. Оси координат на рисунке обычно называются «вертикальными» ( z ), «продольными» ( x ) и «боковыми» ( y ) и вращаются вместе с всадником, как показано на рисунке. справа (заключительный сердечный валок спирали американских горок [7]).Следует отметить, что внешняя сила, действующая на всадника, определяется выражением «ускорение».
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешенияТаблица 1 дает максимально допустимое ускорение, которому должен подвергаться пассажир, сидя на американских горках или в космическом корабле. Например, при взлете пассажир может подвергаться постоянному линейному ускорению , , x более 12 с или, в качестве альтернативы, постоянному линейному ускорению , x не более чем на 1 .5 с. Этот тип продолжительных периодов постоянного большого ускорения маловероятен для американских горок, но применим во время запуска космического корабля. Это также может быть достигнуто в карусели, движущейся с постоянной угловой скоростью, когда гонщик обращен к центру, например, при классической поездке на роторе, или на центрифуге NASA 20 g Ames Research Center.
Таблица 1. Допустимые ускорения аттракционов (т.е. значения для a – g ) для направлений x , y и z в зависимости от времени воздействия [6].
| Допустимое ускорение | 0,2 с | 1,5 с | ||||
|---|---|---|---|---|---|---|
| мин. | макс | мин. | макс | мин. | макс | |
| a x | −2,0 г | +6,0 г | -1,5 г | +5.0 г | -1,5 г | +2,5 г |
| a y | −3,0 г | + 3,0 г | −2,5 г | +2,5 г | −2,0 г | +2.0 г |
| a z | −2,0 г | +6,0 г | -1.5 г | +5.0 г | -1,1 г | +2.0 г |
Рисунки 2 и 3 представляют собой графики зависимости ускорения от времени начала, изображающие рекомендуемые воздействия ускорения для различных значений: a z и a x . Важно отметить, что они изображают порог допустимого начала ускорения или рывка как. На рисунке 4 изображен типичный график зависимости ускорения от времени для американских горок с наложенными огибающими соответствующего ускорения от времени начала (рывка).
Увеличить Уменьшить Сбросить размер изображения
Рисунок 2. Рекомендуемая максимальная длительность ускорения для и, а также для отрицательных значений, и. Также показаны рекомендованные максимальные (пунктирные) и минимальные (сплошные) скорости начала или рывков, основанные на [6].
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешенияУвеличить Уменьшить Сбросить размер изображения
Рисунок 3. Рекомендуемая максимальная продолжительность ускорения для и, а также для отрицательных значений, и. Также показаны рекомендованные максимальные (пунктирные) и минимальные (сплошные) скорости начала или рывков, основанные на [6].
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешенияУвеличить Уменьшить Сбросить размер изображения
Рис. 4. Пример анализа «вертикальной» (+ z ) диаграммы зависимости ускорения от времени для езды близко к спине в спирали американских горок [7].Тонкие горизонтальные линии представляют максимально допустимую продолжительность, тогда как более толстые горизонтальные линии представляют фактическую экспозицию на этом уровне. Сплошные наклонные линии представляют среднее ускорение во время соревнования. Пунктирные линии представляют максимальное и минимальное начало ускорения. Согласно [6] «воздействие ускорения патрона всегда должно быть ниже оболочки, образованной трапецией, которая нарисована путем приложения начального ускорения, максимального постоянного ускорения и ускорения задней кромки».
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешенияНастоящие американские горки — это сложные трехмерные искаженные звери с изгибами, петлями и спиралями, и инженер должен объединить все ускорения и убедиться, что экспозиция пассажиров остается в допустимых расчетных пределах. Обратите внимание, что оси координат в таблице 1 прикреплены к человеку, как показано на рисунке 1, и перемещаются и вращаются вместе с всадником во время езды.
В большинстве американских горок изгибы имеют наклон для минимизации боковых сил (, , , , ).Пока положение тела по существу с «вертикальной» ( z ) осью (позвоночником), перпендикулярной гусенице, силы в направлении x относительно невелики, за исключением во время запусков и торможений. В других типах аттракционов или на американских горках, например гонщики вращаются относительно трассы, особенно важно учитывать комбинации векторов ускорения. Максимально допустимое воздействие ускорения в каждом направлении, показанное в таблице 1, затем уменьшается за счет комбинации, как указано в «графиках яиц» на рисунке 5.Можно отметить, что как a x , так и a y достигают гораздо меньших значений, чем a z .
Увеличить Уменьшить Сбросить размер изображения
Рис. 5. «Графики яиц», показывающие допустимый комбинированный эффект a x , a y и a z ускорений для продолжительности менее t = 0.2 с, вместе с кроликами для иллюстрации координат. Первый график показывает комбинации для a z и a x , тогда как второй график показывает комбинации a y с a z , который идентичен графику яиц для комбинации a y с a x . Кроме того, для иллюстрации были включены данные акселерометра от поездки в середине поезда по спирали американских горок, собранные датчиком WDSS [8].Небольшой наклон данных на графике слева может отражать неидеально выровненный датчик, вызывая утечку между компонентами z и x .
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешения«Яйцевые» графики, изображенные на рисунке 5, обычно определяются как набор эллиптических кривых.
Рассмотрим следующие утверждения: «Она вырвала телефон из его рук»; «Автобус резко остановился»; или «Вагоны дергались и тряслись, когда поезд двигался вперед».Что они нам говорят?
За рулем автомобиля мы можем наблюдать эффекты скорости, ускорения и производных более высокого порядка. Более опытный водитель ускоряется плавно, тогда как ученик может двигаться рывками. Переключение передач с помощью ручного сцепления может привести к дрожанию автомобиля на дороге, вызывая рывки и треск.
Рывок и щелчок можно наблюдать в различных областях физики и техники. В физике и технике при возникновении вибрации всегда следует учитывать рывки и щелчки, особенно когда это возбуждение вызывает мультирезонансные режимы вибрации.Их также следует учитывать всегда, когда происходит переход, например: запуск и останов; взлет и посадка; и ускорение и замедление.
Ускорение без рывков — это просто статическая нагрузка, и поэтому одно только постоянное ускорение не может вызвать вибрацию. В механическом цехе инструментальщик может повредить фрезу или работу, если установка начнет вибрировать. Эта вибрация возникает из-за рывков и щелчков.
В машиностроении важно следить за тем, чтобы кулачковый толкатель не соскакивал с распредвала.Это также важно в производственных процессах, поскольку быстрые изменения ускорения режущего инструмента могут привести к преждевременному износу инструмента и привести к неровной и шероховатой поверхности.
В гражданском строительстве железнодорожные пути и дороги должны быть спроектированы для плавного выхода из прямого участка в кривую, и обычно используется переход, называемый клотоидой, которая является частью спирали Корню (также называемой спиралью Корню). Спираль Эйлера). Когда используется клотоида, изменение ускорения не является резким, а уровни рывков и, возможно, рывков значительно снижаются.Если переход между разными радиусами кривизны происходит внезапно, переход неудобен для пассажиров и потенциально опасен, поскольку может привести к тому, что автомобиль или поезд вылетит с дороги или рельсового пути. Инженеры-конструкторы с хорошей физикой пытаются создать постепенный рывок и постоянную резкость, что дает плавное увеличение радиального ускорения или, предпочтительно, нулевое резкое движение, постоянный рывок и линейное увеличение радиального ускорения. Подобно тому, как инженеры дорог и железных дорог проектируют рывки и щелчки, используя клотоидный переход, дизайнеры американских горок разрабатывают петли и спирали для американских горок [11, 12].
В бегах борзых скорость может быть более 18 м / с −1 , а резкий переход от прямого к круговому повороту приводит к большей частоте несчастных случаев и травм.
5.1. Теоретическая модель: свободное падение и движение гармонического осциллятора
В предыдущей статье прыжки на батуте анализировались как комбинация свободного падения и движения гармонического осциллятора [9]. Максимальная сила, направленная вверх от батута на тело массой м , выражается как, дающее максимальное ускорение.Из теоретической модели в [9], объединяющей гармоническое движение со свободным падением, общее время между двумя прыжками может быть выражено с помощью параметра N как
, где — период небольших отскоков, когда ступни не покидают коврик.
По мере того, как ступни достигают мата, ускорение увеличивается как часть синусоидальной функции, которая проходит через ноль, когда прыгун проходит положение равновесия (в момент, когда ускорение равно 0, а сила от мата равна мг , компенсируя для гравитации).
Для той части цикла прыжков, когда батутник находится в воздухе, ускорение является постоянным, а рывок и все более высокие производные равны нулю. Когда гимнастка находится в контакте с батутом, рывок можно описать гармонической функцией, и каждая дополнительная производная добавляет коэффициент ω и сдвигает синус на косинус или косинус на отрицательный синус соответственно. Значение рывка равно нулю при максимальном ускорении. Когда ускорение достигает нуля, рывок имеет максимальное значение, когда гимнастка идет вниз, и максимальное отрицательное значение, когда гимнастка идет вверх.Может быть очень небольшое отставание из-за естественного демпфирования внутри батутной системы.
В теоретической модели рывок становится ступенчатой функцией в моменты, когда ступни достигают мата или отрываются от него. Это приводит к особенностям высших производных. Производная ступенчатой функции может быть формально описана дельта-функцией Дирака, которая может быть реализована с использованием ряда различных аналитических функций. Каждая последующая производная дельта-функции приносит дополнительный максимум или минимум.Ширина и высота приближенной дельта-функции и ее производных зависят от реализации.
5.2. Аутентичные данные батута
На рис. 6 показаны данные акселерометра вместе с их производной, рывком, для пяти последовательных прыжков на гимнастическом батуте, где сила на прыгуне достигает (и ускорение достигает).
Увеличить Уменьшить Сбросить размер изображения
Рисунок 6. Ускорение (синий, в единицах г ) и рывок (красный, в секундах) во время пяти последовательных прыжков на гимнастическом батуте. Красные точки показывают необработанные данные о рывках. Обратите внимание, что ускорение — | г | когда гимнастка находится в воздухе и максимум, когда ковер находится в нижней мертвой точке. Щелчок и треск показаны вместе с ускорением и рывком на рисунке 7.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешенияИз уравнения (1) мы находим, что максимальная сила примерно соответствует соотношению примерно 3 между временем цикла и периодом малых колебаний.На рисунке 6 показаны 4 периода примерно за 6,5 с, что дает период 0,54 с для небольших отскоков или, что также является фактором, добавленным для каждой последующей производной.
Данные акселерометра были собраны с частотой дискретизации 100 Гц с использованием спортивного устройства GPS, и производная в заданное время была получена из точек данных, собранных непосредственно до и после этого времени. Эти необработанные данные о рывках показаны точками на рисунке 6 и показывают большие колебания, тогда как более гладкая сплошная линия показывает 10-балльное скользящее среднее.
За цикл прыжка наблюдались два максимума рывков. Максимум соприкосновения или переднего края, где максимум рывка был положительным и произошел почти сразу после того, как ступни батутиста коснулись мата, и максимум отделяющего или заднего края, где максимум рывка был отрицательным и произошел до отделения ступней батутиста от ковра. Исходя из теоретических соображений, мы ожидаем максимум около, тогда как пять максимумов контакта в необработанных данных о рывках находились между и.Усреднение приводит к более медленному нарастанию, чем в необработанных данных, а также к меньшим пиковым значениям рывка.
На рис. 7 показаны скользящие средние по 10 точкам для более высоких производных, щелчки и треск для одного из прыжков. Как и ожидалось, каждая производная привносит дополнительный коэффициент к максимуму около ω : минимум щелчка составляет приблизительно, наблюдается, как и ожидалось, когда ускорение является максимальным, тогда как треск имеет минимальное и максимальное значения вокруг.
Увеличить Уменьшить Сбросить размер изображения
Рисунок 7. Ускорение в единицах г (синий, сплошной), толчок (красный, пунктирный, — -), щелчок (зеленый, пунктирный,), треск (пурпурный, пунктирный, ––) во время одного прыжка в гимнастическом упражнении батут. Обратите внимание, что максимальный щелчок произошел, когда гимнастка впервые соприкоснулась с ковром, то есть во время переходного периода, хотя большие отрицательные значения привязки происходят, когда ускорение является наибольшим, с теоретическим значением. Ускорение и рывки для одного и того же набора данных показаны на рисунке 6.
Загрузить рисунок:
Стандартное изображение Изображение высокого разрешенияВ дополнение к этим ожидаемым максимумам и минимумам, мы находим два боковых максимума для щелчка при переходе от воздуха к мату или наоборот, и один минимум щелчка во время контакта ступней с ковриком и максимум, когда ступни уходят. коврик.Процедура усреднения заставляет рывок и более высокие производные «перетекать» во временной интервал, когда гимнастка находится в воздухе. Значения вне времени контакта являются результатом численных процедур для вывода и усреднения, а также могут рассматриваться как приближение дельта-функции Дирака (для рывка) и ее производных (для рывка, потрескивания).
Американские горки включают в себя переходы между различными типами движения. Если радиус кривизны при переходе резко изменяется, это также приводит к внезапному изменению ускорения — рывку.В качестве примера мы рассмотрим гипотетическую круговую петлю, которая внезапно переходит в прямую, что означает переход от (по крайней мере) к нижней части за очень короткое время (и наоборот на пути к петле). Для петли высотой 20 м скорость будет не менее 20 м / с −1 внизу. Для расстояния между осями колес, которое обычно составляет около 1 м, это приведет к изменению вертикальной силы не менее чем за 0,05 с, что соответствует рывку примерно 80 г с -1 .Кроме того, произойдет внезапное изменение угловой скорости с на 0, что даст угловое ускорение. Эта комбинация, как было известно, приводила к хлыстовым травмам в горках американских горок начала 20-го века, например, в горках. на Кони-Айленде [10]. Дизайнер американских горок Вернер Стенгель описал, как была введена клотоида, чтобы избежать резких изменений радиуса кривизны [11]. Также используются другие математические формы, в которых все производные непрерывны [11, 12].
Механические тормоза в старых американских горках часто приводят к резким остановкам.В этих случаях не только быстрые изменения силы, действующей на тело, способствуют возможному дискомфорту, но также и неравномерное распределение силы по туловищу всадника. Резкие рывки и щелчки в американских горках также сокращают срок службы конструкции и автомобилей. Также стоит учитывать градиенты силы, действующей на тело.
Рывок — обычное повседневное явление, но редко упоминается при обучении механике. Тем не менее, минимизация рывков — важный аспект, начиная с плавного вождения автомобиля или автобуса и заканчивая дизайном американских горок и других аттракционов.Человеческая толерантность к ускорению была измерена и хорошо изучена. Человеческая толерантность к рывкам и щелчкам еще недостаточно изучена. Тем не менее, дизайнеры американских горок ограничивают их, чтобы повысить комфорт пассажиров. Пассажирам американских горок нужно время, чтобы почувствовать изменения ускорения и отрегулировать напряжение мышц или перенести такие состояния, как хлыстовая травма. Даже когда безопасность человека не является проблемой, физики и инженеры затрачивают значительные усилия на проектирование, оптимизируя рывки и устраняя щелчки при поездках на американских горках, чтобы сократить техническое обслуживание и продлить срок службы аттракциона.
Дифференциальные уравнения — механические колебания
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметкиКажется, вы используете устройство с «узкой» шириной экрана (, т.е. , вероятно, вы используете мобильный телефон). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме.Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 3-11: Механические колебания
Пришло время взглянуть на приложение дифференциальных уравнений второго порядка. Мы собираемся взглянуть на механические колебания.В частности, мы рассмотрим массу, которая свисает с пружины.
Вибрации могут возникать практически во всех отраслях техники, поэтому то, что мы собираемся делать здесь, можно легко адаптировать к другим ситуациям, обычно с помощью простого изменения обозначений.
Давайте установим ситуацию. Мы собираемся начать с пружины длины \ (l \), называемой естественной длиной, и мы собираемся зацепить за нее объект с массой \ (m \). Когда объект прикреплен к пружине, пружина растянется на \ (L \).Мы будем называть положением равновесия положение центра тяжести объекта, когда он висит на пружине без движения.
Ниже представлен эскиз пружины с прикрепленным к ней предметом и без него.
Как показано на рисунке, мы предполагаем, что все силы, скорости и смещения в направлении вниз будут положительными. Все силы, скорости и смещения в направлении вверх будут отрицательными.
Также, как показано на скетче выше, мы будем измерять все смещения массы из положения равновесия.Следовательно, положение \ (u = 0 \) будет соответствовать центру тяжести массы, когда она висит на пружине и находится в состоянии покоя (, т.е. без движения).
Теперь нам нужно разработать дифференциальное уравнение, которое даст смещение объекта в любой момент \ (t \). Во-первых, вспомните второй закон движения Ньютона.
\ [ma = F \]В этом случае мы будем использовать вторую производную смещения, \ (u \), для ускорения, и поэтому Ньютон \ [mu » = F \ left ({t, u, u ‘} \ right) \]
Теперь нам нужно определить все силы, которые будут действовать на объект.Мы предположим, что на объект действуют четыре силы. Два, которые всегда будут воздействовать на объект, и два, которые могут или не могут воздействовать на объект.
Вот список сил, которые будут действовать на объект.
- Гравитация, \ (F_ {g} \)
Конечно, сила тяжести всегда действует на объект. Эта сила равна
\ [{F_g} = мг \] - Пружина, \ (F_ {s} \)
Мы собираемся предположить, что закон Гука будет определять силу, которую пружина оказывает на объект.Эта сила всегда будет присутствовать и равна
. \ [{F_s} = — k \ left ({L + u} \ right) \]Закон Гука гласит, что сила, прикладываемая пружиной, будет равняться жесткости пружины \ (k> 0 \), умноженной на смещение пружины от ее естественной длины. Для нашей установки смещение от естественной длины пружины составляет \ (L + u \), а знак минус стоит там, чтобы гарантировать, что сила всегда имеет правильное направление.
Давайте удостоверимся, что эта сила делает то, что мы от нее ожидаем.Если объект находится в состоянии покоя в своем положении равновесия, смещение равно \ (L \), а сила просто \ (F_ {s} = –kL \), которая будет действовать в восходящем положении, как и должно быть, поскольку пружина была растянута. от его естественной длины.
Если пружина была растянута дальше вниз от положения равновесия, то \ (L + u \) будет положительным, а \ (F_ {s} \) будет отрицательным, действуя, чтобы подтянуть объект обратно вверх, как это должно быть.
Затем, если объект был перемещен выше точки равновесия, но еще не достиг своей естественной длины, то \ (u \) будет отрицательным, но все же меньше, чем \ (L \), и поэтому \ (L + u \) будет положительным, и снова \ (F_ {s} \) будет отрицательным, действуя, чтобы подтянуть объект вверх.
Наконец, если объект был перемещен вверх, так что пружина теперь сжата, тогда \ (u \) будет отрицательным и больше, чем \ (L \). Следовательно, \ (L + u \) будет отрицательным, и теперь \ (F_ {s} \) будет действовать положительно, чтобы толкнуть объект вниз.
Итак, похоже, что эта сила будет действовать так, как мы ожидали.
- Демпфирование, \ (F_ {d} \)
Следующая сила, которую нам нужно учитывать, — это демпфирование.Эта сила может присутствовать, а может и не присутствовать для любой данной проблемы.
Демпферы противодействуют любому движению. Есть несколько способов определить демпфирующую силу. Мы воспользуемся следующим.
\ [{F_d} = — \ gamma \, u ‘\]где \ (\ gamma> 0 \) — коэффициент демпфирования. Давайте задумаемся на минутку, как эта сила будет действовать. Если объект движется вниз, то скорость (\ (u ‘\)) будет положительной, а \ (F_ {d} \) будет отрицательной и будет тянуть объект обратно вверх.Аналогично, если объект движется вверх, скорость (\ (u ‘\)) будет отрицательной, и поэтому \ (F_ {d} \) будет положительным и будет толкать объект обратно вниз.
Другими словами, демпфирующая сила, как мы ее определили, всегда будет действовать, чтобы противодействовать текущему движению объекта, и поэтому будет действовать, чтобы гасить любое движение в объекте.
- Внешние силы, \ (F (t) \)
Это ловушка всей силы. Если есть какие-то другие силы, которые мы решаем воздействовать на наш объект, мы объединяем их здесь и называем хорошими.Обычно мы называем \ (F (t) \) функцией принуждения.
Объединение всего этого дает нам следующее для Второго закона Ньютона.
\ [mu » = mg — k \ left ({L + u} \ right) — \ gamma u ‘+ F \ left (t \ right) \]Или, переписав, получаем
\ [mu » + \ gamma u ‘+ ku = mg — kL + F \ left (t \ right) \]Теперь, когда объект находится в состоянии покоя в своем положении равновесия, на объект действуют ровно две силы: сила тяжести и сила пружины.Кроме того, поскольку объект находится в состоянии покоя (, т.е. не движется), эти две силы должны нейтрализовать друг друга. Это означает, что у нас должно быть
\ [\ begin {уравнение} mg = kL \ label {eq: eq1} \ end {уравнение} \]Использование этого во втором законе Ньютона дает нам окончательную версию дифференциального уравнения, с которым мы будем работать.
\ [\ begin {уравнение} mu » + \ gamma u ‘+ ku = F \ left (t \ right) \ label {eq: eq2} \ end {уравнение} \]Наряду с этим дифференциальным уравнением мы будем иметь следующие начальные условия.
\ [\ begin {уравнение} \ begin {выровнено} u \ left (0 \ right) & = {u_0} \ hspace {0,25 дюйма} {\ mbox {Начальное смещение от положения равновесия}} {\ mbox {.}} \\ u ‘\ left (0 \ right) & = {{u’} _ 0} \ hspace {0,25 дюйма} {\ mbox {Начальная скорость}} {\ mbox {.}} \ end {align} \ label {eq : eq3} \ end {уравнение} \]Обратите внимание, что мы также будем использовать \ (\ eqref {eq: eq1} \) для определения жесткости пружины \ (k \).
Хорошо. Давайте начнем с некоторых конкретных случаев.
Свободные, незатухающие колебания
Это простейший случай, который мы можем рассмотреть. Свободные или ненасильственные колебания означают, что \ (F (t) = 0 \), а незатухающие колебания означают, что \ (\ gamma = 0 \). В этом случае дифференциальное уравнение принимает вид
\ [mu » + ku = 0 \]В целом это достаточно просто решить. Характеристическое уравнение имеет корни:
\ [г = \ pm \, \, i \, \ sqrt {\ frac {k} {m}} \]Обычно это сокращается до
\ [r = \ pm \, {\ omega _0} \, i \]где,
\ [\ omega {_0} = \ sqrt {\ frac {k} {m}} \]и \ ({\ omega _0} \) называется собственной частотой.Напомним также, что \ (m> 0 \) и \ (k> 0 \), поэтому мы можем гарантировать, что эта величина не будет комплексной. Тогда решение в этом случае —
\ [\ begin {уравнение} u \ left (t \ right) = {c_1} \ cos \ left ({{\ omega _0} \, t} \ right) + {c_2} \ sin \ left ({{\ omega _0} \, t} \ right) \ label {eq: eq4} \ end {Equation} \]Мы можем записать \ (\ eqref {eq: eq4} \) в следующей форме:
\ [\ begin {уравнение} u \ left (t \ right) = R \ cos \ left ({{\ omega _0} t — \ delta} \ right) \ label {eq: eq5} \ end {уравнение} \], где \ (R \) — амплитуда смещения, а \ (\ delta \) — фазовый сдвиг или фазовый угол смещения.
Когда смещение имеет форму \ (\ eqref {eq: eq5} \), обычно легче работать. Однако проще найти константы в \ (\ eqref {eq: eq4} \) из начальных условий, чем найти амплитуду и фазовый сдвиг в \ (\ eqref {eq: eq5} \) из начальных условий. . Итак, чтобы привести уравнение в форму в \ (\ eqref {eq: eq5} \), мы сначала поместим уравнение в форму в \ (\ eqref {eq: eq4} \), найдем константы, \ (c_ {1} \) и \ (c_ {2} \), а затем преобразуйте это в форму в \ (\ eqref {eq: eq5} \).
Итак, предполагая, что у нас есть \ (c_ {1} \) и \ (c_ {2} \), как нам определить \ (R \) и \ (\ delta \)? Начнем с \ (\ eqref {eq: eq5} \) и воспользуемся идентификатором триггера, чтобы записать его как
\ [\ begin {уравнение} u \ left (t \ right) = R \ cos \ left (\ delta \ right) \ cos \ left ({{\ omega _0} t} \ right) + R \ sin \ left ( \ delta \ right) \ sin \ left ({{\ omega _0} t} \ right) \ label {eq: eq6} \ end {уравнение} \]Теперь \ (R \) и \ (\ delta \) являются константами, поэтому, если мы сравним \ (\ eqref {eq: eq6} \) с \ (\ eqref {eq: eq4} \), мы увидим, что
\ [{c_1} = R \ cos \ delta \ hspace {0. 2} \\ & {\ mbox {Metric:}} g = 9.2} \ end {align *} \]Это не стандартные 32,2 фута / с 2 или 9,81 м / с 2 , но их использование сделает некоторые цифры немного лучше.
В метрической системе масса предметов дана в килограммах ( кг, ) и нам нечего делать. Однако в британской системе нам обычно дают вес объекта в фунтах (да, фунты — это единицы веса, а не массы…), и поэтому нам нужно будет вычислить массу для этих задач.
На этом этапе мы, вероятно, должны проработать пример всего этого, чтобы увидеть, как это работает.
Пример 1 Объект весом 16 фунтов растягивает пружину на \ (\ frac {8} {9} \) ft самостоятельно. Нет демпфирования и внешних сил, действующих на систему. Пружина первоначально смещается на 6 дюймов вверх от положения равновесия и получает начальную скорость вниз 1 фут / сек. Найдите смещение в любой момент времени \ (t \), \ (u (t) \). Показать решениеСначала нам нужно настроить IVP для проблемы. {8} / {} _ {9}}} = 18 \]
Теперь мы можем настроить IVP.
\ [\ frac {1} {2} u » + 18u = 0 \ hspace {0,25 дюйма} u \ left (0 \ right) = — \ frac {1} {2} \ hspace {0,25 дюйма} u ‘\ слева (0 \ справа) = 1 \]Для начальных условий вспомните, что смещение / движение вверх отрицательно, а смещение / движение вниз положительно. Кроме того, поскольку мы решили делать все в футах, нам пришлось преобразовать начальное смещение в футы.
Теперь, чтобы решить эту проблему, мы можем либо пройти через характеристическое уравнение, либо просто перейти к формуле, которую мы вывели выше.{1} / {} _ {2}}}} = \ sqrt {36} = 6 \]
Общее решение, вместе с его производной, тогда
\ [\ begin {align *} u \ left (t \ right) & = {c_1} \ cos \ left ({6t} \ right) + {c_2} \ sin \ left ({6t} \ right) \\ u ‘\ left (t \ right) & = — 6 {c_1} \ sin \ left ({6t} \ right) + 6 {c_2} \ cos \ left ({6t} \ right) \ end {align *} \]Применение начальных условий дает
\ [\ begin {align *} — \ frac {1} {2} = u \ left (0 \ right) & = {c_1} \ hspace {0. 2}} = \ frac {{\ sqrt {10}}} {6} = 0.{1} / {} _ {2}}}} \ right) = — 0,32175 \]Мы должны быть осторожны с этой деталью. Фазовый угол, указанный выше, находится в квадранте IV, но есть также угол в квадранте II, который также будет работать. Мы получаем этот второй угол, добавляя \ (\ pi \) к первому углу. Итак, на самом деле у нас есть два угла. Их
\ [\ begin {align *} {\ delta _1} & = — 0,32175 \\ {\ delta _2} & = {\ delta _1} + \ pi = 2,81984 \ end {align *} \]Нам нужно решить, какой из этих фазовых сдвигов правильный, потому что только один будет правильным.Для этого напомним, что
\ [\ begin {align *} {c_1} & = R \ cos \ delta \\ {c_2} & = R \ sin \ delta \ end {align *} \]Теперь, поскольку мы предполагаем, что \ (R \) положительно, это означает, что знак \ (\ cos \ delta \) будет таким же, как знак \ (c_ {1} \) и знак \ (\ sin \ delta \) будет таким же, как знак \ (c_ {2} \). Итак, для этого конкретного случая мы должны иметь \ (\ cos \ delta <0 \) и \ (\ sin \ delta> 0 \). Это означает, что фазовый сдвиг должен быть в квадранте II, поэтому второй угол — это тот, который нам нужен.
Итак, после всего этого смещение в любой момент времени \ (t \) равно.
\ [u \ left (t \ right) = 0,52705 \ cos \ left ({6t — 2,81984} \ right) \]Вот эскиз смещения за первые 5 секунд.
Теперь давайте посмотрим на немного более реалистичную ситуацию. Никакая вибрация не будет длиться вечно. Итак, давайте добавим демпфер и посмотрим, что теперь будет.
Свободные демпфированные колебания
Мы по-прежнему будем предполагать, что на систему не будет действовать никаких внешних сил, за исключением, конечно, демпфирования. В этом случае будет дифференциальное уравнение.
\ [mu » + \ gamma u ‘+ ku = 0 \]где \ (m \), \ (\ gamma \) и \ (k \) — все положительные константы. 2} — 4mk}}} {{2m}} \]
У нас будет три кейса.2} & <4mk \\ \ gamma & <2 \ sqrt {mk} \\ \ gamma & <{\ gamma _ {CR}} \ end {align *} \]
и называется при демпфировании.
Давайте рассмотрим здесь несколько примеров с демпфированием.
Пример 2 Возьмите систему пружины и массы из первого примера и прикрепите к ней демпфер, который будет оказывать усилие в 12 фунтов при скорости 2 фута / с. Найдите смещение в любой момент времени \ (t \), \ (u (t) \). Показать решениеМасса и жесткость пружины уже были найдены в первом примере, поэтому мы не будем выполнять здесь работу.Однако нам нужно найти коэффициент демпфирования. Для этого мы будем использовать приведенную выше формулу демпфирующей силы с одной модификацией. Исходная формула демпфирующей силы:
\ [{F_d} = — \ gamma u ‘\]Однако помните, что сила и скорость всегда действуют в противоположных направлениях. Итак, если скорость направлена вверх (, т.е. отрицательная), сила будет направлена вниз (, т.е. положительная), и, таким образом, минус в формуле компенсируется минусом в скорости.Аналогично, если скорость направлена вниз (, т. Е. положительное), сила будет направлена вверх (, т.е. отрицательная), и в этом случае знак минус в формуле будет отменен по сравнению с минусом в силе. Другими словами, мы можем отбросить знак минус в формуле и использовать
\ [{F_d} = \ gamma u ‘\], а затем просто игнорируйте любые знаки силы и скорости.
Это дает нам следующий коэффициент демпфирования
\ [12 = \ gamma \ left (2 \ right) \ hspace {0.25 дюймов} \ Rightarrow \ hspace {0,25 дюйма} \ gamma = 6 \]Тогда IVP для этого примера —
\ [\ frac {1} {2} u » + 6u ‘+ 18u = 0 \ hspace {0,25 дюйма} u \ left (0 \ right) = — \ frac {1} {2} \ hspace {0,25 дюйма} и ‘\ влево (0 \ вправо) = 1 \]Перед тем как решать, давайте посмотрим, какое у нас демпфирование. Для этого нам нужен только критический коэффициент демпфирования.
\ [{\ gamma _ {CR}} = 2 \ sqrt {km} = 2 \ sqrt {\ left ({18} \ right) \ left ({\ frac {1} {2}} \ right)} = 2 \ sqrt 9 = 6 \]Итак, похоже, у нас критическое демпфирование.{- 6т}} \]
Вот эскиз смещения в течение первых 3 секунд.
Обратите внимание, что «вибрация» в системе на самом деле не настоящая вибрация, как мы склонны думать о них. В случае критического затухания не будет реальных колебаний около точки равновесия, которые мы склонны связывать с колебаниями. Демпфирование в этой системе достаточно сильное, чтобы заставить «вибрацию» утихнуть, прежде чем она когда-либо действительно получит шанс сделать что-нибудь в плане колебаний.
Пример 3 Возьмите систему пружины и массы из первого примера, и на этот раз давайте прикрепим к ней демпфер, который будет оказывать усилие в 17 фунтов при скорости 2 фута / с. Найдите смещение в любой момент времени \ (t \), \ (u (t) \). Показать решениеИтак, единственная разница между этим примером и предыдущим — это демпфирующая сила. Итак, найдем коэффициент демпфирования
\ [17 = \ gamma \ left (2 \ right) \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0.25 дюймов} \ gamma = \ frac {{17}} {2} = 8.5> {\ gamma _ {CR}} \]Итак, похоже, что на этот раз мы преодолели демпфирование, поэтому мы должны ожидать получения двух реальных различных корней из характеристического уравнения, и оба они должны быть отрицательными. IVP для этого примера:
\ [\ frac {1} {2} u » + \ frac {{17}} {2} u ‘+ 18u = 0 \ hspace {0,25 дюйма} u \ left (0 \ right) = — \ frac {1 } {2} \ hspace {0,25 дюйма} u ‘\ left (0 \ right) = 1 \]Этот пример немного сложнее, чем в предыдущем примере, поэтому мы проделаем пару шагов, предоставив вам заполнить пробелы.{- 14.5208 \, \, t}} \ end {align *} \]
Вот набросок смещения для этого примера.
Обратите внимание на интересную вещь о смещении здесь. Несмотря на то, что в этом случае мы «чрезмерно» демпфированы, на самом деле для затухания вибрации требуется больше времени, чем в случае критического демпфирования. Иногда это происходит, хотя не всегда избыточное демпфирование позволяет вибрации продолжаться дольше, чем критический случай демпфирования.
Также обратите внимание, что, как и в случае критического демпфирования, мы не получаем вибрации в том смысле, в котором мы обычно о них думаем. Опять же, демпфирование достаточно сильное, чтобы заставить вибрацию затухать достаточно быстро, так что мы не видим много, если вообще видим колебания, которые мы обычно связываем с вибрациями.
Давайте рассмотрим еще один пример, прежде чем переходить к следующему типу вибраций.
Пример 4 Возьмите систему пружины и массы из первого примера, и для этого примера давайте прикрепим к ней демпфер, который будет оказывать силу 5 фунтов при скорости 2 фута / с.Найдите смещение в любой момент времени \ (t \), \ (u (t) \). Показать решениеИтак, получим коэффициент демпфирования.
\ [5 = \ gamma \ left (2 \ right) \ hspace {0.25in} \ Rightarrow \ hspace {0.25in} \ gamma = \ frac {5} {2} = 2.5Итак, на этот раз демпфирование недостаточно. Учитывая первые два примера, это не должно вызывать удивления. IVP для этого примера:
\ [\ frac {1} {2} u » + \ frac {5} {2} u ‘+ 18u = 0 \ hspace {0,25 дюйма} u \ left (0 \ right) = — \ frac {1} { 2} \ hspace {0.{- 1}} \ left ({\ frac {{- 0,04583}} {{- 0,5}}} \ right) = 0,09051 \ hspace {0,25 дюйма} {\ mbox {OR}} \ hspace {0,25 дюйма} {\ delta _2} = {\ delta _1} + \ pi = 3.2321 \ end {align *} \]Как и в случае незатухающего случая, мы можем использовать коэффициенты косинуса и синуса, чтобы определить, какой фазовый сдвиг мы должны использовать. Коэффициент косинуса (\ (c_ {1} \)) отрицательный, поэтому \ (\ cos \ delta \) также должен быть отрицательным. Точно так же коэффициент синуса (\ (c_ {2} \)) также отрицательный, и поэтому \ (\ sin \ delta \) также должен быть отрицательным.{- \ frac {{5t}} {2}}} \ cos \ left ({\ frac {{\ sqrt {119}}} {2} t — 3.2321} \ right) \]
Вот набросок этого смещения.
В этом случае мы наконец получили то, что мы обычно считаем настоящей вибрацией. Фактически, это точка критического демпфирования. По мере увеличения коэффициента демпфирования критический коэффициент демпфирования будет первым, при котором истинные колебания смещения не возникнут. Для всех значений коэффициента демпфирования больше этого ( i.е. чрезмерное демпфирование) мы также не увидим истинных колебаний смещения.
С физической точки зрения критическое (и избыточное) демпфирование обычно предпочтительнее недостаточного демпфирования. Подумайте об амортизаторах в вашей машине. Когда вы ударяетесь о неровность, вы не хотите тратить следующие несколько минут, подпрыгивая вверх и вниз, пока гаснет вибрация, создаваемая неровностью. Вы хотите, чтобы движение было как можно меньше. Другими словами, вы захотите установить амортизаторы в вашем автомобиле так, чтобы демпфирование было хотя бы критическим, чтобы вы могли избежать колебаний, которые будут возникать из-за недостаточно демпфированного корпуса.
Пришло время взглянуть на системы, в которых мы позволяем другим внешним силам воздействовать на объект в системе.
Незатухающие вынужденные колебания
Сначала рассмотрим незатухающий корпус. Дифференциальное уравнение в этом случае —
\ [му » + ку = F \ влево (т \ вправо) \]Это просто неоднородное дифференциальное уравнение, и мы знаем, как его решить. Общее решение —
\ [u \ left (t \ right) = {u_c} \ left (t \ right) + {U_P} \ left (t \ right) \], где дополнительным решением является решение проблемы свободной и незатухающей вибрации.Чтобы получить конкретное решение, мы можем использовать либо неопределенные коэффициенты, либо вариацию параметров, в зависимости от того, что нам проще для данной функции принуждения.
Есть особый тип форсирующей функции, на которую мы должны обратить внимание, поскольку она приводит к некоторым интересным результатам. Предположим, что вынуждающая функция — это простая периодическая функция вида
\ [F \ left (t \ right) = {F_0} \ cos \ left ({\ omega \, t} \ right) \ hspace {0,25 дюйма} {\ mbox {OR}} \ hspace {0.25 дюймов} F \ left (t \ right) = {F_0} \ sin \ left ({\ omega \, t} \ right) \]Для целей этого обсуждения мы будем использовать первый. Используя это, IVP становится
\ [mu » + ku = {F_0} \ cos \ left ({\ omega \, t} \ right) \]Дополнительное решение, как указано выше, составляет всего
\ [{u_c} \ left (t \ right) = {c_1} \ cos \ left ({{\ omega _0} t} \ right) + {c_2} \ sin \ left ({{\ omega _0} t} \ верно)\]где \ ({\ omega _0} \) — собственная частота.
Мы должны быть осторожны при поиске конкретного решения. Причина этого станет ясна, если мы воспользуемся неопределенными коэффициентами. С неопределенными коэффициентами наше предположение о форме конкретного решения будет:
\ [{U_P} \ left (t \ right) = A \ cos \ left ({\ omega \, t} \ right) + B \ sin \ left ({\ omega \, t} \ right) \]Теперь это предположение будет проблемой, если \ ({\ omega _0} = \ omega \). Если бы это произошло, предположение для конкретного решения было в точности дополнительным решением, поэтому нам нужно было бы добавить \ (t \).2}} \ right)}} \ cos \ left ({\ omega t} \ right) \ end {align *} \]
Если бы мы использовали синусоидальную форму функции принуждения, мы могли бы получить аналогичную формулу.
В этом случае нам нужно будет добавить \ (t \) к предположению для конкретного решения.
\ [{U_P} \ left (t \ right) = At \ cos \ left ({{\ omega _0} t} \ right) + Bt \ sin \ left ({{\ omega _0} t} \ right) \]Обратите внимание, что мы пошли дальше и признали, что \ ({\ omega _0} = \ omega \) в нашем предположении.2} + k = — m \ left ({\ frac {k} {m}} \ right) + k = 0 \]
Итак, первые два члена фактически выпадают (что очень хорошо…), и это дает нам
\ [2m {\ omega _0} B \ cos \ left ({\ omega t} \ right) — 2m {\ omega _0} A \ sin \ left ({\ omega t} \ right) = {F_0} \ cos \ влево ({\ omega t} \ right) \]Теперь установим коэффициент равным.
\ [\ begin {align *} & \ cos \ left ({\ omega t} \ right) \ ,: & 2m {\ omega _0} B & = {F_0} & \ Rightarrow \ hspace {0.25 дюймов} B & = \ frac {{{F_0}}} {{2m {\ omega _0}}} \\ & \ sin \ left ({\ omega t} \ right) \ ,: & 2m {\ omega _0} A & = 0 & \ Rightarrow \ hspace {0,25 дюйма} A & = 0 \ end {align *} \]В данном случае конкретным будет,
\ [{U_P} \ left (t \ right) = \ frac {{{F_0}}} {{2m {\ omega _0}}} t \ sin \ left ({{\ omega _0} t} \ right) \ ]Тогда смещение для этого случая составляет
\ [\ begin {align *} u \ left (t \ right) & = {c_1} \ cos \ left ({{\ omega _0} t} \ right) + {c_2} \ sin \ left ({{\ omega _0} t} \ right) + \ frac {{{F_0}}} {{2m {\ omega _0}}} t \ sin \ left ({{\ omega _0} t} \ right) \\ u \ left ( t \ right) & = R \ cos \ left ({{\ omega _0} t — \ delta} \ right) + \ frac {{{F_0}}} {{2m {\ omega _0}}} t \ sin \ слева ({{\ omega _0} t} \ right) \ end {align *} \]в зависимости от формы, которую вы предпочитаете для смещения.
Итак, в чем смысл этих двух случаев? Что ж, в первом случае \ ({\ omega _0} \ ne \ omega \) наша функция смещения состоит из двух косинусов и всегда хороша и хорошо себя ведет.
Напротив, второй случай, \ ({\ omega _0} = \ omega \), будет иметь некоторые серьезные проблемы при увеличении \ (t \). Добавление \ (t \) в частное решение будет означать, что мы увидим колебание, амплитуда которого нарастает с увеличением \ (t \).Этот случай называется резонанс , и мы, как правило, хотели бы избежать этого любой ценой.
В этом случае резонанс возник, если предположить, что вынуждающая функция равна
\ [F \ left (t \ right) = {F_0} \ cos \ left ({{\ omega _0} \, t} \ right) \]У нас также была бы возможность резонанса, если бы мы предположили вынуждающую функцию формы.
\ [F \ left (t \ right) = {F_0} \ sin \ left ({{\ omega _0} \, t} \ right) \]Мы также должны позаботиться о том, чтобы не предполагать, что функция принуждения будет в одной из этих двух форм.Форсирующие функции могут иметь самые разные формы. Если мы столкнемся с функцией принуждения, отличной от той, которая используется здесь, вам придется пройти через неопределенные коэффициенты или изменение параметров, чтобы определить конкретное решение.
Пример 5 К пружине прикреплен предмет весом 3 кг, который сам растянет пружину на 392 мм. В системе отсутствует демпфирование и форсирующая функция вида \ [F \ left (t \ right) = 10 \ cos \ left ({\ omega \, t} \ right) \]прикреплен к объекту, и система будет испытывать резонанс.Если объект изначально смещен на 20 см вниз от его положения равновесия и задана скорость 10 см / сек вверх, найдите смещение в любой момент времени \ (t \).
Показать решениеПоскольку мы находимся в метрической системе, нам не нужно находить массу в том виде, в каком она нам дана. Кроме того, для всех расчетов мы будем переводить все значения длины в метры.
Первое, что нам нужно сделать, это найти \ (k \).
\ [k = \ frac {{mg}} {L} = \ frac {{\ left (3 \ right) \ left ({9.8} \ right)}} {{0.392}} = 75 \]Нам говорят, что система испытывает резонанс, поэтому давайте продолжим и получим собственную частоту, чтобы мы могли полностью настроить IVP.
\ [{\ omega _0} = \ sqrt {\ frac {k} {m}} = \ sqrt {\ frac {{75}} {3}} = 5 \]Тогда IVP для этого будет
\ [3u » + 75u = 10 \ cos \ left ({5t} \ right) \ hspace {0,25 дюйма} u \ left (0 \ right) = 0,2 \ hspace {0,25 дюйма} u ‘\ left (0 \ right ) = — 0.1 \]Мудрое решение, здесь особо нечего делать. Дополнительным решением является свободное незатухающее решение, которое легко получить, и для конкретного решения мы можем просто использовать формулу, полученную нами выше.
Тогда общее решение
\ [\ begin {align *} u \ left (t \ right) & = {c_1} \ cos \ left ({5t} \ right) + {c_2} \ sin \ left ({5t} \ right) + \ frac {{10}} {{2 \ left (3 \ right) \ left (5 \ right)}} t \ sin \ left ({5t} \ right) \\ u \ left (t \ right) & = {c_1 } \ cos \ left ({5t} \ right) + {c_2} \ sin \ left ({5t} \ right) + \ frac {1} {3} t \ sin \ left ({5t} \ right) \ end {выровнять*}\]Применение начальных условий дает смещение в любой момент времени \ (t \).{1} / {} _ {5}}}} \ right) = — 0,099669 \ hspace {0,25 дюйма} {\ delta _2} = {\ delta _1} + \ pi = 3,041924 \ end {align *} \]
В этом случае коэффициент при косинусе положительный, а коэффициент при синусе отрицательный. Это заставляет \ (\ cos \ delta \) быть положительным, а \ (\ sin \ delta \) — отрицательным. Это означает, что фазовый сдвиг должен быть в квадранте IV, и поэтому на этот раз правильный фазовый сдвиг будет первым.
Тогда смещение становится,
\ [и \ влево (т \ вправо) = 0.200998 \ cos \ left ({5t + 0,099669} \ right) + \ frac {1} {3} t \ sin \ left ({5t} \ right) \]Вот эскиз смещения для этого примера.
Пришло время взглянуть на последний случай вибрации.
Принудительные демпфированные колебания
Это полномасштабный случай, когда мы рассматриваем все возможные силы, которые могут воздействовать на систему. Дифференциальное уравнение для этого случая:
\ [mu » + \ gamma u ‘+ ku = F \ left (t \ right) \]Функция смещения на этот раз будет
\ [u \ left (t \ right) = {u_c} \ left (t \ right) + {U_P} \ left (t \ right) \], где дополнительное решение будет решением для случая со свободным демпфированием, а частное решение будет найдено с использованием неопределенных коэффициентов или вариации параметра, в зависимости от того, что наиболее удобно для использования.
В связи с этим случаем следует отметить несколько моментов. Во-первых, из нашей работы в случае свободного затухания мы знаем, что дополнительное решение будет приближаться к нулю при увеличении \ (t \). Из-за этого дополнительное решение в данном случае часто называют переходным решением .
Кроме того, из-за такого поведения смещение будет все больше и больше походить на конкретное решение по мере увеличения \ (t \), и поэтому конкретное решение часто называют устойчивым решением или принудительным откликом .
Прежде чем покинуть этот раздел, давайте поработаем еще один пример. Как и в предыдущих примерах, мы оставим большую часть деталей, чтобы вы могли их проверить.
Пример 6 Возьмите систему из последнего примера и добавьте демпфер, который будет оказывать силу 45 Ньютонов при скорости 50 см / сек. Показать решениеИтак, все, что нам нужно сделать, это вычислить коэффициент демпфирования для этой задачи, а затем извлечь все остальное из предыдущей задачи.Коэффициент демпфирования
\ [\ begin {align *} {F_d} & = \ gamma u ‘\\ 45 & = \ gamma \ left ({0.5} \ right) \\ \ gamma & = 90 \ end {align *} \]IVP для этой проблемы есть.
\ [3u » + 90u ‘+ 75u = 10 \ cos \ left ({5t} \ right) \ hspace {0,25 дюйма} u \ left (0 \ right) = 0,2 \ hspace {0,25in} u’ \ left ( 0 \ right) = — 0,1 \]Дополнительным решением для этого примера является
\ [\ begin {align *} {u_c} \ left (t \ right) & = {c_1} {{\ bf {e}} ^ {\ left ({- 15 + 10 \ sqrt 2} \ right) t} » } + {c_2} {{\ bf {e}} ^ {\ left ({- 15-10 \ sqrt 2} \ right) t}} \\ {u_c} \ left (t \ right) & = {c_1} {{\ bf {e}} ^ {- 0. {- 0.{- 29.1421t}} + \ frac {1} {{45}} \ sin \ left ({5t} \ right) \]Вот эскиз смещения для этого примера.
Специальное периодическое движение — Физика колледжа: OpenStax
Сводка
- Опишите простой гармонический осциллятор.
- Объясните связь между простым гармоническим движением и волнами.
Колебания системы, в которой результирующая сила может быть описана законом Гука, имеют особое значение, потому что они очень распространены.Это также простейшие колебательные системы. Простое гармоническое движение (SHM) — это название, данное колебательному движению для системы, в которой результирующая сила может быть описана законом Гука, и такая система называется простым гармоническим осциллятором . Если результирующая сила может быть описана законом Гука и нет демпфирования (за счет трения или других неконсервативных сил), то простой гармонический осциллятор будет колебаться с равным смещением по обе стороны от положения равновесия, как показано для объекта на пружине на рисунке 1.Максимальное смещение от равновесия называется амплитудой [латекс] \ boldsymbol {X}. [/ Latex] Единицы измерения амплитуды и смещения такие же, но зависят от типа колебаний. Для объекта на пружине единицы измерения амплитуды и перемещения — метры; тогда как для звуковых колебаний у них есть единицы давления (а для других типов колебаний есть еще другие единицы). Поскольку амплитуда — это максимальное смещение, она связана с энергией колебаний.
ПРИЕМНЫЙ ЭКСПЕРИМЕНТ: SHM И МРАМОР
Найдите миску или таз, имеющий изнутри форму полусферы.Поместите мрамор внутрь чаши и периодически наклоняйте чашу, чтобы мрамор катился со дна чаши к одинаково высоким точкам по бокам чаши. Почувствуйте силу, необходимую для поддержания этого периодического движения. Что такое восстанавливающая сила и какую роль эта сила играет в простом гармоническом движении (SHM) мрамора?
Рис. 1. Объект, прикрепленный к пружине, скользящей по поверхности без трения, представляет собой несложный простой гармонический осциллятор. При смещении из состояния равновесия объект совершает простое гармоническое движение с амплитудой X и периодом T .Максимальная скорость объекта достигается при прохождении через равновесие. Чем жестче пружина, тем меньше период T . Чем больше масса объекта, тем больше период T .Что такого важного в простом гармоническом движении? Одна особенность заключается в том, что период [latex] \ boldsymbol {T} [/ latex] и частота [latex] \ boldsymbol {f} [/ latex] простого гармонического осциллятора не зависят от амплитуды. Струна гитары, например, будет колебаться с одной и той же частотой, независимо от того, мягко она или сильно нажата.Поскольку период постоянен, в качестве часов можно использовать простой гармонический осциллятор.
Два важных фактора действительно влияют на период простого гармонического осциллятора. Период связан с тем, насколько жесткая система. Очень жесткий объект имеет большую постоянную силы [latex] \ boldsymbol {k}, [/ latex], что приводит к тому, что система имеет меньший период. Например, вы можете отрегулировать жесткость трамплина — чем она жестче, тем быстрее она вибрирует и тем короче ее период. Период также зависит от массы колебательной системы.Чем массивнее система, тем больше период. Например, тяжелый человек на трамплине подпрыгивает вверх и вниз медленнее, чем легкий.
Фактически, масса [латекс] \ boldsymbol {m} [/ latex] и силовая постоянная [латекс] \ boldsymbol {k} [/ latex] — это только факторов, которые влияют на период и частоту простого гармонического движения. .
ПЕРИОД ПРОСТОГО ГАРМОНИЧЕСКОГО ОСЦИЛЛЯТОРА
Период простого гармонического осциллятора равен
[латекс] \ boldsymbol {T = 2 \ pi} [/ latex] [латекс] \ boldsymbol {\ sqrt {\ frac {m} {k}}} [/ латекс]
и, поскольку [latex] \ boldsymbol {f = 1 / T}, [/ latex], частота простого гармонического генератора равна
[латекс] \ boldsymbol {f \: =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {2 \ pi} \ sqrt {\ frac {k} {m}}}.[/ латекс]
Обратите внимание, что ни [латекс] \ boldsymbol {T} [/ latex], ни [латекс] \ boldsymbol {f} [/ latex] не зависят от амплитуды.
ПРИЕМНЫЙ ЭКСПЕРИМЕНТ: МАССА И КОЛЕБАНИЯ ЛИНЕЙКИ
Найдите две одинаковые деревянные или пластиковые линейки. Плотно прикрепите один конец каждой линейки к краю стола так, чтобы длина каждой линейки, выступающей из стола, была одинаковой. На свободный конец одной линейки прикрепите тяжелый предмет, например несколько крупных монет. Выщипывайте концы линейок одновременно и наблюдайте, какая из них претерпевает больше циклов за период времени, и измерьте период колебаний каждой из линейок.
Пример 1: Расчет частоты и периода колебаний: плохие амортизаторы в автомобиле
Если амортизаторы в автомобиле выходят из строя, автомобиль будет раскачиваться при малейшей провокации, например, при наезде на неровности дороги и после остановки (см. Рисунок 2). Вычислите частоту и период этих колебаний для такого автомобиля, если масса автомобиля (включая его груз) составляет 900 кг, а силовая постоянная [латекс] (\ boldsymbol {k}) [/ латекс] системы подвески равна [латекс] \ boldsymbol {6.4 \ textbf {N / m}}. [/ Latex]
Стратегия
Частота колебаний автомобиля будет соответствовать частоте простого гармонического осциллятора, как указано в уравнении [latex] \ boldsymbol {f = \ frac {1} {2 \ pi} \ sqrt {\ frac {k} {m}} }. [/ latex] Приведены и масса, и силовая постоянная.
Решение
- Введите известные значения k и m :
[латекс] \ boldsymbol {f =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {2 \ pi} \ sqrt {\ frac {k} {m}}} [/ латекс] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {2 \ pi} \ sqrt {\ frac {6.{-1} = 1,36 \ textbf {Hz}}. [/ Latex]
[латекс] \ boldsymbol {T =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {f}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {1.356 \ textbf {Hz}}} [/ latex] [latex] \ boldsymbol {= 0.738 \ textbf {s}}. [/ latex]
Обсуждение
Значения [latex] \ boldsymbol {T} [/ latex] и [latex] \ boldsymbol {f} [/ latex] кажутся подходящими для прыгающей машины.Вы можете наблюдать эти колебания, если сильно надавите на конец автомобиля и отпустите.
Если бы была сделана фотография прыгающего автомобиля с временной выдержкой, когда он проезжал мимо, фара образовала бы волнообразную полосу, как показано на рисунке 2. Точно так же на рисунке 3 показан объект, подпрыгивающий на пружине, оставляющий волнообразный «след». своего положения на движущейся полосе бумаги. Обе волны являются синусоидальными функциями. Все простые гармонические движения тесно связаны с синусоидальными и косинусоидальными волнами.
Рисунок 2. Прыгающий автомобиль совершает волнообразное движение. Если восстанавливающая сила в системе подвески может быть описана только законом Гука, тогда волна является синусоидальной функцией. (Волна — это след от фар при движении автомобиля вправо.) Рисунок 3. Вертикальное положение объекта, подпрыгивающего на пружине, записывается на полоске движущейся бумаги, оставляя синусоидальную волну.Смещение как функция времени t при любом простом гармоническом движении, то есть таком, в котором результирующая восстанавливающая сила может быть описана законом Гука, определяется как
[латекс] \ boldsymbol {x (t) = X \ cos} [/ latex] [латекс] \ boldsymbol {\ frac {2 \ pi {t}} {T}}, [/ латекс]
где [латекс] \ boldsymbol {X} [/ latex] — амплитуда.В [latex] \ boldsymbol {t = 0}, [/ latex] начальное положение — [latex] \ boldsymbol {x_0 = X}, [/ latex], а смещение колеблется назад и вперед с периодом [latex] \ boldsymbol {T}. [/ Latex] (Когда [latex] \ boldsymbol {t = T}, [/ latex] мы снова получаем [latex] \ boldsymbol {x = X} [/ latex], потому что [latex] \ boldsymbol {\ cos2 \ pi = 1}.). [/ latex] Кроме того, из этого выражения для [latex] \ boldsymbol {x}, [/ latex] скорость [latex] \ boldsymbol {v} [/ latex] как функция время вычисляется по:
[латекс] \ boldsymbol {v (t) = — v _ {\ textbf {max}} \ sin} [/ latex] [латекс] \ boldsymbol {(\ frac {2 \ pi {t}} {T})} , [/ латекс]
где [латекс] \ boldsymbol {v _ {\ textbf {max}} = 2 \ pi {X / T} = X \ sqrt {k / m}}.[/ latex] Объект имеет нулевую скорость при максимальном смещении — например, [latex] \ boldsymbol {v = 0} [/ latex], когда [latex] \ boldsymbol {t = 0}, [/ latex] и в это время [latex] \ boldsymbol {x = X}. [/ latex] Знак минус в первом уравнении для [latex] \ boldsymbol {v (t)} [/ latex] указывает правильное направление скорости. Например, сразу после начала движения скорость отрицательна, потому что система движется обратно к точке равновесия. Наконец, мы можем получить выражение для ускорения, используя второй закон Ньютона.[Тогда у нас есть [латекс] \ boldsymbol {x (t), \: v (t), \: t,} [/ latex] и [latex] \ boldsymbol {a (t)}, [/ latex] величины необходимо для кинематики и описания простого гармонического движения.] Согласно второму закону Ньютона, ускорение составляет [латекс] \ boldsymbol {a = F / m = kx / m}. [/ latex] Итак, [латекс] \ boldsymbol { a (t)} [/ latex] также является функцией косинуса:
[латекс] \ boldsymbol {a (t) = -} [/ latex] [латекс] \ boldsymbol {\ frac {kX} {m}} [/ latex] [латекс] \ boldsymbol {\ cos} [/ latex] [латекс] \ boldsymbol {\ frac {2 \ pi {t}} {T}}. [/ латекс]
Следовательно, [латекс] \ boldsymbol {a (t)} [/ latex] прямо пропорционален [латексу] \ boldsymbol {x (t)} и в противоположном ему направлении.[/ латекс]
На рисунке 4 показано простое гармоническое движение объекта на пружине и представлены графики [латекс] \ boldsymbol {x (t), \: v (t),} [/ latex] и [латекс] \ boldsymbol {a ( t)} [/ latex] от времени.
Рис. 4. Графики x ( t ) , v ( t ) и a ( t ) по сравнению с t для движения объект на пружине. Суммарная сила, действующая на объект, может быть описана законом Гука, поэтому объект совершает простое гармоническое движение.Обратите внимание, что исходное положение имеет максимальное значение вертикального смещения X ; v изначально равно нулю, а затем отрицательно по мере движения объекта вниз; и начальное ускорение отрицательное, возвращается к положению равновесия и становится нулевым в этой точке.Наиболее важным моментом здесь является то, что эти уравнения математически просты и справедливы для всех простых гармонических движений. Они очень полезны при визуализации волн, связанных с простым гармоническим движением, включая визуализацию того, как волны складываются друг с другом.
Проверьте свое понимание 1
Предположим, вы взяли струну банджо. Вы слышите одну ноту, которая начинается вслух и постепенно затихает. Опишите, что происходит со звуковыми волнами с точки зрения периода, частоты и амплитуды по мере уменьшения громкости звука.
Проверьте свое понимание 2
Няня толкает ребенка на качелях. В точке, где качели достигают [латекса] \ boldsymbol {x}, [/ latex], где будет находиться соответствующая точка на волне этого движения?
ФЕТ ИССЛЕДОВАНИЯ: МАССЫ И ВЕСНА
Реалистичная лаборатория масс и пружин.Подвесьте массы к пружинам и отрегулируйте жесткость и демпфирование пружины. Вы даже можете замедлить время. Перенесите лабораторию на разные планеты. На диаграмме показана кинетическая, потенциальная и тепловая энергия каждой пружины.
Рисунок 5. Массы и пружиныКонцептуальные вопросы
1: Какие условия должны быть выполнены для создания простого гармонического движения?
2: (a) Если частота для некоторого колебания непостоянна, может ли колебание быть простым гармоническим движением?
(b) Можете ли вы привести примеры гармонического движения, в котором частота может зависеть от амплитуды?
3: Приведите пример простого гармонического осциллятора, особо отметив, что его частота не зависит от амплитуды.
4: Объясните, почему вы ожидаете, что объект, сделанный из жесткого материала, будет вибрировать с большей частотой, чем аналогичный объект, сделанный из губчатого материала.
5: Когда вы проезжаете грузовой автомобиль с прицепом по шоссе, вы замечаете, что его прицеп медленно подпрыгивает вверх и вниз. Более вероятно, что прицеп сильно загружен или почти пустой? Поясните свой ответ.
6: Некоторые люди модифицируют автомобили, чтобы они были намного ближе к земле, чем когда они были изготовлены.Стоит ли устанавливать более жесткие пружины? Поясните свой ответ.
Задачи и упражнения
1: Тип часов с кукушкой отслеживает время, заставляя массу подпрыгивать на пружине, обычно что-то милое, вроде херувима в кресле. Какая силовая постоянная необходима для получения периода 0,500 с для массы 0,0150 кг?
2: Если жесткость пружины простого гармонического осциллятора удвоится, на какой коэффициент потребуется изменить массу системы, чтобы частота движения оставалась прежней?
3: А 0.Подвешенный на пружине груз весом 500 кг колеблется с периодом 1,50 с. Какую массу нужно добавить к объекту, чтобы изменить период до 2,00 с?
4: В зависимости от того, сколько свободы действий (как в процентах, так и по массе) у вас будет при выборе массы объекта в предыдущей задаче, если вы не хотите, чтобы новый период был больше 2,01 с или меньше 1,99 с. ?
5: Предположим, вы прикрепляете объект с массой [латекс] \ boldsymbol {m} [/ latex] к вертикальной пружине, первоначально находящейся в состоянии покоя, и позволяете ему подпрыгивать вверх и вниз.Вы высвобождаете объект из состояния покоя на исходной длине упора пружины. (a) Покажите, что пружина оказывает восходящее усилие [латекс] \ boldsymbol {2.00 \ textbf {mg}} [/ latex] на объект в его самой нижней точке. (b) Если пружина имеет силовую постоянную [латекс] \ boldsymbol {10.0 \ textbf {Н / м}} [/ latex] и объект массой 0,25 кг приводится в движение, как описано, найдите амплитуду колебания. (c) Найдите максимальную скорость.
6: Дайвер на трамплине совершает простое гармоническое движение.Ее масса 55,0 кг, период движения 0,800 с. Следующий дайвер — мужчина, период простых гармонических колебаний которого составляет 1,05 с. Какова его масса, если масса доски ничтожна?
7: Предположим, что доска для прыжков в воду, на которой никого нет, подпрыгивает вверх и вниз, совершая простое гармоническое движение с частотой 4,00 Гц. Доска имеет полезную массу 10,0 кг. Какова частота простого гармонического движения дайвера весом 75,0 кг на доске?
8:
Рисунок 6. В этой детской игрушке используются пружины, чтобы развлекать младенцев. (кредит: Humboldthead, Flickr)Устройство, изображенное на рисунке 6, развлекает младенцев, удерживая их от блужданий. Ребенок подпрыгивает в ремне безопасности, подвешенном к дверной коробке с помощью пружины.
(a) Если пружина тянется на 0,250 м, поддерживая ребенка весом 8,0 кг, какова ее жесткость?
(b) Сколько времени на один полный прыжок этого ребенка? (c) Какова максимальная скорость ребенка, если амплитуда его отскока равна 0.200 м?
9: Парашютист весом 90,0 кг, подвешенный на парашюте, подпрыгивает вверх и вниз с периодом 1,50 с. Каков новый период колебаний, когда второй парашютист массой 60,0 кг свисает с ног первого, как показано на рис. 7.
Рис. 7. На колебания одного парашютиста вот-вот повлияет второй парашютист. (Источник: армия США, www.army.mil)
Глоссарий
- амплитуда
- максимальное смещение от положения равновесия объекта, колеблющегося вокруг положения равновесия
- простое гармоническое движение
- колебательное движение в системе, где результирующая сила может быть описана законом Гука
- простой генератор гармоник
- устройство, реализующее закон Гука, такое как груз, прикрепленный к пружине, при этом другой конец пружины соединен с жесткой опорой, такой как стена
Решения
Проверьте свое понимание 1
Частота и период практически не изменились.При уменьшении громкости уменьшается только амплитуда.
Проверьте свое понимание 2
[latex] \ boldsymbol {x} [/ latex] — максимальная деформация, соответствующая амплитуде волны. Точка на волне будет либо на самом верху, либо на самом низу кривой.
Задачи и упражнения
1:
[латекс] \ boldsymbol {2.37 \ textbf {Н / м}} [/ латекс]
3:
0.389 кг
6:
94,7 кг
9:
1.94 с
.

 1)
1)