Калькулятор восьмеричной системы счисления вычитание. Калькулятор систем счисления с решением. Заем единицы из старшего разряда
С помощю этого онлайн калькулятора можно перевести целые и дробные числа из одной системы счисления в другую. Дается подробное решение с пояснениями. Для перевода введите исходное число, задайте основание сисемы счисления исходного числа, задайте основание системы счисления, в которую нужно перевести число и нажмите на кнопку «Перевести». Теоретическую часть и численные примеры смотрите ниже.
Результат уже получен!
Перевод целых и дробных чисел из одной системы счисления в любую другую − теория, примеры и решения
Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:
Пронумеруем это число справа налево начиная с нуля:
Тогда число 6372 можно представить в следующем виде:
Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.
Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:
Тогда число 1287.923 можно представить в виде:
1287.923 =1000+200+80 +7+0.9+0.02+0.003 = 1·10 3 +2·10 2 +8·10 1 +7·10 0 +9·10 -1 +2·10 -2 +3·10 -3 .
В общем случае формулу можно представить в следующем виде:
Ц n ·s n +Ц n-1 ·s n-1 +…+Ц 1 ·s 1 +Ц 0 ·s 0 +Д -1 ·s -1 +Д -2 ·s -2 +…+Д -k ·s -k
где Ц n -целое число в позиции n , Д -k — дробное число в позиции (-k), s — система счисления.
Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр {0,1,2,3,4,5,6,7,8,9}, в восьмеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7}, в двоичной системе счисления — из множества цифр {0,1}, в шестнадцатеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15.
| Таблица 1 | |||
|---|---|---|---|
| Система счисления | |||
| 10 | 2 | 8 | 16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E | 15 | 1111 | 17 | F |
Перевод чисел из одной системы счисления в другую
Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.
Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:
1 ·2 6 +0 ·2 5 +1 ·2 4 +1 ·2 3 +1 ·2 2 +0 ·2 1 +1 ·2 0 +0 ·2 -1 +0 ·2 -2 +1 ·2 -3 =64+16+8+4+1+1/8=93.125
Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:
Пример 3 . Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:
Здесь A -заменен на 10, B — на 11, C — на 12, F — на 15.
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.
Пример 4 . Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||||||
| 158 | 79 | 2 | |||||
| 1 | 78 | 39 | 2 | ||||
| 1 | 38 | 19 | 2 | ||||
| 1 | 18 | 9 | 2 | ||||
| 1 | 8 | 4 | 2 | ||||
| 1 | 4 | 2 | 2 | ||||
| 0 | 2 | 1 | |||||
| 0 |
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111
. Следовательно можно записать:
1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111
. Следовательно можно записать:
159 10 =10011111 2 .
Пример 5 . Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147 (см. Рис. 2). Следовательно можно записать:
615 10 =1147 8 .
Пример 6 . Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7 . Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | ||
| x | 2 | |
| 0 | 0.428 | |
| x | 2 | |
| 0 | 0.856 | |
| x | 2 | |
| 1 | 0.712 | |
| x | 2 | |
| 1 | 0.424 | |
| x | 2 | |
| 0 | 0.848 | |
| x | 2 | |
| 1 | 0.696 | |
| x | 2 | |
| 1 | 0.392 |
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью.
Следовательно можно записать:
0.214 10 =0.0011011 2 .
Пример 8 . Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | ||
| x | 2 | |
| 0 | 0.25 | |
| x | 2 | |
| 0 | 0.5 | |
| x | 2 | |
| 1 | 0.0 |
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2.
0.125 10 =0.001 2 .
Пример 9 . Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | ||
| x | 16 | |
| 3 | 0.424 | |
| x | 16 | |
| 6 | 0.784 | |
| x | 16 | |
| 12 | 0.544 | |
| x | 16 | |
| 8 | 0.704 | |
| x | 16 | |
| 11 | 0.264 | |
| x | 16 | |
| 4 | 0.224 |
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
Следовательно имеем:
0.214 10 =0.36C8B4 16 .
Пример 10 . Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | ||
| x | 8 | |
| 4 | 0.096 | |
| x | 8 | |
| 0 | 0.768 | |
| x | 8 | |
| 6 | 0.144 | |
| x | 8 | |
| 1 | 0.152 | |
| x | 8 | |
| 1 | 0.216 | |
| x | 8 | |
| 1 | 0.728 |
Получили:
0.512 10 =0.406111 8 .
Пример
11
. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:
Далее объединяя эти результаты получим:
159.125 10 =10011111.001 2 .
Пример 12 . Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим.
Как мы складываем в десятичной системе счисления?
Давайте вспомним о том, как мы складываем числа уже привычным нам способом, в десятичной .
Самое главное стоит понять разряды. Вспомните алфавит каждой СС и тогда вам станет легче.
Сложение в двоичной системе ничем не отличается от сложения в десятичной системе. Главное помнить, алфавит содержит всего две цифры: 0 и 1. Поэтому когда мы складываем 1 + 1, то получаем 0, и увеличиваем число еще на 1 разряд. Посмотрите на пример выше:
- Начинаем складывать как и привыкли справа налево. 0 + 0 = 0, значит записываем 0. Переходим к следующему разряду.
- Складываем 1 + 1 и получаем 2, но 2 нет в двоичной системе счисления, а значит мы записываем 0, а 1 добавляем к следующему разряду.

- У нас получается в этом разряде три единицы складываем 1 + 1 + 1 = 3, этой цифры также быть не может. Значит 3 – 2 = 1. И 1 добавляем к следующему разряду.
- У нас вновь получается 1 + 1 = 2. Мы уже знаем, что 2 быть не может, значит записываем 0, а 1 добавляем к следующему разряду.
- Складывать больше нечего, значит в ответе получаем: 10100.
Один пример мы разобрали, второй решите самостоятельно:
Так же как и в любых других системах счисления необходимо помнить Алфавит. Давайте попробуем сложить выражение.
- Все как обычно, начинаем складывать справа налево. 4 + 3 = 7.
- 5 + 4 = 9. Девяти быть не может, значит из 9 вычитаем 8, получаем 1. И еще 1 добавляем к следующему разряду.
- 3 + 7 + 1 = 11. Из 11 вычитаем 8, получаем 3. И единицу добавляем к следующему разряду.
- 6 + 1 = 7.
- Складывать далее нечего. Ответ: 7317.
А теперь проделайте сложение самостоятельно:
- Выполняем уже знакомые нам действия и не забываем про алфавит.
 2 + 1 = 3.
2 + 1 = 3. - 5 + 9 = 14. Вспоминаем Алфавит: 14 = Е.
- С = 12. 12 + 8 = 20. Двадцати нет в шестнадцатеричной системе счисления. Значит из 20 вычитаем 16 и получаем 4. И единицу добавляем к следующему разряду.
- 1 + 1 = 2.
- Больше складывать нечего. Ответ: 24Е3.
Вычетание в системах счисления
Вспомним, как мы это делаем в десятичной системе счисления.
- Начинаем слева направо, от меньшего разряда к большему. 2 – 1 = 1.
- 1 – 0 = 1.
- 3 – 9 = ? Тройка меньше девяти, поэтому позаимствуем единицу из старшего разряда. 13 – 9 = 4.
- Из последнего разряда мы взяли единицу для предыдущего действия, поэтому 4 – 1 = 3.
- Ответ: 3411.
- Начинаем как обычно. 1 – 1 = 0.
- 1 – 0 = 1.
- От 0 отнять единицу нельзя. Поэтому заберем один разряд у старшего. 2 – 1 = 1.
- Ответ: 110.
А теперь решите самостоятельно:
- Ничего нового, главное помнить алфавит.
 4 – 3 = 1.
4 – 3 = 1. - 5 – 0 = 5.
- От 3 отнять 7 мы сразу не можем, для этого нам необходимо заимствовать единицу у более старшего разряда. 11 – 7 = 4.
- Помним, что заимствовали единицу ранее, 6 – 1 = 5.
- Ответ: 5451.
Возьмем предыдущий пример, и посмотрим каков будет результат в шестнадцатеричной системе. Такой же или другой?
- 4 – 3 = 1.
- 5 – 0 = 5.
- От 3 отнять 7 мы сразу не можем, для этого нам необходимо заимствовать единицу у более старшего разряда. 19 – 7 = 12. В шестнадцатеричной системе 12 = С.
- Помним, что заимствовали единицу ранее, 6 – 1 = 5
- Ответ: 5С51
Пример для самостоятельного решения:
Умножение в системах счисления
Давайте запомним раз и навсегда, что умножение в любой системе счисления на единицу, всегда даст тоже самое число.
- Каждый разряд умножаем на единицу, как обычно справа налево, и получаем число 6748;
- 6748 умножаем на 8 и получаем число 53984;
- Проделываем операцию умножения 6748 на 3.
 Получаем число 20244;
Получаем число 20244; - Складываем все 3 числа, по правилам. Получаем 2570988;
- Ответ: 2570988.
В двоичной системе умножать очень легко. Мы всегда умножаем либо на 0, либо на единицу. Главное, это внимательно складывать. Давайте попробуем.
- 1101 умножаем на единицу, как обычно справа налево, и получаем число 1101;
- Проделываем эту операцию еще 2 раза;
- Складываем все 3 числа внимательно, помним про алфавит, не забывая про лесенку;
- Ответ: 1011011.
Пример для самостоятельного решения:
- 5 х 4 = 20. А 20 = 2 х 8 + 4. Остаток от деления записываем в число – это будет 4, а 2 держим в уме. Проделываем эту процедуру справа налево и получаем число 40234;
- При умножении на 0, получаем четыре 0;
- При умножении на 7, у нас получается число 55164;
- Теперь складываем числа и получаем – 5556634;
- Ответ: 5556634.
Пример для самостоятельного решения:
Все как обычно, главное вспомните алфавит. Буквенные цифры, для удобства переводите в привычную для себя систему счисления, как умножите, переводите обратно в буквенное значение.
Буквенные цифры, для удобства переводите в привычную для себя систему счисления, как умножите, переводите обратно в буквенное значение.
Давайте для наглядности разберем умножение на 5 числа 20А4.
- 5 х 4 = 20. А 20 = 16 + 4. Остаток от деления записываем в число – это будет 4, а 1 держим в уме.
- А х 5 + 1 = 10 х 5 + 1 = 51. 51 = 16 х 3 + 3. Остаток от деления записываем в число – это будет 3, а 3 держим в уме.
- При умножении на 0, получаем 0 + 3 = 3;
- 2 х 5 = 10 = А; В итоге у нас получается А334; Проделываем эту процедуру с двумя другими числами;
- Помним правило умножения на 1;
- При умножении на В, у нас получается число 1670С;
- Теперь складываем числа и получаем – 169В974;
- Ответ: 169В974.
Пример для самостоятельного решения.
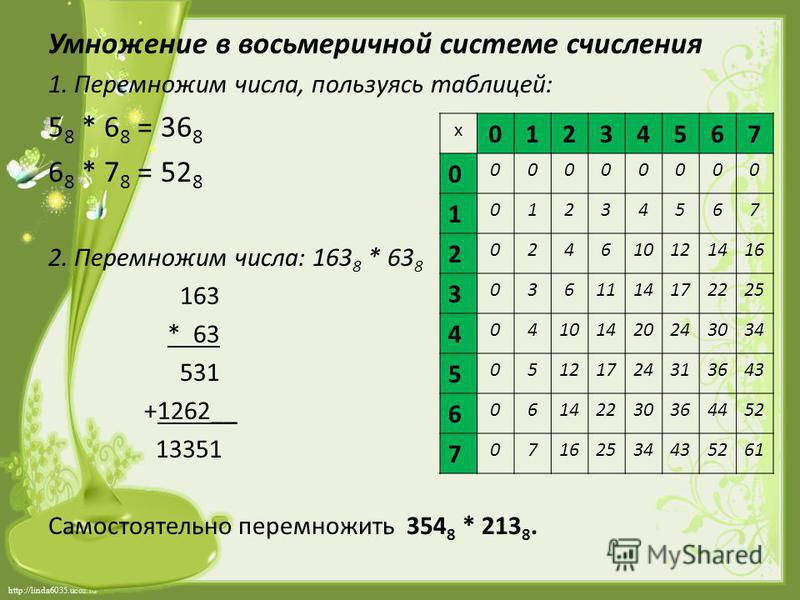
Рассмотрим основные
арифметические операции: сложение,
вычитание, умножение и деление.
Правила выполнения этих операций в
десятичной системе хорошо известны —
это сложение, вычитание, умножение
столбиком и деление углом. Эти правила применимы и ко всем другим
позиционным системам счисления. Только
надо пользоваться особыми таблицами
сложения и умножения для каждой системы.
Эти правила применимы и ко всем другим
позиционным системам счисления. Только
надо пользоваться особыми таблицами
сложения и умножения для каждой системы.
1. Сложение
Таблицы сложения легко составить, используя правила счета.
При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.
Пример 1. Сложим числа 15 и 6 в различных системах счисления .
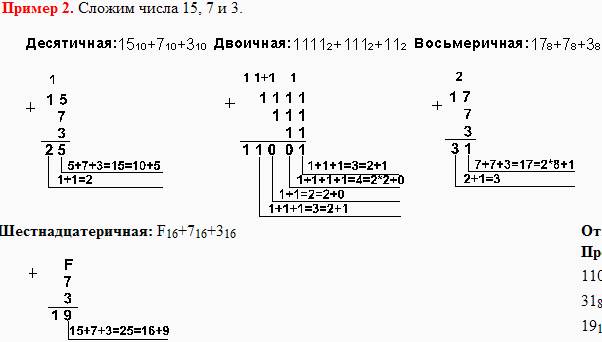
Пример 2. Сложим числа 15, 7 и 3.
|
Шестнадцатеричная : F 16 +7 16 +3 16 |
15+7+3 = 25 10 = 11001 2 = 31 8 = 19 16 . Проверка: 11001 2 = 2 4 + 2 3 + 2 0 = 16+8+1=25, 31 8 = 3 . 8 1 + 1 . 8 0 = 24 + 1 = 25, 19 16 = 1 . 16 1 + 9 . 16 0 = 16+9 = 25. |
Пример 3.
Сложим числа
141,5 и 59,75
.
Ответ: 141,5 + 59,75 = 201,25 10 = 11001001,01 2 = 311,2 8 = C9,4 16
Проверка. Преобразуем полученные суммы к десятичному виду :
11001001,01 2 = 2 7 + 2 6 + 2 3 + 2 0 + 2 -2 = 201,25
311,2 8 = 3 . 8 2 + 1 . 8 1 + 1 . 8 0 + 2 . 8 -1 = 201,25
C9,4 16 = 12 . 16 1 + 9 . 16 0 + 4 . 16 -1 = 201,25
2. Вычитание
|
Вычитание в двоичной системе счисления
заем |
Вычитание в шестнадцатеричной системе счисления
Заем единицы из старшего разряда |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Вычитание в восьмеричной системе счисления
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Заем единицы из старшего разряда
Пример
4. Вычтем
единицу из чисел 10
2
,
10
8
и 10
16
Вычтем
единицу из чисел 10
2
,
10
8
и 10
16
Пример 5. Вычтем единицу из чисел 100 2 , 100 8 и 100 16 .
Пример 6. Вычтем число 59,75 из числа 201,25.
Ответ: 201,25 10 — 59,75 10 = 141,5 10 = 10001101,1 2 = 215,4 8 = 8D,8 16 .
Проверка. Преобразуем полученные разности к десятичному виду:
10001101,1 2 = 2 7 + 2 3 + 2 2 + 2 0 + 2 -1 = 141,5;
215,4 8 = 2 . 8 2 + 1 . 8 1 + 5 . 8 0 + 4 . 8 -1 = 141,5;
8D,8 16 = 8 . 16 1 + D . 16 0 + 8 . 16 -1 = 141,5.
Примеры перевода чисел в различные системы счисления
Пример №1
Переведем число 12 из десятичной в двоичную систему счисления
Решение
Переведем число 12 10
в 2-ичную систему счисления, при помощи последовательного деления на 2, до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.
В результате будет получено число из остатков деления записанное справа налево.
| 12 | : | 2 | = | 6 | остаток: 0 |
| 6 | : | 2 | = | 3 | остаток: 0 |
| 3 | : | 2 | = | 1 | остаток: 1 |
| 1 | : | 2 | = | 0 | остаток: 1 |
12 10 = 1100 2
Пример №2
Переведем число 12.3 из десятичной в двоичную систему счисления
12.3 10 = 1100.010011001100110011001100110011 2
РешениеПереведем целую часть 12 числа 12.3 10 в 2-ичную систему счисления, при помощи последовательного деления на 2, до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.
| 12 | : | 2 | = | 6 | остаток: 0 |
| 6 | : | 2 | = | 3 | остаток: 0 |
| 3 | : | 2 | = | 1 | остаток: 1 |
| 1 | : | 2 | = | 0 | остаток: 1 |
12 10 = 1100 2
Переведем дробную часть 0. 3
числа 12.3 10 в 2-ичную систему счисления, при помощи последовательного умножения на 2, до тех пор, пока в дробной части произведения не получиться ноль или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.
3
числа 12.3 10 в 2-ичную систему счисления, при помощи последовательного умножения на 2, до тех пор, пока в дробной части произведения не получиться ноль или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.
| 0.3 | · | 2 | = | 0 .6 |
| 0.6 | · | 2 | = | 1 .2 |
| 0.2 | · | 2 | = | 0 .4 |
| 0.4 | · | 2 | = | 0 .8 |
| 0.8 | · | 2 | = | 1 .6 |
| 0.6 | · | 2 | = | 1 .2 |
| 0.2 | · | 2 | = | 0 .4 |
| 0.4 | · | 2 | = | 0
. 8 8
|
| 0.8 | · | 2 | = | 1 .6 |
| 0.6 | · | 2 | = | 1 .2 |
| 0.2 | · | 2 | = | 0 .4 |
| 0.4 | · | 2 | = | 0 .8 |
| 0.8 | · | 2 | = | 1 .6 |
| 0.6 | · | 2 | = | 1 .2 |
| 0.2 | · | 2 | = | 0 .4 |
| 0.4 | · | 2 | = | 0 .8 |
| 0.8 | · | 2 | = | 1 .6 |
| 0.6 | · | 2 | = | 1 .2 |
| 0.2 | · | 2 | = | 0 .4 |
| 0.4 | · | 2 | = | 0 .8 |
| 0.8 | · | 2 | = | 1 .6 |
| 0.6 | · | 2 | = | 1
. 2 2
|
| 0.2 | · | 2 | = | 0 .4 |
| 0.4 | · | 2 | = | 0 .8 |
| 0.8 | · | 2 | = | 1 .6 |
| 0.6 | · | 2 | = | 1 .2 |
| 0.2 | · | 2 | = | 0 .4 |
| 0.4 | · | 2 | = | 0 .8 |
| 0.8 | · | 2 | = | 1 .6 |
| 0.6 | · | 2 | = | 1 .2 |
0.3 10 = 0.010011001100110011001100110011 2
12.3 10 = 1100.010011001100110011001100110011 2
Пример №3
Переведем число 10011 из двоичной системы в десятичную систему счисления
Решение
Переведем число 10011 2 в десятичную систему счисления, для этого сначала запишем позицию каждой цифры в числе с права налево, начиная с нуля
Каждая позиция цифры будет степенью числа 2, так как система счисления 2-ичная.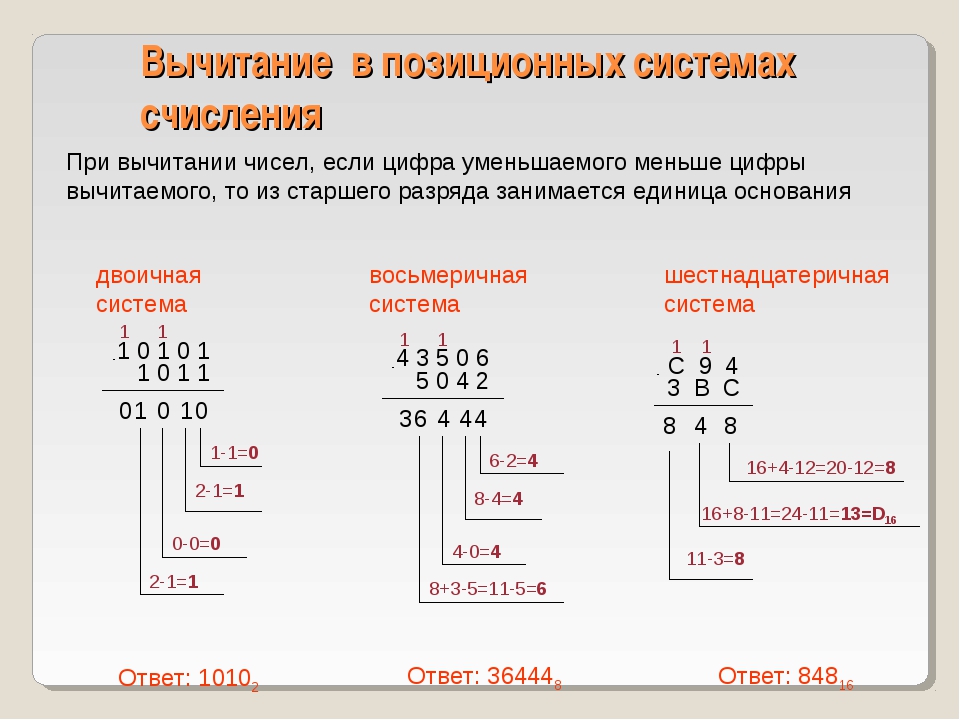 Необходимо последовательно умножить каждое число 10011 2 на 2 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Необходимо последовательно умножить каждое число 10011 2 на 2 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
10011 2 = 1 ⋅ 2 4 + 0 ⋅ 2 3 + 0 ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 19 10
Пример №4
Переведем число 11.101 из двоичной системы в десятичную систему счисления
11.101 2 = 3.625 10
РешениеПереведем число 11.101 2 в десятичную систему счисления, для этого сначала запишем позицию каждой цифры в числе
Каждая позиция цифры будет степенью числа 2, так как система счисления 2-ичная. Необходимо последовательно умножить каждое число 11.101 2 на 2 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
11.101 2 = 1 ⋅ 2 1 + 1 ⋅ 2 0 + 1 ⋅ 2 -1 + 0 ⋅ 2 -2 + 1 ⋅ 2 -3 = 3.625 10
Пример №5
Переведем число 1583 из десятичной системы в шестнадцатеричную систему счисления
1583 10 = 62F 16
РешениеПереведем число 1583 10
в 16-ичную систему счисления, при помощи последовательного деления на 16, до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.
В результате будет получено число из остатков деления записанное справа налево.
| 1583 | : | 16 | = | 98 | остаток: 15, 15 = F |
| 98 | : | 16 | = | 6 | остаток: 2 |
| 6 | : | 16 | = | 0 | остаток: 6 |
1583 10 = 62F 16
Пример №6
Переведем число 1583.56 из десятичной системы в шестнадцатеричную систему счисления
1583.56 10 = 62F.8F5C28F5C28F5C28F5C28F5C28F5C2 16
РешениеПереведем целую часть 1583 числа 1583.56 10 в 16-ичную систему счисления, при помощи последовательного деления на 16, до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.
| 1583 | : | 16 | = | 98 | остаток: 15, 15 = F |
| 98 | : | 16 | = | 6 | остаток: 2 |
| 6 | : | 16 | = | 0 | остаток: 6 |
1583 10 = 62F 16
Переведем дробную часть 0. 56
числа 1583.56 10 в 16-ичную систему счисления, при помощи последовательного умножения на 16, до тех пор, пока в дробной части произведения не получиться ноль или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.
56
числа 1583.56 10 в 16-ичную систему счисления, при помощи последовательного умножения на 16, до тех пор, пока в дробной части произведения не получиться ноль или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.
| 0.56 | · | 16 | = | 8 .96 |
| 0.96 | · | 16 | = | 15 .36, 15 = F |
| 0.36 | · | 16 | = | 5 .76 |
| 0.76 | · | 16 | = | 12 .16, 12 = C |
| 0.16 | · | 16 | = | 2 .56 |
| 0.56 | · | 16 | = | 8 .96 |
| 0.96 | · | 16 | = | 15 .36, 15 = F |
0. 36 36
| · | 16 | = | 5 .76 |
| 0.76 | · | 16 | = | 12 .16, 12 = C |
| 0.16 | · | 16 | = | 2 .56 |
| 0.56 | · | 16 | = | 8 .96 |
| 0.96 | · | 16 | = | 15 .36, 15 = F |
| 0.36 | · | 16 | = | 5 .76 |
| 0.76 | · | 16 | = | 12 .16, 12 = C |
| 0.16 | · | 16 | = | 2 .56 |
| 0.56 | · | 16 | = | 8 .96 |
| 0.96 | · | 16 | = | 15 .36, 15 = F |
| 0.36 | · | 16 | = | 5 .76 |
| 0.76 | · | 16 | = | 12 .16, 12 = C |
| 0.16 | · | 16 | = | 2
. 56 56
|
| 0.56 | · | 16 | = | 8 .96 |
| 0.96 | · | 16 | = | 15 .36, 15 = F |
| 0.36 | · | 16 | = | 5 .76 |
| 0.76 | · | 16 | = | 12 .16, 12 = C |
| 0.16 | · | 16 | = | 2 .56 |
| 0.56 | · | 16 | = | 8 .96 |
| 0.96 | · | 16 | = | 15 .36, 15 = F |
| 0.36 | · | 16 | = | 5 .76 |
| 0.76 | · | 16 | = | 12 .16, 12 = C |
| 0.16 | · | 16 | = | 2 .56 |
0.56 10 = 0.8F5C28F5C28F5C28F5C28F5C28F5C2 16
1583.56 10 = 62F.8F5C28F5C28F5C28F5C28F5C28F5C2 16
Пример №7
Переведем число A12DCF из шестнадцатеричной системы в десятичную систему счисления
A12DCF 16 = 10563023 10
РешениеПереведем число A12DCF 16 в десятичную систему счисления, для этого сначала запишем позицию каждой цифры в числе с права налево, начиная с нуля
Каждая позиция цифры будет степенью числа 16, так как система счисления 16-ичная. Необходимо последовательно умножить каждое число A12DCF 16 на 16 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Необходимо последовательно умножить каждое число A12DCF 16 на 16 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
2
Каждая позиция цифры будет степенью числа 16, так как система счисления 16-ичная. Необходимо последовательно умножить каждое число A12DCF.12A 16 на 16 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
A 16 = 10 10
D 16 = 13 10
C 16 = 12 10
F 16 = 15 10
A12DCF.12A 16 = 10 ⋅ 16 5 + 1 ⋅ 16 4 + 2 ⋅ 16 3 + 13 ⋅ 16 2 + 12 ⋅ 16 1 + 15 ⋅ 16 0 + 1 ⋅ 16 -1
Каждая позиция цифры будет степенью числа 2, так как система счисления 2-ичная.
 Необходимо последовательно умножить каждое число 1010100011 2 на 2 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.
Необходимо последовательно умножить каждое число 1010100011 2 на 2 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.1010100011 2 = 1 ⋅ 2 9 + 0 ⋅ 2 8 + 1 ⋅ 2 7 + 0 ⋅ 2 6 + 1 ⋅ 2 5 + 0 ⋅ 2 4 + 0 ⋅ 2 3 + 0 ⋅ 2 2 + 1 ⋅ 2 1 + 1 ⋅ 2 0 = 675 10
Переведем число 675 10 в 16-ичную систему счисления, при помощи последовательного деления на 16, до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.
| 675 | : | 16 | = | 42 | остаток: 3 |
| 42 | : | 16 | = | 2 | остаток: 10, 10 = A |
| 2 | : | 16 | = | 0 | остаток: 2 |
675 10 = 2A3 16
Системы счисления — презентация онлайн
Системы счисленияВашему вниманию представлены теоретический материал, примеры решения задач и
упражнения для тренировки по теме «Системы счисления».
 Некоторые упражнения и
Некоторые упражнения ирассуждения в тексте основываются на результатах выполнения предыдущих упражнений.
Поэтому для лучшего понимания и закрепления материала рекомендуется при прочтении
текста выполнять задания сразу.
Цифра – это письменный знак, изображающий число. Система счисления – это способ
записи чисел и сопоставления этим записям реальных значений.
В древнейшие времена числа обозначались прямолинейными пометками «палочками»:
одна палочка изображала единицу, две – двойку, … . Для изображения больших чисел этот
способ неудобен. Поэтому с течением времени были созданы знаки для бóльших чисел. У
некоторых народов (древнегреческая, славянская, армянская и древнегрузинская нумерация)
для изображения чисел использовались буквы алфавита. Для отличия цифр от букв над
цифрами писали черточки (у славян — «титло»):
= 1,
= 40,
= 200. Этот способ до сих
пор сохранился в римских цифрах.
В позднейшем своем виде римские цифры1 выглядят так:
I = 1, V = 5, X = 10, L = 50, C = 100, D = 500, M = 1000.

Все целые числа записываются с помощью повторения этих цифр. При этом, если бóльшая
цифра стоит перед меньшей, то они складываются; если меньшая цифра стоит перед
большей (в этом случае она не может повторяться), то меньшая вычитается из большей.
Одна и та же цифра ставится подряд не более трех раз.
Примеры:
2002 = M M I I, 1999 = M C M X C I X, 300 = C C C, 400 = C D.
Арифметические действия с такими числами производить очень неудобно, поэтому
римские цифры используются для нумерации томов, разделов и глав книг, обозначения
номера века или тысячелетия (XIX век, II тысячелетие до н. э.), порядкового номера монарха
(Карл V, Екатерина II) и т. п.
Системы счисления, устроенные таким образом, называют аддитивными.
Упражнение 1
А) Запишите в десятичной системе счисления числа XCI, XXIII, CDLXXII, MCMXIX.
Б) Запишите римскими цифрами числа 17, 48, 293, 965, 2010.
1
Подробнее о римских цифрах можно прочесть по ссылке http://ru.
 wikipedia.org/wiki/Римские_цифры
wikipedia.org/wiki/Римские_цифрыВ Древнем Вавилоне примерно за 40 веков до нашего времени создалась поместная
(позиционная) нумерация, то есть такой способ изображения чисел, при котором одна и та
же цифра может обозначать разные числа в зависимости от места, занимаемого этой цифрой.
Например, в числе 52 цифра 5 обозначает пять десятков: 50 = 5⋅10, а в числе 578 та же цифра
обозначает пять сотен: 500 = 5⋅102. Позиции, в которых располагаются цифры, называют
разрядами. Единица каждого разряда в десятичной системе имеет своё название: единицы,
десятки, сотни, тысячи, десятки тысяч, сотни тысяч, миллион и т.д., десятые, сотые,
тысячные, десятитысячные и т. д.
В недесятичной позиционной системе счисления для представления чисел выбираются
некоторые символы (цифры), а остальные числа получаются в результате каких-либо
операций над цифрами данной системы счисления. Количество цифр, используемых для
записи чисел, называется основанием системы счисления (это натуральное число).
 Заметим,
Заметим,что основание системы счисления равно числу единиц какого-либо разряда, объединяемых в
единицу более старшего разряда. Цифры в системе с основанием b > 0 принимают значения
от нуля до b – 1. Например, в десятичной системе счисления десять цифр: 0, 1, 2, …, 9; в
системе с основанием 2 имеем две цифры – ноль и единица, в системе с основанием 8 –
цифры: 0, 1, 2, 3, 4, 5, 6, 7. Если основание больше 10, то для обозначения цифр могут
использоваться буквы латинского алфавита.
Например, в шестнадцатеричной системе счисления:
Цифры в 16-ричной системе
0 1 2 3 4 5 6 7 8 9 A
B
C
D
E
F
Значения в десятичной системе 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Для того, чтобы указать, в какой системе счисления записано число, основание
системы счисления пишут в качестве нижнего индекса рядом с числом. Поскольку чаще
всего мы работаем с десятичной системой счисления, то основание 10 не пишем.
Упражнение 2
Выпишите цифры в тринадцатеричной системе счисления и их значения в десятичной
системе счисления
Любое число в позиционной системе счисления можно представить в виде суммы,
каждое слагаемое которой равно произведению цифры на единицу соответствующего ей
разряда.
 При этом единицу каждого разряда можно записать в виде степени какого-либо
При этом единицу каждого разряда можно записать в виде степени какого-либочисла. Мы привыкли к десятичной системе счисления, в ней числа представляются в виде:
α n α n −1 … α 2 α 1 α 0 , α −1 …α − k =
k
=αn·10n + αn–1·10n–1 + … + α2·102 + α1·10 + α0 + α −1·10−1 + …+ α −k·10− ,
где αn, αn–1, …, α2, α1, α0, α −1, …, α −k – цифры данного числа: α0 – число единиц, α1 –
число десятков, α2 – число сотен и т. д. Черта над записью (при буквенной записи)
используется для того, чтобы отличать записанные подряд цифры числа от произведения
переменных.
Например, разложение по степеням десяти имеет вид:
2390847,516 = 2·106 + 3·105 + 9·104 + 0·103 + 8·102 + 4·10 + 7·100 + 5·10-1 + 1·10-2 + 6·10-3
Аналогично в системе счисления с основанием b число будет представлено в виде:
α n α n −1 … α 2 α 1 α 0 , α −1 …α − k =
k
= αn·bn + αn–1·bn–1 + … + α2·b2 + α1·b1 + α0·b0 + α −1·b−1 + …+ α −k· b − .
Например, разложение числа в восьмеричной системе записывается по степеням числа 8:
4273,518 = 4·83 + 2·82 + 7·8 + 3·80 + 5·8-1 + 1·8-2
Упражнение 3
Запишите числа в виде разложения по степеням основания системы счисления:
А) 101001110,01012; 2548; 2D716
Перевод чисел из системы с основанием b в десятичную
Правило 1.
 При переводе чисел из системы счисления с основанием b в десятичную систему
При переводе чисел из системы счисления с основанием b в десятичную системусчисления необходимо пронумеровать разряды целой части справа налево, начиная с
нулевого, и в дробной части, начиная с разряда сразу после запятой слева направо
(начальный номер -1). Затем вычислить сумму произведений соответствующих значений
разрядов на основание системы счисления в степени, равной номеру разряда.
Например, переведём в десятичную систему двоичное число
5 4 3 2 1 0 −1 −2 −3
110101, 0 1 1 2 = 1 ⋅ 2 5 + 1 ⋅ 2 4 + 0 ⋅ 2 3 + 1 ⋅ 2 2 + 0 ⋅ 21 + 1 ⋅ 2 0 + 0 ⋅ 2 −1 + 1 ⋅ 2 − 2 + 1 ⋅ 2 −3 =
1 1
3
= 32 + 16 + 4 + 1 + + = 53 = 53,375
4 8
8
Переведём в десятичную систему шестнадцатеричное число
2 1 0 −1 −2
6 А 9, С 1 16 = 616 ⋅ 16 2 + А16 ⋅ 161 + 916 ⋅ 16 0 + С16 ⋅ 16 −1 + 116 ⋅ 16 − 2 =
= 6 ⋅ 16 2 + 10 ⋅ 161 + 9 ⋅ 16 0 + 12 ⋅ 16 −1 + 1 ⋅ 16 − 2 =
12
1
193
= 1536 + 160 + 9 + +
= 1705
= 1705,75390625
16 256
256
Упражнение 4
Переведите в десятичную систему числа 101001110,01012; 2548; 2D716
Перевод целых чисел из десятичной системы в систему с основанием b
Правило 2.
 Для перевода целого числа в систему с основанием b нужно разделить это число
Для перевода целого числа в систему с основанием b нужно разделить это числона b и запомнить остаток от деления. Полученное частное вновь делится на b, а остаток
запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю.
Остатки от деления на b выписываются в порядке, обратном их получению.
Поясним алгоритм перевода на примере перевода десятичного числа 20 в двоичную
систему. Разделим число 20 на 2 столбиком. Деление будем производить до тех пор, пока
целая часть от деления не станет равной нулю.
Если внимательно посмотреть на процесс деления:
20 = 2·10 + 0 = 2·(2·5 + 0) + 0 = 2·(2·[2·2 +1]+ 0) + 0 = 2·(2·[2·{2·1+0} +1]+ 0) + 0 =
2·(2·[2·{2·(2·0 + 1)+0} +1] + 0) + 0 = 25·0 + 24·1 + 23·0 + 22·1 + 2·0 + 0 = 101002 ,
то можно заметить, что остатки от деления образуют последовательность 00101 – т. е. число
10100, записанное в обратном порядке. Таким образом, чтобы записать число в двоичной
системе, нужно записать остатки, получающиеся в процессе деления, только в обратном
порядке.
 Аналогично поступают и в случае системы с другим основанием.
Аналогично поступают и в случае системы с другим основанием.20 = 81·2 + 80·4 = 248
20 = 161·1 + 160·4 = 1416
Упражнение 5
Переведите
десятичное
число
973
в
двоичную,
четверичную,
восьмеричную
и
шестнадцатеричную системы
Перевод чисел, меньших единицы, из десятичной системы в систему с основанием b
Правило 3. Для перевода числа, меньшего единицы, из десятичной системы в систему с
основанием b нужно:
1) умножить дробную часть числа на b, после чего целая часть запоминается;
2) отбросить целую часть числа после умножения; если дробная часть равна нулю, то
перейти к шагу 3), иначе – к шагу 1)
3) выписать целые части после запятой в порядке их получения.
Примеры:
1. 0,09375 переводим в двоичную систему:
0,09375 ⋅ 2 = 0,1875; 0,1875 ⋅ 2 = 0,375; 0,375 ⋅ 2 = 0,75; 0,75 ⋅ 2 = 1,5; 0,5 ⋅ 2 = 1,0.
Получаем ответ: 0,0937510 = 0,000112.
2. 0,0732421875 переводим в 16-ричную систему:
0,0732421875 ⋅ 16 = 1,171875; 0,171875 ⋅ 16 = 2,75;
0,75 ⋅ 16 = 12 (в 16-ричной системе это значение шестнадцатеричной цифры C).

Получаем ответ: 0, 073242187510 = 0,12С16.
3. Переведём число 0,3125 в двоичную, четверичную, восьмеричную и шестнадцатеричную
системы. Заметим, что для сокращения записи процесс умножения удобно записывать в
виде следующей схемы:
Умножение производится для числа, стоящего справа от вертикальной черты (то есть с
отброшенной целой частью), а целая часть, получающаяся в результате умножения,
записывается слева от вертикальной черты и представляет собой очередную цифру числа
в новой системе счисления.
0,3125 = 0,01012 = 0,114 = 0,248 = 0,516
Заметим, что результатом может быть как конечная, так и бесконечная (возможно,
периодическая) дробь в системе счисления с основанием b. Если период выделить не
удается, то приходится обрывать умножение на каком-либо шаге и довольствоваться
приближенной записью исходного числа в системе с основанием b.
Пример 4.
Переведем в двоичную, восьмеричную и шестнадцатеричную системы число 0,26.

Заметим, что в дробной части каждый раз получается новое число, и процесс
умножения может продолжаться довольно долго. Поэтому мы обрываем процесс умножения
на некотором шаге и получаем приближённые значения: 0,26 ≈ 0,01000012, 0,26 ≈ 0,205078.
В процессе умножения на 16 замечаем, что после умножения 0,76 на 16 получили 12,16,
а после отбрасывания целой части нужно будет на 16 умножать число 0,16, которое мы уже
умножали выше. Значит, далее процесс умножения будет повторять уже пройденные шаги,
то есть мы имеем бесконечную периодическую дробь. При записи ответа десятичные
значения 15 и 12 заменяем на шестнадцатеричные цифры F и C. В результате получаем
0,26 = 0,4(28F5C)16.
Упражнение 6
Переведите десятичное число 0,8125 в двоичную, четверичную, восьмеричную и
шестнадцатеричную системы.
Упражнение 7
Переведите
десятичное
число 0,92
в
двоичную,
четверичную,
шестнадцатеричную системы (получить пять знаков после запятой).

восьмеричную
и
Перевод чисел с целой и дробной частью
из десятичной системы в систему с основанием b
Правило 4. Для перевода числа с целой и дробной частью из десятичной системы в систему с
основанием b нужно перевести отдельно целую часть по правилу 2 и отдельно дробную
часть по правилу 3, а результаты сложить.
Например, переведём число 20,3125 в двоичную систему. Выше мы уже перевели отдельно
целую 20 = 101002 и дробную часть 0,3125 = 0,01012. Следовательно, 20,3125 = 10100,01012.
Упражнение 8
Переведите десятичное число 813,6875 в двоичную, четверичную, восьмеричную и
шестнадцатеричную системы.
Арифметические действия в недесятичных позиционных системах счисления
Арифметические действия над числами в любой позиционной системе счисления
производятся по тем же правилам, что и в десятичной системе. При этом нужно только
пользоваться теми таблицами сложения и умножения, которые соответствуют данному
основанию b системы счисления.

Например, таблицы сложения и умножения в двоичной системе имеют вид:
Таблица сложения
Таблица умножения
+ 0 1
0 0 1
1 1 10
× 0 1
0 0 0
1 0 1
Поясним, как получается 12+12=102. Напомним, что основание системы счисления
равно числу единиц какого-либо разряда, объединяемых в единицу более старшего разряда.
В нашем случае мы складываем как раз количество единиц, равное основанию системы
счисления, значит, получаем единицу следующего разряда, которая записывается как 102.
Составим таблицы сложения и умножения в четверичной системе:
Таблица сложения
+
0
1
2
3
0 1 2 3
0 1 2 3
1 2 3 10
2 3 10 11
3 10 11 12
Поясним, как заполняются эти таблицы.
Таблица умножения
×
0
1
2
3
0
0
0
0
0
1 2 3
0 0 0
1 2 3
2 10 12
3 12 21
Прибавление нуля к некоторому числу всегда дает это число. Прибавление единицы к
числу x равносильно переходу к числу, следующему за x.
 За единицей в четверичной
За единицей в четверичнойсистеме следует число 24, затем 34, а добавление к последнему ещё одной единицы дает
четыре единицы, которые в системе с основанием 4 объединяются в единицу следующего
разряда, то есть 104. Заметим, что прибавление двойки равносильно прибавлению единицы, а
затем ещё одной единицы, то есть третья строка таблицы сложения получается
прибавлением единицы к числам в предыдущей строке. Аналогично четвертая строка
получается прибавлением единицы к числам из предыдущей строки.
Умножение на ноль всегда дает ноль, а умножение числа на единицу дает само это
число. Умножение числа x на два означает, что нужно прибавить это число к самому себе,
поэтому третья строка (и третий столбец) таблицы умножения совпадает с диагональю
таблицы сложения. Заметим, что осталось заполнить всего одну ячейку таблицы – результат
умножения 34 на 34. Умножение числа x на три равносильно тому, что к результату
умножения на два нужно прибавить x.
 Согласно таблице умножения 34×24=124.
Согласно таблице умножения 34×24=124.Следовательно, нам нужно к 124 прибавить 34. По таблице сложения 24+34=114, откуда
124+34=104+24+34=104+114=214.
Упражнение 9
Составьте таблицы сложения и умножения для семеричной системы.
Сложим два числа в двоичной системе. Запишем их столбиком друг под
другом, и будем складывать по отдельности числа в каждом разряде, начиная с
правого. В крайнем правом разряде складываем две единицы, получаем 102, ноль
пишем в соответствующем разряде, а единица переносится в следующий разряд, что на
рисунке отмечено точкой над вторым разрядом справа. Аналогично рассуждаем в
следующих разрядах. В последнем (крайнем левом) разряде мы складываем две единицы и
получаем 102, но поскольку произошёл перенос из соседнего разряда, то добавляем ещё
единицу и получаем 112, то есть записываем единицу в соответствующий разряд и единицу
переносим в следующий. Таким образом, 1101012 + 1011012 = 11000102. Для проверки
переведём слагаемые и результат в десятичную систему: 53 + 45 = 98.

Аналогично производится умножение: 11012 · 10112 = 100011112, проверка: 13 · 11 = 14.
Аналогично выполняются действия в системах с другим основанием.
Например, сложим два семеричных числа 5057 и 347. Запишем числа в столбик и
будем проводить сложение поразрядно. В младшем разряде нам нужно сложить 57
и 47. Если мы добавим 27 к 57, то получим единицу следующего разряда, то есть 107.
Складывая 47 и 57, мы добавляем ещё 27 к 107 и получаем 127. Пишем две единицы в
младший разряд результата, а единица переносится в следующий разряд. В следующем
разряде нужно прибавить запомненную единицу к 37, а в последнем разряде остаётся
переписать 57.
Рассмотрим теперь пример умножения семеричных чисел 2367 и 27. По
таблице умножения в семеричной системе 67×27=157, пять пишем в последний
разряд результата, а единицу переносим в следующий разряд. Далее 37×27=67, и
прибавляем единицу, перенесённую из младшего разряда, получаем 107, то есть ноль пишем,
а единицу переносим в соседний разряд.
 Наконец, 27×27=47, и прибавляем единицу,
Наконец, 27×27=47, и прибавляем единицу,перенесённую из предыдущего разряда, получаем 57. Таким образом, 2367×27=5057.
5
0 1,
2, 3
4
6
42
0
+1
6
+3
33
4
2
1
2
3
21
0
3
+1
15
правому краю. Если числа содержат дробную часть, то
5
умножение ведём, не обращая внимания на запятые, а в
×
+4
2
1
0
4
13
0
2
+1
11
3
0
3
1
5
5
5
+1
6
+1
+1
1
7
7
Поясним процесс умножения многозначных чисел.
Как и в десятичной системе при умножении в столбик
числа записываем друг под другом, выравнивая по
результате запятой отделим столько разрядов, сколько
10
составляют в сумме количества разрядов после запятой в
3
1 5 5 6, 0 0 3
7
множителях.
Для наглядности промежуточные результаты будем записывать подробно. Перемножим
числа 501,47 и 2,367.
 По таблице умножения в семеричной системе 47×67=337, 17×67=67,
По таблице умножения в семеричной системе 47×67=337, 17×67=67,07×67=07, 57×67=427. Эти числа записаны мелким синим шрифтом в первой строке после
черты, отделяющей сомножители от промежуточных вычислений. Теперь записываем
результат умножения на 67. Заметим, что в последнем разряде получилось двузначное число,
значит, младший разряд этого числа будет записан в этом же разряде, а старший даст
перенос в следующий разряд. Отметим это во второй строке (также мелким синим шрифтом)
как «+3» в том разряде, куда произошёл перенос. Во втором разряде справа 67 + 37 =127, то
есть две единицы в текущем разряде и одну единицу переносим в следующий разряд. В
следующем разряде 07 + 17 = 17, и в последнем разряде два пишем, а 4 переносим в
следующий разряд. Итак, получили результат умножения на цифру 6: 421237. Аналогично
рассуждаем при умножении на другие цифры второго сомножителя. Осталось сложить
результаты умножения на отдельные цифры. В последнем разряде имеем только число 3, во
втором разряде справа 27 + 57 = 107, значит, ноль пишем в этом разряде а единицу переносим
в следующий (отмечая это как «+1» в третьем столбце справа).
 В третьем справа разряде
В третьем справа разряде17+47+17=67, что отмечено в верхней строке результата, да ещё нужно прибавить единицу,
перешедшую из предыдущего разряда, то есть снова имеем 107. Далее (27+07+37)+17=67 и в
следующий разряд ничего переносить не надо. В следующих столбиках 47+17+07=57, 27+37=57
и единица в крайнем левом разряде. В первом сомножителе была одна цифра после запятой,
во втором – две, значит, в результате будет 1+2=3 цифры после запятой. Итак, получили
501,47 × 2,367 = 1556,0037.
Упражнение 10
Выполните действия:
А) 10001111102 + 10110001012 ; 620,28 + 1453,38 ; 348,116 + 2D4,416.
Б) 11001102×1100102 ; 177,48 × 23,48; в) 10,616 × 2A,816 .
В*) 11000010102 – 100000112 ; 1520,58 – 403,28; 368,A16 – 239,D16.
Г*) 1001110002 : 11012 ; 43438 : 318; A3B16 : 1B16 .
Перевод чисел из системы с основанием s в систему с основанием r
Для перевода числа из системы с основанием s в систему с основанием r требуется
записать число в виде суммы
∑α s
i
i
, где цифры αi и s выражены в новой r-системе, и
i
выполнить соответствующие арифметические действия по правилам r-системы.

Например, переведем число 21045 в семеричную систему счисления. Заметим, что
промежуточные действия нами выполнены выше.
21045 = 27⋅ 537 +17⋅ 5 72 +07⋅ 517 +47⋅ 5 07 =27⋅2367+17⋅347 +47 =5057+347 +47 =5467
Поскольку выполнение действий в системе счисления с основанием, отличным от 10,
производить затруднительно, то обычно используют следующее правило:
Правило 5. Для перевода числа из одной системы в другую используют десятичную систему
в качестве промежуточной (переводят число сначала из системы с основанием s в
десятичную систему по правилу 1, а потом из десятичной – в систему с основанием r по
правилу 4). Если основания старой и новой систем счисления являются степенями числа 2,
то в качестве промежуточной используют двоичную систему (правила 6 и 7).
Поясним это правило на числе 21045 из рассмотренного выше примера. Переведем это
число сначала в десятичную систему:
21045 = 2⋅53+1⋅52+0⋅5+4⋅50 = 2⋅125 + 1⋅25 + 4 = 279
Теперь переведем это число из десятичной системы в семеричную, получим 279 = 5467.
Таким образом, 21045 = 279 = 5467. Получили тот же самый результат, что и выше.
Упражнение 11
Переведите :
А) число 1002123 в пятеричную и семеричную системы,
Б) число 20145 в троичную и семеричную системы,
В) число 5467 в троичную и пятеричную системы.
Перевод чисел из системы с основанием 2m в систему с основанием 2n
В системах, основаниями которых являются степени числа 2, процесс перевода
упрощается, если в качестве промежуточной системы используется двоичная. Прежде, чем
сформулировать правила перевода чисел, составим таблицу, в которой выпишем
представление чисел от нуля до 16 в системах, основаниями которых являются степени
двойки. Эту таблицу рекомендуем выучить.
основание
4
0
0
1
1
10
2
11
3
100
10
101
11
110
12
111
13
1000
20
1001
21
1010
22
1011
23
1100
30
1101
31
1110
32
1111
33
10
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
2
16
10000
100
8
0
1
2
3
4
5
6
7
10
11
12
13
14
15
16
17
16
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
20
10
Заметим, что цифры в четверичной системе могут быть представлены двоичным кодом,
состоящим не более, чем из двух цифр; цифры в восьмеричной системе – кодами не более,
чем из трёх двоичных цифр; цифры в шестнадцатеричной системе – кодами не более, чем из
четырёх цифр.
 Если к двоичным кодам приписать начальные нули, то можем утверждать,
Если к двоичным кодам приписать начальные нули, то можем утверждать,что четверичные цифры записываются двузначными кодами, восьмеричные – трёхзначными,
а шестнадцатеричные – четырёхзначными. Длина кодов не случайна, а связана с тем, что
4=22, 8=23, 16=24, то есть длина кода равна показателю степени двойки.
Заметим также, что код двузначных чисел в 4-ой, 8-ой и 16-ой системах может быть
получен, если записать рядом коды каждой цифры (с приписанными начальными нулями).
Например, 234 = 10 112, 158 = 001 1012, 1016 = 0001 00002. Эта закономерность позволяет
сформулировать правила перевода чисел в системах, основания которых являются степенями
двойки.
Правило 6. Для перевода числа из системы с основанием 2m в двоичную достаточно
представить в двоичной записи каждую цифру числа (дописывая при необходимости нули
так, чтобы каждая цифра в исходной системе была представлена m двоичными цифрами).
Примеры
Переведём число 424538 из восьмеричной и число 5D16 из шестнадцатеричной системы
в двоичную.

Поскольку 8=23, то каждую цифру первого числа нужно представить трёхзначным
кодом:
424538 = 100 010 100 101 0112.
Поскольку 16=24, то каждую цифру второго числа нужно представить четырёхзначным
кодом:
5D16 = 0101 11012.
Во втором примере начальный ноль записан для наглядности, в ответе его писать не нужно.
Итак, получили 424538 = 1000101001010112 ; 5D16 = 10111012.
Правило 7. Для перевода двоичного числа в систему с основанием 2n достаточно разбить
цифры числа на группы по n цифр (отсчитывая от запятой влево и, если есть дробная часть,
вправо) и осуществить перевод каждой группы отдельно.
Примеры
Переведём
число
10101000101011,11012
в
четверичную,
восьмеричную
и
шестнадцатеричную системы.
Для перевода в четверичную систему (4=22) разобьём цифры числа на группы по
2 цифры (отсчитывая от запятой влево и вправо) и осуществим перевод каждой группы
отдельно:
10 10 10 00 10 10 11,11 012 = 2220223,314
Для перевода в восьмеричную систему (8=23) разобьём цифры числа на группы по
3 цифры (отсчитывая от запятой влево и вправо).
 При этом требуется дописать начальный
При этом требуется дописать начальныйноль в крайней левой группе и два нуля в конце числа. После этого осуществим перевод
каждой группы отдельно:
010 101 000 101 011,110 1002 = 25053,648
Для перевода в шестнадцатеричную систему (16=24) разобьём цифры числа на группы
по 4 цифры (отсчитывая от запятой влево и вправо), дописав начальные нули в крайней
левой группе. После этого осуществим перевод каждой группы отдельно:
0010 1010 0010 1011,11012 = 2A2B, D 16
Упражнение 12
Переведите:
А) 2131220304 в восьмеричную и шестнадцатеричную системы,
Б) число 2F61B16 в четверичную и восьмеричную системы.
Перевод чисел с периодической дробной частью
Переведем число 0,63(17)8 в 4-ную систему счисления.
Переведем сначала число из восьмеричной системы в двоичную. Представляем каждую
3
цифру двоичным кодом (т.к. 8=2 , то группы должны содержать по три цифры):
0,63(17)8 = 0,110 011 (001 111)2
2
Т. к. 4=2 , то отделяем в двоичной записи группы по две цифры (при этом период
повторим несколько раз):
0,63(17)8 = 0, 11 00 11 00 11 11 00 11 11 00 11 11 … 2
Переводим каждую группу из двух двоичных цифр в четверичную систему:
0,63(17)8 = 0, 3 0 3 0 3 3 0 3 3 0 3 3 … 4
Выделяем в полученном числе период.
 Заметим, что повторяются три цифры – две
Заметим, что повторяются три цифры – дветройки и ноль, то есть периодом может быть либо последовательность 330, либо 303, либо
033. Для того, чтобы найти ту цифру, с которой начинается период, будем группировать по
три цифры и сдвигаться на цифру от запятой вправо, если последовательности, стоящие в
соседних скобках, окажутся не одинаковыми:
0,63(17)8 = 0, ( 3 0 3 ) ( 0 3 3 ) 0 3 3 0 3 3 … 4
0,63(17)8 = 0, 3 ( 0 3 0 ) ( 3 3 0 ) 3 3 0 3 3 … 4
0,63(17)8 = 0, 3 0 ( 3 0 3 ) ( 3 0 3 ) ( 3 0 3 ) 3 … 4
Таким образом, 0,63(17)8 = 0,30(303)4 .
Упражнение 13
Перевести число 0,11(12)4 в двоичную, восьмеричную и шестнадцатеричную системы.
Решения и ответы к упражнениям
Упражнение 1
А) 91, 23, 472, 1919
Б) XVII, XLVIII, CCXCIII, CMLXV, MMX
Упражнение 2
Цифры в 13-ричной системе
0 1 2 3 4 5 6 7 8 9 A
B
C
Значения в десятичной системе 0 1 2 3 4 5 6 7 8 9 10 11 12
Упражнение 3
а) 101001110,01012 = 1·2-4 + 0·2-3 + 1·2-2 + 0·2-1 + 0·20 + 1·2 + 1·22 + 1·23 + 0·24 + 0·25 +
+ 1·26 + 0·27 + 1·28;
б) 2548 = 4·80 + 5·81 + 2·82;
в) 2D716 = 7⋅160 + D·161 + 2·162
Упражнение 4
101001110,01012 = 1·2-4 + 0·2-3 + 1·2-2 + 0·2-1 + 0·20 + 1·2 + 1·22 + 1·23 + 0·24 + 0·25 +
+ 1·26 + 0·27 + 1·28 = 0,0625 + 0,25 + 2 + 4 + 8 + 64 + 512 = 588,3125
2548 = 4·80 + 5·81 + 2·82 = 4 + 40 + 128 = 172
2D716 = 716⋅160 + D16·161 + 216·162 = 7 + 13·16 + 2·256 = 727
Упражнение 5
973
2
972 486
2
1 486 243
2
0 242 121 2
1 120 60
1 60
0
973 = 11110011012
2
30
30
0
2
15
14
1
2
7
6
1
2
3
2
1
2
1
0
1
2
0
973 = 330314
973 = 17158
Упражнение 6
0,8125 = 0,11012 = 0,314 = 0,648 = 0,D16
Упражнение 7
0,92 ≈ 0,111012, 0,92 ≈ 0,322324, 0,92 ≈ 0,727028, 0,92 = 0,(EB851)16
Упражнение 8
813,6875 = 1100101101,10112 = 30231,234 = 1455,548 = 32D,B16.

973 = 3CD16
Упражнение 9
0
0
1
2
3
4
5
6
+
0
1
2
3
4
5
6
1
1
2
3
4
5
6
10
2
2
3
4
5
6
10
11
3
3
4
5
6
10
11
12
4
4
5
6
10
11
12
13
5
5
6
10
11
12
13
14
×
0
1
2
3
4
5
6
6
6
10
11
12
13
14
15
0
0
0
0
0
0
0
0
1
0
1
2
3
4
5
6
Упражнение 10
A) 10000000112; 2273,58; 61C,516
перенос
1
0
1
1
1
1
1
1 0 0 0 1 1
+ 1 0 1 1 0 0
1
1 1 1 0
0 1 0 1
1 0 1 0 0 0 0 0 0 1 1
перенос
2
2
2
1
1
1 4 5 3 , 3
+
6 2 0 , 2
2 2 7 3 , 5
3 4
+ 2 D
8
8
8
4
, 1
, 4
6 1 C , 5
8
Б) 10011111011002; 4666,28; 2B7,F16
×
перенос
0
0 0
1 1 0
1 1 0 0
1
0
0
0
1
1
1
1
1 1
1
0 0
1 0
0 0
0 0
1 1
1 0
0
1
0
0
0
0
0
0
0
0
1
0
0
1
0
0
1
0
1 0
1 0
0 0
0
1 0 0 1 1 1 1 1 0 1 1 0 0
2
2
2
2
16
16
16
2
0
2
4
6
11
13
15
3
0
3
6
12
15
21
24
4
0
4
11
15
22
26
33
5
0
5
13
21
26
34
42
6
0
6
15
24
33
42
51
1
7 7,
2 3,
×
34
+3
4
+3
3
+2
2
+1
34
+2
20
0
7
7
6
25
+2
25
+1
14
4
5
7
6
16
+1
16
+1
10
3
7
7
0
3
+1
14
+2
25
+1
15
+1
4
4
12
8
×
8
0
4 6 6 6, 2 0
1 0,
2 A,
6
8
8
0
+3
30
0
8
3
A
0
+3
3C
C
A
3
2
0
C
2
0
C
2
A
+1
17
2 B 7, F 0
8
16
16
16
В*) 10100001112 ; 1356,18 ; 12E,D16
1 1
перенос
0 0 0 0 1
-1
+10
–
1 0
1 5 2
0
1
0
2
-1
+10-1
+10-1
+10
1 0 0 0 0
0
1
1
2
1 0 0 0 0
1
1
1
2
, 5
8
3 6
3
, 2
8
– 2 3
9
,
D
16
1 1 1 5
, 3
8
1 2
E
, D
16
перенос
-1
–
4 0
0
+10
-1
8
,
+10-1
A
16
+10
Г*) 110002 ; 1338; 6116 .

1 0 0 1 1 1 0 0 02 1 1
1 1 0 1
1 1
0 12
4 3 4 38 3 18
0 0 02
3 1
1 1 0 1
1 2 4
1 1 0 1
1 1 3
0
1 3
1 1 3
1 1 3
A
3 B16
1 B16
A
2
6 116
1 B
1 B
0
0
38
Упражнение 11
А) 1010103 = 273 = 20435 = 5407,
Б) 40225 = 254 = 2002223 = 5127,
В) 5467 = 279 = 1011003 = 21045.
Упражнение 12
А) 2131220304 = 1001110110100011002
100 111 011 010 001 1002 = 4732148 ; 0010 0111 0110 1000 11002 = 2768C16
Б) 2F61B16 = 001011110110000110112
10 11 11 01 10 00 01 10 112 = 2331201234 ; 101 111 011 000 011 0112 = 5730338.
Упражнение 13
0,11(12)4 = 0, 01 01 01 10 01 10 01 10 01 10 … 2
0, 01010110011001100110 … 2 = 0,010(0110)2
0, 010 101 100 110 011 001 100 110 … 2 = 0,25(4631)8
0, 0101 0110 0110 0110 0110 … 2 = 0,5(6)16
Деление в шестнадцатеричной системе счисления онлайн калькулятор. Арифметические операции с числами в позиционных системах счисления
Назначение сервиса . Онлайн-калькулятор предназначен для сложения двоичных чисел в прямом, обратном и дополнительном кодах.
Онлайн-калькулятор предназначен для сложения двоичных чисел в прямом, обратном и дополнительном кодах.
Вместе с этим калькулятором также используют следующие:
Перевод чисел в двоичную, шестнадцатеричную, десятичную, восьмеричную системы счисления
Умножение двоичных чисел
Формат представления чисел с плавающей запятой
Пример №1
. Представить число 133,54 в форме числа с плавающей точкой.
Решение
. Представим число 133.54 в нормализованном экспоненциальном виде:
1.3354*10 2 = 1.3354*exp 10 2
Число 1.3354*exp 10 2 состоит из двух частей: мантиссы M=1.3354 и экспоненты exp 10 =2
Если мантисса находится в диапазоне 1 ≤ M Представление числа в денормализованном экспоненциальном виде
.
Если мантисса находится в диапазоне 0,1 ≤ M Представим число в денормализованном экспоненциальном виде: 0.13354*exp 10 3
Пример №2
. Представить двоичное число 101.10 2 в нормализованном виде, записать в 32-битом стандарте IEEE754.
Таблица истинности
Вычисление пределов
Арифметика в двоичной системе счисления
Арифметические действия в двоичной системе выполняются так же, как и в десятичной. Но, если в десятичной системе счисления перенос и заём осуществляется по десять единиц, то в двоичной — по две единицы. В таблице представлены правила сложения и вычитания в двоичной системе счисления.
Но, если в десятичной системе счисления перенос и заём осуществляется по десять единиц, то в двоичной — по две единицы. В таблице представлены правила сложения и вычитания в двоичной системе счисления.
- При сложении в двоичной системе системе счисления двух единиц в данном разряде будет 0 и появится перенос единицы в старший разряд.
- При вычитании из нуля единицы производится заём единицы из старшего разряда, где есть 1 . Единица, занятая в этом разряде, даёт две единицы в разряде, где вычисляется действие, а также по единице, во всех промежуточных разрядах.
Сложение чисел с учетом их знаков на машине представляет собой последовательность следующих действий:
- преобразование исходных чисел в указанный код;
- поразрядное сложение кодов;
- анализ полученного результата.

При выполнении операции в дополнительном (модифицированном дополнительном) коде если в результате сложения в знаковом разряде возникает единица переноса, она отбрасывается.
Операция вычитания в ЭВМ выполняется через сложение по правилу: Х-У=Х+(-У). Дальнейшие действия выполняются также как и для операции сложения.
Пример №1
.
Дано: х=0,110001; y= -0,001001, сложить в обратном модифицированном коде.
Дано: х=0,101001; y= -0,001101, сложить в дополнительном модифицированном коде.
Пример №2
. Решить примеры на вычитание двоичных чисел, используя метод дополнения до 1 и циклического переноса.
а) 11 — 10.
Решение
.
Представим числа 11 2 и -10 2 в обратном коде.
Двоичное число 0000011 имеет обратный код 0,0000011
Сложим числа 00000011 и 11111101
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | |||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | ||||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 |
В 2-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 3-й разряд.
Поэтому записываем 0, а 1 переносим на 3-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | |||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | ||||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | |||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Возник перенос из знакового разряда.
 Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).
Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Результат сложения: 00000001. Переведем в десятичное представление . Для перевода целой части необходимо умножить разряд числа на соответствующую ему степень разряда.
00000001 = 2 7 *0 + 2 6 *0 + 2 5 *0 + 2 4 *0 + 2 3 *0 + 2 2 *0 + 2 1 *0 + 2 0 *1 = 0 + 0 + 0 + 0 + 0 + 0 + 0 + 1 = 1
Результат сложения (в десятичном представлении): 1
б) 111-010
Представим числа 111 2 и -010 2 в обратном коде.
Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Двоичное число 0000111 имеет обратный код 0,0000111
Двоичное число 0000010 имеет обратный код 1,1111101
Сложим числа 00000111 и 11111101
В 0-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 1-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | |||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 |
В 1-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 2-й разряд.
Поэтому записываем 0, а 1 переносим на 2-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | ||||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 |
В 2-ом разряде возникло переполнение (1 + 1 + 1 = 11). Поэтому записываем 1, а 1 переносим на 3-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | |||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 |
В 3-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 4-й разряд.
Поэтому записываем 0, а 1 переносим на 4-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | ||||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 0 |
В 4-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 5-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | |||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 |
В 5-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 6-й разряд.
Поэтому записываем 0, а 1 переносим на 6-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | ||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 |
В 6-ом разряде возникло переполнение (1 + 1 = 10). Поэтому записываем 0, а 1 переносим на 7-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 |
В 7-ом разряде возникло переполнение (1 + 1 = 10).
 Поэтому записываем 0, а 1 переносим на 8-й разряд.
Поэтому записываем 0, а 1 переносим на 8-й разряд.
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
Возник перенос из знакового разряда.
 Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).
Добавим его (т.е. 1) к полученному числу (тем самым осуществляя процедуру циклического переноса).
В итоге получаем:
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
Результат сложения: 00000101
Получили число 00000101. Для перевода целой части необходимо умножить разряд числа на соответствующую ему степень разряда.
00000101 = 2 7 *0 + 2 6 *0 + 2 5 *0 + 2 4 *0 + 2 3 *0 + 2 2 *1 + 2 1 *0 + 2 0 *1 = 0 + 0 + 0 + 0 + 0 + 4 + 0 + 1 = 5
Результат сложения (в десятичном представлении): 5
Сложение двоичных вещественных чисел с плавающей запятой
В компьютере любое число может быть представлено в формате с плавающей точкой. Формат с плавающей точкой показан на рисунке:
Формат с плавающей точкой показан на рисунке:
Например, число 10101 в формате с плавающей точкой можно записать так:
В компьютерах используется нормализованная форма записи числа, в которой положение запятой всегда задается перед значащей цифрой мантиссы, т.е. выполняется условие:
b -1 ≤|M|Нормализованное число —
это число, у которого после запятой идет значащая цифра (т.е. 1 в двоичной системе счисления). Пример нормализации:
0,00101*2 100 =0,101*2 10
111,1001*2 10 =0,111001*2 101
0,01101*2 -11 =0,1101*2 -100
11,1011*2 -101 =0,11011*2 -11
При сложении чисел с плавающей точкой выравнивание порядков выполняют в сторону большего порядка:
Алгоритм сложения чисел с плавающей точкой:
- Выравнивание порядков;
- Сложение мантисс в дополнительном модифицированном коде;
- Нормализация результата.
Пример №4
.
A=0,1011*2 10 , B=0,0001*2 11
1. Выравнивание порядков;
A=0,01011*2 11 , B=0,0001*2 11
2. Сложение мантисс в дополнительном модифицированном коде;
Сложение мантисс в дополнительном модифицированном коде;
MA доп.мод. =00,01011
MB доп.мод. =00,0001
00,01011
+ 00,00010
=
00,01101
A+B=0,01101*2 11
3. Нормализация результата.
A+B=0,1101*2 10
Пример №3 . Записать десятичное число в двоично-десятичной системе счисления и сложить два числа в двоичной системе счисления.
Примечание:
Выполнять действия можно только в одной системе счисления, если вам даны разные системы счисления, сначала переведите все числа в одну систему счисления
Если вы работаете с системой счисления, основание которой больше 10 и у вас в примере встретилась буква, мысленно замените её цифрой в десятичной системе, проведите необходимые операции и переведите результат обратно в исходную систему счисления
Сложение:
Все помнят, как в начальной школе нас учили складывать столбиком, разряд с разрядом. Если при сложении в разряде получалось число больше 9, мы вычитали из него 10, полученный результат записывали в ответ, а 1 прибавляли к следующему разряду. Из этого можно сформулировать правило:
Из этого можно сформулировать правило:
- Складывать удобнее «столбиком»
- Складывая поразрядно, если цифра в разряде > больше самой большой цифры алфавита данной Системы счисления, вычитаем из этого числа основание системы счисления.
- Полученный результат записываем в нужный разряд
- Прибавляем единицу к следующему разряду
Сложить 1001001110 и 100111101 в двоичной системе счисления
1001001110 |
100111101 |
1110001011 |
Ответ: 1110001011
Сложить F3B и 5A в шестнадцатеричной системе счисления
Ответ: FE0
Вычитание:Все помнят, как в начальной школе нас учили вычитать столбиком, разряд из разряда. Если при вычитании в разряде получалось число меньше 0, мы то мы «занимали» единицу из старшего разряда и прибавляли к нужной цифре 10, из нового числа вычитали нужное. Из этого можно сформулировать правило:
Из этого можно сформулировать правило:
- Вычитать удобнее «столбиком»
- Вычитая поразрядно, если цифра в разряде
- Производим вычитание
Вычесть из 1001001110 число 100111101 в двоичной системе счисления
1001001110 |
100111101 |
100010001 |
Ответ: 100010001
Вычесть из F3B число 5A в шестнадцатеричной системе счисления
Ответ: D96
Самое главное, не забывайте про то, что у вас в распоряжении только цифры данной системы счисления, так же не забывайте про переходы между разрядными слагаемыми.
Умножение:
Умножение в других системах счисления происходит точно так же, как и мы привыкли умножать.
- Умножать удобнее «столбиком»
- Умножение в любой системе счисления происходит по тем же правилам, что и в десятичной.
 Но мы можем использовать только алфавит, данный системы счисления
Но мы можем использовать только алфавит, данный системы счисления
Умножить 10111 на число 1101 в двоичной системе счисления
10111 |
1101 |
10111 |
10111 |
10111 |
100101011 |
Ответ: 100101011
Умножить F3B на число A в шестнадцатеричной системе счисления
Ответ: 984E
Ответ: 984E
Самое главное, не забывайте про то, что у вас в распоряжении только цифры данной системы счисления, так же не забывайте про переходы между разрядными слагаемыми.Деление в других системах счисления происходит точно так же, как и мы привыкли делить.
- Делить удобнее «столбиком»
- Деление в любой системе счисления происходит по тем же правилам, что и в десятичной.
 Но мы можем использовать только алфавит, данный системы счисления
Но мы можем использовать только алфавит, данный системы счисления
Пример:
Разделить 1011011 на число 1101 в двоичной системе счисления
Разделить F 3 B на число 8 в шестнадцатеричной системе счисления
Самое главное, не забывайте про то, что у вас в распоряжении только цифры данной системы счисления, так же не забывайте про переходы между разрядными слагаемыми.
НЕПОЗИЦИОННЫЕ
Непозиционные системы счисления
Непозиционные системы счисления появились исторически первыми. В этих системах значение каждого цифрового символа постоянно и не зависит от его положения. Простейшим случаем непозиционной системы является единичная, для которой для обозначения чисел используется единственный символ, как правило это черта, иногда точка, которых всегда ставится количество, соответствующее обозначаемому числу:
- 1 — |
- 2 — ||
- 3 — |||, и т.
 д.
д.
Таким образом, этот единственный символ имеет значение единицы , из которой последовательным сложением получается необходимое число:
||||| = 1+1+1+1+1 = 5.
Модификацией единичной системы является система с основанием, в которой есть символы не только для обозначения единицы, но и для степеней основания. Например, если за основание взято число 5, то будут дополнительные символы для обозначения 5, 25, 125 и так далее.
Примером такой системы с основанием 10 является древнеегипетская, возникшая во второй половине третьего тысячеления до новой эры. В этой системе имелись следующие иероглифы:
- шест — единицы,
- дуга — десятки,
- пальмовый лист — сотни,
- цветок лотоса — тысячи.
Числа получались простым сложением, порядок следования мог быть
любым. Так, для обозначения, например, числа 3815, рисовали три цветка
лотоса, восемь пальмовых листов, одну дугу и пять шестов. Более сложные
системы с дополнительными знаками — старая греческая, римская. Римская
также использует элемент позиционной системы — большая цифра, стоящая
перед меньшей, прибавляется, меньшая перед большей — вычитается: IV = 4,
но VI = 6, этот метод, правда, применяется исключительно для
обозначения чисел 4, 9, 40, 90, 400, 900, 4000, и производных их
сложением.
Римская
также использует элемент позиционной системы — большая цифра, стоящая
перед меньшей, прибавляется, меньшая перед большей — вычитается: IV = 4,
но VI = 6, этот метод, правда, применяется исключительно для
обозначения чисел 4, 9, 40, 90, 400, 900, 4000, и производных их
сложением.
Новогреческая и древнерусская системы использовали в качестве цифр 27 букв алфавита, где ими обозначалось каждое число от 1 до 9, а также десятки и сотни. Такой подход обеспечил возможность записывать числа от 1 до 999 без повторений цифр.
В старорусской системе для обозначения больших чисел использовались специальные обрамления вокруг цифр.
В качестве словесной системы номерации до сих пор практически
везде используется непозиционная. Словесные системы нумерации сильно
привязаны в языку, и общие их элементы в основном относятся к общим
принципам и названиям больших чисел (триллион и выше). Общие принципы,
положенные в основу современных словесных нумераций вредполагают
формирование обозначения посредством сложения и умножения значений
уникальных названий.
Арифметические операции в двоичной системе счисления
Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения.
Правило выполнения операции сложения одинаково для всех систем счисления: если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд. При вычитании, если необходимо, делают заем.
Аналогично выполняются арифметические действия в восьмеричной, шестнадцатеричной и других системах счисления. При этом необходимо учитывать, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления.
Арифметические операции в восьмеричной системе счисления
Для представления чисел в восьмеричной системе счисления используются восемь цифр(0, 1, 2, 3, 4, 5, 6, 7), так как основа восьмеричной системы счисления равна8. Все операции производятся посредством этих восьми цифр. Операции сложения и умножения в восьмеричной системе счисления производятся с помощью следующих таблиц:
Операции сложения и умножения в восьмеричной системе счисления производятся с помощью следующих таблиц:
Таблицы сложения и умножения в восьмеричной системе счисления
|
Пример 5 .Вычесть восьмеричные числа 5153- 1671и2426,63- 1706,71 |
Пример 6 .Умножить восьмеричные числа51 16и16,6 3,2 |
Арифметические операции в шестнадцатеричной системе счисления
Для представления чисел в шестнадцатеричной системе счисления используются шестнадцать цифр:0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. В шестнадцатеричной системе числошестнадцатьпишется как10. Выполнение арифметических операций в шестнадцатеричной системе производится как и в десятиричной системе, но при выполнении арифметических операций над большими числами необходимо использовать таблицы сложения и умножения чисел в шестнадцатеричной системе счисления.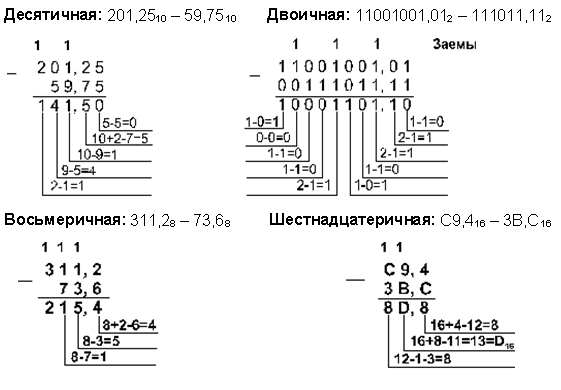
Таблица сложения в шестнадцатеричной системе счисления
Таблица умножения в шестнадцатеричной системе счисления
|
Пример 7 .Сложить шестнадцатеричные числа |
Сложение и вычитание чисел в любой позиционной системе счисления выполняется поразрядно. Для нахождения суммы складываются единицы одного и того же разряда, начиная с единиц первого разряда (справа). Если сумма единиц складываемого разряда превышает число, равное основанию системы, то из этой суммы выделяется единица старшего разряда, которая и добавляется к соседнему разряду слева. Поэтому сложение можно производить непосредственно, как и в десятичной системе, в «столбик», используя таблицу сложения однозначных чисел.
Например, в системе счисления с основанием 4 таблица сложения имеет такой вид:
Еще проще таблица сложения в двоичной системе счисления:
| 0 + 0 = 0 | 0 + 1 = 1 | 1 + 1 = 10.
|
|
Пример: |
Вычитание выполняем так же, как и в десятичной системе: подписываем вычитаемое под уменьшаемым и производим вычитание чисел в разрядах, начиная с первого. Если вычитание единиц в разряде невозможно, «занимаем» единицу в высшем разряде и преобразуем ее в единицы соседнего правого разряда.
|
Пример: 2311 4 — 1223 4 .
|
С помощю этого онлайн калькулятора можно перевести целые и дробные числа из одной системы счисления в другую. Дается подробное решение с пояснениями. Для перевода введите исходное число, задайте основание сисемы счисления исходного числа, задайте основание системы счисления, в которую нужно перевести число и нажмите на кнопку «Перевести». Теоретическую часть и численные примеры смотрите ниже.
Результат уже получен!
Перевод целых и дробных чисел из одной системы счисления в любую другую − теория, примеры и решения
Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:
Пронумеруем это число справа налево начиная с нуля:
Тогда число 6372 можно представить в следующем виде:
6372=6000+300+70+2 =6·10 3 +3·10 2 +7·10 1 +2·10 0 .
Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.
Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:
Тогда число 1287.923 можно представить в виде:
1287.923 =1000+200+80 +7+0.9+0.02+0.003 = 1·10 3 +2·10 2 +8·10 1 +7·10 0 +9·10 -1 +2·10 -2 +3·10 -3 .
В общем случае формулу можно представить в следующем виде:
Ц n ·s n +Ц n-1 ·s n-1 +…+Ц 1 ·s 1 +Ц 0 ·s 0 +Д -1 ·s -1 +Д -2 ·s -2 +…+Д -k ·s -k
где Ц n -целое число в позиции n , Д -k — дробное число в позиции (-k), s — система счисления.
Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр {0,1,2,3,4,5,6,7,8,9}, в восьмеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7}, в двоичной системе счисления — из множества цифр {0,1}, в шестнадцатеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15. В таблице Таб.1 представлены числа в разных системах счисления.
В таблице Таб.1 представлены числа в разных системах счисления.
| Таблица 1 | |||
|---|---|---|---|
| Система счисления | |||
| 10 | 2 | 8 | 16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E | 15 | 1111 | 17 | F |
Перевод чисел из одной системы счисления в другую
Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.
Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:
1 ·2 6 +0 ·2 5 +1 ·2 4 +1 ·2 3 +1 ·2 2 +0 ·2 1 +1 ·2 0 +0 ·2 -1 +0 ·2 -2 +1 ·2 -3 =64+16+8+4+1+1/8=93.125
Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:
Пример 3 . Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:
Здесь A -заменен на 10, B — на 11, C — на 12, F — на 15.
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.
Пример 4 . Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||||||
| 158 | 79 | 2 | |||||
| 1 | 78 | 39 | 2 | ||||
| 1 | 38 | 19 | 2 | ||||
| 1 | 18 | 9 | 2 | ||||
| 1 | 8 | 4 | 2 | ||||
| 1 | 4 | 2 | 2 | ||||
| 0 | 2 | 1 | |||||
| 0 |
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111
. Следовательно можно записать:
1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111
. Следовательно можно записать:
159 10 =10011111 2 .
Пример 5 . Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147 (см. Рис. 2). Следовательно можно записать:
615 10 =1147 8 .
Пример 6 . Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7 . Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | ||
| x | 2 | |
| 0 | 0.428 | |
| x | 2 | |
| 0 | 0.856 | |
| x | 2 | |
| 1 | 0.712 | |
| x | 2 | |
| 1 | 0.424 | |
| x | 2 | |
| 0 | 0.848 | |
| x | 2 | |
| 1 | 0.696 | |
| x | 2 | |
| 1 | 0.392 |
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011
.
Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011
.
Следовательно можно записать:
0.214 10 =0.0011011 2 .
Пример 8 . Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | ||
| x | 2 | |
| 0 | 0.25 | |
| x | 2 | |
| 0 | 0.5 | |
| x | 2 | |
| 1 | 0.0 |
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
В третьем этапе получилось 0. Следовательно, получился следующий результат:
0.125 10 =0.001 2 .
Пример 9 . Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | ||
| x | 16 | |
| 3 | 0.424 | |
| x | 16 | |
| 6 | 0.784 | |
| x | 16 | |
| 12 | 0.544 | |
| x | 16 | |
| 8 | 0.704 | |
| x | 16 | |
| 11 | 0.264 | |
| x | 16 | |
| 4 | 0.224 |
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B.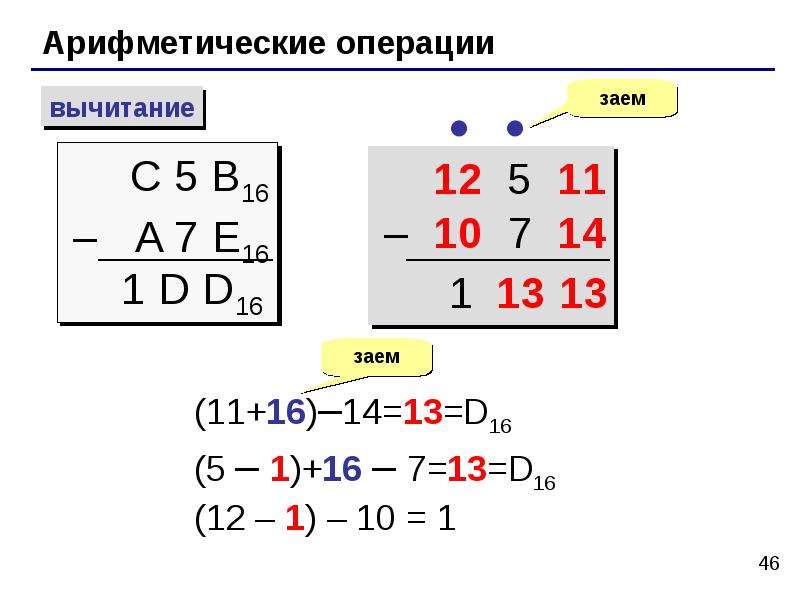 Следовательно имеем:
Следовательно имеем:
0.214 10 =0.36C8B4 16 .
Пример 10 . Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | ||
| x | 8 | |
| 4 | 0.096 | |
| x | 8 | |
| 0 | 0.768 | |
| x | 8 | |
| 6 | 0.144 | |
| x | 8 | |
| 1 | 0.152 | |
| x | 8 | |
| 1 | 0.216 | |
| x | 8 | |
| 1 | 0.728 |
Получили:
0.512 10 =0.406111 8 .
Пример
11
. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8). Далее объединяя эти результаты получим:
Далее объединяя эти результаты получим:
159.125 10 =10011111.001 2 .
Пример 12 . Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим.
Глава 8 Альтернативы десятке . Код. Тайный язык информатики
Число 10 — исключительно важное для человека. У большинства из нас по десять пальцев на руках и на ногах, и мы, конечно, предпочитаем, чтобы и тех, и других было по десять. Поскольку на пальцах удобно считать, человек выстроил всю систему счисления на основании числа 10.
Как упоминалось в предыдущей главе, такая система называется «система с основанием 10», или «десятеричная». Она кажется нам столь естественной, что поначалу сложно даже найти альтернативу. Действительно, когда видим число 10, нас тянет представить, что оно означает, например, десять уток.
Единственная причина, по которой возникает такая ассоциация, в том, что уток столько же, сколько и пальцев у нас на руках. Если бы у человека было иное количество пальцев, то и считали бы мы по-другому, и число 10 означало бы нечто иное. Например, число 10 может указывать и на такое количество уток.
Если бы у человека было иное количество пальцев, то и считали бы мы по-другому, и число 10 означало бы нечто иное. Например, число 10 может указывать и на такое количество уток.
Или так.
Или даже так.
Как только мы поймем, в каком случае 10 означает двух уток, можно будет приступать к разговору о представлении чисел при работе с переключателями, проводами, лампочками и реле (далее — и с компьютерами).
Что, если бы у людей было всего по четыре пальца на руке, как у мультяшек? Вероятно, нам бы даже не пришло в голову разрабатывать десятеричную систему счисления. Напротив, мы бы считали нормальным, естественным, разумным, неизбежным, неопровержимым и бесспорно верным построить систему счисления с основанием 8. Она называлась бы не десятеричной, а восьмеричной, или системой с основанием 8.
Если бы наша система счисления была построена на основании 8, то вот этот символ нам бы не требовался:
9.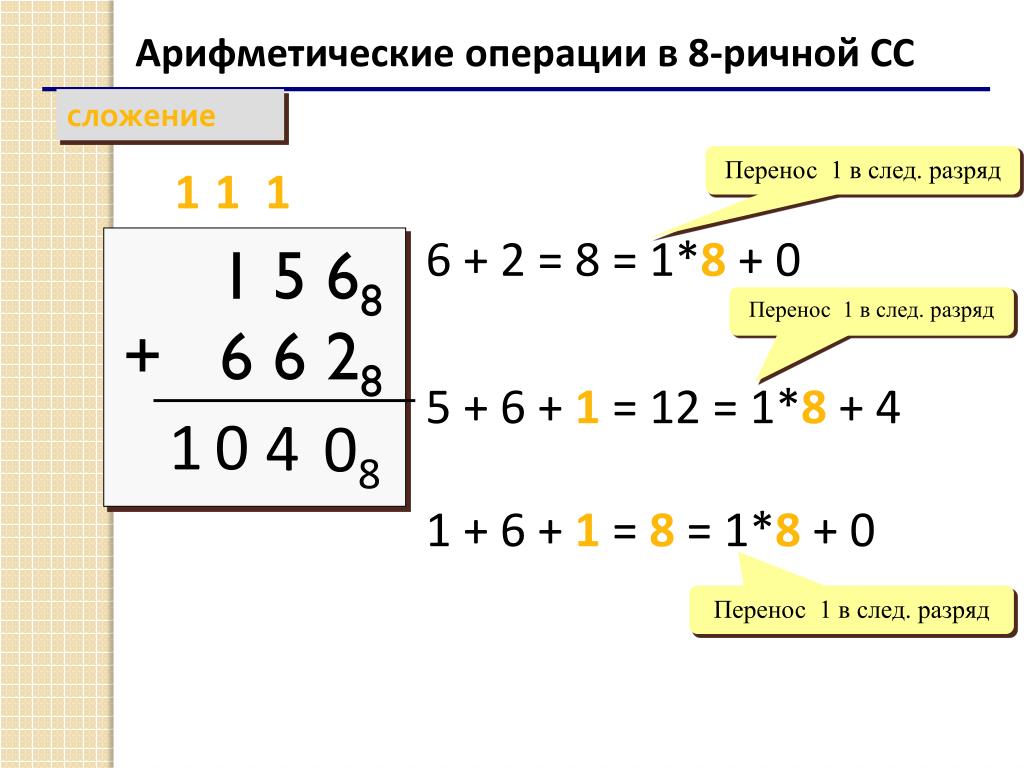
Покажите этот символ мультяшке, и герой спросит: «Что это? Зачем это нужно?» Если задуматься, то и без этого символа можно обойтись:
8.
В десятеричной системе счисления нет специального символа для десятки, соответственно в восьмеричной системе счисления его нет для восьмерки.
В десятеричной системе счисления мы считаем: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а потом 10. В восьмеричной системе считаем: 0, 1, 2, 3, 4, 5, 6, 7, а потом что? Цифры кончились. Остается лишь 10, и это правильный ответ. В восьмеричной системе за 7 следует 10. Но в таком случае 10 соответствует не десяти пальцам, которые есть на двух руках у человека. В восьмеричной системе 10 — это количество пальцев у мультяшек.
Давайте считать дальше на четырехпалых ступнях.
Имея дело с иными системами счисления, кроме десятеричной, можно не путаться, если называть число 10 «один-ноль». Аналогично 13 будет «один-три», а 20 — «два-ноль». Чтобы вообще обойтись без путаницы, можно говорить «два-ноль с основанием восемь» или «два-ноль восьмеричных».
Чтобы вообще обойтись без путаницы, можно говорить «два-ноль с основанием восемь» или «два-ноль восьмеричных».
Даже когда у нас кончатся пальцы на руках и ногах, можно и далее считать в восьмеричной системе. В принципе, процесс не отличается от счета в десятеричной, просто мы пропускаем все числа, в которых есть 8 или 9. Естественно, конкретные числа обозначают уже другие величины.
0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, 20, 21, 22, 23, 24, 25, 26, 27, 30, 31, 32, 33, 34, 35, 36, 37, 40, 41, 42, 43, 44, 45, 46, 47, 50, 51, 52, 53, 54, 55, 56, 57, 60, 61, 62, 63, 64, 65, 66, 67, 70, 71, 72, 73, 74, 75, 76, 77, 100…
Последнее число называется «один-ноль-ноль». Это общее количество пальцев мультяшки, умноженное само на себя.
При записи десятеричных и восьмеричных чисел можно избежать путаницы, записывая все числа с нижними индексами, обозначающими принадлежность к той или иной системе счисления. Нижний индекс ДЕСЯТЬ означает «основание десять», то есть десятеричную систему, а нижний индекс ВОСЕМЬ — «основание восемь», или восьмеричную систему.
Нижний индекс ДЕСЯТЬ означает «основание десять», то есть десятеричную систему, а нижний индекс ВОСЕМЬ — «основание восемь», или восьмеричную систему.
Итак, Белоснежка повстречала 7ДЕСЯТЬ, или 7ВОСЕМЬ, гномов.
У мультяшек по 8ДЕСЯТЬ, или 10ВОСЕМЬ, пальцев на руке.
Бетховен написал 9ДЕСЯТЬ, или 11ВОСЕМЬ, симфоний.
У человека 10ДЕСЯТЬ, или 12ВОСЕМЬ, пальцев на руках.
В году 12ДЕСЯТЬ, или 14ВОСЕМЬ, месяцев.
В двух неделях 14ДЕСЯТЬ, или 16ВОСЕМЬ, дней.
Паспорт выдают в 16ДЕСЯТЬ, или 20ВОСЕМЬ, лет.
В сутках 24ДЕСЯТЬ, или 30ВОСЕМЬ, часов.
В латинице 26ДЕСЯТЬ, или 32ВОСЕМЬ, букв.
В английской кварте 907ДЕСЯТЬ, или 1134, граммов.
В покерной колоде 52ДЕСЯТЬ, или 64ВОСЕМЬ, карт.
Самый известный адрес по Сансет-Стрип — 77ДЕСЯТЬ, или 115ВОСЕМЬ.
Длина поля для американского футбола — 91ДЕСЯТЬ, или 131ВОСЕМЬ, метров.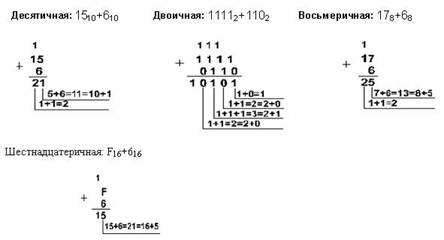
На старте женского одиночного зачета в Уимблдонском турнире — 128ДЕСЯТЬ, или 200ВОСЕМЬ, участниц.
Площадь Мемфиса равна 640ДЕСЯТЬ, или 1000ВОСЕМЬ, квадратных километров.
Обратите внимание: в этом списке есть несколько круглых восьмеричных чисел. Круглым называется число, оканчивающееся на один или несколько нулей. Если десятеричное число оканчивается двумя нулями, значит, оно кратно 100ДЕСЯТЬ, а 100ДЕСЯТЬ — это 10ДЕСЯТЬ, умноженное на 10ДЕСЯТЬ. В восьмеричной системе два нуля в конце числа означают, что число кратно 100ВОСЕМЬ, то есть 10ВОСЕМЬ умножить на 10ВОСЕМЬ (или 8ДЕСЯТЬ умножить на 8ДЕСЯТЬ, что равно 64ДЕСЯТЬ).
Возможно, вы также заметили, что такие круглые восьмеричные числа, как 100ВОСЕМЬ, 200ВОСЕМЬ и 400ВОСЕМЬ, в десятеричной системе соответствуют 64ДЕСЯТЬ, 128ДЕСЯТЬ и 256ДЕСЯТЬ, и все эти десятеричные числа — степени двойки. Это логично. Например, число 400ВОСЕМЬ, равно 4ВОСЕМЬ умножить на 10ВОСЕМЬ и умножить на 10ВОСЕМЬ, и все это — степени двойки. Всякий раз при умножении степени двойки на степень двойки мы получаем еще одну степень двойки.
Всякий раз при умножении степени двойки на степень двойки мы получаем еще одну степень двойки.
В следующей таблице даны некоторые степени двойки в десятеричном и восьмеричном представлении.
Степень двойки
Десятеричная система
Восьмеричная система
20
1
1
21
2
2
22
4
4
23
8
10
24
16
20
25
32
40
26
64
100
27
128
200
28
256
400
29
512
1000
210
1024
2000
211
2048
4000
212
4096
10 000
Круглые числа из правого столбца подсказывают, что системы счисления, отличающиеся от десятеричной, удобны для работы с двоичными кодами.
Структурно восьмеричная система аналогична десятеричной. Отличия лишь в деталях. Например, каждая позиция в восьмеричном числе — это цифра, умноженная на степень восьмерки.
Следовательно, восьмеричное число 3725ВОСЕМЬ можно разбить:
3725ВОСЕМЬ = 3000ВОСЕМЬ + 700ВОСЕМЬ + 20ВОСЕМЬ + 5ВОСЕМЬ.
Эту последовательность можно переписать несколько иначе. Например, при помощи степеней восьмерки в их десятеричном представлении:
3725ВОСЕМЬ = 3 ? 512ДЕСЯТЬ +
7 ? 64ДЕСЯТЬ +
2 ? 8ДЕСЯТЬ +
5 ? 1.
То же самое, записанное при помощи степеней восьмерки в восьмеричном представлении:
3725ВОСЕМЬ = 3 ? 1000ВОСЕМЬ +
7 ? 100ВОСЕМЬ +
2 ? 10ВОСЕМЬ +
5 ? 1.
А можно сделать вот так:
3725ВОСЕМЬ = 3 ? 83 +
7 ? 82 +
2 ? 81 +
5 ? 80.
Если выполнить эти расчеты в десятеричной системе, получится 2005ДЕСЯТЬ. Таким образом восьмеричные числа преобразуются в десятеричные.
Таким образом восьмеричные числа преобразуются в десятеричные.
Восьмеричные числа складываются и перемножаются в точности как десятеричные. Разница в том, что таблицы умножения и сложения для восьмеричных чисел строятся иначе. Вот таблица сложения восьмеричных чисел.
Например, 5ВОСЕМЬ + 7ВОСЕМЬ = 14ВОСЕМЬ, то есть восьмеричные числа можно складывать в столбик.
Начинаем справа: 5 плюс 3 равно 10, 0 пишем, 1 в уме; 1 плюс 3 плюс 4 равно 10, 0 пишем, 1 в уме; 1 плюс 1 плюс 6 равно 10.
Аналогично дважды два и в восьмеричной системе равно четырем. Но трижды три не равно девяти. А как? Трижды три равно 11ВОСЕМЬ, это столько же, сколько и 9ДЕСЯТЬ. Далее полностью приведена восьмеричная таблица умножения.
Здесь у нас 4 ? 6 равно 30ВОСЕМЬ, но 30ВОСЕМЬ равно 24ДЕСЯТЬ, то есть 4 ? 6 в десятеричной системе.
Восьмеричная система счисления столь же полноценна, как и десятеричная.
Мы разработали систему счисления для мультяшек. Теперь давайте создадим такую же систему для омаров. У омаров нет пальцев, но на кончиках передних лап у них клешни. Омарам подойдет четверичная система счисления с основанием четыре.
Теперь давайте создадим такую же систему для омаров. У омаров нет пальцев, но на кончиках передних лап у них клешни. Омарам подойдет четверичная система счисления с основанием четыре.
Вот как считают в четверичной системе: 0, 1, 2, 3, 10, 11, 12, 13, 20, 21, 22, 23, 30, 31, 32, 33, 100, 101, 102, 103, 110 и т. д.
Не буду подробно останавливаться на четверичной системе, поскольку мы приближаемся к более важному вопросу. Как видите, здесь каждая позиция в числе соответствует степени четверки.
В четверичной системе счисления число 31 232 можно записать следующим образом:
31 232ЧЕТЫРЕ = 3 ? 256ДЕСЯТЬ +
1 ? 64ДЕСЯТЬ +
2 ? 16ДЕСЯТЬ +
3 ? 4ДЕСЯТЬ +
2 ? 1ДЕСЯТЬ.
Что равнозначно записи:
31 232ЧЕТЫРЕ = 3 ? 10 000ЧЕТЫРЕ +
1 ? 1000ЧЕТЫРЕ +
2 ? 100ЧЕТЫРЕ +
3 ? 10ЧЕТЫРЕ +
2 ? 1ЧЕТЫРЕ.
А это то же самое, что и:
31 232ЧЕТЫРЕ = 3 ? 44 +
1 ? 43 +
2 ? 42 +
3 ? 41 +
2 ? 40.
Если мы выполним вычисления в десятичной системе счисления, то обнаружим, что 31 232ЧЕТЫРЕ — это 878ДЕСЯТЬ.
Теперь мы сделаем еще один прыжок, на этот раз окончательный. Представьте, что мы дельфины и можем использовать для подсчета два плавника. В данном случае мы имеем дело с системой счисления с основанием 2, или двоичной, или, иначе, бинарной (от лат. binary — «двойной», «состоящий из двух частей»). Понятно, что у нас будет только две цифры: 0 и 1.
С нулем и единицей мало что можно сделать, и, чтобы привыкнуть к двоичным числам, требуется практика. Проблема в том, что сразу заканчиваются цифры. Например, на следующем рисунке показано, как дельфин считает на плавниках.
Да, в двоичной системе счисления за 1 следует 10. Это странно, однако это не должно удивлять. Независимо от того, какую систему счисления мы используем, всякий раз, когда у нас заканчиваются отдельные цифры, первое двузначное число всегда 10. В двоичной системе счисления мы считаем:
В двоичной системе счисления мы считаем:
0, 1, 10, 11, 100, 101, 110, 111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111, 10000, 10001…
Эти числа могут показаться большими, но на самом деле это не так. Скорее, двоичные числа очень быстро становятся длинными, а не большими.
Количество голов у людей — 1ДЕСЯТЬ, или 1ДВА.
Количество плавников у дельфинов — 2ДЕСЯТЬ, или 10ДВА.
Количество чайных ложек в столовой ложке — 3ДЕСЯТЬ, или 11ДВА.
Количество сторон у квадрата — 4ДЕСЯТЬ, или 100ДВА.
Количество пальцев на одной человеческой руке — 5ДЕСЯТЬ, или 101ДВА.
Количество конечностей у насекомых — 6ДЕСЯТЬ, или 110ДВА.
Количество дней в неделе — 7ДЕСЯТЬ, или 111ДВА.
Количество музыкантов в октете — 8ДЕСЯТЬ, или 1000ДВА.
Количество планет в Cолнечной системе, включая Плутон, — 9ДЕСЯТЬ, или 1001ДВА.
Количество центнеров в тонне — 10ДЕСЯТЬ, или 1010ДВА.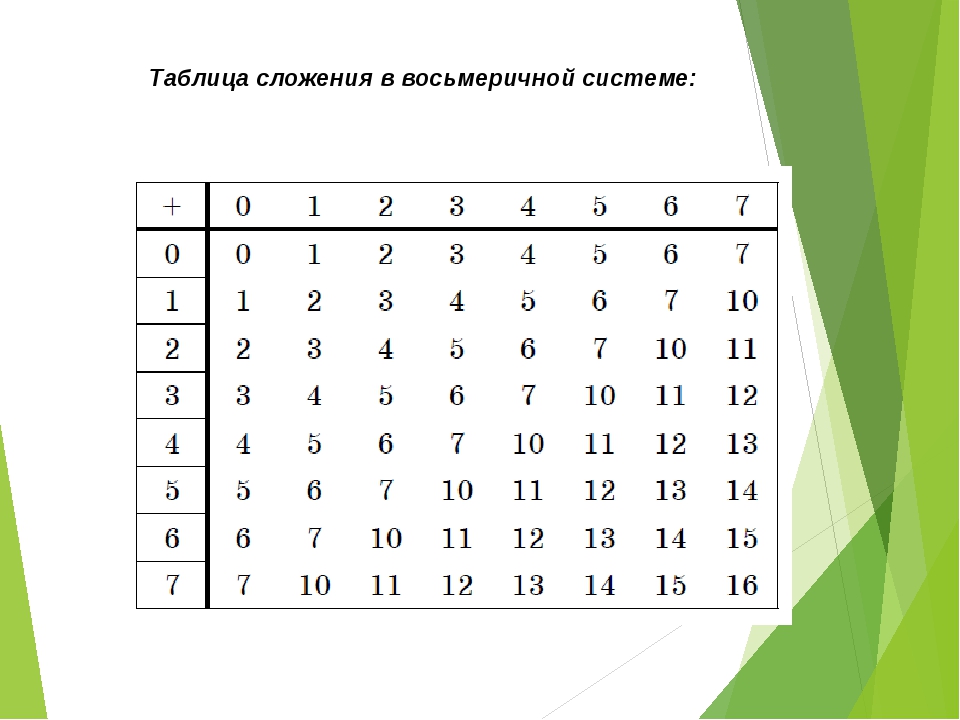
В двоичном числе, состоящем из большого количества цифр, позиции знаков соответствуют степени двойки.
Таким образом, каждый раз, когда встречаем двоичное число, состоящее из единицы и следующих за ней нулей, мы понимаем, что это число соответствует какой-либо из степеней двойки. Эта степень равна количеству нулей в этом двоичном числе. Вот наша расширенная таблица степеней двойки, демонстрирующая такое правило.
Допустим, у нас есть двоичное число 101101011010. Его можно записать так:
101101011010ДВА = 1 ? 2048ДЕСЯТЬ +
0 ? 1024ДЕСЯТЬ +
1 ? 512ДЕСЯТЬ +
1 ? 256ДЕСЯТЬ +
0 ? 128ДЕСЯТЬ +
1 ? 64ДЕСЯТЬ +
0 ? 32ДЕСЯТЬ +
1 ? 16ДЕСЯТЬ +
1 ? 8ДЕСЯТЬ +
0 ? 4ДЕСЯТЬ +
1 ? 2ДЕСЯТЬ +
0 ? 1ДЕСЯТЬ.
Или:
101101011010ДВА = 1 ? 211 +
0 ? 210 +
1 ? 29 +
1 ? 28 +
0 ? 27 +
1 ? 26 +
0 ? 25 +
1 ? 24 +
1 ? 23 +
0 ? 22 +
1 ? 21 +
0 ? 20.
Если просто сложить все слагаемые в десятичной системе, получим 2048 + 512 + 256 + 64 + 16 + 8 + 2, что составляет 2906ДЕСЯТЬ.
Для более легкого преобразования двоичных чисел в десятичные можно использовать следующую схему.
Эта схема позволяет конвертировать числа, содержащие до восьми двоичных разрядов; ее можно легко расширить. Введите до восьми цифр в восемь верхних полей, по одной цифре в каждый квадрат. Выполните восемь операций умножения и введите их результаты в восемь нижних полей. Сложите числа в этих восьми полях для получения окончательного результата. Этот пример демонстрирует процесс нахождения десятичного эквивалента двоичного числа 10010110.
Преобразовать десятичные числа от 0 до 255 в двоичные не так просто, однако вы можете использовать следующую схему.
Процесс преобразования сложнее, чем кажется, поэтому внимательно следуйте указаниям. Поместите десятичное число (меньшее или равное 255) в верхний левый квадрат. Разделите это число (делимое) на первый делитель (128), как показано на схеме. Поместите целую часть в нижнее поле (левый нижний квадрат), а остаток от деления — в поле справа (второй квадрат в верхнем ряду). Этот первый остаток является делимым, которое будет участвовать в следующей операции деления, где в качестве делителя используется число 64.
Разделите это число (делимое) на первый делитель (128), как показано на схеме. Поместите целую часть в нижнее поле (левый нижний квадрат), а остаток от деления — в поле справа (второй квадрат в верхнем ряду). Этот первый остаток является делимым, которое будет участвовать в следующей операции деления, где в качестве делителя используется число 64.
Помните, что каждая целая часть будет равна либо 0, либо 1. Если делимое меньше делителя, то целая часть от деления будет равна 0, а остаток — самому делимому. Если делимое больше или равно делителю, то целая часть от деления будет равна 1, а остаток — разности между делимым и делителем. Вот как преобразуется число 150.
Если вам нужно сложить или перемножить два двоичных числа, вероятно, будет легче выполнить вычисления в двоичной системе, не преобразуя числа в десятичные. Это должно понравиться. Представьте, как быстро вы могли бы освоить сложение, если бы потребовалось запомнить только это.
Давайте с помощью этой таблицы сложим два двоичных числа.
Начиная с правого столбца: 1 плюс 0 равно 1. Второй столбец справа: 0 плюс 1 равно 1. Третий столбец: 1 плюс 1 равно 0, 1 в уме. Четвертый столбец: 1 (перенесенное значение) плюс 0 плюс 0 равно 1. Пятый столбец: 0 плюс 1 равно 1. Шестой столбец: 1 плюс 1 равно 0, 1 в уме. Седьмой столбец: 1 (перенесенное значение) плюс 1 плюс 0 = 10.
Таблица умножения даже проще, чем таблица сложения, поскольку ее можно составить, используя два базовых правила умножения: умножая на 0, получаем 0, умножение на 1 не влияет на исходное число.
Вот процесс умножения числа 13ДЕСЯТЬ на число 11ДЕСЯТЬ в двоичной системе счисления.
Результат — 143ДЕСЯТЬ.
Люди, работающие с двоичными числами, часто предваряют их нулями, то есть пишут нули слева от первой 1, например 0011 вместо 11. Это совершенно не влияет на значение, а служит исключительно для красоты. В следующей таблице перечислены первые шестнадцать двоичных чисел и их десятичные эквиваленты.
Двоичное число
Десятичное число
0000
0
0001
1
0010
2
0011
3
0100
4
0101
5
0110
6
0111
7
1000
8
1001
9
1010
10
1011
11
1100
12
1101
13
1110
14
1111
15
Давайте рассмотрим список двоичных чисел. Обратите внимание на каждый из четырех вертикальных столбцов, состоящих из нулей и единиц, и заметьте, как эти цифры чередуются в столбцах сверху вниз:
в крайнем правом столбце — 0 и 1;
во втором столбце справа — два 0 и две 1;
в следующем столбце — четыре 0 и четыре 1;
в крайнем левом столбце — восемь 0 и восемь 1.
В этом есть порядок, не так ли? Действительно, вы можете легко написать следующие шестнадцать двоичных чисел, просто повторив первые шестнадцать и добавив 1 в начале.
Двоичное число
Десятичное число
10000
16
10001
17
10010
18
10011
19
10100
20
10101
21
10110
22
10111
23
11000
24
11001
25
11010
26
11011
27
11100
28
11101
29
11110
30
11111
31
Вот еще один способ смотреть на это: при выполнении подсчета в двоичном формате крайняя цифра справа (также называемая младшим разрядом) поочередно принимает значения 0 и 1. Каждый раз, когда она изменяется с 1 на 0, вторая цифра справа, следующая за младшим разрядом, также изменяется либо с 0 на 1, либо с 1 на 0. Так что каждый раз, когда двоичная цифра изменяется с 1 на 0, следующая за ней цифра также меняется либо с 0 на 1, либо с 1 на 0.
Каждый раз, когда она изменяется с 1 на 0, вторая цифра справа, следующая за младшим разрядом, также изменяется либо с 0 на 1, либо с 1 на 0. Так что каждый раз, когда двоичная цифра изменяется с 1 на 0, следующая за ней цифра также меняется либо с 0 на 1, либо с 1 на 0.
При записи больших десятичных чисел мы используем запятые через каждые три знака для облегчения их восприятия[11]. Например, если вы увидите число 12000000, вероятно, придется подсчитать количество цифр, однако, увидев число 12,000,000, вы сразу поймете, что оно означает 12 миллионов.
Двоичные числа очень быстро могут стать весьма длинными. Например, 12 миллионов в двоичной системе счисления записывается так: 101101110001101100000000. Чтобы такое число было легче воспринимать, каждые четыре двоичных разряда обычно разделяются пробелами (1011 0111 0001 1011 0000 0000). Далее в этой книге мы рассмотрим более сжатый способ записи двоичных чисел.
Сведя систему счисления к двоичным цифрам 0 и 1, мы достигли предела. Далее упрощать некуда. Более того, двоичная система соединяет арифметику с электричеством. В предыдущих главах мы рассматривали переключатели, провода, лампочки и реле, и любой из этих объектов может отображать двоичные цифры 0 и 1.
Далее упрощать некуда. Более того, двоичная система соединяет арифметику с электричеством. В предыдущих главах мы рассматривали переключатели, провода, лампочки и реле, и любой из этих объектов может отображать двоичные цифры 0 и 1.
Провод может представлять собой двоичную цифру. Если по нему идет ток, то двоичная цифра равна 1, если нет — 0.
Переключатель может представлять собой двоичную цифру. Если переключатель включен, или замкнут, то двоичная цифра равна 1, если переключатель выключен, или разомкнут, то двоичная цифра — 0.
Лампочка может представлять собой двоичную цифру. Если лампочка горит, то двоичная цифра равна 1, если нет — 0.
Телеграфное реле может представлять собой двоичную цифру. Если реле замкнуто, то двоичная цифра равна 1, если разомкнуто — 0.
Двоичные цифры имеют непосредственное отношение к компьютерам.
Примерно в 1948 году американский математик Джон Тьюки (род. 1915)[12] осознал, что в будущем словосочетание «двоичная цифра» (binary digit), вероятно, приобретет гораздо большее значение — по мере распространения компьютеров. Он решил создать новое, более короткое слово, чтобы заменить эти громоздкие пять слогов, и рассматривал такие варианты, как bigit и binit, но остановился на коротком, простом, элегантном и просто замечательном слове bit («бит»).
1915)[12] осознал, что в будущем словосочетание «двоичная цифра» (binary digit), вероятно, приобретет гораздо большее значение — по мере распространения компьютеров. Он решил создать новое, более короткое слово, чтобы заменить эти громоздкие пять слогов, и рассматривал такие варианты, как bigit и binit, но остановился на коротком, простом, элегантном и просто замечательном слове bit («бит»).
Перевод чисел из одной системы счисления в другую. Правила перевода чисел из одной системы счисления в другую
Способы перевода чисел из одной системы счисления в другую.
Перевод чисел из одной позиционной системы счисления в другую: перевод целых чисел.
Чтобы перевести целое число из одной системы счисления с основанием d1 в другую с основанием d2 необходимо последовательно делить это число и получаемые частные на основание d2 новой системы до тех пор, пока не получится частное меньше основания d2. Последнее частное — старшая цифра числа в новой системе счисления с основанием d2, а следующие за ней цифры — это остатки от деления, записываемые в последовательности, обратной их получению. Арифметические действия выполнять в той системе счисления, в которой записано переводимое число.
Последнее частное — старшая цифра числа в новой системе счисления с основанием d2, а следующие за ней цифры — это остатки от деления, записываемые в последовательности, обратной их получению. Арифметические действия выполнять в той системе счисления, в которой записано переводимое число.
Пример 1. Перевести число 11(10) в двоичную систему счисления.
Ответ: 11(10)=1011(2).
Пример 2. Перевести число 122(10) в восьмеричную систему счисления.
Ответ: 122(10)=172(8).
Пример 3. Перевести число 500(10) в шестнадцатеричную систему счисления.
Ответ: 500(10)=1F4(16).
Перевод чисел из одной позиционной системы счисления в другую: перевод правильных дробей.
Чтобы перевести правильную дробь из системы счисления с основанием d1 в систему с основанием d2, необходимо последовательно умножать исходную дробь и дробные части получающихся произведений на основание новой системы счисления d2. Правильная дробь числа в новой системе счисления с основанием d2 формируется в виде целых частей получающихся произведений, начиная с первого.
Если при переводе получается дробь в виде бесконечного или расходящегося ряда, процесс можно закончить при достижении необходимой точности.
При переводе смешанных чисел, необходимо в новую систему перевести отдельно целую и дробную части по правилам перевода целых чисел и правильных дробей, а затем оба результата объединить в одно смешанное число в новой системе счисления.
Пример 1. Перевести число 0,625(10) в двоичную систему счисления.
Ответ: 0,625(10)=0,101(2).
Пример 2. Перевести число 0,6(10) в восьмеричную систему счисления.
Ответ: 0,6(10)=0,463(8).
Пример 2. Перевести число 0,7(10) в шестнадцатеричную систему счисления.
Ответ: 0,7(10)=0,В333(16).
Перевод двоичных, восьмеричных и шестнадцатеричных чисел в десятичную систему счисления.
Для перевода числа P-ичной системы в десятичную необходимо использовать следующую формулу разложения:
аnan-1…а1а0=аnPn+ аn-1Pn-1+…+ а1P+a0 .
Пример 1. Перевести число 101,11(2) в десятичную систему счисления.
Ответ: 101,11(2)= 5,75(10) .
Пример 2. Перевести число 57,24(8) в десятичную систему счисления.
Ответ: 57,24(8) = 47,3125(10) .
Пример 3. Перевести число 7A,84(16) в десятичную систему счисления.
Ответ: 7A,84(16)= 122,515625(10) .
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления и обратно.
Для перевода числа из восьмеричной системы счисления в двоичную необходимо каждую цифру этого числа записать трехразрядным двоичным числом (триадой).
Пример: записать число 16,24(8) в двоичной системе счисления.
Ответ: 16,24(8)= 1110,0101(2) .
Для обратного перевода двоичного числа в восьмеричную систему счисления, необходимо исходное число разбить на триады влево и вправо от запятой и представить каждую группу цифрой в восьмеричной системе счисления. Крайние неполные триады дополняют нулями.
Пример: записать число 1110,0101(2) в восьмеричной системе счисления.
Ответ: 1110,0101(2)= 16,24(8) .
Для перевода числа из шестнадцатеричной системы счисления в двоичную необходимо каждую цифру этого числа записать четырехразрядным двоичным числом (тетрадой).
Пример: записать число 7A,7E(16) в двоичной системе счисления.
Ответ: 7A,7E(16)= 1111010,0111111(2) .
Примечание: незначащие нули слева для целых чисел и справа для дробей не записываются.
Для обратного перевода двоичного числа в шестнадцатеричную систему счисления, необходимо исходное число разбить на тетрады влево и вправо от запятой и представить каждую группу цифрой в шестнадцатеричной системе счисления. Крайние неполные триады дополняют нулями.
Пример: записать число 1111010,0111111(2) в шестнадцатеричной системе счисления.
Сдающим ЕГЭ и не только…
Странно, что в школах на уроках информатики обычно показывают ученикам самый сложный и неудобный способ перевода чисел из одной системы в другую. Это способ заключается в последовательном делении исходного числа на основание и сборе остатков от деления в обратном порядке.
Например, нужно перевести число 810 10 в двоичную систему:
Результат записываем в обратном порядке снизу вверх. Получается 81010 = 11001010102
Если нужно переводить в двоичную систему довольно большие числа, то лестница делений приобретает размер многоэтажного дома. И как тут собрать все единички с нулями и ни одной не пропустить?
В программу ЕГЭ по информатике входят несколько задач, связанных с переводом чисел из одной системы в другую. Как правило, это преобразование между 8- и 16-ричными системами и двоичной. Это разделы А1, В11. Но есть и задачи с другими системами счисления, как например, в разделе B7.
Для начала напомним две таблицы, которые хорошо бы знать наизусть тем, кто выбирает информатику своей дальнейшей профессией.
Таблица степеней числа 2:
| 2 1 | 2 2 | 2 3 | 2 4 | 2 5 | 2 6 | 2 7 | 2 8 | 2 9 | 2 10 |
| 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 |
Она легко получается умножением предыдущего числа на 2.
 Так, что если помните не все эти числа, остальные нетрудно получить в уме из тех, которые помните.
Так, что если помните не все эти числа, остальные нетрудно получить в уме из тех, которые помните.
Таблица двоичных чисел от 0 до 15 c 16-ричным представлением:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 0000 | 0001 | 0010 | 0011 | 0100 | 0101 | 0110 | 0111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 | 1111 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
Недостающие значения тоже нетрудно вычислить, прибавляя по 1 к известным значениям.

Перевод целых чисел
Итак, начнем с перевода сразу в двоичную систему. Возьмём то же число 810 10 . Нам нужно разложить это число на слагаемые, равные степеням двойки.
- Ищем ближайшую к 810 степень двойки, не превосходящую его. Это 2 9 = 512.
- Вычитаем 512 из 810, получаем 298.
- Повторим шаги 1 и 2, пока не останется 1 или 0.
- У нас получилось так: 810 = 512 + 256 + 32 + 8 + 2 = 2 9 + 2 8 + 2 5 + 2 3 + 2 1 .
Способ 1
: Расставить 1 по тем разрядам, какие получились показатели у слагаемых. В нашем примере это 9, 8, 5, 3 и 1. В остальных местах будут стоять нули. Итак, мы получили двоичное представление числа 810 10 = 1100101010 2
. Единицы стоят на 9-м, 8-м, 5-м, 3-м и 1-м местах, считая справа налево с нуля.
Способ 2 : Распишем слагаемые как степени двойки друг под другом, начиная с большего.
810 =
А теперь сложим эти ступеньки вместе, как складывают веер: 1100101010 .
Вот и всё. Попутно также просто решается задача «сколько единиц в двоичной записи числа 810?».
Ответ — столько, сколько слагаемых (степеней двойки) в таком его представлении. У 810 их 5.
Теперь пример попроще.
Переведём число 63 в 5-ричную систему счисления. Ближайшая к 63 степень числа 5 — это 25 (квадрат 5). Куб (125) будет уже много. То есть 63 лежит между квадратом 5 и кубом. Тогда подберем коэффициент для 5 2 . Это 2.
Получаем 63 10 = 50 + 13 = 50 + 10 + 3 = 2 * 5 2 + 2 * 5 + 3 = 223 5 .
Ну и, наконец, совсем лёгкие переводы между 8- и 16-ричными системами. Так как их основанием является степень двойки, то перевод делается автоматически, просто заменой цифр на их двоичное представление. Для 8-ричной системы каждая цифра заменяется тремя двоичными разрядами, а для 16-ричной четырьмя. При этом все ведущие нули обязательны, кроме самого старшего разряда.
При этом все ведущие нули обязательны, кроме самого старшего разряда.
Переведем в двоичную систему число 547 8 .
| 547 8 = | 101 | 100 | 111 |
| 5 | 4 | 7 |
Ещё одно, например 7D6A 16 .
| 7D6A 16 = | (0)111 | 1101 | 0110 | 1010 |
| 7 | D | 6 | A |
Переведем в 16-ричную систему число 7368. Сначала цифры запишем тройками, а потом поделим их на четверки с конца:
736 8 = 111 011 110 = 1 1101 1110 = 1DE 16
.
Переведем в 8-ричную систему число C25 16 . Сначала цифры запишем четвёрками, а потом поделим их на тройки с конца:
C25 16 = 1100 0010 0101 = 110 000 100 101 = 6045 8
.
Теперь рассмотрим перевод обратно в десятичную. Он труда не представляет, главное не ошибиться в расчётах. Раскладываем число на многочлен со степенями основания и коэффициентами при них. Потом всё умножаем и складываем.
E68 16 = 14 * 16 2 + 6 * 16 + 8 = 3688
.
732 8 = 7 * 8 2 + 3*8 + 2 = 474
.
Раскладываем число на многочлен со степенями основания и коэффициентами при них. Потом всё умножаем и складываем.
E68 16 = 14 * 16 2 + 6 * 16 + 8 = 3688
.
732 8 = 7 * 8 2 + 3*8 + 2 = 474
.
Перевод отрицательных чисел
Здесь нужно учесть, что число будет представлено в дополнительном коде. Для перевода числа в дополнительный код нужно знать конечный размер числа, то есть во что мы хотим его вписать — в байт, в два байта, в четыре. Старший разряд числа означает знак. Если там 0, то число положительное, если 1, то отрицательное. Слева число дополняется знаковым разрядом. Беззнаковые (unsigned) числа мы не рассматриваем, они всегда положительные, а старший разряд в них используется как информационный.
Для перевода отрицательного числа в двоичный дополнительный код нужно перевести положительное число в двоичную систему, потом поменять нули на единицы и единицы на нули. Затем прибавить к результату 1.
Итак, переведем число -79 в двоичную систему. Число займёт у нас один байт.
Переводим 79 в двоичную систему, 79 = 1001111. Дополним слева нулями до размера байта, 8 разрядов, получаем 01001111. Меняем 1 на 0 и 0 на 1. Получаем 10110000. К результату прибавляем 1, получаем ответ 10110001 . Попутно отвечаем на вопрос ЕГЭ «сколько единиц в двоичном представлении числа -79?». Ответ — 4.
Прибавление 1 к инверсии числа позволяет устранить разницу между представлениями +0 = 00000000 и -0 = 11111111. В дополнительном коде они будут записаны одинаково 00000000.
Перевод дробных чисел
Дробные числа переводятся способом, обратным делению целых чисел на основание, который мы рассмотрели в самом начале. То есть при помощи последовательного умножения на новое основание с собиранием целых частей. Полученные при умножении целые части собираются, но не участвуют в следующих операциях. Умножаются только дробные. Если исходное число больше 1, то целая и дробная части переводятся отдельно, потом склеиваются.
Переведем число 0,6752 в двоичную систему.
| 0 | ,6752 |
| *2 | |
| 1 | ,3504 |
| *2 | |
| 0 | ,7008 |
| *2 | |
| 1 | ,4016 |
| *2 | |
| 0 | ,8032 |
| *2 | |
| 1 | ,6064 |
| *2 | |
| 1 | ,2128 |
Процесс можно продолжать долго, пока не получим все нули в дробной части или будет достигнута требуемая точность. Остановимся пока на 6-м знаке.
Получается 0,6752 = 0,101011 .
Если число было 5,6752, то в двоичном виде оно будет 101,101011 .
Результат уже получен!
Системы счисления
Существуют позиционные и не позиционные системы счисления. Арабская система счисления, которым мы пользуемся в повседневной жизни, является позиционной, а римская − нет. В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:
В позиционных системах счисления позиция числа однозначно определяет величину числа. Рассмотрим это на примере числа 6372 в десятичном системе счисления. Пронумеруем это число справа налево начиная с нуля:
Тогда число 6372 можно представить в следующем виде:
6372=6000+300+70+2 =6·10 3 +3·10 2 +7·10 1 +2·10 0 .
Число 10 определяет систему счисления (в данном случае это 10). В качестве степеней взяты значения позиции данного числа.
Рассмотрим вещественное десятичное число 1287.923. Пронумеруем его начиная с нуля позиции числа от десятичной точки влево и вправо:
Тогда число 1287.923 можно представить в виде:
1287.923 =1000+200+80 +7+0.9+0.02+0.003 = 1·10 3 +2·10 2 +8·10 1 +7·10 0 +9·10 -1 +2·10 -2 +3·10 -3 .
В общем случае формулу можно представить в следующем виде:
Ц n ·s n +Ц n-1 ·s n-1 +…+Ц 1 ·s 1 +Ц 0 ·s 0 +Д -1 ·s -1 +Д -2 ·s -2 +…+Д -k ·s -k
где Ц n -целое число в позиции n
, Д -k — дробное число в позиции (-k), s
— система счисления.
Несколько слов о системах счисления.Число в десятичной системе счисления состоит из множества цифр {0,1,2,3,4,5,6,7,8,9}, в восьмеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7}, в двоичной системе счисления — из множества цифр {0,1}, в шестнадцатеричной системе счисления — из множества цифр {0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}, где A,B,C,D,E,F соответствуют числам 10,11,12,13,14,15.В таблице Таб.1 представлены числа в разных системах счисления.
| Таблица 1 | |||
|---|---|---|---|
| Система счисления | |||
| 10 | 2 | 8 | 16 |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E | 15 | 1111 | 17 | F |
Перевод чисел из одной системы счисления в другую
Для перевода чисел с одной системы счисления в другую, проще всего сначала перевести число в десятичную систему счисления, а затем, из десятичной системы счисления перевести в требуемую систему счисления.
Перевод чисел из любой системы счисления в десятичную систему счисления
С помощью формулы (1) можно перевести числа из любой системы счисления в десятичную систему счисления.
Пример 1. Переводить число 1011101.001 из двоичной системы счисления (СС) в десятичную СС. Решение:
1 ·2 6 +0 ·2 5 +1 ·2 4 +1 ·2 3 +1 ·2 2 +0 ·2 1 +1 ·2 0 +0 ·2 -1 +0 ·2 -2 +1 ·2 -3 =64+16+8+4+1+1/8=93.125
Пример 2. Переводить число 1011101.001 из восьмеричной системы счисления (СС) в десятичную СС. Решение:
Пример 3 . Переводить число AB572.CDF из шестнадцатеричной системы счисления в десятичную СС. Решение:
Здесь A -заменен на 10, B — на 11, C — на 12, F — на 15.
Перевод чисел из десятичной системы счисления в другую систему счисления
Для перевода чисел из десятичной системы счисления в другую систему счисления нужно переводить отдельно целую часть числа и дробную часть числа.
Целую часть числа переводится из десятичной СС в другую систему счисления — последовательным делением целой части числа на основание системы счисления (для двоичной СС — на 2, для 8-ичной СС — на 8, для 16-ичной — на 16 и т.д.) до получения целого остатка, меньше, чем основание СС.
Пример 4 . Переведем число 159 из десятичной СС в двоичную СС:
| 159 | 2 | ||||||
| 158 | 79 | 2 | |||||
| 1 | 78 | 39 | 2 | ||||
| 1 | 38 | 19 | 2 | ||||
| 1 | 18 | 9 | 2 | ||||
| 1 | 8 | 4 | 2 | ||||
| 1 | 4 | 2 | 2 | ||||
| 0 | 2 | 1 | |||||
| 0 |
Как видно из Рис. 1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111
. Следовательно можно записать:
1, число 159 при делении на 2 дает частное 79 и остаток 1. Далее число 79 при делении на 2 дает частное 39 и остаток 1 и т.д. В результате построив число из остатков деления (справа налево) получим число в двоичной СС: 10011111
. Следовательно можно записать:
159 10 =10011111 2 .
Пример 5 . Переведем число 615 из десятичной СС в восьмеричную СС.
| 615 | 8 | ||
| 608 | 76 | 8 | |
| 7 | 72 | 9 | 8 |
| 4 | 8 | 1 | |
| 1 |
При приведении числа из десятичной СС в восьмеричную СС, нужно последовательно делить число на 8, пока не получится целый остаток меньшее, чем 8. В результате построив число из остатков деления (справа налево) получим число в восьмеричной СС: 1147 (см. Рис. 2). Следовательно можно записать:
615 10 =1147 8 .
Пример 6 . Переведем число 19673 из десятичной системы счисления в шестнадцатеричную СС.
| 19673 | 16 | ||
| 19664 | 1229 | 16 | |
| 9 | 1216 | 76 | 16 |
| 13 | 64 | 4 | |
| 12 |
Как видно из рисунка Рис.3, последовательным делением числа 19673 на 16 получили остатки 4, 12, 13, 9. В шестнадцатеричной системе счисления числе 12 соответствует С, числе 13 — D. Следовательно наше шестнадцатеричное число — это 4CD9.
Для перевода правильных десятичных дробей (вещественное число с нулевой целой частью) в систему счисления с основанием s необходимо данное число последовательно умножить на s до тех пор, пока в дробной части не получится чистый нуль, или же не получим требуемое количество разрядов. Если при умножении получится число с целой частью, отличное от нуля, то эту целую часть не учитывать (они последовательно зачисливаются в результат).
Рассмотрим вышеизложенное на примерах.
Пример 7 . Переведем число 0.214 из десятичной системы счисления в двоичную СС.
| 0.214 | ||
| x | 2 | |
| 0 | 0.428 | |
| x | 2 | |
| 0 | 0.856 | |
| x | 2 | |
| 1 | 0.712 | |
| x | 2 | |
| 1 | 0.424 | |
| x | 2 | |
| 0 | 0.848 | |
| x | 2 | |
| 1 | 0.696 | |
| x | 2 | |
| 1 | 0.392 |
Как видно из Рис.4, число 0.214 последовательно умножается на 2. Если в результате умножения получится число с целой частью, отличное от нуля, то целая часть записывается отдельно (слева от числа), а число записывается с нулевой целой частью. Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011
.
Если же при умножении получиться число с нулевой целой частью, то слева от нее записывается нуль. Процесс умножения продолжается до тех пор, пока в дробной части не получится чистый нуль или же не получим требуемое количество разрядов. Записывая жирные числа (Рис.4) сверху вниз получим требуемое число в двоичной системе счисления: 0.0011011
.
Следовательно можно записать:
0.214 10 =0.0011011 2 .
Пример 8 . Переведем число 0.125 из десятичной системы счисления в двоичную СС.
| 0.125 | ||
| x | 2 | |
| 0 | 0.25 | |
| x | 2 | |
| 0 | 0.5 | |
| x | 2 | |
| 1 | 0.0 |
Для приведения числа 0.125 из десятичной СС в двоичную, данное число последовательно умножается на 2. В третьем этапе получилось 0. Следовательно, получился следующий результат:
В третьем этапе получилось 0. Следовательно, получился следующий результат:
0.125 10 =0.001 2 .
Пример 9 . Переведем число 0.214 из десятичной системы счисления в шестнадцатеричную СС.
| 0.214 | ||
| x | 16 | |
| 3 | 0.424 | |
| x | 16 | |
| 6 | 0.784 | |
| x | 16 | |
| 12 | 0.544 | |
| x | 16 | |
| 8 | 0.704 | |
| x | 16 | |
| 11 | 0.264 | |
| x | 16 | |
| 4 | 0.224 |
Следуя примерам 4 и 5 получаем числа 3, 6, 12, 8, 11, 4. Но в шестнадцатеричной СС числам 12 и 11 соответствуют числа C и B. Следовательно имеем:
Следовательно имеем:
0.214 10 =0.36C8B4 16 .
Пример 10 . Переведем число 0.512 из десятичной системы счисления в восьмеричную СС.
| 0.512 | ||
| x | 8 | |
| 4 | 0.096 | |
| x | 8 | |
| 0 | 0.768 | |
| x | 8 | |
| 6 | 0.144 | |
| x | 8 | |
| 1 | 0.152 | |
| x | 8 | |
| 1 | 0.216 | |
| x | 8 | |
| 1 | 0.728 |
Получили:
0.512 10 =0.406111 8 .
Пример
11
. Переведем число 159.125 из десятичной системы счисления в двоичную СС. Для этого переведем отдельно целую часть числа (Пример 4) и дробную часть числа (Пример 8).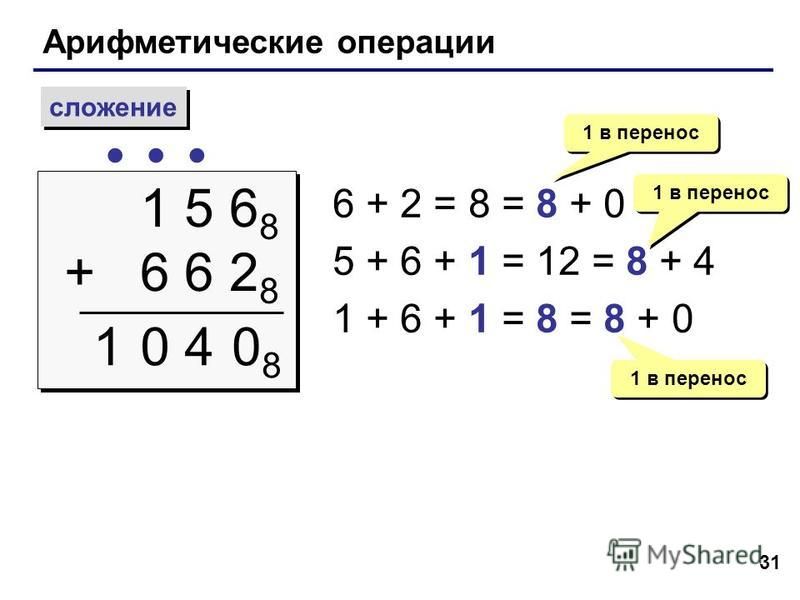 Далее объединяя эти результаты получим:
Далее объединяя эти результаты получим:
159.125 10 =10011111.001 2 .
Пример 12 . Переведем число 19673.214 из десятичной системы счисления в шестнадцатеричную СС. Для этого переведем отдельно целую часть числа (Пример 6) и дробную часть числа (Пример 9). Далее объединяя эти результаты получим.
При переводе чисел из десятичной системы счисления в любую другую, всегда отдельно (по разным правилам) переводится целая и дробная части.
Перевод целой части
Для того, чтобы перевести число из десятичной системы счисления, в любую другую, нужно выполнять целочисленное деление исходного числа на основание той системы счисления, в которую нужно перевести число. При этом важен остаток от деления и частное. Частное нужно делить на основание до тех пор, пока не останется 0. После этого все остатки нужно выписать в обратном порядке — это и будет число в новой системе счисления.
Например, перевод — числа 25 из десятичной системы счисления в двоичную будет выглядеть следующим образом:
Выписав остатки в обратном порядке, получим 25 10 =11001 2 .
Если Вы задумаетесь, то можете легко заметить, что при переводе абсолютно любого числа в двоичную систему счисления самый последний остаток (то есть, самая первая цифра в результате) всегда будет равен самому последнему частному, которое оказалось меньше основания той системы счисления, в которую мы переводим число. Поэтому, деление часто останавливают раньше, чем частное станет равным нулю — в тот момент, когда частное станет просто меньше основания. Например:
Перевод из десятичной системы счисления в любую другую систему счисления производится по абсолютно точно таким же правилам. Вот пример перевода 393 10 в шестнадцатеричную систему счисления:
Выписав остатки в обратном порядке, получим 393 10 =189 16 .
Нужно понимать, что остатки получаются в десятичной системе счисления. При делении на 16 могут появиться остатки не только от 0 до 9, но также и остатки от 10 до 15. Каждый остаток — это всегда ровно одна цифра в той системе счисления, в которую осуществляется перевод.
Например, если при переводе в шестнадцатеричную систему счисления Вы получили такие остатки (выписаны в порядке, как они должны быть записаны в числе): 10, 3, 15, 7, то в шестнадцатеричной системе счисления этой последовательности остатков будет соответствовать число A3F7 16 (некоторые по ошибке записывают число как 103157 16 — понято же, что это совсем другое число, и что если так делать, то получится, что ни в каком шестнадцатеричном числе не появится цифры от A до F).
Перевод дробной части
При переводе дробной части, в отличие от перевода целой части — нужно не делить, а умножать на основание той системы счисления, в которую мы переводим. При этом каждый раз отбрасываются целые части, а дробные части — снова умножаются. Собрав целые части в том порядке, как они были получены — получается дробная часть числа в нужной системе счисления.
Одна операция умножения даёт ровно один дополнительный знак в системе счисления, в которую осуществляется перевод.
При этом существует два условия завершения процесса:
1) в результате очередного умножения Вы получили ноль в дробной части. Понятно, что дальше этот ноль сколько ни умножай — он всё равно останется нулём. Это означает, что число перевелось из десятичной системы счисления в нужную точно.
Понятно, что дальше этот ноль сколько ни умножай — он всё равно останется нулём. Это означает, что число перевелось из десятичной системы счисления в нужную точно.
2) не все числа возможно перевести точно. В таком случае обычно переводят с некоторой точностью. При этом сначала определяют, сколько знаков после запятой будет нужно — именно такое количество раз и нужно будет выполнить операцию умножения.
Вот пример перевода числа 0.39 10 в двоичную систему счисления. Точность — 8 разрядов (в данном случае точность перевода выбрана произвольно):
Если выписать целые части в прямом порядке, то получим 0.39 10 =0.01100011 2 .
Самый первый ноль (на рисунке перечёркнут синим) выписывать не нужно — так как он относится не к дробной части, а к целой. Некоторые по ошибке записывают этот ноль после запятой, когда выписывают результат.
Вот так будет выглядеть перевод числа 0.39 10 в шестнадцатеричную систему счисления. Точность — 8 разрядов в данном случае точность снова выбрана произвольно:
Если выписать целые части в прямом порядке, то получим 0. 39 10 =0.63D700A3 16 .
39 10 =0.63D700A3 16 .
При этом Вы, наверное, заметили, что целые части при умножении получаются в десятичной системе счисления. Эти целые части, полученные при переводе дробной части числа следует интерпретировать точно так же, как и остатки при переводе целой части числа. То есть, если при переводе в шестнадцатеричную систему счисления целые части получились в таком порядке: 3, 13, 7, 10, то соответствующее число будет равно 0.3D7A 16 (а не 0.313710 16 , как некоторые иногда ошибочно записывают).
Перевод числа с целой и дробной частью
Чтобы выполнить перевод числа с целой и дробной частью, нужно отдельно перевести целую часть, а отдельно — дробную, и поэтом эти две части записать вместе.
Например, 25.39 10 =11001.01100011 2 (переводы целой и дробной части — смотрите выше).
Перевод небольших целых чисел из десятичной системы счисления в двоичную в уме
Поскольку при работе с различными системами счисления, особенно при разработке программ, очень часто возникает необходимость
перевода небольших целых чисел, то, вообще говоря, имеет смысл запомнить для первых 16 чисел (от 0 до 15).
Но если разобраться, как легко в уме переводить небольшие целые числа от 0 до 15 из десятичной системы счисления в двоичную, то значительную часть таблицы Вы сможете просто вычислять в уме каждый раз, когда это будет нужно. Проделывайте эту операцию много раз, и в какой-то момент Вы сами не сможете понять — Вы уже запомнили таблицу или всё ещё вычисляете.
Итак, чтобы перевести небольшое положительное целое число от 0 до 15 из десятичной системы счисления в двоичную, первое, что нужно понять — это что каждой позиции в двоичном числе соответствует степень двойки. При этом степени двойки для позиций от 0 до 3 запомнить очень просто — это числа 1, 2, 4 и 8:
А число 10 — это 2 плюс 8:
Ну а число 0 — грех не запомнить, так как, чтобы его получить, ничего не нужно складывать.
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней двойки:
Таблица 4. Степени числа 2
Степени числа 2
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 5. Степени числа 8
Пример. Число перевести в десятичную систему счисления.
3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 6. Степени числа 16
Пример. Число перевести в десятичную систему счисления.
4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в двоичную систему счисления.
5. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в шестнадцатеричную систему счисления.
7. Чтобы перевести число из двоичной системы в восьмеричную, его нужно разбить на триады (тройки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую триаду нулями, и каждую триаду заменить соответствующей восьмеричной цифрой (табл. 3).
3).
Пример. Число перевести в восьмеричную систему счисления.
8. Чтобы перевести число из двоичной системы в шестнадцатеричную, его нужно разбить на тетрады (четверки цифр), начиная с младшего разряда, в случае необходимости дополнив старшую тетраду нулями, и каждую тетраду заменить соответствующей восьмеричной цифрой (табл. 3).
Python | Операции с числами
Операции с числами
Последнее обновление: 20.06.2017
Арифметические операции
Python поддерживает все распространенные арифметические операции:
+
Сложение двух чисел:
print(6 + 2) # 8
—
Вычитание двух чисел:
print(6 - 2) # 4
*
Умножение двух чисел:
print(6 * 2) # 12
/
Деление двух чисел:
print(6 / 2) # 3.0
//
Целочисленное деление двух чисел:
print(7 / 2) # 3.
 5
print(7 // 2) # 3
5
print(7 // 2) # 3
Данная операция возвращает целочисленный результат деления, отбрасывая дробную часть
**
Возведение в степень:
print(6 ** 2) # Возводим число 6 в степень 2. Результат - 36
%
Получение остатка от деления:
print(7 % 2) # Получение остатка от деления числа 7 на 2. Результат - 1
В данном случае ближайшее число к 7, которое делится на 2 без остатка, это 6. Поэтому остаток от деления равен 7 — 6 = 1
При последовательном использовании нескольких арифметических операций их выполнение производится в соответствии с их приоритетом. В начале выполняются операции с большим приоритетом. Приоритеты операций в порядке убывания приведены в следующей таблице.
Операции | Направление |
** | Справо налево |
* / // % | Слева направо |
+ — | Слева направо |
Пусть у нас выполняется следующее выражение:
number = 3 + 4 * 5 ** 2 + 7 print(number) # 110
Здесь начале выполняется возведение в степень (5 ** 2) как операция с большим приоритетом, далее результат умножается на 4 (25 * 4), затем происходит сложение
(3 + 100) и далее опять идет сложение (103 + 7).
Чтобы переопределить порядок операций, можно использовать скобки:
number = (3 + 4) * (5 ** 2 + 7) print(number) # 224
Следует отметить, что в арифметических операциях могут принимать участие как целые, так и дробные числа. Если в одной операции участвует целое число (int) и число с плавающей точкой (float), то целое число приводится к типу float.
Арифметические операции с присвоением
Ряд специальных операций позволяют использовать присвоить результат операции первому операнду:
+=
Присвоение результата сложения
-=
Присвоение результата вычитания
*=
Присвоение результата умножения
/=
Присвоение результата от деления
//=
Присвоение результата целочисленного деления
**=
Присвоение степени числа
%=
Присвоение остатка от деления
Примеры операций:
number = 10 number += 5 print(number) # 15 number -= 3 print(number) # 12 number *= 4 print(number) # 48
Функции преобразования чисел
Ряд встроенных функций в Python позволяют работать с числами. В частности, функции int() и float()
позволяют привести значение к типу int и float соответственно.
В частности, функции int() и float()
позволяют привести значение к типу int и float соответственно.
Например, пусть у нас будет следующий код:
first_number = "2" second_number = 3 third_number = first_number + second_number
Мы ожидаем, что «2» + 3 будет равно 5. Однако этот код сгенерирует исключение, так как первое число на самом деле представляет строку. И чтобы все заработало как надо, необходимо привести строку к числу с помощью функции int():
first_number = "2" second_number = 3 third_number = int(first_number) + second_number print(third_number) # 5
Аналогичным образом действует функция float(), которая преобразует в число с плавающей точкой. Но вообще с дробными числами надо учитывать, что результат операций с ними может быть не совсем точным. Например:
first_number = 2.0001 second_number = 5 third_number = first_number / second_number print(third_number) # 0.40002000000000004
В данном случае мы ожидаем получить число 0.40002, однако в конце через ряд нулей появляется еще какая-то четверка. Или еще одно выражение:
print(2.0001 + 0.1) # 2.1001000000000003
В этот случае для округления результата мы можем использовать функцию round():
first_number = 2.0001 second_number = 0.1 third_number = first_number + second_number print(round(third_number, 4)) # 2.1001
Первый параметр функции — округляемое число, а второй — сколько знаков после запятой должно содержать получаемое число.
Представление числа
При обычном определении числовой переменной она получает значение в десятичной системе. Но кроме десятичной в Python мы можем использовать двоичную, восьмеричную и шестнадцатеричную системы.
Для определения числа в двоичной системе перед его значением ставится 0 и префикс b:
x = 0b101 # 101 в двоичной системе равно 5
Для определения числа в восьмеричной системе перед его значением ставится 0 и префикс o:
a = 0o11 # 11 в восьмеричной системе равно 9
Для определения числа в шестнадцатеричной системе перед его значением ставится 0 и префикс x:
y = 0x0a # a в шестнадцатеричной системе равно 10
И с числами в других системах измерения также можно проводить арифметические операции:
x = 0b101 # 5
y = 0x0a # 10
z = x + y # 15
print("{0} in binary {0:08b} in hex {0:02x} in octal {0:02o}". format(z))
format(z))
Для вывода числа в различных системах исчисления используются функция format, которая вызывается у строки. В эту строку передаются различные форматы. Для двоичной системы «{0:08b}», где число 8 указывает, сколько знаков должно быть в записи числа. Если знаков указано больше, чем требуется для числа, то ненужные позиции заполняются нулями. Для шестнадцатеричной системы применяется формат «{0:02x}». И здесь все аналогично — запись числа состоит из двух знаков, если один знак не нужен, то вместо него вставляется ноль. А для записи в восьмеричной системе испольуется формат «{0:02o}».
Результат работы скрипта:
15 in binary 00001111 in hex 0f in octal 17
Восьмеричная система счисления
СИСТЕМА Восьмеричных чисел
Восьмеричная система счисления, или система счисления с основанием 8, широко используется в компьютерах. Потому что
его связь с двоичной системой, это полезно при программировании некоторых типов
компьютеры.
Внимательно посмотрите на сравнение двоичной и восьмеричной систем счисления в таблице 1-3. Ты сможешь видите, что одна восьмеричная цифра эквивалентна трем двоичным цифрам.Следующее примеры преобразования восьмеричного числа 225 8 в двоичное и обратно далее проиллюстрируйте это сравнение:
Таблица 1-3. — Двоичное и восьмеричное сравнение
Блок и номер
Термины, которые вы выучили в десятичной и двоичной части, также используются с восьмеричная система.
Единица остается единым объектом, а число остается символом, используемым для обозначения один или несколько единиц.
Основание (основание)
Как и в других системах, основание — это количество символов, используемых в
система. В восьмеричной системе используются восемь символов — от 0 до 7. Основание или основание системы счисления — это
обозначается нижним индексом 8.
Позиционное обозначение
Восьмеричная система счисления — это позиционная система счисления. Так же, как десятичный система использует степень 10, а двоичная система использует степень 2, восьмеричная система использует степень 8 для определения значения позиции числа.Следующая гистограмма показывает позиции и мощность базы:
Помните, что степень или экспонента указывает, сколько раз основание умножается на себя. Значение этого умножения выражается в базе 10, как показано ниже:
Все числа слева от точки счисления являются целыми числами, а числа справа дробные числа.
MSD и LSD
При определении старших и младших цифр восьмеричного числа используйте те же
правила, которые вы использовали с другими системами счисления. Крайняя слева цифра от
Точка счисления — это MSD, а крайняя правая точка от точки счисления — это LSD.
Пример:
Если число является целым числом, MSD — это ненулевая цифра, крайняя слева от точка счисления, а LSD — это цифра слева от точки счисления.И наоборот, если число является только дробью, ненулевая цифра, ближайшая к точке счисления — это MSD, а LSD — это ненулевая цифра, крайняя справа от точки системы счисления.
Сложение восьмеричных чисел
Сложить восьмеричные числа несложно, если вы помните, что в любое время сумма двух цифр превышает 7, производится перенос. Сравните два примера, показанных ниже:
Таблица восьмеричного сложения в таблице 1-4 будет вам полезна, пока вы привык складывать восьмеричные числа.Чтобы использовать таблицу, просто следуйте инструкциям, приведенным в этот пример:
Добавьте: 6 8 и 5 8
Таблица 1-4. — Таблица восьмеричного сложения
Найдите цифру 6 в столбце X на рисунке. Затем найдите 5 в Y
столбец. Точка в области Z , где пересекаются эти два столбца, является суммой.
Следовательно,
Затем найдите 5 в Y
столбец. Точка в области Z , где пересекаются эти два столбца, является суммой.
Следовательно,
Если вы используете концепции сложения, которые вы уже изучили, вы готовы добавить восьмеричные числа.
Проработайте решения следующих проблем:
Как упоминалось ранее в этом разделе, каждый раз сумма столбца чисел превышает 7, производится перенос. Может быть произведено более одного переноски, если их три или нужно добавить дополнительные числа, как в этом примере:
Сумма возрастающего и первого слагаемых составляет 6 8 с переносом.Сумма 6 8 а второе слагаемое — 5 8 с переносом. Вы должны записать 5 8 и сложите два переноса и уменьшите их до суммы, как показано ниже:
Теперь попробуем несколько практических задач:
Q. 24 Добавить:
24 Добавить:
Q.25 Добавить:
Q.26 Добавить:
Q.27 Добавить:
Q.28 Добавить:
Q.29 Добавить:
Работа с восьмеричным Octal в языке программирования C
Домой » Язык программирования C
Восьмеричное значение имеет 8-значные значения от 0 до 7, с основанием 8. (Подробнее о компьютерных системах счисления), здесь мы узнаем , как работать с восьмеричными значениями на языке программирования c?
Представление восьмеричных чисел в программировании на C
В языке программирования C восьмеричное число представлено предшествующим числом «0» , таким образом, восьмеричное число может быть записано как «0123» (что эквивалентно 83 в десятичном формате ).
Присвоение восьмеричного числа в переменной
В программировании на C нет специального типа данных для хранения восьмеричных значений, восьмеричное число — это целочисленное значение , и вы можете сохранить его в целочисленном типе типов данных (char, short или int).
Предположим, у нас есть значение в восьмеричном формате «0123» (83 в десятичном формате).
Мы сохраняем «0123» в переменной типа unsigned char (83 — это небольшое значение, которое может храниться в байтах).
Рассмотрим следующие утверждения
беззнаковый символ a = 0123;
Печать числа в восьмеричном формате
Чтобы напечатать целое число в восьмеричном формате, «% o» используется в качестве спецификатора формата в операторе printf ().
Рассмотрим код, который печатает значение a …
#includeint main () { беззнаковый символ a = 0123; printf ("значение a (в восьмеричном формате):% o \ n", a); printf ("значение a (в десятичной системе):% d \ n", a); возврат 0; }
Выход
значение a (в восьмеричном формате): 123
значение a (в десятичной системе): 83
Чтение значения в восьмеричном формате
«% o» можно использовать с оператором scanf () для чтения значения в восьмеричном формате от пользователя.
Рассмотрим следующий код
#includeint main () { беззнаковое целое число; printf ("Ввести восьмеричное значение:"); scanf ("% o", & num); printf ("Введено значение в восьмеричном формате:% o \ n", num); printf ("Введено значение в десятичном формате:% d \ n", число); возврат 0; }
Выход
Вводное значение в восьмеричном формате: 12345
Введено значение в восьмеричном формате: 12345.
Введено значение в десятичном формате: 5349
Объявление целочисленного массива путем присвоения восьмеричных значений
Рассмотрим следующий пример, где целочисленный массив объявляется с восьмеричными значениями и печатается в обоих форматах: Decimal и Octal.
#includeint main () { int arr [] = {0100, 0101, 0123, 0761, 10}; int i; printf ("Элементы массива \ n"); для (я = 0; я <5; я ++) printf ("Десятичное:% d, Восьмеричное:% o \ n", arr [i], arr [i]); возврат 0; }
Выход
Элементы массива
Десятичный: 64, восьмеричный: 100
Десятичный: 65, восьмеричный: 101
Десятичный: 83, восьмеричный: 123
Десятичный: 497, восьмеричный: 761
Десятичный: 10, восьмеричный: 12
Подробнее. ..
..
ОБЪЯВЛЕНИЕ
ОБЪЯВЛЕНИЕ
десятичных, двоичных, восьмеричных, шестнадцатеричных чисел!
Обзор
- Почему?
- Десятичное
- Двоичное
- Восьмеричное
- Шестнадцатеричное
- Преобразования!
- Математика!
Почему?
Знание того, как информация используется и кодируется, очень полезно при отладке и сжатии информации.0) = 458 в десятичном формате
Восьмеричные значения более компактны, чем двоичные, поэтому часто использовались вместо них. Сегодня большинство значений представлены в шестнадцатеричном формате для еще большей компактности данных.
Шестнадцатеричный
Каждая цифра может быть одним из 16 значений (следовательно, шестнадцатеричным): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E или F, где A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.
Каждый раз, когда мы добавляем цифру, мы умножаем эту цифру на значение 16 и складываем его. 0) = 43981 в десятичной системе счисления
0) = 43981 в десятичной системе счисления
Конверсии!
Пример:
123 = 0b1111011 = 0o173 = 0x7B
Десятичное в двоичное и двоичное в десятичное
Начните с наибольшей степени 2, которую вы можете, от десятичного значения, которое равно или меньше этого значения, здесь значение равно 64, так что у нас есть один в этом месте: 0b1000000. Затем мы проверяем, какое значение осталось представить: 123 - 64 = 59. Следующее снижение мощности - 32, поэтому мы добавляем единицу в этом месте и получаем: 0b100000. Мы продолжаем это, пока не представим значение 123.Затем мы складываем все эти значения вместе. В итоге должно получиться 0b1111011 = 0b1000000 + 0b100000 + 0b10000 + 0b10000 + 0b1000 + 0b10 + 0b1. Для фактического использования просто сложите цифры вместе и поставьте ноль везде, где вы не можете использовать степень 2.
Чтобы перейти от двоичного к десятичному, мы будем использовать наш процесс, описанный ранее.
Двоичное в восьмеричное и восьмеричное в двоичное
Если мы посмотрим на пример, мы можем заметить, что если мы префикс нули до тех пор, пока количество двоичных цифр не делится на 3 (здесь 00 1111011), затем сгруппируем двоичные цифры в группы по 3 (2 ^ 3 = 8). 4 = 16) вместо этого. Мы получим следующие группы: 0111, 1011
4 = 16) вместо этого. Мы получим следующие группы: 0111, 1011
Если мы сможем преобразовать каждую группу в шестнадцатеричные значения и получить: 7, B! Шестнадцатеричный! Мы также можем распознать, как и с восьмеричным числом, что 0111 = 7 и 1011 = B. Со временем вы сможете распознавать закономерности, а не преобразовывать значения.
Краткие справки
Краткий справочник по двоично-восьмеричным числам
0b0 = 0o0
0b1 = 0o1
0b10 = 0o2
0b11 = 0o3
0b100 = 0o4
0b101 = 0o5
0b110 = 0o6
0b111 = 0o24binary 00002 0x07
0b10 = 0x2
0b11 = 0x3
0b100 = 0x4
0b101 = 0x5
0b110 = 0x6
0b111 = 0x7
0b1000 = 0x8
0b1001 = 0x9
b 0x11 0x11 0x2400 = 0x9 0xD
0b1110 = 0xE
0b1111 = 0xF
Удобный конвертер можно найти здесь из RapidTables: https: // www.rapidtables.com/convert/number/index.html
Математика! (Прямо как десятичный!)
Сложение и вычитание
Двоичное
0b0101 + 0b1010 = 0b1111
5 + 10 = 15
0b01 + 0b01 = 0b10
1 + 1 = 2
0b1010 - 0b0101 = 0b0101
10 - 516o000 0
43 + 5
4o000 = 0o30
10 + 14 = 24
0o71 - 0o32 = 0o37
57-26 = 31
Умножение и деление
Двоичное
0b10 * 0b100 = 0b1000
2 * 4 = 8
0b01111 / 0101
= 0 / 3 = 5
Связанные
Radix и дополнение с уменьшенным Radix в цифровой электронике
Чаще всего используются дополнения до единиц, двоек, девяток и десяти. Помимо этих дополнений, есть еще много дополнений, с которыми в большинстве своем люди не знакомы. Для нахождения вычитания в системе счисления используются дополнения. Если r является основанием системы счисления, тогда возможны два типа дополнений, то есть r и (r-1). Мы можем найти дополнение числа r и дополнение числа (r-1), здесь r - основание системы счисления. Дополнение r также известно как дополнение к корню , дополнение (r-1), дополнение к корню с уменьшенным основанием .
Помимо этих дополнений, есть еще много дополнений, с которыми в большинстве своем люди не знакомы. Для нахождения вычитания в системе счисления используются дополнения. Если r является основанием системы счисления, тогда возможны два типа дополнений, то есть r и (r-1). Мы можем найти дополнение числа r и дополнение числа (r-1), здесь r - основание системы счисления. Дополнение r также известно как дополнение к корню , дополнение (r-1), дополнение к корню с уменьшенным основанием .
Если основание числа равно 2, то мы можем найти дополнение числа до 1 и 2. Точно так же, если число является восьмеричным числом, мы можем найти его дополнение к 7 и 8.
Существует следующая формула для нахождения дополнений r и (r-1):
r 's = дополнение = (r n ) 10 -N
(r-1) дополнение = {(r n ) 10 -1} -N
В приведенных выше формулах
- n - количество цифр в номере.

- N - заданное число.
- r - основание или основание числа.
Преимущества дополнения r's
Это следующие преимущества использования дополнения r:
- В дополнении r мы можем дополнительно использовать существующую схему сложения, что означает отсутствие специальной схемы.
- Нет необходимости определять, больше ли значение minuend и subtrahend, потому что результат автоматически имеет правильный знак.
- Отрицательные нули удаляются дополнением к r.
Давайте рассмотрим несколько примеров, чтобы понять, как мы можем вычислить дополнение r и (r-1) к двоичным, десятичным, восьмеричным и шестнадцатеричным числам.
Пример 1: (1011000) 2
Это число имеет основание 2, что означает, что это двоичное число. Итак, для двоичных чисел значение r равно 2, а r-1 равно 2-1 = 1. Итак, мы можем вычислить дополнение числа до 1 и 2.
Дополнение до 1 числа 1011000 рассчитывается как
.
= {(2 7 ) 10 -1} - (1011000) 2
= {(128) 10 -1} - (1011000) 2
= {(127) 10 } - (1011000) 2
= 1111111 2 -1011000 2
= 0100111
Дополнение до 2 числа 1011000 рассчитывается как
. = (2 7 ) 10 - (1011000) 2
= (128) 10 - (1011000) 2
= 10000000 2 -1011000 2
= 01010008
Пример 2: (155) 10
Это число имеет основание 10, что означает, что это десятичное число.Итак, для десятичных чисел значение r равно 10, а r-1 равно 10-1 = 9. Итак, мы можем вычислить дополнение числа до 10 и 9.
Дополнение до 9 числа 155 рассчитывается следующим образом:
= {(10 3 ) 10 -1} - (155) 10
= (1000-1) -155
= 999-155
= (844) 10
Дополнение до 10 числа 1011000 рассчитывается как
.
= (10 3 ) 10 - (155 10
= 1000-155
= (845) 10
Пример 3: (172) 8
Это число имеет основание 8, что означает, что это восьмеричное число.Итак, для восьмеричных чисел значение r равно 8, а r-1 равно 8-1 = 7. Итак, мы можем вычислить дополнение числа до 8 и 7.
Дополнение до 7 числа 172 рассчитывается как
. = {(8 3 ) 10 -1} - (172) 8
= ((512) 10 -1) - (132) 8
= (511) 10 - (122) 10
= (389) 10
= (605) 8
Дополнение числа 172 до 8 рассчитывается как:
= (8 3 ) 10 - (172) 8
= (512) 10 -172 8
= 512 10 -122 10
= 390 10
= 606 8
Пример 4: (F9) 16
Это число имеет основание 16, что означает, что это шестнадцатеричное число. Итак, для шестнадцатеричных чисел значение r равно 16, а r-1 равно 16-1 = 15. Итак, мы можем вычислить дополнение числа до 16 и 15.
Итак, для шестнадцатеричных чисел значение r равно 16, а r-1 равно 16-1 = 15. Итак, мы можем вычислить дополнение числа до 16 и 15.
Дополнение до 15 числа F9 рассчитывается как:
{(16 2 ) 10 -1} - (F9) 16
(256-1) 10 -F9 16
255 10 -249 10
(6) 10
(6) 16
Дополнение до 16 числа F9 рассчитывается как:
{(16 2 ) 10 } - (F9) 16
256 10 -249 10
(7) 10
(7) 16
Восьмеричная система счисления
- Определение и преобразование
Под названием «Восьмеричная система счисления» мы можем понять, что это разновидность системы счисления.Итак, прежде чем мы узнаем восьмеричную систему счисления, позвольте нам сначала узнать, что такое система счисления? Система счисления, также известная как система счисления, представляет собой систему именования, представления или выражения чисел. В математике мы можем называть или представлять числа в различных формах. Четыре основных способа представления чисел - это двоичная система счисления, десятичная система счисления, шестнадцатеричная система счисления и восьмеричная система счисления. Теперь дайте нам знать все концепции системы счисления вместе с их типами, преобразованиями и примерами.
В математике мы можем называть или представлять числа в различных формах. Четыре основных способа представления чисел - это двоичная система счисления, десятичная система счисления, шестнадцатеричная система счисления и восьмеричная система счисления. Теперь дайте нам знать все концепции системы счисления вместе с их типами, преобразованиями и примерами.
Что такое система счисления?
Система счисления - это способ или система письма, которые мы используем для выражения чисел. Это математическое обозначение, используемое для представления чисел данного набора с использованием цифр или других символов в логической манере. Система счисления позволяет нам представить каждое число уникальным образом. Он представляет собой арифметическую и алгебраическую структуру фигур. Не только это, но также позволяет нам выполнять арифметические операции, такие как сложение, вычитание и деление.
Значение цифры в числе обычно определяется:
Типы систем счисления
В математике мы можем представлять числа в различных типах, но четыре основные системы счисления:
-
Десятичная система счисления (Base- 10)
-
Двоичная система счисления (Base- 2)
-
Восьмеричная система счисления (Base-8)
-
Шестнадцатеричная система счисления (Base- 16)
Восьмеричное число Система
Восьмеричная система счисления - это система с основанием восемь и числа от 0 до 7. Это одна из классификаций систем счисления, помимо двоичных чисел, десятичных и шестнадцатеричных чисел. Символ восьмеричного числа используется для обозначения чисел с основанием 8. Существуют различные применения и важность восьмеричных чисел. Одно из наиболее распространенных его применений - основы работы с компьютером. Мы можем преобразовать восьмеричные числа в десятичные числа, двоичные числа в восьмеричные числа, где нам сначала нужно преобразовать двоичное число в десятичное число, а десятичное число в восьмеричное число.Итак, давайте сначала обсудим восьмеричное число с его определением, таблицей, примером и применением.
Это одна из классификаций систем счисления, помимо двоичных чисел, десятичных и шестнадцатеричных чисел. Символ восьмеричного числа используется для обозначения чисел с основанием 8. Существуют различные применения и важность восьмеричных чисел. Одно из наиболее распространенных его применений - основы работы с компьютером. Мы можем преобразовать восьмеричные числа в десятичные числа, двоичные числа в восьмеричные числа, где нам сначала нужно преобразовать двоичное число в десятичное число, а десятичное число в восьмеричное число.Итак, давайте сначала обсудим восьмеричное число с его определением, таблицей, примером и применением.
Что такое восьмеричная система счисления?
Система счисления с основанием «восемь» известна как восьмеричная система счисления и использует числа от 0 до 7, то есть 0, 1, 2, 3, 4, 5, 6 и 7. Мы можем взять пример , чтобы лучше понять концепцию. Как мы уже знаем, любое число с основанием 8 называется восьмеричным числом, например \ [24_ {8} \], \ [109_ {8} \], \ [55_ {8} \] и т. Д.
Д.
Просто как восьмеричные числа представлены с основанием 8, таким же образом двоичное число представлено с основанием 2, десятичное число с основанием 10, а шестнадцатеричное число представлено с основанием 16.{-3} \] ...… и т. Д.
↑
Восьмеричная точка
Чтобы преобразовать восьмеричное число в двоичное, преобразование должно выполняться путем преобразования каждого числа из восьмеричной цифры в двоичную. Каждую цифру необходимо преобразовать в 3-битное двоичное число, и результат будет двоичным эквивалентом восьмеричного числа.
Преобразование из восьмеричного в двоичное
| Восьмеричный символ | Двоичный эквивалент |
| 0 | 8 000 |
| 2 | 010 |
| 3 | 011 |
| 4 | 9704 101 |
| 6 | 110 |
| 7 | 111 |
Пример 1) Преобразовать \ [(8} \.
Решение 1) Чтобы преобразовать восьмеричное в двоичное и наоборот, нам понадобится эта таблица преобразования. Согласно таблице восьмеричное значение \ [(145056) _ {8} \] может быть преобразовано в двоичное как
\ [(001 \: 100 \: 101 \:. 101 \: 110) _ {2} \ ]
Преобразование двоичного числа в восьмеричное
Мы можем использовать ту же таблицу для преобразования двоичного числа в восьмеричное. И для этого мы сначала должны сгруппировать двоичное число в группу из трех битов и записать его восьмеричный эквивалент.
Пример 2) Преобразование двоичного числа \ [(11001111) _ {2} \] в восьмеричное
Решение 2) Трехбитовая группа двоичных чисел может быть записана как 011 001 111, потому что мы должны добавить ноль перед каждым числом, чтобы завершите группировку в виде трех двоичных цифр.Следовательно, восьмеричные числа будут 3, 1, 7, т. Е. \ [(317) _ {8} \]
Преобразование восьмеричного числа в десятичное
Метод, который мы используем для преобразования восьмеричного числа в его десятичный эквивалент, чрезвычайно просто. {0} \] = 207
{0} \] = 207
Преобразование десятичного числа в восьмеричное
Мы можем преобразовать число из десятичного в восьмеричное, разделив число на 8, используя повторное деление метод, который обычно известен как метод двойного прикосновения.Делаем повторное деление и находим остаток. Вот пример.
Пример 4) Преобразуйте десятичное число 158 в восьмеричное.
Решение 4) Мы должны разделить число 158 на 8 следующим образом:
Изображение будет загружено в ближайшее время
Следовательно, в восьмеричном формате значение будет \ [236_ {8} \]
Восьмеричные числа Восьмеричное. Преобразование десятичных чисел в двоично-десятичное Цифровая логика Проектирование Электроника
CS302 - Цифровая логика и дизайн
Урок Нет.04
НОМЕР СИСТЕМЫ И КОДЫ
восьмеричный Номера
восьмеричный Система счисления также предоставляет удобный способ представить длинная строка двоичного кода
номера. Восьмеричное число - это основание 8
система счисления с цифрами
от 0 до 7.
Восьмеричный
Восьмеричное число - это основание 8
система счисления с цифрами
от 0 до 7.
Восьмеричный
система преобладала в более ранние цифровые системы и не используется в современных цифровой
систем особенно когда Доступно шестнадцатеричное число.Каждая цифра восьмеричного числа банка
представляют собой 3-битное двоичное число. В Двоичные числа и Перечислены восьмеричные эквиваленты в
Стол 4,1
Десятичное
двоичный
восьмеричное
0
000
0
1
001
1
2
010
2
3
011
3
4
100
4
5
101
5
6
110
6
7
111
7
Стол 4.1
восьмеричный Эквиваленты десятичного и Двоичные числа
Подсчет Восьмеричное число Система
Подсчет
Octal похож на подсчет в
любая другая система счисления. Максимум
Максимум
значение представлен одним восьмеричным цифра 7. Для представления большие значения комбинация из
два или должно быть больше восьмеричных цифр использовал.Таким образом, десятичная 8 равна представлены комбинацией
108. Нижний индекс 8 указывает число - восьмеричное 10 и не десятичный десятичный. В Восьмеричные числа
для Десятичные числа от 8 до 30 являются перечислено в таблице 4.2
Десятичное
восьмеричное
Десятичное
восьмеричное
Десятичное
восьмеричное
8
10
16
20
24
30
9
11
17
21
25
31
10
12
18
22
26
32
11
13
19
23
27
33
12
14
20
24
28
34
13
15
21
25
29
35
14
16
22
26
30
36
15
17
23
27
31
37
Стол
4. 2
2
Подсчет с использованием восьмеричных чисел
Двоичный в Восьмеричное преобразование
Преобразование Из двоичного в восьмеричное - это очень просто. Двоичная строка разделен на малые
группы 3 бита, начиная с младший значащий бит. Каждый 3-битная двоичная группа заменен на его
восьмеричный эквивалент.
111010110101110010110
двоичный Число
111 010 110 101 110 010110 Делится на группы из 3-х битов
7 2 6 5 6 2 6
Замена каждая группа своим восьмеричным числом эквивалент
Таким образом 111010110101110010110 представлен в Восьмеричный по 7265626
31
CS302 - Цифровая логика и дизайн
двоичный струны, которые не могут быть точно разделен на целое количество 3-битных групп
предполагается
добавить 0 в
наиболее значимые биты для
завершить группу.
1101100000110
двоичный Число
1 101 100 000 110
Разделение на группы по 3 бита
001 101 100 000 110
Добавление три нуля, чтобы завершить группа
1 5 4 0 6
Замена каждая группа своим восьмеричным числом эквивалент
Восьмеричный к Двоичное преобразование
Преобразование из восьмеричного обратно в двоичный тоже очень просто.Каждый цифра восьмеричной
Номерзаменен эквивалентным двоичным строка из 3 бит
1726
восьмеричный Число
001 111 010 110
Замена каждая восьмеричная цифра своим 3-битный двоичный эквивалент
От десятичного до Восьмеричное преобразование
Там два метода преобразования от десятичного до восьмеричного.В первый метод -
Косвенный Метод и второй метод повторяется Метод деления.
1. Косвенный
Метод
Косвенный
Метод
десятичный число может быть преобразовано в его восьмеричный эквивалент косвенно первыми
конвертация десятичное число в его двоичный эквивалент и затем преобразование двоичного к
Восьмеричный.
2. Повторно Метод деления на 8
Метод повторного деления имеет обсуждалось ранее и используется для преобразования
десятичный Числа в двоичные и Шестнадцатеричный путем многократного деления десятичное число 2
и 16 соответственно. Десятичное число можно напрямую преобразовать в восьмеричный с помощью повторяется
дивизия.Десятичное число делится на 8 (основание значение восьмеричного номер
).
преобразование десятичного числа 2075 в Восьмеричный с использованием Repeated Метод деления на 8 -
показано на Таблица 4.3. Восьмеричный эквивалент 207510 составляет 40338.
Номер
Частное после деления
Остаток после деления
2075
259
3
259
32
3
8
4
0
4
0
4
Стол
4. 3
3
восьмеричный Эквивалент десятичных чисел с использованием повторного Дивизион
Восьмеричный к Десятичное преобразование
Преобразование Преобразование восьмеричных чисел в десятичное выполняется двумя способами. Первый метод -
г. Косвенный метод и Второй метод - это Метод суммы весов.
1. Косвенный Метод
косвенный метод конвертации Восьмеричное число в десятичное номер должен быть первым конвертировать
восьмеричный число в двоичное, а затем Двоичное в десятичное.
32
CS302 - Цифровая логика и дизайн
2. Сумма весов Метод
Восьмеричный номер может быть напрямую преобразовано в десятичное число используя сумму вес
метод. Шаги преобразования с использованием метод суммы весов показаны.
4033
восьмеричный номер
4 х 83 + 0 х 82 + 3 х 81 + 3 х 80
Письмо число в выражение
(4 х 512) + (0 х 64) + (3 х 8) + (3 х 1)
2048 + 0 + 24 + 3
Суммирование Вес
2075
десятичный эквивалент
восьмеричный Дополнение и Вычитание
номеров в восьмеричном формате может быть добавлено и вычтено напрямую, не имея к
конвертировать
их в десятичные или двоичные
эквиваленты. Правила
Сложение и вычитание
то есть
Правила
Сложение и вычитание
то есть
раньше складывать и вычитать числа в Десятичное или двоичное число системы применяются к Восьмеричный
Дополнение и вычитание. Восьмеричный Сложение и вычитание позволяет использовать большие двоичные числа быть
быстро добавлено и вычтено.
1. Восьмеричный Дополнение
Перенести
1
Номер 1
7
6
0
2
Номер 2
5
7
7
1
Сумма
1
5
5
7
3
3.Восьмеричный Вычитание
Заем
1
1
Номер 1
7
6
0
2
Номер 2
5
7
7
1
Разница
1
6
1
1
Рабочий с разными двоичными представительства
Там
разные способы
представление чисел в двоичном формате. Четыре способа
представляющие
Четыре способа
представляющие
двоичный числа уже были обсуждали.
Без знака двоичный
Знаковая величина форма
2-х Форма дополнения
Плавающий точечное обозначение
разные представления помогают в обработка номеров. За пример 2
дополнение основанные на числах со знаком помогают в обработка положительных и отрицательные числа.Плавающий
балла обозначения помогают в обращении числа, имеющие целое число и дробная часть. Цифровой системы
в целом разрешить обработку нескольких значения данных, которые того же типа. За Например, один
Номерпредставлен с использованием беззнакового двоичный файл не может использоваться для выполнять арифметические действия операции
с другое число представлено используя знаковые обозначения.Поэтому перед цифровым система как
компьютер способен обрабатывать данные, которые у него есть быть прямо проинформированным типы данных и
манера в
которыми они были
представлен в
машина.
Когда компьютерные программы написано, как правило, в качестве первого шаг программы разные
переменных и их типы данных объявлены и определены.Во время выполнения программы когда-либо
конкретный переменная доступна через Компьютер это знает точно тип данных и тип
операций что может быть выполнено на Это.
33
CS302 - Цифровая логика и дизайн
Альтернативный формы двоичных представительства
Там есть много разных способов представляют собой двоичные числа, кроме 4
представительство что мы обсуждали.Многие из эти альтернативные представления используются для
поддержка конкретные приложения и требования. Предвзятый код или Используется лишний код по
плавающий номера точек для представления положительный и отрицательный значения экспоненты.
Во многих приложения, в которых Digital Системы используются, Цифровые системы взаимодействовать
с
реальный мир. За
например, цифровой контроллер
управляет двигателем, который
позиции солнечной
За
например, цифровой контроллер
управляет двигателем, который
позиции солнечной
панель к указывать на солнце, чтобы извлечь максимум солнечной энергии энергия. Контроллеру требуется к
точно знать угол, под которым панель указывает; это может быть определено
позиция вал двигателя в отношении некоторых ориентир.Вал позиция имеет
для кодирования в какой-то подходящий формат, чтобы иметь использовать к контроллеру. А датчик вала на основе на
г. Код Грея используется для чтения угловое положение вал двигателя.
угловое положение вал двигателя может отображаться на 7-сегментном дисплее панель
в пересчете на Десятичные числа.Код BCD используется для отображения десятичной дроби цифры на 7 сегменте
Дисплей Панели.
The Дополнительный код
Рассмотреть
диапазон десятичных чисел +7
до -8. Эти положительные и
отрицательное десятичное число
Эти положительные и
отрицательное десятичное число
номера может быть представлен 2-дополнительное представление. Величина положительный
и отрицательные числа не могут быть легко сравнить как положительный и отрицательный числа
представлены в Форма дополнения 2 не представлен на единообразном увеличивающийся масштаб.
диапазон десятичных чисел от +7 до -8 представлен с использованием Excess-8 код, который
назначает 0000 до -8 наименьшее число в диапазоне от 1111 до +7 самое большое число в
ассортимент. Код Excess-8 можно получить добавление числа к наименьшее число -8 в диапазон
таких что результат нулевой. Цифра 8.Номер 8 добавляется ко всем оставшиеся
десятичный числа от -7 до наивысший номер +7. В Превышение-8 представлено представлено
в таблице 4.4.
Десятичное
2-х
Превышение-8
Десятичное
2-х
Превышение-8
Дополнение
Дополнение
0
0000
1000
-8
1000
0000
1
0001
1001
-7
1001
0001
2
0010
1010
-6
1010
0010
3
0011
1011
-5
1011
0011
4
0100
1100
-4
1100
0100
5
0101
1101
-3
1101
0101
6
0110
1110
–2
1110
0110
7
0111
1111
–1
1111
0111
Рисунок
4. 4
4
Превышение-8 Код Представление десятичной дроби числа в диапазоне от 7 до -8
The Код BCD
двоичный Кодированный десятичный (BCD) код: используется для представления десятичной дроби цифры в двоичном формате. BCD
Код- это 4-битный двоичный код; в первые 10 комбинаций представляют десятичные цифры от 0 до 9.
34
CS302 - Цифровая логика и дизайн
Осталосьшесть 4-битных комбинаций 1010, 1011, 1100, 1101, 1110 и 1111 считаются быть
недействительно и не существует.
BCD-код, представляющий десятичные цифры от 0 до 9 показаны в Таблица 4.4
Десятичное
BCD
Десятичное
BCD
0
0000
5
0101
1
0001
6
0110
2
0010
7
0111
3
0011
8
1000
4
0100
9
1001
Стол 4.4
BCD представление десятичных цифр от 0 до 9
Написать 17, два кода BCD для 1 и 7 используются 0001 и 0111. две цифры -
считается отдельный. Обычный метод представления десятичной дроби 17 используя
без знака двоичный код равен 10001. Телефон клавиатура с цифрами 0 до 9 генерирует BCD коды
для нажатые клавиши.
Мост цифровые системы отображают значение счета или время в десятичный на 7-сегментном светодиоде дисплей
панели. Поскольку отображаемые числа в десятичной системе счисления, поэтому используется код BCD к
дисплей десятичные числа. Рассмотрим 2-значное 7-сегментное дисплей, который может отображать количество
значение от 0 до 99.Чтобы отобразить две десятичные цифры два отдельные коды BCD применяется в
г. два 7-сегментных дисплея входы схемы.
BCD Дополнение
Многозначный Номера BCD могут быть добавлены вместе.
23
0010 0011
45
0100 0101
68
0110 1000
два 2-значных числа в двоично-десятичном коде добавляются и генерируют результат в BCD.в например
минимум значащие цифры 3 и 5 сложите до 8, что является допустимым BCD-представление. так же
большинство значащие цифры 2 и 4 сложите до 6, что также является действительный BCD представление.
Рассмотреть следующий пример, где наименее значимый числа в сумме составляют номер
больше чем 9, для которых нет действующий код BCD
23
0010 0011
48
0100 1000
71
0110 1011
Для Числа BCD, которые в сумме составляют неверный номер BCD или генерировать перенос числа 6
(0110) - это добавлен к неверному номеру.Если результат переносится, он добавляется к следующий самый значительный
цифра. Таким образом,
35
CS302 - Цифровая логика и дизайн
0011
1000
1011
11 генерируется который является недопустимым BCD номер
0110
6 эт добавлено
1 0001
Перенос - это сгенерированный, который добавлен к результат следующего наиболее значимый цифры
1
0110
0111
ответ: 0111 0001
The Серый код
Код Грея не иметь какие-либо веса, назначенные его битовые позиции.В Серый код
не является позиционный код. Серый код отличается от беззнаковый двоичный код как
подряд значения кода Грея различаются всего на один бит. Таблица 4.5 показывает серый Код
представительство десятичных чисел от 0 до 9.
Десятичное
Серый
двоичный
0
0000
0000
1
000 1
0001
2
00 11
0010
3
001 0
0011
4
0 110
0100
5
011 1
0101
6
01 01
0110
7
010 0
0111
8
1 100
1000
9
110 1
1001
Стол 4.5
серый Кодовое представление десятичного числа значения
биты выделены жирным шрифтом изменение в последовательные значения Грея представление кода
36
CS302 - Цифровая логика и дизайн
серый Код приложения
Рисунок 4,1
двоичный и на основе кода Грея Датчики вала
диаграмма показывает диск подключен к валу вращающаяся машина.В затемненный
площадей на диск указывает проводку площадь при напряжении +5 вольт. Незаштрихованные участки
указывают непроводящая область. Три стационарные щетки A, B и C коснуться поверхности
вращающийся диск. Три кисти подключаются к трем светодиодам лампы через провода. Как диск
вращается кисти соприкасаются с проводящей областью и утепленная территория.
три Светодиоды отображают положение вращающийся вал в условиях 3-х битных чисел. Таким образом, если диск
на вправо вращается в против часовой стрелки на 450, кисть A входит в связаться с
проводящих полоса на 5 вольт, которая включает светодиод, указывающий Двоичный 001.
Если диск непрерывный его вращения, после поворота еще 450, кисть B -
контакты с проводящей полосой и кисть A соприкасается с непроводящим полоска.
Таким образом Светодиод подключен к щетке B горит, указывая двоичный 010. Таким образом, в любой момент время,
светодиода указать угловой положение вращающегося вал.
Предположить что три кисти A, B и C не выровнены правильно и кисть B это
немного впереди щеток A и C. Теперь, если диск вращается 900 из начальная позиция.Щетка A
будет в контакт с проводящим полоса, кисть B из-за ее несоосность также будет в
контакты с проводящей полосой и кисть C будет в контакт с изолированным полоска. Таким образом,
когда диск вращает Светодиоды покажут 001, за которым следует 011 для короткая продолжительность, когда
г. диск вращается от 900 до 910, а затем до 010.Таким образом, из-за несоосность счет значение
прыгнул от 1 до 3, а затем обратно к 2.
Рассмотреть диск, показанный на правильно. Проведение и непроводящие полосы следовать
а Серый Кодовый образец 000, 001, 011, 010, 110, 111, 101 и 100, представляющие десятичный 0, 1, 2,
3, 4, 5, 6 и 7. Теперь даже если кисти смещены, светодиоды всегда будет отображать
правильно значение счета.Таким образом серый Кодирующий датчик вала позволяет угловое положение
вал быть определяется даже тогда, когда кисти смещен.
буквенно-цифровой Коды
Все представление изучено так далеко разрешить десятичные числа быть представленным в
двоичный. Цифровые системы также обрабатывают текстовая информация как при редактировании документы.Таким образом, каждые
письмо алфавит, верхний регистр и нижний регистр, вдоль со знаками препинания следует
37
CS302 - Цифровая логика и дизайн
иметь представление. Числа также написано в текстовой форме например, 2 июня 2003 г.
ASCII Код является общепринятым код, позволяющий 128 символы и символы быть
представлено.
ASCII Код
Код ASCII (американский Стандартный код для Обмен информацией) является 7-битным код
, представляющий 128 уникальных кодов, которые представляют алфавит символы от A до Z в нижнем чехол
и верхний регистр, десятичная дробь цифры от 0 до 9, знаки препинания и контроль символы.
ASCII коды 011 0000 (30ч) на 011 1001 (39h) представляет числа от 0 до 9
ASCII коды 110 0001 (61h) на 111 1010 (7Ah) представляют строчные буквы от а до z
ASCII коды 100 0001 (41h) на 101 1010 (5Ah) представляют заглавные буквы от A до Z
ASCII коды 000 0000 (0h) на 001 1111 (1Fh) представляют 32 Control символы.
Расширенный Код ASCII
Только 7-битный код ASCII имеет 128 уникальных кодов чего недостаточно для представляют
некоторые графические символы отображаются на Компьютерные экраны. 8-битный код расширенный ASCII
Коддает 256 уникальных кодов. Расширенный 128 уникальных коды представляют собой графические символы
, который стали неофициальными стандарт, используемый поставщиками их собственная интерпретация эти
графический коды.
Четность Метод
двоичный информация, которая может быть текст или числа обрабатываются, хранится и передан.
Хотя цифровые системы чрезвычайно надежный, но все же есть вероятность, что один бит получает
поврежден. То есть 1 меняется на 0 или 0 изменяется на 1. Многие системы используют бит четности для обнаружения
ошибок.А ошибка на основе единой четности схема обнаружения не очень практически эффективный и более
разрабатывать и надежные схемы имеют был разработан и реализовано для обнаружения и правильный
кратный битовые ошибки. Тем не менее использование бита четности помочь в понимании базовый
концепция обнаружение ошибок.
Рассмотреть что 8-битный расширенный Код ASCII используется для передавать текстовые сообщения с
один расположение к другому удаленному место расположения.Дополнительный бит с добавлением 8 данных биты, составляющие
всего из девять бит. 8-битный содержат информацию который должен быть сохранен или передан и
за дополнительную плату бит четности добавляется к проверьте на наличие ошибок что может произойти во время хранилище или
передача информация. Две схемы используются, Четная четность или Нечетная четность по существу
г. две схемы идентичны кроме очень незначительного разница.
Четный Метод четности
информация 10001101 должна быть передана в удаленное место. Паритет битовая ошибка
обнаружение принят метод, чтобы указать, если информация была испорчен, когда это достигает
г. другой конец. В четном Метод паритета количество 1 с считается в информации и
в зависимости по количеству единиц в сообщение добавленной четности бит либо установлен в 0, либо 1
сделать общее количество единиц, которые будут даже (четность)
8-битные данные 10001101 имеют четное количество единиц, поэтому бит четности, который это
добавлено установлен на 0.9-битное сообщение это 10001101 0. бит четности указан в Смелый.
Предположим сообщение, полученное на другой конец провода показывает биты, чтобы быть 10101101 0,
г. подчеркнутый бит изменился от 0 до 1. До передача сообщения, пользователи на обоих
концов провод согласился что они будут отправлять и получение сообщений с помощью даже
38
CS302 - Цифровая логика и дизайн
паритет.Таким образом, приемник на получение 9-битного сообщения выполняет быструю проверку четности. Всего
номер биты, включая четность бит должен составлять четное номер. Однако в этом чехол
г. цифры 1 в сообщении сложите до 5, что означает что немного было поврежден.
Нет способ, которым получатель может знать местонахождение поврежденный бит в сообщение.
единственное решение - запросить отправитель повторно передать сообщение. Если два бита получают испорченный
во время трансмиссия, 10100101 0 тогда общее количество единиц остается прежним и
приемник не сможет обнаружить ошибка. Если 3 бита получают поврежден, 10100001 0 пользователь
будет все еще быть в состоянии обнаружить это произошла ошибка, однако нет возможности определить, если
сингл бит или 3-бит, или 5-бит, или 7-битная ошибка произошел.
Нечетный паритет идентичен, за исключением что оба отправителя и получатель соглашаются отправь
информация с использованием нечетной четности и бит четности установлен или очищен так, чтобы общее количество
1с в сообщение, включая четность битовые суммы до нечетного Число.

 Вычитаем во втором разряде: 4-2 = 2.
Вычитаем во втором разряде: 4-2 = 2.