Урок 27. решение уравнений вида: х ∙ 8 = 26 + 70, х : 6 = 18 ∙ 5, 80 : х = 46 – 30 — Математика — 4 класс
Математика, 4 класс
Урок № 27. Решение уравнений вида: х · 8 = 26 + 70, х : 6 = 18 · 5,80 : х = 46 – 30
Перечень вопросов, рассматриваемых в теме:
— как решать уравнения вида: x∙ 8 = 26 + 70, x : 6 = 18 ∙ 5, 80 : x = 46 – 30
— какой алгоритм решения данных уравнений?
Глоссарий по теме:
Уравнение – это равенство с неизвестным числом. Неизвестное число обозначают латинской буквой.
Алгоритм — последовательность действия (шагов)
Решить уравнение – это значит найти такое значение неизвестного числа, при котором равенство будет верным.
Основная и дополнительная литература по теме урока:
1. Моро М.И., Бантова М.А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.1 — М.; Просвещение, 2017. – с.80
2. Моро М.И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 1. М.; Просвещение, 2016. – с.34,35
И. Математика. Рабочая тетрадь 4 класс. Часть 1. М.; Просвещение, 2016. – с.34,35
3. Волкова С.И. Математика. Проверочные работы 4 класс. М.; Просвещение, 2017. – с.44-45.
4. Волкова С.И. Математика. Тесты 4 класс. М.; Просвещение, 2017. – с.40-41.
5. Кочергина А.В. Учим математику с увлечением (Методическая библиотека). М.: 5 за знания, 2007. – с.159.
Теоретический материал для самостоятельного изучения
Вспомните, как связаны между собой числа при умножении.
Посмотрите, множитель 20, множитель 3, произведение 60.
Если 60 разделить на 20, получится 3.
Если 60 разделить на 3, получится 20.
Значит, если произведение разделить на один из множителей, то получится другой множитель. Это правило потребуется при решении уравнений, в которых неизвестен один из множителей.
20 ∙ 3 = 60
60 : 20 = 3
60 : 3 = 20
Решим уравнение:
произведение неизвестного числа и числа 7 равно числу 91. В нем неизвестен первый множитель.
13 умножить на 7 получим 91. Получили верное равенство:
91 равно девяносто одному. Значит, решили правильно.
А теперь догадайтесь, как решить уравнение: произведение неизвестного числа и числа 7 равно сумме чисел восьмидесяти и одиннадцати. Найдем значение выражения в правой части уравнения: 80 плюс 11 равно 91. Тем самым мы получили уравнение, которое уже умеем решать. Посмотрите, как записывается решение этого уравнения и его проверка.
Вспомним, как связаны между собой числа при делении.
Посмотрите: делимое 15, делитель 3, частное равно пяти.
Если делитель 3 умножить на частное 5, получим делимое 15.
Если делимое 15 разделить на частное 5, получим делитель 3.
15 : 3 = 5
3 ∙ 5 = 15
15 : 5 = 3
Знание связей между делимым, делителем и частным потребуется для решения уравнений, в которых неизвестен один из компонентов: делимое или делитель. Посмотрите, как решаются такие уравнения. В первом уравнении неизвестно делимое. Чтобы его найти, нужно делитель 3 умножить на частное 9.
Посмотрите, как решаются такие уравнения. В первом уравнении неизвестно делимое. Чтобы его найти, нужно делитель 3 умножить на частное 9.
Во втором уравнении неизвестен делитель. Чтобы его найти, нужно делимое 45 разделить на частное 3.
А как решить такое уравнение? Вычислим произведение в правой части: 18 умножить на 5 получим 90. Получается уравнение, в котором неизвестно делимое. Вы уже знаете, как его решать. Выполним проверку решения уравнения. Подставим число 540 вместо икс, вычислим левую часть и правую часть выражения: 90 равно 90. Значит уравнение решили верно.
Задания тренировочного модуля:
1.К каждой позиции первого столбца подберите соответствующую позицию второго.91 : х = 13 | x = 20 |
х : 21=4 | x = 7 |
24 ∙x = 96 | x = 84 |
x∙ 3 = 60 | x = 4 |
Правильный ответ:
91 : х = 13 | x = 7 |
х : 21= 4 | x = 84 |
24 ∙x = 96 | x = 4 |
x∙3 = 60 | x = 20 |
2. Выполните вычисления и выделите верный ответ:
Выполните вычисления и выделите верный ответ:
7 ∙x = 140 : 2
Варианты ответов: 10, 400, 2
Правильный вариант:
10
3.Решите уравнение, подчеркните правильный ответ:
(80 : у) ∙ 700 = 2800
Варианты ответов:
2, 4, 20
Правильные варианты:
20
Найди закономерность и продолжи ряд — математические закономерности
Закономерность — это регулярные устойчивые взаимосвязи в количествах, свойствах и явлениях объектов. В математической закономерности нужно найти алгоритм, согласно которому в цепочке чисел происходит их повторение, изменение или замещение в соответствии с установленным правилом.
В чем смысл игры?
Игры такого рода развивают умение выделять закономерности в последовательном ряде элементов. Для этого сначала нужно внимательно рассмотреть задание: сравнить соседние объекты и попробовать определить правило закономерности.
Решить задачу можно с помощью простого счета, обобщения по какому-либо признаку или простого анализа рисунка, текста или схемы.
Как научить ребенка находить закономерности?
Маленьким детям, для решения задач на поиски закономерностей, понадобится только смекалка и воображение. Достаточно лишь объяснить, как можно установить закономерность между звеньями ряда. Если задачу решить не получается, то вместо прямых подсказок следует задать дополнительные вопросы, не раскрывая решение задачи полностью.
В любом случае, пользы будет больше, если ребенок решит, хотя бы одну задачу самостоятельно, нежели взрослый просто расскажет, как её решать.
Рассмотрим способы, которые помогут ребенку понять закономерности и последовательности в заданиях.
Инструкция по решению числовых последовательностей:
- Найти разницу между двумя рядом стоящими числами
- Определить алгоритм построения последовательности
- Применить алгоритм к следующей паре чисел
- Использовать алгоритм для определения следующего числа в ряду
Инструкция по нахождению закономерностей в заданиях с геометрическими фигурами:
- Рассмотреть фигуры и разделить их, на повторяющиеся группы
- Определить какой элемент изменился в группе
- Решить, какая именно фигура отсутствует или является лишней.

Задания для 1 класса
Задание 1
Раскрась дорожки для зайчика и белочки, сохраняя закономерность.
Решение: Белочка и зайчик бегут по разным дорожкам. У каждой дорожки есть своя закономерность. У зайчика повторяется 3 цвета на дорожке: красный, голубой, жёлтый, а у белочки 4: зеленый, коричневый, фиолетовый, жёлтый.
В этом задании можно обратить внимание на то, что обе дорожки состоят из 12 кругов. Но количество повторяющихся цветов разное.
Задание 2
Найди закономерность в ряду геометрических фигур.
Решение: В этом ряду нужно обратить внимание на размеры фигур, а не на цвет и форму. Сначала идет одна большая фигура, а за ней две маленькие, далее они повторяются.
Задание 3
Нарисуйте в четвертом квадрате правильный ответ.
Решение: Рассмотрев внимательно рисунок, мы увидим, что круги в квадратах исчезают по одному, против часовой стрелки.
Задание 4
Соблюдая закономерность, продолжи ряд чисел до 10. Сформулируй правило, которое действует в этой закономерности. Используя это правило, придумай свою закономерность.
Решение: В этом ряду каждая цифра увеличивается на 2 относительно предыдущей – мы вычислили правило для данной закономерности. Значит, чтобы продолжить ряд, мы прибавим к каждой следующей цифре по 2. Ответ будет выглядеть так: 2,4,6,8,10.
Чтобы придумать подобную закономерность, нужно использовать сформулированное выше правило: например, 1,3,5,7,9.
Задания для 2 класса
Задание 1
Найди закономерность и в пустом квадрате нарисуй нужное количество кругов.
Решение: В таблице в первом горизонтальном ряду количество кругов увеличивается на 1. Во втором ряду увеличивается на 2.
Задание 2
В цепочке чисел найди закономерность и вставь пропущенные числа
- 95, 90, 85, 80, 75,_, 65,_, _,50
Решение: В цепочке чисел можно выделить пары: 95 -90, 85 – 80 и далее. Каждый раз, в паре, число уменьшается на 5. Значит, после 75 запишем 70, после 65 — 60, а затем 55 .
Задание 3
Найди закономерность и продолжи последовательность.
- 2, 3, 5, 8, …, …, …, …
Решение: В этой цепочке чисел к каждому последующему числу прибавляется предыдущее. 2+3=5+3=8+5=13+8=21+13=34 и далее.
Задание 4
В поезде едут геометрические фигуры. Нарисуйте фигуры, в четвёртом вагоне, соблюдая закономерность их расположения.
Решение: В поезде едут геометрические фигуры: квадрат, треугольник, прямоугольник и круг. В трёх вагонах все места заняты фигурами, в определённом порядке. Расставим их и в четвертом вагоне: Круг в нём будет располагаться в нижнем левом углу, квадрат в верхнем левом, треугольник поедет в правом нижнем, а прямоугольник – в левом верхнем углу.
В трёх вагонах все места заняты фигурами, в определённом порядке. Расставим их и в четвертом вагоне: Круг в нём будет располагаться в нижнем левом углу, квадрат в верхнем левом, треугольник поедет в правом нижнем, а прямоугольник – в левом верхнем углу.
Задания для 3 класса
Задание 1
Рассмотрите картинку и найдите закономерность в задаче.
Решение: В таблице мы увидим такую закономерность:
8-5=3, то есть число увеличилось на 3; далее 14-8=6, соответственно, число увеличилось на 6. В последней связке 23-14=9 число увеличилось на 9. Мы делаем вывод, что каждое следующее число увеличивается на предыдущее значение+3. Таким образом, следующее число увеличивается на 9+3=12. 23 + 12 = 35. Ответ: 35.
Задание 2
В пустые клетки вставьте геометрические фигуры, сохраняя закономерность.
Решение: Чтобы выполнить задание, нужно фигуры расставить по порядку, друг за другом, соблюдая последовательность. Значит, после прямоугольника стоит круг, треугольник и квадрат и т. д.
д.
Задание 3
Найди закономерность и продолжи ряды:
- 12, 23, 34, 45, 56…
- 13, 24, 35, 46…
Решение: В этой задаче каждая последующая цифра увеличивается так: десятки на один десяток и единицы на одну единицу. 12=10+2, 23=20+3, 34=30+5 и т. д.
Задание 4
Продолжи ряд, сохраняя закономерность.
- 12, 36, 13, 39, 14, 42, 15,…
Решение: В числовой цепочке выделяем пары чисел. Первая пара:12 и 36. 12×3=36, далее по порядку: 13×3=39. Умножая каждый раз на 3, цифры, следующие по порядку (12,13,14,15…), мы продолжаем последовательный ряд. Ответ: 45.
Задания для 4 класса
Задание 1
Найди ошибку в бусах.
Решение: В первых бусах повторяются квадрат и круг, значит лишний шестой круг. Во вторых бусах, повторяется закономерность: круг, два треугольника, два круга, лишний – восьмой, по счету, круг.
Задание 2
Определите закономерность. Найдите лишнее число.
- 8, 16, 20, 24, 32, 40, 48, 56, 64, 72.
Решение: В этом числовом ряду таблица умножения на 8. Ответ: число 20 – лишнее.
Задание 3
Каких геометрических фигур не хватает? Дорисуй их, соблюдая закономерность в таблице:
Решение: Определить, какой элемент изменился во втором и последующих рядах, можно, выделив последовательность: ромб, трапеция, шестиугольник и параллелограмм. Во втором ряду недостает шестиугольника, в третьем — ромба, в четвертом – параллелограмма и трапеции.
Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнееКак решить любую проблему: пошаговый алгоритм (4 шага, метод McKinsey и другие методики)
Встречались ли вам на вашем жизненном пути проблемы, которые вы не знали, как решить? Скорее всего, да. И каким же образом вы их решили? Предприняли мозговой штурм и нашли решение сами? Обратились за помощью к друзьям или специалистам требуемого профиля? Просто «забили» на проблему, и она через время перестала быть таковой?
И каким же образом вы их решили? Предприняли мозговой штурм и нашли решение сами? Обратились за помощью к друзьям или специалистам требуемого профиля? Просто «забили» на проблему, и она через время перестала быть таковой?
Вы найдете намного больше новых способов решения любых проблем, если пройдете нашу программу «ТРИЗ на практике: творческий подход на работе и в жизни». Аббревиатура ТРИЗ расшифровывается как «теория решения изобретательских задач», однако сама теория применима не только к сфере науки и изобретательства, но и к бизнесу, личной жизни и другим сферам.
Но кое-что новое для себя в плане подходов к решению проблем вы сможете найти прямо сейчас в этой статье. Например, как решить любую проблему за 4 шага.
Как решить любую проблему за 4 шага?
Мы не просто так написали, что для решения проблемы нужно сделать именно 4 шага. Так считает автор книги «4 шага к решению всех проблем. Разговор с эффективным психологом» Полина Гавердовская, медицинский психолог и гештальт-терапевт [П. Гавердовская, 2016]. Мы перечислим эти шаги, а потом рассмотрим подробнее, что же имеется в виду:
Гавердовская, 2016]. Мы перечислим эти шаги, а потом рассмотрим подробнее, что же имеется в виду:
- Шаг первый – отказаться от стереотипов.
- Шаг второй – пресечь манипуляцию.
- Шаг третий – стать честным с собой и другими.
- Шаг четвертый – прекратить страдать от любви и начать радоваться ей.
Итак, начнем. Что такое стереотипы? Это заранее сформированные мыслительные оценки и модели поведения. Могут ли заранее сформированные оценки помочь в решении какой-то новой проблемы? Иногда да, но чаще нет. Особенно, если действовать приходится в быстро меняющейся ситуации, для которой нужны принципиально новые подходы.
Идем дальше. Что такое манипуляция? Это психологическое воздействие с целью изменить поведение или решение человека. Решите ли вы возникшую проблему, если будете исходить из интересов другого человека, который вами манипулирует? Если ваши цели полностью совпадают, тогда да. Такое бывает крайне редко, поэтому, скорее всего, под воздействием чувства ложной вины или ложно понятого долга, кои умело внушают манипуляторы, вы вряд ли найдете решение проблем, которое вас устроит.
Теперь поговорим о том, как стать честным с собой и другими. На самом деле тяжелее всего быть честным с самим собой. Над всеми нами довлеют стереотипы, как правильно жить и что нужно делать. Нам с детства навязывают так называемые «общечеловеческие ценности», хотя все люди разные. И даже взяв за основу, что все одинаково сильно хотят быть счастливыми, придется признать, что понимание счастья у всех разное.
Собственно, именно поэтому первым шагом к решению проблемы должно стать избавление от стереотипов. Так вы сможете честно сказать себе, чего вы хотите на самом деле. И так быстрее отпадет необходимость говорить другим заученные банальности, которые те другие будут принимать за чистую монету, мешать двигаться к цели и решать актуальные для вас проблемы.
И, наконец, пора прекратить страдать от любви и начать радоваться ей. Полина Гавердовская, как вы уже поняли, специализируется на психологии межличностных отношений [П. Гавердовская, 2016]. Однако если в этой фразе заменить слово «любовь» на слово «работа», смысл останется прежним. Поэтому в большинстве случаев такой пошаговый алгоритм из четырех шагов является практически универсальным и позволяет решать любые проблемы, даже если ранее вы не знали, что вам делать и как вам быть.
Поэтому в большинстве случаев такой пошаговый алгоритм из четырех шагов является практически универсальным и позволяет решать любые проблемы, даже если ранее вы не знали, что вам делать и как вам быть.
Всегда ли эти шаги достаточны для решения проблемы? Если проблема лежит в сфере межличностных отношений или работы в качестве рядового наемного сотрудника, тогда, в принципе, достаточны. Но как быть, если вы топ-менеджер в крупной компании или собственник бизнеса? Все вышеприведенные шаги полностью актуальны, однако требуют детализации, и, скажем так, немного другого наполнения. Тем не менее универсальные подходы существуют и для деловой сферы. Это, в частности, метод McKinsey.
Метод McKinsey: как решить любую проблему?
Итак, как решить же любую проблему по методу McKinsey? Пошаговый алгоритм подробно описан в книге, которую написал Итан Расиел «Метод McKinsey. Использование техник ведущих стратегических консультантов для решения личных и деловых задач», но для начала мы сделаем небольшой исторический экскурс, чтобы понять истоки метода [И. Расиел, 2012].
Расиел, 2012].
Консалтинговая фирма McKinsey была образована в 1923 году и изначально сориентирована на решение проблем клиентов, преимущественно представителей крупного бизнеса. Каждый сотрудник фирмы – это своего рода универсальный специалист, решающий любые проблемы. Причем фраза «решу любую вашу проблему» от сотрудников фирмы не была простым бахвальством или попыткой выдать желаемое за действительное. Фирма McKinsey действительно решала все проблемы, за которые бралась.
Автор проработал в этой фирме 3 года, с 1989 по 1992-й, затем опросил несколько десятков бывших сотрудников, и это все вместе позволило сложить пошаговый алгоритм решения любой проблемы, который и получил условное название метод McKinsey. Приступим к его рассмотрению.
Факты, структура, гипотеза
Итак, поиск решения всегда должен опираться на факты, иметь внятную структуру, основываться на выдвижении и анализе различных гипотез. Именно поэтому в McKinsey всегда начинают со сбора фактов, которые могли бы пролить свет на разные аспекты существующей проблемы. Далее команда консультантов выдвигает гипотезу, как можно решить проблему, и приступает к поиску фактов, которые или подтверждают или опровергают возможность решения проблемы предложенным способом [И. Расиел, 2012].
Далее команда консультантов выдвигает гипотезу, как можно решить проблему, и приступает к поиску фактов, которые или подтверждают или опровергают возможность решения проблемы предложенным способом [И. Расиел, 2012].
Помимо тщательного сбора фактов, в McKinsey столь же важным считают структурирование мышления при поиске решения. Для этого, как минимум, проблема должна быть подробно описана, однако при этом описание не должно быть избыточным. В описании проблемы и изложении фактов консультанты руководствуются принципом «ВИСИ», что означает «взаимно исключающие, совместно исчерпывающие».
Как это выглядит на практике? Проблему разбивают на подпроблемы, после чего анализируют, является ли описание проблемы исчерпывающим и является ли каждая из подпроблем независимой от других. Например, если компания-производитель задается вопросом, как ей увеличить продажи производимой продукции, стартовый список подпроблем будет следующим:
- Усовершенствовать розничную торговлю.

- Улучшить маркетинг.
- Сократить издержки на производство продукции.
Почему мы не видим в списке модернизацию производства? Потому что это один из вариантов сокращения издержек на производство, и если внести его в стартовый список, этот список окажется избыточным [И. Расиел, 2012]. Почему мы не видим в списке повышение качества продукции, что всегда помогает борьбе за внимание покупателей? Потому что это составляющая маркетинга.
Таким образом, пункты стартового списка не должны пересекаться и в этом смысле они являются взаимоисключающими и соответствующими принципу «ВИСИ». При этом пункты должны охватить и исчерпать проблему полностью. Что касается прочих расширяющих их идей, они впоследствии вносятся в список в качестве подпунктов. Это все позволит выдвинуть рабочую гипотезу, как решить проблему.
Отметим, что гипотеза не обязательно будет учитывать все ранее собранные факты, сформулированные пункты и подпункты. Для гипотезы нужно ровно столько фактов и пунктов, чтобы она стала рабочей. Допустим, если увеличить продажи собственной продукции можно лишь с помощь усовершенствования розничной торговли, этого консультантам фирмы McKinsey полностью достаточно для генерации рабочей гипотезы. Другими словами, шаги должны быть необходимыми и достаточными.
Допустим, если увеличить продажи собственной продукции можно лишь с помощь усовершенствования розничной торговли, этого консультантам фирмы McKinsey полностью достаточно для генерации рабочей гипотезы. Другими словами, шаги должны быть необходимыми и достаточными.
Далее остается лишь собрать дополнительные факты и перепроверить, действительно ли потенциал улучшения работы розницы является достаточным, чтобы увеличить объемы сбыта до тех, которые кажутся на данный момент оптимальными. Например, нет смысла до бесконечности увеличивать потенциал сбыта, если пока нет возможности производить больше. В общем, нужно правильно понимать суть проблемы, чтобы найти верное решение.
Реальная проблема и адекватное решение
Тут мы подходим к еще одному важному моменту, на который указывает автор книги, посвященной методу McKinsey. Важно определиться, имеет консультант дело с реальной проблемой или мнимой. Это как если бы в конце 90-х производители пейджеров озадачились темой завоевания рынка, когда им на пятки наступают подешевевшие мобильные телефоны. Понятно, что в этих условиях нужно думать не про модернизацию производства пейджеров, а о том, как соответствовать изменившимся запросам рынка.
Понятно, что в этих условиях нужно думать не про модернизацию производства пейджеров, а о том, как соответствовать изменившимся запросам рынка.
Из этого вытекает следующий вывод: нельзя подгонять факты под решение. Когда решение кажется очевидным, всегда есть соблазн отбросить факты, которые не вписываются в «идеальную картину мира», и работать лишь с тем, что вам нравится. Это часто становится ловушкой, в которую попадают люди, желающие видеть только то, что им кажется правильным. В лучшем случае такой подход ведет к потерям времени на проработку деталей, которые не дают верного решения, в худшем случае это приведет к неправильным решениям.
И даже когда решение со всех точек зрения выглядит логичным и правильным, нужно убедиться, что оно подходит клиенту. Это многоаспектный момент. Так, вряд ли стоит предлагать модернизацию производства стоимостью несколько сотен миллионов долларов, если у клиента нет таких средств и нет возможностей взять такой кредит. С другой стороны, не стоит предлагать сэкономить тем фирмам и компаниям, которые желают рисковать и инвестировать в будущее, пусть даже сейчас есть готовое и недорогое решение.
В качестве примера Итан Расиел приводит ситуацию, когда крупный холдинг на заре спутниковой эры решил наладить спутниковую связь между офисами, разбросанными по всему миру. Ввиду того, что фирма McKinsey получила заказ на поиск возможностей сокращения издержек, консультанты предложили решить проблему с помощью обычной телефонной связи, что обошлось бы в разы дешевле. На что получили ответ, что холдинг нуждается в масштабных проектах и от идеи спутниковой связи между офисами отказываться не намерен даже во имя большой экономии [И. Расиел, 2012].
Бывают и другие случаи, когда существенного сокращения издержек можно добиться, буквально слегка подкорректировав политику продаж. Так, автор описывает случай, когда около половины финансовых издержек банка приходились лишь на одну услугу, продажи которой не превышали 5% от всех заказов услуг этого банка [И. Расиел, 2012]. Причем изначально заказчик был настроен скептически к консультантам фирмы и даже подозревал их в некомпетентности.
К слову, если речь идет о решении чьей-то проблемы, всегда нужно быть готовым к сопротивлению. Любая компания состоит из работающих в ней людей, и предлагаемые меры могут напрямую затронуть их работу, должность, зарплату. Если у некоторых из этих людей есть смутное подозрение, что они причастны к проблемам своей компании, они будут всячески саботировать попытки помочь.
Если таковые находятся в топ-менеджменте и ближнем кругу лиц, которым доверяет руководство, лучше не лезть на рожон, а переформулировать проблему так, чтобы она не выглядела, как затрагивающая чьи-то интересы. Главное сориентироваться вовремя, иначе консультанта могут заподозрить либо в некомпетентности, либо в попытке уклониться от реальных трудностей. Кроме того, в этом случае лучше продумать предлагаемые меры так, чтобы их можно было внедрять постепенно, не разрушая существующую систему. Что, к слову, вполне коррелирует с общеизвестным принципом «80 на 20».
Принцип Парето «80 на 20» и «Закон квадратов»
Широко известный принцип Парето гласит, что 20% усилий приносят 80% результата. Это не значит, что остальные 20% результата и 80% усилий не нужны вовсе. Однако когда речь идет о стратегических задачах, важно сосредоточиться на самом главном. Поэтому, если встает вопрос «как увеличить прибыль», следует сначала уточнить, что является основным источником прибыли.
Это не значит, что остальные 20% результата и 80% усилий не нужны вовсе. Однако когда речь идет о стратегических задачах, важно сосредоточиться на самом главном. Поэтому, если встает вопрос «как увеличить прибыль», следует сначала уточнить, что является основным источником прибыли.
В качестве примера автор приводит работу с брокерской конторой, как раз и занимавшейся поиском возможностей для дополнительной прибыли. Оказалось, что основную прибыль приносят 10 клиентов, с которыми работают 3 брокера, что применительно к штату конторы вписывалось в упомянутый принцип. Консультанты McKinsey предложили увеличить число брокеров, обслуживавших ведущих клиентов, что ускорило решение всех вопросов крупных заказчиков и в конечном счете привело к увеличению прибыли [И. Расиел, 2012].
Сосредоточиться на главном стоит и потому, что, как образно заметил коллега автора книги, «не надо пытаться вскипятить океан». Анализировать нужно лишь те факторы, которые влияют на результат, а не все доступные данные. Так, «Закон квадратов» гласит, что, если решаемая проблема возросла в 2 раза, время на ее решение увеличится в 4 раза. Поэтому, если задачу не упростить вовремя, существует риск потратить на поиск ее решения много времени. При этом не факт что найденное в результате анализа множества второстепенных факторов решение будет адекватным [И. Расиел, 2012].
Так, «Закон квадратов» гласит, что, если решаемая проблема возросла в 2 раза, время на ее решение увеличится в 4 раза. Поэтому, если задачу не упростить вовремя, существует риск потратить на поиск ее решения много времени. При этом не факт что найденное в результате анализа множества второстепенных факторов решение будет адекватным [И. Расиел, 2012].
Тут, как говорится, «срывайте низко висящий плод». Иногда не нужно анализировать тонны фактов, чтобы найти, что можно улучшить прямо сейчас. Это не означает отказаться работать над проблемой. Это означает, что доступные по ресурсам и несложные по исполнению шаги нужно делать прямо сейчас, как только вы увидели возможность с их помощью решить хотя бы часть проблемы. Это нечто сродни идее, как разобраться с большим потоком дел и рутины: то, что можно сделать за 2 минуты, сделайте прямо сейчас.
Подытожим вкратце, что нам рассказала про метод McKinsey книга Итана Расиела:
- Поиск решения и само решение должны опираться на факты.

- Проблему необходимо разобрать на самодостаточные и не пересекающиеся подпроблемы.
- Для каждой подпроблемы нужно продумать ключевые подпункты, которые помогут ее детализировать.
- Факты, пункты и подпункты должны быть достаточными, но не должны быть избыточными.
- Для рабочей гипотезы в поиске решения проблемы использовать ровно то количество фактов и пунктов, которые делают гипотезу рабочей.
- Убедиться, что перед вами реальная проблема, а не мнимая.
- Не подгонять факты под решение.
- Убедиться, что найденное решение подходит для данной ситуации.
- Быть готовым к сопротивлению отдельных представителей заказчика.
- Переформулировать проблему, если в существующем виде она вызывает много разногласий.
- Применять принцип «80 на 20».
- Применять «Закон квадратов».
- «Не пытаться вскипятить океан».
- «Срывать низко висящий плод».
В книге Расиела «Метод McKinsey. Использование техник ведущих стратегических консультантов для решения личных и деловых задач» можно найти и другие, более банальные, но не менее действенные рекомендации, помогающие решать любые проблемы [И. Расиел, 2012]. Например, совет научиться излагать суть проблемы и ее решения за 30 секунд, что позволит быстрее находить поддержку в решении проблем.
Расиел, 2012]. Например, совет научиться излагать суть проблемы и ее решения за 30 секунд, что позволит быстрее находить поддержку в решении проблем.
Или, к примеру, в конце дня записывать 3 самых главных вещи, которые вам удалось сделать или узнать за день. Со временем эти записи будут стимулировать ваше мышление, когда вы возьметесь их перечитывать. Кроме того, Итан Расиел считает, что во многих случаях «лучше дать хороший пас, чем пытаться забить гол». В переводе со спортивного языка на деловой язык командного взаимодействия это значит, что не нужно пытаться решать все проблемы в одиночку. Это, кстати, актуально для любой сферы, не только для бизнеса.
И, конечно, всегда в работе над проблемой нужно делать остановку и отвечать себе на вопрос, насколько ваши теперешние действия ведут (или не ведут) к конечной цели – решению проблемы.
Так в чем же все-таки суть метода McKinsey? Суть в том, что при всем многообразии проблем их можно решить с помощью универсальных шагов. Не нужно каждый раз применять их все сразу. Нужно выбрать самые подходящие и воплотить их в жизнь. Именно так поступают люди, решающие любые проблемы.
Не нужно каждый раз применять их все сразу. Нужно выбрать самые подходящие и воплотить их в жизнь. Именно так поступают люди, решающие любые проблемы.
Некоторые задачи можно и вовсе решить за несколько шагов. Если вы пока не топ-менеджер или собственник компании, и ваши задачи не так масштабны, как завоевание новых рынков или сокращение издержек производства при многомиллионных оборотах, вам могут подойти упрощенные схемы, как решить любую проблему. Рассмотрим несколько популярных методик.
Как решить любую проблему: полезные методики
Начнем эту часть статьи с того, что книга Итана Расиела вовсе не единственная с таким названием. Точно так называется книга Алана Баркера «Как решить любую проблему» [А. Баркер, 2014]. Как заявляет сам автор, его книга учит иначе смотреть на проблемы. Автор, много лет посвятивший бизнес-консалтингу, считает, что самое главное – это сделать мышление более гибким. Тогда человек сможет выйти даже из тупиковой ситуации. А в идеале вообще перестанет в такие ситуации попадать.
В книге очень много сказано о необходимости отказаться от шаблонного мышления и понять, что проблема может иметь множество правильных решений, а не одно-единственное верное, как привыкло думать большинство людей. Вот эту убежденность, что правильное решение всего одно, Алан Баркер называет «проклятием правильного ответа», просто потому что в современном мире это уже давно не так [А. Баркер, 2014]. Как избежать этого «проклятия правильного ответа»? В этом поможет наша программа «ТРИЗ на практике: творческий подход на работе и в жизни» и несколько популярных методик, о которых мы расскажем прямо сейчас.
Квадрат Декарта
Люди традиционно тратят очень много времени на переживания о вещах, которые вряд ли когда-то случатся. А если и случатся, сегодняшние переживания вряд ли помогут решению проблемы в далеком будущем, когда будут другое время, другие законы, другой темп жизни. Поэтому вместо того чтобы до бесконечности гонять по кругу вопрос «Что будет, если это случится», ответьте еще на несколько вопросов:
- Что будет, если это случится?
- Что будет, если это не случится?
- Чего не будет, если это случится?
- Чего не будет, если это не случится?
После ответа на эти вопросы решение проблемы с большой степенью вероятности придет само. Так работает квадрат Декарта и позволяет решать любые проблемы. Кстати, пользоваться этим алгоритмом можно практически для любых проблем, как больших, так и маленьких, как сиюминутных так и возможных или кажущихся в будущем.
Так работает квадрат Декарта и позволяет решать любые проблемы. Кстати, пользоваться этим алгоритмом можно практически для любых проблем, как больших, так и маленьких, как сиюминутных так и возможных или кажущихся в будущем.
На сегодняшний день существует масса интерпретаций «квадрата Декарта», которые даже не всегда можно распознать с первого взгляда. Так, если вас не устраивает ситуация на работе, существует 4 способа действия:
- Изменить свое поведение в сложившейся ситуации – обсудить и добиться изменения условий, научиться делать то, что требуется.
- Изменить ситуацию – перейти в другой отдел, начать борьбу за свои права.
- Выйти из ситуации – уволиться.
- Пересмотреть отношение к ситуации – найти положительные стороны в том, что есть, и смириться, что любая работа неидеальна.
Если хорошо подумать, одно из этих действий вам придется выбрать и предпринять, когда вы ответите на 4 ранее приведенных вопроса. Принципиальный момент, на который указывает автор статьи: формулировать проблему нужно так, чтобы главным действующим лицом были вы сами [М. Долгий, 2019]. Пока в вашем понимании в ваших проблемах виноват кто угодно, кроме вас, ни одну проблему решить не получится.
Долгий, 2019]. Пока в вашем понимании в ваших проблемах виноват кто угодно, кроме вас, ни одну проблему решить не получится.
Смена фокуса
Фраза «со стороны виднее» весьма популярна, но точна лишь отчасти. Со стороны увидеть решение проблемы можно лишь тогда, когда вы в курсе всех нюансов ситуации. А кто знает все нюансы ситуации лучше, чем вы сами? Однако пока вы находитесь внутри проблемы, вы не увидите ее со стороны. Что делать?
Для начала нужно «убежать» от проблемы физически и отвлечься от нее эмоционально: пойти на прогулку, тренировку, концерт, в любое другое место, где вам гарантирована легкая физическая и положительная эмоциональная нагрузка. После того как вы сделаете небольшой перерыв в обдумывании проблемы, у вас получится сменить фокус и увидеть свою ситуацию глазами стороннего наблюдателя.
Поедание слона
Технику поедания слона очень любят рекомендовать различные пособия по тайм-менеджменту. Суть в том, что задачу или проблему нужно разбить на максимальное мелкие составляющие, решение (поедание!) которых не займет много времени и не отнимет много сил. Это что касается тайм-менеджмента.
Это что касается тайм-менеджмента.
Для решения проблемы по методу поедания слона можно действовать еще проще: подходить и «откусывать» от своей проблемы кусок, который вы в состоянии переработать. Не стоит тратить много времени на размышления, с какой стороны начать.
Если проблема сложная настолько, что не ясно, как к ней подступиться, попробуйте подступиться с любой стороны наугад. Нередко таким способом можно быстрее выйти на оптимальное решение, нежели долго анализируя все факты и факторы.
Практика «Хоопонопоно»
И, наконец, мы можем посоветовать вам книгу «#Хоопонопоно. 4 фразы, которые решат любую вашу проблему, даже если вы не верите в чудеса» [Л. Бодэн, 2016]. Забегая вперед, назовем эти волшебные фразы:
- «Мне очень жаль» – так вы признаете свои ошибки.
- «Прости» – далее следует попросить прощения за свои ошибки.
- «Спасибо» – это благодарность за разрешение забыть те воспоминания, которые мешают двигаться вперед.

- «Я люблю тебя» – без комментариев.
Если для вас так с ходу не совсем очевидно, как эти 4 фразы, решат любую вашу проблему, для начала можно ознакомиться с практикой «Хоопонопоно» в общих чертах. Так вам будет проще понимать рекомендации и пояснения из книги.
Итак, мы познакомили вас с наиболее действенными и универсальными методами, как решить любую проблему. Найдите время на изучение нашей программы «ТРИЗ на практике: творческий подход на работе и в жизни», и ваш мозг будет готов мыслить нестандартно и находить решение там, где его, казалось бы, не существует.
А еще вас ждет один вопрос по обсуждаемой в статье теме. Мы же желаем вам успешно справляться с любыми проблемами. Но еще лучше, чтобы проблем у вас не было вообще!
4 класс, уравнение, решение уравнений, примеры и задачи
Дата публикации: .
Решение уравнений
1. Реши уравнения на сложение и вычитание целых чисел.
| 5456 — х = 2343 | х + 3217 = 7898 | у — 4325 = 346 |
| 9949 — y = 6957 | 1202 — y = 722 | y + 4890 = 8979 |
2. Реши уравнения на умножение и деление целых чисел.
| 45 * х = 225 | х * 18 = 108 | у : 25 = 12 |
| 44 * y = 176 | 224 : y = 32 | y * 40 = 360 |
3. Реши уравнения на сложение и вычитание дробей.
| 3 1⁄8 — х = 2 1⁄8 | х + 4 1⁄3 = 7 3⁄9 | у — 5 8⁄7 = 1⁄14 |
| 12 1⁄15 — y = 1 1⁄5 | 4 1⁄2 — y = 2 1⁄8 | y + 13 1⁄4 = 2 4⁄8 |
4. Реши уравнения на умножение и деление дробей.
| 45 * х = 225 | х * 17 = 108 | у : 25 = 12 |
| 49 * y = 176 | 224 : y = 32 | y * 40 = 360 |
Текстовые задачи и уравнения
Составь уравнения к задачам и реши их.
2. Одновременно в противоположных направлениях из города выехали велосипедист и мотоциклист и продолжили движение в течении 3 часов. Мотоциклист двигался со скоростью 40 км/час, а велосипедист – со скоростью 15 км/час. Сколько километров проехал мотоциклист? Сколько километров проехал велосипедист? На сколько километров мотоциклист проехал больше, чем велосипедист?
3. Из деревни А в село Б вышел пешеход. Через 2 часа он остановился на отдых и отдыхал в течении одного часа. Затем он продолжил свой путь и пришел в село Б через 6 часов после часового отдыха. Какова скорость пешехода, если расстояние между деревней А и селом Б равно Х км?
4. В городе есть 4 улицы: Южная, Северная, Восточная и Западная. На Южной улице живет 10 % от всех жителей города. На Восточной живет на 1 3⁄5 больше, чем на Южной улице. На Северной улице живет в 2 раза больше, чем на Южной улице. Сколько жителей живет на каждой улице, если всего городе зарегистрировано 1 миллион человек?
Сколько жителей живет на каждой улице, если всего городе зарегистрировано 1 миллион человек?
Общие задачи.
1. Запиши числа, которые содержат:
| 9 | сот. | 1 | дес. | 2 | ед. | = _____ | 3 | сот. | 0 | дес. | 7 | ед. | = _____ | |
| 6 | сот. | 0 | дес. | 6 | ед. | = _____ | 3 | сот. | 5 | дес. | 0 | ед. | = _____ | |
| 0 | сот. | 5 | дес. | 0 | ед. | = _____ | 9 | сот. | 8 | дес. | 5 | ед. | = _____ | |
2. Заполни таблицу.
| e | 300 | 356 | 353 | 389 | 342 | 384 | 382 |
| e-90 | . .. .. | … | … | … | … | … | … |
| | |||||||
| f | 451 | 451 | 461 | 441 | 431 | 471 | 481 |
| f+80 | … | … | … | … | … | … | … |
3. Заполните таблицу
| Слагаемое | 410 | 109 | 358 | ||||
| Слагаемое | 301 | 259 | 758 | 420 | 294 | 273 | 193 |
| Сумма | 772 | 816 | 881 | 689 |
4. Заполните таблицу
| Уменьшаемое | 161 | 972 | 291 | 494 | 741 | ||
| Вычитаемое | 284 | 216 | 714 | 269 | 161 | ||
| Разница | 32 | 6 | 178 | 33 |
5. Вычисли и выполни проверку.
Вычисли и выполни проверку.
| 458 | 146 | 185 | 164 | 703 | |||||
| — | 132 | + | 15 | — | 50 | + | 10 | — | 58 |
| … | … | … | … | … | |||||
| 773 | 374 | 308 | 659 | 351 | |||||
| + | 241 | — | 214 | + | 247 | — | 487 | + | 220 |
| … | … | … | … | … | |||||
6. Вычисли и выполни проверку.
| 375 | 319 | 782 | 684 | 862 | |||||
| — | 198 | — | 226 | — | 737 | — | 522 | — | 622 |
| … | … | … | … | … | |||||
| 627 | 325 | 777 | 597 | 908 | |||||
| — | 139 | — | 307 | — | 121 | — | 496 | — | 720 |
| … | … | … | … | … | |||||
7. Реши уравнения
Реши уравнения
| 9 | + | x | = | 26 | y | + | 26 | = | 68 | x | + | 7 | = | 93 | ||
| x | = | … | y | = | … | x | = | … |
8. Реши уравнения
| 15 | — | x | = | 8 | y | — | 13 | = | 24 | x | — | 9 | = | 56 | ||
| x | = | … | y | = | … | x | = | … |
9. Реши уравнения
| 37 | — | x | = | 13 | y | + | 21 | = | 45 | x | — | 32 | = | 58 | ||
| x | = | … | y | = | … | x | = | … |
10. Сколько единиц каждого разряда в числах:
Сколько единиц каждого разряда в числах:
Уравнения на сложение и вычитание. Тренироваочне материалы. Вариант № 1.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 3 = 6 y + 25 = 28 51 — x = 34 67 — y = 1
2) x + 28 = 89 y + 3 = 53 59 — x = 49 13 — y = 6
3) x + 27 = 63 y + 72 = 88 74 — x = 41 77 — y = 28
4) x + 14 = 81 y + 30 = 83 90 — x = 53 72 — y = 17
5) x + 84 = 87 y + 5 = 18 28 — x = 17 35 — y = 2
6) x + 3 = 94 y + 9 = 18 95 — x = 46 70 — y = 9
7) x + 6 = 63 y + 23 = 26 76 — x = 44 78 — y = 73
8) x + 6 = 46 y + 17 = 89 9 — x = 7 72 — y = 55
9) x + 59 = 90 y + 7 = 76 83 — x = 29 67 — y = 41
10) x + 19 = 24 y + 2 = 36 52 — x = 48 1 — y = 0
Уравнения на сложение и вычитание.
 Вариант № 2.
Дата:______________ ФИО:_________________________________ Оценка:__________
Вариант № 2.
Дата:______________ ФИО:_________________________________ Оценка:__________
Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 11 = 78 y + 52 = 57 72 — x = 38 38 — y = 12
2) x + 21 = 93 y + 7 = 81 94 — x = 70 42 — y = 37
3) x + 0 = 35 y + 8 = 11 71 — x = 56 29 — y = 6
4) x + 15 = 18 y + 65 = 77 58 — x = 24 43 — y = 20
5) x + 77 = 91 y + 57 = 75 23 — x = 2 10 — y = 1
6) x + 8 = 58 y + 22 = 91 92 — x = 1 57 — y = 3
7) x + 3 = 20 y + 25 = 67 91 — x = 73 5 — y = 3
8) x + 54 = 73 y + 4 = 71 72 — x = 23 82 — y = 3
9) x + 2 = 95 y + 44 = 88 22 — x = 12 8 — y = 5
10) x + 32 = 97 y + 30 = 37 93 — x = 74 40 — y = 3
Уравнения на сложение и вычитание. Вариант № 3.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 7 = 40 y + 76 = 77 16 — x = 1 90 — y = 64
2) x + 21 = 26 y + 47 = 65 73 — x = 35 54 — y = 15
3) x + 6 = 21 y + 19 = 74 42 — x = 35 10 — y = 2
4) x + 70 = 75 y + 65 = 91 45 — x = 12 70 — y = 59
5) x + 13 = 30 y + 28 = 39 61 — x = 15 5 — y = 0
6) x + 23 = 50 y + 4 = 8 79 — x = 69 69 — y = 0
7) x + 3 = 4 y + 10 = 78 7 — x = 3 92 — y = 23
8) x + 64 = 83 y + 45 = 81 73 — x = 27 25 — y = 3
9) x + 14 = 41 y + 15 = 22 62 — x = 60 43 — y = 29
10) x + 6 = 85 y + 18 = 58 87 — x = 35 59 — y = 4
Уравнения на сложение и вычитание. Вариант № 4.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 28 = 56 y + 8 = 20 94 — x = 15 80 — y = 66
2) x + 54 = 71 y + 0 = 4 40 — x = 32 35 — y = 32
3) x + 2 = 28 y + 47 = 85 92 — x = 66 35 — y = 19
4) x + 59 = 87 y + 13 = 18 45 — x = 4 51 — y = 36
5) x + 76 = 82 y + 2 = 41 54 — x = 33 33 — y = 2
6) x + 8 = 18 y + 36 = 81 22 — x = 6 75 — y = 60
7) x + 68 = 74 y + 28 = 36 90 — x = 46 42 — y = 13
8) x + 1 = 3 y + 70 = 90 36 — x = 17 72 — y = 3
9) x + 4 = 5 y + 27 = 60 60 — x = 13 44 — y = 30
10) x + 16 = 18 y + 7 = 18 16 — x = 15 76 — y = 50
Уравнения на сложение и вычитание. Вариант № 5.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 21 = 35 y + 7 = 9 30 — x = 28 73 — y = 40
2) x + 33 = 75 y + 5 = 60 1 — x = 0 62 — y = 59
3) x + 28 = 30 y + 26 = 71 79 — x = 28 74 — y = 66
4) x + 74 = 90 y + 0 = 9 67 — x = 26 55 — y = 35
5) x + 8 = 9 y + 7 = 59 1 — x = 0 29 — y = 24
6) x + 15 = 63 y + 4 = 10 79 — x = 47 35 — y = 3
7) x + 20 = 23 y + 8 = 54 73 — x = 59 6 — y = 2
8) x + 18 = 25 y + 1 = 53 25 — x = 4 86 — y = 23
9) x + 20 = 31 y + 29 = 99 18 — x = 5 71 — y = 3
10) x + 0 = 1 y + 40 = 44 75 — x = 39 43 — y = 13
Уравнения на сложение и вычитание.
 Вариант № 6.
Дата:______________ ФИО:_________________________________ Оценка:__________
Вариант № 6.
Дата:______________ ФИО:_________________________________ Оценка:__________
Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 15 = 17 y + 2 = 13 22 — x = 10 25 — y = 3
2) x + 32 = 42 y + 1 = 4 21 — x = 11 77 — y = 2
3) x + 71 = 94 y + 42 = 44 59 — x = 26 9 — y = 7
4) x + 29 = 68 y + 45 = 54 48 — x = 1 80 — y = 6
5) x + 23 = 50 y + 34 = 44 68 — x = 16 24 — y = 9
6) x + 33 = 82 y + 3 = 35 74 — x = 47 90 — y = 80
7) x + 64 = 91 y + 40 = 91 27 — x = 17 24 — y = 5
8) x + 74 = 94 y + 45 = 98 32 — x = 9 8 — y = 3
9) x + 9 = 17 y + 18 = 22 93 — x = 24 30 — y = 3
10) x + 9 = 18 y + 9 = 40 18 — x = 7 70 — y = 27
Уравнения на сложение и вычитание. Вариант № 7.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 17 = 91 y + 21 = 22 32 — x = 3 8 — y = 0
2) x + 17 = 81 y + 1 = 10 77 — x = 35 99 — y = 83
3) x + 27 = 55 y + 6 = 18 15 — x = 4 67 — y = 58
4) x + 91 = 97 y + 10 = 54 60 — x = 27 12 — y = 8
5) x + 0 = 27 y + 27 = 31 5 — x = 1 32 — y = 25
6) x + 10 = 60 y + 33 = 34 15 — x = 11 14 — y = 12
7) x + 3 = 50 y + 28 = 35 10 — x = 5 29 — y = 5
8) x + 0 = 1 y + 18 = 93 56 — x = 25 44 — y = 14
9) x + 5 = 22 y + 30 = 74 31 — x = 25 42 — y = 7
10) x + 7 = 63 y + 11 = 81 53 — x = 41 3 — y = 1
Уравнения на сложение и вычитание. Вариант № 8.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 54 = 72 y + 63 = 77 64 — x = 12 89 — y = 27
2) x + 2 = 39 y + 6 = 33 16 — x = 7 40 — y = 13
3) x + 16 = 29 y + 17 = 46 12 — x = 1 70 — y = 6
4) x + 14 = 27 y + 12 = 13 88 — x = 27 22 — y = 19
5) x + 4 = 28 y + 7 = 34 41 — x = 9 27 — y = 24
6) x + 44 = 56 y + 81 = 100 35 — x = 29 55 — y = 41
7) x + 0 = 6 y + 31 = 88 50 — x = 5 83 — y = 33
8) x + 0 = 18 y + 10 = 50 51 — x = 1 92 — y = 50
9) x + 44 = 46 y + 14 = 99 85 — x = 27 88 — y = 33
10) x + 10 = 77 y + 60 = 94 47 — x = 6 91 — y = 51
Уравнения на сложение и вычитание. Вариант № 9.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 5 = 6 y + 0 = 6 61 — x = 47 47 — y = 14
2) x + 3 = 84 y + 2 = 9 72 — x = 46 64 — y = 49
3) x + 71 = 87 y + 5 = 8 41 — x = 30 58 — y = 8
4) x + 44 = 67 y + 25 = 32 3 — x = 1 75 — y = 10
5) x + 84 = 100 y + 23 = 31 9 — x = 6 22 — y = 18
6) x + 6 = 30 y + 42 = 51 74 — x = 26 23 — y = 22
7) x + 45 = 69 y + 2 = 4 6 — x = 1 74 — y = 17
8) x + 0 = 22 y + 17 = 23 76 — x = 35 79 — y = 74
9) x + 4 = 23 y + 41 = 90 65 — x = 32 78 — y = 44
10) x + 13 = 20 y + 8 = 78 89 — x = 32 9 — y = 6
Уравнения на сложение и вычитание.
 Вариант № 10.
Дата:______________ ФИО:_________________________________ Оценка:__________
Вариант № 10.
Дата:______________ ФИО:_________________________________ Оценка:__________
Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 9 = 34 y + 19 = 25 98 — x = 46 50 — y = 14
2) x + 0 = 81 y + 12 = 58 91 — x = 16 50 — y = 26
3) x + 34 = 42 y + 7 = 12 94 — x = 58 39 — y = 25
4) x + 0 = 5 y + 16 = 29 98 — x = 83 69 — y = 37
5) x + 0 = 23 y + 10 = 22 58 — x = 49 36 — y = 20
6) x + 66 = 67 y + 21 = 35 79 — x = 71 77 — y = 51
7) x + 44 = 50 y + 47 = 53 67 — x = 26 48 — y = 5
8) x + 5 = 69 y + 13 = 22 2 — x = 0 28 — y = 15
9) x + 79 = 88 y + 79 = 94 70 — x = 59 94 — y = 39
10) x + 20 = 48 y + 2 = 5 57 — x = 56 72 — y = 59
Уравнения на сложение и вычитание. Вариант № 11.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 3 = 89 y + 14 = 48 95 — x = 57 64 — y = 16
2) x + 1 = 11 y + 1 = 8 10 — x = 4 90 — y = 66
3) x + 17 = 21 y + 5 = 58 11 — x = 6 6 — y = 5
4) x + 20 = 28 y + 16 = 41 31 — x = 7 86 — y = 73
5) x + 76 = 92 y + 38 = 91 90 — x = 52 76 — y = 37
6) x + 16 = 44 y + 29 = 55 57 — x = 55 61 — y = 1
7) x + 1 = 14 y + 12 = 32 25 — x = 6 5 — y = 2
8) x + 18 = 59 y + 25 = 33 26 — x = 18 42 — y = 37
9) x + 19 = 57 y + 10 = 31 51 — x = 26 46 — y = 15
10) x + 18 = 20 y + 43 = 57 47 — x = 2 97 — y = 14
Уравнения на сложение и вычитание. Вариант № 12.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 17 = 44 y + 6 = 56 18 — x = 4 26 — y = 9
2) x + 5 = 82 y + 5 = 12 42 — x = 24 99 — y = 60
3) x + 3 = 38 y + 0 = 5 73 — x = 2 79 — y = 51
4) x + 19 = 84 y + 52 = 67 19 — x = 6 81 — y = 4
5) x + 27 = 73 y + 5 = 27 85 — x = 84 91 — y = 8
6) x + 69 = 90 y + 85 = 92 29 — x = 15 36 — y = 23
7) x + 15 = 67 y + 88 = 89 86 — x = 84 15 — y = 2
8) x + 44 = 48 y + 11 = 54 40 — x = 38 17 — y = 7
9) x + 37 = 87 y + 5 = 66 55 — x = 3 10 — y = 5
10) x + 0 = 14 y + 19 = 45 99 — x = 14 67 — y = 20
Уравнения на сложение и вычитание. Вариант № 13.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 85 = 97 y + 67 = 71 13 — x = 6 44 — y = 7
2) x + 62 = 93 y + 23 = 90 19 — x = 17 59 — y = 41
3) x + 46 = 52 y + 2 = 6 65 — x = 2 16 — y = 7
4) x + 20 = 42 y + 68 = 92 46 — x = 32 72 — y = 28
5) x + 64 = 77 y + 7 = 58 54 — x = 20 52 — y = 32
6) x + 41 = 95 y + 48 = 54 52 — x = 14 58 — y = 42
7) x + 91 = 96 y + 5 = 9 60 — x = 12 15 — y = 1
8) x + 40 = 51 y + 17 = 30 8 — x = 1 63 — y = 37
9) x + 18 = 42 y + 51 = 100 4 — x = 1 87 — y = 28
10) x + 75 = 77 y + 16 = 67 88 — x = 1 34 — y = 15
Уравнения на сложение и вычитание.
 Вариант № 14.
Дата:______________ ФИО:_________________________________ Оценка:__________
Вариант № 14.
Дата:______________ ФИО:_________________________________ Оценка:__________
Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 10 = 15 y + 1 = 2 12 — x = 0 70 — y = 55
2) x + 50 = 78 y + 8 = 70 44 — x = 25 71 — y = 55
3) x + 24 = 32 y + 21 = 44 77 — x = 55 52 — y = 24
4) x + 42 = 85 y + 11 = 52 20 — x = 11 77 — y = 31
5) x + 2 = 10 y + 13 = 45 74 — x = 28 3 — y = 2
6) x + 1 = 4 y + 11 = 15 36 — x = 4 52 — y = 36
7) x + 44 = 45 y + 4 = 8 80 — x = 78 23 — y = 8
8) x + 58 = 88 y + 6 = 14 3 — x = 1 73 — y = 28
9) x + 17 = 38 y + 14 = 17 48 — x = 14 28 — y = 22
10) x + 61 = 69 y + 9 = 51 21 — x = 7 29 — y = 1
Уравнения на сложение и вычитание. Вариант № 15.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 4 = 98 y + 73 = 88 86 — x = 46 91 — y = 39
2) x + 6 = 8 y + 25 = 50 96 — x = 73 46 — y = 29
3) x + 63 = 100 y + 9 = 34 85 — x = 71 6 — y = 1
4) x + 6 = 12 y + 44 = 70 46 — x = 45 51 — y = 25
5) x + 14 = 26 y + 56 = 79 54 — x = 29 29 — y = 15
6) x + 19 = 66 y + 16 = 85 27 — x = 3 39 — y = 7
7) x + 24 = 47 y + 70 = 86 9 — x = 4 23 — y = 17
8) x + 4 = 32 y + 7 = 16 44 — x = 6 79 — y = 17
9) x + 2 = 3 y + 3 = 34 61 — x = 53 88 — y = 32
10) x + 31 = 62 y + 8 = 25 86 — x = 13 11 — y = 3
Уравнения на сложение и вычитание. Вариант № 16.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 7 = 13 y + 4 = 5 64 — x = 15 97 — y = 59
2) x + 10 = 80 y + 47 = 54 42 — x = 34 98 — y = 62
3) x + 83 = 85 y + 32 = 33 61 — x = 8 10 — y = 3
4) x + 36 = 76 y + 24 = 43 44 — x = 28 59 — y = 30
5) x + 42 = 68 y + 5 = 49 87 — x = 61 6 — y = 4
6) x + 39 = 70 y + 2 = 69 89 — x = 66 55 — y = 11
7) x + 9 = 82 y + 49 = 92 73 — x = 4 76 — y = 31
8) x + 31 = 91 y + 52 = 88 91 — x = 22 68 — y = 22
9) x + 3 = 7 y + 7 = 21 7 — x = 4 47 — y = 41
10) x + 9 = 19 y + 22 = 83 10 — x = 2 19 — y = 15
Уравнения на сложение и вычитание. Вариант № 17.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 36 = 50 y + 46 = 87 93 — x = 0 67 — y = 39
2) x + 34 = 49 y + 9 = 17 7 — x = 3 85 — y = 79
3) x + 53 = 56 y + 2 = 9 69 — x = 24 13 — y = 10
4) x + 6 = 13 y + 1 = 2 85 — x = 55 64 — y = 62
5) x + 1 = 14 y + 6 = 7 25 — x = 18 64 — y = 12
6) x + 8 = 24 y + 39 = 56 50 — x = 32 20 — y = 10
7) x + 41 = 100 y + 16 = 46 79 — x = 10 99 — y = 4
8) x + 49 = 89 y + 82 = 90 55 — x = 32 88 — y = 68
9) x + 10 = 12 y + 14 = 29 47 — x = 29 59 — y = 43
10) x + 7 = 26 y + 22 = 78 75 — x = 38 65 — y = 17
Уравнения на сложение и вычитание.
 Вариант № 18.
Дата:______________ ФИО:_________________________________ Оценка:__________
Вариант № 18.
Дата:______________ ФИО:_________________________________ Оценка:__________
Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 44 = 45 y + 1 = 4 80 — x = 78 32 — y = 27
2) x + 12 = 59 y + 7 = 59 51 — x = 46 43 — y = 28
3) x + 42 = 63 y + 10 = 22 91 — x = 66 4 — y = 3
4) x + 18 = 23 y + 11 = 16 76 — x = 2 47 — y = 8
5) x + 0 = 1 y + 4 = 6 48 — x = 12 28 — y = 6
6) x + 29 = 38 y + 31 = 95 47 — x = 27 100 — y = 67
7) x + 66 = 67 y + 19 = 74 60 — x = 35 72 — y = 59
8) x + 20 = 95 y + 3 = 95 54 — x = 6 1 — y = 0
9) x + 33 = 85 y + 35 = 68 20 — x = 6 69 — y = 18
10) x + 0 = 15 y + 0 = 1 41 — x = 40 32 — y = 27
Уравнения на сложение и вычитание. Вариант № 19.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 100.
Реши уравнения на сложение и вычитание.
1) x + 8 = 20 y + 20 = 43 57 — x = 51 55 — y = 29
2) x + 2 = 13 y + 44 = 90 3 — x = 2 69 — y = 58
3) x + 13 = 58 y + 23 = 61 33 — x = 13 11 — y = 9
4) x + 1 = 41 y + 45 = 70 57 — x = 23 30 — y = 0
5) x + 58 = 61 y + 20 = 36 51 — x = 28 81 — y = 62
6) x + 6 = 35 y + 3 = 7 36 — x = 33 24 — y = 15
7) x + 77 = 80 y + 3 = 100 8 — x = 7 11 — y = 7
8) x + 5 = 39 y + 10 = 77 77 — x = 60 36 — y = 21
9) x + 33 = 42 y + 0 = 8 61 — x = 5 53 — y = 50
10) x + 4 = 34 y + 86 = 98 20 — x = 19 16 — y = 10
Уравнения на сложение и вычитание. Вариант № 1.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 350 = 665 y + 151 = 539 619 — x = 130 169 — y = 136
2) x + 208 = 362 y + 31 = 46 585 — x = 296 667 — y = 236
3) x + 314 = 502 y + 53 = 472 88 — x = 86 809 — y = 785
4) x + 91 = 800 y + 62 = 573 202 — x = 183 904 — y = 419
5) x + 13 = 599 y + 256 = 917 90 — x = 62 538 — y = 211
6) x + 449 = 903 y + 462 = 852 292 — x = 128 778 — y = 114
7) x + 304 = 721 y + 266 = 294 749 — x = 280 357 — y = 177
8) x + 394 = 413 y + 503 = 612 902 — x = 753 711 — y = 188
9) x + 306 = 996 y + 30 = 69 440 — x = 330 971 — y = 35
10) x + 180 = 632 y + 142 = 569 533 — x = 373 279 — y = 37
Уравнения на сложение и вычитание. Вариант № 2.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 247 = 725 y + 25 = 710 634 — x = 618 45 — y = 9
2) x + 72 = 375 y + 3 = 351 182 — x = 51 997 — y = 240
3) x + 24 = 102 y + 133 = 216 778 — x = 775 151 — y = 95
4) x + 28 = 84 y + 107 = 248 684 — x = 46 49 — y = 46
5) x + 215 = 343 y + 1 = 710 709 — x = 20 899 — y = 336
6) x + 345 = 594 y + 184 = 276 828 — x = 593 454 — y = 330
7) x + 242 = 722 y + 414 = 594 106 — x = 63 770 — y = 754
8) x + 1 = 70 y + 12 = 56 766 — x = 670 182 — y = 66
9) x + 20 = 28 y + 643 = 778 477 — x = 340 133 — y = 76
10) x + 98 = 598 y + 6 = 8 202 — x = 61 703 — y = 490
Уравнения на сложение и вычитание. Вариант № 3.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 365 = 918 y + 307 = 469 177 — x = 106 956 — y = 760
2) x + 842 = 935 y + 149 = 364 867 — x = 765 479 — y = 167
3) x + 11 = 690 y + 8 = 32 966 — x = 555 706 — y = 673
4) x + 589 = 924 y + 479 = 499 784 — x = 728 906 — y = 866
5) x + 422 = 962 y + 378 = 411 599 — x = 284 946 — y = 914
6) x + 13 = 69 y + 65 = 75 808 — x = 322 185 — y = 75
7) x + 712 = 763 y + 219 = 622 954 — x = 207 118 — y = 62
8) x + 702 = 761 y + 131 = 501 966 — x = 402 639 — y = 373
9) x + 444 = 534 y + 789 = 812 193 — x = 180 18 — y = 0
10) x + 340 = 677 y + 52 = 212 65 — x = 42 978 — y = 117
Уравнения на сложение и вычитание. Вариант № 4.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 82 = 537 y + 369 = 377 457 — x = 106 466 — y = 392
2) x + 17 = 830 y + 184 = 264 99 — x = 4 995 — y = 628
3) x + 123 = 175 y + 129 = 659 600 — x = 1 663 — y = 28
4) x + 580 = 783 y + 583 = 746 934 — x = 383 211 — y = 208
5) x + 119 = 727 y + 10 = 697 455 — x = 175 743 — y = 618
6) x + 49 = 526 y + 458 = 504 782 — x = 240 957 — y = 52
7) x + 597 = 984 y + 538 = 554 136 — x = 40 14 — y = 5
8) x + 200 = 501 y + 387 = 685 955 — x = 822 400 — y = 189
9) x + 12 = 303 y + 317 = 702 876 — x = 48 393 — y = 382
10) x + 248 = 306 y + 311 = 601 411 — x = 353 8 — y = 7
Уравнения на сложение и вычитание. Вариант № 5.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 224 = 569 y + 25 = 982 900 — x = 556 525 — y = 67
2) x + 529 = 541 y + 360 = 400 577 — x = 416 961 — y = 333
3) x + 266 = 563 y + 563 = 624 828 — x = 751 108 — y = 69
4) x + 305 = 326 y + 43 = 64 968 — x = 792 997 — y = 813
5) x + 100 = 248 y + 27 = 836 127 — x = 93 893 — y = 575
6) x + 696 = 975 y + 210 = 215 78 — x = 48 203 — y = 45
7) x + 17 = 458 y + 145 = 458 79 — x = 66 886 — y = 683
8) x + 55 = 328 y + 201 = 239 69 — x = 16 251 — y = 150
9) x + 420 = 501 y + 84 = 183 801 — x = 381 238 — y = 40
10) x + 135 = 248 y + 183 = 233 735 — x = 535 565 — y = 227
Уравнения на сложение и вычитание. Вариант № 6.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 123 = 169 y + 813 = 849 789 — x = 128 327 — y = 227
2) x + 190 = 777 y + 213 = 261 257 — x = 218 942 — y = 272
3) x + 288 = 664 y + 194 = 287 504 — x = 499 529 — y = 483
4) x + 147 = 444 y + 113 = 427 242 — x = 143 104 — y = 96
5) x + 697 = 929 y + 153 = 246 490 — x = 15 186 — y = 58
6) x + 65 = 251 y + 10 = 268 544 — x = 42 699 — y = 192
7) x + 312 = 888 y + 246 = 878 528 — x = 187 260 — y = 77
8) x + 246 = 795 y + 699 = 964 377 — x = 116 238 — y = 213
9) x + 52 = 102 y + 35 = 293 322 — x = 43 179 — y = 79
10) x + 20 = 77 y + 89 = 857 206 — x = 55 475 — y = 362
Уравнения на сложение и вычитание. Вариант № 7.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 112 = 330 y + 484 = 676 228 — x = 81 379 — y = 173
2) x + 362 = 445 y + 403 = 796 926 — x = 793 732 — y = 38
3) x + 480 = 505 y + 472 = 475 508 — x = 318 29 — y = 13
4) x + 29 = 220 y + 454 = 791 829 — x = 159 659 — y = 309
5) x + 84 = 612 y + 18 = 156 630 — x = 355 460 — y = 456
6) x + 116 = 463 y + 434 = 488 848 — x = 627 940 — y = 531
7) x + 15 = 986 y + 7 = 16 91 — x = 28 771 — y = 165
8) x + 252 = 419 y + 949 = 958 599 — x = 479 439 — y = 243
9) x + 59 = 513 y + 234 = 573 288 — x = 180 137 — y = 134
10) x + 32 = 106 y + 78 = 304 694 — x = 589 290 — y = 38
Уравнения на сложение и вычитание. Вариант № 8.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 117 = 246 y + 15 = 19 913 — x = 74 304 — y = 21
2) x + 378 = 576 y + 103 = 581 850 — x = 180 421 — y = 345
3) x + 179 = 927 y + 150 = 232 389 — x = 329 775 — y = 172
4) x + 130 = 330 y + 270 = 537 278 — x = 165 28 — y = 7
5) x + 866 = 918 y + 430 = 867 844 — x = 502 190 — y = 72
6) x + 40 = 394 y + 514 = 670 856 — x = 823 487 — y = 75
7) x + 53 = 54 y + 3 = 5 111 — x = 108 396 — y = 299
8) x + 232 = 556 y + 66 = 95 593 — x = 155 205 — y = 189
9) x + 124 = 889 y + 258 = 868 271 — x = 59 709 — y = 50
10) x + 107 = 263 y + 730 = 738 873 — x = 437 916 — y = 202
Уравнения на сложение и вычитание. Вариант № 9.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 184 = 862 y + 75 = 106 227 — x = 66 863 — y = 527
2) x + 469 = 678 y + 329 = 333 984 — x = 643 916 — y = 188
3) x + 383 = 875 y + 2 = 146 819 — x = 171 159 — y = 81
4) x + 315 = 398 y + 535 = 751 437 — x = 411 742 — y = 296
5) x + 266 = 775 y + 106 = 109 965 — x = 857 298 — y = 239
6) x + 59 = 330 y + 104 = 134 563 — x = 531 790 — y = 434
7) x + 158 = 250 y + 630 = 792 343 — x = 48 408 — y = 279
8) x + 131 = 229 y + 248 = 345 905 — x = 51 373 — y = 366
9) x + 318 = 632 y + 112 = 219 109 — x = 26 764 — y = 456
10) x + 376 = 396 y + 31 = 244 881 — x = 714 728 — y = 710
Уравнения на сложение и вычитание. Вариант № 10.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 112 = 116 y + 146 = 255 150 — x = 89 696 — y = 361
2) x + 27 = 36 y + 70 = 274 250 — x = 130 453 — y = 279
3) x + 558 = 883 y + 21 = 791 364 — x = 10 191 — y = 2
4) x + 698 = 775 y + 352 = 857 845 — x = 681 895 — y = 605
5) x + 274 = 635 y + 806 = 990 489 — x = 56 686 — y = 382
6) x + 738 = 839 y + 100 = 125 105 — x = 44 975 — y = 964
7) x + 36 = 41 y + 75 = 104 953 — x = 173 552 — y = 321
8) x + 281 = 391 y + 100 = 444 886 — x = 865 957 — y = 790
9) x + 150 = 595 y + 168 = 355 274 — x = 94 768 — y = 625
10) x + 42 = 533 y + 35 = 274 56 — x = 54 650 — y = 506
Уравнения на сложение и вычитание. Вариант № 11.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 101 = 381 y + 145 = 380 480 — x = 90 289 — y = 97
2) x + 46 = 459 y + 479 = 836 382 — x = 281 569 — y = 371
3) x + 173 = 245 y + 173 = 751 75 — x = 38 607 — y = 557
4) x + 130 = 278 y + 53 = 95 189 — x = 110 515 — y = 436
5) x + 512 = 889 y + 36 = 52 34 — x = 22 994 — y = 89
6) x + 210 = 992 y + 138 = 562 322 — x = 318 118 — y = 89
7) x + 51 = 362 y + 23 = 25 338 — x = 22 948 — y = 458
8) x + 95 = 135 y + 219 = 415 878 — x = 875 803 — y = 541
9) x + 246 = 468 y + 257 = 288 543 — x = 90 327 — y = 299
10) x + 234 = 572 y + 217 = 428 230 — x = 114 710 — y = 481
Уравнения на сложение и вычитание. Вариант № 12.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 135 = 582 y + 48 = 109 879 — x = 585 668 — y = 494
2) x + 796 = 957 y + 78 = 225 835 — x = 739 52 — y = 2
3) x + 58 = 379 y + 432 = 759 388 — x = 87 204 — y = 188
4) x + 71 = 355 y + 344 = 348 329 — x = 169 409 — y = 287
5) x + 526 = 971 y + 337 = 919 604 — x = 193 73 — y = 30
6) x + 197 = 521 y + 165 = 637 402 — x = 222 474 — y = 20
7) x + 454 = 951 y + 525 = 662 251 — x = 171 214 — y = 54
8) x + 159 = 338 y + 372 = 433 963 — x = 618 727 — y = 688
9) x + 237 = 854 y + 261 = 498 498 — x = 418 456 — y = 403
10) x + 638 = 921 y + 65 = 92 92 — x = 85 566 — y = 82
Уравнения на сложение и вычитание. Вариант № 13.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 210 = 523 y + 448 = 987 226 — x = 55 302 — y = 98
2) x + 812 = 871 y + 74 = 320 266 — x = 255 363 — y = 241
3) x + 287 = 886 y + 124 = 415 853 — x = 445 896 — y = 447
4) x + 109 = 202 y + 745 = 819 387 — x = 329 976 — y = 735
5) x + 562 = 648 y + 36 = 42 175 — x = 50 692 — y = 249
6) x + 357 = 418 y + 630 = 755 79 — x = 31 192 — y = 156
7) x + 201 = 382 y + 157 = 409 752 — x = 61 307 — y = 83
8) x + 235 = 252 y + 306 = 539 781 — x = 390 617 — y = 524
9) x + 138 = 545 y + 128 = 220 332 — x = 301 67 — y = 8
10) x + 13 = 571 y + 384 = 426 121 — x = 45 505 — y = 448
Уравнения на сложение и вычитание. Вариант № 14.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 193 = 889 y + 214 = 282 798 — x = 670 746 — y = 539
2) x + 219 = 935 y + 424 = 429 73 — x = 15 30 — y = 28
3) x + 28 = 795 y + 10 = 19 164 — x = 42 993 — y = 919
4) x + 301 = 315 y + 17 = 50 405 — x = 249 498 — y = 476
5) x + 8 = 9 y + 43 = 48 95 — x = 14 958 — y = 24
6) x + 234 = 480 y + 104 = 327 909 — x = 387 1 — y = 0
7) x + 200 = 294 y + 148 = 318 472 — x = 35 597 — y = 533
8) x + 202 = 535 y + 150 = 699 913 — x = 318 11 — y = 0
9) x + 348 = 482 y + 103 = 326 483 — x = 52 183 — y = 69
10) x + 1 = 122 y + 18 = 188 582 — x = 567 420 — y = 75
Уравнения на сложение и вычитание. Вариант № 15.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 368 = 452 y + 219 = 889 754 — x = 389 494 — y = 225
2) x + 717 = 784 y + 91 = 390 506 — x = 314 516 — y = 261
3) x + 442 = 502 y + 145 = 988 15 — x = 6 204 — y = 130
4) x + 247 = 985 y + 30 = 795 68 — x = 36 402 — y = 384
5) x + 393 = 644 y + 7 = 176 803 — x = 162 962 — y = 114
6) x + 25 = 293 y + 767 = 912 101 — x = 95 359 — y = 75
7) x + 5 = 299 y + 13 = 53 693 — x = 504 654 — y = 130
8) x + 187 = 222 y + 50 = 717 328 — x = 139 647 — y = 404
9) x + 407 = 909 y + 74 = 309 573 — x = 305 371 — y = 166
10) x + 117 = 235 y + 263 = 914 87 — x = 14 249 — y = 58
Уравнения на сложение и вычитание. Вариант № 16.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 543 = 960 y + 354 = 831 446 — x = 371 559 — y = 68
2) x + 399 = 404 y + 319 = 515 845 — x = 463 55 — y = 11
3) x + 739 = 903 y + 319 = 379 276 — x = 67 860 — y = 293
4) x + 78 = 237 y + 14 = 234 992 — x = 576 993 — y = 376
5) x + 437 = 506 y + 249 = 323 361 — x = 207 149 — y = 76
6) x + 2 = 155 y + 30 = 201 423 — x = 288 591 — y = 105
7) x + 45 = 95 y + 55 = 955 746 — x = 167 261 — y = 137
8) x + 5 = 142 y + 262 = 486 405 — x = 127 491 — y = 337
9) x + 95 = 220 y + 467 = 860 169 — x = 113 905 — y = 149
10) x + 9 = 41 y + 890 = 948 228 — x = 218 397 — y = 41
Уравнения на сложение и вычитание. Вариант № 17.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 188 = 221 y + 126 = 857 42 — x = 23 278 — y = 88
2) x + 7 = 24 y + 817 = 890 143 — x = 134 970 — y = 258
3) x + 109 = 214 y + 0 = 5 971 — x = 884 860 — y = 356
4) x + 27 = 708 y + 5 = 43 82 — x = 49 160 — y = 102
5) x + 662 = 981 y + 94 = 177 304 — x = 264 912 — y = 566
6) x + 134 = 447 y + 124 = 354 670 — x = 232 480 — y = 170
7) x + 218 = 265 y + 632 = 696 223 — x = 136 154 — y = 45
8) x + 58 = 269 y + 99 = 100 10 — x = 9 724 — y = 503
9) x + 909 = 991 y + 72 = 545 861 — x = 712 142 — y = 25
10) x + 97 = 982 y + 309 = 812 768 — x = 674 625 — y = 399
Уравнения на сложение и вычитание. Вариант № 18.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 536 = 880 y + 316 = 637 966 — x = 273 833 — y = 745
2) x + 536 = 941 y + 259 = 517 30 — x = 21 954 — y = 832
3) x + 907 = 984 y + 638 = 655 587 — x = 5 844 — y = 87
4) x + 415 = 967 y + 467 = 801 454 — x = 309 559 — y = 458
5) x + 573 = 628 y + 662 = 954 308 — x = 174 902 — y = 14
6) x + 689 = 935 y + 13 = 181 200 — x = 74 850 — y = 149
7) x + 210 = 260 y + 1 = 33 507 — x = 470 977 — y = 577
8) x + 321 = 519 y + 147 = 299 149 — x = 51 221 — y = 96
9) x + 72 = 714 y + 66 = 78 155 — x = 66 626 — y = 14
10) x + 175 = 593 y + 276 = 429 908 — x = 62 914 — y = 859
Уравнения на сложение и вычитание. Вариант № 19.
Дата:______________ ФИО:_________________________________ Оценка:__________Решение уравнений с числами до 1000.
Реши уравнения на сложение и вычитание.
1) x + 51 = 382 y + 19 = 58 653 — x = 233 3 — y = 2
2) x + 661 = 799 y + 604 = 804 97 — x = 73 827 — y = 759
3) x + 515 = 800 y + 4 = 901 193 — x = 114 83 — y = 82
4) x + 74 = 773 y + 235 = 255 422 — x = 212 761 — y = 24
5) x + 106 = 134 y + 70 = 230 172 — x = 151 565 — y = 503
6) x + 260 = 525 y + 356 = 671 36 — x = 9 608 — y = 562
7) x + 12 = 87 y + 60 = 166 120 — x = 24 966 — y = 84
8) x + 419 = 491 y + 731 = 770 679 — x = 147 983 — y = 279
9) x + 115 = 712 y + 250 = 696 681 — x = 481 416 — y = 388
10) x + 52 = 732 y + 127 = 692 113 — x = 110 798 — y = 712
Интерфакс-Недвижимость / План по восстановлению прав дольщиков в IV квартале 2021 года выполнили 11 регионов РФ
9 февраля 2022, 17:33
Москва.
 9 февраля. ИНТЕРФАКС-НЕДВИЖИМОСТЬ — Одиннадцать регионов РФ выполнили план по восстановлению прав дольщиков в IV квартале 2021 года, сообщили в пресс-службе Фонда развития территорий.
9 февраля. ИНТЕРФАКС-НЕДВИЖИМОСТЬ — Одиннадцать регионов РФ выполнили план по восстановлению прав дольщиков в IV квартале 2021 года, сообщили в пресс-службе Фонда развития территорий.
«В IV квартале 2021 года 11 регионов показали хорошее исполнение мероприятий по восстановлению прав дольщиков», — говорится в сообщении.
Среди них — Московская, Самарская, Новосибирская, Костромская, Саратовская, Волгоградская области, Санкт-Петербург, Хабаровский край и ряд других.
«Эти регионы выполнили все, что было предусмотрено по дорожным картам, или выполнили что-то сверх плана и защитили еще больше граждан», — подчеркнул гендиректор Фонда Константин Тимофеев.
Отмечается, что ряд регионов, напротив, не выполнили взятые обязательства. Среди них — Тамбовская, Липецкая, Рязанская, Свердловская области, Севастополь и другие. Так, суммарно они заявили на IV квартал 20 проблемных объектов, но проблемы 1,4 тыс. дольщиков там не решили.
Тимофеев отметил, что ведется работа с регионами по данным объектам. В частности, устанавливаются сроки и план решения проблем.
В частности, устанавливаются сроки и план решения проблем.
«Если нам не могут назвать сроки, то мы рекомендуем заявлять такие объекты в Фонд и решать проблемы вместе», — пояснил Тимофеев.
Напомним, всего в IV квартале 2021 года субъекты собственными силами восстановили права почти 13,4 тыс. пострадавших дольщиков 223 проблемных объектов.
Фонд защиты прав дольщиков (с 1 января 2022 года вошел в Фонд развития территорий) был зарегистрирован в форме публично-правовой компании в октябре 2017 года. Застройщики обязаны перечислять в него взносы в размере 1,2% от ДДУ по всем новым объектам. В случае необходимости средства фонда могут быть направлены на достройку проблемных объектов или выплату компенсаций.
В США арестовали супругов за отмывание биткоинов на 4,5 млрд долларов
ФБР обвиняет их в сговоре с хакерами, которые в 2016 году взломали биржу Bitfinex и похитили почти 120 тысяч токенов. Пока обвиняемых отпустили под залог в 8 млн долларов
Пока обвиняемых отпустили под залог в 8 млн долларов
В США арестовали супружескую пару за отмывание биткоинов на 4,5 млрд долларов. ФБР обвиняет гражданина России и Соединенных Штатов Илью Лихтенштейна и его супругу Хизер Морган в сговоре с хакерами, которые в 2016 году взломали биржу Bitfinex. Тогда были похищены почти 120 тысяч токенов на сумму 71 млн долларов, уточняет американский Минюст. По сегодняшнему курсу ущерб исчисляется миллиардами.
Bitfinex, считавшаяся на тот момент третьей по популярности биржей в мире, заявила о взломе в августе 2016 года. После похищения торги были приостановлены на несколько дней, биткоин упал на 13%. Большая часть токенов, связанных с этим взломом, отслеживалась и была занесена в черный список. Поэтому похитителям было сложно их отмыть. Часть украденного на сумму в 700 млн долларов им удалось вывести через даркнет, когда рынок отвлекся на листинг биржи Coinbase на NASDAQ, пишет агентство Elliptic.
Оставшиеся 3,5 млрд долларов хакеры пытались отмыть всего неделю назад, и это заметили на бирже. Минюст США 9 февраля сообщил об аресте причастных ко взлому, биткоины были изъяты. По данным ФБР, Лихтенштейн и Морган провели 2 тысячи несанкционированных транзакций на кошелек россиянина, а затем вывели деньги на свои счета.
Минюст США 9 февраля сообщил об аресте причастных ко взлому, биткоины были изъяты. По данным ФБР, Лихтенштейн и Морган провели 2 тысячи несанкционированных транзакций на кошелек россиянина, а затем вывели деньги на свои счета.
По данным Crunchbase, 34-летний Илья Лихтенштейн — сооснователь стартапа MixRank, который разрабатывает ПО для маркетинговых компаний. 31-летняя Хизер Морган основала сервис по копирайтингу SalesFolk. Суд обвинил хакеров в двух заговорах — в целях отмывания денег и обмана Соединенных Штатов. Им грозит до 25 лет лишения свободы.
Суд предложил выпустить супругов под залог, правительство потребовало установить его в 10 млн долларов. Адвокаты хакеров назвали сумму «смехотворной», и суд выпустил Морган за 3 млн долларов, Лихтенштейна — за 5 млн долларов, пишет Bloomberg. Остается вопросом, по какому курсу оценивать сумму ущерба, говорит генеральный директор «Крипто-А» Алена Нариньяни:
Алена Нариньяни генеральный директор «Крипто-А»
По оценке аналитической компании Chainalysis, в 2021 году хакеры украли криптовалюту на сумму 14 млрд долларов. Ущерб от преступлений, связанных с цифровыми валютами, вырос почти на 79% по сравнению с 2020 годом.
Ущерб от преступлений, связанных с цифровыми валютами, вырос почти на 79% по сравнению с 2020 годом.
Добавить BFM.ru в ваши источники новостей?
AirPods не подключаются к Apple Watch? Как исправить
Не можете подключить наушники AirPods к своим Apple Watch? Ниже мы расскажем о разных способах, которые могут помочь вам решить эту проблему.
Вы можете подключить AirPods или другие Bluetooth-наушники к своим смарт-часам для звонков, для прослушивания ответов Siri и прослушивания своих голосовых записей. Для всего этого можно использовать и динамик Apple Watch.
Для прослушивания музыки и подкастов к Apple Watch обязательно нужно подключать наушники. Через динамик смарт-часов музыку послушать нельзя.
К тому же, для долгих телефонных разговоров удобнее использовать AirPods, подключенные к часам.
Способы ниже актуальны для всех моделей AirPods (1, 2, 3 поколения, Pro, Max) и всех моделей Apple Watch с современными версиями watchOS.
Большинство решений ниже актуальны также для беспроводных наушников Beats, Samsung Galaxy, Pixel и др. Они помогут решить проблемы и с подключением устройств для отслеживания здоровья к Apple Watch.
1. Узнайте, как подключать Bluetooth-устройства к Apple Watch
AirPods
Когда вы подключаете наушники AirPods к одному из своих устройств Apple, они автоматически подключаются и ко всем остальным вашим устройствам. Это значит, что как только вы подключите наушники к своему iPhone, они автоматически станут доступны и для Mac, iPad, Apple Watch и других ваших устройств. Вам не нужно подключать AirPods к каждому из устройств вручную.
Это актуально и для наушников Beats.
Сторонние Bluetooth-наушники
Сторонние Bluetooth-наушники нужно подключать ко всем устройствам Apple вручную. Если вы подключите свои сторонние наушники к iPhone, то на Apple Watch и Mac они не появятся автоматически.
Способ подключения сторонних Bluetooth-наушников к Apple Watch зависит от их бренда. В целом шаги для всех наушников схожи.
В целом шаги для всех наушников схожи.
Вот как подключить Bluetooth-устройство к Apple Watch:
1) Нажмите колёсико Digital Crown на своих Apple Watch и зайдите в «Настройки» > Bluetooth. Убедитесь, что Bluetooth включен.
2) Включите свои Bluetooth-наушники с помощью кнопки или просто вынув их из футляра.
3) Нажмите кнопку Bluetooth-подключения на наушниках. Часто это та же кнопка, что и кнопка включения. Прочтите инструкцию к наушникам. В большинстве случаев нужно зажать кнопку, чтобы активировать режим подключения по Bluetooth. Некоторые наушники сообщат вам о том, что они готовы к подключению, звуковым сигналом.
4) Через несколько секунд ваши наушники появятся на экране настроек Bluetooth на ваших Apple Watch. Выберите их, чтобы подключить. Если они не появились, то ещё раз проверьте, что правильно активировали режим подключения на аксессуаре. Можете также выключить и включить Bluetooth на Apple Watch.
2. Проверьте, чтобы AirPods были заряжены
Перед тем, как переходить к последующим способам, проверьте, что ваши беспроводные наушники заряжены. Если это не так, то они не подключатся к вашим Apple Watch.
Примечание: Если зарядка от ваших Apple Watch недалеко, поместите на неё свои смарт-часы на несколько минут.
3. Отключите AirPods от iPhone, iPad или Mac
Ваши AirPods подключены к вашему iPhone, Mac или другому устройству поблизости? Из-за этого у вас может не получаться подключить AirPods к Apple Watch.
Чтобы проверить подключение на iPhone и iPad зайдите в «Настройки» > Bluetooth. Если рядом с названием ваших AirPods есть надпись «Подключено», нажмите значок «i» рядом с ними, а затем «Отключить». Вы также можете открыть пункт управления и через него отключить Bluetooth.
На Mac нажмите значок Bluetooth в пункте управления macOS или в строке меню. Если AirPods подключены, их значок будет синим. Нажмите название AirPods, чтобы отключить наушники. Это также можно сделать через «Системные настройки» > Bluetooth, нажав на AirPods правой кнопкой мыши и выбрав «Отключить».
Нажмите название AirPods, чтобы отключить наушники. Это также можно сделать через «Системные настройки» > Bluetooth, нажав на AirPods правой кнопкой мыши и выбрав «Отключить».
Когда ваши AirPods или другие Bluetooth-наушники будут отключены от всех остальных устройств, попробуйте подключить их к своим Apple Watch. В этот раз всё должно получиться.
Примечание: Пока вы не вставите наушники AirPods в свои уши, на экране Apple Watch может не появиться слово «Подключено».
4. Выберите Bluetooth-устройство для вывода
Когда Apple Watch воспроизводят какой-то звук, на их экране отображается значок AirPlay (треугольник с тремя кругами сверху). Нажмите этот значок и выберите свои AirPods или другие Bluetooth-наушники. Если AirPods находятся вне футляра, а сторонние наушники включены, то они должны подключиться к вашим Apple Watch через пару секунд.
Вы также можете выбрать устройство вывода аудио, нажав значок AirPlay в пункте управления своих Apple Watch. Чтобы его открыть, проведите вверх от нижнего края экрана смарт-часов.
Чтобы его открыть, проведите вверх от нижнего края экрана смарт-часов.
5. AirPods не подключаются к Apple Watch во время звонков?
Иногда AirPods могут не подключаться к Apple Watch только во время обычных или звонков по FaceTime. Возможно, это баг watchOS. К счастью, есть решение.
1) В приложении «Музыка» включите какую-нибудь песню и выберите свои AirPods. Наушники подключатся и начнут воспроизводить музыку.
2) Теперь на часах начните вызов. Вы услышите своего собеседника через наушники.
6. Отключите и включите Bluetooth
1) Зайдите в приложение «Настройки» и выберите секцию Bluetooth.
2) Пролистайте вниз и отключите Bluetooth.
3) Подождите примерно 30 секунд и снова включите Bluetooth.
7. Включите Авиарежим
1) Откройте пункт управления свайпом вверх от нижнего края экрана.
2) Нажмите значок Авиарежима с самолётом.
3) Через 30 секунд ещё раз нажмите этот значок, чтобы выключить Авиарежим.
Теперь, когда вы выберите свои AirPods как устройство для вывода аудио, всё должно получиться.
8. Закройте приложения на Apple Watch
Нажмите боковую кнопку смарт-часов и смахните влево приложения. Чтобы закрыть их, нажмите красный значок «x».
9. Перезагрузите Apple Watch
Зажмите боковую кнопку своих Apple Watch и проведите по слайдеру отключения вправо. Подождите примерно минуту и нажмите эту же кнопку для включения Apple Watch.
10. Поместите AirPods в футляр
На отключение и включение Apple Watch уйдёт около двух минут. В это время поместите свои AirPods в их футляр для зарядки и закройте крышку.
Если у вас сторонние наушники, отключите и включите их способом, описанным в инструкции от них.
Когда Apple Watch снова включатся, выньте AirPods из чехла и снова попытайтесь подключить их к смарт-часам. Должно получиться.
Должно получиться.
11. Забудьте AirPods и подключите их заново
Вы можете полностью отвязать AirPods от всех своих устройств с одним Apple ID.
1) Откройте приложение «Настройки» и выберите Bluetooth.
2) Если там отображаются ваши AirPods, нажмите значок (i) рядом с ним, а затем нажмите «Забыть устройство».
3) Перезагрузите свои Apple Watch, заранее поместив AirPods в футляр.
4) Теперь откройте крышку футляра и нажмите кнопку на задней его стороне. Лампочка на футляре станет белой. После этого наушники появятся на экране настроек Bluetooth на Apple Watch. Выберите их для подключения.
12. Обновите систему Apple Watch и AirPods
Если у вас устаревшая версия watchOS, следует установить последнюю доступную версию системы. Также стоит обновить прошивку AirPods. Ваш iPhone автоматически обновляет прошивку AirPods без вашего ведома. Вы можете только проверить, какая версия у вас сейчас стоит.
Вы можете только проверить, какая версия у вас сейчас стоит.
13. Сделайте сброс AirPods
Если проблема всё ещё не решена, попробуйте сделать сброс своих AirPods. После этого подключите их к своему iPhone.
14. Сбросьте настройки сети на iPhone
На Apple Watch нет своих настроек сети, но вы можете сбросить их на своём iPhone. Для этого зайдите в «Настройки» > «Основные» > «Перенос или сброс iPhone» > «Сброс» > «Сбросить настройки сети».
После этого подключите свои AirPods к iPhone. Они должны автоматически подключиться и к Apple Watch.
15. Сделайте сброс Apple Watch
Всё ещё не получается? Проверьте, подключаются ли AirPods к другим устройствам. Если наушники работают отлично, то проблема в ваших Apple Watch. Исправить её можно сбросом.
Оцените пост
[всего: 0 рейтинг: 0]
Смотрите похожее
AirPods Apple WatchКак собрать кубик Рубика 4×4
Месть Рубика — это версия кубика Рубика 4×4. Это тоже венгерское изобретение, разработанное Себестени Петером. Эту извилистую головоломку можно использовать как 2x2x2, не поворачивая внешние слои, или как 3x3x3, если вращать только внешние слои. Есть около 7,4 × 10 45 возможных перестановок для этой головоломки.
Это тоже венгерское изобретение, разработанное Себестени Петером. Эту извилистую головоломку можно использовать как 2x2x2, не поворачивая внешние слои, или как 3x3x3, если вращать только внешние слои. Есть около 7,4 × 10 45 возможных перестановок для этой головоломки.
Имеет 24 ребра, 24 центра и 8 угловых полей. У него такой же основной механизм, как у кубика Рубика, но в этом случае 4 центральные части удерживаются вместе скрытым центром.Чтобы разобрать его, вытащите центральную часть с помощью отвертки. Повторная сборка может быть сложной, если у вас нет четырех запасных рук.
Играйте с симулятором Rubik’s Revenge
Пазлы-кубики 2×2, 4×4 и 5×5
Вариации
Так же, как кубик Рубика, 4×4 имеет множество модификаций формы, построенных на одном и том же внутреннем механизме.
Axis Cube — куб в решенном положении, но он меняет свою форму, когда вы его перемешиваете.
Октаэдр – центры становятся углами, а углы становятся центрами.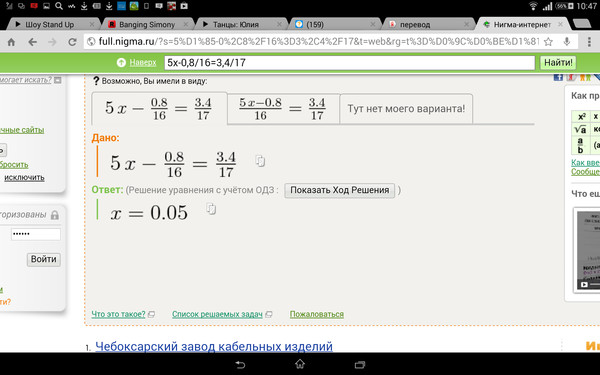
Fisher Cube — мать модов формы.
Перевязанный куб – с некоторыми частями, соединенными вместе. 2×2 в 2×2 от Meffert’s.
Ветряная мельница – со слегка скрученным сердечником.
Mastermorphix – 4-цветный оборотень с подушками.
4-цветный оборотень. Мы также должны упомянуть кубики Ghost и Mirror 4×4.
Как решить 4×4
Решение сложнее, чем классический метод кубика Рубика, но если вы умеете собирать 3х3х3, то и с этим у вас не должно возникнуть трудностей.Мы решаем 4×4, группируя 4 центра и пары ребер вместе, и, наконец, решаем его как 3×3. Некоторые спидкуберы могут решить этот куб менее чем за 30 секунд, так что это не так сложно!
Обозначение
Мы используем буквы для обозначения поворотов на кубике, подобно обозначениям кубика Рубика. Глубокие повороты возникают, когда мы перемещаем две буквы вместе, но мы можем определить повороты среза, когда перемещаем только второй слой. Мы будем использовать официальное обозначение NxNxN:
Мы будем использовать официальное обозначение NxNxN:
F – Наружная передняя грань по часовой стрелке
U’ – Наружная лицевая сторона против часовой стрелки
L2 – Двойной поворот левой грани (180 o )
Две лицевые грани Fw вместе: по часовой стрелке.Для кубов NxNxN мы отмечаем, сколько слоев нужно захватить, но мы можем игнорировать это для куба 4×4, поскольку числа всегда равны 2: 2Rw’ . В других учебниках используются строчные буквы для обозначения двойных поворотов.
f – Строчные буквы обозначают повороты внутреннего среза. U’ = Uw’ U
Шаг 1: Два соседних центра
Поскольку у 4×4 нет фиксированной центральной части, которая определяет цвет каждой грани, мы должны вычислить цветовую схему из цветов угловых частей.
На изображении показана наиболее распространенная цветовая схема, авторское право на которую принадлежит бренду Рубика, поэтому другие производители избегают ее, заменяя оранжевый на фиолетовый или реорганизовывая лица. Если у вас на кубике есть логотип Рубика, вам нужно использовать его.
Если у вас на кубике есть логотип Рубика, вам нужно использовать его.
Сначала решим белых и желтых смежных центров. Если вы не можете найти углы, имеющие эти два цвета рядом друг с другом, то это должно быть хорошо.
Этот шаг не должен быть проблемой, потому что нет решенных частей, которые мы могли бы испортить.Используйте этот короткий алгоритм, чтобы вставить кусок сверху на передний слой.
Дв’ Пр’ Дв
Когда белая грань готова, попробуйте построить желтый блок 2×2 на противоположной стороне, переместив белую грань вниз.
С заполненным белым центром внизу: Rw U Rw’ и Rw U2 Rw’
Шаг 2: оставшиеся четыре центра
Переместите готовые центры влево и вправо, чтобы они не мешались.Постройте первый блок, затем следите за цветовой схемой для следующих.
Используйте те же алгоритмы, что и выше, с белым и желтым центром слева и справа: Rw U Rw’
Шаг 3.
 Сопряжение ребер
Сопряжение ребер
Центральные блоки готовы, теперь нужно соединить края. Используйте приведенные ниже алгоритмы для присоединения двух ребер из переднего левого и переднего правого ребер. В зависимости от их положения приходится использовать два зеркальных алгоритма. Убедитесь, что над нижней частью края (отмеченной стрелками) нет полного ребра, потому что этот алгоритм нарушит его.
Когда совпадающие фигуры находятся рядом на одном уровне (3-е изображение), вам нужно перевернуть ту, что справа, вверх дном, чтобы выполнить одно из движений.
Первый случай: Uw L’ U’ L Uw’ Второй случай: Uw’ R U R’ Uw Рядом: R U’ B’ R2
Когда вы дойдете до двух последних ребер, вы не сможете использовать несовпадающие пары ребер в верхнем слое, потому что все они уже спарены.У нас есть отдельный алгоритм для решения двух последних ребер. Используйте описанный выше прием R U’ B’ R2 , если части не выровнены правильно.
Последние кромки: Dw R F’ U R’ F Dw’
Шаг 4: Решите как 3×3
С этого момента мы можем закончить сборку куба как 3×3, поворачивая только внешние слои. Прочтите здесь, как собрать кубик Рубика , если вам нужна дополнительная помощь, но пока не закрывайте эту страницу, потому что по мере продвижения вперед вы можете столкнуться с одним из случаев четности.
4×4 уменьшен до 3×3
Шаг 5: Случаи четности
Когда вы доберетесь до последнего слоя, вы можете оказаться в ситуации, когда куб кажется неразрешимым. Например, когда вы достигаете желтого креста и один край кажется ориентированным неправильно, или вы находите две части в правильном месте, когда позиционируете углы последнего слоя. Посмотрите, какой из длинных алгоритмов ниже решает вашу ситуацию.
Переориентация 2 и 3 :
r2 B2 U2 l – U2 r’ U2 r – U2 F2 r F2 – l’ B2 r2
То же, но без срезов:
Rw2 R2 B2 U2 – Lw L’ U2 Rw’ – R U2 Rw R’ – U2 F2 Rw R’ – F2 Lw’ L – B2 Rw2 R2
Поменять местами 4 и 5 :
Rw2 f2 U2 Fw2 – D Rw2 U2 Fw2 – U’ Fw2 L2 U2 – B2 Lw2 U
Тот же алгоритм без перемещений среза:
– Dw Fw2 Fw2 Rw2 Fw2 U2 Fw2 – U’ Fw2 L2 U2 – B2 Lw2 U
Поменять местами 1 и 4 :
F2 R2 B’ — D’ B R2 F’ U — Fw2 F L2 — f2 Lw2 — f2 l2 U’ (ok)
Тот же алгоритм без перемещений среза:
F2 R2 B’ — D’ B R2 F’ U — Fw2 F L2 — Fw2 F2 Lw2 — Fw2 F2 Lw2 L2 U’
Подробнее о 4×4 Parity
Решите любой куб NxNxN
Комментарии
Solve 4/5*x=56 Tiger Algebra Solver
Переставить:
Переставить уравнение, вычитая то, что находится справа от знака равенства из обеих частей уравнения: =0
Пошаговое решение:
Шаг 1 :
4
Упростить —
5
Уравнение в конце шага 1 :
4 (— • х) - 56 = 0 5
Шаг 2 :
Преобразование целого в виде эквивалентной дроби:
2. 1 Вычитание целого из дроби
1 Вычитание целого из дроби
Преобразуйте целое в виде дроби, используя 5 в качестве знаменателя:
56 56 • 5
56 = —— = ——————
1 5
Эквивалентная дробь: Полученная таким образом дробь выглядит иначе, но имеет то же значение, что и целое
Общий знаменатель: Эквивалентная дробь и другая дробь, участвующая в вычислении, имеют один и тот же знаменатель
Сложение дробей, имеющих общий знаменатель:
2.2 Складываем две эквивалентные дроби
Складываем две эквивалентные дроби, которые теперь имеют общий знаменатель
Объединяем числители вместе, подводим сумму или разность к общему знаменателю, затем приводим к наименьшему виду, если возможно:
4x - (56 • 5) 4х - 280
знак равно
5 5
Шаг 3:
Вытягивание подобное Условия:
3.1 Вытащить как факторы:
4x — 280 = 4 • (x — 70)
11 Уравнение в конце шага 3:
4 • (х - 70)
———————————— = 0
5
Шаг 4 :
Если дробь равна нулю:
4.1 Если дробь равна нулю...
Если дробь равна нулю, ее числитель, часть, которая находится над дробной чертой, должна равняться нулю.
Теперь, чтобы избавиться от знаменателя, Тигр умножает обе части уравнения на знаменатель.
Вот как:
4•(x-70)
———————— • 5 = 0 • 5
5
Теперь в левой части 5 уравновешивает знаменатель, а в правой части ноль, умноженный на что-либо, по-прежнему равен нулю.
Теперь уравнение принимает форму:
4 • (x-70) = 0
Уравнения, которые никогда не бывают истинными :
4.2 Решение : 4 = 0
Это уравнение не имеет решения.
A ненулевая константа никогда не равна нулю.
Уравнение одного переменного уравнения:
4.3 Решить: x-70 = 0
Добавить 70 к обеим сторонам уравнения:
x = 70
Один раствор был найден:
x = 70Как решить для переменной как часть дроби
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно
или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному агенту, указанному ниже. Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как решить 3/4+х=5/4?
#color(blue)(«Понимание сложения и вычитания дробей»)#
Задержите мысль на мгновение, что когда вы применяете процесс, скажем, #6-2#, вы манипулируете счетами.
Теперь рассмотрим дробь (рациональное число). Имеем структуру:
#» «(«count»)/(«индикатор размера того, что вы считаете»)#
Используя собственные имена для них, мы имеем:
#» «(«числитель»)/(«знаменатель»)#
Индикатор размера сообщает вам, сколько из того, что вы считаете, необходимо, чтобы сделать что-то целое (полная 1)
Итак,
Для #1/2# требуется 2 из них, чтобы составить целое, но у нас есть счет 1 из них.
Для # 2/16 # требуется 16 из них, чтобы составить целое, но у нас есть счет 2 из них
‘~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Хорошо! Вернемся к #6-2#
Запишите это как #6/1-2/1″ «larr» обычно так не делается»#
Знаменатели (индикаторы размера) одинаковы, поэтому мы можем #ul(«непосредственно»)# применить вычитание счетчиков
, ………………………………………….. …………………………………………………………….
Итак, если вы хотите добавить вычесть счетчики, вам нужно сделать индикаторы размера одинаковыми.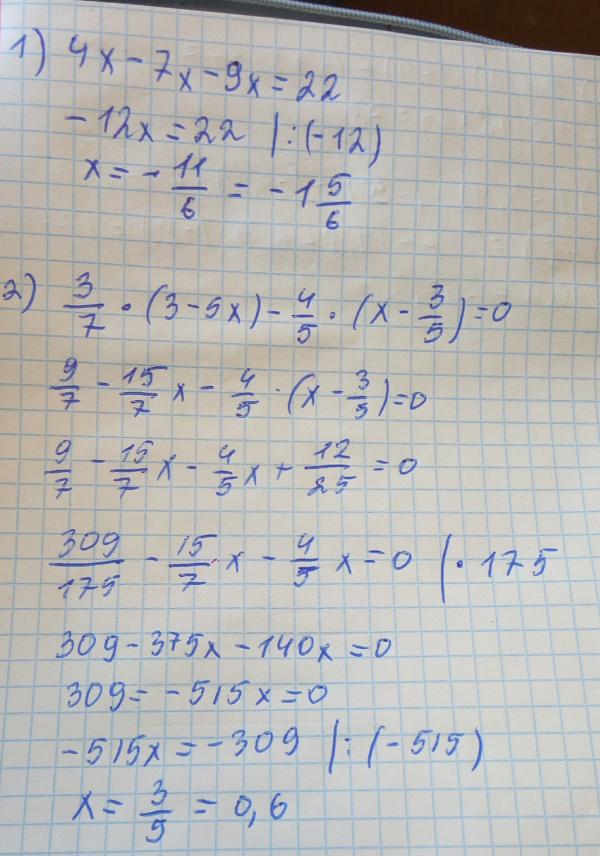 В противном случае вы пытаетесь выполнить эквивалентную операцию, как в следующем примере.
В противном случае вы пытаетесь выполнить эквивалентную операцию, как в следующем примере.
#2/(«ящик яблок»)» «-» «3/(«отдельные яблоки»)#
Вам нужно преобразовать индикатор размера «коробки яблок» в индикатор размера «отдельных яблок», прежде чем вы сможете определить, сколько яблок у вас осталось.
‘~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ ~~
#color(blue)(«Ответ на вопрос»)#
#3/4+x=5/4#
Вычесть #цвет(синий)(3/4)# с обеих сторон
#цвет(коричневый)(3/4цвет(синий)(-3/4)+x=5/4цвет(синий)(-3/4)#
Но #3/4-3/4=0#
#0+х=5/4-3/4#
#х=5/4-3/4#
Индикаторы размера (знаменатели) одинаковы, поэтому мы можем напрямую вычесть количество.
#х=(5-3)/4 = 2/4#
Но #2/4# эквивалентно #1/2#
#x=1/2#
Решение дробей для неизвестных X
Использование калькулятора
Найти неизвестное значение
x с этим калькулятором дробей.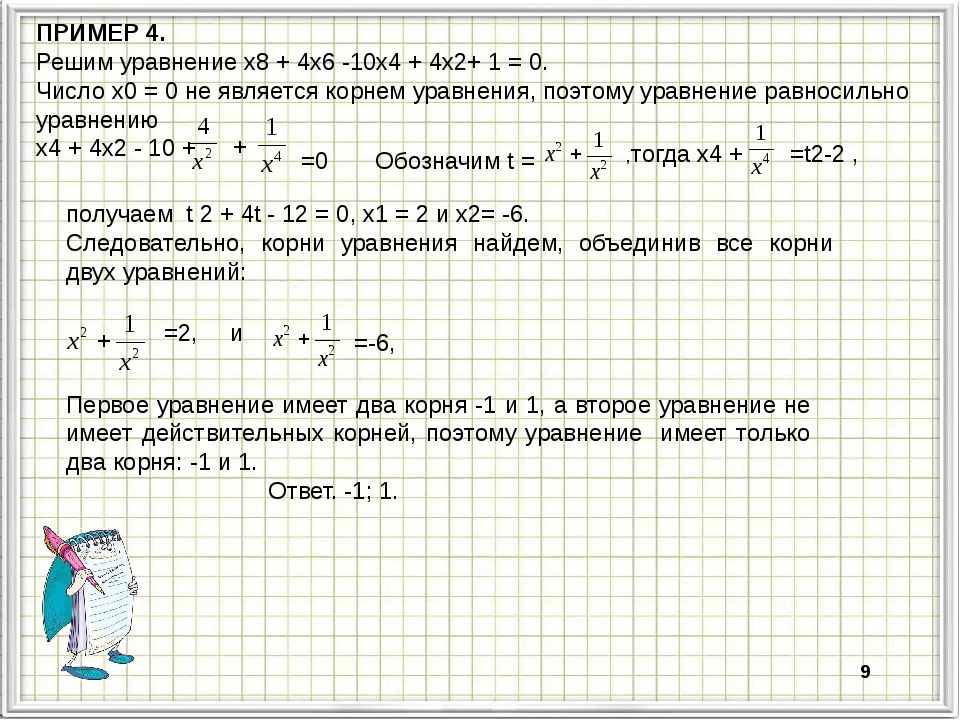 Найдите отсутствующую дробную переменную в пропорции, используя перекрестное умножение для вычисления неизвестной переменной.
х . Решить пропорцию между 2 дробями и вычислить недостающую дробную переменную в равенствах.
Найдите отсутствующую дробную переменную в пропорции, используя перекрестное умножение для вычисления неизвестной переменной.
х . Решить пропорцию между 2 дробями и вычислить недостающую дробную переменную в равенствах.
Введите 3 значения и 1 неизвестное. Например, введите x/45 = 1/15. Калькулятор пропорций решает х .
Как найти x в дробях
Найдите x, умножив и упростив уравнение, чтобы найти x.
Пример: Учитывая уравнение 4/10 = x/15, найдите x.
- Крест умножить дроби
4 * 15 = 10 * х - Решите уравнение для x
х = (4 * 15) / 10 - Упростить для x
х = 6
Для проверки работы подставьте результат 6 обратно в исходное уравнение
4/10 = 6/15
Крест перемножьте дроби и вы получите
4 * 15 = 6 * 10
60 = 60
Поскольку 60 = 60 верно, вы можете быть уверены, что x = 6 — правильный ответ.
Дробь с нулевым знаменателем не определена.
Дробь с нулевым числителем равна 0.
Почему работает калькулятор перекрестного умножения дробей?
Перекрестное умножение работает, потому что вы просто умножаете обе части уравнения на 1. Поскольку умножение чего-либо на 1 не меняет его значения, вы получите эквивалентное уравнение.
Например, посмотрите на это уравнение:
\( \dfrac{a}{b} = \dfrac{c}{d} \)
Если вы умножите обе части на 1, используя знаменатели из другой части уравнения, вы получите:
\( \dfrac{a}{b} \times \dfrac{d}{d} = \dfrac{c}{d} \times \dfrac{b}{b} \)
Обратите внимание, что это ничего не меняет, потому что умножение чего-либо на 1 не меняет его значения.Итак, теперь у вас есть:
\( \dfrac{a \times d}{b \times d} = \dfrac{b \times c}{b \times d} \)
Поскольку знаменатели здесь тоже одинаковые, b × d, вы можете удалить их и сказать, что:
\( а \умножить на d = b \умножить на с \)
Что является результатом перекрестного умножения исходного уравнения:
\( \dfrac{a}{b} = \dfrac{c}{d} \)
Каталожные номера
Cross Multiply от Math Is Fun на http://www. mathsisfun.com/
mathsisfun.com/
Как собрать кубик 4×4 — Месть Рубика
Введение
Кубик 4x4x4 — следующая головоломка в серии кубиков Рубика, известная какМесть Рубика . Хотя кажется, что это намного сложнее, чем знаменитая 3×3, решение мести Рубика 4×4 очень похоже на нее и требует изучения лишь нескольких дополнительных алгоритмов.
Сначала научитесь собирать куб 3×3
Чтобы собрать кубик 4х4, вам нужно сначала узнать, как собрать кубик Рубика 3х3. Если вы не знакомы с решением или не помните его, просмотрите решение 3×3, прежде чем продолжить. Лучше всего освоить решение 3×3, прежде чем переходить на 4×4, хотя это и не обязательно.Перемещение нотаций
Те же правила обозначения хода применяются и для куба 4×4, с двумя отличиями:1. Строчные буквы означают поворот 2 слоев соответствующей грани.

2. «2» перед буквой лицевой стороны (например, 2R) означает перемещение только внутреннего слоя соответствующей грани.
[ р ]
[ 2Р ]
Механика
Механика 4х4 немного отличается от классического кубика Рубика 3х3. Нет единой центральной части, а есть 4 центральные части каждого цвета; поэтому они не фиксируются в своих положениях.Нет фиксированных центральных частей: В кубе 4×4 нет фиксированных центральных частей, что означает, что эти центральные части могут перемещаться по кубу и заменять друг друга местами (в отличие от 3×3, где желтые всегда остаются напротив белых, например ).Это означает, что мы не можем определить цветовую схему куба, глядя на центральные части (мы будем использовать память или угловые части). Как уже упоминалось, есть 4 центральных элемента для каждого цвета. Для 4 центральных частей, собранных вместе, мы называем центральный блок . (На изображении: пример решенного красного центрального блока)
Несколько граней: каждая грань в кубе 4×4 имеет идентичную кромку вокруг куба, то есть существует 2 кромки каждого типа (например, 2 желто-красных кромки). На втором этапе мы собираемся соединить их вместе. Для двух одинаковых краев, соединенных вместе, мы называем краевым блоком . (На изображении: пример парного красно-синего реберного блока)
На втором этапе мы собираемся соединить их вместе. Для двух одинаковых краев, соединенных вместе, мы называем краевым блоком . (На изображении: пример парного красно-синего реберного блока)
Решение
Шаг 1 Шаг 2 Шаг 3 Шаг 4Шаг 1: Сборка центральных частей
Первый шаг заключается в том, чтобы полностью собрать 6 центральных блоков, всего 24 элемента. Мы начнем с решения 1-го центрального блока . Удачи!В этом руководстве для начала я выбрал желтый цвет .Собрать первый центральный блок должно быть довольно легко, так как нет деталей, которые нужно сохранять. Вот как вы должны подойти к этому: начните с сопоставления 2 центральных частей рядом друг с другом и поднесите к ним 3-ю и 4-ю части.
Пример: сборка 4-го центрального элемента.
Решение:[ r’ F r ]
Объяснение: , выполняя движение r’ , вы опустите верхнюю правую желтую центральную часть на верхней грани на лицевую сторону (теперь она будет смежно с центральной частью на лицевой стороне), затем F Переместите , чтобы выровнять обе детали по правой стороне лицевой стороны, и, наконец, переместите r , чтобы вывести их обе вверх на верхнюю грань и сформировать полный желтый центральный блок.
Если бы желтая деталь на передней панели находилась в другом положении на передней панели (из 4 возможных), вы могли бы просто сделать несколько F-поворотов, чтобы отрегулировать ее. То же самое касается верхней грани.
Я сделал инструкции для этой части короткими, так как это интуитивно понятная часть. Просто найдите время, чтобы попрактиковаться в движениях куба 4×4, и вскоре вы освоите способность интуитивно создавать центральные блоки.
2-й центральный блок: Вторым центральным блоком, который нужно решить, должен быть , цвет которого противоположен по цвету предыдущему, который мы только что решили: Поскольку мы только что решили решить желтый центральный блок, теперь мы должны решить . белый центральный блок (Это относится только к кубам оригинальной цветовой схемы! Где желтый цвет противоположен белому, красный — оранжевому, а синий — зеленому.)
Переверните куб так, чтобы желтый центральный блок оказался внизу. Способ решения белого центрального блока заключается в перемещении белых центральных частей по одной (или попарно) на верхнюю грань (конечно, не повреждая решенный центральный блок внизу).
Поскольку сохраняются только нижняя и верхняя части посередине, вы можете свободно переворачивать: F / B / R / L слоев.
Способ «загрузки» центральной части с боковой грани (F / B / R / L) в верхнюю грань заключается в использовании следующих движений:
Пример: загрузка 2 белых центральных частей с грани F (одинаково для всех граней).
Решение: [ r’ F2 r ]
Объяснение: так как мы должны сохранить центральные части внизу, просто сделать движение вправо/влево недостаточно. Поэтому мы делаем ход r’ и опускаем небелые центральные фигуры вверху на поверхность F, затем меняем их местами с 2 белыми фигурами, выполняя F2 . (В данный момент на задней стороне есть 2 желтые фигуры, которые вернутся в исходное положение на следующем ходу).Теперь мы, наконец, изменим ход r’, выполнив ход r . Белые фигуры теперь правильно расположены на верхней грани, а все желтые фигуры на нижней остались невредимыми.
Это важная идея для понимания решения 4×4. Это похоже на движение «лифта », мы спускаем «лифт» к фигурам, которые хотим переместить, «загружаем» фигуры в «лифт» и поднимаем их вверх в решенное положение. Таким образом, мы можем позиционировать фигуры, сохраняя при этом уже решенные фигуры.
Когда 3 центральных элемента находятся сверху:
Здесь реализована та же идея: мы также воспользуемся идеей лифта. На самом деле алгоритм почти аналогичен
Решение: [ r’ F r ]
Разница лишь в том, что нам нужно сделать только один F-поворот, потому что одна белая фигура уже была «внутри» лифта.
Если 3 белые детали сверху или деталь на лицевой стороне расположены иначе, чем в примере, все, что вам нужно сделать, это всего лишь несколько поворотов U / F, чтобы отрегулировать их, как на изображении, и решить.
3-й центральный блок: мы можем выбрать любой из оставшихся четырех цветов в качестве третьего блока для решения.
В этом руководстве я выбрал красный .
Лучше всего повернуть (перевернуть) куб так, чтобы решенные центральные блоки (желтый и белый) оказались на правой и левой гранях.
Сделайте несколько ходов r/r’ & U/F/B/D , чтобы сформировать 2 соседние красные фигуры. Поверните (переверните) куб так, чтобы они появились на верхней грани (желтые и белые по-прежнему на правой и левой гранях).Затем сделайте несколько разворотов, если необходимо, чтобы выровнять 2 красных центральных элемента на левой стороне верхней грани (см. изображение для пояснений левой/правой внутренней стороны) (может быть и правая сторона, я лично привык к левой, так как я правша), как в примере ниже (правое изображение):
Пример: образует 2 соседних красных элемента.
Решение: [ U’r U ]
Объяснение: мы сделаем U’ ход (поэтому, когда мы сделаем r ход, две красные фигуры станут рядом друг с другом, а не по диагонали), затем мы сделаем r движение, чтобы соединить 2 красные центральные части, и, наконец, мы сделаем движение U , чтобы выровнять их обе слева.
Сбор оставшихся 2 частей: Лучший способ сделать это — расположить одну красную центральную часть с левой стороны (внутренняя левая) куба, а вторую — с правой стороны, затем сделать r/r’ двигаться, чтобы соединить их. В следующем примере обе оставшиеся части находятся на правой стороне (внутренней правой) куба (одна находится на верхней грани):
Решение: [ F2 r’ F r ]
Объяснение: Сначала мы сделаем ход F2 , чтобы переместить одну фигуру в левую сторону (так что следующий ход r’ не повлияет на нее, и она соединится с фигурой, которая сейчас находится сверху) (Причина мы делаем F2, а не F’, потому что на следующем ходу мы хотим, чтобы они образовали пары рядом друг с другом, а не по диагонали).Затем мы сделаем ход r’ , чтобы соединить фигуры в пары. Теперь сделаем движение F , чтобы выровнять обе части по правой стороне лицевой стороны. Наконец, мы сделаем ход r , чтобы собрать их в окончательное положение на верхней грани, чтобы все 4 красных центральных элемента были полностью собраны.
*Приведенный выше пример применим ко всем возможным случаям, так как, выполняя ходы «п/р» и «П/Б/Н/Н», вы можете расположить 2 оставшиеся центральные фигуры в одном и том же положении и решить таким же образом.
4-й центральный блок: Четвертый центральный блок, который нужно решить, противоположен по цвету тому, который мы только что собрали,
означает оранжевый (опять же, относится только к исходным кубикам цветовой схемы, где оранжевый противоположен красному).
Сначала мы перевернем куб вверх дном, чтобы красный центр оказался на нижней грани (желто-белый остается на левой и правой гранях). Нам нужно перенести все оранжевые центральные части на верхний слой. Надеюсь, некоторые из них уже есть.
Мы воспользуемся принципом «лифта», чтобы загрузить оранжевые элементы наверх, не повреждая красные элементы внизу. Вот пример того, как это делается:
Решение: [ r’ F’ r U ]
Пояснение: сначала мы сделаем ход r’ , чтобы снести «лифт» с неоранжевыми центральными фигурами наверху. Затем мы сделаем ход F’ , чтобы загрузить фигуру в лифт (правильно делать F’, а не F2, чтобы совпасть рядом с оранжевой фигурой сверху).Затем мы сделаем движение r , чтобы поднять лифт обратно в решенное положение. Наконец, мы сделаем движение U , чтобы выровнять обе части по левой стороне центра (чтобы «освободить» лифт для следующих двух частей).
Затем мы сделаем ход F’ , чтобы загрузить фигуру в лифт (правильно делать F’, а не F2, чтобы совпасть рядом с оранжевой фигурой сверху).Затем мы сделаем движение r , чтобы поднять лифт обратно в решенное положение. Наконец, мы сделаем движение U , чтобы выровнять обе части по левой стороне центра (чтобы «освободить» лифт для следующих двух частей).
Собираем оставшиеся 2 центральные детали: Лучший способ собрать оставшиеся 2 детали — перемещать по одной детали в верхний слой, используя принцип лифта:
Решение: [ r’ F r ]
(Если вы забыли, мы не можем просто сделать ход [r], потому что внизу есть красные центральные фигуры, которые нужно сохранить)
Пояснение: делаем ход r’ (снос «лифта»), затем делаем ход F , чтобы загрузить в него оранжевую фигуру, наконец делаем r переместите, чтобы загрузить оранжевую центральную часть в решенную позицию.(Примечание: опять же, используя принцип лифта, ни одна красная центральная часть или желто-белая часть не пострадала).
Теперь мы снова применим ту же самую идею для последней центральной части:
Решение: [ F2 r’ F r ]
Объяснение: Сначала мы сделаем F2 движение, чтобы расположить оранжевую фигуру на левой внутренней стороне куба (мы делаем F2, а не F, потому что мы хотим, чтобы она совпадала с другой оранжевой фишкой, которая будет спускайтесь дальше).Затем делаем ход r’ (спуск на лифте), затем ход F , чтобы загрузить обе части в «лифт». Наконец, мы загрузим обе части с ходом r и решим весь оранжевый центральный блок.
5-й и 6-й центральные блоки: Последние 2 центральных блока собираются одновременно, так как при решении 1 цвета другие цветные блоки автоматически окажутся в противоположном центре, который является единственным доступным центром.
Важно! Эти центры можно решить правильно, а неправильно .Давайте выберем зеленый цвет , чтобы узнать его правильное положение (из 2 доступных мест). По исходной цветовой схеме, когда желтый цвет сверху, а красный цвет на лицевой грани — зеленый должен быть справа .
По исходной цветовой схеме, когда желтый цвет сверху, а красный цвет на лицевой грани — зеленый должен быть справа .
Переверните куб так, чтобы будущая зеленая грань оказалась сверху.
Решение этих двух последних центров проще, чем кажется, и это делается только с помощью движений r2 и U/B.
1) Сначала возьмите 2 соседних зеленых элемента на верхний слой (скорее всего он уже там) и выровняйте их по левому краю.Вот как это сделать:
Поместите зеленую центральную часть с левой стороны, используя U ходов. Сделайте ход r2 и посмотрите, образовались ли 2 соседние зеленые фигуры на верхней грани. Если это так, сделайте движение U/U’ , чтобы выровнять их по левой стороне, и сделайте еще одно движение r2 , чтобы перевернуть и вернуть все на место.
Если после выполнения первого хода r2 у вас нет соседних зеленых цветов, переверните ход r2 и сделайте несколько ходов D (посмотрите на нижнюю грань, чтобы увидеть, сколько нужно), поэтому, когда вы снова сделаете еще один ход r2, зеленая часть будет перемещена вверх и совпадет с зеленой частью, которая уже там.
Пример: Нижняя грань выглядит так: (поворот x)
Решение: [ D’ r2 U’ r2 ]
В этом случае зеленой пары сверху уже нет (обозначения смотрите только на левом изображении).
Объяснение: сначала требуется ход D/D’ , чтобы следующий ход r2 образовал соседнюю пару зеленых центров сверху. Затем ход r2 , чтобы совместить 2 зеленые фигуры вместе (подъемник поднимается вверх), затем ход U’ , чтобы выровнять обе зеленые фигуры с левой стороны («выгрузка» из лифта).Наконец, движение r2 переворачивает все остальные части на место (лифт опускается).
2) Соединяем две другие зеленые части в верхнюю грань: Здесь есть два варианта: только одна часть внизу или обе части внизу.
Если одна деталь сверху: более легкий случай. Совместите зеленую центральную часть внизу с левой стороной нижней грани (с помощью D/D’) таким образом, чтобы к следующему ходу r2 она совпала со второй зеленой частью. Сделайте ход r2 и сопоставьте 2 зеленые центральные части. Затем просто сделайте движение D/D, чтобы выровнять обе части по правой стороне нижнего центра. Наконец, сделайте ход r2, чтобы загрузить обе фигуры наверх. Все зеленые фигуры собраны, а все синие фигуры находятся внизу (все центральные части собраны!)
Сделайте ход r2 и сопоставьте 2 зеленые центральные части. Затем просто сделайте движение D/D, чтобы выровнять обе части по правой стороне нижнего центра. Наконец, сделайте ход r2, чтобы загрузить обе фигуры наверх. Все зеленые фигуры собраны, а все синие фигуры находятся внизу (все центральные части собраны!)
Пример:
Решение: [ D r2 D’ r2 ]
Если обе части находятся внизу: возможны 2 случая- рядом или по диагонали друг к другу-
Диагональ: [ r2 D/D’ r2 ] .Объяснение: сделайте ход r2 так, чтобы одна зеленая фишка поднялась вверх на верхний слой. Затем сделайте движение D/D’ , чтобы переместить оставшуюся зеленую фигуру внизу во второе доступное место с левой стороны, чтобы она рядом совпадала со второй фигурой, которая в данный момент находится сверху, как только она вернется вниз в следующий раз. переехать. Теперь сделайте ход r2 , чтобы опустить зеленую фигуру. Зеленые центральные части теперь расположены рядом друг с другом. Продолжайте в соответствии с приведенными ниже инструкциями для смежных случаев.
Продолжайте в соответствии с приведенными ниже инструкциями для смежных случаев.
Смежный: [ r2 D2 r2 ] . Объяснение: выровняйте обе зеленые фигуры по левой стороне центральной области внизу (сделав несколько ходов D/D’ ), затем сделайте ход r2 (принцип лифта), сделайте ход D2 , чтобы положить обе зеленые фигуры в правую сторону (чтобы они были подняты вверх следующим ходом), и, наконец, измените ход r2 , чтобы вывести центры зелени на верхнюю грань и полностью решить зеленый (и синий!) Центральный блок!.(см. пример ниже)
Пример: Нижняя часть выглядит так: (поворот x)
Решение: [ D’ r2 D2 r2 ]
Вот и все! Вы правильно собрали все 6 центральных блоков друг с другом. Я рекомендую вам остановиться на этом и попрактиковаться в сборке всех центральных блоков куба 4×4, пока вы не почувствуете себя комфортно, делая это интуитивно. Опытному сборщику кубика Рубика 3×3 не составит большого труда сделать это за день или два.
Шаг 2. Соедините все кромки
Второй шаг заключается в объединении всех реберных частей с их идентичными близнецами на кубе 4×4 в реберных блоков .Нужно решить 12 краевых блоков, то есть всего 24 краевых элемента. На изображении справа вы можете увидеть пример двух бело-синих краев, соединенных вместе в один краевой блок (бело-синий краевой блок).Перестановки краевых блоков вокруг куба совершенно бессмысленны на этом шаге.
Решение первых 4 граничных блоков:
Здесь нужно объединить краевые части в блоки и сохранить их на верхней и нижней гранях (= 8 доступных мест).Начнем с 4 сверху). Помните, что вы можете делать любые ходы U/D/B/R/L/F, которые вы хотите, так как они не влияют на центральные фигуры.
Вот как это делается:
Найдите 2 одинаковых ребра, расположенных как на картинке, затем выполните следующий алгоритм:
Алгоритм: [ d R U R’ d’ ]
Этот алгоритм объединяет две краевые части в блок и сохраняет их на верхней грани, не повреждая центральную часть. Вот как: сделав ход d , две крайние фигуры соединится. Затем с помощью перемещения R сформированный краевой блок переместится вверх в верхний слой. Затем мы сделаем ход U/U’/U2 , чтобы закрепить блок наверху (чтобы он не опустился на следующем ходу — R’). Мы будем делать U/U’/U2 в соответствии с краевыми блоками вверху, если нет решенных краевых блоков, то это не имеет значения. Если есть уже решенные блоки — мы хотим убедиться, что вместо этого их не сняли.Наконец, мы сделаем R’ d’ , чтобы вернуть все остальные детали на место.
Вот как: сделав ход d , две крайние фигуры соединится. Затем с помощью перемещения R сформированный краевой блок переместится вверх в верхний слой. Затем мы сделаем ход U/U’/U2 , чтобы закрепить блок наверху (чтобы он не опустился на следующем ходу — R’). Мы будем делать U/U’/U2 в соответствии с краевыми блоками вверху, если нет решенных краевых блоков, то это не имеет значения. Если есть уже решенные блоки — мы хотим убедиться, что вместо этого их не сняли.Наконец, мы сделаем R’ d’ , чтобы вернуть все остальные детали на место.
Используя этот метод, вы сможете быстро соединить и сохранить сверху/снизу первые 8 граничных блоков.
Как вставить крайние части в чехол выше?
Сначала поместите обе фигуры на одну грань, используя движения R2/L2/F2/B2 и движения U/D. Вот быстрый алгоритм перемещения 2 ребер в нужное положение (см. изображение):
Решение: [ L’ U L ]
С помощью этого простого алгоритма вы сможете правильно расположить 2 ребра, которые находятся на одной грани и имеют одинаковый цвет на общей грани (если нет, просто сделайте U-образный ход) в нужный корпус. Затем просто выполните соответствующий алгоритм [ d R U R’ d’ ] , и обе части будут объединены в пары и сохранены на верхней грани.
Затем просто выполните соответствующий алгоритм [ d R U R’ d’ ] , и обе части будут объединены в пары и сохранены на верхней грани.
Используя описанный выше метод, вы сможете перевести все 8 первых пар ребер в положение простого регистра. Начните с более легких ребер, которые уже находятся в этом положении. Чем меньше краевых кусочков останется, тем легче получится.
Если у вас уже есть парные ребра на сторонах куба (например, между передней и правой гранями), просто сделайте простой R/R’/L/L’, чтобы поместить его на верхний слой.Для парных рёбер на нижней просто сделайте двойное движение боковой грани, чтобы вывести её на верхнюю грань.
Пример: решение 4-го реберного блока.
Решение: [ L D’ L’ ] [ d’ L’ U L d ]
Объяснение: в этом примере видно, что 3 реберных блока уже сформированы, а четвертый разделен на грани F. В первых 3 ходах (первые скобки) мы двигаемся вокруг ребра внизу в «идеальный» случай, когда они оба находятся на боковых гранях с разными цветами на грани F, а затем просто решим это так, как описано выше (это тот же алгоритм, только слева — L вместо R)
Теперь все 4 крайних блока сверху сформированы, переходим к следующим:
Решение блоков с 5-го по 8-й ребро:
Переверните куб вверх дном, чтобы все парные реберные блоки оказались на нижнем слое. Теперь просто сделайте то же самое для следующих 4 пар ребер, используя те же алгоритмы и идеи, что и выше. Единственное отличие состоит в том, что для уже решенного реберного блока на боковых гранях: вместо перемещения R выполните – [R U R’] для загрузки реберного блока в верхний слой с сохранением нижних реберных блоков.
Теперь просто сделайте то же самое для следующих 4 пар ребер, используя те же алгоритмы и идеи, что и выше. Единственное отличие состоит в том, что для уже решенного реберного блока на боковых гранях: вместо перемещения R выполните – [R U R’] для загрузки реберного блока в верхний слой с сохранением нижних реберных блоков.
Пример: решение 8-й пары.
Решение: [ d’ L’ U L d ]
(точно так же, как обсуждалось выше)
В этом примере формируются все краевые блоки внизу, а также формируются еще 3 блока на верхней грани.Осталось решить только одну. В нашем случае это будет красно-белая часть (вторая часть находится между передней и левой гранями). Решается точно так же, как показано в последнем примере.
После решения всех 8 краевых блоков на верхней/нижней гранях переходите к последним четырем:
Решение последних 4 граничных блоков:
Решение последних 4 граничных блоков немного сложнее, но очень короткое. Здесь мы хотим, чтобы 2 части с двумя краями были с цветом на их общей стороне (как на изображении ниже).
Следующий алгоритм решает обе пары ребер одновременно, сохраняя все остальные реберные блоки и центральные части:
Алгоритм: [ d R F’ U R’ F d’ ]
Это важный алгоритм; это алгоритм, который вам нужно запомнить, чтобы собрать кубик 4×4 наизусть. Потратьте некоторое время, чтобы получить его.
С помощью этого алгоритма вы решите все 4 последние пары ребер.
Если ребра не имеют одинакового цвета на их общей грани, как в примере ниже, используйте следующую последовательность движений:
Решение: [ R F’ U R’ F ]
Объяснение: этот алгоритм перевернет 2 ребра между передней и правой гранями.Теперь части будут совпадать для случая, описанного выше.
Если только одна пара ребер имеет одинаковый цвет на взаимной грани, а вторая пара не имеет (или даже не одинаковых ребер), все равно выполнить алгоритм! Таким образом, вы решите 1 крайний блок из 4 оставшихся, и продолжайте, пока все 4 не будут решены.
Вот и все! Теперь все краевые части уже должны быть спарены друг с другом. Вы можете заметить, что кубик выглядит как обычный кубик Рубика 3×3, и именно так вы собираетесь его сейчас собирать, как описано в инструкциях к следующему шагу.
Шаг 3. Сборка кубика Рубика 3×3 (до последнего слоя)
Кубик теперь действительно похож на обычный кубик Рубика 3x3x3! Считайте центральные блоки одной центральной частью, а краевые блоки — отдельными краевыми частями. =На изображениях выше вы можете видеть, что части 4×4 расположены так же, как , как куб 3×3.
Итак, с этого момента просто продолжайте собирать кубик, как это был кубик Рубика 3×3, до последнего слоя (непосредственно перед ориентацией последнего слоя).
Причина решения только до последнего слоя, а не завершения куба, заключается в том, что в кубе 4×4 могут возникнуть 2 особых случая, которые невозможны в кубе 3×3.Их называют паритетами.
Шаг 4. Решение последнего уровня (четности OLL и PLL)
Вот возможные случаи, которые могут произойти при решении куба 4×4:OLL паритет:
[ r U2 x r U2 r U2 r’ U2 l U2 r’ U2 r U2 r’ U2 r’ ]
Контроль четности PLL: (вид сверху)
[ 2R2 U2 2R2 u2 2R2 2U2 ]
Что такое четность OLL?
Четность OLL — это когда не ориентирован только один граничный блок. Это невозможный случай в обычном кубе 3х3. Этот случай решается по алгоритму выше. Важно выполнить алгоритм четности OLL, если необходимо, перед решением последнего слоя , потому что он не сохраняет позиции частей последнего слоя. Вероятность встретить четность OLL во время решения 4×4 составляет 50%.
Это невозможный случай в обычном кубе 3х3. Этот случай решается по алгоритму выше. Важно выполнить алгоритм четности OLL, если необходимо, перед решением последнего слоя , потому что он не сохраняет позиции частей последнего слоя. Вероятность встретить четность OLL во время решения 4×4 составляет 50%.
Что такое четность PLL?
Четность PLL — это когда только 2 ребра остаются нерешенными, а остальная часть куба полностью собрана. Этот случай также не может произойти на кубе 3×3 (причины ниже) и устраняется алгоритмом четности PLL.Алгоритм четности PLL сохраняет все фрагменты, кроме фрагментов переключенных ребер, и поэтому может использоваться в конце решения (после решения всех других фрагментов последнего слоя). Вероятность встретить четность PLL во время решения 4×4 составляет 50%.
Внимание! Вы можете столкнуться со странным случаем PLL, когда решаются все фигуры, но, например, 2 угла. Это из-за четности PLL. После применения алгоритма четности PLL это станет разрешимым случаем PLL.
Объяснение обозначений: Контроль четности PLL использует движение внутреннего слоя.Цифра «2», показанная перед указанной буквой грани, означает перемещение внутреннего слоя ее грани. Пример: [2R] = [r R’]. Перемещение «2R» можно выполнить, переместив оба слоя, выполнив r, а затем вернув грань R назад, выполнив R’. Перемещение «2R2» означает перемещение этого внутреннего слоя дважды. Вы можете увидеть примеры изображений во вступительном разделе выше.
Почему четность PLL происходит на кубах 4×4, а на обычном кубе 3×3 это невозможно?
Причина в механике и математике кубика Рубика.Как вы знаете, переместить только 2 ребра, сохранив при этом все остальные, невозможно* (алгоритм U-perm затрагивает 3 ребра, что является минимально возможным). Переместить только одну фигуру заведомо невозможно (куда она пойдет без переключения другой фигурой?).
Таким образом, случай, когда необходимо поменять местами только 2 ребра, является невозможным для куба 3×3. Однако на кубе 4×4 это не совсем 2 штуки, а 4 штуки , и 4 штуки нужно переключать между и возможный случай.
Однако на кубе 4×4 это не совсем 2 штуки, а 4 штуки , и 4 штуки нужно переключать между и возможный случай.
(* По крайней мере, не легальными ходами, единственный возможный способ сделать это — разобрать 2 части, разбив куб и собрав его неправильно (куб станет неразборным)
Те же правила применяются ко всем кубам (3×3, 4×4, 5×5 и т.д..)
Как насчет паритета OLL?
Четность OLL происходит и в кубе 4×4 по тем же причинам. Минимальное количество элементов ориентации при сохранении всех остальных элементов равно 2 (применяется для всех размеров кубов).Следовательно, в кубе 3х3 не может быть неориентированным только 1 ребро. В то время как в кубе 4×4 на самом деле это 2 разных реберных элемента (хотя мы рассматриваем их как «один реберный блок»), где — это возможный случай.
Разобравшись с паритетами, продолжим и закончим сборку куба 4х4:
Если после выполнения шага 3 (решение куба до последнего слоя) вы заметили, что имеет место четность OLL — тогда примените алгоритм и продолжите решение последнего слоя, используя технику решения 3×3. При необходимости также примените алгоритм PLL.
При необходимости также примените алгоритм PLL.
Вот и все! Вы только что собрали Месть Рубика 4×4! Просто сохраняйте и тренируйтесь в сборке кубика 4×4, пока вы не сможете сделать это без использования этого руководства. Вы будете рады узнать, что для этого вам нужно запомнить всего 4 алгоритма (2 четности + 2 алгоритма из шага 2)! Поздравляем!
Добавить Rubiksplace.com в Избранное!Надеюсь, вам понравилось собирать кубик Месть Рубика 4×4 .Приглашаем вас оставить комментарий на нашей странице в Facebook и написать о своем опыте решения проблемы.
Прочтите мое руководство по лучшим скоростным кубикам 4×4
Где я просматриваю лучшие на сегодняшний день кубики 4×4, текущие мировые рекорды, выбор лучших кубов и где их взять. Они намного быстрее и приятнее в разгадывании и стоят обычно меньше оригинальных рубиков 4х4.
Калькулятор дробей
Этот калькулятор выполняет базовые и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти
дробное значение из нескольких дробных операций. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти
дробное значение из нескольких дробных операций. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила для выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целым числом и дробной частью. Смешанные числа (смешанные дроби или смешанные числа) Оставьте один пробел между целым числом и дробью
и используйте косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т. е.1/2
е.1/2
• сложение дробей и смешанных чисел: 8/5 + 6 2/7
• деление целых чисел и дробей: 5 ÷ 1/2
• сложные дроби: 5/8 : 2 2/3
• десятичная дробь: 0,625
• Дробь до десятичной: 1/4
• Дробь до процента: 1/8 %
• сравнение дробей: 1/4 2/3
• умножение дроби на целое число: 6 * 3/4
• квадратный корень дроби: sqrt(1/16)
• сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22
• выражение со скобками: 1 /3 * (1/2 — 3 3/8)
• составная дробь: 3/4 от 5/7
• дроби, кратные: 2/3 от 3/5
• разделить, чтобы найти частное: 3/5 ÷ 2 /3
Калькулятор следует известным правилам порядка операций .Наиболее распространенные мнемоники для запоминания этого порядка операций:
PEMDAS — Скобки, Экспоненты, Умножение, Деление, Сложение, Вычитание.
BEDMAS — Скобки, Экспоненты, Деление, Умножение, Сложение, Вычитание
BODMAS — Скобки, Порядок, Деление, Умножение, Сложение, Вычитание.
