Восьмеричная система счисления. Шестнадцатеричная система счисления. Правило перевода целых десятичных чисел в систему счисления с основанием
Для начала вспомним, что такое позиционная система счисления.
Позиционная система счисления – это система счисления, в которой количественный эквивалент цифры зависит от её положения (позиции) в записи числа.
На этом уроке мы с вами познакомимся с восьмеричной и шестнадцатеричной системами счисления, узнаем правила перевода из восьмеричной и шестнадцатеричной систем счисления в десятичную и наоборот. Также изучим правило перевода целых десятичных чисел в систему счисления с основание q.
Начнём с восьмеричной системы счисления.
Восьмеричная система
счисления – это позиционная система счисления с основанием 8. В
алфавит восьмеричной системы счисления входят цифры от 0 до 7 включительно.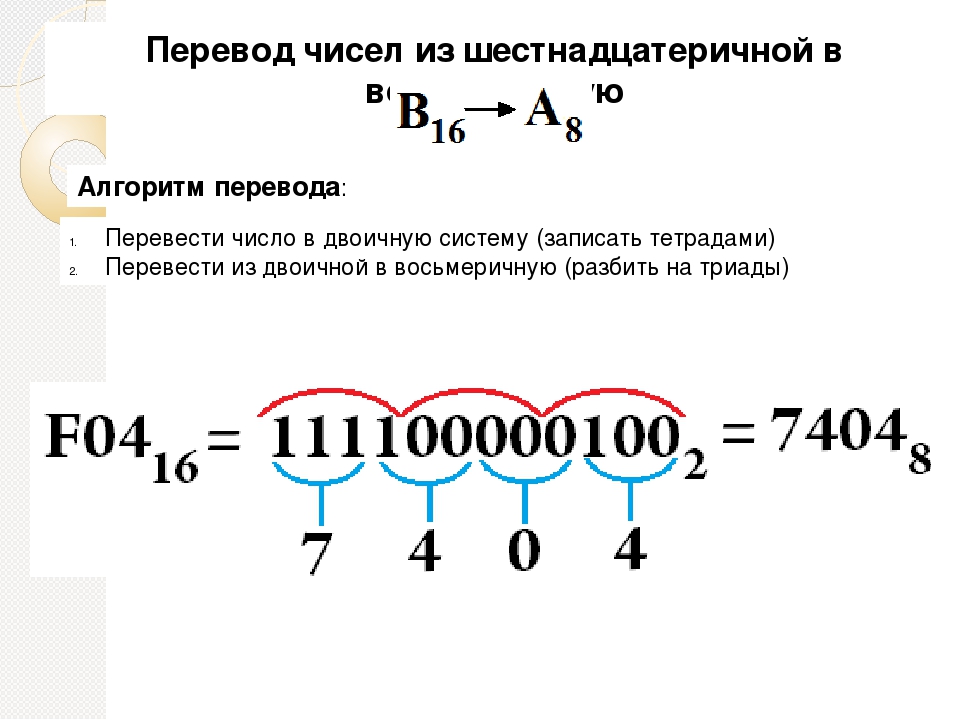
Мы с вами уже узнали, как записывается развёрнутая форма записи числа. Она выглядит следующим образом:
Из этой формулы можно вывести развёрнутую форму записи целого восьмеричного числа:
Посмотрим, как это выглядит на примере. Нам дано следующее число: 41538. Давайте распишем его по формуле. Ставим равно. Для начала проставим над цифрами степени для восьмёрки справа налево, начиная с нуля.
После равно пишем первую цифру 4 и умножаем её на 83. Ставим плюс. Далее запишем вторую цифру 1, умноженную на 82. Снова ставим плюс. Записываем цифру 5 и умножаем её на 81. И плюс последняя цифра 3, умноженная на 80.
Мы с вами расписали исходное число в развёрнутой форме целого восьмеричного числа.
Правило для перевода из
восьмеричной системы счисления в десятичную очень простое.
Достаточно расписать число в развёрнутой форме записи, а затем вычислить
значение получившегося выражения.
Давайте переведём наше число из восьмеричной системы счисления в десятичную. Оно уже у нас расписано в развёрнутой записи. Нам осталось сосчитать. Обратимся к математике и распишем степени числа восемь.
Теперь осталось всё посчитать. Ставим равно.
Мы получили число 2 155. Это число представлено в десятичной системе счисления.
А теперь давайте переведём число 125 из десятичной системы счисления в восьмеричную.
Это правило похоже на перевод из десятичной в двоичную систему счисления, но в данном случае мы будем делить на число 8.
Само правило
звучит следующим образом: для перевода целого десятичного числа в восьмеричную
систему счисления следует последовательно выполнять деление данного числа и
получаемых целых частных на 8 до тех пор, пока не получим частное, равное 0. В
результате нужно записать в одну строку, справа налево все остатки, начиная с
последнего.
Переведём наше число. Делим его на 8. Получим 15, а в остатке 5. Обведём остаток в кружок.
Теперь число 15 делим на 8. Получим 1. В остатке 7. Снова обведём это число.
1 больше 0. Значит делим число 1 на 8. Получим 0. А в остатке 1. Обводим наш остаток.
Теперь осталось после равно записать все остатки справа налево.
12510 = 1758
Мы перевели число 125 в восьмеричную систему счисления.
А теперь давайте узнаем, что такое шестнадцатеричная система счисления.
Шестнадцатеричная система счисления – это позиционная система счисления с основанием 16. В алфавит этой системы входят цифры от 0 до 9 и буквы А, B, C, D, Е, F. Эти буквы обозначают в десятичной системе числа от 10 до 15 соответственно.
Для представление целого шестнадцатеричного числа в развёрнутой форме записи нужно использовать следующую формулу:
Распишем предоставленное
шестнадцатеричное число A6E
в развёрнутой форме.
Ставим знак равно. Снова проставим степени для шестнадцати над цифрами нашего числа справа налево.
Пишем букву А и умножаем её на 162. Ставим плюс. Пишем цифру 6, умноженную на 161 и прибавляем букву Е, умноженную на 160.
Для перевода целого шестнадцатеричного числа в десятичную систему счисления нужно перейти к его развёрнутой записи, заменить буквы на соответствующие им цифры в десятичной системе счисления и вычислить значение получившегося выражения.
Наше число уже записано в развёрнутой форме. Нам осталось заменить буквы на соответствующие им десятичной системе числа и сосчитать. Ставим равно. Буква А соответствует числу 10 в десятичной системе счисления. Запишем число 10 и умножаем его на 162.
Ставим плюс и перепишем число 6, умноженное на 161.
Снова ставим плюс. Букве
Е соответствует число 14 в десятичной системе счисления.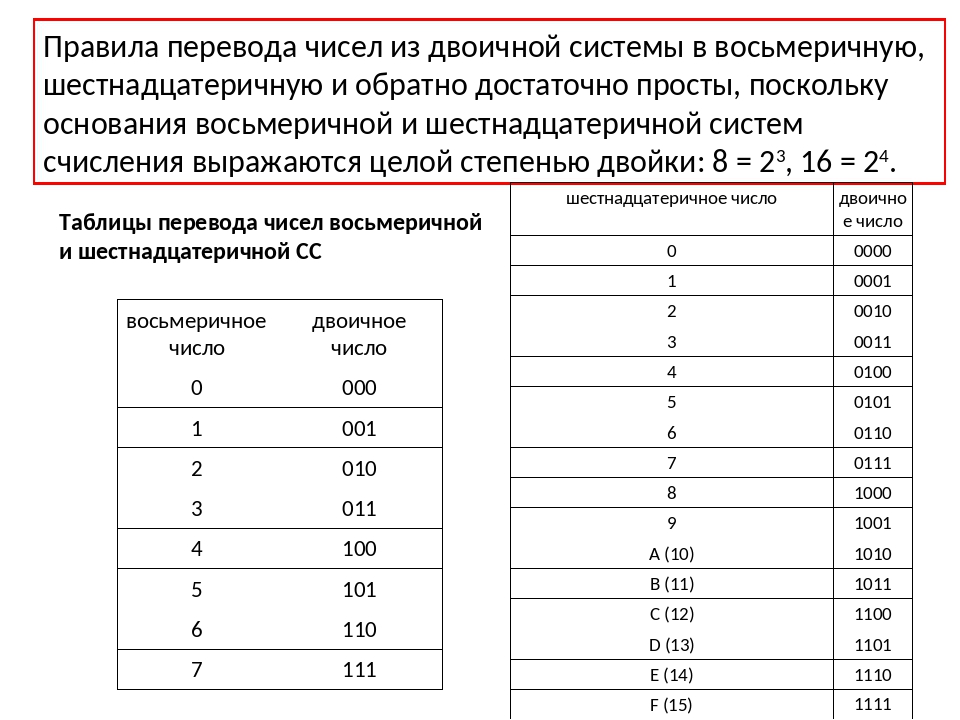 Пишем число 14,
умноженное на 160.
Ставим равно.
Пишем число 14,
умноженное на 160.
Ставим равно.
Прежде, чем всё это сосчитать снова обратимся к математике и распишем степени числа шестнадцать.
162 = 256.
162 ·10 = 2 560
Ставим плюс.
161 = 16.
161 · 6 = 96.
Снова ставим плюс.
160 = 1.
160 · 14 = 14.
Ставим равно.
Мы получили 2 670 в десятичной системе счисления.
Для перевода целого десятичного числа в шестнадцатеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 16 до тех пор, пока не получим частное, равное 0. В результате нужно записать в одну строку, справа налево все остатки, начиная с последнего, при необходимости, заменяя цифры на соответствующие им буквы в шестнадцатеричной системе счисления.
Переведём число 350 в
шестнадцатеричную систему счисления.
Делим наше число на 16, получим 21, остаток 14. Выделим его.
Делим 21 на 16. Получим 1 и 5 в остатке. Обводим наш остаток.
1 больше 0. Делим 1 на 16, получим 0 и 1 в остатке. И снова выделяем остаток 1.
Теперь запишем все числа справа налево. Записываем следующие цифры: 1, 5.
35010 = 15.
Так как в шестнадцатеричной системе счисления числу 14 соответствует буква Е, то пишем её после 5.
35010 = 15E16.
Мы с вами перевели число 350 в шестнадцатеричную систему счисления.
Вы, наверное, заметили, что все правила перевода целого десятичного числа в любую систему счислению с другим основанием похожи.
Давайте изучим общее правило перевода целых десятичных чисел в любую систему счисления с основание q.
Для того, чтобы перевести целое десятичное число в систему счисления с основанием q нужно:
1. Последовательно
выполнять деление данного числа и получаемых целых частных на основание новой
системы счисления до тех пор, пока не получим частное, равное нулю.
Последовательно
выполнять деление данного числа и получаемых целых частных на основание новой
системы счисления до тех пор, пока не получим частное, равное нулю.
2. Полученные остатки, которые являются цифрами числа в новой системе счисления, привести в соответствии с алфавитом новой системы счисления.
3. Составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.
Вам предоставлена таблица соответствия десятичных, двоичных, восьмеричных и шестнадцатеричных чисел от 0 до 20. Числа от 0 до 20 подразумевают собой десятичную систему счисления.
А теперь давайте выполним задание.
Переведём одно и то же число 247 в двоичную, восьмеричную и шестнадцатеричную системы счисления и сравним получившиеся числа.
Для начала переведём из
десятичной в двоичную систему счисления. Для этого будем использовать таблицу,
так как число большое. В ней будет две строки.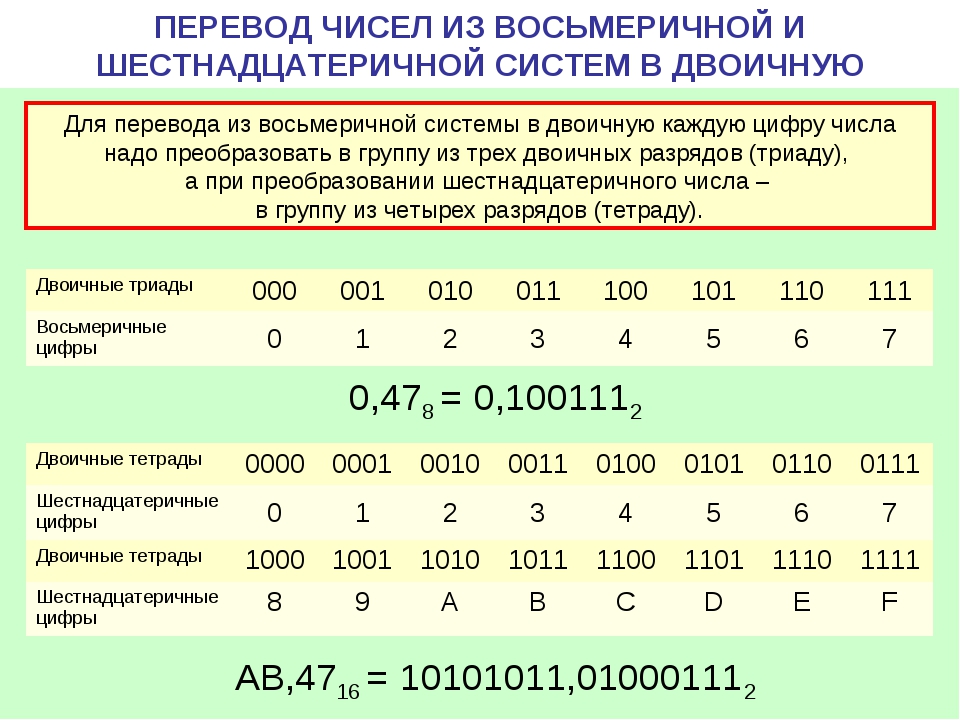 В первую строку первого столбца
запишем наше число.
В первую строку первого столбца
запишем наше число.
Делим его на 2. Получим 123 и 1 в остатке. 123 запишем во вторую ячейку первой строки, а 1 – в первую ячейку второй строки.
Далее 123 разделить на 2 и получим 61 и 1 в остатке. 61 запишем после числа 123, а остаток один под число 123.
Далее 61 : 2 = 30 и остаток – 1. Запишем их в таблицу.
30 : 2 = 15, а остаток равен 0. Снова запишем их в таблицу в соответствующие ячейки.
При делении 15 на 2 получим 7 и 1 в остатке. Снова заполняем таблицу.
Далее 7 : 2 = 3 и 1 в остатке. Запишем в соответствующие ячейки наши числа.
3 :2 = 1 и 1 в остатке. Занесём данные в таблицу.
И делим 1 на 2, получим 0 и 1 в остатке. 0 писать не будет. Занесём только наш остаток в ячейку.
А теперь соберём все наши
цифры в число в двоичной системе. Записываем их поочерёдно справа налево.
24710 = 111101112.
А сейчас переходим к переводу в восьмеричную систему счисления числа 247.
Делим 247 на 8. Получим 30 и 7 в остатке. Обведём остаток от деления.
Далее 30 делим на 8, получим 3 и 6 в остатке. Выделяем остаток.
3 делим на 8, получаем 0 и 3 в остатке. Обводим остаток.
Теперь запишем все остатки справа налево и получим число в восьмеричной системе счисления.
24710 = 3678.
Нам осталось перевести наше число в шестнадцатеричную систему счисления. Делим 247 на 16. Получим 15 и 7 в остатке. Обведём остаток.
Теперь делим 15 на 16, получим 0. А остаток от деления равен 15. Выделим его.
А сейчас запишем наши
цифры справа налево в соответствии с алфавитом шестнадцатеричной системы
счисления. Число 15 — это буква F
в этой системе счисления. Ставим её на первое место.
24710 = F716
Задание выполнено. Давайте сравним все наши получившиеся числа.
Как можем видеть – все они одинаковые, но записаны разными цифрами, потому что они представлены в различных системах счисления. Это можно увидеть, если обратить внимание на основания чисел.
А теперь пришла пора довести итоги урока. Сегодня мы узнали, что такое восьмеричная и шестнадцатеричная системы счисления, какие действия нужно выполнить для перевода целого десятичного числа в систему счисления с основанием q.
Также мы сегодня научились переводить числа из восьмеричной и шестнадцатеричной систем счисления в десятичную и наоборот.
Как перевести из десятичной в восьмеричную онлайн
Большинство людей привыкло использовать числа десятичной системы измерения, но иногда их необходимо перевести в восьмеричную. Это можно сделать при помощи специальных онлайн-сервисов.
Это можно сделать при помощи специальных онлайн-сервисов.
Читайте также: Перевод из восьмеричной в десятичную онлайн
Способы перевода
Рассмотрим самые популярные и удобные онлайн-сервисы для перевода чисел из десятичной системы счисления в восьмеричную.
Способ 1: Calculatori.ru
Онлайн-ресурс Calculatori.ru представляет собой набор калькуляторов различной направленности. Среди них имеется и инструмент, который позволяет производить перевод чисел из десятичной системы в восьмеричную.
Онлайн-сервис Calculatori.ru
- После перехода на главную страницу сервиса по ссылке выше щелкните по пункту «Перевод чисел из одной системы счисления в любую другую онлайн», который расположен в разделе «Информатика».
- В единственное поле открывшегося окна введите числовое значение, которое требуется преобразовать. В блоке настроек «Его система счисления» переставьте радиокнопку в позицию «Десятичная».
 В списке параметров «Перевести в» выберите вариант «Восьмеричную». Затем нажмите кнопку «Перевести».
В списке параметров «Перевести в» выберите вариант «Восьмеричную». Затем нажмите кнопку «Перевести». - После этого в том же окне отобразится итоговый результат перевода.
Способ 2: Math.Semestr
Ещё один онлайн-сервис калькуляторов Math.Semestr также имеет в своем арсенале возможность преобразовывать числа из десятичной системы счисления в восьмеричную.
Онлайн-сервис Math.Semestr
- После перехода по указанной выше ссылке на главную страницу Math.Semestr щелкните по пункту «Информатика онлайн» в блоке «Калькуляторы по направлениям».
- На открывшейся странице в блоке «Онлайн-калькулятор по информатике» щелкните по ссылке «Перевод чисел онлайн».
- Откроется форма калькулятора преобразования значений. В поле «Число» введите значение, которое требуется преобразовать. Из выпадающего списка «Перевод из системы счисления» выберите пункт «10».
 Из раскрывающегося перечня «Перевести в систему счисления» выберите вариант «8». Кроме того, с помощью выпадающего списка можно указать количество отображаемых знаков после запятой для дробных чисел, что в предыдущем рассматриваемом сервисе отсутствовало. После того как все вышеуказанные значения введены, нажмите кнопку «Решить».
Из раскрывающегося перечня «Перевести в систему счисления» выберите вариант «8». Кроме того, с помощью выпадающего списка можно указать количество отображаемых знаков после запятой для дробных чисел, что в предыдущем рассматриваемом сервисе отсутствовало. После того как все вышеуказанные значения введены, нажмите кнопку «Решить».
Внимание! Для корректной работы скриптов сайта рекомендуем отключить на данном сервисе расширения в браузере или инструменты для блокировки рекламы, если они у вас активированы.
- После этого в окне веб-обозревателя отобразится не только ответ, но и весь алгоритм преобразования.
Способ 3: Calc.ru
Следующий сервис калькуляторов, который позволяет среди прочих возможностей перевести числовое значение из десятичной системы счисления в восьмеричную, называется Calc.ru. Рассмотрим алгоритм действий в нем.
Онлайн-сервис Calc.ru
- После перехода на главную страницу сервиса Calc.
 ru по указанной выше ссылке щелкните по элементу «Интернет, информатика, инструменты веб мастера, генераторы паролей, размеры экранов», который расположен в разделе «Калькуляторы онлайн».
ru по указанной выше ссылке щелкните по элементу «Интернет, информатика, инструменты веб мастера, генераторы паролей, размеры экранов», который расположен в разделе «Калькуляторы онлайн». - В открывшемся списке калькуляторов выберите вариант «Перевод систем счисления онлайн» и щелкните по нему.
- В единственное поле открывшейся формы калькулятора введите числовое значение, которое требуется преобразовать. В первом выпадающем списке выберите вариант «десятичной». Во втором выпадающем списке выберите пункт «восьмеричную». Затем нажмите кнопку «Перевести».
- После этого сервис выполнит расчет и результат отобразится в окне браузера.
Как видим, алгоритм преобразования чисел из десятичной системы счисления в восьмеричную через онлайн-сервисы довольно прост и мало чем отличается на разных ресурсах. Единственный значительный плюс сервиса Math.Semestr перед остальными аналогами заключается в возможности оперировать не только с целыми, но и с дробными числовыми значениями, а также в возможности для пользователя видеть весь процесс расчета.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТПеревод чисел между системами исчисления в Excel.
В мире существует множество различных способов записи чисел и систем исчисления. В текущем столетии самыми популярными являются системы исчисления:
• Двоичная;
• Восьмеричная;
• Десятеричная;
• Шестнадцатеричная.
Программа «Excel» предусматривает возможность обработки информации в этих системах.
Для удобства перевода чисел из различных систем в привычную большинству пользователей десятеричную систему, а так же перевода чисел между восьмеричной, двоичной, шестнадцатеричной системами существует целый ряд функций. Эти функции позволяют произвести перевод чисел из одной системы в другую.
Рассмотрим эти функции:
• ДЕС.В.ДВ( ) – переводит десятичные числа в двоичные;
• ДЕС.В.ВОСЬМ( ) – переводит десятичные числа в восьмеричные;
• ДЕС.В.ШЕСТН( ) – переводит десятичные числа в шестнадцатеричные;
• ВОСЬМ.В.ДВ() – переводит восьмеричные в двоичные;
• ВОСЬМ.В.ДЕС() – переводит восьмеричные десятичные;
• ВОСЬМ.В.ШЕСТН() – переводит восьмеричные в шестнадцатеричные;
• ШЕСТН.В.ВОСЬМ() – переводит шестнадцатеричные в восьмеричные;
• ШЕСТН.В.ДВ() – переводит шестнадцатеричные в двоичные;
• ШЕСТН.В.ДЕС() – переводит шестнадцатеричные в десятичные;
• ДВ.В.ВОСЬМ() – переводит двоичные в восьмеричные;
• ДВ.В.ДЕС() – переводит двоичные в десятичные;
• ДВ.В. ШЕСТН() – переводит двоичные в шестнадцатеричные.
Пример использования:
• Установить курсор в ячейку, которой будет присвоено значение;
• Выбрать необходимую функцию при помощи мастера функций в зависимости от того в какую систему исчисления вы хотите перевести число;
• В появившемся окне указать ячейку с переводимым числом или прописать само число;
• Указать количество разрядов – количество знаков в написании числа при необходимости (для функций перевода в десятичную систему количество разрядов не указывается).
• Нажать «Enter» или «Ok».
Как преобразовать восьмеричное в шестнадцатеричное на примере
Используя следующие два метода, мы можем преобразовать восьмеричную систему счисления в шестнадцатеричную систему счисления.
1. Преобразуйте восьмеричное число в двоичное , а затем преобразуйте двоичное число в шестнадцатеричное.
2. Преобразуйте восьмеричное число в десятичное , а затем преобразуйте десятичное число в шестнадцатеричное.
Переведем восьмеричное число в шестнадцатеричную систему счисления.
Восьмеричный Двоичный Шестнадцатеричный
Преобразуем (56) 8 в шестнадцатеричное число.
Шаг 1: Преобразование (56)
8 в двоичный Чтобы преобразовать восьмеричное число в двоичное, нам нужно выразить каждое восьмеричное значение, используя 3 двоичных бита.
Двоичный эквивалент 5 равен (101) 2 .
Двоичный эквивалент 6 равен (110) 2 .
= (56) 8
= (101)(110)
= (101110) 2
Шаг 2: Преобразование (101110)
2 в шестнадцатеричное числоЧтобы преобразовать двоичное число в шестнадцатеричное, нам нужно сгруппировать каждые 4 двоичных бита и вычислить значение [Слева направо].
(101110)
2 в шестнадцатеричном формате= (101110) 2
= (10)(1110)
= (2)(14)
= (2е) 16
14 эквивалентных шестнадцатеричных чисел e .
Этот метод относительно прост по сравнению с описанным ниже.
Восьмеричный Десятичный Шестнадцатеричный
Шаг 1: Преобразование (56)
8 в десятичное число= 5*8 1 +6*8 0
= 40+6
= (46) 10
Шаг 2: Преобразование (46)
10 в шестнадцатеричное число16|46 ---- 16| 2 - 14= (2е) 16
Темы, которые могут вам понравиться
Программа Pythonдля преобразования восьмеричного числа в шестнадцатеричное
В этой статье я создал несколько программ на Python для преобразования восьмеричного числа, введенного пользователем, в его эквивалент шестнадцатеричное значение.Вот список программ:
- Восьмеричное преобразование в шестнадцатеричное с использованием List и , а Loop
- Использование строки и в то время как Цикл
- Использование методов int() и hex()
- Использование пользовательской функции
- Использование класса
Примечание — Перед созданием этих программ, если вы не знаете о шагах, используемых для преобразования, см.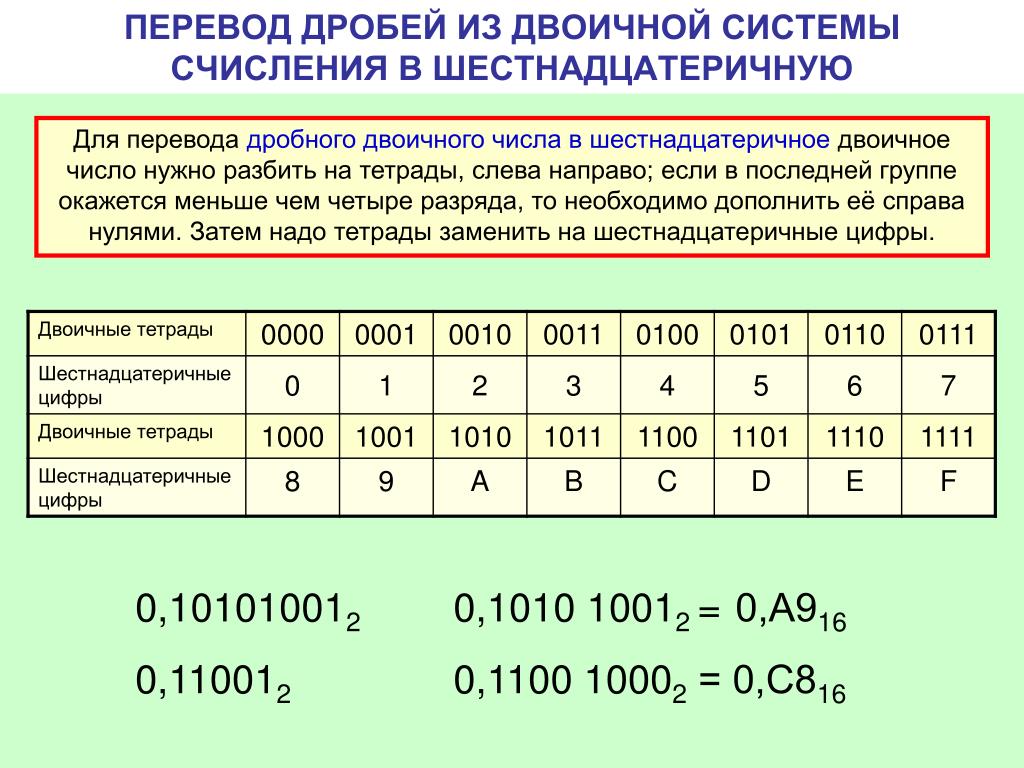 в восьмеричные в шестнадцатеричные шаги и формулы, чтобы получить все необходимые вещи.
в восьмеричные в шестнадцатеричные шаги и формулы, чтобы получить все необходимые вещи.
Восьмеричное преобразование в шестнадцатеричное с использованием списка и цикла while
Чтобы преобразовать восьмеричное число в шестнадцатеричное в Python, вы должны попросить пользователя ввести восьмеричное число, а затем преобразовать это число в его эквивалентное шестнадцатеричное значение. Вопрос в том, напишите программу Python для преобразования восьмеричного числа в шестнадцатеричный, используя список и цикл while . Вот его ответ:
print("Введите восьмеричное число:")
восьмеричное число = целое (ввод ())
проверка = 0
я = 0
десятичное число = 0
в то время как восьмеричное число! = 0:
rem = восьмерка% 10
если rem>7:
проверка = 1
ломать
десятичное число = десятичное число + (рем * (8 ** i))
я = я + 1
восьмеричное число = целое (восьмеричное число/10)
если чек == 0:
я = 0
шестнадцатеричное число = []
в то время как десятичное число != 0:
рем = десятичная % 16
если рем < 10:
бэр = бэр + 48
еще:
бэр = бэр + 55
рем = хр(рем)
шестнадцатеричный.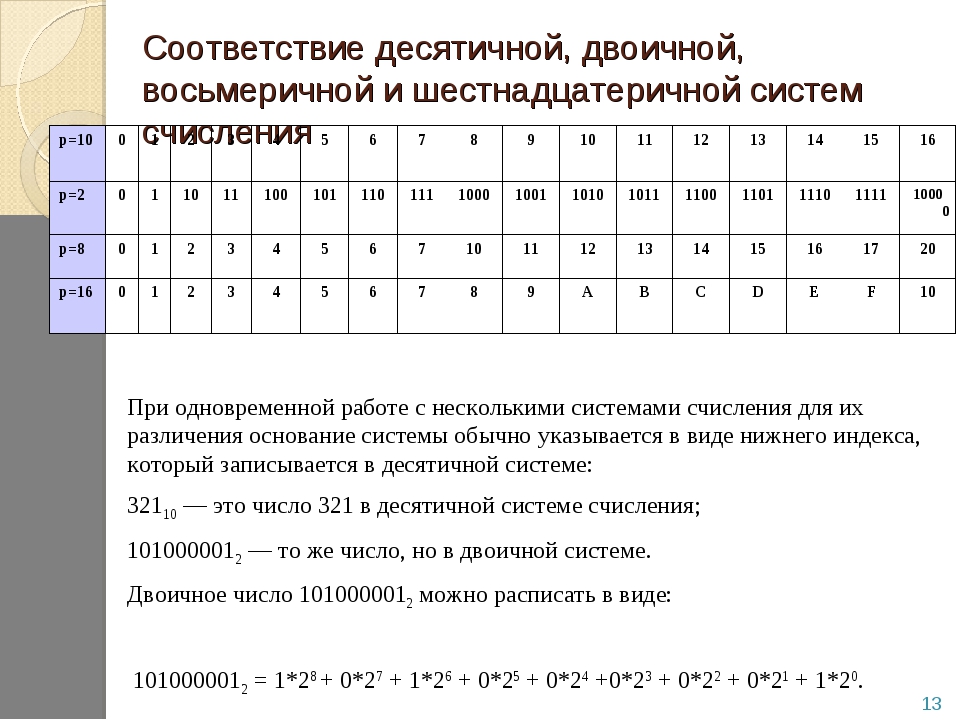 вставить (я, рем)
я = я + 1
десятичное число = целое (десятичное число / 16)
print("\nЭквивалентное шестнадцатеричное значение: ")
я = я - 1
пока я >= 0:
печать (конец = шестнадцатеричное число [я])
я = я - 1
Распечатать()
еще:
print("\nНеверный ввод!")
вставить (я, рем)
я = я + 1
десятичное число = целое (десятичное число / 16)
print("\nЭквивалентное шестнадцатеричное значение: ")
я = я - 1
пока я >= 0:
печать (конец = шестнадцатеричное число [я])
я = я - 1
Распечатать()
еще:
print("\nНеверный ввод!")
Вот первоначальный вывод этой программы на Python:
Теперь введите ввод, скажем, 4720 в виде восьмеричного числа и нажмите клавишу ENTER , чтобы преобразовать и распечатать его.
эквивалентное шестнадцатеричное значение, как показано на снимке экрана ниже:
В приведенной выше программе следующий блок кода:
, а восьмеричное число!=0:
rem = восьмерка% 10
если rem>7:
проверка = 1
ломать
десятичное число = десятичное число + (рем * (8 ** i))
я = я + 1
восьмеричное число = целое (восьмеричное число/10)
используется для преобразования данного восьмеричного числа в его эквивалентное десятичное значение. Чтобы получить подробную информацию о коде, см.
в восьмеричное в десятичное в Python. И следующий блок кода:
Чтобы получить подробную информацию о коде, см.
в восьмеричное в десятичное в Python. И следующий блок кода:
, а десятичное число != 0:
рем = десятичная % 16
если рем < 10:
бэр = бэр + 48
еще:
бэр = бэр + 55
рем = хр(рем)
hexdecnum.insert(i, rem)
я = я + 1
десятичное число = целое (десятичное число / 16)
используется для преобразования десятичного числа в шестнадцатеричное. Чтобы узнать подробнее о работе с кодом, обратитесь к разделу «Десятичная система счисления в шестнадцатеричной системе счисления в Python
».Восьмеричное преобразование в шестнадцатеричное с использованием строки и цикла while
Теперь эта программа создается с использованием строки вместо списка , который использовался в предыдущей программе.Конец = используется для пропуска печати автоматического перехода на новую строку.
print("Введите восьмеричное число: ", end="")
онум = целое (ввод ())
chk = i = dnum = 0
в то время как онум!=0:
рем = онум % 10
если rem>7:
проверка = 1
ломать
dnum = dnum + (rem * (8 ** i))
я = я + 1
онум = интервал (онум / 10)
если чек == 0:
хнум = ""
в то время как dnum != 0:
рем = число % 16
если рем < 10:
бэр = бэр + 48
еще:
бэр = бэр + 55
рем = хр(рем)
hnum = hnum + rem
число = целое (число / 16)
число = число [::-1]
print("\nЭквивалентное шестнадцатеричное значение =", hnum)
еще:
print("\nНеверный ввод!")
Вот пример запуска с вводом восьмеричного числа 7123 :
Следующий оператор:
указывает, что обратная строка, хранящаяся в hnum , инициализируется как hnum . То есть строка, хранящаяся в hnum , переворачивается.
То есть строка, хранящаяся в hnum , переворачивается.
Восьмеричное преобразование в шестнадцатеричное с использованием int() и hex()
Эта программа создана с использованием двух предопределенных функций, а именно int() и hex() для выполнения одной и той же работы, т.е. преобразования восьмеричного в шестнадцатеричное. int() возвращает целочисленный эквивалент значения, переданного в качестве аргумента. И hex() возвращает шестнадцатеричный эквивалент значения, переданного в качестве аргумента.
print("Введите восьмеричное число: ", end="")
онум = ввод ()
число = целое (онум, 8)
hnum = шестнадцатеричный (dnum)
print("\nЭквивалентное шестнадцатеричное значение =", hnum)
Вот пример запуска с пользовательским вводом 7302 :
Примечание - Чтобы пропустить первые два символа и сделать заглавными шестнадцатеричных цифр.Замените следующий (последний) оператор:
print("\nЭквивалентное шестнадцатеричное значение =", hnum)
с новым заявлением, как указано ниже:
print("\nЭквивалентное шестнадцатеричное значение =", hnum[2:]. upper())
upper())
Теперь вывод с тем же пользовательским вводом, что и в предыдущем примере, выглядит так:
Примечание. Чтобы реализовать пользовательский код для преобразования нижнего регистра в верхний, см. раздел Нижний регистр в верхний в Python.
Восьмеричное преобразование в шестнадцатеричное с использованием функции
Эта программа создана с использованием определяемой пользователем функции с именем OctToHex() .Эта функция получает значение (восьмеричное) в качестве аргумента и возвращает его эквивалентное шестнадцатеричное значение, используя методы int() и hex() .
по умолчанию OctToHex(o):
вернуть шестнадцатеричный (int (o, 8))
print("Введите восьмеричное число: ", end="")
онум = ввод ()
hnum = OctToHex(onum)
print("\nЭквивалентное шестнадцатеричное значение =", hnum[2:].upper())
Восьмеричное преобразование в шестнадцатеричное с использованием класса
Это последняя программа, созданная с использованием класса и объекта. То есть создается объект об класса
Взломщик кодов . Используя этот объект, функция-член с именем OctToHex() получает доступ с помощью оператора точка (.) .
То есть создается объект об класса
Взломщик кодов . Используя этот объект, функция-член с именем OctToHex() получает доступ с помощью оператора точка (.) .
класс CodesCracker:
def OctToHex(self, o):
вернуть шестнадцатеричный (int (o, 8))
print("Введите восьмеричное число: ", end="")
онум = ввод ()
ob = Взломщик кодов()
hnum = ob.OctToHex(onum)
print("\nЭквивалентное шестнадцатеричное значение =", hnum[2:].upper())
Та же программа на других языках
Онлайн-тест Python
« Предыдущая программа Следующая программа »
Восьмеричный код в шестнадцатеричный Конвертер - Восьмеричный в шестнадцатеричный
Восьмеричное число в шестнадцатеричное
Восьмеричное преобразование в шестнадцатеричное
Восьмеричное преобразование в шестнадцатеричное - Восьмеричная система счисления представляет собой систему счисления с основанием 8, или октябрь для краткости, и использует цифры от 0 до 7. Восьмеричные числа можно получить, группируя последовательные двоичные числа в группы по три (справа налево).
Восьмеричные числа можно получить, группируя последовательные двоичные числа в группы по три (справа налево).
Старая система счисления, основанная на компьютере, — «восьмеричная» или основание «8». Восьмеричные цифры: 0, 1, 2, 3, 4, 5, 6 и 7. Значение «восемь» записывается как «1 восемь и 0» или 10 8 .
Технически существует множество различных компьютерных языковых протоколов для восьмеричного, но мы, в основном, просто используем простую математическую систему.
Забавный факт: Некоторые племена Нового Света используют основные 8 систем счисления; вместо того, чтобы считать десять пальцев, они считают восемь промежутков между пальцами.Голубые аборигены в фильме «Аватар» использовали восьмеричное число, потому что на их руках было всего четыре пальца.
Таблица преобразования восьмеричного числа в шестнадцатеричное приведена ниже, чтобы понять, как восьмеричные числа представлены в шестнадцатеричной системе счисления. восьмерично-шестнадцатеричный калькулятор используется для преобразования восьмеричных чисел в шестнадцатеричные для быстрого преобразования.
Шестнадцатеричная система счисления
Как упоминалось выше, в десятичной математике нет одной одиночной цифры, представляющей значение «десять». Вместо этого мы обычно используем две цифры, 1 и 0: «10." Но в шестнадцатеричной математике столбцы обозначают числа, кратные 16!
У нас есть числа от 0 до 9 по основанию десять и от 0 до 7 по основанию восемь. Точно так же у нас есть числа от 0 до 3 по основанию 4. Как мы знаем, есть представляют собой цифры от 0 до единицы меньше основания в любой базовой системе. Это означает, что нам нужны «цифры» от 0 до 15 в шестнадцатеричном формате. Для этого нам понадобятся одиночные цифры, представляющие «десять», «одиннадцать», «двенадцать». , "тринадцать", "четырнадцать" и "пятнадцать". Но мы не используем цифры для представления 10, 11, 12, 13, 14 и 15.Итак, вместо этого мы используем буквы. То есть шестнадцать «чисел», считая в шестнадцатеричном формате, таковы:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
, где
10 = A
12 = C
12 = C
13 = D
14 = E
15 = F
Другими словами, в «регулярных» числах, A IS » 10», «В» — «11», «С» — «12», «D» — «13», «E» — «14», а «F» — 15. Вот почему шестнадцатеричные числа выглядят такими странными. Но в обычном режиме преобразования работают легко.
Вот почему шестнадцатеричные числа выглядят такими странными. Но в обычном режиме преобразования работают легко.
Где мы можем использовать шестнадцатеричный формат?
Преобразование значений RGB (для изображения в вашем графическом ПО) в шестнадцатеричное (для соответствующего цвета фона на веб-странице), шестнадцатеричная система счисления может быть полезной.
Графические программы работают со значениями цвета для RGB (красный-зеленый-синий). Каждый из этих цветовых компонентов имеет значения от 0 до 255 где-то. Эти значения могут быть преобразованы между 00 и FF в шестнадцатеричные значения. Если вы перечислите компоненты RGB цвета в виде строки из трех чисел, вы можете получить R: 204, G: 51, B: 255, что в HTML-кодировании переводится в светло-фиолетовый цвет #CC33FF.Обратите внимание, что CC16= 20410, 5110= 3316 и FF16= 25510.
С другой стороны, если у вас есть код для #9, в вашей графической программе он будет транслироваться в темно-красный R: 153, G: 0, B: 51. Другими словами, для преобразования между вашей графической программой и кодировкой вашей веб-страницы используйте шестнадцатеричное число не как шестизначное число, а как трехзначное число, и преобразуйте эти пары цифр в соответствующие RGB. ценности. Или просто используйте наш конвертер hex в RGB для лучшего преобразования.
Другими словами, для преобразования между вашей графической программой и кодировкой вашей веб-страницы используйте шестнадцатеричное число не как шестизначное число, а как трехзначное число, и преобразуйте эти пары цифр в соответствующие RGB. ценности. Или просто используйте наш конвертер hex в RGB для лучшего преобразования.
Преобразование восьмеричного в шестнадцатеричный не самый простой способ. Вы можете использовать наш восьмеричный преобразователь в шестнадцатеричный для быстрого преобразования. Наш восьмеричный конвертер — это удобный инструмент для студентов, преподавателей и начинающих, которые хотят преобразовать число в шестнадцатеричное без использования ручных формул.
Для большего количества преобразований между двоичными, десятичными и шестнадцатеричными числовыми системами вы можете использовать наш бесплатный конвертер десятичных чисел в шестнадцатеричные, двоичных в шестнадцатеричные, шестнадцатеричных в двоичные, шестнадцатеричных в восьмеричные.
| Двоичный | Десятичный | шестнадцатеричных | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1 | 1 | 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10 | 2 | 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11 | 3 | 3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 100 | 4 | 4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 101 | 5 | 5 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 110 | 6 | 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 111 | 7 | 7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1000 | 8 | 8 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1001 | 9 | 9 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1010 | 10 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1011 | 11 | B | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1100 | 12 | С | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1101 9 0362 | 13 | D | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1110 | 14 | Е | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1111 | 15 | F | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10000 | 16 | 10 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10001 | 17 | 11 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
и т. д. д. | и т.д. | и т.д.
Как записать 64 в шестнадцатеричном формате (с основанием 16)? 64 равно 34 в шестнадцатеричной форме Преобразование из/в десятичные, шестнадцатеричные, восьмеричные и двоичные числа.Калькулятор преобразования восьмеричной базы.
Здесь вы можете найти ответ на такие вопросы, как: конвертировать восьмеричное число 64 в шестнадцатеричный калькулятор
Таблица десятичных, двоичных, шестнадцатеричных и восьмеричных диаграмм+
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Декабрь | Шестигранный | Октябрь | бен | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16 | 10 | 20 | 10000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 17 | 11 | 21 | 10001 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18 | 12 | 22 | 10010 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19 | 13 | 23 | 10011 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20 | 14 | 24 | 10100 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21 | 15 | 25 | 10101 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 22 | 16 | 26 | 10110 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23 | 17 | 27 | 10111 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24 | 18 | 30 | 11000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 25 | 19 | 31 | 11001 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26 | 1А | 32 | 11010 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27 9036 2 | 1B | 33 | 11011 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 28 | 1C | 34 | 11100 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 29 | 1D | 35 | 11101 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30 | 1E | 36 | 11110 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 31 | 1F | 37 | 11111 |
| Декабрь | Шестигранный | Октябрь | бен |
|---|---|---|---|
| 32 | 20 | 40 | 100000 |
| 33 | 21 | 41 | 100001 |
| 34 | 22 | 42 | 100010 |
| 35 | 23 | 43 | 100011 |
| 36 | 24 | 44 | 100100 |
| 37 | 25 | 45 | 100101 |
| 38 | 26 | 46 | 100110 |
| 39 | 27 | 47 | 100111 |
| 40 | 28 | 50 | +101000 |
| 41 | 29 | 51 | 101001 |
| 42 | 2А | 52 | 101010 |
| 2B | 53 | 101011 | |
| 44 | 2C | 54 | 101100 |
| 45 | 2D | 55 | 101101 |
| 46 | 2E | 56 | 101110 |
| 47 | 2F | 57 | 101111 |
| Декабрь | Шестигранный | Октябрь | бен |
|---|---|---|---|
| 48 | 30 | 60 | 110000 |
| 49 | 31 | 61 | 110001 |
| 50 | 32 | 62 | 110010 |
| 51 | 33 | 63 | 110011 |
| 52 | 34 | 64 | 110100 |
| 53 | 35 | 65 | 110101 |
| 54 | 36 | 66 | 110110 |
| 55 | 37 | 67 | 110111 |
| 56 | 38 | 70 | 111000 |
| 57 | 39 | 71 | 111001 |
| 58 | 3A | 72 | 111010 |
| 3B | 73 | 111011 | |
| 60 | 3C | 74 | 111100 |
| 61 | 3D | 75 | 111101 |
| 62 | 3E | 76 | 111110 |
| 63 | 3F | 77 | 111111 |
| Декабрь | Шестигранный | Октябрь | бен | |
|---|---|---|---|---|
| 80 | 50 | 120 | 1010000 | |
| 81 | 51 | 121 | 1010001 | |
| 82 | 52 | 122 | 1010010 | |
| 83 | 53 | 123 | 1010011 | |
| 84 | 54 | 124 | 1010100 | |
| 85 | 55 | 125 | 1010101 | |
| 86 | 56 | 126 | 1010110 | |
| 87 | 57 | 127 | 1010111 | |
| 88 | 58 | 130 | 1011000 | |
| 89 | 59 | 131 | 1011001 | |
| 90 | 5А | 132 | 1011010 9 0362 | |
| 91 | 5B | 133 | 1011011 | |
| 92 | 5C | 134 | 1011100 | |
| 93 | 5D | 135 | 1011101 | |
| 94 | 5E | 136 | 1011110 | |
| 95 | 5F | 137 | 1011111 | 9 90 344 |
| Декабрь | Шестигранный | Октябрь | бен | |
| 96 | 60 | 140 | 1100000 | |
| 97 | 61 | 141 | 1100001 | |
| 98 | 62 | 142 | 1100010 | |
| 99 | 63 | 143 | 1100011 | |
| 100 | 64 | 144 | 1100100 | |
| 101 | 65 | 145 | 1100101 | |
| 102 | 66 | 146 | 1100110 | |
| 103 | 67 | 147 | 1100111 | |
| 104 | 68 | 150 | 1101000 | |
| 105 | 69 | 151 | 1101001 | |
| 106 | 6А | 152 | 11 01010 | |
| 107 | 6B | 153 | 1101011 | |
| 108 | 6C | 154 | 1101100 | |
| 109 | 6D | 155 | 1101101 | |
| 110 | 6E | 156 | 1101110 | |
| 111 | 90 344 | |||
| Декабрь | Шестигранный | Октябрь | бен | |
| 112 | 70 | 160 | 1110000 | |
| 113 | 71 | 161 | 1110001 | |
| 114 | 72 | 162 | 1110010 | |
| 115 | 73 | 163 | 1110011 | |
| 116 | 74 | 164 | 1110100 | |
| 117 | 75 | 165 | 1110101 | |
| 118 | 76 | 166 | 1110110 | |
| 119 | 77 | 167 | 1110111 | |
| 120 | 78 | 170 | 1111000 | |
| 121 | 79 | 171 | 1111001 | |
| 122 | 7А | 172 | 9036 1 1111010||
| 123 | 7Б | 173 | 1111011 | |
| 124 | 7C | 174 | 1111100 | |
| 125 | 7D | 175 | 1111101 | |
| 126 | 7E | 176 | 1111110 | |
| 127 | 7F | 177 | ||
| Декабрь | Шестигранный | Октябрь | бен | |
| 128 | 80 | 200 | 10000000 | |
| 129 | 81 | 201 | 10000001 | |
| 130 | 82 | 202 | 10000010 | |
| 131 | 83 | 203 | 10000011 | |
| 132 | 84 | 204 | 10000100 | |
| 133 | 85 | 205 | 10000101 | |
| 134 | 86 | 206 | 10000110 | |
| 135 | 87 | 207 | 10000111 | |
| 136 | 88 | 210 | 10001000 | |
| 137 | 89 | 211 | 10001001 | |
| 138 | 8А | 212 9 0362 | 10001010 | |
| 139 | 8B | 213 | 10001011 | |
| 140 | 8C | 214 | 10001100 | |
| 141 | 8D | 215 | 10001101 | |
| 142 | 8E | 216 | 21000 | 10001110 |
| 143 | 8F | 217 | 210001111 |
| Декабрь | Шестигранный | Октябрь | бен | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 160 | А0 | 240 | 10100000 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 161 | A1 | 241 | 10100001 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 162 | А2 | 242 | 10100010 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 163 | А3 | 243 | 10100011 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 164 | А4 | 244 | 10100100 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 165 | А5 | 245 | 10100101 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 166 | A6 | 246 | 10100110 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 167 | A7 | 247 | 10100111 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 168 | A8 | 250 | 10101000 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 169 | А9 | 251 | 10101001 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 170 | АА | 252 9 0362 | 10101010 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 171 | АВ | 253 | 10101011 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 172 | AC | 254 | 10101100 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 173 | А. Д. Д. | 255 | 10101101 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 174 | АЕ | 256 | 10101110 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 175 | АФ | 257 |
| Декабрь | Hex | Октябрь | Bin | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 176 | B0 | 260 | 10110000 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 177 | B1 | 261 | 10110001 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 178 | B2 | 262 | 10110010 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 179 | В3 | 263 | 10110011 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 180 | В4 | 264 | 10110100 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 181 | В5 | 265 | 10110101 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 182 | В6 | 266 | 10110110 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 183 | В7 | 267 | 10110111 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 184 | В8 | 270 | 10111000 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 185 | В9 | 271 | 10111001 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 186 | БА | 272 9 0362 | 10111010 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 187 | BB | 273 | 10111011 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 188 | до н. э. э. | 274 | 10111100 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 189 | BD | 275 | 10111101 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 190 | БЭ | 276 | 10111110 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 191 | БФ | 277 | 11 | 1 111
| Декабрь | Шестигранный | Октябрь | бен | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 192 | С0 | 300 | 11000000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 193 | C1- | 301 | 11000001 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 194 | С2 | 302 | 11000010 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 195 | С3 | 303 | 11000011 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 196 | С4 | 304 | 11000100 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 197 | С5 | 305 | 11000101 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 198 | С6 | 306 | 11000110 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 199 | С7 | 307 | 11000111 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 200 | С8 | 310 | 11001000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 201 | С9 | 311 | 11001001 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 202 | СА | 312 9 0362 | 11001010 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 203 | СВ | 313 | 11001011 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 204 | CC | 314 | 11001100 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 205 | CD- | 315 | 11001101 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 206 | CE | 316 | 11001110 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 207 | CF | 317 | 11||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Декабрь | Шестигранный | Октябрь | бен | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 208 | D 0 | 320 | 11010000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 209 | D1 | 321 | 11010001 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 210 | D2 | 322 | 11010010 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 211 | D3 | 323 | 11010011 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 212 | D4 | 324 | 11010100 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 213 | Д5 | 325 | 11010101 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 214 | D6 | 326 | 11010110 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 215 | Д7 | 327 | 11010111 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 216 | D8 | 330 | 11011000 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 217 | D9 | 331 | 11011001 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 218 | DA | 332 9 0362 | 11011010 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 219 | DB | 333 | 11011011 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 220 | DC | 334 | 11011100 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 221 | DD | 335 | 11011101 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 222 | ДЭ | 336 | 11011110 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 223 | ДФ | 337 | 111 11
Декабрь | Шестигранный | Октябрь | бен | 16 | 10 | 20 | 10000 | 17 | 11 | 21 | 10001 | 18 | 12 | 22 | 10010 | 19 | 13 | 23 | 10011 | 20 | 14 | 24 | 10100 | 21 | 15 | 25 | 10101 | 22 | 16 | 26 | 10110 | 23 | 17 | 27 | 10111 | 24 | 18 | 30 | 11000 | 25 | 19 | 31 | 11001 | 26 | 1А | 32 | 11010 | 27 9036 2 | 1B | 33 | 11011 | 28 | 1C | 34 | 11100 | 29 | 1D | 35 | 11101 | 30 | 1E | 36 | 11110 | 31 | 1F | 37 | 11111 |
Отказ от ответственности Несмотря на то, что мы прилагаем все усилия для обеспечения точности информации, представленной на этом веб-сайте, мы не даем никаких гарантий в отношении этой информации. |


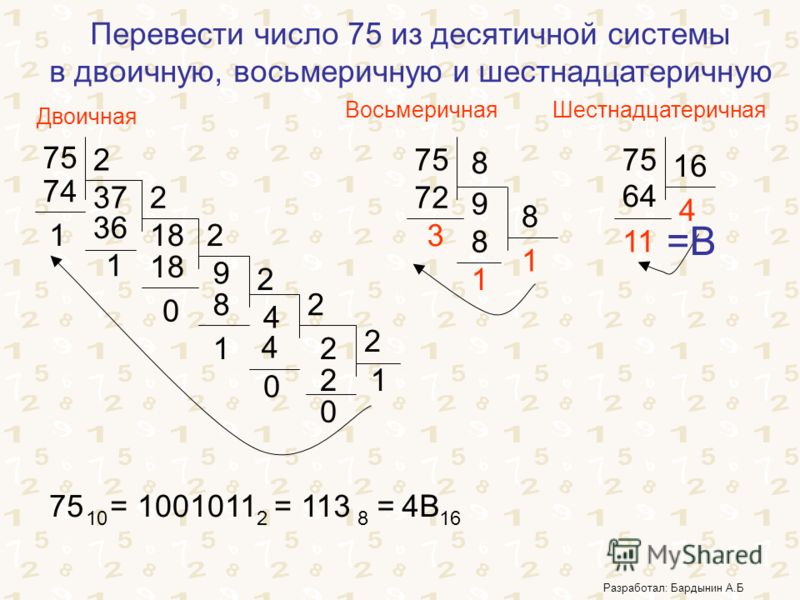 Преобразователь магнитодвижущей силы. Преобразователь напряженности магнитного поля. Преобразователь магнитного потока.Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксов Конвертер передачи данных Конвертер типографских единиц и единиц цифровой обработки изображений Конвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
Преобразователь магнитодвижущей силы. Преобразователь напряженности магнитного поля. Преобразователь магнитного потока.Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксов Конвертер передачи данных Конвертер типографских единиц и единиц цифровой обработки изображений Конвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица  Первоначально письменное представление чисел с помощью символов развивалось независимо, но как только торговля между странами и континентами стала широко распространенной, люди учились и заимствовали друг у друга, и системы счисления, используемые в настоящее время, были созданы посредством коллективного знания.
Первоначально письменное представление чисел с помощью символов развивалось независимо, но как только торговля между странами и континентами стала широко распространенной, люди учились и заимствовали друг у друга, и системы счисления, используемые в настоящее время, были созданы посредством коллективного знания. Даже сегодня люди, которые учатся считать или хотят проиллюстрировать мысль о счете в разговоре, часто используют пальцы. В некоторых культурах для счета также использовались пальцы ног, промежутки между пальцами и суставы пальцев. Любопытно, что числа представлены «цифрами» — тем же словом, которое используется для обозначения пальцев рук и ног в английском и многих других языках.
Даже сегодня люди, которые учатся считать или хотят проиллюстрировать мысль о счете в разговоре, часто используют пальцы. В некоторых культурах для счета также использовались пальцы ног, промежутки между пальцами и суставы пальцев. Любопытно, что числа представлены «цифрами» — тем же словом, которое используется для обозначения пальцев рук и ног в английском и многих других языках.  Например, XI равно 11, а IX равно 9. Правило вычитания не является универсальным, оно работает только для следующих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, и вместо них последовательно записываются числа.
Например, XI равно 11, а IX равно 9. Правило вычитания не является универсальным, оно работает только для следующих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, и вместо них последовательно записываются числа.  Так, например, 32 будет записано (используя соответствующие символы) как CCCTT.Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати.
Так, например, 32 будет записано (используя соответствующие символы) как CCCTT.Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати. 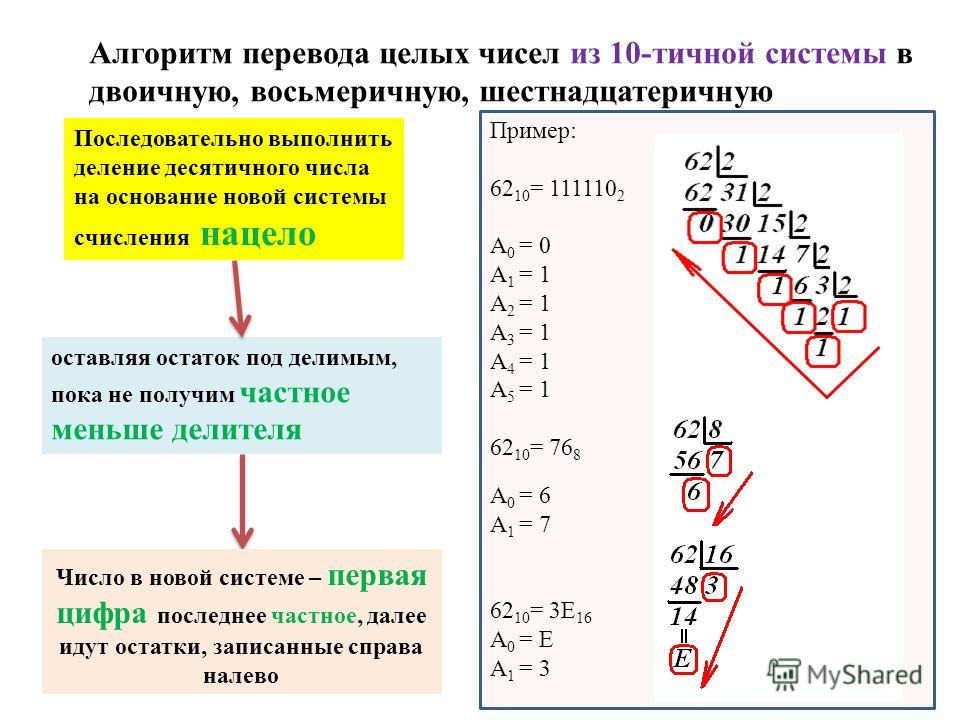 Например, при подсчете очков команд-победителей или подсчете предметов или дней люди в западном мире и некоторых других регионах часто писали четыре вертикальные линии, затем пересекали их пятой горизонтальной линией и повторяли процесс.Например, в части А) на картинке человек, считающий дошел до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал писать счетные метки, пока не получил в сумме двенадцать. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи.Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике.
Например, при подсчете очков команд-победителей или подсчете предметов или дней люди в западном мире и некоторых других регионах часто писали четыре вертикальные линии, затем пересекали их пятой горизонтальной линией и повторяли процесс.Например, в части А) на картинке человек, считающий дошел до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал писать счетные метки, пока не получил в сумме двенадцать. Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи.Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике.  Например, в системе счисления 10 у нас есть следующее:
Например, в системе счисления 10 у нас есть следующее:  Сложение по основанию 2 аналогично сложению по основанию 10. Чтобы увеличить число на единицу:
Сложение по основанию 2 аналогично сложению по основанию 10. Чтобы увеличить число на единицу: 
 Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами.
Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами. 
 В английском языке, например, есть слово, обозначающее 1000, и указывается, сколько существует тысяч, вплоть до 999 999. Затем следует слово миллион, обозначающее 1 000 000. В японском языке есть слово, обозначающее 10 000, после чего приращение продолжается до 99 999 999, за которым следует специальное слово для 100 000 000.
В английском языке, например, есть слово, обозначающее 1000, и указывается, сколько существует тысяч, вплоть до 999 999. Затем следует слово миллион, обозначающее 1 000 000. В японском языке есть слово, обозначающее 10 000, после чего приращение продолжается до 99 999 999, за которым следует специальное слово для 100 000 000.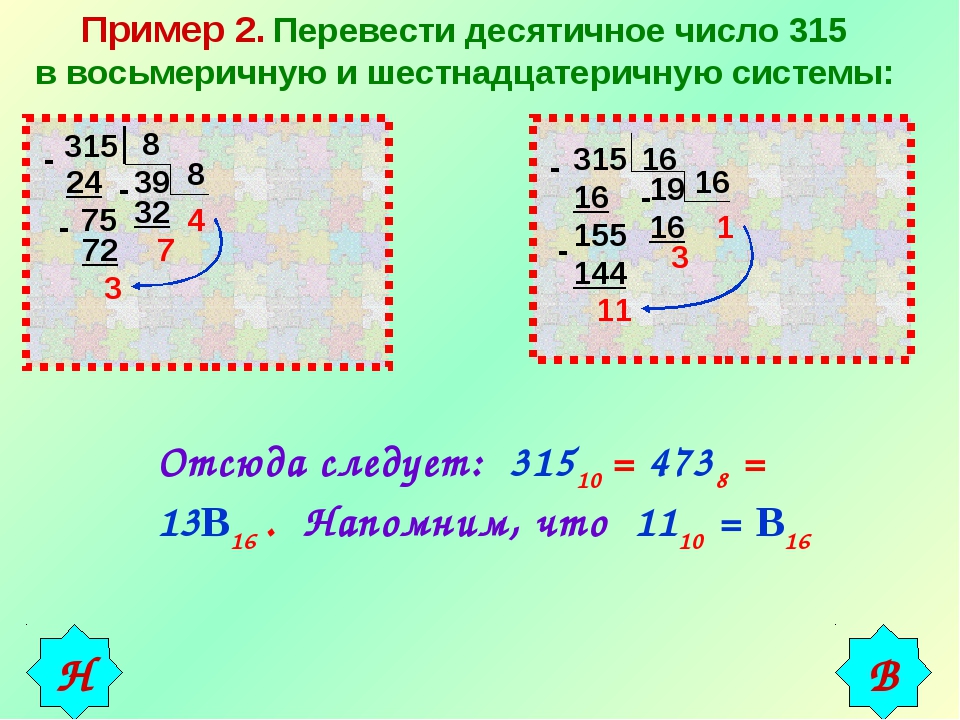 Нечетные числа, с другой стороны, представляют изменение, движение, сущность, которая нуждается в завершении и развитии, и жизнь. Согласно этому поверью, считается плохой приметой дарить живым людям четное количество цветов — это количество обычно отводится на похороны.
Нечетные числа, с другой стороны, представляют изменение, движение, сущность, которая нуждается в завершении и развитии, и жизнь. Согласно этому поверью, считается плохой приметой дарить живым людям четное количество цветов — это количество обычно отводится на похороны. Это подразумевает, что жизнь окончена, и относится к смерти.
Это подразумевает, что жизнь окончена, и относится к смерти.  Это суеверие настолько сильно, что люди насмехаются и всячески оскорбляют тех, у кого в номере, квартире или телефоне стоит цифра 39. Один из таких случаев, по слухам, издевательств привел к трагедии, когда кандидат в депутаты, занявший 39-е место в бюллетене для голосования, подвергся насмешкам проезжающих мимо водителей, что привело к дорожно-транспортному происшествию.Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят.
Это суеверие настолько сильно, что люди насмехаются и всячески оскорбляют тех, у кого в номере, квартире или телефоне стоит цифра 39. Один из таких случаев, по слухам, издевательств привел к трагедии, когда кандидат в депутаты, занявший 39-е место в бюллетене для голосования, подвергся насмешкам проезжающих мимо водителей, что привело к дорожно-транспортному происшествию.Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят.  цифра
система (или система счисления) — система записи для обозначения чисел; тот
это математическая запись для представления чисел данного набора с использованием цифр или
другие символы последовательно.
цифра
система (или система счисления) — система записи для обозначения чисел; тот
это математическая запись для представления чисел данного набора с использованием цифр или
другие символы последовательно. Основание 10 указывает на то, что мы используем 10 различных символов.
Основание 10 указывает на то, что мы используем 10 различных символов.  система
система
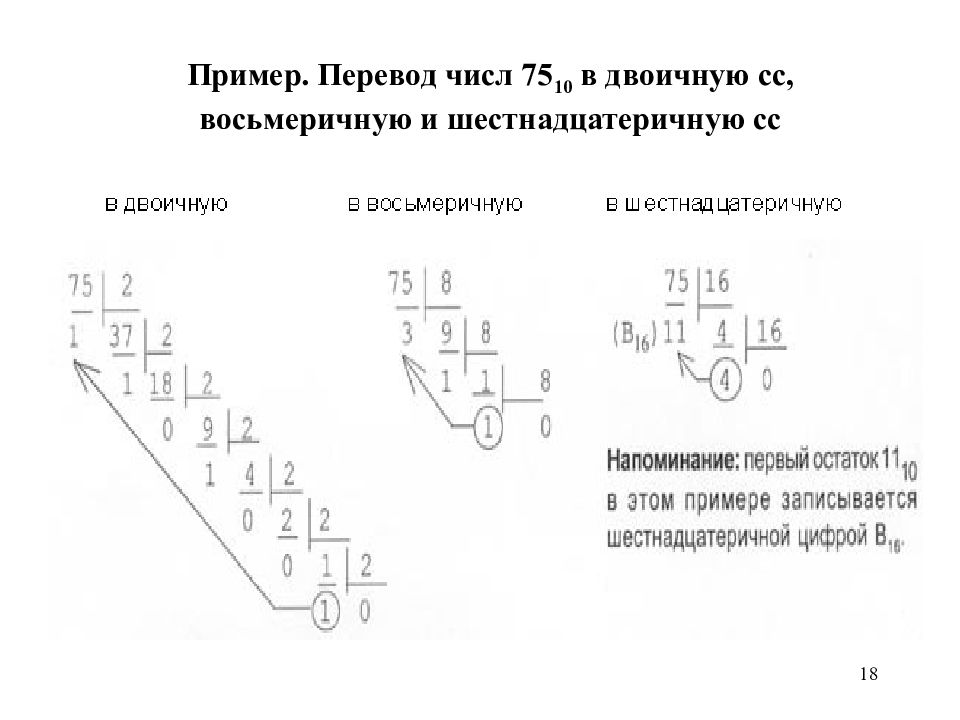 А = 10. В = 11, С = 12,
D = 13, E = 14, F = 15 также называется системой счисления с основанием 16.
А = 10. В = 11, С = 12,
D = 13, E = 14, F = 15 также называется системой счисления с основанием 16.


