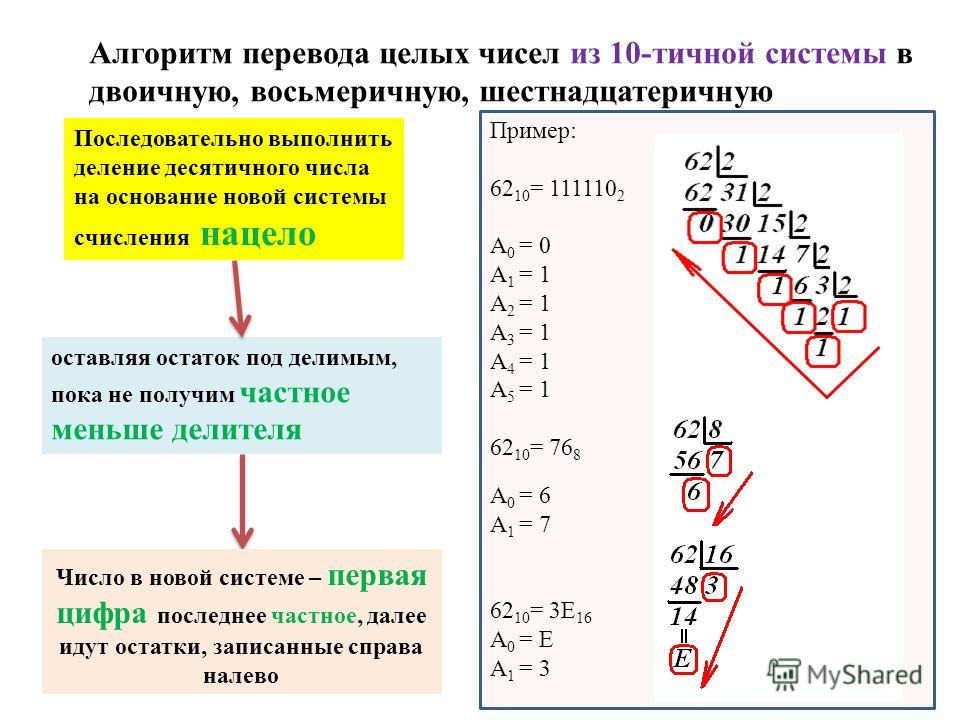
«Перевод целых чисел из десятичной системы счисления в другие системы счисления»
Тема урока: Перевод целых чисел из десятичной системы счисления в другие системы счисления.
Учитель информатики: Жданов С.Н.
Цели урока:
1. Сформировать у учащихся навыки и умения переводить целые числа из десятичной системы счисления в другие системы счисления.
2. Развить умение анализировать, сравнивать, обобщать.
3. Воспитать чувство взаимопомощи, ответственности.
Оборудование: компьютер, проектор, интерактивная доска, раздаточный материал.
План урока:
• Организационный момент.
• Цели и задачи урока.
• Повторение изученного материала.
• Разбор заданий ЕГЭ по теме «Базы данных».
• Закрепление материала в виде теста.
• Подведение итогов, выставление оценок.
Ход урока
•
Организационный момент.
• Цели урока. (слайд 2)
• Сколько лет каждому из вас в 8-ричной или 16-ричной системах счисления?
• «10», «11», «100», «101» — такой была бы шкала оценок в школе в двоичной системе счисления.
• Проверка домашнего задания
У доски учащиеся показывают решения задач(выборочно).
Пока ребята готовятся отвечать, остальные выполняют задание по карточкам.
Задание. Заполните таблицу: (слайд 3)
|
Число |
Система счисления |
Основание системы счисления |
Десятичное представление |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предлагаемые числа: 1345, 10012, 1113, 123,36, 0,1012
• Изложение нового материала
Алгоритм
перевода целых чисел из десятичной системы счисления в другие системы
счисления. (слайд 4)
(слайд 4)
• Последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получится частное, меньше делителя.
• Полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления.
• Составить число в новой системе счисления, записывая его, начиная с последнего частного и собрав последовательно все остатки в обратном порядке.
Пример 1 (слайд 5)
Перевести десятичное число 23 в двоичную систему счисления (2310 -> Х2)
Получаем 2310 = 101112
Пример 2 (слайд 6)
9810 -> Х8
Получаем 9810 = 1428
Пример 3 (слайд 7)
18010 -> Х16
Получаем 18010 = В416
• Закрепление изученного материала (слайд 8)
Решите задачи:
№1
Переведите десятичное число 2014 в:
• двоичную систему счисления; ответ: 11111011110
• восьмеричную систему счисления; ответ: 3736
• шестнадцатеричную систему счисления; ответ: 7DЕ
№2
• 15610 -> Х 5
• 32110 -> Х9
• 21310 -> Х3
Ответы: а) 11115, b) 3869, c) 212203
Проверка усвоенного материала в виде компьютерного теста (слайды 9 — 14)
Тест установлен на
ученические компьютеры. После завершения теста ребята сразу видят результаты
своей работы (слайд 15 )
После завершения теста ребята сразу видят результаты
своей работы (слайд 15 )
• Итоги урока
Оценить работу класса и назвать учащихся, отличившихся на уроке. Выставить оценки за тестовую работу.
Домашнее задание (слайд 16)
• Знать алгоритм перевода целых чисел из десятичной системы счисления в другие системы счисления.
• Заполнить следующую таблицу:
|
|
Х8 |
Х10 |
Х16 |
|
110101 |
|
|
|
|
|
217 |
|
|
|
|
|
261 |
|
|
|
|
|
4АС |
Тест
1. 25710
-> А8
25710
-> А8
a) 402
b) 401
c) 40
d) 104
2. 2710 -> А2
а) 1101
b) 1011
c) 11111
d) 11011
3. 2810 -> А8
a) 33
b) 24
c) 34
d) 43
4. 50210 -> А16
a) 1F6
b) 1E6
c) 6F1
d) 1F
5. 25410 -> А16
a) 1514
b) EF
c) 1415
d) FE
Список литературы:
1. Угринович Н.Д. Информатика и ИКТ. Профильный уровень: учебник для 10 класса / М: БИНОМ. Лаборатория знаний, 2010.
2. Чернобабова К.В., Шаповалова Е.А. Использование VBA для тестового контроля знаний // Информатика и образование. 2008. №4.
3.
Соколова О.Л. Универсальные поурочные
разработки по информатике: 10 класс. – М.: ВАКО, 2008.
– М.: ВАКО, 2008.
Перевод произвольных чисел из одной системы счисления в другую — В помощь ученику — Информатика — Блог учителя
1. Перевод произвольных чисел
Перевод произвольных чисел, т.е. чисел, содержащих целую и дробную части, осуществляется в два этапа. Отдельно переводится целая часть, отдельно — дробная. В итоговой записи полученного числа целая часть отделяется от дробной запятой (точкой).
Пример 9. Перевести число 17,2510 в двоичную систему счисления.
| Переводим целую часть: | Переводим дробную часть: |
17 2 1 8 2 0 4 2 0 2 2 0 1 | 0, 25 ×2 0 50 ×2 1 00 |
Получаем: 17,2510=1001,012
Пример 10. Перевести
число 124,2510 в восьмеричную систему.
Перевести
число 124,2510 в восьмеричную систему.
| Переводим целую часть: | Переводим дробную часть: |
124 8 4 15 8 7 1 | 0, 25 ×8 2 00 |
Получаем: 124,2510=174,28
2. Перевод чисел из системы счисления с основанием 2 в систему счисления с основанием 2
nПеревод целых чисел. Если основание q-ичной системы счисления является степенью числа 2, то перевод чисел из q-ичной системы счисления в 2-ичную и обратно можно проводить по более простым правилам. Для того, чтобы целое двоичное число записать в системе счисления с основанием q=2n, нужно:
1. Двоичное число разбить справа налево на группы по n цифр в каждой.
2.
Если в последней левой группе окажется
меньше n разрядов, то ее надо дополнить
слева нулями до нужного числа разрядов.
3. Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2n.
Пример 11. Число 1011000010001100102 переведем в восьмеричную систему счисления.
Разбиваем число справа налево на триады и под каждой из них записываем соответствующую восьмеричную цифру:
101 | 100 | 001 | 000 | 110 | 010 |
5 | 4 | 1 | 0 | 6 | 2 |
Получаем восьмеричное представление исходного числа: 5410628.
Пример 12. Число
10000000001111100001112 переведем в
шестнадцатеричную систему счисления.
Число
10000000001111100001112 переведем в
шестнадцатеричную систему счисления.
Разбиваем число справа налево на тетрады и под каждой из них записываем соответствующую шестнадцатеричную цифру:
0010 | 0000 | 0000 | 1111 | 1000 | 0111 |
4 | 0 | 0 | F | 8 | 7 |
Получаем шестнадцатеричное представление исходного числа: 400F8716.
Перевод дробных чисел. Для того, чтобы дробное двоичное число записать в системе счисления с основанием q=2n, нужно:
1.
Двоичное число разбить слева направо на
группы по n цифр в
каждой.
2. Если в последней правой группе окажется меньше n разрядов, то ее надо дополнить справа нулями до нужного числа разрядов.
3. Рассмотреть каждую группу как n-разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием q=2n.
Пример 13. Число 0,101100012 переведем в восьмеричную систему счисления.
Разбиваем число слева направо на триады и под каждой из них записываем соответствующую восьмеричную цифру:
000, | 101 | 100 | 010 |
0, | 5 | 4 | 2 |
Получаем восьмеричное представление исходного числа: 0,5428.
Пример 14. Число
0,1000000000112 переведем
в шестнадцатеричную систему
счисления. Разбиваем число слева направо на
тетрады и под каждой из них записываем
соответствующую шестнадцатеричную цифру:
Разбиваем число слева направо на
тетрады и под каждой из них записываем
соответствующую шестнадцатеричную цифру:
0, | 1000 | 0000 | 0011 |
0, | 8 | 0 | 3 |
Получаем шестнадцатеричное представление исходного числа: 0,80316
Перевод произвольных чисел. Для того, чтобы произвольное двоичное число записать в системе счисления с основанием q=2n, нужно:
1. Целую часть данного двоичного числа разбить справа налево, а дробную — слева направо на группы по n цифр в каждой.
2. Если в последних левой и/или правой группах окажется меньше n разрядов, то их надо дополнить слева и/или справа нулями до нужного числа разрядов;
3. Рассмотреть каждую
группу как n-разрядное двоичное число и
записать ее соответствующей цифрой в
системе счисления с основанием q=2n
Рассмотреть каждую
группу как n-разрядное двоичное число и
записать ее соответствующей цифрой в
системе счисления с основанием q=2n
Пример 15. Число 111100101,01112 переведем в восьмеричную систему счисления.
Разбиваем целую и дробную части числа на триады и под каждой из них записываем соответствующую восьмеричную цифру:
111 | 100 | 101, | 011 | 100 |
7 | 4 | 5, | 3 | 4 |
Получаем восьмеричное представление исходного числа: 745,348.
Пример 16. Число
11101001000,110100102 переведем в
шестнадцатеричную систему счисления.
Разбиваем целую и дробную части числа на тетрады и под каждой из них записываем соответствующую шестнадцатеричную цифру:
0111 | 0100 | 1000, | 1101 | 0010 |
7 | 4 | 8, | D | 2 |
Получаем шестнадцатеричное представление исходного числа: 748,D216.
Перевод чисел из систем счисления с
основанием q=2n в двоичную систему. Для того,
чтобы произвольное число, записанное в
системе счисления с основанием q=2n,
перевести в двоичную систему счисления,
нужно каждую цифру этого числа заменить ее
n-значным эквивалентом в двоичной системе
счисления.
Пример 17. Переведем шестнадцатеричное число 4АС3516 в двоичную систему счисления.
В соответствии с алгоритмом:
4 | А | С | 3 | 5 |
0100 | 1010 | 1100 | 0011 | 0101 |
Получаем: 10010101100001101012.
Задания для самостоятельного выполнения
1. Переведите целые числа из десятичной системы счисления в двоичную:
а)513; в)600; д)602; ж)1000;
б)2304; г)5001; е)7000; з)8192.
2. Переведите десятичные дроби в двоичную систему счисления (ответ записать с шестью двоичными знаками):
а)0,4622; в)0,5198; д)0,5803; ж)0,6124;
б)0,7351;
г)0,7982; е)0,8544;
з)0,9321.
3. Переведите смешанные десятичные числа в двоичную систему счисления:
а)40,5; б)31,75; в)124,25; г)125,125.
4. Переведите целые числа из десятичной в восьмеричную систему счисления:
а) 8700; б)8888; в)8900; г)9300.
5. Переведите целые числа из десятичной в шестнадцатеричную систему счисления:
а)266; б)1023; в)1280; г)2041.
6. Переведите числа из десятичной системы счисления в восьмеричную:
а) 0,43; б) 37,41; в) 2936; г)481,625.
7. Переведите числа из десятичной системы счисления в шестнадцатеричную:
а) 0,17; б)43,78; в)25,25; г)18,5.
8. Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основанием 2, 8, 10 и 16.
Основание 2 | Основание 8 | Основание 10 | Основание 16 |
101010 |
|
|
|
| 127 |
|
|
|
| 321 |
|
|
|
| 2А |
9. Переведите двоичные числа в
восьмеричную систему счисления:
Переведите двоичные числа в
восьмеричную систему счисления:
а)1010001001011; в)1011001101111; д)110001000100;
б)1010,00100101; г)1110,01010001; е)1000,1111001.
10. Переведите двоичные числа в шестнадцатеричную систему счисления:
а)1010001001011; в)1011001101111; д)110001000100;
б)1010,00100101; г)1110,01010001; е)100,1111001.
11. Переведите восьмеричные и шестнадцатеричные числа в двоичную систему счисления:
а)2668; в)12708; д)10,238;
б)26616; г)2а1916; е)10,2316.
12. Осуществите перевод чисел по схеме А10» А16 » А2 » А8:
а) 16547; б) 21589; | в) 8512; г) 7756; | д) 5043; е)
2323. |
13. Перевести числа из восьмеричной системы счисления в шестнадцатеричную:
а) 12754; | б) 1515; | в) 7403. |
14. Перевести числа из шестнадцатеричной системы счисления в восьмеричную:
а) 1АЕ2; | б) 1С1С; | в) 34Е. |
15. Сколько разрядов будет в числе, если записать его в восьмеричной системе счисления:
а) 101110102; б) 110011110001112; | в) А18С16; г) 1375ВЕ16. |
16. Сколько разрядов будет в числе, если записать его в шестнадцатеричной системе счисления:
а) 101110102; б) 110011110001112; | в) 777318; г)
1011548. |
17. Сравните числа:
а) 12516 и 1111000101012; б) 7578 и 11100101012; в) А2316 и 12328; | г) 12,2516 и 111,1000101012; д) 63,57518 и 11100,101012; е) В,А16 и 11,38. |
[PDF] Задания для самостоятельного выполнения по теме «Системы счисления»
Download Задания для самостоятельного выполнения по теме «Системы счисления»…
Задания для самостоятельного выполнения по теме «Системы счисления» 1. Переведите целые числа из десятичной системы счисления в двоичную: а)513; б)2304;в)600; г)5001;
д)602; е)7000;
ж)1000; з)8192.
2. Переведите десятичные дроби в двоичную систему счисления (ответ записать с шестью двоичными знаками): а)0,4622; б)0,7351;
в)0,5198; д)0,5803; г)0,7982; е)0,8544;
ж)0,6124; з)0,9321.
3. Переведите смешанные десятичные числа в двоичную систему счисления: а)40,5;
б)31,75;
в)124,25;
г)125,125.
4. Переведите целые числа из десятичной в восьмеричную систему счисления: а) 8700;
б)8888;
в)8900;
г)9300.
5. Переведите целые числа из десятичной в шестнадцатеричную систему счисления: а)266;
б)1023;
в)1280;
г)2041.
6. Переведите числа из десятичной системы счисления в восьмеричную: а) 0,43;
б) 37,41;
в) 2936;
г)481,625.
7. Переведите числа из десятичной системы счисления в шестнадцатеричную: а) 0,17;
б)43,78;
в)25,25;
г)18,5.
8. Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основанием 2, 8, 10 и 16. Основание Основание 2 8 101010 127
Основание 10
Основание 16
321 2А 9. Переведите двоичные числа в восьмеричную систему счисления: а)1010001001011; б)1010,00100101;
в)1011001101111; г)1110,01010001;
д)110001000100; е)1000,1111001.
10. Переведите двоичные числа в шестнадцатеричную систему счисления:
а)1010001001011; б)1010,00100101;
в)1011001101111; г)1110,01010001;
д)110001000100; е)100,1111001.
11. Переведите восьмеричные и шестнадцатеричные числа в двоичную систему счисления: а)2668; б)26616;
в)12708; г)2а1916;
д)10,238; е)10,2316.
12. Осуществите перевод чисел по схеме А10» А16 » А2 » А8: а) 16547; в) 8512; б) 1589; г) 7756;
д) 5043; е) 2323.
13. Перевести числа из восьмеричной системы счисления в шестнадцатеричную: а) 12754; б) 1515;
в) 7403.
14. Перевести числа из шестнадцатеричной системы счисления в восьмеричную: а) 1АЕ2;
б) 1С1С;
в) 34Е.
15. Сколько разрядов будет в числе, если записать его в восьмеричной системе счисления: а) 101110102; б) 110011110001112;
в) А18С16; г) 1375ВЕ16.
16. Сколько разрядов будет в числе, если записать его в шестнадцатеричной системе счисления: а) 101110102; б) 10011110001112;
в) 777318; г) 1011548.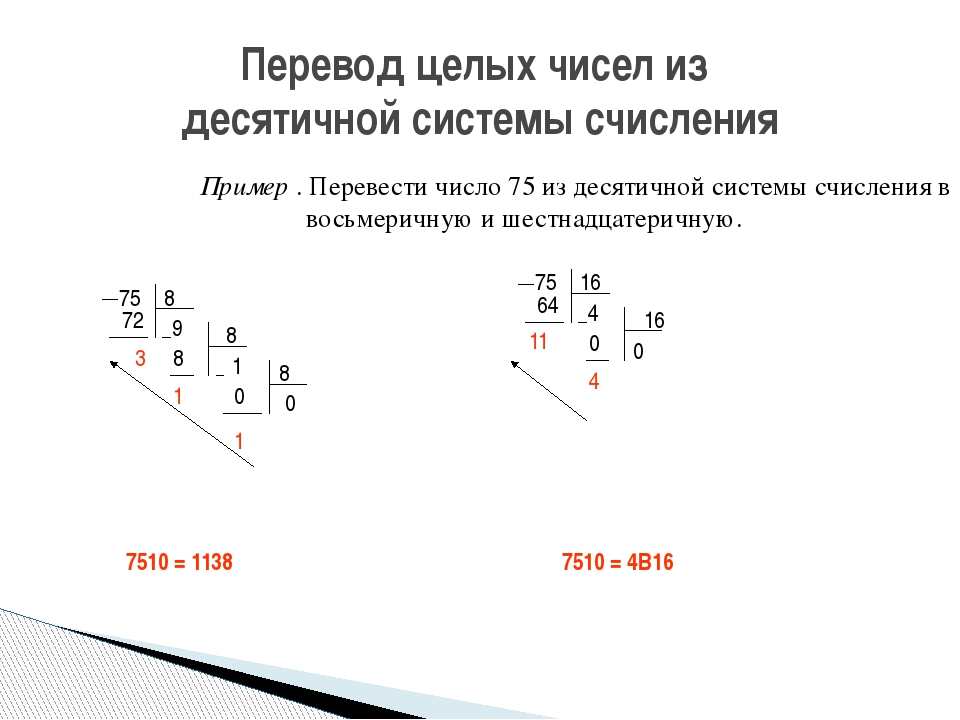
17. Сравните числа: а) 12516 и 1111000101012; б) 7578 и 11100101012; в) А2316 и 12328;
г) 12,2516 и 111,1000101012; д) 63,57518 и 11100,101012; е) В,А16 и 11,38.
Домашнее задание к 19.12.13г: № 1, 4, 5, 8, 9, 10, 11, 17. При выполнении домашнего задания используйте программу Калькулятор
Конвертер десятичного числа в восьмеричное
Десятичная в восьмеричную
Десятичная система счисления для широкой публики является наиболее знакомой системой счисления среди двоичной, восьмеричной и шестнадцатеричной систем счисления. База 10 имеет только 10 символов: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Тогда как восьмеричная система представляет 7 чисел как одну из систем счисления. Таким образом, основание 8 имеет только восемь символов: 0, 1, 2, 3, 4, 5, 6 и 7.
Преобразование десятичного числа в восьмеричное
Существуют различные методы преобразования десятичного числа в восьмеричное, прямое или косвенное.Вам нужно преобразовать десятичное число в другую систему счисления косвенным методом (например, двоичную или шестнадцатеричную), затем вы можете преобразовать его в двоичное число, преобразовав каждую цифру из шестнадцатеричной системы счисления в двоичную и используя группировку из восьмеричной системы счисления.
Давайте понять это с примером
9000 9000
98 на восьмеричное число
первый преобразовать его в двоичный или шестнадцатеричный номер,
= (98) 10
= (1×2 6 + 1×2 5 + 0x2 4 + 0x2 3 + 0x2 2 + 1×2 1 + 0x2 0 ) 0 ) 10 Двоичное преобразование
= (6×16 1 + 2×16 0 ) 10 Шестнадцатеричное преобразование
Поскольку основанием двоичного и шестнадцатеричного чисел являются 2 и 16 соответственно.
= (1100010) 2 или (62) 16
Затем преобразуйте каждую цифру шестнадцатеричного числа в 4 бита двоичного числа, а каждую группу из 3 битов преобразуйте из младшего значащего двоичного числа.
= (001 100 010) 2 или (0110 0010) 2
= (001 100 010) 2
= (1 4 2) 8
= (142) 8
Это единственный ручной способ преобразования десятичного числа в восьмеричное.
Однако существует два прямых метода преобразования десятичного числа в восьмеричное: преобразование в остаток и преобразование в деление. Они объясняются, как показано ниже.
- Конвертация с остатками (для целочисленной части) 3
- преобразование с остатками (для дробной части)
- Преобразование десятичного числа в восьмеричное с использованием списка и в цикле
- Использование метода oct()
- Использование функции
- Использование класса
- Исходные значения, десятичное число=346 (вводится пользователем), i=0
- Условие (из в то время как цикл ) десятичное число!=0 или 346!=0 оценивается как истинное, поэтому программа поток идет внутри цикла
- decnum%8 или 346%8 или 2 инициализируется до rem
- И используя следующий оператор:
octnum. вставка(я, рем)
вставка(я, рем)
значение rem инициализируется до octnum[i] . Итак, octnum[i] или octnum[0] = 2 - i+1 или 0+1 или 1 инициализируется как i
- int(decnum/8) или int(346/8) или 43 инициализируется до denum
- Условие , в то время как цикл снова оценивается с новым значением десятичное число
- То есть условие десятичное число!=0 или 43!=0 снова оценивается как истинное, поэтому выполнение программы входит внутрь цикла.Этот процесс продолжается до тех пор, пока условие не будет оценено как ложное .
- Таким образом, список octnum содержит эквивалентное восьмеричное значение заданного пользователем десятичного числа во время выполнения
- После выхода из цикла уменьшить значение i . Потому что перед условием в то время как цикл оценивается как false, значение i было увеличено на
- Теперь напечатайте octnum[] перечислите один за другим от последнего индекса до 0 th index
- Первая позиция предназначена для чисел от нуля до девяти, то есть число в первой позиции должно быть умножено на десять в степени нуля.
- Число во второй позиции умножается на десять в степени один.
- Число в третьей позиции умножается на десять в степени двойки и так далее, пока числа во всех позициях не будут исчерпаны.

- Если число заканчивается нулем, последний ноль заменяется единицей: e.г. 100 (4) + 1 (1) = 101 (5). Здесь числа с основанием 10 используются в скобках для сравнения.

- Если число оканчивается на единицу, но не на все единицы, то первый ноль справа заменяется единицей, а все последующие за ним справа становятся нулями: 1011 (11) + 1 (1) = 1100.
- Если в исходном числе все единицы, то все они заменяются нулями и впереди добавляется единица: 111 (7) + 1 (1) = 1000 (8).
- 1+1 дает 0, с одним переносом
- 1+1+1 дает 1, с одним переносом
- 1+1 дает 0, с одним переносом
- 1+1+1 дает 1, с одним переносом
- 1 +1 дает 10
Десятичная к восьмерию преобразование с остатками (для целочисленной части)
Это просто метод, включающий деление числа, которое необходимо преобразовать.Пусть десятичное число равно N, затем разделите это число на восемь, потому что основание восьмеричной системы счисления равно восьми. Обратите внимание, что оставшееся значение будет: 0, 1, 2, 3, 4, 5, 6 или 7. Разделите оставшееся десятичное число снова, пока оно не станет 0, и отметьте каждый оставшийся шаг. Затем напишите остатки снизу вверх (или в обратном порядке), которые будут восьмеричным числом заданного десятичного числа.
Пример — Десятичные 210 до восьмеричного номера
210/8 = 26 2 остаток 2
26/8 = 3 остаток 2
3/8 = 0 остаток 3
сейчас, напишите остаток снизу вверх (в обратном порядке), это 322, что эквивалентно восьмеричному числу десятичного целого числа 210.
Преобразование десятичной дроби в восьмеричную с остатками (для дробной части)
Пусть часть десятичной дроби будет M, затем умножьте ее на 8, так как основание восьмеричного числа равно 8. Обратите внимание на значение целой части: 0, 1 , 2, 3, 4, 5, 6 и 7. Снова умножьте оставшееся десятичное число, пока оно не станет 0, и запишите каждое целое число в результате каждого шага. Затем запишите результаты целой части, которые представляют собой число восьмеричной дроби, равное десятичному числу.
Пример – Десятичное дробное число 0.140869140625 в восьмеричном число
0,140869140625 х 8 = 0,12695313 Результирующих Целые 1
0,12695313 × 8 = 0,01562504 Результирующих Целые 1
0,01562504 × 8 = 0,12500032 Результирующих Целые 0
0,12500032 х 8 = 0,00000256 Результирующей Integer 1
0,00000256 x 8=0,000020544 Результирующее целое число 1
И так далее…
Теперь запишите полученные целые части, 0. 11010, что эквивалентно восьмеричной дроби 0,140869140625 десятичной дроби.
11010, что эквивалентно восьмеричной дроби 0,140869140625 десятичной дроби.
Вам не нужно преобразовывать десятичные числа в восьмеричные с помощью этих сложных процедур, так как наш преобразователь десятичных чисел в восьмеричные лучше всего подходит для преобразования этих чисел друг в друга. Наш конвертер может легко и точно преобразовать целые и дробные десятичные числа в восьмеричные.
Для большего количества преобразований между двоичными, десятичными и шестнадцатеричными числовыми системами вы можете использовать наш бесплатный преобразователь десятичных чисел в шестнадцатеричные, двоичных в шестнадцатеричные, шестнадцатеричных в двоичные, восьмеричных в шестнадцатеричные и восьмеричных в десятичные.
десятичных чисел в восьмеричной Таблица
| Десятичный | восьмиштырьковый |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 10 |
| 9 | 11 |
| 10 | 12 |
| 11 | 13 |
| 12 | 14 |
| 13 | 15 |
| 14 | 16 |
| 15 | 17 |
| 16 | 20 |
Преобразование целого числа из десятичного в восьмеричное — Преобразование — ДИкласс
В этом уроке мы научимся преобразовывать десятичное число в восьмеричное.
Прежде чем мы углубимся в основную тему, давайте немного поговорим о десятичной и восьмеричной системах счисления, с которыми мы будем работать в этом уроке.
Десятичная система счисления состоит из 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Таким образом, любое число, которое мы используем в нашей повседневной жизни, фактически находится в десятичной системе счисления.
В восьмеричной системе счисления мы используем восемь цифр.
0, 1, 2, 3, 4, 5, 6 и 7
Восьмеричное число подразумевает основание 8
Как преобразовать десятичное число в восьмеричное?
Чтобы преобразовать десятичное число в восьмеричное, мы делим число на 8 до тех пор, пока делимое не станет меньше 8.
Преобразование десятичного числа 20 в восьмеричную форму
Итак, наше делимое равно 20, и поскольку мы находим восьмеричное число 20, мы разделим его на 8. Таким образом, делитель равен 8.
Шаг 1
----------------
Дивиденд = 20
Делитель = 8
Частное = 2
8 ) 20 ( 2
16
----
4
Разделив 20 на 8, получим в остатке 4. Итак, 1-й остаток = 4
Дивиденд за шаг 2 = частное шага 1
Итак, делимое за шаг 2 = 2
Шаг 2
------------------
Дивиденд = 2
Поскольку дивиденд меньше 8, мы остановимся здесь и скопируем дивиденд как последний остаток.Итак, 2-й ремайдер = 2
Итак, 1-й остаток = 4
Дивиденд за шаг 2 = частное шага 1
Итак, делимое за шаг 2 = 2
Шаг 2
------------------
Дивиденд = 2
Поскольку дивиденд меньше 8, мы остановимся здесь и скопируем дивиденд как последний остаток.Итак, 2-й ремайдер = 2
Рассчитанный остаток выглядит следующим образом.
1-й остаток = 4
2-й остаток = 2
Чтобы найти восьмеричное число, мы должны просмотреть остаток снизу.
Итак, 20 (основание 10) = 24 (основание 8)
В качестве альтернативы, (20) 10 = (24) 8
Где (основание 10) означает, что число находится в десятичной системе счисления и (основание 8) означает, что число находится в восьмеричной системе счисления.
Преобразование десятичного числа 110 в восьмеричную форму
Итак, наше делимое равно 110, а делитель равен 8.
Шаг 1
----------------
Дивиденд = 110
Делитель = 8
Частное = 13
8 ) 110 ( 13
96
-----
6
Разделив 110 на 8, получим в остатке 6. Итак, 1-й остаток = 6
Дивиденд за шаг 2 = частное шага 1
Итак, делимое за шаг 2 = 13
Шаг 2
----------------
Дивиденд = 13
Делитель = 8
Частное = 1
8 ) 13 ( 1
8
-----
5
Разделив 13 на 8, получим в остатке 5.
Итак, 1-й остаток = 5
Дивиденд за шаг 2 = частное шага 1
Итак, делимое за шаг 2 = 1
Шаг 3
------------------
Дивиденд = 1
Поскольку дивиденд меньше 8, мы остановимся здесь и скопируем дивиденд как последний остаток.Итак, 3-й ремайдер = 1
Итак, 1-й остаток = 6
Дивиденд за шаг 2 = частное шага 1
Итак, делимое за шаг 2 = 13
Шаг 2
----------------
Дивиденд = 13
Делитель = 8
Частное = 1
8 ) 13 ( 1
8
-----
5
Разделив 13 на 8, получим в остатке 5.
Итак, 1-й остаток = 5
Дивиденд за шаг 2 = частное шага 1
Итак, делимое за шаг 2 = 1
Шаг 3
------------------
Дивиденд = 1
Поскольку дивиденд меньше 8, мы остановимся здесь и скопируем дивиденд как последний остаток.Итак, 3-й ремайдер = 1
Рассчитанный остаток выглядит следующим образом.
1-й остаток = 6
2-й остаток = 5
3-й остаток = 1
Чтобы найти восьмеричное число, мы должны просмотреть остаток снизу.
Итак, 110 (основание 10) = 156 (основание 8)
Альтернативно, (110) 10 = (156) 8
Программа Python для преобразования десятичного числа в восьмеричное — Pencil Programmer
Проблема: Напишите программу на Python для преобразования десятичного числа в соответствующее восьмеричное представление.
Пример:
Ввод: 8 Выход: 10. Вход: 15. Выход: 17
Преобразование десятичных к восьмерированию в Python с использованием петлей
Стандартный способ преобразования десятичной к восьмерию — разделить десятичный на 8 до тех пор, пока он не уменьшится до 0
после окончания отдела, если мы сложим остатки восходящим образом, результирующее значение будет эквивалентным восьмеричным числом.
decimal = int(input("Введите десятичное число: "))
восьмеричное = 0
ctr = 0.
temp = десятичный #copying номер
#вычисление восьмеричного числа с использованием цикла while
в то время как (температура > 0):
восьмеричный + = ((TEMP% 8) * (10 ** CTR)) #Stacking остатки
temp = int(temp/8) #обновление дивидендов
ctr += 1
print("Двоичный файл {x}: {y}".format(x=decimal,y=octal)) Вывод :
Введите десятичное число: 15
Двоичное число 15: 17
Преобразование десятичного числа в восьмеричное в Python с помощью Recursion
в восьмеричное с помощью рекурсии, мы передаем частное (делимое/8) следующему рекурсивному вызову и выводим остаточное значение (деленное%8).
Мы повторяем процесс до тех пор, пока число не уменьшится до нуля (т. е. до тех пор, пока десятичное число не станет > 0).
Поскольку рекурсия реализует стек, остатки печатаются снизу вверх, и мы получаем эквивалентное восьмеричное число.
по умолчанию detoOct (десятичный):
если (десятичное > 0):
dectoOct((int)(десятичное число/8))
печать (десятичный% 8, конец = '')
decimal = int(input("Введите десятичное число: "))
print("Восьмеричный: ", end='')
dectoOct(decimal) Вывод :
Введите десятичное число: 8
Восьмеричное: 10
Преобразование десятичного числа в восьмеричное с помощью метода oct()
восьмеричное представление десятичного числа, переданного в качестве параметра.
Возвращает восьмеричное число в виде 0oxyz , где xyz — фактическое значение восьмеричного числа.
>>> печать (октябрь (15))
0o17 Прокомментируйте ниже свои сомнения или предложения, если они у вас есть.
Программа Python для преобразования десятичных чисел в восьмеричные
Эта статья создана для описания некоторых программ на Python, для преобразования десятичного числа, введенного пользователем во время выполнения к его эквивалентному восьмеричному значению. Вот список программ:
Примечание — Перед созданием этих программ, если вы не знаете об этапах преобразования, см. Шаги преобразования десятичного числа в восьмеричное и пример, чтобы получить каждый необходимые вещи по теме.
Преобразование десятичного числа в восьмеричное с использованием списка и цикла while
Чтобы преобразовать десятичное число в восьмеричное в Python, вы должны попросить пользователя ввести число в десятичной системе счисления,
затем преобразуйте это число в его эквивалентное значение в восьмеричной системе счисления, как показано в программе, приведенной ниже. Вопрос в том, напишите программу Python для преобразования десятичного числа в восьмеричное, используя список и цикл while . Вот его ответ:
Вопрос в том, напишите программу Python для преобразования десятичного числа в восьмеричное, используя список и цикл while . Вот его ответ:
print("Введите десятичное число:")
десятичное число = целое (ввод ())
я = 0
восьмеричное число = []
в то время как десятичное число!=0:
бэр = десятичное число% 8
восьмеричный.вставить (я, рем)
я = я + 1
десятичное число = целое (десятичное число/8)
print("\nЭквивалентное восьмеричное значение: ")
я = я-1
пока я>=0:
печать (восьмеричное число [i], конец = "")
я = я-1
печать()
Вот пример запуска:
Теперь введите ввод, скажем, 346 в виде десятичного числа, затем нажмите клавишу ENTER , чтобы преобразовать и распечатать
его эквивалентное восьмеричное значение, как показано на снимке ниже:
Пробный запуск вышеуказанной программы с пользовательским вводом 346 выглядит так:
Модифицированная версия предыдущей программы
Это модифицированная версия предыдущей программы. Эта программа использует end= , чтобы пропустить печать автоматического перехода на новую строку, используя print()
Эта программа использует end= , чтобы пропустить печать автоматического перехода на новую строку, используя print()
print("Введите десятичное число: ", end="")
числовое число = целое (ввод ())
я = 0
онум = []
в то время как dnum!=0:
onum.insert(i, число % 8)
я = я + 1
число = целое (число / 8)
print("\nЭквивалентное восьмеричное значение = ", end="")
я = я-1
пока я>=0:
печать (онум [я], конец = "")
я = я-1
печать()
Вот пример запуска с пользовательским вводом 3112 в виде десятичного числа:
Десятичное число в восьмеричное с помощью oct()
Метод oct() возвращает восьмеричный эквивалент значения, переданного в качестве аргумента.
print("Введите десятичное число: ", end="")
числовое число = целое (ввод ())
онум = окт (днум)
print("\nЭквивалентное восьмеричное значение = ", onum)
Вот его пример запуска с вводом десятичного числа как 1234 :
Примечание — Чтобы пропустить первые два символа восьмеричного числа, добавьте [2:] после onum во время печати. То есть замените следующий оператор (из приведенной выше программы):
То есть замените следующий оператор (из приведенной выше программы):
print("\nЭквивалентное восьмеричное значение = ", onum)
с приведенным ниже заявлением:
print("\nЭквивалентное восьмеричное значение = ", onum[2:])
Теперь вывод выглядит так:
Преобразование десятичного числа в восьмеричное с использованием функции
Эта программа создана с использованием как пользовательских, так и предопределенных функций.Пользовательская функция с именем DecToOct() получает значение в качестве аргумента и возвращает его восьмеричный эквивалент, используя метод oct() .
деф DecToOct(d):
возврат окт (г)
print("Введите десятичное число: ", end="")
числовое число = целое (ввод ())
onum = DecToOct(dnum)
print("\nЭквивалентное восьмеричное значение =", onum[2:])
Используя следующий оператор:
Значение переменной dnum (хранит введенное пользователем десятичное число) передается в функцию DecToOct() . И эта функция возвращает эквивалентное восьмеричное значение. Поэтому это значение (восьмеричное) возвращается и инициализируется
онум переменная. Теперь выведите значение переменной onum как восьмеричный эквивалент заданного десятичного числа.
И эта функция возвращает эквивалентное восьмеричное значение. Поэтому это значение (восьмеричное) возвращается и инициализируется
онум переменная. Теперь выведите значение переменной onum как восьмеричный эквивалент заданного десятичного числа.
Преобразование десятичного числа в восьмеричное с использованием класса
Эта программа создана с использованием класса, объектно-ориентированной функции Python. То есть класс с именем CodesCracker создается с помощью функции-члена с именем DecToOct() .Чтобы получить доступ к функции-члену класса, объект класса может быть использован. Поэтому объект с именем obj создается из класса CodesCracker для доступа к его члену. функция с именем DecToOct() с использованием оператора точка (.) .
класс CodesCracker:
def DecToOct (я, д):
возврат окт (г)
print("Введите десятичное число: ", end="")
числовое число = целое (ввод ())
obj = взломщик кодов()
onum = obj. DecToOct(dnum)
print("\nЭквивалентное восьмеричное значение =", onum[2:])
DecToOct(dnum)
print("\nЭквивалентное восьмеричное значение =", onum[2:])
Та же программа на других языках
Онлайн-тест Python
« Предыдущая программа Следующая программа »
Восьмеричная система счисления, объяснение преобразования восьмеричного в десятичное и десятичного в восьмеричное
В этой статье объясняется восьмеричная система счисления.Метод преобразования десятичного числа в восьмеричное и восьмеричного в десятичное число также был объяснен на примере.
Что такое восьмеричная система счисления?
Система счисления, в которой используются только восемь цифр, а именно. 0, 1, 2, 3, 4, 5, 6-7 называется восьмеричной системой счисления. Основанием или основанием этой системы счисления является 8. Все цифры от 0 до 7 в восьмеричной системе имеют то же значение, что и в десятичной системе. Однако десятичные числа от 8 до 15 представлены как 10, 11, 12, 13, 14, 15, 16 и 17 соответственно в восьмеричной системе.
В восьмеричной системе счисления каждая значащая позиция имеет позиционный вес. Наименее значащая позиция имеет вес 8 0 , т.е. 1; старшим значащим позициям присваивается вес в возрастающих степенях числа 8, т. Е. 8 1 , 8 2 , 8 3 и т. д. соответственно.
Преобразование десятичного числа в восьмеричное:
Чтобы преобразовать десятичное число в восьмеричное, десятичное число последовательно делится на 8, пока не будет получено 0 в частном.Остаток на каждом шаге деления при чтении в обратном порядке дает эквивалентное восьмеричное число. Эта процедура преобразования десятичного числа в восьмеричное аналогична методу двойного мазка.
В следующем примере поясняется способ преобразования десятичного числа в восьмеричное.
Предположим, задано десятичное число (444,456) 10 , и нам нужно преобразовать его в эквивалентное восьмеричное число. В качестве самого первого шага мы разделим целую и дробную часть десятичного числа.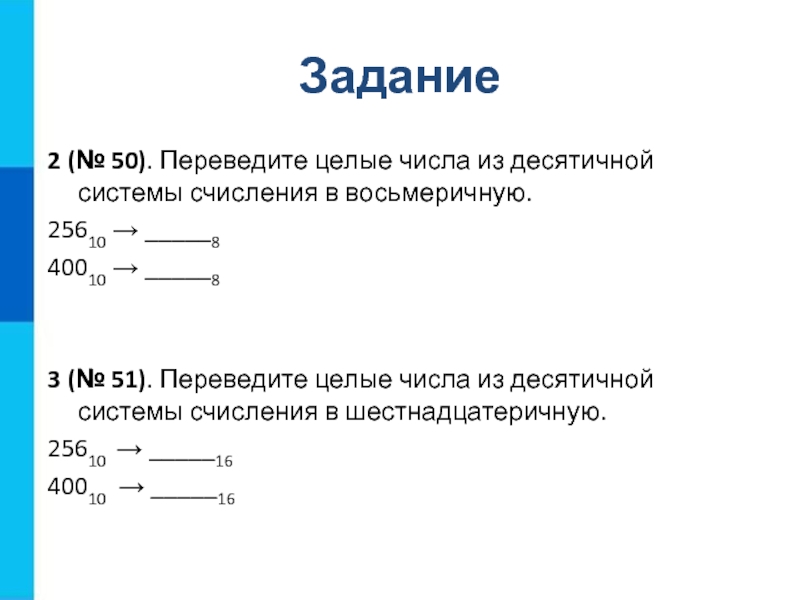
Чтобы преобразовать целую часть десятичного числа в восьмеричное, мы будем делить целое число на 8 несколько раз, пока не будет получено нулевое частное. Запишите остаток на каждом шаге деления и расположите их в обратном порядке. Это показано ниже.
| Отдел | Сгенерированный остаток |
| 8) 444 | |
| 8) 55 | 4 |
| 8) 6 | 7 |
| 8) 0 | 6 |
Если читать остатки снизу вверх, десятичное число (444) 10 эквивалентно восьмеричному (674) 8 .
Чтобы преобразовать дробную часть десятичного числа в восьмеричное, непрерывно умножайте дробь на 8. Запишите перенос в целочисленной позиции при каждом умножении. Процесс умножения прекращается, когда получаются значащие цифры. Перенос при чтении в прямом порядке дает восьмеричную форму десятичной дроби. Это показано ниже.
Это показано ниже.
| Умножение | Сгенерированный перенос в целочисленной позиции |
| 8×0.456 = 3,648 | 3 |
| 8×0,648 = 5,184 | 5 |
| 8×0,184 = 1,472 | 1 |
| 8×0,472 = 3,776 | 3 |
| 8×0,776 = 6,208 | 6 |
Чтение переноса сверху вниз дает эквивалентное восьмеричное число. Следовательно, десятичное (0,456) 10 эквивалентно восьмеричному (0,35136) 8 .
Таким образом, десятичное число (444.456) 10 эквивалентно восьмеричному (674.35136) 8 .
Преобразование восьмеричных чисел в десятичные:
Каждая значащая позиция в восьмеричной системе имеет позиционный вес. Наименее значащая позиция имеет вес 8 0 , т.е. 1; старшим значащим позициям присваивается вес в возрастающих степенях числа 8, т. Е. 8 1 , 8 2 , 8 3 и т. д. соответственно. Однако цифры после восьмеричной точки имеют вес 8 -1 , 8 -2 , 8 -3 и т. д.
1; старшим значащим позициям присваивается вес в возрастающих степенях числа 8, т. Е. 8 1 , 8 2 , 8 3 и т. д. соответственно. Однако цифры после восьмеричной точки имеют вес 8 -1 , 8 -2 , 8 -3 и т. д.
Рассмотрим восьмеричное число (237,45) 8 . Преобразуем это в десятичное число. Прежде всего, присвоение соответствующего веса; умножьте цифры на их позиционный вес и сложите их вместе. Это показано ниже.
Таким образом, десятичный номер. равно 159,578125, что соответствует восьмеричному числу (237,45) 8 .
Преобразование десятичных чисел в восьмеричные • Конвертер чисел • Популярные конвертеры единиц • Компактный калькулятор • Онлайн-конвертеры единиц измерения Конвертер скорости и скоростиПреобразователь углаПреобразователь топливной экономичности, расхода топлива и экономии топливаКонвертер чиселКонвертер единиц информации и хранения данныхКурсы обмена валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиПреобразователь угловой скорости и частоты вращенияПреобразователь ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииПреобразователь момента силыПреобразователь крутящего моментаУдельный объем Энергия, теплота сгорания (на массу) КонвертерУдельная энергия, теплота сгорания (на объем) Конвертер erКонвертер температурного интервалаКонвертер коэффициента теплового расширенияКонвертер теплового сопротивленияКонвертер теплопроводностиКонвертер удельной теплоемкостиПлотность теплоты, плотность пожарной нагрузкиКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объемного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер массового потокаКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер абсолютной вязкости KS Конвертер натяженияПреобразователь проницаемости, проницаемости, паропроницаемостиПреобразователь коэффициента пропускания паров влагиПреобразователь уровня звукаПреобразователь чувствительности микрофонаПреобразователь уровня звукового давления (SPL)Преобразователь уровня звукового давления с выбираемым эталонным давлениемПреобразователь яркостиПреобразователь силы светаПреобразователь освещенностиПреобразователь разрешения цифрового изображенияПреобразователь частоты и длины волныПреобразователь оптической мощности (диоптрий) в фокусное расстояниеОптическая мощность ( диоптрия) → Увеличение (X) КонвертерПреобразователь электрического зарядаЛинейный преобразователь плотности зарядаПреобразователь поверхностной плотности зарядаКонвертер объемной плотности зарядаПреобразователь электрического токаПреобразователь линейной плотности токаПреобразователь плотности поверхностного токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь удельного электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электрической проводимостиПреобразователь уровняПреобразователь емкостиПреобразователь индуктивности, дБ·м·Гау Ватт и другие единицы измерения.
 Преобразователь магнитодвижущей силы. Преобразователь напряженности магнитного поля.Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксов Конвертер передачи данных Конвертер типографских единиц и единиц цифровой обработки изображений Конвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица
Преобразователь магнитодвижущей силы. Преобразователь напряженности магнитного поля.Преобразователь радиоактивного распадаПреобразователь радиационного воздействияИзлучение. Конвертер поглощенной дозыКонвертер метрических префиксов Конвертер передачи данных Конвертер типографских единиц и единиц цифровой обработки изображений Конвертер единиц измерения объема пиломатериаловКалькулятор молярной массыПериодическая таблица Обзор
Приложение-калькулятор для iPhone
Число — это абстрактное математическое понятие, представляющее количество. Используется при счете. Числа использовались с древних времен, сначала в виде счетных меток — царапин на дереве или кости, а затем в виде более абстрактных систем.Существует несколько способов представления чисел в числовых системах. Некоторые из них сегодня не используются.
Различные способы представления чисел
Некоторые исследователи считают, что понятие числа возникло независимо в разных регионах. Первоначально письменное представление чисел с помощью символов развивалось независимо, но как только торговля между странами и континентами стала широко распространенной, люди учились и заимствовали друг у друга, и системы счисления, используемые в настоящее время, были созданы посредством коллективного знания.
Индуистско-арабские цифры
Индо-арабская система счисления сегодня является одной из наиболее широко используемых в мире. Первоначально она была разработана в Индии и усовершенствована персидскими и арабскими математиками. В средние века он распространился в западном мире через торговлю, чтобы заменить римскую систему счисления. В дальнейшем он был изменен и получил широкое распространение во всем мире из-за европейской торговли и колонизации. Это система с основанием 10, что означает, что она основана на числах, кратных десяти, и использует десять символов для представления всех чисел.
Десять — обычное число для счета, потому что у людей десять пальцев, а части тела исторически часто использовались для счета. Даже сегодня люди, которые учатся считать или хотят проиллюстрировать мысль о счете в разговоре, часто используют пальцы. В некоторых культурах для счета также использовались пальцы ног, промежутки между пальцами и суставы пальцев. Любопытно, что числа представлены «цифрами» — тем же словом, которое используется для обозначения пальцев рук и ног в английском и многих других языках.
Надпись на латыни и римскими цифрами на Адмиралтейской арке в Лондоне.Он гласит: ANNO: DECIMO: EDWARDI: SEPTIMI: REGIS: VICTORIÆ: REGINÆ: CIVES: GRATISSIMI: MDCCCCX: (На десятом году правления короля Эдуарда VII, королеве Виктории, от наиболее благодарных граждан, 1910 г.).
Римские
Римские цифры использовались в Римской империи и Европе до 14 века. Они до сих пор используются в некоторых контекстах, например, на часах, для обозначения часов. Римские цифры основаны на семи числах, записанных буквами латинского алфавита:
Порядок важен в римской системе, потому что большее число, за которым следует меньшее, означает, что два должны быть добавлены, но меньшее число перед большее означает, что меньшее число вычитается из большего.Например, XI равно 11, а IX равно 9. Правило вычитания не является универсальным, оно работает только для следующих чисел: IV, IX, XL, XC, CD и CM. В некоторых случаях правила вычитания не используются, и вместо них последовательно записываются числа.
Системы в других культурах
Люди во многих географических регионах имели системы представления чисел, подобные римским или индуистско-арабским. Например, некоторые славянские народы использовали кириллицу для представления чисел, таких как от 1 до 9, кратных 10 и кратных 100, со специальными символами для больших чисел, а также символами для отличия цифр от букв.Система счисления на иврите использует еврейский алфавит для представления чисел от одного до десяти, кратных десяти, 100, 200, 300 и 400. Остальные числа представлены как кратные или суммы. Греческая система счисления также похожа.
В некоторых культурах используются более простые представления, такие как вавилонская система, которая имеет только два клинописных символа, для одного (чем-то напоминающего букву «Т») и для десяти (немного похожего на букву «С»). Так, например, 32 будет записано (используя соответствующие символы) как CCCTT.Египетская система была очень похожа, за исключением того, что были дополнительные символы для нуля, ста, одной тысячи, десяти тысяч, ста тысяч и одного миллиона, а также специальные обозначения для дробей. Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати.
Числа в культуре майя имели символы ноль, один и пять со специальными обозначениями для чисел выше девятнадцати.
Унарная система счисления. Метки счета в различных культурах
Унарная система
Унарная система представляет каждое число с тем же количеством символов, что и его значение.Эти символы обычно одинаковы, поэтому, если 1 представлено буквой A, то 5 будет представлено как AAAAA. Когда дети учатся считать, их учителя часто используют эту систему, чтобы помочь создать связь между конкретной, простой для понимания системой и более абстрактным представлением чисел. Эта система также иногда используется в играх и других простых вычислениях. В разных странах для этого могут использоваться разные виды представительства. Например, при подсчете очков команд-победителей или подсчете предметов или дней люди в западном мире и некоторых других регионах часто писали четыре вертикальные линии, затем пересекали их пятой горизонтальной линией и повторяли процесс.Например, в части А) на картинке человек, считающий дошел до четырех, зачеркнул его, затем снова дошел до четырех, зачеркнул и продолжал писать счетные метки, пока не получил в сумме двенадцать.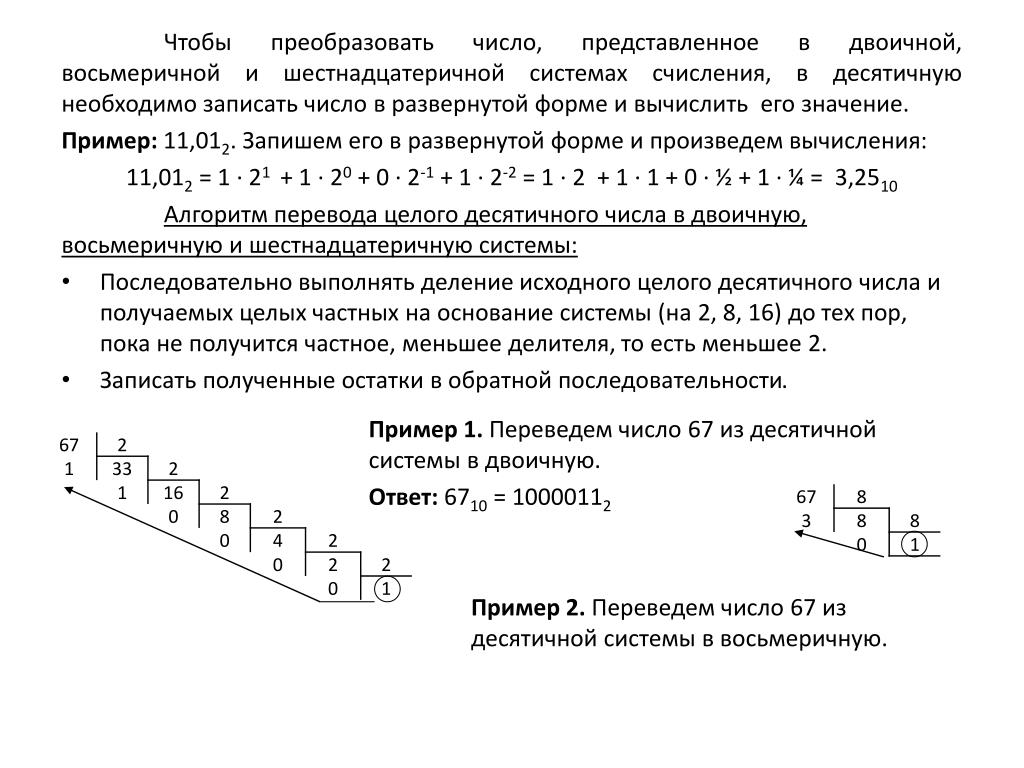 Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи.Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике.
Люди, которые используют или исторически использовали китайские иероглифы в своих системах письма, например, в Китае, Японии и Корее, используют определенный китайский иероглиф с пятью штрихами, чтобы сделать то же самое. В части Б) на картинке человек считает до пяти, завершая иероглиф, а затем начинает новый иероглиф, продолжая счет до семи.Порядок штрихов предопределен, как показано на рисунке. Унарная система также используется в информатике.
Арифмометр, использующий десятичную систему, и микропроцессорный чип, использующий двоичную систему.
Позиционная система
Позиционная система работает с основанием. Например, в системе счисления 10 у нас есть следующее:
Чтобы получить окончательное значение представленного числа, необходимо сложить все значения в каждой позиции. Это удобный способ представления чисел, поскольку он позволяет работать с числами относительно большими по значению, не занимая много места для их записи.
Пример: 3102 = 3 × 10³ + 1 × 10² + 0 × 10¹ + 2 × 10⁰
Двоичная система счисления
Двоичная система счисления широко используется в математике и информатике. Он основан на двух символах «0» и «1» для представления всех возможных чисел. Другими словами, это система с основанием 2. Числа представляются следующим образом: 0=0, 1=1, а начиная с 2 используется принцип сложения. Сложение по основанию 2 аналогично сложению по основанию 10. Чтобы увеличить число на единицу:
Художественное представление двоичных чисел
Чтобы сложить два числа, их выравнивают друг под другом, и для каждого места 0+0 дает 0, 1+0 дает 1, а 1+1 дает 10, где 0 ставится на эту позицию, а 1 переносится на следующую позицию.Например:
11111 (31)
+1011 (11)
———————————
101010 (42)
В этом случае, работая справа налево:
Таким образом, складывая это вместе, мы получаем 101010.
Вычитание работает по тому же принципу, за исключением того, что вместо переноса единиц мы «заимствуем» их. Умножение также похоже на умножение по основанию 10. Умножение на 0 дает 0, а умножение 1 на 1 дает 1. Так, например:
Умножение также похоже на умножение по основанию 10. Умножение на 0 дает 0, а умножение 1 на 1 дает 1. Так, например:
101 (5)
× 10 (2)
———————————
000
101
———————————
1010 (10)
Деление и вычисление квадратных корней также очень похожи на основание 10.
Классификация номеров
Все номера можно разделить на подмножества. Некоторые из приведенных ниже подмножеств частично перекрываются.
Долг — отрицательное число
Отрицательные числа
Отрицательные числа — это числа, представляющие отрицательное значение.Перед ними ставится знак минус. Например, если у человека А нет денег и он должен 5 долларов человеку Б, то у человека А есть -5 долларов. Здесь –5 – отрицательное число.
Рациональные числа
Рациональные числа — это числа, которые можно представить в виде дробей, где знаменатель — натуральное число, отличное от нуля, а числитель — целое число. Например, и 3/4, и -10/5 (то же, что и -2) являются рациональными числами.
Натуральные числа
Натуральные числа — это положительные числа (включая 0), а не дроби, например 7 или 86 766 575 675 456.
Целые числа
Целые числа включают нули, отрицательные и положительные числа, не являющиеся дробями. Примеры включают -65 и 11 223.
Комплексные числа
Комплексные числа — это все числа, являющиеся суммой одного действительного числа и произведением другого действительного числа и квадратного корня из отрицательной единицы.
Простые числа
Простые числа — это натуральные числа больше единицы, которые дают целое число только при делении на единицу или само по себе. Некоторые примеры: 3, 5 и 11.2 57 885 161 −1 — самое большое известное простое число на зиму 2013 года. Оно содержит 17 425 170 цифр. Простые числа используются в криптографии с открытым ключом, системе кодирования данных, часто используемой для безопасного обмена данными в Интернете, например, в онлайн-банкинге.
Интересные факты о числах
Китайские цифры для защиты от мошенничества
Числительные для защиты от мошенничества
Для предотвращения мошенничества при написании чисел в бизнесе и коммерции в китайском языке используются специальные сложные символы, которые трудно подделать, добавив лишние штрихи. Это сделано потому, что обычно используемые китайские иероглифы для чисел слишком просты, и их значение легко изменить, добавив штрихи.
Это сделано потому, что обычно используемые китайские иероглифы для чисел слишком просты, и их значение легко изменить, добавив штрихи.
Современный счет в торговле
Некоторые языки в странах, где в настоящее время используется 10-кратная система счисления, по-прежнему отражают то, что в прошлом были распространены другие системы счисления. Например, в английском языке есть специальное слово для обозначения двенадцати, «дюжина», которое в настоящее время используется в основном для подсчета яиц, выпечки, вина и цветов. У кхмеров есть специальные слова, основанные на древней системе счисления по основанию 20, для подсчета фруктов.
Группировка чисел
И в Китае, и в Японии принята индийско-арабская система счисления, но большие числа группируются по 10 000, и это отражено в языке. В английском языке, например, есть слово, обозначающее 1000, и указывается, сколько существует тысяч, вплоть до 999 999. Затем следует слово миллион, обозначающее 1 000 000. В японском языке есть слово, обозначающее 10 000, после чего приращение продолжается до 99 999 999, за которым следует специальное слово для 100 000 000.
Несчастливые числа
Леонардо да Винчи. Тайная вечеря. Церковь Святой Марии Благодати (Санта-Мария-делле-Грацие), Милан, Италия.
В западной традиции число 13 считается несчастливым. Многие считают, что это взято из иудео-христианской традиции, где тринадцать было числом учеников Иисуса Христа во время Тайной вечери, после которой тринадцатый ученик, Иуда, предал Иисуса. Также среди викингов существовало суеверие, что один из тринадцати собравшихся людей умрет в следующем году.
В России и многих странах бывшего СССР все четных чисел считаются несчастливыми. Возможно, эта традиция возникла из веры в то, что четные числа полны, стабильны и статичны, неподвижны и, следовательно, неживы. Нечетные числа, с другой стороны, представляют изменение, движение, сущность, которая нуждается в завершении и развитии, и жизнь. Согласно этому поверью, считается плохой приметой дарить живым людям четное количество цветов — это количество обычно отводится на похороны.
В странах, говорящих на китайском, японском и корейском языках, число 4 считается несчастливым, поскольку оно произносится так же, как и «смерть». В некоторых случаях все числа, в которых есть четверка, считаются несчастливыми. Например, в здании может не быть этажей 4, 14 и 24. В Китае число 7 также является несчастливым, потому что оно представляет собой духовный мир и призраков. Седьмой месяц китайского календаря именуется «призрачным месяцем», когда открывается связь между мирами живых и духов.В Японии другим несчастливым числом является 9 , произношение которого совпадает со словом «страдание».
В Италии 17 — несчастливое число, потому что, когда его римское представление «XVII» переставляется, оно читается как VIXI или «vixi», что переводится с латыни как «я жил». Это подразумевает, что жизнь окончена, и относится к смерти.
666 — еще одно несчастливое число, называемое в Библии «числом зверя». Иногда считают, что это число 616, но чаще встречается 666. Это относится к антихристу или сатане. Его происхождение спорно, но некоторые ученые считают, что 666 — это транслитерация на иврит, а 616 — на латынь имени императора Нерона, связанного с гонениями на христиан и с тираническим и кровавым правлением. Некоторые также считают Нерона поджигателем во время большого пожара в Риме, хотя его причастность оспаривается историками.
Это относится к антихристу или сатане. Его происхождение спорно, но некоторые ученые считают, что 666 — это транслитерация на иврит, а 616 — на латынь имени императора Нерона, связанного с гонениями на христиан и с тираническим и кровавым правлением. Некоторые также считают Нерона поджигателем во время большого пожара в Риме, хотя его причастность оспаривается историками.
В Афганистане, особенно в Кабуле и его окрестностях 39 считается проклятым или постыдным числом, связанным с проституцией.Это связано с историей о сутенере, у которого в номерном знаке и номере квартиры была цифра 39. Некоторые обвиняют власти и подразделения организованной преступности в распространении этого суеверия для получения прибыли от покупки и продажи автомобилей с «оскорбительными» номерными знаками. Это суеверие настолько сильно, что люди насмехаются и всячески оскорбляют тех, у кого в номере, квартире или телефоне стоит цифра 39. Один из таких случаев, по слухам, издевательств привел к трагедии, когда кандидат в депутаты, занявший 39-е место в бюллетене для голосования, подвергся насмешкам проезжающих мимо водителей, что привело к дорожно-транспортному происшествию.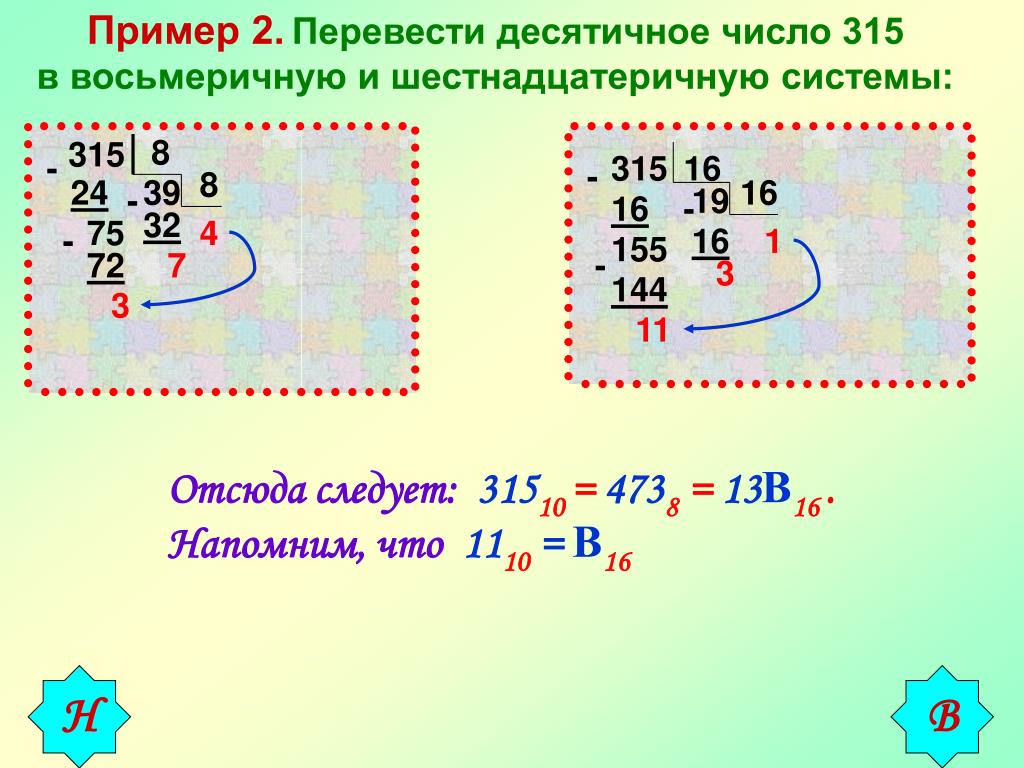 Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят.
Телохранители, опасаясь за его жизнь, застрелили двух причастных к делу людей. Эти утверждения опровергаются телохранителями и парламентарием, и никаких обвинений им не предъявлено, поэтому неясно, городская ли это легенда или реальный случай, но в Кабуле об этом говорят.
Справочная информация
Эта статья была написана Катериной Юрий
Вам трудно перевести единицу измерения на другой язык? Помощь доступна! Разместите свой вопрос в TCTerms и через несколько минут получите ответ от опытных технических переводчиков.
Конвертер десятичных чисел в восьмеричные | Convertopedia
Используйте приведенный ниже онлайн-инструмент преобразования, чтобы преобразовать любое десятичное число в восьмеричное число:Также попробуйте:
Десятичное число
Целое число, десятичная точка и дробное значение объединяются в десятичное число. Десятичная точка отделяет целую часть числа от дробной части числа. Каждая цифра десятичного числа может быть любым числом от 0 до 9. Любое значение меньше 1 записывается справа от десятичной точки.Десятичные числа также известны как число с основанием 10 или счетное число . Разрядное значение десятичного числа варьируется в зависимости от степени 10, начиная слева от десятичной точки. Точно так же разрядное значение цифр, оставшихся до десятичной точки, изменяется в зависимости от деления степени десятков.
Любое значение меньше 1 записывается справа от десятичной точки.Десятичные числа также известны как число с основанием 10 или счетное число . Разрядное значение десятичного числа варьируется в зависимости от степени 10, начиная слева от десятичной точки. Точно так же разрядное значение цифр, оставшихся до десятичной точки, изменяется в зависимости от деления степени десятков.
Восьмеричное число
Восьмеричные числа используют только цифры от 0 до 7. Он известен как base-8 число . Позиционное значение каждой цифры восьмеричного числа варьируется в зависимости от степени 8, начиная справа (младшая значащая цифра).Первое однозначное число в восьмеричной системе — 0, а последнее — 7. Точно так же первое двузначное восьмеричное число — 10, последнее — 77 и так далее. Восьмеричная система счисления широко использовалась в первых компьютерах.
Десятичная к восьмерикальной конверсии Пример
Конвертировать 582
10 к восьмерию 582 10 582 10 = 1106 8
5
859 10 = 1533 8
Read Подробнее: как преобразовать десятичное число на восьмеричное число
десятичных до
десятичных до
| 30189 | |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 10 |
| 9 | 11 |
| 10 | 12 |
| 11 | 13 |
| 12 | 0187|
| 13 | 15 |
| 14 | 16 |
| 15 | 17 |
| 16 | 20 |
| 50 | 62 |
| 100 | 144 |
Также попробуйте:
Другие преобразователи
.