Как переводить из десятичной в восьмеричную систему. Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно
Лабораторная работа №1
Тема: Система счисления. Перевод целых десятичных чисел в двоичную, восьмеричную, шестнадцатиричную систему счисления. (1 час), СРСП(1 час).
Десятичная система счисления
Название «десятичная» объясняется тем, что в основе этой системы лежит основание десять. В этой системе для записи чисел используются десять цифр — 0, 1, 2, 3, 4 , 5, 6, 7, 8, 9.
Десятичная система является позиционной, так как значение цифры в записи десятичного числа зависит от ее позиции, или местоположения, в числе.
Позицию, отводимую для цифры числа, называют разрядом.
Например, запись 526 означает, что число состоит из 5 сотен, 2 десятков и 6 единиц, Цифра 6 стоит в разряде единиц. Цифра 2 — в разряде десятков цифра 5-в разряде сотен.
Это число записать в виде суммы:
526=5*10 2 +2*10 1 +6*10 0
в этой записи число 10-основание системы счисления.
Для записи десятичных дробей используются отрицательные значения степеней основания. Например, число 555,55 в развернутой форме записывается следующим образом:
555,55 10 = 5*10 2 + 5*10 1 + 5*10°+ 5*10- 1 +5*10- 2 .:
Перевод целых десятичных чисел в двоичную систему счисления.
При переводе десятичного числа в двоичное нужно это число делить на 2. Чтобы перевести целое положительное десятичное число в двоичную систему счисления, нужно это число разделить на 2. Полученное частное снова разделить на 2 и т.д. до тех пор, пока частное не окажется меньше 2. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
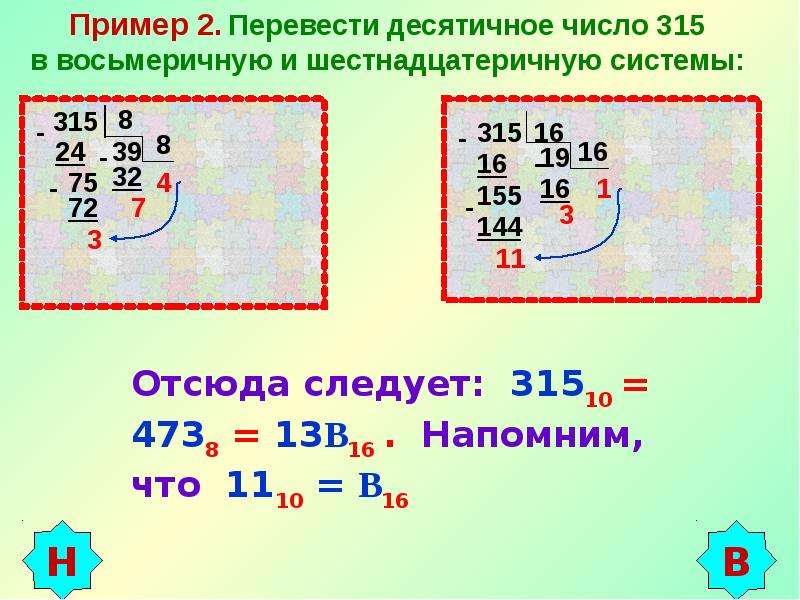
Пример. Число 891 перевести из десятичной системы в двоичную систему счисления.
Решение:
1:2=0, 1 (старшая цифра двоичного числа)
Записываем в одну строку последнее частное и все остатки, начиная с последнего.
Ответ: 891 10 =1101111011 2
Перевод десятичных дробей в двоичную систему счисления
Перевод десятичных дробей в двоичную систему счисления заключается в поиске целых частей при умножении на 2.
Пример. Переведем десятичную дробь 0,322 в двоичную систему счисления.
Чтобы найти первую после запятой цифру двоичной дроби, нужно умножить заданное число на 2 и выделить целую часть произведения.
Решение:
0,322 10 8,83 10
0.322*2=0.644 0 8:2=4 остаток 0
0.644*2=1.288 1 4:2=2 остаток 0
0.288*2=0.576 0 2:2=1 остаток 0
0.576*2=1.152 1 1:2=0 остаток 1
0,3222 10 =0.0101 2 0.83*2=1.66 целая часть равна 1
0.66*2=1.32 целая часть равна 1
0.32*2=0.64 целая часть равна 0
0.64*2=1.28 целая часть равна 1
Ответ: 8,83=1000,1101
Перевод десятичных чисел в восьмеричную систему счисления
Для перевода числа из десятичной системы в восьмеричную применяется тот же прием, что и при переводе в двоичную систему.
Преобразуемое число делят на 8 по правилам десятичной системы с запоминанием остатка, который, конечно, не превышает 7. Если полученное частное больше 7, его тоже делят на 8, сохраняя остаток.
Решение:
(старшая цифра двоичного числа).
Ответ: 891 10 =1573 8
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней двойки:
Таблица 4. Степени числа 2
Пример.
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 5. Степени числа 8
Степени числа 8
Пример. Число перевести в десятичную систему счисления.
3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 6. Степени числа 16
Пример. Число перевести в десятичную систему счисления.
4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в двоичную систему счисления.
5. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в восьмеричную систему счисления.
6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в шестнадцатеричную систему счисления.
Для микросхем компьютера важно лишь одно. Либо сигнал есть (1), либо его нет (0). Но записывать программы в двоичном коде — дело нелегкое. На бумаге получаются очень длинные комбинации из нулей и единиц. Человеку их тяжело.Использование привычной всем десятичной системы в компьютерной документации и программировании очень неудобно. Преобразования из двоичной в десятичную системы и обратно — весьма трудоемкие процессы.
Происхождение восьмеричной системы, так же как и десятичной, связывают со счетом на пальцах. Но считать нужно не пальцы, а промежутки между ними. Их как раз восемь.
Решением проблемы стала восьмеричная . По крайней мере на заре компьютерной техники. Когда разрядность процессоров была невелика. Восьмеричная система позволила с легкостью переводить как двоичные числа в восьмеричные, так и наоборот.
Восьмеричная система счисления — система счисления с основанием 8. Для представления чисел в ней используются цифры от 0 до 7.
Преобразование
Для того чтобы перевести число в двоичное, необходимо заменить каждую цифру восьмеричного числа на тройку из двоичных цифр. Важно лишь запомнить, какая двоичная комбинация соответствует цифрам числа. Их совсем немного. Всего восемь!Во всех системах счисления, кроме десятичной, знаки читаются по одному. Например, в восьмеричной системе число 610 произносится «шесть, один, ноль».
Видео по теме
У компонентов электронных машин, к которым относятся и компьютеры, есть только два различимых состояния: есть ток и нет тока. Их обозначают «1» и «0» соответственно. Поскольку таких состояний только два, многие процессы и операции в электронике можно описать с помощью двоичных чисел.
Инструкция
Делим десятичное число на два до тех пор, пока не получим неделимый на два остаток. На шаге получим остаток 1 (если число было нечетным) или 0 (если делимое делится на два без остатка). Все эти остатки обязательно должны быть учтены. Последнее частное, полученное в результате такого пошагового деления, всегда будет единицей.
Записываем последнюю единицу в старший разряд искомого двоичного , а полученные в процессе остатки записываем за этой единицей в обратном порядке. Здесь надо быть внимательным и не пропускать нули.
Таким образом, числу 235 в двоичном коде будет соответствовать число 11101011.
Теперь переведем в двоичную систему счисления дробную часть десятичного числа.
Тогда десятичному дробному числу 235.62 соответствует двоичное дробное 11101011.100111.
Видео по теме
Обратите внимание
Двоичная дробная часть числа будет конечной, только если дробная часть исходного числа конечна и заканчивается на 5. Простейший случай: 0.5 х 2 = 1, следовательно 0.5 в десятичной системе — это 0.1 в двоичной.
Источники:
- Перевод десятичных чисел в двоичную систему счисления в 2019
Двоичная или бинарная система счисления применяется для отображения электронной информации. Любое число можно записать в двоичном виде. Двоичная система используется во всех вычислительных машинах. Каждая запись в них кодируется по определенным правилам с помощью набора двух символов: 0 и 1. Перевести двоичное число в его десятичное представление, более удобное пользователю, можно с помощью разработанного алгоритма.
Инструкция
Представьте число в виде записи степеней по 2. Для этого все восемь цифр последовательно умножаем на число 2, возведенное в . Степень должна соответствовать разряду цифры. Разряд считается от нуля, начиная с младшего, самого правого символа двоичного числа . Все восемь составленных произведений запишите в .
Десятичная система счисления – одна из самых распространенных в математической теории. Однако с появлением информационных технологий, двоичная система получила не менее широкое распространение, поскольку она является основным способом представления информации в компьютерной памяти.
Инструкция
Преобразование из десятичной системы в двоичную реализуется как для целых чисел, так и для дробных. Перевод целого десятичного числа производится методом последовательного деления его на 2. При этом количество итераций (действий) увеличивается до тех пор, пока частное не станет равно нулю, а итоговое двоичное

Например, преобразования числа 19 выглядит так:19/2 = 18/2 + 1 = 9, в остатке – 1, пишем 1;9/2 = 8/2 + 1 = 4, в остатке – 1, пишем 1;4/2 = 2, остаток отсутствует, пишем 0;2/2 = 1, остаток отсутствует, пишем 0;1/2 = 0 + 1, в остатке – 1, пишем 1.Итак, после метода последовательного деления к числу 19 получилось двоичное число 10011.
1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 12 | 1100 | 110 | 22 |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.
Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.
Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.
3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т. е.
е.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Т. е.
е.
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
Быстрый переход между двоичной, 8-ичной и 16-ичной системами
Быстрый переход между двоичной, восьмеричной и шестнадцатеричной системами
Как перевести число из одной недесятичной системы в другую недесятичную? Можно, например, сначала перевести его в десятичную, а потом из десятичной в нужную систему.
Но в случае, если перевод осуществляется между двоичной, восьмеричной и шестнадцатеричной системами, всё оказывается гораздо проще.
Чтобы быстро перейти от двоичной системы к восьмеричной, необходимо разбить двоичное число на так называемые триады – группы по три цифры, начиная от младших разрядов и заканчивая старшими. В случае, если при этом последняя триада из старших цифр оказывается неполной (содержит одну или две цифры), нужно дополнить ее до трех цифр, приписав нужное количество нулей. Например, разбив на триады число 11011102, получим
Например, разбив на триады число 11011102, получим
001 101 110
Теперь нужно просто воспользоваться таблицей соответствия двоичных триад восьмеричным цифрам:
0002 = 08
0012 = 18
0102 = 28
0112 = 38
1002 = 48
1012 = 58
1102 = 68
1112 = 78
Исходя из таблицы, наше число равно 1568. По той же таблице можно совершать обратный переход из восьмеричной системы в двоичную.
Аналогично можно переводить числа из двоичной системы в 16-ичную и обратно. Для этого нужно разбить двоичное число на группы по 4 цифры (эти группы называются «тетрадами») и воспользоваться таблицей соответствия шестнадцатеричных цифр двоичным тетрадам.
Замечание. Данный способ применим только к двоичной, четверичной, восьмеричной и шестнадцатеричной системам, то есть, к системам с основанием 2n, где n – целое число.
Онлайн калькулятор
для перевода чисел в двоичную, восьмеричную и шестнадцатеричную системы
Для получения пошагового объяснения перевода чисел в двоичную, восьмеричную и шестнадцатеричную системы вы можете воспользоваться калькулятором вверху страницы. Введите число, которое вы собираетесь перевести из одной системы в другую, а также выберите соответствующие системы счисления (из какой и в какую будете переводить).
Как перевести из десятичной в восьмеричную. Перевод чисел в двоичную, шестнадцатеричную, десятичную, восьмеричную системы счисления
Лабораторная работа №1
Тема: Система счисления. Перевод целых десятичных чисел в двоичную, восьмеричную, шестнадцатиричную систему счисления. (1 час), СРСП(1 час).
(1 час), СРСП(1 час).
Десятичная система счисления
Название «десятичная» объясняется тем, что в основе этой системы лежит основание десять. В этой системе для записи чисел используются десять цифр — 0, 1, 2, 3, 4 , 5, 6, 7, 8, 9.
Десятичная система является позиционной, так как значение цифры в записи десятичного числа зависит от ее позиции, или местоположения, в числе.
Позицию, отводимую для цифры числа, называют разрядом.
Например, запись 526 означает, что число состоит из 5 сотен, 2 десятков и 6 единиц, Цифра 6 стоит в разряде единиц. Цифра 2 — в разряде десятков цифра 5-в разряде сотен.
Это число записать в виде суммы:
526=5*10 2 +2*10 1 +6*10 0
в этой записи число 10-основание системы счисления. Для каждой цифры числа основание 10 возводится в степень, зависящую от позиции цифры, и умножается на эту цифру. Степень основания для единиц равна нулю, для десятков — единице, для сотен – двум и т.д.
Для записи десятичных дробей используются отрицательные значения степеней основания. Например, число 555,55 в развернутой форме записывается следующим образом:
Например, число 555,55 в развернутой форме записывается следующим образом:
555,55 10 = 5*10 2 + 5*10 1 + 5*10°+ 5*10- 1 +5*10- 2 .:
Перевод целых десятичных чисел в двоичную систему счисления.
При переводе десятичного числа в двоичное нужно это число делить на 2. Чтобы перевести целое положительное десятичное число в двоичную систему счисления, нужно это число разделить на 2. Полученное частное снова разделить на 2 и т.д. до тех пор, пока частное не окажется меньше 2. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример. Число 891 перевести из десятичной системы в двоичную систему счисления.
Решение:
1:2=0, 1 (старшая цифра двоичного числа)
Записываем в одну строку последнее частное и все остатки, начиная с последнего.
Ответ: 891 10 =1101111011 2
Перевод десятичных дробей в двоичную систему счисления
Перевод десятичных дробей в двоичную систему счисления заключается в поиске целых частей при умножении на 2.
Пример. Переведем десятичную дробь 0,322 в двоичную систему счисления.
Чтобы найти первую после запятой цифру двоичной дроби, нужно умножить заданное число на 2 и выделить целую часть произведения.
Решение:
0,322 10 8,83 10
0.322*2=0.644 0 8:2=4 остаток 0
0.644*2=1.288 1 4:2=2 остаток 0
0.288*2=0.576 0 2:2=1 остаток 0
0.576*2=1.152 1 1:2=0 остаток 1
0,3222 10 =0.0101 2 0.83*2=1.66 целая часть равна 1
0.66*2=1.32 целая часть равна 1
0.32*2=0.64 целая часть равна 0
0.64*2=1.28 целая часть равна 1
Ответ: 8,83=1000,1101
Перевод десятичных чисел в восьмеричную систему счисления
Для перевода числа из десятичной системы в восьмеричную применяется тот же прием, что и при переводе в двоичную систему.
Преобразуемое число делят на 8 по правилам десятичной системы с запоминанием остатка, который, конечно, не превышает 7. Если полученное частное больше 7, его тоже делят на 8, сохраняя остаток.
Решение:
(старшая цифра двоичного числа).
Ответ: 891 10 =1573 8
Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.
1. Для перевода двоичного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 2, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней двойки:
Таблица 4. Степени числа 2
Пример.
2. Для перевода восьмеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 8, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней восьмерки:
Таблица 5. Степени числа 8
Пример. Число перевести в десятичную систему счисления.
3. Для перевода шестнадцатеричного числа в десятичное необходимо его записать в виде многочлена, состоящего из произведений цифр числа и соответствующей степени числа 16, и вычислить по правилам десятичной арифметики:
При переводе удобно пользоваться таблицей степеней числа 16:
Таблица 6. Степени числа 16
Степени числа 16
Пример. Число перевести в десятичную систему счисления.
4. Для перевода десятичного числа в двоичную систему его необходимо последовательно делить на 2 до тех пор, пока не останется остаток, меньший или равный 1. Число в двоичной системе записывается как последовательность последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в двоичную систему счисления.
5. Для перевода десятичного числа в восьмеричную систему его необходимо последовательно делить на 8 до тех пор, пока не останется остаток, меньший или равный 7. Число в восьмеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в восьмеричную систему счисления.
6. Для перевода десятичного числа в шестнадцатеричную систему его необходимо последовательно делить на 16 до тех пор, пока не останется остаток, меньший или равный 15. Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Число в шестнадцатеричной системе записывается как последовательность цифр последнего результата деления и остатков от деления в обратном порядке.
Пример. Число перевести в шестнадцатеричную систему счисления.
Для представления чисел в микропроцессоре используется двоичная система счисления
.
При этом любой цифровой сигнал может иметь два устойчивых состояния: «высокий уровень» и «низкий уровень». В двоичной системе счисления для изображения любого числа используются две цифры, соответственно: 0 и 1. Произвольное число x=a n a n-1 ..a 1 a 0 ,a -1 a -2 …a -m
запишется в двоичной системе счисления как
x = a n ·2 n +a n-1 ·2 n-1 +…+a 1 ·2 1 +a 0 ·2 0 +a -1 ·2 -1 +a -2 ·2 -2 +…+a -m ·2 -m
где a i
— двоичные цифры (0 или 1).
Восьмеричная система счисления
В восьмеричной системе счисления базисными цифрами являются цифры от 0 до 7. 8 единиц младшего разряда объединяются в единицу старшего.
Шестнадцатеричная система счисления
В шестнадцатеричной системе счисления базисными цифрами являются цифры от 0 до 15 включительно. Для обозначения базисных цифр больше 9 одним символом кроме арабских цифр 0…9 в шестнадцатеричной системе счисления используются буквы латинского алфавита:
Для обозначения базисных цифр больше 9 одним символом кроме арабских цифр 0…9 в шестнадцатеричной системе счисления используются буквы латинского алфавита:
10 10 = A 16 12 10 = C 16 14 10 = E 16
11 10 = B 16 13 10 = D 16 15 10 = F 16 .
Например, число 175 10 в шестнадцатеричной системе счисления запишется как AF 16 . Действительно,
10·16 1 +15·16 0 =160+15=175
В таблице представлены числа от 0 до 16 в десятичной, двоичной, восьмеричной и шестнадцатеричной системах счисления.
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
Двоично-восьмеричные и двоично-шестнадцатеричные преобразования
Двоичная система счисления удобна для выполнения арифметических действий аппаратными средствами микропроцессора, но неудобна для восприятия человеком, поскольку требует большого количества разрядов. Поэтому в вычислительной технике помимо двоичной системы счисления широкое применение нашли восьмеричная и шестнадцатеричная системы счисления для более компактного представления чисел.
Поэтому в вычислительной технике помимо двоичной системы счисления широкое применение нашли восьмеричная и шестнадцатеричная системы счисления для более компактного представления чисел.
Три разряда восьмеричной системы счисления реализуют все возможные комбинации восьмеричных цифр в двоичной системе счисления: от 0 (000) до 7(111). Чтобы преобразовать двоичное число в восьмеричное, нужно объединить двоичные цифры в группы по 3 разряда (триады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от него тоже можно добавить незначащие нули до заполнения всех триад. Затем каждая триада заменяется восьмеричной цифрой.
Пример: Преобразовать число 1101110,01 2 в восьмеричную систему счисления.
Объединяем двоичные цифры в триады справа налево. Получаем
001 101 110,010 2 = 156,2 8 .
Чтобы перевести число из восьмеричной системы в двоичную, нужно каждую восьмеричную цифру записать ее двоичным кодом:
156,2 8 = 001 101 110,010 2 .
Четыре разряда шестнадцатеричной системы счисления реализуют все возможные комбинации шестнадцатеричных цифр в двоичной системе счисления: от 0 (0000) до F(1111). Чтобы преобразовать двоичное число в шестнадцатеричное, нужно объединить двоичные цифры в группы по 4 разряда (тетрады) в две стороны, начиная от разделителя целой и дробной части. При необходимости слева от исходного числа нужно добавить незначащие нули. Если число содержит дробную часть, то справа от нее тоже нужно добавить незначащие нули до заполнения всех тетрад. Затем каждая тетрада заменяется шестнадцатеричной цифрой.
Пример: Преобразовать число 1101110,11 2 в шестнадцатеричную систему счисления.
Объединяем двоичные цифры в тетрады справа налево. Получаем
0110 1110,1100 2 = 6E,C 16 .
Чтобы перевести число из шестнадцатеричной системы в двоичную, нужно каждую шестнадцатеричную цифру записать ее двоичным кодом.
1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 10 | 3 |
| 4 | 100 | 11 | 4 |
| 5 | 101 | 12 | 10 |
| 6 | 110 | 20 | 11 |
| 7 | 111 | 21 | 12 |
| 8 | 1000 | 22 | 13 |
| 9 | 1001 | 100 | 14 |
| 10 | 1010 | 101 | 20 |
| 11 | 1011 | 102 | 21 |
| 12 | 1100 | 110 | 22 |
| 13 | 1101 | 111 | 23 |
| 14 | 1110 | 112 | 24 |
| 15 | 1111 | 120 | 30 |
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 8 |
| 9 | 9 |
| 10 | |
| 11 | |
| 12 | 10 |
| 13 | 11 |
| 14 | 12 |
| 15 | 13 |
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.
Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.
Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.
3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:
Это и есть десятичная запись нашего числа, т. е.
е.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.
Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.
4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
Т. е.
е.
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
| 0 | 0 |
| 1 | 1 |
| 10 | 2 |
| 11 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:
Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно
Перевод чисел между системами счисления, основания которых являются степенями числа 2 (q = 2 n), может производиться по более простым алгоритмам. Такие алгоритмы могут применяться для перевода чисел между двоичной (q = 2 1), восьмеричной (q = 2 3) и шестнадцатеричной (q = 2 4) системами счисления.
Перевод чисел из двоичной системы счисления в восьмеричную. Для записи двоичных чисел используются две цифры, то есть в каждом разряде числа возможны 2 варианта записи. Решаем показательное уравнение:
2 = 2 i . Так как 2 = 2 1 , то i = 1 бит.
Каждый разряд двоичного числа содержит 1 бит информации.
Для записи восьмеричных чисел используются восемь цифр, то есть в каждом разряде числа возможны 8 вариантов записи. Решаем показательное уравнение:
Решаем показательное уравнение:
8 = 2 i . Так как 8 = 2 3 , то i = 3 бита.
Каждый разряд восьмеричного числа содержит 3 бита информации.
Таким образом, для перевода целого двоичного числа в восьмеричное его нужно разбить на группы по три цифры, справа налево, а затем преобразовать каждую группу в восьмеричную цифру. Если в последней, левой, группе окажется меньше трех цифр, то необходимо ее дополнить слева нулями.
Переведем таким способом двоичное число 101001 2 в восьмеричное:
101 001 2 => 1 × 2 2 + 0 × 2 1 + 1 × 2 0 0 × 2 2 + 0 × 2 1 + 1 × 2 0 => 51 8 .
Для упрощения перевода можно заранее подготовить таблицу преобразования двоичных триад (групп по 3 цифры) в восьмеричные цифры:
| Двоичные триады | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
| Восьмеричные цифры | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
Для перевода дробного двоичного числа (правильной дроби) в восьмеричное необходимо разбить его на триады слева направо и, если в последней, правой, группе окажется меньше трех цифр, дополнить ее справа нулями.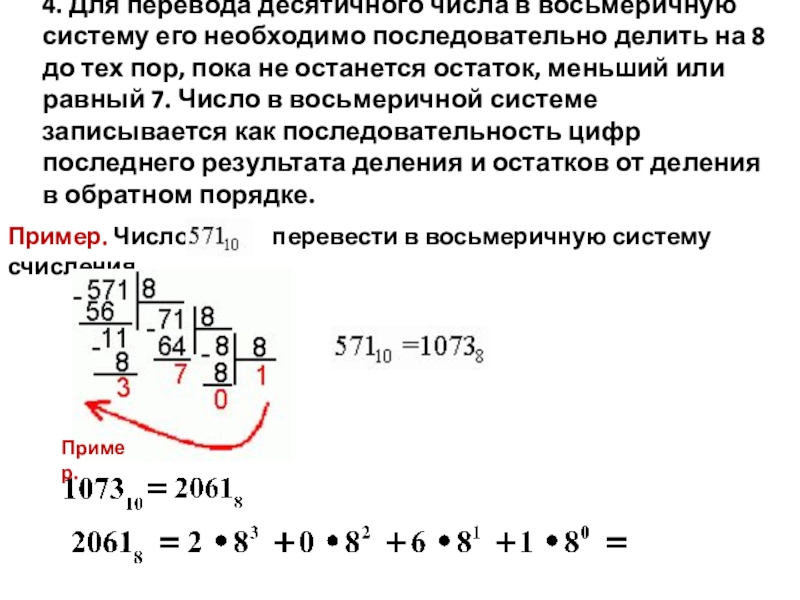 Далее необходимо триады заменить на восьмеричные числа.
Далее необходимо триады заменить на восьмеричные числа.
Например, преобразуем дробное двоичное число А 2 = 0,110101 2 в восьмеричную систему счисления:
| Двоичные триады | 110 | 101 |
| Восьмеричные цифры | 6 | 5 |
Получаем: А 8 = 0,65 8 .
Перевод чисел из двоичной системы счисления в шестнадцатеричную. Для записи шестнадцатеричных чисел используются шестнадцать цифр, то есть в каждом разряде числа возможны 16 вариантов записи. Решаем показательное уравнение:
16 = 2 i . Так как 16 = 2 4 , то i = 4 бита.
Каждый разряд шестнадцатеричного числа содержит 4 бита информации.
Таким образом, для перевода целого двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры (тетрады), начиная справа, и, если в последней левой группе окажется меньше четырех цифр, дополнить ее слева нулями.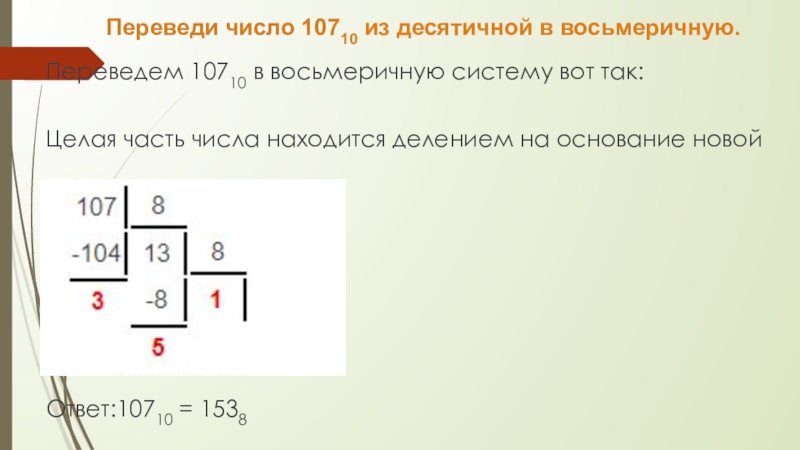 Для перевода дробного двоичного числа (правильной дроби) в шестнадцатеричное необходимо разбить его на тетрады слева направо и, если в последней правой группе окажется меньше четырех цифр, то необходимо дополнить ее справа нулями.
Для перевода дробного двоичного числа (правильной дроби) в шестнадцатеричное необходимо разбить его на тетрады слева направо и, если в последней правой группе окажется меньше четырех цифр, то необходимо дополнить ее справа нулями.
Затем надо преобразовать каждую группу в шестнадцате-ричную цифру, воспользовавшись для этого предварительно составленной таблицей соответствия двоичных тетрад и шестнадцатеричных цифр.
Переведем целое двоичное число А 2 = 101001 2 в шестнадцатеричное:
Получаем: А 16 = 0,D4 16 .
Для того чтобы преобразовать любое двоичное число в восьмеричную или шестнадцатеричную системы счисления, необходимо произвести преобразования по рассмотренным выше алгоритмам отдельно для его целой и дробной частей.
Перевод чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную.
Для перевода чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную необходимо цифры числа преобразовать в группы двоичных цифр. Для перевода из восьмеричной системы в двоичную каждую цифру числа надо преобразовать в группу из трех двоичных цифр (триаду), а при преобразовании шестнадцатеричного числа — в группу из четырех цифр (тетраду).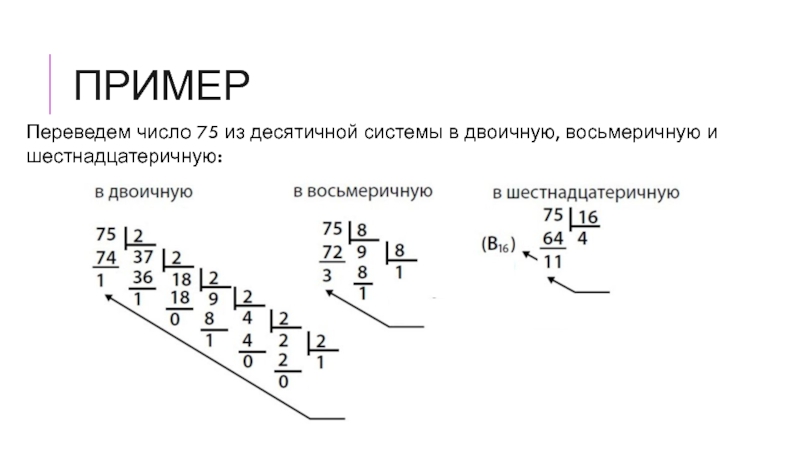
Например, преобразуем дробное восьмеричное число А 8 = 0,47 8 в двоичную систему счисления:
В результате имеем: А 2 = 10101011 2
3адания
1.16. Составить таблицу соответствия двоичных тетрад и шестнадцатеричных цифр.
1.17. Перевести в восьмеричную и шестнадцатеричную системы счисления следующие целые числа: 1111 2 , 1010101 2 .
1.18. Перевести в восьмеричную и шестнадцатеричную системы счисления следующие дробные числа: 0,01111 2 , 0,10101011 2 .
1.19. Перевести в восьмеричную и шестнадцатеричную системы счисления следующие числа: 11,01 2 , 110,101 2 .
1.20. Перевести в двоичную систему счисления следующие числа: 46,27 8 , ЕF,12 16 .
1.21. Сравнить числа, выраженные в различных системах счисления: 1101 2 и D 16 ; 0,11111 2 и 0,22 8 ; 35,63 8 и 16,С 16 .
Урок 10. Перевод десятичных чисел в другие системы счисления. Правило перевода целого числа
Урок 10. Перевод десятичных чисел в другие системы счисления. Правило перевода целого числа
Правило перевода целого числа
Восьмеричной системой счисления называется позиционная система счисления с основанием 8. Для записи чисел в восьмеричной системе счисления используются цифры: 0, 1, 2, 3, 4, 5, 6, 7.
На основании формулы (1) для целого восьмеричного числа можно записать:
Например: 10638 = 1 • 83 + 0 • 82 + 6 • 81 + 3 • 80 = 56310.
Таким образом, для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.
Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в новой системе счисления составляется последовательной записью полученных остатков, начиная с последнего.
Пример 6. Переведём десятичное число 103 в восьмеричную систему счисления.
10310 = 1478
Шестнадцатеричная система счисленияОснование: q = 16.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, В, С, D, Е, F.
Здесь только десять цифр из шестнадцати имеют общепринятое обозначение 0,…, 9. Для записи цифр с десятичными количественными эквивалентами 10, 11, 12, 13, 14, 15 обычно используются первые пять букв латинского алфавита.
Таким образом, запись 3AF16 означает:
Пример 7. Переведём десятичное число 154 в шестнадцатеричную систему счисления.
Переведём десятичное число 154 в шестнадцатеричную систему счисления.
15410 = 9А16
Презентация «Системы счисления»
Презентация «Системы счисления» (Open Document Format)
Ссылки на ресурсы ЕК ЦОР
Федеральный центр информационных образовательных ресурсов:
Правило перевода целых десятичных чисел в систему счисления с основанием qДля перевода целого десятичного числа в систему счисления с основанием g следует:
1) последовательно выполнять деление данного числа и получаемых целых частных на основание новой системы счисления до тех пор, пока не получим частное, равное нулю;
2) полученные остатки, являющиеся цифрами числа в новой системе счисления, привести в соответствие с алфавитом новой системы счисления;
3) составить число в новой системе счисления, записывая его, начиная с последнего полученного остатка.
Представим таблицу соответствия десятичных, двоичных, восьмеричных и шестнадцатеричных чисел от О до 2010.
В Единой коллекции цифровых образовательных ресурсов (http://sc.edu.ru/) размещена интерактивная анимация «Преобразование десятичного числа в другую систему счисления» (135050). С её помощью можно понаблюдать за переводом произвольного целого числа от 0 до 512 в позиционную систему счисления, основание которой не превышает 16.
В размещённой там же виртуальной лаборатории «Цифровые весы» (135009) вы сможете освоить ещё один способ перевода целых десятичных чисел в другие системы счисления — метод разностей.
Презентация «Системы счисления»
Презентация «Системы счисления» (Open Document Format)
Ссылки на ресурсы ЕК ЦОР
Федеральный центр информационных образовательных ресурсов:
Компьютерные» системы счисленияВ компьютерной технике используется двоичная система счисления, обеспечивающая ряд преимуществ по сравнению с другими системами счисления:
• двоичные числа представляются в компьютере с помощью достаточно простых технических элементов с двумя устойчивыми состояниями;
• представление информации посредством только двух состояний надёжно и помехоустойчиво;
• двоичная арифметика наиболее проста;
• существует математический аппарат, обеспечивающий логические преобразования двоичных данных.
Обмен информацией между компьютерными устройствами осуществляется путём передачи двоичных кодов. Пользоваться такими кодами из-за их большой длины и зрительной однородности человеку неудобно. Поэтому специалисты (программисты, инженеры) на некоторых этапах разработки, создания, настройки вычислительных систем заменяют двоичные коды на эквивалентные им величины в восьмеричной или шестнадцатеричной системах счисления. В результате длина исходного слова сокращается в три, четыре раза соответственно. Это делает информацию более удобной для рассмотрения и анализа.
С помощью ресурса «Интерактивный задачник, раздел “Системы счисления”» (128659), размещённого в Единой коллекции цифровых образовательных ресурсов, можно проверить, насколько прочно вы усвоили изученный в этом параграфе материал.
САМОЕ ГЛАВНОЕСистема счисления — это знаковая система, в которой приняты определённые правила записи чисел. Знаки, с помощью которых записываются числа, называются цифрами, а их совокупность — алфавитом системы счисления.
Система счисления называется позиционной, если количествен-ный эквивалент цифры зависит от её положения (позиции) в записи числа. Основание позиционной системы счисления равно количеству цифр, составляющих её алфавит.
Основанием позиционной системы счисления может служить любое натуральное число q > 1.
В позиционной системе счисления с основанием q любое число может быть представлено в виде:
Здесь:
А — число;
q — основание системы счисления;
a i — цифры, принадлежащие алфавиту данной системы счисления;
n — количество целых разрядов числа;
m — количество дробных разрядов числа;
q i — «вес» i-то разряда.
1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?
2. Найдите дополнительную информацию об унарной, позиционных и непозиционных системах счисления. Чем они различаются? Приведите примеры.
Найдите дополнительную информацию об унарной, позиционных и непозиционных системах счисления. Чем они различаются? Приведите примеры.
3. Цифры каких систем счисления приведены на рис. 1.1?
4. Объясните, почему позиционные системы счисления с основаниями 5, 10, 12 и 20 называют системами счисления анатомического происхождения.
5. Как от свёрнутой формы записи десятичного числа перейти к его развёрнутой форме?
6. Запишите в развёрнутой форме числа:
а) 143,51110;
б) 1435118;
в) 14351116;
г) 1435,118
7. Вычислите десятичные эквиваленты следующих чисел:
а) 1728;
б) 2ЕА16;
в) 1010102;
г) 10,12;
д) 2436.
8. Укажите, какое из чисел 1100112, 1114, 358 и 1В16 является:
а) наибольшим;
б) наименьшим.
9. Какое минимальное основание имеет система счисления, если в ней записаны числа 123, 222, 111, 241? Определите десятичный эквивалент данных чисел в найденной системе счисления.
10. Верны ли следующие равенства?
а) 334 = 217;
б) 338 = 214.
11. Найдите основание х системы счисления, если:
а) 14x = 910;
б) 2002x. = 13010.
12. Переведите целые числа из десятичной системы счисления в двоичную:
а) 89;
б) 600;
в) 2010.
13. Переведите целые числа из десятичной системы счисления в восьмеричную:
а) 513;
б) 600;
в) 2010.
14. Переведите целые числа из десятичной системы счисления в шестнадцатеричную:
а) 513;
б) 600;
в) 2010.
15. Заполните таблицу, в каждой строке которой одно и то же число должно быть записано в системах счисления с основаниями 2, 8, 10 и 16.
Электронное приложение к уроку
| Презентации, плакаты, текстовые файлы | Вернуться к материалам урока | Ресурсы ЭОР |
Cкачать материалы урока
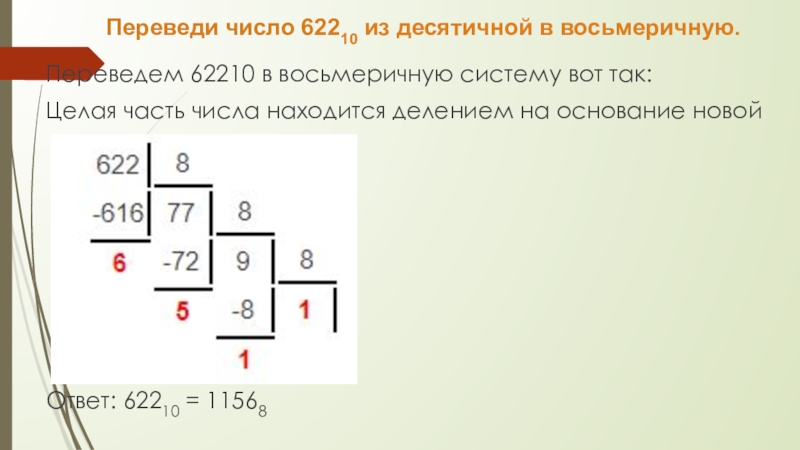
как преобразовать десятичное 64 в восьмеричное
Как записать 64 в восьмеричном формате (с основанием 8)?
Преобразование из/в десятичные, шестнадцатеричные, восьмеричные и двоичные числа.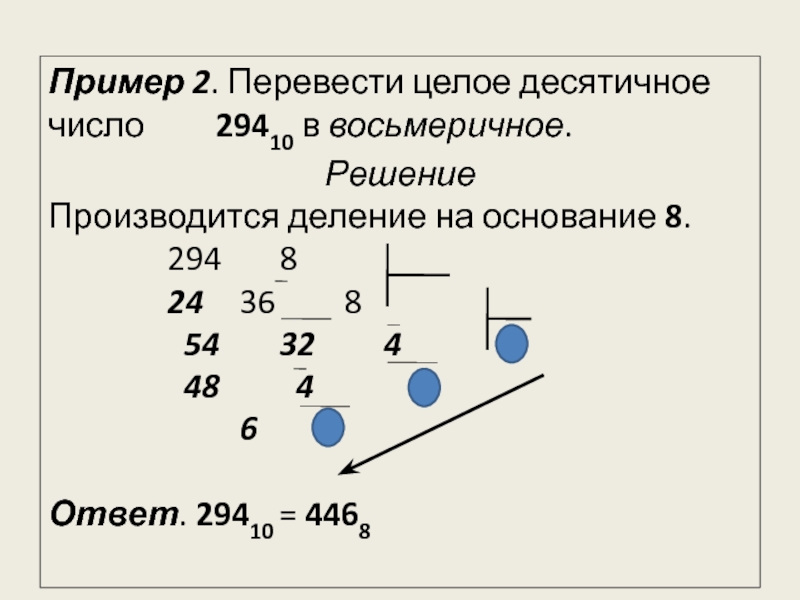 Калькулятор преобразования десятичной базы.
Здесь вы можете найти ответ на такие вопросы, как: как преобразовать десятичное 64 в восьмеричное или десятичное в восьмеричное преобразование.
Калькулятор преобразования десятичной базы.
Здесь вы можете найти ответ на такие вопросы, как: как преобразовать десятичное 64 в восьмеричное или десятичное в восьмеричное преобразование.
Таблица десятичных, двоичных, шестнадцатеричных и восьмеричных диаграмм
| декабря | гекса | октября | 0 | |
|---|---|---|---|---|
| 0 | 0 | 9002 00 | ||
| 1 | 1 | 1 | 1 | |
| 2 | 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 | |
| 4 | 4 | 4 | 100 | |
| 5 | 5 | 5 | 101 | |
| 6 | 6 | 6 | 110 | |
| 7 | 7 | 7 | 111 | |
| 8 | 8 | 10 | 1000 | |
| 9 | 9 | 11 | 1001 | 1001 |
| 10 | A | 12 | 1010 | |
| 11 | B | 13 | 1011 | 1011 | 90 020
| 12 | С | 14 | 1100 | |
| 13 | D | 15 | 1 101 | |
| 14 | Е | 16 | 1110 | |
| 15 | F | 17 | 1111 |
| Декабрь | Шестигранный | Октябрь | бен |
|---|---|---|---|
| 16 | 10 | 20 | 10000 |
| 17 | 11 | 21 | 10001 |
| 18 | 12 | 22 | 10010 |
| 19 | 13 | 23 | 10011 |
| 20 | 14 | 24 | 10100 |
| 21 | 15 | 25 | 10101 |
| 22 | 16 | 26 | 10110 |
| 23 | 17 | 27 | 10111 |
| 24 | 18 | 30 | 11000 |
| 25 | 19 | 31 | 11001 |
| 26 | 1A | 32 | 11010 |
| 27 9002 3 | 1B | 33 | 11011 |
| 28 | 1C | 34 | 11100 |
| 29 | 1D | 35 | 11101 |
| 30 | 1E | 36 | 11110 |
| 31 | 1F | 37 | 11111 |
| Декабрь | Шестигранный | Октябрь | бен |
|---|---|---|---|
| 32 | 20 | 40 | 100000 |
| 33 | 21 | 41 | 100001 |
| 34 | 22 | 42 | 100010 |
| 35 | 23 | 43 | 100011 |
| 36 | 24 | 44 | 100100 |
| 37 | 25 | 45 | 100101 |
| 38 | 26 | 46 | 100110 |
| 39 | 27 | 47 | 100111 |
| 40 | 28 | 50 | 101 000 |
| 41 | 29 | 51 | 101001 |
| 42 | 2А | 52 | 101010 |
| 2B | 53 | 101011 | |
| 44 | 2C | 54 | 101100 |
| 45 | 2D | 55 | 101101 |
| 46 | 2E | 56 | 101110 |
| 47 | 2F | 57 | 101111 |
| Декабрь | Шестигранный | Октябрь | бен |
|---|---|---|---|
| 48 | 30 | 60 | 110000 |
| 49 | 31 | 61 | 110001 |
| 50 | 32 | 62 | 110010 |
| 51 | 33 | 63 | 110011 |
| 52 | 34 | 64 | 110100 |
| 53 | 35 | 65 | 110101 |
| 54 | 36 | 66 | 110110 |
| 55 | 37 | 67 | 110111 |
| 56 | 38 | 70 | 111000 |
| 57 | 39 | 71 | 111001 |
| 58 | 3A | 72 | 111010 |
| 3B | 73 | 111011 | |
| 60 | 3C | 74 | 111100 |
| 61 | 3D | 75 | 111101 |
| 62 | 3E | 76 | 111110 |
| 63 | 3F | 77 | 111111 |
| Декабрь | Шестигранный | Октябрь | бен |
|---|---|---|---|
| 64 | 40 | 100 | +1000000 |
| 65 | 41 | 101 | 1000001 |
| 66 | 42 | 102 | 1000010 |
| 67 | 43 | 103 | 1000011 |
| 68 | 44 | 104 | 1000100 |
| 69 | 45 | 105 | 1000101 |
| 70 | 46 | 106 | 1000110 |
| 71 | 47 | 107 | 1000111 |
| 72 | 48 | 110 | 1001000 |
| 73 | 49 | 111 | 1001001 |
| 74 | 4А | 112 | 1001010 9 0023 |
| 75 | 4B | 113 | 1001011 |
| 76 | 4C | 114 | 1001100 |
| 77 | 4D | 115 | 1001101 |
| 78 | 4E | 116 | 1001110 |
| 79 | 4F | 117 | 1001111 |
| Декабрь | Шестигранный | Октябрь | бен |
|---|---|---|---|
| 80 | 50 | 120 | 1010000 |
| 81 | 51 | 121 | 1010001 |
| 82 | 52 | 122 | 1010010 |
| 83 | 53 | 123 | 1010011 |
| 84 | 54 | 124 | 1010100 |
| 85 | 55 | 125 | 1010101 |
| 86 | 56 | 126 | 1010110 |
| 87 | 57 | 127 | 1010111 |
| 88 | 58 | 130 | 1011000 |
| 89 | 59 | 131 | 1011001 |
| 90 | 5А | 132 | 1011010 9 0023 |
| 91 | 5B | 133 | 1011011 |
| 92 | 5C | 134 | 1011100 |
| 93 | 5D | 135 | 1011101 |
| 94 | 5E | 136 | 1011110 |
| 95 | 5F | 137 | 1011111 |
| Декабрь | Шестигранный | Октябрь | бен | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 96 | 60 | 140 | 1100000 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 97 | 61 | 141 | 1100001 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 98 | 62 | 142 | 1100010 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 99 | 63 | 143 | 1100011 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 100 | 64 | 144 | 1100100 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 101 | 65 | 145 | 1100101 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 102 | 66 | 146 | 1100110 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 103 | 67 | 147 | 1100111 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 104 | 68 | 150 | 1101000 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 105 | 69 | 151 | 1101001 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 106 | 6А | 152 | 11 01010 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 107 | 6B | 153 | 1101011 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 108 | 6C | 154 | 1101100 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 109 | 6D | 155 | 1101101 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 110 | 6E | 156 | 1101110 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 111 |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Д.
Д. 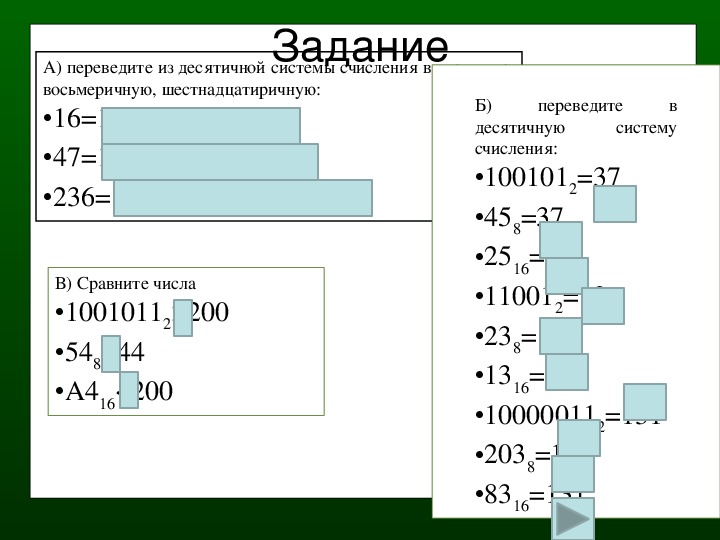 э.
э. 
 д.
д.
 Соответственно при каждом делении остаток становится старшим битом восьмеричного числа.
Соответственно при каждом делении остаток становится старшим битом восьмеричного числа.
 Возьмите десятичное число в качестве входных данных и сохраните его в переменной decimalnum.
Возьмите десятичное число в качестве входных данных и сохраните его в переменной decimalnum.  Десятичная точка отделяет целую часть числа от дробной части числа. Каждая цифра десятичного числа может быть любым числом от 0 до 9. Любое значение меньше 1 записывается справа от десятичной точки.Десятичные числа также известны как числа с основанием 10 или счетные числа. Разрядное значение десятичного числа варьируется в зависимости от степени 10, начиная слева от десятичной точки. Точно так же разрядное значение цифр, оставшихся до десятичной точки, изменяется в зависимости от деления степени десятков.
Десятичная точка отделяет целую часть числа от дробной части числа. Каждая цифра десятичного числа может быть любым числом от 0 до 9. Любое значение меньше 1 записывается справа от десятичной точки.Десятичные числа также известны как числа с основанием 10 или счетные числа. Разрядное значение десятичного числа варьируется в зависимости от степени 10, начиная слева от десятичной точки. Точно так же разрядное значение цифр, оставшихся до десятичной точки, изменяется в зависимости от деления степени десятков. 




 э.
э.  э.
э.