| 1. |
Мгновенная скорость
Сложность: лёгкое |
1 |
| 2. |
Задача на исследование аргумента функции
Сложность: лёгкое |
2 |
3.
|
Средняя скорость движения точки
Сложность: лёгкое |
1 |
| 4. |
Нахождение скорости и ускорения
Сложность: среднее |
2 |
5.
|
Изменение функции в точке
Сложность: среднее |
2 |
| 6. |
Скорость изменения функции
Сложность: среднее |
1 |
7.
|
Скорость и ускорение
Сложность: сложное |
4 |
| 8. |
Доказательство с применением производной
Сложность: сложное |
4,2 |
9.
|
Вычисление производной Сложность: сложное | 5 |
Задачи, приводящие к понятию производной — урок. Алгебра, 10 класс.
Задача 1 (о скорости движения). Материальная точка движется по прямой, на которой заданы начало отсчёта, единица измерения (метр) и направление. Закон движения задан формулой \(s=s(t)\), где \(t\) — время (в секундах), \(s(t)\) — расстояние материальной точки от начала отсчёта (её координата) в момент времени \(t\) (в метрах). Найти скорость движения материальной точки в момент времени \(t\) (в \(м/с\)).
Найти скорость движения материальной точки в момент времени \(t\) (в \(м/с\)).
Решение. Пусть в момент времени \(t\) материальная точка была в положении \(T\).
В момент времени t+Δt материальная точка будет в точке \(K\), то есть OK=st+Δt.
Значит, за Δt секунд материальная точка переместилось из \(T\) в точку \(K\). Имеем: TK=OK−OT=st+Δt−s(t). Полученную разность мы назвали приращением функции: st+Δt−s(t)=Δs. Итак, TK=Δs(м). Средняя скорость vср движения материальной точки за промежуток времени t;t+Δt равна vср=ΔsΔt \((м/с)\).
А скорость \(v(t)\) в момент времени \(t\) (мгновенная скорость) — это тоже скорость движения за промежуток времени t;t+Δt, но Δt выбирается очень маленьким, почти равным нулю, то есть Δt→0. Это значит, что v(t)=limΔt→0vср.
Итак,
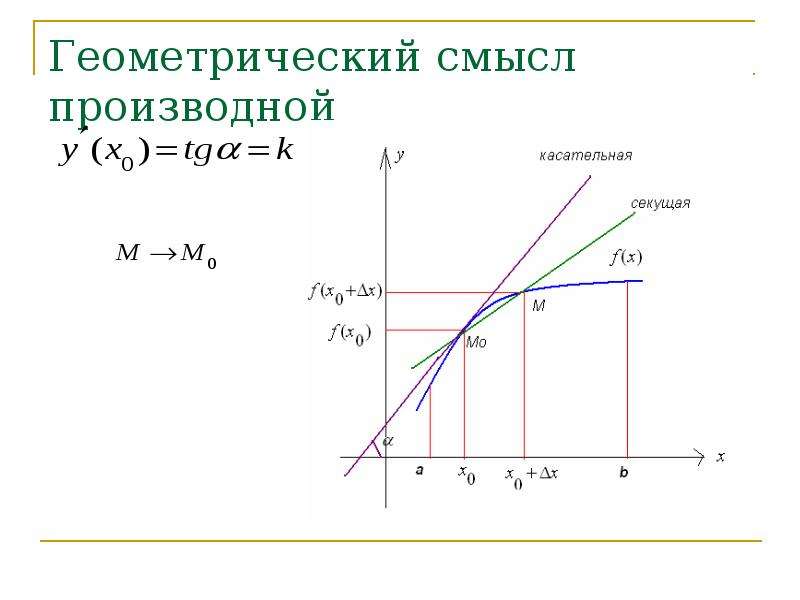
Задача 2 (о касательной к графику функции). На графике функции \(y=f(x)\) взяли точку \(M(a;f(a))\) и в этой точке провели касательную к графику функции. Необходимо определить угловой коэффициент этой касательной.
Необходимо определить угловой коэффициент этой касательной.
Решение. Дадим аргументу приращение Δx и рассмотрим на графике точку \(P\) с абсциссой a+Δx. Ордината точки \(P\) равна fa+Δx. Угловой коэффициент секущей \(MP\) равен тангенсу угла между секущей и осью \(x\): kсек=ΔyΔx.
При Δx, стремящемся к нулю, точка \(P\) будет приближаться по графику к точке \(M\). При этом касательная будет предельным положением секущей. Значит, угловой коэффициент касательной равен kкас=limΔx→0kсек. Используя приведённую выше формулу для kсек, получаем:
kкас=limΔx→0ΔyΔx.
Производная функции, её геометрический и физический смысл
Презентация на тему: «Понятие опроизводной функции,
её геометрический
и
физический смысл»
Цели урока:
ОБУЧАЮЩАЯ:
1) Ввести определение производной функции на основе задач физики,
рассматривая при этом физический смысл производной.
2) Выяснить геометрический смысл производной дифференцируемой
функции.

3) Научиться решать задачи на данную тему, используя полученные знания.
РАЗВИВАЮЩАЯ:
1) Способствовать развитию общения как метода научного познания,
синтетического мышления, смысловой памяти и произвольного внимания.
2) Развитие навыков исследовательской деятельности.
ВОСПИТАТЕЛЬНАЯ:
1) Способствовать развитию творческой деятельности.
2) Развивать у учащихся коммуникативные компетенции,
потребности к самообразованию.
Вопросы:
1. История возникновения производной
функции.
2. Понятие производной.
3. Геометрический смысл производной.
4. Физический (механический) смысл
производной.
1. История возникновения производной
функции
Раздел математики, в котором изучаются производные и их применение к
исследованию
функций,
называется
дифференциальным
исчислением.
Приращения вида Δf, представляющие собой разности, играют заметную роль при
работе с производными.
 Естественно поэтому появление латинского корня differentia
Естественно поэтому появление латинского корня differentia(разность) в названии calculis differentialis нового исчисления, которое переводится
как исчисление разностей; это название появилось уже в конце 17в., т.е. при
рождении нового метода.
Термин «производная» является буквальным переводом на русский французского
слова deriveе, которое ввёл в 1797г. Ж.Лагранж, он же ввёл современные
обозначения у’ , f’. Такое название отражает смысл понятия: функция f'(x) происходит
из f(x), является производным от f(x). И.Ньютон называл производную функцию
флюксией, а саму функцию – флюентой. Г.Лейбниц говорил о дифференциальном
отношении и ввёл обозначение производной df/dx.
Слово «экстремум» происходит от латинского extremum (крайний). Maximum
переводится как наибольший, а minimum – наименьший.
« – величественная пирамида математических наук»
Наполеон I Бонапарт
Рано изучил сочинения
Евклида и Архимеда,
Галлея (друга Ньютона).

В 16 лет стал преподавать математику в
Артиллерийском училище в Турине.
В 19 лет стал профессором математических
наук.
В 23 года стал академиком и иностранным
членом Берлинской академии наук.
Автор трудов по вариационному исчислению,
математическому анализу, теории чисел, алгебре,
дифференциальным уравнениям.
Его работы по математике, астрономии и
механике составляют 14 томов.
Император Франции сделал учёного сенатором,
графом империи и командором ордена Почетного
легиона.
1736 — 1813
Выдающийся
французский
математик,
ввел
термин «ПРОИЗВОДНАЯ» и её современное
обозначение.
2. Понятие производной
Пусть х — произвольная точка, лежащая в некоторой
окрестности точки х0 (окрестность точки х0 — это
интервал (а; б), x0 (а; б)).
Разность х-х0 называется приращением аргумента:
∆x=х-x0. Отсюда x=x0+∆x.
Разность
f(x)-f(x0)
называется
функции: ∆f=f(x)-f(x0) или
приращением
∆f=f(х0+∆x)–f(х0).

Отсюда, f(х0+∆x)=f(х0)+∆f.
2. Понятие производной
Производной функции y=f(x) в точке х0
называется
предел
отношения
приращения функции ∆f к приращению
аргумента ∆x, стремящегося к «нулю»:
f
y` lim
x 0 x
f ( x 0 x) f ( x)
y` lim
x 0
x
2. Понятие производной
Четыре обозначения для производной:
2. Понятие производной
2. Понятие производной
Правило нахождения производной функции
y=f(x) в точке х0:
1.
2.
3.
4.
Найти значение функции в точке x0+∆x: f(x0+∆x)
Найти приращение функции: ∆f=f(x0+∆x)-f(x0)
Найти отношение приращения функции к приращению
аргумента: f
f ( x0 x) f ( x0 )
x
x
Найти предел отношения приращения функции к
аргумента к нулю:
f ( x x) f ( x )
y ‘ lim
x 0
0
0
x
2. Понятие производной
Пример: Дана функция y=x2. Найти её производную в
произвольной точке и в точке х=3.

Решение:
1. f(x0+∆x)=(х+∆x)2;
2. ∆f=(х+∆x)2-х2=x2+2x∆x+(∆x)2-x2=2х∆x+(∆x)2;
3.
y
y ‘ Lim
Lim (2 x x) 2 x
x 0 x
x 0
, т.е. y’=(x2)’=2x;
4. при х=3 получим y’(3)=2*3=6.
Ответ: y’=2x; y’(3)=6
Пример: Воспользовавшись определением производной,
3x 1
.
найти производную функцииy
2x 5
Решение: Дадим x приращение x, тогда y получит приращение y:
3 x x 1 3x 1 3x 3 x 1 2 x 5 3x 1 2 x 2 x 5
2 x x 5 2 x 5
2 x x 5 2 x 5
17 x
.
2 x 2 x 5 2 x 5
y
Так как
то
y
17 x
17
,
x x 2 x 2 x 5 2 x 5
2 x 2 x 5 2 x 5
y
17
17
lim
.
2
x 0 x
x 0 2 x 2 x 5 2 x 5
2 x 5
y lim
Ответ:
17
y
.
2
2 x 5
3. Геометрический смысл
производной.
Лейбниц
Это кто?
Г.В.
«Если продолжить одно из
маленьких
звеньев
ломаной,
составляющей
кривую линию, то эта
продолженная
таким
образом сторона будет
называться касательной к
кривой»
А
4
С
А
В
Tg A=3/ 3
A=7/4
tg В -?
Tg B= 3/3
B=4/7
7
3
С
tg A-?
3
В
Вычислите tgα, если
α = 135°, 120°, 150°.

=-1
=- 3
=- 3/3
Угловой коэффициент прямой.
Прямая проходит через начало
координат и точку Р(3; -1). Чему
равен ее угловой коэффициент?
1 3k
1
k
3
Найдите угловые
коэффициенты прямых:
2
1
1
4
2
3
3
4
3. Геометрический смысл
производной.
3. Геометрический смысл производной
Возьмем на непрерывной кривой L две точки М и М1:
Через точки М и М1 проведем
секущую и обозначим через φ
угол наклона секущей.
y
М1
f(x+ Δx )
f(x )
x
φ
0
y
М
х
x+Δx
х
y f ( x x) f ( x)
tg
x
x
При
x→0 в силу непрерывности функции
y также
стремится к нулю, поэтому точка М1 неограниченно
приближается по кривой к точке М, а секущая ММ1 переходит в
касательную.
tg tg
lim lim
x 0
x 0
3. Геометрический смысл производной.
f ( x x ) f ( x )
y
lim
tg
k
x 0
x
Производная f ’(x) равна угловому
y коэффициенту касательной к
графику функции y = f(x) в точке, абсцисса которой равна x.

Если точка касания М имеет координаты (x0; y0 ), угловой
коэффициент касательной есть k = f ’(x0 ).
Уравнение
Уравнение прямой с угловым коэффициентом:
y y 0 к (x — x0 )
касательной
Уравнение
нормали
Прямая, перпендикулярная касательной в точке касания,
f ‘ ( x0 )
называется нормалью к кривой.
kнорм
1
1
1
y y0
( x x0 )
kкас f ‘ ( x0 )
f ‘ ( x0 )
Пример:
точке x0 = 3.
Найти уравнение касательной и нормали для функции f(x)=x2 в
Решени
е:
1) y 3 f 3 x f 3 3 x 2 32 9 2 3 x x 2 9 6 x x 2 ,
2)
6 x x 2
x 6 x
f 3 lim
lim
lim 6 x 6.
x 0
x 0
x 0
x
x
y f x0 f x0 x x0 уравнение касательной
y f x0
1
x x0 — уравнение нормали
f x0
3)
yкас 9 6 x 3
yкас 6 x 9
13.11.2020
f x0 0 .
1
x 3
6
1
1
yнорм x 9 .
6
2
Ответ: yкас 6 x 9
yнорм 9
1
1
yнорм x 9 .

6
2
3. Физический (механический)
смысл производной
Исаак
Это кто?
Ньютон
«Когда
величина
является
максимальной
или
минимальной, в этот момент
она не течет ни вперед, ни
назад»
3. Физический (механический)
смысл производной
0
s
S(t) за время t
S’(t) V(t) V’(t) a(t)
S(t) — перемещение точки за время t
V(t) – скорость точки в момент t
a(t) – ускорение точки в момент t
3. Физический (механический)
смысл производной
Пример: Точка движется прямолинейно по закону
S(t) = 2 t ³ — 3 t. Вычислите скорость движения точки:
а) в момент времени t;
б) в момент времени t=2с.
Решение:
а)
б)
3
2
2
v(t ) s (t ) (2t 3t ) 2 3t 3 1 6t 3
v(2) 6 22 3 21( м / c)
Ответ: V(t)=6t2-3; V(2)=21 м/с
3. Физический (механический) смысл производной
Пример: Материальная точка движется
по закону 9
2
S (t ) t 7t 6 (м).

Найти
2
В какой момент времени (с) скорость
точки будет равна 12,8 м/c ?
Решение:
S’(t) V(t)
Найти
S (t ) 9t 7 V (t ) V (t ) 12,8
9t 7 12,8
9t 19,8 t = 2,2 (с).
3. Физический (механический)
смысл производной
Пример: Материальная точка движется прямолинейно по
закону х(t)=t³- 4t²
Найдите скорость и ускорение в момент времени t=5с.
Решение:
2
2
v(t ) ( x(t )) 3t 4 2t 3t 8t
v(5) 3 5 8 5 75 40 35( м / с)
2
a(t ) (v(t )) (3t 8t ) 6t 8
2
a(5) 6 5 8 22( м / с )
2
Ответ: V(5)=35 м/c; a(5)=22 м/с2
3. Физический (механический)
смысл производной
x(t ) (t 1) , где t 0;10
3
1. Найти среднюю скорость движения на указанном отрезке
x(10) x(0) 93 ( 1)3 730
cp
73 м с
10 0
10
10
2. Найти мгновенную скорость в момент времени t=3 сек.
(t ) x’ (t ) 3(t 1) 2
мгн (3) 3(3 1) 2 3 4 12 м с
3. Найти ускорение при t=3 сек
a(t ) ‘ (t ) 6(t 1)
Ответ: Vср=73 м/с;
V(3)=12 м/c; a(3)=12 м/с2
a(3) 12 м 2
с
S, км
B
45
III
C
3.
 Физический (механический)
Физический (механический)смысл производной
Определите среднюю скорость
движения
на каждом из
четырех участков :
II
IV
A
10
I
D
0
1
3
3,5
I : Vср
10 0 10
10 км
ч
1 0
1
II : Vср
45 30 15
7.5 км
ч
3 1
2
8
III : Vср
45 45
0
0 км
ч
3,5 3 0,5
IV : Vср
45 0 45
10 км
ч
8 3.5 4.5
t, ч
3. Физический (механический) смысл производной
Пример: Две материальные
точки
движутся
прямолинейно
по законам s1(t) = 1 — 6t + 2,5t 2 и
s2(t) = -3+ 2t + 0,5t 2. Определить в какой момент
времени скорости их
будут равны.
Решение:
1) V1 (t ) (2.5t 2 6t 1)’ 5t 6
(формула нахождения скорости движения 1 тела )
2) V2 (t ) (0.5t 2 2t 3)’ t 2
(формула нахождения скорости движения 2 тела )
3) по условию в момент времени t 0
подсказк
а
v(t ) S (t )
их скорости равны, т.
 е.
е.5t 0 6 t 0 2
t0 2
Ответ: при t0 = 2 с
3. Физический (механический) смысл производной
Задача по химии
Пример: Пусть количество вещества,
вступившего в химическую реакцию задается
зависимостью р( t ) = t 2/2 + 3t –3 (моль). Найти
скорость химической реакции через 3 секунды.
РЕШЕНИЕ:
1) v( t ) = p`( t ) = t + 3,
2) v(3) = p`(3) = 3 + 3 = 6 (моль/сек)
подсказк
а
v(t ) Р (t )
Ответ: 6 моль / сек
3. Физический (механический) смысл производной
Пример: Тело, подброшенное вверх движется
по закону s(t) = 4+ 8t – 5t 2 . Найдите:
1) скорость тела в начальный момент времени;
2) наибольшую высоту подъёма тела.
РЕШЕНИЕ:
1) v (t) = s’(t) = 8 – 10t — скорость тела;
2) t= 0, v(0) = s’(0) = 8 м/с – скорость тела в
начальный момент времени
подсказк
а
v(t ) S (t )
3) s (0,8)= 4+ 8·0,8 – 5· 0,64
=7,2 м – максимальная
высота броска тела.
Ответ: 8 м/с ; 7,2 м.

УСТНО!
Задача по физике
Точка движется прямолинейно по закону
S (t) = t3 – 2t2.
Выберите какой из формул задается скорость
движения точки в момент времени t.
S (t ) v(t )
1) 3t2 – 2; 2) t2 – 4t; 3)3t2 – 4t; 4) t4 – 2t3
Ответ: 3
УСТНО!
Задача по экономике
Объем продукции V цеха в течение дня
зависит от времени по
V(t) = -5/3t3+15/2t2+50t+70.
Вычислите производительность труда П(t).
V (t ) П (t ).
Ответ: П(t) = -5t2+15t+50
Подведём итог:
1. Что называется касательной к графику
функции в точке?
2. В чем заключается геометрический смысл
производной?
3. Сформулируйте алгоритм нахождения
уравнения касательной?
4. В чём заключается физический смысл
производной?
Выберете смайлик, соответствующий вашему
настроению и состоянию после проведенного урока
тревожно, не уверен в себе
спокойно, у меня все получится
безразлично, что будет, то и будет
Домашнее задание:
Написать конспект занятия.
 Выделить
Выделитьформулы и определения.
13.11.2020
40
Используемая литература:
1.
Учебник Колмогорова А.Н. «Алгебра и начала анализа 10-11»
2.
Алгебра и начала математического анализа: Учеб. Для 10-11 кл. для учащихся
общеобразовательных учреждений (базовый уровень) / Под редакцией А.Г.
Мордковича. – М.: Мнемозина, 2009.
3.
Алгебра и начала математического анализа: Задачник, Для 10-11 кл. для учащихся
общеобразовательных учреждений (базовый уровень) / Под редакцией А.Г.
Мордковича. – М.: Мнемозина, 2009.
4.
Алгебра и начала анализа. Самостоятельные и контрольные работы для 10-11
классов. / Ершова А.П., Голобородько В.В. – М.: ИЛЕКСА, 2010
5.
ЕГЭ 2010. Математика. Задача В8. Рабочая тетрадь / Под редакцией А.Л.Семенова и
И.В.Ященко – M.: Издательство МЦНМО, 2010
6.
МАТЕМАТИКА СБОРНИК ТЕСТОВ ПО ПЛАНУ ЕГЭ 2009. Учебно-методическое
пособие. под редакцией А. Г. Клово, Д. А. Мальцева; Ростов-на-Дону.
 НИИ школьных
НИИ школьныхтехнологий
Математика онлайн
Решение математики онлайн
Math34.biz – это современный способ решения математики, в том числе для сравнения самостоятельных решений с машинными вычислениями.
Пользование сервисом удобно и понятно каждому человеку, попавшему на сайт впервые. Сразу выбираете нужный калькулятор, вводите необходимые данные по вашей задаче и нажимаете кнопку «Решение». За считанные секунды ответ готов.
Чтобы не возникало трудностей с вводом данных, мы подготовили специальную статью Как вводить данные? Помимо правил написания формул и чисел, в ней вы можете увидеть, как правильно вводятся различные константы и математические функции.
О калькуляторах
По мере возможности добавляются новые математические калькуляторы. На сегодняшний день их более 85.
Если не удалось найти нужный калькулятор, которым может быть решена ваша математическая задача, или есть предложение по улучшению имеющегося калькулятора, пожалуйста, сообщите об этом на почту info@math34. biz
biz
Преимущества
1. Бесплатно
Решение математики онлайн не будет вам стоить ни копейки. Наш сервис абсолютно бесплатный и доступен любому пользователю интернета.
2. Без регистрации
Для пользования калькуляторами не требуется регистрации на сайте, отнимая время на заполнение почтовых ящиков и других личных данных.
3. Подробные решения
На многие задачи вы получите пошаговый развернутый ответ, что позволяет понять, каким образом было получено решение задачи.
4. Разные способы решения задач
Для популярных калькуляторов доступны разные методы решения задач, если они применимы, что позволяет, во-первых, лучше понять, как решается задача известным вам способом, а, во-вторых, научиться решать ту же самую задачу альтернативными методами.
5. Точность вычислений
В полученном ответе не приходится сомневаться, ведь мощная система расчета обеспечивает высокую точность при решении математических задач онлайн.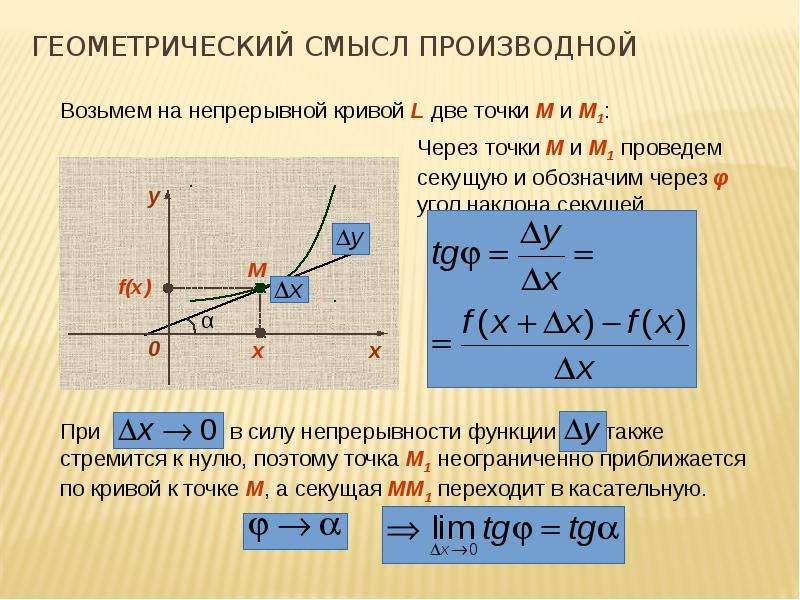
Однако, мы не исключаем возможность каких-либо ошибок, ведь известно, что алгоритмы пишутся хотя и очень умными, но всё же людьми. В случае обнаружения ошибки, пожалуйста, не поленитесь и сообщите нам о ней.
Определение производной, ее геометрический и физический смысл
Вопросы занятия:
· познакомиться с понятием производной;
· познакомиться с геометрическим и физическим смыслом производной.
Материал урока.
Прежде чем приступить к изучению нового материала, давайте выполним упражнение.
Упражнение.
Давайте рассмотрим одну физическую задачу.
Пусть ёжик движется по дорожке из домика. Домик будем считать точкой отсчёта и
обозначим её точкой O. Единицей измерения выберем метр, и укажем
направление движения ёжика. Закон движения ёжика задан формулой S = s(t),
где t – время (в секундах), S(t)
– положение ёжика на дорожке (говоря математическим языком – координата
движущегося ёжика) в момент времени t по отношению к началу отсчёта. Давайте найдём скорость движения ёжика в момент времени t. Скорость
будем измерять в м/с. В данном случае ёжика будем рассматривать как
материальную точку.
Давайте найдём скорость движения ёжика в момент времени t. Скорость
будем измерять в м/с. В данном случае ёжика будем рассматривать как
материальную точку.
Предположим, что в момент времени t ёжик находился в точке M, тогда OM = S(t). Дадим аргументу t приращение и рассмотрим, где же окажется ёжик в момент времени t + Δt. Очевидно, что ёжик переместиться из точки M, например, в точку P. Тогда отрезок OP равен S (t + Δt).
Значит, если за Δt
секунд ёжик переместился из точки M в точку P,
то отрезок MP равен OP
– OM ,
то есть разности S
(t + Δt) –
S(t),
то есть отрезок MP = ΔS
метров, причём перемещение из точки M в точку P
произошло за Δ t
секунд.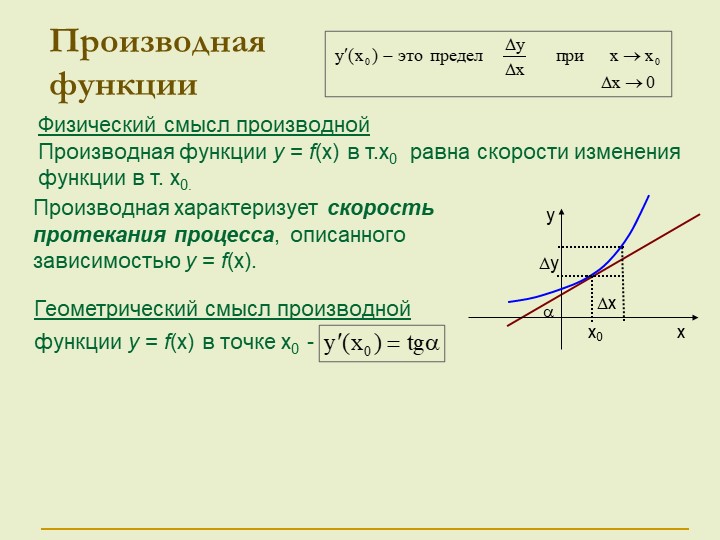 Давайте вычислим среднюю скорость движения ёжика за промежуток времени
от t до t
+ Δt.
Давайте вычислим среднюю скорость движения ёжика за промежуток времени
от t до t
+ Δt.
Прежде чем сформулировать вторую задачу, давайте определим такое понятие как «касательная к плоской кривой». При изучении функций в курсе алгебры базовой школы, мы уже встречались с термином касательная.
Например, мы говорили, что график функции y = x2 касается оси Ox в точке x = 0, то есть ось Ox является касательной к параболе в точке x = 0.
Однако возникает вопрос, что такое касательная? Казалось бы, все очень просто: касательная к графику функции – это такая прямая, которая имеет с графиком функции одну общую точку. Тогда почему нельзя назвать касательной ось Oy? Ведь с параболой эта ось тоже имеет только одну общую точку.
Давайте посмотрим, как же определить
касательную.
Пусть дана кривая L, на ней выбрана точка M. Возьмём на ней ещё одну точку P, проведём секущую MP. Теперь давайте будем приближать точку P к точке M по кривой L. Секущая MP будет менять своё положение, как бы поворачиваясь вокруг точки M. Продолжая приближать точку P к точке M, мы достигнем такого положения прямой MP, которое будет предельным, эту прямую, которая является предельным положением секущей и называют касательной к кривой L в точке M.
Учитывая только что сформулированное определение, нетрудно доказать, что касательной к графику функции y = x2 в точке о будет ось Ox.
Теперь давайте рассмотрим задачу.
Пусть дан график функции y = f(x).
На нем выбрана точка M
(a;
f(a))
и в этой точке к графику функции проведена касательная.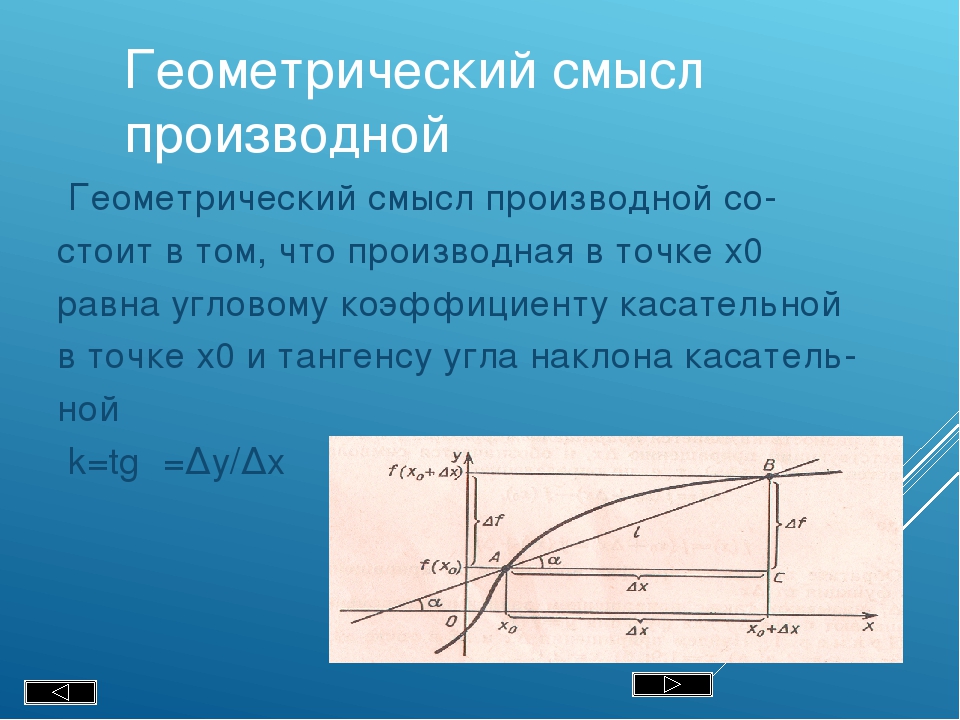 Давайте найдём угловой
коэффициент касательной.
Давайте найдём угловой
коэффициент касательной.
Давайте дадим аргументу приращение Δx и рассмотрим на графике точку P с абсциссой a + Δx. Тогда ордината точки P равна f(a + Δx). На прошлых уроках, мы говорили, что отношение приращения функции к приращению аргумента – это угловой коэффициент прямой, то есть угловой коэффициент секущей MP равен отношению Δy к Δx. Еcли же Δx стремиться к нулю, то точка P начнёт приближаться к точке M по графику функции. Поскольку предельное положение секущей – это касательная, то получим, что угловой коэффициент касательной к графику функции равен пределу углового коэффициента секущей при Δx стремящемся к нулю.
Подставляя вместо углового коэффициента
секущей формулу, получим, что угловой коэффициент касательной равен пределу
отношения Δy к Δx,
при Δx стремящемся к нулю.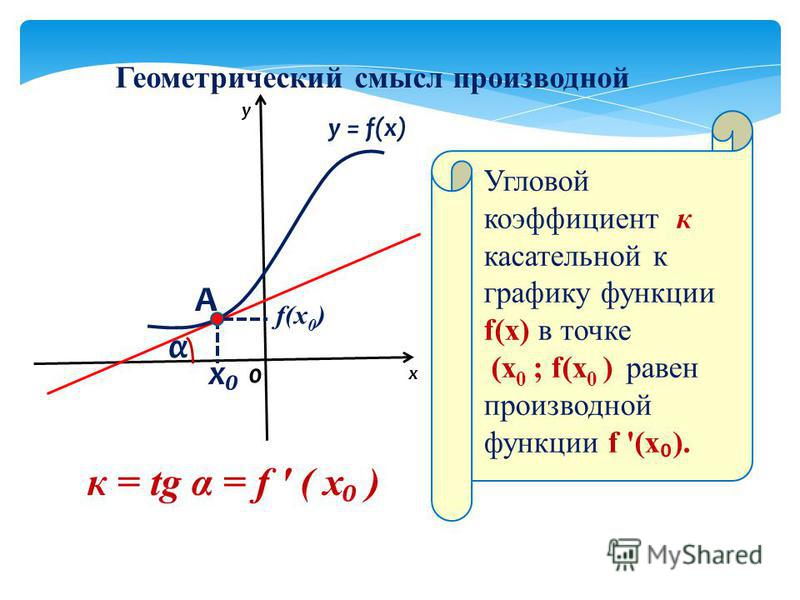
Однако, стоит заметить, что не все касательные имеют угловой коэффициент. Например, если касательной к графику функции в точке является прямая x = a, то угловой коэффициент этой касательной не существует.
Итак, сегодня мы рассмотрели две задачи, в результате решения которых получили оду и туже формулу – предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю.
Мы рассмотрели всего две задачи, однако при решении задач из других областей науки, например, экономики, химии, приходят к этой же формуле.
Определение.
Пусть функция y = f(x) определена в
некотором интервале, содержащем внутри себя точку x0.
Дадим аргументу приращение Δx
такое, чтобы не выйти из этого интервала. Найдём соответствующее приращение
функции Δy, при переходе от точки x0
к точке x + x0
и составим отношение Δy/Δx,
если существует предел этого отношения при Δx
стремящемся к нулю, то указанный предел называют производной функции y
= f(x)
в точке x0
и обозначают f‘(x0).
Для обозначения производной часто используют символ y‘.
Отметим, что y‘ = f‘(x) – это новая функция, но, естественно, связанная с функцией y = f(x), определённая во всех точках x, в которой существует указанный выше предел.
Эту функцию называют производная функции y = f(x).
На предыдущих уроках мы нашли производные некоторых функций.
Учитывая, введённые понятия и определение можно сказать, что рассмотренные нами задачи показывают физический и геометрический смысл производной.
Физический смысл производной.
Геометрический смысл производной.
Давайте сформулируем алгоритм нахождения производной функции
y = f(x).
Давайте рассмотрим данный алгоритм на
примере.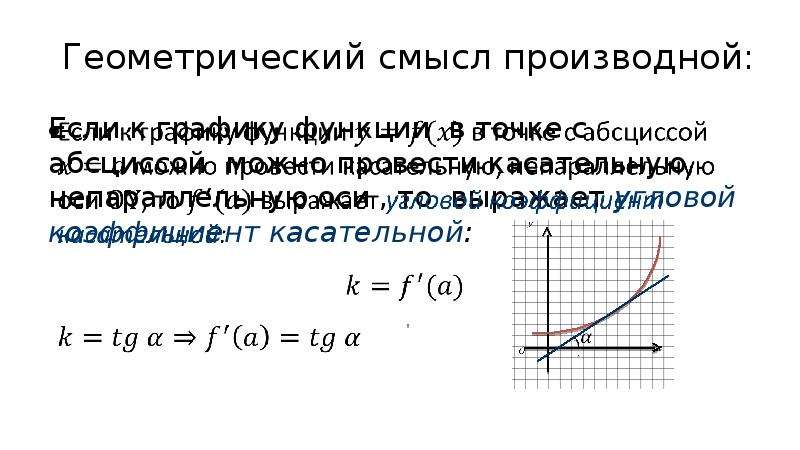
Пример.
Рассмотрим ещё один пример.
Пример.
Если функция y = f(x) имеет производную в точке x, то её называют дифференцируемой в точке x. Процедуру нахождения производной функции y = f(x) называют дифференцированием функции y = f(x).
Давайте теперь попробуем найти связь между понятиями непрерывности и дифференцируемости функции в точке.
Пусть функция y
= f(x)
дифференцируема в точке x.
Тогда, пользуясь геометрическим смыслом производной, в точке M
(x; f(x))
можно
провести касательную, причём, угловой коэффициент этой касательной равен f'(x).
То есть в точке M не
может быть разрыва, то есть функция y = f(x) непрерывна в точке икс.
Сформулируем это более строго. Если функция y = f(x) дифференцируема в точке x, то она и непрерывна в этой точке.
Обратное утверждение не верно. Примером этого может служить функция y = │x│. Эта функция непрерывна везде, в том числе и в точке x = 0, но касательной в точке x = 0 существует. Если в некоторой точке к графику функции нельзя провести касательную, то в этой точке не существует производная.
А теперь давайте попробуем ответить на вопрос: можно ли по графику функции сделать вывод по её дифференцируемости?
Если в некоторой точке к графику функции можно
провести касательную, не перпендикулярную оси абсцисс, то в этой точке функция
дифференцируема. Если в некоторой точке касательная к графику функции не
существует или она перпендикулярна оси абсцисс, то в этой точке функция
недефференцируема.
Например.
Раздел математики, который изучает производные функции и их применения, называется дифференциальным исчислением. Это исчисление возникло из решений задач на проведение касательных к кривым, на вычисление скорости движения, на отыскание наибольших и наименьших значений функции.
Ряд задач дифференциального исчисления был решён ещё в древности Архимедом, разработавшим способ проведения касательной.
Архимед построил касательную к спирали, носящей его имя.
Аполлоний – к эллипсу, гиперболе и параболе.
Но общего метода, пригодного для построения касательной к любой кривой плоскости в произвольной её точке найдено не было.
Более общим и важным для развития дифференциального исчисления был метод построения касательных Ферма.
Задача нахождения скорости изменения
функции была впервые решена Ньютоном. Ньютон пришёл к понятию производной
исходя из вопросов механики.
Основываясь на результатах Ферма и некоторых других выводах, Лейбниц в 1684 году опубликовал первую статью по дифференциальному исчислению, в которой были изложены основные правила дифференцирования.
Термин «производная» впервые встречается у француза Луи Арбогаста. Этим термином стал пользоваться Лагранж, который и ввёл обозначения y’ и f‘(x).
Формула выражающая определение производной. Геометрический и физический смысл производной
Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.
В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна . Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.
Запомним определение:
Производная — это скорость изменения функции.
На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?
Как вы думаете, какая из них быстрее растет?
Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.
Вот другой пример.
Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:
На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная , — разная. Что касается Матвея — у его дохода производная вообще отрицательна.
Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?
На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.
Производная функции обозначается .
Покажем, как найти с помощью графика.
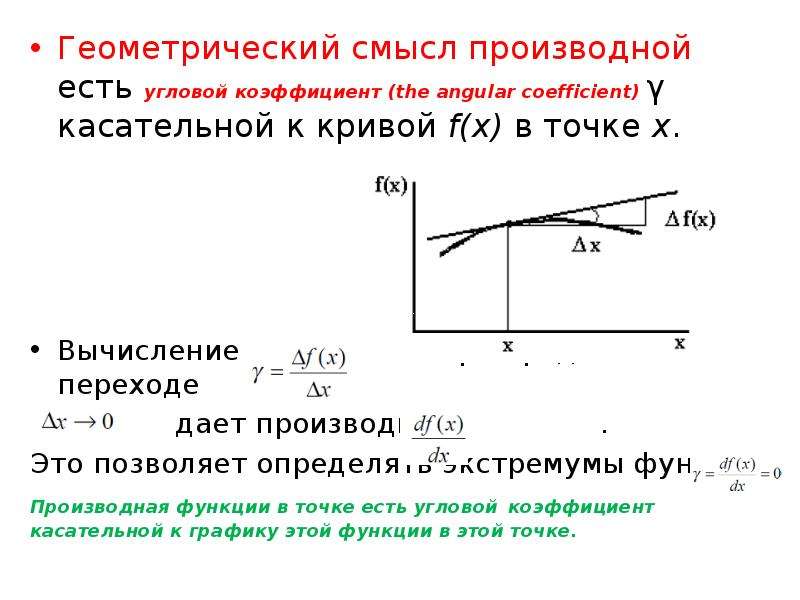
Нарисован график некоторой функции . Возьмем на нем точку с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной .
Производная функции в точке равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.
Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .
Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.
Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника :
Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике под номером .
Такие задачи часто встречаются в ЕГЭ по математике под номером .
Есть и другое важное соотношение. Вспомним, что прямая задается уравнением
Величина в этом уравнении называется угловым коэффициентом прямой . Она равна тангенсу угла наклона прямой к оси .
.
Мы получаем, что
Запомним эту формулу. Она выражает геометрический смысл производной.
Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
Другими словами, производная равна тангенсу угла наклона касательной.
Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.
Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.
В точке функция возрастает. Касательная к графику, проведенная в точке , образует острый угол ; с положительным направлением оси . Значит, в точке производная положительна.
Значит, в точке производная положительна.
В точке наша функция убывает. Касательная в этой точке образует тупой угол ; с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке производная отрицательна.
Вот что получается:
Если функция возрастает, ее производная положительна.
Если убывает, ее производная отрицательна.
А что же будет в точках максимума и минимума? Мы видим, что в точках (точка максимума) и (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.
Точка — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке с «плюса» на «минус».
В точке — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».
Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.
Если производная положительна, то функция возрастает.
Если производная отрицательная, то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
Запишем эти выводы в виде таблицы:
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| + | 0 | — | 0 | + |
Сделаем два небольших уточнения. Одно из них понадобится вам при решении задачи . Другое — на первом курсе, при более серьезном изучении функций и производных.
Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая :
В точке касательная к графику горизонтальна, и производная равна нулю. Однако до точки функция возрастала — и после точки продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.
Знак производной не меняется — она как была положительной, так и осталась.
Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.
А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется
Дата: 20.11.2014
Таблица производных.
Производная — одно из главных понятий высшей математики. В этом уроке мы познакомимся с этим понятием. Именно познакомимся, без строгих математических формулировок и доказательств.
Это знакомство позволит:
Понимать суть несложных заданий с производной;
Успешно решать эти самые несложные задания;
Подготовиться к более серьёзным урокам по производной.
Сначала — приятный сюрприз.)
Строгое определение производной основано на теории пределов и штука достаточно сложная. Это огорчает. Но практическое применение производной, как правило, не требует таких обширных и глубоких знаний!
Для успешного выполнения большинства заданий в школе и ВУЗе достаточно знать всего несколько терминов
— чтобы понять задание, и всего несколько правил
— чтобы его решить. И всё. Это радует.
И всё. Это радует.
Приступим к знакомству?)
Термины и обозначения.
В элементарной математике много всяких математических операций. Сложение, вычитание умножение, возведение в степень, логарифмирование и т.д. Если к этим операциям добавить ещё одну, элементарная математика становится высшей. Эта новая операция называется дифференцирование. Определение и смысл этой операции будут рассмотрены в отдельных уроках.
Здесь же важно понять, что дифференцирование — это просто математическая операция над функцией. Берём любую функцию и, по определённым правилам, преобразовываем её. В результате получится новая функция. Вот эта новая функция и называется: производная.
Дифференцирование — действие над функцией.
Производная — результат этого действия.
Так же, как, например, сумма — результат сложения. Или частное — результат деления.
Зная термины, можно, как минимум, понимать задания.) Формулировки бывают такие: найти производную функции; взять производную; продифференцировать функцию; вычислить производную
и т. п. Это всё одно и то же.
Разумеется, бывают и более сложные задания, где нахождение производной (дифференцирование) будет всего лишь одним из шагов решения задания.
п. Это всё одно и то же.
Разумеется, бывают и более сложные задания, где нахождение производной (дифференцирование) будет всего лишь одним из шагов решения задания.
Обозначается производная с помощью штришка вверху справа над функцией. Вот так: y» или f»(x) или S»(t) и так далее.
Читается игрек штрих, эф штрих от икс, эс штрих от тэ, ну вы поняли…)
Штрих также может обозначать производную конкретной функции, например: (2х+3)» , (x 3 )» , (sinx)» и т.д. Часто производная обозначается с помощью дифференциалов, но такое обозначение в этом уроке мы рассматривать не будем.
Предположим, что понимать задания мы научились. Осталось всего ничего — научиться их решать.) Напомню ещё раз: нахождение производной — это преобразование функции по определённым правилам. Этих правил, на удивление, совсем немного.
Чтобы найти производную функции, надо знать всего три вещи. Три кита, на которых стоит всё дифференцирование. Вот они эти три кита:
Вот они эти три кита:
1. Таблица производных (формулы дифференцирования).
3. Производная сложной функции.
Начнём по порядку. В этом уроке рассмотрим таблицу производных.
Таблица производных.
В мире — бесконечное множество функций. Среди этого множества есть функции, которые наиболее важны для практического применения. Эти функции сидят во всех законах природы. Из этих функций, как из кирпичиков, можно сконструировать все остальные. Этот класс функций называется элементарные функции. Именно эти функции и изучаются в школе — линейная, квадратичная, гипербола и т.п.
Дифференцирование функций «с нуля», т.е. исходя из определения производной и теории пределов — штука достаточно трудоёмкая. А математики — тоже люди, да-да!) Вот и упростили себе (и нам) жизнь. Они вычислили производные элементарных функций до нас. Получилась таблица производных, где всё уже готово.)
Вот она, эта табличка для самых популярных функций. Слева — элементарная функция, справа — её производная.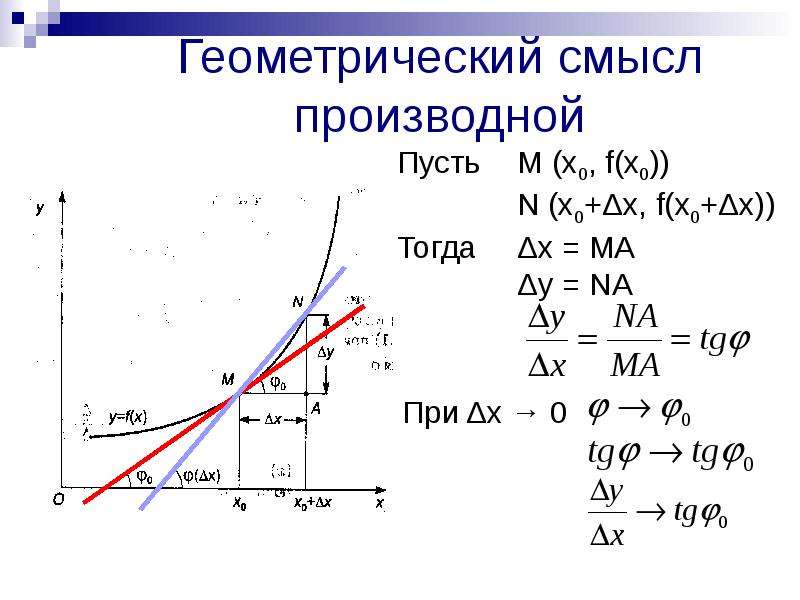
Рекомендую обратить внимание на третью группу функций в этой таблице производных. Производная степенной функции — одна из самых употребительных формул, если только не самая употребительная! Намёк понятен?) Да, таблицу производных желательно знать наизусть. Кстати, это не так трудно, как может показаться. Попробуйте решать побольше примеров, таблица сама и запомнится!)
Найти табличное значение производной, как вы понимаете, задание не самое трудное. Поэтому очень часто в подобных заданиях встречаются дополнительные фишки. Либо в формулировке задания, либо в исходной функции, которой в таблице — вроде и нету…
Рассмотрим несколько примеров:
1. Найти производную функции y = x 3
Такой функции в таблице нет. Но есть производная степенной функции в общем виде (третья группа). В нашем случае n=3. Вот и подставляем тройку вместо n и аккуратно записываем результат:
(x 3) » = 3·x 3-1 = 3x 2
Вот и все дела.
Ответ: y» = 3x 2
2. Найти значение производной функции y = sinx в точке х = 0.
Это задание означает, что надо сначала найти производную от синуса, а затем подставить значение х = 0 в эту самую производную. Именно в таком порядке! А то, бывает, сразу подставляют ноль в исходную функцию… Нас же просят найти не значение исходной функции, а значение её производной. Производная, напомню — это уже новая функция.
По табличке находим синус и соответствующую производную:
y» = (sin x)» = cosx
Подставляем ноль в производную:
y»(0) = cos 0 = 1
Это и будет ответ.
3. Продифференцировать функцию:
Что, внушает?) Такой функции в таблице производных и близко нет.
Напомню, что продифференцировать функцию — это просто найти производную этой функции. Если забыть элементарную тригонометрию, искать производную нашей функции достаточно хлопотно.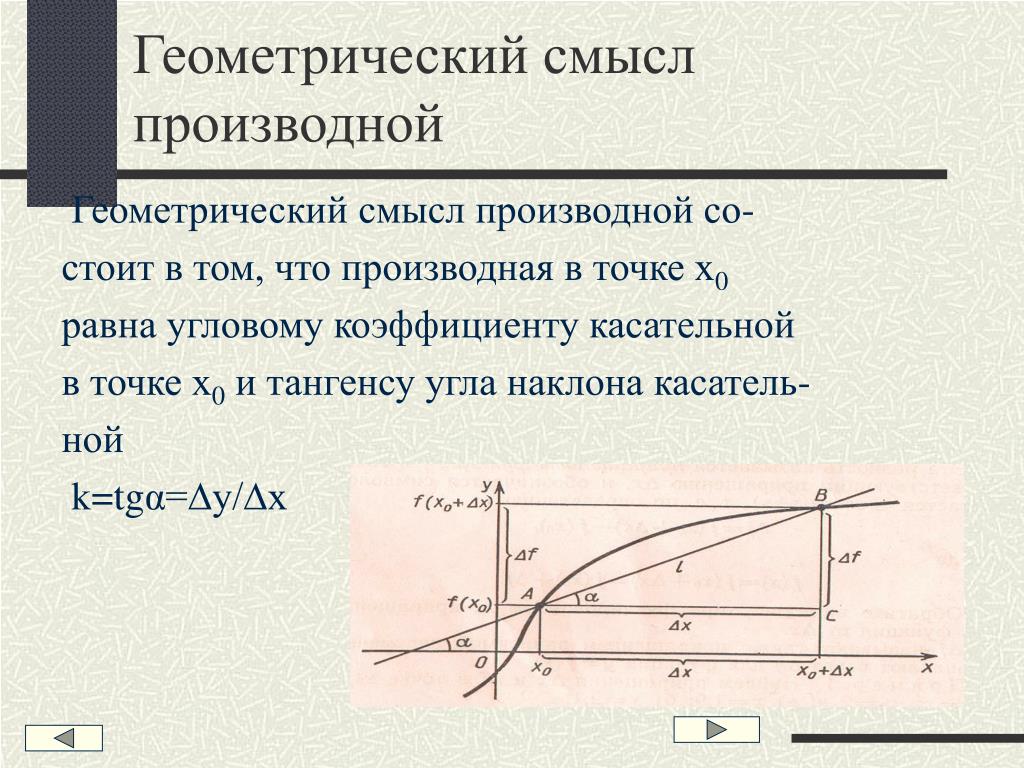 Таблица не помогает…
Таблица не помогает…
Но если увидеть, что наша функция — это косинус двойного угла , то всё сразу налаживается!
Да-да! Запомните, что преобразование исходной функции до дифференцирования вполне допускается! И, случается, здорово облегчает жизнь. По формуле косинуса двойного угла:
Т.е. наша хитрая функция есть не что иное, как y = cosx . А это — табличная функция. Сразу получаем:
Ответ: y» = — sin x .
Пример для продвинутых выпускников и студентов:
4. Найти производную функции:
Такой функции в таблице производных нет, разумеется. Но если вспомнить элементарную математику, действия со степенями… То вполне можно упростить эту функцию. Вот так:
А икс в степени одна десятая — это уже табличная функция! Третья группа, n=1/10. Прямо по формуле и записываем:
Вот и всё. Это будет ответ.
Надеюсь, что с первым китом дифференцирования — таблицей производных — всё ясно. Осталось разобраться с двумя оставшимися китами. В следующем уроке освоим правила дифференцирования.
Осталось разобраться с двумя оставшимися китами. В следующем уроке освоим правила дифференцирования.
При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из данной функции y=f(x) получать новую функцию, которую называют производной функцией (или просто производной) данной функции f(x) и обозначают символом
Тот
процесс, с помощью которого из данной
функции f(x)
получают новую функцию f
» (x)
,
называют дифференцированием
и состоит он из следующих трех шагов:
1)
даем аргументу x
приращение
x
и определяем соответствующее приращение
функции
y
= f(x+
x)
-f(x)
;
2)
составляем отношение
3)
считая x
постоянным, а
x
0,
находим
,
который обозначаем черезf
» (x)
,
как бы подчеркивая тем самым, что
полученная функция зависит лишь от того
значения x
,
при котором мы переходим к
пределу.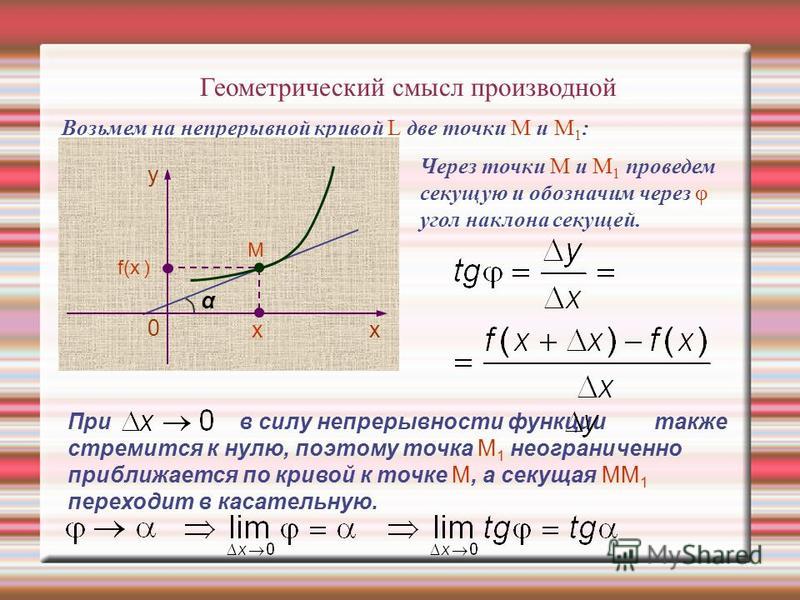 Определение
:
Производной
y » =f » (x)
данной
функции y=f(x)
при
данном x
называется предел отношения приращения
функции к приращению аргумента при
условии, что приращение аргумента
стремится к нулю, если, конечно, этот
предел существует, т.е. конечен.
Таким
образом,
Определение
:
Производной
y » =f » (x)
данной
функции y=f(x)
при
данном x
называется предел отношения приращения
функции к приращению аргумента при
условии, что приращение аргумента
стремится к нулю, если, конечно, этот
предел существует, т.е. конечен.
Таким
образом,
,
или
Заметим,
что если при некотором значении x
,
например при x=a
,
отношение
при
x
0
не стремится к конечному пределу, то в
этом случае говорят, что функция f(x)
при x=a
(или в точке x=a
)
не имеет производной или не дифференцируема
в точке x=a
.
2. Геометрический смысл производной.
Рассмотрим график функции у = f (х), дифференцируемой в окрестностях точки x 0
f(x)
Рассмотрим
произвольную прямую, проходящую через
точку графика функции — точку А(x 0 ,
f
(х 0))
и пересекающую график в некоторой точке
B(x;f(x)).
Такая прямая (АВ) называется секущей.
Из ∆АВС: АС = ∆x;
ВС =∆у; tgβ=∆y/∆x
.
Так как АС || Ox, то ALO = BAC = β (как соответственные при параллельных). Но ALO — это угол наклона секущей АВ к положительному направлению оси Ох. Значит, tgβ = k — угловой коэффициент прямой АВ.
Теперь будем уменьшать ∆х, т.е. ∆х→ 0. При этом точка В будет приближаться к точке А по графику, а секущая АВ будет поворачиваться. Предельным положением секущей АВ при ∆х→ 0 будет прямая (a), называемая касательной к графику функции у = f (х) в точке А.
Если
перейти к пределу при ∆х → 0 в равенстве
tgβ
=∆y/∆x,
то получим
илиtg
=f
«(x 0),
так как
-угол
наклона касательной к положительному
направлению оси Ох
,
по определению производной. Но tg
= k — угловой коэффициент касательной,
значит, k = tg
= f
«(x 0).
Итак, геометрический смысл производной заключается в следующем:
Производная функции в точке x 0 равна угловому коэффициенту касательной к графику функции, проведенной в точке с абсциссой x 0 .
3.
 Физический смысл производной.
Физический смысл производной. Рассмотрим движение точки по прямой. Пусть задана координата точки в любой момент времени x(t). Известно (из курса физики), что средняя скорость за промежуток времени равна отношению расстояния, пройденного за этот промежуток времени, на время, т.е.
Vср = ∆x/∆t. Перейдем к пределу в последнем равенстве при ∆t → 0.
lim Vср (t) = (t 0) — мгновенная скорость в момент времени t 0 , ∆t → 0.
а lim = ∆x/∆t = x»(t 0) (по определению производной).
Итак, (t) =x»(t).
Физический смысл производной заключается в следующем: производная функции y = f (x ) в точке x 0 — это скорость изменения функции f (х) в точке x 0
Производная применяется в физике для нахождения скорости по известной функции координаты от времени, ускорения по известной функции скорости от времени.
(t) = x»(t) — скорость,
a(f) = »(t) — ускорение, или
Если известен закон движения материальной точки по окружности, то можно найти угловую скорость и угловое ускорение при вращательном движении:
φ = φ(t) — изменение угла от времени,
ω = φ»(t) — угловая скорость,
ε
= φ»(t)
— угловое ускорение, или ε
= φ»(t).
Если известен закон распределения массы неоднородного стержня, то можно найти линейную плотность неоднородного стержня:
m = m(х) — масса,
x , l — длина стержня,
р = m»(х) — линейная плотность.
С помощью производной решаются задачи из теории упругости и гармонических колебаний. Так, по закону Гука
F = -kx, x – переменная координата, k- коэффициент упругости пружины. Положив ω 2 =k/m, получим дифференциальное уравнение пружинного маятника х»(t) + ω 2 x(t) = 0,
где ω = √k/√m частота колебаний (l/c), k — жесткость пружины (H/m).
Уравнение вида у» + ω 2 y = 0 называется уравнением гармонических колебаний (механических, электрических, электромагнитных). Решением таких уравнений является функция
у = Asin(ωt + φ 0) или у = Acos(ωt + φ 0), где
А — амплитуда колебаний, ω — циклическая частота,
φ 0 — начальная фаза.
Многие удивятся неожиданному расположению этой статьи в моём авторском курсе о производной функции одной переменной и её приложениях.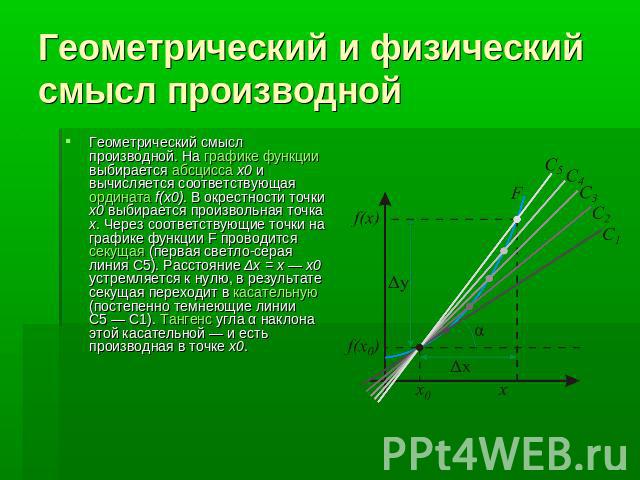 Ведь как оно было ещё со школы: стандартный учебник в первую очередь даёт определение производной, её геометрический, механический смысл. Далее учащиеся находят производные функций по определению, и, собственно, только потом оттачивается техника дифференцирования с помощью таблицы производных
.
Ведь как оно было ещё со школы: стандартный учебник в первую очередь даёт определение производной, её геометрический, механический смысл. Далее учащиеся находят производные функций по определению, и, собственно, только потом оттачивается техника дифференцирования с помощью таблицы производных
.
Но с моей точки зрения, более прагматичен следующий подход: прежде всего, целесообразно ХОРОШО ПОНЯТЬ предел функции , и, в особенности, бесконечно малые величины . Дело в том, что определение производной базируется на понятии предела , которое слабо рассмотрено в школьном курсе. Именно поэтому значительная часть молодых потребителей гранита знаний плохо вникают в саму суть производной. Таким образом, если вы слабо ориентируетесь в дифференциальном исчислении либо мудрый мозг за долгие годы успешно избавился от оного багажа, пожалуйста, начните с пределов функций . Заодно освоите/вспомните их решение.
Тот же практический смысл подсказывает, что сначала выгодно научиться находить производные
, в том числе производные сложных функций
. Теория теорией, а дифференцировать, как говорится, хочется всегда. В этой связи лучше проработать перечисленные базовые уроки, а может и стать мастером дифференцирования
, даже не осознавая сущности своих действий.
Теория теорией, а дифференцировать, как говорится, хочется всегда. В этой связи лучше проработать перечисленные базовые уроки, а может и стать мастером дифференцирования
, даже не осознавая сущности своих действий.
К материалам данной страницы рекомендую приступать после ознакомления со статьёй Простейшие задачи с производной , где, в частности рассмотрена задача о касательной к графику функции. Но можно и повременить. Дело в том, что многие приложения производной не требуют её понимания, и неудивительно, что теоретический урок появился достаточно поздно – когда мне потребовалось объяснять нахождение интервалов возрастания/убывания и экстремумов функции. Более того, он довольно долго находился в теме «Функции и графики », пока я всё-таки не решил поставить его раньше.
Поэтому, уважаемые чайники, не спешите поглощать суть производной, как голодные звери, ибо насыщение будет невкусным и неполным.
Понятие возрастания, убывания, максимума, минимума функцииМногие учебные пособия подводят к понятию производной с помощью каких-либо практических задач, и я тоже придумал интересный пример. Представьте, что нам предстоит путешествие в город, до которого можно добраться разными путями. Сразу откинем кривые петляющие дорожки, и будем рассматривать только прямые магистрали. Однако прямолинейные направления тоже бывают разными: до города можно добраться по ровному автобану. Или по холмистому шоссе – вверх-вниз, вверх-вниз. Другая дорога идёт только в гору, а ещё одна – всё время под уклон. Экстремалы выберут маршрут через ущелье с крутым обрывом и отвесным подъемом.
Представьте, что нам предстоит путешествие в город, до которого можно добраться разными путями. Сразу откинем кривые петляющие дорожки, и будем рассматривать только прямые магистрали. Однако прямолинейные направления тоже бывают разными: до города можно добраться по ровному автобану. Или по холмистому шоссе – вверх-вниз, вверх-вниз. Другая дорога идёт только в гору, а ещё одна – всё время под уклон. Экстремалы выберут маршрут через ущелье с крутым обрывом и отвесным подъемом.
Но каковы бы ни были ваши предпочтения, желательно знать местность или, по меньшей мере, располагать её топографической картой. А если такая информация отсутствует? Ведь можно выбрать, например, ровный путь, да в результате наткнуться на горнолыжный спуск с весёлыми финнами. Не факт, что навигатор и даже спутниковый снимок дадут достоверные данные. Поэтому неплохо бы формализовать рельеф пути средствами математики.
Рассмотрим некоторую дорогу (вид сбоку):
На всякий случай напоминаю элементарный факт: путешествие происходит слева направо
. Для простоты полагаем, что функция непрерывна
на рассматриваемом участке.
Для простоты полагаем, что функция непрерывна
на рассматриваемом участке.
Какие особенности у данного графика?
На интервалах функция возрастает , то есть каждое следующее её значение больше предыдущего. Грубо говоря, график идёт снизу вверх (забираемся на горку). А на интервале функция убывает – каждое следующее значение меньше предыдущего, и наш график идёт сверху вниз (спускаемся по склону).
Также обратим внимание на особые точки. В точке мы достигаем максимума , то есть существует такой участок пути, на котором значение будет самым большим (высоким). В точке же достигается минимум , и существует такая её окрестность, в которой значение самое маленькое (низкое).
Более строгую терминологию и определения рассмотрим на уроке об экстремумах функции
, а пока изучим ещё одну важную особенность: на промежутках функция возрастает, но возрастает она с разной скоростью
. И первое, что бросается в глаза – на интервале график взмывает вверх гораздо более круто
, чем на интервале . Нельзя ли измерить крутизну дороги с помощью математического инструментария?
И первое, что бросается в глаза – на интервале график взмывает вверх гораздо более круто
, чем на интервале . Нельзя ли измерить крутизну дороги с помощью математического инструментария?
Идея состоит в следующем: возьмём некоторое значение (читается «дельта икс»)
, которое назовём приращением аргумента
, и начнём его «примерять» к различным точкам нашего пути:
1) Посмотрим на самую левую точку: минуя расстояние , мы поднимаемся по склону на высоту (зелёная линия). Величина называется приращением функции , и в данном случае это приращение положительно (разность значений по оси – больше нуля). Составим отношение , которое и будет мерИлом крутизны нашей дороги. Очевидно, что – это вполне конкретное число, и, поскольку оба приращения положительны, то .
Внимание!
Обозначение являются ЕДИНЫМ
символом, то есть нельзя «отрывать» «дельту» от «икса» и рассматривать эти буквы отдельно. Разумеется, комментарий касается и символа приращения функции.
Разумеется, комментарий касается и символа приращения функции.
Исследуем природу полученной дроби содержательнее. Пусть изначально мы находимся на высоте 20 метров (в левой чёрной точке). Преодолев расстояние метров (левая красная линия), мы окажемся на высоте 60 метров. Тогда приращение функции составит метров (зелёная линия) и: . Таким образом, на каждом метре этого участка дороги высота увеличивается в среднем на 4 метра …не забыли альпинистское снаряжение? =) Иными словами, построенное отношение характеризует СРЕДНЮЮ СКОРОСТЬ ИЗМЕНЕНИЯ (в данном случае – роста) функции.
Примечание : числовые значения рассматриваемого примера соответствуют пропорциям чертежа лишь приблизительно.
2) Теперь пройдём то же самое расстояние от самой правой чёрной точки. Здесь подъём более пологий, поэтому приращение (малиновая линия) относительно невелико, и отношение по сравнению с предыдущим случаем будет весьма скромным. Условно говоря, метров и скорость роста функции
составляет . То есть, здесь на каждый метр пути приходится в среднем
пол метра подъёма.
То есть, здесь на каждый метр пути приходится в среднем
пол метра подъёма.
3) Маленькое приключение на склоне горы. Посмотрим на верхнюю чёрную точку, расположенную на оси ординат. Предположим, что это отметка 50 метров. Снова преодолеваем расстояние , в результате чего оказываемся ниже – на уровне 30-ти метров. Поскольку осуществлено движение сверху вниз (в «противоход» направлению оси ), то итоговое приращение функции (высоты) будет отрицательным : метров (коричневый отрезок на чертеже). И в данном случае речь уже идёт о скорости убывания функции: , то есть за каждый метр пути этого участка высота убывает в среднем на 2 метра. Берегите одежду на пятой точке.
Теперь зададимся вопросом: какое значение «измерительного эталона» лучше всего использовать? Совершенно понятно, 10 метров – это весьма грубо. На них запросто уместится добрая дюжина кочек. Да что там кочки, внизу может быть глубокое ущелье, а через несколько метров – другая его сторона с дальнейшим отвесным подъёмом. Таким образом, при десятиметровом мы не получим вразумительной характеристики подобных участков пути посредством отношения .
Таким образом, при десятиметровом мы не получим вразумительной характеристики подобных участков пути посредством отношения .
Из проведённого рассуждения следует вывод – чем меньше значение , тем точнее мы опишем рельеф дороги. Более того, справедливы следующие факты:
– Для любой точки подъемов можно подобрать значение (пусть и очень малое), которое умещается в границах того или иного подъёма. А это значит, что соответствующее приращение высоты будет гарантированно положительным, и неравенство корректно укажет рост функции в каждой точке этих интервалов.
– Аналогично, для любой точки склона существует значение , которое полностью уместится на этом склоне. Следовательно, соответствующее приращение высоты однозначно отрицательно, и неравенство корректно покажет убыль функции в каждой точке данного интервала.
– Особо интересен случай, когда скорость изменения функции равна нулю: . Во-первых, нулевое приращение высоты () – признак ровного пути. А во-вторых, есть другие любопытные ситуации, примеры которых вы видите на рисунке. Представьте, что судьба завела нас на самую вершину холма с парящими орлами или дно оврага с квакающими лягушками. Если сделать небольшой шажок в любую сторону, то изменение высоты будет ничтожно мало, и можно сказать, что скорость изменения функции фактически нулевая. В точках наблюдается именно такая картина.
А во-вторых, есть другие любопытные ситуации, примеры которых вы видите на рисунке. Представьте, что судьба завела нас на самую вершину холма с парящими орлами или дно оврага с квакающими лягушками. Если сделать небольшой шажок в любую сторону, то изменение высоты будет ничтожно мало, и можно сказать, что скорость изменения функции фактически нулевая. В точках наблюдается именно такая картина.
Таким образом, мы подобрались к удивительной возможности идеально точно охарактеризовать скорость изменения функции. Ведь математический анализ позволяет устремить приращение аргумента к нулю: , то есть сделать его бесконечно малым .
По итогу возникает ещё один закономерный вопрос: можно ли для дороги и её графика найти другую функцию , которая сообщала бы нам обо всех ровных участках, подъёмах, спусках, вершинах, низинах, а также о скорости роста/убывания в каждой точке пути?
Что такое производная? Определение производной.Геометрический смысл производной и дифференциала
Пожалуйста, прочитайте вдумчиво и не слишком быстро – материал прост и доступен каждому! Ничего страшного, если местами что-то покажется не очень понятным, к статье всегда можно вернуться позже. Скажу больше, теорию полезно проштудировать несколько раз, чтобы качественно уяснить все моменты (совет особенно актуален для студентов-«технарей», у которых высшая математика играет значительную роль в учебном процессе).
Скажу больше, теорию полезно проштудировать несколько раз, чтобы качественно уяснить все моменты (совет особенно актуален для студентов-«технарей», у которых высшая математика играет значительную роль в учебном процессе).
Естественно, и в самом определении производной в точке заменим на :
К чему мы пришли? А пришли мы к тому, что для функции по закону ставится в соответствие другая функция , которая называется производной функцией (или просто производной) .
Производная характеризует скорость изменения функции . Каким образом? Мысль идёт красной нитью с самого начала статьи. Рассмотрим некоторую точку области определения функции . Пусть функция дифференцируема в данной точке. Тогда:
1) Если , то функция возрастает в точке . И, очевидно, существует интервал (пусть даже очень малый), содержащий точку , на котором функция растёт, и её график идёт «снизу вверх».
2) Если , то функция убывает в точке . И существует интервал, содержащий точку , на котором функция убывает (график идёт «сверху вниз»).
3) Если , то бесконечно близко около точки функция сохраняет свою скорость постоянной. Так бывает, как отмечалось, у функции-константы и в критических точках функции , в частности в точках минимума и максимума .
Немного семантики. Что в широком смысле обозначает глагол «дифференцировать»? Дифференцировать – это значит выделить какой-либо признак. Дифференцируя функцию , мы «выделяем» скорость её изменения в виде производной функции . А что, кстати, понимается под словом «производная»? Функция произошла от функции .
Термины весьма удачно истолковывает механический смысл производной
:
Рассмотрим закон изменения координаты тела , зависящий от времени , и функцию скорости движения данного тела . Функция характеризует скорость изменения координаты тела, поэтому является первой производной функции по времени: . Если бы в природе не существовало понятия «движение тела», то не существовало бы и производного
понятия «скорость тела».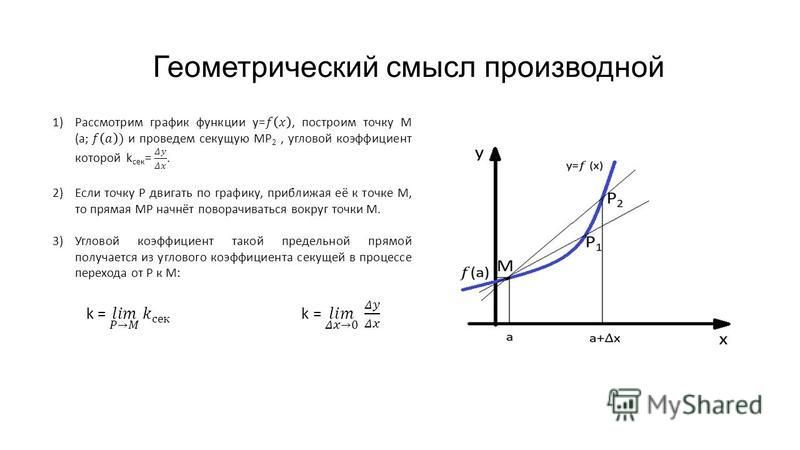
Ускорение тела – это скорость изменения скорости, поэтому: . Если бы в природе не существовало исходных понятий «движение тела» и «скорость движения тела», то не существовало бы и производного понятия «ускорение тела».
Когда человек сделал первые самостоятельные шаги в изучении математического анализа и начинает задавать неудобные вопросы, то уже не так-то просто отделаться фразой, что «дифференциальное исчисление найдено в капусте». Поэтому настало время набраться решимости и раскрыть тайну появления на светтаблицы производных и правил дифференцирования . Начало положено в статьео смысле производной , которую я настоятельно рекомендую к изучению, поскольку там мы как раз рассмотрели понятие производной и начали щёлкать задачи по теме. Этот же урок носит ярко выраженную практическую направленность, более того,
рассматриваемые ниже примеры, в принципе, можно освоить и чисто формально (например, когда нет времени/желания вникать в суть производной). Также крайне желательно (однако опять не обязательно) уметь находить производные «обычным» методом – хотя бы на уровне двух базовых занятий:
Как найти производную?и
Производная сложной функции.
Также крайне желательно (однако опять не обязательно) уметь находить производные «обычным» методом – хотя бы на уровне двух базовых занятий:
Как найти производную?и
Производная сложной функции.
Но без чего-чего сейчас точно не обойтись, так это безпределов функций . Вы должны ПОНИМАТЬ, что такое предел и уметь решать их, как минимум, на среднем уровне. А всё потому, чтопроизводная
функции в точке определяется формулой:
Напоминаю обозначения и термины: называютприращением аргумента ;
– приращением функции;
– это ЕДИНЫЕ символы («дельту» нельзя «отрывать» от «икса» или «игрека»).
Очевидно, что является «динамической» переменной,– константой и результат вычисления предела– числом(иногда – «плюс» либо «минус» бесконечностью) .
В качестве точки можно рассмотреть ЛЮБОЕ значение, принадлежащееобласти определения функции, в котором существует производная.
Примечание : оговорка «в котором существует производная» –в общем случае существенна ! Так, например, точкахоть и входит в область определения функции, но производной
там не существует. Поэтому формула
Поэтому формула
не применима в точке,
и укороченная формулировка без оговорки будет некорректна. Аналогичные факты справедливы и для других функций с «обрывами» графика, в частности, для арксинуса и арккосинуса.
Таким образом, после замены , получаем вторую рабочую формулу:
Обратите внимание на коварное обстоятельство, которое может запутать чайника: в данном пределе «икс», будучи сам независимой переменной, исполняет роль статиста, а «динамику» задаёт опять же приращение . Результатом вычисления предела
является производная функция.
Исходя из вышесказанного, сформулируем условия двух типовых задач:
– Найти производную в точке , используя определение производной.
– Найти производную функцию , используя определение производной. Эта версия, по моим наблюдениям, встречается заметно чаще и ей будет уделено основное внимание.
Принципиальное отличие заданий состоит в том, что в первом случае требуется найти число (как вариант, бесконечность) , а во втором –
функцию
. Кроме того, производной может и вовсе не существовать.
Кроме того, производной может и вовсе не существовать.
Как ?
Составить отношение и вычислить предел.
Откуда появилась таблица производных и правила дифференцирования? Благодаря единственному пределу
Кажется волшебством, но в
действительности – ловкость рук и никакого мошенничества. На уроке Что такое производная? я начал рассматривать конкретные примеры, где с помощью определения нашёл производные линейной и квадратичной функции. В целях познавательной разминки продолжим тревожитьтаблицу производных , оттачивая алгоритм и технические приёмы решения:
По сути, требуется доказать частный случай производной степенной функции, который обычно фигурирует в таблице: .
Решение технически оформляется двумя способами. Начнём с первого, уже знакомого подхода: лесенка начинается с дощечки, а производная функция – с производной в точке.
Рассмотрим некоторую
(конкретную) точку, принадлежащуюобласти определения
функции, в которой существует производная.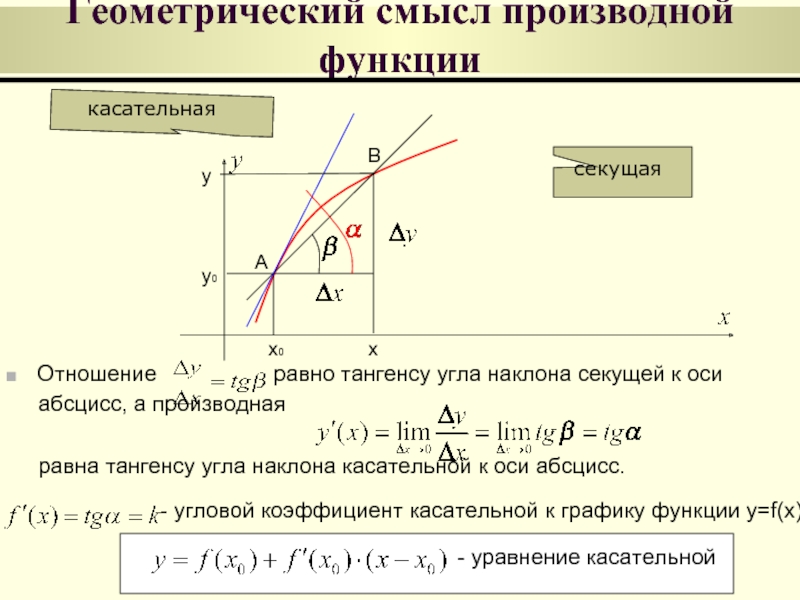 Зададим в данной точке приращение (разумеется, не выходящее за рамки
о/о
-я)
и составим соответствующее приращение функции:
Зададим в данной точке приращение (разумеется, не выходящее за рамки
о/о
-я)
и составим соответствующее приращение функции:
Вычислим предел:
Неопределённость 0:0 устраняется стандартным приёмом, рассмотренным ещё в первом веке до нашей эры. Домножим
числитель и знаменатель на сопряженное выражение :
Техника решения такого предела подробно рассмотрена на вводном уроке о пределах функций .
Поскольку в качестве можно выбрать ЛЮБУЮ точкуинтервала
То, осуществив замену, получаем:
В который раз порадуемся логарифмам:
Найти производную функции , пользуясь определением производной
Решение : рассмотрим другой подход к раскрутке той же задачи. Он точно такой же, но более рационален с точки зрения оформления. Идея состоит в том, чтобы в начале решения избавиться от
подстрочного индекса и вместо буквы использовать букву.
Рассмотрим произвольную
точку, принадлежащуюобласти определения
функции(интервалу), и зададим в ней приращение.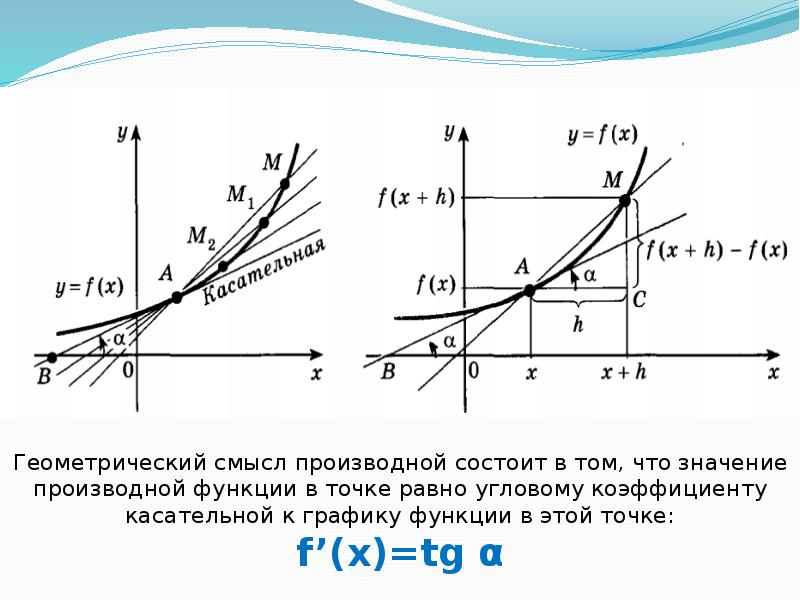 А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
А вот здесь, кстати, как и в большинстве случаев, можно обойтись без всяких оговорок, поскольку логарифмическая функция дифференцируема в любой точке области определения.
Тогда соответствующее приращение функции:
Найдём производную:
Простота оформления уравновешивается путаницей, которая может
возникнуть у начинающих (да и не только). Ведь мы привыкли, что в пределе изменяется буква «икс»! Но тут всё по-другому: – античная статуя, а– живой посетитель, бодро шагающий по коридору музея. То есть «икс» – это «как бы константа».
Устранение неопределённости закомментирую пошагово:
(1) Используем свойство логарифма .
(2) В скобках почленно делим числитель на знаменатель.
(3) В знаменателе искусственно домножаем и делим на «икс» чтобы
воспользоваться замечательным пределом , при этом в качествебесконечно малой величины выступает.
Ответ : по определению производной:
Или сокращённо:
Предлагаю самостоятельно сконструировать ещё две табличные формулы:
Найти производную по определению
В данном случае составленное приращение сразу же удобно привести к общему знаменателю. Примерный образец оформления задания в конце урока (первый способ).
Примерный образец оформления задания в конце урока (первый способ).
Найти производную по определению
А тут всё необходимо свести к замечательному пределу . Решение оформлено вторым способом.
Аналогично выводится ряд других табличных производных . Полный список можно найти в школьном учебнике, или, например, 1- м томе Фихтенгольца. Не вижу особого смысла переписывать из книг и доказательства правил дифференцирования – они тоже порождены
формулой .
Переходим к реально встречающимся заданиям: Пример 5
Найти производную функции , используя определение производной
Решение : используем первый стиль оформления. Рассмотрим некоторую точку, принадлежащую, и зададим в ней приращение аргумента. Тогда соответствующее приращение функции:
Возможно, некоторые читатели ещё не до конца поняли принцип, по которому нужно составлять приращение . Берём точку(число) и находим в ней значение функции:, то есть в функцию
вместо «икса» следует подставить. Теперь берём
Составленное приращение функции бывает выгодно сразу же упростить
. Зачем? Облегчить и укоротить решение дальнейшего предела.
Зачем? Облегчить и укоротить решение дальнейшего предела.
Используем формулы , раскрываем скобки и сокращаем всё, что можно сократить:
Индейка выпотрошена, с жаркое никаких проблем:
В итоге:
Поскольку в качестве можно выбрать любое действительное число, то проведём заменуи получим.
Ответ :по определению.
В целях проверки найдём производную с помощью правил
дифференцирования и таблицы:
Всегда полезно и приятно знать правильный ответ заранее, поэтому лучше мысленно либо на черновике продифференцировать предложенную функцию «быстрым» способом в самом начале решения.
Найти производную функции по определению производной
Это пример для самостоятельного решения. Результат лежит на поверхности:
Вернёмся к стилю №2: Пример 7
Давайте немедленно узнаем, что должно получиться. По правилу дифференцирования сложной функции :
Решение : рассмотрим произвольную точку, принадлежащую, зададим в ней приращение аргументаи составим приращение
Найдём производную:
(1) Используем тригонометрическую формулу
(2)
Под синусом раскрываем скобки, под косинусом приводим подобные слагаемые.
(3) Под синусом сокращаем слагаемые, под косинусом почленно делим числитель на знаменатель.
(4) В силу нечётности синуса выносим «минус». Под косинусом
указываем, что слагаемое .
(5) В знаменателе проводим искусственное домножение, чтобы использовать первый замечательный предел . Таким образом, неопределённость устранена, причёсываем результат.
Ответ :по определению Как видите, основная трудность рассматриваемой задачи упирается в
сложность самого предела + небольшое своеобразие упаковки. На практике встречаются и тот и другой способ оформления, поэтому я максимально подробно расписываю оба подхода. Они равноценны, но всё-таки, по моему субъективному впечатлению, чайникам целесообразнее придерживаться 1-го варианта с «икс нулевым».
Пользуясь определением, найти производную функции
Это задание для самостоятельного решения. Образец оформлен в том же духе, что предыдущий пример.
Разберём более редкую версию задачи:
Найти производную функции в точке, пользуясь определением производной.
Во-первых, что должно получиться в сухом остатке? Число Вычислим ответ стандартным способом:
Решение : с точки зрения наглядности это задание значительно проще, так как в формулевместо
рассматривается конкретное значение.
Зададим в точке приращениеи составим соответствующее приращение функции:
Вычислим производную в точке:
Используем весьма редкую формулу разности тангенсов и в который раз сведём решение кпервому
замечательному пределу:
Ответ :по определению производной в точке.
Задачу не так трудно решить и «в общем виде» – достаточно заменить наили простов зависимости от способа оформления. В этом случае, понятно, получится не число, а производная функция.
Пример 10 Используя определение, найти производную функциив точке
Это пример для самостоятельного решения.
Заключительная бонус-задача предназначена, прежде всего, для студентов с углубленным изучением математического анализа, но и всем остальным тоже не помешает:
Будет ли дифференцируема функция в точке?
Решение : очевидно, что кусочно-заданная функциянепрерывна в точке, но будет ли она там дифференцируема?
Алгоритм решения, причём не только для кусочных функций, таков:
1)
Находим
левостороннюю производнуюв данной точке:
.
2) Находим правостороннюю производнуюв данной точке: .
3) Если односторонние производныеконечны и совпадают:
, то функциядифференцируема в точкеи
геометрически здесь существует общая касательная (см. теоретическую часть урока Определение и смысл производной ).
Если получены два разных значения: (одно из которых может оказаться и бесконечным) , то функция не дифференцируема в точке.
Если же обе односторонние производные равны бесконечности
(пусть даже разных знаков), то функция не
дифференцируема в точке , но там существует бесконечная производная и общая вертикальная касательная к графику(см. Пример 5 урока Уравнение нормали ) .
Понятие производной ее геометрический и физический смысл. Определение производной, её геометрический смысл. VI. Лабораторная работа
Перед прочтением информации на текущей странице советуем посмотреть видео о производной и её геометрическом смысле
Также смотрите пример вычисления производной в точке
Касательной к линии l в точке М0 называется прямая М0Т — предельное положение секущей М0М, когда точка М стремится к М0 вдоль данной линии (т.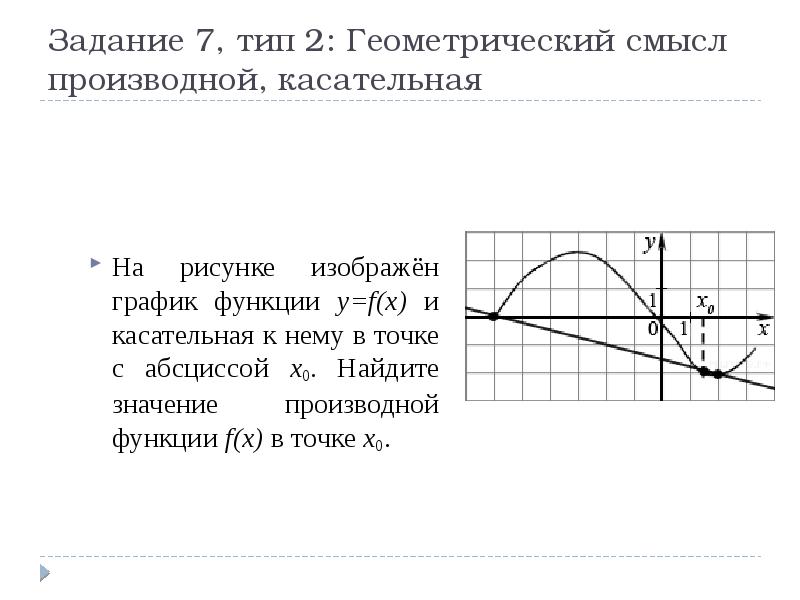 е. угол устремится к нулю) произвольным образом.
е. угол устремится к нулю) произвольным образом.
Производной функции у = f{x) в точке x0 называется предел отношения приращения этой функции к приращению аргумента, когда последнее стремится к нулю. Производную функции у = f{x) в точке х0 и учебниках обозначают символом f»(x0). Следовательно, по определению
Термин «производная» (а также «вторая производная») ввел Ж. Лагранж (1797), к тому же он дал обозначения y’, f’(x), f”(x) (1770,1779). Обозначение dy/dx впервые встречается у Лейбница (1675).
Производная функции y = f(х) при х = xо равна угловому коэффициенту касательной к графику данной функции в точке Мо(хо, f(xо)), т. е.
где а — угол наклона касательной к оси Ох прямоугольной декартовой системы координат.
Уравнение касательной к линии у = f(x) в точке Мо(хо, уо) принимает вид
Нормалью к кривой в некоторой ее точке называется перпендикуляр к касательной в той же точке. Если f(x0) не равно 0, то уравнение нормали к линии у = f(x) в точке Мо(хо, уо) запишется так:
Физический смысл производной
Если x = f(t) — закон прямолинейного движения точки, то x’ = f’(t) — скорость этого движения в момент времени t. Быстрота протекания
физических, химических и других процессов выражается с помощью производной
.
Быстрота протекания
физических, химических и других процессов выражается с помощью производной
.
Если отношение dy/dх при х->х0 имеет предел справа (или слева), то он называется производной справа (соответственно производной слева). Такие пределы называются односторонними производными .
Очевидно, функция f{x) определенная в некоторой окрестности точки х0, имеет производную f’{x) тогда и только тогда, когда односторонние производные существуют и равны между собой.
Геометрическое истолкование производной как углового коэффициента касательной к графику распространяется и на этот случай: касательная в данном случае параллельна оси Оу.
Функция, имеющая производную в данной точке, называется дифференцируемой в этой точке. Функция, имеющая производную в каждой точке данного промежутка, называется дифференцируемой в этом промежутке. Если промежуток является замкнутым, то на концах его имеются односторонние производные.
Операция нахождения производной называется
.
Для выяснения геометрического значения производной рассмотрим график функции y = f(x). Возьмем произвольную точку М с координатами (x, y) и близкую к ней точку N (x + $\Delta $x, y + $\Delta $y). Проведем ординаты $\overline{M_{1} M}$ и $\overline{N_{1} N}$, а из точки М — параллельную оси ОХ прямую.
Отношение $\frac{\Delta y}{\Delta x} $ является тангенсом угла $\alpha $1, образованного секущей MN с положительным направлением оси ОХ. При стремлении $\Delta $х к нулю точка N будет приближаться к M, а предельным положением секущей MN станет касательная MT к кривой в точке M. Таким образом, производная f`(x) равна тангенсу угла $\alpha $, образованного касательной к кривой в точке M (х, y) с положительным направлением к оси ОХ — угловому коэффициенту касательной (рис.1).
Рисунок 1. График функции
Вычисляя значения по формулам (1), важно не ошибиться в знаках, т.к. приращение может быть и отрицательным.
Точка N, лежащая на кривой, может стремиться к M с любой стороны.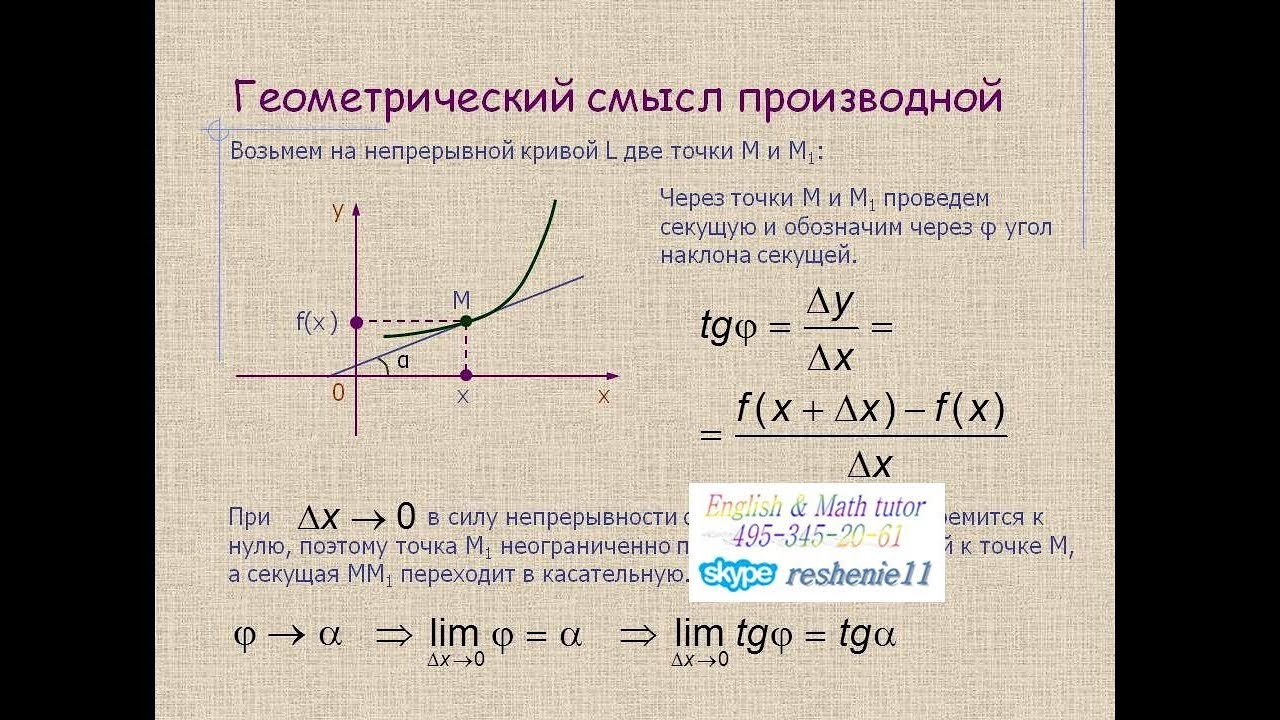 Так, если на рисунке 1, касательной придать противоположное направление, угол $\alpha $ изменится на величину $\pi $, что существенно повлияет на тангенс угла и соответственно угловой коэффициент.
Так, если на рисунке 1, касательной придать противоположное направление, угол $\alpha $ изменится на величину $\pi $, что существенно повлияет на тангенс угла и соответственно угловой коэффициент.
Вывод
Следует вывод, что существование производной связано с существованием касательной к кривой y = f(x), а угловой коэффициент — tg $\alpha $ = f`(x) конечный. Поэтому касательная не должна быть параллельной оси OY, иначе $\alpha $ = $\pi $/2, а тангенс угла будет бесконечным.
В некоторых точках непрерывная кривая может не иметь касательной или иметь касательную параллельную оси OY (рис.2). Тогда в этих значениях функция не может иметь производную. Подобных точек может быть сколько угодно много на кривой функции.
Рисунок 2. Исключительные точки кривой
Рассмотрим рисунок 2. Пусть $\Delta $x стремится к нулю со стороны отрицательных или положительных значений:
\[\Delta x\to -0\begin{array}{cc} {} & {\Delta x\to +0} \end{array}\]
Если в данном случае отношения (1) имеют конечный придел, он обозначается как:
В первом случае — производная слева, во втором — производная справа.
Существование предела говорит о равносильности и равенстве левой и правой производной:
Если же левая и правая производные неравны, то в данной точке существуют касательные не параллельные OY (точка М1, рис.2). В точках М2, М3 отношения (1) стремятся к бесконечности.
Для точек N лежащих слева от M2, $\Delta $x $
Справа от $M_2$, $\Delta $x $>$ 0, но выражение также f(x + $\Delta $x) — f(x) $
Для точки $M_3$ слева $\Delta $x $$ 0 и f(x + $\Delta $x) — f(x) $>$ 0, т.е. выражения (1) и слева, и справа положительны и стремятся к +$\infty $ как при приближении $\Delta $x к -0, так и к +0.
Случай отсутствия производной в конкретных точках прямой (x = c) представлен на рисунке 3.
Рисунок 3. Отсутствие производных
Пример 1
На рисунке 4 изображен график функции и касательной к графику в точке с абсциссой $x_0$. Найти значение производной функции в абсциссе.
Решение. Производная в точке равна отношению~приращения функции к приращению аргумента. Выберем на касательной две точки с целочисленными координатами. Пусть, например, это будут точки F (-3,2) и C (-2.4).
Выберем на касательной две точки с целочисленными координатами. Пусть, например, это будут точки F (-3,2) и C (-2.4).
Лекция: Понятие о производной функции, геометрический смысл производной
Понятие о производной функции
Рассмотрим некоторую функцию f(x), которая будет непрерывной на всем промежутке рассмотрения. На рассматриваемом промежутке выберем точку х 0 , а также величину функции в данной точке.
Итак, давайте рассмотрим график, на котором отметим нашу точку х 0 , а также точку (х 0 + ∆х). Напомним, что ∆х – это расстояние (разница) между двумя выбранными точками.
Так же стоит понимать, что каждому х соответствует собственное значение функции у.
Разница значений функции в точке х 0 и (х 0 + ∆х) называется приращением данной функции: ∆у = f(х 0 + ∆х) — f(х 0).
Давайте обратим внимание на дополнительную информацию, которая имеется на графике – это секущая, которая названа КL, а также треугольник, который она образует с интервалами KN и LN.
Угол, под которым находится секущая, называется её углом наклона и обозначается α. Легко можно определить, что градусная мера угла LKN так же равна α.
А теперь давайте вспомним соотношения в прямоугольном треугольнике tgα = LN / KN = ∆у / ∆х.
То есть тангенс угла наклона секущей равен отношению приращения функции к приращению аргумента.
В свое время, производная – это предел отношения приращения функции к приращению аргумента на бесконечно малых интервалах.
Производная определяет скорость, с которой происходит изменение функции на некотором участке.
Геометрический смысл производной
Если найти производную любой функции в некоторой точке, то можно определить угол, под которым будет находится касательная к графику в данной токе, относительно оси ОХ. Обратите внимание на график – угол наклона касательно обозначается буквой φ и определяется коэффициентом k в уравнении прямой: y = kx + b.
То есть можно сделать вывод, что геометрическим смыслом производной является тангенс угла наклона касательной в некоторой точке функции.
Производная функции.
1. Определение производной, её геометрический смысл.
2.Производная сложной функции.
3. Производная обратной функции.
4. Производные высших порядков.
5. Параметрически заданные функции и неявно.
6. Дифференцирование функций, заданных параметрически и неявно.
Введение.
Источником дифференциального исчисления были два вопроса, выдвинутые запросами науки и техники в 17 веке.
1) Вопрос о вычислении скорости при произвольно заданном законе движения.
2) Вопрос о нахождении (с помощью вычислений) касательной к кривой произвольно заданной.
Задачу проведения касательной к некоторым кривым решил ещё древнегреческий учёный Архимед (287-212 г.г. до н.э.), пользуясь методом вычерчивания.
Но только в 17 и 18 веках в связи с прогрессом естествознания и техники эти вопросы получили должное развитие.
Одним из важных вопросов при изучении любого физического явления обычно является вопрос о скорости, быстроте происходящего явления.
Скорость с которой движется самолёт или автомобиль, всегда служит важнейшим показателем его работы. Быстрота прироста населения того или иного государства является одной из основных характеристик его общественного развития.
Первоначальная идея скорости ясна каждому. Однако для решения большинства практических задач этой общей идеи недостаточно. Необходимо иметь такое количественное определение этой величины, которую мы называем скоростью. Потребность в таком точном количественном определении исторически послужила одним из основных побудителей к созданию математического анализаю. Целый раздел математического анализа посвящен решению этой основной задачи и выводам из этого решения. К изучению этого раздела мы и переходим.
Определение производной, её геометрический смысл.
Пусть дана функция определённая в некотором интервале (а,в) и непрерывная в нём.
1. Дадим аргументу х приращение , тогда функция получит
приращение :
2. Составим отношение .
Составим отношение .
3. Переходя к пределу в при и, предполагая, что предел
существует, получим величину , которую называют
производной функции по аргументу х .
Определение. Производной функции в точке называется предел отношения приращения функции к приращению аргумента , когда →0.
Значение производной очевидно зависит от точки х , в которой оно найдено, поэтому производная функции есть в свою очередь некоторая функция от х . Обозначается .
По определению имеем
или (3)
Пример. Найти производную функции .
1. ;
Производной функции f (x) в точке х0 называется предел (если он существует) отношения приращения функции в точке х0 к приращению аргумента Δх, если прирост аргумента стремится к нулю и обозначается f ‘(x0). Действие нахождения производной функции называется дифференцированием.
Производная функции имеет такой физический смысл: производная функции в заданной точке — скорость изменения функции в заданной точке.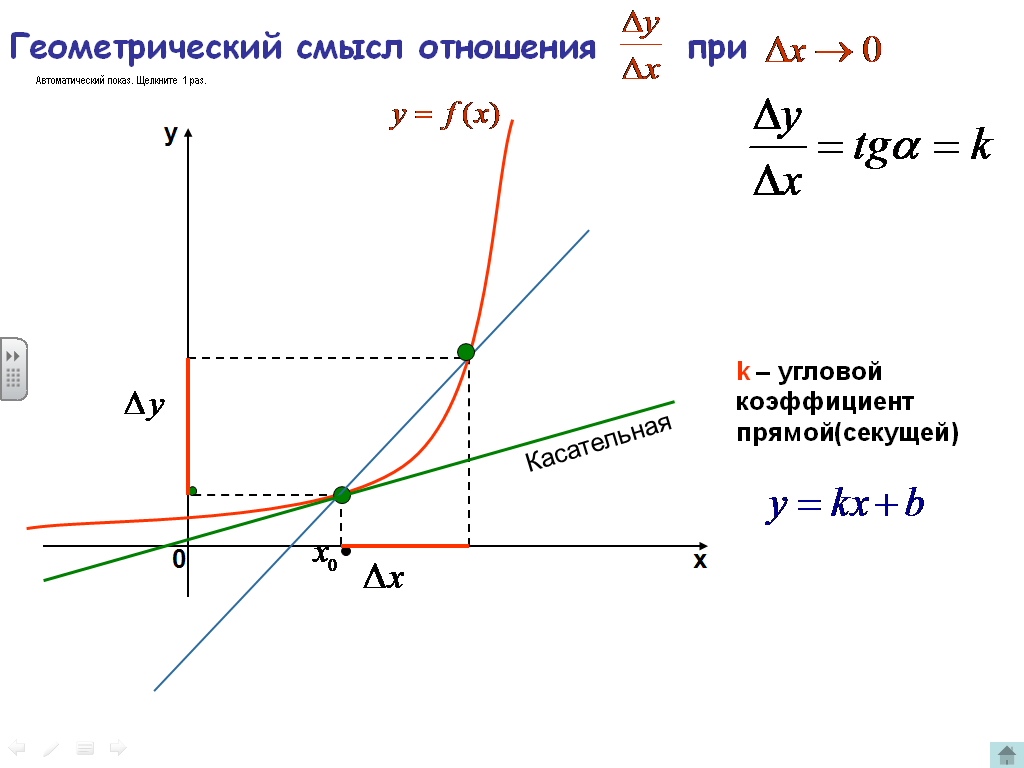
Геометрический смысл производной . Производная в точке x0 равна угловому коэффициенту касательной к графику функции y=f(x) в этой точке.
Физический смысл производной. Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки:
Понятие дифференциала, его свойства. Правила дифференцирования. Примеры.
Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.Дифференциал функции y = f(x) равен произведению её производной на приращение независимой переменной x (аргумента).
Это записывается так:
или
Или же
Свойства дифференциала
Дифференциал обладает свойствами, аналогичными свойствам производной:
К основным правилам дифференцирования
относят:
1) вынесение постоянного множителя за знак производной
2) производная суммы, производная разности
3) производная произведения функций
4) производная частного двух функций (производная дроби)
Примеры.
Докажем формулу: По определению производной имеем:
Произвольный множитель можно выносить за знак предельного перехода (это известно из свойств предела), поэтому
Например:
Найти производную функции
Решение:
Воспользуемся правилом вынесения множителя за знак производной:
Достаточно часто приходится сначала упрощать вид дифференцируемой функции, чтобы, воспользоваться таблицей производных и правилами нахождения производных. Следующие примеры это наглядно подтверждают.
Формулы дифференцирования. Применение дифференциала в приближенных вычислениях. Примеры.
Применение дифференциала в приближенных вычислениях позволяет использовать дифференциал для приближенных вычислений значений функции.
Примеры
.
С помощью дифференциала вычислить приближенно
Для вычисления данного значения применим формулу из теории
Введем в рассмотрение функцию а заданную величину представим в виде
тогда Вычислим
Подставляя все в формулу, окончательно получим
Ответ:
16. Правило Лопиталя для раскрытия неопределенностей вида 0/0 Или ∞/∞. Примеры.
Правило Лопиталя для раскрытия неопределенностей вида 0/0 Или ∞/∞. Примеры.
Предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
1)
17. Возрастание и убывание функции. Экстремум функции. Алгоритм исследования функции на монотонность и экстремум. Примеры .
Функция возрастает на интервале, если для любых двух точек этого интервала, связанных отношением , справедливо неравенство . То есть, большему значению аргумента соответствует большее значение функции, и её график идёт «снизу вверх». Демонстрационная функция растёт на интервале
Аналогично, функция убывает на интервале, если для любых двух точек данного интервала, таких, что , справедливо неравенство . То есть, большему значению аргумента соответствует меньшее значение функции, и её график идёт «сверху вниз». Наша убывает на интервалах убывает на интервалах .
Экстремумы
Точку называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство .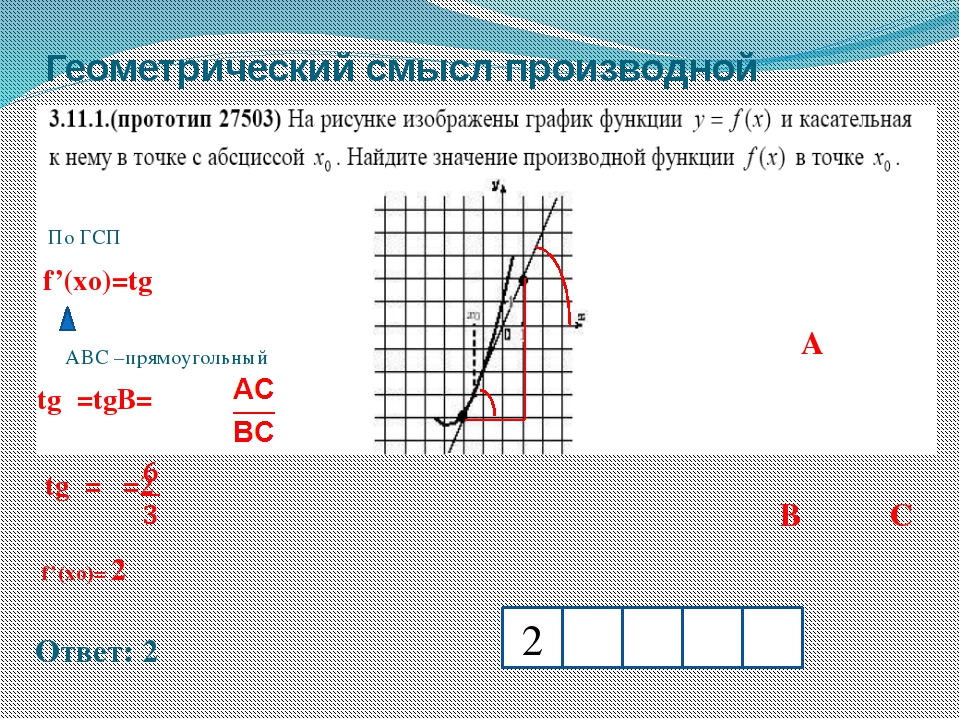 Значение функции в точке максимума называют максимумом функции
и обозначают .
Значение функции в точке максимума называют максимумом функции
и обозначают .
Точку называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство . Значение функции в точке минимума называют минимумом функции
и обозначают .
Под окрестностью точки понимают интервал , где — достаточно малое положительное число.
Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции
.
Чтобы исследовать функцию на монотонность
, воспользуйтесь следующей схеме:
— Найдите область определения функции;
— Найдите производную функции и область определения производной;
— Найдите нули производной, т.е. значение аргумента, при которых производная равна нулю;
— На числовом лучи отметьте общую часть области определения функции и области определения ее производной, а на ней — нули производной;
— Определите знаки производной на каждом из полученных промежутков;
— По знакам производной определите, на которых промежутках функция возрастает, а на каких спадает;
— Запишите соответствующие промежутки через точку с запятой.
Алгоритм исследования непрерывной функции y = f(x) на монотонность и экстремумы
:
1) Найти производную f ′(x).
2) Найти стационарные (f ′(x) = 0) и критические (f ′(x) не существует) точки функции y = f(x).
3) Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
4) Сделать выводы о монотонности функции и ее точках экстремума.
18. Выпуклость функции. Точки перегиба. Алгоритм исследования функции на выпуклость (Вогнутость) Примеры .
выпуклой вниз на интервале Х, если ее график расположен не ниже касательной к нему в любой точке интервала Х.
Дифференцируемая функция называется выпуклой вверх на интервале Х, если ее график расположен не выше касательной к нему в любой точке интервала Х.
Точка формула называется точкой перегиба графика
функции y=f(x), если в данной точке существует касательная к графику функции (она может быть параллельна оси Оу) и существует такая окрестность точки формула, в пределах которой слева и справа от точки М график функции имеет разные направления выпуклости.
Нахождение интервалов на выпуклость:
Если функция y=f(x) имеет конечную вторую производную на интервале Х и если выполняется неравенство (), то график функции имеет выпуклость направленную вниз (вверх) на Х.
Эта теорема позволяет находитьть промежутки вогнутости и выпуклости функции, нужно лишь на области определения исходной функции решить неравенства и соответственно.
Пример
: Выяснить промежутки, на которых график функцииВыяснить промежутки, на которых график функции имеет выпуклость направленную вверх и выпуклость направленную вниз. имеет выпуклость направленную вверх и выпуклость направленную вниз.
Решение:
Областью определения этой функции является все множество действительных чисел.
Найдем вторую производную.
Область определения второй производной совпадает с областью определения исходной функции, поэтому, чтобы выяснить интервалы вогнутости и выпуклости, достаточно решить и соответственно. Следовательно, функция выпуклая вниз на интервале формула и выпуклая вверх на интервале формула.
19) Асимптоты функции. Примеры.
Прямая называется вертикальной асимптотой графика функции , если хотя бы одно из предельных значений или равно или .
Замечание. Прямая не может быть вертикальной асимптотой, если функция непрерывна в точке . Поэтому вертикальные асимптоты следует искать в точках разрыва функции.
Прямая называется горизонтальной асимптотой графика функции , если хотя бы одно из предельных значений или равно .
Замечание. График функции может иметь только правую горизонтальную асимптоту или только левую.
Прямая называется наклонной асимптотой графика функции , если
ПРИМЕР:
Задание. Найти асимптоты графика функции
Решение. Область определения функции:
а) вертикальные асимптоты: прямая — вертикальная асимптота, так как
б) горизонтальные асимптоты: находим предел функции на бесконечности:
то есть, горизонтальных асимптот нет.
в) наклонные асимптоты :
Таким образом, наклонная асимптота: .
Ответ. Вертикальная асимптота — прямая .
Наклонная асимптота — прямая .
20) Общая схема исследования функции и построение графика. Пример.
a.
Найти ОДЗ и точки разрыва функции.
b. Найти точки пересечения графика функции с осями координат.
2. Провести исследование функции с помощью первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания.
3. Исследовать функцию с помощью производной второго порядка, то есть найти точки перегиба графика функции и интервалы его выпуклости и вогнутости.
4. Найти асимптоты графика функции: а) вертикальные, b) наклонные.
5. На основании проведенного исследования построить график функции.
Заметим, что перед построением графика полезно установить, не является ли данная функция четной или нечетной.
Вспомним, что функция называется четной, если при изменении знака аргумента значение функции не меняется: f(-x)
= f(x)
и функция называется нечетной, если f(-x)
= -f(x)
.
В этом случае достаточно исследовать функцию и построить её график при положительных значениях аргумента, принадлежащих ОДЗ. При отрицательных значениях аргумента график достраивается на том основании, что для четной функции он симметричен относительно оси Oy , а для нечетной относительно начала координат.
Примеры. Исследовать функции и построить их графики.
Область определения функции D(у)= (–∞; +∞). Точек разрыва нет.
Пересечение с осью Ox : x = 0,у= 0.
Функция нечетная, следовательно, можно исследовать ее только на промежутке }
Определение производной
Определение производнойПроизводная
Концепция производной лежит в основе исчисления и
современная математика. Определение производной может быть
подошел двумя разными способами. Один геометрический (как наклон
кривой), а другой — физический (как скорость изменения).
Исторически была (и, может быть, до сих пор) борьба между
математиков, который из двух иллюстрирует концепцию
производная лучше и какая из них более полезна.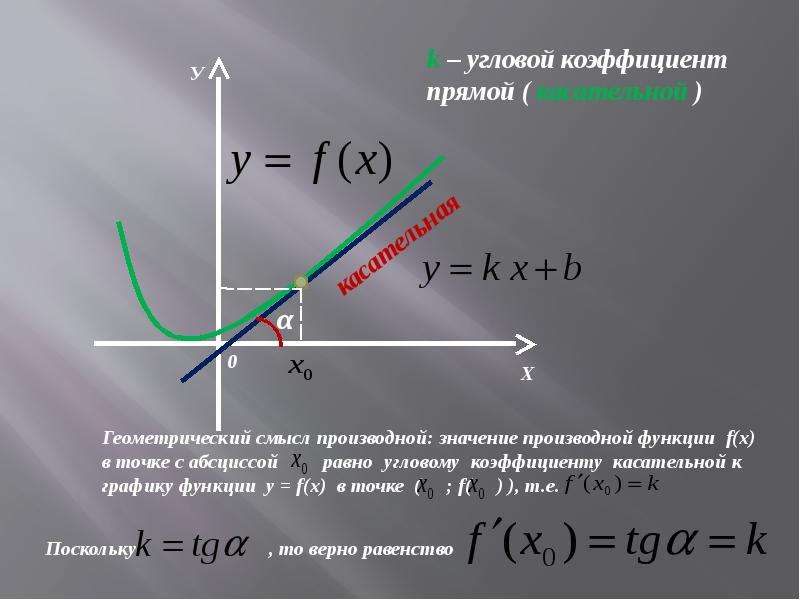 Мы не будем останавливаться
на этом и представит оба понятия. Наш акцент будет
об использовании производной в качестве инструмента.
Мы не будем останавливаться
на этом и представит оба понятия. Наш акцент будет
об использовании производной в качестве инструмента.
Если мы теперь предположим, что А и В очень близки друг к другу, мы приблизиться к тому, что называется мгновенной скоростью .Из Конечно, если А и В находятся близко друг к другу, то время, которое требуется на проезд из А в Б тоже будет мало. Действительно, предположим, что при time t = a , мы находимся в точке A. Если время, затраченное на то, чтобы добраться до точки B, равно , тогда мы будем в B во время . Если расстояние от А до В, тогда средняя скорость является
Мгновенная скорость (в точке A) будет найдена при уменьшении и уменьшении.
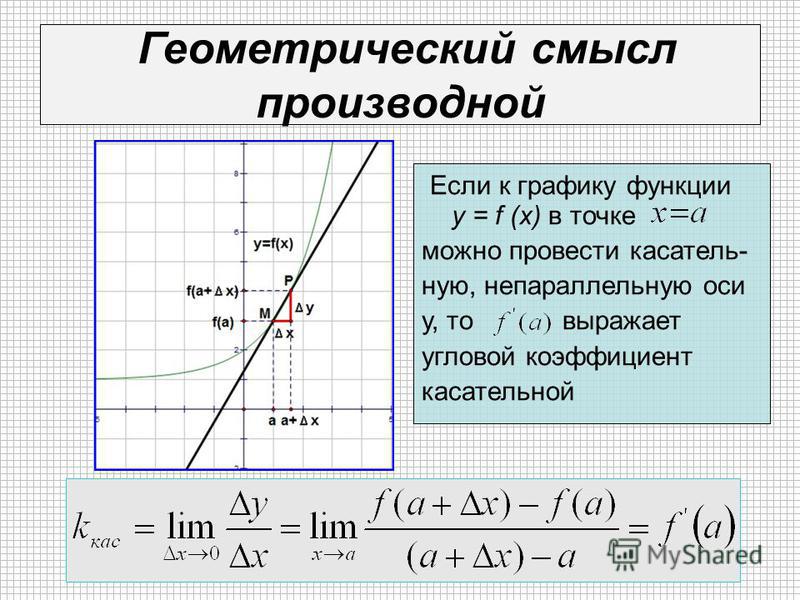 Здесь мы естественным образом сталкиваемся с понятием
предела. Действительно, у нас есть
Здесь мы естественным образом сталкиваемся с понятием
предела. Действительно, у нас есть
Если f ( t ) описывает позицию в момент времени t , то .В этом случае мы имеем
Пример. Рассмотрим параболическое движение, заданное функцией
ф ( т ) = т 2 . Мгновенная скорость при t = a определяется выражением
С
мы заключаем, что мгновенная скорость в t = a равна 2 a .
Это понятие скорости может быть расширено, чтобы найти скорость изменения любой переменной по отношению к любой другой переменной.Например, объем газа зависит от температуры газа. Таким образом, в этом случае переменными являются V (объем) как функция T (температура). В общем, если мы имеем y = f ( x ), то средняя скорость изменения y по отношению к x от x = к к
,
куда
,
является
Как и прежде, мгновенная скорость изменения y относительно до x при x = a ,
Обозначение. Теперь самое сложное. Так как мы не можем
продолжайте писать «Мгновенная скорость», выполняя вычисления,
нам нужно придумать для него подходящее обозначение. Если мы напишем
дх для
мало, то можно использовать обозначение
Теперь самое сложное. Так как мы не можем
продолжайте писать «Мгновенная скорость», выполняя вычисления,
нам нужно придумать для него подходящее обозначение. Если мы напишем
дх для
мало, то можно использовать обозначение
Это обозначение введено Лейбницем. (Вильгельм Готфрид Лейбниц (1646-1716) и Исаак Ньютон (1642-1727) считаются изобретатели исчисления.) Рассмотрим функцию y = f ( x ) и ее график.Напомним, что график функции представляет собой набор точек (то есть ( x , f ( x )) для x из домена функции f ). Мы можем нарисовать график в плоскости с горизонтальной осью (обычно называемой осью x) и вертикальная ось (обычно называемая осью Y).
Зафиксируйте точку на графике, скажем
( x 0 , f ( x 0 )). Если граф как
геометрическая фигура «хорошая» (т.е. гладкой) вокруг этой точки, это
естественно задаться вопросом, можно ли найти уравнение прямой
линия, «касающаяся» графика в этой точке.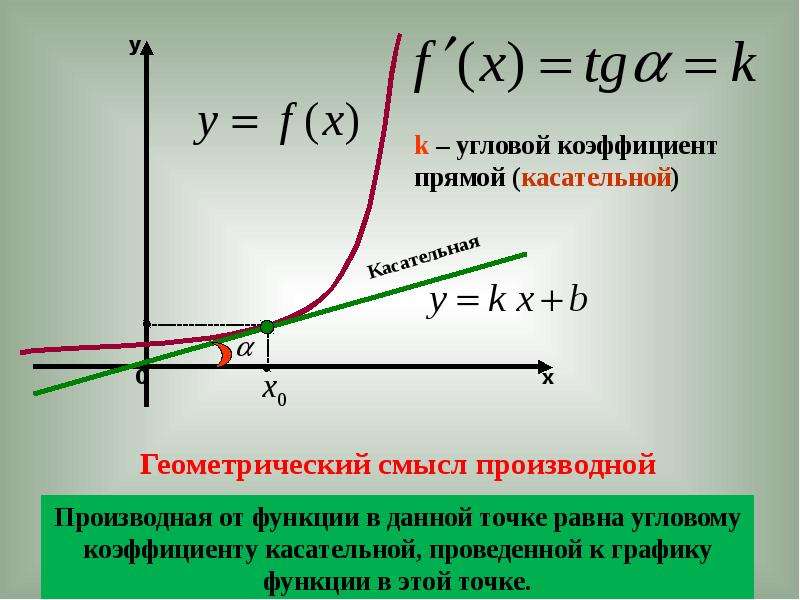 Такая прямая линия
называется касательной в рассматриваемой точке. То
понятие касательной можно рассматривать в более общем виде.
Такая прямая линия
называется касательной в рассматриваемой точке. То
понятие касательной можно рассматривать в более общем виде.
(Обратите внимание, что касательная может не существовать. Мы обсудим это случай позже.) Один из способов найти касательную — рассмотреть точек ( x , f ( x )) на графике, где x очень близко к х 0 .Затем проведите прямую, соединяющую обе точки (см. картинка ниже):
Как видите, когда x все ближе и ближе к x 0 ,
линии все ближе и ближе к касательной. Поскольку все эти
линии проходят через точку
( x 0 , f ( x 0 )), их уравнения будут
определить, найдя их наклон: Наклон линии
прохождение через точки
( x 0 , f ( x 0 )) и ( x , f ( x )) (где
)
дан кем-то
Сама касательная будет иметь уклон м , что очень близко к м ( x ), когда само x очень близко к x 0 .
 Это
концепция предела еще раз!
Это
концепция предела еще раз!
Другими словами, мы имеем
Итак, уравнение касательной имеет вид
Обозначение. Написание «м» для наклона касательной
не несет достаточно информации; мы хотим следить за
функция f ( x ) и точка x 0 в наших обозначениях. Общее
используемые обозначения
м = f ‘ ( х 0 ).
В этом случае уравнение касательной принимает вид
у — f ( х 0 ) = f ‘( х 0 ) ( х — х 5 ) 10 х 5
куда
Последнее замечание: иногда удобнее вычислить ограничения, когда переменная приближается к 0. Один из способов сделать это — сделать перенос по оси абсцисс. Действительно, если мы установим ч = х — х 0 , получаем
[Назад] [Следующий] [Тригонометрия] [Исчисление] [Геометрия] [Алгебра] [Дифференциальные уравнения] [Комплексные переменные] [Матричная алгебра] С.
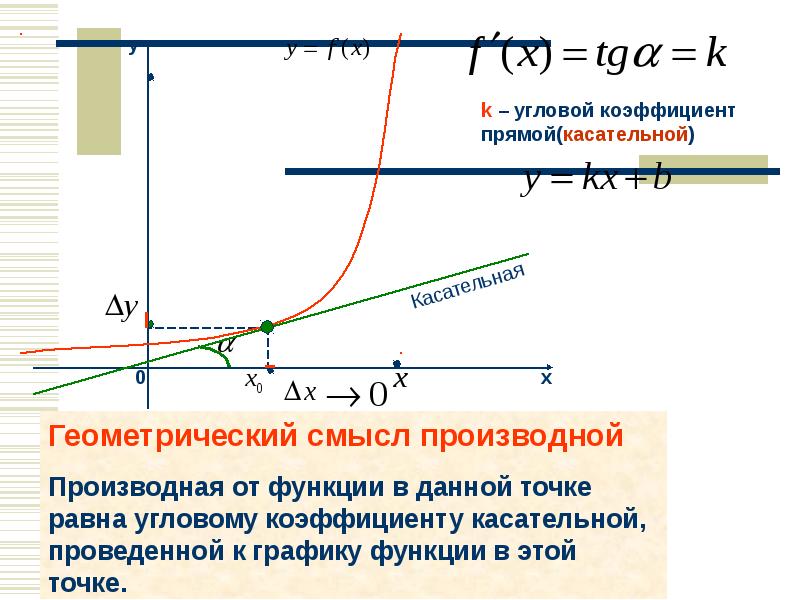 Домашняя страница OS MATHematics
Домашняя страница OS MATHematics
Вам нужна дополнительная помощь? Пожалуйста, разместите свой вопрос на нашем S.O.S. Математика CyberBoard.
Мохамед А. Хамси
Copyright 1999-2022 MathMedics, LLC. Все права защищены.
Связаться с нами
Математика Медикс, ООО. — П.О. Box 12395 — Эль-Пасо, Техас 79913 — США
пользователей онлайн за последний час
1.8: Геометрическая интерпретация производных
Напомним, что если \(y=f(x),\), то для любого действительного числа \(\Delta x\)
\[\frac{\Delta y}{\Delta x}=\frac{f(x+\Delta x)-f(x)}{\Delta x}\] — средняя скорость изменения \(y\ ) по \(x\) на интервале \([x, x+\Delta x]\) (см. \((1.2 .7)) .\) Теперь, если график \(y\) представляет собой прямую линию, то есть если \(f(x)=m x+b\) для некоторых действительных чисел \(m\) и \(b,\), то \((1.8.1)\) есть \(m,\) наклон линии. В самом деле, прямая линия характеризуется тем, что \((1.8 .1)\) одинаково для любых значений \(x\) и \(\Delta x . {\prime}(a)\), проходящую через \((a, f(a))\) касательная к графику \(f\) в точке \((a, f(a)) .{2}(x)\] в точке \(x=\frac{\pi}{4}\).
{\prime}(a)\), проходящую через \((a, f(a))\) касательная к графику \(f\) в точке \((a, f(a)) .{2}(x)\] в точке \(x=\frac{\pi}{4}\).
- Ответить
-
\(y=3\left(t-\frac{\pi}{4}\right)+\frac{3}{2}\)
|
Основополагающие рабочие инструменты исчисления, производных и интегралов пронизывают все аспекты моделирования природы в физических науках. Производная функции может быть геометрически интерпретирована как наклон кривой математической функции f(x), построенной как функция от x.Но его последствия для моделирования природы гораздо глубже, чем это может подразумевать это простое геометрическое приложение. В конце концов, вы можете представить себе, как рисуете конечные треугольники, чтобы определить наклон, так почему же производная так важна? Его важность заключается в том, что многие физические величины, такие как скорость, ускорение, сила и т. Интеграл функции может быть геометрически интерпретирован как площадь под кривой математической функции f(x), построенной как функция от x. Вы можете увидеть, как рисуете большое количество блоков, чтобы аппроксимировать площадь под сложной кривой, получая лучший ответ, если вы используете больше блоков. Интеграл дает вам математический способ рисования бесконечного числа блоков и получения точного аналитического выражения для площади. Это очень важно для геометрии — и чрезвычайно важно для физических наук, где определения многих физических объектов могут быть выражены в математической форме, такой как площадь под кривой.Площадь маленького блока под кривой можно представить как ширину полосы, взвешенную (то есть умноженную на) на высоту полосы. Многие свойства непрерывных тел зависят от взвешенных сумм, которые, если быть точными, должны быть бесконечными взвешенными суммами — проблема, созданная специально для интеграла. |
Индекс Производные понятия Интегральные понятия |
Вся элементарная математика — Учебное пособие — Принципы анализа
Производные. Инкременты аргумента и функции. Дифференцируемая функция.Геометрический смысл производной. Наклон касательной. Касательное уравнение.
Механическое значение производной. Мгновенная скорость. Ускорение.
Производный. Рассмотрим функцию y = F = F ( x ) в двух очках: x 4 0 и x 0 5 +: F ( x 4 0 ) и F ( х 0 + ). Здесь означает небольшое изменение аргумента, называемое приращением аргумента ; соответственно разность между двумя значениями функции: f ( x 0 + ) – f ( x 0 ) называется приращением 11 функции4. Производное функции Y = F ( x ) в точке x 0 — это предел:
Здесь означает небольшое изменение аргумента, называемое приращением аргумента ; соответственно разность между двумя значениями функции: f ( x 0 + ) – f ( x 0 ) называется приращением 11 функции4. Производное функции Y = F ( x ) в точке x 0 — это предел:
Если этот предел существует, то функция F ( x ) является дифференцируемой функцией в точке x 0 . Производная функции f ( x ) помечается как:
Геометрический смысл производной. Рассмотрим график функции y = f ( x ) :
Из рис.1 мы видим, что для любых двух точек А и В графика функции:
где — угол наклона секущей АВ.
Таким образом, коэффициент разности равен наклону секущей. Если зафиксировать точку А и сдвинуть точку В к А, то неограниченно уменьшится и будет приближаться к 0, а секущая АВ будет приближаться к касательной АС.
 Отсюда предел разностного отношения равен наклону касательной в точке А. Отсюда следует: производная функции в точке есть наклон касательной графика этой функции в этой точке.
Отсюда предел разностного отношения равен наклону касательной в точке А. Отсюда следует: производная функции в точке есть наклон касательной графика этой функции в этой точке. Касательное уравнение. Теперь составим уравнение касательной к графику функции в точке A ( x 0 , f ( x 0 4 ) 900). В общем случае уравнение прямой линии с наклоном F ( x 4 0 ) имеет форму:
y = F ( x 0 ) x + б .Чтобы найти B Bell Использовать тот факт, что касательная линия проходит через точку A:
F ( x 0 F ( x 4 0 ) x 4 0 + B , , следовательно, B = F ( x 4 0 5 ) — F ( x 4 0 ) x 0 , и подставляя это выражение вместо B , хорошо получите уравнение касательного: y = F ( x 4 0 ) + F ( x 0 ) ( х – х 0 ) .
Механическое значение производной. Рассмотрим простейший случай: движение материальной точки вдоль координатной линии, причем задан закон движения, т.е. координата х этой движущейся точки есть известная функция х ( t ) времени t . Во время интервала времени от T 4 0 до T 0 + Точечное перемещение равно: x ( T 0 +) — x ( t 0 ) = , а его средняя скорость равна: v a = / . При 0 среднее значение скорости приближается к определенному значению, которое называется мгновенной скоростью v ( t 0 ) материальной точки в момент t 0 . Но согласно производному определению у нас есть:
, следовательно, V ( V ( T 0 ) = X ( T 0 ), IE A Производная координата по отношению ко времени скорость.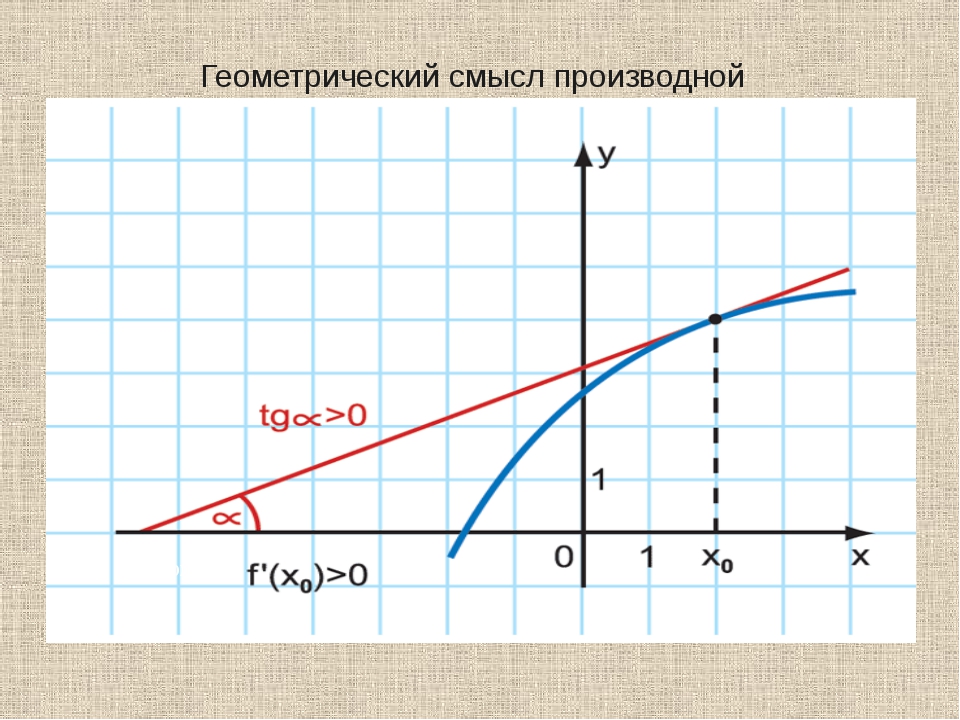 Это механическое значение производной. Аналогично этому, ускорение является производной скорости по времени : a = v ( t ).
Это механическое значение производной. Аналогично этому, ускорение является производной скорости по времени : a = v ( t ).
Каков физический смысл производной? – Greedhead.net
Каков физический смысл производной?
Производная определяется как мгновенная скорость изменения в данной точке. Обычно мы различаем два вида функций, неявные и явные функции.Явные функции — это функции, в которых известное значение независимой переменной «х» напрямую приводит к значению зависимой переменной «у».
Каков геометрический смысл дифференцируемости?
Геометрическая интерпретация дифференцируемости Грубо говоря, если мы «увеличим» график функции вблизи точки, и график будет выглядеть очень близко к прямой, то функция будет дифференцируемой в этой точке.
Каково геометрическое значение dy dx?
Геометрический смысл производной в точке Производная [f'(x) или dy/dx] функции y = f(x) в точке P(x, y) (если она существует) равна наклону (или градиенту ) касательной к кривой y = f(x) в точке P(x, y).
Каковы 2 определения производной?
К определению производной можно подойти двумя разными способами. Один из них геометрический (как наклон кривой), а другой — физический (как скорость изменения).
Что такое производная?
Производная — это мгновенная скорость изменения функции по отношению к одной из ее переменных. Это эквивалентно нахождению наклона касательной к функции в точке.
Что такое геометрическая интерпретация?
Напротив, «интерпретировать геометрически» просто означает взять что-то, что изначально/по своей сути не входит в сферу геометрии, и представить это визуально с помощью чего-то другого, кроме уравнений или просто чисел (т.г., таблицы).
Что означает геометрическое представление?
Геометрическое представление L — это представление в решетке подпространств векторного пространства над некоторым телом.
Что такое геометрическое значение?
Это просто означает, как вы можете геометрически интерпретировать что-то в обсуждаемой теме. Поскольку у геометрии есть много аспектов, есть много способов интерпретировать вещи геометрически.
Поскольку у геометрии есть много аспектов, есть много способов интерпретировать вещи геометрически.
Что такое английское значение слова «геометрический»?
1.относительно, или следуя методам и принципам геометрии. 2. состоящий из точек, линий, кривых или поверхностей, образованный ими или характеризуемый ими.
Что вы подразумеваете под производным определением?
производная, в математике скорость изменения функции по отношению к переменной. Геометрически производную функции можно интерпретировать как наклон графика функции или, точнее, как наклон касательной в точке.
Каково геометрическое определение производных?
Геометрическая идея производной — это просто обобщение понятия наклона.Мы приходим к концепции, которую называем производной, когда пытаемся вычислить наклон кривой, которая не является прямой линией. Геометрическое определение производной, к которому мы придем, будет очень похоже на приведенное выше определение наклона.
Как называется производная функции?
Геометрическое определение производной. Производная функции f (x) при x = x0, обозначаемая f'(x0) или (x0), может быть наивно определена как наклон графика f при x = x0. Проблема в том, что мы не сказали, что мы подразумеваем под наклоном произвольного графика в точке.Однако мы знаем, что мы подразумеваем под наклоном линии.
Что такое производная кривой?
К определению производной можно подойти двумя разными способами. Один из них геометрический (как наклон кривой), а другой — физический (как скорость изменения).
Как понять геометрическую интуицию для производной?
Чтобы понять геометрическую интуицию для производной, нам нужно повторить понятие из алгебры: наклон. В обычных курсах исчисления предполагается, что вы хорошо разбираетесь в этой концепции.Однако, по моему опыту, большинство студентов, достигших уровня исчисления, не имеют с ним необходимого знакомства.
Геометрический и физический смысл производной 1 вариант. Определение производной. Его физический и геометрический смысл
Производной функции f(x) в точке x0 является предел (если он существует) отношения приращения функции в точке x0 к приращению аргумента Δx, если приращение аргумента стремится к нулю и обозначается через f ‘(x0).Действие по нахождению производной функции называется дифференцированием.
Производная функции имеет следующий физический смысл: производная функции в заданной точке — скорость изменения функции в данной точке.
Геометрический смысл производной … Производная в точке x0 равна наклону касательной к графику функции y = f(x) в этой точке.
Физический смысл производной. Если точка движется вдоль оси x и ее координата изменяется по закону x(t), то мгновенная скорость точки равна:
Дифференциальное понятие, его свойства. Правила дифференциации. Примеры.
Правила дифференциации. Примеры.
Определение. Дифференциал функции в некоторой точке х есть основная, линейная часть приращения функции. Дифференциал функции y = f(x) равен произведению ее производной на приращение независимой переменной x (аргумент).
Записывается так:
или
Или
Дифференциальные свойства
Дифференциал обладает свойствами, аналогичными свойствам производной:
К К основным правилам дифференцирования относятся:
1) вынесение знака постоянного множителя из производной
2) производная суммы, производная разности
3) производная произведения функций
4) производная частного двух функций (производная дроби)
Примеры.
Докажем формулу: По определению производной имеем:
Произвольный множитель можно вынести за знак предельного перехода (это известно из свойств предела), поэтому
Например: Найдите производную функции
Решение: Воспользуемся правилом вынесения множителя из-под знака производной :
Довольно часто сначала приходится упростить вид дифференцированной функцию для того, чтобы пользоваться таблицей производных и правилами нахождения производных. Следующие примеры наглядно это подтверждают.
Следующие примеры наглядно это подтверждают.
Формулы дифференцирования. Дифференциальное применение в приближенных расчетах. Примеры.
Использование дифференциала в приближенных вычислениях позволяет использовать дифференциал для приближенных вычислений значений функции.
Примеры .
Используя дифференциал, вычислить приблизительно
Для вычисления заданного значения применить формулу из теории
Введем в рассмотрение функцию и представим заданное значение в виде
, затем Вычислим
Подставляя все в формулу, окончательно получаем
Ответ:
16.Правило Лопиталя для раскрытия неопределенностей вида 0/0 Or ∞ / ∞. Примеры.
Предел отношения двух бесконечно малых или двух бесконечно больших величин равен пределу отношения их производных.
1)
17. Увеличение и уменьшение функции. Экстремальная функция. Алгоритм исследования функции на монотонность и экстремум. Примеры.
Примеры.
Функция является возрастающей на отрезке , если для любых двух точек этого отрезка, связанных соотношением, выполняется неравенство.То есть большему значению аргумента соответствует большее значение функции, а ее график идет «снизу вверх». Демонстрационная функция растет на интервале
Аналогично функция убывает на на отрезке, если для любых двух точек данного отрезка таких, что неравенство верно. То есть большему значению аргумента соответствует меньшее значение функции, а ее график идет «сверху вниз». Наш уменьшается с интервалами уменьшается с интервалами.
Экстремумы Точка называется точкой максимума функции y = f(x), если неравенство выполняется для всех x из ее окрестности. Значение функции в точке максимума называют максимальной функцией и обозначают.
Точка называется точкой минимума функции y = f(x), если неравенство выполняется для всех x из ее окрестности. Значение функции в точке минимума называют минимумом функции и обозначают.
Под окрестностью точки понимается интервал , где – достаточно малое положительное число.
Точки минимума и максимума называются точками экстремума, а значения функции, соответствующие точкам экстремума, называются экстремумами функции .
Для исследования функции на монотонности используйте следующую схему:
— Найдите область определения функции;
— Найти производную функции и область определения производной;
— Найти нули производной, т.е. значение аргумента, при котором производная равна нулю;
— На числовых лучах отметьте общей частью область определения функции и область определения ее производной, а на ней — нули производной;
— Определить знаки производной на каждом из полученных интервалов;
— По знакам производной определить, через какие промежутки функция возрастает, а через какие убывает;
— Запишите соответствующие пробелы через точку с запятой.
Алгоритм исследования непрерывной функции y = f(x) на монотонность и экстремумы :
1) Найти производную f′(x).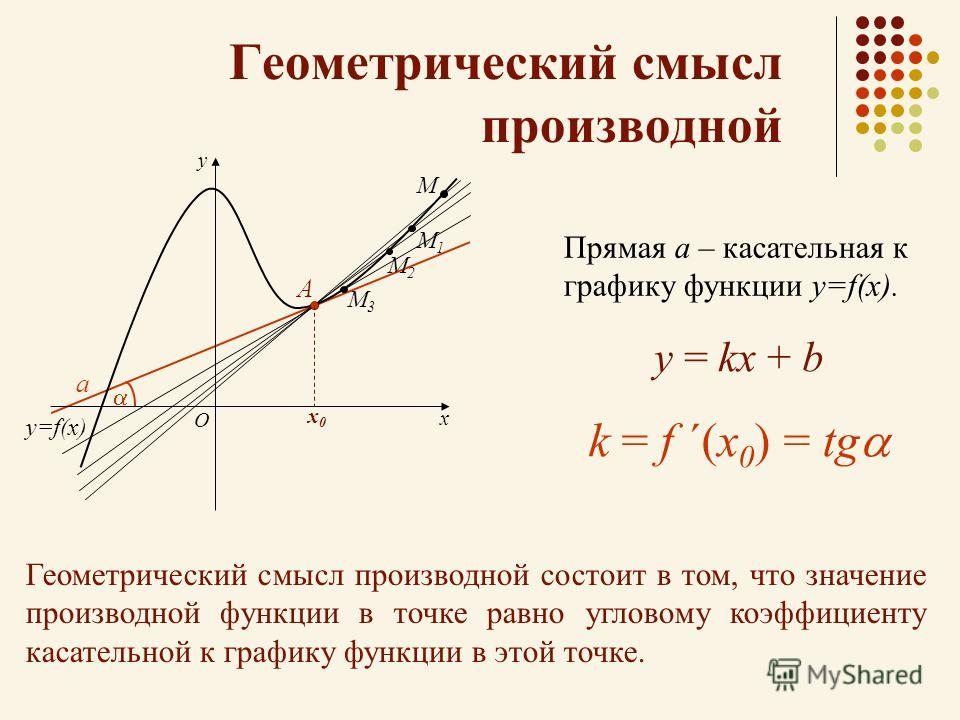
2) Найти стационарные (f ′ (x) = 0) и критические (f ′ (x) не существует) точки функции y = f (x).
3) Отметить стационарные и критические точки на числовой прямой и определить знаки производной на полученных отрезках.
4) Сделать выводы о монотонности функции и ее экстремальных точках.
18.Выпуклость функции. Точки перегиба. Алгоритм исследования функции на выпуклость (вогнутость) Примеры .
выпуклая вниз на отрезке X, если ее график расположен не ниже касательной к ней в любой точке отрезка X.
Дифференцируемая функция называется выпуклой вверх на интервале X, если ее график расположен не выше касательной к ней в любой точке интервала X.
Точка формулы называется точкой перегиба функции у = f(x), если в данной точке есть касательная к графику функции (может быть параллельна оси Оу) и есть такая окрестность точечной формулы, в пределах которой график функции имеет разные направления выпуклости влево и вправо от точки М.
Нахождение интервалов выпуклости:
Если функция y = f(x) имеет конечную вторую производную на отрезке X и выполняется неравенство (), то график функции имеет выпуклость, направленную вниз (вверх) на X.
Эта теорема позволяет найти интервалы вогнутости и выпуклости функции; надо только решить неравенства и, соответственно, на область определения исходной функции.
Пример : Найдите интервалы, на которых график функции Найдите интервалы, на которых график функции имеет восходящую выпуклость и нисходящую выпуклость.имеет выпуклость вверх и выпуклость вниз.
Решение: Областью определения этой функции является весь набор действительных чисел.
Найдем вторую производную.
Область определения второй производной совпадает с областью определения исходной функции, поэтому для нахождения интервалов вогнутости и выпуклости достаточно решить и соответственно. Следовательно, функция выпукла вниз по интервальной формуле и выпукла вверх по интервальной формуле.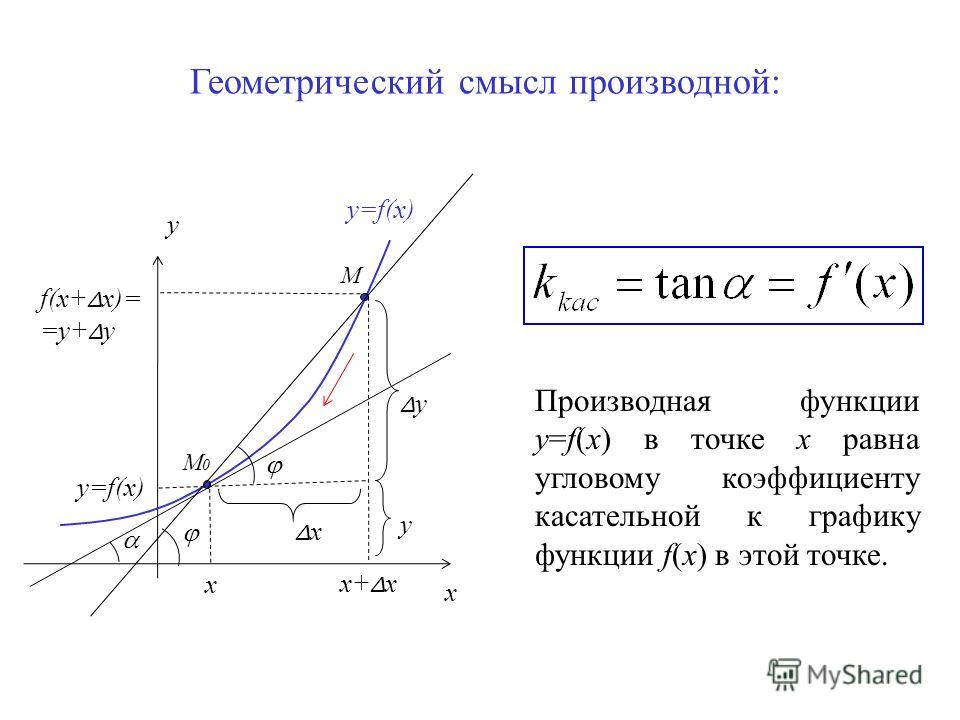
19) Асимптоты функции. Примеры.
Прямая называется вертикальной асимптотой графиком функции, если хотя бы одно из предельных значений равно или .
Комментарий. Прямая не может быть вертикальной асимптотой, если функция непрерывна в точке. Поэтому вертикальные асимптоты следует искать в точках разрыва функции.
Прямая линия называется горизонтальной асимптотой графиком функции, если хотя бы одно из предельных значений или равно.
Комментарий. График функции может иметь только правую горизонтальную асимптоту или только левую.
Прямая линия называется наклонной асимптотой графиком функции
ПРИМЕР:
Упражнение. Найдите асимптоты графика функции
Раствор. Объем функции:
а) вертикальные асимптоты: прямая — вертикальная асимптота, начиная с
б) горизонтальные асимптоты: находим предел функции на бесконечности:
, то есть горизонтальных асимптот нет.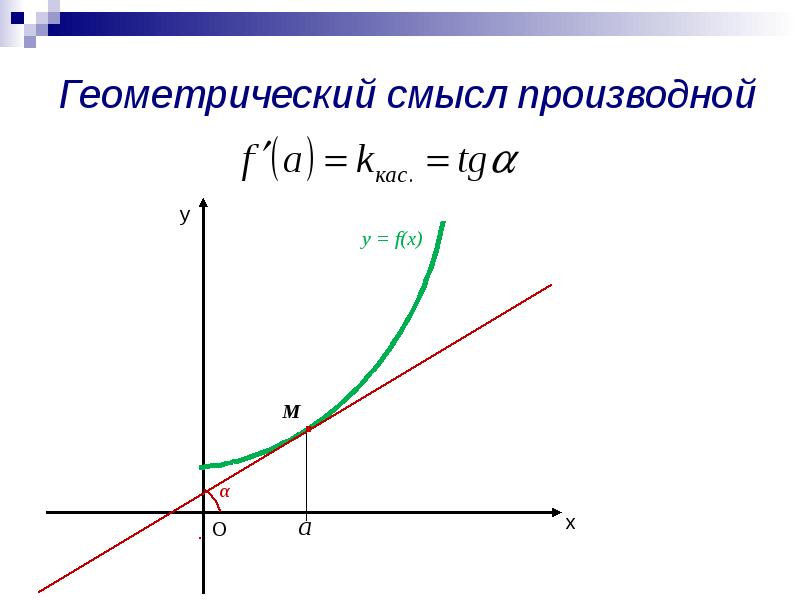
в) наклонные асимптоты:
Таким образом, наклонная асимптота равна:.
Ответ. Вертикальная асимптота прямая.
Наклонная асимптота прямая.
20) Общая схема исследования функции и построения графика. Пример.
а.
Найти ОДЗ и точки останова функции.
б. Найдите точки пересечения графика функции с осями координат.
2.Провести исследование функции по первой производной, то есть найти точки экстремума функции и интервалы возрастания и убывания.
3. Исследуйте функцию с помощью производной второго порядка, т. е. найдите точки перегиба графика функции и интервалы ее выпуклости и вогнутости.
4. Найдите асимптоты графика функции: а) вертикального, б) наклонного.
5. На основе исследования построить график функции.
Обратите внимание, что перед построением графика полезно определить, является ли заданная функция четной или нечетной.
Напомним, что функция вызывается, даже если значение функции не меняется при изменении знака аргумента: f (-x) = f (x) и функция называется нечетной, если f (-x) = -f(x). (2)) + 5\ ]
(2)) + 5\ ]
Нам нужно найти производную в точке 2.(2)) + 5 = \]
\[=-16+32-12+5=9\]
Вот и все, мы нашли окончательный ответ. Итого, скорость нашей материальной точки в момент времени $t=2c$ будет равна 9 м/с.
Пример № 2
Материальная точка движется по закону:
где $x$ — расстояние от точки отсчета в метрах, $t$ — время в секундах, отсчитываемое от начала движения. В какой момент времени его скорость была равна 3 м/с?
Смотрите, в прошлый раз от нас требовалось найти $v$ в момент времени 2 с, а в этот раз требуется найти тот самый момент, когда эта скорость будет равна 3 м/с.(2)) = 0 \]
Полученное число означает, что в момент времени 4 с$v$ движения материальной точки по вышеописанному закону она как раз будет равна 3 м/с.
Ключевые точки
В заключение еще раз пройдемся по самому главному пункту сегодняшней задачи, а именно по правилу перевода расстояния в скорость и ускорение. Итак, если в нашей задаче прямо описан закон, прямо указывающий расстояние от материальной точки до точки отсчета, то по этой формуле можно найти любую мгновенную скорость (это всего лишь производная). И более того, мы также можем найти ускорение. Ускорение, в свою очередь, равно производной скорости, т.е. второй производной расстояния. Такие задачи достаточно редки, поэтому сегодня мы их не разбирали. Но если вы видите в условии слово «ускорение», пусть вас это не пугает, достаточно просто найти другую производную.
И более того, мы также можем найти ускорение. Ускорение, в свою очередь, равно производной скорости, т.е. второй производной расстояния. Такие задачи достаточно редки, поэтому сегодня мы их не разбирали. Но если вы видите в условии слово «ускорение», пусть вас это не пугает, достаточно просто найти другую производную.
Надеюсь, этот урок поможет вам подготовиться к ЕГЭ по математике.
Математические задачи находят применение во многих науках.К ним относятся не только физика, химия, инженерия и экономика, но и медицина, экология и другие дисциплины. Одним из важных понятий, которым необходимо овладеть, чтобы найти решения важных дилемм, является производная функции. Физический смысл его вовсе не так сложно объяснить, как может показаться непосвященному в суть вопроса. Достаточно просто найти для этого подходящие примеры в реальной жизни и обычных бытовых ситуациях. На самом деле любой автомобилист ежедневно справляется с подобной задачей, когда смотрит на спидометр, определяя скорость своего автомобиля в конкретный момент фиксированного времени. Ведь именно в этом параметре и заключается суть физического смысла производной.
Ведь именно в этом параметре и заключается суть физического смысла производной.
Как найти скорость
Любой пятиклассник легко может определить скорость движения человека по дороге, зная пройденное расстояние и время в пути. Для этого нужно разделить первое из заданных значений на второе. Но не каждый молодой математик знает, что в этот момент находится отношение приращений функции и аргумента. Действительно, если представить движение в виде графика, отложив путь по ординате, а время по абсциссе, то это будет именно так.
Однако скорость пешехода или любого другого объекта, которую мы определяем на большом участке пути, считая движение равномерным, вполне может различаться. В физике известны многие формы движения. Его можно выполнять не только с постоянным ускорением, но и произвольно замедлять и увеличивать. Следует отметить, что в этом случае линия, описывающая движение, уже не будет прямой линией. Графически он может принимать самые сложные конфигурации. Но для любой из точек на графике всегда можно провести касательную, представленную линейной функцией.
Для уточнения параметра изменения водоизмещения в зависимости от времени необходимо укоротить измеряемые отрезки. Когда они станут бесконечно малыми, расчетная скорость будет мгновенной. Этот опыт помогает нам определить производную. Из такого рассуждения логически вытекает и его физический смысл.
Геометрически
Известно, что чем выше скорость тела, тем круче график зависимости перемещения от времени, а значит и угол наклона касательной к графику в определенной точке.Индикатором таких изменений может служить тангенс угла между осью абсцисс и линией касательной. Именно он определяет значение производной и рассчитывается отношением длин противолежащего катета к прилежащему в прямоугольном треугольнике, образованном перпендикуляром, опущенным из некоторой точки на оси абсцисс.
Это геометрическое значение первой производной. Физическая проявляется в том, что величина противоположной ноги в нашем случае представляет собой пройденный путь, а соседней — время. В данном случае их отношением является скорость. И снова приходим к выводу, что мгновенная скорость, определяемая при стремлении обоих интервалов к бесконечно малому, есть сущность, указывающая на ее физический смысл. Второй производной в этом примере будет ускорение тела, демонстрирующее, в свою очередь, степень изменения скорости.
В данном случае их отношением является скорость. И снова приходим к выводу, что мгновенная скорость, определяемая при стремлении обоих интервалов к бесконечно малому, есть сущность, указывающая на ее физический смысл. Второй производной в этом примере будет ускорение тела, демонстрирующее, в свою очередь, степень изменения скорости.
Примеры нахождения производных в физике
Производная является показателем скорости изменения любой функции, даже если она не является движением в прямом смысле этого слова.Чтобы наглядно продемонстрировать это, приведем несколько конкретных примеров. Предположим, что сила тока в зависимости от времени изменяется по следующему закону: I = 0,4t 2. Требуется найти значение скорость изменения этого параметра в конце 8-й секунды процесса. Обратите внимание, что само желаемое значение, как можно судить из уравнения, постоянно увеличивается.
Для ее решения требуется найти первую производную, физический смысл которой был рассмотрен ранее. Здесь dI /
дт = 0,8
t … Далее находим для t =8
получаем, что скорость изменения силы тока равна 6,4
А /
с .
Здесь считается, что сила тока измеряется в амперах, а время, соответственно, в секундах.
Здесь dI /
дт = 0,8
t … Далее находим для t =8
получаем, что скорость изменения силы тока равна 6,4
А /
с .
Здесь считается, что сила тока измеряется в амперах, а время, соответственно, в секундах.
Все изменчиво
Видимый мир, состоящий из материи, постоянно претерпевает изменения, находясь в движении различных процессов, происходящих в нем.Для их описания можно использовать различные параметры. Если они объединены зависимостью, то математически записываются в виде функции, графически отображающей их изменения. А где есть движение (в какой бы форме оно ни выражалось), там же существует и производная, физический смысл которой мы и рассматриваем в настоящий момент.
По этому поводу следующий пример… Допустим температура тела изменяется по закону T =0,2
т 2
… Найдите скорость, с которой он прогревается в конце 10-й секунды. Задача решается аналогично описанному в предыдущем случае. То есть находим производную и подставляем значение
т = 10
, получаем Т = 0,4
т = 4.
Это означает, что окончательный ответ равен 4 градусам в секунду, то есть процесс нагрева и изменение температуры, измеряемое в градусах, происходит именно с такой скоростью.
Задача решается аналогично описанному в предыдущем случае. То есть находим производную и подставляем значение
т = 10
, получаем Т = 0,4
т = 4.
Это означает, что окончательный ответ равен 4 градусам в секунду, то есть процесс нагрева и изменение температуры, измеряемое в градусах, происходит именно с такой скоростью.
Решение практических задач
Конечно, в жизни все гораздо сложнее, чем в теоретических задачах. На практике значение величин обычно определяют в ходе эксперимента. В этом случае используются приборы, дающие показания при измерениях с определенной погрешностью. Поэтому при расчетах приходится иметь дело с приблизительными значениями параметров и прибегать к округлению неудобных чисел, а также к другим упрощениям.Принимая это во внимание, мы снова переходим к проблемам физического смысла производной, принимая во внимание, что они являются лишь определенной математической моделью сложных процессов, происходящих в природе.
Извержение
Представьте, что происходит извержение вулкана. Насколько он может быть опасен? Чтобы прояснить этот вопрос, необходимо рассмотреть множество факторов. Мы постараемся учесть один из них.
Из пасти «огненного монстра» вертикально вверх выбрасываются камни, имеющие начальную скорость с момента выхода.Необходимо рассчитать, насколько они могут достигать максимальной высоты.
Чтобы найти искомое значение, составим уравнение зависимости высоты Н, измеряемой в метрах, от других величин. К ним относятся начальная скорость и время. Величину ускорения считаем известной и примерно равной 10 м/с 2.
Частная производная
Рассмотрим теперь физический смысл производной функции немного с другой стороны, ибо само уравнение может содержать не одну, а несколько переменных.Например, в предыдущей задаче зависимость высоты подъема камней, выбрасываемых из жерла вулкана, определялась не только изменением временных характеристик, но и величиной начальной скорости. Последняя рассматривалась постоянное, фиксированное значение. Но в других задачах с совсем другими условиями все могло быть иначе. Если величин, от которых зависит комплексная функция, несколько, расчеты производятся по приведенным ниже формулам.
Последняя рассматривалась постоянное, фиксированное значение. Но в других задачах с совсем другими условиями все могло быть иначе. Если величин, от которых зависит комплексная функция, несколько, расчеты производятся по приведенным ниже формулам.
Физический смысл частной производной следует определять, как и в обычном случае.Это скорость изменения функции в определенный момент при увеличении параметра переменной. Он рассчитывается таким образом, что все остальные компоненты принимаются постоянными, а переменным считается только один. Дальше все происходит по обычным правилам.
Понимая физический смысл производной, нетрудно привести примеры решения запутанных и сложных задач, ответ на которые позволяет найти аналогичные знания. Если у нас есть функция, описывающая расход топлива в зависимости от скорости автомобиля, мы можем рассчитать, при каких параметрах последний расход бензина будет наименьшим.
В медицине можно предсказать, как отреагирует организм человека на лекарство, назначенное врачом. Прием препарата влияет на множество физиологических показателей. К ним относятся изменения артериального давления, частоты сердечных сокращений, температуры тела и многое другое. Все они зависят от дозы принимаемого лекарственного средства. Эти расчеты помогают предвидеть ход лечения как при благоприятных проявлениях, так и при нежелательных случайностях, которые могут фатально сказаться на изменениях в организме больного.
Прием препарата влияет на множество физиологических показателей. К ним относятся изменения артериального давления, частоты сердечных сокращений, температуры тела и многое другое. Все они зависят от дозы принимаемого лекарственного средства. Эти расчеты помогают предвидеть ход лечения как при благоприятных проявлениях, так и при нежелательных случайностях, которые могут фатально сказаться на изменениях в организме больного.
Несомненно, важно понимать физический смысл производной в технических вопросах, в частности в электротехнике, электронике, проектировании и строительстве.
Тормозной путь
Рассмотрим следующую задачу. Двигаясь с постоянной скоростью, автомобиль, подъезжая к мосту, должен был затормозить за 10 секунд до въезда, так как водитель заметил дорожный знак, запрещающий движение со скоростью более 36 км/ч. Нарушил ли водитель правила, если тормозной путь можно описать формулой S = 26t — t 2 ?
После вычисления первой производной находим формулу скорости, получаем v = 28 — 2t.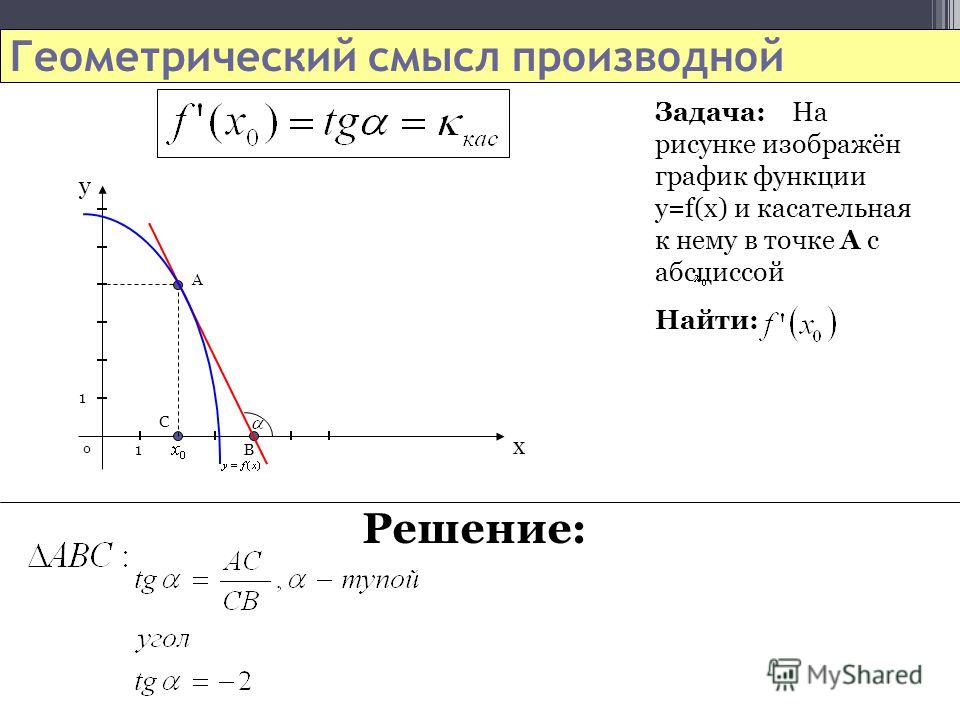 Далее подставляем в указанное выражение значение t = 10.
Далее подставляем в указанное выражение значение t = 10.
Так как это значение было выражено в секундах, то скорость получается 8 м/с, значит 28,8 км/ч. Это дает возможность понять, что водитель вовремя начал тормозить и не нарушал ПДД, а значит и ограничение скорости, указанное на знаке.
Это доказывает важность физического смысла производной. Пример решения этой задачи демонстрирует широту использования этого понятия в различных сферах жизни. В том числе и в бытовых ситуациях.
Производная в экономике
До XIX века экономисты в основном оперировали средними величинами, будь то производительность труда или цена продукции. Но с какого-то момента предельные значения стали более необходимыми для эффективных прогнозов в этой области. К ним относятся предельная полезность, доход или стоимость. Понимание этого дало толчок к созданию совершенно нового инструмента экономических исследований, который существует и развивается уже более ста лет.
Для составления таких расчетов, где преобладают такие понятия, как минимум и максимум, просто необходимо понимать геометрический и физический смысл производной.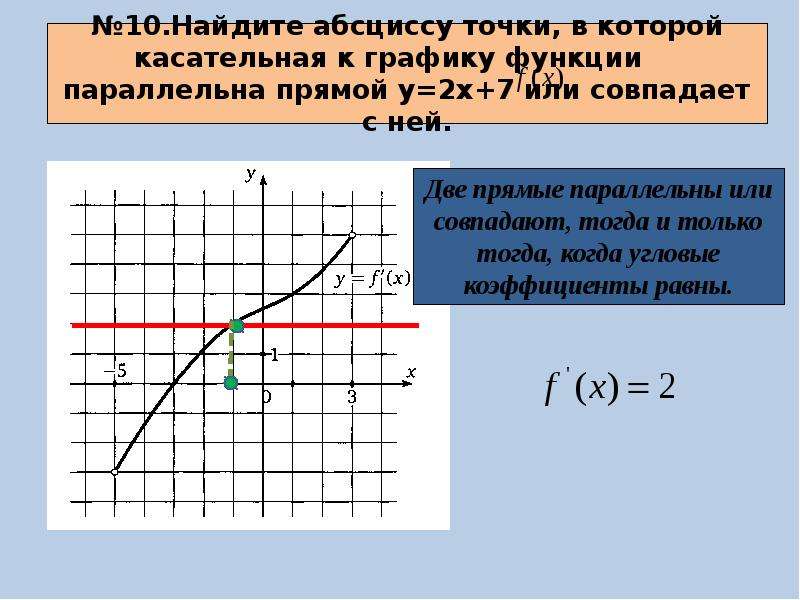 Среди создателей теоретической базы этих дисциплин можно назвать таких выдающихся английских и австрийских экономистов, как У. Джевонс, К. Менгер и другие. Конечно, не всегда удобно использовать предельные значения в экономических расчетах. И, например, квартальные отчеты не обязательно вписываются в существующую схему, но тем не менее применение такой теории во многих случаях может быть полезным и эффективным.
Среди создателей теоретической базы этих дисциплин можно назвать таких выдающихся английских и австрийских экономистов, как У. Джевонс, К. Менгер и другие. Конечно, не всегда удобно использовать предельные значения в экономических расчетах. И, например, квартальные отчеты не обязательно вписываются в существующую схему, но тем не менее применение такой теории во многих случаях может быть полезным и эффективным.
Алгебраический и геометрический смысл производной
Примечание: Это первая часть серии производных концепций.Вторая часть — «Производная в контексте реальной жизни», а третья — «Производная и проблема максимальной площади».
***
Если мы хотим получить наклон линии, нам нужны две точки. Предположим, точки имеют координаты и , мы узнали, что наклон описывается формулой .
На рисунке 1 у нас есть линия, касательная к функции в точке, где координаты равны . Проблема, породившая исчисление, заключается в том, чтобы получить наклон этой касательной. Однако есть проблема. Нам нужны две точки для вычисления наклона, но у нас есть только одна точка.
Однако есть проблема. Нам нужны две точки для вычисления наклона, но у нас есть только одна точка.
Обратите внимание, что слово касательная в этой задаче отличается от определения касательной к окружности, потому что ясно, что линия будет пересекать график более чем в одной точке.
Рисунок 1 – Прямая l, касательная к функции f в точке P.
Используя концепцию пределов, мы можем решить эту проблему. Во-первых, мы создаем точку с единицами координат x справа от координаты x .Затем мы проводим линию, секанс линия к функции.
Рисунок 2. Секущая проведена через точку P.
Фактически координаты были бы и понятно, что наклон секущей описывается формулой
Если мы хотим аппроксимировать наклон касательной, разумно двигаться в направлении фиксированной. Нажмите здесь, чтобы изучить диаграмму выше с помощью GeoGebra.
Из исследования GeoGebra выше, если мы движемся к , мы наблюдаем следующее:
1.) Значение подходов .

 д., определяются как мгновенные скорости изменения какой-либо другой величины. Производная может дать вам точное мгновенное значение для этой скорости изменения и привести к точному моделированию желаемой величины.
д., определяются как мгновенные скорости изменения какой-либо другой величины. Производная может дать вам точное мгновенное значение для этой скорости изменения и привести к точному моделированию желаемой величины. Например, нахождение центра масс непрерывного тела включает взвешивание каждого элемента массы по его расстоянию от оси вращения, процесс, для которого необходим интеграл, если вы хотите получить точное значение.Огромное количество физических задач включает в свои решения такие бесконечные суммы, что делает интеграл важным инструментом для ученого-физика.
Например, нахождение центра масс непрерывного тела включает взвешивание каждого элемента массы по его расстоянию от оси вращения, процесс, для которого необходим интеграл, если вы хотите получить точное значение.Огромное количество физических задач включает в свои решения такие бесконечные суммы, что делает интеграл важным инструментом для ученого-физика.