Формулы по тригонометрии 10 класс – Формулы по тригонометрии 10 класс шпаргалка - Управленческое образование

Содержание

73 формулы тригонометрии

На странице вы найдете все формулы тригонометрии в удобном для использования оформлении. Формулы структурированы в блоки по количеству аргументов, степеням, арифметическим операциям над ними.

Все формулы тригонометрии

Основные тригонометрические тождества

{\tg \alpha = \dfrac {\sin \alpha}{ \cos \alpha} = \dfrac{1}{\ctg \alpha}}

{\ctg \alpha = \dfrac {\cos \alpha}{ \sin \alpha} = \dfrac{1}{\tg \alpha}}

{\sin ^2 \alpha + \cos ^2 \alpha = 1}

{1+\tg^2\alpha=\dfrac{1}{\cos^2\alpha}}

{1+\ctg^2\alpha=\dfrac{1}{\sin^2\alpha}}

{\tg\alpha \cdot \ctg\alpha=1}

Формулы двойного угла (аргумента)

{\sin(2\alpha)=2 \cdot \cos \alpha \cdot \sin \alpha}

{\sin(2\alpha)=\dfrac{2 \cdot \tg \alpha}{1+\tg ^2 \alpha}=\dfrac{2 \cdot \ctg \alpha}{1+\ctg ^2 \alpha}=\dfrac{2}{\tg \alpha + \ctg \alpha}}

{\cos(2\alpha)=\cos ^2 \alpha- \sin ^2 \alpha = 2 \cdot \cos ^2 \alpha- 1 = 1- 2 \cdot \sin ^2 \alpha}

{\cos(2\alpha)=\dfrac{1 -\tg ^2 \alpha}{1+\tg ^2 \alpha}=\dfrac{\ctg ^2 \alpha- 1}{\ctg ^2 \alpha +1}=\dfrac{\ctg \alpha-\tg \alpha}{\ctg \alpha + \tg \alpha}}

{\tg(2\alpha) = \dfrac{2 \cdot \tg \alpha}{1-\tg ^2 \alpha}=\dfrac{2 \cdot \ctg \alpha}{\ctg ^2 \alpha- 1}=\dfrac{2}{\ctg \alpha- \tg \alpha}}

{\ctg(2\alpha) = \dfrac{\ctg ^2 \alpha-1}{2 \cdot \ctg \alpha}=\dfrac{\ctg \alpha- \tg \alpha}{2}}

Формулы тройного угла (аргумента)

{\sin(3\alpha)=3 \cdot \sin \alpha- 4 \cdot \sin ^3 \alpha}

{\cos(3\alpha)= 4 \cdot \cos ^3 \alpha- 3 \cdot \cos \alpha}

{\tg(3\alpha)= \dfrac{3 \cdot \tg \alpha- \tg ^3 \alpha}{1-3 \cdot \tg ^2 \alpha}}

{\ctg(3\alpha)= \dfrac{\ctg ^3 \alpha- 3 \cdot \ctg \alpha}{3 \cdot \ctg ^2 \alpha -1}}

Формулы понижения степени тригонометрических функций

Вторая степень

{\sin ^2 \alpha = \dfrac{1-\cos(2\alpha)}{2}}

{\cos ^2 \alpha = \dfrac{1+\cos(2\alpha)}{2}}

{\tg ^2 \alpha = \dfrac{1-\cos(2\alpha)}{1+\cos(2\alpha)}}

{\ctg ^2 \alpha = \dfrac{1+\cos(2\alpha)}{1-\cos(2\alpha)}}

{(\sin \alpha- \cos \alpha)^2=1-\sin(2 \alpha)}

{(\sin \alpha+ \cos \alpha)^2=1+\sin(2 \alpha)}

Третья степень

{\sin ^3 \alpha = \dfrac{3 \cdot \sin(\alpha)-\sin(3 \alpha)}{4}}

{\cos ^3 \alpha = \dfrac{3 \cdot \cos(\alpha)+\cos(3 \alpha)}{4}}

{\tg ^3 \alpha = \dfrac{3 \cdot \sin (\alpha)-\sin(3 \alpha)}{3 \cdot \cos (\alpha)+\cos(3 \alpha)}}

{\ctg ^3 \alpha = \dfrac{3 \cdot \cos (\alpha)+\cos(3 \alpha)}{3 \cdot \sin (\alpha)-\sin(3 \alpha)}}

Четвёртая степень

{\sin ^4 \alpha = \dfrac{3-4 \cdot \cos(2 \alpha)+\cos(4 \alpha)}{8}}

{\cos ^4 \alpha = \dfrac{3+4 \cdot \cos(2 \alpha)+\cos(4 \alpha)}{8}}

Пятая степень

{\sin ^5 \alpha = \dfrac{10 \cdot \sin(\alpha)-5 \cdot \sin(3 \alpha)+\sin(5 \alpha)}{16}}

{\cos ^5 \alpha = \dfrac{10 \cdot \cos(\alpha)+5 \cdot \cos(3 \alpha)+\cos(5 \alpha)}{16}}

Формулы половинного угла (аргумента)

{\sin \Big( \dfrac{\alpha}{2} \Big)=\pm \sqrt{\dfrac{1-\cos \alpha}{2}}}

{\cos \Big( \dfrac{\alpha}{2} \Big)=\pm \sqrt{\dfrac{1+\cos \alpha}{2}}}

{\tg \Big( \dfrac{\alpha}{2} \Big)= \dfrac{1-\cos \alpha}{\sin \alpha}= \dfrac{\sin \alpha}{1+\cos \alpha}}

{\ctg \Big( \dfrac{\alpha}{2} \Big)= \dfrac{1+\cos \alpha}{\sin \alpha}= \dfrac{\sin \alpha}{1-\cos \alpha}}

Формулы понижения степени половинного угла (аргумента)

{\sin ^2 \Big( \dfrac{\alpha}{2} \Big)=\dfrac{1-\cos \alpha}{2}}

{\cos ^2 \Big( \dfrac{\alpha}{2} \Big)=\dfrac{1+\cos \alpha}{2}}

{\tg ^2 \Big( \dfrac{\alpha}{2} \Big)=\dfrac{1-\cos \alpha}{1+\cos \alpha}}

{\ctg ^2 \Big( \dfrac{\alpha}{2} \Big)=\dfrac{1+\cos \alpha}{1-\cos \alpha}}

Формулы сложения аргументов

{\sin(\alpha + \beta)=\sin \alpha \cdot \cos \beta + \cos \alpha \cdot \sin \beta}

{\cos(\alpha + \beta)=\cos \alpha \cdot \cos \beta- \sin \alpha \cdot \sin \beta}

{\tg(\alpha + \beta)= \dfrac{\tg \alpha + \tg \beta}{1-\tg \alpha \cdot \tg \beta}}

{\ctg(\alpha + \beta)= \dfrac{\ctg \alpha \cdot \ctg \beta-1}{\ctg \alpha + \ctg \beta}}

Формулы вычитания аргументов

{\sin(\alpha- \beta)=\sin \alpha \cdot \cos \beta- \cos \alpha \cdot \sin \beta}

{\cos(\alpha- \beta)=\cos \alpha \cdot \cos \beta+ \sin \alpha \cdot \sin \beta}

{\tg(\alpha- \beta)= \dfrac{\tg \alpha- \tg \beta}{1+\tg \alpha \cdot \tg \beta}}

{\ctg(\alpha- \beta)= \dfrac{\ctg \alpha \cdot \ctg \beta+1}{\ctg \alpha- \ctg \beta}}

Формулы суммы тригонометрических функций

{\sin \alpha+ \sin \beta=2 \cdot \sin \big( \dfrac{\alpha + \beta}{2} \big) \cdot \cos \big( \dfrac{\alpha- \beta}{2} \big)}

{\cos \alpha+ \cos \beta=2 \cdot \cos \big( \dfrac{\alpha + \beta}{2} \big) \cdot \cos \big( \dfrac{\alpha- \beta}{2} \big)}

{\tg \alpha + \tg \beta = \dfrac{\sin(\alpha + \beta)}{\cos \alpha \cdot \cos \beta}}

{\ctg \alpha + \ctg \beta = \dfrac{\sin(\alpha + \beta)}{\cos \alpha \cdot \cos \beta}}

{\sin (\alpha)+\cos(\alpha)=\sqrt{2} \cdot \sin \Big( \alpha+ \dfrac{\pi}{4} \Big)}

Формулы разности тригонометрических функций

{\sin \alpha- \sin \beta=2 \cdot \sin \big( \dfrac{\alpha- \beta}{2} \big) \cdot \cos \big( \dfrac{\alpha+ \beta}{2} \big)}

{\cos \alpha- \cos \beta=-2 \cdot \sin \big( \dfrac{\alpha + \beta}{2} \big) \cdot \sin \big( \dfrac{\alpha- \beta}{2} \big)}

{\tg \alpha- \tg \beta = \dfrac{\sin(\alpha- \beta)}{\cos \alpha \cdot \cos \beta}}

{\ctg \alpha- \ctg \beta = \dfrac{\sin(\alpha + \beta)}{\sin \alpha \cdot \sin \beta}}

{\sin (\alpha)-\cos(\alpha)=\sqrt{2} \cdot \sin \Big( \alpha- \dfrac{\pi}{4} \Big)}

Формулы произведения тригонометрических функций

{\sin \alpha \cdot \sin \beta = \dfrac{\cos (\alpha- \beta)-\cos(\alpha + \beta)}{2}}

{\sin \alpha \cdot \cos \beta = \dfrac{\sin (\alpha- \beta)+\sin(\alpha + \beta)}{2}}

{\cos \alpha \cdot \cos \beta = \dfrac{\cos (\alpha- \beta)+\cos(\alpha + \beta)}{2}}

{\tg \alpha \cdot \tg \beta = \dfrac{\cos(\alpha- \beta)- \cos(\alpha+\beta)}{\cos(\alpha- \beta)+ \cos(\alpha+\beta)}=\dfrac{\tg \alpha + \tg \beta}{\ctg \alpha + \ctg \beta}}

{\ctg \alpha \cdot \ctg \beta = \dfrac{\cos(\alpha- \beta)+ \cos(\alpha+\beta)}{\cos(\alpha- \beta)- \cos(\alpha+\beta)}=\dfrac{\ctg \alpha + \ctg \beta}{\tg \alpha + \tg \beta}}

{\tg \alpha \cdot \ctg \beta = \dfrac{\sin(\alpha- \beta)+ \sin(\alpha+\beta)}{\sin(\alpha+ \beta)- \sin(\alpha-\beta)}}

Формулы произведения тригонометрических функций в степени

{\sin ^2 (\alpha) \cdot \cos ^2 (\alpha) = \dfrac{1-\cos(4 \alpha)}{8}}

{\sin ^3 (\alpha) \cdot \cos ^3 (\alpha) = \dfrac{3 \cdot \sin(2 \alpha)- \sin(6 \alpha)}{32}}

{\sin ^4 (\alpha) \cdot \cos ^4 (\alpha) = \dfrac{3-4 \cdot \cos(4 \alpha)+ \cos(8 \alpha)}{128}}

{\sin ^5 (\alpha) \cdot \cos ^5 (\alpha) = \dfrac{10 \cdot \sin (2 \alpha)-5 \cdot \sin(6 \alpha)+\sin (10 \alpha)}{512}}

Все формулы тригонометрии на одном листе

На этой картинке собраны все формулы тригонометрии для печати. Листо можно распечатать и использовать при решении задач ЕГЭ или вырезать таблицы и использовать как шпаргалку. Распечатанный лист можно применять как справочный материал при решении задач по тригонометрии в 10 и 11 классе.

Все формулы тригонометрии на одном листе

Просмотров страницы: 15 333

mnogoformul.ru

Урок по теме «Тригонометрические формулы». 10-й класс

Разделы: Математика, Конкурс «Презентация к уроку»

Презентация к уроку

Загрузить презентацию (1,2 МБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели урока. (Cлайд 1-3)

Дидактические:

обобщить и систематизировать знания учащихся по теме;
продолжить формирование умений и навыков по применению тригонометрических формул;
проконтролировать степень усвоения знаний, умений и навыков по теме.

Развивающие:

совершенствовать, развивать умения и навыки по решению задач на применение тригонометрических формул;

развивать умения и навыки в работе с тестами;

продолжить работу по развитию логического мышления, математической речи и памяти.

Воспитательные:

продолжить формирование навыков эстетического оформления записей в тетради;
приучать к умению общаться и выслушивать других;
воспитание сознательной дисциплины;
развитие творческой самостоятельности и инициативы;
стимулировать мотивацию и интерес к изучению тригонометрии.

Задачи урока:

повторить определение синуса, косинуса, тангенса, котангенса числа ;
повторить формулы приведения, формулы двойного угла, формулы сложения;
повторить основное тригонометрическое тождество и формулы, выражающие связь между тангенсом и косинусом, между котангенсом и синусом.
научить применять полученные знания при решении задач.

Тип урока: урок обобщения и систематизации знаний.

Оборудование: учебники, компьютер, мультимедийный проектор.

Ход урока: (слайд 4)
Организационный момент, вступительная беседа.

Блиц-опрос.

Закрепление знаний и умений.

Самостоятельная работа (тест) .

Проверка самостоятельной работы.

Это интересно.

Подведение итогов урока.

Домашнее задание.

1. Организационный момент.

Для успешного решения задач по тригонометрии необходимо уверенное владение многочисленными формулами. Тригонометрические формулы надо помнить. Но это не значит, что их надо заучивать все наизусть, главное запоминать не сами формулы, а алгоритмы их вывода. Любую тригонометрическую формулу можно довольно быстро получить, если твердо знать определения и основные свойства функций sin, cos, tg, ctg,соотношение sin
2+ cos²=1 и формулы сложения. Каждый раз выводить нужную формулу, например, для преобразования тригонометрического уравнения время уйдет достаточно много. Поэтому круг формул, которые необходимо знать, должен быть достаточно широким.

Разучивание тригонометрических формул в школе не для того чтобы вы всю оставшуюся жизнь вычисляли синусы и косинусы, а для того чтобы ваш мозг приобрел способность работать. “Дороги не те знания, которые отлагаются в мозгу, как жир; дороги те, которые превращаются в умственные мышцы” писал Г. Спесер, английский философ и социолог.

Так вот, давайте сегодня на уроке работать активно, внимательно, будем поглощать знания с большим желанием, ведь они вам пригодятся.

Тема нашего урока: “Тригонометрические формулы”- последний урок по данной теме, следующий – контрольная работа.

2. Блиц-опрос (по формулам в форме математического диктанта). (Слайд 5-7)

Проверка проводится на уроке с выставлением оценок. (Приложение 1)

“5” — 12; “4” — 10 – 11; “3” — 7 – 9; “2” — 0 – 6

3. Закрепление знаний и умений. (Слайд 8-10)

4. Самостоятельная работа обучающего характера в форме теста, с последующей проверкой на уроке. (Слайд 11)

5. Проверка самостоятельной работы (проверка теста проводится на уроке, оценки выставляются выборочно). (Слайд 12)

6. Это интересно. (Слайд 13-17)

Зарождение тригонометрии относится к глубокой древности. Еще задолго до новой эры вавилонские ученые умели предсказывать солнечные и лунные затмения. Это позволяет сделать вывод о том, что им были известны простейшие сведения из тригонометрии. Само название “тригонометрия” греческого происхождения, обозначающее “измерение треугольников”. Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры. Гиппарх является автором первых тригонометрических таблиц. [5]

Тригонометрия в ладони

Значения синусов и косинусов углов “находятся” на вашей ладони. Протяните руку и разведите как можно сильнее пальцы, так как показано на слайде. Сейчас мы измерим углы между вашими пальцами. (Возьмем два прямоугольных треугольника с углами 30°и 45° и приложим вершину нужного угла к бугру Луны на ладони. Бугор Луны находится на пересечении продолжений мизинца и большого пальца. Одну сторону угла совмещаем с мизинцем, а другую сторону — с одним из остальных пальцев)

Смотрите, я прикладываю угол в 30°; оказывается, это угол

— между мизинцем и безымянным пальцем;

— между мизинцем и средним пальцем — 45°;

— между мизинцем и указательным пальцем — 60°;

— между мизинцем и большим пальцем — 90°;

И это у всех людей без исключения.

Если пальцы считать лучами, исходящими из бугра Луны на ладони, то, если совместить (сжать) пальцы с мизинцем, угол между лучами будет равен 0°, то есть можно считать, что направление мизинца соответствует началу отсчета углов, то есть 0°, а поэтому введем нумерацию пальцев:

№0 — Мизинец

№1 — Безымянный

№2 — Средний

№3 -Указательный

№4 — Большой

№0 Мизинец 0°
№1 Безымянный 30°

№2 Средний 45°

№3 Указательный 60°

№4 Большой 90°

n — номер пальца

Значения синуса и косинуса угла по “ладони” приведено в таблице.

Примечание. Для определения косинуса угла отсчет пальцев происходит от большого пальца руки. [6]

Значения синуса

Значения косинуса

7. Итоги урока.

8. Домашнее задание. (Cлайд 18)

“Проверь себя”, стр. 166

Спасибо, урок окончен! (Cлайд 19)

Используемая литература

Алимов Ш.А., Колягин Ю.М. и др. Алгебра и начала анализа: учеб. Для общеобразовательных учреждений. – 16-е изд. – М.: Просвещение, 2010.

Макеева А.В. Карточки по тригонометрии. 10-11 классы: Дидактический материал для учителя — ОАО “Издательство “Лицей”, Саратов, 2002.

Изучение алгебры и начал анализа 10-11: Методические рекомендации к учеб.; кн. для учителя / Н.Е.Федорова, М.В. Ткачева. – М.: Просвещение, 2007.

Дидактические материалы по алгебре и началам анализа для 10 класс/М.И. Шабунин, М.В. Ткачева и др. -2-е изд. — М.: Просвещение, 2007.

Решетников Н.Н. Материалы курса “Тригонометрия в школе” лекции 1-8. – М.: Педагогический университет “Первое сентября”, 2006

Газета “Первое сентября. Математика”. — №6, 2004.

Сборники заданий к ЕГЭ 2002, 2011.

Электронная поддержка урока:
Авторская презентация “Тригонометрические формулы”.

Авторский тест “Тригонометрические формулы”.

Приложение
15.04.2012
urok.1sept.ru
Все формулы по тригонометрии
Все формулы по тригонометрии
Подождите пару секунд пока подгрузятся формулы
Основные тригонометрические тождества
$$sin^2x+cos^2x=1$$
$$tgx= \frac{sinx}{cosx}$$
$$ctgx= \frac{cosx}{sinx}$$
$$tgxctgx=1$$
$$tg^2x+1= \frac{1}{cos^2x}$$
$$ctg^2x+1= \frac{1}{sin^2x}$$
Формулы двойного аргумента (угла)
$$sin2x=2cosxsinx$$
\begin{align} sin2x &=\frac{2tgx}{1+tg^2x}\\ &= \frac{2ctgx}{1+ctg^2x}\\ &= \frac{2}{tgx+ctgx} \end{align}
\begin{align} cos2x & = \cos^2x-sin^2x\\ &= 2cos^2x-1\\ &= 1-2sin^2x \end{align}
\begin{align} cos2x & = \frac{1-tg^2x}{1+tg^2x}\\ &= \frac{ctg^2x-1}{ctg^2x+1}\\ &= \frac{ctgx-tgx}{ctgx+tgx} \end{align}
\begin{align} tg2x & = \frac{2tgx}{1-tg^2x}\\ &= \frac{2ctgx}{ctg^2x-1}\\ &= \frac{2}{ctgx-tgx} \end{align}
\begin{align} ctg2x & = \frac{ctg^2x-1}{2ctgx}\\ &= \frac{2ctgx}{ctg^2x-1}\\ &= \frac{ctgx-tgx}{2} \end{align}
Формулы тройного аргумента (угла)
$$sin3x=3sinx-4sin^3x$$
$$cos3x=4cos^3x-3cosx$$
$$tg3x= \frac{3tgx-tg^3x}{1-3tg^2x}$$
$$ctg3x= \frac{ctg^3x-3ctgx}{3ctg^2x-1}$$
Формулы половинного аргумента (угла)
$$sin^2 \frac{x}{2}= \frac{1-cosx}{2}$$
$$cos^2 \frac{x}{2}= \frac{1+cosx}{2}$$
$$tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}$$
$$ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}$$
\begin{align} tg \frac{x}{2} & = \frac{1-cosx}{sinx}\\ &= \frac{sinx}{1+cosx} \end{align}
\begin{align} ctg \frac{x}{2} & = \frac{1+cosx}{sinx}\\ &= \frac{sinx}{1-cosx} \end{align}
Формулы квадратов тригонометрических функций
$$sin^2x= \frac{1-cos2x}{2}$$
$$cos^2x= \frac{1+cos2x}{2}$$
$$tg^2x= \frac{1-cos2x}{1+cos2x}$$
$$ctg^2x= \frac{1+cos2x}{1-cos2x}$$
$$sin^2 \frac{x}{2}= \frac{1-cosx}{2}$$
$$cos^2 \frac{x}{2}= \frac{1+cosx}{2}$$
$$tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}$$
$$ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}$$
Формулы кубов тригонометрических функций
$$sin^3x= \frac{3sinx-sin3x}{4}$$
$$cos^3x= \frac{3cosx+cos3x}{4}$$
$$tg^3x= \frac{3sinx-sin3x}{3cosx+cos3x}$$
$$ctg^3x= \frac{3cosx+cos3x}{3sinx-sin3x}$$
Формулы тригонометрических функций в четвертой степени
$$sin^4x= \frac{3-4cos2x+cos4x}{8}$$
$$cos^4x= \frac{3+4cos2x+cos4x}{8}$$
Формулы сложения аргументов
$$sin(\alpha + \beta) = sin \alpha cos \beta + cos \alpha sin \beta$$
$$cos(\alpha + \beta) = cos \alpha cos \beta — sin \alpha sin \beta$$
$$tg(\alpha + \beta)= \frac{tg \alpha + tg \beta}{1 — tg \alpha tg \beta}$$
$$ctg(\alpha + \beta)= \frac{ctg \alpha ctg \beta -1}{ctg \alpha + ctg \beta}$$
$$sin(\alpha — \beta) = sin \alpha cos \beta — cos \alpha sin \beta$$
$$cos(\alpha — \beta) = cos \alpha cos \beta + sin \alpha sin \beta$$
$$tg(\alpha — \beta)= \frac{tg \alpha — tg \beta}{1 + tg \alpha tg \beta}$$
$$ctg(\alpha — \beta)= \frac{ctg \alpha ctg \beta +1}{ctg \alpha — ctg \beta}$$
Формулы суммы тригонометрических функций
$$sin\alpha + sin\beta = 2sin \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}$$
$$cos\alpha + cos\beta = 2cos \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}$$
$$tg\alpha + tg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta}$$
$$ctg\alpha + ctg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta}$$
$$(sin\alpha + cos\alpha)^2= 1+sin2\alpha$$
Формулы разности тригонометрических функций
$$sin\alpha — sin\beta = 2sin \frac{\alpha — \beta }{2} \cdot cos \frac{\alpha + \beta }{2}$$
$$cos\alpha — cos\beta = -2sin \frac{\alpha + \beta }{2} \cdot sin \frac{\alpha — \beta }{2}$$
$$tg\alpha — tg\beta = \frac{sin(\alpha — \beta) }{cos \alpha cos \beta}$$
$$ctg\alpha — ctg\beta = — \frac{sin(\alpha — \beta) }{sin \alpha sin \beta}$$
$$(sin\alpha + cos\alpha)^2= 1-sin2\alpha$$
Формулы произведения тригонометрических функций
$$sin\alpha \cdot sin\beta = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{2}$$
$$sin\alpha \cdot cos\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{2}$$
$$cos\alpha \cdot cos\beta = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{2}$$
\begin{align} tg\alpha \cdot tg\beta & = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{cos(\alpha — \beta)+cos(\alpha + \beta)}\\ &= \frac{tg\alpha + tg\beta}{ctg\alpha + ctg\beta} \end{align}
\begin{align} ctg\alpha \cdot ctg\beta & = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{cos(\alpha — \beta)-cos(\alpha + \beta)}\\ &= \frac{ctg\alpha + ctg\beta}{tg\alpha + tg\beta} \end{align}
$$tg\alpha \cdot ctg\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha — \beta)}$$
www.100formul.ru
Открытый урок по алгебре «Формулы тригонометрии», 10 класс
Конспект открытого урока алгебры теме
« Тригонометрические формулы» (10 класс)
Выполнила : учитель математики
МБОУ СОШ р.п. Мухен Кушнарь Л.А.
Урок входит в раздел программы « Тригонометрические формулы». На данный раздел в программе отводится 19 уроков. Урок обобщения проводится в конце изучения темы и предшествует контрольной работе.
Самоанализ урока.
Основная цель данного урока- обобщить полученные по теме знания, закрепить навыки решения простейших примеров по данной теме, подготовиться к контрольной работе. Так как группа сформирована в основном из слабых учащихся, имеющих большие пробелы в знаниях по математике, у них сформировано негативное отношение к урокам математики еще со школы. Поэтому на уроках математике ставится трудная задача вызвать интерес к изучению математики и сформировать познавательную мотивацию к учебной деятельности. Поэтому на уроках необходимо применять различные методы и формы работы. Одной из таких форм и является образец данного урока- форма игры. Такая работа позволяет развивать познавательный интерес к изучению математики.
Средства урока: карточки-задания, тестовые задания, доска, самостоятельная работа, слово учителя.
Разнообразные задания разного уровня сложности позволяют выбрать для себя те задания, которые по силам конкретному учащемуся.
Методы :
По организации учебно-познавательной деятельности: устные и письменные ответы учащихся;
По характеру управления учебной работой: работа под руководством учителя и учащихся- консультантов;
По степени самостоятельности мышления: репродуктивный;
Методы стимулирования интереса: игровые моменты, соревновательная атмосфера;
Методы стимулирования долга и ответственности: работа в группах, взаимоконтроль, взаимопомощь;
Методы контроля и самоконтроля: работа в группах, индивидуальные задания, самооценка и взаимооценка результатов работы.
Формы обучения:
Индивидуальная, групповая, фронтальная.
Цели урока:
Закрепить и обобщить знания по теме «Тригонометрические формулы».
Развивать познавательный интерес к изучению математики.
Активизировать навыки самостоятельной работы.
Вырабатывать умение работать в коллективе, воспитывать ответственность, аккуратность.
Ход урока:
Оргмомент. Сообщение целей урока. (3 мин)
«Математика уступает свои крепости лишь сильным и смелым». (А.П. Конфорович – автор научно-популярных книг «Математика лабиринта»
«Великая книга природы может быть прочтена только теми, кто знает язык, на котором она написана, и этот язык – математика.» Галилей
Сегодня на уроке мы должны повторить формулы тригонометрии, закрепить все те знания и умения, которые появились у вас при изучении темы.
Для этого вся группа разделится на три бригады. Из числа учащихся назначается координатор(помощник) , который помогает учителю. Каждая бригада выбирает себе командира. ( распределение на бригады проводилось заранее). Наш урок будет состоять из туров. Каждый учащийся выполняет всю работу на уроке на зачетных листах. . За каждый тур вы будете зарабатывать математические: «степы» Заработанные степы зачисляться на счет команды. За урок каждый из вас может получить оценки , которые вы можете выкупить на заработанные деньги. За урок вы можете получить по две оценки: в командном зачете и в личном.
Расценки на оценки:
В личном зачете: В командном зачете:
Оц. «5» -более 6 степов более 25 степов
Оц. «4» -5-6 степов 20-24 степа
Оц. «3» -2-4 степа 16-19 степов
1тур: Разминка. (5 мин)
Вопросы к разминке: (1 вопрос – 1 степ)
В каких четвертях лежит уголα, если sinα<0? (4,3четв.)
Чему равен sin7 π? (0)
Какой знак имеет cos150º? (-)
В каких пределах находится sinα? (-1≤х≤1) 2 команда
cosα>0, в какой четверти расположен угол α? (1,4)
Чему равен cos 45 º? ( √2/2)
Сколько градусов составляет дуга в π рад? (180°)
Чему равен tgα? (sina/cosa)
Чему равен ctgα? (cosa/ sina)
Сколько радиан составляет 360º? (2П)
11. Что называется углом в 1 радиан?
Ответ: угол в 1 радиан – это такой центральный угол, длина дуги которого равна радиусу окружности. 1радиан ≈ 57º.
12.½ пи
Игорь — Работа координатора: (координатор с объяснением решает пример у доски) (10 мин)
Вычислить:
sin2α, если cosα=, ‹α‹2π
После того, как координатор решит пример, часть записей с доски убирается, и учащиеся самостоятельно восстанавливают пример у себя в зачетных листах.
восстановить запись
2 тур: (10 мин)
Игра «Домино» Восстановить формулы 1 чел с бригады в это время проходит конкурс шифровальщиков
Конкурс шифровальщиков.
По 1 учащемуся из каждой бригады восстановить формулы тригонометрии Остальные учащиеся принимают участие в конкурсе шифровальщиков.
Тур Конкурс шифровальщиков: каждая команда получает задание с 8 примерами, ответы к которым зашифрованы буквами. Из этих букв должны сложить слово. Каждый учащийся решает не менее одного примера. ( один пример-2 степа).
е
к
н
о
с
у
я
—
45
—
40
π
1 бригада:
Ответ: косеканс
КООРДИНАТОР, КОСЕКАНС — одна из тригонометрических функций, обозначаемая ( — аргумент) и определяемая формулой
,
1.=
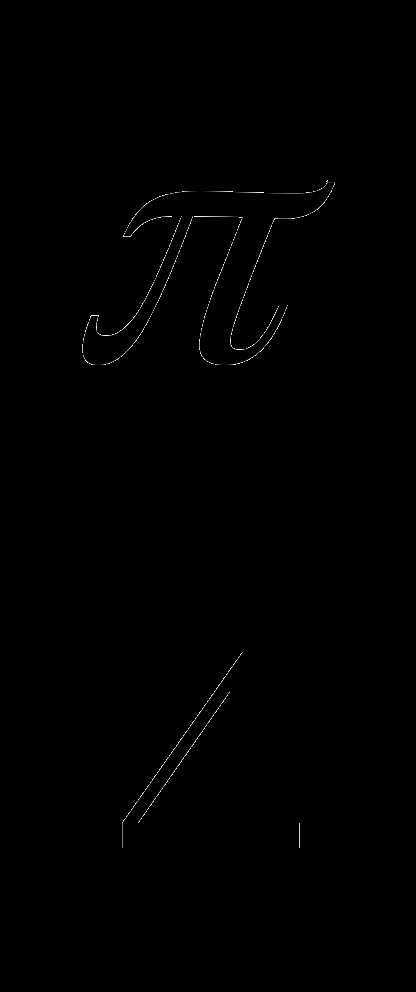2.sin(-30º)=
3.cos²15º- sin²15º=
4. sin()=
5. cosα=, α=?
6. cos=
7. 72º=
8. sin=
2 бригада:
й
л
м
о
п
т
ф
0
—
18
—
1
Ответ: Птоломей
2sin15º cos15º=
cos(π-)=
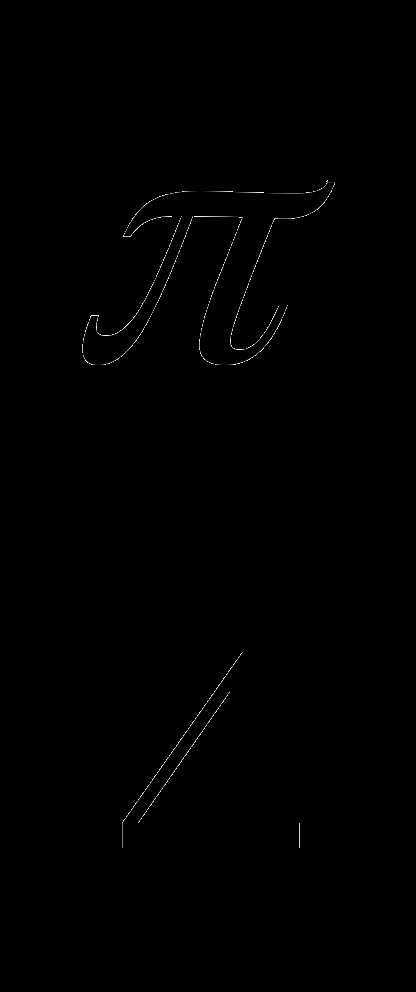sin=
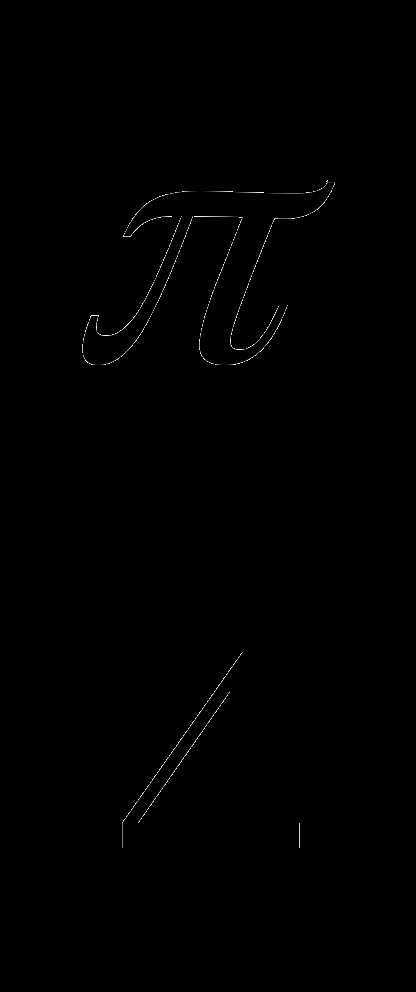60º=
cos45º=

=
sin8π=
sin(π)=
3 бригада:
к
п
с
т
у
ь
х
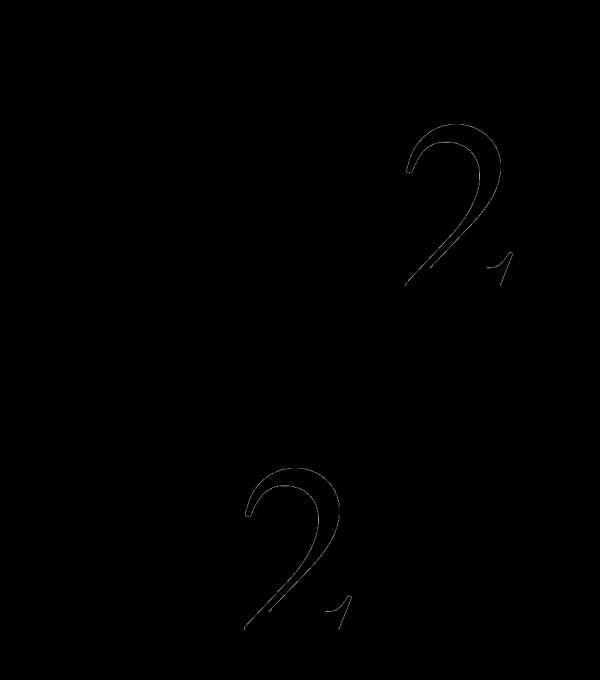
135
1
-1
0
136
Ответ: Питискус
π=
sin=
sin =
cos60º=
cos124 π=
sin(-45º)=
2 sin135º cos135º=
sin=
Та команда, которая первой закончит работу, получает дополнительное задание. ( Кроссворд)
тур: карточка 1 Решение индивидуальное и защита 1 примера на доске
тур карточка 2 Решение индивидуальное и защита 1 примера на доске
тур карточка 3 Решение индивидуальное и защита 1 примера на доске
Тур «Тест»
Резервный. Тур « Кто вернее?» (10 мин) ( групповая работа) защита одного примера на доске
(Резервное время) Найти; Вычислить; Упростить.
Найти:
а) cosα, если sinα = , <α< π
б) sinα, если cosα = —, <α< π
в) tgα, если sinα = — , < α<2 π
Вычислить:
а) 2 sin75ºcos75º
б) cos ²75º- sin ²75º
в) sin cos+ sin cos
Упростить:
а) 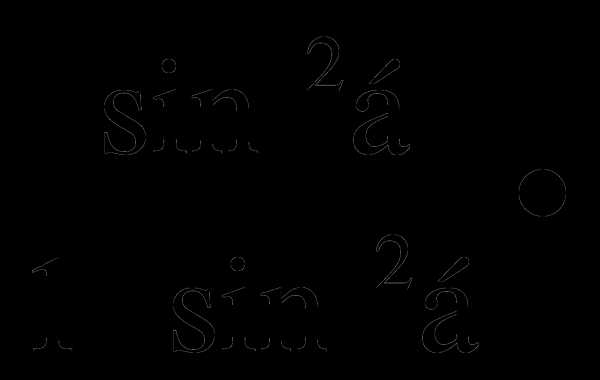ctg ²α
б) ( sin α- cosα)²+( sin α+ cosα) ² -2
в)
Вывод. Подведение итогов.
Учитель подводит итоги, отмечает работу отдельных учащихся.
Капитаны каждой команд сдают ведомость учета работы каждой команды, и игроки выкупают на заработанные баллы оценки. Каждый учащийся сдают свои листы и учитель проверяет с последующим выставлением оценок.
1. «Восстанови формулы». Один учащийся у интерактивной доски дописывает формулы:
tg α =
sin² α +cos² α = 1
1+ tg²α =
sin(-α) = — sin α
tg (-α) = — tg α
ctg α =
tg α∙ ctg α = 1
1+ ctg²α =
cos (-α) = cos α
ctg (-α) = — ctg α
cos² α = 1- sin² α
sin² α = 1- cos² α
tg α =
ctg α =
Задание
Решение
Ответ
Формулы
1
Упростить выражение:
2
Упростить выражение:
3
Упростить выражение:

Задание
Решение
Ответ
Формулы
1
Вычислить:
Синус суммы
2
Вычислить:
Косинус суммы
3
Вычислить:
Тангенс разности
4
Вычислить:
Зная, что , .
Синус суммы

Задание
Решение
Ответ
Формулы
1
Упростить выражение:
2
Найти , если известно, что , .
ТЕСТ
Задание #1
Вопрос:
Вычисли:
Выберите один из 5 вариантов ответа:
1) 2) 3) 4) 5)
Задание #2
Вопрос:
Вычисли:
Выберите один из 5 вариантов ответа:
1) 2) 3) 4) 5)
Задание #3
Вопрос:
Упрости выражение:
Выберите один из 5 вариантов ответа:
1) 2) 3) 4) 5)
Задание #5
Вопрос:
Упрости выражение:
Выберите один из 5 вариантов ответа:
1) 2) 3) 4) 5)
Задание #6
Вопрос:
Вычисли:
Выберите один из 5 вариантов ответа:
1) 2) 3) 4) 5)
Задание #7
Вопрос:
Упрости выражение
Выберите один из 5 вариантов ответа:
1) 2) 3) 4) 5)
Задание #8
Вопрос:
Вычисли:
Выберите один из 5 вариантов ответа:
1)
2) 1
3)
4) 1/2
5)
Задание #9
Вопрос:
Упрости выражение:
Выберите один из 5 вариантов ответа:
1)
2)
3)
4)
5)
Задание #10
Вопрос:
Вычисли:
Выберите один из 5 вариантов ответа:
1) 2) 3)
4) 5)
Ответы:
1) (1 б.) Верные ответы: 5;
2) (1 б.) Верные ответы: 5;
3) (1 б.) Верные ответы: 1;
5) (1 б.) Верные ответы: 5;
6) (1 б.) Верные ответы: 4;
7) (1 б.) Верные ответы: 2;
8) (1 б.) Верные ответы: 2;
9) (1 б.) Верные ответы: 3;
10) (1 б.) Верные ответы: 1;
КОД 551-542-231

1.тригонометрия
2. косинус
3. ордината
4. тангенс
5. мнемоническое
6 эйлер
ИНДИВИДУАЛЬНЫЙ ЛИСТ УЧЕТА
УЧЕНИКА 10 КЛАССА______________________________
ответы
Карточка 1
Карточка 2
Карточка 3
Тест
Код:
Кроссворд
3 бригада: Конкурс шифровальщиков:
к
п
с
т
у
ь
х
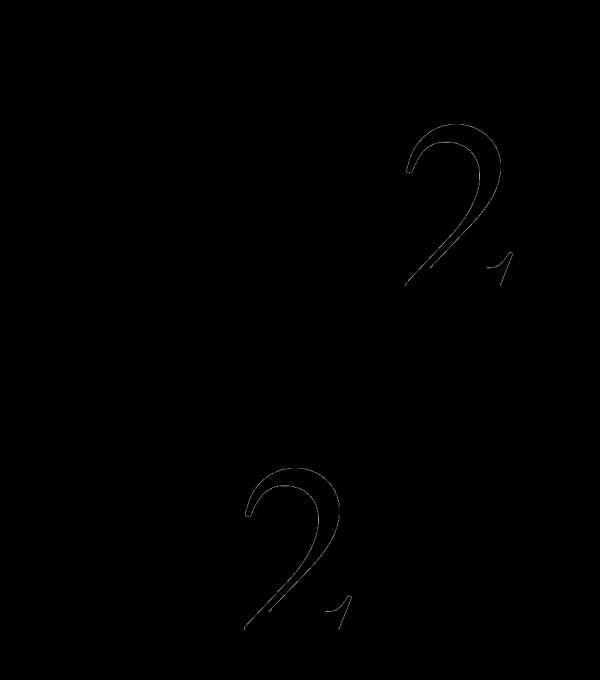
135
1
-1
0
136
π=
sin=
sin =
cos60º=
cos124 π=
sin(-45º)=
2 sin135º cos135º=
sin=
2 бригада: Конкурс шифровальщиков:
й
л
м
о
п
т
ф
0
—
18
—
1
1. 2sin15º cos15º=
2. cos(π-)==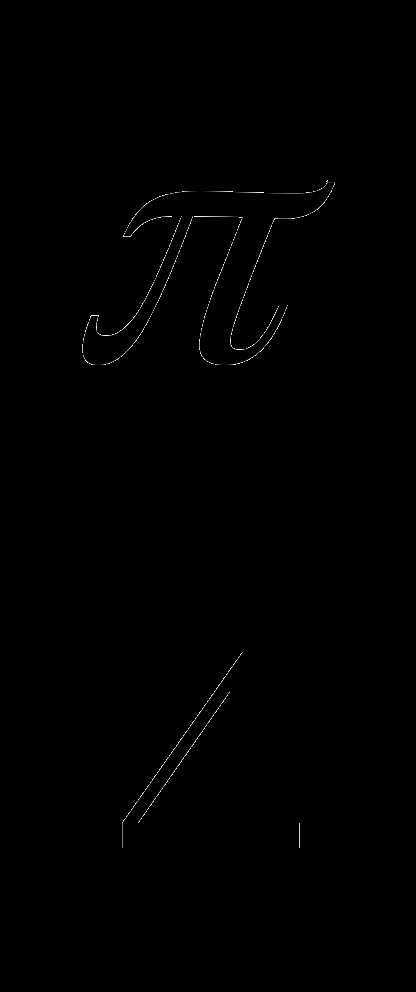
3. sin=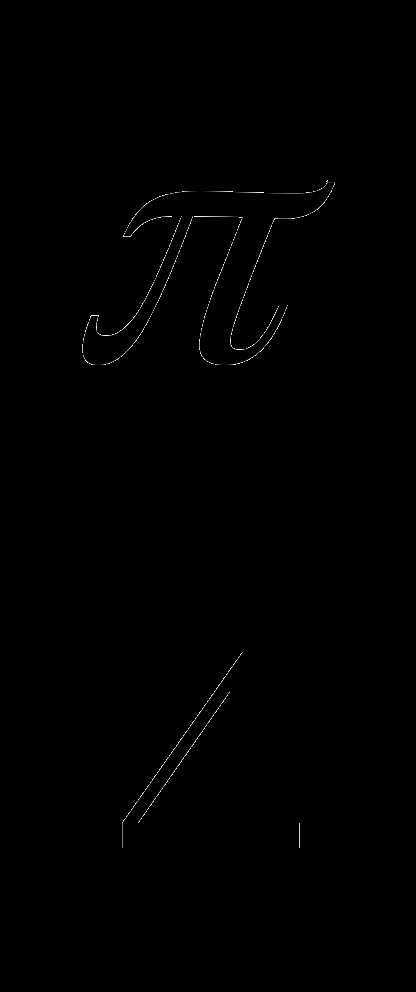
4. 60º=
5. cos45º=
6. =
7. sin8π=
8. sin(π)=
1 бригада Конкурс шифровальщиков:
=
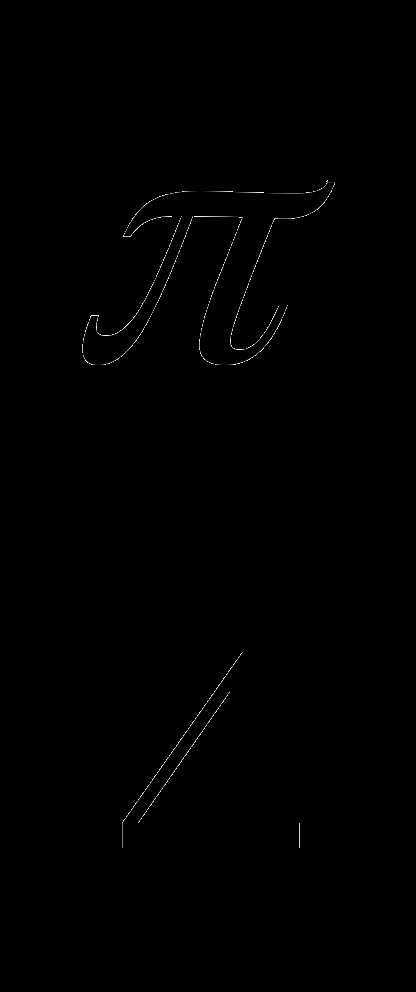2. sin(-30º)=
3. cos²15º- sin²15º=
4. sin()=
5. cosα=, α=?
6. cos=
7. 72º=
8. sin=
е
к
н
о
с
у
я
—
45
—
40
π

infourok.ru
Учебно-методический материал по алгебре (10 класс) по теме: Основные формулы по тригонометрии
По теме: методические разработки, презентации и конспекты
Контроль знаний основных формул по алгебре и началам анализа учащихся 10 класса при подготовке к ЕГЭ.
Материал служит для контроля знаний тригонометрических формул при подготовке к ЕГЭ….
Основные формулы тригонометрии
Основные формулы тригонометрии, которые необходимы при подготовке к ЕГЭ по математике…
ФОРМУЛЫ ПО ТРИГОНОМЕТРИИ ИСПОЛЬЗУЕМЫЕ НА ЕГЭ
каждый год выпускаю классы и имею подборку тригонометрических формул используемых в обеих частях ЕГЭ, которыми хочу поделиться с Вами….
Основные формулы по геометрии
Формулы по геометрии…
Индивидуальные карточки по алгебре для 10 класса на тему: «Основные формулы тригонометрии»
Цель: сформировать целостное представление об основных понятиях тригонометрии.Задачи:обобщить и систематизировать материал о тригонометрических функциях;изучить методы и способы нахождения значений тр…
Урок по алгебре в 10-м классе по теме «Основные формулы sinа и cosа»
урок в 10-м классе по алгебре на тему: «Основные формулы sinа и cosа». УМК: . Алгебра и начала анализа. 10 класс: Учебник для общеобразовательных учреждений/С.М. Никольский, М.К. Потапов, Н….
Основные формулы по физике
Основные формулы по физике…
nsportal.ru
Обобщающий урок в 10 классе по теме:»Основные тригонометрические формулы»
Тема урока: Основные тригонометрические формулы.
( 2 часа)
Тип урока: повторения и обобщения знаний.
Цели урока:
Повторить, обобщить, знания учащихся по изученной теме, осуществить проверку знаний учащихся по наиболее важным разделам пройденного материала; корректировать знания учащихся; подготовить их к предстоящей контрольной работе.
Развивать навыки устной и самостоятельной работы, прививать умение выслушивать других учащихся, дополнять их ответы; развивать внимательность, память, логическое мышление.
Активизировать мыслительную деятельность учащихся путём применения информационных технологий.
Ход урока.
Вступительное слово учителя.
Сегодня мы проводим обобщающий урок по теме: «Основные тригонометрические формулы» и начать его мне хотелось бы со слов математика и кораблестроителя А.Н. Крылова, который сказал:
«Теория без практики мертва или бесплодна, практика без теории невозможна или пагубна. Для теории нужны знания, для практики, сверх всего того, и умение».
( см. презентация)
Постановка целей урока. (формулируются учащимися).
Устная работа.
Учитель:
— Давайте вспомним , что мы называем единичной окружностью?
— Какие направления угла поворота вам известны?
— Какие углы при этом получаются?
Групповая работа .
Каждой группе предлагается карточка с заданием ( задания дифференцированы по уровню сложности).
Задание объясняет учитель: «В таблицу рядом с окружностью вы должны поставить ту букву, в которую перейдёт конец единичного радиуса (1;0) при повороте на заданный угол α». По истечении 3-4 минут выполнения задания учитель вызывает по одному ученику от каждой группы, которые записывают полученную из выбранных семи букв фразу на доске. Первая буква Т записывается учителем после всех написанных букв. В результате всех верно полученных ответов должна получиться известная фраза А.В.Суворова:
« Тяжело в ученье легко в бою»
Групповая работа со слайдами. (см презентация)

— Какова главная цель введения в этот параграф единичной окружности и понятия поворота точки вокруг начала координат?
— пожалуйста, дайте определение синуса угла ; косинуса угла; тангенса и котангенса угла.
Задание №1. Определение синуса и косинуса угла.
— А теперь давайте определим зависимость между синусом и косинусом одного и того же угла. Чем она выражается?
____________________________________________
— Как называется это тождество?
— Какую основную задачу можно выполнить , зная это тождество?
_________________________________________________________
Задание №2. Зависимость между синусом и косинусом одного и того же аргумента.
А теперь пришло время вспомнить не менее важные формулы: формулы приведения. Устная работа по слайдам.
Задание № 3. Формулы приведения.
Результаты своей деятельности при выполнении заданий 1-3 учащиеся заносят в таблицу и сдают учителю на проверку.
№
слайда
значения
№
слайда
Зависимость м/д
и
№
слайда
Формулы
приведения
1
1
1
2
2
2
3
3
3
4
4
4
5
5
5
6
6
6
7
7
7
8
8
8
9
9
9
10
10
10
Индивидуальная работа. Применение формул тригонометрии к решению задач.
Учащимся предлагается задание по выбору. «Упростить выражение». Задание оценивается по количеству набранных баллов.
(смотри приложение)
Презентация проекта: « Об истории тригонометрии»
( подготовлена учащимися)
Итог урока. Сообщение оценок за групповую работу.
Домашнее задание. ( см. презентация.)
Литература:
Алгебра и начала анализа: учеб. для 10-11 кл.-14 изд.- М.: Просвещение,2006.
Алгебра и начала анализа. 10 класс: поурочные планы по учебнику Ш.А. Алимова и др — Ч.II/ авт.-сост.Г.И.Григорьева. — Волгоград: Учитель,2006.
Газета « Математика в школе» фестиваль « Открытый урок»
infourok.ru
Презентация к уроку по алгебре (10 класс) на тему: Урок-зачет по теме «Тригонометрические формулы» для 10 класса
Урок-зачет по теме «Тригонометрические формулы». 10-й класс
Разработан учителем математики высшей квалификационной категории Азаровой О.Е., МБОУ СОШ № 9 г. Уфа
“Дороги не те знания, которые отлагаются в мозгу, как жир; дороги те, которые превращаются в умственные мышцы”
Герберт Спенсер, английский философ и социолог.
Цели урока. (Cлайд 1-3)
Дидактические:
обобщить и систематизировать знания учащихся по теме;
продолжить формирование умений и навыков по применению тригонометрических формул;
проконтролировать степень усвоения знаний, умений и навыков по теме.
Развивающие:
совершенствовать, развивать умения и навыки по решению задач на применение тригонометрических формул;
развивать умения и навыки в работе с тестами;
продолжить работу по развитию логического мышления, математической речи и памяти.
Воспитательные:
продолжить формирование навыков эстетического оформления записей в тетради;
приучать к умению общаться и выслушивать других;
воспитание сознательной дисциплины;
развитие творческой самостоятельности и инициативы;
стимулировать мотивацию и интерес к изучению тригонометрии.
Задачи урока:
повторить определение синуса, косинуса, тангенса, котангенса числа ;
повторить формулы приведения, формулы двойного угла, формулы сложения;
повторить основное тригонометрическое тождество и формулы, выражающие связь между тангенсом и косинусом, между котангенсом и синусом.
научить применять полученные знания при решении задач.
Тип урока: урок обобщения и систематизации знаний.
Оборудование: учебники, компьютер, мультимедийный проектор.
Ход урока:
Организационный момент, вступительная беседа.
Блиц-опрос.
Закрепление знаний и умений.
Самостоятельная работа (тест) .
Проверка самостоятельной работы.
Это интересно.
Подведение итогов урока.
Домашнее задание.
1. Организационный момент.
Для успешного решения задач по тригонометрии необходимо уверенное владение многочисленными формулами. Тригонометрические формулы надо помнить. Но это не значит, что их надо заучивать все наизусть, главное запоминать не сами формулы, а алгоритмы их вывода. Любую тригонометрическую формулу можно довольно быстро получить, если твердо знать определения и основные свойства функций sin, cos, tg, ctg,соотношение sin2+ cos2=1 и формулы сложения. Каждый раз выводить нужную формулу, например, для преобразования тригонометрического уравнения время уйдет достаточно много. Поэтому круг формул, которые необходимо знать, должен быть достаточно широким.
Разучивание тригонометрических формул в школе не для того чтобы вы всю оставшуюся жизнь вычисляли синусы и косинусы, а для того чтобы ваш мозг приобрел способность работать.
Так вот, давайте сегодня на уроке работать активно, внимательно, будем поглощать знания с большим желанием, ведь они вам пригодятся.
Тема нашего урока: “Тригонометрические формулы”- последний урок по данной теме, следующий – контрольная работа.
2. Блиц-опрос (по формулам в форме математического диктанта). (Слайд 4-6)

Проверка проводится на уроке с выставлением оценок. (Приложение 1)
“5” — 12; “4” — 9 – 10; “3” — 6 – 8; “2” — 0 – 5
3. Закрепление знаний и умений. (Слайд 7-9)
4. Самостоятельная работа обучающего характера в форме теста, с последующей проверкой на уроке. (Слайд 10)
5. Проверка самостоятельной работы (проверка теста проводится на уроке, оценки выставляются выборочно). (Слайд 11)
1 вариант 2 вариант
Г) б)
Б) в)
Г) г)
Б) а)
6. Это интересно. (Слайд 12-16)
Зарождение тригонометрии относится к глубокой древности. Еще задолго до новой эры вавилонские ученые умели предсказывать солнечные и лунные затмения. Это позволяет сделать вывод о том, что им были известны простейшие сведения из тригонометрии. Само название “тригонометрия” греческого происхождения, обозначающее “измерение треугольников”. Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры. Гиппарх является автором первых тригонометрических таблиц. [5]
Тригонометрия в ладони
Значения синусов и косинусов углов “находятся” на вашей ладони. Протяните руку и разведите как можно сильнее пальцы, так как показано на слайде. Сейчас мы измерим углы между вашими пальцами. (Возьмем два прямоугольных треугольника с углами 30°и 45° и приложим вершину нужного угла к бугру Луны на ладони. Бугор Луны находится на пересечении продолжений мизинца и большого пальца. Одну сторону угла совмещаем с мизинцем, а другую сторону — с одним из остальных пальцев)
Смотрите, я прикладываю угол в 30°; оказывается, это угол
— между мизинцем и безымянным пальцем;
— между мизинцем и средним пальцем — 45°;
— между мизинцем и указательным пальцем — 60°;
— между мизинцем и большим пальцем — 90°;
И это у всех людей без исключения.
Если пальцы считать лучами, исходящими из бугра Луны на ладони, то, если совместить (сжать) пальцы с мизинцем, угол между лучами будет равен 0°, то есть можно считать, что направление мизинца соответствует началу отсчета углов, то есть 0°, а поэтому введем нумерацию пальцев:
№0 — Мизинец
№1 — Безымянный
№2 — Средний
№3 -Указательный
№4 — Большой
№0 Мизинец 0°
№1 Безымянный 30°
№2 Средний 45°
№3 Указательный 60°
№4 Большой 90°
n — номер пальца
Значения синуса и косинуса угла по “ладони” приведено в таблице.
Примечание. Для определения косинуса угла отсчет пальцев происходит от большого пальца руки. [6]
Значения синуса
№ пальца
Угол

0
0
1
30°
2
45°
3
60°
4
90°
Значения косинуса
№ пальца
Угол

4
0°
3
30°
2
45°
1
60°
0
90°
7. Итоги урока.
8. Домашнее задание. (Cлайд 17)
“Проверь себя”, стр. 166
Спасибо, урок окончен! (Cлайд 18)
Используемая литература
Алимов Ш.А., Колягин Ю.М. и др. Алгебра и начала анализа: учеб. Для общеобразовательных учреждений. – 16-е изд. – М.: Просвещение, 2010.
Макеева А.В. Карточки по тригонометрии. 10-11 классы: Дидактический материал для учителя — ОАО “Издательство “Лицей”, Саратов, 2002.
Изучение алгебры и начал анализа 10-11: Методические рекомендации к учеб.; кн. для учителя / Н.Е.Федорова, М.В. Ткачева. – М.: Просвещение, 2007.
Дидактические материалы по алгебре и началам анализа для 10 класс/М.И. Шабунин, М.В. Ткачева и др. -2-е изд. — М.: Просвещение, 2007.
Решетников Н.Н. Материалы курса “Тригонометрия в школе” лекции 1-8. – М.: Педагогический университет “Первое сентября”, 2006
Электронная поддержка урока:
Авторская презентация “Тригонометрические формулы”.
Авторский тест “Тригонометрические формулы”.
nsportal.ru