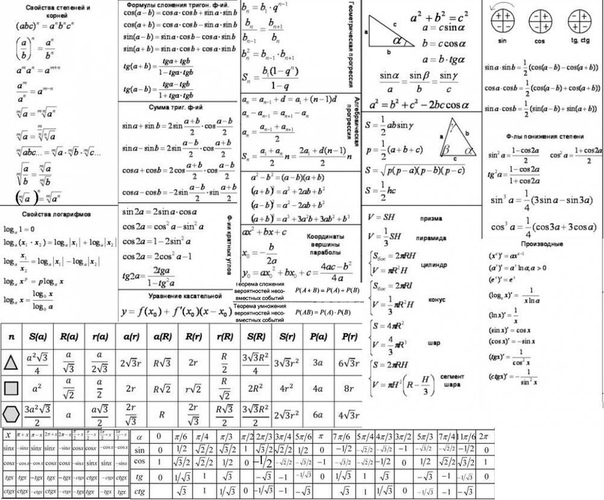
Формулы по геометрии 11 класс: Основные формулы геометрия 7-11 класс

Содержание

Формулы по геометрии с 7-9 классы :: dredmitvisearch

Материал и по алгебре, и по геометрии в виде сборника 431 формул и правил вы можете получить здесь. Радиус окружности, вписанной в прямоугольный треугольник. Через любые две точки Если две. Геометрия. Слайд 1 Справочник по геометрии 7 9 класс МБОУ СОШ с. Восток Автор:Чучуй Любовь Анатольевна. Собраны основные формулы по курсу геометрии 7 9 классов.

Геометрии класс по теме:. Готовьтесь к экзамену эффективно с нами. Пожалуйста. Добавил: Дата: 07 Октябрь 2012, 23:40, Воскресенье Загрузок: 3231. Описание:. Знание формул по геометрии является основой для успешной подготовки и.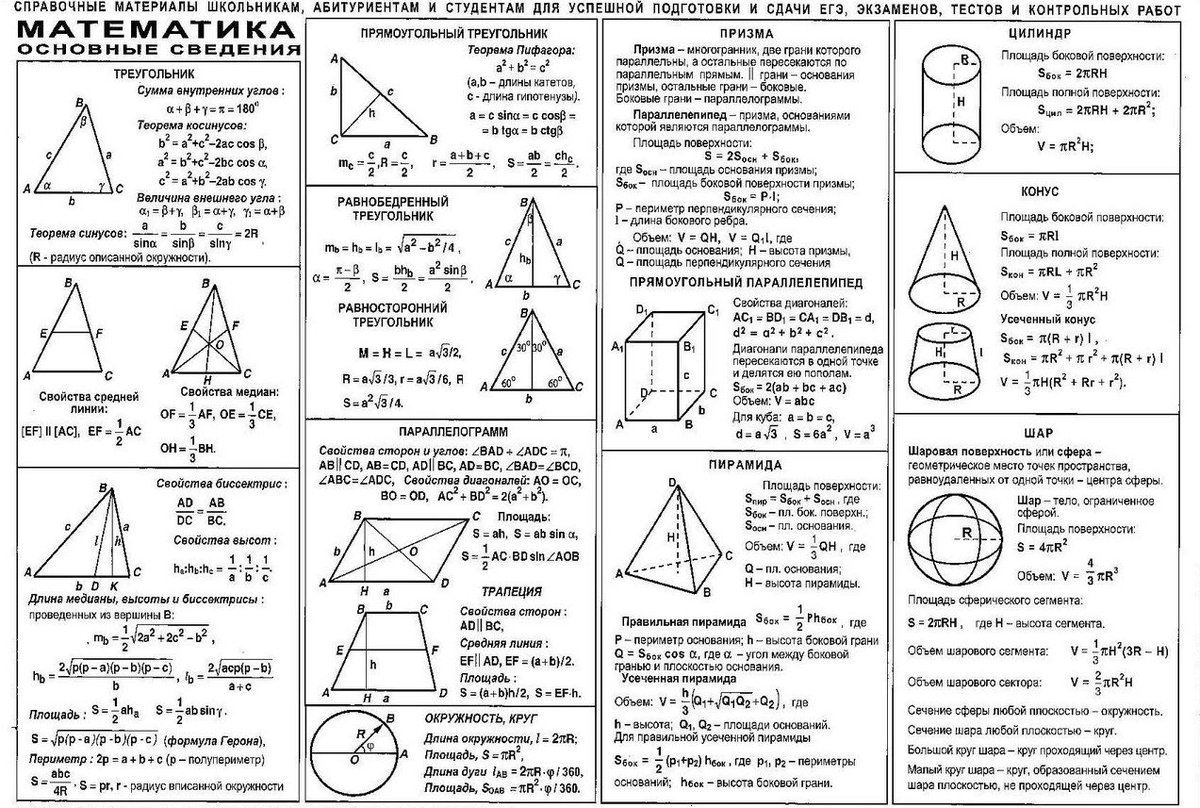

Формулы по геометрии. Дата: 07 Октябрь 2012, 23:40, Воскресенье Загрузок: 3231. Описание:. Справочный материал по геометрии для 7 11 классов. Радиус вписанной и описанной окружности. Теоремы.

Все формулы по алгебре и геометрии. Формулы по геометрии для учащихся старших классов. Для работы на уроках и дома, для подготовки к экзамену за курс Работа над созданием справочника продолжается Номинация: интерактивная презентация к урокам. На нашем сайте представлены основные формулы из курса геометрии, для. Тригонометрия. Формулы по геометрии. Геометрия. . В данном разделе.

Формулы треугольника, окружности. Теория по геометрии 7 9 класс. Все формулы и шпаргалки для подготовки к ОГЭ 9 класс. Площадь параллелограмма. На нашем сайте представлены основные формулы из курса геометрии, для быстрого. Способы нахождения площадей в. Радиус описанной окружности правильного многоугольника. Напишите пожалуйста формулы по геометрии за 7 9 классы. Радиус вписанной и описанной. Качайте формулы здесь.

Работа над созданием справочника продолжается. Весь справочный.

Собраны основные формулы по геометрии, которые необходимы. Формулы. Добавил. Площадь и объем пирамиды, конуса, треугольника, многоугольника. Формулы по геометрии для учащихся старших классов. Все формулы раздела. Формулы, таблицы, справочники. По математике, алгебре и геометрии для учащихся 5 11 классов. Среди. Шпаргалка по математике для 4 класса. Площадь параллелограмма, площадь треугольника, площадь круга. Собраны основные. Материал охватывает 7 9 классы. Презентация к уроку.

Вместе с Формулы по геометрии с 7-9 классы часто ищут

формулы по геометрии егэ.

все формулы по геометрии шпаргалка.

все формулы по алгебре.

формулы по геометрии 8 класс площади.

формулы геометрии 10-11 класс.

все формулы по геометрии за 7-9 класс атанасян.

формулы по геометрии огэ.

формулы по геометрии 9 класс векторы

Читайте также:

Гдз 4 класс английский язык кучма смотреть бесплатно

Рабочия тетрадь по математике 6 класс ерина

Гдз по истории 6 класс данилов сизова кузнецов без скачивания спиши.ру

Тематические тесты по геометрии. Основные формулы стереометрии.

Тип ПОЛабораторная работа PASCOActivInspire (Promethean)SMART NotebookПрезентация PowerPointAнимационный Flash-роликУрок для ActivTableElite Panaboard (Panaboard)HitachiМастер-классMimioStudio™RM Easiteach Next Generation (TriumphBoard, Panaboard, Legamaster)Interwrite WorkSpace (Interwrite)IP board (IPBoard /Julong)Интересный материал

ПредметАстрономияИнформатикаГеографияОкружающий мирБиологияНемецкий языкОбщественные наукиМатематикаТатарский языкОРКСЭкономикаИностранный языкМХКВоспитательная работа (классный час)Русский языкОБЖГеометрияАнглийский языкТехнологияПриродоведениеОбществознаниеВнеурочное занятиеЕстественные наукиФизикаХимияЛитератураИсторияПравоИЗОЧерчениеМузыкаФранцузский языкДругое

Уровень образованияДошкольное образованиеНачальная школаСредняя школаСтаршая школаВысшая школаСредне-специальное образованиеСреднее образованиеПрофессиональное образованиеСпециальное образованиеДистанционное обучениеВнеурочные занятияДополнительное образование

Вид урокаМетодические рекомендацииРазработка урокаИграФрагмент урокаВнеурочные занятияДидактический материалШаблонСценарий

Классдошкольное1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 классне зависит от класса

Площадь сферы

На этом уроке мы поговорим о формуле для вычисления площади поверхности сферы.

Узнаем, какой многогранник называется описанным около сферы. А также решим несколько задач на применение формулы для вычисления площади сферы.

Прежде чем приступить к рассмотрению данной темы, давайте вспомним, что такое сфера.

Итак, сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. Причём, данная точка называется центром сферы, а данное расстояние – радиусом сферы.

Ранее вы уже познакомились с понятием касательной плоскости к сфере, её свойством, а также с признаком касательной плоскости к сфере.

Вспомним их. Итак, плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере

, а их общая точка называется точкой касания плоскости и сферы.

Свойство касательной плоскости к сфере: радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Признак касательной плоскости к сфере: если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.

Перейдём к рассмотрению вопроса о нахождении площади сферы.

В отличие от боковых поверхностей цилиндра и конуса сферу нельзя развернуть так, чтобы получилась плоская фигура.

Поэтому для сферы не подходит способ определения и вычисления площади поверхности с помощью развертки.

Для определения площади сферы воспользуемся понятием описанного многогранника.

Определение:

Многогранник называется описанным около сферы (шара), если сфера касается всех его граней.

При этом сфера называется вписанной в многогранник.

Говорят, что сфера касается грани многогранника, если плоскость грани является касательной к сфере и точка касания принадлежит грани. Понятно, что центр О сферы с радиусом , вписанной в многогранник, находится на расстоянии, равном радиусу сферы, от каждой из плоскостей, содержащих грани многогранника.

На экране вы видите примеры описанных около сферы многогранников.

Тетраэдр, куб и октаэдр называются описанными около сферы. В свою очередь, сфера называется вписанной в многогранник. Обратите внимание, плоскость каждой грани многогранника является касательной к сфере.

Рассмотрим последовательность описанных около данной сферы многогранников. То есть пусть около сферы описан многогранник, который имеет граней.

Будем неограниченно увеличивать число граней так, чтобы при этом наибольший размер каждой грани многогранника стремился к нулю.

Наибольшим размером грани мы будем называть наибольшее расстояние между двумя точками грани. Например, если грань является прямоугольником, то её наибольший размер равен диагонали. Представим себе, что количество граней многогранника стало бесконечно много. Тогда площадь поверхности многогранника будет приближаться к площади сферы.

За площадь сферы можно принять предел последовательности площадей поверхностей этих многогранников при стремлении к нулю наибольшего размера каждой грани, который равен . Существование этого предела мы докажем при изучении объема шара.

Таким образом, площадь сферы можно вычислить по формуле , где – радиус сферы.

Задача: найдите площадь сферы, радиус которой равен см.

Решение: запишем формулу для вычисления площади сферы.

По условию задачи радиус сферы равен см. Подставим длину радиуса в формулу. Получим, что площадь сферы равна . Запишем ответ.

Задача: площадь сферы равна см². Найдите радиус сферы.

Решение: запишем формулу для вычисления площади сферы.

И выразим из неё радиус. Получили, что радиус сферы можно вычислить по формуле: . Не забудем записать ответ.

Задача: площадь сечения сферы, проходящего через её центр, равна см². Найдите площадь сферы.

Решение: запишем формулу для вычисления площади сферы.

Рассмотрим внимательно рисунок.

Напомним, что сечение сферы плоскостью есть окружность. Так как по условию задачи сечение сферы проходит через её центр, то сечение будет иметь радиус равный радиусу сферы .

Площадь сечения (окружности) вычисляется по формуле . Отсюда, найдём радиус (см).

Подставим найденный радиус в формулу для вычисления площади сферы. Посчитаем. Получим, что площадь сферы равна .

Запишем ответ.

Задача: около сферы описан куб с ребром, равным см. Вычислите площадь сферы.

Решение: запишем формулу для вычисления площади сферы.

Напомним, что многогранник называется описанным около сферы, если сфера касается всех его граней.

При этом плоскость каждой грани куба является касательной к сфере. А по свойству касательной плоскости к сфере: радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.

Значит, диаметр нашей сферы равен длине ребра куба (см). Отсюда, радиус сферы равен (см).

Подставим радиус сферы в формулу для вычисления площади сферы. Посчитаем. Получим, что площадь сферы равна .

Не забудем записать ответ.

Итоги:

На этом уроке мы вспомнили формулу для вычисления площади поверхности сферы. Узнали, что многогранник называется описанным около сферы (шара), если сфера касается всех его граней. При этом сфера называется вписанной в многогранник.

4.2 Уравнение прямой | Аналитическая геометрия

\начать{выравнивать*} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y-7}{x-3} &= \frac{1-7}{-6-3} \\ \frac{y-7}{x-3} &= \frac{-6}{-9} \\ \frac{y-7}{x-3} &= \frac{2}{3} \\ y — 7 &= \frac{2}{3} \left( x — 3 \right) \\ y &= \frac{2}{3}x — 2 + 7 \\ \следовательно y &= \frac{2}{3}x + 5 \конец{выравнивание*}

\((1;-\frac{11}{4})\) и \((\frac{2}{3}; -\frac{7}{4})\)

\начать{выравнивать*} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y + \frac{11}{4}}{x-1} &= \frac{-\frac{7}{4} + \frac{11}{4}}{\frac{2}{ 3} — 1} \\ \frac{y + \frac{11}{4}}{x-1} &= \frac{1}{-\frac{1}{3}} \\ \frac{y + \frac{11}{4}}{x-1} &= -3 \\ y + \frac{11}{4} &= -3 (x — 1) \\ y &= -3x + 3 — \frac{11}{4} \\ \поэтому y &= -3x + \frac{1}{4} \конец{выравнивание*}

\начать{выравнивать*} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y-1}{x+2} &= \frac{6-1}{3+2} \\ \frac{y-1}{x+2} &= \frac{5}{5} \\ у — 1 &= х + 2 \\ \поэтому у &= х + 3 \конец{выравнивание*}

\начать{выравнивать*} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y-3}{x-2} &= \frac{5-3}{3-2} \\ \frac{y-3}{x-2} &= 2 \\ у — 3 &= 2(х — 2) \\ у &= 2х — 4 + 3\\ \поэтому y &= 2x — 1 \конец{выравнивание*}

\((1;-5)\) и \((-7;-5)\)

\начать{выравнивать*} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y+5}{x-1} &= \frac{-5+5}{-7-1} \\ \frac{y+5}{x-1} &= 0 \\ у + 5 &= 0\\ \поэтому у &= -5 \конец{выравнивание*}

\((-4;0)\) и \((1;\frac{15}{4})\)

\начать{выравнивать*} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y-0}{x+4} &= \frac{\frac{15}{4}-0}{1+4} \\ \ frac {y} {x + 4} & = \ frac {\ frac {15} {4} {5} \\ \frac{y}{x+4} &= \frac{15}{20} \\ y &= \frac{3}{4} \left( x+4 \right) \\ \поэтому y &= \frac{3}{4}x + 3 \конец{выравнивание*}

\начать{выравнивать*} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y-t}{x-s} &= \frac{s — t}{t — s}\\ \frac{y-t}{x-s} &= \frac{-(t — s)}{t — s}\\ \frac{y-t}{x-s} &= -1\\ y — t &= -(x — s)\\ у &= -х + с + т \конец{выравнивание*}

\((-2;-8)\) и \((1;7)\)

\начать{выравнивать*} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y+8}{x+2} &= \frac{7+8}{1+2} \\ \frac{y+8}{x+2} &= \frac{15}{3} \\ \frac{y+8}{x+2} &= 5 \\ у + 8 &= 5(х + 2)\\ у + 8 &= 5х + 10\\ у &= 5x + 2 \конец{выравнивание*}

\((2p;q)\) и \((0;-q)\)

\начать{выравнивать*} \frac{y-y_1}{x-x_1} &= \frac{y_2-y_1}{x_2-x_1} \\ \frac{y-q}{x-2p} &= \frac{-q-q}{0 — 2p} \\ \frac{y-q}{x-2p} &= \frac{-2q}{-2p} \\ \frac{y-q}{x-2p} &= \frac{q}{p} \\ y — q &= \frac{q}{p} \left( x — 2p \right) \\ y — q &= \frac{q}{p}x — 2q \\ \поэтому y &= \frac{q}{p}x — q \конец{выравнивание*}

Использование и переписывание формул в геометрии

Использование геометрических формул без перестановки

Иногда вы можете использовать формулу в геометрии, просто подставляя значения, которые вы знаете для каждой переменной. Например, если вы хотите найти периметр ( P ) прямоугольника, вам нужно знать длину ( l ) и ширину ( w ) прямоугольника. Если вам дано, что длина равна 10 футам, а ширина — 8 футам, то вы подставляете эти значения в формулу для периметра.

Пример периметра

Допустим, вы хотите найти объем стаканчика в форме конуса , который шел в комплекте с лакомством из снежного конуса.Формула объема конуса показана ниже.

Итак, чтобы вычислить объем ( V ), вы измерили высоту конуса ( h ) 6 дюймов и радиус ( r ) дюймов ( r ) . Теперь вы подставляете числовые значения в формулу.

Преобразование формул

В этих двух примерах вам просто нужно подставить значения, которые вы знаете для каждой переменной, и затем вы можете легко вычислить количество, которое хотите узнать. Это не всегда так. Бывают случаи, когда вам может потребоваться сначала переписать уравнение, прежде чем вы сможете подставить значения, которые вы знаете.

Например, вы знаете объем ( V ) цилиндра и радиус ( r ), но не знаете высоту ( h ) Вы можете изменить формулу для объема цилиндра и решить ее для ч с помощью алгебры.

Затем разделите обе части уравнения, чтобы получить ч само по себе.

Предположим, вам нужно, чтобы площадь ( A ) треугольника была равна 36 кв. длина основания ( b ) треугольника. С этим можно разобраться, но сначала нужно взять формулу площади треугольника и решить ее для b .

Теперь вы подставляете известные вам значения, чтобы найти основание треугольника.

Итоги урока

На этом уроке вы научились пользоваться геометрическими формулами без какой-либо перестановки. Вы сделали это, просто подставив значения, которые вы знали, и рассчитали количество, которое вы хотели знать. Затем вы рассмотрели примеры, в которых вам нужно было изменить формулу с помощью алгебры, прежде чем вы могли подставить значения, которые вы знали. Вы узнали, что геометрические формулы действительно полезны для расчета величин, связанных с геометрическими фигурами.

Глава 11: Векторы и геометрия пространства

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 8604

vecd} [1] {\ overset {- \! — \! \ rightharpoonup} {\ vphantom {a} \ smash {# 1}}} \) \ (\ newcommand {\ id} {\ mathrm {id}} \ ) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range }\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\ mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle} \) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span} }\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{ \mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm} [1]{\| #1 \|}\) \( \newco mmand{\inner}[2]{\langle #1, #2 \rangle}\) \(\newcommand{\Span}{\mathrm{span}}\)

Авторы

11. 1: Векторы на плоскости
Некоторые величины, такие как сила, определяются в терминах размера (также называемого величиной) и направления. Величина, имеющая величину и направление, называется вектором.
11.2: Векторы в пространстве
Векторы — полезный инструмент для решения двумерных задач. Однако жизнь протекает в трех измерениях. Чтобы расширить использование векторов до более реалистичных приложений, необходимо создать основу для описания трехмерного пространства.
11.3: Скалярное произведение
Скалярное произведение, по сути, говорит нам, какая часть вектора силы приложена в направлении вектора движения. Скалярное произведение также может помочь нам измерить угол, образованный парой векторов, и положение вектора относительно осей координат. Он даже обеспечивает простой тест, чтобы определить, пересекаются ли два вектора под прямым углом.
11. 4: Перекрестное произведение
В этом разделе мы разработаем операцию, называемую перекрестным произведением, которая позволяет нам найти вектор, ортогональный двум заданным векторам.Вычисление крутящего момента является важным применением векторных произведений, и мы более подробно рассмотрим крутящий момент позже в этом разделе.
11.5: Уравнения прямых и плоскостей в пространстве
Чтобы написать уравнение прямой, мы должны знать две точки на прямой или мы должны знать направление прямой и по крайней мере одну точку через которую проходит линия. В двух измерениях мы используем понятие наклона для описания ориентации или направления линии. В трех измерениях мы описываем направление линии, используя вектор, параллельный линии.В этом разделе мы рассмотрим, как использовать уравнения для описания линий и плоскостей в пространстве.
11.6: Квадратичные поверхности
Мы изучали векторы и векторные операции в трехмерном пространстве и разработали уравнения для описания линий, плоскостей и сфер. В этом разделе мы используем наши знания о плоскостях и сферах, которые являются примерами трехмерных фигур, называемых поверхностями, для изучения множества других поверхностей, которые можно изобразить в трехмерной системе координат.
11.7: Цилиндрические и сферические координаты
Декартова система координат обеспечивает простой способ описания расположения точек в пространстве. Однако некоторые поверхности трудно смоделировать с помощью уравнений, основанных на декартовой системе. Как следует из названия, цилиндрические координаты полезны для решения задач, связанных с цилиндрами. Точно так же сферические координаты полезны для решения задач, связанных со сферами.
11R: Обзорные упражнения по главе 11

Участники

Гилберт Стрэнг (MIT) и Эдвин «Джед» Херман (Харви Мадд) со многими сотрудничающими авторами. Этот контент от OpenStax лицензирован по лицензии CC-BY-SA-NC 4. 0. Скачать бесплатно на http://cnx.org.

Наверх
- Оглавление
- 11.1: Векторы на плоскости

Была ли эта статья полезной?
Да
Нет

Тип изделия
Глава
укрытие
решения
Лицензия
CC BY-NC-SA
Показать страницу Содержание
нет
Включено
да
Метки
1. расчет: да

МАТЕМАТИКА G11: Алгебра II

Описание

Опираясь на свою работу с линейными, квадратичными и экспоненциальными функциями, учащиеся расширяют свой набор функций, включая полиномиальные, рациональные и радикальные функции. Учащиеся тесно работают с выражениями, определяющими функции, и продолжают расширять и оттачивать свои способности моделировать ситуации и решать уравнения, включая решение квадратных уравнений над набором комплексных чисел и решение показательных уравнений с использованием свойств логарифмов. Стандарты математической практики применяются на протяжении всего курса и вместе со стандартами содержания предписывают учащимся воспринимать математику как последовательный, полезный и логичный предмет, который использует их способность разбираться в проблемных ситуациях.

О загружаемых ресурсах

Обзор курса «Алгебра II» : предоставление рекомендаций по разработке учебных материалов путем объединения информации из Единых основных стандартов обучения штата Нью-Йорк, моделей содержания PARCC, пояснений к стандартам NYSED и прогрессии.

A Story of Functions Карта учебного плана и обзор 9–12 : предоставляет учителям четкое представление о модулях на каждом уровне обучения с 9 по 12 классы.

Инструкции по созданию строительных лесов для ELL, Справочник по математике : предоставьте преподавателям рекомендации о том, как пользоваться учебными материалами на EngageNY, и предоставьте дополнительные строительные леса для учащихся ELL в соответствии с их уровнем владения английским языком.

загрузок

Могут быть случаи, когда наши загружаемые ресурсы содержат гиперссылки на другие веб-сайты. Эти гиперссылки ведут на веб-сайты, опубликованные или управляемые третьими сторонами.UnboundEd и EngageNY не несут ответственности за содержание, доступность или политику конфиденциальности этих веб-сайтов.

Кредиты

С сайта EngageNY.org Департамента образования штата Нью-Йорк. Алгебра II. Доступно на веб-сайте вовлечения.org/resource/high-school-алгебра-ii; по состоянию на 29 мая 2015 г.

Читать заметки, формулы, уравнения, вопросы и многое другое

Координатная геометрия — это раздел математики, в котором положение точки описывается на плоскости. Он состоит из одной из важнейших частей математики. По определению координатной геометрии вы можете легко проанализировать важность этой главы, где бы ни была плоскость, это просто означает, что есть координата.Он обеспечивает связь между алгеброй и геометрией через графики линий и кривых. Это в основном помогает нам найти точки на плоскости. Его использование распространяется во всех областях, таких как тригонометрия, исчисление, размерная геометрия и т. д. И этот предмет имеет очевидные применения в статистике, физике и в реальной жизни для области строительства, эскиз здания — это чистая геометрия, в астрофизике, чтобы найти расстояние между планетами, координатная геометрия очень помогает. На JEE Mains или других вступительных экзаменах экзаменатор пытается проверить вашу силу, используя концепцию координатной геометрии.В физике используется Закон Ньютона, Закон Движения, Закон Гравитации, Все виды сил даже в измерении Координатная геометрия.

Почему Координатная геометрия?
Геометрия, как логическая система, является средством, и даже самым мощным средством, позволяющим детям почувствовать силу человеческого духа, принадлежащего их собственному духу.- H. FREUDENTHAL

Координатная геометрия Пример из реальной жизни
В детстве вы играли в игру Людо
В этой игре вы прошли самый длинный путь.Вы когда-нибудь задумывались, почему вы используете этот путь, если ваша единственная цель — поместить токен в конечную точку, поскольку у нас есть еще один вариант — выбрать наименьший путь, который напрямую помещает наш токен в конечную точку.
Онлайн-подготовка к JEE Main/NEET
Crack JEE 2021 с онлайн-программой подготовки к JEE/NEET
Начинай сейчас
Ответ заключается в том, чтобы сделать игру более интересной, поэтому они определили некоторые координаты в игре, где мы можем хранить наши жетоны, и обязательно пересечь все эти координаты, чтобы сделать игру более интересной.
Оооо! вы изучаете координатную геометрию с детства
Изучив эту главу, вы точно поймете, каким образом Examiner настроил для вас Людо.
Теперь возьмем другой пример
Предположим, вы и ваши школьные друзья планируете отправиться на экскурсию.
Первое, что приходит в голову, это найти место встречи и место встречи должно быть кратчайшим расстоянием для всех.
Итак, как вы выбираете место встречи?
Сначала вы начинаете делиться своим домашним местоположением.
Во-вторых, вы выбираете место, куда каждый может легко добраться. Причина достижения зависит от наличия транспорта.
В-третьих, вы выбираете точку в направлении вашего тура, чтобы он занимал меньше времени.
Все планирование выполняется с использованием координатной геометрии.

Примечания по координатной геометрии
Прямые линии: На предыдущих занятиях вы были знакомы с прямыми линиями. Теперь в этом разделе вы изучите некоторые важные свойства линии, когда прямые определяются в координатах.
Наклон линии: В координатной плоскости линия пересекает ось x и образует с осью x два дополнительных угла. Угол, образуемый линией с положительным направлением оси x и измеренный против часовой стрелки, называется наклоном линии.
Окружность: Окружность определяется как множество всех точек на координатной плоскости, равноудаленных от фиксированной точки на плоскости.

Парабола: Парабола определяется как множество всех точек координатной плоскости, равноудаленных от фиксированной точки и фиксированной прямой линии на плоскости.

Эллипс: Эллипс определяется как множество всех точек на плоскости, сумма расстояний которых от двух фиксированных точек на плоскости является постоянной величиной.

Гипербола: Гипербола — это множество всех точек на плоскости, разность расстояний которых от двух фиксированных точек на плоскости является постоянной величиной.

Важные уравнения координатной геометрии

Важные уравнения координатной геометрии

Важные термины координатной геометрии
Координата точки на плоскости
Уклон и уклон
Угол между двумя пересекающимися прямыми, точка их пересечения, параллельные прямые и коллинеарные прямые
Фокус и эксцентриситет
Директриса
Широкая кишка прямой кишки

Советы, которые помогут вам в подготовке координатной геометрии
Лучший способ решить вопрос — использовать простые методы.
Всегда помните об общем уравнении геометрии, если вы не можете ответить на какой-либо вопрос, попробуйте сделать данное уравнение похожим на общее уравнение, например, для. каждый получит, чье это уравнение, если вы видите, что степень y равна 2, а степень x равна 1, значит, это уравнение параболы, и теперь попытайтесь сделать его таким же похожим на общее уравнение, теперь оно выглядит просто, и вы можете легко см. значение a равно 1.
Важные термины, определенные в этой теме, являются основным ключевым моментом решения всех типов задач.
Короткий трюк для решения вопроса с множественным выбором заключается в том, что поместите координатные точки от варианта ответа к заданному вопросу, помните одну вещь, данный вариант может обмануть вас в любом месте, поэтому будьте осторожны.

Лучшая книга по координатной геометрии:
Книги NCERT по математике являются одним из самых важных учебных материалов, поскольку эта книга охватывает все темы. Начните с книги NCERT, пример, приведенный в NCERT, прост и ясен.Большинство важных понятий и теорий вы поймете, просто решив приведенные примеры. А также решить все проблемы (в т.ч. прочие проблемы) NCERT. Если вы сделаете это, ваш базовый уровень подготовки будет пройден.
Затем вы можете обратиться к книгам «Координаты» Амита М. Агарвала, Cengage Mathematics Coordinate Geometry или RD Sharma. Координатная геометрия очень красиво объяснена в книге Арихант Алгебра, и есть много вопросов с кристально ясными концепциями.Но опять же, выбор справочника зависит от вас, найдите книгу, которая лучше всего подходит вам, в зависимости от того, насколько хорошо вы разбираетесь в концепциях и сложности вопросов, которые вам нужны. Вместо того, чтобы ссылаться на все книги, просто придерживайтесь одной хорошей книги, но для отработки большего количества задач вы можете обратиться к другим книгам.

Математика по главам Примечания к инженерным экзаменам
Геометрия
Геометрия — это все о формах и их свойствах.
Если вы любите играть с предметами или рисовать, то геометрия для вас!
Геометрию можно разделить на:

Плоская геометрия касается плоских фигур, таких как линии, круги и треугольники… формы, которые можно нарисовать на листе бумаги

Solid Geometry — это трехмерные объекты, такие как кубы, призмы, цилиндры и сферы.
Подсказка: Попробуйте нарисовать некоторые формы и углы, когда будете учиться… это помогает.
Точка, линия, плоскость и тело
Точка не имеет размеров, только положение
Линия одномерная
Плоскость двухмерная (2D)
Твердое тело трехмерное (3D)
Почему?
Почему мы занимаемся геометрией? Чтобы открывать закономерности, находить площади, объемы, длины и углы и лучше понимать окружающий мир.
Плоская геометрия
Плоская геометрия — это формы на плоской поверхности (как на бесконечном листе бумаги).

Полигоны
Многоугольник — это двухмерная фигура, состоящая из прямых линий. Треугольники и прямоугольники являются многоугольниками.
Вот еще:

Круг
Теоремы о кругах (расширенная тема)

Символы
В геометрии используется много специальных символов.Вот краткая ссылка для вас:
Геометрические символы

Конгруэнтные и подобные

Углы
Типы уголков

Использование чертежных инструментов

Преобразования и симметрия
Преобразования:
Симметрия:

Координаты

Дополнительные темы плоской геометрии
Пифагор

Конические профили

Теоремы круга
Треугольные центры
Тригонометрия
Тригонометрия — отдельная тема, поэтому вы можете посетить:

Твердотельная геометрия
Solid Geometry — это геометрия трехмерного пространства, в котором мы живем.