Простая информатика — Система счисления
Система счисления – это способ записи чисел. Обычно, числа записываются с помощью специальных знаков – цифр (хотя и не всегда). Если вы никогда не изучали данный вопрос, то, по крайней мере, вам должны быть известны две системы счисления – это арабская и римская. В первой используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и это позиционная система счисления. А во второй – I, V, X, L, C, D, M и это непозиционная система счисления.
В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, а в непозиционных – нет. Например:
11 – здесь первая единица обозначает десять, а вторая – 1.
II – здесь обе единицы обозначают единицу.
345, 259, 521 – здесь цифра 5 в первом случае обозначает 5, во втором – 50, а в третьем – 500.
XXV, XVI, VII – здесь, где бы ни стояла цифра V, она везде обозначает пять единиц. Другими словами, величина, обозначаемая знаком V, не зависит от его позиции.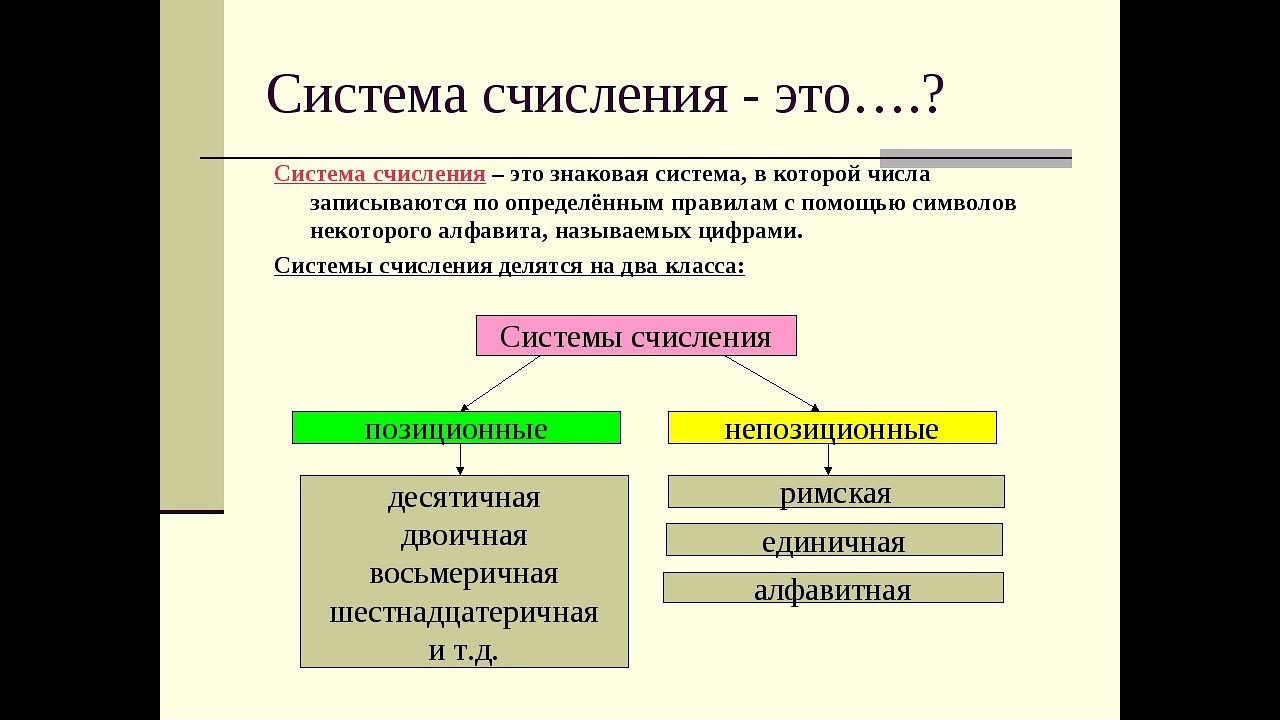
Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, чем в непозиционных, т.к. математические операции осуществляются по несложным алгоритмам (например, умножение в столбик, сравнение двух чисел).
В мире наиболее распространены позиционные системы счисления. Помимо знакомой всем с детства десятичной (где используется десять цифр от 0 до 9), в технике широкое распространение нашли такие системы счисление как двоичная (используются цифры 0 и 1), восьмеричная и шестнадцатеричная.
Следует отметить, важную роль нуля. «Открытие» этой цифры в истории человечества сыграло большую роль в формировании позиционных систем счисления.
Основание системы счисления – это количество знаков, которое используется для записи цифр.
Разряд — это позиция цифры в числе. Разрядность числа — количество цифр, из которых состоит число (например, 264 — трехразрядное число, 00010101 — восьмиразрядное число). Разряды нумеруются справа на лево (например, в числе 598 восьмерка занимает первый разряд, а пятерка — третий).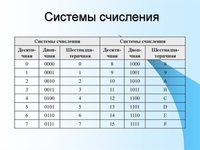
Итак, в позиционной системе счисления числа записываются таким образом, что каждый следующий (движение справа на лево) разряд больше другого на степень основания системы счисления. (придумать схему)
Одно и тоже число (значение) можно представить в различных системах счисления. Представление числа при этом различно, а значение остается неизменным.
Двоичная система счисления
В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)
Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.
В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются.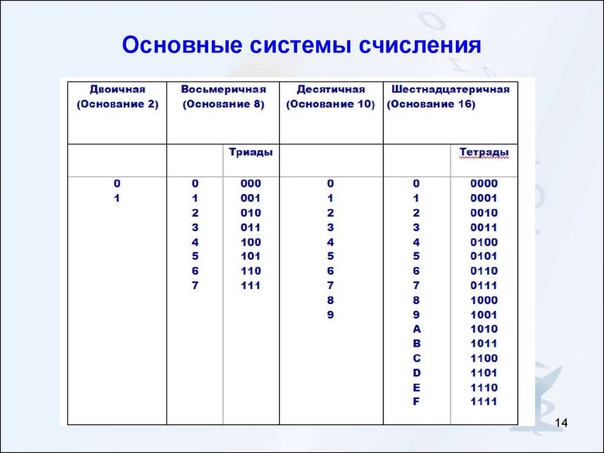 И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.
И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.
Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.
Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.
Перевод чисел из двоичной системы счисления в десятичную
Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.
В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т. д. Например:
д. Например:
1476 = 1000 + 400 + 70 + 6
Можно пойти еще дальше и разложить так:
1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100
Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 — это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.
Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:
10001001 = 1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20
Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:
1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
Т. е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:
е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:
100010012 = 13710
Почему двоичная система счисления так распространена?
Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:
77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)
Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:
Это и есть число 77 в двоичном представлении. Проверим:
Восьмеричная система счисления
Итак, современное «железо понимает» лишь двоичную систему счисления. Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.
В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:
000 – 0
001 – 1
010 – 2
011 – 3
100 – 4
101 – 5
110 – 6
111 – 7
Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки и заменить их соответствующими им цифрами из восьмеричной системы счисления.
1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135
Т.е число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 10111012 = 1358.
Обратный перевод. Допустим, требуется перевести число 1008 (не заблуждайтесь! 100 в восьмеричной системе – это не 100 в десятичной) в двоичную систему счисления.
1008 = 1 0 0 = 001 000 000 = 001000000 = 10000002
Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме:
6728 = 6 * 82 + 7 * 81 + 2 * 80 = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 44210
1008 = 1 * 8
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется в компьютерной науке из-за легкости перевода в нее двоичных чисел.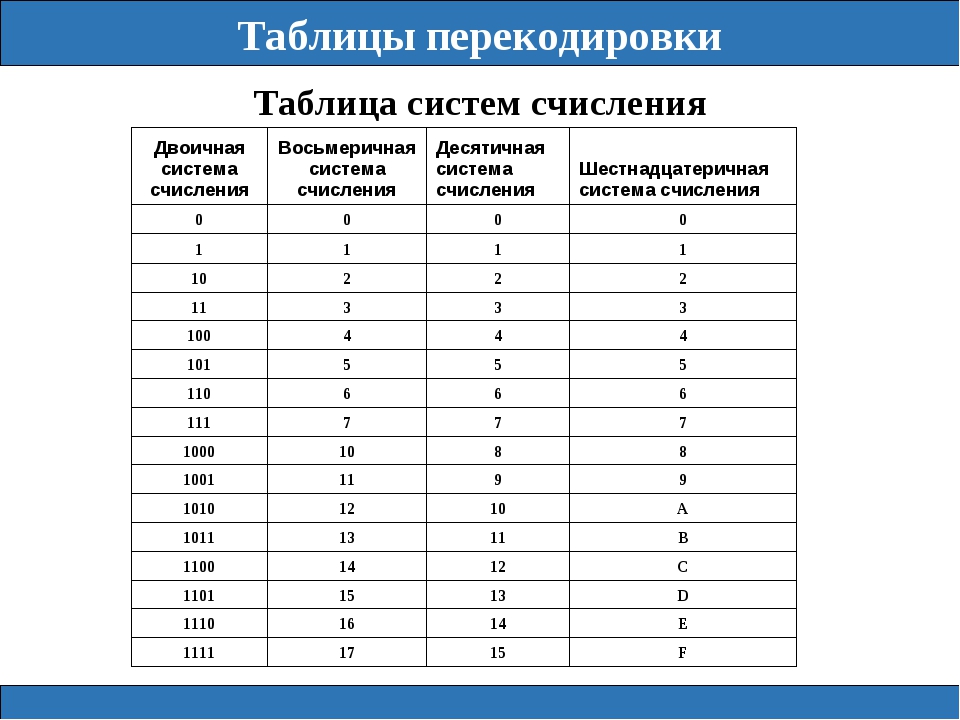 При шестнадцатеричной записи числа получаются более компактными.
При шестнадцатеричной записи числа получаются более компактными.
В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15).
При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифра шестнадцатеричной системе счисления:
Например:
10001100101 = 0100 1100 0101 = 4 C 5 = 4C5
Если потребуется, то число 4C5 можно перевести в десятичную систему счисления следующим образом (C следует заменить на соответствующее данному символу число в десятичной системе счисления – это 12):
4C5 = 4 * 162 + 12 * 161 + 5 * 160 = 4 * 256 + 192 + 5 = 1221
Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи — это FF.
FF = 15 * 161 + 15 * 160 = 240 + 15 = 255
255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF. Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние
Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние
1.3. Системы счисления. Основы информатики: Учебник для вузов
1.3. Системы счисления
Система счисления – это способ записи чисел с помощью заданного набора специальных знаков (цифр).
Существуют системы позиционные и непозиционные.
В непозиционных системах счисления вес цифры не зависит от позиции, которую она занимает в числе. Так, например, в римской системе счисления в числе XXXII (тридцать два) вес цифры X в любой позиции равен просто десяти.
В позиционных системах счисления вес каждой цифры изменяется в зависимости от ее позиции в последовательности цифр, изображающих число.
Любая позиционная система характеризуется своим основанием. Основание позиционной системы счисления – это количество различных знаков или символов, используемых для изображения цифр в данной системе.
За основание можно принять любое натуральное число – два, три, четыре, шестнадцать и т. д. Следовательно, возможно бесконечное множество позиционных систем.
Десятичная система счисления
Пришла в Европу из Индии, где она появилась не позднее VI века н. э. В этой системе 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, однако информацию несет не только цифра, но и место, на котором цифра стоит (то есть ее позиция). В десятичной системе счисления особую роль играют число 10 и его степени: 10, 100, 1000 и т. д. Самая правая цифра числа показывает число единиц, вторая справа – число десятков, следующая – число сотен и т. д.
Двоичная система счисления
В этой системе всего две цифры – 0 и 1. Особую роль здесь играет число 2 и его степени: 2, 4, 8 и т. д. Самая правая цифра числа показывает число единиц, следующая цифра – число двоек, следующая – число четверок и т. д. Двоичная система счисления позволяет закодировать любое натуральное число – представить его в виде последовательности нулей и единиц. В двоичном виде можно представлять не только числа, но и любую другую информацию: тексты, картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко реализуется технически.
В двоичном виде можно представлять не только числа, но и любую другую информацию: тексты, картинки, фильмы и аудиозаписи. Инженеров двоичное кодирование привлекает тем, что легко реализуется технически.
Восьмеричная система счисления
В этой системе счисления 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Цифра 1, указанная в самом младшем разряде, означает, как и в десятичном числе, просто единицу. Та же цифра 1 в следующем разряде означает 8, в следующем – 64 и т. д. Число 100 (восьмеричное) есть не что иное, как 64 (десятичное). Чтобы перевести в двоичную систему, например, число 611 (восьмеричное), надо заменить каждую цифру эквивалентной ей двоичной триадой (тройкой цифр). Легко догадаться, что для перевода многозначного двоичного числа в восьмеричную систему нужно разбить его на триады справа налево и заменить каждую триаду соответствующей восьмеричной цифрой.
Шестнадцатеричная система счисления
Запись числа в восьмеричной системе счисления достаточно компактна, но еще компактнее она получается в шестнадцатеричной системе. В качестве первых 10 из 16 шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве остальных 6 цифр используют первые буквы латинского алфавита: A, B, C, D, E, F. Цифра 1, записанная в самом младшем разряде, означает просто единицу. Та же цифра 1 в следующем – 16 (десятичное), в следующем – 256 (десятичное) и т. д. Цифра F, указанная в самом младшем разряде, означает 15 (десятичное). Перевод из шестнадцатеричной системы в двоичную и обратно производится аналогично тому, как это делается для восьмеричной системы.
В качестве первых 10 из 16 шестнадцатеричных цифр взяты привычные цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, а вот в качестве остальных 6 цифр используют первые буквы латинского алфавита: A, B, C, D, E, F. Цифра 1, записанная в самом младшем разряде, означает просто единицу. Та же цифра 1 в следующем – 16 (десятичное), в следующем – 256 (десятичное) и т. д. Цифра F, указанная в самом младшем разряде, означает 15 (десятичное). Перевод из шестнадцатеричной системы в двоичную и обратно производится аналогично тому, как это делается для восьмеричной системы.
Таблица 1. Соответствие между первыми несколькими натуральными числами всех трех систем счисления
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРессистема счисления. Виды систем счисления
В курсе информатики, вне зависимости, школьном или университетском, особое место уделяется такому понятию как системы счисления.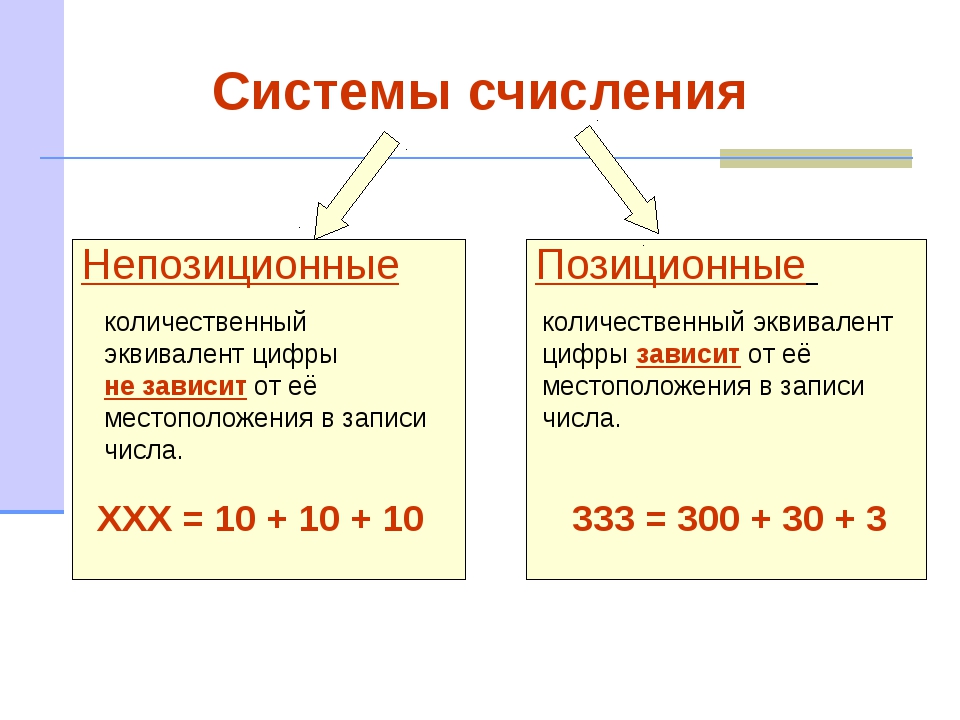 Как правило, на него выделяют несколько уроков или практических занятий. Основная цель — не только усвоить основные понятия темы, изучить виды систем счисления, но и познакомиться с двоичной, восьмеричной и шестнадцатеричной арифметикой.
Как правило, на него выделяют несколько уроков или практических занятий. Основная цель — не только усвоить основные понятия темы, изучить виды систем счисления, но и познакомиться с двоичной, восьмеричной и шестнадцатеричной арифметикой.
Что это значит?
Начнем с определения основного понятия. Как отмечает учебник «Информатика», система счисления — это система записи чисел, в которой используется специальный алфавит или определенный набор цифр.
В зависимости от того, меняется ли значение цифры от ее положения в числе, выделяют две: позиционную и непозиционную системы счисления.
В позиционных системах значение цифры меняется вместе с ее положением в числе. Так, если взять число 234, то цифра 4 в ней означает единицы, если же рассмотреть число 243, то тут она будет уже означать десятки, а не единицы.
В непозиционных системах значение цифры статично, вне зависимости от ее положения в числе. Наиболее яркий пример – палочковая система, где каждая единица обозначается с помощью черточки. Неважно, куда вы припишите палочку, значение числа измениться лишь на единицу.
Неважно, куда вы припишите палочку, значение числа измениться лишь на единицу.
Непозиционные системы
К непозиционным системам счисления относятся:
- Единичная система, которая считается одной из первых. В ней вместо цифр использовались палочки. Чем их было больше, тем больше было значение числа. Встретить пример чисел, записанных таким образом, можно в фильмах, где речь идет о потерянных в море людях, заключенных, которые отмечают каждый день с помощью зарубок на камне или дереве.
- Римская, в которой вместо цифр использовались латинские буквы. Используя их, можно записать любое число. При этом его значение определялось с помощью суммы и разницы цифр, из которых состояло число. Если слева от цифры находилось меньшее число, то левая цифра вычиталась из правой, а если справа цифра была меньше или равна цифре слева, то их значения суммировались. Например, число 11 записывалось как XI, а 9 – IX.
- Буквенные, в которых числа обозначались с помощью алфавита того или иного языка.
 Одной из них считается славянская система, в которой ряд букв имел не только фонетическое, но и числовое значение.
Одной из них считается славянская система, в которой ряд букв имел не только фонетическое, но и числовое значение. - Вавилонская система счисления, в которой использовалось всего два обозначения для записи – клинья и стрелочки.
- В Египте тоже использовались специальные символы для обозначения чисел. При записи числа каждый символ мог использоваться не более девяти раз.
Позиционные системы
Большое внимание уделяется в информатике позиционным системам счисления. К ним относятся следующие:
- двоичная;
- восьмеричная;
- десятичная;
- шестнадцатеричная;
- шестидесятеричная, используемая при счете времени (к примеру, в минуте — 60 секунд, в часе — 60 минут).
Каждая из них обладает своим алфавитом для записи, правилами перевода и выполнения арифметических операций.
Десятичная система
Данная система является для нас наиболее привычной. В ней используются цифры от 0 до 9 для записи чисел. Они также носят название арабских. В зависимости от положения цифры в числе, она может обозначать разные разряды – единицы, десятки, сотни, тысячи или миллионы. Ее мы пользуемся повсеместно, знаем основные правила, по которым производятся арифметические операции над числами.
В зависимости от положения цифры в числе, она может обозначать разные разряды – единицы, десятки, сотни, тысячи или миллионы. Ее мы пользуемся повсеместно, знаем основные правила, по которым производятся арифметические операции над числами.
Двоичная система
Одна из основных систем счисления в информатике – двоичная. Ее простота позволяет компьютеру производить громоздкие вычисления в несколько раз быстрее, нежели в десятичной системе.
Для записи чисел используется лишь две цифры – 0 и 1. При этом, в зависимости от положения 0 или 1 в числе, его значение будет меняться.
Изначально именно с помощью двоичного кода компьютеры получали всю необходимую информацию. При этом, единица означала наличие сигнала, передаваемого с помощью напряжения, а ноль – его отсутствие.
Восьмеричная система
Еще одна известная компьютерная система счисления, в которой применяются цифры от 0 до 7. Применялась в основном в тех областях знаний, которые связаны с цифровыми устройствами. Но в последнее время она употребляется значительно реже, так как на смену ей пришла шестнадцатеричная система счисления.
Но в последнее время она употребляется значительно реже, так как на смену ей пришла шестнадцатеричная система счисления.
Двоично-десятичная система
Представление больших чисел в двоичной системе для человека – процесс довольно сложный. Для его упрощения была разработана двоично-десятичная система счисления. Используется она обычно в электронных часах, калькуляторах. В данной системе из десятичной системы в двоичную преобразуется не все число, а каждая цифра переводится в соответствующий ей набор нулей и единиц в двоичной системе. Аналогично происходит и перевод из двоичной системы в десятичную. Каждая цифра, представленная в виде четырехзначного набора нулей и единиц, переводится в цифру десятичной системы счисления. В принципе, нет ничего сложного.
Для работы с числам в данном случае пригодится таблица систем счисления, в которой будет указано соответствие между цифрами и их двоичным кодом.
Шестнадцатеричная система
В последнее время все большую популярность приобретает в программировании и информатике система счисления шестнадцатеричная.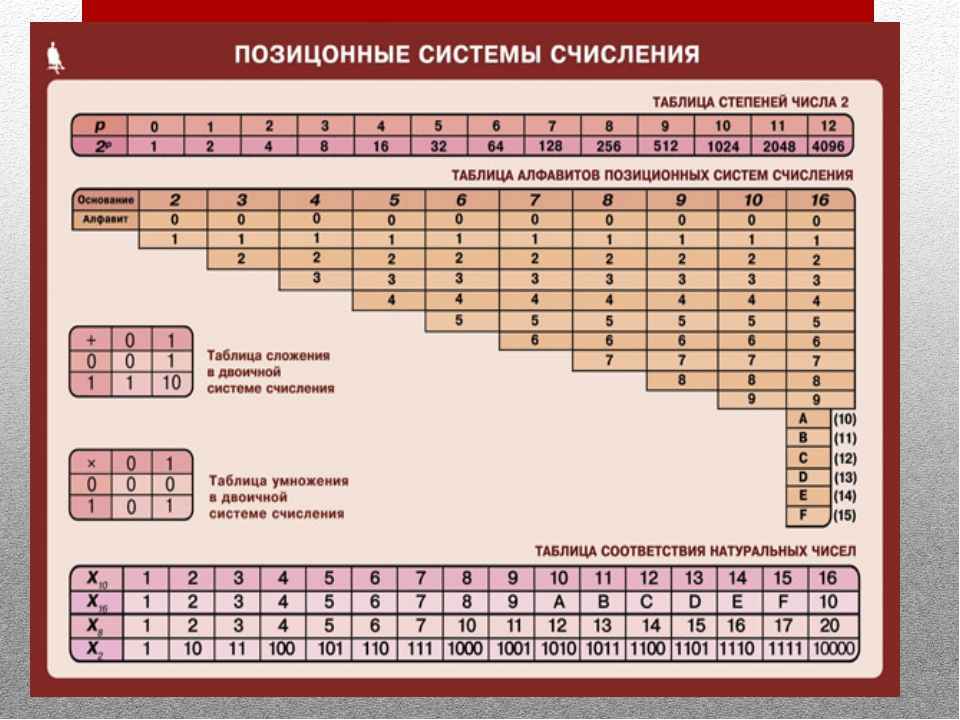 В ней используются не только цифры от 0 до 9, но и ряд латинских букв – A, B, C, D, E, F.
В ней используются не только цифры от 0 до 9, но и ряд латинских букв – A, B, C, D, E, F.
При этом, каждая из букв имеет свое значение, так A=10, B=11, C=12 и так далее. Каждое число представляется в виде набора из четырех знаков: 001F.
Перевод чисел: из десятичной в двоичную
Перевод в системах счисления чисел происходит по определенным правилам. Наиболее часто встречается перевод из двоичной в десятичную систему и наоборот.
Для того, чтобы перевести число из десятичной системы в двоичную, необходимо последовательно делить его на основание системы счисления, то есть, число два. При этом, остаток от каждого деления необходимо фиксировать. Так будет происходить до тех пор, пока остаток от деления не будет меньше или равен единице. Проводить вычисления лучше всего в столбик. Затем полученные остатки от деления записываются в строку в обратном порядке.
Например, переведем число 9 в двоичную систему:
Делим 9, так как число не делится нацело, то берем число 8, остаток будет 9 – 1 = 1.
После деления 8 на 2 получаем 4. Снова делим его, так как число делится нацело – получаем в остатке 4 – 4 = 0.
Проводим ту же операцию с 2. В остатке получаем 0.
В итоге деления у нас получается 1.
Далее записываем все полученные нами остатки в обратном порядке, начиная с итога деления: 1001.
Вне зависимости от итоговой системы счисления, перевод чисел из десятичной в любую другую будет происходить по принципу деления числа на основу позиционной системы.
Перевод чисел: из двоичной в десятичную
Довольно легко переводить числа и в десятичную систему счисления из двоичной. Для этого достаточно знать правила возведения чисел в степень. В данном случае, в степень двойки.
Алгоритм перевода следующий: каждую цифру из кода двоичного числа необходимо умножить на двойку, причем, первая двойка будет в степени m-1, вторая – m-2 и так далее, где m – количество цифр в коде. Затем сложить результаты сложения, получив целое число.
Для школьников этот алгоритм можно объяснить проще:
Для начала берем и записываем каждую цифру, умноженную на двойку, затем проставляем степень двойки с конца, начиная с нуля. Потом складываем полученное число.
Потом складываем полученное число.
Для примера разберем с вами полученное ранее число 1001, переведя его в десятичную систему, и заодно проверим правильность наших вычислений.
Выглядеть это будет следующим образом:
1*23 + 0*22+0*21+1*20= 8+0+0+1 =9.
При изучении данной темы удобно использовать таблицу со степенями двойки. Это существенно уменьшит количество времени, необходимое для проведения вычислений.
Другие варианты перевода
В некоторых случаях перевод может осуществляться между двоичной и восьмеричной системой счисления, двоичной и шестнадцатеричной. В таком случае можно пользоваться специальными таблицами или же запустить на компьютере приложение калькулятор, выбрав во вкладке вид вариант «Программист».
Арифметические операции
Вне зависимости от того, в каком виде представлено число, с ним можно проводить привычные для нас вычисления. Это может быть деление и умножение, вычитание и сложение в системе счисления, которую вы выбрали. Конечно, для каждой из них действуют свои правила.
Конечно, для каждой из них действуют свои правила.
Так для двоичной системы разработаны свои таблицы для каждой из операций. Такие же таблицы используются и в других позиционных системах.
Заучивать их необязательно – достаточно просто распечатать и иметь под рукой. Также можно воспользоваться калькулятором на ПК.
Одна из важнейших тем в информатике – система счисления. Знание этой темы, понимание алгоритмов перевода чисел из одной системы в другую – залог того, что вы сможете разобраться в более сложных темах, таких как алгоритмизация и программирование и сможете самостоятельно написать свою первую программу.
|
Вопреки распространённому заблуждению, двоичная система счисления была придумана не инженерами-конструкторами ЭВМ, а математиками и философами задолго до появления компьютеров, ещё в 17 веке. |
| Тема: Кодирование числовой информации. | ||
| Требования к знаниям и умениям: Знать: определения — система счисления, позиционная система счисления, непозиционная система счисления, основание системы счисления, алфавит системы счисления, разряд числа, представление числа в развернутой форме. Системы счисления используемые в ЭВМ. Уметь: представлять число в развернутой форме; перевести десятичное число в любую систему счисления; перевести число из любой системы счисления в десятичную; переводить числа из 2-ой систему напрямую в 8-ю и обратно; |
||
| Конспект | Кодирование информации в компьютере | Скачать |
| Конспект | Системы счисления. | Скачать |
| Конспект | Перевод из 10-й системы в 2-ю и обратно. | Скачать |
| Конспект | Действия в 2-системе. | Скачать |
| Конспект | Перевод чисел из 10-системы в 8-систему и обратно. | Скачать |
| Конспект | Перевод чисел из 10-системы в 16-систему и обратно. | Скачать |
| Конспект | Перевод из 2-й системы напрямую в 8-ю и 16-ю. |
Скачать |
| Тренинг «Системы счисления» | Пройти | |
| Тренинг «Алфавит системы счисления» | Пройти | |
| Тренинг «Системы счисления»-2 | Пройти | |
| Тренинг «Позиционные и непозиционные системы»-1 | Пройти | |
| Тренинг «Позиционные и непозиционные системы»-2 | Пройти | |
| Тренинг «Позиционные и непозиционные системы»-3 | Пройти | |
| Тренинг «Определения алфавит и основание» | Пройти | |
| Тренинг «Определи основание системы счисления»-1 | Пройти | |
| Тренинг «Определи основание системы счисления»-2 | Пройти | |
| Тренинг «Цифры в системе счисления» | Пройти | |
| Тренинг «Определи основание системы счисления»-3 | Пройти | |
| Тренинг «Викторина системы счисления» | Пройти | |
| Тренинг «Викторина системы счисления»-2 | Пройти | |
| Кроссворд «Системы счисления» | Пройти | |
| Тренинг «Правило перевода из 10-системы в другие»-1 | Пройти | |
| Тренинг «Правило перевода из 10-системы в другие»-2 | Пройти | |
| Двоичная система счисления | ||
| Тренинг «Двоичная система счисления» | Пройти | |
| Тренинг «Правило перевода из 10-системы в 2-ю»-1 | Пройти | |
| Тренинг «Правило перевода из 10-системы в 2-ю»-2 | Пройти | |
| Тренинг «Викторина» | Пройти | |
| Тренинг «Перевод из 10-й в 2-ю систему счисления» | Пройти | |
| Тренинг «Перевод из 2-й в 10-ю систему счисления» | Пройти | |
| Тренинг «Узнай число» | Пройти | |
| Тренинг «Количество нулей и единиц» | Пройти | |
| Тренинг «Расставь по порядку» | Пройти | |
| Тренинг «Определи последующее число» | Пройти | |
| Группа упражнений «Двоичная система» | Пройти | |
| Восьмеричная система счисления | ||
| Тренинг «Восьмеричная система» | Пройти | |
| Тренинг «Восьмеричная система»-2 | Пройти | |
| Тренинг «Викторина восьмеричная система» | Пройти | |
| Тренинг «Правило перевода из 10-системы в 8-ю»-1 | Пройти | |
| Тренинг «Правило перевода из 10-системы в 8-ю»-2 | Пройти | |
| Тренинг «Расставь по порядку»-2 | Пройти | |
| Тренинг «Перевод из 10 в 8-ю систему счисления» | Пройти | |
| Тренинг «Перевод из 8 в 10-ю систему счисления» | Пройти | |
| Тренинг «Перевод из 10 в 8-ю систему счисления»-2 | Пройти | |
| Тренинг «Перевод из 8 в 10-ю систему счисления»-2 | Пройти | |
| Группа упражнений «Восьмеричная система» | Пройти | |
| Шестнадцатеричная система счисления | ||
| Тренинг «Шестнадцатеричная система» | Пройти | |
| Тренинг «Правило перевода из 10-системы в 16-ю»-1 | Пройти | |
| Тренинг «Правило перевода из 10-системы в 16-ю»-2 | Пройти | |
| Тренинг «Викторина шестнадцатеричная система» | Пройти | |
Тренинг «Соответствие чисел в 10 и 16 сист. счисления» счисления» |
Пройти | |
| Тренинг «Соответствие чисел в 10 и 16 сист. счисления»-2 | Пройти | |
| Тренинг «Расставь по порядку»-3 | Пройти | |
| Тренинг «Соответствие чисел в 10 и 16 сист. счисления»-3 | Пройти | |
| Тренинг «Соответствие чисел в 10 и 16 сист. счисления»-4 | Пройти | |
| Тренинг «Перевод из 10-й в 16-ю систему счисления» | Пройти | |
| Тренинг «Перевод из 16-й в 10-ю систему счисления» | Пройти | |
| Группа упражнений «Шестнадцатеричная система» | Пройти | |
| Обобщение и систематизация | ||
| Тренинг «Машинные системы счисления» | Пройти | |
| Тренинг «Определи систему счисления» | Пройти | |
| Тренинг «Кто хочет стать миллионером» | Пройти | |
| Тренинг «Обыграй компьютер» | Пройти | |
| Тренинг «Определи систему счисления»-2 | Пройти | |
Тренинг «Системы счисления. Обобщение»-1 Обобщение»-1 |
Пройти | |
| Тренинг «Системы счисления. Обобщение»-2 | Пройти | |
| Тренинг «Системы счисления. Обобщение»-3 | Пройти | |
| Тренинг «Системы счисления. Обобщение»-4 | Пройти | |
| Тренинг «Системы счисления. Обобщение»-5 | Пройти | |
| Группа упражнений «Системы счисления обобщение» | Пройти | |
| На оценку | ||
| Тест «Системы счисления»-1 | Пройти | |
| Тест «Двоичная система-1» | Пройти | |
| Тест «Двоичная система-2» | Пройти | |
| Тест «Двоичная система-3» (обратный перевод) | Пройти | |
| Тест «Двоичная система-4» (обратный перевод) | Пройти | |
| Тест «Двоичная система-5» (количество) | Пройти | |
| Тест «Восьмеричная система-1» | Пройти | |
| Тест «Восьмеричная система-2» | Пройти | |
| Тест «Восьмеричная система-3» (обратный перевод) | Пройти | |
| Тест «Восьмеричная система-4» (обратный перевод) | Пройти | |
| Тест «Шестнадцатеричная система-1» | Пройти | |
| Тест «Шестнадцатеричная система-2» | Пройти | |
| Тест «Шестнадцатеричная система-3» (обратный перевод) | Пройти | |
| Тест «Шестнадцатеричная система-4» (обратный перевод) | Пройти | |
| Тест «Двоичная система-6» (числа от 1 до 10 триады) | Пройти | |
| Тест «Двоичная система-7» (числа от 1 до 15 тетрады) | Пройти | |
Тест «Системы счисления. Итог»-1 Итог»-1 |
Пройти | |
| Тест «Системы счисления. Итог»-2 | Пройти | |
| Тест «Системы счисления. Итог»-3 | Пройти | |
| Контрольная работа «системы счисления« | Открыть | |
Страница не найдена | Кафедра физики твердого тела ПетрГУ
http://secretary.rid.go.th/ http://rtlabs.nitk.ac.in/ http://www.ei.ksue.edu.ua/ http://www.unajma.edu.pe/ http://www.drbrambedkarcollege.ac.in/
Home Page – Revisedhttps://www.hsri.or.th/ https://www.agrft.uni-lj.si/ http://www4.fe.usp.br/ https://www.cnba.uba.ar/
Homebak hocam 2yildir kullandigim siteye gelip kod ekliyorsun not yazip kodlarini siliyorum (insan olan utanir kusura bakma hocam diyip giderdi) kendine dusmanmi ariyorsun? belliki sen disli birine denk gelmemissin hayatin boyunca ama ben cok ugrastim cokta denk geldim bu sekilde tanimadigin birini tehtit etmen ya deli oldugunu gosterir yada tecrubesizligini sen bana isimi ogretecegine once baskalarina ait olan sitelere girmemeyi ogren ondan sonra bana isimi ogretirsin ben cok takintili bir adamim beni kotu bir insan olmaya zorlama rica ediyorum bak lutfen birbirimizi uzmeyelim emin ol bu site felan umrumdami saniyorsun? olay tamamen prensip meselesi sen benim yatakodama gelip beraber yatacagiz diyorsun oyle bir olay yok isine bak oldu 10 kisi daha cagir 500 kod eklesin herkes yorumbacklink isimi yapiyorsun? sacmalamissin daha fazla beni muatap etme kendinle yaptigin terbiyesizligin farkina var illa darbe yiyincemi aklin basina gelecek anlamiyorum ki o kadar yaziyorum ki birbirimize kotuluk yapmayalim kalp kirmayalim birbirimizi uzmeyelim sana daha once boyle notlar yazan bir linkci gordun mu Allah askina ben bazen goruyorum ana baci duymadigim kufurler yaziyor adamlar birbirine sen benim gibi bir insani uzuyorsun ama lutfen.
 . 8yildir ben kimseyle ortak site kullanmadim babam gelse onunlada kullanmam en hassas oldugum konudur bu bir daha kod eklememeni siddetle tavsiye ediyorum yoksa farkli seyler olur ve kendine nur topu gibi manyak bir dusman edinirsin bos yere bu polemigi uzatiyorsun haksiz olan sensin kod disinde birsey yazmak istersen yazabilirsin ama rica ediyorum isi inada bindirme senden ERDEMLİ DÜRÜST VE OLGUN bir davranis bekliyorum beni anladigini umuyorum ve tekrar inşAllah kod eklemeyecegini umuyorum olumlu olumsuz notunu buraya yazablirsin bende bir daha bu siteyi kullanmiyacagim sanada kullandirmam tabiki is site isi degil prensip isi.. ihtiyacin olabilir site sayin azdir bunlar dogal seyler ben gerekirse kendim eklerim senin kodlarini oyle bir durumda kendi kodlarimida silerim sadece senin olur ama o son not garip bir insan oldugunu dusunduruyor bana ve inan ugrasacak vaktim de kafamda yok kendine sardirma hepimiz ekmek davasindayiz senle isim yok benden sana kotulukte gelmez ama beni zorlama lutfen.
. 8yildir ben kimseyle ortak site kullanmadim babam gelse onunlada kullanmam en hassas oldugum konudur bu bir daha kod eklememeni siddetle tavsiye ediyorum yoksa farkli seyler olur ve kendine nur topu gibi manyak bir dusman edinirsin bos yere bu polemigi uzatiyorsun haksiz olan sensin kod disinde birsey yazmak istersen yazabilirsin ama rica ediyorum isi inada bindirme senden ERDEMLİ DÜRÜST VE OLGUN bir davranis bekliyorum beni anladigini umuyorum ve tekrar inşAllah kod eklemeyecegini umuyorum olumlu olumsuz notunu buraya yazablirsin bende bir daha bu siteyi kullanmiyacagim sanada kullandirmam tabiki is site isi degil prensip isi.. ihtiyacin olabilir site sayin azdir bunlar dogal seyler ben gerekirse kendim eklerim senin kodlarini oyle bir durumda kendi kodlarimida silerim sadece senin olur ama o son not garip bir insan oldugunu dusunduruyor bana ve inan ugrasacak vaktim de kafamda yok kendine sardirma hepimiz ekmek davasindayiz senle isim yok benden sana kotulukte gelmez ama beni zorlama lutfen. . zaten kafamda bir dunya sorun var hayat acimasiz hayat zor benim derdim bana yetiyor butun ictenligim ve iyi niyetim ile sana bu notu yaziyorum bu kadar sozden sonra kod ekleyecegini sanmiyorum birde seninle ugrasmayayim guzel kardesim arkadasim lutfen rica ediyorum LUTFEN barış her zaman erdemli insanlarin isidir lutfen ayni olgunluk ile senden olumlu donusunu bekliyorum eger yazdiklarimda kalp kirici yada incitici birsey varsa lutfen kusura bakma 1-2defa kontrol ettim ama belki gozumden kacmis olabilir hakkini helal et ve en iyisi ikimiz icinde helallesip bu isi noktalamaktir inan kotu biri degilim selam ve sevgiyle..
. zaten kafamda bir dunya sorun var hayat acimasiz hayat zor benim derdim bana yetiyor butun ictenligim ve iyi niyetim ile sana bu notu yaziyorum bu kadar sozden sonra kod ekleyecegini sanmiyorum birde seninle ugrasmayayim guzel kardesim arkadasim lutfen rica ediyorum LUTFEN barış her zaman erdemli insanlarin isidir lutfen ayni olgunluk ile senden olumlu donusunu bekliyorum eger yazdiklarimda kalp kirici yada incitici birsey varsa lutfen kusura bakma 1-2defa kontrol ettim ama belki gozumden kacmis olabilir hakkini helal et ve en iyisi ikimiz icinde helallesip bu isi noktalamaktir inan kotu biri degilim selam ve sevgiyle..
Информатика егэ 1 задание, объяснение и разбор
На уроке рассмотрено решение 1 задание ЕГЭ по информатике 2017: дается подробное объяснение и разбор заданий
Объяснение задания 1 ЕГЭ по информатике
1-я тема характеризуется, как задания базового уровня сложности,
время выполнения – примерно 1 минута,
максимальный балл — 1
«Перевод всех используемых в задании чисел в десятичную систему сам по себе не является ошибкой, но приводит к лишним вычислениям и увеличению вероятности арифметической ошибки»
ФГБНУ «Федеральный институт педагогических измерений»
Системы счисления и представление информации в памяти ПК
Для решения 1 задания следует вспомнить и повторить следующие темы:
Двоичная система счисления
Количество цифр или основание системы: 2
Цифры (алфавит): 0, 1
Перевод чисел из 10-й системы счисления в двоичную:
Перевод чисел из 10-й сист.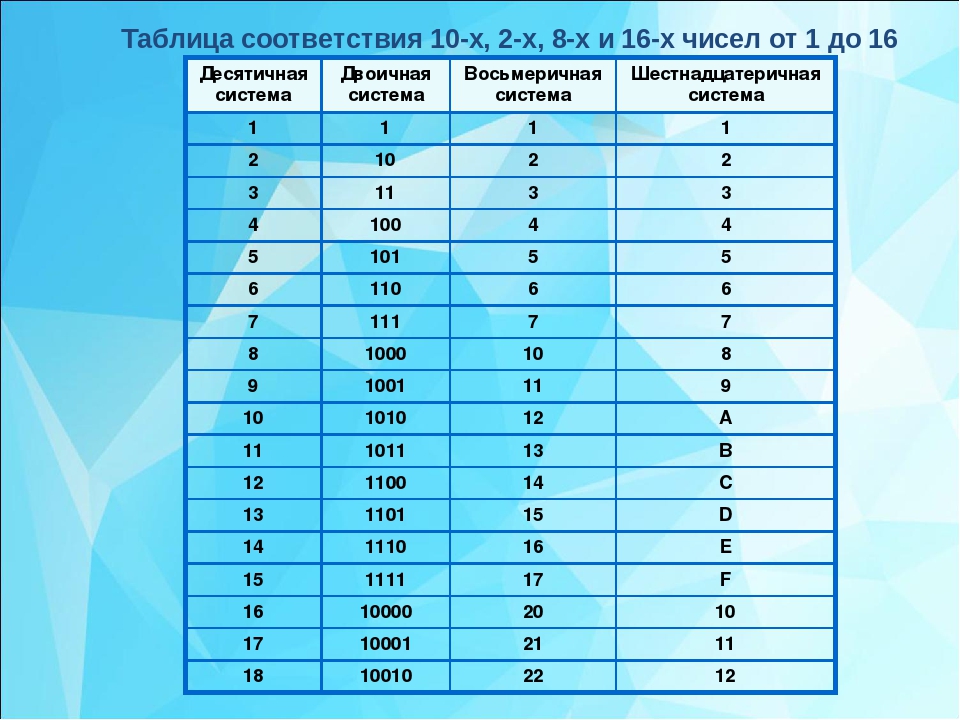 сч-я в двоичную
сч-я в двоичную
Егифка ©:
Перевод чисел из 2-й системы счисления в 10-ую:
Перевод чисел из 2-й сист. сч-я в 10-ую
Егифка ©:
При работе с большими числами, лучше использовать разложение по степеням двойки:
Разложение по степеням двойки
Егифка ©:
Восьмеричная система счисления
Количество цифр или основание системы: 8
Цифры (алфавит): 0, 1, 2, 3, 4, 5, 6, 7
Перевод чисел из 10-й системы счисления в 8-ую
Перевод чисел из 10-й сист. сч-я в 8-ую
Перевод чисел из 8-й сист. сч-я в 10-ую
Перевод чисел из 8-й системы счисления в 10-ую
Перевод чисел из 8-й сист. сч-я в 2-ую и обратно триадами
Перевод из 8-й сист. сч-я в 2-ую и обратно триадами
Егифка ©:
Шестнадцатеричная система счисления
Количество цифр или основание системы: 16
Цифры (алфавит): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A (10), B (11), C (12), D (13), E (14), F (15)
Перевод чисел из 10-й системы счисления в 16-ую
Перевод из 10-й сист. сч-я в 16-ую
сч-я в 16-ую
Перевод из 16-й системы счисления в 10-ую
Перевод из 16-й сист. сч-я в 10-ую
Перевод чисел из 2-й сист. сч-я в 16-ую и обратно тетрадами
Перевод из 2-й с. сч-я в 16-ую и обратно тетрадами
Егифка ©:
Полезности для двоичной системы счисления:
26 = 64 ≤ 126 7, 126 = 11111102 (7 цифр)
32 = 25 = 1000002
31 = 25-1 = 111112
15 = 11112, 30 = 111102, 60 = 1111002, 120 = 11110002
1024 512 256 128 64 32 16 8 4 2 1 210 29 28 27 26 25 24 23 22 21 20
X10,X8 X2 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111
X10 X16 X2 0 0 0000 1 1 0001 2 2 0010 3 3 0011 4 4 0100 5 5 0101 6 6 0110 7 7 0111 8 8 1000 9 9 1001 10 A 1010 11 B 1011 12 C 1100 13 D 1101 14 E 1110 15 F 1111
- нужно перевести a-1 в двоичную систему счисления;
- сделать инверсию битов: заменить все нули на единицы и единицы на нули в пределах разрядной сетки
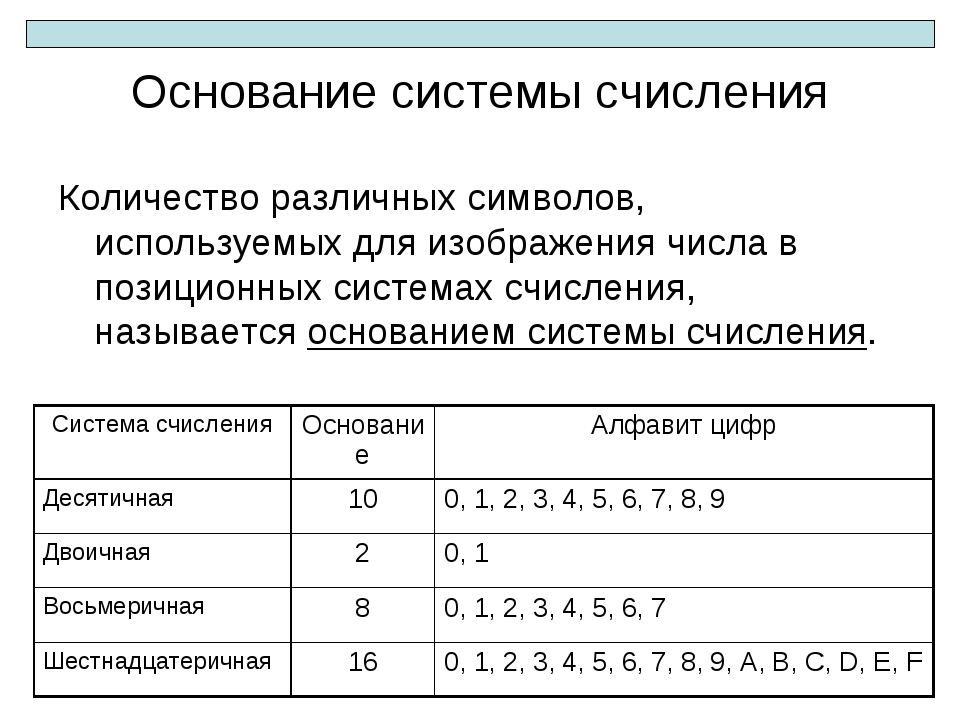
Тренировка работы с системами счисления (эти задания отсутствуют в ЕГЭ с 2021г.
 )
)
✍ Решение:
- В шестнадцатеричной с-ме счисления числа от 10 до 15 представлены буквами латинского алфавита: A-10, B-11, C-12, D-13, E-14, F-15.
- Необходимо вспомнить двоичные коды чисел от 1 до 15 (см. теорию выше на странице), так как для перевода 16-ричного в двоичную с-му достаточно каждую цифру отдельно записать в виде четверки двоичных цифр (тетрады):
2 A C 1 0010 1010 1100 0001
Результат: 6
Подробный разбор 1 задания с объяснением просмотрите на видео:
1_2: Демоверсия ЕГЭ 2018 информатика (ФИПИ):
Сколько существует целых чисел x, для которых выполняется неравенство 2A16<x<618?
В ответе укажите только количество чисел.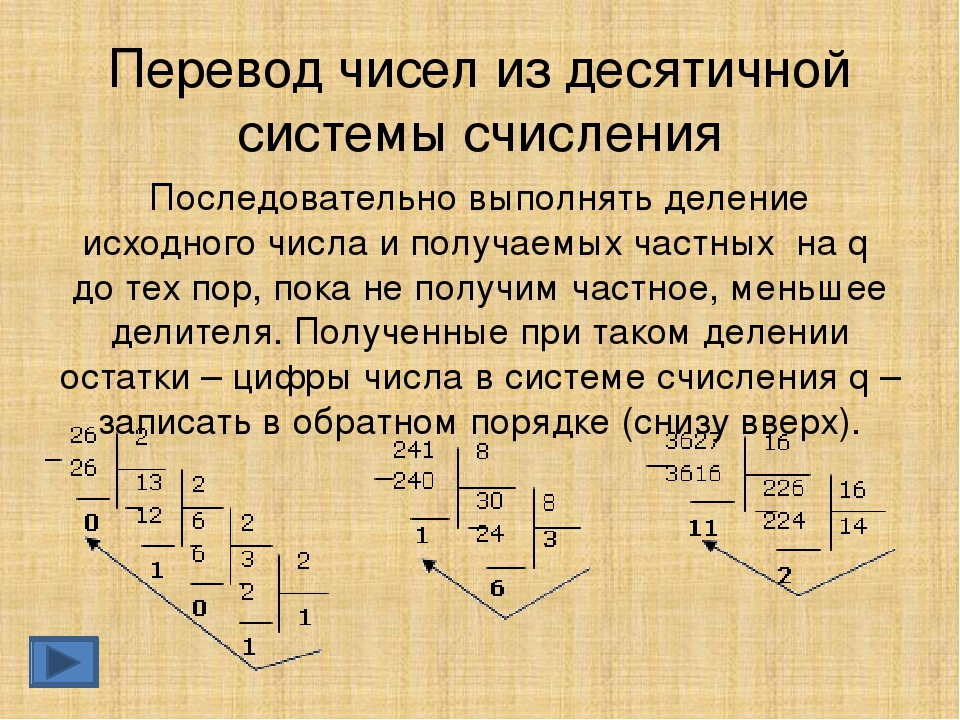
Подобные задания для тренировки
✍ Решение:
- Переведем 2A16 в десятичную систему счисления:
2A16 = 2*161+10*160 = 32 + 10 = 42
618 = 6*81+1*80 = 48 + 1 = 49
42
<), то количество целых, удовлетворяющих условию:49 - 42 - 1 = 6
Результат: 6
Подробное решение данного 1 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
1_3: ГВЭ 11 класс по информатике 2018 (ФИПИ):
Сколько значащих цифр в двоичной записи десятичного числа 129?
1) 6
2) 2
3) 7
4) 8
✍ Решение:
- Выполним перевод из десятичной с-мы счисления в двоичную делением на 2, справа будем записывать остатки:
129 / 1 64 / 0 32 / 0 16 / 0 8 / 0 4 / 0 2 / 0 1
10000001
 Их 8, и все они значащие (незначащими могут быть только нули слева, например, 010 — это то же самое, что 10). Правильный ответ под номером 4
Их 8, и все они значащие (незначащими могут быть только нули слева, например, 010 — это то же самое, что 10). Правильный ответ под номером 4Результат: 4
1_4: (контрольный вариант экзаменационной работы 2018 года, С.С. Крылов, Д.М. Ушаков):
Сколько существует натуральных чисел x, для которых выполняется неравенство
10101128?
В ответе укажите только количество чисел.
✍ Решение:
Подробный разбор решения тренировочного варианта предлагаем посмотреть на видео:
1_5: вариант № 1, 2019 Информатика и ИКТ Типовые экзаменационные варианты (10 вариантов), С.С. Крылов, Т.Е. Чуркина::
Вычислите значение выражения AE16 – 1916.
В ответе запишите вычисленное значение в десятичной системе счисления.
Подобные задания для тренировки
✍ Решение:
- Переведем уменьшаемое и вычитаемое в десятичную систему счисления:
1 0 A E = 10*161 + 14*160 = 160 + 14 = 174* A16 соответствует числу 10 в десятичной системе счисления
* E16 соответствует числу 14 в десятичной системе счисления
1 0 19 = 1*161 + 9*160 = 16 + 9 = 25
174 - 25 = 149
Результат: 149
1_6: с сайта К. Полякова, вариант 104 со ссылкой на Носкина А.Н.:
Петя и Коля загадывают натуральные числа. Петя загадал число Х, а Коля число У. После того, как Петя прибавил к Колиному числу 9, а Коля к Петиному числу 20, сумма полученных чисел при записи в двоичной системе счисления представляет собой пять единиц.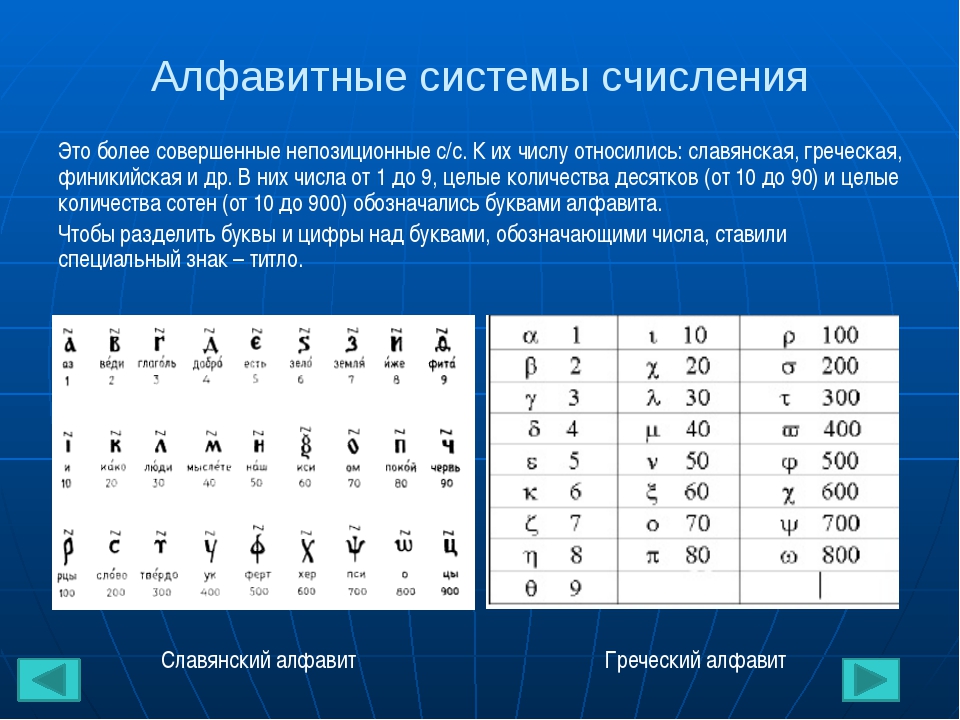
Чему равна изначальная сумма загаданных мальчиками чисел? Ответ запишите в двоичной системе счисления. Основание указывать не надо.
✍ Решение:
- Перепишем условие задачи в более понятном виде:
(x + 9) + (y + 20) = 111112 (x + y)2 = ?
111112 = 3110 31 - 20 - 9 = 2
210 = 102
Результат: 10
1_7: с сайта К. Полякова, вариант 105 со ссылкой на Куцырь Е.В.:
Укажите наибольшее четырёхзначное восьмеричное число, четверичная запись которого содержит ровно 2 тройки, не стоящие рядом. В ответе запишите только само восьмеричное число, основание системы счисления указывать не нужно.
В ответе запишите только само восьмеричное число, основание системы счисления указывать не нужно.
✍ Решение:
- Вспомним, что в восьмеричной системе максимальная цифра 7, а в четверичной — 3. Попробуем выполнить перевод наибольшего восьмеричного числа в четверичную систему, не учитывая условие с нестоящими подряд тройками. Выполним перевод через двоичную систему счисления:
77778 - максимальное четырехзначное восьмеричное число Перевод в двоичную с.с: 7 7 7 7 111 111 111 111 Перевод из двоичной с.с. в четверичную осуществляется делением на группы по две цифры: 11 11 11 11 11 11 3 3 3 3 3 3
11 10 11 10 10 10 3 2 3 2 2 24
111 011 101 010 7 3 5 2
Результат: 7352
1_8: с сайта К.
 Полякова, вариант 109 со ссылкой на Носкина А.Н.:
Полякова, вариант 109 со ссылкой на Носкина А.Н.:
Задан отрезок [a, b]. Число a – наименьшее число, восьмеричная запись которого содержит ровно 3 символа, один из которых – 3. Число b – наименьшее число, шестнадцатеричная запись которого содержит ровно 3 символа, один из которых – F.
Определите количество натуральных чисел на этом отрезке (включая его концы).
✍ Решение:
- Перепишем условие задачи в более понятном виде, подставив значения для чисел a и b:
a: 1038 - наименьшее трехразрядное восьмеричное число, одна из цифр которого – 3 b: 10F16- наименьшее трехразрядное 16-е число, одна из цифр которого – F
1038 = 6710 10F16 = 27110 [a,b] = [67,271] длина отрезка = 271 - 67 + 1 (включая его концы) = 205
Результат: 205
1_9: 2020 (Тематические тренировочные задания, 2020 г. , Самылкина Н.Н., Синицкая И.В., Соболева В.В.):
, Самылкина Н.Н., Синицкая И.В., Соболева В.В.):
Для хранения целого числа со знаком используется один байт.
Сколько единиц содержит внутреннее представление числа (-116)?
✍ Решение:
-
Для перевода отрицательного числа в двоичную систему счисления воспользуемся следующим алгоритмом:
- Из модуля исходного числа вычтем единицу:
|-116| - 1 = 115
11510 = 11100112
01110011
10001100
Результат: 10001100
Компьютерные системы счисления — Определение систем счисления, типы систем счисления, восьмеричная система счисления, десятичная система счисления, шестнадцатеричная система счисления
Домой » Разное
Какие системы счисления в компьютере?
Системы счисления — это метод представления чисел в архитектуре компьютерной системы, каждое значение, которое вы сохраняете или получаете в / из памяти компьютера, имеет определенную систему счисления.
Архитектура компьютера поддерживает следующие системы счисления.
- Двоичная система счисления
- Восьмеричная система счисления
- Десятичная система счисления
- Шестнадцатеричная (шестнадцатеричная) система счисления
1) Двоичная система счисления
В двоичной системе счисления всего две цифры: 0 и 1 . Каждое число (значение) представляет собой 0 и 1 в этой системе счисления. Основание двоичной системы счисления — 2, потому что в ней всего две цифры.
2) Восьмеричная система счисления
В восьмеричной системе счисления всего восемь (8) цифр от 0 до 7 .Каждое число (значение) представляет собой 0,1,2,3,4,5,6 и 7 в этой системе счисления. Основание восьмеричной системы счисления — 8, потому что в ней всего 8 цифр.
3) Десятичная система счисления
В десятичной системе счисления всего десять (10) цифр от 0 до 9 . Каждое число (значение) представляет собой 0,1,2,3,4,5,6, 7,8 и 9 в этой системе счисления. Основание десятичной системы счисления — 10, потому что в ней всего 10 цифр.
Основание десятичной системы счисления — 10, потому что в ней всего 10 цифр.
4) Шестнадцатеричная система счисления
Шестнадцатеричная система счисления имеет шестнадцать (16) буквенно-цифровых значений от 0 до 9 и от A до F .Каждое число (значение) представляет собой 0,1,2,3,4,5,6, 7,8,9, A, B, C, D, E и F в этой системе счисления. Основа шестнадцатеричной системы счисления — 16, потому что она имеет 16 буквенно-цифровых значений. Здесь A равно 10 , B равно 11 , C равно 12 , D равно 13 , E равно 14 и F равно 15 .
Таблица систем счисления с основанием, используемыми цифрами, представлением, представлением на языке C:
| Система счисления | База | Используемые цифры | Пример | C Присвоение языка |
| Двоичный | 2 | 0,1 | (11110000) 2 | int val = 0b11110000; |
| восьмеричное | 8 | 0,1,2,3,4,5,6,7 | (360) 8 | int val = 0360; |
| Десятичный | 10 | 0,1,2,3,4,5,6,7,8,9 | (240) 10 | int val = 240; |
| Шестнадцатеричный | 16 | 0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F |
(F0) 16 | int val = 0xF0; |
Преобразования системы счисления
Есть три типа конвертации:- От десятичной системы счисления к другой системе счисления
[например: от десятичной системы счисления к двоичной системе счисления] - Другая основа в десятичной системе счисления
[например: двоичная система счисления в десятичную систему счисления] - Другая база в другую базу
[например: двоичная система счисления в шестнадцатеричную систему счисления]
От десятичной системы счисления к другой системе счисления
Преобразовать систему счисления из в десятичную систему счисления в с любой другой системой счисления довольно просто; вам нужно выполнить всего два шага:
A) Разделите число (десятичное число) на основание целевой базовой системы (в которой вы хотите преобразовать число: двоичное (2), восьмеричное (8) и шестнадцатеричное (16)). )).
)).
B) Запишите остаток от шага 1 как младший значащий бит (LSB) в последний шаг как старший значащий бит (MSB).
| Преобразование десятичного числа в двоичное | Результат |
|
Десятичное число: (12345) 10 |
Двоичное число: (11000000111001) 2 |
| Десятичное преобразование в восьмеричное | Результат |
|
Десятичное число: (12345) 10 |
Восьмеричное число: (30071) 8 |
| Преобразование десятичного числа в шестнадцатеричное | Результат |
|
Пример 1 Десятичное число: (12345) 10 |
Шестнадцатеричное число: (3039) 16 |
|
Пример 2 Десятичное число: (725) 10 |
Шестнадцатеричное число: (2D5) 16 Преобразует 10, 11, 12, 13, 14, 15 в его эквивалент.  .. .. A, B, C, D, E, F |
Другая система счисления в десятичную систему счисления
Чтобы преобразовать систему счисления из в любую другую базовую систему в десятичную систему счисления , вам нужно выполнить всего три шага:
A) Определите базовое значение исходной системы счисления (которое вы хотите преобразовать), а также определить позицию цифр из LSB (позиция первой цифры — 0, позиция второй цифры — 1 и т. д.).
B) Умножьте каждую цифру на соответствующее умножение значения позиции и базы исходной системы счисления.
C) Добавьте значение, полученное на шаге B.
Пояснения к примерам:
Приведенные ниже экзамены содержат следующие строки:
A) Строка 1 содержит ЦИФРОВ числа (которое будет преобразовано).
B) Строка 2 содержит POSITION каждой цифры в системе счисления.
C) Строка 3 содержит умножение: ЦИФРА * ОСНОВА ^ ПОЛОЖЕНИЕ .
D) Строка 4 содержит результат вычисления шага C .
E) И затем сложите каждое значение шага D , полученное значение будет десятичным числом.
| Преобразование двоичного числа в десятичное | |
|
Двоичное число: (11000000111001) 2 |
| Восьмеричное преобразование в десятичное | Результат |
|
Восьмеричное число: (30071) 8 |
= 12288 + 0 + 0 + 56 + 1 = 12345 Десятичное число: (12345) 10 |
| Преобразование шестнадцатеричного числа в десятичное | Результат |
|
Шестнадцатеричное число: (2D5) 16 |
= 512 + 208 + 5 = 725 Десятичное число: (725) 10 |
ОБЪЯВЛЕНИЕ
ОБЪЯВЛЕНИЕ
Система счисления и компьютерные науки Пример бесплатного эссе
Сравните различные форматы представления чисел в компьютерах.
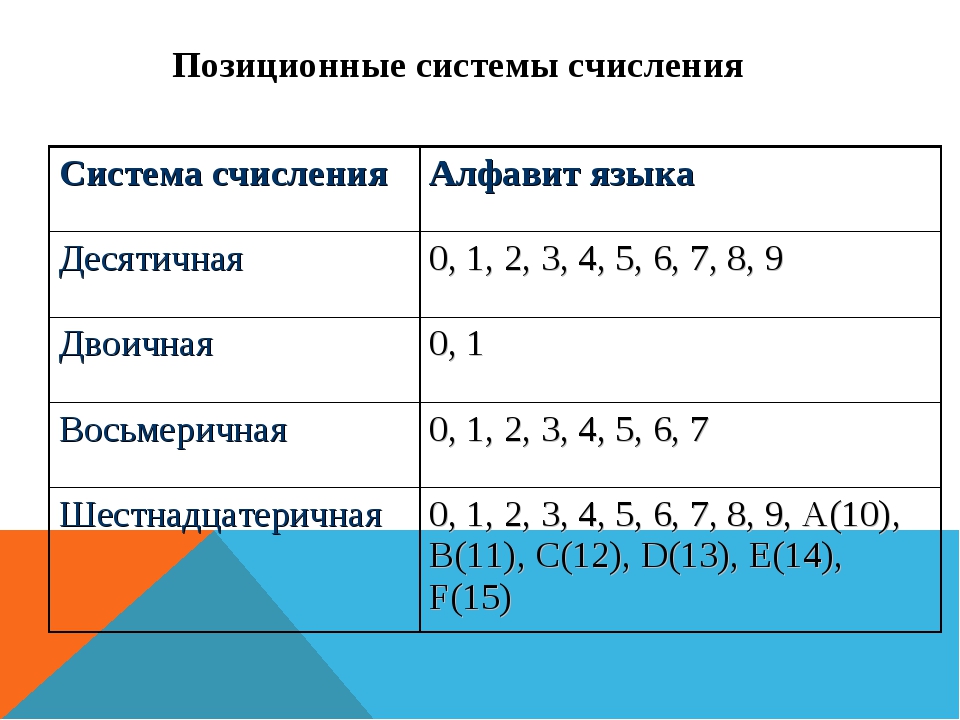 Кратко обсудите с помощью примеров. Назовите наиболее популярное представление чисел и почему вы так думаете
Кратко обсудите с помощью примеров. Назовите наиболее популярное представление чисел и почему вы так думаете
Система счисления — это способ представления чисел. Мы привыкли использовать десятичную систему счисления (основание 10). Другие распространенные системы счисления включают шестнадцатеричную (основание 16), восьмеричную (основание 8) и двоичную (основание 2). Что касается компьютерных систем, системы счисления можно разделить на четыре категории:
- Десятичная система счисления
- Двоичная система счисления
- Восьмеричная система счисления
- Шестнадцатеричная система счисления
Десятичная система счисления
Термин «десятичный» происходит от латинского префикса «deci», что означает десять.
Не используйте источники плагиата. Получите собственное эссе на
«Системы счисления и информатика»
Получите нестандартную бумагуНОВИНКА! интеллектуальное сопоставление с писателем
В десятичной системе счисления десять цифр от 0 до 9. Потому что в этой системе десять цифр; ее также называют десятичной или десятичной системой счисления. Десятичное число всегда следует писать с нижним индексом 10, например. X10. Но поскольку это наиболее широко используемая система счисления в мире, нижний индекс обычно понимается и игнорируется в письменной работе.
Потому что в этой системе десять цифр; ее также называют десятичной или десятичной системой счисления. Десятичное число всегда следует писать с нижним индексом 10, например. X10. Но поскольку это наиболее широко используемая система счисления в мире, нижний индекс обычно понимается и игнорируется в письменной работе.
Однако, когда многие системы счисления рассматриваются вместе, всегда следует ставить нижний индекс, чтобы различать системы счисления.
Двоичная система счисления
Для обозначения чисел используются две цифры, а именно 1 и 0. В отличие от десятичных чисел, где значение разряда увеличивается в десять раз, в двоичной системе значения разряда увеличиваются в 2 раза, двоичные числа записываются как X2, рассмотрим двоичное число, такое как 10112. Крайняя правая цифра имеет разрядное значение 1–20, в то время как крайнее левое значение имеет разряд 1–23.
Узнайте смету стоимости вашей бумаги
«Вы должны согласиться с условиями предоставления услуг и политикой конфиденциальности»
Восьмеричная система счисления
Состоит из восьми цифр в диапазоне от 0 до 7. Разряд восьмеричных чисел увеличивается в восемь раз справа налево.
Разряд восьмеричных чисел увеличивается в восемь раз справа налево.
Шестнадцатеричная система счисления
Это система счисления с основанием 16, которая состоит из шестнадцати цифр в диапазоне от 0 до 9 и букв A-F, где A эквивалентно 10, от B до 11 до F, что эквивалентно 15 в системе с основанием десять.Разрядность шестнадцатеричных чисел увеличивается в шестнадцать раз.
Шестнадцатеричное число может быть обозначено с помощью нижнего индекса 16 или заглавной буквы H справа от числа. Например, 94B можно записать как 94B16 или 94BH.
Самое популярное представление номера
Самым популярным представлением чисел среди вышеперечисленных четырех, на мой взгляд, является десятичная система счисления. Это потому, что он не ограничивает нас в использовании его нижнего индекса 10, например X10, как и другие системы счисления.Как это понимает большинство из нас.
Что вы подразумеваете под точностью представления числа с плавающей запятой в стандарте IEEE? Объясните на небольшом примере
IEEE стандартизировал компьютерное представление двоичных чисел с плавающей запятой в IEEE 754 (также известном как IEC 60559) в 1985 году. Новая версия IEEE 754-2008 была опубликована в августе 2008 года после семилетнего процесса пересмотра под председательством Дэна. Зурас и отредактированный Майком Коулишоу. Он заменил как IEEE 754-1985 (двоичная арифметика с плавающей запятой), так и стандарт IEEE 854-1987 для Radix-независимой арифметики с плавающей запятой.Текущая версия IEEE 754-2019, опубликованная в июле 2019 года, является производной и заменяет IEEE 754-2008 после процесса пересмотра, начатого в сентябре 2015 года под председательством Дэвида Г. Хоу и отредактированным Майком Коулишоу. Он включает в себя в основном пояснения и исправления, но также включает некоторые новые рекомендуемые операции. Стандарт предусматривает множество тесно связанных форматов, три из которых особенно широко используются в компьютерном оборудовании и языках:
Новая версия IEEE 754-2008 была опубликована в августе 2008 года после семилетнего процесса пересмотра под председательством Дэна. Зурас и отредактированный Майком Коулишоу. Он заменил как IEEE 754-1985 (двоичная арифметика с плавающей запятой), так и стандарт IEEE 854-1987 для Radix-независимой арифметики с плавающей запятой.Текущая версия IEEE 754-2019, опубликованная в июле 2019 года, является производной и заменяет IEEE 754-2008 после процесса пересмотра, начатого в сентябре 2015 года под председательством Дэвида Г. Хоу и отредактированным Майком Коулишоу. Он включает в себя в основном пояснения и исправления, но также включает некоторые новые рекомендуемые операции. Стандарт предусматривает множество тесно связанных форматов, три из которых особенно широко используются в компьютерном оборудовании и языках:
одинарной точности
Одинарная точность обычно используется для представления типа «float» в семействе языков C (хотя это не гарантируется).Это двоичный формат, занимающий 32 бита (4 байта), а его значащий формат имеет точность 24 бита (около 7 десятичных цифр).
Двойная точность
Двойная точность обычно используется для представления типа «double» в семействе языков C (хотя это не гарантируется). Это двоичный формат, который занимает 64 бита (8 байтов), а его значащая часть имеет точность 53 бита (около 16 десятичных цифр).
Двойной удлиненный
Двойной расширенный также называется форматом «расширенной точности».Это двоичный формат, который занимает не менее 79 бит (80, если правило скрытых / неявных битов не используется), а его значащий формат имеет точность не менее 64 бит (около 19 десятичных цифр). Формат, удовлетворяющий минимальным требованиям (64-битная точность, 15-битная экспонента, что соответствует 80 битам), обеспечивается архитектурой x86. Как правило, на таких процессорах этот формат может использоваться с «длинным двойным» в семействе языков C (стандарты C99 и C11 «Расширение арифметики с плавающей запятой IEC 60559 — Приложение F» рекомендуют использовать 80-битный расширенный формат как «Длинный дубль», если таковой имеется).
Например, если b = 10, p = 7 и e-max = 96, то e-min =? 95, значащее удовлетворяет 0? с? 9,999,999, а показатель степени удовлетворяет? 101? д? 90. Следовательно, наименьшее ненулевое положительное число, которое может быть представлено, составляет 1 × 10 × 101, а наибольшее — 9999999 × 1090 (9,999999 × 1096), поэтому полный диапазон чисел составляет от? 9,999999? 1096 до 9,999999? 1096. . Числа? B1? Emax и b1? Emax (здесь? 1? 10? 95 и 1? 10? 95) являются наименьшими (по величине) нормальными числами; ненулевые числа между этими наименьшими числами называются субнормальными числами.
Компьютерные науки
Приложения в наши дни, CS / SE движется к
Информатика — это изучение компьютеров и вычислительных систем. В отличие от инженеров-электриков и компьютерных инженеров, компьютерные ученые в основном занимаются программным обеспечением и программными системами; это включает их теорию, дизайн, разработку и применение. Основные области изучения компьютерных наук включают искусственный интеллект, компьютерные системы и сети, безопасность, системы баз данных, взаимодействие человека с компьютером, зрение и графику, численный анализ, языки программирования, программную инженерию, биоинформатику и теорию вычислений.
Хотя умение программировать необходимо для изучения информатики, это только один элемент области знаний. Ученые-информатики разрабатывают и анализируют алгоритмы для решения программ и изучают производительность компьютерного оборудования и программного обеспечения. Проблемы, с которыми сталкиваются компьютерные ученые, варьируются от абстрактных (определение того, какие проблемы могут быть решены с помощью компьютеров и сложности алгоритмов, которые их решают), до материальных (разработка приложений, которые хорошо работают на портативных устройствах, которые просты в использовании и которые соблюдать меры безопасности.Его области можно разделить на теоретические и практические дисциплины. Теория вычислительной сложности очень абстрактна, в то время как компьютерная графика делает упор на реальные приложения.
Разница между CS / SE / CE
Компьютерная инженерия (CE)
Он занимается проектированием, разработкой и эксплуатацией компьютерных систем. По своей сути компьютерная инженерия концентрируется на цифровых аппаратных устройствах и компьютерах, а также на программном обеспечении, которое ими управляет. Компьютерная инженерия делает упор на решении проблем с цифровым оборудованием и программно-аппаратным интерфейсом.
Компьютерная инженерия делает упор на решении проблем с цифровым оборудованием и программно-аппаратным интерфейсом.
Программная инженерия (SE)
Занимается созданием и сопровождением программных систем. Он больше ориентирован на программное обеспечение и уделяет больше внимания крупным программным приложениям, чем компьютерная инженерия. Он более прикладной, чем информатика, уделяя больше внимания всему процессу разработки программного обеспечения, от идеи до конечного продукта.
Компьютерные науки
Он фокусируется на понимании, проектировании и разработке программ и компьютеров. По своей сути компьютерные науки концентрируются на данных, преобразовании данных и алгоритмах.На курсах продвинутого уровня представлены специализированные методы программирования и конкретные области применения. Программа CS менее структурирована, чем программы CE и SE, что дает студентам большую гибкость для углубления или расширения в различных областях приложений или в основах компьютерных наук.
В Интернете
Когда вы вводите слова на веб-странице поисковой системы, она так быстро возвращает вам результаты. (Алгоритмы поиска, параллельные вычисления)
Игра в компьютерные науки
- Современные игры выглядят потрясающе, со всеми их крутыми трехмерными эффектами, и все это визуализируется в реальном времени, когда вы играете и постоянно меняете игровую среду.(Компьютерная графика)
- Враги в игре кажутся «умными» и могут учиться на ваших действиях. (Искусственный интеллект)
- Мы и десятки других игроков можем играть онлайн одновременно, и при этом большую часть времени игра будет отзывчивой. (Сеть, архитектура клиент-сервер)
Загрузка носителя (юридически)
- Программы обмена файлами, такие как Bit-Torrent, могут работать намного быстрее, чем простая загрузка с веб-сайта.(Сеть, распределенные алгоритмы)
- Разве не удивительно, что когда вы загружаете файл, он всегда попадает на ваш компьютер в первозданном виде, даже если ему пришлось пройти тысячи миль по ненадежным медным проводам? (Надежные сетевые протоколы, обнаружение и исправление ошибок)
- Высококачественные фотографии, аудио и видео можно сильно сжать (от 1/10 до 1/100 исходного размера) без большой потери качества.
 (Алгоритмы сжатия потерь)
(Алгоритмы сжатия потерь)
Покупки в Интернете
- Вы можете быть уверены в том, что никто не украдет номер вашей кредитной карты, пока вы делаете покупки в Интернете.(Сетевая безопасность, криптография)
- Продавец может отслеживать, какие товары есть в наличии, и сообщать результаты в режиме реального времени на своем веб-сайте. (Базы данных, веб-программирование)
- Некоторые другие приложения информатики: использование наших мобильных телефонов, невротическое обновление ваших страниц в Facebook, Instagram, Twitter, отслеживание профилей других людей и путешествия в самолете.
Будущее компьютерных наук
Будущее информатики может быть не слишком светлым.Компьютеры стали настолько широко распространенной технологией, что я думаю, что изучение вычислительной техники может скоро быть отнесено к другим академическим дисциплинам, и компьютерная наука может потерять свою независимость как академический предмет. Меня не удивит, если через 20 лет отделы информационных технологий вымрут. Вычислительная техника уже породила несколько академических факультетов, таких как информационные технологии, программная инженерия и компьютерная инженерия, которые редко интегрируются в учебную программу факультета компьютерных наук. В последнее время возникли и другие вычислительные дисциплины, такие как научные вычисления / вычислительная наука, наука об управлении, цифровая графика и компьютерные игры / виртуальная реальность.
Вычислительная техника уже породила несколько академических факультетов, таких как информационные технологии, программная инженерия и компьютерная инженерия, которые редко интегрируются в учебную программу факультета компьютерных наук. В последнее время возникли и другие вычислительные дисциплины, такие как научные вычисления / вычислительная наука, наука об управлении, цифровая графика и компьютерные игры / виртуальная реальность.
% PDF-1.4
%
162 0 объект
>>>] / ON [256 0 R] / Order [] / RBGroups [] >> / OCGs [256 0 R] >> / PageLabels 153 0 R / Pages 155 0 R / Type / Catalog / ViewerPreferences >>>
эндобдж
163 0 объект
> / Шрифт >>> / Поля 149 0 R >>
эндобдж
159 0 объект
> поток
2019-04-08T11: 37: 59 + 05: 302021-07-16T15: 44: 31 + 05: 302021-07-16T15: 44: 31 + 05: 30 Adobe InDesign CS6 (Windows) uuid: 98387d9b-453b-4128- a146-f9f06186aed1xmp.did: 71640CFE67F3E6119306C8311DE9562Cxmp.ID: 38A215A1C459E9118A99846CA80138BDproof: pdfxmp.iid: 37A215A1C459E9118A99846CA80138BDxmp. did: A95EA8083946E911A063E224536B60ACxmp.did: 71640CFE67F3E6119306C8311DE9562Cdefault
did: A95EA8083946E911A063E224536B60ACxmp.did: 71640CFE67F3E6119306C8311DE9562Cdefault
 0 21.0 615.0 805.8] / Тип / Страница >>
эндобдж
50 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / Rotate 0 / TrimBox [21.0 21.0 615.0 805.8] / Type / Page >>
эндобдж
58 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / Shading> / XObject >>> / Rotate 0 / TrimBox [21.0 21.0 615.0 805.8] / Type / Page >>
эндобдж
70 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / Rotate 0 / TrimBox [21.0 21.0 615.0 805.8] / Type / Page >>
эндобдж
72 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / Rotate 0 / TrimBox [21.0 21.0 615.0 805.8] / Тип / Страница >>
эндобдж
74 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / Rotate 0 / TrimBox [21.0 21.0 615.0 805.8] / Type / Page >>
эндобдж
83 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / Rotate 0 / TrimBox [21.0 21.0 615.0 805.8] / Type / Page >>
эндобдж
85 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / Rotate 0 / TrimBox [21.
0 21.0 615.0 805.8] / Тип / Страница >>
эндобдж
50 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / Rotate 0 / TrimBox [21.0 21.0 615.0 805.8] / Type / Page >>
эндобдж
58 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / Shading> / XObject >>> / Rotate 0 / TrimBox [21.0 21.0 615.0 805.8] / Type / Page >>
эндобдж
70 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / Rotate 0 / TrimBox [21.0 21.0 615.0 805.8] / Type / Page >>
эндобдж
72 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / Rotate 0 / TrimBox [21.0 21.0 615.0 805.8] / Тип / Страница >>
эндобдж
74 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / Rotate 0 / TrimBox [21.0 21.0 615.0 805.8] / Type / Page >>
эндобдж
83 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / Rotate 0 / TrimBox [21.0 21.0 615.0 805.8] / Type / Page >>
эндобдж
85 0 объект
> / ExtGState> / Font> / ProcSet [/ PDF / Text] / XObject >>> / Rotate 0 / TrimBox [21.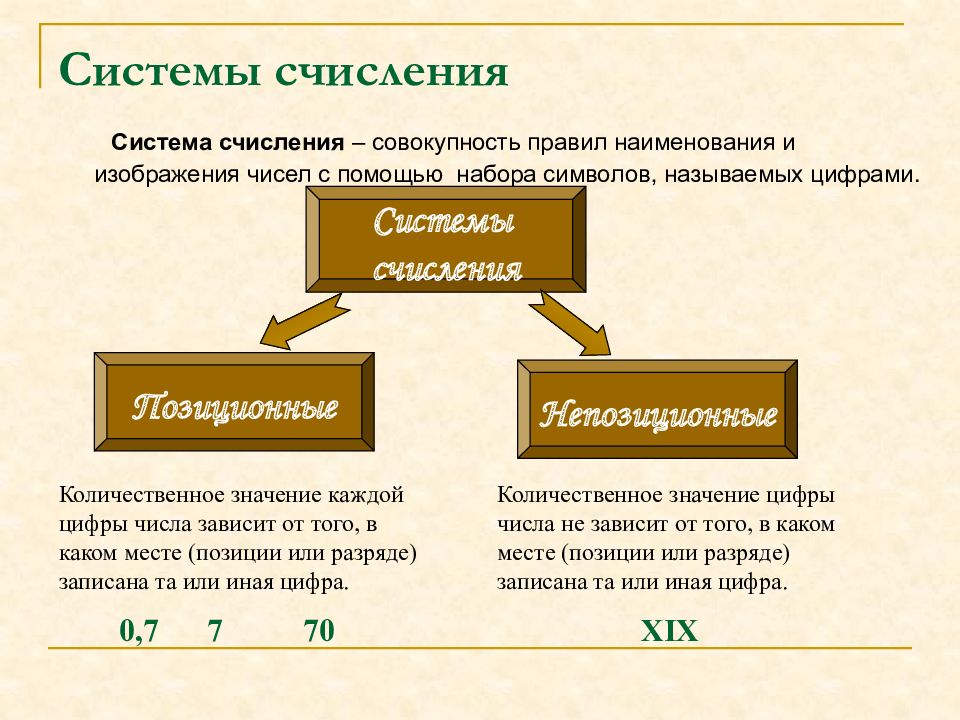 0 21.0 615.0 805.8] / Type / Page >>
эндобдж
277 0 объект
> поток
HWrk /) \ VIqS% R «
0 21.0 615.0 805.8] / Type / Page >>
эндобдж
277 0 объект
> поток
HWrk /) \ VIqS% R « Зачем нужны различные системы счисления в информатике?
Автор: проф.Фазаль Рехман Шамиль
Зачем нужны различные системы счисления в информатике?
Компьютеры не понимают человеческие языки. Итак, для обработки команд и инструкций, данных программистами, они используют разные системы, обычно известные как системы счисления.
Наиболее широко используемые системы счисления:
- двоичный
- восьмеричное
- Десятичное
- Шестнадцатеричный
Все они одинаково важны.В статье ниже вы узнаете, что это за числа и некоторые из их приложений.
1. Двоичная система
Двоичная система, известная как система счисления Base-2, используется компьютерами для работы. Все данные, хранящиеся в компьютере, состоят из двоичных чисел. Это наиболее широко используемая система.
Двоичный состоит из двух единиц 0 и 1 , известных как бит.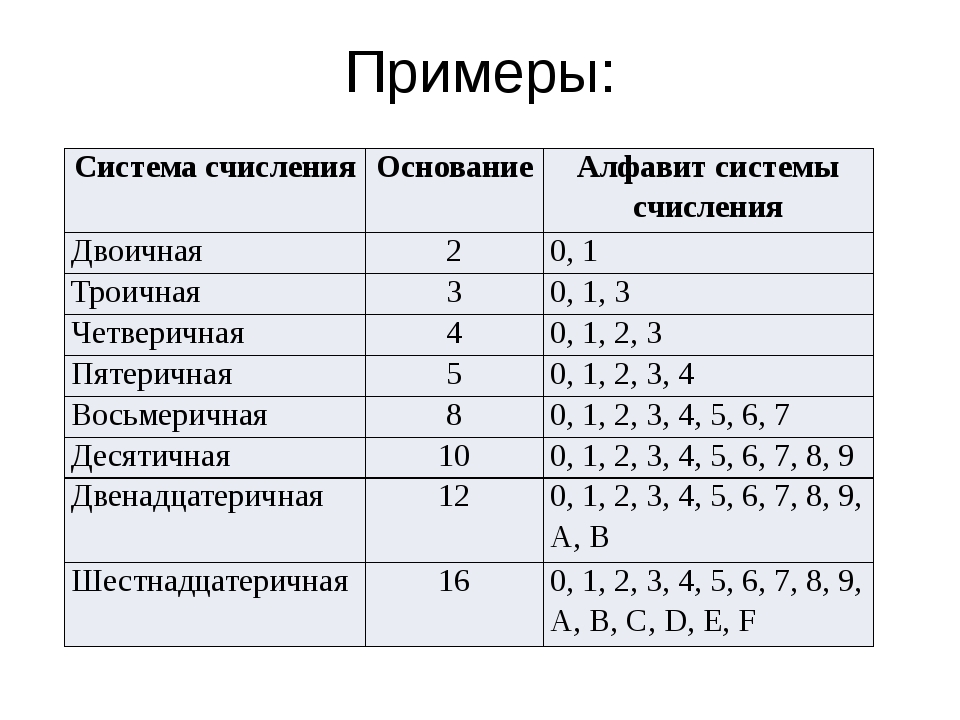 По отдельности бит 0 означает НЕТ (Ложь), а 1 бит означает ДА (Истина).
По отдельности бит 0 означает НЕТ (Ложь), а 1 бит означает ДА (Истина).
Эти биты объединены в группу из 8 байтов для представления нескольких символов и значений.Один байт может представлять 256 значений в зависимости от расположения битовых единиц.
Двоичные файлы хранятся в компьютерных данных как «Машинный код». Таким образом, его центральный процессор может выполнять программы, установленные компьютерными учеными.
В двоичной системе нет представления для отрицательных целых чисел, потому что у нас есть только 0 и 1. Нет знака -ve нет знака + ve. Поэтому для представления таких чисел и выполнения аналогичных операций программисты используют дополнение до двух.
Вы можете найти дополнение до двух двоичных чисел с помощью калькулятора дополнения до двух.
Примечание :
Исходный код не следует путать с машинным кодом. Исходный код разработан программистами на таких языках, как HTML, Python и т. Д.
Д.
Чтобы понять этот исходный код, компьютер преобразует его в двоичные числа, машинный код.
Использование двоичной системы счисления:
- Может использоваться для представления пикселей изображения.
- Он также используется для обозначения включения и выключения в цепи.
- Верные и ложные утверждения.
- ASCII
Двоичное преобразование:
Хотя он в основном используется в компьютерах, люди также могут легко изучить эту систему.
Пример :
Преобразует 345 в двоичное число.
Решение :
- Выполните повторное деление на 345 с 2 в качестве делителя.
- Начинайте писать снизу вверх. 10010
- Полный 8-битный байт с добавлением нулей слева. 00010010
2. Восьмеричная система счисления
База-8 — это система счисления, в которой в качестве основания используется 8. В этой системе используются 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Все эти представления можно расположить по-разному, чтобы получить больше восьмеричных представлений.
В этой системе используются 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7. Все эти представления можно расположить по-разному, чтобы получить больше восьмеричных представлений.
Восьмеричная система счисления немного сбивает с толку и требует практики, чтобы понять ее полностью. Восьмеричное число обычно выражается индексом 8, например .
Компьютеры не могут читать восьмеричные числа напрямую.Вот почему они сначала преобразуются в двоичные.
В восьмеричных числах цифры выше 7 представлены иначе. Например, 8 представлено как 10, что на самом деле является 1 + 0, а не десятичным числом 10. Чтобы еще больше прояснить это.
Восьмеричные числа:
| Десятичное число | 3-битное двоичное число | Восьмеричное число |
0 |
000 |
0 |
1 |
001 |
1 |
2 |
010 |
2 |
3 |
011 |
3 |
4 |
100 |
4 |
5 |
101 |
5 |
6 |
110 |
6 |
7 |
111 |
7 |
8 |
001 000 |
10 (1 + 0) |
9 |
001 001 |
11 (1 + 1) |
Использование восьмеричных чисел:
- В UNIX
- Вычислительная графика
- Защита файлов
Восьмеричное преобразование:
Восьмеричное преобразование очень похоже на преобразование в двоичном формате.
Пример :
Преобразование 130 в восьмеричное.
Решение :
- Выполнить повторное деление на 130.
- Начинайте писать снизу вверх.
(202) 8
3. Десятичная система
Десятичная система, также известная как система счисления с основанием 10, — это система счисления, с которой знаком почти каждый человек. Разобраться в этой системе может даже необразованный человек.
Причина в том, что мы используем его в повседневной жизни в финансах, считая и т. Д. Числа, используемые в денарной системе: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В денарной системе значение каждого числа увеличивается в 10 раз при движении справа налево. Например, в числе 56 цифра 5 в 10 раз дороже, чем цифра 6.
Использование десятичной системы счисления:
- Финансы
- Календарь
- Подсчет
Десятичное преобразование:
В десятичном преобразовании особо нечего делать, потому что мы используем эту систему счисления. Это означает, что используемые нами числа уже представлены в денарной системе.
Это означает, что используемые нами числа уже представлены в денарной системе.
Но мы можем научиться преобразовывать двоичные числа в десятичную систему.
Пример :
Преобразует 10010101 в десятичное.
Решение:
- Сначала запишите 2 под каждым битом с той же мощностью, что и его позиция.
- Теперь умножьте числа на соответствующий двоичный бит и сложите их.то есть
= 128 + 16 + 4 + 1
= 149
4. Шестнадцатеричная система
Последняя и самая сложная система счисления — шестнадцатеричная. Это сложно выучить по сравнению с другими системами счисления.
Эта система счисления делает несколько удобных вещей такими, как представление байтов. Для представления 8-битного байта двоичных чисел требуется только 2 шестнадцатеричных числа.
Он также известен как основание-16, а цифры и алфавиты, используемые в этой системе: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. .
.
Алфавит A представляет десятичное число 10, B представляет десятичное число 11 и так далее.
Использование шестнадцатеричного числа:
- Ячейки памяти
- Устранение ошибок
- Для определения цветов на веб-страницах, например, оттенок красного представлен как ff0000.
| Десятичное число | 4-битное двоичное число | Шестнадцатеричное число |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | С |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
| 16 | 0001 0000 | 10 (1 + 0) |
| 17 | 0001 0001 | 11 (1 + 1) |
Шестнадцатеричное преобразование:
Для преобразования десятичного числа в шестнадцатеричное используется тот же метод, что и для восьмеричного преобразования.
Пример :
Преобразование 510 в шестнадцатеричное.
Решение :
- Выполнить повторное деление на 510.
- Пишите снизу вверх и используйте соответствующие алфавиты там, где это необходимо.
14 = E, 15 = F, 1 = 1
- Следовательно,
510 = (1FE) 16
Заключение
Каждая система счисления важна и имеет различные применения.Именно благодаря этим системам счисления современные компьютеры могут выполнять гораздо больше задач, чем старые.
Хотя эти системы используются в компьютерном программировании, их можно легко изучить, потому что в конечном итоге все они связаны с десятичной системой счисления, которую используют люди.
Информатика — Преобразование системы счисления и математические операции в программировании | Луис Карлос
Стенограммы
1. Презентация и превью курса: добро пожаловать в систему счисления Curse.Меня зовут Карлос, и я мог работать только инженером по телекоммуникациям. У меня семилетний опыт работы тренером в области математики и информатики, и мои основные цели — расширить наши знания в этой области. Система счисления более здорового личного развития и успеха использует различные области информатики, такие как система, сеть, безопасность и программирование. В конце курса вы сможете определять разные системы счисления, охватывать числа двух разных размеров и выполнять математические операции с разными системами счисления.Vickers делится на модели, для начинающих и для продвинутых. В начальной части вы узнаете, что такое востребованные, используемые для сокрытия цифр на футболках и для продвинутой части. Вы узнаете методы преобразования, привязки всех членов и выполнения сложения и вычитания, используя разные элементы места. Идеальные студенты для дискурса — это те, кто изучает информатику или просто хочет расширить свои знания.
Презентация и превью курса: добро пожаловать в систему счисления Curse.Меня зовут Карлос, и я мог работать только инженером по телекоммуникациям. У меня семилетний опыт работы тренером в области математики и информатики, и мои основные цели — расширить наши знания в этой области. Система счисления более здорового личного развития и успеха использует различные области информатики, такие как система, сеть, безопасность и программирование. В конце курса вы сможете определять разные системы счисления, охватывать числа двух разных размеров и выполнять математические операции с разными системами счисления.Vickers делится на модели, для начинающих и для продвинутых. В начальной части вы узнаете, что такое востребованные, используемые для сокрытия цифр на футболках и для продвинутой части. Вы узнаете методы преобразования, привязки всех членов и выполнения сложения и вычитания, используя разные элементы места. Идеальные студенты для дискурса — это те, кто изучает информатику или просто хочет расширить свои знания. Единственное требование — это удовольствие учиться, а остальное я сделаю, чтобы помочь вам не стесняться смотреть наше предварительное видео, если вы в пределах пяти.Мы обсуждали гигантов
2. Обзор курса: Меня зовут Уиш Карлос, я из Particle. Я буду вашим инструктором в следующие 90 минут, где вы научитесь преобразовывать числа. Используя различные покупки, давайте начнем с проклятия обзора во вводной части, с основной стороны, каковы системы нумерации? Различные области использования и изложения различаются по своим номерам. Основное внимание в дискурсе уделяется преобразованию между различными системами нумерации с использованием простых и дробных чисел.После создания азиатов-открытий вы научитесь делать сложения и вычитания. Использование различных покупок — это
3. Введение: привет. В этой первой главе я собираюсь поговорить о важности чисел в информатике. Вы используете символы во все моменты нашей жизни. А иногда в наши дни символы выражают числовые значения. Десятичная система счисления используется чаще.
Единственное требование — это удовольствие учиться, а остальное я сделаю, чтобы помочь вам не стесняться смотреть наше предварительное видео, если вы в пределах пяти.Мы обсуждали гигантов
2. Обзор курса: Меня зовут Уиш Карлос, я из Particle. Я буду вашим инструктором в следующие 90 минут, где вы научитесь преобразовывать числа. Используя различные покупки, давайте начнем с проклятия обзора во вводной части, с основной стороны, каковы системы нумерации? Различные области использования и изложения различаются по своим номерам. Основное внимание в дискурсе уделяется преобразованию между различными системами нумерации с использованием простых и дробных чисел.После создания азиатов-открытий вы научитесь делать сложения и вычитания. Использование различных покупок — это
3. Введение: привет. В этой первой главе я собираюсь поговорить о важности чисел в информатике. Вы используете символы во все моменты нашей жизни. А иногда в наши дни символы выражают числовые значения. Десятичная система счисления используется чаще. Мы использовали десятичное высвобождение в разные моменты. Например, когда вы делаете математические упражнения в школе, когда ходите по магазинам и видите цены, когда вы идете на футбольный матч, и вы видите количество голов в шраме.Барт. Существуют и другие разные системы счисления, и основное различие между ними — это количество используемых символов. Они важны в таких областях, как электроника информатики или микропроцессоры. Эти разные системы счисления используют эти области, потому что компьютерам легче понять информацию в определенном формате. Современный компьютер работает по принципу двух состояний: включено и выключено. Эти два состояния реагируют на то, что они либо есть буквы, либо отсутствуют в настоящее время, либо отсутствуют.Включенное состояние — это сегмент со значением один, если электрический ток присутствует, а выключенное состояние — это застоявшееся с нулевым значением. Если нет электрического тока. Вот почему мы переходим в двоичную систему, потому что как два состояния, два разных состояния, орбита каждой двоичной цифры — это просто один ноль или единица, которая напрямую соответствует одному переключателю в схеме UF, вот этот переключатель, и если он находится в положении, I соответствует нуль.
Мы использовали десятичное высвобождение в разные моменты. Например, когда вы делаете математические упражнения в школе, когда ходите по магазинам и видите цены, когда вы идете на футбольный матч, и вы видите количество голов в шраме.Барт. Существуют и другие разные системы счисления, и основное различие между ними — это количество используемых символов. Они важны в таких областях, как электроника информатики или микропроцессоры. Эти разные системы счисления используют эти области, потому что компьютерам легче понять информацию в определенном формате. Современный компьютер работает по принципу двух состояний: включено и выключено. Эти два состояния реагируют на то, что они либо есть буквы, либо отсутствуют в настоящее время, либо отсутствуют.Включенное состояние — это сегмент со значением один, если электрический ток присутствует, а выключенное состояние — это застоявшееся с нулевым значением. Если нет электрического тока. Вот почему мы переходим в двоичную систему, потому что как два состояния, два разных состояния, орбита каждой двоичной цифры — это просто один ноль или единица, которая напрямую соответствует одному переключателю в схеме UF, вот этот переключатель, и если он находится в положении, I соответствует нуль. Переключатель открыт, и если это закрытое положение, клюв откликается на визит.Если вы наденете много переключателей вместе, вы не сможете представить больше чисел, больше нулей и единиц. Таким образом, вместо одной цифры вы подняли группы с восьми, что соответствует поклевкам. Пошел байк, ответ на восемь однозначных цифр. Вы можете увидеть другой пример. Два переключателя. И если они находятся в позиции, я и позиция вижу, что они открыты, что соответствует нулевому значению. Если они на месте. B в позиции D, они замкнуты и соответствуют значению один. Компьютер. Используйте миллионы выключателей. Единственная уловка заключается в том, что вы используете этот ввод, сделанный изображениями, звуком или другими типами файлов.Вам просто нужно преобразовать два нуля этого файла, и компьютер понимает такую информацию.
4. Типы системы счисления: Здравствуйте. Это глава о различных типах систем счисления. Система счисления — это любая система, которую мы использовали для представления различных чисел.
Переключатель открыт, и если это закрытое положение, клюв откликается на визит.Если вы наденете много переключателей вместе, вы не сможете представить больше чисел, больше нулей и единиц. Таким образом, вместо одной цифры вы подняли группы с восьми, что соответствует поклевкам. Пошел байк, ответ на восемь однозначных цифр. Вы можете увидеть другой пример. Два переключателя. И если они находятся в позиции, я и позиция вижу, что они открыты, что соответствует нулевому значению. Если они на месте. B в позиции D, они замкнуты и соответствуют значению один. Компьютер. Используйте миллионы выключателей. Единственная уловка заключается в том, что вы используете этот ввод, сделанный изображениями, звуком или другими типами файлов.Вам просто нужно преобразовать два нуля этого файла, и компьютер понимает такую информацию.
4. Типы системы счисления: Здравствуйте. Это глава о различных типах систем счисления. Система счисления — это любая система, которую мы использовали для представления различных чисел.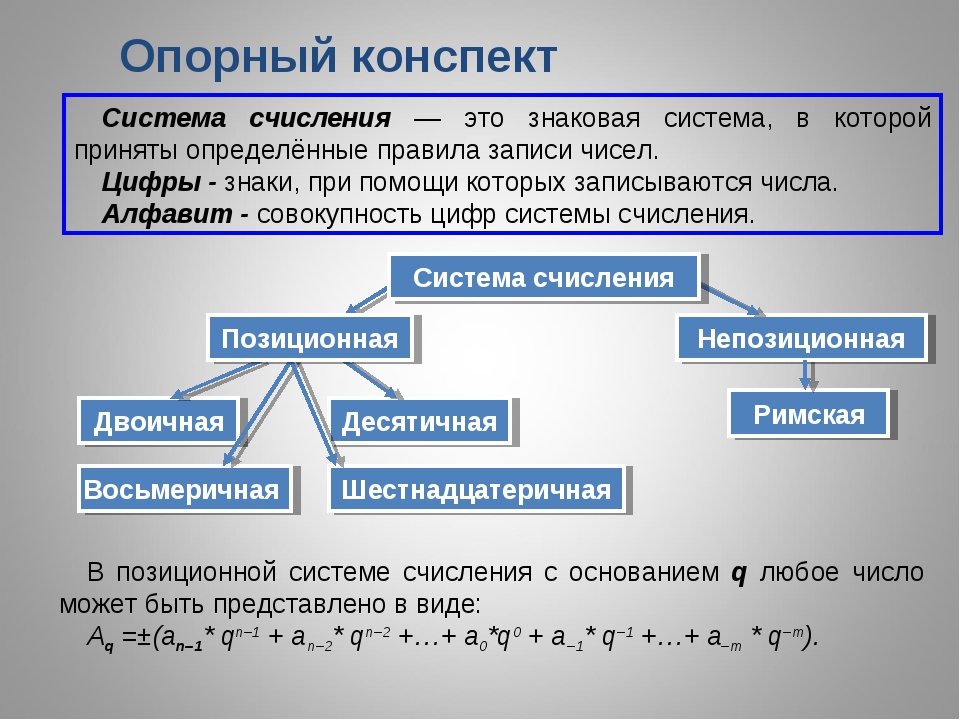 У нас есть четыре основных типа. Десятичное число, которое используется чаще всего, двоичное, конец восьмеричного числа, десятичное число выхода. Эти меньше деревьев больше используются в некоторых областях, помимо информатики, которыми я буду заниматься. Я представляю различные типы систем счисления, которые использовал Стэн И.F. 10 различных значений для представления одной цифры в этой двоичной системе счисления. У меня есть два разных значения для представления действительного в этом Bice Bice для системы нумерации артикулов на вид, у меня есть восемь разных значений для представления одной цифры и, наконец, десятичная дробь выхода. К 16 годам у меня есть 16 различных значений для представления одной цифры 10 чисел от нуля до девяти и шесть букв от A до F. Как я собираюсь представить различные системы счисления в следующей жизни между Берланти, я собираюсь списать прибор с числа в ребята с десятичных чисел.Я напишу 10. Сделайте двоичными для чисел Octel восемь и выйдите из десятичных чисел.
У нас есть четыре основных типа. Десятичное число, которое используется чаще всего, двоичное, конец восьмеричного числа, десятичное число выхода. Эти меньше деревьев больше используются в некоторых областях, помимо информатики, которыми я буду заниматься. Я представляю различные типы систем счисления, которые использовал Стэн И.F. 10 различных значений для представления одной цифры в этой двоичной системе счисления. У меня есть два разных значения для представления действительного в этом Bice Bice для системы нумерации артикулов на вид, у меня есть восемь разных значений для представления одной цифры и, наконец, десятичная дробь выхода. К 16 годам у меня есть 16 различных значений для представления одной цифры 10 чисел от нуля до девяти и шесть букв от A до F. Как я собираюсь представить различные системы счисления в следующей жизни между Берланти, я собираюсь списать прибор с числа в ребята с десятичных чисел.Я напишу 10. Сделайте двоичными для чисел Octel восемь и выйдите из десятичных чисел.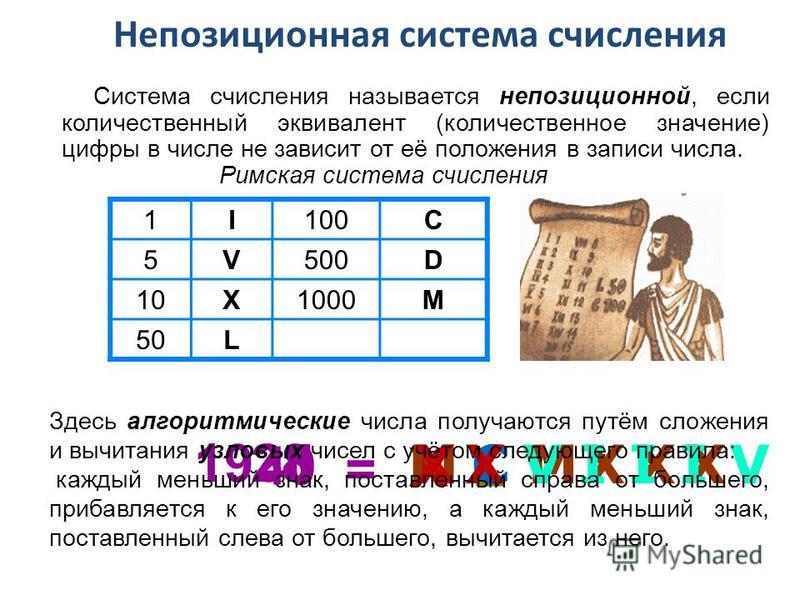 16. Зачем. Я использую auto и exit decimal и просто не использую двоичные числа только потому, что когда вы говорите об информации в компьютере? U F много битов и укусов для представления информации множеством нулей и единиц. Octel и десятичная система выхода — это всего лишь короткий путь, удобный способ представления двоичного числа. Почему? Потому что в автоматической системе счисления одной цифрой можно представить три двоичных разряда. Что делает число больше диаграмм, и в выходной десятичной системе с одной цифрой, которую я могу представить для двоичных ставок, давайте рассмотрим только два примера, где у меня есть одно первое двоичное число с девятью битами 0110101 ноль, а с местной системой счисления я использовал всего три цифры для представления этой информации.Наконец, второй пример с восемью битами 01110101 Я использую только две цифры для представления этих восьми ставок.
5. Десятичная система: Здравствуйте, Industries. Я собираюсь показать вам некоторые свойства без десятичной системы.
16. Зачем. Я использую auto и exit decimal и просто не использую двоичные числа только потому, что когда вы говорите об информации в компьютере? U F много битов и укусов для представления информации множеством нулей и единиц. Octel и десятичная система выхода — это всего лишь короткий путь, удобный способ представления двоичного числа. Почему? Потому что в автоматической системе счисления одной цифрой можно представить три двоичных разряда. Что делает число больше диаграмм, и в выходной десятичной системе с одной цифрой, которую я могу представить для двоичных ставок, давайте рассмотрим только два примера, где у меня есть одно первое двоичное число с девятью битами 0110101 ноль, а с местной системой счисления я использовал всего три цифры для представления этой информации.Наконец, второй пример с восемью битами 01110101 Я использую только две цифры для представления этих восьми ставок.
5. Десятичная система: Здравствуйте, Industries. Я собираюсь показать вам некоторые свойства без десятичной системы. Эта система используется больше всего в нашей жизни. Так почему мы называем простую систему? Просто потому, что для представления цифры в десятичном числе вы можете использовать разные значения от 0 до 9, это блюдо. Это разные значения разряда, которые могут быть представлены подставкой с положительным и отрицательным показателем степени.Если говорить о внутренней части, экспоненты положительные? А для дифракции все части экспоненты теперь отрицательные, что делает пример Джастина, где я собираюсь составить число 156. Это число состоит из уличных цифр и трех разных замаскированных белых. Положительный только потому, что я нашел число без дробных частей. Теперь я собираюсь составить число в разных белых и разных значениях разряда и умножить каждое справа. Таким образом, укусы с соответствующими показателями степени соответствующими цифрами И при определении я определю все значения Итак, 156 равно 10, взорвать на умноженное на соответствующую цифру, закончить с 10 показателями при умножении на пять, отредактировать с 10 показателями, ноль умножить на шесть.
Эта система используется больше всего в нашей жизни. Так почему мы называем простую систему? Просто потому, что для представления цифры в десятичном числе вы можете использовать разные значения от 0 до 9, это блюдо. Это разные значения разряда, которые могут быть представлены подставкой с положительным и отрицательным показателем степени.Если говорить о внутренней части, экспоненты положительные? А для дифракции все части экспоненты теперь отрицательные, что делает пример Джастина, где я собираюсь составить число 156. Это число состоит из уличных цифр и трех разных замаскированных белых. Положительный только потому, что я нашел число без дробных частей. Теперь я собираюсь составить число в разных белых и разных значениях разряда и умножить каждое справа. Таким образом, укусы с соответствующими показателями степени соответствующими цифрами И при определении я определю все значения Итак, 156 равно 10, взорвать на умноженное на соответствующую цифру, закончить с 10 показателями при умножении на пять, отредактировать с 10 показателями, ноль умножить на шесть. Это даст мне 100, умноженные на единицу, оканчивающуюся на. Затем мы развернем на пять, добавив один, умноженный на шесть. Итоговый результат, как мы и ожидали, — 156.
6. Преобразование десятичных чисел в двоичные: в строке я собираюсь преобразовать десятичные числа в двоичные числа. Техника, которую я собираюсь использовать, — это метод деления, при котором я собираюсь сделать несколько делений на два десятичного числа, которое я хочу преобразовать. В этом первом примере я собираюсь скрыть двоичный файл 252. Первый шаг — это деление на два от исходного числа, и я получаю деление на частное и напоминание об этом числе.250. Разделите на два. Я получаю вопрос от 125, а остаток от нуля. В следующей ситуации я воспользуюсь предыдущим вопросом. 125. Разделите на два. Я получаю вопрос с 62, а остальные с первого. Я остановил ситуацию, когда у меня ноль. Результат определения Indyk Oceans в двоичном формате дается мне остатком. Последнее напоминание, которое я получил, это самый старший бит двоичного числа, а первый остаток, который я получаю, — это младшие значащие биты.
Это даст мне 100, умноженные на единицу, оканчивающуюся на. Затем мы развернем на пять, добавив один, умноженный на шесть. Итоговый результат, как мы и ожидали, — 156.
6. Преобразование десятичных чисел в двоичные: в строке я собираюсь преобразовать десятичные числа в двоичные числа. Техника, которую я собираюсь использовать, — это метод деления, при котором я собираюсь сделать несколько делений на два десятичного числа, которое я хочу преобразовать. В этом первом примере я собираюсь скрыть двоичный файл 252. Первый шаг — это деление на два от исходного числа, и я получаю деление на частное и напоминание об этом числе.250. Разделите на два. Я получаю вопрос от 125, а остаток от нуля. В следующей ситуации я воспользуюсь предыдущим вопросом. 125. Разделите на два. Я получаю вопрос с 62, а остальные с первого. Я остановил ситуацию, когда у меня ноль. Результат определения Indyk Oceans в двоичном формате дается мне остатком. Последнее напоминание, которое я получил, это самый старший бит двоичного числа, а первый остаток, который я получаю, — это младшие значащие биты. Таким образом, конечный результат до конца и 50 в десятичном виде — это единица 11 11010 Следующий пример.Я собираюсь преобразовать 78 в двоичное 78. Разделим на два. Дайте нам вопросы по оставшимся вопросам. Нуль. Предыдущее частное используется для следующей ситуации. 39. Разделите на два. Когда я получаю ноль, я получаю вопрос из 19 и оставшуюся часть из одного. Indyk, Ocean Я перестал объезжать и получил окончательный номер в своем напоминании. 1001110 В последнем примере я собираюсь преобразовать 177 в двоичное. Давайте сделаем первую ситуацию. 177. Разделите на два. Задайте мне вопрос из 88 оставшихся когда-либо выигранных.Предыдущий вопрос используется в следующем Дивизионе 88. Разделите на, чтобы получить часть от 44 и остаток от нуля. Этот процесс останавливается, когда вопрос равен нулю, и я получаю окончательное число. В моем остатке. 10110001 Видно, да? Окончательные результаты. Вещи
7. Преобразование десятичного числа в восьмеричное: в этом вы чувствуете? Я собираюсь показать вам, как преобразовать десятичные числа в восьмеричные.
Таким образом, конечный результат до конца и 50 в десятичном виде — это единица 11 11010 Следующий пример.Я собираюсь преобразовать 78 в двоичное 78. Разделим на два. Дайте нам вопросы по оставшимся вопросам. Нуль. Предыдущее частное используется для следующей ситуации. 39. Разделите на два. Когда я получаю ноль, я получаю вопрос из 19 и оставшуюся часть из одного. Indyk, Ocean Я перестал объезжать и получил окончательный номер в своем напоминании. 1001110 В последнем примере я собираюсь преобразовать 177 в двоичное. Давайте сделаем первую ситуацию. 177. Разделите на два. Задайте мне вопрос из 88 оставшихся когда-либо выигранных.Предыдущий вопрос используется в следующем Дивизионе 88. Разделите на, чтобы получить часть от 44 и остаток от нуля. Этот процесс останавливается, когда вопрос равен нулю, и я получаю окончательное число. В моем остатке. 10110001 Видно, да? Окончательные результаты. Вещи
7. Преобразование десятичного числа в восьмеричное: в этом вы чувствуете? Я собираюсь показать вам, как преобразовать десятичные числа в восьмеричные.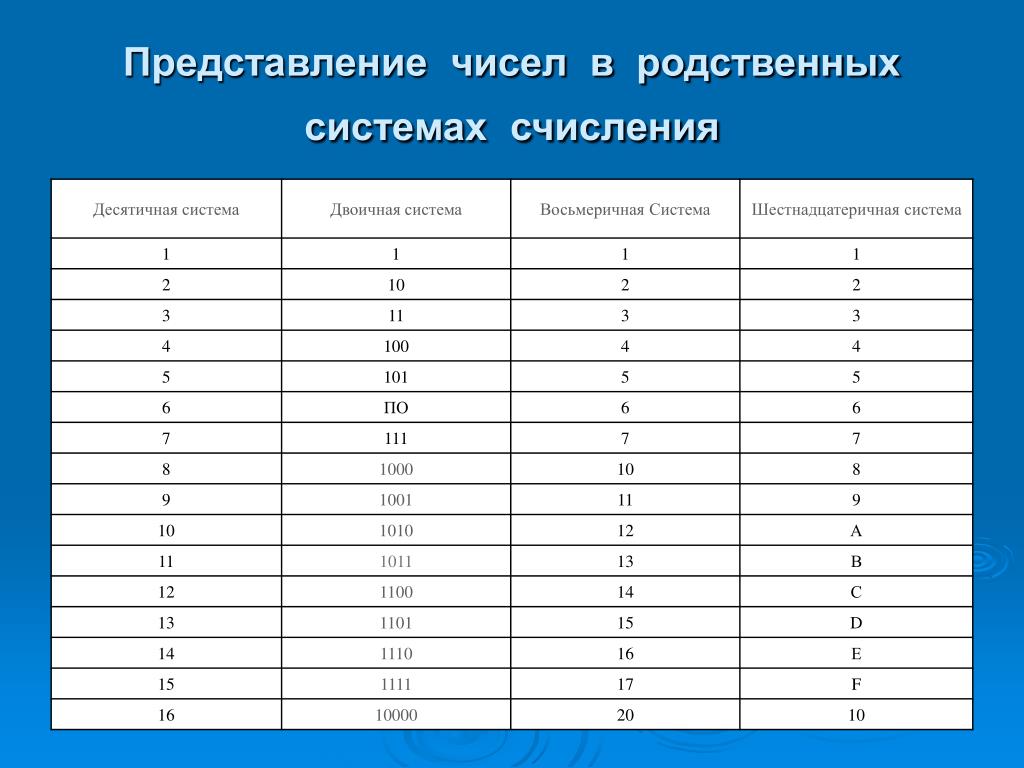 Первый Met, который я собираюсь использовать, — это методы деления, которые использовались в предыдущей главе. При преобразовании десятичных чисел в двоичные используется вместо деления на два.Чтобы получить двоичные числа, вы разделите их на восемь. Чтобы получить числа Octel, вы можете увидеть первый пример деления 250 на восемь. Вы получили предупреждение 31. Напоминание о том, что во втором дивизионе вы сделаете разделение с предыдущей частью на восемь и получите предупреждение о дереве и оставшихся семи в финале. Итару голень. Вы собираетесь разделить три на восемь и получить вопрос ноль, а остальные три. Вы все равно получите окончательное число 372 в Octel, данное командой. Либо второй метод, который я использую, — это их преобразование из десятичного числа в двоичное на первом этапе, а на втором этапе — преобразование из двоичного в Octel.Используя эту таблицу соответствия, сначала выполните преобразование десятичной дроби в двоичную. Из предыдущей главы вы узнали, что чем 50 в десятичной системе дано 11111010 в двоичной системе счисления.
Первый Met, который я собираюсь использовать, — это методы деления, которые использовались в предыдущей главе. При преобразовании десятичных чисел в двоичные используется вместо деления на два.Чтобы получить двоичные числа, вы разделите их на восемь. Чтобы получить числа Octel, вы можете увидеть первый пример деления 250 на восемь. Вы получили предупреждение 31. Напоминание о том, что во втором дивизионе вы сделаете разделение с предыдущей частью на восемь и получите предупреждение о дереве и оставшихся семи в финале. Итару голень. Вы собираетесь разделить три на восемь и получить вопрос ноль, а остальные три. Вы все равно получите окончательное число 372 в Octel, данное командой. Либо второй метод, который я использую, — это их преобразование из десятичного числа в двоичное на первом этапе, а на втором этапе — преобразование из двоичного в Octel.Используя эту таблицу соответствия, сначала выполните преобразование десятичной дроби в двоичную. Из предыдущей главы вы узнали, что чем 50 в десятичной системе дано 11111010 в двоичной системе счисления. После того, как у вас есть двоичное число, вы хотите создать группы из трех басов с исходным двоичным числом и использовать таблицу соответствия, чтобы увидеть соответствующее число Отто, которое вы можете увидеть здесь. 0111, когда 1010 примечаний, которые вы редактируете слева 10, чтобы сделать эти три группы из трех битов для использования этой таблицы. Во втором примере я конвертирую 78 в auto, используя первое значение 78.Разделите на восемь. Дайте мне предупреждение девять и напоминание шесть во втором девятом дивизионе. Разделите на восемь. Задайте мне один вопрос и напомните один, а в последнем дивизионе один разделите на восьмой. Дайте мне предупреждение, равное нулю и остатку. Один последний номер Octel 116. Используя второй метод, я собираюсь преобразовать десятичное число 70 18 в двоичное 1001110. А теперь я собираюсь объединить трибуты в группы. 001, что соответствует единице в окто, 0011 в окто и 110 шестерке в дяде. Последний пример преобразования с 177 в автоматический сначала встретился с делением десятичного числа на восемь.
После того, как у вас есть двоичное число, вы хотите создать группы из трех басов с исходным двоичным числом и использовать таблицу соответствия, чтобы увидеть соответствующее число Отто, которое вы можете увидеть здесь. 0111, когда 1010 примечаний, которые вы редактируете слева 10, чтобы сделать эти три группы из трех битов для использования этой таблицы. Во втором примере я конвертирую 78 в auto, используя первое значение 78.Разделите на восемь. Дайте мне предупреждение девять и напоминание шесть во втором девятом дивизионе. Разделите на восемь. Задайте мне один вопрос и напомните один, а в последнем дивизионе один разделите на восьмой. Дайте мне предупреждение, равное нулю и остатку. Один последний номер Octel 116. Используя второй метод, я собираюсь преобразовать десятичное число 70 18 в двоичное 1001110. А теперь я собираюсь объединить трибуты в группы. 001, что соответствует единице в окто, 0011 в окто и 110 шестерке в дяде. Последний пример преобразования с 177 в автоматический сначала встретился с делением десятичного числа на восемь. 177. Разделите на восемь Gift, как 22 частное, а остаток вычтено. Единица 22. Разделить на коэффициент ненависти два и остаток от шести и в последнем делении разделить на восемь предостережений ноль и остаток два. Окончательный результат до 61 в Octel. Используя второй метод, я собираюсь произвести преобразование из десятичного числа в двоичное. 177 равно 10110001. Составьте группы из трех долей, и вы получите 010110001. Это дает до 61, используя таблицу соответствия между двоичными числами и числами Octel.
8. Преобразование десятичного числа в шестнадцатеричное: Здравствуйте.В этой главе я собираюсь произвести преобразование десятичных чисел в десятичные числа. Первое, что я собираюсь использовать, это методы деления, которые я собираюсь разделить на 16 десятичных чисел, пока не получу окончательное десятичное число для выхода. Пример 250. Разделите на 16 частное от 15 и оставшуюся часть, затем введите букву второй итерации. 15. Разделите на 16 частное нуля и остаток. 15 Буква f Не забывайте, что для недоступности представления цифр U F 16 различных значений от нуля до F конечный результат 250 в десятичном виде — это F A в exas Immel.
177. Разделите на восемь Gift, как 22 частное, а остаток вычтено. Единица 22. Разделить на коэффициент ненависти два и остаток от шести и в последнем делении разделить на восемь предостережений ноль и остаток два. Окончательный результат до 61 в Octel. Используя второй метод, я собираюсь произвести преобразование из десятичного числа в двоичное. 177 равно 10110001. Составьте группы из трех долей, и вы получите 010110001. Это дает до 61, используя таблицу соответствия между двоичными числами и числами Octel.
8. Преобразование десятичного числа в шестнадцатеричное: Здравствуйте.В этой главе я собираюсь произвести преобразование десятичных чисел в десятичные числа. Первое, что я собираюсь использовать, это методы деления, которые я собираюсь разделить на 16 десятичных чисел, пока не получу окончательное десятичное число для выхода. Пример 250. Разделите на 16 частное от 15 и оставшуюся часть, затем введите букву второй итерации. 15. Разделите на 16 частное нуля и остаток. 15 Буква f Не забывайте, что для недоступности представления цифр U F 16 различных значений от нуля до F конечный результат 250 в десятичном виде — это F A в exas Immel.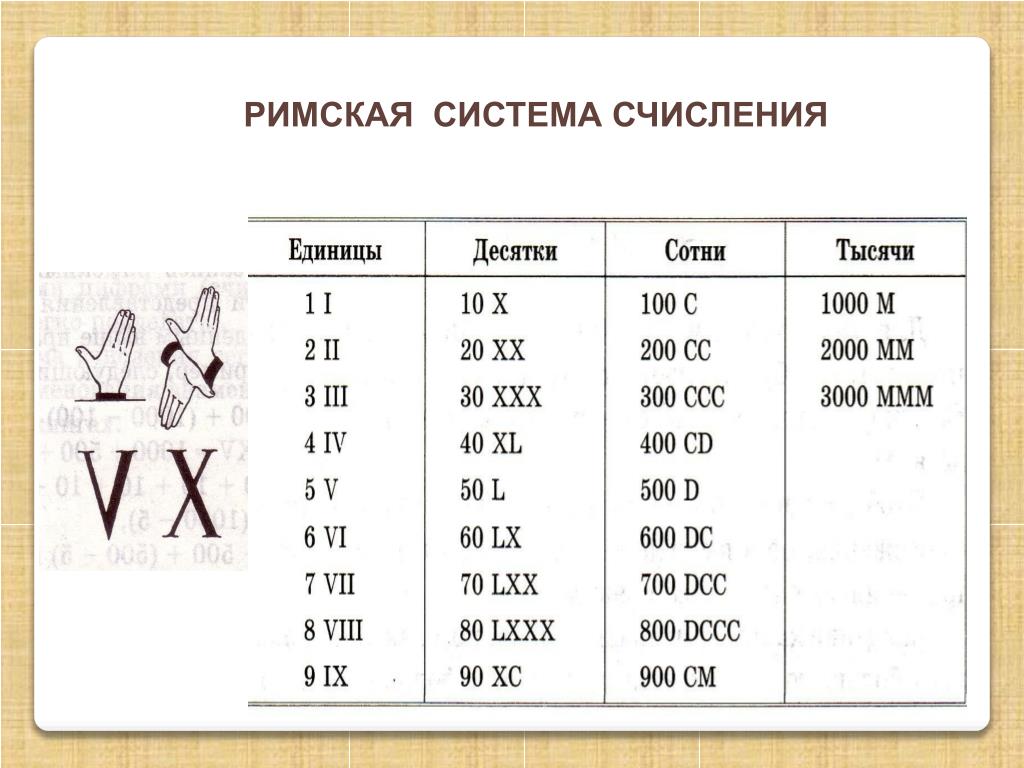 Второй используемый метод — это преобразование из предназначенного в двоичный на первом этапе, а на втором этапе из двоичного в десятичный. Я просто использовал это значение, потому что в предыдущей главе я преобразовал десятичные вычисления в двоичные. У меня просто этот результат в двоичном формате. Если вы думаете, что получить результат за один шаг проще, просто сделав деление на 16, вы можете использовать первый метод, теперь сделайте расчет. 250 равно 11111010 в двоичном формате, что составляет две группы из четырех битов. Я получаю 1111 — это буква f, а 1010 — это буква.Второй пример. Преобразование из десятичного числа 78 в десятичное число выхода 78. Разделите на 16. Дайте мне четвертый вопрос и напоминание. 14 Letter e far Разделите на 16. Дайте мне нулевой берег и остаток прочь. Четыре. Окончательные результаты. 70 18 Десятичное число для E в десятичном формате на выходе с использованием второго значения, первое Govert из десятичного числа в двоичное 78 в десятичном формате равно 1001110 при создании двоичного числа.
Второй используемый метод — это преобразование из предназначенного в двоичный на первом этапе, а на втором этапе из двоичного в десятичный. Я просто использовал это значение, потому что в предыдущей главе я преобразовал десятичные вычисления в двоичные. У меня просто этот результат в двоичном формате. Если вы думаете, что получить результат за один шаг проще, просто сделав деление на 16, вы можете использовать первый метод, теперь сделайте расчет. 250 равно 11111010 в двоичном формате, что составляет две группы из четырех битов. Я получаю 1111 — это буква f, а 1010 — это буква.Второй пример. Преобразование из десятичного числа 78 в десятичное число выхода 78. Разделите на 16. Дайте мне четвертый вопрос и напоминание. 14 Letter e far Разделите на 16. Дайте мне нулевой берег и остаток прочь. Четыре. Окончательные результаты. 70 18 Десятичное число для E в десятичном формате на выходе с использованием второго значения, первое Govert из десятичного числа в двоичное 78 в десятичном формате равно 1001110 при создании двоичного числа. Две группы запретов, которые я получаю: 0100 Это число четыре и 1110 Это результаты поиска букв для a в последнем примере преобразования с 177 для выхода из десятичного числа.Сначала метод деления меньше 77, деление на 16, частное 11 и остальное, когда 11 делится на 16. Предупреждаю, чтобы ноль и остаток не учитывались. 11. Буква B Конечный результат 177 в десятичной системе счисления равен единице B в десятичной системе счисления, используя сначала второй метод, преобразование десятичного числа в двоичное. 177. Кишечник — 1011 0001, разделенный на две группы. Я получаю 1011 буквы B и 0001 номер один.
9. Преобразование двоичного числа в десятичное: Здравствуйте. В предыдущих главах они узнали, как преобразовывать десятичные числа в двоичные Octel и выходить из десятичных чисел.В следующих главах мы постараемся охватить двоичные числа и другие основы. Начнем с преобразования двоичных чисел в десятичные по их системе, использующей основу, и, как и идея, основанию дерева, каждая цифра имеет разные веса.
Две группы запретов, которые я получаю: 0100 Это число четыре и 1110 Это результаты поиска букв для a в последнем примере преобразования с 177 для выхода из десятичного числа.Сначала метод деления меньше 77, деление на 16, частное 11 и остальное, когда 11 делится на 16. Предупреждаю, чтобы ноль и остаток не учитывались. 11. Буква B Конечный результат 177 в десятичной системе счисления равен единице B в десятичной системе счисления, используя сначала второй метод, преобразование десятичного числа в двоичное. 177. Кишечник — 1011 0001, разделенный на две группы. Я получаю 1011 буквы B и 0001 номер один.
9. Преобразование двоичного числа в десятичное: Здравствуйте. В предыдущих главах они узнали, как преобразовывать десятичные числа в двоичные Octel и выходить из десятичных чисел.В следующих главах мы постараемся охватить двоичные числа и другие основы. Начнем с преобразования двоичных чисел в десятичные по их системе, использующей основу, и, как и идея, основанию дерева, каждая цифра имеет разные веса. Чтобы получить десятичные числа из двоичного числа, вы должны произвести умножение каждого значения на каждую цифру и соответствующий белый цвет в финале. У вас все ценности. Посмотрим на первый пример. 11011 Это пятизначное число с пятью разными весами, которое вы можете увидеть в конюшне справа от этой жизни.Теперь я собираюсь произвести умножение каждого значения Digit, и соответствующее ожидание 11011 равно для объяснения и многократно умножено на, когда закончилось, чтобы удалить запись, умноженную на одно редактирование, чтобы расширить до умножения на ноль. Это ноль, всегда U F — бит со значением ноль, конечный результат — ноль, и что мы, чтобы объяснить, умножили его на один добавленный вес, чтобы расширить ноль, умноженный на единицу, вы получите окончательный результат. 16 закончились восьмиголовым умом, чтобы отредактировать его одним, то получится 27 в десятичной системе счисления.Во втором примере, который я показываю вам, преобразование 10011 в двоичном формате в их символ равно do, объясненное для умножения на единицу в остроумие, чтобы объяснить запись, умноженную на ноль.
Чтобы получить десятичные числа из двоичного числа, вы должны произвести умножение каждого значения на каждую цифру и соответствующий белый цвет в финале. У вас все ценности. Посмотрим на первый пример. 11011 Это пятизначное число с пятью разными весами, которое вы можете увидеть в конюшне справа от этой жизни.Теперь я собираюсь произвести умножение каждого значения Digit, и соответствующее ожидание 11011 равно для объяснения и многократно умножено на, когда закончилось, чтобы удалить запись, умноженную на одно редактирование, чтобы расширить до умножения на ноль. Это ноль, всегда U F — бит со значением ноль, конечный результат — ноль, и что мы, чтобы объяснить, умножили его на один добавленный вес, чтобы расширить ноль, умноженный на единицу, вы получите окончательный результат. 16 закончились восьмиголовым умом, чтобы отредактировать его одним, то получится 27 в десятичной системе счисления.Во втором примере, который я показываю вам, преобразование 10011 в двоичном формате в их символ равно do, объясненное для умножения на единицу в остроумие, чтобы объяснить запись, умноженную на ноль. Это нулевое редактирование снова с нулем, и мы, чтобы объяснить это, когда умножаем на единицу и, наконец, добавляем, мы расширяем ноль, умножая на единицу, вы получаете 16 закончилось. Мы редактируем с единицей в десятичной системе счисления, вы получаете результат с 19, а в последнем примере — с отключением преобразования. 10 10 10 в Бина B два десятичных числа do, умноженные на пять, с нулевым результатом, дерево с двумя показателями, умноженное на один, с нулевым окончанием, снова отредактируйте, чтобы объяснить это, один умноженный на единицу снова с нулем, вы получите окончательный результат из 32 объявлений с восемью редактировать с 2 42 в десятичной системе
10.Преобразование двоичных чисел в восьмеричные: в этой главе вы узнаете, как преобразовать двоичные числа в автоматические. Это не новость для вас, потому что, когда вы научитесь преобразовывать десятичные итоговые числа, вы будете использовать методы dis. Первый. Пример. У меня есть двоичное число, состоящее из девяти цифр, и я собираюсь преобразовать его из двоичного в восьмизначное.
Это нулевое редактирование снова с нулем, и мы, чтобы объяснить это, когда умножаем на единицу и, наконец, добавляем, мы расширяем ноль, умножая на единицу, вы получаете 16 закончилось. Мы редактируем с единицей в десятичной системе счисления, вы получаете результат с 19, а в последнем примере — с отключением преобразования. 10 10 10 в Бина B два десятичных числа do, умноженные на пять, с нулевым результатом, дерево с двумя показателями, умноженное на один, с нулевым окончанием, снова отредактируйте, чтобы объяснить это, один умноженный на единицу снова с нулем, вы получите окончательный результат из 32 объявлений с восемью редактировать с 2 42 в десятичной системе
10.Преобразование двоичных чисел в восьмеричные: в этой главе вы узнаете, как преобразовать двоичные числа в автоматические. Это не новость для вас, потому что, когда вы научитесь преобразовывать десятичные итоговые числа, вы будете использовать методы dis. Первый. Пример. У меня есть двоичное число, состоящее из девяти цифр, и я собираюсь преобразовать его из двоичного в восьмизначное. Первый шаг — разделить двоичные числа на группы из трех заявок, вы получите 010, что соответствует двум в Octel, 111 ответ семи в Octel и 100 ответ слишком далеко в окто.Последнее число — 174. Следующий пример преобразования 10101 из двоичного в окто-формат. Сделаем отображение. Отъедает число 010, которое отвечает в сумме ах, и 1015 в Octel. Финальный номер 25 в Octel. В последнем примере преобразование отключено, когда 10111 из двоичного кода в октавы делит число 110 на шесть в дяде и 1117 в Octel. Конечный номер 67
11. Преобразование из двоичного в шестнадцатеричное: Мэри для выхода из десятичного преобразования. Это последняя глава о преобразовании двоичных чисел в другую основу. Как и в предыдущей главе, когда я раскрыл двоичное значение для общего числа.Если. Исходное число и F делят число на группы по четыре ставки для этого случая. У меня есть оригинальный номер 01010101100 Теперь я собираюсь сделать эту складку от пердежа. 0101 В конюшне вы видите, что это номер 501, дорогой, снова номер пять, а 1100 — это буква c.
Первый шаг — разделить двоичные числа на группы из трех заявок, вы получите 010, что соответствует двум в Octel, 111 ответ семи в Octel и 100 ответ слишком далеко в окто.Последнее число — 174. Следующий пример преобразования 10101 из двоичного в окто-формат. Сделаем отображение. Отъедает число 010, которое отвечает в сумме ах, и 1015 в Octel. Финальный номер 25 в Octel. В последнем примере преобразование отключено, когда 10111 из двоичного кода в октавы делит число 110 на шесть в дяде и 1117 в Octel. Конечный номер 67
11. Преобразование из двоичного в шестнадцатеричное: Мэри для выхода из десятичного преобразования. Это последняя глава о преобразовании двоичных чисел в другую основу. Как и в предыдущей главе, когда я раскрыл двоичное значение для общего числа.Если. Исходное число и F делят число на группы по четыре ставки для этого случая. У меня есть оригинальный номер 01010101100 Теперь я собираюсь сделать эту складку от пердежа. 0101 В конюшне вы видите, что это номер 501, дорогой, снова номер пять, а 1100 — это буква c. Мое последнее число — 55 c в десятичной системе счисления. Преобразование второго числа с 111101 в десятичное. Я собираюсь снова сделать группы по четыре удара. Я поставил результат «Запреты на воздух левой ноги» во второй группе 0011 Это улица в десятичном формате на выходе и 1101 Это последняя буква D в изгнании.Десятичная дробь Окончательные результаты три d. Второй пример Преобразование выключено. 1010110 Чтобы выйти из десятичного разделения на группы по четыре доли, я получаю 0101 — это пять, а 0110 — это число шесть. Окончательные результаты 56 в десятичной системе счисления
12. Преобразование из восьмеричного в двоичное: Давайте теперь сделаем преобразование из автоматического в двоичное в числах. Чтобы сделать это преобразование, я должен преобразовать каждую цифру Octel в группы из трех двоичных цифр. Первый пример, число до 141 в восьмицилиндре Цифра два в Octel представлена деревом, обращающимся к двоичному значению 010 в Octel 100 и единице в безумном.001 Конечное число 010100001 В двоичном формате.
Мое последнее число — 55 c в десятичной системе счисления. Преобразование второго числа с 111101 в десятичное. Я собираюсь снова сделать группы по четыре удара. Я поставил результат «Запреты на воздух левой ноги» во второй группе 0011 Это улица в десятичном формате на выходе и 1101 Это последняя буква D в изгнании.Десятичная дробь Окончательные результаты три d. Второй пример Преобразование выключено. 1010110 Чтобы выйти из десятичного разделения на группы по четыре доли, я получаю 0101 — это пять, а 0110 — это число шесть. Окончательные результаты 56 в десятичной системе счисления
12. Преобразование из восьмеричного в двоичное: Давайте теперь сделаем преобразование из автоматического в двоичное в числах. Чтобы сделать это преобразование, я должен преобразовать каждую цифру Octel в группы из трех двоичных цифр. Первый пример, число до 141 в восьмицилиндре Цифра два в Octel представлена деревом, обращающимся к двоичному значению 010 в Octel 100 и единице в безумном.001 Конечное число 010100001 В двоичном формате. Второй пример. Преобразование выключено. 123 из восьмиугольника в двоичный. Преобразование первой цифры в единицу до тех пор, пока я не получу 001 Ответ на 2-й визит в Arkle 010. Цифровой выбит 011 Мой последний номер в двоичном формате — 001010011 в двоичном, а в последнем примере преобразование отключено. 315 в двоичном формате First Digital Street. Я получаю 011 2-я цифра — единица. Я получаю 001, а третья цифра — пять. Я получаю хлопья 10 Мой последний номер 011001101
13. Преобразование восьмеричных чисел в десятичные: я собираюсь начать с преобразования восьмеричных чисел.В первых случаях Octel преобразовывает две десятичные дроби в систему Octel в качестве основы и, как и в других базах, каждая цифра как разные белые. Чтобы получить окончательное десятичное число, вы должны сначала умножить каждую цифру значения и соответствующий белый, а в последнем сыне все значения. Пример. Число 34 34 состоит из двух цифр и двух разных весов при единичном и нулевом показателе степени. Делаем умножение.
Второй пример. Преобразование выключено. 123 из восьмиугольника в двоичный. Преобразование первой цифры в единицу до тех пор, пока я не получу 001 Ответ на 2-й визит в Arkle 010. Цифровой выбит 011 Мой последний номер в двоичном формате — 001010011 в двоичном, а в последнем примере преобразование отключено. 315 в двоичном формате First Digital Street. Я получаю 011 2-я цифра — единица. Я получаю 001, а третья цифра — пять. Я получаю хлопья 10 Мой последний номер 011001101
13. Преобразование восьмеричных чисел в десятичные: я собираюсь начать с преобразования восьмеричных чисел.В первых случаях Octel преобразовывает две десятичные дроби в систему Octel в качестве основы и, как и в других базах, каждая цифра как разные белые. Чтобы получить окончательное десятичное число, вы должны сначала умножить каждую цифру значения и соответствующий белый, а в последнем сыне все значения. Пример. Число 34 34 состоит из двух цифр и двух разных весов при единичном и нулевом показателе степени. Делаем умножение. Я получаю три, умноженные на восемь показателей. Один закончился с четырьмя умноженными на восемь показателей. Нулевой конечный результат — это прибавление к 24 неделям, что дает мне результат, равный восьми в десятичной системе счисления.Второй пример Обратитесь достаточно, когда меньше 27 2 десятичных 127 равно единице, умноженной на восемь степеней. Добавим, мы вообще умножаем на восемь показателей. Один закончился с семью умноженными на восемь показателей. Ноль вы получите 64, прибавив 16 к семи. Конечный результат в десятичном формате — 87. При окончательном преобразовании 531 в окто-значении равно пяти, умноженным на восемь степеней для редактирования с деревом, умноженным на восемь степеней. Один при этом мы бы хотели умножить на восемь показателей. Ноль вы получите 320 редактирования с 24 7 с одним.Конечный результат в десятичной системе счисления — 345.
14. Преобразование из восьмеричного в шестнадцатеричное: до двух яиц, преобразование десятичных чисел, чтобы исключить такое преобразование.
Я получаю три, умноженные на восемь показателей. Один закончился с четырьмя умноженными на восемь показателей. Нулевой конечный результат — это прибавление к 24 неделям, что дает мне результат, равный восьми в десятичной системе счисления.Второй пример Обратитесь достаточно, когда меньше 27 2 десятичных 127 равно единице, умноженной на восемь степеней. Добавим, мы вообще умножаем на восемь показателей. Один закончился с семью умноженными на восемь показателей. Ноль вы получите 64, прибавив 16 к семи. Конечный результат в десятичном формате — 87. При окончательном преобразовании 531 в окто-значении равно пяти, умноженным на восемь степеней для редактирования с деревом, умноженным на восемь степеней. Один при этом мы бы хотели умножить на восемь показателей. Ноль вы получите 320 редактирования с 24 7 с одним.Конечный результат в десятичной системе счисления — 345.
14. Преобразование из восьмеричного в шестнадцатеричное: до двух яиц, преобразование десятичных чисел, чтобы исключить такое преобразование.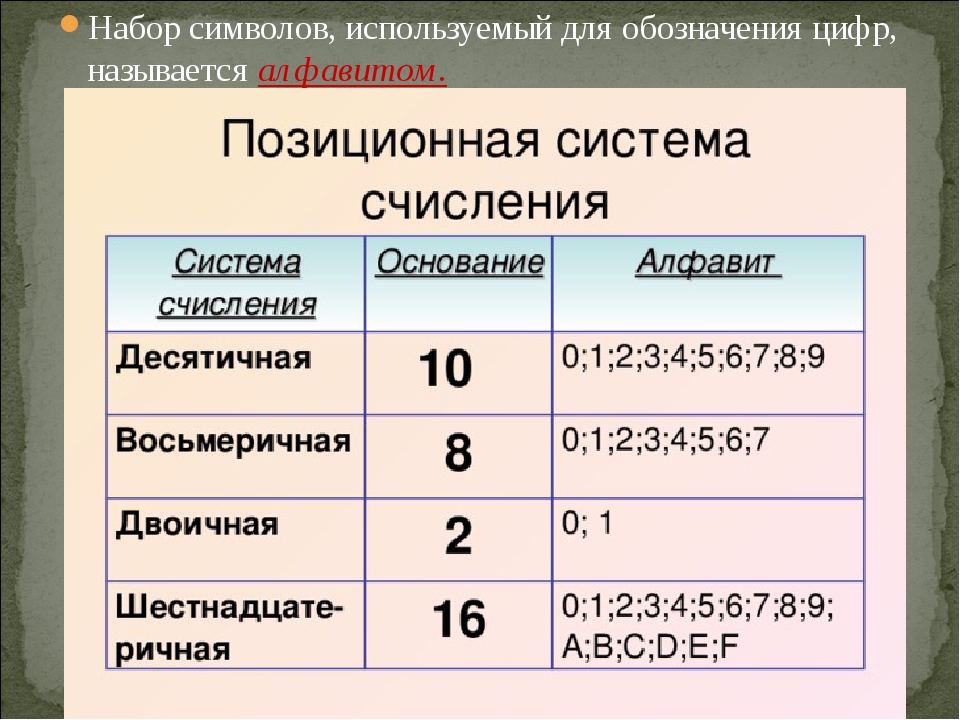 Во-первых, мне нужно преобразовать каждую цифру октела в двоичное число из трех битов. В первом примере у меня есть номер 71 в Octel, и я получаю его от этого числа. Цифра семь составляет 111 в двоичной системе, а цифра — 001 в двоичной системе. Присоединяясь к этому номеру, я собираюсь сделать две группы по четыре удара, и я получу 0011 и 1001. Мое окончательное число, которое дают эти две группы, это улица из этой первой группы и девять из этой второй группы 39 в десятичной системе счисления.Используйте мое последнее преобразование числа во второе число с 104 из Octo, чтобы выйти из десятичного числа, чтобы группа отключилась на три доли. Я получаю 001 000 и 100, присоединяясь к дебатам и составляя две группы дальних битов. Я получаю 0010 «Он все еще на выходе» и 0100 «На выходе». Мое последнее число 24 в десятичной системе счисления. Наконец, мой последний пример. Преобразование 237 из Octo в десятичное преобразование, преобразование первой цифры два равно 010, Дерево в статье — 011, а семь в октябре — 111, что делает группу отключенной для битов.
Во-первых, мне нужно преобразовать каждую цифру октела в двоичное число из трех битов. В первом примере у меня есть номер 71 в Octel, и я получаю его от этого числа. Цифра семь составляет 111 в двоичной системе, а цифра — 001 в двоичной системе. Присоединяясь к этому номеру, я собираюсь сделать две группы по четыре удара, и я получу 0011 и 1001. Мое окончательное число, которое дают эти две группы, это улица из этой первой группы и девять из этой второй группы 39 в десятичной системе счисления.Используйте мое последнее преобразование числа во второе число с 104 из Octo, чтобы выйти из десятичного числа, чтобы группа отключилась на три доли. Я получаю 001 000 и 100, присоединяясь к дебатам и составляя две группы дальних битов. Я получаю 0010 «Он все еще на выходе» и 0100 «На выходе». Мое последнее число 24 в десятичной системе счисления. Наконец, мой последний пример. Преобразование 237 из Octo в десятичное преобразование, преобразование первой цифры два равно 010, Дерево в статье — 011, а семь в октябре — 111, что делает группу отключенной для битов. Я получаю 1001 «Это номер девять» на выходе и 1111 «F» в яйцах.Конечное число — девять F в десятичной системе счисления.
15. Преобразование из шестнадцатеричного в двоичное: после преобразования из десятичного числа в два десятичных числа я собираюсь выполнить преобразование в двоичные числа. Чтобы выполнить такое преобразование, я должен преобразовать каждую десятичную цифру выхода в группы из четырех двоичных цифр. Как вы можете видеть в первом примере, номер два I в десятичной системе NZ равен 0010 от цифры до и 1010 от цифры a. Присоединение к двум группам. Я получаю свой финал по их номеру 00101010, сейчас это последний номер.Второй пример. Преобразование 45 в десятичной дроби на выходе для Байдена Мэри, делающего группы из четырех долей. Я получаю 0100 из цифры для и 0101 из цифры пять. Присоединяясь к двум группам, я получаю 01000101 и в последнем примере конверсия отключена. 34 B из яиц, доступных для двоичного кода. Сейчас если. Три группы из четырех битов 0011 из дерева цифр в X: десятичная дробь, 0100 из цифры для и 1011 из цифр в выходной десятичной системе.
Я получаю 1001 «Это номер девять» на выходе и 1111 «F» в яйцах.Конечное число — девять F в десятичной системе счисления.
15. Преобразование из шестнадцатеричного в двоичное: после преобразования из десятичного числа в два десятичных числа я собираюсь выполнить преобразование в двоичные числа. Чтобы выполнить такое преобразование, я должен преобразовать каждую десятичную цифру выхода в группы из четырех двоичных цифр. Как вы можете видеть в первом примере, номер два I в десятичной системе NZ равен 0010 от цифры до и 1010 от цифры a. Присоединение к двум группам. Я получаю свой финал по их номеру 00101010, сейчас это последний номер.Второй пример. Преобразование 45 в десятичной дроби на выходе для Байдена Мэри, делающего группы из четырех долей. Я получаю 0100 из цифры для и 0101 из цифры пять. Присоединяясь к двум группам, я получаю 01000101 и в последнем примере конверсия отключена. 34 B из яиц, доступных для двоичного кода. Сейчас если. Три группы из четырех битов 0011 из дерева цифр в X: десятичная дробь, 0100 из цифры для и 1011 из цифр в выходной десятичной системе. Мое последнее двоичное число — 0011 01001011
16. Преобразование из шестнадцатеричного в десятичное: выход из преобразования десятичных чисел.Сначала я расскажу о преобразовании выходных десятичных чисел. Два десятичных числа соответствуют системе символов Bice 16 и, как и другие, основывают каждую цифру как разные белые. Чтобы получить окончательное десятичное число, я сначала делаю умножение каждого значения Digit и соответствующего белого, а в последнем Sam All — все значения. Пример. Число 23 в выходном десятичном формате, это число как две цифры и два разных белого цвета. 16 единиц степени и 16 единиц степени равны нулю, делающие умножение. Я получаю два, умноженные на 16 показателей, когда добавляю поток, умноженный на 16 показателей.Ноль равен нулю 32, заканчивающемуся улицей 35. В десятичной дроби мое последнее число, что делает второе преобразование Govert F единиц в выходное десятичное число два. Десятичная дробь делает тусклое умножение 15 умноженным на 16 степеней. Один закончился с одним, умноженным на 16 показателей.
Мое последнее двоичное число — 0011 01001011
16. Преобразование из шестнадцатеричного в десятичное: выход из преобразования десятичных чисел.Сначала я расскажу о преобразовании выходных десятичных чисел. Два десятичных числа соответствуют системе символов Bice 16 и, как и другие, основывают каждую цифру как разные белые. Чтобы получить окончательное десятичное число, я сначала делаю умножение каждого значения Digit и соответствующего белого, а в последнем Sam All — все значения. Пример. Число 23 в выходном десятичном формате, это число как две цифры и два разных белого цвета. 16 единиц степени и 16 единиц степени равны нулю, делающие умножение. Я получаю два, умноженные на 16 показателей, когда добавляю поток, умноженный на 16 показателей.Ноль равен нулю 32, заканчивающемуся улицей 35. В десятичной дроби мое последнее число, что делает второе преобразование Govert F единиц в выходное десятичное число два. Десятичная дробь делает тусклое умножение 15 умноженным на 16 степеней. Один закончился с одним, умноженным на 16 показателей. Нуль. Мой окончательный результат — прибавление 240 на одну ногу. 141 это мой итоговый результат на их цив. Наконец, преобразование из дерева e из десятичного числа в два десятичного числа, производящего умножение. Я получаю 14, умноженные на 16 показателей, а также добавляем Дэна, умноженного на 16.Объясни это. Один закончился деревом, умноженным на 16 показателей. Нуль. Мой окончательный результат — 3747 в десятичной системе счисления.
17. Преобразование из шестнадцатеричного в восьмеричное: выход из десятичного числа в преобразование числа. Dutra assortment Выход из десятичного числа два Натуральное число. Я должен разбить его на два шага. Во-первых, сжатие от точного символа к двоичному числу с использованием групп из четырех битов, а на втором этапе посредством сортировки двоичное число превращается в пиломатериал, используя сначала группы из трех ударов в двоичное число. Пример.Число шесть в десятичной форме выхода. Разделив число на группы по четыре бита, я получу 01 10 из цифры шесть и 1010 из цифры.
Нуль. Мой окончательный результат — прибавление 240 на одну ногу. 141 это мой итоговый результат на их цив. Наконец, преобразование из дерева e из десятичного числа в два десятичного числа, производящего умножение. Я получаю 14, умноженные на 16 показателей, а также добавляем Дэна, умноженного на 16.Объясни это. Один закончился деревом, умноженным на 16 показателей. Нуль. Мой окончательный результат — 3747 в десятичной системе счисления.
17. Преобразование из шестнадцатеричного в восьмеричное: выход из десятичного числа в преобразование числа. Dutra assortment Выход из десятичного числа два Натуральное число. Я должен разбить его на два шага. Во-первых, сжатие от точного символа к двоичному числу с использованием групп из четырех битов, а на втором этапе посредством сортировки двоичное число превращается в пиломатериал, используя сначала группы из трех ударов в двоичное число. Пример.Число шесть в десятичной форме выхода. Разделив число на группы по четыре бита, я получу 01 10 из цифры шесть и 1010 из цифры. Теперь я собираюсь разделить провидческое число на группы по три доли, и я получу 001 101 010, что соответствует действительному числу. 152 второй пример. Достаточно смелости. Три A от X, A от десятичной дроби до восьмеричного делают две группы по четыре доли. Я получаю 0011 из цифрового дерева и 1010 из цифры, составляющей две группы из трех долей. Я получаю 111, что соответствует семи в окто, и 010, что соответствует двум в автоматическом режиме.Это мой последний номер. Во избежание, например, преобразование из дерева будет из десятичного числа на выходе в AKEL, что сделает три группы по четыре доли. Я получаю 0011 из цифрового дерева 0001 из цифры один и один зоопарк 11 из цифры, делающей группу из трех битов, я получаю 001100 011011, и мое окончательное число 1433 в ужасе.
18. Преобразование десятичного числа в двоичное с помощью дробных чисел: Здравствуйте. В следующих видеороликах я покажу вам, как выполнять преобразование чисел с дробными частями. Во-первых, я собираюсь начать с преобразования десятичных чисел в двоичные.
Теперь я собираюсь разделить провидческое число на группы по три доли, и я получу 001 101 010, что соответствует действительному числу. 152 второй пример. Достаточно смелости. Три A от X, A от десятичной дроби до восьмеричного делают две группы по четыре доли. Я получаю 0011 из цифрового дерева и 1010 из цифры, составляющей две группы из трех долей. Я получаю 111, что соответствует семи в окто, и 010, что соответствует двум в автоматическом режиме.Это мой последний номер. Во избежание, например, преобразование из дерева будет из десятичного числа на выходе в AKEL, что сделает три группы по четыре доли. Я получаю 0011 из цифрового дерева 0001 из цифры один и один зоопарк 11 из цифры, делающей группу из трех битов, я получаю 001100 011011, и мое окончательное число 1433 в ужасе.
18. Преобразование десятичного числа в двоичное с помощью дробных чисел: Здравствуйте. В следующих видеороликах я покажу вам, как выполнять преобразование чисел с дробными частями. Во-первых, я собираюсь начать с преобразования десятичных чисел в двоичные. Вы знаете, что десятичные числа могут состоять из двух частей, а в части учителя и дробной части, которая может быть разделена запятой, вы можете видеть, что в этом примере у вас есть целая часть для 57 и дифракция всей части 375, преобразующая целую часть, которую вы знаете, из в предыдущих главах вам нужно разделить число на два. И с напоминанием у вас есть результат Дерри преобразования из десятичного числа в двоичный, начиная с этого первого примера и преобразования из Inti jher. Барт, я разделю на два.Я получаю свои предупреждения и напоминание в следующем разделе. Я воспользуюсь предыдущим предупреждением и получу снова. И новое предупреждение, и новое напоминание. Эти изменения прекращаются, когда я получаю предупреждение о нулевом значении, а остаток даст мне результат в двоичном формате внутренних частей с числом de final, равным 111 001001. Чтобы получить мои дробные части, я должен умножить дробную часть на два. Я получаю этот результат, и в следующем его соотношении я буду использовать дробную часть умножения и снова умножу на два, и снова получу новый результат — это умножение на два.
Вы знаете, что десятичные числа могут состоять из двух частей, а в части учителя и дробной части, которая может быть разделена запятой, вы можете видеть, что в этом примере у вас есть целая часть для 57 и дифракция всей части 375, преобразующая целую часть, которую вы знаете, из в предыдущих главах вам нужно разделить число на два. И с напоминанием у вас есть результат Дерри преобразования из десятичного числа в двоичный, начиная с этого первого примера и преобразования из Inti jher. Барт, я разделю на два.Я получаю свои предупреждения и напоминание в следующем разделе. Я воспользуюсь предыдущим предупреждением и получу снова. И новое предупреждение, и новое напоминание. Эти изменения прекращаются, когда я получаю предупреждение о нулевом значении, а остаток даст мне результат в двоичном формате внутренних частей с числом de final, равным 111 001001. Чтобы получить мои дробные части, я должен умножить дробную часть на два. Я получаю этот результат, и в следующем его соотношении я буду использовать дробную часть умножения и снова умножу на два, и снова получу новый результат — это умножение на два. Что ж, остановись, когда я получу ноль при умножении на два, или я получу периодическое число. Результат в двоичном формате дается входящей частью замаскированного умножения 0110, которую вы можете видеть в последней строке. Таким образом, результат дробной части — это четыре бита 0110, а конечный результат — внутренний парк. 111 001001 кома и дробная часть 0110 Теперь сделаем еще один пример, преобразовав это число с помощью части намерения 351 и дробной части 59375. Я начну с части в учителе, поэтому я сделаю деление на два и получу частное и остаток в следующем делении.Я воспользуюсь предыдущим предостережением и снова получу новую смесь и новое напоминание. Это прекратится, когда я получу ноль Indyk Ocean, а остаток даст мне результат в двоичном формате. Так что моя в Тишере часть равна 101011 одна одна. Теперь сделаем преобразование дробной части. Умножу на два и получу такой результат. И в следующей роли я буду использовать дифракцию всей части, умножу ее на два и получу, и вы снова получите результат.
Что ж, остановись, когда я получу ноль при умножении на два, или я получу периодическое число. Результат в двоичном формате дается входящей частью замаскированного умножения 0110, которую вы можете видеть в последней строке. Таким образом, результат дробной части — это четыре бита 0110, а конечный результат — внутренний парк. 111 001001 кома и дробная часть 0110 Теперь сделаем еще один пример, преобразовав это число с помощью части намерения 351 и дробной части 59375. Я начну с части в учителе, поэтому я сделаю деление на два и получу частное и остаток в следующем делении.Я воспользуюсь предыдущим предостережением и снова получу новую смесь и новое напоминание. Это прекратится, когда я получу ноль Indyk Ocean, а остаток даст мне результат в двоичном формате. Так что моя в Тишере часть равна 101011 одна одна. Теперь сделаем преобразование дробной части. Умножу на два и получу такой результат. И в следующей роли я буду использовать дифракцию всей части, умножу ее на два и получу, и вы снова получите результат. Я остановлю эту ситуацию, когда у меня будет ноль или периодическое число.Внутренняя часть умножения даст мне окончательный результат в двоичном формате. 10011 ноль — мои окончательные результаты. И внутренняя часть с дробной частью — это 101 011111 Goldman, а моя дробная часть — 10011. И в следующем и последнем примере преобразования из десятичной системы в двоичную Выключите число 71, запятую 10, начиная с части Тишера при делении на два. Я получаю свой Коциан и Напоминание, и я использую вопрос для следующего деления на два и получу ядерный океан и напоминание. Это прекратится, когда я получу ноль в предупреждении, а остаток даст мне окончательный результат в двоичном формате 1000 11, когда и, наконец, дифракция ALS Part zero Goma 10.Множественная жизнь, чтобы получить этот результат, и я остановлю умножение, когда получу ноль или периодическое число. В этом случае я получу не ноль, а периодическое число. Вы можете видеть, что во второй строке и в правиле less у вас тот же результат.
Я остановлю эту ситуацию, когда у меня будет ноль или периодическое число.Внутренняя часть умножения даст мне окончательный результат в двоичном формате. 10011 ноль — мои окончательные результаты. И внутренняя часть с дробной частью — это 101 011111 Goldman, а моя дробная часть — 10011. И в следующем и последнем примере преобразования из десятичной системы в двоичную Выключите число 71, запятую 10, начиная с части Тишера при делении на два. Я получаю свой Коциан и Напоминание, и я использую вопрос для следующего деления на два и получу ядерный океан и напоминание. Это прекратится, когда я получу ноль в предупреждении, а остаток даст мне окончательный результат в двоичном формате 1000 11, когда и, наконец, дифракция ALS Part zero Goma 10.Множественная жизнь, чтобы получить этот результат, и я остановлю умножение, когда получу ноль или периодическое число. В этом случае я получу не ноль, а периодическое число. Вы можете видеть, что во второй строке и в правиле less у вас тот же результат.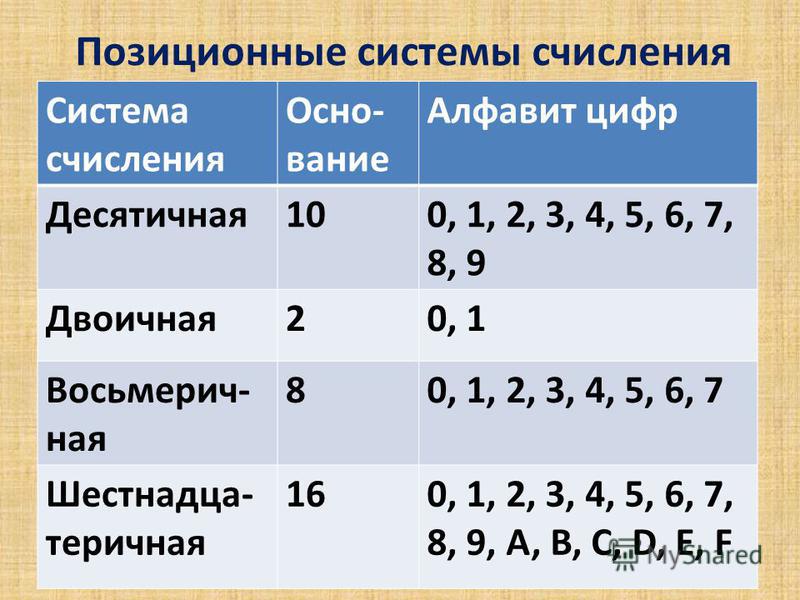 Итак, этот 0011 повторится снова. Начиная с этого столбца с нуля, это будет повторяться снова 0011 Итак, мое последнее число, дробная часть — 00011, и do для последних битов повторится снова, приятель. С этической точки зрения, окончательное число — это часть напитка Фишера с дробной частью.Часть учителя дана 1000111 комой, а дробная часть — 00 01 Когда с этими четырьмя заключительными ударами повторно
19. Преобразование двоичного числа в десятичное с использованием дробных чисел: преобразование двоичного числа в десятичное. На первых уроках вы научитесь преобразовывать числа учителя из двоичных в десятичные. В этой главе вы узнаете, как преобразовать числа с помощью в дробную часть из двоичного числа с двумя десятичными. В чем основная разница между этим? Эти две разные части числа, целая часть? Мы будем использовать положительные показатели, а дробная часть — отрицательные показатели.Если вы видите в этой таблице значения выключены, отрицательные показатели с by stew дадут вам значения больше нуля и меньше, чем один.
Итак, этот 0011 повторится снова. Начиная с этого столбца с нуля, это будет повторяться снова 0011 Итак, мое последнее число, дробная часть — 00011, и do для последних битов повторится снова, приятель. С этической точки зрения, окончательное число — это часть напитка Фишера с дробной частью.Часть учителя дана 1000111 комой, а дробная часть — 00 01 Когда с этими четырьмя заключительными ударами повторно
19. Преобразование двоичного числа в десятичное с использованием дробных чисел: преобразование двоичного числа в десятичное. На первых уроках вы научитесь преобразовывать числа учителя из двоичных в десятичные. В этой главе вы узнаете, как преобразовать числа с помощью в дробную часть из двоичного числа с двумя десятичными. В чем основная разница между этим? Эти две разные части числа, целая часть? Мы будем использовать положительные показатели, а дробная часть — отрицательные показатели.Если вы видите в этой таблице значения выключены, отрицательные показатели с by stew дадут вам значения больше нуля и меньше, чем один. Первый пример. Я собираюсь преобразовать это число в Они простые, из двоичного в десятичный, и в конце вы получите эти результаты, начиная с анти-jher части с положительными показателями. Если вы не забыли преобразовать из двоичного кода в десятичный, вам нужно умножить каждую цифру значения на соответствующий белый, с основанием и положительными показателями, начиная с и собираясь получить единицу, умноженную на два показателя.Ноль закончился умножением на единицу для объяснения. Вход закончился с умножением одного на два показателя. Шесть закончились тем, что один умножили на, чтобы объяснить, и семь добавили, а один умножили на два показателя СПИДа. Конечный результат, как вы и ожидали, будет 457 в десятичной системе с преобразованием дробной части числа. Другое дело, что у вас есть отрицательные показатели, и вы сделаете расчет, не умноженный на два показателя минус два, один редактор умножил на два показателя минус поток. Конечный результат — 0.355 и ответ на эту дробную часть второго примера преобразования.
Первый пример. Я собираюсь преобразовать это число в Они простые, из двоичного в десятичный, и в конце вы получите эти результаты, начиная с анти-jher части с положительными показателями. Если вы не забыли преобразовать из двоичного кода в десятичный, вам нужно умножить каждую цифру значения на соответствующий белый, с основанием и положительными показателями, начиная с и собираясь получить единицу, умноженную на два показателя.Ноль закончился умножением на единицу для объяснения. Вход закончился с умножением одного на два показателя. Шесть закончились тем, что один умножили на, чтобы объяснить, и семь добавили, а один умножили на два показателя СПИДа. Конечный результат, как вы и ожидали, будет 457 в десятичной системе с преобразованием дробной части числа. Другое дело, что у вас есть отрицательные показатели, и вы сделаете расчет, не умноженный на два показателя минус два, один редактор умножил на два показателя минус поток. Конечный результат — 0.355 и ответ на эту дробную часть второго примера преобразования. Разделите каждое число 10 1110.11011 на два десятичных числа из двоичного числа в десятичное, начиная с части Индонезии. Что 01110 равно двум показателям пяти, умноженным на один редактор. Это слишком объяснено для умножения на ноль, добавленного к дереву двух показателей, умноженного на одно редактирование, чтобы объяснить и умножить на. Один закончился двумя показателями, один умножился на один, и, наконец, Эдвардс, два показателя степени, умножили ноль на ноль. Мой окончательный результат такой же: 32 с восьмью, с четырьмя с двумя 46 в их символе.Дробные части равняются 11011. И при вычислении с отрицательными показателями у меня будет два показателя минус при умножении на единицу, добавленных с двумя показателями минус два, умноженными на одну голову, с двумя показателями минус улица, умноженными на ноль, в конце будут два показателя минус четыре, умноженные на единицу. закончился двумя показателями минус пять, умноженными на один, и это даст 0,8437 пять окончательных результатов 46,84375 в их символе.
Разделите каждое число 10 1110.11011 на два десятичных числа из двоичного числа в десятичное, начиная с части Индонезии. Что 01110 равно двум показателям пяти, умноженным на один редактор. Это слишком объяснено для умножения на ноль, добавленного к дереву двух показателей, умноженного на одно редактирование, чтобы объяснить и умножить на. Один закончился двумя показателями, один умножился на один, и, наконец, Эдвардс, два показателя степени, умножили ноль на ноль. Мой окончательный результат такой же: 32 с восьмью, с четырьмя с двумя 46 в их символе.Дробные части равняются 11011. И при вычислении с отрицательными показателями у меня будет два показателя минус при умножении на единицу, добавленных с двумя показателями минус два, умноженными на одну голову, с двумя показателями минус улица, умноженными на ноль, в конце будут два показателя минус четыре, умноженные на единицу. закончился двумя показателями минус пять, умноженными на один, и это даст 0,8437 пять окончательных результатов 46,84375 в их символе. 20. Преобразование десятичного числа в другое основание с использованием дробных чисел: преобразование десятичного числа в другое основание.Этот вид преобразования очень похож, как и преобразование из десятичного числа в двоичное. Это мой первый пример числа от 78 до 50 в десятичной дроби. И если я хочу преобразовать это число в другие части Tischer базовой темы, я должен разделить число на основание, чтобы остаток от деления. Дайте мне окончательный результат внутренней части в новом Bice, сделав этот практический пример первым преобразованием части учителя в число покупок, верно? Мне нужно разделить число на восемь.Я получаю предупреждение и напоминание, когда количество предупреждений равно нулю. Напоминание. Дайте мне окончательный результат для целой части. 78 в десятичной системе счисления равно 116 в восьмеричной системе счисления, используя устройства 16, преобразующие десятичную дробь в 16. Целая часть. Я сделал деление на 16. Я получаю частное и напоминание, когда я получаю ноль в океанах, Напоминание Дайте мне окончательный результат.
20. Преобразование десятичного числа в другое основание с использованием дробных чисел: преобразование десятичного числа в другое основание.Этот вид преобразования очень похож, как и преобразование из десятичного числа в двоичное. Это мой первый пример числа от 78 до 50 в десятичной дроби. И если я хочу преобразовать это число в другие части Tischer базовой темы, я должен разделить число на основание, чтобы остаток от деления. Дайте мне окончательный результат внутренней части в новом Bice, сделав этот практический пример первым преобразованием части учителя в число покупок, верно? Мне нужно разделить число на восемь.Я получаю предупреждение и напоминание, когда количество предупреждений равно нулю. Напоминание. Дайте мне окончательный результат для целой части. 78 в десятичной системе счисления равно 116 в восьмеричной системе счисления, используя устройства 16, преобразующие десятичную дробь в 16. Целая часть. Я сделал деление на 16. Я получаю частное и напоминание, когда я получаю ноль в океанах, Напоминание Дайте мне окончательный результат. 70 18 Decimal равно четырем e в Bice 16 для преобразования дифракционной части ALS Сначала мне нужно умножить Defection части LPA на базовое значение, которое я хочу взять дробную часть в качестве значения, чтобы умножить на следующем шаге дробные части, которые я получить столбец десерт, который я буду использовать в следующем умножении и остановлюсь, когда получу ноль или периодическое число.Окончательный результат преобразования дает этот Форт-Коллинз. Тизерная часть замаскированного умножения для основного права на преобразование из подставки, чтобы купить его от нулевой комы до 50 в десятичной системе, равняется нулю комы до нуля в Bice, верно? И конечный результат — это целая часть и дробная часть u F 116, равная нулю в окто, как окончательные результаты для выходного десятичного преобразования, я должен умножить дифракцию на 16. И когда я получаю ноль или периодическое число в умножении , часть anti jher, дайте мне окончательный результат.Нулевая кома до 50 в десятичной системе равна нулю комы для нуля в тисках 16, а конечный результат — внутренняя часть с дробной частью, целой частью для E и дробной частью для нуля.
70 18 Decimal равно четырем e в Bice 16 для преобразования дифракционной части ALS Сначала мне нужно умножить Defection части LPA на базовое значение, которое я хочу взять дробную часть в качестве значения, чтобы умножить на следующем шаге дробные части, которые я получить столбец десерт, который я буду использовать в следующем умножении и остановлюсь, когда получу ноль или периодическое число.Окончательный результат преобразования дает этот Форт-Коллинз. Тизерная часть замаскированного умножения для основного права на преобразование из подставки, чтобы купить его от нулевой комы до 50 в десятичной системе, равняется нулю комы до нуля в Bice, верно? И конечный результат — это целая часть и дробная часть u F 116, равная нулю в окто, как окончательные результаты для выходного десятичного преобразования, я должен умножить дифракцию на 16. И когда я получаю ноль или периодическое число в умножении , часть anti jher, дайте мне окончательный результат.Нулевая кома до 50 в десятичной системе равна нулю комы для нуля в тисках 16, а конечный результат — внутренняя часть с дробной частью, целой частью для E и дробной частью для нуля.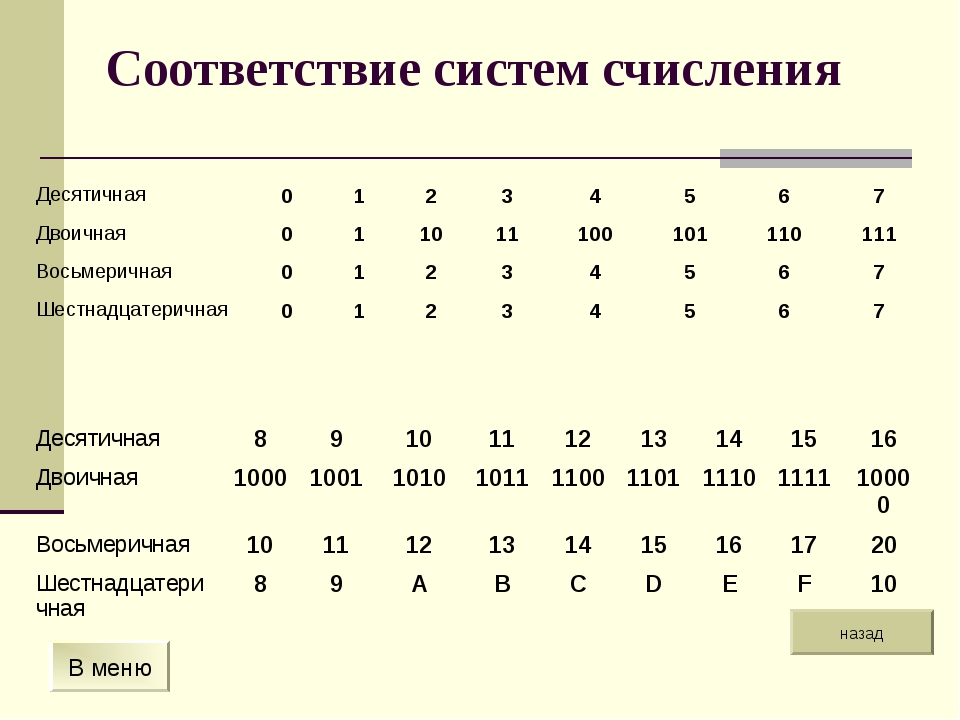 Если я хочу скрыться по этому простому номеру. Две другие покупки отличаются от восьми и 16. Во-первых, внутренние части в этом примере я хочу покрыть, чтобы купить 20, и я собираюсь разделить на 20, чтобы получить индийские части jher. Я получаю частное в напоминании, и я остановлюсь, когда у меня будет ноль на Kocian. Напоминание.Дай мне окончательный результат. В устройстве 20 у вас есть 20 различных значений для представления. Цифра в смерти покупает числа от 0 до 9, а буквы от A до G 876 в их символе равны двум деревам G в Bice. 20. Дробная часть. Мне нужно умножить на 20, и когда я получу ноль или замаскированное периодическое число, ноль. Эта часть умножения в учителе даст мне окончательные результаты в Bice 20 zero Coma. Восемь в базе 10 равняется нулю комы G в Bice 20. Таким образом, окончательный результат состоит в том, чтобы обработать G для внутренней коры и G для дробной части.
21.Преобразование двоичного кода в другой базис с использованием дробных чисел: преобразование двоичного в другой базис.
Если я хочу скрыться по этому простому номеру. Две другие покупки отличаются от восьми и 16. Во-первых, внутренние части в этом примере я хочу покрыть, чтобы купить 20, и я собираюсь разделить на 20, чтобы получить индийские части jher. Я получаю частное в напоминании, и я остановлюсь, когда у меня будет ноль на Kocian. Напоминание.Дай мне окончательный результат. В устройстве 20 у вас есть 20 различных значений для представления. Цифра в смерти покупает числа от 0 до 9, а буквы от A до G 876 в их символе равны двум деревам G в Bice. 20. Дробная часть. Мне нужно умножить на 20, и когда я получу ноль или замаскированное периодическое число, ноль. Эта часть умножения в учителе даст мне окончательные результаты в Bice 20 zero Coma. Восемь в базе 10 равняется нулю комы G в Bice 20. Таким образом, окончательный результат состоит в том, чтобы обработать G для внутренней коры и G для дробной части.
21.Преобразование двоичного кода в другой базис с использованием дробных чисел: преобразование двоичного в другой базис. Вы узнаете из предыдущего видео о долге. Чтобы выполнить преобразование из двоичного числа два Octel или десятичного числа выхода, вы должны разделить дальновидное число на группы по три доли, чтобы получить пластичную цифру. Корреспондент Octel Digit и Split в четыре раза обыгрывает Divine по каждому номеру, чтобы попасть к корреспонденту Exas Immel. Замаскированные цифры. Я собираюсь показать вам, как преобразовать число 11011 в кому. 011 В двоичном коде Octel я могу отображать питание группами по три доли, и я получаю 011011011 Эти три группы из трех долей совпадают, если для одного и того же значения одна и та же цифра.Это дерево ручья, дерево Коулмана. Это число в восьмеричном формате, которое нужно покрыть, чтобы выйти из десятичной складки льда. Это число в группах дальних ударов, и я получаю 0001 Соответствует цифре 110. 11 ответом на это должен быть ответ 0110 на цифру шесть. Мое последнее число — один Б. Гольдман, шестерка в десятичном разряде на выходе, и это еще один пример.
Вы узнаете из предыдущего видео о долге. Чтобы выполнить преобразование из двоичного числа два Octel или десятичного числа выхода, вы должны разделить дальновидное число на группы по три доли, чтобы получить пластичную цифру. Корреспондент Octel Digit и Split в четыре раза обыгрывает Divine по каждому номеру, чтобы попасть к корреспонденту Exas Immel. Замаскированные цифры. Я собираюсь показать вам, как преобразовать число 11011 в кому. 011 В двоичном коде Octel я могу отображать питание группами по три доли, и я получаю 011011011 Эти три группы из трех долей совпадают, если для одного и того же значения одна и та же цифра.Это дерево ручья, дерево Коулмана. Это число в восьмеричном формате, которое нужно покрыть, чтобы выйти из десятичной складки льда. Это число в группах дальних ударов, и я получаю 0001 Соответствует цифре 110. 11 ответом на это должен быть ответ 0110 на цифру шесть. Мое последнее число — один Б. Гольдман, шестерка в десятичном разряде на выходе, и это еще один пример. Число 1110 Coma 1111 Делая это, нумерация групп разделена на три доли. Чтобы получить свой номер Octel, я получаю 001 Want go 0 one go one 100 1674 в окто преобразовании в десятичную дробь на выходе разделить число на группы по четыре ставки 1110 Goma 1111 Две цифры — это дробная часть.Если мое последнее число — E, если теперь, если я хочу преобразовать два других, используя разные степени двойки, то преобразование не будет прямым. Во-первых, мне нужно преобразовать из двоичного в десятичное, а на втором этапе мне нужно преобразовать из десятичного в устройство, которое я хочу охватить на втором этапе, из десятичного в устройство, которое я хочу, я использую метод деления, чтобы получить внутреннюю часть Часть В окончательной части Bice и дробной части я использовал умножение. Я должен услышать диаграмму, и у меня есть двоичное число, исходное двоичное число сначала преобразовано в десятичное.Затем у меня есть десятичное число, и в этом примере я собираюсь преобразовать его в устройство.
Число 1110 Coma 1111 Делая это, нумерация групп разделена на три доли. Чтобы получить свой номер Octel, я получаю 001 Want go 0 one go one 100 1674 в окто преобразовании в десятичную дробь на выходе разделить число на группы по четыре ставки 1110 Goma 1111 Две цифры — это дробная часть.Если мое последнее число — E, если теперь, если я хочу преобразовать два других, используя разные степени двойки, то преобразование не будет прямым. Во-первых, мне нужно преобразовать из двоичного в десятичное, а на втором этапе мне нужно преобразовать из десятичного в устройство, которое я хочу охватить на втором этапе, из десятичного в устройство, которое я хочу, я использую метод деления, чтобы получить внутреннюю часть Часть В окончательной части Bice и дробной части я использовал умножение. Я должен услышать диаграмму, и у меня есть двоичное число, исходное двоичное число сначала преобразовано в десятичное.Затем у меня есть десятичное число, и в этом примере я собираюсь преобразовать его в устройство. Семь, чтобы получить число к семи. Внутреннюю часть разделю на семь и напоминание. Дайте мне окончательный результат на семь и отклонение друг от друга, я умножу на семь и внутреннюю часть умножения. Дайте мне дробную часть результатов в базе седьмой, приведя пример. Конверсия пошла 101 Goma 0112 на семь. Сначала преобразование из двоичного в десятичное. Итак, я умножу каждую цифру на соответствующую белую, основание f на единицу, умноженную на два показателя степени, кроме единицы, умноженной на два показателя степени, также закончилось единицей, умноженной на два показателя степени.Ноль, я уверен, в десятичной форме для дифракционных деталей внутренних частей ALS — это единица, умноженная на два показателя степени минус два, заканчивающаяся на единицу, умноженную на, чтобы объяснить, что в моей отрасли это дает мне число нулевая запятая 375 в десятичной системе. Итак, мое последнее число в символе — одно дерево. Целая часть запятой 375 в десятичной системе. Это первый шаг от преобразования, который теперь выполняет второй шаг, преобразование десятичного числа в семь I f в Дубае.
Семь, чтобы получить число к семи. Внутреннюю часть разделю на семь и напоминание. Дайте мне окончательный результат на семь и отклонение друг от друга, я умножу на семь и внутреннюю часть умножения. Дайте мне дробную часть результатов в базе седьмой, приведя пример. Конверсия пошла 101 Goma 0112 на семь. Сначала преобразование из двоичного в десятичное. Итак, я умножу каждую цифру на соответствующую белую, основание f на единицу, умноженную на два показателя степени, кроме единицы, умноженной на два показателя степени, также закончилось единицей, умноженной на два показателя степени.Ноль, я уверен, в десятичной форме для дифракционных деталей внутренних частей ALS — это единица, умноженная на два показателя степени минус два, заканчивающаяся на единицу, умноженную на, чтобы объяснить, что в моей отрасли это дает мне число нулевая запятая 375 в десятичной системе. Итак, мое последнее число в символе — одно дерево. Целая часть запятой 375 в десятичной системе. Это первый шаг от преобразования, который теперь выполняет второй шаг, преобразование десятичного числа в семь I f в Дубае. Вот номер символа, теперь я собираюсь преобразовать его в азиатскую часть, используя методы деления.Я сделаю деление на семь. Я получаю частное и напоминание. Когда значение Coche int равно нулю, напоминание даст мне окончательный результат в базе седьмой. Таким образом, результат равен 16 по основанию седьмого. Чтобы получить дробную часть, я реально умножаю отклонение части LPA от десятичного числа на семь. И когда я получаю ноль при умножении на периодическое число, внутренняя часть умножения дает мне замаскированный окончательный результат. Вы можете видеть это в первом ряду, и в этом аэро у вас те же результаты.Итак, это периодический номер. Эти числа будут повторяться снова, так что окончательное число к семи равно нулю комы. 2424 Периодические итоговые результаты: 16 для учителей и 2 для периодических. Для дробных частей
22. Бинарное дополнение: Мэри Дополнение. Сложение Divine Eri очень похоже на сложение десятичных чисел, но вместо вас значения Stan представляют одну цифру, используемую для значений, представляющих одну цифру.
Вот номер символа, теперь я собираюсь преобразовать его в азиатскую часть, используя методы деления.Я сделаю деление на семь. Я получаю частное и напоминание. Когда значение Coche int равно нулю, напоминание даст мне окончательный результат в базе седьмой. Таким образом, результат равен 16 по основанию седьмого. Чтобы получить дробную часть, я реально умножаю отклонение части LPA от десятичного числа на семь. И когда я получаю ноль при умножении на периодическое число, внутренняя часть умножения дает мне замаскированный окончательный результат. Вы можете видеть это в первом ряду, и в этом аэро у вас те же результаты.Итак, это периодический номер. Эти числа будут повторяться снова, так что окончательное число к семи равно нулю комы. 2424 Периодические итоговые результаты: 16 для учителей и 2 для периодических. Для дробных частей
22. Бинарное дополнение: Мэри Дополнение. Сложение Divine Eri очень похоже на сложение десятичных чисел, но вместо вас значения Stan представляют одну цифру, используемую для значений, представляющих одну цифру. Так что со значениями возможны разные комбинации. Отображение отключило возможные комбинации, если сумма ударов 10 и 20 равна нулю и нести ее.Ноль между — это ноль, а ударьте два — это один какой-то один и несите его. Нулевой удар один равен единице, а второй — нулю. Сумма равна единице, перенос с нулем. И, наконец, если первый удар равен единице, а второй — один, какой-то ноль, и неси его. Если ты не понимаешь, как я это делаю, Сэм, тебе будет сложно. Вы можете Шторм преобразовать двоичного Сэма в десятичный Сэм, и вы увидите окончательные результаты Божественного Эри в этой меньшей строке, которую вы получите в двоичном блюзе. Единица в двоичном формате равна единице в десятичной системе счисления плюс один кишечный. Число один в двоичном формате равно единице в десятичном, так что я могу сделать это изменение с двоичного на десятичное в десятичном значении плюс один, промышленный уровень равен интересам кишечника.Снова преобразование в двоичное значение равно 10 в двоичном формате. Этот ноль — тот же результат, а этот несет немного.
Так что со значениями возможны разные комбинации. Отображение отключило возможные комбинации, если сумма ударов 10 и 20 равна нулю и нести ее.Ноль между — это ноль, а ударьте два — это один какой-то один и несите его. Нулевой удар один равен единице, а второй — нулю. Сумма равна единице, перенос с нулем. И, наконец, если первый удар равен единице, а второй — один, какой-то ноль, и неси его. Если ты не понимаешь, как я это делаю, Сэм, тебе будет сложно. Вы можете Шторм преобразовать двоичного Сэма в десятичный Сэм, и вы увидите окончательные результаты Божественного Эри в этой меньшей строке, которую вы получите в двоичном блюзе. Единица в двоичном формате равна единице в десятичной системе счисления плюс один кишечный. Число один в двоичном формате равно единице в десятичном, так что я могу сделать это изменение с двоичного на десятичное в десятичном значении плюс один, промышленный уровень равен интересам кишечника.Снова преобразование в двоичное значение равно 10 в двоичном формате. Этот ноль — тот же результат, а этот несет немного.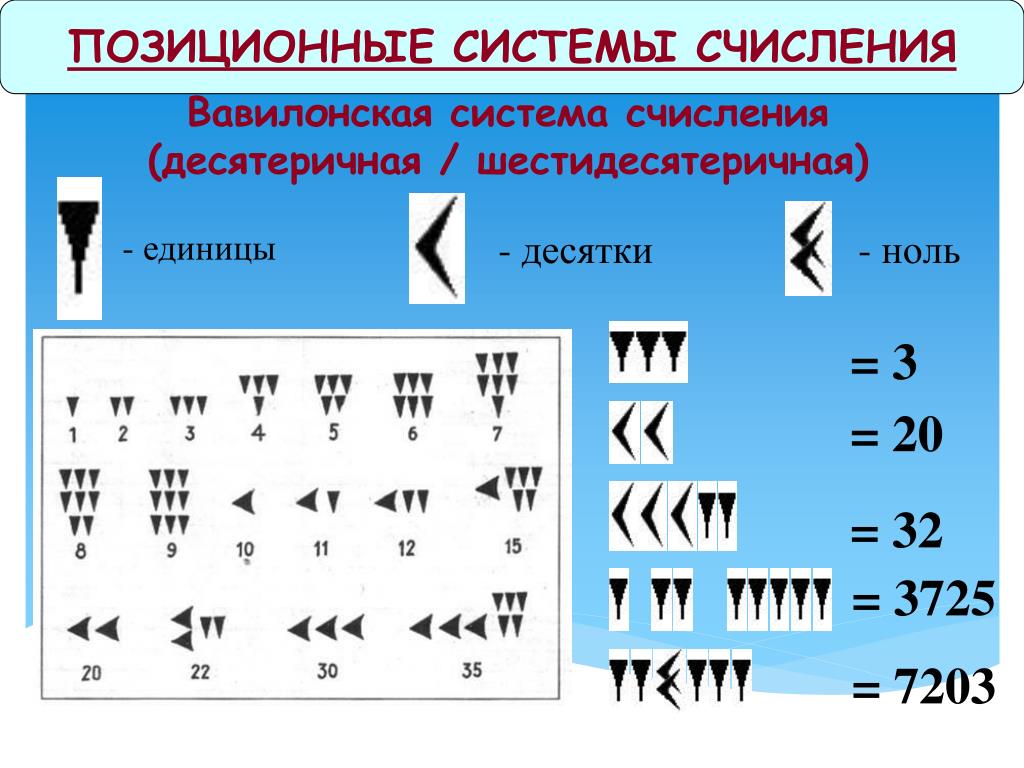 Когда мы использовали десятичную систему, у нас также есть биение несущей, когда результат превышает девять. В этом примере пять синих девяток равны четырем несу, что дает результат. 14. Я вам сейчас покажу. Еще три примера. Сложение двух чисел пошло на ноль. Получил 1010 с 011101 и сделал расчет. Ноль блюза, один — 11 Синий ноль — один ноль плюс один, когда? Когда Блюз.Когда эта последняя строка? Так что это ноль. Неси это. Когда? Когда. Блюз Когда Блюз единица — это единица с Единицей несущей, когда синий ноль плюс ноль — это когда и когда. Блюз-ноль — это один, и я тебя, Питер. Мои окончательные результаты. 1110111 В двоичном формате. Следующий пример сложения 11100101 с Когда Когда? 010111 И первый расчет — один. Проиграть один — ноль. Несите 11 плюс ноль плюс один — нулевая несущая. Когда сейчас я снова вижу, когда Польша Польша едина. Керри это когда 10 р. Ноль. Один ноль плюс один — это когда синий ноль равен единице.Когда тяги уходят в ноль, когда вы несете одно и снова дерево, то когда вы его несете, результат меньше.
Когда мы использовали десятичную систему, у нас также есть биение несущей, когда результат превышает девять. В этом примере пять синих девяток равны четырем несу, что дает результат. 14. Я вам сейчас покажу. Еще три примера. Сложение двух чисел пошло на ноль. Получил 1010 с 011101 и сделал расчет. Ноль блюза, один — 11 Синий ноль — один ноль плюс один, когда? Когда Блюз.Когда эта последняя строка? Так что это ноль. Неси это. Когда? Когда. Блюз Когда Блюз единица — это единица с Единицей несущей, когда синий ноль плюс ноль — это когда и когда. Блюз-ноль — это один, и я тебя, Питер. Мои окончательные результаты. 1110111 В двоичном формате. Следующий пример сложения 11100101 с Когда Когда? 010111 И первый расчет — один. Проиграть один — ноль. Несите 11 плюс ноль плюс один — нулевая несущая. Когда сейчас я снова вижу, когда Польша Польша едина. Керри это когда 10 р. Ноль. Один ноль плюс один — это когда синий ноль равен единице.Когда тяги уходят в ноль, когда вы несете одно и снова дерево, то когда вы его несете, результат меньше. Итак, мои последние воспоминания, когда когда ноль перешел в единицу, когда 100 и, наконец, последний пример. 110101 закончился на 1010 пошел один, начиная расчет, когда блюз Когда равен нулю, несет один, когда плюс ноль плюс один равен нулю. Carrier пошел, когда синий пошел, ноль — это ноль, несущий один, и снова, когда Blues zero pull, Went zero, нес один, плюс один, плюс ноль, это ноль, несущий один. Теперь я нахожу один город с одним.Итак, мой окончательный результат получился, когда 00000 в двоичном формате
23. Двоичное вычитание: в этом видео я собираюсь показать вам, как вычитать два двоичных числа с помощью дополнения до двух, Демет, которое я собираюсь использовать как преобразование вычитания. Я собираюсь преобразовать вычитание в новое сложение с отрицательными числами, используя два дополнения в таблице, вы можете увидеть разницу между внутренними числами Гнанта и двумя дополнительными числами. В застойных числах вы просто найдете положительные числа. А с помощью дополнения до двух вы можете преобразовать положительные числа в отрицательные.
Итак, мои последние воспоминания, когда когда ноль перешел в единицу, когда 100 и, наконец, последний пример. 110101 закончился на 1010 пошел один, начиная расчет, когда блюз Когда равен нулю, несет один, когда плюс ноль плюс один равен нулю. Carrier пошел, когда синий пошел, ноль — это ноль, несущий один, и снова, когда Blues zero pull, Went zero, нес один, плюс один, плюс ноль, это ноль, несущий один. Теперь я нахожу один город с одним.Итак, мой окончательный результат получился, когда 00000 в двоичном формате
23. Двоичное вычитание: в этом видео я собираюсь показать вам, как вычитать два двоичных числа с помощью дополнения до двух, Демет, которое я собираюсь использовать как преобразование вычитания. Я собираюсь преобразовать вычитание в новое сложение с отрицательными числами, используя два дополнения в таблице, вы можете увидеть разницу между внутренними числами Гнанта и двумя дополнительными числами. В застойных числах вы просто найдете положительные числа. А с помощью дополнения до двух вы можете преобразовать положительные числа в отрицательные. Что отличает это от типа чисел, положительных и отрицательных значений, так это наиболее значимый бит. Если вы говорите о положительных числах, старший бит равен нулю. Что касается отрицательных чисел, старший бит — это тот, который вы видите в токе таблицы. Избегайте положительных моментов. Два минуса. Вы просто использовали два дополнения, как вы можете увидеть здесь пример. Семь. Положительный 0111 Как я уже сказал, первая оставшаяся доля равна нулю, а минус семь начинается с единицы, потому что это отрицательное число, а остальные доли равны 000 Как мне сделать расчет, чтобы дать отрицательное число, чтобы получить отрицательное число .Легко начать справа налево. Выключите число, когда найдете 1-ю 1. Вы изменили все биты, нули, единицу и два нуля и получили отрицательное число. В этом примере у меня положительное число 20, и я получаю минус 20 с помощью этой техники. 1-й 1 бит этого дерева изменится на перевернутый, и вы получите минус 20 — 101100 Второй пример из числа 18 я получу минус, сражаясь с дополнением до двух, число, начинающееся справа налево.
Что отличает это от типа чисел, положительных и отрицательных значений, так это наиболее значимый бит. Если вы говорите о положительных числах, старший бит равен нулю. Что касается отрицательных чисел, старший бит — это тот, который вы видите в токе таблицы. Избегайте положительных моментов. Два минуса. Вы просто использовали два дополнения, как вы можете увидеть здесь пример. Семь. Положительный 0111 Как я уже сказал, первая оставшаяся доля равна нулю, а минус семь начинается с единицы, потому что это отрицательное число, а остальные доли равны 000 Как мне сделать расчет, чтобы дать отрицательное число, чтобы получить отрицательное число .Легко начать справа налево. Выключите число, когда найдете 1-ю 1. Вы изменили все биты, нули, единицу и два нуля и получили отрицательное число. В этом примере у меня положительное число 20, и я получаю минус 20 с помощью этой техники. 1-й 1 бит этого дерева изменится на перевернутый, и вы получите минус 20 — 101100 Второй пример из числа 18 я получу минус, сражаясь с дополнением до двух, число, начинающееся справа налево. Я получаю 1-ю единицу, и я верну эти четыре доли слева, и я получу 10111 ноль с долей слева, потому что это отрицательное число.Теперь сделаю вычитание. Два числа. 16 минус девять. Я собираюсь преобразовать в сложение с положительным числом, а отрицательное число 16 отправить с минус девять. Итак, я убираю два дополнения от девяти, чтобы получить минус девять девять в десятичной дроби. Положительное значение — 01001. Это моя первая 1, поэтому я собираюсь инвертировать оставшиеся запреты и получаю 10111 минус ночь в десятичном виде. Вычисление 16 минус девять равно этому вычислению. Если я сделал вычитание, но собираюсь преобразовать в сложение от 16 до минус девять с дополнением двойки, и я получу это число 000111 Перенос пшеницы игнорируется, поэтому мои удары слева равны нулю.Так что это положительное число. Это число в десятичной системе счисления составляет 7 16, с минус девятью цифрами в десятичной системе счисления. Мой второй пример. Девять. Вычитание с 17 равняется девяти. Отредактируйте с минус 17, чтобы я не заметил комплимент зуба.
Я получаю 1-ю единицу, и я верну эти четыре доли слева, и я получу 10111 ноль с долей слева, потому что это отрицательное число.Теперь сделаю вычитание. Два числа. 16 минус девять. Я собираюсь преобразовать в сложение с положительным числом, а отрицательное число 16 отправить с минус девять. Итак, я убираю два дополнения от девяти, чтобы получить минус девять девять в десятичной дроби. Положительное значение — 01001. Это моя первая 1, поэтому я собираюсь инвертировать оставшиеся запреты и получаю 10111 минус ночь в десятичном виде. Вычисление 16 минус девять равно этому вычислению. Если я сделал вычитание, но собираюсь преобразовать в сложение от 16 до минус девять с дополнением двойки, и я получу это число 000111 Перенос пшеницы игнорируется, поэтому мои удары слева равны нулю.Так что это положительное число. Это число в десятичной системе счисления составляет 7 16, с минус девятью цифрами в десятичной системе счисления. Мой второй пример. Девять. Вычитание с 17 равняется девяти. Отредактируйте с минус 17, чтобы я не заметил комплимент зуба. 17 17 010001 Это моя первая 1. Я собираюсь инвертировать эти пять долей слева и получаю 101111. Теперь производим вычисления. Не забудьте поставить нули слева, потому что это положительное число. Если у вас есть один слева, это означает, что это отрицательное число. Хорошо, сделаем дополнение до 17.Я получаю 001001, заканчивающийся на 101111 Это Дайте мне результат от 111000 Бит слева — это Гэри Бит. В этой части вы узнаете, что результат отрицательный. Если вы снова сделаете два дополнения, вы пойдете. Вы собираетесь дать вам абсолютное число от этого отрицательного числа. Я добавляю два и получаю 001000 Это восемь в десятичной системе счисления. Таким образом, это число минус восемь девять минус 17 минус восемь в десятичной системе счисления.
24. Введение в арифметические операции с разными основаниями: Здравствуйте.В этом последнем разделе вы собираетесь объединить преобразование и загадочные операции, которые вы узнали из предыдущих глав. Во втором разделе вы узнаете, как выполнить преобразование.
17 17 010001 Это моя первая 1. Я собираюсь инвертировать эти пять долей слева и получаю 101111. Теперь производим вычисления. Не забудьте поставить нули слева, потому что это положительное число. Если у вас есть один слева, это означает, что это отрицательное число. Хорошо, сделаем дополнение до 17.Я получаю 001001, заканчивающийся на 101111 Это Дайте мне результат от 111000 Бит слева — это Гэри Бит. В этой части вы узнаете, что результат отрицательный. Если вы снова сделаете два дополнения, вы пойдете. Вы собираетесь дать вам абсолютное число от этого отрицательного числа. Я добавляю два и получаю 001000 Это восемь в десятичной системе счисления. Таким образом, это число минус восемь девять минус 17 минус восемь в десятичной системе счисления.
24. Введение в арифметические операции с разными основаниями: Здравствуйте.В этом последнем разделе вы собираетесь объединить преобразование и загадочные операции, которые вы узнали из предыдущих глав. Во втором разделе вы узнаете, как выполнить преобразование. Использование различных покупок — это тушение 8, 10 и 16. И в разделе, где вы познакомитесь с моими операциями Edit Matic, сложением и вычитанием с помощью устройства, вы собираетесь присоединиться к этим двум разделам и научитесь делать загадочные операции с использованием четырех основных Bisys.
25. Шестнадцатеричное и восьмеричное сложение: добавление Octel и выходных десятичных чисел.В следующих видео я буду использовать отрицательные и положительные числа для сложения и вычитания. Я сделаю различие между ними. Если старший бит равен нулю. Я говорю о положительных числах. Вы можете добавить ноль, который стоит перед числом. Смерть. Не меняйте значение этого числа. А если самый значительный, то он равен единице. Я говорю об отрицательных числах, о тех, которые не попали в число. Не меняйте это значение на отрицательное число. Первый. Пример. Дерево в десятичной системе счисления равно 011 в двоичной системе счисления.Этот ноль слева означает, что число теперь положительное и изменится на отрицательное дерево.
Использование различных покупок — это тушение 8, 10 и 16. И в разделе, где вы познакомитесь с моими операциями Edit Matic, сложением и вычитанием с помощью устройства, вы собираетесь присоединиться к этим двум разделам и научитесь делать загадочные операции с использованием четырех основных Bisys.
25. Шестнадцатеричное и восьмеричное сложение: добавление Octel и выходных десятичных чисел.В следующих видео я буду использовать отрицательные и положительные числа для сложения и вычитания. Я сделаю различие между ними. Если старший бит равен нулю. Я говорю о положительных числах. Вы можете добавить ноль, который стоит перед числом. Смерть. Не меняйте значение этого числа. А если самый значительный, то он равен единице. Я говорю об отрицательных числах, о тех, которые не попали в число. Не меняйте это значение на отрицательное число. Первый. Пример. Дерево в десятичной системе счисления равно 011 в двоичной системе счисления.Этот ноль слева означает, что число теперь положительное и изменится на отрицательное дерево. Я должен сделать комплимент соку, так что минусовое дерево в десятичной системе счисления равно 101 в двоичной системе счисления. Чтобы изменить это двоичное число с трех ударов на восемь ударов. У меня остался один, и я получаю 1111, когда 01 в двоичном формате. Это число не меняется при выходе из десятичного числа равно F D. Теперь, сделав наш первый пример сложения с числами Octel, число 37 добавлено с 25 в восьмом первом шаге Преобразование из Отто в двоичное Создание двух групп.Три удара. Я получаю 011 из третьей цифры и 111 из цифр. Семерка 010 Передняя цифра два и 101 из цифры пять. Складываем эти два числа. Используя конюшню, я получаю 000110100. У меня было три удара, которые оставили 30 ударов, просто чтобы это число было положительным, потому что последний бит был равным единице, если я не добавляю уличные удары, поэтому я получаю ноль из этого дерева. 2 группы И для этих последних групп дерева 064 в Octel — это мой последний номер, теперь во втором выпуске всего 15 для трех в Octel Сложение этих двух чисел Во-первых, преобразование из 82 способов в, и я получаю 001 из цифры единица и 101 из пятой цифры 100 передняя цифра для и 011 из третьей цифры.
Я должен сделать комплимент соку, так что минусовое дерево в десятичной системе счисления равно 101 в двоичной системе счисления. Чтобы изменить это двоичное число с трех ударов на восемь ударов. У меня остался один, и я получаю 1111, когда 01 в двоичном формате. Это число не меняется при выходе из десятичного числа равно F D. Теперь, сделав наш первый пример сложения с числами Octel, число 37 добавлено с 25 в восьмом первом шаге Преобразование из Отто в двоичное Создание двух групп.Три удара. Я получаю 011 из третьей цифры и 111 из цифр. Семерка 010 Передняя цифра два и 101 из цифры пять. Складываем эти два числа. Используя конюшню, я получаю 000110100. У меня было три удара, которые оставили 30 ударов, просто чтобы это число было положительным, потому что последний бит был равным единице, если я не добавляю уличные удары, поэтому я получаю ноль из этого дерева. 2 группы И для этих последних групп дерева 064 в Octel — это мой последний номер, теперь во втором выпуске всего 15 для трех в Octel Сложение этих двух чисел Во-первых, преобразование из 82 способов в, и я получаю 001 из цифры единица и 101 из пятой цифры 100 передняя цифра для и 011 из третьей цифры. Я снова добавил 30. Это осталось только для того, чтобы это число было положительным. Теперь, добавляя, я получаю 000110000, и мое последнее число в Octel — 060. Наконец, пример с выходными десятичными числами. При добавлении одного I к преобразованию дерева от 16 до двух, я получаю 0001 из первой цифры и 1010 из первой цифры I, 0010 переднюю цифру и 0011 из цифр. Три. Делая сложение, я получаю 00111101, делаю две группы из четырех битов, и я получаю свой последний выход. Десятичное число равно дереву
26. Шестнадцатеричное и восьмеричное вычитание: я промышленность, не так ли? Я сделаю вычитание с помощью авто и выйду из десятичных чисел на глаз.И к 16-му числа я собираюсь начать с чисел Octel и найду два числа 14 и 37 в окто. Сначала я сделаю преобразование в двоичные числа. 14 в Octel равно 001 из цифры один и 100 из цифры для В этом числе три дайте мне 011 и цифры семь. Дайте мне один. Пошел один. Теперь я собираюсь преобразовать вычитание в сложение. Так что я должен сделать двойной комплимент от этого числа, и я получаю 10 000 Когда? Теперь я могу сложить эти два числа и получить окончательное двоичное число 111 01 Когда 01 вы увидите, что наиболее значимая доля равна единице.
Я снова добавил 30. Это осталось только для того, чтобы это число было положительным. Теперь, добавляя, я получаю 000110000, и мое последнее число в Octel — 060. Наконец, пример с выходными десятичными числами. При добавлении одного I к преобразованию дерева от 16 до двух, я получаю 0001 из первой цифры и 1010 из первой цифры I, 0010 переднюю цифру и 0011 из цифр. Три. Делая сложение, я получаю 00111101, делаю две группы из четырех битов, и я получаю свой последний выход. Десятичное число равно дереву
26. Шестнадцатеричное и восьмеричное вычитание: я промышленность, не так ли? Я сделаю вычитание с помощью авто и выйду из десятичных чисел на глаз.И к 16-му числа я собираюсь начать с чисел Octel и найду два числа 14 и 37 в окто. Сначала я сделаю преобразование в двоичные числа. 14 в Octel равно 001 из цифры один и 100 из цифры для В этом числе три дайте мне 011 и цифры семь. Дайте мне один. Пошел один. Теперь я собираюсь преобразовать вычитание в сложение. Так что я должен сделать двойной комплимент от этого числа, и я получаю 10 000 Когда? Теперь я могу сложить эти два числа и получить окончательное двоичное число 111 01 Когда 01 вы увидите, что наиболее значимая доля равна единице. Итак, это отрицательное число. Я просто добавляю один, который остановился на числе, чтобы сделать группы из трех и четырех ударов, чтобы преобразовать число из двоичного в автоматический и выйти из преобразования децибел из двоичного в Отто. Я делаю эти три группы из трех долей, и я получаю 755 в окто, конвертируя в яйца десятичное число, если две группы по четыре доли, и я получаю число A D и конвертирую из двоичного в десятичное. Вы знаете, что это отрицательное число. И если я сделаю два дополнения, я собираюсь преобразовать это отрицательное число в его положительное число с положительным сигналом.И это число — это положительное число, равное 19. Итак, окончательный результат в десятичной системе счисления равен минус 19. Теперь, используя десятичные числа для выхода, я нашел два дерева чисел для десятичного числа на выходе и 71 в формате на 16, сделав сначала преобразование в двоичное. Я получаю 0011 из дерева цифр 0100 из цифры для. И из этого числа я получаю 0111 из цифр семь и 0001 из цифры один, что делает это число двойным комплиментом.
Итак, это отрицательное число. Я просто добавляю один, который остановился на числе, чтобы сделать группы из трех и четырех ударов, чтобы преобразовать число из двоичного в автоматический и выйти из преобразования децибел из двоичного в Отто. Я делаю эти три группы из трех долей, и я получаю 755 в окто, конвертируя в яйца десятичное число, если две группы по четыре доли, и я получаю число A D и конвертирую из двоичного в десятичное. Вы знаете, что это отрицательное число. И если я сделаю два дополнения, я собираюсь преобразовать это отрицательное число в его положительное число с положительным сигналом.И это число — это положительное число, равное 19. Итак, окончательный результат в десятичной системе счисления равен минус 19. Теперь, используя десятичные числа для выхода, я нашел два дерева чисел для десятичного числа на выходе и 71 в формате на 16, сделав сначала преобразование в двоичное. Я получаю 0011 из дерева цифр 0100 из цифры для. И из этого числа я получаю 0111 из цифр семь и 0001 из цифры один, что делает это число двойным комплиментом. Я получаю 10001111 Теперь я могу сложить эти два числа, и результат будет 1100 0011 в двоичном формате.Это отрицательное число, потому что старший бит со значением один теперь преобразует это двоичное число в ночное число. Я получаю 703 и получаю десятичное число для выхода. Смотрите дерево. Наконец, это отрицательное число. Если бы я использовал комплимент «Двойка», я бы знал число, но с положительным значением. Положительный сигнал. Таким образом, это число минус 61 в десятичной системе счисления.
27. Сложение и вычитание по всем базам: Здравствуйте. В этом видео я покажу вам мое состояние и вычитание, используя разные числа, основанные на числах, вы можете сложить комбинацию из различных лучших чисел, которые вы выучите.Единственная уловка заключается в том, что когда вы используете Bice 8 16 и десятичный, вы должны преобразовать его в двоичный, чтобы получить видение A. После того, как вы сделаете добавление в двоичном формате, у вас будет полученный двоичный файл, чтобы вы могли снова выполнить преобразование в устройство, которое вы хотите в финале.
Я получаю 10001111 Теперь я могу сложить эти два числа, и результат будет 1100 0011 в двоичном формате.Это отрицательное число, потому что старший бит со значением один теперь преобразует это двоичное число в ночное число. Я получаю 703 и получаю десятичное число для выхода. Смотрите дерево. Наконец, это отрицательное число. Если бы я использовал комплимент «Двойка», я бы знал число, но с положительным значением. Положительный сигнал. Таким образом, это число минус 61 в десятичной системе счисления.
27. Сложение и вычитание по всем базам: Здравствуйте. В этом видео я покажу вам мое состояние и вычитание, используя разные числа, основанные на числах, вы можете сложить комбинацию из различных лучших чисел, которые вы выучите.Единственная уловка заключается в том, что когда вы используете Bice 8 16 и десятичный, вы должны преобразовать его в двоичный, чтобы получить видение A. После того, как вы сделаете добавление в двоичном формате, у вас будет полученный двоичный файл, чтобы вы могли снова выполнить преобразование в устройство, которое вы хотите в финале.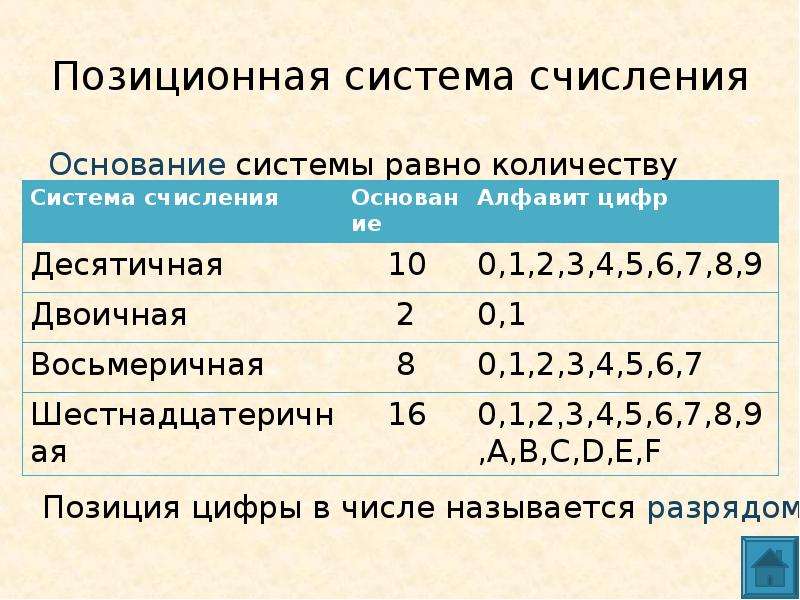 Приведем первый пример. Я хочу сделать добавление 12 в десятичном формате на выходе и 21 в BIST 10. Первый шаг — преобразовать два байта, также 12 в десятичный ответ два. Бас два равен 0001 из числа один и 0010 из числа, чтобы покрыть 21 в десятичной системе счисления вам F, чтобы использовать методы деления.Теперь, когда у вас есть два числа, давайте сделаем сложение. Таким образом, вы получите это окончательное число в двоичном формате. Вы можете преобразовать это число в окто-число и полностью преобразовать 047 в десятичное число при выходе в семь и в десятичное 39 39. Теперь, когда я хочу произвести вычитание, это то же самое. Сначала я хочу преобразовать это намерение 8 16 в двоичное, а затем второе число. Я должен сделать комплимент сока, чтобы убрать комплимент двойки со второго числа. Если у вас когда-нибудь будет положительное число, оно будет отрицательным.После комплимента двойки я складываю положительное число и отрицательное число, и я получаю окончательное число в двоичном долге окончательных покупок.
Приведем первый пример. Я хочу сделать добавление 12 в десятичном формате на выходе и 21 в BIST 10. Первый шаг — преобразовать два байта, также 12 в десятичный ответ два. Бас два равен 0001 из числа один и 0010 из числа, чтобы покрыть 21 в десятичной системе счисления вам F, чтобы использовать методы деления.Теперь, когда у вас есть два числа, давайте сделаем сложение. Таким образом, вы получите это окончательное число в двоичном формате. Вы можете преобразовать это число в окто-число и полностью преобразовать 047 в десятичное число при выходе в семь и в десятичное 39 39. Теперь, когда я хочу произвести вычитание, это то же самое. Сначала я хочу преобразовать это намерение 8 16 в двоичное, а затем второе число. Я должен сделать комплимент сока, чтобы убрать комплимент двойки со второго числа. Если у вас когда-нибудь будет положительное число, оно будет отрицательным.После комплимента двойки я складываю положительное число и отрицательное число, и я получаю окончательное число в двоичном долге окончательных покупок. Я хочу, чтобы я испортил двоичное число покупок долга два, сделав один пример 37 в Octel, вычитая с одним A в выходном десятичном значении 37, получается 011 единица. Хочу один? Эта первая улица бьет из дерева цифр, а второе дерево бьет из цифр. Семь 0001 — это первая цифра этого числа в десятичной системе счисления, а 1010 — это первая цифра этого числа.Теперь я собираюсь дополнить это число до двух. Это число было положительным, а теперь оно отрицательное, потому что старший бит, производящий сложение, я получаю это число. Положительное число Бит переноса игнорируется. Теперь я могу преобразовать в Octel номер 05 в Octel 05 в десятичное число выхода и 05 в десятичное число. Теперь делаем второй пример 12 в Octel Subtraction. Сорняки 20 в десятичной системе счисления. 12 равно 001 010 в двоичном формате и 20. Используя метод деления, я получаю в двоичном формате 010100 Делая комплименты двойкам.Это число. Используйте это, чтобы дополнить их. Основание наиболее значимого ритма от 0 до 1.
Я хочу, чтобы я испортил двоичное число покупок долга два, сделав один пример 37 в Octel, вычитая с одним A в выходном десятичном значении 37, получается 011 единица. Хочу один? Эта первая улица бьет из дерева цифр, а второе дерево бьет из цифр. Семь 0001 — это первая цифра этого числа в десятичной системе счисления, а 1010 — это первая цифра этого числа.Теперь я собираюсь дополнить это число до двух. Это число было положительным, а теперь оно отрицательное, потому что старший бит, производящий сложение, я получаю это число. Положительное число Бит переноса игнорируется. Теперь я могу преобразовать в Octel номер 05 в Octel 05 в десятичное число выхода и 05 в десятичное число. Теперь делаем второй пример 12 в Octel Subtraction. Сорняки 20 в десятичной системе счисления. 12 равно 001 010 в двоичном формате и 20. Используя метод деления, я получаю в двоичном формате 010100 Делая комплименты двойкам.Это число. Используйте это, чтобы дополнить их. Основание наиболее значимого ритма от 0 до 1. После сложения я получаю 110110. Это число теперь отрицательное, что делает преобразование в окто. Я получаю 66 преобразований в десятичную форму выхода. Я получил F шесть и теперь делаю двойной комплимент этому окончательному результату. Я получаю номер, но с положительным сигналом. Это число с положительным сигналом. Итак, это число в двоичном формате ese минус 10
После сложения я получаю 110110. Это число теперь отрицательное, что делает преобразование в окто. Я получаю 66 преобразований в десятичную форму выхода. Я получил F шесть и теперь делаю двойной комплимент этому окончательному результату. Я получаю номер, но с положительным сигналом. Это число с положительным сигналом. Итак, это число в двоичном формате ese минус 10
Компьютерные науки: двоичный
/ ru / информатика / аппаратно-программное обеспечение / содержание /
двоичный
На протяжении всей истории почти каждая цивилизация использовала десятичную систему счисления с 10 цифрами : от нуля до девяти.Все числа, которые мы можем придумать, используют некоторую комбинацию этих 10 цифр.
Компьютеры, однако, работают иначе. Вместо этого они используют систему счисления, в которой всего две цифры : единица и ноль. Эта система называется двоичная , и ваш компьютер использует ее постоянно.
Посмотрите видео ниже, чтобы узнать больше о том, как компьютеры используют двоичный код.
Компьютеры нуждаются в информации для того, чтобы делать то, что они делают. Эта цифровая информация, или данных , состоит из того, что называется битами .Бит — это сокращение от двоичной цифры , что означает, что каждый бит на самом деле представляет собой просто одно число: либо , либо , либо , ноль .
Эти биты можно комбинировать для создания более крупных единиц, таких как байты, мегабайты и т. Д., Которые мы используем для измерения наших файлов. Чем больше файл, тем больше в нем битов. Так что что-то вроде видео с высоким разрешением на самом деле состоит из миллионов и миллионов единиц и нулей.
Но как именно эти единицы и нули объединяются и позволяют компьютеру функционировать? Давайте подумаем о двоичном коде как о выключателе света . Представьте, что один представляет выключатель света на , а ноль представляет на . В двоичном режиме индикатор горит или выключен, других возможных состояний нет.
Представьте, что один представляет выключатель света на , а ноль представляет на . В двоичном режиме индикатор горит или выключен, других возможных состояний нет.
Эти биты объединены в различные комбинации единиц и нулей, и они образуют своего рода код . Затем ваш компьютер быстро обрабатывает этот код и переводит его в данные, сообщая ему, что делать.
Вам может быть интересно, почему компьютеры используют двоичную систему вместо десятичной, которую мы используем для подсчета вещей в нашей повседневной жизни.Как упоминалось выше, двоичный файл имеет два состояния: выключено и включено. Если бы компьютеры использовали десятичную систему, вместо этого было бы 10 состояний , и им пришлось бы работать намного больше , чтобы обработать их все. Компьютерам проще обрабатывать двоичные файлы, к тому же они занимают меньше места.
Подобно тому, как атомы составляют все вокруг нас в реальном мире, все в цифровом мире можно разбить на двоичные. И хотя мы их не видим, это всего лишь куча единиц и нулей.
И хотя мы их не видим, это всего лишь куча единиц и нулей.
/ ru / информатика / языки программирования / содержание /
Система счисления для класса 11
Система счисления — это способ представления всего в виде цифр. Есть четыре типа системы счисления.
1. Двоичная система счисления
Двоичная система счисления может содержать две цифры 0 и 1. Таким образом, основание двоичной системы счисления равно 2. Двоичные числа представлены цифрой 2 в качестве индекса значения.
Примеры двоичных чисел:
- (1101) 2
- (1110.011) 2
2. Десятичная система счисления
Десятичная система счисления может содержать цифры от 0 до 9. Таким образом, основание десятичной системы счисления — 10. Десятичные числа представлены с 10 в качестве индекса значения.
Примеры десятичных чисел:
- (1234) 10
- (55,34) 10
3.
 Восьмеричная система счисления
Восьмеричная система счисления Восьмеричная система счисления может содержать цифры от 0 до 7 .Таким образом, основание восьмеричной системы счисления — 8. Восьмеричные числа представлены с 8 в качестве нижнего индекса к значению.
Примеры восьмеричных чисел:
- (561) 8
- (17,54) 8
4. Шестнадцатеричная система счисления
Шестнадцатеричная система счисления может содержать цифры от 0 до 9 и алфавиты от A до F, где
A = 10
B = 11
C = 12
D = 13
E = 14
F = 15
Таким образом, основание шестнадцатеричной системы счисления — 16.Шестнадцатеричные числа представлены индексом 16 к значению.
Примеры шестнадцатеричных чисел: :
- (A74) 16
- (91.B3) 16
Преобразование числовой системы
1.
 Преобразование десятичной системы в двоичную
Преобразование десятичной системы в двоичную To Чтобы получить двоичный эквивалент десятичного числа, десятичное число следует многократно разделить на 2 остатка записи, получаемого на каждом шаге.
Это должно продолжаться до тех пор, пока последнее частное не станет равным 1.Остатки следует записывать снизу вверх, чтобы получить двоичный эквивалент десятичного числа.
- (17) 10 = (?) 2 = (10001) 2
2. Преобразование десятичного в восьмеричное
Для получения восьмеричного эквивалента десятичного числа , десятичное число следует многократно разделить на 8 остатков записи, получаемых на каждом шаге.
Это должно продолжаться до тех пор, пока последнее частное не станет меньше 8.Остатки следует записывать снизу вверх, чтобы получить восьмеричный эквивалент десятичного числа.
3. Преобразование десятичного числа в шестнадцатеричное
Чтобы получить шестнадцатеричный эквивалент десятичного числа, десятичное число следует многократно разделить на 16 остатков записи, получаемых на каждом шаге.
Это должно продолжаться до тех пор, пока последнее частное не станет меньше 16. Остатки следует записывать снизу вверх, чтобы получить шестнадцатеричный эквивалент десятичного числа.
4. Преобразование двоичного числа в десятичное
Чтобы получить десятичный эквивалент двоичного числа, отдельные цифры двоичного числа должны быть умножены на степени 2, начиная с крайней правой цифры, умноженной на 2 0 , вторая последняя цифра умножается на 2 1 , третья последняя цифра умножается на 2 2 и так далее до самой левой цифры.
Пример :
5.Преобразование восьмеричного числа в десятичное
Чтобы получить десятичный эквивалент восьмеричного числа, отдельные цифры восьмеричного числа должны быть умножены на степень 8, начиная с крайней правой цифры, умноженной на 8 0 , вторая последняя цифра умножена на 8 1 , третья последняя цифра умножается на 8 2 и так далее до самой левой цифры.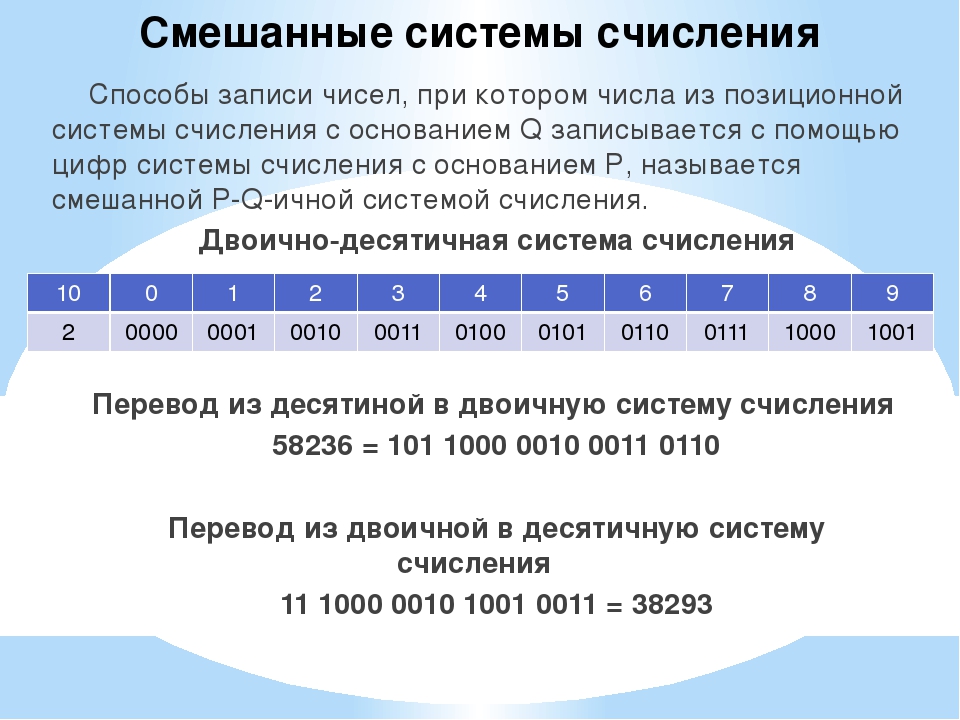
Пример:
** Стрелки представляют значения для умножения.
6. Преобразование шестнадцатеричного числа в десятичное
Чтобы получить десятичный эквивалент шестнадцатеричного числа, отдельные цифры шестнадцатеричного числа следует умножить на степень 16, начиная с крайней правой цифры, умноженной на 16 0 , вторая последняя цифра умножена на 16 1 , третья последняя цифра умножается на 16 2 и так далее до самой левой цифры.
В случае букв от A до F коды алфавитов должны быть умножены на степень 16.
Пример:
** Стрелки представляют значения, которые необходимо умножить.
7. Преобразование восьмеричного числа в двоичное
Чтобы получить двоичный эквивалент восьмеричного числа, отдельные цифры восьмеричного числа должны быть преобразованы в двоичные группы по три цифры.
Например, чтобы получить двоичный эквивалент восьмеричного числа 127 , мы можем предпринять следующие шаги:
Двоичный эквивалент 7 — 111
Двоичный эквивалент 2 — 010
Двоичный эквивалент 1 — 001
Итак, двоичный эквивалент из (127) 8 это:
8.Преобразование шестнадцатеричного числа в двоичное
Чтобы получить двоичный эквивалент шестнадцатеричного числа, отдельные цифры шестнадцатеричного числа должны быть преобразованы в двоичное в группах по четыре цифры.
Например, чтобы получить двоичный эквивалент шестнадцатеричного числа A27, мы можем предпринять следующие шаги:
Двоичный эквивалент 7 — 0111
Двоичный эквивалент 2 — 0010
Двоичный эквивалент A (10) — 1010
Итак, двоичный эквивалент (A27) 16 :
9.Преобразование двоичного числа в восьмеричное
Чтобы получить восьмеричный эквивалент двоичного числа, цифры двоичного числа должны быть разделены на группы из трех цифр, начиная с самой правой цифры.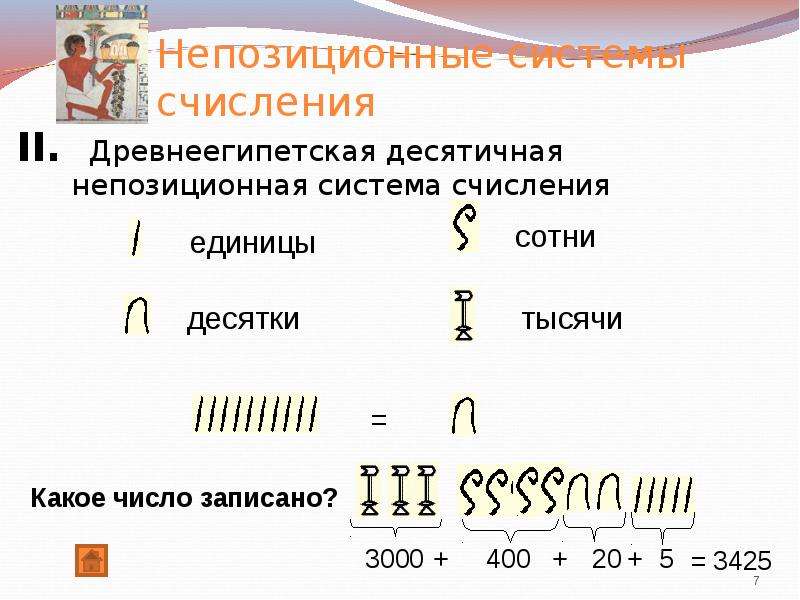 Затем эти группы следует преобразовать в соответствующие десятичные числа.
Затем эти группы следует преобразовать в соответствующие десятичные числа.
Например, чтобы получить восьмеричный эквивалент двоичного числа 101011, мы можем предпринять следующие шаги:
101011 делится на группы из трех цифр:
(101) (011)
Десятичный эквивалент 011 равен 3
Десятичный эквивалент 101 — 5
Восьмеричный эквивалент 101011 2 :
10.Преобразование двоичного числа в шестнадцатеричное
Чтобы получить шестнадцатеричный эквивалент двоичного числа, цифры двоичного числа должны быть разделены на группы по четыре цифры, начиная с крайней правой цифры. Затем эти группы следует преобразовать в соответствующие десятичные числа.
Например, чтобы получить восьмеричный эквивалент двоичного числа 1011101011, мы можем предпринять следующие шаги:
1011101011 делится на группы из четырех цифр как:
(0010) (1110) (1011)
Примечание: нули — это заполняется в начале самой левой группы двоичных цифр, если количество цифр меньше четырех.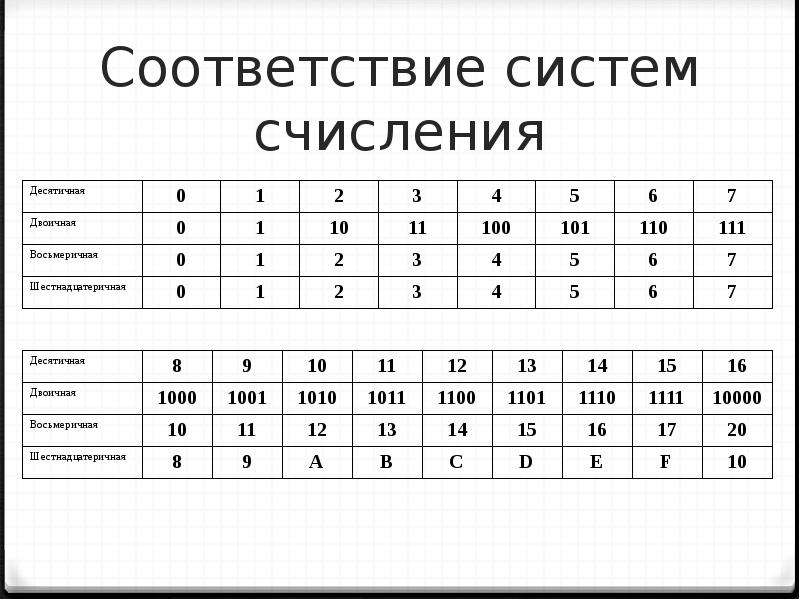
Десятичный эквивалент 1011 — 11 (B)
Десятичный эквивалент 1110 — 14 (E)
Десятичный эквивалент 0010 — 2
Шестнадцатеричный эквивалент 1011101011 2 — это:
Двоичное сложение
Двоичные числа можно складывать так же, как и обычные числа, но в случае двоичных чисел сумма всегда равна 0 или 1. Правила сложения двоичных чисел следующие:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 0 с переносом 1
Пример 1:
Сумма в приведенном выше примере выполняется с помощью следующих шагов:
1 + 1 = 10 = 0 с переносом 1.
1 + 0 + 1 = 10 = 0 с переносом 1
1 + 1 + 0 = 10 = 10 = 0 с переносом 1
1 + 1 + 1 = 10 + 1 = 11 = 1 с переносом 1
1 +1 +1 = 11
Пример 2:
Теги урока: двоичная система счисления, двоичное преобразование в десятичное, десятичная система счисления, десятичное преобразование в двоичное, десятичное в шестнадцатеричное преобразование, десятичное преобразование в восьмеричное, шестнадцатеричная система счисления, шестнадцатеричное преобразование в десятичное, шестнадцатеричное преобразование в двоичное, преобразование системы счисления, восьмеричное Система счисления, восьмеричное преобразование в десятичное, восьмеричное преобразование в двоичное.


 Великий немецкий учёный Лейбниц считал:
Великий немецкий учёный Лейбниц считал:
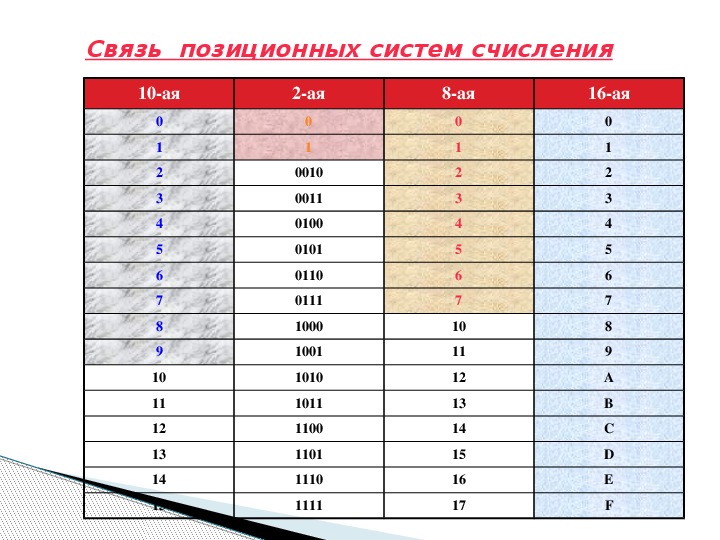 Таких элементов достаточно много: намагниченный или не намагниченный сердечник, открытый или закрытый транзистор и др. Для десятичной системы счисления понадобилось бы, к примеру, устройство с 10 устойчивыми состояниями. Это значительно усложнило бы схему ЭВМ.
Таких элементов достаточно много: намагниченный или не намагниченный сердечник, открытый или закрытый транзистор и др. Для десятичной системы счисления понадобилось бы, к примеру, устройство с 10 устойчивыми состояниями. Это значительно усложнило бы схему ЭВМ.
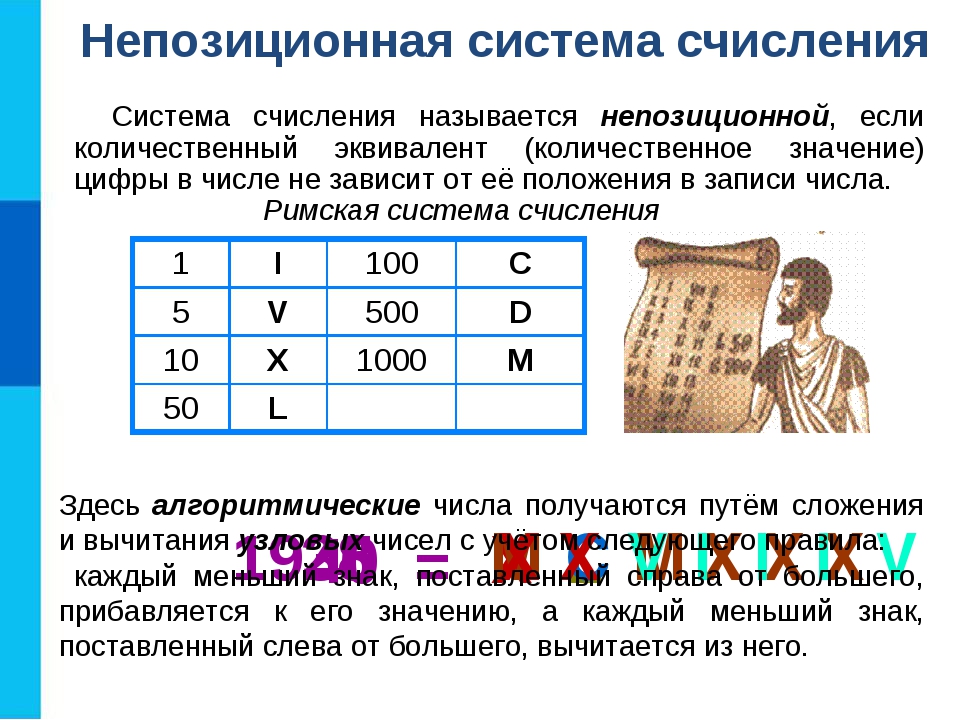 Затем преобразованное число складывается с уменьшаемым:
Затем преобразованное число складывается с уменьшаемым:
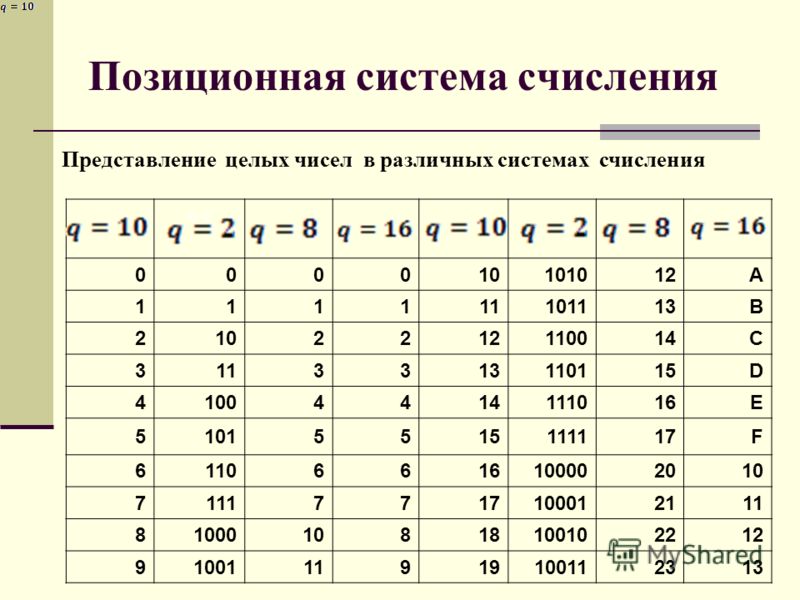 Но все достоинства этой системы делают такой недостаток не столь существенным.
Но все достоинства этой системы делают такой недостаток не столь существенным.
