Алгебра логики. Понятие высказывания
Для проектирования, оптимизации и описания компьютерных схем широко используется алгебра логики, которая устанавливает закономерности формирования и преобразования логических функций.
Логика появилась приблизительно в IV веке до нашей эры. Основоположником формальной логики принято считать выдающегося древнегреческого философа Аристотеля. Он систематизировал различные научные сведения, сформулировал формы и правила логического мышления. Труды, посвященные логике, Аристотель описал в цикле философских сочинений, известных под названием «Органон».
Впервые алгебраические методы для решения традиционных логических задач применил основатель математической логики английский математик и логик Джордж Буль. Свои исследования он опубликовал в работах «Математический анализ логики» (1847), «Логическое исчисление» (1848), «Исследование законов мышления» (1854).
Спустя почти 100 лет в 1938 году выдающийся американский математик и инженер Клод Шеннон показал, что алгебра логики применима для описания самых разнообразных процессов, в том числе и для функционирования релейно-контактных и электронно-ламповых схем.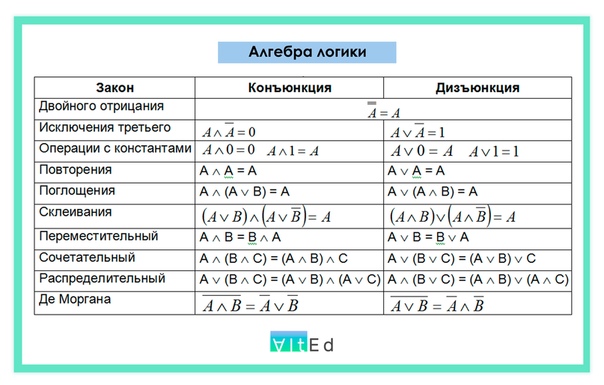
Высказывание
Исследования в алгебре логики тесно связаны с изучением высказываний, вызвано это тем, что высказывания являются одним из основных видов носителей информации. С помощью высказываний устанавливаются свойства, взаимосвязи между объектами.
В формальной логике Аристотель определяет высказывание следующим образом:
Высказывание — это языковое образование, в отношении которого имеет смысл говорить о его истинности или ложности.
Однако, определение Аристотеля не является математически точным и порождает ряд парадоксов и противоречий. Это связано с тем, что Аристотель проблему определения высказывания заменяет проблемой определения истинности или ложности предложения.
Например, рассмотрим предложение: «Это предложение является ложным»
- Пусть предложение истинно. Тогда это противоречит его собственному утверждению.
- Пусть предложение ложно. Тогда следует, что предложение на самом деле истинно.
Значит, предложению нельзя приписать какое-либо значение истинности, следовательно, оно не является высказыванием.
Причина данного парадокса лежит в структуре построения указанного предложения: оно ссылается на свое собственное значение. Таким образом, необходимы определенные ограничения на допустимые формы высказываний:
- Определение. Высказывание называется простым (элементарным), если никакая его часть сама не является высказыванием.
- Алгебра логики отвлекается от смысловой содержательности высказываний.
Введение таких ограничений дает возможность изучать высказывания алгебраическими методами, т.е. позволяет ввести операции над элементарными высказываниями и с их помощью строить и изучать составные высказывания.
Cоставное высказывание
Определение. Cоставное (cложное) высказывание – это высказывание, построенное из простых высказываний, с помощью логических связок (операций).
В обычной речи, в качестве подобных связок, употребляются «и», «или», «не», «либо…, либо…», «если…, то…», «тогда и только тогда, когда …». Эти связки трактуются как логические операции над высказываниями.
| Логическая операция | Логическая связка | Формальный знак |
|---|---|---|
| Конъюнкция (логическое умножение) | «и» | &, ∧ |
| Дизъюнкция (логическое сложение) | «или» | ∨, + |
| Инверсия (логическое отрицание) | «не» | ¬ |
| Разделительная дизъюнкция (исключающее ИЛИ) | «либо…, либо…» | ⊕, Δ |
| Импликация (логическое следование) | «если…, то…» | ⇒, → |
| Эквивалентность (равносильность) | «тогда и только тогда, когда» | ≡, ↔, ⇔ |
Алгебра логики изучает строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
Учебный курс «Информатика»
 Триггер
ТриггерЛогика очень древняя наука. Ещё в античные времена была известна
Другой закон логики — закон непротиворечивости. Если сказать: «Во время своих странствий Платон был в Египте И не был Платон в Египте», то очевидно, любое высказывание, имеющее такую форму, всегда будет ложно.
 Если из теории следуют два противоречащих друг другу вывода, то такая теория безусловно неправильная (ложная) и должна быть отвергнута.
Если из теории следуют два противоречащих друг другу вывода, то такая теория безусловно неправильная (ложная) и должна быть отвергнута.
Ещё один закон, известный в древности — закон отрицания: «Если НЕ верно, что Платон НЕ был в Египте, то значит, Платон был в Египте».
Формальная логика основана на “высказываниях”. “Высказывание” — это основной элемент логики, определяемый как повествовательное предложение, относительно которого можно однозначно сказать, истинное или ложное утверждение оно содержит.
Например: Листва на деревьях опадает осенью. Земля прямоугольная.
Первое высказывание содержит истинную информацию, а второе — ложную. Вопросительное, побудительное и восклицательное предложения не являются высказываниями, так как в них ничего не утверждается и не отрицается.
Пример предложений, не являющихся высказываниями: Не пейте сырую воду! Кто не хочет быть счастливым?
Высказывания могут быть и такими: 2>1, Н2О+SO3=h3SO4.

Приведённые выше примеры высказываний являются простыми. Но из простых высказываний можно получить сложные, объединив их с помощью логических связок. Логические связки — это слова, которые подразумевают определённые логические связи между высказываниями. Основные логические связки издавна употребляются не только в научном языке, но и в обыденном, — это “и”, “или”, “не”, “если … то”, “либо … либо” и другие известные нам из русского языка связки. В рассмотренных нами трёх законах формальной логики использовались связки “и”, “или”, “не”, “если … то” для связи простых высказываний в сложные.
Высказывания бывают общими, частными и единичными. Общее высказывание начинается со слов: всё, все, всякий, каждый, ни один. Частное высказывание начинается со слов: некоторые, большинство и т.п. Во всех других случаях высказывание является единичным.

Формальная логика была известна в средневековой Европе, она развивалась и обогащалась новыми законами и правилами, но при этом вплоть до 19 века она оставалась обобщением конкретных содержательных данных и её законы сохраняли форму высказываний на разговорном языке.
В 1847 году английский математик Джордж Буль, преподаватель провинциального университета в маленьком городке Корке на юге Англии разработал алгебру логики.
Алгебра логики очень проста, так как каждая переменная может принимать только два значения: истинно или ложно. Трудность изучения алгебры логики возникает из-за того, что для обозначения переменных принимают символы 0 и 1, которые по написанию совпадают с обычными арифметическими единицей и нулём. Но совпадение это только внешнее, так как смысл они имеют совсем иной.
 е. ложно. Высказывание заменилось на логическое выражение, которое строится из логических переменных (А, В, Х, …) и логических операций (связок).
е. ложно. Высказывание заменилось на логическое выражение, которое строится из логических переменных (А, В, Х, …) и логических операций (связок).
В алгебре логики знаки операций обозначают лишь три логические связки ИЛИ, И, НЕ.
1.Логическая операция ИЛИ. Логическую функцию принято задавать в виде таблицы. В левой части этой таблицы перечисляются все возможные значения аргументов функции, т.е. входные величины, а в правой указывается соответствующее им значение логической функции. Для элементарных функций получается таблица истинности данной логической операции. Для операции ИЛИ таблица истинности имеет вид:
Операцию ИЛИ называют также логическим сложением, и потому её можно обозначать знаком «+».
Рассмотрим сложное единичное высказывание: «Летом я поеду в деревню или в туристическую поездку». Обозначим через А простое высказывание «Летом я поеду в деревню», а через В — простое высказывание «Летом я поеду в туристическую поездку».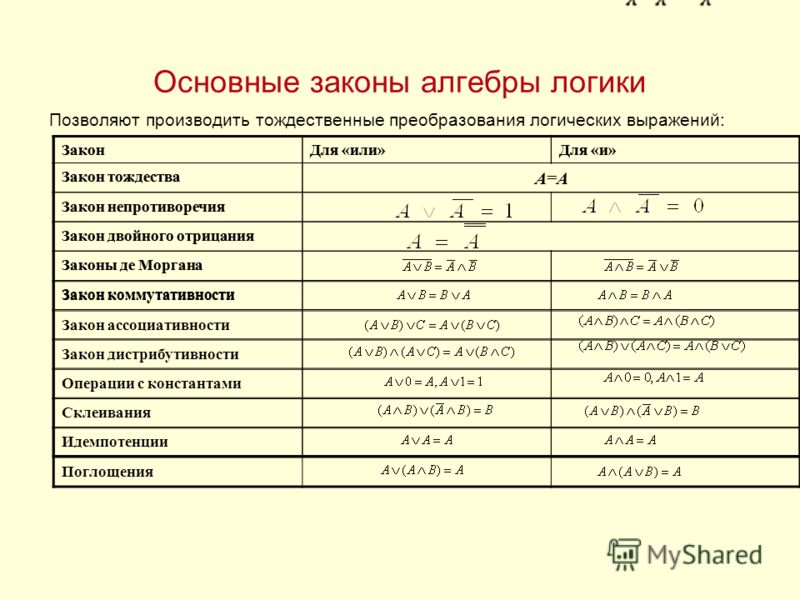 Тогда логическое выражение сложного высказывания имеет вид А+В, и оно будет ложным только, если ни одно из простых высказываний не будет истинным.
Тогда логическое выражение сложного высказывания имеет вид А+В, и оно будет ложным только, если ни одно из простых высказываний не будет истинным.
2. Логическая операция И. Таблица истинности для этой функции имеет вид:
Из таблицы истинности следует, что операция И — это логическое умножение
В формальной логике операции логического умножения соответствуют связки и, а, но, хотя.
3. Логическая операция НЕ. Эта операция является специфичной для алгебры логики и не имеет аналога в обычной алгебре. Она обозначается чертой над значением переменной, либо знаком приставки перед значением переменной:
Читается в обоих случаях одинаково «Не А». Таблица истинности для этой функции имеет вид:
В вычислительной технике операцию НЕ называют отрицанием или инверсией, операцию ИЛИ — дизъюнкцией, операцию И — конъюнкцией. Набор логических функций “И”, “ИЛИ”, “НЕ” является функционально полным набором или базисом алгебры логики. С помощью него можно выразить любые другие логические функции, например операции “строгой дизъюнкции”, “импликации” и “эквивалентности” и др. Рассмотрим некоторые из них.
Набор логических функций “И”, “ИЛИ”, “НЕ” является функционально полным набором или базисом алгебры логики. С помощью него можно выразить любые другие логические функции, например операции “строгой дизъюнкции”, “импликации” и “эквивалентности” и др. Рассмотрим некоторые из них.
Логическая операция “строгая дизъюнкция”. Этой логической операции соответствует логическая связка “либо … либо”. Таблица истинности для этой функции имеет вид:
Операция “строгая дизъюнкция” выражается через логические функции “И”, “ИЛИ”, “НЕ” любой из двух логических формул:
и иначе называется операцией неравнозначности или “сложения по модулю 2”, так как при сложении чётного количества единиц, результатом будет “0”, а при сложении нечётного числа единиц, результат станет равен “1”.
Логическая операция “импликация”. Выражение, начинающееся со слов если, когда, коль скоро и продолжающееся словами то, тогда, называется условным высказыванием или операцией «импликация». Таблица истинности для этой функции имеет вид:
Таблица истинности для этой функции имеет вид:
Операцию “импликация” можно обозначить по-разному:
Эти выражения эквивалентны и читаются одинаково: «Игрек равен импликации от А и В». Операция “импликация” выражается через логические функции “ИЛИ”, “НЕ” в виде логической формулы
Логическая операция “эквивалентность” (равнозначность). Этой логической операции соответствуют логические связки “если и только если”, «тогда и только тогда, когда». Таблица истинности для этой функции имеет вид:
Операция “эквивалентность” обозначается по-разному. Выражения
обозначают одно и тоже, и можно сказать, что А эквивалентна В, если и только если они равнозначны. Логическая операция “эквивалентность” выражается через логические функции “И”, “ИЛИ”, “НЕ” в виде логической формулы
С помощью алгебры логики можно очень кратко записать законы формальной логики и дать им математически строгое доказательство.
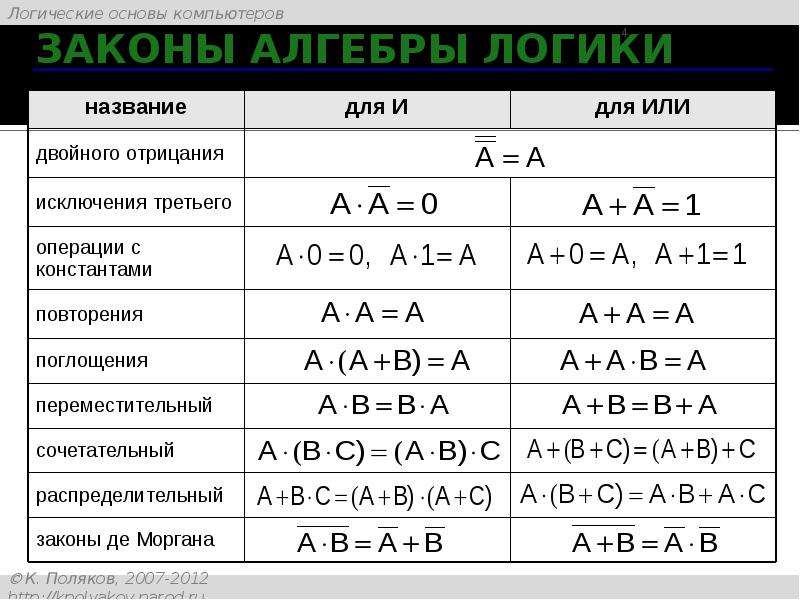
В алгебре логики, как в элементарной, справедливы переместительный (закон коммутативности), сочетательный (закон ассоциативности) и распределительный (закон дистрибутивности) законы, а также аксиома идемпотентности (отсутствие степеней и коэффициэнтов) и др., в записях которых используются логические переменные, принимающие только два значения — логический ноль и логическая единица. Применение этих законов позволяет производить упрощение логических функций, т.е. находить для них выражения, имеющие наиболее простую форму. Основные аксиомы и законы алгебры логики приведены в таблице:
Примеры использования основных аксиом и законов:| 1. |
Найди высказывания
Сложность: лёгкое |
1 |
2.
|
Определения связок
Сложность: лёгкое |
1 |
| 3. |
Обозначение логических операций
Сложность: среднее |
3 |
4.
|
Вид высказывания
Сложность: среднее |
2 |
| 5. |
Порядок действий
Сложность: среднее |
2 |
6.
|
Логическое выражение
Сложность: среднее |
2 |
| 7. |
Составление сложных высказываний
Сложность: сложное |
3 |
8.
|
Как на ЕГЭ. Количество наборов
Сложность: сложное |
1 |
Алгебра логики: основные понятия
Алгебра логики — раздел математики. Она оперирует логическими высказываниями.
Логическое высказывание — любое предложение в повествовательной форме, о котором можно однозначно сказать, истинно оно или ложно. Примеры логических высказываний:
- «Москва — столица России» (высказывание истинно).
- «После зимы наступает осень» (высказывание ложно).

Простое высказывание — логическое высказывание, состоящее из одного утверждения.
Сложное высказывание — логическое высказывание, состоящее из нескольких утверждения, объединенных с помощью «связок»: союзов «и», «или (либо)», частицы «не», связки «если, то» и др. Примеры сложных высказываний:
1. «Иван сдает экзамен по физике и информатике».
Высказывание содержит два утвеждения, объединенных «и»:
- Утверждение1: «Иван сдает экзамен по физике».
- Утверждение2: «Иван сдает экзамен по информатике».
2. «Игорь решил записаться в секцию по воллейболу или баскетболу».
Высказывание содержит два утвеждения, объединенных «или»:
- Утверждение1: «Игорь решил записаться в секцию по воллейболу».
- Утверждение2: «Игорь решил записаться в секцию по баскетболу».
3. «Если Илья будет много готовиться самостоятельно и будет заниматься с репетитором, то он поступит в ВУЗ».
Высказывание содержит три утвеждения, объединенных связкой «если, то» и союзом «и»:
- Утверждение1: «Илья будет много готовиться самостоятельно».
- Утверждение2: «Илья будет заниматься с репетитором».
- Утверждение2: «Илья поступит в ВУЗ».
Логические операции — «связки»: союзы и частицы естественного языка, образующие из простых высказываний сложные, представленные в формальном виде . Подробно основные логические операции рассмотрены в этой статье.
Логическое выражение — простое или сложное логическое высказывание, представленное в формальном виде. Примеры логических выражений:
- простое: A,
- сложное: AVB→C,
где A, B, C — утверждения;
Λ, V, → — логические операции.
Законы алгебры логики — законы, позволяющие преобразовывать логические выражения. Основные законы рассмотрены в этой этой статье.
Логическая переменная — переменная, которая может принимать значение 1 (истина) или 0 (ложь).
Логическая функция — функция, аргументы и значение которой могут принимать значение 1 (истина) или 0 (ложь).
Таблица истинности — таблица, которая используется для описания логических функций, в частности отдельных логических операций. Примеры таблиц истинности для часто используемых логических операций.
Диаграммы Эйлера-Венна — диаграммы, которые служат для наглядного представления всех вариантов пересечения нескольких множеств. В качестве множеств могут использоваться простые логические высказывания. Диаграмма строится для логического высказывания, которое содержит от одного до трех утверждений
О том, как строить такие диаграммы, можно прочесть в статье: «Диаграммы Эйлера-Венна». Типовые задачи на множества подробно разобраны в статье «Как решать задачи с помощью диаграмм Эйлера-Венна».
Перейти к решению задач на алгебру логики из демо ЕГЭ
Основы алгебры логики в одной странице — Сайт учителя информатики Лосева А.
 В.
В.Скачать шпаргалку «Основы алгебры логики в одной странице»
Логические операции
Инверсия (отрицание)
Инверсия — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда исходное высказывание ложно.
В выражениях обозначается ¬A или .
Читается «НЕ» (например, «не А»).
Конъюнкция (логическое умножение)
Конъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда истинны оба исходных высказывания.
В выражениях обозначается A ∧ B или A & B (знак может не указываться — AB).
Читается «И» (например, «А и Б»)
Дизъюнкция (логическое сложение)
Дизъюнкция — это логическая операция, образующая сложное высказывание, истинное тогда, когда истинно хотя бы одно из исходных высказываний.
В выражениях обозначается A ∨ B, иногда A + B.
Читается «ИЛИ» (например, «А или Б»)
Импликация (следование)
Импликация — это логическая операция, образующая сложное высказывание, ложное тогда и только тогда, когда первое исходное высказывание истинно, а второе — ложно.
В выражениях обозначается A ⇒ B или A → B.
Читается «ЕСЛИ…ТО» (например, «если А, то Б»)
Эквивалентность (равнозначность)
Эквивалентность — это логическая операция, образующая сложное высказывание, истинное тогда и только тогда, когда значения исходных высказываний совпадают.
В выражениях обозначается A ⇔ B или A ≡ B.
Читается «ТОГДА И ТОЛЬКО ТОГДА, КОГДА» (например, «А тогда и только тогда, когда Б»)
Таблицы истинности
Статью подготовил учитель информатики Лосев Антон Владимирович
Алгебра логики
Как мы уже говорили, любое логическое высказывание — это повествовательное предложение, про которое можно сказать истинно оно или ложно, но оно не может быть одновременно истинным и ложным. Как правило, любое логическое высказывание описывает свойства или состояние объекта (Лето было дождливым. Я был рад встретить старого друга.) или утверждает что-то об отношениях между объектами (Лев крупнее тигра. Тимур и Руслан — друзья). Логические высказывания (далее просто высказывания) обычно обозначаются латинскими буквами A, B, C и т. д. Если высказывание истинно, то его значение равно 1, если ложно — оно равно 0 (нулю).
Как правило, любое логическое высказывание описывает свойства или состояние объекта (Лето было дождливым. Я был рад встретить старого друга.) или утверждает что-то об отношениях между объектами (Лев крупнее тигра. Тимур и Руслан — друзья). Логические высказывания (далее просто высказывания) обычно обозначаются латинскими буквами A, B, C и т. д. Если высказывание истинно, то его значение равно 1, если ложно — оно равно 0 (нулю).
Пример 1
Найти значения следующих высказываний:
- A = «Париж — столица Франции»
- B = «2+3 = 2*3»
- С = «Луна вращается вокруг Земли»
Высказывания A и C являются истинными, высказывание B — ложным, то есть: A = 1, B = 0, C = 1.
Пример 2
Какие предложения являются высказываниями?
- Давай, убери свою комнату.
- Приходи сегодня на стадион играть в футбол.

- Зачем ты выкинула эту игрушку?
- Где находится школа?
В отношении этих предложений невозможно сказать, истинны они или ложны.
Не являются высказываниями повелительные и вопросительные предложения, потому что они не обладают свойством быть истинным или ложным.
Пример 3
Являются ли высказываниями следующие предложения?
- 2x + 8 > 20.
- Завтра я сдам экзамен по математике на «отлично»!
- Черепахи не летают, потому что холодильник закрыт.
- Я — сладкоежка, значит я люблю кататься на лыжах.
Являются ли они высказываниями? На первый взгляд — да. Но невозможно определить, истинны они или ложны. Чтобы понять истинно или ложно первое высказывание, необходимы дополнительные сведения. Вот если бы было написано так: «2х+8>20, при х > 6», то это было бы логическим высказыванием. О втором высказывании также нельзя сказать, истинно оно или ложно, потому что оно неопределённо и зависит от воли случая. Можно хорошо подготовиться, но если попадётся сложный билет или будет строгий экзаменатор, то можно получить и «тройку». А можно выучить только один билет, и, если тебе повезёт — попадётся именно он, тогда ты получишь «пятёрку». Ну а высказывания под номерами 3 и 4 — вообще бессмысленны, что также не позволяет назвать их логическими высказываниями. Логическими высказываниями также не могут быть бессмысленные предложения, а также высказывания, в которых присутствует неопределённость или недостаток информации.
Можно хорошо подготовиться, но если попадётся сложный билет или будет строгий экзаменатор, то можно получить и «тройку». А можно выучить только один билет, и, если тебе повезёт — попадётся именно он, тогда ты получишь «пятёрку». Ну а высказывания под номерами 3 и 4 — вообще бессмысленны, что также не позволяет назвать их логическими высказываниями. Логическими высказываниями также не могут быть бессмысленные предложения, а также высказывания, в которых присутствует неопределённость или недостаток информации.
Логические высказывания бывают простыми и сложными. Высказывание называется простым (элементарным), если оно является неделимым и никакая его часть сама не является высказыванием.
Пример 4
Даны два простых неделимых высказывания:
- Отец старше сына
- Отец младше деда
Эти два высказывания можно объединить в одно: «Отец старше сына, но младше деда». Получилось сложное высказывание.
Получилось сложное высказывание.
Сложным (составным) называется высказывание, составленное из простых высказываний.
Логические элементы эвм. алгебра логики. законы алгебры логики.
Для описания логики функционирования аппаратных и программных средств ЭВМ используется алгебра логики или, как ее часто называют, булева алгебра.Основоположником этого раздела математики был Дж. Буль.
Булева алгебра оперирует с логическими переменными, которые могут принимать только два значения: истина или ложь, обозначаемые соответственно 1 и 0.
основной системой счисления ЭВМ является двоичная СС, в которой также используются только две цифры: 1 и 0. Таким образом, одни и те же цифровые устройства ЭВМ могут применяться для обработки как числовой информации в двоичной СС, так и логических переменных.
Совокупность значений логических переменных x1, x2, …, xn называется набором переменных.
Общее число ФАЛ n переменных определяется возведением числа 4 в степень n, т. е. 4n. Существуют четыре ФАЛ одной логической переменной.
е. 4n. Существуют четыре ФАЛ одной логической переменной.
Функции F0(х) = 0 и F3(х) = 1 являются константами (функции не изменяются при изменении аргумента). Функция F1(х) = х повторяет значение аргумента х. Функция F2(x) называется отрицанием переменной или инверсией и обозначается так:
F2(x) = .
Из оставшихся десяти логических функций широкое распространение имеют функции F1(х) (конъюнкцияилилогическое умножение) и F7(х) (дизъюнкцияилилогическое сложение), которые совместно с функцией инверсии составляют функционально полную систему логических функций. С помощью этих трех функций можно представить (аналитически выразить) любую сколь угодно сложную логическую функцию. Очень важной для вычислительной техники является логическая функция исключающее ИЛИ (неравнозначность, сложение по модулю два). Функция исключающее ИЛИ обозначается символом A. Ниже приведены таблицы истинности для этих трех функций.
| Инверсия | |
| х | |
| x2 | x1 | x2 U x1 | x2 U x1 | x2A x1 |
Логические переменные, объединенные знаками логических операций, составляют логические выражения. При определении значения логического выражения принято следующее старшинство (приоритет) логических операций: сначала выполняется инверсия, затем конъюнкция и в последнюю очередь — дизъюнкция. Для изменения указанного порядка используют скобки.
При определении значения логического выражения принято следующее старшинство (приоритет) логических операций: сначала выполняется инверсия, затем конъюнкция и в последнюю очередь — дизъюнкция. Для изменения указанного порядка используют скобки.
В алгебре логики рассматриваются переменные, которые могут принимать только два значения: 0 и 1.
Кодирование информации. Кодовая таблица. Система кодирования ASCII. Система кодирования UNICODE.
Кодирование информации— это процесс формирования определенного представления информации.
все числа в компьютере представляются с помощью нулей и единиц (а не десяти цифр, как это привычно для людей). Иными словами, компьютеры обычно работают в двоичной системе счисления, поскольку при этом устройства для их обработки получаются значительно более простыми. Ввод чисел в компьютер и вывод их для чтения человеком может осуществляться в привычной десятичной форме, а все необходимые преобразования выполняют программы, работающие на компьютере.
Кодовая таблица
в кодовой таблице представлено определенное количество строк и только два столбца:
- в одном столбце указаны цифровые (в нашем случае двоичные) коды -слова, как сочетания элементов алфавита, расположенные в определенной последовательности;
- в другом столбце — их значения (нецифровой смысл, т. е. значения кодов).
Определение
Кодовая таблица — это совокупность цифровых (двоичных) кодов и их значений.
Самая распространенная система кодирования латиницы — ASCII — использует 7 бит на символ. Другие алфавиты обычно кодируются более сложным образом.Используются две основные кодировки латиницы — ASCII и EBCDIC (Extended Binary Coded Decimal Information Code), применяемая системами AS/400, System/370, System/390 и z90 фирмы IBM. Операции сравнения в современных процессорах реализованы как неразрушающее вычитание — мы производим те же действия, что и при обычном двоичном вычитании, но запоминаем не сам результат, а лишь флаги знака, переноса и равенства результата нулю. На основании значений этих флагов определяем результат сравнения: если разность равна нулю, сравниваемые символы одинаковы, если она положительна или отрицательна, один из символов больше или меньше другого.
На основании значений этих флагов определяем результат сравнения: если разность равна нулю, сравниваемые символы одинаковы, если она положительна или отрицательна, один из символов больше или меньше другого.
В кодировке ASCII (American Standard Code for Information Interchange — Американский стандартный код обмена информацией), например, все символы латиницы, цифры и большинство распространенных знаков препинания обозначаются кодами от 0 до 127, при этом коды букв расставлены в соответствии с латинским алфавитом. В США, как и в других англоязычных странах, латинский алфавит используется в неизмененном виде, а для передачи звуков, отсутствовавших в оригинальном латинском языке, применяется причудливая орфография. Большинство других европейских алфавитов обходит проблему несоответствия фонетик путем расширения набора символов латиницы — например, в немецком языке добавлены буквы o, a, u и ?. Другие языки имеют множество различных акцентов и диакритических символов, расставляемых над буквами для указания особенностей произношения. itatx eto po-russki, smenite kodirovku). Естественно, совместить такое сопоставление и алфавитную сортировку невозможно.
itatx eto po-russki, smenite kodirovku). Естественно, совместить такое сопоставление и алфавитную сортировку невозможно.
Стандартным решением в таких случаях является использование для сравнения и лексикографической сортировки промежуточных таблиц, в которых для каждого допустимого кода указан его номер в лексикографическом порядке. На уровне системы команд процессоры этого обычно не делают, но на уровне библиотек языков высокого уровня это осуществляется очень часто.
Статьи к прочтению:
Элемент Музыка
Похожие статьи:
-
Базовыми операциями алгебры логики
операции логического умножения – конъюнкции ( ), логического сложения – дизъюнкции ( ), исключающего или – (A), логического отрицания – инверсии ( )….
-
Системы функций алгебры логики
Рассмотрим теорему Жегалкина, которая играет важную роль в алгебре логики.
 Теорема Жегалкина. Любая булева функция может быть представлена многочленом…
Теорема Жегалкина. Любая булева функция может быть представлена многочленом…
Алгебра и логика | Дом
В этом журнале публикуются результаты последних исследований в области современной общей алгебры и логики, рассматриваемых преимущественно с алгебраической точки зрения. Алгебраические статьи, составляющие основную часть содержания, посвящены исследованиям в таких областях, как упорядоченные, почти без кручения, нильпотентные и метабелевы группы; кольца изоморфизма; алгебры Ли; подгруппы Фраттини; и кластеры алгебр.В области логики журнал освещает такие темы, как иерархические множества, логические автоматы и рекурсивные функции.
Алгебра и логика — перевод рецензируемого журнала Алгебра и логика , издания Сибирского фонда алгебры и логики и Института математики СО РАН.
Дополнительная информация доступна на сайте редакции по следующей ссылке:
http://math.nsc.ru/~alglog/
- Публикует последние исследования в области современной общей алгебры и логики, рассматриваемые преимущественно с алгебраической точки зрения.

- Содержит статьи по алгебре, составляющие основную часть содержания и посвященные исследованиям в таких областях, как упорядоченные, почти без кручения, нильпотентные и метабелевы группы; кольца изоморфизма; алгебры Ли; подгруппы Фраттини; и кластеры алгебр.
Информация журнала
- Главный редактор
- Издательская модель
- Гибридный.Как публиковаться у нас, в том числе в открытом доступе
Показатели журнала
- 0,753 (2020)
- Импакт-фактор
- 0,668 (2020)
- Пятилетний импакт-фактор
- 12 411 (2020)
- Загрузки
Алгебра логики: с чего на самом деле начал Буль
Аннотация
Хотя концепция булевой алгебры уходит своими корнями в алгебру логики, алгебра логики девятнадцатого века была схемой символизации логических отношений как алгебраических таким образом, чтобы логические выводы могли быть выполнены с помощью алгебраических манипуляций. Буль написал три работы по логике, но именно в первой из них, 1847 г. «Математический анализ логики, будучи эссе на пути к исчислению дедуктивной логики» , можно найти наиболее тщательное алгебраическое развитие. Однако ни один из трех подходов не имел адекватного отношения к экзистенциальным утверждениям, и, по сути, ни один из последователей Буля также не имел с ними адекватного отношения, хотя некоторые из более поздних версий алгебры логики существенно улучшили трактовку Буля. Несмотря на эти улучшения, в течение приблизительно пятидесяти лет, составлявших период, когда алгебра логики была основным направлением математических исследований в логике, логики так и не пришли к согласию относительно единой системы обозначений.Наконец, на рубеже веков термин «алгебра логики» стал использоваться в современном смысле булевой алгебры, и поэтому то, что Буль начал в 1847 году, теперь по существу скрыто.
Буль написал три работы по логике, но именно в первой из них, 1847 г. «Математический анализ логики, будучи эссе на пути к исчислению дедуктивной логики» , можно найти наиболее тщательное алгебраическое развитие. Однако ни один из трех подходов не имел адекватного отношения к экзистенциальным утверждениям, и, по сути, ни один из последователей Буля также не имел с ними адекватного отношения, хотя некоторые из более поздних версий алгебры логики существенно улучшили трактовку Буля. Несмотря на эти улучшения, в течение приблизительно пятидесяти лет, составлявших период, когда алгебра логики была основным направлением математических исследований в логике, логики так и не пришли к согласию относительно единой системы обозначений.Наконец, на рубеже веков термин «алгебра логики» стал использоваться в современном смысле булевой алгебры, и поэтому то, что Буль начал в 1847 году, теперь по существу скрыто.
Информация
Опубликовано: январь 1994 г.
Впервые доступно в Project Euclid: 6 марта 2008 г.
Темы:
Начальный: 03-03
Вторичный: 01А55 , 03G05 , 06-03 , 06E99
Права: Copyright © 1994 The Review of Modern Logic
Алгебраическая логика – обзор
2 Логика уравнений и их модели
В начале 20-го века понятия абстрактной алгебры, алгебраической логики и универсальной алгебры появляются, в частности, в работах Альфреда Тарского и Гаррета Биркгофа.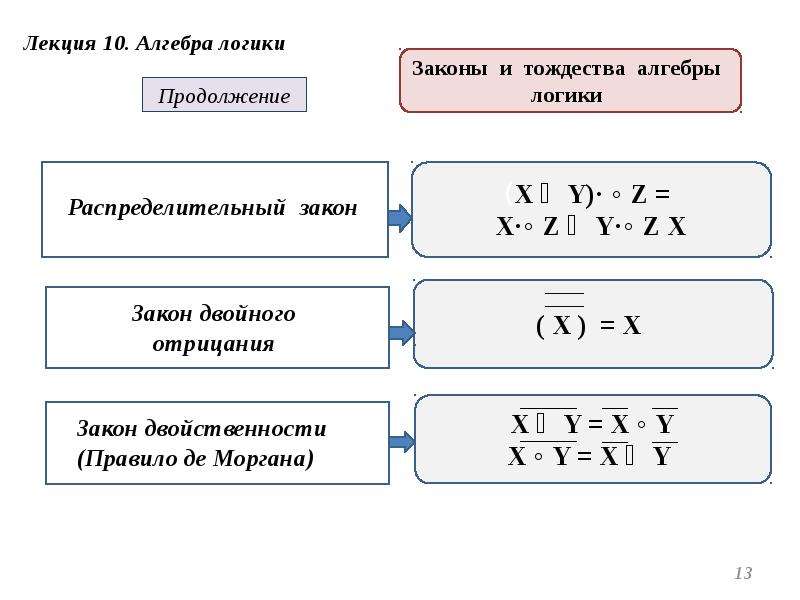 Функциональные символы и равенства на логическом уровне интерпретируются операциями над алгебрами.
Функциональные символы и равенства на логическом уровне интерпретируются операциями над алгебрами.
В эквациональной логике формулы строятся из предиката равенства и членов первого порядка, т. е. правильно построенных выражений, построенных на множестве F функциональных символов с арностью (числом аргументов) и множестве X переменных. Набор термов обозначается T(F,X). Переменные терма могут быть конкретизированы подстановками, определенными как отображения σ из подмножества переменных в термы и расширены на термы с сохранением их структуры.
Обозначается эквациональная аксиома или равенство (∀ X , l = r ), где X — множество переменных, встречающихся в терминах l и r . Из набора аксиом можно вывести новые равенства с помощью правил вывода. Система вывода для эквациональной логики представлена на рисунке 1.
Рисунок 1. Правила вывода для логики уравнений E , обозначаемое Th(E), представляет собой набор равенств, которые можно получить, начиная с E , применяя правила вывода, приведенные на рисунке 1. Мы пишем
Мы пишем
E⊦s=tif(s=t)∈Th(E).
Более компактной системой вывода является так называемая замена равных равными: для набора E аксиом мы пишем s ↔ E t , если есть равенство l = r (или r = l ) в E , так что подтермин s в позиции ω , обозначенный s | Ω , представляет собой экземпляр σ ( л ) л для некоторого замещения σ и, если T просто отличается от S , содержащим σ ( R ) в положении ω , что обозначается как t = s [ σ ( r )] ω .Рефлексивное транзитивное замыкание вышеуказанного симметричного отношения обозначается ↔*E. Это отношение конгруэнтности, частное множества термов T(F,X) по ↔*E обозначается T(F,X)/E, а класс эквивалентности терма t обозначается 〈 t 〉 E .
Следующая теорема Биркгофа [Birkhoff, 1935] устанавливает эквивалентность между двумя системами вывода для вывода равенства:
E⊦s=tiffs↔*Et.
Модели эквациональной логики — это F-алгебры, представляющие собой непустые множества (называемые носителями), с операциями, интерпретирующими символы в F.Отображения, сохраняющие интерпретации символов, называются гомоморфизмами.
В непустом классе C F-алгебр могут существовать две особенно интересные алгебры: одна — это начальная алгебра I, такая, что для любой алгебры A в C существует единственный гомоморфизм ϕ:I→A Другая — это свободная алгебра T над набором переменных X такая, что: для любой алгебры A в C и любого назначения ν: X→A ν можно расширить с помощью единственного гомоморфизма ϕ:T→A.
Обратите внимание, что по определению начальную алгебру также можно рассматривать как свободную алгебру над пустым набором переменных.Когда он существует, он уникален с точностью до изоморфизма.
Учитывая набор E аксиом равенства, алгебра A является моделью E , если для каждой аксиомы s = t в E , для любого назначения s 0 переменных и t в носитель A, ν ( s ) = ν ( t ). Мы также говорим, что в A справедливо равенство s = t , и это обозначается A⊧s=t.Mod(E) обозначает набор моделей E . Основная теорема Биркгофа [Birkhoff, 1935] связывает модели и эквациональную дедукцию: для любого набора аксиом E , для любых термов s , t∈T(F,X),
Мы также говорим, что в A справедливо равенство s = t , и это обозначается A⊧s=t.Mod(E) обозначает набор моделей E . Основная теорема Биркгофа [Birkhoff, 1935] связывает модели и эквациональную дедукцию: для любого набора аксиом E , для любых термов s , t∈T(F,X),
Mod(E)⊧s =tiffT(F,X)/E⊧s=tiffE⊦s=tiffs↔*Et
т.е. валидность в моделях эквивалентна замене равенства на равное, поэтому семантическая проверка может быть достигнута полностью синтаксически. Мы пишем s = E t тогда и только тогда, когда Mod(E)⊧s=t.Благодаря этим результатам обозначения s = E t и s↔*Et могут использоваться взаимозаменяемо.
В классе алгебр, являющихся моделями E , свободной алгеброй над X является (изоморфна) алгебра T(F,X)/E. В классе алгебр, являющихся моделями E , исходной алгеброй является (изоморфная) алгебра T(F)/E.
Когда указана только арность функций, легко построить такие термины, как разделить (2, 0), которые не имеют интерпретаций. Введя тип Nat для натуральных чисел и Nat + для ненулевых натуральных чисел, и набрав функцию разделить с рангом Nat , Nat + 050 Nat 09 09 09 09 Nat такие письменные термины не удовлетворяют ограничению ввода. Сортировки были введены для классификации терминов и типизации аргументов и результатов функций. В многообразной подписи функция F имеет ранг (или тип) F : S 1 … S N ↦ S , с S I , s в наборе сортов S и переменные тоже типизированы, например x : s означает, что переменная x имеет вид s .Многосортные термины строятся на многосортных сигнатурах и классифицируются в соответствии с их видами. Многосортные алгебры имеют носители, соответствующие каждому сорту, и операции с отсортированными аргументами.
Введя тип Nat для натуральных чисел и Nat + для ненулевых натуральных чисел, и набрав функцию разделить с рангом Nat , Nat + 050 Nat 09 09 09 09 Nat такие письменные термины не удовлетворяют ограничению ввода. Сортировки были введены для классификации терминов и типизации аргументов и результатов функций. В многообразной подписи функция F имеет ранг (или тип) F : S 1 … S N ↦ S , с S I , s в наборе сортов S и переменные тоже типизированы, например x : s означает, что переменная x имеет вид s .Многосортные термины строятся на многосортных сигнатурах и классифицируются в соответствии с их видами. Многосортные алгебры имеют носители, соответствующие каждому сорту, и операции с отсортированными аргументами.
Правила дедукции для эквациональной дедукции, представленные на рисунке 1, обобщаются на многосортную структуру при условии, что нет пустой сортировки . Goguen и Meseguer сделали точный анализ возможных проблем, которые могут возникнуть, когда эта гипотеза не выполняется [Meseguer and Goguen, 1985].Чтобы правила вывода, показанные на рис. 1, оставались в силе для многосортной логики, следует рассматривать только модели с непустыми сортировками.
Goguen и Meseguer сделали точный анализ возможных проблем, которые могут возникнуть, когда эта гипотеза не выполняется [Meseguer and Goguen, 1985].Чтобы правила вывода, показанные на рис. 1, оставались в силе для многосортной логики, следует рассматривать только модели с непустыми сортировками.
Такая структура типов обеспечивает концептуальную ясность и обнаружение многих ошибок. Однако реализация строгой типизации в многосортной логике довольно жесткая и не обладает выразительной силой, необходимой для обработки ошибок и пристрастности, см. обзор Mosses и все различные подходы к решению этих проблем [Mosses, 1997]. Один из них, начатый в 1977 году Гогеном, приводит к [Goguen and Meseguer, 1987], где предлагается структура типов с сортировкой по порядку, делающая многие кажущиеся частичными или проблематичными функции полными и четко определенными на правом подвиде.Эта структура типа с сортировкой по порядку обеспечивается частичным упорядочением множества сортировок, которое интерпретируется как включение множества в алгебры с сортировкой по порядку. Например, отношение подсортировки Nat < Int интерпретируется как включение N ⊆ Z натуральных чисел в целые числа в стандартной модели. Кроме того, операторные символы, такие как _+_, могут иметь перегруженные объявления, например _+_: Nat Nat -> Nat, _+_: Int Int -> Int, которые необходимы для получения того же результата при ограничении аргументами те же подвиды.Перегрузка — это синтаксическая возможность обработки операторов, определенных для разных подмножеств, которые могут пересекаться, для достижения своего рода полиморфизма. Кроме того, такие операторы в общем случае являются частичными функциями, что выражается благодаря отношению подсорта.
Например, отношение подсортировки Nat < Int интерпретируется как включение N ⊆ Z натуральных чисел в целые числа в стандартной модели. Кроме того, операторные символы, такие как _+_, могут иметь перегруженные объявления, например _+_: Nat Nat -> Nat, _+_: Int Int -> Int, которые необходимы для получения того же результата при ограничении аргументами те же подвиды.Перегрузка — это синтаксическая возможность обработки операторов, определенных для разных подмножеств, которые могут пересекаться, для достижения своего рода полиморфизма. Кроме того, такие операторы в общем случае являются частичными функциями, что выражается благодаря отношению подсорта.
Хотя все основные результаты эквациональной логики обобщаются на случай многих сортировок, дедукция сортировки по порядку более тонкая [Goguen, 1992]. Например, замена equals на equals и переписывание терминов требуют тщательного анализа, который был начат в [Goguen et al ., 1985] и получил дальнейшее развитие в [Isakowitz and Gallier, 1988; Кирхнер и др.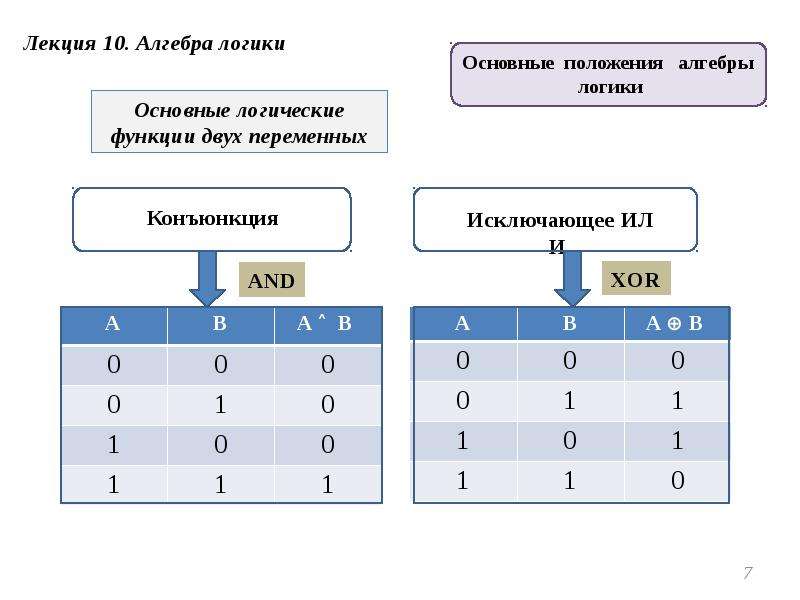 ., 1988].
., 1988].
Все эти концепции использовались для определения семантики нескольких спецификаций и языков программирования. Отметим два из них.
Язык программирования OBJ возник в результате новаторской работы Гогена в Калифорнийском университете в Лос-Анджелесе [Goguen and Tardo, 1979; Goguen and Malcolm, 2000] в конце семидесятых годов, позже полностью разработанная в SRI International Гогеном, Месегером и несколькими приглашенными сотрудниками [Futatsugi et al ., 1985; Goguen и др. ., 1987; Jouannaud и др. ., 1992; Кирхнер и др. ., 2000]. OBJ — это язык алгебраического программирования, последние версии которого (OBJ-2 [Futatsugi et al ., 1985] и OBJ-3 [Goguen et al ., 1987]) основаны на эквациональной логике с сортировкой по порядку. Программы представляют собой сортированные по порядку эквациональные спецификации, а вычисления представляют собой упорядоченную по порядку эквациональную дедукцию [Kirchner et al . , 1988].
, 1988].
В конце 1990-х годов инициатива CoFI была создана и спонсирована рабочей группой IFIP WG1.3. Это была открытая совместная работа по созданию общей структуры для алгебраической спецификации и разработки вместе с так называемым общим языком алгебраической спецификации Casl, языком спецификации общего назначения, основанным на логике первого порядка [Astesiano et al . , 2002], который также поддерживает частичные функции и подсортировку. Casl был разработан с целью включения многих существующих языков спецификаций и реализации наиболее важных функций алгебраических спецификаций.
Вклад в философию нотации [продолжение в томе. 7, нет. 3] на JSTOR
Перейти к основному содержанию Есть доступ к библиотеке? Войдите через свою библиотекуВесь контент Картинки
Поиск JSTOR Регистрация Вход-
Поиск
- Расширенный поиск
- Изображения
-
Просматривать
-
По тематике
Журналы и книги -
По названию
Журналы и книги - Издатели
- Коллекции
- Изображения
-
По тематике
-
Инструменты
- Рабочее пространство
- Анализатор текста
- Серия JSTOR Understanding
- Данные для исследований
Логика как алгебра | Математическая ассоциация Америки
Цель Логика как алгебра ясно выражена в предисловии:
.…чтобы показать, что логику можно (и, возможно, следует) рассматривать с алгебраической точки зрения. При таком рассмотрении многие из его основных понятий оказываются старыми друзьями, знакомыми алгебраическими понятиями, «замаскированными» под логическую одежду. Более того, становится более ясной связь между основными теоремами предмета и известными теоремами алгебры. Даже доказательства часто выигрывают в простоте.
С этой целью авторы Пол Халмос и Стивен Гивант написали краткий увлекательный текст, предназначенный как для любителей, так и для профессионалов, для которого требуется только курс современной алгебры в качестве основы.
Поскольку одним из возможных вариантов использования этой книги является текст курса, может оказаться полезным краткое изложение ее содержания:
- Что такое логика?
Вводная притча и мини-логика подготавливают читателя к встрече с логикой высказываний. - Исчисление высказываний
Достаточно традиционное развитие логики высказываний.
- Булева алгебра
Основы булевых алгебр, мотивированные их сходством с исчислением высказываний.Содержит хороший пример силы алгебраического метода: доказательство непротиворечивости логики высказываний путем демонстрации того, что множество предложений является нетривиальной булевой алгеброй. - Универсальная булева алгебра
Каталог терминологии и фактов о булевых подалгебрах, гомоморфизмах, идеалах, фильтрах и т. д. Кульминацией является теорема Стоуна о представлении, которая используется для доказательства того, что исчисление высказываний индуцирует свободную булеву алгебру. (Эта глава кажется особенно полезной для студентов в качестве обзора абстрактной алгебры.) - Логика через алгебру
Ядро книги, доказывающее полноту и правильность булевой логики. - Решетки и бесконечные операции
Краткое отступление, без привязки к логике. (Это немного озадачивает, так как было бы легко упомянуть бесконечные конъюнкции и дизъюнкции наряду с бесконечными инф и суп. )
) - Монадическое исчисление предикатов
Представлена теория одного квантора в булевой логике (т.е., каждое высказывание имеет не более одного квантора) и применяет его к классическим силлогизмам.
Проза Логика как Алгебра элегантна и ясна. Основанный на заметках из курса, который Халмош читал несколько раз, текст создает у читателя впечатление, будто он заглянул на эти лекции. Тон разговорный: теоремы и доказательства возникают естественно и лишь изредка выделяются из основного текста. В результате книгу приятно читать.
В качестве текста курса курс «Логика как алгебра» подойдет для курса «Введение в алгебраическую логику», хотя инструкторы должны знать, что в нем нет упражнений.Это, безусловно, естественным образом ведет к «Алгебраической логике » Халмоша, , которая развивает теорию множественных кванторов с помощью полиадических алгебр.
Тем не менее, я считаю, что есть лучший выбор учебников для Введения в логику (в отличие от Алгебраической логики). Одним из примеров является «Математическая логика » Эббингауза, Флума и Томаса. Частичный список его оглавления иллюстрирует часть того, что отсутствует в Логика как алгебра: Синтаксис языков первого порядка, Семантика языков первого порядка, Теорема Левенгейма-Скулема и Теорема компактности, Расширения первого порядка. Логика порядка и ограничения формального метода (включая теорему Гёделя о неполноте).Халмош и Гиван упоминают компактность, но ничего не говорят о ее удивительной силе. И их подход не поддается четкому разграничению синтаксиса и семантики. К сожалению, это усугубляется несколькими ключевыми типографскими ошибками в теореме о дедукции и вокруг нее на странице 91: символ семантического следствия используется, когда (я почти уверен) имелся в виду синтаксический символ.
Одним из примеров является «Математическая логика » Эббингауза, Флума и Томаса. Частичный список его оглавления иллюстрирует часть того, что отсутствует в Логика как алгебра: Синтаксис языков первого порядка, Семантика языков первого порядка, Теорема Левенгейма-Скулема и Теорема компактности, Расширения первого порядка. Логика порядка и ограничения формального метода (включая теорему Гёделя о неполноте).Халмош и Гиван упоминают компактность, но ничего не говорят о ее удивительной силе. И их подход не поддается четкому разграничению синтаксиса и семантики. К сожалению, это усугубляется несколькими ключевыми типографскими ошибками в теореме о дедукции и вокруг нее на странице 91: символ семантического следствия используется, когда (я почти уверен) имелся в виду синтаксический символ.
У меня есть еще одна последняя проблема, которая имеет более личный характер. Как логик, у меня есть некоторые проблемы с тоном, который книга принимает по отношению к логике.Рассмотрим разницу между названием пятой главы «Логика через алгебру» и названием книги «Логика как алгебра». Первый указывает маршрут к независимому субъекту, что нормально; второй отдает первенство алгебре, что кажется неуместным.
Первый указывает маршрут к независимому субъекту, что нормально; второй отдает первенство алгебре, что кажется неуместным.
Это было бы мелкой придиркой, если бы не соответствие, установленное между логикой и безмыслием в притче первой главы «Что такое логика?» Он появляется в разделе, озаглавленном «Считать или думать». Во втором абзаце нам говорится: «Содержанием логики являются предложения и выводы, а методы логики — перечисление (счет) и комбинаторность (упорядочение).Это приводит к проблеме подсчета количества матчей в турнире на выбывание с 1025 игроками. Даны три решения: подсчет каждого раунда и сложение суммы, подсчет и использование геометрического ряда для подсчета суммы и «чистая мысль». — понимая, что каждый игрок, кроме чемпиона, проиграет ровно один матч, поэтому будет сыграно 1024 матча. Суть в том, что «чистая мысль всегда лучше, чем бездумный подсчет». Кто может не согласиться? Но в этом контексте логика изображался как метод счета, и остается предположить, что алгебраический метод, который будет представлен, ближе к чистому мышлению. Эта переписка повторяется на протяжении всей книги.
Эта переписка повторяется на протяжении всей книги.
Возможно, это безобидно, если читатель — профессиональный математик. Но я предполагаю, что у студента, впервые познакомившегося с логикой через «Логика как алгебра », вряд ли возникнет желание изучать ее дальше. Эта книга, безусловно, не дает ей стимула для этого. Даже для профессионала я бы рекомендовал сбалансировать этот подход с альтернативой, такой как Абрахама Робинсона «Введение в теорию моделей и метаматематику алгебры», , просто чтобы укрепить идею о том, что две дисциплины, алгебра и логика, поддерживают друг друга.
И последнее замечание: обсуждавшаяся выше притча о теннисе уже появлялась в работе Халмоша. В «Математике как творческом искусстве» (см. его Selecta: Expository Writing) он используется для иллюстрации того, что абстрактная математика — это нечто большее, чем просто счет. В этой обстановке я не мог не согласиться.
Марк Джонсон — доцент кафедры математики и информатики Центрального колледжа. Помимо логики, его интересы включают Билла Эванса, Телониуса Монка, Миннесотских близнецов и буррито размером с вашу голову.
Помимо логики, его интересы включают Билла Эванса, Телониуса Монка, Миннесотских близнецов и буррито размером с вашу голову.
Истоки булевой алгебры в логике классов: Джордж Буль, Джон Венн и К. С. Пирс
Введение
Рис. 1. Слева направо: Пионеры булевой алгебры Джордж Буль, Джон Венн и Чарльз Сандерс Пирс (Источник: MacTutor History of Mathematics Archive)
Практически в один и тот же день в 1847 году выдающимися британскими математиками были опубликованы две крупные новые работы по логике: «Формальная логика » [3] Августа Де Моргана (1806–1871) и «Математический анализ логики » [1] Джордж Буль (1815–1864).Оба автора стремились расширить границы традиционной логики, разработав общий метод представления и обработки логически обоснованных выводов или, как объяснил Де Морган в письме Булю от 1847 г., разработать «механические способы совершения переходов с обозначениями, которые представляют нашу логику». головная работа» [7, с. 25]. В отличие от метода, предложенного Де Морганом, подход Буля предпринял важный шаг, явно приняв для этой цели алгебраические методы. Как позже провозгласил сам Де Морган, «г.Булевское обобщение форм логики, безусловно, самое смелое и оригинальное. . . (цитируется по [4, с. 174]).
головная работа» [7, с. 25]. В отличие от метода, предложенного Де Морганом, подход Буля предпринял важный шаг, явно приняв для этой цели алгебраические методы. Как позже провозгласил сам Де Морган, «г.Булевское обобщение форм логики, безусловно, самое смелое и оригинальное. . . (цитируется по [4, с. 174]).
Несмотря на явно алгебраический характер, смелый и оригинальный подход Буля привел к очень странной новой системе алгебры. Например, среди законов, которые выполняются в системе, можно найти как стандартный закон дистрибутивности умножения над сложением \(x(y+z)=xy+xz\), так и необычный на вид двойной закон дистрибутивности сложения над умножением \ (x+yz=(x+y)(x+z).\) В своей зрелой работе по логике An Investigation of the Laws of Thought [2], опубликованной в 1854 г., Буль дополнительно исследовал, каким образом законы этой алгебраической системы сходны и отличаются от законов стандартной алгебры, а также как причины, по которым он удовлетворяет этим различным законам. По иронии судьбы, Законы Мышления изначально не были хорошо приняты; Буль и его друг, понесшие расходы на его первоначальную печать, вероятно, не возместили свои затраты. Абстрактная структура булевой алгебры, которая в конечном итоге развилась из работ Буля, стала, однако, не только важной областью изучения математики, но и мощным инструментом проектирования и изучения электронных схем и компьютерной архитектуры.
По иронии судьбы, Законы Мышления изначально не были хорошо приняты; Буль и его друг, понесшие расходы на его первоначальную печать, вероятно, не возместили свои затраты. Абстрактная структура булевой алгебры, которая в конечном итоге развилась из работ Буля, стала, однако, не только важной областью изучения математики, но и мощным инструментом проектирования и изучения электронных схем и компьютерной архитектуры.
Из работ многочисленных людей, которые внесли свой вклад в историю рождения и развития булевой алгебры, мы создали три основных исходных модуля проекта, подходящие для студентов вводных или промежуточных курсов дискретной математики:
- проект, в котором исследуется применение булевой алгебры к проблеме проектирования схем, представленный в статье Convergence Applications of Boolean Algebra: Claude Shannon and Circuit Design;
-
проект, который исследует структуру булевой алгебры как абстрактной аксиоматизированной структуры, представленный в статье Convergence , Булева алгебра как абстрактная структура: Эдвард В.
 Хантингтон и аксиоматизация;
Хантингтон и аксиоматизация; - настоящий проект «Происхождение булевой алгебры в логике классов: Джордж Буль, Джон Венн и К. С. Пирс», который развивает элементарную теорию множеств на основе исходных отрывков из собственных работ Буля и двух первых математиков, внесших изменения в Подход Буля к логике.
Все три проекта являются частью большой коллекции, опубликованной в Convergence, , и весь вводный курс по дискретной математике может быть изучен на основе подборки проектов из этой коллекции.Дополнительные проекты см. в разделе «Основные исторические источники в классе: дискретная математика и информатика».
Наш проект «Истоки булевой алгебры в логике классов: Джордж Буль, Джон Венн и К. С. Пирс» готов для студентов, а исходный код Latex также доступен для преподавателей, которые могут захотеть изменить проект для студентов. Подробные «Примечания для инструктора», представленные далее, также прилагаются к самому проекту.
Рис. 2. Нижняя треть витража, посвященного Джорджу Булю, в Линкольнском соборе в Линкольне, Англия, где родился Буль (Источник: Wikimedia Commons)
2. Нижняя треть витража, посвященного Джорджу Булю, в Линкольнском соборе в Линкольне, Англия, где родился Буль (Источник: Wikimedia Commons)
Заметки для инструктора
Проект «Истоки булевой алгебры в логике классов: Джордж Буль, Джон Венн и К. С. Пирс» предназначен для вводного или среднего курса дискретной или конечной математики, включающего изучение элементарной теории множеств. Без явного введения современных обозначений для операций над множествами проект развивает современное понимание этих операций и их основных свойств в контексте ранних попыток разработать символическую алгебру для логики.Хотя проект фокусируется на том, что сейчас можно было бы назвать «введением в теорию множеств», он также закладывает основу для более абстрактного обсуждения булевой алгебры как дискретной аксиоматизированной структуры. Соответственно, этот проект можно также использовать в качестве введения в один или оба сопутствующих проекта, описанных ниже, в любом курсе, который рассматривает булеву алгебру с точки зрения математики или информатики. Помимо определенного уровня математической зрелости, соответствующего типичному опыту исчисления I, для этого проекта не требуется предварительных условий.Сильные учащиеся на уровне, предшествующем математическому анализу, также могут выполнить предыдущие разделы этого проекта.
Помимо определенного уровня математической зрелости, соответствующего типичному опыту исчисления I, для этого проекта не требуется предварительных условий.Сильные учащиеся на уровне, предшествующем математическому анализу, также могут выполнить предыдущие разделы этого проекта.
Начиная с работ Буля об использовании символической алгебры для представления логических классов в его Исследование законов мышления [2] (раздел 2), этот проект вводит операции логического сложения (т.т. е. объединение множеств), логическое умножение (т. е. пересечение множеств) и логическое различие (т. е. различие множеств) и исследует определенные ограничения, наложенные на их использование Булем, которые с тех пор были сняты. Вводятся также основные законы этих операций, разработанные и обоснованные Булем; эти обоснования частично основывались на его определениях операций и частично на аналогии его символов с символами «стандартной алгебры». Раздел 3) и Чарльза Сандерса Пирса в его «Об усовершенствовании логического исчисления Буля» [5] (Раздел 4), при этом уровень абстракции неуклонно возрастает в этих разделах.Проект завершается (раздел 5) кратким изложением того, как «Алгебра логики» Буля соотносится с элементарной теорией множеств в том виде, в каком она обычно представлена сегодня, и обсуждается, как элементарная теория множеств (если рассматривать ее как алгебраическую структуру) служит конкретным примером булева алгебра. Стандартные (студенческие) обозначения и свойства для операций теории множеств, используемых сегодня, включены и сравниваются со стандартными (студенческими) обозначениями и аксиомами для булевой алгебры в этом разделе. Вопросы, связанные с использованием языка и операциями над множествами, которые вызывают трудности у многих учащихся, но которые игнорируются или не признаются современными авторами учебников, также подробно рассматриваются в трудах Буля и Венна (разделы 3 и 4) и дополнительно исследуются в рамках проекта.
Вводятся также основные законы этих операций, разработанные и обоснованные Булем; эти обоснования частично основывались на его определениях операций и частично на аналогии его символов с символами «стандартной алгебры». Раздел 3) и Чарльза Сандерса Пирса в его «Об усовершенствовании логического исчисления Буля» [5] (Раздел 4), при этом уровень абстракции неуклонно возрастает в этих разделах.Проект завершается (раздел 5) кратким изложением того, как «Алгебра логики» Буля соотносится с элементарной теорией множеств в том виде, в каком она обычно представлена сегодня, и обсуждается, как элементарная теория множеств (если рассматривать ее как алгебраическую структуру) служит конкретным примером булева алгебра. Стандартные (студенческие) обозначения и свойства для операций теории множеств, используемых сегодня, включены и сравниваются со стандартными (студенческими) обозначениями и аксиомами для булевой алгебры в этом разделе. Вопросы, связанные с использованием языка и операциями над множествами, которые вызывают трудности у многих учащихся, но которые игнорируются или не признаются современными авторами учебников, также подробно рассматриваются в трудах Буля и Венна (разделы 3 и 4) и дополнительно исследуются в рамках проекта. вопросы в этих разделах.
вопросы в этих разделах.
Следуя усовершенствованиям, внесенным в символическую алгебру Буля руками Венна и Пирса, этот проект дает учащимся возможность своими глазами увидеть, как протекает процесс разработки и уточнения математической системы, как математики делают и объясняют свой выбор на этом пути, а также то, как со временем изменились стандарты строгости в этом отношении.Таким образом, помимо развития свойств теории множеств как конкретного конкретного примера булевой алгебры, проект способен исследовать множество математических тем, в том числе понятие обратной операции, понятие двойственности, вопросы, связанные с математическими обозначения, а также стандарты строгости и доказательства. Следуя одной или нескольким из этих тем в рамках проекта, преподаватели имеют значительную свободу действий в адаптации проекта к своим целям для конкретной группы студентов. Инструктору рекомендуется заранее проработать все упражнения, чтобы определить, какие из них он может пропустить.Например, раздел 4 можно было бы полностью опустить, если бы инструктор решил не исследовать доказательства свойств элементарного множества с более абстрактной точки зрения, которую принял Пирс. Для полного завершения проекта требуется примерно две недели.
Следуя одной или нескольким из этих тем в рамках проекта, преподаватели имеют значительную свободу действий в адаптации проекта к своим целям для конкретной группы студентов. Инструктору рекомендуется заранее проработать все упражнения, чтобы определить, какие из них он может пропустить.Например, раздел 4 можно было бы полностью опустить, если бы инструктор решил не исследовать доказательства свойств элементарного множества с более абстрактной точки зрения, которую принял Пирс. Для полного завершения проекта требуется примерно две недели.
Два сопутствующих проекта по булевой алгебре также доступны в качестве продолжения этого вводного проекта, каждый из которых или оба могут также использоваться независимо от проекта Буля-Венна-Пирса. Кроме того, любой из двух сопутствующих проектов можно использовать в качестве предварительного или дополняющего другого сопутствующего проекта.
Сопутствующий проект «Булевая алгебра как абстрактная структура: Эдвард В. Хантингтон и аксиоматизация» исследует раннюю аксиоматизацию булевой алгебры как абстрактной структуры на основе чтения статьи Хантингтона 1904 года «Наборы независимых постулатов для алгебры логики». В дополнение к введению теперь стандартных аксиом для структуры булевой алгебры, проект иллюстрирует, как использовать эти постулаты для доказательства некоторых основных свойств булевых алгебр. Конкретные вопросы проекта также дают учащимся возможность попрактиковаться в использовании символических обозначений и побуждают их анализировать логическую структуру выраженных в количественном выражении утверждений.В проекте также исследуется использование Хантингтоном двузначной булевой алгебры на \(K = \{0, 1\}\) — впервые изученной Джорджем Булем в его работе по логике классов — в качестве модели для установления независимости и непротиворечивость одного из его наборов постулатов. В заключительном разделе проекта обсуждаются современные (студенческие) обозначения и аксиомы для булевых алгебр, а также предлагаются несколько практических упражнений для закрепления идей, разработанных в предыдущих разделах.
В дополнение к введению теперь стандартных аксиом для структуры булевой алгебры, проект иллюстрирует, как использовать эти постулаты для доказательства некоторых основных свойств булевых алгебр. Конкретные вопросы проекта также дают учащимся возможность попрактиковаться в использовании символических обозначений и побуждают их анализировать логическую структуру выраженных в количественном выражении утверждений.В проекте также исследуется использование Хантингтоном двузначной булевой алгебры на \(K = \{0, 1\}\) — впервые изученной Джорджем Булем в его работе по логике классов — в качестве модели для установления независимости и непротиворечивость одного из его наборов постулатов. В заключительном разделе проекта обсуждаются современные (студенческие) обозначения и аксиомы для булевых алгебр, а также предлагаются несколько практических упражнений для закрепления идей, разработанных в предыдущих разделах.
Сопутствующий проект «Применение булевой алгебры к проектированию схем: Клод Шеннон», основанный на новаторской статье Шеннона «Символический анализ реле и коммутационных цепей» [6], начинается с краткого обзора двух основных исторических предшественников работы Шеннона: Оригинальная работа Буля по логике и работа Хантингтона по аксиоматизации.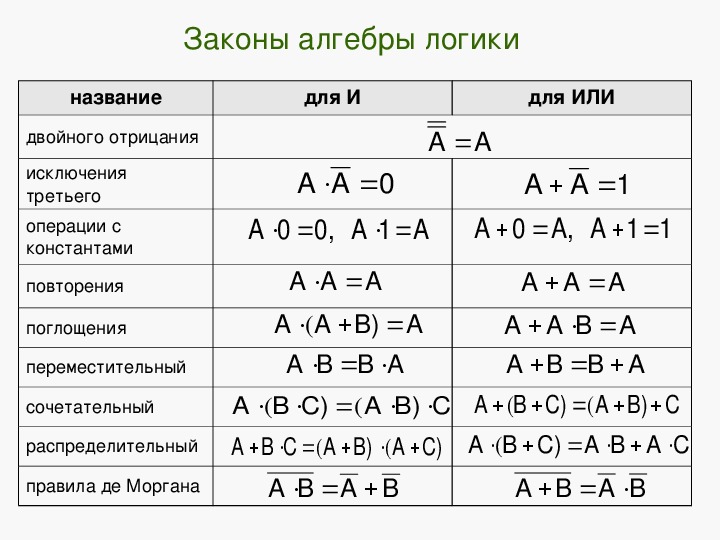 Затем проект разрабатывает стандартные свойства булевой алгебры в конкретном контексте схем и дает учащимся практику использования этих свойств для упрощения логических выражений. Двузначная булева алгебра на \(K = \{0, 1\}\) снова играет центральную роль в этой работе. Проект завершается исследованием концепции «дизъюнктивной нормальной формы» для логических выражений, опять же в контексте схем.
Затем проект разрабатывает стандартные свойства булевой алгебры в конкретном контексте схем и дает учащимся практику использования этих свойств для упрощения логических выражений. Двузначная булева алгебра на \(K = \{0, 1\}\) снова играет центральную роль в этой работе. Проект завершается исследованием концепции «дизъюнктивной нормальной формы» для логических выражений, опять же в контексте схем.
Реализация со учащимися любого из этих проектов может быть достигнута путем индивидуальной работы, работы в малых группах и/или обсуждения в классе; рекомендуется сочетание этих учебных стратегий, чтобы воспользоваться разнообразием вопросов, включенных в проект.
Загрузите проект «Истоки булевой алгебры в логике классов: Джордж Буль, Джон Венн и К. С. Пирс» в виде файла pdf, готового для использования в классе.
Загрузите редактируемый исходный файл Latex для этого проекта.
Дополнительные проекты см. в разделе «Основные исторические источники в классе: дискретная математика и информатика».
Библиография
[1] Буль, Г., Математический анализ логики, MacMillan, Barclay & MacMillan, Cambridge, 1847.Репринт Open Court, La Salle, 1952.
[2] Буль, Г., Исследование законов мысли, на которых основаны математические теории логики и вероятностей, Уолтон и Маберли, Лондон, 1854. Перепечатка Dover Publications, Нью-Йорк, 1958.
[3] Де Морган, А., Формальная логика: или Исчисление вывода, необходимое и вероятное, Тейлор и Уолтон, Лондон, 1847.
[4] Меррилл, Д., Август Де Морган и логика отношений, Клювер, Дордрехт, 1990.
[5] Пирс, К. С., Об усовершенствовании логического исчисления Буля, Proceedings of the American Academy of Arts and Sciences, 7 (1867), 250–261. Перепечатано в Собрании статей Чарльза Сандерса Пирса , Том III: Точная логика, К. Хартсхорн и П. Вайс (редакторы), Oxford University Press, Лондон, 1967, 3-15.
[6] Шеннон, К.Э., Символический анализ реле и коммутационных цепей, Американский институт инженеров-электриков, 57 (1938), 713-723. Перепечатано в Claude Elwood Shannon: Collected Papers, NJA Sloane and AD Wyner (редакторы), IEEE Press, New York, 1993, 471-495.
Перепечатано в Claude Elwood Shannon: Collected Papers, NJA Sloane and AD Wyner (редакторы), IEEE Press, New York, 1993, 471-495.
[7] Smith, G.C., The Boole-DeMorgan Correspondence, 1842-1864, Clarendon Press, Oxford, 1982.
[8] Venn, J., Symbolic Logic, MacMillan, London, 1894. Переиздание Chelsea, Bronx, 1971.
Подтверждение
Разработка учебных материалов по дискретной математике была частично поддержана Национальным научным фондом в рамках программы усовершенствования курсов, учебных планов и лабораторий в рамках грантов DUE-0717752 и DUE-0715392, за что авторы выражают особую признательность.Любые мнения, выводы и заключения или рекомендации, выраженные в этом материале, принадлежат авторам и не обязательно отражают точку зрения Национального научного фонда.
Логика и алгебра — 1-е издание — Альдо Урсини — Пауло Альяно
Содержание
«Приглашенные доклады Логика доказательств с операторами сложности, С. Артемов и А. Чуприна За пределами s-семантики: теория наблюдаемых, М. Комини и Г. Леви Логика коммутирующих отношений эквивалентности, Д.Финберг, М. Майнетти и Г.-К. Rota Proof-Nets: параллельный синтаксис для теории доказательств, J.-Y. Жирар Магари и другие об онтологическом доказательстве Гёделя, П. Хайек, конечно порожденные алгебры и арифметика Магари, Л. Хендрикс и Д. де Йонг, бабочка и змей, Дж. Ламбек, сопряженные в бикатегориях и среди них, Ф. Уильям Лоувер, экспоненциальная алгебра, А. Категорные эквивалентности Макинтайра для многообразий, Р. Маккензи, Булева универсальная алгебра, А. Ф. Пиксли, реструктуризация математической логики: подход, основанный на прагматизме Пирса, Р.Вилле «Развитие исследований в области алгебры в Италии с 1850 по 1940 год», Дж. Заппа, статьи «Критерий для решения проблемы семантического соответствия», Дж. Агуцци и У. Модильяни, замечания об алгебрах Магари для PA и IDelta0+EXP, Л. Беклемишев, неразрешимость в слабых теориях принадлежности, Д. БеллЭ и Ф.
Артемов и А. Чуприна За пределами s-семантики: теория наблюдаемых, М. Комини и Г. Леви Логика коммутирующих отношений эквивалентности, Д.Финберг, М. Майнетти и Г.-К. Rota Proof-Nets: параллельный синтаксис для теории доказательств, J.-Y. Жирар Магари и другие об онтологическом доказательстве Гёделя, П. Хайек, конечно порожденные алгебры и арифметика Магари, Л. Хендрикс и Д. де Йонг, бабочка и змей, Дж. Ламбек, сопряженные в бикатегориях и среди них, Ф. Уильям Лоувер, экспоненциальная алгебра, А. Категорные эквивалентности Макинтайра для многообразий, Р. Маккензи, Булева универсальная алгебра, А. Ф. Пиксли, реструктуризация математической логики: подход, основанный на прагматизме Пирса, Р.Вилле «Развитие исследований в области алгебры в Италии с 1850 по 1940 год», Дж. Заппа, статьи «Критерий для решения проблемы семантического соответствия», Дж. Агуцци и У. Модильяни, замечания об алгебрах Магари для PA и IDelta0+EXP, Л. Беклемишев, неразрешимость в слабых теориях принадлежности, Д. БеллЭ и Ф. Парламенто Бесконечное лямбда-исчисление и бессмысленные модели, А. Берардуччи Компьютерное исследование трехэлементных группоидов, Дж. Бремен и С.Н. Идеальные свойства конгруэнтностей Барриса, И. Чайда, Дуализируемость вообще и Эндуализируемость в частности, Б.А. Дэйви Гиперординалы и нестандартные альфа-модели, М. Ди Нассо, Некоторые заметки о количественном определении подслов и их индукции, Ф. Феррейра, Исследования в области автоматизированной дедукции как основы вероятностной теории доказательств, П. Форчери, П. Джентилини и М.Т. Мольфино Идемпотентные простые алгебры, К. Кернс. Пересмотр математической части статьи Магари «Введение в метаморальность», Р. Магари и Г. Сими. Некоторые аспекты категориальной семантики для полиморфного лямбда-исчисления, М. Е. Использование отражения Майетти. Условия выводимости, С.Мэтьюз и А.К. Базы Стоуна Симпсона, псевдоним Конструктивное содержание каменного представления, С. Негри О k-перестановочности для категорий T-алгебр, М.К. Педиккио Слабый против сильного Тезис Боэция: проблема анализа следственной импликации, К.
Парламенто Бесконечное лямбда-исчисление и бессмысленные модели, А. Берардуччи Компьютерное исследование трехэлементных группоидов, Дж. Бремен и С.Н. Идеальные свойства конгруэнтностей Барриса, И. Чайда, Дуализируемость вообще и Эндуализируемость в частности, Б.А. Дэйви Гиперординалы и нестандартные альфа-модели, М. Ди Нассо, Некоторые заметки о количественном определении подслов и их индукции, Ф. Феррейра, Исследования в области автоматизированной дедукции как основы вероятностной теории доказательств, П. Форчери, П. Джентилини и М.Т. Мольфино Идемпотентные простые алгебры, К. Кернс. Пересмотр математической части статьи Магари «Введение в метаморальность», Р. Магари и Г. Сими. Некоторые аспекты категориальной семантики для полиморфного лямбда-исчисления, М. Е. Использование отражения Майетти. Условия выводимости, С.Мэтьюз и А.К. Базы Стоуна Симпсона, псевдоним Конструктивное содержание каменного представления, С. Негри О k-перестановочности для категорий T-алгебр, М.К. Педиккио Слабый против сильного Тезис Боэция: проблема анализа следственной импликации, К.
