Алгоритм графический примеры – 2.2. Графический способ описания алгоритма.

18. Способы описания алгоритмов. Основы графического способа.

Алгоритмы можно записывать не только при помощи слов. В настоящее время различают несколько способов описания алгоритмов:

1. Словесный, т.е. записи на естественном языке, описание словами последовательности выполнения алгоритма.

Например: Записать алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел. Алгоритм может быть следующим: задать два числа; если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма; определить большее из чисел; заменить большее из чисел разностью большего и меньшего из чисел; повторить алгоритм с шага

2. Формульно-словесный, аналогично пункту 1, плюс параллельная демонстрация используемых формул.

В качестве примера можно привести ведение лекций преподавателем (словесный способ) с одновременной записью формул на доске (формульный).

3. Графический, т.е. с помощью блок-схем.

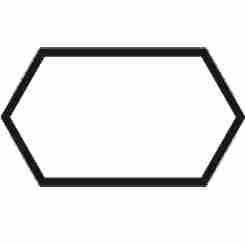
Графический способ представления алгоритмов является более компактным и наглядным по сравнению со словесным. При графическом исполнении алгоритм изображается в виде последовательности связанных между собой блочных символов, каждый из которых соответствует выполнению одного из действий. Такое графическое представление называется схемой алгоритма или блок-схемой. В блок-схеме каждому типу действий (вводу исходных данных, вычислению значений выражений, проверке условий, управлению повторением действий, окончанию обработки и т.п.) соответствует геометрическая фигура, представленная в виде блочного символа. Блочные символы соединяются линиями переходов, определяющими очередность выполнения действий. Символы, наиболее часто употребляемые в блок-схемах.

При выполнении схем соблюдают следующие правила:

Все блоки в схеме нумеруются положительными целыми числами.

Соединительные линии не должны пересекаться между собой

Если этого избежать не удается (или схема переносится на другой лист), то на линиях делают разрывы и обозначают соединителями.

На линиях должны указываться стрелки, обозначающие последовательность выполнения действий (стрелки не ставят если процесс идет сверху вниз или слева направо).

Программный, т.е. тексты на языках программирования.

19. Структуры алгоритмов. Основные виды вычислительных процессов. Примеры.

Все многообразие сложных алгоритмов строится всего лишь из трех основных видов вычислительных процессов (им соответсвуют типовые структуры алгоритмов):

Линейный (линейная структура алгоритма).

Разветвленный (разветвленная структура алгоритма).

Циклический (циклическая структура алгоритма).

Линейный вычислительный процесс предполагает выполнение одной и той же последовательности действий при любых допустимых исходных данных.

Разветвленный вычислительный процесс предполагает выбор одного из двух или нескольких возможных направлений алгоритма (ветви) в зависимости от результата проверки некоторого условия или условий. Количество ветвей всегда больше числа проверяемых условий.

Циклический вычислительный процесс предполагает неоднократное выполнение одной и той же последовательности действий для заданного набора исходных данных. Повторяющаяся цепочка действий называется тело цикла. Существует 2 вида циклических процессов: арифметический и цикл по условию.

Арифметический — цикл с изменяемым параметром или цикл с явно заданным числом повторений. Для организации такого цикла в алгоритм вводят специальную переменную (параметр цикла, счетчик), которая изменяет свое значение при каждом выполнении тела цикла от начального до конечного с заданным шагом.

Циклы по условию — число повторений заранее не известно. Управляются с помощью заданного условия. В зависимости от месторасположения условия (до или после тела цикла) существует две разновидности — цикл с предусловием и цикл с постусловием.

Цикл с постусловием — тело цикла выполняется всегда хотя бы один раз.

Циклические вычислительные процессы позволяют создавать компактные алгоритмы и программы.

Линейный алгоритм

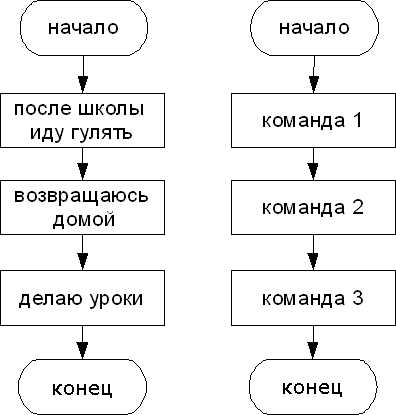
Разветвляющийся алгоритм

Циклический алгоритм

studfiles.net

Графическое описание алгоритма

Графическое изображение алгоритма – это представление его в виде схемы, состоящей из последовательности блоков (геометрических фигур), каждый из которых отображает содержание очередного шага алгоритма. А внутри фигур кратко записывают действие, выполняемое в этом блоке. Такую схему называют блок-схемой или структурной схемой алгоритма, или просто схемой алгоритма.

Правила изображения фигур сведены в единую систему программной документации (дата введения последнего стандарта ГОСТ 19.701.90 – 01.01.1992).

По данному ГОСТу графическое изображение алгоритма – это схема данных, которая отображает путь данных при решении задачи и определяет этапы их обработки.

Таблица 1. Основные типы блоков

Наименование	Обозначение	Пояснение
1	2	3
Пуск – останов		Начало, конец алгоритма, останов, вход, выход в подпрограмму
Процесс		Вычислительная операция или группа операций
Решение		Разветвление в алгоритме, проверка условий
Модификация		Начало цикла
Предопределенный процесс		Программа, стандартная подпрограмма
Ввод-вывод		Ввод-вывод в общем виде

Продолжение таблицы 1

1	2	3
Документ		Вывод результатов на бумагу
Дисплей		Ввод-вывод данных на дисплей
Линии потока		Соединительные линии между блоками алгоритмов
Соединители		Разрыв линий потока на странице, на разных страницах

Типы алгоритмов

Алгоритмы бывают линейные, разветвляющиеся и циклические.

Линейный алгоритм не содержит логических условий, имеет одну ветвь обработки и изображается линейной последовательностью связанных друг с другом блоков. Условное изображение линейного алгоритма может быть представлено на рис. 1.1

Рис. 1.1. Условное изображение линейного алгоритма.

Пример простейшего линейного процесса

Наиболее часто в практике программирования требуется организовать расчет некоторого арифметического выражения при различных исходных данных. Например, такого:

где x > 0 – вещественное, m – целое.

Разработка алгоритма обычно начинается с составления схемы. Продумывается оптимальная последовательность вычислений, при которой, например, отсутствуют повторения. При написании алгоритма рекомендуется переменным присваивать те же имена, которые фигурируют в заданном ариф­метическом выражении либо иллюстрируют их смысл.

Для того чтобы не было «длинных» операторов, исходное выражение полезно разбить на ряд более простых. В нашей задаче предлагается схема вычислений, представленная на рис. 1.2.

Рис. 1.2. Схема линейного процесса

Она содержит ввод и вывод исходных данных, линейный вычислительный процесс, вывод полученного результата. Заметим, что выражение 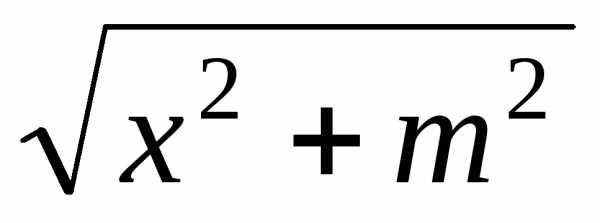вычисляется только один раз. Введя дополнительные переменныеa, b, c, мы разбили сложное выражение на ряд более простых.

Разветвляющийся алгоритм содержит одно или несколько логических условий и имеет несколько ветвей обработки.

Условное изображение разветвления представлено на рис. 1.3. Структура РАЗВЕТВЛЕНИЕ предусматривает проверку условия, после которого вычислительный процесс развивается по одной из двух ветвей (в зависимости от ответа на поставленный в условии вопрос). Каждый из путей (ветвей) ведет к общему выходу.

Рис. 1.3. Условное изображение разветвляющегося алгоритма

studfiles.net

18.Словесно формульный способ описания алгоритмов.

При словесно-формульном способе алгоритм записывается в виде текста с формулами по пунктам, определяющим последовательность действий.

Пусть, например, необходимо найти значение следующего выражения:

у = 2а – (х+6).

Словесно-формульным способом алгоритм решения этой задачи может быть записан в следующем виде:

1. Ввести значения а и х.

2. Сложить х и 6.

3. Умножить a на 2.

4. Вычесть из 2а сумму (х+6).

5. Вывести у как результат вычисления выражения.

19.Графический способ описания алгоритмов.

Графический способ описания (блок-схема)

Для составления алгоритма в виде блок-схемы применяются следующие основные графические изображения.

20.Псевдокоды.

Псевдокод представляет собой систему обозначений и правил, предназначенную для единообразной записи алгоритмов.

Псевдокод занимает промежуточное место между естественным и формальным языками. С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой строны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи.

В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя.

Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются.

Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций.

Примером псевдокода является школьный алгоритмический язык в русской нотации (школьный АЯ), описанный в учебнике А.Г. Кушниренко и др. «Основы информатики и вычислительной техники», 1991. Этот язык в дальнейшем мы будем называть просто «алгоритмический язык».

21.Структура данных. Классификация структур данных.

Структура данных (англ.data structure) — программная единица, позволяющая хранить и обрабатывать множество однотипных и/или логически связанных данныхввычислительной технике. Для добавления, поиска, изменения и удаления данных структура данных предоставляет некоторый набор функций, составляющих её интерфейс.

Структуры данных формируются с помощью типов данных,ссылоки операций над ними в выбранномязыке программирования.

Некоторые структуры:

• Массив(функция с конечной областью определения) — простая совокупность элементов данных одного типа, средство оперирования группой данных одного типа. Отдельный элемент массива задается индексом. Массив может быть одномерным, двумерным и т.д. Разновидностями одномерных массивов переменной длины являются структуры типа кольцо, стек, очередь и двухсторонняя очередь.

• Запись(декартово произведение) — совокупность элементов данных разного типа. В простейшем случае запись содержит постоянное количество элементов, которые называют полями. Совокупность записей одинаковой структуры называется файлом. (Файлом называют также набор данных во внешней памяти, например, на магнитном диске). Для того, чтобы иметь возможность извлекать из файла отдельные записи, каждой записи присваивают уникальное имя или номер, которое служит ее идентификатором и располагается в отдельном поле. Этот идентификатор называют ключом.

Классификация структур данных м.б. выполнена  по различным признаками.

1) По сложности: простые и интегрированные. Простые (базовые, примитивные) структуры — это такие, которые не могут быть распределены на составные части.  Структурированные(интегрированные, композитные, сложные) — такие структуры данных, составными частями которых есть другие структуры данных — простые ли, в свою очередь, интегрированные. Интегрированные структуры данных конструируются программистом.

2). По способу представления: физическая и логическая. Физическая структура данных — это способ физического представления данных в памяти компьютера. Логическая или абстрактная структура — это рассмотрение структуры данных без учета его представления в машинной памяти.  В общем случае между логической и соответствующей ей физической структурами существует расхождения, степень которого зависит от самой структуры и особенностей той среды, в котором она должна быть отображенной. Вследствие этого расхождения существуют процедуры, которые осуществляют отображение логической структуры в физическую, и, наоборот, физической структуры в логическую.

3). По наличию связей между элементами данных: несвязные и связные. Несвязные структуры характеризуются отсутствием связей между элементами структуры. Связные структуры характеризуются наличием связи. Примерами несвязных структур есть векторы, массивы, строки, стеки, очереди; примеры связных структур — связные списки.

4).  По изменчивости: статические, полустатические, динамические. Изменчивость, то есть изменение числа элементов и (ли) связей между элементами структуры.  Статические — к этой группе относят массивы, множества, записи, таблицы.  Полустатические — это стеки, очереди, деки, дерева. Динамические — линейные и разветвленные связные списки, графы, дерева.

5). По характеру упорядоченности элементов в структуре: линейные инелинейные. Линейные структуры в зависимости от характера взаимного расположения элементов в памяти разделяют на структуры с последовательнымраспределением элементов в памяти  (векторы, строки, массивы, стеки, очереди) иструктуры с произвольным связным распределением элементов в памяти (односвязные и двусвязные линейные списки).  Нелинейные структуры — многосвязные списки, дерева, графы.

6). По виду памяти, используемой для сохранности данных: структуры данных для оперативной  и для внешней памяти. Структуры данных для оперативной памяти — это данные, размещенные в статической и динамической памяти компьютера. Все вышеприведенные структуры данных — это структуры для оперативной памяти.   Структуры данных для внешней памяти называют файловыми    структурами или файлами. Примерами файловых структур есть последовательные файлы, файлы, организованные разделами, В- деревья.

studfiles.net

Графические средства ms Word для изображения схем алгоритмов

Лабораторная работа № 1

Понятие алгоритма. Схемы алгоритмов.

Цель: изучить понятие алгоритма, его свойства, способы представления, основные элементы блок-схем; научиться применять программные средства для построения схем данных

Теоретический материал

Алгоритм — точное предписание исполнителю совеpшить определенную последовательность действий для достижения поставленной цели за конечное число шагов.

Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение самого термина «алгоритм» связано с математикой. Это слово происходит от Algorithmi – латинского написания имени Мухаммеда аль-Хорезми (787 – 850) выдающегося математика средневекового Востока. В своей книге «Об индийском счете» он сформулировал правила записи натуральных чисел с помощью арабских цифр и правила действий над ними столбиком. В дальнейшем алгоритмом стали называть точное предписание, определяющее последовательность действий, обеспечивающую получение требуемого результата из исходных данных.

В XII в. был выполнен латинский перевод его математического трактата, из которого европейцы узнали о десятичной позиционной системе счисления и правилах арифметики многозначных чисел. Именно эти правила в то время называли алгоритмами.

Данное выше определение алгоритма нельзя считать строгим – не вполне ясно, что такое «точное предписание» или «последовательность действий, обеспечивающая получение требуемого результата».

Поэтому обычно формулируют несколько общих свойств алгоритмов, позволяющих отличать алгоритмы от других инструкций.

Такими свойствами являются:

• Дискретность (прерывность, раздельность) – алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.

• Определенность – каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.

• Результативность (конечность) – алгоритм должен приводить к решению задачи за конечное число шагов.

• Массовость – алгоритм решения задачи разрабатывается в общем виде, то есть, он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.

На основании этих свойств иногда дается определение алгоритма, например: “Алгоритм – это последовательность математических, логических или вместе взятых операций, отличающихся детерменированностью, массовостью, направленностью и приводящая к решению всех задач данного класса за конечное число шагов”.

Такая трактовка понятия “алгоритм” является неполной и неточной.

Во-первых, неверно связывать алгоритм с решением какой-либо задачи. Алгоритм вообще может не решать никакой задачи.

Во-вторых, понятие “массовость” относится не к алгоритмам как к таковым, а к математическим методам в целом. Решение поставленных практикой задач математическими методами основано на абстрагировании – мы выделяем ряд существенных признаков, характерных для некоторого круга явлений, и строим на основании этих признаков математическую модель, отбрасывая несущественные признаки каждого конкретного явления. В этом смысле любая математическая модель обладает свойством массовости. Если в рамках построенной модели мы решаем задачу и решение представляем в виде алгоритма, то решение будет “массовым” благодаря природе математических методов, а не благодаря “массовости” алгоритма.

 

Требования, предъявляемые к алгоритму

Первое правило – при построении алгоритма, прежде всего, необходимо задать множество объектов, с которыми будет работать алгоритм. Формализованное (закодированное) представление этих объектов носит название данных. Алгоритм приступает к работе с некоторым набором данных, которые называются входными, и в результате своей работы выдает данные, которые называются выходными. Таким образом, алгоритм преобразует входные данные в выходные. Это правило позволяет сразу отделить алгоритмы от “методов” и “способов”. Пока мы не имеем формализованных входных данных, мы не можем построить алгоритм.

Второе правило – для работы алгоритма требуется память. В памяти размещаются входные данные, с которыми алгоритм начинает работать, промежуточные данные и выходные данные, которые являются результатом работы алгоритма. Память является дискретной, т.е. состоящей из отдельных ячеек. Поименованная ячейка памяти носит название переменной. В теории алгоритмов размеры памяти не ограничиваются, т.е. считается, что мы можем предоставить алгоритму любой необходимый для работы объем памяти.

В языках программирования распределение памяти осуществляется декларативными операторами (операторами описания переменных). При запуске программы транслятор языка анализирует все идентификаторы в тексте программы и отводит память под соответствующие переменные.

Третье правило – дискретность. Алгоритм строится из отдельных шагов (действий, операций, команд). Множество шагов, из которых составлен алгоритм, конечно.

Четвертое правило – детерменированность. После каждого шага необходимо указывать, какой шаг выполняется следующим, либо давать команду остановки.

Пятое правило – сходимость (результативность). Алгоритм должен завершать работу после конечного числа шагов. При этом необходимо указать, что считать результатом работы алгоритма.

Виды алгоритмов

Виды алгоритмов как логико-математических средств отражают указанные компоненты человеческой деятельности и тенденции, а сами алгоритмы в зависимости от цели, начальных условий задачи, путей ее решения, определения действий исполнителя подразделяются следующим образом:

• Механические алгоритмы, или иначе детерминированные, жесткие (например, алгоритм работы машины, двигателя и т.п.). Механический алгоритм задает определенные действия, обозначая их в единственной и достоверной последовательности, обеспечивая тем самым однозначный требуемый или искомый результат, если выполняются те условия процесса, задачи, для которых разработан алгоритм.

• Гибкие алгоритмы, например стохастические, т.е. вероятностные и эвристические:

• Вероятностный (стохастический) алгоритм дает программу решения задачи несколькими путями или способами, приводящими к вероятному достижению результата.

• Эвристический алгоритм (от греческого слова “эврика”) – это такой алгоритм, в котором достижение конечного результата программы действий однозначно не предопределено, так же как не обозначена вся последовательность действий, не выявлены все действия исполнителя. К эвристическим алгоритмам относят, например, инструкции и предписания. В этих алгоритмах используются универсальные логические процедуры и способы принятия решений, основанные на аналогиях, ассоциациях и прошлом опыте решения схожих задач.

На всех этапах подготовки к алгоритмизации задачи широко используется структурное представление алгоритма.

Схемы данных

Структурная (блок-, граф-) схема алгоритма – графическое изображение алгоритма в виде схемы связанных между собой с помощью стрелок (линий перехода) блоков – графических символов, каждый из которых соответствует одному шагу алгоритма. Внутри блока дается описание соответствующего действия.

Графическое изображение алгоритма широко используется перед программированием задачи вследствие его наглядности, т.к. зрительное восприятие обычно облегчает процесс написания программы, ее корректировки при возможных ошибках, осмысливание процесса обработки информации.

Можно встретить даже такое утверждение: “Внешне алгоритм представляет собой схему – набор прямоугольников и других символов, внутри которых записывается, что вычисляется, что вводится в машину и что выдается на печать и другие средства отображения информации “. Здесь форма представления алгоритма смешивается с самим алгоритмом.

Конфигурацию, перечень и размеры условных изображений, а также правила построения схем алгоритмов устанавливает ГОСТ 19.701–90 «Схемы алгоритмов, программ, данных и систем».

Алгоритм выражен последовательностью графических символов, выполняющих определенные функции, и наличием связей между ними – линий, стрелок (потоками информации). Основное направление – сверху вниз и слева направо, при этом стрелки, указывающие направления, можно не ставить.

Перечень основных элементов блок-схем

Элемент блок-схемы	Наименование	Содержание
	Блок вычислений (вычислительный блок)	Вычислительные действия или последовательность действий
	Логический блок (блок условия)	Выбор направления выполнения алгоритма в зависимости от некоторого условия
	Блок ввода-вывода данных	Общее обозначения ввода (вывода) данных (вне зависимости от физического носителя)
	Начало (конец)	Начало или конец алгоритма, вход или выход в подпрограмме
	Процесс пользователя (подпрограмма)	Вычисление по стандартной программе или подпрограмме
	Блок модификации	Функция выполняет действия, изменяющие пункты (например, заголовок цикла) алгоритма
	Соединитель	Указание связи прерванными линиями между потоками информации в пределах одного листа
	Межстраничные соединения	Указание связи между информацией на разных листах

Базовые алгоритмические конструкции

Базовые структуры алгоритмов— это определенный набор блоков и стандартных способов их соединения для выполнения типичных последовательностей действий.

К основным структурам относятся следующие:

Линейныминазываются алгоритмы, в которых действия осуществляются последовательно друг за другом. Стандартная блок-схема линейного алгоритма приводится ниже:

Рис. 1 Фрагмент линейного алгоритма

Разветвляющимсяназывается алгоритм, в котором действие выполняется по одной из возможных ветвей решения задачи, в зависимости от выполнения условий. В отличие от линейных алгоритмов, в которых команды выполняются последовательно одна за другой, в разветвляющиеся алгоритмы входит условие, в зависимости от выполнения или невыполнения которого выполняется та или иная последовательность команд (действий).

В качестве условия в разветвляющемся алгоритме может быть использовано любое понятное исполнителю утверждение, которое может соблюдаться (быть истинно) или не соблюдаться (быть ложно). Такое утверждение может быть выражено как словами, так и формулой. Таким образом, алгоритм ветвления состоит из условия и двух последовательностей команд.

В зависимости от того, в обоих ветвях решения задачи находится последовательность команд или только в одной разветвляющиеся алгоритмы делятся на полные и не полные (сокращенные).

Стандартные блок-схемы разветвляющегося алгоритма приведены ниже:

Рис. 2 Фрагменты разветвляющихся алгоритмов

Циклическимназывается алгоритм, в котором некоторая часть операций (тело цикла — последовательность команд) выполняется многократно. Однако слово «многократно» не значит «до бесконечности». Организация циклов, никогда не приводящая к остановке в выполнении алгоритма, является нарушением требования его результативности — получения результата за конечное число шагов.

Перед операцией цикла осуществляются операции присвоения начальных значений тем объектам, которые используются в теле цикла. В цикл входят в качестве базовых следующие структуры:

• блок проверки условия

• блок, называемый телом цикла

Существуют три типа циклов:

• Цикл с предусловием

• Цикл с постусловием

• Цикл с параметром (разновидность цикла с предусловием)

Если тело цикла расположено после проверки условий , то может случиться, что при определенных условиях тело цикла не выполнится ни разу. Такой вариант организации цикла, управляемый предусловием, называется циклом c предусловием.

Возможен другой случай, когда тело цикла выполняется по крайней мере один раз и будет повторяться до тех пор, пока не станет ложным условие. Такая организация цикла, когда его тело расположено перед проверкой условия, носит название цикла с постусловием.

Цикл с параметромявляется разновидностью цикла с предусловием. Особенностью данного типа цикла является то, что в нем имеется параметр, начальное значение которого задается в заголовке цикла, там же задается условие продолжения цикла и закон изменения параметра цикла. Механизм работы полностью соответствует циклу с предусловием, за исключением того, что после выполнения тела цикла происходит изменение параметра по указанному закону и только потом переход на проверку условия.

Стандартные блок-схемы циклических алгоритмов приведены ниже:

Рис. 3. Фрагменты циклических алгоритмических конструкций

В некоторых случаях при наличии одинаковых последовательностей указаний (команд) для различных данных с целью сокращения записи также выделяют вспомогательный алгоритм.

Вспомогательный (подчиненный) алгоритм (процедура) – алгоритм, ранее разработанный и целиком используемый при алгоритмизации конкретной задачи.

Применение программных средств для построения схем данных

При составлении схемы алгоритма следует придерживаться определенных стандартов в изображении элементов схемы. Для изображения схем алгоритмов могут использоваться разнообразные программные средства, в частности, графические возможности текстового процессора MS Office Word и программа Microsoft Visio.

В MS Office Word 2003 средства, позволяющие строить схемы алгоритмов, сосредоточены на панели инструментов Рисование (рис. 4, а), а в MS Word 2010 – на вкладке Вставка и открываются щелчком мыши на кнопке Фигуры (рис. 4, б).

Методика изображения схемы алгоритма заключается в следующем:

1. Запустите текстовый процессор.

2. Раскройте на экране панель Рисование, выполнив команды меню Вид  Панели инструментов  Рисование или щелчком мышью на кнопке Панель рисования .

3. Щелкните на кнопке Автофигуры этой панели, наведите указатель мыши на команду Блок-схема и выберите в раскрывшемся меню графических примитивов нужный элемент щелчком мыши. Назначение элемента высвечивается в контекстной подсказке.

4. Перейдите в рабочее поле документа, нажмите левую кнопку мыши и, не отпуская ее, нарисуйте элемент схемы алгоритма.

5. Щелкните правой кнопкой по нарисованной фигуре и выберите в контекстом меню команду Добавить текст, чтобы можно было вписать текст внутри элемента.

6. Еще раз щелкните правой кнопкой по фигуре и выберите в контекстом меню команду Формат автофигуры.

7. В открывшемся одноименном диалоге перейдите на вкладку Размер и установите в полях высота и ширина необходимые размеры, например, высота 1,5 см, ширина 3 см.

Помните, что значения высоты и ширины должны быть кратны 5 мм, а ширина фигуры должна быть больше высоты в 1,5-2 раза.

8. Перейдите на вкладку Цвета и линии и в поле толщина установите нужное значение, например, 1 пт. После этого нажмите кнопку ОК.

9. Щелкните указателем мыши внутри нарисованной фигуры и введите необходимый текст. Тип шрифта выбирается в раскрывающемся списке кнопки Шрифт (), а размер – в раскрывающемся списке кнопки Выбрать размер шрифта (). Выравнивание текста осуществляется кнопками , расположенными на панели инструментов Форматирование.

10. Для изображения связей между фигурами щелкните на кнопкеАвтофигуры панели Рисование, наведите указатель мыши на команду Соединительные линии и выберите нужный тип линии в раскрывшемся меню.

11. Соедините две фигуры между собой выбранной линией с помощью мыши при нажатой левой кнопке.

12. Для выравнивания фигур друг относительно друга их необходимо выделить (для этого надо щелкать левой кнопкой мыши по фигурам при нажатой клавише SHIFT), а затем щелкнуть на кнопке Рисование панели Рисование, навести указатель мыши на команду Выровнять/распределить и выбрать в раскрывшемся меню нужный инструмент выравнивания/распределения (рис. 5).

13. Когда все элементы схемы алгоритма будут нарисованы, щелкните мышью по кнопке Выбор объектов () панели Рисование, нажмите левую кнопку мыши и, не отпуская ее, обведите пунктирным прямоугольником все нарисованные элементы. Они окажутся выделенными. После этого щелкните правой кнопкой мыши по любому выделенному элементу и в контекстном меню выполните команды Группировка  Группировать. Все нарисованные элементы и связи между ними будут сгруппированы в один графический объект.

studfiles.net

Алгоритм и его свойства. Примеры алгоритмов

Разделы: Информатика

---

Цель занятия: познакомить учащихся с понятием алгоритма, исполнителями алгоритмов, примерами алгоритмов в жизни, алгоритмическим способом решения задач, закрепить полученные знания с помощью электронного теста, развивать навыки самоконтроля.

Ход урока

1. Организационный момент.
2. Подготовка к изучению нового материала. (ознакомление с планом и целью занятия) .
3. Изучение нового материала. (просмотр электронного урока с использованием мультимедиа проектора) . Слайды + текст лекции.
4. По ходу урока учащиеся конспектируют определения и отвечают на вопросы.
5. Закрепление темы занятия (работа уч-ся на компьютере) . Электронный тест с последующей самопроверкой. Решение алгоритмических задач.
6. Подведение итогов. Выставление оценок с учетом процентного выполнения теста.
7. Задание на дом. (выучить определения, привести примеры алгоритмов из жизненной практики.)

Изучение нового материала.

Один из важнейших этапов решения задач на ЭВМ – составление алгоритма. О том, что такое алгоритмы, какими общими свойствами они обладают и как исполняются, мы и поговорим на этом уроке.

В 1983 году отмечалось 1200-летие со дня рождения одного из величайших ученых Средней Азии и средневекового Востока Мухамада ибн Мусы аль-Хорезми. Он написал ряд трактатов по арифметике и алгебре, в том числе книгу «Арифметика индусскими цифрами» – о счете с помощью десяти цифр и правилах арифметических действий с числами.

Имя ученого аль-Хорезми превратилось в понятие algorithmi, первоначально обозначавшее десятичную систему исчисления и правила арифметических действий в этой системе. Отсюда и возник современный научный термин «алгоритм».

Каждый из нас ежедневно использует различные алгоритмы: инструкции, правила, рецепты и т.п. Обычно мы это делаем не задумываясь. Например, открывая дверь ключом, никто не размышляет над тем, в какой последовательности выполнять действия. Однако чтобы научить кого-нибудь открывать дверь, придется четко указать и сами действия, и порядок их выполнения. То же потребуется и при указании маршрута поездки.

Сравним эти алгоритмы. На первый взгляд, между ними нет ничего общего. Одно дело – открывать дверь, другое – ехать в гости. Но если приглядеться внимательно, можно заметить существенное сходство между ними. Прежде всего, это строгий порядок выполнения действий.

Демонстрация слайда 1. /Приложение/

Мы можем теперь сказать, что алгоритм – это организованная последовательность действий. Данную формулировку, конечно, нельзя считать определением алгоритма. Например, мы не объяснили, что означают слова «организованная» и «действия». Скажем сразу: абсолютно строгого определения алгоритма не существует. Алгоритм – это одно из тех основных понятий (категорий) математики, которые не обладают формальным определением в терминах более простых понятий, а абстрагируются непосредственно из опыта.

На слайде еще одно задание. Выполните его, используя для записи ответа любой текстовый редактор или бумагу и карандаш.

Демонстрация слайда 2. /Приложение/

Сравните свой ответ с правильным.

Правильный алгоритм:

1. Налить в чайник воду.
2. Зажечь спичку.
3. Открыть кран газовой горелки.
4. Поднести спичку к горелке.
5. Поставить чайник на плиту.
6. Ждать, пока вода закипит.
7. Выключить газ.

Демонстрация слайда 3. /Приложение/

Рассмотренные нами алгоритмы составлены для исполнения человеком. Но человек далеко не единственный возможный исполнитель алгоритмов. Все живые существа и даже отдельные клетки исполняют различные алгоритмы. Способны на это и созданные человеком устройства – роботы-манипуляторы и станки с программным управлением. Но прежде чем составлять алгоритм решения задачи, нужно узнать, какие действия предполагаемый исполнитель способен выполнить.

Поясним сказанное на примере. Допустим, нужно решить квадратное уравнение.

Десятикласснику требуется минимум инструкций, потому что он уже знает способ решения.

Восьмикласснику понадобятся намного более сложные инструкции, потому что он этого еще не проходил.

Теперь мы можем уточнить понятие алгоритма: это организованная последовательность действий, допустимых для некоторого исполнителя.

Рассмотрим информационный процесс редактирования текста. При работе с текстом возможны различные операции: удаление, копирование, перемещение или замена его фрагментов. Что необходимо для того, чтобы преобразовать текст?

• Первое. Требуется исполнитель.
• Второе. Процесс должен быть разбит на этапы, понятные исполнителю.
• Третье. Должно быть определено начальное состояние текста и его требуемое конечное состояние.

Теория алгоритмов имеет большое практическое значение. Алгоритмический тип деятельности важен не только как одна из эффективных форм труда человека. Через алгоритмизацию, через расчленение сложных действий на всё более простые, на действия, выполнение которых доступно машинам, пролегает путь к автоматизации различных процессов.

Далее под алгоритмом будет пониматься конечная последовательность указаний, адресованных исполнителю, четко и однозначно задающая процесс решения задач какого-либо типа во всех деталях и позволяющая получить за конечное число шагов результат, однозначно определяемый исходными данными.

Такое свойство алгоритма, как однозначность результата при заданных исходных данных, называется определенностью (детерминированностью) .

Заметим, что большинство алгоритмов могут выполняться при достаточно разнообразных наборах исходных данных, то есть использоваться для решения не какой-либо одной задачи, а целого класса подобных задач. Это свойство алгоритма называется массовостью.

С алгоритмами человек встречается на каждом шагу.

Пример 1. Дан угол. Необходимо провести биссектрису. (Есть способ, как, пользуясь линейкой и циркулем, можно решить эту задачу.)

Пример 2. Даны два целых числа. Необходимо найти их разность. (Имеется правило, в котором ясно изложен весь порядок действий с цифрами данных чисел.)

В приведенных примерах речь идет о том, как сложную работу представить в виде последовательности простых действий. Вычитание многоразрядных чисел сводится к действиям с цифрами. При делении угла пополам выполняются несложные построения линейкой и циркулем.

Однако высказанные соображения следует дополнить. Ведь правила вычитания формулируются для любых многоразрядных чисел, а не для каких-то конкретных двух. Инструкция проведения биссектрисы тоже такова, что, пользуясь ею, можно разделить пополам любой угол. То есть каждому алгоритму присуща массовость – пригодность для решения не какой-либо одной, а целого класса задач.

Далее под алгоритмом будет пониматься конечная последовательность указаний, адресованных исполнителю, четко и однозначно задающая процесс решения задач какого-либо типа во всех деталях и позволяющая получить за конечное число шагов результат, однозначно определяемый исходными данными.

Такое свойство алгоритма, как однозначность результата при заданных исходных данных, называется определенностью (детерминированностью) .На этом занятии мы познакомились с такими важнейшими понятиями, как алгоритм, исполнитель, система команд исполнителя, узнали основные свойства алгоритма.

Закрепление темы:

Алгоритмические задачи

№1. Старик должен переправить на лодке через реку волка, козу и капусту. Лодка может выдержать только старика и одного “пассажира”. В каком порядке старик перевезет пассажиров? Не забудь, что волк может съесть козу, а коза – капусту. Найди 2 варианта решения.

Алгоритм решения задачи:

1 вариант	2 вариант
1) __________________________	1) _________________________
2) _________________________	2) _________________________
3) __________________________	3) _________________________

и т.д.

№2 Два мальчика и двое взрослых должны переправиться на другую сторону реки на плоту, который выдерживает либо двух мальчиков, либо одного мальчика и одного взрослого. Как осуществить переправу? Найди несколько способов решения этой задачи.

Алгоритм решения задачи:

	1 способ	2 способ	3 способ
1 шаг
2 шаг
3 шаг
4 шаг
5 шаг

Обозначения: 1м- один мальчик, 2м – два мальчика, 1в – один взрослый.

1. Практикум по решению задач

Злоумышленник поменял местами действия в алгоритме вычисления среднего арифметического из квадратного корня трёх чисел:

Присвоить а значение (а²+в²+с²) /3.

Вести а,в,с

Сообщить “Среднее арифметическое квадратов равно”

Сообщить а.

Восстановите правильный порядок действий.

2. Исправьте следующий алгоритм решения уравнения (х-2) (х+2) =0:

Присвоить х значение +-2.

Сообщить “Корни уравнения равны”.

Сообщить первое значение х.

Сообщить второе значение х.

3. Автомобиль проехал три участка пути разной длины с разными скоростями. Составьте алгоритм нахождения средней скорости автомобиля.

4. Проснувшись утром, школьник почувствовал недомогание. Находившийся рядом злоумышленник тут же составил для него следующий алгоритм:

Измерить температуру.

Если температура выше 37⁰, то:

Вызвать врача.

Пойти в школу.

Несмотря на недомогание, школьник исправил этот алгоритм, добавив всего две строки. Какие строки добавил школьник?

5. Запишите в виде алгоритмов правила определения знака:

А) произведения двух действительных чисел;

Б) суммы двух действительных чисел.

6. В записи алгоритма вычисления значения выражения (х²— 5х+5) / (х⁶— 4х²+3)

Злоумышленник одно действие поставил не на свое место. Вот как стал выглядеть алгоритм:

1. ввести х
2. если х⁶— 4х² + 3=0, то:
3. сообщить “При таком х значение выражения не определено”.
4. иначе:
5. присвоить у значение (х²— 5х +5) /(х⁶- 4х²+3) .
6. конец ветвления.
7. сообщить у.

Верните действие на свое место.

Электронный тест

1.Которые из документов являются алгоритмами?

а) Правило правописания приставок, оканчивающихся на з,с(да)

б) Программа телепередач

в) Кулинарный рецепт приготовления блюда

г) Инструкция по сборке проданного в разобранном виде шкафа

2. В каких случаях правильно заканчивается предложение: Алгоритм – это

а) конечная последовательность действий, приводящая к искомому результату при любых допустимых исходных данных

б) указание на выполнение действий

в) конечный набор понятных некоторому исполнителю команд, выполнение которых приводит к однозначному решению поставленной задачи

г) программа в машинных кодах

3. Расчлененность алгоритма на отдельные элементарные действия – это

а) Дискретность

б) Определенность

в) Массовость

г) Детерминированность

4. Которые из документов являются алгоритмами?

А) Каталог книг в библиотеке

Б) Порядок набора международного телефонного номера

В) Рецепт приготовления клея

Г) Настенный календарь на текущий год

Подведение итогов. Выставление оценок с учетом процентного выполнения теста.

Задание на дом. (выучить определения, привести примеры алгоритмов из жизненной практики.)

5.02.2007

urok.1sept.ru

Способы описания алгоритмов | Студентик.РФ

Существуют следующие способы описания (представления) алгоритмов:

1. словесное описание;
2. описание алгоритма с помощью   математических  формул;
3. графическое описание алгоритма в виде блок-схемы;
4. описание алгоритма с помощью псевдокода;
5. комбинированный способ изображения алгоритма с   использованием словесного, графического и др. способов.

Словесное описание алгоритма представляет собой описание структуры алгоритма на естественном языке. Например, к приборам бытовой техники, как правило, прилагается инструкция по эксплуатации, т.е. словесное описание алгоритма, в соответствии с которым данный прибор должен использоваться.

Графическое описание алгоритма в виде блок-схемы – это описание структуры алгоритма с помощью геометрических фигур с линиями связи.

Блок схема алгоритма – это графическое представление метода решения задачи, в котором используются специальные символы для отображения операций.

Символы, из которых состоит блок-схема алгоритма, определяет ГОСТ 19.701-90. Этот ГОСТ соответствует международному стандарту оформления алгоритмов, поэтому блок-схемы алгоритмов, оформленные согласно ГОСТ 19.701-90, в разных странах понимаются однозначно.

Псевдокод – описание структуры алгоритма на естественном, но частично формализованном языке. В псевдокоде используются некоторые формальные конструкции и общепринятая математическая символика. Строгих синтаксических правил для записи псевдокода не предусмотрено.

Рассмотрим простейший пример. Пусть необходимо описать алгоритм вывода на экран монитора наибольшего значения из двух чисел.

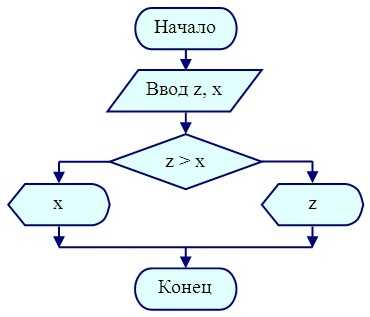
Рисунок 1 — Пример описания алгоритма в виде блок-схемы

Описание этого же алгоритма на псевдокоде:

1. Начало
2. Ввод чисел: Z, X
3. Если Z > X то Вывод Z
4. Иначе вывод Х
5. Конец

Каждый из перечисленных способов изображения алгоритмов имеет и достоинства и недостатки. Например, словесный способ отличается многословностью и отсутствием наглядности, но дает возможность лучше описать отдельные операции. Графический способ более наглядный, но часто возникает необходимость описать некоторые операции в словесной форме. Поэтому при разработке сложных алгоритмов лучше использовать комбинированный способ.

xn--d1acjinvhdf.xn--p1ai

Блок-схемы алгоритмов. ГОСТ. Примеры — Блог программиста

Схема — это абстракция какого-либо процесса или системы, наглядно отображающая наиболее значимые части. Схемы широко применяются с древних времен до настоящего времени — чертежи древних пирамид, карты земель, принципиальные электрические схемы. Очевидно, древние мореплаватели хотели обмениваться картами и поэтому выработали единую систему обозначений и правил их выполнения. Аналогичные соглашения выработаны для изображения схем-алгоритмов и закреплены ГОСТ и международными стандартами.

На территории Российской Федерации действует единая система программной документации (ЕСПД), частью которой является Государственный стандарт — ГОСТ 19.701-90 «Схемы алгоритмов программ, данных и систем» [1]. Не смотря на то, что описанные в стандарте обозначения могут использоваться для изображения схем ресурсов системы, схем взаимодействия программ и т.п., в настоящей статье описана лишь разработка схем алгоритмов программ.

Рассматриваемый ГОСТ практически полностью соответствует международному стандарту ISO 5807:1985.

Содержание:

1. Элементы блок-схем алгоритмов
2. Примеры блок-схем
3. Нужны ли блок-схемы? Альтернативы

Элементы блок-схем алгоритмов

Блок-схема представляет собой совокупность символов, соответствующих этапам работы алгоритма и соединяющих их линий. Пунктирная линия используется для соединения символа с комментарием. Сплошная линия отражает зависимости по управлению между символами и может снабжаться стрелкой. Стрелку можно не указывать при направлении дуги слева направо и сверху вниз. Согласно п. 4.2.4, линии должны подходить к символу слева, либо сверху, а исходить снизу, либо справа.

Есть и другие типы линий, используемые, например, для изображения блок-схем параллельных алгоритмов, но в текущей статье они, как и ряд специфических символов, не рассматриваются. Рассмотрены лишь основные символы, которых всегда достаточно студентам.

Терминатор начала и конца работы функции	Терминатором начинается и заканчивается любая функция. Тип возвращаемого значения и аргументов функции обычно указывается в комментариях к блоку терминатора.
Операции ввода и вывода данных	В ГОСТ определено множество символов ввода/вывода, например вывод на магнитные ленты, дисплеи и т.п. Если источник данных не принципиален, обычно используется символ параллелограмма. Подробности ввода/вывода могут быть указаны в комментариях.
Выполнение операций над данными	В блоке операций обычно размещают одно или несколько (ГОСТ не запрещает) операций присваивания, не требующих вызова внешних функций.
Блок, иллюстрирующий ветвление алгоритма	Блок в виде ромба имеет один вход и несколько подписанных выходов. В случае, если блок имеет 2 выхода (соответствует оператору ветвления), на них подписывается результат сравнения — «да/нет». Если из блока выходит большее число линий (оператор выбора), внутри него записывается имя переменной, а на выходящих дугах — значения этой переменной.
Вызов внешней процедуры	Вызов внешних процедур и функций помещается в прямоугольник с дополнительными вертикальными линиями.
Начало и конец цикла	Символы начала и конца цикла содержат имя и условие. Условие может отсутствовать в одном из символов пары. Расположение условия, определяет тип оператора, соответствующего символам на языке высокого уровня — оператор с предусловием (while) или постусловием (do … while).
Подготовка данных	Символ «подготовка данных» в произвольной форме (в ГОСТ нет ни пояснений, ни примеров), задает входные значения. Используется обычно для задания циклов со счетчиком.
Соединитель	В случае, если блок-схема не умещается на лист, используется символ соединителя, отражающий переход потока управления между листами. Символ может использоваться и на одном листе, если по каким-либо причинам тянуть линию не удобно.
Комментарий	Комментарий может быть соединен как с одним блоком, так и группой. Группа блоков выделяется на схеме пунктирной линией.

Примеры блок-схем

В качестве примеров, построены блок-схемы очень простых алгоритмов сортировки, при этом акцент сделан на различные реализации циклов, т.к. у студенты делают наибольшее число ошибок именно в этой части.

Сортировка вставками

Массив в алгоритме сортировки вставками разделяется на отсортированную и еще не обработанную части. Изначально отсортированная часть состоит из одного элемента, и постепенно увеличивается.

На каждом шаге алгоритма выбирается первый элемент необработанной части массива и вставляется в отсортированную так, чтобы в ней сохранялся требуемый порядок следования элементов. Вставка может выполняться как в конец массива, так и в середину. При вставке в середину необходимо сдвинуть все элементы, расположенные «правее» позиции вставки на один элемент вправо. В алгоритме используется два цикла — в первом выбираются элементы необработанной части, а во втором осуществляется вставка.

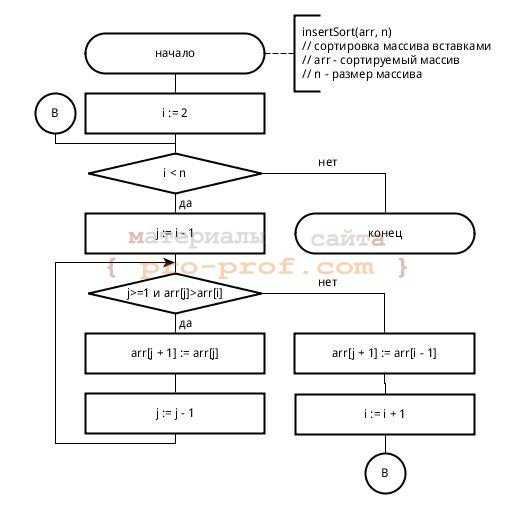Блок-схема алгоритма сортировки вставками

В приведенной блок-схеме для организации цикла используется символ ветвления. В главном цикле (i < n) перебираются элементы необработанной части массива. Если все элементы обработаны — алгоритм завершает работу, в противном случае выполняется поиск позиции для вставки i-того элемента. Искомая позиция будет сохранена в переменной j в результате выполнения внутреннего цикла, осуществляющем сдвиг элементов до тех пор, пока не будет найден элемент, значение которого меньше i-того.

На блок-схеме показано каким образом может использоваться символ перехода — его можно использовать не только для соединения частей схем, размещенных на разных листах, но и для сокращения количества линий. В ряде случаев это позволяет избежать пересечения линий и упрощает восприятие алгоритма.

Сортировка пузырьком

Сортировка пузырьком, как и сортировка вставками, использует два цикла. Во вложенном цикле выполняется попарное сравнение элементов и, в случае нарушения порядка их следования, перестановка. В результате выполнения одной итерации внутреннего цикла, максимальный элемент гарантированно будет смещен в конец массива. Внешний цикл выполняется до тех пор, пока весь массив не будет отсортирован.

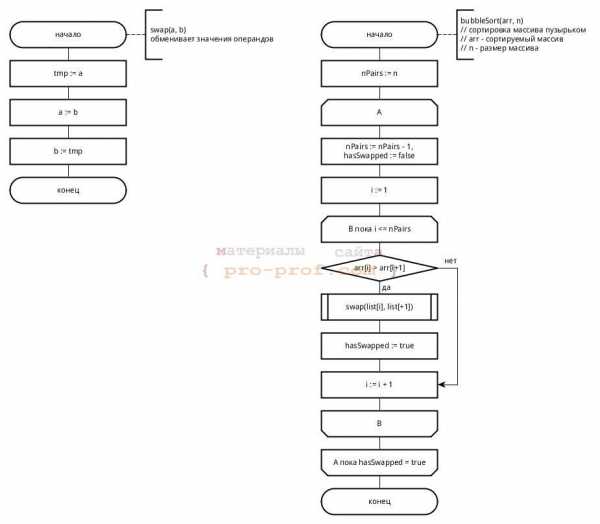Блок-схема алгоритма сортировки пузырьком

На блок-схеме показано использование символов начала и конца цикла. Условие внешнего цикла (А) проверяется в конце (с постусловием), он работает до тех пор, пока переменная hasSwapped имеет значение true. Внутренний цикл использует предусловие для перебора пар сравниваемых элементов. В случае, если элементы расположены в неправильном порядке, выполняется их перестановка посредством вызова внешней процедуры (swap). Для того, чтобы было понятно назначение внешней процедуры и порядок следования ее аргументов, необходимо писать комментарии. В случае, если функция возвращает значение, комментарий может быть написан к символу терминатору конца.

Сортировка выбором

В сортировке выбором массив разделяется на отсортированную и необработанную части. Изначально отсортированная часть пустая, но постепенно она увеличивается. Алгоритм производит поиск минимального элемента необработанной части и меняет его местами с первым элементом той же части, после чего считается, что первый элемент обработан (отсортированная часть увеличивается).

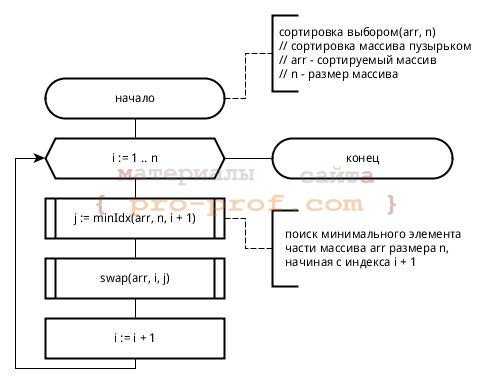Блок-схема сортировки выбором

На блок-схеме приведен пример использования блока «подготовка», а также показано, что в ряде случаев можно описывать алгоритм более «укрупнённо» (не вдаваясь в детали). К сортировке выбором не имеют отношения детали реализации поиска индекса минимального элемента массива, поэтому они могут быть описаны символом вызова внешней процедуры. Если блок-схема алгоритма внешней процедуры отсутствует, не помешает написать к символу вызова комментарий, исключением могут быть функции с говорящими названиями типа swap, sort, … .

На блоге можно найти другие примеры блок-схем:

Часть студентов традиционно пытается рисовать блок-схемы в Microsoft Word, но это оказывается сложно и не удобно. Например, в MS Word нет стандартного блока для терминатора начала и конца алгоритма (прямоугольник со скругленными краями, а не овал). Наиболее удобными, на мой взгляд, являются утилиты MS Visio и yEd [5], обе они позволяют гораздо больше, чем строить блок-схемы (например рисовать диаграммы UML), но первая является платной и работает только под Windows, вторая бесплатная и кроссплатфомренная. Все блок-схемы в этой статье выполнены с использованием yEd.

Нужны ли блок-схемы? Альтернативы

Частные конторы никакие блок-схемы не используют, в книжках по алгоритмам [6] вместо них применяют словесное описание (псевдокод) как более краткую форму. Возможно блок-схемы применяют на государственных предприятиях, которые должны оформлять документацию согласно требованиям ЕСПД, но есть сомнения — даже для регистрации программы в Государственном реестре программ для ЭВМ никаких блок-схем не требуется.

Тем не менее, рисовать блок-схемы заставляют школьников (примеры из учебников ГОСТ не соответствуют) — выносят вопросы на государственные экзамены (ГИА и ЕГЭ), студентов — перед защитой диплом сдается на нормоконтроль, где проверяется соответствие схем стандартам.

Разработка блок-схем выполняется на этапах проектирования и документирования, согласно каскадной модели разработки ПО, которая сейчас почти не применяется, т.к. сопровождается большими рисками, связанными с ошибками на этапах проектирования.

Появляются подозрения, что система образования прогнила и отстала лет на 20, однако аналогичная проблема наблюдается и за рубежом. Международный стандарт ISO 5807:1985 мало чем отличается от ГОСТ 19.701-90, более нового стандарта за рубежом нет. Там же производится множество программ для выполнения этих самых схем — Dia, MS Visio, yEd, …, а значит списывать их не собираются. Вместо блок-схем иногда применяют диаграммы деятельности UML [6], однако удобнее они оказываются, разве что при изображении параллельных алгоритмов.

Периодически поднимается вопрос о том, что ни блок-схемы, ни UML не нужны, да и документация тоже не нужна. Об этом твердят программисты, придерживающиеся методологии экстремального программирования (XP) [7], ходя даже в их кругу нет единого мнения.

В ряде случаев, программирование невозможно без рисования блок-схем, т.к. это один процесс — существуют визуальные языки программирования, такие как ДРАКОН [8], кроме того, блок-схемы используются для верификации алгоритмов (формального доказательства их корректности) методом индуктивных утверждений Флойда [9].

В общем, единого мнения нет. Очевидно, есть области, в которых без чего-то типа блок-схем обойтись нельзя, но более гибкой альтернативы нет. Для формальной верификации необходимо рисовать подробные блок-схемы, но для проектирования и документирования такие схемы не нужны — я считаю разумным утверждение экстремальных программистов о том, что нужно рисовать лишь те схемы, которые помогают в работе и не требуют больших усилий для поддержания в актуальном состоянии [10].

Список использованных источников:

1. ГОСТ 19.701–90 (ИСО 5807–85) «Единая система программной документа­ции».
2. Алгоритм. Свойства алгоритма \ https://pro-prof.com/archives/578
3. Алгоритмы сортировки слиянием и быстрой сортировки \ https://pro-prof.com/archives/813
4. yEd Graph Editor \ http://www.yworks.com/products/yed
5. Книги: алгоритмы \ https://pro-prof.com/books-algorithms
6. Рамбо Дж., Якобсон А., Буч Г. UML: специальный справочник. -СПб.: Питер, 2002. -656 с.
7. Кент Бек Экстремальное программирование: разработка через тестирование – СПб.: Питер – 2003
8. Визуальный язык ДРАКОН \ http://drakon.su/
9. Шилов Н.В. Верификация шаблонов алгоритмов для метода отката и метода ветвей и границ. Моделирование и анализ информационных систем, ISSN 1818 – 1015, т.18, №4, 2011
10. Брукс Ф., Мифический человеко — месяц или как создаются программные системы. СПб. Символ Плюс, 1999 — 304 с. ил.

pro-prof.com