Задания из огэ по математике – задания, ответы, решения. Обучающая система Дмитрия Гущина.

Тест №2 ОГЭ по математике |

Тестовые задания №2 ОГЭ по математике. Теория к заданию №2 и разбор типовых вариантов по ссылке под тестами!⇓⇓⇓

Лимит времени: 0

Информация

Тренировочные варианты типовых тестовых заданий №2 ОГЭ по математике. После ответа вы найдете объяснение и пояснение ко всем вариантам. Успехов в подготовке! 😉

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

1. С ответом
2. С отметкой о просмотре

1. Задание 1 из 5

   В магазине продаются обои шириной 1±0,05 м. Какую ширину не могут иметь обои?

   Правильно
   
   1. 1,02 м Ответ неверный. Число 1,02 попадает в допустимый интервал.
   2. 0,94 м Правильный ответ. Число 0,94 не принадлежит интервалу допустимых значений.
   3. 1,00 м Неверно. Число 1,0 принадлежит указанному в условии диапазону чисел.
   4. 1,05 м Вариант неверный. Число 1,05 включено в интервал допустимых значений.

   Решение:

   Решение задания сводится к определению интервала допустимых значений, который находится в промежутке чисел. Значит, ширина обоев не может быть за пределами диапазона 0,95-1,05.  Очевидно, что нам не подходит число 0,94 м.

   Неправильно
   
   1. 1,02 м Ответ неверный. Число 1,02 попадает в допустимый интервал.
   2. 0,94 м Правильный ответ. Число 0,94 не принадлежит интервалу допустимых значений.
   3. 1,00 м Неверно. Число 1,0 принадлежит указанному в условии диапазону чисел.
   4. 1,05 м Вариант неверный. Число 1,05 включено в интервал допустимых значений.

   Решение:

   Решение задания сводится к определению интервала допустимых значений, который находится в промежутке чисел. Значит, ширина обоев не может быть за пределами диапазона 0,95-1,05.  Очевидно, что нам не подходит число 0,94 м.

   Решение задания сводится к определению интервала допустимых значений, который находится в промежутке чисел. Значит, ширина обоев не может быть за пределами диапазона 0,95-1,05.  Очевидно, что нам не подходит число … 🙂

2. Задание 2 из 5

   В таблице приведены расстояния от Солнца до четырёх планет Солнечной системы. Какая из планет самая близкая к Солнцу?

   Планета	Марс	Сатурн	Уран	Юпитер
   Расстояние (в км)	2,3*108	1,42*109	2,9*109	7,8*108

   Правильно

   Наименьшее расстояние определяется по 2 критериям:

   1. Нахождение множителя с наименьшим показателем степени, в нашем случае 10⁸
   2. Сравнение чисел, предшествующих степени: 2,3 < 7,8. Меньшее из них первое, а значит, Марс находится ближе к Солнцу.
   Неправильно

   Наименьшее расстояние определяется по 2 критериям:

   1. Нахождение множителя с наименьшим показателем степени, в нашем случае 10⁸
   2. Сравнение чисел, предшествующих степени: 2,3 < 7,8. Меньшее из них первое, а значит, Марс находится ближе к Солнцу.

   Наименьшее расстояние определяется по 2 критериям:

   1. Нахождение множителя с наименьшим показателем степени.
   2. Сравнение чисел, предшествующих степени.

3. Задание 3 из 5

   Куриные яйца в зависимости от их массы подразделяют на пять категорий: высшая, отборная, первая, вторая и третья. Определите к какой категории относится яйцо массой 48,5 г:

   Категория	Масса одного яйца, не менее, г
   Высшая	75
   Отборная	65
   Первая	55
   Вторая	45
   Третья	35

   Правильно

   1) первая

   Ответ неверный. Число 48,5 меньше 55,0, а значит не входит в диапазон масс.

   2) вторая

   Верный ответ. Число 48,5 находится в промежутке чисел 45-55.

   3) третья

   Неверный ответ. Число 48,5 не принадлежит допустимому интервалу значений для третьей категории, так как 48,5 больше 35,0

   4) отборная

   Неверно. Число 48,5 много меньше 65,0, а значит не входит в диапазон масс.

   Решение:

   В таблице приведены массы яиц по категориям. Для определения подходящей категории, необходимо вычислить допустимые значения чисел по массе, то есть определить интервал. Например, масса 48,5 г больше 45 г, но меньше 55,0 г, то есть выполняется условие интервала 45-55.

   Неправильно

   1) первая

   Ответ неверный. Число 48,5 меньше 55,0, а значит не входит в диапазон масс.

   2) вторая

   Верный ответ. Число 48,5 находится в промежутке чисел 45-55.

   3) третья

   Неверный ответ. Число 48,5 не принадлежит допустимому интервалу значений для третьей категории, так как 48,5 больше 35,0

   4) отборная

   Неверно. Число 48,5 много меньше 65,0, а значит не входит в диапазон масс.

   Решение:

   В таблице приведены массы яиц по категориям. Для определения подходящей категории, необходимо вычислить допустимые значения чисел по массе, то есть определить интервал. Например, масса 48,5 г больше 45 г, но меньше 55,0 г, то есть выполняется условие интервала 45-55.

   В таблице приведены массы яиц по категориям. Для определения подходящей категории, необходимо вычислить допустимые значения чисел по массе, то есть определить интервал.

4. Задание 4 из 5

   Площадь территории Казахстана составляет 2,7 млн км². Как эта величина записывается в стандартном виде?

   Правильно

   Решение задания сводится к двух действиям:

   1. Нахождение числа в стандартном виде, то есть из интервала 1≤ |a| < 10, в нашем случае это 2,7;
   2. Приставка «миллион» означает множитель с показателем степени 6. То есть 2,7 млн км² – это величина равная км².

   1) 2,7 • 10⁵  км²

   Ответ неверный. Миллион – это показатель степени равный 6.

   2)  270 • 10⁵  км²

   Ответ неверный. 270 • 10⁵ не является числом в стандартном виде, а приставка «миллион» означает степень 6. К стандартному виду относятся числа, где перед множителем с показателем степени идет цифра из интервала: 1≤ |a| <10.

   3)  270 • 10⁶ км²

   Ответ неверный.  не является числом в стандартном виде. К стандартному виду относятся числа, где перед множителем с показателем степени идет цифра из интервала: 1≤ |a| <10.

   4)   2,7 • 10⁵ км²

   Верный ответ. Миллион – это  а 2,7 – число в стандартном виде и удовлетворяет условию 1≤ |a| <10.

   Неправильно

   Решение задания сводится к двух действиям:

   1. Нахождение числа в стандартном виде, то есть из интервала 1≤ |a| < 10, в нашем случае это 2,7;
   2. Приставка «миллион» означает множитель с показателем степени 6. То есть 2,7 млн км² – это величина равная км².

   1) 2,7 • 10⁵  км²

   Ответ неверный. Миллион – это показатель степени равный 6.

   2)  270 • 10⁵  км²

   Ответ неверный. 270 • 10⁵ не является числом в стандартном виде, а приставка «миллион» означает степень 6. К стандартному виду относятся числа, где перед множителем с показателем степени идет цифра из интервала: 1≤ |a| <10.

   3)  270 • 10⁶ км²

   Ответ неверный.  не является числом в стандартном виде. К стандартному виду относятся числа, где перед множителем с показателем степени идет цифра из интервала: 1≤ |a| <10.

   4)   2,7 • 10⁵ км²

   Верный ответ. Миллион – это  а 2,7 – число в стандартном виде и удовлетворяет условию 1≤ |a| <10.

   Решение задания сводится к двух действиям:

   • Нахождение числа в стандартном виде, то есть из интервала 1≤ |a| < 10.
   • Приставка «миллион» означает множитель с показателем степени 6.

5. Задание 5 из 5

   Во время мероприятия в спортивной секции результаты оценивались в баллах. Команды получили такие результаты:

   Команда	Прыжки в длину	Бег на 60 м	Эстафета	Метание мяча
   «Медведи»	2	4	1	2
   «Звезда»	1	3	3	1
   «Старт»	3	2	2	3
   «Победители»	4	1	3	4

   По итогам побеждала команда, набравшая наибольшее суммарное количество баллов. Какая команда заняла третье место?

   Правильно

   Первое и последнее места занимают команды, набравшие в сумме наибольшее и наименьшее количество баллов. Необходимо подсчитать число баллов для всех представленных команд, складываем числа из строчек:

   — команда «Медведи»: 2+4+1+2=9;

   — команда «Звезда»: 1+3+3+1=8;

   — команда «Старт»: 3+2+2+3=10;

   — команда «Победители»: 4+1+3+4=12.

   Неправильно

   Первое и последнее места занимают команды, набравшие в сумме наибольшее и наименьшее количество баллов. Необходимо подсчитать число баллов для всех представленных команд, складываем числа из строчек:

   — команда «Медведи»: 2+4+1+2=9;

   — команда «Звезда»: 1+3+3+1=8;

   — команда «Старт»: 3+2+2+3=10;

   — команда «Победители»: 4+1+3+4=12.

   Первое и последнее места занимают команды, набравшие в сумме наибольшее и наименьшее количество баллов. Необходимо подсчитать число баллов для всех представленных команд, складываем числа из строчек.

spadilo.ru

Разбор и решение задания №10 ОГЭ по математике |

---

Графики функций

---

В десятом задании ОГЭ по математике идет работа с графиками функций. В большинстве случаев требуется установить соответствие между графиком функции и математическим выражением (формулой). В задании сопоставляется различная информация о функциях. Необходимо находить и  использовать в выполнении задания область определения функции, ее промежутки возрастания и убывания, промежутки знакопостоянства, нули функции, уметь читать графики функций. Работать надо с функциями, описывающими прямую пропорциональную зависимость, линейными функциями, гиперболами, квадратичными функциями.

Хотя на самом экзамене мы ожидаем работу именно с графиками функций, тем не менее в некоторых заданиях дается вместо рисунков их описание. Это делается, чтобы подчеркнуть те детали, на которые надо обратить внимание при работе с графиками функций.

Задание № 5 несложное, тем не менее последние задания придуманы таким образом, чтобы любознательным школьникам было над чем подумать.

Ответом в задании 10 является набор цифр, описывающий соответствие между различными объектами.

---

Теория к заданию №10

---

Так как в данном задании речь идет о функциях и их графиках, приведем основные понятия и формулы.

На произвольном примере ознакомимся с исследованием функции:

• область определения и множество значений
• корни и критические точки
• промежутки возрастания  убывания

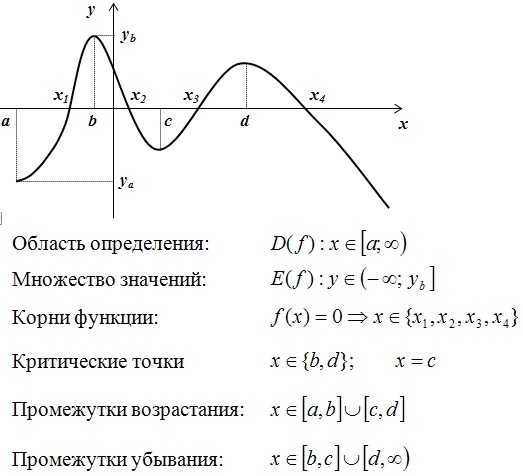
Теперь рассмотрим данный материал на линейной функции:

y = kx + b

где  k – угловой коэффициент, b – свободный член

Рассмотрим случай квадратичной функции:

Также вспомним, что такое коренная функция и модуль:

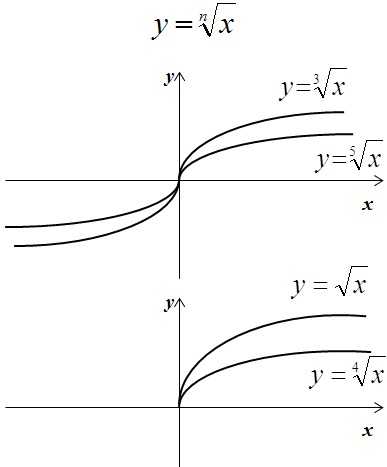
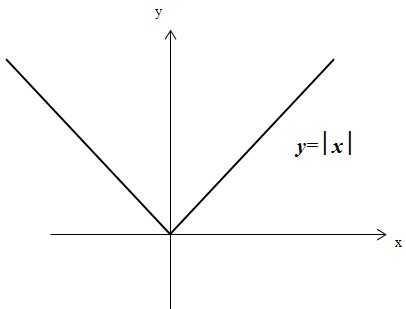
Я разобрал три случая — случай с параболой и влияние коэффициентов на вид параболы — в первом примере. Во втором примере разобрана гипербола и общие закономерности зависимости общего вида графика от математического выражения. Третий случай рассматривает прямую и варианты её построения в зависимости от коэффициентов.

---

Разбор типовых вариантов задания №10 ОГЭ по математике

---

Первый вариант задания (параболы)

На рисунках изображены графики функций вида

y = ax² + bx + c

Установите соответствие между знаками коэффициентов a и c и графиками функций.

Коэффициенты:

А) a > 0, c > 0

Б) a < 0, c > 0

В) a > 0, c < 0

Графики:

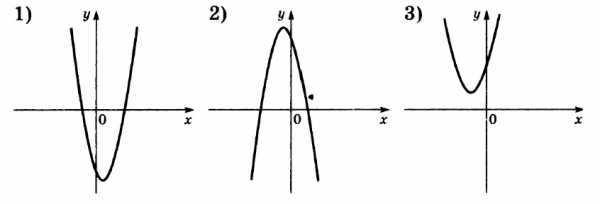
Решение:

Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида

y = ax² + bx + c

Коэффициент a определяет направление ветвей параболы: если a > 0, то ветви направлены вверх, а если  a < 0, то ветви направлены вниз.

Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a < 0.

У первой и третьей ветви направлены вверх, то есть a > 0.

Далее мы смотрим, на что влияет коэффициент c.

Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:

если c > 0, то вершина параболы расположена выше оси х

если c < 0, то вершина параболы расположена ниже оси x

Так, у первой параболы c < 0, у второй и третьей c > 0.

Из всего вышеперечисленного можно найти ответ:

А) 3

Б) 2

В) 1

---

Второй вариант задания (гиперболы)

Установите соответствие между функциями и их графиками.

Функции:

A) y = -3/x

Б) y = 3/x

В) y = 1/(3x)

Графики:

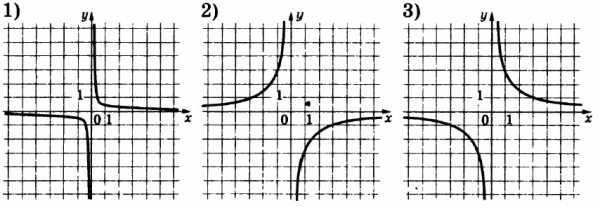
Решение:

В данной ситуации можно воспользоваться двумя подходами — можно руководствоваться общими соображениями, а можно просто решить задачу подстановкой. Я рекомендую решать задачу общими соображениями, а проверять подстановкой.

Общие правила:

• если уравнение гиперболы положительное (то есть не стоит знак -, как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти
• если перед уравнением гиперболы стоит знак — (как в первом случае), то график лежит во второй и четвертой четвертях

Таким образом можно сразу определить, что первое уравнение соответствует графику под номером 2.

Второе правило, которым я пользуюсь, звучит так:

• чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости

и наоборот:

• чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям

Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.

Ответ:

A) 2

Б) 3

В) 1

---

Третий вариант задания (линейный график)

Установите соответствие между функциями и их графиками.

Функции:

A) y = 3x

Б) y = -3x

В) y = (1/3)x

Графики:

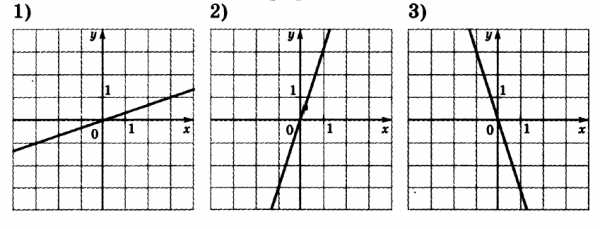
Решение:

Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:

y = kx + b

График данной функции зависит от k и b.

• если k < 0,  то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
• если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
• коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если  b > 0, то выше ноля в точке y = b
• если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1

Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.

Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.

Ответ:

A) 2

Б) 3

В) 1

---

Четвертый вариант задания  (демонстрационный вариант ОГЭ 2017)

Установите соответствие между графиками функций и формулами, которые их задают.

1) y = x²

2) y = x/2

3) y = 2/x

Решение:

Для решения данной задачи необходимо знать вид графиков функций, а именно:

y = x² — парабола, в общем виде это y = ax²+bx+c, но в нашем случае b = c = 0, а а = 1

x/2 — прямая, в общем виде график прямой имеет вид y = ax + b, в нашем случае b = 0,  а = 1/2

y = 2/x — гипербола, в общем виде график функции y = a/x + b, в данном примере b = 0, a = 2

Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая — В.

Ответ:

А 1

Б 3

В 2

spadilo.ru

Разбор и решение задания №11 ОГЭ по математике |

---

Арифметические и геометрические прогрессии

---

В одиннадцатом задании мы сталкиваемся с прогрессиями — общими понятиями.

Конечно, по каждой теме можно придумать очень сложные задачи, но на самом ОГЭ по этой теме они обычно простые.Главным здесь является понимание, что такое арифметическая и что такое геометрическая прогрессия.

Ответом в задании 11 является целое число или конечная десятичная дробь.

---

Теория к заданию №11

---

Начнем теоретическую справку об определениях прогрессий.

Арифметическая прогрессия:

Последовательность, у которой задан первый член a1, а каждый следующий равен предыдущему, сложенному с одним и тем же числом d, называется арифметической прогрессией.

a_n+1 = a_n + d

где d – разность прогрессии

Геометрическая прогрессия:

Последовательность, у которой задан первый член b1 не равен 0, а каждый следующий равен предыдущему, умноженному на одно и то же число q не равное 0, называется геометрической прогрессией.

b_n+1 = b_n q

где q – знаменатель прогрессии

В первом варианте я разобрал, как найти разность арифметической прогрессии, если известны два её члена. Во втором варианте разобрано нахождение неизвестного члена геометрической прогрессии из ряда членов прогрессии. В третьем варианте представлено объяснение по поиску n-ого члена арифметической прогрессии.

---

Разбор типовых вариантов задания №11 ОГЭ по математике.

---

Первый вариант задания (нахождение разности прогрессии)

Дана арифметическая прогрессия a(n) в которой

a (3) = 6,9

a (16) = 26,4

Найдите разность прогрессии.

Решение:

Чтобы найти разность прогрессии в нашем случае, нужно разделить разницу между значениями членов прогрессии на количество членов (в нашем случае — это между 3 и 16).

Находим разницу между значениями  a (3) и a (16):

a (3) — a (16) = 26,4 — 6,9 = 19,5

Находим количество членов:

16 — 3 = 13

Находим разность прогрессии:

19,5 / 13 = 1,5

Ответ: 1,5

---

Второй вариант задания (нахождение неизвестного члена)

Выписано несколько последовательных членов геометрической прогрессии:

-1, x, -49, -343, ….

Найдите x.

Решение:

Для того, чтобы найти x, необходимо вначале вычислить знаменатель прогрессии — для этого необходимо разделить последующий член на предыдущий:

-343 / -49 = 7

Затем, зная знаменатель прогрессии мы можем найти x, разделив последующий член (-49) на уже известный знаменатель 7.

x = -49 / 7 = -7

Ответ: -7

---

Третий вариант задания (нахождение n-ого члена)

Выписаны первые несколько членов арифметической прогрессии:  10, 6, 2, …

Найдите 101 член.

Решение:

Для решения данной задачи воспользуемся формулой, задающей арифметическую прогрессию:

a_n = a₁ + (n-1) • d

В нашем случае:

a₁ = 10

d = 6 — 10 = -4

Подставляем значения в формулу:

a₁₀₁ = 10 + (101-1) • (-4) = -390

Ответ: -390

---

Четвертый вариант задания (демонстрационный вариант ОГЭ 2017)

В последовательности чисел первое число равно 6, а каждое следующее больше предыдущего на 4. Найдите пятнадцатое число.

Решение:

В данном задании нас проверяют на знание формулы арифметической прогрессии:

где n — номер члена прогрессии, d — разность, а а1 — первый член.

Решение:

Подставим в общую формулу известные из условия значения:

d = 4,

а1 = 6,

n = 15,

получим:

a15 = 6 + (15 — 1) • 4

вычислив, получаем значение 15 члена:

a15 = 62

Ответ: 62

spadilo.ru

Разбор и решение задания №13 ОГЭ по математике |

---

Расчеты по формулам

---

Перейдем к рассмотрению тестового задания ОГЭ по математике — задания №13. В данном задании нам необходимо поработать с формулами — либо просто подставить значения в формулу и провести вычисления, либо вначале выразить неизвестную величину, а затем произвести подстановку.

Итак, рассмотрим конкретные типовые примеры.

---

Разбор типовых вариантов задания №13 ОГЭ по математике

---

Первый вариант задания

Мощность постоянного тока (в ваттах) вычисляется по формуле P = I²R, где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 224 Вт, а сила тока равна 4 А.

Решение:

Выразим сопротивление R:

R = P / I²

Подставим значения в полученную формулу:

R = 224 / 4² = 224 / 16 = 14 ом

Ответ: 14

---

Второй вариант задания

В фирме «Родник» стоимость (в рублях) колодца из железобетонных колец рассчитывается по формуле:

С = 6000 + 4100•n,

где n — число колец, установленных в колодце.

Пользуясь этой формулой, рассчитайте стоимость колодца из 7 колец. Ответ укажите в рублях.

Решение:

В данном случае выражать из формулы нам ничего не требуется, поэтому подставим в данную форму лу значение n = 7:

С = 6000 + 4100•7 = 6000 + 28700 = 34700

Ответ: 34700

---

Третий вариант задания

Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой

t_F = 1,8 • t_C + 32,

где t_C — температура в градусах Цельсия, t_F — температура в градусах Фаренгейта.

Какая температура по шкале Фаренгейта соответствует -25° по шкале Цельсия?

Решение:

Подставляем значение -25 в формулу:

t_F = 1,8 • (-25) + 32 = -45 + 32 = -13

Ответ: -13

---

Четвертый вариант задания (демонстрационный вариант 2017)

Период колебания математического маятника T (в секундах) приближенно можно вычислить по формуле:

T = 2 • √l 

где l — длина нити (в метрах). Пользуясь этой формулой, найдите длину нити маятника (в метрах), период колебаний которого составляет 3 секунды.

Решение:

Выразим из формулы l, для этого возведем обе части в квадрат, получим:

T ² = 4 • l ,

тогда:

l  = T ² / 4

Подставляя значения из условия, получаем:

l = 3 ² / 4 = 9 / 4 = 2,25

Ответ 2,25

spadilo.ru

Разбор и решение задания №20 ОГЭ по математике |

---

Анализ геометрических высказываний

---

В 20 задании из приведенных утверждений необходимо выбрать одно или несколько правильных. Утверждения из общего теоретического курса геометрии, поэтому, какие-то определенные рекомендации здесь дать нельзя, кроме как полного повторения теоретического курса. Другое дело, что если вы точно не знаете какое-либо утверждение, то решить задачу можно наоборот — выбирая и отсеивая неправильные. Это задание не имеет какого либо подхода к решению, однако ниже я привел несколько разобранных задач.

---

Разбор типовых вариантов задания №20 ОГЭ по математике

---

Первый вариант задания

Какие из следующих утверждений верны?

1. Все диаметры окружности равны между собой.
2. Угол, вписанный в окружность, равен соответствующему центральному углу, опирающемуся на ту же дугу.
3. Любые два равносторонних треугольника подобны.

Решение:

Все диаметры окружности всегда равны между собой — это даже интуитивно понятно. Что касается второго утверждения, то оно неверно — вписанный угол всегда в два раза меньше центрального. А вот третье утверждение тоже верно — треугольники могут быть подобны по трем углам, а у равносторонних треугольников они всегда равны.

Ответ: 1,3.

---

Второй вариант задания

Какие из следующих утверждений верны?

1. Все высоты равностороннего треугольники равны.
2. Существуют три прямые, которые проходят через одну точку.
3. Если диагонали параллелограмма равны, то он является ромбом.

Решение:

Первое утверждение верно, так как у равностороннего треугольника все стороны равнозначны, а значит и все элементы, проведенные к ним, тоже. Второе утверждение тоже верно, так как нет ограничений на количество произвольных прямых, проходящих через одну точку. Третье утверждение неверно — если диагонали равны, то это либо прямоугольник, либо квадрат.

Ответ: 1,2.

---

Третий вариант задания

Какие из следующих утверждений верны?

1. Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.
2. Любой прямоугольник можно вписать в окружность.
3. Через заданную точку плоскости можно провести единственную прямую.

Решение:

Первое утверждение верно из общих свойств треугольника — сумма двух сторон всегда больше третьей. Второе утверждение тоже верно — действительно, любой прямоугольник можно вписать в окружность. ретье утверждение неверно, так как я писал уже чуть выше, что нет ограничений на количество произвольных прямых, проходящих через одну точку.

---

Четвертый вариант задания (демонстрационный вариант 2017)

Укажите номера верных утверждений.

1. Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2. Треугольник со сторонами 1, 2, 4 существует.
3. Если в ромбе один из углов равен 90° , то такой ромб — квадрат.
4. В любом параллелограмме диагонали равны.

Решение:

Проанализируем каждое из утверждений:

1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.

Да, такое утверждение в геометрии есть, с дополнением » и только одну» :

«Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой, и причем только одну.»

2) Треугольник со сторонами 1, 2, 4 существует.

Для существования треугольника должно выполняться следующее правило:

Сумма двух сторон всегда больше третьей. В данном случае это не так, так как 1 + 2 < 4

3) Если в ромбе один из углов равен 90° , то такой ромб — квадрат.

Действительно, ромб — параллелограмм с равными сторонами, если у него один из углов будет равен 90°, а значит и все остальные, то тогда он станет квадратом.

4) В любом параллелограмме диагонали равны.

Нет, такого утверждения в геометрии нет, они равны только в квадрате и прямоугольнике.

Ответ: 1,3

spadilo.ru

Решение задания 23 из ОГЭ по математике

Данная статья посвящена решению примеров заданий 23 из ОГЭ по математике. В этих заданиях школьников обычно просят построить график той или иной функции, а затем указать, при каких значениях параметра этот график пересекается с неким другим графиком, касается его или же, к примеру, имеет с ним несколько точек пересечения. Ну и тому подобное. В данной статье вы найдёте разбор примеров решения заданий 23 из ОГЭ по математике от профессионального репетитора, на протяжении многих лет занимающегося подготовкой школьников к этому экзамену.

Примеры решения заданий 23 из ОГЭ по математике

Пример 1. Постройте график функции     Определите, при каких значениях прямая имеет с графиком ровно одну общую точку.

Построение графика функции всегда нужно начинать с указания области определения этой функции. В данном случае ограничения на эту область задаются тем, что в знаменателе не должно быть нуля, потому что деление на нуль не имеет математического смысла. То есть областью определения данной функции являются все числа, за исключением 1. Записать это можно следующим образом:

   

После того, как мы указали область определения исходной функции, можно попробовать её упростить. Для этого вынесем минус в знаменателе за скобку и сократим. В результате получим следующее выражение:

   

График данной функции получается из графика функции путём её отражения относительно оси OX и параллельного переноса всех точек на 0,25 единичного отрезка вниз. При этом мы должны удалить из этого графика точку , потому что она не входит в область определения исходной функции. То есть искомый график выглядит следующим образом:

Теперь отвечаем на главный вопрос задачи. Графиком функции является прямая, проходящая через начало координат. При этом в зависимости от коэффициента эта прямая имеет разный наклон относительно оси

OX. Когда это прямая имеет ровно одну общую точку с изображённым графиком? Только в двух случаях. Рассмотрим их по отдельности.

Первый случай. Когда данная прямая касается изображённого графика. Это ситуация изображена на рисунке:

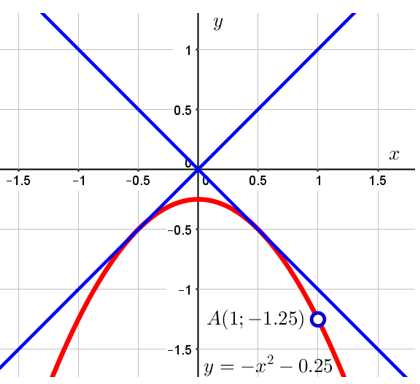
Сложность состоит в том, чтобы определить значения , при которых эта ситуация реализуется. Для решения этой задачи можно использовать несколько различных подходов. Используем наиболее типичный.

Суть в том, что в точке касания графики проходят через одну и ту же точку на координатной плоскости. Значит, в этой точке имеет место равенство:

   

Дискриминант последнего квадратного уравнения равен

yourtutor.info