Карточка 1 1) Найти АВ 2) Найти угол АСВ, если угол АОВ = 84° 3) 4) Найдите площадь равностороннего треугольника, отсекаемого от данного треугольника его средней линией, если площадь данного треугольника равна 48см2. 5) Периметр равностороннего треугольника АВС равен 24см. Найдите длину средней линии этого треугольника. | Карточка 2 1) Найти угол АСВ, если угол АОВ равен 160° 2) 3) Найдите площадь данного равностороннего треугольника, если площадь треугольника, отсекаемого от него средней линией, равна 6 см2. 4) Средняя линия равностороннего треугольника АВС равна 8см. Найдите периметр этого треугольника 5) Из квадрата со стороной 10см вырезан прямоугольник со сторонами 3см и 4см. Найдите площадь оставшейся части. | Карточка 3 1) Найти угол ВАС, если угол ВОС = 160° 2) Найдите площадь прямоугольного треугольника, если его гипотенуза равна 16см, а один из углов треугольника равен 45°.
3) Найти угол ВАС
4) Найти длину меньшей средней линии треугольника 5) В прямоугольнике одна сторона равна 28см, а диагональ равна 35см. Найдите площадь прямоугольника. | |
Карточка 4 1) Найти угол ВАС
2) Найти угол АОВ, если угол АСВ = 25° 3) Найти площадь четырёхугольника 4) Найти длину большей высоты параллелограмма 5) Найти косинус угла | Карточка 5 1) В треугольнике АВС угол В равен 46°, угол С равен 71°, ВD – биссектриса. Найдите угол АDВ. 2) Найти радиус окружности, если АВ = 12см, ОА = 13см. 3) Найти длину отрезка НМ, Если АМ=3см, АН=НС=2 4) Найти угол ВОС, если угол ВАС = 70° 5) Найти площадь треугольника АВС, если высота, проведённая к одной из его сторон равна 11, а средняя линия, параллельная этой стороне, равна 10. | Карточка 6 1) Найти угол АОВ, если точки А и В делят окружность на две дуги в отношении 9 : 11. 2) Найти площадь параллелограмма 3) КВСD — параллелограмм. Найдите длину отрезка АВ. 4) Найдите косинус угла 5) Найдите площадь четырёхугольника | |
Карточка 7 1) Найти угол 3, если угол 1 равен 40°, а угол 2 равен 55°. 2) Основания трапеции равны 48 и 24, высота 4. Найдите площадь трапеции. 3) На рисунке изображён параллелограмм. Найти: х. 4) Из квадрата со стороной 8см вырезан прямоугольник со сторонами 3см и 2см. Найдите площадь оставшейся части. 5) Стороны прямоугольника равны 10 и 24. Найдите радиус окружности, описанной около этого прямоугольника. | Карточка 8 1) Средняя линия трапеции равна 11, а меньшее основание равно 5. Найдите большее основание трапеции. 2) Найдите угол α 3) Прямоугольный треугольник вписан в окружность. Найдите радиус этой окружности. 4) Найдите тангенс угла А. 5) Из прямоугольника со сторонами 8см и 10см вырезан квадрат со стороной 5см. Найдите площадь оставшейся части. | Карточка 9 1) Найдите тангенс угла А. 2) Найти длину медианы проведённой из вершины прямого угла. 3) Стороны параллелограмма равны 10 и 35. Высота, опущенная на первую сторону, равна 21. Найдите высоту, опущенную на вторую сторону. 4) Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах. 5) Найти площадь трапеции. | |
Карточка 10 1) Найти больший угол параллелограмма АВСD 2) 3) Найти угол ОСD 4) ВС = 8, соsВ = 0,8 Найти АВ 5) АВСD — равнобедренная трапеция Найти угол АВC | Карточка 11 1) Найти меньший угол параллелограмма АВСD 2) Найти угол ОСD 3) 4) 5) Найти тангенс угла С | Карточка 12 1) АВСD — равнобедренная трапеция Найти угол АDC Найти угол ОDС 2) 3) АС = 6, соsA = 0,6 Найти АВ 4) 5) Найти площадь параллелограмма | |
Карточка 13 1) В трапеции АВСD АВ=СD ∟ВDА=18° и ∟ВDС=97°. Найдите угол АВD. 2) Найдите тангенс угла АОВ 3) Найдите расстояние от точки А до середины отрезка СВ 4) Найдите угол АВС 5) Колесо имеет 8 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы. | Карточка 14 1) В трапеции АВСD АВ=СD ∟ВDА=40° и ∟ВDС=24°. Найдите угол АВD. 2) Найдите расстояние от точки А до середины отрезка СВ Найдите котангенс угла АОВ 3) 4) Найдите угол АВС 5) Угол АОВ = 63°. Найдите угол АСВ. | Карточка 15 1) В трапеции АВСD АВ=СD ∟ВDА=24° и ∟ВDС=70°. Найдите угол АВD. 2) Найдите расстояние от точки А до середины отрезка СВ 3) Найдите котангенс угла АОВ 4) Из квадрата Вырезали прямоугольник. Найдите площадь получившейся фигуры. 5) Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 2,6 м и 3,6 м? | |
Карточка 16 1) Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3,4 м и 4,6 м? 2) Сколько спиц в колесе, если угол между соседними спицами равен 40°? 3) Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85. 4) Найдите тангенс угла АОВ 5) Найдите площадь фигуры | Карточка 17 1) Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 20 см. Сколько потребуется таких дощечек? 2) Сколько спиц в колесе, если угол между соседними спицами равен 9°? 3) Колесо имеет 40 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы. 4) Найдите тангенс угла АОВ 5) Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота средней опоры 3,1 м, высота большей опоры 3,3 м. Найдите высоту малой опоры. | Карточка 18 1) Пол комнаты, имеющей форму прямоугольника со сторонами 6 м и 7 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек? 2) Сколько спиц в колесе, если угол между соседними спицами равен 15°? 3) Колесо имеет 6 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы. 4) Найдите котангенс угла АОВ 5) Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,5 м, высота средней опоры 2,65 м. Найдите высоту большей опоры. | |
Карточка 19 1) Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,95 м, высота большей опоры 3,65 м. Найдите высоту средней опоры. 2) Сколько потребуется кафельных плиток квадратной формы со стороной 15 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 2,7 м и 3 м? 3) Человек ростом 1,8 м стоит на расстоянии 10 м от столба, на котором висит фонарь на высоте 7,8 м. Найдите длину тени человека в метрах. 4) Найдите площадь трапеции 5) Прямые m и n параллельны. Найдите ∟3, если ∟1 = 117°, ∟2 = 24°. | Карточка 20 1) Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,25 м, высота большей опоры 2,85 м. Найдите высоту средней опоры. 2) Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3,4 м и 4,2 м? 3) Человек ростом 1,6 м стоит на расстоянии 15 м от столба, на котором висит фонарь на высоте 9,6 м. Найдите длину тени человека в метрах. 4) Найдите площадь трапеции 5) Прямые m и n параллельны. Найдите ∟3, если ∟1 = 74°, ∟2 = 39°. | Карточка 21
80 см. Расстояние между точками А и В составляет 41 м. Найдите высоту, на которую поднимается лестница (в метрах). 2) Человек ростом 1,5 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 10,5 м. Найдите длину тени человека в метрах. 3) Найдите площадь трапеции 4) 5) Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности. | |
Карточка 22
сторону на два отрезка. Каковы длины этих отрезков? 2) 3) Найдите тангенс угла АВС 4) 5) На отрезке AB выбрана точка C так, что AC=6 и BC=4. Построена окружность с центром A , проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности. | Карточка 23 1) 2) MN и АВ – диаметры окружности. ∟NВА=73°. Найти угол NMB 3) ∟DMC=24°. Найдите угол СМА. 4)Найти площадь трапеции. 5) Найти площадь параллелограмма | Карточка 24 1) Прямая касается окружности в точке K . Точка O – центр окружности. Хорда КМ образует с касательной угол, равный 7°. Найдите величину угла ОМК 2) Найти площадь трапеции 3) 4) Найти радиус окружности 5) В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB. |
intolimp.org
ОГЭ. Модуль «Геометрия». Тренировочные и тематические тесты. (9 класс)
Вариант 1
1. Дан параллелограмм , внешний угол при вершине равен . Найдите , если — высота.
2. Дан треугольник , внешние углы при вершинах и равны соответственно и . Найдите .
3. Дана равнобокая трапеция , внешний угол при вершине равен . Найдите , если — высота.
4. Дан параллелограмм , внешний угол при вершине равен . Найдите , если — высота.
5. Дан треугольник , внешние углы при вершинах и равны соответственно и . Найдите .
6. Дана равнобокая трапеция , внешний угол при вершине равен . Найдите , если — высота.
Вариант 2
1. В равнобедренном треугольнике внешний угол при вершине равен . Найдите величину . Ответ дайте в градусах.
2. В треугольнике внешний угол при вершине равен . Найдите величину внешнего угла при вершине , если Ответ дайте в градусах.
3. В равнобедренном треугольнике угол равен . Найдите внешний угол при вершине . Ответ дайте в градусах.
4. В равнобедренном треугольнике внешний угол при вершине равен . Найдите величину . Ответ дайте в градусах.
5. В треугольнике внешний угол при вершине равен . Найдите величину внешнего угла при вершине , если . Ответ дайте в градусах.
Вариант 3
1. Дан параллелограмм , внешний угол при вершине равен . Найдите , если — высота.
2. Дан треугольник , внешние углы при вершинах и равны соответственно и . Найдите .
3. Дана равнобокая трапеция , внешний угол при вершине равен . Найдите , если — высота.
4. Дан параллелограмм , внешний угол при вершине равен . Найдите , если — высота.
5. Дан треугольник , внешние углы при вершинах и равны соответственно и . Найдите .
Вариант 4
1. Дан параллелограмм , угол . Найдите внешний угол про вершине , если — высота.
2. Дана равнобокая трапеция , внешний угол при вершине равен . Найдите , если — высота.
3. Дан параллелограмм , угол . Найдите внешний угол про вершине , если — высота.
4. Дан треугольник , внешние углы при вершинах и равны соответственно и . Найдите .
5. Дана равнобокая трапеция , равен . Найдите внешний угол при вершине , если — высота.
infourok.ru
Банк ОГЭ — Геометрия
15:12:2016Центральный угол AOB опирается на хорду АВ так, что угол ОАВ равен 60°. Найдите длину хорды АВ, если радиус окружности равен 8.
Показать решение
15:12:2016Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
Показать решение
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=10 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Показать решение
28:08:2015Какое из следующих утверждений верно?
1)Все углы ромба равны.
2)Если стороны одного четырёхугольника соответственно равны сторонам другого четырёхугольника, то такие четырёхугольники равны.
3)Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.
Показать решение
28:08:2015В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.
Показать решение
28:08:2015Высота BH ромба ABCD делит его сторону AD на отрезки AH=44 и HD=11. Найдите площадь ромба.
Показать решение
28:08:2015В треугольнике ABC угол C равен 90°, AC=12, tg A=(2√10)/3. Найдите AB.
Показать решение
27:08:2015В треугольнике ABC известно, что AC=BC. Внешний угол при вершине B равен 146°. Найдите угол C. Ответ дайте в градусах.
Показать решение
Задача по геометрии. Задание 26 (ОГЭ)
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 28.
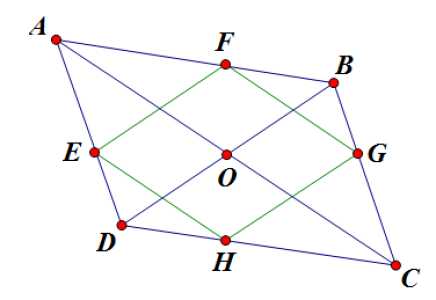
Решение.
По условию отношение диагоналей параллелограмма равно 28, .
Пусть , тогда . (1)
Точка — точка пересечения диагоналей параллелограмма. Из соображений симметрии диагонали ромба пересекаются в этой же точке. То есть отрезок — половина диагонали ромба. Вспомним, что диагонали ромба являются биссектрисами углов. Этот факт нам понадобится в дальнейшем.
Рассмотрим треугольник .
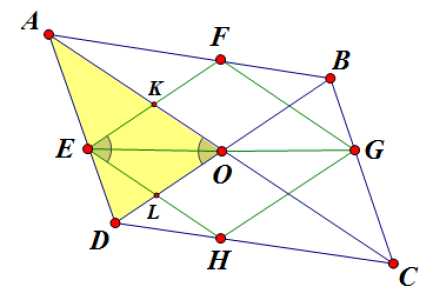
Так как стороны ромба параллельны диагоналям параллелограмма, четырехугольник — параллелограмм. ; — биссектриса углов и .
Биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам. Так как — биссектриса треугольника , :
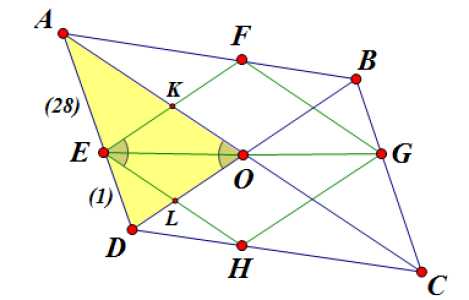
Из подобия треугольников и следует, что , отсюда . Тогда из соотношения (1) выразим сторону ромба:
Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними:
Площадь ромба равна произведению квадрата его стороны и синуса угла между сторонами, то есть
Ответ:
И. В. Фельдман, репетитор по математике.
ege-ok.ru
Подготовка к ОГЭ по геометрии 2015 | Геометрия
Подготовка к ОГЭ по геометрии 2015 | Геометрия — просто!Добрый день, друзья! Сегодня мы будем заниматься подготовкой к ОГЭ по геометрии. Для того, чтобы точно ответить на 5 вопросов модуля «Геометрия», необходимо знать основные геометрические фигуры, правила, которые с ними связаны и конечно же формулы. Так что давайте, попробуем.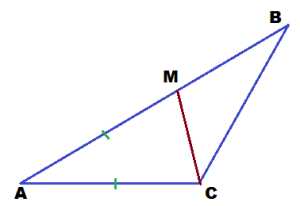 
Задача 1. Дан треугольник АВС. На стороне АВ выбрана точка М таким образом, что АМ=АС. Угол А в треугольнике АВС равен 10º, а угол С этого же треугольника равен 166º. Найти угол МСВ. Решение: Нам дано, что АМ=АС. А это значит, что треугольник АМС — равнобедренный. А мы знаем, что в равнобедренном треугольнике углы при основании равны.
Задача 1. Дан треугольник АВС. На стороне АВ выбрана точка М таким образом, что АМ=АС. Угол А в треугольнике АВС равен 10º, а угол С этого же треугольника равен 166º. Найти угол МСВ. Решение: Нам дано, что АМ=АС. А это значит, что треугольник АМС — равнобедренный. А мы знаем, что в равнобедренном треугольнике углы при основании равны.Угол при вершине треугольника АМС равен 10º. А мы знаем, что сумма внутренних углов треугольника равна 180º. Значит, на остальные 2 угла треугольника приходится 180-10 = 170º. Но углы в треугольнике АМС равны. Значит, каждый из них равен 170/2 = 85º. Угол АСМ равен 85º. Но этот угол входит в состав угла АСВ, который равен 166º. Значит, на долю другого угла, а именно МСВ приходится 166 — 85 = 81º. Ответ: угол МСВ равен 81º.
Задача 2. В окружности центральный угол МОК равен 122°. Найти длину большей дуги, если длина меньшей дуги равна 183. Решение: Длина дуги окружности зависит от величины центрального угла, который опирается на эту дугу. l=пRn/180, где l- длина дуги, n-величина центрального угла. 183 = 122пR/180 пR = 183*180/122 Большая дуга окружности измеряется центральным углом, который равен 360-122 = 238. Отсюда находим длину большей дуги: l=пRn/180 = 183*180/122 * 238/180 = 183*238/122 = 238*1.5 = 357. Ответ: Длина большей дуги равна 357.
Задача 3. Основания равнобедренной трапеции равны 8 и 18, а её боковые стороны равны 13. Найти площадь трапеции. Решение: Перед тем, как приступить к решению этой задачи, необходимо сделать дополнительное построение, а именно — опустить высоты из вершин В и С на основание АД. Слева и справа получим 2 прямоугольных треугольника, которые равны между собой по гипотенузе и острому углу. Значит, АМ=КД. Получается, что основание АД разбито на 3 отрезка АМ, МК и КД. МК = ВС = 8. АМ=КД = (18-8):2 = 5. Из треугольника АВМ, зная гипотенузу АВ=13, катет АМ=5, находим ВМ. ВМ = √13² — 5² = √169-25 = √144 = 12. Высота трапеции равна 12. Площадь трапеции находим по формуле: S = (8+18)/2 * 12 = 156. Ответ: Площадь трапеции 156.
Задача 4. В треугольнике АВС АВ=ВС=35, АС=42. Найти длину медианы ВМ. Решение: поскольку в треугольнике 2 стороны равны, это треугольник — равнобедренный. А в равнобедренном треугольнике медиана угла при вершине является одновременно биссектрисой и высотой. Получается, что треугольник АВМ — прямоугольный. АВ=35, АМ=1/2 АС = 21. По теореме Пифагора находим длину медианы. ВМ² = √35² — 21² = √(35-21)(35+21) = √14*56 = √14*14*4 = 14*2 = 28. Ответ: Длина медианы равна 28.
Задача 5. В трапеции АВСД основания равны 4 и 1, а её площадь равна 35. Найти площадь треугольника АВС. Решение: площадь трапеции равна произведению полу-суммы оснований на высоту. Отсюда, высота трапеции равна 35:2,5 = 14. Площадь треугольника АВС равна половине произведения основания на высоту. Основание треугольника равно 1, высота 14. Площадь равна 7. Ответ: площадь треугольника равна 7.
На сегодня всё. Успехов и до новых задач! В субботу 28 марта девятиклассники пишут пробный ОГЭ по математике. Ни пуха, ни пера!
Вам так же будет интересно:
Оставить комментарий
Подготовка к ОГЭ, геометрия, 8-9 класс. Тестовые задания и ответы.
Подготовка к ГИА. Раздел Геометрия. 9 класс.
1. Средняя линия трапеции равна 45, а меньшее основание равно 37. Найдите большее основание трапеции.
2. Чему равен больший угол равнобедренной трапеции, если известно, что разность противолежащих углов равна 72°? Ответ дайте в градусах.
3. Найдите высоту ромба, сторона которого равна , а острый угол равен 60°.
4. Найдите меньшую диагональ ромба, стороны которого равны 11, а острый угол равен 60°.
5. В квадрате расстояние от точки пересечения диагоналей до одной из его сторон равно 15. Найдите периметр этого квадрата.
6. В прямоугольнике диагональ делит угол в отношении 1:2, меньшая его сторона равна 11. Найдите диагональ данного прямоугольника.
7. Меньшая сторона прямоугольника равна 56, диагонали пересекаются под углом 60°. Найдите диагонали прямоугольника.
8. Диагональ параллелограмма образует с двумя его сторонами углы 29° и 58°. Найдите больший угол параллелограмма. Ответ дайте в градусах.
9. В треугольнике ABC AC = BC, угол C равен 120o, . Найдите AB.
10. В треугольнике ABC , угол C равен 120o. Найдите высоту AH.
11. В треугольнике ABC AC = BC = 6, высота AH равна 3. Найдите угол C. Ответ дайте в градусах.
12. В равностороннем треугольнике ABC высота CH равна . Найдите стороны этого треугольника.
13. В треугольнике ABC угол C равен 90o, CH — высота, угол A равен 30o, AB = 2. Найдите AH.
14. В треугольнике ABC угол C равен 90o, угол A равен 30o, . Найдите AB.
15. На рисунке угол 1 равен 48o, угол 2 равен 26o, угол 3 равен 40o. Найдите угол 4. Ответ дайте в градусах.
16. В треугольнике ABC угол A равен 60o, угол B равен 82o. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
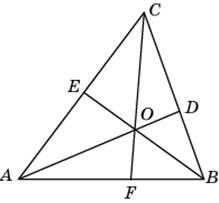
17. В треугольнике ABC угол A равен 30o, угол B равен 86o, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах.
18. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 4o. Найдите меньший угол этого треугольника. Ответ дайте в градусах.
19. Острые углы прямоугольного треугольника равны 69oи 21o. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
20. В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.
21. Острый угол прямоугольного треугольника равен 40o. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.
22. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на .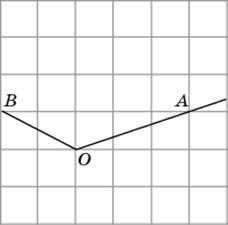 
23. Основания равнобедренной трапеции равны 76 и 48. Тангенс острого угла равен. Найдите высоту трапеции.
24. Большее основание равнобедренной трапеции равно 56. Боковая сторона равна 9. Синус острого угла равен . Найдите меньшее основание.
25. Основания равнобедренной трапеции равны 3 и 27. Боковые стороны равны 15. Найдите синус острого угла трапеции.
26. В параллелограмме ABCD AB=5, AD=8,. Найдите большую высоту параллелограмма.
27. В треугольнике ABC AC=BC=5,. Найдите синус внешнего угла при вершине A.
28.В треугольнике ABC угол C равен 90o, CH — высота, AH = 49, . Найдите BH.
ОТВЕТЫ:
1. | 2. | 3. | 4. | 5. | 6. | 7. | 8. | 9. | 10. |
53 | 126 | 4,5 | 11 | 120 | 22 | 112 | 93 | 6 | 3 |
11. | 12. | 13. | 14. | 15. | 16. | 17. | 18. | 19. | 20. |
30 | 4 | 1,5 | 4 | 114 | 49 | 56 | 41 | 48 | 36 |
21. | 22. | 23. | 24. | 25. | 26. | 27. | 28. | ||
65 | 2 | 17 | 42 | 0,6 | 7 | 0,4 | 25 |
kopilkaurokov.ru
Карточка 1 Я ЗНАЮ ГЕОМЕТРИЮ 1) Найти АВ 2) Найти угол АСВ, если угол АОВ = 84° 3) 4) Найдите площадь равностороннего треугольника, отсекаемого от данного треугольника его средней линией, если площадь данного треугольника равна 48см2. 5) Периметр равностороннего треугольника АВС равен 24см. Найдите длину средней линии этого треугольника. | Карточка 2 Я ЗНАЮ ГЕОМЕТРИЮ 1) Найти угол АСВ, если угол АОВ равен 160° 2) 3) Найдите площадь данного равностороннего треугольника, если площадь треугольника, отсекаемого от него средней линией, равна 6 см2. 4) Средняя линия равностороннего треугольника АВС равна 8см. Найдите периметр этого треугольника 5) Из квадрата со стороной 10см вырезан прямоугольник со сторонами 3см и 4см. Найдите площадь оставшейся части. | Карточка 3 Я ЗНАЮ ГЕОМЕТРИЮ 1) Найти угол ВАС, если угол ВОС = 160° 2) Найдите площадь прямоугольного треугольника, если его гипотенуза равна 16см, а один из углов треугольника равен 45°.
3) Найти угол ВАС
4) Найти длину меньшей средней линии треугольника 5) В прямоугольнике одна сторона равна 28см, а диагональ равна 35см. Найдите площадь прямоугольника. | |
Карточка 4 Я ЗНАЮ ГЕОМЕТРИЮ 1) Найти угол ВАС
2) Найти угол АОВ, если угол АСВ = 25° 3) Найти площадь четырёхугольника 4) Найти длину большей высоты параллелограмма 5) Найти косинус угла | Карточка 5 Я ЗНАЮ ГЕОМЕТРИЮ 1) В треугольнике АВС угол В равен 46°, угол С равен 71°, ВD – биссектриса. Найдите угол АDВ. 2) Найти радиус окружности, если АВ = 12см, ОА = 13см. 3) Найти длину отрезка НМ, Если АМ=3см, АН=НС=2 4) Найти угол ВОС, если угол ВАС = 70° 5) Найти площадь треугольника АВС, если высота, проведённая к одной из его сторон равна 11, а средняя линия, параллельная этой стороне, равна 10. | Карточка 6 Я ЗНАЮ ГЕОМЕТРИЮ 1) Найти угол АОВ, если точки А и В делят окружность на две дуги в отношении 9 : 11. 2) Найти площадь параллелограмма 3) КВСD — параллелограмм. Найдите длину отрезка АВ. 4) Найдите косинус угла 5) Найдите площадь четырёхугольника | |
Карточка 7 Я ЗНАЮ ГЕОМЕТРИЮ 1) Найти угол 3, если угол 1 равен 40°, а угол 2 равен 55°. 2) Основания трапеции равны 48 и 24, высота 4. Найдите площадь трапеции. 3) На рисунке Изображён параллелограмм. Найти х. 4) Из квадрата со стороной 8см вырезан прямоугольник со сторонами 3см и 2см. Найдите площадь оставшейся части. 5) Стороны прямоугольника равны 10 и 24. Найдите радиус окружности, описанной около этого прямоугольника. | Карточка 8 Я ЗНАЮ ГЕОМЕТРИЮ 1) Средняя линия трапеции равна 11, а меньшее основание равно 5. Найдите большее основание трапеции. 2) Найдите угол α 3) Прямоугольный треугольник вписан в окружность. Найдите радиус этой окружности. 4) Найдите тангенс угла А. 5) Из прямоугольника со сторонами 8см и 10см вырезан квадрат со стороной 5см. Найдите площадь оставшейся части. | Карточка 9 Я ЗНАЮ ГЕОМЕТРИЮ 1) Найдите тангенс угла А. 2) Найти длину медианы проведённой из вершины прямого угла. 3) Стороны параллелограмма равны 10 и 35. Высота, опущенная на первую сторону, равна 21. Найдите высоту, опущенную на вторую сторону. 4) Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах. 5) Найти площадь трапеции. | |
Карточка 10 Я ЗНАЮ ГЕОМЕТРИЮ 1) Найти больший угол параллелограмма АВСD 2) 3) Найти угол ОСD 4) ВС = 8, соsВ = 0,8 Найти АВ 5) АВСD — равнобедренная трапеция Найти угол АВC | Карточка 11 Я ЗНАЮ ГЕОМЕТРИЮ 1) Найти меньший угол параллелограмма АВСD 2) Найти угол ОСD 3) 4) 5) Найти тангенс угла С | Карточка 12 Я ЗНАЮ ГЕОМЕТРИЮ 1) АВСD — равнобедренная трапеция Найти угол АDC Найти угол ОDС 2) 3) АС = 6, соsA = 0,6 Найти АВ 4) 5) Найти площадь параллелограмма | |
Карточка 13 Я ЗНАЮ ГЕОМЕТРИЮ 1) В трапеции АВСD АВ=СD ∟ВDА=18° и ∟ВDС=97°. Найдите угол АВD. 2) Найдите тангенс угла АОВ 3) Найдите расстояние от точки А до середины отрезка АВ 4) Найдите угол АВС 5) Колесо имеет 8 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы. | Карточка 14 Я ЗНАЮ ГЕОМЕТРИЮ 1) В трапеции АВСD АВ=СD ∟ВDА=40° и ∟ВDС=24°. Найдите угол АВD. 2) Найдите расстояние от точки А до середины отрезка АВ Найдите котангенс угла АОВ 3) 4) Найдите угол АВС 5) Угол АОВ = 63°. Найдите угол АСВ. | Карточка 15 Я ЗНАЮ ГЕОМЕТРИЮ 1) В трапеции АВСD АВ=СD ∟ВDА=24° и ∟ВDС=70°. Найдите угол АВD. 2) Найдите расстояние от точки А до середины отрезка АВ 3) Найдите котангенс угла АОВ 4) Из квадрата Вырезали прямоугольник. Найдите площадь получившейся фигуры. 5) Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 2,6 м и 3,6 м? | |
Карточка 16 Я ЗНАЮ ГЕОМЕТРИЮ 1) Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3,4 м и 4,6 м? 2) Сколько спиц в колесе, если угол между соседними спицами равен 40°? 3) Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 40 и 85. 4) Найдите тангенс угла АОВ 5) Найдите площадь фигуры | Карточка 17 Я ЗНАЮ ГЕОМЕТРИЮ 1) Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 20 см. Сколько потребуется таких дощечек? 2) Сколько спиц в колесе, если угол между соседними спицами равен 9°? 3) Колесо имеет 40 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы. 4) Найдите тангенс угла АОВ 5) Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота средней опоры 3,1 м, высота большей опоры 3,3 м. Найдите высоту малой опоры. | Карточка 18 Я ЗНАЮ ГЕОМЕТРИЮ 1) Пол комнаты, имеющей форму прямоугольника со сторонами 6 м и 7 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 25 см. Сколько потребуется таких дощечек? 2) Сколько спиц в колесе, если угол между соседними спицами равен 15°? 3) Колесо имеет 6 спиц. Найдите величину угла (в градусах), который образуют две соседние спицы. 4) Найдите котангенс угла АОВ 5) Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,5 м, высота средней опоры 2,65 м. Найдите высоту большей опоры. | |
Карточка 19 Я ЗНАЮ ГЕОМЕТРИЮ 1) Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,95 м, высота большей опоры 3,65 м. Найдите высоту средней опоры. 2) Сколько потребуется кафельных плиток квадратной формы со стороной 15 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 2,7 м и 3 м? 3) Человек ростом 1,8 м стоит на расстоянии 10 м от столба, на котором висит фонарь на высоте 7,8 м. Найдите длину тени человека в метрах. 4) Найдите площадь трапеции 5) Прямые m и n параллельны. Найдите ∟3, если ∟1 = 117°, ∟2 = 24°. | Карточка 20 Я ЗНАЮ ГЕОМЕТРИЮ 1) Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 2,25 м, высота большей опоры 2,85 м. Найдите высоту средней опоры. 2) Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3,4 м и 4,2 м? 3) Человек ростом 1,6 м стоит на расстоянии 15 м от столба, на котором висит фонарь на высоте 9,6 м. Найдите длину тени человека в метрах. 4) Найдите площадь трапеции 5) Прямые m и n параллельны. Найдите ∟3, если ∟1 = 74°, ∟2 = 39°. | Карточка 21 Я ЗНАЮ ГЕОМЕТРИЮ
80 см. Расстояние между точками А и В составляет 41 м. Найдите высоту, на которую поднимается лестница (в метрах). 2) Человек ростом 1,5 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 10,5 м. Найдите длину тени человека в метрах. 3) Найдите площадь трапеции 4) 5) Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности. | |
Карточка 22 Я ЗНАЮ ГЕОМЕТРИЮ
сторону на два отрезка. Каковы длины этих отрезков? 2) 3) Найдите тангенс угла АВС 4) 5) На отрезке AB выбрана точка C так, что AC=6 и BC=4. Построена окружность с центром A , проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности. | Карточка 23 Я ЗНАЮ ГЕОМЕТРИЮ 1) 2) MN и АВ – диаметры окружности. ∟NВА=73°. Найти угол NMB 3) ∟DMC=24°. Найдите угол СМА. 4) Найти площадь трапеции. 5) Найти площадь параллелограмма | Карточка 24 Я ЗНАЮ ГЕОМЕТРИЮ 1) Прямая касается окружности в точке K . Точка O – центр окружности. Хорда КМ образует с касательной угол, равный 7°. Найдите величину угла ОМК 2) Найти площадь трапеции 3) 4) Найти радиус окружности 5) В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB. |
videouroki.net
