Справочный материал огэ математика 9 класс 2018 – Материал для подготовки к ЕГЭ (ГИА) по алгебре (9, 11 класс) на тему: Справочный материал для подготовки к ОГЭ и ЕГЭ по математике | скачать бесплатно

ОГЭ 2018 Математика Новый полный справочник

УДК 373:512
ББК 22.14я721
М52
Мерзляк, А.Г.
М52
Математика : Новый полный справочник для подготовки к ОГЭ / А.Г. Мерзляк, В.Б. Полонский,
М.С. Якир. — Москва : АСТ, 2017. — 447,[1] сил Новый полный справочник для подготовки к ОГЭ)
ISBN
978 5 17 096817 Самый популярный справочник для подготовки к ОГЭ)
Cправочник содержит материал курса Математика в объёме, проверяемом на государственной итоговой аттестации.
Структура книги соответствует современному кодификатору элементов содержания по предмету, на основе которого формируются контрольные измерительные материалы (КИМы)
основного государственного экзамена (ОГЭ).
Справочник состоит из двух глав. Первая глава Арифметика. Алгебра соответствует содержанию курсов математики классов и алгебры 7–9 классов основной школы, вторая глава Геометрия — содержанию курса геометрии 7–9 классов.
Помимо теоретического материала в справочнике представлено значительное количество разобранных примеров, иллюстрирующих основные методы и приёмы решения задач. Ко всем заданиям в конце пособия даны ответы для самопроверки.
Работа с пособием позволит повторить все основные темы курса математики за 5–9 классы и успешно подготовиться к сдаче ОГЭ.
Справочник адресован выпускникам 9 х классов.
УДК 373:512
ББК я 5 17 096816 Новый полный справочник для подготовки к ОГЭ)
ISBN
978 5 17 096817 Самый популярный справочник для подготовки к ОГЭ)
© Мерзляк А.Г., Полонский В.Б.,
Якир МС ООО Издательство АСТ»

ОГЛАВЛЕНИЕ
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ГЛАВА АРИФМЕТИКА. АЛГЕБРА 1. Натуральные числа . . . . . . . . . . . . . . . . . . . . 17 1.1. Десятичная запись натуральных чисел. . . . 17 1.2. Арифметические действия над натуральными числами.
Степень с натуральным показателем . . . . . 18 1.3. Делимость натуральных чисел . . . . . . . . . . 20 1.4. Признаки делимости. . . . . . . . . . . . . . . . . . . 21 1.5. Простые и составные числа . . . . . . . . . . . . . 22 1.6. Наибольший общий делитель.
Наименьшее общее кратное . . . . . . . . . . . . . 24 1.7. Деление с остатком . . . . . . . . . . . . . . . . . . . . Примеры заданий № 1 . . . . . . . . . . . . . . . . . . . . . 27
§ 2. Дроби . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 2.1. Обыкновенная дробь. Основное свойство дроби. Сравнение дробей . . . . . . . . . . . . . . . 31 2.2. Арифметические действия с обыкновенными дробями . . . . . . . . . . . . . . 34 2.3. Десятичная дробь.
Сравнение десятичных дробей . . . . . . . . . . . 35 2.4. Арифметические действия с десятичными дробями . . . . . . . . . . . . . . . . 37 2.5. Нахождение части от целого и целого по его части. . . . . . . . . . . . . . . . . . . 39

ОГЛАВЛЕНИЕ. Представление обыкновенной дроби в виде десятичной. Бесконечные периодические десятичные дроби . . . . . . . . . . . . . . . . . . . . . 40 2.7. Округление чисел . . . . . . . . . . . . . . . . . . . . . Примеры заданий
№ 2 . . . . . . . . . . . . . . . . . . . . . 43 2.8. Проценты . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 2.9. Нахождение процентов от величины и величины по её процентам . . . . . . . . . . . 48 2.10. Отношение. Процентное отношение . . . . . 49 2.11. Пропорции . . . . . . . . . . . . . . . . . . . . . . . . . . 50 2.12. Прямая и обратная пропорциональные зависимости . . . . . . . . . . . . . . . . . . . . . . . . Примеры заданий № 3 . . . . . . . . . . . . . . . . . . . . . 53
§ 3. Рациональные числа . . . . . . . . . . . . . . . . . . 57 3.1. Целые числа. Рациональные числа . . . . . . . 57 3.2. Координатная прямая . . . . . . . . . . . . . . . . . 58 3.3. Модуль числа.
Сравнение рациональных чисел . . . . . . . . . 59 3.4. Арифметические действия с рациональными числами . . . . . . . . . . . . . Примеры заданий № 4 . . . . . . . . . . . . . . . . . . . . . 62
§ 4. Целые выражения. . . . . . . . . . . . . . . . . . . . . 66 4.1. Буквенное выражение
(выражение с переменными).
Алгебраические выражения . . . . . . . . . . . . 66 4.2. Свойства степени с натуральным показателем . . . . . . . . . . . . . 67 4.3. Одночлен . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69 4.4. Многочлен. Степень многочлена.
Корень многочлена с одной переменной . . . 70 4.5. Сложение, вычитание и умножение многочленов . . . . . . . . . . . . . . . . . . . . . . . . . 72

ОГЛАВЛЕНИЕ. Квадрат суммы и квадрат разности.
Формула разности квадратов . . . . . . . . . . . . 73 4.7. Формулы суммы кубов и разности кубов . . . . . . . . . . . . . . . . . . . . . . 75 4.8. Разложение многочленов на множители. . . Примеры заданий № 5 . . . . . . . . . . . . . . . . . . . . . 77
§ 5. Дробные выражения . . . . . . . . . . . . . . . . . . . 82 5.1. Алгебраические (рациональные) дроби . . . 82 5.2. Тождество. Тождественные преобразования выражений . . . . . . . . . . . . . 83 5.3. Основное свойство рациональной дроби. Сокращение дробей . . . . . . . . . . . . . . . . . . . . 83 5.4. Действия с алгебраическими дробями. . . . . Примеры заданий № 6 . . . . . . . . . . . . . . . . . . . . . 88 5.5. Степень с нулевыми целым отрицательным показателями . . . . . . . . . . . 94 5.6. Стандартный вид числа . . . . . . . . . . . . . . . . Примеры заданий № 7 . . . . . . . . . . . . . . . . . . . . . 96
§ 6. Корень из числа . . . . . . . . . . . . . . . . . . . . . . . 99 6.1. Квадратный корень. Арифметический квадратный корень . . . . . . . . . . . . . . . . . . . . 99 6.2. Свойства арифметического квадратного корня . . . . . . . . . . . . . . . . . . . . 100 6.3. Тождественные преобразования выражений, содержащих квадратные корни . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102 6.4. Корень третьей степени . . . . . . . . . . . . . . . . 104 6.5. Запись корня с помощью степени с дробным показателем . . . . . . . . . . . . . . . . . 104 6.6. Понятие об иррациональном числе. Десятичные приближения иррациональных чисел . . . . . . . . . . . . . . . . . 105

ОГЛАВЛЕНИЕ. Понятие о множестве. Числовые множества. Множество действительных чисел . . . . . . . Примеры заданий № 8 . . . . . . . . . . . . . . . . . . . . . 109
§ 7. Уравнения с одной переменной . . . . . . . . . . 114 7.1. Общие сведения об уравнениях с одной переменной . . . . . . . . . . . . . . . . . . . 114 7.2. Линейное уравнение с одной переменной . . 117 7.3. Квадратное уравнение . . . . . . . . . . . . . . . . . 118 7.4. Теорема Виета . . . . . . . . . . . . . . . . . . . . . . . . 121 7.5. Квадратный трёхчлен. Разложение квадратного трёхчлена на множители . . . . Примеры заданий № 9 . . . . . . . . . . . . . . . . . . . . . 124 7.6. Рациональные уравнения. . . . . . . . . . . . . . . 128 7.7. Метод замены переменной . . . . . . . . . . . . . . Примеры заданий № 10 . . . . . . . . . . . . . . . . . . . . 131
§ 8. Функции. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 134 8.1. Понятие функции. Область определения и область значений функции . . . . . . . . . . . . 134 8.2. Способы задания функции . . . . . . . . . . . . . . 135 8.3. График функции . . . . . . . . . . . . . . . . . . . . . . 137 8.4. Нули функции. Промежутки знакопостоянства. Возрастание и убывание функции. Наибольшее и наименьшее значения функции . . . . . . . . 139 8.5. Чтение графиков функций,
отображающих реальные процессы. . . . . . . 142 8.6. Линейная функция и её свойства.
Прямая пропорциональность. . . . . . . . . . . . 144 8.7. Обратная пропорциональная зависимость.
Функция y = , где k 0, и её свойства . . . Примеры заданий № 11 . . . . . . . . . . . . . . . . . . . . 149
k
x

ОГЛАВЛЕНИЕ. Квадратичная функция и её свойства . . . . . 164 8.9. Функция и её свойства . . . . . . . . . 169 8.10. График функции
. . . . . . . . . . . . . 170 8.11. Функция y = | x | и её свойства . . . . . . . . . . 170 8.12. Решение уравнений графическим методом . . . . . . . . . . . . . . . . . Примеры заданий № 12 . . . . . . . . . . . . . . . . . . . . 173
§ 9. Уравнения с двумя переменными . . . . . . . . 184 9.1. Решение уравнения с двумя переменными.
График уравнения. . . . . . . . . . . . . . . . . . . . . 184 9.2. Системы уравнений с двумя переменными. Решение систем уравнений графическим методом . . . . . . . . . . . . . . . . . . 186 9.3. Методы решения систем двух уравнений с двумя переменными . . . . . . . . . . . . . . . . . . Примеры заданий № 13 . . . . . . . . . . . . . . . . . . . . 194
§ 10. Текстовые задачи . . . . . . . . . . . . . . . . . . . . 199 10.1. Решение текстовых задач с помощью уравнений . . . . . . . . . . . . . . . . Примеры заданий № 14 . . . . . . . . . . . . . . . . . . . . 202 10.2. Решение текстовых задач с помощью систем уравнений . . . . . . . . . . . Примеры заданий № 15 . . . . . . . . . . . . . . . . . . . . 209 10.3. Решение текстовых задач арифметическим способом . . . . . . . . . . . . . Примеры заданий № 16 . . . . . . . . . . . . . . . . . . . . 213
§ 11. Неравенства . . . . . . . . . . . . . . . . . . . . . . . . . 216 11.1. Числовые неравенства и их свойства . . . . . 216 11.2. Оценка значений числовых выражений с помощью свойств числовых неравенств . . . . . . . . . . . . . . . . . . . . . . . . . . 218
y
x
y
x
3

ОГЛАВЛЕНИЕ. Общие сведения о неравенствах с одной переменной . . . . . . . . . . . . . . . . . . . 220 11.4. Числовые промежутки . . . . . . . . . . . . . . . . 222 11.5. Линейные неравенства с одной переменной.
Системы линейных неравенств . . . . . . . . . 223 11.6. Квадратные неравенства . . . . . . . . . . . . . . Примеры заданий № 17 . . . . . . . . . . . . . . . . . . . . 228
§ 12. Числовые последовательности . . . . . . . . . 234 12.1. Понятие последовательности . . . . . . . . . . . 234 12.2. Способы задания последовательности . . . . 235 12.3. Арифметическая прогрессия . . . . . . . . . . . 238 12.4. Сумма n первых членов арифметической прогрессии . . . . . . . . . . . . . 239 12.5. Геометрическая прогрессия.
Формула сложных процентов . . . . . . . . . . 240 12.6. Сумма n первых членов геометрической прогрессии . . . . . . . . . . . . . 244 12.7. Сумма бесконечной геометрической прогрессии, модуль знаменателя которой меньше единицы . . . . . . . . . . . . . . . . . . . . . Примеры заданий № 18 . . . . . . . . . . . . . . . . . . . . 245
§ Элементы комбинаторики, теории вероятностей, описательной статистики . . 249 13.1. Комбинаторные задачи.
Перебор вариантов . . . . . . . . . . . . . . . . . . . 249 13.2. Комбинаторные правила суммы и произведения . . . . . . . . . . . . . . . . . . . . . . 251 13.3. Представление данных в виде таблиц, диаграмм, графиков . . . . . . . . . . . . . . . . . . 253 13.4. Статистика.
Статистические характеристики . . . . . . . . 255 13.5. Частота и вероятность случайного события . . . . . . . . . . . . . . . . . . . . . . . . . . . . 257

ОГЛАВЛЕНИЕ. Достоверные и невозможные события.
Равновозможные события. Классическое определение вероятности . . . . . . . . . . . . . . 259 13.7. Представление о геометрической вероятности . . . . . . . . . . . . . . . . . . . . . . . . . Примеры заданий № 19 . . . . . . . . . . . . . . . . . . . . ГЛАВА ІІ
ГЕОМЕТРИЯ
§ Простейшие геометрические фигуры
и их свойства . . . . . . . . . . . . . . . . . . . . . . . . 273 14.1. Прямая, луч, отрезок.
Измерение отрезков . . . . . . . . . . . . . . . . . . 273 14.2. Угол. Измерение углов . . . . . . . . . . . . . . . . 275 14.3. Смежные и вертикальные углы . . . . . . . . . 277 14.4. Перпендикулярные прямые. Угол между пересекающимися прямыми. Перпендикуляр и наклонная.
Расстояние от точки до прямой . . . . . . . . . Примеры заданий № 20 . . . . . . . . . . . . . . . . . . . . 279
§ 15. Параллельные прямые . . . . . . . . . . . . . . . . 282 15.1. Признаки параллельности прямых . . . . . . 282 15.2. Свойства параллельных прямых . . . . . . . . Примеры заданий № 21 . . . . . . . . . . . . . . . . . . . . 285
§ 16. Треугольник . . . . . . . . . . . . . . . . . . . . . . . . . 287 16.1. Элементы треугольника.
Равные треугольники . . . . . . . . . . . . . . . . . 287 16.2. Виды треугольников . . . . . . . . . . . . . . . . . . 290 16.3. Признаки равенства треугольников . . . . . 291

ОГЛАВЛЕНИЕ. Свойства равнобедренного треугольника . . . 292 16.5. Признаки равнобедренного треугольника. . . 293 16.6. Сумма углов треугольника. Свойство внешнего угла треугольника . . . . . . . . . . . 295 16.7. Неравенство треугольника.
Зависимость между величинами сторон и углов треугольника . . . . . . . . . . . . . . . . . 297 16.8. Признаки равенства прямоугольных треугольников. Свойства прямоугольного треугольника . . . . . . . . . . . . . . . . . . . . . . . . 298 16.9. Терема Фалеса. Теорема о пропорциональных отрезках . . . . . . . . . . 301 Средняя линия треугольника . . . . . . . . . . 302 Подобные треугольники . . . . . . . . . . . . . . 303 Признаки подобия треугольников . . . . . . Примеры заданий № 22 . . . . . . . . . . . . . . . . . . . . 308 16.13. Метрические соотношения в прямоугольном треугольнике . . . . . . . . 314 16.14. Теорема Пифагора . . . . . . . . . . . . . . . . . . 314 16.15. Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника . . . . . . . . . . . . . . . . . . . . . . . 315 Синус, косинус, тангенс и котангенс угла от 0 до 180 . . . . . . . . . . . . . . . . . . . . 318 Теорема косинусов . . . . . . . . . . . . . . . . . . 321 Теорема синусов . . . . . . . . . . . . . . . . . . . . Примеры заданий № 23 . . . . . . . . . . . . . . . . . . . . 323
§ 17. Окружность и круг . . . . . . . . . . . . . . . . . . . 328 17.1. Понятие о геометрическом месте точек.
Примеры ГМТ . . . . . . . . . . . . . . . . . . . . . . . 328 17.2. Окружность и круг, их элементы . . . . . . . 329 17.3. Свойства элементов окружности . . . . . . . . 331 17.4. Касательная и секущая к окружности . . . 332

ОГЛАВЛЕНИЕ. Взаимное расположение двух окружностей . . . . . . . . . . . . . . . . . . . . . . . . 334 17.6. Окружность, описанная около треугольника . . . . . . . . . . . . . . . . . . . . . . . . 335 17.7. Окружность, вписанная в треугольник . . . 337 17.8. Центральные и вписанные углы.
Градусная мера дуги окружности . . . . . . . 339 17.9. Длина окружности . . . . . . . . . . . . . . . . . . . Примеры заданий № 24 . . . . . . . . . . . . . . . . . . . . 342
§ 18. Многоугольник . . . . . . . . . . . . . . . . . . . . . . 349 18.1. Четырёхугольник и его элементы . . . . . . . 349 18.2. Параллелограмм и его свойства . . . . . . . . . 351 18.3. Признаки параллелограмма . . . . . . . . . . . . 353 18.4. Прямоугольник, ромб, квадрат . . . . . . . . . Примеры заданий № 25 . . . . . . . . . . . . . . . . . . . . 356 18.5. Трапеция. Средняя линия трапеции . . . . . 361 18.6. Четырёхугольник,
вписанный в окружность . . . . . . . . . . . . . . 364 18.7. Четырёхугольник,
описанный около окружности . . . . . . . . . . 365 18.8. Сумма углов выпуклого многоугольника . . . 365 18.9. Правильные многоугольники. . . . . . . . . . . Примеры заданий № 26 . . . . . . . . . . . . . . . . . . . . 368
§ 19. Площадь и объём . . . . . . . . . . . . . . . . . . . . . 374 19.1. Понятие площади многоугольника.
Площадь прямоугольника . . . . . . . . . . . . . 374 19.2. Площадь параллелограмма и трапеции. . . 376 19.3. Формулы для нахождения площади треугольника . . . . . . . . . . . . . . . . . . . . . . . . 377 19.4. Площадь круга. Площадь сектора . . . . . . . 379 19.5. Формулы объёмов прямоугольного параллелепипеда, куба и шара . . . . . . . . . . Примеры заданий № 27 . . . . . . . . . . . . . . . . . . . . 381

ОГЛАВЛЕНИЕ 20. Декартовые координаты на плоскости . . . 388 20.1. Координатная плоскость . . . . . . . . . . . . . . 388 20.2. Формула расстояния между двумя точками. Координаты середины отрезка. . 390 20.3. Уравнение фигуры.
Уравнение окружности. . . . . . . . . . . . . . . . 391 20.4. Общее уравнение прямой. Уравнение прямой с угловым коэффициентом . . . . . . 393 20.5. Графическая интерпретация неравенств с двумя переменными . . . . . . . . . . . . . . . . Примеры заданий
№ 28 . . . . . . . . . . . . . . . . . . . . 396
§ 21. Векторы на плоскости. . . . . . . . . . . . . . . . . 399 21.1. Понятие вектора. Модуль вектора. Коллинеарные векторы.
Равные векторы. . . . . . . . . . . . . . . . . . . . . . 399 21.2. Координаты вектора . . . . . . . . . . . . . . . . . . 402 21.3. Сложение и вычитание векторов . . . . . . . . 404 21.4. Умножение вектора на число . . . . . . . . . . . 407 21.5. Разложение вектора по двум неколлинеарным векторам. . . . . . . . . . . . . 408 21.6. Скалярное произведение векторов. . . . . . . Примеры заданий
№ 29 . . . . . . . . . . . . . . . . . . . . 412
§ 22. Геометрические преобразования . . . . . . . . 416 22.1. Движение фигуры.
Параллельный перенос . . . . . . . . . . . . . . . . 416 22.2. Осевая симметрия . . . . . . . . . . . . . . . . . . . . 418 22.3. Центральная симметрия. . . . . . . . . . . . . . . 420 22.4. Поворот . . . . . . . . . . . . . . . . . . . . . . . . . . . . 423 22.5. Гомотетия. Подобие фигур . . . . . . . . . . . . . Примеры заданий № 30 . . . . . . . . . . . . . . . . . . . . Ответы к примерам заданий . . . . . . . . . . . . . . . . 434

ВВЕДЕНИЕ
На основной государственный экзамен (ОГЭ) по математике выносятся темы, рассматриваемые в курсах математики 5–6 классов, алгебры и геометрии классов. Основой подготовки к ОГЭ является организация систематического повторения материала, изученного в 5–9 классах. Существует целый ряд способов реализации этой задачи. Например, можно использовать школьные учебники.
Неудобства такого подхода очевидны во первых,
надо иметь под рукой все школьные учебники по математике соответствующих этапов её изучения;
во вторых, поиск необходимого материала может привести к немалой потере времени. Гораздо удобней использовать пособие, в котором в краткой форме изложены базовые факты определения, теоремы, формулы, свойства математических объектов и т. п. Именно такую книгу выдержите в руках. Она представляет собой справочник для подготовки к
ОГЭ по математике.
Это пособие содержит не только теоретический материал, необходимый для решения вариантов
ОГЭ, но и значительное количество разобранных примеров, иллюстрирующих основные методы и приёмы решения задач.
Данный справочник выполняет также и свою традиционную роль — позволяет быстро найти нужную информацию какими свойствами обладает степень с целым показателем, чему равна сумма первых членов геометрической прогрессии, как найти дробь от числа, по какой формуле можно вычислить площадь трапеции и т. п
14
ВВЕДЕНИЕ
Справочник состоит из двух глав. Первая глава
«Арифметика. Алгебра соответствует содержанию курсов математики 5–6 классов и алгебры 7–9 классов основной школы, вторая глава Геометрия содержанию курса геометрии 7–9 классов. Каждая из глав разбита на параграфы. Их содержание отвечает кодификатору, на основании которого формируются задания для проведения ОГЭ по математике.
Понятно, что для успешного написания ОГЭ необходимо уметь решать задачи. Поэтому в справочник включён обширный дидактический материал.
Каждый параграф содержит одну или две (в зависимости от объёма материала) проверочные работы в рубрике Примеры заданий. Такое название рубрики связано стем, что большинство представленных в ней задач аналогичны или близки по содержанию и форме к заданиям, предлагавшимся враз ные годы на ОГЭ по математике.
Большинство проверочных работ состоит из двух частей. Задания второй части более сложные. Поэтому советуем приступать к их решению после того,
как будут выполнены задания первой части.
Некоторые задания первой части представляют собой задачи, решение которых заключается в выборе одного правильного ответа из четырёх предложенных. Для таких задач в рубрике Ответы к примерам заданий указан номер правильного ответа.
Желаем вам успешной сдачи основного государственного экзамена по математике

ГЛАВА I
АРИФМЕТИКА.
АЛГЕБРА

перейти в каталог файлов

metodich.ru

Баллы по математике ОГЭ 2017

Баллы по математике ОГЭ 2017 — 9 класс

Критерии оценивания ОГЭ по математике и баллы за задания можно найти в демоверсии КИМ.

Первичный балл — это предварительный балл, который получается путем прямого суммирования числа правильных ответов, каждый из которых имеет определенный коэффициент. Каждое выполненное задание оценивается от 1 и более баллов. Первичные баллы переводятся в отметки по пятибалльной шкале.

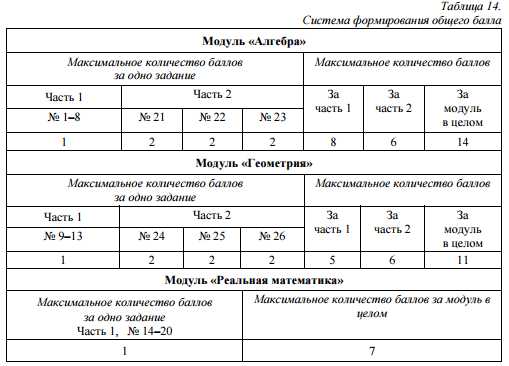
Максимальный балл ОГЭ 2017 по математике — 32 

Из них – за модуль «Алгебра» – 14 баллов, за модуль «Геометрия» – 11 баллов, за модуль «Реальная математика» – 7 баллов.

Минимальный балл 

Рекомендуемый минимальный результат выполнения экзаменационной работы по математике – 8 баллов, набранные в сумме за выполнение заданий всех трёх модулей, при условии, что из них не менее 3 баллов по модулю «Алгебра», не менее 2 баллов по модулю «Геометрия» и не менее 2 баллов по модулю «Реальная математика».

Перевод баллов ОГЭ по математике в оценки.

Разработанная специалистами ФГБНУ «ФИПИ» шкала перевода первичных баллов в отметки по пятибалльной шкале для проведения ОГЭ носят РЕКОМЕНДАТЕЛЬНЫЙ ХАРАКТЕР. 

Таблица оценок ОГЭ 2017

Отметка по пятибалльной шкале	2	3	4	5
Суммарный балл за работу в целом	0-7	8-14	15-21	22-32

Шкала оценивания ОГЭ от ФИПИ — скачать

Распределение баллов ОГЭ по заданиям отражена в демонстрационном варианте в файле спецификация.

Результаты экзамена могут быть использованы при приеме обучающихся в профильные классы средней школы. Ориентиром при отборе в профильные классы могут быть показатели, примеры нижних границ которых приведены ниже:

— для естественнонаучного профиля: 18 баллов, из них не менее 10 по алгебре, не менее 6 по геометрии;

— для экономического профиля: 18 баллов, из них не менее 9 по алгебре, 3 по геометрии, 5 по реальной математике;

— для физико-математического профиля: 19 баллов, из них не менее 11 по алгебре, 7 по геометрии.

Смотрите также:

— демоверсии ОГЭ 2017 по математике

— официальный сайт ОГЭ

ucthat-v-skole.ru

Справочные материалы ОГЭ — Сайт учителя

Справочные материалы ОГЭ — Сайт учителя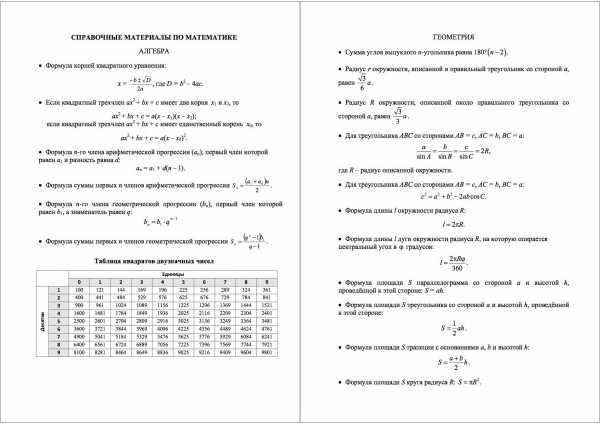

Скачать в PDF

 

 

 

 

Поделиться ссылкой:

Похожее

Навигация по записям

timur-ovchinnikov.ru