решение и разбор типовых вариантов по всем предметам
Как проводится и проверяется?
Экзамен длится несколько часов, продолжительность зависит от выбранного предмета. Место проведения определяется министерством образования на муниципальном уровне в содействии с представителями исполнительной власти РФ. Оно должно отвечать общегосударственным требованиям безопасности и оснащенности системой видеонаблюдения.
Проведение ЕГЭ подвергается строжайшему контролю. Распределение выпускников по пунктам проведения экзамена начинается в 9.00, начало экзамена в 10.00 по местному времени.
Учащиеся распределяются по аудиториям, занимают свои места. Получив КИМы, выслушивают инструктаж и заполняют бланки под присмотром инструктора.
Если выпускнику понадобится выйти из аудитории, он сможет сделать это только в сопровождении наблюдателя.
Тестовая часть проверяется специализированными компьютерными программами, а часть С экспертами региональной экзаменационной комиссии.
Что понадобится и от чего придется отказаться на ЕГЭ?
Отправляясь на ЕГЭ по любому предмету необходимо иметь при себе паспорт, две-три черные гелевые ручки. При необходимости можно взять с собой бутылочку питьевой воды и что-то из еды, к примеру, плитку шоколада. При каких-либо специфических заболеваниях разрешается взять нужные лекарственные препараты.
Для учащихся с особыми образовательными потребностями допускается применение специальных технических средств.
Каждый предмет имеет свои особенности. Так на экзамене по физике, химии и географии разрешается применение калькуляторов и линеек.
Телефоны, другие средства связи и личные вещи, недопустимые на экзамене, располагаются у входа в аудиторию в специально отведенном для этих целей месте.
Если выпускник нарушает правила или порядок проведения ЕГЭ, организатор или наблюдатель имеют право удалить его с экзамена.
spadilo.ru
Разбор и решение задания №15 ОГЭ по математике |
Практические задачи по геометрии
15 задание — применение знания геометрии в окружающем мире. Самые распространенные задания — на прямоугольные треугольники и вычисление расстояния по теореме Пифагора, а также определение положения стрелок в градусах. Итак, перейдем к рассмотрению примеров.
Разбор типовых вариантов задания №15 ОГЭ по математике
Первый вариант задания
Какой угол (в градусах) образуют минутная и часовая стрелки часов в 18:00?
Решение:
Данный пример несложный — стрелки образуют прямую, а значит, угол равен 180 градусов.
Ответ: 180
Второй вариант задания
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 3,2 метра от земли. Длина троса равна 4 метра. Найдите расстояние от основания флагштока до места крепления троса на земле. Ответ дайте в метрах.
Решение:
Так как на чертеже — прямоугольный треугольник, применяем теорему Пифагора:
4² = 3,2² + x²
16 = 10,24 + x²
x² = 16 — 10,24
x² = 5,76
x = √5,76
x = 2,4 метра
Ответ: 2,4 метра
Третий вариант задания
Какой угол (в градусах) описывает минутная стрелка за 4 минуты?
Решение:
Вначале найдем сколько в одной минуте градусов — так как в круге 60 минут и 360 градусов, то:
360 / 60 = 6 градусов — в одной минуте
В 4 минутах, соответственно:
6 • 4 = 24 градуса
Ответ: 24
Четвертый вариант задания (демонстрационный вариант 2017)
Наклонная балка поддерживается тремя столбами, стоящими вертикально на равном расстоянии друг от друга. Длины двух меньших столбов — 60 см и 90 см. Найдите длину большего столба. Ответ дайте в см.
Решение:
В данном задании необходимо применить знания из геометрии, а именно:
«Средняя линия трапеции равна среднему арифметическому двух оснований.»
Нам известна средняя линия — средний столб, и малое основание — малый столб.
Из этих данных находим большее основание:
( Малое основание + Большее основание ) / 2 = Средняя линия
( 60 + Большее основание ) / 2 = 90
Можем переписать в виде уравнения, где х — Большее основание
( 60 + х ) / 2 = 90
Решая, получаем:
х = 120
Ответ: 120 см.
spadilo.ru
Разбор и решение задания №18 ОГЭ по математике |
Треугольники, четырёхугольники, многоугольники и их элементы
В 18 задании нас ждут задачи с четырехугольниками, а именно трапецией, ромбами и произвольными параллелограммами. Необходимо знать формулы вычисления площади всех вышеперечисленных четырехугольников, а также их свойства.
В демонстрационном варианте ОГЭ предлагается задание, связанное с нахождением площади фигуры.
Как найти площадь треугольника, трапеции, параллелограмма, круга и сектора?
С одной стороны, мы знаем соответствующие формулы. Для выполнения большинства заданий этого будет вполне достаточно, но иногда надо проявить и определенную сообразительность. В некоторых случаях будет разумно представить
заданную геометрическую фигуру как сумму или как разность более простых фигур. Безусловно, площадь измеряется в соответствующих единицах. Например, если длины сторон фигуры заданы в сантиметрах, то вычисляемая площадь автоматически измеряется в квадратных сантиметрах. Чтобы не загромождать условие задачи информацией, которая при ее решении фактически не используется, единицы измерения, если они не существенны, не указаны.
Ответом в задании 16 является целое число или конечная десятичная дробь.
Теория к заданию №18
Приступим к разбору теории.
Выпуклый четырехугольник:

Правильный многоугольник:
- Правильным многоугольником называется многоугольник, у которого все стороны и углы равны между собой.
- Около всякого правильного многоугольника можно описать окружность и в него вписать окружность, причём центры этих окружностей совпадают.

Ниже я привожу формулы для вычисления элементов произвольного правильного многоугольника:

Разберем пример четырехугольника — ромб.
Параллелограмм, все стороны которого равны называется ромбом.
- Диагональ ромба является его осью симметрии.
- Диагонали взаимно перпендикулярны.
- Диагонали являются биссектрисами углов.

Трапеция:
Четырёхугольник, у которого две стороны параллельны, а другие не параллельны, называется трапецией.

Ниже я разобрал типовые примеры 11 задания. Давайте приступим к их рассмотрению.
Разбор типовых вариантов задания №18 ОГЭ по математике
Первый вариант задания
Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 35° и 30°. Найдите меньший угол параллелограмма.
Решение:
Найдем угол BAD — это сумма углов, на которые диагональ делит этот угол, поэтому:
∠BAD = 35° + 30° = 65°
Вспоминаем, что в параллелограмме противоположные углы равны, а соседние в сумме дают 180°.
Значит:
∠ABC = ∠ADC = 180 — 65 = 115°
∠BAD = ∠BCD = 65°
Так как нас просят найти меньший угол, то это 65.
Ответ: 65
Второй вариант задания
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основаниям равен 45°. Найдите площадь трапеции.
Решение:
Площадь трапеции равна произведению полусуммы оснований, умноженную на высоту. Основания нам известны из условия, необходимо самим найти высоту:
После проведения высоты, у нас получается прямоугольный треугольник. Прямоугольный — потому что высота проводится к основанию под углом 90 градусов. Один из углов равен 45°, значит, и второй тоже, так как сумма острых углов в прямоугольном треугольнике равна 90°. Следовательно, треугольник равнобедренный.
Проведя еще одну высоту, мы получим прямоугольник в центре, та с противоположной стороной, равной основанию 3.
Так как трапеция равнобедренная, то и треугольники равны, значит оставшаяся длина делится пополам:
( 9 — 3 ) / 2 = 3
А так как треугольники равнобедренные, то и высота равна 3.
Отсюда можем найти площадь:
S = ( a + b ) • h / 2 = ( 3 + 9 ) • 3 / 2 = 18
Ответ: 18
Третий вариант задания
Основания трапеции равны 10 и 11. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Решение:
Средняя линия трапеции является еще и средней линией для треугольников, на которые трапецию поделила её диагональ. Средняя линия треугольника равна половине основания, поэтому отрезки, на которые делит диагональ среднюю линию, будут равны:
10 / 2 = 5
11 / 2 = 5,5
Так как нас просят найти больший из отрезков, то ответ 5,5.
Ответ: 5,5
Четвертый вариант задания (демонстрационный вариант 2017)
Найдите площадь трапеции, изображённой на рисунке.

Решение:
Для решения необходимо помнить и знать формулу для вычисления площади трапеции, а это
«полусумма оснований умноженная на высоту»
Непонятно, зачем нам дана информация о значениях длин отрезков, тем не менее решение выглядит так:
- Верхнее основание равно 7
- Нижнее основание равно 9 + 12 = 21
- Полусумма (21 + 7) / 2 = 14
- Высота равна 12
Таким образом, площадь равна 14 • 12 = 168 см²
Ответ: 168
spadilo.ru
Разбор и решение задания №17 ОГЭ по математике |
Окружность, круг и их элементы
В 17 задании ОГЭ по математике необходимо решить простую задачу по геометрии. Для успешного решения необходимо обладать базовыми знаниями по геометрии вообще, так как сложно выделить какую-то одну тему, по которой даны задания. Это относится ко всему модулю геометрии. Я рекомендую повторить понятия центральные и вписанные углы, свойства касательных к окружности, взаимосвязь между радиусом описанной или вписанной окружности в геометрические фигуры — в первую очередь прямоугольный треугольник и квадрат.
По спецификации ОГЭ здесь могут встретиться задания, связанные с необходимостью нахождения длин, углов и площадей.
Ответом в задании 17 является целое число или конечная десятичная дробь.
Теория к заданию №17
Несмотря на то, что в задании №17 могут потребоваться любые знания по геометрии, в данном разделе мы разберем теорию по теме «окружность».
Начнем рассмотрение с понятия вписанная окружность:
- Центр окружности, вписанной в треугольник, лежит на пересечении биссектрис треугольника.
- Если окружность вписана в произвольный четырехугольник, тогда попарные суммы противолежащих сторон равны между собой: a + b = c + d
Длинна окружности и площадь:

Касательная и секущая:
- Касательная – прямая, имеющая с окружностью одну общую точку.
- Секущая – прямая, имеющая с окружностью две общие точки.

Описанная окружность и её свойства:
- Центр окружности, описанной около треугольника, лежит на пересечении серединных перпендикуляров к его трем сторонам.
- Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы.
- Около трапеции можно описать окружность только тогда, когда трапеция равнобочная.
- Если окружность описана около произвольного четырехугольника, тогда попарные суммы противолежащих углов равны между собой.

Хорда – отрезок, соединяющий две точки окружности.
- Диаметр, делящий хорду пополам, перпендикулярен хорде.
- В окружности равные хорды равноудалены от центра окружности.
- Отрезки пересекающихся хорд связаны равенством:

Центральный и вписанный углы:
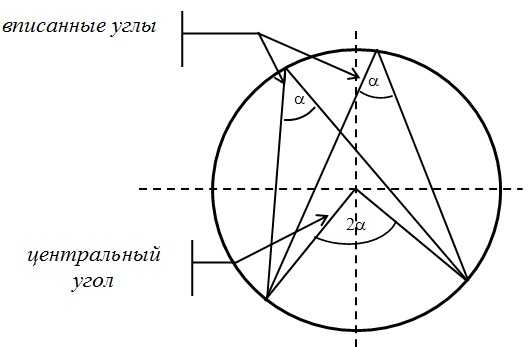
Ниже я разобрал три различных примера 10 задания. Если у вас остались пожелания, или вы хотите разобрать задачу, которой здесь нет, напишите об этом в комментарии.
Разбор типовых вариантов заданий №17 ОГЭ по математике
Первый вариант задания
Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
Решение:
Внимательно посмотрим на рисунок. Угол ABC опирается на дугу ADC, а угол CAD — на дугу DC. Угол, который нам необходимо найти — ABD, опирается на дугу AD — которая является частью дуги ADC за вычетом дуги DC. Значит, угол ABD равен разности углов ABC и CAD:
∠ABD = 92 — 60 = 32
Ответ: 32°
Второй вариант задания
Касательные в точках A и B к окружности с центром O пересекаются под углом 2º. Найдите угол ABO. Ответ дайте в градусах.

Решение:
Во-первых, касательные равны между собой по длине, а значит треугольник с основанием AB равнобедренный. Угол при вершине этого треугольника равен 2 градуса по условию, значит углы при основании равны:
(180 — 2) / 2 = 89°
Во-вторых, касательные перпендикулярны радиусу, то есть угол между ними и радиусом равен 90 градусов.
Заметим, что угол ABO, который необходимо найти, является частью угла между касательной и радиусом, а именно за вычетом угла, который мы нашли в первом пункте. Значит, этот угол равен:
90 — 89 = 1°
Ответ: 1
Третий вариант задания
В треугольнике ABC известно, что AC = 16, BC = 12, угол C равен 90º. Найдите радиус описанной около этого треугольника окружности.

Решение:
Для решения необходимо вспомнить, что центр описанной около прямоугольного треугольника окружности расположен в середине гипотенузы. То есть гипотенуза является диаметром, а её половина — радиусом.
По теореме Пифагора найдем гипотенузу AB:
AB² = BC² + AC² = 12² + 16² = 144 + 256 = 400
AB = √400 = 20
Гипотенуза равна 20, значит радиус — 10.
Ответ: 10
Четвертый вариант задания (демонстрационный вариант 2017)
Найдите длину хорды окружности радиусом 13 см, если расстояние от центра окружности до хорды равно 5 см. Ответ дайте в см.

Решение:
Для решения данной задачи необходимо провести радиус окружности к точке начала хорды:

Получаем прямоугольный треугольник, где гипотенуза c — радиус и равна 13 см, b — расстояние до хорды — 5 см. По теореме Пифагора находим катет a:
a² + b² = c²
a² = c² — b² = 13² — 5² = 169 — 25 = 144
Откуда
а = √144 = 12
Но а — лишь половина хорды, поэтому вся хорда равна 2 • а = 24
Ответ: 24
spadilo.ru
Разбор и решение задания №4 ОГЭ по математике |
Числа, вычисления и алгебраические выражения
Четвертое задание в модуле алгебре проверяет знания в области обращения со степенями и подкоренными выражениями.
При выполнении задания №4 ОГЭ по математике проверяются не только навыки выполнения вычисления и преобразований числовых выражений, но и умение преобразовывать алгебраические выражения. Возможно, потребуется выполнить действия со степенями с целым показателем, с многочленами, тождественные преобразования рациональных выражений.
В соответствии с материалами проведения основного экзамена могут быть задания, в которых потребуется выполнение тождественных преобразований рациональных выражений, разложение многочленов на множители, использование процентов и пропорций, признаков делимости.
Ответом в задании 4 является одна из цифр 1; 2; 3; 4 соответствующая номеру предложенного варианта ответа к заданию.
Теория к заданию №4
Из теоретического материала нам пригодятся правила обращения со степенями:

Правила работы с подкоренными выражениями:
В моих разобранных вариантах представлены данные правила — в разборе первого варианта третьего задания представлены правила обращения со степенями, а во втором и третьем варианте разобраны примеры работы подкоренными выражениями.
Разбор типовых вариантов задания №4 ОГЭ по математике
Первый вариант задания
Какое из данных ниже выражений при любых значениях n равно произведению 121 • 11n ?
- 121n
- 11n+2
- 112n
- 11n+3
Решение:
Для решения данной задачи необходимо вспомнить следующие правила обращения со степенями:
- при умножении степени складываются
- приделении степени вычитаются
- при возведении степени в степень степени перемножаются
- при извлечении корня степени делятся
Кроме того, для решения необходимо представить 121 как степень 11, а именно это 112.
121 • 11n = 112 • 11n
С учетом правила умножения, складываем степени:
112 • 11n = 11n+2
Следовательно, нам подходит второй ответ.
Ответ: 2
Второй вариант задания
Значение какого из данных ниже выражений является наибольшим?
- 3√5
- 2√11
- 2√10
- 6,5
Решение:
Для решения данного задания нужно привести все выражения к общему виду — представить выражения в виде подкоренных выражений:
Переносим 3 под корень:
3√5 = √(3² •5) = √(9•5) = √45
Переносим 2 под корень:
2√11 = √(2² • 11) = √(4 • 11) =√44
Переносим 2 под корень:
2√10 = √(2² • 10) = √(4 • 10) =√40
Возводим 6,5 в квадрат:
6,5 = √(6,5²) = √42,25
Посмотрим на все получившиеся варианты:
- 3√5 = √45
- 2√11 = √44
- 2√10 = √40
- 6,5 = √42,25
Следовательно, правильный ответ первый
Ответ: 1
Третий вариант задания
Какое из данных чисел является рациональным?
- √810
- √8,1
- √0,81
- все эти числа иррациональны
Решение:
Для решения этой задачи нужно действовать следующим образом:
Сначала разберемся, степень какого числа рассмотрена в данном примере — это число 9, так как его квадрат 81, и это уже чем-то похоже на выражения в ответах. Далее рассмотрим формы числа 9 — это могут быть:
0,9
90
Рассмотри каждое из них:
0,9 = √(0,9)² = √0,81
90 = √(90²) = √8100
Следовательно, число √0,81 является рациональным, остальные же числа
хотя и похожи на форму 9 в квадрате, не являются рациональными.
Таким образом, правильный ответ третий.
Ответ: 3
Четвертый вариант задания
По просьбе подписчика моего сообщества Спадило Дианы, привожу разбор следующего задания №4:
Какое из данных ниже чисел является значением выражения?
Решение:
Заметим, что в знаменателе присутствует разность (4 — √14), от которой нам необходимо избавиться. Как же это сделать?
Для этого вспоминаем формулу сокращенного умножения, а именно разность квадратов! Чтобы правильно её применить в этом задании необходимо помнить правила обращения с дробями. В данном случае вспоминаем, что дробь не изменяется, если числитель и знаменатель домножить на одно и то же число или выражение. Для разности квадратов нам не хватает выражения (4 + √14), значит, домножим на него числитель и знаменатель.
После этого в числителе получим 4 + √14, а в знаменателе разность квадратов: 4² — (√14)². После этого знаменатель легко вычисляется:
16 — 14 = 2
Суммарно наши действия выглядят так:
Ответ: 4
Хотите, чтобы ваше задание я разобрал и представил здесь? Подписывайтесь на мою группу Спадило и присылайте задание в личные сообщения группы!
Пятый вариант задания (демонстрационный вариант ОГЭ 2017)
Значение какого из выражений является рациональным числом?
- √6-3
- √3•√5
- (√5)²
- (√6-3)²
Решение:
В данном задании у нас проверяют навыки операций с иррациональными числами.
Разберем каждый вариант ответа в решении:
1) √6-3
√6 само по себе является иррациональным числом, для решения подобных задач достаточно помнить, что рационально извлечь корень можно из квадратов натуральных чисел, например, 4, 9, 16, 25…
При вычитании из иррационального числа любого другого, кроме его же самого, приведет вновь к иррациональному числу, таким образом, в этом варианте получается иррациональное число.
2) √3•√5
При умножении корней, мы можем извлечь корень из произведения подкоренных выражений, то есть:
√3•√5 = √(3•5) = √15
Но √15 является иррациональным, поэтому данный вариант ответа не подходит.
3) (√5)²
При возведении квадратного корня в квадрат, мы получаем просто подкоренное выражение (если уж быть точнее, то подкоренное выражение по модулю, но в случае числа, как в данном варианте, это не имеет значения), поэтому:
(√5)² = 5
Данный вариант ответа нам подходит.
4) (√6-3)²
Данное выражение представляет продолжение 1 пункта, но если √6-3 иррациональное число, то никакими известными нам операциями перевести в рациональное его нельзя.
Ответ: 3
spadilo.ru
Тест №9 ОГЭ по математике |
Тестовые задания №9 ОГЭ по математике. Теория к заданию №9 и разбор типовых вариантов по ссылке под тестами!⇓⇓⇓
Лимит времени: 0
Информация
Тренировочные варианты типовых тестовых заданий №9 ОГЭ по математике. После ответа вы найдете объяснение и пояснение ко всем вариантам. Успехов в подготовке! 😉
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- С ответом
- С отметкой о просмотре
Задание 1 из 5
В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что сумма выпавших очков равна 5. Результат округлите до тысячных.
ПравильноГрани игральных костей имеют номера от 1 до 6. При бросании трех кубиков сумма в 5 очков может получиться при выпадении одной из комбинаций:
1+1+3
1+2+2
1+3+1
2+1+2
2+2+1
3+1+1
Таким образом получается 6 благоприятных исходов. При бросании 3 кубиков суммарное количество комбинаций равно: 63 = 216. Получается, вероятность выпадения 5 очков: P = 6 / 216 = 0,028
НеправильноГрани игральных костей имеют номера от 1 до 6. При бросании трех кубиков сумма в 5 очков может получиться при выпадении одной из комбинаций:
1+1+3
1+2+2
1+3+1
2+1+2
2+2+1
3+1+1
Таким образом получается 6 благоприятных исходов. При бросании 3 кубиков суммарное количество комбинаций равно: 63 = 216. Получается, вероятность выпадения 5 очков: P = 6 / 216 = 0,028
Определите общее количество возможных комбинаций, количество возможных комбинаций, когда сумма выпавших чисел равна 5 и найдите их частное.
Задание 2 из 5
Экзамен по химии содержит 40 билетов, Артем не знает 5 из них. Найдите вероятность того, что ему не попадется невыученный билет.
ПравильноПусть событие A – Артем выбрал билет, ответ на который он знает. Тогда число возможных благоприятных исходов этого события: 40–5=35. Зная, что общее число исходов равно 40, получим вероятность события A:
P = 35 / 40 = 0,875
НеправильноПусть событие A – Артем выбрал билет, ответ на который он знает. Тогда число возможных благоприятных исходов этого события: 40–5=35. Зная, что общее число исходов равно 40, получим вероятность события A:
P = 35 / 40 = 0,875
Зная общее количество билетов и количество выученных Артемом билетов, находим частное этих чисел.
Задание 3 из 5
В соревнованиях по лыжному спорту участвуют 7 спортсменов из России, 1 из Германии и 2 лыжника из Норвегии. Стартовый номер участников определяется жребием. Определите вероятность того, что под первым номером будет стартовать немец.
ПравильноТак как Германия на соревновании представила одного спортсмена, то вероятность того, что он будет стартовать под любым номер, равна 1 доли от общего числа участников. Зная, что всего в соревновании участвует 10 спортсменов, находим, что искомая вероятность равна: 1/10 (0,1).
НеправильноТак как Германия на соревновании представила одного спортсмена, то вероятность того, что он будет стартовать под любым номер, равна 1 доли от общего числа участников. Зная, что всего в соревновании участвует 10 спортсменов, находим, что искомая вероятность равна: 1/10 (0,1).
Так как Германия на соревновании представила одного спортсмена, то вероятность того, что он будет стартовать под любым номер, равна 1 доли от общего числа участников. Зная, что всего в соревновании участвует 10 спортсменов, находим, что искомая вероятность равна: 1/10 (0,1).
Задание 4 из 5
На новогодние подарки в этом году купили 20 пазлов, 8 с изображение замков и 12 с животными. Подарки распределяются случайным образом между 20 детьми, среди которых есть Стас. Определите вероятность того, что Стасу достанется пазл с замком.
ПравильноОбозначим A – Стасу выпал пазл с замком. Число возможных благоприятных исходов для события A равно 8 (исходя из общего количества пазлов с замком). Всего возможно исходов 20 (всего было 20 детей), следовательно, вероятность равна: P = 8 / 20 = 0,4
НеправильноОбозначим A – Стасу выпал пазл с замком. Число возможных благоприятных исходов для события A равно 8 (исходя из общего количества пазлов с замком). Всего возможно исходов 20 (всего было 20 детей), следовательно, вероятность равна: P = 8 / 20 = 0,4
Найдите частное между общим количеством пазлов и пазлов с замками.
Задание 5 из 5
В магазине канцтоваров продаётся 112 ручек, из них 17 красные, 44 зелёные, 29 фиолетовые, ещё есть синие и чёрные, их поровну. Найдите вероятность того, что при случайном выборе одной ручки будет выбрана красная или чёрная ручка.
ПравильноОбозначим через событие А выбор черной ручки, а через событие В – выбор красной ручки. Число исходов, благоприятных для события А равно:
(112 — 17 — 44 — 29) / 2 = 11
(из общего числа ручек вычитаем все цветные, а затем делим на 2, поэтому что черных и синих одинаковое количество). Получается, продается всего 11 черных ручек.
Число благоприятных исходов для события В равно 17. Всего исходов 112. Учитывая, что нельзя одновременно выбрать и черную и красную ручки, а всего продается 112 ручек, получаем, что вероятность события А или события В, равно сумме вероятностей этих событий:
P (A+B) = 11/112 + 17/112 = 28/112 = 0,25
НеправильноОбозначим через событие А выбор черной ручки, а через событие В – выбор красной ручки. Число исходов, благоприятных для события А равно:
(112 — 17 — 44 — 29) / 2 = 11
(из общего числа ручек вычитаем все цветные, а затем делим на 2, поэтому что черных и синих одинаковое количество). Получается, продается всего 11 черных ручек.
Число благоприятных исходов для события В равно 17. Всего исходов 112. Учитывая, что нельзя одновременно выбрать и черную и красную ручки, а всего продается 112 ручек, получаем, что вероятность события А или события В, равно сумме вероятностей этих событий:
P (A+B) = 11/112 + 17/112 = 28/112 = 0,25
Зная общее количество ручек, определите вероятность выбора синей ручки, затем, найдите вероятность выбора красной или синей, как сумму обеих вероятностей.
spadilo.ru
Тест по типовым заданиям №9 ОГЭ по русскому |
(1)Бабушка велела мне сходить на увал по землянику.
— (2)Я повезу ягоды в город, продам и куплю тебе пряник.
— (3)Конем, баб?
— (4)Конем, конем.
(5)Пряник конем! (6)Это ж мечта всех деревенских малышей. (7)Он белый-белый, этот конь. (8)А грива у него розовая, хвост розовый, глаза розовые, копыта тоже розовые.
(9)Вот с орлами дяди Левонтия и отправился я по землянику, чтобы трудом своим заработать пряник. (10)Я брал старательно и скоро покрыл дно туеска. (11)Левонтьевские ребятишки сначала ходили тихо, но скоро послышалась возня. (12)Бьются братья богатырские, катаются по земле, всю землянику раздавили.
(13)Вскоре они решили спуститься к Фокинской речке, побрызгаться. (14)Мне тоже хотелось, но я не решался уйти с увала, потому что еще не набрал полную посудину.
— (15)Бабушки Петровны испугался! (16)Эх ты! – закривлялся Санька.
— (17)А хочешь, все ягоды съем? – сказал я.
— (18)Слабо!
— (19)Мне слабо! – хорохорился я, искоса глядя в туесок. – (20)Вот! (21)Ешьте вместе со мной!
(22)Навалилась левонтьевская орда, и ягоды вмиг исчезли.
(23)Тоска на сердце – предчувствует оно встречу с бабушкой, отчет и расчет.
(24)Тихо плелся я за левонтьевскими ребятами из лесу.
— (25)А ты в туес травы натолкай, сверху ягод – и готово дело! – сказал, посоветовавшись с братьями, Санька и помчался домой.
(26)А я остался. (27)Набил травою туго туесок, собрал несколько горсток ягодок, заложил ими траву – получилось земляники даже с копной…
(28)На кухне бабушка кому-то обстоятельно рассказывала:
— …(29)Культурная дамочка, в шляпке. «(30)Я эти вот ягодки все куплю». (31)Пожалуйста, милости прошу. (32)Ягодки-то, говорю, сиротинка горемышный собирал…
(33)Тут я провалился сквозь землю вместе с бабушкой и уже не мог и не желал разбирать, что говорила она дальше, потому что закрылся полушубком, забился в него, чтобы скорее помереть.
(34)Дед успокаивал меня, обтирая большой рукой слезы, которые крупной земляникой сыпанули из моих глаз.
— (35)Попроси прошшенья, легонько подтолкнул он меня в спину.
(36)Я ступил в избу и завел:
— (37)Я больше… (38)Я больше… — и ничего не мог дальше сказать.
— (39)Ладно уж, умывайся да садись трескать! – все еще непримиримо, но уже без грозы, без громов оборвала меня бабушка.
(40)И срамила же она меня! (41)И обличала же! (42)Только теперь, поняв до конца в какую бездонную пропасть ввергло меня плутовство и на какую «кривую дорожку» оно меня еще уведет, коли за лихим людом потянулся на разбой, я уже заревел не просто раскаиваясь, а испугавшись, что пропал, что ни прощенья, ни возврата нету…
(43)Не зная, что делать, как жить дальше, я разглаживал заплатку на штанах, вытягивал из нее нитки. (44)А когда поднял голову, увидел перед собой…
(45)Я зажмурился и снова открыл глаза. (46)Еще раз зажмурился, еще раз открыл.
(47)По скобленому кухонному столу, будто по огромной земле, с пашнями, лугами и дорогами, на розовых копытцах скакал белый конь с розовой гривой.
— (48)Бери, бери, че смотришь? (49)Глядишь, зато еще когда омманешь баушку…
(50)Сколько лет с тех пор прошло! (51)Сколько событий минуло. (52)Нет в живых дедушки, нет и бабушки, да и моя жизнь клонится к закату, а я все не могу забыть бабушкиного пряника – того дивного коня с розовой гривой.
(по В.П. Астафьеву)
В предложениях 22 – 27 найдите предложение с обособленным обстоятельством. Запишите его номер.
spadilo.ru
