Примеры ОГЭ по математике | Геометрия
Примеры ОГЭ по математике | Геометрия — просто! Добрый день, друзья!
Добрый день, друзья!
Сегодня мы будем решать примеры ОГЭ по математике —
четвёртое задание, а именно уравнения.
В этом задании представлены разные виды уравнений: линейные, квадратные, дробные, а также системы уравнений.
Для каждого из видов есть свои методы решения, о чём мы и поговорим сегодня.
Задача 1. Решить уравнение (х-9)² = (х-3)²
Решение: Не смотря на квадраты, это уравнение линейное, и его можно решать двумя способами.
Способ 1. х² — 18х + 81 = х² — 6х + 9
18х — 6х = 81 — 9
12х = 72
х = 6
Способ 2. (х-9)² — (х-3)² = 0
(х-9+х-3)(х-9-х+3) = 0
(2х-12)(-6) = 0
(-12)(х-6) = 0
х = 6
Ответ: 6
Задача 2. Решить уравнение (х+3)² + (х-7)² = 2х²
Решение: Это уравнение также приводится к линейному уравнению:
х²+6х+9+х²-14х+49=2х²
14х — 6х = 9 + 49
8х = 58
х = 7,25
Ответ: 7,25
Задача 3. Решите уравнение х² — 4х + 35 = -9х² + 11х + 45
Решение: Уравнение квадратное.
Приводим его к каноническому виду и проверяем дискриминант.
10х² — 15х — 10 = 0 Делим правую и левую часть уравнения на 5
2х² — 3х — 2 = 0
Поскольку свободный член имеет знак -,
то уравнение ВСЕГДА будет иметь 2 корня.
_3±√(9 + 4•2•2)_ = _3±5_
2•2 4
х1 = 2 х2 = -0,5
Ответ: -0,5; 2
Задача 4. Решите уравнение х²/2 +3х + 4 = 0
Решение: В первую очередь освобождаемся от дроби в левой части уравнения.
Для этого правую и левую часть уравнения умножаем на 2.
х² + 6х + 8 = 0 Это приведённое квадратное уравнение.
И проще всего его решать по теореме Виета.
Сумма корней приведённого квадратного уравнения равна второму коэффициенту с противоположным знаком, а произведение корней равно свободному члену.
Другими словами:
х1 + х2 = -6
х1•х2 = 8
Начинаем с произведения. Раскладываем число 8 на множители и подбираем их таким образом, чтобы в сумме они дали -6.
Это очевидно -2 и -4.
Произведение двух отрицательных чисел даёт нам положительное число,
а их сумма также отрицательна.
Ответ: -4; -2
Задача 5. Решите уравнение х² + 3,5х = 2
Решение: Это уравнение по теореме Виета будет решить сложнее,
чем предыдущее, потому что второй множитель — дробный.
В таком случае домножим правую и левую часть уравнения на 2.
2х² + 7х = 4
2х² + 7х — 4 = 0 Придётся решать это уравнение как полное.
_-7±√(49 + 4•2•4)_ = _-7±9_
2•2 4
х1 = -4 х2 = 0,5
Ответ: -4; 0,5
Задача 6. Решить уравнение х² — 6(х — 4) — 4х + 1 = 0
Решение: х² — 6(х — 4) — 4х + 1 = х² — 6х + 24 — 4х + 1 = х² — 10х + 25 = 0
Если внимательно присмотреться, то можно увидеть
формулу сокращённого умножения — квадрат разности двух чисел х и 5.
х² — 10х + 25 = (х — 5)²
Поэтому корень данного уравнения будет один.
Ответ: 5
Задача 7. Решить уравнение -2х² + 7х = 9
Решение: Перенесём число 9 в левую часть уравнения,
а затем умножим правую и левую часть уравнения на (-1).
2х² — 7х + 9 = 0 Имеем полное квадратное уравнение.
_7±√(49 — 4•2•9)_ = _7±√(-23)_ Дискриминант получился отрицательный.
2•2 4 Корней нет.
Ответ: нет решений.
Задача 8. Решите уравнение 2(х² — 40) = -х² + 6(х + 4) + 1
Решение: Раскрываем скобки, приводим подобные
2х² — 80 = -х² + 6х + 24 + 1 2х² — 80 + х² — 6х — 24 — 1 = 0
3х² — 6х — 105 = 0 Делим правую и левую часть уравнения на 3
х² — 2х — 35 = 0 И опять теорема Виета.
Множители числа 35: 7 и 5.
Свободный член отрицательный, значит корни имеют разные знаки.
Теперь надо их правильно расставить.
Сумма равна +2, значит положительное число по модулю больше,
чем отрицательное.
А теперь уже просто.
х1 = 7; х2 = -5
Ответ: -5; 7
Задача 9. Решите уравнение х²/2 — 1/2 = х•(х+5)/6
Решение: Как в предыдущих примерах с дробями, избавляемся от дробей путём умножения правой и левой части уравнения на 6.
3х² — 3 = х(х+5)
3х² — 3 = х² + 5х
2х² — 5х — 3 = 0
_5±√(25 + 4•2•3)_ = _5±7_
2•2 4
х1 = 3, х2 = -0,5
Ответ: -0,5; 3
На сегодня всё. Успехов и до новых задач!
Вам так же будет интересно:
Оставить комментарий
geometriyaprosto.ru
Темы, входящие в ГИА (ОГЭ) по курсу математики
Темы, входящие в ГИА (ОГЭ) по курсу математики — ЕГЭ физмат Skip to content- Числа и вычисления
- Натуральные числа
- Десятичная система счисления. Римская нумерация
- Арифметические действия над натуральными числами
- Степень с натуральным показателем
- Делимость натуральных чисел. Простые и составные числа, разложение натурального числа на простые множители
- Признаки делимости на 2, 3, 5, 9, 10
- Наибольший общий делитель и наименьшее общее кратное
- Деление с остатком
- Дроби
- Обыкновенная дробь, основное свойство дроби. Сравнение дробей
- Арифметические действия с обыкновенными дробями
- Нахождение части от целого и целого по его части
- Десятичная дробь, сравнение десятичных дробей
- Арифметические действия с десятичными дробями
- Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной
- Рациональные числа
- Целые числа
- Модуль (абсолютная величина) числа
- Сравнение рациональных чисел
- Арифметические действия с рациональными числами
- Степень с целым показателем
- Числовые выражения, порядок действий в них, использование скобок. Законы арифметических действий
- Действительные числа
- Квадратный корень из числа
- Корень третьей степени
- Нахождение приближенного значения корня с помощью калькулятора
- Понятие об иррациональном числе. Десятичные приближения иррациональных чисел. Действительные числа как бесконечные десятичные дроби
- Сравнение действительных чисел
- Измерения, приближения, оценки
- Единицы измерения длины, площади, объема, массы, времени, скорости
- Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире
- Представление зависимости между величинами в виде формул
- Проценты. Нахождение процента от величины и величины по ее проценту
- Отношение, выражение отношения в процентах
- Пропорция. Пропорциональная и обратно пропорциональная зависимости
- Округление чисел. Прикидка и оценка результатов вычислений. Выделение множителя – степени десяти в записи числа
- Натуральные числа
- Алгебраические выражения
- Буквенные выражения (выражения с переменными)
- Буквенные выражения. Числовое значение буквенного выражения
- Допустимые значения переменных, входящих в алгебраические выражения
- Подстановка выражений вместо переменных
- Равенство буквенных выражений, тождество. Преобразования выражений
- Свойства степени с целым показателем
- Многочлены
- Многочлен. Сложение, вычитание, умножение многочленов
- Формулы сокращенного умножения: квадрат суммы и квадрат разности; формула разности квадратов
- Разложение многочлена на множители
- Квадратный трехчлен. Теорема Виета. Разложение квадратного трехчлена на линейные множители
- Степень и корень многочлена с одной переменной
- Алгебраическая дробь
- Алгебраическая дробь. Сокращение дробей
- Действия с алгебраическими дробями
- Рациональные выражения и их преобразования
- Свойства квадратных корней и их применение в вычислениях
- Буквенные выражения (выражения с переменными)
- Уравнения и неравенства
- Уравнения
- Уравнение с одной переменной, корень уравнения
- Линейное уравнение
- Квадратное уравнение, формула корней квадратного уравнения
- Решение рациональных уравнений
- Примеры решения уравнений высших степеней. Решение уравнений методом замены переменной. Решение уравнений методом разложения на множители
- Уравнение с двумя переменными; решение уравнения с двумя переменными
- Система уравнений; решение системы
- Система двух линейных уравнений с двумя переменными; решение подстановкой и алгебраическим сложением
- Уравнение с несколькими переменными
- Решение простейших нелинейных систем
- Неравенства
- Числовые неравенства и их свойства
- Неравенство с одной переменной. Решение неравенства
- Линейные неравенства с одной переменной
- Системы линейных неравенств
- Квадратные неравенства
- Решение текстовых задач арифметическим способом
- Решение текстовых задач алгебраическим способом
- Числовые последовательности
- Понятие последовательности
- Арифметическая и геометрическая прогрессии
- Арифметическая прогрессия. Формула общего члена арифметической прогрессии
- Формула суммы первых нескольких членов арифметической прогрессии
- Геометрическая прогрессия. Формула общего члена геометрической прогрессии
- Формула суммы первых нескольких членов геометрической прогрессии
- Сложные проценты
- Уравнения
- Функции и графики
- Числовые функции
- Понятие функции. Область определения функции. Способы задания функции
- График функции, возрастание и убывание функции, наибольшее и наименьшее значения функции, нули функции, промежутки знакопостоянства, чтение графиков функций
- Примеры графических зависимостей, отражающих реальные процессы
- Функция, описывающая прямую пропорциональную зависимость, ее график
- Линейная функция, ее график, геометрический смысл коэффициентов
- Функция, описывающая обратно пропорциональную зависимость, ее график. Гипербола
- Квадратичная функция, ее график. Парабола. Координаты вершины параболы, ось симметрии
- График функции
- График функции
- График функции
- Использование графиков функций для решения уравнений и систем
- Числовые функции
- Координаты на прямой и плоскости
- Координатная прямая
- Изображение чисел точками координатной прямой
- Геометрический смысл модуля
- Числовые промежутки: интервал, отрезок, луч
- Декартовы координаты на плоскости
- Декартовы координаты на плоскости; координаты точки
- Координаты середины отрезка
- Формула расстояния между двумя точками плоскости
- Уравнение прямой, угловой коэффициент прямой, условие параллельности прямых
- Уравнение окружности
- Графическая интерпретация уравнений с двумя переменными и их систем
- Графическая интерпретация неравенств с двумя переменными и их систем
- Координатная прямая
- Геометрия
- Геометрические фигуры и их свойства. Измерение геометрических величин
- Начальные понятия геометрии
- Угол. Прямой угол. Острые и тупые углы. Вертикальные и смежные углы. Биссектриса угла и ее свойства
- Прямая. Параллельность и перпендикулярность прямых
- Отрезок. Свойство серединного перпендикуляра к отрезку. Перпендикуляр и наклонная к прямой
- Понятие о геометрическом месте точек
- Треугольник
- Высота, медиана, биссектриса, средняя линия треугольника; точки пересечения серединных перпендикуляров, биссектрис, медиан, высот или их продолжений
- Равнобедренный и равносторонний треугольники. Свойства и признаки равнобедренного треугольника
- Прямоугольный треугольник. Теорема Пифагора
- Признаки равенства треугольников
- Неравенство треугольника
- Сумма углов треугольника. Внешние углы треугольника
- Зависимость между величинами сторон и углов треугольника
- Теорема Фалеса
- Подобие треугольников, коэффициент подобия. Признаки подобия треугольников
- Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от до
- Решение прямоугольных треугольников. Основное тригонометрическое тождество. Теорема косинусов и теорема синусов
- Многоугольники
- Параллелограмм, его свойства и признаки
- Прямоугольник, квадрат, ромб, их свойства и признаки
- Трапеция, средняя линия трапеции; равнобедренная трапеция
- Сумма углов выпуклого многоугольника
- Правильные многоугольники
- Окружность и круг
- Центральный, вписанный угол; величина вписанного угла
- Взаимное расположение прямой и окружности
- Окружность, вписанная в треугольник
- Окружность, описанная около треугольника
- Вписанные и описанные окружности правильного многоугольника
- Измерение геометрических величин
- Длина отрезка, длина ломаной, периметр многоугольника. Расстояние от точки до прямой
- Длина окружности
- Градусная мера угла, соответствие между величиной угла и длиной дуги окружности
- Площадь прямоугольника
- Площадь параллелограмма
- Площадь трапеции
- Площадь треугольника
- Площадь круга, площадь сектора
- Формулы объема прямоугольного параллелепипеда, куба, шара
- Векторы на плоскости
- Вектор, длина (модуль) вектора
- Равенство векторов
- Операции над векторами (сумма векторов, умножение вектора на число)
- Угол между векторами
- Коллинеарные векторы, разложение вектора по двум неколлинеарным векторам
- Координаты вектора
- Скалярное произведение векторов
- Геометрические фигуры и их свойства. Измерение геометрических величин
- Статистика и теория вероятностей
- Описательная статистика
- Представление данных в виде таблиц, диаграмм, графиков
- Средние результатов измерений
- Вероятность
- Частота события, вероятность
- Равновозможные события и подсчет их вероятности
- Представление о геометрической вероятности
- Комбинаторика
- Решение комбинаторных задач: перебор вариантов, комбинаторное правило умножения
- Описательная статистика
egefizmat.ru
Структура ОГЭ 2018 по математике
Демонстрационный вариант ОГЭ 2018 по математике
Шкала пересчета баллов ФИПИ 2018
Справочные материалы (выдаются на экзамене каждому)
ОГЭ 2018 по математике состоит из двух частей.
- В первой части 20 заданий (1 — 20) базового уровня сложности, каждое из которых оценивается в 1 балл.
- Во второй части 6 заданий (21 — 26) повышенного и высокого уровня сложности, каждое из которых оценивается в 2 балла.
Всего за экзамен можно набрать 32 балла.
Время, которое отводится на экзамен — 235 минут.
Первая часть
Первая часть состоит из двух модулей:
Ответом к каждому заданию первой части является число, цифра или последовательность цифр. Ответы на задания первой части проверяются компьютером.
Вторая часть
Вторая часть состоит из двух модулей:
Ответом к каждому заданию второй части является письменное решение, которое проверяется двумя независимыми экспертами. Они проставляют в протокол оценки за каждое задание второй части. В случае, если оценки двух экспертов расходятся, назначается третий.
Выставление оценок за работу
- Оценка за экзаменационную работу выставляется по следующим критериям:
| Количество баллов | Оценка |
| 0 – 7 | 2 |
| 8 – 14 | 3 |
| 15 – 21 | 4 |
| 22 – 32 | 5 |
- Оценка по алгебре выставляется по следующим критериям:
| Количество баллов за модуль алгебра |
Оценка |
| 0 – 4 | 2 |
| 5 – 10 | 3 |
| 11 – 15 | 4 |
| 16 – 20 | 5 |
- Оценка по геометрии выставляется по следующим критериям:
| Количество баллов за модуль геометрия |
Оценка |
| 0 – 2 | 2 |
| 3 – 4 | 3 |
| 5 – 7 | 4 |
| 8 – 12 | 5 |
Результаты ОГЭ, в частности, ОГЭ по математике, влияют на дальнейшую судьбу 9-классника:
- для кого-то баллы, набранные на ОГЭ, важны для поступления в профильный класс или лицей,
- для кого-то это возможность получить аттестат и поступить в техникум,
- для кого-то это возможность улучшить годовую оценку по предмету.
В любом случае, успешная сдача экзамена — необходимый шаг, который каждому нужно совершить в своей жизни.
И это несложно!
Начать обучение.
epmat.ru
Математика. Задачи для подготовки к ОГЭ
Задачи для подготовки к ОГЭ
-1. Арифметический минимум
0. Справочник по математике
1. Числа и вычисления
Натуральные числа
Действительные числа
2. Алгебраические выражения
Выражения и многочлены
Алгебраические дроби I
Алгебраические дроби II
Степени с целым показателем
Квадратный корень
3. Уравнения и неравенства
Линейные уравнения
Квадратные уравнения
Рациональные уравнения
Системы двух уравнений
Числовые неравенства
Линейные неравенства
Системы линейных неравенств
Квадратные неравенства
4. Числовые последовательности
Последовательности
Арифметическая прогрессия
Геометрическая прогрессия
5. Геометрия
Основные понятия и теоремы геометрии
Вычисление длин I
Вычисление длин II
Вычисление углов I
Вычисление углов II
Вычисление площадей I
Вычисление площадей II
Тригонометрия
Векторы на плоскости
6. Практико-ориентированные задачи
Текстовые задачи I
Текстовые задачи II
Зависимости между величинами в виде формул
Чтение графиков реальных зависимостей
Прикладные задачи геометрии
Статистика
Теория вероятностей
7. Официальные варианты работ
Тренировочная работа ГИА по математике 6 мая 2014 года
Диагностическая работа ГИА по математике 17 апреля 2014 года
Демонстрационный вариант ГИА (ОГЭ) по математике 2015 (ноябрь)
Диагностическая работа по подготовке к ОГЭ март 2015 (аналог реального варианта)
Типовой вариант 1 ОГЭ 2015 Ященко И.В. с ответами и решениями
Типовой вариант 2 ОГЭ 2015 Ященко И.В. с ответами и решениями
Типовой вариант 21 ОГЭ 2015 Ященко И.В. с ответами и решениями
Пробный вариант ОГЭ (ГИА) 2016 Санкт-Петербург
ОГЭ Демо 2017 по математике
ОГЭ Демо 2018 по математике Решение ОГЭ Демо 2018 по математике
ОГЭ 2017 Типовой вариант 1 по математике Ященко
ОГЭ 2017 Типовой вариант 2 по математике Ященко
ОГЭ Демо 2019 по математике Решение ОГЭ Демо 2019 по математике
смотрите еще Математика. Задачи по алгебре и Математика. Задачи по геометрии
Смотрите:
- ОГЭ 2015 по математике. Типовой вариант 1 Ященко И.В. с ответами и решениями
- Задачи для ОГЭ. Вычисление углов II
- ОГЭ 2015 по математике. Решение типового варианта 21
- Пробный вариант ОГЭ (ГИА) 2016 Санкт-Петербург
www.itmathrepetitor.ru
Тест №4 ОГЭ по математике |
Тестовые задания №4 ОГЭ по математике. Теория к заданию №4 и разбор типовых вариантов по ссылке под тестами!⇓⇓⇓
Лимит времени: 0
Информация
Тренировочные варианты типовых тестовых заданий №4 ОГЭ по математике. После ответа вы найдете объяснение и пояснение ко всем вариантам. Успехов в подготовке! 😉
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…
Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
- С ответом
- С отметкой о просмотре
Задание 1 из 5
Найдите значение выражения
ПравильноЧтобы возвести степень в степень, основание оставляем неизменным, а показатели степени перемножаем 7 5∙(-6)= 7 -30. При делении показатели степени записываются в виде разности:
7 -30-(-31) = 7 1 = 7
НеправильноЧтобы возвести степень в степень, основание оставляем неизменным, а показатели степени перемножаем 7 5∙(-6)= 7 -30. При делении показатели степени записываются в виде разности:
7 -30-(-31) = 7 1 = 7
Чтобы возвести степень в степень, основание оставляем неизменным, а показатели степени перемножаем 7 5∙(-6)= 7 -30. При делении показатели степени записываются в виде разности:
Задание 2 из 5
Найдите значение выражения
ПравильноЧтобы избавиться от корня, возводим каждое число в знаменателе в квадрат:
сокращаем дробь и делим числитель на знаменатель, записываем ответ в виде десятичной дроби:
6 / 75 = 0,08
НеправильноЧтобы избавиться от корня, возводим каждое число в знаменателе в квадрат:
сокращаем дробь и делим числитель на знаменатель, записываем ответ в виде десятичной дроби:
6 / 75 = 0,08
Чтобы избавиться от корня, возводим каждое число в знаменателе в квадрат:
сокращаем дробь и делим числитель на знаменатель, записываем ответ в виде десятичной дроби!
Задание 3 из 5
Найдите значение выражения
(√15-√12)(√12+√15)
ПравильноЧтобы найти значение выражения, необходимо воспользоваться формулой сокращенного умножения – разность квадратов:
(a-b)(a+b)= a2-b2
(√15-√12)(√12+√15)= (√15)2— (√12)2
При возведение квадратного корня во 2 степень, остается только подкоренное выражение:
15 — 12 = 3
НеправильноЧтобы найти значение выражения, необходимо воспользоваться формулой сокращенного умножения – разность квадратов:
(a-b)(a+b)= a2-b2
(√15-√12)(√12+√15)= (√15)2— (√12)2
При возведение квадратного корня во 2 степень, остается только подкоренное выражение:
15 — 12 = 3
Чтобы найти значение выражения, необходимо воспользоваться формулой сокращенного умножения – разность квадратов:
(a-b)(a+b)= a2-b2
(√15-√12)(√12+√15)= (√15)2— (√12)2
При возведение квадратного корня во 2 степень, остается только подкоренное выражение.
Задание 4 из 5
Найдите значение выражения
√54 / √6
ПравильноДля решения необходимо воспользоваться правилом: частное корней равно корню из частного: √(54/6) = √9 = 3
НеправильноДля решения необходимо воспользоваться правилом: частное корней равно корню из частного: √(54/6) = √9 = 3
Для решения необходимо воспользоваться правилом: частное корней равно корню из частного!
Задание 5 из 5
Найдите значение выражения:
(√26+7)2+(√26-7)2
ПравильноЧтобы найти ответ необходимо воспользоваться формулами сокращенного умножения – квадрат суммы: (a+b)2= a2+2ab+b2 и квадрат разности: (a-b)2=a2-2ab+b2
(√26)2+2∙7√26+72 + (√26)2-2∙7√26+72
Далее приводим подобные слагаемые.
НеправильноЧтобы найти ответ необходимо воспользоваться формулами сокращенного умножения – квадрат суммы: (a+b)2= a2+2ab+b2 и квадрат разности: (a-b)2=a2-2ab+b2
(√26)2+2∙7√26+72 + (√26)2-2∙7√26+72
Далее приводим подобные слагаемые.
Чтобы найти ответ необходимо воспользоваться формулами сокращенного умножения!
spadilo.ru
Формулы для ЕГЭ и ГИА (ОГЭ) по математике
Формулы для ЕГЭ и ГИА (ОГЭ) по математике
Чтобы легко решать задачи на экзамене, нужно знать формулы по математике. Все говорят об этом, но никто не говорит о том, какие формулы нужно знать прежде всего, а какие — не имеют никакого отношения к экзаменам. В этом посте я предлагаю вашему вниманию 7 листов формул по математике для подготовки к ГИА (ОГЭ) и ЕГЭ, которые вы наверняка встречали в Сети. Но, кроме этого, я добавлю свои комментарии о том, какие формулы вам обязательно нужно знать, а какие можно выучить «потом».
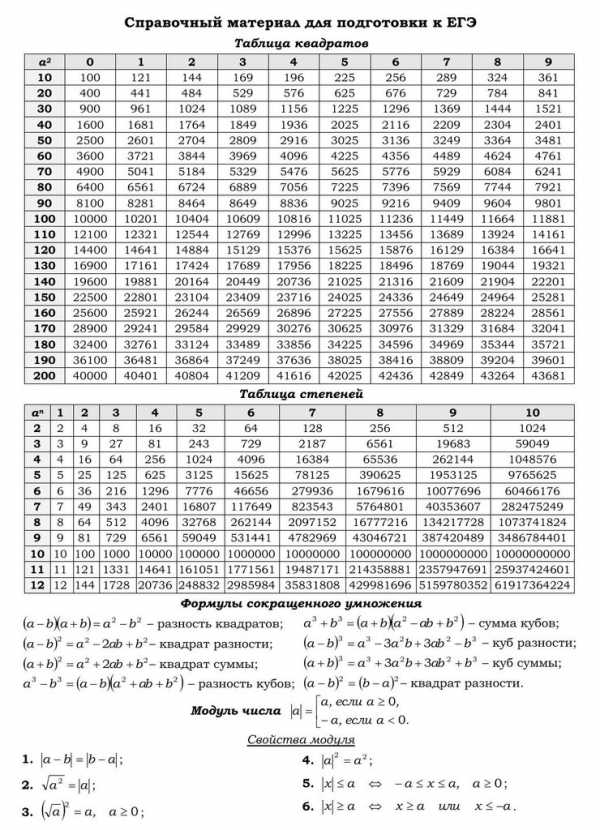

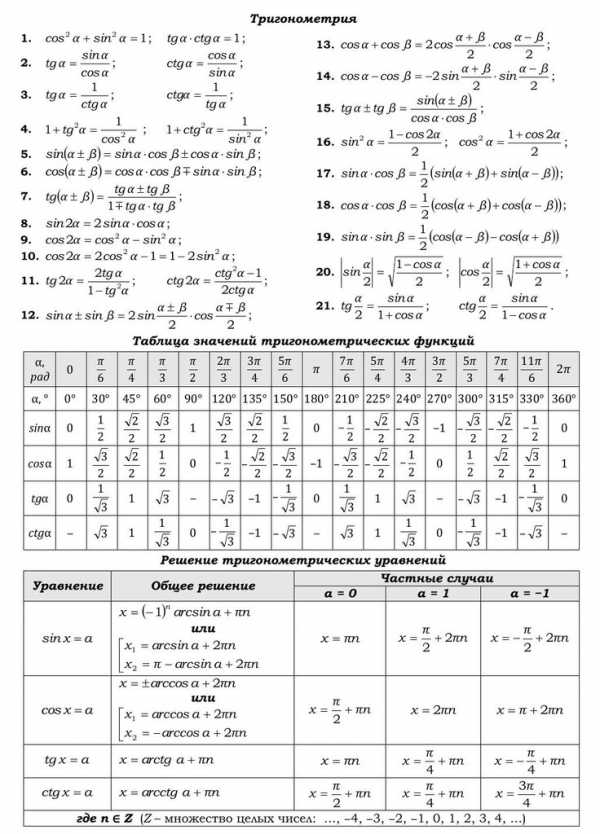





Также вам может пригодиться:
specclass.ru
Разбор и решение задания №5 ОГЭ по математике |
Анализ графиков
Перейдем к рассмотрению пятого задания. В данном случае нам необходимо соотнести значения на графике. По значению одной оси определить значение на второй оси. Задание также выполнено не в абстрактной форме, а на конкретных примерах, например соотнести значение температуры с днями в месяце.
Разбор типовых вариантов задания №5 ОГЭ по математике
Первый вариант задания
На рисунке показано, как изменялась температура воздуха на протяжении одних суток. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. Найдите наименьшее значение температуры в первой половине суток. Ответ дайте в градусах Цельсия.
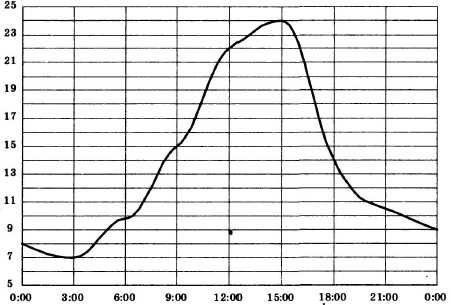
Решение:
Смотрим на график и ищем первую половину суток: это график до 12 часов. Значит, будем искать минимум в первой половине: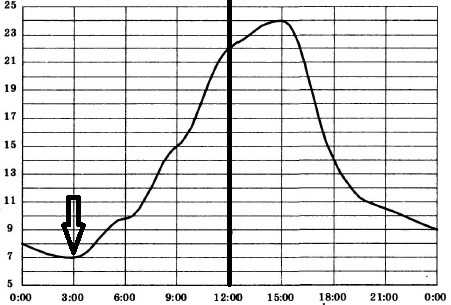
Находим минимум — смотрим на значение по оси y, на которой откладывается температура. Это значение 7.
Ответ: 7
Второй вариант задания
На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Н*м. Чему равен крутящий момент (в Н-м), если двигатель делает 2500 оборотов в минуту?
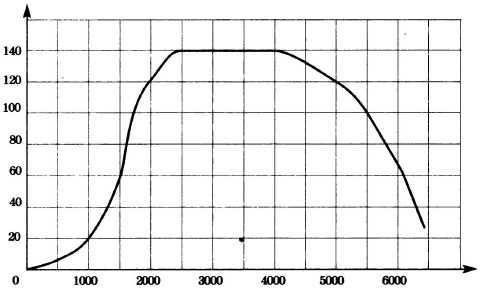
Решение:
Ищем значение 2500 оборотов в минуту и смотрим, чему равно значение y.
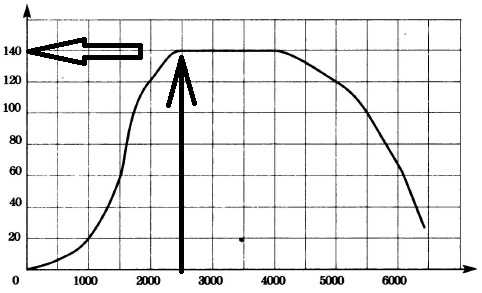
Ответ: 140
Третий вариант задания
При работе фонарика батарейка постепенно разряжается, и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по рисунку, на сколько вольт упадёт напряжение с 6-го по 56-й час работы фонарика.
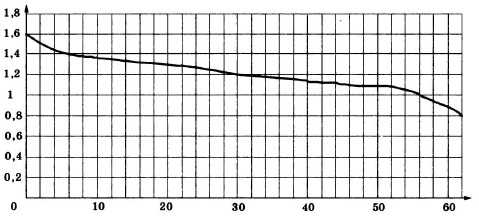
Решение:
Найдем значения напряжения в 6 и 56 час работы:
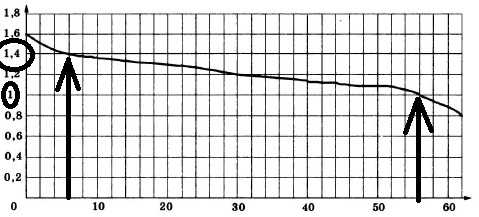
В 6 часов значение напряжения 1,4В , в 56 — 1 В. Разница в значениях — 0,4.
Ответ: 0,4
Четвертый вариант задания (демонстрационный вариант 2017)
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). На какой высоте (в километрах) давление составит 540 миллиметров ртутного столба?
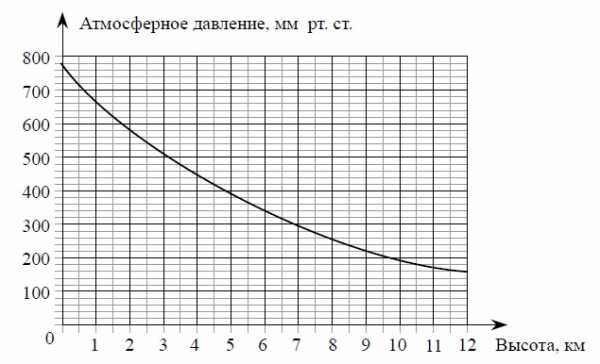
Решение:
Данное задание демонстрирует нам, как функции и графики функций встречаются нам в повседневной жизни, и демонстрируют нам необходимость умения работать с ними. Зависимость давления от высоты — это не что иное, как функция y (давление) от x (высота).
Для решения этой задачи, нужно сопоставить значению функции ее аргумент: значению давления — высоту.
Находим значение 540 на вертикальной оси (y). Мы не видим точной отметки, однако можем посчитать, что деления между 500 и 600 разделены на 5 дополнительных делений, если основное деление — 100, а дополнительных 5, то одно дополнительное это:
100 / 5 = 20 мм.
Значит, значению 540 соответствуют два деления выше 500 — 2 по 20 мм.
Далее ищем аргумент функции (высоту) следующим образом:
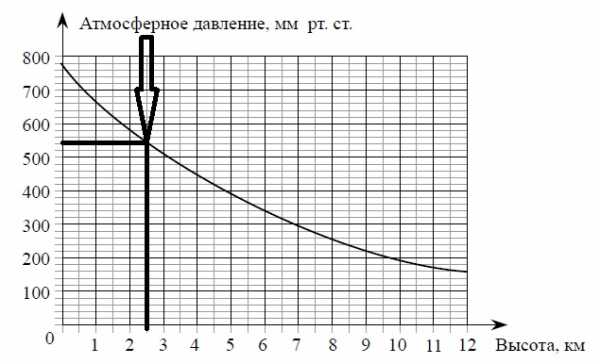
Видим, что значение высоты находится ровно между 2 и 3 километрами, значит высота равна 2,5 км.
Ответ: 2,5 км.
spadilo.ru
