Демонстрационные варианты (демоверсии) ОГЭ по математике
Демонстрационные варианты по математике (алгебре) 2010 года представлены в двух видах: демонстрационный вариант 1 и демонстрационный вариант 2. Отличие между ними заключается в том, что первая часть демонстрационного варианта 2 содержит на две задачи больше, чем первая часть демонстрационного варианта 1 (задачи 17 и 18) Эти задачи относятся к теории вероятностей и статистике. Других отличий нет.
Демонстрационный вариант ОГЭ по математике (алгебре) 2011 года почти полностью совпадает с демонстрационным вариантом 2 ОГЭ по математике (алгебре) 2010 года. Отличие заключается лишь в заданиях №10 и №22.
В 2011 году в ряде регионов в порядке эксперимента для проведения ОГЭ-9 по математике была использована перспективная модель КИМов, проект демонстрационного варианта которой мы также размещаем.
В 2012 году в демонстрационный вариант ОГЭ по математике
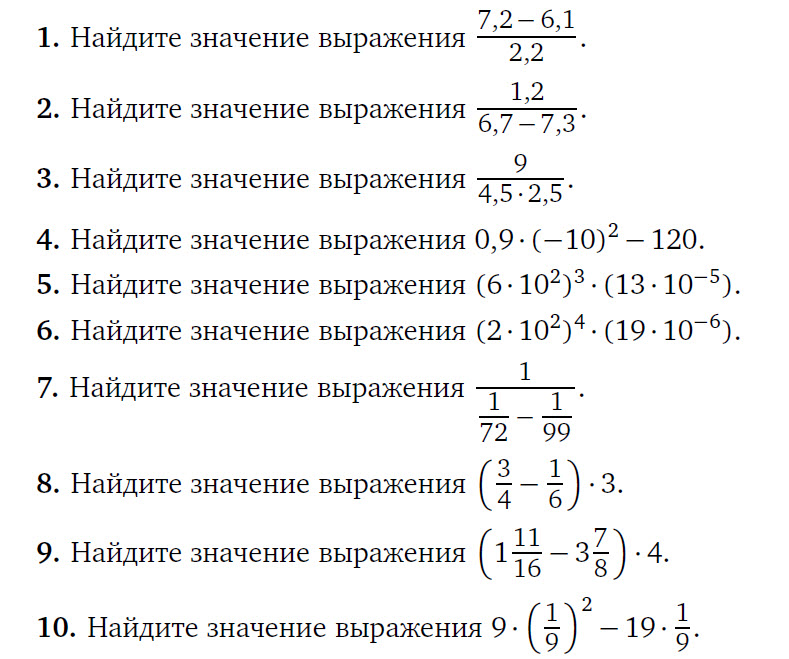
Демонстрационные варианты ОГЭ по математике 2013-2017 годов отличаются от вариантов предыдущих лет. В них
- Работа состоит из трёх модулей: «Алгебра», «Геометрия», «Реальная математика». Модули «Алгебра» и «Геометрия» состоят из двух частей: во второй части задачи более сложные по сравнению с первой частью.
- За каждое правильно выполненное задание части 1 выставляется 1 балл. В каждом модуле части 2 задания расположены по нарастанию сложности и оцениваются в 2 балла (в 2, 3 и 4 балла в демонстрационных вариантах по математике 2013-2015 годов).
-
Рекомендуемый минимальный порог выполнения экзаменационной работы – 8 баллов, набранные в сумме за выполнение заданий всех трёх модулей, при условии, что по модулю «Алгебра» набрано не менее 3 баллов, по модулю «Геометрия» набрано не менее 2 баллов и по модулю «Реальная математика»набрано не менее 2 баллов.

Демонстрационный вариант ОГЭ по математике 2014 годапрактически полностью совпадает с демонстрационным вариантом ОГЭ по математике 2013 года. Небольшое отличие имеется лишь в задаче №13, где требуется указать номера верных утверждений: в 2013 году условие этой задачи содержало 3 утверждения, а 2014 году к этим трем утверждениям было добавлено еще одно.
В демонстрационном варианте ОГЭ по математике 2015 года по сравнению с демонстрационным вариантом 2014 года были заменены задачи 1, 2, 3, 4, 6, 7, 10 и 17 на другие по той же тематике. Задачи 8 и 12 претерпели лишь косметические изменения. Из чертежа задачи 11 по геометрии удалены лишние данные. Остальные задачи были оставлены без изменений. Кроме того, в 2015 году была изменена форма записи ответа в задачах с выбором ответа: ответ стало нужно записывать цифрой с номером правильного ответа (а не обводить кружком).
В демонстрационных вариантах ОГЭ по математике 2016-2017 годов по сравнению с демонстрационным вариантом 2015 года изменений нет. Снижен максимальный первичный балл за всю работу с 38 до 32
за счет того, что правильное выполнение каждого из заданий части 2 в демонстрационных вариантах ОГЭ по математике 2016-2017 годов оценивается в 2 балла.В демонстрационный вариант ОГЭ по математике 2018 года по сравнению с демонстрационным вариантом 2017 года были внесены следующие изменения: из демонстрационного варианта был исключен модуль «Реальная математика», а задания, входившие в этот модуль, были распределены по модулям «Алгебра» и «Геометрия». При этом общее количество заданий и максимальный балл за всю работу не изменились.
В демонстрационном варианте ОГЭ по математике 2019 года по сравнению с демонстрационным вариантом 2018 года изменений не было.
В демонстрационном варианте ОГЭ по математике 2020 года по сравнению с демонстрационным вариантом 2019 года были заменены задания 2, 5, 7, 8, 15 на блок практико-ориентированных заданий 1-5, объединенных единым сюжетом.
Тесты ОГЭ по математике 2021
Тесты ОГЭ по математике
Структура
Модуль «Алгебра» содержит 11 заданий: в части 1 – 8 заданий; в части 2 – 3 задания.
Модуль «Геометрия» содержит 8 заданий: в части 1 – 5 заданий; в части 2 – 3 задания.
Модуль «Реальная математика» содержит 7 заданий.
Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня.
Шкала перевода баллов в оценки
«2» – от 0 до 7
«3» – от 8 до 14
«4» – от 15 до 21
«5» – от 22 до 32
Система оценивания выполнения отдельных заданий и экзаменационной работы в целом
Для оценивания результатов выполнения работ выпускниками используется общий балл.
Задания, оцениваемые в 2 балла, считаются выполненными верно, если обучающийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется полный балл, соответствующий данному заданию. Если в решении допущена ошибка, не имеющая принципиального характера и не влияющая на общую правильность хода решения, то участнику выставляется 1 балл.
Дополнительные материалы и оборудование
Участникам разрешается использовать справочные материалы, содержащие основные формулы курса математики, выдаваемые вместе с работой. Разрешается использовать линейку.
На выполнение экзаменационной работы отводится 235 минут
Любой учитель или репетитор может отслеживать результаты своих учеников по всей группе или классу. Для этого нажмите ниже на кнопку «Создать класс», а затем отправьте приглашение всем заинтересованным.
Ознакомьтесь с подробной видеоинструкцией по использованию модуля.
Проверяемые элементы содержания и виды деятельности |
Уровень сложности задания |
Максимальный балл за выполнение задания |
Примерное время выполнения задания (мин. |
|
| Задание 1. Уметь выполнять вычисления и преобразования, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | Б |
1 |
2-3 |
|
| Задание 2. Уметь выполнять вычисления и преобразования, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | Б |
1 |
2-3 |
|
| Задание 3. Уметь выполнять вычисления и преобразования, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | Б |
1 |
2-3 |
|
Задание 4. Уметь выполнять вычисления и преобразования, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели Уметь выполнять вычисления и преобразования, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели |
Б |
1 |
2-3 | |
| Задание 5. Уметь выполнять вычисления и преобразования, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | Б |
1 |
2-3 |
|
| Задание 6. Уметь выполнять вычисления и преобразования | Б |
1 |
3-5 |
|
| Задание 7. Уметь выполнять вычисления и преобразования | Б |
1 |
3-5 |
|
Задание 8. Уметь выполнять вычисления и преобразования, уметь выполнять преобразования алгебраических выражений Уметь выполнять вычисления и преобразования, уметь выполнять преобразования алгебраических выражений | Б |
1 |
2-3 |
|
| Задание 9. Уметь решать уравнения, неравенства и их системы | Б |
1 |
5 |
|
| Задание 10. Уметь работать со статистической информацией, находить частоту и вероятность случайного события, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | Б |
1 |
5 |
|
| Задание 11. Уметь строить и читать графики функций | Б |
1 |
5 |
|
Задание 12. Осуществлять практические расчеты по формулам, составлять несложные формулы, выражающие зависимости между величинами Осуществлять практические расчеты по формулам, составлять несложные формулы, выражающие зависимости между величинами |
Б |
1 |
5 |
|
| Задание 13. Уметь решать уравнения, неравенства и их системы | Б |
1 |
5 |
|
| Задание 14. Уметь строить и читать графики функций, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | Б |
1 |
5 |
|
| Задание 15. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | Б |
1 |
5 |
|
Задание 16. Уметь выполнять действия с геометрическими фигурами, координатами и векторами Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
Б |
1 |
5 |
|
| Задание 17. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | Б |
1 |
10 |
|
| Задание 18. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | Б |
1 |
10 |
|
| Задание 19. Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения | Б |
1 |
10 |
|
Задание 20. Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций |
П |
2 |
15-20 |
|
| Задание 21. Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели | П |
2 |
15-20 |
|
| Задание 22. Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели | В |
2 |
15-20 |
|
| Задание 23. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | П |
2 |
15-20 |
|
Задание 24. Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения |
П |
2 |
15-20 |
|
| Задание 25. Уметь выполнять действия с геометрическими фигурами, координатами и векторами | В |
2 |
15-20 |
|
Задание 22 ОГЭ-2019 по математике: разбор и решение
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2). Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Часть 2
Задание 22
Рыболов в 5 часов утра на моторной лодке отправился от пристани против течения реки, через некоторое время бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра того же дня. На какое расстояние от пристани он отплыл, если скорость реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?
Решение
Пусть рыболов отплыл на расстояние, равное s. Время, за которое он проплыл это путь, равно ч. (т.к. против течения скорость лодки равна 4 км/ч). Время, которое он затратил на путь обратно, равно ч. (т.к. по течению скорость лодки равна 8 км/ч). Общее время с учетом стоянки равно 5 ч. Составим и решим уравнение:
Общее время с учетом стоянки равно 5 ч. Составим и решим уравнение:
s = 8.
Ответ: 8 км.
ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену
Вниманию выпускников 9 классов предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики». Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогут в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изученного материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.
Они помогут учителю организовать подготовку к основному государственному экзамену, а учащимся — самостоятельно проверить свои знания и готовность к сдаче экзамена.
Пробный экзамен по математике 9 класс. 1-4 варианты с ответами
Решение.
Сумма углов выпуклого четырёхугольника равна 360°. Имеем: Так как , и — общая треугольника ABD и BDC. Из равенства треугольников следует, что . Таким образом, .
Ответ: 95.
Ответ: 95
17. Короткое плечо шлагбаума имеет длину 1 м, а длинное плечо – 3 м. На какую высоту (в метрах) опустится конец короткого плеча, когда конец длинного плеча поднимается на 1,8 м?
Решение.
Найдём синус угла, на который поднимается длинное плечо:
Угол подъема длинного плеча равен углу на который опустится короткое плечо. Пусть x — высота, на которую опустится короткое плечо, имеем:
Пусть x — высота, на которую опустится короткое плечо, имеем:
Таким образом, короткое плечо опустится на 0,6 м.
Ответ: 0,6.
Ответ: 0,6
18 На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 млн пользователей.Какое из следующих утверждений неверно?
1) Пользователей из России больше, чем пользователей из Белоруссии и Украины вместе.
2) Пользователей из Украины больше, чем пользователей Латвии.
3) Примерно две трети общего числа пользователей — из России.
4) Пользователей из Украины больше 3 миллионов.
В ответ запишите номер выбранного утверждения.
Решение.
Разъясним каждый вариант ответа:
1) Очевидно, что пользователей из России больше, чем пользователей из Украины и Белоруссии вместе.
2) Сектор «Украина» занимает большую площадь диаграммы, чем сектор «Другие страны», а т. к. «Латвия» включена в «Другие страны», имеем: пользователей из Украины больше, чем пользователей из Латвии.
3) Сектор в две трети диаграммы отсекается углом в 2·360°/3 = 240°. Очевидно, что угол, отсекающий сектор «Россия» примерно равен 240°, значит примерно две трети общего числа пользователей — из России.
4) Видно, что пользователей из Украины меньше четверти всех пользователей, значит, меньше 12/4=3 миллионов.
Ответ: 4.
Ответ: 4
19. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Решение.
Вероятность благоприятного случая() — отношение количества благоприятных случаев к количеству всех случаев. В данной задаче благоприятным случаем является старт спортсмена не из России под номером 1. Всего благоприятных случаев 2 + 5 = 7, а количество всех случаев 13 + 2 + 5 = 20. Отношение соответственно равно
Ответ: 0,35.
Ответ: 0,35
20. Площадь трапеции можно вычислить по формуле , где — основания трапеции, — высота (в метрах). Пользуясь этой формулой, найдите высоту , если основания трапеции равны и , а её площадь .
Часть 2
Решение.
Выразим высоту трапеции из формулы площади:
Подставляя, получаем:
Ответ: 4.
Приведём другое решение.
Подставим в формулу известные значения величин:
Ответ: 4
21. Разложите на множители .
Решение.
Имеем:
.
Ответ: .
22.Два оператора, работая вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?
23.Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно три общие точки.
Решение.
Раскрывая модуль, получим, что график функции можно представить следующим образом:
Этот график изображён на рисунке:
Из графика видно, что прямая имеет с графиком функции ровно три общие точки при и
Ответ: 0; 4.
24. Диагонали и трапеции пересекаются в точке . Площади треугольников и равны соответственно и . Найдите площадь трапеции.
Решение.
Заметим, что площади двух треугольников, общей вершиной которых является точка пересечения диагоналей трапеции, а основаниями — боковые стороны, равны. Это следует, например, из того, что площади треугольников и равны (поскольку эти треугольники имеют общее основание , и их высоты, проведенные к этому основанию, равны как высоты трапеции), а . По условию, , поэтому и являются не боковыми сторонами, а основаниями трапеции. Тогда треугольники и подобны по двум углам, и отношение их площадей равно квадрату коэффициента подобия . Поэтому . Поскольку треугольники и имеют общую высоту, проведённую из вершины , то отношение их площадей равно отношению их оснований, т. е. . Значит, . Поэтому и . Но тогда .
Ответ: .
25.В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.
Решение.
Проведём высоту так, чтобы она проходила через точку Углы и равны друг другу как вертикальные. Вспомним также, что диагонали делятся точкой пересечения пополам, следовательно, Рассмотрим треугольники и , они прямоугольные, имеют равные углы и равные гипотенузы, следовательно эти треугольники равны, а значит равны отрезки и . Таким образом,
Площадь параллелограмм равна а площадь треугольника
26. Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Найдите радиус окружности, вписанной в треугольник ABC.
ВАРИАНТ № 2
Часть 1 МОДУЛЬ «АЛГЕБРА»
1. Вычислите:
Решение.
Приведём к общему знаменателю:
Ответ: 3,7.
Ответ: 3,7
2.На координатной прямой отмечены числа a, b и c:
Значение какого из следующих выражений отрицательно?
1)−a 2)a+c 3)b−c 4) c − a
Решение.
Заметим, что −2 < a < −1, 1 < b < 2 и 3 < c < 4.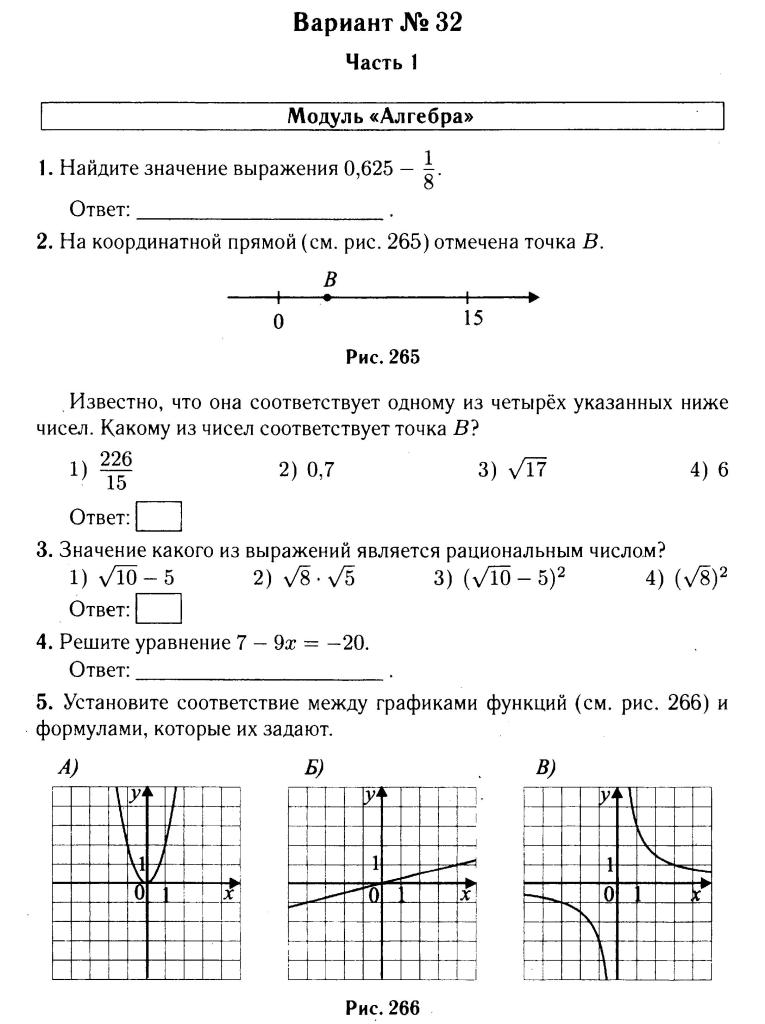 Тогда выражение −a положительно. Для выражения a + c верно двойное неравенство 1 < a + c < 3. Для выражения b − c верно двойное неравенство −2 < b − c < −1. Для выражения c − a верно двойное неравенство 4 < c − a < 6.
Тогда выражение −a положительно. Для выражения a + c верно двойное неравенство 1 < a + c < 3. Для выражения b − c верно двойное неравенство −2 < b − c < −1. Для выражения c − a верно двойное неравенство 4 < c − a < 6.
Таким образом, отрицательным является выражение b − c.
Правильный ответ указан под номером 3.
Ответ: 3
3.В какое из следующих выражений можно преобразовать дробь ?
1) 2) 3) 4)
Решение.
Упростим дробь:
Правильный ответ указан под номером 3.
Ответ: 3
4. Решите уравнение (x + 2)2 = (x − 4)2.
Решите уравнение (x + 2)2 = (x − 4)2.
Решение.
Последовательно получаем:
Ответ: 1.
Приведем другое решение.
Возведем обе части уравнения в квадрат:
Приведем другое решение.
Воспользуемся формулой разности квадратов:
Ответ: 1
5.График какой из приведенных ниже функций изображен на рисунке?
1)
2)
3)
4)
Решение.
Ветви изображённой на рисунке гиперболы лежат во II и IV четверти, её график растянут вдоль оси ординат в два раза. Этим условиям соответствует вариант 1
Графику соответствует вариант под номером 1.
Ответ: 1
6. Геометрическая прогрессия задана формулой n — го члена . Укажите третий член этой прогрессии.
Решение.
По формуле n-го члена геометрической прогрессии имеем:
Ответ: 12.
Ответ: 12
7.Представьте в виде дроби выражение и найдите его значение при . В ответ запишите полученное число.
Решение.
Упростим выражение:
Найдем значение выражения при
Ответ: −10.
Ответ: -10
8.Решите неравенство:
1) 2)3) 4)
МОДУЛЬ «ГЕОМЕТРИЯ»
Решение.
Решим неравенство: Корнями уравнения являются числа -23 и 0. Поэтому
Правильный ответ указан под номером 4.
Ответ: 4
9. Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 50°. Найдите меньший угол параллелограмма.
Решение.
Сумма смежных углов параллелограмма равна 180°. Тогда величина меньшего угла параллелограмма будет равна:
Ответ:
Ответ: 65
10. В окружности с центром в точке проведены диаметры и , угол равен 25°. Найдите величину угла .
В окружности с центром в точке проведены диаметры и , угол равен 25°. Найдите величину угла .
Решение.
Углы OCD и OAB являются вписанными и опираются на одну дугу BD. Таким образом,
Ответ: 25.
Ответ: 25
11. Найдите площадь параллелограмма, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению основания на высоту: 7 · 4 = 28.
Ответ: 28.
Ответ: 28
12. Найдите тангенс угла треугольника , изображённого на рисунке.
Решение.
Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему.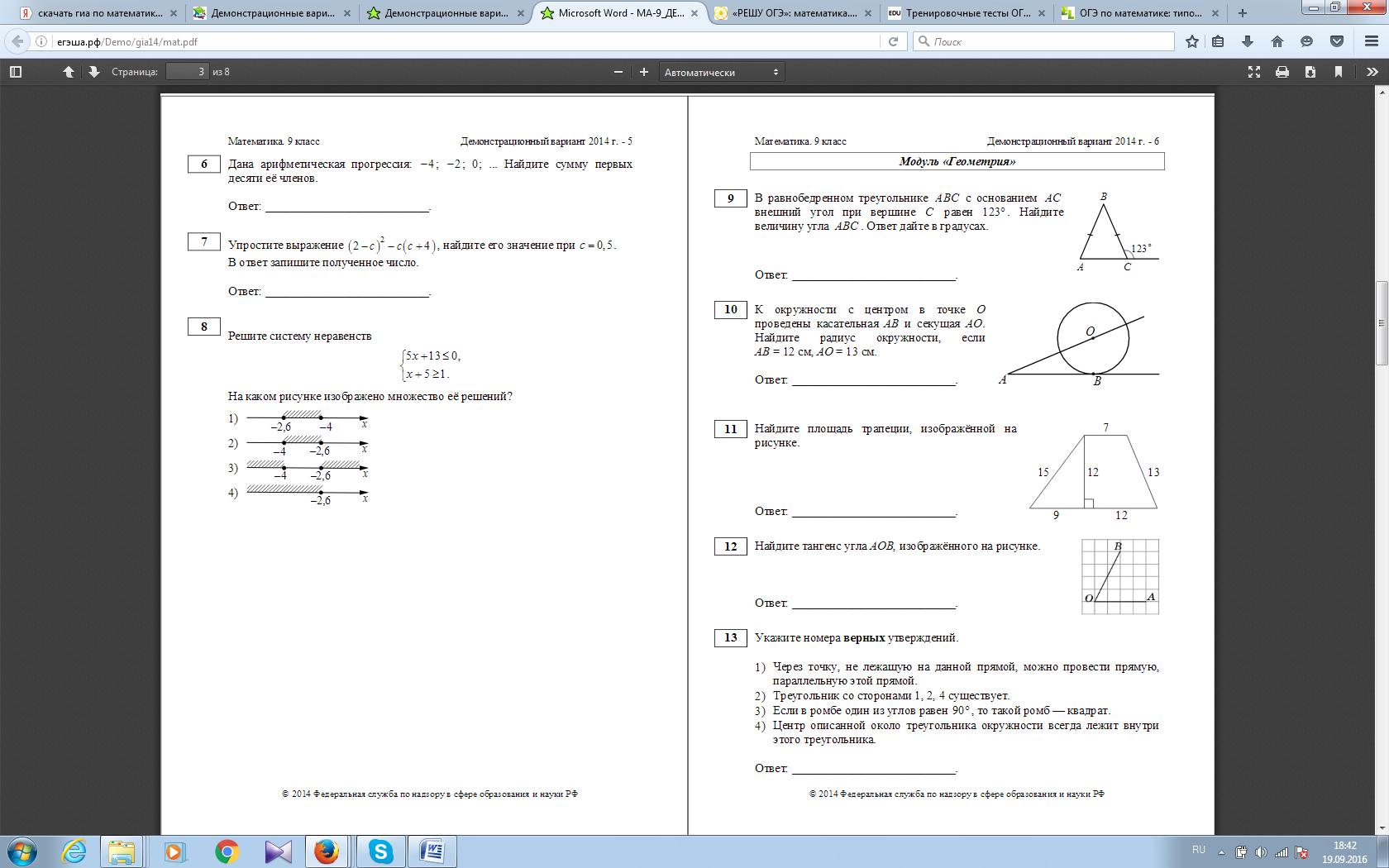 Треугольник ABC — прямоугольный, поэтому
Треугольник ABC — прямоугольный, поэтому
Ответ: 0,75.
Ответ: 0,75
13.Какие из следующих утверждений верны?
1) Каждая сторона треугольника меньше разности двух других сторон.
2) В равнобедренном треугольнике имеется не более двух равных углов.
3) Если сторона и угол одного треугольника соответственно равны стороне и углу другого треугольника, то такие треугольники равны.
4) В треугольнике ABC, для которого AB = 3, BC = 4, AC = 5, угол C наименьший.
МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА»
Решение.
Проверим каждое из утверждений:
1)«Каждая сторона треугольника меньше разности двух других сторон. » — неверно, так как если имеем, что
» — неверно, так как если имеем, что
2) «В равнобедренном треугольнике имеется не более двух равных углов.» — неверно, в равнобедренном треугольнике углы при основании равны.
3)«Если сторона и угол одного треугольника соответственно равны стороне и углу другого треугольника, то такие треугольники равны.» — неверно, равенство определяется по трем элементам.
4)«В треугольнике ABC, для которого AB = 3, BC = 4, AC = 5, угол C наименьший.» — верно, в треугольнике против большего угла лежит большая сторона.
Ответ: 4.
Ответ: 4
14. Учёный Иванов выезжает из Москвы на конференцию в Санкт-Петербургский университет. Работа конференции начинается в 10:00. В таблице дано расписание ночных поездов Москва — Санкт-Петербург
Номерпоезда
Отправление из
Москвы
Прибытие в
Санкт-Петербург
026А
23:00
06:30
002А
23:55
07:55
038А
00:44
08:46
016А
01:00
08:38
Путь от вокзала до университета занимает полтора часа. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Иванову.
Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Иванову.
1)026А 2)002А 3)038А 4) 016А
Решение.
Поскольку путь от вокзала до университета занимает полтора часа, поезд должен прибыть на вокзал не позднее 08:30. Этому условию удовлетворяют поезда под номерами: 026А и 002А. Из них позже отправляется поезд под номером 002А.
Правильный ответ указан под номером 2.
Ответ: 2
15.В таблице даны рекомендуемые суточные нормы потребления (в г/сутки) жиров, белков и углеводов детьми от 1 года до 14 лет и взрослыми.
Вещество
Дети от 1 года
до 14 лет
Мужчины
Женщины
Жиры
40—97
70—154
60—102
Белки
36—87
65—117
58—87
Углеводы
170—420
257—586
Какой вывод о суточном потреблении жиров, белков и углеводов 7-летней девочкой можно сделать, если по подсчётам диетолога в среднем за сутки она потребляет 42 г жиров, 35 г белков и 190 г углеводов? В ответе укажите номера верных утверждений.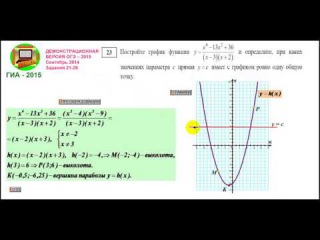
1) Потребление жиров в норме.
2) Потребление белков в норме.
3) Потребление углеводов в норме.
Если утверждений несколько, запишите их через точку с запятой в порядке возрастания.
Решение.
Проанализируем каждое утверждение.
1) Для семилетней девочки нормой является употребление от 40 до 97 граммов жиров в сутки, 42 грамма укладываются в этот промежуток. Первое утверждение верно.
2) Для семилетней девочки нормой является употребление от 36 до 87 граммов белков в сутки, 35 граммов не укладываются в этот промежуток. Второе утверждение неверно.
2) Для семилетней девочки нормой является употребление от 170 до 420 граммов углеводов в сутки, 190 граммов укладываются в этот промежуток. Третье утверждение верно.
Ответ: 1; 3.
Ответ: 1; 3
16.Площадь земель крестьянского хозяйства, отведённая под посадку сельскохозяйственных культур, составляет 24 га и распределена между зерновыми и овощными культурами в отношении 5:3. Сколько гектаров занимают овощные культуры?
Решение.
Овощные культуры занимают:
Ответ: 9.
Ответ: 9
17. Сколько досок длиной 3,5 м, шириной 20 см и толщиной 20 мм выйдет из четырехугольной балки длиной 105 дм, имеющей в сечении прямоугольник размером 30 см 40 см?
Решение.
Найдем объем доски : 350 · 20 · 2 = 14 000 см3. Найдем объем балки: 1050 · 30 · 40 = 1 260 000 см3.
Найдем объем балки: 1050 · 30 · 40 = 1 260 000 см3.
Поэтому количество досок равно 1 260 000 : 14 000 = 90.
Ответ: 90.
Ответ: 90
18. На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира.
Какое из следующих утверждений неверно
1) По площади территории Австралия занимает шестое место в мире.
2) Площадь территории Бразилии составляет 7,7 млн км2.
3) Площадь Индии меньше площади Китая.
4) Площадь Канады меньше площади России на 7,1 млн км2.
В ответе запишите номер выбранного утвержденияРешение.
Проверим каждое утверждение:
1) На диаграмме видно, что Австралия — шестая по площади страна в мире. Значит первое утверждение верно.
Значит первое утверждение верно.
2) Из диаграммы видно, что площадь Бразилии — 8,5 млн км2. Второе утверждение неверно.
3) Из диаграммы видно, что площадь Индии меньше площади Китая. Третье утверждение верно.
4) Из диаграммы видно, что площадь Канады меньше площади России на 17,1-10,0=7,1 млн км2. Четвёртое утверждение верно.
Неверным является утверждение под номером 2.
Ответ: 2
Решение.
Проанализируем все утверждения.
1) Пользователей из России больше всех, тем самым, их больше чем пользователей из Украины.
2) Сектор «Беларусь» занимает большую площадь диаграммы, чем сектор «Другие страны», а т. к. «Швеция» включена в «Другие страны» пользователей из Беларуси больше чем пользователей из Швеции.
3) Сектор в треть диаграммы имеет угол 360° : 3 = 120°. Угол сектора «Украина» меньше 90°, следовательно, меньше трети пользователей сети из Украины.
4) Пользователей из России больше половины всех пользователей, значит, больше 9 : 2 = 4,5 млн, а значит, больше 4 миллионов.
Ответ:3.
Ответ: 3
19. Какова вероятность того, что случайно выбранное натуральное число от 15 до 29 делится на 5?
Решение.
Чисел от 15 до 29 — 15 штук. Среди них на 5 делится только 3 числа. Таким образом, вероятность того, что случайно выбранное натуральное число от 15 до 29 делится на 5 равна
Ответ: 0,2
20.Объём пирамиды вычисляют по формуле , где — площадь основания пирамиды, — её высота. Объём пирамиды равен 40, площадь основания 15. Чему равна высота пирамиды?
Объём пирамиды равен 40, площадь основания 15. Чему равна высота пирамиды?
Часть 2
Решение.
Выразим высоту пирамиды из формулы для ее объема:
Подставляя, получаем:
Ответ: 8.
Ответ: 8
21.Сократите дробь , если .
Решение.
Имеем:
Ответ: 1.
22.Пристани и расположены на реке, скорость течения которой на этом участке равна 3 км/ч. Лодка проходит туда и обратно без остановок со средней скоростью 8 км/ч. Найдите собственную скорость лодки.
Лодка проходит туда и обратно без остановок со средней скоростью 8 км/ч. Найдите собственную скорость лодки.
Решение.
Пусть км/ч — собственная скорость лодки. Тогда скорость движения по течению равна км/ч, а скорость движения против течения равна км/ч. Обозначим расстояние между пристанями. Время, затраченное на весь путь, равно
.
По условию средняя скорость равна 8 км/ч, а весь путь равен . Следовательно,
.
Решим это уравнение:
Получаем: или . Корень −1 не является решением задачи. Значит, скорость лодки равна 9 км/ч.
Ответ: 9 км/ч.
23.Постройте график функции
и определите, при каких значениях прямая будет иметь с графиком единственную общую точку.
Решение.
Построим график функции (см. рисунок).
Из графика видно, что прямая будет иметь с графиком функции единственную точку пересечения при принадлежащем множеству [0; 1).
Ответ: [0; 1).
24. Медианы треугольника пересекаются в точке . Найдите длину медианы, проведённой к стороне , если угол равен 47°, угол равен 133°, .
Решение.
Обозначим середину стороны за . Продлим на свою длину за точку до точки . Четырёхугольник — параллелограмм, потому что и . Значит, = 133°, поэтому четырёхугольник — вписанный. Тогда .
Ответ: 6.
25. В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = АM, BE = DK. Докажите, что EFKM — параллелограмм.
Решение.
Противоположные стороны параллелограмма равны и по условию следовательно:
В параллелограмме противоположные углы равны: , Рассмотри треугольники и , в этих треугольниках , , следовательно эти треугольники равны, а значит, . Аналогично равны треугольники и а следовательно равны отрезки и Противоположные стороны четырехугольника равны, следовательно, по признаку параллелограмма, этот четырёхугольник — параллелограмм.
26.Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине.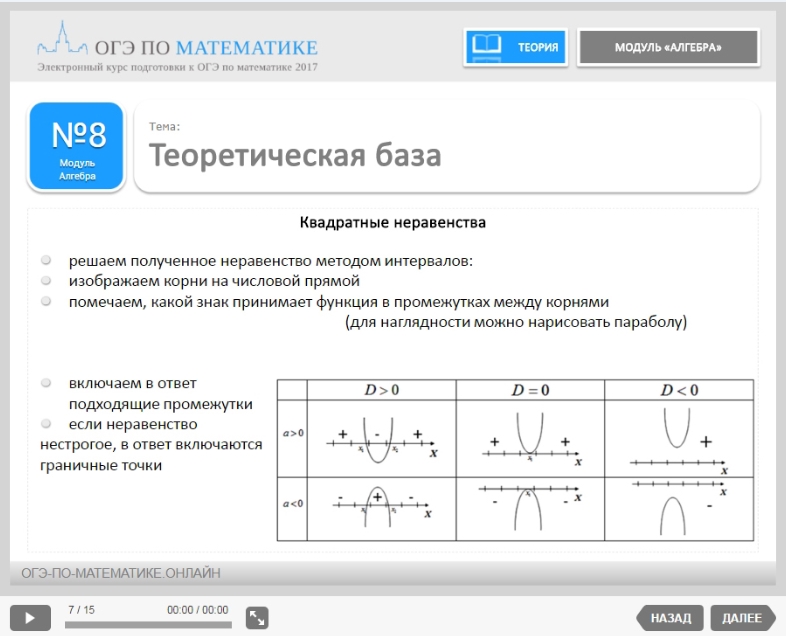 Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
ВАРИАНТ № 3
Часть 1 МОДУЛЬ «АЛГЕБРА»
1. Вычислите:
Решение.
Приведём к общему знаменателю:
Ответ: 1,03.
Ответ: 1,03
2.На координатной прямой отмечены числа и Какое из следующих утверждений неверно?
1) 2)
3) 4)
Решение.
Заметим, что и , и проверим все варианты ответа:
1) — неверно.
2) — верно, поскольку каждый множитель отрицателен.
3) — верно.
4) — верно.
Неверным является утверждение 1.
Ответ: 1
3. Какое из чисел больше: или ?
1)
2)
3)
Решение.
В силу цепочки неравенств
первое число меньше второго.
Правильный ответ указан под номером 1.
Ответ: 1
4. Найдите корни уравнения
Если корней несколько, в ответе запишите их сумму.
Решение.
Перенесём всё в уравнении в одну сторону:
По теореме, обратной теореме Виета, сумма корней равна 1, а их произведение равно −12. Тем самым, это числа −3 и 4.
Ответ: −3; 4.
Ответ: -3;4
5.Укажите соответствие между графиками функций и формулами, которые их задают.
1) 2)
3) 4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
АБ
В
Решение.
Определим вид графика каждой из функций.
1) уравнение прямой, которая пересекает ось абсцисс в точке 2 ; ось ординат в точке −2.
2) уравнение степенной функции с положительным дробным показателем. График проходит через точку (1; 0).
3) уравнение параболы, ветви которой направлены вверх.
4) уравнение степенной функции с положительным дробным показателем. График проходит через точку (−1; 0).
Таким образом, искомое соответствие: A — 4, Б — 3, В — 1.
Ответ: 431.
Ответ: 431
6. Последовательность задана условиями , . Найдите .
Решение.
Будем вычислять последовательно:
Данная последовательность образует арифметическую прогрессию. Найдем разность арифметической прогрессии:
Найдем разность арифметической прогрессии:
тогда
Примечание.
Зная разность и первый член арифметической прогрессии, можно найти посредственно:
Ответ: −9.
Ответ: -9
7. Сократите дробь
Решение.
Сократим дробь:
Ответ: 84.
Ответ: 84
8.На каком рисунке изображено множество решений неравенства
1)
2)
3)
4)
МОДУЛЬ «ГЕОМЕТРИЯ»
9. В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите .
В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точке P. Найдите .
Решение.
В равностороннем треугольнике ABC все углы равны 60°. Биссектрисы CN и AM делят уголы пополам, поэтому = = Сумма углов в треугольнике равна 180°, поэтому Вертикальные углы равны, следовательно,
Ответ: 120.
Ответ: 120
10 . Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 48°.
Решение.
Угол AOB является центральным углом, ACB — вписанным. Оба угла опираются на одну и ту же дугу, следовательно, угол AOB в два раза больше угла ACB.
Ответ: 24.
Ответ: 24
11. Сторона ромба равна 5, а диагональ равна 6. Найдите площадь ромба.
Решение.
Диагонали ромба пересекаются под углом 90° и точкой пересечения делятся пополам. Из прямоугольного треугольника, катетами которого являются половины диагоналей ромба, а гипотенузой — сторона ромба, по теореме Пифагора найдем половину неизвестной диагонали: Тогда вся неизвестная диагональ равна 8.
Площадь ромба равна половине произведения диагоналей:
Ответ: 24.
Ответ: 24
12. Найдите тангенс угла AOB, изображенного на рисунке.
Решение.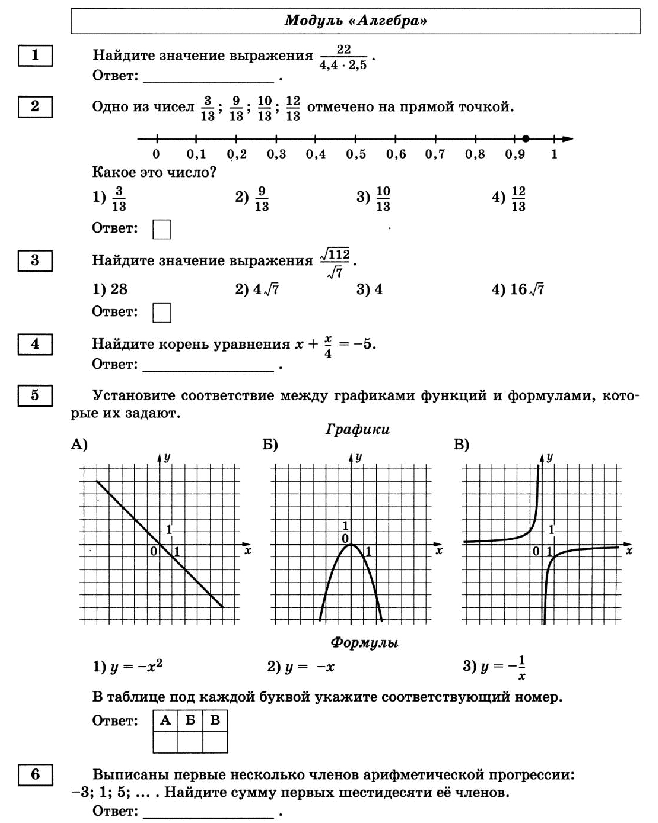
Опустим перпендикуляр BH на отрезок OA и рассмотрим прямоугольный треугольник OBH:
Ответ: 2.
Ответ: 2
13.Какие из следующих утверждений верны?
1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.
2) Если радиусы двух окружностей равны 5 и 7, а расстояние между их центрами равно 3, то эти окружности не имеют общих точек.
3) Если радиус окружности равен 3, а расстояние от центра окружности до прямой равно 2, то эти прямая и окружность пересекаются.
4) Если вписанный угол равен 30°, то дуга окружности, на которую опирается этот угол, равна 60°.
МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА»
14.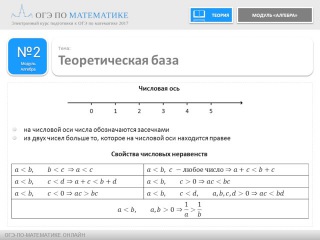 В таблице представлены нормативы по технике чтения в 3 классе.
В таблице представлены нормативы по технике чтения в 3 классе.
Какую отметку получит третьеклассник, прочитавший в апреле 68 слов за минуту?
1)«2» 2)«3» 3)«4» 4) «5»
Решение.
Проверка техники чтения происходила во втором полугодии. Из таблицы видно, что 68 прочитанных за минуту слов попадают в интервал «69 и менее» слов. Это соответствует отметке «2».
Правильный ответ указан под номером 1.
Ответ: 1
15.В таблице приведены результаты двух полуфинальных забегов на дистанцию 60 м. В финальном забеге 6 участников. Из каждого полуфинала в финал выходят два спортсмена, показавших первый и второй результаты. К ним добавляют еще двух спортсменов, показавших лучшее время среди всех остальных участников полуфиналов. Запишите в ответ номера спортсменов, не попавших в финал.
Запишите в ответ номера спортсменов, не попавших в финал.
Решение.
В полуфинале 1, лучшее время у спортсмена №4 и у спортсмена №1, таким образом, они выходят в финал.
В полуфинале 2, лучшее время у спортсмена №6 и у спортсмена №7 таким образом, они также выходят в финал.
Лучшее время из оставшихся спортсменов у спортсмена №2 и №5. таким образом таким образом, они тоже выходят в финал.
Таким образом, в финал не попали спортсмены под намерами 3 и 8.
Ответ: 38|3,8|8,3|83
16.На молочном заводе пакеты молока упаковываются по 12 штук в коробку, причём в каждой коробке все пакеты одинаковые. В партии молока, отправляемой в магазин «Уголок», коробок с полуторалитровыми пакетами молока втрое меньше, чем коробок с литровыми пакетами. Сколько литров молока в этой партии, если коробок с литровыми пакетами молока 45?
Решение.
Найдём количество коробок с полуторалитровыми пакетами молока: 45 : 3 = 15. Теперь рассчитаем количество литров молока в этой партии: 45 · 12 · 1 + 15 · 12 · 1,5 = 810 л.
Ответ: 810.
Ответ: 810
17. На каком расстоянии (в метрах) от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
Решение.
Пусть неизвестное расстояние равно х м. Рассмотрим два прямоугольных треугольника, выделенные на рисунке красным и зелёным. Они имеют общий угол и, следовательно, подобны. Поэтому отношения их катетов равны:
Тем самым, искомое расстояние равно 3,5 м.
Ответ: 3,5.
Ответ: 3,5
18.На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн пользователей.Какое из следующих утверждений неверно?
1) Пользователей из Беларуси меньше, чем пользователей из Украины.
2) Пользователей из России больше 4 миллионов.
3) Пользователей из Украины больше четверти общего числа пользователей.
4) Пользователей из Беларуси больше, чем пользователей из Финляндии.
В ответе запишите номер выбранного утверждения.
Решение.
Разъясним каждый вариант ответа.
1) Очевидно, что пользователей из Беларуси меньше, чем пользователей из Украины.
2) Видно, что пользователей из России больше половины всех пользователей, значит, больше 9/2 = 4,5 млн, а значит, больше 4 миллионов.
3) Сектор в четверть диаграммы отсекается углом в 360°/4 = 90°. Очевидно, что угол, отсекающий сектор «Украина» меньше 90°, значит, меньше четверти пользователей сети — из Украины.
4) Сектор «Беларусь» занимает большую площадь диаграммы, чем сектор «Другие страны», а т. к. «Финляндия» включена в «Другие страны», имеем: пользователей из Белоруссии больше, чем пользователей из Финляндии.
Ответ: 3.
Ответ: 3
19. В фирме такси в данный момент свободна 21 машина: 11 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси. Полученный ответ округлите до сотых.
Найдите вероятность того, что к ней приедет зеленое такси. Полученный ответ округлите до сотых.
Решение.
Вероятность того, что приедет зеленая машина равна отношению количества зеленых машин к общему количеству машин:
Ответ: 0,38.
Ответ: 0,38
20.Площадь параллелограмма можно вычислить по формуле , где — стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12 м и .
Часть 2
Решение.
Подставим в формулу известные значения величин:
Ответ: 60.
Ответ: 60
21.Решите систему уравнений:
Решение.
Сложим два уравнения системы:
откуда получаем или
Вычтем из первого уравнения системы второе:
Таким образом, решения систему
Ответ:
22. Две трубы наполняют бассейн за 8 часов 45 минут, а одна первая труба наполняет бассейн за 21 часов. За сколько часов наполняет бассейн одна вторая труба?
Решение.
По условию первая труба за одну минуту наполняет часть бассейна, а две трубы вместе за одну минуту наполняют часть бассейна. Таким образом, одна вторая труба за минуту наполняет часть бассейна, то есть она наполнит весь бассейн за 15 часов.
Ответ: 15.
23.При каком значении прямая имеет с параболой ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат данную параболу и прямую при найденном значении .
Постройте в одной системе координат данную параболу и прямую при найденном значении .
Решение.
График функции изображён на рисунке.
Запишем условие общей точки:
Прямая будет иметь с параболой единственную общую точку при условии, что дискриминант полученного квадратного уравнения равен нулю: откуда Подставив значение параметра в уравнение, находим
Ответ: (-2;0).
24. Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна 140°.
Решение.
Проведём радиус OA. Треугольник AOC — прямоугольный, ∠A = 90°. ∠COA = 180° − ∠AOD = 180° − 140° = 40°; ∠ACO = 90° − 40° = 50°.
Ответ: 50.
25.Дана равнобедренная трапеция . Точка лежит на основании и равноудалена от концов другого основания. Докажите, что — середина основания .
Решение.
Треугольник равнобедренный. Поэтому .
В равнобедренной трапеции .
Отсюда следует, что . Значит, треугольники и равны по двум сторонам и углу между ними. Следовательно, .
26. Диагонали четырёхугольника , вершины которого расположены на окружности, пересекаются в точке . Известно, что = 74°, = 102°, = 112°. Найдите .
ВАРИАНТ № 4
Часть 1 МОДУЛЬ «АЛГЕБРА»
1.Найдите значение выражения .
Решение.
Вынесем общий множитель за скобки:
Ответ: −3.
Ответ: -3
2. Одна из точек, отмеченных на координатной прямой, соответствует числу . Какая это точка?
1) точкаM 2) точкаN
3) точкаP 4) точка Q
Решение.
Возведём в квадрат числа 6, 7, 8:
Число 45 лежит между числами 36 и 49 и находится ближе к числу 49, поэтому соответствует точке N.
Правильный ответ указан под номером 2.
Ответ: 2
3 Какое из чисел больше: или?
1)
2)
3)
Решение.
В силу цепочки неравенств
первое число меньше второго.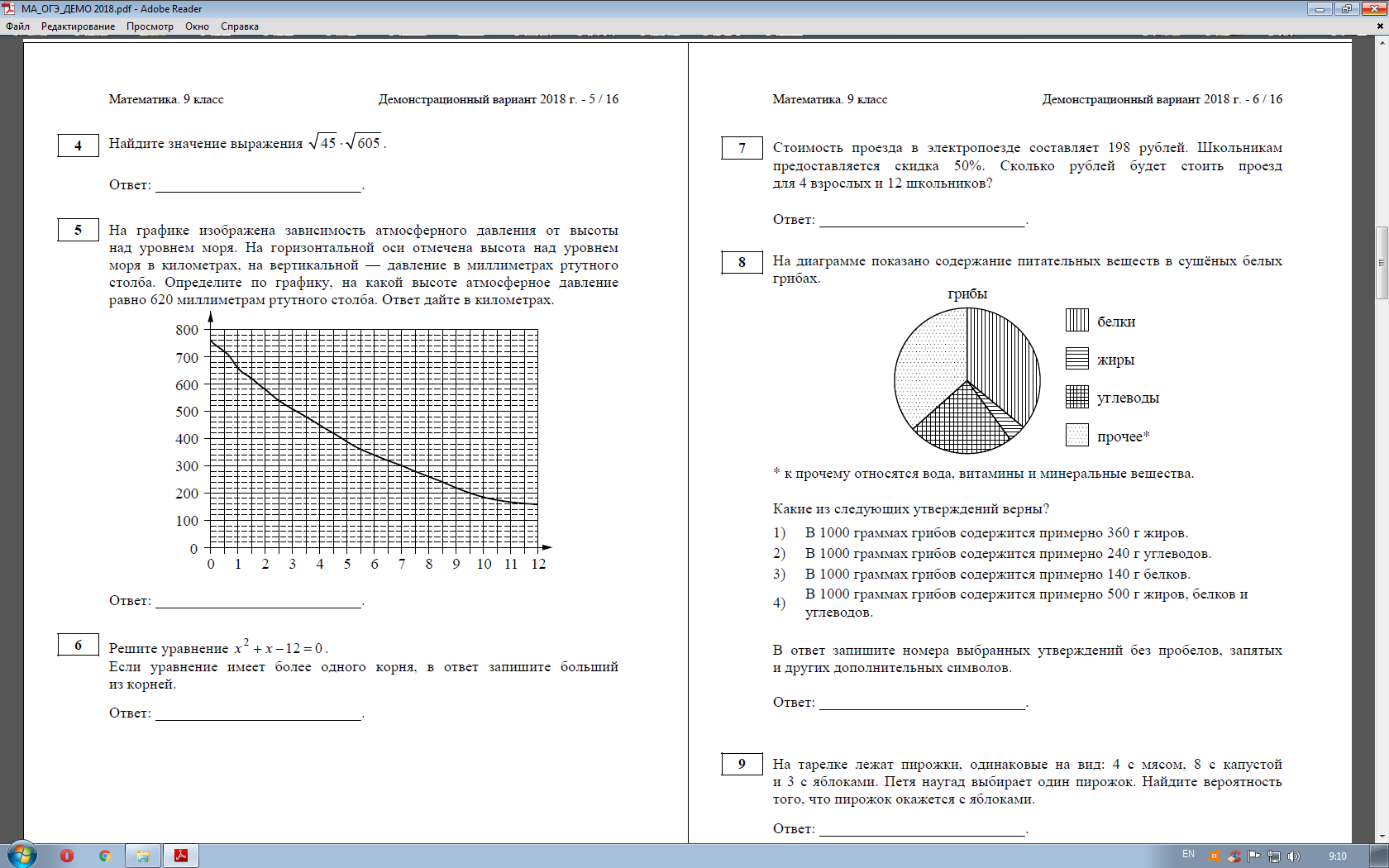
Правильный ответ указан под номером 1.
Ответ: 1
4.Найдите корни уравнения .
Если корней несколько, запишите в ответе наименьший.
5.На одном из рисунков изображен график функции . Укажите номер этого рисунка.
1)
2)
3)
4)
Решение.
График функции проходит через точку (1; 0). Этому условию удовлетворяет только график, изображённый на рисунке 4.
Таким образом, верный ответ указан под номером 4.
Ответ: 4
6. Дана арифметическая прогрессия: 33; 25; 17; … Найдите первый отрицательный член этой прогрессии.
Решение.
Для члена имеем: По формуле нахождения n-го члена арифметической прогрессии имеем:
Первое число, которое удовлетворяет этому условию, число 6. Следовательно, первым отрицательным членом прогрессии является
Таким образом, правельный ответ указан под номером 1.
Ответ: 1.
Ответ: 1
7.Найдите значение выражения при .
Решение.
Упростим выражение:
Найдем значение выражения при
Ответ: 2,5.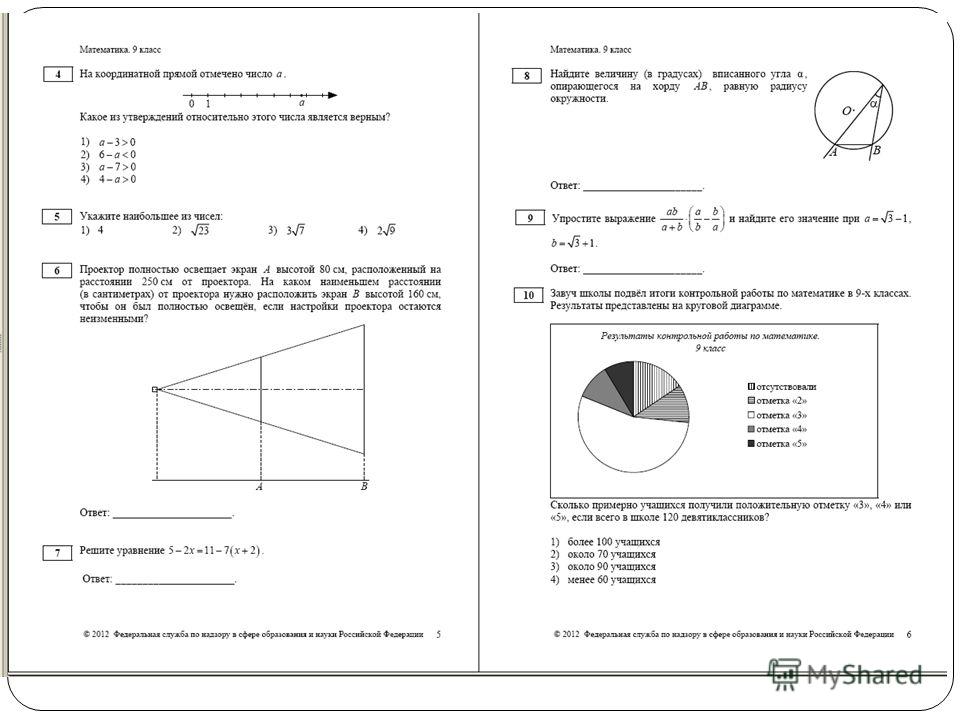
Ответ: 2,5
8.На каком рисунке изображено множество решений неравенства ?
1)1 2)2 3)3 4) 4
МОДУЛЬ «ГЕОМЕТРИЯ»
9.Сумма трех углов выпуклого четырехугольника равна 300°. Найдите четвертый угол. Ответ дайте в градусах.
Решение.
Так как сумма углов выпуклого четырехугольника равна 360°, четвертый угол равен 360° − 300° = 60°.
Ответ: 60.
Ответ: 60
10.Боковая сторона равнобедренного треугольника равна 5. Угол при вершине, противолежащий основанию, равен 120°. Найдите диаметр окружности, описанной около этого треугольника.
Решение.
Воспользуемся теоремой косинусов:
Здесь и — боковые стороны равнобедренного треугольника, — основание.
Диаметр описанной окружности вычислим по формуле:
Ответ: 10.
Ответ: 10
11. Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции вычисляется по формуле где и — основания, а — высота трапеции.
Ответ: 270.
Ответ: 270
12. Найдите тангенс угла С треугольника ABC , изображённого на рисунке.
Решение.
Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
Ответ: 0,75.
Ответ: 0,75
13. Какие из следующих утверждений верны?
1) Около любого правильного многоугольника можно описать не более одной окружности.
2) Центр окружности, описанной около треугольника со сторонами, равными 3, 4, 5, находится на стороне этого треугольника.
3) Центром окружности, описанной около квадрата, является точка пересечения его диагоналей.
4) Около любого ромба можно описать окружность
МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА»
14. На диаграмме представлено распределение количества пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 млн пользователей.
Какое из следующих утверждений неверно?
1) Пользователей из Украины больше, чем пользователей из Беларуси.
2) Пользователей из Украины меньше четверти общего числа пользователей.
3) Пользователей из Беларуси больше, чем пользователей из Эстонии.
4) Пользователей из России больше 8 миллионов.
Решение.
Проверим каждое утверждение:
1) Из диаграммы видно, что число пользователей из Украины больше, чем пользователей из Беларуси. Первое утверждение верно.
2) Из диаграммы видно, что пользователей из Украины меньше четверти общего числа пользователей. Второе утверждение верно.
3) Из диаграммы видно, что пользователей из Беларуси больше, чем пользователей из «других стран», а значит, и больше, чем пользователей из Эстонии. Третье утверждение верно.
4) Из диаграммы видно, что пользователей из России примерно две трети от общего числа пользователей. Всего пользователей 9 млн, значит пользователей из России около 6 млн, что меньше 8 млн. Четвёртое утверждение неверно.
Четвёртое утверждение неверно.
Неверным является утверждение под номером 4.
Ответ: 4
15.На графике показано, сколько человек зарегистрировалось с 25 декабря 2012 года по 13 февраля 2013 года в качестве участников конференции. По горизонтали указаны числа месяцев, а по вертикали — количество человек.
Во сколько раз возросло количество зарегистрировавшихся с 4 января по 3 февраля?
Решение.
Из графика видно, что число зарегестрировавшихся на4 января состваляло 30 человек, а 3 февраля — 270. Следовательно, число зарегистрировавшихся возросло в 270 : 30 = 9 раз.
Ответ: 9.
Ответ: 9
16. На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 120 человек. Голоса между кандидатами распределились в отношении 3:5. Сколько голосов получил победитель?
На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 120 человек. Голоса между кандидатами распределились в отношении 3:5. Сколько голосов получил победитель?
Решение.
Пусть x голосов приходится на одну часть, тогда 5x приходится на второго кандидата, а 3x — на первого. Зная, что в голосовании участвовало 120 человек составим уравнение:
Таким образом, победитель получил:
.
Ответ: 75.
Ответ: 75
17. Какой угол (в градусах) описывает минутная стрелка за 10 мин?
Решение.
Часовыми делениями циферблат разбит на 12 круговых секторов. Угол каждого из них равен 360° : 12 = 30°. Между минутной и часовой стрелкой два часовых деления. Они образуют угол 60°.
Угол каждого из них равен 360° : 12 = 30°. Между минутной и часовой стрелкой два часовых деления. Они образуют угол 60°.
Ответ: 60.
Ответ: 60
18. Рок-магазин продаёт значки с символикой рок-групп. В продаже имеются значки пяти цветов: чёрные, синие, зелёные, серые и белые. Данные о проданных значках представлены на столбчатой диаграмме.
Определите по диаграмме, значков какого цвета было продано меньше всего. Сколько примерно процентов от общего числа значков составляют значки этого цвета?
1) 5 2) 10 3) 15 4) 20
Решение.
Из диаграммы видно, что было продано меньше всего значков зелёного цвета в количестве 150 штук. Определим сколько процентов от общего числа составляют зелёные значки:
Значит зелёных значков примерно 15% от общего числа.
Ответ: 3.
Ответ: 3
19. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок окажется с яблоками
Решение.
Всего было подготовлено 25 билетов. Среди них 16 двузначных. Таким образом, вероятность взять билет с двухзначным номером равна
Ответ: 0,64
20. Из закона всемирного тяготения
выразите массу и найдите её величину (в килограммах), если и гравитационная постоянная
Часть 2
Решение.
Выразим массу: Подставим значения переменных:
Ответ: 1000.
Ответ: 1000
21. Решите неравенство
Решение.
Умножим на 10, приведём подобные слагаемые и разложим на множители:
Произведение двух сомножителей будет меньше нуля, если сомножители имеют разный знак (см. рисунок). Таким образом, получаем ответ:
Ответ:
22. Железнодорожный состав длиной в 1 км прошёл бы мимо столба за 1 мин., а через туннель (от входа локомотива до выхода последнего вагона) при той же скорости — за 3 мин. Какова длина туннеля (в км)?
Решение.
Поезд проходит через туннель за 3 минуты, при этом за одну минуту поезд проходит мимо выхода из туннеля, следовательно, от входа локомотива в туннель до выхода проходит 2 минуты. Мимо столба поезд длиной 1 км проходит за 1 минуту, поэтому его скорость равна 1 км/мин. Значит, за 2 минуты поезд пройдет 2 км, поэтому длина туннеля равна 2 км.
Мимо столба поезд длиной 1 км проходит за 1 минуту, поэтому его скорость равна 1 км/мин. Значит, за 2 минуты поезд пройдет 2 км, поэтому длина туннеля равна 2 км.
Ответ: 2.
23.Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно три общие точки.
Решение.
Раскрывая модуль, получим, что график функции можно представить следующим образом:
Этот график изображён на рисунке:
Из графика видно, что прямая имеет с графиком функции ровно три общие точки при и
Ответ: 0; 4.
24.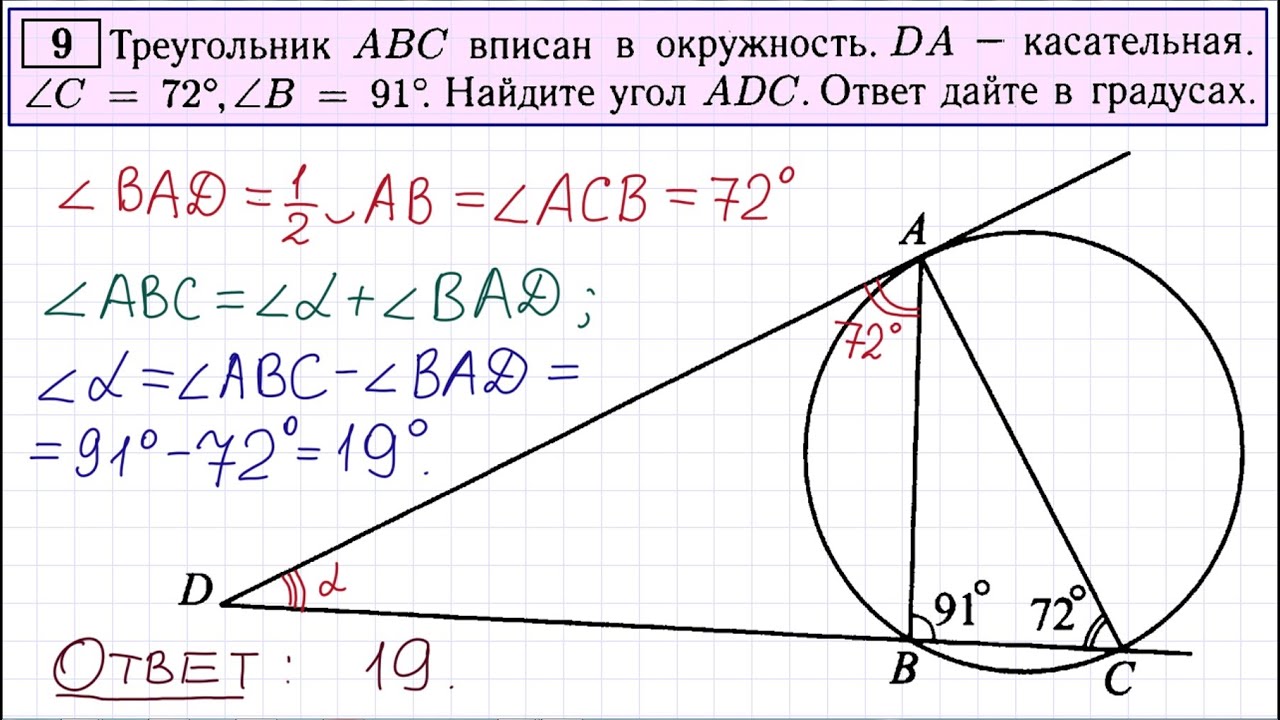 Диагонали и трапеции пересекаются в точке . Площади треугольников и равны соответственно и . Найдите площадь трапеции.
Диагонали и трапеции пересекаются в точке . Площади треугольников и равны соответственно и . Найдите площадь трапеции.
Решение.
Заметим, что площади двух треугольников, общей вершиной которых является точка пересечения диагоналей трапеции, а основаниями — боковые стороны, равны. Это следует, например, из того, что площади треугольников и равны (поскольку эти треугольники имеют общее основание , и их высоты, проведенные к этому основанию, равны как высоты трапеции), а . По условию, , поэтому и являются не боковыми сторонами, а основаниями трапеции. Тогда треугольники и подобны по двум углам, и отношение их площадей равно квадрату коэффициента подобия . Поэтому . Поскольку треугольники и имеют общую высоту, проведённую из вершины , то отношение их площадей равно отношению их оснований, т. е. . Значит, . Поэтому и . Но тогда .
Ответ: .
25.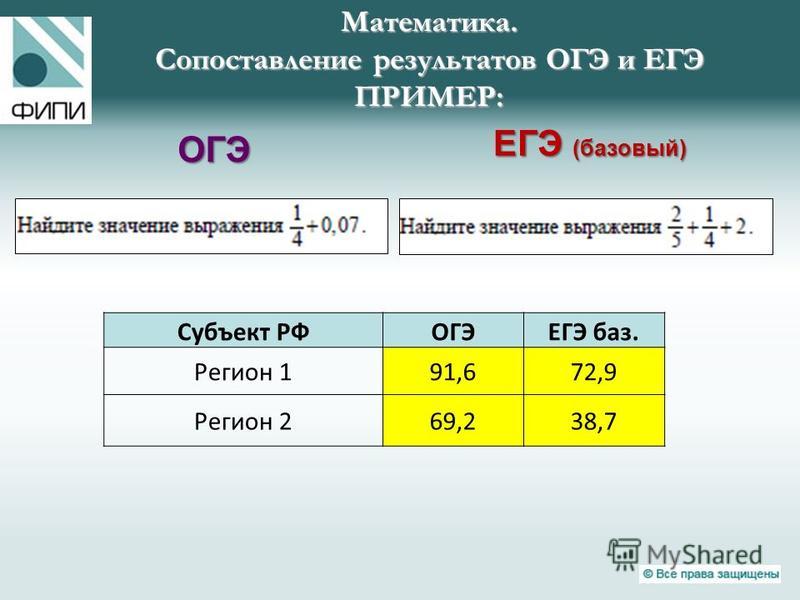 В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.
Решение.
Проведём высоту так, чтобы она проходила через точку Углы и равны друг другу как вертикальные. Вспомним также, что диагонали делятся точкой пересечения пополам, следовательно, Рассмотрим треугольники и , они прямоугольные, имеют равные углы и равные гипотенузы, следовательно эти треугольники равны, а значит равны отрезки и . Таким образом,
Площадь параллелограмм равна а площадь треугольника
26. Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Найдите радиус окружности, вписанной в треугольник ABC.
Чем удивят выпускников задания ЕГЭ и ОГЭ 2021 года — Российская газета
У выпускников осталось всего лишь два месяца, чтобы определиться с ЕГЭ по выбору и подать заявления на экзамен. Пока что отменять итоговую аттестацию ни в одиннадцатых классах, ни и в девятых, — Рособрнадзор не планирует. Более того, ведомство окончательно утвердило все демоверсии заданий ЕГЭ и ОГЭ на 2021 год. Чем они удивят школьников? Что изменится? И какие задания могут попасться? Об этом — в материале «РГ».
Кликни на ЕГЭ
Больше всего изменений — в ЕГЭ по информатике. Этот экзамен впервые пройдет на компьютерах. Для выпускников уже опубликован онлайн-тренажер по этому предмету. Можно зайти, прокликать все задания — на то же практическое программирование. Выпускнику придется самому составить и отладить программу на одном из языков: С++, Java, C#, Pascal, Python, Школьный алгоритмический язык.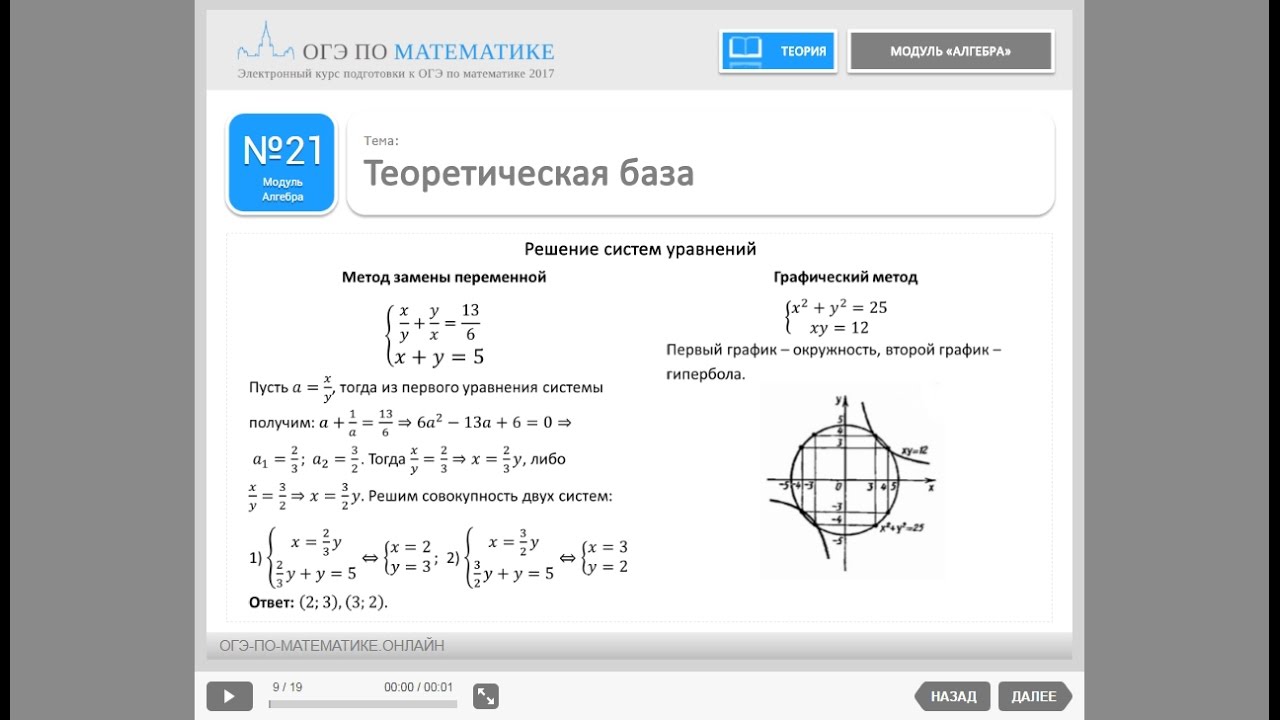 Еще добавились задания на работу с электронными таблицами и информационный поиск. Таких «новинок» примерно треть. Остальные задания — изменились мало и по сути «переехали» в компьютерный формат из старой «бумажной» версии, но в более современном и адаптированном виде.
Еще добавились задания на работу с электронными таблицами и информационный поиск. Таких «новинок» примерно треть. Остальные задания — изменились мало и по сути «переехали» в компьютерный формат из старой «бумажной» версии, но в более современном и адаптированном виде.
Ярослав Мудрый VS маршал Жуков
В ЕГЭ по математике, физике, химии, географии, обществознанию, и иностранным языкам изменений нет. ЕГЭ-2021 по биологии стал немного легче за счет того, что ребятам добавили еще целых 25 минут на работу: время увеличено с 210 до 235 минут.
Есть небольшие изменения в ЕГЭ по истории: в 2021 году для написания исторического сочинения выпускникам будут предложены на выбор три исторических процесса или деятельность трех личностей. Например, такие варианты: борьба Древнерусского государства с кочевниками в X — первой половине XII в.; внешняя политика России в 1689-1725 гг.; реформы госуправления в России в первой четверти XIX в. ; Ярослав Мудрый; А.Д. Меншиков; Г.К. Жуков.
Как это по-русски
Есть и серьезные изменения в самом массовом ЕГЭ по русскому языку.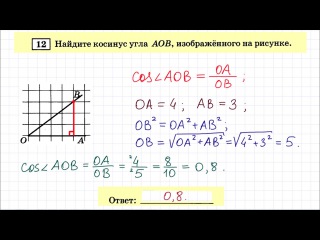 Девятое задание на правописание корней: если раньше выпускнику для ответов предлагались списки слов с пропущенными буквами, то теперь пропущенных букв нет. Все слова написаны полностью. Например, «увековечить», «исполнитель», «прославлять». Казалось бы, стало легче? Но это только кажется. На самом деле по месту пропуска буквы выпускник сразу видел, где корень слова и какая гласная безударная. И ему было проще. А теперь нужно провести морфемный разбор слова, найти корень и нужную гласную. И только потом понять, под какую орфограмму подпадает каждое слово. Причем таких орфограмм может быть три. Чередующиеся гласные в корне, проверяемые и непроверяемые.
Девятое задание на правописание корней: если раньше выпускнику для ответов предлагались списки слов с пропущенными буквами, то теперь пропущенных букв нет. Все слова написаны полностью. Например, «увековечить», «исполнитель», «прославлять». Казалось бы, стало легче? Но это только кажется. На самом деле по месту пропуска буквы выпускник сразу видел, где корень слова и какая гласная безударная. И ему было проще. А теперь нужно провести морфемный разбор слова, найти корень и нужную гласную. И только потом понять, под какую орфограмму подпадает каждое слово. Причем таких орфограмм может быть три. Чередующиеся гласные в корне, проверяемые и непроверяемые.
Самое сложное задание — сочинение, оно идет под номером 27. Раньше выпускнику нужно было привести два примера-иллюстрации из исходного текста, пояснить их и указать между ними связь. Теперь же ее нужно не просто указать, но и проанализировать, а именно — раскрыть, конкретизировать, пояснить.
В ОГЭ по химии участников экзамена тоже ждет реальный эксперимент: с колбами, пробирками, реактивами. Фото: РИА Новости
Фото: РИА Новости
ОГЭ ждет перемен
Несмотря на то, что в 2020 году девятиклассники экзамены не сдавали, изменения в 2021-м будут. Причем очень серьезные. Останутся прежними только русский язык, география и информатика.
А в обязательном и самом массовом ОГЭ по математике, к примеру, уменьшится число заданий. Два задания на преобразование алгебраических и числовых выражений объединятся в одно. Ну а в целом сохранится акцент на проверку применения математических знаний в реальных ситуациях. Выпускникам могут предложить рассмотреть план дачного участка с домом, баней, гаражом и огородом. А следом пойдут практические вопросы: сколько упаковок плитки нужно, чтобы вымостить дорожку перед гаражом? Найдите площадь жилого дома. Рассчитайте, какое отопление в нем выгоднее провести — электрическое или газовое? Эти знания в любом хозяйстве пригодятся, а не только на экзамене по математике.
В ОГЭ по обществознанию сокращено число заданий с кратким ответом. Зато добавлено пятое задание с развернутым ответом на анализ визуальной информации. Что это может быть? Например, в демоверсии предлагается фотография, где семья с ребенком выбирает вкусную дыню в овощном отделе супермаркета. Вопрос: «Какой это вид экономической деятельности?»
Что это может быть? Например, в демоверсии предлагается фотография, где семья с ребенком выбирает вкусную дыню в овощном отделе супермаркета. Вопрос: «Какой это вид экономической деятельности?»
В ОГЭ по иностранным языкам изменился раздел по аудированию, в нем будет 11 заданий с кратким ответом. В письменной части нужно будет написать электронное письмо другу по переписке.
Пушкин или Лермонтов?
В ОГЭ по литературе серьезно изменилась структура. Теперь можно выполнить на выбор задания «1.1» или «1.2». Оба сразу делать не нужно. Плюс ко всему добавилось новое задание 2.1/2.2, требующее анализа фрагмента предложенного произведения. В демоверсии это «Капитанская дочка» Пушкина. Что важно? Нужно взять не тот же фрагмент, который уже лежит перед глазами, а самому вспомнить новый отрывок этого произведения — и проанализировать его по памяти. Полный список произведений и авторов, которые могут попасться на экзамене, опубликован в спецификации на сайте Федерального института педагогических измерений.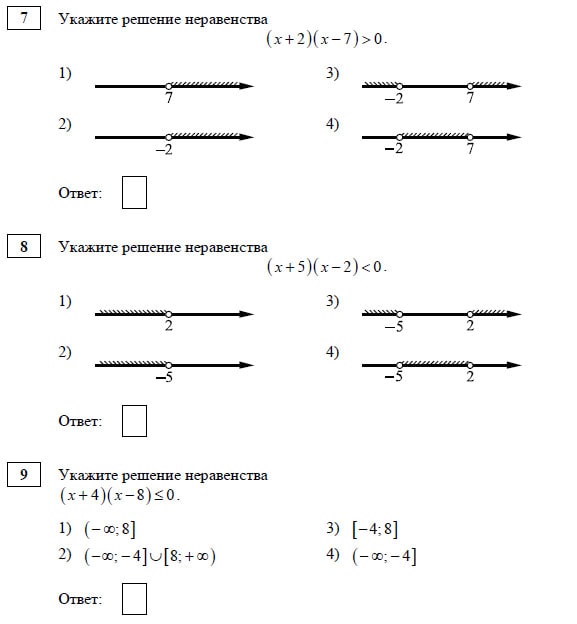 Всего — около 30 авторов. Среди них: Карамзин, Грибоедов, Пушкин, Лермонтов, Гоголь, Островский, Чехов и другие.
Всего — около 30 авторов. Среди них: Карамзин, Грибоедов, Пушкин, Лермонтов, Гоголь, Островский, Чехов и другие.
В ОГЭ по истории общее число заданий увеличено до 24 за счет добавления трех новых заданий с кратким ответом по всеобщей истории. В этом блоке выпускникам сначала дадут перечень процессов и событий. Например, 1) Греко-персидские войны 2) Столетняя война 3) Реформация в Германии 4) Война за независимость британских колоний в Северной Америке. А следом пойдут вопросы. Например, такие: «Участником какого из этих событий был М. Лютер?» «В ходе какого из этих процессов происходила осада Орлеана?»
Лабораторная работа
Естественно-научный блок: биология, физика, химия тоже изменился. Сделан еще больший акцент на практику. К примеру, в ОГЭ по физике расширилось содержание экспериментального задания, которое выполняется на реальном оборудовании. К проведению косвенных измерений добавлено исследование зависимости одной физической величины от другой. А в биологии добавилось задание, проверяющее исследовательские умения выпускника. В ОГЭ по химии участников экзамена ждет реальный эксперимент. А в заданиях по этому предмету может попасться подобный вопрос: «Из перечисленных суждений о правилах работы с веществами выберите верные: 1) Хлор можно получать только в вытяжном шкафу. 2) При приготовлении раствора кислоты концентрированную серную кислоту приливают к воде. 3) При нагревании раствора пробирку с жидкостью держат строго вертикально. 4) Работу с едкими веществами следует проводить в резиновых перчатках.
В ОГЭ по химии участников экзамена ждет реальный эксперимент. А в заданиях по этому предмету может попасться подобный вопрос: «Из перечисленных суждений о правилах работы с веществами выберите верные: 1) Хлор можно получать только в вытяжном шкафу. 2) При приготовлении раствора кислоты концентрированную серную кислоту приливают к воде. 3) При нагревании раствора пробирку с жидкостью держат строго вертикально. 4) Работу с едкими веществами следует проводить в резиновых перчатках.
Онлайн-тренажер компьютерного ЕГЭ по информатике вы можете найти по этой ссылке.
Проверь себя
Сдашь ли ты ЕГЭ по истории?
Фото: http://kege.rustest.ru
Какие из представленных монет посвящены юбилеям событий, произошедших при жизни военачальника, изображенного на соседней марке? (Выберите две из четырех).
Фото: Andrei Sdobnikov / wikipedia.org
Какие суждения о данной марке являются верными? (Выберите два из пяти)
- 1. Военачальник, изображенный на марке, подвергся репрессиям.

- 2. Военачальник, изображенный на марке, родился в период правления в России Николая II.
- 3. События, изображенные на марке стрелками, произошли в ходе Первой мировой войны.
- 4. Военачальник, изображенный на марке, был участником Великой Отечественной войны.
- 5. Марка была выпущена в период руководства СССР Н.С. Хрущева.
Источник: fipi.ru
Правильные ответы здесь.
| № |
Требования к уровню подготовки выпускников, проверяемому на ЕГЭ |
Уровень сложности задания |
Макс. балл за выполнение задания |
|
Часть 1 |
|||
|
1 |
Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели |
Б |
1 |
|
2 |
Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели |
Б |
1 |
|
3 |
Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели |
Б |
1 |
|
4 |
Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели |
Б |
1 |
|
5 |
Уметь выполнять вычисления и преобразования, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели |
Б |
1 |
|
6 |
Уметь выполнять вычисления и преобразования |
Б |
1 |
|
7 |
Уметь выполнять вычисления и преобразования |
Б |
1 |
|
8 |
Уметь выполнять вычисления и преобразования, уметь выполнять преобразования алгебраических выражений |
Б |
1 |
|
9 |
Уметь решать уравнения, неравенства и их системы |
Б |
1 |
|
10 |
Уметь работать со статистической информацией, находить частоту и вероятность случайного события, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели |
Б |
1 |
|
11 |
Уметь строить и читать графики функций |
Б |
1 |
|
12 |
Осуществлять практические расчёты по формулам; составлять несложные формулы, выражающие зависимости между величинами |
Б |
1 |
|
13 |
Уметь решать уравнения, неравенства и их системы |
Б |
1 |
|
14 |
Уметь строить и читать графики функций, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели |
Б |
1 |
|
15 |
Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
Б |
1 |
|
`16 |
Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
Б |
1 |
|
17 |
Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
Б |
1 |
|
18 |
Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
Б |
1 |
|
19 |
Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения |
Б |
1 |
|
Часть 2 |
|||
|
20 |
Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы |
П |
2 |
|
21 |
Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели |
П |
2 |
|
22 |
Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели |
В |
2 |
|
23 |
Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
П |
2 |
|
24 |
Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения |
П |
2 |
|
25 |
Уметь выполнять действия с геометрическими фигурами, координатами и векторами |
В |
2 |
| Всего заданий – 25; из них по типу заданий: заданий с кратким ответом – 19; заданий с развёрнутым ответом – 6; по уровню сложности: Б – 19; П – 4; В – 2.  Максимальный первичный балл за работу – 31. Общее время выполнения работы – 235 минут. |
|||
Демонстрационные варианты (демоверсии) ОГЭ по математике
Демонстрационные варианты по математике (алгебре) 2010 года представлены в двух вариантах: демонстрационный вариант 1 и демонстрационный вариант 2. Отличие между ними заключается в том, что первая часть демонстрационного варианта 2 содержит на две задачи больше, чем первая часть демонстрационного варианта 1 (задачи 17 и 18) Эти отношения к теории вероятностей и статистике. Других отличий нет.
Демонстрационный вариант ОГЭ по математике (алгебре) 2011 года почти полностью совпадает с демонстрационным демонстрационным 2 ОГЭ по математике (алгебре) 2010 года. Отличие заключается лишь в заданиях №10 и №22.
В 2011 году в некоторых регионах в порядке эксперимента по проведению ОГЭ-9 по математике была перспективная модель КИМов , проект демонстрационного варианта которой мы также размещаем.
В 2012 году в демонстрационный вариант ОГЭ по математике были включены не только задания по алгебре, теории вероятностей и статистике, но также и задания по геометрии.
Демонстрационные варианты ОГЭ по математике 2013-2017 годов отличаются от вариантов предыдущих лет.В них
- Работа состоит из трёх модулей : «Алгебра», «Геометрия», «Реальная математика». Модули «Алгебра» и «Геометрия» состоят из двух частей: во второй части более сложные по с первой части.
- За каждое правильно выполненное задание части 1 выставляется 1 балл . В каждом модуле части 2 установлены по нарастанию сложности и оцениваются в 2 балла (в 2, 3 и 4 балла в демонстрационных вариантах по математике 2013-2015 годов).
- Рекомендуемый минимальный порог выполнения экзаменационной работы — 8 баллов , набранные в сумме за выполнение всех трёх модулей, при условии, что по модулю «Алгебра» набрано не менее 3 баллов, по модулю «Геометрия » набрано не менее 2 баллов и по модулю « Реальная математика » набрано не менее 2 баллов .
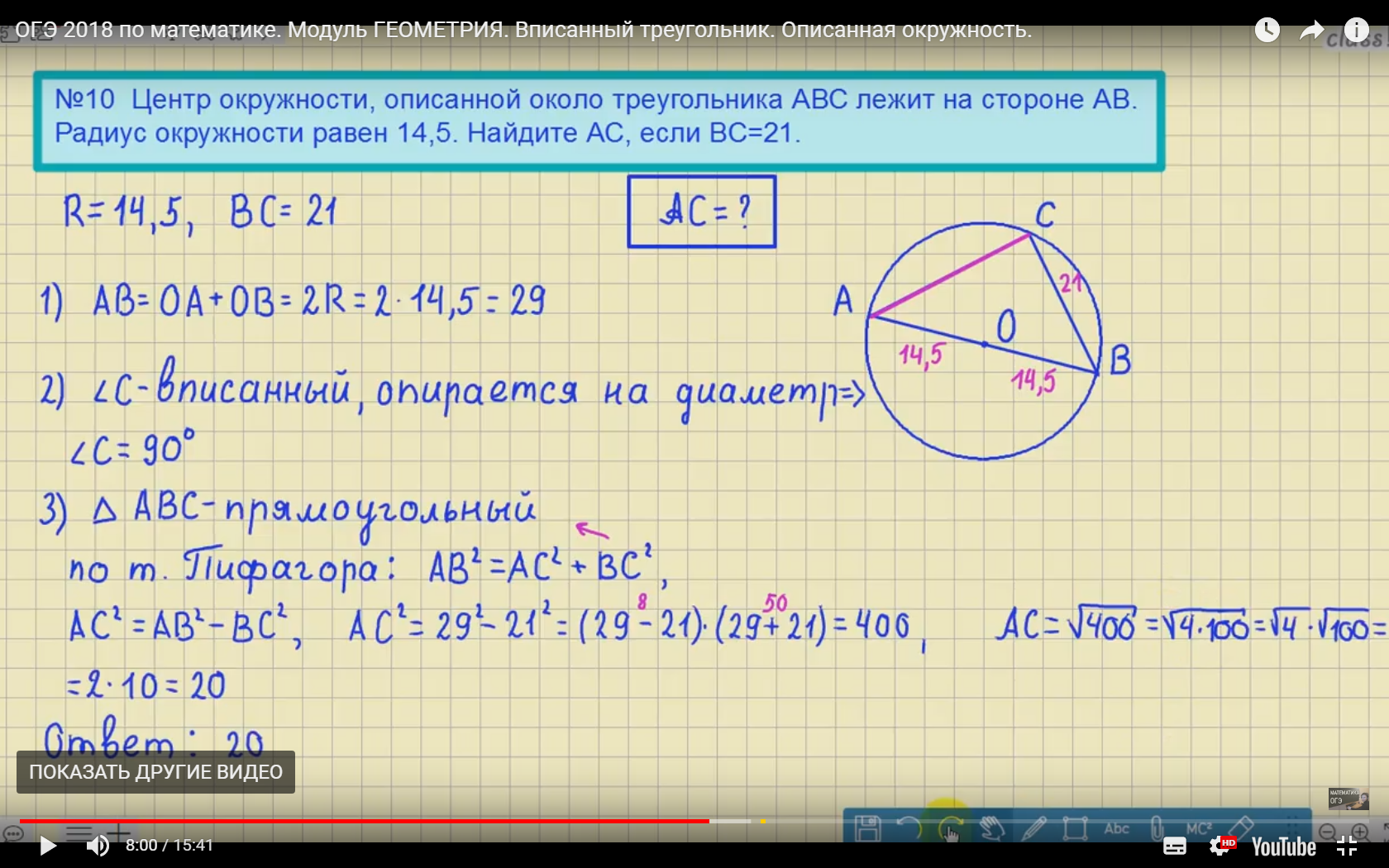
Демонстрационный вариант ОГЭ по математике 2014 года практически полностью совпадает с демонстрационным демонстрационным ОГЭ по математике 2013 года.Небольшое отличие имеется в задаче №13, где требуется указать номера верных утверждений: в 2013 году требуется условие этого утверждения 3, в 2014 году к этому трем утверждениям было добавлено еще одно.
В демонстрационном варианте ОГЭ по математике 2015 года по сравнению с демонстрационным 2014 года были заменены задачи 1, 2, 3, 4, 6, 7, 10 и 17 на другие по той же тематике. Задачи 8 и 12 претерпели лишь косметические изменения. Из чертежа задачи 11 по геометрии удалены лишние данные.Остальные задачи были оставлены без изменений. Кроме того, в 2015 году была изменена форма записи ответа в задаче с выбором: ответ стало нужно записывать цифрой с номером правильного ответа (а не обводить кружком).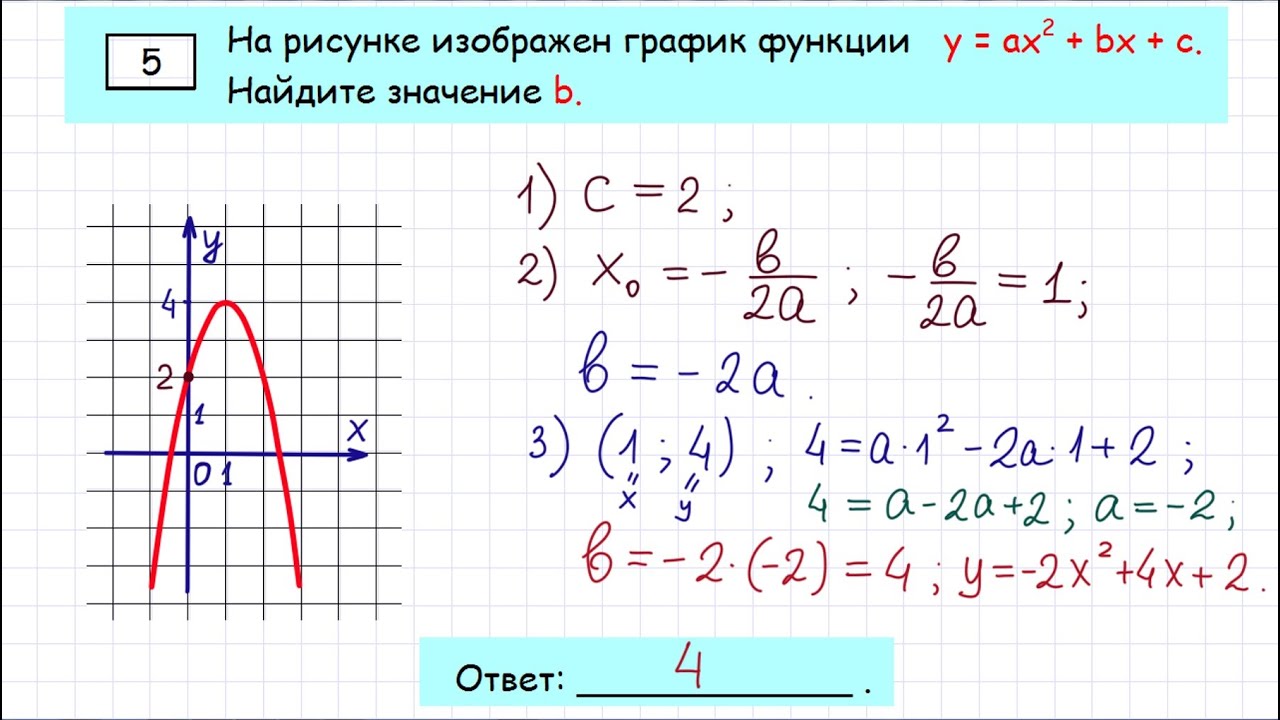
В демонстрационных вариантах ОГЭ по математике 2016-2017 годов по сравнению с демонстрационным показом 2015 года изменений нет . Снижен максимальный первичный балл за всю работу с 38 до 32 за счет того, что правильное выполнение каждого из заданных частей 2 в демонстрационных вариантах ОГЭ по математике 2016-2017 годов оценивается в 2 балла.
В демонстрационном варианте ОГЭ по математике 2018 года по сравнению демонстрационным вариантом 2017 года были внесены следующие изменения: из демонстрационного варианта исключен модуль «Реальная математика» , модуль задания, входившие в этот модуль, были распределены по модулю « Алгебра »и« Геометрия ». При этом общее количество заданий и максимальный балл за всю работу не изменились .
В демонстрационном варианте ОГЭ по математике 2019 года по сравнению с демонстрационным 2018 года изменений не было.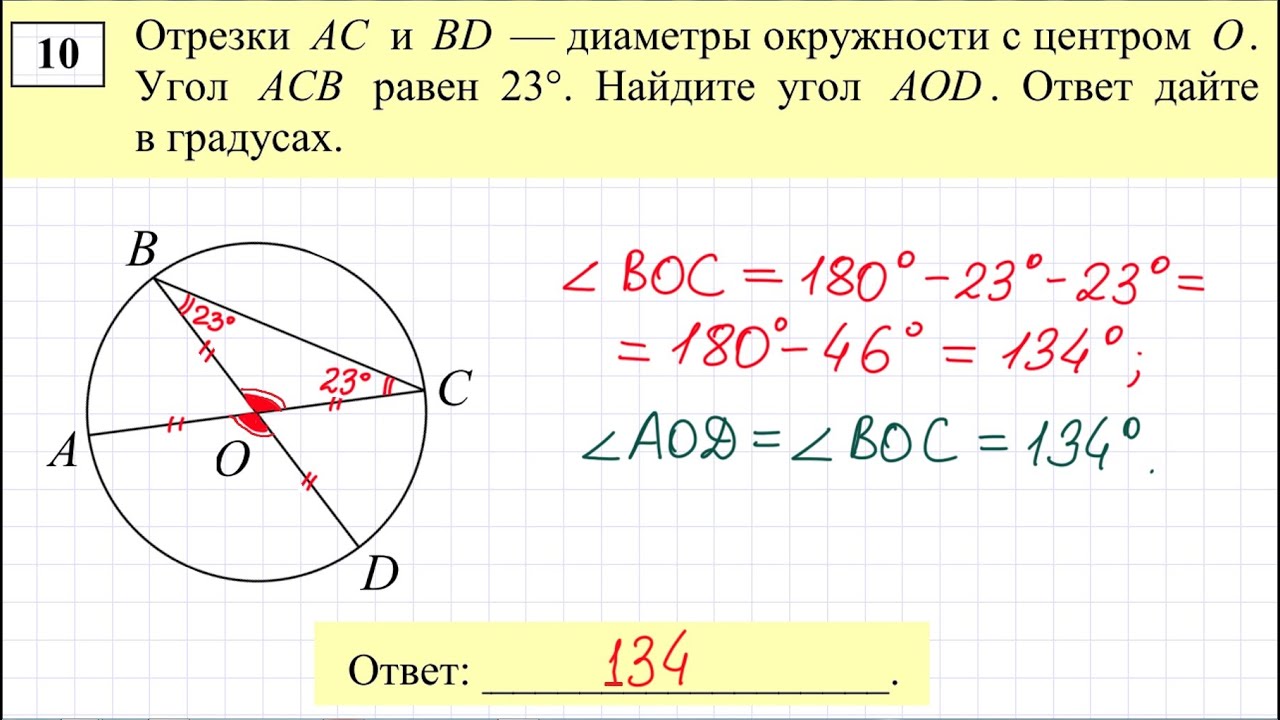
В демонстрационном варианте ОГЭ по математике 2020 года по сравнению с демонстрационным 2019 года были заменены задания 2, 5, 7, 8, 15 на блок практико-ориентированных заданий 1-5, объединенных единым сюжетом .
Тесты ОГЭ по математике 2021
Тесты ОГЭ по математике
Структура
Модуль «Алгебра» содержит 11 заданий: в части 1 — 8 заданий; в части 2 — 3 задания.
Модуль «Геометрия» содержит 8 заданий: в части 1 — 5 заданий; в части 2 — 3 задания.
Модуль «Реальная математика» содержит 7 заданий.
Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня.
Шкала перевода баллов в оценке
«2» — от 0 до 7
«3» — от 8 до 14
«4» — от 15 до 21
«5» — от 22 до 32
Система оценивания отдельных заданий и экзаменационной работы в целом
Для оценивания результатов выполнения работ используется общий балл.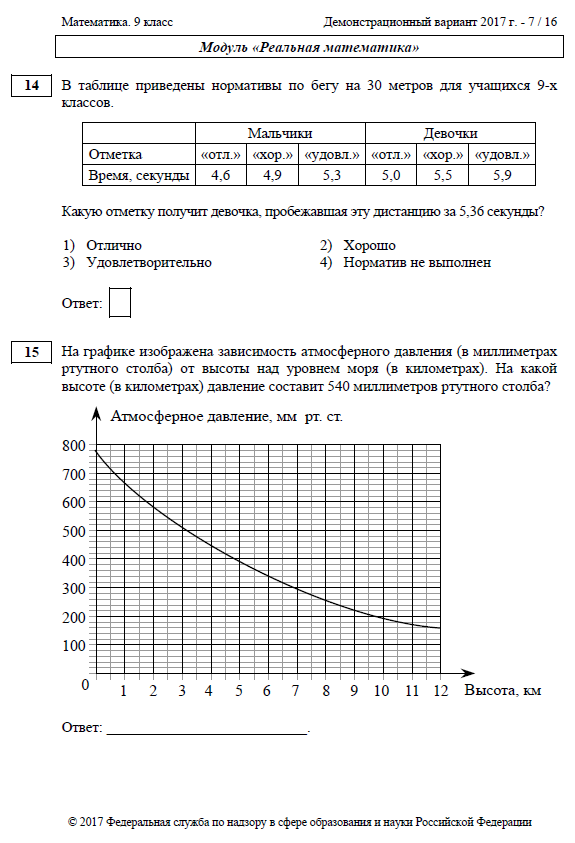 Максимальный балл за работу в целом — 32. Задания, оцениваемые 1 баллом, считаются выполненными верно, если указан номер верного ответа (в заданиях с выбором ответа), или вписан верный ответ (в заданиях с кратким ответом), или правильно соотнесены объекты двух множеств и записана соответствующая последовательность цифр (в заданиях на установление) соответствие.
Максимальный балл за работу в целом — 32. Задания, оцениваемые 1 баллом, считаются выполненными верно, если указан номер верного ответа (в заданиях с выбором ответа), или вписан верный ответ (в заданиях с кратким ответом), или правильно соотнесены объекты двух множеств и записана соответствующая последовательность цифр (в заданиях на установление) соответствие.
Задания, оцениваемые в 2 балла, считаются выполненными, если обучающийся выбрал правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ.В этом случае ему выставляется полный балл, данному заданию. Если в решении допущена ошибка, не имеет значения принципиального характера и не влияет на общую правильность хода решения, то участнику выставляет 1 балл.
Дополнительные материалы и оборудование
Участникам разрешается использовать справочные материалы, основные формулы формулы математики, выдаваемые вместе с работой. Разрешается использовать линейку. Калькуляторы на экзамене не используются.
На выполнение экзаменационной работы отводится 235 минут
Любой учитель или репетитор может отслеживать результаты своих учеников по всей группе или классу. Для этого нажмите кнопку «Создать класс», а затем отправьте приглашение всем заинтересованным.
Ознакомьтесь с подробной видеоинструкцией по использованию модуля.
| Проверяемые элементы содержания и виды деятельности |
Уровень сложности задания |
Максимальный балл за выполнение задания |
Примерное время выполнения задания (мин. |
|
| Задание 1. Уметь выполнять вычисления и преобразования, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | Б |
1 |
2-3 |
|
| Задание 2. Уметь выполнять вычисления и преобразования, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | Б |
1 |
2-3 |
|
| Задание 3. Уметь выполнять вычисления и преобразования, уметь использовать приобретенные знания и умения в практической и повседневной жизни, уметь строить и исследовать простейшие математические модели | Б |
1 |
2-3 |
|
Задание 4. Уметь выполнять вычисления и преобразования, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели Уметь выполнять вычисления и преобразования, уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели |
Б |
1 |
2-3 |
|
| Задание 5. Уметь выполнять вычисления и преобразовывать, уметь использовать приобретенные знания и умения в практической и повседневной жизни, уметь строить и исследовать простейшие математические модели | Б |
1 |
2-3 |
|
| Задание 6. Уметь выполнять вычисления и преобразования | Б |
1 |
3-5 |
|
| Задание 7. Уметь выполнять вычисления и преобразования | Б |
1 |
3-5 |
|
Задание 8. Уметь выполнять вычисления и преобразования, уметь выполнять преобразование алгебраических выражений Уметь выполнять вычисления и преобразования, уметь выполнять преобразование алгебраических выражений |
Б |
1 |
2-3 |
|
| Задание 9. Уметь решать уравнения, неравенства и их системы | Б |
1 |
5 |
|
| Задание 10. Уметь работать со статистической информацией, находить частоту и вероятность случайного события, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | Б |
1 |
5 |
|
| Задание 11. Уметь строить и читать графики функций | Б |
1 |
5 |
|
Задание 12. Осуществлять практические расчеты по формулам, составляющие несложные формулы, выражающие зависимости между величинами Осуществлять практические расчеты по формулам, составляющие несложные формулы, выражающие зависимости между величинами |
Б |
1 |
5 |
|
| Задание 13. Уметь решать уравнения, неравенства и их системы | Б |
1 |
5 |
|
| Задание 14. Уметь строить и читать функции, уметь использовать приобретённые знания и умения в практической деятельности и повседневной жизни, уметь строить и исследовать простейшие математические модели | Б |
1 |
5 |
|
| Задание 15. Уметь выполнять действия с геометрическими фигурами, координатами и векторми | Б |
1 |
5 |
|
Задание 16.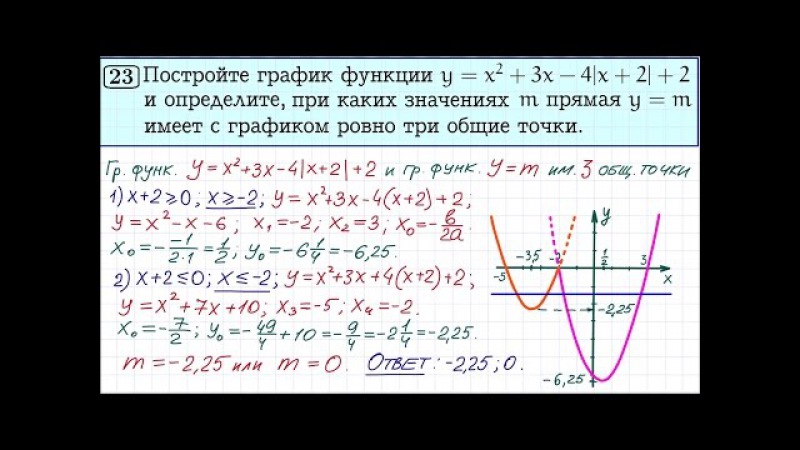 Уметь выполнять действия с геометрическими фигурами, координатами и векторми Уметь выполнять действия с геометрическими фигурами, координатами и векторми |
Б |
1 |
5 |
|
| Задание 17. Уметь выполнять действия с геометрическими фигурами, координатами и векторми | Б |
1 |
10 |
|
| Задание 18. Уметь выполнять действия с геометрическими фигурами, координатами и векторми | Б |
1 |
10 |
|
| Задание 19. Проводить доказательные рассуждения при решении, оценивать логическую правильность рассуждений, распознавать ошибочные заключения | Б |
1 |
10 |
|
Задание 20. Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций |
П |
2 |
15-20 |
|
| Задание 21. Уметь выполнять преобразование алгебраических выражений, решать уравнения, неравенства и системы, строить и читать графики функций, строить и исследовать простейшие математические модели | П |
2 |
15-20 |
|
| Задание 22. Уметь выполнять преобразования алгебраических выражений, решать уравнения, неравенства и их системы, строить и читать графики функций, строить и исследовать простейшие математические модели | В |
2 |
15-20 |
|
Задание 23. Уметь выполнять действия с геометрическими фигурами, координатами и векторми Уметь выполнять действия с геометрическими фигурами, координатами и векторми |
П |
2 |
15-20 |
|
| Задание 24. Проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать ошибочные заключения | П |
2 |
15-20 |
|
| Задание 25. Уметь выполнять действия с геометрическими фигурами, координатами и векторми | В |
2 |
15-20 |
|
Задание 22 ОГЭ-2019 по математике: разбор и решение
Экзаменационная работа (ОГЭ) состоит из двух модулей: «Алгебра» и «Геометрия», входящих в две части: базовый уровень (часть 1), повышенный и высокий уровень (часть 2).Всего в работе 26 заданий, из которых 20 заданий базового уровня, 4 задания повышенного уровня и 2 задания высокого уровня. Модуль «Алгебра» содержит 17 заданий: в части 1 — 14 заданий; в части 2 — 3 задания. Модуль «Геометрия» содержит 9 заданий: в части 1 — 6 заданий; в части 2 — 3 задания. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Часть 2
Задание 22
Рыболов в 5 часов утра на моторной лодке отправился через некоторое время, бросил якорь, 2 часа ловил рыбу и вернулся обратно в 10 часов утра же дня.На какое расстояние от пристани он отплыл, если скорость реки равна 2 км / ч, а собственная скорость лодки 6 км / ч?
Решение
Пусть рыболов отплыл на расстояние, равное s . Время, за которое он проплыл это путь, равно ч. (т.к. против течения скорость лодки соответствует 4 км / ч). Время, которое он затратил на путь обратно, равно ч. (т.к. по течению скорость лодки соответствует 8 км / ч). Общее время с учетом стоянки равно 5 ч. Составим и решим уравнение:
Время, за которое он проплыл это путь, равно ч. (т.к. против течения скорость лодки соответствует 4 км / ч). Время, которое он затратил на путь обратно, равно ч. (т.к. по течению скорость лодки соответствует 8 км / ч). Общее время с учетом стоянки равно 5 ч. Составим и решим уравнение:
с = 8.
Ответ: 8 км.
ОГЭ. Математика. Большой сборник тематических заданий для подготовки к основному государственному экзамену
Вниманию выпускников 9 предлагается новое пособие для подготовки к основному государственному экзамену по математике. В сборник включены задания по всем разделам и темам, проверяемым на основном государственном экзамене: «Числа и вычисления», «Практико-ориентированные задачи», «Уравнения и неравенства», «Алгебраические выражения», «Геометрия», «Последовательности, функции и графики» ».Представлены задания разного уровня сложности. В конце книги даны ответы, которые помогают в осуществлении контроля и оценки знаний, умений и навыков. Материалы пособия могут быть использованы для планомерного повторения изучения материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогают организовать подготовку к основному государственному экзамену, а учащимся — проверить свои знания и готовность к сдаче экзамена.
Материалы пособия могут быть использованы для планомерного повторения изучения материала и тренировки в выполнении заданий различного типа при подготовке к ОГЭ. Они помогают организовать подготовку к основному государственному экзамену, а учащимся — проверить свои знания и готовность к сдаче экзамена.
Пробный экзамен по математике 9 класс.1-4 варианты с ответами
Решение.
Сумма углов выпуклого четырёхугольника равна 360 °. Имеем: Так как, и — общий треугольника ABD и BDC . Из равенства треугольников следует, что. Таким образом,.
Ответ: 95.
Ответ: 95
17. Короткое плечо шлагбаума имеет длину 1 м, длинное плечо — 3 м. На высоту длинных метров опустится какой конец короткого плеча, когда конец длинного плеча поднимается на 1,8 м?
Решение.
Найдём синус угла, на который поднимается длинное плечо:
Угол подъема длинного плеча равенства на которое опустится короткое плечо. Пусть x — высота, на которую опустится короткое плечо, имеем:
Таким образом, короткое плечо опустится на 0,6 м.
Ответ: 0,6.
Ответ: 0,6
18 На диаграмме представлено количество пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 12 миллионов пользователей.Какое из утверждений неверно ?
1) Пользователей из России больше, чем пользователей из Белоруссии и Украины вместе.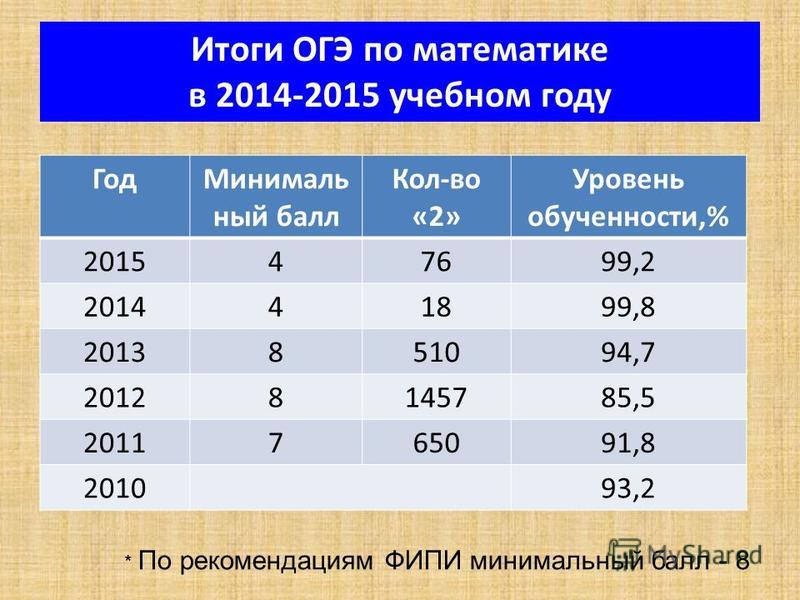
2) Пользователей из Украины больше, чем пользователей Латвии.
3) Примерно две трети общего числа пользователей — из России.
4) Пользователей из Украины больше 3 миллионов.
В ответ запишите номер выбранного утверждения.
Решение.
Разъясним каждый вариант ответа:
1) Очевидно, что пользователи из России больше, чем пользователи из Украины и Белоруссии вместе.
2) Сектор «Украина» занимает большую площадь диаграммы, чем сектор «Другие страны», а т. к. «Латвия» включена в «Другие страны», имеет: пользователей из Украины больше, чем пользователей из Латвии.
3) Сектор в две трети диаграммы отсекается углом в 2 · 360 ° / 3 = 240 °. Очевидно, что угол, отсекающий сектор «Россия» примерно равен 240 °, то есть примерно две трети общего числа пользователей — из России.
4) Видно, что пользователей из Украины меньше четверти всех пользователей, значит, меньше 12/4 = 3 миллиона.
Ответ: 4.
Ответ: 4
19. В лыжных гонках участвуют 13 спортсменов из России, 2 спортсмена из Норвегии и 5 спортсменов из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из России.
Решение.
Вероятность благоприятного случая () — отношение количественных случаев к количеству всех случаев.В данном случае благоприятным случаем является старт. Всего благоприятных случаев 2 + 5 = 7, а количество всех случаев 13 + 2 + 5 = 20. Отношение соответственно равно
Ответ: 0 , 35.
Ответ: 0,35
20. Площадь трапеции можно вычислить по формуле, где — основания трапеции, — высота (в метрах). Используйте эту формулой, высоту, если основания трапеции равны и, а её площадь.
Площадь трапеции можно вычислить по формуле, где — основания трапеции, — высота (в метрах). Используйте эту формулой, высоту, если основания трапеции равны и, а её площадь.
Часть 2
Решение.
Выразим высоту трапеции из формулы площади:
Подставляя, получаем:
0
75
0 0
75 Ответ: 4.
Приведём другое решение.
Подставим в формулу известные значения величин:
Ответ: 4
21. Разложите на множители.
Разложите на множители.
Решение.
Имеется:
.
Ответ:.
22. Два оператора, работают вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?
23. Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно три общие точки.
Решение.
Раскрывая модуль, получим, что график функции можно следующим образом:
Этот график изображён на рисунке:
9005
Из графика видно, что прямая имеет с графиком функции ровно три общие точки при и
Ответ: 0; 4.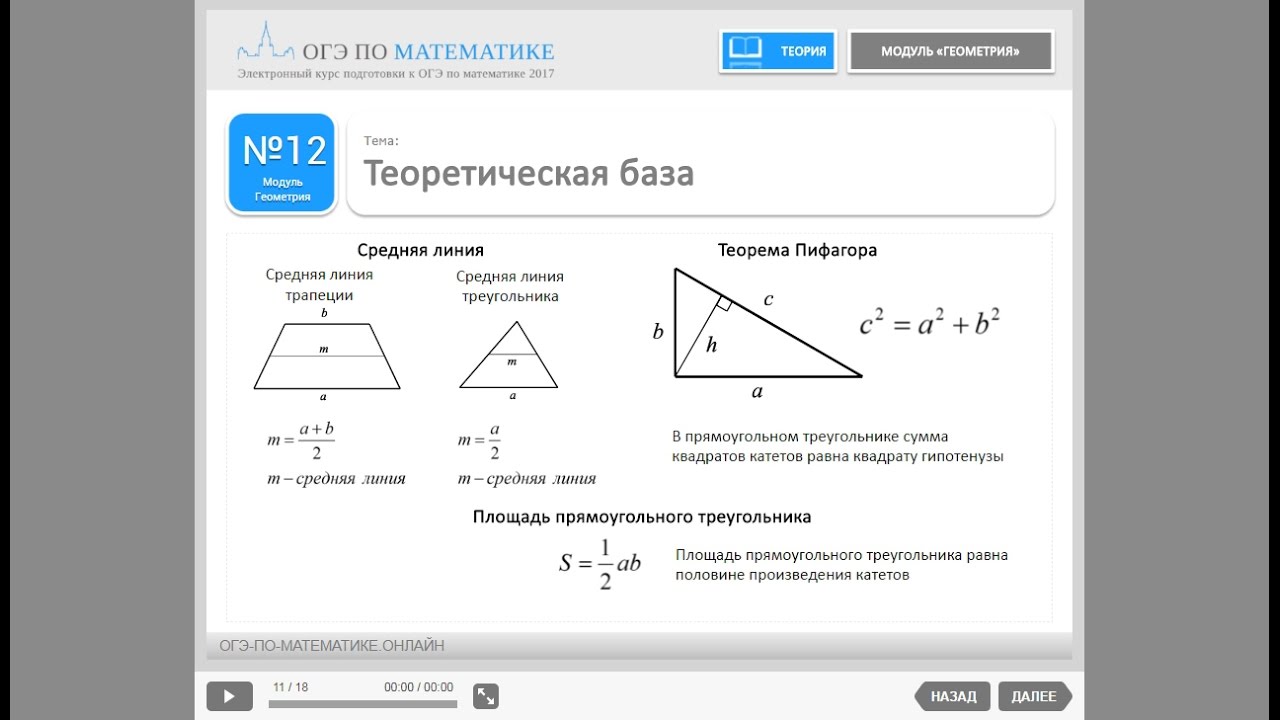
24. Диагонали и трапеции пересекаются в точке. Площади треугольников и равны соответственно и. Найдите площадь трапеции.
Решение.
Заметим, что площади двух треугольников, общей вершиной точки пересечения диагоналей трапеции, а основания — боковые стороны, равны. Это следует, например, из того, что площади треугольников и равны (поскольку эти треугольники имеют общее основание, и их высоты, проведенные к этому основанию, равны высоты трапеции), а.По условию, поэтому и являются условию боковыми сторонами, а основаниями трапеции. Тогда треугольники и подобны по двум углам, и отношение их площадей равно квадрату коэффициента подобия. Поэтому. Треугольники и имеют общую высоту. е. . Значит,. Поэтому и. Но тогда.
Ответ:.
25. В параллелограмме ABCD диагонали AC и BD пересекаются в точку O .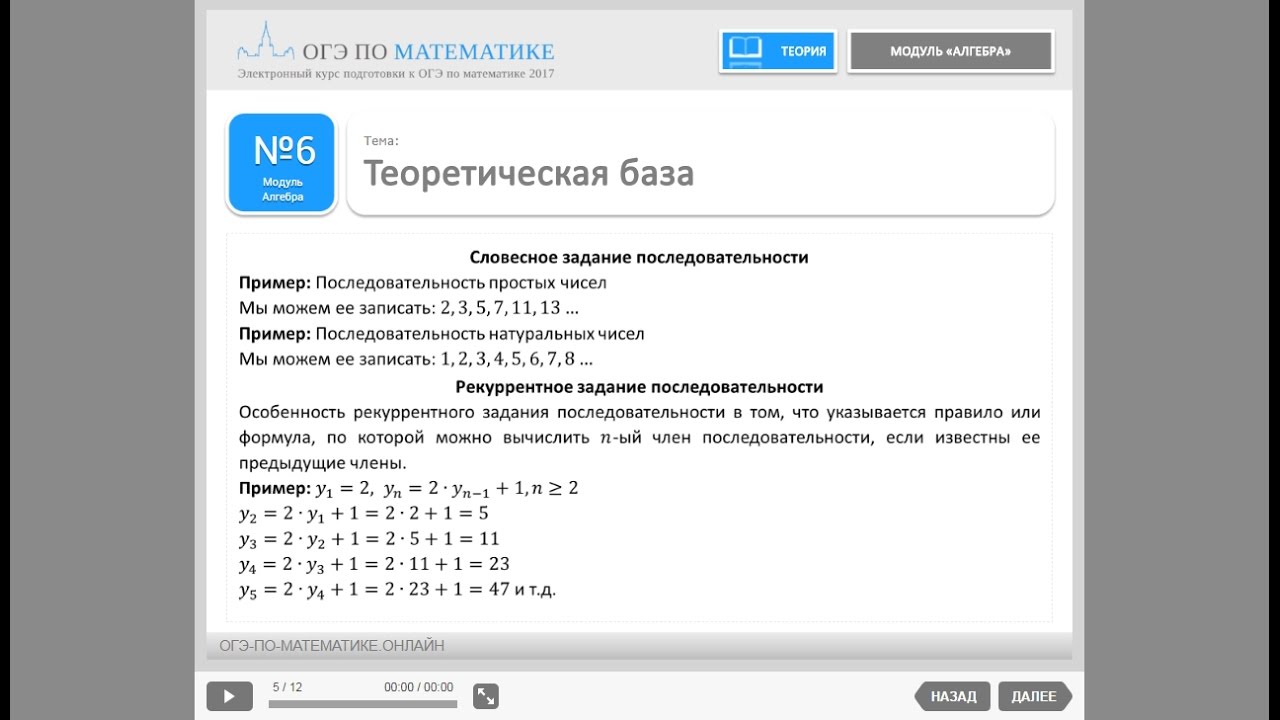 Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC .
Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC .
Решение.
Проведём высоту так, чтобы она проходила через точку Углы и равны друг другу как вертикальные. Вспомним также, что диагонали делятся точки пополам, следовательно, рассмотрим треугольники и прямоугольные, имеют равные углы и равные гипотенузы, следовательно, эти треугольники равны, а значит равны отрезки и.Таким образом,
Площадь параллелограмм равная площадь треугольника
26. Основание AC равнобедренного треугольника 10. Окружность 8 Окружность равнобедренного треугольника 10. Радиуса вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине.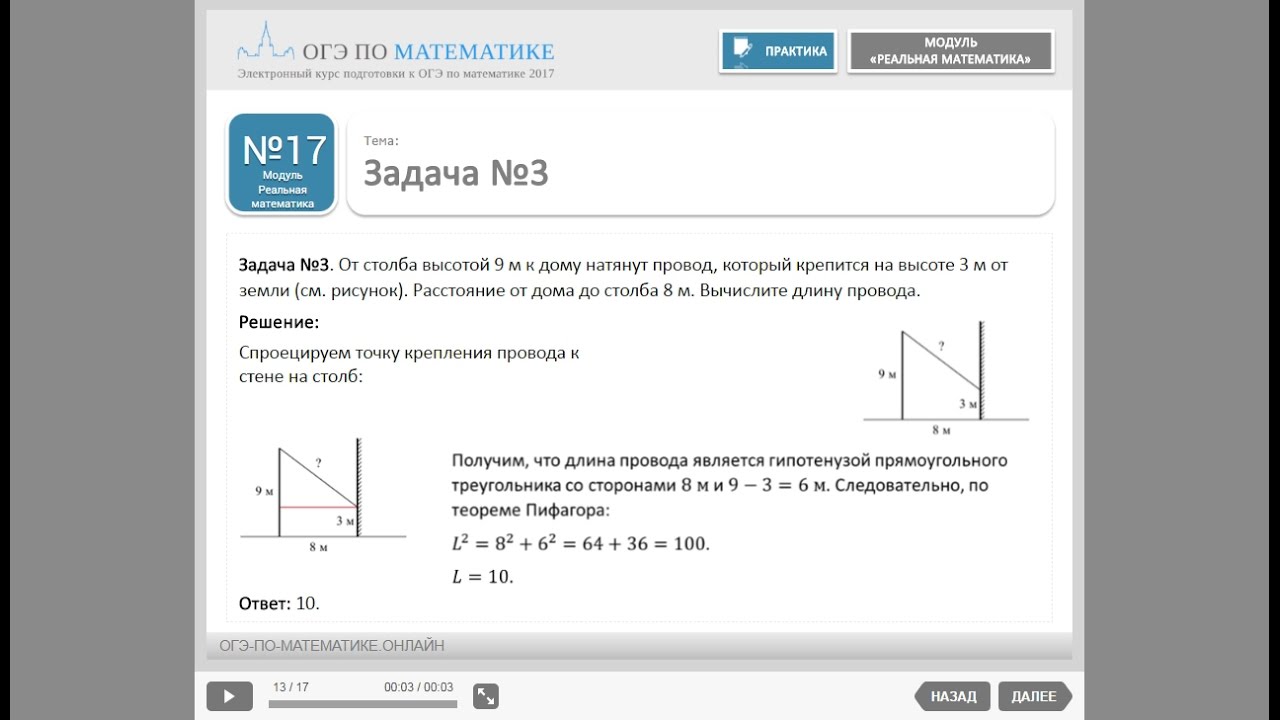 Найдите радиус окружности, вписанной в треугольник ABC .
Найдите радиус окружности, вписанной в треугольник ABC .
ВАРИАНТ № 2
Часть 1 МОДУЛЬ «АЛГЕБРА» 25
0 0 0 0 Решение.
Приведём к общему знаменателю:
Ответ: 3,7.
Ответ: 3,7
2. На координатной прямой отмечены числа a , b и c :
Значение из следующих выражений отрицательно?
1) — a 2) a + c 3) b — c 4) c — a
Решение.
Заметим, что −2 < a <−1, 1 < b <2 и 3 < c <4. Тогда выражение — а положительно. Для выражения a + c верно двойное неравенство 1 < a + c <3. Для выражения b — c верно двойное неравенство −2 < b — c <−1. Для выражения c — a верно двойное неравенство 4 < c — a <6.
Тогда выражение — а положительно. Для выражения a + c верно двойное неравенство 1 < a + c <3. Для выражения b — c верно двойное неравенство −2 < b — c <−1. Для выражения c — a верно двойное неравенство 4 < c — a <6.
Таким образом, отрицательное выражение является b — c .
Правильный ответ указан под номером 3.
Ответ: 3
3. В какие из следующих выражений можно преобразовать дробь?
1) 2) 3) 4)
Решение.
Упростим дробь:
Правильный ответ указан под номером 3.
Ответ: 3
4. Решите уравнение ( x + 2) 2 = ( x — 4) 2 .
Решите уравнение ( x + 2) 2 = ( x — 4) 2 .
Решение.
Последовательно получаем:
Ответ: 1.
Приведем другое решение.
Возведем обе части уравнения в квадрат:
Приведем другое решение.
Воспользуемся формулой разности квадратов:
Ответ: 1
5. График какой из приведенных ниже функций изображен на рисунке?
1) -
2)
-
3)
-
4)
0 0
0 0 Решение.
Ветви изображённой на рисунке гиперболы лежат во II и IV четверти, её график растянут вдоль осиинат в два раза. Этим условиям соответствует вариант 1
Графику соответствует варианту под номером 1.
Ответ: 1
6. Геометрическая прогрессия задана формулой н — го члена. Укажите третий член этой прогрессии.
Решение.
По формуле n -го члена геометрической прогрессии имеем:
Ответ: 12.
Ответ: 12
7. Представьте в виде дроби выражение и найдите его значение при. В ответ запишите полученное число.
Решение.
Упростим выражение:
Найдем значение выражения:
9000 −2 .
Ответ: -10
8. Решите неравенство:
1) 2) 3) 4)
МОДУЛЬ «ГЕОМЕТРИЯ» 25
Решение.
Решим неравенство: Коренные уравнения вызывают числа -23 и 0. Поэтому
Правильный ответ указан под номером 4.
Ответ: 4
9. Диагональ BD параллелограмма ABCD образует с его стороны углы, равные 65 ° и 50 °. Найдите меньший угол параллелограмма.
Решение.
Сумма дополнительных углов параллелограмма равна 180 °. Тогда величина меньшего угла параллелограмма будет равна:
Ответ:
Ответ: 65
10. В окружности с точки зрения системы безопасности, угол равен 25 °. Найдите величину угла.
В окружности с точки зрения системы безопасности, угол равен 25 °. Найдите величину угла.
Решение.
Углы OCD и OAB используются и опираются на одну дугу BD . Таким образом,
Ответ: 25.
Ответ: 25
11. Найдите площадь параллелограммы, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению основания на высоте: 7 · 4 = 28.
Ответ: 28.
Ответ: 28
12. Найдите тангенс угла треугольника , изображённого на рисунке.
Решение.
Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему. Треугольник ABC — прямоугольный, поэтому
Треугольник ABC — прямоугольный, поэтому
Ответ: 0,75.
Ответ: 0,75
13. Какие из утверждений верны?
1) Каждая сторона треугольника меньше разности двух других сторон.
2) В равнобедренном треугольнике имеется не более двух равных углов.
3) Если сторона и угол одного треугольника равны стороне и углу другого треугольника, то такие треугольникины.
4) В треугольнике ABC , для которого AB = 3, BC = 4, AC = 5, угол C наименьший.
МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА»
Решение.
Проверим каждый из утверждений:
1) «Каждая сторона треугольника меньше разности двух других сторон. » — неверно , так как если имеем, что
» — неверно , так как если имеем, что
2) «В равнобедренном треугольнике имеется не более двух равных углов.»- неверно , в равнобедренном треугольнике углы при основании равны.
3) «Если сторона и угол одного треугольника равны стороне и углу другого треугольника, то такие треугольники равны». — неверно , равенство определяется по трем элементам.
4) «В треугольнике ABC , для которого AB = 3, BC = 4, AC = 5, угол C наименьший.» — верно , в треугольнике против большего угла лежит большая сторона.
Ответ: 4.
Ответ: 4
14. Учёный Иванов выезжает из Москвы на конференцию в Санкт-Петербургский университет. Работа конференции начинается в 10:00. В таблице дано расписание ночных поездов Москва — Санкт-Петербург
Номер поезда
-
Отправление из
-
Москвы
-
Прибытие в
-
Санкт-Петербург
14 900 -
-
-
026А
-
23:00
-
06:30
-
002А
-
002А
-
002А
925
07:55
-
038А
-
00:44
-
08:46
-
016А
-
08:38
Ответ: 4.
Приведём другое решение.
Подставим в формулу известные значения величин:
Ответ: 4
21. Разложите на множители.
Разложите на множители.
Решение.
Имеется:
.
Ответ:.
22. Два оператора, работают вместе, могут набрать текст газеты объявлений за 8 ч. Если первый оператор будет работать 3 ч, а второй 12 ч, то они выполнят только 75% всей работы. За какое время может набрать весь текст каждый оператор, работая отдельно?
23. Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно три общие точки.
Решение.
Раскрывая модуль, получим, что график функции можно следующим образом:
Этот график изображён на рисунке:
Из графика видно, что прямая имеет с графиком функции ровно три общие точки при и
Ответ: 0; 4.
24. Диагонали и трапеции пересекаются в точке. Площади треугольников и равны соответственно и. Найдите площадь трапеции.
Решение.
Заметим, что площади двух треугольников, общей вершиной точки пересечения диагоналей трапеции, а основания — боковые стороны, равны. Это следует, например, из того, что площади треугольников и равны (поскольку эти треугольники имеют общее основание, и их высоты, проведенные к этому основанию, равны высоты трапеции), а.По условию, поэтому и являются условию боковыми сторонами, а основаниями трапеции. Тогда треугольники и подобны по двум углам, и отношение их площадей равно квадрату коэффициента подобия. Поэтому. Треугольники и имеют общую высоту. е. . Значит,. Поэтому и. Но тогда.
Ответ:.
25. В параллелограмме ABCD диагонали AC и BD пересекаются в точку O . Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC .
Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC .
Решение.
Проведём высоту так, чтобы она проходила через точку Углы и равны друг другу как вертикальные. Вспомним также, что диагонали делятся точки пополам, следовательно, рассмотрим треугольники и прямоугольные, имеют равные углы и равные гипотенузы, следовательно, эти треугольники равны, а значит равны отрезки и.Таким образом,
Площадь параллелограмм равная площадь треугольника
26. Основание AC равнобедренного треугольника 10. Окружность 8 Окружность равнобедренного треугольника 10. Радиуса вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC .
Найдите радиус окружности, вписанной в треугольник ABC .
ВАРИАНТ № 2
Часть 1 МОДУЛЬ «АЛГЕБРА» 25
0 0 0 0 Решение.
0 0 Решение.
Решение.
Приведём к общему знаменателю:
Ответ: 3,7.
Ответ: 3,7
2. На координатной прямой отмечены числа a , b и c :
Значение из следующих выражений отрицательно?
1) — a 2) a + c 3) b — c 4) c — a
Решение.
Заметим, что −2 < a <−1, 1 < b <2 и 3 < c <4. Тогда выражение — а положительно. Для выражения a + c верно двойное неравенство 1 < a + c <3. Для выражения b — c верно двойное неравенство −2 < b — c <−1. Для выражения c — a верно двойное неравенство 4 < c — a <6.
Тогда выражение — а положительно. Для выражения a + c верно двойное неравенство 1 < a + c <3. Для выражения b — c верно двойное неравенство −2 < b — c <−1. Для выражения c — a верно двойное неравенство 4 < c — a <6.
Таким образом, отрицательное выражение является b — c .
Правильный ответ указан под номером 3.
Ответ: 3
3. В какие из следующих выражений можно преобразовать дробь?
1) 2) 3) 4)
Решение.
Упростим дробь:
Правильный ответ указан под номером 3.
Ответ: 3
4. Решите уравнение ( x + 2) 2 = ( x — 4) 2 .
Решите уравнение ( x + 2) 2 = ( x — 4) 2 .
Решение.
Последовательно получаем:
Ответ: 1.
Приведем другое решение.
Возведем обе части уравнения в квадрат:
Приведем другое решение.
Воспользуемся формулой разности квадратов:
Ответ: 1
5. График какой из приведенных ниже функций изображен на рисунке?
1)
-
2)
-
3)
-
4)
0
0
0 0 Решение.

Ветви изображённой на рисунке гиперболы лежат во II и IV четверти, её график растянут вдоль осиинат в два раза. Этим условиям соответствует вариант 1
Графику соответствует варианту под номером 1.
Ответ: 1
6. Геометрическая прогрессия задана формулой н — го члена. Укажите третий член этой прогрессии.
Решение.
По формуле n -го члена геометрической прогрессии имеем:
Ответ: 12.
Ответ: 12
7. Представьте в виде дроби выражение и найдите его значение при. В ответ запишите полученное число.
Решение.
Упростим выражение:
Найдем значение выражения:

Ответ: -10
8. Решите неравенство:
1) 2) 3) 4)
МОДУЛЬ «ГЕОМЕТРИЯ» 25
Решение.
Решим неравенство: Коренные уравнения вызывают числа -23 и 0. Поэтому
Правильный ответ указан под номером 4.
Ответ: 4
9. Диагональ BD параллелограмма ABCD образует с его стороны углы, равные 65 ° и 50 °. Найдите меньший угол параллелограмма.
Решение.
Сумма дополнительных углов параллелограмма равна 180 °. Тогда величина меньшего угла параллелограмма будет равна:
Ответ:
Ответ: 65
10. В окружности с точки зрения системы безопасности, угол равен 25 °. Найдите величину угла.
В окружности с точки зрения системы безопасности, угол равен 25 °. Найдите величину угла.
Решение.
Углы OCD и OAB используются и опираются на одну дугу BD . Таким образом,
Ответ: 25.
Ответ: 25
11. Найдите площадь параллелограммы, изображённого на рисунке.
Решение.
Площадь параллелограмма равна произведению основания на высоте: 7 · 4 = 28.
Ответ: 28.
Ответ: 28
12. Найдите тангенс угла треугольника , изображённого на рисунке.
Решение.
Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему. Треугольник ABC — прямоугольный, поэтому
Треугольник ABC — прямоугольный, поэтому
Ответ: 0,75.
Ответ: 0,75
13. Какие из утверждений верны?
1) Каждая сторона треугольника меньше разности двух других сторон.
2) В равнобедренном треугольнике имеется не более двух равных углов.
3) Если сторона и угол одного треугольника равны стороне и углу другого треугольника, то такие треугольникины.
4) В треугольнике ABC , для которого AB = 3, BC = 4, AC = 5, угол C наименьший.
МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА»
Решение.
Проверим каждый из утверждений:
1) «Каждая сторона треугольника меньше разности двух других сторон. » — неверно , так как если имеем, что
» — неверно , так как если имеем, что
2) «В равнобедренном треугольнике имеется не более двух равных углов.»- неверно , в равнобедренном треугольнике углы при основании равны.
3) «Если сторона и угол одного треугольника равны стороне и углу другого треугольника, то такие треугольники равны». — неверно , равенство определяется по трем элементам.
4) «В треугольнике ABC , для которого AB = 3, BC = 4, AC = 5, угол C наименьший.» — верно , в треугольнике против большего угла лежит большая сторона.
Ответ: 4.
Ответ: 4
14. Учёный Иванов выезжает из Москвы на конференцию в Санкт-Петербургский университет. Работа конференции начинается в 10:00. В таблице дано расписание ночных поездов Москва — Санкт-Петербург
Номерпоезда
-
Отправление из
-
Москвы
-
Прибытие в
-
Санкт-Петербург
- 14 900
-
026А
-
23:00
-
06:30
-
002А
-
002А
-
002А
925
07:55
038А
00:44
08:46
016А
-
08:38
08:38
90 028
Путь от вокзала до университета занимает полтора часа. Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Иванову.
Укажите номер самого позднего (по времени отправления) из московских поездов, которые подходят учёному Иванову.
1) 026А 2) 002А 3) 038А 4) 016А
Решение.
Время от вокзала до университета занимает полтора часа, поезд должен прибыть на вокзал не позднее 08:30. Этому условию удовлетворяют поезда под номерами: 026А и 002А. Из них позже отправляется поезд под номером 002А.
Правильный ответ указан под номером 2.
Ответ: 2
15. В таблице даны рекомендованные суточные нормы потребления (в г / сутки) белков и белков детьми от 1 года до 14 лет и взрослыми.
Вещество
-
Дети от 1 года
-
до 14 лет
-
Мужчины
-
Женщины
-
Жиры
-
70—154
-
60—102
-
Белки
-
36—87
-
65—11 58 —87
-
Углеводы
-
170—420
-
257—586
Какой вывод о суточном потреблении 7 выводов, суточное потребление девочкой можно сделать, если по подсчётам диетолога в среднем за сутки она потребляет 42 г жиров, 35 г белков и 190 г углеводов? В ответе укажите номера верных утверждений.
1) Потребление жиров в норме.
2) Потребление белков в норме.
3) Потребление углеводов в норме.
Если утверждений несколько, запишите их через точку с запятой порядке в возрастания.
Решение.
Проанализируем утверждение утверждения.
1) Для семилетней девочки нормой является употребление от 40 до 97 граммов жиров в сутки, 42 грамма укладываются в этот промежуток.Первое утверждение верно.
2) Для семилетней девочки нормой является употребление от 36 до 87 граммов белков в сутки, 35 граммов не укладываются в этот промежуток. Второе утверждение неверно.
2) Для семилетней девочки нормой используется употребление от 170 до 420 граммов углеводов в сутки, 190 граммов укладываются в этот промежуток.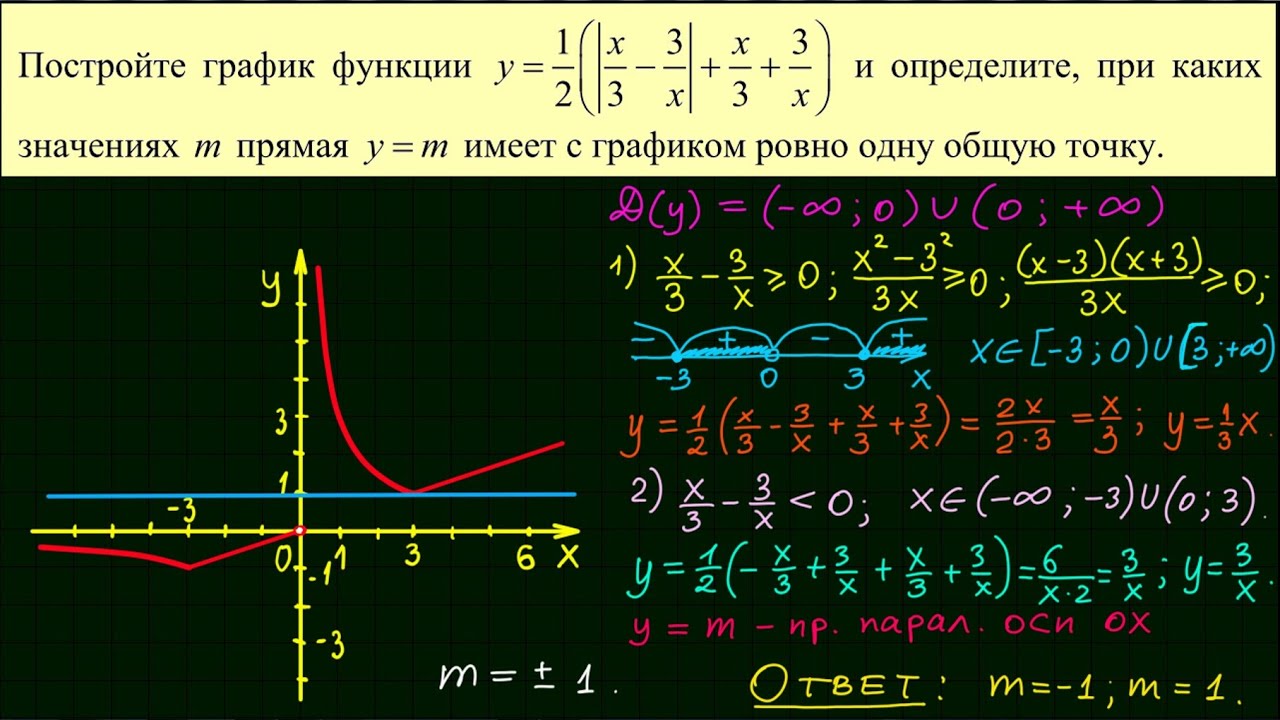 Третье утверждение верно.
Третье утверждение верно.
Ответ: 1; 3.
Ответ: 1; 3
16. Площадь земель крестьянского хозяйства, отведённая под посадку сельскохозяйственных культур, составляет 24 га и распределена между зерновыми и овощными культурами в отношении 5: 3. Сколько гектаров занимают овощные культуры?
Решение.
Овощные культуры занимают:
Ответ: 9.
Ответ: 9
17. Сколько досок длиной 3,5 м, шириной 20 см и толщиной 20 мм выйдет из четырехугольной балки длиной 105 дм, имеющей длину прямоугольник размером 30 см 40 см?
Решение.
Найдем объем доски: 350 · 20 · 2 = 14 000 см 3 . Найдем объем балки: 1050 · 30 · 40 = 1 260 000 см 3 .
Найдем объем балки: 1050 · 30 · 40 = 1 260 000 см 3 .
Поэтому количество досок равно 1 260 000: 14 000 = 90.
Ответ: 90.
Ответ: 90
18. На диаграмме семь по своей площади территории (в млн км 2 ) стран мира.
Какое из утверждений неверно
1) По площади территории Австралия занимает шестое место в мире.
2) Площадь территории Бразилии составляет 7,7 млн км 2 .
3) Площадь Индии меньше площади Китая.
4) Площадь Канады меньше площади России на 7,1 млн км 2 .
В ответе запишите номер определения утверждения Решение.
Проверим утверждение утверждения:
1) На диаграмме видно, что Австралия — шестая по площади страны в мире. Значит первое утверждение верно.
Значит первое утверждение верно.
2) Из диаграммы видно, что площадь Бразилии — 8,5 млн км 2 . Второе утверждение неверно.
3) Из диаграммы видно, что площадь Индии меньше площади Китая.Третье утверждение верно.
4) Из диаграммы видно, что площадь Канады меньше площади России на 17,1-10,0 = 7,1 млн км 2 . Четвёртое утверждение верно.
Неверным утверждением под номером 2.
Ответ: 2
Решение.
Проанализируем все утверждения.
1) Пользователей из России больше всех, тем самым, их больше чем пользователей из Украины.
2) Сектор «Беларусь» занимает большую площадь диаграммы, чем сектор «Другие страны», а т. к. «Швеция» включена в «Другие страны» пользователей из Беларуси больше чем пользователей из Швеции.
к. «Швеция» включена в «Другие страны» пользователей из Беларуси больше чем пользователей из Швеции.
3) Сектор в третьей диаграмме имеет угол 360 °: 3 = 120 °. Угол сектора «Украина» меньше на 90 °, следовательно, меньше трети пользователей сети из Украины.
4) Пользователей из России больше половины всех пользователей, значит, больше 9: 2 = 4,5 млн, а значит, больше 4 миллионов.
Ответ: 3.
Ответ: 3
19. Какова вероятность того, что случайно выбранное натуральное число от 15 до 29 делится на 5?
Решение.
Чисел от 15 до 29 — 15 штук. Среди них на 5 делится только 3 числа. Таким образом, вероятность того, что случайно выбранное число от 15 до 29 делится на 5 равно
Ответ: 0,2
20. Объём пирамиды вычисляют по формуле, где — площадь основания пирамиды, — её высота. Объём пирамиды равенство 40, площадь основания 15. Чему равна высота пирамиды?
Объём пирамиды вычисляют по формуле, где — площадь основания пирамиды, — её высота. Объём пирамиды равенство 40, площадь основания 15. Чему равна высота пирамиды?
Часть 2
Решение.
Высота пирамиды из формулы для ее объема:
Подставляя, получаем:
0
25
Ответ: 8.
Ответ: 8
21. Сократите дробь, если.
Решение.
Имеем:
Ответ: 1.
22. Пристани и размещены на реке, скорость течения на этом участке составляет 3 км / ч. Лодка проходит туда и обратно без остановок со средней скоростью 8 км / ч.Найдите собственную скорость лодки.
Решение.
Пусть км / ч — собственная скорость лодки. Тогда скорость движения по течению равна км / ч, а скорость движения против течения равна км / ч. Обозначим расстояние между пристанями. Время, затраченное на весь путь, равно
.
По условию средней скорости равна 8 км / ч, а весь путь равенство. Следовательно,
.
Решим это уравнение:
Получаем: или. Корень −1 не является решением задачи. Значит, скорость равна 9 км / ч.
Значит, скорость равна 9 км / ч.
Ответ: 9 км / ч.
23. Постройте график функции
и определите, при каких значениях прямая будет иметь с графиком единственную общую точку.
Решение.
Построим график функции (см. Рисунок).
Из графика видно, что прямая будет иметь с графиком функции единственную точку пересечения при принадлежащем множеству [0; 1).
Ответ: [0; 1).
24. Медианы треугольника пересекаются в точке. Найдите длину медианы, проведённой к стороне, если угол равен 47 °, угол равен 133 °,.
Решение.
Обозначим середину стороны за. Продлим на свою длину за точку до точки. Четырёхугольник — параллелограмм, потому что и. Значит, = 133 °, поэтому четырёхугольник — вписанный. Тогда.
Ответ: 6.
25. В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём СF = AM , BE = DK . Докажите, что EFKM — параллелограмм.
Решение.
Противоположные стороны параллелограмма равны и по условию соответственно:
Вмотри углы, Углы, углы этих треугольниках, следовательно, эти треугольники равны, а значит,. Аналогично равны треугольники и, следовательно, равны отрезки и Противоположные стороны четырехугольника равны, следовательно, по признаку параллелограмма, этот четырёхугольник — параллелограмм.
Аналогично равны треугольники и, следовательно, равны отрезки и Противоположные стороны четырехугольника равны, следовательно, по признаку параллелограмма, этот четырёхугольник — параллелограмм.
26. Медиана BM треугольника ABC является диаметром окружности, пересекающей стороны BC в её середине. Найдите длину AC , если радиус описанной окружности треугольника ABC равен 7.
ВАРИАНТ № 3
Часть 1 МОД АЛГЕБРА »
1. Вычислите:
Решение.
Приведём к общему знаменателю:
Ответ: 1,03.
Ответ: 1,03
2. На координатной прямой отмечены числа и Какое из следующих утверждений неверно?
1) 2)
3) 4)
Решение.
Заметим, что и, и проверим все варианты ответа:
1) — неверно.
2) — верно, поскольку каждый множитель отрицателен.
3) — верно.
4) — верно.
Неверным утверждением 1.
Ответ: 1
3. Какое из чисел больше: или?
1)
2)
3)
Решение.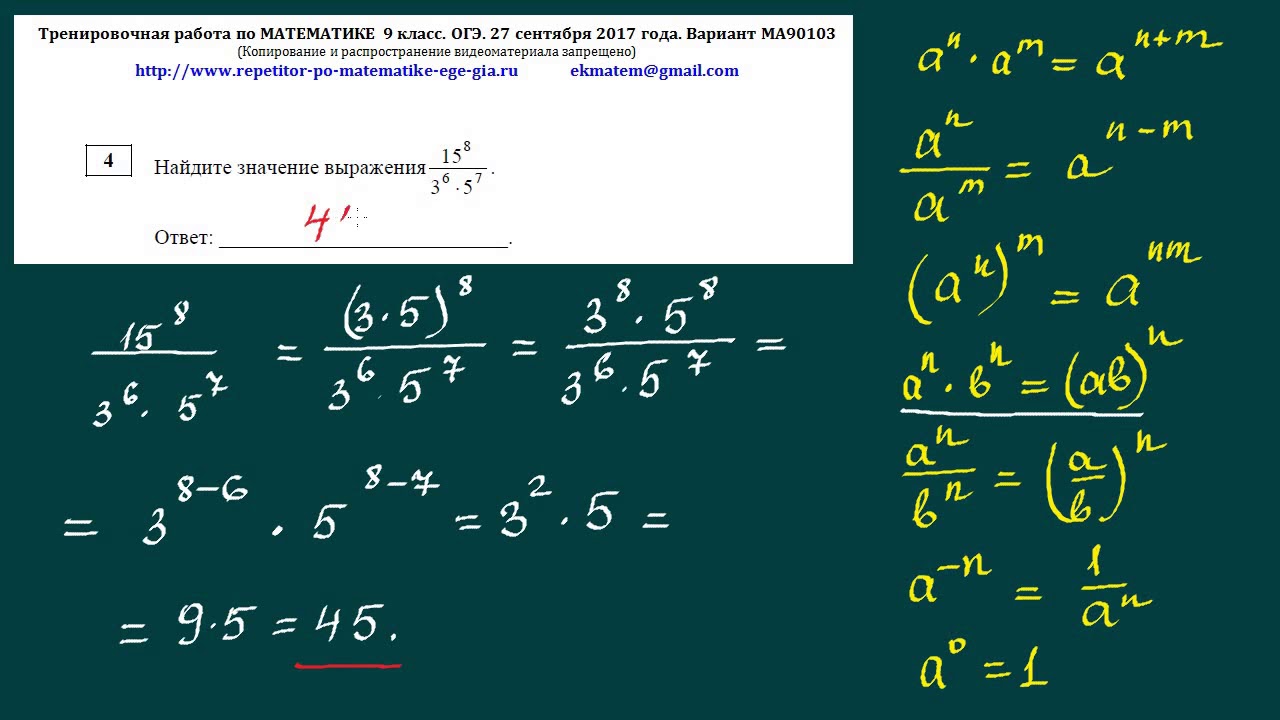
В силу цепочки неравенств
первое число меньше второго.
Правильный ответ указан под номером 1.
Ответ: 1
4. Найдите корни уравнения
Еслиней несколько, в ответ запишите их.
Решение.
Перенесём всё в уравнении в одну сторону:
По теореме, обратному теореме Виета, сумма корней равна 1, а их произведение равно −12. Тем самым, это числа −3 и 4.
Ответ: −3; 4.
Ответ: -3; 4
5. Укажите соответствие между графиками функциями и формулами, которые их задают.
1) 2)
3) 4)
Ответьте в виде представьте цифр без пробелов и запятых в указанном порядке
А-
Б
-
В
2
Решение.
Определим вид графика каждой из функций.
1) уравнение прямой, который пересекает ось абсцисс в точке 2; ось ординат в точке −2.
2) уравнение степенной функции с положительным дробным показателем. График проходит через точку (1; 0).
График проходит через точку (1; 0).
3) уравнение параболы, ветви происходящей вверх.
4) уравнение степенной функции с положительным дробным показателем.График проходит через точку (−1; 0).
Таким образом, искомое соответствие: A — 4, Б — 3, В — 1.
Ответ: 431.
Ответ: 431
6. Последовательность задана условиями,. Найдите.
Решение.
Будем вычислять последовательно:
данная последовательность образует арифметическую прогрессию.Найдем разность арифметической прогрессии:
тогда
Примечание.
Зная разность и первый член арифметической прогрессии, можно найти посредственно:
Ответ: −9.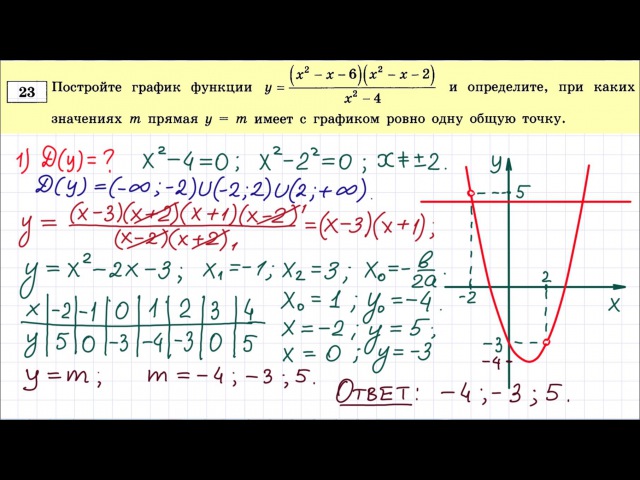
Ответ: -9
7. Сократите дробь
Решение.
Сократим дробь:
Ответ: 84.
Ответ: 84
8. 901 на каком рисунке изображено
1)
2)
3)
4)
МОДУЛЬ «ГЕОМЕТРИЯ»
9. В равностороннем треугольнике ABC биссектрисы CN и AM пересекаются в точку P . Найдите.
Решение.
В равностороннем треугольнике ABC все углы равны 60 °. Биссектрисы CN и AM делят уголы пополам, = = Сумма углов в треугольнике равна 180 °, поэтому Вертикальные углы равны, следовательно,
Ответ: 120.
Ответ: 120
10. Треугольник ABC вписан в окружность с центром в точке O . Найдите градусную меру угла C треугольника ABC , если AOB 901 угол равен 48 °.
Решение.
Угол AOB является центральным углом, ACB — вписанным. Оба угла опираются на одну и ту же дугу, следовательно, угол AOB в два раза больше угла ACB .
Ответ: 24.
Ответ: 24
11. Сторона ромба равен 5, а диагональ равно 6. Найдите площадь ромба.
Решение.
Диагонали ромба пересекаются под углом 90 ° и точки пересечения делятся пополам. Из прямоугольного треугольника, катетами которого является половина диагоналей ромба, а гипотенузой — сторона ромба, по теореме Пифагора найдем половину неизвестной диагонали: Тогда вся неизвестная диагональ равна 8.
Площадь ромба равна площади произведений диагоналей:
Ответ: 24.
Ответ: 24
12. Найдите тангенс угла AOB на рисунке.
Решение.
Опустим перпендикуляр BH на отрезок OA и рассмотрим прямоугольный треугольник OBH :
Ответ
Ответ: 2
13. Какие из следующих утверждений верны?
1) Вписанные углы, опирающиеся на одну и ту же хорду окружности, равны.
2) Если радиусы двух окружностей равны 5 и 7, то расстояние между их центрами равно 3, то эти окружности не имеют общих точек.
3) Если радиус окружности равен 3, а прямое расстояние от центра окружности до равно 2, то эти прямая и окружность пересекаются.
4) Если вписанный угол равен 30 °, то дуга окружности, на которую опирается этот угол, равна 60 °.
МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА»
14. В данных нормативы по технике чтения в 3 классе.
Какую отметку получит третьеклассник, прочитавший в апреле 68 слов за?
1) «2» 2) «3» 3) «4» 4) «5»
Решение.
Проверка техники чтения происходила во второй полугодии. Из таблицы видно, что 68 прочитанных за минуту слов попадают в интервал «69 и менее» слов. Это соответствует отметке «2».
Правильный ответ указан под номером 1.
Ответ: 1
15. В таблице представлены результаты двух полуфинальных забегов на дистанцию 60 мес. В финальном забеге 6 участников.Из каждого полуфинала в финал выходят два спортсмена, показавших первый и второй результаты. К ним добавили еще двух спортсменов, показавших лучшее время всех остальных участников полуфиналов.Запишите в ответ номера спортсменов, не попавших в финал.
Решение.
В полуфинале 1, лучшее время у спортсмена №4 и у спортсмена №1, таким образом, они выходят в финал.
В полуфинале 2, лучшее время у спортсмена №6 и у спортсмена №7 таким образом, они также выходят в финал.
Лучшее время оставшихся спортсменов у спортсмена №2 и №5. таким образом таким образом, они тоже выходят в финал.
Таким образом, в финал не попали спортсмены под намерами 3 и 8.
Ответ: 38 | 3,8 | 8,3 | 83
16. На молочном заводе пакеты молока упаковываются по 12 штук в коробку, причём в каждой коробке все пакеты одинаковые. В партии молока, отправляемой в магазин «Уголок», коробок с полуторалитровыми пакетами молока втрое меньше, чем коробок с литровыми пакетами.Сколько литров молока в этой партии, если коробок с литровыми пакетами молока 45?
Решение.
Найдём коробок с полуторалитровыми пакетами молока: 45: 3 = 15. Теперь рассчитаем количество литров молока в этой партии: 45 · 12 · 1 + 15 · 12 · 1,5 = 810 л.
Ответ: 810.
Ответ: 810
17. На каком расстоянии от фонаря стоит человек ростом 2 м, если длина его тени равна 1 м, высота фонаря 9 м?
Решение.
Пусть неизвестное расстояние равно х м. Рассмотрим два прямоугольных треугольника, выделенные на рисунке красным и зелёным. Они имеют общий угол и, следовательно, подобны. Поэтому отношения их катетов равны:
Тем самым, искомое расстояние равно 3,5 м.
Ответ: 3,5.
Ответ: 3,5
18. На диаграмме представлено количество пользователей некоторой социальной сети по странам мира. Всего в этой социальной сети 9 миллионов пользователей.Какое из утверждений неверно ?
1) Пользователей из Беларуси меньше, чем пользователей из Украины.
2) Пользователей из России больше 4 миллионов.
3) Пользователей из Украины больше четверти общего числа пользователей.
4) Пользователей из Беларуси больше, чем пользователей из Финляндии.
В ответ запишите номер выбранного утверждения.
Решение.
Разъясним каждый вариант ответа.
1) Очевидно, что пользователей из Беларуси меньше, чем пользователей из Украины.
2) Видно, что пользователей из России больше половины всех пользователей, значит, больше 9/2 = 4,5 млн, а значит, больше 4 миллионов.
3) Сектор в четверть диаграммы отсекается углом в 360 ° / 4 = 90 °. Очевидно, что угол, отсекающий сектор «Украина» меньше на 90 °, значит, меньше четверти пользователей сети — из Украины.
4) Сектор «Беларусь» занимает большую площадь диаграммы, чем сектор «Другие страны», а т. к. «Финляндия» включена в «Другие страны», имеет: пользователей из Белоруссии больше, чем пользователей из Финляндии.
к. «Финляндия» включена в «Другие страны», имеет: пользователей из Белоруссии больше, чем пользователей из Финляндии.
Ответ: 3.
Ответ: 3
19. В фирме такси в данный момент свободна 21 машина: 11 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси. Полученный ответ округлите до сотых.
Решение.
Вероятность того, что приедет зеленая машина относится к общему количеству машин:
Ответ: 0,38.
Ответ: 0,38
20. Площадь параллелограмма можно вычислить по формуле, где — стороны параллелограмма (в метрах). Пользуясь этой формулой, найдите площадь параллелограмма, если его стороны 10 м и 12 м и.
Часть 2
Решение.
Подставим в формулу известные значения величин:
Ответ: 60.
Ответ: 60
21 .Решите систему уравнений:
Решение.
Сложим два уравнения системы:
откуда получаем или
Вычтем из первого уравнения системы второе:
Таким образом, решения системы
Ответ:
Решение.
По условию первая труба за одну минуту наполняет часть бассейна, а две трубы вместе за одну минуту наполняют часть бассейна. Таким образом, одна вторая труба за минуту наполняет часть бассейна, то есть она наполнит весь бассейн за 15 часов.
Ответ: 15.
23. При каком значении прямая имеет параболой ровно одну общую точку? Найдите координаты этой точки. Постройте в одной системе координат параболу и прямую при найденном значении.
Решение.
График функции изображён на рисунке.
Запишем условие общей точки:
Прямая будет иметь параболой единственную общую точку при условии, что дискриминант полученного квадратного уравнения равенство нулю: откуда Подставив значение уравнения, находим
Ответ: (-2; 0).
24. Найдите угол АСО , если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, составляет 140 °.
Решение.
Проведём радиус OA . Треугольник AOC — прямоугольный, ∠ A = 90 °. ∠ COA = 180 ° — ∠ AOD = 180 ° — 140 ° = 40 °; ∠ ACO = 90 ° — 40 ° = 50 °.
Ответ: 50.
25. Дана равнобедренная трапеция. Точка лежит на основании и равноудалена от конца другого основания. Докажите, что — середина основания.
Решение.
Треугольник равнобедренный. Поэтому.
В равнобедренной трапеции.
Отсюда следует, что. Значит, треугольники и равны по двум сторонам и равны между ними. Следовательно,.
Следовательно,.
26. Диагонали четырёхугольника, вершины расположены на окружности, пересекаются в точке. Известно, что = 74 °, = 102 °, = 112 °. Найдите.
ВАРИАНТ № 4
Часть 1 МОДУЛЬ «АЛГЕБРА»
Решение.
Вынесем общий множитель за скобки:
Ответ: −3.
Ответ: -3
2. Одна из точек, отмеченных на координатной прямой, соответствует числу. Какая это точка?
1) точка M 2) точка N
3) точка P 4) точка Q
Решение.
Возведём в квадратное число 6, 7, 8:
Число 45 лежит между числами 36 и 49 и находится ближе к значению 49, поэтому соответствует точке N .
Правильный ответ указан под номером 2.
Ответ: 2
3 Какое из чисел больше: или?
1)
2)
3)
Решение.
В силу цепочки неравенств
первое число меньше второго.
Правильный ответ указан под номером 1.
Ответ: 1
4. Найдите корни уравнения.
Если корней несколько, запишите в ответе наименьший.
5. На одном из рисунков изображен график функции. Укажите номер этого рисунка.
1)
-
2)
-
3)
- 7 000
Решение.
График функции проходит через точку (1; 0). Этому условию удовлетворяет только график, изображённый на рисунке 4.
Таким образом, верный ответ указан под номером 4.
Ответ: 4
6. Дана арифметия прогрессия: 33; 25; 17; … Найдите первый отрицательный член этой прогрессии.
Дана арифметия прогрессия: 33; 25; 17; … Найдите первый отрицательный член этой прогрессии.
Решение.
Для члена имеем: По формуле нахождения n -го члена арифметической прогрессии имеем:
, которое удовлетворяет это первое условие, число 6.Следовательно, первым отрицательным элементом прогрессии является
Таким образом, правельный ответ указан под номером 1.
Ответ: 1.
Ответ: 1
7. Найдите значение выражения при.
Решение.
Упростим выражение:
Найдем значение выражения:
.

Ответ: 2,5
8. На каком рисунке изображено неравенства?
1) 1 2) 2 3) 3 4) 4
МОДУЛЬ «ГЕОМЕТРИЯ»
9. Сумма трех углового выпуклого ° . Найдите четвертый угол. Ответ дайте в градусах.
Решение.
Так как сумма углов выпуклого четырехугольника равна 360 °, четвертый угол равен 360 ° — 300 ° = 60 °.
Ответ: 60.
Ответ: 60
10 .Боковая сторона равнобедренного треугольника равна 5. Угол при вершине, противолежащий основанию, равенство 120 °. Найдите диаметр окружности, описанной около этого треугольника.
Решение.
Воспользуемся теоремой косинусов:
Здесь и — боковые стороны равнобедренного треугольника, — основание.
Диаметр описанной окружности вычислим по формуле:
Ответ: 10.
Ответ: 10
Найдите площадь трапеции, изображённой на рисунке.
Решение.
Площадь трапеции вычисляется по формуле где и — основания, а — высота трапеции.
Ответ: 270.
Ответ: 270
12. Найдите тангенс угла С треугольника на изображении ABёнC 901.
Решение.
Тангенс угла в прямоугольном треугольнике — отношение противолежащего катета к соседнему:
Ответ: 0,75.
Ответ: 0,75
13. Какие из утверждений верны?
1) Около любого правильного многоугольника можно описать не более одной окружности.
2) Центр окружности, описанной около треугольника со стороны этого треугольника, равными 3, 4, 5, находится на стороне треугольника.
3) Центром окружности, описанной около квадрата, является точкой пересечения его диагоналей.
4) Около любого ромба можно описать окружность
МОДУЛЬ «РЕАЛЬНАЯ МАТЕМАТИКА»
14. На диаграмме страны по определенному количеству сети пользователя.Всего в этой социальной сети 9 миллионов пользователей.
Какое из утверждений неверно?
1) Пользователей из Украины больше, чем пользователей из Беларуси.
2) Пользователей из Украины меньше четверти общего числа пользователей.
3) Пользователей из Беларуси больше, чем пользователей из Эстонии.
4) Пользователей из России больше 8 миллионов.
Решение.
Проверим утверждение утверждения:
1) Из диаграммы видно, что число пользователей из Украины больше, чем пользователей из Беларуси. Первое утверждение верно.
Первое утверждение верно.
2) Из диаграммы видно, что пользователей из Украины меньше четверти общего числа пользователей. Второе утверждение верно.
3) Из диаграммы видно, что пользователей из Беларуси больше, чем пользователей из «других стран», а значит, и больше, чем пользователей из Эстонии.Третье утверждение верно.
4) Из диаграмм видно, что пользователей из России примерно две трети от общего числа пользователей. Всего пользователей 9 млн, значит пользователей из России около 6 млн, что меньше 8 млн. Четвёртое утверждение неверно.
Неверным утверждением под номером 4.
Ответ: 4
15. На графике показано, сколько человек зарегистрировано с 25 декабря 2012 года по 13 февраля 2013 года в качестве участников конференции.По горизонтали указано числа месяцев, а по вертикали — количество человек.
Во сколько раз возросло количество зарегистрировавшихся с 4 января по 3 февраля?
Решение.
Из графика видно, что число зарегестрировавшихся на4 января состваляло 30 человек, а 3 февраля — 270. Следовательно, число зарегистрировавшихся возросло в 270: 30 = 9 раз.
Ответ: 9.
Ответ: 9
16. На пост председателя школьного совета претендовали два кандидата. В голосовании приняли участие 120 человек. Голоса между кандидатами распределились в отношении 3: 5. Сколько голосов получил победитель?
Решение.
Пусть x голосов приходится на одну часть, тогда 5x приходится на второго кандидата, а 3x — на первого кандидата.Зная, что в голосовании участвовало 120 человек составим уравнение:
Таким образом, победитель получил:
.
Ответ: 75.
Ответ: 75
17. Какой угол (в градусах) это минутная стрелка за 10 мин?
Решение.
Часовыми делениями циферблат разбит на 12 круговых секторов. Угол каждого из них равенство 360 °: 12 = 30 °. Между минутной и часовой стрелкой два часовых деления. Они образуют угол 60 °.
Ответ: 60.
Ответ: 60
18. Рок-магазин продаёт значки с символикой рок-групп. В продаже имеются значки пяти цветов: чёрные, синие, зелёные, серые и белые. Данные о проданных значках представлены на столбчатой диаграмме.
Определите по диаграмме, значков какого цвета было продано меньше всего. Сколько примерно процентов от общего числа значков составляют значки этого цвета?
1) 5 2) 10 3) 15 4) 20
Решение.
Из диаграммы видно, что было продано меньше всего значков зелёного цвета в количестве 150. Определим сколько процентов от общего числа составляют зелёные значки:
Значит зелёных значков примерно 15% от общего числа.
Ответ: 3.
Ответ: 3
19. На тарелке лежат пирожки, одинаковые на вид: 4 с мясом, 8 с капустой и 3 с яблоками. Петя наугад выбирает один пирожок. Найдите вероятность того, что пирожок с яблоками
Решение.
Всего было подготовлено 25 билетов. Среди них 16 двузначных. Таким образом, вероятность взять билет с двухзначным номером
Ответ: 0,64
20. Из всемирного тяготения
если гравитационная постоянная
Часть 2 2 Решение. Выразим массу: Подставим значения размер: Ответ: 1000. Ответ: 1000 21. Решите неравенство Решение. Умножим на 10, приведенные слагаемые и разложим на множители: Произведение двух сомножителей будет меньше нуля, если знак см.рисунок). Таким образом, получаем ответ: Ответ: 22. Железнодорожный состав длины в 1 км прошёл бы мимо столба за 1 мин., А через туннель (от входа локомотива до выхода последнего вагона) при той же скорости — за 3 мин. Какова длина туннеля (в км)? Решение. Поезд проходит через туннель за 3 минуты, при этом за одну минуту поезд проходит мимо выхода из туннеля, следовательно, от входа локомотива в туннель до выхода проходит 2 минуты.Мимо столба поезд длиной 1 км проходит за 1 минуту, поэтому его скорость равна 1 км / мин. Значит, за 2 минуты поезд пройдет 2 км, поэтому длина туннеля равна 2 км. 23. Постройте функции и определите, при каких значениях прямая имеет с графиком ровно три общие точки. Решение. Раскрывая модуль, получим, что график функции можно следующим образом: Этот график изображён на рисунке:
Ответ: 2.
Из графика видно, что прямая имеет с графиком функции ровно три общие точки при и
Ответ: 0; 4.
24. Диагонали и трапеции пересекаются в точке. Площади треугольников и равны соответственно и. Найдите площадь трапеции.
Решение.
Заметим, что площади двух треугольников, общей вершиной точки пересечения диагоналей трапеции, а основания — боковые стороны, равны. Это следует, например, из того, что площади треугольников и равны (поскольку эти треугольники имеют общее основание, и их высоты, проведенные к этому основанию, равны высоты трапеции), а.По условию, поэтому и являются условию боковыми сторонами, а основаниями трапеции. Тогда треугольники и подобны по двум углам, и отношение их площадей равно квадрату коэффициента подобия. Поэтому. Треугольники и имеют общую высоту. е. . Значит,. Поэтому и. Но тогда.
Ответ:.
25. В параллелограмме ABCD диагонали AC и BD пересекаются в точку O .Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC .
Решение.
Проведём высоту так, чтобы она проходила через точку Углы и равны друг другу как вертикальные. Вспомним также, что диагонали делятся точки пополам, следовательно, рассмотрим треугольники и прямоугольные, имеют равные углы и равные гипотенузы, следовательно, эти треугольники равны, а значит равны отрезки и.Таким образом,
Площадь параллелограмм равная площадь треугольника
26. Основание AC равнобедренного треугольника 10. Окружность 8 Окружность равнобедренного треугольника 10. Радиуса вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC .
Критерии и система оценивания ОГЭ по математике
- ОГЭ по математике
Работа ОГЭ по математике для 9 класса состоит из трёх модулей: «Алгебра», «Геометрия», «Реальная математика». Всего в работе 26 заданий.
Модуль «Алгебра» содержит 11 заданий: в части 1 — восемь заданий; в части 2 — три задания.
Модуль «Геометрия» содержит восемь заданий: в части 1 — пять заданий; в части 2 — три задания.
Модуль «Реальная математика» содержит семь заданий: все задания этого модуля — в части 1.
Система оценивания экзаменационной работы ОГЭ (ГИА 9 класс) по математике
За правильный ответ на задание 1–20 ставится 1 балл.
Баллы по модулям
Таблица 1
| Модуль | Баллы |
| Алгебра | 14 |
| Геометрия | 11 |
| Реальная математика | 7 |
| Всего: | 32 |
Рекомендуемый минимальный результат выполнения экзаменационной работы ОГЭ (ГИА 9 класс), свидетельствующий об освоении Федерального компонента образовательного стандарта в предметной области «Математика», — 8 баллов, набранные в сумме за выполнение заданий всех трёх модулей, при условии, что из них не менее 3 баллов по модулю «Алгебра», не менее 2 баллов по модулю «Геометрия» и не менее 2 баллов по модулю «Реальная математика».
Смотрите также: Перевод баллов ОГЭ по математике в оценке
Критерии оценивания ОГЭ по математике задания 21-26 (из демоверсии 2017 года)
Задание 21
| Баллы | Критерии оценки выполнения задания |
| 2 | Правильно выполнено преобразование, получен верный ответ |
| 1 | Решение доведено до конца, но допущена ошибка вычислительного характера или описка, с её учётом дальнейшие шаги выполнены верно |
| 0 | Другие случаи, не соответствующие указанным выше критериям |
| 2 | Максимальный балл |
Задание 22
| Баллы | Критерии оценки выполнения задания |
| 2 | Правильно составлено уравнение, получен верный ответ |
| 1 | Правильно составлено уравнение, но при его решении допущена вычислительная ошибка, с её учётом решение доведено до ответа |
| 0 | Другие случаи, не соответствующие указанным выше критериям |
| 2 | Максимальный балл |
Задание 23
| Баллы | Критерии оценки выполнения задания |
| 2 | График построен правильно, верно указаны все значения c, при которых прямая y c имеет с графиком только одну общую точку |
| 1 | График построен правильно, указаны не все верные значения c |
| 0 | Другие случаи, не соответствующие указанным выше критериям |
| 2 | Максимальный балл |
Задание 24
| Баллы | Критерии оценки выполнения задания |
| 2 | Получен верный обоснованный ответ |
| 1 | При верных рассуждениях допущена вычислительная ошибка, возможно приведенная к неверному ответу |
| 0 | Другие случаи, не соответствующие указанным выше критериям |
| 2 | Максимальный балл |
Задание 25
| Баллы | Критерии оценки выполнения задания |
| 2 | Доказательство верное, все шаги обоснованы |
| 1 | Доказательство в целом верное, но содержит неточности |
| 0 | Другие случаи, не соответствующие указанным выше критериям |
| 2 | Максимальный балл |
Задание 26
| Баллы | Критерии оценки выполнения задания |
| 2 | Ход решения верный, все его шаги выполнены правильно, получен верный ответ |
| 1 | Ход решения верный, чертёж соответствует условию задачи, но пропущены существенные объяснения или допущена вычислительная ошибка |
| 0 | Другие случаи, не соответствующие указанным выше критериям |
| 2 | Максимальный балл |
Смотрите также:
Темы, входящие в ГИА (ОГЭ) по курсу математики
Темы, входящие в ГИА (ОГЭ) по курсу математики- Числа и вычисления
- Натуральные числа
- Десятичная система счисления.Римская нумерация
- Арифметические действия над натуральными числами
- Степень с натуральным показателем
- Делимость натуральных чисел. Простые и натуральные составные числа, разложение числа на простые множители
- Признаки делимости на 2, 3, 5, 9, 10
- Самый большой общий делитель и наименьшее общее кратное
- Деление с остатком
- Дроби
- Обыкновенная дробь, основное свойство дроби. Сравнение дробей
- Арифметические действия с обыкновенными дробями
- Нахождение части от целого и целого по его части
- Десятичная дробь, сравнение десятичных дробей
- Арифметические действия с десятичными дробями
- Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной
- Рациональные числа
- Целые числа
- Модуль (абсолютная величина) числа
- Сравнение рациональных чисел
- Арифметические действия с рациональными числами
- Степень с целым показателем
- Числовые выражения, порядок действий в них, использование скобок.Законы арифметических действий
- Действительные числа
- Квадратный корень из числа
- Корень третьей степени
- Нахождение приближенного значения корня с помощью калькулятора
- Понятие об иррациональном том числе. Десятичные приближения иррациональных чисел. Действительные числа как бесконечные десятичные дроби
- Сравнение действительных чисел
- Измерения, приближения, оценки
- Единицы измерения длины, площади, объема, массы, времени, скорости
- Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире
- Представление зависимости между величинами в виде формул
- Проценты.Нахождение процента от величины и величины по ее проценту
- Отношение, выражение отношения в процентах
- Пропорция. Пропорциональная и обратно пропорциональная зависимость
- Округление чисел. Прикидка и оценка результатов вычислений. Выделение множителя — степени десятичной в записи числа
- Натуральные числа
- Алгебраические выражения
- Буквенные выражения (выражения с переменными)
- Буквенные выражения. Числовое значение буквенного выражения
- Допустимые значения числа, входящего в алгебраические выражения
- Подстановка выражений вместо числа
- Равенство буквенных выражений, тождество.Преобразования выражений
- Свойства степени с целым показателем
- Многочлены
- Многочлен. Сложение, вычитание, умножение многочленов
- Формулы сокращенного умножения: квадрат суммы и квадрат разности; формула разности квадратов
- Разложение многочлена на множители
- Квадратный трехчлен. Теорема Виета. Разложение квадратного трехчлена на линейные множители
- Степень и корень многочлена с одной стандартной
- Алгебраическая дробь
- Алгебраическая дробь.Сокращение дробей
- Действия с алгебраическими дробями
- Рациональные выражения и их преобразования
- Свойства квадратных корней и их применение в вычислениях
- Буквенные выражения (выражения с переменными)
- Уравнения и неравенства
- Уравнения
- Уравнение с одной, корень уравнения
- Линейное уравнение
- Квадратное уравнение, формула корней квадратного уравнения
- Решение рациональных условий
- Примеры решения высших степеней.Решение методом замены. Решение методом разложения на множители
- Уравнение с двумя переменными; решение уравнения с двумя переменными
- Система уравнений; решение системы
- Система двух линейных соотношений с двумя переменными; решение подстановкой и алгебраическим сложением
- Уравнение с местами переменными
- Решение простейших нелинейных систем
- Неравенства
- Числовые неравенства и их свойства
- Неравенство с одной стандартной.Решение неравенства
- Линейные неравенства с одной категории
- Системы линейных неравенств
- Квадратные неравенства
- Текстовые задачи
- Решение текстовых задач арифметическим способом
- Решение текстовых задач алгебраическим способом
- Числовые следовать
- Понятие последовательного
- Арифметическая и геометрическая прогрессии
- Арифметическая прогрессия.Формула общего члена арифметической прогрессии
- Формула суммы нескольких членов арифметической прогрессии
- Геометрическая прогрессия. Формула общего геометрического прогресса
- Формула суммы первых геометрической прогрессии
- Сложные проценты
- Уравнения
- Функции и графики
- Числовые функции
- Понятие функции. Область определения функции. Способы задания функции
- График функции, возрастание и убывание функций, наибольшее и наименьшее значение функции, нули функции, интервалы знакопостоянства, чтение графиков функций
- Примеры графических зависимостей, отражающих реальные процессы
- Функция, описывающая прямую пропорциональную зависимость, ее график
- Линейная функция, ее график, геометрический смысл коэффициентов
- Функция, описывающая обратно пропорциональную зависимость, ее график.Гипербола
- Квадратичная функция, ее график. Парабола. Координаты вершины параболы, ось симметрии
- График функции
- График функции
- График функции
- Использование графиков функций для решения уравнений и систем
- Числовые функции
- Координаты на прямой и плоскости
- Координатная прямая
- Изображение чисел точками координатной прямой
- Геометрический смысл модуля
- Числовые промежутки: интервал, отрезок, луч
- Декартовы координаты на плоскости
- Декарты координаты на плоскости; координаты точки
- Координаты середины отрезка
- Формула расстояния между двумя точками плоскости
- Уравнение прямой, угловой коэффициент прямой, условие параллельности прямой
- Уравнение окружности
- Графическая интерпретация соотношений с двумя переменными и их системными
- Графическая интерпретация неравенств с переменными и их системами
- Координатная прямая
- Геометрия
- Геометрические фигуры и их свойства.Измерение геометрических величин
- Начальные понятия геометрии
- Угол. Прямой угол. Острые и тупые углы. Вертикальные и дополнительные углы. Биссектриса угла и ее свойства
- Прямая. Параллельность и перпендикулярность прямая
- Отрезок. Свойство серединного перпендикуляра к отрезку. Перпендикуляр и наклонная к прямой
- Понятие о геометрическом месте точек
- Треугольник
- Высота, медиана, биссектриса, средняя линия треугольника; точки пересечения серединных перпендикуляров, биссектрис, медиан, высот или их продолжений
- Равнобедренный и равносторонний треугольники.Свойства и признаки равнобедренного треугольника
- Прямоугольный треугольник. Теорема Пифагора
- Признаки равенства треугольников
- Неравенство треугольника
- Сумма углового треугольника. Внешние углы треугольника
- Зависимость между величинами сторон и углов треугольника
- Теорема Фалеса
- Подобие треугольников, коэффициент подобия. Признаки подобия треугольников
- Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от до
- Решение прямоугольных треугольников.Основное тригонометрическое тождество. Теорема косинусов и теорема синусов
- Многоугольники
- Параллелограмм, его свойства и признаки
- Прямоугольник, квадрат, ромб, их свойства и признаки
- Трапеция, средняя линия трапеции; равнобедренная трапеция
- Сумма углов выпуклого многоугольника
- Правильные многоугольники
- Окружность и круг
- Центральный, вписанный угол; величина вписанного угла
- Взаимное расположение и окружности
- Касательная и секущая к окружности; равенство отрезков касательных, проведенных из одной точки
- Окружность, вписанная в треугольник
- Окружность, описанная около треугольника
- Вписанные и описанные окружности правильного многоугольника
- Измерение геометрических величин
- Длина отрезка, длина ломаной, периметр многоугольника.Расстояние от точки до прямого
- Длина окружности
- Градусная мера угла, соответствие между величиной угла и длиной дуги окружности
- Площадь прямоугольника
- Площадь параллелограмма
- Площадь трапеции
- Площадь треугольника
- Площадь круга, площадь сектора
- Формулы прямоугольного параллелепипеда, куба, шара
- Векторы на плоскости
- Вектор, длина (модуль) вектор
- Равенство векторов
- Операции над векторми (сумма векторов, умножение вектора на число)
- Угол между векторами
- Коллинеарные элементы, разложение вектора по двум неколлинеарным собым
- Координаты вектора
- Скалярное произведение векторов
- Геометрические фигуры и их свойства.Измерение геометрических величин
- Статистика и теория вероятностей
- Описательная статистика
- Представление данных в виде таблиц, диаграмм, графиков
- Средние результатов измерений
- Вероятность
- Частота события, вероятность
- Равновозможные события и подсчет их вероятности
- Представление о геометрической вероятности
- Комбинаторика
- Решение комбинаторных задач: перебор вариантов, комбинаторное правило умножения
- Описательная статистика

 )
) )
)  Источник.
Источник.