ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ФОРМУЛЫ | Социальная сеть работников образования
Образование — то, что остается после того, как забыто все, чему учили в школе.
Игорь Хмелинский, новосибирский учёный, ныне работающий в Португалии, доказывает, что без прямого запоминания текстов и формул развитие абстрактной памяти у детей затруднительно. Приведу выдержки из его статьи «Уроки образовательных реформ в Европе и странах бывшего СССР»
Заучивание наизусть и долговременная память
Незнание таблицы умножения имеет и более серьезные последствия, чем неспособность обнаружить ошибки в расчетах на калькуляторе. Наша долговременная память работает по принципу ассоциативной базы данных, то есть, одни элементы информации при запоминании оказываются связанными с другими на основе ассоциаций, установленных в момент знакомства с ними. Поэтому, чтобы в голове образовалась база знаний в какой-либо предметной области, например, в арифметике, нужно для начала выучить хоть что-то наизусть. Далее, вновь поступающая информация попадет из кратковременной памяти в долговременную, если в течение короткого промежутка времени (несколько дней) мы столкнемся с нею многократно, и, желательно, в разных обстоятельствах (что способствует созданию полезных ассоциаций). Однако при отсутствии в постоянной памяти знаний из арифметики, вновь поступающие элементы информации связываются с элементами, которые к арифметике никакого отношения не имеют – например, личностью преподавателя, погодой на улице и т.п. Очевидно, такое запоминание никакой реальной пользы учащемуся не принесет – поскольку ассоциации уводят из данной предметной области, то никаких знаний, относящихся к арифметике, учащийся вспомнить не сможет, кроме смутных идей о том, что он вроде бы что-то когда-то об этом должен был слышать. Для таких учащихся роль недостающих ассоциаций обычно выполняют разного рода подсказки – списать у коллеги, воспользоваться наводящими вопросами в самой контрольной, формулами из списка формул, которым пользоваться разрешено, и т.п. В реальной жизни, без подсказок, такой человек оказывается совершенно беспомощным и неспособным применить имеющиеся у него в голове знания.
Формирование математического аппарата, при котором формулы не заучиваются, происходит медленнее, нежели в противном случае. Почему? Во-первых, новые свойства, теоремы, взаимосвязи между математическими объектами почти всегда используют какие-то особенности ранее изученных формул и понятий. Концентрировать внимание ученика на новом материале будет сложнее, если эти особенности не смогут извлекаться из памяти за короткий промежуток времени. Во-вторых, незнание формул наизусть препятствует поиску решения содержательных задач с большим количеством мелких операций, в которых требуется не только провести определенные преобразования, но и выявить последовательность этих ходов, анализируя применение нескольких формул на два-три шага вперед.
Практика показывает, что интеллектуальное и математическое развитие ребенка, формирование его базы знаний и навыков, происходит значительно быстрее, если большая часть используемой информации (свойства и формулы) находиться в голове. И чем прочнее и дольше она там удерживается, тем лучше.
НАДО ЛИ ВАС ДАЛЬШЕ УБЕЖДАТЬ В ТОМ, ЧТО ФОРМУЛЫ НАДО ЗНАТЬ НАИЗУСТЬ?
nsportal.ru
Основные формулы по математике — Математика — Теория, тесты, формулы и задачи
Знание формул по математике является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по математике, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении математических задач. На этой странице сайта представлены основные формулы по школьной математике.
Изучать основные формулы по школьной математике онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (адрес электронной почты и ссылки в социальных сетях здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
математика в формулах и таблицах
19
Сибирский государственный университет телекоммуникаций и информатики
В.И. Агульник, Б.П. Зеленцов
в формулах и таблицах
Справочное пособие
Новосибирск
2000 г.
В.И.Агульник, Б.П.Зеленцов.
Математика в формулах и таблицах. Справочное пособие
Справочное пособие содержит формулы, таблицы, графики по математике, охватывающие основные разделы элементарной математики — алгебры и геометрии. Оно предназначено для абитуриентов при подготовке к вступительным экзаменам, а также для студентов дневного и заочного обучения при изучении высшей математики и других дисциплин.
Кафедра высшей математики
Рецензент: И.И.Резван
Утверждено редакционно-издательским советом СибГУТИ в качестве учебного пособия.
Сибирский государственный университет телекоммуникаций и информатики, 2000 г.
В.И.Агульник, Б.П.Зеленцов, 2000 г.
ОГЛАВЛЕНИЕ
ЧИСЛА, ДРОБИ, МОДУЛИ…………………………………
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ …………
СТЕПЕНИ И КОРНИ ……………………………………….
КВАДРАТНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА ………
ПРОГРЕССИИ ………………………………………………
ЛОГАРИФМЫ ………………………………………………
ТРИГОНОМЕТРИЯ ………………………………………
ОСНОВНЫЕ ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ ……………
ПЛАНИМЕТРИЯ …………………………………………
СТЕРЕОМЕТРИЯ …………………………………………
ЛИТЕРАТУРА …………………………………………………
1. ЧИСЛА, ДРОБИ, МОДУЛИ
n
N
— множество
натуральных чисел

d = НОД (n, m) — наибольший общий делитель n и m
k = НОК (n, m) — наименьшее общее кратное n и m
Z = множество целых чисел
Q = -множество рациональных чисел (дробей)
R – множество действительных чисел
Арифметические операции с дробями:
; 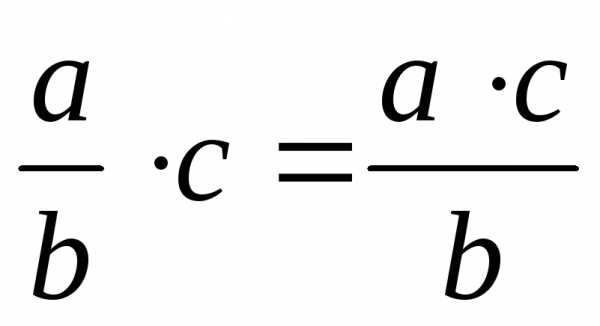 ;
; 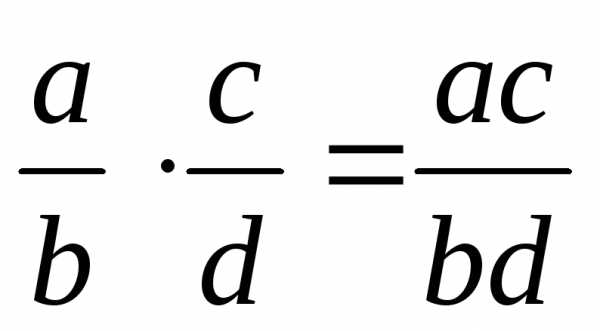 ;
;
 ;
; 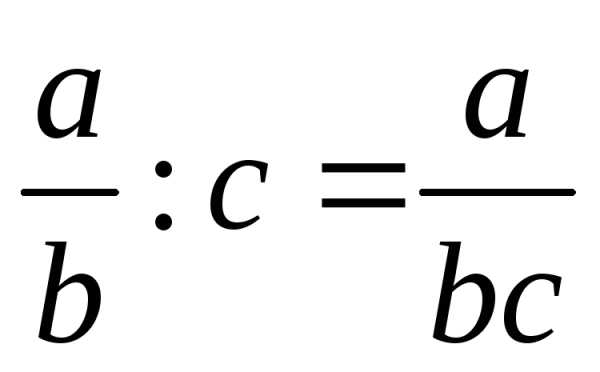 ;
;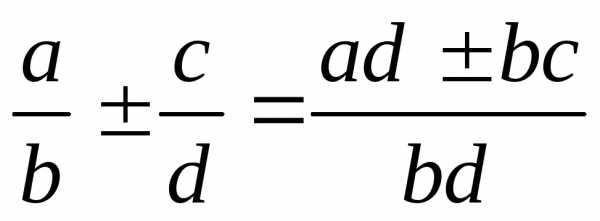 ;
;
Пропорция 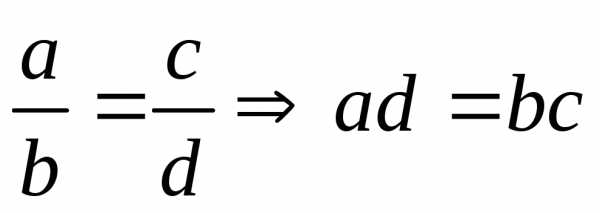 ;
;
Модуль числа. Определение: ;
Свойства модуля:
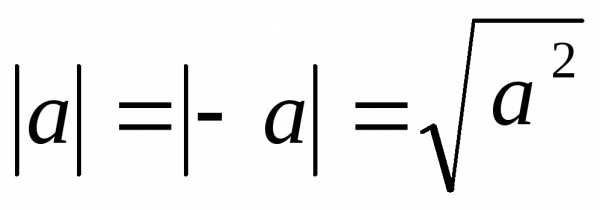
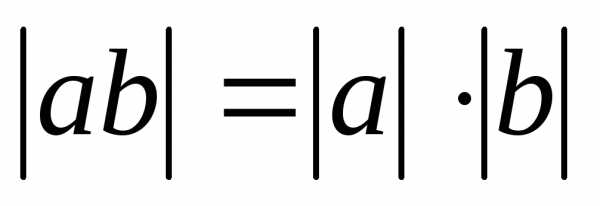 ; ;
; ;
a
a+b
a-b
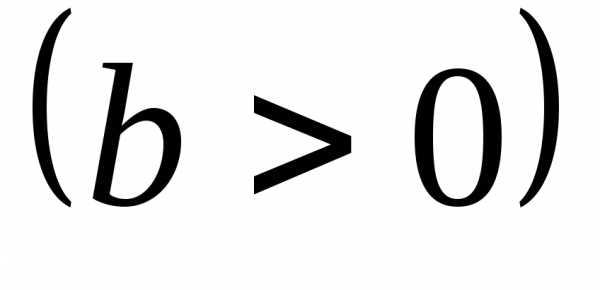 ;x
;x;
a
a+b
a-b
x2. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
; ;
;
;
;
; ;
3. СТЕПЕНИ И КОРНИ
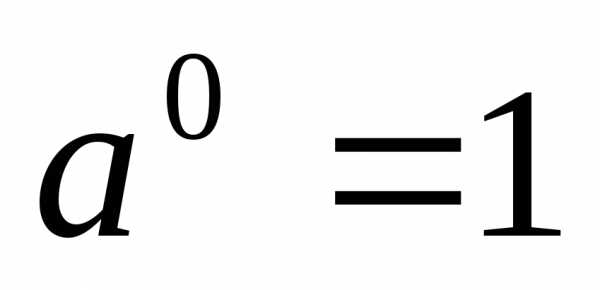 ;
; 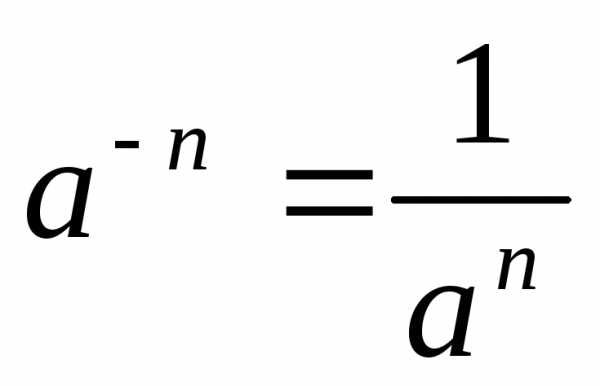 ; ;;
; ;;
; 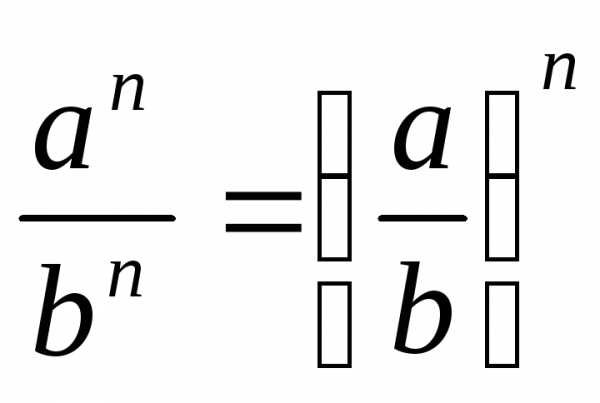 ;
;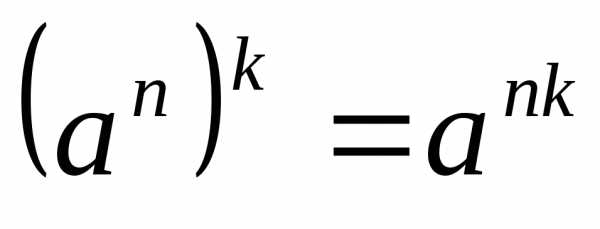 ;
; 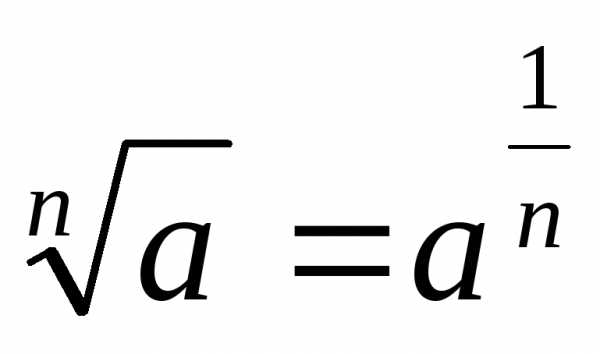 ;
;
; ; 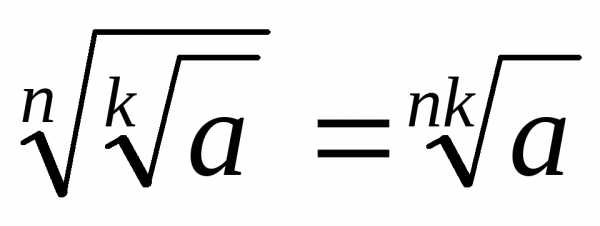 ;
;
4. КВАДРАТНЫЕ УРАВНЕНИЯ
; 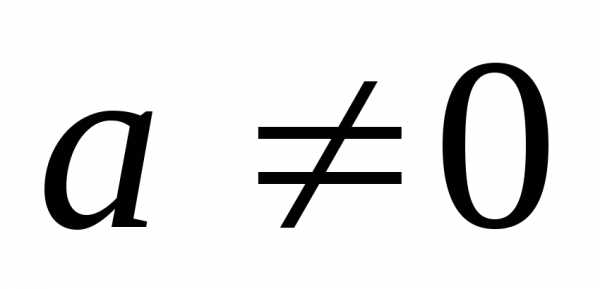
Корни уравнения:
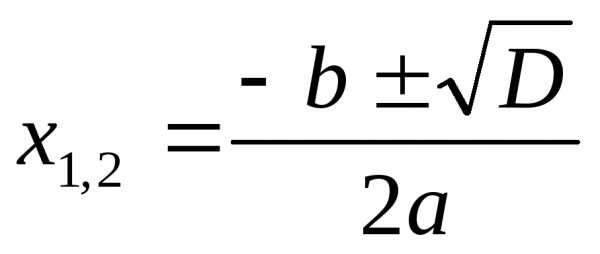 ,
где
,
где —
дискриминант.
—
дискриминант.
Формулы Виета:
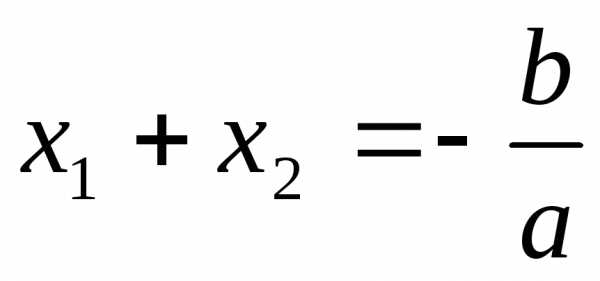 ;
;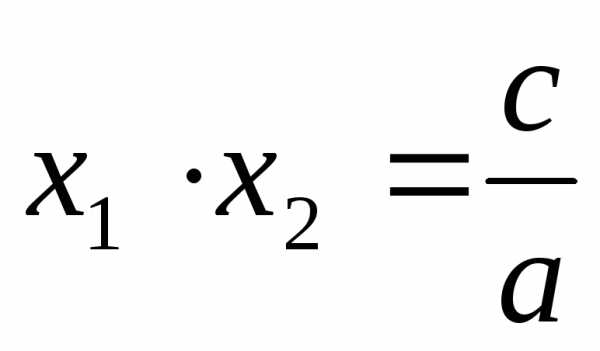 .
.
Разложение квадратного трехчлена на множители:
.
Приведенное
уравнение:
;
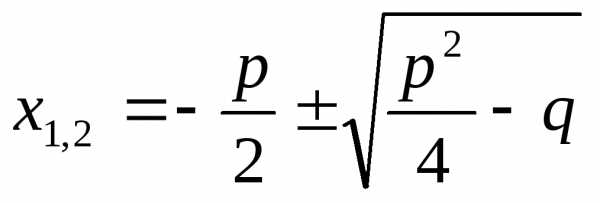 .
.
Квадратное неравенство:
Если D>0
, a>0,
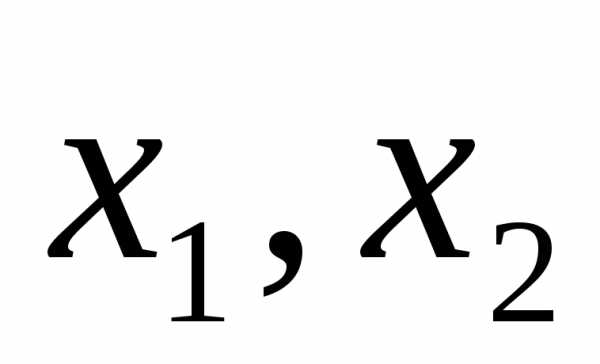 -корни
квадратного
трехчлена,
-корни
квадратного
трехчлена,
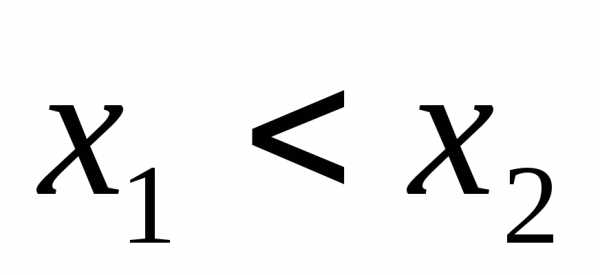 ,
то
,
то
;
.
5. ПРОГРЕССИИ
Арифметическая прогрессия:
Общий член:
,,
где
Сумма членов .
Геометрическая прогрессия
Общий член:
, где
 — знаменатель
прогрессии;
— знаменатель
прогрессии;
Сумма членов .
Сумма геометрической
прогрессии (при
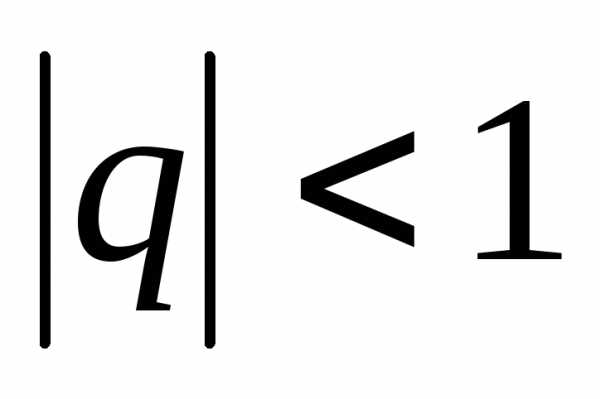 ):
):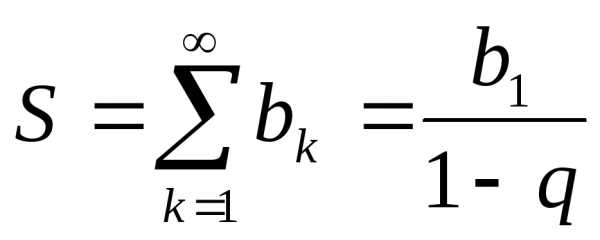 .
.
Некоторые суммы:
; ;
;
; ;
6. ЛОГАРИФМЫ
Логарифм числа
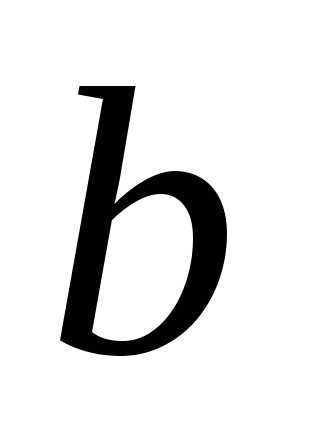 по
основанию
по
основанию :
:
.
Основное
логарифмическое тождество: 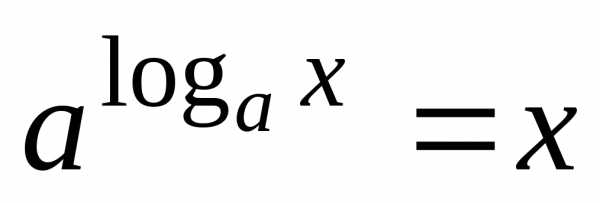 .
.
Свойства логарифмов:
; ;
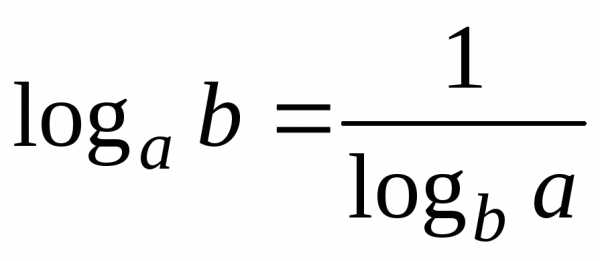 ; ;.
; ;.
Десятичные
логарифмы
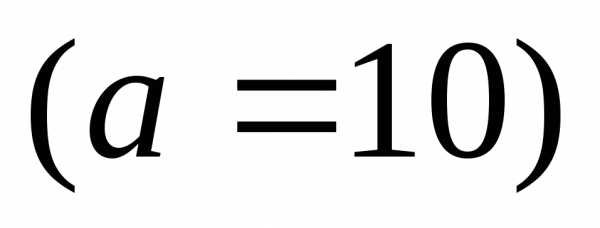 :.
:.
Натуральные логарифмы :.
Логарифмические неравенства:
.
Показательные неравенства:
.
7. ТРИГОНОМЕТРИЯ
7.1. Основные соотношения
;
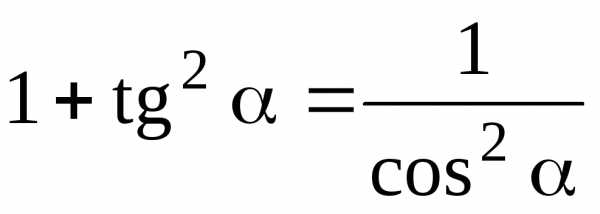 ;
; 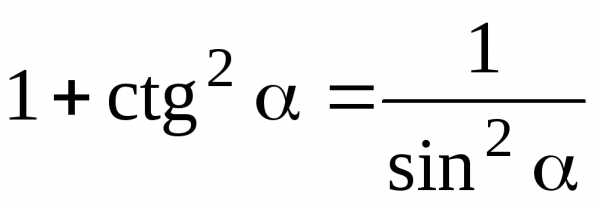 ;
;
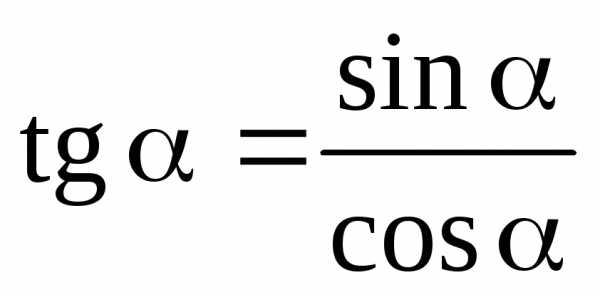 ;
; 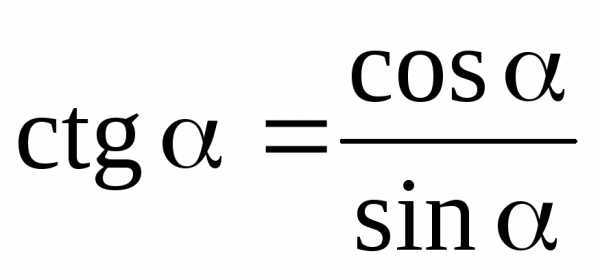 ;;
;;
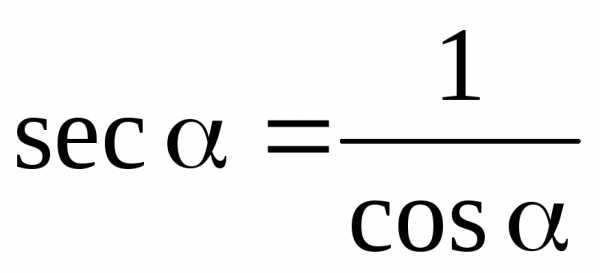 ;
; 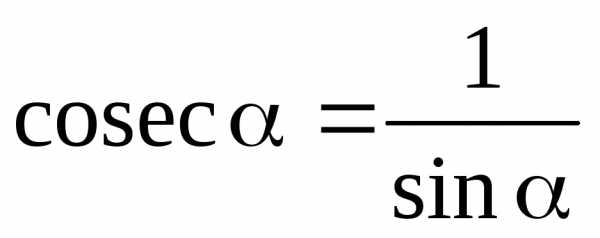 ;
;
7.2. Перевод из радианной меры углов в градусную и обратно:
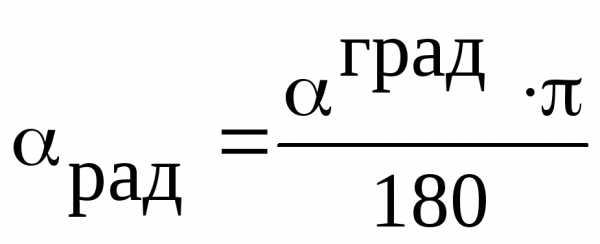 ;
; 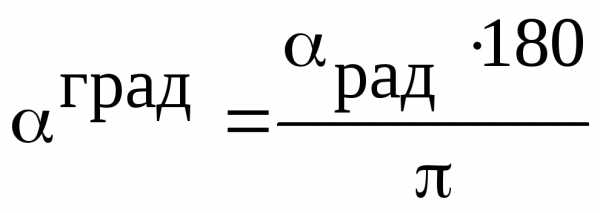 ;
;
7.4. Знаки тригонометрических функций
7.5. Формулы сложения
; ;
; ;
; ;
; ;
7.6. Формулы двойных углов
;
;
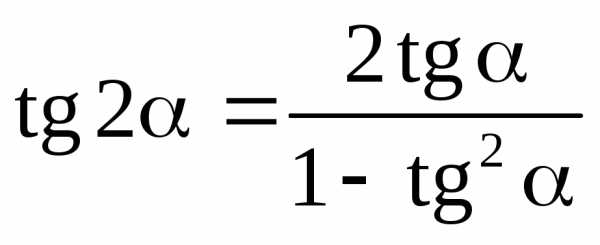 ;
; 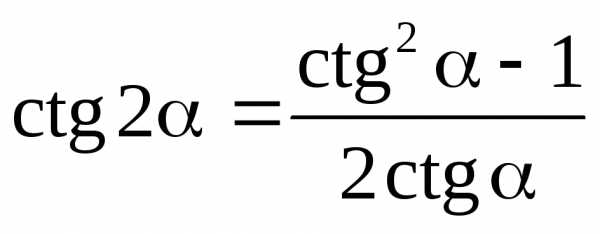 ;
;
7.7. Формулы тройных углов
; ;
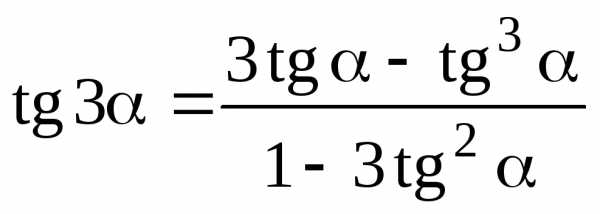 ; ;
; ;
7.8. Формулы половинных углов
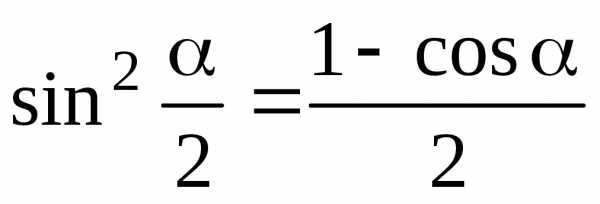 ;
; 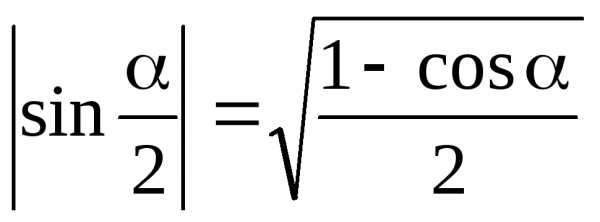 ;
;
; 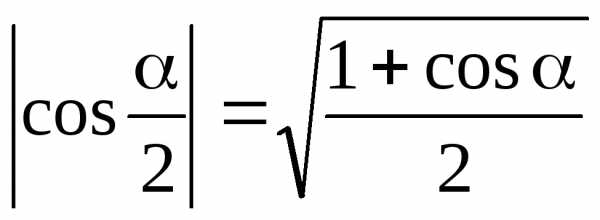 ;
;
;
Универсальная тригонометрическая подстановка, используемая для решения тригонометрических уравнений:
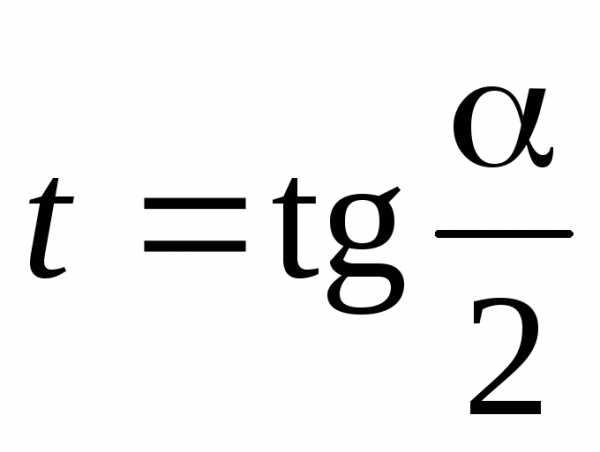
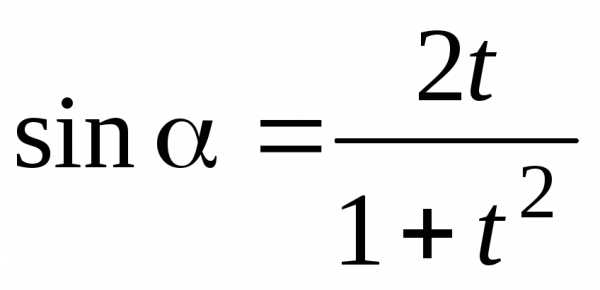 ;
; 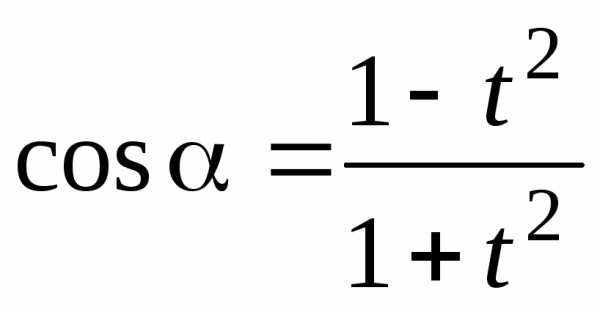 ;
; 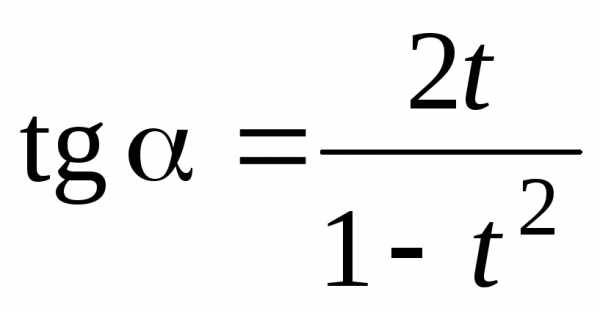 ;
;7.9. Формулы приведения
-
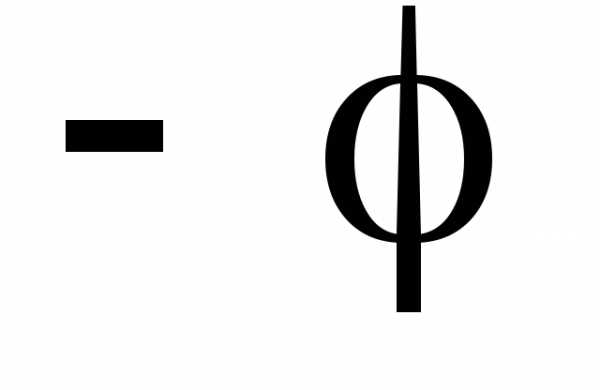
sin
– sin
cos
sin
– cos
sin
cos
cos
sin
– cos
sin
cos
tg
–tg
ctg
tg
ctg
tg
ctg
–ctg
tg
ctg
tg
ctg
7.10. Формулы преобразования суммы и разности
; ;
; ;
, где ;
; ;
; .
7.11. Формулы преобразования произведения
; ;
.
7.12. Обратные тригонометрические функции
;
;
;
.
7.13. Простейшие тригонометрические уравнения
1)
; 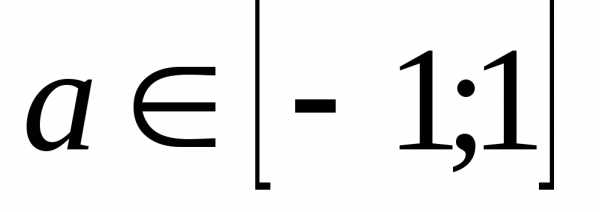 ;.
;.
Частные случаи: ;;
; 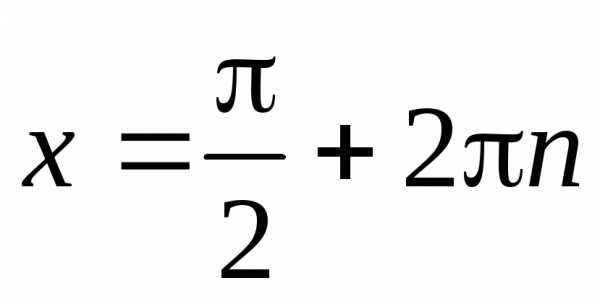 ;
;
; 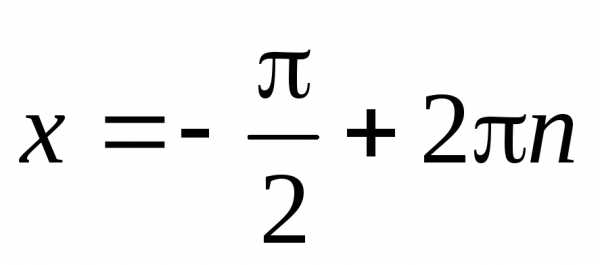 .
.
2)
;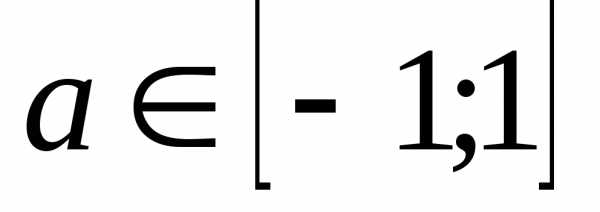 ;.
;.
Частные случаи: ;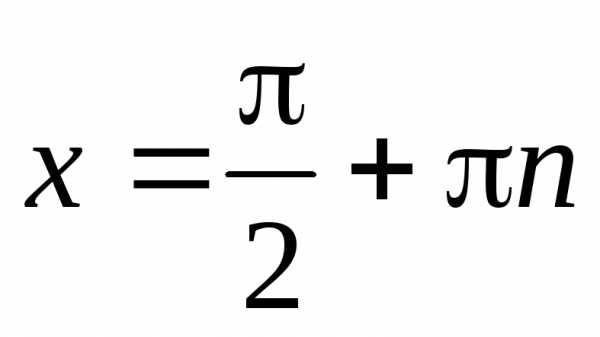 ;
;
; 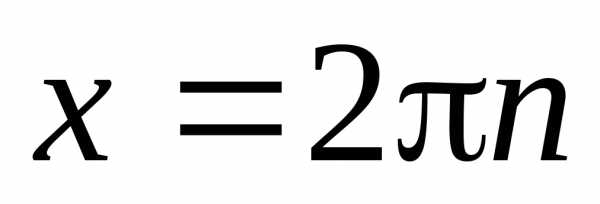 ;
;
; .
3)
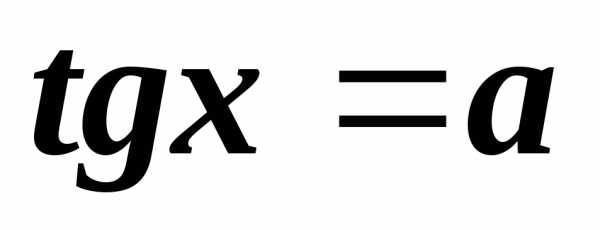 ,;.
,;.
4) ;;.
8. Графики основных элементарных функций
Парабола
Гипербола
Y
Y
y0
x0
x0
X
X
y0
Логарифмическая кривая
Экспонента
Y
a>1
0<a<1
Y
a>1
1
X
0<a<1
y = log a x
y = ax
X
Синусоида
Y
1
/2
-
2
X
y = sin x
y = cos x
Y
Тангенсоида
/2
0
X
y = ctg x
y = tg x
10. ПЛАНИМЕТРИЯ
Треугольник
10.1.1. Основные соотношения
A,B,C – вершины aa,b,c – стороны ,, — углы
— неравенства треугольника; ;
теорема проекций
теорема синусов
теорема косинусов
10.1.2. Замечательные линии и точки в теугольнике
ma, mb, mc — медианы
ha, hb, hc — высоты
la, lb , lc — биссектрисы
p —
полупериметр,

r — радиус вписанной окружности
R – радиус описанной окружности
; ;
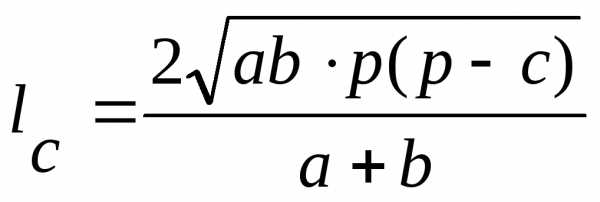 ;
; 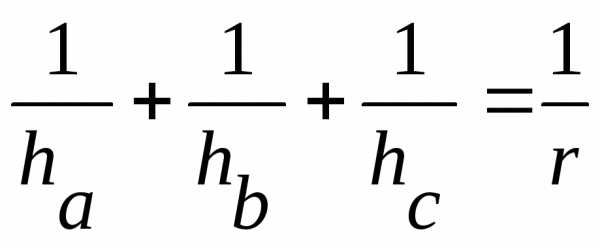 ;
;
10.1.3. Формулы площади треугольника
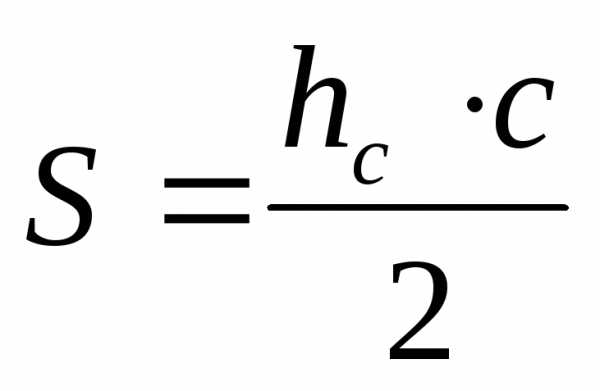
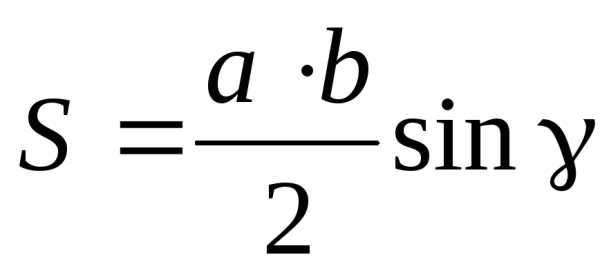
studfiles.net
Основные формулы по геометрии — Математика — Теория, тесты, формулы и задачи
Знание формул по геометрии является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по математике. Формулы по геометрии, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении геометрических задач. На этой странице сайта представлены основные формулы по школьной геометрии.
Изучать основные формулы по школьной геометрии онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (адрес электронной почты и ссылки в социальных сетях здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
educon.by
Формулы элементарной математикИ
Степени и корни
Если
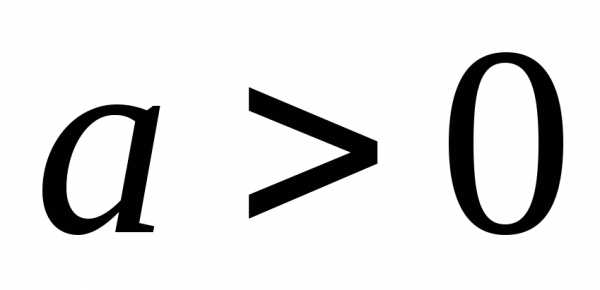 ,
,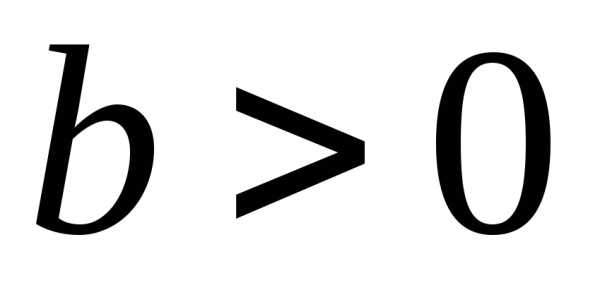 ,
то:
,
то:
;;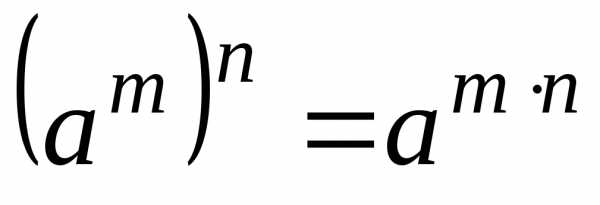 ;
;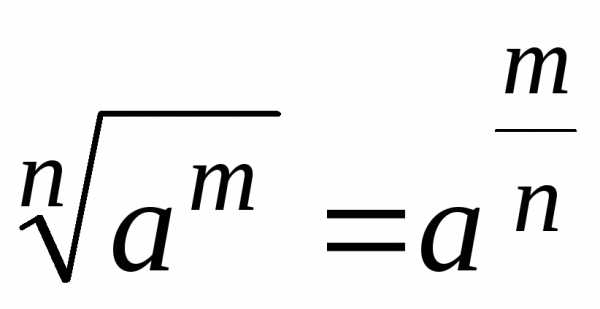 ,
,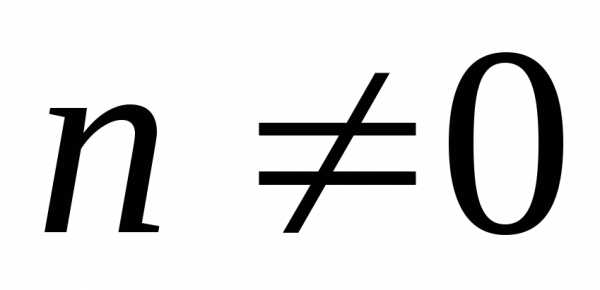 ;
; 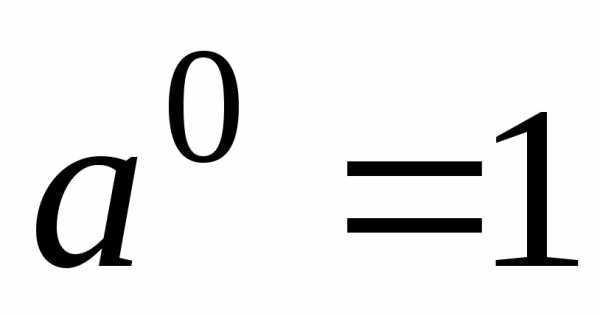 ;
;
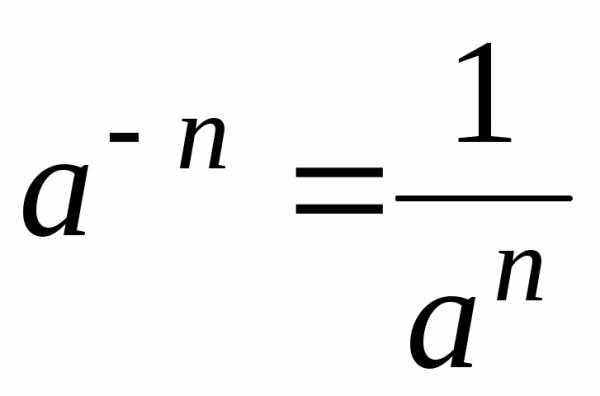 ,
,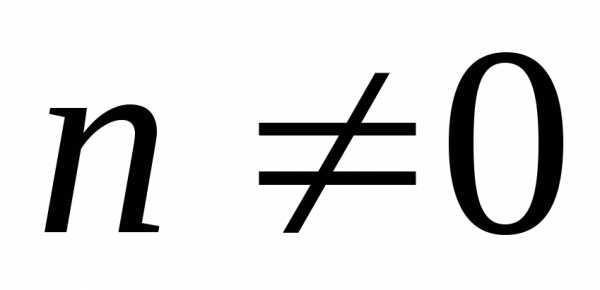 ;,
;,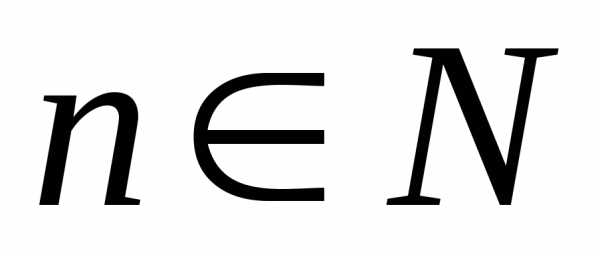 ;
;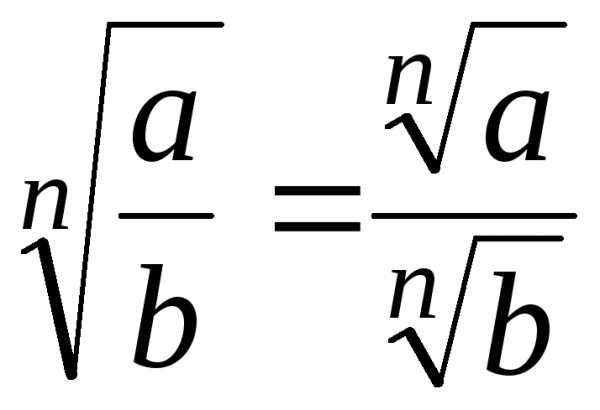 ,
,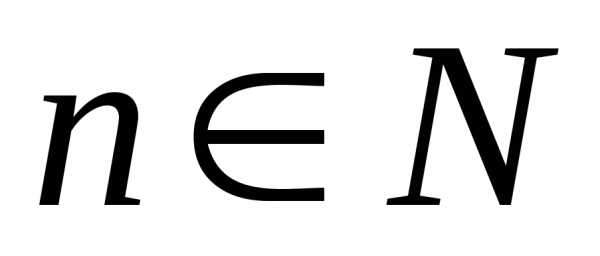 .
.
Формулы сокращенного умножения
– квадрат суммы или разности;
– разность квадратов;
– куб суммы;
– сумма кубов;
– куб разности;
– разность кубов;
3. Квадратное уравнение
Если
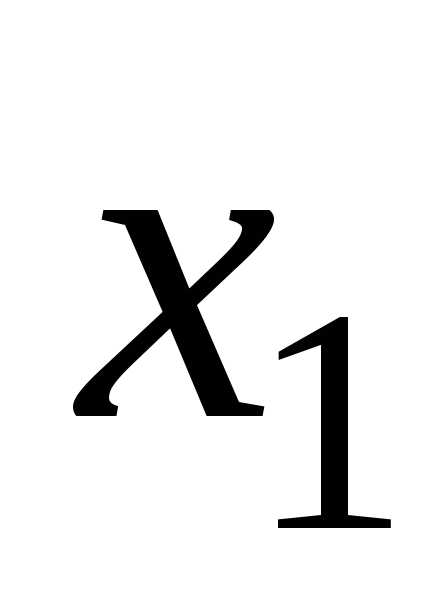 и
и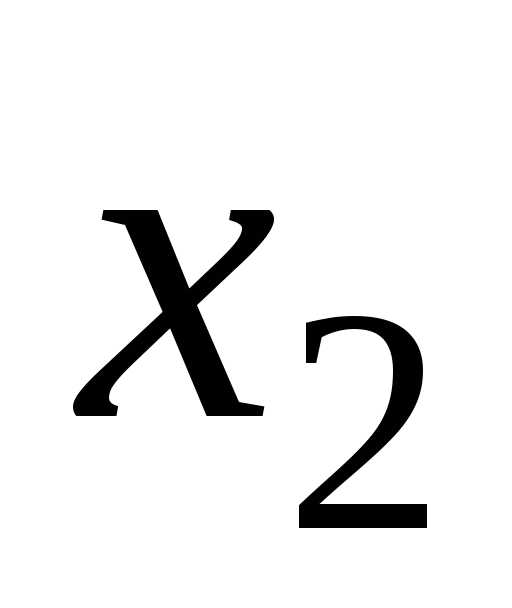 — корни квадратного уравнения,
то
— корни квадратного уравнения,
то
;.
4. Логарифмы
Если
,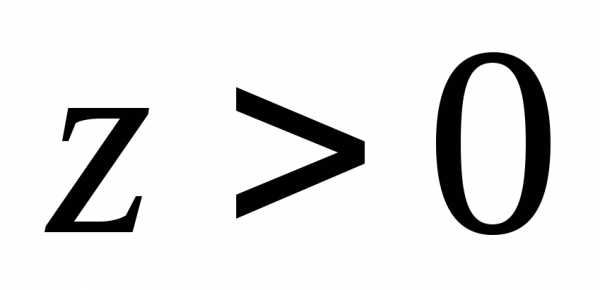 ,
,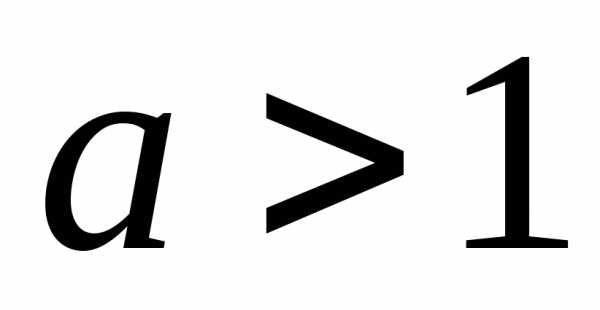 ,
,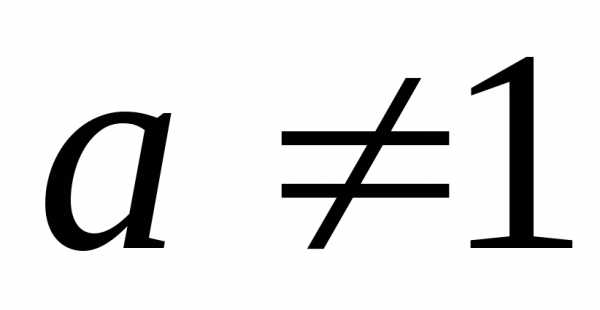 ,
то:
,
то:
– определение логарифма;
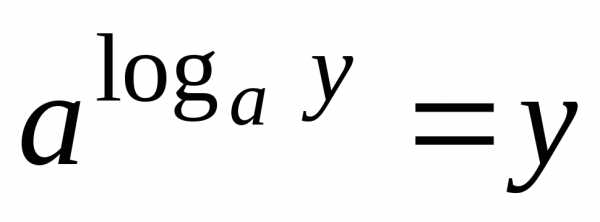 – основное логарифмическое тождество;
– основное логарифмическое тождество;– логарифм произведения;
– логарифм частного;
– логарифм степени;
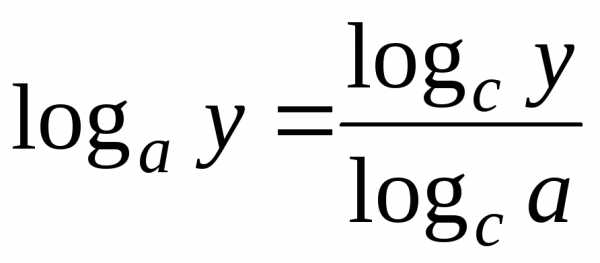 – формула перехода;
– формула перехода;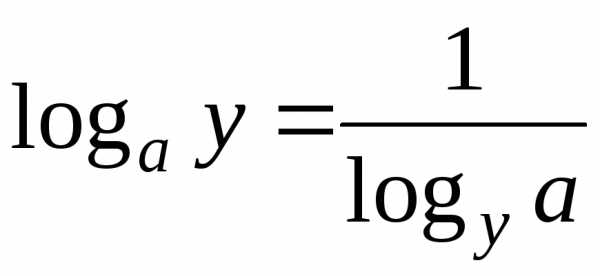 ,;
8)
,;
8)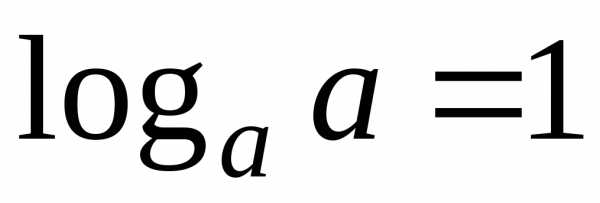 ;
9)
;
9)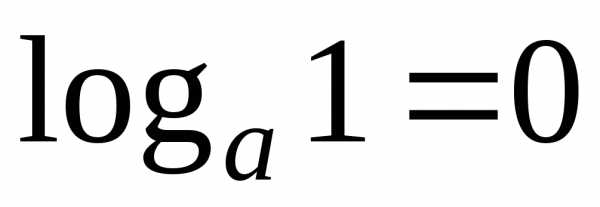 .
.
5. Основные тригонометрические тождества
1)
2)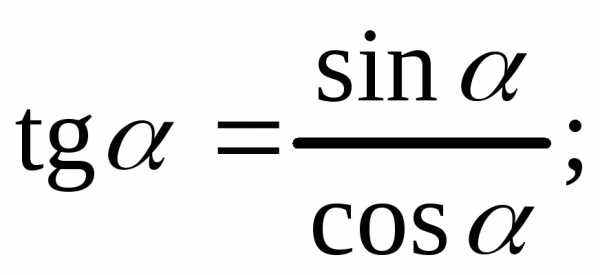 3)
3)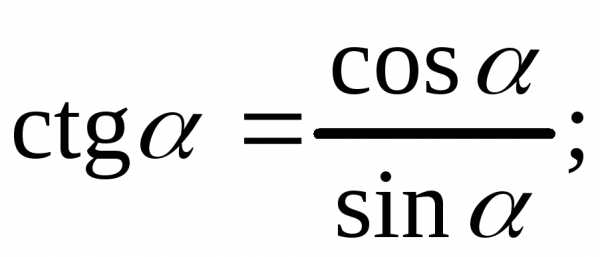
4)
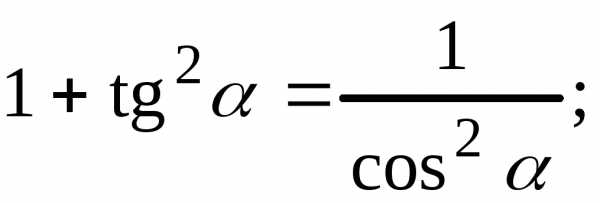 5) 6)
5) 6)
6. Значения тригонометрических функций некоторых аргументов
7. Формулы двойного угла
1) 2)
3)
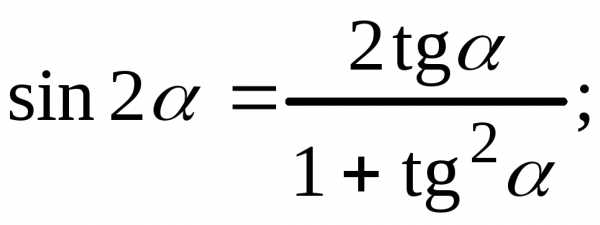 4)
4)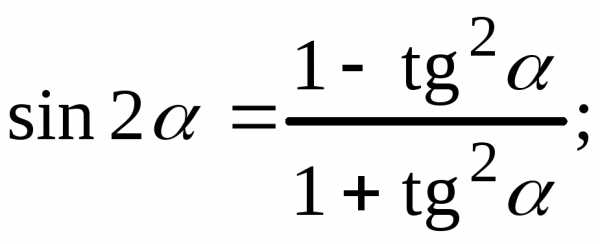 5)
5)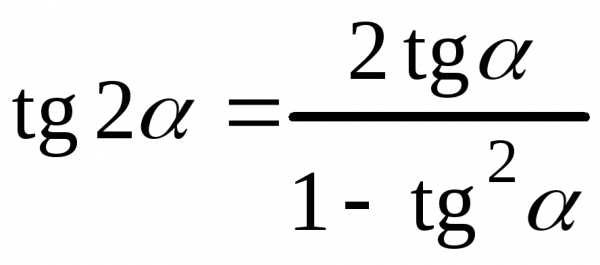
8. Формулы понижения степени
1) 2)
9. Преобразование произведения тригонометрических функций в сумму
1)
2)
3)
Приложение 2
Таблица тригонометрических функций sinx,cosx.
|
Угол, |
sin x |
cos x |
Угол, |
sin x |
cos x |
Угол, |
sin x |
cos x |
|
град |
град |
град | ||||||
|
0 |
0 |
1,0000 | ||||||
|
1 |
0,0175 |
0,9998 |
31 |
0,5150 |
0,8572 |
61 |
0,8746 |
0,4848 |
|
2 |
0,0349 |
0,9994 |
32 |
0,5299 |
0,8480 |
62 |
0,8829 |
0,4695 |
|
3 |
0,0523 |
0,9986 |
33 |
0,5446 |
0,8387 |
63 |
0,8910 |
0,4540 |
|
4 |
0,0698 |
0,9976 |
34 |
0,5592 |
0,8290 |
64 |
0,8988 |
0,4384 |
|
5 |
0,0872 |
0,9962 |
35 |
0,5736 |
0,8192 |
65 |
0,9063 |
0,4226 |
|
6 |
0,1045 |
0,9945 |
36 |
0,5878 |
0,8090 |
66 |
0,9135 |
0,4067 |
|
7 |
0,1219 |
0,9925 |
37 |
0,6018 |
0,7986 |
67 |
0,9205 |
0,3907 |
|
8 |
0,1392 |
0,9903 |
38 |
0,6157 |
0,7880 |
68 |
0,9272 |
0,3746 |
|
9 |
0,1564 |
0,9877 |
39 |
0,6293 |
0,7771 |
69 |
0,9336 |
0,3584 |
|
10 |
0,1736 |
0,9848 |
40 |
0,6428 |
0,7660 |
70 |
0,9397 |
0,3420 |
|
11 |
0,1908 |
0,9816 |
41 |
0,6561 |
0,7547 |
71 |
0,9455 |
0,3256 |
|
12 |
0,2079 |
0,9781 |
42 |
0,6691 |
0,7431 |
72 |
0,9511 |
0,3090 |
|
13 |
0,2250 |
0,9744 |
43 |
0,6820 |
0,7314 |
73 |
0,9563 |
0,2924 |
|
14 |
0,2419 |
0,9703 |
44 |
0,6947 |
0,7193 |
74 |
0,9613 |
0,2756 |
|
15 |
0,2588 |
0,9659 |
45 |
0,7071 |
0,7071 |
75 |
0,9659 |
0,2588 |
|
16 |
0,2756 |
0,9613 |
46 |
0,7193 |
0,6947 |
76 |
0,9703 |
0,2419 |
|
17 |
0,2924 |
0,9563 |
47 |
0,7314 |
0,6820 |
77 |
0,9744 |
0,2250 |
|
18 |
0,309 |
0,9511 |
48 |
0,7431 |
0,6691 |
78 |
0,9781 |
0,2079 |
|
19 |
0,3256 |
0,9455 |
49 |
0,7547 |
0,6561 |
79 |
0,9816 |
0,1908 |
|
20 |
0,3420 |
0,9397 |
50 |
0,7660 |
0,6428 |
80 |
0,9848 |
0,1736 |
|
21 |
0,3584 |
0,9336 |
51 |
0,7771 |
0,6293 |
81 |
0,9877 |
0,1564 |
|
22 |
0,3746 |
0,9272 |
52 |
0,7880 |
0,6157 |
82 |
0,9903 |
0,1392 |
|
23 |
0,3907 |
0,9205 |
53 |
0,7986 |
0,6018 |
83 |
0,9925 |
0,1219 |
|
24 |
0,4067 |
0,9135 |
54 |
0,8090 |
0,5878 |
84 |
0,9945 |
0,1045 |
|
25 |
0,4226 |
0,9063 |
55 |
0,8192 |
0,5736 |
85 |
0,9962 |
0,0872 |
|
26 |
0,4384 |
0,8988 |
56 |
0,8290 |
0,5592 |
86 |
0,9976 |
0,0698 |
|
27 |
0,4540 |
0,8910 |
57 |
0,8387 |
0,5446 |
87 |
0,9986 |
0,0523 |
|
28 |
0,4695 |
0,8829 |
58 |
0,8480 |
0,5299 |
88 |
0,9994 |
0,0349 |
|
29 |
0,4848 |
0,8746 |
59 |
0,8572 |
0,5150 |
89 |
0,9998 |
0,0175 |
|
30 |
0,5000 |
0,8660 |
60 |
0,8660 |
0,5000 |
90 |
1 |
0,0000 |
При ложение 3
Таблица тригонометрических функций tgx.
|
Угол, |
Угол, |
tg x |
Угол, |
Угол, |
tg x |
Угол, |
Угол, |
tg x |
|
град. |
рад. |
град. |
рад. |
град. |
рад. | |||
|
0 |
0 |
0 | ||||||
|
1 |
0,02 |
0,0175 |
31 |
0,54 |
0,6009 |
61 |
1,06 |
1,8040 |
|
2 |
0,03 |
0,0349 |
32 |
0,56 |
0,6249 |
62 |
1,08 |
1,8807 |
|
3 |
0,05 |
0,0524 |
33 |
0,58 |
0,6494 |
63 |
1,10 |
1,9626 |
|
4 |
0,07 |
0,0699 |
34 |
0,59 |
0,6745 |
64 |
1,12 |
2,0503 |
|
5 |
0,09 |
0,0875 |
35 |
0,61 |
0,7002 |
65 |
1,13 |
2,1445 |
|
6 |
0,10 |
0,1051 |
36 |
0,63 |
0,7265 |
66 |
1,15 |
2,2460 |
|
7 |
0,12 |
0,1228 |
37 |
0,65 |
0,7536 |
67 |
1,17 |
2,3559 |
|
8 |
0,14 |
0,1405 |
38 |
0,66 |
0,7813 |
68 |
1,19 |
2,4751 |
|
9 |
0,16 |
0,1584 |
39 |
0,68 |
0,8098 |
69 |
1,20 |
2,6051 |
|
10 |
0,17 |
0,1763 |
40 |
0,70 |
0,8391 |
70 |
1,22 |
2,7475 |
|
11 |
0,19 |
0,1944 |
41 |
0,72 |
0,8693 |
71 |
1,24 |
2,9042 |
|
12 |
0,21 |
0,2126 |
42 |
0,73 |
0,9004 |
72 |
1,26 |
3,0777 |
|
13 |
0,23 |
0,2309 |
43 |
0,75 |
0,9325 |
73 |
1,27 |
3,2709 |
|
14 |
0,24 |
0,2493 |
44 |
0,77 |
0,9657 |
74 |
1,29 |
3,4874 |
|
15 |
0,26 |
0,2679 |
45 |
0,79 |
1,0000 |
75 |
1,31 |
3,7321 |
|
16 |
0,28 |
0,2867 |
46 |
0,80 |
1,0355 |
76 |
1,33 |
4,0108 |
|
17 |
0,30 |
0,3057 |
47 |
0,82 |
1,0724 |
77 |
1,34 |
4,3315 |
|
18 |
0,31 |
0,3249 |
48 |
0,84 |
1,1106 |
78 |
1,36 |
4,7046 |
|
19 |
0,33 |
0,3443 |
49 |
0,86 |
1,1504 |
79 |
1,38 |
5,1446 |
|
20 |
0,35 |
0,3640 |
50 |
0,87 |
1,1918 |
80 |
1,40 |
5,6713 |
|
21 |
0,37 |
0,3839 |
51 |
0,89 |
1,2349 |
81 |
1,41 |
6,3138 |
|
22 |
0,38 |
0,4040 |
52 |
0,91 |
1,2799 |
82 |
1,43 |
7,1154 |
|
23 |
0,40 |
0,4245 |
53 |
0,93 |
1,3270 |
83 |
1,45 |
8,1443 |
|
24 |
0,42 |
0,4452 |
54 |
0,94 |
1,3764 |
84 |
1,47 |
9,5144 |
|
25 |
0,44 |
0,4663 |
55 |
0,96 |
1,4281 |
85 |
1,48 |
11,430 |
|
26 |
0,45 |
0,4877 |
56 |
0,98 |
1,4826 |
86 |
1,50 |
14,301 |
|
27 |
0,47 |
0,5095 |
57 |
0,99 |
1,5399 |
87 |
1,52 |
19,081 |
|
28 |
0,49 |
0,5317 |
58 |
1,01 |
1,6003 |
88 |
1,54 |
28,636 |
|
29 |
0,51 |
0,5543 |
59 |
1,03 |
1,6643 |
89 |
1,55 |
57,290 |
|
30 |
0,52 |
0,5774 |
60 |
1,05 |
1,7321 |
90 |
1,57 |
studfiles.net
