Вопросы»Базовый уровень по математике с решениями. Задание 19. ЕГЭ 2016.|Поступи в ВУЗ
Базовый уровень по математике с решениями. Задание 19. ЕГЭ 2016.
создана: 06.10.2015 в 11:15
…………………………………………
liliana :
В задании 19 базового уровня предложены задачи на тему «Делимость натуральных чисел». Чтобы решить такую задачу, надо хорошо знать признаки делимости натуральных чисел.
Признаки делимости.
Признаки делимости на 2, 3, 4, 6, 8, 9, 11, 5, 25, 10, 100, 1000.
1. Признак делимости на 2. Число делится на 2, если его последняя цифра — ноль или делится на 2. Числа, делящиеся на два, называются чётными, не делящиеся на два – нечётными.
2. Признак делимости на 4. Число делится на 4, если две его последние цифры — нули или образуют число, которое делится на 4.
3. Признак делимости на 8. Число делится на 8, если три его последние цифры — нули или образуют число, которое делится на 8.
4. Признаки делимости на 3
5. Признак делимости на 6. Число делится на 6, если оно делится на 2 и на 3.
6. Признак делимости на 5. Число делится на 5, если его последняя цифра — ноль или 5.
7. Признак делимости на 25. Число делится на 25, если две его последние цифры — нули или образуют число, которое делится на 25.
8. Признак делимости на 10. Число делится на 10, если его последняя цифра — ноль.
9. Признак делимости на 100. Число делится на 100, если две его последние цифры – нули.
10. Признак делимости на 1000. Число делится на 1000, если три его последние цифры -нули.
11. Признак делимости на 11. На 11 делятся только те числа, у которых сумма цифр, стоящих на нечётных местах, либо равна сумме цифр, стоящих на чётных местах, либо отличается от неё на число, делящееся на 11. (Например, 12364 делится на 11, т.к. 1+3+4=2+6.)
Задание 19 (1). Приведите пример трёхзначного числа, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9.
Решение.
Разложим число 20 на слагаемые различными способами:
1) 20 = 9 + 9 + 2
2) 20 = 9 + 8 + 3
3) 20 = 9 + 7 + 4
4) 20 = 9 + 6 + 5
5) 20 = 8 + 8 + 4
6) 20 = 8 + 7 + 5.
Находим сумму квадратов в каждом разложении и проверяем, делится ли она на 3 и не делится на 9?
Замечаем, что, если в разложении 2 числа делятся на 3, то сумма квадратов на 3 не делится.
92+92+22 не делится на 3
При разложении способами (1)−(4) суммы квадратов чисел не делятся на 3.
При разложении способом (5) сумма квадратов делится на 3 и на 9.
Разложение шестым способом удовлетворяет условиям задачи. Таким образом, условию задачи удовлетворяет любое число, записанное цифрами 5, 7 и 8, например, числа 578 или 587 или 785 и т.д.
www.postupivuz.ru
Задание №19 ЕГЭ по математике базового уровня |
Свойства чисел
Задание №19 ЕГЭ по математике весьма необычно. Для его решения необходимо применить знания в области теории чисел. Тем не менее, задание является весьма решаемым, однако для школьников с оценкой хорошо и ниже я рекомендовал бы оставить это задание на последнюю очередь. Перейдем к рассмотрению типового варианта.
Разбор типовых вариантов заданий №19 ЕГЭ по математике базового уровня
Первый вариант задания (демонстрационный вариант 2018)
Найдите трехзначное число, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9. В ответе укажите какое-нибудь оно такое число.
Алгоритм выполнения:
- Ввести условные обозначения.
- Записать условия с помощью условных обозначений.
- Преобразовать полученные выражения.
- Логически рассуждая перебрать все возможные варианты, проверить их соответствие условиям.
Решение:
Обозначим первую цифру числа x, а вторую – y. Тогда третье число с учетом суммы цифр равной 20 будет равно 20 – (x + y). (x + y) обязательно меньше 10, иначе сумма равная 20 не получится.
По условию сумма квадратов цифр делится на 3, но не делится на 9. Запишем сумму квадратов цифр:
x 2 + y2 + (20 – (x + y))2
Преобразуем полученное выражение. Преобразуем квадрат разности с учетом формулы приведения.
Квадрат разности двух выражений равен сумме квадратов этих выражений минус удвоенное произведение первого и второго выражений.
(20 – (x + y))2 = 400 -40(x + y) + (x + y)2
Подставим получившееся выражение в начальное, получим:
x 2 + y2 + (20 – (x + y))2 = x 2 + y2 + 400 — 40(x + y) + (x + y)2
Квадрат суммы двух выражений равен сумме квадратов этих выражений плюс удвоенное произведение первого и второго выражений.
(x + y)2= x2 + 2xy + y2
Подставим:
x 2 + y2 + (20 – (x + y))2 = x 2 + y2 + 400 — 40(x + y) + (x + y)2 = x 2 + y2 + 400 — 40(x + y) + x2 + 2xy + y2
Приведем подобные слагаемые(сложим x2 с x2 и y2 с y2), получим:
x 2 + y2 + 400 — 40(x + y) + x2 + 2xy + y2 = 2x 2 + 2y2 + 2 · 200 — 2 · 20(x + y) + 2xy
Вынесем множитель 2 за скобку:
2x 2 + 2y2 + 2 · 200 — 2 · 20(x + y) + 2xy = 2(x 2 + y2 + 200 — 20(x + y) + xy)
Для удобства объединим 200 и 20(x + y) и вынесем 20 за скобку, получим:
2(x 2 + y2 + 20(10 — (x + y)) + xy)
Множитель 2 – четный, поэтому он никак не влияет на делимость на 3 или 9. Можем его не брать в расчет и рассматривать выражение:
x 2 + y2 + 20(10 — (x + y)) + xy
Предположим, что и x, и y делятся на 3. Тогда x 2 + y2 + xy делится на 3, а 20(10 — (x + y)) – не делится. Следовательно, и вся сумма x 2 + y2 + 20(10 — (x + y)) + xy на 3 не делится.
Предположим, что на 3 делится только одна цифра. Тогда, учитывая, что (x + y) обязательно меньше 10, иначе сумма равная 20 не получится, подберем возможные пары.
(3;8), (6;5), (6;7), (6;8), (9;2), (9;4), (9;5), (9;7), (9;8).
Методом подстановки проверим, соответствуют эти пары условию.
x 2 + y2 + 20(10 — (x + y)) + xy = 3 2 + 82 + 20(10 — (3 + 8)) + 3 · 8 = 9 + 64 – 20 + 24 = 77
x 2 + y2 + 20(10 — (x + y)) + xy = 6 2 + 52 + 20(10 — (6 + 5)) + 6 · 5 = 36 + 25 – 20 + 30 = 71
x 2 + y2 + 20(10 — (x + y)) + xy = 6 2 + 72 + 20(10 — (6 + 7)) + 6 · 7 = 36 + 49 – 60 + 42 = 67
x 2 + y2 + 20(10 — (x + y)) + xy = 6 2 + 82 + 20(10 — (6 + 8)) + 6 · 8 = 36 + 64 – 80 + 48 = 68
x 2 + y2 + 20(10 — (x + y)) + xy = 9 2 + 22 + 20(10 — (9 + 2)) + 9 · 2 = 81 + 4 – 20 + 18 = 83
x 2 + y2 + 20(10 — (x + y)) + xy = 9 2 + 42 + 20(10 — (9 + 4)) + 9 · 4 = 81 + 16 – 60 + 36 = 73
Ни одна из полученных сумм не удовлетворяет условию «сумма квадратов цифр делится на 3, но не делится на 9».
Следующие пары можно не проверять, так как они дают уже имеющиеся тройки цифр.
Предположим, что ни одна из цифр числа не делится на 3.
Возможные пары:
(4;7), (5;7), (5;8), (7;8).
Проверим:
x 2 + y2 + 20(10 — (x + y)) + xy = 4 2 + 72 + 20(10 — (4 + 7)) + 4 · 7 = 16 + 49 – 20 + 28 = 73
x 2 + y2 + 20(10 — (x + y)) + xy = 5 2 + 72 + 20(10 — (5 + 7)) + 5 · 7 = 25 + 49 – 40 + 35 = 69
Сумма 69 удовлетворяет условию «сумма квадратов цифр делится на 3, но не делится на 9». Следовательно, подходят цифры 5,7,8 в любом порядке.
Ответ: 578
Второй вариант задания
На 6 карточках написаны цифры 1; 2; 3; 6; 9; 9 (по одной цифре на каждой карточке). В выражении □ + □□ + □□□ вместо каждого квадратика положили карточку из набора. Оказалось, что полученная сумма делится на 10. Найдите эту сумму. В ответе укажите какое-нибудь одно такое число.
Алгоритм выполнения:
- Вспомнить признак делимости на 10.
- Разместить последние цифры каждого слагаемого таким образом, чтобы в сумме получилось 10.
- Расположить оставшиеся карточки в произвольном порядке.
Решение:
1. Если сумма делится на 10 нацело, то последняя цифра должна быть 0, остальные цифры значения не имеют.
2. В первый квадрат поместим цифру 1, в следующем числе на последнем месте – цифру 3 (или 6), а в третьем – цифру 6 (или 3), получим (сумма 1+3+6=10):
3. Остальные цифры заполним произвольно, например, так:
и получится сумма
1+23+996 = 1020.
Ответ: 1020
Третий вариант задания
На 6 карточках написаны цифры 1; 2; 2; 3; 5; 7 (по одной цифре на каждой карточке). В выражении □ + □□ + □□□ вместо каждого квадратика положили карточку из набора. Оказалось, что полученная сумма делится на 20. Найдите эту сумму. В ответе укажите какое-нибудь одно такое число.
Алгоритм выполнения:
- Вспомнить признак делимости на 10 и сформулировать признак делимости на 20.
- Разместить последние цифры каждого слагаемого таким образом, чтобы в сумме получилось 10.
- Разместить предпоследние цифры каждого слагаемого таким образом, чтобы в сумме получилось четное число в результате с учетом суммы первых цифр.
- Расположить оставшиеся карточки в произвольном порядке.
Решение:
1. Чтобы сумма делилась на 20, она должна заканчиваться на 0 и вторая цифра с конца должна быть четной (делиться на 2). Чтобы в конце суммы получить 0, первые три карточки следует выбрать так:
2. Чтобы вторую цифру получить четной, можно взять карточки 2 и 7 (к ней будет добавляться еще 1 от первой суммы 10):
3. В последнее место помещаем оставшуюся цифру 1, в результате имеем:
и сумма равна:
2+23+175=200.
Ответ: 200
spadilo.ru
Решение всех прототипов задания 19 (база ЕГЭ).
Задача 1366. Найдите шестизначное натуральное число, которое записывается только цифрами 2 и 0 и делится на 24. В ответе укажите какое-нибудь одно такое число.
Решение показать
Искомое натуральное число делится на 24, следовательно, оно делится на 3 и на 8.
Число делится на 3, если сумма его цифр кратна 3.
Число делится на 8, если три его последние цифры делятся на 8 или являются нулями.
Чтобы искомое число делилось на 3, оно должно состоять из шести цифр 2, или из трех цифр 2 и трех цифр 0.
222 не делится на 8, поэтому первый вариант нас не устраивает.
Значит искомое число состоит трех цифр 2 и трех цифр 0.
На 8 в этом случае делится, например, такое число: 222000
Ответ: 222000
Задача 1376. Найдите трехзначное натуральное число, которое при делении на 4, на 5 и на 6 дает в остатке 2 и все цифры которого четные. В ответе укажите какое-нибудь одно такое число.
Решение показать
Сначала найдем число, которое делится на , на и на .
Если число делится на , то его последняя цифра или .
Если число делится на , то две его последние цифры образуют число, которое делится на , или две его последние цифры нули.
Если число делится на , то оно делится на и на , так как .
Если число делится на , то его последняя цифра — четная. И если число делится на , то сумма его цифр делится на .
Тогда для двух последних цифр искомого числа существуют такие варианты:
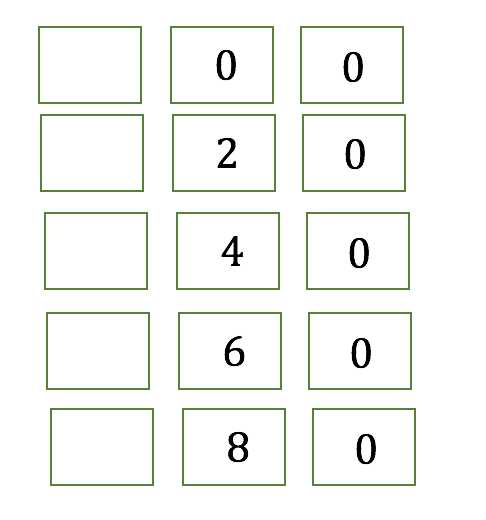
Так как сумма цифр числа делится на , и все цифры четные, получаем такие варианты для первой цифры:

Далее. По условию искомое число при делении на , на и на дает в остатке . Это значит, что если из искомого числа вычесть , то мы получим число, которое делится без остатка на , на и на . То есть чтобы получить искомое число, нужно к числам, записанным в таблице прибавить .
Таким образом, искомым числом может быть одно из следующих:

Ответ: или или или или или .
Задача 1398. Вычеркните в числе 181615121 три цифры так, чтобы получившееся число делилось на 12. В ответе укажите какое-нибудь одно такое число.
Решение показать
Так как искомое число делится на , следовательно, оно делится на и на ().
Следовательно, две его последние цифры образуют число, которое делится на , или две его последние цифры нули (признак делимости на ). И сумма его цифр делится на (признак делимости на ).
Таким образом, точно нужно вычеркнуть последнюю цифру, чтобы две последние цифры образовывали число , которое делится на :
181615121
Теперь нужно вычеркнуть еще две цифры так, чтобы сумма цифр числа делилась на . Сумма всех оставшихся цифр равна Ближайшие числа, которые делятся на это, , , .
Получить не получится, так как — нужно вычеркнуть только одну цифру , а нужно вычеркнуть две.
Чтобы получить нужно из вычесть — это также не получится сделать, зачеркнув две цифры.
Чтобы получить нужно из вычесть . . Значит, нужно вычеркнуть цифру и цифру .
То есть так:
181615121
или так:
181615121
или так:
181615121
Аналогичным образом можно попробовать получить сумму цифр , и т.д.
Но нам достаточно того, что получилось.
Ответ: или .
Задача 6089. Найдите трехзначное число , обладающее следующими свойствами:
В ответе укажите какое-нибудь одно такое число.
Решение показать
Задача 6100. Найдите четырехзначное число, кратное 15, произведение цифр которого больше 35 но меньше 45. В ответе укажите какое-нибудь одно такое число.
Решение показать
Если число кратно , то оно делится на и на ()
Если число делится на , то его последняя цифра или .
Последняя цифра не может быть , так как в этом случае произведение цифр будет равно нулю. Следовательно, последняя цифра равна .
Отсюда произведение трех оставшихся цифр больше чем и меньше чем .
Итак, у нас есть произведение трех цифр, которое больше чем но меньше чем . Следовательно, произведение трех первых цифр равно .
Тогда возможные варианты искомого числа (порядок первых трех цифр произвольный):
1185
1245
Кроме того, поскольку искомое число еще делится на , сумма всех цифр числа, включая последнюю цифру делится на .
Сумма цифр числа 1245 делится на .
Следовательно, искомое число равно . (Также нам подойдут все числа, полученные из числа перестановкой первых трех цифр.)
Ответ: .
Задача 6112. Найдите четырехзначное число, кратное 12, произведение цифр которого равно 10. В ответе укажите какое-нибудь одно такое число.
Решение показать
Если число кратно , то оно делится на и на .
Следовательно, две его последние цифры образуют число, которое делится на , или две его последние цифры нули (признак делимости на ). И сумма его цифр делится на (признак делимости на ).
Последние цифры не могут быть нулями, так как в этом случае произведение цифр будет равно нулю.
Число раскладывается на множители двумя способами:
— этот вариант нам не подходит, так как не является цифрой.
.
Следовательно, число можно представить в виде произведения четырех множителей как .
Таким образом, число, которое мы ищем записывается цифрами , сумма которых равна 9. Следовательно число, записанное этими цифрами делится на .
Две последние цифры должны составлять число, которое делится на — это может быть или .
Таким образом, получим числа
1512 (или 5112)
или
1152
Ответ: или или .
Задача 6123. Найдите четырехзначное число, кратное 44, любые две соседние цифры которого отличаются отличаются на 1. В ответе укажите какое-нибудь одно такое число.
Решение показать
Если число кратно , то оно делится на и на .
Следовательно, две его последние цифры образуют число, которое делится на , или две его последние цифры нули (признак делимости на ). Последние две цифры не могут быть нулями, так как по условию любые две соседние цифры числа отличаются отличаются на 1.
Число делится на 11, если сумма цифр, стоящих на четных местах равна сумме цифр, стоящих на нечетных местах, или разность этих сумм кратна 11. (Признак делимости на 11).
Последними двумя двумя цифрами могут быть, например, 12 или 32 — числа 12 и 32 делятся на 4 и цифры, составляющие эти числа отличаются на 1.
Тогда это могут быть, например, числа
3212
или
1232
В обоих числах суммы цифр стоящих на четных и нечетных местах равны 4.
также подходят числа 1012, 3432, 5456, 5676.
Ответ: 3212, 1232, 1012, 3432, 5456, 5676.
Задача 6134. Найдите четырехзначное число, кратное 66, все цифры которого различны и четны. В ответе укажите какое-нибудь одно такое число.
Решение показать
Если число кратно , то оно делится на , на и на .
Следовательно, его последняя цифра четная, сумма цифр делится на 3, сумма цифр, стоящих на четных местах равна сумме цифр стоящих на нечетных местах, или разность этих сумм кратна 11.
Последнее невозможно, так как все цифры четные.
Так как сумма цифр, стоящих на четных местах равна сумме цифр стоящих на нечетных местах и сумма всех цифр делится на 3, каждая сумма делится на 3.
Этим условиям удовлетворяют, например, числа:
6402
6204
4620
2640
2046
4026
Ответ: 6402, 6204, 4620, 2640, 2046, 4026
Задача 6176. Найдите трехзначное число, кратное 70, все цифры которого различны, а сумма квадратов цифр делится на 5, но не делится на 25. В ответе укажите какое-нибудь одно такое число.
Решение показать
Если число кратно , то оно делится на , и на .
Следовательно, последняя цифра — 0.
Выпишем трехзначные числа, кратные 70:
140, 210, 280, 350, 420, 490, 560, 630, 700, 770, 840, 910, 980.
Вычеркнем содержащие одинаковые цифры:
140, 210, 280, 350, 420, 490, 560, 630, 700, 770, 840, 910, 980.
Сумма квадратов цифр делится на 5, но не делится на 25 у чисел 210, 420, 630, 840, 980
Ответ: 210, 420, 630, 840, 980
Задача 6186. Найдите трехзначное натуральное число, большее 400 но меньшее 650, которое делится на каждую свою цифру, и все цифры которого различны и не равны нулю. В ответе укажите какое-нибудь одно такое число.
Решение показать
Так как число больше 400 но меньше 650, первой цифрой числа могут быть цифры 4, 5 или 6.
Рассмотрим случай, когда первая цифра 4. Тогда число делится на 4, следовательно две его последние цифры образуют число, которое делится на 4. Если число делится на 4, оно также делится на 2.
Кроме того, любое число делится на 1.
Из этих соображений нам подойдет число 412.
Ответ: например, 412.
Задача 6198. Найдите трехзначное натуральное число большее 500, которое при делении на 5 и на 8 дает равные ненулевые остатки и средняя цифра которого является средним арифметическим крайних цифр. В ответе укажите какое-нибудь одно такое число.
Решение показать
Найдем числа, которые делятся без остатка на 5 и на 8. Так как 5 и 8 взаимно простые числа, искомое число за вычетом остатка должно делиться на 40.
Так как искомое число за вычетом остатка делится на 4 и оканчивается на 0, вторая цифра числа обязательно четная.
Чтобы получить искомое число, нужно к числу, которое делится на 40 без остатка прибавить остаток.
Остатком от деления на 5 могут быть числа 1, 2, 3, 4. Следовательно, остаток от деления искомого числа на 5 и на 8 может быть одним из этих чисел.
Пусть первая цифра числа равна 5. Чтобы получить четную цифру на втором месте, остаток должен быть нечетным.
Тогда возможны варианты:
531 (остаток 1)
543 (остаток 3)
Вычтем остаток из этих чисел и проверим, делятся ли полученные числа на 40 без остатка. Ни 530, ни 540 на 40 не делятся.
Пусть первая цифра равна 6. Тогда, чтобы получить четную цифру на втором месте, остаток должен быть четным.
Возможны варианты:
642 (остаток 2)
654 (остаток 4)
Вычтем остаток из этих чисел и проверим, делятся ли полученные числа на 40 без остатка. Число 640 делится на 40 без остатка.
Можно продолжить эти рассуждения и получит другие числа.
Ответ: 642.
Задача 6220. Найдите трехзначное натуральное число, кратно 4, сумма цифр которого равна их произведению. В ответе укажите како-нибудь одно такое число.
Решение показать
Сумма трех цифр равна их произведению, например, в том случае, если это цифры 1, 2, 3.
Составим из этих цифр число, которое делится на 4. Две последние цифры этого числа должны образовать число, которое делится на 4. Это может быть 12 или 32. В таком случае искомым числом может быть одно из чисел 321 или 132.
Ответ: 312, 132.
Задача 9600. Цифры четырехзначного числа, кратного 5, записали в обратном порядке. Затем из первого числа вычли второе и получили 1458. В ответе укажите какое-нибудь одно такое число.
Решение показать
Если число делится кратно 5, то его последняя цифра 0 или 5. 0 не может быть последней цифрой, так в этом случае при записи числа в обратном порядке получим трехзначное число.
Итак, последняя цифра искомого числа 5 и мы имеем такую ситуацию:
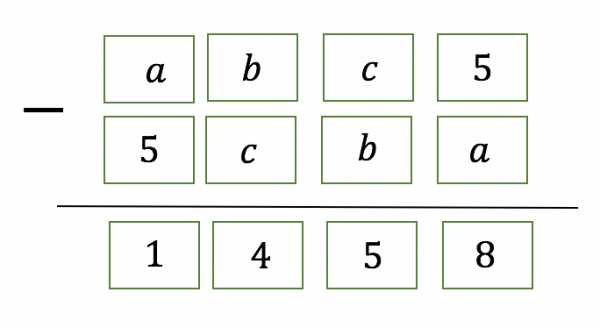
Очевидно, что .
Получим:
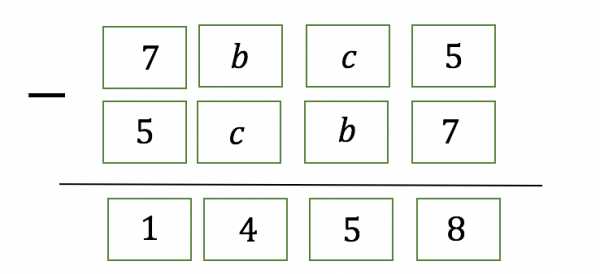
При вычитании в разряде десятков мы из заняли 1. Поэтому получаем: . Отсюда .
При вычитании в разряде сотен мы к добавили 10. Поэтому получаем: . Отсюда . Получили такое же соотношение и .
Поэтому нас устраивает четырехзначное число, у которого первая цифра равна 7, последняя равна 5, а вторая меньше третьей на 6. Например, 7285.
Ответ: 7285.
Задача 9616. Найдите четырехзначное число, которое в три раза меньше четвертой степени некоторого натурального числа. В ответе укажите какое-нибудь одно такое число.
Решение показать
Искомое четырехзначное число можно получить, если разделить четвертую степень какого-нибудь натурального числа на 3. Если четвертая степень натурального числа делится на 3, то само число тоже делится на 3.
Возьмем, например, число 9. . .
Итак, четырехзначное число 2187 в 3 раза меньше, чем .
Ответ: 2187.
ege-ok.ru
Задание 19. Математика ЕГЭ 2018 (базовый уровень): разбор и решение

Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 11 класс. Базовый уровень
Учебник входит в УМК по математике для 10-11 классов, изучающих предмет на базовом уровне. Теоретический материал разделен на обязательный и дополнительный, система заданий дифференцирована по уровню сложности, каждый пункт главы завершается контрольными вопросами и заданиями, а каждая глава — домашней контрольной работой. В учебник включены темы проектов и сделаны ссылки на интернет-ресурсы.
КупитьЗадание 19
На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно –3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно –8.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Решение
А) Пусть среди написанных чисел
x – положительных
y – отрицательных
z – нулей
| Среднее арифметическое чисел = | сумма чисел |
| количество чисел |
Тогда имеем, что
- сумма положительных чисел равна 4x
- сумма отрицательных чисел равна –8y
- сумма всех чисел ряда 4x + (–8y) + 0z = –3(x + y + z)
4(x – 2y + 0z) = –3(x + y + z)
Т.к. левая часть равенства кратна 4, то и правая часть равенства должна быть кратна 4, значит
x + y + z (количество чисел) кратно 4.
40 < x + y + z < 48,
x + y + z = 44
Значит на доске написано 44 числа.
Б) Рассмотрим равенство 4x + (–8y) + 0z = –3(x + y + z)
4x – 8y = – 3x – 3y – 3z
4x + 3x + 3z = 8y – 3y
7x + 3z = 5y
Отсюда получаем, т.к. z ≥ 0 (количество нулей в ряду)
7x < 5y
x < y
Значит положительных чисел меньше, чем отрицательных.
В) Т.к. x + y + z = 44,подставим это значение в равенство 4x + (–8y) + 0z = –3(x + y + z),
получим
4x – 8y = (–3 · 44)/4
x – 2y = –33
x = 2y – 33
Учитывая, что x + y + z = 44, имеем x + y ≤ 44, подставим x = 2y – 33 в данное неравенство
2y – 33 +y ≤ 44
3y ≤ 77
y ≤ 25, учитывая, что x = 2y – 33 получаем x ≤ 17.
Тогда положительных чисел не больше 17.
Ответ: а) 44; б) отрицательных; в) 17.

ЕГЭ-2018. Математика (60х90/16) 10 тренировочных вариантов экзаменационных работ для подготовки к единому государственному экзамену. Профильный уровень
Издание содержит 10 тренировочных вариантов экзаменационных работ для подготовки к ЕГЭ. Каждый вариант составлен в полном соответствии с требованиями ЕГЭ, включает задания профильного уровня. Структура вариантов едина. В конце пособия даны ответы на все задания.
Купить
rosuchebnik.ru
