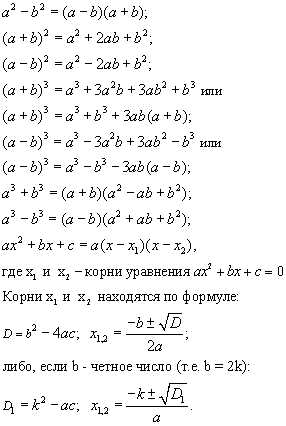| (Ф. Хаусдорф.) ‘ quotes[1]='»Математика — это язык, на котором написана книга природы.»(Г. Галилей) ‘ quotes[2]='»Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели.»(А. Маркушевич) ‘ quotes[3]='»Рано или поздно всякая правильная математическая идея находит применение в том или ином деле.»(А.Н. Крылов) ‘ quotes[4]='»Если вы хотите участвовать в большой жизни, то наполняйте свою голову математикой. Она окажет вам потом огромную помощь во всей вашей работе.»(М.И. Калинин) ‘ quotes[5]='»Разве ты не заметил, что способный к математике изощрен во всех науках в природе?»(Платон) ‘ quotes[6]='»Математика есть лучшее и даже единственное введение в изучение природы.»(Д.И. Писарев) ‘ quotes[7]='»Вдохновение нужно в геометрии не меньше, чем в поэзии.»(А.С. Пушкин) ‘ quotes[8]='»Геометрия полна приключений, потому что за каждой задачей скрывается приключение мысли. Решить задачу – это значит пережить приключение.»(Н.Е. Жуковский) ‘ quotes[10]='»Химия – правая рука физики, математика – ее глаз.»(М.В. Ломоносов) ‘ quotes[11]='»Математику уже затем учить надо, что она ум в порядок приводит.»(М.В. Ломоносов) ‘ quotes[12]='»Математика — это язык, на котором говорят все точные науки.»(Н.И. Лобачевский) ‘ quotes[13]='»Именно математика дает надежнейшие правила: кто им следует – тому не опасен обман чувств.»(Л. Эйлер) ‘ quotes[14]='»Числа не управляют миром, но они показывают, как управляется мир.»(И. Гете) ‘ quotes[15]='»Было бы легче остановить Солнце, легче было сдвинуть Землю, чем уменьшить сумму углов в треугольнике или свести параллели к схождению…»(В.Ф. Каган) ‘ quotes[16]='»Счет и вычисления — основа порядка в голове.»(Песталоцци) ‘ quotes[17]='»Величие человека — в его способности мыслить.»(Б. Паскаль) ‘ quotes[18]='»Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.»(Д.Пойа) ‘ quotes[19]='»Предмет математики столь серьезен, что не следует упускать ни одной возможности сделать его более занимательным.»(Б. Паскаль) ‘ quotes[20]='»В математических вопросах нельзя пренебрегать даже самыми мелкими ошибками.»(И. Ньютон) ‘ quotes[21]='»Первое условие, которое надлежит выполнять в математике, — это быть точным, второе — быть ясным и, насколько можно, простым.»(Л. Карно) ‘ quotes[22]='»Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое.»(М.В. Остроградский) ‘ quotes[23]='»Математика — это цепь понятий: выпадет одно звенышко — и не понятно будет дальнейшее.»(Н.К. Крупская) ‘ quotes[24]='»Математика уступает свои крепости лишь сильным и смелым.»(Ю.А. Шиханович) ‘ quotes[26]='»В каждой естественной науке заключено столько истины, сколько в ней есть математики.»(И. Кант) ‘ var whichquote= Math.floor(Math.random()*(quotes.length)) document.write(quotes[whichquote]) |
free-math.ru
Все главные формулы по математике — Математика — Теория, тесты, формулы и задачи
Оглавление:
Формулы сокращенного умножения
К оглавлению…
Квадрат суммы:
Квадрат разности:
Разность квадратов:
Разность кубов:
Сумма кубов:
Куб суммы:
Куб разности:
Последние две формулы также часто удобно использовать в виде:
Квадратное уравнение и формула разложения квадратного трехчлена на множители
К оглавлению…
Пусть квадратное уравнение имеет вид:
Тогда дискриминант
находят по формуле:Если D > 0, то квадратное уравнение имеет два корня, которые находят по формуле:
Если D = 0, то квадратное уравнение имеет один корень (его кратность: 2), который ищется по формуле:
Если D < 0, то квадратное уравнение не имеет корней. В случае когда квадратное уравнение имеет два корня, соответствующий квадратный трехчлен может быть разложен на множители по следующей формуле:
Если квадратное уравнение имеет один корень, то разложение соответствующего квадратного трехчлена на множители задается следующей формулой:
Только в случае если квадратное уравнение имеет два корня (т.е. дискриминант строго больше ноля) выполняется Теорема Виета. Согласно Теореме Виета, сумма корней квадратного уравнения равна:
Произведение корней квадратного уравнения может быть вычислено по формуле:
Парабола
График параболы задается квадратичной функцией:
При этом координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины:
Игрек вершины параболы:
Свойства степеней и корней
К оглавлению…
Основные свойства степеней:
Последнее свойство выполняется только при n > 0. Ноль можно возводить только в положительную степень.
Основные свойства математических корней:
Для арифметических корней:
Последнее справедливо: если n – нечетное, то для любого a; если же n – четное, то только при a больше либо равном нолю. Для корня нечетной степени выполняется также следующее равенство:
Для корня четной степени имеется следующее свойство:
Формулы с логарифмами
К оглавлению…
Определение логарифма:
Определение логарифма можно записать и другим способом:
Свойства логарифмов:
Логарифм произведения:
Логарифм дроби:
Вынесение степени за знак логарифма:
Другие полезные свойства логарифмов:
Арифметическая прогрессия
К оглавлению…
Формулы n-го члена арифметической прогрессии:
Соотношение между тремя соседними членами арифметической прогрессии:
Формула суммы арифметической прогрессии:
Свойство арифметической прогрессии:
Геометрическая прогрессия
К оглавлению…
Формулы n-го члена геометрической прогрессии:
Соотношение между тремя соседними членами геометрической прогрессии:
Формула суммы геометрической прогрессии:
Формула суммы бесконечно убывающей геометрической прогрессии:
Свойство геометрической прогрессии:
Тригонометрия
К оглавлению…
Пусть имеется прямоугольный треугольник:
Тогда, определение синуса:
Определение косинуса:
Определение тангенса:
Определение котангенса:
Основное тригонометрическое тождество:
Простейшие следствия из основного тригонометрического тождества:
Формулы двойного угла
Синус двойного угла:
Косинус двойного угла:
Тангенс двойного угла:
Котангенс двойного угла:
Тригонометрические формулы сложения
Синус суммы:
Синус разности:
Косинус суммы:
Косинус разности:
Тангенс суммы:
Тангенс разности:
Котангенс суммы:
Котангенс разности:
Тригонометрические формулы преобразования суммы в произведение
Сумма синусов:
Разность синусов:
Сумма косинусов:
Разность косинусов:
Сумма тангенсов:
Разность тангенсов:
Сумма котангенсов:
Разность котангенсов:
Тригонометрические формулы преобразования произведения в сумму
Произведение синусов:
Произведение синуса и косинуса:
Произведение косинусов:
Формулы понижения степени
Формула понижения степени для синуса:
Формула понижения степени для косинуса:
Формула понижения степени для тангенса:
Формула понижения степени для котангенса:
Формулы половинного угла
Формула половинного угла для тангенса:
Формула половинного угла для котангенса:
Тригонометрические формулы приведения
Формулы приведения задаются в виде таблицы:
Тригонометрическая окружность
По тригонометрической окружности легко определять табличные значения тригонометрических функций:
Тригонометрические уравнения
К оглавлению…
Формулы решений простейших тригонометрических уравнений. Для синуса существует две равнозначные формы записи решения:
Для остальных тригонометрических функций запись однозначна. Для косинуса:
Для тангенса:
Для котангенса:
Решение тригонометрических уравнений в некоторых частных случаях:
Геометрия на плоскости (планиметрия)
К оглавлению…
Пусть имеется произвольный треугольник:
Тогда, сумма углов треугольника:
Площадь треугольника через две стороны и угол между ними:
Площадь треугольника через сторону и высоту опущенную на неё:
Полупериметр треугольника находится по следующей формуле:
Формула Герона для площади треугольника:
Площадь треугольника через радиус описанной окружности:
Формула медианы:
Свойство биссектрисы:
Формулы биссектрисы:
Основное свойство высот треугольника:
Формула высоты:
Еще одно полезное свойство высот треугольника:
Теорема косинусов:
Теорема синусов:
Радиус окружности, вписанной в правильный треугольник:
Радиус окружности, описанной около правильного треугольника:
Площадь правильного треугольника:
Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):
Радиус окружности, вписанной в прямоугольный треугольник:
Радиус окружности, описанной вокруг прямоугольного треугольника:
Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):
Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:
Длина средней линии трапеции:
Площадь трапеции:
Площадь параллелограмма через сторону и высоту опущенную на неё:
Площадь параллелограмма через две стороны и угол между ними:
Площадь квадрата через длину его стороны:
Площадь квадрата через длину его диагонали:
Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):
Площадь прямоугольника через две смежные стороны:
Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:
Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):
Свойство касательных:
Свойство хорды:
Теорема о пропорциональных отрезках хорд:
Теорема о касательной и секущей:
Теорема о двух секущих:
Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):
Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):
Свойство центральных углов и хорд:
Свойство центральных углов и секущих:
Условие, при выполнении которого возможно вписать окружность в четырёхугольник:
Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:
Сумма углов n-угольника:
Центральный угол правильного n-угольника:
Площадь правильного n-угольника:
Длина окружности:
Длина дуги окружности:
Площадь круга:
Площадь сектора:
Площадь кольца:
Площадь кругового сегмента:
Геометрия в пространстве (стереометрия)
К оглавлению…
Главная диагональ куба:
Объем куба:
Объём прямоугольного параллелепипеда:
Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):
Объём призмы:
Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):
Объём кругового цилиндра:
Площадь боковой поверхности прямого кругового цилиндра:
Объём пирамиды:
Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):
Объем кругового конуса:
Площадь боковой поверхности прямого кругового конуса:
Длина образующей прямого кругового конуса:
Объём шара:
Площадь поверхности шара (или, другими словами, площадь сферы):
Координаты
К оглавлению…
Длина отрезка на координатной оси:
Длина отрезка на координатной плоскости:
Длина отрезка в трёхмерной системе координат:
Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы):
Таблица умножения
К оглавлению…
Таблица квадратов двухзначных чисел
К оглавлению…
Расширенная PDF версия документа «Все главные формулы по школьной математике»:
К оглавлению…
educon.by
Тригонометрические формулы по алгебре в 10 классе
Инфоурок › Математика › Другие методич. материалы › Тригонометрические формулы по алгебре в 10 классеНайдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсемирная историяВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеДругоеДругойЕстествознаниеИЗО, МХКИзобразительное искусствоИностранные языкиИнформатикаИскусствоИспанский языкИсторияИстория РоссииИстория Средних вековИтальянский языкКлассному руководителюКультурологияЛитератураЛитературное чтениеЛогопедияМатематикаМировая художественная культураМузыкаМХКНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирОсновы безопасности жизнедеятельностиПриродоведениеРелигиоведениеРисованиеРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФинский языкФранцузский языкХимияЧерчениеЧтениеШкольному психологуЭкология
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:
Общая информация
Номер материала: ДБ-404796
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарийinfourok.ru
Все формулы по математике
На этой странице собраны все формулы, необходимые для сдачи контрольных и самостоятельных работ, экзаменов по по алгебре, геометрии, тригонометрии, стереометрии и другим разделам математики.
Здесь вы можете скачать или посмотреть онлайн все основные тригонометрические формулы, формулу площади круга, формулы сокращенного умножения, формула длины окружности, формулы приведения и многие другие.
Можно так же распечатать необходимые сборники математических формул.
Успехов в учебе!
Формулы Арифметики:
Формулы Алгебры:
Геометрические Формулы:
Арифметические формулы:
Законы действий над числамиПереместительный закон сложения: a + b = b + a.
Сочетательный закон сложения: (a + b) + с = a + (b + c).
Переместительный закон умножения: ab = ba.
Сочетательный закон умножения: (ab)с = a(bc).
Распределительный закон умножения относительно сложения: (a + b)с = aс + bс.
Распределительный закон умножения относительно вычитания: (a — b)с = aс — bс.
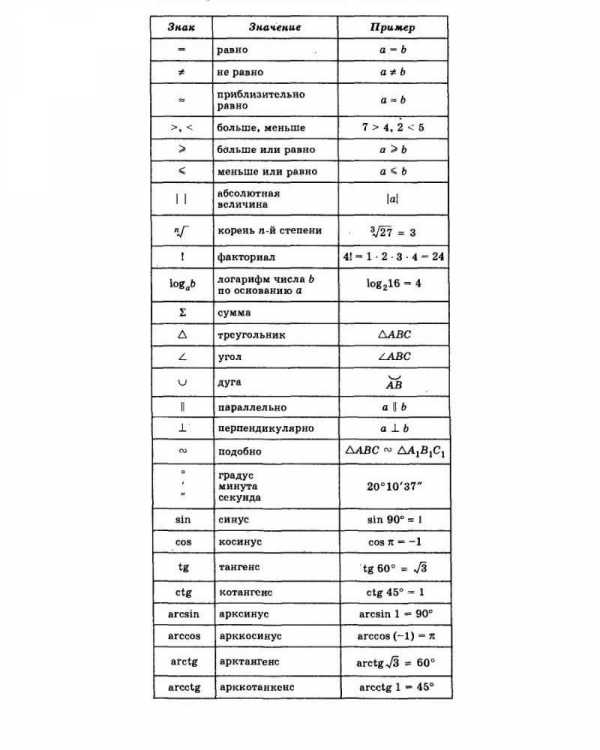
Некоторые математические обозначения и сокращения:
Признаки делимости
Признаки делимости на «2»
- Число, делящееся на «2» без остатка называется чётным, не делящееся – нечётным. Число делится на «2» без остатка, если его последняя цифра чётная (2, 4, 6, 8) или ноль
Признаки делимости на «4»
- Число делится на «4» без остатка, если две последние его цифры нули или в сумме образуют число, делящееся без остатка на «4»
Признаки делимости на «8»
- Число делится на «8» без остатка, если три последние его цифры нули или в сумме образуют число, делящееся без остатка на «8» (пример: 1 000 — три последние цифры «00», а при делении 1 000 на 8 получается 125; 104 — две последние цифры «12» делятся на 4, а при делении 112 на 4 получается 28; и.т.д.)
Признаки делимости на «3» и на «9»
- Без остатка на «3» делятся только те числа, у которых сумма цифр делится без остатка на «3»; на «9» — только те, у которых сумма цифр делится без остатка на «9»
Признаки делимости на «5»
- Без остатка на «5» делятся числа, последняя цифра которых «0» или «5»
Признаки делимости на «25»
- Без остатка на «25» делятся числа, две последние цифры которых нули или в сумме образуют число, делящееся без остатка на «25» (т.е. числа, оканчивающиеся на «00», «25», «50», «75»
Признаки делимости на «10», «100» и на «1 000»
- Без остатка на «10» делятся только те числа, последняя цифра которых ноль, на «100» — только те числа, у которых две последние цифры нули, на «1000» — только те числа, у которых три последние цифры нули
Признаки делимости на «11»
- Без остатка на «11» делятся только те числа, у которых сумма цифр, занимающих нечётные места, либо равна сумме цифр, занимающих чётные места, либо отличается от неё на число, делящееся на «11»
Абсолютная величина — формулы (модуль)
|a| ? 0, причём |a| = 0 только если a = 0; |-a|=|a| |a2|=|a|2=a2 |ab|=|a|*|b| |a/b|=|a|/|b|, причём b ? 0; |a+b|?|a|+|b| |a-b|?|a|-|b|Формулы Действия с дробями
Формула обращения конечной десятичной дроби в рациональную дробь:
Пропорции
<span «>Два равных отношения образуют пропорцию:
Основное свойство пропорцииad = bc
Нахождение членов пропорции
Пропорции, равносильные пропорции : Производная пропорция — следствие данной пропорции в видеСредние величины
Некоторые конечные числовые ряды
Алгебра:
Тождественные преобразования алгебраических и тригонометрических выражений
Свойства степеней
- Для любых x, y и положительных a и b верны равенства:
Свойства арифметических корней
Для любых натуральных n и k, больших 1, и любых неотрицательных a и b верны равенства:Многочлены
Для любых a, b и c верны равенства:
Свойства числовых неравенств
1) Если a < b, то при любом c: a + с < b + с.
2) Если a < b и c > 0, то aс < bс.
3) Если a < b и c < 0, то aс > bс.
4) Если a < b, a и b одного знака, то 1/a > 1/b.
5) Если a < b и c < d, то a + с < b + d, a — d < b — c.
6) Если a < b, c < d, a > 0, b > 0, c > 0, d > 0, то ac < bd.
7) Если a < b, a > 0, b > 0, то
8) Если , то
Соотношения между тригонометрическими функциями одного и того же аргумента
(здесь и в дальнейшем запись n є Z означает, что n – любое целое число)Формулы сложения:
Формулы двойного аргумента:
Формулы тройного аргумента:
Формулы Прогрессии:
Арифметическая прогрессия
(a1 – первый член; d – разность; n – число членов; an – n-й член; Sn – сумма n первых членов):
Геометрическая прогрессия
(b1 – первый член; q – знаменатель; n – число членов; bn – n-й член; Sn – сумма n первых членов, S – сумма бесконечной геом. прогрессии):
Производная
Основные правила дифференцирования:
- Логарифмы:
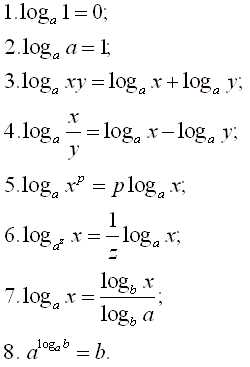
- Координаты и векторы
1. Расстояние между точками A1(x1;y1) и A2(x2;y2) находится по формуле:
2. Координаты (x;y) середины отрезка с концами A1(x1;y1) и A2(x2;y2) находится по формулам:
3. Уравнение прямой с угловым коэффициентом и начальной ординатой имеет вид:
y = kx + q.
Угловой коэффициент k представляет собой значение тангенса угла, образуемого прямой с положительным направлением оси Ox, а начальная ордината q – значение ординаты точки пересечения прямой с осью Oy.
4. Общее уравнение прямой имеет вид: ax + by + c = 0.5. Уравнения прямых, параллельных соответственно осям Oy и Ox, имеют вид:
ax + by + c = 0.6. Условия параллельности и перпендикулярности прямых y1=kx1+q1 и y2=kx2+q2 соответственно имеют вид:
7. Уравнения окружностей с радиусом R и с центром соответственно в точках O(0;0) и C(xo;yo) имеют вид:
8. Уравнение:представляет собой уравнение параболы с вершиной в точке, абсцисса которой
- Прямоугольная декартова система координат в пространстве
1. Расстояние между точками A1(x1;y1;z1) и A2(x2;y2;z2) находится по формуле:
2. Координаты (x;y;z) середины отрезка с концами A1(x1;y1;z1) и A2(x2;y2;z2) находятся по формулам:
3. Модуль вектора заданного своими координатами, находится по формуле:
4. При сложении векторов их соответствующие координаты складываются, а при умножении вектора на число все его координаты умножаются на это число, т.е. справедливы формулы:
5. Единичный вектор сонаправленный с вектором находится по формуле:
6. Скалярным произведением векторов называется число:
где — угол между векторами.
7. Скалярное произведение векторов
8. Косинус угла между векторами и находится по формуле:
9. Необходимое и достаточное условие перпендикулярности векторов и имеет вид:10. Общее уравнение плоскости, перпендикулярной вектору имеет вид:
ax + by + cz + d = 0.11. Уравнение плоскости, перпендикулярной вектору и проходящей через точку (xo;yo;zo), имеет вид:
a(x — xo) + b(y — yo) + c(z — zo) = 0.12. Уравнение сферы с центром O(0;0;0) записывается в виде:
- Комбинаторика и бином Ньютона
1) Число перестановок из n элементов находится по формуле:
2) Число размещений из n элементов по m находится по формуле:
3) Число сочетаний из n элементов по m находится по формуле:
4) Справедливы следующие свойства сочетаний:
5) Формула бинома Ньютона имеет вид:
Сумма показателей чисел a и b равна n.
6) (k+1)-й член находится по формуле:
7) Число сочетаний также можно найти по треугольнику Паскаля.
Треугольник Паскаля (до n=7):
8) Сумма биномиальных коэффициентов равна 2n.
9) Чтобы найти биномиальный коэффициент следующего члена, нужно биномиальный коэффициент предыдущего члена умножить на показатель числа a и разделить на кол-во предыдущих членов.
- Пределы
- Теоремы о пределах
- Замечательные пределы
- Неопределенные интегралы
Геометрия
advice-me.ru
Алгебра 10-11 классы — Всё для чайников
- Главная
- Видеотека
- Естествознание
- Физика
- Математика
- Химия
- Биология
- Экология
- Обществознание
- Обществознание — как наука
- Иностранные языки
- История
- Психология и педагогика
- Русский язык и литература
- Культурология
- Экономика
- Менеджмент
- Логистика
- Статистика
- Философия
- Бухгалтерский учет
- Технические науки
- Черчение
- Материаловедение
- Сварка
- Электротехника
- АСУТП и КИПИА
- Технологии
- Теоретическая механика и сопромат
- САПР
- Метрология, стандартизация и сертификация
- Геодезия и маркшейдерия
- Программирование и сеть
- Информатика
- Языки программирования
- Алгоритмы и структуры данных
- СУБД
- Web разработки и технологии
- Архитектура ЭВМ и основы ОС
- Системное администрирование
- Создание программ и приложений
- Создание сайтов
- Тестирование ПО
- Теория информации и кодирования
- Функциональное и логическое программирование
- Программы
- Редакторы и компиляторы
- Офисные программы
- Работа с аудио видео
- Работа с компьютерной графикой и анимацией
- Автоматизация бизнеса
- Прочие
- Музыка
- Природное земледелие
- Рисование и живопись
- Естествознание
- Библиотека
- Естествознание
- Физика
- Математика
- Химия
- Биология
- Экология
- Астрономия
- Обществознание
- Естествознание
forkettle.ru
Основные формулы математики
Дорогие друзья! Весь справочный материал вы найдете на страницах «Математика», «Алгебра» и «Геометрия» моего сайта. По многим разделам ( там, где кликабельные заголовки) имеется пояснительный материал с примерами.
Уважаемые родители! Если Вы ищите репетитора по математике для Вашего ребёнка, то это объявление для Вас. Предлагаю скайп-репетиторство: подготовка к ОГЭ, ЕГЭ, ликвидация пробелов в знаниях. Ваши выгоды очевидны:
1) Ваш ребенок находится дома, и Вы можете быть за него спокойны;
2) Занятия проходят в удобное для ребенка время, и Вы даже можете присутствовать на этих занятиях. Объясняю я просто и доступно на всем привычной школьной доске.
3) Другие важные преимущества скайп-занятий додумаете сами!
Напишите мне по адресу: [email protected] или сразу добавляйтесь ко мне в скайп, и мы обо всём договоримся. Цены доступные.
P.S. Возможны занятия в группах по 2-4 учащихся.
С уважением Татьяна Яковлевна Андрющенко.
Друзья! На этой странице я предлагаю вам получить все формулы математики (и алгебры и геометрии) за 7-11 классы. Разумеется, бесплатно. Пройдите по ссылке.
Трудно решать примеры и задачи, не имея под рукой формул. Так что получите, распечатайте и пользуйтесь на здоровье! Инструкция по распечатке сборника формул здесь! Воспользуйтесь ею, и Вы получите удобную книжечку. Желаю вам легко повторить и запомнить все формулы. Удачи!
Дорогие друзья! Готовитесь к ОГЭ или ЕГЭ? Вам в помощь «Справочник по геометрии 7-9». Подробнее здесь.
Дорогие друзья! Если вас затрудняют задачи на проценты, то вам поможет книга «Как решать задачи на проценты». Как её получить — смотрите здесь!
Дорогие друзья! По вашим просьбам я сделала подборку всех правил и формул по математике для 5 класса. Этот небольшой справочник будет полезен и детям и их родителям, ведь зная, что именно должен выучить учащийся в 5 классе, взрослым будет легче помочь и проконтролировать своего ребенка! А когда учебный год закончится, и учебники будут сданы в библиотеку — у вас останется мой справочник, а значит, и возможность летом все повторить и отлично подготовиться к 6 классу! Справочник МАТЕМАТИКА 5. Переходите по ссылке здесь!
Дорогие друзья! Не секрет, что некоторые дети испытывают трудности при умножении и делении в столбик. Чаще всего это связано с недостаточным знанием таблицы умножения. Предлагаю подучить таблицу умножения с помощью лото. Посмотреть видео презентацию здесь. Скачать лото здесь.
www.mathematics-repetition.com
Математика.10 класс. Формулы сложения.docx — План урока по математике на …
Раздел 10.4.A. Тригонометрия
Тема: Формулы сложения
Дата: 27.031.04.2017
Date:
Класс: 10 g
Урок № 12
Ожидаемые
результаты данного
урока
Learning objectives that
this
is
contributing to
Цели урока
Learning objectives
lesson
Критерии успеха
Языковые цели
language objectives
Привитие ценностей
Межпредметные связи
Навыки использования
ИКТ
Первоначальные
знания
Школа: НИШ ХБН г. Атырау
Имя учителя: Адилгалиева Ж.С
Количество
присутствующих:
Количество
отсутствующих:
АТ 10.5.выводить и применять формулы приведения, формулы сложения,
формулы двойного/половинного аргумента, формулы преобразования
суммы и разности тригонометрических функций в произведение, формулы
преобразования произведения тригонометрических функций в сумму при
решении задач
отработать навыки использования тригонометрических формул сложения,
двойного аргумента и преобразования суммы в произведение;
рассмотреть построение графиков функций, полученные путем сжатия,
растяжения и перемещения исходных графиков тригонометрических функций;
сформировать умение применять формулы сложения и их свойства, а так же
свойства функций при решение заданий различной степени сложности;
Учащиеся достиг цели, если
выводит и применяет формулы приведения, формулы сложения, формулы
двойного/половинного аргумента, формулы преобразования суммы и разности
тригонометрических функций в произведение, формулы преобразования
произведения тригонометрических функций в сумму при решении задач
Учащиеся понимают и объясняют, как использовать графические калькуляторы
Предметная лексика и терминология.
sin, cos, tan (синус, косинус, тангенс)
угол возвышения/понижения
инверсия, горизонтальная, ось (оси), область определения.
арксинус, арккосинус, арктангенс
формула приведения/сложения
преобразование в точке пересечения, преобразование функции
Серия полезных фраз для диалога/письма
Давать четкие, точно выраженные указания по использованию калькулятора,
например:
Ввести функцию.
Перейти в {Режим} в 3 ряду.
Выбрать НАСТРОЙКА/УВЕЛИЧЕНИЕ.
Установить расстояние (интервал).
Настроить yMax/yMin.
Нажать на кнопку
Использовать стрелкууказатель
Уважение, сотрудничество, открытость
Привитие ценностей осуществляется посредством/через парную и групповую виды
работ.
Power point
Имеет представления о тригонометрических функциях
Ход урока
Этапы урока
Planned timings
Первый урок
First lesson
1 мин
Актуализация
опорных знаний
Запланированная деятельность на уроке
Planned activities
Приветствие учащихся, проверка готовности к уроку,
мотивация учащихся, объявляет план урока
Включение в деловой ритм, подготовка класса к работе
Активировать знания, необходимые для изучения новой темы
Организация учащихся на постановку темы и целей урока
Актуализация познавательного интереса к изучаемой теме
Ресурсы
Resources
znanio.ru
