Олимпиада по математике 9 класс, задания, уравнения, задачи с ответами
Курс математики в 9 классе посвящен достаточно серьезным темам. Ученики знакомятся с решением квадратных неравенств, понятиями множества и подмножества, числовыми функциями и прогрессиями. Участие в олимпиадах по математике для учеников 9 класса является хорошей возможностью подготовки к предстоящей ГИА.
На этой странице предложены реальные примеры олимпиадных заданий по математике. Ученикам предложены уравнения и задачи с решениями и ответами.
Данный материал может использоваться на занятиях для подготовки к олимпиаде, а также во время проведения контрольных или итоговых работ по математике. Подробные решения задач, расписанные внизу страницы помогут провести работу над ошибками и восполнить пробелы в знаниях учащихся.
Уравнения
1. Решите уравнение: − − 3 = 0
2. Решите уравнение: − + 2 = 0
3. Решите уравнение: − + 4 = 0
4. Решите уравнение: ( + )( + + 2) = 3
5. Решите уравнение: x4 − + 18 = 0
6. Решите уравнение: ( − − 16)( − + 2) = 88
7. Решите уравнение: ( + )( + − 5) = 84
8. Решите уравнение: ( − 1)( + 1) − 4( − 11) = 0
9. Решите уравнение: + − − + + 5 = 0
10. При каких с не имеет корней уравнение: − + с = 0
Задачи
Задача №1
Можно ли представить дробь 2/7 в виде суммы двух дробей, числители которых равны 1, а знаменатели — различные целые числа?
Задача №2
Токарь и его ученик, работая одновременно, обычно выполняют задание за 4 часа. При этом производительность труда токаря в 2 раза выше производительности ученика. Получив такое же задание, и, работая по очереди, они справились с заданием за 9 часов работы. Какую часть задания выполнил ученик токаря.
Задача №3
Стрелок десять раз выстрелил по стандартной мишени и выбил 90 очков. Сколько попаданий было в семерку, восьмерку и девятку, если десяток было четыре, а других попаданий и промахов не было?
Задача №4
На столе лежат 2005 монет. Двое играют в следующую игру: ходят по очереди; за ход первый может взять со стола любое нечетное число монет от 1 до 99, второй – любое четное число монет от 2 до 100. Проигрывает тот, кто не сможет сделать ход. Кто выиграет при правильной игре?
Задача №5
Имеются два сосуда, в первом из них 1 л воды, второй сосуд пустой. Последовательно проводятся переливания из первого сосуда во второй, из второго в первый и т. д., причем доля отливаемой воды составляет последовательно 1/2, 1/3, 1/4 и т. д. от количества воды в сосуде, из которого вода отливается. Сколько воды будет в сосудах после 2007 переливаний?
Ответы к уравнениям
| Уравнение | № 1 | № 2 | № 3 | № 4 | № 5 |
| Ответ | ± | нет корней |
± | -1; 3 | ±; ± |
| Уравнение | № 6 | № 7 | № 8 | № 9 | № 10 |
| Ответ | -4; 5 | -3; 4 | нет корней | ±1; ± | c > 36 |
Ответы к задачам
Задача 1
Можно. Например, 2/7=1/4+1/28.
Задача 2
Ученик выполнит 1\2 часть задания
Задача 3
Так как стрелок попадал лишь в семерку, восьмерку и девятку в остальные шесть выстрелов, то за три выстрела (по одному разу в семерку, восьмерку и девятку) он наберет 24 очка. Тогда за оставшиеся 3 выстрела надо набрать 26 очков. Что возможно при единственной комбинации 8 + 9 + 9 = 26. Итак, в семерку стрелок попал 1 раз, в восьмерку – 2 раза, в девятку – 3 раза.
Задача 4
Опишем стратегию первого игрока. Первым ходом он должен взять со стола 85 монет. Каждым следующим, если второй игрок берет х монет, то первый игрок должен взять 101 – x монет (он всегда может это сделать, потому что если х – четное число от 2 до 100, то (101 – x) – нечетное число от 1 до 99). Так как 2005 = 101 × 19 + 85 + 1, то через 19 таких «ответов» после хода первого на столе останется 1 монета, и второй не сможет сделать ход, т. е. проиграет.
Задача 5
«Просчитав» несколько первых переливаний, нетрудно обнаружить, что после первого, третьего, пятого переливаний в обоих сосудах будет по ½ л воды. Необходимо доказать, что так будет после любого переливания с нечетным номером. Если после переливания с нечетным номером 2k-1 в сосудах было по ½ л, то при следующем переливании из второго сосуда берется 1/(2k + 1) часть, так что в первом сосуде оказывается — 1/2 + (2/2(2k + 1)) = (k + 1)/(2k + 1) (л). При следующем переливании, имеющем номер 2k + 1, из него берется 1/(2k + 2) часть и остается (k + 1)/(2k + 1)-(k + 1)/((2k + 1)(2k + 1)) = 1/2 (л). Поэтому после седьмого, девятого и вообще любого нечетного переливания в сосудах будет по ½ л воды.
Другие классы
Обновлено: , автор: Валерия Токареваruolimpiada.ru
Недельные домашние задания для подготовки к ОГЭ по математике для 9 класса
Главная / Старшие классы / Алгебра Скачать34.87 КБ, 430702.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015
Скачать 36.07 КБ, 430704.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015 Скачать34.82 КБ, 430705.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015
Скачать35.31 КБ, 430707.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015
Скачать34.18 КБ, 430708.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015
Скачать76.41 КБ
76.34 КБ, 430711.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015
Скачать75.63 КБ, 430713.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015
Скачать67.64 КБ, 430714.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015
Скачать79.12 КБ, 430716.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015
Скачать 97.49 КБ, 430718.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015 Скачать101.84 КБ, 430719.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015
Скачать78.79 КБ, 430720.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015
Скачать89.1 КБ, 430722.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015
Скачать
91.75 КБ, 430723.docx
52.91 КБ, 430724.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015
Скачать64.85 КБ, 430726.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015
Скачать65.17 КБ, 430728.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015
Скачать39.67 КБ, 430729.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015
Скачать 37.57 КБ, 430730.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015 Скачать408.74 КБ, 430732.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015
Скачать170.25 КБ, 430734.docx Автор: Эльснер Мария Владимировна, 21 Мар 2015
Данный материал предназначен для подготовки к ОГЭ по математике для 9 класса. Подобраны прототипы по алгебре и геометрии для успешного выполнения части В
Автор: Эльснер Мария Владимировна
Похожие материалы
| Тип | Название материала | Автор | Опубликован |
|---|
pedportal.net
Решебник (ГДЗ) по математике за 9 класс
Решебники, ГДЗ
-
1 Класс
- Математика
- Русский язык
- Английский язык
- Информатика
- Немецкий язык
- Литература
- Человек и мир
- Природоведение
- Основы здоровья
- Музыка
- Окружающий мир
-
2 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Украинский язык
- Немецкий язык
- Литература
- Человек и мир
- Природоведение
- Основы здоровья
- Музыка
- Окружающий мир
- Технология
-
3 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Украинский язык
- Немецкий язык
- Литература
- Музыка
- Окружающий мир
- Испанский язык
-
4 Класс
- Математика
- Русский язык
- Белорусский язык
- Английский язык
- Информатика
- Украинский язык
- Немецкий язык
- Литература
- Человек и мир
- Основы здоровья
- Музыка
- Окружающий мир
megaresheba.ru
Задания «ОГЭ математика- 2 часть 21-26задания» (9класс)
21 задание
1’.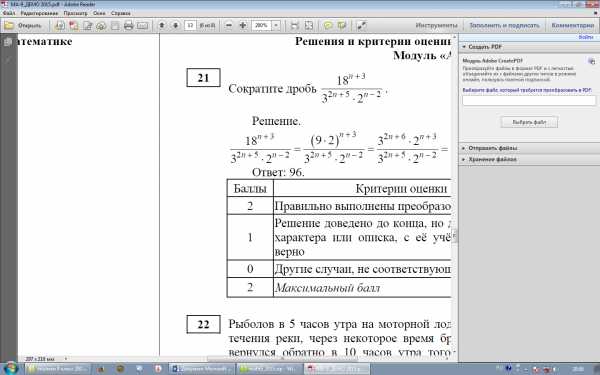
2’.
3’.
4’.
5’.
6’.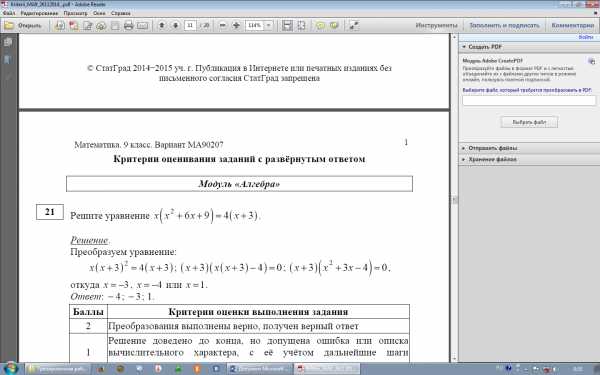
7’.
8’.
9’.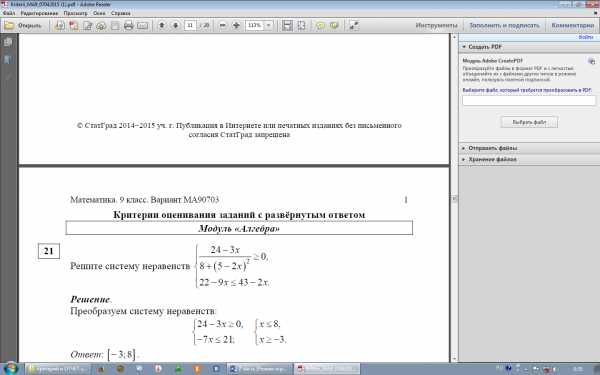
10’.
11’.Решите систему уравнений
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11. Решите неравенство
12. Решите систему уравнений
13. Решите систему уравнений
14. Решите систему уравнений
15. Выполните преобразования
16. Выполните преобразования
17. Решить неравенство
18. Решите уравнение
19.
20.
21.
22.
infourok.ru
