Спецкурс по математике 11 класс
Муниципальное бюджетное общеобразовательное учреждение
«Гимназия № 3 г. Горно-Алтайска»
На кафедре учителей
математики и информатики
МБОУ « Гимназия № 3
Протокол № 2
от « 29 » августа 2016г.
Руководитель кафедры:______/И.Н.Шарикова/
«Согласовано»
с методическим советом,
протокол №___
« _30___ » ___09______.2016г.
_______/О.М.Казанцева/
«Утверждаю»
Директор МБОУ Гимназия № 3 г.Горно-Алтайска
______ /В.В. Техтиекова/
Приказ № 14
от «__30__»_____________.2016г.
РАБОЧАЯ ПРОГРАММА
спецкурса
по математике для учащихся 11 класса
«Подготовка к единому
государственному экзамену»
(68часов)
Составитель : Голвко Валентина Васильевна,
МБОУ «Гимназия №3 г. Горно-Алтайска»
2. Пояснительная записка
Актуальность курса:
Данная программа элективного курса своим содержанием рассчитана для учащихся 11 классов. Этот курс предлагает учащимся знакомство с математикой как с общекультурной ценностью, выработкой понимания ими того, что математика является инструментом познания окружающего мира и самого себя. На занятиях этого курса есть возможность устранить пробелы ученика по тем или иным изученным темам. Учитель помогает выявить слабые места ученика, оказывает помощь при систематизации материала, готовит правильно оформлять экзаменационные бланки ответов. Навыки решения математических задач необходимы всякому ученику, желающему хорошо подготовиться и успешно сдать экзамены по математике, добиться значимых результатов при участии в математических конкурсах и олимпиадах.
Структура курса:
Особенность элективного курса «Подготовка к ЕГЭ» состоит в том, что для занятий по математике предлагаются небольшие фрагменты, относящиеся к различным разделам школьной математики.
Каждое занятие направлено на то, чтобы развить интерес школьников к предмету, познакомить их с новыми идеями и методами, расширить представление об изучаемом в основном курсе материале, а главное, прорешать интересные задачи.
Данный курс является базовым общеобразовательным, отражает обязательную для всех школьников инвариативную часть образования и направлен на успешное завершение общеобразовательной подготовки обучающихся.
Элективный курс « Подготовка к ЕГЭ» рассчитан на 34 часа и предусматривает повторное рассмотрение теоретического материала по математике, а кроме этого, нацелен на более глубокое рассмотрение отдельных тем, поэтому имеет большое общеобразовательное значение, способствует развитию логического мышления, намечает и использует целый ряд межпредметных связей (прежде всего с физикой и геометрией, химией, биологией, информатикой, историей возникновения математики).
Цели данного курса:
Оказание индивидуальной и систематической помощи выпускнику при повторении, обобщении и систематизации курса алгебры и геометрии и подготовке к экзаменам;
Создание целостного представления о теме и значительно расширить спектр задач, посильных для учащихся.
Задачи курса:
-подготовить учащихся к экзаменам;
-дать ученику возможность проанализировать и раскрыть свои способности;
Для работы с учащимися применимы такие формы работы, как лекция, семинар, практические занятия.
Предлагаемый курс является развитием системы ранее приобретенных программных знаний. Все свойства, входящие в спецкурс, и их доказательства не вызовут трудности у учащихся, т.к. не содержат громоздких выкладок, а каждое предыдущее готовит последующее. При направляющей роли учителя школьники могут самостоятельно сформулировать новые для них свойства и даже доказать их. Все должно располагать к самостоятельному поиску и повышать интерес к изучению предмета.
Организация на занятиях может несколько отличается от урочной: ученику необходимо давать время на размышление, учить рассуждать, выдвигать гипотезы. В курсе заложена возможность дифференцированного обучения. При решении ряда задач необходимо рассмотреть несколько случаев. Одной группе учащихся полезно дать возможность самим открыть эти случаи. В другой — учитель может сузить требования и рассмотреть один из случаев.
Таким образом, программа применима для различных групп школьников.
-ориентация на совершенствование навыков познавательной, организационной деятельности;
-компенсация недостатков обучения по математике.
Требования к уровню освоения курса:
-Материал курса должен быть освоен на базовом уровне. Учитель может провести самостоятельные работы, пробный экзамен, зачёты по конкретным темам.
-Организация и проведение аттестации учащихся
-Основными результатами освоения содержания элективного курса учащимися может быть определенный набор общеучебных умений, а также опыт внеурочной деятельности, содержательно связанной с предметным полем – математикой. При этом должна использоваться преимущественно качественная оценка выполнения заданий, а также итоговое тестирование учащихся.
-Начинается курс с ознакомительной вводной лекции. Следующее за ней занятие посвящается входному тестированию, цели которого:
-составить представление учителя об уровне базовых знаний учащихся, выбравших курс.
-коррекция в связи с этим уровня подачи материала по данному курсу.
При прослушивании блоков лекционного материала и проведения семинара, закрепляющего знания учащихся, предусматривается индивидуальное или групповое домашнее задание, содержащее элементы исследовательской работы, задачи для самостоятельного решения. Защита решений и результатов исследований проводится на выделенном для этого занятии и оценивается по пятибалльной системе или системе «зачет-незачет», в зависимости от уровня подготовленности группы.
Возможная форма итоговой аттестации:
Итоговая контрольная работа (по заданиям ЕГЭ прошлых лет).
Ожидаемый результат изучения курса:
учащийся должен знать/понимать/:
-существо понятия алгоритма; примеры алгоритмов;
-как используются математические формулы, уравнения и неравенства;
-примеры их применения для решения математических и практических задач;
-как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
-значение математики как науки и значение математики в повседневной жизни, а также как прикладного инструмента в будущей профессиональной деятельности
-решать задания, по типу приближенных к заданиям ЕГЭ
-иметь опыт (в терминах компетентностей):
-работы в группе, как на занятиях, так и вне, работы с информацией, в том числе и получаемой посредством Интернет
Методические рекомендации по реализации программы:
Основным дидактическим средством для предлагаемого курса являются тексты рассматриваемых типов задач, которые могут быть выбраны из разнообразных сборников, различных вариантов ЕГЭ или составлены самим учителем .Курс обеспечен раздаточным материалом, подготовленным на основе прилагаемого ниже списка литературы.
Для более эффективной работы учащихся целесообразно в качестве дидактических средств использовать плакаты с опорными конспектами или медиа ресурсы, банк заданий(интернет ФИПИ).
Минимум содержание учебного материала:
Концептуальную основу курса составляет идея подготовки учащихся к сдаче единого государственного экзамена по математике. Поэтому в содержание курса включены основные ключевые темы школьного курса математики, входящие в материалы ЕГЭ. Выделены основные содержательные линии:
Выражения и их преобразования.
Уравнения.
Неравенства.
Производная. Первообразная.
Каждая линия (блок) содержит систематизированный справочный материал, примеры на применение каждого вида справочного материала, варианты разного уровня заданий для самостоятельной работы, набор заданий для самостоятельного составления теста и список дополнительной литературы.
4. Содержание курса
Вводная лекция «Чем занимается алгебра».
Предмет, изучению которого посвящен данный курс. Исторические сведения. Связь с базовым курсом школьной математики. Организационные моменты о формах работы с элективным курсом. Входное тестирование.
Об эволюции понятия числа.
Историческая справка о развитии понятия числа (экскурс в историю математики).
4. Основные законы и формулы алгебры.
Основные законы алгебры. Исторические справки. Формулы сокращенного умножения, их применение в различных сферах деятельности человека.
Уравнение
Основные понятия, относящиеся к уравнениям. Что значит решить уравнение. Виды уравнений. Классификация уравнений. Наиболее важные приемы преобразования уравнений.
Определение линейного уравнения. Классификация линейных уравнений. Алгоритм решения линейного уравнения. Примеры задач, решение которых сводится к решению линейных уравнений. Линейные уравнения с параметрами. Решение квадратных уравнений в мировой математике. Определение квадратного уравнения. Разновидности квадратных уравнений. Способы решения квадратных уравнений Решение уравнений нестандартного вида. Квадратные уравнения с параметром Системы уравнений.
Функции
Виды функций, чтение графиков различных зависимостей.
Логарифмы Определение логарифма. Классификация заданий. Алгоритм решения логарифмического уравнения, неравенства. Примеры задач.
Неравенства Определение и классификация неравенств. Алгоритм решения линейного неравенства, неравенств, решаемых методом интервалов. Примеры задач, решение которых сводится к решению неравенств .Системы неравенств.
Итоговый тест соответствующий ЕГЭ.
Критерии оценки.
Правильный ответ в зависимости от сложности задания оцениваются от 1балла до 4 баллов. Экзамен состоит из 2-х частей уровень В(15 заданий ) и уровень С — С1,С2 по 2балла; С3,С4 по 3 балла; С5,С6 по 4балла.
Требования к уровню подготовки учащихся
Основные образовательные результаты:
Учащиеся должны уметь:
— выполнять преобразования различных математических выражений, связанных с доказательством тождеств, приведением выражений к стандартному виду;
— уметь решать различные виды уравнений и неравенств, распознавать их, определять метод их решения, использовать свойства функций;
— записывать функции школьного курса математики в виде формул, использовать свойства функций для решения математических задач (решение уравнений), строить и «узнавать» графики функций, «читать» свойства функций по графику;
— вычислять производные функций, находить их первообразные, «читать» графики производной, исследовать функции с помощью производной, решать задания на геометрический и физический смысл производной, вычислять площадь криволинейной трапеции.
учащийся должен знать/понимать/:
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
значение математики как науки и значение математики в повседневной жизни, а также как прикладного инструмента в будущей профессиональной деятельности
решать задания, по типу приближенных к заданиям ЕГЭ
иметь опыт (в терминах компетентностей):
работы в группе, как на занятиях, так и вне,
работы с информацией, в том числе и получаемой посредством Интернет
Планирование занятий элективного курса
№
Тема
Кол-во часов
Прим
дата
Примечание
Числа и выражения. Контроль на входе
2
Числа и выражения. Все действия с Rчислами. Свойства действий.
2
Тождественные преобразования алгебраических выражений. Формулы сокращенного умножения.
2
Тождественные преобразования алгебраических выражений.
2
Тождественные преобразования выражений, содержащих корни натуральной степени
2
Рациональные уравнения
2
Рациональные уравнения
2
Иррациональные уравнения
2
Системы уравнений
2
Рациональные неравенства и системы неравенств
2
Модули. Уравнения и неравенства с модулем
2
Модули. Уравнения и неравенства с модулем
2
Показательные уравнения
2
Показательные и логарифмические неравенства
2
Тригонометрические функции и тригонометрические выражения.
2
Тригонометрические выражения, тригонометрические уравнения и неравенства.
2
Функция. Свойства функций.
2
Тождественные преобразования степенных выражений.
2
Повторение темы «Показательные функции, уравнения и неравенства».
2
Производная. Исследование функций с помощью производной.
2
Прогрессии.
2
Логарифмы.
2
Логарифмические уравнения.
2
Решение логарифмических уравнений и неравенств. Исследование логарифмических функций
2
Задания, содержащие логарифмы
2
Тождественные преобразования логарифмических выражений, нахождение их значений.
2
Повторение темы «Тригонометрические функции, уравнения и неравенства»
2
Повторение темы «Тригонометрические функции, уравнения и неравенства»
2
Иррациональные неравенства
2
Тест ЕГЭ (раздел В)
2
Интегралы и производные
2
Геометрические задачи
2
Тестовые задачи и задачи на «проценты»
2
Повторение. Выполнение тестовых заданий
2
КИМы (открытый банк заданий ФИПИ -интернет)
Текущая аттестация качества усвоения курса: выполнение теста по завершении повторения каждого блока.
Итоговая аттестация качества усвоения курса: выполнение итогового теста.
Информационно-методическое обеспечение
1. С.И.Колесникова Решение сложных задач ЕГЭ по математике. 9-11 классы.- М.: ВАКО ,2011.-288с.
2. В.Н.Литвиненко Геометрия. Готовимся к ЕГЭ 11 класс. М.: Просвещение,2012. – 160с.
3. В.Н.Литвиненко , Г.К.Безрукова Задачи по стереометрии 10-11 классы. –М.: Школьная пресса,2005.-92с.
4. Сагателова Л.С. Практическая геометрия. Комбинации геометрических тел. 10-11 классы: методическое пособие с электронным приложением. М.: Планета, 2011.- 336с.
5. Единый государственный экзамен 2007г. Сергиев Посад: ФОЛИО,2007-164с.
6. В.В.Кочагин, М.Н.Кочагина Интенсивная подготовка к ЕГЭ. Математика. Тематические тренировочные задания.- М.: Эскмо , 2013-160с.
7. ЕГЭ – 2013 – 2014 г. Математика: типовые экзаменационные вырианты: 30 вариантов/под ред. А.Л.Ссемёнова, И.В.Ященко/- М.: Национальное образование, 2013,2014 г, — 192с.
8. А.М. Титаренко. Форсированный курс подготовки к экзамену по математике. (Практикум и теоретический материал) -М.: Эскмо , 2005-336с.
9. И.Л. Гусева,С.А., Пушкин, Н.В., Рыбакова Сборник тестовых заданий для тематического контроля . Алгебра и начала анализа 10-11 классы.- М.: Интеллект-центр ,2009.- 224с.
10. А.С. Бортаковский , В.М.Завалюкин и др. Сборник задач по математике для поступающих в вузы. Под редюР.Н.Молодожниковой .- М.: Изд-во МАИ, 1995. – 464с.
11. Крамер В.С. Повторяем и систематизируем школьный курс алгебры. – М.: Просвещение, 1990
12. Математика в понятиях, определениях и терминах. Ч.I. Пособие для учителей. Под ред. Л.В.Сабинина. М., «Просвещение», 2005
13. Шарыгин И.Ф. Факультативный курс по математике. Решение задач: Учеб.пособие для 10 кл. сред. шк. – М.: Просвещение, 1989
14. Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. 3-е издание, дополненное и переработанное. – М.: Илекса, Харьков: Гимназия, 2002
infourok.ru
Спецкурс по математике 10-11 класс
| «Рассмотрено» Руководитель МО _____ /Бутко Е.Ю./ ФИО Протокол №_ __от «30» августа 2016 г. | «Согласовано» Заместитель руководителя по УВР МБОУ «СОШ № 14» _____ /__Рубанова Е.А./ ФИО « 30 » августа 2016 г. | «Утверждено» Руководитель МБОУ «СОШ № 14» ___________ /_Полякова_В.А.__ / ФИО Приказ № от «30 » _августа_2016 г. |
РАБОЧАЯ ПРОГРАММА ПЕДАГОГА
Беловой Виктории Васильевны,
спецкурс
«Функции помогают уравнениям»
10-11 классы
Утверждено на заседании педагогического совета
протокол № ____
от «30 » августа 2016 г.
2016 – 2017 учебный год
город Нижневартовск
Пояснительная записка
Предлагаемый курс «Функции помогают уравнениям» является предметно-ориентированным и предназначен для расширения и углубления теоретических и практических знаний учащихся в 10-11 классах общеобразовательных учреждений и рассчитан на 140 часов.
Функциональная линия просматривается в курсе алгебры, начиная с 7 класса. Возникает потребность обобщить, углубить и систематизировать вопросы, связанные с областью определения функции, множеством значений, четностью и нечетностью, периодичностью функций, а также их взаимосвязи с решением уравнений и неравенств. Многие задания ЕГЭ требуют аккуратного применения вопросов, связанных с периодичностью функций, их монотонностью, нахождением промежутков убывания и возрастания, точек экстремума и экстремумов функций.
Программа данного курса ориентирована на приобретение обучающимися определенного опыта решения задач, связанных со знанием свойств функций, эффективными методами, которые позволят школьнику решать многие типичные задачи быстро, коротким способом, экономя экзаменационное время на более сложные (нестандартные) задания. Изучение данного курса тесно связано с такими дисциплинами, как алгебра, алгебра и начала анализа.
Данный курс представляется особенно актуальным и современным, так как расширяет, углубляет и систематизирует знания учащихся, готовит их к более осмысленному пониманию теоретических сведений и применению их на практике.
Цель курса:
Углубление и расширение знаний, умений и навыков учащихся по алгебре и началам анализа, подготовка к сдаче ЕГЭ и обучению в вузах, где математика является профилирующим предметом
Задачи курса:
овладение системой знаний о свойствах функций и их применением при решении уравнений и неравенств;
овладение эффективными методами решения типичных и нестандартных задач, обучение умению выбирать рациональные способы решения и обосновывать сделанный выбор;
обучение эвристическим приемам общего характера, ценным для математического развития личности, применяемым в исследовательской деятельности;
формирование логического мышления учащихся;
вооружение учащихся специальными умениями и навыками, позволяющими им самостоятельно добывать знания;
приобретение опыта решения задач прикладного характера, позволяющего осмысленно подойти к профориентационному выбору;
подготовка к ЕГЭ: формирование у учащихся умений и навыков решения задач части С (С 1, С 3, С5).
Требования к уровню подготовки учащихся
Личностные результаты:
готовность и способность к образованию и самообразованию на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;
осознанный выбор будущей профессии на основе понимания ее ценностного содержания и возможностей реализации собственных жизненных планов.
Метапредметные результаты:
владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания для изучения различных сторон окружающей действительности;
расширение и систематизация знаний учащихся, которые позволяют осмысленно понимать теоретический материал, решать практические задачи из разных предметных областей.
Предметные результаты:
овладение системой знаний о свойствах функций, позволяющей применять их в различных предметных областях;
овладение нестандартными способами решения уравнений и неравенств;
овладение навыками описания процессов с помощью математических моделей – уравнений или неравенств;
владение терминологией, описывающей функциональные зависимости.
Краткое содержание курса:
10 класс.
Свойства функций в решении уравнений и неравенств.
Нахождение области определения функции в зависимости от параметра. Нахождение значений параметра функции по области определения. Алгоритм исследования существования корней уравнения с учетом множества значений функции. Рациональные способы решения уравнений и неравенств с исследованием области допустимых значений. Понятие равносильного перехода. Решение иррациональных уравнений и неравенств. Неравенства, содержащих модуль, вида ǀf(x)ǀ ˂ǀg(x)ǀ,
ǀf(x)ǀ ˂g(x).
Тригонометрические уравнения и системы.
Тождественные преобразования в решении тригонометрических уравнений. О сужении и расширении области определения уравнения в процессе преобразований. Форма записи множества решений уравнений и систем. Методы искусственных преобразований. Решение тригонометрических уравнений методом экстремальных значений. Нестандартные тригонометрические подстановки.
Производная и касательная.
Определение числа корней уравнения с помощью производной. Производная при доказательстве неравенств. Связь между корнями дифференцируемой функции и корнями производной. Производная и наглядно — графический метод в решении задач. Понятие дифференциального уравнения.
11 класс.
Показательные уравнения и неравенства.
Правила равносильных переходов при решении показательных и логарифмических неравенств. Решение неравенств вида a f(x) ˃ a g (x), log a f(x) ˃0, log a f(x) ˃ log a g (x).
Уравнения и неравенства, содержащие сложную экспоненту a(x)b(x)=cb(x)logca(x) .
Неравенства c переменным основанием вида a(x)f(x) ˃ a(x) g (x), log a(х) f(x) ˃0, log a(х) f(x) ˃ log a(х) g (x). Использование нестандартных приемов решения стандартных уравнений и неравенств. Метод «Мини-максов».
Задачи с параметром.
Использование монотонности и экстремальных свойств функций. Симметрия в задачах. Решение относительно параметра. Функционально-графический подход в решении задач с параметрами. Производная и параметры. Задачи с логическим содержанием.
Задачи с параметрами в заданиях единого государственного экзамена.
\
Календарно-тематическое планирование
Литература
1. Математика. 10-11 классы. Функции помогают уравнениям: элективный курс/авт.-сост. Ю.В. Лепехин.- Волгоград: Учитель,2009.
2. Шарыгин И.Ф.,. Голубев В.И. Факультативный курс по математике: Решение задач: Учебное пособие для 11 кл. сред. Шк.-М.: Просвещение, 1991.
3. Колесникова С.И. Математика. Интенсивный курс подготовки к Единому государственному экзамену.- М.: Айрис-пресс, 2004.
4. Четвериков А. «Задачи с параметрами»-газета «Математика»№13 2007.
5. Севрюков П.Ф., Смоляков А.Н. «Школа решения задач с параметрами»-М.: Илекса; Народное образование; Ставрополь: Сервисшкола, 2007.
6. Шахмейстер А.Х. «Задачи с параметрами в ЕГЭ»-СПб.: «ЧеРо-на-Неве», 2004.
Методическое обеспечение
ДМ (Презентация) «Применение свойств функции для решения уравнений. Подготовка к ЕГЭ».
ДМ «Решение уравнений методом «Мини-максов». Подготовка к ЕГЭ».
ДМ «Множество значений сложной функции. Исследование функции элементарными методами».
ДМ «Задачи с параметрами. В помощь старшеклассникам при подготовке к экзаменам».
Методическое обеспечение
Урок по алгебре и началам анализа
Класс — 11
Тема – «Функционально-графический подход к решению задач с параметрами»
Учебно-методическое обеспечение: УМК любого автора, так как урок ориентирован на подготовку к ЕГЭ
Время реализации занятий – 40 минут
Оборудование и материалы для урока: компьютер, проектор, экран, презентация для сопровождения урока, раздаточный материал учащихся.
Медиапродукт: Среда — Microsoft Office PowerPoint, Paint.
Вид медиапродукта: наглядная презентация учебного материала, образовательный комплекс
Тип урокапроблемно-исследовательский, комбинированный
Цели урока
изучить функционально-графический подход к решению задач с параметрами
Задачи урока
1. Сформировать у школьников личностную мотивацию к изучению данной темы.
2. Развивать у учащихся умение пользоваться опорными знаниями, для получения новых знаний.
3. Развивать у учащихся мышление (умение выделять существенные признаки и делать обобщения).
4. Развивать у учащихся навыки творческого подхода к решению задач и навыки исследовательской работы над задачей.
Знания, умения, навыки и качества, которые актуализируют/приобретут/закрепят/др. ученики в ходе урока
умение пользоваться опорными знаниями, для получения новых знаний;
умение выделять существенные признаки и делать обобщения;
навыки творческого подхода к решению задач и навыки исследовательской работы над задачей.
Подробный конспект урока
Мотивация учащихся
Мотивация (выявление проблемы успешной сдачи ЕГЭ).
Ход и содержание урока
I этап – актуализация знании и опыта,
подготовка к изучению новой темы (8 мин)
II этап – изучение вопроса «Изучение функционально-графического подхода к решению задач с параметром» (8 мин)
III этап – изучение строения задачи с параметром (14 мин)
IV этап – подведение итогов «Творческая лаборатория» (7 мин)
V этап – подведение итогов, рефлексия (3 мин)
Проверка и оценивание ЗУНКов
Учащиеся должны объединиться в группы по 5 человек, подготовить и представить свой проект задачи с параметром. Хорошо, красиво, грамотно выполненный проект будет подведением итога урока, оценкой работы учителя и ответом на вопрос «Чему ребята научились на уроке?»
Рефлексия деятельности на уроке
Что нового вы узнали на уроке?
Чему вы научились?
Какое у вас настроение в конце урока?
Можете ли вы научить этому способу решения задач товарища?
Домашнее задание
Составить две задачи с параметром, используя полученные знания, если их оформить по одинаковому образцу, то в классе будет свой сборник задач для подготовки к ЕГЭ.
В помощь учителю
Использованные источники и литература (если имеются)
Внеурочная работа по математике в контексте реализации инновационных технологий. Дидактические материалы для организации деятельности обучаемых: учеб. пособие∕авт.-сост.: А.Т. Лялькина, Е.В. Чудаева и др. – Саранск, 2007
Черкасов О.Ю., Якушев А.Г. Математика: интенсивный курс подготовки к экзамену. – 6-е изд., — М.: Рольф, 2002.
Экзаменационные материалы для подготовки к единому государственному экзамену. Математика. ЕГЭ – 2007. Составитель: Клово А.Г. – М.: ООО «РУСТЕСТ»,2006.
Обоснование, почему данную тему оптимально изучать с использованием медиа-, мультимедиа, каким образом осуществить
Данную тему оптимально изучать с использованием мультимедиа, так как это позволит показать учащимся движение графиков функций и продемонстрировать поэтапное решение задач графическим способом.
Советы по логическому переходу от данного урока к последующим
Данную тему удобно изучать в конце учебного года, в рамках системы уроков по подготовке учащихся к ЕГЭ.
Тема урока: «Функционально-графический подход к решению задач с параметрами».
Тип урока: комбинированный.
Вид урока: проблемно-исследовательский.
Цель урока: изучить функционально-графический подход к решению задач.
Задачи урока:
1. Сформировать у школьников личностную мотивацию к изучению данной темы.
2. Развивать у учащихся умение пользоваться опорными знаниями, для получения новых знаний.
3. Развивать у учащихся мышление (умение выделять существенные признаки и делать обобщения).
4. Развивать у учащихся навыки творческого подхода к решению задач и навыки исследовательской работы над задачей.
Оборудование: мультимедийный терминал, съемный диск поэтапного показа урока, индивидуальный раздаточный материал для учащихся.
План урока:
1. Сформирование у школьников личностной мотивации к изучению данной темы.
2. Показ применения темы урока в деятельности каждого ученика 11 класса.
3. Повторение опорных знаний.
4. Изучение функционально-графического подхода к решению задач с параметрами.
5. Творческая лаборатория (работа в группах: создание и защита мини-проекта).
6. Подведение итога урока, рефлексия.
7. Домашнее задание.
Ход урока:
I этап – актуализация знании и опыта,
подготовка к изучению новой темы (8 мин)
1.Мотивация (выявление проблемы успешной сдачи ЕГЭ). Математическое моделирование социальной задачи.2. Тренировочные упражнения.
3. Повторение способов построения графиков с помощью преобразования
4. Решение уравнений.
Вводная беседа.
Тестовая работа с последующей самопроверкой
Адаптационно-развивающий диалог
Вызов учащихся к доске.
Устные ответы на вопросы.
Работа с тестом,
Самопроверка,
Самооценка
Устные ответы на вопросы учителя
Работа у доски и в тетрадях
II этап– изучение вопроса «Изучение функционально-графического подхода к решению задач с параметром» (8 мин)
1. Изучение нового материала2. Составление алгоритма решения
3. Подведение итогов
Объяснение
Разноуровневая
самостоятельная работа
Устные ответы на вопросы учителя
Работа по алгоритму
Выбор уровня сложности, решение самостоятельной работы
III этап – изучение строения задачи с параметром (14 мин)
1. Анализ строения задачи с параметром2. Технология составления задач с параметром
3. Практическая работа
Объяснение у доски
Постановка задач по исследованию свойств её графического образа
На экране проецирует поэтапное составление задачи, её решение, и оформление
Изучение строения задачи, работа в тетради
Анализ технологической схемы
Анализ видеофрагм., запись образца решения в тетрадь
IV этап – подведение итогов «Творческая лаборатория» (7 мин)
Организация творческой работыГрупповая работа
V этап – подведение итогов, рефлексия (3 мин)
1. Подведение итогов2. Домашнее задание
Беседа с использованием таблицы
Проецируется на экран
Групповая работа,
подведение итогов
Запись в дневники
Сценарий урока.
— Здравствуйте ребята! Тема нашего урока «Функционально-графический подход к решению задач с параметрами» (слайд 1)
-Задачи с параметрами – самый сложный раздел школьного курса математики, в учебнике алгебры 10 – 11 класса нет ни одного параграфа отводимого на изучение данной темы, а сборник для подготовки к ЕГЭ содержит задачи, с параметрами начиная с части «А» Данное противоречие порождает проблему:
Как в сложившейся ситуации успешно подготовиться к сдаче ЕГЭ по математике?
Что такое «параметр» и где это понятие может встретиться нам в жизни?
Решением данной проблемы мы и займемся сегодня на уроке (слайд 2).
— Запишите число, сегодня 14 марта. Скоро весенние каникулы, а там не успеете оглянуться и вы — выпускники, после сдачи ЕГЭ вы можете захотеть продолжить образование и стать абитуриентами, пройдет лето и многие из вас станут студентами.
Составим математическую модель этой ситуации (слайд 3)
Выпускники – сдача ЕГЭ – абитуриенты – студенты
— Задача: Как выпускнику стать студентом? Какие проблемы могут стоять в данной задаче?
Предполагаемые ответы: Проблема сдать ЕГЭ. Проблема поступить в ВУЗ. Другие проблемы.
— Хорошо. Решим задачу поэтапно. Сравним количество выпускников школы и с количеством детей поступивших в ВУЗ.
1. По каким причинам не все выпускники допускаются к сдаче ЕГЭ?
Предполагаемые ответы: Проблемы с учебой. Проблемы со здоровьем.
2. В каком случае ученики, сдавшие ЕГЭ, не могут подать документы в ВУЗ и стать абитуриентами?
Предполагаемые ответы: Плохо сдал ЕГЭ. Нет желания учиться дальше. Армия. Другие причины.
3. По каким причинам не все абитуриенты становятся студентами?
Предполагаемые ответы: Высокий проходной балл. Другие причины.
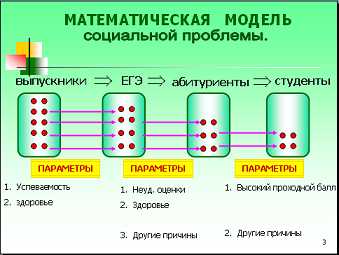
Посмотрите внимательно на полученную схему. Решая, разные проблемы, мы получили одинаковые ответы (на слайде выделяются слова учеба и здоровье).
Какой вывод можно сделать?
Предполагаемые ответы: все проблемы данной задачи могут быть решены при наличии хорошего здоровья и успешной учебы.
От кого зависят данные параметры?
Предполагаемые ответы: от каждого ученика лично.
Вы не задумываясь ответили мне на вопрос о параметрах. Давайте уточним, какой значение имело слово параметр в данной задаче?
Предполагаемые ответы: условия, причины, зависимость от чего-либо.
Значит, мы можем условия, причины, зависимость от чего-либо заменить одним словом параметр.
Вот мы и вышли на понятие параметра и определили личностный мотив каждого ученика 11 класса (слайд 4): для продолжения образования, для саморазвития и интеллектуального роста вам необходимо прилежно и осознанно учиться в школе и заботиться о своем здоровье. В этом вам помогает государство, оно поддерживает творческую, талантливую молодежь (программа «Образование» слайд). И заботится о сохранении её здоровья (программа «Здоровье» слайд).
В толковом словаре дано общее определение понятия параметр:
«Параметр – величина, характеризующая основные свойства системы или явления».
В (слайд5) математике ярким и всем известным с 8 класса уравнением с параметром является уравнение квадратного трехчлена: . В зависимости от коэффициентов и дискриминанта , график данного уравнения может иметь различное положение на координатной плоскости. 
Определение: В уравнениях (неравенствах) коэффициенты при неизвестных или свободные члены заданные не конкретными числовыми значениями, а обозначенные буквами называются параметрами.
Решить уравнение с параметром это значит, для каждого значения параметра найти значения x, удовлетворяющие условию этой задачи. 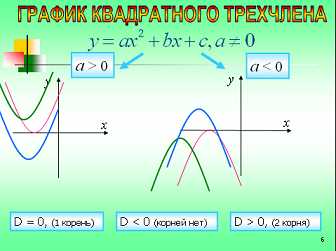
Как (слайд 6) зависит от коэффициента а график квадратичной функции?
Предполагаемые ответы: направление ветвей параболы, если а положительно, то ветви параболы направлены вверх, если а – отрицательно, то ветви параболы, направлены вниз
Что зависит от дискриминанта?
Предполагаемые ответы: количество решений квадратного уравнения. Если , то решений нет, если , один корень, если то уравнение имеет два корня (слайд 6)
Рассмотрим преобразование построение графика функций в зависимости от параметра на примере функции абсолютной величины числа.
Что является графиком данной функции?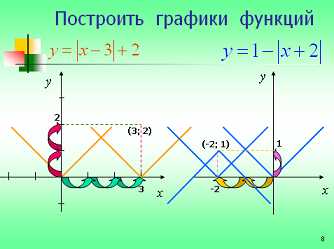
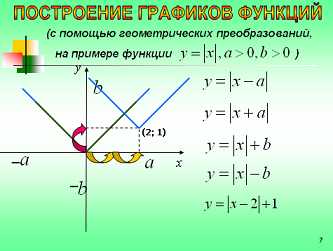
Предполагаемые ответы: «прямой угол», с вершиной в начале координат, образованный биссектрисами первого и второго квадранта (четверти) на координатной плоскости.
(просмотр слайда 7, с комментариями учителя ).
— Примените полученные знания для самостоятельного решения двух задач на построение графиков функций.
(проверка: сравнение своей работы со слайдом 8).
— Молодцы все кто успешно справился с заданием. Ребята, встаньте, пожалуйста. Расправьте плечи, встряхните руками, поверните голову налево, направо и тихонечко сядьте.
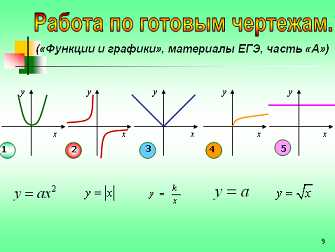
— Переходим к заданиям раздела «В». (Слайд 9). Вам предложены изображения пяти графиков функций, и даны пять формул. Сопоставьте формулу и её графический образ.
Предполагаемые ответы:
1 ученик. Формула задает квадратичную функцию, её графиком является парабола, 1 рисунок.
2 ученик. Формула задает функцию абсолютной величины числа, её графиком является «прямой угол», 3 рисунок.
3 ученик. Формула задает обратную пропорциональность, её графиком является гипербола, 2 рисунок.
4 ученик. Формула задает прямую пропорциональность, её графиком является прямая, 5 рисунок.
5 ученик. Формула задает «полупараболу», направленную вдоль оси абсцисс, рисунок 4.
На каких чертежах изображены графики четных функций?
Предполагаемые ответы: 1,3.
Какие функции определены на всей числовой оси?
Предполагаемые ответы: 1,3,5
Какие функции имеют неотрицательное множество значений?
Предполагаемые ответы: 1,3,4.
Какие функции являются возрастающими на всей области определения?
Предполагаемые ответы: 4,5.
(слайд 10) Очень хорошо. Эти знания нам пригодятся при решении заданий части «В».
Запишем схему решения уравнений графическим способом.
1. строим графики и .
2. находим точки пересечения графиков.
3. выписываем ответ.
Рассмотрим образец решения задачи с параметром. (слайд 11)
Задача. Решите уравнение . (1 способ решения – аналитический)
Решение. Заметим, что левая часть уравнения неотрицательна при всех значениях неизвестной, следовательно, при отрицательном значении параметра решений нет. Если параметр , то уравнение принимает вид , и имеет один корень . При положительном значении параметра а, данное уравнение имеет два корня .
Ответ: при , корней нет;
при , один корень ; 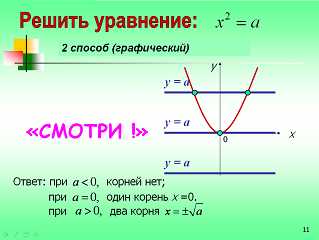
при , два корня .
2 –ой способ решения – графический.
Построим в одной системе координат графики обеих частей уравнения: параболу и семейство прямых , которые движутся вдоль оси ординат. По рисунку записываем ответ.
— Какой вывод можно сделать, сравнивая два способа решения задачи?
Предполагаемые ответы: графический способ понятнее. Графическим способом задача решается быстрее. На рисунке все решение видно.
Да. Достаточно одного взгляда, чтобы определить количество корней уравнения в зависимости от параметра а. Я могла бы вам ничего, не объясняя сделать чертеж, и написать одно слово «Смотри!», именно так поступали древнегреческие учителя, обучая своих учеников доказательству теоремы Пифагора.
А мы вернемся к параметрам (слайд 12) (2 ученика выходят к доске, остальные работают в тетрадях)
Затем сверяем решение с образцом на далее представленных слайдах (вторично проговаривая шаги решения).
(слайд 13) Задача. При каких значениях параметра а уравнение имеет единственное решение?
Решение. Записываем данное уравнение в виде . Построим графический образ обеих частей уравнения. Левая часть представляет собой «прямой угол», ветви направлены вниз, вершина (2;3). Правая часть представляет семейство прямых параллельных оси абсцисс. Из чертежа видно, что единственное решение возможно при .
Ответ: 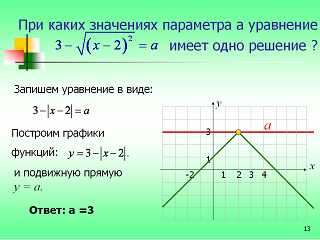
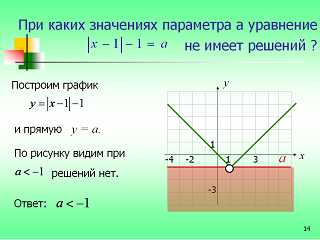
(слайд 14) Задача. При каких значениях параметра а уравнение не имеет решений?
Решение. Построим графический образ обеих частей уравнения. Левая часть представляет собой «прямой угол», ветви направлены вверх, вершина (1;-1). Правая часть представляет семейство прямых параллельных оси абсцисс. Из чертежа видно, что решений нет при .
Ответ:
Кто самостоятельно справился с задачей, поднимите руки. Очень хорошо!
(слайд 15) Давайте сделаем вывод о решении задач с параметром графическим способом в общем виде.
Задачу с параметром будем рассматривать как функцию . Алгоритм решения:
1. строим графический образ.
2. пересекаем полученное изображение прямыми параллельными оси абсцисс.
3. Считываем нужную информацию.
Рассмотрим образец решения задачи с параметром.
(слайд 16) Устная работа по готовому рисунку (просмотр и обсуждение решения задачи с пошаговыми комментариями учителя).


(слайд 17) Закрепим полученные знания, самостоятельным решением задачи по выбору.
Вам предлагается найти при каких значениях параметра а, уравнение будет иметь два решения. Уровень сложности задачи – определите самостоятельно. 1 минута.
Проверяем.
Кто выбрал первый рисунок? Какие ответы получились?
Предполагаемые ответы: Сверяем по слайду
Кто выбрал второй рисунок? Какие ответы получились?
Предполагаемые ответы: Сверяем по слайду
Кто выбрал третий рисунок? Какие ответы получились?
Предполагаемые ответы: Сверяем по слайду
Молодцы! Вы очень хорошо поработали. И перед следующим этапом урока мы сделаем зарядку для глаз, выполнив упражнение «Стрельба глазами»: мальчики стреляют в девочек, а девочки в мальчиков. При этом можно поворачиваться в разные стороны. Постарайтесь попасть не менее 10 раз.
(слайд 18) Переходим к самой трудной части урока: решению задач с параметром части «С».
Вариант №3, стр. 39, «С – 5».
(слайд 19) Задача. Найти сумму целых значений параметра а при которых уравнение имеет три корня.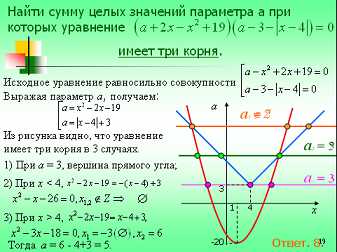

Решение. Запишем уравнение в виде совокупности . Построим в одной системе координат параболу (ветви вверх, вершина (1;- 20)), и «прямой угол» (ветви направлены вверх, вершина (4:3)). Будем пересекать полученный образ прямыми параллельными оси абсцисс. Три решения возможны в трех случаях. Рассмотрим их отдельно: а = 3, в вершине прямого углаа. Раскроем знак модуля.
1) При , имеем , или , решая это уравнение находим, что корни не удовлетворяют условию задачи ().
2) При , имеем , или , решая это уравнение находим, корни х = -3 (не удовлетворяет условию) и х = 6.
Вычисляем .
Искомые значения а = 3 и а = 5, их сумма равна 8.
Ответ: 8.
— Чтобы до конца понять и осмыслить задачу, нужно разобраться в том, как она устроена. Вы не задумывались, почему маленькие дети часто ломают игрушки? Они их не ломают, они пытаются выяснить: почему едет машинка, и почему кукла говорит «мама». Вот и мы сейчас узнаем технологию составления данных задач.
(слайд 20) Прошу в творческую лабораторию.
Проанализируем решенную задачу.
-Как мы её решали?
Предполагаемые ответы: большую задачу разбили на две части.
-Что мы делали дальше?
Предполагаемые ответы: нашли знакомые функции и построили их графики.
И последний шаг?
Предполагаемые ответы: воспользовались знаниями, полученными на уроке, и нашли значения параметра а.
(слайд 21) Прекрасно!
Чтобы составить такую задачу, пойдем обратным путем.
1. возьмем два уравнения, графики которых мы умеем строить.
2. построим графический образ.
3. объединим произведением оба уравнения, приравняв их к нулю.
4. заменим букву у буквой а, и получим уравнение с параметром.
5. зададим вопрос (глядя на рисунок), сформулируем условие задачи.
Рассмотрим, как работает этот алгоритм (просмотр мультимедийного слайда 22)
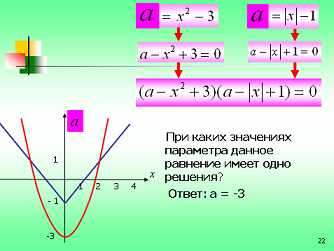

(слайд 23) Известный венгерский математик Пойа писал: «Умение решать задачи – практическое искусство, подобное плаванию, или катанию на лыжах ..: научиться этому можно лишь подражая избранным образцам и постоянно тренируясь…».
Вам предстоит потренироваться в составлении задач с параметром. Для этого вы объединитесь в группы по 5 человек, подготовите и представите свой проект. Пример карточки (слайд 24). Хорошо, красиво, грамотно выполненный проект будет подведением итога нашего урока, оценкой моей работы и ответом на вопрос «Чему я вас научила?»
Подготовка и защита проекта. 5 минут
Подведем итог урока (слайд 25).
-Что нового вы узнали на уроке?
Предполагаемые ответы: новый метод решения задач с параметрами.
-Чему вы научились?
Предполагаемые ответы: Решать задачи. Сами научились составлять задачи.
(слайд 26) Домашнее задание. Составить две задачи с параметром, используя полученные знания, если вы их оформите по одинаковому образцу, то в классе будет свой сборник задач для подготовки к ЕГЭ.
А сейчас расслабьтесь. После такого плодотворного урока, вспомните что-нибудь приятное и представьте, что вам подарили шикарный подарок! С такой приятной улыбкой мы заканчиваем урок.
(слайд 27) Всем спасибо. Всего хорошего!
Литература
Алгебра и начала анализа: учеб. для 10 – 11 кл. общеобразоват. учреждений∕Ш. А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. – 10-е изд. – М.: Просвещение, 2002. – 384с.
Внеурочная работа по математике в контексте реализации инновационных технологий. Дидактические материалы для организации деятельности обучаемых: учеб. пособие∕авт.-сост.: А.Т. Лялькина, Е.В. Чудаева и др. – Саранск, 2007
Черкасов О.Ю., Якушев А.Г. Математика: интенсивный курс подготовки к экзамену. – 6-е изд., — М.: Рольф, 2002. – 432 с. (Домашний репетитор).
Экзаменационные материалы для подготовки к единому государственному экзамену. Математика. ЕГЭ – 2007. Составитель: Клово А.Г. – М.: ООО «РУСТЕСТ»,2006.
infourok.ru
Программа спецкурса по математике » Математика абитуриенту»,11 класс
Программа спецкурса «Математика абитуриенту»
Пояснительная записка
Программа рассчитана на 68 часов. Она предназначена для повышения эффективности подготовки учащихся 11 класса к итоговой аттестации по математике за курс старшей школы и предусматривает их подготовку к дальнейшему математическому образованию. Разработана в соответствии с Государственным стандартом по математике для 5 – 11 классов.
Курс по математике в 11 классе « Математика абитуриенту» представляет расширенное изучение теоретического материала укрупненными блоками. Курс рассчитан на учеников общеобразовательного класса, желающих основательно подготовиться к ЕНТ. В результате изучения этого курса будут использованы приемы парной, групповой деятельности для осуществления элементов самооценки, взаимооценки, умение работать с математической литературой и выделять главное.
Цель обучения курса:
- систематизация и обобщение имеющихся знаний;
- ликвидация пробелов;
- знакомить учащихся со способами решения задач, содержащих параметр.
- обобщить понятия: «уравнение», «система уравнений»;
- систематизировать основные приёмы решения уравнений, систем уравнений и научиться применять их в нестандартных ситуациях;
- обобщить понятия: «неравенство», «система неравенств»;
- систематизировать основные методы решения неравенств, систем неравенств; научиться применять их в новых нестандартных ситуациях;
- подготовка к ЕНТ.
Задачи курса:
— формирование и развитие личностных качеств учащихся, адекватных полноценной математической деятельности;
— формирование умений, навыков, необходимых для полноценного функционирования в современном обществе.
В результате изучения курса все учащиеся должны
овладеть следующими умениями, задающими уровень обязательной подготовки:
— находить область определения и область значений заданной числовой функции;
определять промежутки возрастания и убывания функции;
определять является ли заданная функция четной, нечетной;
— решать рациональные неравенства методом интервалов;
— помнить значения тригонометрических функций для значений аргумента 0, п/6, п/4, п/3, п/2;
— определять знаки тригонометрических функций по четвертям;
— решать тригонометрические уравнения на основе использования основных тригонометрических тождеств;
-вычислять производную степенной функции с натуральным показателем;
-выносить постоянный множитель за знак производной;
-находить производную многочлена;
-применять производную к нахождению промежутков возрастания и убывания исследуемых функций;
-с помощью производной находить экстремумы исследуемых функций, их наибольшие и наименьшие значения;
— применять производную к построению графиков исследуемых функций.
-находить первообразную степенной функции;
-находить первообразную многочлена;
-исследовать свойства степенной функции с натуральным показателем по заданному графику;
-проверять, является ли целое число корнем n-ой степени (п=3,4, 5) из данного числа;
-использовать свойства корней для упрощения вычислений; представлять степень с рациональным показателем в виде корня;
-решать показательные уравнения и неравенства;
-в простейших случаях определять логарифм числа по данному основанию;
— применять свойства логарифмов для упрощения несложных логарифмических выражений;
— решать логарифмические уравнения и неравенства;
-различать и показывать на моделях прямую и правильную призмы, прямоугольный параллелепипед, куб, пирамиду, правильную пирамиду, указывать их основные элементы;
-изображать на рисунках треугольные и четырехугольные призмы и пирамиды и, их элементы;
— решать задачи на нахождение элементов, вычисление площадей поверхностей, объемов параллелепипеда, прямой и правильной призмы, правильной пирамиды;
-вычислять площади поверхностей и объемы цилиндра и конуса;
-различать сферу и шар;
-использовать соответствующие формулы для вычислений площади поверхности сферы и объема шара.
Содержание курса:
- Задачи с целыми числами. Признаки делимости.( 2ч)
- Действительные числа.
Преобразования алгебраических выражений( 4ч)
- Уравнения и неравенства, методы их решения ( 24ч)
- Решение линейных уравнений и неравенств.
- Решение квадратных уравнений и неравенств.
- Решение рациональных, дробно-рациональных и иррациональных уравнений и неравенств.
- Решение тригонометрических уравнений и неравенств
- Показательные и логарифмические уравнения и неравенства
- Решение систем уравнений и неравенств
- Уравнения высших степеней.
- Решение систем уравнений и неравенств
- Функции (8ч)
- Область определения и множество значений функции
- Графики функций
- Преобразования тригонометрических выражений. Обратные тригонометрические функции
- Производная и ее применение (4ч)
Производная функции у= хп (n е Z).,элементарных функций
Производные суммы, произведения и частного
Производная тригонометрических функций
Применение производной к исследованию функций
Наибольшее и наименьшее значения функции на промежутке
- Первообразная. Интеграл. Площади криволинейных трапеций (4ч)
- Решение уравнений, содержащих параметры: ( 4ч)
- Исследование квадратного трехчлена.
- Теорема Виета.
- Расположение корней квадратного трехчлена.
- Необходимые условия в задачах с параметрами.
- Квадратные неравенства с параметрами.
- Дробно-рациональные уравнения и неравенства, содержащие параметр.
- Прогрессии ( 2ч)
- определение числовой последовательности
- способы задания числовых последовательностей
- монотонные последовательности
- арифметическая прогрессия.
- формула п-го члена арифметической прогресии
- понятие арифметической прогрессии
- формула п-го члена фрифметической прогрессии
- сумма первых n членов арифметической прогрессии
- геометрическая прогрессияю, формула n-го члена геометрической прогрессии
- понятие геометрической прогрессии
- формула n-го члена геометрической прогрессии
- сумма первых n членов геометрической прогрессии
9. Решение задач на составление уравнений, на проценты (4ч)
10. Решение геометрических задач ( 12 ч)
- Планиметрия. Задачи на вычисление
- Стереометрия. Задачи на вычисление
№ урока
Тема занятия
Кол. часов
Дата
измен
прим.
1-2
Задачи с целыми числами. Признаки делимости.
2
3-6
Действительные числа. Преобразования алгебраических выражений
4
7-10
Уравнения и неравенства первой и второй степени.
4
11-12
Уравнения высших степеней. Рациональные неравенства
2
13-16
Иррациональные уравнения и неравенства
4
17-22
Системы уравнений и неравенств
6
23-24
Область определения и множество значений функции
2
25-26
Графики функций
2
27-30
Преобразования тригонометрических выражений. Обратные тригонометрические функции
4
31-34
Решение тригонометрических уравнений, неравенств и систем уравнений
4
35-38
Производная. Исследование функций с помощью производной
4
39-42
Первообразная. Интеграл. Площади криволинейных трапеций
4
43-46
Показательные и логарифмические уравнения и неравенства
4
47-48
Прогрессии
2
49-52
Решение задач на составление уравнений ,на проценты
4
53-56
Решение уравнений, содержащих параметры
4
57-62
Планиметрия. Задачи на вычисление
6
63-68
Стереометрия. Задачи на вычисление
6
Итого
68
Календарно-тематическое планирование
(2час в неделю, всего 68ч)
используемая литература:
1. Повторяем и систематизируем школьный курс алгебры начал анализа, В.С. Крамор,»просвещение»;
2. Задачи по математике. Уравнения и неравества, Москва «Наука»
3. Тригонометрические уравнения и неравенства, И.Т. Бородуля, Москва»Просвещение»;
4. Уравнения и неравенства, содержащие параметры, Г.А. Ястребинский, Москва «Просвещение»;
5. Повторяем и систематизируем школьный курс геометрии, В.С. Крамор, «Просвещение»;
6. Сборники тестовых заданий для подготовки к ЕНТ.
Просмотр содержимого документа
«Программа спецкурса по математике » Математика абитуриенту»,11 класс »
Программа спецкурса «Математика абитуриенту»
Пояснительная записка
Программа рассчитана на 68 часов. Она предназначена для повышения эффективности подготовки учащихся 11 класса к итоговой аттестации по математике за курс старшей школы и предусматривает их подготовку к дальнейшему математическому образованию. Разработана в соответствии с Государственным стандартом по математике для 5 – 11 классов.
Курс по математике в 11 классе « Математика абитуриенту» представляет расширенное изучение теоретического материала укрупненными блоками. Курс рассчитан на учеников общеобразовательного класса, желающих основательно подготовиться к ЕНТ. В результате изучения этого курса будут использованы приемы парной, групповой деятельности для осуществления элементов самооценки, взаимооценки, умение работать с математической литературой и выделять главное.
Цель обучения курса:
систематизация и обобщение имеющихся знаний;
ликвидация пробелов;
знакомить учащихся со способами решения задач, содержащих параметр.
обобщить понятия: «уравнение», «система уравнений»;
систематизировать основные приёмы решения уравнений, систем уравнений и научиться применять их в нестандартных ситуациях;
обобщить понятия: «неравенство», «система неравенств»;
систематизировать основные методы решения неравенств, систем неравенств; научиться применять их в новых нестандартных ситуациях;
подготовка к ЕНТ.
Задачи курса:
— формирование и развитие личностных качеств учащихся, адекватных полноценной математической деятельности;
— формирование умений, навыков, необходимых для полноценного функционирования в современном обществе.
В результате изучения курса все учащиеся должны
овладеть следующими умениями, задающими уровень обязательной подготовки:
— находить область определения и область значений заданной числовой функции;
определять промежутки возрастания и убывания функции;
определять является ли заданная функция четной, нечетной;
— решать рациональные неравенства методом интервалов;
— помнить значения тригонометрических функций для значений аргумента 0, п/6, п/4, п/3, п/2;
— определять знаки тригонометрических функций по четвертям;
— решать тригонометрические уравнения на основе использования основных тригонометрических тождеств;
-вычислять производную степенной функции с натуральным показателем;
-выносить постоянный множитель за знак производной;
-находить производную многочлена;
-применять производную к нахождению промежутков возрастания и убывания исследуемых функций;
-с помощью производной находить экстремумы исследуемых функций, их наибольшие и наименьшие значения;
— применять производную к построению графиков исследуемых функций.
-находить первообразную степенной функции;
-находить первообразную многочлена;
-исследовать свойства степенной функции с натуральным показателем по заданному графику;
-проверять, является ли целое число корнем n-ой степени (п=3,4, 5) из данного числа;
-использовать свойства корней для упрощения вычислений; представлять степень с рациональным показателем в виде корня;
-решать показательные уравнения и неравенства;
-в простейших случаях определять логарифм числа по данному основанию;
— применять свойства логарифмов для упрощения несложных логарифмических выражений;
— решать логарифмические уравнения и неравенства;
-различать и показывать на моделях прямую и правильную призмы, прямоугольный параллелепипед, куб, пирамиду, правильную пирамиду, указывать их основные элементы;
-изображать на рисунках треугольные и четырехугольные призмы и пирамиды и, их элементы;
— решать задачи на нахождение элементов, вычисление площадей поверхностей, объемов параллелепипеда, прямой и правильной призмы, правильной пирамиды;
-вычислять площади поверхностей и объемы цилиндра и конуса;
-различать сферу и шар;
-использовать соответствующие формулы для вычислений площади поверхности сферы и объема шара.
Содержание курса:
Задачи с целыми числами. Признаки делимости.( 2ч)
Действительные числа.
Преобразования алгебраических выражений( 4ч)
Уравнения и неравенства, методы их решения ( 24ч)
Решение линейных уравнений и неравенств.
Решение квадратных уравнений и неравенств.
Решение рациональных, дробно-рациональных и иррациональных уравнений и неравенств.
Решение тригонометрических уравнений и неравенств
Показательные и логарифмические уравнения и неравенства
Решение систем уравнений и неравенств
Уравнения высших степеней.
Решение систем уравнений и неравенств
Функции (8ч)
Область определения и множество значений функции
Графики функций
Преобразования тригонометрических выражений. Обратные тригонометрические функции
Производная и ее применение (4ч)
Производная функции у= хп (n е Z).,элементарных функций
Производные суммы, произведения и частного
Производная тригонометрических функций
Применение производной к исследованию функций
Наибольшее и наименьшее значения функции на промежутке
Первообразная. Интеграл. Площади криволинейных трапеций (4ч)
Решение уравнений, содержащих параметры: ( 4ч)
Исследование квадратного трехчлена.
Теорема Виета.
Расположение корней квадратного трехчлена.
Необходимые условия в задачах с параметрами.
Квадратные неравенства с параметрами.
Дробно-рациональные уравнения и неравенства, содержащие параметр.
Прогрессии ( 2ч)
способы задания числовых последовательностей
монотонные последовательности
арифметическая прогрессия.
формула п-го члена арифметической прогресии
понятие арифметической прогрессии
формула п-го члена фрифметической прогрессии
сумма первых n членов арифметической прогрессии
геометрическая прогрессияю, формула n-го члена геометрической прогрессии
понятие геометрической прогрессии
формула n-го члена геометрической прогрессии
сумма первых n членов геометрической прогрессии
9. Решение задач на составление уравнений, на проценты (4ч)
10. Решение геометрических задач ( 12 ч)
| № урока | Тема занятия | Кол. часов | Дата | измен | прим. |
| 1-2 | Задачи с целыми числами. Признаки делимости. | 2 | |||
| 3-6 | Действительные числа. Преобразования алгебраических выражений | 4 | |||
| 7-10 | Уравнения и неравенства первой и второй степени. | 4 | |||
| 11-12 | Уравнения высших степеней. Рациональные неравенства | 2 | |||
| 13-16 | Иррациональные уравнения и неравенства | 4 | |||
| 17-22 | Системы уравнений и неравенств | 6 | |||
| 23-24 | Область определения и множество значений функции | 2 | |||
| 25-26 | Графики функций | 2 | |||
| 27-30 | Преобразования тригонометрических выражений. Обратные тригонометрические функции | 4 | |||
| 31-34 | Решение тригонометрических уравнений, неравенств и систем уравнений | 4 | |||
| 35-38 | Производная. Исследование функций с помощью производной | 4 | |||
| 39-42 | Первообразная. Интеграл. Площади криволинейных трапеций | 4 | |||
| 43-46 | Показательные и логарифмические уравнения и неравенства | 4 | |||
| 47-48 | Прогрессии | 2 | |||
| 49-52 | Решение задач на составление уравнений ,на проценты | 4 | |||
| 53-56 | Решение уравнений, содержащих параметры | 4 | |||
| 57-62 | Планиметрия. Задачи на вычисление | 6 | |||
| 63-68 | Стереометрия. Задачи на вычисление | 6 | |||
| итого | 68 |
Календарно-тематическое планирование
(2час в неделю, всего 68ч)
Используемая литература:
Повторяем и систематизируем школьный курс алгебры начал анализа, В.С. Крамор,»просвещение»;
Задачи по математике. Уравнения и неравества, Москва «Наука»
Тригонометрические уравнения и неравенства, И.Т. Бородуля, Москва»Просвещение»;
Уравнения и неравенства, содержащие параметры, Г.А. Ястребинский, Москва «Просвещение»;
Повторяем и систематизируем школьный курс геометрии, В.С. Крамор, «Просвещение»;
Сборники тестовых заданий для подготовки к ЕНТ.
Государственная средняя общеобразовательная школа №28
Программа
спецкурса по математике
« Математика абитуриенту»
для учащихся 11 класса
Разработала : учитель математики
высшей категории СОШ №28
Дроздова Людмила Евгеньевна
2013 год
kopilkaurokov.ru
Программа спецкурса по математике для 10-11 классов
Пояснительная записка
Цели обучения математике в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека.
Исторически сложились две стороны назначения математического образования: практическая, связанная с созданием и применением инструментария, необходимого человеку в его продуктивной деятельности, и духовная, связанная с мышлением человека, с овладением определенным методом познания и преобразования мира математическим методом.
Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира: пространственные формы и количественные отношения – от простейших, усваиваемых в непосредственном опыте людей, до достаточно сложных, необходимых для развития научных и технологических идей. Без конкретных математических знаний затруднено понимание принципов устройства и использования современной техники, восприятие научных знаний, восприятие и интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. Каждому человеку в своей жизни приходится выполнять достаточно сложные расчеты, пользоваться общеупотребительной вычислительной техникой, находить в справочниках и применять нужные формулы, владеть практическими приемами геометрических измерений и построений, читать информацию, представленную в виде таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др.
Без базовой математической подготовки невозможна постановка образования современного человека. В школе математика служит опорным предметом для изучения смежных дисциплин. В послешкольной жизни реальной необходимостью в наши дни становится непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. И наконец, все больше специальностей, требующих высокого уровня образования, связано с непосредственным применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, биология, психология и многое другое). Таким образом, расширяется круг школьников, для которых математика становится профессионально значимым предметом.
Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющегося в определенных умственных навыках. В процессе математической деятельности в арсенал приемов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления, воспитании умений действовать по заданному алгоритму и конструировать новые. В ходе решения задач – основной учебной деятельности на уроках математики – развиваются творческая и прикладная стороны мышления.
Использование в математике наряду с естественным нескольких математических языков дает возможность развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства.
Математическое образование вносит свой вклад в формирование общей культуры человека. Необходимым компонентом общей культуры в ее современном толковании является общее знакомство с методами познания действительности, что включает понимание диалектической взаимосвязи математики и действительности, представление о предмете и методе математики, его отличиях от методов естественных и гуманитарных наук, об особенностях применения математики для решения научных и прикладных задач. Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идеи симметрии. Изучение математики развивает воображение, пространственные представления. История развития математического знания дает возможность пополнить запасы историко-научных знаний школьников, сформировать у них представления о математике как части общечеловеческой культуры. Знакомство с основными историческими вехами возникновения и развития математической науки, судьбами великих открытий, именами людей, творивших науку, должно войти в интеллектуальный багаж каждого культурного человека.
Роль математической подготовки в общем образовании современного человека ставит следующие цели обучения математике в школе:
овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе;
формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
Основная задача обучения математике в школе заключается в обеспечении прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому человеку, достаточных для изучения смежных дисциплин и продолжения образования.
Наряду с решением основной задачи расширенное и углубленное изучение математики предусматривает формирование у учащихся устойчивого интереса к предмету, выявление и развитие их математических способностей, ориентацию на профессии, существенным образом связанные с математикой, подготовку к обучению в вузе.
Занятия курса призваны помочь ученику осознать степень своего интереса к предмету и оценить возможности овладения им, с тем, чтобы он смог сделать сознательный выбор в пользу дальнейшего углубленного либо обычного изучения математики. Интерес и склонности учащегося к математике должны всемерно подкрепляться и развиваться. Учащиеся должны приобрести умения решать задачи более высокой сложности, точно и грамотно формулировать изученные теоретические положения и излагать собственные рассуждения при решении задач и доказательствах теорем, правильно пользоваться математической терминологией и символикой, применять рациональные приемы вычислений и тождественных преобразований, использовать наиболее употребительные эвристические приемы и т.д.
В программу включены ряд дополнительных вопросов, непосредственно примыкающих к курсу алгебры и начал анализа и расширяющих и углубляющих его по основным идейным линиям. Включены также самостоятельные разделы, которые в настоящее время не изучаются, но являются важными содержательными компонентами системы непрерывного математического образования.
Включение дополнительных вопросов преследует две цели:
создание в совокупности с основными разделами курса базы для удовлетворения интересов и развития способностей учащихся, имеющих склонность к математике;
восполнение содержательных пробелов основного курса, придающее содержанию расширенного и углубленного изучения необходимую целостность.
Расширенное и углубленное изучение математики предполагает наполнение курса разнообразными, интересными и сложными задачами, овладение основным программным материалом на более высоком уровне.
Для поддержания и развития интереса к предмету в программу включены занимательные задачи, сведения из истории математики.
Цель: создать условия для расширенного и углубленного изучения материала, удовлетворения познавательных интересов и развития способностей учащихся в соответствии с основными темами курса алгебры и начал анализа 10-11 классов.
Задачи: формировать у учащихся сознательное и прочное овладение системой математических знаний, умений, навыков; систематизировать, расширить и углубить знания по алгебре и началам анализа; детально расширить темы, недостаточно глубоко изучаемые в школьном курсе и, как правило, вызывающие затруднения у учащихся; развивать математические способности учащихся; способствовать вовлечению учащихся в самостоятельную исследовательскую деятельность.
Срок реализации программы – 2 года.
Содержание программы
10 класс
Учебно-тематический план
10 класс
| Решение текстовых задач. | 6/12 |
| Корень степени n. | 2/4 |
| Логарифмы. | 2/4 |
| Показательные и логарифмические уравнения и неравенства. | 6/12 |
| Синус и косинус угла. | 2/4 |
| Тангенс и котангенс угла. | 2/4 |
| Тригонометрические уравнения и неравенства. | 5/10 |
| Элементы теории вероятностей. | 3/6 |
| Итого | 34 часов/68 часов |
Содержание программы
11 класс
Учебно-тематический план
11 класс
| Функции и их графики | 5/10 |
| Производная | 5/10 |
| Применение производной | 5/10 |
| Первообразная и интеграл | 6/12 1/2 |
| Уравнения. Неравенства. Системы. Нестандартные методы решения уравнений и неравенств. | 13/26 |
| Итого | 34 часа/68 часов |
Ожидаемый результат. В результате изучения данного курса учащиеся должны
знать:
основные приемы решений рациональных, иррациональных, показательных, логарифмических, тригонометрических уравнений, неравенств и их систем;
правила преобразований выражений, графиков функций;
способы решения текстовых и других задач;
четко основные определения, формулы и свойства;
уметь:
выполнять тождественные преобразования рациональных, логарифмических, тригонометрических и других выражений;
строить графики элементарных и более сложных функций;
решать задачи, уравнения, неравенства, системы, предусмотренные программой курса;
применять аппарат математического анализа к решению задач;
Формы работы.
привлечение учащихся к составлению таблиц, графиков, изготовлению наглядного, дидактического, раздаточного материала, подготовке презентаций;
использование на занятиях игровых моментов: конкурсов, математических боев, КВН и др.;
изучение, конспектирование учащимися материала из дополнительной литературы;
использование компьютерных, тестовых и других технологий;
Темы творческих работ
(для подготовки к семинарским занятиям)
1) Теорема Пифагора и диофантовы уравнения.
2) Пифагор, Герон, Евклид – известные древнегреческие ученые.
3) Большая теорема Ферма.
4) Известные диофантовы уравнения.
5) Король любителей – П. Ферма.
6) Воплощенный анализ – Л. Эйлер.
7) Величественная пирамида – Ж. Лагранж.
8) Король математиков – К. Гаусс.
Темы исследовательских работ
Уравнения и неравенства с параметром.
2) Задачи, приводящие к дифференциальным уравнениям.
Глоссарий
Абстрагирование – мысленное отвлечение, обособление от тех или иных сторон, свойств или связей предметов и явлений для выделения существенных их признаков.
Алгоритм – совокупность действий, правил для решения данной задачи.
Анализ – метод научного исследования путём рассмотрения отдельных сторон, свойств, составных частей чего-нибудь.
Аналогия — сходство в каком-нибудь отношении между явлениями , предметами, понятиями.
Дедукция – способ рассуждения, при котором новое положение выводится чисто логическим путём от общих положений к частным выводам.
Индукция — способ рассуждения от частных фактов, положений к общим выводам.
Исследование – поиск информации по какой-либо проблеме, за которым следует ее обобщение (написание исследовательской работы или заключения).
Конкретизация – представление в конкретном виде.
Конспект — систематическая, логическая связанная запись, объединяющая план, тезисы, выписки.
Практика — после того как основные идеи были изложены, необходимо предоставить учащимся время на выполнение упражнений.
Прикладные курсы — входят в состав профиля обучения, обязательны для посещения, реализуются за счет школьного компонента и выполняют две функции: «поддерживают» изучение основных профильных предметов и служат для внутри профильной специализации обучения.
Реферат – письменный доклад или выступление по определённой теме, в которой обобщается информация из одного или нескольких источников.
Синтез — метод исследования какого-нибудь явления в его единстве и взаимной связи частей, обобщение, сведение в единое целое данных, добытых анализом.
Тестирование – форма измерения знаний учащихся, основанная на применении педагогических тестов.
Тренинг — метод активного обучения, направленный на развитие ЗУНов.
Список использованной литературы:
1.М.И.Шабунин. Математика для поступающих в ВУЗы.
2.В.А.Гольдич. Алгебра. Решение уравнений и неравенств. Школьная программа.
3.И.Ф.Шарыгин, В.И. Голубев. Факультативный курс по математике.
4.В.С.Лютикас. Факультативный курс по математике.
5.О.Б.Епишева, В.И. Крупич. Учить школьников учиться математике.
Список литературы для учителя и учащихся:
1.А.Г.Мерзляк, В.Б.Полонский, М.С.Якир. Алгебраический тренажер. «Илекса» «Гимназия», Москва-Харьков, 1998.
2.Р.Б.Райхмист. Графики функций. Задачи и упражнения. «Школа-пресс», Москва,
1997г.
3.Г.А.Ястребинецкий. Уравнения и неравенства с параметрами. «Просвещение»,
Москва,1972г.
4.И.Т.Бородуля. Тригонометрические уравнения и неравенства. «Просвещение», Москва, 1998.
5.А.П.Ершова, В.В.Голобородько. Самостоятельные и контрольные работы. Алгебра и начала анализа. 10-11 кл. Разноуровневые дидактические материалы.
6.С.В.Кравцов и др. Методы решения задач по алгебре: от простых до самых сложных.
7.В.Г.Брагин, А.И.Грабовский. Все предметы школьной программы в схемах и таблицах. Алгебра. Геометрия.
8.В.С.Крамор. Повторяем и систематизируем школьный курс алгебры и начал анализа, «Просвещение», 1990.
9.В.С.Крамор, А.А.Михайлов. Тригонометрические функции, «Просвещение», 1983.
10.А.Мерзляк и др. Тригонометрия. Задачник к школьному курсу. 8-11 кл. «АСТ-ПРЕСС: Магистр-S», 1998.
11.Л.О.Денищева и др. Учимся решать уравнения и неравенства. 10-11кл.
12.М.И.Башмаков и др. Задачи по математике. Алгебра и анализ.
13.Б.Г.Зив. Тесты по алгебре и началам анализа. 10-11кл.
14.Г.Г.Левитас. Карточки для коррекции знаний по алгебре. 10-11кл.
15.Е.С.Канин и др. Упражнения по началам математического анализа в 10-11кл.
16.И.Т.Бородуля. Показательная и логарифмическая функции (задачи и упражнения).
17.М.И.Шабунин. Математика для поступающих в ВУЗы. Уравнения и системы уравнений.
18.Р.Д.Лукин и др. Устные упражнения по алгебре и началам анализа.
infourok.ru
Программа спецкурса по математике для 10—11-х классов по теме «Избранные вопросы математики»
Разделы: Математика
Пояснительная записка
Цели обучения математике в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека.
Исторически сложились две стороны назначения математического образования: практическая, связанная с созданием и применением инструментария, необходимого человеку в его продуктивной деятельности, и духовная, связанная с мышлением человека, с овладением определенным методом познания и преобразования мира математическим методом.
Практическая полезность математики обусловлена тем, что ее предметом являются фундаментальные структуры реального мира: пространственные формы и количественные отношения – от простейших, усваиваемых в непосредственном опыте людей, до достаточно сложных, необходимых для развития научных и технологических идей. Без конкретных математических знаний затруднено понимание принципов устройства и использования современной техники, восприятие научных знаний, восприятие и интерпретация разнообразной социальной, экономической, политической информации, малоэффективна повседневная практическая деятельность. Каждому человеку в своей жизни приходится выполнять достаточно сложные расчеты, пользоваться общеупотребительной вычислительной техникой, находить в справочниках и применять нужные формулы, владеть практическими приемами геометрических измерений и построений, читать информацию, представленную в виде таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др.
Без базовой математической подготовки невозможна постановка образования современного человека. В школе математика служит опорным предметом для изучения смежных дисциплин. В послешкольной жизни реальной необходимостью в наши дни становится непрерывное образование, что требует полноценной базовой общеобразовательной подготовки, в том числе и математической. И наконец, все больше специальностей, требующих высокого уровня образования, связано с непосредственным применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, биология, психология и многое другое). Таким образом, расширяется круг школьников, для которых математика становится профессионально значимым предметом.
Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющегося в определенных умственных навыках. В процессе математической деятельности в арсенал приемов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирования вскрывают механизм логических построений, вырабатывают умения формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления, воспитании умений действовать по заданному алгоритму и конструировать новые. В ходе решения задач – основной учебной деятельности на уроках математики – развиваются творческая и прикладная стороны мышления.
Использование в математике наряду с естественным нескольких математических языков дает возможность развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства.
Математическое образование вносит свой вклад в формирование общей культуры человека. Необходимым компонентом общей культуры в ее современном толковании является общее знакомство с методами познания действительности, что включает понимание диалектической взаимосвязи математики и действительности, представление о предмете и методе математики, его отличиях от методов естественных и гуманитарных наук, об особенностях применения математики для решения научных и прикладных задач. Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идеи симметрии. Изучение математики развивает воображение, пространственные представления. История развития математического знания дает возможность пополнить запасы историко-научных знаний школьников, сформировать у них представления о математике как части общечеловеческой культуры. Знакомство с основными историческими вехами возникновения и развития математической науки, судьбами великих открытий, именами людей, творивших науку, должно войти в интеллектуальный багаж каждого культурного человека.
Роль математической подготовки в общем образовании современного человека ставит следующие цели обучения математикев школе:
- овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, для продолжения образования;
- интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых для продуктивной жизни в обществе;
- формирование представлений об идеях и методах математики, о математике как форме описания и методе познания действительности;
- формирование представлений о математике как части общечеловеческой культуры, понимания значимости математики для общественного прогресса.
Основная задача обучения математике в школе заключается в обеспечении прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому человеку, достаточных для изучения смежных дисциплин и продолжения образования.
Наряду с решением основной задачи расширенное и углубленное изучение математики предусматривает формирование у учащихся устойчивого интереса к предмету, выявление и развитие их математических способностей, ориентацию на профессии, существенным образом связанные с математикой, подготовку к обучению в вузе.
Занятия курса призваны помочь ученику осознать степень своего интереса к предмету и оценить возможности овладения им, с тем, чтобы он смог сделать сознательный выбор в пользу дальнейшего углубленного либо обычного изучения математики. Интерес и склонности учащегося к математике должны всемерно подкрепляться и развиваться. Учащиеся должны приобрести умения решать задачи более высокой сложности, точно и грамотно формулировать изученные теоретические положения и излагать собственные рассуждения при решении задач и доказательствах теорем, правильно пользоваться математической терминологией и символикой, применять рациональные приемы вычислений и тождественных преобразований, использовать наиболее употребительные эвристические приемы и т.д.
В программу включены ряд дополнительных вопросов, непосредственно примыкающих к курсу алгебры и начал анализа и расширяющих и углубляющих его по основным идейным линиям. Включены также самостоятельные разделы, которые в настоящее время не изучаются, но являются важными содержательными компонентами системы непрерывного математического образования.
Включение дополнительных вопросов преследует две цели:
- создание в совокупности с основными разделами курса базы для удовлетворения интересов и развития способностей учащихся, имеющих склонность к математике;
- восполнение содержательных пробелов основного курса, придающее содержанию расширенного и углубленного изучения необходимую целостность.
Расширенное и углубленное изучение математики предполагает наполнение курса разнообразными, интересными и сложными задачами, овладение основным программным материалом на более высоком уровне.
Для поддержания и развития интереса к предмету в программу включены занимательные задачи, сведения из истории математики.
Программа составлена на основе изучения курса алгебры и начал анализа по учебнику «Алгебра и начала анализа: учебник для 10-11 кл. общеобразовательных учреждений / [С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин]. – М.: Просвещение, 2006.
Цель программы:
- создать условия для расширенного и углубленного изучения материала, удовлетворения познавательных интересов и развития способностей учащихся в соответствии с основными темами курса алгебры и начал анализа 10-11 классов.
Задачи программы:
- формировать у учащихся сознательное и прочное овладение системой математических знаний, умений, навыков;
- систематизировать, расширить и углубить знания по алгебре и началам анализа; детально расширить темы, недостаточно глубоко изучаемые в школьном курсе и, как правило, вызывающие затруднения у учащихся;
- развивать математические способности учащихся;
- способствовать вовлечению учащихся в самостоятельную исследовательскую деятельность.
Класс гимназический, универсальный.
Срок реализации программы – 2 года.
Содержание программы
10 класс
| Название раздела, темы | Теоретический раздел программы |
| Рациональные уравнения и неравенства | Деление многочленов с остатком.
Алгоритм Евклида. Теорема Безу. Корень многочлена. |
| Решение текстовых задач | Задачи на проценты. Задачи на смеси и сплавы. Задачи на совместную работу. Разные задачи. |
| Корень степени n | Функция у = х и ее график. |
| Логарифмы | Десятичные логарифмы. Степенные функции. Преобразование выражений, содержащих логарифмы. |
| Показательные и логарифмические уравнения и неравенства | Показательные уравнения. Логарифмические уравнения. Уравнения с модулем. Уравнения с параметром. Показательные и логарифмические неравенства. Неравенства с модулем. Неравенства с параметром. Графический способ решения уравнений и неравенств. |
| Синус и косинус угла | Примеры использования арксинуса и
арккосинуса. Формулы для арксинуса и арккосинуса. |
| Тангенс и котангенс угла | Примеры использования арктангенса и
арккотангенса. Формулы для арктангенса и арккотангенса. |
| Тригонометрические уравнения и неравенства | Тригонометрические уравнения. Замена неизвестного t = sin x + cos x. Тригонометрические неравенства. Уравнения и неравенства с модулем. Уравнения и неравенства с параметром. |
| Элементы теории вероятностей | Математическое ожидание. Сложный опыт. Формула Бернулли. Закон больших чисел. |
Учебно-тематический план
10 класс
| Наименование раздела, темы | Количество часов по теме |
| Рациональные уравнения.
Неравенства. Деление многочленов с остатком. Алгоритм Евклида. Теорема Безу. Корень многочлена. |
3/6 |
| Решение текстовых задач. Задачи на проценты. Задачи на смеси и сплавы. Задачи на совместную работу. Разные задачи. |
6/12 |
| Корень степени n. Функция у = х и ее график. |
2/4 |
| Логарифмы. Десятичные логарифмы. Степенные функции. Преобразование выражений, содержащих логарифмы. |
2/4 |
| Показательные и логарифмические
уравнения и неравенства. Показательные уравнения. Логарифмические уравнения. Уравнения с модулем. Уравнения с параметром. Показательные и логарифмические неравенства. Неравенства с модулем. Неравенства с параметром. Графический способ решения уравнений и неравенств. |
6/12 |
| Синус и косинус угла. Примеры использования арксинуса и арккосинуса. Формулы для арксинуса и арккосинуса. |
2/4 |
| Тангенс и котангенс угла. Примеры использования арктангенса и арккотангенса. Формулы для арктангенса и арккотангенса. |
2/4 |
| Тригонометрические уравнения и
неравенства. Тригонометрические уравнения. Замена неизвестного t = sin x + cos x. Тригонометрические неравенства. Уравнения и неравенства с модулем. Уравнения и неравенства с параметром. |
5/10 |
| Элементы теории вероятностей. Математическое ожидание. Сложный опыт. Формула Бернулли. Закон больших чисел. |
3/6 |
| Итого | 35 часов/70 часов |
Содержание программы
11 класс
| Название раздела, темы | Теоретический раздел программы |
| Функции и их графики | Основные способы преобразования графиков. Графики функций, связанных с модулем. Графики сложных функций. Разрывные функции. |
| Производная | Непрерывность функций, имеющих производную. Дифференциал. Производная сложных функций. Производная обратной функции. |
| Применение производной | Теоремы о среднем. Производные высших порядков. Выпуклость и вогнутость графика функции. Асимптота. Формула и ряд Тейлора. |
| Первообразная и интеграл | Замена переменной. Интегрирование по частям. Применение определенных интегралов в геометрических и физических задачах. Понятие дифференциального уравнения. Задачи, приводящие к дифференциальным уравнениям. |
| Уравнения. Неравенства. Системы. Нестандартные методы решения уравнений и неравенств | Уравнения с дополнительными условиями. Неравенства с дополнительными условиями. Уравнения и неравенства с модулями. Метод интервалов для непрерывных функций. Использование областей существования функций. Использование неотрицательности функций. Использование ограниченности функций. Использование свойств синуса и косинуса. Использование числовых неравенств. Использование производной для решения уравнений и неравенств. Уравнения с параметром. Неравенства с параметром. |
Учебно-тематический план
11 класс
| Название раздела, темы | Количество часов по теме |
| Функции и их графики Основные способы преобразования графиков Графики функций, связанных с модулем Графики сложных функций Разрывные функции Решение заданий по теме из КИМов ЕГЭ |
5/10 |
| Производная Непрерывность функций, имеющих производную Дифференциал. Дифференциальные уравнения Производная сложных функций Производная обратной функции Решение заданий по теме из КИМов ЕГЭ |
5/10 |
| Применение производной Теоремы о среднем Производные высших порядков Выпуклость и вогнутость графика функции. Асимптота Формула и ряд Тейлора Решение заданий по теме из КИМов ЕГЭ |
5/10 |
| Первообразная и интеграл Замена переменной Интегрирование по частям Применение определенных интегралов в геометрических и физических задачах Понятие дифференциального уравнения Задачи, приводящие к дифференциальным уравнениям Решение заданий по теме из КИМов ЕГЭ |
6/12 1/2 |
| Уравнения. Неравенства. Системы.
Нестандартные методы решения уравнений и
неравенств Уравнения с дополнительными условиями Неравенства с дополнительными условиями Уравнения и неравенства с модулями Метод интервалов для непрерывных функций Использование областей существования функций Использование неотрицательности функций Использование ограниченности функций Использование свойств синуса и косинуса Использование числовых неравенств Использование производной для решения уравнений и неравенств Уравнения с параметром Неравенства с параметром Решение заданий по теме из КИМов ЕГЭ |
13/26 |
| Итого | 34 часа/68 часов |
Требования к математической подготовке учащихся
В результате изучения данного курса учащиеся должны
знать:
- основные приемы решений рациональных, иррациональных, показательных, логарифмических, тригонометрических уравнений, неравенств и их систем;
- правила преобразований выражений, графиков функций;
- способы решения текстовых и других задач;
- четко основные определения, формулы и свойства;
уметь:
- выполнять тождественные преобразования рациональных, логарифмических, тригонометрических и других выражений;
- строить графики элементарных и более сложных функций;
- решать задачи, уравнения, неравенства, системы, предусмотренные программой курса;
- применять аппарат математического анализа к решению задач;
Формы, методы, способы и средства реализации программы
- привлечение учащихся к составлению таблиц, графиков, изготовлению наглядного, дидактического, раздаточного материала, подготовке презентаций;
- использование на занятиях игровых моментов: конкурсов, математических боев, КВН и др.;
- изучение, конспектирование учащимися материала из дополнительной литературы;
- использование компьютерных, тестовых и других технологий;
Учебно-методическое обеспечение программы
- специальная справочная литература;
- методическая литература;
- дидактический и раздаточный материал;
- набор КИМов ЕГЭ прошлых лет.
Список литературы по программе:
- А.Г.Мерзляк, В.Б.Полонский, М.С.Якир. Алгебраический тренажер. «Илекса» «Гимназия», Москва-Харьков, 1998.
- Р.Б.Райхмист. Графики функций. Задачи и упражнения. «Школа-пресс», Москва, 1997.
- Г.А.Ястребинецкий. Уравнения и неравенства с параметрами. «Просвещение», Москва, 1972.
- И.Т.Бородуля. Тригонометрические уравнения и неравенства. «Просвещение», Москва, 1998.
- А.П.Ершова, В.В.Голобородько. Самостоятельные и контрольные работы. Алгебра и начала анализа. 10-11 кл. Разноуровневые дидактические материалы.
- С.В.Кравцов и др. Методы решения задач по алгебре: от простых до самых сложных.
- М.И.Шабунин. Математика для поступающих в ВУЗы. Уравнения и системы уравнений.
- М.И.Шабунин. Математика для поступающих в ВУЗы. Неравенства и системы неравенств.
- В.А.Гольдич. Алгебра. Решение уравнений и неравенств. Школьная программа.
- В.Г.Брагин, А.И.Грабовский. Все предметы школьной программы в схемах и таблицах. Алгебра. Геометрия.
- В.С.Крамор. Повторяем и систематизируем школьный курс алгебры и начал анализа, «Просвещение», 1990.
- В.С.Крамор, А.А.Михайлов. Тригонометрические функции, «Просвещение», 1983.
- А.Мерзляк и др. Тригонометрия. Задачник к школьному курсу. 8-11 кл. «АСТ-ПРЕСС: Магистр-S», 1998.
- Л.О.Денищева и др. Учимся решать уравнения и неравенства. 10-11кл.
- М.И.Башмаков и др. Задачи по математике. Алгебра и анализ.
- Б.Г.Зив. Тесты по алгебре и началам анализа. 10-11кл.
- Р.Д.Лукин и др. Устные упражнения по алгебре и началам анализа..
- Г.Г.Левитас. Карточки для коррекции знаний по алгебре. 10-11кл.
- Е.С.Канин и др. Упражнения по началам математического анализа в 10-11кл.
- И.Т.Бородуля. Показательная и логарифмическая функции (задачи и упражнения).
7.06.2009
xn--i1abbnckbmcl9fb.xn--p1ai
Рабочая программа спецкурса по математике в 10 – 11 классы.
Рабочая программа спецкурса по математике в 10 – 11кл. разработана на основе федерального компонента государственного образовательного стандарта среднего (полного) общего образования по математике, примерной программы среднего (полного) общего образования по математике (базовый уровень).
Нормативные правовые документы, на основании которых разработана рабочая программа:
Федеральный закон от 29.12.2012 года № 273-ФЗ (ред. От 07 мая 2013 года) «Об образовании в Российской Федерации»
Постановление Главного государственного санитарного врача Российской Федерации от 29.12.2010 № 189 (ред. от 24.11.2015) «Об утверждении СанПиН 2.4.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях» (зарегистрировано в Минюсте России 03.03.2011г. № 19993.
Постановление Главного государственного санитарного врача Российской Федерации от 24.11.2015 № 81 «О внесении изменений № 3 в СанПиН 2.4.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях».
Данный курс является базовым общеобразовательным и направлен на завершение общеобразовательной подготовки обучающихся.
Цель данного курса: оказание индивидуальной и систематической помощи выпускнику при систематизации, обобщении и повторении курса алгебры и подготовке к экзаменам.
Задачи курса:
1) подготовить учащихся к экзаменам;
2) дать ученику возможность проанализировать и раскрыть свои способности;
Предлагаемый курс является развитием системы ранее приобретенных программных знаний, его цель — создать целостное представление о теме и значительно расширить спектр задач, посильных для учащихся.
.Функции спецкурса:
ориентация на совершенствование навыков познавательной, организационной деятельности;
компенсация недостатков обучения по математике.
Место предмета в базисном учебном плане
Спецкурс по математике «Практикум по решению задач» рассчитан на 136 часов для работы с учащимися 10 и 11 классов. Предусматривает повторное рассмотрение теоретического материала по математике, а кроме этого, нацелен на более глубокое рассмотрение отдельных тем, поэтому имеет большое общеобразовательное значение, способствует развитию логического мышления, намечает и использует целый ряд межпредметных связей (прежде всего с физикой и историей).
п.п.Наименование
10 класс
11 класс
Количество часов
Количество часов
1
Количество часов в неделю
2
2
2
Количество часов в 1 полугодии
32
32
3
Количество часов во II полугодии
36
36
4
Количество часов в учебном году
68
68
Тематическое планирование
Содержание и методические рекомендацииАрифметика. Законы действий с числами. Правила действий с десятичными и обыкновенными дробями, положительными и отрицательными числами. Пропорции. Сравнение чисел.
Основная цель – проверить навыки счета с целью составления индивидуальных планов коррекции вычислительных навыков.
Выражения и их преобразования: определение многочлена и операции с многочленами, равенств двух многочленов, разложение многочлена на множители, деление многочлена на многочлен, теорема Безу.
Основная цель – расширить и углубить знания и умения, связанные с тождественными преобразованиями рациональных , иррациональных, логарифмических, степенных выражений.
Текстовые задачи
Проценты, сплавы, смеси. Движение. Путь, скорость. Работа, производительность.
Основная цель — совершенствовать навыки решения задач , научить обучающихся давать обоснования при решении задач, опираясь на теоретические сведения.
Методические рекомендации
Эта тема введена в связи с тем, что такого типа задачи встречаются в КИМах ЕГЭ . Задачи, которые будут рассматриваться, соответствуют степени трудности задач, предлагаемых на ЕГЭ. Необходимо включать задачи, взятые из окружающей жизни, задачи, естественным образом связанные со знакомыми обучающимся вещами, опытом. Контроль усвоения материала можно провести по желанию обучающегося в виде домашней контрольной работы.
Задачи на прогрессию
Арифметическая и геометрическая прогрессии. Убывающая геометрическая прогрессия
Основная цель — развивать навыки решения задач, связанных с прогрессиями.
Методические рекомендации
Повторить определения арифметической и геометрической прогрессий, их характеристических свойств, формул, которые применяются при решении задач на прогрессии. На занятиях рассмотреть более сложные задачи, где присутствуют различные функции, которые образуют некоторую прогрессию.
Решение геометрических задач
Треугольники. Четырехугольники. Вписанная в многоугольник и описанная около многоугольника окружности. Площади. Комбинации тел. Объемы тел. Решение геометрических задач повышенной трудности.
Основная цель — обобщить знания и умения обучающихся по курсу планиметрии, стереометрии.
Обучающиеся должны уметь: проводить полные обоснования при решении задач, используя для этого изученные теоретические сведения; освоить определенный набор приемов решения геометрических задач и уметь применять их в задачах на вычисление, доказательство; овладеть общими методами геометрии (преобразований, векторный, координатный) и применять их при решении геометрических задач, вычислять значения геометрических величин (длин, углов, площадей, объемов), используя изученные формулы, а также аппарат алгебры, начала анализа и тригонометрии.
Методические рекомендации
Повторить и обобщить знания и умения обучающихся по геометрии. Разобрать решения некоторых нестандартных задач, наиболее часто встречающихся. Особое внимание уделить на решение задач, где участвуют несколько тел. Тему завершить домашней контрольной работой.
Уравнения
Многочлены. Рациональные уравнения. Иррациональные уравнения. Тригонометрические уравнения. Уравнения с модулями. Уравнение с двумя неизвестными. Системы уравнений с двумя неизвестными. Уравнения с параметром. Системы уравнений с параметром.
Основная цель — обобщить и систематизировать имеющиеся у обучающихся сведения об уравнениях, системах и методах их решения. Сформировать умение решать уравнения с модулями, параметрами.
При изучении темы обучающиеся должны знать: определение многочлена, выполнять действия с многочленами, раскладывать многочлен на множители. Знать формулы разложения многочлена разности и суммы кубов, разности хп — уп и суммы х2п+1 – у2п+1 , теорему Безу и ее следствие о делимости многочлена на линейный двучлен. Знать, какие уравнения называются равносильными, уравнения-следствия, какие операции приводят к появлению посторонних корней, какие – к потере. Уметь применять нестандартные приемы при решении уравнений и их систем.
Показательные и логарифмические уравнения. Показательные и логарифмические неравенства. Основная цель — обобщить и систематизировать знания умения обучающихся по теме. Научить обучающихся применять нестандартные приемы при решении уравнений и их систем., а также применять графики для решения неравенств и их систем.
Методические рекомендации
Дать определения показательного, логарифмического уравнения, показательного, логарифмического неравенства с одной переменной, повторить теоремы , которые используются при решении неравенств. Повторить свойства функций. Задания для занятий можно брать из сборников для поступающих в вузы и для подготовки к ЕГЭ. При выполнении практических заданий обучающихся можно разбить на группы, работу в группах давать различной степени сложности и оценить результаты. Тему завершить домашней контрольной работой.
Сначала желательно повторить определение многочлена и операции с многочленами, особое внимание уделить равенству двух многочленов, разложению многочлена на множители, делению многочлена на многочлен, теорему Безу. Далее дать определение равносильных уравнений и уравнений-следствий, теоремы, при которых уравнения переходят в равносильные уравнения. Рассмотреть различные способы решения уравнений и их систем, более подробно разобрать функционально-графический метод решения уравнений и метод оценки. Задания для занятий можно брать из сборников для подготовки к ЕГЭ. При выполнении практических заданий обучающихся можно разбить на группы, работу в группах давать различной степени сложности и оценить результаты. Тему завершить домашней контрольной работой.
Неравенства
Тригонометрические неравенства. Иррациональные неравенства. Неравенства с параметром. Смешанные неравенства.
Основная цель — обобщить и систематизировать имеющиеся у обучающихся сведения о неравенствах, системах и методах их решения, познакомить с неравенствами Коши и Бернулли, научить применять их, сформировать умение решать неравенства с параметрами.
При решении неравенств целесообразно обращаться к графическим образам.
Показательные и логарифмические неравенства будут изучаться позже.
Методические рекомендации
Напомнить определение неравенства с одной переменной, определения равносильных неравенств, повторить теоремы , которые используются при решении неравенств, метод интервалов. Повторить свойства функций. Задания обучающимся давать различной степени трудности, чтобы каждые смог бы выбрать те задания, которые ему по силам. В конце провести контрольную работу по двум темам.
Функции
Наибольшее, наименьшее значения функции (без использования производной). Производная, её геометрический смысл. Применение производной к исследованию функций и нахождению наибольшего и наименьшего значений. Первообразная. Вычисление площадей криволинейных трапеций. Сложная функция. Область определения и множество значений функции. Решение уравнений, неравенств и их систем с помощью применения свойств функций (нестандартные задачи).
Основная цель — совершенствовать навыки и умения применять методы дифференциального исчисления и методы интегрирования для решения задач.
В результате изучения темы обучающиеся должны уметь: находить значения функций, заданных формулой, таблицей, графиком; проводить исследование функций; строить и читать графики функций; владеть основными приемами преобразования графиков и применять их при построении графиков; уметь преобразовывать выражения, содержащие обратные тригонометрические функции. Существенное внимание следует уделить решению разнообразных задач, связанных с исследованием функций, и нахождению первообразных в сложных случаях.
Методические рекомендации
Знать свойства функций, сложных функций и уметь применять свои знания при нахождении области определения функции и множества значений функции, находить наибольшее и наименьшее значения функции без использования производной. Повторить свойства обратных тригонометрических функций. После изучения темы провести контрольную работу.
Решение различных задач повышенной сложности (6ч)
Основная цель — научить обучающихся решать нестандартные задания и задания повышенной сложности, взятые из материалов ЕГЭ и сборников для поступающих в вузы.
Последние занятия рассчитаны на то, что обучающиеся в основном самостоятельно будут отыскивать ход решения задачи, его оформления. Работу можно организовать в виде пар или небольших групп. Потом провести зачетную работу, сделать анализ решений и допущенных ошибок.
Методические рекомендации
При проведении занятий применять различные формы и методы, а именно: уроки-практикумы, уроки-зачеты, урок вопросов и ответов, урок-семинар, групповая и индивидуальная работа. Обучающимся, которые принимают активное участие в работе, выставлять полученные отметки в журнал. Заранее доводить до сведения обучающихся уровень сложности тех или иных заданий. За две-три недели до зачета довести до сведения обучающихся примерный перечень вопросов и задач.
Материал курса должен быть освоен на базовом уровне. Учитель может провести самостоятельные работы, пробный экзамен, зачёты по конкретным темам.
Основными результатами освоения содержания спецкурса учащимися может быть определенный набор универсальных учебных действий, а также опыт внеурочной деятельности, содержательно связанной с предметным полем – математикой. При этом должна использоваться преимущественно качественная оценка выполнения заданий, а также итоговое тестирование учащихся.
Начинается курс с ознакомительной вводной лекции. Следующее за ней занятие посвящается входному тестированию, цели которого:
Составить представление учителя об уровне базовых знаний учащихся.
Коррекция в связи с этим уровня подачи материала по данному курсу.
При прослушивании блоков лекционного материала и проведении семинара, закрепляющего знания учащихся, предусматривается индивидуальное или групповое домашнее задание, содержащее элементы исследовательской работы, задачи для самостоятельного решения. Защита решений и результатов исследований проводится на выделенном для этого занятии и оценивается по пятибалльной системе или системе «зачет-незачет», в зависимости от уровня подготовленности группы. На последнем уроке при изучении каждой темы проводится тестирование, короткая (10-15) минут контрольная работа, самостоятельная работа или защита минипроектов, исследовательских работ или домашних.
Возможная форма итоговой аттестации:
Ожидаемый результат изучения курса
знать/понимать:
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
значение математики как науки и значение математики в повседневной жизни, а также как прикладного инструмента в будущей профессиональной деятельности
решать задания, по типу приближенных к заданиям ЕГЭ (части А и части В)
иметь опыт (в терминах компетентностей):
работы в группе, как на занятиях, так и вне,
работы с информацией, в том числе и получаемой посредством Интернет
Методические рекомендации по реализации программы
Основным дидактическим средством для предлагаемого курса являются тексты рассматриваемых типов задач, которые могут быть выбраны из разнообразных сборников, различных вариантов ЕГЭ или составлены самим учителем.
Курс обеспечен раздаточным материалом, подготовленным на основе прилагаемого ниже списка литературы.
Тематическое планирование спецкурса по математике для 10 – 11 классов «Практикум решения задач по математике»
23.09-29.09
Текстовые задачи
10
9-12
Проценты, сплавы, смеси, растворы
4
30.09-06.10
07.10-13.10
13-16
Движение
4
14.10-20.10
21.10-27.10
17-18
Работа, производительность.
2
06.11-12.11
19-22
Задачи на прогрессию
4
13.11-19.11
20.11-26.11
Решение геометрических задач
8
23-24
Треугольники. Правильные многоугольники.
2
27.11-03.12
25-26
Площади плоских фигур
2
04.12-10.12
27-28
Окружность и круг
2
11.12-17.12
29-30
Параллельность и перпендикулярность прямых. Элементы тригонометрии
2
18.12-24.12
Уравнения
10
31-32
Решение рациональных уравнений
2
25.12-28.12
33-34
Решение иррациональных уравнений
2
10.01-14.01
35-36
Решение показательных уравнений
2
15.01-21.01
37-38
Решение логарифмических уравнений
2
22.01-28.01
39-40
Решение тригонометрических уравнений.
2
29.01-04.02
Неравенства
10
41-42
Решение линейных неравенств и их систем
2
05.02-11.02
43-44
Равносильность при решении иррациональных неравенств.
2
12.02-18.02
45-46
Показательные и логарифмические неравенства
2
19.02-25.02
47-48
Тригонометрические неравенства
2
26.02-04.03
49-50
Решение неравенств с модулем.
2
05.03-11.03
Функции
10
51-52
Степенные функции
2
12.03-18.03
53-54
Показательные и логарифмические функции
2
28.03-03.04
55-56
Построение графика функции с модулем
2
04.04-10.04
57-58
Решение различных задач на применение свойств функций и построение их графиков
2
11.04-17.04
59-60
Решение задач ЕГЭ
2
18.04-24.04
61-64
Решение тригонометрических уравнений. № 13 ЕГЭ
4
25.04-02.05
03.05-10.05
65-66
Задача № 17 ЕГЭ
2
11.05-17.05
67-68
Резерв
2
18.05-24.05
11 класс 2017/18уч. год
68
23.09-29.09
Текстовые задачи
10
9-12
Проценты, сплавы, смеси, растворы
4
30.09-06.10
07.10-13.10
13-16
Движение
4
14.10-20.10
21.10-27.10
17-18
Работа, производительность.
2
06.11-12.11
Решение геометрических задач
8
19-20
Треугольники. Правильные многоугольники
2
13.11-19.11
21-22
Площади плоских фигур
2
20.11-26.11
23-24
Окружность и круг
2
27.11-03.11
25-26
Параллельность и перпендикулярность прямых. Элементы тригонометрии
2
04.12-10.12
Показательные и логарифмические уравнения и неравенства.
10
27-28
Свойства показательной функции.
2
11.12-17.12
29-30
Методы решения показательных уравнений и неравенств. Решение нестандартных показательных уравнений и неравенств.
2
18.12-24.12
31-32
Свойства логарифмической функции.
2
25.12-28.12
33-36
Методы решения логарифмических уравнений и неравенств. Решение нестандартных логарифмических уравнений и неравенств.
4
10.01-14.01
15.01-21.01
Задачи стереометрии
10
37-38
Различные способы построения сечений
2
22.01-28.01
39-40
Проектированию на плоскость
2
29.01-04.02
41-42
Задачи на комбинацию стереометрических тел
2
05.02-11.02
43-44
Метод координат
2
12.02-18.02
45-46
Задачи ЕГЭ
2
19.02-25.02
Тригонометрические уравнения и неравенства.
8
47
Обзор методов решений тригонометрических уравнений.
1
26.02-04.03
48-50
Практикум по решению нестандартных тригонометрических уравнений.
3
26.02-04.03
05.03-11.03
51-52
Практикум по решению тригонометрических неравенств.
2
12.03-18.03
53-54
Задачи ЕГЭ
2
28.03-03.04
Решение различных задач повышенной сложности
6
55-56
Понятие “задача с параметрами” Использование геометрических интерпретаций при анализе решения задач с параметрами.
2
04.04-10.04
57-58
Задачи, сводящиеся к исследованию квадратного трехчлена.
2
11.04-17.04
59-60
Оценка правой и левой части уравнений и неравенств.
2
18.04-24.04
12
Решение вариантов ЕГЭ
6
25.04-02.05
03.05-09.05
10.05-17.05
Резерв
2
18.05-24.05
ВСЕГО
136
Оптимальный банк заданий для подготовки учащихся. Единый государственный экзамен 2017. Математика. Учебное пособие./ А.В. Семенов, А.С. Трепалин, П.И. Захаров; под ред. И.В. Ященко; Московский центр непрерывного математического образования. – М.: Интеллект-Центр, 2016 – 17г..
ЕГЭ 2016. Математика: Тематические тренировочные задания/ В.В. Кочагин, М.Н. Кочагина. – М. Эксмо, 2016.
ЕГЭ 2013. Математика: Сдаем без проблем/ В.В. Кочагин, М.Н. Кочагина. – М. Эксмо, 2012.
М.И. Сканави «Полный сборник решений задач для поступающих в ВУЗы». Москва. «Альянс – В». 1999 год.
ЕГЭ. Практикум по математике: Решение уравнений и неравенств. Преобразование алгебраических выражений / Ю.В. Садовничий. – М.: Издательство «Экзамен», 2012
ЕГЭ 2015. Математика. Типовые экзаменационные варианты: 36 вариантов/ под ред. И.В. Ященко — М.: Издательство «Национальное образование», 2015 – 2016
Все новые издания по ЕГЭ – 2017.
Интернет – источники:
www.fipi.ru
ege.edu.ru
http://ege-study.ru
www.reshuege.ru
www.alexlarin.net
www.mathus.ru/
http://dvd.ege-study.ru/
www.1september.ru
www.math.ru
www.allmath.ru
www.uztest.ru
http://schools.techno.ru/tech/index.html
http://www.catalog.alledu.ru/predmet/math/more2.html
http://shade.lcm.msu.ru:8080/index.jsp
http://wwwexponenta.ru/
http://comp-science.narod.ru/
http://methmath.chat.ru/index.html
http://www.mathnet.spb.ru/
http://vip.km.ru/vschool/demo/education.asp?subj=292
http:// education.bigli.ru
http://schools.techno.ru/tech/index.html
infourok.ru
Программа спецкурса по математике для 10-11 класса
Программа спецкурса по математике
«Избранные вопросы математики»
10 — 11 класс
Пояснительная записка
Математическое образование в системе основного общего образования занимает одно из ведущих мест, что определяется безусловно практической значимостью математики, ее возможностями, в развитии формирования мышления человека, ее вкладом в создание представлений о научных методах познания действительности.
Основная задача обучения математики в школе, обеспечить прочное, сознательное овладение учащимися математических знаний и умений необходимых в повседневной жизни и трудовой деятельности каждого человека, достаточных для изучения смежных дисциплин и продолжения образования.
Наряду с решением основной задачи данный курс предусматривает формирование у учащихся устойчивого интереса к предмету, выявление развития математических способностей, ориентацию на профессии, требующие математической подготовки.
Главное, этот курс поможет учащимся 10 — 11 классов систематизировать свои математические знания, поможет с разных точек зрения взглянуть на другие, уже известные темы, расширить круг математических вопросов, не изучаемых в школьном курсе.
Тем самым данный спецкурс ведет целенаправленную подготовку ребят к аттестации по математике в форме ЕГЭ.
Цель курса:
На основе коррекции базовых математических знаний учащихся за курс 5-11 классов совершенствовать математическую культуру, развивать творческие способности учащихся, помогающие в овладении математическими знаниями и умениями для сдачи ЕГЭ.
Задачи курса:
Расширить математические представления учащихся по некоторым темам.
Акцентировать внимание учащихся на единых требованиях к правилам оформления заданий второй части ЕГЭ.
Совершенствовать технику решения сложных задач.
Настоящая программа написана на основании следующих нормативных документах:
Федеральный закон « Об образовании в Российской федерации» от 29 декабря 2012 г.№273_фз
Федеральный государственный образовательный стандарт ООО
Приказ Министерства образования России от 05.03.2004 г.№1089 «Об утверждении федерального компонента государственных стандартов начального, основного общего и среднего ( полного) общего образования»
Приказ Минобразования РФ от 09.03.2004г.№1312» Об утверждении Федерального базисного учебного плана примерных учебных планов для общеобразовательных учреждений РФ , реализующих программы общего образования»
Распоряжение Министерства образования Ульяновской области от 15 марта 2012 г. № 929-р г. Ульяновск « Об утверждении регионального базисного учебного плана и примерных учебных планов для общеобразовательных учреждений Ульяновской области , реализующих программы общего образования»
САНПиН24.2.2821-10,зарегистрированно в Минюсте РФ 3 марта 2011 г регистрационный номер №19993.
Учебный план МБОУ СОШ №2 МО « Барышский район « на 2015-2016 учебный год
Программы. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала математического анализа. 10-11 классы / авт-сост. И.И. Зубарева, А.Г. Мордкович. – 2-е изд., испр. и доп. – М.: Мнемозина, 2013.
Программы общебразовательных учреждений. Геометрия. 7-11. классы./ под ред. Т.А. Бурмистровой. – М.: «Просвещение», 2013.
Так же данная программа написана с использованием научно-методических и методических рекомендаций:
Методические рекомендации по организации предпрофильной подготовки и профильного обучения. Математика. / Авт.-сост. Ф.С. Мухаметзянова Ф.С.; Под редакцией Т.Ф. Есенковой, В.В. Зарубиной. — Ульяновск: УИПКПРО, 2005.
Программа рассчитана на 35 час в 10 классе и 35 час в 11 классе, включает в себя основные разделы курса 8-11 классов общеобразовательной школы и ряда дополнительных вопросов, непосредственно примыкающих к этому курсу и углубляющим его по основным темам.
Реализация задач данного спецкурса осуществляется за счет создания общей атмосферы сотрудничества, использовании различных форм организации деятельности учащихся, показа значимости приобретаемых знаний.
Методические рекомендации по реализации программы
Основным дидактическим средством для предлагаемого курса являются тексты рассматриваемых типов задач, которые могут быть выбраны из разнообразных сборников, различных вариантов ЕГЭ или составлены самим учителем.
Курс обеспечен раздаточным материалом, подготовленным на основе прилагаемого ниже списка литературы.
Методы и формы обучения
Для реализации целей и задач курса предполагается использовать следующие формы проведения занятий: лекции, практикумы по решению задач, семинары. Для получения эффективных результатов имеет смысл использовать компьютер интерактивную доску, которые помогут как в реализации результатов работы с данными вопросами, так и при решении математических задач.
Эффективность усвоения изучаемого материала отслеживается через выполнение индивидуальных самостоятельных работ. Итоговый контроль предусматривает выполнение контрольной работы, включающей разноуровневые задания, рассматриваемые на занятиях. Результат освоения курса считается положительным, если ученик выполнил 75% контрольной работы (материалы самостоятельных и контрольных работ формируются согласно открытого банка заданий ФИПИ).
Требования к уровню подготовки обучающихся
В результате изучения данного курса учащиеся должны уметь:
проводить тождественные преобразования иррациональных, показательных, логарифмических и тригонометрических выражений.
решать иррациональные, логарифмические и тригонометрические уравнения и неравенства.
решать системы уравнений изученными методами.
строить графики элементарных функций и проводить преобразования графиков, используя изученные методы.
применять аппарат математического анализа к решению задач.
применять основные методы геометрии (проектирования, преобразований, векторный, координатный) к решению геометрических задач.
Содержание курса и распределение часов по темам
ЛитератураЛитература для учителя
М.И Башмаков. «Алгебра и начала анализа». Москва. «Просвещение». 1992 г.
И.Ф Шарыгин. «Факультативный курс по математике. Решение задач. 10 кл.». Москва. «Просвещение» 1990 год.
И.Ф. Шарыгин «Факультативный курс по математике. Решение задач. 11 кл» Москва. «Просвещение». 1991 год.
В.В. Вавилов, И.И. Мельников «Задачи по математике. Уравнения и неравенства». Справочное пособие. Издательство «Наука» 1988 год.
М.И. Сканави «Полный сборник решений задач для поступающих в ВУЗы». Москва. «Альянс – В». 1999 год.
М.И. Сканави «Сборник задач по математике», «Высшая школа» 1973 год.
С.И. Колесникова «Математика. Интенсивный курс подготовки к ЕГЭ», Айрис Пресс. 2007 год.
«Алгебра и начала анализа 10-11кл.», авт. А.Г. Мордкович, изд Мнемозина., 2006 г.
Математика ЕГЭ, вступительные экзамены, изд. Легион, 2004 г.
Е.А. Семенко., «Обобщение и повторение по курсу алгебры основной школы». Краснодар., 2003 г.
С.А. Шестаков, П.И. Захаров «ЕГЭ-2010. Математика, задача С1» М.МЦНМО 2010 год
И.Н. Сергеев, В.Ц. Панферов «ЕГЭ-2010. Математика, задача С3» М.МЦНМО 2010 год
В.А. Смирнов. «ЕГЭ-2010. Математика, задача С2» М.МЦНМО 2010 год
Р.К. Гордин «ЕГЭ-2010. Математика, задача С4» М.МЦНМО 2010 год
А.И. Козко, В.С.Панферов, И.Н.Сергеев. «ЕГЭ-2010. Математика, задача С5.Задачи с параметрами» М.МЦНМО 2010 год
Литература для ученика
И.Ф Шарыгин. «Факультативный курс по математике. Решение задач. 10 кл.». Москва. «Просвещение» 1990 год.
И.Ф. Шарыгин «Факультативный курс по математике. Решение задач. 11 кл»
«Алгебра и начала анализа 10-11кл.», авт. А.Г. Мордкович, изд Мнемозина., 2006 г
С.А. Шестаков, П.И. Захаров «ЕГЭ-2010. Математика, задача С1» М.МЦНМО 2010 год
И.Н. Сергеев, В.Ц. Панферов «ЕГЭ-2010. Математика, задача С3» М.МЦНМО 2010 год
В.А. Смирнов. «ЕГЭ-2010. Математика, задача С2» М.МЦНМО 2010 год
Р.К. Гордин «ЕГЭ-2010. Математика, задача С4» М.МЦНМО 2010 год
А.И. Козко, В.С.Панферов, И.Н.Сергеев. «ЕГЭ-2010. Математика, задача С5.Задачи с параметрами» М.МЦНМО 2010 год
Б.Г.Гедман «Логарифмические и показательные уравнения и неравенства», ОЛВЗМШ, Москва, 2003 год
Н.Я.Виленкин и др. Алгебра и математический анализ 10-11 кл. Учебное пособие Мнемозина, Москва, 2006год
infourok.ru
