Математика — Infourok
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классы1 класс2 класс3 класс4 класс5 класс6 класс
Выберите учебник:
Все учебники»Испанский язык», Анурова И.В., Соловцова Э.И.»Математика», Виленкин Н.Я., Жохов В.И. и др.»Математика», Зубарева И.И., Мордкович А.
«Математика», Бунимович Е.А., Дорофеев Г.В., Суворова С.Б. и др.»Математика», Мерзляк А.Г., Полонский В.Б., Якир М.С./ Под ред. Подольского В.Е.»Математика», Ткачёва М.В.»Математика», Ткачёва М.В.»Математика (базовый уровень)», Мордкович А.Г., Смирнова И.М.»Математика (в 2 книгах)», Давыдов В.В.,Горбов С.Ф., Микулина Г.Г., Савельева О.В.»Математика (в 2 книгах)», Давыдов В.В.,Горбов С.Ф., Микулина Г.Г., Савельева О.В.»Математика (в 2 книгах)», Давыдов В.В.,Горбов С.Ф., Микулина Г.Г.»Математика (в 2 книгах)», Александрова Э.И.»Математика (в 2 книгах)», Александрова Э.И.»Математика (в 2 книгах)», Александрова Э.И.»Математика (в 2 книгах)», Александрова Э.И.»Математика (в 2 частях)», Аргинская И.И., Бененсон Е.П., Итина Л.С., Кормишина С.Н.»Математика (в 2 частях)», Дорофеев Г.В., Миракова Т.Н., Бука Т.Б.»Математика (в 2 частях) «, Истомина Н.Б. «Математика (в 2 частях)», Моро М.И., Волкова С.И., Степанова С.В.»Математика (в 2 частях) «, Чекин А.Л.»Математика (в 2 частях)», Дорофеев Г.В., Миракова Т.
О., Рыдзе О.А. и др. / Под ред. Булычёва В.А.»Математика (в 2 частях)», Минаева С.С., Рослова Л.О., Рыдзе О.А. и др. / Под ред. Булычёва В.А.»Математика (в 2 частях)», Минаева С.С., Рослова Л.О., Рыдзе О.А. и др. / Под ред. Булычёва В.А.»Математика (в 2 частях)», Минаева С.С., Рослова Л.О. и др. / Под ред. Булычёва В.А.»Математика (в 2 частях)», Муравин Г.К., Муравина О.В.»Математика (в 2 частях)», Муравин Г.К., Муравина О.В.»Математика (в 2 частях)», Муравин Г.К., Муравина О.В.»Математика (в 2 частях)», Муравин Г.К., Муравина О.В.»Математика (в 2 частях)», Рудницкая В.Н., Кочурова Е.Э., Рыдзе О.А.»Математика (в 2 частях)», Рудницкая В.Н., Юдачёва Т.В.»Математика (в 2 частях)», Рудницкая В.Н., Юдачёва Т.В.»Математика (в 2 частях)», Рудницкая В.Н., Юдачёва Т.В.»Математика (в 2 частях)», Башмаков М.И.»Математика (в 2 частях)», Башмаков М.И.»Математика (в 2 частях)», Аргинская И.И., Ивановская Е.И., Кормишина С.Н.»Математика (в 2 частях)», Дорофеев Г.В., Миракова Т.Н., Бука Т.Б.»Математика (в 2 частях)», Миракова Т.
Е., Козлова С.А., Тонких А.П.»Математика (в 3-х частях)», Демидова Т.Е., Козлова С.А., Тонких А.П.»Математика (в 3-х частях)», Демидова Т.Е., Козлова С.А., Тонких А.П.»Математика (для обучающихся с интеллектуальными нарушениями) (в 2 частях) *», Алышева Т.В.»Математика (для обучающихся с интеллектуальными нарушениями) (в 2 частях)*», Алышева Т. В.»Математика (для обучающихся с интеллектуальными нарушениями) (в 2 частях)*», Алышева Т.В.»Математика (для обучающихся с интеллектуальными нарушениями) (в 2 частях)*», Алышева Т.В., Яковлева И.М.»Математика (для обучающихся с интеллектуальными нарушениями) *», Перова М.Н., Капустина Г.М.»Математика (для обучающихся с интеллектуальными нарушениями) *», Капустина Г.М., Перова М.Н.»Математика (для обучающихся с интеллектуальными нарушениями) *», Алышева Т.В.»Математика (для обучающихся с интеллектуальными нарушениями) *», Эк В.В.»Математика (для обучающихся с интеллектуальными нарушениями) *», Антропов А.П., Ходот А.Ю., Ходот Т.Г.»Математика (для обучающихся с интеллектуальными нарушениями) *», Фадеева С.
Учебник для специальных (коррекционных) образовательных учреждений VIII вида*», Эк В.В.»Математика. Учебник для специальных (коррекционных) образовательных учреждений VIII вида*», Перова М.Н.»Математика. Учебник для специальных (коррекционных) образовательных учреждений VIII вида*», Антропов А.П., Ходот А.Ю., Ходот Т.Г.»Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углублённый уровни) (в 2 частях)», Ч.1.: Мордкович А.Г., Семенов П.В.;Ч .2.: Мордкович А.Г. и др., под ред. Мордковича А.Г.»Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый уровень)», Муравин Г.К., Муравина О.В.»Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый уровень)», Муравин Г.К., Муравина О.В.»Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый уровень) (в 2 частях)», Ч.
, Карп А.П.Выберите тему: Все темы
Распоряжение Правительства Российской Федерации от 24 декабря 2013 г. N 2506-р г. Москва
1. Утвердить прилагаемую Концепцию развития математического образования в Российской Федерации.
2. Минобрнауки России утвердить в 3-месячный срок план мероприятий по реализации Концепции развития математического образования в Российской Федерации.
Председатель Правительства
Российской Федерации
Д.Медведев
Прим. ред.: текст распоряжения опубликован на официальном интернет-портале правовой информации http://www.pravo.gov.ru, 27.12.2013.
Концепция развития математического образования в Российской Федерации
Настоящая Концепция представляет собой систему взглядов на базовые принципы, цели, задачи и основные направления развития математического образования в Российской Федерации.
I. Значение математики в современном мире и в России
Математика занимает особое место в науке, культуре и общественной жизни, являясь одной из важнейших составляющих мирового научно-технического прогресса.
Изучение математики играет системообразующую роль в образовании, развивая познавательные способности человека, в том числе к логическому мышлению, влияя на преподавание других дисциплин. Качественное математическое образование необходимо каждому для его успешной жизни в современном обществе. Успех нашей страны в XXI веке, эффективность использования природных ресурсов, развитие экономики, обороноспособность, создание современных технологий зависят от уровня математической науки, математического образования и математической грамотности всего населения, от эффективного использования современных математических методов. Без высокого уровня математического образования невозможны выполнение поставленной задачи по созданию инновационной экономики, реализация долгосрочных целей и задач социально-экономического развития Российской Федерации, модернизация 25 млн. высокопроизводительных рабочих мест к 2020 году. Развитые страны и страны, совершающие в настоящее время технологический рывок, вкладывают существенные ресурсы в развитие математики и математического образования.
Россия имеет значительный опыт в математическом образовании и науке, накопленный в 1950-1980 годах. Форсированное развитие математического образования и науки, обеспечивающее прорыв в таких емких стратегических направлениях, как информационные технологии, моделирование в машиностроении, энергетике и экономике, прогнозирование природных и техногенных катастроф, биомедицина, будет способствовать улучшению положения и повышению престижа России в мире. Система математического образования, сложившаяся в России, является прямой наследницей советской системы. Необходимо сохранить ее достоинства и преодолеть серьезные недостатки. Повышение уровня математической образованности сделает более полноценной жизнь россиян в современном обществе, обеспечит потребности в квалифицированных специалистах для наукоемкого и высокотехнологичного производства.
II. Проблемы развития математического образования
В процессе социальных изменений обострились проблемы развития математического образования и науки, которые могут быть объединены в следующие основные группы.
1. Проблемы мотивационного характера
Низкая учебная мотивация школьников и студентов связана с общественной недооценкой значимости математического образования, перегруженностью образовательных программ общего образования, профессионального образования, а также оценочных и методических материалов техническими элементами и устаревшим содержанием, с отсутствием учебных программ, отвечающих потребностям обучающихся и действительному уровню их подготовки. Все это приводит к несоответствию заданий промежуточной и государственной итоговой аттестации фактическому уровню подготовки значительной части обучающихся.
2. Проблемы содержательного характера
Выбор содержания математического образования на всех уровнях образования продолжает устаревать и остается формальным и оторванным от жизни, нарушена его преемственность между уровнями образования. Потребности будущих специалистов в математических знаниях и методах учитываются недостаточно. Фактическое отсутствие различий в учебных программах, оценочных и методических материалах, в требованиях промежуточной и государственной итоговой аттестации для разных групп учащихся приводит к низкой эффективности учебного процесса, подмене обучения «натаскиванием» на экзамен, игнорированию действительных способностей и особенностей подготовки учащихся.
Математическое образование в образовательных организациях высшего образования оторвано от современной науки и практики, его уровень падает, что обусловлено отсутствием механизма своевременного обновления содержания математического образования, недостаточной интегрированностью российской науки в мировую.
3. Кадровые проблемы
В Российской Федерации не хватает учителей и преподавателей образовательных организаций высшего образования, которые могут качественно преподавать математику, учитывая, развивая и формируя учебные и жизненные интересы различных групп обучающихся. Сложившаяся система подготовки, профессиональной переподготовки и повышения квалификации педагогических работников не отвечает современным нуждам. Выпускники образовательных организаций высшего образования педагогической направленности в своем большинстве не отвечают квалификационным требованиям, профессиональным стандартам, имеют мало опыта педагогической деятельности и опыта применения педагогических знаний.
Подготовка, получаемая подавляющим большинством студентов по направлениям математических и педагогических специальностей, не способствует ни интеллектуальному росту, ни требованиям педагогической деятельности в общеобразовательных организациях. Преподаватели образовательных организаций высшего образования в большинстве своем оторваны как от современных направлений математических исследований, включая прикладные, так и от применений математики в научных исследованиях и прикладных разработках своей образовательной организации высшего образования. Система дополнительного профессионального образования преподавателей недостаточно эффективна и зачастую просто формальна в части совершенствования математического образования.
III. Цели и задачи Концепции
Цель настоящей Концепции — вывести российское математическое образование на лидирующее положение в мире. Математика в России должна стать передовой и привлекательной областью знания и деятельности, получение математических знаний — осознанным и внутренне мотивированным процессом.
Изучение и преподавание математики, с одной стороны, обеспечивают готовность учащихся к применению математики в других областях, с другой стороны, имеют системообразующую функцию, существенно влияют на интеллектуальную готовность школьников и студентов к обучению, а также на содержание и преподавание других предметов.
Задачами развития математического образования в Российской Федерации являются:
модернизация содержания учебных программ математического образования на всех уровнях (с обеспечением их преемственности) исходя из потребностей обучающихся и потребностей общества во всеобщей математической грамотности, в специалистах различного профиля и уровня математической подготовки, в высоких достижениях науки и практики;
обеспечение отсутствия пробелов в базовых знаниях для каждого обучающегося, формирование у участников образовательных отношений установки «нет неспособных к математике детей», обеспечение уверенности в честной и адекватной задачам образования государственной итоговой аттестации, предоставление учителям инструментов диагностики (в том числе автоматизированной) и преодоления индивидуальных трудностей;
обеспечение наличия общедоступных информационных ресурсов, необходимых для реализации учебных программ математического образования, в том числе в электронном формате, инструментов деятельности обучающихся и педагогов, применение современных технологий образовательного процесса;
повышение качества работы преподавателей математики (от педагогических работников общеобразовательных организаций до научно-педагогических работников образовательных организаций высшего образования), усиление механизмов их материальной и социальной поддержки, обеспечение им возможности обращаться к лучшим образцам российского и мирового математического образования, достижениям педагогической науки и современным образовательным технологиям, создание и реализация ими собственных педагогических подходов и авторских программ;
поддержка лидеров математического образования (организаций и отдельных педагогов и ученых, а также структур, формирующихся вокруг лидеров), выявление новых активных лидеров;
обеспечение обучающимся, имеющим высокую мотивацию и проявляющим выдающиеся математические способности, всех условий для развития и применения этих способностей;
популяризация математических знаний и математического образования.
IV. Основные направления реализации Концепции
1. Дошкольное и начальное общее образование
Система учебных программ математического образования в дошкольном и начальном образовании при участии семьи должна обеспечить:
в дошкольном образовании — условия (прежде всего предметно-пространственную и информационную среду, образовательные ситуации, средства педагогической поддержки ребенка) для освоения воспитанниками форм деятельности, первичных математических представлений и образов, используемых в жизни;
в начальном общем образовании — широкий спектр математической активности (занятий) обучающихся как на уроках, так и во внеурочной деятельности (прежде всего решение логических и арифметических задач, построение алгоритмов в визуальной и игровой среде), материальные, информационные и кадровые условия для развития обучающихся средствами математики.
2. Основное общее и среднее общее образование
Математическое образование должно:
предоставлять каждому обучающемуся возможность достижения уровня математических знаний, необходимого для дальнейшей успешной жизни в обществе;
обеспечивать каждого обучающегося развивающей интеллектуальной деятельностью на доступном уровне, используя присущую математике красоту и увлекательность;
обеспечивать необходимое стране число выпускников, математическая подготовка которых достаточна для продолжения образования в различных направлениях и для практической деятельности, включая преподавание математики, математические исследования, работу в сфере информационных технологий и др.
В основном общем и среднем общем образовании необходимо предусмотреть подготовку обучающихся в соответствии с их запросами к уровню подготовки в сфере математического образования.
Необходимо предоставить каждому учащемуся независимо от места и условий проживания возможность достижения соответствия любого уровня подготовки с учетом его индивидуальных потребностей и способностей. Возможность достижения необходимого уровня математического образования должна поддерживаться индивидуализацией обучения, использованием электронного обучения и дистанционных образовательных технологий. Возможность достижения высокого уровня подготовки должна быть обеспечена развитием системы специализированных общеобразовательных организаций и специализированных классов, системы дополнительного образования детей в области математики, системы математических соревнований (олимпиад и др.). Соответствующие программы могут реализовываться и организациями высшего образования (в том числе в рамках существующих и создаваемых специализированных учебно-научных центров университетов, а также сетевых форм реализации образовательных программ).
Достижение какого-либо из уровней подготовки не должно препятствовать индивидуализации обучения и закрывать возможности продолжения образования на более высоком уровне или изменения профиля.
Необходимо стимулировать индивидуальный подход и индивидуальные формы работы с отстающими обучающимися, прежде всего привлекая педагогов с большим опытом работы.
Совершенствование содержания математического образования должно обеспечиваться в первую очередь за счет опережающей подготовки и дополнительного профессионального образования педагогов на базе лидерских практик математического образования, сформировавшихся в общеобразовательных организациях.
3. Профессиональное образование
Система профессионального образования должна обеспечивать необходимый уровень математической подготовки кадров для нужд математической науки, экономики, научно-технического прогресса, безопасности и медицины. Для этого необходимо разработать современные программы, включить основные математические направления в соответствующие приоритетные направления модернизации и технологического развития российской экономики.
Студенты, изучающие математику, включая информационные технологии, и их преподаватели должны участвовать в математических исследованиях и проектах. Преподавателям математических факультетов классических университетов необходимо вести признаваемые профессиональным сообществом фундаментальные исследования, а их студенты должны уделять значительно больше времени, чем в настоящее время, решению творческих учебных и исследовательских задач. Преподаватели математических кафедр технических университетов должны вести исследования в фундаментальной математике или в прикладных профильных областях, выполнять работы по заказу организаций, в которых принимают участие и студенты (аналогично для экономических и других образовательных организаций высшего образования), преподаватели математических кафедр педагогических вузов должны работать со школьниками, участвовать в разработке аттестационных материалов, учебных пособий для школьников. Студентам (в том числе готовящимся стать учителями и воспитателями в организациях, осуществляющих образовательную деятельность) необходимо решать задачи элементарной математики в зоне своего ближайшего развития, в существенно большем объеме, чем сегодня, проходить практику в школе, используя эту деятельность как основу и мотивирующий фактор для получения психолого-педагогических знаний.
Взаимодействие органов, осуществляющих управление в сфере образования, образовательных организаций высшего образования и общеобразовательных организаций должно быть ориентировано на поддержку прихода в школу лучших выпускников математических факультетов педагогических образовательных организаций высшего образования, выпускников профильных специальностей классических университетов. Необходимо обеспечить лучшим выпускникам, обучавшимся по программам математической направленности образовательных организаций высшего образования и имеющим склонности и способности к педагогической работе, возможность преподавать в образовательной организации высшего образования.
4. Дополнительное профессиональное образование, подготовка научно-педагогических работников образовательных организаций высшего образования и научных работников научных организаций, математическая наука
Для успешных преподавателей должна быть обеспечена возможность их профессионального роста в форме научной и прикладной работы, дополнительного профессионального образования, включая стажировку в организациях — лидерах фундаментальных и прикладных исследований в области математики и математического образования.
Важной является поддержка в России мировых организаций, решающих задачу подготовки исследователей и преподавателей высшего уровня, в том числе создание научно-образовательных центров мирового уровня, приглашающих ученых для проведения исследовательской работы и участия в разработке образовательных программ.
Образовательные организации высшего образования и научные центры должны обеспечить передовой уровень фундаментальных и прикладных исследований в области математики и их использование в математическом образовании. Необходимо усилить интеграцию российских математических исследований в мировую науку, обеспечить достижение математическими факультетами ведущих российских университетов высоких позиций в мировых рейтингах, а также рост качества, количества и цитируемости работ российских математиков, привлекательность российского математического образования для лучших иностранных студентов и профессоров. Должна повыситься мобильность студентов, аспирантов и молодых кандидатов наук, должно развиваться сотрудничество между образовательными организациями высшего образования и исследовательскими институтами.
Для решения задач настоящей Концепции предусматривается доработать систему оценки труда с учетом специфики деятельности и международной практики оценки труда преподавателей математики, научно-педагогических работников образовательных организаций высшего образования и научных работников научных организаций, занятых по профилю математики.
Образовательные организации высшего образования и исследовательские центры должны участвовать в работе по математическому просвещению и популяризации математических знаний среди населения России.
5. Математическое просвещение и популяризация математики, дополнительное образование
Для математического просвещения и популяризации математики предусматривается:
обеспечение государственной поддержки доступности математики для всех возрастных групп населения;
создание общественной атмосферы позитивного отношения к достижениям математической науки и работе в этой области, понимания важности математического образования для будущего страны, формирование гордости за достижения российских ученых;
обеспечение непрерывной поддержки и повышения уровня математических знаний для удовлетворения любознательности человека, его общекультурных потребностей, приобретение знаний и навыков, применяемых в повседневной жизни и профессиональной деятельности.
Система дополнительного образования, включающая математические кружки и соревнования, является важнейшей частью российской традиции математического образования и должна быть обеспечена государственной поддержкой. Одновременно должны развиваться такие новые формы, как получение математического образования в дистанционной форме, интерактивные музеи математики, математические проекты на интернет-порталах и в социальных сетях, профессиональные математические интернет-сообщества.
V. Реализация Концепции
Реализация настоящей Концепции обеспечит новый уровень математического образования, что улучшит преподавание других предметов и ускорит развитие не только математики, но и других наук и технологий. Это позволит России достигнуть стратегической цели и занять лидирующее положение в мировой науке, технологии и экономике.
Реализация настоящей Концепции будет способствовать разработке и апробации механизмов развития образования, применимых в других областях.
Математика
Числовые последовательности 2021
Автор: Кочиева Изаура Тамазовна
Цель урока: ввести понятие «числовая последовательность», «n-й член последовательности»; познакомить учащихся с видами последовательностей и способами задания последовательности.
Элементы теории графов 2021
Автор: Епихина Лена Вячеславовна
Теория графов широко применяется в решении экономических и управленческих задач, в программировании, химии, конструировании и изучении электрических цепей, коммуникации, психологии, социологии, лингвистике и в других областях.
Для чего строят графы: чтобы отобразить отношения на множествах. По сути, графы помогают визуально представить всяческие сложные взаимодействия: аэропорты и рейсы между ними, разные отделы в компании, молекулы в веществе.
Методическая разработка урока «Умножение обыкновенных дробей» 2021
Автор: Малиева Виктория Викторовна
Цели урока: расширение понятийной базы по теме «Действия с обыкновенными дробями»: вывести правило умножения дробей, сформировать умение умножать обыкновенные дроби. В ходе урока учащиеся смогут применить правило при решении упражнений.
умножение дробей
Современный урок математики в старших классах 2021
Автор: Емченко Римма
В процессе обучения меня всегда привлекают новые и оригинальные методы к изложению учебного материала.
С целью увлечения школьников предметом, я пользуюсь современными информационными технологиями, благодаря которым и достигаю более высокого уровня в обучении ребят. Таким образом, в свои презентации к урокам я включаю так называемые «МЕМы», которые так любят современные дети.
Методическая разработка практического занятия с применением дистанционных образовательных технологий по теме «Тела вращения» 2021
Автор: Дурнина Светлана Владимировна
Задачи урока: систематизировать знания обучающихся, обобщить изученный материал по теме «Тела вращения», формировать умение решать задачи практического содержания и профессиональной направленности.
дистанционные технологии, задачи с практическим содержанием, тела вращения
Видеоурок «Процент.
Основные действия и задачи с процентами»
2021Автор: Епифанцева Инна Владимировна
Целью курса является обобщить методы решения задач с экономическим содержанием повышенного уровня сложности, при помощи построения и исследования математических моделей, выработать умение использовать приобретенные знания в практической деятельности и повседневной жизни. Курс предназначен для учащихся, которые предполагают сдавать ЕГЭ по математике профильный уровень (учащиеся 9–11-х классов).
проценты
Методическая разработка занятия по основам математического моделирования «Циклоида» 2021
Автор: Гуляева Ирина Владимировна
Цель: формирование представлений о необычных кривых на примере циклоиды.
Основные направления работы по использованию регионального компонента при изучении математики в начальной школе 2021
Автор: Гарбузова Людмила Ивановна
Профессия педагога одна из самых важных и значимых в жизни современного общества. Быть педагогом – это призвание. Это значит, хотеть и уметь снова, и снова проживать детство с каждым ребенком, видеть мир его глазами, удивляться и познавать вместе с ним. Несомненно, обучение и воспитание детей непростое дело. Учитель начальных классов – это педагог-универсал, умеющий творчески работать. Главная цель учителя – развить даже самые крошечные задатки ребёнка, которые с рождения заложены в каждом. В умении разглядеть искру, не дать ей погаснуть, и состоит талант педагога.
Очень трудно не поддаться влиянию и остаться самим собой. Педагог – это созидатель, творец, ему открыт главный ларец – ларец с детскими сердцами, которые ждут тепла, доброго слова, новых знаний и готовы всегда отвечать взаимностью.
Тезисы к проектно-исследовательской работе: «Теорема Пифагора и способы ее доказательства» 2021
Автор: Хасиева Алета Хасанбековна
Цели и задачи исследования: изучить историю открытия теоремы Пифагора; в наиболее простой и интересной форме преподать содержание теоремы Пифагора; показать разнообразие способов доказательства теоремы Пифагора.
Тезисы к исследовательской работе «Золотое сечение» 2021
Автор: Хасиева Алета Хасанбековна
Цели и задачи: поиск закономерностей «золотого сечения» в живой и неживой природе, выявить и изучить проявление «золотого сечения» и производных в окружающем нас мире; описать геометрический смысл «золотого сечения», определить возможности применения «золотого сечения» в различных областях искусства и архитектуры.
Исследовательская работа «Золотое сечение» 2021
Автор: Хасиева Алета Хасанбековна
Цели и задачи: поиск закономерностей «золотого сечения» в живой и неживой природе, выявить и изучить проявление «золотого сечения» и производных в окружающем нас мире; описать геометрический смысл «золотого сечения», определить возможности применения «золотого сечения» в различных областях искусства и архитектуры.
проектная деятельность, исследовательская деятельность, золотое сечение
Проектно-исследовательская работа: «Теорема Пифагора и способы ее доказательства» 2021
Автор: Хасиева Алета Хасанбековна
Представлена проектно-исследовательская работа по теме «Теорема Пифагора и способы ее доказательства».
теорема Пифагора
Теория графов при решении задач 2021
Автор: Темирова Залина Аликовна
Теория графов – раздел математики и информатики, нашедший широкое применение в современных прикладных задачах. В первую очередь, это задачи поиска маршрута на картах, но её применение не ограничивается навигационными приложениями. Графы возникают там, где между данными существуют какие-либо нелинейные связи. Например, это могут быть компьютеры, соединённые в сеть. Или же это могут быть задачи, которые надо выполнить в каком-то порядке, причём некоторые задачи надо выполнять строго после каких-то других.
Существуют алгоритмы, позволяющие вычислить оптимальный порядок выполнения таких задач.
графы, теория графов
Решение задач с экономическим содержанием 2021
Автор: Цховребова Ирина Валериевна
Экзаменационные задания по математике (профильный уровень) содержат задачу с экономическим содержанием под №17. Это задание повышенного уровня сложности, которое оценивается максимально в 3 балла. Для того, чтобы успешно решать подобные задачи, ученики должны не только владеть определенным математическим инструментарием, но и уметь строить простейшие математические модели по заданным условиям.
При подготовке учащихся к решению данных задач возникает ряд вопросов, которые надо с ними предварительно обсудить.
Презентация «Объем, единицы объема» 2021
Автор: Вакина Лидия Николаевна
Цель урока: закрепить умения находить площадь поверхности и объем прямоугольного параллелепипеда.
объем
Конспект урока по математике в 5-м классе «Решение задач на движение» 2021
Автор: Белова Елена Анатольевна
На уроке рассматриваются разные виды движения и разные способы решения задач.
Цель урока: научиться решать задачи на движение, используя формулу пути.
задачи на движение
Различные подходы к решению уравнений и систем уравнений 2021
Автор: Хасиева Алета Хасанбековна
Для успешного исследования многих задач повышенной трудности важно уметь пользоваться не только традиционными способами решения, но и нетрадиционными. Нестандартные методы решения уравнений и систем уравнений – это такие методы, для которых в курсе математики не существует общего алгоритма решения. Нестандартные задачи способствуют повышению интереса изучению математики и выбор метода их решения вызывает не меньший интерес, повышают логику мышления.
Умение применять нетрадиционные пути решений требует углубленного уровня подготовки для обучающихся. Использование нетрадиционных методов решения уравнений и систем уравнений являются наиболее эффективными и незаменимыми в решении заданий повышенной трудности. Уравнения, неравенства системы уравнений и неравенств имеют широкий спектр применения не только в математике, но и в физике и химии. Решение многих прикладных задач не обходятся без их использования. Уравнения, неравенства системы уравнений и неравенств играют большую роль в формировании научного мировоззрения учащихся, в реализации межпредметных связей, которые содействуют пониманию строения всей системы наук и роли научного метода в познании и практике.
одаренные дети
Свойства сложения. Закрепление изученного.
2-й класс (программа «Школа России»)
2021Автор: Петрова Елена Вениаминовна
Цели урока: повторить и обобщить материал, изученный на предыдущих уроках; совершенствовать вычислительные навыки и умение решать текстовые задачи.
математика, УМК «Школа России», сложение
Урок математики по теме «Сложение и вычитание». 1-й класс 2021
Автор: Шашлова Лариса Михайловна
Представлена презентация к уроку в 1-м классе по теме «Сложение и вычитание».
математика, сложение и вычитание чисел
Метапредметный урок «Битва за Москву» 2021
Автор: Попова Наталья Дмитриевна
Цель урока: познакомить детей с подвигом советского народа во время битвы под Москвой. Задачи: совершенствовать вычислительные навыки и навыки устного счет в пределах 100, развивать логическое мышление, внимание; развивать умение рассуждать.
математика,
Битва за Москву,
Великая Отечественная война 1941-1945 гг.
Новые образовательные практики в обучении 2021
Авторы: Герасимов Александр Сергеевич, Герасимова Татьяна Николаевна
В настоящее время необходимо организовывать процесс обучения таким образом, чтобы обучающиеся могли овладеть универсальными учебными действиями, тесно связанные с достижением метапредметных результатов. В статье представлен опыт работы по достижению метапредметных результатов через предметную деятельность, а также выход через метапредметную деятельность – на предметное содержание и предметные результаты.
межпредметные связи, универсальные учебные действия, интеграция
Использование математических сказок на уроке математики 2021
Автор: Поздеева Римма Викторовна
Математические сказки могут существенно повысить интерес обучающихся на уроке при изучении любой темы.
Сказки воздействуют на воображение, ассоциативное мышление, создают картинно-образный облик мира. Самостоятельное сочинение подобной сказки приносит большую пользу для развития творческой личности ученика. Работа по созданию математических сказок увлекательна, но она требует значительных усилий не только со стороны ученика, но и учителя. Для начала учитель знакомит с уже написанными авторскими математическими сказками. Затем помогает ребятам определить тему своей сказки, пояснив, что ценность работы будет заключаться в том, чтобы в сюжетную линию сказки были, например, включены свойства чисел или геометрических фигур. Изначально можно вместе с ребенком сформулировать основную мысль будущей сказки, определить с какой целью она будет написана и чему она должна научить слушателей.
Развитие познавательной деятельности учащихся с ОВЗ на уроках математики 2021
Автор: Калачева Татьяна Александровна
При активизации познавательной деятельности учащихся с ОВЗ учитывают дефекты их познавательной деятельности.
Поиски эффективных методов обучения и методических приемов, активизирующих мысли учащихся, стимулирующих их к приобретению знаний, являются целью работы. Повышение активности учащихся достигается совокупностью методов организации и управления учебно-познавательной деятельностью, которые принято называть активными. Индуктивный путь ориентирован на особенности развития мышления детей с ОВЗ.
активизация познавательной деятельности, дидактическая игра
Разработка открытого урока по геометрии «Пирамида. Решение задач». 10-й класс 2021
Автор: Мазуренко Наталья Ивановна
Цели урока: повторить понятие пирамиды, основные виды пирамиды; повторить элементы пирамиды: основание, боковые грани, вершина, боковые рёбра, высота пирамиды, высота боковой грани; формирование умений учащихся в решении тематических задач; расширить представления учеников о пространственной геометрической фигуре – пирамиде – через усвоение достижений культуры человечества.
геометрия, пирамида
Применение инновационных инструментов цифровых ресурсов 2021
Автор: Злобова Людмила Викторовна
Представлена презентация о применение инновационных инструментов образовательных цифровых ресурсов (интернет-ресурсов).
Дивергентное мышление при решении задач и проблемных ситуаций в школе 2021
Автор: Владимиров Валерий Михайлович
Одним из методов повышения интеллектуальных способностей является дивергентное мышление.
С точки зрения психологии – это способность отказываться от стереотипных методов, видение множества оригинальных идей и подходов к решению задачи, что называют креативность. И это довольно высокий уровень мышления человека, ученику для решения задачи иногда хватает одной идеи. Поэтому опустимся чуть ниже светил науки и рассмотрим другой подход, более подходящий к школьному образованию.
Дивергентное мышление
Открытое занятие по ФЭМП в старшей группе «Путешествие в страну математики» 2021
Автор: Гаджимагамедова Аният Надировна
Цель занятия: создание благоприятных условий для формирования элементарных математических представлений дошкольников.
старшая группа
Рабочая тетрадь по внеклассной работе. Задачи на разрезание 2021
Автор: Кузнецова Валентина Алексеевна
Задачи на разрезание и на сравнение углубляют знание по математике, развивают логическое мышление, поэтому — это один из важных моментов необходимо включать при внеклассной работе по математике в 6-х классах.
задачи на разрезание
Игра кодирование 2021
Автор: Кузнецова Валентина Алексеевна
Цель: Заинтересовать обучающихся для выполнения задания.
Задачи: повторить правила сложения, вычитания, умножения и деления рациональных чисел; повторить вычисление квадратного корня.
Открытый урок в 7-м классе по алгебре по теме «Арифметические действия над многочленами» 2021
Автор: Хидирова Ирина Мухадзировна
Цели урока: обобщение и систематизация знаний, умений, навыков учащихся при выполнении арифметических действий над многочленами; организовать работу класса по закреплению темы «Умножение одночлена на многочлен»; повторение понятий одночлен и его стандартный вид, многочлен и его стандартный вид; применение алгоритма умножения одночлена на многочлен на практике.
Многочлен
Факультет компьютерных технологий и прикладной математики
На факультете компьютерных технологий и прикладной математики подготовку ведут высококвалифицированные специалисты: академик РАН, 10 докторов наук, 34 кандидата наук.
Студенты факультета работают в 9 современных комьютерных классах и в Интернет-центре. Ежегодно более 60% выпускников факультета компьютерных технологий и прикладной математики поступают в магистратуру и аспирантуру.
Гранты и проекты
Достижения
Кафедра математического моделирования.
Бабешко Владимир Андреевич. Является одним из авторов открытия нового физического явления: существования высокочастотного резонанса в полуограниченных средах с неоднородностями. Почетный сенатор Высшей техническо-экономической школы г. Берлина, член Американского акустического и химического обществ. На протяжении многих лет проводил исследования, поддержанные грантами РФФИ, президента РФ, CRDF др. Награжден орденом Почета, орденом «Знак Почета», орденом Дружбы народов, медалью «Герой труда Кубани», медалью им. Вавилова и премией Всесоюзного общества «Знание» им. Вавилова.
Бессарабов Николай Васильевич.
Автор учебника «Базы данных. Модели, языки, структуры и семантика», вышедшем в издательстве «Интуит» (г. Москва) в 2013 году. Один из организаторов подготовки студентов к IT олимпиадам различного уровня. Под его руководством студенты дважды выигрывали международный конкурс студенческих работ CIS Student Innovator и неоднократно становились призерами международной олимпиады «IT-планета» в конкурсах компаний InterSystems и Oracle. Являлся неоднократно исполнителем по проектам, поддержанным научными фондами.
Зарецкая Марина Валерьевна. На протяжении многих лет являлась исполнителем по проектам, поддержанным грантами РФФИ, президента РФ, CRDF и др. На протяжении многих лет являлась руководителем проектов, поддержанных грантами РФФИ. Является руководителем проектов, исследования в рамках которых ведутся при поддержке РФФИ и Администрации Краснодарского края.
Павлова Алла Владимировна. На протяжении многих лет являлась исполнителем по проектам, поддержанным грантами РФФИ, президента РФ, CRDF и др.
На протяжении многих лет являлась руководителем проектов, поддержанных грантами РФФИ. Является руководителем проектов, исследования в рамках которых ведутся при поддержке РФФИ и Администрации Краснодарского края.
Рубцов Сергей Евгеньевич. Неоднократно являлся исполнителем по проектам, поддержанным грантами РФФИ, президента РФ, CRDF и др.
Сыромятников Павел Викторович. Руководит проектами, поддержанными различными научными фондами и организациями. Награждался дипломами и медалями международных Салонов изобретений и инновационных технологий.
Кафедра прикладной математики.
Уртенов Махамет Али Хусеевич. Награжден нагрудным знаком «Почетный работник высшего профессионального образования РФ». Лауреат премии администрации Краснодарского края в области науки, образования и культуры. Награжден медалью, диплом и почетным званием в 2013 г. Член Отделения научно-методического совета по математике Министерства образования и науки РФ в ЮФО, член диссертационных советов
Коваленко Анна Владимировна.
Награждена серебряной медалью и дипломом от министра образования и науки РФ на X Московском международном салоне инноваций и инвестиций (2010 г.). Почетная грамота победителя Всероссийского «Молодежного научно-инновационного конкурса» (УМНИК) фонда содействия развитию малых форм предприятий в научно-технической сфере на право получения гранта (УМНИК-2-10-2) (2010-2011 гг.). Лауреат премии администрации Краснодарского края в области науки, образования и культуры. Награждена медалью, диплом и почетным званием в 2013 г.
Халафян Алексан Альбертович. Награжден почетной грамотой Министерства образования и науки Российской федерации, 2014. Лауреат премии администрации Краснодарского края в области образования за 2008. Награжден серебряной медалью на Х МОСКОВСКОМ МЕЖДУНАРОДНОМ САЛОНЕ ИННОВАЦИЙ И ИНВЕСТИЦИЙ, 2010.
Лебедев Константин Андреевич. Награжден дипломом 65 лауреата Премии за 2012 год международной академической издательской компании Наука /Интерпериодика за лучшую публикацию в издаваемых ею журналах.
Стипендиаты
Ежегодно студенты факультета компьютерных технологий и прикладной математики являются стипендиатами Президента РФ, Правительства России, Администрации края, Совета вуза, «ОАО ФИЛИП МОРРИС КУБАНЬ», фонда В. Потанина, фонда О. Дерипаски
Ученые назвали правильный ответ в спорном примере из школьного курса математики — Общество
МОСКВА, 1 августа. /Корр. ТАСС Олеся Кулинчик, Александра Рыжкова/. Правильный ответ в примере из школьной математики с делением и умножением, породившем споры в социальных сетях, — «16». Об этом ТАСС заявили известные российские математики.
28 июля один из пользователей опубликовал в Twitter пример из школьной программы по математике: «8:2(2+2)=?». Обсуждение примера вызвало широкий резонанс, и перешло на международный уровень, пользователи разных стран получали ответ «16» или «1».
Российский математик, доктор физико-математических наук, первый декан факультета математики Высшей школы экономики Сергей Ландо рассказал ТАСС, что правильный ответ в России будет 16.
«На территории Российской Федерации деление и умножение имеют равные приоритеты. В США или Англии может быть другой порядок. В России сначала выполняется операция в скобках, потом деление на эту сумму, а потом результат умножается на следующий множитель. Правильный ответ — 16», — сказал он. Ландо добавил, что в подобных спорных случаях специалисты стараются обозначить порядок операций скобками.
Заведующий кафедры высшей математики Национального исследовательского университета «Московский институт электронной техники» (НИУ МИЭТ) Александр Прокофьев подтвердил ТАСС, что правильный ответ — 16, и объяснил, почему пример вызвал столько споров.
«Ошибаются, как я полагаю, преимущественно взрослые. У школьников вопросов быть не должно. Первой выполняется операция в скобках, затем, согласно приоритету арифметических действий, деление и умножение — они являются равноправными и выполняются слева направо. Студенты привыкают отделять косой чертой числитель от знаменателя, поэтому путаются в данном примере, полагая, что умножение двойки на скобку расположено в знаменателе», — сказал Прокофьев.
С ними согласилась и заведующая кафедры «Математика» Российского университета транспорта Людмила Кочнева. «Если бы стояла скобка после знака деление, то правильным ответом была бы единица. Если бы после восьмерки была горизонтальная черта — знак дробного деления — а внизу 2(2+2), это была бы единица. А раз все это в строчку, вы должны делать операции в том порядке, в котором они написаны. Восемь делим на два, четыре умножаем на 2+2, получается 16. Это просто манера записи, ничего интересного — чисто арифметическая задача, но все-таки более опрятно надо писать сам пример», — пояснила она.
Математика для школьников — Учёба.ру
Для того, чтобы по-настоящему понять математику, школы недостаточно — там дают лишь базовые знания по предмету и алгоритмы решения типовых задач. Если вы хотите «прокачать» и развить свои навыки, необходимо дополнительное математическое образование. Тем более, исторически сложилось так, что именно российская кружковая и олимпиадная система считается одной из самых эффективных в мире.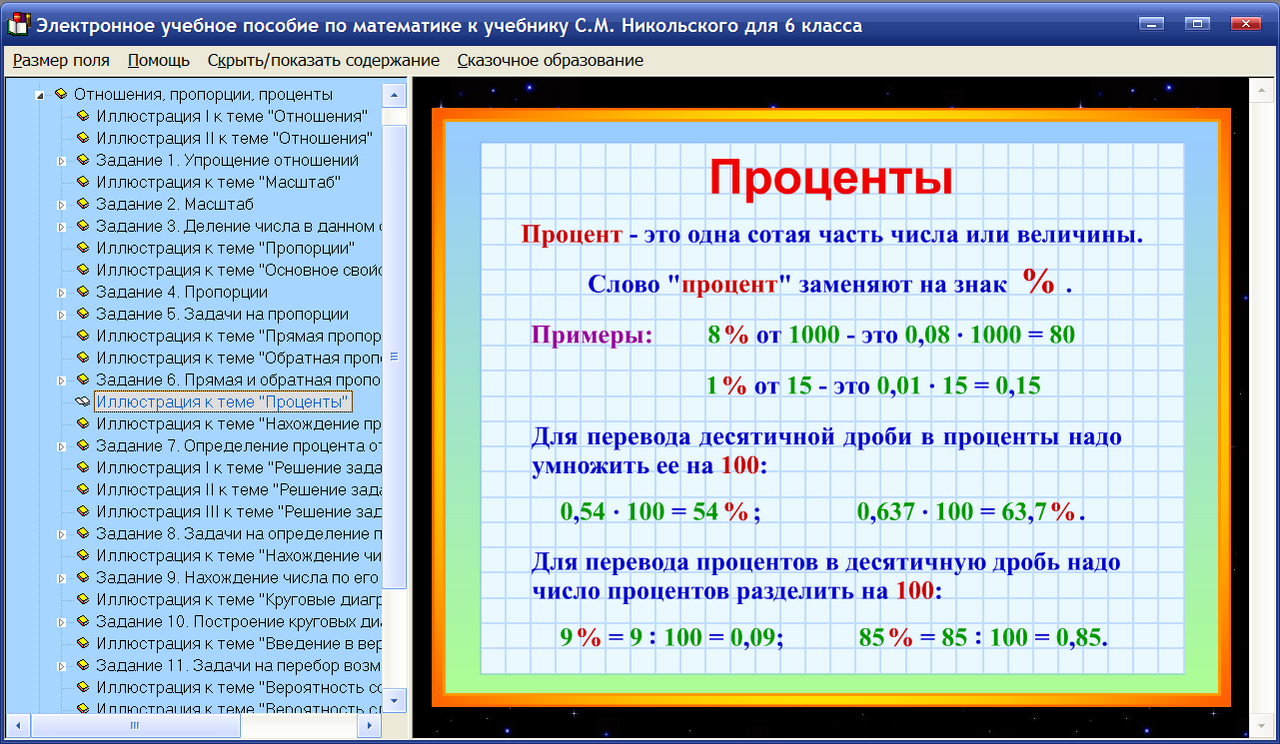
Она учит мыслить, рассуждать, доказывать. Кружки онлайн-школы «Систематика» сочетают в себе традиции математического образования и самые современные подходы к созданию среды интеллектуального развития.
Как построено обучение?
Математические кружки — это гордость отечественной математической школы, благодаря этой системе, в создании которой принимали участие выдающиеся математики, выросло не одно поколение ученых и просто умных образованных людей. Традиционно занятия проходят так: выдается листок с задачами, которые ученик решает и сдает, после этого проходит разбор. Новое в этой отработанной десятилетиями системе — возможность проводить кружки в онлайн режиме, что в наше время существенно облегчает процесс, делает его более системным, позволяет следить за успехами, при этом не затрачивая времени на дорогу.
В «Систематике» занятия проходят в живой, непринужденной атмосфере в формате видеоконференции на платформе Zoom. В небольших группах — от 4 до 10 человек — все имеют возможность высказаться и задать вопрос, но при необходимости можно и уединиться, отключив видео и звук, сосредоточиться на решении задач.
Преподаватели «Систематики» — выпускники и студенты старших курсов Мехмата МГУ и МФТИ, молодые математики, когда-то призёры, а нынче — организаторы олимпиад, что очень вдохновляет.
Вот, что пишут ученики о своих преподавателях: «Педагог Михаил очень доходчиво и спокойно и объясняет, никто из ребят не остается в стороне обсуждения». «Светлана ведет занятия в темпе ребят. Для каждого находит свой подход и каждого успевает подбодрить». «Нравится учитель Ксения. Она живо общается с детьми, старается, чтобы получался диалог».
Какие есть программы?
Олимпиадная математика
Заниматься олимпиадной математикой обычно приходят те ребята, которым уже мало школьной программы, кто хочет двигаться дальше — научиться решать сложные задачи, находить красивые решения, нестандартно мыслить. На онлайн-курсе «Систематики» для школьников предлагается семь уровней сложности: если после первого занятия выяснится, что учиться слишком сложно (или очень легко), уровень можно поменять.
Поначалу может показаться, что олимпиадные задачи невозможно решить — чтобы втянуться рекомендуется смотреть видео с разборами: сначала вы следите за способом мышления преподавателя, а потом эти же подходы и методы применяете в решении других задач. А дальше все становится легко и интересно.
Занятия проходят в мини-группах на платформе Zoom. Всего работает 50 групп, что очень удобно, поскольку можно выбрать удобные для себя дни и время обучения. Школа предлагает и индивидуальные занятия для олимпиадников. Уроки с репетитором могут проводиться как по общей программе, так и по составленной непосредственно под ученика.
Узнать подробнее
Школьная математика
Онлайн-кружок школьной математики будет полезен тем, кто только начинает свое погружение в этот предмет и хочет устранить пробелы в знаниях. Цель обучения — выявить «слабые места» и закрыть их. План занятий составлен по школьной программе на базе учебников Виленкина, Мерзляка и Никольского и рассчитан на учеников с 3 по 7 класс.
На уроках ребята с преподавателем разбирают тему и решают по ней задачи. Чтобы закрепить результат занятия, дома обязательно нужно выполнить домашнее задание и сдать его на проверку.
«Две задачи на неделю»
Чтобы заразить математикой как можно больше людей, в «Систематике» разработали бесплатный курс «Две задачи на неделю» — для тех, кому от 9 до 99 лет. Идея заключается в том, чтобы показать красоту математики, внести ее в жизнь, заинтересовать детей и взрослых. Каждую неделю участникам курса предлагается для решения две интересные олимпиадные задачи, потом открывается видео с их разбором. В конце курса — а рассчитан он 10 недель, — выдается сертификат. Эта программа — отличная возможность познакомиться со школой перед выбором кружка.
Узнать подробнее
Олимпиада по математике
Полученные на уроках знания школьники могут применить буквально сразу же. Ведь «Систематика» проводит собственную олимпиаду по математике, где за призы сражаются ученики 1-9 классов.
Олимпиада проходит дважды в год: осенью и зимой. В этом году 24 октября состоится Девятая международная олимпиада «Систематики», а в следующем году 30 января пройдет зимняя олимпиада. Участие в олимпиаде бесплатное, а победа дает приятные призы — бонусные рубли на личный счёт в школе и скидки на обучение. Кроме того, участие в математических олимпиадах — это еще и возможность расширить круг общения и познакомиться с умными и целеустремленными сверстниками.
Подробнее об олимпиаде
ТРИЗ и шахматы
Задача «Систематики» не просто научить математике, она шире — научить думать, творить, расшевелить мозги и поддерживать их в тонусе. Для того, чтобы развивать аналитическое, изобретательское мышление здесь работает кружок «ТРИЗ» — Теория решения изобретательских задач. На занятиях уделяется время работе над личным проектом для каждого ученика, созданию моделей, изобретений, технологий. Среда единомышленников и опытных педагогов вдохновляет на творческое развитие и поиск нестандартных решений.
Кружок «Шахматы» — это комбинация практики, теории и решения игровых задач, занятия проходят в Zoom и на платформе Lichess.
Репетитор по математике онлайн — математическая школа «Альфа»
Онлайн-занятие проходит на интерактивной платформе один на один с репетитором. Для комфортной связи и удобства мы используем Skype и интерактивную доску. Программу обучения составляют индивидуально под каждого ученика. Длительность урока — 50 минут.
Что нужно для занятий?
- Компьютер / ноутбук / планшет
- Выход в интернет
- Микрофон и наушники
НЕ РЕКОМЕНДУЕМ использовать для занятий телефон! Это создает большие неудобства и ученику, и учителю во время работы и изучения материала.
Оптимальная скорость интернета для бесперебойной связи 1 Мб/с, рекомендуемый браузер — Google Chrome.
Занятия могут проходить когда и где угодно: дома, во время отдыха на свежем воздухе и даже в поездке. А если у ученика не получается, урок можно отменить и запланировать его на любое удобное время.
Присутствие родителей во время занятия НЕ ОБЯЗАТЕЛЬНО! Взрослые смогут в любое время после урока просмотреть запись встречи, чтобы увидеть, как проводилась работа.
Уроки на платформе
Мы разработали программы уроков для 1 — 11 классов, по которым ученики могут подготовиться:
- к сдаче государственных экзаменов (ЕГЭ, ОГЭ),
- по отдельным темам,
- к контрольным или самостоятельным работам,
- к олимпиадам.
Каждый репетитор в онлайн-школе Альфа практикует индивидуальный подход. В самом начале обучения они определяют особенности восприятия информации ученика, длительность удержания концентрации внимания, чтобы составить максимально эффективный план обучения (комбинирование разного рода упражнений, активных/пассивных видов работы, самостоятельной и совместной деятельности ученика и учителя, теоретического и игрового материала).
Интерактивная доска
Репетитор-онлайн работает с интерактивной доской так же активно, как и ученик. Здесь они вместе решают основные и дополнительные задания. Доска синхронно отображает все действия, поэтому ученик видит все записи и пометки репетитор на доске.
Чтобы ознакомиться с основами работы с интерактивной доской, просмотрите обучающее видео.
Если во время урока возникнут проблемы, ученику оперативно оказывают помощь и сами преподаватели, и круглосуточная служба поддержки.
Скайп для связи с репетитором!
Общение и обратная связь с учеником проходит через Скайп при помощи функции «демонстрация экрана». Поскольку ребенок работает с платформой через личный кабинет, а преподаватель будет сопровождать его и следить за ходом выполнения заданий.
Обратная Связь от репетитора
Репетитор высылает на почту отчёт об успехах ребёнка каждые 2 недели после 4 пройденных занятий. В этом документе родители смогут найти пройдённые темы, комментарий по урокам и рекомендации репетитора.
Кроме того, в личном кабинете видна полная программа запланированного занятия. При желании ее в любой момент можно подкорректировать и согласовать с репетитором.
Обратная связь – активный помощник в обучении:
- показывает прогресс ученика;
- демонстрирует, сколько времени понадобилось для устранения пробелов в проблемной теме;
- визуализирует пройденные темы;
- позволяет корректировать план на усмотрение родителя/ученика;
Обратная связь – это ненавязчивый контакт учителя с родителем.
С ее помощью можно отрегулировать программу, чтобы сделать процесс обучения комфортным для всех участников.
А еще она дает родителям лишний повод гордиться своим ребенком, который проделывает такой же огромный труд, как и репетитор.
Выпускная программа
Выпускная программа по математике в Университете Рутгерса предлагает курсы обучения, ведущие к получению степеней доктора философии. и М.С. Быстрая ссылка на обзор нашего доктора философии. программа здесь. M.S. Степень имеет два варианта: математический финансовый вариант и традиционный (сейчас редко используемый) вариант.
В аспирантуру математического факультета входят около 65 активных членов кафедры математики, а также около 20 других преподавателей других факультетов Университета Рутгерса.Наш факультет охватывает широкий спектр областей знаний.
Осенью 2016 г. на постоянной основе работали 76 кандидатов наук.
студенты в нашей программе. Мы стремимся способствовать успеху наших студентов. В рамках этого обязательства мы смогли постоянно оказывать финансовую поддержку почти всем нашим докторантам в виде ассистентов, стипендий и исследовательских фондов. Программа для выпускников в прошлом успешно использовала поддержку групп студентов в виде различных федеральных грантов.В 2009 году мы получили финансирование для стипендий для выпускников через программу GAANN (Помощь выпускникам в областях, нуждающихся в национальных потребностях), которая использовалась в основном для предоставления стипендий для поступающих студентов в течение следующих трех лет; 11 студентов поступили в нашу докторантуру. Программа с поддержкой стипендий GAANN в период с 2010 по 2012 год. Осенью 2012 года мы получили еще один грант GAANN, в рамках которого было предоставлено не менее девяти стипендий с 2012 по 2016 год.
В дополнение к примерно 45 курсам для выпускников, проводимым каждый год, являются многочисленные еженедельные семинары и коллоквиум во второй половине дня в пятницу.
Кроме того, каждый учебный год проводится ряд специальных циклов лекций и конференций. Семинары по другим программам, таким как количественная биология (ранее BIOMAPS), информатика, DIMACS, физика, статистика и исследования операций, легко доступны и могут быть интересны. Региональные, национальные и международные встречи по математике и смежным предметам часто проводятся в Rutgers.
Программа последипломного образования по математике в Rutgers расширена за счет близости к основным академическим учреждениям в Нью-Йорке и Принстоне, а также к нескольким промышленным исследовательским лабораториям в Нью-Джерси.
Для получения дополнительной информации свяжитесь с нами.
| UGC Профессор | ||||
Профессор Др. Субрата Маджумдар (Алгебра) Магистр наук (Радж.), Доктор философии (Бирмингем) | ||||
| Профессор | ||||
| 01. | Д-р Ахил Чандра Пол, (Анализ) M. Sc. И М. Фил. (Радж.), Доктор философии (Банарас) | |||
| 02. | Д-р М. Абдул Латиф, (Теория решеток) M. Sc. (Радж.), Доктор философии (Радж.) | |||
03. | Д-р М. Вазед Али Праманик, (гидродинамика) M. Sc. (Радж.), Доктор философии (Каляни) | |||
| 04. | МиссисНазма Султана, (Компьютерное программирование) M. Sc. (Радж.), Обучение в Великобритании | |||
| 05. | Д-р Зульфикар Али, (Дифференциальные уравнения, интервальный анализ, теория фиксированной точки) M. Sc. (Джахангирнагар), доктор философии (Япония) | |||
| 06. | Доктор.Насима Ахтер, (алгебра, топология) M.  Sc. (Радж.), M.Sc. (Канада), доктор философии (Радж.) | |||
| 07. | Доктор М. Ашабул Хок, (Водные волны) M. Sc. (Радж.), Доктор философии (Япония), Postdoc. (Германия) | |||
| 08. | Д-р М.Асадуззаман, (Функциональный анализ) M. Sc. (Радж.), Доктор философии (Япония) | |||
| 09. | Д-р Шули Шамим Шанта, (Численный анализ) M. Sc. (Радж.), Доктор философии (Япония.), Постдок. (Южная Корея) | |||
10. | Доктор.Хосне Ара Жасмин, (вычислительная гидродинамика) M. Sc. И М. Фил. (Raj.), M. Sc. (Кембридж, Великобритания), Кандидат наук. (Манчестер, Великобритания) | |||
| 11. | Доктор Квази Селина Султана, (алгебра) M. Sc., M. Phil. & Кандидат наук. (Радж.) | |||
| 12. | Д-р М. Лутфор Рахман (гидродинамика) M. Sc. & Кандидат наук. (Радж.) | |||
| 13. | Д-р М. Сазувар Райхан, (Теория решеток) M.Sc. (Raj.), Ph.D. (Радж.) | |||
| 14. | Доктор.Калян Кумар Дей, (Алгебра) Магистр и доктор философии (Радж.) | |||
| 15. | Д-р Джогендра Натх Праманик, (астрофизика) M.Sc. (Raj.), M.S. (Китай), Ph.D. (Радж) | |||
| 16. | Д-р Мохд. Алтаб Хоссейн, (Топология и дифференциальная геометрия) М.Sc. (Радж.), Доктор философии (Радж) | |||
17. | Д-р Гоур Чандра Пол, (астрофизика) M. Sc. (Радж.), Доктор философии (Радж), постдок. (Малайзия) | |||
| Доцент | ||||
| 01. | Доктор Шули Ахтер, (Теория решеток) M. Sc. (Радж.), Доктор философии (Радж) | |||
| 02. | Доктор медицины Сахадат Хоссейн, (Нечеткая математика) M.  Sc. (Raj.), M.Phil. (Радж), доктор философии (Радж) | |||
| 03. | Доктор.М. Харунор Рашид, (Оптимизация, нечеткая математика) M. Sc. (Raj.), M.Phil. (Радж), доктор философии (Китай) | |||
| Доцент | ||||
| 01. | Доктор Мэриленд Илиас Хоссейн M.  Sc. (Университет Раджшахи), доктор философии (Университет Раджшахи) | |||
| 02. | Г-н Абдул Малек M.Sc. (Университет Раджшахи), M.Phil. (Университет Раджшахи) | |||
| 03. | Г-н МД. Масум Муршед (Учебный отпуск в Японии, Университет Канадзавы) M.Sc. (Университет Раджшахи), стажировка в Португалии | |||
| 04. | Г-н Мэриленд Джакир Хоссейн M.Sc. (Университет Раджшахи), M.Phil. (Университет Раджшахи) | |||
05. | Г-н М. Рабиул Хак (Учебный отпуск в Японии, Университет Тохоку) M.Sc. (Университет Раджшахи), стажировка в Португалии | |||
| 06. | Г-н Амитабх Кумер Гальдер (Учебный отпуск в Канаде, Университет Далхаузи) Магистр наук (Университет Раджшахи) | |||
| 07. | г-н М. Абдул Куддус M.Sc. (Университет Раджшахи), магистр наук (Таиланд) | |||
| 08. | Г-н А.Х.М. Рашедуннаби (Учебный отпуск в Японии, Университет Сайтамы) M.Sc. (Университет Раджшахи) | |||
| 09. | Госпожа Шамим Ара M.Sc. (Университет Раджшахи) | |||
| Преподаватель | ||||
Научно-исследовательский опыт математики (REM) — математический факультет — НИУ ВШЭ
«Опыт исследований в математике» — это программа, предназначенная для студентов и аспирантов, специализирующихся в математике или строго связанных областях.
Участники будут работать над исследовательскими проектами под индивидуальным руководством выдающихся московских математиков, преподавателей или исследователей математического факультета НИУ ВШЭ или Математического института им. В. А. Стеклова. Участие бесплатное и зависит от выбора на основании резюме и писем поддержки.
Студенты должны работать со своими наставниками лично в Москве или онлайн в течение не менее 23 дней, с 20 июня t h и 20 августа th 2021.Взаимодействие студента и репетитора очень индивидуализировано, и точный формат работы во многом зависит от методов репетитора и опыта студентов. Однако студенты могут рассчитывать на работу над оригинальным исследовательским проектом, предложенным наставником, иметь пару личных встреч в неделю с наставником в течение всего проекта. Конечно, перед приездом в Москву необходимо провести некоторую предварительную работу по предложению наставника, а во время REM требуется интенсивная работа между встречами.
По результатам проекта ожидается письменный отчет.
Поощряется сотрудничество с другими учащимися, а летние классы, открытые для всех, летом могут быть доступны по определенным темам.
Кто может подать заявку: Подать заявку может любой студент из российских или зарубежных университетов, обучающийся в бакалавриате или магистратуре (или эквивалентном в зависимости от страны) по математике или строго смежным областям.
Финансовая поддержка: Программа REM проводится совместно с Летним университетом НИУ ВШЭ, предлагая различные курсы по разным темам.Однако студентам, участвующим в REM, доступна финансовая поддержка. Для студентов, участвующих в REM, мы предоставляем:
· Бесплатное участие в программе, бесплатные кредиты.
· Базовое проживание в Москве (если вы не участвуете онлайн) доступно для ограниченного количества студентов.
Мы НЕ предоставляем:
· Путевые расходы и местные расходы, кроме проживания.
· Финансовая поддержка кредитов Летнего университета НИУ ВШЭ, не являющихся частью исследовательской практики по математике.
Например, студент может приехать в Москву для участия в REM, иметь бесплатное проживание и свободный доступ к REM, а также использовать личные (или домашние) средства для оплаты дорожных расходов и лекций по русскому языку в Летнем университете НИУ ВШЭ.
Как подать заявку : Заявки на REM должны быть отправлены Мауро Мариани на [email protected] и должны включать:
· Подробное академическое резюме. Пожалуйста, укажите ваше гражданство, так как это важно для оценки времени на получение визы.
· Мотивационное письмо, в котором вы подробно объясняете свои интересы и цели по математике, включая область, в которой вы хотели бы работать во время REM. Не стесняйтесь называть преподавателей, с которыми вам будет интересно работать.
· Письмо поддержки от академика, который с вами контактировал.
Крайний срок подачи заявок: 18 апреля -е для нерусских студентов и 10 мая -е для российских студентов (это означает, что студенты, которые учатся в России и не нуждаются в визе).
Более поздние заявки также могут быть приняты при условии, что у них будет достаточно времени, чтобы с комфортом предоставить студентам визу и подготовить предварительные материалы. Также обратите внимание, что вам нужно подать отдельную заявку на обе программы, если вы также хотите участвовать в Летнем университете Вышки.
В течение трех рабочих дней с момента подачи заявления вы получите уведомление о том, что ваше заявление получено. Окончательный ответ о приеме кандидата требует больше времени и в основном зависит от наличия преподавателей для обучения кандидата.
Важная дополнительная информация: обратите внимание:
· Точный период участия согласовывается между студентом и преподавателем.
· Каждый студент может участвовать в онлайн или офлайн формате. Однако это не всегда вариант, который можно свободно выбирать, и он зависит от: будущего развития продолжающейся пандемии и правовых ограничений, которые могут различаться в зависимости от страны происхождения; наличие наставников по каждому формату; общие проблемы безопасности.
Мы считаем, что личное сотрудничество — более эффективный формат для математических исследований, но безопасность людей является приоритетом.
· Летние классы предлагаются преподавателями на общественных началах. Вы не можете рассчитывать на летние занятия по какой-либо теме по математике. Тем не менее, участие бесплатное и открыто для всех.
· Список проектов, предложенных преподавателями, доступен здесь.
За дополнительной информацией обращайтесь по адресу [email protected].
Как RU поддерживает регулярные контактные часы и академическую честность во время удаленных занятий
Вы также можете услышать Dr.Флер Зельденруст расскажет о своем опыте использования здесь.
Согласно Keuzegids Universiteiten 2020, Radboud University был признан одним из лучших традиционных университетов для программ общего бакалавриата в Нидерландах уже почти сто лет.
С 2019 года Radboud University присоединился к рейтингу преподавателей Times Higher Education Europe, который сравнивает университеты на основе их результатов в области образования. Radboud University занял 24-е место среди 258 университетов.
Флер Зельденруст — доцент кафедры нейрофизиологии Института мозга, познания и поведения Дондерса. Помимо проведения исследований в качестве вычислительного нейробиолога, Флер также преподает математику студентам первого курса биологии по курсу «Математика для биологов».
Вызов
По словам Флер, для большинства студентов, поступающих на ее курс, математика никогда не была их главной заботой во время учебы в средней школе, поскольку их внимание было сосредоточено в основном на биологии.
«У студентов очень разноплановое образование. Из голландских старшеклассников кто-то изучает математику А, а кто-то — математику Б. У нас также довольно большое количество иностранных студентов, и эти ученики также имеют разное школьное образование ».
Когда Флер приступила к разработке этого курса в апреле 2019 года, одной из самых больших проблем, с которыми столкнулась Флер, было разработать курс, который подошел бы этой разнообразной группе студентов.
«Вы не хотите усложнять задачу для тех, кто не имеет большого образования в математике, но вы хотите сохранить интерес для тех, кто имеет».
Эта проблема работы с большой группой разноплановых студентов еще более усугубилась в 2020 году из-за протоколов изоляции и социального дистанцирования COVID-19.
«Мое первое беспокойство в начале этого периода было, если нет лекций или учебных пособий, как мне поддерживать связь со своими учениками и как я могу отслеживать их.”
По сути, Флер хотела убедиться, что, несмотря на отсутствие часов физического контакта, она все еще могла отслеживать успехи своих учеников и вмешиваться, когда они приближались к препятствиям в их соответствующих учебных поездках.
Еще одна серьезная проблема, вызванная COVID-19, заключалась в проведении безопасных формирующих и итоговых оценок. Хотя существовало очевидное решение — удаленный контроль, Флер и ее команда в Radboud думали, что это было очень агрессивно, когда дело касалось частной жизни учащихся, а также контрпродуктивно для обучения и успеваемости учащихся.
«Когда дело доходит до прокторинга, существуют серьезные проблемы с конфиденциальностью. Студенты должны установить программное обеспечение, которое может получить доступ ко всем файлам на вашем компьютере, которое отслеживает, кто знает что, а затем сохраняет их в базах данных, которых нет в Европе. Так что европейские законы не действуют. Некоторые студенты также сказали, что они чувствовали себя очень некомфортно и нервничали, если у них было ощущение, что кто-то наблюдает за ними все время ».
В качестве последнего примечания Флер также упомянула, что в большинстве своих тестов она позволяет студентам использовать таблицы формул и калькуляторы.
Большинство решений для контроля работают на основе программного обеспечения для отслеживания взгляда, которое срабатывает, если они замечают «подозрительное» движение глаз.
«Проблема в том, что мои ученики не всегда смотрят на экран, они смотрят на свой лист формул или свой калькулятор. Поэтому из-за этого программы удаленного контроля получают слишком много ложных срабатываний »
Решение
Чтобы справиться с проблемой разнообразия учебных заведений, Флер решила назначить предварительные учебные материалы и тесты до начала официального курса.
«В основном перед началом курса мы говорили, что это тот уровень, который мы ожидаем от вас. Мы дали им два теста и сказали, что вы можете проводить их сколько угодно, но я надеюсь, что вы это поймете, а если вы этого не сделаете, то вот материал, с которым вы можете практиковаться. Обычно сюда входили такие темы, как экспоненты и дроби, и другие подобные темы ».
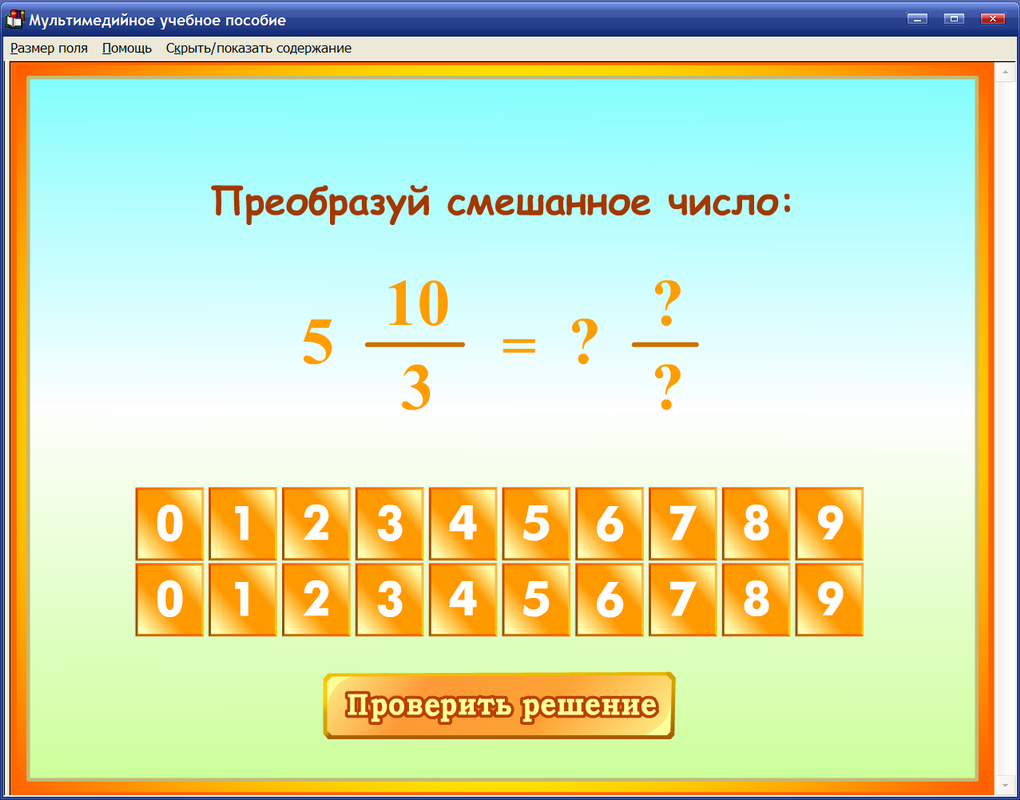
Поскольку инструмент SOWISO включает в себя вопросы, задаваемые случайным образом, учащимся, которые повторно проходили эти начальные тесты, всегда предоставлялись новые вопросы теста с каждой новой попыткой.Таким образом, учащиеся не только получили возможность пересдать тесты, но и Флер смогла убедиться, что результаты тестов учащихся действительно отражают их математические знания, поскольку учащиеся не могут набирать более высокие баллы, просто запоминая вопросы теста и их ответы. соответствующие решения. Вдобавок ко всему, ко всем назначенным практическим материалам прилагалась автоматическая персонализированная обратная связь, которая также помогала студентам еще больше укрепить свои базовые знания, не обращая внимания на учителя.
Когда дело дошло до перехода к онлайн-обучению в ответ на протоколы COVID-19, половина работы была уже сделана для Флер, поскольку все материалы класса уже были онлайн. Все теоретические и практические материалы были в сети с помощью инструмента SOWISO, и она также записала все свои лекции за последний год.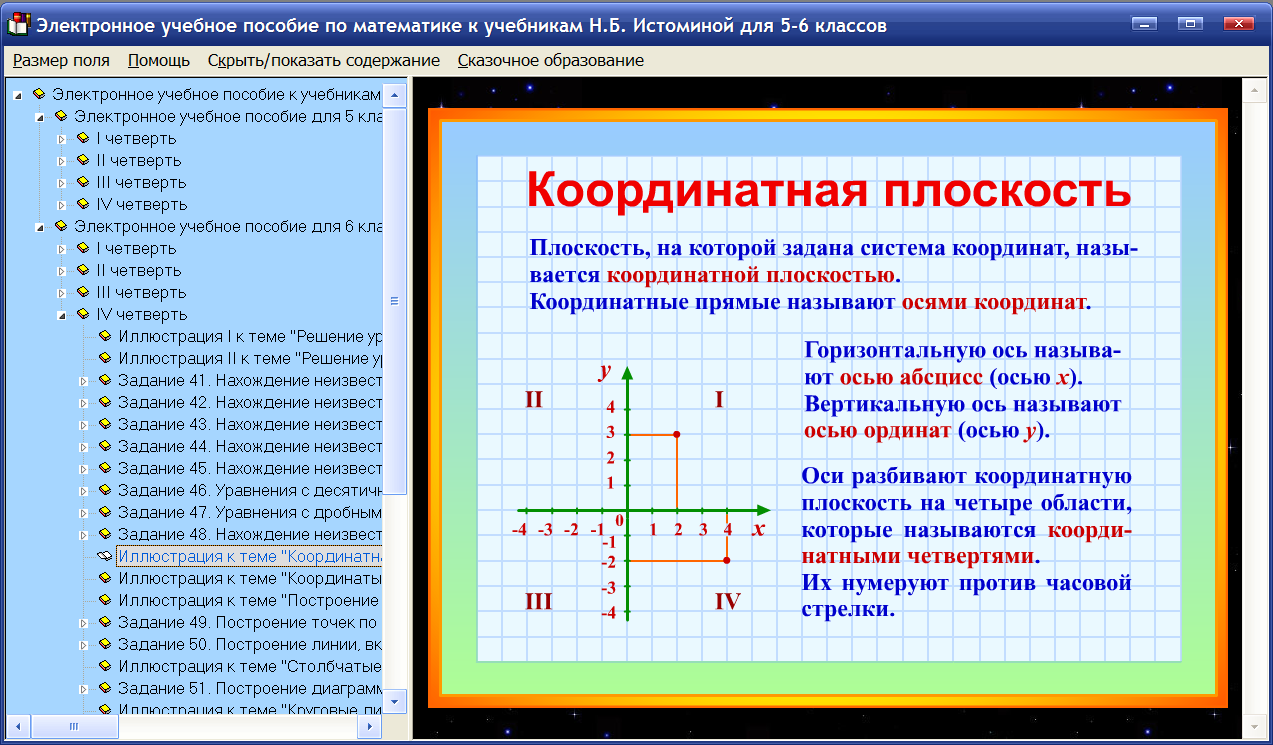
Как было сказано ранее, теперь задача заключалась в том, чтобы убедиться, что она по-прежнему хорошо видит успехи своих учеников.
«Это действительно странно, когда студентов больше нет в кампусе, и вы их больше не видите.Так что становится очень легко пропустить любые проблемы, с которыми могут столкнуться ваши ученики ».
Имея это в виду, Флер начала проводить еженедельные диагностические тесты, которые проверяли ее учеников по всем темам, которые обсуждались в каждую соответствующую неделю. У каждого ученика было по 3 попытки пройти каждый еженедельный диагностический тест, и результат был установлен на 75%.
«Но если у них возникнут проблемы, они могут просто связаться со мной, чтобы получить дополнительные попытки или продление. Это был просто способ их отслеживать.Поэтому, если они не сдадут тест до крайнего срока или не пройдут его, они не будут связываться со мной, а я скорее свяжусь с ними ».
Флер смогла легко проводить эти еженедельные диагностические тесты без особых дополнительных усилий с ее стороны, потому что эти тесты очень легко создать, взяв из существующей базы данных SOWISO рандомизируемых упражнений.
Все это можно затем автоматически проверять и оценивать.
Наконец, когда дело дошло до вопроса сохранения академической честности во время удаленных итоговых тестов, Флер использовала инструмент SOWISO, чтобы студенты загружали сопроводительные рукописные заметки к их попыткам ответа.
«Конечно, они дают свои ответы в электронной программе, но они все еще обычно делают свои выводы вручную. Итак, теперь мы попросили их загрузить их, поэтому по каждому вопросу я хочу видеть несколько примечаний. Это может быть просто небольшой комментарий или что-то в этом роде, просто чтобы помочь мне понять вашу аргументацию ».
Помимо вышеуказанной меры, Флер также использовала функцию рандомизации SOWISO, чтобы убедиться, что каждый студент получил рандомизированный порядок вопросов для своей оценки, а также рандомизированные переменные для каждого конкретного вопроса.Другими словами, каждый ученик получил разную последовательность вопросов, и хотя каждый конкретный вопрос имел одинаковую структуру скелета во всех тестах, конкретные переменные каждого вопроса были разными для каждого ученика.
Результаты
Когда дело дошло до ее разнообразного класса, Флер нашла самостоятельный аспект SOWISO весьма полезным, поскольку теперь она могла лучше справляться с разными уровнями обучения между учениками.
«Студенты с большим объемом базовых знаний могут быстро просмотреть материал и показать с помощью тестов, что они усвоили материал, в то время как студенты с меньшими базовыми знаниями имеют возможность практиковаться почти бесконечно, потому что задания продолжают рандомизироваться.”
Еженедельные диагностические тесты также имели большой успех в ее классе, Флер поняла, что это может быть лучший способ гарантировать, что между ней и ее учениками всегда будет какой-то тип общения.
«Таким образом, я смог действительно поговорить со студентами и спросить их, что происходит, и иногда возникали проблемы, о которых я даже не думал. Оказалось, что у одного студента нет ноутбука. Другой студент с трудом мог сосредоточиться.
Некоторые из иностранных студентов вернулись домой, так что они только поселились. Мы смогли обсудить все это и многое другое. Это может показаться странным, но еженедельные тесты стали точкой контакта. Так что все прошло хорошо »Флер также обнаружила, что, заставляя студентов загружать свои собственные рукописные заметки в свои тесты с цифровым администрированием, она также предоставляла студентам еще одну возможность обучения.
«Я заставил их проверять свои экзамены. Итак, в основном после того, как они сдают экзамен, и после того, как я его просматриваю, я просто сообщаю им их результаты, а также то, что было не так, а что было правильным, чтобы они могли увидеть правильное разработанное решение и сравнить его со своими собственными заметками.Это означает, что они действительно учатся на экзаменах. Они видят, что они сделали неправильно, и, что более важно, на каком этапе они пошли не так »,
В конце концов, уроки Флер имели такой успех, что Флер получила Премию для младших преподавателей Учебного института биологических наук Университета Радбауд за ее работу с курсом и успехи своих студентов.
Математическое и компьютерное моделирование
* 01.04.02 Информатика и прикладная математика
27.04.03 Системный анализ и контроль
СТОИМОСТЬ ОБУЧЕНИЯ
271000 руб. / Год
ОПИСАНИЕ ПРОГРАММЫ
Программа предлагает углубленную фундаментальную подготовку в области математики и вовлекает студентов в исследовательскую и проектную деятельность с самого начала курса. Сферы деятельности программы включают, помимо прочего: математическое моделирование сложных систем, квантовую оптику и квантовую информатику, исследования магнитных наносистем.Чтобы обеспечить участие студентов в международном исследовательском процессе, часть обучения проводится на английском языке. Студенты участвуют в международных научных конференциях и международных стажировках.
АКТУАЛЬНОСТЬ ПРОГРАММЫ
Развитие информационных технологий и нанотехнологий включено в перечень приоритетов Стратегии научно-технологического развития Российской Федерации.
Магистерская программа математического моделирования направлена на подготовку исследователей в области математического моделирования наносистем и информационных технологий.Без таких специалистов прогресс в этой области невозможен. В связи с быстрым развитием отрасли, нынешний высокий спрос на таких специалистов вряд ли сократится в ближайшие годы.
Студенты программы активно участвуют в исследованиях, финансируемых за счет международных грантов (совместные проекты с Германией, Финляндией и Исландией), национальных грантов, таких как гранты Российского научного фонда, президентских грантов и т.п., а также в выполнении государственных контрактов.
ПЕРСПЕКТИВЫ ЗАНЯТОСТИ
Студенты и выпускники программы работают в университетах, исследовательских учреждениях и компаниях, таких как:
- Университет ИТМО
- Университет Дьюка, Дарем, Северная Каролина (США)
- Университет Ватерлоо, Канада
- Принстонский университет, США,
- ICERM, США
- Microsoft, Редмонд, США
- SunGard, Стокгольм, Швеция
- Мэрилендский университет, США
- Геофизический институт, Университет Аляски, Фэрбенкс, США
- Институт Иоффе
- Яндекс
- Оракул
- Т-Системс
- Центр речевых технологий
- Программное обеспечение Veeam
- Девэкспертс
- Группа компаний Геоскан
- Возвращение к разведке
- Cardsmobile
СТУДЕНЧЕСКАЯ СТАЖИРОВКА
Студенты проходят практику в научно-исследовательских учреждениях и компаниях, работающих в области информационных технологий (см.
Выше), и которые входят в число потенциальных будущих работодателей для выпускников.
Л. Посицельский — Леонид Посицельский
Домашняя страница Леонида Посицельского
Я математик, специализирующийся на гомологической алгебре. Я написал статьи о двойственности Кошуля, полубесконечных когомологиях, матричных факторизациях, производных категориях второго рода, когомологиях Галуа и смешанных мотивах с конечными коэффициентами.
С весны 2008 г. я работал старшим научным сотрудником, а с осени 2013 г. — и.о. ведущего научного сотрудника лаборатории алгебры и теории чисел (http: // www.iitp.ru/ru/researchlabs/277.htm) Института проблем передачи информации. С 2011 по 2014 год работал доцентом (http://www.hse.ru/org/persons/35825480) кафедры математики (http://math.hse.ru/) Высшей школы. экономики. Иногда я читал курсы повышения квалификации в Независимом Московском университете (http://www.mccme.ru/ium/english/).
Мои препринты в arXiv доступны по ссылке http://arxiv.
org/a/positselski_l_1.html или http://arxiv.org/a/positselski_l_1.atom
Расширенная версия моей весенней презентации 2014 года о соответствии комодуля-контрамодуля доступна по адресу http://positselski.narod.ru/co-contra.pdf Мои лекции весной 2011 года о двойственности Кошуля (на русском языке) доступны по адресу http://positselski.narod.ru/co-contra.pdf /erb-files.narod.ru/ Мои лекции весны 2009 года о соответствии комодуля-контрамодуля и представлениях бесконечномерных алгебр Ли (также на русском языке) доступны на сайте http: // club.pdmi.ras.ru/moodle/course/view.php?id=10
Мои мемуары «Два вида производных категорий, двойственность Кошуля и соответствие между модулями и модулями» были опубликованы Американским математическим обществом в 2011 году. См. Http://www.ams.org/bookstore-getitem/item=MEMO-212 -996 и http://www.ams.org/journals/memo/2011-212-996/S0065-9266-2010-00631-8/home.html
Моя монография «Гомологическая алгебра полумодулей и полумодулей», содержащая приложения, написанные совместно с Сергеем Архиповым (http: // www.
math.toronto.edu/cms/arkhipov-sergey/) и Дмитрия Румынина (http://www2.warwick.ac.uk/fac/sci/maths/people/staff/dmitriy_rumynin/), опубликованных Birkhauser Basel в 2010 г. См. Http://www.springer.com/birkhauser/mat Mathematics/book/978-3-0346-0435-2
Моя книга «Квадратичные алгебры», написанная совместно с Александром Полищуком (http://www.uoregon.edu/~apolish/), была опубликована Американским математическим обществом в 2005 году. См. Http://www.ams.org/ книжный магазин? fn = 20 & arg1 = ulectseries & item = ULECT-37
Я получил докторскую степень.D. из Гарвардского университета в 1998 году. Расширенная версия моей диссертации доступна в архивах препринтов K-теории по адресу http://www.math.uiuc.edu/K-theory/0730/. находится в архиве arXiv по адресу http://arxiv.org/abs/1405.0965
Моя самая первая статья была опубликована в журнале Functional Analysis and its Applications в 1991 году. См. Http://mi.mathnet.ru/rus/faa/v25/i4/p74 (русский язык; обратите внимание на ошибку в названии) или http: / /dx.
doi.org/10.1007/BF01080085 (английский).
Другими моими соавторами являются Роман Безрукавников (http://en.wikipedia.org/wiki/Roman_Bezrukavnikov), Александр Браверман (http://research.brown.edu/myresearch/Alexander_Braverman) и Александр Вишик (http: // www. .nottingham.ac.uk / математика / люди / alexander.vishik).
Я не могу упомянуть здесь всех своих учителей, но большую часть математики, которую я когда-либо знал, я узнал от Майкла Финкельберга (http://www.hse.ru/org/persons/2806441/index.html) и Аркадия Вайнтроба (http : // www.uoregon.edu/~vaintrob/).
Чтобы посмотреть мою фотографию, щелкните ссылку «Профиль человека» в левом кадре. Чтобы получить доступ к списку моих публикаций с гиперссылками, щелкните ссылку «Публикации». Мое расширенное резюме с резюме исследования (устаревшее) доступно по адресу http://www.iitp.ru/upload/content/277/positselskiCV.pdf. Последнюю версию резюме можно найти по адресу http://positselski.narod. ru / cv.pdf
Черновики моих незаконченных работ время от времени выкладываются на странице http: // positselski.
narod.ru
Мои вопросы и ответы на mathoverflow.net доступны на странице http://mathoverflow.net/users/2106/
Эта домашняя страница больше не обслуживается должным образом, а некоторые ссылки и информация, приведенные выше, могут быть устаревшими. С осени 2018 года работаю научным сотрудником Института математики Чешской академии наук в Праге. Моя домашняя страница на сайте Института математики находится по адресу http://users.math.cas.cz/~positselski/
Журнал вычислительной и инженерной математики
Добро пожаловать на сайт журнала «Вычислительная и инженерная математика»!
Учредитель:
Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Южно-Уральский государственный университет (национальный исследовательский университет)»
ФГАОУ ВО ЮУрГУ
- Обзорные статьи,
- Вычислительная математика,
- Инженерная математика,
- Краткие заметки,
- Personalia.
Раздел «Краткие заметки» содержит доклады аспирантов и магистров в области публикации.
Раздел «Персоналии» содержит биографические статьи о выдающихся ученых.
Основная цель публикации — популяризация фундаментальных и прикладных математических исследований, обеспечивающих развитие вычислительной техники и решение актуальных инженерно-технических задач.Предпочтительно к публикации статьи, посвященные комплексным исследованиям математических моделей, математическим методам в инженерной практике для реализации инновационных проектов, решению прикладных задач с использованием необходимого программного обеспечения и расширенных возможностей компьютеров.
В журнале публикуются оригинальные статьи о
1) комплексном исследовании математических моделей,
2) математических методах в инженерной практике для реализации инновационных проектов,
3) решении практических задач с использованием необходимого программного обеспечения и расширенных возможностей компьютеров.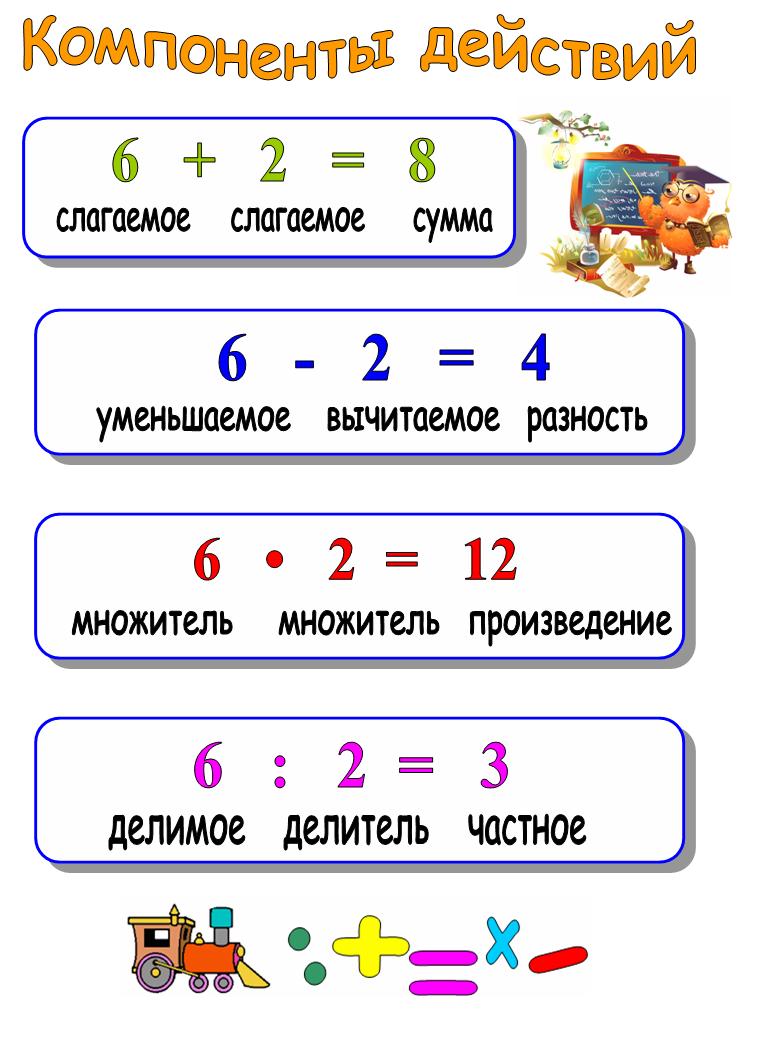
.
Целью является сбор лучших российских и зарубежных статей по актуальным для России и мирового научного сообщества темам компьютерной инженерии и математической инженерии.
Задачи:
Обеспечить информационную платформу для ведущих ученых и практиков для диалога и обмена результатами исследовательской и проектной деятельности по широкому и эффективному применению математического моделирования в инженерной практике и компьютерных технологиях.
Активно общаюсь с научным сообществом ведущих отечественных и зарубежных вузов.
Содействовать развитию международного сотрудничества ЮУрГУ с мировыми научно-исследовательскими центрами.
Журнал основан в 2014 году.
Периодичность — ежеквартально.
Свидетельство о регистрации СМИ ПИ № ФС77-57143 от 11.03.2014 , выдано Федеральной службой по надзору в сфере связи, информационных технологий и связи.
