Информатика как решать системы счисления – Системы счисления - Информатика и ИКТ - Управленческое образование

Содержание

Простая информатика — Система счисления

Система счисления – это способ записи чисел. Обычно, числа записываются с помощью специальных знаков – цифр (хотя и не всегда). Если вы никогда не изучали данный вопрос, то, по крайней мере, вам должны быть известны две системы счисления – это арабская и римская. В первой используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 и это позиционная система счисления. А во второй – I, V, X, L, C, D, M и это непозиционная система счисления.

В позиционных системах счисления количество, обозначаемое цифрой в числе, зависит от ее позиции, а в непозиционных – нет. Например:

11 – здесь первая единица обозначает десять, а вторая – 1.
II – здесь обе единицы обозначают единицу.

345, 259, 521 – здесь цифра 5 в первом случае обозначает 5, во втором – 50, а в третьем – 500.

XXV, XVI, VII – здесь, где бы ни стояла цифра V, она везде обозначает пять единиц. Другими словами, величина, обозначаемая знаком V, не зависит от его позиции.

Сложение, умножение и другие математические операции в позиционных системах счисления выполнить легче, чем в непозиционных, т.к. математические операции осуществляются по несложным алгоритмам (например, умножение в столбик, сравнение двух чисел).

В мире наиболее распространены позиционные системы счисления. Помимо знакомой всем с детства десятичной (где используется десять цифр от 0 до 9), в технике широкое распространение нашли такие системы счисление как двоичная (используются цифры 0 и 1), восьмеричная и шестнадцатеричная.

Следует отметить, важную роль нуля. «Открытие» этой цифры в истории человечества сыграло большую роль в формировании позиционных систем счисления.

Основание системы счисления – это количество знаков, которое используется для записи цифр.

Разряд — это позиция цифры в числе. Разрядность числа — количество цифр, из которых состоит число (например, 264 — трехразрядное число, 00010101 — восьмиразрядное число). Разряды нумеруются справа на лево (например, в числе 598 восьмерка занимает первый разряд, а пятерка — третий).

Итак, в позиционной системе счисления числа записываются таким образом, что каждый следующий (движение справа на лево) разряд больше другого на степень основания системы счисления. (придумать схему)

Одно и тоже число (значение) можно представить в различных системах счисления. Представление числа при этом различно, а значение остается неизменным.

Двоичная система счисления

В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.)

Чтобы научиться понимать числа в двоичной системе счисления, сначала рассмотрим, как формируются числа в привычной для нас десятичной системе счисления.

В десятичной системе счисления мы располагаем десятью знаками-цифрами (от 0 до 9). Когда счет достигает 9, то вводится новый разряд (десятки), а единицы обнуляются и счет начинается снова. После 19 разряд десятков увеличивается на 1, а единицы снова обнуляются. И так далее. Когда десятки доходят до 9, то потом появляется третий разряд – сотни.

Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.

Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.
Перевод чисел из двоичной системы счисления в десятичную

Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 10001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и т.д. Например:

1476 = 1000 + 400 + 70 + 6

Можно пойти еще дальше и разложить так:

1476 = 1 * 103 + 4 * 102 + 7 * 101 + 6 * 100

Посмотрите на эту запись внимательно. Здесь цифры 1, 4, 7 и 6 — это набор цифр из которых состоит число 1476. Все эти цифры поочередно умножаются на десять возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы.

Аналогично можно разложить и любое двоичное число. Только основание здесь будет 2:

10001001 = 1*2⁷ + 0*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 0*2² + 0*2¹ + 1*2⁰

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 10001001:

1*2⁷ + 0*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 0*2² + 0*2¹ + 1*2⁰ = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

Т.е. число 10001001 по основанию 2 равно числу 137 по основанию 10. Записать это можно так:

10001001₂ = 13710
Почему двоичная система счисления так распространена?

Дело в том, что двоичная система счисления – это язык вычислительной техники. Каждая цифра должна быть как-то представлена на физическом носителе. Если это десятичная система, то придется создать такое устройство, которое может быть в десяти состояниях. Это сложно. Проще изготовить физический элемент, который может быть лишь в двух состояниях (например, есть ток или нет тока). Это одна из основных причин, почему двоичной системе счисления уделяется столько внимания.
Перевод десятичного числа в двоичное

Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 77 его двоичную запись:

77 / 2 = 38 (1 остаток)
38 / 2 = 19 (0 остаток)
19 / 2 = 9 (1 остаток)
9 / 2 = 4 (1 остаток)
4 / 2 = 2 (0 остаток)
2 / 2 = 1 (0 остаток)
1 / 2 = 0 (1 остаток)

Собираем остатки вместе, начиная с конца: 1001101. Это и есть число 77 в двоичном представлении. Проверим:

1001101 = 1*2⁶ + 0*2⁵ + 0*2⁴ + 1*2³ + 1*2² + 0*2¹ + 1*2⁰ = 64 + 0 + 0 + 8 + 4 + 0 + 1 = 77

Восьмеричная система счисления

Итак, современное «железо понимает» лишь двоичную систему счисления. Однако человеку трудно воспринимать длинные записи нулей и единиц с одной стороны, а с другой – переводит числа из двоичной в десятичную систему и обратно, достаточно долго и трудоемко. В результате, часто программисты используют другие системы счисления: восьмеричную и шестнадцатеричную. И 8 и 16 являются степенями двойки, и преобразовывать двоичное число в них (так же как и выполнять обратную операцию) очень легко.

В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7). Каждой цифре соответствуют набор из трех цифр в двоичной системе счисления:

000 – 0
001 – 1
010 – 2
011 – 3
100 – 4
101 – 5
110 – 6
111 – 7

Для преобразования двоичного числа в восьмеричное достаточно разбить его на тройки и заменить их соответствующими им цифрами из восьмеричной системы счисления. Разбивать на тройки нужно начинать с конца, а недостающие цифры в начале заменить нулями. Например:

1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135

Т.е число 1011101 в двоичной системе счисления равно числу 135 в восьмеричной системе счисления. Или 1011101₂ = 1358.

Обратный перевод. Допустим, требуется перевести число 1008 (не заблуждайтесь! 100 в восьмеричной системе – это не 100 в десятичной) в двоичную систему счисления.

100₈ = 1 0 0 = 001 000 000 = 001000000 = 10000002

Перевод восьмеричного числа в десятичное можно осуществить по уже знакомой схеме:

6728 = 6 * 8² + 7 * 8¹ + 2 * 8⁰ = 6 * 64 + 56 + 2 = 384 + 56 + 2 = 44210
1008 = 1 * 8² + 0 * 8¹ + 0 * 8⁰ = 6410

Шестнадцатеричная система счисления

Шестнадцатеричная система счисления, так же как и восьмеричная, широко используется в компьютерной науке из-за легкости перевода в нее двоичных чисел. При шестнадцатеричной записи числа получаются более компактными.

В шестнадцатеричной системе счисления используются цифры от 0 до 9 и шесть первых латинских букв – A (10), B (11), C (12), D (13), E (14), F (15).

При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не делится нацело, то первая четверка дописывается нулями впереди. Каждой четверке соответствует цифра шестнадцатеричной системе счисления:

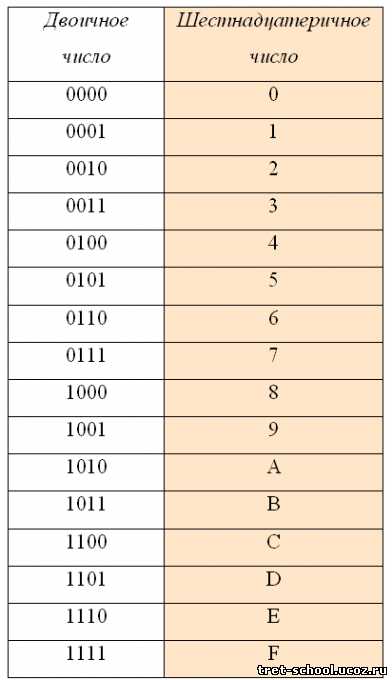
Например:
10001100101 = 0100 1100 0101 = 4 C 5 = 4C5

Если потребуется, то число 4C5 можно перевести в десятичную систему счисления следующим образом (C следует заменить на соответствующее данному символу число в десятичной системе счисления – это 12):

4C5 = 4 * 162 + 12 * 161 + 5 * 160 = 4 * 256 + 192 + 5 = 1221

Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи — это FF.

FF = 15 * 161 + 15 * 160 = 240 + 15 = 255

255 – это максимальное значение одного байта, равного 8 битам: 1111 1111 = FF. Поэтому с помощью шестнадцатеричной системы счисления очень удобно кратко (с помощью двух цифр-знаков) записывать значения байтов. Внимание! Состояний у 8-ми битного байта может быть 256, однако максимальное значение – 255. Не забывайте про 0 – это как раз 256-е состояние

informatic.my1.ru

Задания к зачётной работе «Система счисления. Перевод чисел. Арифметические операции в разных системах счисления»

Разделы: Информатика

Ход занятия

Вариант 1

1. Переведите числа из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную системы счисления.

а) 948;
б) 763;
в) 994,125;
г) 523,25;
д) 203,82.

2. Переведите числа в десятичную систему счисления.

а) 111000111₂;
б) 100011011₂;
в) 1001100101,1001₂;
г) 1001001,011₂;
д) 335,7₈;
е) 14C,A₁₆.

3. Выполните сложение чисел.

а) 1110101010₂+10111001₂;
б) 10111010
2+10010100₂;
в) 111101110,1011₂+1111011110,1₂;
г) 1153,2₈+1147,32₈;
д) 40F,4₁₆+160,4₁₆.

4. Выполните вычитание чисел.

а) 1000000100₂-101010001₂;
б) 1010111101₂-111000010₂;
в) 1101000000,01₂-1001011010,011₂;
г) 2023,5₈-527,4₈;
д) 25E,6₁₆-1B1,5₁₆.

5. Выполните умножение чисел.

а) 1001011₂*1010110₂;
б) 1650,2₈*120,2₈;
в) 19,4₁₆*2F,8₁₆.

Вариант 2

а) 563;
б) 264;
в) 234,25;
г) 53,125;
д) 286,16.

2. Переведите числа в десятичную систему счисления.

а) 1100010010₂;
б) 10011011₂;
в) 1111000001,01₂;
г) 10110111,01₂;
д) 416,1₈;
е) 215,7₁₆.

3. Выполните сложение чисел.

а) 10111111₂+110010000₂;
б) 110010100₂+1011100001₂;
в) 1000000101,0101₂+1010000110,01₂;
г) 1512,4₈+1015,2₈;
д) 274,5₁₆+DD,4₁₆.

4. Выполните вычитание чисел.

а) 1000001001₂-111110100₂;
б) 1111000101₂-1100110101₂;
в) 1100110101,1₂-1011100011,01₂;
г) 1501,34₈-1374,5₈;
д) 12D,3₁₆-39,6₁₆.

5. Выполните умножение чисел.

а) 111101₂*1010111₂;
б) 1252,14₈*76,04₈;
в) 66,68₁₆*1E,3₁₆.

Вариант 3

а) 279;
б) 281;
в) 841,375;
г) 800,3125;
д) 208,92.

2. Переведите числа в десятичную систему счисления.

а) 1100111001₂;
б) 10011101₂;
в) 1111011,001₂;
г) 110000101,01₂;
д) 1601,56₈;
е) 16E,B4₁₆.

3. Выполните сложение чисел.

а) 1000100001₂+1011100110₂;
б) 1101110011₂+111000101₂;
в) 1011011,01₂+1000101110,1001₂;
г) 665,1₈+1217,2₈;
д) 30C,7₁₆+2А1,8₁₆.

4. Выполните вычитание чисел.

а) 11110010₂-10101001₂;
б) 1110100001₂-1011001001₂;
в) 1101001010,1₂-1011101001,11011₂;
г) 166,14₈-143,2₈;
д) 287,А₁₆-62,8₁₆.

5. Выполните умножение чисел.

а) 1001001₂*100010₂;
б) 324,2₈*122,12₈;
в) F,4₁₆*38,6₁₆.

Вариант 4

а) 737;
б) 92;
в) 934,25;
г) 413,5625;
д) 100,94.

2. Переведите числа в десятичную систему счисления.

а) 1110000010₂;
б) 1000100₂;
в) 110000100,001₂;
г) 1001011111,00011₂;
д) 665,42₈;
е) 246,18₁₆.

3. Выполните сложение чисел.

а) 11110100₂+110100001₂;
б) 1101110₂+101001000₂;
в) 1100110011,1₂+111000011,101₂;
г) 1455,04₈+203,3₈;
д) 14Е,8₁₆+184,3₁₆.

4. Выполните вычитание чисел.

а) 1000010101₂-100101000₂;
б) 1001011011₂-101001110₂;
в) 111111011,101₂-100000010,01₂;
г) 341,2₈-275,2₈;
д) 249,5₁₆-ЕЕ,А₁₆.

5. Выполните умножение чисел.

а) 1001000₂*1010011₂;
б) 412,5₈*13,1₈;
в) 3B,A₁₆*10,4₁₆.

Ответы

Вариант 1

Задание 1	Задание 2	Задание 3
а) 948₁₀=1110110100₂=1664₈=3B4₁₆; б) 763₁₀=1011111011₂=1373₈=2FB₁₆; в) 994,125₁₀=1111100010,001₂=1742,1₈=3Е2,2₁₆; г) 523,25₁₀=1000001011,01₂=1013,2₈=20В,4₁₆; д)203,82₁₀=11001011,1101₂=313,6436₈=СВ,D1EB₁₆.	а) 445₁₀; б) 283_10; в) 613,5625₁₀; г) 73,375₁₀; д) 221,875₁₀; е) 332,625₁₀.	а) 10001100011₂; б) 101001110₂; в) 10111001101,0011₂; г) 2322,52₈; д) 56F,8₁₆.
	Задание 4	Задание 5
	а) 10110011₂; б) 11111011₂; в)11100101,111₂; г) 1274,1₈; д) AD,1₁₆.	а) 1100100110010₂; б) 222576,04₈; в) 4AF,6₁₆.

Вариант 2

Задание 1	Задание 2	Задание 3
а) 563₁₀=1000110011₂=1063₈=233₁₆; б) 264₁₀=100001000₂=410₈=108₁₆; в) 234,25₁₀=11101010,01₂=352,2₈=EA,4_16; г) 53,125₁₀=110101,001₂=65,1₈=35,2₁₆; д) 286,16₁₀=100011110,00101₂=436,1217₈=11E,28F5C₁₆.	а) 786₁₀; б) 155₁₀; в) 961,25₁₀; г) 183,25₁₀; д) 270,125₁₀; е) 533,4375₁₀.	а) 1001001111_2; б) 10001110101₂; в)10010001011,1001₂; г) 2527,6₈; д) 351,9₁₆.
	Задание 4	Задание 5
	а) 10101₂; б) 10010000₂; в) 010010,01₂; г) 104,64₈; д) F3,D₁₆.	а) 1010010111011₂; б) 122542,206₈; в) С13,638₁₆.

Вариант 3

Задание 1	Задание 2	Задание 3
а) 279₁₀=100010111₂=427₈=117₁₆; б) 281₁₀=100011001₂=431₈=119_16; в) 841,375₁₀=1101001001,011₂=1511,3₈=349,6₁₆; г) 800,3125₁₀=1100100000,0101₂=1440,24₈=320,5₁₆; д)208,92₁₀=11010000,11101₂=320,727₈=D0,EB851₁₆.	а) 825₁₀; б) 157₁₀; в) 123,125₁₀; г) 389,25₁₀; д) 897,71875₁₀; е) 366,703125₁₀.	а) 10100000111₂; б) 10100111000₂; в)1010001001,1101₂; г) 2104,3₈; д) 5AD,F₁₆.
	Задание 4	Задание 5
	а) 1001001₂; б) 11011000₂; в) 1100000,10101₂ г) 22,74₈; д) 225,2₁₆.	а) 100110110010₂; б) 42035,524₈; в) 35B,B8₁₆.

Вариант 4

Задание 1	Задание 2	Задание 3
а) 737₁₀=1011100001₂=1341₈=2E1₁₆; б) 92₁₀=1011100₂=134₈=5С₁₆; в) 934,25₁₀=1110100110,01₂=1646,2₈=3А6,4₁₆; г) 413,5625₁₀=110011101,1001₂=635,44₈=19D,9₁₆; д) 100,94₁₀=1100100,1111₂=144,7412₈=64,F0A3D₁₆.	а) 898₁₀; б) 68₁₀; в) 388,125₁₀; г) 607,09375₁₀; д) 437,53125₁₀; е) 582,09375₁₀.	а) 1010010101₂; б) 110110110₂; в) 1001111011,001₂; г) 1660,34₈; д) 2D2,B₁₆.
	Задание 4	Задание 5
	а) 11101101₂; б) 100001101₂; в) 11111001,011₂; г) 44₈; д) 15А,B₁₆.	а) 1011101011000₂; б) 5626,15₈; в) 3С8,Е8₁₆.

12.02.2010

Поделиться страницей:

urok.1sept.ru

двоичная, восьмеричная, шестнадцатеричная — урок. Информатика, 8 класс.

Для кодирования информации в компьютере вместо привычной десятичной системы счисления используется двоичная система счисления.

Двоичной системой счисления люди начали пользоваться очень давно. Древние племена Австралии и островов Полинезии использовали эту систему в быту. Так, полинезийцы передавали необходимую информацию, выполняя два вида ударов по барабану: звонкий и глухой. Это было примитивное представление двоичной системы счисления.

Двоичной системой счисления называется позиционная система счисления с основанием \(2\).

Для записи чисел в ней использовали только две цифры: \(0\) и \(1\).

Для обозначения системы счисления, в которой представляется число, используют нижний индекс, указывающий основание системы. Например, 110112 — число в двоичной системе счисления.

Цифры в двоичном числе являются коэффициентами его представления в виде суммы степеней с основанием \(2\), например:

1012=1 ·22+0 ·21+1 ·20.

В десятичной системе счисления это число будет выглядеть так:

1012=4+0+1=5.

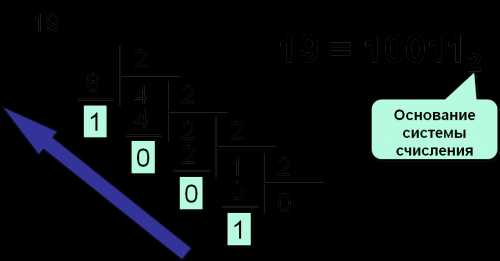
Для перевода целого десятичного числа в двоичную систему счисления нужно последовательно выполнять деление данного числа и получаемых целых частных на \(2\) до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём десятичное число \(13\) в двоичную систему счисления. Рассмотренную выше последовательность действий (алгоритм перевода) можно изобразить так:

Получили 1310=11012.

Пример:

Если десятичное число достаточно большое, то более удобен следующий способ записи рассмотренного выше алгоритма:

\(224\)	\(112\)	\(56\)	\(28\)	\(14\)	\(7\)	\(3\)	\(1\)
\(0\)	\(0\)	\(0\)	\(0\)	\(0\)	\(1\)	\(1\)	\(1\)

22410=111000002.

Восьмеричной системой счисления называется позиционная система счисления с основанием \(8\).

Для записи чисел в восьмеричной системе счисления используются цифры: \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\).

Для перевода целого восьмеричного числа в десятичную систему счисления следует перейти к его развёрнутой записи и вычислить значение получившегося выражения.

Для перевода целого десятичного числа в восьмеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на 8 до тех пор, пока не получим частное, равное нулю. Исходное число в двоичной системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём восьмеричное число 154368 в десятичную систему счисления.

154368=1 ·84+5 ·83+4 ·82+3 ·81+6 ·80=694210

Пример:

Переведём десятичное число \(94\) в восьмеричную систему счисления.

9410=1368

Шестнадцатеричной системой счисления называется позиционная система счисления с основанием \(16\).

Для записи чисел в шестнадцатеричной системе счисления используются цифры: \(0\), \(1\), \(2\), \(3\), \(4\), \(5\), \(6\), \(7\), \(8\), \(9\) и латинские буквы A, B, C, D, E, F. Буквы A, B, C, D, E, F имеют значения 1010, 1110, 1210, 1310, 1410, 1510.

Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Для перевода целого десятичного числа в шестнадцатеричную систему счисления следует последовательно выполнять деление данного числа и получаемых целых частных на \(16\) до тех пор, пока не получим частное, равное нулю. Исходное число в системе счисления составляется последовательной записью полученных остатков, начиная с последнего.

Пример:

Переведём шестнадцатеричное число \(2\)\(A7\) в десятичное. В соответствии с вышеуказанными правилом представим его в виде суммы степеней с основанием \(16\):

2A716=2 ·162+10 ·161+7 ·160=512+160+7=679.

Пример:

Переведём десятичное число \(158\) в шестнадцатеричную систему счисления.

15810=9E16.

Для перевода числа из любой позиционной системы счисления в десятичную необходима использовать развернутую формулу числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами.

Для перевода целых чисел десятичной системы счисления в число любой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы счисление, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.

www.yaklass.ru

Урок информатики в 9-м классе. Тема: «Системы счисления»

Разделы: Информатика, Конкурс «Презентация к уроку»

Презентации к уроку

Загрузить презентацию (387,8 кБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Загрузить презентацию (131,3 кБ)

Тип урока: Урок изучения новой темы.

Дидактическая цель: создать условия для актуализации и закрепления учебной информации

Цель урока:

Образовательная:

знакомство с понятием «система счисления»;
умение различать виды систем счисления и применять их на практическом занятии;
умение правильно записывать числа в системах счисления;
формирование способности для применения правил перевода чисел из одной системы счисления в другие.

Развивающая:

развивать логическое мышление, умение обобщать, конкретизировать;
формирование внимания, умения наблюдать и закреплять знания;

Воспитательная:

воспитывать самостоятельность, уважительное отношение друг к друг;
воспитание информационной культуры учащихся.

Методы обучения: наглядный, информационно-развивающий, опрос.

Формы организации познавательной деятельности: индивидуальная.

Средства обучения: учебник Семакина “Информатика и ИКТ. 9 класс. ” учебник для 9 класса общеобразовательных учреждений, рабочие тетради, авторучки, проектор, компьютер, компьютерная презентация по теме урока.

План урока:

Организационный момент.
Изучение нового материала.
Физкультминутка.
Формирование умений, навыков.
Домашнее задание

Ход урока

1. Организационный момент.

Приветствие, проверка присутствующих. Мы сегодня начинаем изучение новой темы. Данная тема очень важна. Хотелось бы отметить умение решать задачи на систему счисления дает возможность набрать более высокие баллы, что очень важно при сдаче ЕГЭ и поступлении в ВУЗЫ. Открываем тетрадки, записываем сегодняшнее число и тему: СИСТЕМЫ СЧИСЛЕНИЯ.

План темы

Историческая справка
Определение системы счисления
Виды системы счисления
Правила перевода чисел из одной системы счисления в другую

2. Объяснение нового материала (по плану, приложение 3)

2.1. Историческая справка

Люди научились считать еще в незапамятные времена. Сначала они просто различали один предмет перед ними или нет. Если предмет был не один, то говорили «много». Постепенно появилось слово для обозначения двух предметов. Счет парами очень удобен.

Наиболее древней и простой «счетной машиной» издавна являются пальцы рук и ног. И даже в наше время еще пользуются этим «счетным прибором», который всегда при нас. На пальцах можно решать примеры не только в пределах десяти. В древние времена люди ходили босиком. Поэтому они могли пользоваться для счета пальцами как рук, так и ног.

Записывали числа поначалу совсем просто: делали зарубки на куске дерева или кости. На этой кости тридцать тысяч лет назад сделаны нарезки, они показывают, что уже тогда наши предки умели не только считать, но и записывать результаты счета!

Когда понадобилось записывать большие числа, то для пятерок и десяток стали придумывать новые знаки. Вот как египтяне записывали число 3 246:

Запомнить большие числа трудно, поэтому к «счетной машине» рук и ног добавляли механические приспособления. Веревочные счеты с узелками применялись и в России, и во многих странах Европы. Остатками этого способа является практикуемое еще до сих пор завязывание узелков на носовых платках «на память». Так, одни пользовались для запоминания чисел камешками, зернами, веревкой с узелками, другие — палочками с зарубками. Это были первые счетные приборы, которые в конце концов привели к образованию различных систем счисления

2.2. Система счисления — это совокупность правил и приемов записи чисел с помощью набора цифровых знаков.

позиционные, когда значение каждой цифры числа определяется ее позицией в записи числа;
непозиционные, когда значение цифры в числе не зависит от ее места в записи числа.

Непозиционные СС. Единичная система счисления. Находки археологов на стоянках первобытных людей свидетельствуют о том, что первоначально количество предметов отображали равным количеством каких-либо значков (бирок): зарубок, черточек, точек. Позже значки стали группировать по три или по пять. Такая система записи чисел называется единичной (унарной), так как любое число в ней образуется путем повторения одного знака, символизирующего единицу. Отголоски единичной системы счисления встречаются и сегодня (счетные палочки для обучения счету; полоски, нашитые на рукаве, означают на каком курсе учится курсант военного училища). Неудобства такой системы записи чисел и ограниченность ее применения очевидны: чем большее число надо записать, тем длиннее строка из палочек.

Римская система счисления является непозиционной системой. В ней для записи чисел используются буквы латинского алфавита. При записи чисел в римской системе счисления значением числа является алгебраическая сумма цифр, в него входящих. При этом цифры в записи числа следуют, как правило, в порядке убывания их значений, и не разрешается записывать рядом более трех одинаковых цифр. В том случае, когда за цифрой с большим значением следует цифра с меньшим, ее вклад в значение числа в целом является отрицательным. Типичные примеры, иллюстрирующие общие правила записи чисел в римской система счисления, приведены в таблице.

Таблица 1. Запись чисел в римской системе счисления

1	2	3	4	5	6	7	8	9	10	50	100	500	1000
I	II	III	IV	V	VI	VII	VIII	IX	X	L	C	D	M

Недостатком римской системы является отсутствие формальных правил записи чисел и, соответственно, арифметических действий с многозначными числами. По причине неудобства и большой сложности в настоящее время римская система счисления используется там, где это действительно удобно: в литературе (нумерация глав), в оформлении документов (серия паспорта, ценных бумаг и др.), в декоративных целях на циферблате часов и в ряде других случаев.

Мы с вами более подробно рассмотрим позиционные системы счисления.

В позиционной системе счисления основными понятиями являются понятие алфавита и основания системы счисления.

Алфавитом системы счисления называется совокупность всех цифр.

Количество цифр, необходимых для записи числа в системе, называют основанием системы счисления. Основание системы записывается в справа числа в нижнем индексе: 78₁₀, 1100010₁₂, AF12₁₆ и т. д.

Количество цифр, составляющих алфавит, называется его мощностью.

В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места(разряда), где он расположен. Разряд — номер позиции в числе. Нумеруются справа налево, начиная с нуля.

Пример. Число6184₁₀ запишется в форме многочлена следующим образом:

6184₁₀ = 6*10 ³ +1*10 ² +8*10 ¹ +4*10 ⁰

2.3. Виды систем счисления.

В компьютерах принято использовать 4 основные системы счисления – двоичную, восьмеричную, десятичную и шестнадцатеричную. Именно их подробно рассмотрим.

Десятичная система счисления – в настоящее время наиболее известная и используемая. Древнее изображение десятичных цифр не случайно: каждая цифра обозначает число по количеству углов в ней. Например, 0 — углов нет, 1 — один угол, 2 — два угла и т.д. Написание десятичных цифр претерпело существенные изменения. Форма, которой мы пользуемся, установилась в XVI веке.

Десятичная система впервые появилась в Индии примерно в VI веке новой эры. Индийская нумерация использовала девять числовых символов и нуль для обозначения пустой позиции

Десятичная система использует десять цифр – 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9, а также символы “+” и “–” для обозначения знака числа и запятую или точку для разделения целой и дробной частей числа.

Если взять правило, по которым строятся числа в десятичной системе счисления, заменив основание 10 на натуральное число N, можно построить позиционную систему счисления с основанием N.

В вычислительных машинах используется двоичная система счисления, её основание — число 2. Для записи чисел в этой системе используют только две цифры — 0 и 1. Двоичная система счисления была придумана математиками и философами задолго до появления компьютеров, еще в ХVII — ХIХ веках. Двоичная система удобна для компьютера, но неудобна для человека: числа получаются длинными и их трудно записывать и запоминать. Конечно, можно перевести число в десятичную систему и записывать в таком виде, а потом, когда понадобится перевести обратно, но все эти переводы трудоёмки. Поэтому применяются системы счисления, родственные двоичной — восьмеричная и шестнадцатеричная. Для записи чисел в этих системах требуется соответственно 8 и 16 цифр. В 16-теричной первые 10 цифр общие, а дальше используют заглавные латинские буквы. Шестнадцатеричная цифра A соответствует десятеричному числу 10, шестнадцатеричная B – десятичному числу 11 и т. д. Использование этих систем объясняется тем, что переход к записи числа в любой из этих систем от его двоичной записи очень прост. Ниже приведена таблица соответствия чисел, записанных в разных системах.

Учащиеся заполняют таблицу в тетрадях (приложение 1, таблица 1).

2.4. Правила перевода чисел из одной системы счисления в другую

Перевод чисел из одной системы счисления в другую составляет важную часть машинной арифметики. Рассмотрим основные правила перевода.

1. При переводе числа из двоичной (восьмеричной, шестнадцатеричной) системы в десятичную надо это число представить в виде суммы степеней основания его системы счисления.

Числа 10100110₂ , 703₈ , 23FA1₁₆ перевести в десятичную систему счисления.

10100110₂=1*2⁷+0*2⁶+1*2⁵+0*2⁴+0*2³+1*2²+1*2¹+0*2⁰=128+32+4+2=166₁₀

703₈=7*8²+0*8¹+3*8⁰=448+3=447₁₀

23FA1₁₆=2*16⁴+3*16³+15*16²+10*16¹+1*16⁰=131072+12288+3840+160+1=147361

2. Правило перевода из десятичной системы счисления в систему с основанием q:

1. Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя.

2. Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх).

Пример. Перевести числа из десятичной системы счисления

3. Чтобы перевести число из двоичной системы в восьмеричную (шестнадцатеричную), его нужно разбить на триады (тетрады), начиная с младшего разряда (справа налево), в случае необходимости дополнив старшую триаду (тетраду) нулями, и каждую триаду (тетраду) заменить соответствующей восьмеричной (шестнадцатеричной) цифрой (табл.).

Число 10010110111₂ перевести в восьмеричную и в шестнадцатеричную системы счисления.

4. Для перевода восьмеричного (шестнадцатеричного) числа в двоичное необходимо каждую цифру заменить эквивалентной ей двоичной триадой (тетрадой).

Числа 726₈ и 74С₁₆ перевести в двоичную систему счисления.

726₈= 111 010 110₂

74С₁₆ = 0111 0100 1100₂ (при записи числа первый 0 не пишется)

5. При переходе из восьмеричной системы счисления в шестнадцатеричную и обратно, необходим промежуточный перевод чисел в двоичную систему.

Число FAE₁₆ перевести в восьмеричную систему счисления.

FAE₁₆=111110101110₂

111 110 101 110₂=7656₈

Число 635₈ перевести в шестнадцатеричную систему счисления.

635₈ =110011101₂

1 1001 1101₂=19D₁₆

3. Физкультминутка (см. презентация 2)

4. Формирование умений и навыков

Работа с вопросником. Отвечают устно на вопросы, используя свой конспект.

5. Домашнее задание (приложение 4)

Учить конспект, прочитать §16 по учебнику.
Написать дату своего дня рождения в римской системе счисления.

Подведение итогов урока.

Анализ и оценка успешности достижения цели занятия. Определение перспективы последующей работы.

Приложение 2

4.06.2012

urok.1sept.ru

Информатика егэ 1 задание, объяснение и разбор

На уроке рассмотрено решение 1 задание ЕГЭ по информатике 2017: дается подробное объяснение и разбор заданий

Объяснение задания 1 ЕГЭ по информатике

1-я тема характеризуется, как задания базового уровня сложности, время выполнения – примерно 1 минута, максимальный балл — 1

Системы счисления и представление информации в памяти ПК

Для решения 1 задания следует вспомнить и повторить следующие темы:

Двоичная система счисления

Количество цифр или основание системы: 2
Цифры (алфавит): 0, 1

Перевод чисел из 10-й системы счисления в двоичную:

Перевод чисел из 10-й сист. сч-я в двоичную

Егифка ©:

Перевод чисел из 2-й системы счисления в 10-ую:

Перевод чисел из 2-й сист. сч-я в 10-ую

Егифка ©:

При работе с большими числами, лучше использовать разложение по степеням двойки:

Разложение по степеням двойки

Егифка ©:

Восьмеричная система счисления

Количество цифр или основание системы: 8
Цифры (алфавит): 0, 1, 2, 3, 4, 5, 6, 7

Перевод чисел из 10-й системы счисления в 8-ую

Перевод чисел из 10-й сист. сч-я в 8-ую

Перевод чисел из 8-й сист. сч-я в 10-ую

Перевод чисел из 8-й системы счисления в 10-ую
Перевод чисел из 8-й сист. сч-я в 2-ую и обратно триадами
Перевод из 8-й сист. сч-я в 2-ую и обратно триадами
Егифка ©:
Шестнадцатеричная система счисления
Количество цифр или основание системы: 16
Цифры (алфавит): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A (10), B (11), C (12), D (13), E (14), F (15)
Перевод чисел из 10-й системы счисления в 16-ую
Перевод из 10-й сист. сч-я в 16-ую
Перевод из 16-й системы счисления в 10-ую
Перевод из 16-й сист. сч-я в 10-ую
Перевод чисел из 2-й сист. сч-я в 16-ую и обратно тетрадами
Перевод из 2-й с. сч-я в 16-ую и обратно тетрадами
Егифка ©:
Полезности для двоичной системы счисления:
2⁶ = 64 ≤ 126 7, 126 = 1111110₂ (7 цифр)
если число имеет вид 2^k, то оно записывается в двоичной системе как единица и k нулей, например:
32 = 2⁵ = 100000₂
если число имеет вид 2^k-1, то оно записывается в двоичной системе k единиц, например:
31 = 2⁵-1 = 11111₂
если известна двоичная запись N, то двоичную запись числа 2•N можно легко получить, приписав в конец ноль, например:
15 = 1111₂, 30 = 11110₂, 60 = 111100₂, 120 = 1111000₂
Необходимо также выучить степени двойки, увеличивая степень справа налево:
1024 512 256 128 64 32 16 8 4 2 1 2¹⁰ 2⁹ 2⁸ 2⁷ 2⁶ 2⁵ 2⁴ 2³ 2² 2¹ 2⁰
желательно выучить таблицу двоичного представления цифр от 0 до 7 в виде триад (групп из 3-х битов):
X¹⁰,X⁸ X² 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111
желательно знать таблицу двоичного представления чисел от 0 до 15 (в шестнадцатеричной с-ме – 0-F₁₆) в виде тетрад (групп из 4-х битов):
X₁₀ X₁₆ X₂ 0 0 0000 1 1 0001 2 2 0010 3 3 0011 4 4 0100 5 5 0101 6 6 0110 7 7 0111 8 8 1000 9 9 1001 10 A 1010 11 B 1011 12 C 1100 13 D 1101 14 E 1110 15 F 1111
Перевод отрицательного (-a) в двоичный дополнительный код выполняется следующим образом:
нужно перевести a-1 в двоичную систему счисления;
сделать инверсию битов: заменить все нули на единицы и единицы на нули в пределах разрядной сетки
Решение 1 задания ЕГЭ
Разбор 1 задания ЕГЭ по информатике 2017 года ФИПИ вариант 1 (Крылов С.С., Чуркина Т.Е.):
Сколько единиц в двоичной записи шестнадцатеричного числа 2AC1₁₆?
Подобные задания для тренировки

✍ Решение:
В шестнадцатеричной с-ме счисления числа от 10 до 15 представлены буквами латинского алфавита: A-10, B-11, C-12, D-13, E-14, F-15.
Необходимо вспомнить двоичные коды чисел от 1 до 15 (см. теорию выше на странице), так как для перевода 16-ричного в двоичную с-му достаточно каждую цифру отдельно записать в виде четверки двоичных цифр (тетрады):
2 A C 1 0010 1010 1100 0001
в этой записи 6 единиц
Результат: 6
Подробный разбор 1 задания с объяснением просмотрите на видео:
1 задание. Демоверсия ЕГЭ 2018 информатика (ФИПИ):
Сколько существует целых чисел x, для которых выполняется неравенство 2A₁₆<x<61₈?
В ответе укажите только количество чисел.
Подобные задания для тренировки

✍ Решение:
Переведем 2A₁₆ в десятичную систему счисления:
2A₁₆ = 2*16¹+10*16⁰ = 32 + 10 = 42
Переведем 61₈ в десятичную с-му счисления:
61₈ = 6*8¹+1*8⁰ = 48 + 1 = 49
Получим сравнение:
42
Поскольку в задании дважды строгое сравнение (<), то количество целых, удовлетворяющих условию:
49 - 42 - 1 = 6
Проверим: 43, 44, 45, 46, 47, 48
Результат: 6
Подробное решение данного 1 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
1 задание. ГВЭ 11 класс по информатике 2018 (ФИПИ):
Сколько значащих цифр в двоичной записи десятичного числа 129?
1) 6
2) 2
3) 7
4) 8

✍ Решение:
Выполним перевод из десятичной с-мы счисления в двоичную делением на 2, справа будем записывать остатки:
129 / 1 64 / 0 32 / 0 16 / 0 8 / 0 4 / 0 2 / 0 1
Перепишем остатки снизу вверх, начиная с последней единицы, которая уже не делится на два:
10000001
Посчитаем количество разрядов в получившемся двоичном числе. Их 8, и все они значащие (незначащими могут быть только нули слева, например, 010 — это то же самое, что 10). Правильный ответ под номером 4
Результат: 4
Решение 1 задания ЕГЭ по информатике (контрольный вариант экзаменационной работы 2018 года, С.С. Крылов, Д.М. Ушаков):
Сколько существует натуральных чисел x, для которых выполняется неравенство
101011₂8?
В ответе укажите только количество чисел.

✍ Решение:
Подробный разбор решения тренировочного варианта предлагаем посмотреть на видео:
Разбор 1 задания ЕГЭ вариант № 1, 2019 Информатика и ИКТ Типовые экзаменационные варианты (10 вариантов), С.С. Крылов, Т.Е. Чуркина::
Вычислите значение выражения AE₁₆ – 19₁₆.
В ответе запишите вычисленное значение в десятичной системе счисления.
Подобные задания для тренировки

✍ Решение:
Переведем уменьшаемое и вычитаемое в десятичную систему счисления:
_{1 0} A E = 10*16¹ + 14*16⁰ = 160 + 14 = 174
* A₁₆ соответствует числу 10 в десятичной системе счисления

* E₁₆ соответствует числу 14 в десятичной системе счисления

_{1 0} 19 = 1*16¹ + 9*16⁰ = 16 + 9 = 25
Найдем разность:
174 - 25 = 149
Результат: 149

labs-org.ru
Задание №1. Перевод из одной системы счисления в другую

Автор материалов — Лада Борисовна Есакова.
Системы счисления и их разновидности.
Система счисления – это способ представления, записи чисел с помощью письменных знаков. Количество этих самых знаков (цифр), используемых для записи чисел, называется основанием системы счисления.
Различных систем счисления у разных народов существовало великое множество. Но все их можно поделить на непозиционные и позиционные. Позиционные системы в свою очередь подразделяются на однородные и смешанные.
1. Непозиционные системы счисления.
В непозиционных системах счисления число, обозначаемое цифрой, не зависит от положения цифры в записи числа.
Самым простым примером непозиционной системы счисления является единичная (унарная) система счисления. Это запись числа с помощью повторения зарубок на дощечке или узелков на веревке. Все зарубки, узелки или другие «цифры» абсолютно одинаковы, а потому их порядок не имеет значения, число получается простым суммированием количества символов.
Унарной системой счисления до сих пор пользуются маленькие дети, показывая количество на пальцах.
Еще одной используемой до сих пор почти непозиционной системой счисления является Римская:

Она названа почти непозиционной, потому что в Римской системе, кроме обычного сложения цифр в числе, действует правило: если младшая цифра стоит слева от старшей, она вычитается из суммы.
Т.е. число , а число
Непозиционных систем счисления известно очень много, но мы завершим на этом их рассмотрение. Использование непозиционных систем неудобно, а для очень больших чисел практически невозможно, и к тому же нет возможности записать дроби.
2. Позиционные системы счисления.
В позиционных системах счисления число, обозначаемое цифрой, зависит от положения цифры в записи числа.
Самой популярной позиционной системой является, конечно же, десятичная.
Мы видим, что числа 15 и 51 имеют совсем разные значения, хотя состоят из одних и тех же цифр. Разница обусловлена положением цифры в числе.
Но десятичная система ничем не лучше и не хуже другой позиционной системы, она просто привычная. Число 10 выбрано основанием по количеству пальцев на двух руках (для удобства счета). Однако, в Китае популярной была пятиречная система счисления (по количеству пальцев на одной руке), а двадцатиричная система использовалась у Ацтеков, Майя и некоторых народов Африки (по количеству пальцев на ногах и руках).
Еще одной известной позиционной системой счисления является двенадцатиричная (считали фаланги пальцев (кроме большого) на руке. Элементы двенадцатиричной системы сохранились в Англии: 1 фут = 12 дюймов, 1 шиллинг = 12 пенсов.
Ну и, наконец, незаменимая в наш компьютерный век двоичная система. Почему именно двоичная? Да потому что у компьютера только 2 «пальца», точнее два состояния: «есть ток», «нет тока».
2.1. Однородные системы счисления.
В однородной системе в каждой позиции числа может находиться любая цифра. Примером может быть запись числа в любой позиционной системе счисления (десятичной, двоичной и пр.). Т.е. когда мы пишем число в десятичной системе, в любой позиции мы можем написать цифру от 0 до 9.
2.2. Смешанные системы счисления.
В смешанной системе счисления набор используемых цифр может отличаться в зависимости от позиции. В качестве примера удобно рассмотреть запись времени в формате ЧЧ.ММ.СС (часы.минуты.секунды). В качестве часов может быть использовано число от 00 до 23, в качестве минут и секунд – число от 00 до 59.
Системы счисления. Перевод из одной системы в другую.
1. Порядковый счет в различных системах счисления.
В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».
Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.
Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.
Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):
0 0 0 0
1 1 1 1
2 10 2 2
3 11 10 3
4 100 11 4
5 101 12 10
6 110 20 11
7 111 21 12
8 1000 22 13
9 1001 100 14
10 1010 101 20
11 1011 102 21
12 1100 110 22
13 1101 111 23
14 1110 112 24
15 1111 120 30
Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):
0 0
1 1
2 2
3 3
4 4
5 5
6 6
7 7
8 8
9 9
10
11
12 10
13 11
14 12
15 13
2.Перевод из десятичной системы счисления в любую другую.
Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.
Пример 1. Переведем десятичное число 46 в двоичную систему счисления.
Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.
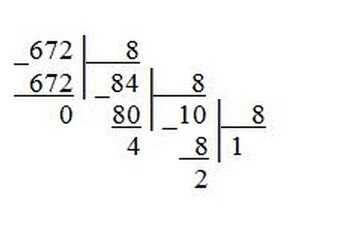
Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.
3. Перевод из любой системы счисления в десятичную.
Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.
Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:

Это и есть десятичная запись нашего числа, т.е.
Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.

Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.

4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).
Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.
Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:
Таблицу соответствия мы научились строить в п.1.
0 0
1 1
10 2
11 3
100 4
101 5
110 6
111 7
Т.е.
Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.
0 0
1 1
10 2
11 3
100 4
101 5
110 6
111 7
1000 8
1001 9
1010 A
1011 B
1100 C
1101 D
1110 E
1111 F
5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.
Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.
Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.
Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:

Десятичные дроби и смешанные числа в разных системах счисления.

Автор — Лада Борисовна Есакова.
Перевод целых чисел из одной системы счисления в другую обычно не вызывает проблем. А вот необходимость перевести десятичную дробь или смешанное число (число с целой и дробной частью) из системы в систему часто ставит в тупик даже сильных учеников.
1. Перевод смешанного числа в десятичную систему счисления из любой другой.
Для перевода смешанного числа в десятичную систему из любой другой следует пронумеровать разряды числа, начиная с нуля, справа налево от младшего целого разряда. Разряды дробной части нумеруются слева направо от -1 в убывающем порядке. Теперь представим число в виде суммы произведений его цифр на основание системы в степени разряда числа и ответ готов.
Пример 1.
Переведите число 105,4 из восьмеричной системы в десятичную.
Решение:
Пронумеруем целые разряды числа справа налево от 0, дробные – слева направо от -1 :
Посчитаем сумму произведений цифр числа на 8 (основание системы) в степени разряда числа:
Ответ:
2. Перевод десятичных дробей из десятичной системы счисления в любую другую.
Для перевода десятичной дроби из десятичной системы в любую другую следует умножать дробь, а затем дробные части произведений, на основание новой системы пока дробная часть не станет равной 0 или до достижения указанной точности. Затем целые части выписать, начиная с первой.
Пример 2
Переведите десятичное число 0,816 в двоичную систему с точностью до сотых.
Решение:
Умножаем дробь 0,816, а затем дробную часть произведения (0,632) на 2 и выписываем целые части, начиная с первой:
Ответ:
Пример 3.
Переведите десятичное число 0,8125 в восьмеричную систему.
Решение:
Умножаем дробь 0,8125, а затем дробную часть произведения (0,5) на 8 и выписываем целые части, начиная с первой:
Ответ:
3. Перевод смешанных чисел из десятичной системы счисления в любую другую
Если необходимо перевести смешанное число из десятичной системы в любую другую, следует перевести целую и дробную части, а затем записать, разделив десятичной запятой.

Пример 4.
Сколько единиц в двоичной записи десятичного числа 14,125?
Решение:
Переведем целую часть числа в двоичную систему:
Переведем дробную часть числа в двоичную систему:
Соединим целую и дробную части:

14,12510 = 1110,0012
Количество единиц равно 4.
Ответ: 4
Ты нашел то, что искал? Поделись с друзьями!
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Двоичная система счисления
Двоичная система счисления — это позиционная система счисления с основанием 2. В этой системе счисления числа записываются с помощью двух символов: 0 и 1. Двоичную цифру называют битом. Двоичная система счисления является основной системой представления информации в памяти компьютера.
Сложение, вычитание и умножение двоичных чисел.
Таблица сложения
Пример: 1001 + 10 = 1011
Таблица вычитания
Пример: 1111101 — 10001 = 1101100
Таблица умножения
Пример: 1111 · 1001 = 10000111
Перевод чисел.
Для перевода десятичного числа в двоичное надо разделить его на 2 и собрать остатки, начиная с последнего частного.
Пример: 73₁₀ = 1001001₂
Для перевода двоичного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания двоичной системы счисления на соответствующие цифры в разрядах двоичного числа.
Пример: требуется перевести двоичное число 10110110 в десятичное. В этом числе 8 цифр и 8 разрядов ( разряды считаются, начиная с нулевого, которому соответствует младший бит). Представим его в виде суммы степеней с основанием 2: 10110110₂ = (1·2⁷)+(0·2⁶)+(1·2⁵)+(1·2⁴)+(0·2³)+(1·2²)+(1·2¹)+(0·2⁰) = 128+32+16+4+2 = 182₁₀

Другие заметки по информатике
edu.glavsprav.ru