Задачи на тему Динамика | Физика
§ 2.
2.1 Какой массы балласт надо сбросить с равномерно опускающегося аэростата, чтобы он начал равномерно подниматься с той же скоростью? Масса аэростата с балластом m = 1600 кг, подъемная сила аэростата F = 12 кН. Считать силу сопротивления Fсопр воздуха одной и той же при подъеме и спуске.РЕШЕНИЕ
2.2 К нити подвешен груз массой m = 1 кг. Найти силу натяжения нити T, если нить с грузом поднимать с ускорением a = 5 м/с2; опускать с тем же ускорением a = 5 м/с2.
РЕШЕНИЕ
2.3 Стальная проволока некоторого диаметра выдерживает силу натяжения Т = 4,4 кН. С каким наибольшим ускорением можно поднимать груз массой m = 400 кг, подвешенный на этой проволоке, чтобы она не разорвалась.
РЕШЕНИЕ
2.4 Масса лифта с пассажирами m = 800 кг. С каким ускорением а и в каком направлении движется лифт, если известно, что сила натяжения троса, поддерживающего лифт Т = 12 кН; 6 кН
РЕШЕНИЕ
2.5 К нити подвешена гиря. Если поднимать гирю с ускорением a1 = 2 м/с2, то сила натяжения нити T1 будет вдвое меньше той силы натяжения T2, при которой нить разорвется. С каким ускорением a1 надо поднимать гирю, чтобы нить разорвалась
РЕШЕНИЕ
2.6 Автомобиль массой m = 1020 кг, двигаясь равнозамедленно, остановился через время t = 5 c, пройдя путь s = 25 м. Найти начальную скорость v0 автомобиля и силу торможения F.
РЕШЕНИЕ
2.7 Поезд массой m = 500 т, двигаясь равнозамедленно, в течение времени t = 1 мин уменьшает свою скорость от v1 = 40 км/ч до v2 = 28 км/ч. Найти силу торможения
РЕШЕНИЕ
2.8 Вагон массой m = 20 т движется с начальной скоростью v0 = 54 км/ч. Найти среднюю силу, действующую на вагон, если известно, что вагой останавливается в течение времени t = 1 мин 40 c; 10 c; 1 c
РЕШЕНИЕ
2.9 Какую силу F надо приложить к вагону, стоящему на рельсах, чтобы вагон стал двигаться равноускоренно и за время t = 30 с прошел путь s = 11 м? Масса вагона 16 т. Во время движения на вагон действует сила трения Fтр, равная 0,05 действующей на него силы тяжести
РЕШЕНИЕ
2.10 Поезд массой m = 500 т после прекращения тяги паровоза под действием силы трения Fтр = 98 кН останавливается через время t = 1 мин. С какой скоростью шел поезд
РЕШЕНИЕ
2.11 Вагон массой m = 20 т движется равнозамедленно, имея начальную скорость v0 = 54 км/ч и ускорение a = -0,3 м/с2. Какая сила торможения F действует на вагон? Через какое время t вагон остановится? Какое расстояние s вагон пройдет до остановки
РЕШЕНИЕ
2.12 Тело массой m = 0,5 кг движется прямолинейно, причем зависимость пройденного телом пути s от времени t дается уравнением s = A — Bt + Ct^2 — Dt^3, где С = 5 м/с2 и D = 1 м/с3. Найти силу, действующую на тело в конце первой секунды движения.
РЕШЕНИЕ
2.13 Под действием силы F = 10 H тело движется прямолинейно так, что зависимость пройденного телом пути s от времени t дается уравнением s = A — Bt + Ct2, где С = 1 м/с2. Найти массу тела.
РЕШЕНИЕ
2.14 Тело массой m = 0,5 кг движется так, что зависимость пройденного телом пути s от времени m дается уравнением s = A*sin(ωt), где A = 5 см и ω = π рад/с. Найти силу, действующую на тело через время 1/6 c после начала движения.
РЕШЕНИЕ
2.15 Молекула массой m = 4,65·10-26 кг, летящая по нормали к стенке сосуда со скоростью v = 600 м/с, ударяется о стенку и упруго отскакивает от нее без потери скорости. Найти импульс силы, полученный стенкой во время удара.
РЕШЕНИЕ
2.16 Молекула массой m = 4,65·10-26 кг, летящая со скоростью v = 600 м/с, ударяется о стенку сосуда под углом α = 60 к нормали и упруго отскакивает от нее без потери скорости. Найти импульс силы Ft, полученный стенкой во время удара.
РЕШЕНИЕ
2.17 Шарик массой m = 0,1 кг, падая с некоторой высоты, ударяется о наклонную плоскость и упруго отскакивает от нее без потери скорости. Угол наклона плоскости к горизонту 30. За время удара плоскость получает импульс силы FΔt = 1,73 Н·с. Какое время t пройдет от момента удара шарика о плоскость до момента, когда он будет находиться в наивысшей точке траектории
РЕШЕНИЕ
2.18 Струя воды сечением S = 6 см2 ударяется о стенку под углом α = 60 к нормали и упруго отскакивает от нее без потери скорости. Найти силу, действующую на стенку, если известно, что скорость течения воды в струе 12 м/с.
РЕШЕНИЕ
2.19 Трамвай, трогаясь с места, движется с ускорением a = 0,5 м/с2. Через время t = 12 с после начала движения мотор выключается и трамвай движется до остановки равнозамедленно. Коэффициент трения на всем пути k = 0,01. Найти наибольшую скорость v и время t движения трамвая. Каково его ускорение а при его равнозамедленном движении? Какое расстояние пройдет трамвай за время движения
РЕШЕНИЕ
2.20 На автомобиль массой m = 1 т во время движения действует сила трения Fтр, равная 0,1 действующей на него силе тяжести mg. Какова должна быть сила тяги F, развиваемая мотором автомобиля, чтобы автомобиль двигался равномерно; с ускорением a = 2 м/с2
РЕШЕНИЕ
2.21 Какой угол с горизонтом составляет поверхность бензина в баке автомобиля, движущегося горизонтально с ускорением a = 2,44 м/с2
РЕШЕНИЕ
2.22 Шар на нити подвешен к потолку трамвайного вагона. Вагон тормозится, и его скорость за время t = 3 с равномерно уменьшается от v1 = 18 км/ч до v2 = 6 км/ч. На какой угол отклонится при этом нить с шаром
РЕШЕНИЕ
2.23 Вагон тормозится, и его скорость за время t = 3,3 с равномерно уменьшается от v1 = 47,5 км/ч до v2 = 30 км/ч. Каким должен быть предельный коэффициент трения k между чемоданом и полкой, чтобы чемодан при торможении начал скользить по полке
РЕШЕНИЕ
2.24 Канат лежит на столе так, что часть его свешивается со стола, и начинает скользить тогда, когда длина свешивающийся части составляет 1/4 его длины. Найти коэффициент трения k каната о стол.
РЕШЕНИЕ
2.25 На автомобиль массой m = 1 т во время движения действует сила трения Fтр , равная 0,1 действующей на него силы тяжести mg . Найти силу тяги F, развиваемую мотором автомобиля, если автомобиль движется с постоянной скоростью в гору с уклоном 1 м на каждые 25 м пути; под гору с тем же уклоном.
РЕШЕНИЕ
2.26 На автомобиль массой m = 1 т во время движения действует сила трения Fтр, равная 0,1 действующей на него силе тяжести mg . Какова должна быть сила тяги F, развиваемая мотором автомобиля, если автомобиль движется с ускорением 1 м/с2 в гору с уклоном 1 м на каждые 25 м пути.
РЕШЕНИЕ
2.27 Тело лежит на наклонной плоскости, составляющей с горизонтом угол α = 4. При каком предельном коэффициенте трения к тело начнет скользить по наклонной плоскости? С каким ускорением а будет скользить тело по плоскости, если коэффициент трения k = 0,03? Какое время t потребуется для прохождения при этих условиях пути s = 100 м ? Какую скорость v будет иметь тело в конце пути
РЕШЕНИЕ
2.28 Тело скользит по наклонной плоскости, составляющей с горизонтом угол α = 45. Пройдя путь s = 36,4 см, тело приобретает скорость v = 2 м/с. Найти коэффициент трения k тела о плоскость.
РЕШЕНИЕ
2.29 Тело скользит по наклонной плоскости, составляющей с горизонтом угол α = 45. Зависимость пройденного пути s от времени t дается уравнением s = Сt^2, где С = 1,73 м/с2. Найти коэффициент трения к тела о плоскость.
РЕШЕНИЕ
2.30 Две гири с массами m1 = 2 кг и m2 = 1 кг соединены нитью и перекинуты через невесомый блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити T. Трением в блоке пренебречь.
РЕШЕНИЕ
2.31 Невесомым блок укреплен на конце стола. Гири 1 и 2 одинаковой массы m1 = m2 = 1 кг соединены нитью и перекинуты через блок. Коэффициент трения гири 2 о стол k = 0,1. Найти ускорение a, с которым движутся гири, и силу натяжения нити Т
РЕШЕНИЕ
2.32 Невесомый блок укреплен в вершине наклонной плоскости, составляющей с горизонтом угол α = 30. Гири 1 и 2 одинаковой массы m1 = m2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити T. Трением гири о наклонную плоскость и трением в блоке пренебречь.
РЕШЕНИЕ
2.33 Невесомый блок укреплен в вершине наклонной плоскости, составляющей с горизонтом угол 30. Гири 1 и 2 одинаковой массы m1 = m2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити Т. Коэффициент трения гири 2 о наклонную плоскость k = 0,1.
РЕШЕНИЕ
2.34 Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы α = 30 и β = 45. Гири 1 и 2 одинаковой массы m = 1 кг соединены нитью и перекинуты через блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити Т. Трением гирь 1 и 2 о наклонные плоскости, а также трением в блоке пренебречь.
РЕШЕНИЕ
2.35 Невесомый блок укреплен в вершине двух наклонных плоскостей, составляющих с горизонтом углы 30 и 45. Гири 1 и 2 одинаковой массы m1 = m2 = 1 кг соединены нитью и перекинуты через блок. Найти ускорение a, с которым движутся гири, и силу натяжения нити Т. Коэффициенты трения гирь 1 и 2 о наклонные плоскости 0,1. Показать, что из формул, дающих решение этой задачи, можно получить, как частные случаи, решения задач
РЕШЕНИЕ
2.36 При подъеме груза массой m = 2 кг на высоту h = 1 м сила F совершает работу A = 78,5 Дж. С каким ускорением поднимается груз
РЕШЕНИЕ
2.37 Самолет поднимается и на высоте h = 5 км достигает скорости v = 360 км/ч. Во сколько раз работа A1, совершаемая при подъеме против силы тяжести, больше работы A2, идущей на увеличение скорости самолета
РЕШЕНИЕ
2.38 Какую работу A надо совершить, чтобы заставить движущееся тело массой m = 2 кг увеличить скорость с v1 = 2 м/с до v2 = 5 м/с; остановиться при начальной скорости v0 = 8 м/с
РЕШЕНИЕ
2.39 Мяч, летящий со скоростью v1 = 15 м/с, отбрасывается ударом ракетки в противоположном направлении со скоростью v2 = 20 м/с. Найти изменение импульса mΔv мяча, если известно, что изменение его кинетической энергии W = 8,75 Дж.
РЕШЕНИЕ
2.40 Камень, пущенный по поверхности льда со скоростью v = 3 м/с, прошел до остановки расстояние s = 20,4 м. Найти коэффициент трения камня о лед.
РЕШЕНИЕ
2.41 Вагон массой m = 20 т, двигаясь равнозамедленно с начальной скоростью v0 = 54 км/ч, под действием силы трения Fтр = 6 кН через некоторое время останавливается. Найти работу сил трения и расстояние s, которое вагон пройдет до остановки.
РЕШЕНИЕ
2.42 Шофер автомобиля, имеющего массу m = 1 т, начинает тормозить на расстоянии s = 25 м от препятствия на дороге. Сила трения в тормозных колодках автомобиля Fтр = 3,84 кН. При какой предельной скорости движения автомобиль успеет остановиться перед препятствием? Трением колес о дорогу пренебречь.
РЕШЕНИЕ
2.43 Трамвай движется с ускорением a = 49,0 см/с. Найти коэффициент трения k, если известно, что 50% мощности мотора идет на преодоление силы трения и 50% на увеличение скорости движения.
РЕШЕНИЕ
2.44 Найти работу A, которую надо совершить, чтобы увеличить скорость движения тела массой m=1 т от v1 = 2 м/с до v2 = 6 м/с на пути s = 10 м. На всем пути действует сила трения 2 Н
РЕШЕНИЕ
2.45 На автомобиль массой M = 1 т во время движения действует сила трения Fтр, равная 0,1 действующей на него силе тяжести mg. Какую массу m бензина расходует двигатель автомобиля на то, чтобы на пути s = 0,5 км увеличить скорость от v1 = 10 км/ч до v2 = 40 км/ч? К.п.д. двигателя n= 0,2, удельная теплота сгорания бензина q = 46 МДж/кг.
РЕШЕНИЕ
2.46 Какую массу m бензина расходует двигатель автомобиля на пути s = 100 км, если при мощности двигателя N = 11 кВт скорость его движения v = 30 км/ч? К.п.д. двигателя 0,22, удельная теплота сгорания бензина q = 46 МДж/кг.
РЕШЕНИЕ
2.47 Найти к.п.д. двигателя автомобиля, если известно, что при скорости движения v = 40 км/ч двигатель потребляет объем V = 13,5 л бензина на пути s = 100 км и развивает мощность N = 12 кВт. Плотность бензина ρ = 0,8*10^3 кг/м3, удельная теплота сгорания бензина q = 46 МДж/кг.
РЕШЕНИЕ
2.48 Камень массой m = 1 кг брошен вертикально вверх с начальной скоростью v0 = 9,8 м/с. Построить график зависимости от времени t кинетической, потенциальной и полной W энергий камня для интервала 0РЕШЕНИЕ
2.49 В условиях предыдущей задачи построить график зависимости от расстояния h кинетической Wк, потенциальной Wn и полной W энергий камня.
РЕШЕНИЕ
2.50 Камень падает с некоторой высоты в течение времени t = 1,43 c. Найти кинетическую и потенциальную энергии камня в средней точке пути. Масса камня 2 кг.
РЕШЕНИЕ
2.51 С башни высотой h = 25 м горизонтально брошен камень со скоростью v0 = 15 м/с. Найти кинетическую и потенциальную энергии камня через время t = 1 c после начала движения. Масса камня m = 0,2 кг.
РЕШЕНИЕ
2.52 Камень брошен со скоростью v0 = 15 м/c под углом 60 к горизонту. Найти кинетическую Wк, потенциальную Wп и полную W энергии камня через время t = l c после начала движения; в высшей точке траектории. Масса камня m = 0,2 кг.
РЕШЕНИЕ
2.53 На толкание ядра, брошенного под углом α = 30 к горизонту, затрачена работа A = 216 Дж. Через какое время t и на каком расстоянии от места бросания ядро упадет на землю? Масса ядра m = 2 кг.
РЕШЕНИЕ
2.54 Тело массой m = 10 г движется по окружности радиусом R = 6,4 см. Найти тангенциальное ускорение ат тела, если известно, что к концу второго оборота после начала движения его кинетическая энергия 0,8 МДж.
РЕШЕНИЕ
2.55 Тело массой m = 1 кг скользит сначала по наклонной плоскости высотой h = 1 м и длиной склона l = 10 м, а затем по горизонтальной поверхности. Коэффициент трения на всем пути k = 0,05. Найти кинетическую энергию Wк тела у основания плоскости; скорость v тела у основания плоскости; расстояние S, пройденное телом по горизонтальной поверхности до остановки.
РЕШЕНИЕ
2.56 Тело скользит сначала по наклонной плоскости составляющей угол α = 8 с горизонтом, а затем по горизонтальной поверхности. Найти коэффициент трения на всем пути, если известно, что тело проходит по горизонтальной плоскости то же расстояние, что и по наклонной плоскости.
РЕШЕНИЕ
2.57 Тело массой m = 3 кг, имея начальную скорость v0 = 0 , скользит по наклонной плоскости высотой h = 0,5 м и длиной склона l = 1 м и приходит к основанию наклонной плоскости со скоростью v = 2,45 м/с. Найти коэффициент трения k тела о плоскость и количество теплоты, выделенное при трении.
РЕШЕНИЕ
2.58 Автомобиль массой m = 2 т движется в гору с уклоном 4 м на каждые 100 м пути. Коэффициент трения k = 0,08. Найти работу, совершаемую двигателем автомобиля на пути S = 3 км, и мощность развиваемую двигателем, если известно, что путь S = 3 км был пройден за время t = 4 мин.
РЕШЕНИЕ
2.59 Какую мощность N развивает двигатель автомобиля массой m = 1 т, если известно, что автомобиль едет с постоянной скоростью v = 36 км/ч по горизонтальной дороге; в гору с уклоном 5 м на каждые 100 м пути; под гору с тем же уклоном
РЕШЕНИЕ
2.60 Автомобиль массой m = 1 т движется при выключенном моторе с постоянной скоростью v = 54 км/ч под гору с уклоном 4 м на каждые 100 м пути. Какую мощность должен развивать двигатель автомобиля, чтобы автомобиль двигался с той же скоростью в гору
РЕШЕНИЕ
2.61 На рельсах стоит платформа массой m1 = 10 т. На платформе закреплено орудие массой m2 = 5 т, из которого производится выстрел вдоль рельсов. Масса снаряда m3 = 100 кг; его начальная скорость относительно орудия v0 = 500 м/с. Найти скорость u платформы в первый момент после выстрела, если платформа стоит неподвижно; платформа двигалась со скоростью v = 18 км/ч и выстрел был произведен в направлении, противоположном направлению ее движения.
РЕШЕНИЕ
2.62 Из ружья массой m1 = 5 кг вылетает пуля массой m = 5 г со скоростью v2 = 600 м/c. Найти скорость v1 отдачи ружья.
РЕШЕНИЕ
2.63 Человек массой m1 = 60 кг, бегущий со скоростью v1 = 8 км/ч, догоняет тележку массой m2 = 80 кг, движущуюся со скоростью v2 = 2,9 км/ч, и вскакивает на нее. С какой скоростью u будет двигаться тележка? С какой скоростью будет двигаться тележка, если человек бежал ей навстречу
РЕШЕНИЕ
2.64 Снаряд массой m1 = 100 кг, летящий горизонтально вдоль железнодорожного пути со скоростью v1 = 500 м/с, попадает в вагон с песком, масса которого m2 = 10 т, и застревает в нем. Какую скорость получит вагон, если вагон стоял неподвижно; вагон двигался со скоростью v2 = 36 км/ч в том же направлении, что и снаряд; вагон двигался со скоростью v2 = 36 км/ч в направлении, противоположном движению снаряда
РЕШЕНИЕ
2.65 Граната, летящая со скоростью v = 10 м/с, разорвалась на два осколка. Больший осколок, масса которого составляла 0,6 массы всей гранаты, продолжал двигаться в прежнем направлении, но с увеличенной скоростью u1 = 25 м/с. Найти скорость u2 меньшего осколка.
РЕШЕНИЕ
2.66 Тело массой m1 = 1 кг, движущееся горизонтально со скоростью v1 = 1 м/с, догоняет второе тело массой m2 = 0,5 кг и неупруго соударяется с ним. Какую скорость и получат тела, если второе тело стояло неподвижно; второе тело двигалось со скоростью v2 = 0,5 м/с в направлении, что и первое тело; второе тело двигалось со скоростью v2 = 0,5 м/с в направлении, противоположном направлению движения первого тела.
РЕШЕНИЕ
2.67 Конькобежец массой M = 70 кг, стоя на коньках на льду, бросает в горизонтальном направлении камень массой m = 3 кг со скоростью v = 8 м/с. На какое расстояние s откатится при этом конькобежец, если коэффициент трения коньков о лед k = 0,02
РЕШЕНИЕ
2.68 Человек, стоящий на неподвижной тележке, бросает в горизонтальном направлении камень массой m = 2 кг. Тележка с человеком покатилась назад, и в первый момент бросания ее скорость была v = 0,1 м/с. Масса тележки с человеком M = 100 кг. Найти кинетическую энергию брошенного камня через время t = 0,5 с после начала движения.
РЕШЕНИЕ
2.69 Тело массой m1 = 2 кг движется навстречу второму телу массой m2 = 1,5 кг и неупруго соударяется с ним. Скорости тел непосредственно перед ударом были v1 = 1 м/с и v2 = 2 м/с . Какое время t будут двигаться эти тела после удара, если коэффициент трения k = 0,05
РЕШЕНИЕ
2.70 Автомат выпускает пули с частотой n = 600 мин-1. Масса каждой пули m = 4 г, ее начальная скорость v = 500 м/с. Найти среднюю силу отдачи при стрельбе.
РЕШЕНИЕ
2.71 На рельсах стоит платформа массой m1 = 10 т. На платформе закреплено орудие массой m2 = 5 т, из которого производится выстрел вдоль рельсов. Масса снаряда m3 = 100 кг, его скорость относительно орудия v0 = 500 м/с. На какое расстояние s откатится платформа при выстреле, если платформа стояла неподвижно; платформа двигалась со скоростью v = 18 км/ч и выстрел был произведен в направлении ее движения; платформа двигалась со скоростью v = 18 км/ч и выстрел был произведен в направлении противоположном направлению ее движения
РЕШЕНИЕ
2.72 Из орудия массой m1 = 5 т вылетает снаряд массой m2 = 100 кг. Кинетическая энергия снаряда при вылете Wк2 = 7,5 МДж. Какую кинетическую энергию Wк1 получает орудие вследствие отдачи
РЕШЕНИЕ
2.73 Тело массой m1 = 2 кг движется со скоростью v1 = 3 м/с и нагоняет тело массой m2 = 8 кг, движущееся со скоростью v2 = 1 м/с. Считая удар центральным, найти скорости u1 и u2 тел после удара, если удар неупругий; упругий.
РЕШЕНИЕ
2.74 Тело массой m1 = 2 кг движется со скоростью v1 = 3 м/с и нагоняет тело массой m2 = 8 кг, движущееся со скоростью v2 = 1 м/с. Найти соотношение между массами тел, чтобы при упругом ударе первое тело остановилось
РЕШЕНИЕ
2.75 Тело массой m = 3 кг движется со скоростью v1 = 4 м/с и ударяется о неподвижное тело такой же массы. Считая удар центральным и неупругим, найти количество теплоты, выделившееся при ударе
РЕШЕНИЕ
2.76 Тело массой m1 = 5 кг ударяется о неподвижное тело массой m2 = 2,5 кг, которое после удара начинает двигаться с кинетической энергией Wк2 = 5 Дж. Считая удар центральным и упругим, найти кинетическую энергию первого тела до и после удара.
РЕШЕНИЕ
2.77 Тело массой m1 = 5 кг ударяется о неподвижное тело массой m2 = 2,5 кг. Кинетическая энергия системы двух тел непосредственно после удара стала Wк = 5 Дж. Считая удар центральным и неупругим, найти кинетическую энергию Wк1 первого тела до удара.
РЕШЕНИЕ
2.78 Два тела движутся навстречу друг другу и соударяются неупруго. Скорости тел до удара были v1 = 2 м/с и v2 = 4 м/с. Общая скорость тел после удара u = 1 м/с и по направлению совпадает с направлением скорости v1. Во сколько раз кинетическая энергия Wк1 первого тела была больше кинетической энергии Wк2 второго тела
РЕШЕНИЕ
2.79 Два шара с массами m1 = 0,2 кг и m2 = 0,1 кг подвешены на нитях одинаковой длины так, что они соприкасаются. Первый шар отклоняют на высоту h0 = 4,5 см и отпускают. На какую высоту h поднимутся шары после удара, если удар упругий; неупругий
РЕШЕНИЕ
2.80 Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули в 1000 раз меньше массы шара. Расстояние от центра шара до точки подвеса стержня l = 1 м. Найти скорость v пули, если известно, что стержень с шаром отклонился от удара пули на угол 10
РЕШЕНИЕ
2.81 Пуля, летящая горизонтально, попадает в шар, подвешенный на невесомом жестком стержне, и застревает в нем. Масса пули m1 = 5 г, масса шара m2 = 0,5 кг. Скорость пули v1 = 500 м/c. При каком предельном расстоянии l от центра шара до точки подвеса стержня шар от удара пули поднимется до верхней точки окружности
РЕШЕНИЕ
2.82 Деревянным молотком, масса которого m1 = 0,5 кг, ударяют о неподвижную стенку. Скорость молотка в момент удара v1 = 1 м/с. Считая коэффициент восстановления при ударе молотка о стенку k = 0,5, найти количество теплоты, выделившееся при ударе
РЕШЕНИЕ
2.83 Деревянным молотком, масса которого m1 = 0,5 кг, ударяют о неподвижную стенку. Скорость молотка в момент удара v1 = 1 м/с. Считая коэффициент восстановления при ударе молотка о стенку k = 0,5, найти импульс силы, полученный стенкой за время удара.
РЕШЕНИЕ
2.84 Деревянный шарик массой m = 0,1 кг падает с высоты h2 = 2 м. Коэффициент восстановления при ударе шарика о пол k = 0,5. Найти высоту h3, на которую поднимется шарик после удара о пол, и количество теплоты, выделившееся при ударе.
РЕШЕНИЕ
2.85 Пластмассовый шарик, падая с высоты h2 = 1 м несколько раз отскакивает от пола. Найти коэффициент восстановления k при ударе шарика о пол, если с момента падения до второго удара о пол прошло время t = 1,3 c.
РЕШЕНИЕ
2.86 Стальной шарик, падая с высоты h2 = 1,5 м на стальную плиту, отскакивает от нее со скоростью v2 = 0,75·v1, где v1 скорость, с которой он подлетает к плите. На какую высоту h3 он поднимется? Какое время t пройдет с момента падения до второго удара о плиту
РЕШЕНИЕ
2.87 Металлический шарик, падая с высоты h2 = 1 м на стальную плиту, отскакивает от нее на высоту h3 = 81 см. Найти коэффициент восстановления при ударе шарика о плиту.
РЕШЕНИЕ
2.88 Стальной шарик массой m = 20 г, падая с высоты h2 = 1 м на стальную плиту, отскакивает от нес на высоту h3 = 81 см. Найти импульс силы, полученный плитой за время удара, и количество теплоты, выделившееся при ударе.
РЕШЕНИЕ
2.89 Движущееся тело массой m1, ударяется о неподвижное тело массой m2. Считая удар неупругим и центральным, найти, какая часть кинетической энергии первого тела переходит при ударе в тепло. Задачу решить сначала в общем виде, а затем рассмотреть случаи m1 = m2; m1 = 9m2.
РЕШЕНИЕ
2.90 Движущееся тело массой m1, ударяется о неподвижное тело массой m2. Считая удар упругим и центральным, найти, какую часть кинетической энергии Wк1 первое тело передает второму при ударе. Задачу решить сначала в общем виде, а затем рассмотреть случаи m1 = m2; m1 = 9m2
РЕШЕНИЕ
2.91 Движущееся тело массой m1 ударяется о неподвижное тело массой m2. Каким должно быть отношение масс m1/m2, чтобы при центральном упругом ударе скорость первого тела уменьшилась в 1,5 раза? С какой кинетической энергией начинает двигаться при этом второе тело, если первоначальная кинетическая энергия первого тела 1 кДж
РЕШЕНИЕ
2.92 Нейтрон масса m0 ударяется о неподвижное ядро атома углерода m = 12m0. Считая удар центральным и упругим, найти, во сколько раз уменьшится кинетическая энергия нейтрона при ударе.
РЕШЕНИЕ
2.93 Нейтрон ударяется о неподвижное ядро атома углерода m = 12m0; атома урана m = 235m0. Считая удар центральным и упругим, найти, какую часть скорости v потеряет нейтрон при ударе.
РЕШЕНИЕ
2.94 На какую часть уменьшится вес тела на экваторе вследствие вращения Земли вокруг оси
РЕШЕНИЕ
2.95 Какой продолжительности T должны были бы быть сутки на Земле, чтобы тела на экваторе не имели веса.
РЕШЕНИЕ
2.96 Трамвайный вагон массой m = 5 т идет по закруглению радиусом R = 128 м. Найти силу бокового давления колес на рельсы при скорости движения v = 9 км/ч.
РЕШЕНИЕ
2.97 Ведерко с водой, привязанное к веревке длиной l = 60 см, равномерно вращается в вертикальной плоскости. Найти наименьшую скорость v вращения ведерка, при которой в высшей точке вода из него не выливается. Какова сила натяжения веревки T при этой скорости в высшей и низшей точках окружности
РЕШЕНИЕ
2.98 Камень, привязанный к веревке длиной l = 50 см, равномерно вращается в вертикальной плоскости. При какой частоте вращения n веревка разорвется, если известно, что она разрывается при десятикратной силе тяжести, действующей на камень
РЕШЕНИЕ
2.99 Камень, привязанный к веревке, равномерно вращается в вертикальной плоскости. Найти массу m камня, если известно, что разность между максимальной и минимальной силами натяжения веревки T = 10 Н.
РЕШЕНИЕ
2.100 Гирька, привязанная к нити длиной l = 30 см, описывает в горизонтальной плоскости окружность радиусом R = 15 см. С какой частотой n вращается гирька
РЕШЕНИЕ
2.101 Гирька массой m = 50 г, привязанная к нити длиной l = 25 см, описывает в горизонтальной плоскости окружность. Частота вращения гирьки n = 2 об/с. Найти силу натяжения нити
РЕШЕНИЕ
2.102 Диск вращается вокруг вертикальной оси с частотой n = 30 об/мин. На расстоянии r = 20 см от оси вращения на диске лежит тело. Каким должен быть коэффициент трения k между телом и диском, чтобы тело не скатилось с диска
РЕШЕНИЕ
2.103 Самолет, летящий со скоростью v = 900 км/ч, делает мертвую петлю. Каким должен быть радиус мертвой петли R, чтобы наибольшая сила, прижимающая летчика к сидению, была равна пятикратной силе тяжести, действующей на летчика; десятикратной силе тяжести, действующей на летчика
РЕШЕНИЕ
2.104 Мотоциклист едет по горизонтальной дороге со скоростью v = 72 км/ч, делая поворот радиусом R = 100 м. На какой угол при этом он должен наклониться, чтобы не упасть при повороте
РЕШЕНИЕ
2.105 К потолку трамвайного вагона подвешен на нити шар. Вагон идет со скоростью v = 9 км/ч по закруглению радиусом R = 36,4 м. На какой угол отклонится при этом нить с шаром
РЕШЕНИЕ
2.106 Длина стержней центробежного регулятора l = 12,5 см. С какой частотой n должен вращаться центробежный регулятор, чтобы грузы отклонялись от вертикали на угол, равный 60; 30
РЕШЕНИЕ
2.107 Шоссе имеет вираж с уклоном α = 10 при радиусе закругления дороги R = 100 м. На какую скорость v рассчитан вираж
РЕШЕНИЕ
2.108 Груз массой m = 1 кг, подвешенный на нити, отклоняют на угол α = 30 и отпускают. Найти силу натяжения нити T в момент прохождения грузом положения равновесия.
РЕШЕНИЕ
2.109 Мальчик массой m = 45 кг вращается на гигантских шагах с частотой n = 16 об/мин. Длина канатов l = 5 м. Какой угол α с вертикалью составляют канаты гигантских шагов? Каковы сила натяжения канатов и скорость вращения мальчика
РЕШЕНИЕ
2.110 Груз массой m = 1 кг, подвешенный на невесомом стержне длиной l = 0,5 м, совершает колебания в вертикальной плоскости. При каком угле отклонения α стержня от вертикали кинетическая энергия груза в его нижнем положении Wк = 2,45 Дж? Во сколько раз при таком угле отклонения сила натяжения стержня в нижнем положении больше силы натяжения стержня в верхнем положении
РЕШЕНИЕ
2.111 Груз массой m, подвешенный на невесомом стержне, отклоняют на угол α = 90 и отпускают. Найти силу натяжения T стержня в момент прохождения грузом положения равновесия.
РЕШЕНИЕ
2.112 Груз массой m = 150 кг подвешен на стальной проволоке, выдерживающей силу натяжения T = 2,94 кН. На какой наибольший угол можно отклонить проволоку с грузом, чтобы она не разорвалась при прохождении грузом положения равновесия
РЕШЕНИЕ
2.113 Камень массой m = 0,5 кг привязан к веревке длиной l = 50 см, равномерно вращается в вертикальной плоскости. Сила натяжения веревки в нижней точке окружности T = 44 Н. На какую высоту h поднимется камень, если веревка обрывается в тот момент, когда скорость направлена вертикально вверх
РЕШЕНИЕ
2.114 Вода течет по трубе диаметром d = 0,2 м, расположенной в горизонтальной плоскости и имеющей закругление радиусом R = 20,0 м. Найти боковое давление воды p, вызванное центробежной силой. Через поперечное сечение трубы за единицу времени протекает масса воды m1 = 300 т/ч.
РЕШЕНИЕ
2.115 Вода течет по каналу шириной b = 0,5 м, расположенному в горизонтальной плоскости и имеющему закругление радиусом R = 10 м. Скорость течения воды v = 5 м/с. Найти боковое давление воды P, вызванное центробежной силой.
РЕШЕНИЕ
2.116 Найти работу A, которую надо совершить, чтобы сжать пружину на l = 20 см, если известно, что сила F пропорциональна сжатию l и жесткость пружины k = 2,94 кН/м.
РЕШЕНИЕ
2.117 Найти наибольший прогиб h рессоры от груза массой m, положенного на ее середину, если статический прогиб рессоры от того же груза h0 = 2 см. Каким будет наибольший прогиб, если тот же груз падает на середину рессоры с высоты H = 1 м без начальной скорости
РЕШЕНИЕ
2.118 Акробат прыгает в сетку с высоты H = 8 м. На какой предельной высоте h над полом надо натянуть сетку, чтобы акробат не ударился о пол при прыжке? Известно, что сетка прогибается на h0 = 0,5 м, если акробат прыгает в нее с высоты H0 = 1 м.
РЕШЕНИЕ
2.119 Груз положили на чашку весов. Сколько делений покажет стрелка весов при первоначальном отбросе, если после успокоения качаний она показывает 5 делений
РЕШЕНИЕ
2.120 Груз массой m = 1 кг падает на чашку весов с высоты H = 10 см. Каковы показания весов F в момент удара, если после успокоения качаний чашка весов опускается на h = 0,5 см
РЕШЕНИЕ
2.121 С какой скоростью v двигался вагон массой m = 20 т, если при ударе о стенку каждый буфер сжался на l = 10 см? Жесткость пружины каждого буфера 1 МН/м.
РЕШЕНИЕ
2.122 Мальчик, стреляя из рогатки, натянул резиновый шнур так, что его длина стала больше на 10 см. С какой скоростью v полетел камень массой m = 20 г
РЕШЕНИЕ
2.123 К нижнему концу пружины, подвешенной вертикально, присоединена другая пружина, к концу которой прикреплен груз. Жесткости пружин равны k1 и k2. Пренебрегая массой пружин по сравнению с массой груза, найти отношение потенциальных энергий этих пружин.
РЕШЕНИЕ
2.124 На двух параллельных пружинах одинаковой длины весит невесомый стержень длиной L = 10 см. Жесткости пружин k1 = 2 Н/м и k2 = 3 Н/м. В каком месте стержня надо подвесить груз, чтобы стержень оставался горизонтальным
РЕШЕНИЕ
2.125 Резиновый мяч массой m = 0,1 кг летит горизонтально с некоторой скоростью и ударяется о неподвижную вертикальную стенку. За время t = 0,01 с мяч сжимается на 1,37 см; такое же время затрачивается на восстановление первоначальной формы мяча. Найти среднюю силу F, действующую на стенку за время удара.
РЕШЕНИЕ
2.126 Гиря массой m = 0,5 кг, привязанная к резиновому шнуру длиной l0, описывает в горизонтальной плоскости окружность. Частота вращения гири n = 2 об/с. Угол отклонения шнура от вертикали 30. Жесткость шнура k = 0,6 кН/м. Найти длину l0 нерастянутого резинового шнура.
РЕШЕНИЕ
2.127 Гирю массой m = 0,5 кг, привязанную к резиновому шнуру длиной l0 = 9,5 см, отклоняют на угол α = 90 и отпускают. Найти длину l резинового шнура в момент прохождения грузом положения равновесия
РЕШЕНИЕ
2.128 Мяч радиусом R = 10 см плавает в воде так, что его центр масс находится на H = 9 см выше поверхности воды. Какую работу надо совершить, чтобы погрузить мяч в воду до диаметральной плоскости
РЕШЕНИЕ
2.129 Шар радиусом R = 6 см удерживается внешней силой под водой так, что его верхняя точка касается поверхности воды. Какую работу произведет выталкивающая сила, если отпустить шар и предоставить ему свободно плавать? Плотность материала шара ρ = 0,5*10^3 кг/м3.
РЕШЕНИЕ
2.130 Шар диаметром D = 30 см плавает в воде. Какую работу надо совершить, чтобы погрузить шар в воду на H = 5 см глубже
РЕШЕНИЕ
2.131 Льдина площадью поперечного сечения S = 1 м2 и высотой h = 0,4 м плавает в воде. Какую работу надо совершить, чтобы полностью погрузить льдину в воду
РЕШЕНИЕ
2.132 Найти силу гравитационного взаимодействия F между двумя протонами, находящимися на расстоянии r = 10-16 м друг от друга. Масса протона m = 1,67*10-27 кг.
РЕШЕНИЕ
2.133 Два медных шарика с диаметрами D1 = 4 см и D2 = 6 см находятся в соприкосновении друг с другом. Найти гравитационную потенциальную энергию этой системы.
РЕШЕНИЕ
2.134 Вычислить гравитационную постоянную G, зная радиус земного шара R, среднюю плотность земли ρ и ускорение свободного падения g у поверхности Земли
РЕШЕНИЕ
famiredo.ru
Сборник задач на динамику. Общие принципы решения. План решения задач
Задачи на тему «динамика» присутствуют как в школьном рассмотрении так и в централизованном тестировании в огромном количестве. Они в целом очень разнообразны и связаны как с прямолинейным, так и с криволинейным движением. Полностью данный раздел классифицировать сложно, но частично можно выделить ряд задач, для которых можно ввести более-менее универсальный план решения:
- задачи на поиск значения силы, исходя из её определения
Для такого типа задач необходимо знать формульное значение силы и искать неизвестные составляющие (сила Гука, сила Кулона, сила Лоренца и т.д.).
Для таких задач универсальность плана очень велика, т.е. даже бездумное использование плана приводит к записи системы уравнений, математически решив которую, можно решить задачу.
Важно: помним, что сила — векторная физическая величина, т.е. для работы с ней нам понадобятся как правила сложения векторов, а соответственно и теоремы Пифагора, синусов/косинусов, так и знания о проекциях.
В данном разделе мы ограничимся динамическими задачами механики. Т.е. будем работать только с силами в механике.
Первый тип задач:
- Во сколько раз отличаются силы тяжести, действующие на тела массами…
- Во сколько раз сила тяжести, действующая на 2 л воды, отличается…
- Силы тяжести, действующие на две чугунные детали, отличаются в…
- Плотность вещества и объём одной детали в k раз больше, чем другой…
- В одном из опытов по проверке закона всемирного тяготения сила притяжения…
- Определите ускорение, вызванное силой тяготения, на высоте…
- На какой высоте от поверхности Земли сила тяготения…
- Какими будут показания динамометра, если к нему подвесить гирю массой…
- Определите вес, силу тяжести и массу ртути, объём которой…
- Будут ли в равновесии рычажные весы…
- Картонный ящик содержит плиток шоколада…
Второй тип задач:
- Тело массой 7,4 кг перемещают по гладкой горизонтальной поверхности, действуя…
- После раскрытия парашюта движение парашютиста стало равномерным…
- Комок ваты массой падает с постоянной скоростью…
www.abitur.by
Банк задач. Динамика. Задачи для абитуриентов [1 — 20]
Динамика. Задачи для абитуриентов.1(РГУНГ 2002). Тело поднимают вверх вдоль наклонной плоскости, прикладывая к нему горизонтальную силу, величина которой вдвое больше действующей на тело силы тяжести. Высота наклонной плоскости 3 м, ее длина 5 м. Найдите ускорение тела, если коэффициент трения равен 0,2. [решение]
2(РГУНГ 2005). В лифте, поднимающемся с ускорением 1,4 м/с2, на пружине жесткостью 700 Н/м висит груз массой 0,5 кг. Чему равно (в мм) удлинение пружины? Ускорение свободного падения 9,8 м/с2. [решение]
3(РГУНГ 2004). Невесомый стержень вращается в горизонтальной плоскости с угловой скоростью 30 c−1. На расстояниях 0,4 м и 0,3 м от оси вращения закреплены грузы, имеющие массы
4(РГУНГ 2003). Замкнутая цепочка массой 157 г надета «с натягом» на жесткий вертикальный цилиндр радиусом 5 см. Когда цилиндр раскрутили до угловой скорости 20 с−1, цепочка с него соскользнула вниз. Чему равно натяжение цепочки? Коэффициент трения цепочки о цилиндр 0,1. Принять π = 3,14. [решение]
5(РГУНГ 2006). Груз массой 3 кг подвешен к потолку лифта с помощью двух нитей, каждая из которых образует с вертикалью угол 60°. Каким будет натяжение каждой нити, если лифт будет опускаться с ускорением, направленным вниз и равным 2 м/с2? [решение]
6(РГУНГ 2006). К невесомой нити длиной 1 м прикреплен шарик массой 200 г, который равномерно вращается в вертикальной плоскости. При какой минимальной угловой скорости вращения произойдет обрыв нити, если она выдерживает максимальную нагрузку 3,8 Н? [решение]
7(РГУНГ 2007). Шарик, подвешенный на легкой нити к потолку, вращается по окружности, лежащей в горизонтальной плоскости, с угловой скоростью 5 рад/с. Найдите расстояние (в см) между точкой подвеса и центром окружности. [решение]
8(РГУНГ 2007). Вверх по наклонной плоскости высотой 9 м и длиной 15 м пущена шайба. Коэффициент трения равен 0,5. Найдите ускорение шайбы. В ответе укажите абсолютную величину ускорения. [решение]
9(РГУНГ 2006). Радиус некоторой планеты в √3 раза меньше радиуса Земли, а ускорение силы тяжести на поверхности планеты в 3 раза
10(МГИЭТ 2002). По наклонной плоскости скользит с ускорением a = 1 м/с2 брусок массой m = 200 г. С какой силой F нужно прижимать брусок перпендикулярно наклонной плоскости, чтобы он начал двигаться равномерно? Коэффициент трения бруска о наклонную плоскость μ = 0,1. [решение]
11(РГУНГ 2002). Невесомый стержень может свободно вращаться вокруг горизонтальной оси, проходящей через точку, которая делит стержень в отношении 1:2. На концах стержня закреплены одинаковые грузы массой 0,5 кг каждый. Стержень приводят в горизонтальное положение. С какой силой действует он на ось сразу после этого. Ускорение свободного падения принять равным 10 м/с2. [решение]
12(МГИЭТ 2003). К вертикальной железной стене «прилипла» намагниченная шайба. К шайбе привязали легкую нить и тянут за нее так, что нить все время остается параллельной стене. Когда нить тянут вертикально вверх, шайба начинает двигаться при минимальной силе F1 = 1,6 Н; когда нить тянут вертикально вниз, шайба приходит в движение при F2 = 0,6 Н. Найдите массу m шайбы. [решение]
13(НГУ). На конце линейки длины L, лежащей на горизонтальной плоскости, находится маленький грузик. Линейку начинают поднимать за тот же конец с постоянной скоростью u, направленной вверх. Через какое время t грузик начнет соскальзывать? Коэффициент трения между грузиком и линейкой μ. [решение]
14(МГУ). Начальный участок трассы скоростного спуска, расположенный вниз по склону горы с углом наклона α = 45° к горизонту, горнолыжник прошел, не отталкиваясь палками. Какую максимальную скорость мог развить спортсмен на этом участке, если его масса
15(МФТИ). Космонавты, высадившиеся на поверхность Марса, измерили период вращения конического маятника (небольшое тело, прикрепленное к нити и движущееся по окружности в горизонтальной плоскости с постоянной скоростью), и он оказался равным T = 3 c. Длина нити l = 1 м. Угол, составляемый нитью с вертикалью, α = 30°. Найдите по эти данным ускорение свободного падения на Марсе. [решение]
16(РГУНГ 2002). Тело массой 1 кг вращается в вертикальной плоскости на нити длиной 2 м. Когда тело при подъеме проходит точку, расположенную на 1 м выше точки подвеса нити, она обрывается. На сколько выше точки подвеса поднимется тело, если натяжение нити перед обрывом было равно 35 Н? [решение]
17(Ш). Вообразим, что строительная техника позволяет возводить сколь угодно высокие сооружения. Какую высоту должна иметь башня, расположенная на экваторе Земли, чтобы тело, находящееся на ее вершине, было невесомым? [решение]
18(Ш). Шайба, скользившая по льду, остановилась через время t = 5 c после удара о клюшку на расстоянии l = 20 м от места удара. Масса шайбы m = 100 г. Определите действовавшую на шайбу силу трения. [решение]
19(Ш). В электронно-лучевой трубке электроны с начальной горизонтальной скоростью v влетают в область электрического поля напряженности
20(Ш). Четырьмя натянутыми нитями груз закреплен на тележке. Силы натяжения горизонтальных нитей соответственно T1 и T2, а вертикальных T3, T4. С каким ускорением тележка движется по горизонтальной плоскости? [решение]
fizportal.ru
Алгоритм решения задач по Динамике
Умение решать задачи на законы Ньютона — является одним из показателей того, что учащийся знает и понимает физику. Тем более, что динамические задачи встречаются не только в «Механике», но и в других разделах физики (например задачи на равновесие и движение частицы в электрическом поле или движение заряженной частицы в магнитном поле).
И самые простые, и более сложные задачи решаются с использованием этого алгоритма, приведенного ниже.
Сам алгоритм сопровождается пояснительными рисунками (для большей наглядности).
Алгоритм решения задач по динамике.
1. Сделать рисунок, на котором изобразить тело (систему тел), о котором идет речь в задаче, и указать направление вектора скорости (если движение равномерное) или направление вектора ускорения (если движение равноускоренное или равнозамедленное) для тела (системы тел).
| Тело на горизонтали | Тело на наклонной плоскости | Cвязанные тела |
2. Указать все силы, действующие на тело (систему тел).
3. Записать уравнение Ньютона (уравнение динамики) в векторной форме (векторная сумма сил, действующих на тело равна равнодействующей ma). Если речь идет о связанных телах, то уравнения Ньютона записываются для каждого тела.
4. Выбрать удобное направление координатных осей (для связанных тел направление координатных осей может отличаться).
5. Спроецировать векторное(-ые) уравнение(-я) на координатные оси.
6. Записать дополнительные кинематические уравнения, если это необходимо и формулы для определения сил.
7. Составить систему уравнений, выделить неизвестные и решить систему получившихся уравнений относительно неизвестных величин.
Большое количество задач, решенных с помощью этого алгоритма, Вы можете найти на нашем сайте.
Вы можете оставить комментарий, или поставить трэкбек со своего сайта.Написать комментарий
fizika-doma.ruдинамика Archives — Физика дома
Автор: admin. Рубрики: Задачи 28 (С2). Опубликовано: Октябрь 19th, 2016Комбинированная задача по физике на условия равновесия тел, имеющих ось вращения, будет интересна выпускникам и десятиклассникам, интересующимися физикой.
Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рисунок). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту 450. Найти модуль силы F, действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.
(подробнее…)
Автор: admin. Рубрики: Задачи 30 (С5). Опубликовано: Август 27th, 2015Точечный отрицательный заряд q= — 1.5*10-12Кл движется в однородных электрическом и магнитном полях. Напряжённость электрического поля Е = 1200 В/м, индукция магнитного поля В = 0,03 Тл. В некоторый момент вмени скорость заряда равна v = 105 м/с и лежит в плоскости векторов В и Е, при этом вектор скорости перпендикулярен вектору Е и составляет с вектором В угол 450. Найдите величину результирующей силы, действующей на заряд со стороны электромагнитного поля в этот момент времени.
(подробнее…)
Автор: admin. Рубрики: Задачи 27 (С1). Опубликовано: Август 17th, 2015Комбинированная задача для подготовки к ЕГЭ по физике, объединяющая темы «Механика» и «Молекулярная физика». Задача полезна для всех, кто готовится к экзамену по физике.
В горизонтальном сосуде, закрытом поршнем, находится разрежённый газ. Максимальная сила трения между поршнем и стенками сосуда составляет Fтр макс, а площадь поршня равна S. На рТ – диаграмме показано, как изменялось давление и температура разряженного газа в процессе его нагревания. Как изменялся объём газа (увеличивался, уменьшался или же оставался неизменным) на участках 1-2 и 2-3? Объяснить причину такого изменения объёма газа в процессе его нагревания, указав, какие физические явления и закономерности Вы использовали для объяснения.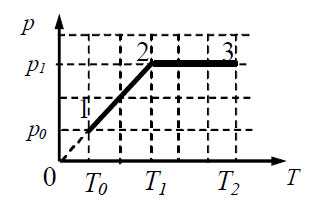
(подробнее…)
Для просмотра данного материала, зарегистрируйтесь!
Теги: динамика, задачи ЕГЭ, закон сохранения энергии, комбинированные задачи, механика, молекулярная, С1, С2, С3, С4, С6, электродинамика
Задача для подготовки к ЕГЭ по физике. С 2015 года в экзамен вновь включены задания со свободным ответом, поэтому вполне вероятно, что данная задача может встретиться в числе заданий этого типа.
Тело без начальной скорости начинает скользить по наклонной плоскости высотой 5 м. Угол наклона 300, коэффициент трения 0,02. Найдите время движения тела по наклонной плоскости. (подробнее…)
Автор: admin. Рубрики: ОГЭ. Опубликовано: Ноябрь 5th, 2014Задача для подготовки ОГЭ по физике по теме «Сила тяжести. Закон всемирного тяготения». Задача может быть полезна и для подготовки к ЕГЭ по физике.
Рассчитайте силу тяжести, действующую на тело массой 12 кг, поднятое над Землёй на расстояние, равное трети земного радиуса. (подробнее…)
Автор: admin. Рубрики: Задачи 28 (С2). Опубликовано: Ноябрь 1st, 2014Комбинированная задача для подготовки к ЕГЭ по физике, объединяющая темы «Кинематика» и «Динамика».
Не смотря на то, что разделение на части А, В, С в ЕГЭ с этого учебного года убрана, по старой привычке я отнесла эту задачу именно к этому разделу (назвать эту задачу задачей под номером 29 — язык пока не поворачивается).
Ледяная гора составляет с горизонтом угол 300. По ней снизу вверх пускают камень, который в течение 2 с проходит расстояние 16 м, после чего соскальзывает вниз. Определить время соскальзывания камня.
(подробнее…)
Данная задача из раздела «Динамика. Движение связанных тел» может быть интересна и учащимся, готовящимся к экзаменам, и учащимся, готовящимся к олимпиадам.
Цепь длиной 1 м лежит на столе так, что её конец свешивается с края стола. При какой длине свешивающейся со стола части цепи, вся цепь начнёт скользить по столу, если коэффициент трения цепи о стол равен 1/3? (подробнее…)
Предыдущие записи »fizika-doma.ru
| Динамика. ИСО Первый закон Ньютона. Принцип относительности Галилея  Инертность. Масса. Плотность  Сила. Второй закон Ньютона Третий закон Ньютона
| Примеры задач Полезные советы по решению задач. Скачать Задания по динамике Скачать Задания для самостоятельного решения Вариант 1 Вариант 2
| Подробный конспект по теме Динамика. Инерция Масса Сила. Первый закон Ньютона Второй и третий законы Ньютона Фильмы по теме Принцип относительности Галилея. Явление инерции. Инертность тел. Основная задача динамики. Движение и силы. Масса тела Зависимость ускорения от массы. Понятие силы Зависимость ускорения от силы Постоянство отношений ускорений взаимодействующих тел Законы Ньютона Первый закон Ньютона. Второй закон Ньютона. Действие и противодействие. Третий закон Ньютона Применение законов Ньютона Динамика движения по окружности. Биографические ссылки: Аристотель Галилей Ньютон Проверьте себя Вариант 1 Ответы |
www.eduspb.com
Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»
Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»
«Физика — 10 класс»
При решении задач на эту тему следует иметь в виду, что моменты силы, инерции и импульса зависят от выбора оси вращения. Кроме этого, нужно обращать внимание на то, что моменты импульса всех тел записываются относительно одной и той же системы отсчёта.
Задача 1.
На блок радиусом r и массой m1 намотана нить, к концу которой привязан груз массой m2 (рис. 6.12).
Груз отпускают, и он движется вниз, раскручивая нить. Определите ускорение груза. Массой нити можно пренебречь.
Р е ш е н и е.
Обозначим на рисунке силы, действующие на блок и груз.
На блок действуют сила тяжести m1, сила реакции опоры и сила натяжения нити.
На груз действуют сила тяжести m2 и сила натяжения ‘.
Согласно второму закону Ньютона в проекции на ось Y для груза запишем:
m2a = m2g — T’. (1)
Согласно основному закону динамики вращательного движения для блока запишем:
Iε = Tr. (2)
Момент инерции блока Связь углового и линейного ускорений а = εr.
Так как по условию задачи нить невесома, то Т = Т’.
Преобразуем уравнение (2): тогда
Подставив это выражение в уравнение (1), получим
Окончательно
Задача 2.
Скамья Жуковского радиусом 1 м со стоящим в центре человеком вращается, делая 2 об/с. Человек переходит на край скамьи. Определите изменение угловой скорости вращения скамьи. Масса человека 50 кг, момент инерции скамьи 30 кг • м2.
Р е ш е н и е.
Так как внешние силы — сила тяжести и сила реакции опоры, направленные параллельно оси вращения, не могут изменить момент импульса системы тел «скамья—человек», то согласно закону сохранения импульса
I1ω1 = I2ω2. (1)
Когда человек находится в центре скамьи, то момент инерции системы равен только моменту инерции скамьи: I1 = Iск.
После того как человек перешёл на край скамьи, момент инерции системы стал равен I2 = Iск + mr2.
Угловая скорость связана с числом оборотов в секунду соотношением ω1 = 2πn.
Подставив найденные выражения в уравнение (1), получим Iск2πn = (Iск + mr2)ω2. Тогда
Изменение угловой скорости
Задача 3.
На наклонную плоскость вкатывается колесо, двигавшееся по горизонтальной поверхности со скоростью 4 м/с. Вся масса колеса сосредоточена в ободе. Определите максимальную высоту, на которую поднимется колесо. Работой силы трения можно пренебречь.
Р е ш е н и е.
Выберем нулевой уровень отсчёта потенциальной энергии так, как показано на рисунке 6.13. Учтём, что момент инерции колеса-обруча I = mR2, а угловая скорость вращения ω = υ/R. Механическая энергия колеса на горизонтальной поверхности равна сумме кинетических энергий поступательного и вращательного движений колеса:
На максимальной высоте механическая энергия равна потенциальной энергии Е2 = mgh. Согласно закону сохранения механической энергии получим Е1 = Е2, или mυ2 = mgh, откуда h = υ2/g = 1,6 м.
Задача 4.
Сплошной цилиндр раскрутили до угловой скорости ω и положили на пол к стенке. Коэффициент трения между стенкой, полом и цилиндром μ, радиус цилиндра R. Определите, сколько оборотов сделает цилиндр до остановки.
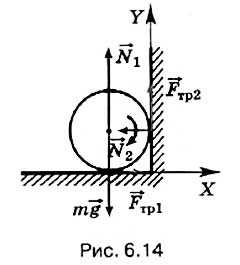
Р е ш е н и е.
Решаем задачу, используя теорему об изменении кинетической энергии. При этом учтём, что ось вращения цилиндра неподвижна, момент инерции цилиндра относительно этой оси равен соответственно кинетическая энергия цилиндра вначале равна
Изменение кинетической энергии равно алгебраической сумме работ сил, действующих на него:
На цилиндр (рис. 6.14) действуют силы тяжести m реакции опоры 1, 2 и силы трения тр1, тр2.
Так как перемещается относительно стенок угла только точка приложения сил трения, то работу совершают только силы трения. В связи с этим справедливо уравнение
Работы сил трения равны Aтp1 = -Fтp12πRn; Aтp2 = -Fтp12πRn, где n — число полных оборотов цилиндра до остановки, а силы трения определяются силами реакции опоры стенок на цилиндр: Fтp1 = μN1; Fтp2 = μN2.
Найдём силы реакции опоры.
По условию задачи цилиндр только вращается, его центр тяжести не движется, следовательно, векторная сумма сил, действующих на него, равна нулю:
m + 1 + 2 + тp1 + тp2 = 0.
В проекциях на оси ОХ и OY имеем
Fтp1 — N2 = 0; (2)
N1 + Fтp2 — mg = 0. (3)
Подставив в уравнения (2) и (3) выражения для сил трения, получим
μN1 — N2 = 0; (4)
N1 + μN2 — mg = 0. (5)
Решая систему уравнений (4) и (5), найдём силы реакции опоры:
Тогда число оборотов до остановки цилиндра
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Законы сохранения в механике — Физика, учебник для 10 класса — Класс!ная физика
Импульс материальной точки — Закон сохранения импульса — Реактивное движение. Успехи в освоении космоса — Примеры решения задач по теме «Закон сохранения импульса» — Механическая работа и мощность силы — Энергия. Кинетическая энергия — Примеры решения задач по теме «Кинетическая энергия и её изменение» — Работа силы тяжести. Консервативные силы — Работа силы упругости. Консервативные силы — Потенциальная энергия — Закон сохранения энергии в механике — Работа силы тяготения. Потенциальная энергия в поле тяготения — Примеры решения задач по теме «Закон сохранения механической энергии» — Основное уравнение динамики вращательного движения — Закон сохранения момента импульса. Кинетическая энергия абсолютно твёрдого тела, вращающегося относительно неподвижной оси — Примеры решения задач по теме «Динамика вращательного движения абсолютно твёрдого тела»
class-fizika.ru
