Физика тема механика – «Раздел 1. Механика Тема 1.1. Кинематика. Механика. Механическое движение. Кинематика Механика – раздел физики, в котором изучается механическое движение.». Скачать бесплатно и без регистрации.

Введение

Министерство транспорта Российской Федерации

Федеральное агентство железнодорожного транспорта

Омский государственный университет путей сообщения

__________________

С. Н. Крохин

Краткий курс механики

Утверждено редакционно-издательским советом университета

в качестве программы и методических указаний по изучению курса «Физика»

для студентов заочной формы обучения

Омск 2006

УДК 530.1(075.8)

ББК 22.3

К83

Краткий курс механики: Программа и методические указания по изучению курса «Физика» / С. Н. Крохин; Омский гос. ун-т путей сообщения. Омск, 2006. 25 с.

Методические указания содержат рабочую программу раздела «Механика» дисциплины «Физика» и краткое теоретическое изложение основныхвопросов этого раздела.

Приведены определения физических величин, их единицы измерения в системе СИ, законы классической механики.

предназначены для самостоятельной работы студентов заочной формы обучения.

Библиогр.: 4 назв. Рис. 7.

Рецензенты: доктор техн. наук, профессор В. А. Нехаев;

канд. физ.-мат. наук, доцент В. И. Струнин.

________________________

© Омский гос. университет

путей сообщения, 2006

О Г Л А В Л Е Н И Е

Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5

1. Рабочая программа дисциплины «Физика». Механика . . . . . . . . . . . . . . . . 6

2. Кинематика и динамика материальной точки. . . . . . . . . . . . . . . . . . . . . . . . 7

3. Кинематика и динамика вращения твердого тела вокруг

неподвижной оси . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14

4. Законы сохранения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .18

Библиографический список. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24

Механика – раздел физики, изучающий закономерности механического движения и причины, вызывающие или изменяющие это движение. Механическое движение есть во всех высших и более сложных формах движения материи (химических, биологических и др.). Эти формы движения изучаются другими науками (химией, биологией и др.).

В основных учебных пособиях [1 – 4] вопросы по изучению механического движения излагаются подробно, зачастую с громоздкими математическими выкладками, что существенно затрудняет самостоятельную работу студентов.

В методических указаниях даны рабочая программа раздела «Механика», определения физических понятий, кратко излагаются основные физические законы и закономерности классической механики, приводится запись этих законов в математической форме.

В разделе «Механика» рассматриваются кинематика и динамика материальной точки, кинематика и динамика вращения твердого тела вокруг неподвижной оси и законы сохранения.

Для изучения раздела «Механика» необходимы знания из математики: элементов векторной алгебры (проекция вектора на ось, скалярное и векторное произведение и т. п.), дифференциального и интегрального исчисления (вычисление простейших производных и нахождение первообразных).

В методических указаниях из-за ограничений по объему издания не отражен экспериментальных материал.

Данные методические указания помогут студентам в самостоятельном изучении курса механики в период экзаменационной сессии.

1. Рабочая программа дисциплины «физика»

МЕХАНИКА

1. Относительность механического движения. Система отсчета. Материальная точка (частица). Радиус-вектор. Траектория. Путь и перемещение. Скорость и ускорение.

2. Прямолинейное и криволинейное движение частицы. Касательное (тангенциальное) и нормальное ускорение.

3. Инерция. Инерциальные системы отсчета. Первый закон Ньютона. Сложение скоростей и принцип относительности в классической механике.

4. Взаимодействие тел. Сила. Инертность. Масса, плотность. Второй и третий законы Ньютона.

5. Силы в механике: гравитационная, тяжести, упругости, вес, выталкивающая, трения (покоя, скольжения, качения, вязкое).

6. Движение тела в поле силы тяжести. Свободное падение. Движение тела под действием нескольких сил. Равнодействующая.

7. Абсолютно твердое тело (АТТ). Центр инерции (центр масс) АТТ и закон его движения. Поступательное и вращательное движение АТТ. Система центра инерции.

8. Угловое перемещение, угловая скорость и угловое ускорение. Связь между кинематическими характеристиками поступательного и вращательного движения.

9. Момент силы. Момент инерции. Теорема Штейнера. Основное уравнение динамики вращательного движения.

10. Изолированная система. Импульс (количество движения) тела. Закон сохранения импульса.

11. Момент импульса (момент количества движения). Собственный момент импульса. Закон сохранения момента импульса.

12. Механическая работа, мощность. Работа постоянной и переменной силы. Работа момента сил при вращательном движении.

13. Кинетическая энергия. Консервативные силы. Потенциальная энергия. Полная механическая энергия. Закон сохранения энергии в механике. Диссипация энергии. Общефизический закон сохранения энергии.

14. Абсолютно упругое и абсолютно неупругое столкновение частиц.

15. Простые механизмы: наклонная плоскость, блок, рычаг. «Золотое правило» механики. КПД механизма.

studfiles.net

Механика — Механика — Темы по физике — Каталог лекций

Определение

---

Механикой называется часть физики, изучающая движение и взаимодействие материальных тел. При этом механическое движение рассматривается как изменение с течением времени взаимного положения тел или их частей в пространстве.

Основоположниками классической механики являются Г. Галилей (1564–1642) и И. Ньютон (1643–1727). Методами классической механики изучается движение любых материальных тел (кроме микрочастиц) со скоростями, малыми по сравнению со скоростью света в вакууме. Движение микрочастиц рассматривается в квантовой механике, а движение тел со скоростями, близкими к скорости света – в релятивистской механике (специальной теории относительности).

Свойства пространства и времени, принятые в классической физике

---

Пространство	Время
1. Трёхмерное 2. Евклидовое 3. Однородное 4. Изотропное 5. Континуальное	1. Одномерное 2. Евклидовое 3. Однородное 4. Необратимое 5. Континуальное

Дадим определения вышеуказанным определениям.
Одномерное пространство — параметрическая характеристика, в которой положение точки описывается одним параметром.
Евклидово пространство и время означает, что сами по себе они не искривлены и описываются в рамках евклидовой геометрии.
Однородность пространства означает, что его свойства не зависят от расстояния до наблюдателя. Однородность времени означает, что оно не растягивается и не сжимается, а течет равномерно. Изотропность пространства означает, что его свойства не зависят от направления. Поскольку время одномерно, то об изотропности его говорить не приходится. Время в классической механике рассматривается как «стрела времени», направленная из прошлого в будущее. Оно необратимо: нельзя вернуться в прошлое и что-то там «подправить».
Пространство, и время континуальны (от лат. continuum – непрерывное, сплошное), т.е. их можно дробить на все более мелкие части сколь угодно долго. Иначе говоря, в пространстве и времени нет «прорех», внутри которых они бы отсутствовали. Механику делят на Кинематику и Динамику

---

Кинематика изучает движение тел как простое перемещение в пространстве, вводя в рассмотрение так называемые кинематические характеристики движения: перемещение, скорость и ускорение.

При этом скорость материальной точки рассматривается как быстрота ее перемещения в пространстве или, с математической точки зрения, как векторная величина, равная производной по времени ее радиус вектора:

---

Ускорение материальной точки рассматривается как быстрота изменения ее скорости или, с математической точки зрения, как векторная величина, равная производной по времени ее скорости или второй производной по времени ее радиус-вектора:

---

Динамика

---

Динамика изучает движение тел в связи с действующими на них силами, оперируя так называемыми динамическими характеристиками движения: массой, импульсом, силой и др.

При этом масса тела рассматривается как мера его инерции, т.е. сопротивляемости по отношению к действующей на данное тело силе, стремящейся изменить его состояние (привести в движение или, наоборот, остановить, или изменить скорость движения). Масса может рассматриваться также как мера гравитационных свойств тела, т.е. его способности взаимодействовать с другими телами, также обладающими массой и находящимися на некотором расстоянии от данного тела. Импульс тела рассматривается как количественная мера его движения, определяемая как произведение массы тела на его скорость: Сила рассматривается как мера механического действия на данное материальное тело со стороны других тел.

[Если Нет рекламы, то отключи AdBlock]

mgh.do.am

2. Механика. Механическое движение.

Понятие механики. Механика – это часть физики, в которой изучают движение тел, взаимодействие тел или, движение тел под каким-либо взаимодействием.

Главная задача механики – это определение местоположения тела в любой момент времени.

Разделы механики: кинематика и динамика. Кинематика – это раздел механики, изучающий геометрические свойства движений без учета их масс и действующих на них сил. Динамика – это раздел механики, изучающий движение тел под действием приложенных к ним сил.

Движение. Характеристики движения. Движение – это изменение положения тела в пространстве с течением времени относительно других тел. Характеристики движения: пройденный путь, перемещение, скорость, ускорение.

Механическое движение – это изменение положение тела (или его частей) в пространстве относительно других тел с течением времени.

Поступательное движение. Демонстрируется видеопоказом с объяснениями.

Равномерное движение тела. Демонстрируется видеопоказом с объяснениями.

Неравномерное механическое движение – это движение, при котором за равные промежутки времени тело совершает неравные перемещения.

Относительность механического движения. Демонстрируется видеопоказом с объяснениями.

Точка отсчёта и система отсчёта в механическом движении. Тело, относительно которого рассматривается движение, называется точкой отсчёта. Система отсчёта в механическом движении – это точка отсчёта и система координат и часами.

Система отсчета. Характеристики механического движения. Система отсчета демонстрируется видеопоказом с объяснениями. Механическое движение имеет характеристики: Траектория; Путь; Скорость; Время.

Траектория прямолинейного движения – это линия, вдоль которой движется тело.

Криволинейное движение. Демонстрируется видеопоказом с объяснениями.

Путь и понятие скалярной величины. Демонстрируется видеопоказом с объяснениями.

Физические формулы и единицы измерения характеристик механического движения:

Обозначение величины	Единицы измерения величины	Формула для определения величины
Путь-s	м, км	S = vt
Время- t	с, час	T = s/v
Скорость —v	м/с, км/ч	V = s/t

Понятие ускорения. Раскрывается демонстрацией видеопоказа, с объяснениями.

Формула для определения величины ускорения:

3. Законы динамики Ньютона.

Великий физик И. Ньютон. И. Ньютон развенчал античные представления, что законы движения земных и небесных тел совершенно различны. Вся Вселенная подчинена единым законам, допускающим математическую формулировку.

Две фундаментальные задачи, решенные физикой И. Ньютона:

1. Создание для механики аксиоматической основы, которая перевела эту науку в разряд строгих математических теорий.

2. Создание динамики, связывающей поведение тела с характеристиками внешних воздействий на него (сил).

Законы динамики И. Ньютона в его авторской редакции:

1. Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

2. Изменение количества движения пропорционально приложенной силе и происходит по направлению той прямой, по которой эта сила действует.

3. Действию всегда есть равное и противоположное противодействие, иначе, взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны.

Первый закон динамики И. Ньютона. Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние.

Понятия инерции и инертности тела. Инерция – это явление, при котором тело стремится сохранить свое первоначальное состояние. Инертность – это свойство тела сохранять состояние движения. Свойство инертности характеризуется массой тела.

Развитие Ньютоном теории механики Галилея. Долгое время считалось, что для поддержания любого движения необходимо осуществлять нескоменсированное внешнее воздействие со стороны других тел. Ньютон разбил эти убеждения, выведенные Галилеем.

Инерциальная система отсчета. Системы отсчёта, относительно которых свободное тело движется равномерно и прямолинейно, называются инерциальными.

Первый закон Ньютона – закон инерциальных систем. Первый закон Ньютона – это постулат о существовании инерциальных систем отсчёта. В инерциальных системах отсчёта механические явления описываются наиболее просто.

Второй закон динамики И. Ньютона. В инерциальной системе отсчёта прямолинейное и равномерное движение может происходить только в том случае, если на тело не действуют другие силы или действие их скомпенсировано, т.е. уравновешено. Демонстрируется видеопоказом с объяснениями.

Принцип суперпозиции сил. Демонстрируется видеопоказом с объяснениями.

Понятие массы тела. Масса – одна из самых фундаментальных физических величин. Масса характеризует сразу несколько свойств тела и обладает рядом важных свойств.

Сила — центральное понятие второго закона Ньютона. Второй закон Ньютона определяет, что тело тогда будет двигаться с ускорением, когда на него действует сила. Сила – мера взаимодействия двух (или больше) тел.

Два вывода классической механики из второго закона И. Ньютона:

1. Ускорение тела напрямую связано с приложенной к телу силой.

2. Ускорение тела напрямую связано с его массой.

Демонстрация прямой зависимости ускорения тела от его массы

Третий закон динамики И. Ньютона. Демонстрируется видеопоказом с объяснениями.

Значение законов классической механики для современной физики. Механика, основанная на законах Ньютона, называется классической механикой. В рамках классической механики хорошо описывается движение не очень маленьких тел с не очень большими скоростями.

Демонстрации:

Физические поля вокруг элементарных частиц.

Планетарная модель атома Резерфорда и Бора.

Движение, как физическое явление.

Поступательное движение.

Равномерное прямолинейное движение

Неравномерное относительное механическое движение.

Видеоанимация системы отсчета.

Криволинейное движение.

Путь и траектория.

Ускорение.

Инерция покоя.

Принцип суперпозиции.

2-й закон Ньютона.

Динамометр.

Прямая зависимость ускорения тела от его массы.

3-й закон Ньютона.

Контрольные вопросы:.

1. Сформулируйте определение и научный предмет физики.

2. Сформулируйте физические свойства, общие для всех явлений природы.

3. Сформулируйте основные этапы эволюции физической картины мира.

4. Назовите 2 основных принципа современной науки.

5. Назовите особенности механистической модели мира.

6. В чем суть молекулярно-кинетической теории.

7. Сформулируйте основные признаки электромагнитной картины мира.

8. Объясните понятие физического поля.

9. Определите признаки и различия электрического и магнитного полей.

10. Объясните понятия электромагнитного и гравитационного полей.

11. Объясните понятие «Планетарная модель атома»

12. Сформулируйте признаки современной физической картины мира.

13. Сформулируйте основные положения современной физической картины мира.

14. Объясните значение теории относительности А. Эйнштейна.

15. Объясните понятие: «Механика».

16. Назовите основные разделы механики и дайте им определения.

17. Назовите основные физические характеристики движения.

18. Сформулируйте признаки поступательного механического движения.

19. Сформулируйте признаки равномерного и неравномерного механического движения.

20. Сформулируйте признаки относительности механического движения.

21. Объясните смысл физических понятий: «Точка отсчёта и система отсчёта в механическом движении».

22. Назовите основные характеристики механического движения в системе отсчета.

23. Назовите основные характеристики траектории прямолинейного движения.

24. Назовите основные характеристики криволинейного движения.

25. Дайте определение физическому понятию: «Путь».

26. Дайте определение физическому понятию: «Скалярная величина».

27. Воспроизведите физические формулы и единицы измерения характеристик механического движения.

28. Сформулируйте физический смысл понятия: «Ускорение».

29. Воспроизведите физическую формулу для определения величины ускорения.

30. Назовите две фундаментальные задачи, решенные физикой И. Ньютона.

31. Воспроизведите основные смыслы и содержание первого закона динамики И. Ньютона.

32. Сформулируйте физический смысл понятия инерции и инертности тела.

33. В чем проявилось развитие Ньютоном теории механики Галилея.

34. Сформулируйте физический смысл понятия: «Инерциальная система отсчета».

35. Почему первый закон Ньютона это закон инерциальных систем.

36. Воспроизведите основные смыслы и содержание второго закона динамики И. Ньютона.

37. Сформулируйте физические смыслы принципа суперпозиции сил, выведенного И. Ньютоном.

38. Сформулируйте физический смысл понятия массы тела.

39. Обоснуйте, что сила является центральным понятием второго закона Ньютона.

40. Сформулируйте два вывода классической механики на основании второго закона И. Ньютона.

41. Воспроизведите основные смыслы и содержание третьего закона динамики И. Ньютона.

42. Объясните значение законов классической механики для современной физики.

Литература:

1. Ахмедова Т.И., Мосягина О.В. Естествознание: Учебное пособие / Т.И. Ахмедова, О.В. Мосягина. – М.: РАП, 2012. – С. 34-37.

studfiles.net

Механика. Конспекты по физике для 10-11 класса. Знаете ли вы? Гравитация :: Класс!ная физика

Для тех, кто хочет хорошо знать физику!
Тесты — задачи по кинематике для 10-11 класса

Здесь представлены конспекты по теме «Механика» для 10-11 классов.
!!! Конспекты с одинаковыми названиями различаются по степени сложности.

1. Гидростатика  ( повторение 7-8 класса)

2. Гидростатика и гидродинамика

3. Законы Ньютона — Механика.

4. Законы сохранения в механике — Механика.

5. Законы сохранения в механике — Механика.

6. Кинематика материальной точки — Механика.

7. Кинематика материальной точки — Механика.

8. Механические колебания 

9. Механические колебания

10. Основные понятия кинематики (повторение 8-9 класса)

11. Основные понятия кинематики

12. Работа и энергия

13. Работа и энергия

14. Силы в механике

15. Силы в механике

16. Статика

 

Механика, законы, конспекты, конспекты по физике, законы сохранения, работа, энергия, силы.

 

ГРАВИТАЦИЯ. ЗНАЕТЕ ЛИ ВЫ?

Знаете ли Вы, что Кеплер задолго до Ньютона склонялся к мысли о «тяжести», действующей между небесными телами, и именно ею объяснил приливы, приписывая их притяжению вод океана Луной.

… до сих пор существуют сомнения в реальности опытов Галилея по бросанию тел с вершины Пизанской падающей башни. Однако известно, что еще при его жизни эту башню использовал один из сторонников Аристотеля для демонстрации различия в падении тел. Как бы то ни было, Галилею удалось установить независимость ускорения свободного падения от природы падающих тел.

… по Аристотелю, сила тяготения по мере приближения к центру Земли сохраняет численное значение, но при его прохождении скачком изменяет направление на противоположное. Именно так описывал Данте свое путешествие через самое глубокое место ада (центр Земли). По теории же Ньютона, сила притяжения должна там обратиться в ноль, поскольку им было показано, что помещенное в тонкую сферическую оболочку тело не испытывает на себе действия сил.

… почти 200 лет назад, в 1801 году, немецкий астроном И.Зольднер рассчитал, опираясь на теорию Ньютона, как должны отклоняться световые лучи в поле тяготения Солнца. Более чем через 100 лет английский астроном О.Лодж ввел термин «гравитационная линза», предсказав, что протяженные космические тела, например галактики, отклоняя лучи от далеких объектов, могут создавать несколько их изображений. В 1979 году такая «линза» была впервые обнаружена.

… на поверхности внутренних спутников Юпитера кратеров намного меньше, чем на поверхности внешних. Объясняется это тем, что из-за приливного влияния и магнитного поля гигантской планеты у ближайших спутников выше тектоническая активность, поэтому их поверхность активно «перерабатывается» и старые кратеры исчезают.

… несмотря на то, что на Землю ежесуточно выпадает примерно десять тысяч тонн космического вещества в виде метеоритов и пыли, такой прирост массы за все время эволюции нашей планеты практически не отразился на периоде ее оборота вокруг своей оси.

… под действием приливного «трения» Земля замедляет свое суточное вращение и через миллиарды лет будет смотреть на Луну все время одной стороной, как смотрит Плутон на свой спутник Харон. Луна к тому времени уйдет, по расчетам, на 553 тысячи километров от Земли, а новый месяц станет равным 47,2 суток.

… по теории относительности, переменное движение тел должно приводить к излучению гравитационных волн. Однако из-за слабости гравитационного взаимодействия зарегистрировать эти волны даже от мощных космических источников пока еще не удалось. Кстати, действие их приемников основано на приливном эффекте.

… к черным дырам — объектам, удерживающим своим чудовищным гравитационным полем даже свет, — теория тяготения Ньютона не применима, хотя сама возможность их существования вытекает из этой теории.

… при свободном падении, ногами вниз, на черную дыру гипотетический наблюдатель растягивался бы в длинную тонкую нить, так как его ноги двигались бы несравненно быстрее, чем голова, и в конце концов он был бы разорван приливными силами невероятной мощи.

… разрушающее действие приливных сил было «продемонстрировано» Юпитером, развалившим в июле 1992 года проходившую в опасной для себя близости к нему комету.

… в 1932 году будущий академик Лев Ландау предсказал, что при смерти (гибели) массивной звезды ее центральная часть сжимается в одно гигантское атомное ядро — нейтронную звезду, удерживаемую силами гравитации. Плотность такого образования должна достигать 100 миллионов тонн на кубический сантиметр! 35 лет спустя нейтронные звезды были открыты английскими радиоастрономами.

… долгие годы астрономы безуспешно искали так называемую скрытую массу Вселенной, предотвращающую своим гравитационным полем разлет галактик из их скоплений и тормозящую расширение Вселенной. Однако, по последним данным, никакая сила тяготения не заставит повернуть назад стремительно разбегающиеся галактики. Вселенная ускоренно расширяется, и этот процесс продлится вечно.

Источник: журнал «Квант»

class-fizika.narod.ru

Физика. Механика

Южный филиал

«Крымский агротехнологический университет»

Национального аграрного университета

Физика. Механика

Методические указания и задания для самостоятельной работы очного и заочного отделений инженерных специальностей

(модуль I, часть 2)

Симферополь, 2008

Методические указания составили:

— доцент, к.т.н. Ю.Ф. Свириденко;

— старший преподаватель В.П. Кунцов.

Рецензенты:

— доцент, к.т.н. Завалий А.А.;

— доцент, к.т.н. Иваненко В.В.

Методические указания рассмотрены и одобрены на заседании кафедры физики и математики

« 24 » марта 2008г., протокол № 7

Методические указания рассмотрены и утверждены на заседании методического совета механического факультета

« 31 » марта 2008г., протокол № 7

Ответственный за выпуск: Ю.Ф. Свириденко

Содержание

1.Тематический план.

2.Литература

3.Правила выполнения и оформления контрольных работ

4.Учебный материал по разделу «Механика»

5.Примеры решения задач

6.Контрольная работа

7.ТАБЛИЦЫ ВАРИАНТОВ

1. ТЕМАТИЧЕСКИЙ ПЛАН.

Содержание программы Часть 1.

Лекции

механика сила движение импульс

2. Литература

1. Трофимова Т.И., Курс физики. — М.:Высш.шк.,1990.

2. Детлав А.А.,Яворский Б.М.Курс физики.,1989.

3. Чолпан П.П. Основы фізики.-К.:Вища шк.,1995.

4. Федишин Я.І.Лабораторний практикум з фізики.-Львів:Світ,2001.

5. Грабовский Р.И. Курс физики для сельскохозяйственных институтов. М., 1966 и последующие издания.

6. .Чертов А.Г. и др. Задачник по физике. М., 1973.

7. Бурдун Г.Д. Справочник по Международной системе единиц. М., 1972

8. Чертов А.Г. Единицы физических величин. М., 1977.

3. Правила выполнения и оформления контрольных работ

1. Каждая работа, присланная на рецензию, должна быть выполнена в отдельной ученической тетради, на обложке которой нужно указать фамилию, инициалы, полный шифр, номер контрольной работы, дату ее отправки, в институт и адрес студента.

2. Задачи контрольной работы должны иметь те номера, под которыми они стоят в методических указаниях. Условия задач необходимо переписывать полностью. Каждую задачу начинать с новой страницы. Для замечаний рецензента следует оставлять поля шириной 4-5 см. Контрольные работы выполняются чернилами синего или фиолетового цвета.

3. Решение задачи должно быть кратко обосновано с использованием законов и положений физики. При необходимости решение следует пояснить чертежом, выполненным карандашом с помощью циркуля и линейки. Обозначения на чертеже и в решении должны соответствовать и поясняться. Не следует обозначать одну и ту же величину разными буквами, а также обозначать различные величины одними и. теми же символами.

4. На каждую контрольную работу требуется 20-30 часов интенсивного труда. Если, несмотря на собственные усилия и полученные консультации, отдельные задачи не решаются, оформите работу, приведя в соответствующих местах ваши попытки решения, изложив коротко ваши соображения и затруднения. Пусть такая работа не будет зачтена, но критические замечания рецензента, его пояснения, ссылки на литературу или письменные консультации по решению конкретных задач помогут вам найти правильное решение.

Во время лабораторно-экзаменационной сессии вам предложат пояснить ход решения задач, входящих в контрольные работы, физический смысл встречающихся в решениях величин, применяемые при вычислениях единицы и т.п. Неудовлетворительные ответы на вопросы по контрольным работам могут повлиять на исход зачета или экзамена.

5. Как правило, задачи решаются в общем виде, т.е. в буквенных выражениях, без вычисления промежуточных величин. Числовые значения подставляются только в окончательную (расчетную) формулу. Если расчетная формула не выражает общеизвестный физический закон, то ее следует вывести. После получения расчетной формулы необходимо: а) пояснить величины, входящие в формулу; б) проверить расчетную формулу, для чего подставить в нее обозначения единиц, входящих в формулу величин, и убедиться, что единицы правой и левой частей формулы совпадают; в) выразить все величины в СИ и выписать их числовые значения в виде столбика; г) подставить в расчетную формулу числовые значения величин и произвести вычисления.

6. Не следует направлять на рецензию обе работы вместе. Вторая работа посылается только после получения рецензии на первую. Одновременная посылка двух контрольных работ расценивается как признак несамостоятельного их выполнения.

7. Получив проверенную работу (как зачтенную, так и незачтенную), студент обязан тщательно изучить все замечания рецензента, уяснить свои ошибки и внести исправления. Повторно оформленная работа высылается на рецензию обязательно вместе с тетрадью, в которой была выполнена незачтенная работа и рецензия на нее.

Замечания и рекомендации, сделанные преподавателями кафедры, следует рассматривать как руководство для подготовки к беседе по решениям задач. Все тетради с контрольными работами нужно сохранять, так как на экзамен студент допускается только при их предъявлении.

8. В конце работы необходимо указать год и место издания методических указаний, перечислить использованную литературу, обязательно указывая авторов учебников и год их издания. Это позволит рецензенту при необходимости дать ссылку на определенную страницу того пособия, которое имеется у вас.

4. Учебный материал по разделу «Механика»

Основные законы и формулы

5.Примеры решения задач

mirznanii.com

МЕХАНИКА | Энциклопедия Кругосвет

Содержание статьи

МЕХАНИКА, раздел физики, в котором изучается движение тел под действием сил. Механика охватывает очень широкий круг вопросов – в ней рассматриваются объекты от галактик и систем галактик до мельчайших, элементарных частиц вещества. В этих предельных случаях выводы механики представляют, конечно, чисто научный интерес. Но предметом механики является также проектирование строений, мостов и механизмов; этот раздел, обычно называемый прикладной механикой, сам по себе достаточно обширен.

Фундаментальное значение для всей этой тематики имеет механика материальной точки, разделяющаяся на кинематику, предметом которой является математическое описание возможных движений материальной точки, и динамику, которая рассматривает движение материальных точек под действием заданных сил. Основные принципы динамики сведены в законы движения, которые в случае материальных точек имеют самый простой вид. Эти законы были впервые сформулированы в 1687 И.Ньютоном. Если материальные точки движутся с очень большими скоростями, то ньютоновские законы движения следует модифицировать в соответствии с теорией относительности; если же это частицы атомных масштабов, то необходима иная формулировка законов движения – так называемая квантовая механика. Ниже будет изложена ньютоновская механика; ее модификациям посвящены статьи ОТНОСИТЕЛЬНОСТЬ; КВАНТОВАЯ МЕХАНИКА.

Протяженное тело можно формально рассматривать как совокупность идеализированных материальных точек, совершенно не имея в виду атомное строение вещества. Выводы о движении таких тел можно делать, исходя из совокупности движений материальных точек. Здесь тоже проводится различие между кинематикой и динамикой и, кроме того, существует статика, изучающая условия равновесия твердых тел, на которые действуют внешние силы. Эти вопросы обсуждаются ниже.

Механические свойства газов и жидкостей в какой-то мере сходны, и законы, которым подчиняется их движение, тоже можно вывести, рассматривая их как системы материальных точек. Этот раздел, обычно называемый «механикой жидкостей и газов», подразделяется на гидростатику и гидродинамику. Им посвящена статья ГИДРОАЭРОМЕХАНИКА. Специальные вопросы течения газов рассматриваются в статье АЭРОДИНАМИКА, а вопросы движения электропроводящих жидкостей и газов – в статье МАГНИТНАЯ ГИДРОДИНАМИКА. Остаются еще три специальных раздела – аналитическая динамика, небесная механика и статистическая механика. Аналитическая динамика – это математическая дисциплина, в центре внимания которой находятся общие методы составления уравнений движения и их решения, а не анализ конкретных механических систем. В небесной механике методы аналитической динамики применяются при изучении чрезвычайно сложного движения планетных систем. Статистическая механика опирается на теорию газов и рассматривает в общем виде поведение системы, содержащей огромное число молекул или атомов, исходя из свойств таких отдельных частиц и законов, управляющих их поведением. По этим вопросам имеются отдельные статьи НЕБЕСНАЯ МЕХАНИКА; СТАТИСТИЧЕСКАЯ МЕХАНИКА.

Подобное деление механики отражает историческое развитие физики и, кроме того, соответствует использованию различных математических методов. В конечном итоге механика и физика как наука составляют единое целое, ибо чем больше мы узнаем, например, о таких явлениях, как свет и электричество, которые обычно не рассматриваются в механике, тем яснее становится их фундаментальная связь с атомными явлениями, тесно связанными с механикой.

Исторически развитие статики началось с Архимеда в 3 в. до н.э. До этого периода и много столетий спустя проблемы динамики обсуждались лишь с качественной стороны и соотносились с принципами, которые мы полагаем сегодня ошибочными либо не имеющими отношения к делу. Начало динамике было положено Ньютоном, который сформулировал законы движения и закон всемирного тяготения, опубликованные в первом издании Математических начал натуральной философии (Philosophiae naturalis principia mathematica, 1687). Ньютону удалось в своей книге заложить основы, а в ряде случаев и далеко продвинуться в изучении динамики, небесной механики, механики твердого тела, гидродинамики и баллистики. Хотя принципы статики к тому времени были хорошо известны, Ньютон впервые рационально обосновал их, показав, как их можно вывести из законов динамики. На протяжении примерно двух столетий после этого механика развивалась путем построения более совершенных математических методов без необходимости внесения каких-либо изменений в основные принципы, и лишь после 1900 развитие теории электромагнетизма и атомной физики потребовало модификации механики для распространения ее принципов на явления, которые она не могла удовлетворительно описывать. Но теория относительности и квантовая механика не отменили ньютоновской теории – она по-прежнему точна, как и раньше, и можно показать, что она строго вытекает из обеих новых теорий в том случае, когда рассматриваемые тела имеют макроскопические размеры и движутся с умеренными скоростями. В остальной части этой статьи мы будем иметь дело только с такими ситуациями.

Механика материальной точки.

Чтобы можно было описывать движение материальной точки, нужно определить ее положение в данный момент. На рис. 1 показана прямоугольная система координат, которая позволяет характеризовать положение материальной точки, находящейся в точке Р, координатами (x, y, z). Поскольку материальная точка не имеет размеров и, следовательно, не может быть ориентирована в том или ином направлении, эти три числа полностью характеризуют ее положение в любой момент. Если раcсматривать их как функции времени t, то функция [x (t), y(t), z (t)] прочерчивает в пространстве траекторию, полностью определяющую движение материальной точки. Основная задача динамики материальной точки – найти зависимость x, y и z от t, если заданы силы, действующие на материальную точку. (Возможна, конечно, задача о нескольких материальных точках, оказывающих силовое воздействие друг на друга; подобные задачи решаются труднее.)

Рассмотрим сначала материальную точку, движущуюся прямолинейно, скажем, вдоль оси x, в отсутствие каких-либо сил. В средневековой механике вслед за Аристотелем утверждалось, что тело движется, пока на него действует сила. Однако Галилей, а за ним и Ньютон установили, что единственное действие силы состоит в изменении движения тела и что в отсутствие силы тело либо остается в покое, либо продолжает двигаться равномерно и прямолинейно. В этом заключается первый закон механики Ньютона. Под равномерным движением подразумевается движение с постоянной скоростью v, при котором путь x, проходимый за время t, равен:

x = vt.

Точнее было бы формулировать это определение, рассматривая короткие интервалы пути и времени: если частица начинает двигаться из точки x₀ в момент времени t₀ и достигает точки х в момент t, то средняя скорость за это время определяется как

Конечно, если материальная точка движется с постоянной скоростью, то нет необходимости говорить о среднем значении. Но если на материальную точку действует сила, то ее движение не является равномерным. В этом случае скорость меняется во времени, и можно говорить о мгновенной скорости v (t) в момент времени t как пределе представленного выше выражения при очень малых интервалах времени и пути. Это записывается следующим образом:

Точно так же можно говорить об изменении скорости во времени, т.е. об ускорении. Если мгновенная скорость изменяется от v₀ в момент t₀ до vв момент t, то среднее ускорение за этот промежуток определяется как

а мгновенное ускорение в момент времени t –

Таким образом, скорость характеризует быстроту изменения положения, а ускорение – быстроту изменения скорости. Рассматривать скорость изменения ускорения и т.д. не имеет особого смысла, поскольку, как это первым понял Ньютон, сила создает лишь ускорение. Действительно, если к небольшому телу приложена сила F, то, как показывает опыт, его ускорение остается постоянным, если сила постоянна, и в любой момент времени ускорение пропорционально этой силе. Данное положение можно записать в виде a ~ F или F ~ a. В этом соотношении коэффициент пропорциональности m есть величина, постоянная для рассматриваемой частицы независимо от того, где и как она движется. Эта величина m называется массой (инертной массой) частицы, и, следовательно, равенство

F = ma

есть установленное опытным путем соотношение между мгновенными значениями величин F и a. В этом суть второго закона Ньютона. Третий закон, который мы приведем в дальнейшем, относится к случаю, когда имеется более одного тела.

Единицы измерения механических величин вводятся следующим образом. На основе эталонов единиц длины и времени – метра и секунды – определяются единицы скорости – метр в секунду (м/с) и ускорения – метр в секунду в квадрате (м/с²). Единица массы килограмм (кг) определяется как масса международного прототипа килограмма, изготовленного из сплава иридия с платиной и хранящегося в Международном бюро мер и весов в Севре под Парижем. Единица силы в системе СИ называется ньютоном (Н) и определяется как сила, сообщающая телу массой 1 кг ускорение 1 м/с². Таким образом, согласно второму закону Ньютона,

1 H = 1 кгЧм/с².

Направление вектора ускорения совпадает с направлением вектора силы.

Тяготение.

Представленное выше определение единицы силы, основанное на незыблемых физических принципах, тем не менее, не удобно для практических измерений. Удобнее исходить из понятия веса, т.е. силы притяжения Земли. Согласно закону всемирного тяготения, сформулированному тоже Ньютоном, между любыми двумя телами во Вселенной действует сила притяжения, пропорциональная произведению масс этих тел и обратно пропорциональная квадрату расстояния между ними. Это положение математически выражается соотношением

где G – универсальная гравитационная постоянная, а m_G и M_G – гравитационные массы тел. Если тела протяженные, то все материальные точки этих тел попарно взаимодействуют друг с другом в соответствии с этой формулой и, чтобы найти полную силу, нужно суммировать все отдельные взаимодействия. В чрезвычайно важном случае тел сферической формы оказывается, что притяжение будет в точности таким, как если бы масса каждого из них находилась в центре сферы.

Предположим теперь, что телу с гравитационной массой m_G и инертной массой m, удерживаемому не очень высоко над поверхностью Земли, предоставляется возможность свободно падать. Сила тяжести ускоряет тело вниз, и мы имеем

где M_G – гравитационная масса Земли, а R – ее радиус. Ускорение падающего тела можно записать в виде

где первый множитель не зависит от свойств тела. Экспериментально установлено, что ускорение несколько изменяется в разных точках на поверхности Земли, поскольку Земля не является идеальной сферой и к тому же вращается. Однако в данном месте оно в точности одно и то же для всех тел. Это означает, что величины m и m_G всегда и всюду пропорциональны, а при надлежащем выборе единиц измерения одинаковы. В таком случае нет необходимости различать гравитационную и инертную массы, и выражение для F_G приобретает вид

где

Аналогично выражению для ускорения a, ускорение силы тяжести g в любой точке дается формулой

Величина g составляет примерно 9,81 м/с² и позволяет определить массу Земли (5,97Ч10²⁴ кг) и ее среднюю плотность, в 5,5 раз превышающую плотность воды. Предположим, теперь, что вес тела равен W. Так как сила веса создает ускорение g, соотношение между массой, весом и ускорением приобретает вид

W = mg.

Между экватором и полюсами на поверхности земли величина g изменяется от 9,78 до 9,83 м/с². Соответственно этому изменяется и вес, но в одной точке вес двух тел с одинаковой массой всегда одинаков, и на этом опытном факте основан гораздо более удобный способ измерения массы и силы, нежели основанный на втором законе Ньютона. Массы двух тел равны, если в одном и том же месте равны их веса.

Импульс и энергия.

Импульс тела р определяется как произведение его массы на скорость:

p = mv.

Эта величина имеет важное значение. В самом деле, предположим, что два тела с массами m и M действуют друг на друга с силой, стремящейся ускорить оба тела. На рис. 2 такую силу создает пружина (происхождение силы может быть любым). Согласно третьему закону Ньютона, в любой момент времени сила, с которой масса m действует на массу M, равна по величине и противоположна по направлению силе, с которой масса M действует на m (действие равно противодействию). Предположим, что в момент времени t₀ скорости масс равны v₀ и V₀. Комбинируя выражение для ускорений со вторым законом Ньютона, мы найдем, что скорости изменяются в соответствии с выражениями

где F_m и F_M – силы, действующие на m и M. Поскольку эти силы равны и противоположно направлены, имеем

откуда, умножая на (t – t₀) получаем

Из этого равенства следует, что хотя отдельные импульсы изменяются, их сумма в момент времени t₀ равна их же сумме в момент t, т.е. в процессе всего движения остается постоянной. Это – так называемый закон сохранения импульса. Он универсален в том смысле, что справедлив независимо от природы сил и длительности их действия между телами.

Работа U, совершаемая силой, приложенной к движущемуся телу, определяется как произведение силы на расстояние:

U = F(x – x₀),

где (как и далее) точки x и x₀ должны выбираться достаточно близко друг к другу, чтобы силу F можно было считать постоянной. Воспользуемся тем, что, как легко доказать, точка, движущаяся с постоянным ускорением, проходит за время (t – t₀) такое же расстояние, как если бы все это время она двигалась со средней скоростью ¹/₂(v + v₀). Таким образом, из выражения для второго закона Ньютона вытекает:

или

Величина ¹/₂mv² называется кинетической энергией. Если обозначить ее через Т, то выражение

U = T – T₀

означает, что работа, совершаемая за любой малый промежуток времени, а следовательно (если просуммировать), и за любой произвольный промежуток времени, равна разности конечной и начальной кинетических энергий. Это положение справедливо независимо от того, какова сила и как она изменяется со временем, а также от того, каково расстояние, на котором она действует.

Путем точно таких же рассуждений можно показать, что тело, обладающее кинетической энергией Т, может совершить работу, равную T – T₀, если его Т уменьшится до величины T₀, или равную Т, если тело в конце останавливается. Таким образом, всю работу, совершенную над телом при его ускорении, можно снова получить, остановив тело. Поэтому движущееся тело можно рассматривать как «носителя» работы. Под энергией понимается способность совершать работу, а запасенная телом кинетическая энергия зависит только от его скорости (и массы) и не зависит от того, как эта скорость была приобретена.

Предположим, что тело массой m поднято на высоту h над поверхностью земли, а затем свободно падает. Если оно падает в течение времени t с постоянным ускорением g, то соотношение между g, h и t можно получить из правила для средних скоростей

где v – скорость, с которой тело ударяется о землю, причем мы положили v₀ = 0, поскольку до начала падения тело покоится. Вновь, поскольку v = gt, можно написать h = v²/2g, а умножив обе части равенства на mg, получим

mgh = ¹/₂mv².

Поскольку mg – вес тела, величина mgh есть работа по подъему тела на высоту h, а ¹/₂mv² – кинетическая энергия тела в момент достижения им земли, равная работе, которую тело может совершить при ударе. Анализируя весь процесс, мы видим, что работа по подъему тела, равная mgh, запасается телом в виде его потенциальной энергии перед тем, как оно начинает падать. По мере падения потенциальная энергия переходит в кинетическую, которая может снова перейти в работу, равную mgh, при ударе тела о землю. Когда тело окончательно приходит в состояние покоя, то на первый взгляд энергия исчезает. Но более тщательный анализ показывает, что она сохранилась в форме усилившегося молекулярного движения в месте падения, т.е. в форме звука и теплоты. В отличие от импульса, энергия принимает разные формы, но при переходе из одной формы в другую полное количество энергии не меняется. Это – так называемый закон сохранения энергии.

В качестве примера применения двух законов сохранения рассмотрим соударение двух шаровых маятников (рис. 3,а). Предположим, что шары маятников имеют одинаковую массу и изготовлены из абсолютно упругого материала. Это означает, что кинетическая энергия при ударе не рассеивается. Пусть V₁ – скорость первого маятника в момент, предшествующий соударению, и нам надо найти v₁ и v₂ – скорости сразу после удара.

При соударении энергия и импульс сохраняются, и мы имеем

Производя сокращения и возводя обе части второго равенства в квадрат, получаем

Эти соотношения могут выполняться одновременно только при v₁v₂ = 0. Таким образом, либо v₁ = 0, либо v₂ = 0, но не то и другое. Поскольку второй шар служит препятствием для первого, в нуль обратится v₁, и в силу закона сохранения импульса системы имеем v₂ = V₁. Первый шар останавливается, а второй движется со скоростью V₁, как показано на рис. 3,б.

Предположим теперь, что на второй шар нанесена мастика, так что при соударении шары прилипают друг к другу и дальше движутся вместе (рис. 3,в). В этом случае v₂ = v₁ и импульс по-прежнему сохраняется, так что

mV₁ = 2mv₁,

откуда v₁ = ¹/₂V₁, т.е. шары будут двигаться со скоростью, которая в два раза меньше начальной скорости первого шара. Начальное значение кинетической энергии равнялось T₁ = ¹/₂mV₁², а конечное значение 2 ґ¹/₂m(¹/₂V₁)² = ¹/₂T₁. Таким образом, кинетическая энергия, равная ¹/₂T₁, рассеивается, причем основная часть этой потери идет на деформацию и нагрев мастики и шаров.

Динамика и статика в трех измерениях.

Чтобы обобщить предыдущие результаты на случай трех измерений, потребуется ввести лишь еще один принцип, который заключается в том, что законы Ньютона справедливы для движения вдоль каждой оси координат независимо от движения по другим осям. Так, если пренебречь сопротивлением воздуха, снаряд вдоль оси z движется с замедлением (рис. 4), а вдоль горизонтальной оси – без внешних сил и без ускорения. Обозначим через t время полета. Половину этого времени снаряд поднимается, а остальное время опускается. Таким образом, его скорость по вертикали изменяется на v_0z за время ¹/₂t, так что

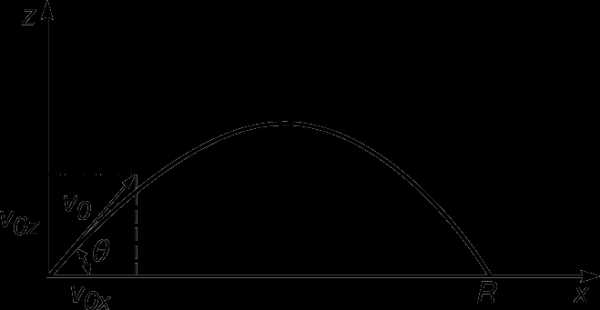
v_0z = ¹/₂gt, t = 2v_0z/g,

и все это время горизонтальное движение происходит со скоростью v_0x и без ускорения. Таким образом, дальность полета равна:

R = v_0xt = 2v_0xv_0z/g.

Если v₀ – начальная скорость, а q – угол возвышения, то легко понять, что v_0x = v₀cosq и v_0x = v₀sinq, так что

и максимальное значение этой величины, равное v₀²/g, достигается при q = 45°.

В приведенном примере начальная скорость v₀ характеризовалась и величиной, и направлением. Такие величины называются векторами, а величины v_0x и v_0z – соcтавляющими или компонентами вектора. (Обычно векторы обозначают полужирными буквами.) Предположим теперь, что в трехмерном пространстве к покоящейся материальной точке приложено несколько сил, под действием которых она остается в покое. О подобной системе сил говорят, что они уравновешены, и законы динамики позволяют определить, каким должно быть соотношение между ними. Если материальная точка покоится и сохраняет это состояние, ее ускорения вдоль осей x, y или z равны нулю, а поскольку ускорения вдоль этих осей не зависят друг от друга, полные силы в каждом из этих трех направлений тоже должны быть равны нулю. (Полная сила, действующая на материальную точку вдоль оси х и стремящаяся привести ее в движение вдоль этой оси, равна сумме x-компонент всех действующих сил; то же самое справедливо и для двух других осей.)

Предположим, что имеются только две силы с компонентами F_1x, F_1y, F_2x и F_2y (для упрощения рисунка ограничимся двумя измерениями). В случае равновесия имеем

F_1x + F_2x = 0 и F_1y + F_2y = 0,

или

F_1x = –F_2x и F_1y = –F_2y.

Так как F_1x и F_1y – компоненты вектора силы F₁, и аналогично F_2x и F_2y – компоненты вектора F₂, то возникает ситуация, показанная на рис. 5, где векторы двух уравновешивающих друг друга сил изображены равными по величине и направленными в противоположные стороны.

Предположим, теперь, что имеются три вектора, причем F₃ уравновешивает F₁ и F₂. В этом случае F_1x + F_2x + F_3x = 0, F_1y + F_2y + F_3y = 0.

Эти соотношения можно переписать в виде

F_1x + F_2x = –F_3x, F_1y + F_2y = –F_3y.

Сравнение с аналогичными соотношениями в случае двух сил показывает, что если мы введем новый вектор R с компонентами

R_x = F_1x + F_2x, R_y = F_1y + F_2y,

который называется равнодействующей сил F₁ и F₂, то R будет в точности уравновешивать F₃. Таким образом, сила R воспроизводит суммарное действие сил F₁ и F₂ в том смысле, что если удалить силы F₁ и F₂, заменив их силой R, то материальная точка по-прежнему останется бы в равновесии. Все сказанное представлено графически на рис. 6,а, где показано сложение компонент. На рис. 6,б вспомогательные линии убраны и оставлены только векторы. Последний рисунок называется параллелограммом сил. Он иллюстрирует один из фундаментальных принципов статики, который, как мы видели, является следствием динамической теории. Этот принцип был установлен С.Стевином (1548–1620), который показал, что если бы это было не так, то имелась бы возможность создать машину, которая производила бы работу, даже если бы к ней не подводилась энергия. Сегодня мы рассматривали бы такую машину как пример нарушения закона сохранения энергии; для Стевина это просто противоречило здравому смыслу, но при этом положения статики тоже обосновывались динамическими соображениями.

Механика твердого тела.

Твердое тело, которое может принимать различные ориентации в пространстве, можно считать состоящим из материальных точек. (Это просто математический прием, позволяющий расширить применимость законов движения материальных точек, но не имеющий ничего общего с гипотезой атомного строения вещества.) Поскольку материальные точки такого тела будут двигаться в разных направлениях с разными скоростями, приходится прибегать к процедуре суммирования.

Рассмотрим систему, изображенную на рис. 7. Сила F, приложенная к тросу, заставляет массу, имеющую форму цилиндра, изменять свою скорость вращения. Будем характеризовать ориентацию цилиндра углом q между радиусом, проведенным из центра цилиндра в некоторую точку на нем, и произвольно выбранным направлением отсчета. Угол q измеряется в радианах; один радиан (примерно 57°) есть центральный угол, стягивающий дугу длиной r на окружности радиуса r. Таким образом, произвольный угол q стягивает дугу s, равную rq, а вся окружность сoответствует углу 2p радиан. Скорость любой точки на окружности равна

где под q /t понимается скорость, с которой изменяется угол q при вращении. Обозначив эту угловую скорость через w, мы наряду с равенством

s = rq

получим

v = rw.

Нетрудно вычислить кинетическую энергию цилиндра, вращающегося вокруг неподвижной оси с угловой скоростью w. Обозначим через m одну из материальных точек цилиндра, расположенную на расстоянии r_m от оси. Ее кинетическая энергия равна ¹/₂m(r_mw)², а полная кинетическая энергия всех материальных точек может быть представлена в виде суммы

или

T = ¹/₂Iw²,

где . Величина I, называемая моментом инерции, зависит от распределения массы в цилиндре и является его характеристикой. Момент инерции можно вычислить путем интегрирования, и для однородного цилиндра он равен ¹/₂Ma², где M – масса цилиндра, а a – его радиус. Если цилиндр вращается свободно и нет сил, которые совершали бы над ним работу, то из закона сохранения энергии следует, что его кинетическая энергия остается постоянной. В таком случае постоянна и величина w, и мы имеем вращательный аналог первого закона Ньютона.

Предположим теперь, что к тросу, намотанному на цилиндр, на короткое время от t₀ до t прилагается сила F и за это время точка, отмеченная на тросе, проходит расстояние от x₀ до х, а цилиндр поворачивается на угол от q₀ до q, причем

x – x₀ = a(q –q₀).

Работа, совершенная при этом силой, равна:

U = F(x – x₀) = Fa(q – q₀),

и точно так же, как при выводе выражения U = ¹/₂mv² – ¹/₂mv₀², мы можем выразить угловое перемещение через среднюю угловую скорость на этом интервале:

q – q₀ = ¹/₂(w +w₀)(t – t₀),

так что

U = ¹/₂Fa(w +w₀)(t – t₀).

За счет этой работы кинетическая энергия цилиндра изменяется от T₀ до T , так что

U = ¹/₂ I(w²– w₀²).

Приравнивая два последних выражения и производя упрощения, получаем выражение

напоминающее формулу для ускорения частицы. Поэтому мы можем ввести угловое ускорение

и тогда для малого интервала от t₀ до t получим L = Ia, т.е. вращательный аналог второго закона Ньютона, в котором величина Fa, вызывающая вращение, обозначена через L. Она называется вращающим моментом.

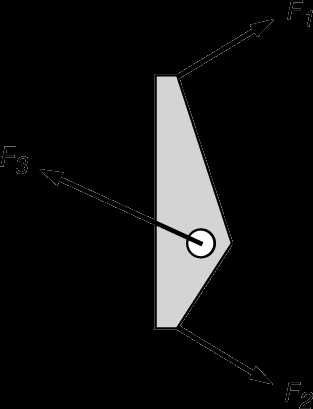
Изложенное можно обобщить на случай, когда отсутствуют неподвижные оси и тело свободно вращается в пространстве. В этом случае имеются три момента инерции, относящиеся к «главным осям». Мы не будем углубляться в рассмотрение этих вопросов. Однако можно вывести второй основной принцип статики для случая твердых тел. Пусть силы F₁ и F_2, приложенные к пластине, которая может вращаться, таковы, что вращения нет (рис. 8). Равновесие означает отсутствие углового ускорения, и поэтому полный вращающий момент равен нулю. Моменты сил F₁ и F₂ компенсируют друг друга при условии:

F₁a₁ = F₂a₂,

т.е. получается закон рычага, известный со времен Архимеда. Удалим ось и заменим ее действие третьей силой, как показано на рис. 9, предполагая, что весом пластины можно пренебречь. Для равновесия всех этих сил нужно, во-первых, чтобы пластина не перемещалась и, следовательно, компоненты сил удовлетворяли условию векторного равновесия и, во-вторых, чтобы не было вращения, т.е. выполнялось выведенное только что соотношение. Оба эти принципа составляют основу теории строительной механики и важны при проектировании мостов и зданий.

Проводившиеся выше рассуждения упрощаются, если пользоваться обозначениями математического анализа, в которых подразумевается предельный переход (t → t₀), так что нет необходимости все время говорить о нем. Ньютон первым применил методы дифференциального и интегрального исчисления при решении физических задач, а последующее развитие механики как науки было делом таких математиков, как Л.Эйлер, Ж.Лагранж, П.Лаплас и К.Якоби, каждый из которых находил в ньютоновской механике источник вдохновения для своих математических изысканий.

www.krugosvet.ru

Часть I. Основы механики и молекулярная физика

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ

РОССИСИЙСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

НЕФТИ И ГАЗА им. И.М. ГУБКИНА

Кафедра физики

ПОСОБИЕ

ДЛЯ ПОДГОТОВКИ К ЭКЗАМЕНАМ ПО КУРСУ ФИЗИКИ

Москва 2002

ОСНОВЫ МЕХАНИКИ.

Кинематика материальной точки и абсолютно твердого тела.

Тема 1. Кинематические характеристики движения.

1. Радиус-вектор. Вектор перемещения. Их выражение через декартовы координаты точки. Сделайте рисунок, укажите соответствующие векторы.

2. Скорость перемещения. Средняя и мгновенная скорости. Сделайте рисунок, укажите направления этих скоростей. Проекции скорости на оси декартовых координат. Модуль скорости.

3. Путь. Его связь с модулем скорости. Что собой представляет путь на графике зависимости скорости от времени? Среднее значение модуля скорости

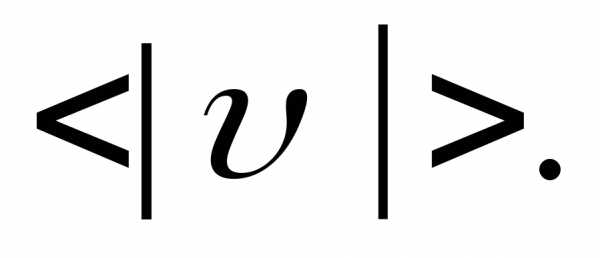
4. Ускорение, его связь со скоростью и радиус-вектором точки. Проекции ускорения на оси декартовых координат. Модуль ускорения. Среднее значение модуля

ускорения .

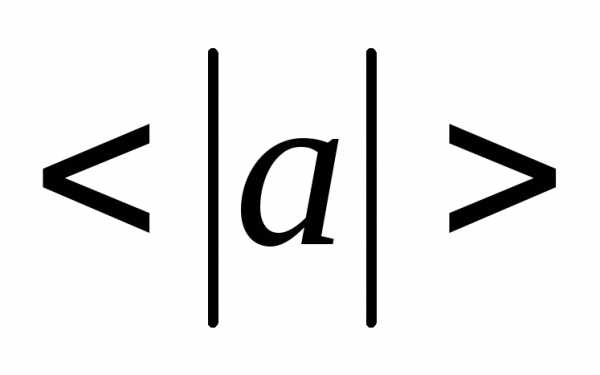5. Неравномерное движение точки по криволинейной траектории. Нормальная а_n и тангенциальная а_τ составляющие ускорения, их связь со скоростью точки. Как они характеризуют изменение скорости? Сделайте рисунок, укажите а_n,а_τ, скорость υ и полное ускорение а.

Тема 2. Кинематические уравнения движения. Равнопеременное движение.

1. Получите на основе дифференциальных уравнений кинематические уравнения движения 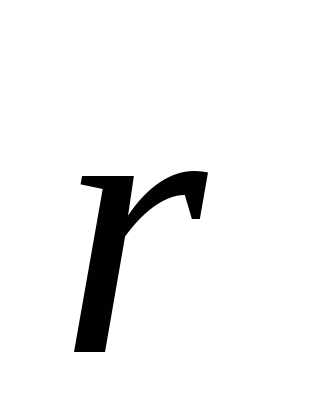(t) и (t) для тела, движущегося с постоянным ускорением . Начальный радиус-вектор 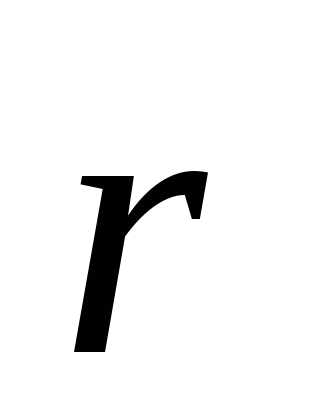₀, начальная скорость тела ₀.

2. Получите на основе дифференциальных уравнений кинематические уравнения движения x(t),y(t), v_x(t) и v_y(t) для тела, брошенного горизонтально с высоты h со скоростью v₀. Укажите оси и начало отсчета координат. Получите уравнение траектории.

3. Получите на основе дифференциальных уравнений кинематические уравнения движения x(t),y(t), v_x(t) и v_y(t) для тела, брошенного со скоростью v₀ под углом а к горизонту. Сделайте рисунок, укажите оси и начало отсчета координат.

4. Получите уравнение траектории для тела брошенного с поверхности земли со скоростью v₀ под углом  к горизонту. Сделайте рисунок, укажите оси и начало отсчета координат.

Тема 3. Кинематика вращательного движения точки.

1. Кинематические характеристики вращательного движения: угол поворота dφ радиус-вектора; угловое перемещение d, угловая скорость угловое ускорение, связь между ними. Сделайте рисунок и укажите направления этих векторов.

2. Связь между линейными (ds, v, а, а_τ, а_n) и угловыми (dφ, ω, ) характеристиками движения точки.

3. Получите кинематические уравнения равноускоренного и равнозамедленного вращения точки φ(t) и (t), используя дифференциальные уравнения:  = dω/dt и ω=dφ/dt (φ — угол поворота, ω -угловая скорость, - угловое ускорение; при t = 0 φ₀ = 0, ω = ω₀).

4. Напишите выражения для средних величин угловой скорости <ω> и углового ускорения <>. Найдите среднее значение угловой скорости за время от начала движения до остновки, если она меняется по закону:

ω = ω₀-At², где ω₀ и А — постоянные величины.

Тема 4. Кинематика абсолютно твердого тела.

1.Дайте определение абсолютно твердого тела (АТТ). Поступательное и вращательное движения АТТ. Какие кинематические характеристики используются для описания этих движений?

Динамика материальной точки, системы материальных точек, АТТ

studfiles.net