1. Элементы кинематики Основные формулы и законы
21
где — перемещение точки за время,- радиус-вектор, определяющий положение точки.
,
где – путь, пройденный точкой за время .
где — тангенциальная составляющая ускорения, направленная по касательной к траектории;- нормальная составляющая ускорения, направленная к центру кривизны траектории (- радиус кривизны траектории в данной точке).
где — начальная скорость, «+» соответствует равноускоренному движению, «-» — равнозамедленному.
где — угол поворота тела,– период вращения;- частота вращения (– число оборотов, совершаемых телом за время).
где — начальная угловая скорость, «+» соответствует равноускоренному вращению, «-» — равнозамедленному.
; ;;
где – расстояние от точки до мгновенной оси вращения.
2. Динамика материальной точки и поступательного движения твердого тела Основные законы и формулы
,
где -масса материальной точки,- скорость движения.
,
где — тангенциальное (касательное) ускорение,
— нормальное(центростремительное) ускорение.
где — коэффициент трения скольжения;— сила нормального давления.
,
где — величина деформации;- коэффициент жесткости.
,
где – гравитационная постоянная,и– массы взаимодействующих точек,- расстояние между точками.
где — число материальных точек (или тел), входящих в систему.
,
где и- массы тел,и- их скорости до взаимодействия.
; .
,
где — проекция силы на направление перемещения;— угол между направлениями силы и перемещения.
,
где – работа за промежуток времени .
, или .
.
Потенциальная энергия тела массой , поднятого над поверхностью земли на высоту,
,
где — ускорение свободного падения.
.
.
studfiles.net
Кинематика и формулы
Площадиl – длина
b — высота, ширина.
Площадь круга:
Кинематика.
Равномерное движение:
a = 0
V = S/t
Ускоренное движение:
a > 0
a = (V – V0 )/ t
S = S0 + V0t ± (at2 )/2
a = (V2 – V02 )/ 2S
Последовательный ряд нечетных чисел:
N-ую:
просто:
Движение под углом к горизонту
Скорость по оси ОХ:
Скорость по оси ОУ:
Максимальное время подъема:
tполн = 2t
Расстояние:
S = Vxtполн.
Максимальная высота:
Движение тела, брошенного горизонтально:
;
Динамика.
F = ma
P = mg
Fтр. = -mN
F = -F
Момент сил.
M=Fl
M1+M2+…+Mn = 0
Пружина.
x – удлинение.
k – кооф. растяжения.
0
ε — относит. удлинение.
l0 – начальная длина
Сила всемирного тяготения
Сила тяжести
Работа и энергия.
;
;
Движение по окр-ти.
;
w — угловая скорость.[рад/с]
v — линейная скорость
n — частота обращения [об./мин.]
T – период обращения [время]
Угловая скорость. Период обращения
; ;
; ;
Для случаев, когда n = [обороты]
;
— частота [1/с = 1 Гц]
— угол.
l – длина дуги.
Импульс.
;
Не упругое вз-вие.
до: после:
в проекции на ось х:
Упругое соударение.
до вз-я: после:
в проекции на ось х:
Реактивное движение:
в проекции на ось х: (вверх)
║
0 изначально.
— импульс газов
Импульс силы.
Механика жидкостей и газов.
Давление. Закон Паскаля
-//- жидкости на дно сосуда.
; F – сила давления
S – поверхность[1Па = 1Н/1]
h – высота уровня жидкости.
Сообщающиеся сосуды
;
Архимедова сила. Атм. давление
;
;
/
вытесненной жидкости цилиндром.
Закон Гука. Растягив. сила.
l –первоначальная длинна стержня
Δl –абсолютное удлинение
S –площадь поперечного сеч.
E –кооф. пропорцион., модуль Юнга, модуль упругости.
— напряженность
-закон Гука
КПД машин.
; [1дж/1с = 1 Вт]
Колебания и волны. Звук.
F – возвращающая сила
k – постоянная возвращающ.
x – смещение
Маятник.
; l – длина маятника
Математический маятник – точка, подвешенная на невесомой и нерастяжимой нити.
Пружинный маятник:
;
— циклическая частота колебаний
Фаза колебаний.
— угловая скорость
— угол поворота
Скорость распространения волн
;
Электромагнитные колебания.
;
— собственна частота колебаний в контуре
;
;
— фаза колебаний
— амплитуда тока
С – скорость в ваакуме
n – абс. показатель преломления среды
Молекулярно-кинетическая
теория
;
— масса молекулы
— молярная масса
; N – число молекул.
Теплоемкость тела.
с – теплоемкость тела
U – внутренняя энергия
А – работа
q – теплота сгорания
!!! Бывает наоборот!
Линейное расширение твердых тел.
— кооф. линейного расширен.
— интервал температур.
Объемное расширение твердых тел.
— кооф. объемного расш. тел.
Свойства газов.
T = const – изотермический
P = const – изобарический
V = const – изохорический
Главный газовый закон:
Закон Менделеева – Клаперона
— концентрация молекул
= 8.31 Дж/моль*К
— кол-во в-ва.
;
;
k = 1.38*10^-23 Дж/К
— среднеквадратичная ск-ть
— средняя кинетич. энергия движ. мол-лы
КПД тепловой машины.
— кол-во теплоты, получ. рабочим телом от нагрев.
— t холод.
— нагреват.
Электричество и магнетизм.
[В/м] ;
Эквипотенциальные пов-ти.
;
l – расстояние
— поверхностная плотность заряда
Закон Кулона
; [Н]
Ф/м
\ эл. постоянная
Электроемкость. Конденсаторы.
[Дж]
W – Энергия
Электроемкость плоского:
Шара:
Параллельное подключение конденсаторов:
Последовательное подключение:
Постоянный электрический ток.
;
; i – плотность тока
— Электродвиж. сила
[В]
— работа, совершенная сторонними силами
— сила эл. поля
Закон Ома для участка цепи.
;
G — кооф. пропрциональности проводника(его проводимость)
;
— удельная проводимость.
— температурный кооф. сопр.
— удельное сопротивление
[1 град. ^ -1]
постоянная:
Последовательное и парал-ное соединение проводников.
Последовательное:
Параллельное:
Закон Ома для полной цепи:
Последоват. соед. батарей:
;
n – кол-во батарей
Параллельное соед. батарей:
;
Работа при перемещении эл. заряда в эл. поле. Потенциал.
;
— потенциал эл. поля
— потенциальная энергия заряда в поле.
Работа и мощность эл. тока:
Напряжение.
Магнитное поле
;
При расположении проводника с током под углом альфа к вектору В.
B – магнитная индукция
I — сила тока
l – длинна проводника
M – макс. момент сил
S – площадь рамки
Сила Лоуренца
;
n – концентр. свободных частиц
v –скорость упор. движ.
S –площадь поперечного сечения проводника
Магнитная прониуаемость.
;
— магнитная прониц. среды
H- напряженность магнитного поля.
Электромагнитная индукция
[Вб]
;
Ф – магнитный поток
;
Самоиндукция.
; [Гн]
;
; W — энергия
Магнитная рамка.
b,a – стороны рамки
S — площадь рамки
Электроны.
;
Электролиты
Оптика
Закон преломления; — ваакум
; ; ;
— относит. показатель преломления.
— скорости света во 2-й и первой средах.
Линзы
d –расстояние предмета от линзы
f –расстояние от изображения до предмета
F – фокус
D –Оптическая сила линзы [диоптрии]
k — увеличение линзы
; ;
;
— длинна волны излучения
— импульс фотона
— частота излучения
В магнитно-преломляющих средах:
В однородно прозрачной среде:
— относит. диэликтрич. проницаемость среды
— относит. магнитная проницаемость среды.
n – постоянная
Уравнение Эйнштейна.
;
А – работа выхода электрона из в-ва
Фотоэффект.
coolreferat.com
Основные понятия кинематики и уравнения
Что представляют собой основные понятия кинематики? Что это вообще за наука и изучением чего она занимается? Сегодня мы поговорим о том, что представляет собой кинематика, какие основные понятия кинематики имеют место в задачах и что они означают. Дополнительно поговорим о величинах, с которыми наиболее часто приходится иметь дело.
Кинематика. Основные понятия и определения

Для начала поговорим о том, что она собой представляет. Одним из наиболее изучаемых разделов физики в школьном курсе является механика. За ней в неопределенном порядке следует молекулярная физика, электричество, оптика и некоторые другие разделы, такие как, например, ядерная и атомная физика. Но давайте подробнее разберемся с механикой. Этот раздел физики занимается изучением механического движения тел. В нем устанавливаются некоторые закономерности и изучаются его способы.
Кинематика как часть механики
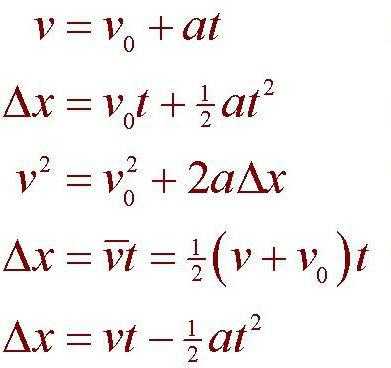
Последняя подразделяется на три части: кинематика, динамика и статика. Эти три поднауки, если их так можно назвать, имеют некоторые особенности. Например, статика изучает правила равновесия механических систем. Сразу же в голову приходит ассоциация с чашами весов. Динамика изучает закономерности движения тел, но при этом обращает внимание на силы, действующие на них. А вот кинематика занимается тем же самым, только в учет силы не принимаются. Следовательно, не учитывается в задачах и масса тех самых тел.
Основные понятия кинематики. Механическое движение

Субъектом в этой науке является материальная точка. Под ней понимается тело, размерами которого, по сравнению с определенной механической системой, можно пренебречь. Это так называемое идеализированное тело, сродни идеальному газу, который рассматривают в разделе молекулярной физики. Вообще, понятие материальной точки, как в механике в общем, так и в кинематике в частности, играет достаточно важную роль. Наиболее часто рассматривается так называемое поступательное движение.
Что это значит и каким оно может быть?
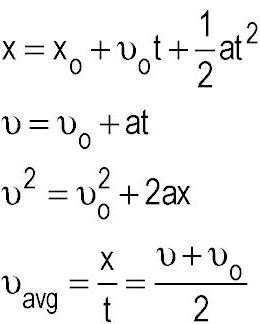
Обычно движения подразделяют на вращательное и поступательное. Основные понятия кинематики поступательного движения связаны в основном с применяемыми в формулах величинами. О них мы поговорим позднее, а пока что вернемся к типу движения. Понятно, что если речь идет о вращательном, то тело крутится. Соответственно, поступательным движением будет называться перемещение тела в плоскости или линейно.
Теоретическая база для решения задач

Кинематика, основные понятия и формулы которой рассматриваем сейчас, имеет огромное количество задач. Это достигается за счет обычной комбинаторики. Один из методов разнообразия здесь – изменение неизвестных условий. Одну и ту же задачу можно представить в разном свете, просто меняя цель ее решения. Требуется найти расстояние, скорость, время, ускорение. Как видите, вариантов целое море. Если же сюда подключить условия свободного падения, простор становится просто невообразимым.
Величины и формулы

Прежде всего сделаем одну оговорку. Как известно, величины могут иметь двоякую природу. С одной стороны, определенной величине может соответствовать то или иное численное значение. Но с другой, она может иметь и направление распространения. Например, волна. В оптике мы сталкиваемся с таким понятием, как длина волны. Но ведь если есть когерентный источник света (тот же самый лазер), то мы имеем дело в пучком плоскополяризованных волн. Таким образом, волне будет соответствовать не только численное значение, обозначающее ее длину, но и заданное направление распространения.
Классический пример
Подобные случаи являются аналогией в механике. Допустим, перед нами катится тележка. По характеру движения мы можем определить векторные характеристики ее скорости и ускорения. Сделать это при поступательном движении (например, по ровному полу) будет чуточку сложнее, поэтому мы рассмотрим два случая: когда тележка закатывается наверх и когда она скатывается вниз.
Итак, представим себе, что тележка едет вверх по небольшому уклону. В таком случае она будет замедляться, если на нее не действуют внешние силы. Но в обратной ситуации, а именно, когда тележка скатывается сверху вниз, она будет ускоряться. Скорость в двух случаях направлена туда, куда движется объект. Это нужно взять за правило. А вот ускорение может изменять вектор. При замедлении оно направлено в противоположную для вектора скорости сторону. Этим объясняется замедление. Аналогичную логическую цепочку можно применить и для второй ситуации.
Остальные величины
Только что мы поговорили о том, что в кинематике оперируют не только скалярными величинами, но и векторными. Теперь сделаем еще один шаг вперед. Кроме скорости и ускорения при решении задач применяются такие характеристики, как расстояние и время. Кстати, скорость подразделяется на начальную и мгновенную. Первая из них является частным случаем второй. Мгновенная скорость — эта та скорость, которую можно найти в любой момент времени. А с начальной, наверное, все и так понятно.
Задача
Немалая часть теории была изучена нами ранее в предыдущих пунктах. Теперь осталось только привести основные формулы. Но мы сделаем еще лучше: не просто рассмотрим формулы, но и применим их при решении задачи, чтобы окончательно закрепить полученные знания. В кинематике используется целый набор формул, комбинируя которые, можно добиться всего, чего нужно для решения. Приведем задачу с двумя условиями, чтобы разобраться в этом полностью.
Велосипедист тормозит после пересечения финишной черты. Для полной остановки ему потребовалось пять секунд. Узнайте, с каким ускорением он тормозил, а также какой тормозной путь успел пройти. Тормозной путь считать линейным, конечную скорость принять равной нулю. В момент пересечения финишной черты скорость была равна 4 метрам в секунду.
На самом деле, задача достаточно интересная и не такая простая, как может показаться на первый взгляд. Если мы попробуем взять формулу расстояния в кинематике (S = Vot +(-) (at^2/2)), то ничего у нас не выйдет, поскольку мы будем иметь уравнение с двумя переменными. Как же поступить в таком случае? Мы можем пойти двумя путями: сначала вычислить ускорение, подставив данные в формулу V = Vo – at или же выразить оттуда ускорение и подставить его в формулу расстояния. Давайте используем первый способ.
Итак, конечная скорость равна нулю. Начальная – 4 метра в секунду. Путем переноса соответствующих величин в левые и правые части уравнения добиваемся выражения ускорения. Вот оно: a = Vo/t. Таким образом, оно будет равно 0,8 метров на секунду в квадрате и будет нести тормозящий характер.
Переходим к формуле расстояния. В нее просто подставляем данные. Получим ответ: тормозной путь равен 10 метрам.
fb.ru
